Три самые сложные задачи из задания 17 ОГЭ (геометрия 1 часть). Ох уж этот ромб… | ОГЭ математика

Задача 1.

Задача с сайта РешуОГЭ

Задача с сайта РешуОГЭ

Задача становится совсем простой, если вспомнить, что ромб это тот же параллелограмм, у которого все стороны равны! Рисуем его как привыкли рисовать параллелограмм:

И что же мы видим сразу? Конечно прямоугольный треугольник (куда же без него в геометрии…) CHD . Да не простой, а с острым углом 60 градусов. Значит второй острый угол равен:

А это уже считай решение, ведь против угла 30 градусов в прямоугольном треугольнике лежит катет равный половине гипотенузы.

Тогда получаем:

А если к этому моменту, вы еще не забыли что это ABCD ромб, то знаете, что отрезок AD=34, отрезок HD =17 (только что нашли), тогда

Получается, что высота разбила сторону на два равных отрезка по 17

Задача 2.

Задача с сайта РешуОГЭ

Задача с сайта РешуОГЭ

И опять держим в голове что это параллелограмм с дополнительным бонусом в виде равных сторон.

Если бы мы знали сторону AD, то легко нашли бы высоту (площадь параллелограмма равна произведению высоты на сторону, к которой эта высота проведена), выразив ее из формулы площади.

Тогда найдем сторону AD. Периметр это сумма длин всех сторон. А у ромба они все одинаковые, тогда:

И всё….из формулы площади находим высоту.

Задача 3.

Задача с сайта РешуОГЭ

Задача с сайта РешуОГЭ

Для удобства обозначу искомый угол красным цветом. И сделаю дополнительное построение (OQ), которое сделает эту задачу устной!

OP=OR=OQ = R видно сто все эти отрезки равны, т.к. являются радиусами одной и той же окружности. В этот ряд равенств можно теперь дописать еще и PQ=QR=OP=OR (стороны ромба)

Всмотревшись в полученный рисунок видим, что треугольник OQR — равносторонний. Все углы равностороннего треугольника равны 60 градусов. В том числе и искомый угол 🙂

Вот такие на первый взгляд непростые задачи оказывается имеют практически устное решение!

Хочешь решать быстро и сразу видеть ответы. Подписывайся на канал. Каждый день новое задание и разбор!

Ваши лайки мой главный мотиватор. Спасибо за прочтение и позитив 🙂

Как решать задачи по геометрии. Часть 1

Геометрическая логика при решении задач

Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.

Это про тебя? Тогда ты попал туда, куда нужно!

Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.

Сразу оговорюсь — без знания теории в геометрии никак. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай). Знать теорию – обязательно!

Ладно, к делу.

Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?

Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.

Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.

К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.

Ладно, давай уже конкретный пример разберем.

Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).

Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.

В геометрии это означает:

1. построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
2. выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
   

Хорошо. Значит, текущая ситуация у нас такова:

Давайте потихоньку развеивать туман.

Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.

Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота. А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.

А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны).

Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).

Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.

Готово. Ответ получен.

Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове. А записывается примерно так:

Двадцать задачек (по безумной, восхитительной геометрии) / Хабр

Предупреждение врача.

Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.

Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.

Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).

Наслаждайтесь. И не говорите, что врач не предупреждал.

1. Сад часов

Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)

«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».

2. Опрокинутый квадрат

(Как по мне, это классика).

3. Это ловушка

В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?

«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».

4.

Три квадратных тарелки

Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?

«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».

5. Красивая стрижка

Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?

«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».

6. Все люди рождены равными

«Ещё одна переделка, которую я предпочитаю оригиналу».

7. Полукруг турдакен

«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».

8. Степенные хорды

Какова площадь круга?

«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»

9.

Сказка о двух кругах

У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.

«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»

10. Doc Oct

У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?

«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».

11. Всё в квадрате

«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».

12. Шип в улье

Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?

«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».

13. Я видел равнобедренных

Все четыре треугольника равнобедренные. Найдите угол.

«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»

14. Зеленый против синего

На картинке больше зелёного цвета или синего (и на сколько)?

«Ещё одна из моих любимых».

15. Резцы по камню

Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?

«Тут самое лучшее — действительно хорошие решения по рассечению площади».

16. Едем, едем, уехалиугольник

Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?

«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»

17. Только один факт

Какова площадь этого квадрата?

«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».

18. Стиральная машина

Какая часть большого квадрата закрашена?

«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».

19. Летающие флаги

У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?

«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».

20. Тигрогон

Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.

«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».

Закат над Квадратным городом

У левого квадрата площадь 4. Какова площадь правого квадрата?

«Мне нравится эта задачка, она напоминает закат над городом скверов.”

---

Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.

Как вы пришли к разработке своих головоломок?

Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.

Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.

Как проходит творческий процесс?

Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.

Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?

Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.

Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.

Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.

Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?

Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!

Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!

Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.

Советы для потенциальных создателей головоломок?

Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.

Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:

1. Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
2. Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
3. Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.

В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы. Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.

Какие задачи использует репетитор по математике на параллелограмм в 8 классе

Предлагаю Вашему вниманию страницы своей коллекции задач по геометрии для 8 класса. Это авторские номера, составлены мной собственноручно к рядовому уроку со средним (но способным) учеником. Репетитору по математике для разработки индивидуального урока.

Задачи репетитора на параллелограмм и свойство угла в 30 градусов.

1) На стороне AB параллелограмма ABCD отмечена середина M. Найдите расстояние от M до AD, если и MC=10 см.

2) Точка P — середина стороны AD параллелограмма ABCD. Известно, что PC=8 см, . Найдите расстояние от P до стороны AB. Задача на дом.

Задачи на биссектрисы углов:
Точка М середина стороны BC параллелограмма ABCD, причем AM и DM — биссектрисы углов BAD и ADC. Найдите DM, если и BC=6 см.

2) На стороне AD параллелограмма ABCD отмечена точка N так, что BN и CN — биссектрисы его углов B и C. Известно, что BN=4 и AD=8см. Найдите градусную меру угла А. (Обратная задача, составленная репетитором на биссектрисы ). Для домашней работы ученика.

Репетитору по математике в копилку красивых задач на параллелограмм

На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN — параллелограмм.

Школьная математика (особенно геометрия) сильно ограничивает репетитора в варьировании простейшими объектами для составления с их участием комбинированных задач под конкретную учебную ситуацию. В начале 8 класса список пройденных теорем и понятий весьма невелик. Поэтому репетитор по математике всегда испытывает определенный недостаток в материале узкого назначения. Простые задачи — однотипные, а сложных не так много. Первые не дают развития, а последние доступны далеко не всем учащимся. Найди что-то интересное посередине — отличительная черта хорошего репетитора по математике. Недавно летом я попал ситуацию, когда со средним учеником 8 класса были перерешены все виды типовых номеров учебника и дидактических материалов (я не беру задачи — клоны). Пришлось составлять оригинальные упражнения. Причем к их подбору я всегда подхожу методически аккуратно и выдерживаю главное правило любого комплекта упражнений: если репетитор по математике разбирает на уроке какую-либо задачу, то аналогичная ей обязательно должна задаваться на дом.

Задача, которая была представлена выше явилась результатом таких поисков. Для того, чтобы получить правильную домашнюю задачу на параллелограмм и треугольники репетитору по математике достаточно симметрично отобразить эти треугольники относительно сторон BC и AD. Вы видите их на рисунке справа. Нужно доказать, что BPDK — параллелограмм.

Как репетитор по математике растягивает задачи?

Как правило, любую задачу можно «дожать» или «растянуть», оптимизируя ее под конкретные цели повторения тех или иных теорем и формул. Я ругулярно комплектую задачи по геометрии несколькими пунктами в графе «докажите». В каждый номер с равносторонними треугольниками репетитору по математике можно посоветовать включить еще один пункт: докажите, что

Вы можете изучить рабочий листочек (план на урок) с этими задачами, который я обычно готовлю каждому ученику. Кликните на него и он откроется в отдельном окне. В него включены еще две задачи на биссектрисы внутренних и внешних углов параллелограмма.

Надеюсь, что репетиторам по базовой математике 8 класса пригодятся предоставленные материалы для работы со средним и даже сильным учеником. Удачного плана на урок!

Репетитор по математике в Москве ( м. Строгино ). А.Н. Колпаков

сложные вопросы геометрии, алгебры, комбинаторики, подготовка к перечневым олимпиадам 1 и 2 уровня: Преподаватели

Цели и задачи программы:

— развитие профессиональных компетенций, методических и практических навыков работы учителей со школьниками;
— повышение профессионального мастерства педагогов, работающих в профильных физико-математических классах и региональных центрах;
— совершенствование навыков работы учителя в обучении мотивированных школьников решению задач высокого уровня сложности, часто встречающихся на вступительных испытаниях и перечневых олимпиадах;
— знакомство слушателей с педагогическим опытом и технологиями работы со школьниками ведущих педагогов России, подготовивших десятки призеров и победителей не только Всероссийской олимпиады школьников по математике, но и многих перечневых олимпиад;
— непосредственное общение педагогов с разработчиками заданий перечневых олимпиад.

Не секрет, что очень достаточно большое количество школьников, начиная работать по программе изучения олимпиадной математики с 3-5 класса, зачастую в 8-9 классе теряют мотивацию, понимая, что не попадут на финальный этап Всероссийской олимпиады, меняют сферу приложения своих талантов или вовсе сосредотачиваются на иных интересах. С другой стороны, часть школьников начинает серьезно заниматься математикой только в старших классах, когда многие важнейшие темы уже не могут быть охвачены в виду недостатка времени. Для таких школьников слабо разработана система кружковых занятий, а педагоги во время основных и факультативных занятий основное внимание уделяют подготовке к ЕГЭ в ущерб содержательной математической части.

Программа нацелена на то, чтобы закрыть этот зазор и дать педагогам материал для работы с подготовленными и мотивированными школьниками, которые нацелены на изучение не столько олимпиадной тематики, сколько серьезному расширению сложных и идейных тем школьной программы.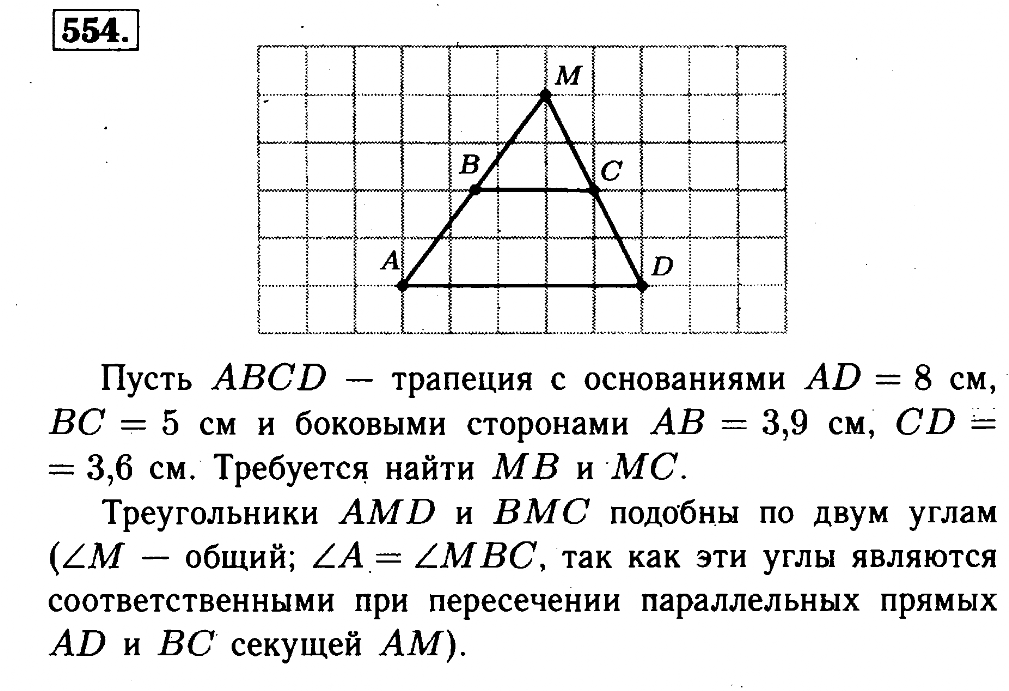 Особое внимание в ходе программы будет уделено не только конкретным темам, но методам и стилям рассуждений, которые мало описаны в учебниках и методических материалах.

Сами методы рассуждений будут проиллюстрированы на разнообразном материале, который часто используется на перечневых олимпиадах. Это даст материал для работы со школьниками 7-11 классов, обучающихся в профильных и предпрофильных классах, в региональных центрах. Отдельно будут рассмотрены ключевые моменты, на которые необходимо обратить внимание в среднем звене, чтобы школьники смогли успешно изучать продвинутый курс школьной математики в старшем звене.

Программа повышения квалификации включает следующие формы работы: лекции, семинары, тематические беседы, групповую работу в режиме «творческой лаборатории», самостоятельную работу, круглый стол.

На программе будут присутствовать руководители ведущих математических кружков России, разработчики заданий перечневых олимпиад, руководители и преподаватели математических программ образовательного центра «Сириус».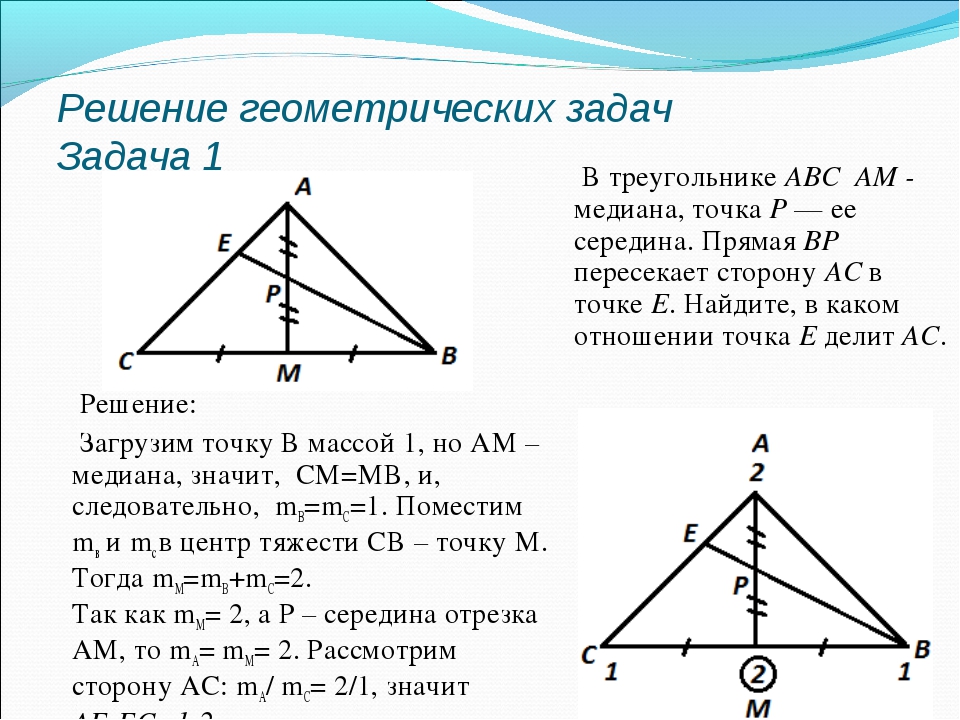

Итоговое мероприятие программы – круглый стол, который предусматривает обсуждение:

— результатов групповой работы слушателей по выбранной теме;
— опыта работы слушателей, осуществляющих обучение в региональных центрах, классах с углубленным изучением математики, кружках, факультативах;

По итогам программы слушатели получают удостоверение о повышении квалификации в объеме 56 часов.

Участники программы получат знания, умения и навыки, позволяющие:

— создавать творческую среду для поддержки и сопровождения детей, одаренных в области математики;
— разрабатывать методы обучения решению задач повышенной сложности по математике, осуществлять качественную подготовку учащихся к участию в перечневых олимпиадах и к решению задач ЕГЭ повышенного уровня сложности;
— осознанно выбирать и использовать образовательные технологии, методы и средства, необходимые для эффективного изучения математики школьниками на углубленном уровне;
— включать задачи на ключевые математические методы в школьный курс на протяжении всего обучения в средней школе.

Приложение для решения задач геометрии ▷ ➡️ Creative Stop ▷ ➡️

Приложение для решения геометрических задач. Геометрия — не ваша сильная сторона, и вам нужна дополнительная помощь. Это нормально. Вот почему я сегодня здесь.

В сегодняшнем уроке я расскажу вам, какие из лучших применения решать геометрические задачи которые можно загрузить на любое устройство, и большинство из них бесплатны и очень просты в использовании.

Разрешить геометрию (Android / iOS)

Один из лучших приложение для решения геометрических задач Это называется Разрешить геометрию, имя, которое не оставляет сомнений в том, какова его «миссия».

Resolve Geometry — особенно полезный ресурс для учеников начальной и средней школы. Его интерфейс очень «чистый» и интуитивно понятный, что облегчает использование пользователем, который может найти решение проблемы в несколько нажатий.

После установки Resolve Geometry на ваше устройство Android o Ios, запустите приложение, нажав кнопку открытый или щелкнув его значок, расположенный на главной странице вашего устройства.

И как только приложение запустится, вы должны увидеть главный экран, содержащий различные геометрические фигуры: Скаленовые треугольники, Равнобедренные треугольники, Равносторонние треугольники, Прямоугольный треугольник, Cuadrado, прямоугольник, Paralelogramo и так далее

Чтобы решить математическую задачу, нажмите на интересующую вас геометрическую фигуру и на открывшемся экране обведите пальцем каждую сторону фигуры.

После прорисовки стороны укажите ее длину: впишите в поле номер длина, нажмите на cm выбрать единицы измерения для стороны и подтвердить операцию, нажав команду добавлять.

Если вы не знаете, какой длины одна сторона фигуры, не вводите ничего в это поле. число, нажмите оранжевый значок увеличительного стекла.

Указав характеристики каждой стороны выбранной геометрической фигуры, прикоснитесь к значок двойного листа (вверху справа) и на открывшемся экране нажмите оранжевую кнопку Решить чтобы решить вашу проблему и увидеть различные шаги, предпринятые алгоритмом.

Вы также можете использовать Solve Geometry на своем ПК, просто зайдите на официальный сайт этого сервиса с помощью любого браузер веб.

Калькулятор геометрии (Android / iOS)

Калькулятор геометрии — еще одно приложение, которое вам следует серьезно рассмотреть, если вы хотите быстро и легко решать геометрические задачи.

Его интерфейс очень похож на предыдущий, поэтому, если вы уже пробовали приложение, которое я показал вам в предыдущем абзаце, у вас не будет проблем с использованием этого другого бесплатного решения.

Прежде чем описывать использование Калькулятора геометрии, я хотел бы уточнить, что для доступа ко всем функциям, включенным в приложение, необходимо совершить покупку некоторых элементов внутри приложения (2,95 евро).

После завершения загрузки калькулятора геометрии на свой Android-устройство или iOS, откройте приложение и на главном экране коснитесь одной из доступных геометрических фигур: треугольник, Cuadrado, прямоугольник, Paralelogramo, и так далее

На открывшемся экране вы можете нажать кнопку значок книги чтобы прочитать соответствующую статью, опубликованную в Википедии, или вы можете нажать на значок треугольника с шестеренкой для выбора параметра для расчета.

Чтобы начать расчет площади, периметра и других параметров, введите в соответствующие поля (напр. a: es h: ) правильные значения и нажмите опцию Сделанный чтобы увидеть окончательный результат операции.

Если вы заметили, что введенные данные неверны, нажмите значок X (вверху), чтобы удалить введенные данные и ввести новые. Однако, чтобы вернуться в начальное меню, нажмите кнопку. < и выберите новую геометрическую фигуру для решения других задач.

Geometryx (Android)

Еще одно полезное приложение решать геометрические задачи es Геометрикс, 100% бесплатный, который, помимо того, что он полный, также очень прост в использовании.

С помощью Geometrix можно рассчитывать значения и параметры форм и геометрических тел: площадь, периметр, объем, координаты центра тяжести, высоту, длину стороны, диагонали, площадь основания, поперечную площадь, общую площадь тела и многое другое.

Как только вы завершите загрузку Geometryx на свой мобильный телефон или планшет, откройте приложение и на главном экране нажмите одну из доступных геометрических фигур: Cuadrado, прямоугольник, Правильный многоугольник, эллипс и так далее

На открывшемся экране введите данные, относящиеся к выбранной геометрической фигуре, в формы, расположенные под разделом Введите ваши входные данные и используйте легенду в правом верхнем углу, чтобы «двигаться» правильным образом.

Как только вы закончите ввод входных данных, приложение автоматически рассчитает площадь, периметр и т. Д. Вы можете увидеть все результаты, прокрутив экран вниз.

Как видите, Geometryx имеет красивую анимацию, которая делает работу с пользователем более увлекательной.

Однако, если рассматриваемые анимации вам не нравятся, вы можете удалить их, нажав на символ (+) и в меню, которое открывается слева, удалив галочка находится рядом со статьей анимации.

Геометрия GeoGebra (Android / iOS)

Еще одно приложение, которое я хочу посоветовать вам попробовать, это Геогебра Геометрия. Это бесплатное приложение, доступное как для Android-устройства как и iOS, он является одним из самых полных, которые вы можете загрузить на свое устройство.

По сравнению с приложениями, которые я упоминал в предыдущих абзацах, он позволяет пользователю создавать геометрические конструкции с чрезвычайной простотой для решения наиболее распространенных геометрических задач.

После установки GeoGebra Geometry на ваше устройство откройте его и используйте инструменты, расположенные вверху, для рисовать желаемые геометрические фигуры.

Для этого щелкните один из доступных вариантов (например, Точка, Право o Многоугольник ) и вставьте выбранный геометрический элемент в плоскость, коснувшись белой области и нажав стрелка внизу справа, чтобы увидеть его характеристики.

После прикосновения к стрелка расположен в правом нижнем углу, нажмите на символ (?) находится слева, выберите пункт Геометрия и в открывшемся меню коснитесь одной из доступных функций.

При выборе одного из вариантов, упомянутых выше, внимательно следуйте инструкциям, которые вы видите на экране, чтобы точно знать, какой «синтаксис» использовать для запись команды правильно, что позволит вам решить проблему.

Напоминаю, что вы также можете получить доступ к услугам, которые предлагает GeoGebra, на вашем компьютере. Для этого подключитесь к официальному сайту GeoGebra или загрузите приложение на Окна 10 и используйте инструменты, которые последний предоставляет в ваше распоряжение.

Другие приложения для решения геометрических задач

Не убедили ли вас решения, о которых я говорил до сих пор? Попробуйте эти:

• Геометрия — калькулятор (Android) — Если вы ищете геометрический калькулятор, который имеет множество функций, но при этом прост в использовании, это приложение для вас. Он имеет интуитивно понятный интерфейс, который позволяет не только легко искать геометрические фигуры, но, прежде всего, решать различные задачи.

 

• Простая геометрия (Android) — Если вы никогда не помните правильные формулы для решения геометрических задач, это приложение поможет вам исправить эту ситуацию. Фактически, простая геометрия — это форма с богатым содержанием, с которой можно легко справиться даже niños. Видеть значит верить!

 

• Геометрия для всех (Android) — Если вы ищете форму, предлагающую дополнительную информацию, вам обязательно стоит попробовать это приложение. Геометрия для всех, по сути, включает в себя не только информацию о формулах, которые следует применять к задачам, связанным с плоскими фигурами, но и твердыми. Это идеальный помощник для общего обзора геометрических формул перед экзаменом в классе.

 

• 3D магометрия (iOS) — это приложение — не простая форма для проверки при необходимости, а многое другое. Mageometry 3D, помимо того, что делает основные геометрические формулы легкодоступными, позволяет вам в несколько касаний решить самые сложные геометрические задачи, в которых пирамиды, параллелепипеды, конусы, сферы и многие другие фигуры являются объектами. Его можно приобрести в App Store по цене 3,49 евро.

Основные формулы по геометрии — Математика — Теория, тесты, формулы и задачи

Знание формул по геометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по геометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении геометрических задач. На этой странице сайта представлены основные формулы по школьной геометрии.

 

Изучать основные формулы по школьной геометрии онлайн:

 

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

 

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Методы решения сложных геометрических задач

‘) вар корзинаStepActive = истина var buybox = document.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode ;[].slice.call(buybox.querySelectorAll(«.вариант-покупки»)).forEach(initCollapsibles) функция initCollapsibles(подписка, индекс) { var toggle = подписка.querySelector(«.Цена-варианта-покупки») подписка.classList.remove(«расширенный») var form = подписка.querySelector(«.форма-варианта-покупки») если (форма && cartStepActive) { вар formAction = form. getAttribute(«действие») form.setAttribute(«действие», formAction.replace(«/checkout», «/cart»)) document.querySelector(«#ecommerce-scripts»).addEventListener(«load», bindModal(form, formAction, timestamp, index), false) } var priceInfo = подписка.querySelector(«.Информация о цене») var PurchaseOption = toggle.parentElement если (переключить && форма && priceInfo) { toggle.setAttribute(«роль», «кнопка») toggle.setAttribute(«tabindex», «0») переключать.addEventListener(«щелчок», функция (событие) { var expand = toggle.getAttribute(«aria-expanded») === «true» || ложный toggle.setAttribute(«aria-expanded», !expanded) form.hidden = расширенный если (! расширено) { покупкаOption. classList.add(«расширенный») } еще { покупкаOption.classList.удалить («расширить») } priceInfo.hidden = расширенный }, ложный) } } функция bindModal (форма, formAction, метка времени, индекс) { var weHasBrowserSupport = window.fetch && Array.from функция возврата () { var Buybox = EcommScripts ? EcommScripts.Buybox : ноль var Modal = EcommScripts ? EcommScripts.Модальный: ноль if (weHasBrowserSupport && Buybox && Modal) { var modalID = «ecomm-modal_» + метка времени + «_» + индекс var modal = новый модальный (modalID) modal. domEl.addEventListener («закрыть», закрыть) функция закрыть () { form.querySelector («кнопка [тип = отправить]»).фокус() } форма.setAttribute( «действие», formAction.replace(«/checkout», «/cart?messageOnly=1») ) form.addEventListener( «Отправить», Buybox.interceptFormSubmit( Буйбокс.fetchFormAction(окно.fetch), Buybox.triggerModalAfterAddToCartSuccess(модальный), консоль.лог, ), ложный ) document. body.appendChild(modal.domEl) } } } функция initKeyControls() { документ.addEventListener(«keydown», функция (событие) { if (document.activeElement.classList.contains(«цена-варианта-покупки») && (event.code === «Пробел» || event.code === «Enter»)) { если (document.activeElement) { event.preventDefault () документ.activeElement.click() } } }, ложный) } функция InitialStateOpen() { var buyboxWidth = buybox.смещениеШирина ;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) { var toggle = option.querySelector(«. цена-варианта-покупки») var form = option.querySelector(«.форма-варианта-покупки») var priceInfo = option.querySelector(«.Информация о цене») если (buyboxWidth > 480) { переключить.щелчок() } еще { если (индекс === 0) { переключать.щелчок() } еще { toggle.setAttribute («ария-расширенная», «ложь») form.hidden = «скрытый» priceInfo.hidden = «скрытый» } } }) } начальное состояниеОткрыть() если (window.buyboxInitialized) вернуть window.buyboxInitialized = истина initKeyControls() })()

Методы решения сложных геометрических задач

Слово «комплекс», фигурирующее в названии этой книги, модифицирует «задачи», а не «геометрию», поэтому читатель, который ищет сборник задач по алгебраической геометрии над полем комплексных чисел, надо искать в другом месте. Перед нами интересный и довольно хорошо подобранный сборник задач по евклидовой плоской геометрии. Задачи элементарны в том смысле, что рассматриваемая здесь геометрия, скорее всего, будет понятна старшекласснику (хотя в этой книге есть темы, которые обычно не изучаются в средней школе, например, теоремы Чевы и Menelaus), но некоторые из них очень сложны.

Книга разделена на четыре главы, посвященные соответственно треугольникам, четырехугольникам, окружностям и геометрическим построениям.Каждая глава разделена на разделы, а часто и на подразделы, состоящие из формулировок (и обычно доказательств) стандартных результатов, за которыми следуют пронумерованные задачи с решениями, расположенными сразу после формулировки. (Всего их 81.) В дополнение к этим пронумерованным задачам последний раздел каждой главы состоит из 20 задач, помеченных как «домашнее задание»; они обычно сопровождаются решениями, некоторые более подробными, чем другие. Используются методы элементарной синтетической геометрии и тригонометрии, но теореме Менелая также придается векторная формулировка, и в одном или двух случаях используется подход геометрического преобразования. Проблемы варьируются по сложности от очевидных до довольно сложных; некоторые требуют доказательств, но многие требуют вычислений или построений.

Соображения по поводу места, очевидно, делают практически невозможным перечисление здесь всех или даже многих задач, но следующая дословная подборка четырех задач, по одной из каждой главы, должна дать разумное представление о том, как они выглядят:

· Рассмотрим разносторонний треугольник ABC с площадью S. Точка P находится внутри треугольника ABC.Проведите три линии через P параллельно каждой стороне треугольника, чтобы сформировать три треугольника с площадями S ₁ , S ₂ и S ₃ . Найти С.

· Дан параллелограмм площади S. Каждая вершина параллелограмма соединена отрезком с серединами двух противоположных сторон. Найдите площадь многоугольника, образованного пересечением всех [так в оригинале] отрезков прямой.

· Пусть AB — диаметр окружности, а CD — хорда. Хорда не перпендикулярна диаметру.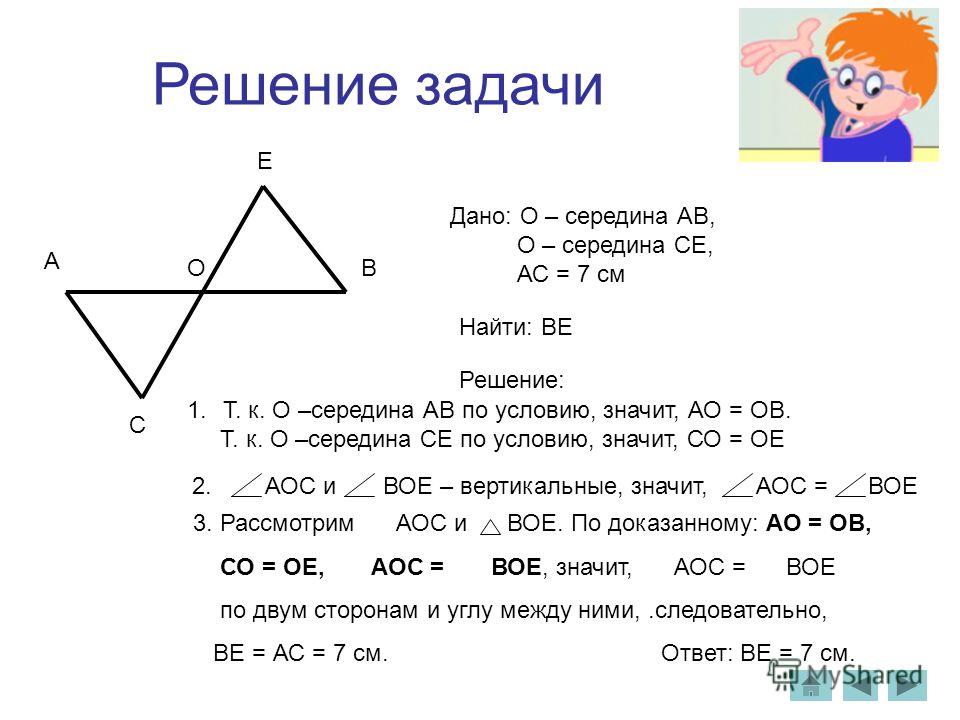 Докажите, что перпендикуляры AE и BF, опущенные из конца диаметра на хорду, делят [sic] хорду CD на равные отрезки CF и DE.

· Построить треугольник по двум его вершинам, A и B, и его ортоцентру, H.

Эти задачи показались мне одними из самых сложных. Другие, как я указал, намного проще и даже тривиальны: например, «Можете ли вы построить угол в 30 ? Есть также некоторые, хотя и не очевидные, но достаточно известные: «Докажите, что если четырехугольники соединены, так что они образуют параллелограмм.

Автор, который, как сказано в предисловии, сначала не любил и не очень хорошо разбирался в геометрии, а потом полюбил ее, приложил особые усилия, чтобы сделать эту книгу как можно более безболезненной для изучающего. На самом деле, явно стремясь «очеловечить» вещи, она создала небольшое приложение из четырех фотографий (три цветных), а также воспроизвела страницу из тетради, которую вела в девятом классе. Такие вещи, конечно, не встретишь во многих учебниках.

В связи с вышеизложенным мне иногда казалось, что автор приложил слишком усилий, чтобы сделать вещи безболезненными; одна или две проблемы, например, сформулированы так, что я счел их слишком приторно юношескими для биркхойзеровского текста. (Задача 28, например, гласит: «Петя нарисовал треугольник со сторонами 11, 13 и 6. Можете ли вы помочь ему оценить площадь треугольника?»).

Кроме того, книга выиграла бы от более тщательного редактирования. Я заметил несколько опечаток (например, те, что перепечатаны выше, а также первый абзац на странице 45, который заканчивается на середине предложения, и подпись к рисунку 3.15, которая гласит: «Угол между двумя секущими (должен быть заменен). Есть еще по крайней мере один содержательный математический вопрос, где автор претендует (на стр. 147) привести доказательство того факта, что четырехугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180 градусам, но на самом деле доказывает только направление «только если».

Однако, к счастью, эти проблемы не умаляют общей ценности этой книги. Хотя он и не задумывался как текст, он, тем не менее, достаточно универсален, чтобы служить нескольким целям и различным группам. Он дает хороший обзор ряда различных тем евклидовой геометрии и дает прекрасную практику для тех, кто готовится к участию в соревнованиях в стиле олимпиады. Кроме того, это хорошее дополнительное чтение для изучающих (или, что более вероятно, учителей) геометрии.В настоящее время я преподаю курс евклидовой геометрии и сомневаюсь, что пройдет много времени, прежде чем я обращусь к этой книге за интересными дополнительными домашними заданиями.

---

Марк Хуначек ([email protected]) преподает математику в Университете штата Айова.

Самая сложная простая задача геометрии – Воскресная головоломка – Принимайте решения

Задача известна как случайные углы Лэнгли и была поставлена ​​в 1922 году. Она также известна как самая сложная простая задача геометрии, потому что ее можно решить элементарными методами, но это сложно и трудоемко.

Вы можете это понять? Посмотрите видео, чтобы узнать о решении.

Сможете ли вы решить самую сложную простую геометрическую задачу?

Или продолжайте читать для объяснения.
.
.

«Все будет хорошо, если вы будете использовать свой разум для принятия решений, и думать только о своих решениях». С 2007 года я посвятил свою жизнь разделению радостей теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.

.
.

.
.
.
.
М
И
Н
Д
.
Д
О
У
Р
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на самую сложную простую задачу по геометрии

Есть два основных принципа решения задачи. Во-первых, сумма всех углов треугольника равна 180 градусам. Во-вторых, в равнобедренном треугольнике против двух равных сторон лежат два равных угла.Если известно, что у треугольника два равных угла, то противоположные стороны равны, а знание двух равных сторон означает, что противоположные углы равны.

Доказательство включает в себя работу с рядом равнобедренных треугольников. Для начала начертите отрезок BG так, чтобы угол CBG был равен 20 градусам.

В треугольнике CBG мы знаем, что один угол равен 20 градусам, а другой равен 80 градусам, всего 100 градусов. Таким образом, сумма углов треугольника равна 180, мы можем решить, что ∠CGB = 80 градусов.Это означает, что треугольник CBG равнобедренный и BC = BG.

Углы CBG и BGE образуют прямую линию, поэтому их сумма должна составлять 180 градусов. Это означает, что угол BGE равен 100 градусам.

Тогда, ориентируясь на треугольник BGE, мы можем решить, что ∠BEG = 40 градусов, потому что это должно быть 180 минус известные углы 40 и 100. В треугольнике BGE два угла равны 40 градусам, так что это еще один равнобедренный треугольник , поэтому BG = GE.

Затем, ориентируясь на треугольник BFC, мы можем решить, что ∠BFC = 50 градусов, что означает, что треугольник BFC является еще одним равнобедренным треугольником.Это означает, что BF = BC.

Мы доказали BC = BG = GE = BF.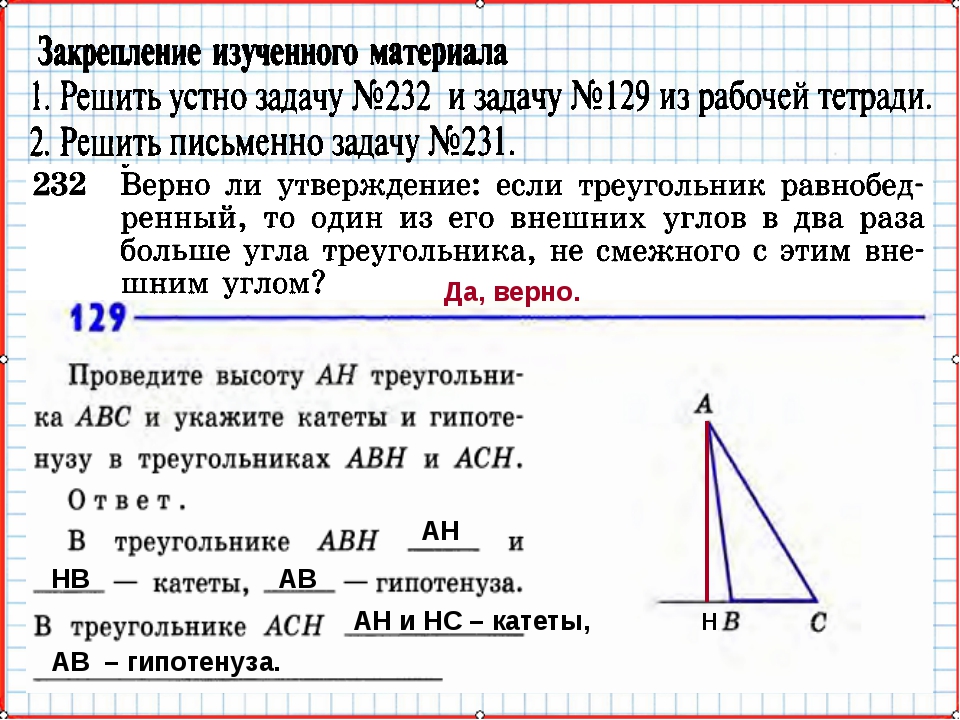

Теперь создадим еще один треугольник BFG. Поскольку BG = BF, мы знаем, что противоположные углы должны быть равны. (Если вы следите за видео, я оговорился с этим шагом в видео на 5:04. Я хотел сказать, что стороны BG и BF равны.)

Третий угол в треугольнике, ∠GBF, равен 60 градусам, таким образом, остальные углы должны составлять половину от 180 – 60. Это (180 – 60)/2 = 60 градусов. Другими словами, все 3 угла равны, поэтому треугольник BFG равносторонний.Все его стороны должны быть равны, поэтому GF = BF.

Мы выяснили много информации. Есть еще один треугольник, который необходимо рассмотреть, поэтому ниже приведена диаграмма, посвященная треугольнику GFE, в которой опущена второстепенная информация.

Мы знаем, что GF = GE, поэтому у нас снова есть равнобедренный треугольник, и мы знаем, что угол при вершине равен 40 градусам. Это означает, что оставшиеся углы составляют половину от 180 – 40, что составляет 70 градусов.

Наконец, мы знаем, что 40 + x должно равняться 70, значит, x = 30 градусов.

Вот и ответ! Значение x равно 30 градусам.

Wikpedia Langley’s 2 Wikpedia Лэнгли. Самая сложная простая задача по геометрии в мире
http://thinkzone.wlonk.com/MathFun/Triangle.htm
https://www.duckware.com/tech/worldshardesteasygeometryproblem.html

Спасибо покровителям!

Кайл
Брайан М. Муни

Вы можете поддержать меня и этот сайт на Patreon.

МОИ КНИГИ

Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

Рейтинги книг по состоянию на январь 2022 г.

(ссылки в США и других странах)
https://mindyourdecisions.com/blog/my-books

Принимайте решения представляет собой сборник из 5 книг:

(1) Радости теории игр: введение в стратегическое мышление
(2) 40 парадоксов логики, вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения
(4) Лучшие приемы ментальной математики
(5) Умножение чисел путем рисования линий

Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 обзорах)

40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (оценка 4,1/5 звезд в 38 обзорах)

Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (оценка 4/5 звезд в 24 отзывах)

Лучшие математические трюки в уме учит, как можно выглядеть гением математики, решая задачи в уме (оценка 4.2/5 звезд на 76 обзорах)

Умножение чисел путем рисования линий Эта книга является справочным пособием для моего видео, которое набрало более 1 миллиона просмотров по геометрическому методу умножения чисел. (оценка 4,3/5 звезд в 30 обзорах)

Загадывайте свои головоломки представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр.Том 1 получил оценку 4,4 / 5 звезд в 87 отзывах.

Математические головоломки, том 2 — это продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)

Math Puzzles Volume 3 — третья книга в серии. (оценка 4,2/5 звезд по 22 отзывам)

KINDLE UNLIMITED

Учителя и студенты со всего мира часто пишут мне о книгах по электронной почте. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно шире по как можно более низкой цене.

В настоящее время вы можете читать большинство моих электронных книг с помощью программы Amazon Kindle Unlimited. Включив подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон / планшет / компьютер и т. Д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте свой местный веб-сайт Amazon, чтобы узнать о доступности и условиях программы.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия , список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, книга результаты (BR)
Мексика, результаты книги (MX)

ТОВАРЫ

Возьмите кружку, футболку и многое другое на официальном сайте товаров: Принимайте решения в Teespring .2}\]

Это возможные значения \(k.\)

Пример — 38

Пусть \(\bar bz + b\bar z = c,\,\,b \ne 1\) — прямая на комплексной плоскости. Если точка \(z{_1}\) является отражением точки \(z{_1}\) через прямую, покажите, что \(c = {\bar z_1}b + {z_2}\bar b,\ )

Решение:

Из рисунка видно, что середина \(АВ\) должна лежать на данной прямой, т.е.e, \(\begin{align}&\frac{{{z_1} + {z_2}}}{2}\end{align}\) должны удовлетворять уравнению прямой. Кроме того, \(AB\) должны быть перпендикулярны данной линии, т.е. комплексные наклоны \(AB\) и данной линии должны составлять 0.

\[\begin{align} &\Стрелка вправо \,\,\,\bar b\left( {\frac{{{z_1} + {z_2}}}{2}} \right) + b\left( { \frac{{{{\bar z}_1} + {{\bar z}_2}}}{2}} \right) = c\,\,\,\,\,\,\,…{ \text{ }}\left( 1 \right) \\\\ &\text{and}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\frac{{{z_1} — {z_2}}}{{{{\bar z}_1} — {{\bar z}_2}}} + \left( {\ frac{{ — b}}{{\ bar b}}} \right) = 0 \\\\&\Стрелка вправо \,\,\,\bar b\left( {{z_1} — {z_2}} \right) — b\left( {{{\bar z}_1} — {{\bar z}_2}} \right) = 0\,\,\,\,\,\,\,\,\, . ..{\ text{}}\left( 2 \right)\\\\& 2 \times \left( 1 \right) — \left( 2 \right)\,\,\,{\text{дает нам требуемое отношение.}}\\\end{align} \]

Пример — 39

Найдите центр описанной окружности треугольника, вершины которого заданы комплексными числами \(z{_1}{\rm{ }},z{_2}{\rm{\;and\; }}z{_3}{\rm {}}.\)

Решение:

Нам нужно найти \(z,\) центр описанной окружности \(O\) треугольника \(PQR.\) В силу того, что он является центром описанной окружности, \(z\) равноудален от \(z{_1}{ \rm{}},z{_2}{\rm{\;и\;}}z{_3}{\rm{}}.\) Следовательно,

\[\begin{align}&\qquad\qquad\left| {г — {г_1}} \право| = \ влево | {г — {г_2}} \право| = \ влево | {z — {z_3}} \right|\\ &\Стрелка вправо \,\,\,(z — {z_1})(\bar z — {{\bar z}_1}) = (z — {z_2}) (\ bar z — {{\ bar z} _2}) = (z — {z_3}) (z — {{\ bar z} _3}) \\\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,&\qquad\qquad\underbrace { \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}_{{\rm{Равенство}}\, {\rm{A}}}\,\,\;\;\;\нижняя скоба {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ ;\;\;\;\;}_{{\rm{Равенство B}}}\\ \end{align}\]

\(\Rightarrow \) Из первых двух членов в приведенном выше равенстве (Равенство \(A\) ) получаем:

\[\begin{gathered} z\, — z{{\bar z}_1} — {z_1}\bar z + {z_1}{{\bar z}_1} = z\, — z{{\bar z}_2} — {z_2}\bar z + {z_2}{{\bar z}_2} \hfill \\\Стрелка вправо \,\,\,\bar z({z_2} — {z_1}) = z( {{\bar z}_1} — {{\bar z}_2}) + {\left| {{z_2}} \right|^2} — {\left| {{z_1}} \right|^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,. 2}({z_1} — {z_2})}}{{{{\bar z}_1}({z_2} — {z_3}) + {{\bar z}_2}({z_3} — {z_1}) + {{\bar z}_3}({z_1} — {z_2})}}\]

Пример — 40

\({z_1},\;{z_2}\;{\rm{and}}\;{z_3}\) — три точки на окружности с центром в начале координат. На окружности выбрана точка \(z\) так, что линия, соединяющая \(z\) и \({z_1}\), перпендикулярна линии, соединяющей \({z_2}\) и \( {z_3}\) . Покажите, что \(z{z_1} + {z_2}{z_3} = 0\)

Решение:

Мы наблюдаем \(\theta  = \phi \), что из-за перпендикулярности двух секущих.

Теперь \(\angle \,SOR + \angle SOQ — \angle SOP = \pi \) , (используя тот факт, что \(\theta  = \phi \) ). Следовательно,

\[\begin{align}& \qquad\;\; \left( {\arg \left({{z_3}} \right) — \arg (z)} \right) + \left( {\arg \left({{z_2}} \right) — \arg (z )} \right) — \left( {\arg \left( {{z_1}} \right) — \arg (z)} \right) = \pi \\ &\Rightarrow \quad \arg \left( {{ z_3}} \right) + \arg \left( {{z_2}} \right) = \pi + \arg \left( {{z_1}} \right) + \arg \left( z \right)\\ & \Rightarrow \quad \arg \left( {{z_2}{z_3}} \right) = \pi + \arg \left( {z{z_1}} \right)\\ &\Rightarrow \quad {z_2}{z_3 } = — z{z_1} \Rightarrow \quad z{z_1} + {z_2}{z_3} = 0\end{align}\]

ПОПРОБУЙТЕ СЕБЯ — IX

В. { + \frac{\pi} {4}}}\bar z = 0\)

(г) \(3z + 3\bar z + 2 = 0\)

Q. 2 Напишите сложные формы для следующих строк

(а) \(х + у + 1 = 0\)

(б) \(\sqrt 3 x — y + 1 = 0\)

(в) \(х = 1\) (г) у = 1

Q. 3 Рассмотрим точку  \(z{_0}\) на окружности \(|z|\; = r\) . Каким будет уравнение касательной в точке \(z{_0}\)  ?

Искусство решения задач

Массовые точки — это метод в евклидовой геометрии, который может значительно упростить доказательство многих теорем о многоугольниках и полезен при решении сложных геометрических задач, связанных с длинами.По сути, это включает в себя использование локальной системы координат для идентификации точек по соотношениям, на которые они делят отрезки прямой. Массовые точки обобщаются барицентрическими координатами.

Геометрия точки массы была изобретена Францем Мебиусом в 1827 году вместе с его теорией однородных координат. Эта техника не прижилась до 1960-х годов, когда нью-йоркские школьники сделали ее популярной. Методика значительно упрощает некоторые задачи. Геометрия точки массы включает в себя систематическое присвоение «веса» точкам с использованием отношений длин, относящихся к вершинам, которые затем можно использовать для вывода других длин, используя тот факт, что длины должны быть обратно пропорциональны их весу (точно так же, как сбалансированный рычаг).Кроме того, точка, разделяющая линию, имеет массу, равную сумме весов на обоих концах линии (например, точка опоры рычага).

Способ систематического присвоения весов точкам включает в себя сначала выбор точки, вокруг которой будет балансировать вся фигура. Оттуда WLOG можно назначить первый вес. Из первого веса можно вывести другие, используя несколько простых правил. Любая линия, проходящая через эту центральную точку, уравновесит фигуру. Если две точки находятся в равновесии, то произведение массы и расстояния от линии равновесия одной точки будет равно произведению массы и расстояния от той же линии равновесия другой точки. Если две точки уравновешены, то точка на балансировочной линии, используемой для их уравновешивания, имеет массу суммы масс двух точек. То есть, если две точки ( и ) имеют массы и , соответственно, третья точка между и которая делится на отношение будет иметь массу .

Примеры

Пример 1

Рассмотрим треугольник с тремя проведенными медианами, точки пересечения которых соответствуют и соответственно. Таким образом, если мы обозначаем точку с весом , также должны иметь вес, поскольку и равноудалены от .С помощью того же процесса мы находим, что должны также иметь вес 1. Теперь, поскольку и оба имеют вес , должны иметь вес (как верно для и ). Таким образом, если мы пометим центроид , мы можем сделать вывод, что это — обратное отношение их весов.

Пример 2

имеет точку на , точку на и точку на . , , и пересекаются в точке . Соотношение есть, а отношение есть. Найдите соотношение

Решение

В этом решении пусть обозначают вес в точке . Так как , пусть , что делает . Теперь посмотрите на . Поскольку (это общее свойство, обычно используемое во многих проблемах с массовыми точками, фактически это то же самое свойство, которое мы использовали выше для определения ), мы имеем . Затем (еще одно свойство массовых точек). Наконец, у нас есть .

~ приключение

Проблемы

2019 AMC 8 Проблемы/Проблема 24

2016 AMC 10A Проблемы/проблема 19

2013 AMC 10B Проблемы/проблема 16

2004 AMC 10B Проблемы/проблема 20

2016 AMC 12A Проблемы/проблема 12

2009 AIME I Проблемы/Проблема 5

2009 AIME I Проблемы/Проблема 4

2001 AIME I Проблемы/Проблема 7

2011 Проблемы AIME II/Проблема 4

1992 AIME Проблемы/Проблема 14

1988 AIME Проблемы/Проблема 12

1989 AIME Проблемы/Проблема 15

1985 AIME Проблемы/Проблема 6

1971 AHSME Проблемы/проблема 26

Видео-лекция

Центральная математическая группа Северной Каролины недавно выпустила лекцию о массовых точках и барицентрических координатах, которую вы можете посмотреть по адресу https://www. youtube.com/watch?v=KQim7-wrwL0.

Самая сложная в мире задача «Простая геометрия»

Вот Самая сложная в мире простая задача по геометрии, как можно найти на веб-странице Кита Эневольдсена Think Zone: Решения обеих этих проблем можно найти далеко ниже, так что будьте осторожны как далеко вы прокручиваете ниже, если вы не хотите видеть ответ. Что делает эти задачи по геометрии такими интересными (и «сложными»), так это то, что только допускается элементарная геометрия (без тригонометрии).Например, основные правила о параллельные и пересекающиеся прямые и углы, образованные: а также простой факты о треугольнике: сумма внутренних углов треугольника в сумме 180° теорема о равнобедренном треугольнике о двух равных углах/сторонах равносторонний треугольник имеет три угла по 60° и три стороны одинаковой длины а также что делает два треугольника равными: Решения, приведенные ниже, разработаны не являются строгими доказательствами , а скорее предоставьте достаточно информации, чтобы сделать истинную решение очень очевидное для большинства читателей. Вы должны щелкнуть, чтобы найти изображения, связанные с этими решениями, чтобы не портить удовольствие тем, кто хочет попробовать найти решение для себя первый. Проблема Один Решение Решение Одно изображение 1. Вычислите некоторые известные углы: ACB = 180-(10+70)-(60+20) = 20° АЕВ = 180-70-(60+20) = 30° 2. Из точки D проведите прямую, параллельную АБ, обозначение пересечения с BC в качестве новой точки F и заключаем: 3.Нарисуйте линию FA маркировка пересечения с DB в качестве новой точки G и заключаем: 4. CFA с двумя углами 20° равнобедренный, поэтому ФК = ФА 5. Проведите линию CG, который делит ACB пополам и заключает: АКГ CAE FC-CE = ФА-АГ = КЭ = ФГ ФГ = ФД, поэтому FE = ФД 6. При двух равных сторонах ДКЭ равнобедренный и заключаем: ДЭФ = 30+х = (180-80)/2 = 50 Ответ: х = 20° Решение второй проблемы Решение Два изображения 1. Вычислите некоторые известные углы: ACB = 180-(20+60)-(50+30) = 20° АЕВ = 180-60-(50+30) = 40° 2. Из точки E проведите прямую, параллельную АБ, обозначение пересечения с AC как новую точку F и сделать вывод: 3. Нарисуйте линию ФБ маркировка пересечения с AE в качестве новой точки G и заключаем: 4. Проведите линию DG. С АД=АВ (нога равнобедренная) и АГ=АВ (каттер равностороннего), заключаем: н.э. = аг. DAG равнобедренный ADG = AGD = (180-20)/2 = 80° 5.Поскольку DGF = 180-80-60 = 40°, заключаем: FDG (с двумя углами по 40°) равнобедренный, поэтому ДФ = ДГ 6. С ЭФ = ЭГ (ноги равностороннего) и ДЭ = ДЭ (тот же отрезок) сделать вывод: Ответ: х = 30° Copyright © 2000-2022 Duckware

Задачи сложной геометрии с решениями

Решения вчерашних задач сложной геометрии

Сегодня я хотел бы опубликовать ответы на три сложных вопроса по геометрии, которые я опубликовал вчера. Если после прочтения приведенных ниже решений вам все еще нужны дополнительные объяснения, не стесняйтесь спрашивать.

Геометрические задачи 5 уровня

1. Длины сторон треугольника равны х , 16 и 31, где х самая короткая сторона. Если треугольник не равнобедренный, каково возможное значение x ?

Решение: По правилу треугольника х лежит между 31 – 16 = 15 и 31 + 16 = 47. То есть имеем 15 < х < 47.Но нам также известно, что х — это длина самой короткой стороны треугольника. Таким образом, x < 16. Следовательно, мы можем использовать любое число от 15 до 16. Например, мы можем создать сетку 15,1 .

Для получения дополнительной информации о правиле треугольника см. следующую статью: Правило треугольника

2. На рисунке выше, если AB = 4, BC = 24 и AD = 26, то CD =

Решение: Задача станет намного проще, если мы «переместим» BC влево, а AB вниз, как показано ниже.

Теперь у нас есть один прямоугольный треугольник, и мы можем либо использовать теорему Пифагора, либо, что еще лучше, заметить, что 26 = (13)(2) и 24 = (12)(2). Таким образом, другая сторона треугольника равна (5)(2) = 10. Итак, мы видим, что CD должно иметь длину 10 – 4 = 6.

Примечание: Если бы мы не заметили, что это кратное треугольнику 5-12-13, то мы бы использовали теорему Пифагора следующим образом.

( x + 4) ² + 24 ² = 26 ²
( x + 4) ² + 576 = 676
( x + 4) ² = 100
х + 4 = 10
х = 6

3. На рисунке выше показан прямоугольный цилиндр диаметром 6 и высотой 9.Если точка   O  является центром верхней части цилиндра, а B  лежит на окружности нижней части цилиндра, каково расстояние по прямой между   O  и B ?

Решение: Нарисуем прямоугольный треугольник внутри цилиндра следующим образом:

Обратите внимание, что нижний катет треугольника равен радиусу окружности (а не диаметру), поэтому он равен 3, а не 6.