Текстовые задачи. Задачи на движение с решениями
Задачи на движение с решениями
перейти к содержанию курса текстовых задач
- Первый турист проехал 2 ч на велосипеде со скоростью 16 км/ч. Отдохнув 2 ч, он отравился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле со скоростью 56 км/ч. На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение
- Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно. Решение
- Поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда. Решение
- Расстояние между станциями A и B равно 103 км. Из A в B вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся до B путь проходил со скоростью, на 4 км/ч большей, чем прежняя. Найти первоначальную скорость поезда, если известно, что оставшийся до B путь был на 23 км длиннее пути, пройденного до задержки, и что на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до нее. Решение
- Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору. Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение
- Автобус проходит расстояние между пунктами A и B по расписанию за 5 ч. Однажды, выйдя из A, автобус был задержан на 10 мин в 56 км от A и, чтобы прибыть в B по расписанию, он должен был оставшуюся большую часть пути двигаться со скоростью, превышающей первоначальную на 2 км/ч. Найти скорость движения автобуса по расписанию и расстояние между пунктами A и B, если известно, что это расстояние превышает 100 км. Решение
- Поезд проходит мимо платформы за 32 с. За сколько секунд поезд проедет мимо неподвижного наблюдателя, если длина поезда равна длине платформы? Решение
- Два поезда отправляются навстречу друг другу с постоянными скоростями, один из А в В, другой из В в А. Они могут встретиться на середине пути, если поезд из А отправится на 1,5 ч раньше. Если бы оба поезда вышли одновременно, то через 6 ч расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение
- От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз на 96 км, потом повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути расстоянии 24 км от А. Решение
- Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В — вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А — первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч? Решение
- Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях — через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение
- Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Решение
- Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся? Решение
Задачи для самостоятельного решения
- Дорога от A до D длиной в 23 км идет сначала в гору, затем — по ровному участку, а потом — под гору. Пешеход, двигаясь из A в D, прошел весь путь за 5 ч 48 мин, а обратно, из D в A, — за 6 ч 12 мин. Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ: 8 км
- В 5 ч утра со станции A вышел почтовый поезд по направлению к станции B, отстоящей от A на 1080 км. В 8 ч утра со станции B по направлению к A вышел пассажирский поезд, который проходил в час на 15 км больше, чем почтовый. Когда встретились поезда, если их встреча произошла в середине пути AB? Ответ: в 5 ч дня
- Из пункта A впунктB отправились три велосипедиста. Первый из них ехал со скоростью 12 км/ч. Второй отправился на 0,5 ч позже первого и ехал со скоростью 10 км/ч. Какова скорость третьего велосипедиста, который отправился на 0,5 ч позже второго, если известно, что он догнал первого через 3 ч после того как догнал второго? Ответ: 15 км/ч
- Два поезда — товарный длиной в 490 м и пассажирский длиной в 210 м — двигались навстречу друг другу по двум параллельным путям. Машинист пассажирского поезда заметил товарный поезд, когда он находился от него на расстоянии 700 м; через 28 с после этого поезда встретились. Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ: 36 км/ч; 54 км/ч
- Турист A и турист B должны были выйти одновременно навстречу друг другу из поселка M ипоселкаN соответственно. Однако турист A задержался и вышел позже на 6 ч. При встрече выяснилось, что A прошел на 12 км меньше, чем B. Отдохнув, туристы одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате A пришел в поселок N через 8 ч, а B пришел в поселок M через 9 ч после встречи. Определить расстояние MN и скорости туристов. Ответ: 84 км; 6 км/ч; 4 км/ч.
- Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был на расстоянии 6 км позади них, а тот момент, когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. На сколько километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист? Ответ: 2 км
- Два туриста вышли одновременно из пункта A в пункт B.Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
- Рыбак проплыл на лодке от пристани против течения 5 км и возвратился обратно на пристань. Скорость течения реки равна 2,4 км/ч. Если бы рыбак греб с той же силой в неподвижной воде озера на лодке с парусом, увеличивающим скорость на 3 км/ч, то он за то же время проплыл бы 14 км. Найти скорость лодки в неподвижной воде. Ответ: 9,6 км/ч
- Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Расстояние, пройденное лодкой по озеру, на 15% меньше расстояния, пройденного по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость движения лодки вниз по реке больше скорости движения по озеру? Ответ: на 20%
- Турист проплыл в лодке по реке из города A в город B и обратно, затратив на это 10 ч. Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч
- По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определить скорости точек. Ответ: 4 м/с; 3 м/с.
- Из точек A и B одновременно начали двигаться два тела навстречу друг другу. Первое в первую минуту прошло 1 м, а в каждую последующую проходило на 0,5 м больше, чем в предыдущую. Второе тело проходило каждую минуту по 6 м. Через сколько минут оба тела встретились, если расстояние между A и B равно 117 м? Ответ: через 12 мин.
- Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по одной и той же речной трассе через 5 ч с момента отплытия. Протяженность всего рейса составила 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем потребовалось столько же времени, сколько на каждые 3 км по течению. Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ: 5/12 км/ч; 2 ч и 3 ч.
Метки движение, текстовые задачи. Смотреть запись.
www.itmathrepetitor.ru
Задачи на движение в одном направлении: примеры и решение
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость с которой объекты сближаются друг с другом называется скоростью сближения.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:
40 · 4 = 160 (км)
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) – это скорость сближения автомобилей
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч)
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) – расстояние между автомобилями
2) 60 — 40 = 20 (км/ч) – скорость сближения автомобилей
3) 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч)
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч)
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) – это скорость сближения пешеходов
2) 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость с которой объекты отдаляются друг от друга называется скоростью удаления.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 2. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.

1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
80 — 40 = 40 (км/ч)
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
40 · 3 = 120 (км)
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
200 : 40 = 5 (ч)
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
naobumium.info
Урок математики в 5-м классе по теме «Задачи на движение по реке»
Тема: Задачи на движение по реке.
Цели:
- обобщить и систематизировать знания по теме «Задачи на движение по реке»;
- проверить знание теоретического материала, умение решать задачи арифметическим способом;
- развивать кругозор, мышление, внимание, культуру математической речи;
- прививать интерес к математике.
Методы обучения: частично-поисковый (эвристический), системные обобщения, самопроверка, взаимопроверка.
Формы организации урока: фронтальная, индивидуальная.
Оборудование: презентация к уроку, листы учета знаний.
ХОД УРОКА
I. Организационный момент
Сообщить учащимся цели урока. Настроить ребят на активную работу.
II. Проверка домашнего задания
№ 391(а).
Собственная скорость теплохода 27км/ч, скорость течения реки 3 км/ч. Сколько времени затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними 120 км?
Решение:
1) Vпо теч.= Vсоб.+ Vтеч. = 27 + 3 = 30 (км/ч).
2) tпо теч.= S : Vпо теч.= 120 : 30 = 4 (ч.)
Ответ: 4 часа.
№ 392.
Катер, имеющий собственную скорость 15 км/ч, проплыл 2 часа по течению реки и 3часа против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
Решение:
1) Vпо теч.= Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
2) Vпр. теч.= Vсоб. – Vтеч.= 15 – 2 = 13 (км/ч.)
3) Sпо теч.= Vпо теч. · tпо теч. = 17 · 2 = 34 (км)
4) Sпр теч.= Vпр. теч.· t пр. теч.=13 · 3 = 39 (км)
5) S=Sпо теч.+ Sпр. теч. = 34 + 39 = 73 (км)
Ответ: 73 км
III. Актуализация знаний
(Фронтальная работа)
Вопросы: (устно или с использованием проектора.)
1. Что такое собственная скорость катера? Ответ:
скорость катера в стоячей воде (озере, пруду).
2. Что такое скорость течения? Ответ: на какое
расстояние относит река предмет за единицу
времени.
3. Как определяется скорость катера по течению
реки? Ответ: как сумма скорости собственной и
течения.
4. Как определяется скорость катера против
течения? Ответ: как разность скорости
собственной и течения.
5. Как определяется скорость движения плота по
реке? Ответ: как скорость течения реки.
Подведем итог:
Vпо течению – сумма V течения и V
собственной.
V против течения – разность Vсобственной и
Vтечения.
Значит, зная Vпо течению и Vпротив течения, можно
найти Vтечения и Vсобственной.
Вспомним задачу на нахождение двух чисел по их сумме и разности.
1) (V по теч. – V пр. теч.) : 2 = Vтеч.
2) Vпо теч. – Vтеч. = Vсоб.
IV. Решение задач
№ 1.
Из четырех скоростей (Vсоб.,Vпо теч.,Vпр. теч.,Vтеч. ) две заданы и изображены отрезком. Вычислите две другие скорости и изобразите их отрезками:
№ 2. Заполним таблицу.
Vсоб, км/ч |
V теч, км/ч |
Vпо теч, км/ч |
Vпр. теч, км/ч |
15 |
3 |
? |
? |
16 |
? |
18 |
? |
13 |
? |
? |
10 |
? |
2 |
11 |
? |
? |
3 |
? |
15 |
? |
? |
28 |
24 |
№ 3
Решим задачу № 393 (а).
Расстояние между двумя причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно, если собственная скорость моторной лодки 10 км/ч, а скорость течения 2 км/ч?
Решение:
1) Vпо теч.= Vтеч.+ Vсоб.= 2 + 10 = 12 (км/ч)
2) Vпр. теч. = Vсоб. – Vтеч.= 10 – 2 = 8 (км/ч)
3) tпо теч.= S : Vпо теч.= 24 : 12 = 2 (ч)
4) tпр. теч.= S : Vпр. теч.= 24 : 8 = 3 (ч)
5) t = tпо теч. + tпр. теч.= 2 + 3 = 5 (ч)
Ответ: 5 часов.
V. Самостоятельная работа
I вариант |
II вариант |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Скорость моторной лодки в стоячей
воде 15км/ч, а скорость течения реки 3 км/ч. Сколько времени потратит моторная лодка на путь от одной пристани до другой и обратно, если расстояние между пристанями 36 км? 2)
|
1) Скорость моторной лодки в стоячей
воде 10 км/ч, а скорость течения реки 2 км/ч. Сколько времени потратит моторная лодка на движение от одной пристани до другой и обратно, если расстояние между пристанями 24 км? 2)
|
VI. Подведение итогов урока
Заполнить карточку самоанализа.
Объявление оценок за урок.
VII. Определение домашнего задания
№ 393 (б), 394 С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. Математика: учебник для 6 кл. общеобразовательных учреждений.– М.: Просвещение, 2008 г.
Презентация
Список литературы:
1. С.М.Никольский, М.К.Потапов, Н.Н.Решетников,
А.В.Шевкин. Математика: учебник для 6 кл.
общеобразовательных учреждений. – М.:
Просвещение, 2008 г.
2. А.В.Шевкин. Обучение решению текстовых
задач в 5-6 классах. – М.: «Русское слово», 2001г.
urok.1sept.ru
Урок математики в 5-м классе «Задачи на движение»
Тема урока: «Задачи на движение»
Количество часов по разделу: 3
Номер урока в разделе: 1
Тип урока: Изучение и первичное закрепление новых знаний
Цель темы: Создать условия для изучения нового вида задач – на встречное движение и движение в одну сторону.
Цели урока:
Образовательная. Обучить учащихся способам решения задач на встречное движение и движение в одну сторону. Обеспечить условия для усвоения всеми учащимися понятий скорости сближения и скорости удаления. Определить уровень восприятия, осмысления и первичного запоминания нового материала, провести коррекцию уровня сформированности умений и навыков в ходе урока.
Развивающая: Развивать умение сравнивать, анализировать, обобщать. Развивать творчество учащихся.
Воспитательная: Воспитывать у учащихся чувство уверенности в своих силах. На примерах задач учить разрешать жизненные вопросы и проблемы.
Уровневые цели для учащихся:
I уровень (базовый)
Понимать формулировку задачи. Уметь находить расстояние, скорость, время. Понимать термины «скорость сближения», «скорость удаления». Уметь решать простейшие задачи на движение в одном направлении и разных направлениях.
II уровень (конструктивный)
Уметь классифицировать задачи. Решать более сложные задачи на движение.
III уровень (творческий)
Уметь решать сложные задачи на движение. Уметь составить задачу по заданной схеме.
Ожидаемый результат:
- Каждый ученик должен проводить классификацию задач по виду движения (в одном направлении, в разных направлениях)
- Уметь выбирать наиболее рациональный способ решения задачи.
- Использовать изученный материал для решения задач в других темах курса.
План урока:
- Организация начала занятий.
- Актуализация опорных знаний.
- Восприятие, осмысление и первичное запоминание нового материала. Проверка усвоения знаний и способов действий. Первичное закрепление знаний и способов действий на трех уровнях. Контроль и самопроверка усвоения знаний и способов действий и коррекция знаний.
- Подведение итогов урока.
- Рефлексия.
- Информация о домашнем задании.
Ход урока
1 этап.
Объявление темы урока, цели урока.
Ученики записывают число и тему урока в тетрадь. Формулируют цель урока.
2 этап.
Актуализация опорных знаний.
1. Выполнить действия:
2. Решить задачу:
Скорость автомобиля 50 км/ч. Сколько километров проедет автомобиль за 2ч, 3ч, а за 5ч? за какое время автомобиль проедет расстояние в 300 км?
3 этап. Объяснение нового материала.
Среди всех задач, которые приходится решать, нередко бывают задачи на движение. В них движутся пешеходы, велосипедисты, мотоциклисты, автомобили, самолеты, поезда и т.д. Нам надо научиться легко решать такие задачи. Чтобы вы научились решать их, мы сегодня разберем новый вид задач – на встречное движение и движение в одну сторону.
Кто и что будет двигаться, нам неважно. План решения от этого не зависит.
Поэтому договоримся, что у нас будут двигаться два путешественника – пешеход Антон и велосипедист Иван. Договоримся, что во всех вариантах задач скорости у них будут одни и те же.
Антон ходит со скоростью 4 км/ч, а Иван ездит со скоростью 20 км/ч.
Задача 1.
Антон и Иван отправились навстречу друг другу из двух пунктов, расстояние между которыми равно 72 км.
а) На какое расстояние они сблизятся за 1ч, 2ч?
б) Через сколько часов они встретятся?
4 + 20 = 24 (км/ч) – за 1 час – скорость сближения
24 ? 2 = 48 (км) – будут через 2 часа
72 : 24 = 3 (ч) – они встретятся
Задача 2.
От места встречи Иван и Антон отправились одновременно в противоположных направлениях друг от друга. На какое расстояние они удалятся друг от друга за 1 ч, за 2 ч?
За каждый час расстояние между ними будет увеличиваться на
4 + 20 = 24 (км/ч) – скорость удаления
24 ? 2 = 48 (км) – расстояние через 2 часа.
Вывод: при движении в разных направлениях
Задача 3.
Антон и Иван отправились одновременно из двух пунктов, расстояние между которыми 72 км., движутся в одном направлении так, что Иван догоняет Антона.
а) На какое расстояние они сблизятся за 1 ч, 2 ч?
б) Через сколько часов Иван догонит Антона?
Расстояние каждый час будет уменьшаться на
20 – 4 = 16 (км/ч) – скорость сближения
16 ? 2 = 32 (км) – расстояние через 2 часа
– Иван догонит Антона
Задача 4.
После того как Иван догнал Антона, они продолжали движение в одном направлении, так что Иван удаляется от Антона. На какое расстояние они удалятся друг от друга за 1 ч, за 2 ч, за 3 ч?
20 – 4 = 16 (км/ч) – скорость удаления
16 ? 2 = 32 (км) – расстояние через 2 часа
16 ? 3 = 48 (км) – расстояние через 3 часа
Вывод: при движении в одном направлении
4 этап. Первичное закрепление.
1. Ответить на вопросы:
- Что называется скоростью сближения? Скоростью удаления?
- Когда скорость сближения равна сумме скоростей путешественников? Когда она равна разности скоростей?
- Когда скорость удаления равна сумме скоросктей путешественников? Когда она равна разности скорстей?
- Антон и Иван начали движение из одного пункта. Чему равна скорость их удаления друг от джруга, если они движутся: а) в одном направлении; б) в противоположных направлениях?
2. Решить задачи №1 (устно) из листа с задачами, которые имеются на каждой парте.
3. Решить задачи №4 – 5 с проверкой у доски
4. Составить задачу по следующей схеме.
5. Самостоятельно решить задачи с листа задач. ( Каждый решает задачи своего уровня сложности)
Задачи на движение.
- Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3ч?
- Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся?
- Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
- Два поезда отошли от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70км/ч. Через сколько часов расстояние между ними будет 260 км?
- Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
- Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4км/ч, скорость второго 5км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа?
- Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние меду которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
- Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие?
- Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км?
- Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость первого 40 км/ч, второго 50 км/ч. Через сколько часов второй догонит первого?
- Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов они встретятся?
- Из села вышел пешеход со скоростью 4 км/ч. Через 3 часа вслед за ним выехал велосипедист со скоростью 10 км/ч. За сколько часов велосипедист догонит пешехода?
- Расстояние от города до села 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?
- Старинная задача. Некий юноша пошел из Москвы к Вологде. Он проходил в день 40 верст. Через день вслед за ним был послан другой юноша, проходивший в день 45 верст. Через сколько дней второй догонит первого?
- Старинная задача. Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака за 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?
- Старинная задача. Из Москвы в Тверь вышли одновременно 2 поезда. Первый проходил в час 39 верст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 верст. Сколько верст от Москвы до Твери?
5 этап. Подведение итогов урока.
Ученики оценивают свою работу.
Рефлексия.
6 этап. Информация о домашнем задании.
Выплнить задачи №403(б), №405
urok.1sept.ru
Решение задач на движение (5 класс)
Тема: Решение задач на движение
Тип урока: урок освоения новой учебной информации
Цель урока: формировать умение анализировать и решать задачи на движение (навстречу друг другу, в противоположных направлениях).
Предметные УУД: умение определять вид задачи, способы решения задачи (навстречу друг другу, в противоположных направлениях), развивать математическую речь учащихся, умение обосновывать свое решение.
Метапредметные УУД:
Регулятивные: планировать свое действие в соответствии с учебным заданием, ставить учебные цели, задавать вопросы на уточнение, адекватно оценивать результаты деятельности, осуществлять самоконтроль;
Познавательные: дополнять условие задачи с недостающими данными, структурировать информацию в виде таблицы, обобщать и анализировать полученные знания;
Коммуникативные: вести диалог с учителем, участвовать в обсуждении содержания материала, эффективно сотрудничать, соотносить свое мнение с мнением других участников учебного коллектива.
Личностные УУД: умения преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести диалог, аккуратности.
Технологическая карта урока
Деятельностьучителя
Задания для учащихся, выполнение которых приведет к достижению планируемых результатов
Деятельность
учеников
Планируемые результаты
предметные
универсальные учебные действия
(УУД)
1. Организационный момент (1 мин)
Создает условия для формирования внутренней потребности учеников во включении в учебную деятельность.
Здравствуйте, ребята! Присаживайтесь! Я надеюсь на вашу отличную работу в течение урока, потому что знаю вы умеете работать быстро и получать хороший результат, умеете думать и рассуждать.
Командир сдает рапорт.
Слушают учителя.
Коммуникативные: уметь совместно договариваться о правилах поведения и общения, следовать им; оформлять свои мысли в устной форме
2. Актуализация знаний. Технология ТРКМ. Стадия «Вызов» (7 мин)
Постановка проблемного вопроса
Предлагаю вам просмотреть видеосюжеты, которые помогут вам сформулировать тему урока
Какие ассоциации возникли? Как их связать с уроком математики?
Как почувствовали эту скорость? Почему на уроках математики важна эта величина?
Вы готовы сформулировать тему сегодняшнего урока, о чем будет идти речь?
Правильно, спасибо. (слайд)
Откройте тетради, запишите 19.12.2017. Классная работа и тему урока Решение задач на движение
Исходя из темы сформулируйте цель урока
Для того, чтобы достичь цель, что мы должны будем сделать?
Какие математические величины характеризуют процесс движения любого объекта?
Запишите в маршрутном листе в первой строке Путь. Скорость. Время.
Во второй строке запишите какими буквами латинского алфавита обозначаются путь, скорость, время.
В третьей строке запишите формулы для нахождения математических величин.
А теперь проверим, что у вас получилось.
Кто заполнил все верно поднимите руку. Кто допустил ошибки? Значит, нужно будет повторить формулы.
Прочитайте самостоятельно задачу в маршрутном листе и попытайтесь решить ее устно:
Из двух пунктов А и В, расстояние между которыми 27 км, отправились одновременно два пешехода. Их скорости 4 км/ч и 5км/ч, какое расстояние будет между ними через 2 часа?
Кто смог решить задачу? Кто не смог? В чем затруднение?
Как решил? Все ли согласны?
Подумайте, как два тела по отношению друг к другу могут двигаться.
Продемонстрируйте движение по первой картинке, прикрепленной на доске.
Определите вид движения и соотнесите схему.
Ребята, напишите вид движения и перечертите схему в маршрутный лист.
А как мы будем решать задачи?
Спасибо, молодцы! На сегодняшнем уроке мы с вами рассмотрим первых два вида движения (навстречу друг другу, в разных направлениях), а решение задач в одном направлении рассмотрим на следующий урок.
Дополним цель нашего урока.
Итак, мы повторили материал? Теперь перейдем ко второму этапу урока. (звездочка)
На доске Решение задач
Цель урока: учиться решать задачи на движение (слайд и прописывается на доске)
Повторить, что мы уже знаем
Узнать новое
Закрепить изученное
s=v*t
v=s:t t=s:v
На доске дополняет учитель цель урока (в одном направлении, в разных направлениях)
Фронтальная, индивидуальная
Учащиеся включаются в активную деятельность
Движение
Формулируют и записывают тему Задачи на движение.
Отвечают на вопросы (Расстояние. Скорость. Время)
Заполняют маршрутный лист Учащиеся комментируют формулы.
Проверяют
Поднимают руку
Испытывают затруднения.
Мы не знаем, как двигались по отношению друг к другу пешеходы.
Навстречу друг другу.
В разные стороны.
Друг за другом.
Демонстрируют движения
В зависимости от видов движения (в одном направлении, в разных направлениях, навстречу друг другу)
Слушают учителя
Знать формулы нахождения пути, скорости и времени движения.
Познавательные: Уметь ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя. Преобразовывать информацию из одной формы в другую)
Коммуникативные: уметь слушать и понимать речь других, оформлять мысли в устной и письменной форме.
Регулятивные: уметь проговаривать последовательность действий на уроке, высказывать свое предположение.
Реализация второго этапа технологии ТРКМ «Осмысление».
Отработка умений решать задачи
Давайте выстроим алгоритм для решения задач на движение
Сейчас будем решать задачи навстречу друг другу и в противоположных направлениях. Кто может подсказать какие новые знания понадобятся при решении задач? Внимательно прочитайте обе задачи. Какие данные одинаковые? Чем отличаются эти задачи? Теперь предлагаю вам выбрать для решения самостоятельно одну из задач.
Кто выбрал 1 задачу?
Кто 2-ю задачу?
Какой вид движения у первой задачи?
Решая задачу, схему чертить не нужно, пояснение тоже не нужно записывать. Только формулы, решение, единицы измерения, ответ. На решение 2 минуты.
Вызывает к доске оформить задачи.
При движении двух участников из двух пунктов навстречу друг другу что происходит с объектами?
Как называется величина, которая равна сумме скоростей этих участников?
Молодцы! Ну, а теперь давайте запишем формулу скорости сближения, когда объекты движутся навстречу друг другу в таблицу в маршрутном листе.
— Как называется математическая величина равная сумме скоростей этих участников?
— Запишите пожалуйста в таблицу в маршрутном листе формулу скорости удаления.
В чем красота 2 способа?
Второй этап подошел к завершению. Какой итог подведем?
Передвигаемся на этап закрепления, но вначале немного отдохнем.
Прочитать внимательно задачу и проанализировать условие и вопрос
Определить вид задачи
Составить схему к задаче
Подобрать нужную формулу
Верно решить задачу
Из двух пунктов А и В выехали навстречу друг другу два велосипедиста. Скорость одного из них 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
• Смоделировать задачу
• Решить с полным объяснением
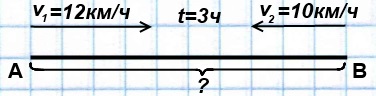
12*3=36 (км) – S первого велосипедиста за 3 ч.
10*3=30 (км) – S второго велосипедиста за 3 ч.
36+30=66 (км) – S между велосипедистами в начале пути
12*3+10*3=(12+10)*3=66 (км)
1) 12+10=22 (км/ч) — скорость сближения велосипедистов
2) 22∙3=66 (км) — было между велосипедистами в начале пути.
Ответ: 66 км.
Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Скорость одного из них — 12 км/ч, скорость другого — 10 км/ч. Какое расстояние будет между ними через 3 часа?
3*(12+10)=66 (км) – S между поездами через 2 часа
Решение:
1) 12 + 10 = 22 (км/ч) – скорость удаления.
2) 22 * 3 = 66 (км) – S между поездами через 2 часа
Ответ: 66 км
На магнитной доске прикрепляют последовательно предложения
Ответы учеников:
Да.
Чтобы найти расстояние, которое было между велосипедистами в начале пути мы складывает скорости первого и второго велосипедиста и умножаем на время
они сближаются
скорость сближения
записывают формулу
Уметь решать задачи на нахождение пути, скорости и времени движения
Уметь находить скорость сближения
Познавательные: уметь извлекать из математических текстов необходимую информацию, устанавливать причинно-следственные связи.
Регулятивные: уметь работать по коллективно составленному плану, проговаривать последовательность действий на уроке.
Коммуникативные: уметь слушать и понимать речь других, оформлять мысли в устной и письменной форме.
Личностные: ориентироваться на успех в учебой деятельности.
Физминутка (1 мин)
V= 5 км/ч, t= 2 ч, S=10 км? S=40 км, t=2 ч, V=30 км/ч? 12^2=144, 11^2=111…….
Выполняют упражнения(хлопок над головой верно, неверно перед собой хлопок)
6. Самостоятельная работа.
А теперь, чтобы проверить уровень усвоения вами темы проведем самостоятельную работу (5 мин) Посмотрите на работу, 3 задание решать без схем, пояснений, только наименование единиц измерения, ответ.
Критерий оценивания:
3 задачи решены верно – «5»;
2 задачи решены верно – «4»;
1 задача решена верно – «3»
Время закончилось, теперь взаимопроверка. Обменяйтесь маршрутными листами с соседом по парте. Критерий оценивания прописан в маршрутном листе.
У кого отметка «5», «4»?
По окончанию урока сдадите маршрутные листы, я еще раз проверю ваши работы и отметки «5» и «4» выставлю в журнал
Молодцы! Справились с заданием.
Ребята, а где нам пригодится тема Задачи на движение в дальнейшем?
Самостоятельная работа
Вариант I
1. Решите задачу.
Сколько километров проползет гигантская слоновая черепаха за 3 часа, если ее скорость 4 км/ч?
2. Определите вид задачи, поставьте +
На движение в противоположных направлениях
Движение навстречу друг другу
На движение
Два велосипедиста выехали одновременно из одного поселка в противоположных направлениях. Через какое время расстояние между ними будет 84 км, если скорость одного из них 16 км/ч, а скорость другого – 12 км/ч?
3. Решить задачу.
От двух станций одновременно навстречу друг другу выехали два поезда, товарный и пассажирский. Скорость товарного поезда 42 км/ч, а скорость пассажирского – 85 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Вариант II
1. Решите задачу.
Сколько километров пробежит гепард за 3 часа, если его скорость 110 км/ч?
2. Определите вид задачи, поставьте +
На движение в противоположных направлениях
Движение навстречу друг другу
На движение
Два велосипедиста выехали одновременно навстречу друг другу из двух сел, расстояние между которыми 54 км. Через какое время они встретятся, если их скорости 12 км/ч и 15 км/ч?
3. Решите задачу
Из одного села в противоположных направлениях одновременно выехали два автомобиля, грузовой и легковой. Скорость грузового автомобиля 54 км/ч, а скорость легкового – 80 км/ч? Какое расстояние будет между ними через 2 часа?
Каждый в маршрутном листе решает задачу по вариантам, уже не парами.
Проверяют работы
Задачи встречаются в ВПР, для успешной сдачи ЕГЭ, отправляясь в школу, на занятия в кружках, мы рассчитываем время, необходимое для того, чтобы не опоздать. Рассчитываем, с какой скоростью будем идти, чтобы быть на месте вовремя. Поэтому нам важно уметь решать задачи на движение.
Уметь самостоятельно решать задачи на нахождение пути, скорости и времени движения.
Регулятивные: уметь проговаривать последовательность действий на уроке, выполнять работу по предложенному плану
7. Итог урока (5 мин).
Наш урок приближается к завершению.
Какая была цель урока?
Как думаете достигли цели?
— Какие трудности были на уроке?
— Что нового узнали на уроке?
— Что понравилось на уроке больше всего?
Ребята, что осталось в таблице у нас незаполненным?
Есть над чем поработать на следующем уроке
На экране памятка
Обучающиеся осуществляют рефлексию. Высказывания учащихся по уроку
Регулятивные: уметь оценивать правильность действия на уровне адекватной ретроспективной оценки
8. Домашнее задание.
Учитель комментирует домашнее задание.
1 задание для всех
2 и 3 на выбор
Для спешного выполнения домашней работы дарю вам памятки с алгоритмом по решению задач, приклейте пожалуйста в тетрадь для правил.
Ребята, в первой задаче в первом варианте в самостоятельной работе что нужно было найти?
Какой ответ получили?
А во втором варианте в первой задаче что нужно было найти?
Какой ответ получили?
Вывод какой?
Спасибо Вам, ребята, за добросовестную и ответственную работу! Спасибо за ваши знания и сотрудничетво!
П. 2.14, № 552 (а), 554 (а) (для всех)
Придумайте по одной задаче к каждому виду движения (навстречу друг другу, в разных направлениях) и решите их
Улитке нужно забраться на дерево высотой 10 метров. За день она поднимается на 4 метра, а за ночь сползает на 3.
Когда она доползет до цели, если стартовала улитка утром в понедельник?
4 м – за день (вечер в воскресенье)
+
6м – за сутки (утро в воскресенье)
5м – за сутки (утро в субботу)
4м – за сутки (утро в пятницу)
3м – за сутки (утро в четверг)
2м – за сутки (утро в среду)
1м – за сутки (утро во вторник)
Записывают домашнее задание
Сколькокило метров проползет черепаха за 3 часа
12 км
Сколько метров пробежит гепард за 3 часа?
330 км
Нужно быть гепардами
infourok.ru
Урок 35. задачи на движение — Математика — 5 класс
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
S | v | t | |
1. | 135 км | 9 км/ч | ____ ч |
2. | ____ м | 12 м/с | 4 с |
3. | 132 м | ____ м/мин | 11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
S | v | t | |
1. | 135 км | 9 км/ч | 15 часов |
2. | 48 м | 12 м/с | 4 с |
3. | 132 м | 12 м/мин | 11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
resh.in.edu.ru
Задачи на движение (5 класс)
Решение задач на движение двух тел.
v = 2 км/чt = 6 ч
s — ?
s = 12 км
v = 3 км/ч
t — ?
s = 2 м
t = 2 мин
v — ?
v = 10м/мин
t = 8 мин
s — ?
v = 6 км/ч
t = 3 ч
s — ?
s = 8 км
t = 2 ч
v — ?
v = 5 м/мин
t = 16 мин
s — ?
s = 12 м
t = 6 ч
v — ?
s = 70 км
v = 14 км/ч
t — ?
v = 6 м/мин
t = 15мин
s — ?
s = 60 см
v = 15 см/с
t — ?
s = 60 км
t = 12 мин
v — ?
Задача 1. Из двух городов, расстояние между которыми равно 65 км, выехали одновременно в противоположных направлениях два автомобиля. Один из них шел со скоростью 80 км/ч, а другой – 110 км/ч. На каком расстоянии друг от друга будут автомобили через 180 мин после выезда?
Задача 2: Одновременно из одного пункта в противоположных направлениях вышли два пешехода. Один из них шёл со скоростью 3,1 км/ч, а другой 2,5 км/ч. Через сколько времени пешеходы удалятся друг от друга на 8,4 км?
Задача 3: Два пешехода находились на расстоянии 3,2 км друг от друга. Они вышли одновременно в противоположных направлениях и через 15 мин оказались на расстоянии 6,8 км друг от друга. Найти скорости пешеходов, если известно, что скорость одного из них на 0,6 км/ч больше скорости другого пешехода.
Задача 4. С двух станций, расстояние между которыми 960 км, одновременно навстречу друг другу вышли два поезда. Скорость одного 90 км/ч, а второго на 20 км/ч меньше. Какое расстояние будет между поездами через 2 ч после выхода?
Задача 5. По шоссе навстречу друг другу едут автобус и мотоциклист. Скорость автобуса 900 м/мин, а скорость мотоциклиста составляет 75% скорости автобуса. Сейчас расстояние между ними 25 км 200 м. Через сколько времени они встретятся?
Задача 6. Из города одновременно в одном и том же направлении выехали два мотоциклиста. Скорость первого из них была больше скорости второго и составляла 72 км/ч. Через 25 мин расстояние между мотоциклистами было равно 5 км. Найдите скорость второго мотоциклиста.
Задача 7. Из города в одном и том же направлении отправились одновременно два автомобиля, скорости которых 75 км/ч и 63 км/ч. На сколько километров отстанет один автомобилист от другого за 3 ч?
Задача 8. Один турист выехал из турбазы на велосипеде, другой на мотороллере, через 2 ч расстояние между ними было 92 км. С какой скоростью ехал турист на мотороллере, если скорость велосипедиста равна 14 км/ч?
Задача 9. Выезжая из села, велосипедист заметил на мосту пешехода, идущего в том же направлении, и догнал его через 12 мин. Найдите скорость пешехода, если скорость велосипедиста 15 км/ч, а расстояние от села до моста 1 км 800 м.
Задача 10. Дорога из села в город проходит через рабочий поселок. Из села в город вышла легковая автомашина со скоростью 1,5 км/мин. В то же самое время из рабочего поселка в город вышла грузовая автомашина со скоростью 1 км/мин. Через 20 мин легковая автомашина догнала грузовую. Найдите расстояние от села до рабочего поселка.
Задача 11. Катер прошел от одной пристани до другой пристани 240 км и вернулся обратно. Найдите среднюю скорость катера на всем пути, если его собственная скорость 18 км/ч, а скорость течения 2 км/ч. Найдите время, затраченное на весь путь.
Задача 12. Путешественник проплыл против течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч.
infourok.ru