Задачи с треугольниками
Задачи по треугольникам с решениями.
Задачи по теме — соотношение между элементами и площадь треугольников.
Пример решения синтетическим методом
Задача: Биссектриса угла прямоугольника делит большую сторону на два отрезка длиной 7 и 9 см. Найти периметр прямоугольника.
Дано: ABCD – прямоугольник; AK – биссектриса;  ; BK = 7 см, KC = 9 см (либо BK = 9 см, KC = 7 см).
; BK = 7 см, KC = 9 см (либо BK = 9 см, KC = 7 см).
Решение задачи:
|
Углы 1 и 2 равны между собой как внутренние разносторонние. С другой стороны, угол 3 равен углу 2, так как AK — биссектриса. Отсюда следует, что угол 1 и угол 3 равны. Но так как эти углы равны, то ∆ABK — равнобедренный. Следовательно, AB = BK. |
|
Дальнейшее решение зависит от того, какой из отрезков равен 7 см, а какой – 9 см.
Если BK = 7 см, KC = 9 см, то AB = BK = 7 см, и периметр равен P = 2∙(7 + 7 + 9) = 46см.
Если BK = 9 см, KC = 7 см, то AB = BK = 9 см, и периметр равен P = 2∙(9 + 9 + 7) = 50 см.
**********************************
Обратите внимание: при решении этой задачи собирались воедино сведения из разных областей геометрии. Результат одного рассуждения использовался для построения следующего.
Примеры решения аналитическим методом
Пример 1. Найти градусные меры смежных углов, если разность их градусных мер равна 50°
- Решение. Обозначим градусные меры смежных углов x и Тогда по теореме о сумме смежных углов
 , а по условию
, а по условию  . Получили систему уравнений
. Получили систему уравнений

Отсюда находим x = 115°, y = 65°.
Пример 2. Доказать, что середины сторон любого четырехугольника являются вершинами параллелограмма.
|
Решение задачи: Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны. Следовательно, если мы докажем параллельность сторон четырехугольника, образованного серединами сторон, то задача будет решена. |
|
- Пусть AC и BD – диагонали четырехугольника. В треугольнике ABC: KL – средняя линия, следовательно, KL||В треугольнике ADC: PQ – средняя линия, следовательно, PQ||AC
- Тогда по признаку параллельных прямых имеем: KL||AC, PQ||AC, отсюда KL|| PQ. Аналогично доказывается параллельность KP и Следовательно, четырехугольник KLPQ – параллелограмм, ч.т.д. (quod erat demonstrandum).
Примеры решения задач по треугольникам алгебраическими методами
Сведение решения задачи к решению уравнения
Периметр прямоугольного треугольника равен 36 см. Гипотенуза AB относится к катету AC как 5:3. Найти стороны треугольника.
Решение задачи.
Дано : ∆ACB;  C = 90°; P = 36 см, AB:AC = 5:3. Найти AB, AC, BC.
C = 90°; P = 36 см, AB:AC = 5:3. Найти AB, AC, BC.
- Обозначим коэффициент пропорциональности через Тогда
 ,
,  . Так как
. Так как  , то
, то  . Отсюда
. Отсюда

Тогда k = 36/12 = 3 см, и стороны треугольника равны:
AB = 3∙5 = 15 см; AС = 3∙3 = 9 см; BC = 3∙4 = 12 см.
Комбинирование геометрического и аналитического методов
|
|
Через точку М внутри треугольника ABC проведены прямые, параллельные сторонам треугольника. Площади образованных при этом треугольников равны |
- Решение. Построим рисунок. Из рисунка видно, что образованные треугольники подобны исходному треугольнику Следовательно,

Тогда

отсюда 
Задачи по треугольникам для закрепления знаний
- н

**********************************************************
22.

Указание. Использовать формулу (2)
**********************************************************
6.

**********************************************************
**********************************************************
**********************************************************
**********************************************************
19.

**********************************************************
18.

**********************************************************
23.

**********************************************************
24.

**********************************************************
28.

**********************************************************
29.

**********************************************************
4.

**********************************************************

**********************************************************

**********************************************************
9.

**********************************************************

zadachi-ru.com.ua
Ключевые задачи по теме Треугольники
Ключевые задачи по теме Треугольники
Наглядная геометрия 7 класс. Ключевые задачи по теме Треугольники



Запомните!
1. Признаки равенства треугольников.
- 1-й. По двум сторонам и углу между ними.
- 2-й. По стороне и двум прилежащим к ней углам.
- 3-й. По трем сторонам.
2. Свойство углов равнобедренного треугольника.
Углы при основании равнобедренного треугольника равны.
3. Обратная теорема.
Если два угла треугольника равны, то треугольник равнобедренный.
4. Свойство биссектрисы равнобедренного треугольника.
Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают.
5. Признаки равнобедренного треугольника. Треугольник является равнобедренным, если:
- а) высота является и медианой;
- б) высота является и биссектрисой;
- в) биссектриса является и медианой.
6. Теорема о свойстве точек серединного перпендикуляра.
- Любая точка серединного перпендикуляра равноудалена от концов отрезка.
- Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.
7. Теорема о пересечении серединных перпендикуляров.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.
Простые вопросы по теме «Треугольники»

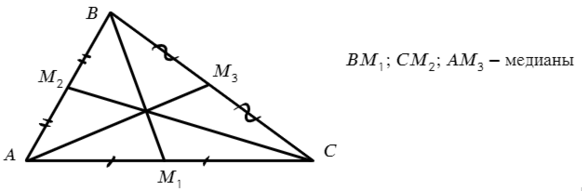
- В треугольнике провели медиану. Сколько треугольников изображено на рисунке?
- Если стороны треугольника продлить, то сколько углов всего образуется, не считая развернутых? А считая и развернутые?
- Верно ли, что биссектриса треугольника лежит на биссектрисе угла?
- Может ли высота треугольника делить сторону пополам?
- Может ли биссектриса треугольника быть перпендикулярной стороне треугольника?
- Верно ли утверждение: «Биссектриса равнобедренного треугольника является высотой и медианой»?
- Является ли любой равнобедренный треугольник равносторонним?
- Является ли любой равносторонний треугольник равнобедренным?
- Может ли биссектриса некоторого равнобедренного треугольника, проведенная к боковой стороне, быть медианой?
- Может ли высота треугольника быть равна его медиане, проведенной из той же вершины?
- Может ли биссектриса треугольника быть равна его высоте, проведенной из той же вершины?
- Существует ли треугольник, периметр которого в 3 раза больше одной из сторон?
- Если медиана образует равные углы с соседними сторонами треугольника, то какой угол она образует с третьей стороной?
- Что для студентов означает слово «медиум»?
- Сколько всего теорем в данной теме?
Непростые вопросы по теме «Треугольники»
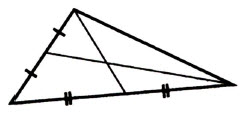
16* В треугольнике провели 2 медианы. Сколько треугольников изображено на рисунке?
17* В треугольнике провели 3 медианы. Сколько треугольников изображено на рисунке?
18* Может ли в треугольнике высота являться медианой, но не являться биссектрисой?
19* Как звучит теорема о свойстве углов равнобедренного треугольника в форме «Если …, то …»?
20* Как звучит утверждение, обратное теореме о свойстве углов равнобедренного треугольника, в форме «Если …, то …»?
21* Может ли медиана треугольника равняться соседней стороне?
22* Может ли биссектриса треугольника равняться соседней стороне?
23* Может ли высота треугольника равняться соседней стороне?
24* Может ли серединный перпендикуляр к стороне треугольника иметь общую точку с каждой из двух других сторон?
25* Может ли серединный перпендикуляр к стороне треугольника делить противоположный угол треугольника пополам?
Ответы на простые и непростые вопросы
- Три. Два маленьких и один данный.
- 12; 24.
- Да.
- Да. В равнобедренном треугольнике.
- Да. В равнобедренном треугольнике.
- Нет. Только биссектриса, проведенная из вершины к основанию.
- Нет.
- Да.
- Да. Если треугольник равносторонний.
- Да. В равнобедренном треугольнике это высота, проведенная к его основанию.
- Да. В равнобедренном треугольнике это биссектриса, проведенная к его основанию.
- Да. Например, равносторонний.
- 90°. Если медиана является биссектрисой, то треугольник равнобедренный и эта медиана является и высотой, проведенной к основанию.
- Медиум — студенческий праздник, знаменующий середину учебы.
- Тринадцать теорем, включая задачу о пересечении серединных перпендикуляров к сторонам треугольника.
16* 8.
17* 16.
18* Нет. Если высота является медианой, то треугольник равнобедренный и эта высота является и биссектрисой.
19* «Если треугольник равнобедренный, то углы при основании равны». 20* «Если у треугольника два угла равны, то треугольник равнобедренный».
21* Да.
22* Да.
23* Да. В прямоугольном треугольнике.
24* Да. В равнобедренном прямоугольном треугольнике.
25* Да. Если треугольник равнобедренный.
Это конспект по геометрии «Ключевые задачи по теме Треугольники». Выберите дальнейшие действия:
uchitel.pro
Теория и задачи по треугольникам (Часть Ⅰ)
 Вертикальные, смежные, соответственные, накрест лежащие углы.
Вертикальные, смежные, соответственные, накрест лежащие углы.
Равенство и подобие треугольников.
Медиана, биссектриса, высота.
Свойства треугольников.
Площадь треугольников.
Кругом одна геометрия — круг друзей, квадрат врагов, треугольник любящих.
Ю. Татаркин
Давай на чистоту: геометрию трудно понимать, если не знаешь определенных теорем и свойств. Я постараюсь донести до тебя понятным языком только необходимое, а ты постарайся разобраться и запомнить!
Что такое луч, прямая, отрезок, угол, треугольник объяснять не буду, иначе кто-то уснет.
Когда небо было ярче, трава зеленее, а ты учился в 7 классе, началось знакомство с геометрией, туда и перенесёмся. Чтобы мы с тобой разговаривали на одном языке, начнем с равных углов.
Смежные углы — два угла, у которых одна сторона общая, а две другие расположены на одной прямой.
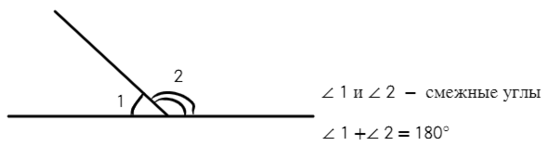
С вертикальными углами проще познакомиться на рисунке:
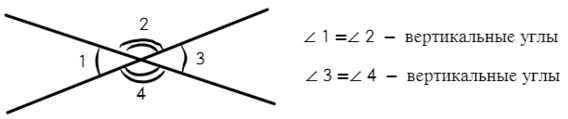
Такими дугами показываем равные углы ∠1 = ∠3 (одной дугой) и ∠2 = ∠4 (двумя дугами)
Теперь об углах при параллельных прямых (параллельные прямые — прямые, которые никогда не пересекутся, сколько бы их не продолжать. Лучше представить рельсы у путей на прямом участке):
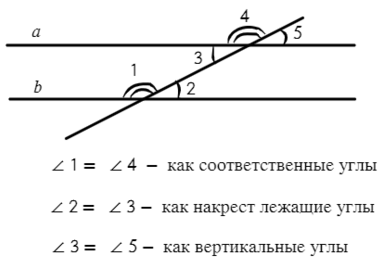
Перейдем к фигурам, а именно к равенству треугольников:
1) Треугольники, у которых две стороны и угол между ними соответственно равны двум сторонам и углу между ними другого треугольника, равны между собой.
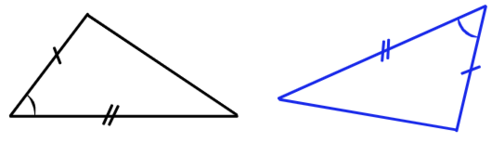
Штрихом и двумя штрихами показывают одинаковые стороны, которые равны между собой. Аналогично равные углы показывает одинаковым количеством дуг. Крайне удобно показывать дано сразу на рисунке.
2) Треугольники, у которых два угла и сторона между ними соответственно равны двум углам и стороне между ними другого треугольника, равны между собой.
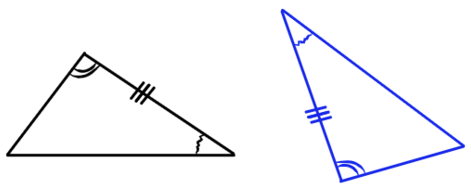
3) Треугольники, у которых три стороны соответственно равны трем сторонам другого треугольника, равны между собой.
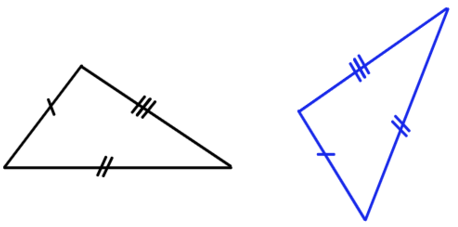
Одинаковые треугольники — это идентичные между собой фигуры, только развернутые. У тебя же не возникает вопроса, равны ли эти телефоны? Ты смотришь на форму, модель и сразу говоришь — идентичны. Так же поступай с треугольниками, только на слово тебе никто не поверит, обязательно нужно доказать один из трех признаков, описанных выше.

А вот эти фигуры какие?

Подобные! У них одинаковая форма, но разный размер. Тогда определим признаки подобных треугольников:
1) Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.
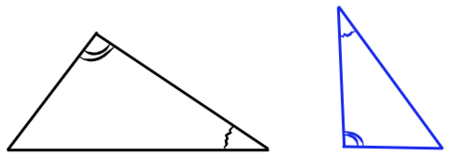
2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
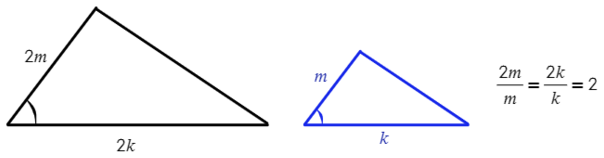
3) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
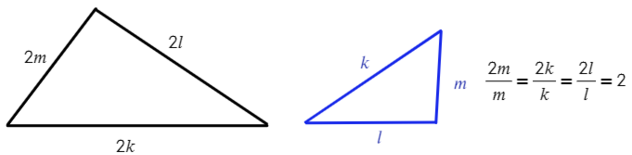
Важное свойство: если в подобных треугольниках отношение сторон равно k, тогда площади этих треугольников будут относится, как k² (покажу на примере задачи №7).
Давай закрепим теорию в задачах.
Введем секретный шифр:
«~» означает подобие
«Δ» означает треугольник
«∠» означает угол
Задача №1. Дано на рисунке:
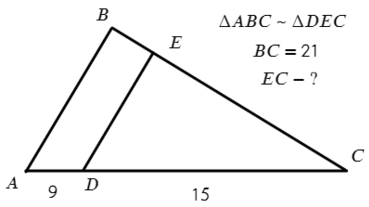
Т.к. треугольники подобны, запишем соотношения сторон против одинаковых углов.
AB II DE, значит ∠A = ∠EDC и ∠B = ∠DEC
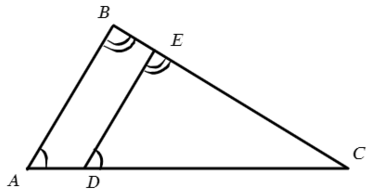
Запишем тогда отношение сторон и выразим нужную сторону EC:
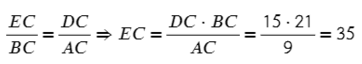
Ответ: 35
Задача №2. Дано на рисунке:
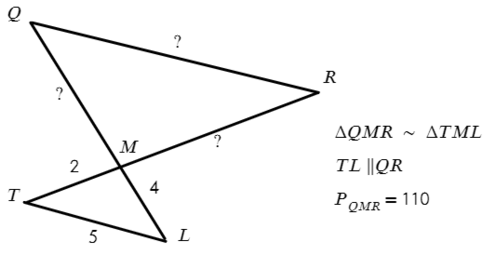
Периметр — это сумма всех сторон. Значит, если периметр отличается в 10 раз, то и стороны тоже в 10 раз.
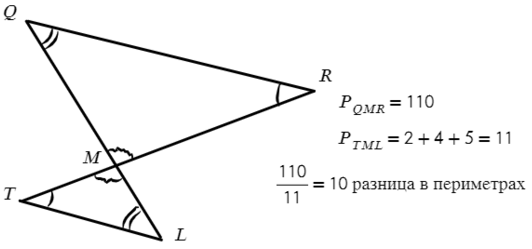
Но мы же знаем, что все стороны должны отличаться в 10 раз, тогда:
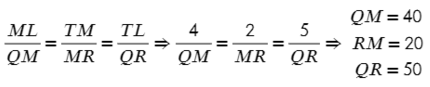
Ответ: 20; 40; 50.
Задача №3. Дано на рисунке:
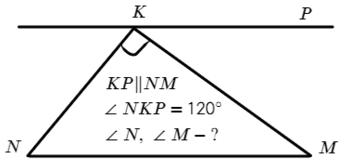
∠NKM = 90° и ∠NKP = 120°, значит ∠MKP = 30°
∠MKP = ∠KMN, как накрест лежащие углы при KP II NM => ∠KMN = 30°
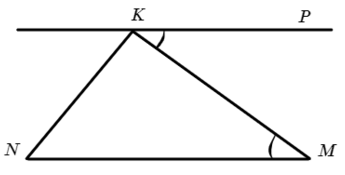
А сумма углов в треугольнике 180°, да-да, не всегда, конечно, но Неевклидовая геометрию оставим на другой раз.
∠KNM = 180 − ∠NKM − ∠KMN = 60°
Ответ: 60° и 30°
Теперь поговорим о самых распространенных отрезках в треугольнике: высота, биссектриса, медиана.
Высота — отрезок, опускающийся на прямую, содержащую противоположную сторону, под углом 90° (такой угол называется прямым).
Обратите внимание, что именно на прямую. В задаче №5 разберем почему.
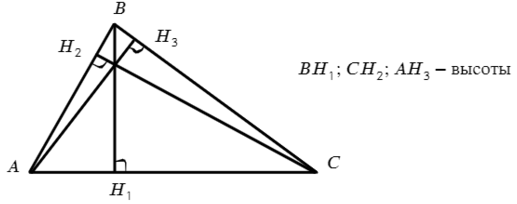
Угол 90° обозначается таким квадратиком у пересечения с прямой.
Биссектриса — луч, делящий угол, из которого выходит, пополам.
Запомнил, как обозначаем одинаковые углы? Одинаковым дугами.
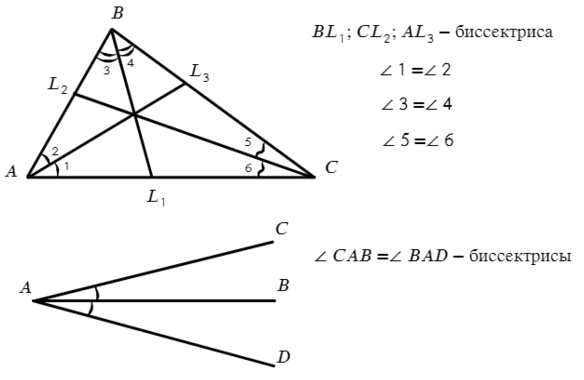
Медиана — отрезок, опускающийся из вершины треугольника на середину противоположной стороны.
Задача №4. Дано на рисунке:
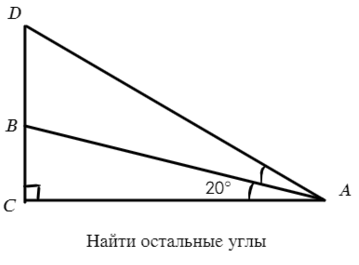
Давай посмотрим, что такое AB? АВ делит угол пополам (одинаковые дуги), значит, это биссектриса => ∠BAD = 20° => ∠CAD = 40°
В Δ CAD: ∠D = 180°− ∠C − ∠CAD = 50°, тогда
В Δ ВAD: ∠DBA = 180° − ∠D − ∠ВAD = 180° − 50° − 20° = 110°
∠DBA и ∠ABC — смежные (их сумма 180°) => ∠ABC = 180° − 110° = 70°
Задача №5. В ΔABC ∠B = 120°; ∠C = 30°. Из вершины А проведена высота, чему равен угол ∠BAH и ∠BAС?
Хороший рисунок — это 50% успеха, а в этой задаче все 90%. Рисуем треугольник примерно с углом 120°:
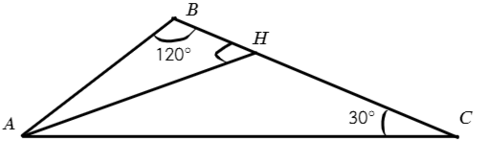
Рисунок получился плохой, а еще проблемы в ΔABH. Сумма углов должна быть 180°, но ∠B = 120° и ∠AHB = 90°, уже 210°! Что-то не так, вернемся к определению высоты — отрезок, опускающийся на прямую, содержащую противоположную сторону, под углом 90°.
Тогда продлим сторону BC, а на нее опустим высоту. Высота получится вне треугольника:
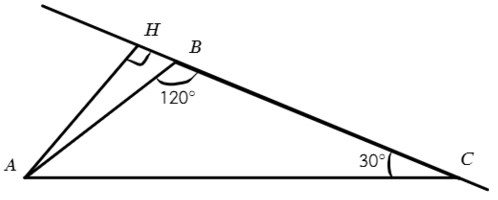
В ΔBAH: ∠HBA = 60° (смежный с ∠ABC) => ∠BAH = 180° − 60° − 90° = 30°
В ΔABC: ∠BAC = 180° − 120° − 30° = 30°
Ответ: 30° и 30°
Получается, что ∠BAC = ∠C = 30°, значит, этот треугольник равнобедренный. А что это такое?
Равнобедренный треугольник — треугольник, у которого две стороны одинаковой длины. Такие стороны называют боковыми, а сторону, которая им не равна, основанием.
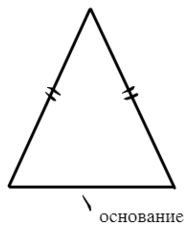 Есть пара крайне полезных свойств в равнобедренном треугольнике:
Есть пара крайне полезных свойств в равнобедренном треугольнике:
1) Углы при основании равнобедренного треугольника равны.
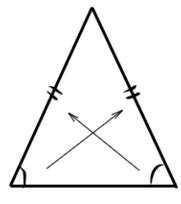
Против равных сторон лежат равные углы. Верно и обратное: если два угла у треугольника равны, то он равнобедренный
2) Медиана, проведенная к основанию треугольника, также является биссектрисой и высотой.
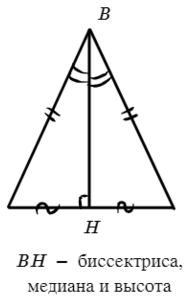
А что будет, если еще и третья сторона получится той же длины? Тогда этот треугольник равносторонний или правильный.
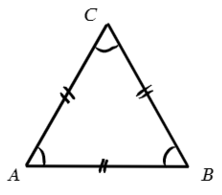
А чему равен каждый угол в равностороннем треугольнике? Сумма 180°, но все углы равны, они лежат против одинаковых сторон. Значит, один угол будет равен 180°/3 = 60°
А есть еще какие-то треугольники? Есть прямоугольный.
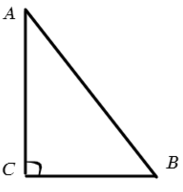
Прямоугольный треугольник — треугольник, у которого один угол равен 90° (прямой угол).
А два угла в треугольнике могут быть по 90°? Нет, тогда третьему углу останется 0°, нарисуешь такой?
Полезные свойства:
1) Катет, лежащий против угла в 30°, равен половине гипотенузы.
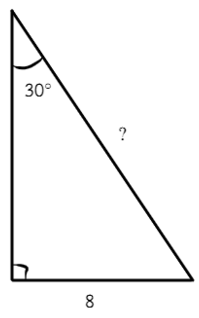
Гипотенуза будет в два раза больше катета и равна 16.
2) Медиана, проведенная из прямого угла, равна половине гипотенузы.
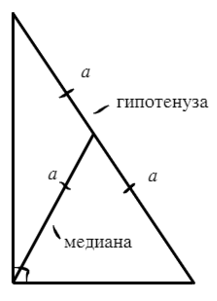
3) Теорема Пифагора
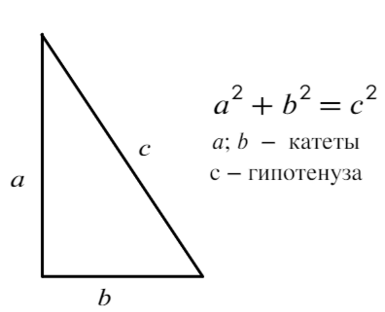
Теорема, которая встречается в 60% задач, а если дан прямоугольный треугольник — в 90%.
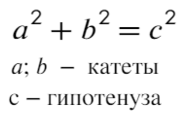
Квадрат гипотенузы (стороны против угла в 90°) равен сумме квадратов катетов.
Теорема Пифагора — это частный случай теоремы косинусов, но о ней мы потом поговорим.
Задача №6. Дано на рисунке:
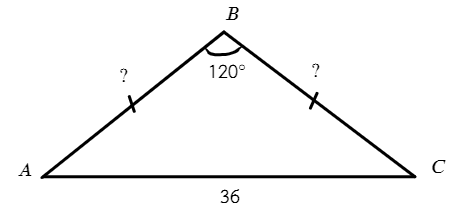
В ΔABC равнобедренный: ∠BAC = ∠BCA = 30°
Опустим высоту из вершины В:
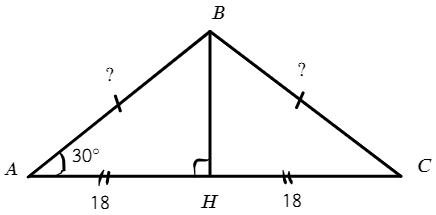
В равнобедренном треугольнике высота так же будет являться биссектрисой и высотой, значит AH = 18.
В ΔABH ∠A = 30°, скажем что BH = a, тогда AB = 2a. (против угла в 30° лежит катет в два раза больше гипотенузы)
В ΔABH по т. Пифагора:
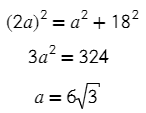
Ответ: 6√3.
Задача №7. ΔMNK ∼ ΔM₁N₁K₁. Площадь ΔMNK = 75, а площадь ΔM₁N₁K₁ = 225. Стороны соотносятся по названию. M₁N₁ = 9, чему равна MN
Вспомним про коэффициент подобия в площадях треугольника: если в подобных треугольниках отношение сторон равно k, тогда площади этих треугольников будут относится, как k²:
225/75 = 3 = k² => k = √3
M₁N₁/MN = k => MN = M₁N₁/k = 9/√3 = 3√3
Ответ: 3√3
Отлично, поздравляю тебя с Beginnerом по геометрии.
Вторая часть по треугольникам − площадь треугольников, свойства треугольников, тригонометрия в прямоугольных треугольниках, что такое синус/косинус, таблицы Брадиса (как пользоваться), теорема синусов и косинусов
Если нашел опечатку, или что-то непонятно − напиши.
ik-study.ru
Решение треугольников, все формулы и примеры
Определение и формулы для решения треугольников
Стороны треугольника обычно обозначают буквами , а противолежащие углы – .
Решение треугольников заключается в отыскании всех неизвестных сторон и всех неизвестных углов треугольника по известным данным.
При решении задач используют теорему косинусов или теорему синусов.
Теоремы для решения треугольников
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной вокруг треугольника окружности:
Также используют условия, которым удовлетворяют стороны треугольника (неравенство треугольника):
и углы
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Решение треугольников
Сегодня на уроке мы подытожим наши знания по разделу «Соотношения между сторонами и углами треугольника».
Прежде чем приступить к решению задач, давайте вспомним основной теоритический материал этой темы.
Формула для вычисления площади треугольника:

Теорема косинусов:

Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема синусов:

Решить треугольник – это значит найти все его элементы (три стороны и три угла) по каким-нибудь известным трем элементам, определяющим треугольник.
К задачам такого плана относятся следующие задачи: решение треугольника по трем сторонам; решение треугольника по трем углам; решение треугольника по двум сторонам и углу между ними; решение треугольника по двум сторонам и углу, не лежащего между ними; решение треугольника по стороне и прилежащим к ней углам; решение треугольников по стороне и произвольным двум углам.
Рассмотрим каждый вид таких задач отдельно.
Начнем с решения треугольника по трем углам.

Запишем теорему синусов и косинусов и подумаем, с помощью какой из них можно решить треугольник.


Обе эти теоремы содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины сторон треугольника.
Попробуем теперь решить треугольник по трем сторонам.
Зная длины всех сторон треугольника, по теореме косинусов можно найти косинусы всех углов треугольника. А, зная косинус угла, сам угол найти несложно. Для этого можно воспользоваться либо калькулятором либо таблицами Брадиса.






Значит в этом случае решить треугольник можно с помощью теоремы косинусов.
Рассмотрим пример.
Задача. Найти углы треугольника, если стороны треугольника равны 25, 20, 17.
Решение.







Ответ:  ;
;  ;
;  .
.
Следующим мы рассмотрим решение треугольника по стороне и прилежащим к ней углам.
Сразу замечаем, что
третий угол найти нетрудно, он равен разности 180° и известных углов  .
.
Запишем теорему синусов.



Из каждого равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной стороны и величину двух прилежащих к ней углов, можно найти все остальные элементы треугольника, используя теорему синусов.









Задача. Решить
треугольник, если одна из сторон треугольника равна  , а углы
прилежащие к этой стороне равны
, а углы
прилежащие к этой стороне равны  и
и
 °
соответственно.
°
соответственно.
Решение.






Ответ: 

 .
.
Задача. Решить
треугольник если две стороны его равны  см и
см и  см
соответственно, а угол между ними равен
см
соответственно, а угол между ними равен  .
.
Решение.






Ответ: 

 .
.
Теперь давайте посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол, который не лежит между ними. Да, можно. Для этого по теореме синусов надо найти второй угол треугольника, а затем и третий угол и по теореме косинусов найти третью сторону треугольника.




То есть и в этом случае треугольник можно решить с помощью теоремы синусов или теоремы косинусов.
Задача. Решить
треугольник, если две его стороны равны  и
и  , а один из
углов, не лежащий между этими сторонами, равен
, а один из
углов, не лежащий между этими сторонами, равен  .
.
Решение.







Ответ: 
 .
.
Итак, давайте обобщим.
Если в треугольнике известны величины трех углов, то решить его нельзя.
Если в треугольнике известны три стороны, то решить такой треугольник можно по теореме косинусов.
Если в треугольнике известна сторона и два любых угла, то решить такой треугольник можно с помощью теоремы синусов.
Если в треугольнике известны две стороны и угол между ними, то решить такой треугольник можно с помощью теоремы косинусов или теоремы синусов.
Если же нам известны две стороны и любой угол, который не лежит между ними, то треугольник можно решить по теореме синусов и косинусов.
videouroki.net
Решение треугольников | Геометрия 9 класс | Примеры решения задач
Содержание страницы:
- – задачи 76 — 77 представлены с примерами решений и ответами по теме «Решение треугольников»;
- – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 — 81;
- – решения, как найти угол, сторону треугольника, объясняются в контрольных работах 82 — 85.
Задача 76.
Дано:Треугольник ΔABC,
стороны треугольника a=10, b=7
Угол A = 60°
Решить треугольник: Угол по сторонам треугольника B, C, сторону c
Решение:
Известно, что формула синуса
, получаем выражение
Sin B = = = = ≈ 0,6062
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы («Четырехзначные математические таблицы» Владимира Модестовича Брадиса)
B = 37°19’
Тогда C = 180° — (60° + 37°19’) = 82°41’
Используя теорему синусов
, получаем равенство
с=≈ 11
Ответ: B = 37°19’; C = 82°41’; c ≈ 11
***
Задача 77.
Дано:
Треугольник ΔABC, стороны треугольника
a=6,3
b=6,3
C = 54°Найти: Угол по сторонам треугольника A, B, сторону c
Решение:
Т.к. a=b=6,3, то треугольник ΔABC — равнобедренный.
Тогда A =B = (180° — 54°): 2 = 63°
Используя теорему синусов
, получаем равенство
с = = ≈ 5,7
Ответ: A =B = 63°; с ≈ 5,7
***
Наверх
Решение треугольников через синус и косинус угла
Задача 78.
Дано:
Треугольник ΔABC
A = 60°
B = 40°c=14
Найти: угол треугольника C, стороны a,b
Решение:
C = 180° — (40° + 60°) = 80°
Используя теорему синусов
, получаем выражение
a = ≈ 12b = ≈ 9
Ответ: C = 80°; a ≈ 12; b ≈ 9
***
Задача 79.
Дано:Треугольник ΔABC
BC=a=6
AC=b=7,3
AB=c=4,8
Найти: углы треугольника A, B, C по сторонам
Решение:
Известно, что формула косинуса
, находим косинус угла B
Cos B = = = = ≈ 0,0998263
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла B
B = 84°16’
Используя формулу теоремы косинусов, находим косинус угла C
Cos C = = =
= ≈ 0,7562785
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла C
C = 40°52’
Тогда угол A равен A =180° — (40°52’ + 84°16’) = 54°52’
Ответ: A = 54°52’ ; C = 40°52’ ; B = 84°16’
***
Задача 80.
Дано:
Треугольник ΔABC
A = 30°
C = 75°
b = 4,5
Найти: угол B, стороны треугольника a,c
Решение:
B = 180° — (30° + 75°) = 75°
Т.к. два угла в треугольнике равны B =C = 75°, тогда треугольник ΔABC — равнобедренный.
Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов
,
находим сторону BC=a
a = ≈ 2,3
Ответ: B = 75°; a ≈ 2,3 ; c = 4,5
***
Задача 81.
Дано:
Треугольник ΔABC, длины трех его сторон
| 1) a=5 , b=c=4 | 2) a=5 , b=9 , c=6 | 3) a=17 , b=15 , c=8 |
Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным
Решение:
1) Т.к. b=c=4, то треугольник ΔABC — равнобедренный, и, значит, остроугольный.
2) Используя формулу теоремы косинусов
, находим косинус угла A
Cos A =
= =0Тогда угол A равен A = 90°. Следовательно, треугольник ΔABC — прямоугольный.
3) Используя формулу теоремы косинусов
, находим косинус угла B
Cos B = == -< 0.
Т.к. значение косинуса угла B меньше нуля, следовательно, угол B — тупой, а треугольник ΔABC — тупоугольный.
***
Наверх
Решение треугольника через угол по сторонам
Задача 82.
Дано:Треугольник ΔABC, два угла и сторона
A = 45°
C = 30°
AD = 3 м
Найти: длину всех сторон треугольника ΔABC = ?
Решение:
Зная размер двух углов в треугольнике ΔABC, находим третий уголB = 180° — (30° + 45°) = 105°
Найдем угол DAB и рассмотрим ΔADC
DAB = 180° — (90° + 45 + 30°) = 15°DAC = 15° + 45° = 60°Используя теорему синусов
, находим сторону AC
AC = (3 • 1) • 2 = 6 (м)
Используя теорему синусов
, находим сторону AB
AB = ≈ 3 (м)
Используя теорему синусов
, находим сторону BC
BC =≈ 4 (м)
Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м.
***
Задача 83.
Дано:
Треугольник ΔABC
Три стороны a = 14, b = 18,
c = 20
Найти:
все углы треугольника ΔABC = ?
Решение:
Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов
Cos C =, находим косинус угла C
Cos C = = ≈ 0,24
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C
C ≈ 76°07’
Используя формулу теоремы косинусов
Cos B =, находим косинус угла B
Cos B = ==≈ 0,4857
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла B
B ≈ 60,941 ≈ 60°57’
Следовательно, A = 180° — (76°13’ + 60°57’) ≈ 42°56’
Ответ: A ≈ 42°56’ ; B ≈ 60°57’ ; C ≈ 76°07’
***
Задача 84.
Дано:
Треугольник ΔEKP, сторона и два угла
EP = 0,75
P = 40°
K = 25°
Найти: сторону треугольника PK = ?
Решение:
Используя теорему синусов
, находим сторону PK
E = 180° — (40° + 25°) =115°Sin 115° = Sin (180° — 65°) = Sin 65°
Тогда
PK = ≈ 1,61
Ответ: PK ≈ 1,61.
***
Задача 85.
Дано:
Треугольник ΔABC, две стороны и угол
b = 18, c = 12
A = 50°
Найти: решить треугольник — определить значение стороны и двух углов
(a, B, C ) = ?
Решение:
Используя формулу теоремы косинусов
, получаем
a = = ≈ 13,8
Используя формулу теоремы косинусов
Cos C =, находим косинус угла C
Cos C == ≈ 0,7457
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C
C ≈ 41°47’
Следовательно, B = 180° — (50° + 41°47’) ≈ 88°13’
Ответ: a ≈ 13,8 ; B ≈ 88°13’ ; C ≈ 41°47’
***
www.petrovskov.ru
Задачи на комбинацию окружности и треугольника
 Продолжаем решать простейшие геометрические задачки.
Продолжаем решать простейшие геометрические задачки.
Разбираем Задачи №6 ЕГЭ по математике.
Сегодня работаем с окружностью, вписанной в треугольник и описанной около треугольника.
Вы можете пройти автотренинг «Планиметрия»
В категорию «Задачи №6» входят также задачи следующих типов + показать
Окружность, вписанная в треугольник
Задача 1.
Площадь треугольника равна 800, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника.

Решение: + показать
Задача 2.
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 66.

Решение: + показать Радиус вписанной окружности в правильный треугольник Итак, Ответ: 22.  – есть
– есть  высоты (
высоты ( ), так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
), так в правильном треугольнике высоты совпадают с медианами, а медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Задача 3.
Сторона правильного треугольника равна  . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.

Решение: + показать
Задача 4.
В треугольнике ABC  . Найдите радиус вписанной окружности.
. Найдите радиус вписанной окружности.

Решение: + показать Найдем гипотенузу по т. Пифагора: Найдем площадь и периметр треугольника, чтобы воспользоваться затем формулой Тогда Ответ: 1. 

 :
:



Задача 5.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 11. Найдите гипотенузу c этого треугольника. В ответе укажите  .
.

Решение: + показать
Задача 6.
Боковые стороны равнобедренного треугольника равны 181, основание равно 38. Найдите радиус вписанной окружности.

Решение: + показать
Задача 7.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Решение: + показать
Задача 8.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 18, 33. Найдите периметр данного треугольника.

Решение: + показать
Окружность, описанная около треугольника
Задача 1.
Найдите радиус окружности, описанной около прямоугольного треугольника  , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1.

Решение: + показать
Задача 2.
Боковые стороны равнобедренного треугольника равны 50, основание равно 60. Найдите радиус описанной окружности этого треугольника.

Решение: + показать Воспользуемся следующей формулой: Площадь будем искать по формуле Герона: Тогда Ответ: 31,25. 



Задача 3.
Сторона AB треугольника ABC равна 28. Противолежащий ей угол C равен 150˚. Найдите радиус окружности, описанной около этого треугольника.

Решение: + показать Согласно т. Синусов Ответ: 28. 



Задача 4.
Угол C треугольника ABC, вписанного в окружность радиуса 47, равен 30˚. Найдите сторону AB этого треугольника.
Решение: + показать
Задача 5.
В треугольнике ABC BC , угол C равен 90°. Радиус описанной окружности этого треугольника равен 17,5. Найдите AC.
, угол C равен 90°. Радиус описанной окружности этого треугольника равен 17,5. Найдите AC.

Решение: + показать В прямоугольном треугольнике гипотенуза – диаметр описанной окружности. Значит, По теореме Пифагора Ответ: 30. 

Задача 6.
Радиус окружности, описанной около правильного треугольника, равен  Найдите сторону этого треугольника.
Найдите сторону этого треугольника.

Решение: + показать
Задача 7.
Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:6:11. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Решение: + показать
Объемный раздел получился… Отдохнем немножко? –>+ показать


Вы может пройти тест «Окружность, описанная около треугольника. Окружность, вписанная в треугольник»
egemaximum.ru

 , а по условию
, а по условию  . Получили систему уравнений
. Получили систему уравнений
 ,
,  . Так как
. Так как  , то
, то  . Отсюда
. Отсюда
 . Найти площадь треугольника.
. Найти площадь треугольника.


