Задачи с уравнениями 7 класс с решением: Методическая разработка по алгебре (7 класс): Решение уравнений. Решение задач с помощью уравнений. 7 класс — Детская игровая комната «Волшебный лес»

Posted on 20.05.202101.09.2020 by alexxlab

Содержание

Методическая разработка по алгебре (7 класс): Решение уравнений. Решение задач с помощью уравнений. 7 класс

Контрольная работа по теме: «Решение уравнений. Решение задач с помощью уравнений»

1 вариант.

№1 Решите уравнения:

a)8х — 7,5 = 6х+1,5 б)4х — (9х — 6) = 46 в) 7х — (х+3) = 3(2х — 1) г)

№2 Решите задачи

а) В трех школах 3080 учащихся. В первой школе в два раза меньше, чем во второй, а в третьей на 80 учащихся больше, чем в первой. Сколько учащихся в каждой школе?

б) На одном складе винограда было вдвое меньше, чем на другом. Когда со второго склада отправили в магазины 16 тонн винограда, а на первый склад привезли 25 тонн, то на обоих складах винограда стало поровну. Сколько винограда было на каждом складе первоначально?

№3 Решите уравнения:

а) б)

Контрольная работа по теме: «Решение уравнений. Решение задач с помощью уравнений»

2 вариант.

№1. Решите уравнение:

а)9х — 8,5 = 7х + 0,5 б)6х – (9х+7) = 11 в) 9х — (3х — 4) = 2(3х+1) г)

№2 Решите задачи

а). Три бригады слесарей изготовили 1085 деталей. Сколько деталей изготовила каждая бригада отдельно. Если известно, что вторая бригада изготовила деталей в 2раза больше, чем первая, а третья на 70 деталей меньше, чем вторая?

б) На первой полке книг в 3 раза больше, чем на второй. Когда с первой полки сняли 11 книг, а на вторую добавили 21 книгу, то книг на полках стало поровну. Сколько было книг на каждой полке первоначально?

№3 Решите уравнения:

а) б)

Контрольная работа по теме: «Решение уравнений. Решение задач с помощью уравнений»

1 вариант.

№1 Решите уравнения:

a)8х — 7,5 = 6х+1,5 б)4х — (9х — 6) = 46 в) 7х — (х+3) = 3(2х — 1) г)

№2 Решите задачи

№3 Решите уравнения:

а) б)

Контрольная работа по теме: «Решение уравнений. Решение задач с помощью уравнений»

2 вариант.

№1. Решите уравнение:

а)9х — 8,5 = 7х + 0,5 б)6х – (9х+7) = 11 в) 9х — (3х — 4) = 2(3х+1) г)

№2 Решите задачи

№3 Решите уравнения:

а) б)

Контрольная работа по теме: «Решение уравнений. Решение задач с помощью уравнений»

1 вариант.

№1 Решите уравнения:

a)8х — 7,5 = 6х+1,5 б)4х — (9х — 6) = 46 в) 7х — (х+3) = 3(2х — 1) г)

№2 Решите задачи

№3 Решите уравнения:

а) б)

Контрольная работа по теме: «Решение уравнений. Решение задач с помощью уравнений»

2 вариант.

№1. Решите уравнение:

а)9х — 8,5 = 7х + 0,5 б)6х – (9х+7) = 11 в) 9х — (3х — 4) = 2(3х+1) г)

№2 Решите задачи

№3 Решите уравнения:

а) б)

Методическая разработка по алгебре (7 класс): Решение задач с помощью уравнений.

Урок открытия нового знания.

7 класс, алгебра. (24.11.17)

Тема: Решение задач с помощью уравнений.

Используемое оборудование: проектор, компьютер, учебник «Алгебра» 7 класс, «Просвещение 2016», авторы Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, под редакцией Г.В. Дорофеева

Цели урока:

Обучающая:

закрепление понятия дробного рационального уравнения;
составление математической модели задачи, перевод условия задачи с обычного языка на математический;
проверка уровня усвоения темы путем проведения проверочной работы.

Развивающая:

развитие умения правильно оперировать полученными знаниями, логически мыслить;
развитие интеллектуальных умений;
развитие умения принимать решения.

Воспитательная:

воспитание познавательного интереса к предмету;
воспитание самостоятельности при решении учебных задач;
воспитание воли и упорства для достижения конечных результатов.

Задачи:

1) актуализировать знание решения уравнений, умение решать задачи при помощи уравнений; добиться усвоения алгоритма решения задач;

2) УУД:

Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,

3) воспитывать чувство товарищества.

Оборудование: презентация, конспект урока, компьютер, проектор.

Ход урока:

1. Инициация.

Здравствуйте, ребята. Чем мы занимались на прошлых уроках? (Решали уравнения и задачи с помощью уравнений)

2. Вхождение или погружение в тему

Какая тема нашего урока. (1 слайд)

Какие цели мы себе можем поставить?

3. Формирование ожиданий учеников.

Я раздам вам волшебные конверты, но чур до конца урока в них не заглядывать.

Актуализация знаний.

( Фронтальный опрос, устная работа с классом.)

Ответьте, пожалуйста, на следующие вопросы:

— Какие равенства называются уравнениями? (2 слайд)

— Какое число называется корнем уравнения? (3 слайд)

— Что значит решить уравнение? (4 слайд)

— Расскажите алгоритм решения уравнений. (5 слайд)

Работать сегодня мы будем в парах. ( пересадить)

Вспомните правила работы в парах. (6 слайд)

(Прислушиваться к мнению соседа, работать дружно, помогать друг другу)

Пример. Решите уравнение (на доске)!!!!! Найди ошибку???? (7 слайд)

-7х+5(2х-3)=6

-7х+10х+15=6

-7х+10х=6-15

3х=-9

х=-9:3

х=-3

Ответ. х=-3

-7х+5(2х-3)=6

-7х+10х-3=6

-7х+10х=6+3

3х=9

х=9:3

х=3

Ответ. х=3

-7х+5(2х-3)=6

-7х+10х-3=6

-7х+10х=6-3

-3х=3

х=3:(-3)

х=-1

Ответ. х=-1

(8 слайд)

Интерактивная лекция и объяснение информации.

Прежде чем приступить к решению задач на движение, давайте вспомним, какие виды движения (передвижения) могут быть рассмотрены в задачах (ехать, идти, плыть, …), (движения по воде и суше, …).

Раз мы рассматриваем задачи на движение какие величины необходимы для решения данных задач (S, V, t). Как они связаны между собой?

(9 слайд)

(10 слайд) Устная задача про катер

(11 слайд) Если мы будем рассматривать задачи на движение по воде, что необходимо помнить (собственная скорость и скорость течения реки).

Запишите данные формулы в тетради.

(12 слайд) Объясните несостоятельность этой ситуации:

Прежде чем приступать к решению задачи необходимо несколько раз внимательно прочитать условие задачи, понять что дано и какую величину обозначить за неизвестную. Как правило, за неизвестное обозначают наименьшую величину.

(13слайд) Рассмотрим пример.

Два поезда, встретившись на разъезде, продолжали движение каждый в своём направлении. Скорость одного из них на 20 км/ч больше скорости другого. Через 3 ч расстояние между ними было 480 км. Найдите скорость каждого поезда.

Решение.

Сделаем рисунок, который поможет нам составить уравнение.

х км/ч х+20 км/ч

3 ч 3 ч

480 км

Составление математической модели:

х км/ч скорость первого поезда;

(х +20) км/ч – скорость второго поезда;

3х км – расстояние, которое проехал первый поезд;

3(х+20) км — расстояние, которое проехал второй поезд;

По условию задачи известно, что через 3 ч расстояние между поездами было 480 км.

(14 слайд)

Составим табличную модель:


I поезд	х	3	3х
II поезд	х+20	3	3(х+20)

Что нам известно про расстояние?

Составьте уравнение и решите его. (каждый сам.)

(15 слайд) взаимопроверка по образцу (обмен тетрадями)

Составим уравнение и решим его:

3х+3(х+20)=480

Работа с составленной моделью.

Решив полученное уравнение, находим х=70.

Ответ на вопрос задачи. 70 км/ч скорость первого поезда, 70+20=90 (км/ч) скорость второго поезда.

После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение.

(16 слайд) Физкультминутка

Быстро встали, улыбнулись.

Выше – выше потянулись

Ну-ка, плечи распрямите,

Поднимите, опустите

Влево, вправо повернитесь,

Рук коленями коснитесь.

Сели, встали. Сели, встали.

И на месте пошагали.

Проработка содержания темы

(17 слайд) Работа в тетрадях.

Задания из учебника «Алгебра 7», Г.В. Дорофеев

№403(а).

Учитель контролирует выполнение задания, отвечает на возникшие вопросы, оказывает помощь слабоуспевающим ученикам. Учащиеся работают парами вместе обсуждают решение задачи.

(Дети читают текст задачи, делают выводы)

Раз в задаче используется скорость и время, значит задача на движение, и как следствие мы будем использовать формулу, связывающую все величины.

Учитель проверяет решение задачи, учащиеся комментируют, как решали задачу.

(18 слайд)

(19 слайд) № 410 ( запас времени) (за х обозначить всех учеников)

Домашнее задание.

Решить в тетрадях

№ 397 , № 403(б),

по выбору 404 (а)

составить задачу на движение по реке.

Рефлексия УД на уроке.

— Итак, над какой темой мы работали? Удалось ли решить поставленную задачу? Каким способом? Какие получили результаты? Что нужно сделать ещё?

— В чём испытывали трудности?

— Где можем применить новые знания? (При решении задач)

— Оцените работу вашего партнёра и себя.

Молодцы. Спасибо за урок.

Эмоциональная разрядка

Откройте конверт и оцените сегодняшний урок

(20 слайд)

Конспект и презентация к у року алгебры в 7 классе «Решение задач с помощью линейных уравнений»

Муниципальное бюджетное общеобразовательное учреждение «Акбулакская средняя общеобразовательная школа № 2 Акбулакского района Оренбургской области»

Конспект урока по алгебре в 7 классе

«Решение задач с помощью линейных уравнений»

подготовила

учитель математики

Гришанова Елена Сергеевна

Акбулак, 2019

Обобщение и систематизация знаний по теме: «Решение задач с помощью линейных уравнений».

Цель: закрепить и обобщить знания учащихся о решении задач с помощью линейных уравнений с одной переменной.
Задачи:

образовательные:

образовательные: повторение, обобщение и систематизация знаний по теме, формирование навыков решения задач по алгоритму, создание условий контроля (самоконтроля) за усвоением знаний и умений;

развивающие:

развивать умение анализировать, сравнивать, обобщать, делать выводы; развивать логическое мышление, творческие способности, смекалку и сообразительность через познавательную деятельность учащихся; развивать умений самостоятельно добывать и применять знания для решения математических задач;

воспитательные:

формировать умение слушать и вступать в диалог, учитывая позицию оппонентов и участвовать в коллективном обсуждении возникающих проблем; повышать мотивацию к обучению через нетрадиционное проведение уроков; воспитывать личностные качества, необходимые для самообразования.

Методы обучения: наглядно-иллюстративный, репродуктивный, беседа, самостоятельная работа.

Формы работы на уроке: классно-урочная, индивидуальная, фронтальная.

Тип урока: комбинированный.

Технические средства обучения:

компьютер, проектор.

Дополнительное оборудование и средства обучения: презентации MS Power Point; распечатанные текстовые материалы для работы на уроке.

Ход урока.

I. Организационный этап.

Приветствие. Настроить учащихся на работу. Организация внимания.

Включаются в деловой ритм урока.

II. Постановка цели и задач урока.

Французский писатель 19 столетия Анатоль Франс однажды заметил: “Учиться можно только весело. Чтобы переваривать знания, надо поглощать их с аппетитом”. Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, будем поглощать знания с большим желанием, ведь они пригодятся вам в дальнейшей жизни.

Через математические знания, полученные в школе, лежит широкая дорога к огромным областям труда и открытий. У нас сегодня с вами своя дорога длиною 40 минут.

Чем мы занимались на прошлых уроках? Чем будем заниматься сегодня на уроке?

Сегодня на уроке перед вами стоит задача – показать, как вы умеете решать линейные уравнения с одной переменной, как решаете задачи с помощью уравнений. Я хочу пожелать всем удачи на пути хорошего и бодрого настроения, правильных ответов.

Любая дорога удачна только в том случае, если вы получаете от неё положительные эмоции. Какой же путь получиться у нас? Поэтому я предлагаю отмечать вам свое настроение на всех этапах нашего урока. Оценивать себя вы будете в зависимости от настроения. Итак, оцените свое настроение в начале урока.

Обобщим знания по теме, будем решать уравнения и задачи с помощью уравнений.

III. Этап актуализации знаний.

1.Работа по карточкам на доске (3 человека)

Карточка № 1

Решить уравнение:

3х+6=2(2х-7)-х

Карточка № 2

Решить уравнение:

4(х-3)=х+6

Карточка № 3

Решить уравнение:

1,8(1-2х)=7,8-(3,6х+6)

Учитель: Для того, чтобы вы смогли активно включиться в работу на уроке, давайте повторим всё, что нам стало известно о линейном уравнении с одной переменной и решении задач с их помощью из предыдущих уроков.

1.Уравнение – это …

2. Что значит решить уравнение?

3. Что же такое корень уравнения?

4. Линейным уравнением с одной переменной называется …

5.Сколько корней может иметь уравнение?

6.Как найти неизвестный множитель, делитель, слагаемое?

7.Как привести подобные слагаемые?

8.Алгоритм решения задач.

Карточка № 1.

3х+6=2(2х-7)-х

3х+6=4х-14-х

3х-3з=-14-6

0х=-20

Ответ: решений нет.

Карточка № 2.

4(х-3)=х+6

4х-12=х+6

4х-х=12+6

3х=18

Х=18:3

Х=6

Ответ: 6.

Карточка № 3.

1,8(1-2х)=7,8-(3,6х+6)

1,8-3,6х=7,8-3,6х-6

-3,6х+3,6х=1.8-1.8

0х=0

Ответ: х — любое число.

IV. Этап решения задач.

Задача № 110 (задача на движение по воде)

Как найти скорость по течению, скорость против течения, как найти путь?

Пусть х – скорость теплохода, тогда скорость по течению равна (х-2,5) км/ч, скорость по течению равна (х+2,5)км/ч, путь, пройденный против течения 3*(х-2,5), путь, пройденный по течению 4*(х+2,5). По условию задачи известно, что путь по течению на 48 км больше, чем против течения. Составлю и решу уравнение.

4*(х+2,5)- 3*(х-2,5)=48

4х+10-3х+7,5=48

Х=48-10-7,5

Х=30,5(км/ч)

Ответ: 30,5 км/ч собственная скорость теплохода.

VI. Физическая минутка.

Утром бабочка проснулась,

Улыбнулась, потянулась!

Раз – росой она умылась,

Два – изящно покружилась,

Три – нагнулась и присела,

На четыре – улетела.

Выполняют зарядку.

VII. Этап самостоятельной работы.

Решить задачи по карточкам (2 варианта)

1) Периметр прямоугольника равен 96 см. Известно, что одна сторона больше другой в 3 раза. Найдите стороны прямоугольника.

2) Периметр прямоугольника равен 150 см. Известно, что одна сторона больше другой в 4 раза. Найдите стороны прямоугольника.

Дополнительное задание:

Решить уравнения:

│3х+2│- 4=0

2│х│+3=0

1)Пусть х — это первая сторона, тогда вторая сторона 3х. По условию задачи известно, что периметр равен 96 см. Составлю и решу уравнение.

(х+3х)*2=96

Х+3х=48

4х=48

Х=48:4

Х=12 (см) первая сторона

3*12=36 (см) вторая сторона

Ответ: 12 см и 36 см.

2) )Пусть х — это первая сторона, тогда вторая сторона 4х. По условию задачи известно, что периметр равен 150 см.Составлю и решу уравнение.

(х+4х)*2=150

Х+4х=75

5х=75

Х=75:5

Х=15 (см) первая сторона

4*15=60 (см) вторая сторона.

Ответ: 15см и 60 см.

1)│3х+2│- 4=0

3х+2-4=0 -3х-2-4=0

3х-2=0 -3х-6=0

3х=2 -3х=6

х=2/3 х = -2

Ответ:2/3; -2.

2) 2│х│+3=0

2х+3=0 -2х+3=0

2х=-3 -2х=-3

Х= -1,5 х=1,5

Ответ: 1,5; — 1,5.

VIII. Этап информации о домашнем задании.

П. 3 № 111, 126 (1) стр.24-25

Записывают задание в дневник. Если есть вопросы по выполнению, задают их учителю.

IX. Рефлексия. Подведение итогов урока.

Если на уроке все задачи и уравнения, которые мы решали, были понятны, покажите радостный смайлик, если нет, то грустный.

Показывают смайлики.

Вариант 1

Периметр прямоугольника равен 96 см. Известно, что одна сторона больше другой в 3 раза. Найдите стороны прямоугольника.

Вариант 2

Периметр прямоугольника равен 150 см. Известно, что одна сторона больше другой в 4 раза. Найдите стороны прямоугольника.

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Конспект по алгебре » Решение задач с помощью уравнений»(7 класс)

Конспект урока. 7 класс. Учебник Алгебра. Ю.М. Калягин. Урок изучения нового материала.

Тема урока. Решение задач с помощью уравнений.

Цели.

Предметные: формировать представление о решении задач с помощью уравнений, изучить алгоритм решения задач с помощью уравнений; развивать умение составлять уравнения по условию задачи, решать линейные уравнения с одной переменной

Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности; ориентироваться на успех в учебной деятельности;

метапредметные: – уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия. Планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки, выявления сделанных ошибок; высказывать свое предположение.

Коммуникативные – уметь оформлять свои мысли в устной форме; слушать и понимать речь других. Совместно договариваться о правилах поведения и общения в школе и следовать им.

Познавательные – уметь ориентироваться в своей системе знаний, отличать новое знание от уже известного с помощью учителя: добывать новые знания; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Ход урока.

1 Орг. Момент.

Приветствие учащихся.Диагностирую эмоциональную обстановку в классе.

(Ребята по просьбе учителя поднимают смайлики, лежащие на партах, соответствующие их настроению).

2.Актуализация знаний.

1)Записать общий вид линейного уравнения.(ах=в).

2)Устно. Назовите свойства уравнений

3)Формулы движения записываем на доске.(S = VT, V = )

4) Формулы работы V –производительность, t –время,A-вся работа( V= )

3. Сообщение темы урока.

Предлагаю решить задачу учебника.

V_тепл =18км/ч

Пристань

V_{течения} = 3 км/ч.

t_путеш.=5ч. t_отдыха= 3ч.Какой вопрос в задаче?(Найти расстояние).Пусть искомое расстояние – Х(км/ч.)

Предлагаю заполнить таблицу. Вспоминаем, что движение по течению V_{теплохода}+ V_{течения}, а против течения V_{теплохода} — V_{течения.}И формулу T =

Учитывая время на берегу 3 часа, и время всего путешествия 5часов, составим уравнение.

Решаем уравнение: = 5-3

=2 , НОК(21;15)=105

Умножим на 105 обе части уравнения и получим:

5Х+7Х=210

12Х=210

Х= 210:12

Х= 17,5(км) — отплыли туристы от пристани.

Ответ: 17,5 км.

— Сформулируйте тему урока.

4.Работа по теме урока.

Предлагаю решить задачу из вводных упражнений №2.Сделать аналогично таблицу и дать ответ.

t(ч)

По течению

7+2

Против течения

7-2

Ответ: t_{по течению}= 5ч.; t_{против течения}= 9 ч.

№ 102(2) .На доске и в тетрадях.

I цех – ? деталей

II цех — ? в 3 раза больше чем I 869 дет.

III цех — ? на139 меньше чем II

Решение. Пусть Х дет. изготовил I цех, тогда II цех изготовил 3Х дет., а III цех — 3Х-139 дет.

Составим уравнение, учитывая условие, что вместе они сделали 869 деталей.

Х+3Х+3Х-139=869

7Х= 869 + 139

7Х =1008

Х =1008: 7

Х = 144(дет.) – I цех. 3Х = 3144 = 432(дет.) – II цех. 432-139 = 293(дет.) – III цех.

Ответ: 144д., 432д., 293д.

№ 106

Решение.

Составим уравнение.

6Х = 4(Х+16)

6Х = 4Х+64

6Х- 4Х= 64

2Х = 64

Х = 64:2

Х = 32(м³) заготовила бригада за день по плану.

Х+16 = 32+16 =48(м³) заготавливала бригада за день сверх плана.

Ответ: 48м³.

Домашнее задание. П. 8 изучить, повторить формулы. Вводные упражнения стр. 54 (1,3), №101.

Рефлексия.

— Что мы сегодня повторили?

— Какие формулы применяли к решению задач?

Покажите с каким настроением вы уходите с урока?(Показывают смайлики).

Спасибо за урок до свидания.

Олимпиада по математике 7 класс, задания, уравнения, задачи с ответами

Усвоить школьную программу по математике могут только те, кто проявляет достаточно упорства. На уроках 7 классе учащиеся знакомятся с такими разделами, как степень с натуральным показателем, одночлен и многочлен, линейная функция, системы линейных уравнений с двумя переменными.

Принимая участие в олимпиадах, ученики углубляют свои знания и совершенствуют навыки, приобретенные на уроках. Но, чтобы добиться высокого результата, нужно долго и усердно готовиться.

На нашем сайте вы найдете олимпиадные задания по математике с ответами и решениями. Предложенные задания помогут подготовиться к олимпиаде. Мы советуем вам использовать их в качестве тренажера как на уроках, так и в ходе внеклассной самостоятельной подготовки.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Уравнения

1. Оба корня уравнения x² – ax + 2 являются натуральными числами. Чему равно a?

2. Решите в натуральных числах уравнение:
zx + 1 = (z + 1)²

3. Решите уравнение:
12 – (4х – 18) = (36 + 5х) + (28 – 6х)

4. Найдите решение уравнения:
7x + 3 (x+0,55) = 5,65

5. Решите уравнение:
10у – 13,5 = 2у — 37,5.

6. Преобразуйте в многочлен:
(4х – 5у)²

7. Представьте выражение в виде квадрата двучлена:
4у2 — 12у + 9

8. Решите уравнение:
8у – (3у + 19) = -3(2у — 1)

9. Решите уравнение:
5х² – 4х = 0

10. Решите систему уравнений:
{ x+2*y = 12
{ 2*x-3*y = -18

Задачи

Задача №1
Из чисел A, B и C одно положительно, одно отрицательно и одно равно 0. Известно, что A = B (B – C). Какое из чисел положительно, какое отрицательно и какое равно 0? Почему?

Задача №2
Последовательность строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на 1. Какое число стоит на 2000 месте?

Задача №3
В XIX-XX веках Россией правили 6 царей династии Романовых. Вот их имена и отчества по алфавиту: Александр Александрович, Александр Николаевич, Александр Павлович, Николай Александрович, Николай Павлович, Павел Петрович. Один раз после брата правил брат, во всех остальных случаях после отца — сын. Как известно, последнего русского царя, погибшего в Екатеринбурге в 1918 году, звали Николаем. Найдите порядок правления этих царей.

Задача №4
Сколько чисел от 1 до 90 делятся на 2, но не делятся на 4?

Задача №5
В трех мешках 114 кг сахара. В первом на 16 кг меньше, чем во втором, а в третьем на 2 кг меньше, чем во втором. Сколько килограммов сахара во втором мешке?

Задача №6
Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не повторяются.

Задача №7
Точка D — середина основания AC равнобедренного треугольника ABC. Точка E — основание перпендикуляра, опущенного из точки D на сторону BC. Отрезки AE и BD пересекаются в точке F. Установите, какой из отрезков BF или BE длиннее.

Задача №8
Пол в гостиной барона Мюнхгаузена вымощен одинаковыми квадратными каменными плитами. Барон утверждает, что его новый ковер (сделанный из одного куска ковролина) закрывает ровно 24 плиты и при этом каждый вертикальный и каждый горизонтальный ряд плит в гостиной содержит ровно 4 плиты, покрытых ковром. Не обманывает ли барон?

Задача №9
Саша выписал первые миллион натуральных чисел, не делящихся на 4. Рома подсчитал сумму 1000 подряд идущих чисел в Сашиной записи. Могло ли у него получиться в результате 20012002?

Задача №10
Автомобиль из A в B ехал со средней скоростью 50 км/ч., а обратно возвращался со скоростью 30 км/ч.. Какова его средняя скорость?

Математические загадки

Загадка №1
Не пользуясь калькулятором и компьютером (в уме) вычислите сумму всех чисел от одного до ста?

Загадка №2
Позавчера Васе было 17 лет. В следующем году ему будет 20 лет. Как такое может быть?

Загадка №3
Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?

Загадка №4
На острове живут два племени: молодцы. Которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник встретил островитянина, спросил его, кто он такой, и когда услышал, что он из племени молодцов, нанял его в проводники. Они пошли и увидели вдали другого островитянина, и путешественник послал своего проводника спросить его, к какому племени он принадлежит. Проводник вернулся и сказал, что тот утверждает, что он из племени молодцов. Спрашивается: был проводник молодцом или лгуном?

Загадка №5
В двух футбольных лигах в сумме 39 команд. Команда играет с каждой командой из своей лиги по одному разу; при этом никаких матчей между лигами не происходит. За победу полагается 3 очка, за ничью — 1 очко, за проигрыш — 0. В прошлом году в одной лиге состоялось на 171 матч больше, чем в другой. Команда «Чемпионы», входящая в одну из лиг, проиграла всего три матча и набрала 32 очка.
Вопрос: со сколькими командами играли «Чемпионы» и сколько раз они сыграли вничью?

Ответы к уравнениям

Уравнение	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	a = 3	z = 2 x = 3	x = — 15¹/₃	x = 0,4	y = -3

Уравнение	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	16х² — 40ху + 25у²	(2у — 3)²	y = 2	x = 0 x=0,8	x = 0,6

Ответы к задачам

Задача 1
Если A = 0, то либо B = 0, либо B – C = 0. Ни то, ни другое невозможно. Поэтому A не 0. Если B = 0, то и A = 0. Это тоже невозможно. Поэтому B не 0. Следовательно, C = 0, и равенство из условия задачи можно переписать в виде A = B. Отсюда следует, что B > 0. Значит, B положительно, а A – отрицательно.

Задача 2
Так как 2000 = 3 x 666 + 2, то 2000-м месте стоит число 5.

Задача 3
Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.

Задача 4
23

Задача 5
44 кг

Задача 6
60 чисел

Задача 7
Отрезок BE длиннее

Задача 8
Примером такой клетчатой фигуры может служить квадрат 6 на 6 без двух подходящих обобщенных диагоналей. Конечно, если трактовать это как ковер в гостиной, получится нечто экстравагантное, но ведь барон не зря слыл незаурядным человеком.

Задача 9
Из любых трёх чисел, идущих в Сашиной записи подряд, одно имеет остаток 1 пр делении на 4, другое – остаток 2, а оставшееся – остаток 3. Значит их сумма при делении на 4 даёт остаток 2. Среди первых 999 Роминых чисел есть ровно 333 таких тройки, сумма чисел в них даёт при делении на 4 такой же остаток, как 333 • 2, то есть 2. Оставшееся число на 4 не делится, поэтому вся сумма не может также давать остаток 2. А 20012002 даёт именно этот остаток.

Задача 10
37,5 км/ч

Ответы на загадки

Загадка 1
5050

Загадка 2
Если нынешний день 1 января, а у Васи день Рождения тридцать первого декабря. Позавчера, т.е. тридцатого декабря ему было еще семнадцать лет. Вчера, т.е. тридцать первого декабря исполнилось восемнадцать лет. В этом году исполнится девятнадцать лет, а в следующем году двадцать лет.

Загадка 3
Всего деливших было трое: дед, его сын и внук

Загадка 4
На острове на данный вопрос никто не мог ответить ничего, кроме того, что он молодец. Так как проводник воспроизвел правильно этот единственно возможный ответ, то ясно, что он молодец.

Загадка 5
«Чемпионы» играли с 23 командами (следовательно, в их лиге 24 команды, а в другой — 15) и сыграли вничью 14 матчей из 23.

Скачайте задания, заполнив форму!

После того как укажете данные, кнопка скачивания станет активной

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

Презентация на тему «Решение задач с помощью систем уравнений» 7 класс

Инфоурок › Алгебра ›Презентации›Презентация на тему «Решение задач с помощью систем уравнений 1 часть» 7 класс

Решение задач с помощью систем уравнений Журнал «Математика» №17/2011

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Решение задач с помощью систем уравнений Журнал «Математика» №17/2011

2 слайд

Описание слайда:

2 см3 4 см3 медь серебро 59 г Плотность меди < плотности серебра на 2г/см3 Журнал «Математика» №17/2011

3 слайд

Описание слайда:

Решение: Пусть плотность меди х г/см3 , плотность серебра у г/см3. По условию задачи разность у и х равна 2, сумма 2х и 4у равна 59. Составим систему уравнений и решим ее. Плотность (г/см3)– масса в граммах одного кубического сантиметра. Журнал «Математика» №17/2011 Журнал «Математика» №17/2011

4 слайд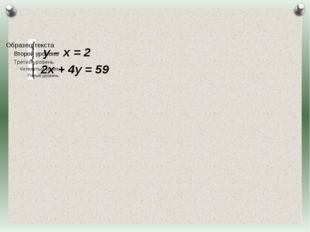

Описание слайда:

у – х = 2 2х + 4у = 59 Журнал «Математика» №17/2011

5 слайд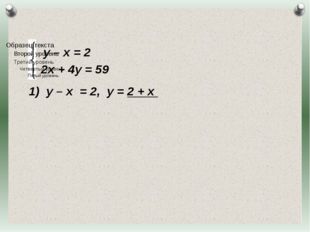

Описание слайда:

у – х = 2 2х + 4у = 59 у – х = 2, у = 2 + х Журнал «Математика» №17/2011

6 слайд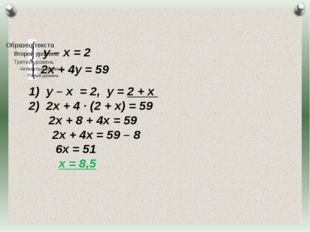

Описание слайда:

у – х = 2 2х + 4у = 59 у – х = 2, у = 2 + х 2х + 4 · (2 + х) = 59 2х + 8 + 4х = 59 2х + 4х = 59 – 8 6х = 51 х = 8,5 Журнал «Математика» №17/2011

7 слайд

Описание слайда:

у – х = 2 2х + 4у = 59 у – х = 2, у = 2 + х 2х + 4 · (2 + х) = 59 2х + 8 + 4х = 59 2х + 4х = 59 – 8 6х = 51 х = 8,5 У = 2 + 8,5 у = 10,5 Ответ: плотность меди 8,5 г/см3, серебра 10,5 г/см3. Журнал «Математика» №17/2011

8 слайд

Описание слайда:

Журнал «Математика» №17/2011

9 слайд

Описание слайда:

Пусть х км/ч – скорость дачника пешком, у км/ч – скорость дачника на велосипеде. По условию задачи у равно 2,4х, сумма 2х и 3у равна 46. Составим систему уравнений и решим ее. Журнал «Математика» №17/2011 Журнал «Математика» №17/2011

10 слайд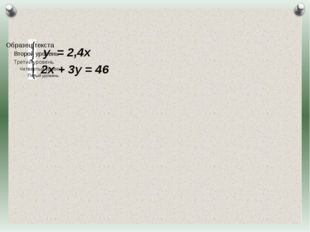

Описание слайда:

у = 2,4х 2х + 3у = 46 Журнал «Математика» №17/2011

11 слайд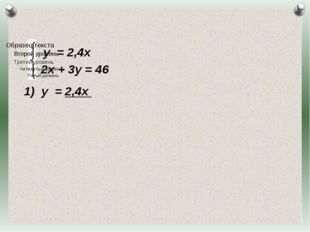

Описание слайда:

у = 2,4х 2х + 3у = 46 у = 2,4х Журнал «Математика» №17/2011

12 слайд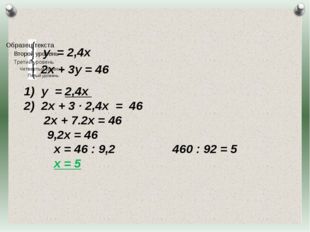

Описание слайда:

у = 2,4х 2х + 3у = 46 у = 2,4х 2х + 3 · 2,4х = 46 2х + 7.2х = 46 9,2х = 46 х = 46 : 9,2 460 : 92 = 5 х = 5 Журнал «Математика» №17/2011

13 слайд

Описание слайда:

у = 2,4х 2х + 3у = 46 у = 2,4х 2х + 3 · 2,4х = 46 2х + 7.2х = 46 9,2х = 46 х = 46 : 9,2 460 : 92 = 5 х = 5 У = 2,4 · 5 у = 12 Ответ: скорость дачника пешком 5км/ч, на велосипеде 12км/ч. Журнал «Математика» №17/2011

14 слайд

Описание слайда:

Журнал «Математика» №17/2011

15 слайд

Описание слайда:

Пусть х гектолитров поступает за одну минуту через первую трубу, у гектолитров через вторую трубу. По условию задачи разность 3у и 4х равна 1, а сумма 5х и у равна 32. Составим систему и решим ее. Журнал «Математика» №17/2011 Журнал «Математика» №17/2011

16 слайд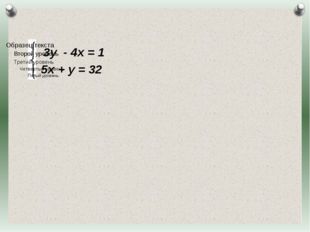

Описание слайда:

3у — 4х = 1 5х + у = 32 Журнал «Математика» №17/2011

17 слайд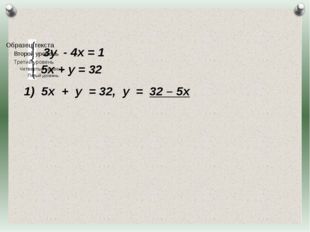

Описание слайда:

3у — 4х = 1 5х + у = 32 5х + у = 32, у = 32 – 5х Журнал «Математика» №17/2011

18 слайд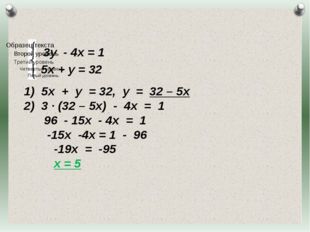

Описание слайда:

3у — 4х = 1 5х + у = 32 5х + у = 32, у = 32 – 5х 3 · (32 – 5х) — 4х = 1 96 — 15х — 4х = 1 -15х -4х = 1 — 96 -19х = -95 х = 5 Журнал «Математика» №17/2011

19 слайд

Описание слайда:

3у — 4х = 1 5х + у = 32 5х + у = 32, у = 32 – 5х 3 · (32 – 5х) — 4х = 1 96 — 15х — 4х = 1 -15х -4х = 1 — 96 -19х = -95 х = 5 У = 32 — 5 · 5 у = 7 Ответ: через первую трубу 5гл /мин, через вторую 7 гл /мин. Журнал «Математика» №17/2011

20 слайд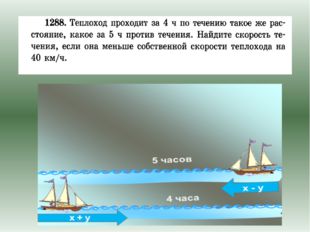

Описание слайда:

Журнал «Математика» №17/2011

21 слайд

Описание слайда:

Пусть х км/ч – собственная скорость теплохода, у км/ч – скорость течения, (х + у)км/ч — скорость по течению, (х – у)км/ч – скорость против течения. По условию задачи разность х и у равна 40, 4(х +у) равно 5(х –у). Журнал «Математика» №17/2011 Журнал «Математика» №17/2011

22 слайд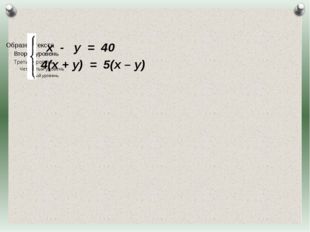

Описание слайда:

х — у = 40 4(х + у) = 5(х – у) Журнал «Математика» №17/2011

23 слайд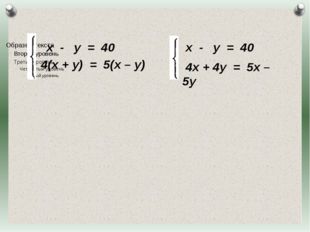

Описание слайда:

х — у = 40 4(х + у) = 5(х – у) х — у = 40 4х + 4у = 5х – 5у Журнал «Математика» №17/2011

24 слайд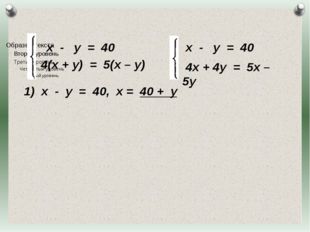

Описание слайда:

х — у = 40 4(х + у) = 5(х – у) х — у = 40, х = 40 + у х — у = 40 4х + 4у = 5х – 5у Журнал «Математика» №17/2011

25 слайд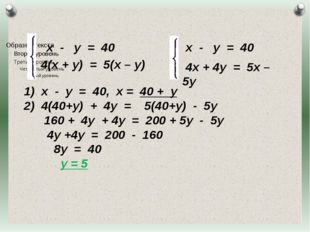

Описание слайда:

х — у = 40 4(х + у) = 5(х – у) х — у = 40, х = 40 + у 4(40+у) + 4у = 5(40+у) — 5у 160 + 4у + 4у = 200 + 5у — 5у 4у +4у = 200 — 160 8у = 40 у = 5 х — у = 40 4х + 4у = 5х – 5у Журнал «Математика» №17/2011

26 слайд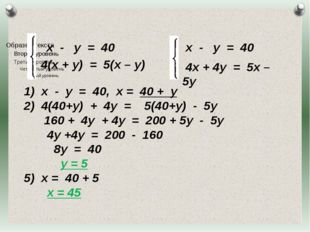

Описание слайда:

х — у = 40 4(х + у) = 5(х – у) х — у = 40, х = 40 + у 4(40+у) + 4у = 5(40+у) — 5у 160 + 4у + 4у = 200 + 5у — 5у 4у +4у = 200 — 160 8у = 40 у = 5 х = 40 + 5 х = 45 х — у = 40 4х + 4у = 5х – 5у Журнал «Математика» №17/2011

27 слайд

Описание слайда:

х — у = 40 4(х + у) = 5(х – у) х — у = 40, х = 40 + у 4(40+у) + 4у = 5(40+у) — 5у 160 + 4у + 4у = 200 + 5у — 5у 4у +4у = 200 — 160 8у = 40 у = 5 х = 40 + 5 х = 45 Ответ: скорость течения равна 5 км/ч. х — у = 40 4х + 4у = 5х – 5у Журнал «Математика» №17/2011

28 слайд

Описание слайда:

Пусть х км/ч – скорость катера по течению, у км/ч – скорость катера против течения. По условию задачи сумма 3х и 4у равна 120, разность 3х и 2у равна 30. 3х + 4у = 120 3х — 2у = 30 Журнал «Математика» №17/2011 Журнал «Математика» №17/2011

29 слайд

Описание слайда:

3х + 4у = 120 3х – 2у = 30 Журнал «Математика» №17/2011

30 слайд

Описание слайда:

3х + 4у = 120 3х – 2у = 30 1) _ 3х + 4у = 120 2) 3х + 4 · 15 = 120 3х – 2у = 30 3х + 60 = 120 ——————————————— 3х = 120 — 60 4у — ( -2у) = 120 — 30 3х = 60 6у = 90 х = 60 : 3 у = 15 х = 20 Журнал «Математика» №17/2011

31 слайд

Описание слайда:

3х + 4у = 120 3х – 2у = 30 1) _ 3х + 4у = 120 2) 3х + 4 · 15 = 120 3х – 2у = 30 3х + 60 = 120 ——————————————— 3х = 120 — 60 4у — ( -2у) = 120 — 30 3х = 60 6у = 90 х = 60 : 3 у = 15 х = 20 Ответ: скорость катера по течению равна 20 км/ч, против течения равна 15 км/ч. Журнал «Математика» №17/2011

32 слайд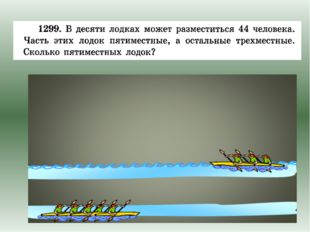

Описание слайда:

Журнал «Математика» №17/2011

33 слайд

Описание слайда:

Пусть х –пятиместных лодок, у — трехместных лодок. По условию задачи сумма х и у равна 10, сумма 5х и 3у равна 44. х + у = 10 5х + 3у = 44 Журнал «Математика» №17/2011 Журнал «Математика» №17/2011

34 слайд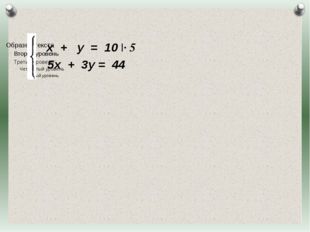

Описание слайда:

х + у = 10 |· 5 5х + 3у = 44 Журнал «Математика» №17/2011

35 слайд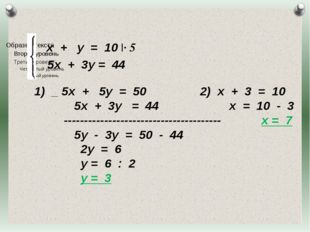

Описание слайда:

х + у = 10 |· 5 5х + 3у = 44 1) _ 5х + 5у = 50 2) х + 3 = 10 5х + 3у = 44 х = 10 — 3 ————————————— х = 7 5у — 3у = 50 — 44 2у = 6 у = 6 : 2 у = 3 Журнал «Математика» №17/2011

36 слайд

Описание слайда:

х + у = 10 |· 5 5х + 3у = 44 1) _ 5х + 5у = 50 2) х + 3 = 10 5х + 3у = 44 х = 10 — 3 ————————————— х = 7 5у — 3у = 50 — 44 2у = 6 у = 6 : 2 у = 3 Ответ: 7 пятиместных лодок. Журнал «Математика» №17/2011

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-169128

Оставьте свой комментарий

Стандарты общего ядра 7 класса

Вот Общие основные стандарты для 7-го класса со ссылками на ресурсы, которые их поддерживают. Мы также поощряем много упражнений и книжную работу.

7 класс | Соотношения и пропорциональные отношения

Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.

7.RP.A.1 Вычислить удельные веса, связанные с соотношениями долей, включая соотношения длин, площадей и других величин, измеренных в одинаковых или разных единицах.Например, если человек проходит 1/2 мили за каждые 1/4 часа, вычислите единичную скорость как сложную долю (1/2) / (1/4) миль в час, что эквивалентно 2 миль в час.

Соотношение — Рецепт шоколадных чипсов Соотношение — приготовить шоколадные чипсы

7.RP.A.2 Распознавать и представлять пропорциональные отношения между количествами.
а. Решите, находятся ли две величины в пропорциональном отношении, например, проверив эквивалентные отношения в таблице или построив график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
г. Определите константу пропорциональности (единицу измерения) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.
г. Изобразите пропорциональные отношения уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, связь между общей стоимостью и количеством товаров может быть выражена как t = pn.
г. Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, уделяя особое внимание точкам (0, 0) и (1, r), где r — удельная ставка.

7.RP.A.3 Используйте пропорциональные отношения для решения многошаговых задач с соотношением шагов и процентов. Примеры: простые проценты, налог, наценки и уценки, чаевые и комиссии, сборы, увеличение и уменьшение процентов, ошибка в процентах.

Разница в процентах Процент ошибок Изменение в процентах

Класс 7 | Система счисления

Применяйте и расширяйте предыдущие представления об операциях с дробями для сложения, вычитания, умножения и деления рациональных чисел.

7.NS.А.1 Применять и расширять предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме.
а. Опишите ситуации, в которых противоположные количества объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что его две составляющие заряжены противоположно.
г. Под p + q понимается число, находящееся на расстоянии | q | от p в положительном или отрицательном направлении в зависимости от того, положительный или отрицательный q.Докажите, что сумма числа и его противоположности равна 0 (аддитивно противоположны). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
г. Под вычитанием рациональных чисел понимается добавление обратного аддитивного числа p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой является абсолютной величиной их разницы, и примените этот принцип в контексте реального мира.
г. Применяйте свойства операций как стратегии для сложения и вычитания рациональных чисел.

Сложение и вычитание положительных и отрицательных чисел

7.NS.A.2 Применяйте и расширяйте предыдущие представления об умножении, делении и дробях для умножения и деления рациональных чисел.
а. Поймите, что умножение расширяется от дробей до рациональных чисел, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1) (- 1) = 1, и правилам умножения чисел со знаком.Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
г. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то — (p / q) = (-p) / q = p / (- q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
г. Применяйте свойства операций как стратегии умножения и деления рациональных чисел.
г. Преобразуйте рациональное число в десятичное с помощью длинного деления; знайте, что десятичная форма рационального числа оканчивается нулями или в конечном итоге повторяется.

7.NS.A.3. Решение реальных и математических задач с использованием четырех операций с рациональными числами. (Вычисления с рациональными числами расширяют правила манипулирования дробями до сложных дробей.)

7 класс | Выражения и уравнения

Используйте свойства операций для создания эквивалентных выражений.

7.EE.A.1 Применяйте свойства операций как стратегии для сложения, вычитания, разложения и расширения линейных выражений с рациональными коэффициентами.

7.EE.A.2. Поймите, что переписывание выражения в различных формах в контексте проблемы может пролить свет на проблему и на то, как соотносятся количества в ней. Например, a + 0,05a = 1,05a означает, что «увеличить на 5%» — это то же самое, что «умножить на 1,05».

Десятичные дроби и проценты

Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.

7.EE.B.3 Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций как стратегии для вычислений с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает прибавку на 10%, она будет дополнительно получать 1/10 своей зарплаты в час, или 2,50 доллара, с новой зарплаты в 27,50 долларов. Если вы хотите разместить штангу для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить штангу на расстоянии примерно 9 дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.

7.EE.B.4. Используйте переменные для представления величин в реальных или математических задачах и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах.
а. Решайте задачи со словами, приводящие к уравнениям вида px + q = r и p (x + q) = r, где p, q и r — конкретные рациональные числа. Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определяя последовательность операций, используемых в каждом подходе.Например, периметр прямоугольника 54 см. Его длина 6 см. Какая у него ширина?
г. Решите проблемы со словами, приводящие к неравенствам вида px + q> r или px + q

7 класс | Геометрия

Рисуйте, конструируйте и описывайте геометрические фигуры и описывайте отношения между ними.

7.G.A.1. Решение проблем, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей из масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе.

7.G.A.2 Нарисуйте (от руки, линейкой, транспортиром и технологией) геометрические фигуры в заданных условиях. Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.

7 класс Учебная программа

Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут с этим навыком. Мы также поощряем много упражнений и книжную работу. Curriculum Home

Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.

7 класс | Division

☐ Понять и уметь использовать Long Division

7 класс | Числа

☐ Различать различные подмножества действительных чисел (подсчет / натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа)

☐ Определите факторизацию данного числа на простые множители и запишите в экспоненциальной форме

☐ Упростите выражения, используя порядок операций (Примечание: выражения могут включать абсолютное значение, квадратные корни и / или целые показатели степени больше 0.)

☐ Сложение, вычитание, умножение и деление целых чисел

☐ Сложить два целых числа (с числовой строкой и без нее)

☐ Развить концептуальное понимание отрицательных и нулевых показателей степени с основанием из десяти и относящихся к дробям и десятичным знакам (например, 10 ^-2 = 0,01 = 1/100)

☐ Распознавать и указывать значение квадратного корня из полного квадрата (до 225)

☐ Определите квадратный корень из неполных квадратов (или более сложных полных квадратов) с помощью калькулятора

☐ Классифицируйте иррациональные числа как неповторяющиеся / не завершающие десятичные дроби

☐ Определите два последовательных целых числа, между которыми лежит квадратный корень из неполного квадратного целого числа меньше 225 (с использованием числовой прямой и без нее)

☐ Признайте разницу между рациональными и иррациональными числами (например,g., исследуйте различные приближения числа пи)

☐ Разместите рациональные и иррациональные числа (приближения) на числовой прямой и выровняйте расположение.

☐ Записывайте числа в экспоненциальном представлении

☐ Заменить числа, записанные в экспоненциальном представлении, на обычные числа

☐ Сравнить числа, записанные в экспоненциальном представлении

☐ Найдите общие делители и наибольший общий делитель двух или более чисел

: Помощь в домашних заданиях и ответы :: Slader

2,1	линейные уравнения; Метод интегрирующих факторов	Проблемы	п.40
2,2	Разделимые уравнения	Проблемы	с.48
2,3	Моделирование с помощью уравнений первого порядка	Проблемы	п.60
2,4	Разница между линейными и нелинейными уравнениями	Проблемы	с.76
2,5	Автономные уравнения и динамика населения	Проблемы	п.88
2,6	Точные уравнения и интегрирующие множители	Проблемы	с.101
2,7	Численное приближение: метод Эйлера	Проблемы	стр.110
2,8	Теорема существования и единственности	Проблемы	стр.120
2.9	Разностные уравнения первого порядка	Проблемы	стр.131
		Проблемы	стр.133

задач со словами системы уравнений | Purplemath

Purplemath

Очень часто словесные задачи с системой уравнений включают в себя смеси или комбинации того или иного вида. Например:

Компания по ландшафтному дизайну разместила два заказа на питомник. Первый заказ был на 13 кустов и 4 дерева на общую сумму 487 долларов.Второй заказ на 6 кустов и 2 дерева составил 232 доллара. В счетах не указана цена за единицу товара. Сколько стоили один куст и одно дерево?

MathHelp.com

Я мог бы попытаться добавить кусты и деревья, чтобы получить 19 кустов и 6 деревьев, но это меня ни к чему не привело, потому что у меня нет промежуточных итогов для кустов и деревьев.Я выберу переменные:

количество кустов: B

количество деревьев: т

С этими переменными я могу составить систему уравнений; каждое уравнение будет представлять одну из транзакций, которые они мне дали:

1-й заказ: 13B + 4 т = 487

2-й порядок: 6B + 2 т = 232

Умножая вторую строку на –2, получаем:

13Б + 4 т = 487

–12B — 4 т = –464

Сложив t -терминов, мы уравняем, и у меня останется B = 23.Решая обратное решение, я получаю, что t = 47. Конечно, в упражнении не запрашивались значения двух переменных. Если перевести обратно на английский, мое решение:

кустов: 23 доллара за штуку

дерева: 47 долларов США за штуку

Вы, вероятно, помните задачи со словом «расстояние», когда у вас была лодка, плывущая по течению, а затем против течения, или самолет, плывущий по ветру (то есть попутный ветер), а затем против ветра (т. Е. встречный ветер).Как только вы научитесь решать системы уравнений, вы увидите больше подобных упражнений.

Пассажирскому реактивному самолету потребовалось три часа, чтобы пролететь 1800 миль в направлении реактивного потока. Обратный путь против реактивного потока занял четыре часа. Какова была скорость реактивного самолета в неподвижном воздухе и скорость реактивного потока?

Когда меня спрашивают о скорости «в неподвижном воздухе» (для самолетов) или «в спокойной воде» (для лодок), они имеют в виду показания спидометра; они относятся только к входу с питанием, независимо от внешних воздействий.

В очень ветреный день вы можете наблюдать, как птицы отчаянно хлопают в воздухе, пытаясь перейти улицу, скажем, из-за дерева во дворе вашего дома. Как бы сильно они ни хлопали, они мало продвинулись вперед или не продвинулись вовсе; иногда кажется, что птица летит назад! Означает ли это, что птица на самом деле не хлопала? Нет; это означало, что попытка скорости птицы (насколько быстро хлопанье двигало птицу в безветренный день) была недостаточно быстрой, чтобы эффективно противодействовать ветру, ударяющему ей в лицо.«Скорость птицы в неподвижном воздухе», за вычетом скорости ветра в обратном направлении, была близка к нулю или даже отрицательна.

То же самое относится и к машинному оборудованию. Если мотор лодки движется со скоростью 10 миль в час (согласно спидометру), но лодка встречает поток воды 15 миль в час в противоположном направлении, то лодка в конечном итоге пойдет на назад и на пять миль. час. Другими словами, показания спидометра не всегда являются фактической скоростью.

Возвращение к упражнению:

Я выберу переменные и настрою систему. В этом случае я буду использовать:

спидометр самолета: p

скорость ветра: Вт

Когда самолет движется «по ветру», скорость самолета с двигателем и скорость ветра складываются; когда самолет летит «против» ветра, скорость ветра будет вычтена из показаний спидометра самолета (то есть из фактической мощности двигателей).

В каждом случае уравнение «расстояние» будет «(комбинированная скорость) умноженное на (время, проведенное на этой скорости) равно (общее пройденное расстояние)»:

со струйным потоком: ( p + w ) (3) = 1800

против струи: ( p — w ) (4) = 1800

Вместо того, чтобы перемножать, я заметил, что если я разделю 3 и 4, у меня будет система, которая уже настроена для решения сложением:

p + w = 600

p — w = 450

Затем, сложив вниз, я получу:

Обратное решение, я вижу, что скорость ветра Вт должна быть 75 миль в час.

скорость реактивного двигателя: 525 миль / ч

скорость ветра: 75 миль / ч

Еще одна тема, которую вы можете увидеть (если не сейчас, то позже в исчислении), — это разложение рациональных выражений с использованием частичных дробей.

Найдите дробное разложение следующего числа:

Знаменатель полиномиальной дроби, которую они мне дали, множится как:

Эти коэффициенты будут знаменателями при разложении на частичные дроби.То есть я буду искать значения A, B и C, которые завершат следующее:

Вышеупомянутое выражение должно быть равно исходной дроби, которую они мне дали. Уравняв их, а затем умножив обе стороны на общий знаменатель, я получу:

5 x + 7 = A ( x + 1) ( x — 1) + B ( x + 2) ( x — 1) + C ( x + 2) ( х + 1)

= A ( x ² — 1) + B ( x ² + x — 2) + C ( x ² + 3 x + 2)

= (A + B + C) x ² + (B + 3C) x + (–A — 2B + 2C) 1

Стандартный способ решения этого большого запутанного уравнения — процесс «сравнения коэффициентов».Два полинома равны, только если коэффициенты при их членах равны. Вот почему я сгруппировал свои термины так, как в последней строке выше; Я сгруппировал все, что было умножено на x ², все, что было умножено на x , и все, что было умножено на 1 (то есть все, что было просто константой, без переменной части).

С левой стороны у меня 5 x + 7, у которого нет термина с x ², поэтому мне нужно думать о «5 x + 7» как 0 x ² + 5 x + 7 дюймов.Это позволит мне создавать новые уравнения, основанные на том факте, что коэффициенты по обе стороны от знака «равно» должны быть одинаковыми. Это дает мне:

x ²: A + B + C = 0

x : B + 3C = 5

1: –A — 2B + 2C = 7

Решая эту систему, я получаю A = –1, B = –1 и C = 2. Тогда разложение на частичную дробь будет:

Что бы вы ни делали, не паникуйте, когда вы столкнетесь с проблемой слов в системе уравнений.Если вы рассмотрите их пошагово, они обычно вполне выполнимы. Тем не менее, вероятно, вам было бы полезно, если бы вы выполняли дополнительные практические задания, просто чтобы помочь вам разобраться в происходящем. Если повезет, ваши тесты пройдут немного быстрее.

URL: https://www.purplemath.com/modules/systprob2.htm

Методическая разработка по алгебре (7 класс): Решение уравнений. Решение задач с помощью уравнений. 7 класс

Методическая разработка по алгебре (7 класс): Решение задач с помощью уравнений.

Конспект и презентация к у року алгебры в 7 классе «Решение задач с помощью линейных уравнений»

Конспект по алгебре » Решение задач с помощью уравнений»(7 класс)

Олимпиада по математике 7 класс, задания, уравнения, задачи с ответами

Скачайте задания, заполнив форму!

Уравнения

Задачи

Математические загадки

Ответы к уравнениям

Ответы к задачам

Ответы на загадки

Скачайте задания, заполнив форму!

Другие классы

Презентация на тему «Решение задач с помощью систем уравнений» 7 класс

Оставьте свой комментарий

Стандарты общего ядра 7 класса

7 класс Учебная программа

: Помощь в домашних заданиях и ответы :: Slader

задач со словами системы уравнений | Purplemath

Purplemath

MathHelp.com

Найдите дробное разложение следующего числа:

Добавить комментарий Отменить ответ