Тренажер «ДРОБИ» | тренажер дробей онлайн | дроби для 5 и 6 класса | Клуб любителей математики
Данный тренажер является третьим в линейке тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.
Работа тренажера также основана на генерации примеров по математике с различными видами дробей, изучаемых в средних классах школы. Решение примеров способствует развитию скорости и качества устного счёта.
Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.
Режимы счёта
На странице настроек режима можно задавать необходимые параметры генерации примеров с дробями для любого класса.
Онлайн тренажер «Дроби» позволяет генерировать примеры с любыми видами дробей, с любым из четырёх арифметических действий.

Кнопки на панели настроек работают по принципу «Вкл/Выкл». Если цвет кнопки зелёный — значит в примерах будут использоваться дроби того типа, который описывает кнопка. Если же цвет серый — этот тип дробей использоваться не будет.
В приложении отсутствуют режимы «Уравнение» и «Сравнение» из-за их избыточной сложности. Работа проходит только в режиме «Пример» с возможным использованием следующих типов дробей:
Разные знаменатели — в примере будут появляться обыкновенные дроби с разными знаменателями.
Неправильные дроби — в примере будут появляться обыкновенные неправильные дроби (числитель больше знаменателя).
Смешанные числа — в примере будут появляться смешанные числа (числа, состоящие из целой и дробной частей).
Десятичные дроби — в примере будут появляться дроби в десятичной записи.
Также имеется возможность включить обязательную проверку ответа на сокращение дробной части числа и выделение целой части числа (если имеется). Понять, нужно ли сокращать ответ можно по красному индикатору * на странице настроек и странице ввода ответа.
Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». Когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.

Процесс счёта

Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звуковые уведомления или перейти к Подробному решению текущего примера.
Вы решаете заданый пример, вводите ответ по частям (целое, числитель, знаменатель) в соответствующие поля с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки ответа Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.
Количество правильных, неправильных ответов и число подсказок можно увидеть в соответствующих индикаторах.
Прогресс и достижения
Приложение также предусматривает небольшой соревновательный момент через получение медалей за безошибочность — правильное решение N примеров подряд.

Если во время решения была использована подсказка, то верный ответ не идет в зачет прогресса. Ошибка же сразу обнуляется весь прогресс. Поэтому будьте максимально осторожны, если хотите получить медаль — один неверный шаг и придется начинать все с начала.
Узнать, получили ли Вы уже медаль за конкретный режим можно на странице «Статистика» в профиле или в самом приложении.
Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.
Подробное решение примеров

В любой момент работы с тренажером вы можете перейти в разделу «Подробного решения примера», если обычной подсказки в виде верного ответа вам не достаточно. Для этого кликните на соответствующую иконку сверху, либо перелестнув страницу вниз.
Здесь вы сможете посмотреть подробное решение примера с дробями со всеми преобразованиями, сокращениями и упрощениями.
Дополнительная информация
Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:
домен сайта + раздел приложения + кодировка данного режима
например: matematika.club/drobi/#60101
Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.
Решение заданий с дробями (основы) – boeffblog.ru

Прежде чем приступать к решению заданий с дробями, необходимо разобраться, что же такое дробь. Это можно сделать, прочитав статью “Как понимать дроби”. Будем надеяться, что с этим Вы уже разобрались. Теперь разберемся с основными действиями над дробями. Поехали.
№1 Сложение и вычитание дробей
В этом типе заданий могут встречаться как обыкновенные дроби, так и десятичные, а еще Вы можете встретить в одном примере сразу и такие, и такие.
Рассмотрим сложение обыкновенных дробей: 
- Первым делом необходимо найти общий знаменатель этих двух дробей, для этого нужно перемножить знаменатели
те что снизумежду собой (25 и 2). То есть, общий знаменатель равен 50. - Затем нужно умножить числитель первой дроби на знаменатель второй дроби (14•2), а числитель второй дроби умножить на знаменатель первой дроби (3•25). Получается крест-накрест.
- Теперь запишем общую дробь:

- Осталось выполнить умножение и сложение:

- В таком виде ответ не получится написать в бланк, нужно привести полученную дробь к десятичному виду, то есть разделить в столбик 103 на 50. Получится 2,06.
При вычитании меняется только знак + на знак –
Например,  .
.
- Находим общий знаменатель (5•4 = 20).
- Умножаем числитель первой дроби на знаменатель второй дроби (1•4 = 4), а числитель второй дроби – на знаменатель первой дроби (3•5 = 15).
- Запишем общую дробь:

- Выполнить умножение и вычитание:

- Разделим в столбик -11 на 20. Получится -0,55.
№2 Умножение и деление дробей
Умножение вообще происходит элементарно: перемножаем числители двух дробей и перемножаем знаменатели двух дробей. Например,  . Приведем к десятичной дроби = 0,45.
. Приведем к десятичной дроби = 0,45.
Деление отличается от умножения лишь тем, что вторая дробь переворачивается (числитель и знаменатель меняются местами). Например,  = 0,9
= 0,9
№3 Возведение дроби в степень
Рассмотрим такой пример: 
 . А далее возводим числитель и знаменатель в квадрат: 12 = 1•1 = 1; 52 = 5•5 = 25. Получим,
. А далее возводим числитель и знаменатель в квадрат: 12 = 1•1 = 1; 52 = 5•5 = 25. Получим, 
Видите, как все просто.
№4 Сложение/вычитание и умножение/деление дроби и числа
Все Вы встречали такие примеры: 3 +  , 8 •
, 8 •  и т д. Что же делать? Как это решать? Да так же как и обычно, только в этом случае целое число нужно переписать в виде дроби. В школе учат, если число умножить на единицу, то в этом случае единица не пишется (5•1 = 5). Логично! Таким образом любое целое число можно записать как это число, умноженное на единицу (5 = 1•5). То же самое и с делением! 3 =
и т д. Что же делать? Как это решать? Да так же как и обычно, только в этом случае целое число нужно переписать в виде дроби. В школе учат, если число умножить на единицу, то в этом случае единица не пишется (5•1 = 5). Логично! Таким образом любое целое число можно записать как это число, умноженное на единицу (5 = 1•5). То же самое и с делением! 3 =  , а также наоборот
, а также наоборот  = 3.
= 3.
Решим первый пример: 3 +  =
=  . Приводим к общему знаменателю (1•2 = 2), и умножаем числитель первой дроби на 2, а числитель второй дроби на 1.
. Приводим к общему знаменателю (1•2 = 2), и умножаем числитель первой дроби на 2, а числитель второй дроби на 1.  = 4,5. При вычитании меняем только знак на минус.
= 4,5. При вычитании меняем только знак на минус.
Решим пример с умножением: 8 •  = 1.
= 1.
Вот мы и познакомились с основными действиями над дробями. Далее рассмотрим решение конкретных заданий с дробями.
Карточки-задания для индивидуальной работы учащихся 5 класса на уроках по теме «Обыкновенные дроби»
Обыкновенные дроби. Правильные и неправильные дроби
1. Запишите в виде дроби:а) три восьмых; б) шесть десятых; в) сорок семь сотых.
2. На выставке представлено 15 телевизоров.
Среди них 11 цветных. Какая часть представленных телевизоров цветные?
3. Запишите три правильные дроби со знаменателем 9, и три неправильные с тем же знаменателем.
В-1
1. Запишите в виде дроби:
а) две пятых; б) семь девятых; в) одиннадцать двадцатых.
2. В коробке лежат 12 мячей. Из них 7 мячей зеленого цвета. Какую часть всех мячей составляют мячи зеленого цвета?
3. Запишите три правильные дроби со знаменателем 7, и три неправильные со знаменателем 6.
В-2
1. Запишите в виде дроби:
а) три десятых; б) четыре девятых; в) двадцать три сотых.
2.В классе 35 учащихся. Из них 23 — ударники.
Какая часть учащихся класса является ударниками?
3. При каких значениях х дробь 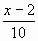 будет правильной?
будет правильной?
В-3
1. Запишите в виде дроби:
а) две десятых; б) семь сотых; в) тринадцать тридцатых.
2. Среди 16 тетрадей 5 тетрадей в линейку, а остальные в клетку. Какую часть всех тетрадей составляют тетради в клетку?
3. При каких значениях х дробь 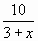 будет неправильной?
будет неправильной?
В-4
1. Туристы прошли лесом 24 км. Это составило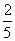 длины их маршрута. Какова длина маршрута?
длины их маршрута. Какова длина маршрута?2. Отметьте на координатном луче точки 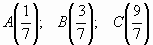 .
.
В-1
1. Турист проехал на машине 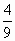 пути, что составило 200 км. Какова длина намеченного пути?
пути, что составило 200 км. Какова длина намеченного пути?
2. Отметьте на координатном луче точки 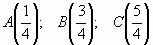 .
.
В-2
1. Какую часть метра составляют: 1 см,
13 см, 3 дм, 7 мм?
2. Отметьте на координатном луче точки 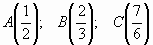 (ед. отрезок 6 клеток)
(ед. отрезок 6 клеток)
В-3
1. Какую часть тонны составляют: 1 кг, 130 кг,
2 ц, 74 ц?
2. Отметьте на координатном луче точки 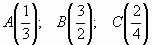 (ед. отрезок 12 клеток)
(ед. отрезок 12 клеток)
В-4
1. Какую часть метра составляют: 1 дм, 3 дм, 7 см ,13 мм?
2. От ленты сначала отрезали 12 м, а потом 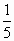 оставшейся части. Найдите первоначальную длину ленты, если во второй раз от неё отрезал 4 м.
оставшейся части. Найдите первоначальную длину ленты, если во второй раз от неё отрезал 4 м.
В-5
1. Какую часть часа составляют 3 мин, 24 сек?
2.В корзине были яблоки. Сначала в неё положили ещё 15 яблок, а затем взяли 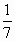 получившихся там яблок. Сколько было яблок в корзине первоначально, если из корзины взяли 20 яблок ?
получившихся там яблок. Сколько было яблок в корзине первоначально, если из корзины взяли 20 яблок ?
В-6
1. Сократите дробь: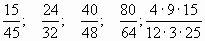
2. Приведите дробь 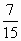 к знаменателю 60.
к знаменателю 60.
В-1
1. Сократите дробь:
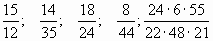
2. Приведите дробь 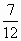 к знаменателю 36. В-2
к знаменателю 36. В-2
1. Сократите дробь:
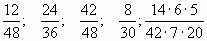
2. Приведите дробь 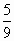 к знаменателю 63.
к знаменателю 63.
В-3
1. Сократите дробь:
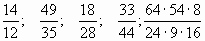
2. Приведите дробь 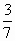 к знаменателю 56.
к знаменателю 56.
В-4
Смешанные числа
1. Запишите в виде смешанных чисел:а) частное 9: 7, б) дробь 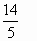
2. Запишите в виде неправильной дроби:
а) 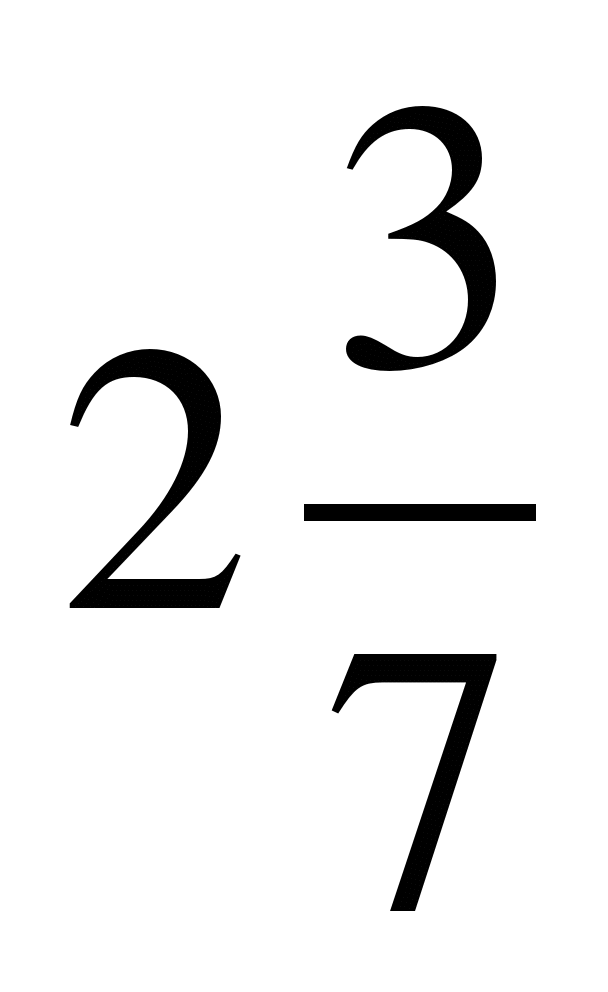 б)
б) 
В-1
1. Запишите в виде смешанных чисел:
а) частное 73 : 10, б) дробь 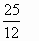
2. Запишите в виде неправильной дроби:
а) 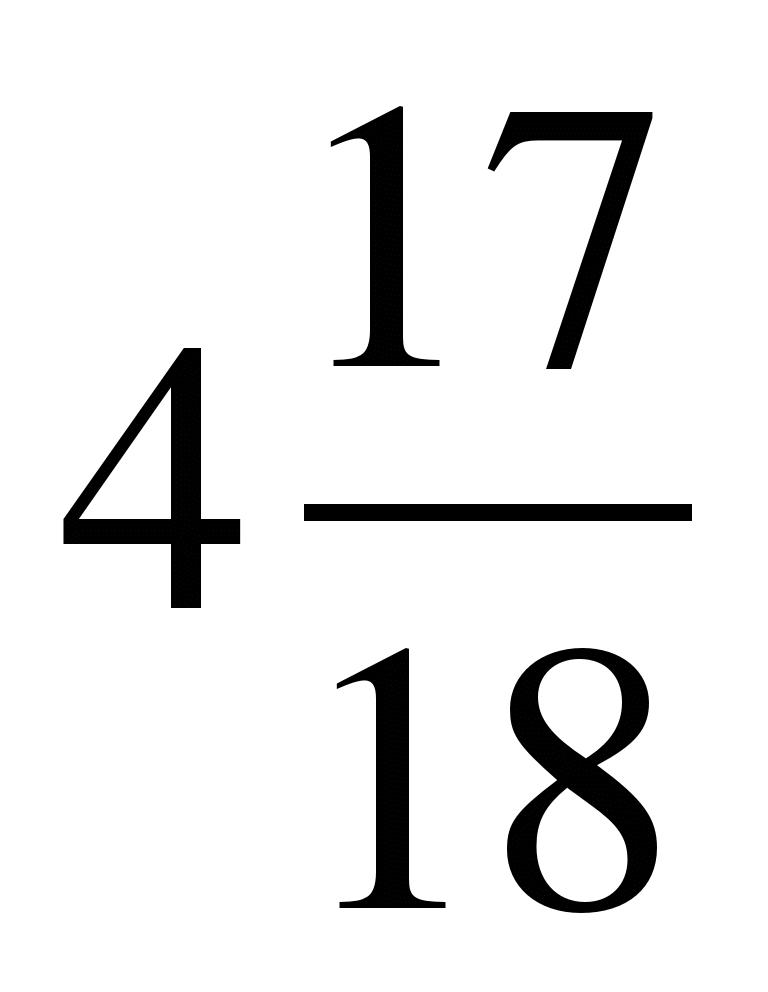 б)
б) 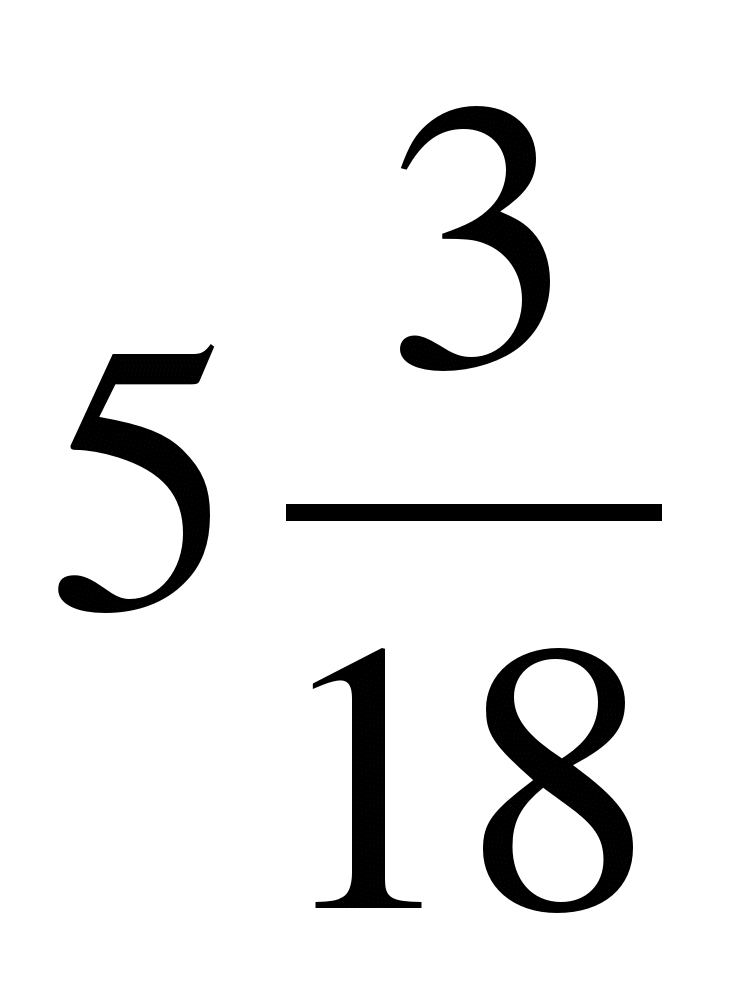
В-2
1. Запишите в виде смешанных чисел:
а) частное 12 : 7, б) дробь 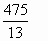
2. Запишите в виде неправильной дроби:
а) 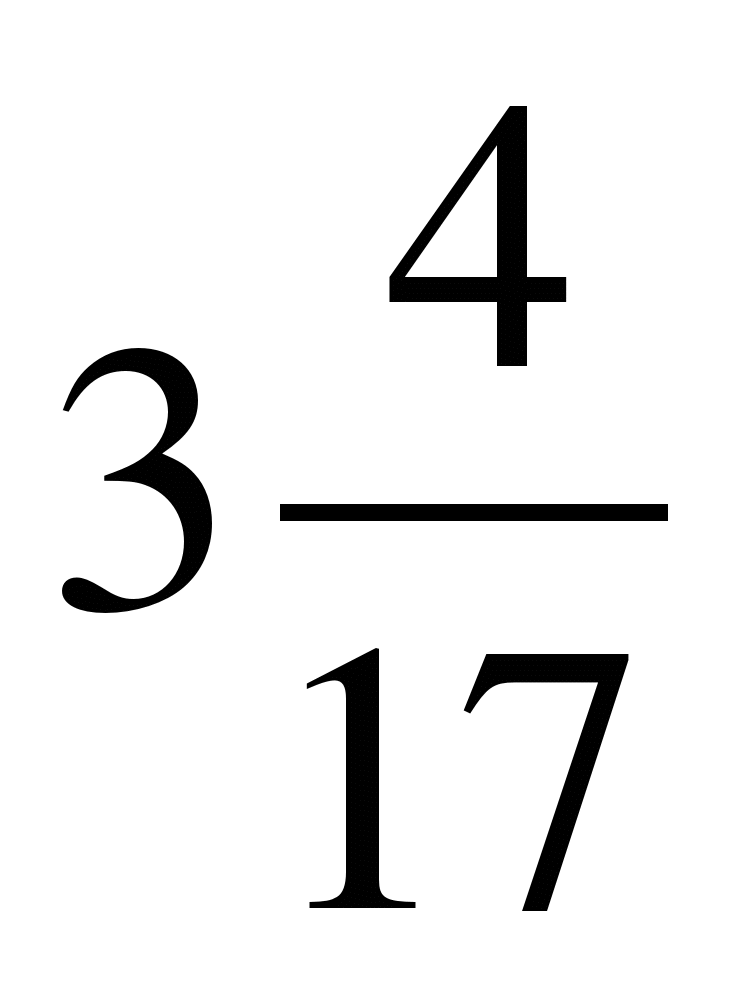 б)
б) 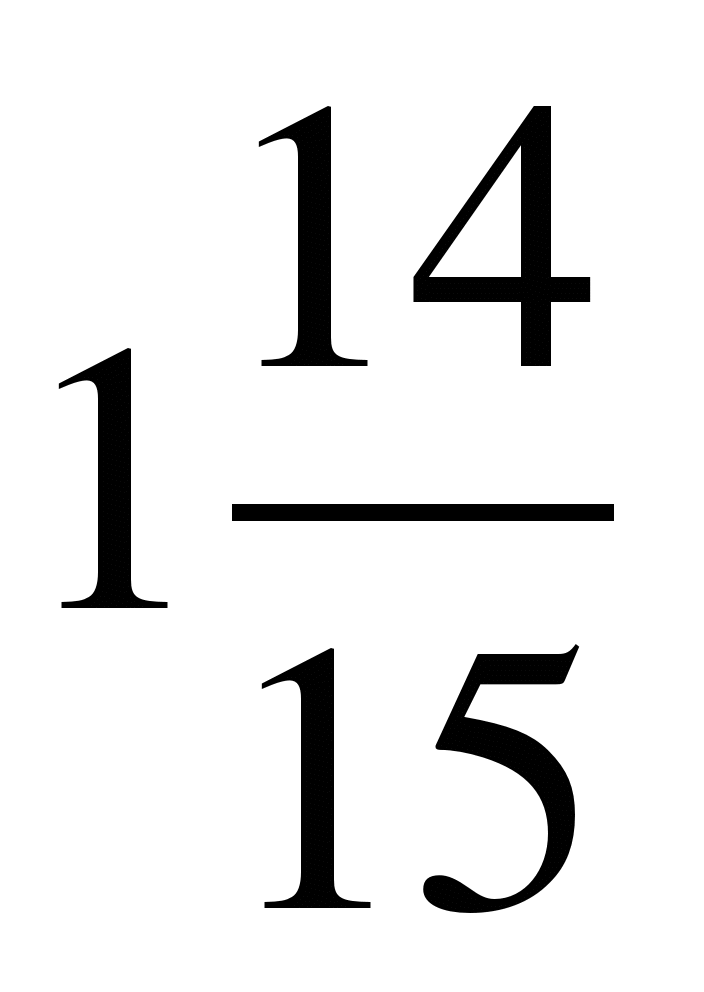
В-3
1. Запишите в виде смешанных чисел:
а) частное 24: 10, б) дробь 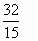
2. Запишите в виде неправильной дроби:
а) 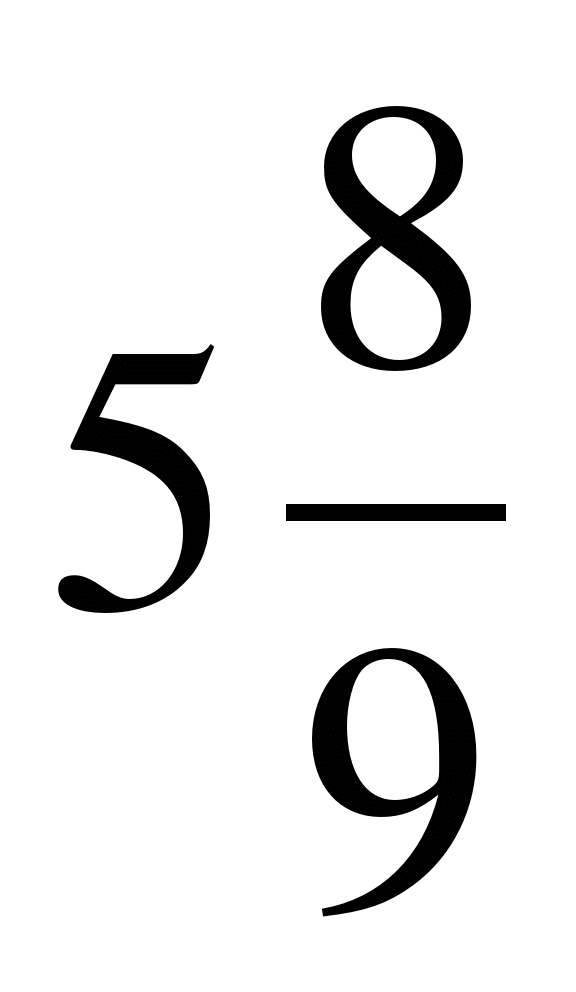 б)
б) 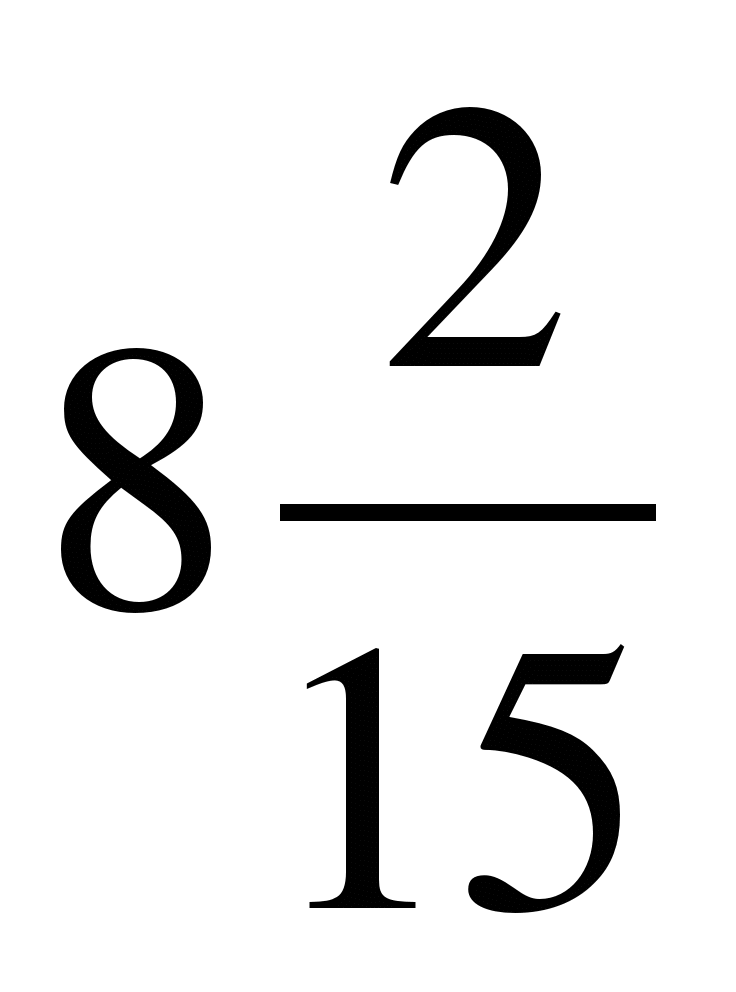
В-4
1. Выдели целую часть из дробей:
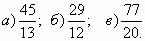
2. Запиши в виде неправильной дроби
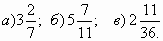
В-5
1. Выдели целую часть из дробей:
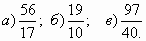
2. Запиши в виде неправильной дроби
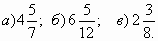
В-6
Сложение и вычитание обыкновенных дробей
1. Выполните сложение:а) 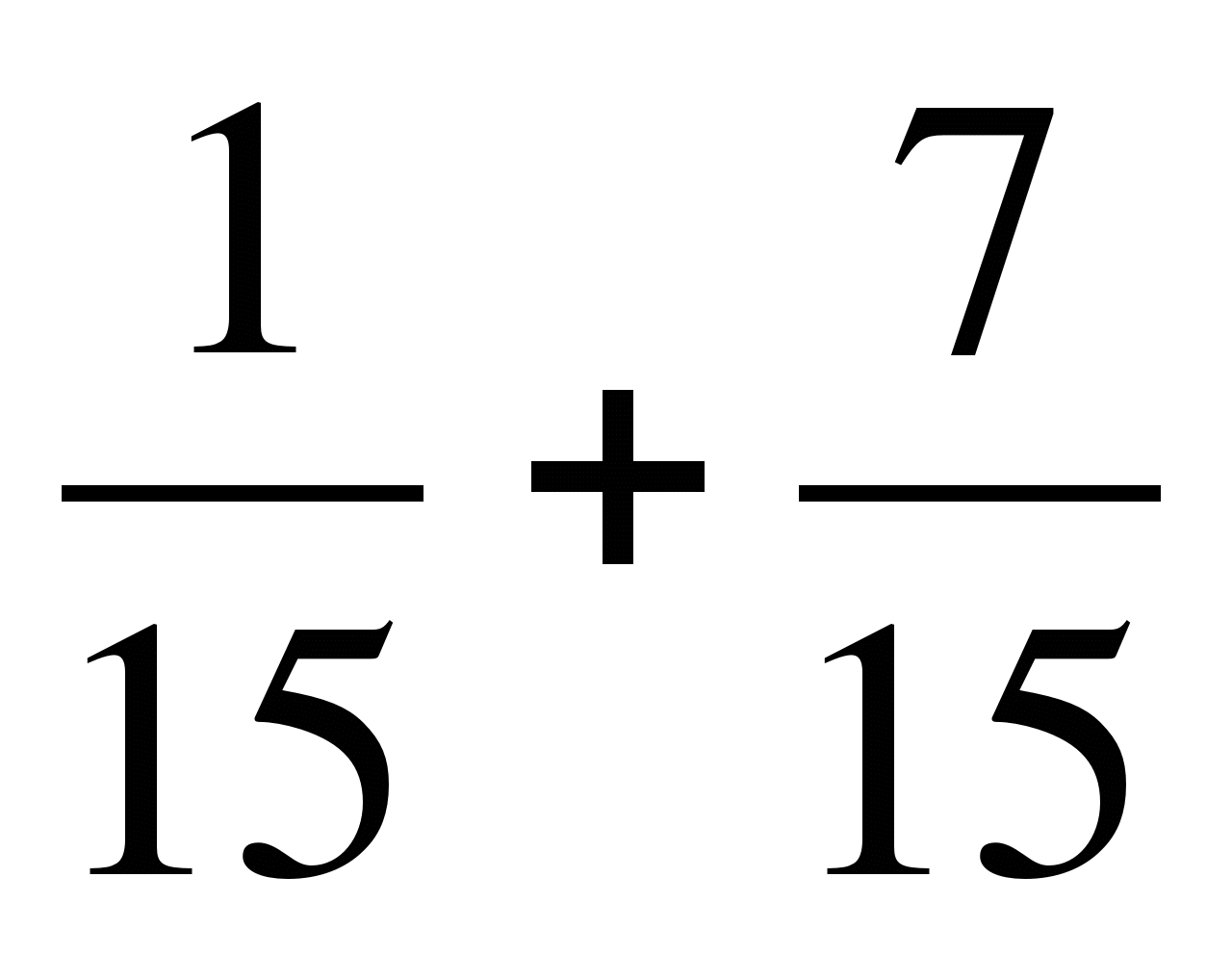 ; б)
; б) 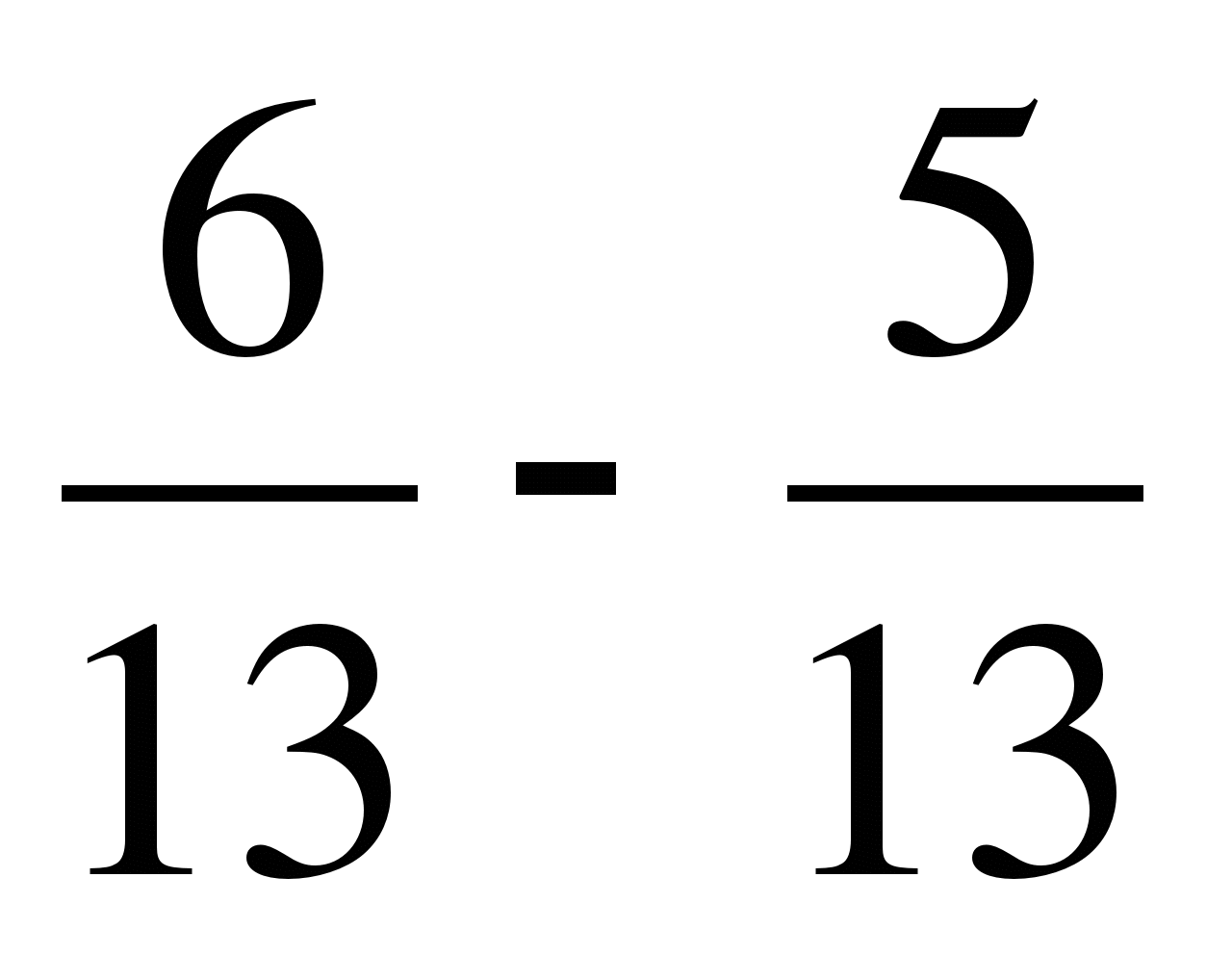 ; в)
; в) 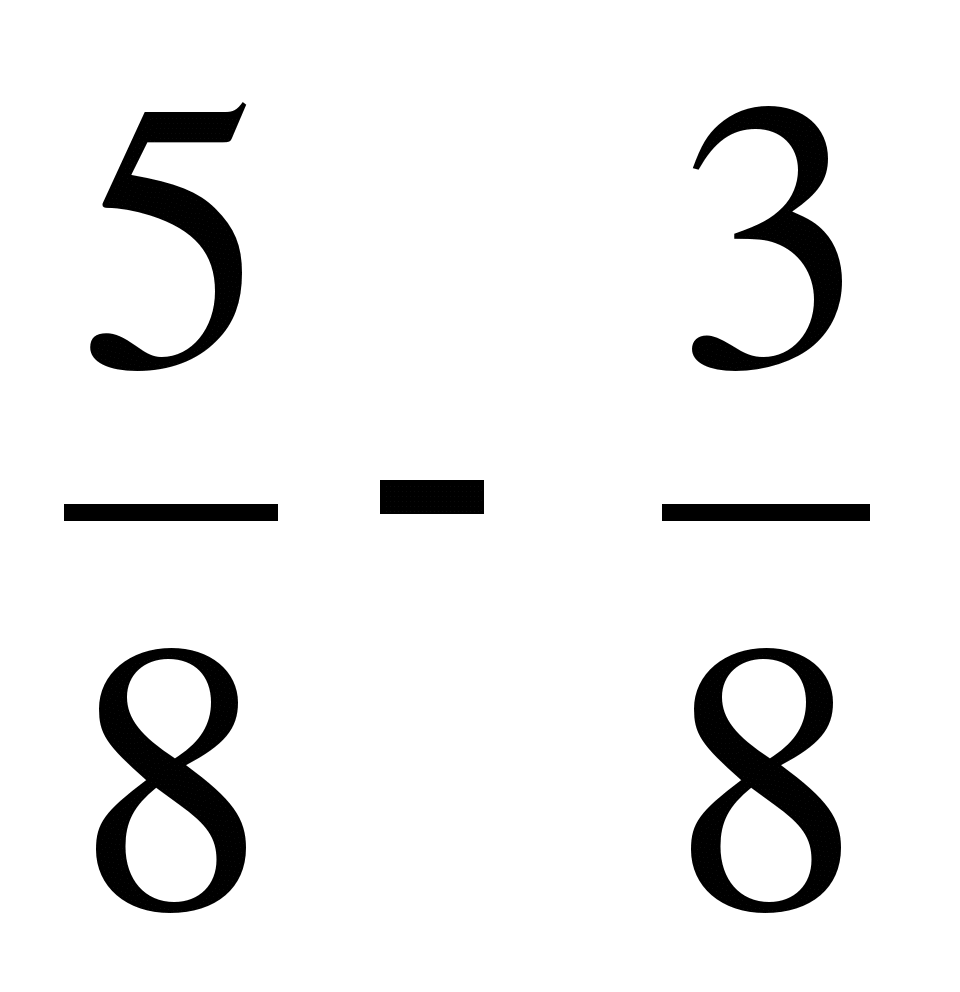
г) 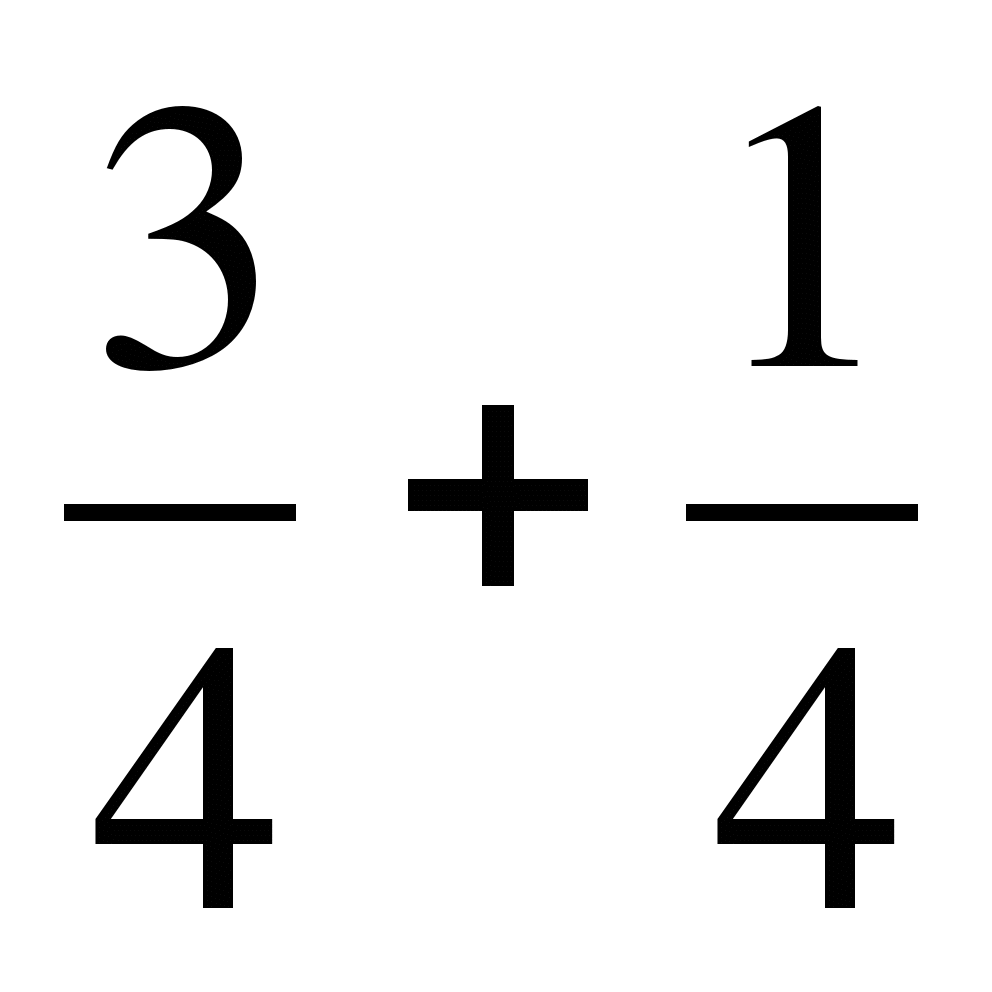 ; д)
; д) 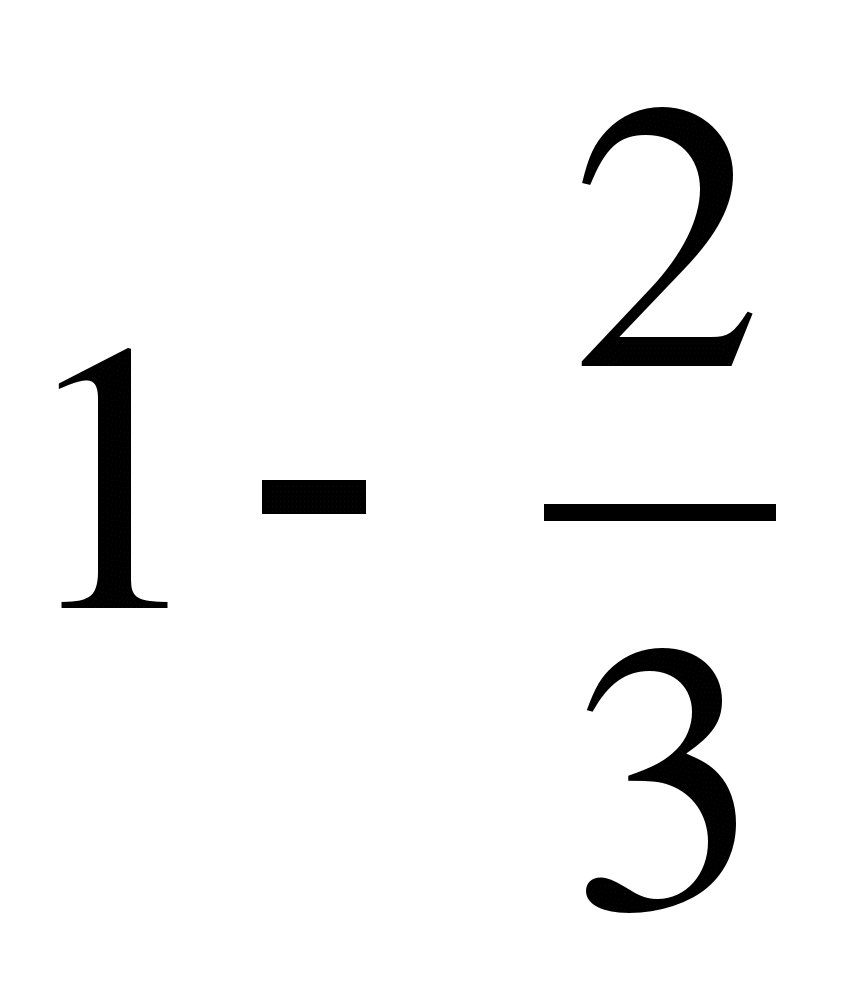 .
.
2. Реши уравнение: 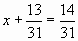 .
.
1в
1. Выполните сложение:
а) 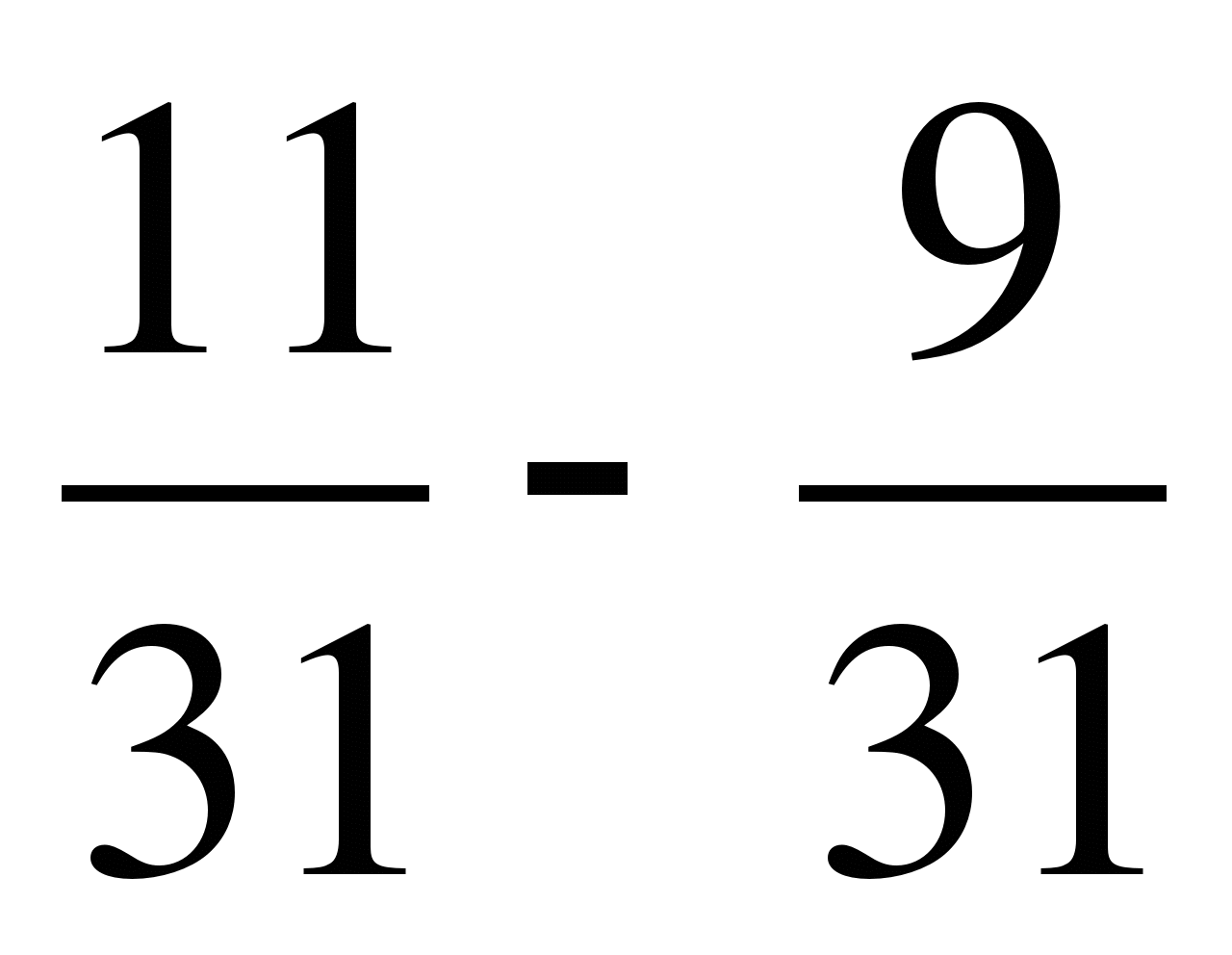 ; б)
; б) 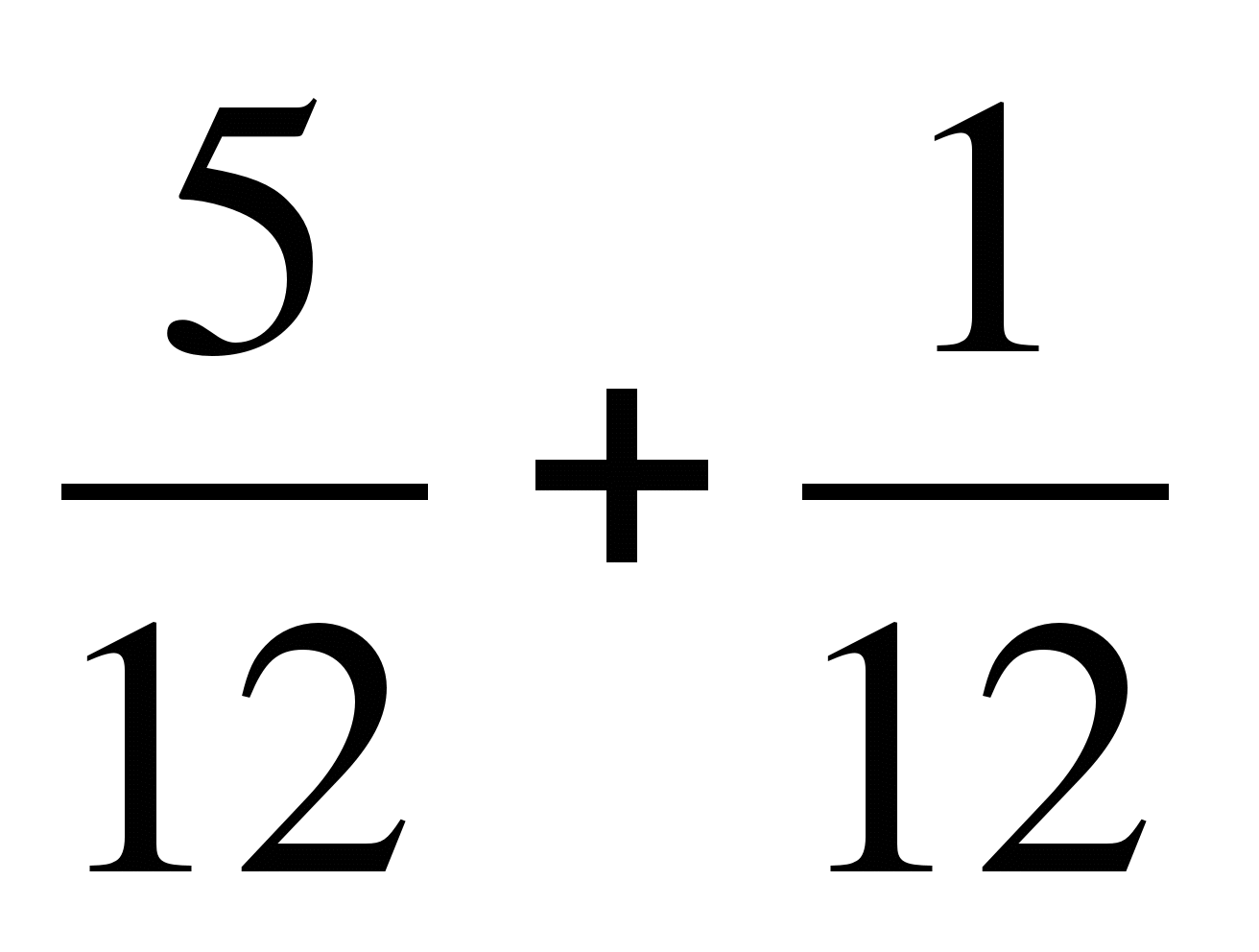 ; в)
; в) 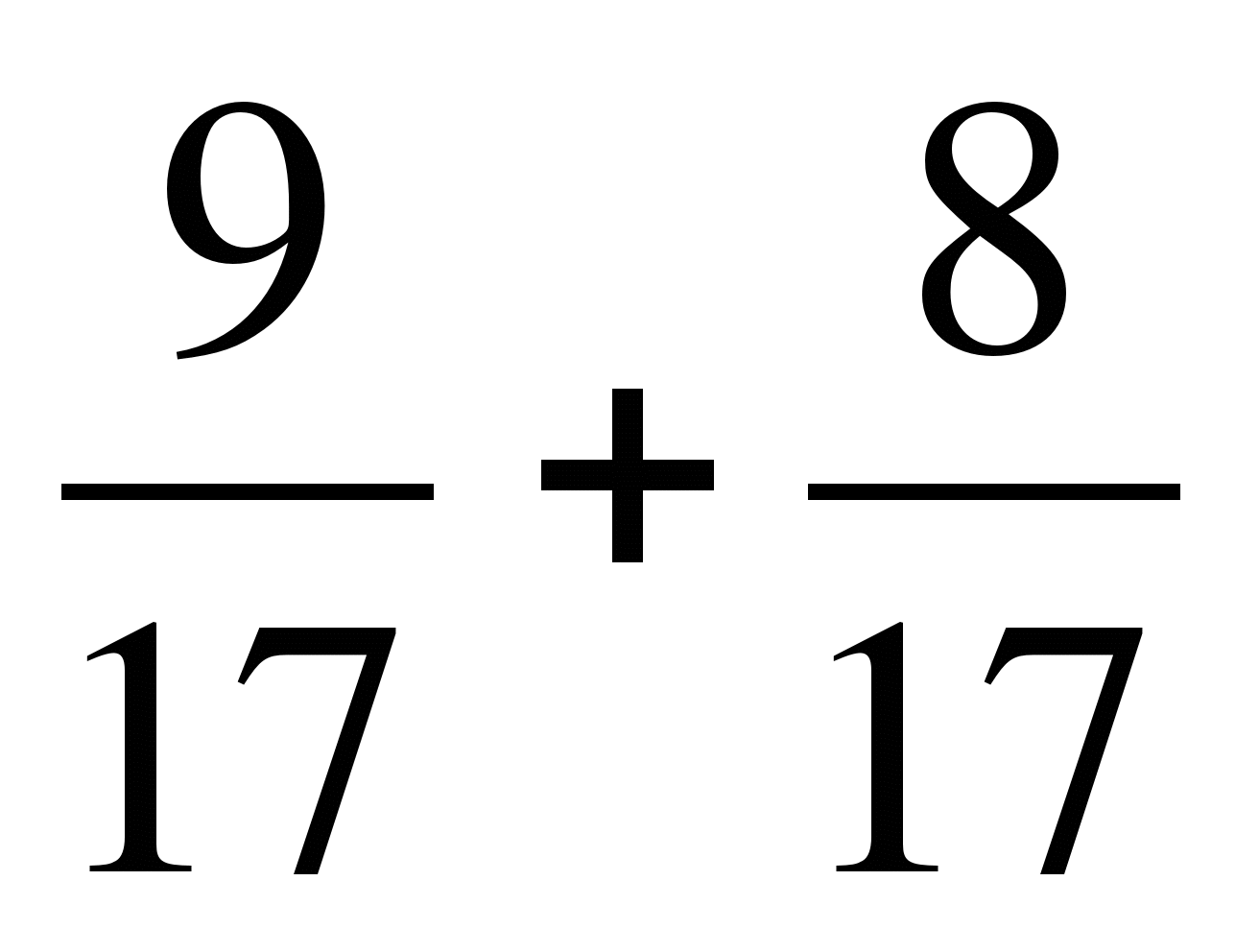
г) 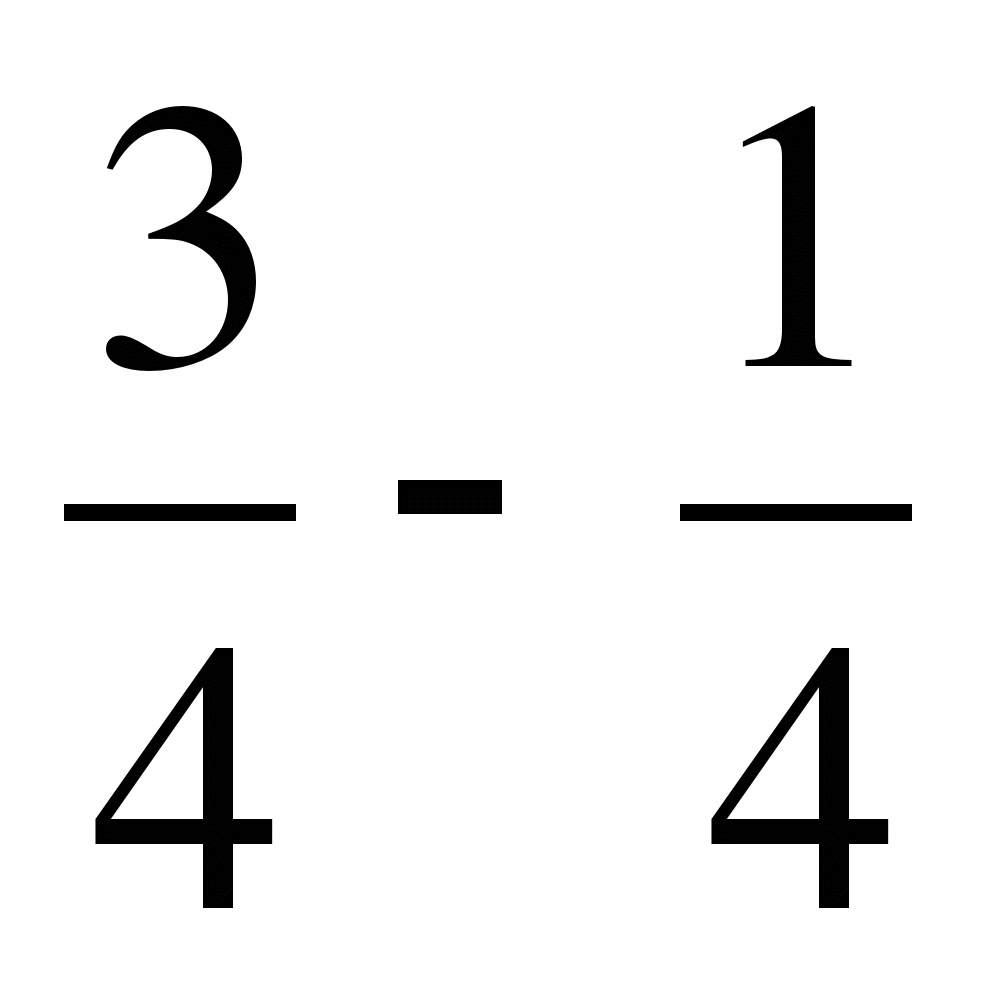 ; д)
; д) 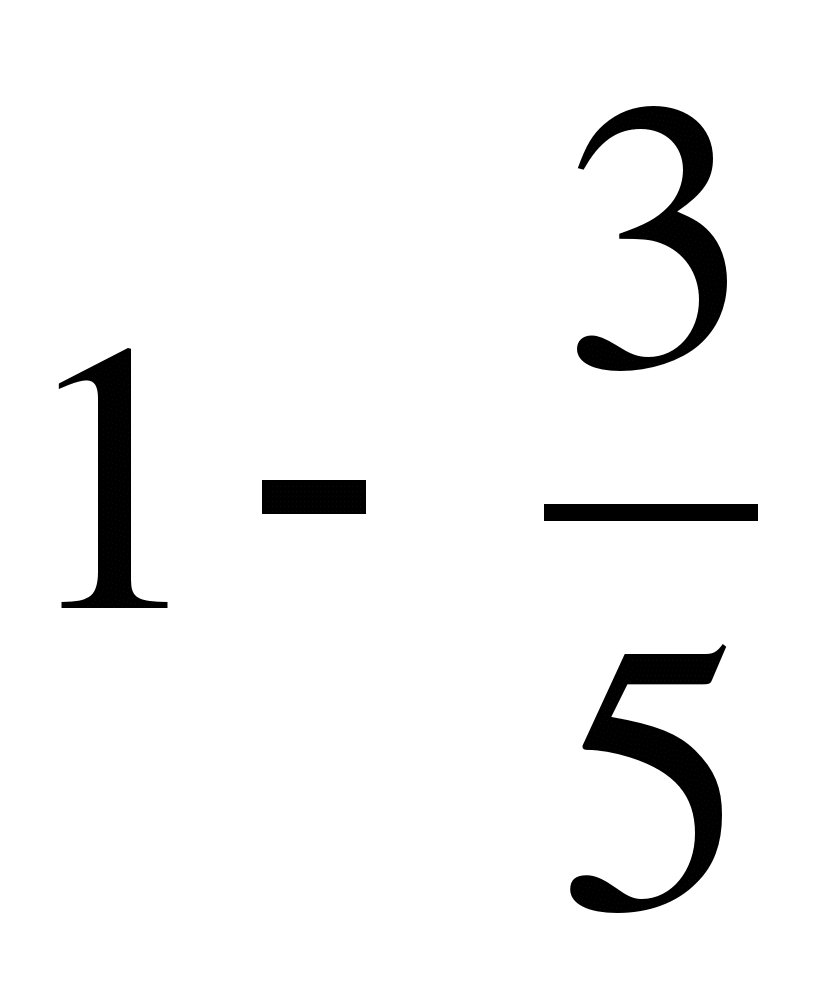 ..
..
2. Реши уравнение: 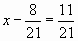 .
.
2в
1. Выполните сложение:
а) 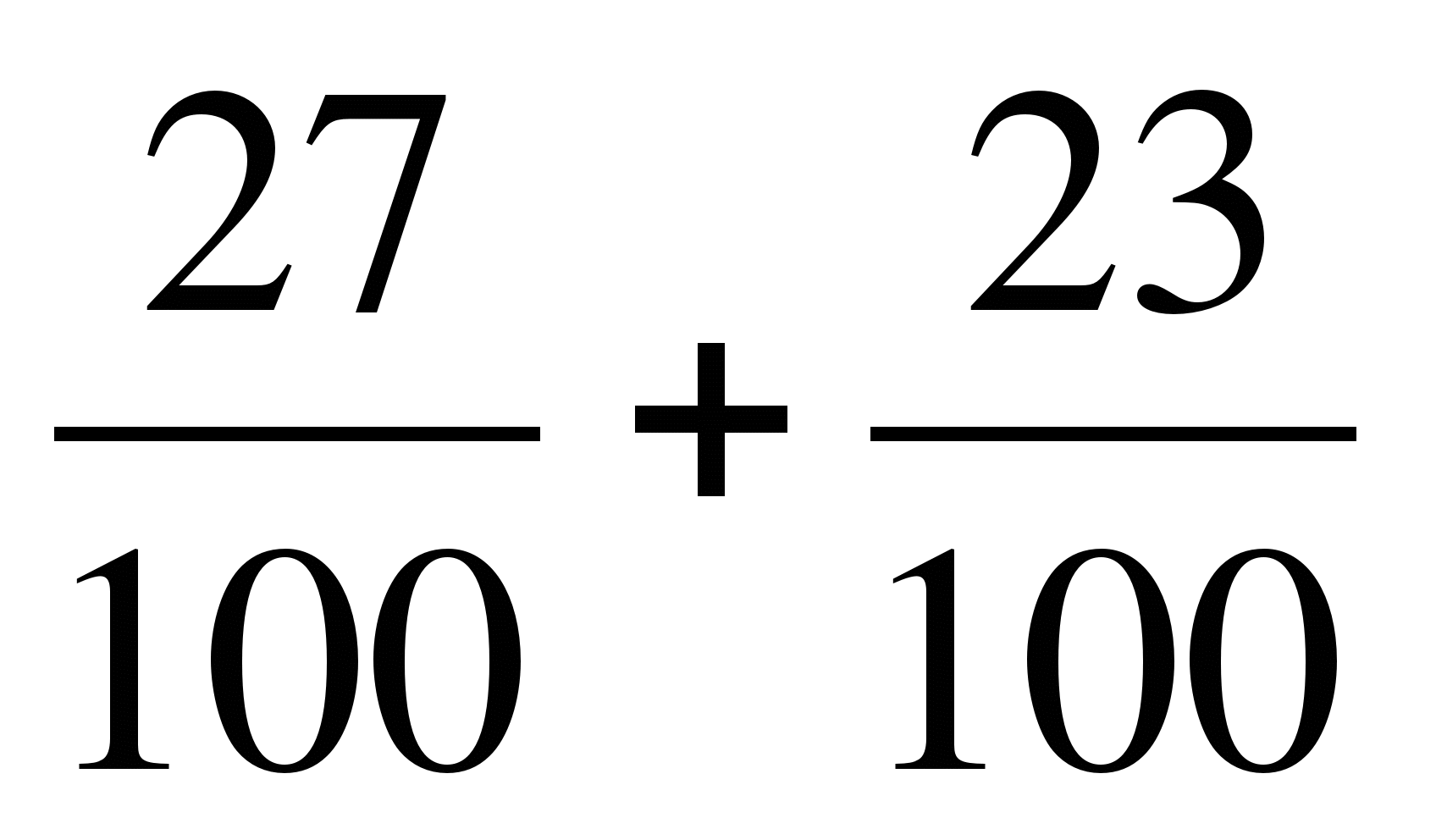 ; б)
; б) 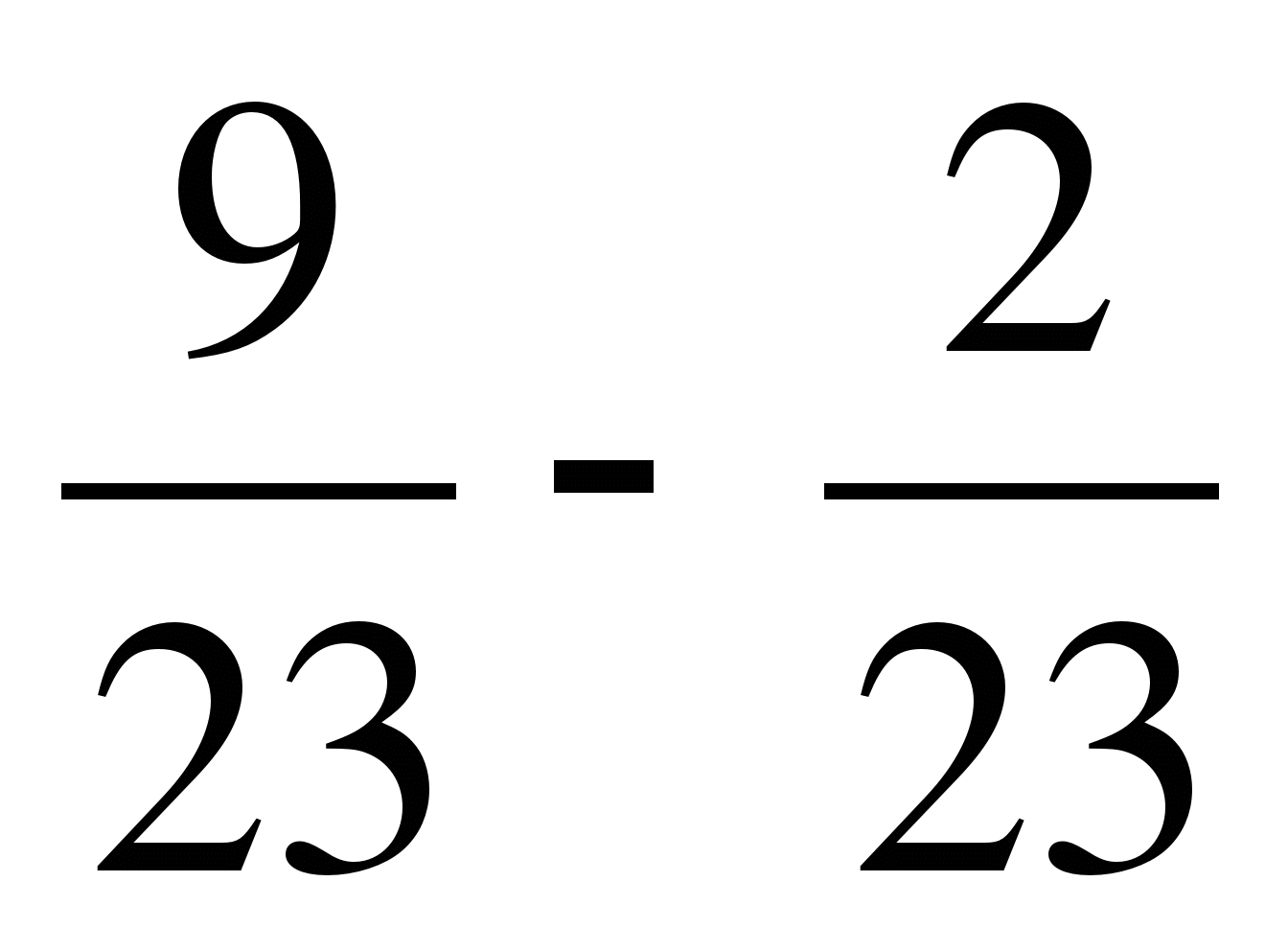 ; в)
; в) 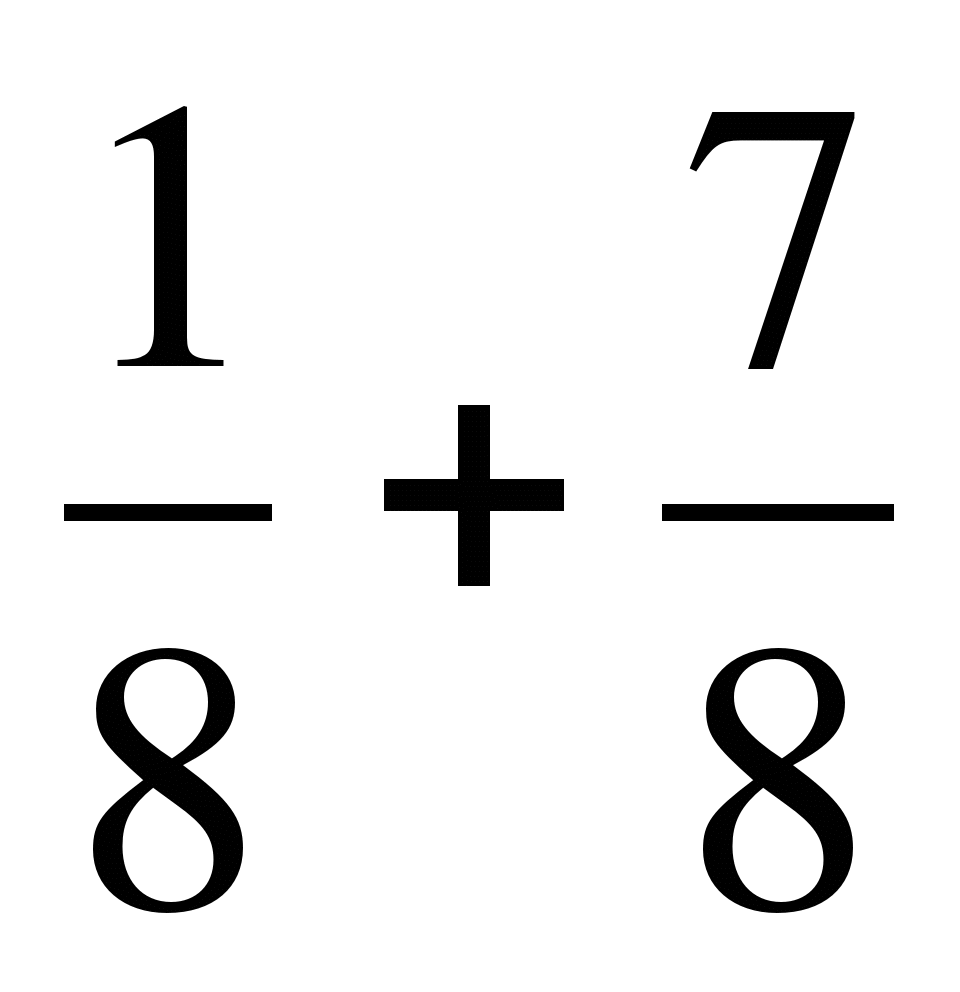
г) 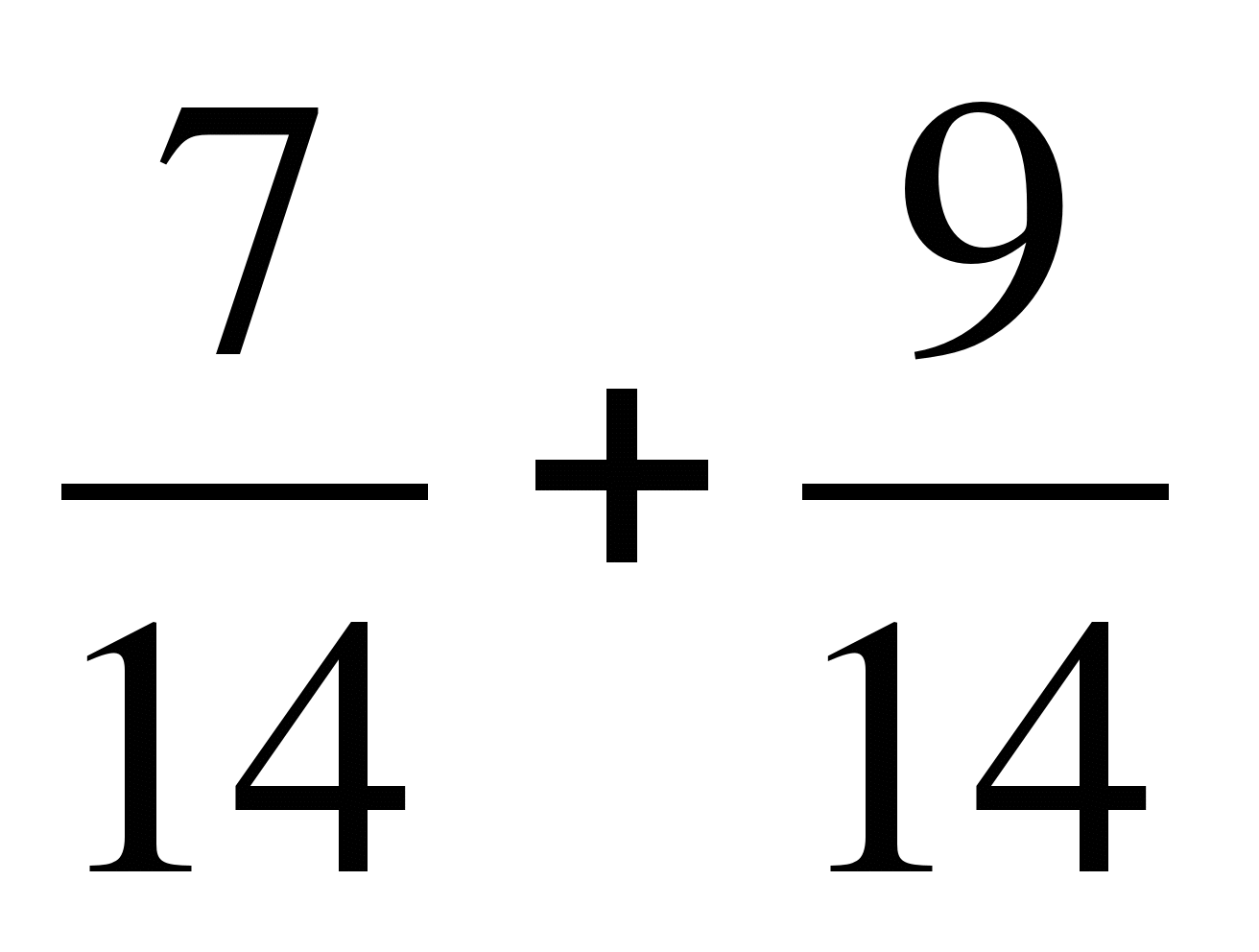 ; д)
; д) 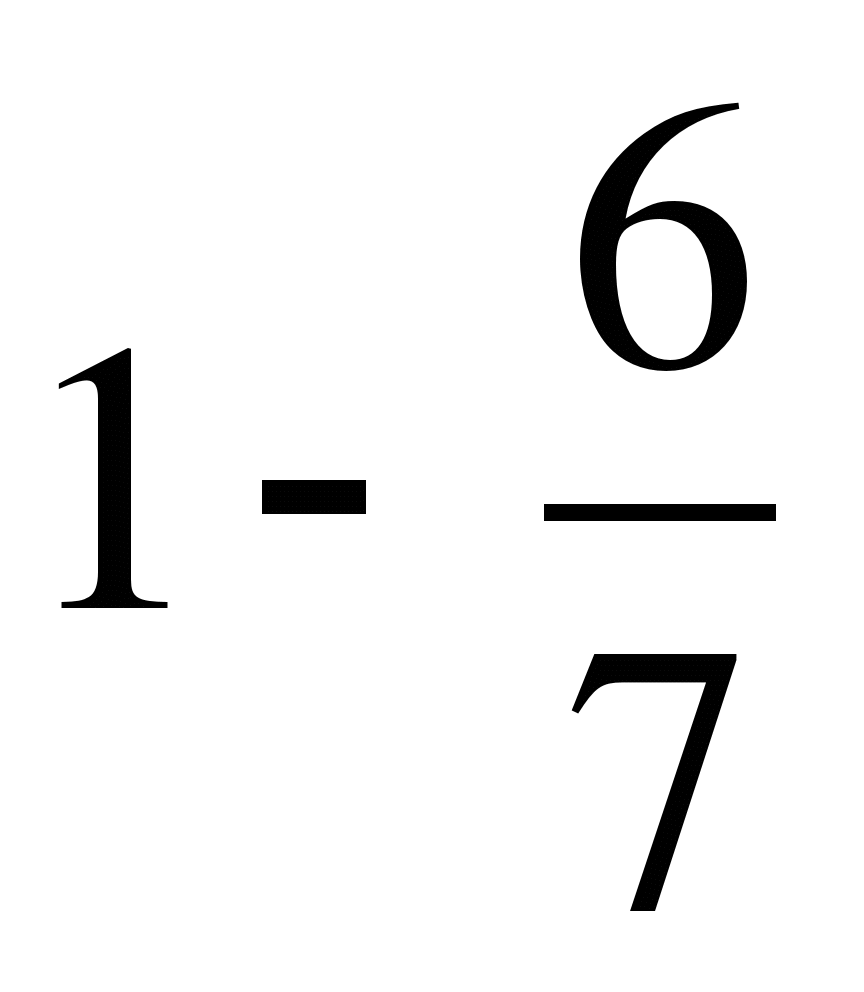 ..
..
2. Вычислите: 
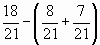 .
.
3в
1. Выполните сложение:
а) 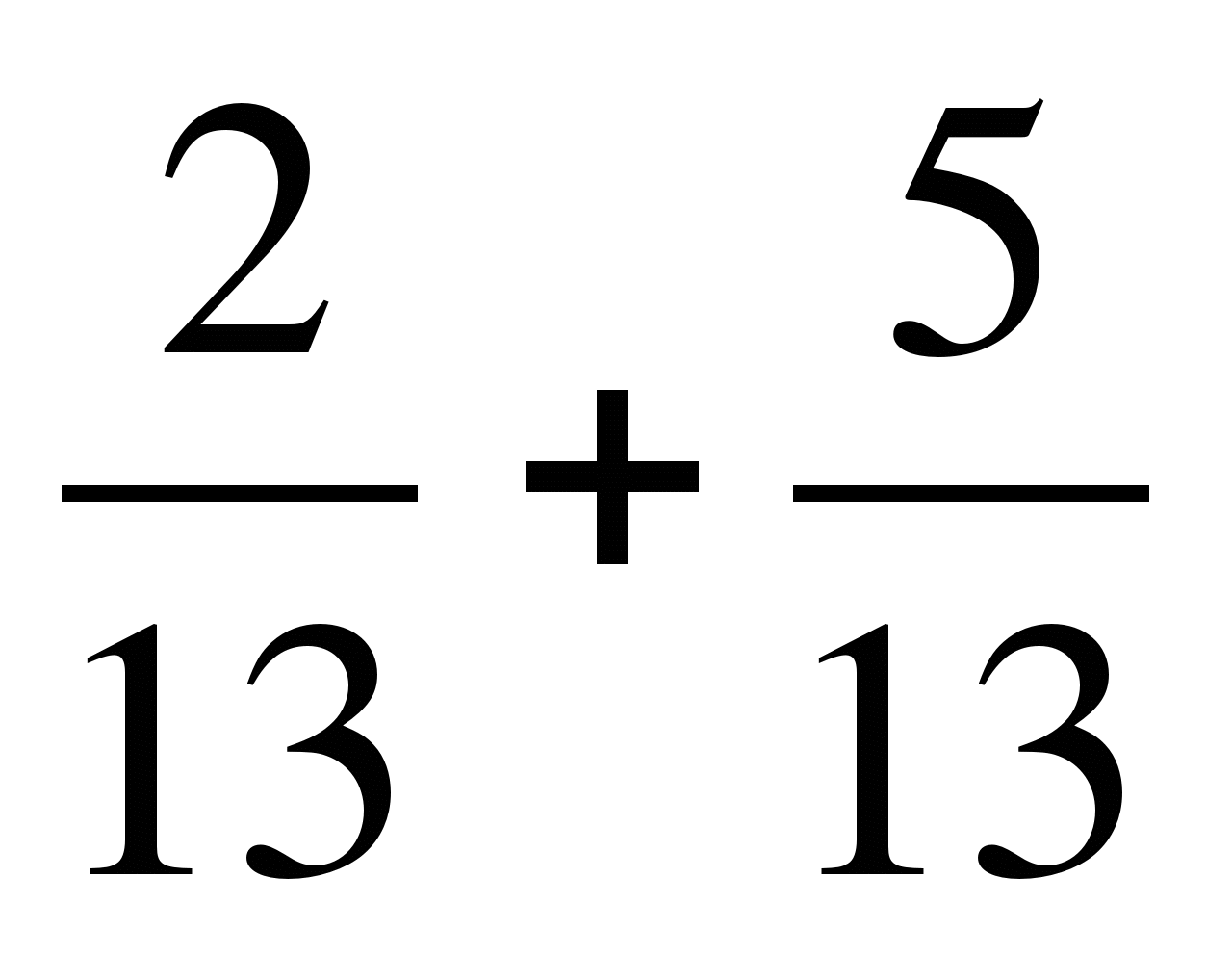 ; б)
; б) 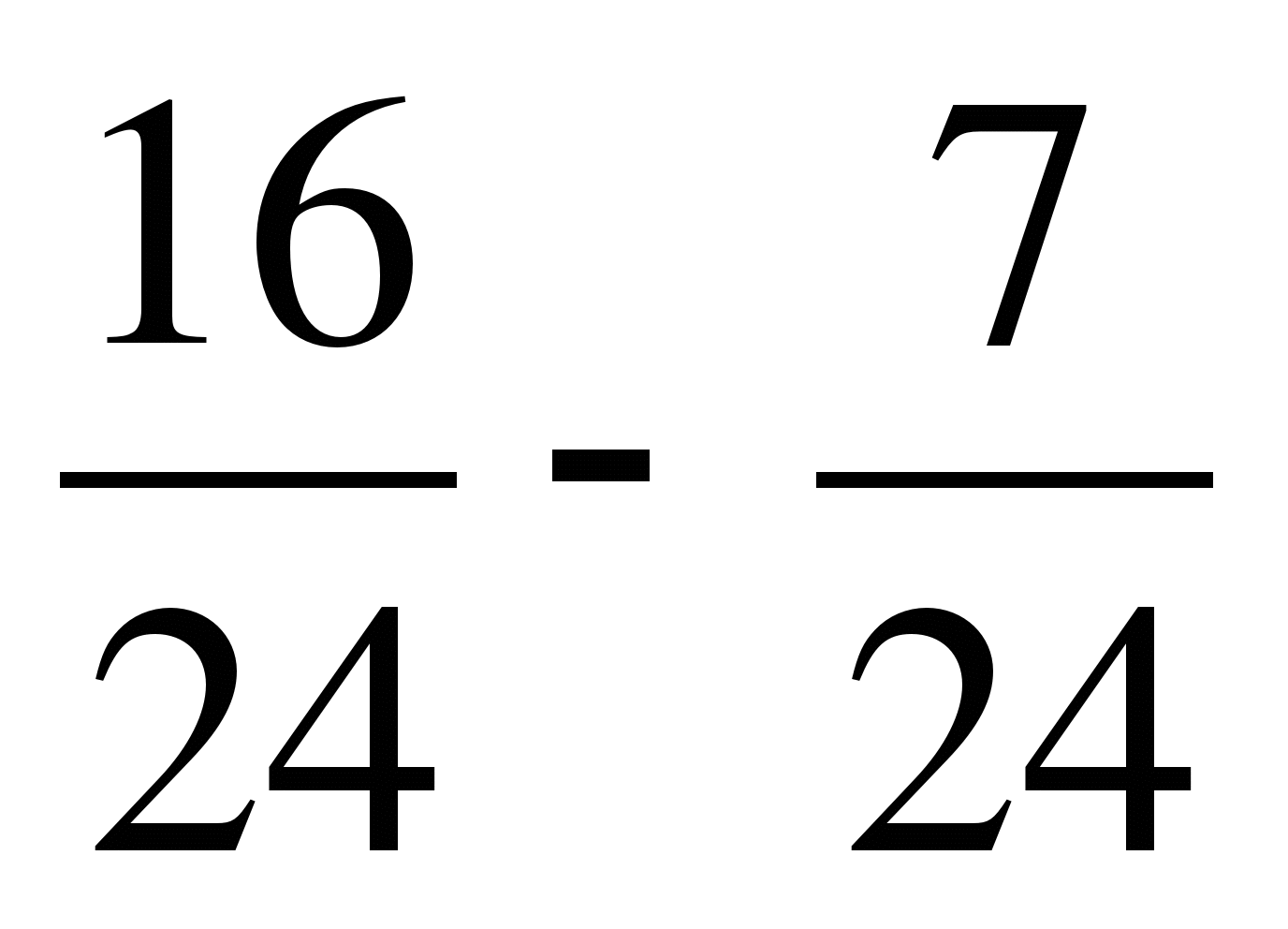 ; в)
; в) 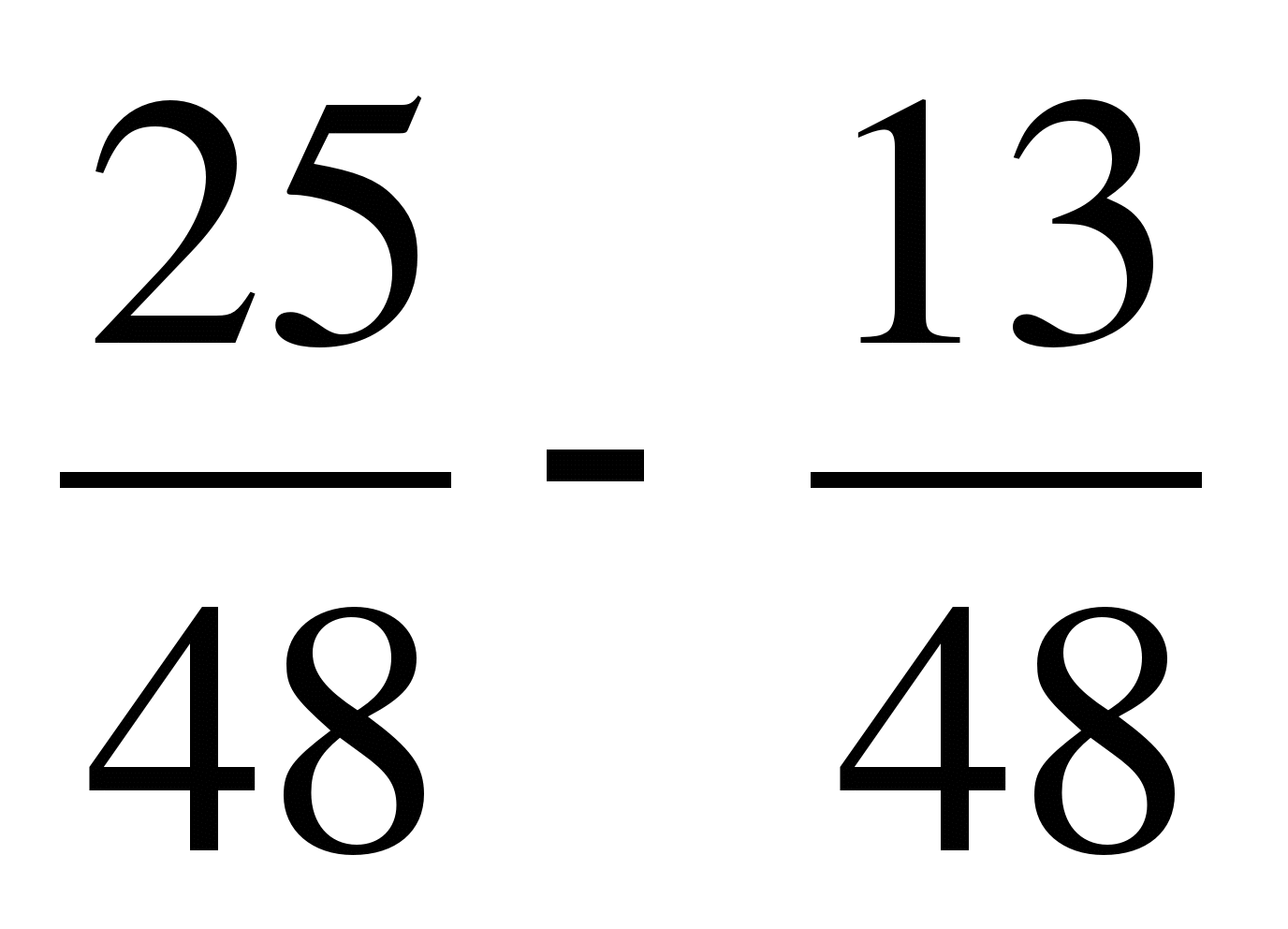
г) 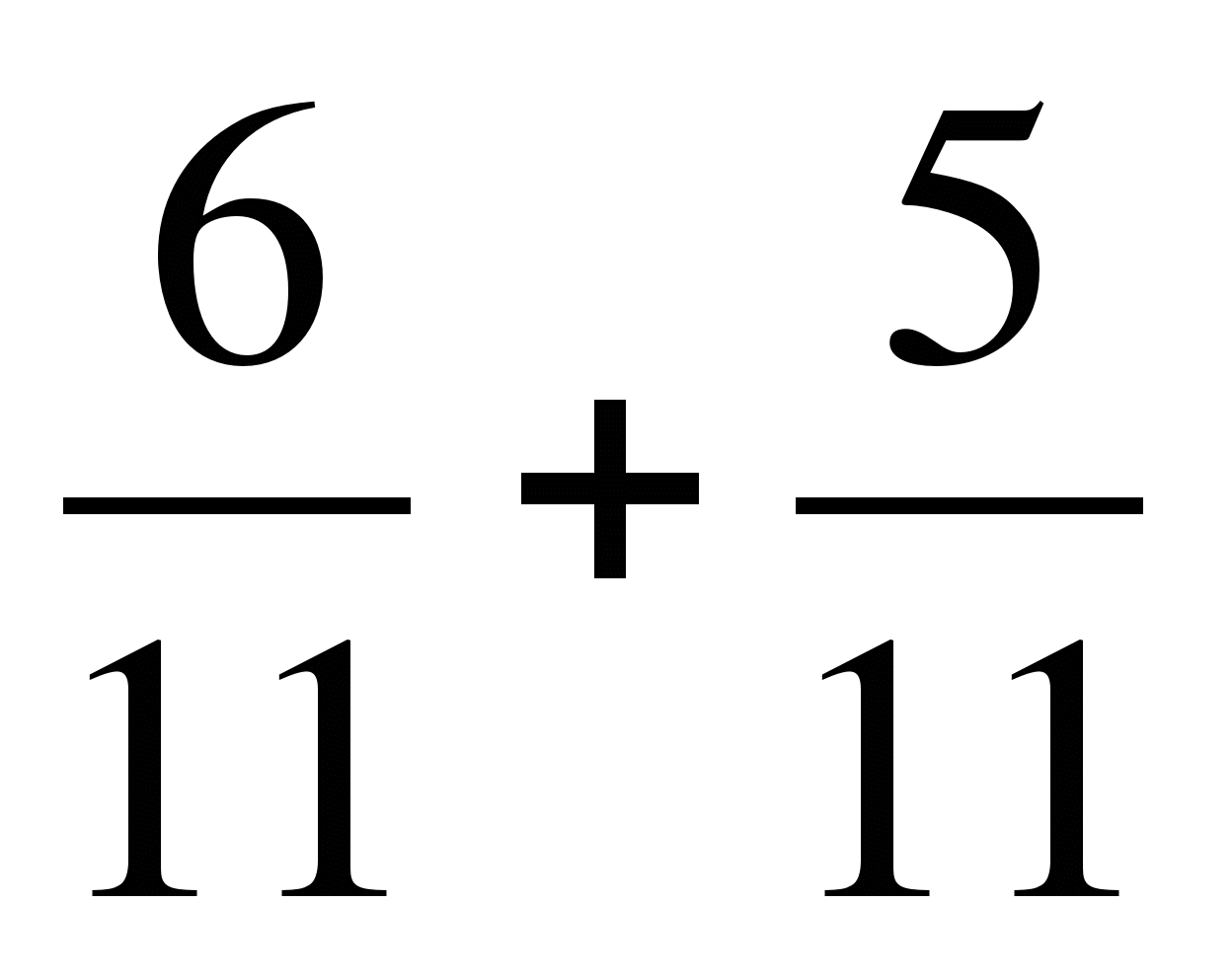 ; д)
; д) 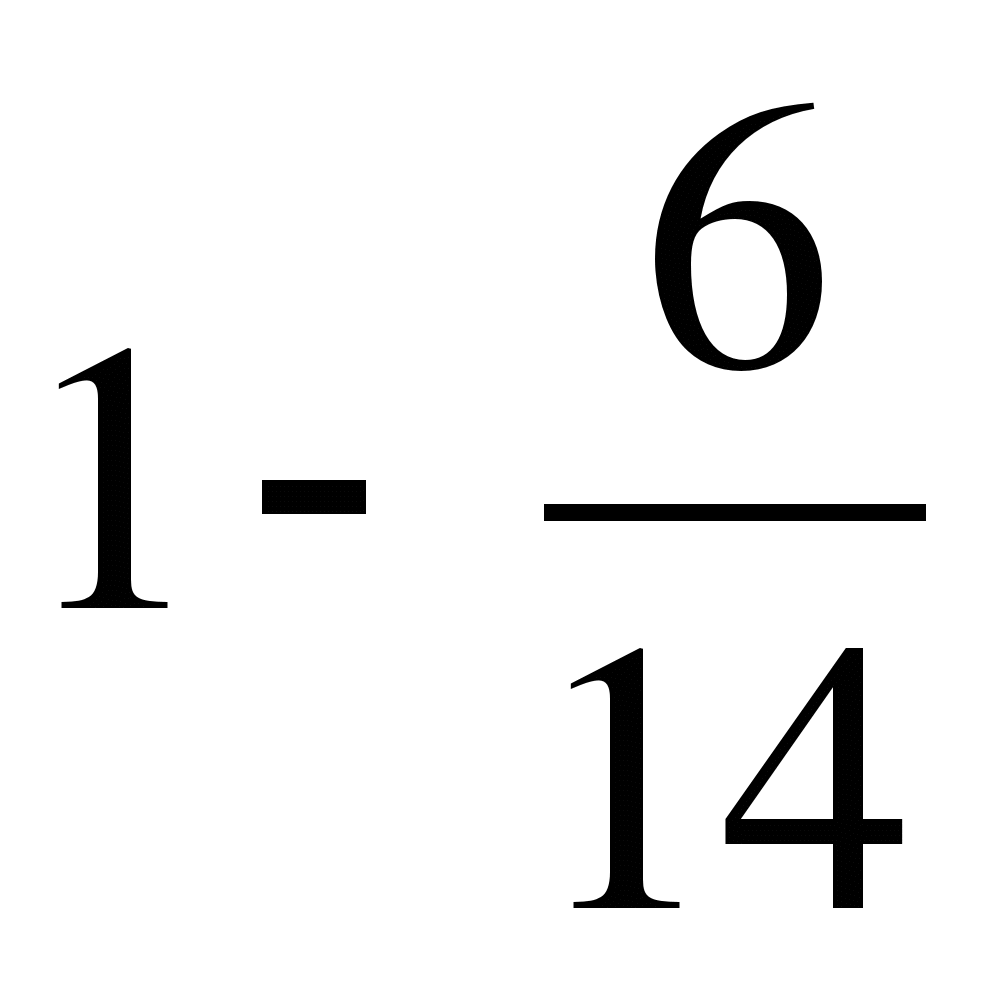 ..
..
2. Вычислите: 
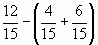 .
.
4в
1. Выполните сложение:
а) 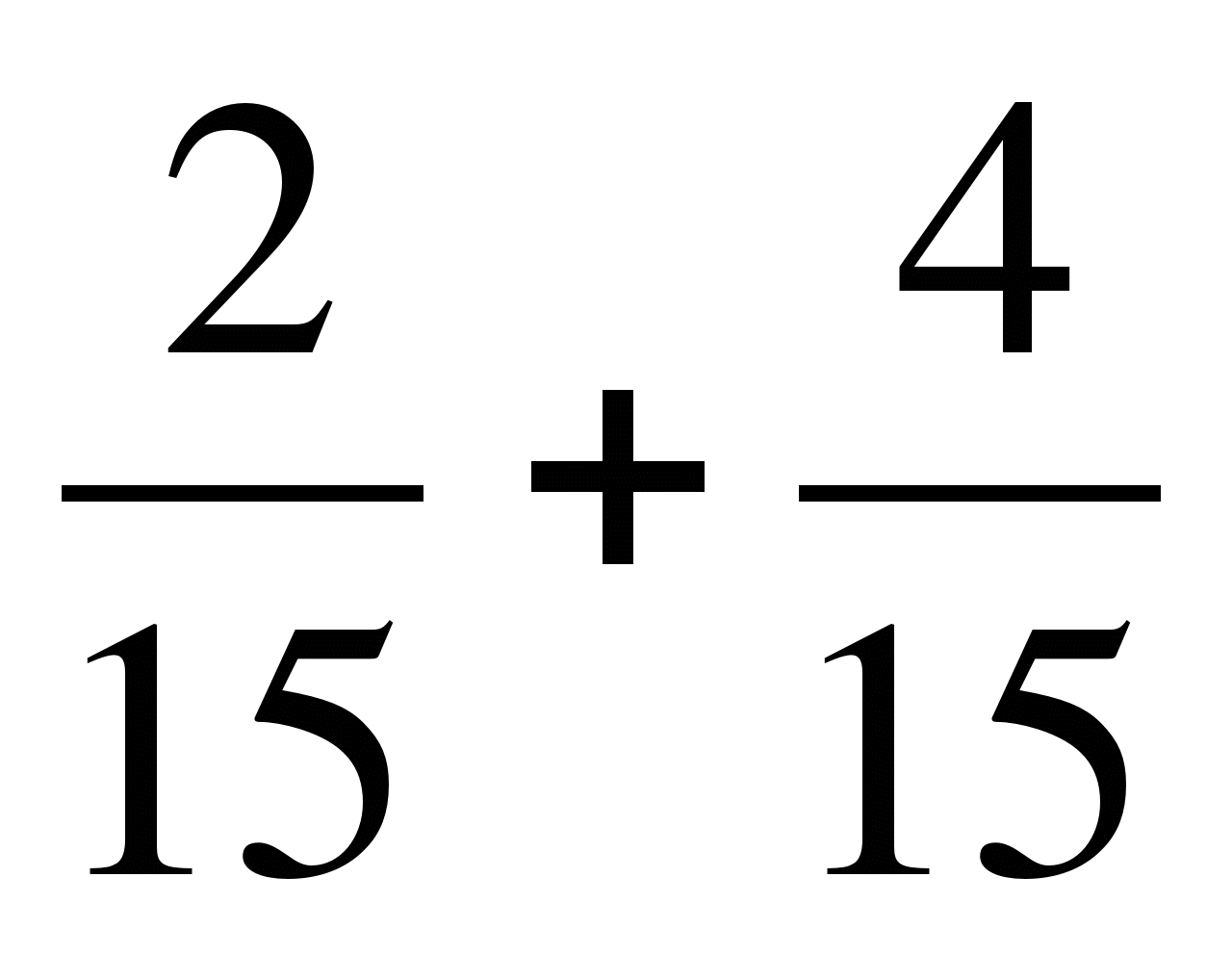 ; б)
; б) 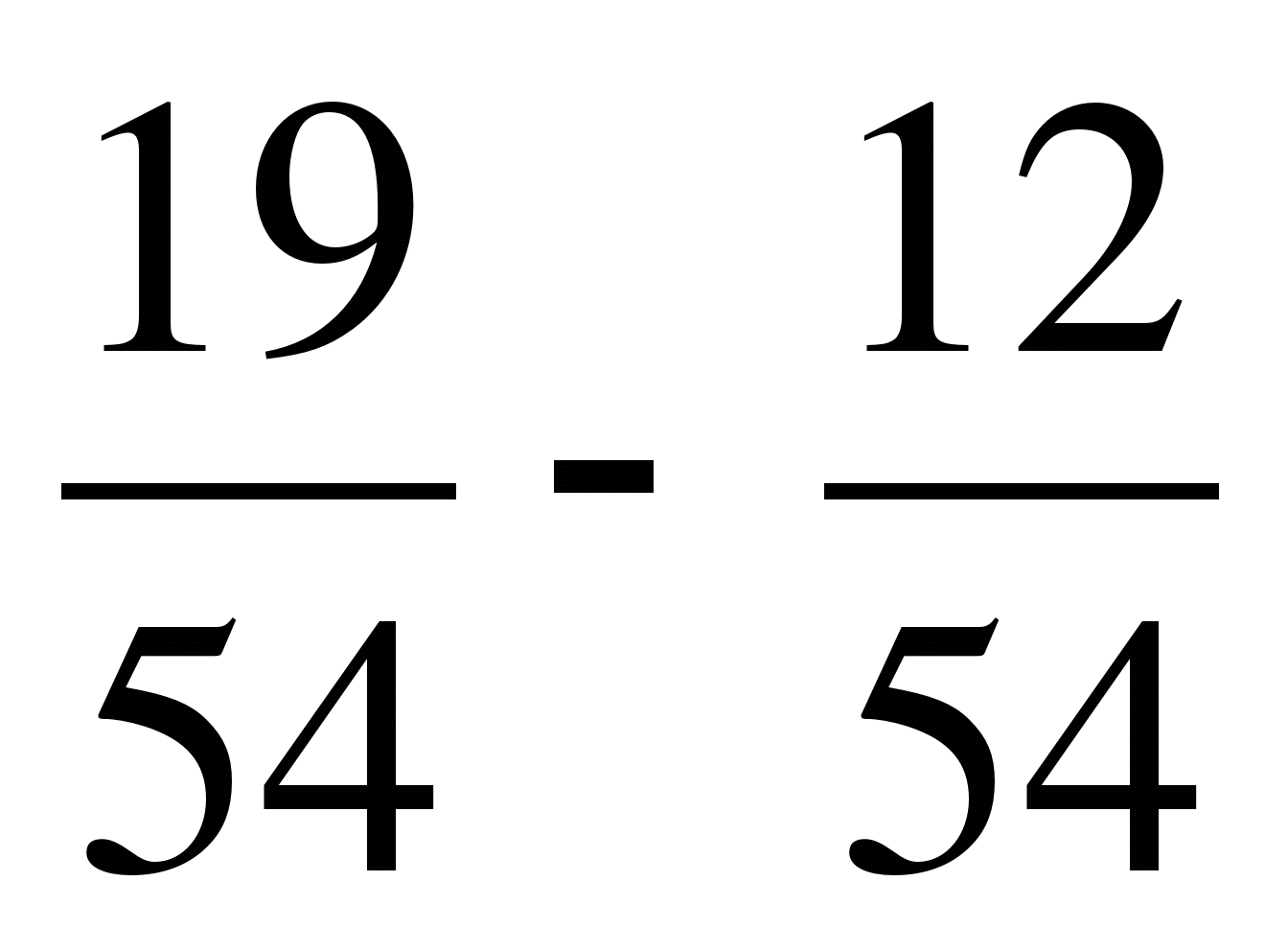 ; в)
; в) 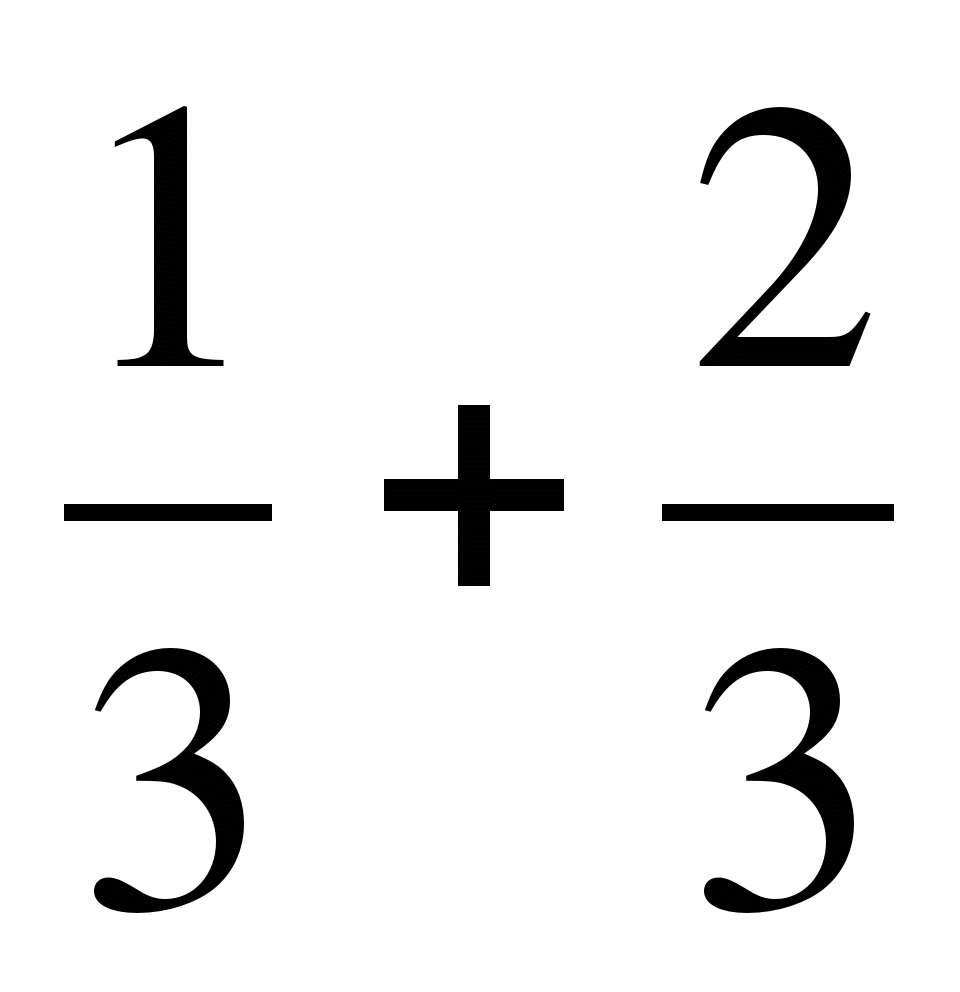 .
.
2. За два дня отремонтировано 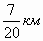
дороги. За 1-ый день отремонтировано
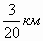 дороги. Сколько километров дороги отремонтировано за 2-й день?
дороги. Сколько километров дороги отремонтировано за 2-й день?
5в
1. Выполните сложение:
а) 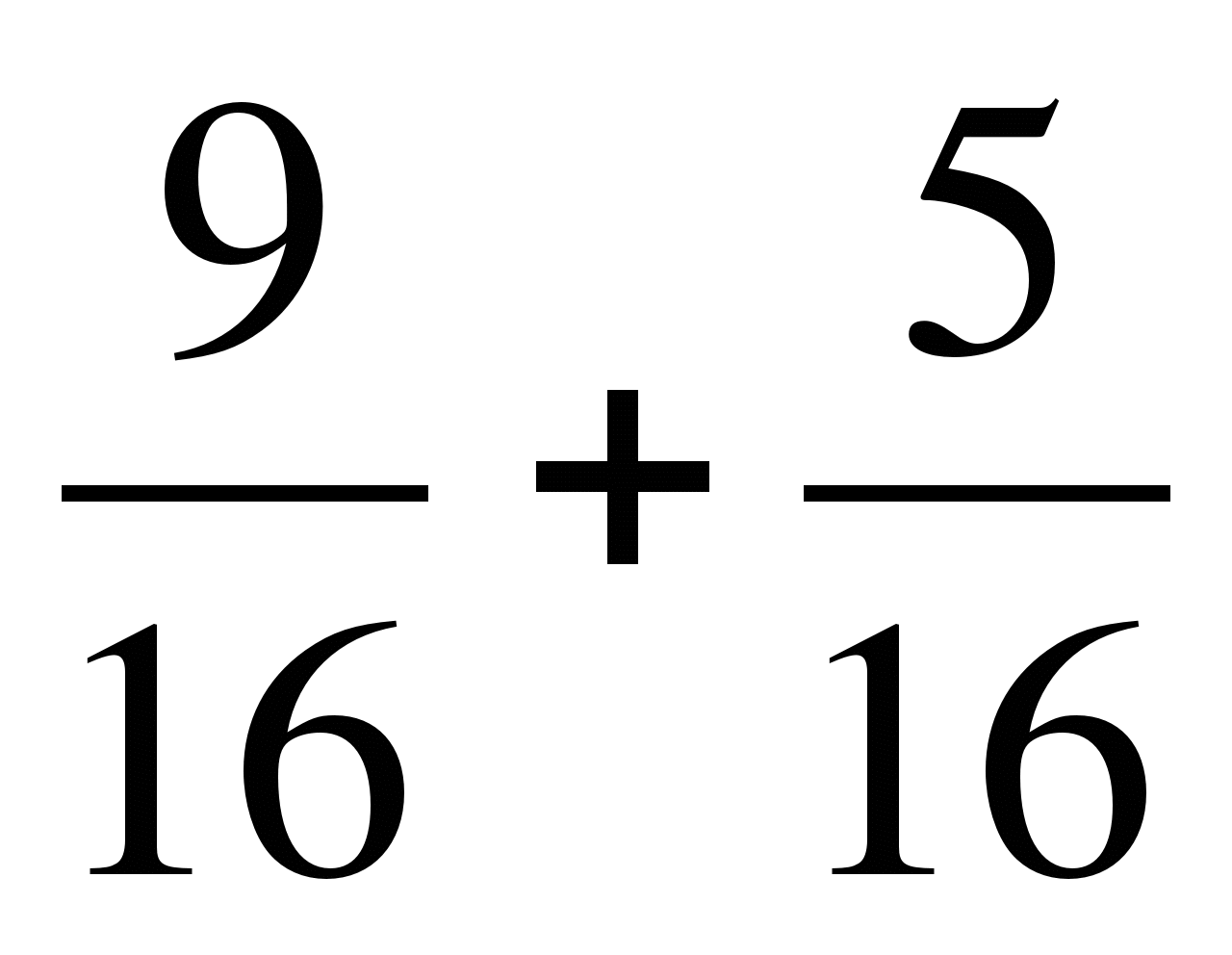 ; б)
; б) 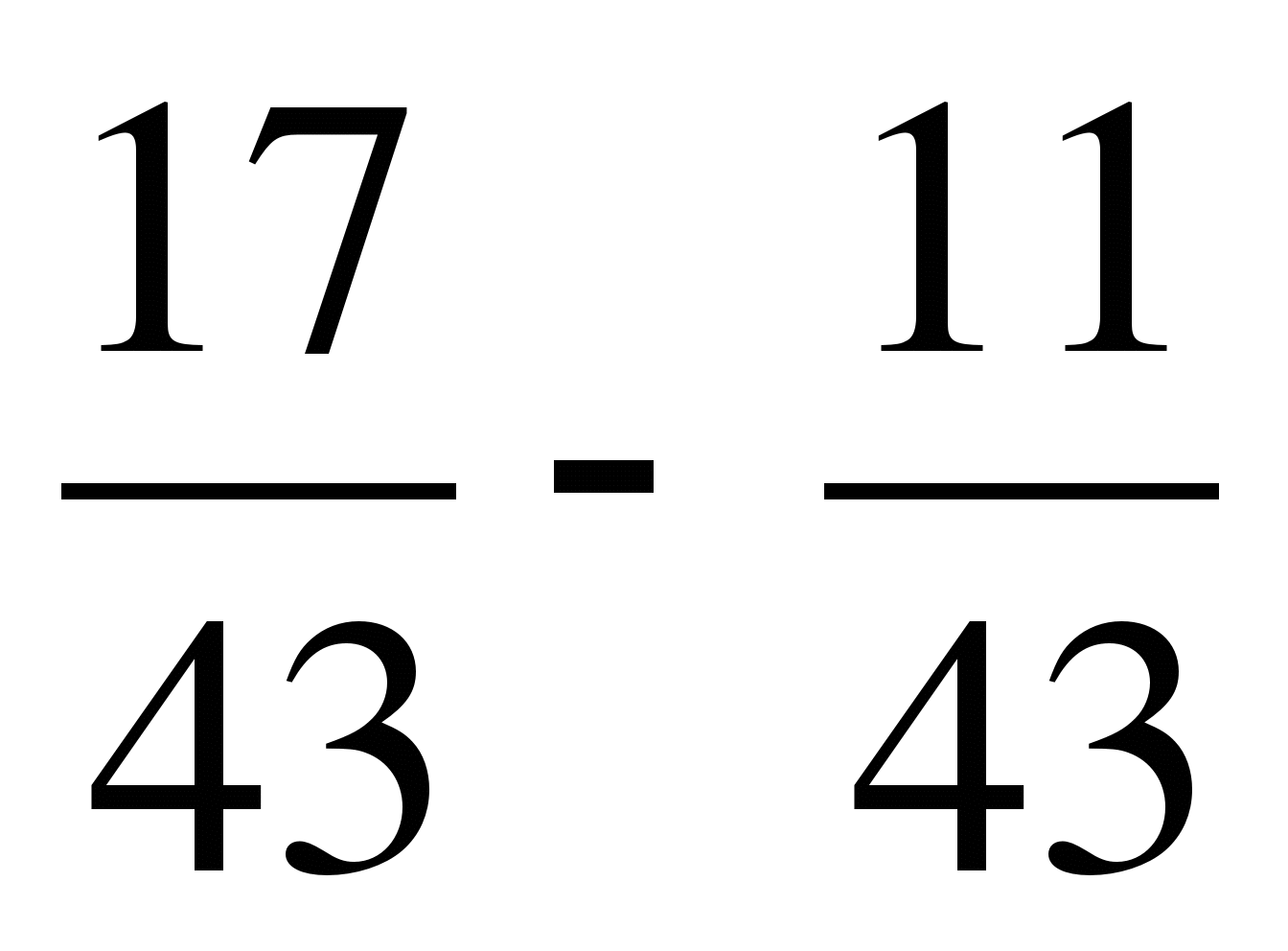 ; в)
; в) 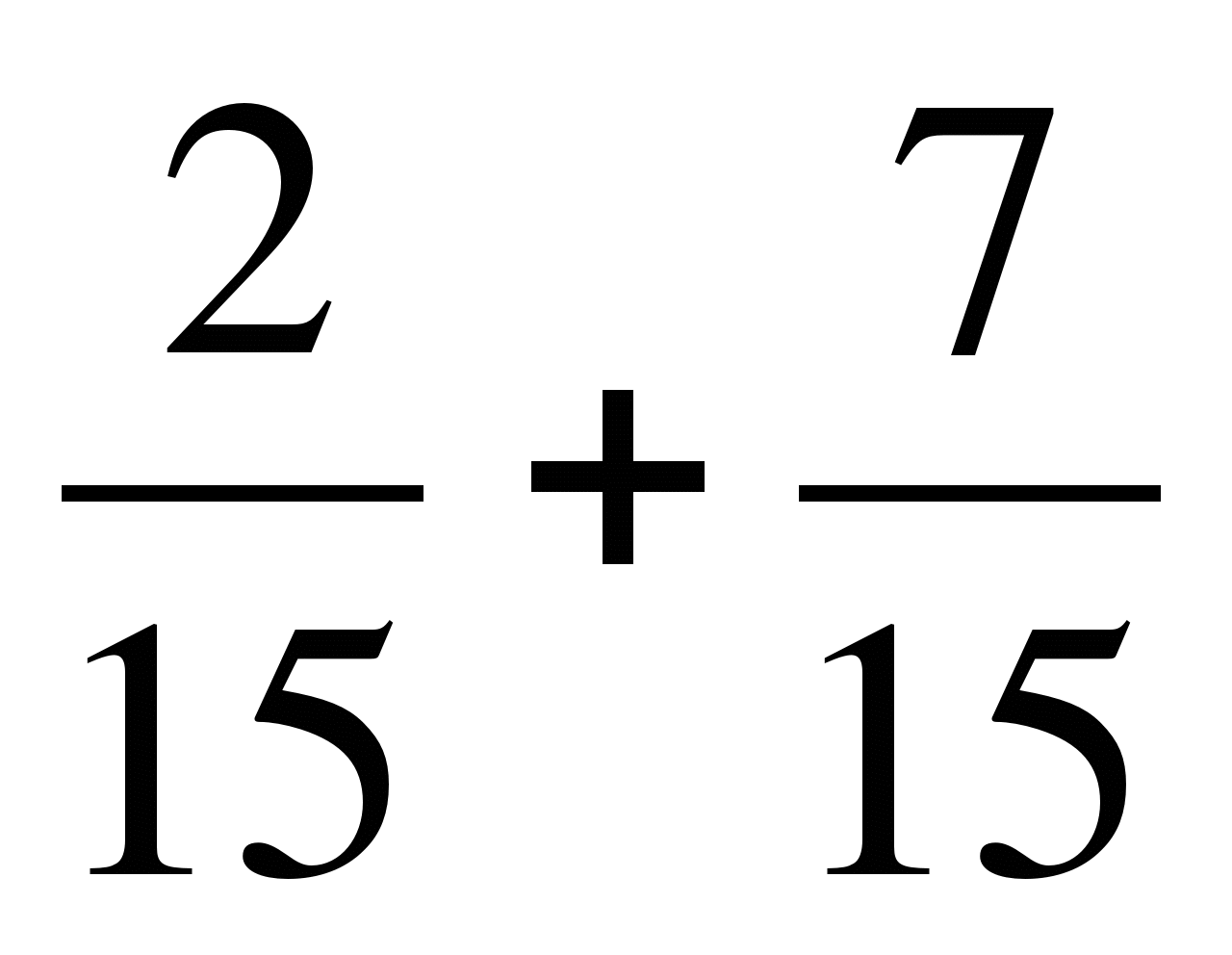 .
.
2. В 1-й день было продано 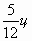 картофеля, а во 2-й день
картофеля, а во 2-й день 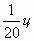 . Сколько центнеров картофеля продано за два дня?
. Сколько центнеров картофеля продано за два дня?
6в
1. Вычислите:
а) 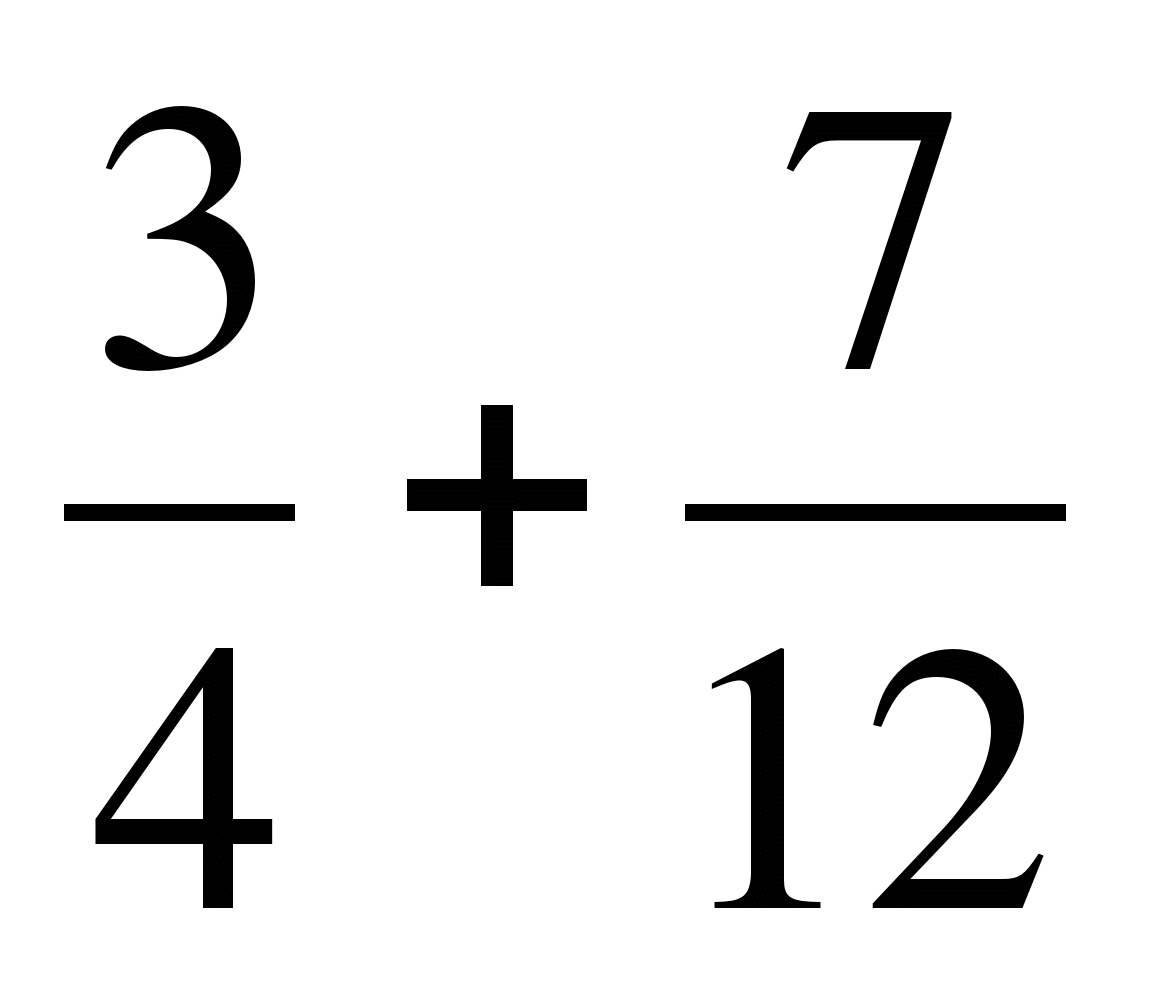 ; б)
; б) 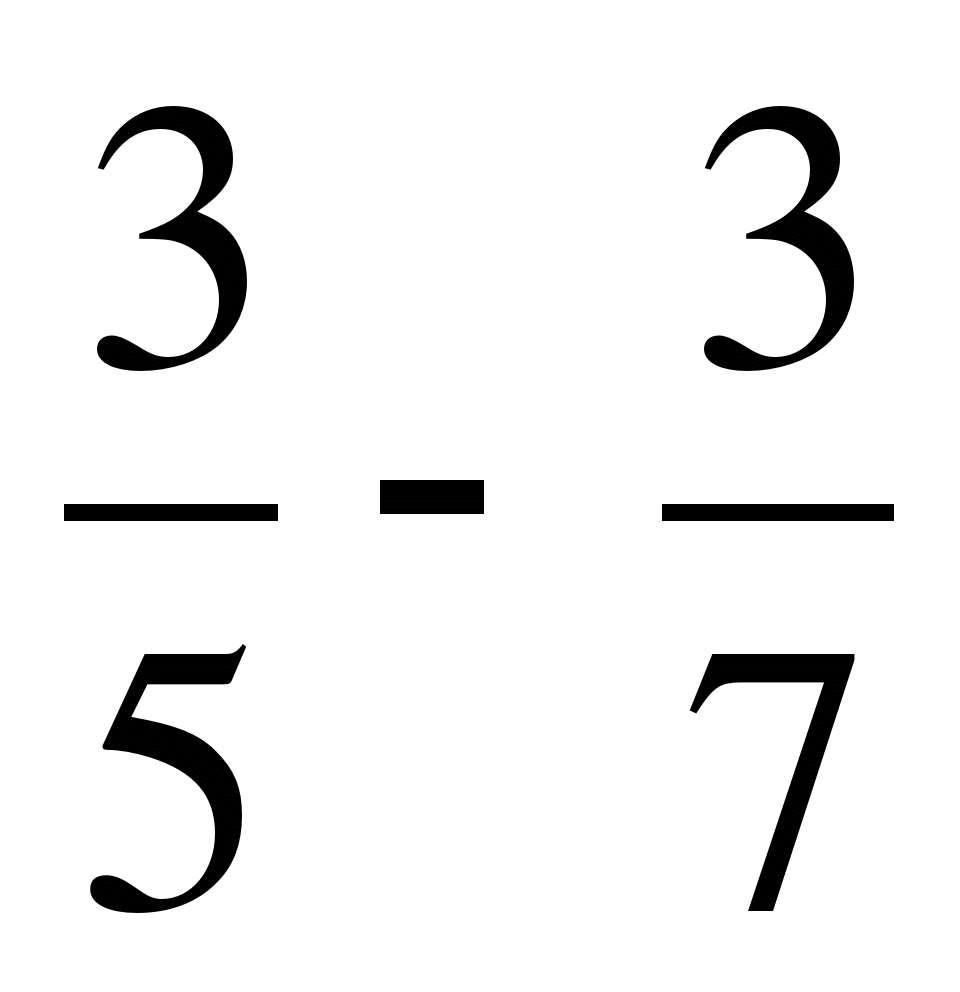 ; в)
; в) 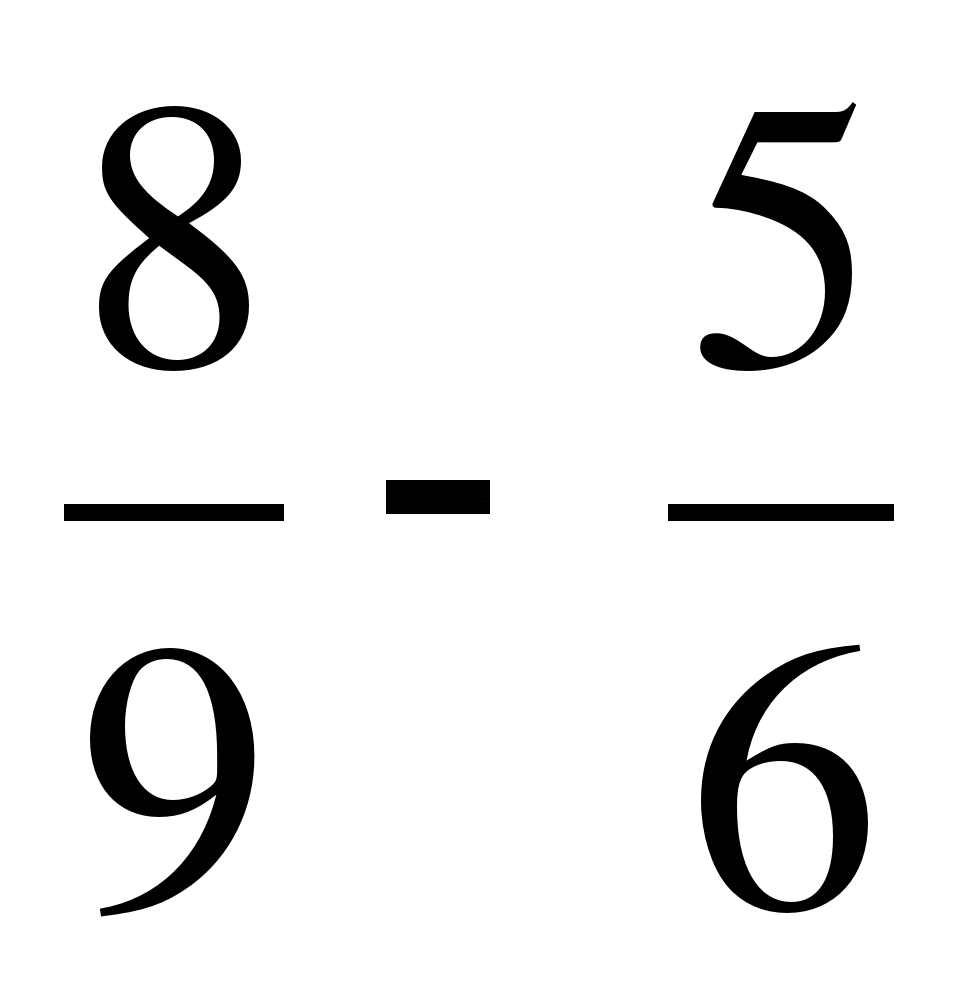 ;
;
г) 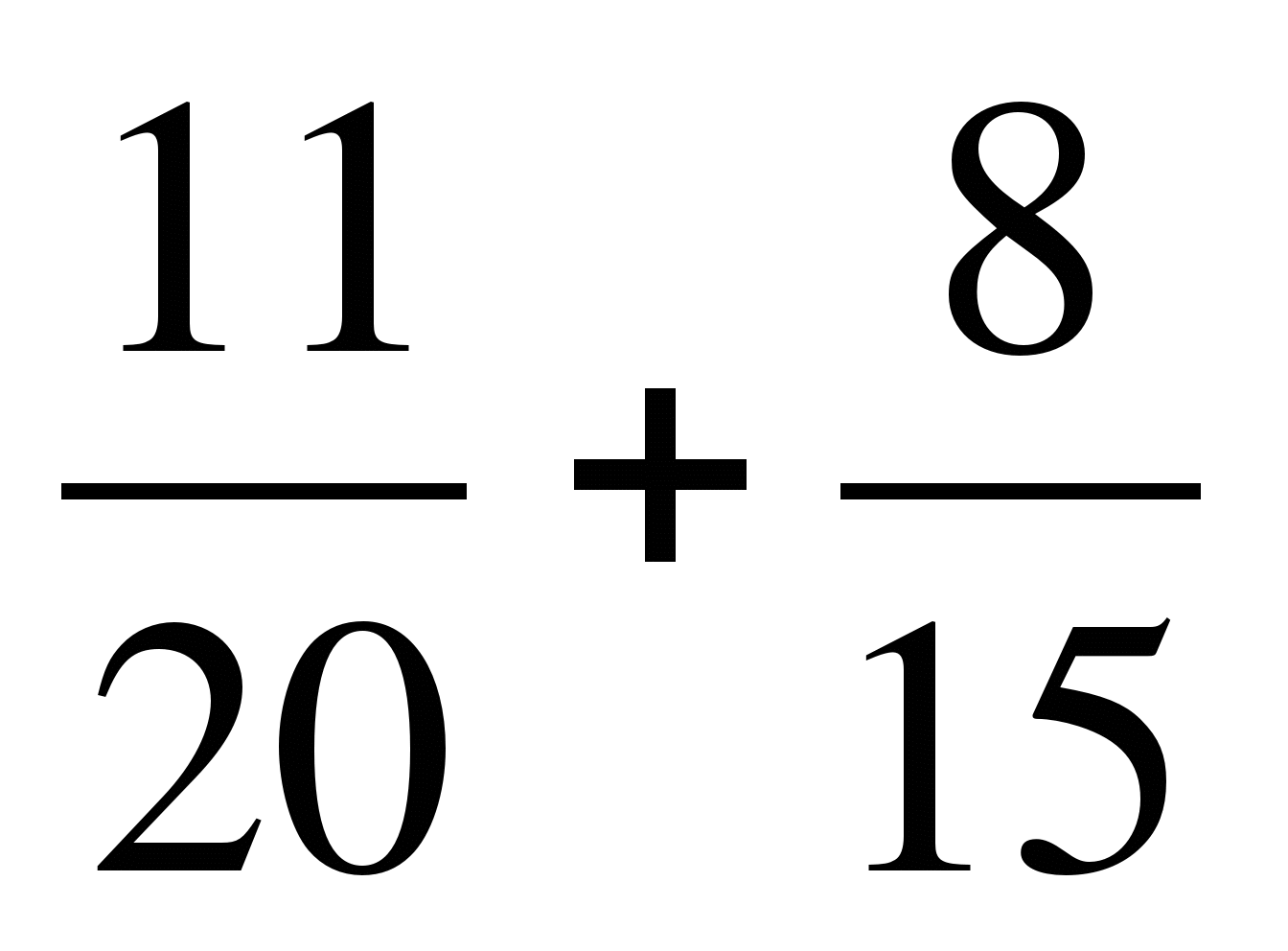 ; д)
; д) 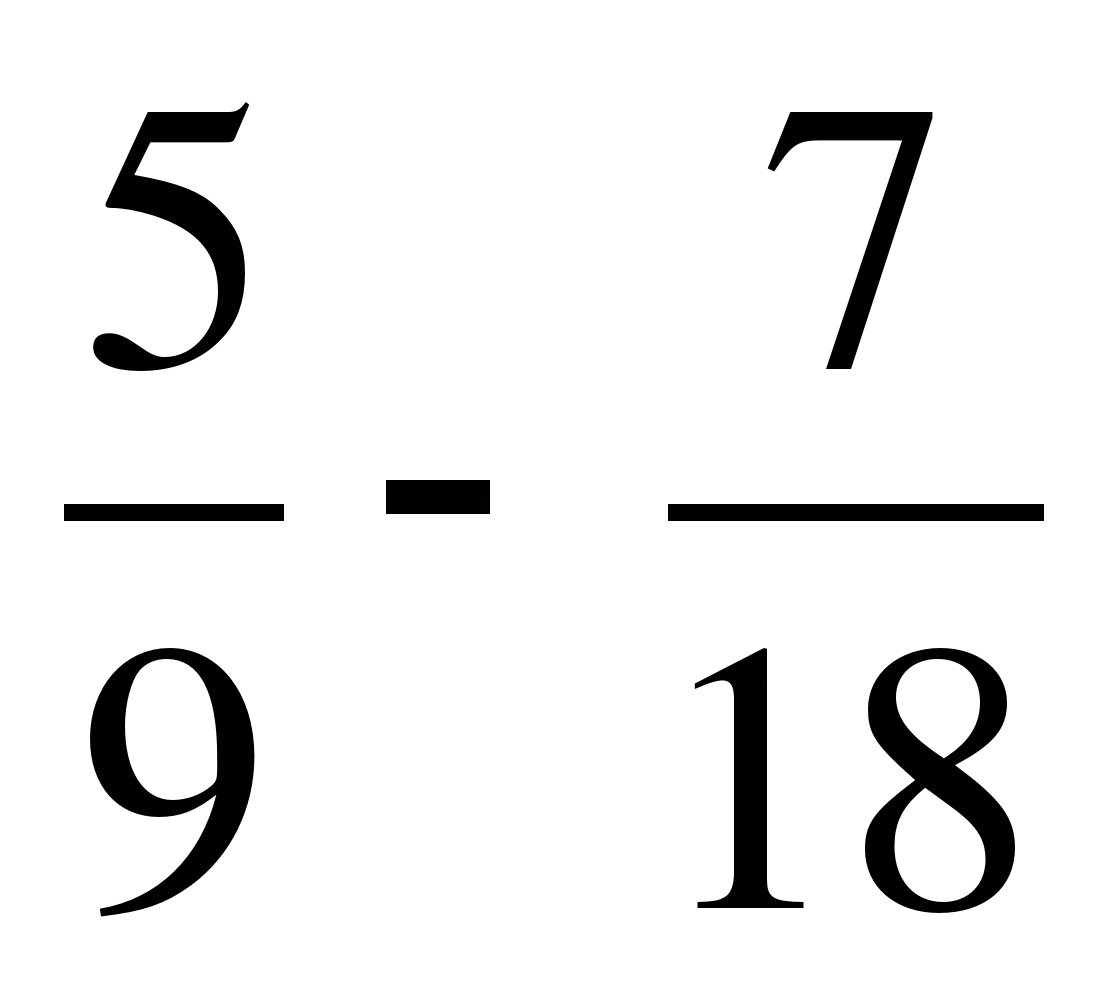
2. Вычислите:
а) 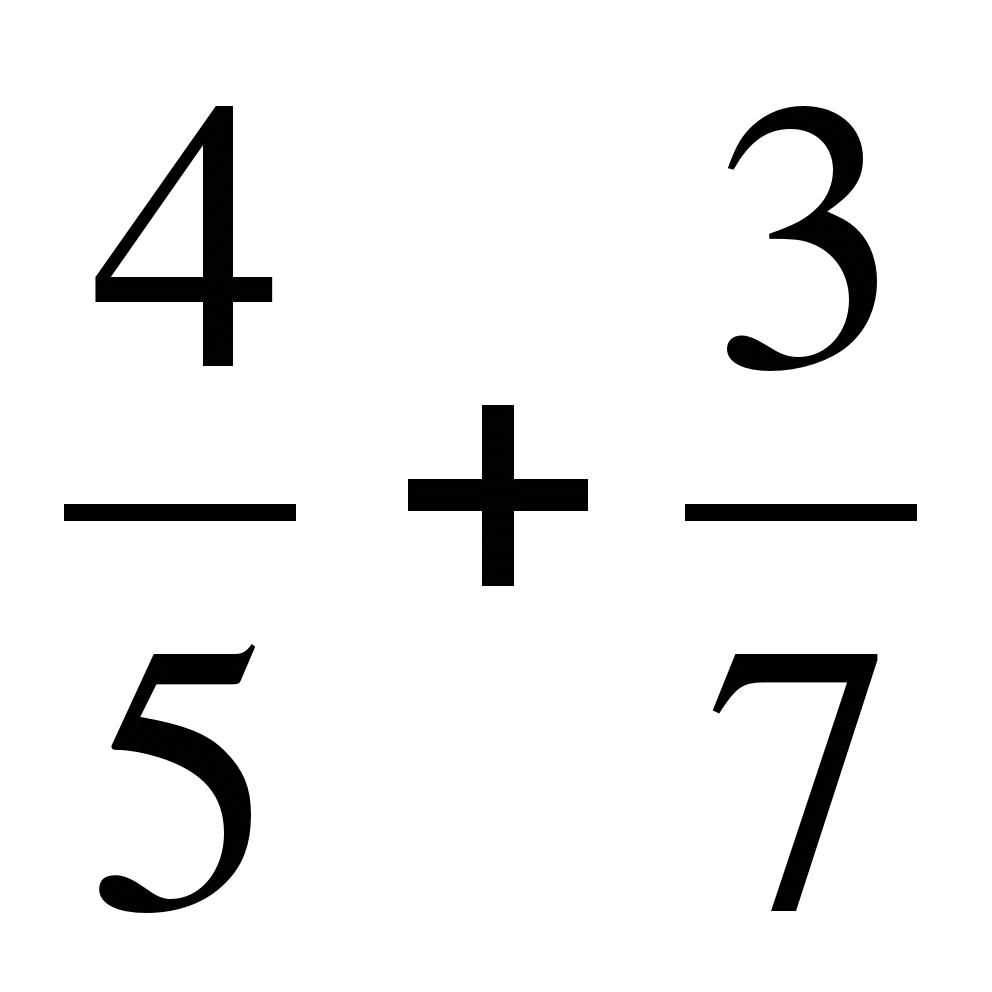 ; б)
; б) 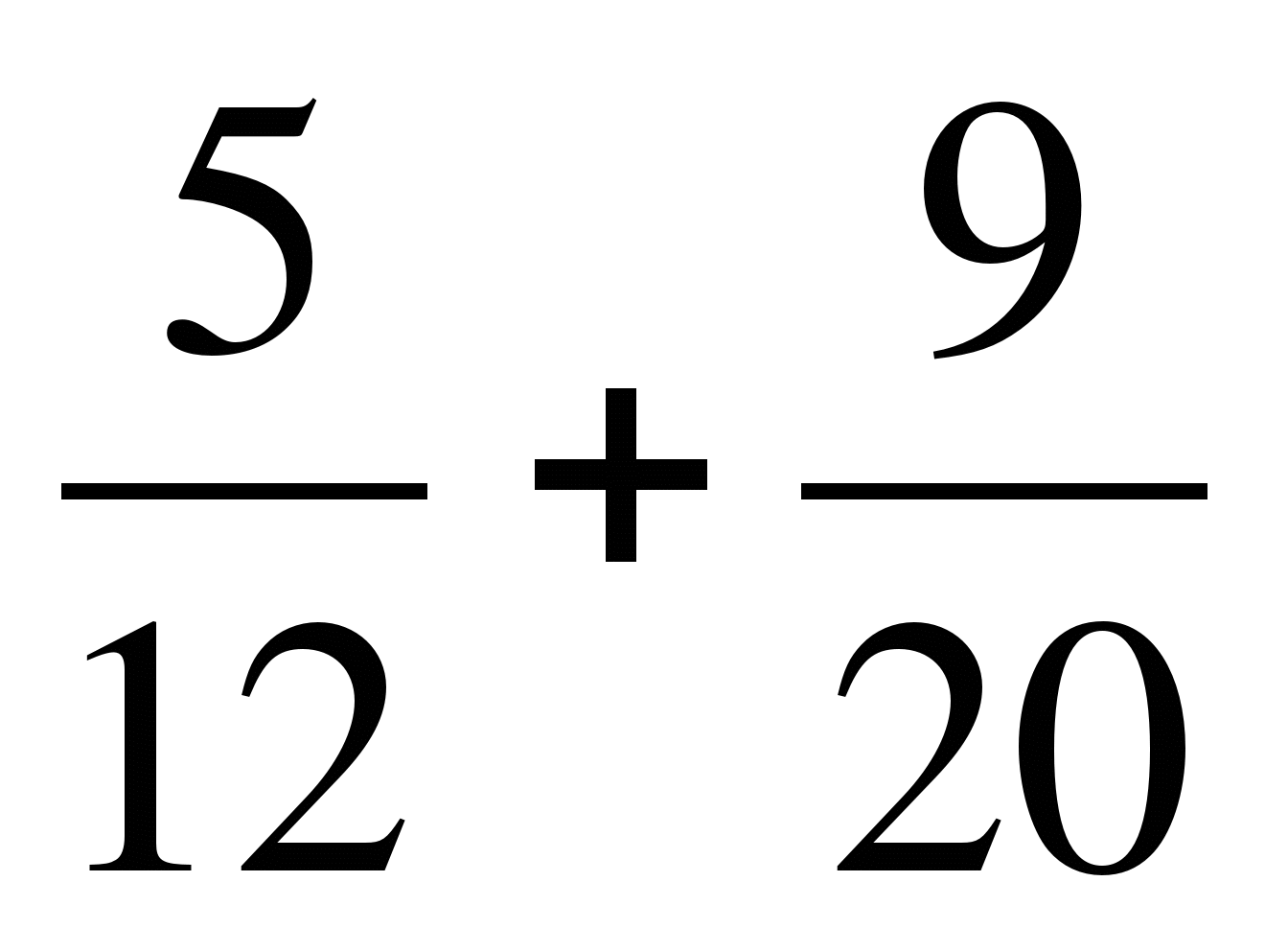 ; в)
; в) 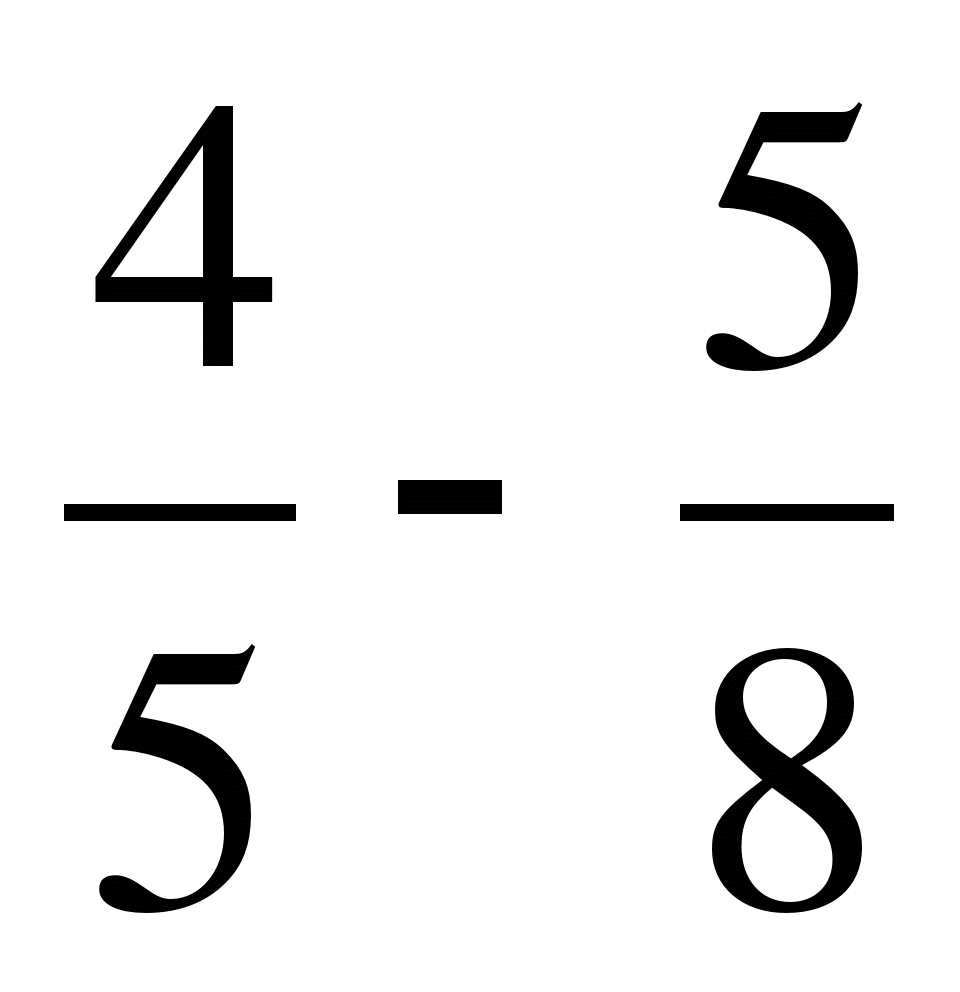 ;
;
г) 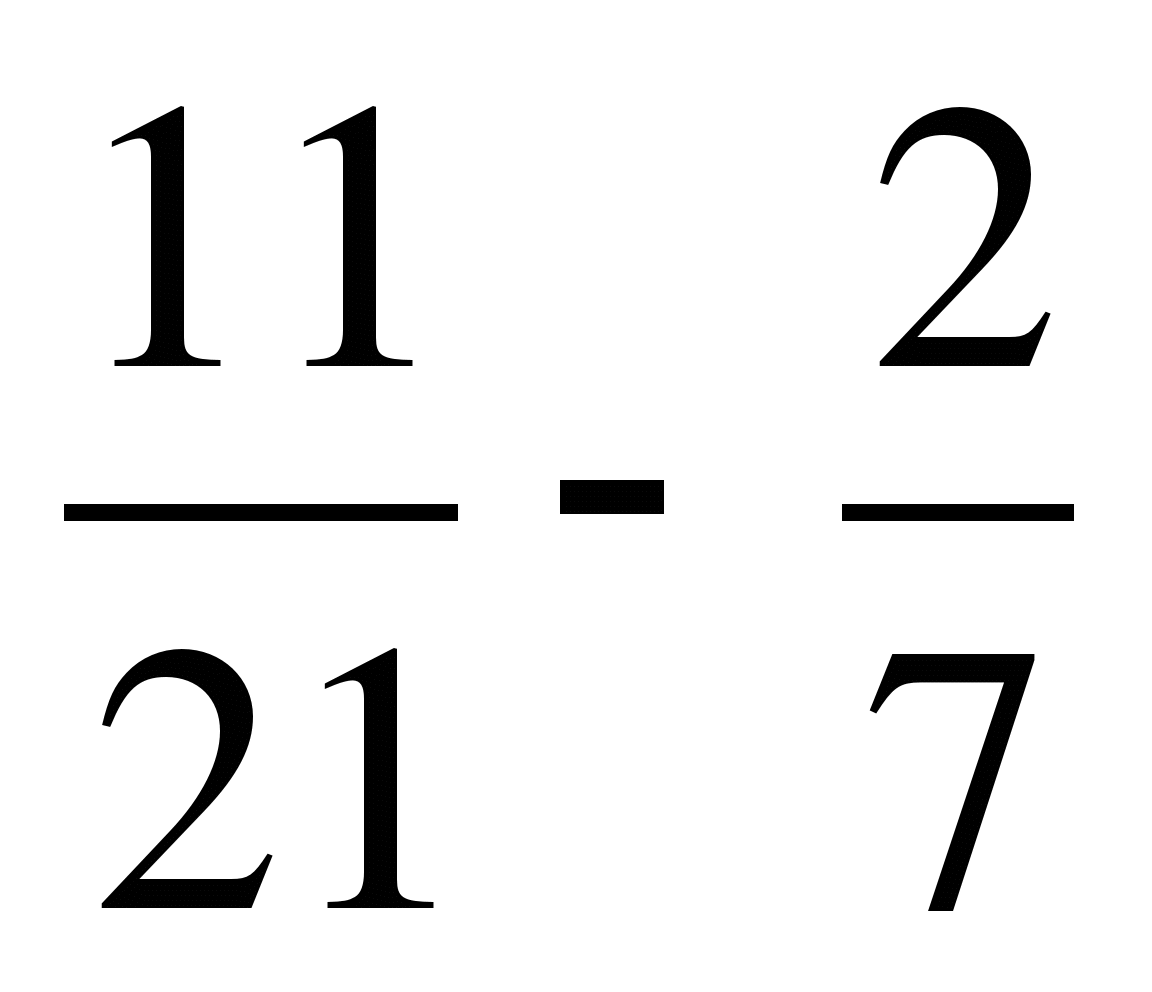 ; д)
; д) 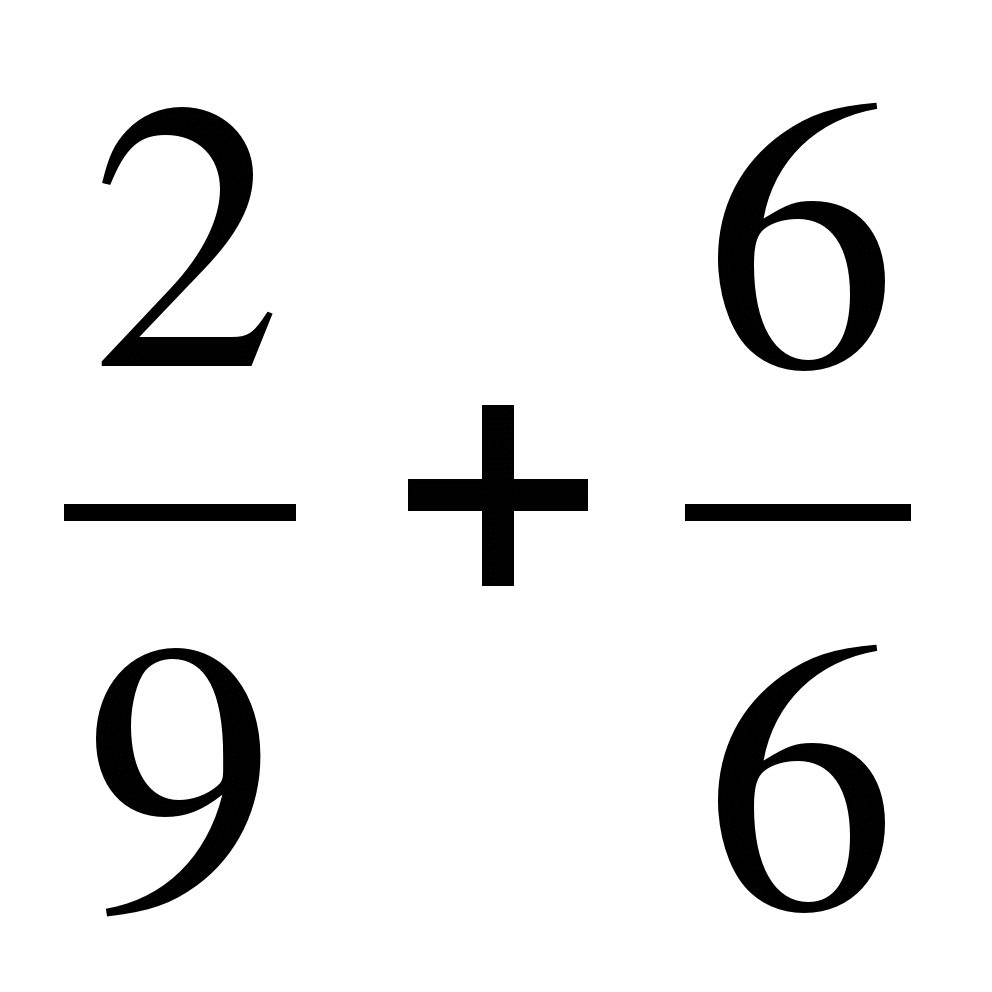
3. Вычислите:
а)  ; б)
; б)  ; в)
; в) 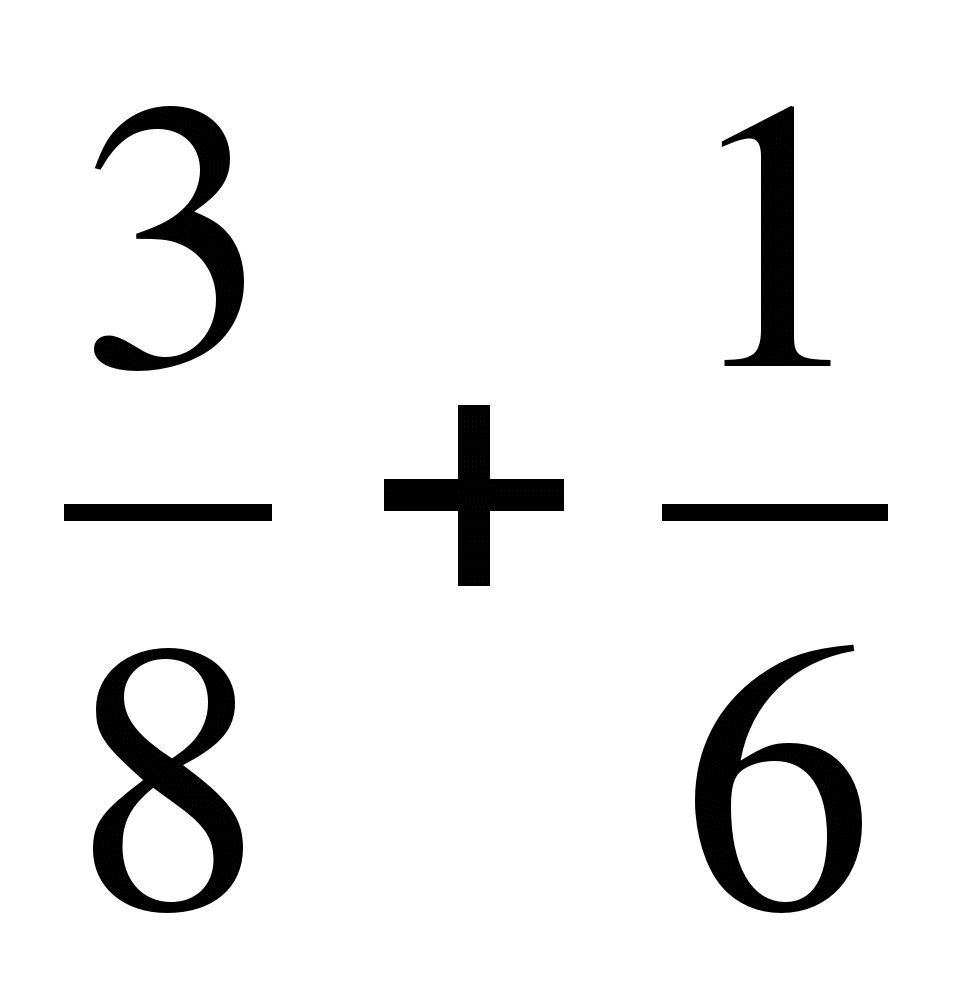 ;
;
г) 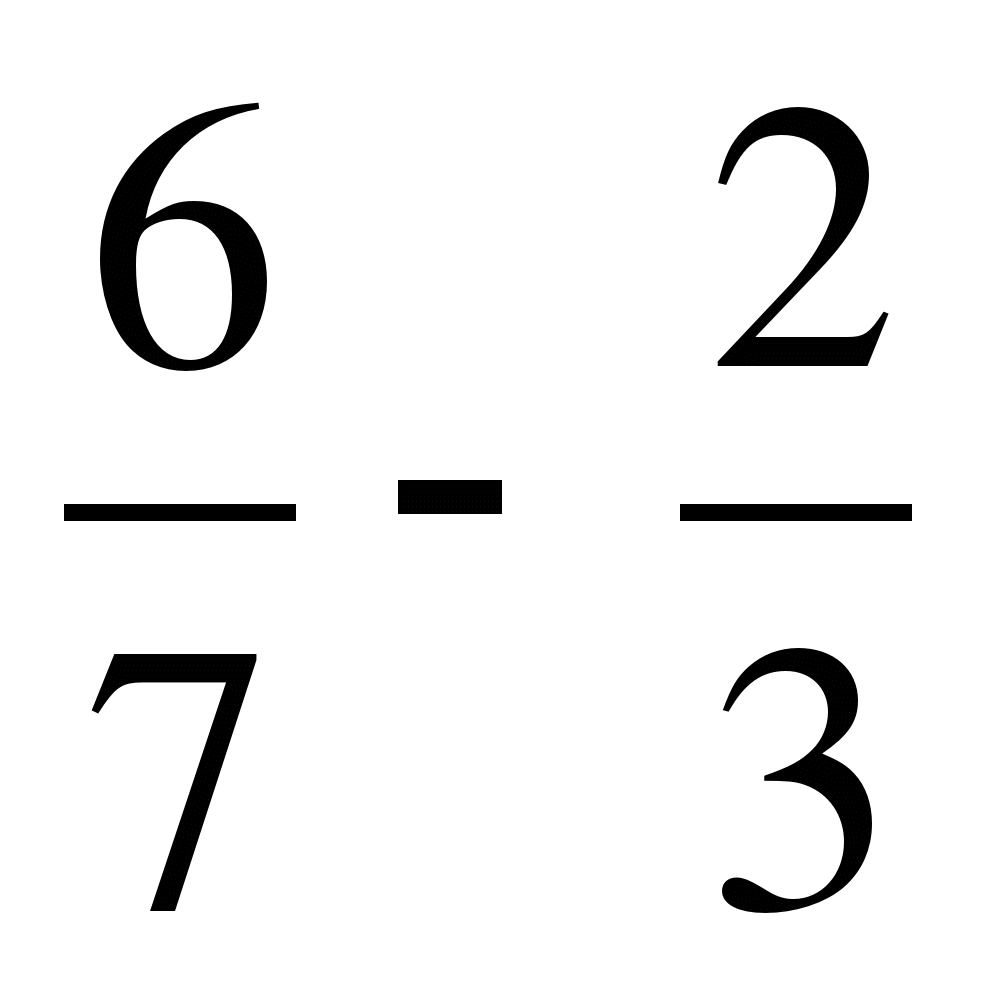 ; д)
; д) 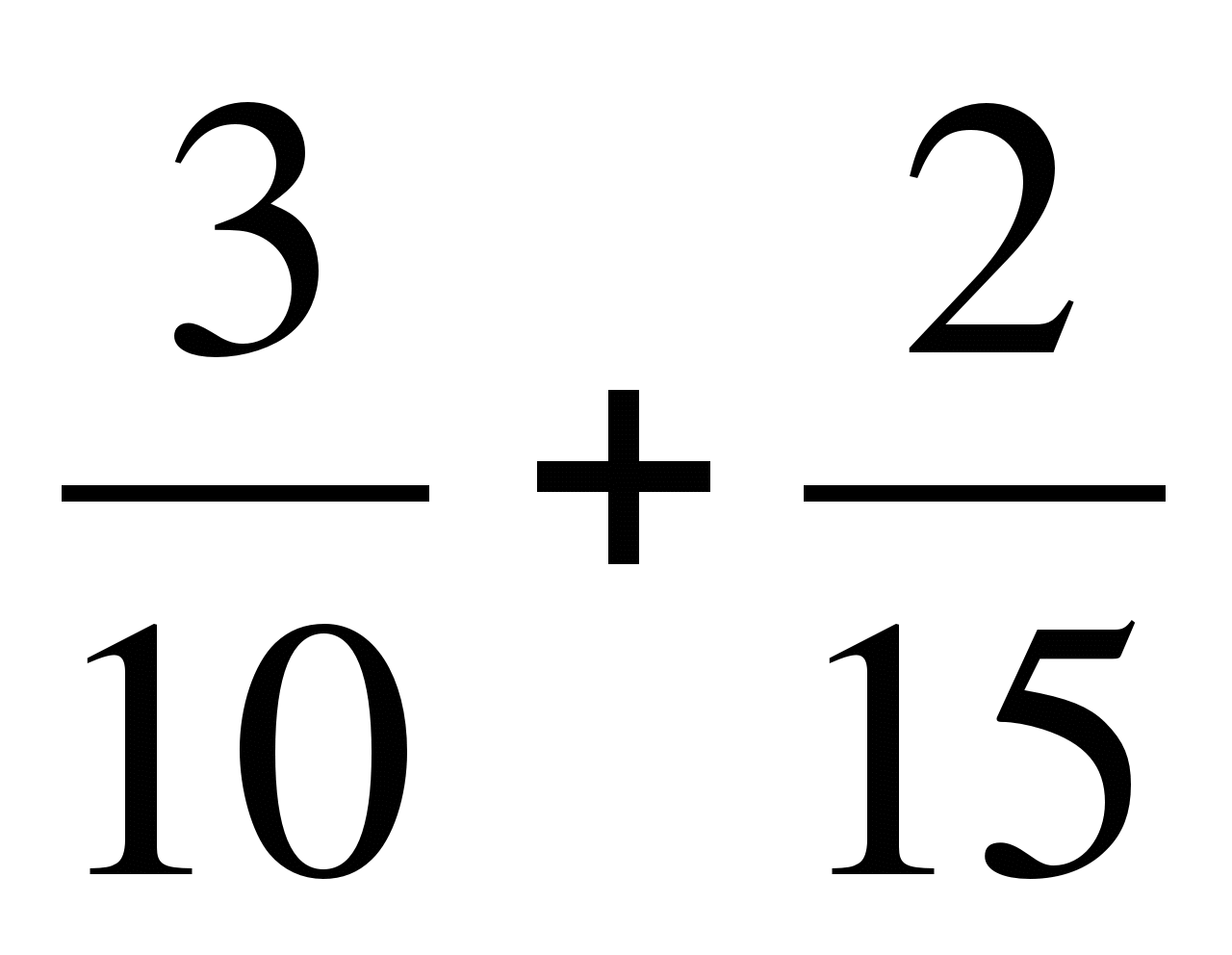
4. Вычислите:
а) 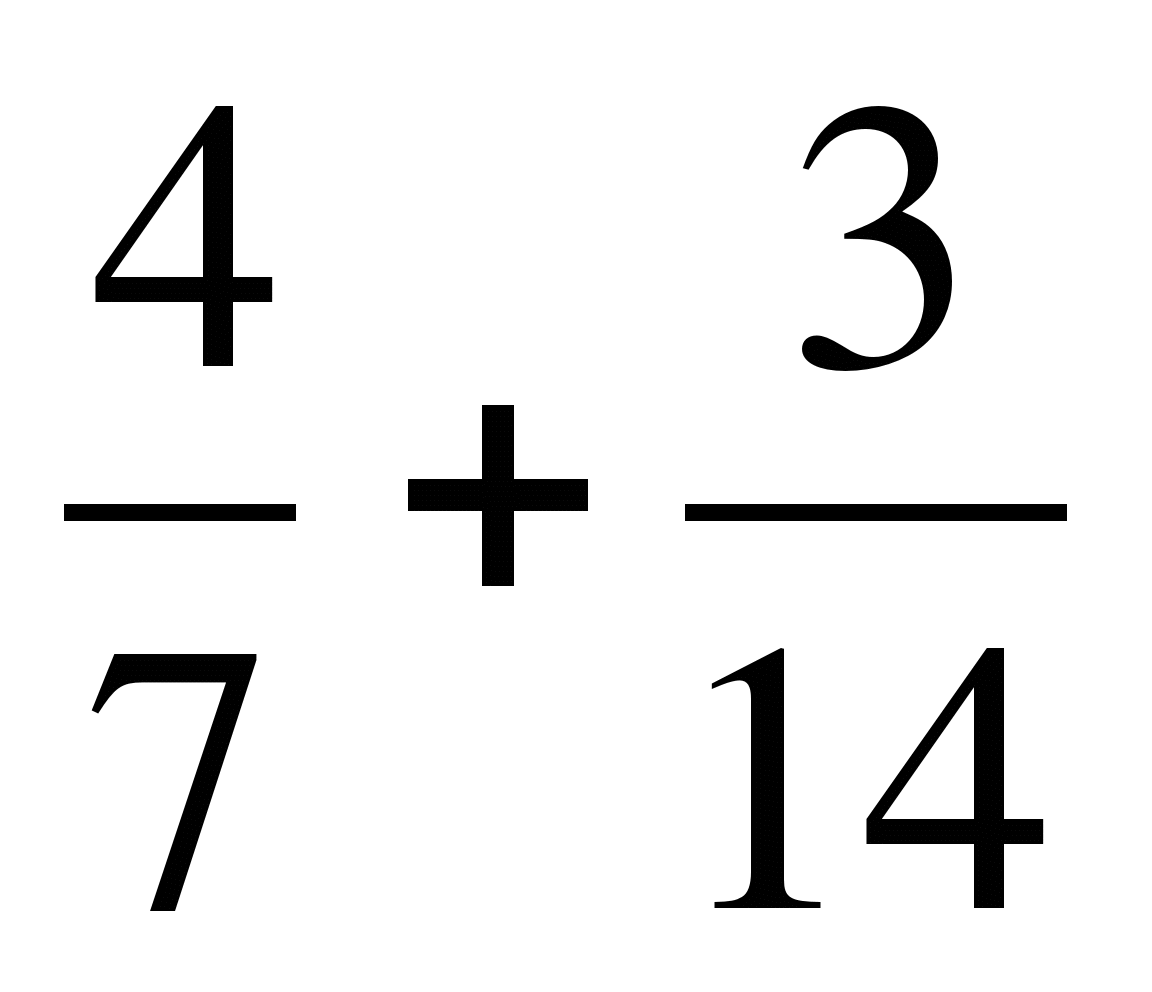 ; б)
; б) 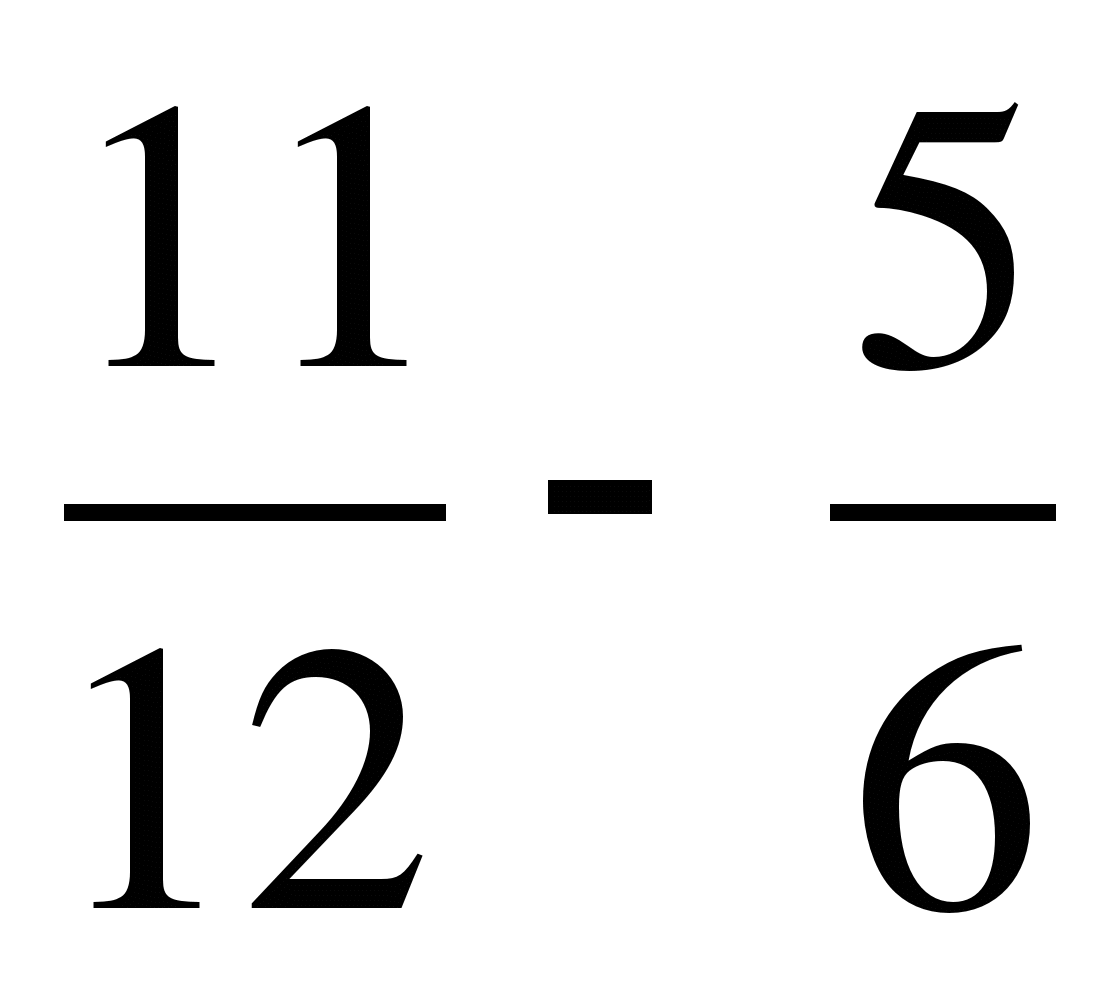 ; в)
; в) 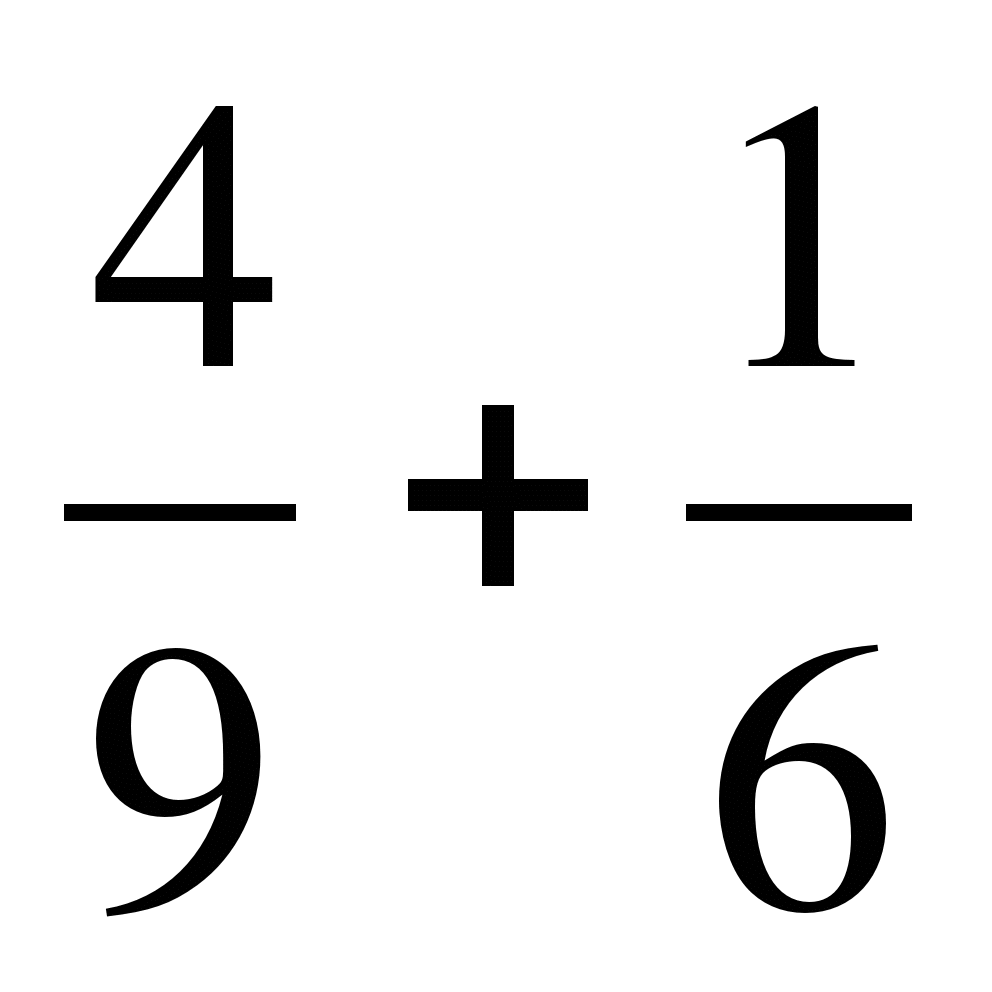 ;
;
г) 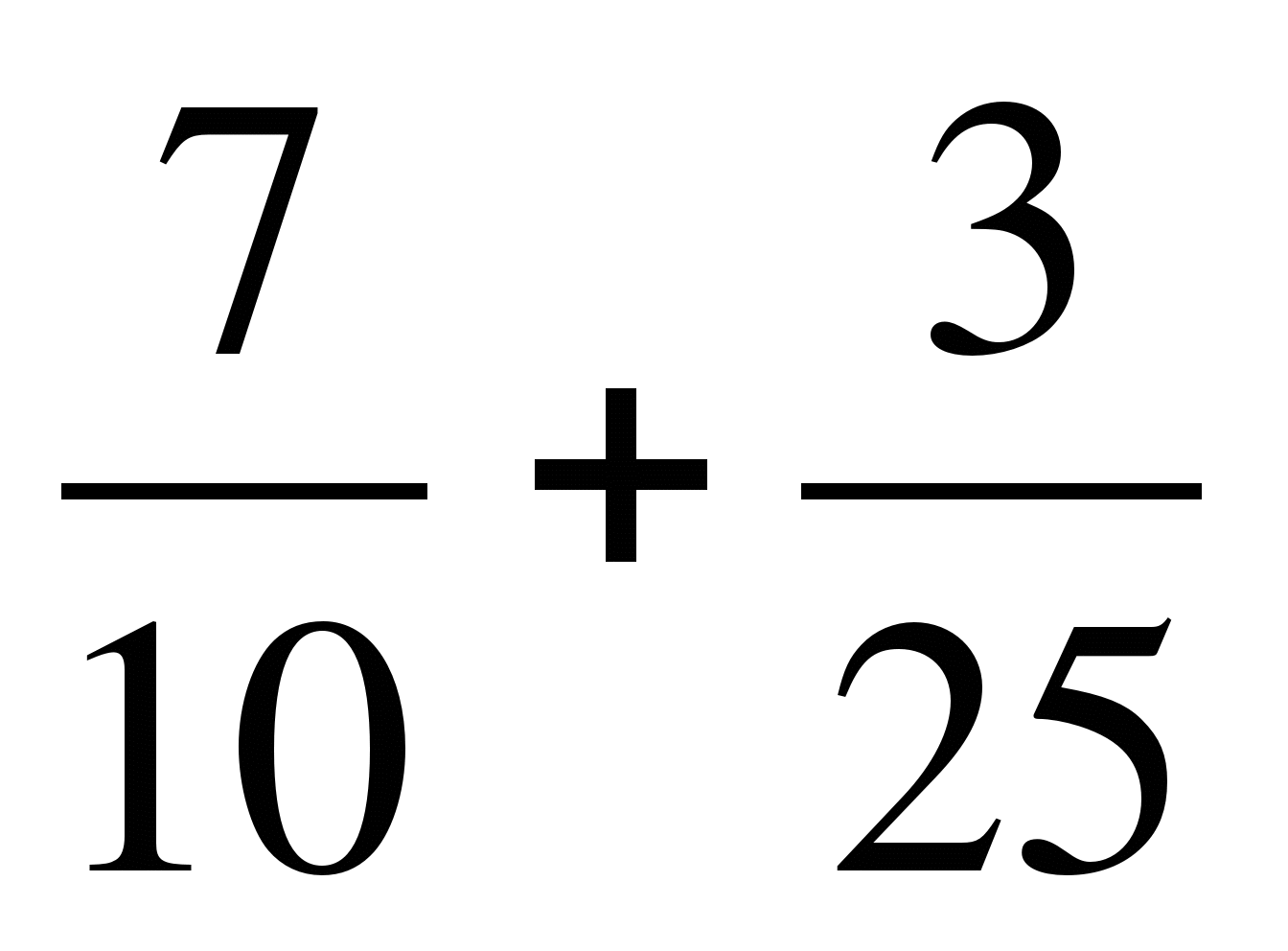 ; д)
; д) 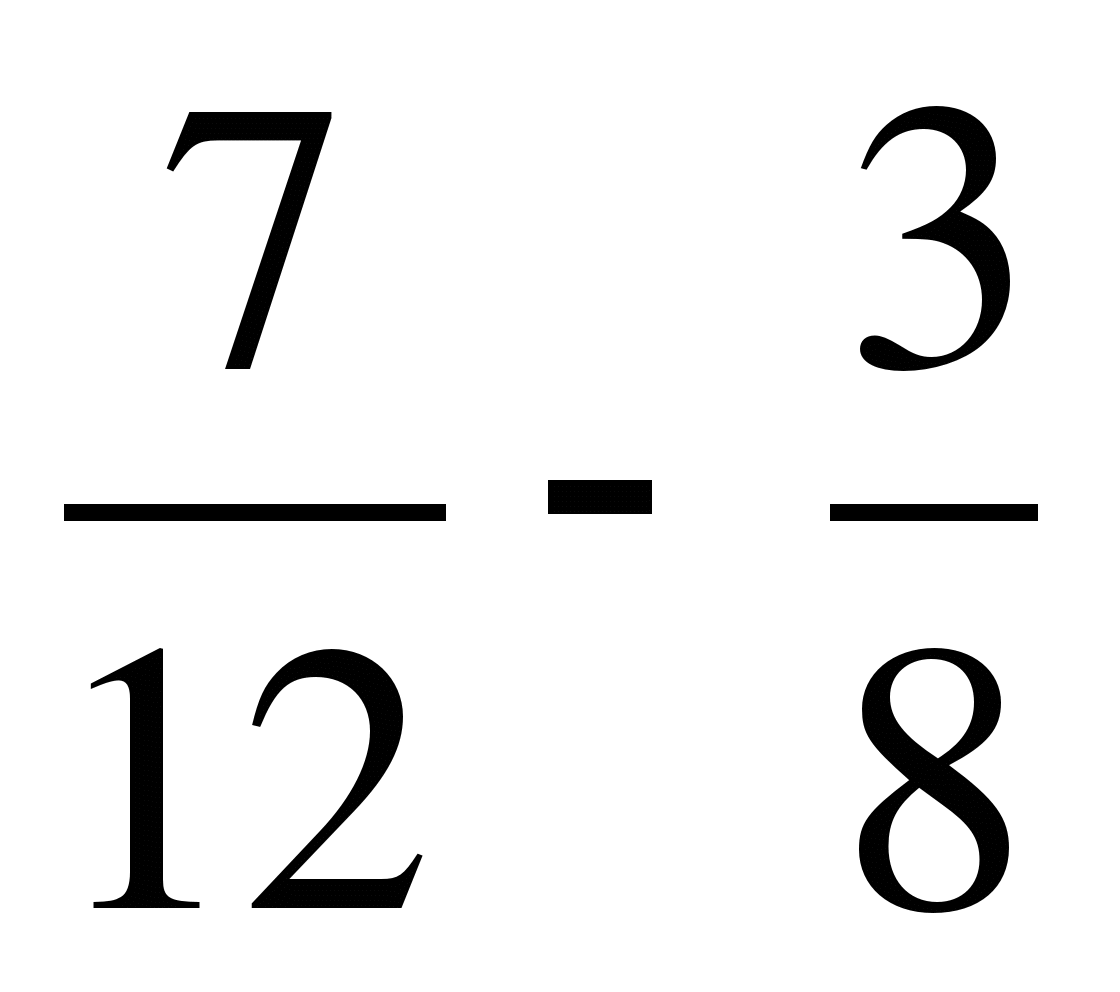
Сложение и вычитание смешанных чисел
1. Вычислите: а) 1-
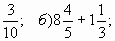 в) 6 — 3
в) 6 — 3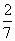 ;
;г) 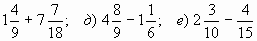
В-1
1. Вычислите: а) 1- 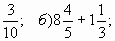 в) 6 — 3
в) 6 — 3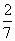 ;
;
г) 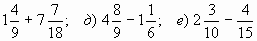
В-1
1. Вычислите: а) 2 — 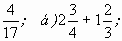 в) 5 + 3
в) 5 + 3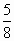 ;
;
г) 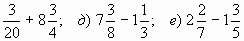
В-2
1. Вычислите: а) 2 — 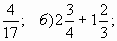 в) 5 + 3
в) 5 + 3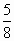 ;
;
г) 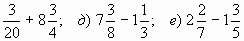
В-2
1. Вычислите: а) 5 — 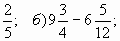 в) 12
в) 12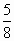 — 3;
— 3;
г) 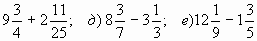
В-3
1. Вычислите: а) 5 — 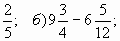 в) 12
в) 12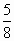 — 3;
— 3;
г) 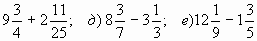
В-3
1. Выполни действия: а)
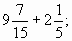 б)
б) 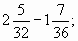
2. Реши уравнение: 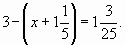
В-1
1. Выполни действия: а) 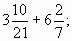 б)
б)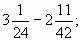
2. Реши уравнение: 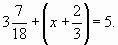
В — 2
Умножение и деление обыкновенной дроби на натуральное число
1. Выполните деление: а) 3 : 8; б) 7: 5; в) 8 : 16.2. Представьте число 6 в виде дроби со знаменателем: а) 1; б) 3.
3. За 6 ч работы было изготовлено 12 деталей.
Сколько часов ушло на 1 деталь?
В-1
1. Выполните деление: а) 3 : 8; б) 7: 5; в) 8 : 16.
2. Представьте число 6 в виде дроби со знаменателем: а) 1; б) 3.
3. За 6 ч работы было изготовлено 12 деталей.
Сколько часов ушло на 1 деталь?
В-1
1. Выполните деление: а) 8 : 9; б) 5: 15; в) 2 : 6.
2. Представьте число 4 в виде дроби со знаменателем : а) 1; б) 2.
3. За 12 руб было куплено 60 тетрадей.
Сколько стоит 1 тетрадь?
В-2
1. Выполните деление: а) 8 : 9; б) 5: 15; в) 2 : 6.
2. Представьте число 4 в виде дроби со знаменателем : а) 1; б) 2.
3. За 12 руб было куплено 60 тетрадей.
Сколько стоит 1 тетрадь?
В-2
1. Выполните действия:
а) 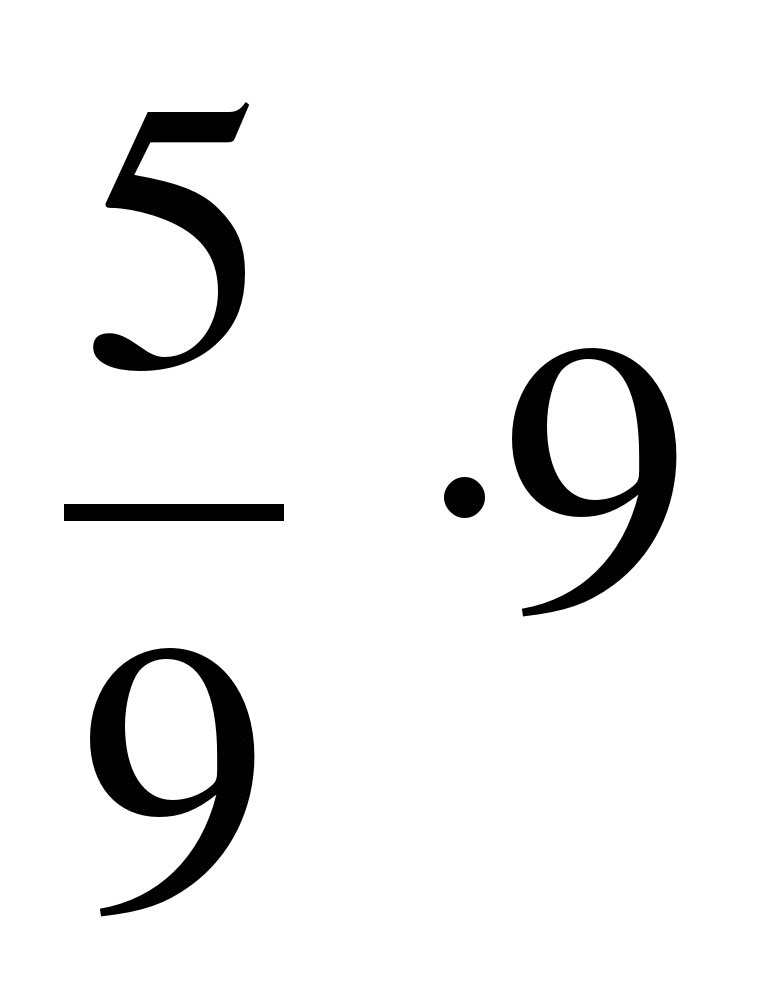 б)
б) 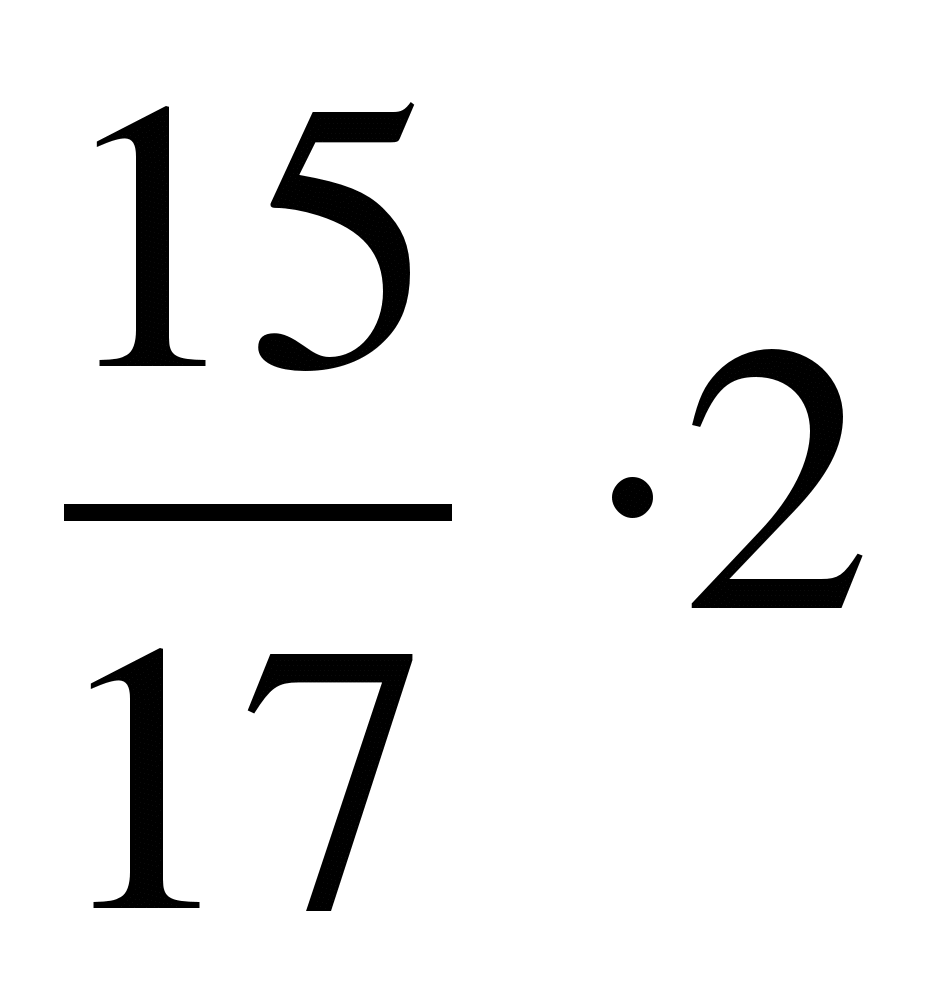 в)
в) 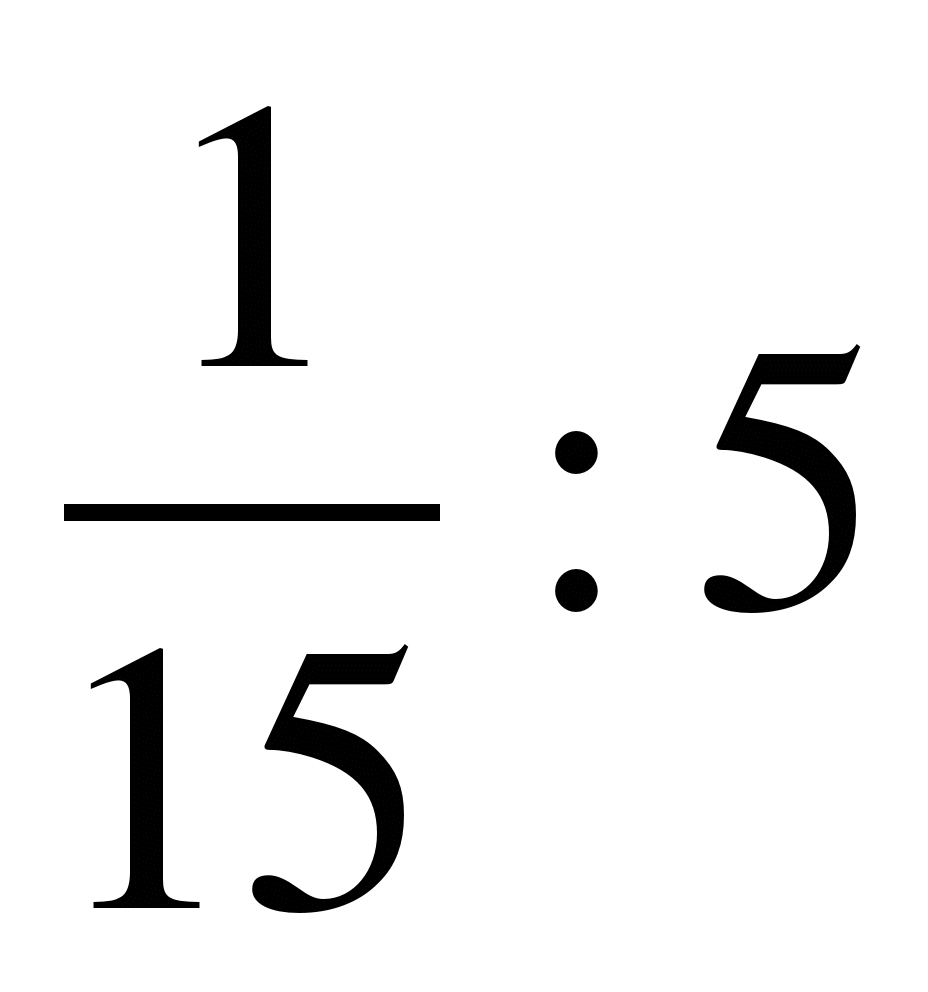 г)
г) 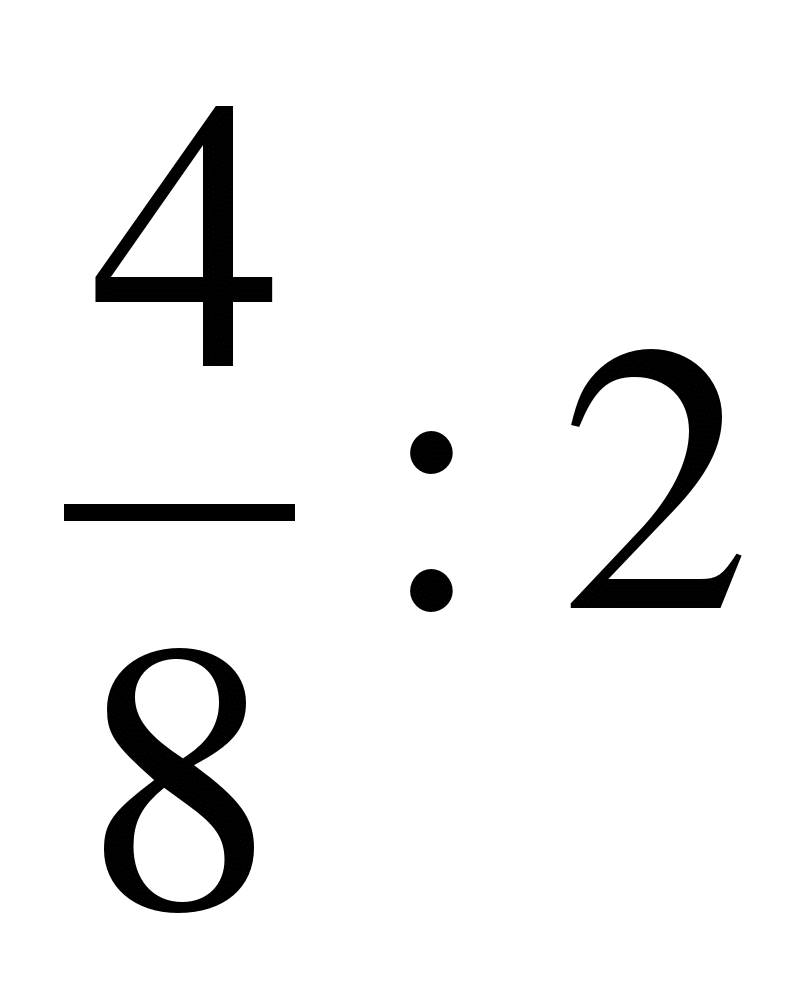
В — 1
1. Выполните действия:
а) 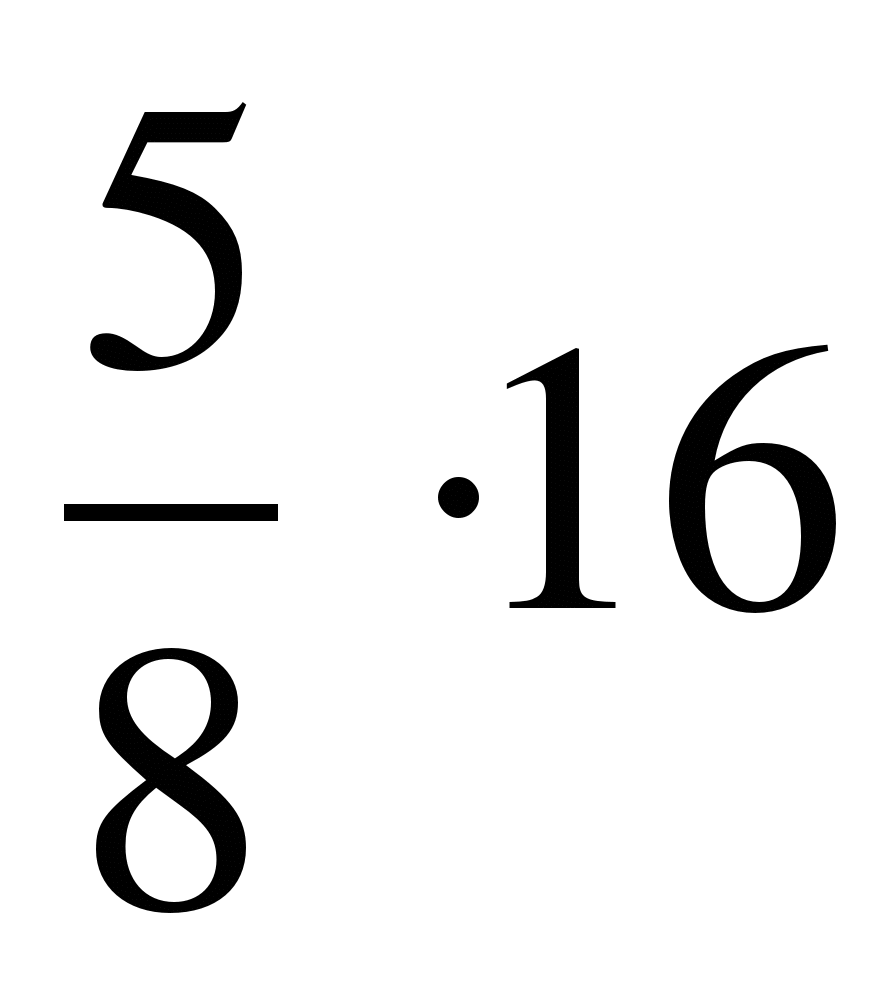 б)
б) 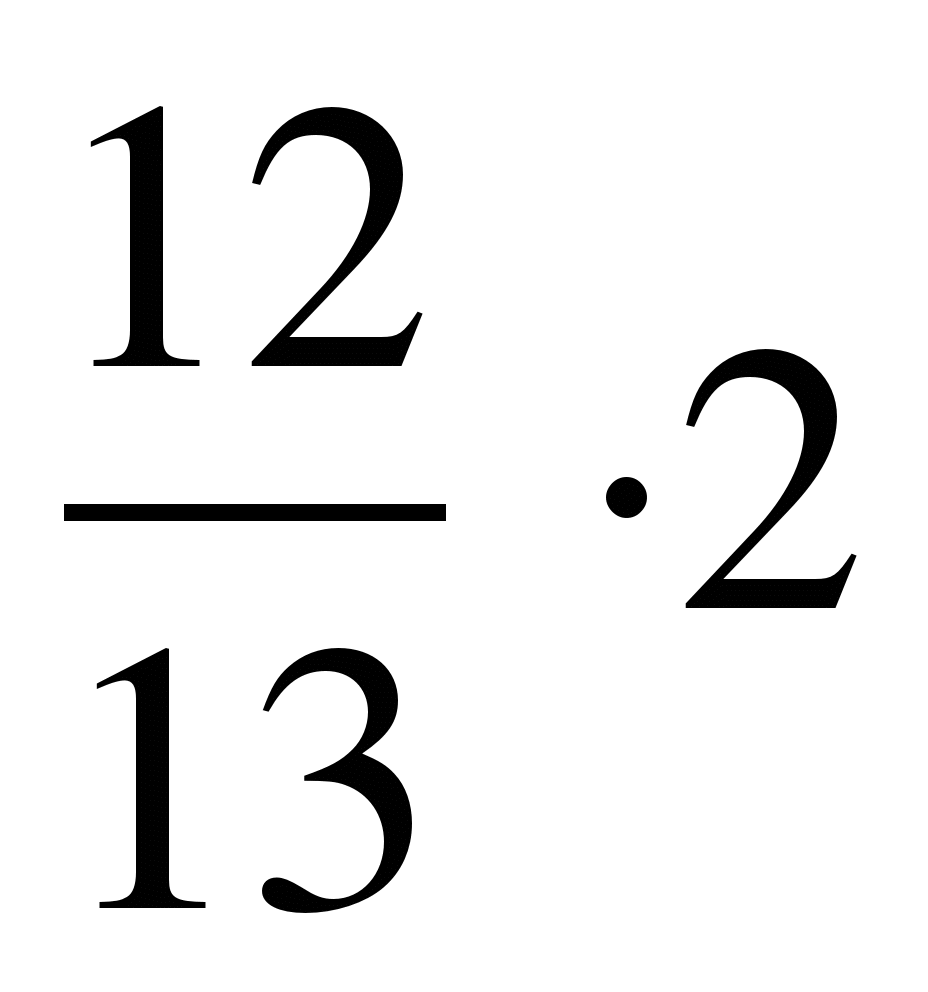 в)
в) 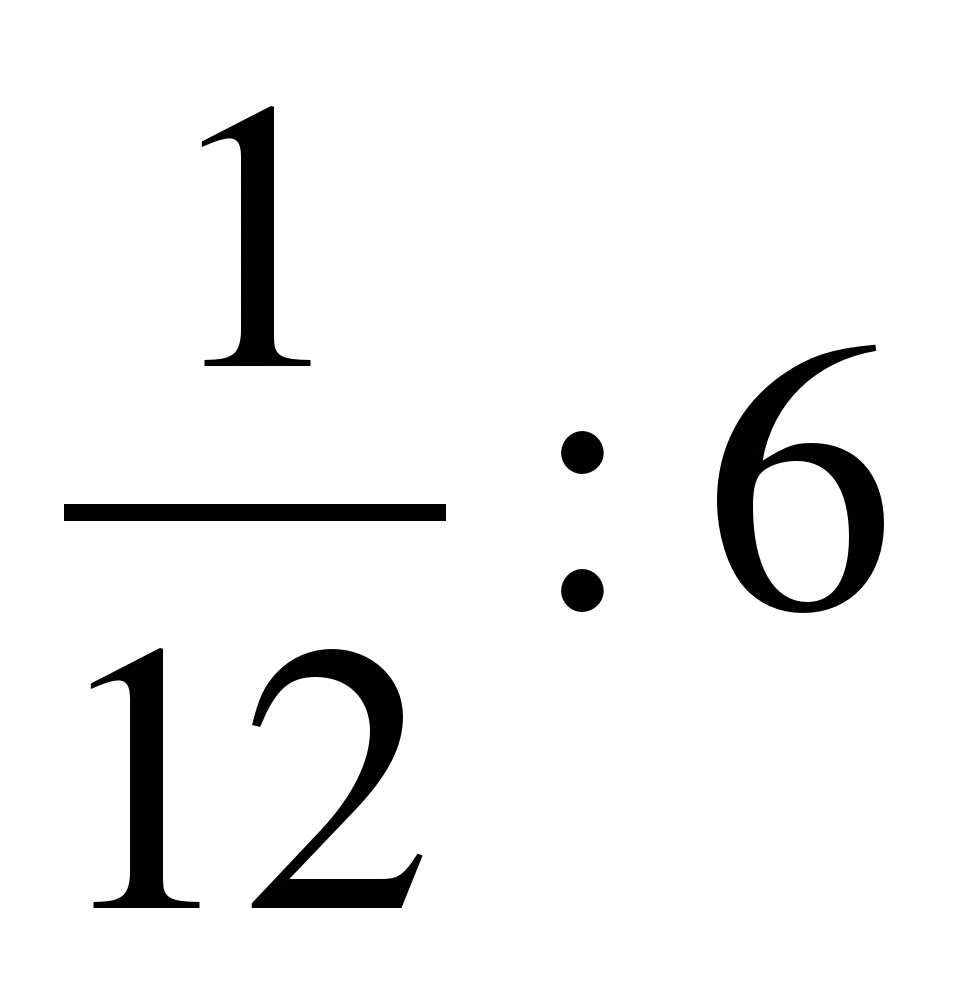 г)
г) 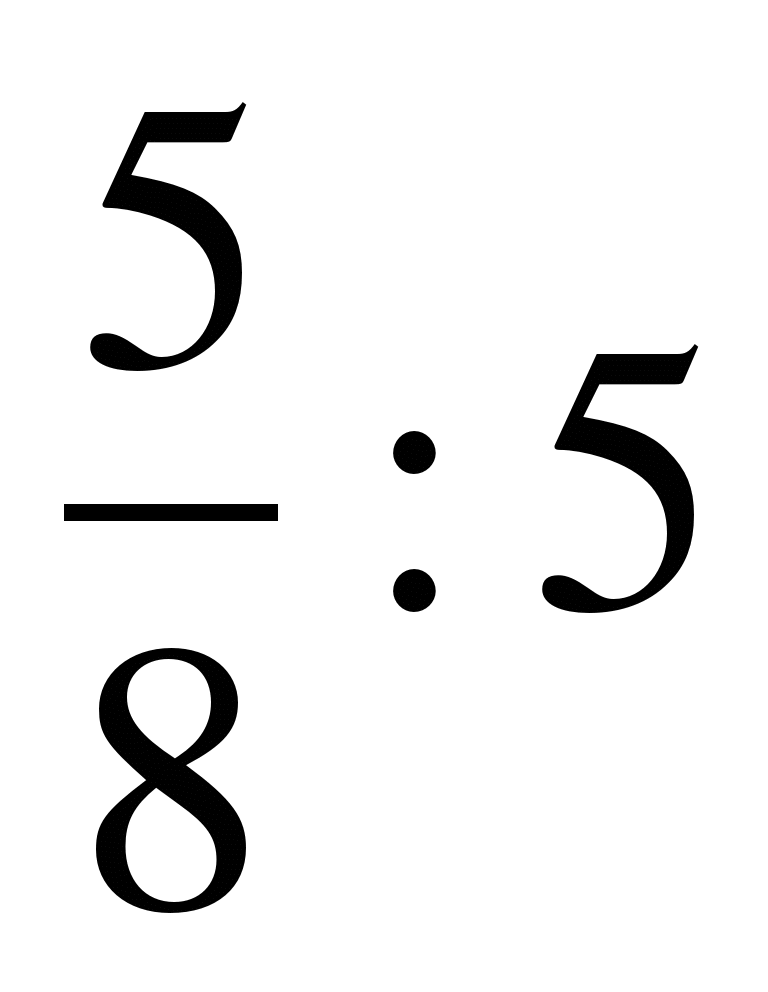
В-2
Действия с дробями, подробно с примерами

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь список материалов и изучать последовательно.
1. Сумма дробей, разность дробей.
Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.
Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.
Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…
Вариант 1 – можно перевести их в обыкновенные и далее вычислять.
Вариант 2 – можно отдельно «работать» с целой и дробной частью.
Примеры (2):

Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.
Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.
Ещё пример:

Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.
Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.
Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.
Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ.
То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.
Теперь посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Способ ВТОРОЙ.
Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.
Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.
Рассмотрим пример:

Видно что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.
Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.
Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.
Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:
— разложить каждое из чисел на ПРОСТЫЕ множители
— выписать разложение БОЛЬШЕГО из них
— умножить его на НЕДОСТАЮЩИЕ множители других чисел
Рассмотрим примеры:
50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5
в разложении большего числа не хватает одной пятёрки
=> НОК(50,60) = 2∙2∙3∙5∙5 = 300
48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3
в разложении большего числа не хватает двойки и тройки
=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144
* Наименьшее общее кратное двух простых чисел равно их произведению
Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Рассмотрим примеры:

*51 = 3∙17 119 = 7∙17
в разложении большего числа не хватает тройки
=> НОК(51,119) = 3∙7∙17
А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.
Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!
— приводим дроби к обыкновенным, если есть целая часть.
— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).
— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).
— если необходимо, то результат сокращаем.
— если необходимо, то выделяем целую часть.
2. Произведение дробей.
Правило простое. При умножении дробей умножаются их числители и знаменатели:
 Примеры:
Примеры:

Если есть возможность сократить дробь на стадии вычисления, то лучше это сделать:

Ещё правило относящееся к умножению!

Примеры, которые мы уже рассмотрели:
Определить, сколько составляет 3/7 от числа 63?

Задача. Весь путь составляет 180 километров. Турист в первый день прошёл 3/10 пути. Сколько километров турист прошёл в первый день?

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм картофеля завезли на базу?

С произведением закончим.
*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.
Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!
С уважением, Александр Крутицких.
Делитесь информацией в социальных сетях.
Урок-Игра по математике, на тему «Действия с обыкновенными дробями»
Тема урока: «Обыкновенные дроби».
Тип урока: урок-игра.
Класс: 5 класс.
Продолжительность урока: 45 минут.
Учебник: Н.Я. Виленкин и др. Математика 5. М., Мнемозина.
Цели урока:
повторить и закрепить действия сложения и вычитания с обыкновенными дробями;
уметь выделять целую часть из неправильной дроби, представлять смешанные числа в виде неправильных дробей.
Оборудование:
проигрыватель;
пластинки;
плакат.
Ход урока:
Урок начинается с песни «Чему учат в школе» (пластинка, проигрыватель).
Учитель объявляет тему, цель урока, обращает внимание учащихся на высказывание Цицерона, записанное на доске:
Без знания дробей никто не может
признаваться знающим математику!
Игра «Кто скорее, кто вернее» (устный счет).
Правило игры: класс делится на 3 команды (по рядам), отвечает тот ученик – член команды, который первым поднимет руку. При правильном ответе принесет команде очко.
сравнить:
и 1 и и и 1
и 0 и и и .
назвать дроби в порядке возрастания:
,
Какая дробь наименьшая? Как называются эти дроби?
выделить целую часть из неправильной дроби:
представить дробные числа в виде неправильных дробей:
перевести:
в метры: 4 дм, 3 м 3 дм, 20 см.
в часы: 30 мин, 15 мин, 45 мин.
решить уравнение:
Число x разделили на 5 и получили . Чему равно число x?
История возникновения дробей (небольшие сообщения трех учащихся от каждой команды по темам «Дроби в Древнем Риме», «Дроби в Древней Греции», «Дроби на Руси», «Дроби в Древнем Египте»).
Игра «Ромашка» на повторение теоретического материала.
Правило игры: на лепестках ромашки написаны задания-вопросы. Нужно открыть лепесток, прочитать задание и ответить на него. Правильный ответ – очко команде.
Вопросы на лепестках:
Что показывают знаменатель и числитель дроби?
Какая дробь равна единице?
Какая дробь называется правильной?
Как выделить целую часть из неправильной дроби?
Какая их двух дробей с равными знаменателями меньше?
Какая дробь называется неправильной?
Какая из двух дробей с одинаковыми знаменателями больше?
Сравни с единицей правильную дробь?
Как из одной дроби вычесть другую, если знаменатели одинаковые?
Какая дробь больше единицы?
Как сложить дроби с одинаковыми знаменателями?
Дроби какого вида называются основными, единичными дробями?
Игра «Лучший счетчик».
Правило игры: дома каждый ученик должен подобрать по данной теме 3-4 примера для устного счета. В каждой команде выбирается «счетчик», который будет защищать честь команды. Примеры предлагают «счетчику» члены других команд до тех пор, пока он не собьется. Затем его сменяет другой «счетчик». Побеждает команда, в которой «счетчик» решил наибольшее количество примеров верно.
Стихотворение «Три десятых», автор В.Лифшиц (читают участники от каждой команды). Это стихотворение раскрывает для чего надо учить эту тему, к чему может привести незнание дробей.
Это кто
Из портфеля
Швыряет в досаде
Ненавистный задачник,
Пенал и тетради
И сует свой дневник,
Не краснея при этом,
Под дубовый буфет,
Чтоб лежал под буфетом?..
Познакомьтесь, пожалуйста:
Костя Жигалин.
Жертва вечных придирок, –
Он снова провален
И шипит,
На растрепанный
Глядя задачник:
– Просто мне не везет!
Просто я неудачник!..
В чем причина
Обиды его и досады?
Что ответ не сошелся
Лишь на три десятых!
И к нему, безусловно,
Придирается
Строгая
Марья Петровна.
Три десятых…
Скажи про такую ошибку
И пожалуй, на лицах
Увидишь улыбку.
Три десятых…
И все же об этой ошибке
Я прошу вас
Послушать меня
Без улыбки…
Если б, строя ваш дом,
Тот, в котором живете,
Архитектор
Немножко
Ошибся
В расчете,–
Что б случилось,
Ты знаешь ли, Костя Жигалин?
Этот дом
Превратился бы
В груду развалин!
Ты вступаешь на мост.
Он надежен и прочен.
А не будь инженер
В чертежах своих точен,
Ты бы, Костя,
Свалившись
В холодную реку,
Не сказал бы спасибо
Тому человеку!
Вот турбина.
В ней вал
Токарями
Расточен.
Если б токарь
В работе
Не очень был точен,
Совершилось бы, Костя,
Большое несчастье:
Разнесло бы турбину
На мелкие части!
Три десятых –
И стены
Возводятся
Косо.
Три десятых –
И рухнут
Вагоны
С откоса.
Ошибись
Только на три десятых
Аптека, –
Станет ядом лекарство,
Убьет человека!
Мы громили и гнали
Фашистскую банду.
Твой отец подавал
Батарее команду.
Ошибись он при этом
Хоть на три десятых, –
Не настигли б снаряды
Фашистов проклятых.
Ты подумай об этом,
Мой друг, хладнокровно,
И скажи –
Не права ль была
Марья Петровна?
Если честно
Подумаешь, Костя, об этом,
То недолго лежать
Дневнику под буфетом!
Игра «Солнышко» – решить примеры.
Правило игры: на лучах солнышка записаны числа, которые надо сложить или вычесть с числом, записанным на солнышке. Правильный ответ – очко команде.
Шуточная задача.
1). Клоун, чтобы посмешить публику сказал, что рост у него км, а вес т. Публика смеялась: всем было ясно, что клоун выбрал неподходящие единицы длины и массы. Скажите, каков рост клоуна в см и каков его вес в кг? (Ответ: 180 см, 80 кг)
2). Клоун предложил кому-нибудь из публики поиграть с ним в такую игру. Он называет дробь. Игрок из публики называет меньшую дробь. Затем клоун называет еще меньшую дробь, игрок из публики – еще меньшую и т.д. Выигрывает тот, кто называет дробь, меньше которой уже дробей нет? Можно ли выиграть в такой игре?
Диктант (по пластинке).
Подведение итогов урока.
Домашнее задание: повторить изученный материал по теме «Дроби».
Наряду с необходимостью считать предметы у людей с древних времен появилась потребность измерять длину, площадь, объем, время и другие величины. Результат измерения не всегда удается выразить натуральным числом. Приходится учитывать и части употребляемой меры. Так возникли дроби.
Дроби в Древнем Египте
Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали …, затем … и т.д., т.е. единичные или основные дроби. У них числитель всегда единица. Египтяне выражали любую дробь в виде суммы только основных дробей. Если, например, в результате измерения получалось дробное число , то для египтян оно представлялось в виде суммы единичных дробей:
Египтяне писали на папирусах, т.е. на свитках, изготовленных из стебля крупных тропических растений – папирус. В папирусе Ахмеса имеются таблицы для представления некоторых дробей в виде суммы единичных дробей.
Дроби в Древнем Риме
У древних римлян асс служил основной единицей измерения массы, а также денежной единицей. Если асс делить на 12 равных частей, то получается унций. Со временем унции стали применяться для измерения любых величин. Так возникли римские двенадцатеричные дроби, т.е. дроби, у которых знаменателем всегда было число 12. Вместо римляне говорили «одна унция», – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной.
Дроби в Древней Греции
В Греции употреблялись наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним – числитель дроби. Например, означало три пятых.
Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями.
Дроби на Руси
Дроби в Древней Руси называли долями, позднее «ломаными числами». В старых руководствах находили следующие названия дробей на Руси:
– половина, полтина, – треть,
– четь, – полтреть,
– полчеть, – полполтреть,
– полполчеть, – полполполтреть (малая треть),
– полполполчеть (малая четь), – пятина,
– седьмина, – десятина



