Уравнения и неравенства с модулем

Репетитору по математике часто приходится сталкиваться с отсутствием у старшеклассников навыков решения простейших уравнений и неравенств с модулем. Между тем среди заданий С3 или С5 из ЕГЭ по математике таковые могут встретиться. Даже если их не будет на экзамене в явном виде, в процессе выполнения некоторых задач из ЕГЭ вам, возможно, придется столкнуться с решением того или иного задания с модулем. Поэтому научиться решать уравнения и неравенства с модулем должен каждый выпускник средней школы. В данной статье рассмотрены некоторые способы их решения. Присутствует также видеоразбор решения одного уравнения, содержащего модуль.
Считается, что чем больше способов решения существует у задачи, тем она интереснее с математической точки зрения. Уравнения и неравенства с модулями можно поэтому смело назвать интересными. Рассмотрим пример.
Решите уравнение: 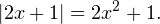
Решение. Постараемся найти как можно большее количество решений данного уравнения. Подробное объяснение решений смотрите в видеоуроке.
Способ №1. Решение возведением в квадрат. Просто возводим обе части уравнения в квадрат. При этом не забываем, что подобное преобразование не является равносильным. Из-за этого могут появиться посторонние корни, поэтому полученные решения необходимо будет проверить прямой подстановкой в исходное уравнение.
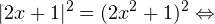
![Rendered by QuickLaTeX.com \[ 4x^2+4x+1=4x^4+4x^2+1\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-532a2f357fb8919edd5159afab9ad466_l3.png)
![Rendered by QuickLaTeX.com \[ 4x^4-4x=0\Leftrightarrow x(x^3-1) = 0\Leftrightarrow \left[\begin{array}{l}x=0,\\ x=1.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-13f51a116116141e641b08a36cb64da9_l3.png)
Путем прямой подстановки полученных решений в исходное уравнение убеждаемся, что посторонних корней среди них нет. На самом деле в данном конкретном задании отсутствует необходимость проверки корней. Возведение обеих частей этого уравнения в квадрат не может привести к приобретению посторонних решений. Подумайте самостоятельно, почему это так.
Способ №2. Метод интервалов. Не совсем верное название, но мы его здесь употребим, поскольку в методической литературе оно встречается. Для решения нам потребуется найти значение переменной 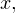 при котором подмодульное выражение обращается в ноль:
при котором подмодульное выражение обращается в ноль: 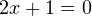
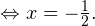 Наносим эту точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.
Наносим эту точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.
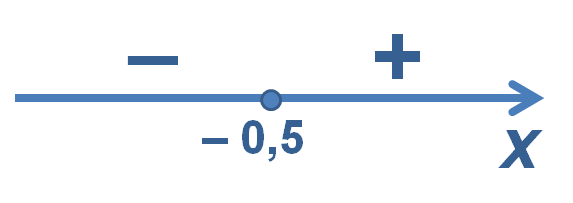
Числовая прямая
Далее на каждом промежутке раскрываем знак модуля в соответствии с полученными данными:
Способ №3. Замена уравнения смешанной системой. Известно, что:
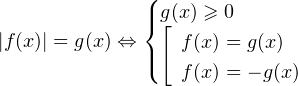
Для тех, кто не знает, какой именно смысл вкладывается в математике в фигурные и квадратные скобки, рекомендую ознакомиться со статьей «Решение систем логарифмических и показательных неравенств». То есть в нашем случае:
![Rendered by QuickLaTeX.com \[ \begin{cases} 2x^2+2\geqslant 0, \\ \left[\begin{array}{l}2x+1 = 2x^2+1, \\ 2x+1 =-2x^2-1.\end{array}\right. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d3948fa0bfe985ef5d1a69696206c3cd_l3.png)
Легко заметить, что первое неравенство выполняется при любом значении 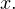 Следовательно, в составе системы на него вообще можно не обращать внимания. Ситуация несколько упрощается:
Следовательно, в составе системы на него вообще можно не обращать внимания. Ситуация несколько упрощается:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}2x+1 = 2x^2+1, \\ 2x+1 =-2x^2-1 \end{array}\right.\Leftrightarrow \left[\begin{array}{l} x=0, \\ x=1.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6be0642796e06ab84528a72b399a058c_l3.png)
Способ №4. Графический. Строим в одной системе координат графики функции 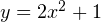 и
и 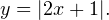 Абсциссы точек их пересечения будут являться решениями уравнения. Метод менее точный, но более наглядный. Видно, что это все те же
Абсциссы точек их пересечения будут являться решениями уравнения. Метод менее точный, но более наглядный. Видно, что это все те же 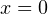 и
и 
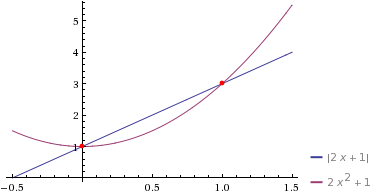
Соответствующие графики функций на одном координатном поле.
На этом список стандартных способов решения данного уравнения с модулем исчерпан. Придумайте свои нестандартные.
Простейшие уравнения с модулем
Пример 1. Решите уравнение: 
Решение. Перепишем уравнение в виде:
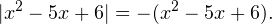
Получается, что модуль выражения равен этому выражению, взятому с противоположным знаком. Такое возможно только в том случае, если данное выражение отрицательно или равно нулю:
![Rendered by QuickLaTeX.com \[ x^2-5x+6\leqslant 0\Leftrightarrow 2\leqslant x\leqslant 3. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0a310ab09168d33aa13cde0788d4de93_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in[2;3].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5a013af4a0ff1fd92a3003066c8cf8cb_l3.png)
Задача для самостоятельного решения №1. Решите уравнение
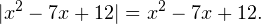
Показать ответ
Ответ:![Rendered by QuickLaTeX.com x\in(-\mathcal{1};3]\cup[4;+\mathcal{1}).](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-46032d8a97c3bb520e479febac55b853_l3.png)
|
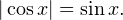
Решение. Исходное уравнение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases} \sin x\geqslant 0, \\ \left[\begin{array}{l} \cos x = \sin x, \\ \cos x = -\sin x \end{array}\right.\end{cases}\Leftrightarrow \begin{cases} 2\pi k\leqslant x\leqslant \pi+2\pi k, \\ \left[\begin{array}{l}x = \frac{\pi}{4}+2\pi n, \\ x = -\frac{\pi}{4}+2\pi z.\end{array}\right.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-074d1bc71b70fde31bcb9088220b70ec_l3.png)
Обе части последних двух уравнений разделили на 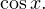 В данном случае
В данном случае  В противном случае
В противном случае 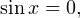 а это невозможно, поскольку
а это невозможно, поскольку 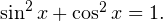
Окончательно, получаем: 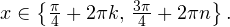
Ответ: 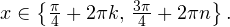
Задача для самостоятельного решения №2. Решите уравнение:
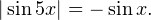
Примечание. Для решения этого задания потребуется знание формулы суммы и разности синусов.
Показать ответ
Ответ: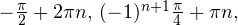
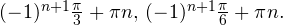
|
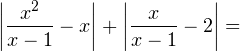
![Rendered by QuickLaTeX.com \[ =\frac{x^2}{x-1}+\frac{x}{x-1}-x-2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7610f222b0f855f3dc23504946c15989_l3.png)
Решение. Перепишем уравнение в виде:
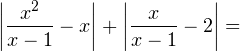
![Rendered by QuickLaTeX.com \[ =\frac{x^2}{x-1}-x+\frac{x}{x-1}-2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9bdc1a135abeae14b5908031d8887ad8_l3.png)
Сумма модулей равна сумме подмодульных выражений. Это возможно только в том случае, когда оба подмодульных выражения неотрицательны:
![Rendered by QuickLaTeX.com \[ \begin{cases}\frac{x^2}{x-1}-x\geqslant 0, \\ \frac{x}{x-1}-2\geqslant 0.\end{cases}\Leftrightarrow \begin{cases}\frac{x}{x-1}\geqslant 0, \\ \frac{2-x}{x-1}\geqslant 0.\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-84ae372e673b4d643757eef2039aabb0_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}x\in(-\mathcal{1};0]\cup(1;+\mathcal{1}), \\ x\in(1;2]\end{cases}\Leftrightarrow x\in(1;2]. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3a0213728762fcd2a8e1b2eeb6911890_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in(1;2].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-eb9d71720b1691043afa1482d86c04f3_l3.png)
Задача для самостоятельного решения №3. Решите уравнение:

Показать ответ
Ответ:![Rendered by QuickLaTeX.com x\in[-2;0]\cup[2;5].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-befd73c50e7ac7104183b7230a3b9a6d_l3.png)
|
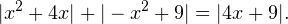
Решение. Сумма модулей равна модулю суммы подмодульных выражений. Это возможно только в том случае, когда оба подмодульных выражения одновременно либо неотрицательны, либо неположительны. То есть:
![Rendered by QuickLaTeX.com \[ (x^2+4x)(-x^2+9)\geqslant 0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-245ffaf848f576ed917aa9bfa233de53_l3.png)
![Rendered by QuickLaTeX.com \[ x(x+4)(3-x)(x+3)\geqslant 0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-abde7529319d261e3e18e413c5fd394c_l3.png)
![Rendered by QuickLaTeX.com \[ x\in[-4;-3]\cup[0;3]. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6fa35da5d18aec962b80a9c4970ed90f_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in[-4;-3]\cup[0;3].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-dc314321a54f554a3f0858f775e75cfb_l3.png)
Задача для самостоятельного решения №4. Решите уравнение:
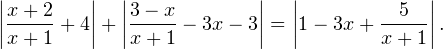
Показать ответ
Ответ:![Rendered by QuickLaTeX.com x\in[-3;-1]\cup[1;4].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-45a03af4fdd5deec1e76f0a95bf37266_l3.png)
Простейшие неравенства с модулем
|
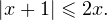
Решение. Исходное неравенство равносильно следующей системе неравенств:
![Rendered by QuickLaTeX.com \[ \begin{cases}x+1\leqslant 2x, \\ x+1\geqslant -2x \end{cases}\Leftrightarrow \begin{cases}x\geqslant 1, \\ x\geqslant -\frac{1}{3}.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5b656630ba4437c654e5bc3555dd9097_l3.png)
Ответ: 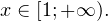
Задача для самостоятельного решения №5. Решите неравенство:
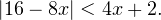
Показать ответ
Ответ: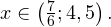
|
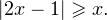
Решение. Исходное неравенство равносильно следующей совокупности неравенств:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}2x-1\geqslant x, \\ 2x-1\leqslant -x\end{array}\right.\Leftrightarrow \left[\begin{array}{l} x\geqslant 1, \\ x\leqslant \frac{1}{3}. \end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9dce8fdab1f260985e56bb02d2a53790_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in\left(-\mathcal{1};\frac{1}{3}\right]\cup[1;+\mathcal{1}).](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ccf77b2896ad96fc27ad113e5147e8a4_l3.png)
Задача для самостоятельного решения №6.
Решите неравенство: 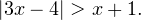
Показать ответ
Ответ: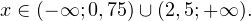 Пример 7. Решите неравенство:
Пример 7. Решите неравенство: 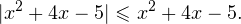
Решение. Исходное неравенство равносильно следующему неравенству:
![Rendered by QuickLaTeX.com \[ x^2 +4x - 5\geqslant 0\Leftrightarrow x\in(-\mathcal{1};-5]\cup[1;+\mathcal{1}). \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c75a231df66a7bd0fd90edb2d78d419b_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in(-\mathcal{1};-5]\cup[1;+\mathcal{1}).](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0162586a982d9a4947e8da6f08140d6c_l3.png)
Задача для самостоятельного решения №8. Решите неравенство:
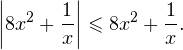
Показать ответ
Ответ:![Rendered by QuickLaTeX.com x\in(-\mathcal{1};0,5]\cup(0;+\mathcal{1}).](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-864f354659ffb86b89038eebf8c06337_l3.png)
|
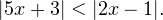
Решение. Исходное неравенство равносильно следующему неравенству:
![Rendered by QuickLaTeX.com \[ (5x+3)^2<(2x-1)^2\Leftrightarrow (3x+4)(7x+2)<0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-dc63fe61671648939960aaf57d8c4713_l3.png)
Ответ: 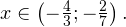
Задача для самостоятельного решения №9. Решите неравенство:
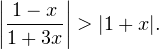
Показать ответ
Ответ: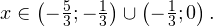
Сергей Валерьевич
Частный преподаватель по математике
yourtutor.info
Уравнения с модулем: учет области значений
Очень часто в уравнениях под знаком модуля стоят довольно сложные конструкции, которые было бы крайне затруднительно раскрывать, а затем решать «напролом». Для таких случаев существует множество приемов и замечаний, позволяющих значительно ускорить вычисления.
Одним из таких приемов является учет области значений модуля (учителя называют это решение методом следствий). Суть его можно описать одним простым предложением: «Сумма неотрицательных чисел равна нулю тогда и только тогда, когда каждое из этих чисел равно нулю».
Сегодня мы продолжаем изучать конструкции, содержащие знак модуля функции и переходим уже к более сложным конструкциям, когда ихдва, либо само уравнение содержит нестандартную функцию.
Немного теории
Для начала вспомним определение модуля: модулем числа $x$ называется либо само это число (при условии, что оно неотрицательное), либо минус это число, если оно отрицательно:
\[\left| x \right|=\left\{ \begin{align}& x,x\ge 0 \\& -x,x<0 \\\end{align} \right.\]
Данная запись является алгебраическим определением, потому что здесь используется только алгебраическая терминология и никак не привлекается геометрия. И именно это определение позволяет нам заключить следующий факт: модуль числа всегда неотрицателен:
\[\left| x \right|\ge 0\]
Именно поэтому его иногда еще называют абсолютным значением, т.е. расстоянием от 0 до этого числа на числовой прямой. И именно тот факт, что модуль функции всегда является неотрицательным числом, позволяет решить целый класс задач, которые иначе решались бы весьма проблематично.
Решаем реальные задачи
Пример № 1
\[\left| x-{{x}^{3}} \right|+\left| {{x}^{2}}+x-2 \right|=0\]
Чтобы решить такое выражение, давайте для начала вспомним, как решается простейшая конструкция с модулем, т.е уравнение вида $\left| f \right|=g$.
Решаются она довольно просто. Рассматривается два случая: в первом случае $f$ неотрицательно — в этом случае модуль функции снимается без всяких изменений и получается, что $f$ равно $g$. А во втором случае $f$ отрицательно — в этом случае модуль раскрывается со знаком «минус», как мы уже знаем из определения. Запишем совокупность систем:
\[\left| f \right|=g=>\left[ \begin{align}& \left\{ \begin{align}& f\ge 0 \\& f=g \\\end{align} \right. \\& \left\{ \begin{align}& f<0 \\& -f=g \\\end{align} \right. \\\end{align} \right.\]
Но все это работает только при условии, что модуль функции в выражении один, а у нас сегодня сразу два. Что делать в такой ситуации?
Давайте заметим, что при сложении двух модулей возникает выражение, значение которого 0. Но, с другой стороны, мы можем записать следующее:
\[\left| x-{{x}^{3}} \right|\ge 0\]
\[\left| {{x}^{2}}+x-2 \right|\ge 0\]
В этом случае сумма вышеописанных двух элементов также будет давать некое число (назовем его $k$), которое больше или равняется 0. При этом от нас требуется, чтобы оно строго равнялось 0. А это значит, что нас устроит только тот вариант, когда каждый из модулей равен 0, т.е. мы можем записать:
\[\left| x-{{x}^{3}} \right|=0\]
\[\left| {{x}^{2}}+x-2 \right|=0\]
Другими словами, сумма двух чисел, каждое из которых не меньше 0, дает в сумме ноль только в том случае, когда каждое из них равняется 0, т.е. требования должны выполняться одновременно. Поэтому запишем систему:
\[\left\{ \begin{align}& \left| x-{{x}^{3}} \right|=0 \\& \left| {{x}^{2}}+x-2 \right|=0 \\\end{align} \right.\]
Модуль функции равен 0, когда подмодульное выражение равно 0, т.е:
\[\left\{ \begin{align}& x-{{x}^{3}}=0 \\& {{x}^{2}}+x-2=0 \\\end{align} \right.\]
Давайте решим каждое из полученных выражений отдельно. Решаем первое:
\[x\left( {{1}^{2}}-{{x}^{2}} \right)=0\]
\[x\left( 1-x \right)\left( 1+x \right)=0\]
\[{{x}_{1}}=0\]
\[{{x}_{2}}=1\]
\[{{x}_{3}}=-1\]
При трех таких значениях тождество обнуляется.
Теперь разберемся со вторым выражением. Будем решать его при помощи формулы Виета:
\[{{x}^{2}}+x-2=0\]
\[\left( x+2 \right)\left( x-1 \right)=0\]
\[{{x}_{1}}=-2\]
\[x=1\]
А теперь вспоминаем, что мы решаем систему уравнений, т.е. нужно из первого и из второго наборов выбрать корни, которые принадлежат каждому из этих наборов. Очевидно, что такой корень только один — $x=1$.
Итого решением первого выражения является единственный корень $x=1$.
Как видите, такое решение оказалось существенно проще стандартного подхода. Здесь достаточно просто заметить,что сумма двух неотрицательных чисел равняется 0 только тогда, когда каждое из этих чисел имеет значение 0.
Пример № 2
Переходим ко второй конструкции:
\[\left| x-2 \right|=-{{x}^{6}}\]
На первый взгляд, можно сказать, что данная конструкция является простейшим уравнением. И, строго говоря, оно хорошо решается по выше записанной формуле, т.е. переходом от выражения с модулем функции к совокупности двух систем. Однако нас смущает степенная функция — степень слишком большая. Поэтому давайте заметим, что функция $f\left( x \right)={{x}^{6}}$ является не просто четной, но и еще неотрицательной на всей числовой оси. А это значит, что $-{{x}^{6}}$ всегда будет либо отрицательной, либо равняться 0. Однако с другой стороны от знака равенства у нас стоит модуль функции — а он всегда неотрицателен. Это значит что, слева значение больше или равно нулю, а справа — меньше или равно. И от нас требуется узнать, когда эти значения друг другу тождественны. Очевидно, что такими они могут быть только тогда, когда каждое из них равняется 0, потому что в противном случае они будут лежать по разные стороны от разделяющего 0, т.е. $\left| x-2 \right|$ будет постоянно отклоняться вправо, а $-{{x}^{6}}$ — влево. Поэтому наше выражением может быть переписано следующим образом:
\[\left\{ \begin{align}& \left| x-2 \right|=0 \\& -{{x}^{6}}=0 \\\end{align} \right.\]
Давайте решим эти конструкции:
\[\left\{ \begin{align}& x-2=0 \\& {{x}^{6}}=0 \\\end{align} \right.\]
Решаем каждое из этих выражений:
\[\left\{ \begin{align}& x=2 \\& x=0 \\\end{align} \right.\]
Мы получаем, что корень должен быть одновременно равен и 2 и 0. Это невозможно, поэтому решением данного выражения является пустое множество. Пусть вас не смущают подобные ответы при решении задач с модулями. Как и при работе с любыми другими функциями, накладывающими ограничения на область определения или значения в рамках задачи, в процессе решения сложных выражений с модулями функции вполне может оказаться, что этих решений просто не существует.
Ключевые моменты
- Сумма двух неотрицательных чисел равна нулю тогда, когда каждое из этих чисел равно нулю. В результате уравнение, которое само по себе далеко не тривиальное, разбивается на систему из двух отдельных уравнений, каждое из которых решается существенно проще.
- Тот факт, что модуль сам по себе является неотрицательным значением, можно использовать и иначе, например, когда с одной стороны стоит модуль функции (эта сторона неотрицательна), а с другой стороны — функция, которая меньше нуля или равна нулю. В этом случае все уравнение сводится к системе из двух уравнений, каждое из которых легко решается.
Как пример, второе вырадением может быть сведено к равенству первого вида следующим образом:
\[\left| x-2 \right|+{{x}^{6}}=0\]
Мы снова видим сумму двух функций, каждая из которых неотрицательна. Запомните этот прием, он очень эффективен при работе со всевозможными функциями, о которых точно известно, что они принимают лишнее отрицательное значение.
Смотрите также:
- Нестандартные уравнения с модулем

- Дробно-рациональные уравнения с модулем

- Как решать квадратные уравнения

- Пробный ЕГЭ 2012. Вариант 9 (без логарифмов)

- Тригонометрические функции

- Тест по задачам B14: средний уровень, 2 вариант

www.berdov.com
Модульные уравнения. Уравнения содержащие модуль.Решение уравнений с модулем.
Как решить простейшее модульное уравнение или уравнение содержащее модуль?
Обычно решение сводится к системе : Уравнения содержащие модуль
Уравнения содержащие модуль
Сразу рассмотрим на примере решение уравнений.
Пример №1:
Решите уравнение | x – 6| = 18.
Решение:
Выражение стоящее под модулем приравниваем к 0:
x-6=0
x=6
Отмечаем 6 на координатной прямой, далее проверяем знак на каждом из получившихся интервалах.
На интервале (-∞; 6) возьмем число 0 и подставим
0-6=-6 получилось отрицательное число, значит на этом интервале будет знак “ – ”
На интервале (6;+∞) возьмем число 7 и подставим
7-6=1 получилось положительное число, значит на этом интервале будет знак “ + ”
 Числовая прямая
Числовая прямаяТеперь решаем уравнения на каждом интервале.
(-∞; 6) здесь получился знак “ – ”, значит выражение под модулем поменяет знаки на противоположные:
-x+6=18
x=-12
Видно, что -12 лежит на интервале (-∞; 6) следовательно, является корнем уравнения.
(6;+∞) здесь получился знак “ + ”, значит выражение под модулем остается без изменения:
x-6=18
x=24
Видно, что 24 лежит на интервале (6;+∞) следовательно, является корнем уравнения.
Ответ: -12 и 24
Пример №2:
Решите уравнение | 2x – 5 |- | 4 — x | = -18.
Решение:
Выражения стоящие под модулем приравниваем к 0:
2x – 5 = 0 и 4 — x = 0
x=2,5 и x=4
Отмечаем x=2,5 и x=4 на координатной прямой, далее проверяем знак на каждом из получившихся интервалах.
На интервале (-∞; 2,5) возьмем число 0 и подставим в каждое выражение
2*0-5=-5 получилось отрицательное число, значит на этом интервале будет знак “ – ”
4-0=4 получилось положительное число, значит на этом интервале будет знак “ + ”
На интервале (2,5; 4) возьмем число 3 и подставим в каждое выражение
2*3-5=1 получилось положительное число, значит на этом интервале будет знак “ + ”
4-3=1 получилось положительное число, значит на этом интервале будет знак “ + ”
На интервале (4; +∞) возьмем число 5 и подставим в каждое выражение
2*5-5=5 получилось положительное число, значит на этом интервале будет знак “ + ”
4-5=-1 получилось отрицательное число, значит на этом интервале будет знак “ – ”
Теперь решаем уравнения на каждом интервале.
(-∞; 2,5) здесь получился знак “ – ” у выражения “ 2x – 5 ”, значит выражение под модулем поменяет знаки на противоположные и знак “ + ” у выражения “ 4 — x ”, значит выражение под модулем остается без изменения:
-2x + 5 — ( 4 — x ) = -18
-2x + 5 — 4 + x = -18
x=19
Видно, что 19 не лежит на интервале (-∞; 2,5) следовательно, не является корнем уравнения.
(2,5; 4) здесь получился знак “ + ” у обоих выражений, значит выражения под модулем останутся без изменений:
2x – 5 — ( 4 — x ) = -18
2x – 5 — 4 + x = -18
3x=-9
x=-3
Видно, что -3 лежит на интервале (2,5; 4) следовательно,не является корнем уравнения.
(4; +∞) здесь получился знак “ – ” у выражения “ 4 — x ”, значит выражение под модулем поменяет знаки на противоположные и знак “ + ” у выражения “ 2x – 5 ”, значит выражение под модулем остается без изменения:
2x – 5 — ( — 4 + x ) = -18
2x – 5 + 4 — x = -18
x=-17
Видно, что -17 лежит на интервале (4; +∞) следовательно,не является корнем уравнения.
Ответ: корней нет
Пример №3:
Решите уравнение ||x|-3|=15.
Решение:
Так как в правой части стоит простое число то распишем на два уравнения (раскроем внешний модуль):
|x|-3=15
|x|-3=-15
Перенесем в обоих уравнениях -3 вправо, получим:
|x|=15+3
|x|=-15+3
|x|=18
|x|=-12 (модуль не может равняться отрицательному числу, следовательно это уравнение не имеет решений)
Раскрываем модуль |x|=18
x=18
x=-18
Ответ: -18 и 18
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
tutomath.ru
Решение уравнения с модулем
 Решение уравнений с модулем. В этой статье я покажу алгоритм решения уравнений, которые содержат несколько выражений под знаком модуля, на примере решения уравнения уровня С1, а затем вы посмотрите ВИДЕОУРОК с подробным разбором тригонометрического уравнения с модулем.
Решение уравнений с модулем. В этой статье я покажу алгоритм решения уравнений, которые содержат несколько выражений под знаком модуля, на примере решения уравнения уровня С1, а затем вы посмотрите ВИДЕОУРОК с подробным разбором тригонометрического уравнения с модулем.
Давайте решим уравнение:

Вспомним, что модуль раскрывается по такому правилу:

Говоря человеческим языком, модуль выражения равен самому выражению, если оно неотрицательно, и выражению с противоположным знаком, если оно меньше нуля.
Таким образом, перед нами стоит задача раскрыть все модули в соответствии со знаками подмодульных выражений.
Будем следовать такому алгоритму:
1. Определим, в каких точках каждое подмодульное выражение меняет знак. Для этого приравняем каждое подмодульное выражение к нулю:
 ,
, 

 ,
, 
Мы получили три точки.
2. Нанесем их на числовую ось:

Эти три числа разбили числовую ось на четыре промежутка:


 ,
, 
 ,
, 


Обратите внимание, что мы включили крайние точки промежутков в оба промежутка. Ничего страшного не случится, если мы эти точки учтем два раза, главное, о них не забыть.
3. Теперь рассмотрим знаки подмодульных выражений на каждом промежутке:
Выражение  меняет знак в точке
меняет знак в точке  . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:
. Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:

Выражение  меняет знак в точке
меняет знак в точке  . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:
. Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:

Выражение  меняет знак в точке
меняет знак в точке  . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:
. Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:
 Мы получили знаки всех подмодульных выражений на каждом промежутке. Теперь раскроем модули на каждом промежутке с учетом этих знаков.
Мы получили знаки всех подмодульных выражений на каждом промежутке. Теперь раскроем модули на каждом промежутке с учетом этих знаков.
Наше уравнение «распадается» на четыре уравнения по количеству числовых промежутков.
4. Решим уравнение на каждом промежутке:
1. 



Решение уравнения на первом промежутке 
2.Раскроем модули на втором промежутке:



Мы получили, что второе уравнение системы является тождеством, то есть второе равенство верно при любом действительном значении  . Следовательно, решением системы будут те значения неизвестного, которые удовлетворяют первому неравенству:
. Следовательно, решением системы будут те значения неизвестного, которые удовлетворяют первому неравенству:
 .
.
3. Раскроем модули на третьем промежутке:




Решение уравнения на третьем промежутке: 
4. Раскроем модули на четвертом промежутке:




Решение уравнения на четвертом промежутке: 
Заметим, что решения нашего уравнения на каждом промежутке принадлежали этому промежутку, то есть удовлетворяли неравенству каждой системы. Однако, так бывает не всегда, и если корень уравнения не удовлетворяет неравенству, значит, соответствующая система не имеет решений.
5. Теперь объединим полученные решения, и запишем ответ:
Ответ: -6≤х≤0, х=12
А сейчас я предлагаю вам посмотреть ВИДЕУРОК с подробным решением уравнения уровня С3:

И.В. Фельдман, репетитор по математике.
ege-ok.ru
Задача с параметром и модулем
Задачи с параметром – наиболее сложные, но зато и самые интересные. Решение такой задачи – всегда исследование, всегда приключение. Тогда вперед, к приключениям!
Задача: Найти все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение
![Rendered by QuickLaTeX.com \[\mid x^2-36 \mid - 8 \mid x-p \mid +2p=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d42c063eace739bbc4b73d3e9544dd29_l3.png)
Относительно переменной  имеет ровно 4 решения.
имеет ровно 4 решения.
Применим графическое решение. Запишем иначе:
![Rendered by QuickLaTeX.com \[\mid x^2-36 \mid = 8 \mid x-p \mid -2p\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-82321bb371a206baa21e08d0a966e5c5_l3.png)
Слева имеем параболу, график которой, вследствие наличия модуля, располагается только в верхней полуплоскости, вся его «подводная» часть отражена вверх:

Рисунок 1. Парабола “в модуле”
Справа имеем «галочку», вершина этой галочки будет перемещаться по прямой  . То, что график выглядит, как «галка», понятно, но как была установлена траектория движения ее вершинки? А вот как:
. То, что график выглядит, как «галка», понятно, но как была установлена траектория движения ее вершинки? А вот как:
![Rendered by QuickLaTeX.com \[y=8 \mid x-p \mid -2p\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8712ab2223acffa07484765bb835d22f_l3.png)
Модуль может быть раскрыт как с плюсом, так и с минусом в зависимости от знака подмодульного выражения:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ y=8( x-p) -2p }}\\{ y=8( p-x) -2p }\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ef18de136ad0418bd7f04e9a3901e655_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ y=8 x-8p -2p }}\\{ y=8p-8x -2p }\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-57a9cf5578835789774bc013eefe1fab_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ y=8x-10p}}\\{ y=6p-8x}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d1b78847e2d39c26e5942232f971808e_l3.png)
Вычитаем уравнения:
![Rendered by QuickLaTeX.com \[16x=16p\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-98588989b614808f0e0cd37f5bb889bd_l3.png)
![Rendered by QuickLaTeX.com \[x = p\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-40bdb0fffd30b32ad15ad1999067e0f1_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[y=8x-10x=-2x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3b6a92855c347505d132272a98ec33a1_l3.png)
Теперь исследуем полученную систему двух графиков. Нас устраивают случаи, когда «галка» 4 раза пересекает параболу. Начинаем двигать нашу галочку слева направо:

Рисунок 2. Галка спускается вниз. Два корня (два пересечения)
В указанном положении будем иметь два корня. Поэтому продолжаем двигать галку вниз:

Рисунок 3. Галка спускается ниже. Три корня (два пересечения и касание)
Когда «галка» своим правым крылом коснется параболы, ее отраженного, внутреннего кусочка, у нас получится три решения. А чуть только мы сдвинемся еще чуть ниже – уже 4. Определим значение параметра при касании, это начальная точка того интервала, который нас интересует.
Определить значение параметра в этом случае просто. Правое крыло «галки» описывается уравнением:  . При касании ордината точки, принадлежащей параболе, и ордината точки, принадлежащей прямой, одинаковы, поэтому приравняем ординаты. Та часть параболы, которой касается прямая, описывается уравнением:
. При касании ордината точки, принадлежащей параболе, и ордината точки, принадлежащей прямой, одинаковы, поэтому приравняем ординаты. Та часть параболы, которой касается прямая, описывается уравнением:
![Rendered by QuickLaTeX.com \[y=36-x^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6f8d6762799979a86009fd6d9d45031c_l3.png)
Тогда, приравняв ординаты, получим:
![Rendered by QuickLaTeX.com \[36-x^2=8x-10p\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-848d3d18370ee77aa85cde60eb40590d_l3.png)
![Rendered by QuickLaTeX.com \[x^2+8x-10p-36=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5895814123356298ef588f587b3859f8_l3.png)
Если общая точка одна, то дискриминант будет равен 0:
![Rendered by QuickLaTeX.com \[D=b^2-4ac=64-4(-10p-36)=64+40p+144=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9af7f2f0843de42b6eef06d16d48cd53_l3.png)
![Rendered by QuickLaTeX.com \[40p=-208\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0682faed0deef86cf582564a31666b03_l3.png)
![Rendered by QuickLaTeX.com \[p=-5,2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3e0e3b50f254fdaf95adb03ee05069db_l3.png)
Сама эта точка нас еще не устраивает, но значения параметра, большие  , уже подходят нам. Выясним, до какого момента будем иметь 4 пересечения:
, уже подходят нам. Выясним, до какого момента будем иметь 4 пересечения:

Рисунок 4. Три корня.
В показанном положении снова будем иметь три пересечения. В этот момент правое крыло «галки» проходит через точку  , тогда
, тогда
![Rendered by QuickLaTeX.com \[8x-10p=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d3152aa05d02f3b368c780805dad2001_l3.png)
![Rendered by QuickLaTeX.com \[8 \cdot 6-10p=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bb0dfcebfaafa489d28945648ba40387_l3.png)
![Rendered by QuickLaTeX.com \[p=4,8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c6bf5e9570186ff4e07068c1fd0fdc38_l3.png)
Итак, найден интервал решений:  .
.
Однако, вдруг это еще не все решения? Сдвинем «галку» еще ниже:

Рисунок 5. Снова три корня.
Видим, что снова, при прохождении левого крыла «галки» через точку  , появились три корня. Небольшой сдвиг еще чуть ниже даст четыре корня, и эта ситуация нас устраивает, следовательно, имеем еще один интервал решений. Определим значение параметра. Левое крыло «галки» описывается уравнением:
, появились три корня. Небольшой сдвиг еще чуть ниже даст четыре корня, и эта ситуация нас устраивает, следовательно, имеем еще один интервал решений. Определим значение параметра. Левое крыло «галки» описывается уравнением:
![Rendered by QuickLaTeX.com \[y=6p-8x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6053424b920019a22b570e4f23e58d71_l3.png)
Подставляем координаты точки в уравнение:
![Rendered by QuickLaTeX.com \[0=6p-8 \cdot 6\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b3783422b08e6bbb07d15e178735e632_l3.png)
![Rendered by QuickLaTeX.com \[p=8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cd33ad7e791e85e8aa36ecef9c0d8bd2_l3.png)
Сдвигаем «галку» еще ниже, и получаем касание:

Рисунок 6. Два пересечения и касание
Приравниваем ординаты:
![Rendered by QuickLaTeX.com \[36-x^2=6p-8x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b39fe7637442516ffb722c5d0a501971_l3.png)
![Rendered by QuickLaTeX.com \[x^2-8x+6p-36=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7f053ca504943de0fcade529c3fc1947_l3.png)
Если общая точка одна, то дискриминант будет равен 0:
![Rendered by QuickLaTeX.com \[D=b^2-4ac=64-4(6p-36)=64-24p+144=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d0376f111366eb66cf44bd168df4eda2_l3.png)
![Rendered by QuickLaTeX.com \[24p=208\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a833b910501e921eb3fd15f06eb74124_l3.png)
![Rendered by QuickLaTeX.com \[p=8\frac{2}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-487bc22172b8f07d071c9c3be1b41dff_l3.png)
Полученное значение параметра нас уже не устраивает: при таком  снова имеем три решения.
снова имеем три решения.
Вот и второй интервал: 
Ответ:  .
.
easy-physic.ru
РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ

Решение уравнений
с модулем.
МБОУ СОШ №46
учитель математики
Дряева Минат Георгиевна.
Г. Владикавказ
2014г.
Слайд 1 . Основные этапы урока:
1⁰. Мотивация учения.
2⁰. Ознакомление учащихся с целями и задачами.
3⁰. Повторение теоретических знаний по данной теме.
4⁰. Устная работа с элементами исследования.
5⁰. Совместная работа учителя и учащихся.
6⁰. Минута отдыха.
7⁰. Нестандартные приемы решения уравнений с модулем.
8⁰. Разноуровневая самостоятельная работа.
9⁰. Постановка домашнего задания.
10⁰. Подведение итогов урока.
Слайд 2 . Во всем дойти до самой сути.
Цель: Обобщение и систематизация, расширение и углубление знаний.
Задачи: 1. Проанализировать различные способы решения уравнений с модулем.
2. Сформировать навык решения различных типов уравнений с модулем.
3. Заинтересовать учащихся в изучении данной темы.
Тип урока: Урок совершенствования знаний (с элементами исследования).
Оборудование: Компьютер, мультимедийный проектор, интерактивная доска,
опорные конспекты, оценочные листы.
Ход урока:
1⁰. Мотивация учения.
Подарите улыбки друг другу ,
Веселыми будьте всегда,
И этим добьётесь удачи,
Успехов во всем и всегда.
А успех нам сегодня так необходим. Прочтите эпиграф , так как он тесно связан с темой нашего урока.
Тема «Решение уравнений с модулем» выбрана мною не случайно. Она является одной из самых сложных тем. В школьной программе ей, на мой взгляд, уделяется недостаточно внимания, не разобраны в системе методы и приемы решения задач с модулем. У многих модуль вызывает страх. Есть замечательные задания с модулем, у которых своя специфика. Попробуем разобрать некоторые из них.
2⁰. Ознакомление учащихся с целями и задачами.
Сегодня мы с вами повторим основные типы уравнений с модулем и проанализируем различные способы их решения.
Слайд 3 . 3⁰. Сначала повторим и систематизируем теоретические знания по данной теме.
Учитель: Дайте определение модуля или абсолютной величины.
Учащиеся :|x|=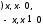 .
.
Учитель: Назовите основные свойства модуля.
Учащиеся: |a|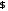 0,
0,
|a|²= a²
|a*b|=|a|*|b|,
|a/b|=|a|/|b|, b≠0
Слайд 4. 4⁰. Устная работа с элементами исследования.
Постановка проблемы:
Для каждого из уравнений указать стрелками соответствующий тип уравнения.
Уравнения
Тип уравнения
Способ решения
|3x-5|=2
|4-3x|=-1
|9-5x|=|7x-5|
|11-3x|=3-2x
2x²+3|x-1|+2=0
|3-x|+|x-5|=1
 ² = 16
² = 16
|f(x)| = a, a- const
Если а>0, то 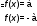
Если а=0, то f(x) = 0
Если а < 0, то корней нет.
|f(x)| = g(x)
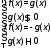
|f(x)| = |g(x)|
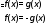
|f1(x)|+ |f₂(x) | +…+|fn(x)|=g(x)
Метод интервалов.
Ответы учащихся:
— Уравнение 1 можно решить, используя определение модуля.
— Уравнение 2 не имеет решений т.к. модуль – величина неотрицательная.
С помощью рассуждений сделаем выводы:
Если |f(x)| = |g(x)| f²(x) – g² (x) = (f (x) – g(x)) (f(x) + g(x)) = 0
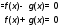
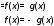
Таким образом, указали способ решения уравнения 3 .
Если |f(x)| = g(x), то g(x)

По определению модуля 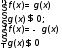
Таким образом, указали способ решения уравнения 4.
— Как же можно решить уравнение 5?
— Рассмотрим два случая т.е. воспользуемся определением модуля.
x-1 0 и x-1<0.
0 и x-1<0.
— Уравнение 7 разве имеет отношение к теме «Модуль»?
— Да, т.к. по свойству корней  ² = |x|, и получим уравнение, содержащее модуль.
² = |x|, и получим уравнение, содержащее модуль.
— А как решить уравнение 6?
— Методом интервалов.
5⁰. Совместная работа учителя и учащихся
Осторожно! Простая задача!
Учиться плавать можно по-разному. Например, сразу броситься в глубокое место, или начать с «лягушатника». Так обстоит дело и в решении сложных задач. Мы пойдем по второму пути, не забывая при этом, что захлебнуться можно и в ванной.
(решение уравнений у доски и в тетрадях).
Пример 1⁰.
|x-3| = 11 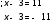
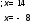
Ответ: -8;14
Пример 2⁰.
|2x-5| = x-1 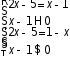
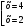
Ответ: 2;4
Пример 3⁰.
|x+3| = |2x-1| 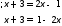
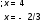
Ответ: -2/3;4
Слайд 6. Пример 4⁰.
|x²-1|+|x²-4|=3.
Воспользуемся методом интервалов. Для этого удобно пользоваться алгоритмом.
(см. опорный конспект).
x²-1=0, x= ±1,
x²-4=0, x= ±2.
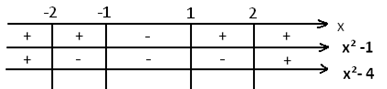
Слайд 7.
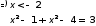
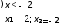
Ответ: Ø.
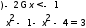
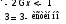
Ответ: -2 x<-1
x<-1
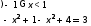

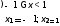
Ответ: x=-1
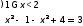
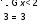
Ответ: 1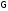 x<2
x<2
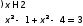
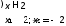
Ответ: x=2
Решив совокупность данных систем, получим:
Ответ: [-2;-1] U {-1} U [1;2) U {2} или [-2;-1] U [1;2]
Этот метод является универсальным методом решения уравнений всех видов, но иногда оказывается не самым рациональным.
Мы проанализировали различные типы уравнений, решаемые с помощью равносильных преобразований.
Слайд 8. Более наглядную картину дает графическое исследование данного уравнения.
Для построения графика функции y=|x²-1|+|x²-4| воспользуемся схемой знаков на рисунке.
y=|x²-1|+|x²-4|= 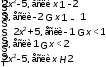
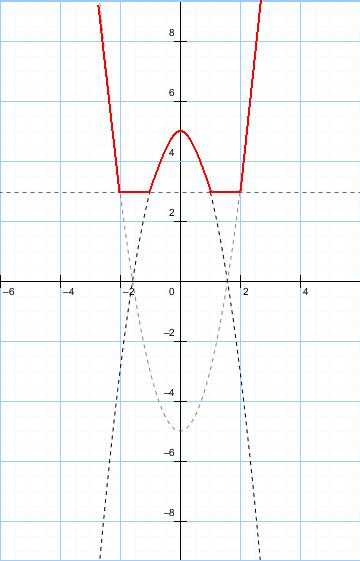
2) Проведем прямую y=3.
По графику очевидно, что графики левой и правой части совпадают (пересекаются) на множестве
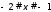 и
и 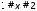
Ответ: [-2;-1] U [1;2]
Мы еще вернемся к данному уравнению.
Слайд 9. 6⁰. Минута отдыха.
— Примем царственную позу. Спина прямая.
— Три раза вдохнем.
— Помассажируем кончики пальцев каждой руки.
— Поставим указательный палец на точку между бровями и массажируем три раза. — Роняем руки.
— Трясем кистями.
— Стряхиваем воду с пальцев.
— Поднимаем и опускаем плечи.
— Твердые и мягкие руки.
— Мельница.
Продолжаем урок.
7⁰. Рассмотрим нестандартные приемы решения уравнений с модулями.
«Умный гору обойдет».
Зачастую по закону зловредности короткое решение более замаскировано, чем длинное. В тех случаях, когда выбранный путь решения сопряжен с большими техническими сложностями, бывает полезно еще раз проанализировать условие задачи, попытаться найти ее конкретные особенности, позволяющие обнаружить нетрадиционную идею.
Слайд 10. Когда модуль можно не раскрывать.
Решение некоторых уравнений может значительно сократить знание ряда свойств модуля:
1. |a|+|b| = a+b a≥0, b≥0;
2. |a| + |b| = |a+b| ab≥0;
3. |a| + |b| = |a-b| ab≤0;
4. |a| — |b| = |a-b| b (a-b) ≥0;
5. |a| — |b| = |a+b| b(a+b) ≤0
(доказательство рассмотрим на факультативных занятиях).
Вернемся к примеру 4:
|x²-1|+|x²-4|=3.
-Посмотрите внимательно. Что вы заметили?
Кто-нибудь из учеников обязательно заметит, что
(x²-1) – (x²-4) = 3 т.е. выполняется условие |a|+|b| = |a-b|.
Применив свойство 3, получим неравенство
(x²-1) (x²-4)≤0.
Решим его методом интервалов.
x²-1=0, x₁=1, x₂=-1
x²-4=0, x₃=2, x₄=-2.

x є [-2;-1] U [1;2].
Ответ: [-2;-1] U [1;2].
Данное уравнение решили тремя способами. Какой способ
— Самый трудный?
— Самый простой?
Пример 5.
|x-2|+|2-3x|=2|x|
Заметим, что |x-2|+|2-3x| = |(x-2)+(2-3x)|=|-2x|=2|x|, т.е. выполняется условие
|a|+|b|=|a+b|.
Используя свойство 2, будем иметь неравенство:
(x-2)(2-3x)≥0,
(x-2)(x-2/3)≤0.
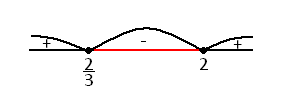
x є [2/3;2]
Ответ: [2/3;2].
Слайд 11. Пример 6.
|x²+6|-|x²-x+6|=|x|
Имеем: |x²+6|-|x²-x+6|=|(x²+6)-(x²-x+6)|=|x|, т.е выполняется условие
|a|-|b|=|a-b|.
Использую свойство 4, получим неравенство x (x²-x+6)≥0
Решив его, получим x≥0.
Ответ: [0;+∞)
8⁰. Разноуровневая самостоятельная работа.
Учащимся выдаются опорные конспекты, рабочие листы и оценочные листы.
(Индивидуальная консультация учителя по мере возникновения затруднений).
Слайд 12. Самостоятельная работа.
1 – ый уровень.
Цель: закрепить умение решать простейшие уравнения, содержащие модули, вида: |f(x)|=a, a –const
Вариант-1
Решите уравнения:
|x|=5 (1 балл)
x= ±5,
Ответ: x₁=-5, x₂=5.
|x+3|=-2 (1 балл)
Нет корней, т.к. модуль – величина неотрицательная.
Ответ: нет корней.
|x²-4|= 0 (1 балл)
x²-4=0
x=±2
Ответ: x₁=-2; x₂=2.
Вариант-2
Решите уравнение:
|x|=8 (1 балл)
x=±8
Ответ: x₁=-8; x₂=8.
2 .|x+7|=-3 (1 балл)
Нет корней, т.к. модуль – величина неотрицательная.
Ответ: нет корней.
3. |x²-9|=0 (1 балл)
x²-9=0,
x=±3
Ответ: x₁=-3; x₂=3.
Проверьте и оцените свою работу (см. на экран). Проставьте количество набранных баллов в оценочный лист.
2 – ой уровень
Цель: закрепить навыки решения уравнений вида:
|f(x)|= g(x) и |f(x)|=|g(x)|.
Вариант – 1
|2x-3|=6-x (2 балла)
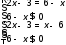
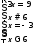
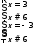
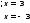
Ответ: x₁=-3, x₂=3
|x-2|=|2x-1| (2 балла)
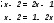
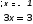
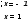
Ответ: x₁=-1, x₂=1.
Вариант – 2
Решение уравнений.
|3x-4|=2x-6 (2 балла)
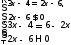
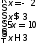
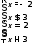
Ответ: нет корней.
|2x-3|=|x-3| (2 балла)
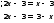
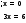
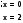
Проверьте и оцените свою работу (см. на экран). Проставьте количество набранных баллов в оценочный лист.
Ответ: x₁=0, x₂=2
3 – ий уровень
Цель: сформировать навык решения уравнений с использованием свойств модуля.
Вариант -1
Решите уравнение:
|2x+5|+|x-3|= 3x+2 (3 балла)
Заметим, что
(2x+5)+(x-3)=3x+2, т.е. выполняется условие
|a|+|b|=a+b
По свойству 1, имеем: 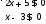
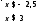 x≥3
x≥3
Ответ: x≥3
2 .Используя свойства, освободитесь от знака модуля .
|x²+x-2|+|x-3|=x²+1 ( 3 балла)
Заметим, что
(x²+x-2)-(x-3)=x²+1, т.е. выполняется условие
|a|+|b|=|a-b|.
Используя свойство 3, получим неравенство
(x²+x-2)(x-3)≤0
Ответ: (x²+x-2)(x-3)≤0.
Вариант – 2
1. Решите уравнение
|x-2|+|x+2|=2|x| (3 балла)
т.к. |x-2|+|x+2|=|(x-2)+(x+2)| = 2|x|, то выполняется условие |a|+|b|= |a+b|.
Используя свойство 2, получим неравенство (x-2)(x+2)≥0
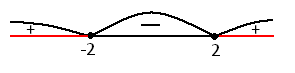 xє (-∞;-2]U [2;+∞)
xє (-∞;-2]U [2;+∞)
Ответ: (-∞;-2]U [2;+∞)
2. Используя свойства, освободитесь от знака модуля
|4x²-1|-|x²-4|=|5x²-5| ( 3 балла)
Заметим, что |4x²-1|-|x²-4|=|4x²-1+x²-4| = |5x²-5| т.е. выполняется условие
| a|-|b|=|a+b|.
Используя свойство 5, получим неравенство:
(x²-4)(5x²-5)≤0. Ответ: (x²-4)(5x²-5)≤0.
Проверьте и оцените свою работу (см. на экран). Проставьте количество набранных баллов в оценочный лист.
Молодцы! Вы прошли 3 уровня усвоения материала. Посчитайте количество набранных баллов.
Если вы набрали от 11 до 13 баллов, то получаете оценку «5».
Если вы набрали от 7 до 10 баллов, то получаете оценку «4».
Если вы набрали от 5 до 6 баллов, то получаете оценку «3».
Сдайте оценочные листы учителю.
Слайд 13. 9⁰. Домашнее задание:
Трем группам (по 2-3 учащихся в каждой) подготовить презентации по темам:
1) Использование понятия расстояния при решении уравнений с модулем.
2) «Вложенные модули»
3) «Красивейшие уравнения».
Остальным — решить уравнения:
1. |x-5|=1
2. |x²-3x|=2x-4
3. |x-2|=|2x-1|
4. |2x-1|+|x|= -5
5. |x-4|+|x-5|=|2x-9|
6. |x²-9|+|x²-4x+3|=0
7. |x-1|+|x-2|=x+3
Слайд 14. 10⁰. Подведение итогов урока:
— Какие типы уравнений мы повторили на уроке?
— какие методы решения уравнений с модулем вы можете выделить?
— какой способ самый эффективный?
— решение каких уравнений вам показалось сложным?
— чему надо уделить особое внимание?
Слайд 15. Используемая литература:
И.И. Гайдуков. «Абсолютная величина»
Изд. «Просвещение», 1968 г.
2) Г.И.Ковалева. «Тренировочные тематические задания повышенной сложности».
Изд. «Учитель», 2009 г.
3) С.В.Кравцев. «Методы решения задач по алгебре».
Изд. «Экзамен», 2005 г.
4) П.И. Горнштейн, А.Г. Мерзляк. «Экзамен по математике и его подводные рифы».
Изд. «Илекса», 2004 г.
Пояснительная записка.
Данный урок проводится в 11-ом классе в 4-ой четверти при повторении. Урок рассчитан на класс, в котором есть учащиеся с математическими способностями.
infourok.ru
УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ – Репетитор по математике
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2016-04-24
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2016-04-2424 Апр 2016
13 Задание (2016) (C1)Диагностические работыУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Задание 13 из Досрочного экзамена, резерв. 16.04.2016
Задание 13. а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку [ ].
].
Решение.
показать
а) Введем замену:  , получим уравнение:
, получим уравнение:

Разложим левую часть на множители способом группировки:


 или
или 
 или
или  .
.
Вернемся к исходной переменной:
 или
или  :
:
Отметим эти значения на линии тангенсов и получим корни:

Корни, лежащие во второй и третьей четверти отстоят от корней, лежащих в первой и четвертой четвертях на промежуток, равный  , то есть на период функции
, то есть на период функции  :
:

б) Выберем корни, принадлежащие промежутку [ ].
].
Этот промежуток выделим дугой:

Получим значения  , принадлежащие указанному промежутку:
, принадлежащие указанному промежутку:




Ответ: а) 
б) 
И.В. Фельдман, репетитор по математике
Инна | Отзывов (6)
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-20
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-2020 Ноя 2014
ВИДЕОЛЕКЦИИВИДЕОТЕКАУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеотека. Построение графиков функций, содержащих модуль
1. Видеолекция. Построение графиков функций, содержащих модуль Далее
Инна | Отзывов (2)
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-20
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-2020 Ноя 2014
ВИДЕОТЕКАВИДЕОУРОКИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеотека. Решение уравнений и неравенств с модулем
1. Видеолекция. Решение уравнений и неравенств с модулем. Далее
Инна | Отзывов нет
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-20
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-11-2020 Ноя 2014
ВИДЕОТЕКАВИДЕОУРОКИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеотека. Решение простейших уравнений с модулем.
Инна | Отзывов нет
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-04-14
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-04-1414 Апр 2014
13 Задание (2016) (C1)ТРИГОНОМЕТРИЯУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Тригонометрическое уравнение с модулем
Решим тригонометрическое уравнение с модулем:

Так как уравнение содержит модуль, нам нужно этот модуль раскрыть по определению модуля.
Рассмотри два случая: Далее
Инна | Отзывов (5)
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-03-31
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2014-03-3131 Мар 2014
15 Задание (2016) (C3)РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Решение системы неравенств с модулем
Решим систему неравенств с модулем из варианта №50 А. Ларина.
 Далее
Далее
Инна | Отзывов (2)
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-11-19
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-11-1919 Ноя 2012
ВИДЕОЛЕКЦИИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеолекция 10. Комбинированные методы решения уравнений и неравенств с модулем
Содержание видеолекции:
1. Как правильно раскрывать модуль с учетом ОДЗ.
2. Решение уравнения

3. Как правильно учитывать условие существования корней при раскрытии модуля.
Далее
Инна | Отзывов нет
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-10-17
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-10-1717 Окт 2012
18 Задание (2015) (C6)ВИДЕОЛЕКЦИИЗАДАЧИ С ПАРАМЕТРОМУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеолекция 7. «Графический метод решения задач с параметрами»
В видеолекции подробно разобрано 7 примеров задач с параметрами, начиная с очень простых и заканчивая реальными заданиями С5 из ЕГЭ. Далее
Инна | Отзывов нет
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-10-17
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-10-1717 Окт 2012
18 Задание (2015) (C6)ВИДЕОЛЕКЦИИЗАДАЧИ С ПАРАМЕТРОМУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Видеолекция «Графический метод решения задач с параметрами»
В видеолекции «Графический метод решения задач с параметрами» подробно разобрано 7 примеров задач с параметрами, начиная с очень простых и заканчивая реальными задачами из Задания 18 ЕГЭ по математике. Далее
Инна | Отзывов нет
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-09-09
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 2012-09-0909 Сен 2012
ВИДЕОЛЕКЦИИОНЛАЙН КУРСЫУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМФУНКЦИИ И ГРАФИКИ
Видеолекция «Построение графика функции, содержащей модуль»
Содержание Видеолекции «Построение графика функции, содержащей модуль»:
1. График функции y=|x|.
2. Построение графика функции y=|x+3|+|2x+1|-x с помощью раскрытия модуля.
3. Построение графика функции y=|x+3|+|2x+1|-x по четырем точкам. Далее
Инна | Отзывов (62)
ege-ok.ru
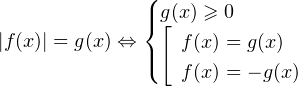
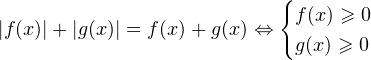
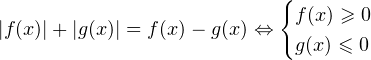
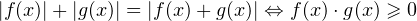

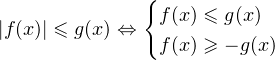

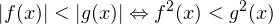



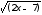 ² = 16
² = 16