Закон Архимеда. Условие плавания тел | LAMPA
Выталкивающую силу называют силой Архимеда, а её формулу, которую мы только что вывели, – законом Архимеда:
FАрхимеда=ρжидкостиgVтелаF_{Архимеда} = \rho_{жидкости} gV_{тела}FАрхимеда=ρжидкостиgVтела
Обратите внимание на то, от каких величин зависит сила Архимеда.
1. От плотности жидкости. Чем плотнее жидкость, тем сильнее она будет выталкивать тело. Поэтому, например, в солёной морской воде плавать легче, чем в пресной речной.

2. От ускорения свободного падения. Фактически – от того, насколько сильно Земля притягивает. Можно сделать вывод, что на других планетах сила Архимеда будет другой – потому что там у ускорения свободного падения другие значения.
3. От объёма тела. Чем больше объём тела, тем сильнее его выталкивает жидкость. Вспомните, как легко удержать под водой маленький мячик (например, мячик для игры в настольный теннис) и как сложно сделать то же самое с большим надувным мячом для игр на пляже.

Закон Архимеда справедлив для тела любой формы – не только кубика. И в формуле будет использоваться объем погруженного тела.

В формуле фигурирует не объём всего тела, а только той его части, что погружена в воду.

То есть, если какая-то часть тела «выглядывает» из воды – она в формуле закона Архимеда не участвует.
Архимедова сила. Физика. 7 класс. Конспект урока
Тип урока: комбинированный.
Цели:
- образовательная: обеспечить усвоение учащимися формулы для расчета архимедовой силы.
- воспитательные: показать связь изучаемого материала с жизнью; познакомить учащихся с практическими применениями закона в технике
- развивающие: развитие познавательной активности и формирование мотивации к дальнейшему применению теоретических знаний в практике; в целях развития научного мировоззрения учащихся, показать роль физического эксперимента в физике
Задачи:
- Сформировать понятие об архимедовой силе, а так же умение выводить формулу, выражающую зависимость этой силы от плотности жидкости (газа) и объема тела, на основе закона Паскаля;
- Продолжить развитие логического мышления, монологической речи и зрительной памяти
- Формирование умений строить определения физических понятий, выбирать рациональные способы выполнения экспериментов.
ТСО: компьютер, проектор, магнитофон.
Наглядность: портрет Архимеда (фотографии опыта Плато – взяты из личной коллекции).
Оборудование и материалы: ведерко Архимеда, стакан с водой, стакан с крепким раствором соли, штатив с муфтой и лапкой, сосуд с отливом, свеча, спички, динамометр, рычаг, два тела равной массы, но неравного объема, резиновый мяч, алюминиевый цилиндр, картофелина, мензурка с касторовым маслом, краски, кисточка.
Для фронтального опыта:
- Мензурка (15 шт.)
- Вода в стакане (15 шт.)
- Динамометр (15 шт.)
- Штатив с муфтой и лапкой (15 шт.)
Использованные источники:
- Крис Окслед, Корин Стокли Физика. Школьный иллюстративный справочник.- М.: «Росмэн», 2000
- Л. А. Друянов Законы природы и их познание книга для внеклассного чтения. – М.: «Просвещение», 1992
- Л. А. Горелов Занимательные опыты по физике. – М.: «Просвещение», 1985
Ресурсы Интернет:
- http://ru.wikipedia.org/wiki
- http://class-fizika.narod.ru
- http://www.physbook.ru/index.php/Kvant.
Ход урока
Эпиграф к уроку:
«Кто овладел творениями Архимеда, будет
меньше удивляться открытиям самых
великих людей нашего времени».Лейбниц
I. Вводное слово учителя
Учитель: Мы в нашей жизни часто сталкиваемся с законом Архимеда: наблюдаем, как плавают рыбки, видим передвижение по реке лодок, пароходов, любим сами плавать, наблюдаем, как в воздухе летают воздушные шары. Сегодня мы с вами еще раз поговорим о законе Архимеда, о том, как он был открыт и как проявляется (зачитываем эпиграф).
II. Повторение (фронтальный опрос)
Учитель: Заполните таблицу:
Величина |
Обозначение |
Формула |
Единицы измерения |
Прибор |
|
1. Объем |
V |
V = Sh |
м3 |
мензурка, линейка |
|
2. Масса |
m |
m = rV |
кг |
весы |
|
3. Вес |
P |
P = mg |
H |
динамометр |
|
4. Давление в жидкостях |
P |
P = rgh |
Па |
манометр |
- Как распространяется давление внутри жидкости?
- Чем объясняется увеличение давления жидкости с глубиной?
- Как распределяется давление в жидкости на одном и том же уровне?
- Какие силы действуют на тело, погруженное в жидкость?
III. Актуализация знаний
Вода – самое удивительное вещество! Одна из основных составляющих жизни. Тончайшим слоем покрывает она 2/3 поверхности земного шара, разделяя континенты. Вода присутствует и в атмосфере в виде пара и мельчайших капелек, из которых состоят дождевые облака. Круговорот воды в природе – это могучие реки Сибири и хрустальные звенящие весенние ручейки, это дожди, ливни, снегопады, утренние туманы и капельки росы на зеленой траве. Изучая химию, биологию, географию, физику, вы будете знакомиться со свойствами воды и не раз поразитесь тому, насколько тесно и неожиданно связана она с нашей жизнью, увидите самые разные ее стороны. Сегодня вы познакомитесь подробно с одним из свойств воды. Хотите узнать каким?
Опыт 1
Погружаем мяч полностью в воду и быстро убираем руку. Мяч «выпрыгивает» из воды.
Учитель: Почему мяч всплыл на поверхность воды?
Ученик: На мяч подействовала сила.
Учитель: Совершенно верно: подействовала сила, которая вытолкнула мяч из воды. Назовем ее выталкивающая сила. Опустим в тот же аквариум цилиндр (Al). Тело утонуло. Действует ли выталкивающая сила в этом случае?
Учитель: Подумайте, как с помощью приборов, которые находятся у вас на столах, проверить действует ли выталкивающая сила на алюминиевый цилиндр?
Опыт 2
Подвесим тело к пружине динамометра. Заметим его показание, затем опустили тело в воду и увидим, что показания динамометра уменьшились.
Сделаем вывод: На любые тела, погруженные в воду, действует выталкивающая сила.
Учитель: Давайте экспериментально выясним, от каких величин зависит выталкивающая сила, а от каких не зависит.
Опыт 3
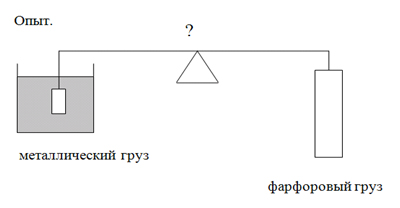
На равноплечном рычаге уравновесили в воздухе 2 груза (металлический и фарфоровый). Подставим один из сосудов, заполненных водой, под металлический груз.
Учитель: Почему нарушается равновесие?
Ответ: На груз, погруженный в воду, действует выталкивающая сила.
Опыт 4
То же самое проделать со вторым грузом.
Учитель: Почему нарушается равновесие?
Ответ: равновесие нарушается, т.к. на другой груз действует выталкивающая сила.
Опыт 5
К обоим грузам поднести сосуды с водой.
Учитель: Почему нарушается равновесие уравновешенного в воздухе рычага с грузами одинакового веса, но различного объема, помещенными в жидкость?
Ответ: На тела действуют различные выталкивающие силы.
Учитель: Почему? От чего они зависят?
Ответ: выталкивающая сила зависит от объема тела (или части тела), погруженного в жидкость. Чем больше объем тела, тем больше выталкивающая сила.
Опыт 6
Учитель: Перед вами два стакана с водой. В первом – картофелина плавает, а во втором – тонет. Как вы думаете, почему?
Ответ: В первом стакане находится крепкий раствор соли, а соленая вода имеет бòльщую плотность, чем пресная вода.
Ответ: В первом.
Учитель: Сделайте вывод, от чего зависит выталкивающая сила?
Вывод: выталкивающая сила зависит от плотности жидкости. Чем больше плотность жидкости, тем больше выталкивающая сила.
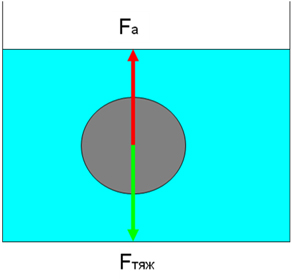
Выталкивающая (Архимедова) сила
Зависит от: |
Не зависит от: |
|
От объёма, погружённой в жидкость, части тела. |
От глубины погружения. |
|
От плотности жидкости, в которую погружено тело. |
От веса тела. |
Учитель: Я предлагаю вам вывести формулу, по которой можно рассчитать выталкивающую силу.
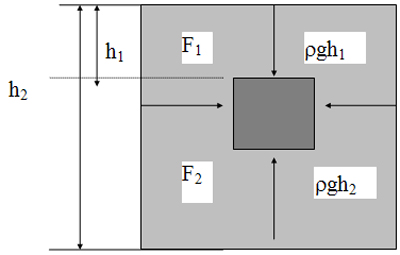
Рис. 1
р снизу > р сверху , т. к.
h3 > h2
р3 = р4
Fa = (р снизу – р сверху) · S
Fa = (ρgh2 – ρgh3) · S
Fa = ρ ж g(h2 – h3) · S, т. к. (h2 – h3) · S = V, то
Fa = ρ ж g Vт – закон Архимеда
Учитель: Мы с вами смогли дать математическую запись знаменитого закона, который во всем мире называют
Проводим опыт с ведерком Архимеда.
Делаем вывод: сила, выталкивающая целиком погруженное в газ или жидкость тело, равна весу газа или жидкости в объеме этого тела.
FA = ρжgVт
«Архимед открыл закон,
Мылся в ванне как-то он,
Полилась на пол вода,
Догадался он тогда.
Сила действует на тело,
Так природа захотела,
Шар летит как самолёт,
Что не тонет, то плывёт!
И в воде груз легче станет,
И тонуть он перестанет,
Океаны вдоль Земли,
Покоряют корабли! »
Учитель: Предание донесло до нас курьезный эпизод, из жизни Архимеда (жившего 250 лет до н. э.), связанный с открытием закона о погружении тел в жидкости. Как Архимед пришел к своему закону? Кто подтолкнул его?
(Класс прослушивает поэму об Архимеде, записанную на магнитофон.)
IV. Закрепление
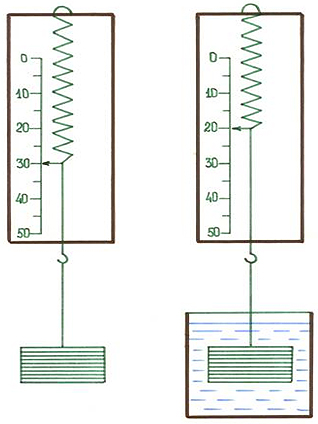
1. Определите, чему равна выталкивающая сила
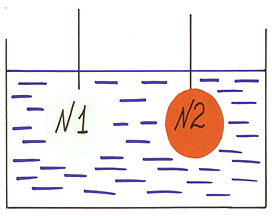
2. Стеклянное (№1) и стальное (№2) тела одинакового объема опущены в воду. Одинаковые ли выталкивающие силы действуют на них?
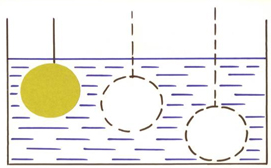
3. Одинаковые ли выталкивающие силы будут действовать на данное тело в жидкости при погружении его на разную глубину?
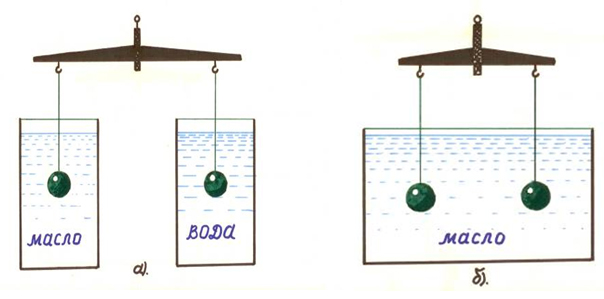
4. Одинаковые шары подвешены к коромыслу весов. В каком случае равновесие нарушится?
5. Учитель: Как долго будет гореть свеча, если ее поместить в сосуд с водой? (проверяем экспериментально)

Ответ: В процессе горения постепенно уменьшается сила тяжести, действующая на свечу. Для ее равновесия выталкивающая (Архимедова) сила должна уменьшаться, а это возможно только с подъемом свечи. Постепенно свеча поднимается и почти вся сгорает
6. Учитель: Налейте в прозрачный стакан касторовое масло на достаточную высоту. Не торопясь, капните в масло каплю подкрашенной обыкновенными акварельными красками воды. Если использовать растворы нескольких цветов, то в стакане с маслом возникнет картина, напоминающая висящие разноцветные шары. Что произойдет с подкрашенными каплями и почему?» (проверяем экспериментально опыт Плато)
Вывод: плотность касторового масла приблизительно равна плотности воды.

7. Ходить по берегу, усеянному галькой, босыми ногами больно. А в воде, погрузившись глубже пояса, ходить по мелким камням не больно. Почему?
8. Пожилые греки рассказывают, что Архимед обладал чудовищной силой. Даже стоя по пояс в воде, он легко поднимал одной левой рукой массу в 1000 кг. Правда, только до пояса, выше поднимать отказывался. Могут ли быть правдой эти рассказы?
(Да, если объем тела большой).
9. Генерал нырнул в жидкость солдатиком и подвергся действию выталкивающих сил. Можно ли утверждать, что жидкость вытолкала генерала в шею.
(Нет. Жидкость толкала генерала в подметки).
10. Собака легко перетаскивает утопающего в воде, однако, на берегу она не может сдвинуть его с места? Почему?
Решите задачи.
- Алюминиевый и медный бруски имеют одинаковые массы. Какой из них легче поднять в воде?
- Чему равна архимедова сила, действующая в воде на полностью погруженный медный брусок массой 890 г?
Учитель: О том, как ведет себя тело, погруженное в жидкость, при разных соотношениях архимедовой силы и силы тяжести, мы поговорим на следующем уроке, посвященному плаванию тел.
V. Домашнее задание
§49, упр.32; подготовка к лабораторной работе № 7 «Определение выталкивающей силы, действующей на погруженное в жидкость тело».
Условия плавания тел ℹ️ основные формулы, принципы, физический смысл выталкивающей силы в законе Архимеда, применение теории, примеры решения задач
Закон Архимеда

Местоположение предмета в пространстве объясняется действующими на него силами. Нарушение баланса приложенных усилий выводит объект из равновесного состояния и даёт старт движению. В газообразной среде и жидкости вертикальный ход тела зависит от пары сил — выталкивающей и тяжести. Закон, описывающий взаимодействие двух основных составляющих, открыл Архимед за три столетия до Рождества Христова.
Физик, математик, инженер
Архимед родился в 287 году до н. э. на Сицилии в греческой колонии Сиракузы. В детстве за воспитание мальчика взялся отец — астроном и математик Фидий. Всестороннее образование юноша получил в Александрии, где занимался изучением трудов Демокрита и Евдокса, общался с Эратосфеном и Кононом. Жизнь в научной столице древнего мира сформировала Архимеда как талантливого исследователя и экспериментатора.
Учёные, повлиявшие на образование Архимеда:
- греческий филолог и географ Эратосфен — вычислил размеры Земли;
- математик и астроном Конон, составлявший прогнозы погоды и календари с указанием времени восхода и заката Солнца;
- в трудах мыслителя Демокрита разработана теория неделимой частицы — атома, которая легла в основу материалистической философии;
- малоазиатский философ Евдокс, которого считают родоначальником интегральных вычислений и теоретической астрономии.
После обучения в Египте Архимед вернулся в Сиракузы, где жил до трагической гибели в 212 году до н. э. За три года до этого римляне начали осаду сицилийского города, который помогал Карфагенскому государству. Инженерный талант греческого математика помогал горожанам сдерживать нападавшие легионы. Осаждённые греки использовали катапульты разного калибра и подъёмные краны, которые при помощи крюков переворачивали вражеские галеры. Кривые зеркала, фокусирующие лучи в одну точку, сжигали неприятельский флот.
Существует несколько вариантов легенды о гибели Архимеда. Но описания совпадают в одном — мыслителя, занятого в этот момент научными изысканиями, убил римский солдат, после того как Сиракузы сдались на милость победителя.
Архимед написал тринадцать трактатов. В книгах учёного определены основные положения гидростатики и теоретической механики. Рассчитывая площади поверхности фигур и объёмы тел, математик заложил основы интегрального и дифференциального вычисления величин. Инженерные разработки великого изобретателя находят применение и в современных конструкциях.
Тело, погружённое в жидкость
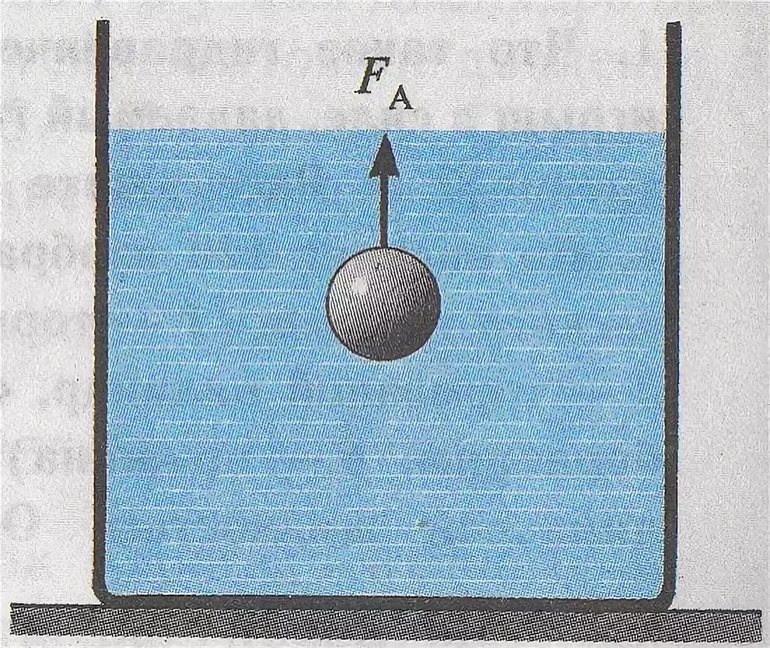
В истории науки известны примеры, когда практические запросы общества приводят к научным открытиям. Подобным образом был открыт основной закон статики. Вычисляя объём царской короны, Архимед погружал символ государственной власти в сосуд с водой. При этом учёный обратил внимание, что предмет, опущенный в жидкость, становится легче. Последующие размышления приводят великого грека к открытию гидростатического закона, названным его именем.
Закон Архимеда гласит, что на тело, погружённое в газовую среду или жидкость, действует сила, равная весу того объёма газа или жидкости, который вытеснило это тело. На языке математики постулат выражается уравнением:
F = gρV.
Смысловое определение математических символов, использованных в формуле:
- F — выталкивающая или архимедова сила;
- g — коэффициент ускорения свободного падения, равный 9,8 м/с²;
- ρ — плотность среды, в которую помещено тело;
- V — объём вытесненной жидкости или газа.
Архимедова сила противоположна силе тяжести и всегда направлена от центра Земли строго по вертикали вверх. В невесомости, где g = 0, закон Архимеда не работает. Взаимодействие двух сил — тяжести Ft и выталкивающей Fa — определяет поведение объекта в пространстве. Наглядным примером проявления силы Архимеда является подъём пузырька воздуха к поверхности воды.
На тело, плавающее на границе сред с разными плотностями, действует суммарная сила:
Fa = (ρ₁V₁ + ρ₂V₂ + ρ₃V₃ +…),
где ρ₁, ρ₂, ρ₃ — плотности различных сред, а V₁, V₂, V₃ — объёмы частей предмета.
Разбирают три варианта развития событий:
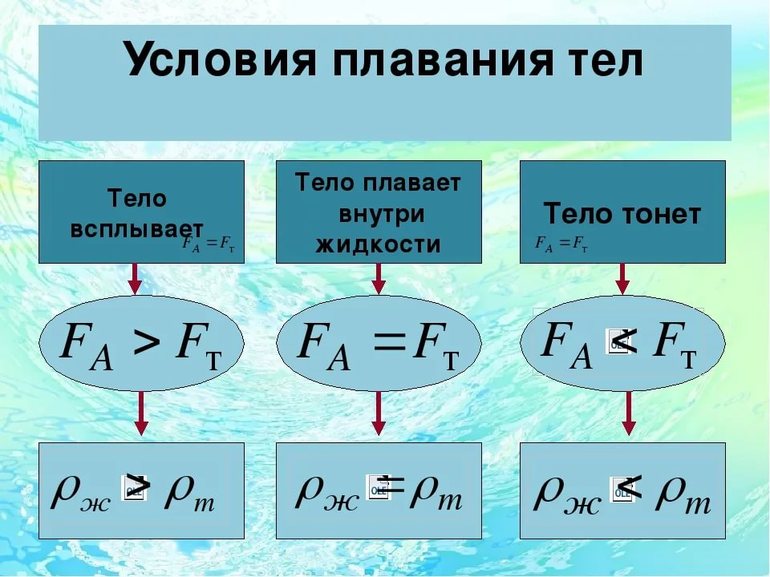
- Если Ft ˂ Fa, то тело начинает всплывать.
- При условии Ft = Fa, объект пребывает в состоянии покоя.
- Если Ft ˃ Fa, то происходит погружение предмета.
Аналогичным образом развивается ситуация, если значения сил заменить величинами плотностей тела и жидкости или газа. То есть, вместо силы тяжести Ft использовать плотность предмета, а взамен выталкивающей силы Fa рассматривать плотность среды, в которую помещён объект.
Корабли не тонут, дирижабли летают
Плавучестью корабля называется способность судна оставаться в равновесном состоянии, не всплывая и не погружаясь на глубину. По закону Архимеда условия плавания тел возникают при равенстве силы тяжести выталкивающей силе. Запас плавучести определяется процентным отношением объёма водонепроницаемой полости выше ватерлинии к объёму всего корабля. Надводные суда рассчитываются с резервом плавучести не менее 50%.
Формула расчёта запаса плавучести:
W = v / V * 100%,
где W — запас плавучести, v — объём отсеков над ватерлинией, V — объём всего корабля.
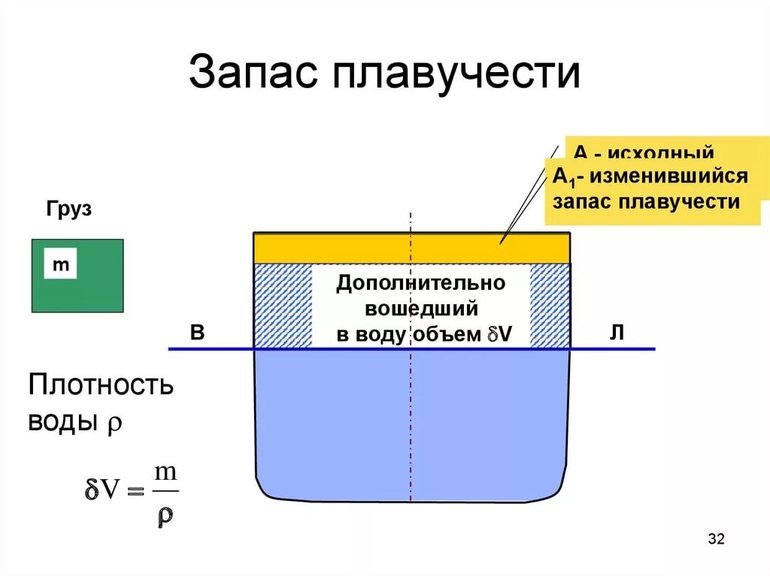
Водоизмещение является основной характеристикой водного транспорта и равно количеству воды, вытесненной подводной частью плавательного средства. Ватерлиния, являясь горизонтальным сечением, обозначается на корпусе и визуально показывает уровень нормального водоизмещения. Вычитание веса судна из водоизмещения представит грузоподъёмность транспортного средства.
В физическом смысле запас плавучести обозначает возможность находиться на поверхности водоёма. Различают нейтральную и отрицательную плавучесть. В первом случае W = 0% и судно погружено в воду до уровня палубы. Малейшее внешнее воздействие приводит к затоплению. Во втором случае корабль не способен держаться на плаву.
Предмет, находящийся в воздухе, также испытывает влияние архимедовой силы. Если подъёмная сила превышает силу тяжести, то тело начинает удаляться от поверхности земли. На этом постулате основан принцип воздухоплавания. В формуле закона Архимеда используется плотность воздуха.
Чтобы летательный аппарат поднялся, оболочку аэростата или дирижабля наполняют газом легче воздуха. Для этого подходят водород и гелий, чьи плотности меньше смеси атмосферных газов. Из-за взрывоопасности водорода чаще применяется гелий.
Идеальным вариантом считается использование в оболочке воздушного шара подогретого воздуха. Горелка устанавливается под отверстием в нижней части сферы. Периодическое включение нагревательного элемента изменяет температуру и плотность воздуха внутри шара, что позволяет регулировать скорость подъёма или спуска.
Решение примеров

Задача 1. Необходимо вычислить выталкивающую силу воды, действующую на сплошное тело цилиндрической формы объёмом 2 м³. Табличное значение плотности воды равно 1 тыс. кг/м³.
Решение. Прежде всего, определяется масса вытесненной воды:
m = ρ * V = 1000 * 2 = 2 тыс. кг.
Вес вытесненной воды, то есть архимедова сила, равны:
P = Fa = g * m = 9,8 * 2000 = 19600 Н.
Задача 2. Требуется определить количество золота в короне, изготовленной из сплава серебра и золота. Вес изделия в воздухе — 2,54 кг. Взвешивание в воде показало результат 2,34 кг.
Решение. На предмет, погружённый в воду, действует архимедова сила:
Fa = gρV = P₁ — P₂,
где P₁ — вес короны в воздухе, P₂ — вес драгоценности в воде, ρ — плотность воды.
Общий объём предмета складывается из объёмов золота и серебра:
V = m₁/ρ₁ + m₂/ρ₂,
где m₁ и ρ₁ — соответственно масса и плотность золота, а m₂ и ρ₂ — масса и плотность серебра.
Поскольку масса является частным от деления веса на коэффициент g, то общий объём короны можно представить формулой:
V = m₁/ρ₁ + 1/ρ₂ * (P₁/g — m₁),
где выражение (P₁/g — m₁) = m₂.

Значение объёма V подставляется в уравнение закона Архимеда:
Fa = g * ρ * (m₁/ρ₁ + 1/ρ₂ * (P₁/g — m₁)) = P₁ — P₂.
Путём математических преобразований определяется m₁:
m₁ = (P₁* (1 — ρ/ρ₂) — P₂)/(g * ρ * (1/ρ₁ — 1/ρ₂)).
Подставив числовые значения коэффициентов и веса короны, получаем ответ: m₁ = 985 г
О существовании трактатов Архимеда европейцам стало известно в XII веке. В это время с арабского языка переводятся труды мусульманских учёных, досконально изучивших работы древнегреческого математика. В XVI столетии методы великого исследователя природы использовал Галилей. Открытия, сделанные Архимедом, послужили фундаментом для развития средневековой механики.
Сила Архимеда
Компьютерная модель позволяет провести ряд экспериментов по теме «Закон Архимеда».
Модель может стать основой самых разнообразных исследовательских работ по данной учебной теме, т. к. допускает широкую вариативность исходных условий.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед.
|
|
|
Теорема 1. Архимеда |
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле:
где ρж – плотность жидкости, Vпт – объем погруженной в жидкость части тела.Модель позволяет провести ряд опытов, в ходе которых можно произвести следующие действия.
- Определять объем тела, погруженного в жидкость.
- Определять вес тела в воздухе и в жидкости.
- Вычислять силу Архимеда, действующую на погруженное тело.
- Вычислять вес вытесненной жидкости.
- Вычислять плотность тела двумя способами (1-ый способ – по массе и объему, 2-ой – по силе Архимеда).
- Проводить экспериментальную проверку закона Архимеда.
В модели предлагается выбор двух вариантов проведения эксперимента.
- С телами одинаковой массы. При выборе тел одинаковой массы, масса каждого цилиндра равна 400 г.
- С телами одинакового объема. При выборе тел одинакового объема, объем каждого тела равен 100 см3.
Предлагаются три цилиндрических тела (из стали, алюминия и меди), соответственно (для расчетов: плотность первого тела = 7800 кг/м3, второго – 2700 кг/м3, третьего – 8900 кг/м3).
В рамках эксперимента можно выбирать жидкость (вода, керосин, бензин).
Задав исходные условия эксперимента можно пронаблюдать результат, нажав кнопку . Экспериментатор может снимать показания с динамометра и измерять изменение высоты жидкости в сосуде.
Плавучесть — Википедия
 Силы, действующие на частично погруженное тело.
Силы, действующие на частично погруженное тело.Плаву́честь — свойство погружённого в жидкость тела оставаться в равновесии, не выходя из воды и не погружаясь дальше, то есть плавать. Также — раздел теории корабля, изучающий плавучесть.
Древнегреческий учёный Архимед сформулировал закон, по которому погружённое тело плавает в равновесии, когда его вес равен весу вытесненного им объёма жидкости.
При этом сила выталкивания, по природе сила давления, зависит от плотности жидкости (ρfluid), а вес (Gravity) от плотности тела (ρobject). Обе силы являются равнодействующими распределённых нагрузок. Понятно, что чем выше плотность жидкости, тем меньшая часть тела погрузится до равновесия. Наоборот, чем больше плотность тела при заданном объёме, тем больше его масса m, и тем глубже оно погрузится.
При отсутствии поверхностного натяжения уравнение равновесия плавающего тела будет выглядеть:
- ρobjectρfluid=Pobjectρfluid⋅g−Pim,{\displaystyle {\frac {\rho _{\mathrm {object} }}{\rho _{\mathrm {fluid} }}}={\frac {P_{\mathrm {object} }}{\rho _{\mathrm {fluid} }\cdot g-P_{\mathrm {im} }}},}
где Pobject{\displaystyle P_{\mathrm {object} }} — вес тела, ρobject{\displaystyle \rho _{\mathrm {object} }} — плотность тела, g{\displaystyle g} — ускорение свободного падения, Pim{\displaystyle P_{\mathrm {im} }} — вес погружённого тела, ρfluid{\displaystyle \rho _{\mathrm {fluid} }} — плотность жидкости.
Считают, что Архимед вывел этот закон, решая задачу определения плотности тела, не прибегая к объёмам. По легенде, ему требовалось узнать, из золота ли сделана корона, весившая столько же, сколько золотой слиток. Прямо измерить объём короны он не мог из-за её сложной формы.[1]
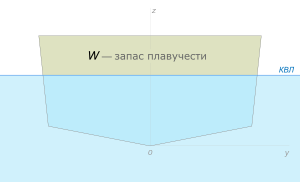 Запас плавучести (показан светло-зелёным)
Запас плавучести (показан светло-зелёным)Запас плавучести[править | править код]
Под плавучестью корабля понимают его способность оставаться на плаву при заданной нагрузке[2]. Эта способность характеризуется запасом плавучести, который выражается как процент объёма водонепроницаемых отсеков выше ватерлинии к общему водонепроницаемому объёму. Любое нарушение непроницаемости ведёт к снижению запаса плавучести. Для корабля (судна), у которого корпус водонепроницаем по главную палубу:
- W=Vh/Vo∗100,{\displaystyle W=V_{h}/V_{o}*100,}
где Vh{\displaystyle V_{h}} — объём подпалубных помещений над ватерлинией, Vo{\displaystyle V_{o}} — весь объём подпалубных помещений.
Уравнение равновесия в этом случае имеет вид:
- P=y(Vo−Vh),{\displaystyle P=y(V_{o}-V_{h}),} или:
- P=yV,{\displaystyle P=yV,}
где P{\displaystyle P} — вес судна, y{\displaystyle y} — плотность воды, V{\displaystyle V} — погружённый объём, и называется основным уравнением плавучести
Из него следует:
- при неизменной плотности y{\displaystyle y} изменение нагрузки P{\displaystyle P} сопровождается пропорциональным изменением погружённого объёма V{\displaystyle V} до достижения нового положения равновесия. То есть, при увеличении нагрузки судно «садится» в воду глубже, при уменьшении всплывает выше.
- при неизменной нагрузке P{\displaystyle P} изменение плотности y{\displaystyle y} сопровождается обратно пропорциональным изменением погружённого объёма V{\displaystyle V}. Так, в пресной воде судно сидит глубже, чем в солёной.
- изменение объёма V{\displaystyle V} при прочих равных сопровождается изменением осадки. Например, при балластировке забортной водой или аварийном затоплении отсеков можно считать, что судно не приняло груз, а увеличило погружённый объём, и осадка увеличилась — судно сидит глубже. При откачке воды происходит обратное.
Физический смысл запаса плавучести — это объём воды, который судно может принять (скажем, при затоплении отсеков), ещё оставаясь на плаву. Запас плавучести 50 % значит, что водонепроницаемый объём выше ватерлинии равен объёму ниже неё. Для надводных кораблей характерны запасы 50÷60 % и выше. Считается, что чем бо́льший запас удалось получить при постройке, тем лучше.
Нейтральная плавучесть[править | править код]
Пример грузовой маркиКогда объём принятой воды (для надводного корабля) в точности равен запасу плавучести, считается что плавучесть утеряна — запас равен 0 %. Действительно, в этот момент корабль погружается по главную палубу и находится в неустойчивом состоянии, когда любое внешнее воздействие может вызвать его уход под воду. А в воздействиях, как правило, недостатка нет. В теории этот случай называется нейтральная плавучесть.
Отрицательная плавучесть[править | править код]
При приёме объёма воды больше чем запас плавучести (или любого груза, большего по весу) говорят, что судно получает отрицательную плавучесть. В этом случае оно неспособно плавать, а может только тонуть.
Поэтому для судна устанавливается обязательный запас плавучести, который оно должно иметь в неповреждённом состоянии для безопасного плавания. Он соответствует полному водоизмещению и маркируется ватерлинией и / или грузовой маркой.
Гипотеза прямобортности[править | править код]
 Пример диаграммы нагрузки, плавучести и осадки судна полным водоизмещением 6000 т
Пример диаграммы нагрузки, плавучести и осадки судна полным водоизмещением 6000 тДля определения влияния переменных грузов на плавучесть пользуются допущением, при котором считается, что прием малых (менее 10 % водоизмещения) грузов не меняет площадь действующей ватерлинии. То есть изменение осадки считается так, словно корпус является прямой призмой. Тогда водоизмещение прямо зависит от осадки.
Исходя из этого, определяется фактор изменения осадки, обычно в т/см:
- q=0,01yS,{\displaystyle q=0,01yS,}
где S{\displaystyle S} — площадь действующей ватерлинии, q{\displaystyle q} означает величину изменения нагрузки в тоннах, необходимую для изменения осадки на 1 см. При обратном расчете он позволяет определить, не вышел ли из допустимых пределов запас плавучести.
- Войткунский Я. И. Справочник по теории корабля. Т. 2. Статика судов. Качка судов.— Л.: Судостроение.— 1986.
- Сизов В. Г. Теория корабля: Учебное пособие для вузов.— Одесса, Феникс.— 2003.