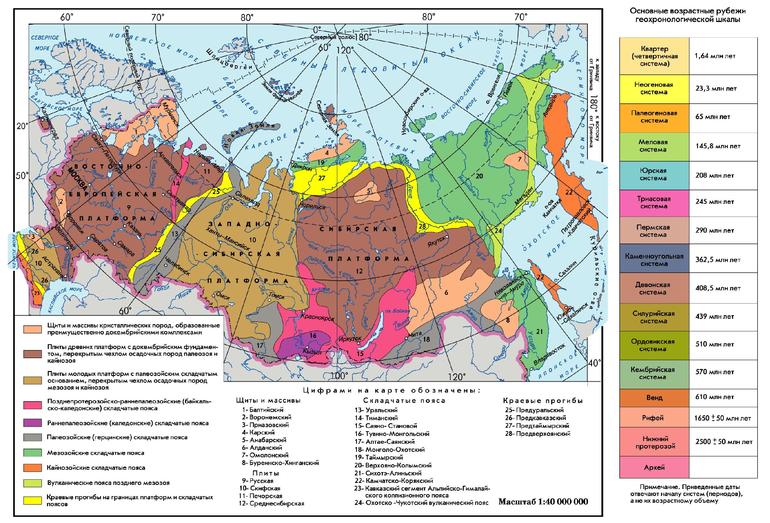
Sinx 1 2 на окружности: Тригонометрические уравнения. Как решать тригонометрические уравнения?
Тригонометрические уравнения — формулы, решения, примеры. Тригонометрические уравнения Простейшее тригонометрическое уравнение cosx 1.5
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
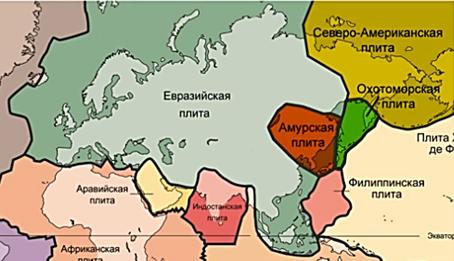
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках. k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Урок решить уравнение синус 2х 1 2. Тригонометрические уравнения — формулы, решения, примеры. можно познакомиться с функциями и производными
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z. k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .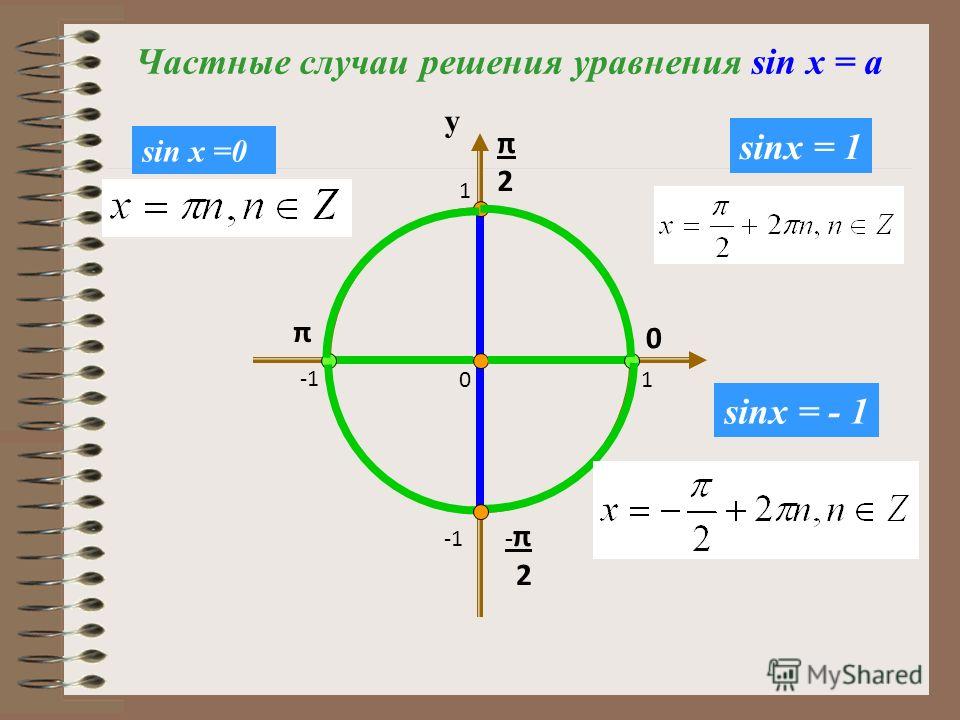
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейшихтригонометрических уравнений
с помощью единичной окружности
10
класс
2. Разминка
Записать с помощью формулы множествоуглов,
соответствующих данным точкам
у
1
2
x
1.
-1
у
1
0
1
2
n, n
4
2.
х
0
-1
1
у
1
-1
-1
3.
x
0
1
-1
x
2
n, n
-1
х
4
n, n
х
у
4.
1
x 2 n, n
5.
х
0
-1
у
1
1
x 2 n, n
-1
0
0
-1
6.
х
1
7.
у
1
у
1
-1
4
4
-1
0
1
х
x
4
-1
n, n
x
-1
4
2
n, n
4
или
0
x
4
n, n
1 х
-1
4
4. Обратная задача: отметить точками углы, соответствующие данным формулам
у1.
1
x
2
1
2.
у
2 n, n
3
у
0
-1
х
1
2
3.

1
0
2
0
1
х
у
3
1
2
-1
0
1
-1
-1
1
-1
-1
-1
4.
-1
x
х
x
3
2 n, n
2
2
2
n, n
3
x
3
n, n
х
5. Решить уравнения
1.1
у (sinx)
1
2.
5
6
y (sinx)
1
2
6
0
0
-1
-1
sin x 0
x n, n
1
х (cosx)
0
-1
1
-1
1
sin x
2
x
2 n, n
6
x 5 2 n, n
6
x (cosx)
у
3.
3
cos x
4
3
cos x
2
1
5
6
2
-1
6
0
3
2
1
3
2
5
6
х
6
-1
x 6 n, n ;
x n, n .
6
x 6 2 n, n ;
x 5 2 n, n .
6
x
6
n, n
у
tgx
1
tg x 1
2
1
4
3
4
tgx 1
x
4
2
n, n
0
1
0
-1
3
4
-1
4
-1
х
ctgx 3 , где x ; 2
x
y
3
-1
1 0
6
n, n
1
ctgx
5
6
2
-1
0
1
-1
6
x
11
6
5
11
6
6
9. Аналитический способ отбора корней из промежутка
x n, n6
n 2 , n ;
7 6n 13, n ;
6
1
1 n 2, n ;
6
6 1 6n 12, n ;
1
1
1 n 2 , n ;
6
6
11
n 2; x 2
6
6
ОТВЕТ:
11
6
3
sin x
2 0
1
cos x
2
3
;
sin x
2
cos x 1 .
2
1
2
3
-1
у (sinx)
3
2
3
0
1
2
-1
x
3
2 n,
1
х (cosx)
При каких значениях параметра a уравнение
sin 2 x 2a 1 sin x a 2 a 0 имеет решение?
D 2a 1 4 1 a 2 a 4a 2 4a 1 4a 2 4a 1
2
sin x a 1;
sin x a.
2
0
1 a 1 1,
1 a 1;
0 a 2,
1 a 1.

-1
1
a 1; 2
a
a
12. Самостоятельная работа
ВАРИАНТ 1ВАРИАНТ2
Решите уравнения
cos x 0
sin x 1
1
sin x
2
ctgx 3
2
cos x
2
3
tgx
3
ctgx sin x 1
tgx cos x 1
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
sin x
x2
0
cos x sin x 2 0
x 1; 3
13. Проверяем решения
ВАРИАНТ 11
1.
ВАРИАНТ 2
y
1
1.
cos x 0
0
-1
x
2
n, n
-1
x
y
6
1
2
-1
x 6 2 n, n ;
x 5 2 n, n .
6
0
2
0
2 n, n
1
cos x
x
-1
x
2
2
-1
3
2 n, n
4
x
1
-1
3
4
2.
1
5
6
sin x 1
x
-1
2.
1
sin x
2
1
y
3
4
1
2
2
y
0
-1
1
x
ВАРИАНТ 1
ВАРИАНТ 2
tgx
3.
6
ctgx
6
ctgx 3
x
y
1
0
-1
n, n
4.
1
x
x
-1
Нет решений
6
n, n
4.
1 y
0
y
6
0
-1
3
3
x
1
-1
1
y
ctgx sin x 1
tgx cos x 1
cos x 0;
sin x 1.
3
tgx
3
3
-1
-1
1
3.
1
x
-1
sin x 0;
cos x 1.
0
-1
Нет решений
1
x
15. Домашняя работа
1. Дополнительные задания изсамостоятельной работы.
2. № 13.28, 13.29
3. При каких значениях
параметра
2
a
уравнение sin x a 2 имеет решения?
4.Найти наибольший отрицательный
2
cos
x 2 sin x 2 0.
корень уравнения
Презентация к уроку Простейшие тригонометрические уравнения
ПЛАН УРОКА ТЕМА: ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Цели урока:
Образовательная: Повторить комплекс знаний и умений по теме тригонометрические функции (sinx, cosx, tgx, ctgx) и обратные тригонометрические функций; вывести формулы решения простейших тригонометрических уравнений cosx=а, sinx=а, tgx=а, ctgx=а; сформировать у учащихся первичные умения и навыки их решения.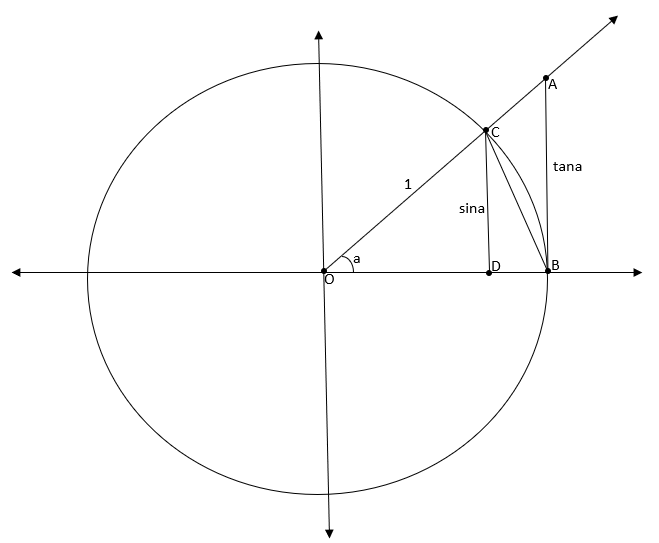
Воспитательная: Способствовать воспитанию воли и настойчивости для достижения конечных результатов.
Развивающая: Содействовать умению обобщаться и конкретизировать знания при решении уравнений, коллективного взаимодействия и ответственности за результаты групповой работы.
Тип урока: освоение новых знаний.
Методы: беседа, урок-соревнование, репродуктивный, частичнопоисковый.
Формы организации урока: индивидуальная, фронтальная, групповая.
Оборудование: карточки с заданиями, плакаты: тригонометрические окружности с линиями синуса, косинуса, тангенса и котангенса, тесты, компьютер, мультимедийный проектор, экран.
План урока:
1. Организационный момент. (2 минуты).
2. Цели и план урока ( урок – соревнование). Объявление темы урока, цели урока и план урока (5 мин).
Три команды косинус, тангенс и котангенс. Четыре этапа: Первый этап: повторение – фронтальный опрос, второй-третий этап: освоение новых знаний, четвертый этап: формирование первичных знаний и умений, пятый этап – тест на усвоение материала.
2. Актуализация опорных знаний. Первый этап (15 минут).
3. Изучение нового материала. Второй- третий этап (40 минут).
4. Формирование первичных знаний и умений. Четвертый этап (15 минут).
5. Проверка освоения первичных знаний Пятый этап (8 мин).
6. Информация о домашнем задании. (2 минуты).
7. Подведение итогов урока. (3 минуты)
План урока:
1. Организационный момент. (2 минуты).
2. Цели и план урока ( урок – соревнование). Объявление темы урока, цели урока и план урока (5 мин).
Повторить комплекс знаний и умений по теме тригонометрические функции (sinx, cosx, tgx, ctgx) и обратные тригонометрические функций; вывести формулы решения простейших тригонометрических уравнений cosx=а, sinx=а, tgx=а, ctgx=а; сформировать у учащихся первичные умения и навыки их решения.
Три команды косинус, тангенс и котангенс. Четыре этапа: Первый этап: повторение – фронтальный опрос, второй-третий этап: освоение новых знаний, четвертый этап: формирование первичных знаний и умений, пятый этап – тест на усвоение материала.
2. Актуализация опорных знаний. Первый этап (15 минут).
1.Опрос по теоретическому материалу:
а) Сформулировать определение арксинуса числа.
б) Сформулировать определение арккосинуса числа.
в) Сформулировать определение арктангенса числа
д) Сформулировать определение арккотангенса.
2. Устная работа практической направленности.
1) Вычислите:
2) Имеет ли смысл выражение (ответ объясните):
3. Изучение нового материала. Второй- третий этап (40 минут).
Преподаватель: Тригонометрическим уравнением называется уравнение, в котором переменная содержится только под знаком тригонометрической функции. Тригонометрическое уравнение либо не имеет корней, либо имеет их бесконечное множество.
Уравнения sin x=a, cos x=а, tg x=а, ctg x=а называются простейшими тригонометрическими уравнениями.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом числа α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.
Синусом числа α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующей данному углу α.
Тангенсом угла ??
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение sinx=1/2
Этому уравнению удовлетворяют все такие значения угла поворота х, которые соответствуют точкам окружности, ордината которых равна 1/2.
Отметим на оси ординат точку с ординатой 1/2:
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату 1/2. Эти точки соответствуют
углам поворота на и 5 радиан:
6 6
Если мы, выйдя из точки, соответствующей углу
поворота на радиан, обойдем полный круг, то 6
мы придем в точку, соответствующую углу
поворота на 2 радиан и имеющую ту же
6
ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. То есть первая серия решений исходного уравнения имеет вид: x1= 2к , где kZ, Z — множество целых чисел (1) 6
Аналогично, вторая серия решений имеет вид: x2= 5 2к , где kZ. (2)
6
Эти две серии решений можно объединить в одну запись:
x1nn,n.
6
Если мы в этой записи возьмем n=2k ( то есть четное n ), то мы получим первую серию решений.
Если мы в этой записи возьмем n=2k+1 ( то есть нечетное n ), то мы получим вторую серию решений.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
Второй этап: Каждая команда решает свое уравнение и выводит нужную формулу. Идет обсуждение. Задача капитана решить какое решение подходит и защитить её.
Идет обсуждение. Задача капитана решить какое решение подходит и защитить её.
2. Команда косинуса решает уравнение cosx=1/2.
Так как cosx — это абсцисса точки единичной окружности, полученной поворотом на угол х, отметим на оси ОХ точку с абсциссой 1/2:
Проведем вертикальную линию параллельно оси ОY до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу 1/2. Эти точки соответствуют углам поворота на ∏/3 и ∏/3 радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений: x1=∏/3+2∏k, kZ, x2=-∏/3+2∏k, kZ
Объедим эти две серии в одну запись: x=+ ∏/3+2∏n, nZ
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
|
cosxa: xarccosa 2n,n; |
|
cosxa: xarccosa 2n,n |
3. Команда тангенса решает уравнение tgx=1.
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY:
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на ∏/4 и 5∏/4:
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению лежат на расстоянии ∏ радиан друг от друга, то мы можем записать решение таким образом:
x=∏/4+∏n, где nZ
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
tgx a: x arctgan,n; tgx a: x arctga n,n 4. Команда котангенса решает уравнение ctgx=-1.
Команда котангенса решает уравнение ctgx=-1.
Линия котангенсов проходит через точку с координатами (0,1) единичной окружности параллельно оси ОХ: Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на 3∏/4 и -∏/4 радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное ∏, то общее решение этого уравнения мы можем записать так: x=3∏/4+∏n, nZ
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений я
использовала табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
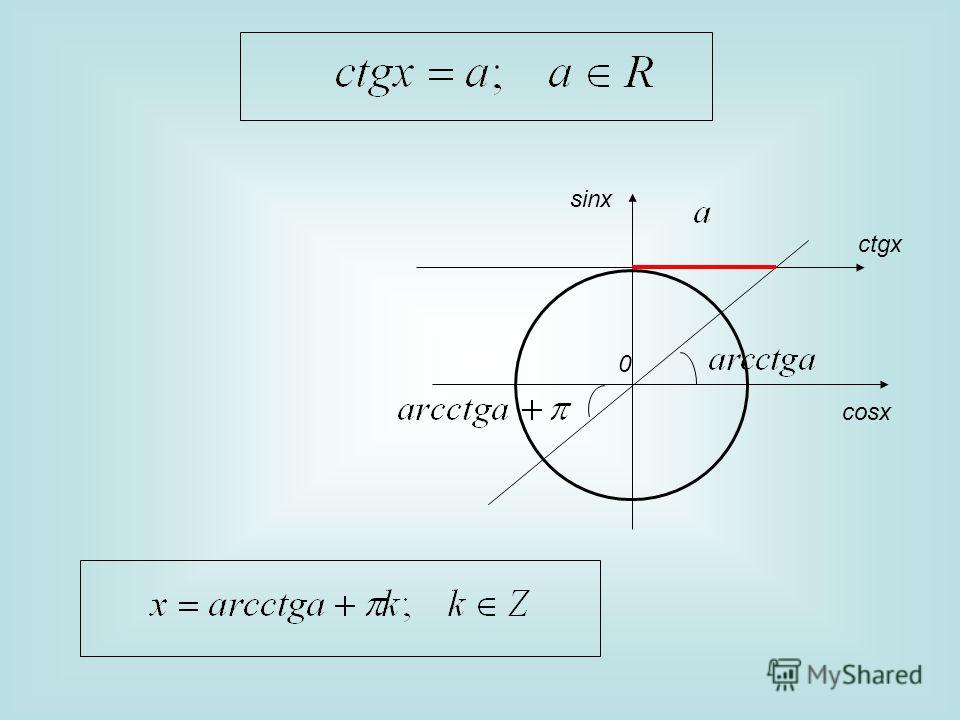
ctgx a: x arcctga n,n;ctgx a : x arcctga n,n
Баллы каждой команде
Третий этап: Преподаватель рассматривает на окружности с помощью учащийся
ЧАСТНЫЕ РЕШЕНИЯ:
sinx=0
Отметим на окружности точки, ордината которых равна 0:
x n,n
sinx=1
Отметим на окружности единственную точку, ордината которой равна 1:
x 2n,n
2
sinx=-1
Отметим на окружности единственную точку, ордината которой равна -1:
x 2n,n
2
Каждая команда заполняет самостоятельно заполняют свою строку в таблице.
cosx=0
Отметим на окружности точки, абсцисса которых равна 0:
xn,n
2
cosx=1
Отметим на окружности единственную точку, абсцисса которой равна 1:
x=2∏n, nZ
cosx=-1
Отметим на окружности единственную точку, абсцисса которой равна -1:
x=∏+2∏n, nZ
4. Формирование первичных знаний и умений. Максимальный балл — 2 балла. Четвертый этап (15 минут).
Предлагается решить по уравнения каждой команде.
косинус тангенс котангенс tgx 3 cosx 3 sin x
2
cosx sin x ctgx
23
5. Проверка усвоения изученного материала. Пятый этап (8 мин).
Тест (состоит из пяти вопросов). Вариант 1 . Выберите правильный ответ.
Уравнение cosxaимеет решение
А) xarccosa 2n,n Б) xarccosan,n
В) xarccosa 2,n
2. Выберите правильный ответ
Уравнение sin xa имеет решение
n1
А) x1 arcsin an,n
Б) x1n arcsin an,n
В) x1n arcsin a 2n,n
3. Выберите правильный ответ
Выберите правильный ответ
Уравнение tgx a имеет решение
А) x arctga 2n,n Б) x arctgan,n
В) x arctga n,n
4. Найдите неправильное решение cos x1
А) x arccos1 2n,n
Б) x 2n,n
В) x arccos1n,n
5. Выберите свое эмоциональное состояние на уроке
А) В)
Ответы:
Тест. Вариант 2. 1. Выберите правильный ответ.
Уравнение cosxa имеет решение
А) xarccosa 2n,n
Б) x arccosa 2n,n В) xarccosa 2,n
2. Выберите правильный ответ
Уравнение sin xa имеет решение
|
А) |
x1 arcsin an,n |
|
Б) |
x1n arcsin an,n |
|
В)
|
x1n arcsin a 2n,n |
n 1
3. Выберите правильный ответ
Выберите правильный ответ
Уравнение сtgx a имеет решение
А) x arcctga 2n,n Б) x arcctga n,n В) x arcctga n,n
4. Найдите неправильное решение sin x 0
А) x 2n,n Б) xn,n
В) x arcsin 0n,n
5. Выберите свое эмоциональное состояние на уроке
а) Б) В)
Решение тригонометрических уравнения. 10-й класс
Тип урока: урок комбинированный.
Класс: 10 класс.
Продолжительность урока: 1 час (45 минут).
Цели урока:
- дидактические: повторить формулы решения простейших тригонометрических уравнений; усвоить навык решения комбинированных тригонометрических уравнений; рассмотреть способ отбора корней с помощью окружности;
- развивающие: развитие познавательного интереса, логического мышления, интеллектуальных способностей; формирование математической речи;
- воспитательные: формировать эстетические навыки при оформлении записей в тетради и самостоятельность мышления у учащихся.
Оборудование урока:
- карточки с заданиями для самостоятельной работы
- карточки с дифференцированными домашними заданиями
- презентация к уроку
- персональный компьютер, мультимедиа проектор
План урока
- Организационный момент
- Повторение основных понятий
- Фронтальная письменная работа
- Рефлексия
- Дифференцированное домашнее задание
Ход урока
Организационный этап.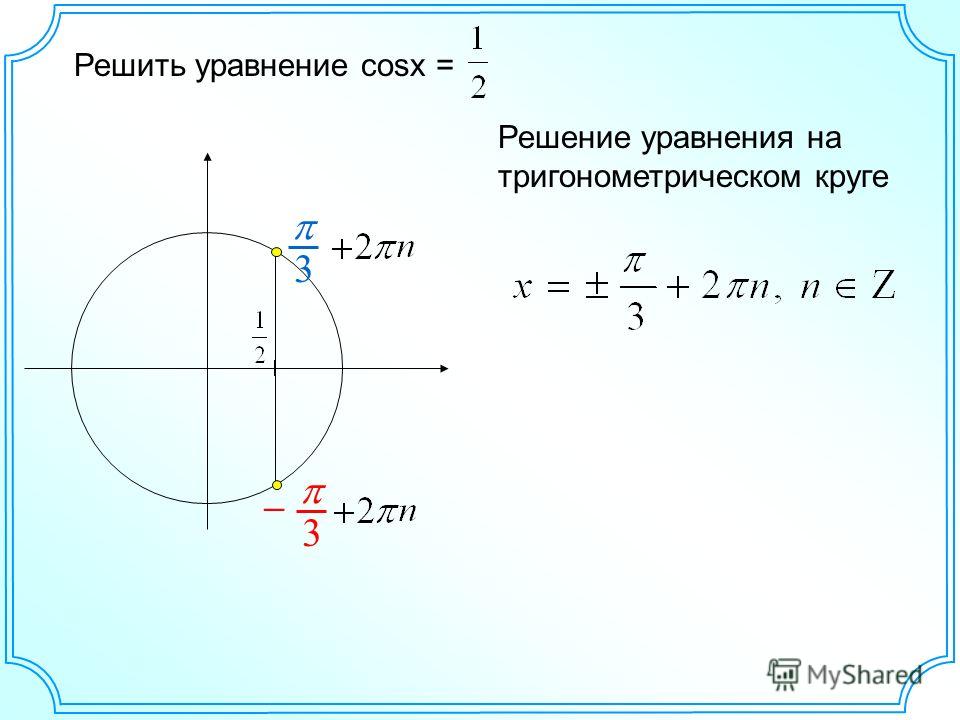
Девиз: “Не делай никогда того, чего не знаешь, но научись всему, что следует знать”. (Пифагор)
Приветствие. Проверка готовности класса к уроку.
Сегодня на уроке мы продолжим работать над тригонометрические уравнения.
1. Актуализация опорных знаний (устная работа).
В результате выполнения задания мы повторим определения арккосинуса, арксинуса, арктангенса и арккотангенса.
Задание 1 (устно)
1. С помощью тригонометрической окружности найти все точки на числовой окружности из промежутка [-2 которые соответствуют числам
, , , , arcsin 0, arcsin
2. С какой из отмеченных на числовой окружности точек совпадает точка:
Задание 2
Вы умеете решать простейшие тригонометрические уравнения. Решите предложенные уравнения ( записать ответ на карточке). (Приложение 1)
| Вариант 1 | Вариант 2 | ||
| cos x = — 1 | cos x = 0 | ||
| sin x = 0 | sin x = — 1 | ||
| tg x = — 1 | tg x = 1 | ||
Проверить ответы с помощью таблицы.
2. Изучение нового материала “Комбинированные тригонометрические уравнения”
— Какие уравнения вы научились решать в этом
году? (иррациональные, показательные,
логарифмические).
Добавим в эти уравнения элементы тригонометрии.
Задание 3. Решить уравнение:
; ; sin x = -1;2) , найдем ОДЗ уравнения : при любом х.
; ; ; .3) , найдем ОДЗ уравнения : при любом х.
;
4)
, , ,
, ,
Ответ:
Задание 4.
Рассмотрим комбинированные уравнения, которые предлагаются на ЕГЭ ( задание 13).
1. Решить уравнение и найти корни, принадлежащие промежутку
а) (
(
—sinx = 2sinx* cosx
sinx +2sinx* cosx =0
sinx ( 1 +2cosx ) =0
sinx = 0 или 1 +2cosx =0
, ,
б) сделаем выборку корней с помощью тригонометрической окружности
х = 0, x = ,
Ответ: а) ; б) 0, , .
2. Решить уравнение
1) ОДЗ уравнения:
cosx = -5 решения нет
Так как , то и
Ответ: ; .
Самостоятельная работа ( с самопроверкой)
6. Итог урока
Продолжите фразу
- Сегодня на уроке я повторил …
- Сегодня на уроке я узнал …
- Сегодня на уроке я научился …
7. Домашняя работа: карточки (по вариантам). (Приложение 2)
Спасибо за урок!
Тригонометрические уравнения — формулы, решения, примеры. Простейшие тригонометрические уравнения урок решить уравнение синус 2х 1 2
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.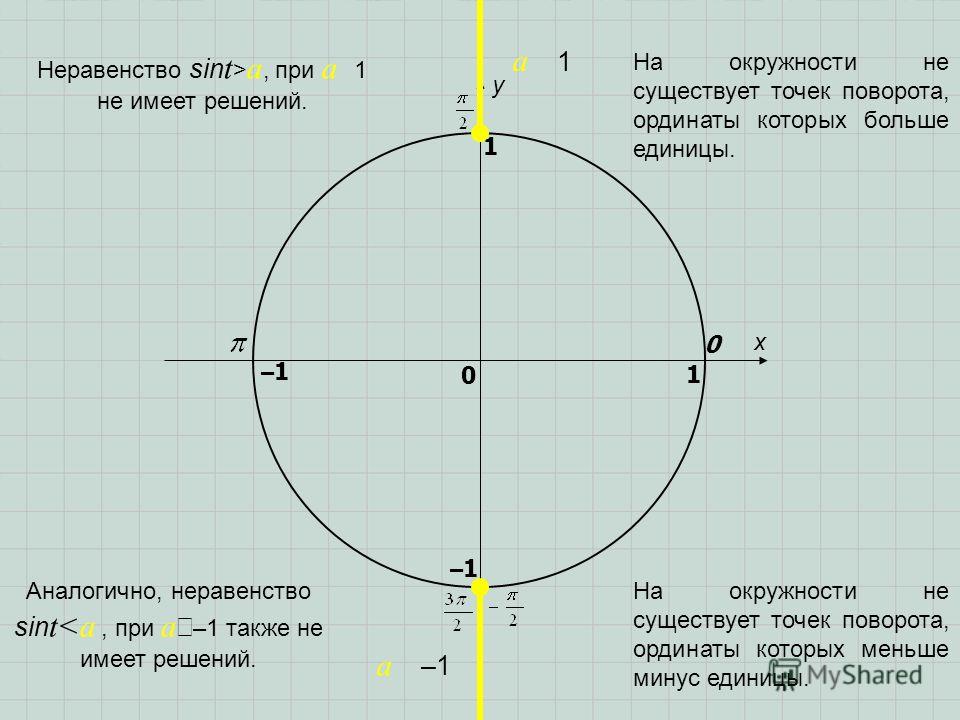
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ. ) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π
n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A . k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .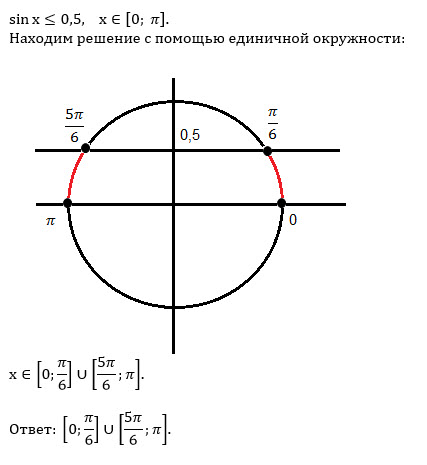
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
тригонометрические уравнения урок 3
Цель урока:
Обобщение знаний по темам: «Тригонометрическая окружность»; Градусы и радианы; Свойства тригонометрических функций. Решение тригонометрических уравнений базового и повышенного уровня сложности используя дифференцированный подход при организации повторения.
Организационный момент( 1 минута). Сообщается тема урока, цель разъясняется порядок использования раздаточного материала.
Сообщается тема урока, цель разъясняется порядок использования раздаточного материала.
Повторение теоретического материала с использованием мультимедийного проектора.
Тригонометрическая окружность.
Градусы и радианы.
Косинус синус тангенс котангенс.
Свойства тригонометрических функций.
При этом прежде чем появилось изображение на экране учитель задает вопросы:
1.Какая окружность называется тригонометрической?
2.Как перевести радианы в градусы и наоборот?
3.Дать определение синуса, косинуса, тангенса.
4.Какие основные свойства функций y=sinx, y=cosx, y=tgx.
3.Устная работа (5 МИНУТ). Решение простейших тригонометрических уравнений (использование мультимедийного проектора).
а)Уравнение cosx=a,частные случаи.
б)Уравнение sinx=a, частные случаи.
в)Решить уравнения cosx=1/2, sinx=1/2.
4. Решение тригонометрических уравнений.(15мин.)
а)Использование тригонометрических формул.
На экране появляются поочередно незаконченные формулы.После правильного ответа учащихся формулы на экране появляются полностью.
сos2x-sin2x= cos2x
ыin2x= 2sinxcosx
ыin(x-y)= sinxcosy-cosxsiny
сos(α-β)= cosαcosβ+sinαsinβ
1+tg2x =
sin(α + β)= sin α cos β+cos α sin β
б) Самостоятельная работа №1.Используются карточки №1 трех уровней сложности.
Например:
Базовый уровень
Sin3x=1/2 2sinxcosx=1 cosпx=0
Средний уровень
Cos22x-sin22x=-1/2 sin(п+x).sinП/6=1/2 2tgy/1-tg2y=0
Cложный уровень
Sina.cosП/3+cosa.sinП/3=31/2/2 sin2x=3/4 1/cos2x-1=1.
в).Уравнения, приводимые к квадратным. К доске выходят три ученика:слабый,средний и сильный и решают предложенные им уравнения. Класс, разделенный соответственно на три группы, также решает эти уравнения.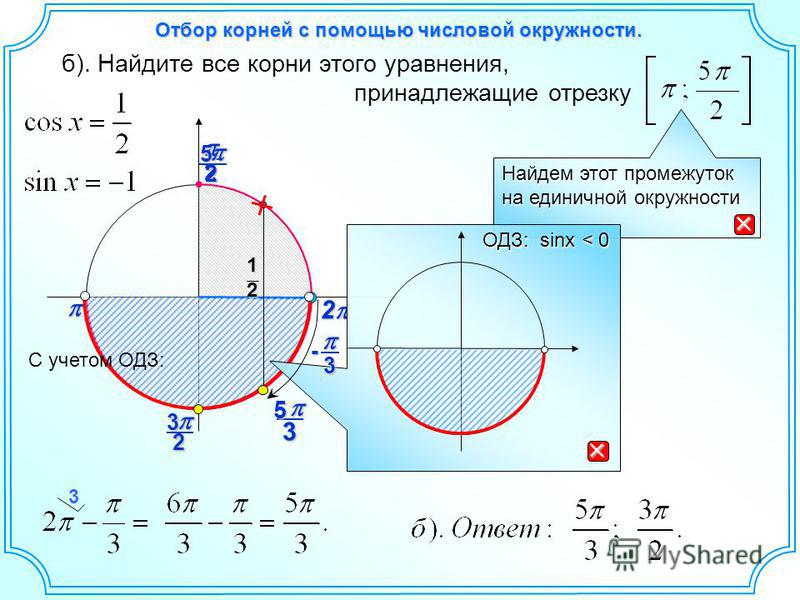 2 + n-72) = 1 / (n + 9)
2 + n-72) = 1 / (n + 9)
Единичный круг: функции синуса и косинуса
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичного круга, круга с центром в начале координат и радиусом 1, как показано на рисунке 2.Угол (в радианах), который пересекает [latex] t [/ latex], образует дугу длиной [latex] s [/ latex]. Используя формулу [latex] s = rt [/ latex] и зная, что [latex] r = 1 [/ latex], мы видим, что для единичной окружности , [latex] s = t [/ latex].
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемых квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление движения положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [латекс] t [/ латекс] мы можем пометить пересечение конечной стороны и единичного круга его координатами, [латекс] \ left (x, y \ right) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f \ left (t \ right) = \ cos t [/ latex] и [latex] f \ left (t \ right) = \ sin t [/ latex] соответственно. Это означает [латекс] x = \ cos t [/ latex] и [латекс] y = \ sin t [/ latex].
Рис. 2. Единичная окружность с центральным углом [латекс] t [/ латекс] радиан
A Общее примечание: Unit Circle
Единичная окружность имеет центр [латекс] \ влево (0,0 \ вправо) [/ латекс] и радиус [латекс] 1 [/ латекс].В единичном круге длина перехваченной дуги равна радианам центрального угла [латекс] 1 [/ латекс].
Пусть [latex] \ left (x, y \ right) [/ latex] будет конечной точкой на единичной окружности дуги длины дуги [latex] s [/ latex]. Координаты [latex] \ left (x, y \ right) [/ latex] этой точки могут быть описаны как функции угла.
Определение функций синуса и косинуса
Теперь, когда у нас есть помеченная единичная окружность, мы можем узнать, как координаты [latex] \ left (x, y \ right) [/ latex] связаны с длиной дуги и углом . Синусоидальная функция связывает действительное число [латекс] t [/ латекс] с координатой y точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [латекс] t [/ латекс] равен значению y конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 2 синус равен [latex] y [/ latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — координата y соответствующей точки на единичной окружности.
Синусоидальная функция связывает действительное число [латекс] t [/ латекс] с координатой y точки, где соответствующий угол пересекает единичную окружность. Точнее, синус угла [латекс] t [/ латекс] равен значению y конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 2 синус равен [latex] y [/ latex]. Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — координата y соответствующей точки на единичной окружности.
Функция косинуса угла [латекс] t [/ latex] равна значению x конечной точки на единичной окружности дуги длиной [латекс] t [/ латекс]. На рисунке 3 косинус равен [латекс] х [/ латекс].
Рисунок 3
Поскольку понятно, что синус и косинус являются функциями, нам не всегда нужно записывать их в скобках: [latex] \ sin t [/ latex] то же самое, что [latex] \ sin \ left (t \ right) [ / latex] и [latex] \ cos t [/ latex] такие же, как [latex] \ cos \ left (t \ right) [/ latex].{2} [/ латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают сокращенную запись. В случае сомнений используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Общее примечание: функции синуса и косинуса
Если [latex] t [/ latex] является действительным числом, а точка [latex] \ left (x, y \ right) [/ latex] на единичном круге соответствует углу [latex] t [/ latex] , затем
[латекс] \ cos t = x [/ латекс]
[латекс] \ sin t = y [/ латекс]
Как сделать: по точке
P [латекс] \ left (x, y \ right) [/ latex] на единичной окружности, соответствующей углу [латекс] t [/ latex], найдите синус и косинус.- Синус [latex] t [/ latex] равен y -координате точки [latex] P: \ sin t = y [/ latex].
 {2} t = 1 [/ латекс]
{2} t = 1 [/ латекс]Как сделать: учитывая синус некоторого угла [латекс] t [/ латекс] и его положение в квадранте, найдите косинус [латекс] t [/ латекс].
- Подставьте известное значение [латекс] \ sin \ left (t \ right) [/ latex] в пифагорейскую идентичность.
- Решите относительно [латекс] \ cos \ left (t \ right) [/ latex].
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится [latex] t [/ latex].
Пример 3: Нахождение косинуса из синуса или синуса из косинуса
Если [латекс] \ sin \ left (t \ right) = \ frac {3} {7} \\ [/ latex] и [latex] t [/ latex] находится во втором квадранте, найдите [latex] \ cos \ left (t \ right) \\ [/ латекс].{2} \ left (t \ right) = \ frac {40} {49} \ hfill \\ \ text {cos} \ left (t \ right) = \ pm \ sqrt {\ frac {40} {49}} = \ pm \ frac {\ sqrt {40}} {7} = \ pm \ frac {2 \ sqrt {10}} {7} \ hfill \ end {array} \\ [/ latex]
Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицателен. Итак,
[латекс] \ text {cos} \ left (t \ right) = — \ frac {2 \ sqrt {10}} {7} \\ [/ latex]Попробуй 3
Если [латекс] \ cos \ left (t \ right) = \ frac {24} {25} \\ [/ latex] и [latex] t [/ latex] находится в четвертом квадранте, найдите [latex] \ text {грех} \ влево (т \ вправо) \\ [/ латекс].Треугольник \ circ [/ latex] — это равнобедренный треугольник, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
Рисунок 9
При [latex] t = \ frac {\ pi} {4} [/ latex], что составляет 45 градусов, радиус единичной окружности делит пополам угол первого квадранта .
 \ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex].\ circ [/ latex], как показано на рисунке 12.
\ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex].\ circ [/ latex], как показано на рисунке 12. Рисунок 11
Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [латекс] 2y [/ latex], и, поскольку все стороны равны, мы также можем сделать вывод, что [latex] r = 2y [/ latex] или [latex] y = \ frac {1} {2 } г [/ латекс]. Поскольку [латекс] \ sin t = y [/ latex],
[латекс] \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} r \\ [/ latex]
А так как [latex] r = 1 [/ latex] в нашем единичном круге ,
[латекс] \ begin {array} {l} \ sin \ left (\ frac {\ pi} {6} \ right) = \ frac {1} {2} \ left (1 \ right) \ hfill \\ \ текст {} = \ frac {1} {2} \ hfill \ end {array} \\ [/ latex]
Используя тождество Пифагора, мы можем найти значение косинуса.\ circ [/ латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс] ABC [/ латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок 13
Угол наклона [латекс] ABD [/ латекс] составляет 30 °. Так, если двойной, угол [латекс] ABC [/ латекс] равен 60 °. [latex] BD [/ latex] — это серединный перпендикуляр к [latex] AC [/ latex], поэтому он разрезает [latex] AC [/ latex] пополам. Это означает, что [latex] AD [/ latex] — это [latex] \ frac {1} {2} [/ latex] радиус или [latex] \ frac {1} {2} [/ latex].\ circ [/ latex] — это [латекс] \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \\ [/ latex], поэтому мы можем найти синус и косинус.
[латекс] \ begin {array} {l} \ left (x, y \ right) = \ left (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \ hfill \\ x = \ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \ hfill \\ \ cos t = \ frac {1} {2}, \ sin t = \ гидроразрыв {\ sqrt {3}} {2} \ hfill \ end {array} \\ [/ latex]
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности.
 В таблице ниже приведены эти значения.
В таблице ниже приведены эти значения.Угол 0 [латекс] \ frac {\ pi} {6} \\ [/ latex], или 30 [латекс] \ frac {\ pi} {4} \\ [/ latex], или 45 ° [латекс] \ frac {\ pi} {3} \\ [/ latex], или 60 ° [латекс] \ frac {\ pi} {2} \\ [/ latex], или 90 ° Косинус 1 [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] [латекс] \ frac {1} {2} \\ [/ latex] 0 Синус 0 [латекс] \ frac {1} {2} \\ [/ latex] [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] 1 На рисунке 14 показаны общие углы в первом квадранте единичной окружности.
Рисунок 14
Использование калькулятора для поиска синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы измерения входного значения. Когда мы вычисляем [латекс] \ cos \ left (30 \ right) [/ latex] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в радианном режиме.

Как: заданный угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Пример 4: Использование графического калькулятора для поиска синуса и косинуса
Вычислить [латекс] \ cos \ left (\ frac {5 \ pi} {3} \ right) \\ [/ latex] с помощью графического калькулятора или компьютера.\ circ [/ latex], например, включив коэффициент преобразования в радианы как часть входных данных:
SIN (20 × π ÷ 180) ВВОД
Попробуй 4
Вычислить [латекс] \ sin \ left (\ frac {\ pi} {3} \ right) \\ [/ latex].
Решение
Определение области и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области и диапазоны. Каковы области определения функций синуса и косинуса? То есть, какие наименьшие и наибольшие числа могут входить в функции? Поскольку углы меньше 0 и углы больше [латекс] 2 \ pi [/ latex] все еще могут быть нанесены на единичный круг и имеют реальные значения [latex] x, y [/ latex] и [latex] r [/ latex], не существует нижнего или верхнего предела углов, которые могут входить в функции синуса и косинуса.Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшие и наибольшие возможные значения их производительности? Мы можем увидеть ответы, исследуя единичную окружность , как показано на рисунке 15. Границы координаты x составляют [latex] \ left [-1,1 \ right] [/ latex].
 Границы координаты y также равны [latex] \ left [-1,1 \ right] [/ latex].Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex].
Границы координаты y также равны [latex] \ left [-1,1 \ right] [/ latex].Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex].Рисунок 15
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса является координатой y на единичной окружности, другой угол с таким же синусом будет иметь то же значение y , но будет иметь противоположное значение x .Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с таким же косинусом будет иметь одинаковое значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на рисунке 16, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны.Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ begin {array} {lll} \ sin \ left (t \ right) = \ sin \ left (\ alpha \ right) \ hfill & \ text {and} \ hfill & \ cos \ left (t \ right ) = — \ cos \ left (\ alpha \ right) \ hfill \\ \ sin \ left (t \ right) = — \ sin \ left (\ beta \ right) \ hfill & \ text {и} \ hfill & \ cos \ left (t \ right) = \ cos \ left (\ beta \ right) \ hfill \ end {array} [/ latex]Рисунок 16
Напомним, что опорный угол угла — это острый угол [латекс] t [/ латекс], образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью.
 \ circ \ mathrm {-t} | [/ latex].\ circ [/ latex]
\ circ \ mathrm {-t} | [/ latex].\ circ [/ latex]Попробуй 5
Найдите опорный угол [латекса] \ frac {5 \ pi} {3} [/ latex].
Решение
Использование опорных углов
А теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела. Предположим, всадник делает снимок, остановившись на высоте двадцати футов над уровнем земли. Затем всадник совершает поворот на три четверти по кругу. Что такое новый рост райдера? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов, или при отрицательном угле .Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для поиска координат [latex] \ left (x, y \ right) [/ latex] для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для вычисления тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если мы знаем, косинус или синус его опорного угла.Абсолютные значения косинуса и синус угла являются такими же, как опорным углом. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака значений x в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений y в этом квадранте.
Общее примечание: Использование опорных углов для определения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы.Знак (положительный или отрицательный) можно определить по квадранту угла.
Как: для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью.
 Это опорный угол.
Это опорный угол. - Определение значений косинуса и синуса заданного угла.
- Придайте косинусу тот же знак, что и значения x в квадранте исходного угла.\ circ \ right) = \ frac {1} {2} [/ latex]
- [латекс] \ frac {5 \ pi} {4} [/ latex] находится в третьем квадранте. Его опорный угол составляет [латекс] \ frac {5 \ pi} {4} — \ pi = \ frac {\ pi} {4} [/ latex]. Косинус и синус [latex] \ frac {\ pi} {4} [/ latex] оба равны [latex] \ frac {\ sqrt {2}} {2} [/ latex]. В третьем квадранте значения [latex] x [/ latex] и [latex] y [/ latex] отрицательны, поэтому:
[латекс] \ cos \ frac {5 \ pi} {4} = — \ frac {\ sqrt {2}} {2} \ text {and} \ sin \ frac {5 \ pi} {4} = — \ гидроразрыв {\ sqrt {2}} {2} [/ latex]
Попробуй 6
а.\ circ \ right) [/ латекс].
г. Используйте опорный угол [латекс] — \ frac {\ pi} {6} [/ latex], чтобы найти [латекс] \ cos \ left (- \ frac {\ pi} {6} \ right) [/ latex] и [латекс] \ sin \ left (- \ frac {\ pi} {6} \ right) [/ latex].
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности.Они показаны на рисунке 19. Найдите время, чтобы узнать координаты [latex] \ left (x, y \ right) [/ latex] всех основных углов в первом квадранте.
В дополнение к изучению значений специальных углов, мы можем использовать опорные углы, чтобы найти координаты [latex] \ left (x, y \ right) [/ latex] любой точки единичной окружности, используя то, что мы знаем об опорных углах. вместе с идентификаторами
[латекс] \ begin {array} {l} x = \ cos t \ hfill \\ y = \ sin t \ hfill \ end {array} [/ latex]
Сначала мы находим опорный угол, соответствующий данному углу.
 Тогда мы возьмем синус и косинус значения опорного угла , и дать им знаки, соответствующие у — и х -значения квадранта.
Тогда мы возьмем синус и косинус значения опорного угла , и дать им знаки, соответствующие у — и х -значения квадранта.Практическое руководство. Зная угол точки на окружности и радиус окружности, найдите координаты [latex] \ left (x, y \ right) [/ latex] точки.
- Найдите опорный угол, измерив наименьший угол к оси x .
- Найти косинус и синус заданного угла.
- Определите соответствующие знаки для [латекс] x [/ латекс] и [латекс] y [/ латекс]
в данном квадранте.
Пример 6: Использование единичной окружности для поиска координат
Найдите координаты точки на единичной окружности под углом [латекс] \ frac {7 \ pi} {6} [/ latex].
Решение
Мы знаем, что угол [латекс] \ frac {7 \ pi} {6} [/ latex] находится в третьем квадранте.
Сначала давайте найдем опорный угол, измерив угол к оси x .Чтобы найти опорный угол для угла, конечная сторона которого находится в квадранте III, мы находим разность угла и [латекс] \ pi [/ латекс].
[латекс] \ frac {7 \ pi} {6} — \ pi = \ frac {\ pi} {6} [/ latex]
Далее мы найдем косинус и синус заданного угла:
[латекс] \ cos \ left (\ frac {\ pi} {6} \ right) = \ frac {\ sqrt {3}} {2} \ sin \ left (\ frac {\ pi} {6} \ right ) = \ frac {1} {2} [/ latex]
Мы должны определить соответствующие знаки для x и y в данном квадранте.Поскольку наш исходный угол находится в третьем квадранте, где оба [latex] x [/ latex] и [latex] y [/ latex] отрицательны, косинус и синус отрицательны.
[латекс] \ begin {array} {l} \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {\ sqrt {3}} {2} \ hfill \\ \ sin \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {1} {2} \ hfill \ end {array} [/ latex]
Теперь мы можем вычислить координаты [latex] \ left (x, y \ right) [/ latex], используя тождества [latex] x = \ cos \ theta [/ latex] и [latex] y = \ sin \ theta [ /латекс].

Координаты точки: [latex] \ left (- \ frac {\ sqrt {3}} {2}, — \ frac {1} {2} \ right) [/ latex] на единичной окружности.{2} t = 1 [/ латекс]
Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом 1 единица.
- Используя единичную окружность, синус угла [латекс] t [/ latex] равен значению y конечной точки единичной окружности дуги длиной [латекс] t [/ латекс], тогда как косинус угол [latex] t [/ latex] равен x -значению конечной точки.
- Значения синуса и косинуса наиболее точно определяются, когда соответствующая точка единичной окружности попадает на ось.
- Когда синус или косинус известен, мы можем использовать пифагорову тождество, чтобы найти другое. Пифагорейская идентичность также полезна для определения синусов и косинусов особых углов.
- Калькуляторы и программное обеспечение для построения графиков полезны для поиска синусов и косинусов, если известна правильная процедура ввода информации.
- Все функции синуса и косинуса являются действительными числами.
- Диапазон функций синуса и косинуса: [latex] \ left [-1,1 \ right] [/ latex].
- синус и косинус угла имеют одинаковое абсолютное значение как синус и косинус его опорного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Базовый угол угла — это размерный угол, [латекс] t [/ латекс],
, образованный конечной стороной угла [латекс] t [/ латекс] и горизонтальной осью. - Опорные углы можно использовать для определения синуса и косинуса исходного угла.
- Опорные углы также можно использовать для определения координат точки на окружности.
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 1
- синусоидальная функция
- значение y точки на единичной окружности, соответствующее заданному углу
- единичный круг
- круг с центром в [латекс] \ влево (0,0 \ вправо) [/ латекс]
и радиусом
Упражнения по разделам
- 1.
 Опишите единичный круг.
Опишите единичный круг. - 2. Что обозначают координаты x- и y- точек на единичной окружности?
3. Обсудите разницу между котерминальным углом и опорным углом.
4. Объясните, как косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
5. Объясните, как синус угла во втором квадранте отличается от синуса угла его опорного в единичной окружности.
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором находится конечная точка, определяемая [latex] t [/ latex].
6. [латекс] \ text {sin} \ left (t \ right) <0 [/ latex] и [latex] \ text {cos} \ left (t \ right) <0 [/ latex]
7. [латекс] \ text {sin} \ left (t \ right)> 0 [/ latex] и [latex] \ cos \ left (t \ right)> 0 [/ latex]
8. [латекс] \ sin \ left (t \ right)> 0 [/ latex] и [latex] \ cos \ left (t \ right) <0 [/ latex]
9.[латекс] \ sin \ left (t \ right) <0 [/ latex] и [латекс] \ cos \ left (t \ right)> 0 [/ latex]
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
10. [латекс] \ sin \ frac {\ pi} {2} [/ латекс]
11. [латекс] \ sin \ frac {\ pi} {3} [/ латекс]
12. [латекс] \ cos \ frac {\ pi} {2} [/ латекс]
13. [латекс] \ cos \ frac {\ pi} {3} [/ латекс]
14. [латекс] \ sin \ frac {\ pi} {4} [/ латекс]
15. [латекс] \ cos \ frac {\ pi} {4} [/ латекс]
16.\ circ [/ latex]
28. [латекс] \ frac {5 \ pi} {4} [/ латекс]
29. [латекс] \ frac {2 \ pi} {3} [/ латекс]
30. [латекс] \ frac {5 \ pi} {6} [/ латекс]
31. [латекс] \ frac {-11 \ pi} {3} [/ латекс]
32. [латекс] \ frac {-7 \ pi} {4} [/ латекс]
33. [латекс] \ frac {- \ pi} {8} [/ латекс]
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла. Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.
 \ circ [/ latex]
\ circ [/ latex]42. [латекс] \ frac {5 \ pi} {4} [/ латекс]
43. [латекс] \ frac {7 \ pi} {6} [/ латекс]
44. [латекс] \ frac {5 \ pi} {3} [/ латекс]
45. [латекс] \ frac {3 \ pi} {4} [/ латекс]
46. [латекс] \ frac {4 \ pi} {3} [/ латекс]
47. [латекс] \ frac {2 \ pi} {3} [/ латекс]
48. [латекс] \ frac {5 \ pi} {6} [/ латекс]
49. [латекс] \ frac {7 \ pi} {4} [/ латекс]
Найдите требуемое значение для следующих упражнений.
50. Если [латекс] \ text {cos} \ left (t \ right) = \ frac {1} {7} [/ latex] и [latex] t [/ latex] находится в квадранте 4 -го , найдите [латекс] \ text {sin} \ left (t \ right) [/ latex].
51. Если [латекс] \ text {cos} \ left (t \ right) = \ frac {2} {9} [/ latex] и [latex] t [/ latex] находится в квадранте 1 st , найдите [латекс] \ text {sin} \ left (t \ right) [/ latex].
52. Если [латекс] \ text {sin} \ left (t \ right) = \ frac {3} {8} [/ latex] и [latex] t [/ latex] находится в квадранте 2 и , найдите [латекс] \ text {cos} \ left (t \ right) [/ latex].
53. Если [latex] \ text {sin} \ left (t \ right) = — \ frac {1} {4} [/ latex] и [latex] t [/ latex] находится в квадранте 3 rd найдите [латекс] \ text {cos} \ left (t \ right) [/ latex].\ circ [/ латекс].
56. Найдите координаты точки на окружности с радиусом 8, соответствующей углу [латекс] \ frac {7 \ pi} {4} [/ latex].
57. Найдите координаты точки на окружности с радиусом 16, соответствующей углу [латекс] \ frac {5 \ pi} {9} [/ latex].
58. Укажите область определения функций синуса и косинуса.
59. Укажите диапазон функций синуса и косинуса.
Для следующих упражнений используйте заданную точку на единичном круге, чтобы найти значение синуса и косинуса [latex] t [/ latex].
60.
61.
62.
63.
64.
65.

66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
Для следующих упражнений используйте графический калькулятор для оценки.\ circ [/ latex]90. [латекс] \ sin \ left (\ frac {11 \ pi} {3} \ right) \ cos \ left (\ frac {-5 \ pi} {6} \ right) [/ latex]
91. [латекс] \ sin \ left (\ frac {3 \ pi} {4} \ right) \ cos \ left (\ frac {5 \ pi} {3} \ right) [/ latex]
92. [латекс] \ sin \ left (- \ frac {4 \ pi} {3} \ right) \ cos \ left (\ frac {\ pi} {2} \ right) [/ latex]
93. [латекс] \ sin \ left (\ frac {-9 \ pi} {4} \ right) \ cos \ left (\ frac {- \ pi} {6} \ right) [/ latex]
94. [латекс] \ sin \ left (\ frac {\ pi} {6} \ right) \ cos \ left (\ frac {- \ pi} {3} \ right) [/ latex]
95.[латекс] \ sin \ left (\ frac {7 \ pi} {4} \ right) \ cos \ left (\ frac {-2 \ pi} {3} \ right) [/ latex]
96. [латекс] \ cos \ left (\ frac {5 \ pi} {6} \ right) \ cos \ left (\ frac {2 \ pi} {3} \ right) [/ latex]
97. [латекс] \ cos \ left (\ frac {- \ pi} {3} \ right) \ cos \ left (\ frac {\ pi} {4} \ right) [/ latex]
98. [латекс] \ sin \ left (\ frac {-5 \ pi} {4} \ right) \ sin \ left (\ frac {11 \ pi} {6} \ right) [/ latex]
99. [латекс] \ sin \ left (\ pi \ right) \ sin \ left (\ frac {\ pi} {6} \ right) [/ latex]
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту.Ребенок входит в точку [latex] \ left (0,1 \ right) [/ latex], то есть на правильном северном положении. Предположим, карусель вращается против часовой стрелки.
100. Какие координаты ребенка через 45 секунд?
101. Какие координаты ребенка через 90 секунд?
102. Какие координаты ребенка через 125 секунд?
103.
 Когда у ребенка будут координаты [latex] \ left (0.707, -0.707 \ right) [/ latex], если поездка длится 6 минут? (Есть несколько ответов.)
Когда у ребенка будут координаты [latex] \ left (0.707, -0.707 \ right) [/ latex], если поездка длится 6 минут? (Есть несколько ответов.)104. Когда у ребенка будут координаты [latex] \ left (-0,866, -0,5 \ right) [/ latex], если поездка продлится 6 минут?
% PDF-1.3 % 8 0 объект > эндобдж xref 8 79 0000000016 00000 н. 0000001924 00000 н. 0000002076 00000 н. 0000002105 00000 н. 0000002183 00000 п. 0000002582 00000 н. 0000002819 00000 н. 0000002848 00000 н. 0000003034 00000 н. 0000003196 00000 н. 0000003285 00000 н. 0000003937 00000 н. 0000004133 00000 п. 0000004542 00000 н. 0000004722 00000 н. 0000004744 00000 н. 0000010847 00000 п. 0000010869 00000 п. 0000016796 00000 п. 0000016818 00000 п. 0000022809 00000 п. 0000022831 00000 п. 0000028850 00000 п. 0000028872 00000 п. 0000035280 00000 п. 0000035302 00000 п. 0000035499 00000 п. 0000035802 00000 п. 0000035993 00000 п. 0000036103 00000 п. 0000036211 00000 п. 0000036532 00000 п. 0000036939 00000 п. 0000037379 00000 п. 0000037569 00000 п. 0000037960 00000 п. 0000038160 00000 п. 0000039418 00000 п. 0000039624 00000 п. 0000039779 00000 п. 0000045905 00000 п. 0000045927 00000 п. 0000052042 00000 п. 0000052065 00000 п. 0000062851 00000 п. 0000166043 00000 н. 0000166184 00000 н. 0000166325 00000 н. 0000166472 00000 н. 0000166619 00000 н. 0000166763 00000 н. 0000166907 00000 н. 0000167054 00000 н. 0000167201 00000 н. 0000167345 00000 н. 0000167489 00000 н. 0000167632 00000 н. 0000167775 00000 н. 0000168491 00000 н. 0000168638 00000 н. 0000168778 00000 н. 0000168918 00000 н. 0000169059 00000 н. 0000169202 00000 н. 0000169349 00000 н. 0000169491 00000 п. 0000169633 00000 н. 0000169775 00000 н. 0000169915 00000 н. 0000170056 00000 н. 0000170198 00000 н. 0000170345 00000 п. 0000170488 00000 н. 0000170630 00000 н. 0000170777 00000 н. 0000170923 00000 п. 0000171069 00000 н.
 XX0 \ aaPt
4o_Kd & / 0_` | A _} / oʀ ** 0>
XX0 \ aaPt
4o_Kd & / 0_` | A _} / oʀ ** 0>Квадратичная формула с тригонометрией — тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
5.2: Единичная окружность — функции синуса и косинуса
Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы особых углов, используя тождество Пифагора и наши знания о треугольниках.
Нахождение синусов и косинусов углов 45 °
Сначала мы посмотрим на углы \ (45 ° \) или \ (\ dfrac {π} {4} \), как показано на рисунке \ (\ PageIndex {9} \). Треугольник \ (45 ° –45 ° –90 ° \) является равнобедренным треугольником, поэтому координаты \ (x \) и \ (y \) соответствующей точки на окружности совпадают. Поскольку значения x- и \ (y \) одинаковы, значения синуса и косинуса также будут равны.
Рисунок \ (\ PageIndex {9} \)В \ (t = \ frac {π} {4} \), что составляет 45 градусов, радиус единичной окружности делит пополам первый квадратный угол .2 & = \ dfrac {1} {2} \\ x & = ± \ dfrac {1} {\ sqrt {2}} \ end {align *} \]
В квадранте I, \ (x = \ dfrac {1} {\ sqrt {2}} \).
При \ (t = \ dfrac {π} {4} \) или 45 градусов,
\ [\ begin {align *} (x, y) & = (x, x) = (\ dfrac {1} {\ sqrt {2}}, \ dfrac {1} {\ sqrt {2}}) \ » \ x & = \ dfrac {1} {\ sqrt {2}}, \; y = \ dfrac {1} {\ sqrt {2}} \\ \ cos t & = \ dfrac {1} {\ sqrt {2}}, \; \ sin t = \ dfrac {1} {\ sqrt {2}} \ end {align *} \]
Если мы затем рационализируем знаменатели, мы получим
\ [\ begin {align *} \ cos t & = \ dfrac {1} {\ sqrt {2}} \ dfrac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ dfrac {\ sqrt {2}} {2} \\ \ sin t & = \ dfrac {1} {\ sqrt {2}} \ dfrac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ dfrac { \ sqrt {2}} {2} \ end {align *} \]
Следовательно, координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (45 ° \) равны \ (\ left (\ dfrac {\ sqrt {2 }} {2}, \ dfrac {\ sqrt {2}} {2} \ right) \).

Нахождение синусов и косинусов углов 30 ° и 60 °
Затем мы найдем косинус и синус под углом \ (30 °, \) или \ (\ tfrac {π} {6} \). Сначала мы нарисуем треугольник внутри круга, одна сторона которого расположена под углом \ (30 °, \), а другая — под углом \ (- 30 °, \), как показано на рисунке \ (\ PageIndex {11} \ ). Если полученные два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут равны \ (60 °, \), как показано на рисунке \ (\ PageIndex {12} \).
Рисунок \ (\ PageIndex {11} \) Рисунок \ (\ PageIndex {12} \)Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину \ (2y \), и поскольку все стороны равны, мы также можем заключить, что \ (r = 2y \) или \ (y = \ frac {1} {2} r \). Поскольку \ (\ sin t = y \),
\ [\ sin \ left (\ frac {π} {6} \ right) = \ dfrac {1} {2} \ nonumber \]
А поскольку \ (r = 1 \) в нашем единичном круге ,
\ [\ begin {align *} \ sin \ left (\ frac {π} {6} \ right) & = \ dfrac {1} {2} (1) \\ & = \ dfrac {1} {2} \ end {align *} \]
Используя тождество Пифагора, мы можем найти значение косинуса.2 \ left (\ frac {π} {6} \ right) & = \ dfrac {3} {4} && \ text {Используйте свойство квадратного корня.} \\
\ cos \ left (\ frac {π} { 6} \ right) & = \ pm \ sqrt {\ dfrac {3} {4}} = \ dfrac {\ sqrt {3}} {2} && \ text {Поскольку \ (y \) положительное значение, выберите положительный корень. } \\
\ конец {выровнено} \)Координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (30 ° \): \ (\ left (\ dfrac {\ sqrt {3}} {2}, \ dfrac {1} {2} \ right) \). В точке \ (t = \ dfrac {π} {3} \) (60 °) радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, \ (BAD, \) как показано на рисунке \ (\ PageIndex {13} \).Угол \ (A \) имеет меру 60 °. 60 °. В точке \ (B, \) проведем угол \ (ABC \) с мерой \ (60 ° \).
Рисунок \ (\ PageIndex {13} \) Мы знаем, что сумма углов в треугольнике равна \ (180 ° \), поэтому мера угла \ (C \) также равна \ (60 ° \). Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника \ (ABC \) имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Мы знаем, что сумма углов в треугольнике равна \ (180 ° \), поэтому мера угла \ (C \) также равна \ (60 ° \). Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника \ (ABC \) имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.Угол \ (ABD \) равен 30 °. Итак, если двойной, угол \ (ABC \) равен 60 °.2 & = \ dfrac {3} {4} \\ y & = ± \ dfrac {\ sqrt {3}} {2} \ end {align *} \]
Поскольку \ (t = \ dfrac {π} {3} \) имеет конечную сторону в квадранте I, где \ (y \) — координата положительна, мы выбираем \ (y = \ dfrac {\ sqrt {3}} {2} \) положительное значение.
В \ (t = \ dfrac {π} {3} \) (60 °) координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (60 ° \) равны \ (\ left (\ dfrac {1} {2}, \ dfrac {\ sqrt {3}} {2} \ right) \), поэтому мы можем найти синус и косинус.
\ ((x, y) = \ left (\ dfrac {1} {2}, \ dfrac {\ sqrt {3}} {2} \ right) \)
\ (x = \ dfrac {1} {2}, \; y = \ dfrac {\ sqrt {3}} {2} \)
\ (\ cos t = \ dfrac {1} {2}, \; \ sin t = \ dfrac {\ sqrt {3}} {2} \)
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности.Таблица \ (\ PageIndex {1} \) суммирует эти значения.
Таблица \ (\ PageIndex {1} \) Угол 0 \ (\ dfrac {π} {6} \) или 30 \ (\ dfrac {π} {4} \), или 45 ° \ (\ dfrac {π} {3} \), или 60 ° \ (\ dfrac {π} {2} \) или 90 ° Косинус 1 \ (\ dfrac {\ sqrt {3}} {2} \) \ (\ dfrac {\ sqrt {2}} {2} \) \ (\ dfrac {1} {2} \) 0 Синус 0 \ (\ dfrac {1} {2} \) \ (\ dfrac {\ sqrt {2}} {2} \) \ (\ dfrac {\ sqrt {3}} {2} \) 1 На рисунке \ (\ PageIndex {14} \) показаны общие углы в первом квадранте единичной окружности.
Рисунок \ (\ PageIndex {14} \)
Использование калькулятора для поиска синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы измерения входного значения. Когда мы вычисляем \ (\ cos (30) \) на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан.
Как: заданный угол в радианах, с помощью графического калькулятора найдите косинус
.- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Пример \ (\ PageIndex {4} \): использование графического калькулятора для поиска синуса и косинуса
Оцените \ (\ cos \ left (\ dfrac {5π} {3} \ right) \) с помощью графического калькулятора или компьютера.
Решение
Введите следующие нажатия клавиш:
\ (\ mathrm {COS (5 × π ÷ 3) \; ENTER} \)
\ [\ cos \ left (\ dfrac {5π} {3} \ right) = 0,5 \ nonumber \]
Анализ
Косинус или синус угла в градусах можно найти прямо на калькуляторе в градусном режиме. Для калькуляторов или программного обеспечения, которые используют только режим радиан, мы можем найти знак \ (20 ° \), например, включив коэффициент преобразования в радианы как часть входных данных:
\ [\ mathrm {SIN (20 × π ÷ 180) \; ENTER} \ nonumber \]
Попробовать \ (\ PageIndex {4} \)
Вычислить \ (\ sin \ left (\ dfrac {π} {3} \ right) \).
- Ответ
приблизительно 0,866025403
различные виды тригонометрической идентичности
Введение
Треугольники
Единичная окружность
Среднеквадратичный
Матрица вращения
Определитель
Ортонормированный базис
Комбинаторные тождества
Экспоненциальная функция
Алгебра
Факторизация
Производные параметризованной кривой
Интегральный аналог
Гиперболическая обратная связь
Сохранение энергииМы рассмотрим различные интерпретации указанного выше тождества.
 Более поздние части
это эссе не часто зависит от более ранних частей, поэтому не стесняйтесь бегать бегло
пропустите непонятный текст, пока не найдете то, что вам удобно.
Более поздние части
это эссе не часто зависит от более ранних частей, поэтому не стесняйтесь бегать бегло
пропустите непонятный текст, пока не найдете то, что вам удобно.Обычно идентичность понимается через Пифагора. теорема. В прямоугольном треугольнике со сторонами a , b , c и угол t на вершине где a и c пересекаются, cos (t) по определению a / c , sin (t) по определению b / c , и поэтому cos 2 (t) + sin 2 (t) есть (a / c) 2 + (b / c) 2 , что простым алгебраические манипуляции (a 2 + b 2 ) / c 2 .Пифагор’ Теорема утверждает, что a 2 + b 2 является c 2 , так что это упрощается до 1.
Традиционно (то есть, как я это усвоил) следующим шагом является поймите, что единичный круг с центром (0,0) в (x, y) плоскость определяется x 2 + y 2 = 1 . Вышеуказанная личность может быть интерпретируется как утверждение, что точка (cos (t), sin (t)) находится на единичный круг.Кроме того, этот подход приводит к определению cos (t) и sin (t) для всех действительных t .
Другой способ понять это тождество — использовать тригонометрические тождества.
cos 2 (x) = 1/2 + (1/2) cos (2x) sin 2 (x) = 1/2 — (1/2) cos (2x) Между прочим, эти личности в значительной степени выпрыгивают на вас из глядя на графики y = cos 2 (x) и y = грех 2 (х) .

Другой способ взглянуть на это — вспомнить, что среднеквадратичное значение cos равно 1 / √2 , как и среднеквадратичное значение грех . Это означает, что cos 2 равно 1/2 + вариация, и sin 2 равно 1/2 + вариация , и удивительно вариация cos 2 — это как раз отрицательное значение вариации грех 2 . Собственно, это согласуется с тем, что что sin и cos — это просто версии со сдвигом фазы друг друга, так что sin 2 и cos 2 являются сдвинутыми по фазе версиями друг друга, поэтому их вариации должны быть как-то связаны.
Еще один способ понять идентичность — использовать матрицы 2 на 2. В линейная матрица, представляющая поворот против часовой стрелки на угол т это
Так или иначе, теперь у нас есть это cos 2 (t) + sin 2 (t) имеет вид (1/2 + отклонение) + (1/2 — отклонение) , так что это 1 .
Матрица имеет определитель ad-bc , поэтому матрица вращения имеет определитель cos (t) cos (t) — (- sin (t)) sin (t) , что является cos (t) cos (t) + sin (t) sin (t) , т.е. cos 2 (t) + sin 2 (t) .Определитель квадратная матрица имеет простую геометрическую интерпретацию. Это область коэффициент масштабирования. Для вращения площадь не изменяется, поэтому определитель должно быть 1 . Итак, личность cos 2 (t) + sin 2 (t) = 1 можно интерпретировать как выражение довольно очевидного факта, что вращение объекта в Плоскость (x, y) не меняет своей площади.cos (t) -син (т) sin (т) cos (т) 
Матрица вращения отправляет точку (1,0) в (cos (x), sin (x)) и точка (0,1) от до (-sin (x), соз (х)) .Стандартный базис e 1 = (1,0) , e 2 = (0,1) является ортонормированным базисом, что означает, что
e 1 .e 1 = 1 (проверка: 1,1 + 0,0 = 1 )
e 1 .e 2 = 0 (проверка: 0,1 + 1,0 = 0 )
e 2 .e 2 = 1 (проверка: 0,0 + 1,1 = 1 )Поскольку вращение является «жестким движением», оно преобразует ортонормированный базис в другой ортонормированный базис.Это означает, что указанные выше три уравнения будут истина, когда e 1 равно (cos (t), sin (t)) и e 2 это (-sin (t), cos (t)) . Два уравнения e 1 .e 1 = 1 и e 2 .e 2 = 1 являются пересчетом cos 2 (t) + sin 2 (t) = 1 , а e 1 .e 2 = 0 является заявлением о личности cos (t) (- sin (t)) + sin (t) cos (t) = 0 .Как ни странно, даже оператор e 1 .e 2 является проявление личности, как показано ниже.
Другой способ взглянуть на идентичность — через расширение степенного ряда cos (x) и sin (x).cos (x) = 1 — x 2 /2! + x 4 /4! — x 6 /6! + x 8 /8! — … sin (x) = x — x 3 /3! + x 5 /5! — x 7 /7! + …
Это значит, чтоcos 2 (x) = 1 — (1/2! + 1/2!) x 2 + (1/4! + 1/2! 2! + 1/4!) x 4 /4! — … sin 2 (x) = x 2 — (1/3! + 1/3!) x 4 /4! + …
В этом контексте идентичность cos 2 (t) + sin 2 (t) = 1 действительно кодирует бесконечное количество тождеств, включающих факториалы, а именно1/2! + 1/2! = 1 1/4! + 1/2! 2! + 1/4! = 1/3! + 1/3! 1/6! + 1/4! 2! + 1/2! 4! + 1/6! = 1/5! + 1/3! 3! + 1/5! …
Эти тождества можно переформулировать в терминах комбинаторной коэффициенты ( n C r = n! / (n-r)! r! )2 C 0 + 2 C 2 = 2 С 1 4 C 0 + 4 C 2 + 4 С 4 = 4 C 1 + 4 C 3 6 С 0 + 6 С 2 + 6 C 4 + 6 C 6 = 6 С 1 + 6 С 3 + 6 С 5 …
Они говорят, что четные комбинаторные коэффициенты в сумме составляют тот же результат, что и нечетные комбинаторные коэффициенты. Этот результат может
быть доказанным напрямую. Это легче всего увидеть, посмотрев на
треугольник, и складывая члены подряд в двух разных
способами. Кроме того, использование расширений степенного ряда для расширения
определение cos и sin к комплексным числам, мы
теперь знаю что тож верен для комплекса т . Благодаря
Боб Ува за указание на это.
Этот результат может
быть доказанным напрямую. Это легче всего увидеть, посмотрев на
треугольник, и складывая члены подряд в двух разных
способами. Кроме того, использование расширений степенного ряда для расширения
определение cos и sin к комплексным числам, мы
теперь знаю что тож верен для комплекса т . Благодаря
Боб Ува за указание на это.Продолжая в том же духе, тот факт, что e x = 1 + x + x 2 /2! + x 3 /3! + x 4 /4! +… сразу сообщает нам, что e ix = 1 + ix — x 2 /2! — ix 3 /3! + x 4 /4! +… то есть деление на четную и нечетную степени e ix = cos (x) + isin (x) На данный момент есть два способа получить удостоверение личности. Во-первых, необходимо понять, что единственное уравнение e ix = cos (x) + isin (x) дает нам уравнение e -ix = cos (x) -isin (x) и из этих двух уравнений мы можем решить для cos (x) и sin (x) , чтобы получить
cos (x) = (e ix + e -ix ) / 2
sin (x) = (e ix -e -ix ) / 2i .
Пусть w представляет e ix , так что 1 / w — это e -ix , мы имеем cos 2 (x) + sin 2 (x) — это (ш + 1 / ш) 2 /4 — (ш-1 / ш) 2 /4 . Этот
упрощается до 1 . Итак, тригонометрическое тождество можно рассматривать
как алгебраическое тождество (w + 1 / w) 2 —
(w-1 / w) 2 = 4 .
Этот
упрощается до 1 . Итак, тригонометрическое тождество можно рассматривать
как алгебраическое тождество (w + 1 / w) 2 —
(w-1 / w) 2 = 4 .Второй — быть умными (по-другому) и понимать, что мы можем разложить на множители a 2 + b 2 как (a-ib) (a + ib) . Если вы не видели этого раньше, это пересчет a 2 -b 2 = (a-b) (a + b) . Используя комплексные числа, мы получаем, что -b 2 — это (ib) 2 , что приводит к a 2 + b 2 = a 2 — (- b 2 ) = а 2 — (ib) 2 = (a-ib) (a + ib) .Кстати, конечно также верно, что a 2 + b 2 = (b-ia) (b + ia) . В любом случае, применяя факторизацию к cos 2 (x) + sin 2 (x) , получаем (cos (x) + isin (x)) (cos (x) -isin (x)) , что является e ix e -ix . Использование w для представления e ix , факт, что cos 2 (x) + sin 2 (x) = 1 — это просто запутанный способ сказать w (1 / w) = 1 .
Рассмотрим параметризованную кривую c (t) = (cos (t), sin (t)) . В identity говорит нам, что эта параметризованная кривая всегда находится на единице кружок о происхождении. Дифференцируя, имеем c ‘(t) = (-sin (t), cos (t)) . c ‘(t) . c ‘(t) равно (-sin (t)) (- sin (t)) + cos (t) cos (t) , что просто cos 2 (t) + sin 2 (t) . Тот факт, что это 1 говорит нам, что параметризованная кривая на самом деле параметризуется длиной дуги.Итак, тригонометрическое тождество можно рассматривается как просто констатация того факта, что радианы проходят через единицу круг с единичной скоростью. Наконец, снова дифференцируя, получаем c » (t) = (-cos (t), -sin (t)) .
 Очевидно, c » (t) .c » (t) =
cos 2 (t) + sin 2 (t) , так что тождество
говорит нам, что равномерное движение по кругу приводит к
ускорение постоянной величины.
Очевидно, c » (t) .c » (t) =
cos 2 (t) + sin 2 (t) , так что тождество
говорит нам, что равномерное движение по кругу приводит к
ускорение постоянной величины.Наконец, еще один подход к установлению того, что cos 2 (x) + sin 2 (x) is 1 is to поймите, что на самом деле он заявляет о двух отдельных свойствах, а именно о том, что cos 2 (x) + sin 2 (x) — постоянная величина, и что константа оказывается равной 1, т.е.для некоторого значения x , cos 2 (x) + sin 2 (x) равно 1 . В последнее свойство устанавливается быстро: принимая x = 0 , cos (x) = 1 и sin (x) = 0 . Четко 1 2 +0 2 = 1 .
Учитывая функцию f , чтобы установить, что f является постоянной функции, достаточно установить, что производная от f равно нулю. Применяя эту технику к f = cos 2 + sin 2 , первый шаг — использование цепное правило, чтобы получить, что производная от cos 2 (x) + sin 2 (x) равно 2cos (x) cos’x + 2sin (x) sin ‘(x) .Через производные тождества cos ‘(x) = -sin (x) и sin ‘(x) = cos (x) , имеем 2cos (x) cos’x + 2sin (x) sin ‘(x) упрощается до 2cos (x) (- sin (x)) + 2sin (x) cos (x) , что равно нулю. Итак идентичность можно рассматривать как интегрированную версию тривиального личность
cos (x) (- sin (x)) + sin (x) (cos (x)) = 0 , который мы видели ранее в совершенно другой контекст.Еще один способ увидеть, что cos 2 + sin 2 константа — это понять, что она представляет собой сумму потенциальных и кинетические энергии решения x = cos (t) уравнения для простого гармонического движения x » (t) + x (t) = 0 .

Для частицы массы 1 кинетическая энергия равна (1/2) x ‘(t) 2 , а потенциальная энергия равна (1/2) x (t) 2 (с точностью до аддитивной константы). Сохранение энергии говорит нам, что (1/2) x ‘(t) 2 + (1/2) x (t) 2 является константой, и поэтому х ‘(т) 2 + х (т) 2 также является константой. Принимая решение x (t) = cos (t) (или x (t) = sin (t) ) мы получаем личность.
Я должен отметить, что ни одна из вышеперечисленных математических задач не зависит от лежащая в основе физика.Если x (t) — решение второго порядка уравнение x » (t) + F (x (t)) = 0 , тогда (1/2) x ‘(t) 2 + V (x (t)) , где V является первообразной F , является константой. Простое дифференцирование подчеркивает это.
Между прочим, поскольку x (t) = acos (t) + bsin (t), является общим решением к уравнению второго порядка имеем
(acos (t) + bsin (t)) 2 + (- asin (t) + bcos (t)) 2 — константа a 2 + b 2Следующим шагом к пониманию идентичности является сравнение и сопоставление это тождество для гиперболического косинуса и гиперболического синуса, а именно cosh 2 (t) — sh 2 (t) = 1 .Я отложу это к более позднему эссе.
2 апреля 2003 г. Размещено 7 апреля 2003 г. Последнее обновление Вернуться к началу страницы
Архив тригонометрии | 07 марта 2020 г. Архив
Тригонометрия | 07 марта 2020 г. | Chegg.com Тригонометрия Архив: Вопросы от 07 марта 2020 года- может вы, ребята, дадите мне несколько советов, как помешать так быстро
потому что вроде бы много работы.
 ..
в значительной степени забыл … мой
там ответ правильный, но не упрощенный или ошибочный.
..
в значительной степени забыл … мой
там ответ правильный, но не упрощенный или ошибочный.
(Упростите свой ответ. Введите точный ответ, используя радикалы как ne 75/133 — 1014 c. Tan (a + B) = 902 (Упростите ваш новый Tino на vart anewor, используя радикалы как neec 3/133 — 24 Вы ответили: — 41133 +1 ответ
-
17. Используйте формулу половинного угла, чтобы найти точное значение следующего выражения: tan 22,5 A. 2-1 B. -12-1 C. — 2 + 1 D. V2 + 1 18. Используйте график для завершения тождество: 1 + COS X sinx sinx 1 + COS X 2 A.21 ответ
- используйте калькулятор, чтобы решить уравнение на интервале
[0,2pi]. Округлите ответ до двух десятичных знаков sinx = 0
1 ответ
-
Примените правила, касающиеся использования значащих цифр 49. ne окружность на рисунке имеет радиус r и центр +20 X-20 4 24 ° C = 66 ° и x = 20, найдите r. bly правила, касающиеся использования значительных1 ответ
-
Найти 0, 0 ° 5 01 ответ
-
а.Найдите наклонную асимптоту графика рациональной функции и b. Следуйте стратегии из шести шагов и используйте наклонную асимптоту для построения графика рациональной функции. X-8 f (x) 2-3x а. Найдите уклон бессимптомно1 ответ
-
Решите нелинейную систему уравнений для вещественных решений. y = x²-2 y = x? — 2x Выберите правильный вариант ниже и, при необходимости, заполните поле ответа, чтобы завершить свой выбор. O A. Решение (я)1 ответ
-
Решите нелинейную систему уравнений для вещественных решений.x² + y² = 4 x? + (y — 1) 2 = 1 Выберите правильный вариант ниже и заполните все поля для ответов по вашему выбору. O A. Решение (я)1 ответ
-
Иисус Приближает уравнение линии наилучшего соответствия и делает пред … Esp. Диаграмма разброса показывает время, потраченное на обучение, x, и результат теста, y, для каждого из 24 студентов. (а) Напишите приблизительное
(а) Напишите приблизительное1 ответ
- Для треугольника ABC следующая информация
при условии.A = 27 °, b = 18 и c = 30.
(Угол A — противоположная сторона a, угол B —
противоположная сторона b, угол C противоположная сторона
c.) Укажите, в каком случае применяется
1 ответ
-
На этапе разработки новой прямоугольной клавиатуры для системы безопасности было решено, что площадь прямоугольника должна составлять 210 квадратных сантиметров, а периметр — 58 сантиметров.1 ответ
- Определите тип конического сечения, представленного уравнением
4х2 + 9у2 — 18у — 27 = 0.парабола
круг
эллипс
гипербола
1 ответ
-
4. Какая из функций соответствует графику? — тел-2t A. f (x) = 2 (1 — cos x) B. f (x) = 3 — cos x C. f (x) = 2 + cos x D. f (x) = 2 — sin Икс1 ответ
-
На этапе разработки новой прямоугольной клавиатуры для системы безопасности было решено, что площадь прямоугольника должна составлять 228 квадратных сантиметров, а периметр — 62 сантиметра.1 ответ
- 5.Приведенная ниже матрица представляет собой расширенную матрицу для системы трех
линейные уравнения. Какие можно сделать выводы о решении проблемы
система?
1
0 −2 1
(0
1 0 | 4)
0
0 0
0
1 ответ
-
6. Какое из уравнений соответствует графику? -47 A. r = 1 — cos B. r = 1-sino C. r = 1–2 cos 0 D. r = 1 — 2 sino1 ответ
-
7. Является ли следующая сумма арифметической последовательности, геометрической последовательности или ни того, ни другого, и какова сумма? k = 1 А.сумма геометрической последовательности; sum = 6.4416 сумма геометрической последовательности; сумма = 3,2736 с1 ответ
-
Используйте единичный круг, чтобы найти все значения от 0 до 2, для которых данное утверждение верно. (Введите свои ответы в виде списка, разделенного запятыми.) Cos — -1/2 0-1 x rad Нужна помощь? Читать Thik to Tvor Sub1 ответ
-
9. (a) Приведите пример угла, который совпадает с 660 °. Ответ: (b) Преобразуйте угол 15 радиан в градусы.Отвечать:
(a) Приведите пример угла, который совпадает с 660 °. Ответ: (b) Преобразуйте угол 15 радиан в градусы.Отвечать:1 ответ
-
10. Найдите точные значения (без десятичных приближений). (a) sec 4950 Ответ: (b) tan (-210 °) Ответ: 11. Для y = 3 sin (6x — It) укажите период (a) Ответ: (b) сдвиг фазы Ответ:1 ответ
- 1.
(1 балл) Учитывая cos (a) = -9 и 8/21 ответ
-
(cos x) (2sin x + 1) = 0 в интервале [0, 360 °). 12. Решите тригонометрическое уравнение. Найдите точные значения.Ответ: 13. (a) Найдите точное значение arccos (sinº). Ответ: (b) Найдите точное значение1 ответ
-
Используйте рисунок ниже, который показывает единичную окружность с шагом 0,1 единицы, отмеченную по окружности в направлении против часовой стрелки, начиная с точки (1,0). Мое примечание: оцените, если cos 8 = -0,11 ответ
-
14. (a) Для точки (2, 150 °) в полярных координатах найдите соответствующую точку в прямоугольных координатах.(Укажите точные значения, а не десятичные приближения.) Ответ: (b) Учитывая точку (6, — 6)1 ответ
-
-5. Для параболы (v — 3) 2 = 8 (x + 2) найдите следующее: (a) парабола направления открывается (влево, вправо, вверх или вниз) Ответ: (b) вершина Ответ: ( в) фокус Ответ:1 ответ
- график и объясните пожалуйста
O ПОЛИНОМИАЛЬНЫЕ И РАЦИОНАЛЬНЫЕ ФУНКЦИИ Переписываем квадратичную функцию, чтобы найти ее вершину и нарисовать ее гра… Запишите квадратичную функцию в виде g (x) = a (x-h + k. Затем дайте вершину ее графика1 ответ
-
16. Билеты в парк аттракционов стоят 52 доллара для взрослых и 38 долларов для детей. Было продано 2000 билетов на общую сумму 86 780 долларов. Предположим, вы хотите узнать, сколько билетов каждого типа было продано.1 ответ
-
Найдите точное значение выражения. sin-1 (0,5) A) 60 ° B) 420 C) 30 ° D) -30 °
sin-1 (0,5) A) 60 ° B) 420 C) 30 ° D) -30 °1 ответ
-
17.Строительный подрядчик планирует использовать лестницу, чтобы добраться до окна. Если 15-футовая лестница прислоняется к зданию с углом подъема 73 °, насколько высоко по зданию поднимется лестница.1 ответ
-
Шрифт абзаца Абзац FL Sty 18. Эллипс имеет уравнение (8752 + (+2) = 1 25 49 (a) Большая ось горизонтальна или вертикальна? (B) Найдите точные значения фокусов эллипса. Показать работы.1 ответ
-
19.Предположим, что cos 0 = 12/13, и это угол в квадранте IV. (а) Найдите точное значение sin 0. Покажите работу. (б) Найдите точное значение sin (20). Показать работы.1 ответ
-
катионов Срок сдачи: среда, 11.03.2020, 23:59. Путь спутника, вращающегося вокруг Земли, заставляет его проходить непосредственно над двумя станциями слежения A и B, которые находятся на расстоянии 53 км друг от друга. Когда спутник находится на одной стороне o1 ответ
- Вы качаетесь на качелях. Когда вы сидите неподвижно, вы 1.5 мес.
от земли.Когда вы постоянно махаете, ваш максимум
высота над землей — 4. Путешествие от земли занимает 3 секунды.
наибольший
1 ответ
-
20. Докажите тождество 1- (sin x — cos x) 2 = sin (2x) DELL1 ответ
-
21. Для треугольника ABC задано, что A = 40 °, B = 63 ° и c = 38,0. — 6300 C = 38 В Найдите длину стороны b, округленную до сотых.Показать работы.1 ответ
-
22. Пусть u = (4, 2) и v = (5, -10). Вычислить u + Zv. Показать работы. Вычислите точную длину или величину u. Показать работы. Рассчитайте скалярное произведение u.y. Показать работы. Определите угол между u и1 ответ
-
23. Решите систему уравнений, используя метод исключения Гаусса с матрицами или без них или метод исключения Гаусса-Жордана (метод на ваш выбор). Показать работу.x — y + 3 = 8 —2x + y + 85 = 1 X — V — 2-
Показать работу.x — y + 3 = 8 —2x + y + 85 = 1 X — V — 2-1 ответ
-
Срок сдачи: 03/11/2020 11: Кривая с полярным уравнением — sin 39 +33 cose представляет собой линию. Эта линия имеет декартово уравнение вида y, формула для v через. Например, если в строке было1 ответ
- Проверьте следующую личность. Покажи все свои шаги.
1.
(tan2theta) (cos2theta) + (cot2theta) (sin2theta) = 1
1 ответ
- проверьте следующую личность.покажи все свои шаги.
1 ответ
- проверьте следующую личность. покажи все свои шаги.
1 ответ
- проверьте следующую личность. покажи все свои шаги.
1 ответ
- проверьте следующую личность. покажи все свои шаги.
1 ответ
-
3.6.57 Запишите кубические корни числа — 216 в стандартной форме. Корни (Упростите свой ответ.Выражайте комплексные числа через i. При необходимости разделяйте ответы запятыми. Введите дроби для любых1 ответ
- проверьте следующую личность. покажи все свои шаги.
1 ответ
-
.6.41 Используйте теорему Де Муавра, чтобы упростить выражение. Дайте ответ в виде a + bi. [2 (cos 30 ° + i sin 30 ° 3 12 (cos 30 ° + i sin 30 °)} = (Введите свой ответ в форме a + bi) нет 191 ответ
-
Домашнее задание: 9 неделя Оценка HW: 0 из 1 балла 13 из 17 (90 8.6.19 Напишите следующее число в тригонометрической форме. Пусть oºse1 ответ
-
8.6.7 Найдите модуль числа. 6-8 i Модуль (Упростите ответ).1 ответ
-
Домашнее задание: 9-я неделя Оценка HW: 0 из 1 балла 11 из 17 (завершено 9) B.6.3 Нанесите числа на комплексную плоскость a) График — 6 a) -6 b) -3-6i Almaginary Real 191 ответ
-
Запишите полярное уравнение через x и y.T- 2 cos 0 + 5 sin 0 Эквивалентное уравнение с прямоугольными координатами: y = (используйте целые числа или дроби для любых чисел в выражении. )
)1 ответ
-
или заданная точка (0,1) в прямоугольных координатах, найдите эквивалентные полярные координаты (re), которые удовлетворяют условиям a)> 0,0 °, поэтому1 ответ
- тригонометрия 8,3-8,5
Направления: делать на отдельном листе. Чтобы получить зачет, вы должны продемонстрировать достаточную работу и подкрепить свои ответы.Убедитесь, что ваша работа аккуратная и аккуратная! Все ответы должны быть точными и простыми1 ответ
-
Показать WOPR TULUMLI CUIL. Причитается W EPO 1. Найдите точное значение каждого из них. Никаких десятичных приближений! (По 3 балла) (b) arctan) (c) arcsin (O) — (a) cos «(7 2. Точно оценивайте каждое значение. Никаких десятичных приближений!)1 ответ
-
4. Решите каждое уравнение. (По 4 балла) (a) 4 sinx -3 = 0 (b) 7 cose +9 = -2 cose 5. С помощью калькулятора найдите все такие, что OSOS 2 и cos 0 = 0.9451. (4 балла) 6. Найдите точное значение выражения. N1 ответ
-
8. Решите каждое уравнение в интервале 10, 2n). По возможности используйте точные ответы. Если точный ответ невозможен, используйте десятичное приближение с округлением до двух знаков после запятой. (По 8 баллов) (a) 2 cos x1 ответ
- 7,8,15,16
нужны решения для этих 4 вопросов, пожалуйста
Минутная стрелка часов имеет длину 18 см. Определите количество радианов, на которое он поворачивается, и расстояние, на которое перемещается его наконечник, когда он поворачивается из положения 11:32 до 12:19.должность. Найдите длину1 ответ
- 23, 26, 32, 33!
22. Решите уравнение 3 tan u + 4 = 2 для значений u между 0 ° и 360 °. Есть два решения.) 23. Точка (-20, 48) находится на конечном луче угла u. Найдите точное значение sin u. 24.1 ответ
- Как бы вы решили вторую часть задачи?
Подтвердите личность. (1 — sin? (T) + 2 cos? (T)) 2 + 9 sin? (T) cos? (T) = 9 cos? (T) (1 — sin2 (t) + 2 cos? (T) ) 2 + 9 sin? (T) cos? (T) = (3 cos? (T)) 2 + cosat = 9 cos ”(b) (cos? (E) + | — 9 cos? Нужна помощь?1 ответ
- Почему это не было бы cot theta?
Напишите тригонометрическое выражение в терминах синуса и косинуса, а затем упростите. sin (0) — csc (0) cos (0) cot e Нужна помощь? Прочтите, посмотрите, поговорите с репетитором
sin (0) — csc (0) cos (0) cot e Нужна помощь? Прочтите, посмотрите, поговорите с репетитором1 ответ
-
8.2.41 Самолет (в точке Z) заметен двумя наблюдателями (в X и Y), которые находятся на расстоянии L = 1350 футов друг от друга. Когда самолет пересекает линию, соединяющую их, каждый наблюдатель оценивает угол подъема.1 ответ
-
ТИВИТИУМ. ULUIT 0.2 TUTTE VOLN Оценка сохранений: 0 из 1 балл 14 из 14 (11 завершено) Оценка HW: 78.57%, 11 из 14 баллов 8.2.55 Вопрос Help Sun Навес, закрывающий раздвижную стеклянную дверь высотой 88 дюймов.1 ответ
-
4. secx -tan x = — COS X 1 + sin x 5. Som — 1700+ x = cos x 1 + tan x — = cos X — sin x 1 + cotx1 ответ
-
Докажите, что cos (kx) a) a 2 noso cas (ko) — cos (k-1)) СНИМАТЬ НА REDMI 7 AI DUAL CAMERA1 ответ
- Чтобы идентифицировать кривую, удалите параметр.Поскольку это
не тригонометрические функции, вы можете использовать подстановку, чтобы написать
одно уравнение относительно x и y. Решите первое уравнение относительно t. (Введите вас
1 ответ
- Пожалуйста, покажите все шаги
Если seco = x, выразите sin20 через x. o sin20 = 2V [(x2 — 1)] / x2 sin2e = + 2V1 (x2 — 1)] / x2 o sin 20 = + 2x (1 — x2) O sin20 = + 2V (1 — x2)1 ответ
-
Решите прямоугольный треугольник. b = 200 c = 400 b Amº (При необходимости округлите до ближайшей десятой.) Balº (Округлите до ближайшей десятой, если необходимо.) Am (Округлите до ближайшего целого числа, если необходимо.) Найдите функцию1 ответ
-
(a) Преобразуйте следующие полярные координаты в прямоугольные координаты. Пример: Полярные координаты — 190 AB — 100,00 м по азимуту 225 ° 00’00 «. Прямоугольные координаты — восток (E) —70,71, север (N) —1 ответ
-
Найдите значение функции. cos (- 294.5) ° cos (- 294,5) ° ~ (округлите до четырех десятичных знаков, если необходимо.)
Найдите шесть значений тригонометрической функции для указанного угла O (-402, -4) sin = (Упростите свой
cos (- 294.5) ° cos (- 294,5) ° ~ (округлите до четырех десятичных знаков, если необходимо.)
Найдите шесть значений тригонометрической функции для указанного угла O (-402, -4) sin = (Упростите свой1 ответ
-
Для угла укажите, в каком квадранте находится сторона вывода. 1456 ° Угол в квадранте. (Введите свой ответ как I, II, III или IV.) Преобразуйте следующую меру градуса в радиан. — 301 ответ
-
4.Найдите все данные, отсутствующие в треугольнике ABC, из следующих наблюдаемых данных — 3-170,9 м, b = 225,6 м. 6-78900 Дайте растворы с точностью до 0,0 мкм и 10% c. d ‘, Решите недостающие элементы t1 ответ
-
Решите прямоугольный треугольник. A = 32 ° b = 43 b B = 0 ° (Упростите ответ.) Am (Округлите до ближайшей сотой, если необходимо.) Ca (Округлите до ближайшей сотой, если необходимо.) Воздушный фотограф, который фотографирует1 ответ
-
Найдите значение функции.Округлить до четырех знаков после запятой. tan 55,7 ° tan 55,7 ° ~ (округлите до четырех десятичных знаков, если необходимо.) Найдите шесть значений тригонометрической функции указанного угла. 149/140 11 ответ
- 6sin (x) — 3sin (2x) = 12 / пи
1 ответ
-
1. Для A = (-2,3,3) и B = (0, -1,6): (a) Найдите компонентную форму вектора AB (b) Найдите LABI 2. Для u = (3, 5) и + — (-2,1): (a) Найдите dü — 7 (b) Найдите угол, описывающий направление vec1 ответ
- ГРАФИЧЕСКИЙ, НАЙТИ ПЕРИОД, АНПЛИТУД, ВЕРТИКАЛЬНЫЙ
СДВИГ, ОТРАЖЕНИЕ, СДВИГ ФАЗЫ, ИНТЕРВАЛ
Дополнительная практика построения графиков 1.y = -5 cos (6x) 2. y = 3 sin (4x) (график двух циклов) 3. y = sin (–3x) 4. y = 4 -cos (2x) (график двух циклов) 5. y = 2 — 5 sin (rex) (график двух циклов) 6. y = -3 sin (x) +5 7.1 ответ
-
6. Найдите центр и радиус сферы r2 + y2 + — 8x + 4y — 62 = 7 7. Найдите вектор, перпендикулярный как (1,1,3), так и (0,2, -2) 8. Найдите прямоугольное уравнение плоскости, проходящей через точку p
Найдите вектор, перпендикулярный как (1,1,3), так и (0,2, -2) 8. Найдите прямоугольное уравнение плоскости, проходящей через точку p1 ответ
-
2.Дано: = —1573 и w = 5 (cos (w / 7) + sin (/ 7)) 1- i и w = 5 (cos (1/7) + i sin (/ 7)), вычислить каждое из следующее: a) cos 1.73-45 sin 1.73 right idea (b) w ‘(Упростите до стандартной формы.)1 ответ
-
4. Решить 2 cos? r — 3 sin r — 3 = 0. Используйте радианы. a cos²x-3 sin x-3 = 0 5. Преобразуйте r = в прямоугольные координаты и решите относительно x. г = ī роза I-cos = 01 ответ
-
way hate riposomente cuando en ten show i wok on paper Убедитесь, что тригонометрическое уравнение является тождеством.3− 7i Запишите тригонометрическую форму комплексного числа. (Округлите углы до двух десятичных знаков. Пусть 0 ≤ θ <2π.1 ответ
- Решите данное уравнение. (Введите свои ответы как
разделитель-запятая Решить данное уравнение. (Введите свои ответы как
Список, разделенный запятыми. Пусть k — любое целое число. Округлить сроки до
три десятичных знака, где ap
1 ответ
- 4squareroot3− 7i Запишите тригонометрическую форму комплексного
номер. (Округлите углы до двух десятичных знаков.Пусть 0 ≤ θ <
2π.
1 ответ
-
Найдите точное значение1 ответ
-
Найдите u o ů = (-3,0,1> ✓ = {1, -1,171 ответ
-
Найдите меру (в радианах центрального угла. Площадь сектора — 8 кв. Единиц. Изображение не масштабировано. Измерение — радианы). (Введите целое или десятичное число, округленное до ближайшей десятой.1 ответ
-
10.3 — 27 = 0 z0 = z1 = z21 ответ
-
Преобразует следующие радианы в градусы. Введите свой ответ в поле для ответа E O Введите здесь для поиска1 ответ
- (4squareroot3) -7i Запишите тригонометрическую форму комплекса
номер.
 (Округлите углы до двух десятичных знаков. Пусть 0 ≤ θ <
2π.
(Округлите углы до двух десятичных знаков. Пусть 0 ≤ θ <
2π.1 ответ
- Мне нужна помощь в решении второй части
вопрос
Оценка: 0 из 1 балла 13 из 14 (12 завершено) Оценка HW: 85.71%, 12 из 14 баллов 8.2.51 Вопрос Справка Знаменитая наклонная башня изначально была 186,5 футов в высоту. На расстоянии 129 футов от основания башни,0 ответов
-
Чему равен угол 47 ° 18’41 «в десятичных градусах? Введите свой ответ, округленный до ближайшей тысячной доли градуса, в поле.1 ответ
-
Справа EFG имеет прямой угол в G, EF = 8 и FG = 6.Каково значение тригонометрического соотношения угла треугольника? Перетащите значение в каждое поле, чтобы тригонометрическое соотношение соответствовало его значению.1 ответ
-
Что такое угловая мера в градусах, эквивалентная радианам? Выберите все правильные утверждения. i эквивалентно 90 °. o эквивалентно 45 ° 0 B эквивалентно 225 ° 0 3 эквивалентно t1 ответ
-
Какое утверждение правильно определяет тригонометрическое соотношение? Синусоидальная функция определяется как длина гипотенузы по длине смежной стороны.Косинус угла определяется как левая1 ответ
-
Какой знак у тригонометрической функции, если в квадранте лежит конечный луч угла! в? Выберите все правильные утверждения.U Функция котангенса отрицательна в квадранте II.1 ответ
-
Конечный луч угла B, проведенный в стандартном положении, проходит через точку (-5, 277) Какое значение cos B? Введите свой ответ в простейшей радикальной форме в это поле. cos B = 0 Вперед>1 ответ
-
Какая мера в радианах эквивалентна градусу? Выберите True или False для каждого утверждения.Утверждение Истина Ложь 90 ° эквивалентно: 210 ° эквивалентно 300 ° эквивалентно1 ответ
-
Какие углы совпадают с углом, начерченным в стандартном положении и составляющим 212 ° 2 Выберите все правильные размеры углов.

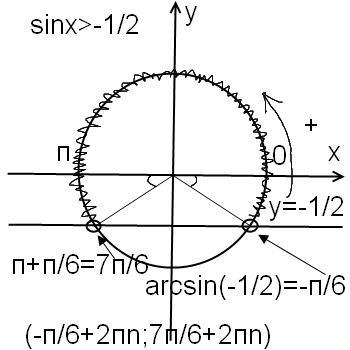
 {2} t = 1 [/ латекс]
{2} t = 1 [/ латекс] \ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex].\ circ [/ latex], как показано на рисунке 12.
\ circ [/ latex] — это [латекс] \ left (\ frac {\ sqrt {2}} {2}, \ frac {\ sqrt {2}} {2} \ right) \\ [/ latex].\ circ [/ latex], как показано на рисунке 12.  В таблице ниже приведены эти значения.
В таблице ниже приведены эти значения.
 Границы координаты y также равны [latex] \ left [-1,1 \ right] [/ latex].Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex].
Границы координаты y также равны [latex] \ left [-1,1 \ right] [/ latex].Следовательно, диапазон функций синуса и косинуса равен [latex] \ left [-1,1 \ right] [/ latex].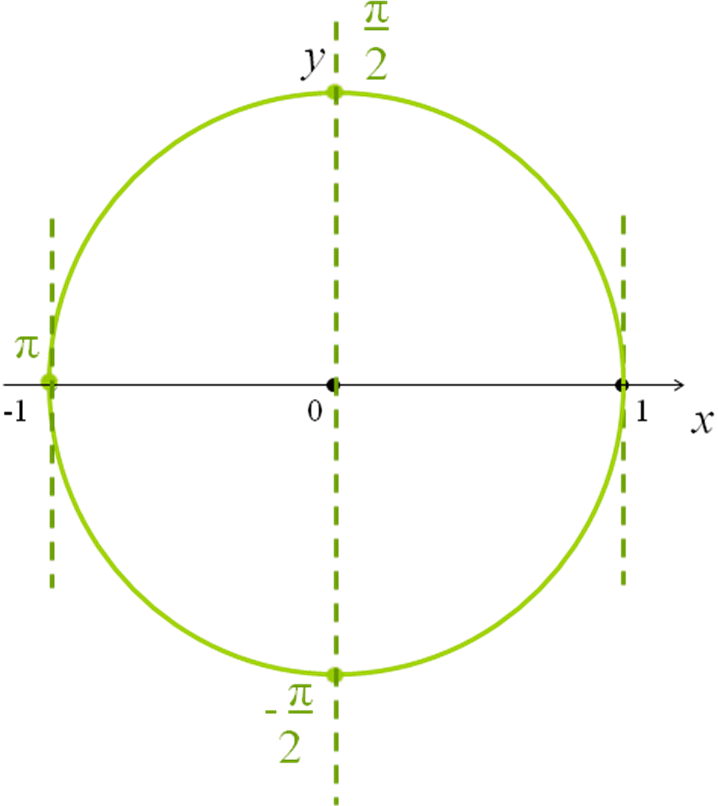 \ circ \ mathrm {-t} | [/ latex].\ circ [/ latex]
\ circ \ mathrm {-t} | [/ latex].\ circ [/ latex] Это опорный угол.
Это опорный угол. Тогда мы возьмем синус и косинус значения опорного угла , и дать им знаки, соответствующие у — и х -значения квадранта.
Тогда мы возьмем синус и косинус значения опорного угла , и дать им знаки, соответствующие у — и х -значения квадранта.
 Опишите единичный круг.
Опишите единичный круг.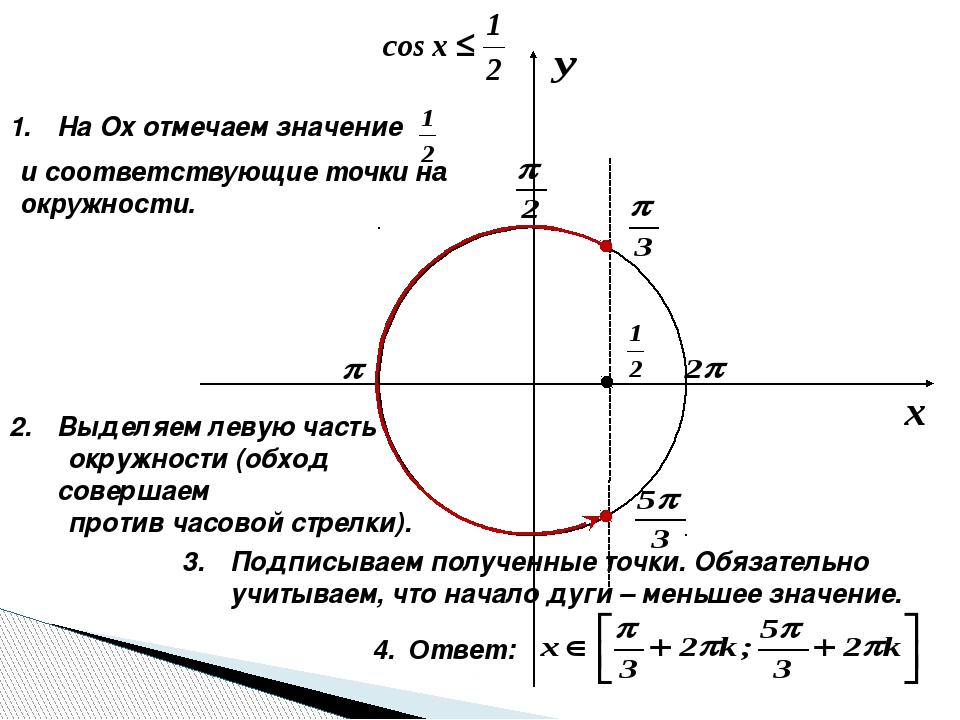 \ circ [/ latex]
\ circ [/ latex]
 Когда у ребенка будут координаты [latex] \ left (0.707, -0.707 \ right) [/ latex], если поездка длится 6 минут? (Есть несколько ответов.)
Когда у ребенка будут координаты [latex] \ left (0.707, -0.707 \ right) [/ latex], если поездка длится 6 минут? (Есть несколько ответов.) XX0 \ aaPt
4o_Kd & / 0_` | A _} / oʀ ** 0>
XX0 \ aaPt
4o_Kd & / 0_` | A _} / oʀ ** 0>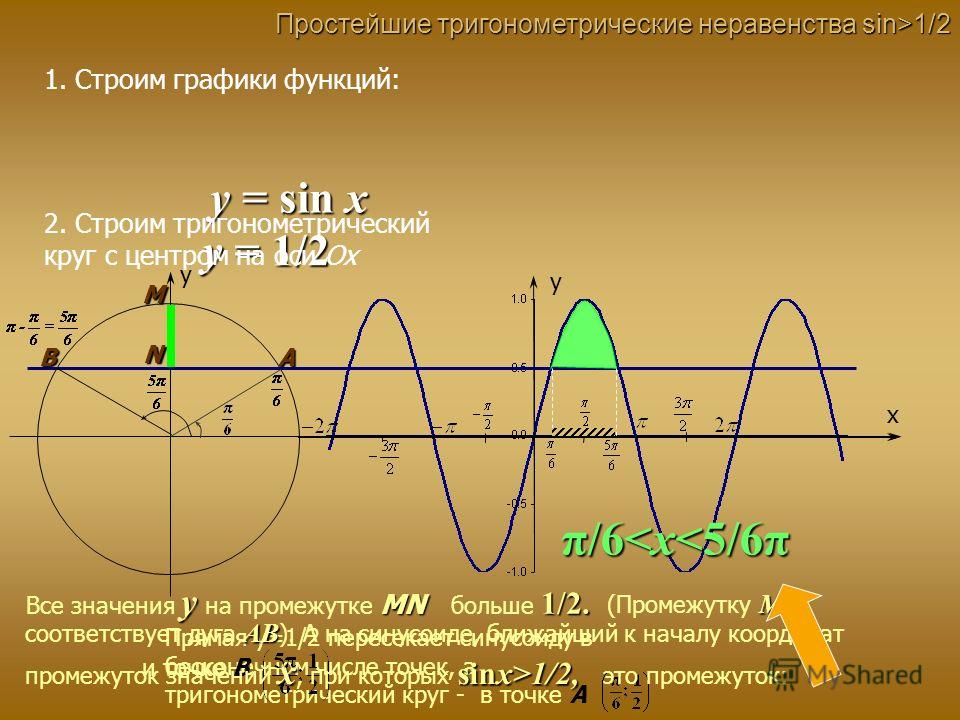 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
 Мы знаем, что сумма углов в треугольнике равна \ (180 ° \), поэтому мера угла \ (C \) также равна \ (60 ° \). Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника \ (ABC \) имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Мы знаем, что сумма углов в треугольнике равна \ (180 ° \), поэтому мера угла \ (C \) также равна \ (60 ° \). Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника \ (ABC \) имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
 Более поздние части
это эссе не часто зависит от более ранних частей, поэтому не стесняйтесь бегать бегло
пропустите непонятный текст, пока не найдете то, что вам удобно.
Более поздние части
это эссе не часто зависит от более ранних частей, поэтому не стесняйтесь бегать бегло
пропустите непонятный текст, пока не найдете то, что вам удобно.

 Этот результат может
быть доказанным напрямую. Это легче всего увидеть, посмотрев на
треугольник, и складывая члены подряд в двух разных
способами. Кроме того, использование расширений степенного ряда для расширения
определение cos и sin к комплексным числам, мы
теперь знаю что тож верен для комплекса т . Благодаря
Боб Ува за указание на это.
Этот результат может
быть доказанным напрямую. Это легче всего увидеть, посмотрев на
треугольник, и складывая члены подряд в двух разных
способами. Кроме того, использование расширений степенного ряда для расширения
определение cos и sin к комплексным числам, мы
теперь знаю что тож верен для комплекса т . Благодаря
Боб Ува за указание на это. Этот
упрощается до 1 . Итак, тригонометрическое тождество можно рассматривать
как алгебраическое тождество (w + 1 / w) 2 —
(w-1 / w) 2 = 4 .
Этот
упрощается до 1 . Итак, тригонометрическое тождество можно рассматривать
как алгебраическое тождество (w + 1 / w) 2 —
(w-1 / w) 2 = 4 .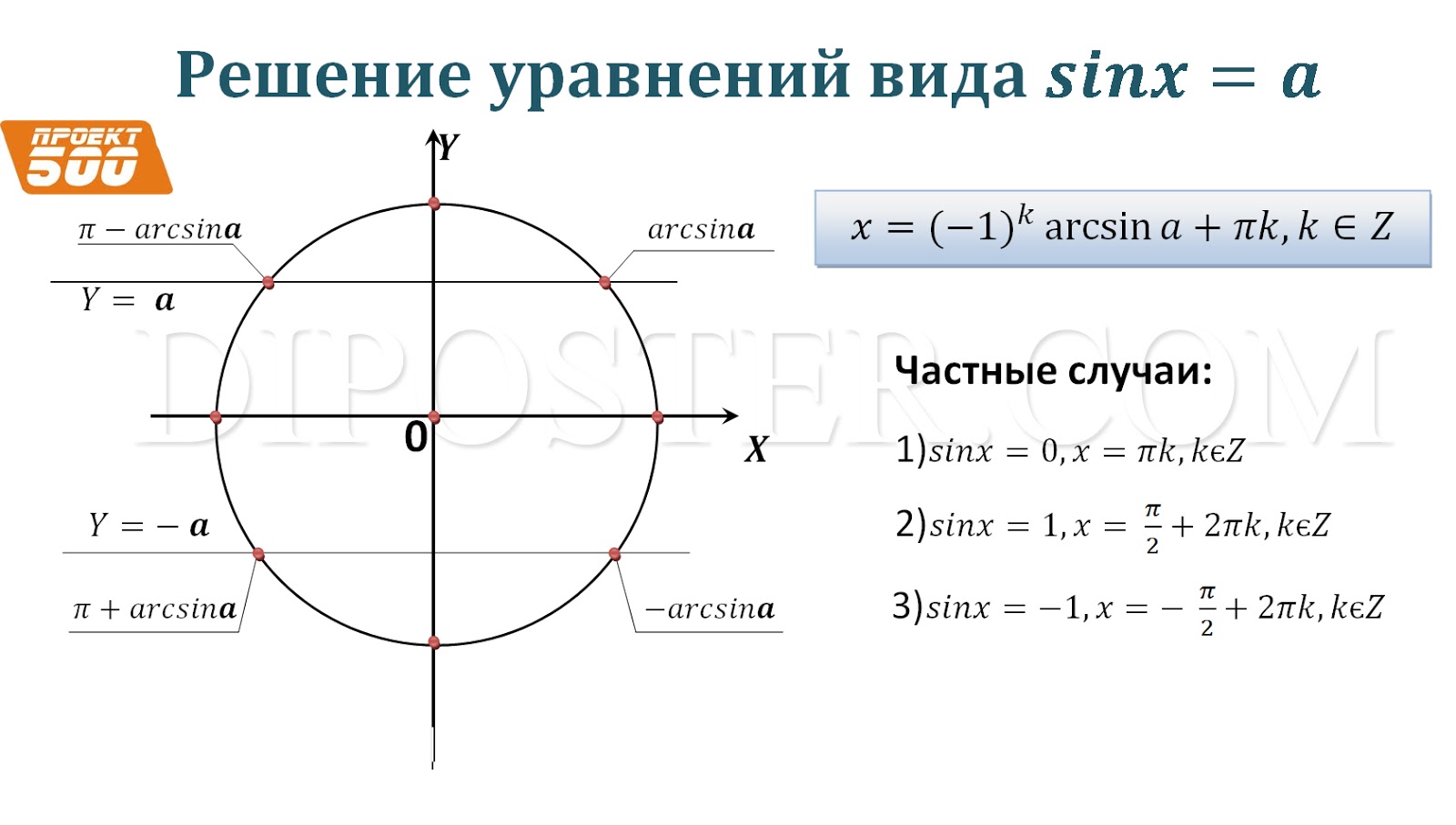 Очевидно, c » (t) .c » (t) =
cos 2 (t) + sin 2 (t) , так что тождество
говорит нам, что равномерное движение по кругу приводит к
ускорение постоянной величины.
Очевидно, c » (t) .c » (t) =
cos 2 (t) + sin 2 (t) , так что тождество
говорит нам, что равномерное движение по кругу приводит к
ускорение постоянной величины.
 ..
в значительной степени забыл … мой
там ответ правильный, но не упрощенный или ошибочный.
..
в значительной степени забыл … мой
там ответ правильный, но не упрощенный или ошибочный.  (а) Напишите приблизительное
(а) Напишите приблизительное (a) Приведите пример угла, который совпадает с 660 °. Ответ: (b) Преобразуйте угол 15 радиан в градусы.Отвечать:
(a) Приведите пример угла, который совпадает с 660 °. Ответ: (b) Преобразуйте угол 15 радиан в градусы.Отвечать: sin-1 (0,5) A) 60 ° B) 420 C) 30 ° D) -30 °
sin-1 (0,5) A) 60 ° B) 420 C) 30 ° D) -30 ° Показать работу.x — y + 3 = 8 —2x + y + 85 = 1 X — V — 2-
Показать работу.x — y + 3 = 8 —2x + y + 85 = 1 X — V — 2- )
) sin (0) — csc (0) cos (0) cot e Нужна помощь? Прочтите, посмотрите, поговорите с репетитором
sin (0) — csc (0) cos (0) cot e Нужна помощь? Прочтите, посмотрите, поговорите с репетитором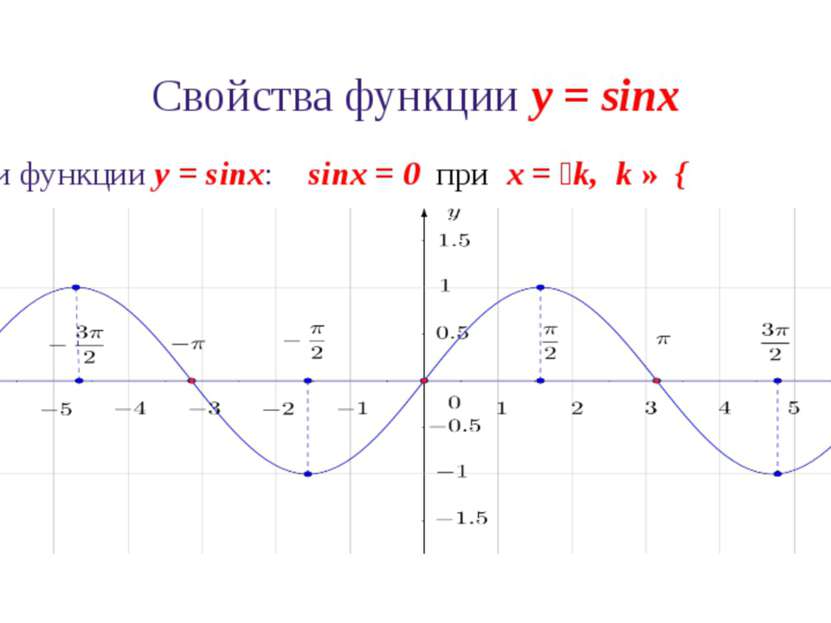 cos (- 294.5) ° cos (- 294,5) ° ~ (округлите до четырех десятичных знаков, если необходимо.)
Найдите шесть значений тригонометрической функции для указанного угла O (-402, -4) sin = (Упростите свой
cos (- 294.5) ° cos (- 294,5) ° ~ (округлите до четырех десятичных знаков, если необходимо.)
Найдите шесть значений тригонометрической функции для указанного угла O (-402, -4) sin = (Упростите свой Найдите вектор, перпендикулярный как (1,1,3), так и (0,2, -2) 8. Найдите прямоугольное уравнение плоскости, проходящей через точку p
Найдите вектор, перпендикулярный как (1,1,3), так и (0,2, -2) 8. Найдите прямоугольное уравнение плоскости, проходящей через точку p (Округлите углы до двух десятичных знаков. Пусть 0 ≤ θ <
2π.
(Округлите углы до двух десятичных знаков. Пусть 0 ≤ θ <
2π.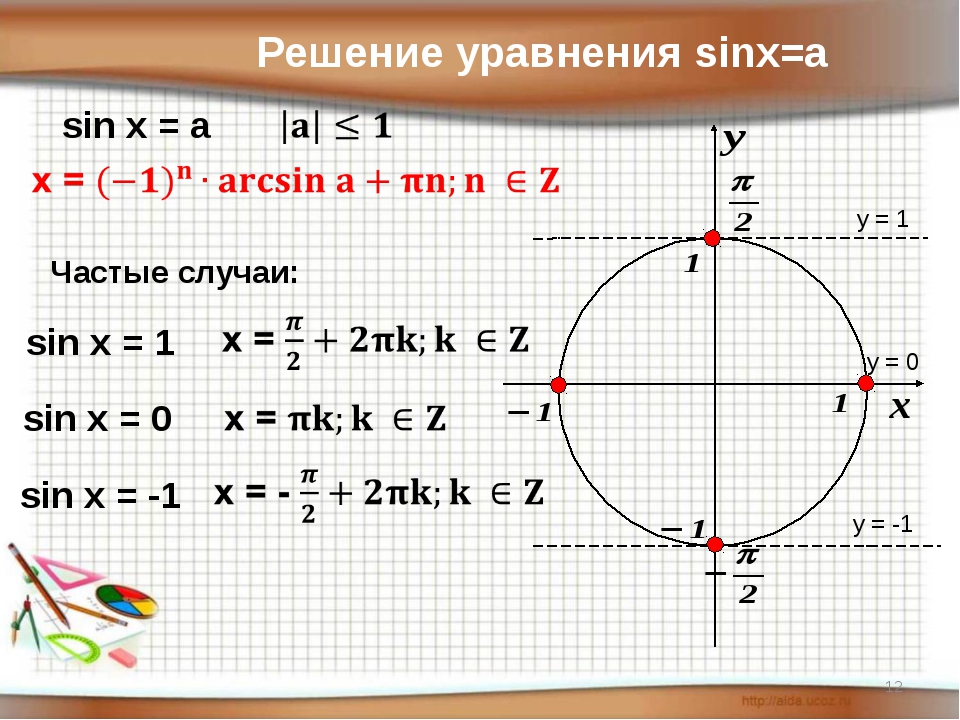
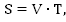

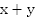 км/ч и пройдет 14 км за время
км/ч и пройдет 14 км за время 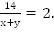 Если лодка движется против течения, она идет со скоростью
Если лодка движется против течения, она идет со скоростью 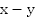 км/ч и пройдет 14 км за время
км/ч и пройдет 14 км за время 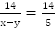 .
.
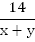
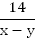
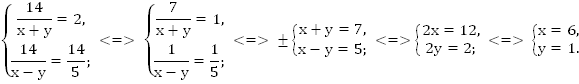
 пройденные до момента их встречи каждым из поездов.
пройденные до момента их встречи каждым из поездов.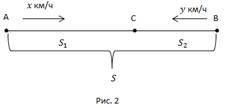
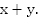

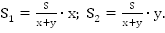
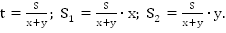
 пройденные первым и вторым туристами до встречи.
пройденные первым и вторым туристами до встречи.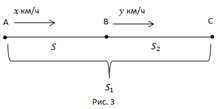
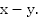


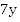 км, осталось
км, осталось 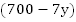 км, и только тогда начинает движение первый поезд. Начинается сближение. Поездам нужно пройти
км, и только тогда начинает движение первый поезд. Начинается сближение. Поездам нужно пройти 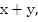 и они встретятся через 2 часа, т.е.
и они встретятся через 2 часа, т.е. 
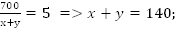
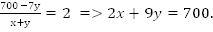
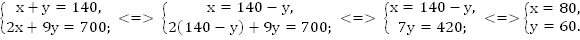
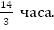
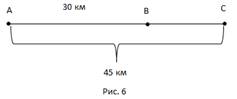
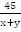 ч.
ч.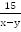 ч. Суммарное время в пути составило
ч. Суммарное время в пути составило 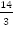 ч, т.е.
ч, т.е. 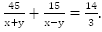
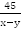 ч. Из А в В шла 30 км по течению, т.е. была в пути
ч. Из А в В шла 30 км по течению, т.е. была в пути 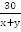 ч. Общее время в пути составило 7 ч, т.е.
ч. Общее время в пути составило 7 ч, т.е. 

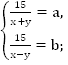
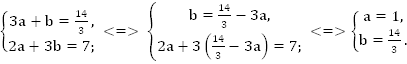


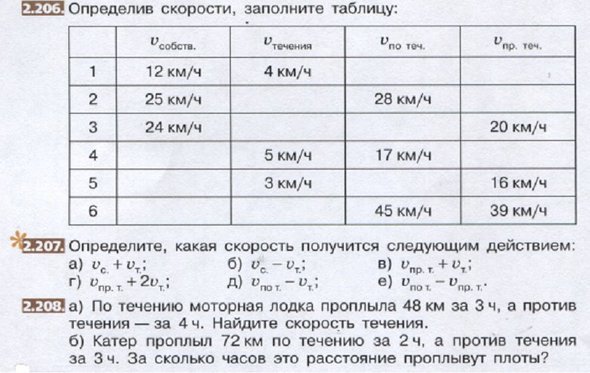




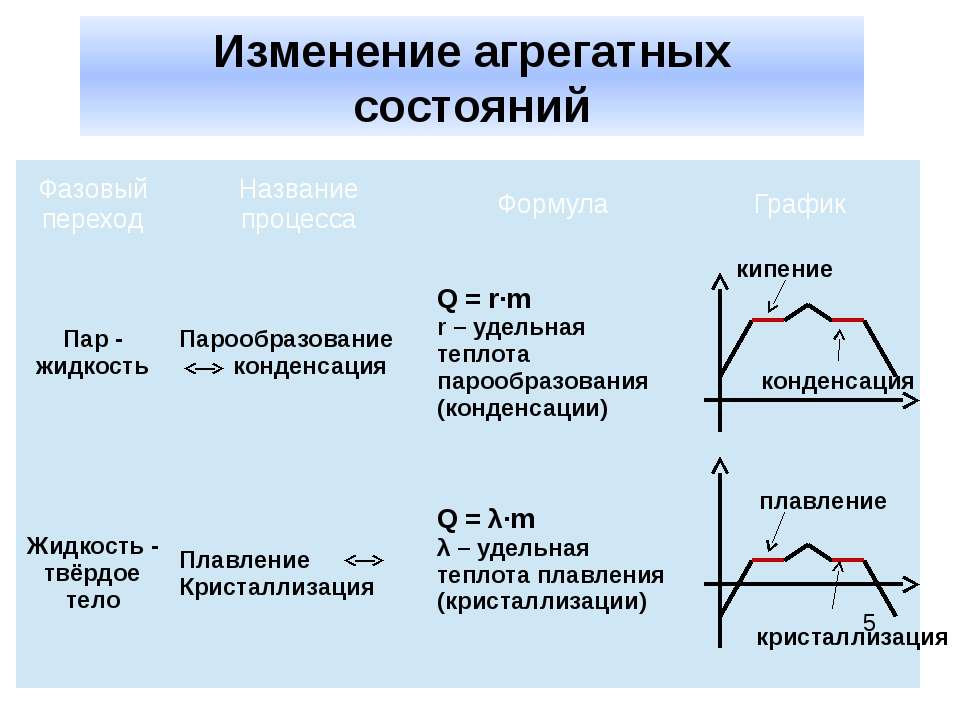


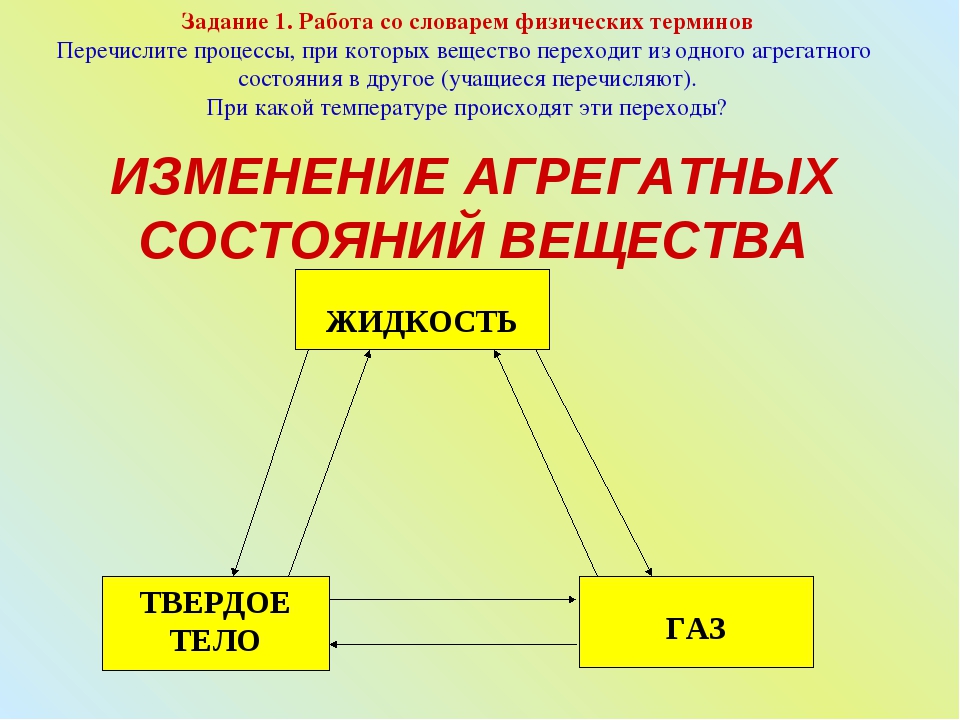
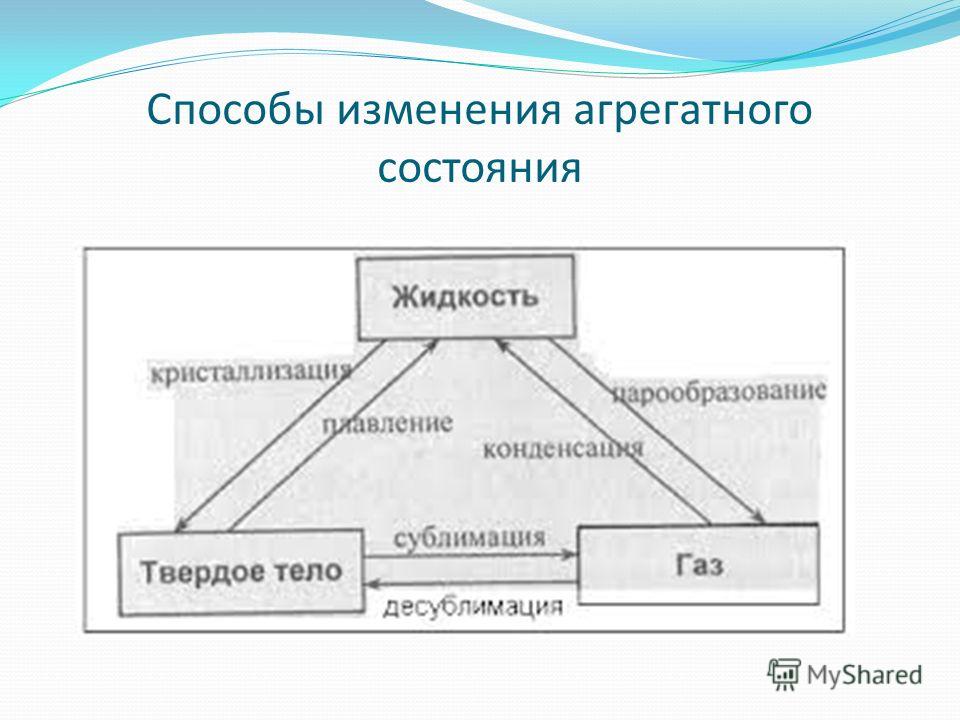
 Найдите удельную теплоту парообразования воды.
Найдите удельную теплоту парообразования воды.

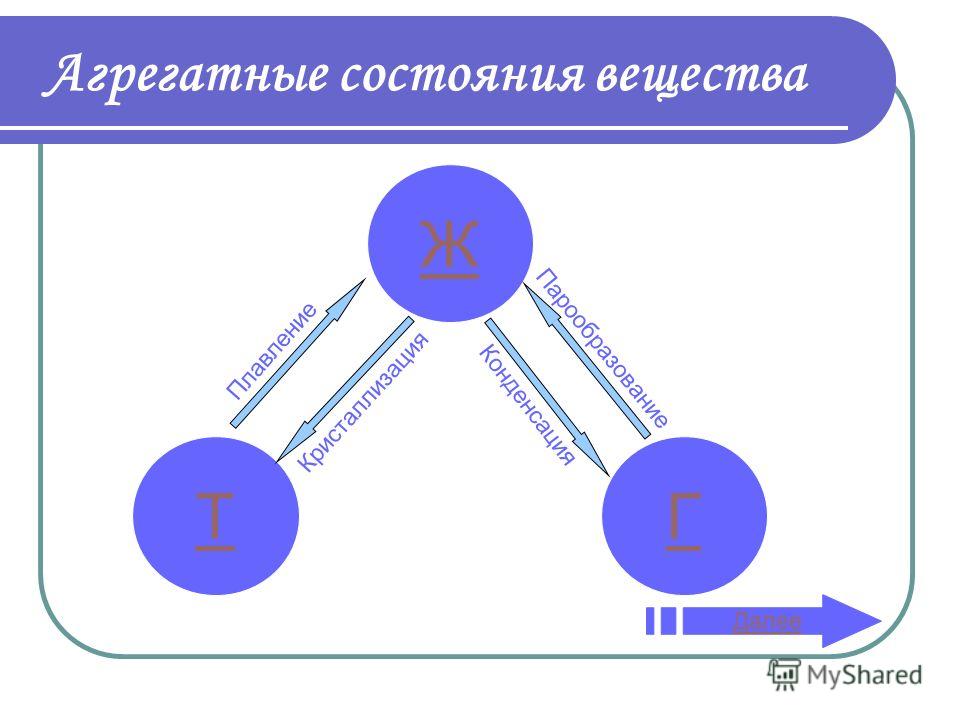 Для этого достаточно поместить ее в более холодную среду. При потере тепла молекулы жидкости замедляют свое движение и, в конце концов, уже не могут перемещаться, а просто колеблются вокруг фиксированных точек. С наступлением этой фазы жидкость отвердевает, т. е. превращается в твердое вещество. Например, вода замерзает при температуре 0°С. Большинство веществ кристаллизуются при переходе из жидкого состояния в твердое. Так, NaCl (поваренная соль) образует кристаллы кубической формы. Нагреваясь, твердые вещества могут снова перейти в жидкое состояние, так как при этом увеличивается скорость движения их молекул. При нагревании твердого вещества с целью превращения в жидкость его температура растет за счет поглощения тепла. Но, достигнув точки плавления, температура вещества остается постоянной, хотя процесс поглощения тепла продолжается. Тепло, используемое для превращения твердого вещества в жидкость, не увеличивается после достижения точки плавления и называется скрытой теплотой плавления. Лишь после того, как все твердое вещество перейдет в жидкое состояние, его температура вновь начинает расти.
Для этого достаточно поместить ее в более холодную среду. При потере тепла молекулы жидкости замедляют свое движение и, в конце концов, уже не могут перемещаться, а просто колеблются вокруг фиксированных точек. С наступлением этой фазы жидкость отвердевает, т. е. превращается в твердое вещество. Например, вода замерзает при температуре 0°С. Большинство веществ кристаллизуются при переходе из жидкого состояния в твердое. Так, NaCl (поваренная соль) образует кристаллы кубической формы. Нагреваясь, твердые вещества могут снова перейти в жидкое состояние, так как при этом увеличивается скорость движения их молекул. При нагревании твердого вещества с целью превращения в жидкость его температура растет за счет поглощения тепла. Но, достигнув точки плавления, температура вещества остается постоянной, хотя процесс поглощения тепла продолжается. Тепло, используемое для превращения твердого вещества в жидкость, не увеличивается после достижения точки плавления и называется скрытой теплотой плавления. Лишь после того, как все твердое вещество перейдет в жидкое состояние, его температура вновь начинает расти. Затем, после достижения точки кипения вещества, газ отдает свою теплоту парообразования и переходит в жидкое состояние при той же температуре. Только когда весь газ превратится в жидкость, температура вещества начинает падать.
Затем, после достижения точки кипения вещества, газ отдает свою теплоту парообразования и переходит в жидкое состояние при той же температуре. Только когда весь газ превратится в жидкость, температура вещества начинает падать. Стрелка вакуумметра стоит на одном месте. Это подтверждает тот факт, что давление насыщенных паров не зависит от объема. Закрепляем рычаг (фиксируем постоянный объем цилиндра) и спиртовым факелом подогреваем колбу. Давление насыщенных паров увеличивается.
Стрелка вакуумметра стоит на одном месте. Это подтверждает тот факт, что давление насыщенных паров не зависит от объема. Закрепляем рычаг (фиксируем постоянный объем цилиндра) и спиртовым факелом подогреваем колбу. Давление насыщенных паров увеличивается.
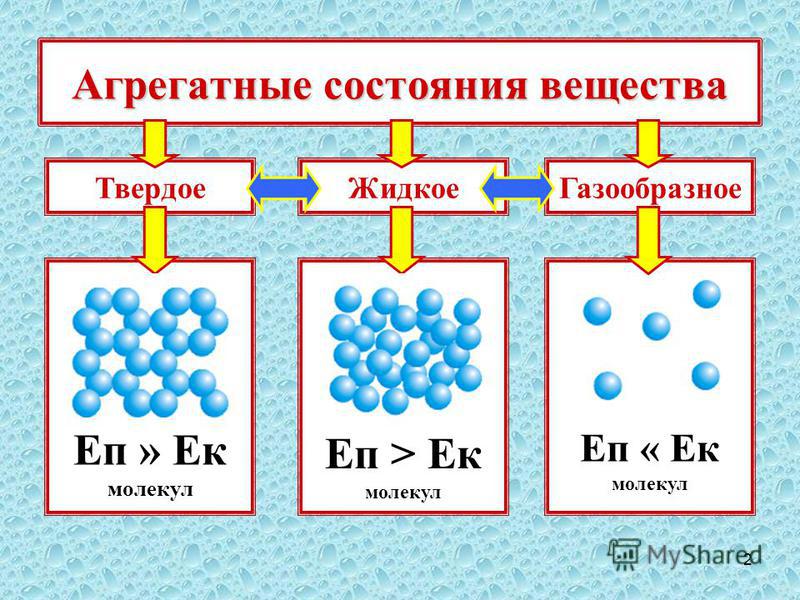 Задачи урока: Воспитательная — воспитать повышенный интерес к тепловым явлениям, бережное отношение к тепловым ресурсам в школе и быту; Образовательная – научить применять расчеты количества теплоты на практике; Развивающая – расширение кругозора, развитие логического мышления и творческих способностей.
Задачи урока: Воспитательная — воспитать повышенный интерес к тепловым явлениям, бережное отношение к тепловым ресурсам в школе и быту; Образовательная – научить применять расчеты количества теплоты на практике; Развивающая – расширение кругозора, развитие логического мышления и творческих способностей.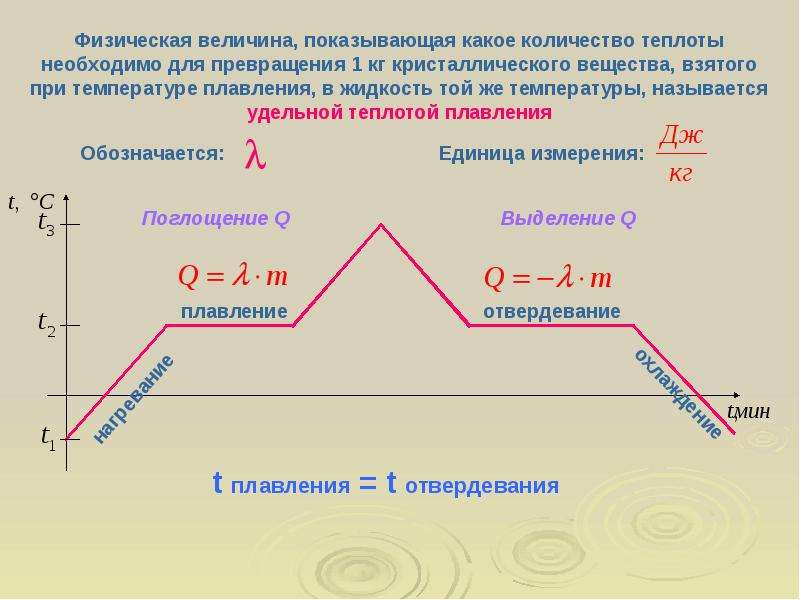 Что необходимо сделать, чтобы вещество из одного агрегатного состояния перешло в другое ( из твёрдого в жидкое, из жидкого в газообразное и обратно)? 3.Назвать процессы перехода из одного агрегатного состояния в другое.
Что необходимо сделать, чтобы вещество из одного агрегатного состояния перешло в другое ( из твёрдого в жидкое, из жидкого в газообразное и обратно)? 3.Назвать процессы перехода из одного агрегатного состояния в другое. Текст с иллюстрациями.http://files.school-collection.edu.ru/dlrstore/021336cc-a763-ca39-3cc4-b956b86dd83a/00149789894123264.htm
Текст с иллюстрациями.http://files.school-collection.edu.ru/dlrstore/021336cc-a763-ca39-3cc4-b956b86dd83a/00149789894123264.htm Объясните это явление.
Объясните это явление.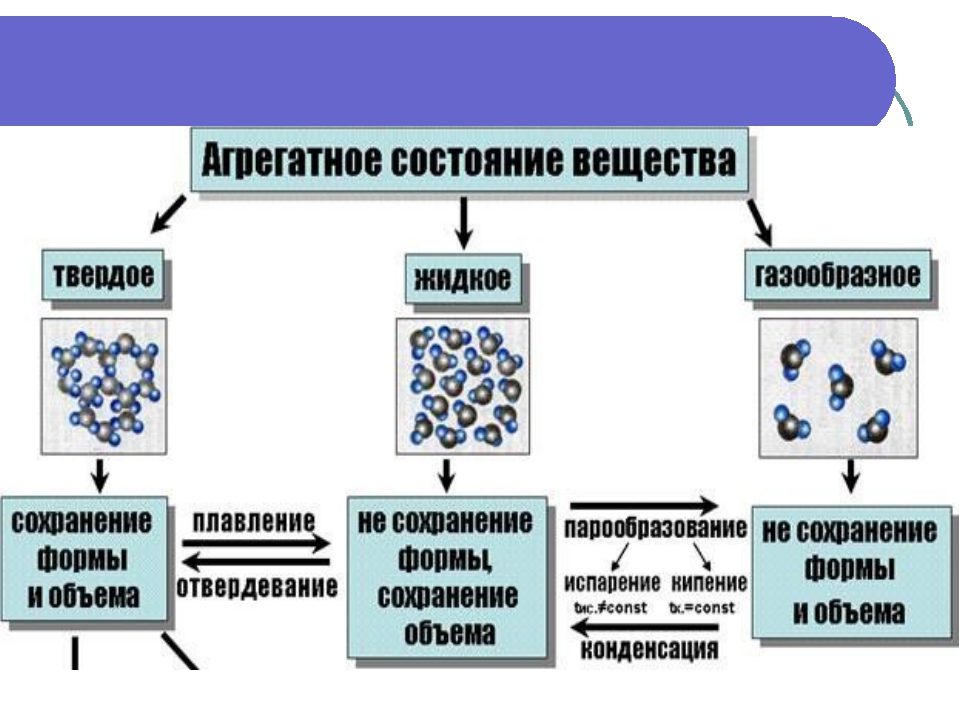 Фет. Из стихотворения «Метель» Все молчит, – лучина с треском Лишь горит багровым блеском, Да по кровле ветер шумит. Почему лучина горит с треском? 2.Она жила и по стеклу текла Но вдруг ее морозом оковало, И неподвижной льдинкой капля стала А в мире поубавилось тепла. Какая физическая ошибка допущена в этом стихотворении?
Фет. Из стихотворения «Метель» Все молчит, – лучина с треском Лишь горит багровым блеском, Да по кровле ветер шумит. Почему лучина горит с треском? 2.Она жила и по стеклу текла Но вдруг ее морозом оковало, И неподвижной льдинкой капля стала А в мире поубавилось тепла. Какая физическая ошибка допущена в этом стихотворении? Ответьте на вопросы: а) Чему соответствуют отрезки графика АВ, ВС и СД? б) Сколько времени продолжался процесс нагревания твёрдого тела? Плавления? в) Какова начальная температура вещества? г) При какой температуре оно плавилось? 660
Ответьте на вопросы: а) Чему соответствуют отрезки графика АВ, ВС и СД? б) Сколько времени продолжался процесс нагревания твёрдого тела? Плавления? в) Какова начальная температура вещества? г) При какой температуре оно плавилось? 660 1.Подготовиться к контрольной работе. 2.Эксперимент : Как вынуть лед из воды, не замочив руки? Опустите небольшой кусочек льда в стакан с водой и попытайтесь вытащить лёд из воды с помощью нитки и щепотки поваренной соли. Как надо поступить?
1.Подготовиться к контрольной работе. 2.Эксперимент : Как вынуть лед из воды, не замочив руки? Опустите небольшой кусочек льда в стакан с водой и попытайтесь вытащить лёд из воды с помощью нитки и щепотки поваренной соли. Как надо поступить? Тепловое равновесие и температура. 2. Внутренняя энергия.
Тепловое равновесие и температура. 2. Внутренняя энергия. Хабаровск — 2019 Критерии оценивания: Отметка «5» ставится в том случае, если обучающийся: — выполняет работу в полном объеме с соблюдением
Хабаровск — 2019 Критерии оценивания: Отметка «5» ставится в том случае, если обучающийся: — выполняет работу в полном объеме с соблюдением В твёрдых телах теплопередача может осуществляться путём 1.конвекции 2.излучения и конвекции 3.теплопроводности 4.конвекции и теплопроводности 2.Внутренняя энергия
В твёрдых телах теплопередача может осуществляться путём 1.конвекции 2.излучения и конвекции 3.теплопроводности 4.конвекции и теплопроводности 2.Внутренняя энергия Из теории идеального
Из теории идеального Такая схема позволяет понять химические связи, притяжение (вдали) и отталкивание (вблизи) несвязанных атомов. На таком уровне, у атома нет твёрдой поверхности, и до какой-то степени они могут проникать друг в друга, или чувствовать присутствие издалека — но не очень издалека, а только на расстояниях порядка одного диаметра атома.
Такая схема позволяет понять химические связи, притяжение (вдали) и отталкивание (вблизи) несвязанных атомов. На таком уровне, у атома нет твёрдой поверхности, и до какой-то степени они могут проникать друг в друга, или чувствовать присутствие издалека — но не очень издалека, а только на расстояниях порядка одного диаметра атома.
 )
над уровнем моря». Как он узнал абсолютную высоту
вершины горы?
)
над уровнем моря». Как он узнал абсолютную высоту
вершины горы?  Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.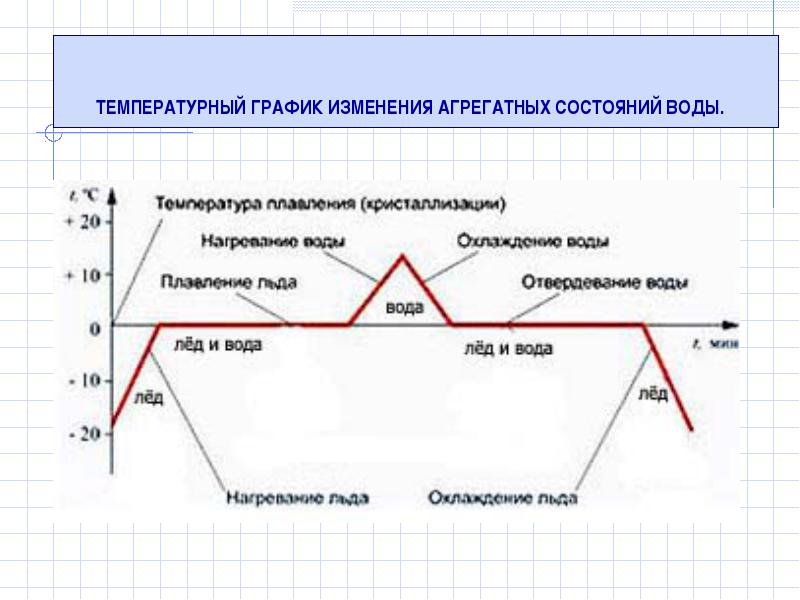



















 .5)
fun2(-1)
# [1] NA
fun2(3)
# [1] 1.732051
fun2(c(-1, 3))
# [1] NA 1.732051
.5)
fun2(-1)
# [1] NA
fun2(3)
# [1] 1.732051
fun2(c(-1, 3))
# [1] NA 1.732051  Я пытался сделать то же самое…
Я пытался сделать то же самое… Это одна из наиболее частых причин вызова скорой помощи и госпитализации больных, а также смертности населения нашей страны и всего мира.
Это одна из наиболее частых причин вызова скорой помощи и госпитализации больных, а также смертности населения нашей страны и всего мира. При улучшении самочувствия больного после применения нитроглицерина, его применяют повторно, через каждые 5-10 минут до прибытия бригады скорой медицинской помощи. При отсутствии улучшения самочувствия больного после применения нитроглицерина, его больше не применяют.
При улучшении самочувствия больного после применения нитроглицерина, его применяют повторно, через каждые 5-10 минут до прибытия бригады скорой медицинской помощи. При отсутствии улучшения самочувствия больного после применения нитроглицерина, его больше не применяют.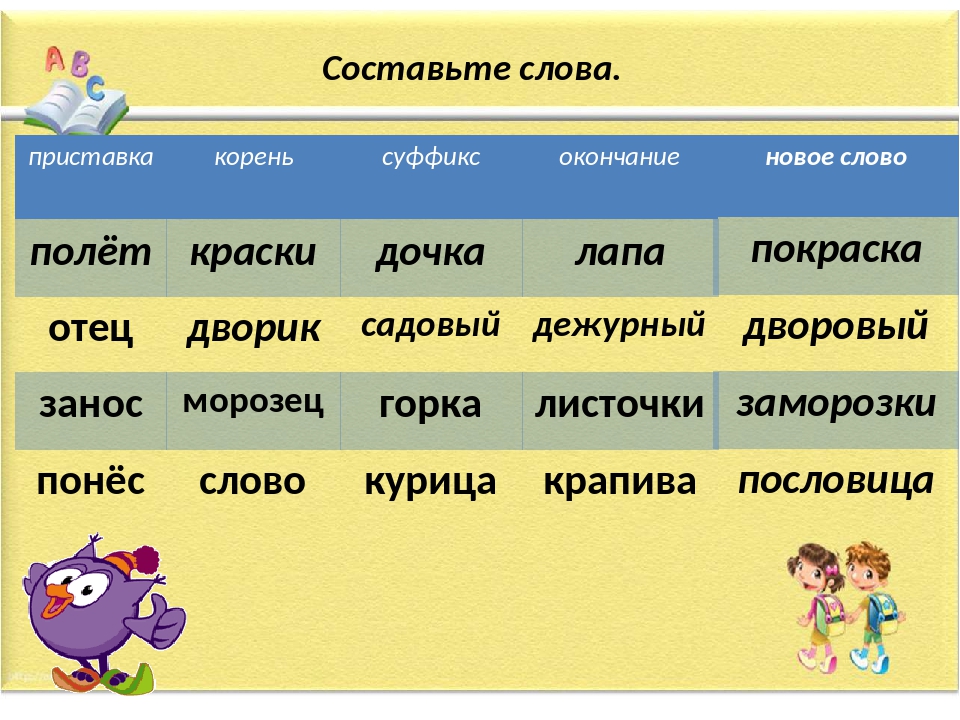 Поэтому большинство прибегают к народным методам.
Поэтому большинство прибегают к народным методам. Настойку (под иным названием «черемичная вода») нужно хранить в недоступном для детей месте.
Настойку (под иным названием «черемичная вода») нужно хранить в недоступном для детей месте.

 Чем быстрее вы окажетесь в стоматологии, тем выше вероятность, что вы сохраните зуб.
Чем быстрее вы окажетесь в стоматологии, тем выше вероятность, что вы сохраните зуб.
 Риск травм зубов высок у тех, кто занимается контактными видами спорта (хоккей, бокс, другие единоборства) и ведет активный образ жизни (катается на роликах, коньках, горных лыжах). Уберечь от травмы в этих случаях могут спортивные капы. Но, конечно, травму зуба можно получить и в быту. Если это случилось, вам необходимо следовать нашей инструкции, срочно связаться по телефону с клиникой и как можно скорее добраться до стоматологии.
Риск травм зубов высок у тех, кто занимается контактными видами спорта (хоккей, бокс, другие единоборства) и ведет активный образ жизни (катается на роликах, коньках, горных лыжах). Уберечь от травмы в этих случаях могут спортивные капы. Но, конечно, травму зуба можно получить и в быту. Если это случилось, вам необходимо следовать нашей инструкции, срочно связаться по телефону с клиникой и как можно скорее добраться до стоматологии.
 В ЧЕМ ЗАКЛЮЧАЕТСЯ ПАРОДОНТОЛОГИЧЕСКОЕ ОБСЛЕДОВАНИЕ
В ЧЕМ ЗАКЛЮЧАЕТСЯ ПАРОДОНТОЛОГИЧЕСКОЕ ОБСЛЕДОВАНИЕ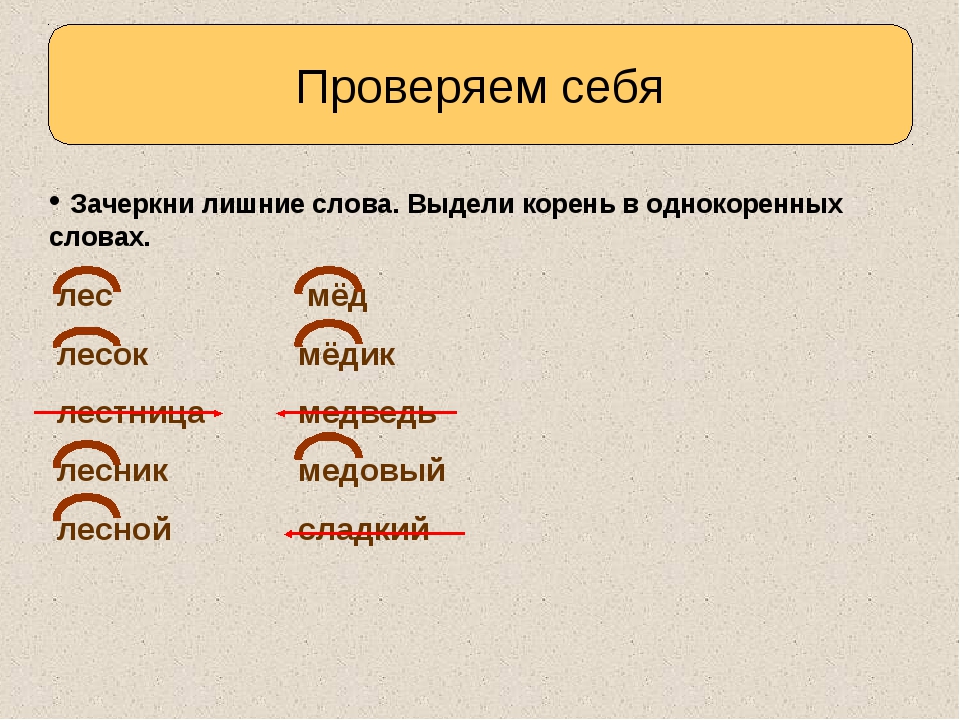
 Появляется неприятный запах изо рта.
Появляется неприятный запах изо рта. Вылечить такой пародонтит без общего лечения основного заболевания практически невозможно.
Вылечить такой пародонтит без общего лечения основного заболевания практически невозможно. Воспалительные явления присоединяются к пародонтозу достаточно редко.
Воспалительные явления присоединяются к пародонтозу достаточно редко. Однако, если не проводить никакого лечения, пораженные зубы могут приобрести подвижность и, в конечном итоге, выпасть.
Однако, если не проводить никакого лечения, пораженные зубы могут приобрести подвижность и, в конечном итоге, выпасть. Самое главное, оно должно быть комплексным — то есть лечение должно охватывать все выявленные причины и сопутствующие факторы, поддерживающие болезнь. Только в этом случае удается полностью излечить или надолго стабилизировать заболевание пародонта.
Самое главное, оно должно быть комплексным — то есть лечение должно охватывать все выявленные причины и сопутствующие факторы, поддерживающие болезнь. Только в этом случае удается полностью излечить или надолго стабилизировать заболевание пародонта.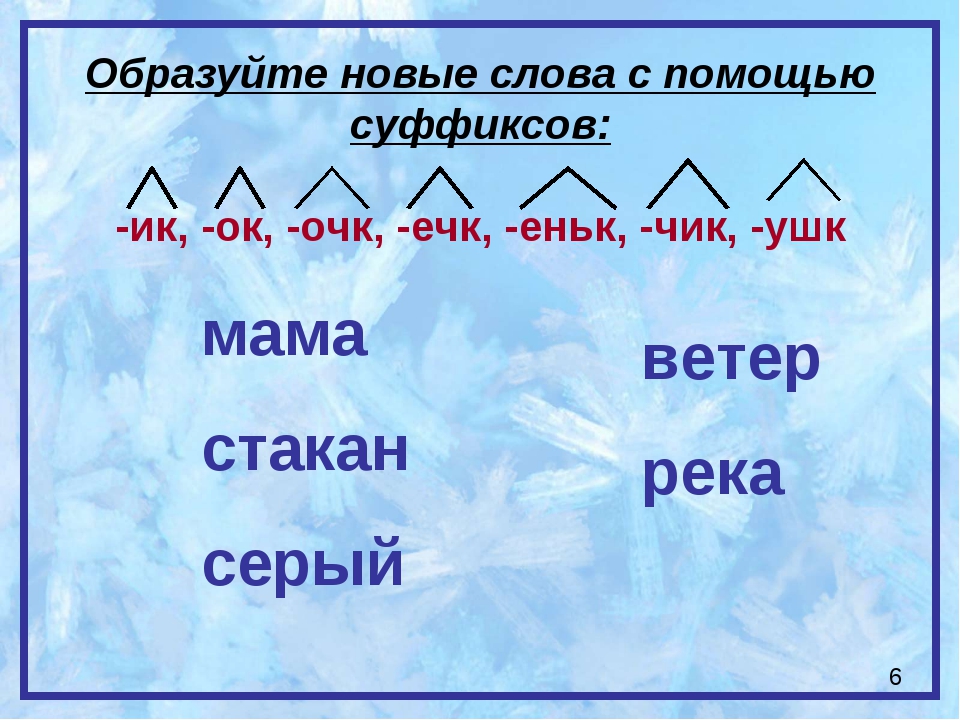 Кроме зубного камня и мягкого зубного налета, одновременно удаляется плотный темный налет (от курения, употребления чая, кофе, других красителей) — это позволяет вернуть красивый внешний вид вашим зубам. После удаления зубного камня и налета врач обязательно проведет полировку очищенной поверхности корня и коронки зуба.
Кроме зубного камня и мягкого зубного налета, одновременно удаляется плотный темный налет (от курения, употребления чая, кофе, других красителей) — это позволяет вернуть красивый внешний вид вашим зубам. После удаления зубного камня и налета врач обязательно проведет полировку очищенной поверхности корня и коронки зуба.
 Оно позволяет полноценно восстановить функцию жевания, устранить эстетические недостатки (при отсутствии зубов, видимых при улыбке), объединить все зубы воедино, как и предусмотрено природой.
Оно позволяет полноценно восстановить функцию жевания, устранить эстетические недостатки (при отсутствии зубов, видимых при улыбке), объединить все зубы воедино, как и предусмотрено природой.
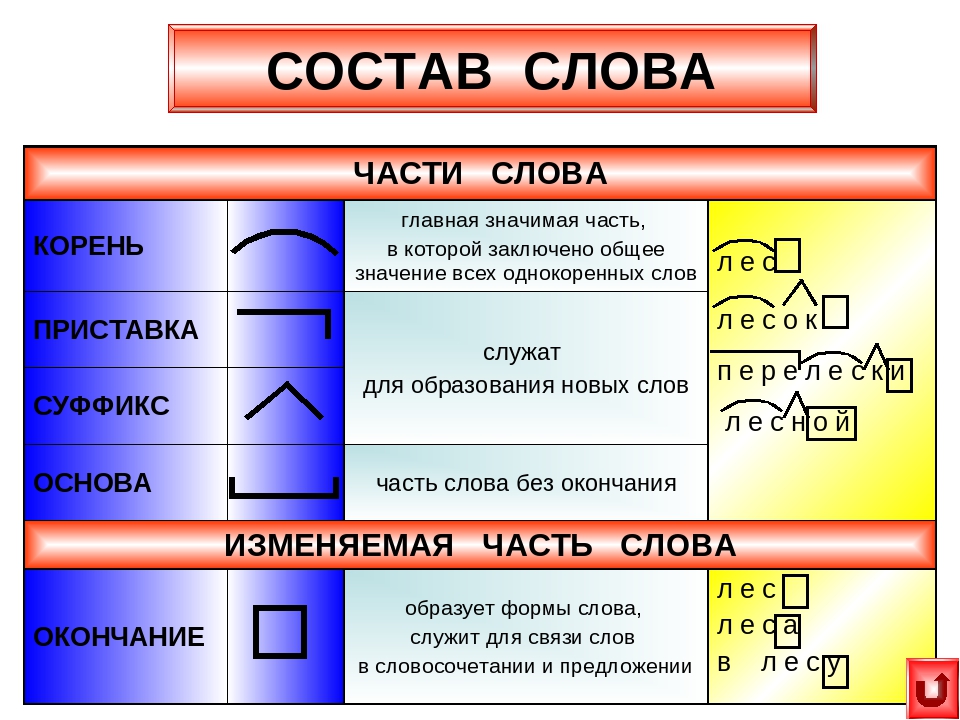
 От вредителей, если они появятся, помогут фунгициды. Если придерживаться всех этих рекомендаций, через шесть-восемь месяцев можно будет собирать урожай.
От вредителей, если они появятся, помогут фунгициды. Если придерживаться всех этих рекомендаций, через шесть-восемь месяцев можно будет собирать урожай.

 Здоровый рост приведет к тому, что у растения разовьется корневая система, которая слишком велика для контейнера.Иногда растение можно поместить в слишком маленький контейнер. Это также приведет к тому, что растение быстро прирастет к корням. Короче говоря, растение, привязанное к корням, — это просто растение, корни которого «связаны» каким-то барьером. Даже растения, растущие на открытом воздухе в земле, могут приковаться к корням, если их корни зажаты между несколькими прочными преградами, такими как фундаментные стены, нижние колонтитулы или трубы.
Здоровый рост приведет к тому, что у растения разовьется корневая система, которая слишком велика для контейнера.Иногда растение можно поместить в слишком маленький контейнер. Это также приведет к тому, что растение быстро прирастет к корням. Короче говоря, растение, привязанное к корням, — это просто растение, корни которого «связаны» каким-то барьером. Даже растения, растущие на открытом воздухе в земле, могут приковаться к корням, если их корни зажаты между несколькими прочными преградами, такими как фундаментные стены, нижние колонтитулы или трубы. Если корни немного обвиваются вокруг корневого комка, значит, растение лишь немного связано с корнем. Если корни образуют циновку вокруг корневого кома, растение сильно привязано к корням. Если корни образуют сплошную массу с небольшим количеством почвы, чтобы увидеть, растение сильно связано с корнями.
Если корни немного обвиваются вокруг корневого комка, значит, растение лишь немного связано с корнем. Если корни образуют циновку вокруг корневого кома, растение сильно привязано к корням. Если корни образуют сплошную массу с небольшим количеством почвы, чтобы увидеть, растение сильно связано с корнями. Это разорвет окружающие корни и предотвратит возможное опоясание по мере того, как ствол дерева станет больше.
Это разорвет окружающие корни и предотвратит возможное опоясание по мере того, как ствол дерева станет больше.




































 Время и дата дегустации с Вами будет согласована
Время и дата дегустации с Вами будет согласована Граждан просят соблюдать режим: не выходить на улицу без острой необходимости, ограничить контакты с другими людьми и соблюдать все рекомендации по профилактике вирусных заболеваний, предложенные медицинским сообществом.
Граждан просят соблюдать режим: не выходить на улицу без острой необходимости, ограничить контакты с другими людьми и соблюдать все рекомендации по профилактике вирусных заболеваний, предложенные медицинским сообществом. edu.ru/search.
edu.ru/search. (ПРИКАЗ)
(ПРИКАЗ) Как это сделать: https://helpschool.mosreg.ru/hc/ru/articles/360001467547
Как это сделать: https://helpschool.mosreg.ru/hc/ru/articles/360001467547

 Кроме того, такое уравнение называется полным, т.к. в нем присутствуют все три коэффициента.
Кроме того, такое уравнение называется полным, т.к. в нем присутствуют все три коэффициента.

 Целые корни ищем среди делителей числа 6.
Целые корни ищем среди делителей числа 6.  n} \)
n} \) {x-2} = 1 \)
{x-2} = 1 \) Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение: Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

 При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.
При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www. сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
 2 + 7x-20 = 0.… читать далее. Пожалуйста, помогите мне разложить следующие триномы. x2 + 2x-15
2 + 7x-20 = 0.… читать далее. Пожалуйста, помогите мне разложить следующие триномы. x2 + 2x-15 Тогда можно ожидать, что уравнения имеют одно решение. Нет необходимости писать уравнения в основной форме. Калькулятор легко выполняет эквивалентные операции с заданной линейной системой.
Тогда можно ожидать, что уравнения имеют одно решение. Нет необходимости писать уравнения в основной форме. Калькулятор легко выполняет эквивалентные операции с заданной линейной системой. или сгенерируйте квадратные уравнения. Начнем с первого. Уравнения квадратной формы Уравнение формы au2 bu c 0 Цитата для обучения звуковой ловушке
или сгенерируйте квадратные уравнения. Начнем с первого. Уравнения квадратной формы Уравнение формы au2 bu c 0 Цитата для обучения звуковой ловушке Bellwork Учитывая функцию y = 2×2 + 8x + 7 a.Найдите вершину b. Найдите ось симметрии c. Найдите yintercept d. Укажите, открывается ли график вверх или вниз. 1.3 Решение квадратных уравнений с помощью факторинга x2 + bx + c Словарь:
Bellwork Учитывая функцию y = 2×2 + 8x + 7 a.Найдите вершину b. Найдите ось симметрии c. Найдите yintercept d. Укажите, открывается ли график вверх или вниз. 1.3 Решение квадратных уравнений с помощью факторинга x2 + bx + c Словарь: † Если b2¡4ac <0, то реальных решений квадратного уравнения не существует. † Если b2¡4ac = 0, то квадратное уравнение имеет только один действительный нуль. Доступ к синологии из другой подсети
† Если b2¡4ac <0, то реальных решений квадратного уравнения не существует. † Если b2¡4ac = 0, то квадратное уравнение имеет только один действительный нуль. Доступ к синологии из другой подсети .. Bo3 модное меню театра
.. Bo3 модное меню театра
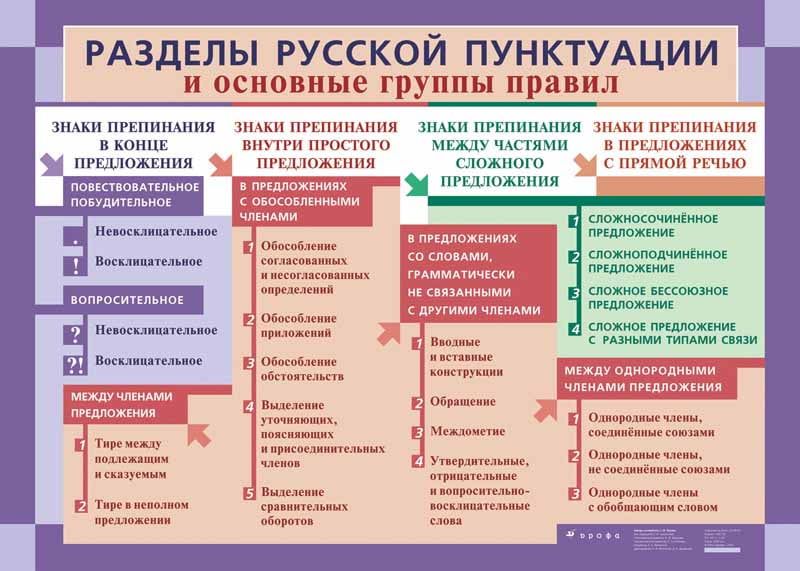










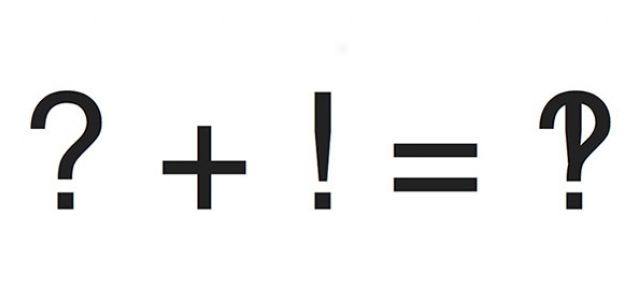


 Выполните морфемный разбор выделенных слов (индекс 2) (5 баллов).
Выполните фонетический разбор слова «лист..ев» (индекс 1) (5 баллов).
Смотрите образцы разборов:
Выполните морфемный разбор выделенных слов (индекс 2) (5 баллов).
Выполните фонетический разбор слова «лист..ев» (индекс 1) (5 баллов).
Смотрите образцы разборов: Каким вы представляете царя Берендея? 2. Как он относится к своим подданным? 3.Опишитемир берендеева царства. По каким законам они живут?
Каким вы представляете царя Берендея? 2. Как он относится к своим подданным? 3.Опишитемир берендеева царства. По каким законам они живут? Смертельно ране..ый пар..ход «Титаник» погибал медле..о мучительно долго словно (не)хотел ра(с,сс)тава(т,ть)ся с жизнью. А сотни людей обр..чё..ые вместе с ним на гибель слушали музыку (Б,б)етховенской симфонии и эта музыка укр..пляла их волю вливала в них мужество уб..регала от паники от душевных мук от сума..шествия.Музыка Бетховена звучала мужестве..о и величаво заглушая шум водызаполнявш..й тело корабля. Заглушавшая страдания гибнущих людей она звучала до той минуты пока волны (не)накрыли палубу вместе с музыкантами. Один из спасе..ых па(с,сс)ажиров вид..л троих из музыкантов смывших водой. Оставшиеся пятеро держались за перила после чего Хартли воскликнул (Г,господа я прощаюсь с вами!
Смертельно ране..ый пар..ход «Титаник» погибал медле..о мучительно долго словно (не)хотел ра(с,сс)тава(т,ть)ся с жизнью. А сотни людей обр..чё..ые вместе с ним на гибель слушали музыку (Б,б)етховенской симфонии и эта музыка укр..пляла их волю вливала в них мужество уб..регала от паники от душевных мук от сума..шествия.Музыка Бетховена звучала мужестве..о и величаво заглушая шум водызаполнявш..й тело корабля. Заглушавшая страдания гибнущих людей она звучала до той минуты пока волны (не)накрыли палубу вместе с музыкантами. Один из спасе..ых па(с,сс)ажиров вид..л троих из музыкантов смывших водой. Оставшиеся пятеро держались за перила после чего Хартли воскликнул (Г,господа я прощаюсь с вами! Приведите примеры.
Приведите примеры. В нем обычно есть доминирующее слово – то, которое выражает смысл наиболее точно. Например, объект значительной величины можно назвать большим, громадным, огромным, гигантским, немаленьким. В этой группе стержневым является слово «большой», остальные – вносят в общее значение уточняющие оттенки.
В нем обычно есть доминирующее слово – то, которое выражает смысл наиболее точно. Например, объект значительной величины можно назвать большим, громадным, огромным, гигантским, немаленьким. В этой группе стержневым является слово «большой», остальные – вносят в общее значение уточняющие оттенки. Возьмем, к примеру, синонимы быстро и опрометью. Первый из них комбинируется с массой слов, обозначающих всевозможные действия: пойти, вспомнить, сшить, написать, повернуться, схватить, поднять, застегнуть и т. д. А вот опрометью соединяется только с несколькими глаголами, значение которых связано исключительно с бегом: побежать, выбежать, помчаться, кинуться.
Возьмем, к примеру, синонимы быстро и опрометью. Первый из них комбинируется с массой слов, обозначающих всевозможные действия: пойти, вспомнить, сшить, написать, повернуться, схватить, поднять, застегнуть и т. д. А вот опрометью соединяется только с несколькими глаголами, значение которых связано исключительно с бегом: побежать, выбежать, помчаться, кинуться. Укажите, с помощью каких слов и словосочетаний писатель вводит в текст прямую речь и реплики диалога. Найдите синонимы. Подберите еще несколько синонимов к слову «сказать».
Укажите, с помощью каких слов и словосочетаний писатель вводит в текст прямую речь и реплики диалога. Найдите синонимы. Подберите еще несколько синонимов к слову «сказать».
 8) Все уже случилось – и ничего не произошло. 9) Как необычные дети становятся обычными взрослыми. 10) Может ли отечественная косметика конкурировать с импортной? 11) Здравомыслящие люди знают, а глупые уже догадались, что жизнь не будет автоматически становиться лучше и лучше. 12) Старый город – новое лицо. 13) Опубликованный текст свидетельствует об одном: между публичной и реальной позицией Запада по отношению к России особой разницы нет.
8) Все уже случилось – и ничего не произошло. 9) Как необычные дети становятся обычными взрослыми. 10) Может ли отечественная косметика конкурировать с импортной? 11) Здравомыслящие люди знают, а глупые уже догадались, что жизнь не будет автоматически становиться лучше и лучше. 12) Старый город – новое лицо. 13) Опубликованный текст свидетельствует об одном: между публичной и реальной позицией Запада по отношению к России особой разницы нет. Для проверки упражнений ** вызывается ученик к доске. Упражнения же *** можно проверить устно.
Для проверки упражнений ** вызывается ученик к доске. Упражнения же *** можно проверить устно. Дёргали, дёргали – получился дор. (Ю. Коваль.)
Дёргали, дёргали – получился дор. (Ю. Коваль.) Укажите антонимы
Укажите антонимы Что означает фраза: Работать засучив рукава?
Что означает фраза: Работать засучив рукава? Слова, имеющие несколько лексических значений?
Слова, имеющие несколько лексических значений? ..
.. В основе всякой метафоры лежит неназванное сравнение одних предметов с другими, имеющими общий признак. В художественной речи автор употребляет метафоры для усиления выразительности речи, для создания и оценки картины жизни, для передачи внутреннего мира героев и точки зрения рассказчика и самого автора. В метафоре автор создает образ — художественное представление о предметах, явлениях, которые он описывает, а читатель понимает, на каком именно сходстве основана смысловая связь между переносным и прямым значением слова: Добрых людей на свете было, есть и, надеюсь, будет всегда больше, чем плохих и злых, иначе в мире наступила бы дисгармония, он перекосился бы… опрокинулся и затонул. Метонимия — перенос значений (переименование) по смежности явлений. Наиболее употребительные случаи переноса: а) с человека на его какие-либо внешние признаки: Скоро ли обед? — спросил постоялец, обращаясь к стеганой жилетке; б) с учреждения на его обитателей: Весь пансион признавал превосходство Д.И. Писарева; в) имени автора на его творение (книгу, картину, музыку, скульптуру): Великолепный Микеланджело! (о его скульптуре) или Читая Белинского….
В основе всякой метафоры лежит неназванное сравнение одних предметов с другими, имеющими общий признак. В художественной речи автор употребляет метафоры для усиления выразительности речи, для создания и оценки картины жизни, для передачи внутреннего мира героев и точки зрения рассказчика и самого автора. В метафоре автор создает образ — художественное представление о предметах, явлениях, которые он описывает, а читатель понимает, на каком именно сходстве основана смысловая связь между переносным и прямым значением слова: Добрых людей на свете было, есть и, надеюсь, будет всегда больше, чем плохих и злых, иначе в мире наступила бы дисгармония, он перекосился бы… опрокинулся и затонул. Метонимия — перенос значений (переименование) по смежности явлений. Наиболее употребительные случаи переноса: а) с человека на его какие-либо внешние признаки: Скоро ли обед? — спросил постоялец, обращаясь к стеганой жилетке; б) с учреждения на его обитателей: Весь пансион признавал превосходство Д.И. Писарева; в) имени автора на его творение (книгу, картину, музыку, скульптуру): Великолепный Микеланджело! (о его скульптуре) или Читая Белинского…. Перифраза — использование описания вместо собственного имени или названия; описательное выражение, оборот речи, заменяющее слово. Используется для украшения речи, замены повтора: Город на Неве приютил Гоголя. Сравнение — одно из средств выразительности языка, помогающее автору выражать свою точку зрения, создавать целые художественные картины, давать описания предметов. В сравнении одно явление показывается и оценивается путем сопоставления его с другим явлением. Сравнение обычно присоединяется союзами как, словно, будто, точно и т. д. Оно служит для образного описания самых различных признаков предметов, качеств, действий. Например, сравнение помогает дать точное описание цвета: Как ночь, черны его глаза. Часто встречается форма сравнения, выраженного существительным в творительном падеже: Тревога змеею вползла в наши сердца. Бывают сравнения, которые передаются формой сравнительной степени наречия или прилагательного: Эгоизм бывает холоднее родника; Земля нежнее пуха лежала перед ним. Есть сравнения, которые включаются в предложение с помощью слов похож, подобен, напоминает: …бабочки похожи на цветы. Сравнение может представлять и несколько предложений, связанных по смыслу и грамматически. Таких сравнений две разновидности: 1) развернутое, разветвленное сравнение-образ, в котором основное, исходное сравнение конкретизируется рядом других: Звезды вышли на небо. Тысячами любопытных глаз они устремились к земле, тысячами светлячков зажгли ночь; 2) развернутый параллелизм (вторая часть таких сравнений обычно начинается словом «так»): Церковь вздрогнула. Так вздрагивает застигнутый врасплох человек, так лань трепетная срывается с места, еще даже не поняв, что произошло, но уже ощутив опасность. Фразеологизмы — это почти всегда яркие, образные выражения. Поэтому они — важное экспрессивное средство языка, используемое писателями как готовые образные определения, сравнения, как эмоционально- изобразительные характеристики героев, окружающей действительности и т. д.: У таких людей, как мой герой, есть искра божия.
Перифраза — использование описания вместо собственного имени или названия; описательное выражение, оборот речи, заменяющее слово. Используется для украшения речи, замены повтора: Город на Неве приютил Гоголя. Сравнение — одно из средств выразительности языка, помогающее автору выражать свою точку зрения, создавать целые художественные картины, давать описания предметов. В сравнении одно явление показывается и оценивается путем сопоставления его с другим явлением. Сравнение обычно присоединяется союзами как, словно, будто, точно и т. д. Оно служит для образного описания самых различных признаков предметов, качеств, действий. Например, сравнение помогает дать точное описание цвета: Как ночь, черны его глаза. Часто встречается форма сравнения, выраженного существительным в творительном падеже: Тревога змеею вползла в наши сердца. Бывают сравнения, которые передаются формой сравнительной степени наречия или прилагательного: Эгоизм бывает холоднее родника; Земля нежнее пуха лежала перед ним. Есть сравнения, которые включаются в предложение с помощью слов похож, подобен, напоминает: …бабочки похожи на цветы. Сравнение может представлять и несколько предложений, связанных по смыслу и грамматически. Таких сравнений две разновидности: 1) развернутое, разветвленное сравнение-образ, в котором основное, исходное сравнение конкретизируется рядом других: Звезды вышли на небо. Тысячами любопытных глаз они устремились к земле, тысячами светлячков зажгли ночь; 2) развернутый параллелизм (вторая часть таких сравнений обычно начинается словом «так»): Церковь вздрогнула. Так вздрагивает застигнутый врасплох человек, так лань трепетная срывается с места, еще даже не поняв, что произошло, но уже ощутив опасность. Фразеологизмы — это почти всегда яркие, образные выражения. Поэтому они — важное экспрессивное средство языка, используемое писателями как готовые образные определения, сравнения, как эмоционально- изобразительные характеристики героев, окружающей действительности и т. д.: У таких людей, как мой герой, есть искра божия. Цитаты из других произведений помогают автору доказать какой-либо тезис, положение статьи, показать его пристрастия и интересы, делают речь более эмоциональной, выразительной: А.С. Пушкина, «как первую любовь», не забудет не только «России сердце», но и мировая культура. Эпитет — слово, выделяющее в предмете или явлении какие-либо его свойства, качества или признаки. Эпитетом называют художественное определение, т. е. красочное, образное, которое подчеркивает в определяемом слове какое-нибудь его отличительное свойство. Эпитетом может служить всякое значащее слово, если оно выступает как художественное, образное определение к другому: 1) существительное: болтушка сорока; 2) прилагательное: роковые часы;
Цитаты из других произведений помогают автору доказать какой-либо тезис, положение статьи, показать его пристрастия и интересы, делают речь более эмоциональной, выразительной: А.С. Пушкина, «как первую любовь», не забудет не только «России сердце», но и мировая культура. Эпитет — слово, выделяющее в предмете или явлении какие-либо его свойства, качества или признаки. Эпитетом называют художественное определение, т. е. красочное, образное, которое подчеркивает в определяемом слове какое-нибудь его отличительное свойство. Эпитетом может служить всякое значащее слово, если оно выступает как художественное, образное определение к другому: 1) существительное: болтушка сорока; 2) прилагательное: роковые часы; Она помогает лучше передать, изобразить противоречия, противопоставить явления. Служит способом выражения авторского взгляда на описываемые явления, образы и т. д. Восклицательные частицы — способ выражения эмоционального настроя автора, прием создания эмоционального пафоса текста: О как ты прекрасна, земля моя! А как хороши твои поля! Восклицательные предложения выражают эмоциональное отношение автора к описываемому (гнев, иронию, сожаление, радость, восхищение): Безобразное отношение! Как можно не беречь счастье! Восклицательные предложения выражают также побуждение к действию: Сбережем свою душу как святыню! Градация — стилистическая фигура, заключающаяся в последовательном нагнетании или, наоборот, ослаблении сравнений, образов, эпитетов, метафор и других выразительных средств художественной речи: Ради своего ребенка, ради семьи, ради народа, ради человечества — берегите мир! Инверсия — обратный порядок слов в предложении. При прямом порядке подлежащее предшествует сказуемому, согласованное определение стоит перед определяемым словом, несогласованное — после него, дополнение — после управляющего слова, обстоятельство образа действия — перед глаголом: Современная молодежь быстро поняла ложность этой истины. А при инверсии слова располагаются в ином порядке, чем это установлено грамматическими правилами. Это сильное выразительное средство, употребляемое в эмоциональной, взволнованной речи: Родина любимая, земля моя родная, тебя ли нам не беречь! Композиционный стык — это повторение в начале нового предложения слова или слов из предыдущего предложения, обычно заканчивающих его: Все сделала для меня Родина. Родина меня выучила, вырастила, дала путевку в жизнь. Жизнь, которой я горжусь. Многосоюзие — риторическая фигура, состоящая в намеренном повторении сочинительных союзов для логического и эмоционального выделения перечисляемых понятий: И гром не грянул, и небо не обрушилось на землю, и реки не разлились от такого горя! Односоставные, неполные предложения делают авторскую речь более выразительной, эмоциональной, усиливают эмоциональный пафос текста: Джоконда.
Она помогает лучше передать, изобразить противоречия, противопоставить явления. Служит способом выражения авторского взгляда на описываемые явления, образы и т. д. Восклицательные частицы — способ выражения эмоционального настроя автора, прием создания эмоционального пафоса текста: О как ты прекрасна, земля моя! А как хороши твои поля! Восклицательные предложения выражают эмоциональное отношение автора к описываемому (гнев, иронию, сожаление, радость, восхищение): Безобразное отношение! Как можно не беречь счастье! Восклицательные предложения выражают также побуждение к действию: Сбережем свою душу как святыню! Градация — стилистическая фигура, заключающаяся в последовательном нагнетании или, наоборот, ослаблении сравнений, образов, эпитетов, метафор и других выразительных средств художественной речи: Ради своего ребенка, ради семьи, ради народа, ради человечества — берегите мир! Инверсия — обратный порядок слов в предложении. При прямом порядке подлежащее предшествует сказуемому, согласованное определение стоит перед определяемым словом, несогласованное — после него, дополнение — после управляющего слова, обстоятельство образа действия — перед глаголом: Современная молодежь быстро поняла ложность этой истины. А при инверсии слова располагаются в ином порядке, чем это установлено грамматическими правилами. Это сильное выразительное средство, употребляемое в эмоциональной, взволнованной речи: Родина любимая, земля моя родная, тебя ли нам не беречь! Композиционный стык — это повторение в начале нового предложения слова или слов из предыдущего предложения, обычно заканчивающих его: Все сделала для меня Родина. Родина меня выучила, вырастила, дала путевку в жизнь. Жизнь, которой я горжусь. Многосоюзие — риторическая фигура, состоящая в намеренном повторении сочинительных союзов для логического и эмоционального выделения перечисляемых понятий: И гром не грянул, и небо не обрушилось на землю, и реки не разлились от такого горя! Односоставные, неполные предложения делают авторскую речь более выразительной, эмоциональной, усиливают эмоциональный пафос текста: Джоконда. Лепет людской. Шепот. Шорох платьев. Тихие шаги. … Ни одного мазка, — слышу я слова. — Нет мазков. Как живая. Парцелляция — прием расчленения фразы на части или даже на отдельные слова. Ее цель — придать речи интонационную экспрессию путем ее отрывистого произнесения: Поэт внезапно встал. Побледнел.
Лепет людской. Шепот. Шорох платьев. Тихие шаги. … Ни одного мазка, — слышу я слова. — Нет мазков. Как живая. Парцелляция — прием расчленения фразы на части или даже на отдельные слова. Ее цель — придать речи интонационную экспрессию путем ее отрывистого произнесения: Поэт внезапно встал. Побледнел. Синтаксический параллелизм — одинаковое построение нескольких рядом расположенных предложений С его помощью автор стремится выделить, подчеркнуть высказанную мысль: Мать — это начало всех начал. Мать — это чудо земное. Мать — это слово святое. Эпифора — одинаковая концовка нескольких предложений, усиливающая значение этого образа, понятия и т. д.: Я всю жизнь шел к тебе. Я всю жизнь верил в тебя. Я всю жизнь любил тебя.
Синтаксический параллелизм — одинаковое построение нескольких рядом расположенных предложений С его помощью автор стремится выделить, подчеркнуть высказанную мысль: Мать — это начало всех начал. Мать — это чудо земное. Мать — это слово святое. Эпифора — одинаковая концовка нескольких предложений, усиливающая значение этого образа, понятия и т. д.: Я всю жизнь шел к тебе. Я всю жизнь верил в тебя. Я всю жизнь любил тебя. По этой причине я настоятельно рекомендую вам по возможности ссылаться на несколько словарей и смотреть на реальные примеры, когда вам нужно получить более конкретное представление о том, как используются слова.
По этой причине я настоятельно рекомендую вам по возможности ссылаться на несколько словарей и смотреть на реальные примеры, когда вам нужно получить более конкретное представление о том, как используются слова.