Обращение по русскому языку: Обращение — урок. Русский язык, 8 класс.
Обращение в русском языке. Примеры и виды обращений
Обращение называет, кому адресована речь. Это слово или словосочетание обозначает, к которому обращается автор. Обращение может относиться и к одушевленному лицу, и к неодушевленному предмету.
Обращение. Примеры
Маша, где ты была?
А мы вас, профессор, давно ищем.
Спи, моя радость, усни.
Ержан, вставай, на работу пора!
Спасибо, сердце, что ты умеешь так любить!
Ах ты, мерзкое стекло! Это врешь ты мне назло. (А.С. Пушкин)
Русь, куда ж несешься ты? (Н.В. Гоголь)
Покажите мне Москву, москвичи! (А. Розенбаум)
Обращение не является членом предложения. Оно может стоять в начале, в середине и в конце предложения. На письме обращение всегда выделяется знаками препинания, а в речи — интонацией.
Основная цель обращения — привлечь внимание, хотя иногда обращение может и выражать отношение к собеседнику:
Милая моя,
Солнышко лесное,
Где, в каких краях
Встретишься со мною.
Ю. Визбор
Какими бывают обращения
Обращением чаще всего служит существительное в именительном падеже или другая часть речи в значении существительного — прилагательное, причастие и так далее.
Примеры обращений
Скажи, дедушка, ты давно приехал?
Эй ты, иди сюда!
Чем вам помочь, любезный?
Провожающие, выйдите из вагона!
Обращениями могут служить собственные имена людей, клички животных, названия по степени родства, профессии, занятию, званию, национальности, возрасту и т.п.
Примеры обращений
Рэкс, ко мне!
Вас к телефону, Иван Иванович.
Света! Пошли в кино.
Так точно, товарищ генерал!
Эй, мужики, как пройти на улицу Ленина?
Смилуйся, государыня рыбка. (А.С. Пушкин)
За мной, читатель! (М.А. Булгаков)
Обращениями могут быть названия предметов и неживой природы, географические названия. В этом случае происходит олицетворение — неодушевленные предметы наделяются человеческими качествами.
В этом случае происходит олицетворение — неодушевленные предметы наделяются человеческими качествами.
Москва, Москва!.. люблю тебя как сын,
Как русский, — сильно, пламенно и нежно!
М.Ю. ЛермонтовШуми, шуми, послушное ветрило,
Волнуйся подо мной, угрюмый океан.
А.С. Пушкин
Краткие и распространенные обращения
Обращение может быть кратким — состоять из одного слова. Обращение не является членом предложения, но может иметь зависимые слова, то есть быть распространенным.
Примеры кратких обращений
Не гонялся бы ты, поп, за дешевизной. (А.С. Пушкин)
Ребята! Не Москва ль за нами? (М.Ю.Лермонтов)
Товарищ, винтовку держи, не трусь! (А.А. Блок)
Каждый труд благослови, удача. (С.А. Есенин)
Примеры распространенных обращений
Бесценный друг, что такое сердце человеческое? (И. Гете)
Забудь, товарищ мой любезный, раздор смешной и бесполезный (А.С. Пушкин)
Как я любил, Кавказ мой величавый, твоих сынов воинственные нравы. (М.Ю. Лермонтов).
Люблю я грусть твоих просторов, мой милый край, святая Русь. (Ф. Сологуб)
Я всю свою звонкую силу поэта тебе отдаю, атакующий класс. (В. В. Маяковский)
А ну-ка песню нам пропой, веселый ветер. (В. Лебедев-Кумач)
Несколько обращений могут идти подряд:
Мама, сестры и товарищи, простите — это не способ (другим не советую), но у меня выходов нет.
Предсмертная записка В.В. Маяковского
В одном предложении может быть даже несколько обращений, направленных к одному адресату, одно из которых только называет слушателя, а другое — оценивает:
Поезжайте, душенька, Илья Ильич! (И.А. Гончаров).
Знаки препинания при обращениях. Как выделяется обращение
Обращение отделяется знаками препинания. Если его произносят без восклицательной интонации, то обращение выделяется запятой в начале или конце предложения или запятыми, если стоит в середине предложения.
Мама, я пришел.
Я пришел, мама.
Я, мама, уже пришел.
Если обращение находится в начале предложения и произносится с восклицательной интонацией, то после него ставится восклицательный знак. При этом первое слово пишется с прописной буквы.
Мама! Я пришел!
Если перед обращением стоит междометие «о», «ах», «а» и тому подобные, они не отделяются запятой от обращения.
О родина святая, какое сердце не дрожит, тебя благославляя. (В.А. Жуковский)
Как хорошо ты, о море ночное! (Ф.И. Тютчев)
Не являются обращениями и не разделяются запятыми междометные выражения боже упаси, господи прости, слава тебе господи и т.п.
Если части распространенного обращения разделены другими членами предложения, то каждая часть выделяется запятыми:
Отколе, умная, бредешь ты, голова? (И.А. Крылов).
В официальных письмах обращения принято записывать на отдельной строке. После обращения в таком случае ставится восклицательный знак.
Уважаемый Иван Иванович! (Слово «уважаемый» входит в состав обращения и запятой не отделяется).
Ты и вы — обращение или подлежащее?
Личные местоимения ты и вы чаще всего в предложении являются подлежащими, а не обращениями.
Ты, царевич, мой спаситель, мой могучий избавитель. (А. С. Пушкин)
Иногда, впрочем, они могут быть обращениями или входить в состав обращений.
Здравствуй, князь ты мой прекрасный! (А.С. Пушкин).
Читайте также: Вводные слова в русском языке. Как ставить запятые?
Обращение (Упражнения и тест)
Упражнение 1.
Выпишите те предложения, в которых есть обращения.
1) Березы белоствольные растите веселей. 2) Шумит земля привольная ветвями тополей. 3) Пусть спокойно в нашей школе спит до осени звонок. 4) Здравствуй солнце здравствуй лес.
Упражнение 2.
Перестройте предложения так, чтобы подлежащие стали обращениями.
1. Ветер споет нам про дикие горы.
2. Мой друг настойчиво добивается цели.
3. Бабушка рассказывает сказку на ночь.
4. Ребята пошли на речку.
5. Мама купила мне книгу.
6. Петя сначала выучил уроки, а потом пошел гулять.
Упражнение 3.
Составьте двенадцать предложений так, чтобы в одних данные слова были подлежащими, а в других — обращениями.
Товарищ, Сергей Петрович, страна родная, читатель, друзья, девушка.
Упражнение 4.
Спишите, расставляя знаки препинания. Вставьте пропущенные буквы.
I. 1) Мой друг отчизн… посвятим души пр…красные порывы! 2) От меня отцу брат милый поклони…ся не забудь. 3) Покажи мне шлем Иван. 4) Поэта дом опальный о Пущин мой ты первый посетил. 5) Играйте, пойте о друзья! 6) Где был ты сын? 7) Последи…я туча рассе…нной бури одна ты несё…ся по ясной лазури. 8) Звезда печальная вечерн…я звезда твой луч осеребрил увядшие р…внины и дремлющий залив и чёрных скал вершины. 9) Простите мирные долины и вы знако¬мых гор вершины и вы знакомые леса. (А. С. Пушкин.)
II. 1) Не буд… товарищ слепым и глухим. Держи товарищ порох сухим. 2) Идите, слов не тратя, на красный наш костёр. Сюда миллионы братьев сюда миллионы сестёр! 3) Веди светло и прямо к работе и боям моя большая мама — республика моя. 4) Слав…те молот и стих землю молодости! 5) Пролетарии стройтесь к последней схватк… . Рабы разгибайте спины и ко¬лени. Армия пролетариев встань стройна.
Упражнение 5.
Спиши, расставляя знаки препинания, подчеркни обращения.
I. Умчались вы дни радости моей. Мы долго кружили по просторному наполне(н,нн)ому птицами заливу и разумеется заблудились. Да в этом ты конечно был прав. Антонина Петровна должно быть и не знает что ты пр_ехал? Конечно говорить об этом было (не)приятно но я разумеется молчал. Нам по правде сказать в этот вечер и ра_влеч(?)ся-то словно бы (не)зачем.
Нам по правде сказать в этот вечер и ра_влеч(?)ся-то словно бы (не)зачем.
II. Это задание он сделает должно быть в срок. Ну-ка дождик теплой влагой ты умой нас огромной рукой. Тебе поем мы песню вечерняя з_ря! К великому моему уд_влению пролетка св_рнула на нашу дорогу. Вам я думаю т_жело жить доктор? Конечно (не)пр_ятно что дома будут бе_покоиться.
III. Спой мне иволга песню пусты(р,нн)ую песню жизни моей. Весна золотобровая весна золотоносая бедовая суровая (не)пр_ставай с вопросами! Предусмотрительный Левинсон еще до приезда разведки пр_ехала она ночью выставил удале(н,нн)ое охр_нение. К счастью Печорин был погруж_н в задумчивость глядя на синие зубцы Кавказа и кажется вовсе не тор_пился в дорогу.
Упражнение 6.
Прочитайте, укажите обращения и объясните расстановку знаков препинания.
1) Пётр Андреич, Максимыч отведёт вас на вашу квартиру. 2) Сын мой Пётр! Письмо твоё мы получили 15 сего месяца.3) Высоко над семьёю гор, Кавказ, твой царственный шатёр сияет. 4) Здравствуй, племя младое, незнакомое! 5) Ты не узнал меня, Прохоров? 6) Как недогадлива ты, няня! 7) Поез¬жайте ты, Трубецкой, и ты, Басманов. 8) Опять я ваш, о юные друзья! 9) О поле, поле! Кто тебя усеял мёртвыми костями? 10) Девицы, красавицы, душеньки, подруженьки, разыграйтесь, девицы, разгуляйтесь, милые! (Из произведений А. С. П у ш к и н а.)
Упражнение 7.
Придумайте примеры предложений с обращениями, чтобы в качестве обращения выступали имя, отчество, фамилия; наименование лица по роду занятий, возрасту, полу, занимаемой должности, месту жительства, национальной принадлежности, родственным и иным отношениям; кличка животного; неодушевленные предметы. Сделайте вывод, какие слова могут выступать в качестве адресата речи.
Упражнение 8.
Запишите предложения, определите, в каких предложениях есть обращения и какими членами предложения являются выделенные слова в остальных примерах.
Сыпь ты, черемуха, снегом, пойте вы, птахи, в лесу.
Сыплетчеремуха снегом, зелень в цвету и росе.
Спой мне, иволга, песню пустынную, песню жизни моей.
Плачет где-то иволга, схоронясь в дупло.
Пока лета не отогнали невинной радости твоей, Спи, милый! Горькие печали не тронут детства тихих дней.
Простите мне, я так люблюТатьяну милую мою.
Прощай, письмо любви! Прощай: она велела…
Татьяна то вздохнет, то охнет; Письмо дрожит в ее руке.
Ах ты, старый конюх, неразумный, Разгадаешь ли, старый, загадку?
Прекрасной дочерью своей гордитсястарый Кочубей.
Ветер, ветер! Ты могуч, ты гоняешь стаи туч…
Свищет ветер, серебряный ветер, В шелковом шелесте снежного шума.
Упражнение 9.
Закончите предложения:
а) о назначении (роли) обращения. Обращение называет того,________________;
б) о способе выражения обращения. Обращение обычно бывает выражено____________________________;
в) об интонационных особенностях обращений. Обращение произносится с особой(_________________)__________________ _________________________________________ ;
г) о том, почему и как нужно отличать обращение от подлежащего. Обращение обычно выражено той же формой имени существительного, что и ___________, поэтому при разборе предложения его нередко __________. Чтобы не ошибиться, нужно помнить, что обращение не входит в _________________________________________ , не является __________________________________ (к нему нельзя поставить вопрос от сказуемого) и произносится с_______________________________ .
Упражнение 10.
Как вы думаете, в какой речи – устной или письменной – чаще используются обращения? Приведите примеры обращений, которые вам приходится использовать в разных ситуациях в течение одного дня. Последите за собой: какое отношение к собеседнику вы выражаете в подборе обращений?
(Сравните: мама, мамочка, мамуля, мамуленька; Анатолий Алексеевич, Анатолий, Толя, Толик, Толечка. )
)
Упражнение 11.
Вспомните, что такое речевая ситуация и как она влияет на выбор языковых средств общения, в том числе и на выбор варианта обращения. Выполнить задание вам поможет высказывание Н.И. Формановской:
…Одному мы можем сказать: уважаемый Александр Ильич, другому (или в других условиях) – Сашенька, а третьему (или в иных условиях) – Санек. И все это будет зависеть от того, кто и кому, в какой обстановке и при каких взаимных отношениях говорит.
Упражнение 12.
Вы переписываетесь с кем-нибудь? В зависимости от чего выбираете обращения? Покажите это: напишите письмо, предварительно определив адресата (кому будете писать), характер письма (официальное, деловое или личное), содержание (о чем хотите сообщить), какие языковые средства лучше использовать для данной ситуации. Не забудьте употребить нужные знаки препинания для выделения обращения.
Упражнение 13.
Припомните, в какой речи роль обращений могут исполнять имена существительные, обозначающие неживые предметы. Прочитайте поэтические строки, спишите, расставив недостающие знаки препинания.
1) Безмолвное море лазурное море стою очарован над бездной твоей. (В.Жуковский)
2) Шуми шуми послушное ветрило волнуйся подо мной угрюмый океан. (А.Пушкин)
3) Что ты клонишь над водами ива макушку свою… И дрожащими листами, словно жадными устами, ловишь беглую струю? (Ф.Тютчев) 4) Тучки небесные вечные странники Степью лазурною цепью жемчужною мчитесь вы, будто как я же, изгнанники с милого севера в сторону южную. (М.Лермонтов) 5) Колокольчики мои цветики степные Что глядите на меня, темно-голубые? (А.К. Толстой)
Упражнение 14.
Спишите, расставляя недостающие знаки препинания. Обозначьте обращения.
а) 1. Что дремучий лес призадумался? (А.Кольцов) 2. Эй, вратарь готовься к бою. (В.Лебедев-Кумач) 3. Присядем друзья перед дальней дорогой. (В.Дыховичный) 4. Эй, костровой за костер огневой ты отвечаешь нам головой. (З.Александрова)
(В.Лебедев-Кумач) 3. Присядем друзья перед дальней дорогой. (В.Дыховичный) 4. Эй, костровой за костер огневой ты отвечаешь нам головой. (З.Александрова)
б) 1. Радуй девочка людей добротой, красой своей. (О.Константинова) 2. Ты проснись Аленушка, уж восходит солнышко. (О.Константинова) 3. Еж не верь словам лисицы, лучше верь друзьям своим. (Г.Скребицкий) 4. Подождите немного леса и поля, я вернусь к вам листочком, травинкой, соломкой. (А.Юрканская) 5. Узнаю тебя рыжая по шубке пушистой, по хвосту роскошному, по поступи осторожной. (О.Константинова) 6. Роза для чего тебе шипы? (А.Юрканская)
Упражнение 15.
Найдите в предложениях обращения. Сделайте вывод, какую позицию в предложении они могут занимать.
1. Здравствуй, племя младое, незнакомое (Пушкин). 2. Учитель! Перед именем твоим позволь смиренно преклонить колени! (Некрасов). 3. Мой друг, отчизне посвятим души прекрасные порывы! (Пушкин). 4. Ох, лето красное! Любил бы я тебя, когда б не зной, да пыль, да комары, да мухи (Пушкин). 5. Родная земля! Назови мне такую обитель, я такого угла не видал, где бы сеятель твой и хранитель, где бы русский мужик не стонал! (Некрасов). 6. Учись, мой сын (Пушкин).
Упражнение 16.
Найдите в предложениях обращения и укажите, чем они отличаются от сходных по форме членов предложения.
1. Пора, мой друг, пора! Покоя сердце просит — летят за днями дни, и каждый час уносит частичку бытия… (Пушкин). — Мой друг нездоров уже несколько дней. 2. Ее мечты всегда были возвышенны и романтичны. — Мечты, мечты, где ваша сладость? (Пушкин). 3. Любезнейший наш друг, о ты, Василий Львович! (Пушкин). — Василий Львович, дядя поэта, тоже писал стихи. 4. Москва — мой любимый город. — Москва! Люблю тебя как сын, как русский, сильно, пламенно и нежно (Лермонтов). — В журнале «Москва» впервые был опубликован роман М. Булгакова «Мастер и Маргарита».
Тест по теме «Обращение»
1. Одно из утверждений неверно. Найдите его.
Одно из утверждений неверно. Найдите его.
1) Обращение — это конструкция, называющая человека (лицо), к которому обращена речь.
2) Обращение, привлекая внимание собеседника, является мощным средством поддержания речевого контакта.
3) В роли обращения обычно употребляются одушевленные существительные в форме именительного падежа, одиночные или с зависимыми словами.
4) В предложении обращения обычно являются подлежащими.
2. С чем нельзя согласиться?
1) Обращение может быть выражено неодушевленным существительным в форме именительного падежа.
2) Обращение не связано синтаксически с членами предложения.
3) Обращение может стоять в любой части предложения.
4) Обращение не может быть выделено на письме знаками препинания.
3. Выберите ошибочное утверждение.
1) Обращение может быть распространено определениями и придаточными предложениями.
2) Обращение, где бы оно ни стояло, отделяется от других членов предложения запятыми.
3) Если обращение окрашено особыми эмоциями и произнесено с восклицательной интонацией, оно оформляется восклицательным знаком.
4) В роли обращения в редких случаях могут выступать личные местоимения ТЫ и ВЫ.
4. Найдите предложения, в которых обращения выражены одушевленным существительным.
1) Здравствуй, солнце да утро веселое!
2) Дни поздней осени бранят обыкновенно, но мне она мила, читатель дорогой.
3) Ускорь шаги, прекрасная весна, поторопи свой радостный приход.
4) Друзья! Вы хоть охрипните, хваля друг дружку, — все ваша музыка плоха.
5. Найдите предложения, в которых обращения выражены неодушевленным существительным.
1) Проснись же, смолкнувшее слово, раздайся с уст моих опять.
2) Свет Родионовна, забуду ли тебя?
3) Ты хочешь меду, сын? — Так жала не страшись.
4) Плачь, душа моя, плачь, моя милая!
6. Найдите предложения, в которых неправильно расставлены знаки препинания.
Найдите предложения, в которых неправильно расставлены знаки препинания.
1) Твой лик, о ночь, не мог меня томить!
2) Внемлите ж, братья, слову брата, пока мы полны юных сил.
3) Умру я скоро. Жалкое наследство о, Родина, оставлю я тебе.
4) Опять я в Москве, любезнейший, Пушкин, действую снова в суде.
7. Установите соответствие:
1) Подлежащее.
2) Обращение.
А. Входит в грамматическую основу предложения. От сказуемого можно поставить вопрос к подлежащему.
Б. Не входит в грамматическую основу предложения, к нему нельзя поставить вопрос от сказуемого.
8. Установите соответствие:
1) «Чем вы, гости, торг ведете и куда теперь плывете?»
2) Гости князю поклонились, вышли вон и в путь пустились.
3) «Вот что, князь, тебя смущает?»
4) Князь у синя моря ходит, с синя моря глаз не сводит.
А. Гости — подлежащее.
Б. Князь — подлежащее.
В. Гости — обращение.
Г. Князь — обращение.
9. Родилась я, милые внуки мои, под Киевом, в тихой деревне. (Н. Некрасов) Это предложение осложнено
1) обращением и вводным словом.
2) вводным словом и словом-предложением.
3) обращением и уточняющим обстоятельством.
4) словом-предложением и обособленным приложением.
10. Нераспространенным обращением осложнено предложение
1) Ты, солнце святое, гори! (А. С. Пушкин)
2) Вы откуда будете, молодые люди? (А. Фадеев)
3) Вперед чужой беде не смейся, голубок. (И. Крылов)
4) Что же ты, моя старушка, приумолкла у окна? (А. С. Пушкин)
11. Распространенным обращением осложнено предложение
1) Петр, куда ты спрятался? (И. С. Тургенев)
2) Он был, о море, твой певец. (А. С. Пушкин)
3) Расскажи свою биографию, Артем! (Н. Островский)
4) Дорогие товарищи, мы спаяны неразрывной дружбой. (Н. Островский)
(Н. Островский)
12. Знаки препинания расставлены правильно в предложении
1) Вы, дядечка помолчите. (А. Чехов)
2) Здравствуй, солнце, да утро веселое! (С. Никитин)
3) Отпусти меня родная, на простор широкий. (Н. Некрасов)
4) Петр Андреевич, Максимыч отведет вас на вашу квартиру. (А. С. Пушкин)
13. Знаки препинания расставлены правильно в предложении
1) Простите, вольные страницы, и край отцов, и тихий Дон. (А. С. Пушкин)
2) Дружная идешь, ты, с нами осень. (С. Щипачев)
3) Я люблю тебя жизнь за весну и за страх, и за ярость. (О. Сулейменов)
4) Так вот судьба твоих сынов, о, Рим, о, грозная держава. (А. С. Пушкин)
14. Для привлечения внимания слушающего к сообщению в устной речи употребляется
1) обращение.
2) вводное слово.
3) слово-предложение.
4) обособленное приложение.
5) уточняющие члены предложения.
15. В каком предложении нет обращения?
I) Зачем ты, Балда. к нам залез?
2) Воротись, поклонися рыбке.
3) Постой, бабушка, постой немножко.’
4) Здравствуй, солнце да утро веселое!
16. В каком предложении нет обращения?
1) Ребята, вероятно, уже все в оборе?
2) Взвейтесь кострами, синие ночи!
3) Ты, видимо, меня не услышал.
4) Пишите нам, уважаемые радиослушатели.
17. В каком предложении есть обращение?
1) Откуда ты идешь?
2) Мой друг, я пишу эти строки в надежде на скорую встречу.
3) Тот, кого любила я, уже слишком далеко.
4) Тебе, великому русскому поэту, я посвящаю эти юношеские стихи.
18. В каком предложении имеется пунктуационная ошибка?
1) Однако я господа, кажется, мешаю вам заниматься.
2) А знаете, Клавочка, я должен вам кое-что сообщить.
3) Кем бы вы тогда стали, Александр Петрович?
4) Ты письмо мое, милый, не комкай.
19. В каком предложении имеется пунктуационная ошибка?
1) Лидия Николаевна, в кухню входить боялась, да и вообще была тихая, пугливая особа.
2) Так что будьте осторожны, дамы и девицы.
3) Брат мой, как я рад тебя видеть!
4) Читатель, любишь ли ты книги?
20. В каком предложении имеется пунктуационная ошибка?
1) Помоги мне, солнце красное.
2) Отдыхающие, будьте взаимно вежливы.
3) Итак, вы в Москве родные мои?
4) Он был, о море, твой певец.
Ответы:
Урок русского языка по теме «Обращение»
Организационный момент. Приветствие учителем учеников, гостей, приветствие учениками гостей. (1 мин)
Определение темы и целей урока. (3 мин)
Ребята, запишем в тетрадях число. Оставим строчку для темы урока, её вы подскажете мне сами чуть позже, и поработаем с текстом. Перед вами текст Л. Н. Толстого, прочитайте его и определите основную мысль текста. Что хотел нам сказать Л.Н.Толстой?
Работа с текстом (текст на карточках, гостям все карточки тоже раздаются).
Укажите, чем осложнены третье и пятое предложения? (Обращениями) Это и есть тема нашего урока. Запишите тему сегодняшнего урока. «Предложение с обращением». (записываю на доске) Нам сегодня с вами нужно многое успеть. Вспомнить, что такое обращение, мы должны научиться легко находить его в тексте, правильно ставить знаки препинания. А еще сегодня на уроке мы будем говорить о здоровом образе жизни, как важно сохранять свое здоровье смолоду.
3. Изучение нового материала.
— Мы будем составлять кластер к определению обращения. Вы знаете, что это такое. А что же значит это слово «кластер»?
Кластер (англ.) –модель, схема, структура свойств определённого термина.
—Давайте вспомним, что называется обращением? (Слово или сочетание слов, называющее того, к кому обращаются с речью.) Откроем учебники (§ 28, стр. 117), убедимся, так ли это. Начинаем заполнять кластер, запишем определение в центр, оставим половину страницы свободной. Презентация.
Слайд. Наблюдение на доске Сравним два предложения и определим, какую синтаксическую функцию выполняет слово «Спорт» в каждом из них.
(Не является членом предложения– занесем в кластер эту грамматическую особенность обращения.
—Давайте попробуем распространить обращение во втором предложении и запишем его. Получается? (Собирай молодость под свои мирные знамена, великий спорт!
Обращение стало распространённым. Это доказывает, что обращения бывают распространённые (несколько слов) и нераспространённые (одно слово) обращения. Сверимся с материалом учебника. Запишем в кластер эту особенность.
Как на письме выделяется обращение? (Запятой или восклицательным знаком.) Работа с таблицей. (слайд).
Запятая и восклицательный знак при обращении
1. Если обращение стоит в начале или в конце предложения, ставится запятая или восклицательный знакНачинайте зарядку, ребята!
Друзья! занимайтесь физкультурой!
2. Если обращение стоит в середине предложения, оно выделяется с двух сторон запятыми.
Не отравляйте, ребята, себя сигаретами.
3. Частица о, стоящая перед обращением, не отделяется от него никакими знаками.
О спорт, ты- мир!
(Н. Некрасов)
Некрасов)
Заполняем кластер. (На письме выделяется запятой, ставится восклицательный знак).
А какова роль обращения в предложении? найдем ответ в учебнике и запишем в кластер (звательная, оценочная, изобразительная). Определите, какова роль обращений в тексте Толстого. (старче — звательная, смерть моя – изобразительная)
С какой интонацией в устной речи произносится обращение? Найдите ответ на этот вопрос в учебнике (со звательной интонацией).
Исторический комментарий (рассказ подготовленного ученика) Интонация имеет такое название «звательная». Всё дело в том, что в древнерусском языке было не шесть падежей, а семь. Как раз седьмой падеж назывался – звательный, т.е. он употреблялся при обращениях. До сих пор этот падеж сохранился в украинском языке, а из русского исчез.
заполняем кластер: Итак, чаще всего обращение в современном русском языке стоит в И.п. и произносится со звательной интонацией.
На доске таблица. Рассмотрим таблицу и сделаем вывод: чем может выражаться обращение.
Чем выражено?Примеры
1. Существительным
2. Частями речи, употребленными в значении существительного:
А) Прилагательным
Б) Причастием
В) Числительным
3. Существительным или прилагательным с «О»
Доброе утро, друзья, начинаем утреннюю гимнастику.
Услышь меня, хорошая, девушке курить вредно!
Обучающиеся 8-х классов, завтра идем в поход!
На первый второй рассчитайсь, первый, шаг вперёд.
О мудрейший, помоги мне избавиться от вредных привычек!
4.Закрепление темы. — Итак, мы выявили следующие признаки обращения: (обращение к кластеру – слайд)
Русские стандарты вежливого обращения сегодня (рассказ подготовленного ученика)
Любое обращение допустимо, когда оно одинаково комфортно для обеих сторон
Придумайте предложение с обращением, чтобы в качестве обращения выступали:
1 ряд: имя и отчество,
2 ряд: род занятий,
3 ряд: неодушевлённый предмет. Тема предложений — здоровый образ жизни. Проговорите получившиеся предложения, интонационно выделяя обращения.
Тема предложений — здоровый образ жизни. Проговорите получившиеся предложения, интонационно выделяя обращения.
КАРТОЧКА 3
Задание 1. Расставьте знаки препинания в предложениях.
И почему же вы ребята предпочитаете курение занятию спортом?
Курильщики вы наносите вред окружающим!
Никогда не забывайте о спорте друзья.
Задание 2. Посмотрите фрагмент текста, внимательно прочитайте его, определите основную мысль и выпишите предложения с обращениями.
Текст. Сегодня в обществе все больше людей борются за здоровый образ жизни. Они не курят, занимаются физкультурой, не едят вредных продуктов. Их главная цель – сберечь здоровье, чтобы вести активную жизнь и дольше прожить.
Молодые люди, помните, что здоровый образ жизни включает в себя несколько составляющих. Если человек хочет следовать такому образу жизни, он отказывается от вредных привычек. То есть не курит, не принимает наркотики, не пьет алкоголя или употребляет его понемногу.
Еще такой человек специально гуляет на свежем воздухе, регулярно проветривает квартиру, делает зарядку или пробежку по утрам, занимается каким-нибудь видом спорта. Так он поддерживает свое тело в хорошей спортивной форме.
Еще один фактор здорового образ жизни – это здоровое питание. Люди, которые его практикуют, соблюдают режим приема пищи, стараются есть только натуральные продукты. Они как можно меньше едят фастфуда, продуктов с красителями и консервантами. У них на столе много свежих овощей и фруктов. Чтобы не вредить организму, такие люди ограничивают себя в жирной, жареной, копченой пище. Ведь вкусная еда не означает, что она полезна. Давайте же, друзья, будем вести здоровый образ жизни.
— Итак, подведем итоги урока. Посмотрите еще раз на информационный кластер и расскажите, что вы знаете об обращении (ответы учащихся).
Выставление и комментарий отметок. ???
Рефлексия. Прием «Инсерт»: отметьте знаком + в конспекте урока то, что вам уже было известно, знаком ! то, что вы узнали сегодня и поняли, знаком ? новое, но непонятное. Проанализируйте, насколько вы усвоили материал, над чем вам еще нужно поработать.
Домашнее задание. 1)приготовить рассказ об обращении по плану с примерами;
2) НА ВЫБОР: а) составить письмо другу о здоровом образе жизни, используя обращения.б) подобрать из рассказа Л. Н. Толстого «После бала» 8-10 предложений с обращениями.
Урок русского языка на тему «Обращение и знаки препинания при нём», 8 класс
Презентация к уроку
PPTX / 2.41 Мб
Обращение и знаки препинания при нём (8 класс)
Автор урока: Стефанова Лариса Михайловна, учитель русского языка и литературы УКП «РДБ» ГОУ РК «Республиканский центр образования»
Цель: расширение и обобщение знаний учащихся об обращении.
Задачи:
— повторить и расширить знания учащихся об обращении, полученные на уроках русского языка в 5 классе;
— показать роль обращения в речи, раскрыть его стилистические особенности;
— формировать умение находить обращения в предложении, тексте, правильно расставлять знаки препинания при них;
— совершенствовать орфографические и пунктуационные навыки учащихся;
— развивать монологическую речь учащихся, учить выразительно читать и правильно интонировать предложения с обращениями, употреблять их с учётом речевой ситуации;
— воспитывать уважение к русскому языку, литературе, любовь к родному краю.
Оборудование:
— Л.А. Тростенцова, Т.А. Ладыженская. Русский язык. 8 класс. – М.: Просвещение, 2014;
— таблица «Знаки препинания при обращении»;
— карточки с заданиями для учащихся составленные на материале произведений С. А. Есенина;
А. Есенина;
— Толковый словарь С. И. Ожегова;
— репродукции картин «Весна. Ручей в лесу», «Дорожка», «Сенокос», «Черёмуха» И. И. Левитана.
Ход урока:
1. Вступительное слово учителя. Эмоциональный настрой учащихся на работу на уроке.
— Добрый день, ребята. Сегодня у нас с вами необычный урок. Он будет построен на произведениях Сергея Александровича Есенина. Основной темой творчества С. А. Есенина является тема Родины, родной природы. Сам поэт признавался: «Моя лирика жива одной большой любовью, любовью к родине. Чувство родины – основное в моем творчестве». Действительно, всё творчество Сергея Есенина проникнуто горячей любовью к родине. Родина в стихах Есенина неотделима от русской природы. Сегодня мы с вами ещё раз убедимся в этом, вспомнив поэтические строки С. А. Есенина. Слайд 1.
2. Этап актуализации знаний. Слайд 2.
— Ребята! А сейчас давайте вместе попробуем определить тему урока. Посмотрите на следующие характеристики и подумайте, о чём мы с вами сегодня будем говорить:
— называет того, к кому обращаются с речью;
— имеет форму именительного падежа и произносится с особой интонацией;
— не является членом предложения;
— может стоять в начале, середине или в конце предложения;
— на письме всегда выделяется запятыми, в особых случаях — восклицательным знаком.
Учащиеся определяют тему урока.
— Совершенно верно, ребята, сегодня мы с вами будем говорить об обращении. Запишите в тетрадях дату и тему урока «Обращение и знаки препинания при нём».
3. Этап целеполагания. Слайд 3.
— Ребята! С обращением мы с вами знакомились в 5 классе. В начале урока мы вспомнили, что вам уже известно об обращении. Какие цели вы для себя ставите на уроке?
Какие цели вы для себя ставите на уроке?
Используется приём «Незаконченное предложение».
Учащимся предлагается закончить предложение:
— Сегодня на уроке я хочу узнать/обобщить/научиться … .
Несколько учащихся высказываются, читают получившиеся предложения (по желанию).
4. Знакомство с новым учебным материалом.
Работа с учебником.
— А сейчас, ребята, давайте обратимся к учебнику.
Чтение параграфа учебника «Обращение и знаки препинания при нём».
Какую новую информацию об обращении вы узнали?
Учащиеся отмечают новые сведения (особенности) обращений:
— обращение может быть распространённым;
— междометие О, частицы АХ, А и другие, стоящие перед обращениями, не отделяются от них запятой.
Работа по таблице «Знаки препинания при обращении». Слайд 4.
— А теперь, ребята, давайте рассмотрим постановку знаков препинания при обращении, в том числе и трудные случаи.
Знаки препинания при обращении
Обращения всегда выделяется запятыми. | [О, …]. [… ,О, …]. [ … ,О]. |
Если обращение произносится с особой интонацией, то после него ставится восклицательный знак. | [О! …]. |
Между двумя обращениями, соединёнными союзами И, ДА (=И), запятая не ставится. | [О и О, …].
|
Междометие О, частицы АХ, А и другие от обращения запятой не отделяются | [… , о О, …]. |
Наблюдение над языковым материалом. Слайд 5.
— Очень важно уметь находить обращения в предложении, отличать их от других слов. Сравните 2 предложения. В каком из них есть обращение? Сделайте вывод о том, чем различаются данные предложения.
1. Я покинул родимый дом,
Голубую оставил Русь.
2. Звени, звени, златая Русь.
Учащиеся выразительно читают и сравнивают два предложения, говорят о том, что во втором предложении есть обращение, делают вывод, чем отличается обращение от других слов:
— произносится с призывной интонацией;
— к нему нельзя задать вопрос;
— не является членом предложения.
5. Отработка полученных знаний, умений и навыков. Выполнение упражнений по карточкам.
Учащиеся выполняют предложенные задания, попутно повторяют изученных ранее орфографические и пунктуационные правил, выделяют орфограммы и пунктограммы.
Также проводится лексическая работа. Учащиеся работают со словарём Ожегова С. И., находят в словаре и объясняют значение неизвестных слов (хата, риза, образа, лонный – лоно, пуща, лития, ладан, ставни, скирда и др.).
Карточка 1. Задание: спишите предложения, вставляя пропущенные буквы и недостающие знаки препинания, найдите в них обращения. Составьте графические схемы предложений 2, 5 и 6. 1. Гой ты Русь моя р…дная, Хаты — в ризах образа. 2. Любя твой день и ночи т…мноту Тебе о родина сл…жил я песню ту. 3. Черёмуха душистая С весною ра…цвела И ветки золотистые Что кудри зав…ла. 4. Сыпь ты черёмуха снегом, Пойте вы птахи в лесу. 5. Мир вам рощи луг и липы Литии медовый ладан! 6. Ни…кий дом с голубыми ставнями, (Не) забыть мне тебя н…когда. 7. Край любимый Сердцу снят…ся Скирды солнца в водах ло(н,нн)ых. |
Самопроверка по эталону. Слайд 6.
Карточка 2. Задание: спишите предложения, вставляя пропущенные буквы и недостающие знаки препинания, найдите в них обращения, выразительно прочитайте предложения, интонационно выделяя обращения. 1. Колокольчик среброзво(н,нн)ый, Ты поёш…? Иль сердцу снит…ся? 2. В…лнуйся неуёмный ветер! 3. Клён ты мой опавший клён зал…денелый, Что стоишь нагнувшись под м…телью белой? 4. Прощай р…дная пуща, Прости златой р…дник. 5. Звёздочки ясные звёзды высокие! Что вы хр…ните в себе, что скрываете? 6. Серебристая дорога Ты зовёш… меня куда? 7. Г…ри звезда моя не падай. Роняй х…лодные лучи. |
Самопроверка по эталону. Слайд 7.
— В своих стихах С. А. Есенин обращается к ветру, роднику, дороге… Он очеловечивает их. Как называется этот приём? Слайд 8.
— Верно, это олицетворение – приём, при котором неодушевлённые предметы изображаются как одушевлённые, они наделяются своими живых существ: даром речи, способностью чувствовать, мыслить. Природа в стихах Есенина живёт и дышит. Подобно человеку она поёт и шепчет, грустит и радуется. Рассмотрите картины художника-пейзажиста И.И.Левитана, подберите к ним есенинские строки.
Чтение предложений с правильным интонированием обращений. Слайды 9-12.
И.И. Левитан «Весна. Ручей в лесу»
Ручей в лесу»
И.И. Левитан «Дорожка»
И.И. Левитан «Сенокос»
И.И. Левитан «Черёмуха»
— Особое место в творчестве Сергея Есенина занимают стихи, обращённые к матери. У каждого человека мать ассоциируется с родным домом. Для Есенина мать является олицетворением родного дома, его Родины. Давайте вспомним эти стихотворения. Слайд 13.
Карточка 3. Задание: спишите предложения, вставляя пропущенные буквы и недостающие знаки препинания, найдите в них обращения, выразительно прочитайте предложения, правильно интонируя обращения. 1. Разбуди меня завтра рано О моя т…рпеливая мать! 2. Ты жива ещё моя старушка? Жив и я. Привет тебе, привет! 3. Милая добрая старая нежная С думами грус…ными ты (не) дружись. 4. Н…чего родная! Успокойся. Это только тягос…ная бредь. |
— Как обращается поэт к матери? Словами каких частей речи выражено обращение? Какую роль выполняют обращения в приведённых примерах?
Учащиеся высказывают своё мнение, говорят о том, что С. А. Есенин с заботой и вниманием относится к матери, ласково обращается к ней. Использованные обращения передают отношение поэта к матери. Также учащиеся делают вывод, что обращение может быть выражено не только именем существительным, но и именем прилагательным.
С. А. Есенин с матерью Татьяной Фёдоровной Есениной
— А сейчас, ребята, вы сами попробуете себя в роли поэта. Задание выполняется устно. Слайды 14-15.
Карточка 4. Задание: восстановите есенинские строки, вставив опущенные обращения. Сравните получившийся у вас вариант с авторским текстом, выразительно прочитайте предложения. 1. … ты мой заброшенный, … ты мой, пустырь, Сенокос некошеный, Лес да монастырь. 2. Тебе одной плету венок, Цветами сыплю стежку серую. … , покойный уголок, Тебя люблю, тебе и верую. 3. … , взмахни крылами, Поставь иную крепь! 4. Я снова здесь, в семье родной, … , задумчивый и нежный! |
— Вы почувствовали, ребята, что быть поэтом – это огромный труд души и сердца. Очень важно не только видеть красоту вокруг себя, но и уметь передать её, выразить свои чувства, эмоции в стихах. И только истинная любовь к родине, к родной природе может найти отклик и вызвать ответные чувства у читателей.
6. Подведение итогов урока. Слайд 16.
— А теперь, ребята, давайте обобщим всё, что мы знаем об обращении.
Карточка 5. Задание: отметьте верные (+) и неверные (-) утверждения. 1) обращение может состоять из нескольких слов; 2) обращение может быть выражено только именем существительным собственным; 3) обращение может быть выражено именем прилагательным; 4) обращение может стоять только в начале предложения; 5) обращение может быть главным и второстепенным членом предложения; 6) обращение на письме всегда выделяется запятыми; 7) обращения употребляются только в разговорном стиле речи. |
Проверка выполнения задания, разбор ошибок.
Верные утверждения: 1, 3, 6.
Неверные утверждения: 2, 4, 5, 7.
— Какую роль играют обращения в речи?
Учащиеся делают вывод о стилистической роли обращений.
— В разговорной речи обращение привлекает внимание собеседника, побуждает к восприятию речи. В художественной речи обращения используются для создания художественного образа. Обращение, как мы с вами отметили, выполняют ещё одну функцию: обращаясь к собеседнику, через название-обращение мы оцениваем его, показываем своё отношение к нему.
Слайд 17. Сергей Есенин не мыслил своей жизни и творчества без России. Каждое стихотворение, каждая строчка поэта – это его признание в любви Родине, родной природе. Есенин любил называть родину Русью – уже в самом этом слове звучит что-то русское, родное… До конца своей жизни поэт сохранил чувство любви к Родине:
Ой ты, Русь, моя родина кроткая,
Лишь к тебе я любовь берегу…
7. Рефлексия. Самооценка учащихся своей работы на уроке и оценка учителя. Слайд 18. Используется приём «Незаконченное предложение». Учащимся предлагается закончить предложение:
— Сегодня на уроке я узнал(а)/обобщил(а)/научился(ась) … .
Учащиеся сравнивают цели, которые они ставили перед собой в начале урока, с достигнутыми результатами, делают вывод, что узнали и чему научились на уроке.
8. Домашнее задание: написать эссе «С чего начинается любовь к Родине?» Слайд 19.
Слайды 20-21. Ссылки на использованные изображения.
Использованные источники:
Ожегов С. И., Шведова Н. Ю. Толковый словарь русского языка. – М.: «АЗЪ», 1996
С. А. Есенин. Собрание сочинений в двух томах. – М.: Современник, 1990
Л. А. Тростенцова, Т. А. Ладыженская. Русский язык. 8 класс. – М.: Просвещение, 2014
Русский язык. 8 класс. – М.: Просвещение, 2014
Тест по русскому языку «Обращение. Знаки препинания при обращении» » 4ЕГЭ
Тест для повторении изученного по разделам «Синтаксис», «Пунктуация».1. Одно из утверждений неверно. Укажите его
1) Обращение — это слово или сочетание слов, называющее того, к кому или чему обращаются с речью.
2) Обращение, привлекая внимание собеседника, является мощным средством поддержания речевого контакта.
3) В роли обращения обычно употребляются одушевленные существительные в форме именительного падежа, одиночные или с зависимыми словами.
4) В предложении обращения обычно являются подлежащими.
2. Укажите предложение с обращением (знаки препинания не расставлены)
1) Ты догадался мой читатель с кем бился доблестный Руслан.
2) Минуй нас пуще всех печалей и барский гнев и барская любовь.
3) Стихнут ветры перестанут бури.
4.) Снеговые горы начинали скрываться в лиловом тумане.
3. Найдите ошибку в оформлении обращения
1) Прощай, прощай, сияние небес!
2) Что же ты, моя старушка, приумолкла у окна?
3) Спой мне иволга песню пустынную, песню жизни моей.
4) Друзья, друзья! Теснее в круг сомкнёмся!
4. Укажите предложения с распространённым обращением (знаки препинания не расставлены)
1) О жизнь моя как ты мне дорога!
2) Сыпь ты черёмуха снегом.
3) Распахни мне объятия свои густолистый развесистый лес!
4) Мы старые друзья с тобою ветер.
5. В каком предложении нет обращения?
I) Зачем ты, Балда, к нам залез?
2) Воротись, поклонися ты рыбке.
3) Постой, друг, постой немножко.
4) Здравствуй, солнце да утро веселое!
6. В каком предложении имеется пунктуационная ошибка?
1) Шуми, шуми с крутой вершины, не умолкай поток седой.
2) Прости, Тригорское, где радость меня встречала столько раз!
3) Брат мой, как я рад тебя видеть!
4) Читатель, любишь ли ты книги?
Ответы
1. 4
4
2. 1
3. 3
4. 1,3
5. 2
6. 1
Самопроверка
«5» — 6,
«4» — 5,
«3» — 4,
«2» — 3.
Урок русского языка в 4-м классе по теме «Предложения с обращениями»
Цель: ознакомление с понятием «обращение».
Задачи:
- Наблюдать над ролью обращений в речи, местом в предложении.
- Рассмотреть постановку знаков препинания при обращении.
- Развивать речь, внимание, мышление, память, творческое воображение.
- Воспитывать интерес к урокам русского языка, самостоятельность.
Оборудование: карточки словарных слов, таблица с языковым материалом, учебник русского языка для 4 класса, толковый словарь Ожегова,фонограмма песни «Лесной олень».
ХОД УРОКА
1. Сообщение темы урока
– Эпиграфом к сегодняшнему уроку являются
слова знаменитого баснописца Древней Греции –
Эзопа.
«При помощи языка люди общаются, решают вопросы,
приветствуют, выражают ласку, радость, получают
знания, развивают культуру».
– Сегодня на уроке мы познакомимся с очень
интересной и важной темой. Каждый из вас должен
быть очень внимательным. Но об этом чуть позже.
2. Минутка чистописания
Об об
3. Словарная работа
1. Корабль, солдат, батон, салют, билет, вагон,
газета, вокзал.
2. Самопроверка.
3. Мне покажут свои тетради….
4. Изучение нового материала
1) – Ребята, положите ручки послушайте меня.
Проверив ваши тетради, хочу сказать, что ты,
Наташа, прекрасно справилась с работой, а ты,
Рома, хуже, чем мог бы это сделать. Скажите, друзья
мои, а почему вы положили ручки? А откуда вы
узнали, что мои слова обращены к вам? Каким было
предложение? Что именно я сказала? РЕБЯТА,
ПОЛОЖИТЕ РУЧКИ. Т.е. я назвала вас « ребята» и
обратилась к вам с просьбой положить ручки.
Т.е. я назвала вас « ребята» и
обратилась к вам с просьбой положить ручки.
– А как узнали Наташа и Рома результаты
словарной работы?
– Вспомните, что именно я сказала?
– Что помогло вам понять, что я говорила именно с
этими ребятами? (Я назвала их имена).
– Так что же это за слово, называющее того, к кому
обращаются с речью?
– Итак, тема нашего урока: «Предложения с
обращениями».
2) На доске:
Давайте же, дети, учиться начнём
И знания светлые нити навек
В свою благодарную память вплетём!Ы. Алтынсарин
– Прочтите строчки « про себя».
– Теперь прочтём эти строчки вслух. Запишите
строчки в тетрадь.
– Найдите обращение в данных строчках.
– Почему вы решили, что это обращение?
– Что такое обращение?
– Словами какой части речи могут быть выражены
обращения?
– Всегда ли обращение – это одно слово? Докажите.
– К слову дети подберите подходящие по смыслу
прилагательные.
– Прочтите ещё раз строчки Ы. Алтынсарина с
прилагательным, подходящим по смыслу к слову
дети.
– Сделайте вывод.
Вывод: Обращением может быть не
только одно слово, но и сочетание слов.
– Выделяется ли обращение интонационно?
– Что соответствует на письме интонационному
выделению?
– Послушайте, какое толкование слова «
обращение» даёт словарь Ожегова. (Индивидуальное
задание ребенку).
– Совпадают ли наши умозаключения, выводы с
толковым словарём?
3) А теперь обратимся к учебнику
и прочтём правила на с. 215-214.
215-214.
5. Закрепление знаний
1) – Обращения не всегда обособляются запятыми.
На доске:
Люди! Берегите природу.
– Запишите предложение в тетрадь.
– Найдите обращение. Почему после него стоит
восклицательный знак?
– В какой части предложения стоит обращение?
– Итак, если обращение стоит в начале
предложения и произносится с сильным чувством,
то после него ставится восклицательный знак.
– Обратите внимание, что после восклицательного
знака слово необходимо писать с большой
буквы
– Приведите примеры предложений с обращениями,
чтобы оно выражало сильное чувство.
2) Комментированное письмо
Друзья, вперёд нас жизнь зовёт.
Ой, Миша, ты испачкался.
Ты сегодня прекрасно отвечала, Юля.
– Где располагается обращение в предложении?
3) Самостоятельная работа (по вариантам)
Изменить предложения, чтобы обращение стояло в начале, в середине, в конце предложения
Помоги мне решить задачу, Ира.
Мама, разреши мне сегодня пойти в кино.
4) Проверка
5) Обобщение
6) Запись предложений под диктовку, разбор их по членам (у доски)
Друзья радуются своим успехам.
Друзья, я радуюсь вашим успехам.
– Каким членом предложения является слово «друзья» в первом предложении? Во втором?
Вывод: Обращение не соединено грамматически ни с одним членом предложения и поэтому не является членом предложения.
– В каком падеже стоит слово-обращение во
втором предложении? (Им. п.), но отличается от
подлежащего звательной интонацией. В
древнерусском языке для обращений существовал
специальный звательный падеж. С формой
звательного падежа можно встретиться у А. С.
Пушкина. (Чего тебе надобно, старче?) Вместо
«старик».
С.
Пушкина. (Чего тебе надобно, старче?) Вместо
«старик».
7) Обобщение по таблице с. 215 № 714
8) Работа в группах
Записать предложение, найти обращение, поставить необходимые знаки препинания.
- Разбуди эту землю, весна.
- Куда ты, ручеёк, течёшь?
- Но ведь тебе, мышка, всюду ходить нельзя.
- Главное, ребята, сердцем не стареть.
- Добро пожаловать, скворцы
9) Проверка
10) Творческая работа (Домашнее задание)
– А сейчас, дети, я предлагаю вам послушать чудесную песню и найти в ней предложения с обращением.
Звучит фонограмма песни «Лесной олень»
– Назовите предложения с обращениями. С какой
просьбой обращается девочка к оленю?
– Итак, представьте себе, что олень выполнил
просьбу девочки, и мы вместе с ней оказались в
сказке. В нашем классе не осталось обычных
мальчиков и девочек, все стали волшебниками.
Вокруг нас сказочные герои: Кот в сапогах, Алиса
из Зазеркалья, Смелый Чиполлино, домовёнок
Кузька и многие другие. Представьте себе, что вы
попали в
трудную ситуацию и вам необходимо написать
мини-письмо сказочному герою с просьбой о помощи.
Но, пожалуйста, не забывайте о вежливых словах и
предложениях с обращениями.
6. Оценивание
7. Итог урока
Предложение с обращением, с прямой речью, диалог 5 класс онлайн-подготовка на Ростелеком Лицей
Предложения с обращением. Прямая речь. Диалог.
Обращение – слово или сочетание слов, называющее того, к кому или к чему обращаются с речью. Обращение обычно записано существительным в именительном падеже или другой частью речи в значении существительного (например, прилагательным). Обращение может стоять в начале, в середине и в конце предложения. Примеры: Вы устали, господа? Король, прощай (В.Пикуль).
Примеры: Вы устали, господа? Король, прощай (В.Пикуль).
Для того, чтобы отличить обращение от подлежащего, выраженного формой именительного падежа, следует учитывать следующее:
· обращение не является членом предложения, не входит в грамматическую основу;
· если в предложении есть обращение, то предложение часто является односоставным с глаголом-сказуемым во втором лице;
· обращение произносится с особой (звательной) интонацией, которая выражается усиленным ударением, паузой.
По значению обращения чаще всего являются наименованиями лиц или названиями, кличками животных. Пример: Вы еще очень скромны, маршал.
Но в художественной речи обращениями могут быть:
· наименования неодушевлённых предметов, отвлечённых понятий. Пример: Судьба, что же сделала ты со мной.
· географические наименования. Пример: Москва, родная ты моя.
Знаки препинания в предложениях с обращениями.
1. Обращения вместе со всеми относящимися к ним словами выделяются (в середине предложения) или отделяются (в начале либо в конце предложения) запятыми, если произносятся без восклицательной интонации. Примеры: Ваше сиятельство, почто так убиваться?; Ах, милая Додо, где мне найти эту палочку?; До свидания, друзья.
2. Если обращение, стоящее в начале предложения, произносится с восклицательной интонацией, то после него ставится восклицательный знак (следующее за обращением слово пишется с прописной буквы). Пример: Друг! Когда же нас свела судьба…
3. Если обращение стоит в конце предложения, то после него ставится тот знак, который требуется содержанием и интонацией самого предложения. Примеры: Жениться Вам надо, господин Горчаков!; Где же ты, мой принц?; Не повезло тебе, дружище. ..
..
Прямой речью называют точное, дословное воспроизведение высказывания какого-либо лица. Прямая речь заключается в кавычки, чтобы указать на то, что слова не принадлежат говорящему.
Пример: Брат спросил: “Где мой учебник?”
Знаки препинания в предложениях с прямой речью.
Прямая речь оформляется при письме особым способом. Для правильного применения знаков препинания необходимо разграничить слова автора и прямую речь. Для нахождения её границ, надо представить, что мы слышим это высказывание.
В комментирующей части обычно присутствует глагол “говорения” (сказал, прошептал, воскликнул и т.д.).
Если слова автора предшествуют прямой речи, после них ставится двоеточие.
Пример: Андрей сказал: “Ты не можешь знать наверняка”.
Если прямая речь содержит восклицательное или вопросительное предложение (Ваня кричал: “С Новым годом!”), то в кавычках ставится не точка, а восклицательный или вопросительный знак.
Если в предложении идет сначала прямая речь, а затем слова автора, то после кавычек ставится тире, а слова автора при этом начинаются со строчной буквы.
Пример: “Дома нет сыра,”- сказала мама.
Вместо точки на конце прямой речи ставится запятая, остальные знаки сохраняются, но комментирующая часть все равно начинается с маленькой буквы.
Диалогом называют разговор двух или нескольких лиц. Диалог состоит из взаимосвязанных реплик собеседников (вопросов, ответов, возражений и т. д.) – отдельных высказываний лиц, принимающих участие в диалоге.
Каждая реплика пишется с новой строки, с заглавной буквы, перед репликой ставится тире.
В диалоге могут присутствовать слова автора. Между репликой и словами автора ставится тире. Слова автора после реплики пишутся со строчной буквы. Если слова автора стоят перед репликой, то после них ставится двоеточие.
Слова автора после реплики пишутся со строчной буквы. Если слова автора стоят перед репликой, то после них ставится двоеточие.
Пример: «Горчаков жаловался драбанту:
— Опять не спал. Вот тут ломило. Всю-то ноченьку.
— А вы скипидаром пробовали? — отвечали ему».
RFE / RL опротестовывает отказ российского суда признать апелляцию на штраф — USAGM
Радио Свободная Европа / Радио Свобода (RFE / RL) опротестовывает отказ российского суда признать апелляцию на штраф
3 марта 2021 г.
Вашингтон, Округ Колумбия — Радио Свободная Европа / Радио Свобода (RFE / RL) опротестовало отклонение сегодня российским судом первых пяти апелляций на штраф государственное СМИ за нарушение правил, требующих навязчивой маркировки контента, просматриваемого его российской аудиторией. Радио Свободная Европа / Радио Свобода подтвердило свою приверженность продолжению обслуживания своей растущей аудитории в России, несмотря на интенсивное давление Кремля.
Президент РСЕ / РС Джейми Флай сказал: «РСЕ / РС отклоняет наложение этих штрафов и не принимает решение российского суда об отклонении нашей апелляции по ним. Мы считаем, что постановление Роскомнадзора о самооценке, фактически предписывающее искажать наши контент-платформы и запугивать нашу аудиторию, является спонсируемым государством посягательством на свободу СМИ, которое нарушает Конституцию России и российский закон о СМИ. RFE / RL продолжит возражать, опротестовывать и обжаловать эти требования.”
Fly продолжил: «RFE / RL не оставит нашу растущую аудиторию в России, которая продолжает заниматься нашей объективной и независимой журналистикой, несмотря на кампанию давления Кремля. РСЕ / РС не остановят эти вопиющие попытки повлиять на нашу редакционную независимость и подорвать нашу способность достучаться до нашей аудитории в тот момент, когда российский народ требует правды ».
Правительство президента России Владимира Путина за последние два десятилетия наложило все более строгие ограничения на способность РСЕ / РС взаимодействовать с аудиторией в России — сначала ограничив способность РСЕ / РС работать с местными филиалами по ретрансляции радиопрограмм, а затем через любое другое время. более ограничительное законодательство о средствах массовой информации «иностранных агентов», которое прямо направлено против Русской службы Радио Свободная Европа / Радио Свобода, сети 24/7 Current Time, четырех проектов местных репортажей, ориентированных на Россию, веб-сайта по проверке фактов, ориентированного на Россию, Татаро-башкирской службы Радио Свободная Европа / Радио Свобода, и трехъязычный Крым Украинской службы Радио Свобода.Проект реалий.
более ограничительное законодательство о средствах массовой информации «иностранных агентов», которое прямо направлено против Русской службы Радио Свободная Европа / Радио Свобода, сети 24/7 Current Time, четырех проектов местных репортажей, ориентированных на Россию, веб-сайта по проверке фактов, ориентированного на Россию, Татаро-башкирской службы Радио Свободная Европа / Радио Свобода, и трехъязычный Крым Украинской службы Радио Свобода.Проект реалий.
Согласно закону об «иностранных агентах», российский регуляторный орган в области Интернета, Роскомнадзор, в последние месяцы ввел в действие и начал применять правила само-маркировки контента, исходящего от средства массовой информации с «иностранными агентами». С 14 января 2021 года Роскомнадзор возбудил 260 дел в отношении RFE / RL за нарушение данных правил; Штрафы уже были наложены московским судом по 142 делам, и мы ожидаем, что этот текущий раунд дел приведет к общей сумме штрафов в размере 980 000 долларов США (71.5 млн руб.).
Правила самооценки Роскомнадзора требуют, чтобы RFE / RL помечало каждый фрагмент текста, видео, аудио или контента социальных сетей заметным заявленным государством заявлением об отказе от ответственности. Видеоконтент должен содержать 15-секундный отказ от ответственности в начале каждого клипа, а отказ от ответственности, опубликованный с текстовыми статьями и сообщениями в социальных сетях, должен публиковаться с размером шрифта, вдвое превышающим размер текста.
Даже несмотря на то, что компания продолжает обжаловать действия Кремля, ей теперь грозит шестидесятидневный срок для соблюдения закона и уплаты соответствующих штрафов или возможного закрытия своих операций в России.
За последние пять лет RFE / RL почти удвоило свою аудиторию в России и сейчас составляет не менее 6,5% взрослого населения России, или почти 6,7 миллиона человек. Несколько русскоязычных репортажных проектов РСЕ / РС предоставляют аудитории репортажи о новостных событиях в своей стране, которых им в противном случае не хватало бы, а также возможность общаться с людьми, местами и историями, которые российские СМИ не показывают. В период с октября 2019 года по сентябрь 2020 года видеороликов, созданных в настоящее время, было просмотрено более 1.5 миллиардов раз на платформах социальных сетей, а количество подписчиков на страницы в социальных сетях Current Time увеличилось более чем вдвое и превысило 5 миллионов; онлайн-аудитория Русской службы Радио Свобода также резко выросла: в 2020 календарном году на всех медиа-платформах было просмотрено 250 миллионов видео.
В период с октября 2019 года по сентябрь 2020 года видеороликов, созданных в настоящее время, было просмотрено более 1.5 миллиардов раз на платформах социальных сетей, а количество подписчиков на страницы в социальных сетях Current Time увеличилось более чем вдвое и превысило 5 миллионов; онлайн-аудитория Русской службы Радио Свобода также резко выросла: в 2020 календарном году на всех медиа-платформах было просмотрено 250 миллионов видео.
О RFE / RL
Radio Free Europe / Radio Liberty — это частная независимая международная новостная организация, программы которой — радио, Интернет, телевидение и мобильная связь — достигают влиятельной аудитории в 23 странах, включая Россию, Украину, Иран, Афганистан, Пакистан. , республики Средней Азии и Кавказа.Он финансируется Конгрессом США через USAGM.
9 лучших сайтов для изучения русского
Вы заслуживаете самого лучшего, но иногда лучшие вещи в жизни — это еще не все, о чем они мечтают.
Caviar имеет свою привлекательность, но холестерин будет подкрадываться к вам.
Водка может быть забавной сейчас, но вы можете пожалеть об этом на следующий день.
Тем не менее, отличные веб-сайты, которые помогут вам выучить русский язык, — это удовольствие, в которое вы действительно можете погрузиться без каких-либо недостатков.
Для всех, кто хочет изучать русский язык, инструменты для изучения русского языка — это не просто роскошь, а необходимость.
Однако использование веб-сайтов для изучения русского языка — одна из маленьких роскошей жизни, поскольку они удобны и заставляют вас чувствовать себя так, как будто вы только что выиграли обучающую лотерею.
Замечательные онлайн-ресурсы по изучению настоящего русского языка очень полезны. Например, вы можете попробовать онлайн-курсы русского языка или сайты, изучающие русский язык.
Кроме того, вам ничто не мешает использовать несколько веб-сайтов для изучения русского языка.Сочетание и сопоставление любимых предметов может дать вам еще более всестороннее русское образование. Думайте о добавлении большего количества веб-сайтов к своему опыту обучения, как о добавлении немного золотого листа к мороженому — конечно, это не важно, но это действительно делает его намного лучше!
Думайте о добавлении большего количества веб-сайтов к своему опыту обучения, как о добавлении немного золотого листа к мороженому — конечно, это не важно, но это действительно делает его намного лучше!
Загрузить: Это сообщение в блоге доступно в виде удобного переносимого PDF-файла, который вы можете можно взять куда угодно. Щелкните здесь, чтобы получить копию. (Скачать)
Зачем использовать сайты для изучения русского языка?
Изучать русский язык через веб-сайты — это удобно .В конце концов, вы можете получить к ним доступ в любое время и в любом месте. Это роскошь, которой не может предложить обучение в классе.
Plus, веб-сайты предлагают широкий спектр полезных материалов , которые помогут вам выучить русский язык. Вы можете смешивать и сопоставлять разные веб-сайты или выбирать свой любимый веб-сайт. Вы можете использовать веб-сайты, чтобы выучить русский язык с нуля или просто сосредоточиться на устранении своих слабых сторон.
Наконец, веб-сайты предлагают что-то для любого изучающего русский язык . Независимо от вашего уровня обучения или стиля обучения, у вас есть отличный веб-сайт.
Так что попробуйте эти девять великолепных веб-сайтов, чтобы изучать русский язык с роскошью, которую вы заслуживаете!
1. Grammatica
Grammatica — это служба подписки, которая предлагает множество полезных функций для российских студентов. В то время как несколько университетов подписываются на него, чтобы помочь своим студентам, отдельные лица также могут подписаться.
Grammatica — это прежде всего текстовый редактор. Вы можете вырезать и вставить любой русский текст в Grammatica, и Grammatica сразу же добавит знаки ударения, чтобы помочь в вашем произношении, предоставит переводы, чтобы помочь вам узнать значения слов, и предложит правила грамматики, которые помогут вам понять правила, которые управляют языком. Это позволяет вам использовать любой русский текст, который вы найдете, в качестве учебного пособия.
Это позволяет вам использовать любой русский текст, который вы найдете, в качестве учебного пособия.
Плюс, если вы хотите ввести слово на русском языке, Grammatica позволяет вам использовать стандартную клавиатуру и транслитерировать то, что вы пишете, на кириллицу. Это очень полезно для всех русских студентов, которые еще не научились печатать на кириллической клавиатуре.
Индивидуальная подписка на Grammatica начинается от 10 долларов в месяц в зависимости от продолжительности подписки.
2. FluentU
FluentU предлагает интересный и гибкий вариант обучения для русских студентов.Эта уникальная программа позволяет вам выбирать свой темп и то, чему вы учитесь, чтобы проложить свой собственный путь к успешному изучению русского языка.
Однако FluentU также предоставляет вам поддержку, чтобы сделать каждое видео полезным для обучения. Видео снабжены субтитрами, и эти субтитры тщательно аннотированы определениями, соответствующими изображениями и несколькими примерами предложений. Если вы хотите увидеть, как другое видео использует слово, вы можете просто щелкнуть это слово.
Более того, FluentU предлагает инновационный режим обучения.В этом режиме видеоклипы, картинки и примеры предложений используются в упражнениях и карточках для увлекательного учебного занятия.
Начните использовать FluentU на веб-сайте или, что еще лучше, загрузите приложение FluentU из магазина iTunes или Google Play.
3. Memrise
Memrise помогает студентам изучать языки. Он предлагает пользователям возможность создавать материалы, соревноваться с друзьями и многое другое.
Memrise предлагает шесть уровневых уроков русского языка.Эти уроки научат вас грамматике и лексике от базового до среднего.
Memrise также предлагает множество материалов, созданных пользователями, например списки лексики, которые вы можете использовать для дальнейшего обучения после того, как закончите уроки с повышенным уровнем.
Базовая версия Memrise бесплатна. Однако покупка про-версии дает вам доступ к большему количеству режимов обучения. Цены на профессиональную версию начинаются от 5 долларов в месяц.
4. Instagram
Конечно, Instagram может не быть популярным местом для языкового образования, но у него есть несколько отличных вариантов.Есть более 13 000 сообщений с тегами #learnRussian, и многие из этих сообщений предлагают отличный учебный материал.
Некоторые аккаунты Instagram используют обычные сообщения в качестве мини-уроков языка. Например, Yes Russian и Russian Up публикуют отличный учебный материал, на усвоение которого уходит всего несколько секунд.
5. Readlang
Readlang предлагает расширение для браузера или загружаемое приложение, которое может превратить любой русскоязычный веб-сайт в полезный урок.
Readlang мгновенно переводит веб-сайты.Однако, в отличие от других служб перевода, Readlang не сразу открывает весь перевод. Вместо этого он позволяет вам выделять слова или фразы, чтобы увидеть их перевод, давая вам возможность попрактиковаться в чтении слов и фраз, которые вы знаете, и помочь с теми, которые вы, возможно, еще не знаете. Кроме того, все, что вы выделяете, сохраняется как флэш-карта, поэтому вы можете легко практиковать их.
Базовая версия доступна для бесплатной загрузки и предоставляет вам 10 переводов фраз в день, а также неограниченное количество карточек и переводов слов.Ежемесячная подписка за 5 долларов дает вам неограниченное количество переводов фраз, слов и карточек.
6. Mango Languages
Mango Languages фокусируется на обучении вас правилам русского языка, практикуясь с полезными фразами на основе распространенных сценариев. Он идеально подходит для русских студентов начального и среднего уровня. Вы выучите и грамматику, и словарный запас легкими, легко усваиваемыми частями. Кроме того, его аудио-примеры призваны дать вам идеальное произношение.
начинаются примерно с 14 долларов.50 в месяц в зависимости от продолжительности подписки. Однако Mango Languages используется многими библиотеками, поэтому вы можете проверить, можете ли вы получить бесплатный доступ через свою локальную библиотеку.
7. LinguaLift
Разработанный командой из Гарварда, Стэнфорда и Оксфорда, LinguaLift был создан, чтобы помочь занятым людям изучать языки.
Тренеры по обучению работают с вами, чтобы составить план обучения и поддержать вас на протяжении всего вашего учебного пути. Ваше образование будет включать слова и фразы, которые вы можете использовать в реальных жизненных ситуациях, и познакомить вас с культурой.Интервальное повторение используется для поощрения долгосрочного запоминания слов.
Кроме того, в LinguaLift вы не найдете старых, устаревших примеров из учебников. Вместо этого LinguaLift сочетает в себе остроумие и обаяние, чтобы сделать уроки более увлекательными (и, возможно, подготовить вас к тому, чтобы научиться так же очаровательно говорить по-русски).
Подписки наLinguaLift начинаются всего с 17 долларов в месяц в зависимости от продолжительности подписки.
8. Центр международного образования
Разработанная Центром международного образования МГУ, эта программа предлагает хороший выбор материалов для начинающих российских студентов.
Включает вводную фонетику, основные слова и фразы, тесты, грамматические правила и информацию о культуре. Программа использует видеоролики с глиняной анимацией для проведения уроков, а вспомогательный текст и упражнения укрепляют ваше обучение.
Также есть медиа-раздел с народными песнями, видеоклипами, играми и упражнениями, так что есть множество отличных материалов для всех, кто изучает русский язык.
Плюс, этот сайт совершенно бесплатный!
9. Ruspeach
Ruspeach предлагает забавные диалоги на основе комиксов, которые помогут вам выучить русский язык.
Каждый диалог содержит аудио- и печатную версию текста вместе с английскими переводами. Каждый диалог вращается вокруг такой темы, как «зоопарк». В конце каждого диалога вы должны пройти тест, чтобы заработать «персики» и открыть следующий урок.
Ruspeach также предлагает ряд игр для проверки вашего обучения и разделы «учебник», чтобы предоставить дополнительные возможности обучения.
Ruspeach предлагает некоторые бесплатные материалы, другие доступны для покупки.Доступ к дополнительным диалогам, тестам и словарным спискам стоит 12,80 долларов в год. Вы также можете выбрать, какие компоненты вы хотите приобрести.
Так что загляните на эти девять отличных веб-сайтов, чтобы выучить русский язык и насладиться некоторыми из маленьких предметов роскоши!
Загрузить: Это сообщение в блоге доступно в виде удобного переносимого PDF-файла, который вы можете можно взять куда угодно. Щелкните здесь, чтобы получить копию. (Скачать)
Если вам понравился этот пост, что-то подсказывает мне, что вам понравится FluentU, лучший способ выучить русский язык с помощью реальных видео.
Погрузитесь в русский язык онлайн!
RFE / RL опротестовывает отказ российского суда признать апелляцию на штраф
ВАШИНГТОН — Radio Free Europe / Radio Liberty (RFE / RL) опротестовало отклонение сегодня российским судом первых пяти апелляций на штрафы, наложенные на государственное СМИ за нарушение правил, требующих навязчивой маркировки контента, просматриваемого его российской аудиторией. Радио Свободная Европа / Радио Свобода подтвердило свою приверженность продолжению обслуживания своей растущей аудитории в России, несмотря на интенсивное давление Кремля.
Президент РСЕ / РС Джейми Флай сказал: «РСЕ / РС отклоняет наложение этих штрафов и не принимает решение российского суда об отклонении нашей апелляции по ним. Мы считаем, что постановление Роскомнадзора о самооценке, фактически предписывающее искажать наши контент-платформы и запугивать нашу аудиторию, является спонсируемым государством посягательством на свободу СМИ, которое нарушает Конституцию России и российский закон о СМИ. RFE / RL продолжит возражать, опротестовывать и обжаловать эти требования.”
Fly продолжил: «RFE / RL не оставит нашу растущую аудиторию в России, которая продолжает заниматься нашей объективной и независимой журналистикой, несмотря на кампанию давления Кремля. РСЕ / РС не остановят эти вопиющие попытки повлиять на нашу редакционную независимость и подорвать нашу способность достучаться до нашей аудитории в тот момент, когда российский народ требует правды ».
Правительство президента России Владимира Путина за последние два десятилетия наложило все более строгие ограничения на способность РСЕ / РС взаимодействовать с аудиторией в России — сначала ограничив способность РСЕ / РС работать с местными филиалами по ретрансляции радиопрограмм, а затем через все более жесткое законодательство о СМИ об «иностранных агентах», которое прямо нацелено на Русскую службу Радио Свободная Европа / Радио Свобода, сеть 24/7 Current Time, четыре проекта местных репортажей, ориентированных на Россию, веб-сайт по проверке фактов, ориентированный на Россию, Татарско-башкирскую службу Радио Свободная Европа / Радио Свобода и трехъязычный Крым Украинской службы Радио Свобода.Проект реалий.
Согласно закону об «иностранных агентах», российский регуляторный орган в области Интернета, Роскомнадзор, в последние месяцы ввел в действие и начал применять правила само-маркировки контента, исходящего от средства массовой информации с «иностранными агентами». С 14 января 2021 года Роскомнадзор возбудил 260 дел в отношении RFE / RL за нарушение данных правил; Штрафы уже были наложены московским судом по 142 делам, и мы ожидаем, что этот текущий раунд дел приведет к общей сумме штрафов в размере 980 000 долларов США (71. 5 млн руб.).
5 млн руб.).
Правила самооценки Роскомнадзора требуют, чтобы RFE / RL помечало каждый фрагмент текста, видео, аудио или контента социальных сетей заметным заявленным государством заявлением об отказе от ответственности. Видеоконтент должен содержать 15-секундный отказ от ответственности в начале каждого клипа, а отказ от ответственности, опубликованный с текстовыми статьями и сообщениями в социальных сетях, должен публиковаться с размером шрифта, вдвое превышающим размер текста.
Даже несмотря на то, что компания продолжает обжаловать действия Кремля, ей теперь грозит шестидесятидневный срок для соблюдения закона и уплаты соответствующих штрафов или возможного закрытия своих операций в России.
За последние пять лет RFE / RL почти удвоило свою аудиторию в России и сейчас составляет не менее 6,5% взрослого населения России, или почти 6,7 миллиона человек. Несколько русскоязычных репортажных проектов РСЕ / РС предоставляют аудитории репортажи о новостных событиях в своей стране, которых им в противном случае не хватало бы, а также возможность общаться с людьми, местами и историями, которые российские СМИ не показывают. В период с октября 2019 года по сентябрь 2020 года видеороликов, созданных в настоящее время, было просмотрено более 1.5 миллиардов раз на платформах социальных сетей, а количество подписчиков на страницы в социальных сетях Current Time увеличилось более чем вдвое и превысило 5 миллионов; онлайн-аудитория Русской службы Радио Свобода также резко выросла: в 2020 календарном году на всех медиа-платформах было просмотрено 250 миллионов видео.
О RFE / RL
RFE / RL полагается на свои сети местных репортеров, чтобы предоставлять точные новости и информацию более чем 41 миллиону человек на 27 языках и в 23 странах, где свобода СМИ ограничена или где профессиональная пресса не полностью развитый.В 2020 финансовом году его видео просмотрели 6,5 миллиардов раз на Facebook, YouTube и Instagram / IGTV. RFE / RL — редакционно-независимая медиакомпания, финансируемая за счет гранта Конгресса США через Агентство США по глобальным СМИ.
—-
ДЛЯ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ ОБРАЩАЙТЕСЬ:
Мартинс Званерс в Вашингтоне (zvanersm@rferl.org, +1.202.457.6948)
Яна Хокувова в Праге (hokuvovaj@rferl.org, +420.221.122.072)
Перевести «призыв» с английского на русский с Mate
Никогда больше не заходите на эту страницу
Загрузите приложение Mate для Mac, которое позволяет переводить прямо в Safari и других приложениях.Двойной щелчок — это все, что нужно. Присоединяйтесь к 800 000 человек, которые уже переводят быстрее.
попробовать бесплатно
Никогда больше не заходите на эту страницу
Получите приложение Mate для iPhone, которое позволяет переводить прямо в Safari, Mail, PDF-файлах и других приложениях. Никакого переключения приложений, никакого копирования и вставки. Присоединяйтесь к 800 000 человек, которые уже переводят быстрее.
Никогда больше не заходите на эту страницу
Установите расширение Mate для Chrome, чтобы переводить слова прямо на веб-страницах с помощью элегантного двойного щелчка.Или выделив предложение. Или даже субтитры Netflix. Присоединяйтесь к 800 000 человек, которые уже переводят быстрее.
Получить бесплатноИнтересно, что больше не значит «обращение». Воспользуйтесь веб-переводчиком Mate, чтобы взглянуть на наши непревзойденные переводы с английского на русский.
Мы прекрасно сделали Mate для macOS, iOS, Chrome, Firefox, Opera и Edge, так что вы можете переводить везде, где есть текст. Больше никаких приложений, переключения вкладок браузера или копирования.
Самая современная система машинного перевода там, где она вам нужна.Легко переводите с английского, русского и еще 101 языка на любой веб-сайт и в любое приложение.
Нужен английский ↔ русский перевод? Мате тебя прикрыл!
Вам нужно перевести электронное письмо, статью или веб-сайт с английского или русского языков для отпуска за границей или деловой поездки? Просто выделите этот текст — Mate переведет его в мгновение ока.
Перевести тексты самому
Прекратите тыкать в друзей и агентства всякий раз, когда вам нужен быстрый перевод с английского на русский.Оснастите себя приложениями и расширениями Mate, чтобы сделать это самостоятельно, быстрее и точнее. Наши приложения интегрируются в iPhone, iPad, Mac и Apple Watch на собственном уровне. Как будто это сделала Apple. Кроме того, вы можете дополнить свой любимый браузер нашими лучшими в своем классе расширениями для Safari, Chrome, Firefox, Opera и Edge.
Мы сделали все возможное, чтобы наша переводческая программа выделялась среди других машинных переводчиков. Mate предназначен для сохранения значения исходного текста и его основной идеи.Переводчики-люди нашли себе пару — это Mate.
Если вы устали копировать данные в Google, Яндекс или Bing, попробуйте Mate. Он не только показывает вам переводы там, где они вам нужны, с помощью элегантного двойного щелчка, но также обеспечивает лучшую конфиденциальность. Мы не отслеживаем, не продаем и не обрабатываем ваши данные. Ваши переводы принадлежат вам. Считайте нас бабел-рыбкой с завязанными глазами, которую превратили в кучу красивых приложений, которые помогут вам с переводами.
Перейти к основному содержанию ПоискПоиск
- Где угодно
Поиск Поиск
Расширенный поиск- Войти | регистр
- Подписка / продление
- Учреждения
- Индивидуальные подписки
- Индивидуальное продление
- Библиотекари
- Выплаты и полные заказы Пакет Чикаго
- Полный цикл и охват содержимого
- Файлы KBART и RSS-каналы
- Разрешения и перепечатки
- Инициатива Чикаго для развивающихся стран
- Даты отправки и претензии
- Часто задаваемые вопросы библиотекарей
- Агенты
- Тарифы, заказы
- Полный пакет Chicago
- Полный охват и содержание
- Даты отправки и претензии
- Часто задаваемые вопросы агента
- Партнеры по издательству
- О нас
- Публикуйте у нас
- Новые журналы
- tners
- Новости прессы
- Подпишитесь на уведомления eTOC
- Пресс-релизы
- СМИ
- и платежи
- Книги издательства Чикагского университета
- Распределительный центр в Чикаго
- Чикагский университет
- Положения и условия
- Заявление о публикационной этике
- Уведомление о конфиденциальности
- Доступность Chicago Journals
- Доступность университета
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
- Свяжитесь с нами
- Запросы СМИ и рекламы
- Открытый доступ в Чикаго
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
Русский язык и литература | New College of Florida
Русский язык и литература Область концентрации
Русский язык в New College предлагает курсы, а также индивидуальные и групповые занятия по языку и литературе.
 Регулярно предлагаемые курсы посвящены литературным достижениям с эпохи сентиментализма в конце 18 века до наших дней. Учебники обычно посвящены важным областям интересов, которые не включены в более формализованные курсовые работы.
Регулярно предлагаемые курсы посвящены литературным достижениям с эпохи сентиментализма в конце 18 века до наших дней. Учебники обычно посвящены важным областям интересов, которые не включены в более формализованные курсовые работы.Студентам также предлагается следить за современными литературными и культурными событиями, особенно с учетом того, что они могут вписаться в континуум литературного производства в России и продолжить работу в соответствующих родственных областях, таких как история, политология и антропология.Студентам предлагается продолжить обучение за пределами кампуса в другом учебном заведении или принять участие в одной из многих доступных программ изучения языка и культуры в США или, в идеале, в России.
студентов New College приняли участие в летних и семестровых программах обучения в МГУ им. М.В. Ломоносова, Санкт-Петербургском государственном университете, Лингвистическом университете в Нижнем Новгороде и в летней программе в Миддлбери-колледже, штат Вермонт. Все без исключения путешествия и учеба оказались неоценимым компонентом AOC студента.
Что я могу сделать с AOC на русском языке и литературе?
Факультет
Недавние тезисы
- Авторитет и авторство: бедственное положение художника в «Отчаянии и приглашении на казнь» Владимира Набокова
- Гоголевский «Шинель» на английском языке: комментарий и перевод
- Вы всегда что-то видите, но никогда не увидишь всего: повествовательные приемы и роль читателя в «Портрете художника в молодости» Джеймса Джойса и «Котик Летаев» Андрея Белого
- Шиллерские идеалы в «Грабителях» и в «Преступлении и наказании» Достоевского
- Новый капитализм: культурные переходы, увиденные в Работы Виктора Пелевина
Дополнительная информация
Учебная программа по русскому языку и литературе
Ознакомьтесь с требованиями к экзамену AOC по русскому языку и литературе и ознакомьтесь с примерами путей получения диплома.
Подробнее читайте здесь
Программа бакалавриата
New College of Florida предлагает более 40 различных специальностей в области гуманитарных, социальных и естественных наук, а также ряд междисциплинарных направлений.
Подробнее читайте здесьИзвестный активист Алексей Навальный снова предстал перед судом в Москве в субботу утром, чтобы предстать перед обвинителями по двум отдельным судебным делам, включая апелляцию, которая, если она будет поддержана, может привести к его освобождению из тюрьмы.
Участнику кампании по борьбе с коррупцией грозит более двух с половиной лет колонии строгого режима за нарушение условий условного приговора, вынесенного за участие в схеме обмана французской косметической фирмы Yves Rocher в 2014 году. В феврале суд постановил, что он не явился регулярно в ФСИН, и его условный приговор был заменен тюремным заключением.
В то же время Навальный ведет дело о клевете из-за комментариев, которые он сделал в отношении 94-летнего ветерана Великой Отечественной войны, которого он обвинил в том, что он «коррумпированный лакей» и «предатель». Игнат Артеменко, бывший солдат Красной Армии, который также воевал с нацистами в качестве партизана, появился в русскоязычном видео RT, призывающем избирателей принять участие в общенациональном голосовании по предлагаемым конституционным поправкам.
Также на rt.com Россия осуждает «вмешательство» Европейского суда по правам человека в требования освободить арестованного оппозиционера Алексея НавальногоОппозиционер обвиняется Следственным комитетом России в публикации «заведомо ложной информации, порочащей честь и достоинство» ветерана.
Ранее на этой неделе Европейский суд по правам человека в Страсбурге заслушал апелляцию адвоката Навального Ольги Михайловой. В заявлении, опубликованном в среду, говорится, что «палата из семи судей Суда решила… указать Правительству России… об освобождении заявителя.


Соляная кислота это что – Кислота соляная — производство и применение
СОЛЯНАЯ КИСЛОТА
Применение соляной кислоты
Соляная кислота широко используется в промышленности при извлечении металлов из руд, травлении металлов и т. д. Также она используется при изготовлении паяльной жидкости, при осаждении серебра и как составная частьцарской водки.
Масштабы применения соляной кислоты в промышленности меньше, чем азотной. Связано это с тем, что соляная кислота вызывает коррозию стальной аппаратуры. К тому же летучие пары её довольно вредны и также вызывают коррозию металлических изделий. Это нужно учитывать при хранении соляной кислоты. Хранят и перевозят соляную кислоту в гуммированных цистернах и бочках, т.е. в сосудах, внутренняя поверхность которых покрыта кислотостойкой резиной, а также в стеклянных бутылях и полиэтиленовой посуде.
Соляная кислота применяется для получения хлоридов цинка, марганца, железа и других металлов, а также хлористого аммония. Соляную кислоту применяют для очистки поверхностей металлов, сосудов, скважин от карбонатов, окислов и других осадков и загрязнений. При этом используют специальные добавки — ингибиторы, которые защищают металл от растворения и коррозии, но не задерживают растворение окислов, карбонатов и других подобных соединений.
HCl применяется в промышленном производстве синтетических смол, каучуков. Используется как сырьё в производстве хлористого метила из метилового спирта, хлористого этила из этилена, хлорвинила из ацетилена.
Первая помощь и методы лечения
При обнаружении признаков отравления требуется вызвать бригаду скорой помощи. В домашних условиях допускается проводить мероприятия, направленные на улучшение состояния пострадавшего. Первая помощь при отравлении соляной кислотой должна проводиться быстро, чтобы уменьшить риск возникновения негативных последствий.
Мероприятия:
- При попадании соляного соединения на кожные покровы места повреждения промывают большим количеством прохладной воды. Длительность обработки составляет не менее получаса.
- При интоксикации парами пострадавшему обеспечивают доступ свежего воздуха, открывают окна, расстегивают тесную одежду.
- Рекомендуется следить за состоянием пациента, при отсутствии признаков жизни проводятся реанимационные действия.
- Пострадавшему от паров разрешается дать выпить теплый чай, воду. Рекомендуется провести полоскание полости носа и рта прохладной водой.
- При передозировке, возникнувшей в результате употребления кислоты внутрь, на живот кладут пузырь со льдом, чтобы исключить либо уменьшить возможное кровотечение.
- Не допускается употребление каких-либо лекарственных средств. Разрешается дать пациенту стакан воды (можно минеральной щелочной). Употреблять жидкость требуется маленькими глотками.
- Не разрешено промывать желудок, пытаться вызвать рвотные позывы в домашних условиях. Подобная первая помощь способна привести к развитию ожогов горла, кровотечению.
Лечение проводится в медицинском учреждении под контролем специалистов.


Терапия:
- Очищение желудка при помощи зонда,
- Использование капельниц с лекарственными растворами,
- Назначение препаратов, снимающих болезненные ощущения,
- Применение медикаментов, направленных на восстановление работы органов и систем,
- При необходимости ингаляции кислородом и искусственная вентиляция легких,
- Проведение реанимационной терапии при отсутствии признаков жизни,
- Подбор витаминов и специального питания.
Лечение проводится в реанимации, а затем в стационаре. Длительность зависит от состояния пациента и степени отравления.
Ожоги и отравление
Каким бы эффективным ни было это средство, оно опасно. Соляная кислота, в зависимости от концентрации, может спровоцировать химические ожоги четырех степеней:
- Возникает лишь покраснение и боль.
- Появляются пузыри с прозрачной жидкостью и отек.
- Формируется некроз верхних слоев кожи. Пузыри заполняются кровью или мутным содержимым.
- Поражение достигает сухожилий и мышц.
Если вещество каким-то образом попало в глаза, надо промыть их водой, а потом содовым раствором. Но в любом случае первым делом надо вызвать скорую.
Попадание кислоты внутрь чревато острыми болями в груди и животе, отеком гортани, рвотными кровавыми массами. Как следствие — тяжелые патологии печени и почек.
А к первым признакам отравления парами относят сухой частый кашель, удушье, повреждение зубов, жжение в слизистых оболочках и боли в животе. Первая неотложная помощь — это умывание и полоскание полости рта водой, а также доступ к свежему воздуху. Настоящую помощь может оказать лишь токсиколог.
Свойства химического спектра
Кислота взаимодействует со многими металлами, солями. Она считается довольно сильной и стоит в одном ряду с серной. Основная реакция проявляется на все группы металлов, находящихся левее от водорода (магний, железо, цинк – электротехнические потенциалы).
Хлороводородный раствор в разбавленном виде вступает в реакцию с солями, но только с теми, которые образованы менее сильными кислотами. Известные всем натрия и кальция карбонат после взаимодействия с ним распадаются на воду и угарный газ.
Азотная кислота
– качественная реакция на солевой раствор. Для ее получения необходимо добавить в этот реактив нитрат серебра, как результат – выпадет осадок белого цвета, с которого получается азотное веществоС помощью данной смеси воды и водорода проводят множество интересных экспериментов. Например, разбавляют его аммиаком. В итоге, получится белый дым, густой, имеющий консистенцию маленьких кристаллов. Метиламин, анилин, диоксид марганца, калий карбонат – реактивы, также поддающиеся под влияние кислоты.
Как и для чего применяют


Пожалуй, это по праву одно из важных веществ, которое встречается и необходимо практически во всех отраслях жизнедеятельности человека.
Локализация области применения:
- Металлургия. Очистка поверхностей от окисленных участков, растворение ржавчины, обработка перед спайкой, лужением. Соляная кислотапомогает извлекать мелкие вкрапления металлов из руд. Цирконий и титан получают, используя способ переведения оксидов в хлориды.
- Промышленность пищевых технологий. Раствор с низкой концентрацией применяется в качестве пищевой добавки. Желатин, фруктоза для диабетиков содержат в своем составе чистый эмульгатор. Обычная сода так же обладает высоким коэффициентом содержания данного вещества. На упаковке товаров увидите его под названием Е507.
- Область медицины. При недостаточном показателе кислотной среды в желудке и проблемах с кишечником. Низкий уровень Ph приводит к появлению рака. Даже при надлежащем питании, витаминов в достатке, опасность не исчезает, необходимо проводить анализы для получения сока из желудочного тракта, ведь при недостаточно кислой среде полезные вещества практически не всасываются, нарушается пищеварение.
- Раствор соли используется как ингибитор – защита от грязи и инфекций, антисептическое действие. Для изготовления клеевых смесей, изделий из керамики. Ним промывают теплообменники.
- Процедура очистки воды для питья тоже не обходится без участия хлора.
- Изготовление каучука, отбеливание тканевых основ.
- Можно ухаживать за линзами с помощью данного раствора.
- Полоскание полости рта в домашних условиях
- Вещество отлично проводит электрический ток.
Как происходит отравление
Соляная кислота – жидкое вещество без цвета, но с характерным резким запахом. Одна из самых сильных кислот, способна растворять некоторые металлы. Легко превращается в газ.
Хлористый водород используется в текстильной промышленности, кожевенном деле, металлургии драгметаллов, при производстве клея, кислот.
Вещество присутствует в желудке в минимальной концентрации. Кислота способствует нормализации пищеварительного процесса, защищает организм от вредных бактерий и микроорганизмов.
При концентрации, превышающей показатель в 24 %, соляная кислота способна нанести необратимый вред человеческому организму. Пары, образующиеся при контакте с воздухом, вызывают раздражение органов зрительной и дыхательной системы.
Выделяют несколько факторов, способных спровоцировать развитие отравления.Факторы:
Интоксикация парами возможна при работе в помещениях с плохой вентиляцией,
Употребление внутрь по неосторожности, чаще происходит у детей,
Попадание соляной кислоты на эпидермис, слизистую оболочку при несоблюдении правил использования реагента.Отравление веществом в домашних условиях у взрослых людей происходит в результате применения без средств защиты кожного покрова, глаз, органов дыхательной системы. Интоксикация способна произойти при неаккуратном переливании кислоты из одной емкости в другую.
Фармакодинамика и фармакокинетика
Что такое кислотность желудочного сока? Это характеристика концентрации Соляной Кислоты в желудке. Кислотность выражается в рН
. В норме в составе желудочного сока должна вырабатываться кислота и принимать активное участие в процессах пищеварения. Формула хлороводородной кислоты: HCl
. Ее продуцируют париетальные клетки, расположенные в фундальных железах, с участием Н+/К+-АТФазы
. Эти клетки выстилают дно и тело желудка. Кислотность желудочного сока сама по себе изменчива и зависит от числа париетальых клеток и интенсивности процессов нейтрализации вещества щелочными компонентами желудочного сока. Концентрация продуцируемой к-ты стабильна и равняется 160 ммоль/л. У здорового человека в норме должно вырабатываться не более 7 и не менее 5 ммоль вещества в час.При недостаточной или избыточной выработке Соляной Кислоты возникают заболевания пищеварительного тракта, ухудшается способность усваивать некоторые и микроэлементы, например, железо. Средство стимулирует выделение желудочного сока, снижает рН
. Активирует пепсиноген
, переводит его в активный фермент пепсин
. Вещество благоприятно воздействует на кислотный рефлекс желудка, замедляет переход не до конца переваренной пищи в кишечник. Замедляются процессы брожения содержимого пищеварительного тракта, исчезает боль, и отрыжка, лучше усваивается железо.После приема внутрь средство частично метаболизируется слюной и желудочной слизью, содержимым 12-перстной кишки. Несвязанное вещество проникает в 12-перстную кишку, где полностью нейтрализуется ее щелочным содержимым.
Другое применение кислоты в быту
Кислотным составом можно легко очистить сантехнику из фаянса от известкового налета и ржавчины, удалить мочевой камень и другие загрязнения. Для большего эффекта к средству добавляют ингибитор (например, уротропин), замедляющий химическую реакцию.
Процедуру проводят следующим образом: кислоту разбавляют водой до достижения 5 %-ной концентрации и добавляют ингибитор из расчета 0,5 г на 1 л жидкости. Полученным составом обрабатывают поверхность и оставляют на 30-40 минут (в зависимости от степени загрязнения), после чего промывают водой.
Слабый кислотный раствор также используется для удаления пятен от ягод, чернил или ржавчины с тканей. Для этого материал замачивают в составе на некоторое время, после чего тщательно ополаскивают и стирают в обычном режиме.
Избавление от накипи в чайнике
Для этой цели используют 3-5 %-ный раствор соляной кислоты, который наливают в чайник и нагревают до 60-80°
С в течение 1-2 часов или до тех пор, пока накипные отложения не распадутся. После этого накипь становится рыхлой и легко удаляется деревянной лопаточкой.Эффективность метода обусловлена тем, что реагент вступает в реакцию с карбонатами магния и кальция и превращает их в растворимые соли. Выделяющийся при этом углекислый газ разрушает слой накипи и придает ему рыхлость. После удаления солевых отложений посуду тщательно моют чистой водой.
Важный момент!
Этот способ не подходит для удаления накипи в эмалированных или алюминиевых чайниках со сколами и трещинами: это приведет к коррозии металла и его сильному повреждению.Получение вещества
Теперь можно поговорить о том, что делают для образования соляной кислоты.
Сначала, посредством сжигания в хлоре водорода, получают главный компонент — газообразный хлороводород. Который потом растворяют в воде. Результатом этой простой реакции становится образование синтетической кислоты.
Еще данное вещество можно получить из абгазов. Это — химические отходящие (побочные) газы. Они образуются при самых разных процессах. К примеру, при хлорировании углеводородов. Находящийся в их составе хлороводород называют абгазным. И кислоту, полученную таким образом, соответственно.
Следует отметить, что в последние годы доля абгазного вещества в общем объеме его производства увеличивается. А кислота, образованная вследствие сжигания в хлоре водорода, вытесняется. Однако справедливости ради нужно отметить, что в ней содержится меньше примесей.


Использование на производстве
Она имеет широкое применение в металлургической, пищевой и медицинской промышленности.
- Металлургии. Применение при паянии, лужении и зачистке металлов.
- Пищевая промышленность. Применение при производстве пищевых регуляторов кислотности, к примеру, Е507.
- Гальванопластика. Используется при травлении.
- Медицине. Находит свое применение при производстве искусственного желудочного сока.
Входит в состав синтетических красителей. Используется при производстве чистящих и моющих средств. Но в жидкостях, предназначенных для бытового использования, концентрация серной кислоты незначительна.
Как добывают соляную кислоту в лабораторных условиях


Производство вещества масштабно, продажа свободна. В условиях лабораторных опытов добывают раствор воздействием серной кислоты высокой концентрации на обычную кухонную соль (натрия хлорид).
Существует 2 метода растворения хлороводорода в воде:
- Водород сжигается в хлоре (синтетический).
- Попутный (абгазный). Суть его в проведении органического хлорирования, дегидрохлорирования.
Вещество хорошо поддается синтезу при пиролизе отходов от хлороорганики. Это случается в результате распада углеводородов при полном дефиците кислорода. Можно использовать так же хлориды металлов, которые являются сырьем неорганических веществ. Если нет серной кислоты концентрированной (электролита), берите разведенную.
Что касается добывания реагента в природных условиях, то чаще всего эту химическую смесь можно встретить в водах вулканических отходов. Хлороводород – это составляющая минералов сильвина (калия хлорид, по виду напоминает кости для игр), бишофита. Все это – методы добыть вещество в промышленности.
В организме человека, данный фермент содержится в желудке. Раствор может быть как кислотой, так и основанием. Одним из распространенных способов добывания, называют сульфатный.
Химические свойства
Хлороводородная кислота, хлористый водород или хлористоводородная кислота – раствор НСl
в воде. Согласно Википедии, вещество относят у группе неорганических сильных одноосновных к-т. Полное название соединения на латинском: Hydrochloricum acid.Формула Соляной Кислоты в химии: HCl
. В молекуле атомы водорода соединяются с атомами галогена – Cl
. Если рассмотреть электронную конфигурацию этих молекул, то можно отметить, что в образовании молекулярных орбиталей соединения принимают участие 1s
-орбитали водорода и обе 3s
и 3p
-орбитали атома Cl
. В химической формуле Соляной Кислоты 1s-
, 3s-
и 3р
-атомные орбитали перекрываются и образуют 1 , 2 , 3 -орбитали. При этом 3s
-орбиталь не носит связывающий характер. Наблюдается смещение электронной плотности к атому Cl
и снижается полярность молекулы, но увеличивается энергия связи молекулярных орбиталей (если рассматривать ее в ряду с другими галогеноводородами
).Физические свойства хлористого водорода. Это прозрачная бесцветная жидкость, обладающая способностью дымиться при соприкосновении с воздухом. Молярная масса химического соединения = 36,6 грамма на моль. При стандартных условиях, при температуре воздуха 20 градусов Цельсия, максимальная концентрация вещества составляет 38% по массе. Плотность концентрированной хлороводородной к-ты в такого рода растворе составляет 1,19 г/см³. В целом же, физические свойства и такие характеристики, как плотность, молярность, вязкость, теплоемкость, температура кипения и pН
, сильно зависят от концентрации раствора. Эти величины подробнее рассматриваются в таблице плотностей. Например, плотность Соляной Кислоты 10% = 1,048 кг на литр. При затвердевании вещество образует кристаллогидраты
разных составов.Химические свойства Соляной Кислоты. С чем реагирует Соляная Кислота? Вещество вступает во взаимодействие с металлами, которые стоят в ряду электрохимических потенциалов перед водородом (железо, магний, цинк и другие). При этом образуются соли и выделяется газообразный H
. С Соляной Кислотой не реагирует свинец, медь, золото, серебро и другие металлы правее водорода. Вещество вступает в реакцию с оксидами металлов, при этом образуя воду и растворимую соль. Гидроксид натрия под действием к-ты образует и воду. Реакция нейтрализации характерна для данного соединения.Разбавленная Соляная Кислота реагирует с солями металлов, которые образованы более слабыми к-ами. Например, пропионовая кислота
слабее, чем соляная. Вещество не взаимодействует с более сильными кислотами. и карбонат натрия
будут образовывать после реакции с HCl
хлорид, угарный газ и воду.Для химического соединения характерны реакции с сильными окислителями, с диоксидом марганца
, перманганатом калия
: 2KMnO4 + 16HCl = 5Cl2 + 2MnCl2 + 2KCl + 8h3O
. Вещество реагирует с аммиаком
, при этом образуется густой белый дым, который состоит из очень мелких кристаллов хлорида аммония. Минерал пиролюзит с Соляной Кислотой также вступает в реакцию, так как содержит диоксид марганца
: MnO2+4HCl=Cl2+MnO2+2h3O
(реакция окисления).Существует качественная реакция на хлороводородную кислоту и ее соли. При взаимодействии вещества с нитратом серебра
выпадает белый осадок хлорида серебра
и образуется азотная к-та
. Уравнение реакции взаимодействия метиламина
с хлористым водородом выглядит следующим образом: HCl + Ch4Nh3 = (Ch4Nh4)Cl
.Вещество реагирует со слабым основанием анилином
. После растворения анилина в воде к смеси прибавляют Соляную Кислоту. В результате основание растворяется и образует солянокислый анилин
(хлорид фениламмония
): (С6Н5Nh4)Cl
. Реакция взаимодействия карбида алюминия с хлористоводородной к-ой: Al4C3+12HCL=3Ch5+4AlCl3
. Уравнение реакции карбоната калия
с к-той выглядит следующим образом: K2CO3 + 2HCl = 2KCl + h3O + CO2.Применение
в металлургии для извлечения руд, удаления ржавчины, окалин, грязи и окислов, паянии и лужении;
при изготовлении синтетических каучуков и смол;
в гальванопластике;
в качестве регулятора кислотности в пищевой промышленности;
для получения хлоридов металлов;
для получения хлора;
в медицине для лечения недостаточной кислотности желудочного сока;
в качестве чистящего и дезинфицирующего средства.
— (НСl), водный раствор хлороводорода, бесцветного газа с резким запахом. Получают действием серной кислоты на поваренную соль, как побочный продукт хлорирования углеводородов, или реакцией водорода и хлора. Соляная кислота используется, для… … Научно-технический энциклопедический словарь
Соляная кислота
— – HCl (СК) (хлористоводородная кислота, хлороводородная кислота, хлористый водород) – это раствор хлороводорода (НСl) в воде, противоморозная добавка. Представляет собой бесцветную жидкость с резким запахом, без взвешенных частиц.… … Энциклопедия терминов, определений и пояснений строительных материаловСОЛЯНАЯ КИСЛОТА
— (хлористоводородная кислота) раствор хлористого водорода в воде; сильная кислота. Бесцветная, дымящая на воздухе жидкость (техническая соляная кислота желтоватая из за примесей Fe, Cl2 и др.). Максимальная концентрация (при 20 .С) 38% по массе,… … Большой Энциклопедический словарьСОЛЯНАЯ КИСЛОТА
— (Acidum muriaticum, Acid, hydrochloricum), раствор хлористого водорода (НС1) в воде. В природе встречается в воде нек рых источников вулканического происхождения, а также находится в желудочном соке (до 0,5%). Хлористый водород может быть получен … Большая медицинская энциклопедияСОЛЯНАЯ КИСЛОТА
— (хлороводородная кислота, хлористоводородная кислота) сильная одноосновная летучая кислота с резким запахом, водный раствор хлористого водорода; максимальная концентрация 38% по массе, плотность такого раствора 1,19 г/см3. Применяют в… … Российская энциклопедия по охране трудаСОЛЯНАЯ КИСЛОТА
— (хлористоводородная кислота) НСl водный раствор хлористого водорода, сильная одноосновная кислота, летучая, с резким запахом; примеси железа, хлора окрашивают её в желтоватый цвет. Поступающая в продажи концентрированная С. к. содержит 37 %… … Большая политехническая энциклопедиясоляная кислота
— сущ., кол во синонимов: 1 кислота (171) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимовСОЛЯНАЯ КИСЛОТА
Современная энциклопедияСоляная кислота
— СОЛЯНАЯ КИСЛОТА, водный раствор хлористого водорода HCl; дымящая на воздухе жидкость с резким запахом. Применяют соляную кислоту для получения различных хлоридов, травления металлов, обработки руд, в производстве хлора, соды, каучуков и др.… … Иллюстрированный энциклопедический словарьсоляная кислота
— (хлороводородная кислота), раствор хлороводорода в воде; сильная кислота. Бесцветная, «дымящая» на воздухе жидкость (техническая соляная кислота желтоватая из за примесей Fe, Cl2 и др.). Максимальная концентрация (при 20°C) 38% по массе,… … Энциклопедический словарьЧем опасно интоксикация
Соляная кислота представляет особую опасность для человеческого организма. При отравлении подобным веществом возможно развитие серьезных осложнений и нарушений функциональности организма.
Осложнения:
- Нарушение работы печени, как следствие токсический гепатит,
- Кровотечение в желудке из-за разрушенных стенок органа,
- Шоковое состояние от боли при попадании кислоты на территорию большой площади,
- При попадании в глаза нарушение зрительных функций,
- Серьезные сбои в работе почек,
- Нарушение дыхательного процесса, удушье, нехватка воздуха,
- Развитие коматозного состояния.
Подобные последствия развиваются постепенно в зависимости от степени отравления.
Вывод
При соблюдении мер предосторожности и правил безопасности соляная кислота станет незаменимым помощником в быту. А приобрести ее по самым доступным ценам можно в нашей компании
Как кислоты. Программа образования предусматривает запоминание учениками названий и формул шести представителей этой группы. И, просматривая предоставленную учебником таблицу, вы замечаете в списке кислот ту, которая стоит первой и заинтересовала вас в первую очередь, — соляную. Увы, на занятиях в школе ни свойства, ни любая другая информация о ней не изучается. Поэтому жаждущие получить знания вне школьной программы ищут дополнительные сведения во всяческих источниках. Но частенько многие не находят нужную информацию. И поэтому тема сегодняшней статьи посвящается именно данной кислоте.
Определение
Соляная кислота является сильной одноосновной кислотой. В некоторых источниках ее могут называть хлоро- и хлористоводородной, а также хлористым водородом.
Физические свойства
Она представляет собой бесцветную и дымящуюся на воздухе едкую жидкость (фото справа). Однако техническая кислота из-за наличия в ней железа, хлора и других добавок имеет желтоватый цвет. Самая большая ее концентрация при температуре 20 о С равняется 38%. Плотность соляной кислоты с такими параметрам равна 1,19г/см 3 . Но это соединение в разной степени насыщенности имеет совершенно разные данные. При уменьшении концентрации происходит снижение числового значения молярности, вязкости и температуры плавления, однако повышается удельная теплоемкость и температура кипения. Затвердевание соляной кислоты любой концентрации дает различные кристаллогидраты.
Химические свойства
Все металлы, которые стоят до водорода в электрохимическом ряду их напряжения, могут взаимодействовать с этим соединением, образуя соли и выделяя газообразный водород. Если их заменить оксидами металлов, то продуктами реакции станут растворимая соль и вода. Такой же эффект будет и при взаимодействии соляной кислоты с гидроксидами. Если же к ней добавить любую соль металлов (например, карбонат натрия), остаток которой был взят из более слабой кислоты (угольной), то образуются хлорид этого металла (натрия), вода и газ, соответствующий кислотному остатку (в данном случае — углекислый).


Получение
Обсуждаемое сейчас соединение образуется, когда в воде растворяют газообразный хлороводород, который можно получить, сжигая водород в хлоре. Соляная кислота, которую получили при помощи такого способа, носит название синтетической. Также источником для добывания этого вещества могут служить абгазы. И такую соляную кислоту будут называть абгазной. В последнее время уровень производства соляной кислоты с помощью этого метода гораздо выше, чем ее получение синтетическим способом, хотя последний дает соединение в более чистом виде. Это все пути его добывания в промышленности. Однако в лабораториях соляную кислоту получают тремя способами (первые два отличаются только температурой и продуктами реакции) при помощи различных видов взаимодействия химических веществ, таких как:
- Воздействие насыщенной серной кислоты на хлорид натрия при температуре 150 о С.
- Взаимодействие приведенных выше веществ в условиях с температурой 550 о С и выше.
- Гидролиз хлоридов алюминия или магния.
Применение
Гидрометаллургия и гальванопластика не могут обойтись без использования соляной кислоты, где она нужна, чтобы очищать поверхность металлов при лужении и паянии и получать хлориды марганца, железа, цинка и других металлов. В пищевой промышленности это соединение знают как пищевую добавку E507 — там это регулятор кислотности, необходимый для того, чтобы изготовить сельтерскую (содовую) воду. Концентрированная соляная кислота также находится в желудочном соке любого человека и помогает переваривать пищу. Во время данного процесса ее степень насыщенности уменьшается, т.к. этот состав разбавляется едой. Однако при продолжительном голодании концентрация соляной кислоты в желудке понемногу увеличивается. А так как данное соединение очень едкое, это может привести к язве желудка.
Заключение
Соляная кислота может быть как полезной, так и вредной для человека. Ее попадание на кожу приводит к появлению сильных химических ожогов, а пары данного соединения раздражают дыхательные пути и глаза
Но если обращаться с этим веществом осторожно, оно может не раз пригодиться в
mr-build.ru
Соляная кислота Википедия
Соляная кислота  (
({{{картинка3D}}}) (
({{{изображение}}})Общие Систематическое
наименованиеХлороводородная кислота Хим. формула H2O:HCl Рац. формула HCl Физические свойства Состояние бесцветная жидкость Молярная масса 36.46 г/моль Плотность 1.19 г/см³ Термические свойства Температура • плавления -30 °C • кипения 48 °C Энтальпия • образования -605.22 кДж/моль Химические свойства Константа диссоциации кислоты pKa{\displaystyle pK_{a}} -10 Растворимость • в воде смешивается Классификация Рег. номер CAS 7647-01-0 Рег. номер EINECS 933-977-5 екс Алиментариус E507 RTECS MW4025000 Безопасность NFPA 704 ru-wiki.ru
Соляная кислота — Википедия. Что такое Соляная кислота
Соля́ная кислота́ (также хлороводоро́дная, хлористоводоро́дная кислота, хлористый водород[1]) — раствор хлороводорода (HCl) в воде, сильная одноосновная кислота. Бесцветная, прозрачная, едкая жидкость, «дымящаяся» на воздухе (техническая соляная кислота — желтоватого цвета из-за примесей железа, хлора и пр.). В концентрации около ω=0,5%{\displaystyle \omega =0,5\%} присутствует в желудке человека, что соответствует pH=pω−lg(ρh3O/μHCl)≅0,86{\displaystyle pH=p\omega -lg(\rho _{H_{2}O}/\mu _{HCl})\cong 0,86}. Максимальная концентрация при 20 °C равна 38 % по массе, плотность такого раствора 1,19 г/см³. Соли соляной кислоты называются хлоридами.
Физические свойства
Физические свойства соляной кислоты сильно зависят от концентрации растворённого хлороводорода:
Конц. (вес),
кг HCl/кгКонц. (г/л),
кг HCl/м³Плотность,
кг/лМолярность
MВодородный
показатель (pH)Вязкость,
мПа·сУдельная
теплоемкость,
кДж/(кг·К)Давление
пара,
ПаТемпература
кипения,
°CТемпература
плавления,
°C10 % 104,80 1,048 2,87 −0,4578 1,16 3,47 0,527 103 −18 20 % 219,60 1,098 6,02 −0,7796 1,37 2,99 27,3 108 −59 30 % 344,70 1,149 9,45 −0,9754 1,70 2,60 1,410 90 −52 32 % 370,88 1,159 10,17 −1,0073 1,80 2,55 3,130 84 −43 34 % 397,46 1,169 10,90 −1,0374 1,90 2,50 6,733 71 −36 36 % 424,44 1,179 11,64 −1,06595 1,99 2,46 14,100 61 −30 38 % 451,82 1,189 12,39 −1,0931 2,10 2,43 28,000 48 −26 При 20 °C, 1 атм (101 кПа)При затвердевании даёт кристаллогидраты составов HCl·H2O, HCl·2H2O, HCl·3H2O, HCl·6H2O.
Химические свойства
- 2Na+2 HCl⟶2 NaCl+ h3↑{\displaystyle {\mathsf {2Na+2\ HCl\longrightarrow 2\ NaCl+\ H_{2}\uparrow }}}
- Mg+2 HCl⟶ MgCl2+ h3↑{\displaystyle {\mathsf {Mg+2\ HCl\longrightarrow \ MgCl_{2}+\ H_{2}\uparrow }}}
- 2Al+6 HCl⟶2 AlCl3+3 h3↑{\displaystyle {\mathsf {2Al+6\ HCl\longrightarrow 2\ AlCl_{3}+3\ H_{2}\uparrow }}}
- Na2O+2 HCl⟶2 NaCl+ h3O{\displaystyle {\mathsf {Na_{2}O+2\ HCl\longrightarrow 2\ NaCl+\ H_{2}O}}}
- MgO+2 HCl⟶ MgCl2+ h3O{\displaystyle {\mathsf {MgO+2\ HCl\longrightarrow \ MgCl_{2}+\ H_{2}O}}}
- Al2O3+6 HCl⟶2 AlCl3+3 h3O{\displaystyle {\mathsf {Al_{2}O_{3}+6\ HCl\longrightarrow 2\ AlCl_{3}+3\ H_{2}O}}}
- NaOH+ HCl⟶ NaCl+ h3O{\displaystyle {\mathsf {NaOH+\ HCl\longrightarrow \ NaCl+\ H_{2}O}}}
- Ba(OH)2+2 HCl⟶ BaCl2+2 h3O{\displaystyle {\mathsf {Ba(OH)_{2}+2\ HCl\longrightarrow \ BaCl_{2}+2\ H_{2}O}}}
- Al(OH)3+3 HCl⟶ AlCl3+3 h3O{\displaystyle {\mathsf {Al(OH)_{3}+3\ HCl\longrightarrow \ AlCl_{3}+3\ H_{2}O}}}
- Na2CO3+2 HCl⟶2 NaCl+ h3O+ CO2↑{\displaystyle {\mathsf {Na_{2}CO_{3}+2\ HCl\longrightarrow 2\ NaCl+\ H_{2}O+\ CO_{2}\uparrow }}}
- 2KMnO4+16 HCl⟶5 Cl2↑+2 MnCl2+2 KCl+8 h3O{\displaystyle {\mathsf {2KMnO_{4}+16\ HCl\longrightarrow 5\ Cl_{2}\uparrow +2\ MnCl_{2}+2\ KCl+8\ H_{2}O}}}
 Соляная кислота (в стакане) взаимодействует с аммиаком
Соляная кислота (в стакане) взаимодействует с аммиаком- Nh4+HCl⟶Nh5Cl{\displaystyle {\mathsf {NH_{3}+HCl\longrightarrow NH_{4}Cl}}}
- HCl+AgNO3→AgCl↓+HNO3{\displaystyle {\mathsf {HCl+AgNO_{3}\rightarrow AgCl{\downarrow }+HNO_{3}}}}
Получение
Соляную кислоту получают растворением газообразного хлороводорода в воде. Хлороводород получают сжиганием водорода в хлоре, полученная таким способом кислота называется синтетической. Также соляную кислоту получают из абгазов — побочных газов, образующихся при различных процессах, например, при хлорировании углеводородов. Хлороводород, содержащийся в этих газах, называется абгазным, а полученная таким образом кислота — абгазной. В последние десятилетия доля абгазной соляной кислоты в объёме производства постепенно увеличивается, вытесняя кислоту, полученную сжиганием водорода в хлоре. Но полученная методом сжигания водорода в хлоре соляная кислота содержит меньше примесей и применяется при необходимости высокой чистоты.
В лабораторных условиях используется разработанный ещё алхимиками способ, заключающийся в действии концентрированной серной кислоты на поваренную соль:
- NaCl+h3SO4→150oCNaHSO4+HCl{\displaystyle {\mathsf {NaCl+H_{2}SO_{4}{\xrightarrow[{}]{150^{o}C}}NaHSO_{4}+HCl}}}
При температуре выше 550 °C и избытке поваренной соли возможно взаимодействие:
- 2NaCl+h3SO4→550oCNa2SO4+2HCl{\displaystyle {\mathsf {2NaCl+H_{2}SO_{4}{\xrightarrow[{}]{550^{o}C}}Na_{2}SO_{4}+2HCl}}}
Возможно получение путём гидролиза хлоридов магния, алюминия (нагревается гидратированная соль):
- MgCl2⋅6h3O→t,oCMgO+2HCl+5h3O{\displaystyle {\mathsf {MgCl_{2}\cdot 6H_{2}O{\xrightarrow[{}]{t,^{o}C}}MgO+2HCl+5H_{2}O}}}
- AlCl3⋅6h3O→t,oCAl(OH)3+3HCl+3h3O{\displaystyle {\mathsf {AlCl_{3}\cdot 6H_{2}O{\xrightarrow[{}]{t,^{o}C}}Al(OH)_{3}+3HCl+3H_{2}O}}}
Эти реакции могут идти не до конца с образованием основных хлоридов (оксихлоридов) переменного состава, например:
- MgCl2+h3O→Mg2OCl2+HCl{\displaystyle {\mathsf {MgCl_{2}+H_{2}O{\xrightarrow[{}]{}}Mg_{2}OCl_{2}+HCl}}}[4]
Хлороводород хорошо растворим в воде. Так, при 0 °C 1 объём воды может поглотить 507 объёмов HCl, что соответствует концентрации кислоты 45 %. Однако при комнатной температуре растворимость HCl ниже, поэтому на практике обычно используют 36-процентную соляную кислоту.
Применение
Промышленность
Медицина
- Естественная составная часть желудочного сока человека. В концентрации 0,3—0,5 %, обычно в смеси с ферментом пепсином, назначается внутрь при недостаточной кислотности.
Особенности обращения

Высококонцентрированная соляная кислота — едкое вещество, при попадании на кожу вызывает сильные химические ожоги. Особенно опасно попадание в глаза. Для нейтрализации ожогов применяют раствор слабого основания, или соли слабой кислоты, обычно питьевой соды.
При открывании сосудов с концентрированной соляной кислотой пары хлороводорода, притягивая влагу воздуха, образуют туман, раздражающий глаза и дыхательные пути человека.
Реагируя с сильными окислителями (хлорной известью, диоксидом марганца, перманганатом калия) образует токсичный газообразный хлор.
В РФ оборот соляной кислоты концентрации 15 % и более — ограничен[5].
Примечания
Ссылки
wiki.sc
Раствор соляной кислоты: свойства и применение
Что представляет собой раствор соляной кислоты? Это – соединение воды (h3O) и хлороводорода (HCl), который является бесцветным термическим газом с характерным запахом. Хлориды отлично растворяются и распадаются на ионы. Соляная кислота является самым известным соединением, которое образует HCl, так что о нем и его особенностях можно рассказать в подробностях.

Описание
Раствор соляной кислоты относится к классу сильных. Он бесцветный, прозрачный и едкий. Хотя техническая соляная кислота имеет желтоватый цвет, обусловленный наличием примесей хлора, железа и прочих элементов. На воздухе «дымится».
Стоит отметить, что данное вещество присутствует и в организме каждого человека. В желудке, если быть точнее, в концентрации 0.5%. Интересно, что этого количества достаточно для полного разрушения бритвенного лезвия. Вещество разъест его всего за неделю.
В отличие от той же серной, кстати, масса соляной кислоты в растворе не превышает 38 %. Можно сказать, что данный показатель – «критическая» точка. Если начать увеличивать концентрацию, то вещество просто будет испаряться, вследствие чего хлороводород просто улетучится вместе с водой. Плюс ко всему, данная концентрация сохраняется лишь при 20 °C. Чем выше температура – тем быстрее протекает испарение.
Взаимодействие с металлами
Раствор соляной кислоты может вступать во многие реакции. В первую очередь с металлами, которые стоят до водорода в ряду электрохимических потенциалов. Это – последовательность, в которой элементы идут по мере увеличения такой свойственной им меры, как электрохимический потенциал (φ0). Данный показатель крайне важен в полуреакциях восстановления катиона. К тому же именно этот ряд демонстрирует активность металлов, проявляемую ими в окислительно-восстановительных реакциях.
Так вот, взаимодействие с ними происходит с выделением водорода в виде газа и с образованием соли. Вот пример реакции с натрием, мягким щелочным металлом: 2Na + 2HCl → 2NaCl +Н2↑.
С другими веществами взаимодействие протекает по похожим формулам. Так выглядит реакция с алюминием, легким металлом: 2Al + 6HCl → 2AlCl3 + 3Н2↑.

Реакции с оксидами
С данными веществами раствор кислоты соляной тоже прекрасно взаимодействует. Оксиды – это бинарные соединения элемента с кислородом, имеющие степень окисления, составляющую -2. Всем известными примерами являются песок, вода, ржавчина, красители, углекислый газ.
Соляная кислота взаимодействует не со всеми соединениями, а лишь с оксидами металлов. Вследствие реакции также образуется растворимая соль и вода. В качестве примера можно привести процесс, происходящий между кислотой и оксидом магния, щелочноземельного металла: MgO + 2HCl → MgCl2 + Н2О.
Реакции с гидроксидами
Так называются неорганические соединения, в составах которых присутствует гидроксильная группа –ОН, в которой атомы водорода и кислорода соединены ковалентной связью. И, поскольку раствор соляной кислоты взаимодействует лишь с гидроксидами металлов, стоит упомянуть, что некоторые из них называются щелочами.
Так что получающаяся в итоге реакция называется нейтрализацией. Ее результатом является образование слабо диссоциирующего вещества (то есть воды) и соли.
В качестве примера можно привести реакцию небольшого объема раствора соляной кислоты и гидроксида бария, мягкого щелочноземельного ковкого металла: Ва(ОН)2 + 2HCl = BaCl2 + 2Н2О.

Взаимодействие с другими веществами
Кроме перечисленного, соляная кислота может вступать в реакции и с соединениями иных типов. В частности, с:
- Солями металлов, которые образованы другими, более слабыми кислотами. Вот пример одной из таких реакций: Na2Co3 + 2HCl → 2NaCl +Н2О + СО2↑. Здесь показано взаимодействие с солью, образованной угольной кислотой (Н2СО3).
- Сильными окислителями. С диоксидом марганца, например. Или с перманганатом калия. Сопровождаются такие реакции выделением хлора. Вот один из примеров: 2KMnO4 +16HCl → 5Cl2↑ + 2MnCl2 + 2KCl + 8Н2О.
- Аммиаком. Это – нитрид водорода с формулой NH3, представляющий собой бесцветный, но резко пахнущий газ. Следствие его реакции с раствором соляной кислоты – масса густого белого дыма, состоящего из мелких кристаллов хлорида аммония. Который, кстати, всем известен, как нашатырь (NH4Cl).Формула взаимодействия следующая: NH3 + HCl → NH4CL.
- Нитратом серебра – неорганическим соединением (AgNO3), являющимся солью азотной кислоты и металла серебра. Вследствие контакта с ним раствора соляной кислоты возникает качественная реакция – образование творожистого осадка хлорида серебра. Который не растворяется в азотной. Выглядит это так: HCL +AgNO3 → AgCl↓ + HNO3.

Получение вещества
Теперь можно поговорить о том, что делают для образования соляной кислоты.
Сначала, посредством сжигания в хлоре водорода, получают главный компонент – газообразный хлороводород. Который потом растворяют в воде. Результатом этой простой реакции становится образование синтетической кислоты.
Еще данное вещество можно получить из абгазов. Это – химические отходящие (побочные) газы. Они образуются при самых разных процессах. К примеру, при хлорировании углеводородов. Находящийся в их составе хлороводород называют абгазным. И кислоту, полученную таким образом, соответственно.
Следует отметить, что в последние годы доля абгазного вещества в общем объеме его производства увеличивается. А кислота, образованная вследствие сжигания в хлоре водорода, вытесняется. Однако справедливости ради нужно отметить, что в ней содержится меньше примесей.

Применение в быту
Во многих чистящих средствах, которыми люди, занимающиеся хозяйством, пользуются регулярно, присутствует определенная доля раствора соляной кислоты. 2-3 процента, а иногда и меньше, но он там есть. Именно поэтому, приводя сантехнику в порядок (вымывая кафель, например), нужно надевать перчатки. Высококислотные средства могут навредить коже.
Еще раствор используют в качестве пятновыводителя. Он помогает избавиться от чернил или ржавчины на одежде. Но чтобы эффект был заметен, надо использовать более концентрированное вещество. Подойдет раствор соляной кислоты в 10%. Он, к слову, превосходно выводит накипь.
Важно правильно хранить вещество. Содержать кислоту в стеклянных емкостях и в местах, куда не доберутся животные и дети. Даже слабый раствор, попавший на кожу или слизистую оболочку, может стать причиной химического ожога. Если это случилось, необходимо срочно промыть участки водой.
В области строительства
Использование соляной кислоты и ее растворов – это популярный способ улучшения множества строительных процессов. Например, ее нередко добавляют в бетонную смесь, чтобы увеличить морозостойкость. К тому же так она быстрее застывает, а стойкость кладки к влаге повышается.
Еще соляную кислоту используют, как очиститель от известняка. Ее 10-процентный раствор – лучший способ борьбы с грязью и следами на красном кирпиче. Для очистки других не рекомендуется его использовать. Структура других кирпичей более чувствительна к воздействию данного вещества.

В медицине
В данной сфере рассматриваемой вещество тоже активно применяется. Разбавленная соляная кислота оказывает следующие действия:
- Переваривает в желудке белки.
- Останавливает развитие злокачественных образований.
- Помогает в лечении онкологических заболеваний.
- Нормализует кислотно-щелочной баланс.
- Служит эффектным средством при профилактике гепатита, сахарного диабета, псориаза, экземы, ревматоидного артрита, желчнокаменной болезни, розовых угрей, астмы, крапивницы и многих других недугов.
В общем, полезный препарат. Если у человека понижена кислотность желудочного сока, то ему не помешает пропить курс медикаментов, в составе которых есть соляная кислота. Неплохим вариантом является «Орто Таурин Эрго». Он увеличивает уровень соляной кислоты в желудочной среде, помогает бороться с бактериями и паразитами.
В голову пришла идея разбавить кислоту и употреблять ее внутрь в таком виде, а не в составе медикаментов? Такое практикуется, но категорически запрещено делать это без врачебной консультации и получения инструкции. Неправильно рассчитав пропорции, можно проглотить избыток раствора соляной кислоты, и просто сжечь себе желудок.
Кстати, еще можно принимать медикаменты, стимулирующие выработку данного вещества. И не только химические. Тот же аир, перечная мята и полынь способствуют этому. Отвары на их основе можно сделать самому, и пропить для профилактики.

Ожоги и отравление
Каким бы эффективным ни было это средство, оно опасно. Соляная кислота, в зависимости от концентрации, может спровоцировать химические ожоги четырех степеней:
- Возникает лишь покраснение и боль.
- Появляются пузыри с прозрачной жидкостью и отек.
- Формируется некроз верхних слоев кожи. Пузыри заполняются кровью или мутным содержимым.
- Поражение достигает сухожилий и мышц.
Если вещество каким-то образом попало в глаза, надо промыть их водой, а потом содовым раствором. Но в любом случае первым делом надо вызвать скорую.
Попадание кислоты внутрь чревато острыми болями в груди и животе, отеком гортани, рвотными кровавыми массами. Как следствие – тяжелые патологии печени и почек.
А к первым признакам отравления парами относят сухой частый кашель, удушье, повреждение зубов, жжение в слизистых оболочках и боли в животе. Первая неотложная помощь – это умывание и полоскание полости рта водой, а также доступ к свежему воздуху. Настоящую помощь может оказать лишь токсиколог.
fb.ru
Хлороводородная кислота — это… Что такое Хлороводородная кислота?
- Хлороводородная кислота
-

Модель молекулы соляной кислоты
Соля́ная (или соляна́я) кислота (хлористоводоро́дная кислота) (Hydrochloric acid) — HCl, раствор хлористого водорода в воде; сильная одноосновная кислота. Бесцветная, «дымящая» на воздухе, сильно едкая жидкость (техническая соляная кислота желтоватая из-за примесей Fe, Cl2 и др.). Максимальная концентрация при 20 °C равна 38 % по массе, плотность такого раствора 1,19 г/см3. Слабые растворы соляной кислоты (до 0,4 %) имеют специфический терпко-кислый вкус, более концентрированные вызывают ожоги полости рта. Соли соляной кислоты называются хлоридами.
Физические свойства
Физические свойства растворов соляной кислоты разных концентраций приведены в таблице:
При 20 °C, 1 атм (101 kPa)Конц. (вес)
c : кг HCl/кгКонц. (г/л)
c : кг HCl/м³Плотность
ρ : кг/лМолярность
MpH Вязкость
η : мПа·сУдельная
теплоемкость
s : кДж/(кг·К)Давление
пара
PHCl : ПаТ
кипения
т.кип.Т
плавления
т.пл.10 % 104,80 1,048 2,87 M −0,5 1,16 3,47 0,527 103 °C −18 °C 20 % 219,60 1,098 6,02 M −0,8 1,37 2,99 27,3 108 °C −59 °C 30 % 344,70 1,149 9,45 M −1,0 1,70 2,60 1,410 90 °C −52 °C 32 % 370,88 1,159 10,17 M −1,0 1,80 2,55 3,130 84 °C −43 °C 34 % 397,46 1,169 10,90 M −1,0 1,90 2,50 6,733 71 °C −36 °C 36 % 424,44 1,179 11,64 M −1,1 1,99 2,46 14,100 61 °C −30 °C 38 % 451,82 1,189 12,39 M −1,1 2,10 2,43 28,000 48 °C −26 °C При затвердевании даёт кристаллогидраты составов HCl·H2O, HCl·2H2O, HCl·3H2O, HCl·6H2O.
Химические свойства











Производство
Соляную кислоту получают растворением газообразного хлороводорода в воде. Хлороводород может быть получен путём взаимодействия концентрированной серной кислоты на хлорид натрия, или сжиганием водорода в атмосфере хлора.
Применение
Промышленность
Медицина
- Составная часть желудочного сока; разведенную соляную кислоту ранее назначали внутрь главным образом при заболеваниях, связанных с недостаточной кислотностью желудочного сока.
Особенности обращения

Соляная кислота — едкое вещество, при попадании на кожу вызывает сильные ожоги. Особенно опасно попадание в глаза. При открывании сосудов с соляной кислотой в обычных условиях образуется туман и пары хлороводорода, которые раздражают слизистые оболочки и дыхательные пути.
Реагируя с такими веществами, как хлорная известь, диоксид марганца, или перманганат калия, образует токсичный газообразный хлор.
Ссылки
Wikimedia Foundation. 2010.
- Хлорофита
- Хлоруксусная кислота
Смотреть что такое «Хлороводородная кислота» в других словарях:
Хлороводородная кислота — (хлористоводородная кислота) то же, что соляная кислота … Российская энциклопедия по охране труда
ХЛОРОВОДОРОДНАЯ КИСЛОТА — то же, что (см.) … Большая политехническая энциклопедия
хлороводородная кислота — то же, что соляная кислота … Энциклопедический словарь
ХЛОРОВОДОРОДНАЯ КИСЛОТА — то же, что соляная кислота … Естествознание. Энциклопедический словарь
СОЛЯНАЯ КИСЛОТА — (хлороводородная кислота), р р хлороводорода в воде; сильная кислота. Бесцв., дымящая на воздухе жидкость (техн. С. к. желтоватая из за примесей Fe, Сl2 и др.). макс. концентрация (при 20 °С) 38% по массе, плотность такого р ра 1,19 г/см3.… … Естествознание. Энциклопедический словарь
соляная кислота — (хлороводородная кислота), раствор хлороводорода в воде; сильная кислота. Бесцветная, «дымящая» на воздухе жидкость (техническая соляная кислота желтоватая из за примесей Fe, Cl2 и др.). Максимальная концентрация (при 20°C) 38% по массе,… … Энциклопедический словарь
СОЛЯНАЯ КИСЛОТА — (хлороводородная кислота, хлористоводородная кислота) сильная одноосновная летучая кислота с резким запахом, водный раствор хлористого водорода; максимальная концентрация 38% по массе, плотность такого раствора 1,19 г/см3. Применяют в… … Российская энциклопедия по охране труда
Соляная кислота — – HCl (СК) (хлористоводородная кислота, хлороводородная кислота, хлористый водород) – это раствор хлороводорода (НСl) в воде, противоморозная добавка. Представляет собой бесцветную жидкость с резким запахом, без взвешенных частиц.… … Энциклопедия терминов, определений и пояснений строительных материалов
СОЛЯНАЯ КИСЛОТА — (хлористоводородная к та, хлороводородная к та), р р НС1 в воде бесцв. жидкость с резким запахом; рильная одноосновная кислота. Хлористый водород НС1 (мол. м. 36,461 ) бесцв. газ с резким запахом, во влажном воздухе сильно дымит; длина связи HЧС1 … Химическая энциклопедия
Список кислот и ангидридов — … Википедия
biograf.academic.ru
О соляной кислоте
Что такое соляная кислота ?
Соляная кислота – это прозрачная бесцветная или желтоватая жидкость без взвешенных или эмульгированных частиц

Соляная кислота представляет собой раствор газообразного хлористого водорода HCl в воде. Последний представляет собой гигроскопичный бесцветный газ с резким запахом. Обычно употребляемая концентрированная соляная кислота содержит 36 – 38% хлористого водорода и имеет плотность 1, 19 г/см3. Такая кислота дымит на воздухе, так как из неё выделяется газообразный HCl; при соединении с влагой воздуха образуются мельчайшие капельки соляной кислоты. Она является сильной кислотой и энергично взаимодействует с большинством металлов. Однако такие металлы, как золото,платина, серебро, вольфрам и свинец, соляной кислотой практически не травятся. Многие недрагоценные металлы, растворяясь в кислоте, образуют хлориды, например цинк:
Zn + 2HCl = ZnCl2 + H2
Чистая кислота бесцветна, а техническая имеет желтоватый оттенок, вызванный следами соединений железа, хлора и других элементов (FeCl3). Часто применяют разбавленную кислоту, содержащую 10% и меньше хлористого водорода. Разбавленные растворы не выделяют газообразного HClи не дымят ни в сухом, ни во влажном воздухе.
Применение соляной кислоты
Соляная кислота широко используется в промышленности при извлечении металлов из руд, травлении металлов и т. д. Также она используется при изготовлении паяльной жидкости, при осаждении серебра и как составная частьцарской водки.
Масштабы применения соляной кислоты в промышленности меньше, чем азотной. Связано это с тем, что соляная кислота вызывает коррозию стальной аппаратуры. К тому же летучие пары её довольно вредны и также вызывают коррозию металлических изделий. Это нужно учитывать при хранении соляной кислоты. Хранят и перевозят соляную кислоту в гуммированных цистернах и бочках, т.е. в сосудах, внутренняя поверхность которых покрыта кислотостойкой резиной, а также в стеклянных бутылях и полиэтиленовой посуде.
Соляная кислота применяется для получения хлоридов цинка, марганца, железа и других металлов, а также хлористого аммония. Соляную кислоту применяют для очистки поверхностей металлов, сосудов, скважин от карбонатов, окислов и других осадков и загрязнений. При этом используют специальные добавки — ингибиторы, которые защищают металл от растворения и коррозии, но не задерживают растворение окислов, карбонатов и других подобных соединений.
HCl применяется в промышленном производстве синтетических смол, каучуков. Используется как сырьё в производстве хлористого метила из метилового спирта, хлористого этила из этилена, хлорвинила из ацетилена.
Отравление соляной кислотой
HCl ядовит. Отравления происходят обычно туманом, образующимся при взаимодействии газа с водяными парами воздуха. HCl поглощается также на слизистых оболочках с образованием кислоты, вызывающей их сильное раздражение. При длительной работе в атмосфере HCl наблюдаются катары дыхательных путей, разрушение зубов, изъязвление слизистой оболочки носа, желудочно-кишечные расстройства. Допустимое содержание HCl в воздухе рабочих помещений не более 0, 005 мг/л. Для защиты используют противогаз, защитные очки, резиновые перчатки, обувь, фартук.
В то же время, наше пищеварение невозможно без соляной кислоты, её концентрация в желудочном соке достаточно высока. Если в организме кислотность понижена, то пищеварение нарушается, и врачи прописывают таким больным приём соляной кислоты перед началом еды.
Применение в быту соляной кислоты
Концентрированная «солянка» смешивается с водой в любой пропорции для бытовых нужд. Сильный раствор этой неорганической кислоты без труда очищает фаянсовую сантехнику от известкового налета и ржавчины, а более слабым можно убрать с тканей пятна ржавчины, чернил, ягодного сока.
Если приглядитесь, на средстве для чистки унитазов «Туалетный утенок» написано, что в состав сходит соляная кислота, поэтому работать с ним нужно в резиновых перчатках и беречь глаза от попадания в них брызг.
Кроме того, без этой кислоты немыслима жизнь ни одного человека – она содержится в желудке и именно благодаря ей пища, попавшая в желудок, растворяется (переваривается).
К тому же, эта кислота служит первым барьером от болезнетворных бактерий, попавших в желудок – они погибают в кислой среде.
Ну а людям, страдающим от гастрита с повышенной кислотностью, эта кислота тоже хорошо знакома. Они даже уменьшают ее действие, чтобы она не разрушала стенки желудка, с помощью специальных препаратов, которые взаимодействуют с ней и уменьшают ее концентрацию.
Самые популярные – это препараты, содержащие оксиды магния и алюминия, например, «Маалокс». Впрочем, есть и экстремальщики, которые пьют пищевую соду, хотя уже доказано, что это приводит лишь к временному облегчению.
xn--c1acbdje2abnav6d.xn--p1ai
свойства, получение, применение :: SYL.ru
В школе вы перешли к изучению такого класса неорганических соединений, как кислоты. Программа образования предусматривает запоминание учениками названий и формул шести представителей этой группы. И, просматривая предоставленную учебником таблицу, вы замечаете в списке кислот ту, которая стоит первой и заинтересовала вас в первую очередь, — соляную. Увы, на занятиях в школе ни свойства, ни любая другая информация о ней не изучается. Поэтому жаждущие получить знания вне школьной программы ищут дополнительные сведения во всяческих источниках. Но частенько многие не находят нужную информацию. И поэтому тема сегодняшней статьи посвящается именно данной кислоте.
Определение
Соляная кислота является сильной одноосновной кислотой. В некоторых источниках ее могут называть хлоро- и хлористоводородной, а также хлористым водородом.
 Физические свойства
Физические свойстваОна представляет собой бесцветную и дымящуюся на воздухе едкую жидкость (фото справа). Однако техническая кислота из-за наличия в ней железа, хлора и других добавок имеет желтоватый цвет. Самая большая ее концентрация при температуре 20оС равняется 38%. Плотность соляной кислоты с такими параметрам равна 1,19г/см3. Но это соединение в разной степени насыщенности имеет совершенно разные данные. При уменьшении концентрации происходит снижение числового значения молярности, вязкости и температуры плавления, однако повышается удельная теплоемкость и температура кипения. Затвердевание соляной кислоты любой концентрации дает различные кристаллогидраты.
Химические свойства
Все металлы, которые стоят до водорода в электрохимическом ряду их напряжения, могут взаимодействовать с этим соединением, образуя соли и выделяя газообразный водород. Если их заменить оксидами металлов, то продуктами реакции станут растворимая соль и вода. Такой же эффект будет и при взаимодействии соляной кислоты с гидроксидами. Если же к ней добавить любую соль металлов (например, карбонат натрия), остаток которой был взят из более слабой кислоты (угольной), то образуются хлорид этого металла (натрия), вода и газ, соответствующий кислотному остатку (в данном случае — углекислый).

Получение
Обсуждаемое сейчас соединение образуется, когда в воде растворяют газообразный хлороводород, который можно получить, сжигая водород в хлоре. Соляная кислота, которую получили при помощи такого способа, носит название синтетической. Также источником для добывания этого вещества могут служить абгазы. И такую соляную кислоту будут называть абгазной. В последнее время уровень производства соляной кислоты с помощью этого метода гораздо выше, чем ее получение синтетическим способом, хотя последний дает соединение в более чистом виде. Это все пути его добывания в промышленности. Однако в лабораториях соляную кислоту получают тремя способами (первые два отличаются только температурой и продуктами реакции) при помощи различных видов взаимодействия химических веществ, таких как:
- Воздействие насыщенной серной кислоты на хлорид натрия при температуре 150оС.
- Взаимодействие приведенных выше веществ в условиях с температурой 550оС и выше.
- Гидролиз хлоридов алюминия или магния.
 Применение
ПрименениеГидрометаллургия и гальванопластика не могут обойтись без использования соляной кислоты, где она нужна, чтобы очищать поверхность металлов при лужении и паянии и получать хлориды марганца, железа, цинка и других металлов. В пищевой промышленности это соединение знают как пищевую добавку E507 — там это регулятор кислотности, необходимый для того, чтобы изготовить сельтерскую (содовую) воду. Концентрированная соляная кислота также находится в желудочном соке любого человека и помогает переваривать пищу. Во время данного процесса ее степень насыщенности уменьшается, т.к. этот состав разбавляется едой. Однако при продолжительном голодании концентрация соляной кислоты в желудке понемногу увеличивается. А так как данное соединение очень едкое, это может привести к язве желудка.
Заключение
Соляная кислота может быть как полезной, так и вредной для человека. Ее попадание на кожу приводит к появлению сильных химических ожогов, а пары данного соединения раздражают дыхательные пути и глаза. Но если обращаться с этим веществом осторожно, оно может не раз пригодиться в деятельности человека.
www.syl.ru

Дроби со степенью: Возведение дроби в степень
0=1;\)Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Возведение дроби в степень Арифметика
Привет, мой друг, тебе интересно узнать все про возведение дроби в степень, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое возведение дроби в степень , настоятельно рекомендую прочитать все из категории Арифметика
При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.
Данное свойство соответствует другой записи свойства № 5 «Степень частного», расмотренного на предыдущей странице.
Примеры возведения в степень дроби.
- возведение в степень дробь» / >
- ( )2 = = =
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой части, превращая смешанное число в неправильную дробь . Об этом говорит сайт https://intellect.icu . После этого возводим в степень и числитель, и знаменатель.
Пример.
Формулу возведения в степень дроби применяют как слева направо, так и справа налево, то есть, чтобы разделить друг на друга степени одинаковыми показателями, можно разделить одно основание на другое, а показатель степени оставить неизменным.
- Пример. Найти значение выражения рациональным способом.
На нашем сайте вы также можете проверить свои вычисления ивозвести число в степень онлайн.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про возведение дроби в степень Надеюсь, что теперь ты понял что такое возведение дроби в степень и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.
 Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
АрифметикаОтрицательная степень чисел и дробей
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
где
a — основание степени
n — показатель степени
Соответственно, an= a · a · a · a… · a
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то она решается довольно просто:
- 23 = 2 · 2 · 2, где
- 2 — основание степени
- 3 — показатель степени
Действия, конечно, можно выполнять и на калькуляторе. Их выбор велик, а доступность иногда на расстоянии одного клика в онлайн. Всё это безусловно можно использовать, но сейчас нам важно подробно разобрать принцип работы, чтобы не упасть в грязь лицом на контрольной по математике.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Число
Вторая степень
Третья степень
1
1
1
2
4
8
3
9
27
4
16
64
5
25
125
6
36
216
7
49
343
8
64
512
9
81
729
10
100
1000
Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления.
 Всего их пять штук — ниже мы их рассмотрим.
Всего их пять штук — ниже мы их рассмотрим.Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0;0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 (0,1).

Примеры
Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины. Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10-9). В школьной программе такие величины редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с разными основаниями, но одинаковыми показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a3 a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
am · an = am + n
Примеры
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
Примеры
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
У нас есть отличная статья на тему — формулы сокращенного умножения, тебе стоит повторить ее!
Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart.
 Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.Запишите ребенка на бесплатный вводный урок математики и начните заниматься с удовольствием уже завтра.
Урок 11. умножение дробей. возведение в степень — Алгебра — 8 класс
Тема: Умножение дробей. Возведение дроби в степень
Содержание модуля (краткое изложение модуля):
Чтобы перемножить обыкновенные дроби, необходимо перемножить их числители, затем перемножить их знаменатели, и первое произведение записать в числитель, а второе – в знаменатель.
Пример:1/3 • 5/7 = (1 • 5)/(3 • 7) = 5/21
Чтобы перемножить рациональные дроби, необходимо перемножить их числители, затем перемножить их знаменатели, и первое произведение записать в числитель, а второе – в знаменатель.a/b • c/d = (a • c)/(b • d) = ac/bd, где
a, b, c и d – многочлены, причем b и d – ненулевые многочлены.
Пример 1:a2/4c • c2/a = (a2 • c2)/4ca = ac/4
Пример 2:(a + b)/a • b/(a2 + 2ab + b2) = (a + b)b/(a(a2 + 2ab + b2)) = (a + b)b/(a(a + b)2) = b/(a(a + b))
Пример 3:(a + b)/(a — b) • (a — b)2 = (a + b)/(a — b) • (a — b)2/1 = (a + b)(a — b) = a2 — b2
Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит вычисления.
Сокращение дробей при расчётах значительно облегчит вычисления.
Чтобы возвести дробь в степень, необходимо возвести в эту степень числитель, а затем возвести в эту степень знаменатель дроби. Первый результат записать в числитель, а второй – в знаменатель.
Пример:(a2/b3)4= (a2)4/(b3)4 = a8/b12
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Умножение дробей. Возведение дроби в степень
Для начала давайте вспомним правило умножения обыкновенных дробей.
Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.
Например
Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.
Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.
Получили, что равенство верно при любых допустимых значениях переменных, т.
 е. является тождеством.
е. является тождеством.Правило умножения рациональных дробей:
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
В буквенном виде это правило записывают так:
Это правило выполняется и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.
Пример 1: умножить дроби.
Решение:
Пример 2: умножить дроби.
Решение:
Пример 3: Представить произведение дробей в виде рациональной дроби.
Решение:
Пример 4: выполнить умножение.
Решение:
Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.
Проверим это равенство на конкретных примерах.
Правило возведения рациональной дроби в степень:
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Пример 5: возвести в третью степень дробь.
Пример 6: возвести во вторую степень дробь.
Пример 7:
Итоги
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Степень обыкновенная дробь. Возведение алгебраической дроби в степень: правило, примеры
На уроке будет рассмотрен более обобщенный вариант умножения дробей — это возведение в степень. Прежде всего, речь будет идти о натуральной степени дроби и о примерах, демонстрирующих подобные действия с дробями. В начале урока, также, мы повторим возведение в натуральную степень целых выражений и увидим, каким образом это пригодится для решения дальнейших примеров.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Возведение алгебраической дроби в степень
1. Правила возведения дробей и целых выражений в натуральную степень с элементарными примерамиПравило возведения обыкновенных и алгебраических дробей в натуральную степень:
Можно провести аналогию со степенью целого выражения и вспомнить, что понимается под возведением его в степень:
Пример 1. .
Как видно из примера, возведение дроби в степень — это частный случай умножения дробей, что изучалось на предыдущем уроке.
Пример 2. а) , б) — минус уходит, т. к. мы возвели выражение в четную степень.
Для удобства работы со степенями вспомним основные правила возведения в натуральную степень:
— произведение степеней;
— деление степеней;
Возведение степени в степень;
Степень произведения.
Пример 3. — это известно нам еще с темы «Возведение в степень целых выражений», кроме одного случая: не существует.
2. Простейшие примеры на возведение алгебраических дробей в натуральную степеньПример 4. Возвести дробь в степень .
Решение. При возведении в четную степень минус уходит:
Пример 5.
 1 = 329
1 = 329Если n = 2, тогда степень квадратом, если n = 3, степень называют кубом. Вычисление квадрата и куба из чисел первого десятка производить достаточно легко. Но с увеличением числа , возводимого в степень, и с увеличением самой степени, вычисления становятся трудоемкими. Для таких вычислении были разработаны специальные таблицы. Также существуют специальные инженерные и online калькуляторы, программные продукты. В качестве простейшего программного для операций со можно использовать табличный редактор Excel.
Источники:
- http://www.bymath.net/studyguide/alg/sec/alg17.html
При решении некоторых технических задач бывает нужно посчитать корень третьей степени . Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).
Вам понадобится
- калькулятор или компьютер
Инструкция
Чтобы посчитать корень степени , воспользуйтесь калькулятором. Желательно, чтобы это был не обычный , а калькулятор, используемый для инженерных расчетов. Однако даже на таком вы не найдете специальную кнопку для извлечения корня третьей степени . Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
Для возведения числа в степень 1/3 наберите на клавиатуре калькулятора само число. После чего нажмите на клавишу «возведение в степень». Такая кнопка, в зависимости от типа калькулятора, может выглядеть как xy (у – в виде верхнего индекса). Так как в большинстве калькуляторов нет возможности работать с обычными (недесятичными) , то вместо числа 1/3 наберите его приблизительное значение: 0,33. Чтобы получить большую точность вычислений, необходимо увеличить количество «троек», например, набрать 0,33333333333333.
 y.
y.Если корень третьей степени приходится систематически, то воспользуйтесь программой MS Excel. Чтобы посчитать корень третьей степени в «Екселе», введите в любую клетку знак «=», а затем, выберите «fx» — вставка функции. В появившемся окошке в списке «Выберите функцию» выберите строку «СТЕПЕНЬ». Нажмите кнопку «Ок». Во вновь появившемся окошке введите в строку «Число» значение числа, из которого нужно извлечь корень . В строку «Степень» введите число «1/3» и нажмите «Ок». В таблицы появится искомое значение кубического корня из исходного числа.
В технических расчетах и при решении многих задач иногда требуется корень , то есть найти такое число, куб которого равен исходному. Для подсчета значения кубического корня достаточно инженерного калькулятора. Однако даже на таком калькуляторе нет специальной клавиши для вычисления кубического корня. Но используя некоторые нехитрые приемы, можно обойтись и без такой кнопки.
Вам понадобится
- инженерный калькулятор или компьютер
Инструкция
Для того чтобы найти кубический корень с помощью калькулятора, возьмите инженерный и наберите на нем исходное число. Затем, нажмите на кнопку возведения в степень. Теперь введите значение показателя . В данном случае он (теоретически) должен равняться 1/3. Но, так как использование обыкновенных дробей даже на инженерном калькуляторе затруднительно, то наберите округленное значение числа 1/3, то есть: 0,33. Затем нажмите на кнопку «=». На индикаторе калькулятора появится искомое значение. Чтобы получить более точное значение, набирайте не две тройки, а , например, 0,333333333333.
Чтобы посчитать кубический корень на компьютере, запустите программу «калькулятор». Если соответствующего значка нет на рабочем столе, проделайте следующее:
— нажмите кнопку «Пуск»;
— выберите пункт меню «Выполнить»;
— введите в появившемся окошке строку «calc».Если появившийся на рабочем столе калькулятор имеет обычный вид (напоминающий «бухгалтерский калькулятор»), то переведите его в режим выполнения расчетов. y». Далее наберите , например, 0,33. Для получения более точного результата, можно набрать более значение показателя степени, например, 0,333333333333. Чтобы получить точный результат, введите показатель степени «1/3» в скобках. То есть нажмите последовательно клавиши «(1/3)».
y». Далее наберите , например, 0,33. Для получения более точного результата, можно набрать более значение показателя степени, например, 0,333333333333. Чтобы получить точный результат, введите показатель степени «1/3» в скобках. То есть нажмите последовательно клавиши «(1/3)».Расчет в программе Excel. Запустите саму программу, нажмите кнопку «=» и выберите функцию «СТЕПЕНЬ». Затем введите то число, из которого требуется извлечь корень степени. После чего, в следующей появившегося окошка наберите дробь «1/3» и нажмите кнопку «Ок».
Видео по теме
Источники:
- как вычислять кубические корни
При решении арифметических и алгебраических задач иногда требуется возвести дробь в квадрат . Проще всего это сделать, когда дробь десятичная – достаточно обычного калькулятора. Однако если дробь обыкновенная или смешанная, то при возведении такого числа в квадрат могут возникнуть некоторые затруднения.
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Yandex.RTB R-A-339285-1
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1
Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени (0 , 5) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a .
 Это можно записать так:
Это можно записать так:Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1
Условие: возведите — 2 в степень 4 .
Решение
Используя определение выше, запишем: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Пример 2
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Пример 3
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ (3 , 14) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи .
От основания степени это не зависит.
Пример 4
Так, (− 9) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
Пример 5
5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1
0 0 — не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Пример 6
Возведите 3 в степень — 2 .
Решение
Используя определение выше, запишем: 2 — 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8: 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8
Пример 7
Возведите 1 , 43 в степень — 2 .
Решение
Переформулируем: 1 , 43 — 2 = 1 (1 , 43) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1 , 43) — 2 = 1 (1 , 43) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1 , 43) — 2 = 10000 20449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .
Пример 8
Пример: 3 − 1 = 1 / 3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Определение 2
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а, потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Пример 9
Вычислите 8 — 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2
После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Пример 10
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь — 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем.
 Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n
Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m nКак возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11
Вычислите приближенное значение 21 , 174367 ….
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
При решении арифметических и алгебраических задач иногда требуется возвести дробь в квадрат . Проще всего это сделать, когда дробь десятичная – достаточно обычного калькулятора. Однако если дробь обыкновенная или смешанная, то при возведении такого числа в квадрат могут возникнуть некоторые затруднения.
Вам понадобится
- калькулятор, компьютер, приложение Excel.
Инструкция
Чтобы возвести десятичную дробь в квадрат , возьмите инженерный , наберите на нем возводимую в квадрат дробь и нажмите на клавишу возведения во вторую степень. На большинстве калькуляторов эта кнопка обозначена как «х²». На стандартном калькуляторе Windows функция возведения в квадрат выглядит как «x^2».
 Например, квадрат десятичной дроби 3,14 будет равен: 3,14² = 9,8596.
Например, квадрат десятичной дроби 3,14 будет равен: 3,14² = 9,8596.Чтобы возвести в квадрат десятичную дробь на обычном (бухгалтерском) калькуляторе, умножьте это число само на себя. Кстати, в некоторых моделях калькуляторов предусмотрена возможность возведения числа в квадрат даже при отсутствии специальной кнопки. Поэтому предварительно ознакомьтесь с инструкцией к конкретному калькулятору. Иногда «хитрого» возведения в степень приведены на задней крышке или на калькулятора. Например, на многих калькуляторах для возведения числа в квадрат достаточно нажать кнопки «х» и «=».
Для возведения в квадрат обыкновенной дроби (состоящей из числителя и знаменателя), возведите в квадрат по отдельности числитель и знаменатель этой дроби. То есть воспользуйтесь следующим правилом:(ч / з)² = ч² / з², где ч – числитель дроби, з – знаменатель дроби.Пример: (3/4)² = 3²/4² = 9/16.
Если возводимая в квадрат дробь – смешанная (состоит из целой части и обыкновенной дроби), то предварительно приведите ее к обыкновенному виду. То есть примените следующую формулу:(ц ч/з)² = ((ц*з+ч) / з)² = (ц*з+ч)² / з², где ц – целая часть смешанной дроби.Пример: (3 2/5)² = ((3*5+2) / 5)² = (3*5+2)² / 5² = 17² / 5² = 289/25 = 11 14/25.
Если в квадрат (не ) дроби приходится постоянно, то воспользуйтесь программой MS Excel. Для этого введите в одну из таблицы следующую формулу: =СТЕПЕНЬ(A2;2) где А2 – адрес ячейки, в которую будет вводиться возводимая в квадрат дробь .Чтобы сообщить программе, что с вводимым числом необходимо обращаться как дробь ю (т.е. не преобразовывать ее в десятичный вид), наберите перед дробь ю цифру «0» и знак «пробел». То есть для ввода, например, дроби 2/3 нужно ввести: «0 2/3» (и нажать Enter). При этом в строке ввода отобразится десятичное представление введенной дроби. Значение и представление дроби непосредственно в сохранится в исходном виде.
 n )} = \frac{1}{ab} $$
n )} = \frac{1}{ab} $$Исчисление II — частичные дроби
Показать мобильное уведомление Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-4: Частичные дроби
В этом разделе мы собираемся взглянуть на интегралы рациональных выражений многочленов и еще раз начнем этот раздел с интеграла, который мы уже можем сделать, чтобы мы могли сопоставить его с интегралами, которые мы будем делать в этом разделе. раздел.2} — x — 6}} \, dx}} & = \ int {{\ frac {4} {{x — 3}} \, — \ frac {1} {{x + 2}} dx}} \ \ & = 4 \ ln \ left | {x — 3} \ right | — \ ln \ left | {x + 2} \ right | + c \ end {align *} \]
Этот процесс взятия рационального выражения и его разложения на более простые рациональные выражения, которые мы можем складывать или вычитать, чтобы получить исходное рациональное выражение, называется разложением частичной дроби . Многие интегралы, включающие рациональные выражения, могут быть получены, если мы сначала сделаем дроби под интегралом.
Итак, давайте сделаем быстрый обзор неполных дробей. Начнем с рационального выражения в форме
\ [f \ left (x \ right) = \ frac {{P \ left (x \ right)}} {{Q \ left (x \ right)}} \], где оба \ (P \ left (x \ right) \) и \ (Q \ left (x \ right) \) являются полиномами, а степень \ (P \ left (x \ right) \) меньше, чем степень \ (Q \ left (x \ right) \).
 k}}} \), \ (k = 1,2,3, \ ldots \)
k}}} \), \ (k = 1,2,3, \ ldots \) Обратите внимание, что первый и третий случаи на самом деле являются частными случаями второго и четвертого случаев соответственно.2} — x — 6}} \, dx}} \] Показать решение
Первый шаг — максимально разложить знаменатель на множители и получить форму разложения на частичные дроби. Это дает
\ [\ frac {{3x + 11}} {{\ left ({x — 3} \ right) \ left ({x + 2} \ right)}} \, = \ frac {A} {{x — 3 }} + \ frac {B} {{x + 2}} \]Следующим шагом будет добавление правой стороны.
\ [\ frac {{3x + 11}} {{\ left ({x — 3} \ right) \ left ({x + 2} \ right)}} \, = \ frac {{A \ left ({x + 2} \ right) + B \ left ({x — 3} \ right)}} {{\ left ({x — 3} \ right) \ left ({x + 2} \ right)}} \]Теперь нам нужно выбрать \ (A \) и \ (B \) так, чтобы числители этих двух были равны для каждого \ (x \).Для этого нам нужно установить числители равными.
\ [3x + 11 = A \ влево ({x + 2} \ right) + B \ left ({x — 3} \ right) \]Обратите внимание, что в большинстве задач мы сразу перейдем от общей формы разложения к этому шагу и не будем беспокоиться о фактическом добавлении терминов. Единственное, что нужно для добавления терминов, — это получить числитель, и мы можем получить его, фактически не записывая результаты сложения.
На данный момент у нас есть один из двух способов продолжить.Один способ всегда будет работать, но зачастую это больше работы. Другой, хотя он не всегда работает, часто оказывается быстрее, когда он действительно работает. В этом случае оба будут работать, поэтому мы воспользуемся более быстрым способом для этого примера. Мы рассмотрим другой метод в следующем примере.
Здесь мы собираемся заметить, что числители должны быть равны для любых x , которые мы хотели бы использовать.
\ [\ begin {align *} x & = — 2: & \ hspace {0,5 дюйма} 5 & = A \ left (0 \ right) + B \ left ({- 5} \ right) & \ hspace {0,25 дюйма } & \ Rightarrow & \ hspace {0,25 дюйма} B & = — 1 \\ x & = 3 \, \, \, \ ,: & \ hspace {0,5 дюйма} 20 & = A \ left (5 \ right) + B \ left (0 \ right) & \ hspace {0,25 дюйма} & \ Rightarrow & \ hspace {0,25 дюйма} A & = 4 \ end {align *} \] В частности, числители должны быть равны для \ (x = — 2 \) и \ (x = 3 \).Итак, давайте подключим их и посмотрим, что у нас получится.
В частности, числители должны быть равны для \ (x = — 2 \) и \ (x = 3 \).Итак, давайте подключим их и посмотрим, что у нас получится.Итак, осторожно выбрав \ (x \), мы получили неизвестные константы, которые быстро выпали.2} — x — 6}} \, dx}} & = \ int {{\ frac {4} {{x — 3}} \, — \ frac {1} {{x + 2}} dx}} \ \ & = \ int {{\ frac {4} {{x — 3}} \, dx}} — \ int {{\ frac {1} {{x + 2}} dx}} \\ & = 4 \ ln \ left | {x — 3} \ right | — \ ln \ left | {x + 2} \ right | + c \ end {align *} \]
Напомним, что для получения этого интеграла мы сначала разбили его на два интеграла, а затем использовали подстановки:
\ [u = x — 3 \ hspace {0,5 дюйма} v = x + 2 \]на интегралы, чтобы получить окончательный ответ.2} + 4 = A \ left ({x + 2} \ right) \ left ({3x — 2} \ right) + Bx \ left ({3x — 2} \ right) + Cx \ left ({x + 2 } \верно)\]
Как и в предыдущем примере, похоже, что мы можем просто выбрать несколько значений \ (x \) и найти константы, так что давайте сделаем это.
\ [\ begin {align *} x & = 0 \, \, \, \, \,: & \ hspace {0,5in} 4 & = A \ left (2 \ right) \ left ({- 2} \ right ) & \ hspace {0,5 дюйма} & \ Rightarrow & \ hspace {0,25 дюйма} A & = — 1 \\ x & = — 2: & \ hspace {0.5 дюймов} 8 & = B \ left ({- 2} \ right) \ left ({- 8} \ right) & \ hspace {0,25 дюйма} & \ Rightarrow & \ hspace {0,25 дюйма} B & = \ frac {1 } {2} \\ x & = \ frac {2} {3} \, \,: & \ hspace {0,5 дюйма} \ frac {{40}} {9} & = C \ left ({\ frac {2 } {3}} \ right) \ left ({\ frac {8} {3}} \ right) & \ hspace {0,25 дюйма} & \ Rightarrow & \ hspace {0,25 дюйма} C & = \ frac {{40} } {{16}} = \ frac {5} {2} \ end {align *} \]Обратите внимание, что в отличие от первого примера большинство коэффициентов здесь дробные.
 2} — 4x}} \, dx}} & = \ int {{- \ frac {1} {x} + \ frac {{\ frac {1} {2}}} {{x + 2}} + \ frac {{\ frac {5} {2}}} {{3x — 2}} \, dx}} \\ & = — \ ln \ left | х \ право | + \ frac {1} {2} \ ln \ left | {x + 2} \ right | + \ frac {5} {6} \ ln \ left | {3x — 2} \ right | + c \ end {align *} \]
2} — 4x}} \, dx}} & = \ int {{- \ frac {1} {x} + \ frac {{\ frac {1} {2}}} {{x + 2}} + \ frac {{\ frac {5} {2}}} {{3x — 2}} \, dx}} \\ & = — \ ln \ left | х \ право | + \ frac {1} {2} \ ln \ left | {x + 2} \ right | + \ frac {5} {6} \ ln \ left | {3x — 2} \ right | + c \ end {align *} \]Опять же, как отмечалось выше, интегралы, генерирующие натуральные логарифмы, очень часто встречаются в этих задачах, поэтому убедитесь, что вы можете их решать. Кроме того, вы смогли правильно сделать последний интеграл, верно? Коэффициент при \ (\ frac {5} {6} \) правильный.2} \]
Теперь есть вариант метода, который мы использовали в первой паре примеров, который здесь будет работать. Есть несколько значений \ (x \), которые позволят нам быстро получить две из трех констант, но нет значения \ (x \), которое просто передало бы нам третью.
В этом примере мы выберем \ (x \), чтобы получить две константы, которые мы можем легко получить, а затем просто выберем другое значение \ (x \), с которым будет легко работать. ( и.е. он нигде не даст больших / беспорядочных чисел), а затем мы воспользуемся тем фактом, что мы также знаем две другие константы, чтобы найти третью.
\ [\ begin {align *} x & = 0: & \ hspace {0,25 дюйма} 18 & = B \ left ({- 3} \ right) & \ hspace {0,15 дюйма} \ Rightarrow \ hspace {0,25 дюйма} B & = — 6 \\ x & = 3: & \ hspace {0,25 дюйма} 18 & = C \ left (9 \ right) & \ hspace {0,15 дюйма} \ Rightarrow \ hspace {0,25 дюйма} C & = 2 \\ x & = 1: & 18 & = A \ left ({- 2} \ right) + B \ left ({- 2} \ right) + C = — 2A + 14 & \ hspace {0.2} — 1}} \, dx}} \]Итак, нам нужно разделить второй интеграл на части. Вот разложение.
\ [\ frac {1} {{\ left ({x — 1} \ right) \ left ({x + 1} \ right)}} = \ frac {A} {{x — 1}} + \ frac { B} {{x + 1}} \]Установка в числителе равного дает,
\ [1 = A \ влево ({x + 1} \ right) + B \ left ({x — 1} \ right) \]Выбор значения \ (x \) дает нам следующие коэффициенты.
\ [\ begin {align *} x & = — 1: & \ hspace {0.2} — 1}} \, dx}} & = \ int {{dx}} + \ int {{\ frac {{\ frac {1} {2}}} {{x — 1}} — \ frac { {\ frac {1} {2}}} {{x + 1}} \, dx}} \\ & = x + \ frac {1} {2} \ ln \ left | {x — 1} \ right | — \ frac {1} {2} \ ln \ left | {x + 1} \ right | + c \ end {align *} \]
Неполные дроби
Способ «разбиения» дробей с многочленами в них.
Что такое неполные дроби?
Мы можем сделать это напрямую:
Как это:
2 х − 2 + 3 х + 1 = 2 (х + 1) + 3 (х − 2) (х − 2) (х + 1)
Что можно упростить с помощью Rational Expressions до:
= 2x + 2 + 3x − 6 х 2 + х − 2х − 2
= 5x − 4 x 2 −x − 2
… но как нам пойти в обратном направлении?
Вот что мы собираемся открыть:
Как найти «части», из которых состоит единичная дробь
(« частичные дроби »).Почему они нам нужны?
Прежде всего … зачем они нам?
Потому что каждая дробная дробь проще .
Это может помочь решить более сложную дробь. Например, это очень полезно в интегральном исчислении.
Частичное разложение на фракции
Итак, позвольте мне показать вам, как это сделать.
Метод называется «Частичное дробное разложение» и выглядит следующим образом:
Шаг 1: Разложите нижнюю часть на множители
Шаг 2: Запишите по одной дробной части для каждого из этих множителей
Шаг 3: Умножаем на нижнюю часть, чтобы у нас больше не было дробей
Шаг 4: Теперь найдите константы A 1 и A 2
Подстановка корней или нулей из (x − 2) (x + 1) может помочь:
И у нас есть ответ:
Это было легко! .
 .. почти слишком просто …
.. почти слишком просто … … потому что может быть намного сложнее !
Теперь мы подробно рассмотрим каждый шаг.
Правильные рациональные выражения
Во-первых, это работает только для правильных рациональных выражений , где степень верха на меньше, чем нижнего.
градуса — это самый большой показатель степени , который имеет переменная.
- Правильно: градус верха меньше градуса низа.
Правильный: градус верха — 1
градуса низа — 3 - Неправильно: степень верха больше или равна степени низа.
Неправильно: градус верха — 2
градуса низа — 1
Если ваше выражение неправильное, сначала выполните полиномиальное деление в столбик.
Факторинг дна
Вы можете разложить нижний многочлен на множители. См. Факторинг в алгебре.
Но не делите их на комплексные числа … вам может потребоваться остановить некоторые множители квадратичными (называемыми неприводимыми квадратиками, потому что любое дальнейшее разложение на множители приводит к комплексным числам):
Пример: (x
2 −4) (x 2 +4)- x 2 −4 можно разложить на (x − 2) (x + 2)
- Но x 2 +4 делить на комплексные числа, поэтому не делайте этого
Итак, лучшее, что мы можем сделать, это:
(х − 2) (х + 2) (х 2 +4)
Таким образом, факторы могут быть комбинацией
- линейные коэффициенты
- неприводимых квадратичных множителей
Если у вас есть квадратичный фактор, вам необходимо включить эту частичную дробь:
B 1 x + C 1 (Ваш квадратичный)
Факторы с показателями
Иногда можно получить множитель с показателем степени, например (x − 2) 3 .
 ..
..Вам нужна частичная дробь для каждой экспоненты от 1 до.
Как это:
Пример:
1 (x − 2) 3
Имеет неполные дроби
A 1 x − 2 + A 2 (x − 2) 2 + A 3 (х − 2) 3
То же самое может случиться и с квадратиками:
Пример:
1 (x 2 + 2x + 3) 2
Имеет неполные фракции:
B 1 x + C 1 x 2 + 2x + 3 + B 2 x + C 2 (x 2 + 2x + 3) 2
Иногда использование корней не решает проблемы
Даже после использования корней (нулей) основания вы можете получить неизвестные константы.
Итак, следующее, что нужно сделать:
О, черт возьми! С этим сложно справиться! Итак, давайте рассмотрим пример, который поможет вам понять:
Большой пример, объединяющий все воедино
Вот вам хороший большой пример!
x 2 +15 (x + 3) 2 (x 2 +3)
- Поскольку (x + 3) 2 имеет показатель степени 2, необходимы два члена (A 1 и A 2 ).
- And (x 2 +3) является квадратичным, поэтому потребуется Bx + C:
x 2 +15 (x + 3) 2 (x 2 +3) = A 1 x + 3 + A 2 (x +3) 2 + Bx + C x 2 +3
Теперь умножаем на (x + 3) 2 (x 2 +3) :
x 2 +15 = (x + 3) (x 2 +3) A 1 + (x 2 +3) A 2 + (x + 3) 2 (Bx + В)
При x = −3 есть ноль (потому что x + 3 = 0), поэтому давайте попробуем это:
(−3) 2 +15 = 0 + ( (−3) 2 +3) A 2 + 0
И упростите его до:
24 = 12A 2
, поэтому A 2 = 2
Заменим A 2 на 2:
x 2 +15 = (x + 3) (x 2 +3) A 1 + 2x 2 +6 + (x + 3) 2 (Bx + C)
Теперь разверните все:
x 2 +15 = (x 3 + 3x + 3x 2 +9) A 1 + 2x 2 +6 + (x 3 + 6x 2 + 9x) B + (x 2 + 6x + 9) C
Соберите вместе степени x:
x 2 +15 = x 3 (A 1 + B) + x 2 (3A 1 + 6B + C + 2) + x (3A 1 + 9B + 6C) + (9A 1 + 6 + 9C)
Разделите степени и запишите систему линейных уравнений:
x 3 : 0 = A 1 + B x 2 : 1 = 3A 1 + 6B + C + 2 x: 0 = 3A 1 + 9B + 6C Константы: 15 = 9A 1 + 6 + 9C Упростите и аккуратно расположите:
0 = А 1 + B -1 = 3A 1 + 6Б + С 0 = 3A 1 + 9Б + 6C 1 = А 1 + С Теперь решите.

Вы можете выбрать свой собственный способ решить эту проблему … Я решил вычесть 4-е уравнение из 2-го, чтобы начать с:
0 = А 1 + B -2 = 2A 1 + 6Б 0 = 3A 1 + 9Б + 6C 1 = А 1 + С Затем вычтите 2 раза первое уравнение из второго:
0 = А 1 + B -2 = 4B 0 = 3A 1 + 9Б + 6C 1 = А 1 + С Теперь я знаю, что B = — (1/2) .

Мы куда-то идем!
И из 1-го уравнения я могу вычислить, что A 1 = + (1/2) .
И из 4-го уравнения я могу вычислить, что C = + (1/2) .
Конечный результат:
A 1 = 1/2 А 2 = 2 B = — (1/2) С = 1/2 И теперь мы можем записать наши дробные дроби:
х 2 +15 (х + 3) 2 (х 2 +3) знак равно 1 2 (х + 3) + 2 (х + 3) 2 + −x + 1 2 (х 2 +3)
Уф! Много работы.Но это может быть сделано.
(Примечание: мне потребовалось почти
час , чтобы сделать это, потому что Пришлось исправить
2 глупые ошибки в пути!)Сводка
- Начните с Правильное Рациональное выражение (если нет, сначала делите)
- Разложите нижнюю часть на:
- линейные коэффициенты
- или «неприводимые» квадратичные множители
- Запишите частичную дробь для каждого множителя (и каждой экспоненты каждого из них)
- Умножьте все уравнение на нижнюю часть
- Решить для коэффициентов по
- подставляем нули снизу
- составление системы линейных уравнений (каждой степени) и решение
- Запишите свой ответ!
5.4 — Неполные дроби
5.4 — Неполные дробиДобавление рациональных выражений
В арифметике вы научились складывать дроби. Вы нашли наименьший общий знаменатель, и затем умножил числитель и знаменатель каждого члена на то, что необходимо для заполните общий знаменатель.

В алгебра, ты нес эту процесс на добавление рациональных выражения. Вы еще раз перемножили числитель и знаменатель каждого срок на то, что отсутствовало в знаменателе этого термина.
с частичной дробью Разложение, мы собираемся обратить процесс и разложить рациональное выражение на два или более простые правильные рациональные выражения, которые были сложены вместе.
Частичное разложение на фракции
Partial Fraction Decomposition работает только для правильных рациональных выражений, то есть степени числитель должен быть меньше степени знаменателя. Если это не так, то вы должны сначала выполнить деление в столбик, а затем выполнить разложение частичной дроби на рациональном часть (остаток по делителю).После того, как вы выполните разложение на частичную дробь, просто добавьте обратно в частную часть от длинного деления.
Обсуждая многочлены в разделе 3.4, мы узнали, что каждый многочлен с вещественным коэффициенты могут быть разложены на множители, используя только линейные и неприводимые квадратичные множители. Это значит, что есть только два типа факторов, о которых мы должны беспокоиться.
Линейные коэффициенты
Если дробные части, на которые мы разлагаем рациональное выражение, должны быть правильными, то Единственное, что может превышать линейный коэффициент, — это постоянная величина.Итак, для каждого линейного фактора в знаменатель, вам понадобится константа больше, чем в числителе.
Неприводимые квадратичные множители.
Если дробные части, на которые мы разлагаем рациональное выражение, должны быть правильными, тогда неприводимый квадратичный фактор может иметь линейный член и / или постоянный член в числителе. Так, для каждого неприводимого квадратичного множителя в знаменателе вам понадобится линейный член и постоянный член в числителе.
Повторяющиеся факторы
Рассмотрим дробь, знаменатель которой равен 8.Означает ли это, что знаменатель каждого складываемый член должен был быть 8? Нет, знаменатели могли быть 2, 4 или 8.
 потому что общий знаменатель между 2, 4 и 8 равен 8. Последствия этого для частичного
дробное разложение состоит в том, что когда у вас есть повторяющийся фактор (фактор с кратностью
кроме одного), вам необходимо включить коэффициент расширения для каждой возможной мощности.
потому что общий знаменатель между 2, 4 и 8 равен 8. Последствия этого для частичного
дробное разложение состоит в том, что когда у вас есть повторяющийся фактор (фактор с кратностью
кроме одного), вам необходимо включить коэффициент расширения для каждой возможной мощности.Например, если у вас есть (x-2) 3 , вам нужно будет включить (x-2), (x-2) 2 и (x-2) 3 .
Показатели степени 2 или 3 не меняют, является ли фактор линейным или квадратичным, а зависит только то, сколько раз фактор есть. Каждый из этих (x-2) факторов получит постоянный член в числитель, потому что x-2 линейен, независимо от того, в какую степень он возведен.
Неправильные дроби
Правильная дробь — это дробь, числитель которой меньше знаменателя. Для рациональных выражений это означает, что степень в числителе меньше, чем степень в знаменателе.Если у вас неправильная дробь, вы сначала Чтобы получить частное и остаток, необходимо выполнить деление в столбик.
Оставить частную в покое, но выполнить разложение на частную дробь. на оставшейся фракции.
Основное уравнение
После создания уравнения в частных долях вы умножаете обе части уравнение по наименьшему общему знаменателю, чтобы избавиться от дробей. В Полученное уравнение без дробей называется основным уравнением.
Техника 1 — Выберите значения для x
Когда есть линейные коэффициенты, самый простой способ сделать декомпозиция, вероятно, заключается в выборе хороших значений для x.
В примере справа мы берем каждый фактор в знаменатель и дайте ему собственный член в правой части. Поскольку каждый фактор в знаменатель является линейным, и рациональные выражения должны быть правильными, a постоянный член был помещен в каждый числитель каждого члена. Мы умножаем на наименьший общий знаменатель, чтобы получить в уравнении без фракции.Это уравнение называется основным уравнением и составляет …
х + 2 = А (х — 4) + В х
«Хорошие» значения для x — это те, которые приводят к тому, что каждый линейный коэффициент нуль.
 В этом случае хороши x = 4 и x = 0. «Хорошие» ценности будут
заставляют каждый член, кроме одного, выпадать из уравнения,
и поэтому вы сможете найти значение переменной очень
быстро.
В этом случае хороши x = 4 и x = 0. «Хорошие» ценности будут
заставляют каждый член, кроме одного, выпадать из уравнения,
и поэтому вы сможете найти значение переменной очень
быстро.Когда вы позволяете x = 0, член B выпадает, и вы получаете …
0 + 2 = A (0-4) или 2 = -4A. Решение, которое дает A = -1/2.
Если вы позволите x = 4, член A выпадет, и вы получите …
4 + 2 = B (4) или 6 = 4B. Решение, которое дает B = 3/2.
После вы нашли значения каждой константы, важно подключить их ценности обратно в разложение. Не останавливайтесь только на A = -1 / 2, B = 3/2, потому что кто-то другой может определил A и B по-разному. Правильный ответ — поместить их обратно в разложение и при необходимости упростить. Упрощение было бы уменьшить количество знаков (по возможности не ставить первый член отрицательным) и исключить составные дроби, вычленив наименьший общий знаменатель числителей.
Примечание: хороших значений ровно столько, сколько разных (разных) линейные факторы. Если есть повторяющиеся линейные множители или неприводимые квадратичные множители факторы (повторяющиеся или нет), у вас не будет достаточно «хороших» значений для выбора. В таких случаях вам нужно будет выбрать удобные, но не очень хорошие значения, а затем подставьте известные константы в уравнение чтобы найти другие константы. Подставьте простые числа, например x = 0, x = 1 и т. Д.
Вам нужно будет выбрать для x столько значений, сколько нужно найти констант.
Метод 2 — Создание системы линейных уравнений
Первый метод выбора значений x работает очень хорошо, когда все факторы различны. линейные факторы. Если есть какие-либо линейные факторы, то первый метод, вероятно, лучше техника для использования. Однако если есть только неприводимые квадратичные множители, то метод выбор значений для x может стать беспорядочным.
Есть другой способ сделать это проблемы (на самом деле, этот метод работают, когда есть линейные факторы, просто что с другим проще и быстрее).

Первая часть процесса такая же. Вперед и запиши разложение, включая постоянные члены по линейным коэффициентам, а также линейные и постоянные члены над неприводимой квадратичной факторы. Затем умножьте на наименьший общий знаменатель, чтобы найти основное уравнение. То же самое. Основное уравнение …
2x 2 + x + 8 = Ax (x 2 + 4) + B (x 2 +4) + Cx + D
Вот и разница.
Перейти вперед и расширить (умножить) основное уравнение…
2x 2 + x + 8 = Ax 3 + 4Ax + Bx 2 + 4B + Cx + D
и перегруппировать условия общими полномочиями переменная x.
2x 2 + x + 8 = Ax 3 + Bx 2 + 4Ax + Cx + 4B + D
Теперь разложите крестики на степень.
2x 2 + x + 8 = (A) x 3 + (B) x 2 + (4A + C) x + (4B + Г) (1)
Следующая часть работает, потому что если два многочлена будут равны, они должно иметь одинаковое количество одинаковых терминов с обеих сторон.Итак, трюк здесь состоит в том, чтобы приравнять обе части уравнения вместе, приравнивая одинаковые члены.
Установите элементы x 3 слева (из которых нет ни одного) равными условиям x 3 на правая (из которых есть A), чтобы прийти к первому уравнению 0 = A. Хорошо, что было довольно просто, и вы уже получили ценность для A.
Установите элементы x 2 слева (из которых 2) равными условиям x 2 справа (из которых есть B), чтобы прийти ко второму уравнению 2 = B.Теперь вы знаете Б.
Для x: 1 слева и 4A + C справа, поэтому 1 = 4A + C.
Для констант: 8 слева и 4B + D справа, поэтому 8 = 4B + D.
Возможно, вам придется решить систему линейные уравнения, но именно поэтому этот раздел, посвященный частным дробям, находится в этом глава. Мы просто освежили наши воспоминания о том, как решить систему линейных уравнения в последнем разделе.

После некоторые решения, мы приходим к A = 0, B = 2, C = 1 и D = 0, и мы готовы чтобы вставить эти значения обратно в исходное разложение, чтобы прийти к окончательному ответу.
Обязательно и при необходимости упростите ответ.
Этот пример на самом деле был довольно простым, потому что вы смогли найти A и B сразу же. Во многих случаях вам нужно будет решить более крупную систему. уравнений, чтобы найти значения.
Как и почему разложение частичной дроби с невычисляемыми квадратиками в знаменателе
Если вы читаете этот пост, вы, вероятно, достигли той точки в вашем курсе исчисления, где вас пытаются научить выполнять интеграцию путем расширения частичной дроби.И если вы похожи на меня, когда я впервые изучал математический анализ, вы, вероятно, почесываете голову и получаете whadafuhhhh ? В чем смысл всего этого ?
Вот что вам нужно знать. Частичное расширение дроби не является методом интегрирования . Это алгебраическая техника. При этом это полезно для упрощения интеграции определенных алгебраических выражений (т. Е. Рациональных выражений), разбивая их на более мелкие и простые куски.2 + x + 1)} \]
Чтобы быстро просмотреть шаги (они должны быть в вашем учебнике или на любом онлайн-ресурсе), методика выполняется следующим образом:
- Убедитесь, что степень знаменателя больше степени числителя. Если нет, сделайте полиномиальное деление в столбик и разложите частичную дробь для любого остатка, который появляется. Для нашей задачи степень знаменателя равна 3, а степень числителя равна 0, так что все готово.
- Разложите на множители числитель и знаменатель выражения (или остаток, если он был получен на шаге 1) и удалите все множители, общие для числителя и знаменателя. Наша проблема уже принята во внимание. Обратите внимание, что квадратичный член в знаменателе не может быть дополнительно разложен на множители.

- Основываясь на множителях в знаменателе, запишите соответствующие частные дроби с неизвестными коэффициентами в числитель. Форма этих терминов приведена в вашем учебнике и во многих других онлайн-ресурсах, поэтому я не буду здесь подробно описывать их.2 + х + 1) \). Кроме того, почему у одного из этих терминов в числителе есть \ (x \)? Ответ на оба эти вопроса дает другой курс — линейная алгебра. Да, я знаю, вы, наверное, еще не пошли по этому пути, и это несправедливо, но такова жизнь. Я постараюсь объяснить это как можно лучше:
Вкратце, решение для неизвестных коэффициентов (что мы сделаем сейчас) даст нам систему из 3 линейно независимых уравнений, потому что знаменатель нашего выражения имеет степень 3. Чтобы получить уникальное решение, мы таким образом, нужны 3 неизвестных значения: \ (A \), \ (B \) и \ (C \).2 + х + 1) \). Тогда мы вернемся к тому, с чего начали — у нас будет только две (линейно независимых) частичных дроби и, следовательно, не будет уникальных значений для \ (A \) и \ (B \). Следовательно, нам всегда нужна одна линейно независимая частичная дробь для каждой степени знаменателя .
Понял? Чтобы найти \ (A \), \ (B \) и \ (C \), мы умножаем обе части уравнения на весь знаменатель нашего исходного выражения и упрощаем:
Затем мы группируем похожие степени \ (x \) в правой части уравнения и приравниваем их соответствующим степеням \ (x \) в левой части уравнения:
Разделив на соответствующие степени \ (x \) в каждом уравнении, мы получим следующую систему из 3-х уравнений с 3-мя неизвестными:
Обратите внимание, что если бы у нас вообще не было члена \ (B \) (т.е.е., если бы \ (B = 0 \)), то мы получили бы \ (A = 0 \) и тогда не было бы возможного решения для \ (C \).
Теперь, когда у нас есть эта система уравнений, мы можем решить ее, используя любой из методов решения одновременных уравнений. Мы могли бы использовать либо метод замены, либо метод исключения, но я собираюсь использовать гибридный подход, добавляя уравнения таким образом, чтобы исключить одно или несколько неизвестных, а затем произвести замену.
 Складывая второе и третье уравнения, исключаем \ (C \):
Складывая второе и третье уравнения, исключаем \ (C \):Теперь мы можем добавить это новое уравнение к первому уравнению, исключить \ (B \) и решить для \ (A \):
Подставляя наше значение \ (A \) обратно в первое уравнение, мы решаем для \ (B \):
И, наконец, подставляя наше значение \ (A \) обратно в третье уравнение, мы решаем для \ (C \):
Итак, теперь мы нашли наши коэффициенты: \ (A = \ frac {1} {3} \), \ (B = — \ frac {1} {3} \) и \ (C = — \ frac {2 } {3} \).Подставляя их обратно в наши дробные части, мы получаем:
Вот и все. Правая часть, наше расширение частичной дроби, позволяет делать то, что мы иначе не могли бы сделать с исходным выражением. Например, было бы невозможно напрямую интегрировать исходное выражение, но мы знаем, как интегрировать эти члены с частичной дробью. Первый член может быть интегрирован с помощью простой u-подстановки, в то время как второй и третий члены потребуют завершения квадрата и выполнения тригонометрической замены (фу!) Эй, никто не сказал, что это будет легко, но, по крайней мере, теперь это возможно.
Причина, по которой частные дроби, как правило, доставляют студентам столько хлопот, заключается в том, что они объединяют целый ряд различных вопросов и методов: полиномиальное деление в столбик, линейную независимость функций и решение систем уравнений и многие другие. Вдобавок ко всему, если конечной целью является интеграция выражения, вам, возможно, придется отказаться от всех других методов интеграции, которые вы только что изучили за последние несколько недель. Ключ к решению задач с частичными дробями — это не торопиться, тщательно записывать правильную форму разложения, а затем методично работать над поиском коэффициентов.Удачи!
Неполные дроби — A Plus Topper
Неполные дроби
Выражение вида \ (\ frac {f (x)} {g (x)} \), где f (x) и g (x) полиномиальны от x, называется рациональной дробью.

- Собственные рациональные функции: Функции вида \ (\ frac {f (x)} {g (x)} \), где f (x) и g (x) — многочлены, а g (x) ≠ 0, называются рациональными функциями от x.
Если степень f (x) меньше степени g (x), то называется правильной рациональной функцией. - Неправильные рациональные функции: Если степень f (x) больше или равна степени g (x), то \ (\ frac {f (x)} {g (x)} \) называется неправильная рациональная функция.
- Частичные дроби: Любая правильная рациональная функция может быть разбита на группу различных рациональных дробей, каждая из которых имеет простой множитель знаменателя исходной рациональной функции. Каждая такая дробь называется частичной дробью.
Если с помощью некоторого процесса мы можем разбить данную рациональную функцию \ (\ frac {f (x)} {g (x)} \) на различные дроби, знаменатели которых являются множителями g (x), то процесс их получения называется разрешением или разложением \ (\ frac {f (x)} {g (x)} \) на его частичные дроби.
Различные случаи частичных дробей
(1) Когда знаменатель состоит из неповторяющихся линейных множителей:
Каждому линейному множителю (x — a), встречающемуся один раз в знаменателе правильной дроби, соответствует единственная частичная дробь вида \ (\ frac {A} {xa} \), где A — постоянная, которую необходимо определить.
Если g (x) = (x — a 1 ) (x — a 2 ) (x — a 3 ) ……. (x — a n ), тогда мы предполагаем, что,
, где A 1 , A 2 , A 3 , ……….A n — константы, можно определить, приравняв числитель L.H.S. в числитель R.H.S. (после L.C.M.) и подставив x = a 1 , a 2 , …… a n .
(2) Когда знаменатель состоит из линейных множителей, некоторые из которых повторяются:
Каждому линейному множителю (x — a), встречающемуся r раз в знаменателе правильной рациональной функции, соответствует сумма r частичных дробей.
Пусть g (x) = (x — a) k (x — a 1 ) (x — a 2 ) …….{2} + bx + c}} \), где A и B — константы, которые необходимо определить.
Пример:
(4) Когда знаменатель состоит из повторяющихся квадратичных множителей:
Каждому неприводимому квадратичному множителю ax 2 + bx + c, встречающемуся r раз в знаменателе правильной рациональной дроби, соответствует сумма r частичные дроби формы.
где A и B — константы, которые необходимо определить.Частичные дроби несобственных рациональных функций
Если степень больше или равна степени g (x), то \ (\ frac {f (x)} {g (x)} \) называется несобственной. рациональная функция и каждая рациональная функция могут быть преобразованы в надлежащую рациональную функцию путем деления числителя на знаменатель.
Делим числитель на знаменатель до тех пор, пока не получим остаток, который имеет меньшую степень, чем знаменатель.Общий метод определения констант
- Выразите данную дробь на ее частичные дроби в соответствии с изложенными выше правилами.
- Затем умножьте обе стороны на знаменатель данной дроби, и вы получите тождество, которое будет сохраняться для всех значений x.
- Приравняйте коэффициенты при одинаковых степенях x в результирующем тождестве и решите уравнения, полученные таким образом, одновременно, чтобы найти различные постоянные короткие методы.Иногда мы подставляем конкретные значения переменной x в тождество, полученное после очистки дробей, чтобы найти некоторые или все константы. Для неповторяющихся линейных коэффициентов значения x используются как те, для которых знаменатель соответствующих долей становится равным нулю.
Частичное разложение на фракции — ChiliMath
Этот метод используется для разложения данного рационального выражения на более простые дроби. Другими словами, если мне дается одна сложная дробь, моя цель — разбить ее на серию «более мелких» компонентов или частей.

Ранее при добавлении / вычитании рациональных выражений мы хотели объединить два или более рациональных выражения в одну дробь, как в примере ниже. Однако разложение частичной фракции ( также известно как расширение частичной фракции ) — это как раз процесс, обратный этому. Ниже приводится иллюстративная диаграмма, показывающая основную концепцию.
Теперь я рассмотрю пять (5) примеров, чтобы продемонстрировать этапы разложения одной дроби на части.
Примеры частичного разложения на фракции
Пример 1: Найдите дробное разложение рационального выражения.
Это простая задача, поэтому рассматривайте ее как вводный пример. Я начну с факторизации знаменателя (выньте x из бинома). Затем я настрою процесс разложения, поместив A и B для каждого из уникальных или различных линейных факторов. Последующие шаги включают в себя избавление от всех знаменателей путем умножения ЖК-дисплея (который является всего лишь исходным знаменателем задачи) по всему уравнению.
В итоге я должен получить простое уравнение, в котором я могу легко сравнить коэффициенты одинаковых членов с обеих сторон уравнения. В результате я получу систему линейных уравнений с переменными A и B, которую можно решить либо методом подстановки, либо методом исключения, в зависимости от того, что я предпочитаю.
- Выносим за скобки знаменатель.
- Создайте отдельные дроби с правой стороны, имея каждый из множителей в качестве знаменателя. У меня есть две частичные дроби с двумя неизвестными значениями числителей, представленных переменными A и B.
- Я хочу исключить все знаменатели. Это можно сделать, умножив обе части уравнения на \ color {blue} LCD = x \ left ({x + 1} \ right).
- Затем я распределяю ЖК-дисплей по каждой стороне уравнения. На этом этапе я стараюсь очень осторожно отслеживать процесс отмены. Я хочу убедиться, что сделаю этот шаг правильно, чтобы избежать ненужных головных болей в дальнейшем.

- Это упрощенное уравнение после правильного выполнения вышеуказанного шага.
- Теперь я умножу все и соберу общие термины, написав их рядом. Пришло время сравнить коэффициенты многочленов. Идея состоит в том, чтобы приравнять соответствующие коэффициенты при одинаковых членах.
- Я приравниваю коэффициенты члена x, выделенного желтым цветом. Кроме того, я приравниваю постоянные члены, как показано зеленым выделением.
- Затем я прихожу к решению двух уравнений с двумя неизвестными.Используйте метод подстановки, чтобы решить для B.
- Это окончательные значения переменных A и B.
- Вставьте решенные значения A и B обратно в исходную установку, чтобы получить окончательный ответ.
Пример 2: Найдите дробное разложение рационального выражения.
Эта задача аналогична примеру 1. Единственное отличие состоит в том, что множители знаменателя — это два линейных бинома.
- Я начинаю с вынесения трехчлена в знаменатель.
Затем я настраиваю частичное разложение на дроби, помещая A и B в качестве числителей. Два различных линейных фактора займут место знаменателей.
- Я хочу удалить все знаменатели, поэтому умножу обе части уравнения на ЖК-дисплей (синий).
- Мне нужно быть осторожным при отмене общих факторов.
- Приведенные здесь шаги в значительной степени являются частью процесса «очистки» и реорганизации общих терминов.
- Пришло время установить соответствие между двумя сторонами уравнения.
Для членов x коэффициенты \ left ({A + B} \ right) = 1, в то время как чистые числа у меня 3A + 5B = — 1.
- У нас есть два уравнения с двумя неизвестными. С этого момента с ним должно быть легко справиться, не так ли? Я предлагаю использовать метод исключения для решения относительно A и B.

Умножьте верхнее уравнение на — \, 3 или — \, 5, затем сложите их, чтобы исключить одну из переменных.
- Это правильные значения A и B.
- Я вернусь к исходной настройке дробных дробей, чтобы заменить значения A и B фактическими числами.
Пример 3: Найдите дробное разложение рационального выражения
В этой задаче знаменатель является произведением отдельного линейного множителя, который повторяется три раза и обозначается показателем 3. Не допускайте ошибки записи трех частичных дробей с общим знаменателем только \ left ({x — 1 } \верно).3}.
- Поскольку у меня есть повторяющийся линейный коэффициент \ left ({x — 1} \ right), возведенный в степень 3, мне нужно учитывать каждую степень, начиная с наименьшей (1) до наибольшей (3).
Вы понимаете, почему эта установка неверна?
Подсказка: Сложите дробные дроби и сравните их знаменатели.
- Удалите все знаменатели, распределив ЖК-дисплей в уравнении.
- Это упрощенная версия после отмены общих факторов.2 член слева. Это очень важный шаг.
- Теперь я могу четко выделить необходимые уравнения, которые будут использоваться для решения отсутствующих переменных.
Уравнение A = 0 — хороший подарок, так как мне не нужно беспокоиться о его алгебраическом решении.
- Используйте тот факт, что A = 0, подключите это ко второму уравнению \ left ({- 2A + B = 5} \ right), чтобы получить B. Наконец, решите относительно C, используя третье уравнение, используя решенные значения A и Б.
Вы получили такие же ответы?
- Запишите исходную схему разложения частичной дроби и замените решенные значения для A, B и C.
Дробь, числитель которой A = 0, исчезнет. Это оставляет нам две дроби в качестве окончательного ответа.
Пример 4: Найдите дробное разложение рационального выражения
Это тот случай, когда знаменатель является произведением различных линейных множителей, некоторые из которых повторяются.

Обратите внимание, что знаменатель этого рационального выражения состоит из двух различных линейных факторов. Первый множитель \ left ({x — 2} \ right) появляется один раз, а второй множитель \ left ({x — 3} \ right) появляется дважды, таким образом повторяется.
- У меня здесь два различных линейных фактора.
\ left ({x — 2} \ right) появляется один раз
\ left ({x — 3} \ right) появляется дважды и обозначается степенью 2
Поэтому я напишу \ left ({x — 2} \ right) в одной неполной фракции, а \ left ({x — 3} \ right) в двух неполных дробях с возрастанием степени от 1 до 2.
- Я исключу все знаменатели, умножив уравнение на соответствующий ЖК-дисплей.
- Опять же, я должен быть осторожен с моими отменами.2 семестр. Это означает, что я должен предоставить нулевых заполнителей для отсутствующего члена x и постоянного члена.
Таким образом, становится легко сравнивать коэффициенты при одинаковых членах в обеих частях уравнения.
Стрелки и цветовая кодировка должны направлять вас в этом процессе.
- Я могу решить эту проблему несколькими способами. Один из способов — использовать метод исключения, чтобы избавиться от C между 2-м и 3-м уравнениями.
Я умножу второе уравнение на 2, а затем добавлю это к третьему уравнению.Я должен получить уравнение, содержащее только A и B. Используйте это «новое» уравнение с 1-м уравнением, чтобы найти значения A и B. Я предлагаю вам попробовать его на бумаге, чтобы вы могли следовать ему.
Как только вы получите значения A и B, вы можете решить относительно C, используя либо 2-е, либо 3-е уравнение, используя обратную подстановку.
- Это правильные значения A, B и C.
- Подставьте значения в исходную настройку частичной дроби, чтобы получить окончательный ответ.
Пример 5: Найдите дробное разложение рационального выражения
Это еще один тип задач при разложении на частичные дроби.
 Разложив знаменатель на множители, я получу следующее.
Разложив знаменатель на множители, я получу следующее.Обратите внимание, что на этот раз у меня есть квадратичный множитель. Вопрос в том, могу ли я еще разложить это на линейные коэффициенты? Я могу попробовать, но очевидно, что уже нельзя исключить из . Фактически, это имеет специальное название неприводимая квадратичная .2 с левой стороны.
Обратите внимание на соответствие коэффициентов в обеих частях уравнения.
- Путем быстрого анализа я знаю, что C = 1 и A = -2.
Поскольку A + B = 0 и A = -2, \ left ({- 2} \ right) + B = 0 влечет B = 2.
- Это правильные значения A, B и C.
- Подставьте значения обратно в исходную настройку частичного разложения на дроби, и все готово!
Практика с рабочими листамиНеполные дроби
В этом разделе мы собираемся обсудить процесс разложения рационального выражения на суммы и разности более простых рациональных выражений.То есть мы хотим знать, какие термины добавляются, чтобы получить определенную долю. Этот процесс называется частичным разложением на фракции .Запись дроби в виде двух или более ТЕРМИНОВ иногда бывает полезна в исчислении. Хотя мы могли бы подождать, пока ваш класс исчисления обсудит эту тему, возможность, которая может найти широкую поддержку среди студентов алгебры колледжей, приложения caluclus больше ориентированы на использование этого процесса как шага в более крупном приложении, чем на обучении самому процессу.По этой причине мы представляем его здесь.
ОБРАЗЕЦ: Вот типичный вопрос:Мы ищем:
Полученные члены называются « частичное разложение на дробь », поскольку каждый член независимо составляет только часть дроби.
Каждый из примеров будет следовать одним и тем же четырем шагам.
ЧЕТЫРЕ ЭТАПА ЧАСТИЧНОГО РАЗЛОЖЕНИЯ
CHECK: Уменьшена ли дробь? Если нет, разделите общие факторы.
ШАГ 1: Напишите шаблон разложения на частичную дробь (см. Текст для объяснения).
ШАГ 2: Умножьте каждую часть уравнения на наименьший общий знаменатель.
ШАГ 3: Найдите неизвестные.
ШАГ 4: Напишите окончательный ответ на разложение на частичную дробь.
Из четырех шагов частичной декомпозиции шаг 3 требует больше всего времени. Мы поговорим о двух методах, которые помогут нам найти неизвестные. Эти два метода называются методом «ключевого числа», примерами 1 и 2, ниже) и «методом сравнения коэффициентов». В некоторых задачах наиболее эффективно использовать комбинацию двух методов (пример 3, ниже).
ПРИМЕР 1: Найдите дробное разложение
CHECK: Уменьшена ли дробь? Да. Между числителем и знаменателем нет общих множителей, а степень числителя меньше степени знаменателя.
ШАГ 1:
ШАГ 2: x + 11 = A (x — 5) + B (x + 3)
Поскольку уравнение в ШАГЕ 2 является тождественным, мы можем подставить любое значение вместо x, и левая часть будет равна правой.Поскольку мы пытаемся найти значения A и B, было бы в наших интересах выбрать значения x, которые делают множители (x — 5) и (x + 3) равными нулю.
Значения x = 5 и x = — 3 называются номерами ключей .
ШАГ 3: Используйте ключевые числа, чтобы найти неизвестные, которые будет легко найти.
если x = 5 если x = — 3 5 + 11 = А (5-5) + В (5 + 3) — 3 + 11 = А (- 3 — 5) + В (- 3 + 3) 16 = 8B 8 = — 8 А В = 2 А = -1 ПРИМЕР 2: Найдите дробное разложение
CHECK: Уменьшена ли дробь? Да.
 Между числителем и знаменателем нет общих множителей, а степень числителя меньше степени знаменателя.
Между числителем и знаменателем нет общих множителей, а степень числителя меньше степени знаменателя.Как и ранее в ПРИМЕРЕ 1, нам выгодно выбрать значения x, при которых множители (x — 1) и x равны нулю. Эти значения (критические значения): x = 1 и
x = 0.ШАГ 3: Используйте ключевые числа, чтобы найти неизвестные, которые будет легко найти.
Но нам все еще нужно найти значение для B.Мы еще раз вернемся к идентичности, определенной в ШАГЕ 2. Помните, поскольку уравнение в ШАГЕ 2 является тождеством, мы можем подставить любое значение для x, и левая часть будет равна правой. Я произвольно выберу x = 2 .если x = 1 если x = 0 1 + 2 + 7 = С (1) 7 = А (- 1) (- 1) С = 10 А = 7 ( 2 ) 2 + 2 ( 2 ) + 7 = A ( 2 — 1) 2 + B ( 2 ) ( 2 — 1) + C ( 2 )
15 = А + 2В + 2С
Но мы уже обнаружили, что C = 10 и A = 7, поэтому
15 = 7 + 2B + 2 (10)
В = — 6
Итак, дробное разложение данной дроби записывается следующим образом:
Сравнение коэффициентовВ некоторых задачах частичной декомпозиции количество неизвестных (A, B, C и т. Д.) больше, чем количество критических значений (или ключевых чисел). В этом случае мы можем объединить метод ключевого числа с методом, называемым сравнением коэффициентов, чтобы найти все неизвестные. Вот что мы подразумеваем под «сравнением коэффициентов».
Если квадратичный слева равен квадратичному справа, то 5 = a, 6 = b и 9 = c.
Формально мы говорим, что : если два многочлена равны, то соответствующие коэффициенты должны быть равны.. Это составляет основу метода, называемого «сравнение коэффициентов», который также можно использовать для поиска неизвестных в разложении на частичные дроби.
 Однако ВСЕГДА быстрее использовать все ключевые числа для поиска неизвестных, прежде чем использовать трудоемкий процесс решения системы уравнений, который часто требуется путем «сравнения коэффициентов». В примере 3 показан метод ключевых чисел в сочетании с «сравнением коэффициентов» для нахождения частичного разложения на дроби.
Однако ВСЕГДА быстрее использовать все ключевые числа для поиска неизвестных, прежде чем использовать трудоемкий процесс решения системы уравнений, который часто требуется путем «сравнения коэффициентов». В примере 3 показан метод ключевых чисел в сочетании с «сравнением коэффициентов» для нахождения частичного разложения на дроби.ПРИМЕР 3: Найдите дробное разложение
ШАГ 3: Единственный номер ключа — x = — 5. Обратите внимание: не существует НАСТОЯЩИХ чисел, которые делали бы (x 2 + 1) равным нулю, поэтому он не дает нам ключевых чисел.
3 (-5) 2 + 2 (-5) — 1 = A (25 + 1) + (-5 B + C) (-5 + 5)
64 = 26 А
А = (64/26) = (32/13)
Поскольку нам еще предстоит найти два неизвестных значения, перейдем к сравнению метода коэффициентов. Во-первых, мы переставляем идентичность на ШАГЕ 2, группируя похожие термины вместе.
3x 2 + 2x — 1 = Ax 2 + A + Bx 2 + 5Bx + Cx + 5C
3 x 2 + 2 x — 1 = ( A + B ) x 2 + ( 5B + C ) x + ( A + 5C )
Коэффициент x 2 слева ( 3 ) должен быть равен коэффициенту x 2 справа ( A + B )
Коэффициент x слева ( 2 ) должен быть равен коэффициент при x справа ( 5B + C )
Постоянный член слева ( — 1 ) должен равняться постоянному члену справа ( A + 5C )Даем нам систему уравнений:
A + B = 3
5B + C = 2
A + 5C = — 1Поскольку мы уже знаем, что A = (32/13), мы можем использовать A + B = 3, чтобы найти, что B = (7/13)
Мы также можем использовать A = (32/13) с A + 5C = — 1 чтобы найти, что C = (- 9/13)
Уравнение 5B + C = 2 можно использовать для проверки правильности расчета B и C:5 (7/13) + (- 9/13) = (26/13) = 2
Затем разложение на частичную дробь записывается следующим образом:
© 1999 Джо Стейг
.
- Собственные рациональные функции: Функции вида \ (\ frac {f (x)} {g (x)} \), где f (x) и g (x) — многочлены, а g (x) ≠ 0, называются рациональными функциями от x.




 Регулярно предлагаемые курсы посвящены литературным достижениям с эпохи сентиментализма в конце 18 века до наших дней. Учебники обычно посвящены важным областям интересов, которые не включены в более формализованные курсовые работы.
Регулярно предлагаемые курсы посвящены литературным достижениям с эпохи сентиментализма в конце 18 века до наших дней. Учебники обычно посвящены важным областям интересов, которые не включены в более формализованные курсовые работы.






 (
( (
( Соляная кислота (в стакане) взаимодействует с аммиаком
Соляная кислота (в стакане) взаимодействует с аммиаком






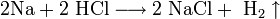
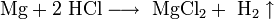
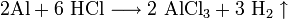
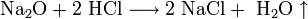
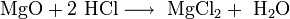
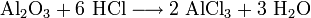
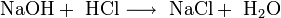
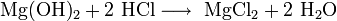
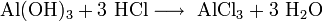
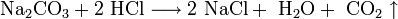
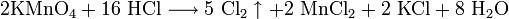


 Физические свойства
Физические свойства
 Применение
Применение Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика Всего их пять штук — ниже мы их рассмотрим.
Всего их пять штук — ниже мы их рассмотрим.
 Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Сокращение дробей при расчётах значительно облегчит вычисления.
Сокращение дробей при расчётах значительно облегчит вычисления. е. является тождеством.
е. является тождеством.
 1 = 329
1 = 329 y.
y. y». Далее наберите , например, 0,33. Для получения более точного результата, можно набрать более значение показателя степени, например, 0,333333333333. Чтобы получить точный результат, введите показатель степени «1/3» в скобках. То есть нажмите последовательно клавиши «(1/3)».
y». Далее наберите , например, 0,33. Для получения более точного результата, можно набрать более значение показателя степени, например, 0,333333333333. Чтобы получить точный результат, введите показатель степени «1/3» в скобках. То есть нажмите последовательно клавиши «(1/3)». Это можно записать так:
Это можно записать так:

 Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n
Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n Например, квадрат десятичной дроби 3,14 будет равен: 3,14² = 9,8596.
Например, квадрат десятичной дроби 3,14 будет равен: 3,14² = 9,8596. n )} = \frac{1}{ab} $$
n )} = \frac{1}{ab} $$ k}}} \), \ (k = 1,2,3, \ ldots \)
k}}} \), \ (k = 1,2,3, \ ldots \)  В частности, числители должны быть равны для \ (x = — 2 \) и \ (x = 3 \).Итак, давайте подключим их и посмотрим, что у нас получится.
В частности, числители должны быть равны для \ (x = — 2 \) и \ (x = 3 \).Итак, давайте подключим их и посмотрим, что у нас получится. 2} — 4x}} \, dx}} & = \ int {{- \ frac {1} {x} + \ frac {{\ frac {1} {2}}} {{x + 2}} + \ frac {{\ frac {5} {2}}} {{3x — 2}} \, dx}} \\ & = — \ ln \ left | х \ право | + \ frac {1} {2} \ ln \ left | {x + 2} \ right | + \ frac {5} {6} \ ln \ left | {3x — 2} \ right | + c \ end {align *} \]
2} — 4x}} \, dx}} & = \ int {{- \ frac {1} {x} + \ frac {{\ frac {1} {2}}} {{x + 2}} + \ frac {{\ frac {5} {2}}} {{3x — 2}} \, dx}} \\ & = — \ ln \ left | х \ право | + \ frac {1} {2} \ ln \ left | {x + 2} \ right | + \ frac {5} {6} \ ln \ left | {3x — 2} \ right | + c \ end {align *} \]
 .. почти слишком просто …
.. почти слишком просто …  ..
..


 потому что общий знаменатель между 2, 4 и 8 равен 8. Последствия этого для частичного
дробное разложение состоит в том, что когда у вас есть повторяющийся фактор (фактор с кратностью
кроме одного), вам необходимо включить коэффициент расширения для каждой возможной мощности.
потому что общий знаменатель между 2, 4 и 8 равен 8. Последствия этого для частичного
дробное разложение состоит в том, что когда у вас есть повторяющийся фактор (фактор с кратностью
кроме одного), вам необходимо включить коэффициент расширения для каждой возможной мощности. В этом случае хороши x = 4 и x = 0. «Хорошие» ценности будут
заставляют каждый член, кроме одного, выпадать из уравнения,
и поэтому вы сможете найти значение переменной очень
быстро.
В этом случае хороши x = 4 и x = 0. «Хорошие» ценности будут
заставляют каждый член, кроме одного, выпадать из уравнения,
и поэтому вы сможете найти значение переменной очень
быстро.


 Складывая второе и третье уравнения, исключаем \ (C \):
Складывая второе и третье уравнения, исключаем \ (C \):





 Разложив знаменатель на множители, я получу следующее.
Разложив знаменатель на множители, я получу следующее.
 Между числителем и знаменателем нет общих множителей, а степень числителя меньше степени знаменателя.
Между числителем и знаменателем нет общих множителей, а степень числителя меньше степени знаменателя. Однако ВСЕГДА быстрее использовать все ключевые числа для поиска неизвестных, прежде чем использовать трудоемкий процесс решения системы уравнений, который часто требуется путем «сравнения коэффициентов». В примере 3 показан метод ключевых чисел в сочетании с «сравнением коэффициентов» для нахождения частичного разложения на дроби.
Однако ВСЕГДА быстрее использовать все ключевые числа для поиска неизвестных, прежде чем использовать трудоемкий процесс решения системы уравнений, который часто требуется путем «сравнения коэффициентов». В примере 3 показан метод ключевых чисел в сочетании с «сравнением коэффициентов» для нахождения частичного разложения на дроби.




 Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.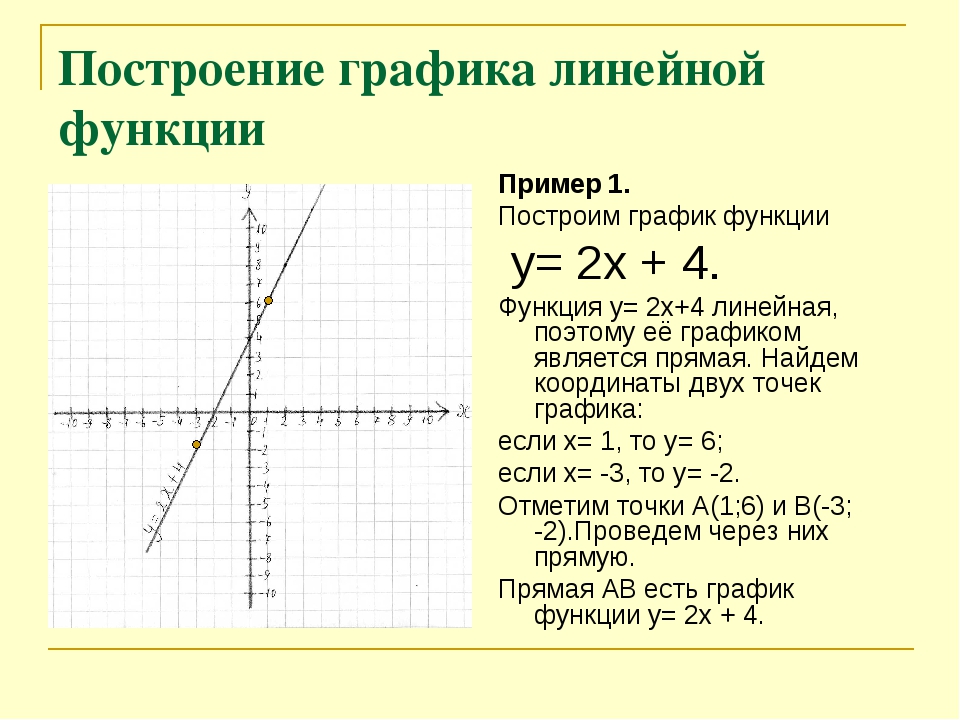 x1 ==26 + 2 21 2 x − 16 − 2 21№ 982. а) x2 − 5 x = 0 , если х ≥ 0, то x = x , имеем х2 – 5х = 0, х(х – 5) = 0,y1 =5 + 21,27 + 21⎛521 ⎞⎛521 ⎞y− +⎜⎜ y − −⎟⎜⎟⎟ = 0 ,⎟⎜2222⎝⎠⎝⎠y2 =х1 = 0, х2 = 5; если х < 0, то x = − x , имеем х2 + 5х = 0,х(х + 5) = 0, х1 = 0, х2 = -5; Ответ: -5; 0; 5;196www.gdz.pochta.ru3х2 + 4х = 0,б) 3x 2 + 4 x = 0 , при х ≥ 0 имеем4⎞44⎛x 2 + x = 0 , x ⎜ x + ⎟ = 0 , х1 = 0, x2 = − ,3⎠33⎝4x = − не удовлетворяет условию х ≥ 0, значит, не является корнем;344⎞4⎛при x < 0 имеем 3х2 – 4х = 0, x2 − x = 0 , x ⎜ x − ⎟ = 0 , х1 = 0, x2 = ,333⎝⎠4x = не удовлетворяет условию х < 0, значит, не является корнем;3Ответ: 0;в) 2 x 2 + x − 3x = 0 , при х ≥ 0 имеем 2х2 + х – 3х = 0,2х2 – 2х = 0, х(х – 1) = 0, х1 = 0, х2 = 1;при х < 0 имеем 2х2 – х – 3х = 0, 2х2 – 4х = 0,х2 – 2х = 0, х(х – 2) = 0, х1 = 0, х2 = 2, х = 2 не удовлетворяет условию x < 0,значит, не является корнем; Ответ: 0; 1;г) 4 x 2 − 3 x + x = 0 , при х ≥ 0 имеем 4х2 – 3х + х = 0,4х2 – 2х = 0, 2х2 – х = 0, х(2х – 1) = 0, х1 = 0, х2 = 0,5;при х < 0 имеем 4х2 + 3х +х = 0, х2 + х = 0, х(х + 1) = 0, х1 = 0, х2 = -1;Ответ: -1; 0; 0,5.№ 983.а) 4 x 2 +xx= 0 , при х ≥ 0 имеем 4 x 2 + = 0 ,xx4х2 + 1 = 0, 4х2 = -1 нет корней;при х < 0 имеем4 x2 +x1= 0 , 4х2 – 1 = 0, x2 = , х1,2 = ±0,5,4−xх = 0,5 – не удовлетворяет условию x < 0, значит, не является корнем;Ответ: — 0,5;б) x2 −3x23x 2=0,= 0 , при х ≥ 0 имеем x2 −xxх2 – 3х = 0, х(х – 3) = 0, х1 = 0, х2 = 3;х = 0 не входит в ОДЗ уравнения;при х < 0 имеем х2 + 3х = 0, х(х + 3) = 0, х1 = 0, х2 = -3; Ответ: ±3;в) x2 −4xx= 0 , при х ≥ 0 имеем x 2 −4x= 0 , х2 – 4 = 0, х = ±2,xх = -2 – не удовлетворяет условию х ≥ 0, значит, не является корнем;при х < 0 имеем х2 + 4 = 0, х2 = -4 нет корней; Ответ: 2;г) 2 x 2 +x2 +x2x= 0 , при х ≥ 0 имеем 2 x 2 + = 0 ,2×21⎞x⎛= 0 , x ⎜ x + ⎟ = 0 , х1 = 0,4⎠4⎝x2 = −1,4197www.gdz.pochta.ruх=0 не корень, т.к.
x1 ==26 + 2 21 2 x − 16 − 2 21№ 982. а) x2 − 5 x = 0 , если х ≥ 0, то x = x , имеем х2 – 5х = 0, х(х – 5) = 0,y1 =5 + 21,27 + 21⎛521 ⎞⎛521 ⎞y− +⎜⎜ y − −⎟⎜⎟⎟ = 0 ,⎟⎜2222⎝⎠⎝⎠y2 =х1 = 0, х2 = 5; если х < 0, то x = − x , имеем х2 + 5х = 0,х(х + 5) = 0, х1 = 0, х2 = -5; Ответ: -5; 0; 5;196www.gdz.pochta.ru3х2 + 4х = 0,б) 3x 2 + 4 x = 0 , при х ≥ 0 имеем4⎞44⎛x 2 + x = 0 , x ⎜ x + ⎟ = 0 , х1 = 0, x2 = − ,3⎠33⎝4x = − не удовлетворяет условию х ≥ 0, значит, не является корнем;344⎞4⎛при x < 0 имеем 3х2 – 4х = 0, x2 − x = 0 , x ⎜ x − ⎟ = 0 , х1 = 0, x2 = ,333⎝⎠4x = не удовлетворяет условию х < 0, значит, не является корнем;3Ответ: 0;в) 2 x 2 + x − 3x = 0 , при х ≥ 0 имеем 2х2 + х – 3х = 0,2х2 – 2х = 0, х(х – 1) = 0, х1 = 0, х2 = 1;при х < 0 имеем 2х2 – х – 3х = 0, 2х2 – 4х = 0,х2 – 2х = 0, х(х – 2) = 0, х1 = 0, х2 = 2, х = 2 не удовлетворяет условию x < 0,значит, не является корнем; Ответ: 0; 1;г) 4 x 2 − 3 x + x = 0 , при х ≥ 0 имеем 4х2 – 3х + х = 0,4х2 – 2х = 0, 2х2 – х = 0, х(2х – 1) = 0, х1 = 0, х2 = 0,5;при х < 0 имеем 4х2 + 3х +х = 0, х2 + х = 0, х(х + 1) = 0, х1 = 0, х2 = -1;Ответ: -1; 0; 0,5.№ 983.а) 4 x 2 +xx= 0 , при х ≥ 0 имеем 4 x 2 + = 0 ,xx4х2 + 1 = 0, 4х2 = -1 нет корней;при х < 0 имеем4 x2 +x1= 0 , 4х2 – 1 = 0, x2 = , х1,2 = ±0,5,4−xх = 0,5 – не удовлетворяет условию x < 0, значит, не является корнем;Ответ: — 0,5;б) x2 −3x23x 2=0,= 0 , при х ≥ 0 имеем x2 −xxх2 – 3х = 0, х(х – 3) = 0, х1 = 0, х2 = 3;х = 0 не входит в ОДЗ уравнения;при х < 0 имеем х2 + 3х = 0, х(х + 3) = 0, х1 = 0, х2 = -3; Ответ: ±3;в) x2 −4xx= 0 , при х ≥ 0 имеем x 2 −4x= 0 , х2 – 4 = 0, х = ±2,xх = -2 – не удовлетворяет условию х ≥ 0, значит, не является корнем;при х < 0 имеем х2 + 4 = 0, х2 = -4 нет корней; Ответ: 2;г) 2 x 2 +x2 +x2x= 0 , при х ≥ 0 имеем 2 x 2 + = 0 ,2×21⎞x⎛= 0 , x ⎜ x + ⎟ = 0 , х1 = 0,4⎠4⎝x2 = −1,4197www.gdz.pochta.ruх=0 не корень, т.к. §31. Формулы корней квадратного уравнения№ 984. а) х2 + 5х – 6 = 0, a = 1, b = 5, c = -6, D = b2 – 4ac = 25 + 4⋅6 = 49;б) x2 – 1,3x + 2 = 0, a = 1, b = -1,3, c = 2, D = b2 – 4ac = 1,69 — 4⋅2 = -6,31;в) х2 – 2,4х + 1 = 0, а = 1, b = -2,.4, с = 1, D = b2 – 4ac = 5,76 – 4 = 1,76;г) х2 – 7х – 4 = 0, a = 1, b = -7, c = -4, D = b2 – 4ac = 49 + 16 = 65.№ 985. а) 3х2 + 2х – 1 = 0, a = 3, b = 2, c = -1, D = b2 – 4ac = 4 + 4⋅3 = 16;б) -х2 + 4х + 3 = 0, a = -1, b = 4, c = 3, D = b2 – 4ac = 16 + 4⋅3 = 28;в) -2х2 + 5х + 3 = 0, a = -2, b = 5, c = 3, D = b2 – 4ac = 25 + 4⋅2⋅3 = 49;г) 4х2 – 5х – 4 = 0, a = 4, b = -5, c = -4, D = b2 – 4ac = 25 + 4⋅4⋅4 = 89.№ 986.
§31. Формулы корней квадратного уравнения№ 984. а) х2 + 5х – 6 = 0, a = 1, b = 5, c = -6, D = b2 – 4ac = 25 + 4⋅6 = 49;б) x2 – 1,3x + 2 = 0, a = 1, b = -1,3, c = 2, D = b2 – 4ac = 1,69 — 4⋅2 = -6,31;в) х2 – 2,4х + 1 = 0, а = 1, b = -2,.4, с = 1, D = b2 – 4ac = 5,76 – 4 = 1,76;г) х2 – 7х – 4 = 0, a = 1, b = -7, c = -4, D = b2 – 4ac = 49 + 16 = 65.№ 985. а) 3х2 + 2х – 1 = 0, a = 3, b = 2, c = -1, D = b2 – 4ac = 4 + 4⋅3 = 16;б) -х2 + 4х + 3 = 0, a = -1, b = 4, c = 3, D = b2 – 4ac = 16 + 4⋅3 = 28;в) -2х2 + 5х + 3 = 0, a = -2, b = 5, c = 3, D = b2 – 4ac = 25 + 4⋅2⋅3 = 49;г) 4х2 – 5х – 4 = 0, a = 4, b = -5, c = -4, D = b2 – 4ac = 25 + 4⋅4⋅4 = 89.№ 986. 28287№ 991. а) 4х2 + 10х – 6 = 0, 2х2 + 5х – 3 = 0, D = 25 + 4⋅2⋅3 = 49 > 0, значит,x1 =−5 + 7 1−5 − 7= , x2 == −3 ;42410= −0, 2 ;2 ⋅ 258+ 228−2= 1 , x2 ==1;в) 3х2–8х + 5 = 0, D = 64 — 4⋅3⋅5 = 4 > 0, значит, x1 =636б) 25х2 + 10х + 1 = 0, D = 100 — 4⋅25 = 0, значит, x = −г) 4х2 + х + 67 = 0, D = 1 — 4⋅4⋅67 < 0, значит, нет корней.№ 992. а) 3х2 + 32х + 80 = 0, D = 1024 — 4⋅3⋅80 = 64 > 0, значит,x1 =−32 + 8−32 − 8202= −4 , x ==−= −6 ;6633б) 100х2 – 160х + 63 = 0, D = 25600 — 4⋅100⋅63 = 400 > 0, значит,x1 =160 + 20160 − 20= 0,9 , x2 == 0,7 ;200200в) 5х2 + 26х – 24 = 0, D = 676 + 4⋅5⋅24 = 1156 > 0, значит,x1 =−26 + 34−26 − 34= 0,8 , x2 == −6 ;1010г) 4х2 – 12х + 9 = 0, D = 144 — 4⋅4⋅9 = 0, значит, x =12= 1,5 .8№ 993.а) х2 = 2х + 48, х2 – 2х – 48 = 0, D = 4 + 4⋅48 = 196 > 0, значит,x1 =2 + 142 − 14= 8 , x2 == −6 ;22б) 6х2 + 7х = 5, 6х2 + 7х – 5 = 0, D = 49 + 4⋅6⋅5 = 169 > 0, значит,x1 =−7 + 13−7 − 132= 0,5 , x2 == −1 ;12123в) х2 = 4х + 96, х2 – 4х – 96 = 0, D = 16 + 4⋅96 = 400 > 0, значит,199www.gdz.pochta.rux1 =4 + 204 − 20= −8 ;= 12 , x2 =32г) 2х2 – 2 = 3х, 2х2 – 3х – 2 = 0, D = 9 + 4⋅2⋅2 = 25 > 0, значит,x2 =3+ 53−5= −0,5 .= 2 , x2 =44№ 994.
28287№ 991. а) 4х2 + 10х – 6 = 0, 2х2 + 5х – 3 = 0, D = 25 + 4⋅2⋅3 = 49 > 0, значит,x1 =−5 + 7 1−5 − 7= , x2 == −3 ;42410= −0, 2 ;2 ⋅ 258+ 228−2= 1 , x2 ==1;в) 3х2–8х + 5 = 0, D = 64 — 4⋅3⋅5 = 4 > 0, значит, x1 =636б) 25х2 + 10х + 1 = 0, D = 100 — 4⋅25 = 0, значит, x = −г) 4х2 + х + 67 = 0, D = 1 — 4⋅4⋅67 < 0, значит, нет корней.№ 992. а) 3х2 + 32х + 80 = 0, D = 1024 — 4⋅3⋅80 = 64 > 0, значит,x1 =−32 + 8−32 − 8202= −4 , x ==−= −6 ;6633б) 100х2 – 160х + 63 = 0, D = 25600 — 4⋅100⋅63 = 400 > 0, значит,x1 =160 + 20160 − 20= 0,9 , x2 == 0,7 ;200200в) 5х2 + 26х – 24 = 0, D = 676 + 4⋅5⋅24 = 1156 > 0, значит,x1 =−26 + 34−26 − 34= 0,8 , x2 == −6 ;1010г) 4х2 – 12х + 9 = 0, D = 144 — 4⋅4⋅9 = 0, значит, x =12= 1,5 .8№ 993.а) х2 = 2х + 48, х2 – 2х – 48 = 0, D = 4 + 4⋅48 = 196 > 0, значит,x1 =2 + 142 − 14= 8 , x2 == −6 ;22б) 6х2 + 7х = 5, 6х2 + 7х – 5 = 0, D = 49 + 4⋅6⋅5 = 169 > 0, значит,x1 =−7 + 13−7 − 132= 0,5 , x2 == −1 ;12123в) х2 = 4х + 96, х2 – 4х – 96 = 0, D = 16 + 4⋅96 = 400 > 0, значит,199www.gdz.pochta.rux1 =4 + 204 − 20= −8 ;= 12 , x2 =32г) 2х2 – 2 = 3х, 2х2 – 3х – 2 = 0, D = 9 + 4⋅2⋅2 = 25 > 0, значит,x2 =3+ 53−5= −0,5 .= 2 , x2 =44№ 994. 442№ 997.а) 0,6х2 + 0,8х – 7,8 = 0, 6х2 + 8х – 78 = 0, 3х2 + 4х – 39 = 0,D = 16 + 4⋅3⋅39 = 484 > 0, значит, x1 =200−4 + 22−4 − 22131= 3 , x2 == − = −4 ;6633www.gdz.pochta.ruб) 0,25х2 – х + 1 = 0, 25х2 – 100х + 100 = 0, х2 – 4х + 4 = 0,D = 16 — 4⋅4 = 0, значит, x =4=2;2в) 0,2х2 – 10х + 125 = 0, 2х2 – 100х + 1250 = 0, х2 – 50х + 625 = 0,D = 2500 — 4⋅625 = 0, значит, x =50= 25 ;2г) 4х2 – 7х – 7,5 = 0, 8х2 – 14х – 15 = 0, D = 106 + 4⋅8⋅15 = 676 > 0, значит,x1 =14 + 2614 − 26= 2,5 , x2 == −0,75 .1616№ 998.
442№ 997.а) 0,6х2 + 0,8х – 7,8 = 0, 6х2 + 8х – 78 = 0, 3х2 + 4х – 39 = 0,D = 16 + 4⋅3⋅39 = 484 > 0, значит, x1 =200−4 + 22−4 − 22131= 3 , x2 == − = −4 ;6633www.gdz.pochta.ruб) 0,25х2 – х + 1 = 0, 25х2 – 100х + 100 = 0, х2 – 4х + 4 = 0,D = 16 — 4⋅4 = 0, значит, x =4=2;2в) 0,2х2 – 10х + 125 = 0, 2х2 – 100х + 1250 = 0, х2 – 50х + 625 = 0,D = 2500 — 4⋅625 = 0, значит, x =50= 25 ;2г) 4х2 – 7х – 7,5 = 0, 8х2 – 14х – 15 = 0, D = 106 + 4⋅8⋅15 = 676 > 0, значит,x1 =14 + 2614 − 26= 2,5 , x2 == −0,75 .1616№ 998. 201www.gdz.pochta.ru№ 1002.I этап: Пустьх – искомое натуральное число, тогда х2 – его квадрат или х + 56.Уравнение: х2 = х + 56.II этап: х2 – х – 56 = 0, D = 1 + 4⋅45 = 225, x1 =1 + 15= 8 , x2 = -7.2III этап: х2 = –7 – не удовлетворяет условию задачи.Так что искомое число 8.
201www.gdz.pochta.ru№ 1002.I этап: Пустьх – искомое натуральное число, тогда х2 – его квадрат или х + 56.Уравнение: х2 = х + 56.II этап: х2 – х – 56 = 0, D = 1 + 4⋅45 = 225, x1 =1 + 15= 8 , x2 = -7.2III этап: х2 = –7 – не удовлетворяет условию задачи.Так что искомое число 8. Найдите площадь фигуры, ограниченной
графиком функции у=3-х2 и прямой у=2х
Найдите площадь фигуры, ограниченной
графиком функции у=3-х2 и прямой у=2х Вычислите площадь фигуры, ограниченной графиком
данной функции, этой касательной и осью ординат.
Вычислите площадь фигуры, ограниченной графиком
данной функции, этой касательной и осью ординат. Вычислите площадь фигуры, ограниченной графиком данной функции,
найденной касательной и прямой х=2
Вычислите площадь фигуры, ограниченной графиком данной функции,
найденной касательной и прямой х=2 Найдите площадь фигуры, ограниченной
линиями х [у]=3, х=1, х=2
Найдите площадь фигуры, ограниченной
линиями х [у]=3, х=1, х=2
 Найдите площадь фигуры, ограниченной
графиком функции у=х2+6х+9 и касательными к этому графику,
проходящими через начало координат.
Найдите площадь фигуры, ограниченной
графиком функции у=х2+6х+9 и касательными к этому графику,
проходящими через начало координат.


 В какой точке отрезка [–8; –4] функция f(x) принимает наименьшее значение.
В какой точке отрезка [–8; –4] функция f(x) принимает наименьшее значение.




 Найдите с .
Найдите с .





 Тесты по русскому языку.Пройти >>
Тесты по русскому языку.Пройти >>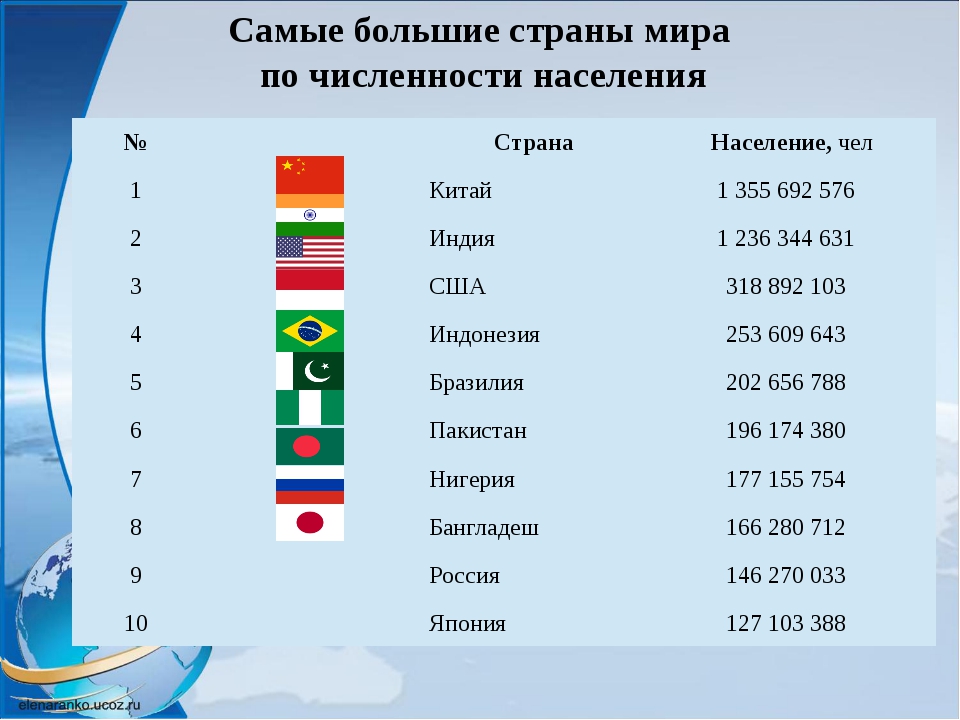 Данные о населении из всех источников оцениваются на предмет полноты, точности и последовательности и при необходимости корректируются.
Данные о населении из всех источников оцениваются на предмет полноты, точности и последовательности и при необходимости корректируются.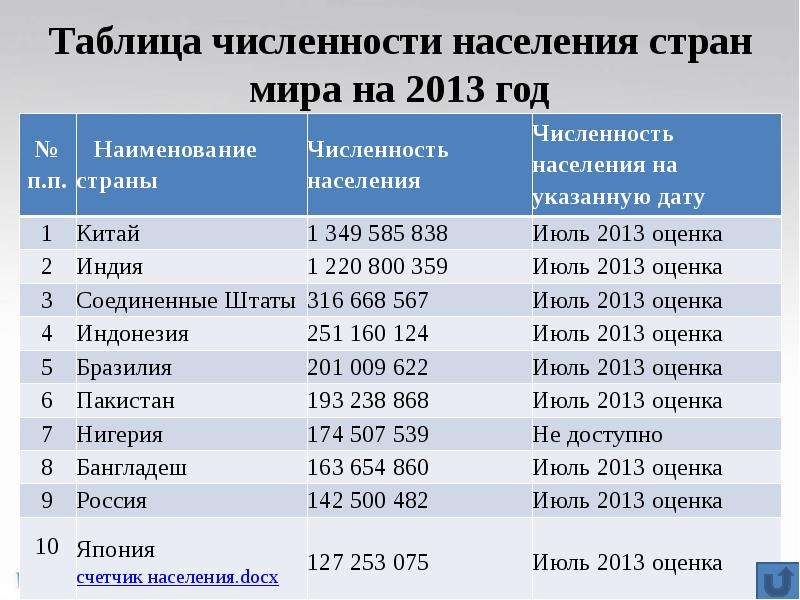 На эти две страны приходятся, соответственно, 19 и 18 процентов мирового населения. Ожидается, что примерно к 2024 году по числу жителей Индия обойдет Китай.
На эти две страны приходятся, соответственно, 19 и 18 процентов мирового населения. Ожидается, что примерно к 2024 году по числу жителей Индия обойдет Китай.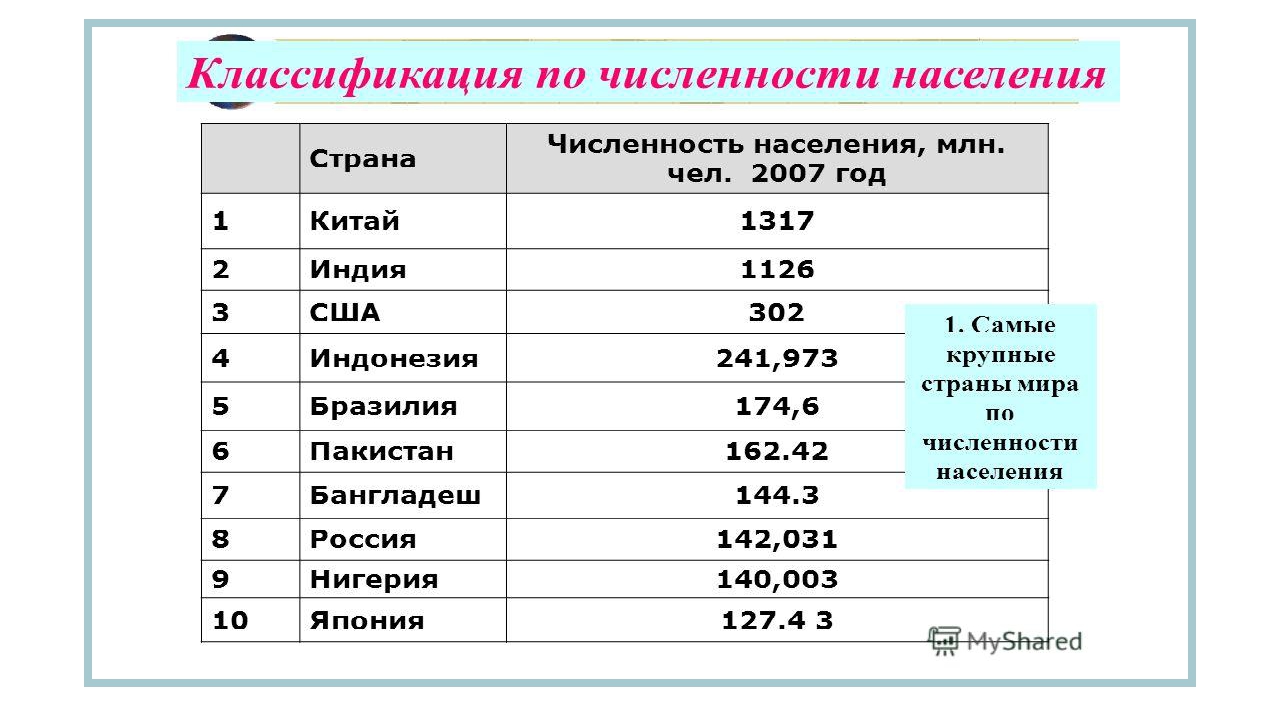 В этой группе — Россия
В этой группе — Россия К такому выводу пришли ученые из Института показателей и оценки здоровья при Медицинской школе Университета Вашингтона в Сиэтле. Исследование опубликовал научный журнал The Lancet.
К такому выводу пришли ученые из Института показателей и оценки здоровья при Медицинской школе Университета Вашингтона в Сиэтле. Исследование опубликовал научный журнал The Lancet. Доля населения мира, живущего в условиях крайней нищеты, к 2015 году снизилась до 10 процентов, но темпы сокращения крайней нищеты замедлились, 19 сентября предупредил Всемирный банк.
Доля населения мира, живущего в условиях крайней нищеты, к 2015 году снизилась до 10 процентов, но темпы сокращения крайней нищеты замедлились, 19 сентября предупредил Всемирный банк. Доклад также предупреждает, что самые слабые данные, необходимые для оценки всеобщего процветания, предоставляются теми странами, которым в большей степени требуется улучшение. Только одна из четырех стран с низким уровнем доходов и четыре из 35 признанных нестабильными и затронутых конфликтами государств может предоставить данные, необходимые для оценки всеобщего процветания, в течение определенного периода времени.
Доклад также предупреждает, что самые слабые данные, необходимые для оценки всеобщего процветания, предоставляются теми странами, которым в большей степени требуется улучшение. Только одна из четырех стран с низким уровнем доходов и четыре из 35 признанных нестабильными и затронутых конфликтами государств может предоставить данные, необходимые для оценки всеобщего процветания, в течение определенного периода времени.
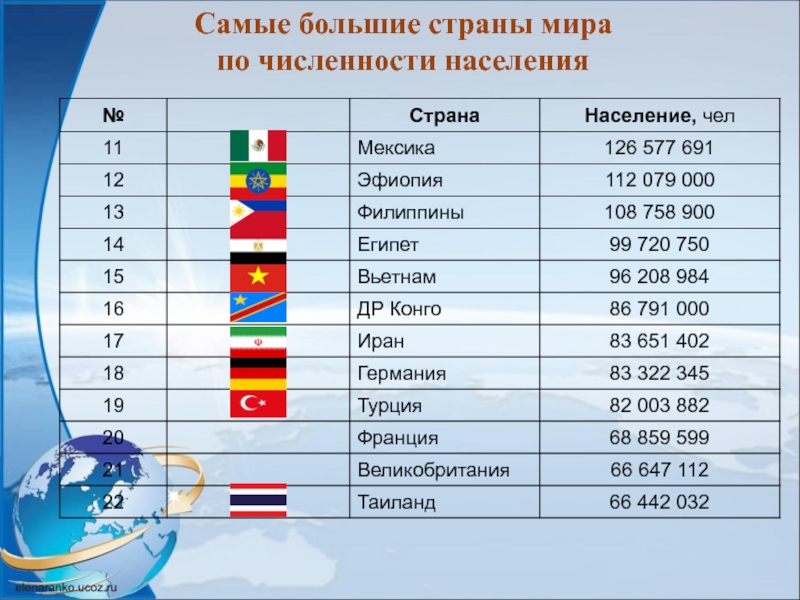
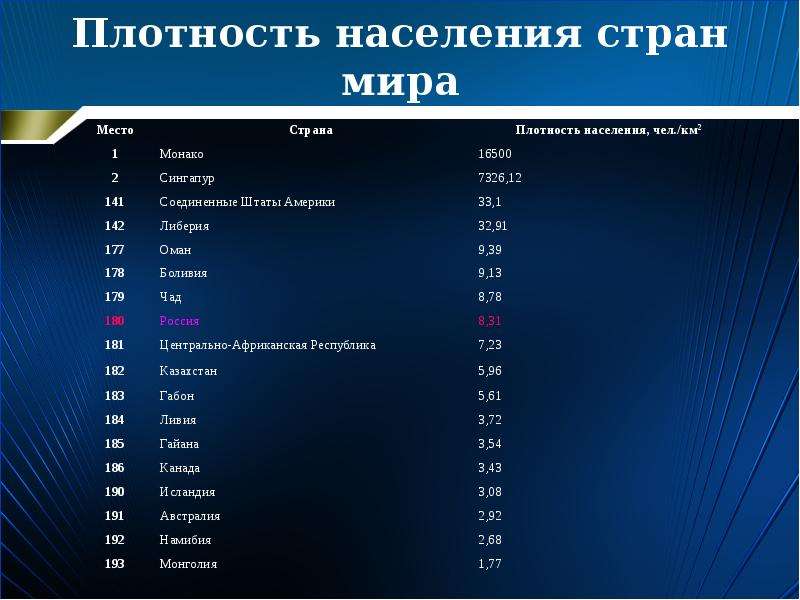


 За последние пять лет десятки миллионов человек пополнили ряды хронически недоедающих, а проблема неполноценного питания в его многочисленных формах остается актуальной для всех стран мира.
За последние пять лет десятки миллионов человек пополнили ряды хронически недоедающих, а проблема неполноценного питания в его многочисленных формах остается актуальной для всех стран мира. Тем не менее тенденция остается неизменной. Анализ всей серии документов по проблематике голода в мире начиная с 2000 года приводит к однозначному выводу: количество хронически голодающих, постоянно снижавшееся на протяжении десятилетий, в 2014 году начало медленно расти и сегодня продолжает свой рост.
Тем не менее тенденция остается неизменной. Анализ всей серии документов по проблематике голода в мире начиная с 2000 года приводит к однозначному выводу: количество хронически голодающих, постоянно снижавшееся на протяжении десятилетий, в 2014 году начало медленно расти и сегодня продолжает свой рост.
 Согласно приводящимся в докладе расчетам, такой переход позволил бы практически полностью нивелировать обусловленные нездоровым рационом питания расходы в сфере здравоохранения, которые, по прогнозам, в 2030 году достигнут 1,3 трлн долл. США в год, и почти на три четверти сократить связанные с рационом социальные издержек в виде выбросов парниковых газов, которые к 2030 году могут составить 1,7 трлн долл. США в год[iv].
Согласно приводящимся в докладе расчетам, такой переход позволил бы практически полностью нивелировать обусловленные нездоровым рационом питания расходы в сфере здравоохранения, которые, по прогнозам, в 2030 году достигнут 1,3 трлн долл. США в год, и почти на три четверти сократить связанные с рационом социальные издержек в виде выбросов парниковых газов, которые к 2030 году могут составить 1,7 трлн долл. США в год[iv].

 Отдел народонаселения.
Отдел народонаселения.











