Плагин комментариев – Отключить комментарии WordPress (Закрыть, Включить, Удалить комментарии) — Плагин для WordPress
Плагины комментариев WordPress — 8 лучших модулей

Привет друзья! Давненько я не писал статьи про создание и настройку блога. Постепенно буду исправляться, поэтому сегодня вам расскажу о том, какие плагины комментариев на wordpress необходимо использовать, чтобы улучшить комментирование блога.
Приведу пример тех модулей, которые были употреблены ранее и которые используются по сей день на блоге seoslim.ru.
Последние новости…
Новость 1. Много времени уделяю своему новому увлечению в сети, которое связано с созданием сайтов (сателлитов) предназначенных для заработка в бирже ссылок Sape, каждый день изучаю горы информации и провожу собственные эксперименты.
Как появятся первые результаты, обязательно об этом напишу, главное не пропустите.
Новость 2. В разделе «Услуги» я сделал очередное обновление. Теперь все желающие могут заказать за копейки анализ сайтов на ТРАСТ и СПАМ. Эта услуга пригодится тем, кто хочет покупать качественные ссылки с других площадок.
Роль комментариев на сайте
Прежде чем продолжить давайте зайдем к вопросу комментирования издалека, скажите все ли вы делаете, чтобы на ваших площадках активно дискутировали посетители, обсуждаю статью и задавая вопросы по ней? Лично я все стараюсь для этого делать, ведь здесь одни только плюсы:
— поведенческие факторы улучшаются;
— позиции сайта растут;
— трафик увеличивается;
— заработок становится больше.
Как-то я уже поднимал противоположную тему «Как убрать комментарии на wordpress» советую прочитать эту статью, где рассказал, как в настройках блога выключить данную функцию.
Конечно, так делать нужно тем, кто создает одностраничники, для продажи товаров или услуг, а также подойдет тем, у кого сайты, созданные для рекламы.

Зато тем, у кого блоги, комментирование обязательно должно быть и вы все должны сделать, чтобы посетители, как можно больше оставляли сообщений.
Подумайте сами, как читатели будут высказывать свое мнение по поводу ваших статей, как смогут похвалить автора или задать собственный вопрос? Для этого и существует специальная форма, расположенная обычно после всех постов.
Лично я заметил, что комментарии хорошо влияют на личностный рост любого блоггера. Когда автор пишет полезный и интересный материал, удовлетворяющий всем потребностям его аудитории, то его будут только благодарить за работу, в результате чего самооценка становится выше «плинтуса», а уверенность в себе только растет.
Теперь посмотрите обратную сторону, когда автора начинают ругать или критиковать. В таком случае можно сделать вывод, что в следующий раз нужно изменить подачу материала и не допускать подобных ошибок.
Делая вывод можно сказать, что комментирование сайтов дополняет статьи, помогает их обновлению и налаживает связь между автором и посетителями.
Например, когда я захожу на любой понравившийся блог и вижу под анонсами статей количество оставленных сообщений равное 0, понимаю что это мертвый блог, у которого пока еще нет своей аудитории, и мне такие статьи не очень интересно читать.
Подборка плагинов для комментирования wordpress сайтов
Далее я расскажу все фишки, которые помогут посетителям охотнее высказывать свое мнение на счет ваших статей, ведь нередко для этого их приходится подтолкнуть.
Russify Comments Number — этот плагин склоняет слово «комментарий» по всем правилам русского языка. Например, «19 комментариев», «3 комментария» и так далее.
Скачиваем модуль, далее его нужно установить и активировать, больше никаких настроек делать не нужно.
TinyMCEComments — данный плагин добавляет в форме для оставления сообщений визуальный редактор, который позволяет выделять текст жирным, курсивом, оставлять ссылки и т.д.
Плагин можете скачать здесь. Как и предыдущий плагин кроме активации больше ничего делать не нужно. Этот модуль я больше не использую, потому что моя тема wordpress с ним конфликтует и выдает ошибку.
Qip Smiles — плагин позволяет добавлять в комментарии различные смайлики. Рекомендую прочитать статью по установке и настройке смайлов «Устанавливаем смайлы на сайте с плагином и без».
Сейчас я вывожу смайлики без этого плагина, так как забочусь о скорости загрузки блога и удобства посетителей.
Highlight Author Comments — плагин, позволяющий выделять высказывания автора другим цветом. Очень удобно посетителям искать ответы автора на их вопросы.
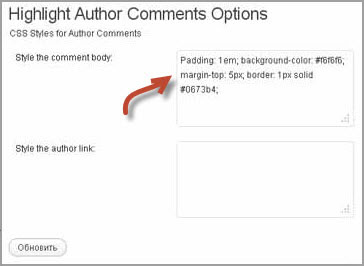
Скачать плагин можно по этой ссылке. После установки нужно будет перейти в настройки плагина и задать в отдельном окне цвет фона, размер шрифта, отступы и рамку.
Недавно в статье «Оформление комментариев автора» я этот плагин заменил PHP кодом, чтобы не создавать лишнюю нагрузку на блог.
Easy Gravatar — этот плагин позволяет выводить в комментариях аватарки. Лично я им не пользовался, так как в мою тему wordpress эта функция встроена автоматически. Скачать его можно вот здесь.
Мне только пришлось прикрепить к почтовому ящику свою аватарку, для того чтобы она отображалась в отзывах на всех ресурсах. Как это сделать можете узнать из статьи «Как создать аватар в комментариях на всех сайтах».
Subscribe to comments — плагин позволяет посетителям подписываться на сообщения к статьям. Рекомендую его к установке всем.

После установки и активации нужно перейти в раздел настроек и отредактировать поля «От», указав имя и адрес отправителя уведомлений.
Comment Redirect + Exclude Pages from Navigation — этот два плагина wordpress, работающие в паре. Первый перенаправляет посетителя оставившего первый комментарий вот на такую страницу. А второй запрещаете показа этой страницы в разделе меню блога и в карте сайта.
Скачать Comment Redirect можете по этой ссылке. После установки и активации создаете обычную страницу, в которой будите благодарить посетителей за первый отзыв к посту.
Далее переходите в настройки плагина и выбираете из выпадающего списка ту страницу, на которую и будет перенаправляться посетитель.

Для того чтобы эта страница не была видна другим пользователям в карте блога, а также в меню, необходимо установить плагин Exclude Pages from Navigation. Скачать его можете здесь.
После установки и активации вы должны обратить внимание, что теперь при создании или редактировании любой страницы появится вот такой виджет.
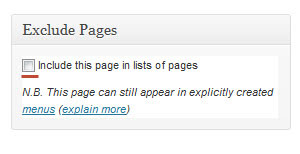
Теперь если вы снимите галочку в форме «Exclude Pages», тогда эта страница не будет отображаться в меню навигации. Таким образом, можно исключать любые страницы. Очень подробно, как сделать страницу «Спасибо за комментарий» читайте по ссылке.
Плагин комментариев Вконтакте для WordPress
Для того чтобы установить связь с посетителями по максимум можно использовать в качестве формы комментариев виджет от Вконтакте. Посмотрите, как это реализовано у меня перед основной формой комментирования.
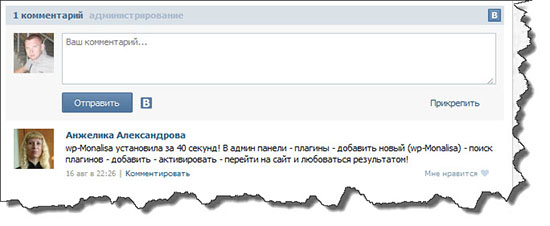
Плюсы:
- Простота в установке.
- Удобное редактирование комментариев.
- Защита от спама.
Минусы:
- Комментарии публикуются без модерации админом.
- Не индексируются ПС, так как хранятся на сервисе Вконтакте.
Более подробно о том, как установить и настроить виджет комментариев Вконтакте на wordpress я рассказал в этой статье.
Ну и в заключении хотелось бы вам еще сказать об одном способе, который подталкивает посетителя, чтобы тот высказал свое мнение — это МОТИВАЦИЯ.
Для этого мною было создано:
Признание. В сайдбаре у меня есть виджет, в котором располагаются лучшие комментаторы за месяц со ссылкой на их ресурс.
Это хороший способ комментирующему привлечь к себе внимание и трафик, так как посещаемость у меня большая, и каждый посетитель видит этот топ.
Конкурс. Например, я раз в месяц награждаю самого активного посетителя денежным призом.
Более подробно об этом я рассказывал в статье «Правила комментирования + КОНКУРС».
В очередной раз побеждает Надежда Суптеля (uspehmoney.ru). Прошу вас прислать мне на почту свои реквизиты WMR для вручения денежного приза.
Подарок. Все те, кто оставляет первый комментарий получают от меня специальный подарок в виде классной книги. Скачать ее можно только на странице «Спасибо за первый комментарий на блоге!», на которую посетитель автоматически перенаправляется после оставленного отзыва.
Я не заставляю повторять вас за мной. Вы можете придумать какие-то свои фишки, заставляющие людей активно комментировать ваши посты, будьте оригинальными.
На этом у меня все. Буду признателен, если вы понажимаете на кнопки социальных сетей под статьей и расскажите, какими способами вы заставляете своих посетителей охотней высказывать мнение. Жду ваших комментариев. Пока!
Вывод комментариев в виджете | WordPress.org Русский
O(@perdyllo)
чтобы после автора выводился текст комментария. Для этого нужно скачивать плагин?
Именно так
https://ru.wordpress.org/plugins/search/Comments+Widget/
Понял. Спасибо. Буду выбирать плагин.
O(@perdyllo)
Долго выбирать не придётся. Первый же по этому запросу и судя по описанию похоже то, что вам надо. Хотя конечно он не единственный среди себе подобных.
https://ru.wordpress.org/plugins/comments-widget-plus/
Да, спасибо за рекомендацию. Установил Comments Widget Plus. Все функции для виджета последних комментариев в нем есть.
Только не пойму, как можно изменить стили в виджете? Мне нужно, чтобы текст комментария в виджете был не #787878, а #000000 . В каком файле нужно править?
Спасибо заранее!
Модератор SeVlad(@sevlad)
wp.me/3YHjQ
Только не пойму, как можно изменить стили в виджете?
В стилях дочерней темы или кастомайзере (внешний вид-настроить) — доп. стили.
Только это уже другой вопрос. См правила форума, п2.
Всё, понял, не буду нарушать правила!
Плагины для комментариев WordPress | Сайт с нуля
Если вы создали собственный блог, неважно какой тематики, то помимо полезных материалов, размещаемых на ресурсе, вам еще нужно подумать об удобстве пользователей. В этой статье рассмотрим плагины для комментариев WordPress которые можно было бы использовать вместо стандартной, не всегда удобной системы комментирования.
Disqus
В последние несколько лет одна из самых популярных систем, функционирует уже 10 лет. Disqus — это сторонний сервис для комментирования на ваших сайтах. Представляет из себя нечто среднее между форумом и социальной сетью. Пользователи могут вести обсуждения, даже не заходя на сам сайт-первоисточник. Сервис сам пришлет им уведомления и продолжить разговор можно прямо из учетки в системе.
Многие посетители и рады бы поблагодарить автора статьи за отличную работу, но просто ленятся проходить стандартную процедуру регистрации. С Disqus эта проблема будет решена. Авторизация доступна при помощи популярных соцсетей: Твиттер, Гугл+ и Фейсбук. Есть и классическая регистрация с логином, электронной почтой и паролем. Заведя один раз учетную запись, в дальнейшем с ее помощью можно комментировать любой сайт, где установлен данный плагин.
Из плюсов стоит отметить, что все комментарии и сопутствующий контент хранится на серверах системы, что снижает нагрузку на хостинг. Возможность поделится целым обсуждением или отдельным комментарием в соцсетях. Если вам интересна тема беседы, можно подписаться на комментарии не оставляя при этом сообщений. Disqus предоставляет возможность монетизировать ресурс, но, к сожалению, только для англоязычных веб-сайтов. И, конечно, бесплатность, сервисом пользуются более двухсот тысяч владельцев сайтов.
Из минусов: Нужно разбираться в настройке или нанимать специалиста, плагин имеет сложную стилизацию. Для установки требуется совершить ряд действий и необходимы хотя бы базовые знания английского. С недавнего времени Disqus ввел плату за отключение рекламы в комментариях, примерно 10 долларов в месяц. Правда, для маленьких веб-сайтов, личных блогов и некоммерческих сайтов будет возможность выборочного вывода рекламы. Полноценный ввод этой схемы планируется на март 2017 года. Ну и небольшой, но минус для русскоязычных пользователей, нет возможности залогиниться через «Вконтакте».
Немного об установке
Зарегистрировавшись в системе (неважно каким способом) Нужно выбрать в меню справа «Add Disqus to Site» и добавить URL вашего сайта, затем, вашу CMS, после чего, установить плагин привычным способом из консоли WP. Для этого заходим в плагины, добавить новый, вбиваем в поиск название и устанавливаем.
Далее, заходим на страницу с установленными плагинами, ищем «Disqus Comment System» и жмем «Configure». Видим такую надпись: «Upgade Disqus Comments» (обновление базы данных), жмем кнопочку «Upgrade». Дальше настраивайте по своему усмотрению, благо настроек хватает. В том числе, и возможность импортировать комментарии, которые были до установки Disqus.
Postmatic
Этот плагин не является сторонним сервисом, а использует встроенную платформу WordPress, но позволяет значительно расширить возможности комментариев на сайте. Пользователи смогут подписаться на интересующие темы и получать уведомления по электронной почте. Отвечать можно прямо по email, это очень удобно, может помочь вести беседу оперативно, для этого комментатору не надо заходить на сайт и искать тему, а в ней новые сообщения, достаточно просто проверить почту. Сразу после отправки, комментарий появится в блоге, что поможет вести диалог, а следовательно, и вовлечь читателей в беседу, тем самым улучшив ПФ сайта.
Из плюсов: используются только собственные ресурсы хостинга и все данные будут полностью вам подконтрольны. Улучшенный шаблон отправки уведомлений по почте. Помимо последних ответов, в нем присутствует Gravatar пользователя и полный архив сообщений. Все это красиво оформлено и выглядит гораздо лучше стандартной системы оповещений WP. Отлично подойдет, если нет надобности с более навороченными комментариями и нужно просто слегка дополнить базовую версию.
Из минусов: Postmatic дополняет стандартный функционал, но не улучшает его радикально.
HyperComments
Удобная и современная система комментирования. Предоставляется как условно-бесплатный продукт, в бесплатной версии (Lite) доступен один сайт с одним модератором. В месяц возможна загрузка не более ста тысяч комментариев и 1000 обращений к API в час, за большее нужно доплачивать.
Персональная годовая лицензия обойдется в 24$ в год, в ней также один сайт, но уже три модератора и 500 тыс. загрузок виджета. Не более 5 тыс. обращений к API в час.
Professional — 120$ за год или по 11$ в месяц. Доступно три сайта, 15 модераторов и 2 млн загрузок, а также, возможность настроить индивидуальный дизайн виджета, аналитика и различные отчеты. Обращений к API 10 тыс.
Enterprise — 480$ в год или 44$ в месяц. Количество сайтов и модераторов не ограничено, 6 млн загрузок и сохранение в вашей базе данных комментариев. Имеется также SSO и SEO. Запросы к API не лимитированы. В каждом из тарифов есть пробная версия с полным функционалом на 14 дней.
Из плюсов: возможность гипперкомментариев, когда читатель выделяет интересный фрагмент текста для дальнейшего обсуждения. Нет надобности каждый раз обновлять страницу, комментарии появляются сразу в режиме real-time. Виджет адаптирован под мобильные платформы. Присутствует панель, которая показывает пользователей, находящихся в данный момент на странице. Хорошая индексация в поисковиках. Авторизация через популярные соцсети, включая «Вконтакте» и «Одноклассники». В этих же социальных сетях можно сделать репост любой понравившейся части статьи, что положительно влияет на продвижение сайта.
Из минусов: если у пользователя нет аккаунта в одной из соцсетей, он не сможет оставить сообщение, если у вас отключены анонимные комментарии. HyperComments не уведомляет читателей о новых добавленных сообщениях, что может быть серьезным недостатком для активных обсуждений. Ну и главным минусом являются ограничения в бесплатной версии, о которых писалось выше.
IntenseDebate
Эта платформа для комментирования была разработана самой WordPress, что делает ее интеграцию в движок практически безболезненной. Отличный конкурент Disqus, бесплатен. Позволяет установить дополнительные виджеты при необходимости: статистику комментариев, активных комментаторов и самых обсуждаемых тем.
Из плюсов нужно выделить дружественный интерфейс формы комментариев, пользователем будет удобно. Моментальное оповещение о новых записях, это касается не только читателей, но и администраторов. Возможность авторизоваться через Фейсбук, Твиттер или Вордпресс, также можно создать учетную запись на самом IntenseDebate, что позволит комментировать другие веб-сайты где установлена эта платформа. Поддержка кросспостинга в Твиттер. Комментарии, добавленные при помощи этого сервиса стабильно индексируется поисковыми системами.
Из минусов: не используются популярные в российском сегменте соцсети: «Вконтакте», «Одноклассники». Отсутствуют real-time сообщения. Это, пожалуй, самые основные недостатки платформы IntenseDebate.
Также стоит прочитать
Плагин Heyoya для голосовых комментариев на сайте WordPress
Хотя существует множество плагинов WordPress для комментариев, все они являются лишь вариацией одного и того же основного подхода.
Посетители переходят в конец вашего поста, вводят свое имя, некоторый текст, и нажимают «Отправить». Если у них есть Gravatar, то вы сможете увидеть изображение профиля. В противном случае это безликий текст на странице сайта.





 Heyoya – плагин комментариев WordPress, который кардинально меняет привычную форму представления комментариев. Он позволяя вам добавлять реальные голосовые комментарии к вашему контенту или голосовые обзоры к вашим продуктам WooCommerce. Вы и ваши посетители сможете записывать и воспроизводить голосовые сообщения в ваших комментариях или разделах отзывов, что создает максимальное интерактивное взаимодействие.
Heyoya – плагин комментариев WordPress, который кардинально меняет привычную форму представления комментариев. Он позволяя вам добавлять реальные голосовые комментарии к вашему контенту или голосовые обзоры к вашим продуктам WooCommerce. Вы и ваши посетители сможете записывать и воспроизводить голосовые сообщения в ваших комментариях или разделах отзывов, что создает максимальное интерактивное взаимодействие.В этом практическом обзоре Heyoya рассмотрим, как именно работает этот плагин и как он изменит ваш веб-сайт WordPress.
Особенности плагина Heyoya
Основная функция Heyoya – добавлять реальные голосовые комментарии на сайт WordPress. Но это не все – в его силах улучшить раздел комментариев и другими способами.
Heyoya не ограничивается голосовыми комментариями – ваши посетители могут оставлять текстовые комментарии, если они предпочитают такой подход.

Плагин работает не только с комментариями – вы можете использовать его для отзывов в вашем магазине электронной коммерции.
Чтобы оставить комментарий / отзыв, посетителям необходимо подтвердить свой адрес электронной почты или использовать социальную регистрацию. Они могут сделать это, используя свою учетную запись в социальной сети (Facebook или Twitter). Это сокращает спам, хотя и добавляет немного больше трения в процесс комментирования. Но в этом кроется и преимущество – вы можете использовать уведомления по электронной почте, чтобы вернуть посетителей на ваш сайт.
Посетители сайта могут использовать поле для «лайка» отдельных комментариев и делиться ими в социальных сетях.
Наконец, вы сможете полностью настроить внешний вид поля для комментариев, а также настроить его функционирование, например запретить ссылки в комментариях.
Как использовать Heyoya
У Heyoya есть специальный плагин интеграции на WordPress.org, очень простой в настройке и использовании.
Базовая настройка
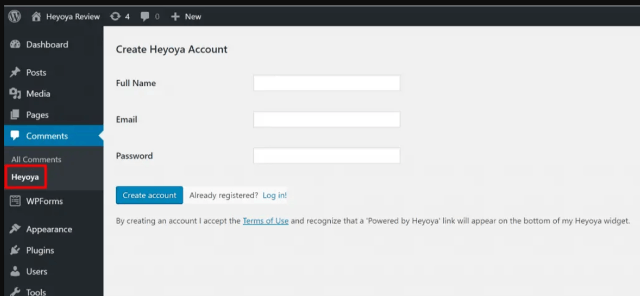
Для начала установите и активируйте бесплатный плагин Heyoya с WordPress.org. Затем перейдите в Комментарии → Heyoya на панели инструментов WordPress, чтобы настроить плагин.
Вам нужно войти в существующую учетную запись Heyoya или создать новую, что вы можете сделать прямо с панели управления WordPress:

После входа в систему можно настроить параметры Heyoya.
Первая настройка: укажите, ведете ли вы блог / контент-сайт или магазин электронной коммерции. Помните, что вы можете использовать голосовой подход Heyoya для комментариев в блогах и обзорах продуктов:
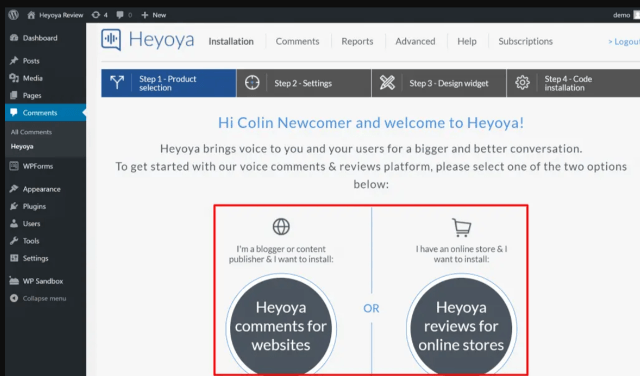

Для этого обзора выберем опцию комментариев блога.
Окно комментариев
С помощью визуального интерфейса вы сможете настроить функциональность окна комментариев Heyoya.
Плагин предоставляет много вариантов:
- Измените весь текст, который появляется в поле.
- Выберите, что можно включить, например, разрешить ли ссылки, электронные письма или повторяющиеся символы.
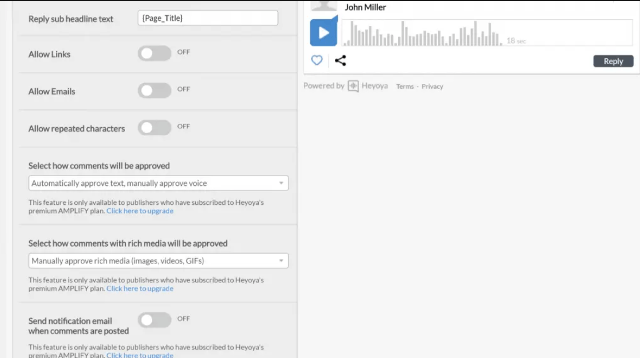
- Выберите способ утверждения комментариев в зависимости от того, какой контент включен.
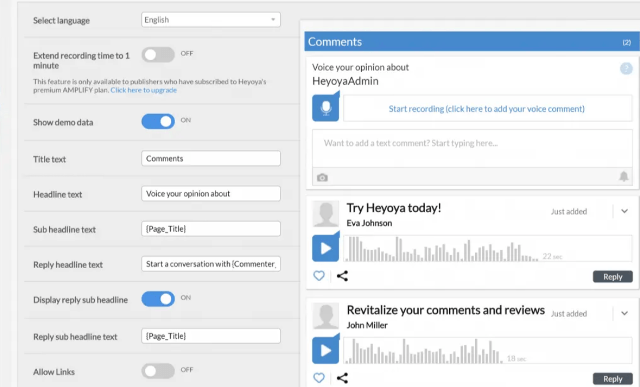

Например, вы можете автоматически утверждать текстовые комментарии, но для голосовых комментариев требуется модерация:

Стили комментариев
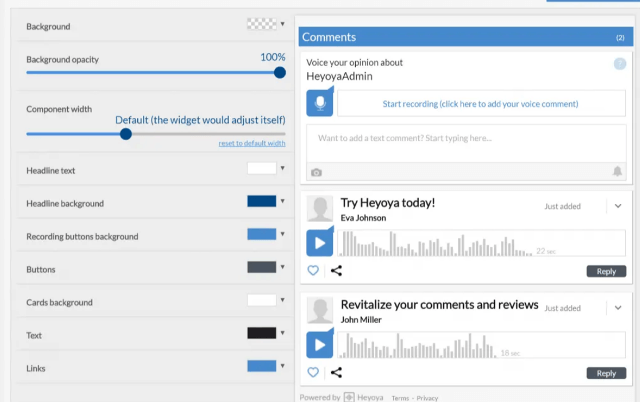
На следующей странице можно настроить внешний вид окна комментария. Благодаря визуальному предварительному просмотру вы увидите, как различные параметры стиля влияют на общий вид комментариев.
Помимо изменения ширины и фона, для всех элементов в окне можно изменять и цвет:

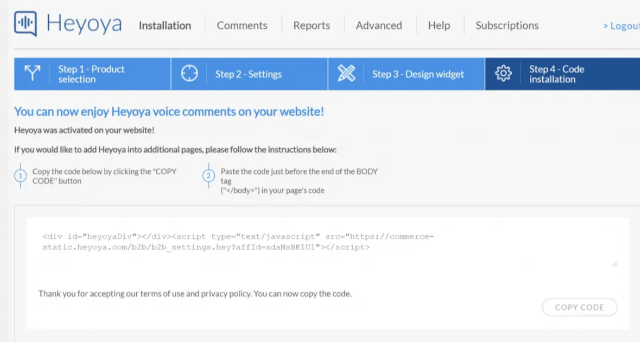
Теперь плагин Heyoya настроен для раздела комментариев. Если захотите использовать комментарии Heyoya и для другого контента, можно вручную добавить фрагмент кода.

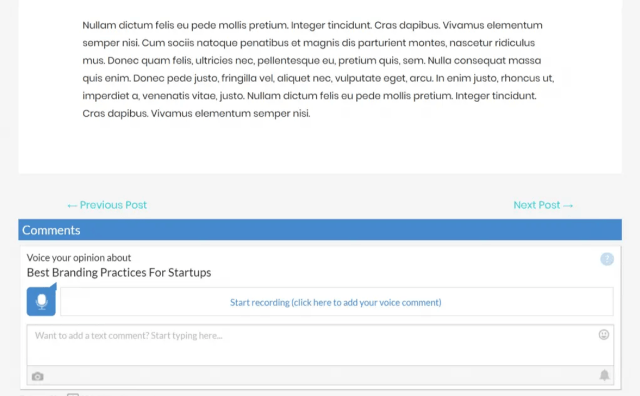
А вот как это выглядит на сайте:

Смотрите также:
Какие лучшие плагины голосовых сообщений подойдут для вашего сайта WordPress.
Как Heyoya работает для комментаторов
Теперь посмотрим на функционал Heyoya с точки зрения ваших посетителей.
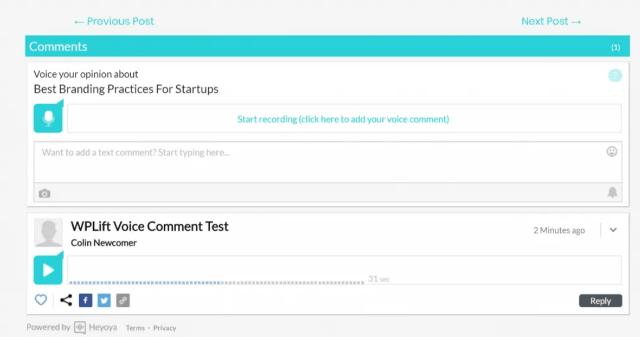
Когда они хотят оставить комментарий, то могут либо ввести текстовое сообщение, либо нажать кнопку «Начать запись» и записать голосовой комментарий.
Перед началом записи голосового комментария Heyoya попросит доступ к микрофону посетителя:
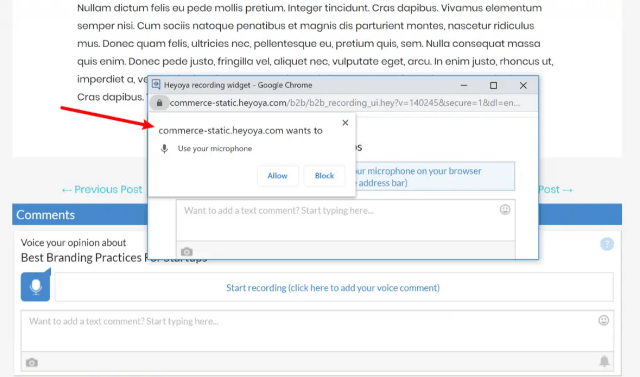

Примечание. Если ваш сайт использует HTTPS, все это будет происходить в реальном интерфейсе, а не как показано на картинке выше, в всплывающем окне.
Затем запуститься таймер обратного отсчета времени, отведенного на голосовой комментарий. По умолчанию пользователи получают 30 секунд. Но можно продлить время записи до минуты, подписавшись на премиум-сервис Heyoya.
Комментаторы также получат возможность прослушать свое голосовое сообщение и повторно записать его при необходимости:
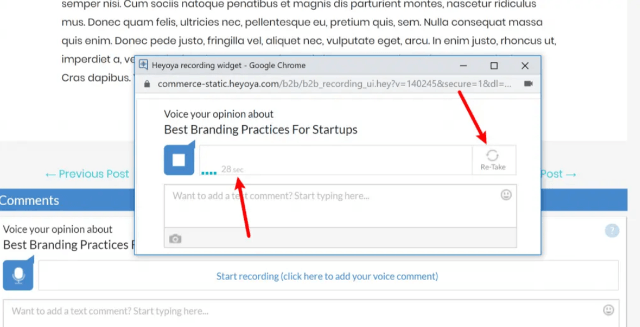

Чтобы отправить свой голосовой комментарий, посетителям необходимо:
- Добавить заголовок.
- Пройти верификацию своей электронной почты. Используя либо социальный логин, либо введя свой адрес электронной почты, нужно перейти по ссылке активации, которую отправляет Heyoya на e-mail. Такая проверка проводится только для первого комментария пользователя.
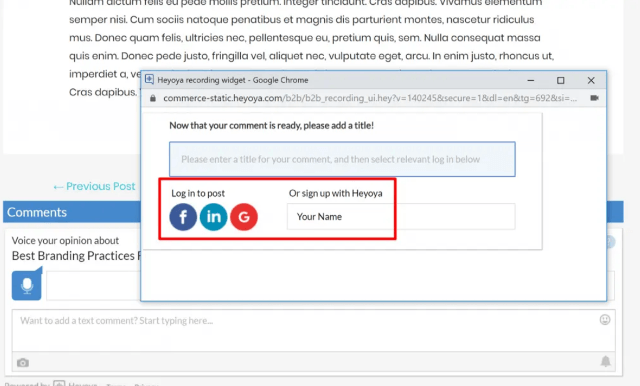

Как только администратор одобрит комментарий, он появится на сайте.
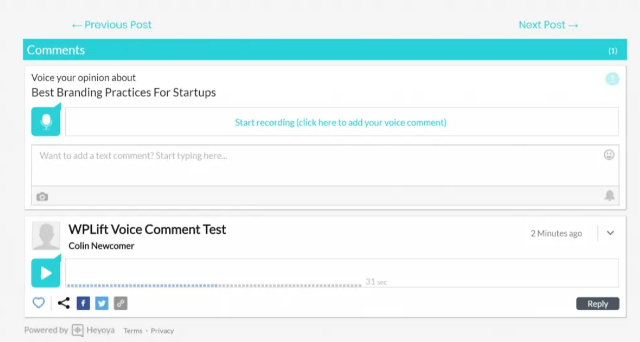
В разделе комментариев люди могут «лайкать» или делиться отдельными голосовыми комментариями в социальных сетях:

Расширенные настройки администратора
Теперь проверим некоторые дополнительные параметры администрирования.
Как администратор, вы сможете модерировать комментарии на вкладке Комментарии, включая предварительное прослушивание голосового сообщения:
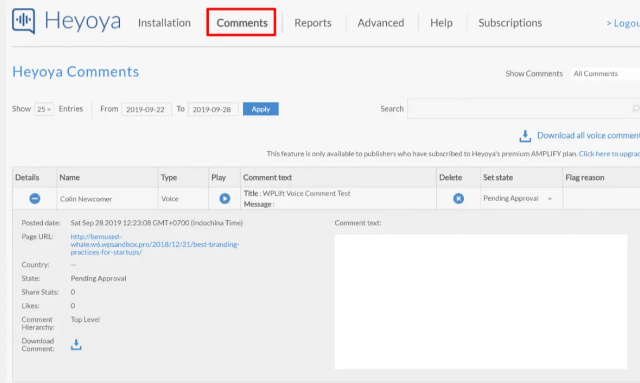

На вкладке «Отчеты» представлена базовая аналитика для:
- Комментариев.
- Голосовых комментариев.
- Прослушанных голосовых комментариев.
- Текстовых комментариев.
- Общих ресурсов (генерируются кнопкой «Поделиться» в разделе комментариев).
- Комментариев с отметкой «Понравилось».
Вкладка «Дополнительно» позволяет:
- Создавать уведомления, которые отправляются через поле для комментариев Heyoya.
- Просматривать список пользователей, которые прокомментировали ваш сайт.
- Добавлять пользовательский брендинг, когда посетители делятся комментариями в социальных сетях (в бесплатной версии используется брендинг Heyoya).
- Импортировать существующие комментарии, загрузив файл. Для этого вы можете использовать инструменты импорта / экспорта WordPress, хотя было бы проще встроить эту функцию.
Цены на Heyoya
Основная услуга Heyoya – бесплатная.
С бесплатной версией посетители смогут оставлять голосовые комментарии до 30 секунд, текстовые комментарии, видео / мультимедиа и многое другое.
Платный план Amplify поможет:
- Увеличить время записи голоса до одной минуты.
- Получить расширенные возможности модерации.
- Предоставить больше возможностей обмена.
- Отправить пользовательские уведомления.
- Выгрузить ваши комментарии с серверов Heyoya, чтобы использовать их в других местах.
План Amplify, как правило, стоит 7 долларов в месяц на один сайт при оплате ежегодно или 8 долларов в месяц при оплате ежемесячно.
Пока трудно спрогнозировать, будет ли этот голосовой подход превосходить текстовые комментарии для ваших конкретных сайтов, но в любом случае это интересно и необычно.
Это эффективно для личных блогов и обзоров, потому что голос делает обзор более аутентичным, что может помочь укрепить доверие.
Бесплатный план Heyoya должен работать нормально для большинства сайтов, что само по себе привлекательно.


Источник: wplift.com


Смотрите также:
Новый плагин для комментариев / Habr
Один из «секретов» успеха Facebook — это его инструменты для интеграции с другими сайтами, так как именно они «приводят» на Facebook большее количество контента (или ссылок на него), что в свою очередь превращает Facebook из обычной социальной сети в мощную платформу, которую пользователи могут использовать самым различным образом.Среди таких инструментов важную роль играют плагины для медиа — сайтов новостных агентств, газет, телеканалов и собственно онлайн-изданий. Плагины позволяют людям легко размещать ссылки на заинтересовавшие их статьи у себя на стене в Facebook и комментировать их, используя свое имя в Facebook вместо того, чтобы регистрироваться на каждом сайте отдельно.
Недавно плагин комментариев для медиа претерпел небольшие изменения, которые стоит иметь в виду, как издателям, так и пользователям:
- Комментарии в плагине отображаются с учетом отношений пользователя и комментаторов и качества комментариев: наверх в плагин поднимаются комментарии от друзей и друзей друзей пользователя и комментарии и ветки с наибольшим количеством ответов и «лайков».
- Рядом с именем комментатора указывается публичная информация из его профиля: возраст, город проживания, где работает, количество общих друзей.
- Дискуссия, которая начинается на сайте, может быть продолжена в ленте пользователя на Facebook: все комментарии, оставленные под статьей на Facebook синхронизируются с комментариями в плагине на сайте, что позволяет сохранять единое обсуждение на сайте и в Facebook. Если кто-то ответит на комментарий пользователя на сайте, то пользователь получит об этом уведомление на Facebook.
- Пользователи могут комментировать не только под своим личным профилем, но и в режиме страницы, если пользователь комментирует в плагине в режиме страницы, то это комментарии будут видны всем поклонникам страницы.
- Все комментарии в плагине и на Facebook теперь организованы в ветки дискуссий
Также изменения коснулись возможностей модерации дискуссии:
- Модераторы могут составлять список слов, которые не могут появляться в комментариях на сайте и также составлять черный список пользователей, которые не могут принимать участие в дискуссии.
- Модераторы могут установить режим премодерации комментариев, все комментарии, которые оставляют пользователи на сайте, будут видны только им самим, их друзьям на Facebook и модераторам. Комментарии появятся на сайте и будут видны всем посетителям только после того, как модератор одобрит комментарий для публикации.
Подробнее почитать о том, как работает новый плагин комментариев можно здесь —
http://developers.facebook.com/blog/post/472
Код для вставки на сайт можно получить здесь — http://developers.facebook.com/docs/reference/plugins/comments/
А, похоже, первый пример внедрения нового плагина в России можно посмотреть на сайте Vesti.ru — например здесь
AnyComment — плагин комментариев для WordPress
В этой записи, я бы хотел обсудить то, как владельцы WordPress блогов общаются со своей аудиторией.
Общение на моем личном примере
Для меня общение с аудиторией происходит посредством переписки и ответа на комментарии к постам. Встроенные комментарии в WordPress имеют следующие минусы:
- нужно ввести много ненужной информации, почту, имя и прочее, чтобы оставить комментарии (даже если программно это можно все убрать, проблемы все равно остаются и не каждый технически понимает как это сделать). Да есть плагины, которые сделают работы за вас, но поймите, что это долго и никто не хочет столько времени возится, чтобы это решить
- оставив комментарии, страница перезагружается (что мне лично не нравится)
- нельзя использовать социальные сети для авторизации
- нужно копаться в коде, чтобы подогнать по стилистике под сайт (что не каждый умеет)
Альтернативы и что с ними не так
Есть альтернативы, такие как например, Disqus.
Но опять же не то, потому что:
- зависимость от третьего сервиса (все комментарии и данные о пользователях хранятся на их серверах)
- нет полного контроля над комментариями
- неизвестно что происходит за сценой, так как комментарии обрабатываются на третьей стороне
- неизвестно как хранятся и обрабатываются данные о подписчиках или читателях сайта
и это лишь самые очевидные причины…
Решение всех проблем (ну, почти)
Именно с этой целью был придуман и создан AnyComment.
А вот ссылка на официальную страницу в репозитории WordPress.
- Актуальная версия: 0.0.1
- Протестировано до версии: 4.9.6
Цель — сделать его лучшим плагином комментариев для WordPress придерживаясь простоты, удобства, скорости работы, учитывая вашу обратную связь.
Описание
Каждый плагин должен решать какую-то проблему и я вкратце расскажу его текущие особенности и некоторые из уже запланированных:
- оставить комментарий без перезагрузки страницы
- возможность авторизоваться через ВК, Твиттер, Facebook, Google, Одноклассники, GitHub
- если пользователь гость, то ему не предлагается ввести кучу полей, показывается обычно поле ввода, как для авторизованного пользователя, после нажатия на поле ввода текста, ему предлагается авторизоваться одним из способов описанных пунктом выше
- ВСЕ комментарии хранятся в вашей базе данных. Никакой зависимости от третьих сервисов (только подключение к API соц. сетей для авторизации)
- простой интерфейс, который будет понятен каждому
- в комментариях пользователи могут видеть с какой соц. сети зашел пользователь
- при добавлении комментария, он попадает в стандартные комментарии от WordPress. Таким образом вы не потеряете ни одного комментария, которые были добавлены до установки плагина
- удобная сводная консоль о плагине, график активных пользователей относительно оставленных комментариев и количество активных пользователей
Планы:
- проводить конкурсы внутри комментариев на лучшего комментатора или на лучший комментарий
- защита от спама: поддержка ReCaptcha от Google, плагина Akismet
- общая статистика комментариев, сколько оставили за последний день, недели, месяц. Сколько всего комментариев, самые активные комментаторы и прочее
- удобная модераторская панель для комфортного управления комментариями
- полная настройка стилистики плагина для совпадения со стилем сайта
- автор будет выделен особенным образом в комментариях
- авто-обновление комментариев когда был добавлен новый комментарий
- подгрузка комментариев в момент прокрутки пользователем к ним
- подключать собственные события для перехвата данных (для статистики и прочего)
- интеграция с другими плагинами
- интеграция с сервисами для добавления гифок
- добавление смайликов
- авторизация через другие соц. сети, такие как GitHub, Dribble и прочие
- для разработчиков: поддержка Markdown
- для разработчиков: подстветка синтаксиса
- поддержка базовых HTML тегов, для форматирования текста
- поддержка визуально редактируемого текста (жирный, курсив и прочее)
Скриншоты
Консоль в админ-центре выглядит следующим образом:
На графике показывается статистика пользователей относительно количества оставленных ими комментариев. Выше отображается количество пользователей которые хоть что-то комментировали и справа общее количество комментариев на сайте.
Далее скрин того как комментарии выглядят на темном фоне, в данном случае задний фон сайта синий, комментарии сами по себе прозрачные и используется белый цвет для текста.
И конечно же вариант для светлых дизайнов.

















 больше числа
больше числа  , если их разность чисел
, если их разность чисел  , если разность
, если разность  ;
;  , если разность
, если разность  ;
; , если разность
, если разность  ;
;  , если разность
, если разность  .
. .
. .
. .
.
 .
.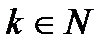 ) следует, что оно истинно и при
) следует, что оно истинно и при 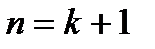 , то оно истинно при всех натуральных значениях п.
, то оно истинно при всех натуральных значениях п. =1;
=1;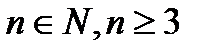 , то
, то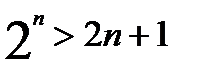
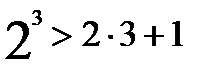 . Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что
. Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что 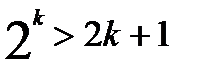 , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что
, и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что 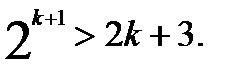
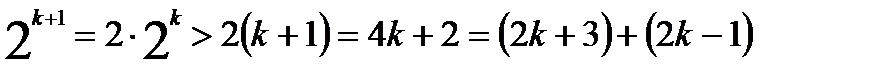 . Итак,
. Итак, 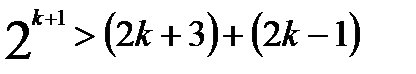 .
.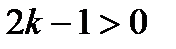 при любом натуральном значении k. Следовательно, тем более
при любом натуральном значении k. Следовательно, тем более 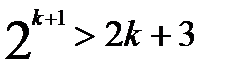 .
.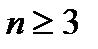 .
.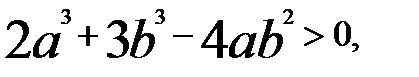 если
если 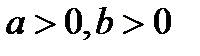 .
.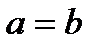 . Получаем
. Получаем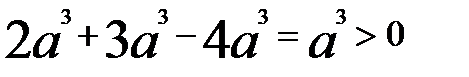 , т.к.
, т.к. 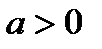
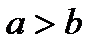 , т.е.
, т.е. 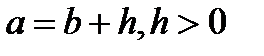 .
.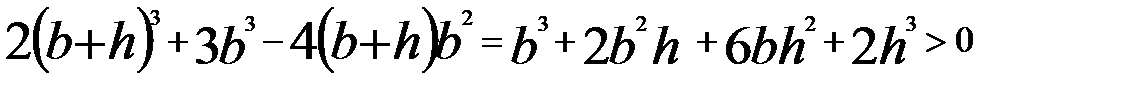 . Неравенство справедливо.
. Неравенство справедливо.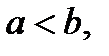 т.е.
т.е. 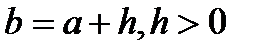 .
.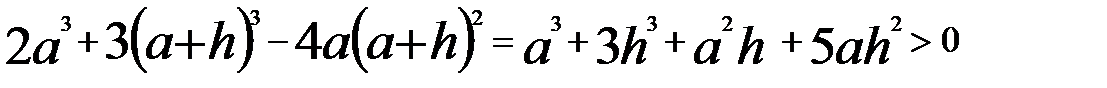 . Неравенство справедливо.
. Неравенство справедливо.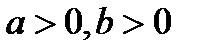 .
.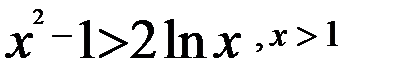
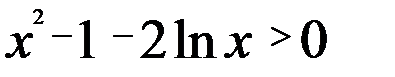 .
.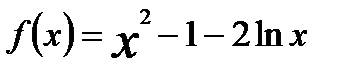 .
.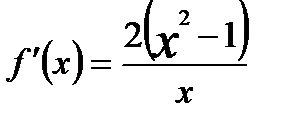 . При
. При 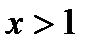 ,
, 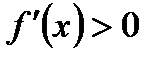 . Это значит, что при
. Это значит, что при 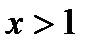
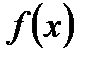 возрастает, причём
возрастает, причём 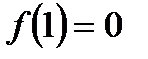 . Поэтому при
. Поэтому при 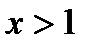
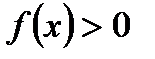 .
.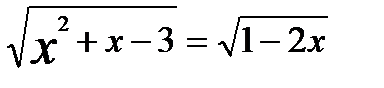 .
.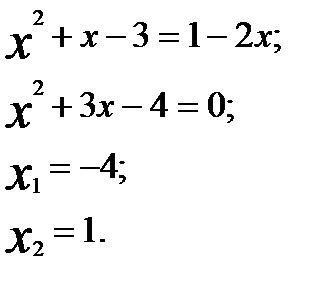
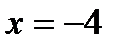 является корнем исходного уравнения.
является корнем исходного уравнения.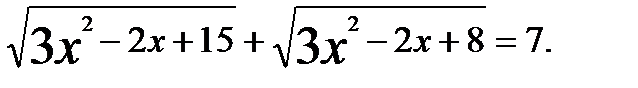
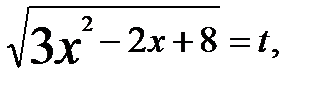 заметим, что
заметим, что 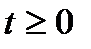 .
.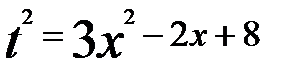 и
и 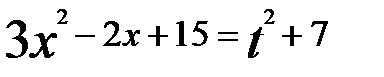 .
.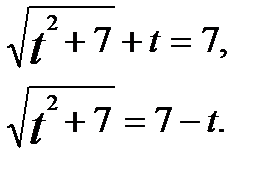
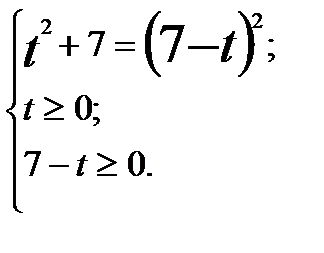
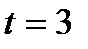 .
.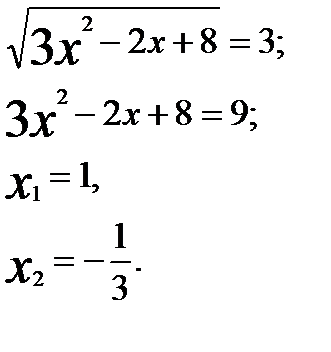
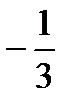 .
.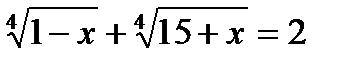 .
.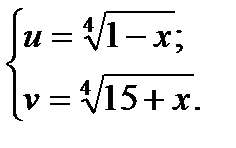
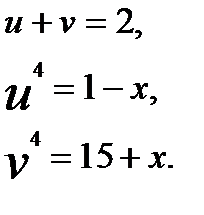
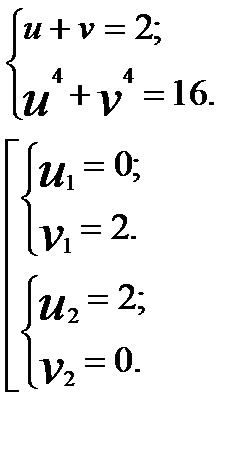
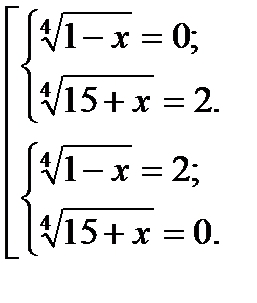
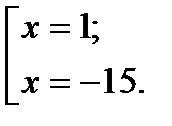
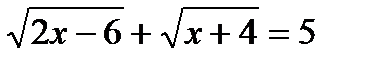 .
.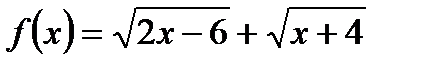 .
.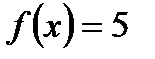 .
.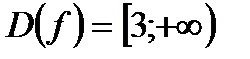 . Функция
. Функция 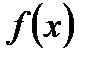 монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что
монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что 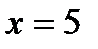 является корнем уравнения.
является корнем уравнения.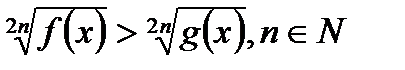 равносильно системе
равносильно системе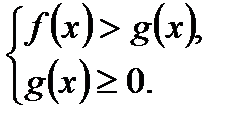
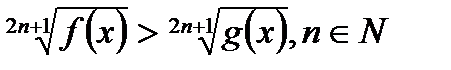 равносильно неравенству
равносильно неравенству 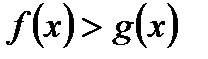 .
.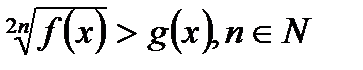 равносильно совокупности систем
равносильно совокупности систем 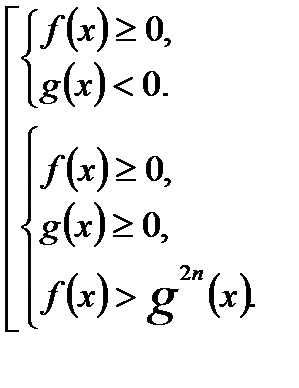
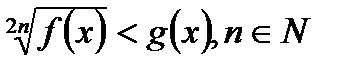 равносильно системе
равносильно системе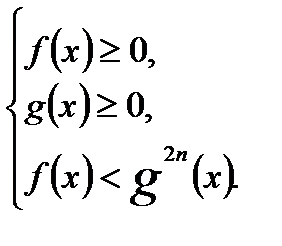
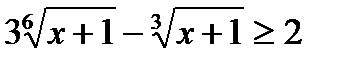 .
.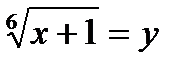 . Тогда исходное неравенство принимает вид:
. Тогда исходное неравенство принимает вид: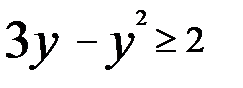 .
.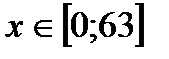 .
.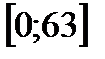 .
.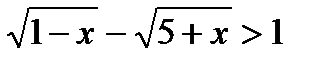 .
.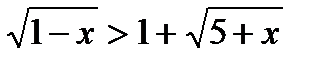 .
.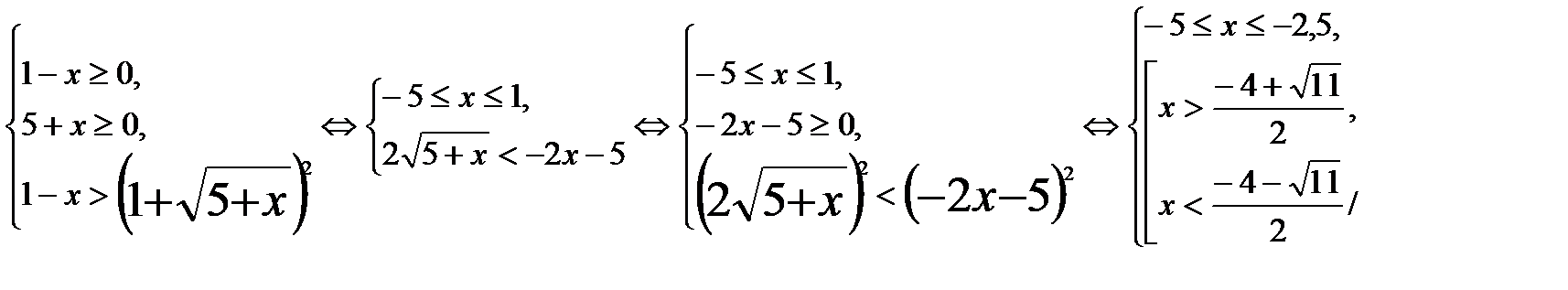 Откуда получаем
Откуда получаем  .
.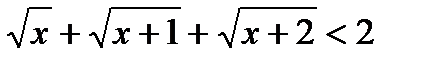 .
.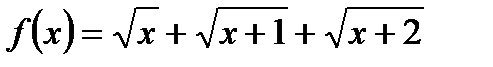 . Область определения этой функции
. Область определения этой функции 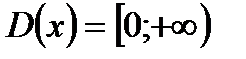 . Функция
. Функция 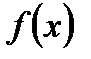 возрастает на всей области определения, причём
возрастает на всей области определения, причём 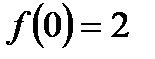 . Значит, неравенство
. Значит, неравенство 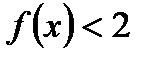 решений не имеет.
решений не имеет. где a – положительное число.
где a – положительное число. 0 .
0 .







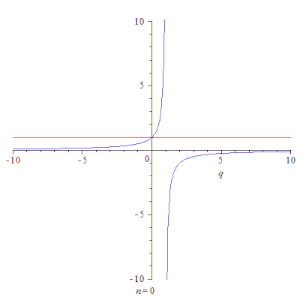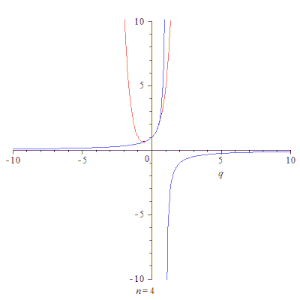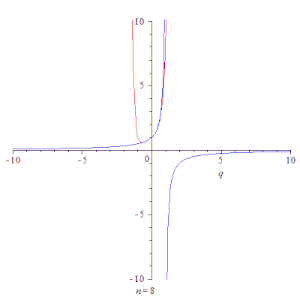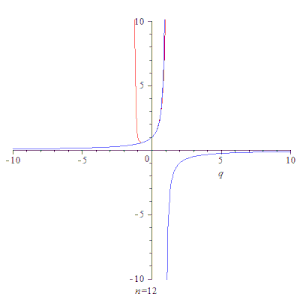 Анимация, показывающая сходимость частичных сумм геометрической прогрессии ∑k=0nqk{\displaystyle \sum \limits _{k=0}^{n}q^{k}} (красная линия) к её сумме 11−q{\displaystyle {1 \over 1-q}} (синяя линия) при |q|<1{\displaystyle |q|<1}.
Анимация, показывающая сходимость частичных сумм геометрической прогрессии ∑k=0nqk{\displaystyle \sum \limits _{k=0}^{n}q^{k}} (красная линия) к её сумме 11−q{\displaystyle {1 \over 1-q}} (синяя линия) при |q|<1{\displaystyle |q|<1}. Последовательность
Последовательность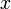 одного натурального переменного, обладающая следующим свойством:
одного натурального переменного, обладающая следующим свойством: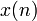 обычно называют членом последовательности
обычно называют членом последовательности 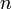 .
.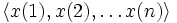 первых
первых 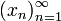 . Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида
. Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида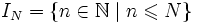 ,
,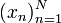 .
.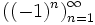 является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид 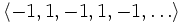 .
.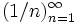 является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид 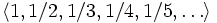 .
.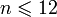 одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида
одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида 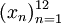 . В частности, пятым членом x5 этой последовательности является слово «май».
. В частности, пятым членом x5 этой последовательности является слово «май».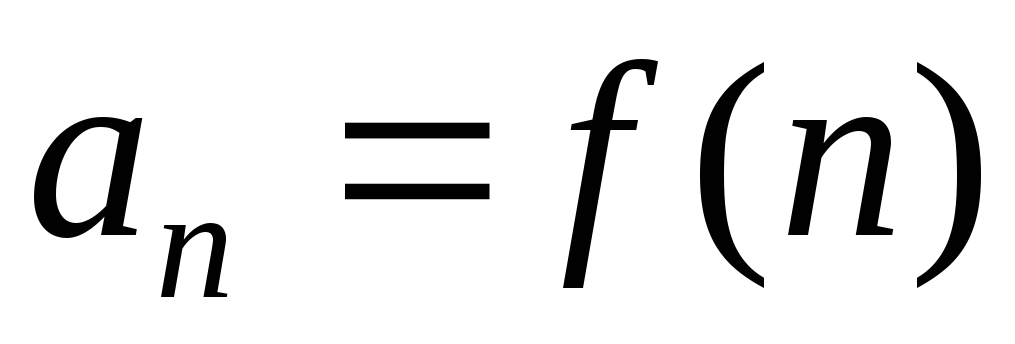 задать на множестве натуральных чисел
задать на множестве натуральных чисел ,
то множество значений функции будет
счетным и каждому номеру
,
то множество значений функции будет
счетным и каждому номеру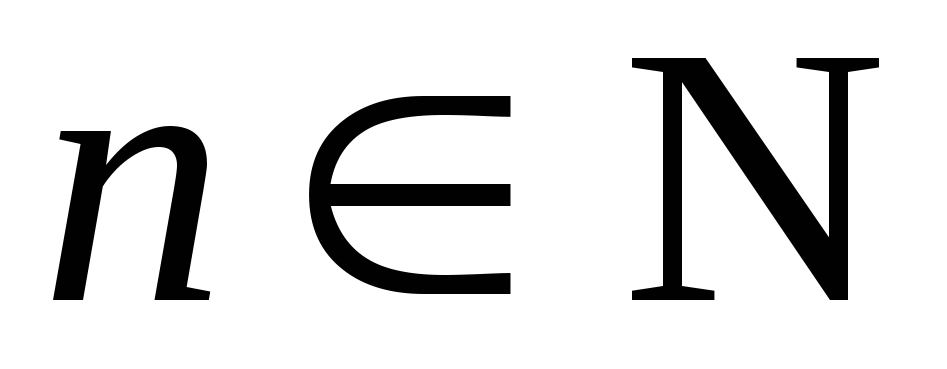 ставится в соответствие число
ставится в соответствие число .
В этом случае говорят, что заданачисловая
последовательность. Числа
.
В этом случае говорят, что заданачисловая
последовательность. Числа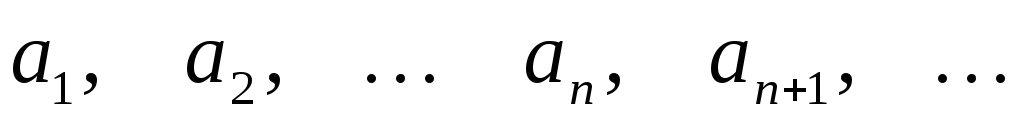 называютэлементамиили членами
последовательности, а число
называютэлементамиили членами
последовательности, а число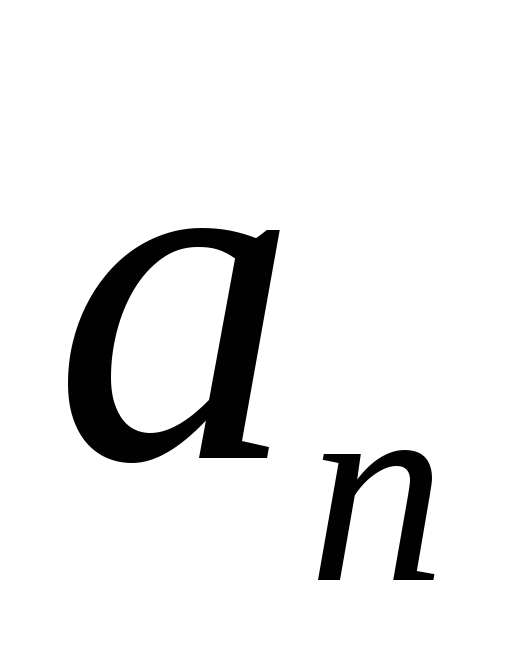 – общим или
– общим или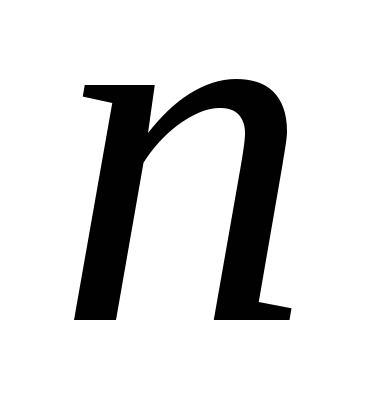 –м
членом последовательности. Каждый
элемент
–м
членом последовательности. Каждый
элемент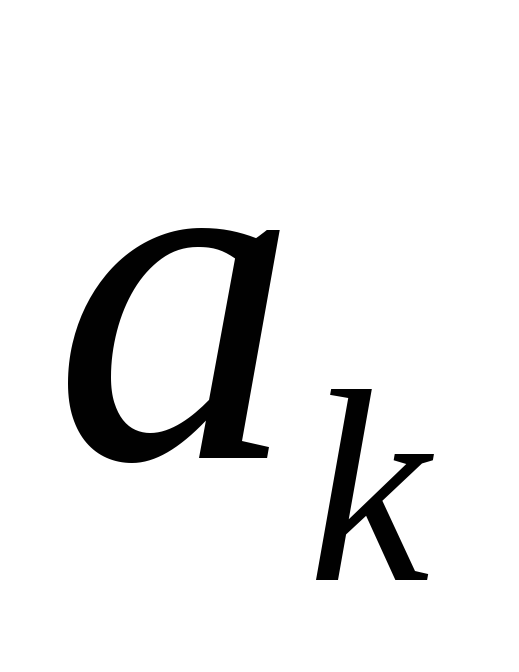 имеет последующий элемент
имеет последующий элемент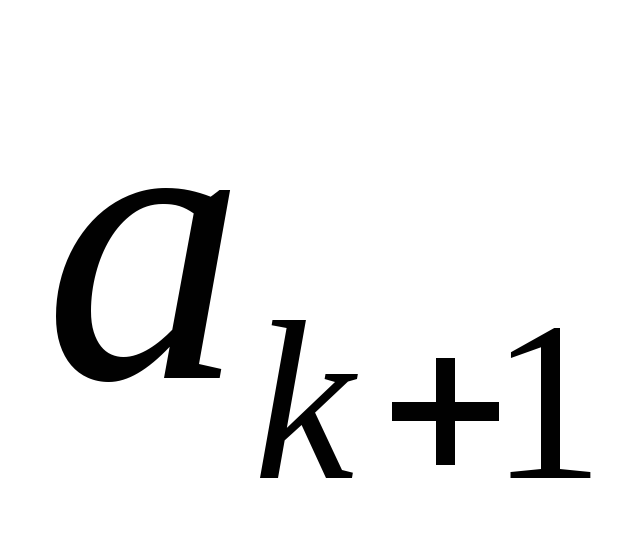 .
Это объясняет употребление термина
«последовательность».
.
Это объясняет употребление термина
«последовательность».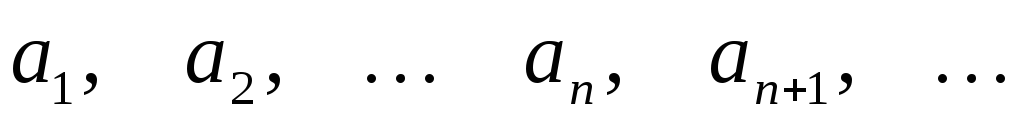 ,
либо указанием закона, по которому
вычисляется элемент с номером
,
либо указанием закона, по которому
вычисляется элемент с номером ,
т.е. указанием формулы ее
,
т.е. указанием формулы ее ‑го
члена
‑го
члена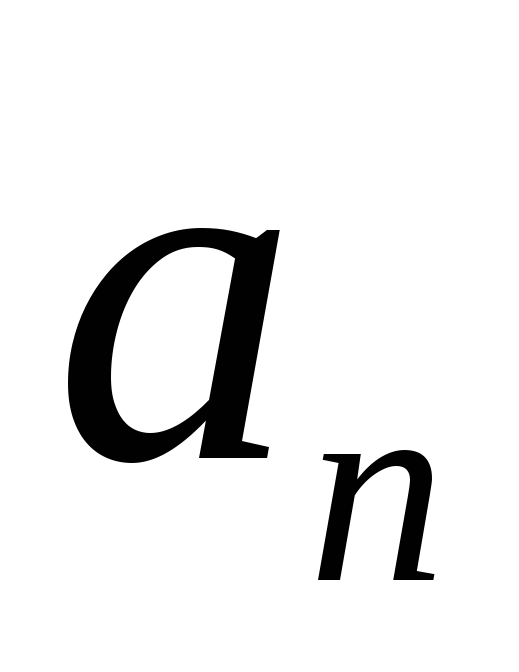 .
.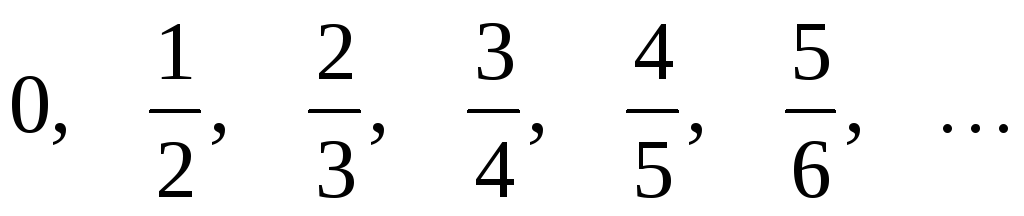 может быть задана формулой:
может быть задана формулой: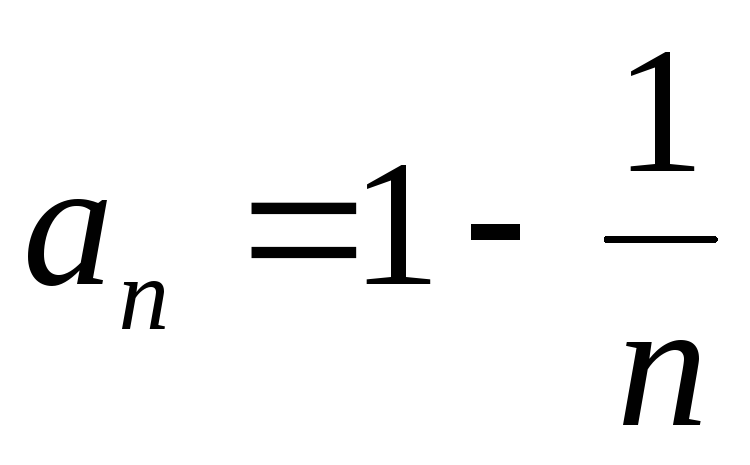 .
.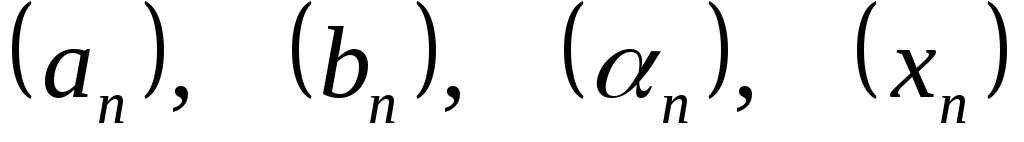 и т.п., где в скобках указывается формула
ее
и т.п., где в скобках указывается формула
ее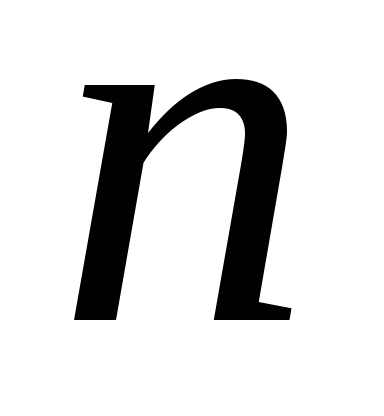 -го
члена.
-го
члена.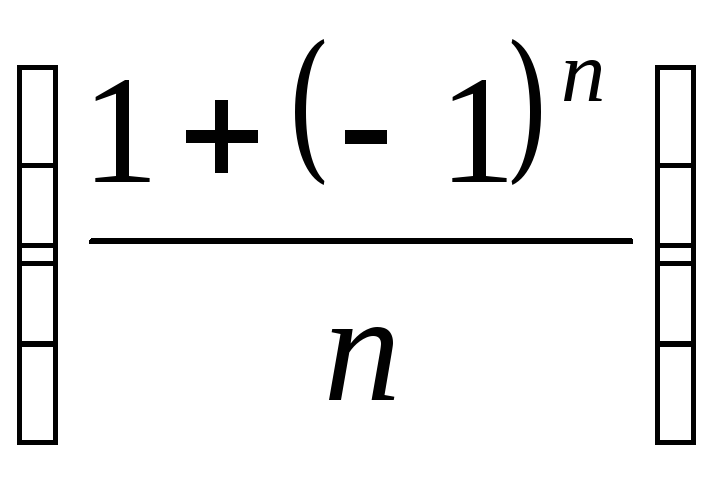 ‑это последовательность
‑это последовательность 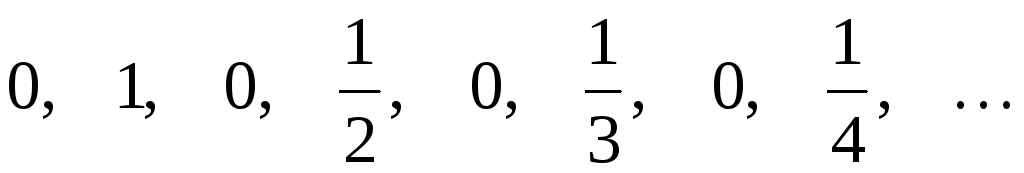
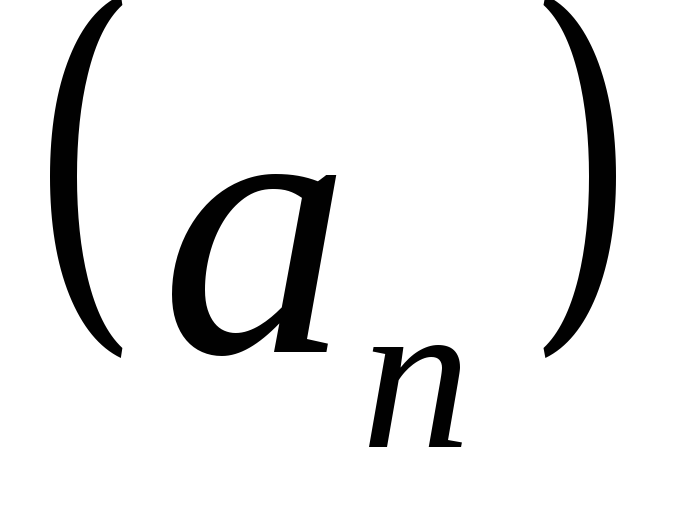 обозначается
обозначается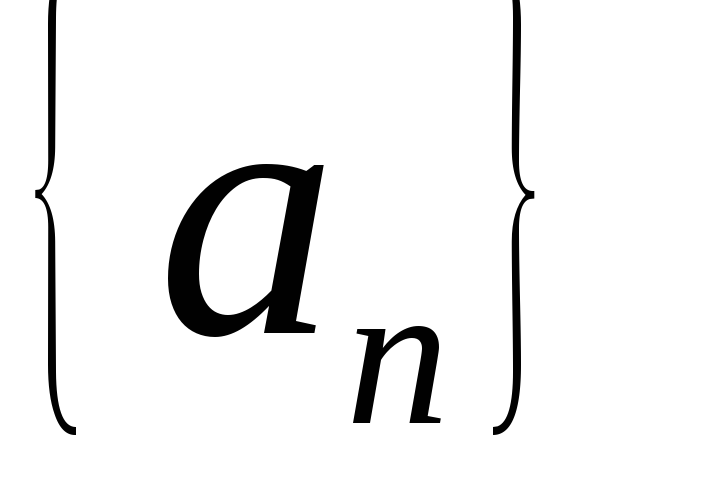 .
.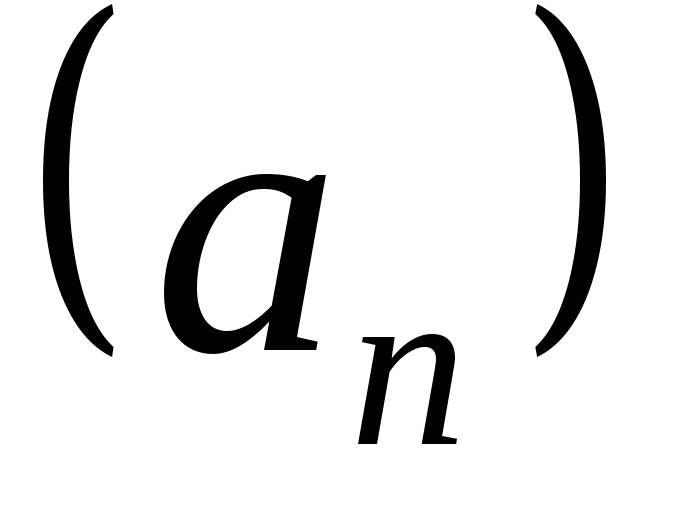 и
и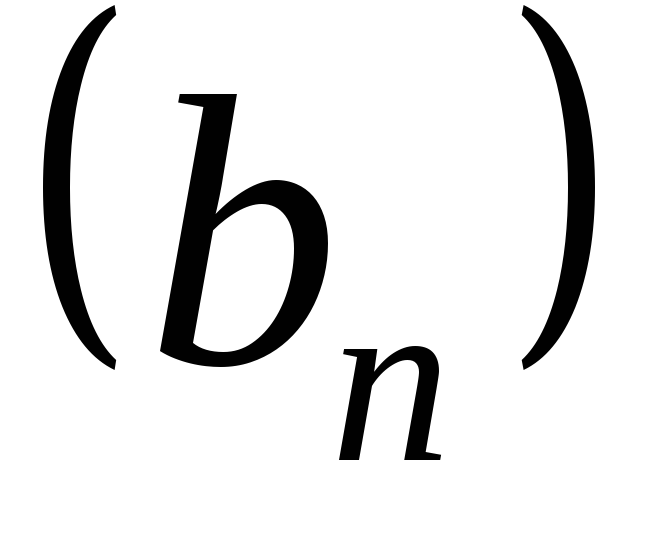 ‑ две последовательности.
‑ две последовательности.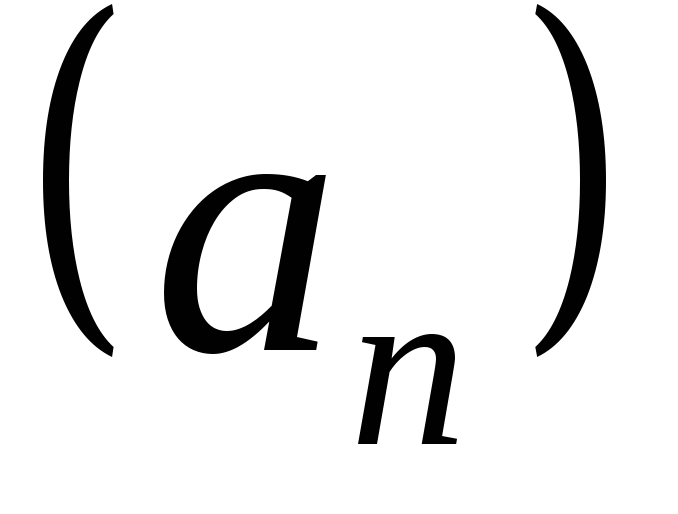 и
и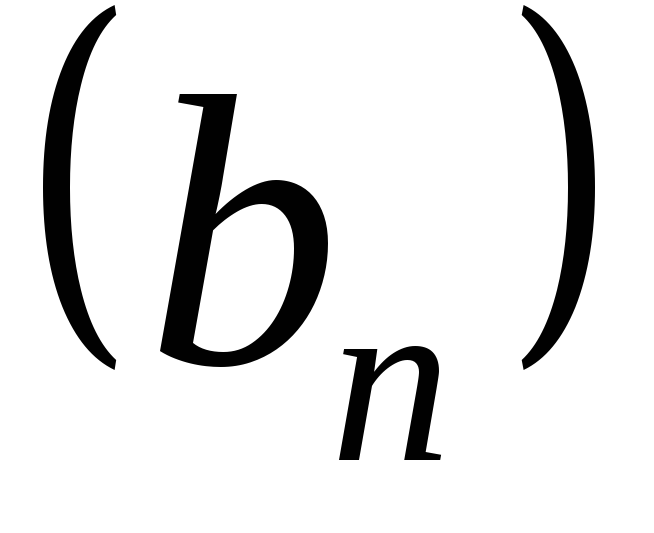 называют последовательность
называют последовательность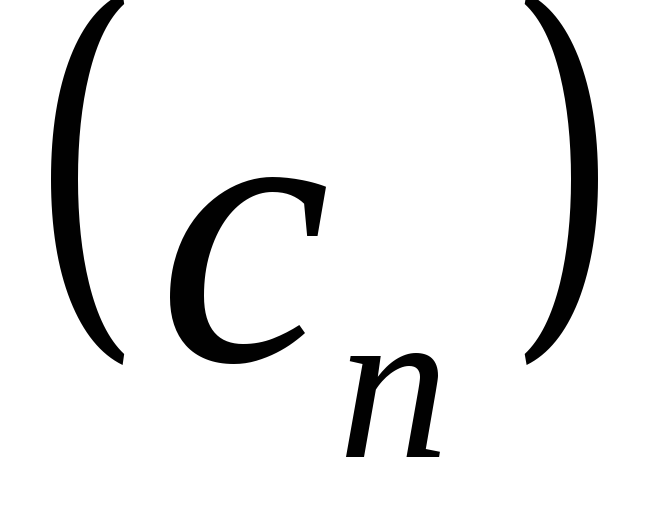 ,
где
,
где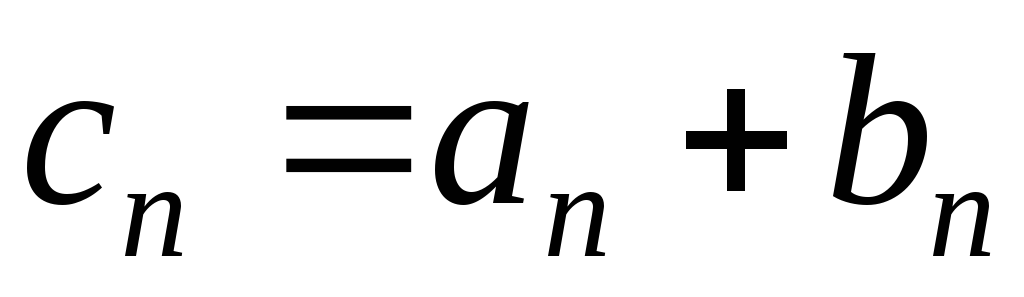 ,
т.е.
,
т.е.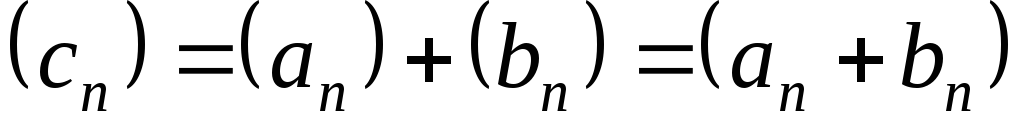 .
.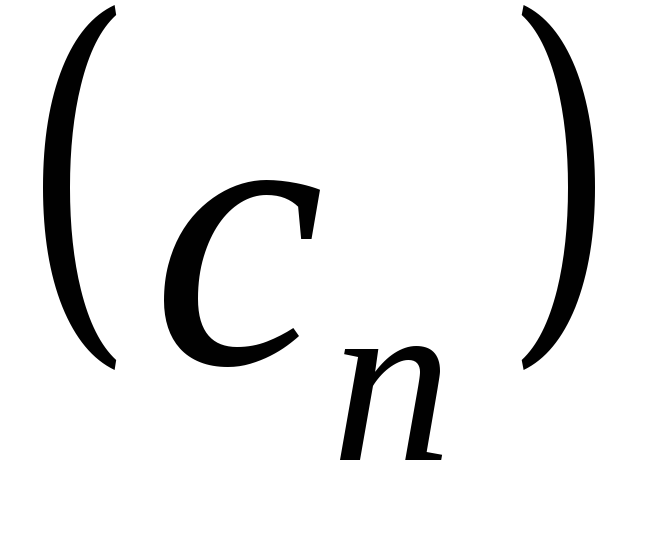 ,
где
,
где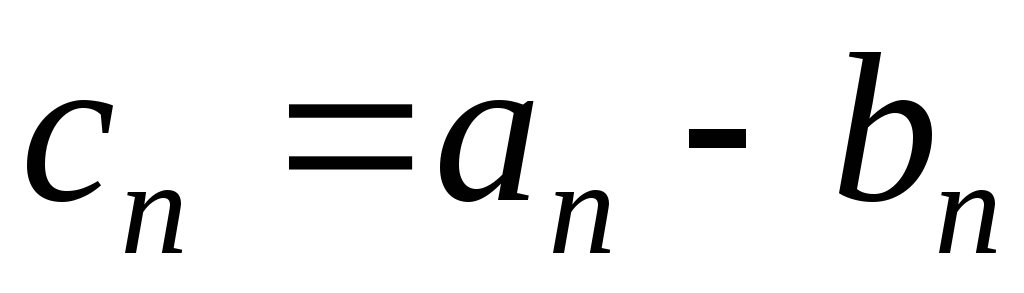 ,
т.е.
,
т.е.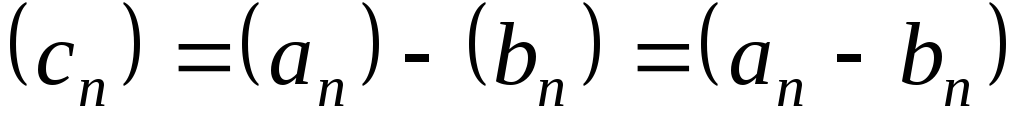 .
. и
и  ‑постоянные, то последовательность
‑постоянные, то последовательность 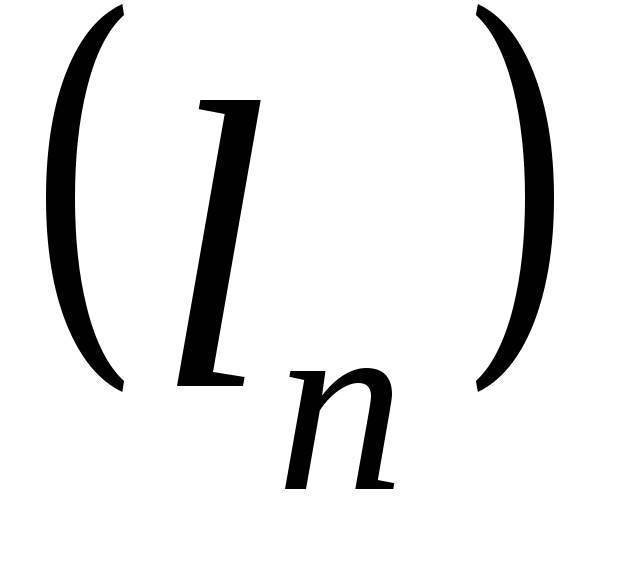 ,
,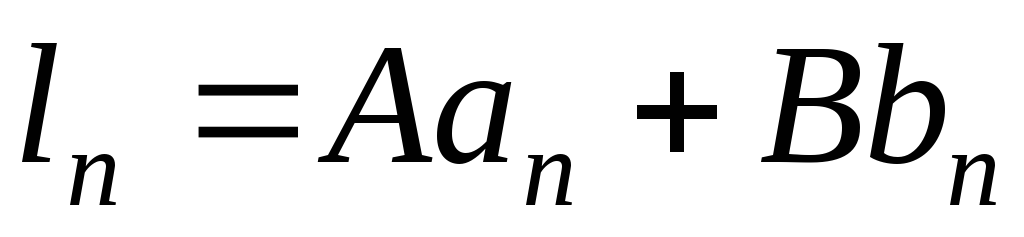 называютлинейной комбинациейпоследовательностей
называютлинейной комбинациейпоследовательностей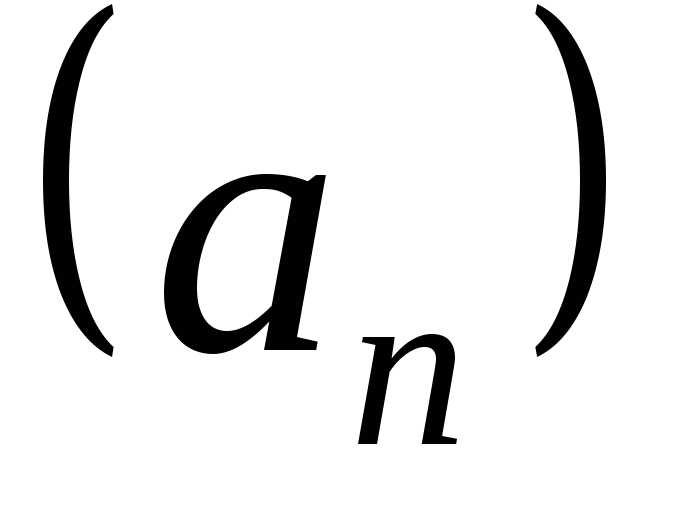 и
и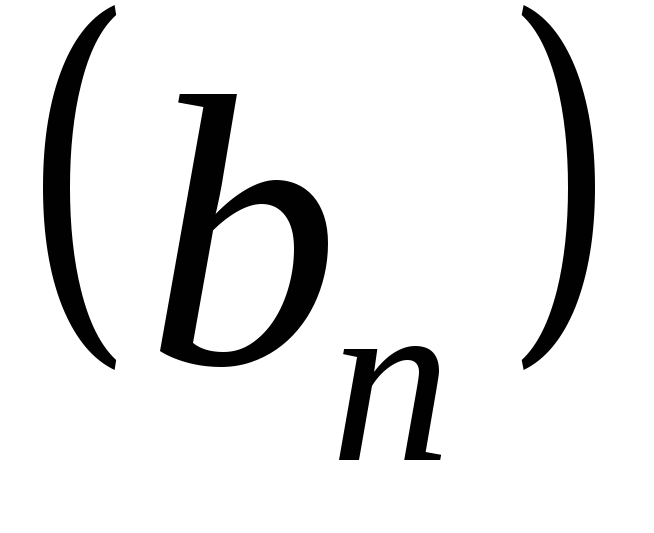 ,
т.е.
,
т.е.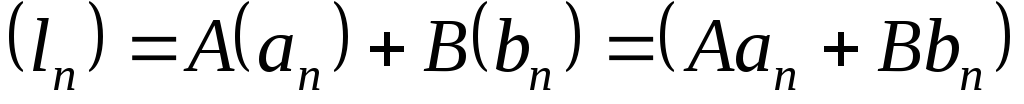 .
.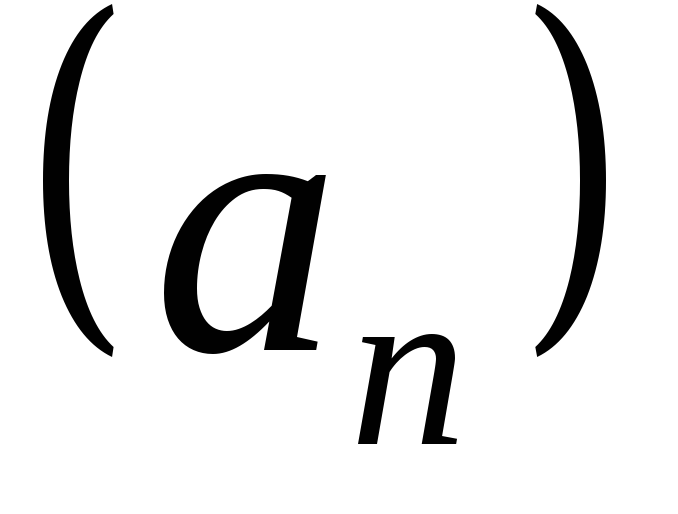 и
и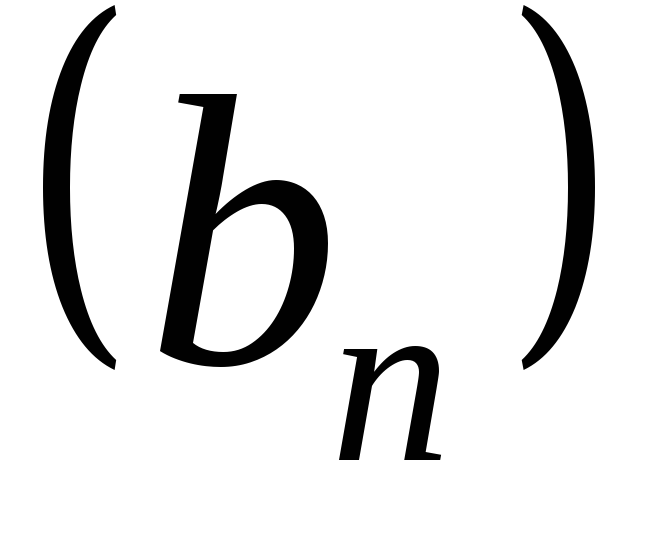 называют последовательность с
называют последовательность с -м
членом
-м
членом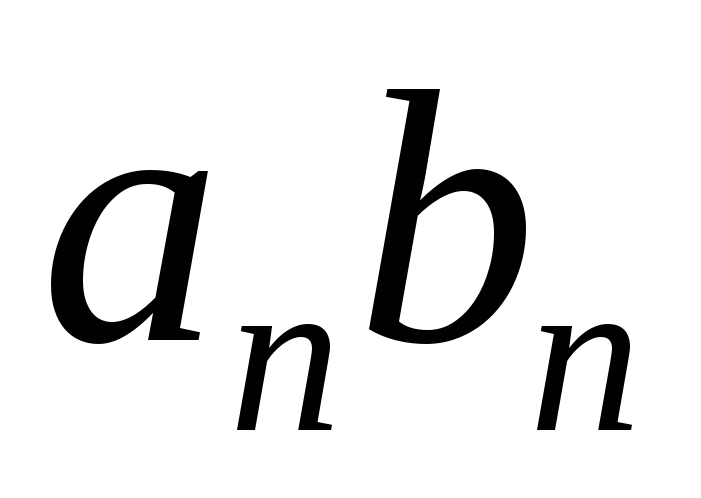 ,
т.е.
,
т.е.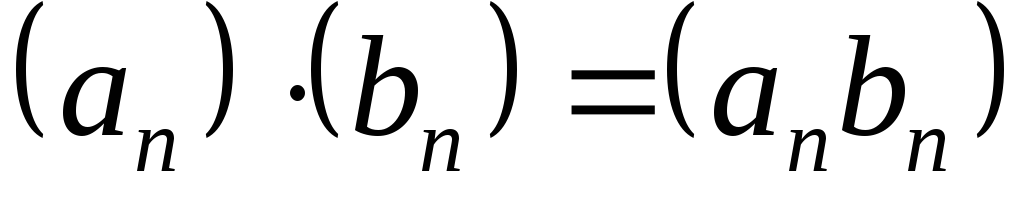 .
.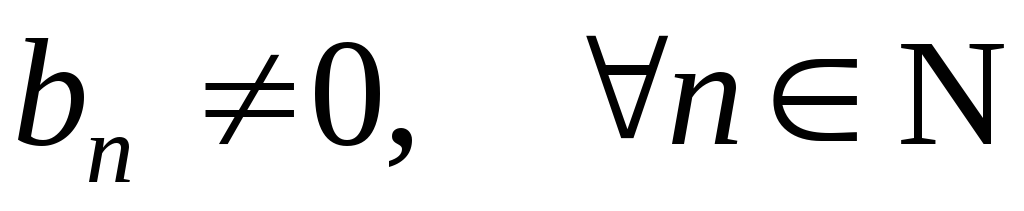 ,
то можно определитьчастное
,
то можно определитьчастное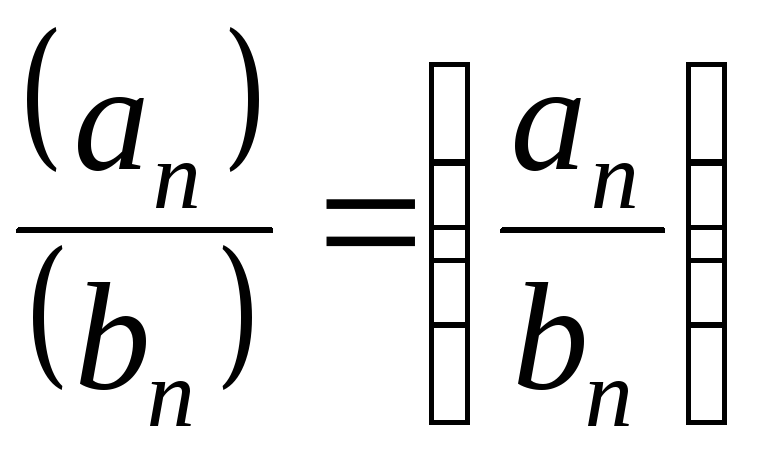 .
.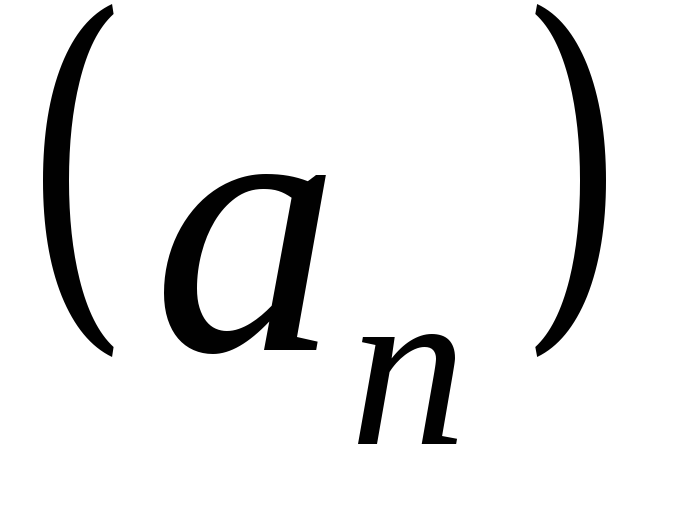 и
и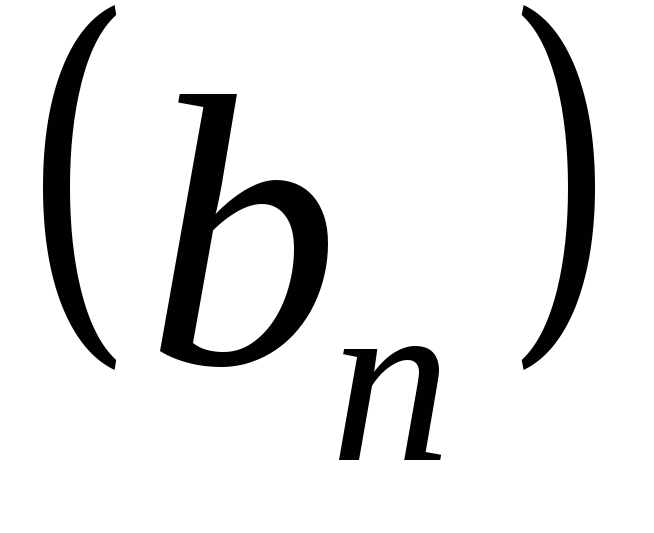 называются ихалгебраическимикомпозициями.
называются ихалгебраическимикомпозициями.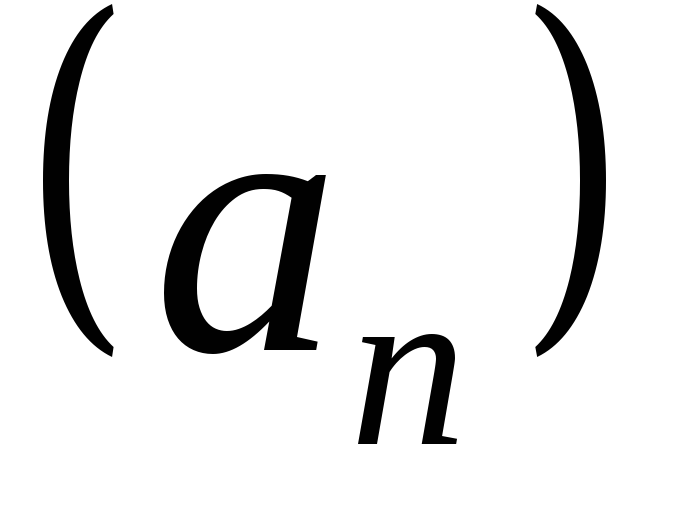 и
и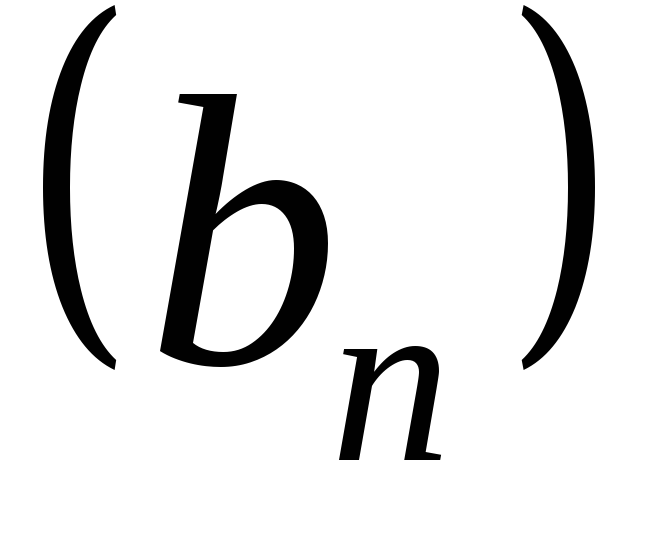 ,
где
,
где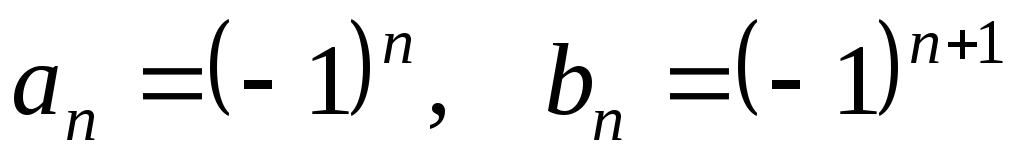 .
Тогда
.
Тогда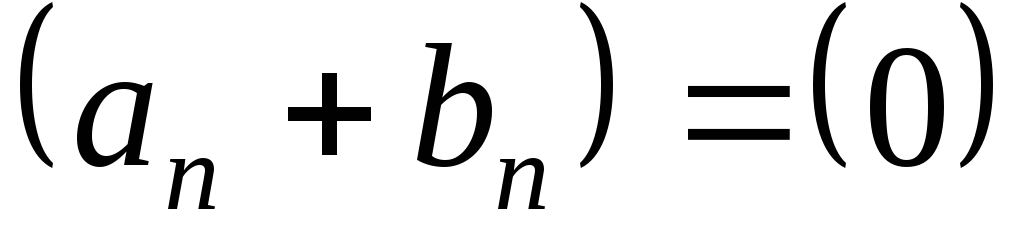 ,
т.е. последовательность
,
т.е. последовательность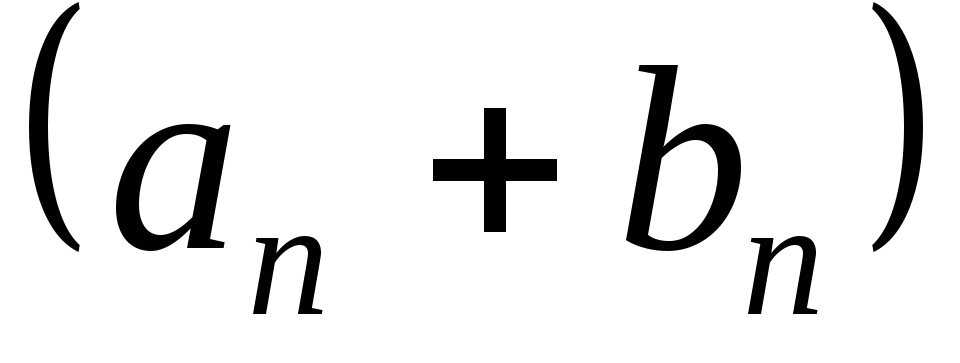 имеет все элементы, равные нулю.
имеет все элементы, равные нулю.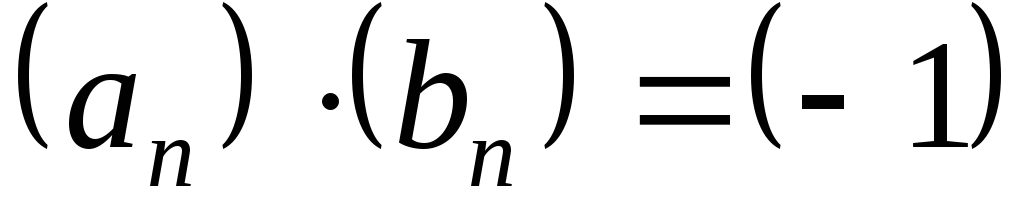 ,
, 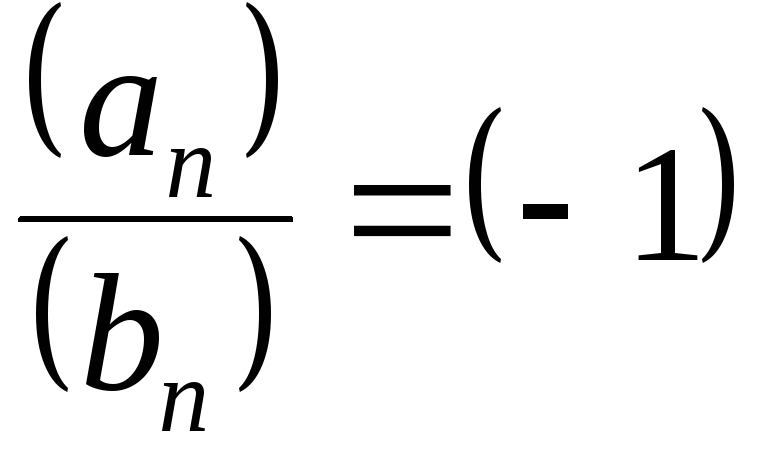 ,
т.е. все элементы произведения и частного
равны
,
т.е. все элементы произведения и частного
равны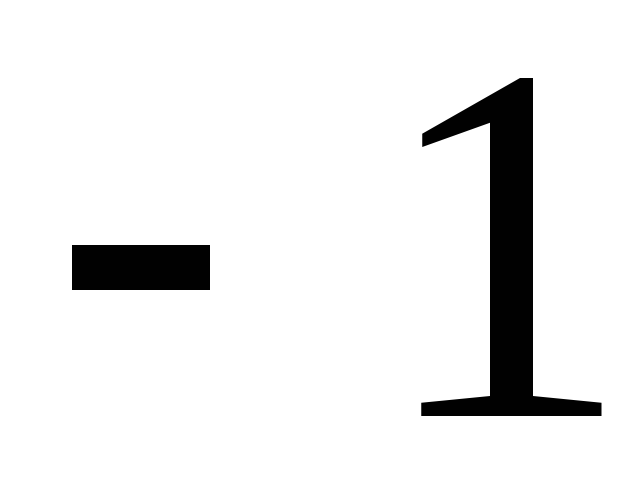 .
.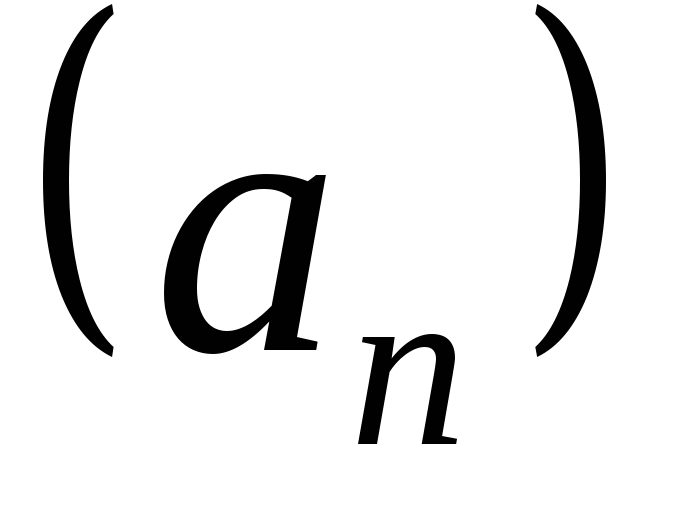 так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемуюподпоследовательностьюпоследовательности
так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемуюподпоследовательностьюпоследовательности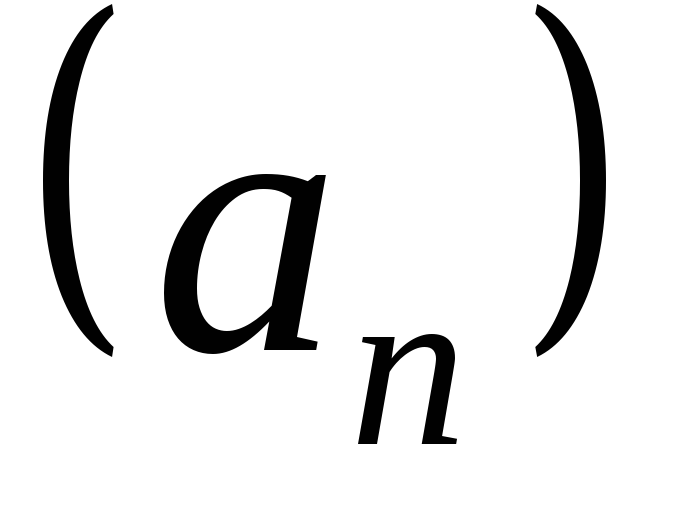 .
Если вычеркнуть несколько первых
элементов последовательности
.
Если вычеркнуть несколько первых
элементов последовательности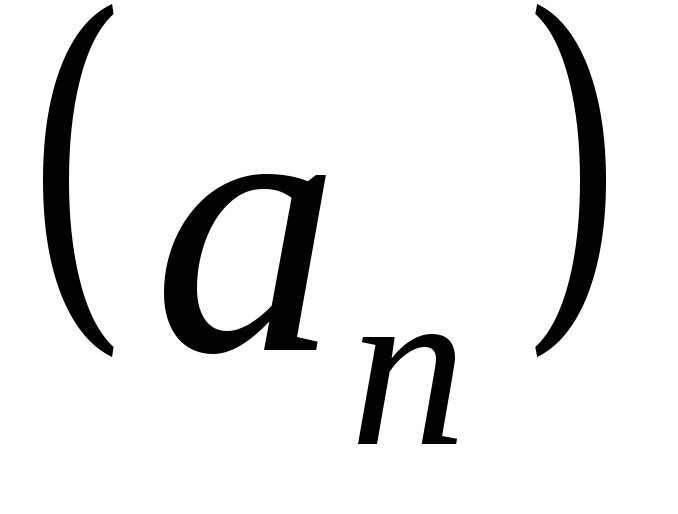 ,
то новую последовательность называютостатком.
,
то новую последовательность называютостатком.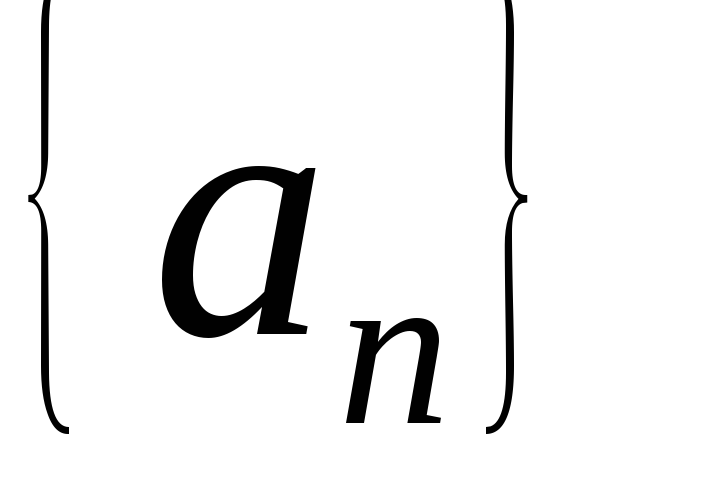 ограничено сверху (снизу). Последовательность
называютограниченной, если она
ограничена сверху и снизу. Последовательность
ограничена тогда и только тогда, когда
ограничен любой ее остаток.
ограничено сверху (снизу). Последовательность
называютограниченной, если она
ограничена сверху и снизу. Последовательность
ограничена тогда и только тогда, когда
ограничен любой ее остаток.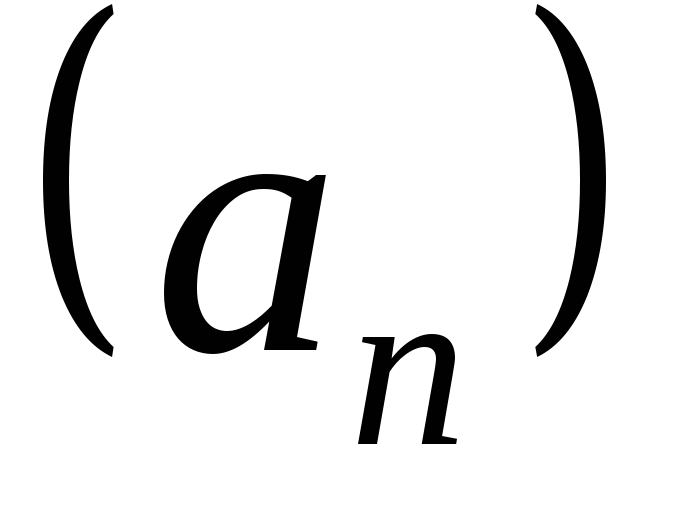 сходится, если существует число
сходится, если существует число такое, что для любого
такое, что для любого существует такое
существует такое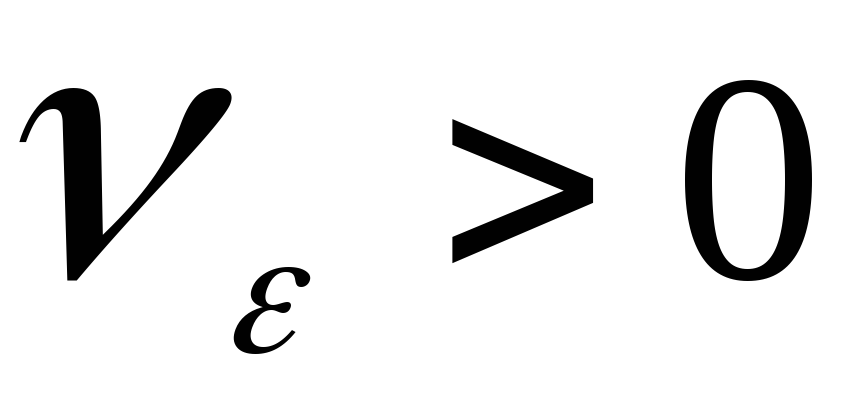 ,
что для любого
,
что для любого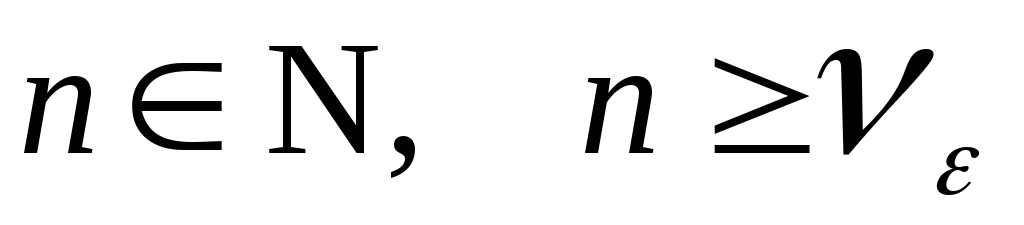 ,
выполняется неравенство:
,
выполняется неравенство: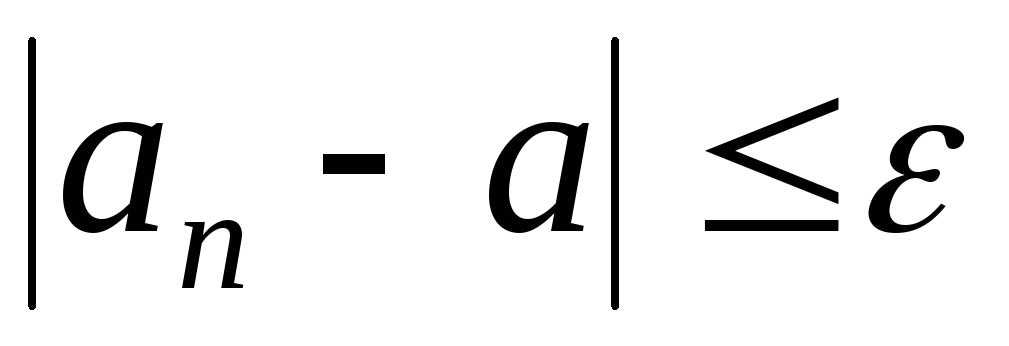 .
. называютпределом последовательности
называютпределом последовательности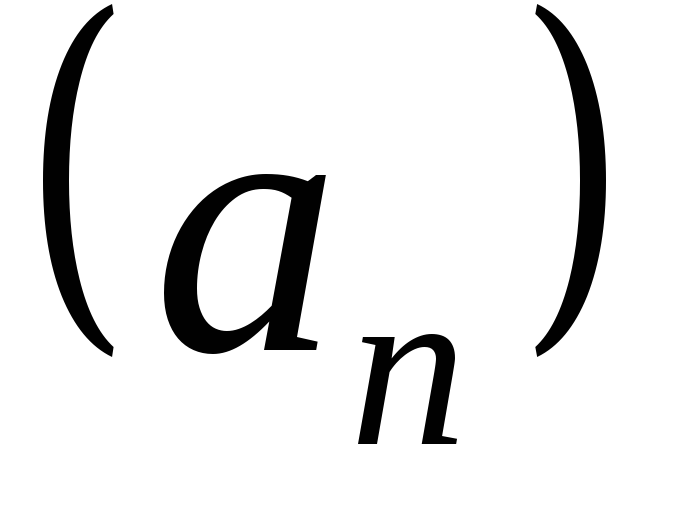 .
При этом записывают
.
При этом записывают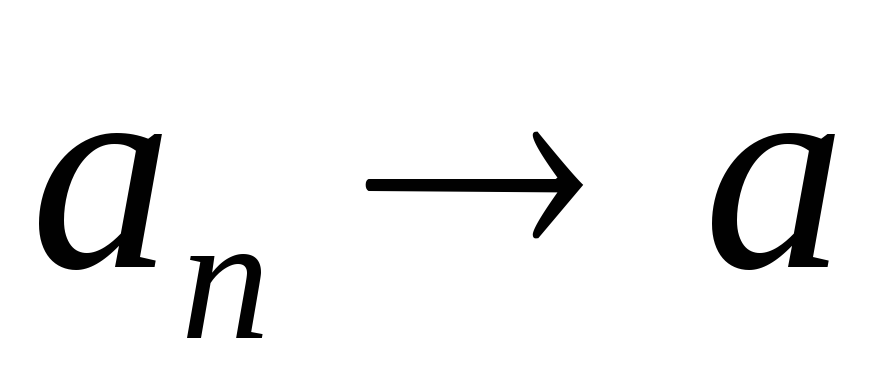 или
или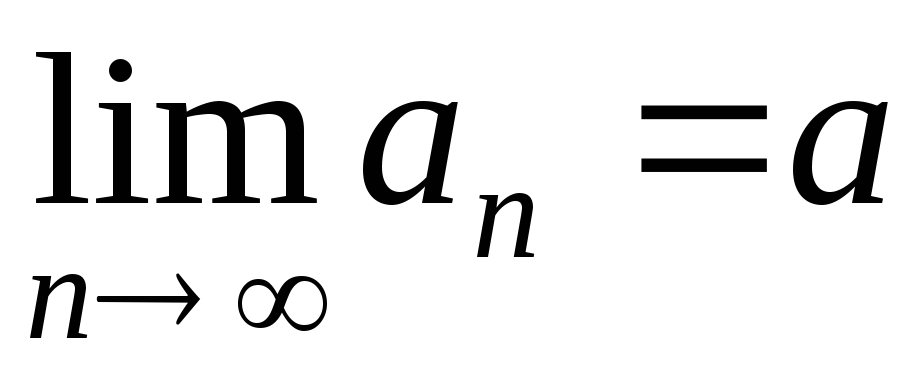 .
.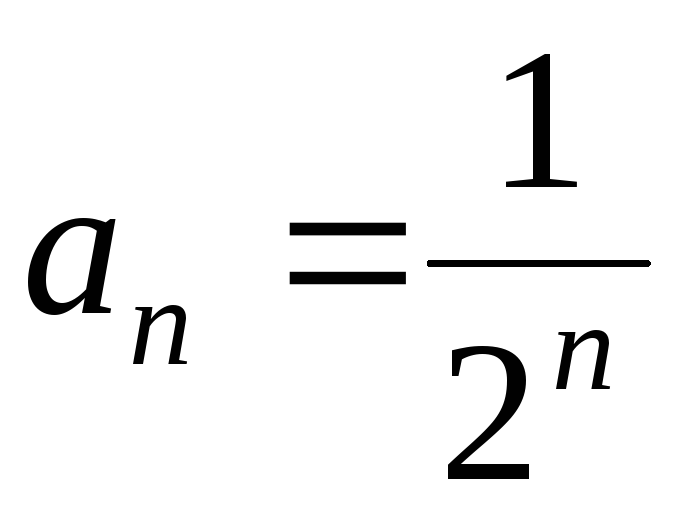 .
.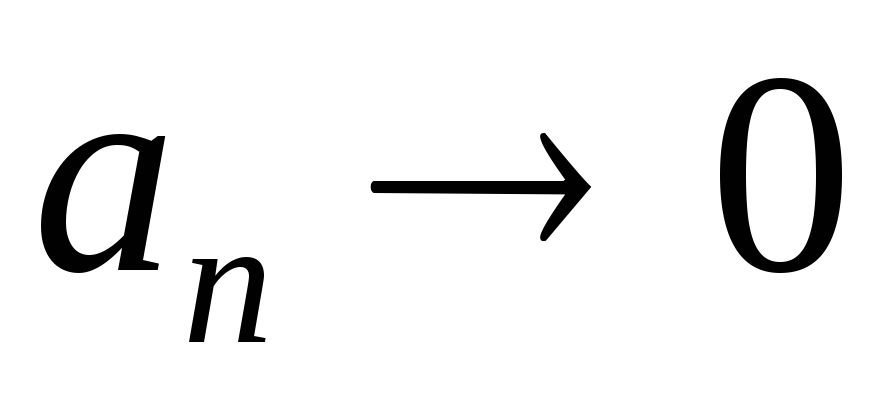 .
Зададим любое число
.
Зададим любое число .
Неравенство
.
Неравенство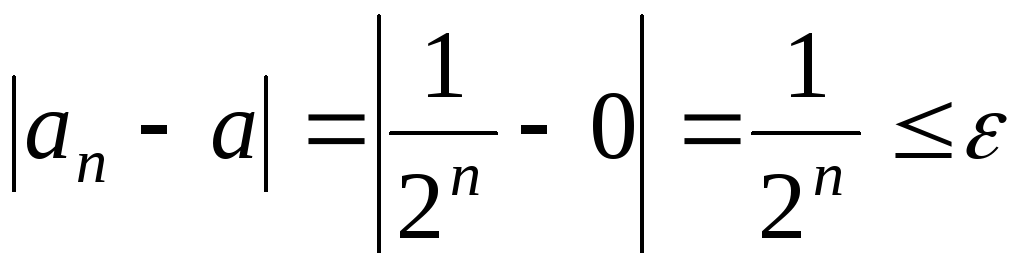 выполняется для
выполняется для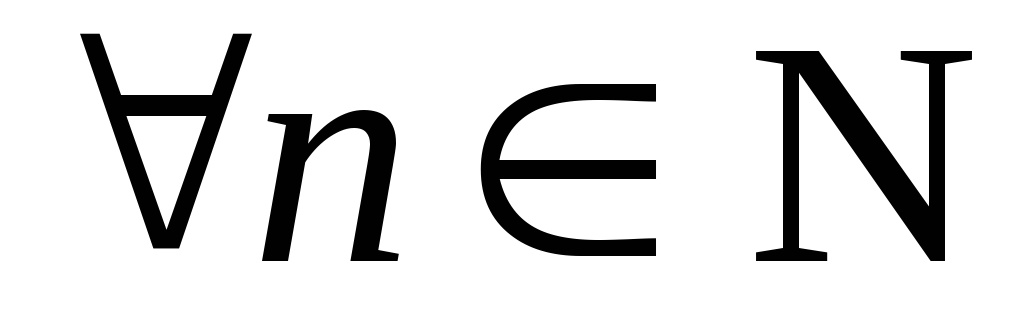 ,
такого, что
,
такого, что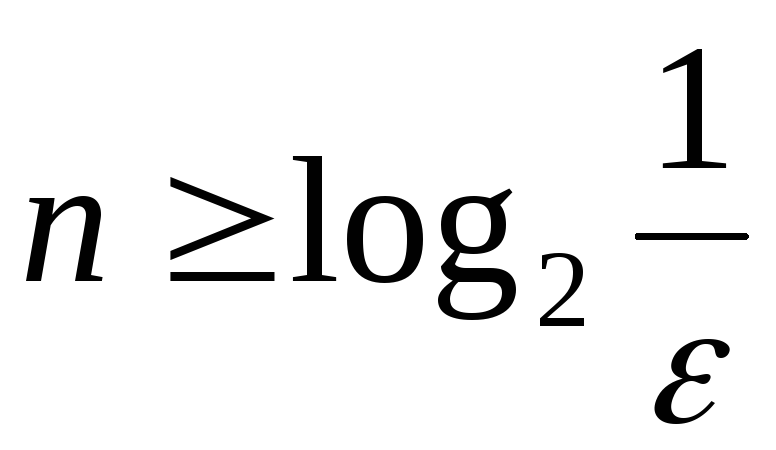 ,
что определение сходимости выполняется
для числа
,
что определение сходимости выполняется
для числа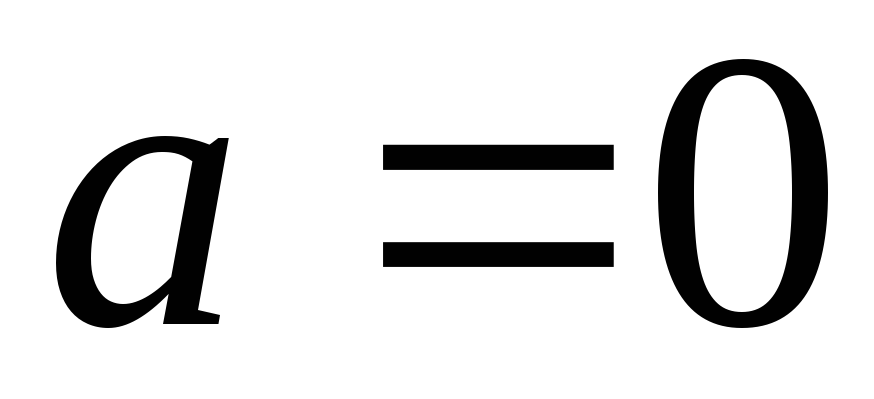 .
Значит,
.
Значит,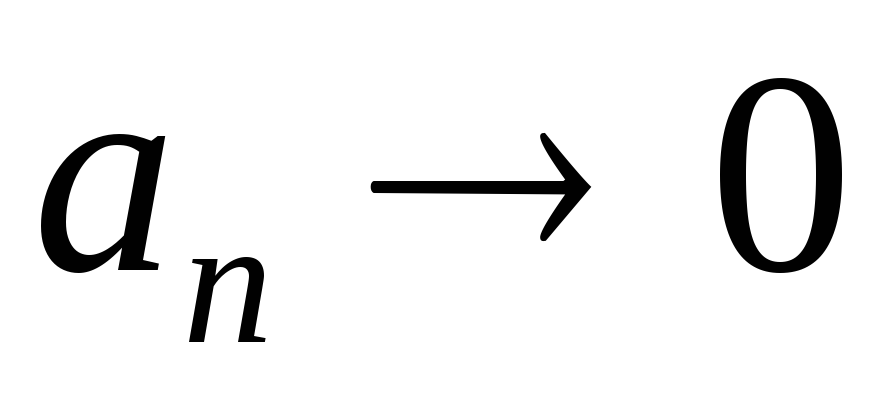 .
.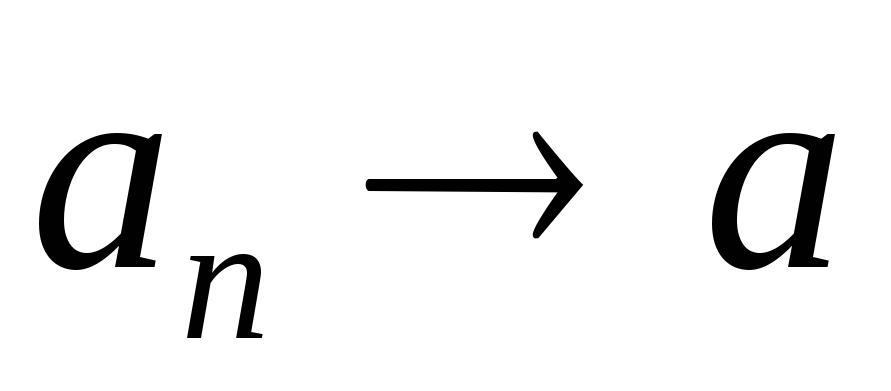 означает, что все члены последовательности
означает, что все члены последовательности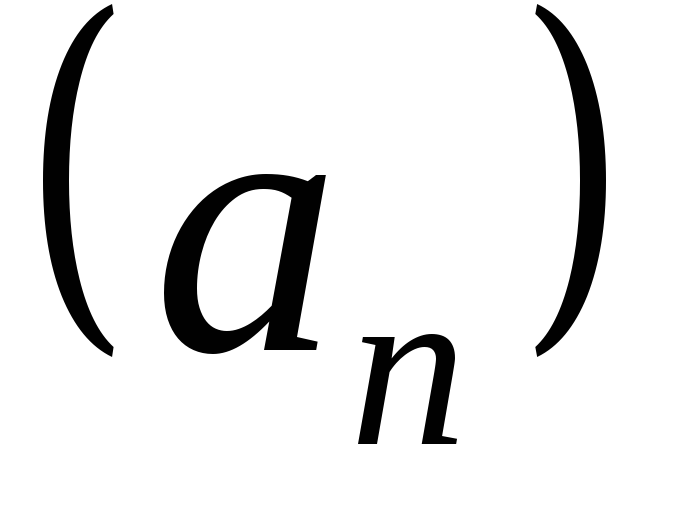 с достаточно большими номерами мало
отличается от числа
с достаточно большими номерами мало
отличается от числа ,
т.е. начиная с некоторого номера
,
т.е. начиная с некоторого номера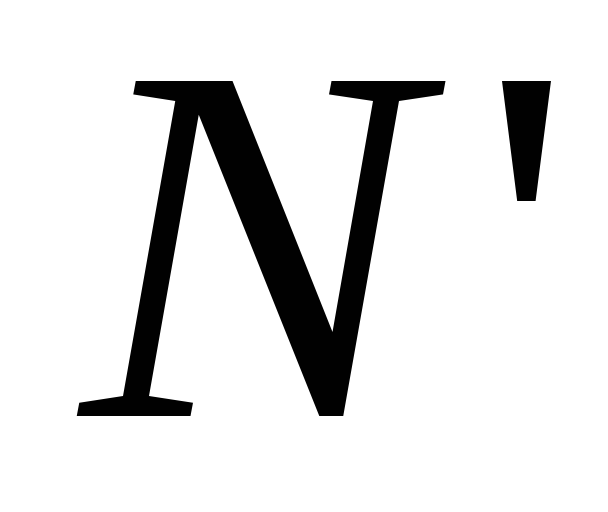 (при
(при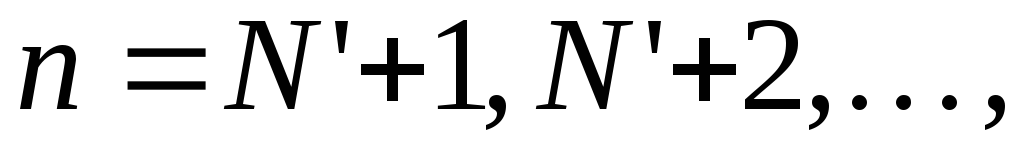 )
элементы последовательности находятся
в интервале
)
элементы последовательности находятся
в интервале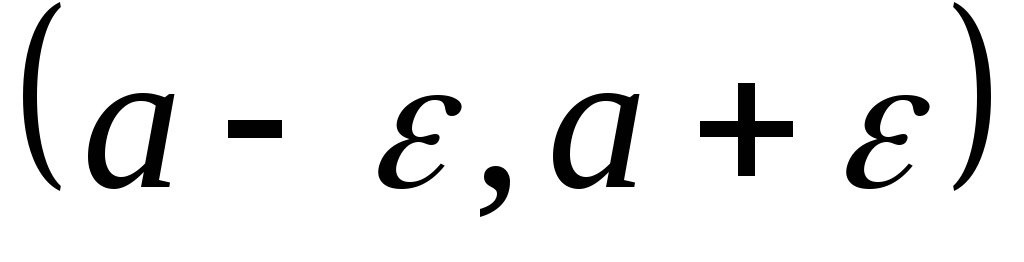 ,
который называется
,
который называется –окрестностью
точки
–окрестностью
точки .
.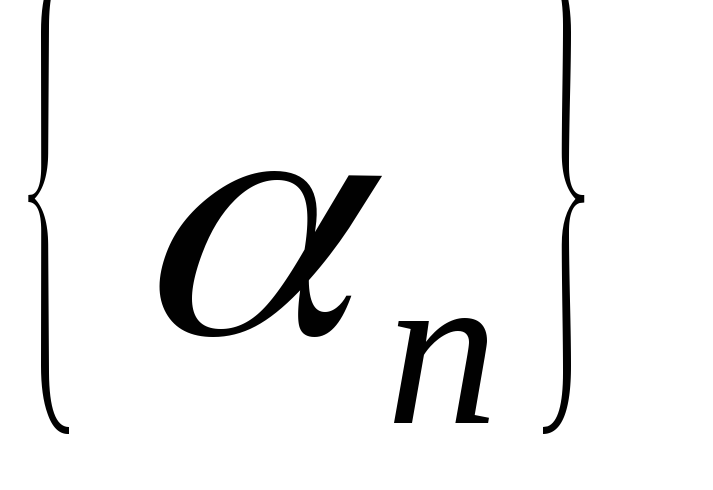 ,
предел которой равен нулю (
,
предел которой равен нулю (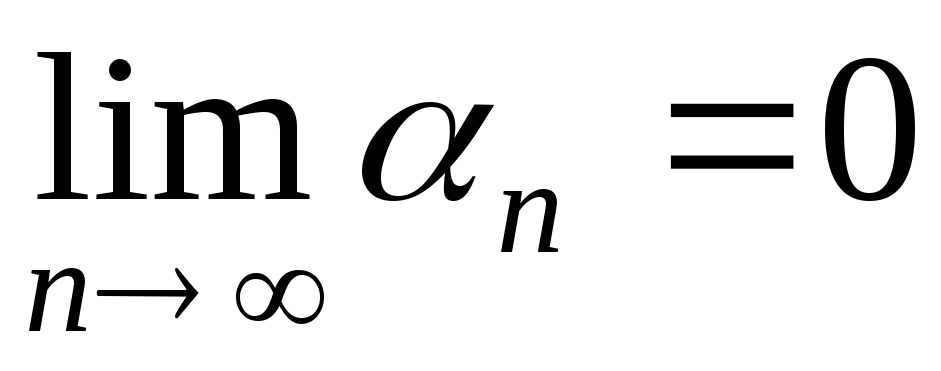 ,
или
,
или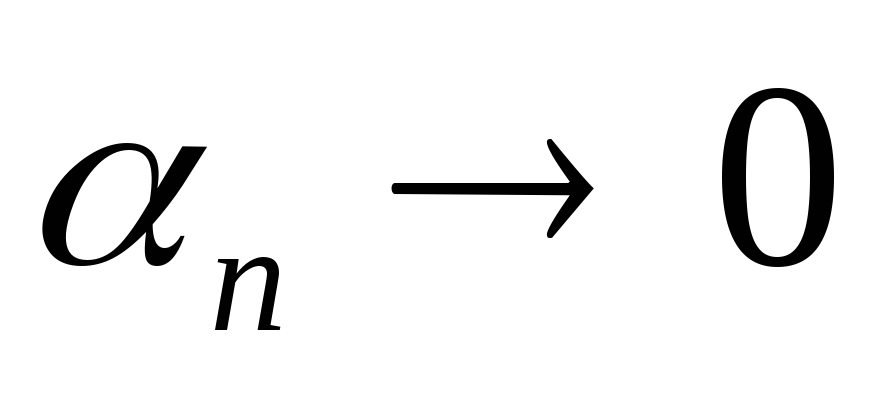 при
при )
называетсябесконечно малой.
)
называетсябесконечно малой.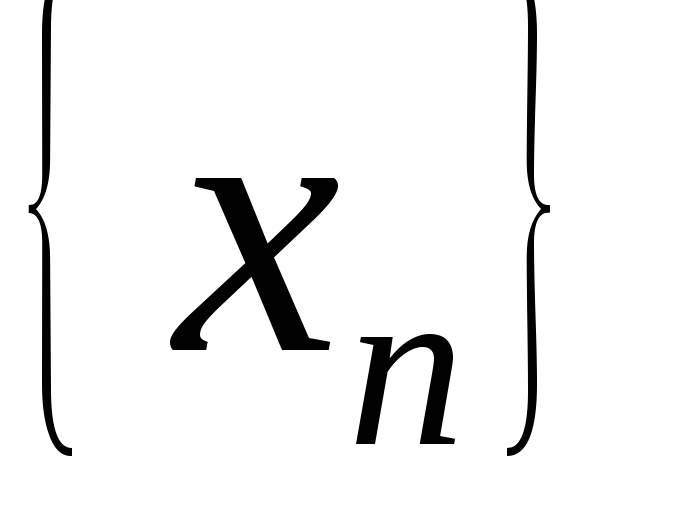 имела предел, необходимо и достаточно
чтобы
имела предел, необходимо и достаточно
чтобы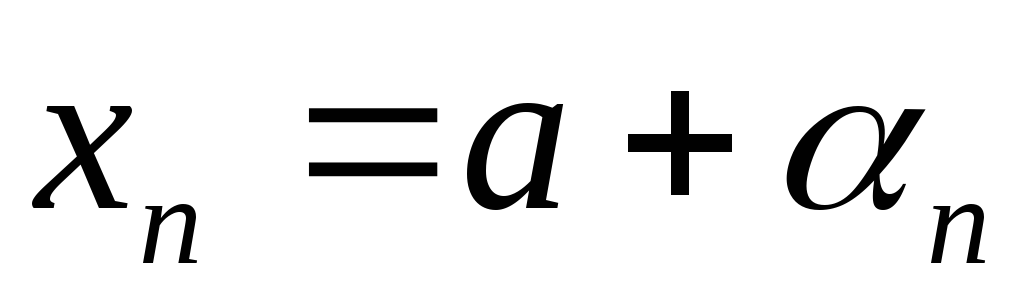 ,
где
,
где – постоянная;
– постоянная;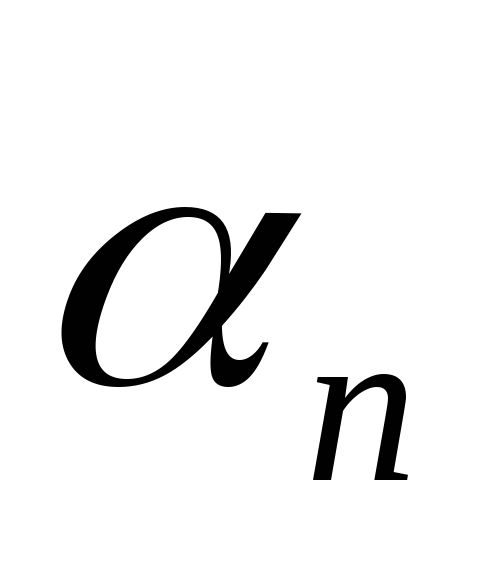 –
бесконечно малая.
–
бесконечно малая.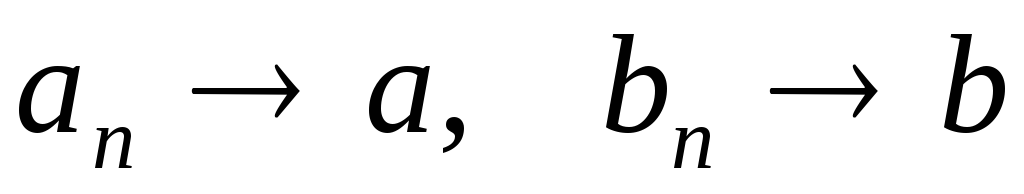 ,
то
,
то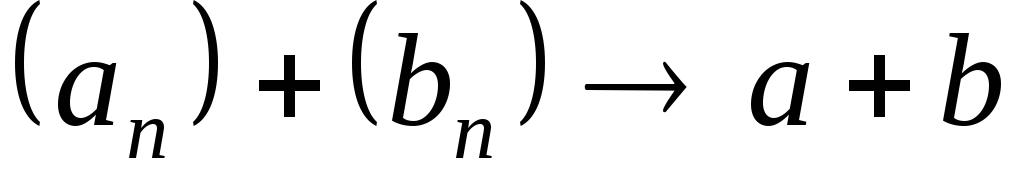 ;
; и
и
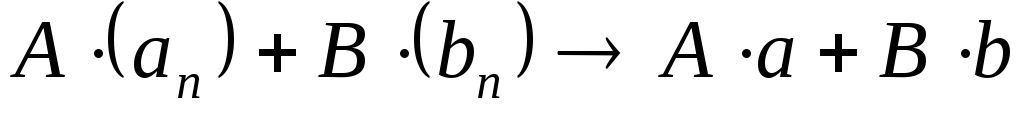 ;
;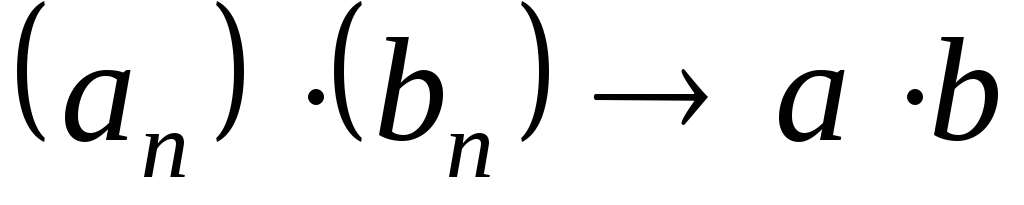 ;
;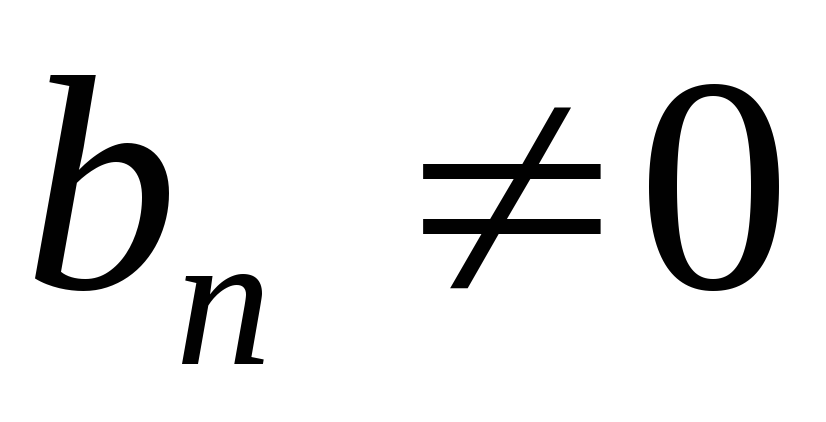 ,
,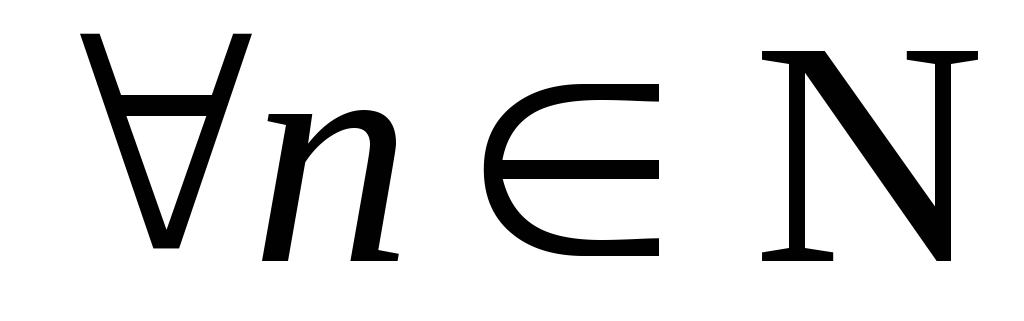 и
и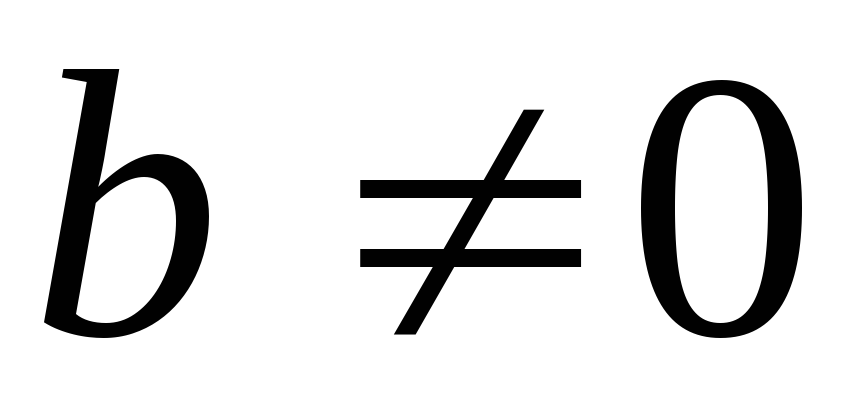 ,
то
,
то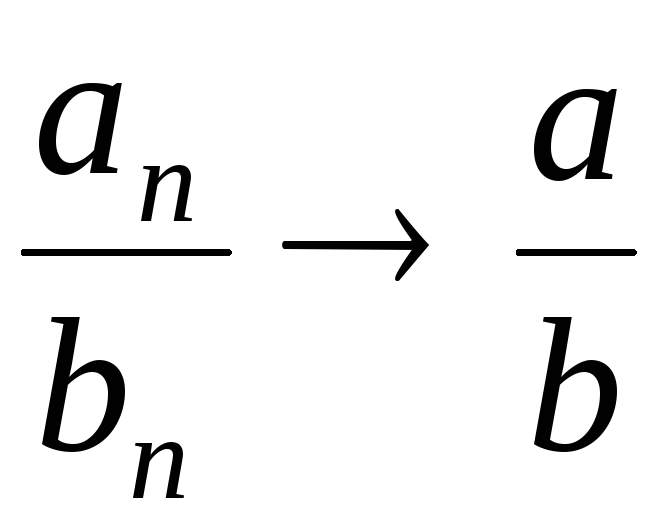 ;
;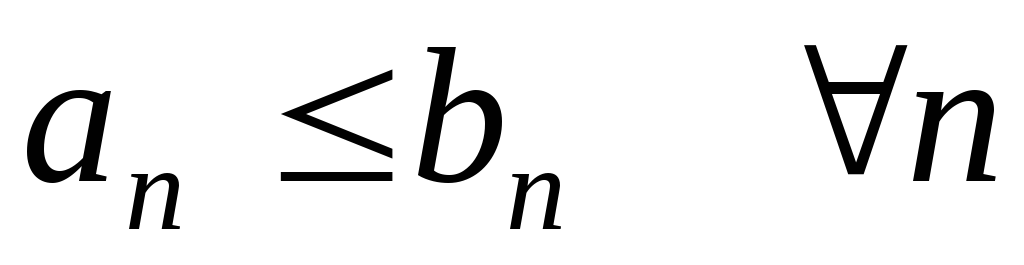 ,
то
,
то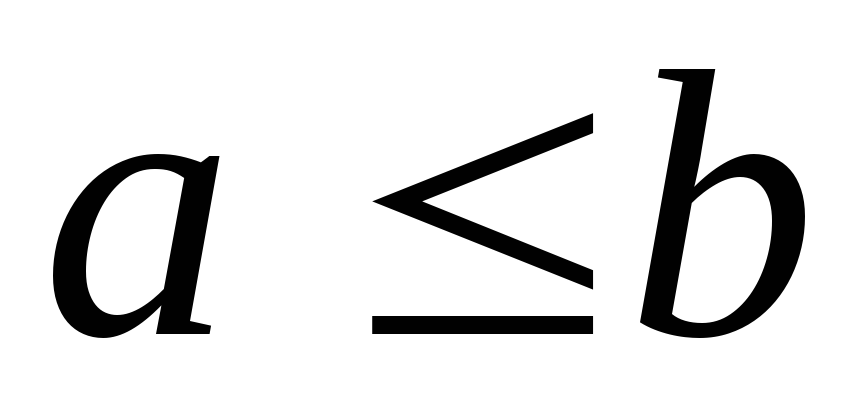 ;
;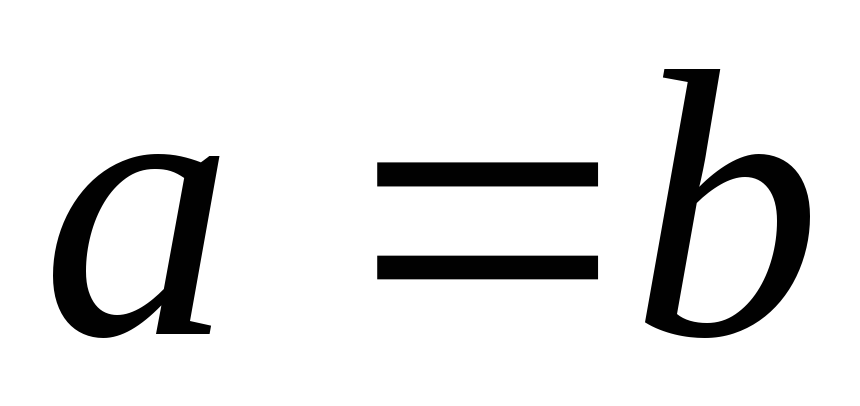 и
и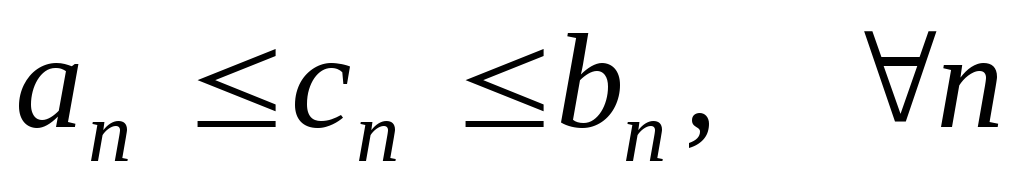 ,
то
,
то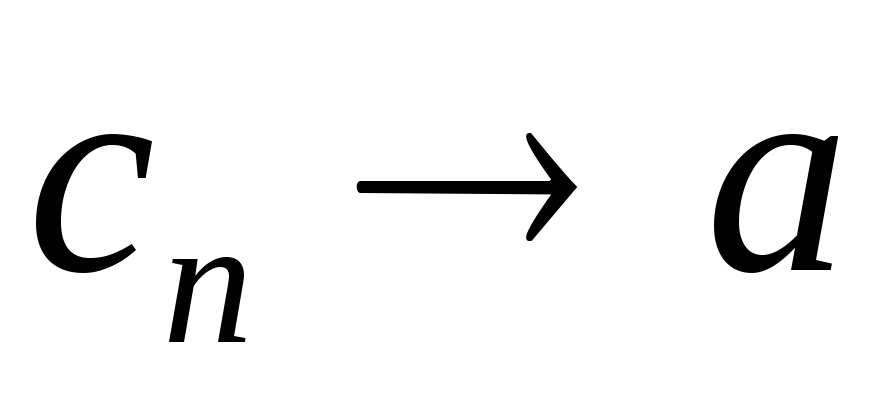 ;
;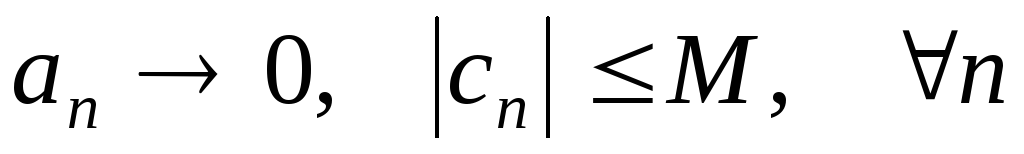 ,
то
,
то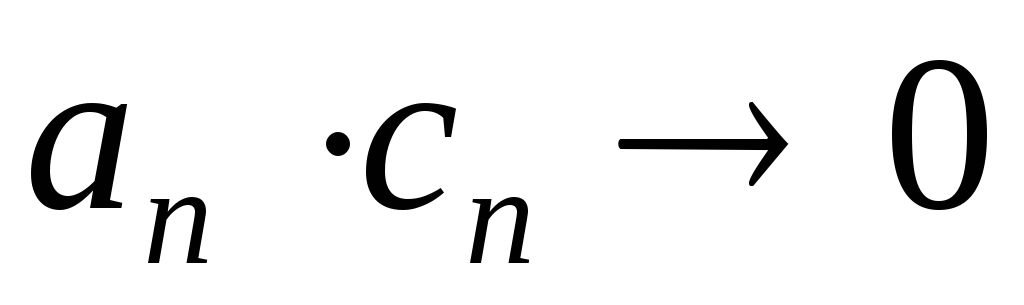 .
. ,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени
,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени числителя и знаменателя).
числителя и знаменателя).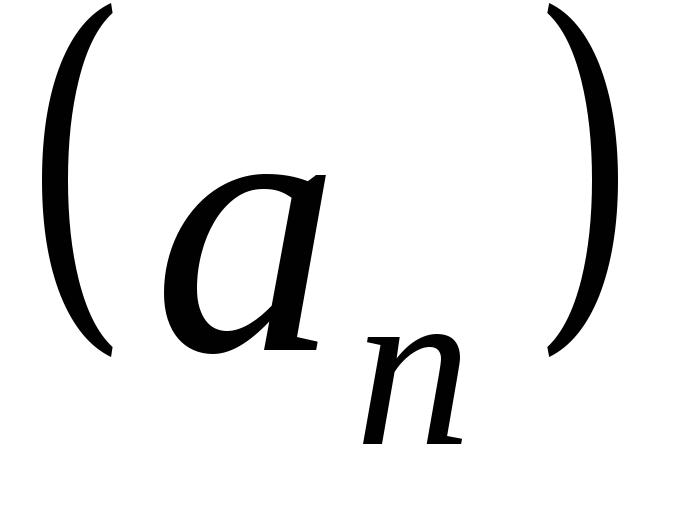 называется:
называется: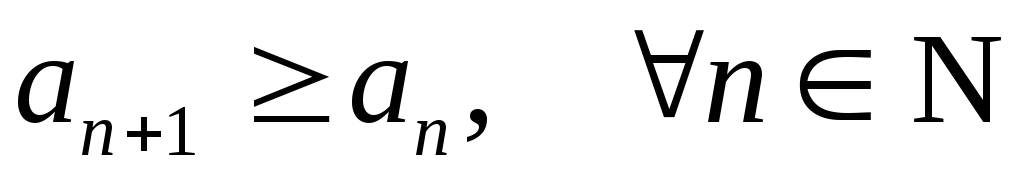 ;
;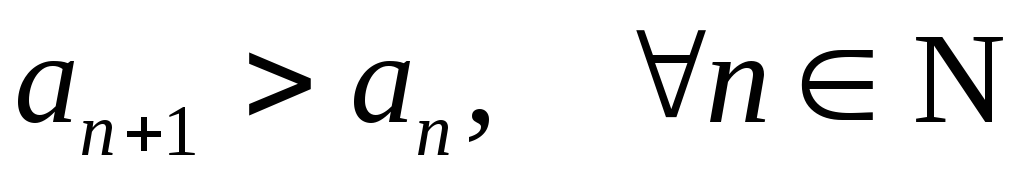 ;
;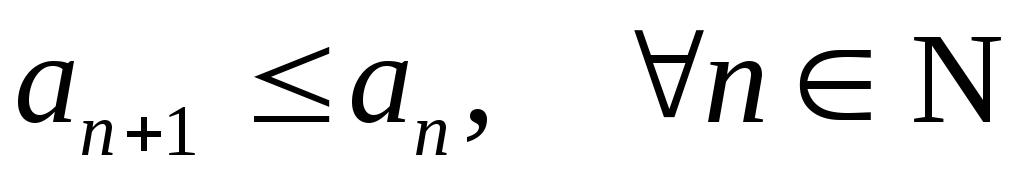 ;
;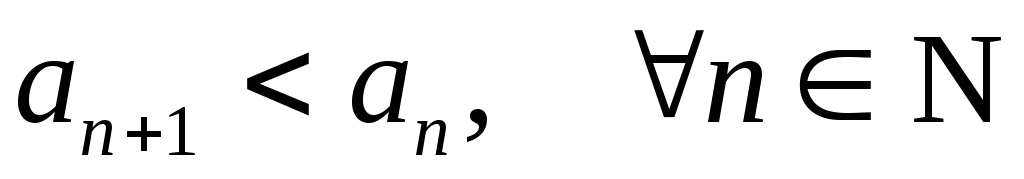 .
.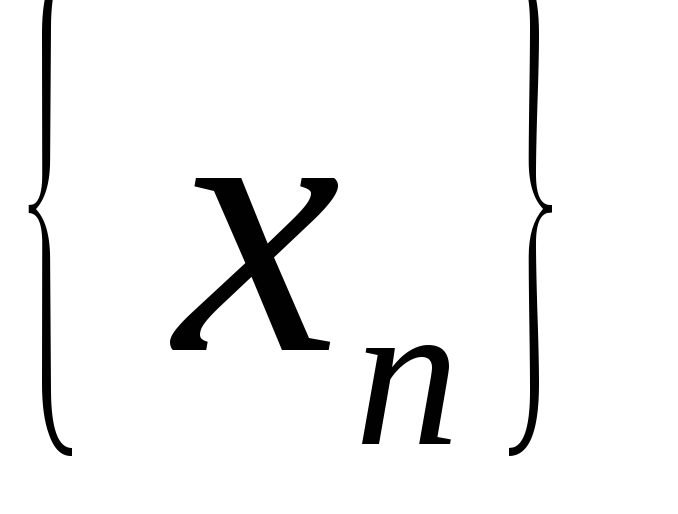 монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани. Тесты по русскому языку.Пройти >>
Тесты по русскому языку.Пройти >> Доски имеют пазы и шипы с четырёх сторон [4]
Доски имеют пазы и шипы с четырёх сторон [4] В последнее время ходит много слухов касательно добавления новых предметов в список обязательных для сдачи на ЕГЭ/ОГЭ. Особенно это касается ОГЭ по иностранному языку, который многие неофициальные сайты объявили обязательным с 2020 года. Но так ли это? В этом вопросе не стоит полагаться на слухи, которые зачастую вводят в заблуждение и повышают и так безмерное волнение выпускников.
В последнее время ходит много слухов касательно добавления новых предметов в список обязательных для сдачи на ЕГЭ/ОГЭ. Особенно это касается ОГЭ по иностранному языку, который многие неофициальные сайты объявили обязательным с 2020 года. Но так ли это? В этом вопросе не стоит полагаться на слухи, которые зачастую вводят в заблуждение и повышают и так безмерное волнение выпускников.



 За все школьные годы вашему ребенку придется решить множество задач, и несмотря на то, что все они кажутся разноплановыми, в алгоритме их решения все же есть общие моменты, и, уяснив их и следуя этому алгоритму, ребенок сможет решить практически любую задачу. Если ученик еще в 1-3 классе освоит тактику решения задач, в старших классах он будет щелкать задачки как семечки не только по математике, но и по физике, химии, геометрии тоже.
За все школьные годы вашему ребенку придется решить множество задач, и несмотря на то, что все они кажутся разноплановыми, в алгоритме их решения все же есть общие моменты, и, уяснив их и следуя этому алгоритму, ребенок сможет решить практически любую задачу. Если ученик еще в 1-3 классе освоит тактику решения задач, в старших классах он будет щелкать задачки как семечки не только по математике, но и по физике, химии, геометрии тоже.


























































 Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.
Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.





 Акробатический манёвр с увеличением угла тангажа (например, ввод в горку) сопровождается положительной перегрузкой — тело весит больше, чем обычно У этого термина существуют и другие значения, см. Перегрузка.
Акробатический манёвр с увеличением угла тангажа (например, ввод в горку) сопровождается положительной перегрузкой — тело весит больше, чем обычно У этого термина существуют и другие значения, см. Перегрузка.
 К обсуждению. Sealle 10:46, 18 апреля 2018 (UTC)
К обсуждению. Sealle 10:46, 18 апреля 2018 (UTC) Акробатический манёвр с увеличением угла тангажа (например, ввод в горку) сопровождается положительной перегрузкой — тело весит больше, чем обычно
Акробатический манёвр с увеличением угла тангажа (например, ввод в горку) сопровождается положительной перегрузкой — тело весит больше, чем обычно











