Биолог профессия это – что за профессия, чем занимается, плюсы и минусы, обучение, требования, описание,для детей, википедия, такой
Профессия — Биолог | Выпускник.Kz
Категория: ПедагогическиеБиология — это не только изучение жуков и различных видов насекомых. Узнайте больше о трудовой деятельности специалистов в этой области и решите, хотите ли вы связать свою жизнь с этой сферой деятельности.
История
Биологи специализируются на исследовании живых организмов. История профессии напрямую связана с зарождением медицины и корнями уходит в древность. Первые труды по описанию различных видов, физиологии и анатомии как человека, так и животных появились в Древней Греции. В те времена философы размышляли об устройстве мира и организмов.
С течением времени знания в области медицины и устройства окружающего мира постепенно увеличивались и развивались. Люди узнавали о полезных свойствах тех или иных видов, учились выращивать скот более крупным и питательным, узнавали новые подробности о внутреннем устройстве тела человека.
Все приостановилось в период Средневековья. Темные времена – это страшное время для всех естествоведов. Наличие знаний о свойствах трав, устройстве организмов и человеческих болезнях приравнивалось к поклонению дьяволу. Лекари, целители, травники – все признавались слугами сатаны и подвергались очищению огнем.
Просветление наступает с эпохой Возрождения. Естественные науки начинают стремительно развиваться. Открываются музеи естествознания, появляются зверинцы и больницы. Наступает эпоха расцвета биологических наук.
Однако, сам термин «биология» возник лишь в 19 веке. Биологию выделяют в отдельную науку, которая объединяет массу ответвлений: зоологию, анатомию, физиологию и т.д. Ранее все эти отрасли знания существовали по отдельности, но именно в 19 веке ученые заметили, что у всего живого есть общие черты, что и привело к обобщению всех естественных наук под крылом биологии.
В наши дни биологи имеют колоссальные возможности в плане технологий и возможностей. Современные механизмы исследований, огромный багаж знаний прошлых лет в совокупности со сверхмощным оборудованием – все это открывает новый этап в профессии биолога и развитии науки.
Краткое описание профессии
Профессия биолога довольно многогранна. Стандартно ее классифицируют по отраслям биологической науки:
- Биолог-ботаник. Данный специалист занимается растениями. Он изучает их свойства, отыскивает новые разновидности и классифицирует виды. Также именно данный специалист выясняет влияние растений на человека и животных.
- Биолог-зоолог. Данный специалист изучает животных и все, что с ними связано, исследует их заболевания и их влияние на человека, занимается поиском новых видов. Зоологи имеют широкий спектр деятельности. Именно они указывают на причины исчезновения видов, стимулируя людей беречь природу.
- Микробиолог. Это специалист, изучающий микроорганизмы. Он знает все о бактериях, проводит различные исследования, направленные на борьбу с ними и способы их полезного применения. Данная отрасль биологической науки стремительно развивается и имеет ряд перспектив.
Каждый из трех основных подразделений биологической науки классифицируется на 10-ки видов знаний, которые еще более узко направлены. Биолог может изучать все и сразу. Это специалист широкого профиля, знающий массу информации об устройстве и принципах жизнедеятельности живых организмов. Именно биология помогает человеку проводить исследования, необходимые для открытия панацеи от страшных заболеваний современности.
Работа у биолога может быть как лабораторной, так и весьма увлекательной, связанной с поездками по всему земному шару. Биологи-исследователи постоянно путешествуют в поиске новых видов и попытках остановить массовое уничтожение лесов.
На каких специальностях учиться
Для того чтобы иметь возможность работать биологом, вам необходимо выбрать одну из таких специализаций в высшем учебном заведении:
- Биология.
- Биотехнология.
- Биоинженерия и биоинформатика.
- Биология и химия (педагогическое образование).
- Водные биоресурсы и аквакультура.
- Почвоведение.
- Медицинская кибернетика.
- Медицинская биофизика.
Чем приходится заниматься на работе и специализации
Работа биолога в основном заключается в постоянном проведении исследовательской деятельности. Спектр ежедневных обязанностей включает:
- Сбор информации, который входит в планирование исследования.
- Подготовка материалов к исследованию. Биолог постоянно изучает информацию. Это необходимо для того, чтобы подобрать методы для эффективного проведения исследования.
- Подбор и разработка необходимого оборудования.
- Непосредственное проведение исследований. Для этого пригодится не только знание биологии, но и отличные навыки в химии.
- Фиксация результатов исследования. Биолог постоянно фиксирует показатели приборов и записывает все виды реакций и процессов.
- Обобщение результатов. В данный этап входит их повторное изучение и обработка.
- Составление выводов. Это уже аналитический вид работ. На основе результатов исследований появляются выводы и рекомендации.
- Путешествия. Это один из излюбленных видов работ. Биологи занимаются изучением видов в естественной среде обитания, фиксируют результаты и описывают их.
- Открытие и описание новых видов. Многие растения и животные все еще не обнаружены человеком.
- Преподавательская деятельность. Обучение студентов и школьников тонкостям биологии и более узких ее отраслей.
Профессия биолога – это интересная и динамично развивающаяся деятельность, дело, которое приносит максимум пользы человеку и природе.
Кому подходит данная профессия
Биолог – это в первую очередь большой любитель природы и всего живого. Данная профессия требует усидчивости, аккуратности и внимательности – эти качества помогут в проведении исследований и наблюдений. Аналитический склад ума сделает исследовательскую деятельность максимально эффективной. Биолог должен обладать хорошо развитой долговременной памятью, так как довольно часто может пригодиться какая-либо информация.
Еще одним качеством для хорошего биолога является отсутствие аллергических реакций на животных и растений. Она может стать помехой при проведении исследований.
Востребованность
Профессия биолога не является востребованной. Обычно вакансии появляются только в университетах и школах. Немногие компании на территории нашего государства занимаются исследовательской деятельностью. На рынке замечается существенный спад интереса к биологии.
Легко ли устроиться на работу
Устроиться на работу довольно сложно, связано это не с высокими требованиями, а с тем, что вакансии появляются крайне редко. При их появлении диплома обычно оказывается недостаточно. Ключевую роль играет опыт и наличие исследовательской практики.
Как обычно строится карьера
Карьера биолога строится в зависимости от сферы применения знаний:
- Педагоги могут вырасти до завучей, деканов и ректоров. Главное, постоянно повышать уровень своих знаний.
- Биологи-исследователи часто становятся заведующими лабораторией и начальниками проектов. Для роста важно проявить себя. Постоянно развиваться, демонстрировать осведомленность и находить материалы для проведения качественных исследований.
Перспективы профессии
Профессия биолога уже давно находится далеко не на пике популярности. Большинство исследований отведено медикам и более узконаправленным профессорам и ученым. Перспективы роста есть всегда. Так биологи могут стать деканами факультетов или же заведующими лабораторией.
Связанные специальности
где учиться, зарплата, плюсы и минусы
Микробиолог специализируется на изучении микроорганизмов, и в первую очередь – тех, что могут вызывать развитие заболеваний у животных и людей. Также он тестирует и разрабатывает лекарственные препараты, различные химические вещества для нужд промышленности, проводит экспертизы и исследования. Профессия относится к категории «человек – природа». Профессия подходит тем, кого интересует химия и биология (см. выбор профессии по интересу к школьным предметам).
Читайте также:
Краткое описание
Микробиология как профессия зародилась вскоре после того, как человечество изобрело достаточно мощные увеличительные приборы, позволяющие рассмотреть микроорганизмы, не доступные обычному человеческому зрению. Сегодня в арсенале микробиологов есть оборудование, с помощью которого они могут изучать мельчайшие частицы, ставить опыты и эксперименты на них, исследовать закономерности развития микробиологических процессов. Чаще всего их работа, так или иначе, сопряжена с медициной, хотя подобные специалисты могут заниматься даже исследованиями и разработками на благо пищевой промышленности.
Особенности профессии
Одна из основных особенностей профессии микробиолога – это высокий уровень ответственности. Достаточно часто его работа направлена на исследование потенциально опасных микроорганизмов, поэтому соблюдение правил безопасности на рабочем месте для таких сотрудников имеет исключительное значение. В целом их трудовые обязанности обычно сводятся примерно к следующим:
- Отбор проб материала, которые подходят для исследовательских целей.
- Посев изучаемых микроорганизмов на среду, которая подходит для их роста и развития, поддержание их жизнеспособности за счет использования специальных питательных растворов.
- Иссле
Биологические профессии и специальности
Какие возможности ждут тех, кто любит биологию и хочет связать с ней жизнь? На кого и куда пойти учиться? Отвечаем на главные вопросы о перспективных биологических профессиях и специальностях.
В этой статье:
Почему биология – наука будущего
Человек всегда ставил перед собой невероятные задачи. И за последние 50 лет мы научились с нуля выращивать внутренние органы, делать пересадки, сложнейшие операции и вылечивать людей с онкологией. Всему этому человек научился, изучая природу и самого себя.
Развитие медицины сегодня достигло таких высот, что врачи ещё на этапе вынашивания ребёнка могут узнать о нём всё: потенциальные болезни, предрасположенности к чему-то, всё это записано в наших генах словно на флешке, главное научиться обрабатывать эти данные.
Всё это говорит только о том, что биология – это не просто наука будущего, а наука, которая создаст это будущее.

Биологические профессии и специальности
Привычные биологические профессии и специальности
Для любителей биологии найдётся много важнейших профессий, известных каждому с детства.
Ветеринар
По сути, это врач для животного. Требования к ветеринарам обычно такие же, как и к обычным врачам – они должны разбираться во всех нюансах своей работы.
Но в этой профессии есть много ответвлений. Например, ветеринары зачастую работают в судмедэкспертизе. Есть даже понятие «судебно-ветеринарная экспертиза». Ещё не стоит забывать, что помимо прикладных ветеринаров есть исследователи.
Учёный
Учёные в теории и на практике изучают особенности дикой природы и человеческого тела, трудятся над разработками в лабораториях и выпускают книги и статьи в научных и научно-популярных изданиях.
Такие люди посвящают себя многолетним исследованиям и разработкам. И некоторые даже становятся лауреатами Нобелевской премии по физиологии или медицине. Кстати, за время существования премии только 2 учёных из России удостоились её – Иван Петрович Павлов и Илья Ильич Мечников.

Количество лауреатов Нобелевской премии по физиологии или медицине по странам
Учёным приходится сложнее всего, ведь без них прогресс во всех сферах останавливается, и та же медицина без них невозможна.
Медик (врач)
Вряд ли нужно рассказывать, кто такой врач, ведь с представителем этой профессии каждый из нас сталкивался в жизни. Врачебные практики делятся на десятки отраслей и специальностей, но главным остаётся одно – помощь людям.
Для будущих врачей мы написали статью «Как поступить в медицинский вуз»
К слову, с 2017 года начать работать врачом стало возможно сразу после окончания вуза, а не после ординатуры. Но выбирая медицину, будьте готовы к тому, что после 6 лет в вузе врачу всё равно придётся учиться и совершенствоваться всю жизнь.
Агроном
Это специалист в области сельского хозяйства. Агрономы лечат растения, создают удобрения и занимаются выведением новых сортов уже знакомых плодов сельского хозяйства.
А поскольку в наши дни всё это стало высокотехнологичной областью, сегодня агроном-селекционер – вновь актуальная профессия!
Биологические профессии и специальности будущего
Но не медиками едиными… В той же медицине появилось много новых профессий. Технологический прогресс сделал возможным работу в абсолютно неизвестных ранее областях.
Генная инженерия
Стоит сказать, что генетика состоит из множества направлений.
Генный инженер – это учёный, который работает над изменениями живых организмов путём изменений в генах. Специалисты данной категории способны развить в организме необходимые им качества, а главное – притупить ненужные.
Без генных инженеров развитие фармацевтики не было бы таким стремительным. Именно благодаря этой профессии становится возможным диагностировать и лечить многие болезни.
Генная инженерия — наука новая, поэтому по этой специальности ведут набор совсем немного вузов. Помимо биологии в программе обычно много математики и информатики, студенты изучают клонирование и трансплантацию клеток, биоинженерию и разные виды химии.

Сколько получают генные инженеры?
Неонатология
Медицина для новорожденных. Хирургия, наблюдение, реанимирование, восстановление недоношенных детей – это малая часть того, чем занимается неонатолог.
Такие врачи присутствуют на родах и полностью обследуют новорожденного для быстрого выявления патологий, а позднее – лечения. Их можно назвать врачами широго профиля: от неврологии до хирургии. Однако работают они именно с младенцами.
Чтобы стать неонатологом, нужно поступить в любой понравившийся вам медицинский вуз на факультет педиатрии.

Сколько получают неонатологи?
Биотехнология
Это наука об использовании живых организмов и биологических процессов для производства ценных продуктов, возможности использования живых организмов, их систем или продуктов их жизнедеятельности для решения технологических задач. Биотехнология находится на стыке клеточной и молекулярной биологии, молекулярной генетики, биохимии и биоорганической химии.
В медицине биотехнологи играют важную роль в создании новых лекарственных препаратов для ранней диагностики и лечения сложных болезней.

Сколько получают биотехнологи?
Медицинская биофизика
Медицинские биофизики – это необыкновенные люди, их профессия включает в себя одновременно медицину, физику и биологию. Такие специалисты – большая ценность в наши дни, ведь когда в одном человеке сочетаются сразу три направления, то он становится универсальным.
Медбиофизики специализируются в большей части на медицине, поэтому могут оказывать медицинскую помощь и диагностику.
Медицинская физика относится к необычным подвидам профессий физика.
Что сдавать для биологической профессии?
Чтобы упростить выбор предметов для сдачи, расскажем о самых распространённых наборах ЕГЭ:
- Русский язык + Математика + Биология + Химия = Медик
- Русский язык + Математика + Биология + Химия + Физика = Учёный
- Русский язык + Математика + Биология = Ветеринар
- Русский язык + Математика + Биология + Химия = Агроном
- Русский язык + Математика + Биология = Генная инженерия
- Русский язык + Математика + Биология = Неонатология
- Русский язык + Математика + Биология + Химия + Физика = Медицинская биофизика
Помните, что точную информацию о необходимых предметах ЕГЭ для каждой конкретной специальности нужно узнавать в самом вузе.
Где получить биологическую специальность?
Чаще всего это можно сделать в медицинском вузе. И если говорить про лучшие вузы сегодня, то, разумеется, можно выделить Первый мед; Сеченовку и РНИМУ имени Пирогова. Они находятся на первых позициях рейтингов уже на протяжении многих лет.
Также по версии рейтинга медицинских вузов «Национальное признание» десятка лучших выглядит следующим образом:

Топ-10 медицинских вузов России в 2019 году
А если с выбором профессии пока есть трудности, пройдите профтестирование или запишитесь на бесплатную консультацию с экспертом.
Читайте также:
Кто такой нейропсихолог?
Нейропсихология — направление психологии, которое только набирает обороты в России. Расскажем, как стать нейропсихологом, чем она отличается от смежных специальностей, и где потом работать.
Профессии, связанные с биологией
Биология — быстроразвивающаяся востребованная наука, а наше время – век биотехнологий и открытий. Лекарство от рака, вакцина против гепатита В, протезирование, выращивание тропических растений в Сибири, технологии переработки мусора с использованием специально выведенных бактерий — все это благодаря профессиям, связанным с биологией. Наверное, поэтому особо любознательные школьники стремятся связать свою жизнь именно с этой наукой и выбрать себе соответствующую профессию. В материалах этой статьи мы расскажем о наиболее популярных и востребованных профессий, связанных с изучением биологии.
Список профессий, связанных с изучением биологии
Список профессий, связанных с биологией, на самом деле очень велик. Охватить абсолютно все вряд ли удастся, но мы постараемся рассказать о наиболее популярных и востребованных профессиях, которые могут заинтересовать старшеклассников.
Агроном
Агроном – это специалист в области земледелия (растениеводства). Он решает когда, где, как и какие растения выращивать. Агроном должен хорошо разбираться в ботанике: знать все существующие и когда-то существовавшие виды сельскохозяйственных культур, все стадии роста растений их особенности. Разбираться в типах почв, климатических условиях, земледельческих технологиях.  Все эти знания помогают ему подобрать качественные семена, правильно их высеять, внести нужное количество удобрений в почву, бороться с вредителями растений. От грамотности человека этой профессии напрямую зависит количество и качество полученного урожая. Часто он занимается еще и подготовкой и организацией самих сельскохозяйственных работ. И, чтобы во всем этом разбираться, качественно выполнять свою работу и получать достойную заработную плату нужно изучать биологию.
Все эти знания помогают ему подобрать качественные семена, правильно их высеять, внести нужное количество удобрений в почву, бороться с вредителями растений. От грамотности человека этой профессии напрямую зависит количество и качество полученного урожая. Часто он занимается еще и подготовкой и организацией самих сельскохозяйственных работ. И, чтобы во всем этом разбираться, качественно выполнять свою работу и получать достойную заработную плату нужно изучать биологию.
Специальность агронома доступна к изучению в любом сельскохозяйственном или аграрном техникуме, вузе России.
Эта профессия подходит людям:
- с крепким физическим здоровьем
- выносливым
- без аллергических реакций на растения, химикаты, составляющие удобрений, солнце
- умеющим принимать быстрые нестандартные решения
Учитель/преподаватель биологии
Учитель/преподаватель биологии – это человек, который со школьной скамьи прививает детям любовь к себе и окружающему миру, помогает разобраться в тайнах живых организмов, растит интерес к ботанике, зоологии и анатомии. Он знает, как появляются бабочки, почему медведь сосет лапу, сколько лет баобабу и чем цветы привлекают пчел. Учитель биологии может рассказать много интересного о природе и человеке.
Если такая профессия по душе, то поступать следует в высшие педагогические учебные заведения. В России их очень много, они есть практически в каждом крупном городе всех регионов страны. Поэтому проблем с выбором, где получить образование, возникнуть не должно.
Профессиональные качества учителя/преподавателя биологии:
- любовь к детям
- грамотность
- умение заинтересовать и донести информацию
- устойчивость к стрессам
- терпеливость
- умение быстро принимать решения
- ответственность
- культура
Эколог
Эколог – человек, занимающийся изучением взаимодействия объектов окружающей среды между собой и влияния на них деятельности человека. Они разбираются во всех катаклизмах и их причинах, работают над внедрением технологий для охраны природы, ее сохранением для будущих поколений. Ежедневно в СМИ звучат упоминания, о тех или иных мероприятиях по защите природы. Проблемы загрязнения окружающей среды, потепления климата, исчезновения видов животных и растений – это все сфера деятельности эколога. Эта профессия тесно связана не только с биологией, но и химиейы, физикой, экологией. Ученые считают, что в будущем профессия «Эколог» станет неотъемлемой в каждой сфере деятельности.
Экологом можно стать, отучившись по любой из специальностей, связанной с охраной окружающей среды и/или рациональным использованием природных ресурсов.
Люди, неравнодушные к состоянию живой природы, умеющие командно работать в экстремальных условиях, целеустремленные, ответственные и смелые найдут себя в этой профессии.
Врач
Врач – самая древняя, благородная и нужная профессия. Получают ее только люди, готовые посвятить себя здоровью каждого человека. Быть врачом почетно и сложно. Нужно уметь сохранять внутреннее спокойствие в случаях, когда человеку помочь невозможно, быть уверенным в собственном выборе методов и действий, быть храбрым и ответственным, ведь иногда приходится поступать во благо больного, но во вред самому себе (например, обследование и лечение людей в местах эпидемий). Во всех специализациях и направлениях медицинской практики применяются знания биологии — лечение травами, профилактика здоровья человека, операции и протезирование. На протяжении всей своей деятельности врачу предстоит учиться для повышения уровня профессионализма.
При поступлении в учебные заведения медицинского направления обязательна сдача экзамена по биологии. Деятельность медика предполагает, что специалист обладает целым рядом личных качеств:
- устойчив к стрессу
- несет ответственность за себя и своих коллег
- внимателен
- умеет принимать скорые правильные решения в сложных ситуациях
- настойчив и усерден в работе
Ветеринар
Ветеринар – это врач, который лечит домашних и сельскохозяйственных животных. Ветеринарные клиники есть в каждом городе. Профессия очень тесно взаимодействует с такими науками, как химия, биология, фармацевтика. Ни одна сельскохозяйственная ферма, занимающаяся животноводством, ни обходится без врача для животных.
Это интересный, увлекательный, очень ответственный, в большей мере умственный труд. Ведь ветеринар должен уметь правильно поставить диагноз, назначить лечение, помочь животному в опасной для жизни ситуации. А внимания будут требовать самые разнообразные представители животного мира: от маленьких хомячков, преданных собак, ласковых кошек до птиц, дельфинов и огромных слонов. Профессия требует храбрости и выдержки, ведь врач работает и с животными дикого мира, совершенно неприрученными и даже опасными. В ходе работы возможны взаимодействия с экологами, инженерами лесного хозяйства, медиками.
Между тем высококвалифицированных ветеринаров не так уж и много. Получить специальность «Ветеринарный врач» можно в аграрных и сельскохозяйственных учебных заведениях.
Если человек ответственный, терпеливый, умный, с детства любит животных, ухаживает за ними и заботится, то направление в выборе профессии для него очевидно.
Инженер лесного хозяйства
Инженер лесного хозяйства — человек, заботящийся о лесе — специалист, который занимается восстановлением лесных запасов, принимает решения о вырубке определенных участков, следит за пожарной и санитарной безопасностью на отведенной лесной территории.
Разбивка городских парков, скверов и другого ландшафтного строительства требует планирования, оценки и реализации со стороны таких профессионалов. Инженер лесного хозяйства принимает непосредственное участие в проведении инвентаризации, ведет кадастрового учет ландшафтов, обеспечивает бесперебойное, рациональное, восполнимое использование лесных ресурсов для народного хозяйства. То есть провести качественную проверку леса с целью выявить сухостой и больные деревья, а так же деревья, подходящие для вырубки в промышленных масштабах, провести мероприятия по пополнению лесного богатства, борьба с незаконным уничтожением леса и подготовка соответствующей рабочей документации – это задачи людей, занимающих должности инженеров лесного хозяйства.
Очень часто взаимодействуют с экологами, многие употребляют названия этих профессий как одной, не различая их функциональных различий.
Успешным специалистом в этой области возможно стать, воспитывая в себе такие качества:
- любовь к природе и неравнодушие к окружающему миру
- внимательность
- высокий уровень развития памяти
- выносливость
- конкретность
Получить высшее образование можно в вузах по специальностям «Лесное дело», «Лесоинженерное дело», «Лесное и лесопарковое хозяйство» и др.
Ландшафтный дизайнер
Ландшафтный дизайнер — человек, занимающийся проектированием парков, скверов, садов и околодомовых территорий. В деятельности объединены знания из растениеводства, дизайна, экологии, архитектуры. Профессия творческая, очень интересная и увлекательная. Ландшафтный дизайнер чаще всего работает с заказчиками, выполняя индивидуальные заказы по облагораживанию территорий. Нужно уметь презентовать дизайн-проект, разбираться в многообразии растительного мира, знать основы установки фонтанов и водоемов. Для этого быть креативным, внимательным, ответственным, исполнительным, любознательным человеком.
Очень востребованная и популярная профессия, особенно в больших городах, где жизнь подчинена модным тенденциям. Самыми престижными учебными заведениями, где обучают этой специальности, являются Московский государственный университет леса, Санкт-Петербургский государственный университет технологии и дизайна и др.
Технолог пищевой промышленности
Технолог пищевой промышленности – специалист, который отвечает за производство качественных безопасных продуктов питания. Он полностью контролирует все работы производственного цикла. Деятельность технолога распространяется на процессы от закупки сырьевых материалов до упаковки уже готового изделия. Его главное назначение — избежать нарушений в технологии производственного процесса, исключить появление непригодной в пищу продукции. Профессия очень важная и ответственная, ведь от этих специалистов напрямую зависит качество еды на столе каждого человека.
Стрессоустойчивость, аккуратность, внимание, высокий уровень интуиции, терпение и ответственность, умение запоминать и воспроизводить большое количество информации – признаки характера людей этой профессии.
Диплом технолога пищевой промышленности можно защитить, успешно окончив вуз по специальности:
- «технология хлеба, кондитерских и макаронных изделий»
- «технология мясной и молочной промышленности»
- «технология бродильных производств и виноделия»
- «технология продуктов питания»
- «технология консервного производства»
Биофизик
Биофизик проводит исследовательскую работу и изучение физических процессов, происходящих внутри организмов. Из названия понятно, что профессия требует глубоких знаний биологии и физики. Но эта деятельность затрагивает все естественные науки, предполагает умение работать в лаборатории и с высокотехнологичной техникой. В работе не бывает предположений, основанных на интуиции. Все заключения делаются на основе экспериментов.
Работа биофизика очень сложная и требует серьезного образовательного уровня. Результаты деятельности, полученные в ходе экспериментов, анализа, исследований, находят свое применение в отраслях сельского хозяйства, экологии, в сфере медицины и биотехнологий.
В характере биофизика должны обязательно присутствовать такие личностные характеристики, как:
- ответственность
- усидчивость
- умение сконцентрироваться на задаче
- усердие и нестандартное мышление
Для получения этой профессии следует поступать в НИИ, политехнические университеты, исследовательские академии.
Биоинженер
Биоинженер – квалифицированный работник, занимающийся изучением материй и организмов с целью создания новых продуктов и для поиска решений вопросов медицины и генетики. Благодаря их деятельности появилось искусственное сердце, всевозможные протезы, сложные медицинские аппараты. Одним из направлений этой области является генетическая инженерия. Результатом работы биоинженеров стало появление инсулина, интерферона, гормона человеческого роста, появились искусственные человеческие органы, ГМО.
Не каждый человек выдержит такой труд. Для работы в этой области нужно иметь:
- аналитический склад ума
- терпение
- ответственность
- скрупулезность и целеустремленность
Получить знания для работы можно в учебных заведениях по специальности «биоинженерия и биоинформатика».
Вместо заключения
Как видно, профессий, связанных с биологией, множество и они часто взаимодействуют или используют научные и труды друг друга. Перед выбором специальности следует максимально изучить ее характеристики, направления, требования, сферы применения, ее актуальность и востребованность, уровень заработной платы, чтобы при поступлении на выбранный факультет не сомневаться, а приложить максимум усилий в сдаче вступительных экзаменов.
7 профессий, связанных с биологией
Нравится биология? Адукар расскажет о семи профессиях, связанных с этим предметом. Конечно, отождествлять урок со спецификой работы не стоит, а вот присмотреться к профессиям, где можно применить знания по предмету, неплохо.
Биолог
Изучает общие свойства и особенности развития живой природы. Специализируется на одном или нескольких направлениях (зоология, ботаника, анатомия, генетика, микробиология и т. д.) либо работает на стыке наук (биохимия, биофизика, биоэкология). Биолог собирает информацию об объекте исследования, к примеру, наблюдает за популяцией. Также проводит эксперименты, анализирует и обобщает полученную информацию, применяет её на практике для решения некоторых проблем. Этот специалист любознателен, наблюдателен, ответственный и терпеливый. Сфера деятельности биолога довольно широка: от высадки растений, продаж лекарств до работы в патентном бюро (изучение специальных текстов). В последнем случае может понадобиться английский язык.
 SPEAK ENGLISH. LIVE ENGLISH!В дружеской атмосфере мы научим тебя понимать английский язык и общаться на нём!Записывайся!
SPEAK ENGLISH. LIVE ENGLISH!В дружеской атмосфере мы научим тебя понимать английский язык и общаться на нём!Записывайся!Выучиться на биолога можно в вузах Беларуси, России и Польши (бакалавриат и магистратура).

Эколог
Неравнодушен к проблемам окружающей среды, хочешь спасти природу от разрушительных действий человека — профессия эколог то, что тебе нужно. Однако прозаичных будней в такой работе больше, чем героических спасательных операций. Экологи следят за соблюдением экологических норм, составляют отчёты по использованию природных ресурсов, утилизации отходов. Они рассчитывают ущерб от причинённого или потенциального вреда для окружающей среды. Кроме знаний по биологии и химии понадобятся умения вести документацию, убеждать руководство в необходимости улучшить производство, чтобы оно не ухудшало состояние окружающей среды. Экологам приходится больше взаимодействовать с обществом, искоренять его недостатки, а уже потом контактировать с природой. Получить профессию эколог можно в БГУ, БГТУ, БарГУ, БрГУ имени А. С. Пушкина, БрГТУ, ВГУ имени П. М. Машерова, ГГУ имени Франциска Скорины, ГрГУ имени Янки Купалы, БГСХА (заочно).

Врач
Врач занимается диагностикой и лечением заболеваний людей. Ежедневное общение с пациентами, среди которых есть неизлечимо больные, огромные физические и психические нагрузки сопровождают работу врача. Во время учёбы приходится буквально зазубривать медицинскую литературу, много практиковаться. Врач не должен быть брезгливым и впечатлительным, воспринимать чужую боль и страдания как собственные. Иначе он не сможет лечить людей. Обзор медицинских вузов и колледжей Беларуси поможет тебе определиться с выбором учебного заведения. К слову, специальности «Стоматология» и «Фармация» самые популярные среди белорусских абитуриентов. Проходные баллы — от 360.
 Подготовься к ЦТ на 100 баллов!Выпускница курсов Адукар 2019 Яна Никуленкова сдала ЦТ по биологии на 100 баллов и поступила на фармацевтический факультет БГМУ. Записывайся!
Подготовься к ЦТ на 100 баллов!Выпускница курсов Адукар 2019 Яна Никуленкова сдала ЦТ по биологии на 100 баллов и поступила на фармацевтический факультет БГМУ. Записывайся!Ветеринар
Он лечит и предупреждает болезни животных, занимается ветеринарно-санитарной экспертизой продуктов животного происхождения (мясо, молоко, рыба, шерсть и т. д.). Если ты не можешь причинить боль животному, чтобы его спасти, данная профессия не для тебя. В Беларуси высшее образование в этой сфере дают ВГАВМ и ГГАУ. Вузы специализируются на сельскохозяйственных животных, так что совершенствоваться в искусстве врачевания остальных братьев наших меньших придётся самому.
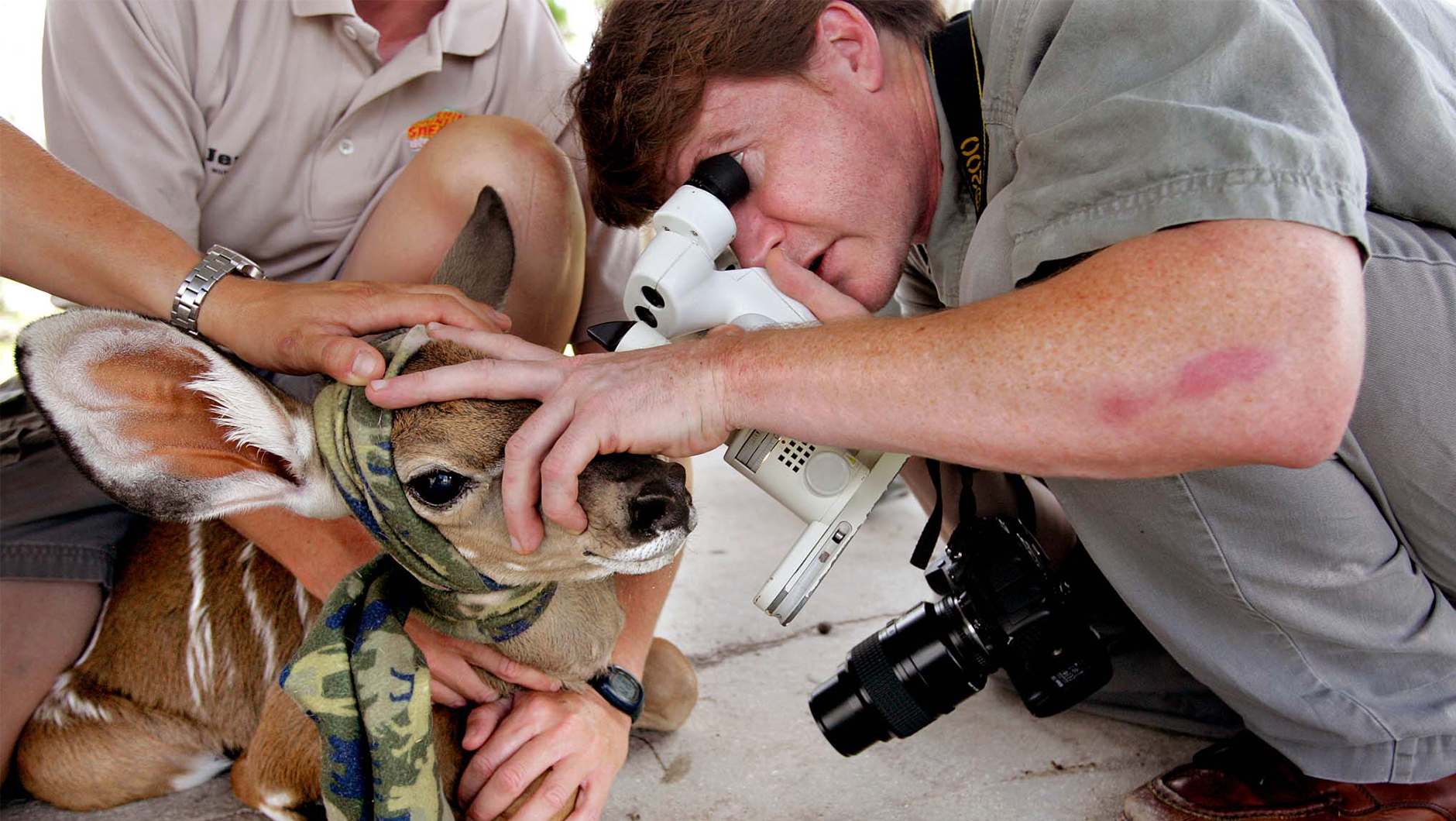
Инженер лесного хозяйства
Эта профессия близка к деятельности эколога. Лес издревле был великой ценностью для людей. Его уважали и почитали. Правда, находились и те, кто смотрел на него исключительно как на источник наживы. Инженер лесного хозяйства следит за сохранностью вверенного ему участка: присекает незаконную вырубку, происки браконьеров, защищает лес от возникновения пожаров. Хватает у него и бумажной работы. Без конфликтов тоже не обходится, ведь нарушители бывают разные. Стрессоустойчивость, умение договариваться с людьми, разъяснять что-либо — неотъемлемые качества данного специалиста. Этому можно научиться в БГТУ и ГГУ имени Франциска Скорины.

Агроном
Кто кормит страну сельскохозяйственной продукцией? Знает, где, когда, как посадить растения и собрать урожай? Правильно, агроном! В нём сочетаются качества исследователя, рачительного хозяина и грамотного менеджера. Он должен быть в курсе последних методов возделывания, удобрения земли и выращивания сельхозкультур, борьбы с вредителями. Агроном составляет производственный план, следит за его выполнением. Этот специалист контролирует всё: от подготовки почвы к посеву до сбора и хранения урожая. Сельский образ жизни по душе? Тогда эта профессия может тебе подойти. Программы БГСХА, ГГАУ и БарГУ к твоим услугам.

Учитель биологии
Хочешь передавать знания подрастающему поколению, готовить увлекательные уроки — работа учителем биологии как раз то, что надо. Есть, правда, несколько «но»: предмет нравится тебе, а вот учеников ещё нужно заинтересовать. Учитель также заполняет много документации, несёт общественную нагрузку. Подумай, что тебя привлекает в профессии учитель, а потом делай выбор. Семь вузов Беларуси готовы обучить преподаванию этого предмета.
Успехов при выборе профессии! Понадобится помощь, чтобы подтянуть биологию, обращайся к нашим преподавателям на курсы подготовки к ЦТ!
***
Если материал был для тебя полезен, не забудь поставить «мне нравится» в наших соцсетях ВКонтакте, Instagram, Facebook, ASKfm и поделись постом с друзьями. А мы сделаем ещё больше материалов, которые пригодятся тебе для учёбы.
Перепечатка материалов с сайта adukar.by возможна только с письменного разрешения редакции. [email protected]

Профессии связанные с биологией: список ТОП-25
Лекарства от старения, диета, излечивающая диабет, способы создания ранее не существовавших живых систем, нейропротезирование, возможность стирать воспоминания и видеть невидимое, а также многое и многое другое. «Что это?» — спросите вы. Речь идет о самых последних научных открытиях в области биологии — дисциплине, которая сегодня является одной из самых динамично развивающихся. Появились новые профессии, связанные с биологическими науками и чрезвычайно востребованные на рынке труда. Поговорим о наиболее популярных из них и самых новых.
Биология — не отдельная наука, замкнутая сама на себе. Это целый комплекс знаний о живом мире, в который входят десятки самостоятельных направлений.
Например, ботаника изучает растения, анатомия — строение организма человека и животных, физиология — работу тела, а также особенности функционирования отдельных систем и органов, гистология — строение тканей, зоология — животных, микология — грибы, вирусология — вирусы, бактериология — бактерии. Более того, каждая из этих областей биологии имеет свои дополнительные ответвления.
В последние годы стали активно развиваться экология — наука об окружающей среде и взаимодействии живых организмов, генетика, изучающая закономерности наследственности, этология, предметом изучения которой является поведение животных, и другие направления науки.
Наконец, появились совершенно новые научные дисциплины, такие, например, как квантовая, синтетическая и вычислительная биология. А также смежные науки, которые существуют на стыке биологических знаний и математики, физики, медицины, химии и т.д.
История возникновения и развития биологии
Отдельной эта отрасль стала не так давно — в XIX веке. Но корни ее зарождения находятся еще в древности.
Прародителем науки можно считать древнегреческого врача Гиппократа, который жил в 4-5 веке до нашей эры. Он первым описал строение тела животных и человека. Ему же принадлежат первые медицинские открытия и способы лечения болезней.
Гиппократ установил связь между здоровьем организма и, например, наследственностью, питанием, влиянием окружающей среды и другими факторами.
Соотечественник врача, философ и ученый Аристотель, живший в 4 веке до нашей эры, систематизировал живую и неживую природу. Он же поделил мир на растения, животных и человека, землю, а также воду и воздух.
Большое исследование мыслитель посвятил животным. Он описал их происхождение, строение, способы размножения и т.д. Считается, что основоположником зоологии, как подраздела биологии, является именно Аристотель.
Еще один древний грек, ученый Теофаст, подарил нам первые знания в области ботаники. Он открыл порядка полутысячи видов растений, а также ввел ряд ботанических терминов.
Древнеримский естествоиспытатель Плиний Старший написал труд из тридцати семи томов, где изложил наиболее полные на тот момент сведения о живых организмах. Называется работа «Естественная история».
Врач и философ Клавдий Гален занимался вскрытием животных и изучением их внутреннего строения и органов. Это помогло ученому сделать открытия в области анатомии, физиологии, неврологии и других дисциплинах. Его методологию по препарированию обезьян и свиней использовали вплоть до 16 века, а открытие Глена о том, что мозг контролирует движение тела до сегодняшнего дня никто не оспаривал.
Древние ученые заложили также основы научной анатомии, эмбриологии, микробиологии, генетики, теории клеток и системы естественного отбора в живой среде.
Изначально биология была предметом интереса ученых, но уже в ХХ веке ее стали изучать в школах и вузах, потому что знание науки дает возможность разбираться во многих других сферах жизни. И конечно, биология стала базовой основой для многих важных профессий.
Топ-5 профессий, связанных с биологией
Ученый-биолог
Сфера изучения специалиста, владеющего этой профессии, чрезвычайно широка. Он изучает законы происхождения и развития живых организмов, способы их взаимодействия между собой и со средой обитания. Эти вопросы касаются всех существ, которые населяют окружающую среду.
Биолог-зоолог может специализироваться в орнитологии (изучение птиц), энтомологии (насекомые), ихтиологии (рыбы), кинологии (собаки), паразитологии (паразиты), иппологии (лошади). В профессии зоолога более двадцати направлений.
Открытия ученых-зоологов используются в медицине, сельском хозяйстве, фармакологии, ветеринарии. Работать зоологи могут в аграрном секторе, зоопарках, природных заповедниках, научно-исследовательских центрах.
Биолог-ботаник изучает растения, их виды, свойства и развитие. Специалист в этой области находит и классифицирует новые разновидности флоры, а также исследует влияние растений на животных и человека. Результаты научных открытий в области ботаники используются в различных технологиях, медицине, производстве лекарств, агрономии, цветоводстве и других фито направлениях науки.
Ученые, которые специализируются на анатомии людей и животных, занимаются изучением строения и физиологии человека. Казалось бы, тема давно изученная. Однако открытия в этой сфере продолжаются. Например, в 2013 году учёные обнаружили ранее неизвестную переднебоковую коленную связку, которая во время травм и вывихов часто повреждается.
В 2018 году Нобелевскую премию за открытие в области физиологии получили американец Джеймс Эллисонс и японец Тасуку Хондзё. Они предложили метод терапии раковых клеток с помощью мобилизации внутренних ресурсов организма, а именно иммунитета. Новая методика позволит отказаться от химических и других агрессивных способов лечения онкологии.
Врач
Это древняя и уважаемая профессия. Существует выражение: врач — первый после Бога. Это значит, что в его руках находится самое главное — жизнь человека. Не случайно к качеству подготовки людей в белых халатах предъявляются особые требования, а специалисты, которые имеют «золотые» руки» и высокую профессиональную квалификацию, чрезвычайно ценятся.
Доктор может быть врачом общей терапии, а также специализироваться в отдельном направлении — кардиологии, урологии, хирургии, эндокринологии, офтальмологии, иммунологии и т.д.
Обучение профессии занимает не менее шести лет с последующей практикой в ординатуре. Квалификация врача требует регулярного подтверждения, а ему самому необходимо регулярно повышать уровень самообразования и осваивать новые медицинские технологии, ведь медицина постоянно развивается
У профессии есть один безусловный «плюс» — ее востребованность. Насколько быстрой и успешной будет карьера — вопрос исключительного желания, старательности будущего врача, а главное его любви к этому сложному, но благородному делу.
Ветеринар
Врачеватели братьев наших меньших всегда оставались в тени «настоящих» врачей. Однако все больше людей заводят дома животных, причем не только традиционных кошек, собак и канареек, но и экзотических хорьков, мини-пигов, шиншилл и енотов.
Не стоит забывать, что практически каждый крупный населенный пункт имеет свой зоопарк и цирк, где также необходимы ветеринары. В последние годы открывается много приютов и гостиниц для животных, в которых руки специалиста придутся как нельзя кстати. Не важно, дикий зверь или домашний, он тоже требует медицинского обслуживания, поддержки, а в случае необходимости и помощи.
Сегодня вузы, которые готовят ветеринаров, не испытывают нужды в абитуриентах. А тот, кто выходит на рынок труда с полученным дипломом, имеет все возможности найти себе занятие по специальности. Всегда востребованы ветеринарные клиники, потому что любовь к животным, к счастью, свойственна современным людям и едва ли в не каждой третьей семье живет какой-нибудь четвероногий.
Агроном
Еще век назад Россия была аграрной страной, и в последние годы наблюдается тенденция к возврату ей этого статуса. Правительство разрабатывает программы по развитию сельского хозяйства, а также возрождению сел и деревень. Поэтому, вне сомнения, профессия агронома будет возрождаться.
Чем занимается агроном? Под его контролем происходит отбор и оценка качества посевного материала. Он следит за проведением посадочных работ, контролирует процесс роста урожая, оценивает здоровье растений на разных этапах, а также объем и качество собранного урожая.
На агрономе также лежит ответственность за состояние почвы, заготовку удобрений, борьбу с вредителями, условия хранения собранных овощей, фруктов, зерновых культур и много другой важной работы, от которой зависит продовольственная и экономическая стабильность большой страны.
Готовят специалистов в области сельского хозяйства сельскохозяйственные институты и академии. Они существуют во многих регионах, а особенно в тех, которые специализируются на развитии этой перспективной отрасли народного хозяйства.
Технолог пищевой промышленности
Человечество давно перешло от сыроедения к продуктам, подвергающимся холодной и тепловой обработке. Чтобы понимать, как происходят эти процессы, необходимо знать особенности пищевых компонентов животного или растительного происхождения. Это первая обязанность человека, чья профессия «технолог пищевой промышленности». Без знания биологии тут не обойтись.
Чтобы готовый продукт получился вкусным, полезным и безопасным для здоровья, специалист должен проконтролировать качество исходного сырья, отследить последовательность процессов и соблюдение технологии, а также оценить конечный результат.
Кроме того, технолог отвечает за соблюдение санитарных норм, обеспечивает условия, подходящие для производства каждого конкретного продукта, следит за количеством отходов после завершения производственного цикла.
Работают технологи в пищевой промышленности, на предприятиях общепита, базах по заготовке и переработке продукции, в многопрофильных фермерских хозяйства, специализированных лабораториях и научно-исследовательских институтах.
И наконец, перечислим специальности , которые пользуются большим спросом и только-только выходят на рынок.
Активно развивающиеся профессии, связанные с биологией
- агрохимик;
- вирусолог;
- диетолог;
- генетик;
- иммунолог;
- фармацевт;
- микробиолог;
- дизайнер-флорист;
- эпидемиолог;
- специалист по обращению с отходами;
- фермер;
- фитотерапевт;
- эколог.
Новые специальности, основа которых — биология
- биогеограф;
- валеолог;
- врач космической медицины;
- врач-радиолог;
- зоопсихолог;
А также целый ряд профессий, связанных с экологией:
- экоаналитик;
- экоаудитор;
- геоэколог;
- гидроэколог;
- медицинский эколог;
- специалист по экологическому проектированию
Автор статьи
Редактор портала Info-Profi, руководитель центра поддержки студенческих проектов ТюмГУ.
Написано статей
Кто такой биолог? Что изучает наука биология?
Биологом именует себя преподаватель этой дисциплины в учебном заведении, специалист в области генетических исследований, сотрудник ботанического сада или зоопарка. Так все-таки, кто такой биолог? Что это за профессия? Кто имеет право считаться биологом? Ответы на эти вопросы — в нашем небольшом исследовании.
Биология – это наука
Наука, которая связана с исследованием всего живого на планете, начиная с микроскопических бактерий, заканчивая физиологическими процессами жизнедеятельности человека.
Человека разумного процессы жизнедеятельности, сходство и различие живых форм, отличия в условиях обитания растений и животных интересовали издавна. Правда, в период мрачного Средневековья за слишком уж видимый интерес к исследованиям можно было и на костер попасть. Другое дело — эпоха Возрождения. Искусство и науки тогда стали в большом почете, основывались целые научные школы, и появились первые музеи естествознания.
Кто такой биолог в древности? Это мог быть и лекарь-травник, и алхимик, и основатель первого зверинца. Сам термин «наука биология» появился лишь в 19-м веке, когда в одно течение объединили все, что относится к изучению живых форм существования на Земле («био» – жизнь, «логос» — наука).

Направления биологии
Биология – это наука о жизни. Такое вот обобщенное понятие. В зависимости от конкретного предмета изучения выделяют отдельные биологические науки:
- Зоология – наука о животном мире.
- Ботаника – изучает мир растений.
- Физиология и анатомия – науки о процессах жизнедеятельности и строении человеческого организма.
- Микробиология и вирусология. Предмет их изучения виден только под микроскопом.
- Морфология – изучает строение и форму живых видов.
В свою очередь, основные направления постепенно разделялись на более узкие специальности и специализации, которых по мере развития науки становится все больше. На сегодня известно более семидесяти направлений биологии. Биология океана, антропология, цитология, нейробиология, экология – это лишь некоторые из них. Профессия биолог объединяет всех представителей тех или иных специализаций и направлений, связанных одной наукой.
Связь с другими науками
В ходе развития мировой науки и техники, благодаря проникновению ученых в глубокие сферы познания, обнаружилась глубокая связь биологии с другими дисциплинами. Кто такой биолог в современном мире? Кроме традиционных зоолога и ботаника, это биофизик, биохимик, специалист по биометрии, космической биологии, биологии труда, бионике. Современный биолог может быть параллельно хорошим инженером, врачом или математиком.
Что делает биолог?
С теорией все более-менее ясно. Но кто такой биолог на практике? Где его рабочее место? Ответ неоднозначен и обширен, как и список специализаций биологии. Все зависит от выбранного направления. Выпускник, окончивший соответствующий факультет вуза, может стать преподавателем в среднеобразовательном учебном заведении, а может продолжить свою связь с наукой и посвятить свою жизнь изучению других живых организмов. Зоологи успешно работают с животными в зоопарках, ботаники в оранжереях и ботанических садах. Биологи-селекционеры трудятся над изобретением новых сортов сельскохозяйственных культур. Вирусологи изучают новые и старые микроорганизмы, их влияние на окружающий мир, экологи следят за чистотой окружающей среды. Широко востребованы в современном мире биологи новой формации – генетики, нейробиологи, космические биологи, биоэнергетики. Специалист биологии может быть ветврачом, агрономом, ландшафтным дизайнером, врачом-лаборантом.

Главные качества биолога
Успешной профессия биолог окажется для тех, кто ощущает себя частью таинственного мира живых организмов, кому интересно общение с природой, изучение окружающей среды.
Любовь к природе становится главной, когда биолог проводит длительные месяцы в путешествиях и экспедициях с целью изучения новых видов флоры и фауны.
Усидчивость и аналитический ум нужны работникам лабораторий, исследовательских центров.
В зависимости от специализации биологу могут понадобиться хорошие отношения с физикой, астрономией, механикой, химией и другими науками.

Плюсы и минусы профессии
Для тех, кто любит все живое в любых его проявлениях, посвятить свою жизнь биологии – уже сплошной плюс. Ничто так не делает человека счастливым, как занятия любимой работой. Профессия биолог, к сожалению, не всегда оценивается достойно в денежном выражении – это минус. Именно низкие зарплаты привели к тому, что интересная для многих профессия вошла в разряд непопулярных. Те же, кто решили все-таки посвятить ей свою жизнь и упорно идут к цели, становятся порой авторами новых открытий и научных сенсаций.
Биология новых направлений, исследования в области генетики, микробиологии, новых биотехнологий занимает второе место в мире в списке перспективных профессий. Особенно рады таким специалистам Канада, США, западные страны, которые занимаются разработками новых технологий.

Выдающиеся биологи
Говоря о биологии как о науке, стоит упомянуть о людях, имена которых известны всему миру. Их открытия внесли огромный вклад в развитие человечества в целом.
- Вавилов Николай (Россия) – генетик в области агрономии, основоположник учения об иммунитете растений.
- Владимир Вернадский (Россия) – основоположник Украинской академии наук, занимался изучением биосферы, стоял у истоков развития биохимии и биофизики.
- Уильям Гарвей (Великобритания) – придворный врач короля, который первым провел исследования и описал систему кровообращения и работу сердца и сосудов в человеческом теле.
- Чарльз Дарвин (Англия) – великий натуралист, создавший систему классификации видов растений.
- Антони Ван Левенгук (Голландия) – натуралист, создавший микроскоп, что позволило проводить изучение организмов, невидимых прежде человеческому глазу.
Кроме них, прославили науку россияне Илья Мечников, Климент Тимирязев, Луи Пастер, Карл Линней, Руслан Меджитов и многие другие ученые-натуралисты.

 = 3.
= 3. на целое число
на целое число  с остатком (нахождение неполного частного
с остатком (нахождение неполного частного  и остатка
и остатка  , таких, что выполняется равенство:
, таких, что выполняется равенство:  ).
). 
 , где
, где 
 .
. является простым. Доказать, что а) имеет место представление
является простым. Доказать, что а) имеет место представление  для некоторого
для некоторого  ; б)
; б)  .
. . Простое число p может попасть только либо в класс
. Простое число p может попасть только либо в класс  , либо в класс
, либо в класс  . Т.к. числа первого класса делятся на 2, 3, поэтому они составные. Числа третьего класса делятся на 2, числа четвертого класса делятся на 3, числа пятого класса делятся на 2.
. Т.к. числа первого класса делятся на 2, 3, поэтому они составные. Числа третьего класса делятся на 2, числа четвертого класса делятся на 3, числа пятого класса делятся на 2. , т.к. первый множитель делится на 12, а третий на 2. ч.т.д.
, т.к. первый множитель делится на 12, а третий на 2. ч.т.д. последняя цифра любого числа повторяется с периодом 4
последняя цифра любого числа повторяется с периодом 4 для любого натурального числа n.
для любого натурального числа n. .
. .
. .
. .
. сумма делится на 133, т.е.
сумма делится на 133, т.е.  , содержащее не менее трех цифр, делилось на 4, необходимо и достаточно, чтобы делилось на 4 число, образованное двумя последними цифрами числа
, содержащее не менее трех цифр, делилось на 4, необходимо и достаточно, чтобы делилось на 4 число, образованное двумя последними цифрами числа  не делится ни на одно из простых чисел, не превосходящих
не делится ни на одно из простых чисел, не превосходящих  , т.е. на
, т.е. на  , то число –
, то число –  . Проверим, делится ли число 2003 на 2,3,5,7,11,13,17,19,23,29,31,37,41,43. Для проверки деления на 2,3,5,7,11,13 применяем признаки делимости. Деление на 17,19,23,29,31,37,41,43 проверяем при помощи деления уголком. 2003 не делится ни на одно из перечисленных простых чисел
. Проверим, делится ли число 2003 на 2,3,5,7,11,13,17,19,23,29,31,37,41,43. Для проверки деления на 2,3,5,7,11,13 применяем признаки делимости. Деление на 17,19,23,29,31,37,41,43 проверяем при помощи деления уголком. 2003 не делится ни на одно из перечисленных простых чисел  — это все простые числа. Число
— это все простые числа. Число  не делится на
не делится на  , где
, где  — простые числа.
— простые числа.

 . Тогда
. Тогда
![Rendered by QuickLaTeX.com \[Z=297n-8=61k-8=21p-8=45m-8=826f-8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-47264cbb5b836ab110e1e2e315bc9681_l3.png)
![Rendered by QuickLaTeX.com \[297=11\cdot3\cdot9\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a40a7236991fbb212197a691c7ab601d_l3.png)
![Rendered by QuickLaTeX.com \[826=2\cdot7\cdot59\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-96a664e97479a84426f1c982c3e78eba_l3.png)
![Rendered by QuickLaTeX.com \[21=7\cdot3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f021588888626d861f2e7784cd7245d7_l3.png)
![Rendered by QuickLaTeX.com \[45=5\cdot9\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-00b64905cd7007b257ad0635fdd2bc5c_l3.png)
![Rendered by QuickLaTeX.com \[Z=2\cdot7\cdot59\cdot61\cdot11\cdot9\cdot3\cdot5-8=74823202\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-81935a4292543b31512dc3f24e395a90_l3.png)
 .
.![Rendered by QuickLaTeX.com \[S=\frac{2+12}{2}\cdot11=77\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2343e19f8bdc74f8b21e92cb29cd0f91_l3.png)
![Rendered by QuickLaTeX.com \[N=77+78\cdot 42+1+3+6+10=3373\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bd2e7f9db85acd075565ec0627fd1b97_l3.png)
 , если сумма оставшихся цифр равна 1808?
, если сумма оставшихся цифр равна 1808? раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна
раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна  . Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна
. Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна  . Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна
. Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна  . Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:
. Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:![Rendered by QuickLaTeX.com \[6892-2610-2610=1672\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9a3471ce36f398825534b9f4d507761b_l3.png)
![Rendered by QuickLaTeX.com \[1672\div 8=209\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ebc3c01c71aef72d3462eb18a86c07d_l3.png)
 . Вторая пара: единицу можем выбрать 73 способами (одна зачеркнута в самом начале), 0 – 111 способами. Следовательно, вторую пару можно выбрать
. Вторая пара: единицу можем выбрать 73 способами (одна зачеркнута в самом начале), 0 – 111 способами. Следовательно, вторую пару можно выбрать  способами.
способами. способов. Итого
способов. Итого  способа.
способа. Как расстояние зависит от времени и скорости?
Как расстояние зависит от времени и скорости? Как решать задачи для 4 класса?
Как решать задачи для 4 класса? В случае опасности заяц может бежать со скоростью 80 км/час
В случае опасности заяц может бежать со скоростью 80 км/час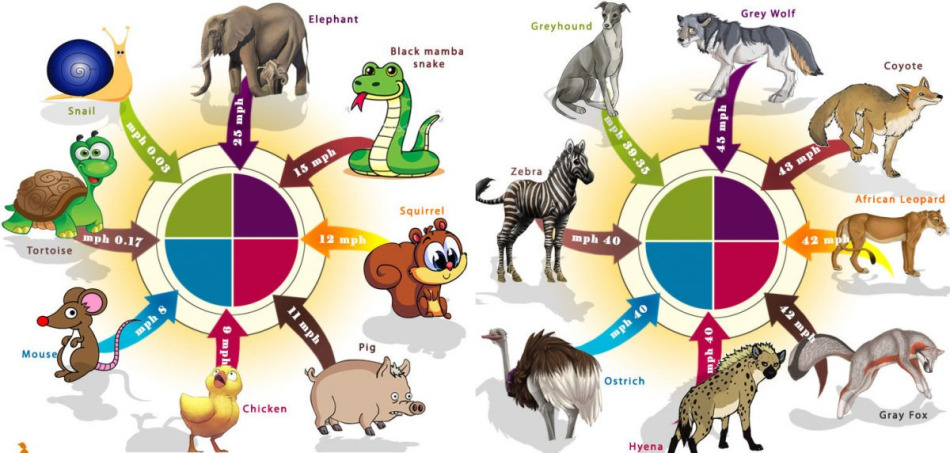 С какой скоростью могут передвигаться разные животные?
С какой скоростью могут передвигаться разные животные?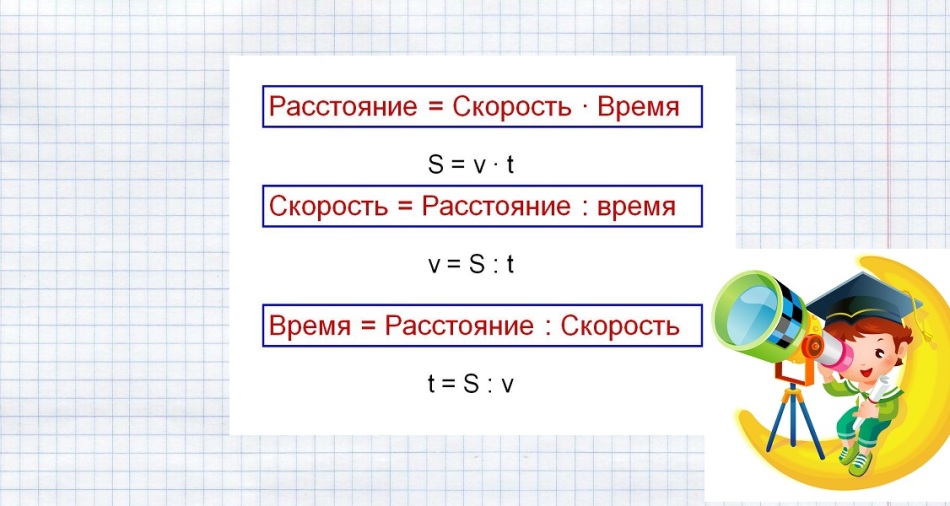 Формулы для решения задач про расстояние, время и скорость
Формулы для решения задач про расстояние, время и скорость Волк может бежать со скоростью 60 км/час
Волк может бежать со скоростью 60 км/час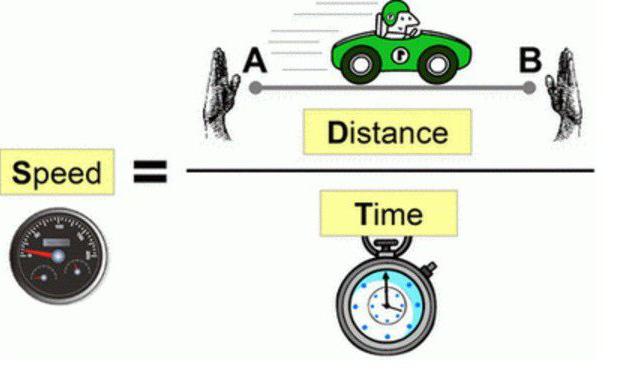


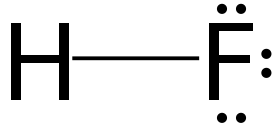
 (
(
 HF в воде. Реактив еще называют фтористоводородной кислотой и плавиковой кислотой. Последнее название связано с тем, что фтороводород получают из содержащего фтор (CaF2) плавикового шпата — очень красивого минерала флюорита, светящегося под ультрафиолетовым излучением или при нагревании.
HF в воде. Реактив еще называют фтористоводородной кислотой и плавиковой кислотой. Последнее название связано с тем, что фтороводород получают из содержащего фтор (CaF2) плавикового шпата — очень красивого минерала флюорита, светящегося под ультрафиолетовым излучением или при нагревании. Плавиковая кислота и ее пары ядовиты. Особенно коварна разбавленная кислота: при попадании на кожу ее брызг человек может вообще ничего не почувствовать, но вещество впитается в кожу и поступит в кровоток. Примерно через сутки проявятся симптомы токсического отравления, отек легких, нарушения работы сердечно-сосудистой системы и ЖКТ, так как соединение образует нерастворимые соли кальция и магния, связывая эти важные для нормального функционирования организма элементы. На коже проявится химический ожог из-за того, что реагент разрушает клетчатку.
Плавиковая кислота и ее пары ядовиты. Особенно коварна разбавленная кислота: при попадании на кожу ее брызг человек может вообще ничего не почувствовать, но вещество впитается в кожу и поступит в кровоток. Примерно через сутки проявятся симптомы токсического отравления, отек легких, нарушения работы сердечно-сосудистой системы и ЖКТ, так как соединение образует нерастворимые соли кальция и магния, связывая эти важные для нормального функционирования организма элементы. На коже проявится химический ожог из-за того, что реагент разрушает клетчатку. фторопластовых) канистрах, контейнерах и кубах. Для больших емкостей используется металлическая обрешетка. Кислоту высокой концентрации допускается перевозить железнодорожным и автомобильным транспортом в железных и стальных цистернах. Температурный режим — не выше +30 °С.
фторопластовых) канистрах, контейнерах и кубах. Для больших емкостей используется металлическая обрешетка. Кислоту высокой концентрации допускается перевозить железнодорожным и автомобильным транспортом в железных и стальных цистернах. Температурный режим — не выше +30 °С.
 (
( (
(
 Медиафайлы на Викискладе
Медиафайлы на Викискладе



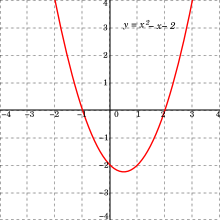 Квадратичный полином с двумя реальными корнями (пересечения х осей) и , следовательно , без каких — либо сложных корней. Некоторые другие квадратичные полиномы имеют свой минимум выше х осей, в этом случае нет никаких действительных корней и два комплексных корня.
Квадратичный полином с двумя реальными корнями (пересечения х осей) и , следовательно , без каких — либо сложных корней. Некоторые другие квадратичные полиномы имеют свой минимум выше х осей, в этом случае нет никаких действительных корней и два комплексных корня. График у = ах 2 + BX + C , где и дискриминант б 2 — 4 переменного тока являются положительными, с
График у = ах 2 + BX + C , где и дискриминант б 2 — 4 переменного тока являются положительными, с Визуализация комплексных корней у = ах 2 + BX + C : парабола поворачивается на 180 ° вокруг своей вершины ( оранжевый ). Ее х -intercepts повернуты на 90 ° вокруг своей средней точки, а декартову плоскость интерпретируются как комплексная плоскость ( зеленый ).
Визуализация комплексных корней у = ах 2 + BX + C : парабола поворачивается на 180 ° вокруг своей вершины ( оранжевый ). Ее х -intercepts повернуты на 90 ° вокруг своей средней точки, а декартову плоскость интерпретируются как комплексная плоскость ( зеленый ). Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда: 13 слайд
Описание слайда: 13 слайд  Описание слайда:
Описание слайда:


 Цели урока:
Цели урока:


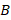 – индукция магнитного поля
– индукция магнитного поля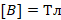
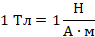
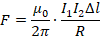








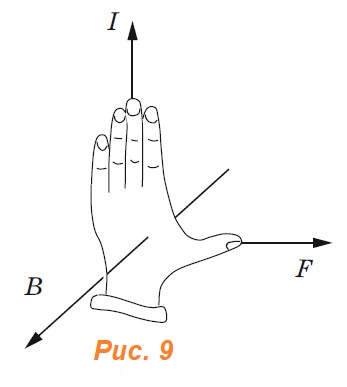
 со стороны магнитного поля зависит от направления электрического тока
со стороны магнитного поля зависит от направления электрического тока 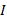 в проводнике и от линий магнитного поля
в проводнике и от линий магнитного поля 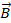

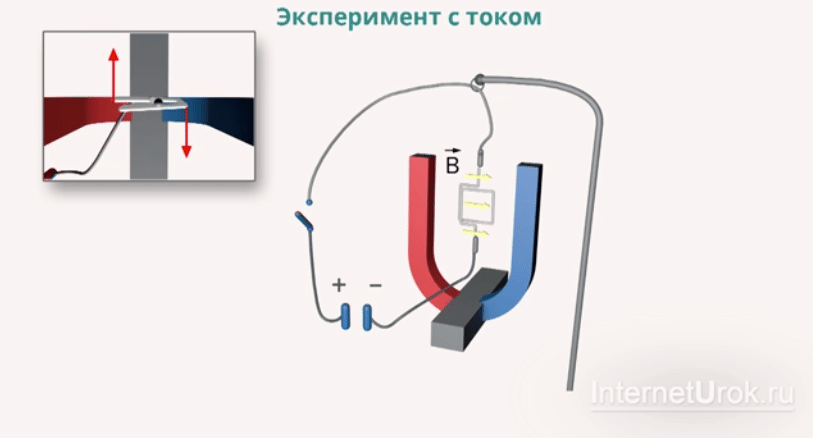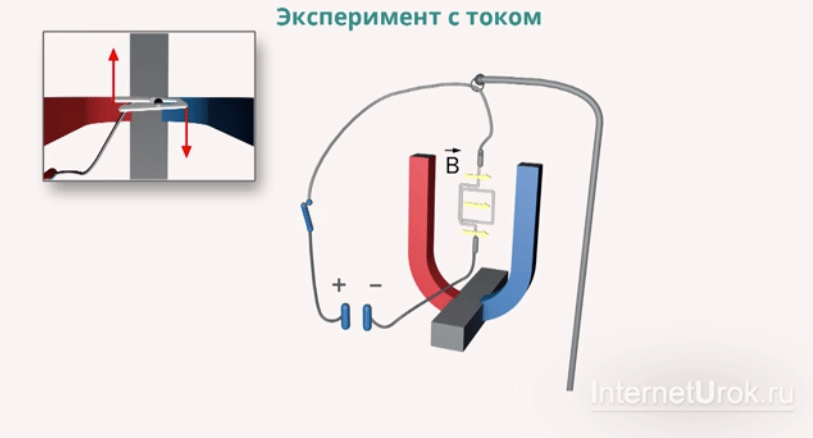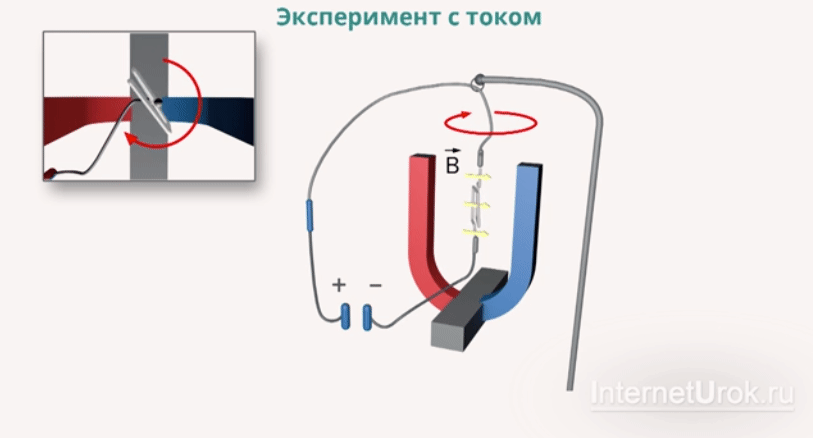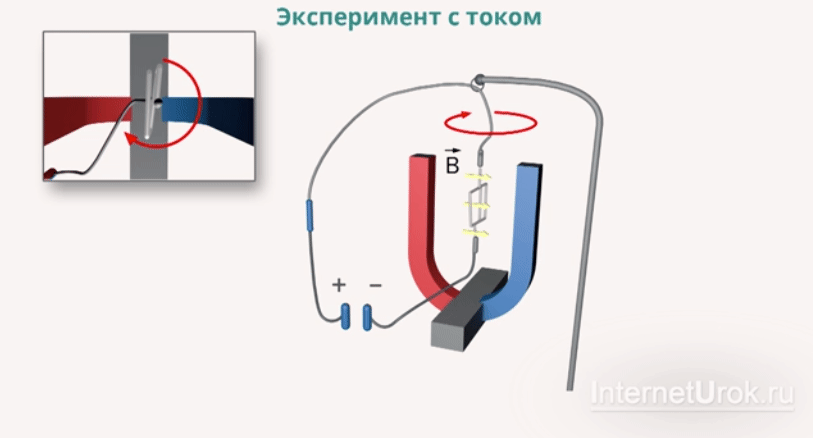
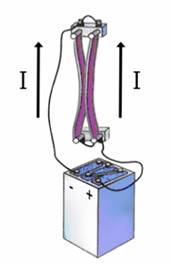
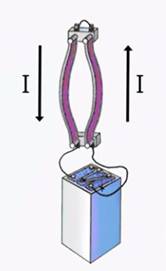
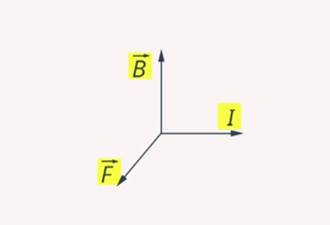
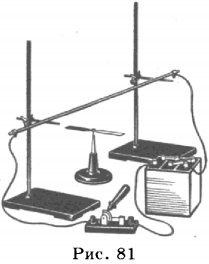
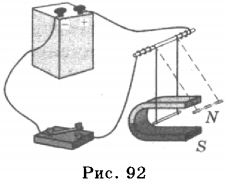
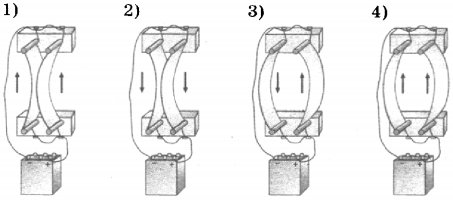
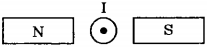
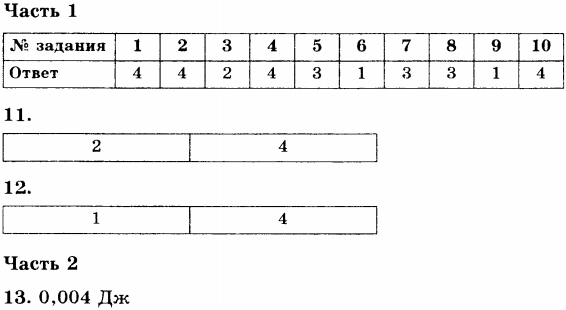
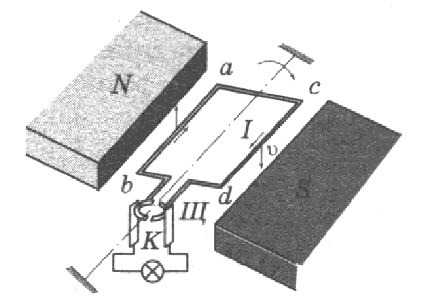
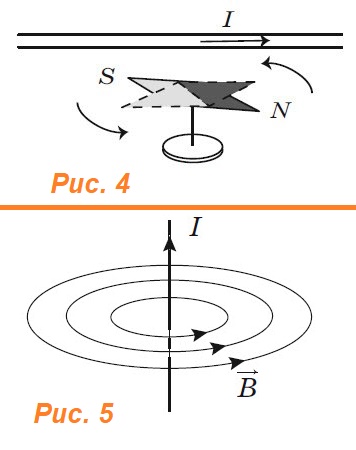
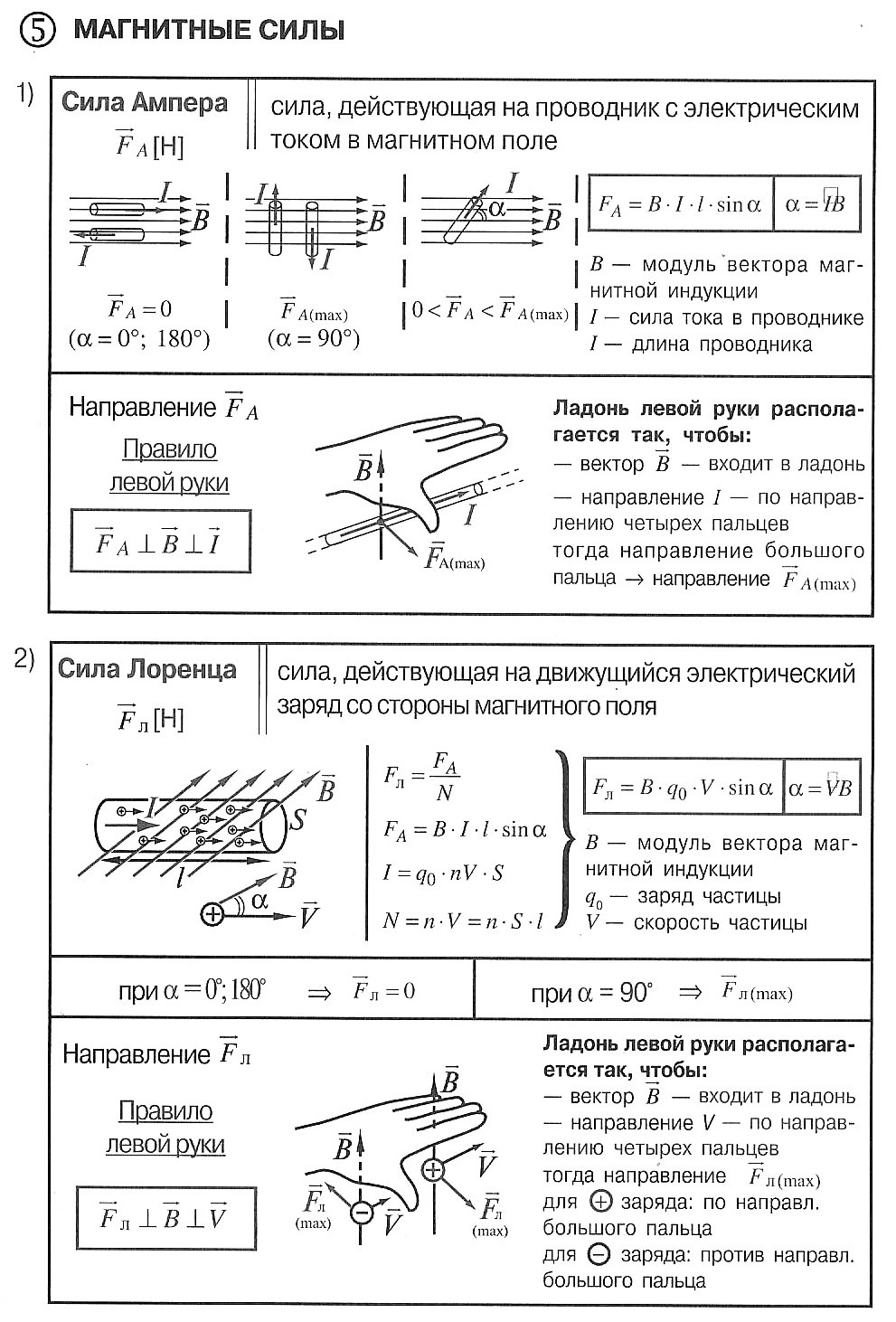
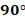 палец левой руки покажет направление действия силы (рис. 17). Сформулированное нами правило называется правилом левой руки.
палец левой руки покажет направление действия силы (рис. 17). Сформулированное нами правило называется правилом левой руки.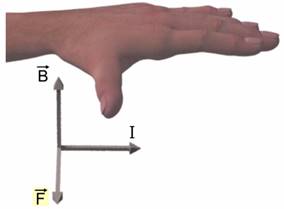

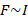
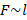
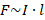
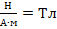 , следовательно, нужно правую часть умножить на модуль магнитной индукции:
, следовательно, нужно правую часть умножить на модуль магнитной индукции: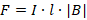
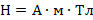

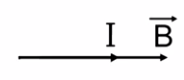
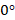
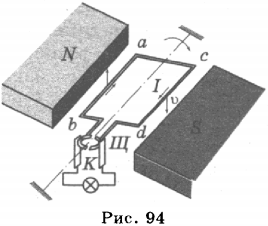
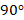 (рис. 22), то сила действия магнитного поля на проводник с током максимальна.
(рис. 22), то сила действия магнитного поля на проводник с током максимальна.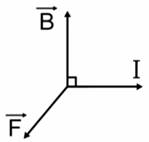
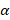 – угол между направлением тока и направлением вектора магнитной индукции:
– угол между направлением тока и направлением вектора магнитной индукции:


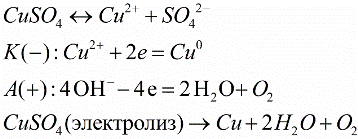
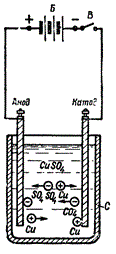
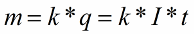
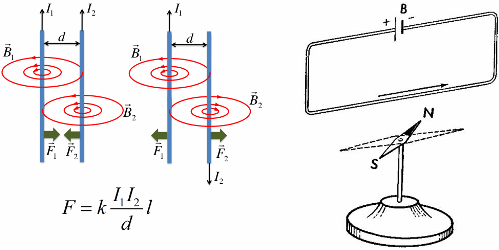










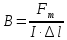 , гдеB– модуль магнитной
индукции,Fmмаксимальная сила,Iсила
тока, ∆l – длина
проводника.
, гдеB– модуль магнитной
индукции,Fmмаксимальная сила,Iсила
тока, ∆l – длина
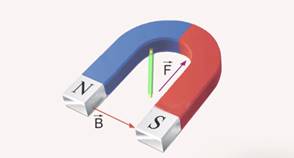
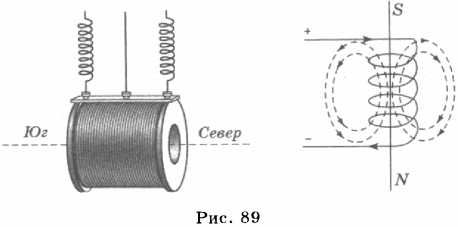
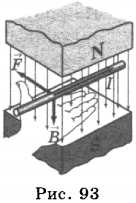
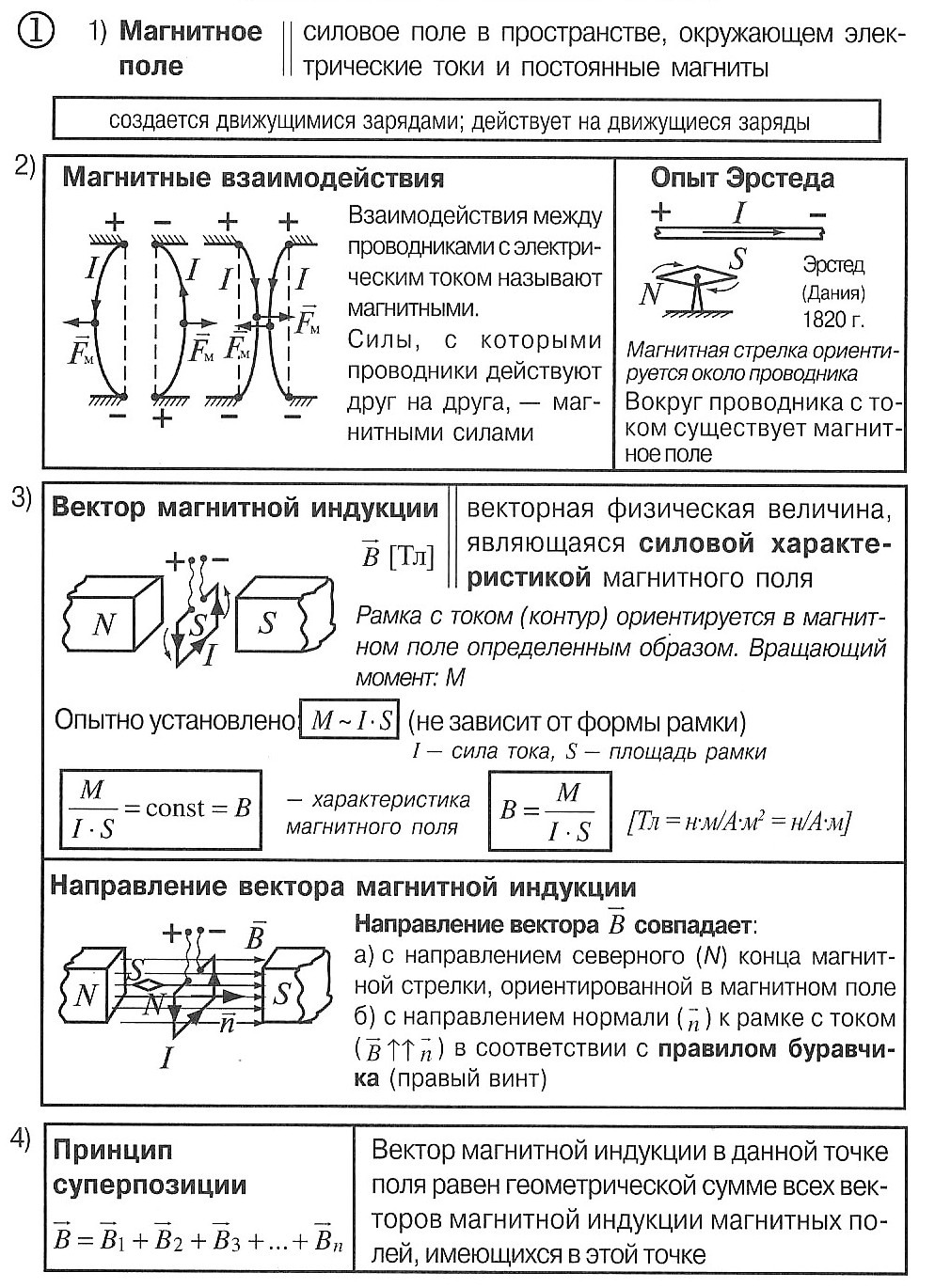
проводника.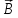 направлен от северного полюса магнита
к южному полюсу.
направлен от северного полюса магнита
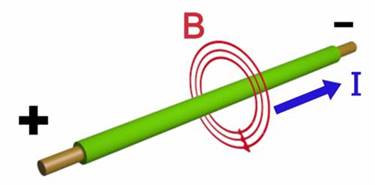
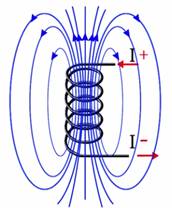
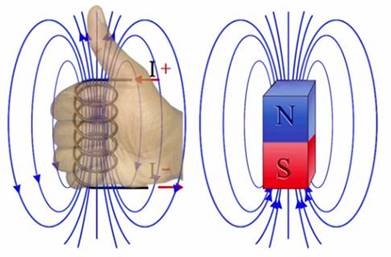
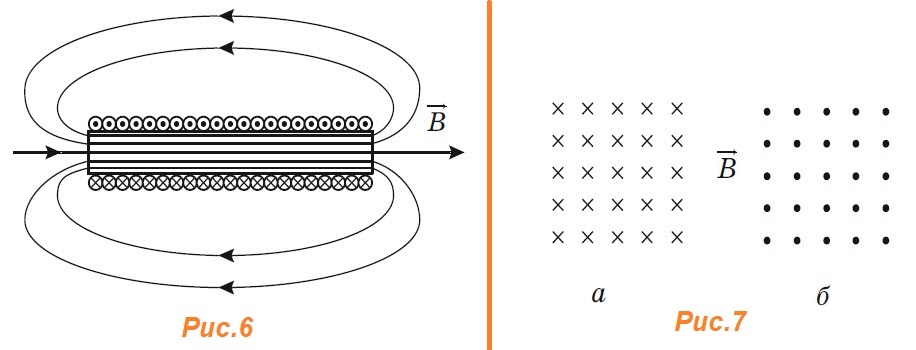
к южному полюсу.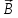 определяют поправилубуравчика:
если направление поступательного
движения буравчика совпадает с
направлением тока в проводнике, то
направление вращения буравчика совпадёт
с направлением вектора
определяют поправилубуравчика:
если направление поступательного
движения буравчика совпадает с
направлением тока в проводнике, то
направление вращения буравчика совпадёт
с направлением вектора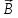 .
.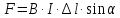 ,
где
,
где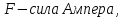
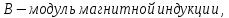
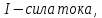
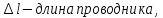
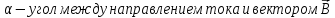 .
.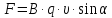 ,
где
,
где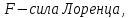
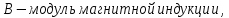
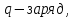
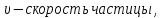
 .
.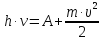 энергия порции света
энергия порции света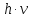 идёт на совершение работы выхода
идёт на совершение работы выхода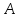 электрона из металла и на сообщение
электрону кинетической энергии
электрона из металла и на сообщение
электрону кинетической энергии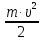 .
.
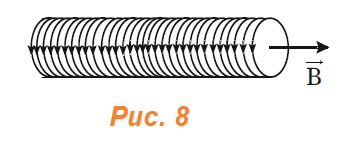
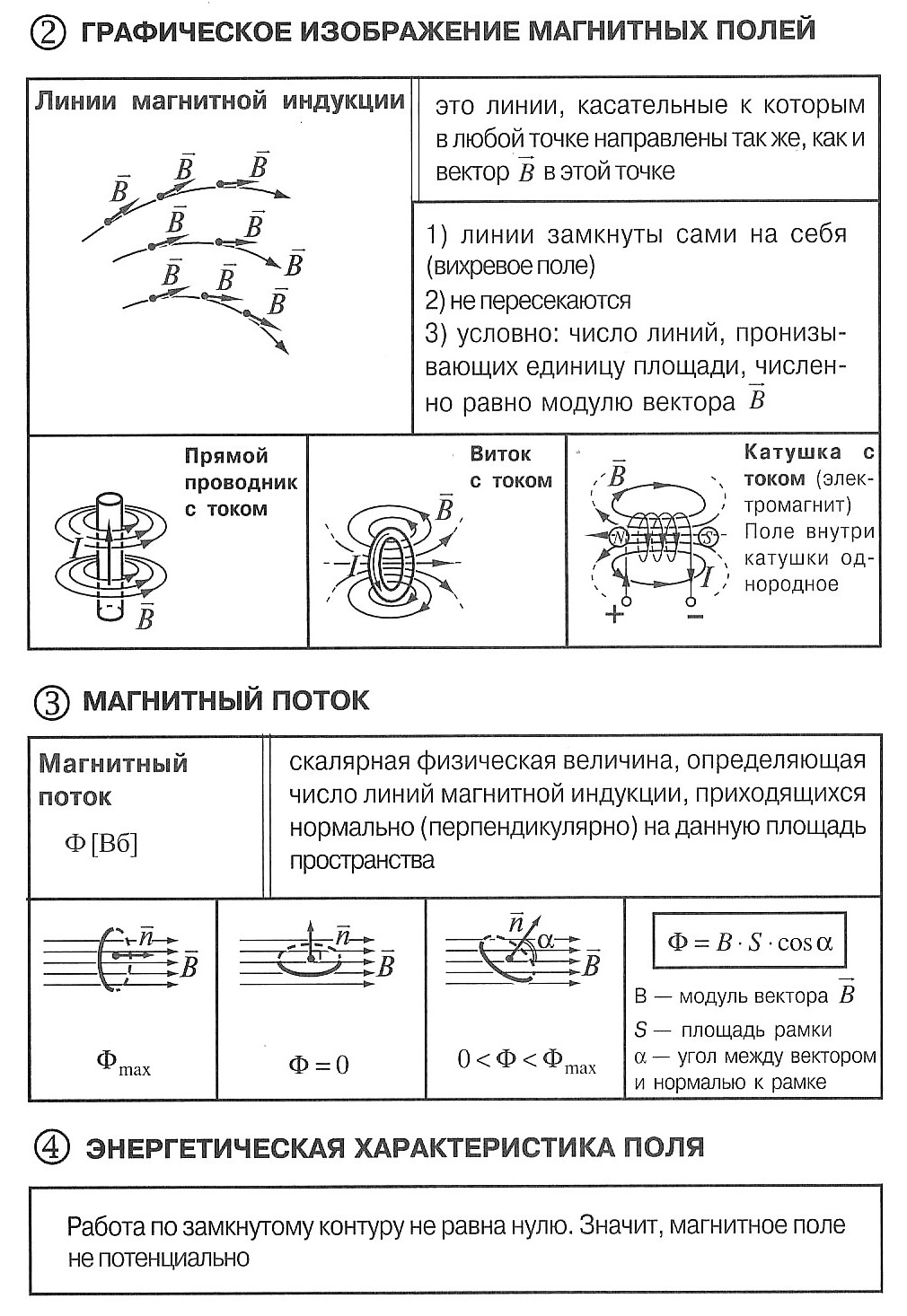
 Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.
Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.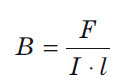 не зависит от свойств проводника и характеризует само магнитное поле.
не зависит от свойств проводника и характеризует само магнитное поле.

 Тесты по русскому языку.Пройти >>
Тесты по русскому языку.Пройти >>



 2Hg + O 2 – 180 кДж, С(тв) + O 2 (г) — СO 2 (г) + 394 кДж «
2Hg + O 2 – 180 кДж, С(тв) + O 2 (г) — СO 2 (г) + 394 кДж «







 . Составьте электронный баланс, укажите ок-ль и вос-ль и расставьте коэффициенты в реакции: Fe2O3 + CO
. Составьте электронный баланс, укажите ок-ль и вос-ль и расставьте коэффициенты в реакции: Fe2O3 + CO  Fe + CO2
Fe + CO2 Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.
Найти значения десятичного логарифма от чисел 100, 1000, 0.1, 0.01, 0.001.

 Но ряд:
Но ряд:
 Натуральный логарифм — это логарифм по основанию e (2,71828182845904).
Натуральный логарифм — это логарифм по основанию e (2,71828182845904).
 Десятичные (lg) и натуральные логарифмы (ln).
Десятичные (lg) и натуральные логарифмы (ln). Но ряд:
Но ряд: Введите свой запрос:
Введите свой запрос: 1)
1)

 Стандартные функции и выражения
Стандартные функции и выражения Результат TRUE, если аргумент нечетный, FALSE – если четный.
Результат TRUE, если аргумент нечетный, FALSE – если четный. Для корректной записи выражений необходимо знать не только как обозначаются те или иные операции, функции и т. п., но также стоит предусмотреть приоритеты их выполнения, математические и логические правила, а также некоторые тонкости самого языка. Для более углубленного изучения выражений, стоит рассмотреть несколько примеров.
Для корректной записи выражений необходимо знать не только как обозначаются те или иные операции, функции и т. п., но также стоит предусмотреть приоритеты их выполнения, математические и логические правила, а также некоторые тонкости самого языка. Для более углубленного изучения выражений, стоит рассмотреть несколько примеров. (a) = exp(a*ln(x))
(a) = exp(a*ln(x)) Аналогичные правила для логарифмов.
Аналогичные правила для логарифмов.
 То есть они дали мне , один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
То есть они дали мне , один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .

 В символах [латекс] \ log_b (xy) = \ log_b (x) + \ log_b (y). [/ Latex]
В символах [латекс] \ log_b (xy) = \ log_b (x) + \ log_b (y). [/ Latex] p) = p \ log_b (x). [/ latex]
p) = p \ log_b (x). [/ latex] В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex]
В символах [латекс] \ log_b \ left (\ frac {x} {y} \ right) = \ log_bx — \ log_by. [/ Latex] {100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс]
{100}) = 4 \ log_2x + 9 \ log_2y-100 \ log_2z. [/ Латекс] z = \ log_bx [/ latex]
z = \ log_bx [/ latex]
 Но 2 в знаменателе нужно убрать. Если мы умножим обе стороны на 2, получим:
Но 2 в знаменателе нужно убрать. Если мы умножим обе стороны на 2, получим:  Это
экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2)
= 8. Следовательно, x = 3.
Это
экспонента, до которой нужно возвести 2, чтобы получить 8. Мы знаем, что 2 (2) (2)
= 8. Следовательно, x = 3. Это показатель степени.
на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, x = 1.
Это показатель степени.
на которое нужно поднять 11, чтобы получить 11.Мы знаем, что 1 (1) = 11.
Следовательно, x = 1.
 7
7 0000007609 00000 н.
0000007807 00000 н.
0000008080 00000 н.
0000008387 00000 н.
0000008743 00000 н.
0000009013 00000 н.
0000009034 00000 н.
0000024051 00000 п.
0000024075 00000 п.
0000024128 00000 п.
0000024341 00000 п.
0000024522 00000 п.
0000025371 00000 п.
0000026217 00000 п.
0000026425 00000 н.
0000026455 00000 п.
0000027362 00000 п.
0000027384 00000 п.
0000027746 00000 п.
0000028077 00000 п.
0000028270 00000 п.
0000030317 00000 п.
0000030781 00000 п.
0000031632 00000 п.
0000031835 00000 п.
0000032685 00000 п.
0000032897 00000 н.
0000033016 00000 п.
0000033318 00000 п.
0000033402 00000 п.
0000034191 00000 п.
0000034395 00000 п.
0000034457 00000 п.
0000034567 00000 п.
0000034594 00000 п.
0000034621 00000 п.
0000034648 00000 п.
0000034799 00000 н.
0000034943 00000 п.
0000035011 00000 п.
0000035079 00000 п.
0000035147 00000 п.
0000035215 00000 п.
0000002443 00000 н.
0000003663 00000 н.
трейлер
]
>>
startxref
0
%% EOF
241 0 объект
>
/ Имена 245 0 руб.
0000007609 00000 н.
0000007807 00000 н.
0000008080 00000 н.
0000008387 00000 н.
0000008743 00000 н.
0000009013 00000 н.
0000009034 00000 н.
0000024051 00000 п.
0000024075 00000 п.
0000024128 00000 п.
0000024341 00000 п.
0000024522 00000 п.
0000025371 00000 п.
0000026217 00000 п.
0000026425 00000 н.
0000026455 00000 п.
0000027362 00000 п.
0000027384 00000 п.
0000027746 00000 п.
0000028077 00000 п.
0000028270 00000 п.
0000030317 00000 п.
0000030781 00000 п.
0000031632 00000 п.
0000031835 00000 п.
0000032685 00000 п.
0000032897 00000 н.
0000033016 00000 п.
0000033318 00000 п.
0000033402 00000 п.
0000034191 00000 п.
0000034395 00000 п.
0000034457 00000 п.
0000034567 00000 п.
0000034594 00000 п.
0000034621 00000 п.
0000034648 00000 п.
0000034799 00000 н.
0000034943 00000 п.
0000035011 00000 п.
0000035079 00000 п.
0000035147 00000 п.
0000035215 00000 п.
0000002443 00000 н.
0000003663 00000 н.
трейлер
]
>>
startxref
0
%% EOF
241 0 объект
>
/ Имена 245 0 руб. YVxp @ => A} ĽXP {Ȇqup>% Qz
YVxp @ => A} ĽXP {Ȇqup>% Qz Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.
Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках. Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться как основание, поскольку все его степени равны 1), как показано в таблице логарифмических законов.
Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться как основание, поскольку все его степени равны 1), как показано в таблице логарифмических законов. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724.
Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724. Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.
Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.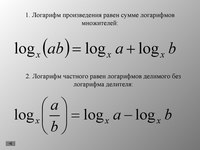
 Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма.
Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма. Обращение к таблицам тогда состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Обращение к таблицам тогда состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов. Это десятичный логарифм
Это десятичный логарифм И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма, заданного b> 0, мы имеем logb bx = x и blogb x = x, когда х> 0 .:
И поскольку f (f − 1 (x)) = x и f − 1 (f (x)) = x, у нас есть следующие обратные свойства логарифма, заданного b> 0, мы имеем logb bx = x и blogb x = x, когда х> 0 .: 00001
00001 ,
, После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить.
После возведения обеих сторон в степень n преобразовать обратно в логарифмическую форму, а затем обратно подставить. Сделайте эту замену, а затем примените степенное свойство логарифмов.
Сделайте эту замену, а затем примените степенное свойство логарифмов. Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
 log2 (8x2y)
log2 (8x2y)

 Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью раскрывается, когда свойства логарифма больше не могут быть применены.



 2) −15≈ − 13,2
2) −15≈ − 13,2

