Что такое ферромагниты – Ферромагнитные вещества ферромагнетики — Справочник химика 21
Магнитная восприимчивость — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 ноября 2016; проверки требуют 7 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 ноября 2016; проверки требуют 7 правок.Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе[1].
Магнитная восприимчивость определяется отношением намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. По своему смыслу восприимчивость является величиной безразмерной.
χ=MH{\displaystyle \chi ={\frac {M}{H}}}, где M{\displaystyle M} — намагниченность вещества под действием магнитного поля, H{\displaystyle H} — напряженность магнитного поля.
Иногда бывает полезно также ввести понятие удельной магнитной восприимчивости, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратных килограммах (кг−1). Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях (моль−1).
Магнитная восприимчивость некоторых веществ[править | править код]
Реальные объекты могут обладать как положительными, так и отрицательными магнитными восприимчивостями. Примером веществ с отрицательной восприимчивостью могут служить диамагнетики — их намагниченность по направлению противоположна приложенному магнитному полю. Положительной восприимчивостью обладают парамагнетики и ферромагнетики.
Магнитная восприимчивость диамагнетиков и парамагнетиков мала (для диамагнетиков она отрицательна) и численно составляет величину порядка 10−4 — 10−6, при этом она практически не зависит от напряжённости приложенного магнитного поля. Заметные отклонения наблюдаются только в области сильных полей или низких температур.
В ферромагнетиках магнитная восприимчивость может достигать весьма больших значений, составляя величины от нескольких десятков до многих тысяч единиц, причём наблюдается её сильная зависимость от напряжённости приложенного поля. Поэтому для удобства используют также дифференциальную магнитную восприимчивость, равную производной намагниченности единицы объёма вещества по напряжённости поля. В отсутствие поля магнитная восприимчивость ферромагнетиков отлична от нуля и имеет некоторое положительное значение χa{\displaystyle \chi _{a}}, называемое начальной магнитной восприимчивостью. С увеличением напряжённости поля величина восприимчивости растёт, пока не достигает некоего максимума χmax{\displaystyle \chi _{\mathrm {max} }}, после чего вновь уменьшается. В области очень сильных полей магнитная восприимчивость ферромагнетиков (при температурах, не очень близких к точке Кюри) падает практически до нуля, сравниваясь с величиной восприимчивости обычных парамагнетиков (эта область параметров называется областью парапроцесса).
Кривая СтолетоваВид зависимости магнитной восприимчивости ферромагнетика от напряжённости намагничивающего поля носит название кривой Столетова и обусловлен сложными механизмами намагничивания
ферромагнетиков. Значения χa{\displaystyle \chi _{a}} и χmax{\displaystyle \chi _{\mathrm {max} }} некоторых ферромагнетиков в нормальных условиях:
Магнитная восприимчивость большинства веществ (за исключением большей части диамагнетиков и некоторых парамагнетиков — щелочных и, в меньшей степени, щёлочноземельных металлов) зависит от температуры вещества. У парамагнетиков магнитная восприимчивость уменьшается с температурой, подчиняясь закону Кюри — Вейса. У ферромагнетиков магнитная восприимчивость с ростом температуры увеличивается, достигая резкого максимума вблизи точки Кюри (см. эффект Гопкинса).
Магнитная восприимчивость антиферромагнетиков увеличивается с ростом температуры до точки Нееля, а затем падает по закону Кюри — Вейса[2].
Магнитная воприимчивость почв зависит от соотношения в ней диа-, пара-, и ферромагнетиков. Она возрастает в почвах, богатых окристаллизованными оксидами железа (что характерно в верхних горизонтах почв аридных районов), резко снижена в оглееных почвах и органических горизонтах, обыкновенно снижается при возрастании выветрелости первичных пород.
Магнит — Википедия
 Подковообразный магнит из альнико — сплава железа, алюминия, никеля и кобальта и стали. Магниты изготовляются в виде подковы для того, чтобы приблизить полюса друг к другу с целью создать сильное магнитное поле, с помощью которого можно поднимать большие куски железа.
Подковообразный магнит из альнико — сплава железа, алюминия, никеля и кобальта и стали. Магниты изготовляются в виде подковы для того, чтобы приблизить полюса друг к другу с целью создать сильное магнитное поле, с помощью которого можно поднимать большие куски железа. 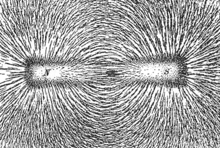 Рисунок линий силового поля магнита, полученный с помощью железных опилок
Рисунок линий силового поля магнита, полученный с помощью железных опилок 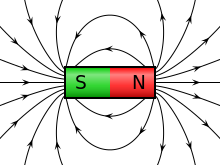
Магни́т — тело, обладающее собственным магнитным полем. Возможно, слово происходит от др.-греч. Μαγνῆτις λίθος (Magnētis líthos), «камень из Магнесии» — от названия региона Магнисия и древнего города Магнесия в Малой Азии[1], где в древности были открыты залежи магнетита.[2]
Простейшим и самым маленьким магнитом можно считать электрон. Магнитные свойства всех остальных магнитов обусловлены магнитными моментами электронов внутри них. С точки зрения квантовой теории поля электромагнитное взаимодействие переносится безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля).
Постоянный магнит — изделие, изготовленное из ферромагнетика, способного сохранять остаточную намагниченность после выключения внешнего магнитного поля. В качестве материалов для постоянных магнитов обычно служат железо, никель, кобальт, некоторые сплавы редкоземельных металлов (как, например, в неодимовых магнитах), а также некоторые естественные минералы, такие как магнетиты. Постоянные магниты применяются в качестве автономных (не потребляющих энергии) источников магнитного поля. Свойства магнита определяются характеристиками размагничивающего участка петли магнитного гистерезиса материала магнита: чем выше остаточная индукция Br и коэрцитивная сила Hc, тем выше намагниченность и стабильность магнита. Характерные поля постоянных магнитов — до 1 Тл (10 кГс).
Электромагнит — устройство, магнитное поле которого создаётся только при протекании электрического тока. Как правило, это катушка-соленоид, со вставленным внутрь ферромагнитным (обычно железным) сердечником с большой магнитной проницаемостью μ≃10000{\displaystyle \mu \simeq 10000}. Характерные поля электромагнитов 1,5—2 Тл определяются так называемым насыщением железа, то есть резким спадом дифференциальной магнитной проницаемости при больших значениях магнитного поля.
Старинная легенда рассказывает о пастухе по имени Магнус (у Льва Толстого в рассказе для детей «Магнит» этого пастуха зовут Магнис). Он обнаружил однажды, что железный наконечник его палки и гвозди сапог притягиваются к чёрному камню. Этот камень стали называть «камнем Магнуса» или просто «магнитом», по названию местности, где добывали железную руду (холмы Магнезии в Малой Азии). Таким образом, за много веков до нашей эры было известно, что некоторые каменные породы обладают свойством притягивать куски железа. Об этом упоминал в 6 веке до нашей эры греческий физик и философ Фалес. Первое научное изучение свойств магнита было предпринято в 13 веке ученым Петром Перегрином. В 1269 году вышло его сочинение «Книга о магните», где он писал о многих фактах магнетизма: у магнита есть два полюса, которые ученый назвал северным и южным; невозможно отделить полюса друг от друга разламыванием. Перегрин писал и о двух видах взаимодействия полюсов — притяжении и отталкивании. К 12—13 векам нашей эры магнитные компасы уже использовались в навигации в Европе, в Китае и других странах мира[3].

В 1600 году вышло сочинение английского врача Уильяма Гильберта «О магните». К известным уже фактам Гильберт прибавил важные наблюдения: усиление действия магнитных полюсов железной арматурой, потерю магнетизма при нагревании и другие. В 1820 году датский физик Ганс Христиан Эрстед на лекции попытался продемонстрировать своим студентам отсутствие связи между электричеством и магнетизмом, включив электрический ток вблизи магнитной стрелки. По словам одного из его слушателей, он был буквально «ошарашен», увидев, что магнитная стрелка после включения тока начала совершать колебания. Большой заслугой Эрстеда является то, что он оценил значения своего наблюдения и повторил опыт. Соединив длинным проводом полюса гальванической батареи, Эрстед протянул провод горизонтально и параллельно свободно подвешенной магнитной стрелке. Как только был включён ток, стрелка немедленно отклонилась, стремясь встать перпендикулярно к направлению провода. При изменении направления тока стрелка отклонилась в другую сторону. Вскоре Эрстед доказал, что магнит действует с некоторой силой на провод, по которому идёт ток.
Открытие взаимодействия между электрическим током и магнитом имело огромное значение. Оно стало началом новой эпохи в учении об электричестве и магнетизме. Это взаимодействие сыграло важную роль в развитии техники физического эксперимента.
Узнав об открытии Эрстеда, французский физик Доминик Франсуа Араго начал серию опытов. Он обмотал медной проволокой стеклянную трубку, в которую вставил железный стержень. Как только замкнули электрическую цепь, стержень сильно намагнитился и к его концу крепко прилипли железные ключи; когда выключили ток, ключи отпали. Араго рассматривал проводник, по которому идёт ток, как магнит. Правильное объяснение этого явления было дано после исследования французского физика Андре Ампера, который установил внутреннюю связь между электричеством и магнетизмом. В сентябре 1820 года он сообщил Французской Академии наук о полученных им результатах.
Затем Ампер в своем «станке» заменил раму свободно подвешенным спиральным проводником. Этот провод при пропускании по нему тока приобретал свойство магнита. Ампер назвал его соленоидом. Исходя из магнитных свойств соленоида, Ампер предложил рассматривать магнетизм как явление, обязанное круговым токам. Он считал, что магнит состоит из молекул, в которых имеются круговые токи. Каждая молекула представляет собой маленький магнитик, располагаясь одноимёнными полюсами в одну и ту же сторону, эти маленькие магнитики и образуют магнит. Проводя вдоль стальной полосы магнитом (несколько раз в одну и ту же сторону), мы заставляем молекулы с круговыми токами ориентироваться в пространстве одинаково. Таким образом, стальная пластинка превратится в магнит. Теперь стал понятен и опыт Араго со стеклянной трубкой, обмотанной медным проводом. Вдвинутый в неё железный стержень стал магнитом потому, что вокруг него шёл ток. Это был электромагнит.
В 1825 году английский инженер Уильям Стёрджен изготовил первый электромагнит, представляющий собой согнутый стержень из мягкого железа с обмоткой из толстой медной проволоки. Для изолирования от обмотки стержень был покрыт лаком. При пропускании тока железный стержень приобретал свойства сильного магнита, но при прерывании тока он мгновенно их терял. Именно эта особенность электромагнитов позволила широко применять их в технике.
Термин «магнит», как правило, используется в отношении объектов, которые имеют собственное магнитное поле даже в отсутствие приложенного магнитного поля. Такое возможно лишь в некоторых классах материалов. В большинстве же материалов магнитное поле появляется в связи с приложенным внешним магнитным полем; это явление известно как магнетизм. Существует несколько типов магнетизма, и каждый материал имеет, по крайней мере, один из них.
В целом поведение магнитного материала может значительно варьироваться в зависимости от структуры материала и, не в последнюю очередь, его электронной конфигурации. Существует несколько типов взаимодействия материалов с магнитным полем, в том числе:
- Ферромагнетики и ферримагнетики — материалы, которые обычно и считаются магнитными. Они притягиваются к магниту достаточно сильно — так, что притяжение ощущается. Только эти материалы могут сохранять намагниченность и стать постоянными магнитами. Ферримагнетики сходны с ферромагнетиками, но слабее них. Различия между ферро- и ферримагнитными материалами связаны с их микроскопической структурой.
- Парамагнетики — такие вещества, как платина, алюминий и кислород, которые слабо притягиваются к магниту. Этот эффект в сотни тысяч раз слабее, чем притяжение ферромагнитных материалов, поэтому он может быть обнаружен только с помощью чувствительных инструментов или очень сильных магнитов.
- Диамагнетики — вещества, намагничивающиеся против направления внешнего магнитного поля. Диамагнитные, по сравнению с пара- и ферромагнитными, вещества, такие как углерод, медь, вода и пластики, отталкиваются от магнита. Все вещества, не обладающие одним из других типов магнетизма, являются диамагнитными; к ним относится большинство веществ. Силы, действующие на диамагнитные объекты от обычного магнита, слишком слабы, однако в сильных магнитных полях сверхпроводящих магнитов диамагнитные материалы, например кусочки свинца, могут пари́ть, а поскольку углерод и вода являются веществами диамагнитными, в мощном магнитном поле могут пари́ть даже органические объекты, например живые лягушки и мыши[4].
Также существуют и другие виды магнетизма, например спиновые стёкла, суперпарамагнетизм, супердиамагнетизм и метамагнетизм.
В системе СИ единицей магнитного потока является вебер (Вб), магнитной проницаемости — генри на метр (Гн/м), напряжённости магнитного поля — ампер на метр (А/м), индукции магнитного поля — тесла.
Вебер — магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 ом проходит количество электричества 1 кулон.
Генри — международная единица индуктивности и взаимной индукции. Если проводник обладает индуктивностью в 1 Гн и ток в нём равномерно изменяется на 1 А в секунду, то на его концах индуктируется ЭДС в 1 вольт. 1 генри = 1,00052 · 109 абсолютных электромагнитных единиц индуктивности.
Тесла — единица измерения индукции магнитного поля в СИ, численно равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.

- Магнитные носители информации: VHS кассеты содержат катушки из магнитной ленты. Видео и звуковая информация кодируется на магнитном покрытии на ленте. Также в компьютерных дискетах и жёстких дисках запись данных происходит на тонком магнитном покрытии. Однако носители информации не являются магнитами в строгом смысле, так как они не притягивают предметы. Магниты в жёстких дисках используются в ходовом и позиционирующем электродвигателях.
- Кредитные, дебетовые и ATM карты — ранние модели всех этих карт имеют магнитную полосу на одной стороне (магнитные полосы постепенно вытесняются микросхемами cмарт-карт). Эта полоса кодирует информацию, необходимую для соединения с финансовым учреждением и связи с их счетами.
- Обычные телевизоры и компьютерные мониторы: телевизоры и компьютерные мониторы, содержащие электронно-лучевую трубку используют электромагнит для управления пучком электронов и формирования изображения на экране. Плазменные панели и ЖК-дисплеи используют другие технологии.
- Громкоговорители и микрофоны: большинство громкоговорителей используют постоянный магнит и токовую катушку для преобразования электрической энергии (сигнала) в механическую энергию (движение, которое создает звук). Обмотка намотана на катушку, прикрепляется к диффузору и по ней протекает переменный ток, который взаимодействует с полем постоянного магнита.
- Другой пример использования постоянных магнитов в звукотехнике — в головке звукоснимателя электрофона и в простейших магнитофонах в качестве экономичной стирающей головки.
 Магнитный сепаратор тяжёлых минералов
Магнитный сепаратор тяжёлых минералов- Электродвигатели и генераторы: некоторые электрические двигатели (так же, как громкоговорители) основываются на комбинации электромагнита и постоянного магнита. Они преобразовывают электрическую энергию в механическую энергию. Генератор, наоборот, преобразует механическую энергию в электрическую энергию путём перемещения проводника через магнитное поле.
- Трансформаторы: устройства передачи электрической энергии между двумя обмотками провода, которые электрически изолированы, но связаны магнитно.
- Магниты используются в поляризованных реле. Такие устройства запоминают своё состояние на время выключения питания.
- Компасы: компас (или морской компас) является намагниченным указателем, который может свободно вращаться и ориентируется на направление магнитного поля, чаще всего магнитного поля Земли.
- Искусство: виниловые магнитные листы могут быть присоединены к живописи, фотографии и другим декоративным изделиям, что позволяет присоединять их к холодильникам и другим металлическим поверхностям.
 Магниты часто используются в игрушках. M-TIC использует магнитные стержни, связанные с металлическими сферами
Магниты редкоземельных элементов в форме эллипсоида, которые притягиваются друг к другу
Магниты часто используются в игрушках. M-TIC использует магнитные стержни, связанные с металлическими сферами
Магниты редкоземельных элементов в форме эллипсоида, которые притягиваются друг к другу- Игрушки: учитывая их способность противостоять силе тяжести на близком расстоянии, магниты часто используются в детских игрушках с забавными эффектами.
- Магниты могут использоваться для производства ювелирных изделий. Ожерелья и браслеты могут иметь магнитную застёжку, или могут быть изготовлены полностью из серии связанных магнитов и чёрных бусин.
- Магниты встречаются в сумках в виде вставленной внутрь закрывающей сумку кнопки намагниченной железной пластины; магниты также вшивают внутрь верхней одежды для закрывания клапана одежды элегантной, невидимой глазу застёжкой.
- Магниты могут поднимать магнитные предметы (железные гвозди, скобы, кнопки, скрепки), которые либо являются слишком мелкими, либо их трудно достать или они слишком тонкие чтобы держать их пальцами. Некоторые отвёртки специально намагничиваются для этой цели.
- Магниты могут использоваться при обработке металлолома для отделения магнитных металлов (железа, стали и никеля) от немагнитных (алюминия, цветных сплавов и т. д.). Та же идея может быть использована в рамках так называемого «Магнитного испытания», в которой кузов автомобиля обследуется с магнитом для выявления областей, отремонтированных с использованием стекловолокна или пластиковой шпатлевки.
- Маглев: поезд на магнитном подвесе, движимый и управляемый магнитными силами. Такой состав, в отличие от традиционных поездов, в процессе движения не касается поверхности рельса. Так как между поездом и поверхностью движения существует зазор, трение исключается, и единственной тормозящей силой является лишь сила аэродинамического сопротивления.
- Магниты используются в фиксаторах мебельных дверей.
- Если магниты поместить в губки, то эти губки можно использовать для мытья тонких листовых немагнитных материалов сразу с обеих сторон, причём одна сторона может быть труднодоступной. Это могут быть, например, стёкла аквариума или балкона.
- Магниты используются для передачи вращающего момента «сквозь» стенку, которой может являться, например, герметичный контейнер электродвигателя. Так была устроена игрушка ГДР «Подводная лодка». Таким же образом в бытовых счётчиках расхода воды передаётся вращение от лопаток датчика на счётный узел.
- Магниты совместно с герконом применяются в специальных датчиках положения. Например, в датчиках дверей холодильников и охранных сигнализаций.
- Магниты совместно с датчиком Холла используют для определения углового положения или угловой скорости вала.
- Магниты используются в искровых разрядниках для ускорения гашения дуги.
- Магниты используются при неразрушающем контроле магнитопорошковым методом (МПК)
- Магниты используются для отклонения пучков радиоактивных и ионизирующих излучений, например при наблюдении в камерах.
- Магниты используются в показывающих приборах с отклоняющейся стрелкой, например, амперметр. Такие приборы весьма чувствительны и линейны.
- Магниты применяются в СВЧ вентилях и циркуляторах.
- Магниты применяются в составе отклоняющей системы электронно-лучевых трубок для подстройки траектории электронного пучка.
- До открытия закона сохранения энергии, было много попыток использовать магниты для построения «вечного двигателя». Людей привлекала, казалось бы, неисчерпаемая энергия магнитного поля постоянного магнита, которые были известны очень давно. Но рабочий макет так и не был построен.
- Магниты применяются в конструкциях бесконтактных тормозов, состоящих из двух пластин, одна — магнит, а другая из алюминия. Одна из них жёстко закреплена на раме, другая вращается с валом. Торможение регулируется зазором между ними.
Из-за того, что человеческие ткани имеют очень низкий уровень восприимчивости к статическому магнитному полю, не существует научных доказательств его эффективности для использования в лечении любых заболеваний[5]. По той же причине отсутствуют научные свидетельства опасности для здоровья человека, связанной с воздействием этого поля. Однако если ферромагнитное инородное тело находится в человеческих тканях, магнитное поле будет взаимодействовать с ним, что может представлять собой серьёзную опасность[6].
В частности, если кардиостимулятор был встроен в грудную клетку пациента, следует держать его подальше от магнитных полей. Именно по этой причине больные с установленным кардиостимулятором не могут быть протестированы с использованием МРТ, которое представляет собой магнитное устройство визуализации внутренних органов и тканей.
Дети иногда могут глотать небольшие магниты из игрушек. Это может быть опасно, если ребёнок проглотил два или более магнита, так как магниты могут повредить внутренние ткани; был зафиксирован как минимум один смертельный случай[7].
Иногда намагниченность материалов становится нежелательной и возникает необходимость в их размагничивании. Размагничивание материалов может быть осуществлено тремя способами:
- нагревание магнита выше температуры Кюри всегда ведёт к размагничиванию;
- сильный удар молотком по магниту, или просто сильный удар ведет к размагничиванию.
- поместить магнит в переменное магнитное поле, превышающее коэрцитивную силу материала, а затем постепенно уменьшать воздействие магнитного поля или вывести магнит из него.
Последний способ применяется в промышленности для размагничивания инструментов, жёстких дисков, стирания информации на магнитных карточках и так далее.
Частичное размагничивание материалов происходит в результате ударов, так как резкое механическое воздействие ведёт к разупорядочению доменов.
Магнитная проницаемость — Википедия
Магни́тная проница́емость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией B{\displaystyle {B}} и напряжённостью магнитного поля H{\displaystyle {H}} в веществе.
Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).
Обычно обозначается греческой буквой μ{\displaystyle \mu }. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).
Впервые этот термин встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») опубликованной в 1881 году[1].
В общем, соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как:
- B→=μH→,{\displaystyle {\vec {B}}=\mu {\vec {H}},}
и μ{\displaystyle \mu } в общем случае здесь следует понимать как тензор, что в компонентной записи имеет вид[2]:
- Bi=μijHj{\displaystyle \ B_{i}=\mu _{ij}H_{j}}
Для изотропных веществ соотношение:
- B→=μH→{\displaystyle {\vec {B}}=\mu {\vec {H}}}
можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру).
В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:
- μr=μμ0{\displaystyle \mu _{r}={\frac {\mu }{\mu _{0}}}},
- где μr{\displaystyle \mu _{r}} — относительная, а μ{\displaystyle \mu } — абсолютная проницаемость, μ0{\displaystyle \mu _{0}} — магнитная постоянная.
Нередко обозначение μ{\displaystyle \mu } используется не для абсолютной, а именно для относительной магнитной проницаемости (при этом μ{\displaystyle \mu } совпадает с таковым в СГС).
Размерность абсолютной магнитной проницаемости в СИ такая же, как размерность магнитной постоянной, то есть Гн/м или Н/А2.
Относительная магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением:
- μr=1+χ,{\displaystyle \mu _{r}=1+\chi ,}
а в Гауссовой системе магнитная проницаемость связана с магнитной восприимчивостью χ соотношением:
- μ=1+4πχ.{\displaystyle \mu =1+4\pi \chi .}
Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля для анизотропных веществ (и, кроме того, от температуры, давления и т. д.).
Также она зависит от скорости изменения поля со временем, в частности, для синусоидального изменения поля — зависит от частоты этого колебания (в этом случае для описания намагничивания вводят комплексную магнитную проницаемость, чтобы описать влияние вещества на сдвиг фазы B относительно H). При достаточно низких частотах — небольшой быстроте изменения поля, её можно обычно считать в этом смысле независимой от частоты.
 Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ0) и диамагнетиков (μd)
Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ0) и диамагнетиков (μd) 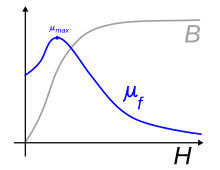
- Магнитная проницаемость сильно зависит от величины поля для нелинейных по магнитной восприимчивости сред (типичный пример — ферромагнетики, для которых характерен магнитный гистерезис). Для таких сред магнитная проницаемость, как независящее от поля число, может указываться приближенно, в линейном приближении.
- Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо выполняется для широкого диапазона изменения величины поля.
Классификация веществ по значению магнитной проницаемости[править | править код]
Подавляющее большинство веществ относятся либо к классу диамагнетиков (μ⪅1{\displaystyle \mu \lessapprox 1}), либо к классу парамагнетиков (μ⪆1{\displaystyle \mu \gtrapprox 1}). Но существует ряд веществ — (ферромагнетики), например железо, обладают более выраженными магнитными свойствами.
Для ферромагнетиков, вследствие гистерезиса, понятие магнитной проницаемости, строго говоря, неприменимо. Однако, в определённом диапазоне изменения намагничивающего поля (в тех случаях, когда можно было пренебречь остаточной намагниченностью, но до насыщения) можно, в лучшем или худшем приближении, всё же представить эту зависимость как линейную (а для магнитомягких материалов ограничение снизу может быть и не слишком практически существенно), и в этом смысле величина магнитной проницаемости бывает измерена и для них.
Магнитная проницаемость сверхпроводников равна нулю, так как материал выталкивает магнитное поле при переходе в сверхпроводящее состояние, иногда говорят, что сверхпроводники — идеальные диамагнетики.
Абсолютная магнитная проницаемость воздуха приблизительно равна магнитной проницаемости вакуума и в технических расчетах принимается равной[3] магнитной постоянной = 4π × 10−7{\displaystyle 4\pi \ \times \ 10^{-7}} Гн/м
Магнитные проницаемости некоторых веществ и материалов[править | править код]
Относительная магнитная проницаемость некоторых[4] веществ[править | править код]
| Парамагнетики, μ>1{\displaystyle \mu >1} | (μ−1)⋅10−6{\displaystyle (\mu -1)\cdot 10^{-6}} | Диамагнетики, μ<1{\displaystyle \mu <1} | (1−μ)⋅10−6{\displaystyle (1-\mu )\cdot 10^{-6}} |
|---|---|---|---|
| Азот | 0,013 | Водород | 0,063 |
| Воздух | 0,38 | Бензол | 7,5 |
| Кислород | 1,9 | Вода | 9 |
| Эбонит | 14 | Медь | 10,3 |
| Алюминий | 23 | Стекло | 12,6 |
| Вольфрам | 176 | Каменная соль | 12,6 |
| Платина | 360 | Кварц | 15,1 |
| Жидкий кислород | 3400 | Висмут | 176 |
Магнитная восприимчивость и магнитная проницаемость некоторых материалов[править | править код]
| Medium | Восприимчивость χm (объемная, СИ) | Проницаемость μ, Гн/м | Относительная проницаемость μ/μ0 | Магнитное поле | Максимум частоты |
|---|---|---|---|---|---|
| Метглас (англ. Metglas) | 1,25 | 1 000 000[5] | при 0,5 Тл | 100 кГц | |
| Наноперм (англ. Nanoperm) | 10⋅10-2 | 80 000[6] | при 0,5 Тл | 10 кГц | |
| Мю-металл | 2,5⋅10-2 | 20 000[7] | при 0,002 Тл | ||
| Мю-металл | 50 000[8] | ||||
| Пермаллой | 1,0⋅10-2 | 8000[7] | при 0,002 Тл | ||
| Электротехническая сталь | 5,0⋅10-3 | 4000[7][нет в источнике] | при 0,002 Тл | ||
| Никель-цинковый Феррит | 2,0⋅10-5 — 8,0⋅10-4 | 16-640 | от 100 кГц до 1 МГц[источник не указан 2897 дней] | ||
| Марганец-цинковый Феррит | >8,0⋅10-4 | 640 (и более) | от 100 кГц до 1 МГц | ||
| Сталь | 1,26⋅10-4 | 100[7] | при 0,002 Тл | ||
| Никель | 1,25⋅10-4 | 100[7] — 600 | при 0,002 Тл | ||
| Неодимовый магнит | 1,05[9] | до 1,2—1,4 Тл | |||
| Платина | 1,2569701⋅10-6 | 1,000265 | |||
| Алюминий | 2,22⋅10-5[10] | 1,2566650⋅10-6 | 1,000022 | ||
| Дерево | 1,00000043[10] | ||||
| Воздух | 1,00000037[11] | ||||
| Бетон | 1[12] | ||||
| Вакуум | 0 | 1,2566371⋅10-6 (μ0) | 1[13] | ||
| Водород | -2,2⋅10-9[10] | 1,2566371⋅10-6 | 1,0000000 | ||
| Фторопласт | 1,2567⋅10-6[7] | 1,0000 | |||
| Сапфир | -2,1⋅10-7 | 1,2566368⋅10-6 | 0,99999976 | ||
| Медь | -6,4⋅10-6 или -9,2⋅10-6[10] | 1,2566290⋅10-6 | 0,999994 | ||
| Вода | -8,0⋅10-6 | 1,2566270⋅10-6 | 0,999992 | ||
| Висмут | -1,66⋅10-4 | 1 | 0,999834 | ||
| Сверхпроводники | −1 | 0 | 0 |
- ↑ Werner von Siemens, Lebenserinnerungen
- ↑ Подразумевается суммирование по повторяющемуся индексу (j), то есть запись следует понимать так: μijHj≡∑j=13μijHj.{\displaystyle \mu _{ij}H_{j}\equiv \sum \limits _{j=1}^{3}\mu _{ij}H_{j}.} Эта запись, как легко видеть, означает умножение вектора слева на матрицу по правилам матричного умножения.
- ↑ Намагничивание стали. Магнитная проницаемость. (неопр.) (недоступная ссылка). Дата обращения 16 июля 2011. Архивировано 19 марта 2011 года.
- ↑ Магнитная проницаемость. Магнитная проницаемость среды. Относительная магнитная проницаемость. Магнитная проницаемость вещества (неопр.) (недоступная ссылка). Дата обращения 16 июля 2011. Архивировано 12 февраля 2012 года.
- ↑ «Metglas Magnetic Alloy 2714A», »Metglas» (неопр.) (недоступная ссылка). Metglas.com. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ «Typical material properties of NANOPERM», »Magnetec» (неопр.) (PDF). Дата обращения 8 ноября 2011.
- ↑ 1 2 3 4 5 6 «Relative Permeability», »Hyperphysics» (неопр.). Hyperphysics.phy-astr.gsu.edu. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ Nickel Alloys-Stainless Steels, Nickel Copper Alloys, Nickel Chromium Alloys, Low Expansion Alloys (неопр.). Nickel-alloys.net. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ Juha Pyrhönen, Tapani Jokinen, Valéria Hrabovcová. Design of Rotating Electrical Machines (неопр.). — John Wiley and Sons, 2009. — С. 232. — ISBN 0-470-69516-1.
- ↑ 1 2 3 4 Richard A. Clarke. Clarke, R. »Magnetic properties of materials», surrey.ac.uk (неопр.). Ee.surrey.ac.uk. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, 568 pp., p.16
- ↑ NDT.net. Determination of dielectric properties of insitu concrete at radar frequencies (неопр.). Ndt.net. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ точно, по определению.
Ферриты — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Феррит.Ферри́ты (оксифе́ры) — соединения оксида железа Fe2O3 с более осно́вными оксидами других металлов, являющиеся ферримагнетиками[1]. Широко применяются в качестве магнитных материалов в радиоэлектронике, радиотехнике и вычислительной технике, поскольку сочетают высокую магнитную восприимчивость с полупроводниковыми или диэлектрическими свойствами.
Ферриты-шпинели[править | править код]
Ферриты со структурой шпинели кристаллизуются в кубической решётке с пространственной группой Fd3m, Z = 8. Их общая формула MeFe2O4, где Me — двухвалентный металл: никель, кобальт, марганец, магний, медь, железо, цинк, кадмий[2].
Ферриты-гранаты[править | править код]
Ферриты со структурой граната кристаллизуются в кубической решётке с пространственной группой Ia3d, Z = 8. Общая формула: Me3Fe5O12, где Me — тяжёлый редкоземельный элемент (от самария до лютеция) или иттрий. Примером широко используемого феррита из этого класса является иттрий-железный гранат Y3Fe5O12[2].
Гексаферриты[править | править код]
Ферриты с гексагональной решёткой (гексаферриты) имеют кристаллическую структуру типа магнетоплюмбита PbFe12O19 с пространственной группой P63/mmc или близкую к ней. В эту группу ферритов входит несколько типов, различающихся общей формулой[2].
Ортоферриты[править | править код]
Ферриты с ромбической решёткой (ортоферриты) имеют кристаллическую структуру типа искажённой структуры перовскита с пространственной группой Pcmn, Z = 4 и общую формулу MeFeO3, где Me — редкоземельный элемент. Ортоферриты, в отличие от трёх вышеописанных групп (ферримагнетиков), при нормальной температуре являются антиферромагнетиками и становятся ферримагнетиками лишь при температуре ниже нескольких кельвинов[2].
Большинство ферритов являются относительно тугоплавкими кристаллическими веществами с достаточно высокой твёрдостью, не растворимыми в воде и органических растворителях. Реагируют с кислотами. При нормальной температуре устойчивы на воздухе, при температурах выше 1000°C могут диссоциировать. На воздухе при таких температурах ферриты, содержащие Fe2+ и Mn2+, могут окисляться[2].
Благодаря сочетанию высоких магнитных свойств и низкой электропроводности ферриты широко применяются в технике высоких частот (более 100 кГц). Ферриты используют в качестве магнитных материалов в радиотехнике, электронике, автоматике, вычислительной технике (ферритовые поглотители электромагнитных волн, антенны, сердечники, элементы памяти, постоянные магниты и т. д.).
Основные способы получения ферритов[править | править код]
Поликристаллические ферриты производят по керамической технологии. Из ферритового порошка, синтезированного из смеси исходных ферритообразующих компонентов и гранулированного со связкой, прессуют изделия нужной формы, которые подвергают затем спеканию при температурах от 900 до 1500 °C на воздухе или в специальной газовой атмосфере. В качестве исходных ферритообразующих компонентов применяются смеси оксидов, гидроксидов, оксалатов и карбонатов (иногда их совместно осаждают из раствора) или совместно упаренные растворы солей (нитраты, сульфаты, двойные сульфаты типа шенитов. Монокристаллы ферритов выращивают зонной плавкой или методами Вернейля или Чохральского, обычно под давлением кислорода в несколько десятков или сотен атмосфер. Для растворимых ферритов используют гидротермальное выращивание в растворах гидроксида или карбоната натрия, хлорида аммония или смеси хлоридов под давлением от 200 до 1200 атмосфер. Монокристаллы некоторых ферритов (при применении в качестве исходных веществ смеси оксидов) выращивают также из растворов в расплаве (смеси PbO + PbF2, PbO + B2O3, BaO + B2O3 или более сложные)[2].
Для выращивания ферритовых плёнок со структурой шпинели обычно применяют метод химических транспортных реакций с хлороводородом или другими галогеноводородами в качестве носителя, а для плёнок феррит-гранатов и гексаферритов используют метод жидкостной эпитаксии из растворов в расплаве, а также метод разложения паров (в качестве газообразных исходных материалов применяются, например, β-дикетонаты металлов)[2].
- Михайлова М., Филиппов В., Муслаков В. Магнитомягкие ферриты для радиоэлектронной аппаратуры. Справочник. — М. Радио и связь, 1983.
- Куневич А. В. Ферриты, каталог М., 1991
- Куневич А. В., Подольский А. В. Сидоров И. Н. «Ферриты: Энциклопедический справочник. Магниты и магнитные системы. Том 1» издательство Лик, 2004 г.
- Журавлев Г.И. Химия и технология ферритов — Ленинград: Химия. Ленингр. отд-ние, 1970. — 191 с.
- Смит, Я., Вейн, Х. Ферриты. — Москва: Иностранная литература, 1962. — 504 с.
- Ситидзе, Ю., Сато, Х. Ферриты. — Москва: Мир, 1964. — 407 с.
Что такое ферритовый магнит? — блог Мира Магнитов
В настоящий момент доля ферритовых магнитов в общем объеме реализации магнитной продукции составляет 75%. Несмотря на такую массовость и распространенность многие не знают, что такое ферритовый магнит и что это за материал. Сегодня вы прочитаете эту статью и устраните этот пробел.История возникновения и развития
Чтобы в полной мере оценить, что такое ферритовый магнит, следует рассмотреть историю его появления. С момента обнаружения магнетизма усилия ученых были направлены на снижение стоимости материалов и улучшение их эксплуатационных качеств. В 1930-х гг. был получен сплав альнико (алюминий-никель-кобальт). Благодаря сочетанию доступной стоимости и хороших магнитных свойств этот материал более 30 лет оставался лидером в изготовлении и потреблении. Практически на протяжении всего этого срока японские исследователи Като и Такей не оставляли попыток найти природный магнитный материал, который бы позволил создать более дешевую и совершенную альтернативу альнико.
Ёгоро Като (Yogoro Kato) и Такеши Такей (Takeshi Takei)
В одном из экспериментов Като и Такей, синтезируя феррит по керамической технологии, заменили оксид железа на оксид кобальта. В тот момент ученые еще не понимали, что они изобрели первый ферритовый магнит и что это открытие увековечит их имена. Коэрцитивная сила нового материала достигала 48-72 кА/м, намного опережая соответствующий параметр альнико. Эстафету японских изобретателей подхватили ученые из компании Филлипс. Найденный ими бариевый феррит позволил достичь еще более высокий показатель коэрцитивной силы – 160 кА/м. Технологически производство нового перспективного материала постоянно совершенствовалось. В лабораториях экспериментировали с исходным сырьем, помолом порошковых компонентов, режимами синтеза ферритов и другими составляющими процесса изготовления магнитов. В итоге удалось с небольшими затратами изготавливать магнитный материал с высоким показателем индукции. Первое коммерческое изделие, выполненное по новой технологии, увидело свет в 1955 году в Японии. Вскоре и в СССР узнали, что такое ферритовый магнит и уже к середине 1960-х гг. освоили его массовый выпуск. Со временем производство с использованием бариевых ферритов было вытеснено стронциевыми. Главное свойство нового материала, обеспечившего его преимущество – экологическая безопасность. Кроме того, стронциевый феррит не требовал тонкой настройки температуры спекания, что позволило упростить технический процесс. До сих пор ферритовые магниты остаются самыми дешевыми среди альтернатив. До 90% их состава приходится на оксид железа. Этот материал очень распространен в виде концентрата природного магнетита. Кроме того, ежегодно металлургическая отрасль производит огромное количество синтетического оксида железа (в качестве отходов). Следовательно, ферритовый порошок купить можно очень дешево. Таким образом, для изготовления ферритовых магнитов существует практически бесконечный источник дешевого сырья, что в сочетании с простотой техпроцесса позволяет этому материалу оставаться мировым лидером в производстве и потреблении.Ферритовые магниты сегодня
Практически во всех сферах, где необходима миниатюризация компонентов, ферритовые магниты вытесняются неодимовыми. В то же время во многих отраслях позиции классического материала остаются очень прочными. Ферритовые магниты кольца используются для подавления шумовых помех, из ферритовых пластин делают магнитные держатели для сварочных работ. Низкая цена – далеко не единственное выгодное свойство ферритов. Также ферритовые магниты обладают следующими преимуществами: 1) Высокий уровень сопротивления электричеству. 2) Устойчивость к коррозии. 3) Стойкость к высоким температурам. Интернет-магазин «Мир магнитов» предлагает вам лучшие цены на качественную магнитную продукцию. Наши консультанты с радостью ответят на любые ваши вопросы, а также помогут подобрать и заказать подходящее изделие.Ферромагнит — это… Что такое Ферромагнит?
Определение
Ферромагнетики — вещества (как правило, в твёрдом кристаллическом или аморфном состоянии), в которых ниже определённой критической температуры (точки Кюри) устанавливается дальний ферромагнитный порядок магнитных моментов атомов или ионов (в неметаллических кристаллах) или моментов коллективизированных электронов (в металлических кристаллах). Ландау предсказал существование диамагнетизма свободных электронов.
Свойства ферромагнетиков
- Ферромагнетики сильно втягиваются в область более сильного магнитного поля.
- Магнитная восприимчивость ферромагнетиков положительна и значительно больше единицы.
- При не слишком высоких температурах ферромагнетики обладают самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий.
Представители ферромагнетиков
Среди химических элементов
Среди химических элементов ферромагнитны переходные элементы Fe, Со и Ni (3 d-металлы) и редкоземельные металлы Gd, Tb, Dy, Er. (См. Таблицу 1)
Таблица 1. — Ферромагнитные металлы
|
|
¹ Js0 — величина намагниченности единицы объёма при абсолютном нуле температуры, называемая спонтанной намагниченностью.
² Tc — критическая температура, связанная с фазовым переходом из парамагнитного в ферромагнитное состояние, называемая точкой Кюри.
Для 3d-металлов и Gd характерна коллинеарная ферромагнитная атомная структура, а для остальных редкоземельных ферромагнетиков — неколлинеарная (спиральная и др.; см. Магнитная структура).
Среди соединений
Ферромагнитны также многочисленные металлические бинарные и более сложные (многокомпонентные) сплавы и соединения упомянутых металлов между собой и с другими неферромагнитными элементами, сплавы и соединения Cr и Mn с неферромагнитными элементами (так называемые Гейслеровы сплавы), соединения ZrZn2 и ZrxM1-xZn2 (где М — это Ti, Y, Hf), Au4V, Sc3In и др. (Таблица 2), а также некоторые соединения металлов группы актиноидов (например, UH3).
| Соединение | Tc, К | Соединение | Tc, К |
|---|---|---|---|
| Fe3AI | 743 | TbN | 43 |
| Ni3Mn | 773 | DyN | 26 |
| FePd3 | 705 | EuO | 77 |
| MnPt3 | 350 | MnB | 578 |
| CrPt3 | 580 | ZrZn2 | 35 |
| ZnCMn3 | 353 | Au4V | 42–43 |
| AlCMn3 | 275 | Sc3ln | 5–6 |
Другие известные
Особую группу ферромагнетиков образуют сильно разбавленные растворы замещения парамагнитных атомов, например Fe или Со в диамагнитной матрице Pd. В этих веществах атомные магнитные моменты распределены неупорядоченно (при наличии ферромагнитного порядка отсутствует атомный порядок). Ферромагнитный порядок обнаружен также в аморфных (метастабильных) металлических сплавах и соединениях, аморфных полупроводниках, в обычных органических и неорганических стёклах, халькогенидах (сульфидах, селенидах, теллуридах) и т. п. Число известных неметаллических ферромагнетиков пока невелико. Это, например, ионные соединения типа La1-x CaxMnO5(0,4 > x > 0,2), EuO, Eu2SiO4, EuS, EuSe, EuI2, CrB3 и т. п. У большинства из них точка Кюри лежит ниже 1 К. Только у соединений Eu, халькогенидов, CrB3 значение Q ~ 100 К.
Применение
Литература
См. также
Wikimedia Foundation. 2010.
Ферромагнитные вещества ферромагнетики — Справочник химика 21
Магнитные свойства. По отношению к магнитному полю все металлы делятся на три группы диамагнитные, парамагнитные и ферромагнитные. К диамагнитным веществам (обладающим отрицательной восприимчивостью к магнитному полю и оказывающим сопротивление силовым его линиям) относятся часть элементов I (Си, Ag, Ли), П группы (Ве, Zn, Сс1, Hg), П1 (Са, 1п, Т1) и IV группы (Се, Зп, РЬ) периодической системы. Металлы щелочных, щелочноземельных элементов, а также большинства -элементов хорошо проводят силовые линии магнитного поля, обладают положительной магнитной восприимчивостью. Они являются парамагнитными веществами и намагничиваются параллельно силовым линиям внешнего магнитного поля. Очень высокой магнитной восприимчивостью обладают Ге, Со, N1, Ос1, Ву. Они являются ферромагнетиками. Ферромагнетики характеризуются температурой, выше которой ферромагнитные свойства металла переходят в парамагнитные. Эта температура называется температурой Кюри. Для железа, кобальта и никеля эта температура составляет 768, 1075 и 362 °С, соответственно. [c.324]К числу ферромагнетиков относятся железо, никель, кобальт, редкоземельные металлы от гадолиния до тулия, их соединения, сплавы, а также сплавы хрома и марганца и др. Особенностью ферромагнитных веществ является большое значение [х, а также то, что они сохраняют намагничивание и после того, как намагничивающее поле прекратило свое действие магнитная проницаемость (X и коэффициент % для них не являются постоянными [c.288]
Магнитные свойства ферромагнитных веществ зависят и от напряженности магнитного поля, и от температуры. Повышение температуры приводит к понижению магнитной восприимчивости и при некоторой температуре, называемой температурой Кюри, она резко снижается. Выше температуры Кюри ферромагнетик ведет себя как парамагнитное вещество. Для ферромагнитных веществ постоянная А равна температуре Кюри. [c.195]
Хотя теория среднего поля не согласуется с экспериментальными данными относительно равновесных критических точек именно потому, что пренебрегает пространственными флуктуациями и поэтому была заменена теорией ренормгруппы [6.6], она нередко позволяет получить хорошее описание неравновесных критических точек, по крайней мере в детерминированных условиях. Происходит это потому, что в неравновесных фазовых переходах, например в лазере или в хорошо перемешиваемых химических системах, пространственные флуктуации в действительности не играют роли. Хотя классическая теория среднего поля предсказывает одни и те же критические показатели для всех равновесных критических точек, таких, как критическая точка жидкость — газ, ферромагнитная критическая точка и т.д., все ее понятия лучше всего проиллюстрировать на переходе от парамагнетика к ферромагнетику. Параметром порядка для такого перехода является намагниченность образца т. Хорошо известно, что намагниченность обусловлена спином электронов в неполных ат-омных оболочках. Спины пребывают на наиниз-шем энергетическом уровне, если все они параллельны (вследствие квантового явления, известного под названием обменного эффекта ). Если температура образца равна нулю, то все спины параллельны, и существует конечная намагниченность — вещество ферромагнитно. Направление вектора намагниченности т не определено в изотропном случае возможны все направления. С ростом температуры Т тепловое движение нарушает идеальную выстроенность спинов. Но при не слишком высоких температурах существует заметная доля спинов, ориентированных в одном и том же направлении. Следовательно, намагниченность [c.372]
Внесение ферромагнитного вещества в магнитное поле приводит к переориентации электронных спинов в некоторых доменах в направлении силовых линий поля, в результате чего магнитный момент вещества растет. С ростом напряженности поля процесс переориентации спинов распространяется на все большее число доменов вплоть до полного магнитного насыщения ферромагнетика. [c.303]
Последовательное рассмотрение КФД должно исходить из всех возможных типов взаимодействия между частицами ферромагнитного вещества в носителе, в пределах частицы, между частицами и атомизированной фазой ферромагнетика. [c.244]
До сих пор речь шла о диамагнитных веществах, в которых отсутствуют неспаренные электроны, и о парамагнитных веществах, где такие электроны есть, но соответствующие им магнитные моменты в отсутствие поля ориентированы беспорядочно. Однако существуют твердые тела, в которых магнитные моменты ориентированы друг относительно друга определенным образом. Это ферромагнитные и антиферромагнитные вещества. К ферромагнитным веществам относятся N1, Со, Ре, некоторые окислы железа, хрома и др. Все ферромагнитные тела разбиты на участки (домены), в каждом из которых магнитные моменты ориентированы параллельно, т. е. и в отсутствие поля каждый домен уже полностью намагничен. Однако весь ферромагнетик в отсутствие поля может быть и не намагничен, так как ориентация доменов в этом случае беспорядочна и магнитные моменты компенсируются. При наложении магнитного поля домены поворачиваются таким образом, что все магнитные моменты устанавливаются параллельно друг другу в направлении поля. Такое коллективное поведение магнитных моментов, приводящее к огромным значениям магнитной восприимчивости (в 10 раз больше, чем у парамагнетиков), характерно именно для ферромагнитных веществ. [c.280]
Аналогичный интерес представляет применение эффекта Мессбауэра к изучению суперпарамагнетизма, который наиболее ярко проявляется при изучении магнитных свойств ультрамалых частиц ферромагнитного вещества. В этом случае каждая частица является однодоменным ферромагнетиком с двумя антипараллельными осями легкого намагничивания, и из-за тепловых флуктуаций в таких частицах должно отсутствовать явление магнитного гистерезиса. [c.76]
В ферримагнитных веществах взаимодействие между атомными магнитными моментами обусловливает антипараллельную ориентацию, как в антиферромагнитных веществах, однако при этом общие моменты в двух противоположных направлениях оказываются не одинаковыми, и результирующий магнитный момент не равен нулю. Свойства ферримагнитных веществ качественно подобны свойствам ферромагнетиков для них характерна температура перехода Кюри, выше которой вещество парамагнитно, а ниже — ферромагнитно. Однако общий магнитный момент, определенный в парамагнитной области, значительно превышает момент, полученный по данным измерения насыщения в ферромагнитной области. [c.819]
Из опыта известно, что для вещества, находящегося в ферромагнитном состоянии, характерно наличие спонтанного намагничивания . Это означает, что макроскопический кристалл ферромагнетика разбивается на ряд областей (доменов), каждая из которых обладает магнитным моментом при отсутствии внешнего магнитного поля. Однако магнитные моменты этих областей в обычных условиях (без внешнего поля) ориентированы беспорядочно, поэтому общий магнитный момент макроскопического ферромагнитного кристалла равен нулю. При наложении внешнего магнитного поля, [c.152]
Однако известно, что в реальных случаях это не так. Направление магнитных моментов флуктуирует во всех магнитных веществах. В ферромагнитных и антиферромагнитных материалах флуктуации магнитного момента отдельного атома около средней величины настолько быстры, что ядра видят только среднюю величину атомного момента, и поэтому магнитное сверхтонкое взаимодействие в точности такое же, как и во внешнем постоянном магнитном поле (возможность наблюдений таких флуктуаций в ферромагнетиках была проанализирована Каганом и Афанасьевым [117]). [c.71]
Магнитные силы могут возникать в тонкодисперсных системах наряду с рассмотренными силами. Их возникновение связано с наличием в дисперсных системах ферромагнетиков. Переработка дисперсных смесей, содержащих ферромагнитные переходные металлы (Ре, Со, Ni) и редкоземельные металлы (0(1, НЬ, Ву, Но, Ег, Тт), при температурах ниже точки Кюри осушествляется в условиях, когда эффект проявления магнитных моментов в неметаллических и металлических кристаллах невелик и не оказывает существенного влияния на физические и механические свойства этих веществ. [c.233]
&

 Два бесконечных параллельных проводника в вакууме
Два бесконечных параллельных проводника в вакууме
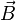 —векторная
величина, являющаяся силовой характеристикой
магнитного
поля
(его действия на заряженные частицы) в
данной точке пространства. Определяет,
с какой силой
—векторная
величина, являющаяся силовой характеристикой
магнитного
поля
(его действия на заряженные частицы) в
данной точке пространства. Определяет,
с какой силой 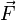 магнитное
поле действует назаряд
магнитное
поле действует назаряд 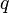 ,
движущийся со скоростью
,
движущийся со скоростью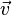 .
.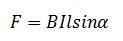
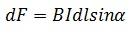
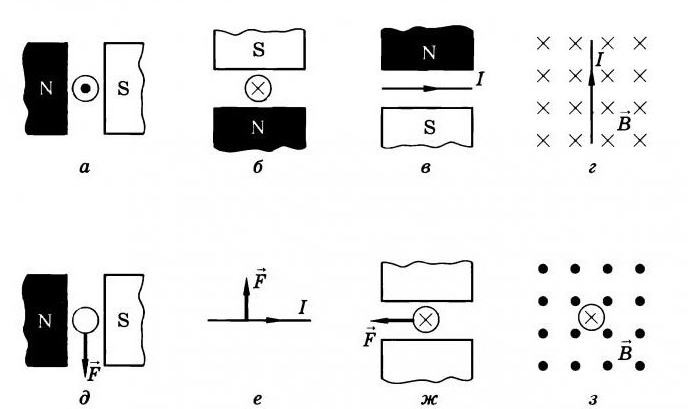
 ЗАКОН АМПЕРА Применение закона
ЗАКОН АМПЕРА Применение закона ЗАКОН АМПЕРА — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
ЗАКОН АМПЕРА — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : где α — угол между векторами магнитной индукции и тока.
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : где α — угол между векторами магнитной индукции и тока. ПРИМЕНЕНИЕ ЗАКОНА Громкоговоритель служит для возбуждения звуковых волн под действием переменного электрического тока, меняющегося со звуковой частотой. В электродинамическом громкоговорителе (динамике) используется действие магнитного поля постоянного магнита на переменный ток в подвижной катушке.
ПРИМЕНЕНИЕ ЗАКОНА Громкоговоритель служит для возбуждения звуковых волн под действием переменного электрического тока, меняющегося со звуковой частотой. В электродинамическом громкоговорителе (динамике) используется действие магнитного поля постоянного магнита на переменный ток в подвижной катушке. Схема устройства громкоговорителя показана на рисунке 1. 22, а. Звуковая катушка ЗК располагается в зазоре кольцевого магнита М. С катушкой жестко связан бумажный конус — диафрагма D. Диафрагма укреплена на упругих подвесах, позволяющих ей совершать вынужденные колебания вместе с подвижной катушкой. По катушке проходит переменный электрический ток с частотой, paвной звуковой частоте сигнала с микрофона или с выхода радиоприемника, проигрывателя, магнитофона. Под действием силы Ампера катушка колеблется вдоль оси громкоговорителя ОО 1 (см. рис. 1. 22, а) в такт с колебаниями токa. Эти колебания передаются диафрагме, и поверхность диафрагмы излучает звуковые волны. Первоклассные громкоговорители воспроизводят без значительных искажений звуковые колебания в диапазоне 40— 15 000 Гц. Но такие устройства очень сложны. Поэтому обычно применяют системы из нескольких громкоговорителей, каждый из которых воспроизводит звук в определенном небольшом интервале частот. Общим недостатком всех громкоговорителей является их малый КПД. Они излучают лишь 1 3% проводимой энергии.
Схема устройства громкоговорителя показана на рисунке 1. 22, а. Звуковая катушка ЗК располагается в зазоре кольцевого магнита М. С катушкой жестко связан бумажный конус — диафрагма D. Диафрагма укреплена на упругих подвесах, позволяющих ей совершать вынужденные колебания вместе с подвижной катушкой. По катушке проходит переменный электрический ток с частотой, paвной звуковой частоте сигнала с микрофона или с выхода радиоприемника, проигрывателя, магнитофона. Под действием силы Ампера катушка колеблется вдоль оси громкоговорителя ОО 1 (см. рис. 1. 22, а) в такт с колебаниями токa. Эти колебания передаются диафрагме, и поверхность диафрагмы излучает звуковые волны. Первоклассные громкоговорители воспроизводят без значительных искажений звуковые колебания в диапазоне 40— 15 000 Гц. Но такие устройства очень сложны. Поэтому обычно применяют системы из нескольких громкоговорителей, каждый из которых воспроизводит звук в определенном небольшом интервале частот. Общим недостатком всех громкоговорителей является их малый КПД. Они излучают лишь 1 3% проводимой энергии. Звук в радиоприемнике, проигрывателе и магнитофоне возникает в результате движения катушки с током в поле постоянного магнита. Наряду с электромеханическими громкоговорителями в настоящее время широкое применение получили громкоговорители, основаннью на пьезоэлектрическом эффекте. Этот эффект проявляется в виде деформации некоторых типов кристаллов в электростатическом поле. Две пьезопластинки склеивают. Пластинки подбирают так, что одна из них увеличивается но длине под действием поля, а другая уменьшается (см. рис. 1. 22, б). В результате получают элемент, который сильно изгибается под действием поля и при переменном электрическом поле создает акустическую волну. Пьезогромкоговорители очень удобны в изготовлении и могут быть совсем маленькими. Вследствие этого они нашли широкое применение в радиотелефонах, мобильных телефонах, ноутбуках и микрокомпьютерах. Взаимодействие токов и пьезоэлектрический эффект положены в основу принципа работы современных громкоговорителей.
Звук в радиоприемнике, проигрывателе и магнитофоне возникает в результате движения катушки с током в поле постоянного магнита. Наряду с электромеханическими громкоговорителями в настоящее время широкое применение получили громкоговорители, основаннью на пьезоэлектрическом эффекте. Этот эффект проявляется в виде деформации некоторых типов кристаллов в электростатическом поле. Две пьезопластинки склеивают. Пластинки подбирают так, что одна из них увеличивается но длине под действием поля, а другая уменьшается (см. рис. 1. 22, б). В результате получают элемент, который сильно изгибается под действием поля и при переменном электрическом поле создает акустическую волну. Пьезогромкоговорители очень удобны в изготовлении и могут быть совсем маленькими. Вследствие этого они нашли широкое применение в радиотелефонах, мобильных телефонах, ноутбуках и микрокомпьютерах. Взаимодействие токов и пьезоэлектрический эффект положены в основу принципа работы современных громкоговорителей.
 ЭЛЕКТРОДИНАМОМЕТР ВЕБЕРА Закон Ампера взаимодействия токов, или, что то же самое, магнитных полей, порождаемых этими токами, используют для устройства весьма распространенного типа электроизмерительных приборов магнитоэлектрических приборов. Они имеют легкую рамку с проволокой, укрепленную на упругом подвесе той или иной конструкции, способную поворачиваться в магнитном поле. Родоначальником всех магнитоэлектрических приборов является электродинамометр Вебера (рис. 4).
ЭЛЕКТРОДИНАМОМЕТР ВЕБЕРА Закон Ампера взаимодействия токов, или, что то же самое, магнитных полей, порождаемых этими токами, используют для устройства весьма распространенного типа электроизмерительных приборов магнитоэлектрических приборов. Они имеют легкую рамку с проволокой, укрепленную на упругом подвесе той или иной конструкции, способную поворачиваться в магнитном поле. Родоначальником всех магнитоэлектрических приборов является электродинамометр Вебера (рис. 4). Именно этот прибор позволил провести классические исследования закона Ампера. Внутри неподвижной катушки У висит на бифилярном подвесе поддерживаемая вилкой llў подвижная катушка C, ось которой перпендикулярна оси неподвижной катушки. При последовательном прохождении тока по катушкам, подвижная катушка стремится стать параллельно неподвижной и поворачивается, закручивая бифилярный подвес. Углы поворота отсчитываются при помощи прикрепленного к раме llў зеркала f.
Именно этот прибор позволил провести классические исследования закона Ампера. Внутри неподвижной катушки У висит на бифилярном подвесе поддерживаемая вилкой llў подвижная катушка C, ось которой перпендикулярна оси неподвижной катушки. При последовательном прохождении тока по катушкам, подвижная катушка стремится стать параллельно неподвижной и поворачивается, закручивая бифилярный подвес. Углы поворота отсчитываются при помощи прикрепленного к раме llў зеркала f.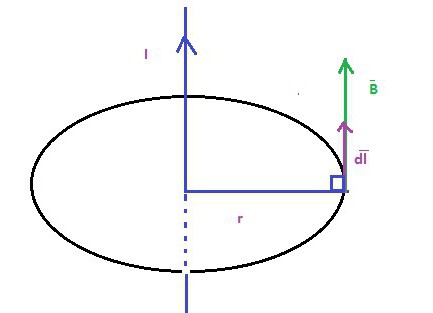
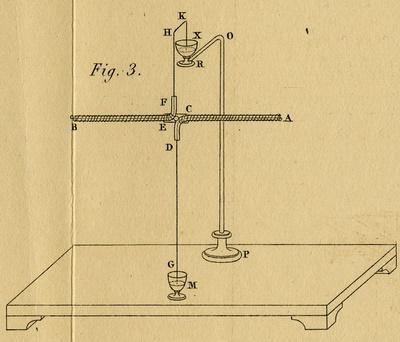

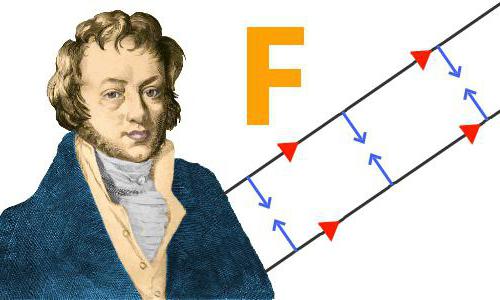
 Сила Ампера является главной составляющей закона Ампера — закона о взаимодействии электрических токов. В нём говорится, что в параллельных проводниках, в которых электрические токи текут в одном направлении, возникает сила притягивания. А в тех проводниках, в которых электрические токи текут в противоположных направлениях, возникает сила отталкивания.
Сила Ампера является главной составляющей закона Ампера — закона о взаимодействии электрических токов. В нём говорится, что в параллельных проводниках, в которых электрические токи текут в одном направлении, возникает сила притягивания. А в тех проводниках, в которых электрические токи текут в противоположных направлениях, возникает сила отталкивания.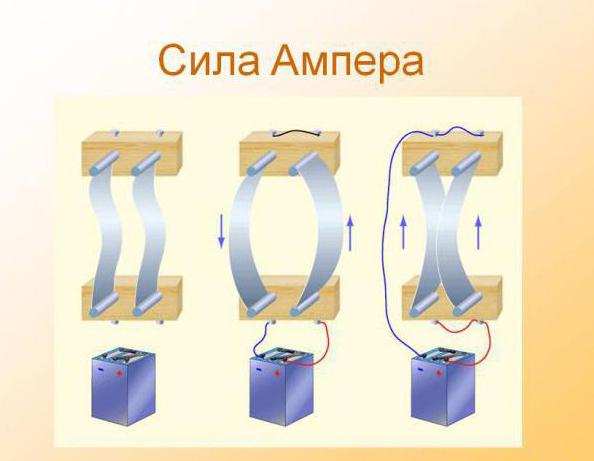 Это сила, с которой магнитное поле влияет на часть проводника, по которому течёт ток. Сам проводник находится в магнитном поле. Сила Ампера прямо зависит от силы тока в проводнике и векторного произведения длины части проводника, множимого на магнитную индукцию.
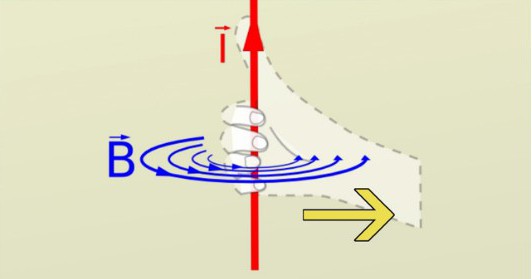
Это сила, с которой магнитное поле влияет на часть проводника, по которому течёт ток. Сам проводник находится в магнитном поле. Сила Ампера прямо зависит от силы тока в проводнике и векторного произведения длины части проводника, множимого на магнитную индукцию.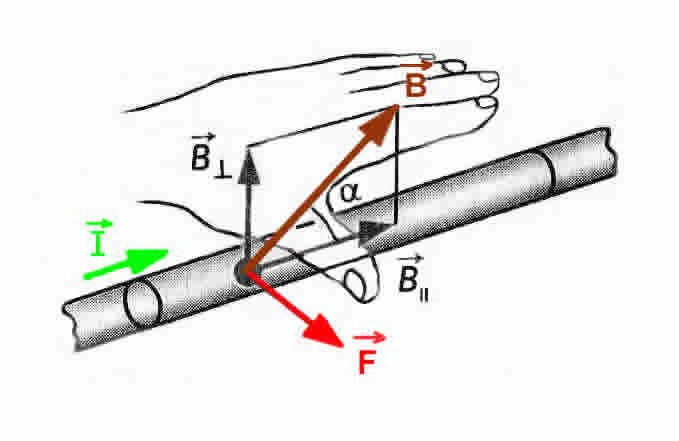 Это правило помогает запомнить направление силы Ампера. Само правило звучит так: если рука занимает такое положение, что линии самой магнитной индукции внешнего поля заходят в ладонь, а пальцы с мизинца по указательный указывают направление в сторону движения тока в проводнике, то отторгнутый по углом в 90 градусов большой палец ладони и будет указывать, куда направлена сила Ампера, действующая на элемент проводника. Могут возникнуть некоторые затруднения при использовании этого правила, но только если угол между током и индукцией поля слишком маленький. Для простоты применения этого правила ладонь часто располагают так, чтобы в неё входил не вектор, а модуль магнитной индукции (как изображено на картинке).
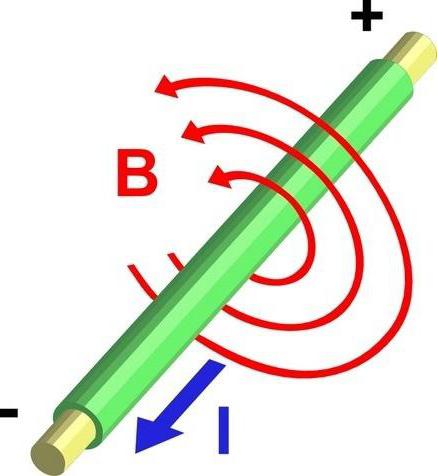
Это правило помогает запомнить направление силы Ампера. Само правило звучит так: если рука занимает такое положение, что линии самой магнитной индукции внешнего поля заходят в ладонь, а пальцы с мизинца по указательный указывают направление в сторону движения тока в проводнике, то отторгнутый по углом в 90 градусов большой палец ладони и будет указывать, куда направлена сила Ампера, действующая на элемент проводника. Могут возникнуть некоторые затруднения при использовании этого правила, но только если угол между током и индукцией поля слишком маленький. Для простоты применения этого правила ладонь часто располагают так, чтобы в неё входил не вектор, а модуль магнитной индукции (как изображено на картинке).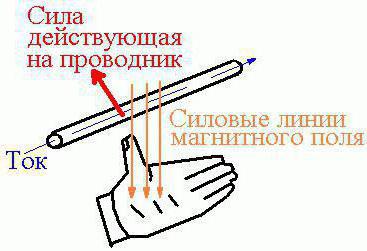 Представьте два бесконечных проводника, которые расположены на определённом расстоянии. По ним протекают токи. Если токи текут в одном направлении, то проводники притягиваются. В противоположном случае они будут отталкиваться один от одного. Поля, которые создают параллельные проводники, направлены встречно друг другу. И чтобы понять, почему они реагируют именно так, вам достаточно вспомнить о том, что одноименные полюса магнитов или одноименные заряды всегда отталкиваются. Для определения стороны направления поля, созданного проводником, следует использовать правило правого винта.
Представьте два бесконечных проводника, которые расположены на определённом расстоянии. По ним протекают токи. Если токи текут в одном направлении, то проводники притягиваются. В противоположном случае они будут отталкиваться один от одного. Поля, которые создают параллельные проводники, направлены встречно друг другу. И чтобы понять, почему они реагируют именно так, вам достаточно вспомнить о том, что одноименные полюса магнитов или одноименные заряды всегда отталкиваются. Для определения стороны направления поля, созданного проводником, следует использовать правило правого винта.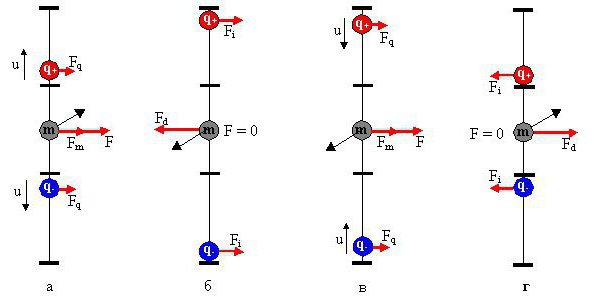 Встретиться с областью применения знания о силе Ампера можно практически на каждом шагу цивилизации. Применение силы Ампера настолько обширно, что среднестатистическому гражданину даже сложно представить себе, что можно делать, зная закон Ампера и особенности применения силы. Так, под действием силы Ампера вращается ротор, на обмотку которого оказывает влияние магнитное поле статора, и ротор приходит в движение. Любое транспортное средство, которое использует электротягу для вращения валов (которые соединяют колеса транспорта), использует силу Ампера (это можно увидеть на трамваях, электровозах, электрических машинах и многих других интересных видах транспорта). Также именно магнитное поле влияет на механизмы, которые являются электрическими приборами, что должны открывать/закрывать что-то (двери лифта, открывающиеся ворота, электрические двери и много других). Другими словами, все устройства, что не могут работать без электричества и имеют движимые узлы, работают благодаря знанию о законе Ампера. Для примера:
Встретиться с областью применения знания о силе Ампера можно практически на каждом шагу цивилизации. Применение силы Ампера настолько обширно, что среднестатистическому гражданину даже сложно представить себе, что можно делать, зная закон Ампера и особенности применения силы. Так, под действием силы Ампера вращается ротор, на обмотку которого оказывает влияние магнитное поле статора, и ротор приходит в движение. Любое транспортное средство, которое использует электротягу для вращения валов (которые соединяют колеса транспорта), использует силу Ампера (это можно увидеть на трамваях, электровозах, электрических машинах и многих других интересных видах транспорта). Также именно магнитное поле влияет на механизмы, которые являются электрическими приборами, что должны открывать/закрывать что-то (двери лифта, открывающиеся ворота, электрические двери и много других). Другими словами, все устройства, что не могут работать без электричества и имеют движимые узлы, работают благодаря знанию о законе Ампера. Для примера: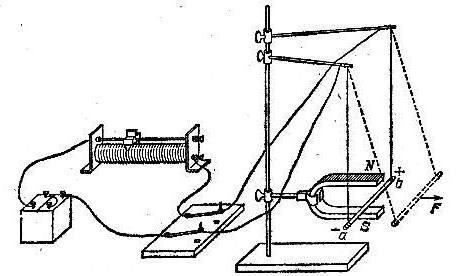 Для того чтобы иметь возможность своими глазами увидеть действие силы Ампера, можно провести дома небольшой эксперимент. Для начала необходимо взять магнит-подкову, в котором между полюсами поместить проводник. Всё желательно воспроизвести так, как на картинке. Если замкнуть ключ, то можно увидеть, что проводник начнёт двигаться, смещаясь от начальной точки равновесия. Можно поэкспериментировать с направлениями пропускания тока и увидеть, что зависимо от направления движения меняется направление отклонения проводника. Из самого эксперимента можно вынести несколько наблюдений, которые подтверждают вышесказанное:
Для того чтобы иметь возможность своими глазами увидеть действие силы Ампера, можно провести дома небольшой эксперимент. Для начала необходимо взять магнит-подкову, в котором между полюсами поместить проводник. Всё желательно воспроизвести так, как на картинке. Если замкнуть ключ, то можно увидеть, что проводник начнёт двигаться, смещаясь от начальной точки равновесия. Можно поэкспериментировать с направлениями пропускания тока и увидеть, что зависимо от направления движения меняется направление отклонения проводника. Из самого эксперимента можно вынести несколько наблюдений, которые подтверждают вышесказанное:




![[-6; 9]. [-6; 9].](/800/600/https/ege-study.ru/wp-content/uploads/2019/09/С54.jpg)
![[-5; 4]. [-5; 4].](/800/600/https/ege-study.ru/wp-content/uploads/2019/09/С54-1.jpg)
![[-4; 4] . [-4; 4] .](/800/600/https/ege-study.ru/wp-content/uploads/2019/09/Т7-7.jpg)





















 Доставка новых самоделок на почту
Доставка новых самоделок на почту













































 Большой круг делит сферу на две полусферы
Большой круг делит сферу на две полусферы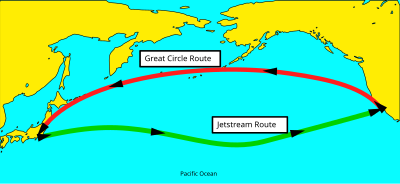
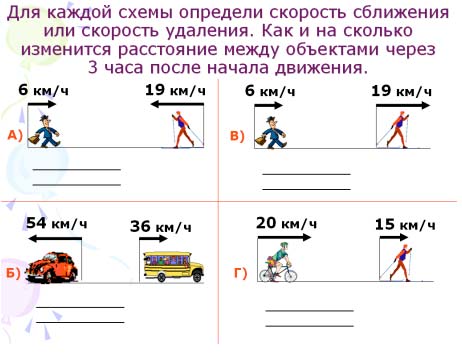


 ) Назовите фигур
) Назовите фигур
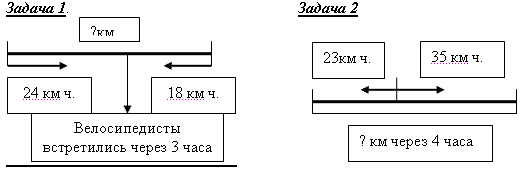
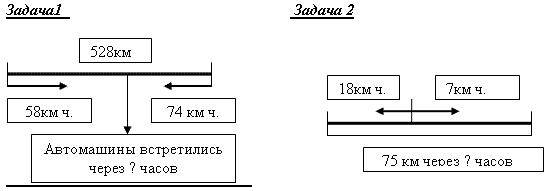
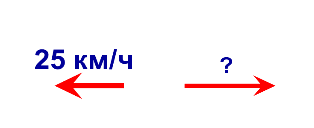 оставление задач по схеме.
оставление задач по схеме.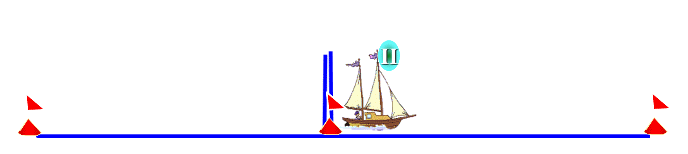













 В настоящее время особую популярность приобрели всевозможные вещи ручной работы. Мастера перестали ограничивать поток своей фантазии и выполняют свои задумки из старых вещей, бумаги и даже мусора. К подобным вещам, которые обретают вторую жизнь, можно отнести изделия из пластиковых бутылок для дома и детей. Из неприглядной пластмассы можно сделать панно, пластмассовый массажный коврик или даже игрушку для малыша.
В настоящее время особую популярность приобрели всевозможные вещи ручной работы. Мастера перестали ограничивать поток своей фантазии и выполняют свои задумки из старых вещей, бумаги и даже мусора. К подобным вещам, которые обретают вторую жизнь, можно отнести изделия из пластиковых бутылок для дома и детей. Из неприглядной пластмассы можно сделать панно, пластмассовый массажный коврик или даже игрушку для малыша. По своей сути малыши являются великими фантазёрами. Их фантазия безгранична и позволяет из совершенно неприглядного предмета создать новую поделку. Прекрасным материалом для творчества деток могут стать пластиковые пробки от бутылок. Их можно не только клеить, скручивать и раскрашивать, тем самым создавая прекрасные панно из пластиковых пробок, декоративные штучки, игрушки и фигурки для дома.
По своей сути малыши являются великими фантазёрами. Их фантазия безгранична и позволяет из совершенно неприглядного предмета создать новую поделку. Прекрасным материалом для творчества деток могут стать пластиковые пробки от бутылок. Их можно не только клеить, скручивать и раскрашивать, тем самым создавая прекрасные панно из пластиковых пробок, декоративные штучки, игрушки и фигурки для дома.

 Рука, как и нога робота, выполняется из четырёх пробок. В трёх крышках сверлятся центральные отверстия, в последней — боковое. Работа по сборке руки выполняется в той же последовательности, что и предыдущая часть тела.
Рука, как и нога робота, выполняется из четырёх пробок. В трёх крышках сверлятся центральные отверстия, в последней — боковое. Работа по сборке руки выполняется в той же последовательности, что и предыдущая часть тела. По своей сути малыши являются великими фантазёрами. Их фантазия безгранична и позволяет из совершенно неприглядного предмета создать новую поделку. Прекрасным материалом для творчества деток могут стать пластиковые пробки от бутылок. Их можно не только клеить, скручивать и раскрашивать, тем самым создавая прекрасные панно из пластиковых пробок, декоративные штучки, игрушки и фигурки для дома.
По своей сути малыши являются великими фантазёрами. Их фантазия безгранична и позволяет из совершенно неприглядного предмета создать новую поделку. Прекрасным материалом для творчества деток могут стать пластиковые пробки от бутылок. Их можно не только клеить, скручивать и раскрашивать, тем самым создавая прекрасные панно из пластиковых пробок, декоративные штучки, игрушки и фигурки для дома.

 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 53°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 53°. Ответ дайте в градусах. .
. Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке. и
и  . Найдите угол ABD. Ответ дайте в градусах.
. Найдите угол ABD. Ответ дайте в градусах. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности? Высота BH ромба ABCD делит его сторону AD на отрезки AH = 24 иHD = 2. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 24 иHD = 2. Найдите площадь ромба. На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B иC. Найдите расстояние от точки A до прямой BC.
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B иC. Найдите расстояние от точки A до прямой BC. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 4 м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5 м?
Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 4 м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5 м? Прямые m и n параллельны. Найдите ∠3, если ∠1 = 88°, ∠2 = 16°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 88°, ∠2 = 16°. Ответ дайте в градусах. Касательные в точках A и B к окружности с центром O пересекаются под углом 10°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 10°. Найдите угол ABO. Ответ дайте в градусах. . Высота ВH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
. Высота ВH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах. Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов). В остроугольном треугольнике ABC высота AH равна 13
В остроугольном треугольнике ABC высота AH равна 13 а сторона AB равна 52. Найдите cosB.
а сторона AB равна 52. Найдите cosB. На окружности с центром O отмечены точки A и B так, что ﮮАОВ = 8° . Длина меньшей дуги AB равна 37. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что ﮮАОВ = 8° . Длина меньшей дуги AB равна 37. Найдите длину большей дуги. . Найдите площадь трапеции.
. Найдите площадь трапеции.

 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах.
Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.










