Deer в множественном числе: Единственное и множественное число существительных в английском языке – Образование множественного числа существительных в английском языке
Единственное и множественное число существительных в английском языке
Всем известно, что существительные бывают единственного и множественного числа. Чтобы из одного предмета сделать несколько, нужно прибавить окончание к слову, означающему этот один предмет. Это правило действует и в русском, и в английском языках. В последнем это окончание –s.
- Table – tables (стол-столы)
- Chair – chairs (стул-стулья)
- Page – pages (страница-страницы)
Но есть вариация этого окончания — -es. Такое окончание прибавляется к тем существительным, которые заканчиваются на –o, —ch, —sh, —x, -(s)s:
- Potato – potatoes
- Inch – inches
- Crash – crashes
- Fax – faxes
- Kiss – kisses
Тем не менее, все не так просто, как кажется на первый взгляд. Дело в том, что в случае с существительными тоже есть неправильные формы. Работают они по принципу неправильных глаголов – полностью меняют свою форму во множественном числе, а не прибавляют окончание –s.
Таблица.
|
|
Единственное число |
Множественное число |
|
Мужчина |
man |
men [men] |
|
Женщина |
woman |
women [‘wimin] |
|
Ребенок |
child |
children |
|
Бык |
ox |
oxen |
|
Мышь |
mouse |
mice |
|
Ступня |
foot |
feet |
|
Зуб |
tooth |
teeth |
|
Гусь |
goose |
geese |
|
Рыба |
fish |
fish |
|
Олень |
deer |
deer |
|
Свинья |
swine |
swine |
|
Овца |
sheep |
sheep |
Не путайте sheep и ship, deer и dear. Sheep – овца, ship – корабль. Deer – олень, dear – дорогой, уважаемый.
Кажется, мы рассмотрели все варианты: и окончание –s, и –es, и «неправильные» формы множественного числа. Самое смешное то, что это и еще не всё.
Ведь существительные делятся не только на единственного и множественного числа. А еще и на исчисляемые и неисчисляемые. Исчисляемые существительные мы можем посчитать. Например, один телефон, два телефона, сорок телефонов и т.д. Неисчисляемые нельзя сосчитать. Действительно, мы даже по-русски не говорим «одна вода, две воды; один песок, три песка». Короче говоря, все, что течет, сыплется и крошится – это неисчисляемые существительные. Еще к таковым относятся абстрактные существительные, то есть любовь, дружба, количество, неопределенность и т.д. Чувства и эмоции, как вы понимаете, тоже нельзя посчитать.
Как связаны понятия числа и исчисляемости друг с другом? Все очень просто – у неисчисляемых существительных нет множественного числа. Что это значит? К ним
- нельзя прибавлять окончания множественного числа –s и –es;
- нельзя ставить артикль a, потому что он обозначает то же самое, что и one; а мы договорились, что неисчисляемые существительные не употребляются с числительными.
Также разница между исчисляемыми и неисчисляемыми состоит в употреблении с ними местоимения «много». Для исчисляемых – это many, для неисчисляемых – much. А если вы путаетесь, то запомните еще одно – a lot of. Оно употребляется со всеми существительными.
- There are many flowers in the vase. – В вазе много цветов.
- There is much water in the vase. – В вазе много воды.
- There are a lot of flowers in the vase. – В вазе много цветов.
- There is a lot of water in the vase. – В вазе много воды.
Образование множественного числа существительных в английском языке
Часть 1.
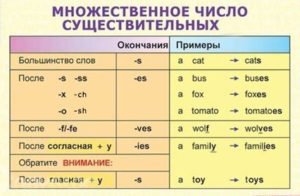
Основным способом образования множественного числа имён существительных является прибавление окончания -s или -es к форме существительного в единственном числе.
| -s | -es |
|---|---|
| a bag — bags a cat — cats a rose — roses | a glass — glasses a fox — foxes a watch — watches a bush — bushes |
Имена существительные, оканчивающиеся на -y с предшествующей согласной, образуют множественное число путём прибавления окончания -es, причём -у меняется на -i. Например, a dictionary — dictionaries.
Но: a boy — boys, a day — days (перед -у стоит гласная). Некоторые имена существительные, оканчивающиеся на -f, -fe, образуют множественное число путём изменения -f на -v и прибавлением окончания -es.
a half — halves
a wolf — wolves
a wife — wives
Но: roof — roofs, safe — safes.
Ряд существительных образуют форму множественного числа особым образом.
| ед. ч. | мн. ч. |
|---|---|
| man woman foot tooth goose mouse child sheep deer datum phenomenon | men women feet teeth geese mice children sheep deer data phenomena |
Часть 2.
«Жили у бабуси два веселых G**SE»
или Как не запутаться в превеликом множестве!
Все мы прекрасно знаем правило образования множественно числа — множественное число образуется путем добавления окончания «s» к существительному в единственном числе. Но все ли знают о том, что здесь, как и во многих других правилах, есть несколько особых случаев, которые надо запоминать? Давайте посмотрим на них и заодно проверим полноту и правильность наших знаний.
Надо помнить о том, что если наше существительное заканчивается на:
— o, — ch, — sh, -ss или — x,
множественное число образуется путем добавления окончания — es.
Example: tomato (помидор) — tomatoes, church (церковь) — churches, bush (куст) — bushes, kiss (поцелуй) — kisses, box (коробка) — boxes.
Только обратите внимание на то, что, если слово иностранного происхождения оканчивается на — o, мы добавляем просто «s»:
Example: kilo (килограмм) — kilos, photo (фотография) — photos, piano (рояль) — pianos, soprano (сопрано) — sopranos.Кроме того, если существительное оканчивается на — y и перед — y стоит согласная буква, мы «y» меняем на «i» и добавляем — es.
Example: baby (малыш, ребенок) — babies, fly (муха) — flies.12 существительных оканчивающихся на — f или — fe, при образовании множественно числа «теряют» — f или — fe, но приобретают — ves.
Вот они:- calf (теленок),
- half (половина),
- knife (нож),
- leaf (лист дерева),
- life (жизнь),
- loaf (буханка, каравай),
- self (сам, себя),
- sheaf (сноп, вязанка),
- shelf (полка),
- thief (вор),
- wife (жена),
- wolf (волк).
Так же следует запомнить ряд существительных, у которых множественное число образуется за счет изменения гласной (а в некоторых случаях, за счет добавления окончания — en / — ren). Example:
- foot (нога, ступня) — feet,
- tooth (зуб) — teeth,
- man (мужчина, человек) — men,
- woman (женщина) — women,
- mouse (мышь) — mice,
- goose (гусь) — geese,
- louse (вошь) — lice,
- child (ребенок) — children,
- ox (бык, вол) — oxen.
И последнее, что стоит запомнить — существительные deer (олень) и sheep (овца) имеют одинаковую форму, как для единственного, так и для множественно числа.
Example: sheep — sheep, deer — deer.
Тест: Множественное число существительных
Образование множественного числа существительных. Слова-исключения

Множественное число существительных английского языка ‹ Грамматика ‹ engblog.ru
Чтобы не пропустить новые полезные материалы, подпишитесь на обновления сайта
Когда мы говорим о предметах, явлениях, людях, мы используем множественное число. В статье мы разберем общие правила образования множественного числа, приведем примеры и укажем слова-исключения, которые не поддаются правилам. И еще в конце статьи вы найдете подробную таблицу, в которой мы собрали все правила, исключения и множество примеров, чтобы у вас под рукой всегда была шпаргалка по форме множественного числа. Начнем?
Основное правило образования множественного числа существительных
- Общее правило подходит большей части существительных в английском, и звучит оно так: к слову в единственном числе нужно добавить —s, и мы получим множественное число.
A spoon – spoons (ложка – ложки).
A dog – dogs (собака – собаки). - Если существительное заканчивается на —s, —ss, —sh, —ch, —tch, —z, —x, то мы добавляем —es.
A brush – brushes (щетка – щетки).
A torch – torches (факел – факелы).
A match – matches (спичка – спички). - Если существительное заканчивается на —y (и —у читается, как русская /и/), то —y исчезает, а добавляется —ies.
A country – countries (страна – страны).
A cherry – cherries (вишня – вишни). - Если существительное заканчивается на —ay, —ey, —oy (-y в конце читается как русская /й/), то мы просто добавляем —s.
A boy – boys (мальчик – мальчики).
A toy – toys (игрушка – игрушки). - Если существительное заканчивается на —о, то добавляем —es.
A tomato – tomatoes (помидор – помидоры).
A hero – heroes (герой – герои).НО!
A piano – pianos (пианино – несколько пианино)
A kilo – kilos (килограмм – килограммы)
A photo – photos (фотография – фотографии)
A video – videos (видео – несколько видео)
A flamingo – flamingos (es) (фламинго – несколько фламинго)
A volcano – volcanos (es) (вулкан – вулканы) - Если существительное заканчивается на —f или —fe, то —f меняется на —v и добавляется —es.
A loaf – loaves (буханка – буханки).
A wife – wives (жена – жёны).
Множественное число «неправильных» существительных
- Некоторые существительные не поддаются никаким правилам. К сожалению, нам не остается ничего другого, как учить наизусть форму множественного числа таких существительных.
- A man – men (мужчина – мужчины).
- A person – people (человек – люди).
- A woman – women (женщина – женщины).
- A mouse – mice (мышь – мыши).
- A foot — feet (нога – ноги).
- A child – children (ребенок – дети).
- A tooth – teeth (зуб – зубы).
- A goose – geese (гусь – гуси).
- An ox – oxen (бык – быки).
- А еще есть существительные, которые имеют одинаковые формы, как в единственном, так и во множественном числе.
- A fish – fish (рыба – рыбы).
- A fruit – fruit (фрукт – фрукты).
- A deer – deer (олень – олени).
- A sheep – sheep (овца – овцы).
- A Swiss – Swiss (швейцарец – швейцарцы).
- Многие слова, заимствованные из греческого и латинского языков, также считаются исключениями из общего правила. И их форму множественного числа тоже надо запоминать. Ниже представлено несколько слов. А более полный список мы собрали в табличке в конце статьи.
- A phenomenon – phenomena (явление – явления).
- A datum – data (информация).
- A formula – formulae (формула – формулы).
- A genius – genii (гений – гении).
Давайте теперь посмотрим, как преподаватель Rebecca с engvid объясняет эту тему на английском языке. Даже если у вас невысокий уровень английского, вы в любом случае поймете, что она рассказывает, так как она говорит медленно и использует уже знакомые нам слова.
Множественное число неисчисляемых существительных английского языка
Все существительные в английском языке можно поделить на две группы: исчисляемые и неисчисляемые. Существительные, которые мы до сих пор разбирали в данной статье, считаются исчисляемыми – они все имеют форму множественного числа. А это значит, что их можно посчитать: один мальчик (a boy) – два мальчика (two boys), один мужчина (a man) – трое мужчин (three men) и т. д.
Но также в английском есть существительные, которые употребляются только в единственном числе, у них просто нет формы множественного числа. Такие существительные называются неисчисляемыми. В русском тоже есть подобные слова: информация (информации), кофе (кофии). К неисчисляемым существительным в английском относятся следующие группы:
- Все сыпучие и жидкие вещества: water (вода), cream (крем), rice (рис).
- Абстрактные понятия: success (успех), happiness (счастье), love (любовь).
- Слова information (информация), advice (совет), money (деньги), news (новости), furniture (мебель).
- Подробный список исчисляемых и неисчисляемых существительных вы найдете в этой статье.
Что же делать, если нам надо посчитать количество этих неисчисляемых существительных? В таком случае мы считаем не сами предметы и явления, а то, чем они измеряются. Например, мы не можем сказать «два сахаров», но мы можем сказать «два килограмма сахара», «две ложки сахара», «два пакетика сахара» – во всех этих случаях мы считаем сахар с помощью единиц измерения сыпучих веществ. Кстати, обратите внимание, что и в русском языке во всех примерах слово «сахар» стоит в единственном числе. У каждого из неисчисляемых существительных свои единицы измерения:
- A bottle of milk – two bottles of milk (бутылка молока – две бутылки молока).
- A kilo of rice – three kilos of rice (килограмм риса – три килограмма риса).
- A glass of juice – ten glasses of juice (стакан сока – десять стаканов сока).
- Словам, с помощью которых мы измеряем неисчисляемые существительные, мы посвятили отдельную статью «Partitive Expressions».
Без правил образования множественного числа невозможно грамотно разговаривать по-английски, ведь эта тема тесно связана с употреблением глаголов, артиклей и других частей речи. Поэтому так важно хорошо разобраться во всех правилах. Не забудьте скачать таблицу, по которой вы всегда сможете сориентироваться и выбрать правильный вариант множественного числа.
↓ Скачать таблицу «Образование множественного числа в английском языке». (*.pdf, 208 Кб)
И еще пройдите тест, чтобы лучше запомнить правила.
ТестМножественное число существительных в английском
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Окончание множественного числа английский — Секреты английскогоСекреты английского языка
Окончание множественного числа английский
 Давайте рассмотрим как меняется окончание у существительных во множественном числе в английском языке. Множественное число — это когда предметов больше чем один. Например, два, три, десять, сто и так далее.
Давайте рассмотрим как меняется окончание у существительных во множественном числе в английском языке. Множественное число — это когда предметов больше чем один. Например, два, три, десять, сто и так далее.
сущ., оканчивающиеся на согласн. звук или гласную e | +s | dog – dogs name – names |
сущ., оканчивающиеся на ss, x, sh, ch, o | + es | kiss – kisses box – boxes brush – brushes church – churches tomato – tomatoes |
сущ., оканчивающиеся на букву y с предшествующей согласной буквой | y → i + es | baby – babies fly — flies Искл. boy-boys, toy — toys |
Исключения
(особые формы образования множественного числа)
Окончание множественного числа английский
| существительные, имеющие одинаковую форму в единственном и множественном числе | deer – deer sheep – sheep swine – swine |
| существительные, оканчивающиеся на f и fe, меняют их во множественном числе на ves | wolf – wolves wife – wives knife – knives |
| существительные, которые во множественном числе меняют гласную в корне без добавления окончания | man – men woman – women tooth – teeth goose – geese foot – feet mouse – mice |
| существительные, имеющие форму только множественного числа | trousers, glasses, clothes, spectacles, scissors, goods |
| существительные, имеющие форму только единственного числа | sugar, milk, money, weather, peace, hair |
| существительные child и ox меняют ед. число на множеств. число путем прибавления нового окончания | child – children ox – oxen |
 Попробуйте образовать множественное число следующих существительных:
Попробуйте образовать множественное число следующих существительных:
a man , a tooth, a mouse, a goose, a sheep, a child, a foot, a woman, a garden, a flower
Должно получиться: men, teeth,mice, geese, sheep, children, feet, women,gardens, flowers.
Другие примеры: a glass — glasses — стакан — стаканы; a fly — flies — муха- мухи, a tomato- tomatoes -помидор — помидоры; a game — games — игра — игры; a river — rivers — река — реки; lady — ladies — дама — дамы;
Окончание множественного числа английский
Чтение окончаний:
Окончания существительных во множественном числе произносятся так:
[s] — если слова оканчиваются звуками [f] [k] [p] [t] [Ɵ] — cliffs, books, shops, cats, myths, months
[ɪz] — если слова оканчиваются звуками [s] [ks] [ʃ] [tʃ] [dʒ] [z] [ʒ] — buses, foxes, brushes, torches, bridges, roses, mirages
[z] — если они заканчиваются на другие звуки — rooms. boys, leaves, lemons, pianos
Чтобы определить, на какой звук заканчивается слово — прочитайте его или посмотрите транскрипцию.
Вконтакте
Одноклассники
Мой мир
Исключения множественного числа в английском (Irregular Plural Nouns)
Большинство исчисляемых существительных образуют множественное число прибавлением окончания -s или -es. Но ограниченное число существительных имеют неправильные формы множественного числа.
Множество английских слов были заимствованы из латинского и греческого языков. Некоторые их них сохранили свои латинские или греческие окончания в единственной (-is, —us, —on, —um, —a, —x) и в множественной форме (antenna → antennae). Однако эти слова также могут иметь английское окончание -s или -es, которое чаще используется в обычной устной речи, а также письме, они считаются более употребительными.
Латинские и греческие окончания множественной формы чаще встречаются в научных и академических трудах и существительные с ними могут отличаться по значению от тех же существительных с английским окончанием. Также есть неправильные формы множественного числа у некоторых названий животных, частей тела, слов для обозначения людей и т.д.
| man → men мужчина → мужчины | woman → women женщина → женщины | child → children ребенок → дети |
| mouse → mice мышь → мыши | louse → lice вошь → вши | ox → oxen бык → быки, рогатый скот |
| foot → feet ступня → ступни | tooth → teeth зуб → зубы | goose → geese гусь → гуси |
| an aircraft → two aircraft воздушное судно → два воздушных судна | an alms → alms подаяние → подаяния |
| a barracks → barracks казарма, барак → казармы, бараки | a bison → five bison бизон → пять бизонов |
| a corps → corps корпус, организация → корпусы, организации | a crossroads → crossroads перекрёсток, пересечение дорог → перекрёстки |
| a deer → two deer один олень → два оленя | a dozen → two dozen дюжина → две дюжины |
| a fish → two fish рыба → две рыбы | a gallows → gallows виселица → виселицы |
| a headquarters → headquarters штаб → штабы | a means → means средство → средства |
| a moose → three moose лось → три лося | an offspring → several offspring отпрыск, продукт → несколько отпрысков, продуктов |
| a series → two series серия, сериал → две серии | one sheep → two sheep одна овца → две овцы |
| a species → different species вид, род → разные виды | a swine → several swine свинья → несколько свиней |
| analysis → analyses анализ → анализы | axis → axes ось → оси |
| basis → bases базис, основа → основы | crisis → crises кризис → кризисы |
| diagnosis → diagnoses диагноз → диагнозы | ellipsis → ellipses эллипсис, многоточие → многоточия |
| emphasis → emphases акцент, эмфаза, подчёркивание, ударение | genesis → geneses происхождение, генезис |
| hypothesis → hypothesies гипотеза → гипотезы | oasis → oases оазис → оазисы |
| paralysis → paralyses паралич → параличи | parenthesis → parentheses вводное слово, отступление → вводные слова, отступления |
| synopsis → synopses синопсис, краткий обзор → краткие обзоры | synthesis → syntheses синтез → синтезы |
| thesis → theses тезис, диссертация → тезисы, диссертации | |
| abacus → abacuses, abaci счёты (как один предмет) → счёты (мн.ч.) | alumnus → alumni выпускник, бывший студент → выпускники |
| apparatus → apparatus, apparatuses аппарат → аппараты | cactus → cactuses, cacti кактус → кактусы |
| calculus → calculi,calculuses исчисление → исчисления | corpus → corpora корпус, свод, тело → корпусы |
| eucalyptus → eucalyptuses,eucalypti эвкалипт → эвкалипты | focus → focuses, foci фокус → фокусы |
| fungus → fungi, funguses грибок, плесень → грибки | genus → genera, genuses род, вид, сорт → виды, сорта |
| hippopotamus → hippopotamuses, hippopotami гиппопотам → гиппопотамы | nucleus → nuclei, nucleuses ядро → ядра |
| octopus → octopuses, octopi осьминог → осьминоги | papyrus → papyri,papyruses папирус → папирусы |
| platypus → platypuses, platypi утконос → утконосы | radius → radii, radiuses радиус → радиусы |
| rhombus → rhombuses, rhombi ромб → ромбы | stimulus → stimuli стимул → стимулы |
| stylus → styluses, styli (техн) игла, перо, щуп → иглы, щупы | syllabus → syllabuses, syllabi учебный план → учебные планы |
| terminus → termini, terminuses конец, конечный пункт → конечные пункты | |
| automaton → automatons, automata автомат, робот → автоматы, роботы | criterion → criteria критерий → критерии |
| phenomenon → phenomena феномен → феномены | polyhedron → polyhedrons, polyhedra многогранник → многогранники |
| octahedron → octahedrons, octahedra октаэдр, восьмигранник → октаэдры | tetrahedron → tetrahedrons, tetrahedra тетраэдр, четырёхгранник → тетраэдры |
| addendum → addenda приложение → приложения | aquarium → aquariums, aquaria аквариум → аквариумы |
| arboretum → arboretums, arboreta дендрарий → дендрарии | atrium → atria, atriums атрий, атриум → атриумы |
| bacterium → bacteria бактерия → бактерии | compendium → compendiums, compendia компендиум → компендиумы |
| curriculum → curriculums, curricula программа (обучения) → программы | datum → data данное → данные |
| emporium → emporiums, emporia торговый центр → торговые центры | equilibrium → equilibriums, equilibria равновесие, уравновешенность |
| erratum → errata опечатка → опечатки | forum → forums, fora форум → форумы |
| maximum → maximums, maxima максимум → максимумы | medium → media способ, средство (связи) → медиа |
| medium → mediums медиум → медиумы | memorandum → memorandums, memoranda меморандум → меморандумы |
| millennium → millenniums, millennia тысячелетие → тысячелетия | planetarium → planetariums, planetaria планетарий → планетарии |
| podium → podiums, podia подиум → подиумы | spectrum → spectra, spectrums спектр → спектры |
| stadium → stadiums, stadia стадион → стадионы | sternum → sterna, sternums грудина → грудины |
| stratum → strata, stratums слой, пласт → слои, пласты | symposium → symposiums, symposia симпозиум → симпозиумы |
| terrarium → terrariums, terraria террарий, террариум → террарии, террариумы | vacuum → vacuums, vacua вакуум → вакуумы |
| vivarium → vivariums, vivaria виварий → виварии | |
| alumna → alumnae выпускница → выпускницы | antenna → radio antennas антенна → радио антенны |
| antenna → insects’ antennae усик → усики насекомых | charisma → charismata харизма |
| dogma → dogmas, dogmata догма → догмы | enigma → enigmas, enigmata загадка, необъяснимое явление → загадки |
| formula → formulas, formulae формула → формулы | stigma → stigmata, stigmas клеймо, пятно → стигмы, стигматы, пятна |
| vertebra → vertebrae, vertebras позвонок → позвонки | |
| apex → apexes, apices высшая точка, вершина → вершины | appendix → appendixes, appendices приложение → приложения |
| index → indexes, indices индекс → индексы | matrix → matrices, matrixes матрица, форма → матрицы, формы |
| vertex → vertexes, vertices вершина, макушка → вершины | vortex → vortexes, vortices водоворот, вихрь → водовороты |
| man → men мужчина → мужчины |
| woman → women женщина → женщины |
| child → children ребенок → дети |
| mouse → mice мышь → мыши |
| louse → lice вошь → вши |
| ox → oxen бык → быки, рогатый скот |
| foot → feet ступня → ступни |
| tooth → teeth зуб → зубы |
| goose → geese гусь → гуси |
| an aircraft → two aircraft воздушное судно → два воздушных судна |
| an alms → alms подаяние → подаяния |
| a barracks → barracks казарма, барак → казармы, бараки |
| a bison → five bison бизон → пять бизонов |
| a corps → corps корпус, организация → корпусы, организации |
| a crossroads → crossroads перекрёсток, пересечение дорог → перекрёстки |
| a deer → two deer один олень → два оленя |
| a dozen → two dozen дюжина → две дюжины |
| a fish → two fish рыба → две рыбы |
| a gallows → gallows виселица → виселицы |
| a headquarters → headquarters штаб → штабы |
| a means → means средство → средства |
| a moose → three moose лось → три лося |
| an offspring → several offspring отпрыск, продукт → несколько отпрысков, продуктов |
| a series → two series серия, сериал → две серии |
| one sheep → two sheep одна овца → две овцы |
| a species → different species вид, род → разные виды |
| a swine → several swine свинья → несколько свиней |
| analysis → analyses анализ → анализы |
| axis → axes ось → оси |
| basis → bases базис, основа → основы |
| crisis → crises кризис → кризисы |
| diagnosis → diagnoses диагноз → диагнозы |
| ellipsis → ellipses эллипсис, многоточие → многоточия |
| emphasis → emphases эмфаза, подчёркивание, выделение |
| genesis → geneses происхождение, генезис |
| hypothesis → hypothesies гипотеза → гипотезы |
| oasis → oases оазис → оазисы |
| paralysis → paralyses паралич → параличи |
| parenthesis → parentheses вводное слово, отступление → вводные слова, отступления |
| synopsis → synopses синопсис, краткий обзор → краткие обзоры |
| synthesis → syntheses синтез → синтезы |
| thesis → theses тезис, диссертация → тезисы, диссертации |
| abacus → abacuses, abaci счёты (как один предмет) → счёты (мн.ч.) |
| alumnus → alumni выпускник, бывший студент → выпускники |
| apparatus → apparatus, apparatuses аппарат → аппараты |
| cactus → cactuses, cacti кактус → кактусы |
| calculus → calculi,calculuses исчисление → исчисления |
| corpus → corpora корпус, свод, тело → корпусы |
| eucalyptus → eucalyptuses, eucalypti эвкалипт → эвкалипты |
| focus → focuses, foci фокус → фокусы |
| fungus → fungi, funguses грибок, плесень → грибки |
| genus → genera, genuses род, вид, сорт → виды, сорта |
| hippopotamus → hippopotamuses, hippopotami гиппопотам → гиппопотамы |
| nucleus → nuclei, nucleuses ядро → ядра |
| octopus → octopuses, octopi осьминог → осьминоги |
| papyrus → papyri, papyruses папирус → папирусы |
| platypus → platypuses, platypi утконос → утконосы |
| radius → radii, radiuses радиус → радиусы |
| rhombus → rhombuses, rhombi ромб → ромбы |
| stimulus → stimuli стимул → стимулы |
| stylus → styluses, styli (техн) игла, перо, щуп → иглы, щупы |
| syllabus → syllabuses, syllabi учебный план → учебные планы |
| terminus → termini, terminuses конец, конечный пункт → конечные пункты |
| automaton → automatons, automata автомат, робот → автоматы, роботы |
| criterion → criteria критерий → критерии |
| phenomenon → phenomena феномен → феномены |
| polyhedron → polyhedrons, polyhedra многогранник → многогранники |
| octahedron → octahedrons, octahedra октаэдр, восьмигранник → октаэдры |
| tetrahedron → tetrahedrons, tetrahedra тетраэдр, четырёхгранник → тетраэдры |
| addendum → addenda приложение → приложения |
| aquarium → aquariums, aquaria аквариум → аквариумы |
| arboretum → arboretums, arboreta дендрарий → дендрарии |
| atrium → atria, atriums атрий, атриум → атриумы |
| bacterium → bacteria бактерия → бактерии |
| compendium → compendiums, compendia компендиум → компендиумы |
| curriculum → curriculums, curricula программа (обучения) → программы |
| datum → data данное → данные |
| emporium → emporiums, emporia торговый центр → торговые центры |
| equilibrium → equilibriums, equilibria равновесие, уравновешенность |
| erratum → errata опечатка → опечатки |
| forum → forums, fora форум → форумы |
| maximum → maximums, maxima максимум → максимумы |
| medium → media способ, средство (связи) → медиа |
| medium → mediums медиум → медиумы |
| memorandum → memorandums, memoranda меморандум → меморандумы |
| millennium → millenniums, millennia тысячелетие → тысячелетия |
| planetarium → planetariums, planetaria планетарий → планетарии |
| podium → podiums, podia подиум → подиумы |
| spectrum → spectra, spectrums спектр → спектры |
| stadium → stadiums, stadia стадион → стадионы |
| sternum → sterna, sternums грудина → грудины |
| stratum → strata, stratums слой, пласт → слои, пласты |
| symposium → symposiums, symposia симпозиум → симпозиумы |
| terrarium → terrariums, terraria террарий, террариум → террарии, террариумы |
| vacuum → vacuums, vacua вакуум → вакуумы |
| vivarium → vivariums, vivaria виварий → виварии |
| alumna → alumnae выпускница → выпускницы |
| antenna → radio antennas антенна → радио антенны |
| antenna → insects’ antennae усик → усики насекомых |
| charisma → charismata харизма |
| dogma → dogmas, dogmata догма → догмы |
| enigma → enigmas, enigmata загадка, необъяснимое явление → загадки |
| formula → formulas, formulae формула → формулы |
| stigma → stigmata, stigmas клеймо, пятно → стигмы, стигматы, пятна |
| vertebra → vertebrae, vertebras позвонок → позвонки |
| apex → apexes, apices высшая точка, вершина → вершины |
| appendix → appendixes, appendices приложение → приложения |
| index → indexes, indices индекс → индексы |
| matrix → matrices, matrixes матрица, форма → матрицы, формы |
| vertex → vertexes, vertices вершина, макушка → вершины |
| vortex → vortexes, vortices водоворот, вихрь → водовороты |
История неправильных форм существительных в английском языке
Чтобы не пропустить новые полезные материалы, подпишитесь на обновления сайта
Вы когда-нибудь задумывались, почему английский язык стал таким популярным во всём мире? Конечно, существует множество различных теорий по этому поводу: и историко-географические, и социально-культурные, и другие. Но всё же каждый, кто пробовал учить, помимо английского, другие языки, ответит однозначно: «Он популярный, потому что учить его сравнительно легко». Ну, к примеру, выучил ты слово «стол» – table – и всё! Никаких тебе «столом», «столе», «столу», а потом еще «столы», «столами», «столов» и прочих сложностей, связанных с падежами, числами, а если ещё вспомнить про склонения… Действительно, если изучение глаголов в английском языке иногда вызывает уныние (мало того что куча неправильных, так ещё и с временами не все понятно :-)), то существительные в английском языке радуют. Отсутствие родов, падежных окончаний и склонений существительных значительно упрощает их изучение и применение в речи. Но так было не всегда…
Давайте обратимся к истории и посмотрим, какой путь прошли английские существительные, прежде чем предстать перед нами. Этот экскурс в историю поможет нам увидеть, откуда произошли неправильные формы существительных в современном английском языке и каковы их корни.
Если мы посмотрим на староанглийский язык, то он особо ничем не отличается от других языков своей группы. В нём были обычные падежи: правда, не 6, как в русском языке, а 4, как в современном немецком языке. И в разных падежах существительные имели различные окончания. Более того, существовало 3 различных склонения существительных, которые, соответственно, склонялись по падежам тремя различными способами. Ну как при этом не радоваться, что мы учим современный английский язык, а не его древний вариант! Итак, посмотрим на три склонения существительных, характерных для древнеанглийского языка и на их падежные окончания.
Первое склонение называлось гласным, а ещё его часто называли сильным, потому что падежные окончания этого склонения отличались друг от друга больше, чем в остальных двух. К нему относились существительные мужского и среднего рода. Рассмотрим слово stan (совр. англ. stone – камень).
Таблица 1. Гласное, сильное склонение
| Падежи | Единственное | Множественное |
|---|---|---|
| Именительный (Nominative) | Stan | Stanas |
| Родительный (Genitive) | Stanes | Stana |
| Дательный (Dative) | Stane | Stanum |
| Винительный (Accusative) | Stan | Stanas |
Второе склонение называлось согласным, и падежные окончания в нём зачастую совпадали, теряя свою различительную силу. Поэтому его называли слабым. Пример – слово nama (совр. англ. name – имя).
Таблица 2. Согласное, слабое склонение
| Падежи | Единственное | Множественное |
|---|---|---|
| Именительный (Nominative) | Nama | Naman |
| Родительный (Genitive) | Naman | Namena |
| Дательный (Dative) | Naman | Namum |
| Винительный (Accusative) | Naman | Naman |
Третье склонение называлось корневым, так как у существительных, принадлежавших к этой группе, в некоторых падежах менялся корневой гласный. Слов таких было немного, но употреблялись в речи они достаточно часто. Пример существительного, принадлежавшего к этой группе, – mann (совр.англ. man – мужчина, человек).
Таблица 3. Корневое склонение
| Падежи | Единственное | Множественное |
|---|---|---|
| Именительный (Nominative) | Mann | Menn |
| Родительный (Genitive) | Mannes | Manna |
| Дательный (Dative) | Menn | Mannum |
| Винительный (Accusative) | Mann | Menn |
При внимательном рассмотрении несложно заметить, что падежные окончания в староанглийских склонениях не очень сильно отличались друг от друга и зачастую совпадали. Окончания, которые совпадают, теряют свою силу показывать различия падежей, поэтому неудивительно, что со временем их просто перестали употреблять. Сильное склонение было превалирующим, потому что количество слов, принадлежащих к нему, значительно превышало все остальные, к тому же они чаще других встречались в речи. Как это обычно происходит в жизни, побеждает сильнейший. Именно поэтому форма множественного числа именительного падежа из гласного склонения (см. Таблицу 1) была взята за правило формирования множественного числа и используется с большинством существительных и сегодня.
Но всё-таки исчезнувшие склонения оставили свой след в языке и немного усложнили жизнь тем, кто изучает английский язык. Такие формы как child – children (ребёнок – дети), ox – oxen (бык – быки), а также форма brethren (собратья), принадлежавшие к согласному склонению, сохранили свою старую форму для множественного числа. Исключения, возникшие в результате корневого склонения, более многочисленны.
Таблица 4. Современные исключения из правила из-за корневого склонения
| Единственное число | Множественное число | Перевод |
|---|---|---|
| Man | Men | Мужчина – мужчины |
| Woman | Women | Женщина – женщины |
| Goose | Geese | Гусь – гуси |
| Tooth | Teeth | Зуб – зубы |
| Foot | Feet | Нога (ступня) – ноги |
| Mouse | Mice | Мышь – мыши |
| Louse | Lice | Вошь – вши |
Интересно, что при переносе значения слова на более современные предметы, «старинная» форма множественного числа не сохраняется. Так, например, исследования показывают, что большинство носителей языка, говоря о компьютерной мышке (computer mouse), во множественном числе используют форму mouses, а не mice. То есть, если слово современное, то и грамматику к нему нужно применять современную, а не историческую.
Ещё одна группа слов, не отвечающая правилам формирования множественного числа, — это те слова, в которых единственное и множественное число совпадают. Это, как известно, представители животного мира: a sheep – sheep (овца – овцы), a deer – deer (олень – олени), a swine – swine (свинья – свиньи), a fish – fish (рыба – рыбы). В этом случае объяснение имеет вполне жизненные основания. По словам ученых, форма не изменилась во множественном числе, потому что эти животные живут стадами, а стадо можно считать единым целым. Что же касается рыб, то многие виды передвигаются в воде, собираясь в косяки, то есть их тоже можно считать одним целым. Конечно, это не объясняет, почему другие виды животных, собирающихся в группы, не подверглись тому же принципу. Но если взглянуть на исторический контекст, охота на диких кабанов и оленей была самой популярной на Британских островах в то время, а овцы – основными стратегически важными животными. Вероятно, именно частота употребления этих слов во множественном числе и вызвала такие изменения.
Конечно, «неправильность» существительных не заканчивается на этих исключениях, существует также большая группа латинских и греческих заимствований, которые сохранили свою множественную форму из языка-оригинала. Большинство из них относится к академической сфере и представляет собой различные термины. Примеры таких слов с объяснениями можно посмотреть в следующем видео.
А если у кого-то есть желание узнать обо всех неправильных формах существительных и систематизировать знания в этом вопросе, видеокурс от Crown Academy English будет очень полезен для этой цели.
Как видите, даже у неправильных форм множественного числа есть вполне логичное объяснение. В истории языка очень интересно покопаться, так многие явления становятся более понятными для запоминания. Также предлагаю пройти тест на множественное число существительных, проверьте свои знания!
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
все правила и исключения —
Поговорим о том, как образуется множественное число в английском языке. Тема довольно простая, но в то же время нудная, т.к. здесь полно правил и исключений. Попробуем разобраться с наименьшими потерями.
Начнем с напоминания о том, что множественное число имеют только исчисляемые существительные, то есть те, которые можно посчитать: a computer (компьютер), a plate (тарелка), a dress (платье), и так далее. Неисчисляемые существительные множественного числа не имеют, их нельзя посчитать: paper (бумага), time (время), information (информация), и так далее. По умолчанию к ним применяются все правила для единственного числа. Подробнее с этой темой можно ознакомиться здесь: существительные и их свойства.
Способы образования множественного числа английских существительных
- В общем случае множественное число образуется путем добавления окончания –s к существительному в форме единственного числа: book – books (книга — книги), bird – birds (птица – птицы), student – students (студент – студенты).
- Если существительное уже оканчивается на –s, –ss, ch, -sh, -x, —o, тогда добавляется окончание –es: bus-buses (автобус – автобусы), dress-dresses (платье – платья), wish – wishes (желание – желания). Это логично, так как все слова, оканчивающиеся на шипящий звук было бы неудобно произносить, добавляя только букву –s. Попробуйте сказать слово лиса, добавив просто –s в конец:
foxs– шипящие звуки просто смешаются друг с другом. Поэтому: fox – foxes (лиса – лисы). - Исключения здесь составляют некоторые существительные на –o, к которым просто добавляется –s как и в общем случае: photo- photos (фотография-фотографии), kilo-kilos (килограмм- килограмы) и некоторые другие. Подавляющее большинство слов в английском относится именно к этим двум категориям – их нужно железно запомнить. Далее еще несколько нюансов.
- Существительные, оканчивающиеся на -y с предшествующей согласной. Здесь y заменяется на -i и добавляется окончание -es : city – cities (город – города), lady – ladies (дама – дамы). Если перед -y идет гласная, то множественное число образуется по общему правилу просто добавлением -s: day – days, monkey – monkeys (обезьяна – обезьяны).
- Существительные, оканчивающиеся на –f. У них буква -f меняется на -v + добавляется окончание –es: wolf – wolves (волк – волки), leaf – leaves (лист – листья).
- Существительные, оканчивающиеся на –fe. У них —fe меняется на -ve + добавляется окончание —s: wife – жена; wives – жены, knife – knives (нож – ножи).
Существительные, множественное число которых образуется не по правилу
Теперь поговорим про те самые остальные нудные правила и исключения, без которых в этой теме, увы, никак. К счастью, их не так уж много, поэтому проще сразу же выучить:
|
man – мужчина |
men – мужчины |
|
woman – женщина |
women – женщины |
|
foot – нога |
feet – ноги |
|
tooth – зуб |
teeth – зубы |
|
goose – гусь |
geese – гуси |
|
mouse – мышь |
mice – мыши |
|
ox – бык |
oxen – быки |
|
child – ребенок |
children – дети |
Особое внимание здесь следует обратить на часто употребляемые нами в речи слова man-men (мужчина-мужчины) и woman-women (женщина-женщины). На первый взгляд они очень похожи, и многие путают их, но следует помнить, что одна буква или звук могут кардинально изменить смысл высказывания.
Существительные, употребляющиеся только во множественном числе
Как и в русском, в английском языке есть такие слова, которые могут быть только множественного числа. Их тоже хорошо бы знать, но их довольно много, поэтому обратите внимание на самые распространенные. Здесь много парных предметов, например: scissors – ножницы, scales – весы, и так далее:
- goods – товар, товары
- clothes – одежда
- stairs – лестница
- glasses −очки
- jeans — джинсы
- pajamas, pyjamas — пижама
- shorts − шорты, трусы
- tights − трико
- tongs– щипцы
- trousers– брюки
- proceeds − доход
- thanks – благодарность
- wages – заработок
- и другие..
Эти существительные стоят всегда во множественном числе, соответственно они требуют сказуемого во множественном числе:
My jeans don’t suit me at all – Мои джинсы совсем мне не подходят.
Если нужно сказать в единственном числе об этих вещах, то надо употреблять выражения типа a pair of jeans – одна пара джинс.
Существительные, у которых форма в единственном и во множественном числе совпадает:
Это еще одна, последняя группа существительных, которые желательно знать. У них одна форма слова как для множественного, так и для единственного числа. Здесь произношение и написание никак не меняются в зависимости от числа:
- craft (корабль – корабли)
- species (вид – виды)
- headquarters (главное управление − центральные органы)
- crossroads (пересечение дорог − перекрестки)
- deer (олень – олени)
- sheep (овца − овцы)
- fish (рыба − рыбы)
- fruit (фрукт − фрукты)
- means (средство − средства)
- salmon (лосось − лососи)
- series (серия − серии)
- swine (свинья – свиньи)
- и другие..
Вот мы и разобрались с темой множественное число в английском. Теперь вас ждет упражнение на закрепление. Обязательно проверьте себя по ответам ниже.
Упражнение на множественное число английских существительных
Образуйте множественное число и проверьте себя по ответам ниже:
- ребенок — child, дети — ?
- way – путь, пути — ?
- ножницы — ?
- shelf полка, полки -?
- гитара — guitar, гитары — ?
- пижама — ?
- orange – апельсин, апельсины — ?
- leaf — лист дерева, листья -?
- life — жизнь, жизни -?
- dog –собака, собаки -?
- skyscraper – небоскреб, небоскребы ?
- foot – нога, ноги?
- рыба – рыбы?
Ответы:
- children
- ways
- scissors
- shelves
- gitars
- pajamas
- oranges
- leaves
- lives
- dogs
- skyscrapers
- feet
- fish
Другие статьи по теме:
Существительные и их свойства
Падежи существительных
Определенный артикль the
Личные местоимения в английском языке
Прилагательные и их виды
Следующий урок >>>




















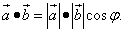 (1)
(1)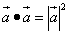 называется скалярным квадратом.
называется скалярным квадратом.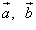 .
Найти скалярное произведение векторов
.
Найти скалярное произведение векторов
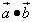 , если их длины и угол между ними представлены
следующими значениями:
, если их длины и угол между ними представлены
следующими значениями: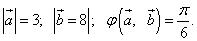
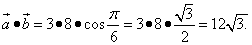
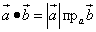 (2)
(2)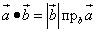 (3)
(3)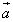 и
и 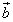 на плоскости определены своими двумя декартовыми прямоугольными координатами
на плоскости определены своими двумя декартовыми прямоугольными координатами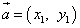
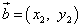 ,
,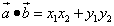 .
.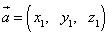
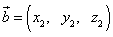 ,
,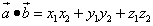 .
.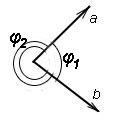
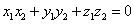 .
.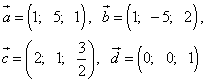 .
.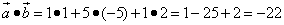 .
.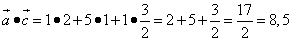 .
.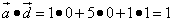 .
.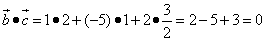 .
.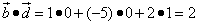 .
.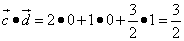 .
.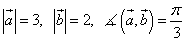 .
.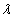 векторы
векторы 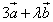 и
и 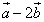 ортогональны (перпендикулярны).
ортогональны (перпендикулярны).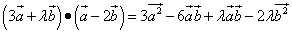 .
.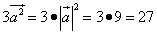
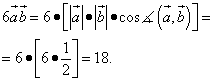
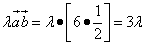
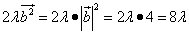 .
.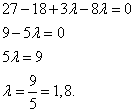
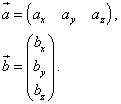
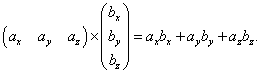
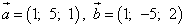
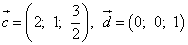 ,
,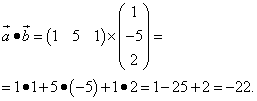
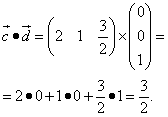
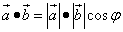 (1)
(1)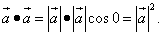
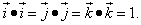
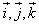
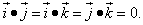
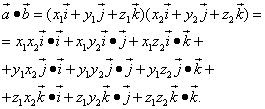
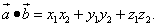
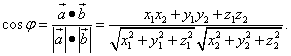
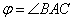 .
.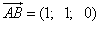 ,
,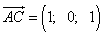 .
.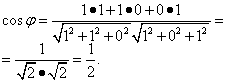
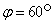 .
.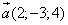
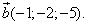
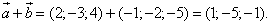
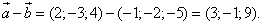
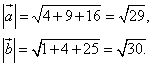
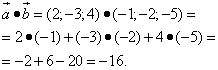
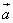 и
и 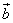 :
: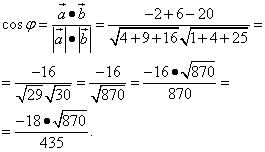
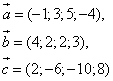
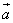 и
и 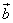 :
: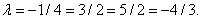
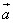 и
и 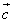 :
: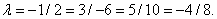
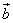 и
и 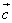 :
: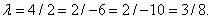
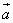 и
и 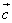 .
.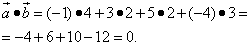
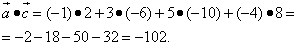
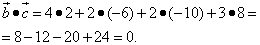
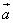 и
и 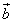 и
и 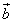 и
и 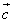 .
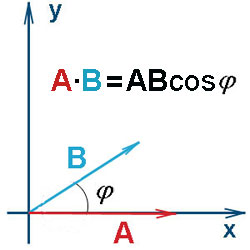
.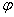 с перемещением S = A.
Из физики известно, что работа силы F при перемещении S равна
с перемещением S = A.
Из физики известно, что работа силы F при перемещении S равна
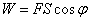 .
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.
.
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.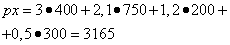

 Позначення кутів і сторін трикутника
Позначення кутів і сторін трикутника
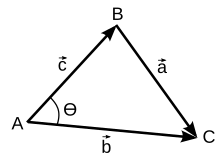 Векторний трикутник
Векторний трикутник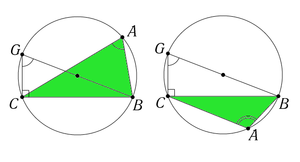
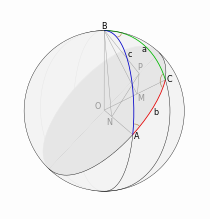 Рисунок к доказательству теоремы синусов с помощью проекций.
Рисунок к доказательству теоремы синусов с помощью проекций.

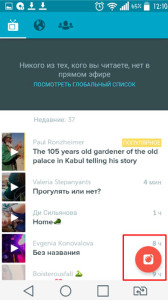
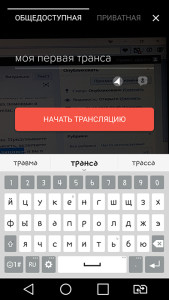
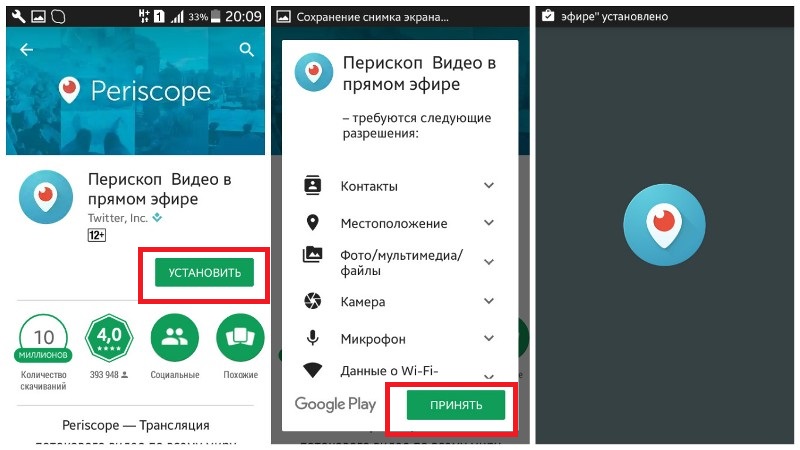
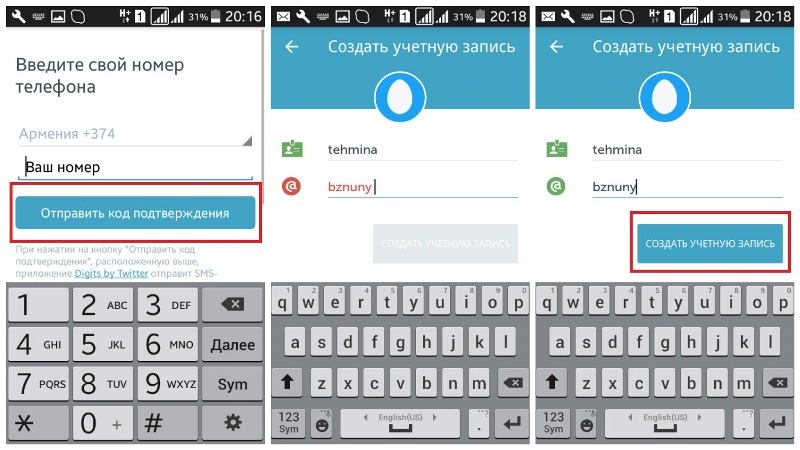
 Благодаря приложению Перископ, можно обзавестись полезными знакомствами. Они могут нести любой характер:
Благодаря приложению Перископ, можно обзавестись полезными знакомствами. Они могут нести любой характер:















 Африканский кистехвостый дикобраз
Африканский кистехвостый дикобраз



 Краснолобая газель
Краснолобая газель 




 Цинодонт Oligokyphus (поздний триас — ранняя юра, современная реконструкция), обратите внимание на развитый шерстяной покров
Цинодонт Oligokyphus (поздний триас — ранняя юра, современная реконструкция), обратите внимание на развитый шерстяной покров









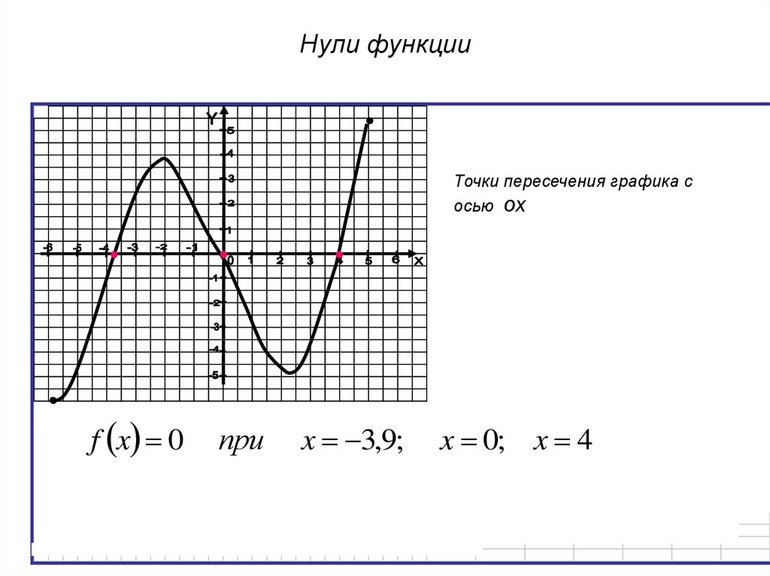

 Евгений Ширяев, преподаватель и руководитель Лаборатории математики Политехнического музея, рассказал АиФ.ru о делении на ноль:
Евгений Ширяев, преподаватель и руководитель Лаборатории математики Политехнического музея, рассказал АиФ.ru о делении на ноль:
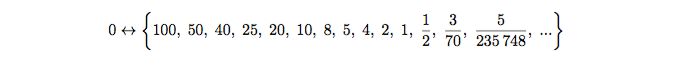

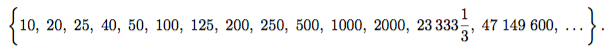

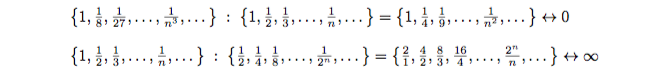


 Реконструкция афарского австралопитека.
Реконструкция афарского австралопитека. «Селам» или DIK 1-1
«Селам» или DIK 1-1  Реконструкция внешности Селам
Реконструкция внешности Селам

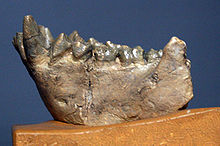 Нижняя челюсть Dryopithecus fontani, вид спереди
Нижняя челюсть Dryopithecus fontani, вид спереди Фрагмент нижней челюсти вида Dryopithecus fontani из Франции (средний миоцен, 11,5 млн л. н.)
Фрагмент нижней челюсти вида Dryopithecus fontani из Франции (средний миоцен, 11,5 млн л. н.)
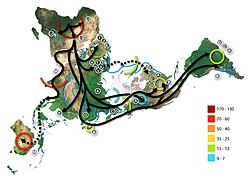 Схема расселения популяций человека разумного в пределах современного ареала. Буквы в кружках обозначают МтДНК-гаплогруппы
Схема расселения популяций человека разумного в пределах современного ареала. Буквы в кружках обозначают МтДНК-гаплогруппы График скорости бега на разные дистанции
График скорости бега на разные дистанции

 часть бассейна наполнится за 1 час.
часть бассейна наполнится за 1 час.  часть работы выполняли каждый час.
часть работы выполняли каждый час. часть бассейна. За сколько часов она наполнит бассейн?
часть бассейна. За сколько часов она наполнит бассейн? часть пути. За сколько часов он пройдет весь путь?
часть пути. За сколько часов он пройдет весь путь? бассейна, а вторая –
бассейна, а вторая –  =
=  (часть бассейна) – наполняют обе трубы за 1 час
(часть бассейна) – наполняют обе трубы за 1 час (двора)
(двора) = 2 (года)
= 2 (года) (водоема) – наполнится через вторую трубу за час.
(водоема) – наполнится через вторую трубу за час. (водоема) – наполнится через третью трубу за час.
(водоема) – наполнится через третью трубу за час. (водоема) – наполнится через три трубы за час.
(водоема) – наполнится через три трубы за час. = 1·
= 1·  = 2,4 (ч)
= 2,4 (ч)
 = 1 (то есть один торт) – вместе три медведя съедят торт за 1 день
= 1 (то есть один торт) – вместе три медведя съедят торт за 1 день Вася и Коля за 1 час
Вася и Коля за 1 час Коля и Петя за 1 час
Коля и Петя за 1 час 2 Пети, 2 Коли, 2 Васи за 1 час
2 Пети, 2 Коли, 2 Васи за 1 час часть своего участка, а второму —
часть своего участка, а второму —  своего участка. Сколько времени понадобится второму трактору, чтобы одному вспахать все поле? (50 ч).
своего участка. Сколько времени понадобится второму трактору, чтобы одному вспахать все поле? (50 ч). стены. За сколько часов они выложили бы стену вместе? (6 ч)
стены. За сколько часов они выложили бы стену вместе? (6 ч)