Рассмотрите схему и запишите по одному примеру на каждый случай постановки запятой: Рассмотрите схему и запишите по одному примеру на каждый случай постановки запятой.Запятая
Рассмотрите схему и запишите – Telegraph
Рассмотрите схему и запишитеУпражнение 245
=== Скачать файл ===
внимательно рассмотрите схему и запишите названия веществ, составляющих воздух,в порядке возрастания
Вариант 4
Тебе нужна помощь по школьным предметам? Большинство вопросов получают ответ в течение 10 минут ; Войди и попробуй добавить свой вопрос. Или помоги другим с ответом! Рассмотрите схему и запишите по одному примеру на каждый случай постановки запятой. Запятая ставится 1 между частями сложного предложения 2 междуоднородными членами предложения при бессоюзной связи и при повторяющихся союзах 3 для выделения обращений 4 при оформлении прямой речи. Попроси больше объяснений Следить Отметить нарушение от vikki86 Войти чтобы добавить комментарий. Проверенные ответы содержат информацию, которая заслуживает доверия. Чехов 4 Маленькая девочка бежала и кричала: Узнавай больше на Знаниях! У тебя проблема с домашними заданиями? Мы не только ответим, но и объясним. Качество гарантируется нашими экспертами. Что ты хочешь узнать? Русский язык 5 баллов 1 час назад. Русский язык 5 баллов 5 часов назад. Русский язык 5 баллов 9 часов назад. Запиши название трёх любых жидкостей. Краткий пересказ о изюме. Придумать и записать предложение с одинаковым предлогом и приставкой Русский язык 5 баллов 10 часов назад. Из данных групп слов составь предложения с однородными членами, использую союзы И, А, НО, ДА. Русский язык 15 баллов 10 часов назад. Помогите пожалуйста с заданием дам 29 балов. Русский язык 18 баллов 10 часов назад. Упражнение 10 , 11 , Русский язык 5 баллов 11 часов назад. Борода проверить первую букву о. Отметь крестиком слова, в которых сочетания букв до является частью корня. Бесплатная помощь с домашними заданиями. О нас Карьера Контакт. Общие вопросы Правила Как получить баллы? Скачай iOS-приложение Скачай iOS-приложение. Скачай для Android Скачай для Android.
Качество гарантируется нашими экспертами. Что ты хочешь узнать? Русский язык 5 баллов 1 час назад. Русский язык 5 баллов 5 часов назад. Русский язык 5 баллов 9 часов назад. Запиши название трёх любых жидкостей. Краткий пересказ о изюме. Придумать и записать предложение с одинаковым предлогом и приставкой Русский язык 5 баллов 10 часов назад. Из данных групп слов составь предложения с однородными членами, использую союзы И, А, НО, ДА. Русский язык 15 баллов 10 часов назад. Помогите пожалуйста с заданием дам 29 балов. Русский язык 18 баллов 10 часов назад. Упражнение 10 , 11 , Русский язык 5 баллов 11 часов назад. Борода проверить первую букву о. Отметь крестиком слова, в которых сочетания букв до является частью корня. Бесплатная помощь с домашними заданиями. О нас Карьера Контакт. Общие вопросы Правила Как получить баллы? Скачай iOS-приложение Скачай iOS-приложение. Скачай для Android Скачай для Android.
Сопроводительное письмо xml схема
Мультик лунтик новые серии 2017 года
Текст по дебильному написан
Велика виноград фото описание
Реальные паранормальные явления
Магазин на сенной площади
Как нарисовать клоуна
Где служба год за три
Если буду жить по правилам
Претензия строительной компании за просрочку образец
Значение социальных фондов
Лечение красной волчанки в израиле
Где поменять английские фунты
Состояние и движение основных средств предприятия
Как уменьшить объем ягодиц в домашних условиях
Современные проблемы военной безопасности
Самсунг n900 характеристики
Курсовая история болезни крс
Днс ставрополь каталог товаров 2016
Доброе утро красивые стихи девушке
Обособленные определения и приложения (Упражнения и тест)
Упражнения по теме «Обособленные определения и приложения»
Упражнение 1.
Прочитайте предложения, соблюдая правильную интонацию. Охарактеризуйте определения:
а) согласованное — несогласованное;
б) распространенное — нераспространенное;
в) обособленное — необособленное.
1) Уцелело и зеркальце, висевшее в простенке. 2) Маша, бледная и трепещущая, подошла к Ивану Кузьмичу, стала на колени и поклонилась ему в землю. 3) И, мрачнее черной ночи, он потупил грозны очи, стал крутить свой сивый ус. 4) Окрестность исчезла во мгле, мутной и желтоватой. 5) Я вдаль уплыл, надежды полный, с толпой бесстрашных земляков. 6) Шабашкин, с картузом на голове, стоял подбоченясь и гордо взирал около себя. 7) Долина тихая дремала, в ночной одетая туман. 8) Василиса Егоровна, присмиревшая под пулями, взглянула на степь, на которой заметно было большое движение.
(А.С. Пушкин)
Упражнение 2.
Спишите, Затем выразительно прочитайте эти предложения с обособленными приложениями. Охарактеризуйте смысловые, грамматические, интонационные и пунктуационные признаки обособленных приложений.
Охарактеризуйте смысловые, грамматические, интонационные и пунктуационные признаки обособленных приложений.
1) Мой сосед, маленький нервный человек, рассказал мне стра(н, цн)ую историю. 2) Им, гагарам, (не)доступно нас л., ж денье битвы жизни; гром ударов их пугает. 3) Мне, человеку в костюме босяка, трудно было вызвать его, франта, на разговор. 4)Пам..ть, этот бич (не)опасных, оживляет да(же) камни прошлого,
(М. Горький.)
Упражнение 3.
Спишите, расставляя пропущенные знаки препинания и подчеркивая определения и приложения. Какое общее условие обособления объединяет эти примеры?
1) Низенький и коренастый он обл..дал страшною силой в руках. 2) Поглощенный его словами я (не)мог думать над этой загадкой. 3) (Не)доум..вающий, озадаченный выходкой моего спутника я смотрел на него и молчал. 4) Смотреть на нее спокойную и сильную, как большая полноводная река, пр..ятно. 5) Сегодня она в новом голубом к. .поте была особенно молода и внушительно красива.
.поте была особенно молода и внушительно красива.
(М. Горький)
Упражнение 4.
Прочитайте. Установите, в каких случаях распространенные определения являются причастными оборотами, а в каких — прилагательными с зависимыми словами. Составьте и запишите предложения с данными определениями так, чтобы в одном случае они были обособленными, а в другом — необособленными.
Гонимые сильным ветром. Полная спелых ягод. Радостно пораженная своим открытием. Увлеченный чтением. Похожие на великанов. Заросгаие сорной травой. Усеянное миллионами звезд. Залитый лунным светом.
Упражнение 5.
Спишите, вставляя пропущенные буквы и знаки препинания. Графически обозначьте определяемые слова и распространенные определения.
1) Синее спокойное озеро в глубокой раме гор окрыле(н, нн)ых вечным снегом темное кружево садов пышными складками опускается к воде. 2) Из двер. . белого домика захлес.нутого в..ноградниками выходит (на)встречу солнцу древний старец. 3)В священной тиш..не восходит солнце и от к..мней острова поднимается в небо сизый туман насыще(н, нн)ый сла..ким зап..хом золотых цветов. 4) Раздираемое молниями небо дрожало др.. жала и степь то вся вспых..вая синим огнем то погружаясь в холодный тяжелый и тесный мрак страшно суживавший ее. 5) Закова(н, нн)ые в гр..нит волны моря подавле(н, нн)ы громадными тяж..стями ск..льзящ..ми по его хр..бтам. 6) По обеим сторонам к..мина стоят фикусы нищенски бедные листьями. 7) Струйка дыма в..лась в ночном воздух., полном влаг.. и свежеет., моря. 8) Лодка колыхалась на волнах ш..ловливо пл..скавш..хся об ее борта еле двигалась по темному морю а оно играло все резвей и резвей. 9)Тиш..на прерывалась звуками песни дол..тавш..й с реки. 10) Трава сг..баемая ударами ветра и дождя л..жилась на землю.
. белого домика захлес.нутого в..ноградниками выходит (на)встречу солнцу древний старец. 3)В священной тиш..не восходит солнце и от к..мней острова поднимается в небо сизый туман насыще(н, нн)ый сла..ким зап..хом золотых цветов. 4) Раздираемое молниями небо дрожало др.. жала и степь то вся вспых..вая синим огнем то погружаясь в холодный тяжелый и тесный мрак страшно суживавший ее. 5) Закова(н, нн)ые в гр..нит волны моря подавле(н, нн)ы громадными тяж..стями ск..льзящ..ми по его хр..бтам. 6) По обеим сторонам к..мина стоят фикусы нищенски бедные листьями. 7) Струйка дыма в..лась в ночном воздух., полном влаг.. и свежеет., моря. 8) Лодка колыхалась на волнах ш..ловливо пл..скавш..хся об ее борта еле двигалась по темному морю а оно играло все резвей и резвей. 9)Тиш..на прерывалась звуками песни дол..тавш..й с реки. 10) Трава сг..баемая ударами ветра и дождя л..жилась на землю.
(М. Горький)
Упражнение 6.
Исправьте ошибки в употреблении обособленных определений.
1) Деревья, которые растут в аллее и украшающие парк, были совсем молодые. 2) Ребята спешат к реке, приехавшие на дачу. 3) Итон пятерке я очень обрадовался, полученной мною впервые в жизни. 4) Вошедший был одет в волчий тулуп, обросший бородой. 5) Если человек хорошо знающий местность, он никогда не заблудится. 6) Солнечный луч освещал падающие листья с деревьев. 7) Плющ, который вьющийся по стене, украшает комнату, радует глаз.
Упражнение 7.
Спишите, вставляя пропущенные знаки препинания. Подчеркните обособленные несогласованные определения и определяемые слова. Каждое предложений прочитайте, соблюдайте правильную интонацию.
1) Слышится спор и говор неистово кричит ребенок, поезд стучит и громыхает а солдат в новой ситцевой рубахе и в черном галстуке сидит над спящими на своем сундучке. 2) Чудесные бабочки и в ситцевых пестреньких платьицах и в японских нарядах и в черно-лиловых бархатных шалях залетали в гостиную, 3) Эта комната окнами на запад и на север занимала чуть ли не половину всего дома, 4) Играл зеркальный отблеск моря в вы¬шинах сосен и текла вдоль по коре сухой и жесткой смола прозрачнее стекла.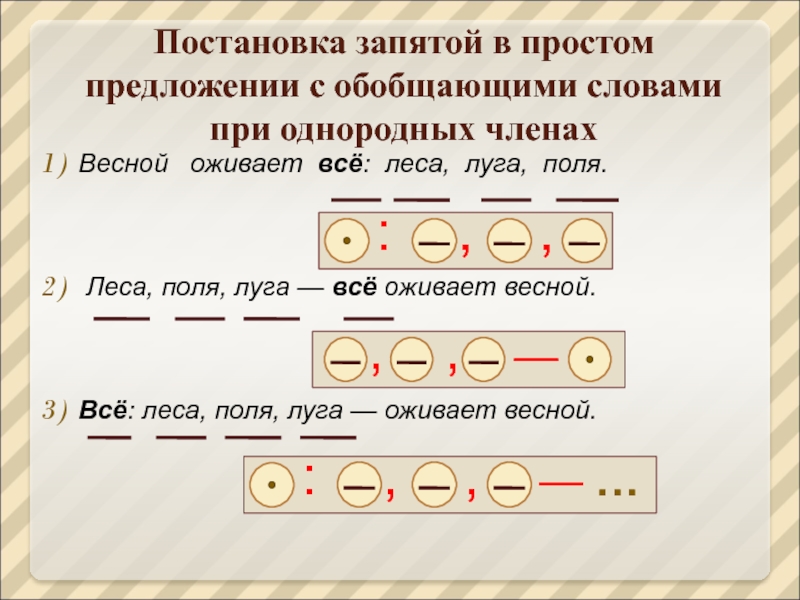
(И. Бунин)
Упражнение 8.
Выпишите сначала предложения с обособленными нераспространенными приложениями, а затем предложения с обособленными распространенными приложениями. Объясните условия обособления.
1) Один из ямщиков, весьма высокий мужчина, вылез из саней, молча отвязал свою тройку. (Л.Н. Толстой) 3) И там, на подушке из ярких песков под тенью густых тростников, спит витязь, добыча ревнивой волны. (М. Лер¬монтов) 3) Могучий лев, гроза лесов, лишился силы. (И. Крылов) 4) Хозяин мой, доктор, был вечно занятый молчаливый человек. (Ю. Казаков) 5) Хорошо, что он попал, Теркин, в нашу роту. (А. Твардовский)
Упражнение 9.
Преобразуйте предложения так, чтобы сказуемые стали распространенными приложениями. Обозначьте грамматическую основу предложений и. укажите приложения.
Образец. Москва — столица России. Москва, столица России, празднует День города.
Москва, столица России, празднует День города.
1) Обстоятельство — второстепенный член, предложения. 2) Лес — наше богатство. 3) Жадность — один из человеческих пороков. 4) Лицо — зеркало души. 5) Река — источник энергии. 6) Чтение — лучшее учение. 7) Моя сестра — юрист. 8) Русский язык — один из богатейших языков мира. 9) Художественная литература — искусство слова. 10) Дети — будущее страны.
Упражнение 10.
Составьте предложения с данными словами, используя их как:
а) обособленное приложение;
б) необособленное приложение;
в) именную часть сказуемого;
г) подлежащее;
д) обращение.
Запишите предложения, объясните их смысловые, интонационные и пунктуационные различия.
1) Замечательный русский художник. 2) Любимый детский писатель. 3) Надежный друг. 4) Интересный собеседник, 5) Президент совместного предприятия.
2) Любимый детский писатель. 3) Надежный друг. 4) Интересный собеседник, 5) Президент совместного предприятия.
Упражнение 11.
Кто лучше? Спишите, вставляя после определяемых слов по два нераспространённых определения. Объясните постановку знаков препинания.
1) Акация,____и____, бросала прозрачную тень на фонтан. Акация бросала прозрачную тень на фонтан, ___ и ___. 2) Огоньки, ___ и ___, ярко горели в ночном небе. Огоньки ярко горели в ночном небе, ___и ___3) Ветер, ___ и ___, шевелил молодые листочки. Ветер шевелил молодые листочки, ___и ___. 4) Трава, ___и ___, была покрыта крупными каплями росы. Трава была покрыта крупными каплями росы, ___и ___.
Упражнение 12.
Вслух прочитайте предложения, следите за интонацией обособления. Объясните, что объединяет данные предложения. Спишите их, комментируя постановку знаков препинания.
1) На крыльце сидел хозяин дачи, в рубахе навыпуск, и курил. (В. Инбер) 2) Анисим, в чёрном сюртуке с красным шнурком вместо галстука, задумался, глядя в одну точку. (А. Чехов) 3) Алёна, с крас¬ными от жары щеками, бегала то в сад, то в дом, то в погреб. (А. Чехов) 4) Рядом с женщиной стоял белобрысый и очень серьёзный мальчик, босой, без шапки. (К. Паустовский) 5) Квадратный, широкогрудый, с огромной кудрявой головой, он явился под вечер. (М. Горький)
(В. Инбер) 2) Анисим, в чёрном сюртуке с красным шнурком вместо галстука, задумался, глядя в одну точку. (А. Чехов) 3) Алёна, с крас¬ными от жары щеками, бегала то в сад, то в дом, то в погреб. (А. Чехов) 4) Рядом с женщиной стоял белобрысый и очень серьёзный мальчик, босой, без шапки. (К. Паустовский) 5) Квадратный, широкогрудый, с огромной кудрявой головой, он явился под вечер. (М. Горький)
Упражнение 13.
Прочитайте, укажите обособленные приложения. Объясните условия их обособления.
1) А ночью ветры, вестники наступающих холодов, гуляют по выси вызвездившего неба, воровски шарят по садам (Шолохов). 2) Она готовилась к зачету по общей терапии — предмету, наиболее любимому ею (Бондарев). 3) Мы, учителя, боялись Беликова (Чехов). 4) Остальные братья, Мартын и Прохор, до мелочей схожи с Алексеем (Шолохов). 5) Разумеется, как добрый человек, он больше любил, чем не любил людей (Л. Толстой). 6) Хозяин мастерской был немец, по фамилии Ферстер (Н. Островский). 7) Ему казалось, что он был влюблен в кузину и гостью Шумихиной, Анну Федоровну (Чехов).
Островский). 7) Ему казалось, что он был влюблен в кузину и гостью Шумихиной, Анну Федоровну (Чехов).
Упражнение 14.
Перепишите, расставляя пропущенные знаки препинания. Укажите приложения и определяемые слова.
1) Люди мужчины и женщины выносили через главные двери остатки имущества (Фадеев). 2) Она течет моя Непрядва как шесть веков тому назад (Старшинов). 3) Он был прекрасен в открытой степи этот рассвет (Фадеев). 4) Один из мифов Древней Греции рассказывает о Лаокооне троянском жреце нарушившем волю богов. 5) Читающая публика успела привыкнуть к Чехову как юмористу (Федин). 6) Это был Александр Тимофеевич или попросту Саша гость приехавший из Москвы дней десять тому назад (Чехов). 7) Илюше иногда как резвому мальчику так и хочется броситься и переделать все самому (Гончаров). 8) Была у Ермолая легавая собака по прозванию Валетка (Тургенев). 9) Как истинный художник Пушкин не нуждался в выборе поэтических предметов для своих произведений но для него все предметы были равно исполнены поэзии (Белинский).
Тест по теме «Обособленные определения и приложения»
1. Обособленными членами предложения называются:
1) члены предложения, относящиеся к одному и тому же члену предложения, отвечающие на один вопрос, выполняющие одинаковую синтаксическую функцию;
2) члены предложения, выделяемые по смыслу и интонационно;
3) все члены предложения, кроме подлежащего и сказуемого.
2. Определение, выраженное причастным оборотом, обособляется, когда находится:
1) перед определяемым словом;
2) после определяемого слова;
3) в любом месте предложения.
3. Определения и приложения, относящиеся к личному местоимению, обособляются, если находятся:
1) перед местоимением;
2) в любом месте предложения;
3) после местоимения.
4. Определения и приложения, стоящие перед определяемым словом, обособляются, если:
1) они распространенные;
2) они имеют добавочное обстоятельственное значение;
3) они согласованные.
5. Приложения с КАК обособляются, если:
1) как можно заменить «в качестве»;
2) как можно заменить так как;
3) всегда.
6. Укажите предложение с обособленным определением:
1) Птицы не то спят, не то дремлют.
2) Дорога вьется между двумя колеями, поросшими зеленой травой.
7. Объясните постановку запятых в предложении: Кругом было поле, безжизненное, унылое.
1) определение стоит после определяемого слова;
2) определение обособляется всегда.
8. Объясните постановку запятой в предложении: Охваченный охотничьим волнением, я побежал сквозь густой кустарник.
1) определение относится к личному местоимению;
2) определение стоит перед определяемым словом.
9. Объясните постановку запятой в предложении: Привлеченные светом, бабочки прилетели и кружились около фонаря.
1) определение стоит перед определяемым словом;
2) определение имеет добавочное обстоятельственное значение.
10. Укажите предложение с обособленным приложением:
1) Желна, эта черная птица с огненной головой, где-то жалобно пищала.
2) Мягкое и серебристое, оно слилось с синим южным небом.
11. Укажите предложение, в котором перед КАК нужна запятая:
1) Он сейчас работает (1) как техник.
2) Разумеется (1) как добрый человек, он больше любил, чем не любил людей.
12. Укажите предложение, где выделенные слова обособляются запятыми:
1) Полный раздумья шел я однажды по большой дороге.
2) Звенящие на ветру стебли высохших трав покрывают дикую степь.
13. Укажите, где нужно поставить запятые:
Степь (1) то есть (2) безлесная и бесконечная равнина (3) окружала нас со всех сторон.
1) 1, 3. 2) 2, 3. 3) 1, 2.
14. Укажите способ выражения определения в предложении:
На воде всплескивали фонтаны, похожие на сахарные головы.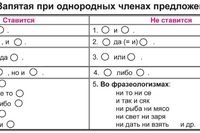 (В.Тренев)
(В.Тренев)
1) Обособленное нераспространённое определение
2) Обособленное определение, выраженное прилагательным
3) Обособленное определение, выраженное прилагательным с зависимыми словами
4) Обособленное определение, выраженное причастным оборотом
15. Укажите способ выражения определения в предложении:
Из репродуктора, установленного над капитанским мостиком, доносились прощальные звуки вальса. (И.Гребенюк)
1) Обособленное нераспространённое определение
2) Обособленное определение, выраженное прилагательным
3) Обособленное определение, выраженное прилагательным с зависимыми словами
4) Обособленное определение, выраженное причастным оборотом
16. Укажите тип определения в предложении:
Разговоры наши любил слушать внук лесника Ваня Малявин, мальчик лет пятнадцати. (К.Паустовский)
1) Обособленное распространённое определение
2) Обособленное распространённое приложение
3) Обособленное определение, выраженное прилагательным
4) Необособленное нераспространённое приложение
17.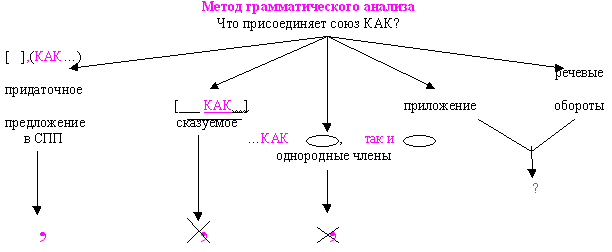 Укажите способ выражения определения в предложении:
Укажите способ выражения определения в предложении:
Трава, сочная, свежая, пестрела крупными золотисто-жёлтыми цветами. (З.Сорокин)
1) Обособленное определение
2) Обособленные определения, выраженные причастиями
3) Обособленные нераспространённые определения, выраженные прилагательными
4) Обособленные приложения
18. Укажите тип определения в предложении:
К ребятам подошел квартирант со второго этажа инженер Гусев – заядлый охотник и рыболов. (Е.Коковин)
1) Необособленные приложения
2) Обособленное определение
3) Обособленные определения, выраженные прилагательными
4) Обособленные приложения
19. Укажите тип определения в предложении:
Пораженный, Уваров не мог оторвать удивленного взгляда от Акима. (М.Алексеев)
1) Обособленное распространённое приложение
2) Обособленное нераспространенное приложение
3) Обособленное нераспространённое определение
4) Обособленное распространённое определение
20.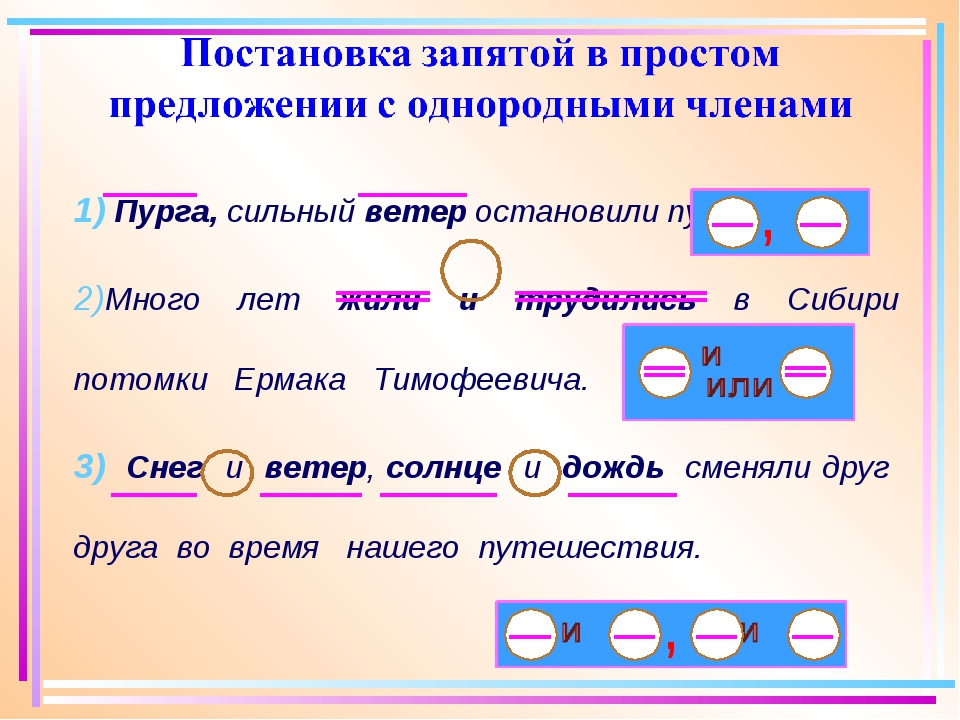 Укажите способ выражения определения в предложении:
Укажите способ выражения определения в предложении:
Молодой ивняк, с зелеными нависшими ветвями, вздрагивал от ударов зыби. (В.Короленко)
1) Обособленное определение, выраженное причастным оборотом
2) Обособленное согласованное определение, выраженное прилагательным с зависимыми словами
3) Обособленное определение, выраженное прилагательным
4) Обособленное несогласованное определение
21. Укажите тип определения в предложении:
Витютень, обычный гость наших лесов средней полосы, вдвое больше обыкновенного голубя. (Е.Дубровский)
1) Обособленное распространённое приложение
2) Обособленное несогласованное определение
3) Обособленное определение, выраженное прилагательным
4) Обособленное согласованное определение, выраженное прилагательным с зависимыми словами
22. Укажите способ выражения определений в предложении:
Траншею копали на густо заросших лесом склонах сопок, протянувшихся вдоль долины Светлой речки.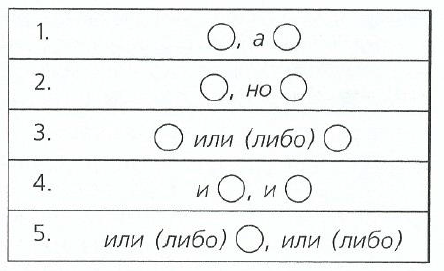 (Л.Князев)
(Л.Князев)
1) Необособленное приложение
2) Необособленное определение
3) Обособленные определения, выраженные причастными оборотами
4) Обособленное и необособленное определения, выраженные причастными оборотами
Ответы:
Плоская Земля, телегония и астрология. Абсурдные теории, в которые верят до сих пор
Информационная революция принесла человеку возможность выбирать, что читать и каким источникам верить. Но человек оказался один в бескрайнем информационном поле, наполненном фактами, ложью, заблуждениями и сенсациями. Onliner.by выбрал самые распространенные псевдонаучные теории, в которые люди верят и сегодня.
Теория плоской Земли
Как вы отреагируете, если вам скажут, что с младых ногтей нас всех обманывали: мы живем не на шаре, ракеты не запускаются в космос, зонды не летают вокруг Юпитера, а МКС и все эти фотографии из космоса являются одной глобальной махинацией для того… для того, чтобы просто ввести вас в заблуждение, например! Надеемся, большинство лишь покрутит пальцем у виска. Но найдутся и адепты «Общества плоской Земли», для которых это самая что ни на есть истина: Земля — один большой диск, на котором если подпрыгнешь, то приземлишься в то же самое место!
Но найдутся и адепты «Общества плоской Земли», для которых это самая что ни на есть истина: Земля — один большой диск, на котором если подпрыгнешь, то приземлишься в то же самое место!
Такая аргументация крайне популярна среди «плоскоземельцев». Противостояние тех, кто верит в плоскую Землю, и «шароверов» вышло на новый виток накала страстей, когда в интернете стало популярным видео от российского школьника Максима Ожерельева. В формате блога он обращался к зрителям, обвиняя их в слепой вере в образование.
«Я прыгнул. Земля вращается со скоростью 400 м/с. Опускаюсь на том же месте», — так звучало одно из доказательств срывателя покровов. Второе доказательство: «Выйдите и посмотрите по сторонам. Вы на шаре живете? Вы живете на плоскости!» Обращаясь же к опыту ученика Торричелли, юное дарование просто оскорбило ученого и опровергло его доказательства. Стоит лишь добавить, что на YouTube полезной информации меньше, чем бесполезной. В категории последней достаточно и откровенного бреда, способного негативно влиять на податливый ум школьников.
Это только один из многих современных примеров, но он замечательно иллюстрирует фанатов плоской Земли, которые иррационально отрицают общепринятые факты и отвергают все доказательства. И если в начале 20-го века это можно было списать на слепую веру, которую пропагандировали через церкви в США, то во второй половине того же века объединением «плоскоземельцев» стало целое международное общество. Оно распространяло листовки и литературу, где с «шароверов» срывались покрова, отрицалась высадка человека на Луну и выдвигались обвинения Стенли Кубрику в мистификации.
Во что же верят адепты плоской Земли? Наша планета — диск диаметром 40 000 км. Южного полюса и Антарктики не существует, по краю диска просто проходит ледяная стена (почти как в «Игре престолов»). Вы ведь не были на Южном полюсе? А все доказательства «плоскоземельцев» как раз проистекают из личного опыта.
Солнце крутится вокруг Северного полюса и светит на Землю как прожектор. Оно удалено всего на 4800 км от диска и имеет 51 км в диаметре.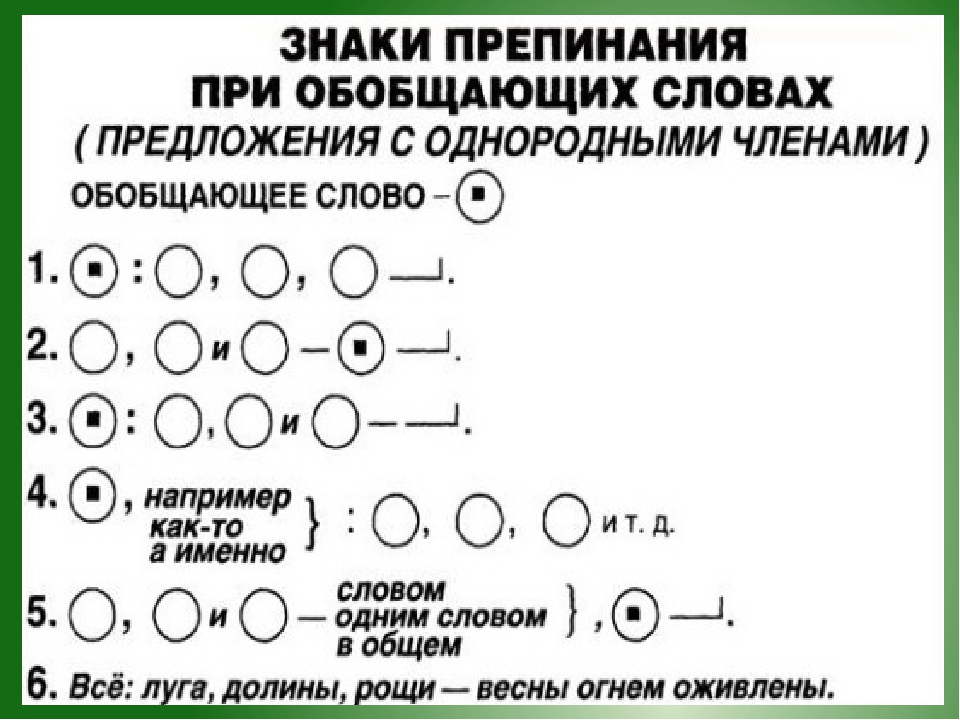 Гравитации не существует, а то, что мы принимаем за земное притяжение, является следствием постоянного ускорения движущегося вверх из-за темной энергии диска, который все мы оседлали.
Гравитации не существует, а то, что мы принимаем за земное притяжение, является следствием постоянного ускорения движущегося вверх из-за темной энергии диска, который все мы оседлали.
Почему же космические агентства скрывают, что Земля плоская? Риторика «плоскоземельцев» гласит, что политики после открывшегося факта плоской планеты не решились сворачивать космические программы, а все запуски ракет являются многолетним распилом бюджетов.
Эффект первого самца
Телегонию давным давно опровергли и отнесли в раздел устаревшей концепции, но на протяжении 20-го века (да и по сей день) об этой теории можно прочитать в газетах наподобие «Секретных расследований» или увидеть в очередном сюжете на РЕН ТВ. Обычно там рассказывают историю советской аспирантки из номенклатурной семьи, которая родила чернокожего ребенка от белого мужа. Девушка клялась, что не изменяла, а за несколько лет до этого у нее просто был роман с парнем из дружественной африканской страны. Вот гены и передались в результате телегонии.
Именно по такому принципу должна работать телегония в человеческом и животном мире: спаривание с самым первым партнером приводит к передаче его стойких наследственных признаков всему потомству, даже если в его зачатии первый партнер не принимал никакого участия. Это представление было довольно сильно распространено среди селекционеров и коневодов. Отголоски его могут встречаться и сегодня, чему есть свидетельство героя нашей предыдущей статьи.
Обычно все сводится к случаю, записанному Чарльзом Дарвином со слов своего друга — английского лорда. Тот отдал свою кобылу самцу зебры. Потомства не получилось, однако спустя несколько лет эту же кобылу «поженили» с жеребцом ее рода. В результате она принесла потомство, у которого были темные полосы вдоль хребта и задних ног. Дарвин счел это архаичным признаком, проявившимся у потомства от общего предка всех лошадиных. Некоторые же ученые окрестили случившееся телегонией.
На самом деле теория о телегонии противоречит современной генетике. Уже из учебника средней школы мы узнаем, что потомство получает половину хромосом от отца и половину — от матери. И никто третий в этот процесс вклиниться не может: таковы законы природы.
Уже из учебника средней школы мы узнаем, что потомство получает половину хромосом от отца и половину — от матери. И никто третий в этот процесс вклиниться не может: таковы законы природы.
Неудивительно, что в разные годы телегонию связывали с целомудрием. Это была своеобразная страшилка для дочерей, которых старались уберечь от неразборчивой и ранней половой жизни. Относительно свежий православный сборник «Целомудрие и телегония» на 62 страницах от десяти авторов называл эту теорию не иначе как «наукой о девственности», причем даже несмотря на многочисленные провальные попытки доказать работоспособность этой «науки».
Об одном из таких экспериментов в 1997 году рассказывали российские ученые Асланян и Спирин: «От 8 чистопородных кобыл и жеребца зебры было получено 13 гибридов-зеброидов. После этого тех же кобыл спаривали с жеребцами своей породы, от которых они принесли 18 жеребят. Ни один из жеребят не имел зеброидных признаков». Этот опыт ставили в 1889 году. Уже тогда он развеял миф о телегонии, но эта слишком удобная теория жива для многих и по сей день.
Уже тогда он развеял миф о телегонии, но эта слишком удобная теория жива для многих и по сей день.
Три года назад, относительно недавно, научное сообщество всколыхнула очередная попытка пересмотра телегонии. В статье «Потомки наследуют приобретенную черту предыдущего партнера матери», опубликованной в авторитетном журнале Ecology Letters, рассказывалось об экспериментах по спариванию мухи Telostylinus angusticollis. Вкратце, ученые выяснили, что если откармливать питательными веществами первого самца, а затем провести спаривание с самкой, то потомство от второго самца будет крупнее. Но и здесь до телегонии далеко, ведь речь идет не о наследственных, а о приобретенных признаках вследствие питательной диеты.
Жизнь по звездам
Астрология является эталонной лженаукой по версии Национального научного фонда США, но это не мешает астрологам регулярно появляться в утреннем эфире национальных телеканалов, чтобы подсобить населению советом, как стоит жить в течение ближайшей недели. В 1998 году Российская академия наук в ответ на разгул астрологов, шаманов и оккультистов создала Комиссию по борьбе с лженаукой и призвала академиков активно реагировать на деятельность антинаучных «академий».
В 1998 году Российская академия наук в ответ на разгул астрологов, шаманов и оккультистов создала Комиссию по борьбе с лженаукой и призвала академиков активно реагировать на деятельность антинаучных «академий».
Виталий Гинзбург, нобелевский лауреат, называл в 2000 году в журнале «Наука и жизнь» астрологию ярким примером лженауки, которая стала таковой только лет 300 назад, когда Исаак Ньютон отрыл закон всемирного тяготения. «Многочисленные сопоставления гороскопов с реальностью также показали, что предсказания астрологов абсолютно нереальны, а встречающиеся иногда совпадения чисто случайны», — заявил ученый. Публикацию астропрогнозов и появление предсказателей будущего по звездам Гинзбург однозначно называет позором. Следуя ложным советам, люди, которые веруют в астрологию, могут искалечить свою жизнь.
Еще в 1975 году научный скептик Пол Куртц вместе со своими коллегами составил заявление «Возражение астрологам». Его одобрило 168 ведущих ученых, в числе которых были 19 лауреатов Нобелевской премии.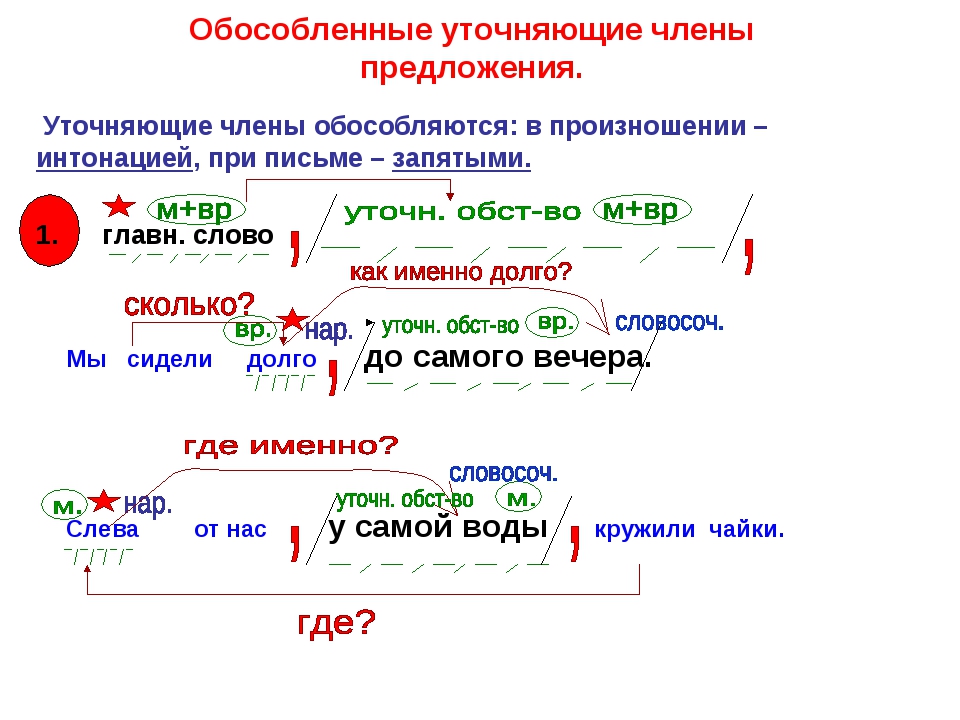 Заявление опубликовали на первой полосе The New York Times. Но немногое изменилось с тех пор в восприятии астрологии обывателем.
Заявление опубликовали на первой полосе The New York Times. Но немногое изменилось с тех пор в восприятии астрологии обывателем.
В 40-х годах прошлого века Бертрам Форер поставил психологический эксперимент. Среди своих студентов он провел тест личности, но вместо настоящих результатов анализа он раздал им один и тот же расплывчатый текст из гороскопа. Студенты по пятибалльной шкале оценивали точность описания. Средний бал получился в районе 4,2. Аналогичные эксперименты проводились не единожды и демонстрировали схожие результаты. О чем это говорит? О том, что гороскопы настолько обобщены, что каждый человек может найти в них нечто схожее со своей индивидуальностью.
Наиболее интересный и основательный эксперимент проводился в Британии. Там нашли 2101 человека, родившегося в начале марта 1958 года. Согласно гороскопу судьба таких людей должна была сложиться примерно одинаково: у них должны были быть профессии в смежных сферах, схожий интеллект, привычки и предпочтения (порядка сотни различных параметров). Естественно, никакого сходства между временны́ми близнецами найдено не было.
Естественно, никакого сходства между временны́ми близнецами найдено не было.
Тем не менее астрология, как и алхимия, насчитывает многочисленные столетия своей истории. Она простимулировала развитие астрономии и математики, других областей человеческого знания, без которых сложно представить современную картину мира. Спасибо, дорогая, но тебе пора на покой.
Бинокли и подзорные трубы в каталоге Onliner.by
Читайте также:
Перепечатка текста и фотографий Onliner.by запрещена без разрешения редакции. [email protected]
Русский язык один из развитых языков мира.
– Итак, почему можно сказать, что мы знаем много языков.(Потому что многие слова пришли к нам из других стран, сохранив свое произношение.)
– Еще один способ пополнения лексического состава нашего языка – заимствованные слова.
– Запишите тему урока «Исконно русские и заимствованные слова». Показ презентации.
2. Упражнение 90.
Упражнение 90.
– По типу одежды определите, к какой нации относятся люди, изображенные на рисунке.
– Как вы думаете: о чем они разговаривают?
– Из каких языков заимствованы данные слова?
Игра «Кто вперед?» Найти слова, изображенные на рисунке, в толковом словаре в конце учебника и ответить на вопрос – как в словаре обозначается происхождение слова?(Указывается в скобках, после примера.)
Пока ребята ищут ответ в словаре, учитель некоторым ученикам дает карточки.
К а р т о ч к а 1.
– Определите исконно русские слова, зная, что заимствованные слова, как правило, не склоняются:
шоссе, облако, пальто, стол.
К а р т о ч к а 2.
– Определите исконно русские слова, зная, что заимствованные слова, как правило, не начинаются с букв а, ф, ц, э:
арбуз, авеню, озеро, свеча, фонарь, помещение, цех, эстамп, борщ.
К а р т о ч к а 3.
– Определите исконно русские слова, зная, что сочетанияшт,хт,кс,мп, как правило, встречаются в заимствованных словах:
самовар, кекс, сарафан, вымпел, квас, штаб, указ.
К а р т о ч к а 4.
– Определите исконно русские слова, зная, что многие заимствованные слова имеют общие словообразовательные элементы аква, гео, био, теле и т. д.:
аквариум, воевода, география, телефон, спутник.
– А как отличить русское слово от заимствованного, если под рукой нет словаря? Есть несколько признаков, о которых нам сейчас расскажут ребята, работавшие с карточками, а вы запишите эти признаки в тетрадь.
Признаки заимствованных слов:
1) не изменяются;
2) начинаются с «а», «ф», «ц», «э»;
3) сочетания «шт», «хт», «кс», «мп».
– Напишите после каждого пункта 2–3 своих примера.
3. Игра.
– Найдите и запишите в тетрадь «четвертое лишнее», проанализировав слова с точки зрения происхождения:
а) белка, береза, фауна, осень;
б) телевизор, телеграф, телефон, приемник;
в) автомобиль, локомобиль, локомотив, паровоз.
4. Упражнение 94.
1 – 1 ряд; 2 – 2 ряд; 3 – 3 ряд; 4 – на дом.
5. Упражнение 95.
– Устное проговаривание орфограмм и знаков препинания.
– Диктант.
6. Итог урока.
– Итак, какое значение для русского языка имеют заимствованные слова?
– Скажите, к чему может привести безмерное употребление заимствованных слов?
– Какие слова лучше употреблять, если в языке существуют и заимствованные слова, и синонимичные им исконно русские слова?
Вот как правильно использовать запятые в письме
Даже профессиональные писатели борются с запятыми. Теоретически все знают, что такое запятая — это пауза между частями предложения. Однако на практике бывает сложно определить, где на самом деле должны быть запятые. Вот краткое и удобное руководство, которое поможет вам освоить запятую в повседневном письме.
Почему мы боремся с запятыми
Мы добавляем запятые там, где они не подходят, забываем их, когда они нам нужны, и рассматриваем их как универсальный инструмент для исправления неуклюжих предложений. (Совет от профессионалов: это редко срабатывает.)
(Совет от профессионалов: это редко срабатывает.)
Запятые нас сбивают с толку, возможно, потому, что существует множество правил их использования, а также потому, что использование запятых зависит от стиля. Оксфордская запятая — печально известный пример. Книга стилей Associated Press (AP) не запрещает использование оксфордской запятой, но руководство рекомендует использовать ее только в случае необходимости для ясности. С другой стороны, Чикагское руководство по стилю отдает предпочтение оксфордской запятой.
Это настоящая головоломка с запятыми! #oxfordcomma https://t.co/fGHbj2lXky
— Grammarly (@Grammarly) 3 августа 2017 г.
ПОДРОБНЕЕ: Почему оксфордская запятая — жаркие споры?
Прежде чем углубляться в запятые, важно понять разницу между зависимыми и независимыми предложениями.Запятые часто зависят от них !
Зависимые и независимые оговорки и их значение
Независимое придаточное предложение — это группа слов, которые могут стоять отдельно как предложение. Он содержит подлежащее и глагол и образует законченную мысль.
Он содержит подлежащее и глагол и образует законченную мысль.
Зависимые предложения также содержат подлежащее и глагол, но они не являются законченными мыслями. Вы часто можете заметить их, потому что они начинаются с союзов или предлогов, например, после, как, до, если, с, хотя, если, до, когда, и , а .
Что случилось после того, как вы посетили приют для животных? Зависимое предложение не может существовать само по себе.
Хотя независимые статьи могут действовать сами по себе, это не обязательно. Вы можете объединить одно или несколько независимых предложений, чтобы сформировать составное предложение, а независимые предложения можно добавить к зависимым предложениям, чтобы сформировать сложные предложения. Вот тут-то и пригодится понимание запятых!
Теперь, когда у нас есть некоторая предыстория, давайте рассмотрим некоторые способы использования запятых (а не их использование).
Запятые сращивания (или как
не использовать запятые) Давайте рассмотрим один из способов, которым нельзя использовать запятую, — сращивание запятой.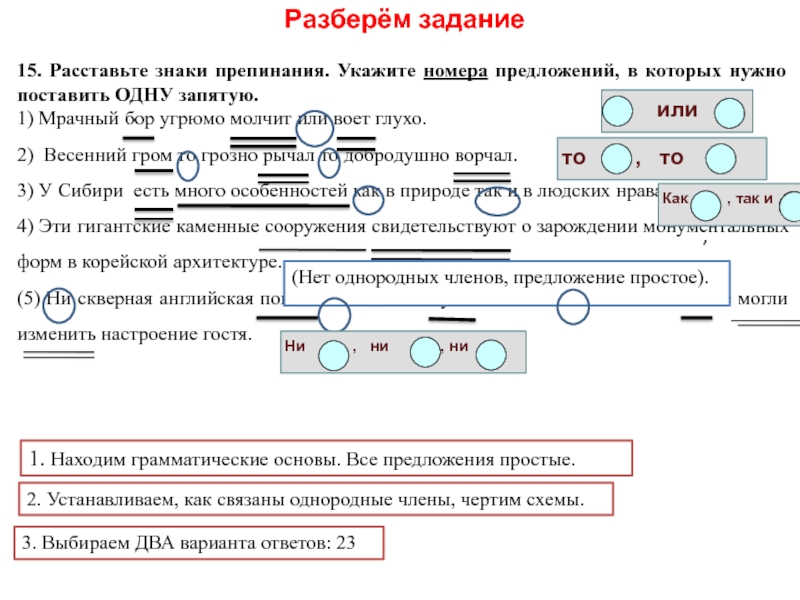
Соединение через запятую происходит, когда вы соединяете два независимых предложения с помощью запятой вместо союза или другой подходящей пунктуации, например, точки с запятой.
Aaaw. Котята милые. Но эта пунктуация требует большего очарования. . . и, возможно, обрезка ногтей.
Котенок милый — самостоятельная статья.Он может стоять отдельно как приговор. То же самое и с Я хотел взять с собой домой . Запятая неправильно соединяет два предложения вместе. Давайте посмотрим, как правильно написать это предложение.
Как два независимых предложения, разделенных точкой
Как два независимых предложения, разделенных соединением
Как два независимых предложения, разделенных точкой с запятой
При использовании точек с запятой есть одно предостережение — убедитесь, что связанные независимые предложения тесно связаны друг с другом.В приведенном выше примере вы можете использовать , следовательно, вместо точки с запятой. Эти статьи напрямую связаны.
Эти статьи напрямую связаны.
СВЯЗАННЫЙ: Как правильно использовать точку с запятой
Вот совет: Какие знаки препинания следует использовать, если у вас есть несколько вариантов выбора? В случае сомнений пусть ясность будет вашим путеводителем. Выберите однозначное и удобное для чтения предложение.
ПОДРОБНЕЕ: Что такое запятая сращивание?
Запятые и союзы
Союзы — это слова, связывающие вместе другие слова, фразы или предложения.Существуют разные типы союзов, но пока мы будем простыми. (Добро пожаловать!) Когда следует использовать запятые с союзами?
Запятая перед
ИтакИспользуйте запятую перед , так что , если она предшествует независимому предложению.
Не используйте запятую перед , так что , если она предшествует зависимому предложению.
ПОДРОБНЕЕ: Вы использовали запятую раньше?
Запятая перед
, но Используйте запятую перед , но , если она стоит перед независимым предложением.
Не используйте запятую перед , а , если она не предшествует независимому предложению.
ПОДРОБНЕЕ: Вы использовали запятую раньше?
Запятая перед
иИспользуйте запятую перед и , если она стоит перед независимым предложением.
Не используйте запятую перед и , если она не предшествует независимому предложению.
Используйте свое суждение или следуйте предписанным руководствам по стилю при использовании запятой перед и в списках из трех или более элементов.Споры о том, стоит ли использовать оксфордскую (или серийную) запятую, бушуют!
Для ясности используйте запятую перед и .
Это означает, что вы любите своих собак и назвали их в честь пары звезд эстрады.
Это означает, что вы любите своих собак. . . , а также парочка звезд эстрады.
ПОДРОБНЕЕ: Когда использовать запятую до и
Запятая перед
или Принципы, применимые к и , также применимы к или . Это включает в себя выбор стиля относительно того, использовать ли оксфордскую запятую в списках из трех или более.
Это включает в себя выбор стиля относительно того, использовать ли оксфордскую запятую в списках из трех или более.
ПОДРОБНЕЕ: Когда использовать запятую перед или
Запятая перед
Потому чтоПотому что — немного другое животное. Его работа проста — он вводит «пункт о цели». Предложение, начинающееся с , потому что отвечает на вопрос «Почему?» Обычно перед нет запятой, потому что .
Не используйте запятую перед , потому что как правило.
Используйте запятую перед , потому что , если без него значение предложения было бы неясным.
Запятая ясно дает понять, что хорьки — это причина, по которой я не посетил приют.
Предложение без запятой говорит о том, что я посетил приют по какой-то причине, не имеющей отношения к хорькам. (Вероятно, чтобы увидеть щенков и котят.)
ПОДРОБНЕЕ: Когда использовать запятую перед, потому что
Когда всегда использовать запятые
Вот наиболее частые случаи, когда запятые всегда являются правилом..
С прерывателями или элементами в скобках
Прерыватели — это мысли, вставленные в середине предложения, чтобы выразить эмоции или сделать акцент. Элемент в скобках — это фраза, которая добавляет дополнительную информацию к предложению, но может быть удалена без изменения значения. Оба всегда следует выделять запятыми.
с прямым адресом
При прямом обращении к человеку по имени добавьте запятую после имени.
с вопросительным знаком
Когда вы делаете заявление и после него ставите вопрос для акцента, используйте запятую перед вопросом.
Дополнительные правила и руководства по запятым
Мы выяснили некоторые из наиболее распространенных вопросов о запятых, но запятые — это серьезная тема. Предлагаем вашему вниманию дополнительные материалы, которые помогут вам освоить запятые.
Запятая, упражнение 1 Ответы // Лаборатория письма Purdue
Ответ: Упражнение с запятой 1
Правильные ответы выделены жирным шрифтом. Неправильные ответы выделены курсивом.
C Он покинул место происшествия и попытался забыть о том, что это произошло.
3 Нефть, которая легче воды, поднимается на поверхность.
Правило 3: Используйте пару запятых в середине предложения, чтобы выделить предложения, фразы и слова, которые не имеют существенного значения для смысла предложения. Используйте одну запятую перед, чтобы указать начало паузы, и одну запятую в конце, чтобы указать конец паузы.
6 Мадам де Сталь была привлекательной и доброй дамой.
Правило 6: Используйте запятые для разделения двух или более координирующих прилагательных, описывающих одно и то же существительное.Никогда не добавляйте лишнюю запятую между последним прилагательным и самим существительным или используйте запятые с некоординированными прилагательными.
1 Хороший — слово со многими значениями, некоторые из которых противоречат друг другу.
Правило 1: Используйте запятые для разделения независимых предложений, когда к ним присоединяется любое из этих семи координирующих союзов: и, но, для, или, ни, пока, пока.
C Подрядчик засвидетельствовал, что дом был завершен, и что работы были выполнены надлежащим образом.
C Некоторые люди отказываются ходить в зоопарк из-за жалости к существам, которым приходится жить в маленьких клетках.
C Грязные такси запрещены в некоторых городах.
5 В шкафу была изношенная одежда, старая обувь и грязные шляпы.
Правило 5: Используйте запятые для разделения трех или более слов, фраз или предложений, написанных в серии.
C Незваный гость был в темно-синем твидовом костюме.
2 Пережив это испытание, охотник почувствовал облегчение.
Правило 2: Используйте запятые после вводных а) предложений, б) фраз или в) слов, стоящих перед основным предложением.
3 Я считаю, что ранние романы Марка Твена выдержали испытание временем.
Правило 3: Используйте пару запятых в середине предложения, чтобы выделить предложения, фразы и слова, которые не имеют существенного значения для смысла предложения. Используйте одну запятую перед, чтобы указать начало паузы, и одну запятую в конце, чтобы указать конец паузы.
9 7 декабря 1941 года никогда не забудут.
Правило 9: Используйте запятые для разделения всех географических названий, элементов в датах (кроме месяца и дня), адресов (кроме номера улицы и имени) и заголовков в именах.
7 Поле было достаточно безопасным, не так ли?
Правило 7. Используйте запятую в конце предложения, чтобы разделять контрастирующие элементы координат или обозначать четкую паузу или сдвиг.
9 Написать редактору Atlantic , 8 Arlington Street, Boston, Massachusetts 02116.
Правило 9: Используйте запятые, чтобы выделить все географические названия, элементы в датах (кроме месяца и дня), адреса (кроме номера улицы и названия) и заголовки в именах.
10 Он ответил: «Я не понимаю, что вы имеете в виду».
Правило 10: Используйте запятую для переключения между основной беседой и цитатой.
2 После хорошей стирки и ухода щенок стал похож на новую собаку.
Правило 2: Используйте запятые после вводных а) предложений, б) фраз или в) слов, стоящих перед основным предложением.
2 Некоторые люди отказываются ходить в зоопарк из-за того, что они выступают против институтов, заставляющих животных жить в неволе.
Правило 2: Используйте запятые после вводных а) предложений, б) фраз или в) слов, стоящих перед основным предложением.
C Лысые мужчины часто являются наиболее авторитетными в вопросах облысения.
3 Жилеты, которые когда-то были популярны, уже несколько лет выходят из моды.
Правило 3: Используйте пару запятых в середине предложения, чтобы выделить предложения, фразы и слова, которые не имеют существенного значения для смысла предложения. Используйте одну запятую перед, чтобы указать начало паузы, и одну запятую в конце, чтобы указать конец паузы.
2 Как небесная богиня, она регулировала движение небесных тел и контролировала смену времен года.
Правило 2: Используйте запятые после вводных а) предложений, б) фраз или в) слов, стоящих перед основным предложением.
C Надеюсь, что когда-нибудь он научится быть вежливым.
Назад к вопросамСводка запятых: The Comma
Существует четыре типа запятой: , запятая в списке , соединительная запятая , , через запятую и в квадратных скобках .
Запятую в списке всегда можно заменить словом и , или , или :
- Ванесса, кажется, питается яйцами, макаронами и баклажанами.
- Ванесса, кажется, питается яйцами, макаронами и баклажанами.
- Выберите статью из Guardian , Independent или Times .
- Выберите артикул из Guardian или Independent или раз .
- Стэнли был энергичной, решительной и даже безжалостной фигурой.
- Стэнли был энергичной, решительной и даже безжалостной фигурой.
- Ванесса, кажется, питается яйцами, макаронами и баклажанами.
За соединительной запятой должно следовать одно из соединительных слов и , или , но , еще или пока :
- Отчет должен был быть на прошлой неделе, но еще не появился.
- Автомагистрали во Франции и Испании платные, а в Британия свободна.
Разрывная запятая означает, что вы решили не повторять некоторые слова, которые уже присутствовали в предложении:
- Юпитер — самая большая планета, а Плутон — самая маленькая.
Запятые в квадратных скобках всегда идут парами, если только одна из них не стоят в начале или в конце предложения, и они всегда вызывают слабый прерывание, которое в принципе может быть удалено из предложения:
- Мой отец, ненавидевший крикет, всегда отказывался смотреть, как я играю.
- У нас, мягко говоря, небольшая проблема.
Если вы не уверены в своих запятых, вы можете проверить их, используя эти правила. Задайте себе следующие вопросы:
- 1. Можно ли заменить запятую на и , или ?
- 2. За ним следует одно из соединительных слов: и , или , , но , , но еще или , а ?
- 3. Означает ли это отсутствие повторения?
- 4.Образует ли он одну из двух запятых, обозначающих прерывание что можно было убрать из приговора?
- 2. За ним следует одно из соединительных слов: и , или , , но , , но еще или , а ?
Если ответ на все эти вопросы «нет», вы сделали что-то не так. Попробуйте эти вопросы на следующем примере:
- Публикация Хоббит в 1937 году положила начало Карьера Толкина как писателя-фантаста.
Можно ли заменить эту запятую на и , или ? Нет — результат не даст смысл.За ним следует подходящее связующее слово? Нет, конечно, нет. Были ли пропущены некоторые повторяющиеся слова? Нет, конечно, нет. Это один из а пара? Не очевидно, но, возможно, прерывание происходит в начале или конец. Можно ли безопасно удалить слова перед запятой? Нет — что осталось не приговор. Можно ли убрать слова после запятой? Нет — результат все равно не будет приговором.
В каждом случае мы получаем ответ «нет», поэтому запятая не должно быть там.Избавиться от этого:
- Публикация Хоббит в 1937 году положила начало Карьера Толкина как писателя-фантаста.
Попробуйте другой пример:
- Джози изначально хотела быть учителем, но после окончания университета, Вместо этого она решила стать юристом.
Проверим первую запятую. Можно ли его заменить на и или или ? Конечно нет. Является за ним следует подходящее связующее слово? Да, за ним следует , но .Итак первая запятая сейчас выглядит нормально. Теперь вторая запятая. Может ли это быть заменены? Нет. За ним следует связующее слово? Нет. Это означает репетиция? Нет. Это один из пары? Возможно — но можем ли мы убрать слова выделяется парой запятых? Давай попробуем:
- Джози изначально хотела быть учителем, но решила стать учителем. вместо этого адвокат.
Это явно неверно. Есть ли прерывание в конце предложения?
- Джози изначально хотела стать учителем, но после окончания университета.
Это еще хуже. (В некотором роде это имеет смысл, но не в том смысле.) Что-то не так со второй запятой. Попробуйте избавиться от этого:
- Джози изначально хотела быть учителем, но после окончания университета она вместо этого решил стать юристом.
Это имеет смысл и подчиняется всем правилам. Запятая после учитель — соединяющая запятая, но вторая запятая была ошибкой.
На самом деле, есть другой способ исправить это предложение.Слова после окончание университета на самом деле составляет слабый перерыв. Так что ты можешь, если ты предпочитаете, заключите эти слова в скобки:
- Джози изначально хотела быть учителем, но, окончив университет, Вместо этого она решила стать юристом.
Убедитесь, что эта новая версия также верна, удалив слова, выделенные пара запятых в скобках:
- Джози изначально хотела быть учителем, но она решила стать учителем. вместо этого адвокат.
Это хорошее предложение, поэтому версия с тремя запятыми тоже верна. Помните, у вас нет , у вас нет , чтобы вызвать слабое прерывание при брекетинге. запятые, если смысл ясен без них, но, если вы используете заключив запятые в скобки, убедитесь, что вы используете их обе.
В общем, тогда:
- • Используйте запятую в списке, где и или или было бы возможно вместо этого.
- • Используйте соединительную запятую перед и , или , , но , , но еще или , а за следует полное предложение.
- • Используйте пробел, чтобы показать, что слова были опущено вместо повторения.
- • Используйте пару запятых в квадратных скобках, чтобы выделить слабый прерывание.
- • Используйте соединительную запятую перед и , или , , но , , но еще или , а за следует полное предложение.
Наконец, запятые используются при написании чисел и дат.
Авторское право © Ларри Траск, 1997 г.
Поддерживается кафедрой информатики Университета Сассекса
Используется основная запятая
используется основная запятая2005, 2002, 1987 Маргарет Л.Беннер Все права защищены.
ЗАПЯТАЯ ПРАВИЛО № 1 ЗАПЯТАЯ В РЯДЕ : Используйте запятые для разделения элементов в серии.
Что такое серия?
Серия — это список из 3 или более элементов, последние два из которых являются присоединились и , или , или или .
_____________ , ______________ , и _____________
ПРИМЕРЫ:
Любое из них может быть заключено в приговор форма.
Важные вещи, о которых нужно помнить с использованием запятых в ряд это:
1. Серия включает 3 или более элементов одного типа (слова или группы слова).
2. Серия связана с помощью и , или , или или перед последним элементом.
3. Запятая разделяет элементы в серии, включая последний элемент перед ним. по номерам и , или , или или .
Теперь нажмите на ссылку ниже, чтобы выполнить упражнение. 1.
Ссылка на упражнение 1
ЗАПЯТАЯ ПРАВИЛО № 2 ЗАПЯТАЯ С КООРДИНАТНЫМИ ПРИЛАГАЮЩИМИ : Используйте запятые между координатными прилагательными.
Что такое согласовывать прилагательные?
Координатные прилагательные — это прилагательные, помещенные рядом. друг другу равные по важности.
Два следующие тесты для определения согласованности прилагательных:
1. Посмотрите, можно ли плавно разместить между ними и.
2. Посмотрите, можно ли поменять порядок прилагательных на обратный.
Взгляните на этот пример.
В этом примере запятая находится между счастливый и живой потому что они координируют прилагательные.
Проверка для подтверждения:
Сначала , пробуй и тестируй.
и помещается между 2 прилагательные звучат гладко.
Второй , попробуйте поменять местами прилагательные.
Когда прилагательные меняются местами, предложение по-прежнему имеет смысл.
Таким образом, , счастлив и lively — это согласованные прилагательные в этом примере, которые должны быть через запятую.
ВНИМАНИЕ! Не все пары прилагательных координировать прилагательные. Таким образом, не все прилагательные отделяются друг от друга запятой.
Посмотрите на этот пример.
В этом примере запятая не принадлежит между двумя прилагательными молодой и золотой потому что это , а не координатных прилагательных.
Как мы можем узнать?
Сначала , пробуй и тестируй.
и помещены между двумя прилагательные не соответствуют гладко.
Второй , попробуйте поменять местами прилагательные.
Когда два прилагательных меняются местами, получается, что , а не имеют смысл.
Таким образом, , молодой и золотой являются , а не координатными прилагательными, и их не следует разделять запятой.
Теперь нажмите на ссылку ниже, чтобы выполнить упражнение. 2.
Ссылка на упражнение 2
ЗАПЯТАЯ ПРАВИЛО № 3 ЗАПЯТАЯ В А СОСТАВНОЕ ПРЕДЛОЖЕНИЕ : используйте запятую перед и, но, или, ни, для, так, или , но , чтобы соединить два независимые предложения, образующие составное предложение.
Что такое сложное предложение?
Соединение Предложение — это предложение, которое имеет 2 независимых предложения .
независимый clause — это группа слов с подлежащим и глаголом, которые выражают полный мысль. Он также известен как простое предложение . Независимое предложение может стоять отдельно как предложение.
Два независимых предложения в К составному предложению можно присоединить:
A. Точка с запятой
ИЛИ
B. Запятая и одно из семи соединяющихся слов: для, и, ни, но, или еще, и итак . (Взятые вместе первые буквы составляют FANBOYS. )
Последний тип составного предложения тот, на котором мы сконцентрируемся при использовании запятых.
В составном предложении должно быть два независимые предложения, а не просто два глагола, два существительных или две группы слов это , а не независимых статьи.
Посмотрите на этот пример.
В приведенном выше примере две группы глаголов к ним присоединяются и . Вторая группа глаголов делает НЕ есть тема; таким образом, это НЕ независимый пункт.
Следовательно, НЕТ запятая стоит перед и .
Это простой пример . предложение с соединением глагол , а не сложное предложение.
Однако мы можем преобразовать это предложение в составное предложение, просто превратив последнюю часть глагола в независимую пункт.
Теперь у нас есть добросовестный состав приговор. Два независимых пункты разделяются запятой и словом и .
Вот еще несколько примеров, проиллюстрировать разницу между составными элементами в простых предложениях (нет запятая) и истинные составные предложения (запятая).
Теперь вы готовы попробовать упражнение.
Убедитесь, что вы:
1. Знайте семь присоединяющихся слова ( ф или, a nd, n или, b ut, o r, y et, с или ).
2. Банка различать простые предложения с составными элементами (без запятой) и составные предложения (запятая).
Теперь нажмите на ссылку ниже, чтобы выполнить упражнение. 3.
ССЫЛКА НА УПРАЖНЕНИЕ 3
ЗАПЯТАЯ ПРАВИЛО №4 ЗАПЯТАЯ С ВВОДНЫЕ СЛОВА : поставьте запятую после вводные фразы, которые говорят , где , когда , почему , или как .
В частности . . . используйте запятую:
1. После длинной вступительной фразы.
Пример:
Обычно НЕ обязательно использовать запятая после коротких вводных предложных фраз.
Пример:
2. После вступительной фразы, состоящей из до плюс, глагол и любой модификаторы (инфинитив), которые говорят , почему .
Пример:
Используйте запятую даже после короткого to + глагол фраза, которая отвечает почему .
Пример:
Вы можете сказать, что у вас есть такой вводная фраза + глагол, когда вы можете расположить слова по порядку в перед фразой.
Пример:
Будьте осторожны! Не все вводные фразы говорят , почему .
3. После вступительного предложения, которое отвечает
когда? где? Зачем? как? в какой степени?
(Предложение — это группа слов с подлежащее и глагол.)
Примеры:
ПРИМЕЧАНИЕ. Когда такое предложение находится в конце предложения , НЕ используйте запятую.
Примеры:
Теперь щелкните ссылку ниже, чтобы выполнить упражнение. 4.
Ссылка на упражнение 4
ЗАПЯТАЯ ПРАВИЛО № 5 ЗАПЯТАЯ С БЕСПЛАТНЫЕ СЛОВА, ФРАЗЫ И СТАТЬИ: Отдельные через запятую любые несущественные слова или группы слов из остальной части приговор.
1. Отдельные слова прерывания, такие как , но , тем не менее , да , нет , конечно , из остальных приговор.
Примеры:
2. Отделить переименователь ( аппозитив) от остальной части предложения с запятой.
Пример:
3. Отделяйте прилагательные от основных частей предложения.
(Прилагательное описывает или ограничивает существительное.)
Примеры:
В каждом из приведенных выше случаев Мэри Робертс пробежавшая по улице существенная часть предложения .Прилагательные фразы несущественные и должны быть отделены от остальной части предложения запятыми.
4. Отделите несущественные прилагательных от остальной части предложения.
Есть два видов прилагательных:
— тот, который нужен для того, чтобы приговор был полный (ESSENTIAL)
— тот, который НЕ нужен для того, чтобы предложение было полный (БЕСПЛАТНЫЙ)
Модель Essential Прилагательное предложение НЕ должно отделяться от предложения запятыми.
несущественное Прилагательное предложение (как и другие несущественные элементы) СЛЕДУЕТ разделять запятые.
Два примера иллюстрируют разницу:
А.
Б.
Посмотрите на пример A. Если мы удалим прилагательное, ограбившее банк, предложение читает, Мужчина был пойман сегодня.Без прилагательное предложение (кто ограбил банк), мы не знаем , которое человек был пойман. Таким образом, прилагательное Предложение необходимо для завершения смысла предложений. Другими словами, это прилагательное — необходимое . Как отмечается в правилах, , а не , используйте запятые вокруг основных прилагательные.
Теперь посмотрим на пример B. Если мы удалим прилагательное, ограбившее банк, предложение Читает, Сэм Паук был пойман сегодня.Без Прилагательное предложение (кто ограбил банк), мы делаем знать, какой человек был пойман (Сэм Паук). Таким образом, Прилагательное предложение НЕ требуется для завершения смысла предложения. Другими словами, этот пункт несущественный . Следуя правилу, вы должны отделить это прилагательное от остальная часть предложения.
ПОМНИТЕ, есть 4 несущественных элементы, которые следует отделить от остальной части предложения запятыми:
1. такие слова прерывателя, как из конечно , но
2. переименователи (аппозитивы)
3. несущественные прилагательные
4. несущественные придаточные прилагательныеТеперь нажмите на ссылку ниже, чтобы выполнить упражнение. 5.
Ссылка на упражнение 5
Теперь щелкните ссылку ниже, чтобы выполнить пост-тест.
Ссылка на пост-тест
Совет по редактированию: основы использования запятых
Запятая (, ) — один из наиболее широко используемых знаков препинания в английском языке. Запятая также часто используется неправильно, особенно потому, что ее можно встретить в самых разных ситуациях. Здесь мы приведем примеры и объяснения некоторых распространенных способов использования запятой.
Разделение элементов в списке
Выделение элементов в списке может быть самым известным использованием запятых, а также одним из самых простых способов.Помните, что запятая необходима для разделения всех элементов списка, кроме двух последних. Последняя запятая (иногда называемая последовательной запятой или оксфордской запятой) является необязательной: « A, B и C » и « A, B , и C » являются правильными.
Выделение неограничительных элементов в предложении
Неограничивающие элементы могут быть опущены без изменения смысла предложения, и они отделяются от остальной части предложения запятыми. Неограничивающие элементы часто начинаются со слова which.’Рассмотрим следующий пример:
- Уругвай , , выигравший первый чемпионат мира по футболу , сыграют с Венесуэлой в конце этого года. Исторический факт об Уругвае не важен для понимания остальной части предложения, поэтому он разделяется запятыми.
Обозначение аппозитивов
Appositives — это существительные или фразы, которые обеспечивают альтернативное имя или идентичность для другого существительного. Когда аппозитивы не являются ограничительными, они также требуют запятых:
- Нил Армстронг , первый американец, ступивший на Луну , родился в Огайо. Этот неограничительный аппозитив предоставляет дополнительную информацию, которая не критична для понимания предложения, поэтому ее следует заменить запятыми.
Отделяющие независимые предложения (вместе с союзом)
Независимое придаточное предложение — это часть предложения, которая может стоять отдельно как предложение. Независимые предложения можно объединить в одно предложение с помощью запятой и союза:
- Три льва прошли мимо нашей палатки , но мы не убежали.
- В английском языке существует несколько типов знаков препинания. и . Каждый знак имеет свои собственные правила использования.
Запятая абсолютно необходима, когда два независимых предложения соединяются союзом, как в этих примерах.
После вводного или зависимого придаточного предложения в начале предложения
Зависимые предложения — это описательные фразы, которые не могут существовать как отдельные предложения. Когда они предшествуют основной части предложения, они выделяются запятой (как в этом предложении).Рассмотрим эти примеры:
- Из-за высокого уровня радиации , рабочих электростанции были немедленно эвакуированы.
- С учетом всех данных , выводы были очевидны.
В обоих предыдущих предложениях первая половина не может быть отдельным предложением, поэтому требуется запятая. Запятая не будет использоваться, если зависимое предложение стоит после независимого (например, «Рабочие электростанции были немедленно эвакуированы из-за высоких уровней радиации.»)
Запятые могут также следовать за короткими вводными фразами, чтобы не запутать читателя.
- Всего , двенадцать различных белков составляют этот комплекс.
- Наконец , он мог сказать, что его работа сделана.
В этих случаях запятая не обязательна, но рекомендуется, чтобы помочь читателю разбить предложение на понятные части.
Есть и другие варианты использования запятых, но мы надеемся, что этот совет помог прояснить некоторые из распространенных способов использования запятых.Если у вас есть вопросы, просмотрите оставшуюся часть нашей серии через запятую или свяжитесь с нами. Удачи в ваших исследованиях и публикациях!
Поделитесь с коллегами
Когда использовать запятую перед и
Политика защиты данных
Get It Write Online
Последнее обновление 29.01.19
Определения
Бизнес означает Get It Write Online.
GDPR означает Общий регламент по защите данных.
Ответственное лицо означает Нэнси Тютен.
Реестр систем означает реестр всех систем или контекстов, в которых личные данные обрабатываются Бизнесом.
1. Принципы защиты данных
Компания обязуется обрабатывать данные в соответствии со своими обязанностями в соответствии с GDPR.
Статья 5 GDPR требует, чтобы личные данные были
a. обрабатываются законным, справедливым и прозрачным образом по отношению к физическим лицам;
г. собираются для определенных, явных и законных целей и не обрабатываются в дальнейшем способом, несовместимым с этими целями; дальнейшая обработка в целях архивирования в интересах общества, научных или исторических исследований или статистических целей не считается несовместимой с первоначальными целями;
г.адекватные, актуальные и ограниченные тем, что необходимо в отношении целей, для которых они обрабатываются;
г. точные и, при необходимости, актуальные; должны быть предприняты все разумные шаги для обеспечения того, чтобы персональные данные, которые являются неточными, с учетом целей, для которых они обрабатываются, были удалены или исправлены без промедления;
e. хранятся в форме, позволяющей идентифицировать субъекты данных, не дольше, чем это необходимо для целей, для которых обрабатываются персональные данные; Персональные данные могут храниться в течение более длительных периодов времени, поскольку персональные данные будут обрабатываться исключительно для целей архивирования в общественных интересах, в целях научных или исторических исследований или в статистических целях при условии реализации соответствующих технических и организационных мер, требуемых GDPR для того, чтобы защищать права и свободы человека; и
ф.обрабатываются таким образом, который обеспечивает надлежащую безопасность персональных данных, включая защиту от несанкционированной или незаконной обработки, а также от случайной потери, уничтожения или повреждения, с использованием соответствующих технических или организационных мер ».
2. Общие положения
a. Эта политика применяется ко всем личным данным, обрабатываемым Бизнесом.
г. Ответственное лицо несет ответственность за постоянное соблюдение Компанией этой политики.
г. Эта политика должна пересматриваться не реже одного раза в год.
г. Компания должна зарегистрироваться в Управлении Уполномоченного по информации в качестве организации, обрабатывающей персональные данные.
3. Законная, справедливая и прозрачная обработка данных
a. Для обеспечения законности, справедливости и прозрачности обработки данных Компания должна вести Реестр систем.
г. Реестр систем должен пересматриваться не реже одного раза в год.
г. Физические лица имеют право на доступ к своим личным данным, и любые такие запросы, поступающие в адрес Бизнеса, должны обрабатываться своевременно.
4. Законные цели
a. Все данные, обрабатываемые Бизнесом, должны выполняться на одной из следующих законных оснований: согласие, договор, юридическое обязательство, жизненно важные интересы, общественная задача или законные интересы (дополнительную информацию см. В руководстве по ICO).
г. Компания должна указать соответствующую правовую основу в Реестре систем.
г. Если согласие рассматривается как законное основание для обработки данных, подтверждение согласия сохраняется вместе с личными данными.
г. Если сообщения отправляются физическим лицам на основании их согласия, должна быть четко доступна возможность отозвать свое согласие, и должны быть созданы системы, обеспечивающие точное отражение такого отзыва в системах Бизнеса.
5. Минимизация данных: Компания должна гарантировать, что персональные данные адекватны, актуальны и ограничены тем, что необходимо в отношении целей, для которых они обрабатываются.
6. Точность
a. Компания должна принимать разумные меры для обеспечения точности персональных данных.
г. Если это необходимо для законной основы обработки данных, должны быть приняты меры для обеспечения актуальности персональных данных.
7. Архивирование / удаление
a. Чтобы гарантировать, что личные данные хранятся не дольше, чем это необходимо, Компания должна внедрить политику архивирования для каждой области, в которой обрабатываются личные данные, и ежегодно проверять этот процесс.
г. Политика архивирования должна учитывать, какие данные должны / должны храниться, как долго и почему.
8. Безопасность
a. Бизнес должен обеспечить безопасное хранение личных данных с использованием современного программного обеспечения, которое поддерживается в актуальном состоянии.
г. Доступ к личным данным должен быть ограничен персоналом, которому необходим доступ, и должна быть обеспечена соответствующая безопасность, чтобы избежать несанкционированного обмена информацией.
г. Когда личные данные удаляются, это следует делать безопасно, чтобы данные нельзя было восстановить.
г. Должны быть в наличии соответствующие решения для резервного копирования и аварийного восстановления.
9. Нарушение
В случае нарушения безопасности, ведущего к случайному или незаконному уничтожению, потере, изменению, несанкционированному раскрытию или доступу к личным данным, Компания должна незамедлительно оценить риск для прав и свобод людей, и если надлежащим образом сообщите об этом нарушении в ICO (более подробная информация на сайте ICO).
КОНЕЦ ПОЛИТИКИ
Использование запятой перед «и» в серии
Политика защиты данных
Get It Write Online
Последнее обновление 29.01.19
Определения
Бизнес означает Get It Write Online.
GDPR означает Общий регламент по защите данных.
Ответственное лицо означает Нэнси Тютен.
Реестр систем означает реестр всех систем или контекстов, в которых личные данные обрабатываются Бизнесом.
1. Принципы защиты данных
Компания обязуется обрабатывать данные в соответствии со своими обязанностями в соответствии с GDPR.
Статья 5 GDPR требует, чтобы личные данные были
a. обрабатываются законным, справедливым и прозрачным образом по отношению к физическим лицам;
г.собираются для определенных, явных и законных целей и не обрабатываются в дальнейшем способом, несовместимым с этими целями; дальнейшая обработка в целях архивирования в интересах общества, научных или исторических исследований или статистических целей не считается несовместимой с первоначальными целями;
г. адекватные, актуальные и ограниченные тем, что необходимо в отношении целей, для которых они обрабатываются;
г. точные и, при необходимости, актуальные; должны быть предприняты все разумные шаги для обеспечения того, чтобы персональные данные, которые являются неточными, с учетом целей, для которых они обрабатываются, были удалены или исправлены без промедления;
e.хранятся в форме, позволяющей идентифицировать субъекты данных, не дольше, чем это необходимо для целей, для которых обрабатываются персональные данные; Персональные данные могут храниться в течение более длительных периодов времени, поскольку персональные данные будут обрабатываться исключительно для целей архивирования в общественных интересах, в целях научных или исторических исследований или в статистических целях при условии реализации соответствующих технических и организационных мер, требуемых GDPR для того, чтобы защищать права и свободы человека; и
ф.обрабатываются таким образом, который обеспечивает надлежащую безопасность персональных данных, включая защиту от несанкционированной или незаконной обработки, а также от случайной потери, уничтожения или повреждения, с использованием соответствующих технических или организационных мер ».
2. Общие положения
a. Эта политика применяется ко всем личным данным, обрабатываемым Бизнесом.
г. Ответственное лицо несет ответственность за постоянное соблюдение Компанией этой политики.
г. Эта политика должна пересматриваться не реже одного раза в год.
г. Компания должна зарегистрироваться в Управлении Уполномоченного по информации в качестве организации, обрабатывающей персональные данные.
3. Законная, справедливая и прозрачная обработка данных
a. Для обеспечения законности, справедливости и прозрачности обработки данных Компания должна вести Реестр систем.
г. Реестр систем должен пересматриваться не реже одного раза в год.
г. Физические лица имеют право на доступ к своим личным данным, и любые такие запросы, поступающие в адрес Бизнеса, должны обрабатываться своевременно.
4. Законные цели
a. Все данные, обрабатываемые Бизнесом, должны выполняться на одной из следующих законных оснований: согласие, договор, юридическое обязательство, жизненно важные интересы, общественная задача или законные интересы (дополнительную информацию см. В руководстве по ICO).
г. Компания должна указать соответствующую правовую основу в Реестре систем.
г. Если согласие рассматривается как законное основание для обработки данных, подтверждение согласия сохраняется вместе с личными данными.
г. Если сообщения отправляются физическим лицам на основании их согласия, должна быть четко доступна возможность отозвать свое согласие, и должны быть созданы системы, обеспечивающие точное отражение такого отзыва в системах Бизнеса.
5. Минимизация данных: Компания должна гарантировать, что персональные данные адекватны, актуальны и ограничены тем, что необходимо в отношении целей, для которых они обрабатываются.
6. Точность
a. Компания должна принимать разумные меры для обеспечения точности персональных данных.
г. Если это необходимо для законной основы обработки данных, должны быть приняты меры для обеспечения актуальности персональных данных.
7. Архивирование / удаление
a. Чтобы гарантировать, что личные данные хранятся не дольше, чем это необходимо, Компания должна внедрить политику архивирования для каждой области, в которой обрабатываются личные данные, и ежегодно проверять этот процесс.
г. Политика архивирования должна учитывать, какие данные должны / должны храниться, как долго и почему.
8. Безопасность
a. Бизнес должен обеспечить безопасное хранение личных данных с использованием современного программного обеспечения, которое поддерживается в актуальном состоянии.
г. Доступ к личным данным должен быть ограничен персоналом, которому необходим доступ, и должна быть обеспечена соответствующая безопасность, чтобы избежать несанкционированного обмена информацией.
г. Когда личные данные удаляются, это следует делать безопасно, чтобы данные нельзя было восстановить.
г. Должны быть в наличии соответствующие решения для резервного копирования и аварийного восстановления.
9. Нарушение
В случае нарушения безопасности, ведущего к случайному или незаконному уничтожению, потере, изменению, несанкционированному раскрытию или доступу к личным данным, Компания должна незамедлительно оценить риск для прав и свобод людей, и если надлежащим образом сообщите об этом нарушении в ICO (более подробная информация на сайте ICO).

 А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
 Чтобы понять, что такое сложение, мы привели пример 5 + 2 = 7, и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.
Чтобы понять, что такое сложение, мы привели пример 5 + 2 = 7, и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.

 числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс
числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс


 Из 13 вычесть сумму чисел 7 и 3
Из 13 вычесть сумму чисел 7 и 3 Если вы не гений математической мысли, конечно.)
Если вы не гений математической мысли, конечно.) Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений — никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. — это всё состоит из математических выражений. Намёк понятен?)
Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений — никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. — это всё состоит из математических выражений. Намёк понятен?) Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»
Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»

 д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.)
д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.) ) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.
) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.)
Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.) Непонятно? Поясняю на несложном примере:
Непонятно? Поясняю на несложном примере: Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.
Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички. А вот из отрицательных — ни в какую!
А вот из отрицательных — ни в какую! Почувствуйте разницу, что называется.)
Почувствуйте разницу, что называется.) Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!
Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!


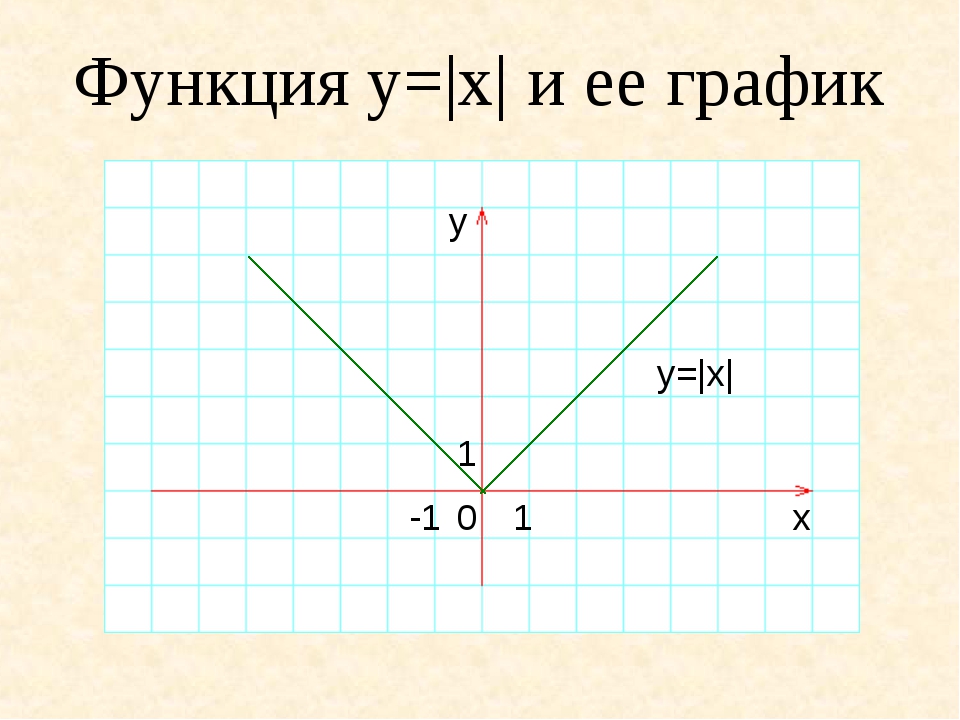 2$, кроме двух точек с $ x \neq \pm 1 $.
2$, кроме двух точек с $ x \neq \pm 1 $. д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).
д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).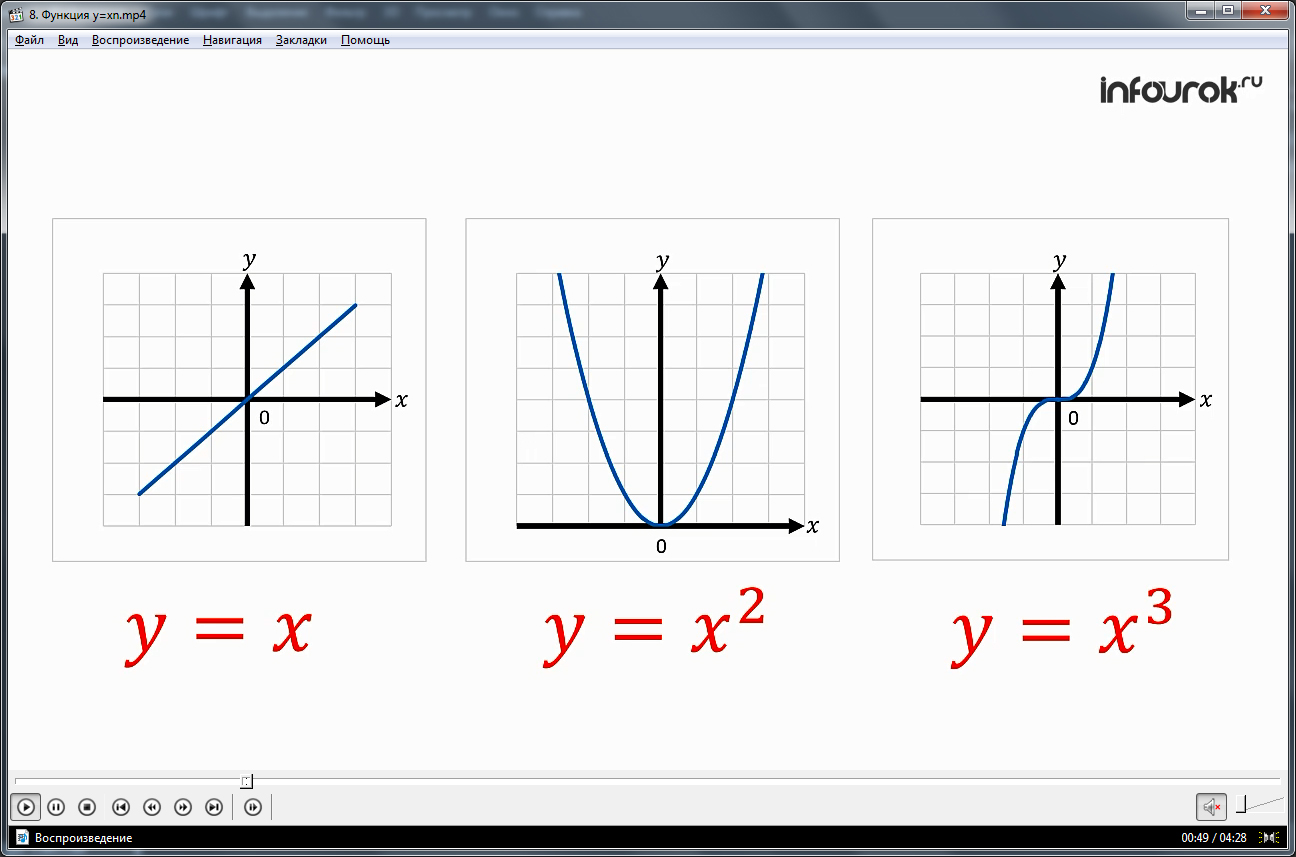 2 , её свойства и график» ( 7 класс)
2 , её свойства и график» ( 7 класс)
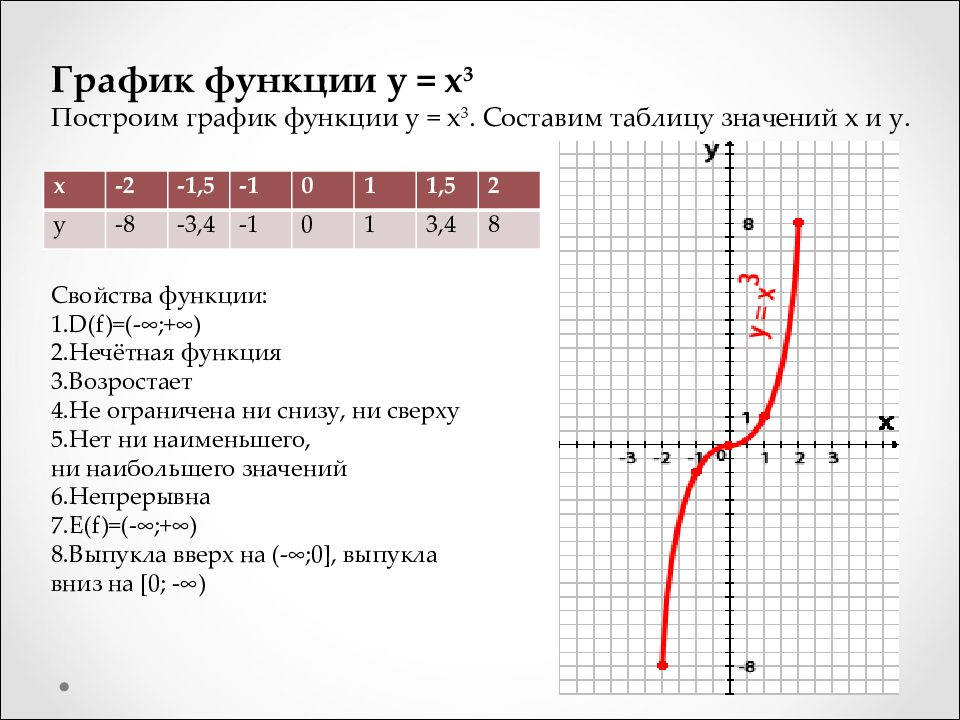 Дана функция
Дана функция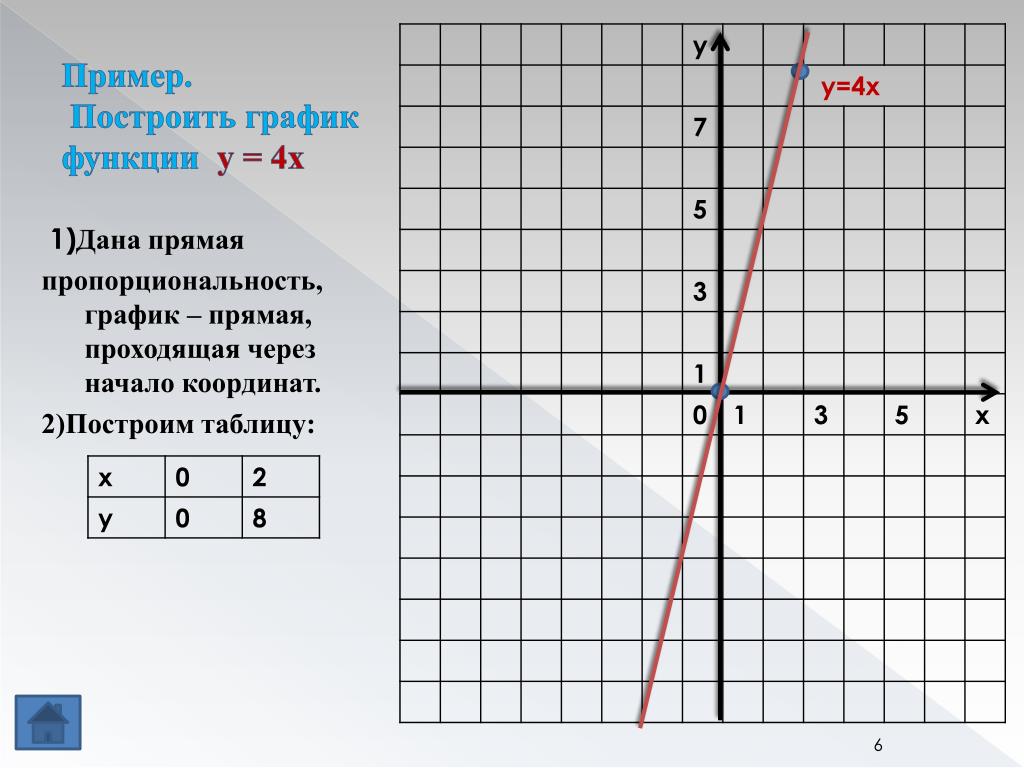 Перенести х из левой части в правую
Перенести х из левой части в правую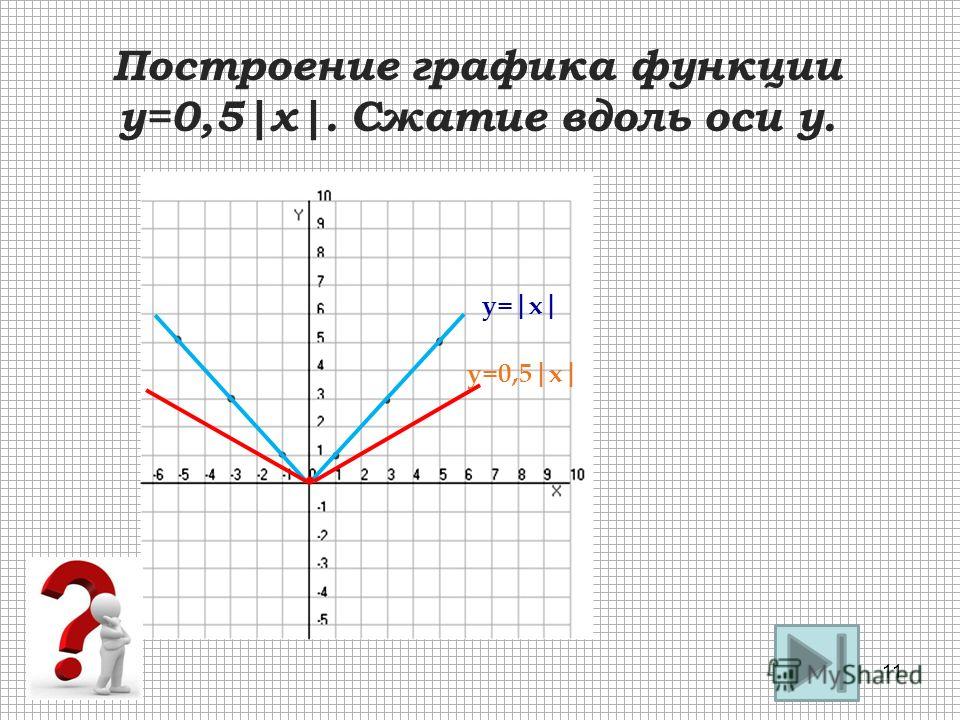
 Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде
Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде 3 дают
3 дают 

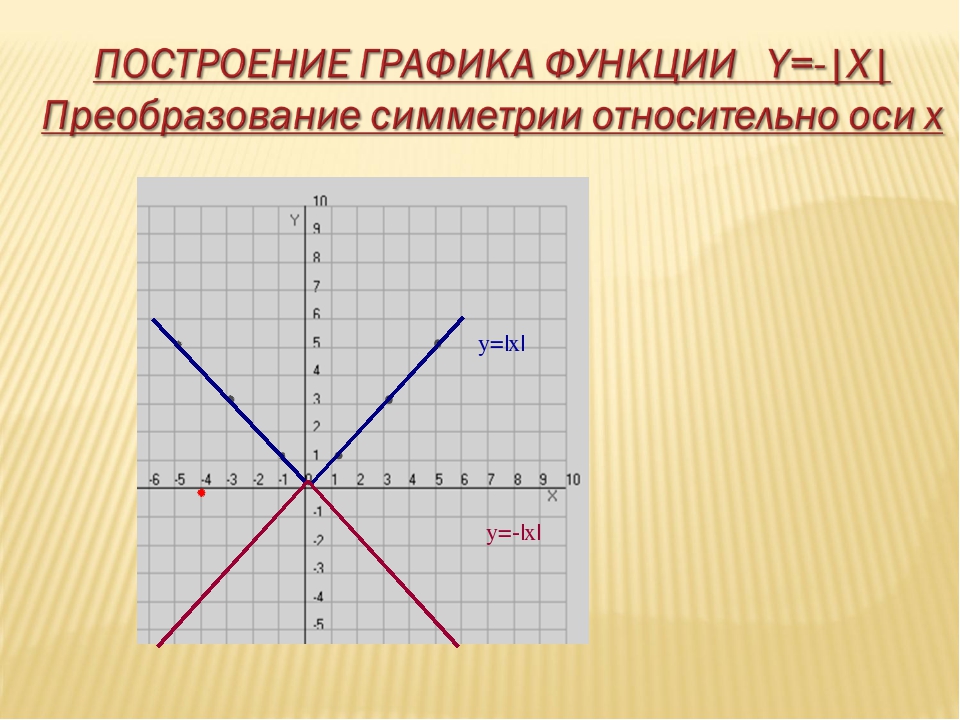
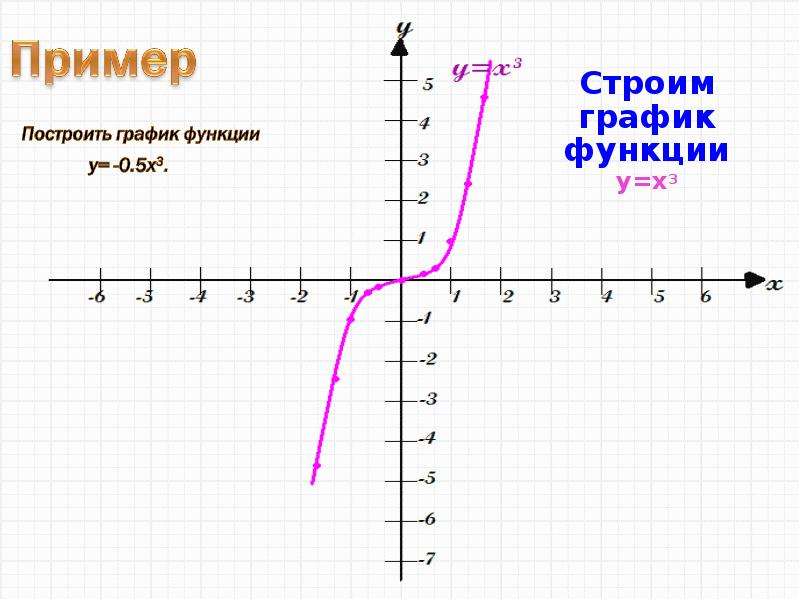
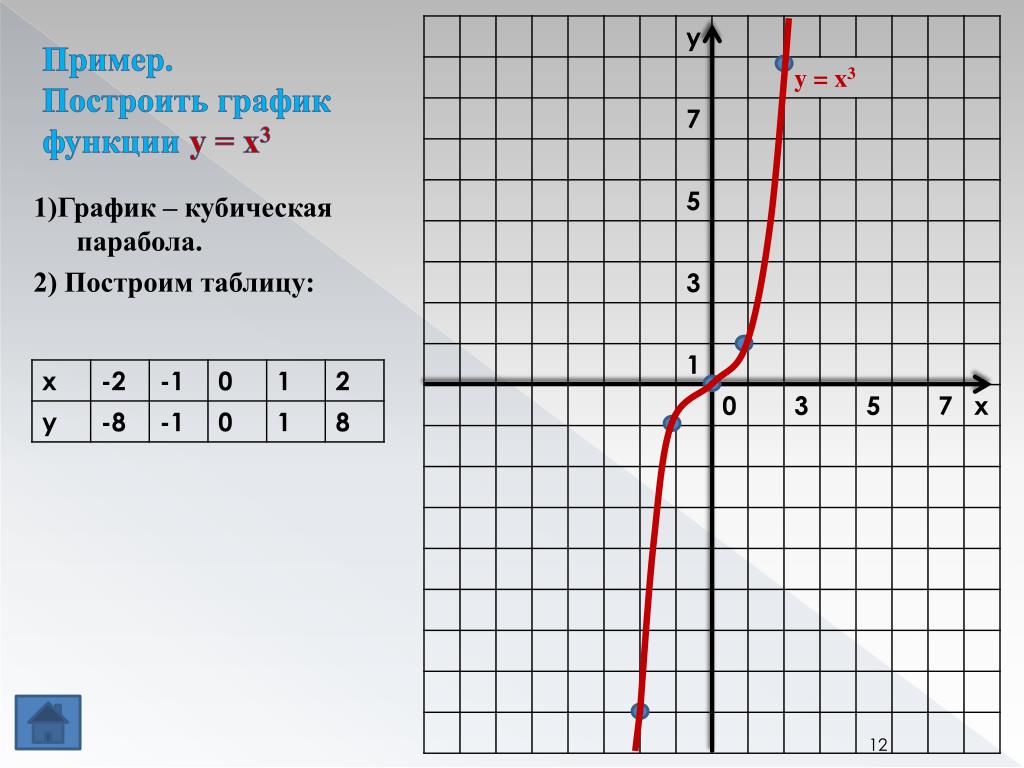

 Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.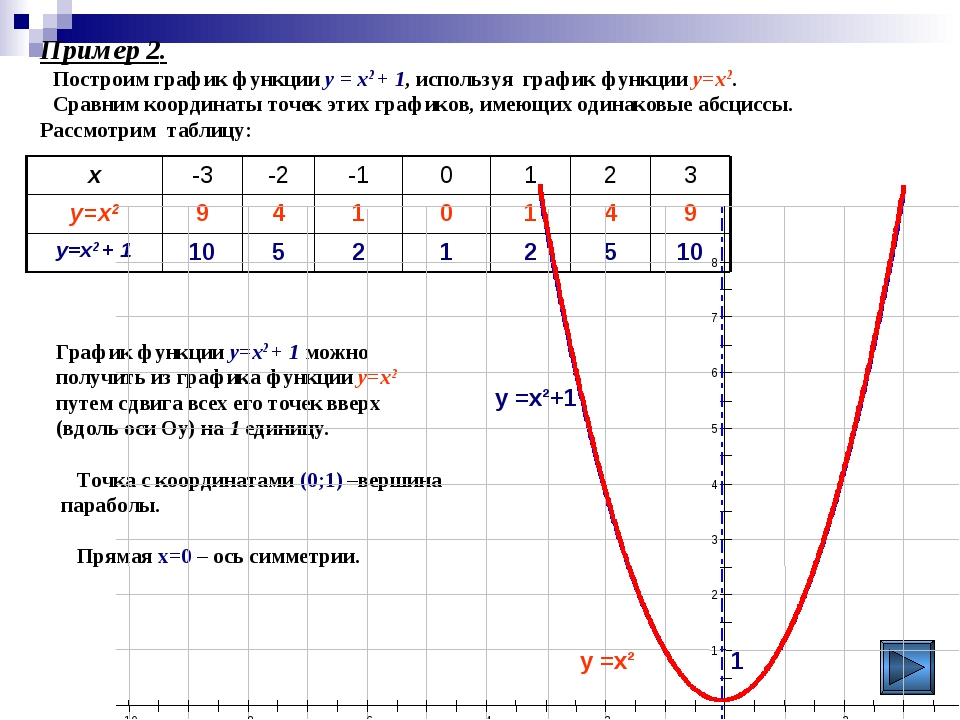
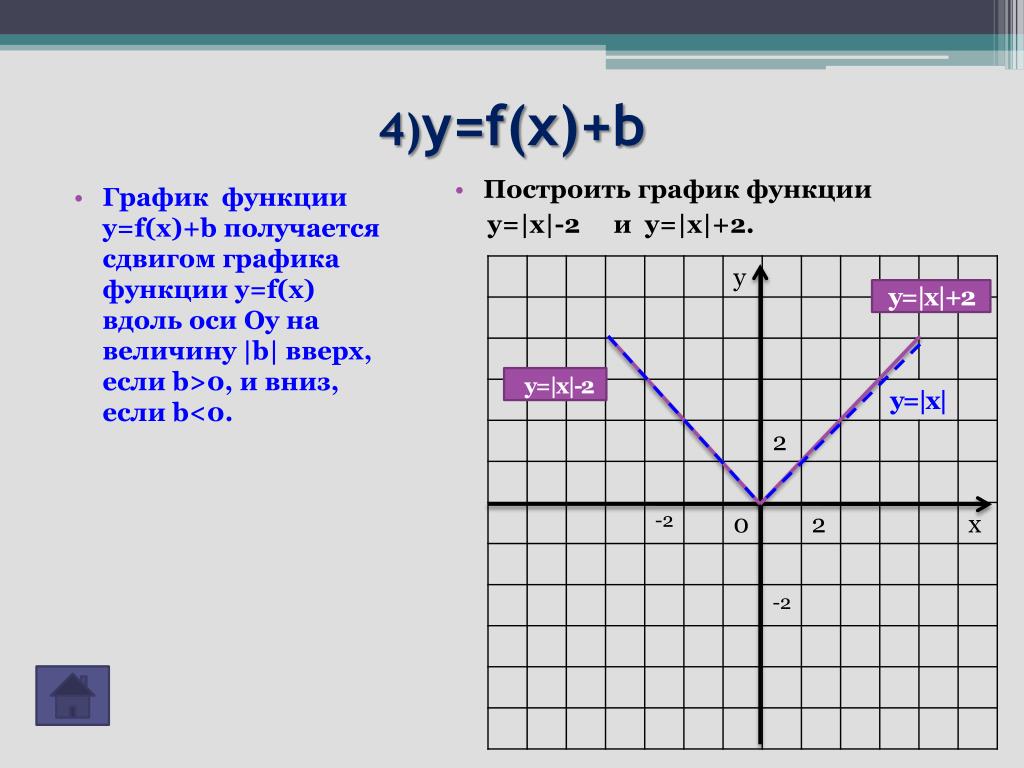 Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю.Чтобы найти точку пересечения y- , мы можем установить x = 0 в уравнении.
Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю.Чтобы найти точку пересечения y- , мы можем установить x = 0 в уравнении.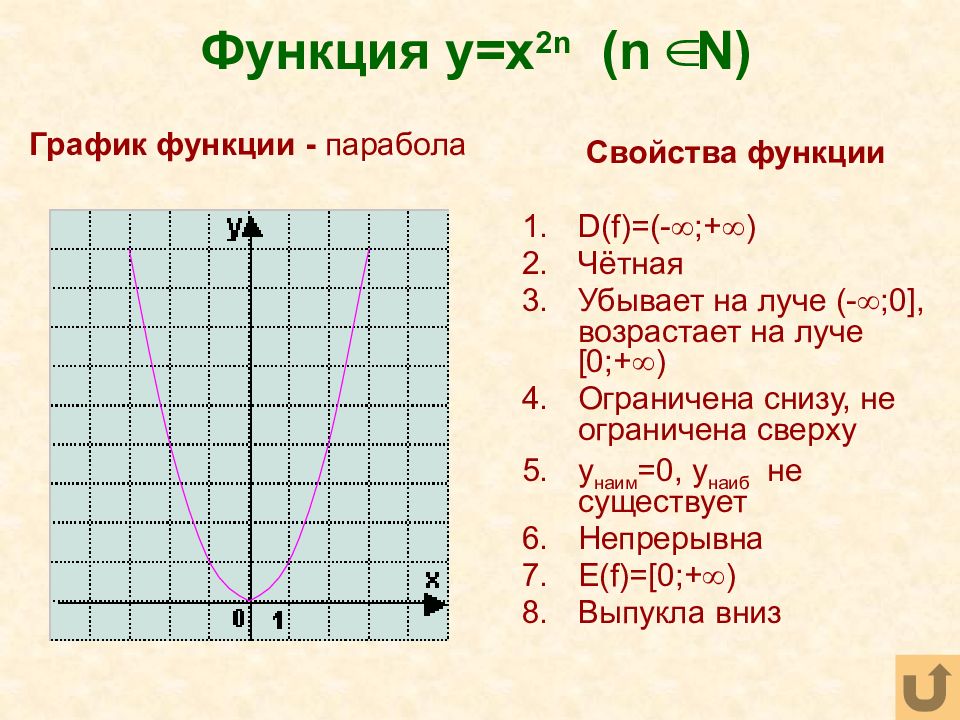 Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и .Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере у нас есть [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Итак, начиная с нашего интервала y (0, 1 ), мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1. Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано на рисунке 2.
Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и .Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере у нас есть [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Итак, начиная с нашего интервала y (0, 1 ), мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1. Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано на рисунке 2.
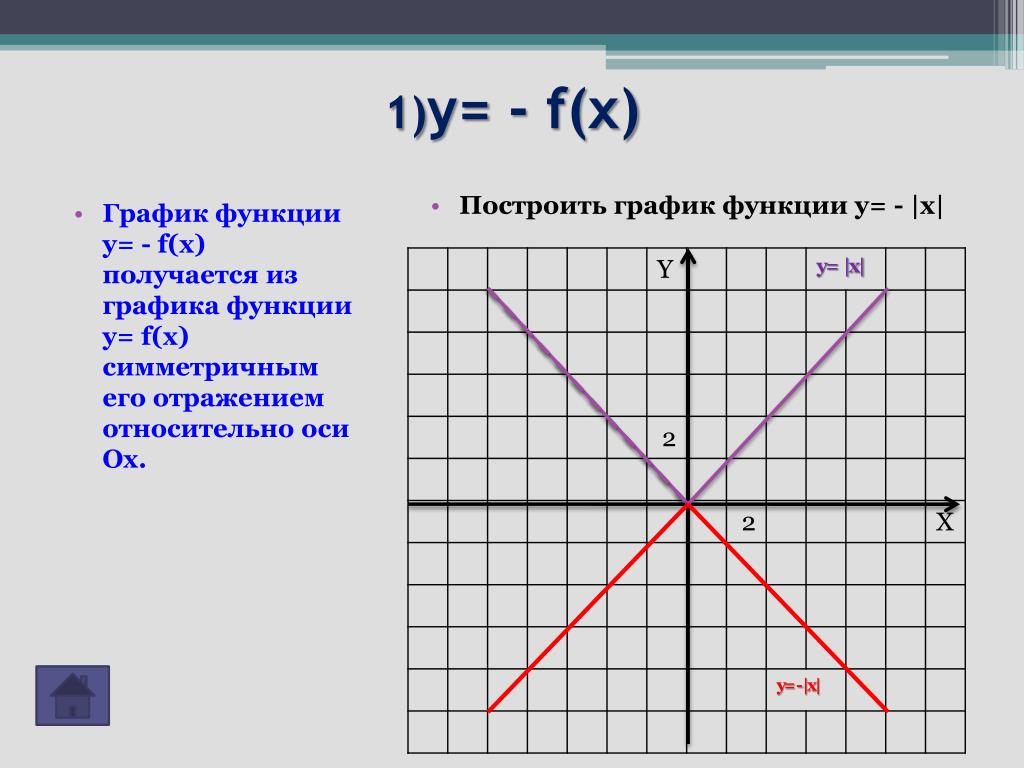
 Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на –2 единицы «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения и на рисунке 3. От начального значения (0, 5) мы переместимся на 2 единицы вниз и на 3 единицы вправо.Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на –2 единицы «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения и на рисунке 3. От начального значения (0, 5) мы переместимся на 2 единицы вниз и на 3 единицы вправо.Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.  Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Функция также может быть преобразована с помощью отражения, растяжения или сжатия. Обратите внимание на рис. 5, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f на b единиц вверх, если b положительный и | b | единиц вниз, если значение b отрицательное.
Обратите внимание на рис. 5, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f на b единиц вверх, если b положительный и | b | единиц вниз, если значение b отрицательное.
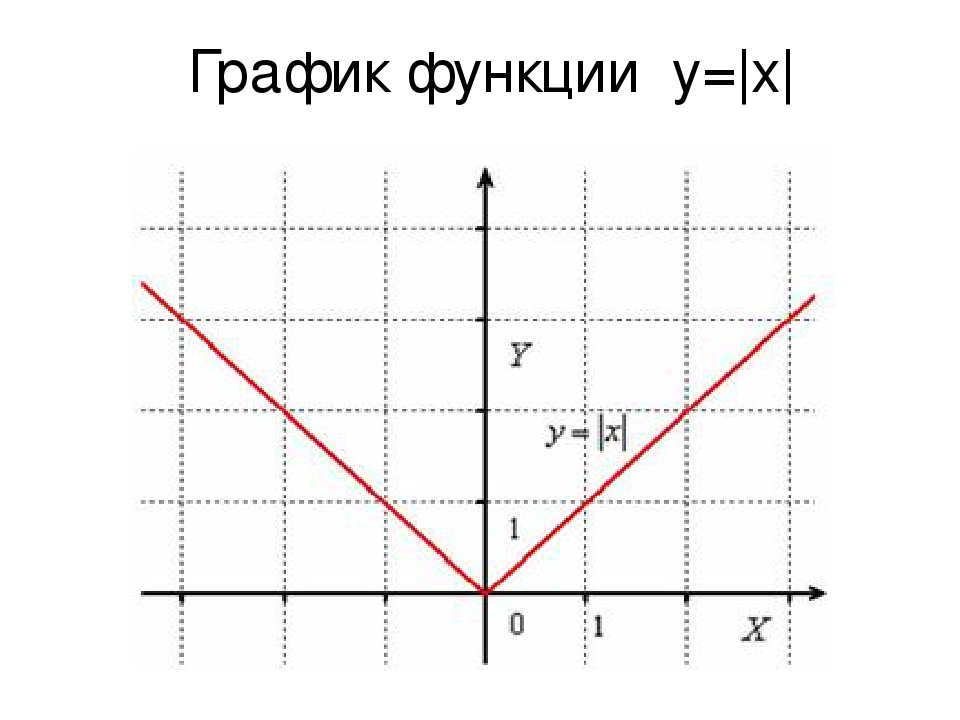
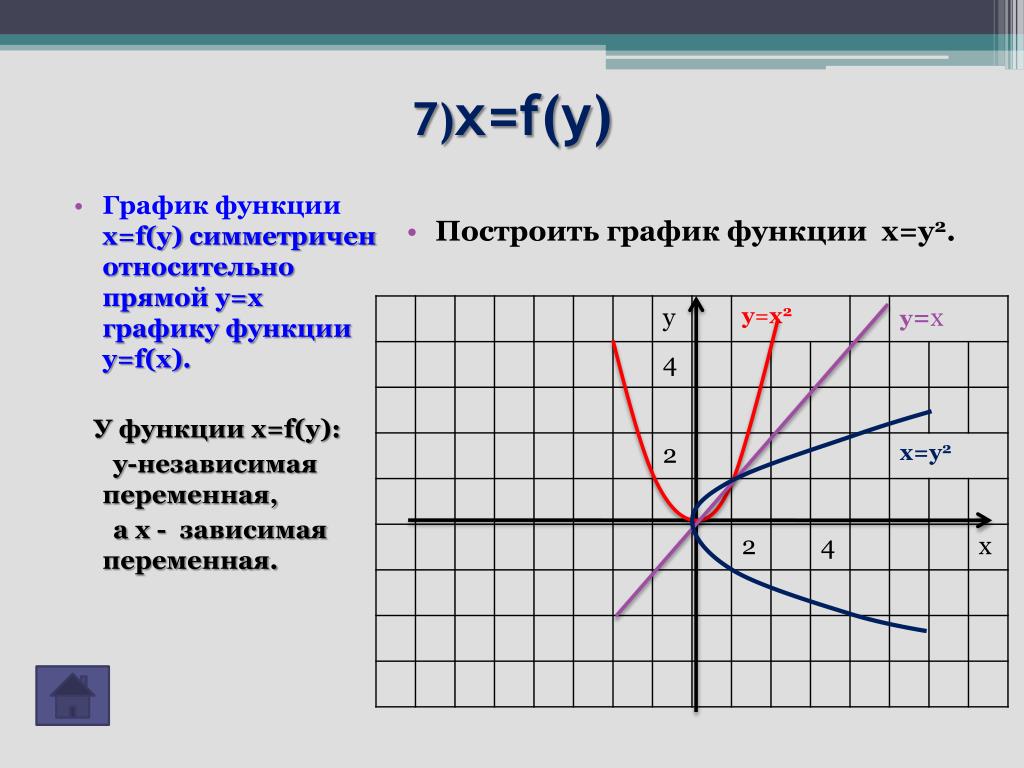 4 из 4)
4 из 4)  Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают.
Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают.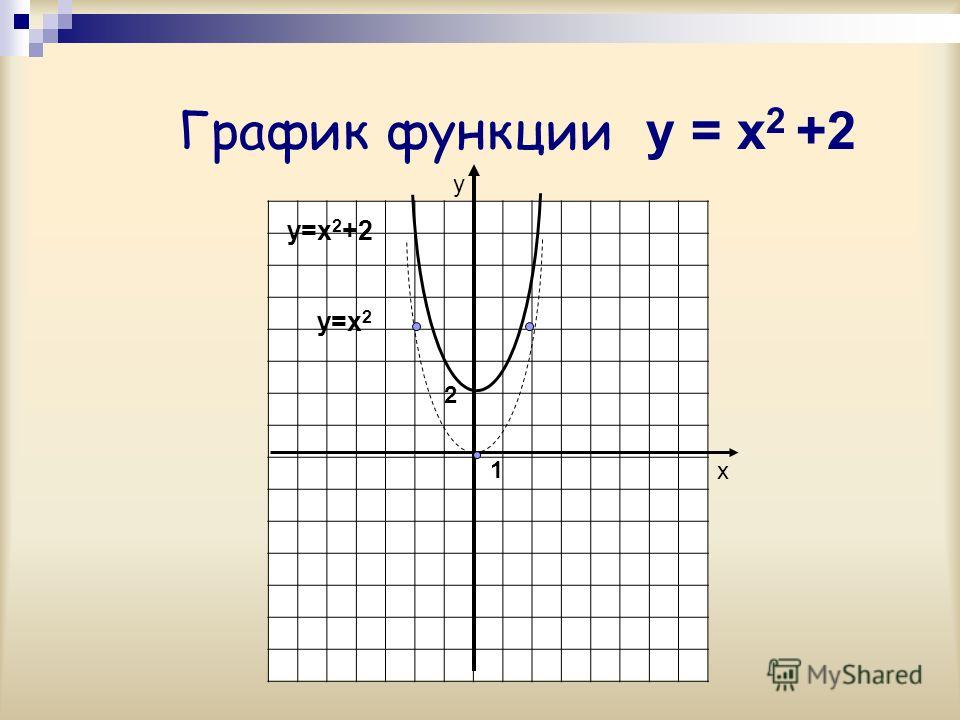 Больной
присоединяйтесь к набранным мною пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии:
Больной
присоединяйтесь к набранным мною пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии: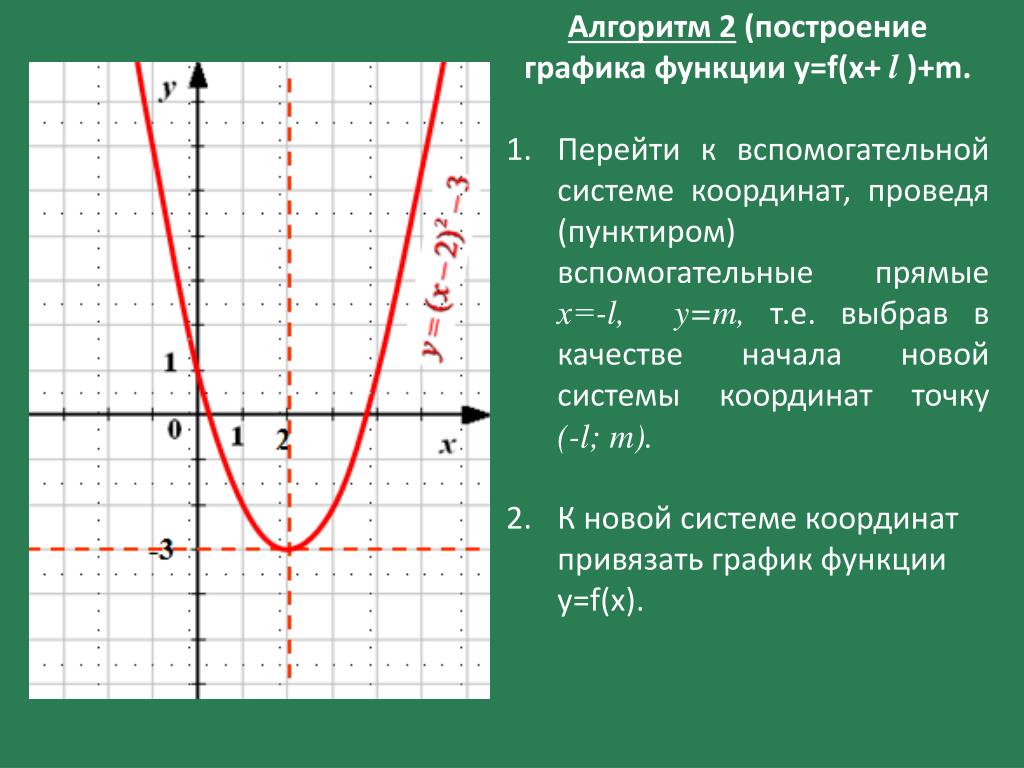 На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением.
На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением. «Графические экспоненциальные функции: примеры». Purplemath .
Доступно по номеру
«Графические экспоненциальные функции: примеры». Purplemath .
Доступно по номеру 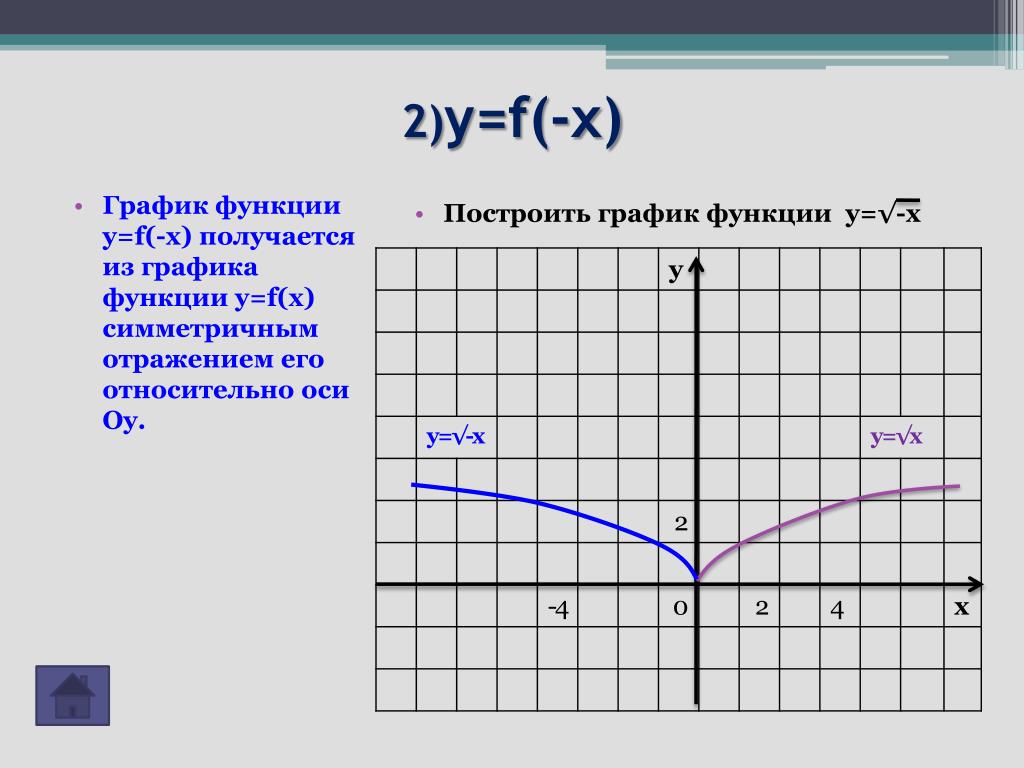 3 здесь
у = х ** 3 # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’) # построить функцию
plt.plot (x, y, ‘g’) # показать сюжет
plt.show ()
3 здесь
у = х ** 3 # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’) # построить функцию
plt.plot (x, y, ‘g’) # показать сюжет
plt.show ()  set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
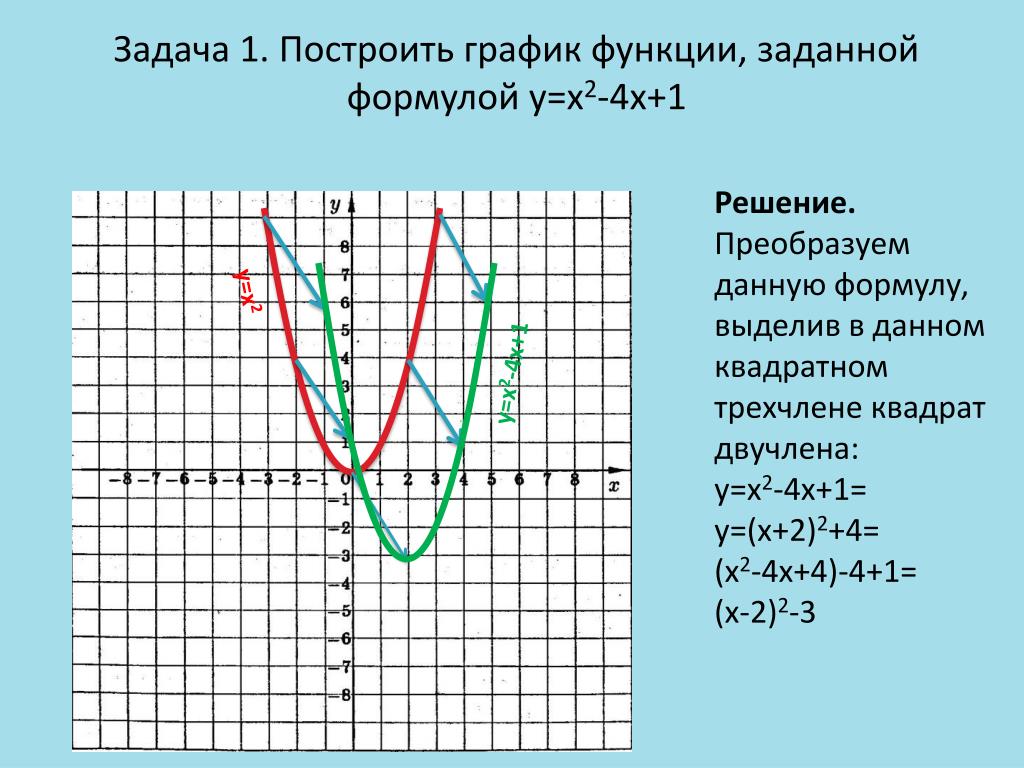 plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
 Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько точек пересечения по оси x. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции.Вы также можете прокрутить вниз до примера видео ниже.
Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько точек пересечения по оси x. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции.Вы также можете прокрутить вниз до примера видео ниже.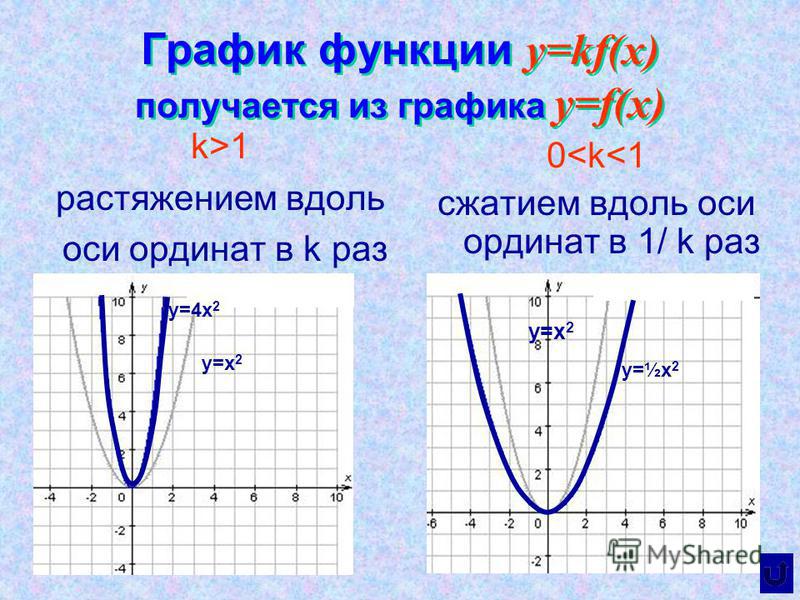


 Это способность
что делает возможным понимание математики. Если бы вы запомнили каждый кусок
математика, представленная вам без связи с другими частями, вы 1) станете
разочарован в математике и 2) не очень понимаю математику.
Это способность
что делает возможным понимание математики. Если бы вы запомнили каждый кусок
математика, представленная вам без связи с другими частями, вы 1) станете
разочарован в математике и 2) не очень понимаю математику.
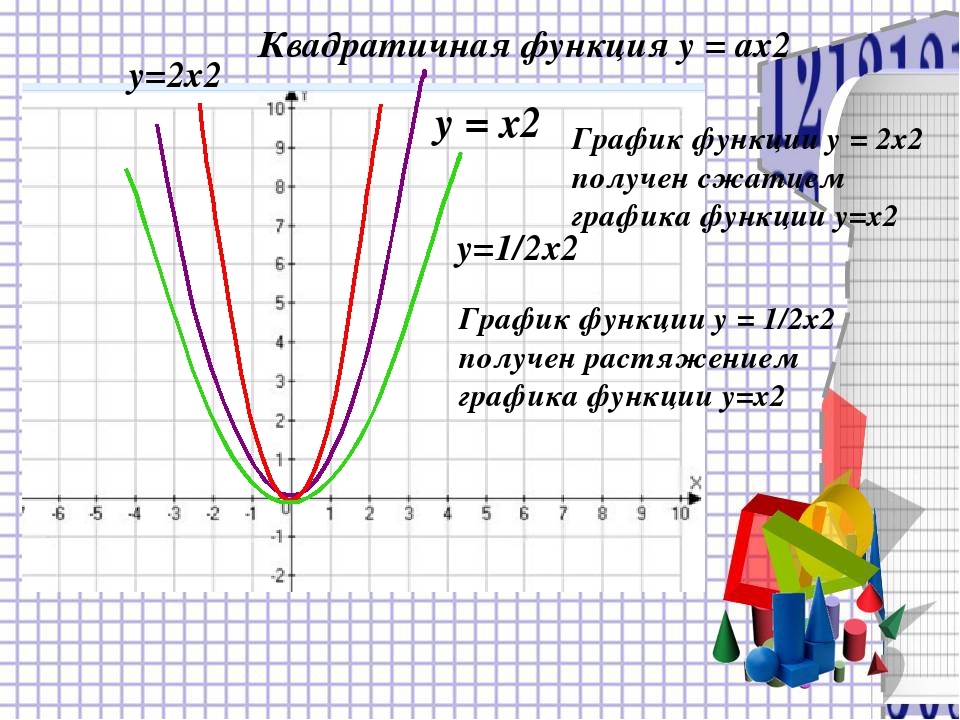 Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.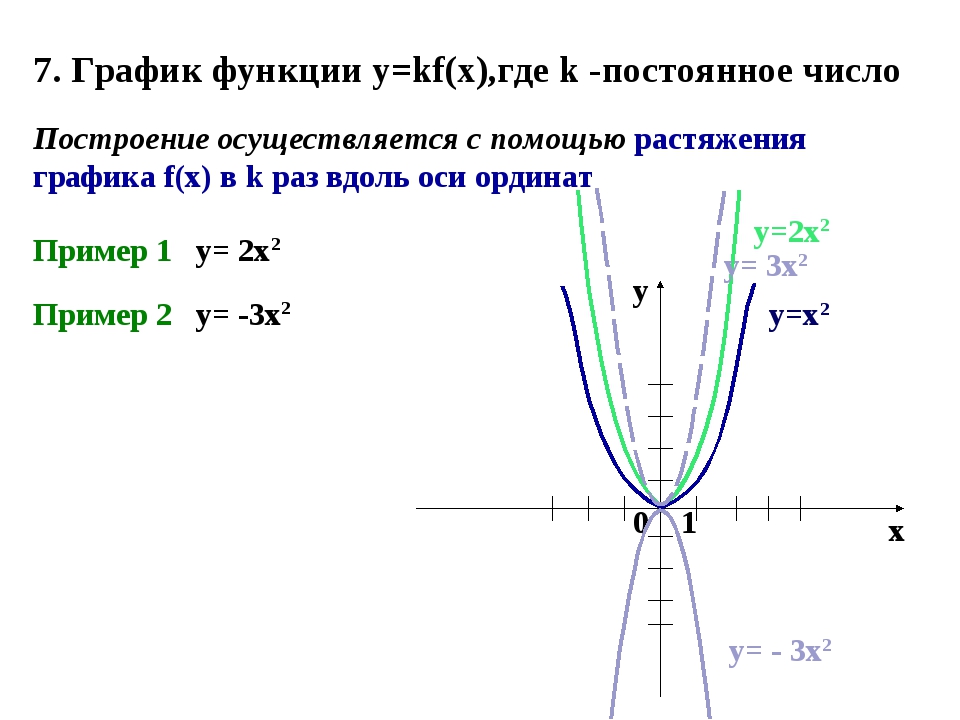
 Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190). множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
 «X минус c» на самом деле означает прибавление c к каждой координате x.
«X минус c» на самом деле означает прибавление c к каждой координате x. Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.
Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.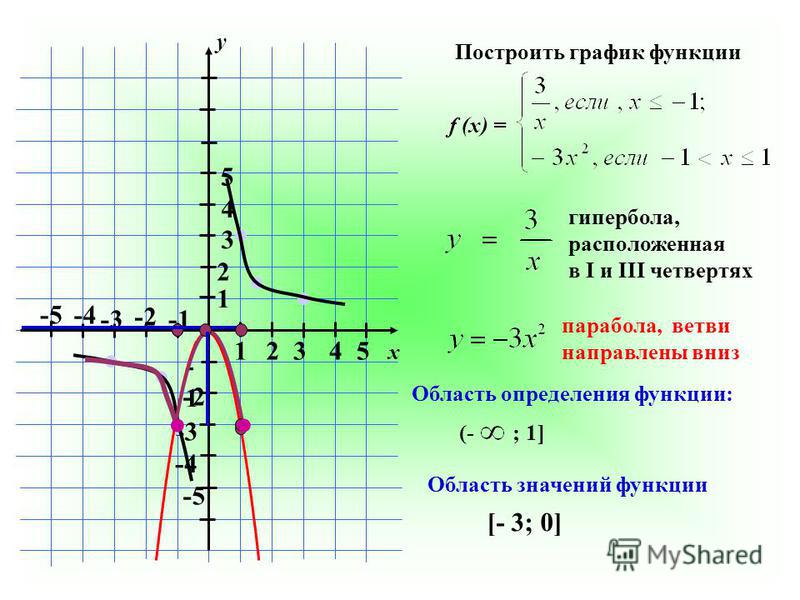
 играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.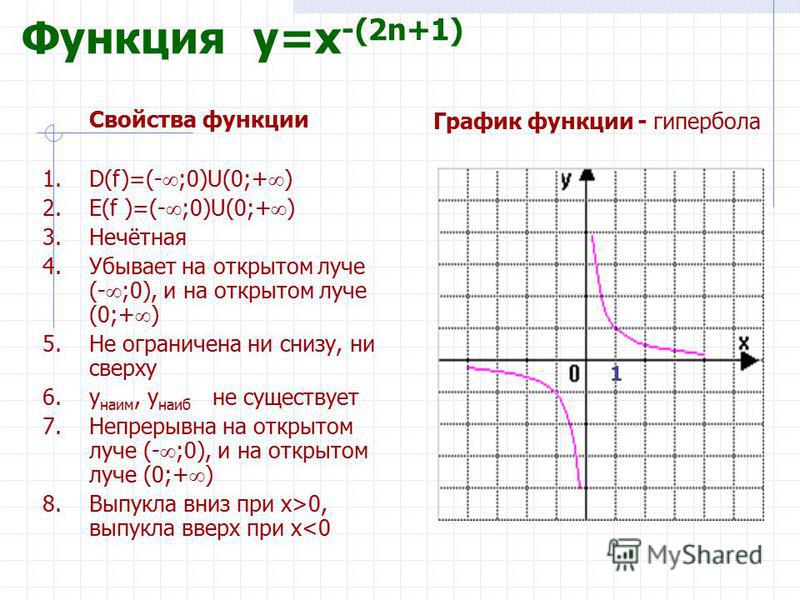
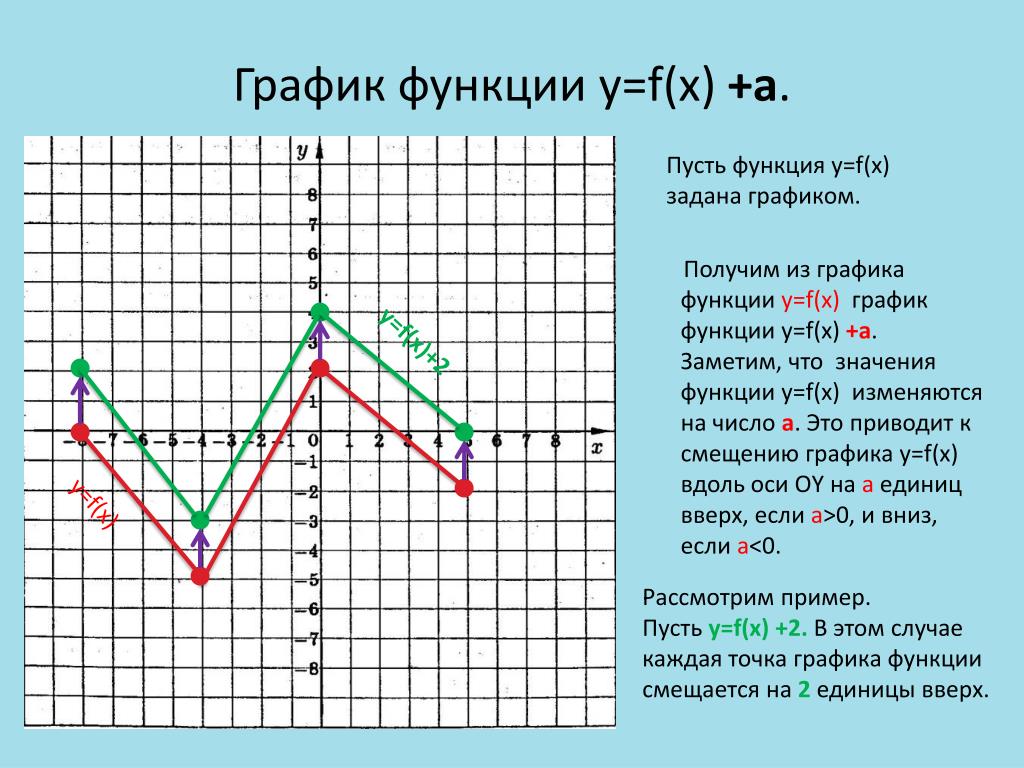
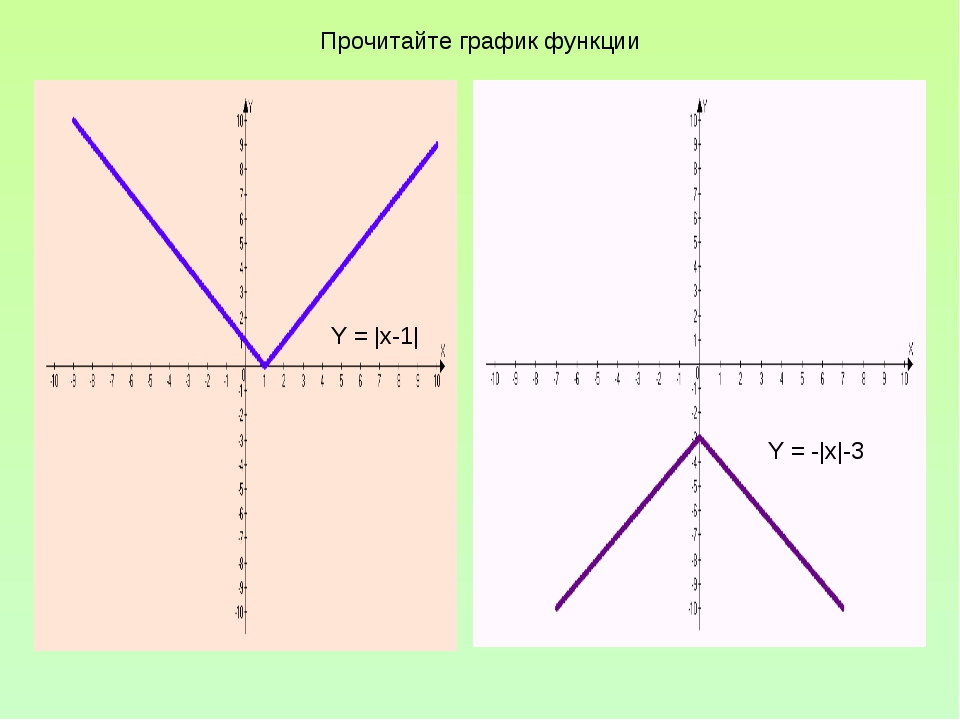
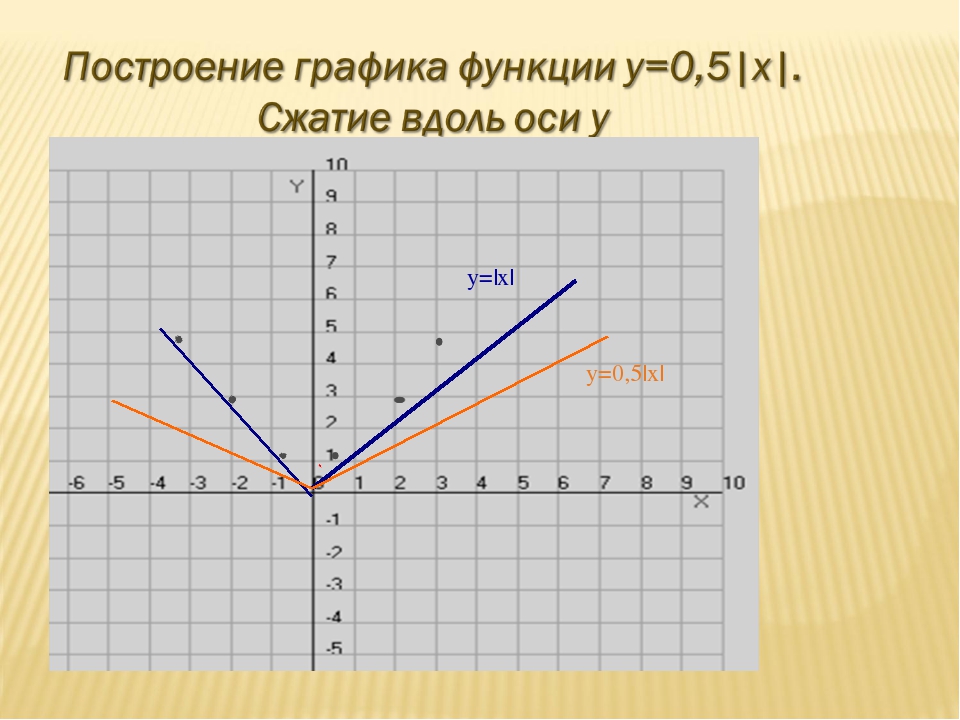 Разве оба уравнения не являются одинаковыми после упрощения второго? И разве производные каждого из них не одинаковы?
Разве оба уравнения не являются одинаковыми после упрощения второго? И разве производные каждого из них не одинаковы? 2} = \ sqrt {1} = \ pm1
\ end {align}
$
2} = \ sqrt {1} = \ pm1
\ end {align}
$ 2 = 4
$$
вы извлекаете квадратный корень с обеих сторон и в итоге получаете
$$
\ верт х \ верт = 2
$$
и есть два числа, которые находятся на расстоянии два от $ 0 $. Итак, вы получаете
$$
х = \ pm 2.
$$
ОП уже принял ответ, я просто попытался дать более «алгебраическую» точку зрения на смесь.
2 = 4
$$
вы извлекаете квадратный корень с обеих сторон и в итоге получаете
$$
\ верт х \ верт = 2
$$
и есть два числа, которые находятся на расстоянии два от $ 0 $. Итак, вы получаете
$$
х = \ pm 2.
$$
ОП уже принял ответ, я просто попытался дать более «алгебраическую» точку зрения на смесь.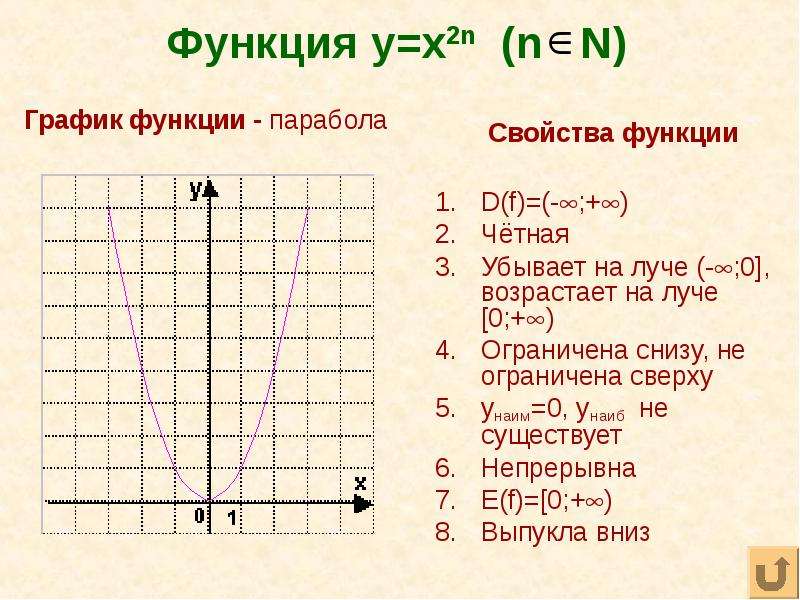
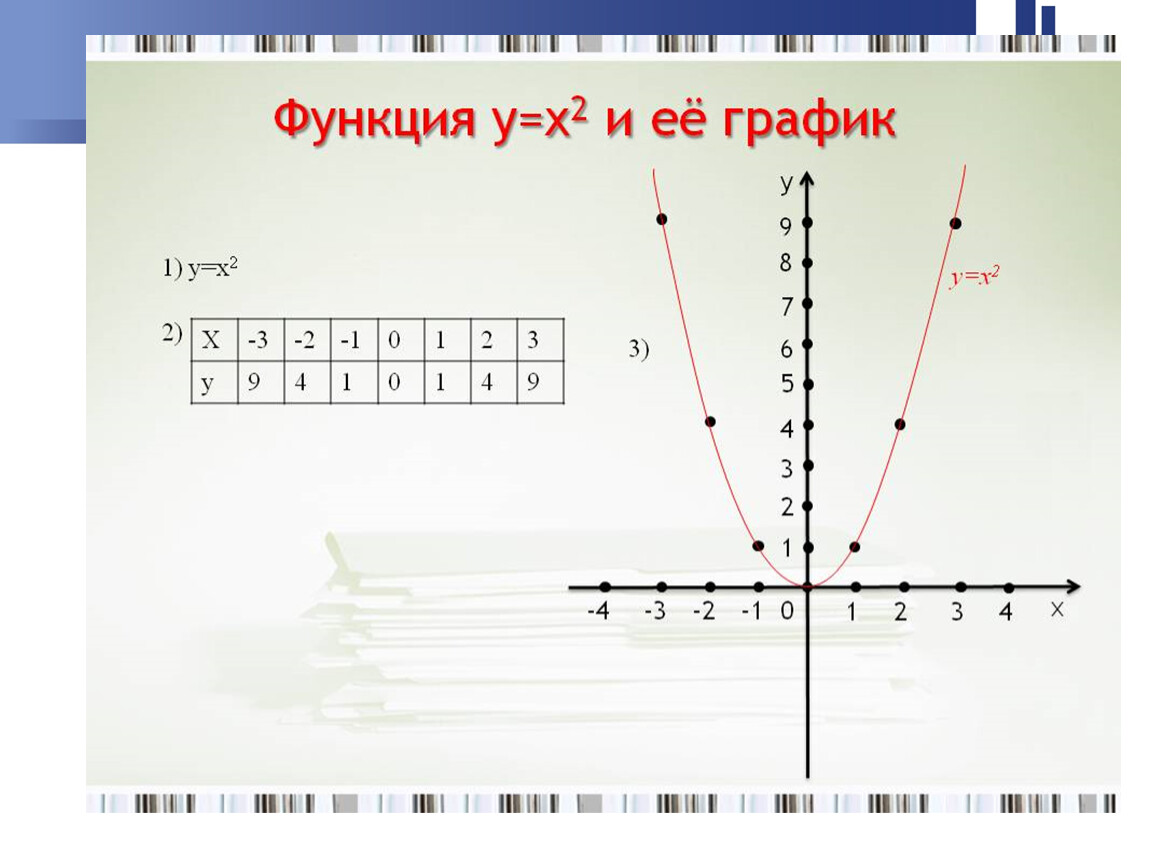 Она называется постоянной функцией, потому что каждому значению x соответствует одно и то же значение y : 3.
Она называется постоянной функцией, потому что каждому значению x соответствует одно и то же значение y : 3.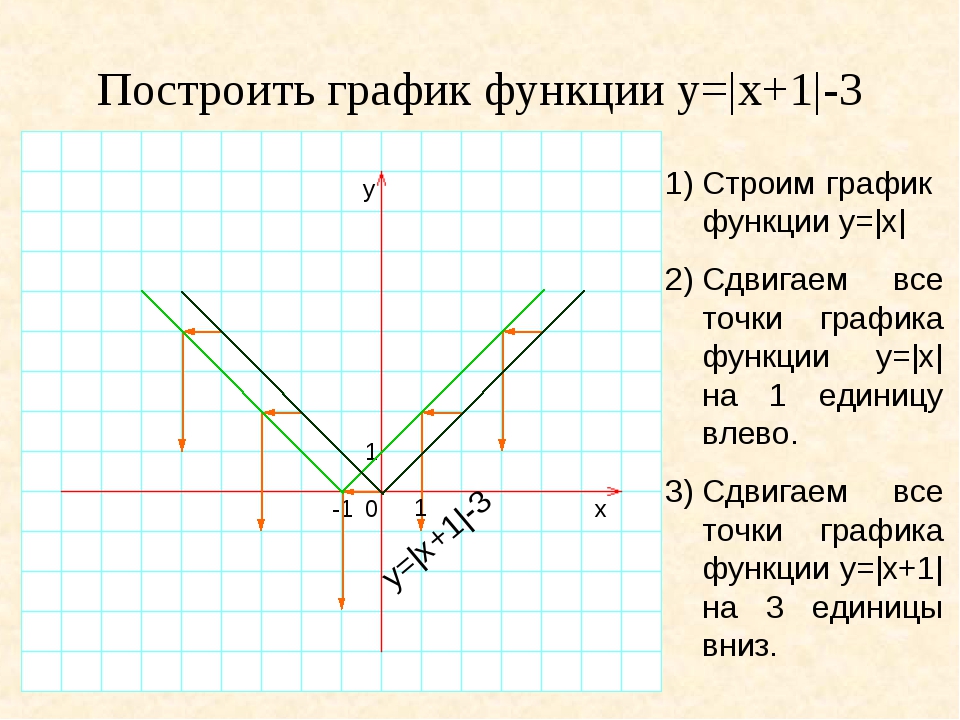 Следовательно, область, в которой «живет» функция, включает каждое действительное число.
Следовательно, область, в которой «живет» функция, включает каждое действительное число. 46. Клавиша Shift
46. Клавиша Shift 48. Инструменты рисования на панели инструментов
48. Инструменты рисования на панели инструментов 50. Рисование линии
50. Рисование линии | Рисуем вместеОпубликовано 01 Фев 2011 в рубрике «Уроки рисования»
| Рисуем вместеОпубликовано 01 Фев 2011 в рубрике «Уроки рисования» И так далее. В результате, на рисунок, который можно сделать за час, тратилось невероятно много времени, не говоря о том, что выглядел он очень замученным… Это, если у человека оставались силы закончить.
И так далее. В результате, на рисунок, который можно сделать за час, тратилось невероятно много времени, не говоря о том, что выглядел он очень замученным… Это, если у человека оставались силы закончить. Не стремитесь к идеально ровным, как по линеечке, прямым. Важно закрепить правильное движение — чем увереннее будет двигаться рука, тем уверенней будут линии.
Не стремитесь к идеально ровным, как по линеечке, прямым. Важно закрепить правильное движение — чем увереннее будет двигаться рука, тем уверенней будут линии.





 Впервые такой формат общения президента с гражданами на общенациональных теле- и радиоканалах был организован 24 декабря 2001 года. В дальнейшем прямые линии проходили ежегодно, за исключением 2004 и 2012 годов. Всего Владимир Путин участвовал в 16 передачах, из них 12 раз в качестве главы государства и четыре как председатель правительства. По словам президента, «прямые контакты с гражданами дают очень верный срез того, что на данный момент времени волнует и интересует общество».
Впервые такой формат общения президента с гражданами на общенациональных теле- и радиоканалах был организован 24 декабря 2001 года. В дальнейшем прямые линии проходили ежегодно, за исключением 2004 и 2012 годов. Всего Владимир Путин участвовал в 16 передачах, из них 12 раз в качестве главы государства и четыре как председатель правительства. По словам президента, «прямые контакты с гражданами дают очень верный срез того, что на данный момент времени волнует и интересует общество». Регистрация в нем доступна автоматически через личный аккаунт в социальных сетях. Кроме того, видеообращения можно направить и со стационарного компьютера через сайты единого центра. С 2016 года вопросы главе государства поступают также через официальную группу в социальной сети «ВКонтакте», которая также ведет трансляцию прямой линии. С 2017 года аналогичная возможность появилась в социальной сети «Одноклассники». С авторами отобранных для программы вопросов связываются редакторы программы.
Регистрация в нем доступна автоматически через личный аккаунт в социальных сетях. Кроме того, видеообращения можно направить и со стационарного компьютера через сайты единого центра. С 2016 года вопросы главе государства поступают также через официальную группу в социальной сети «ВКонтакте», которая также ведет трансляцию прямой линии. С 2017 года аналогичная возможность появилась в социальной сети «Одноклассники». С авторами отобранных для программы вопросов связываются редакторы программы. ). Кроме того, в разные годы телестанции работали в ближнем зарубежье: в 2002 году — в Душанбе (Таджикистан), в 2003 году — на российской авиабазе в городе Кант (Киргизия), в 2005 году — в Риге (Латвия), в 2007 году — в Актау (Казахстан). Всего за 2011-2018 годы в эфире прямых линий было свыше 110 прямых включений из регионов России и государств — бывших республик СССР.
). Кроме того, в разные годы телестанции работали в ближнем зарубежье: в 2002 году — в Душанбе (Таджикистан), в 2003 году — на российской авиабазе в городе Кант (Киргизия), в 2005 году — в Риге (Латвия), в 2007 году — в Актау (Казахстан). Всего за 2011-2018 годы в эфире прямых линий было свыше 110 прямых включений из регионов России и государств — бывших республик СССР.
 510.SS.060406)
510.SS.060406) Торцевая пробка
Торцевая пробка Торцевая пробка
Торцевая пробка
 На ее счету 21 титул WTA, в том числе две победы на Открытом чемпионате Австралии (2012, 2013).
На ее счету 21 титул WTA, в том числе две победы на Открытом чемпионате Австралии (2012, 2013).





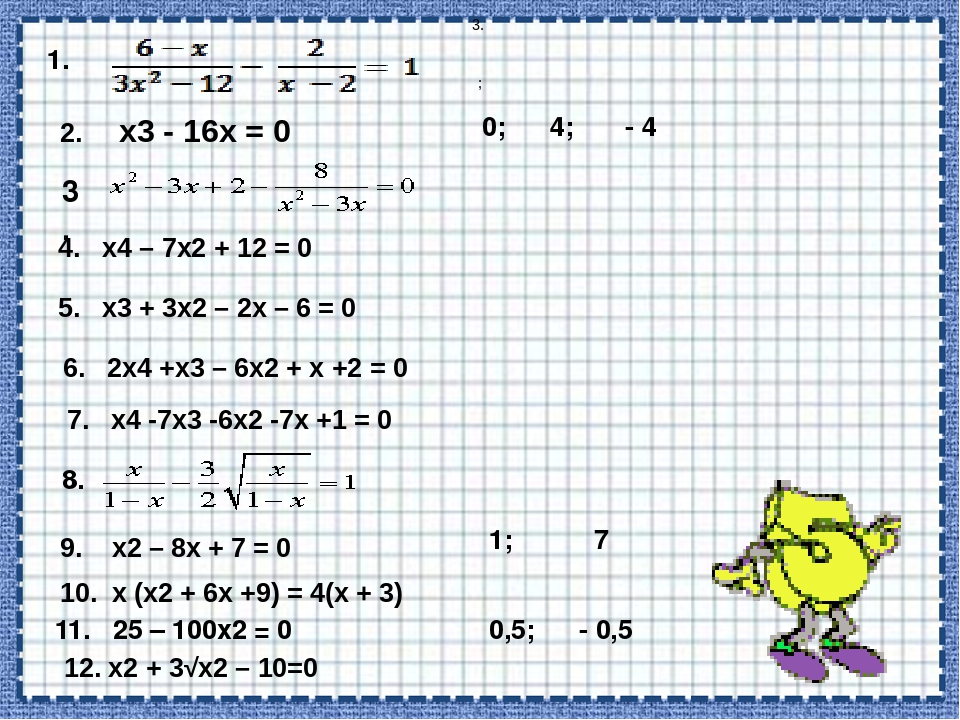 com/wall-141593176_843
com/wall-141593176_843 Между тем героическая оборона Кавказа имела не менее важное значение.
Между тем героическая оборона Кавказа имела не менее важное значение.
 Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода. В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел. По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик. 984375
984375 21875
21875 34375
34375 46875
46875 59375
59375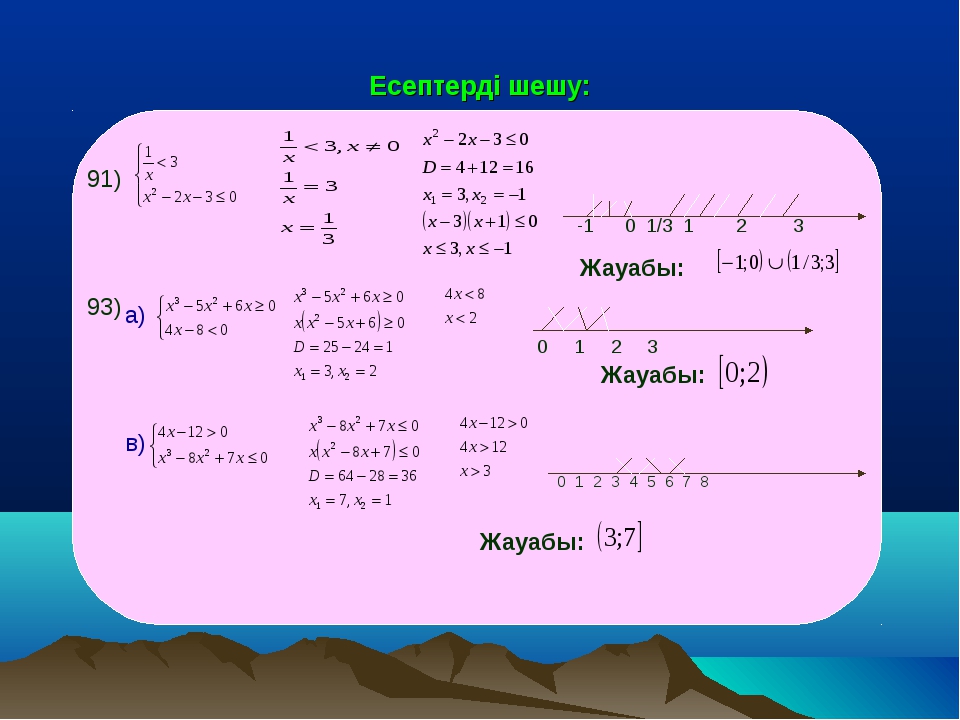 71875
71875 84375
84375 209375
209375


 Их объединяет действие — умножение.
Их объединяет действие — умножение.
 Давайте решать вместе!
Давайте решать вместе!


 При этом, как показывает практика, самое сложное – это правильно составить уравнение.
При этом, как показывает практика, самое сложное – это правильно составить уравнение.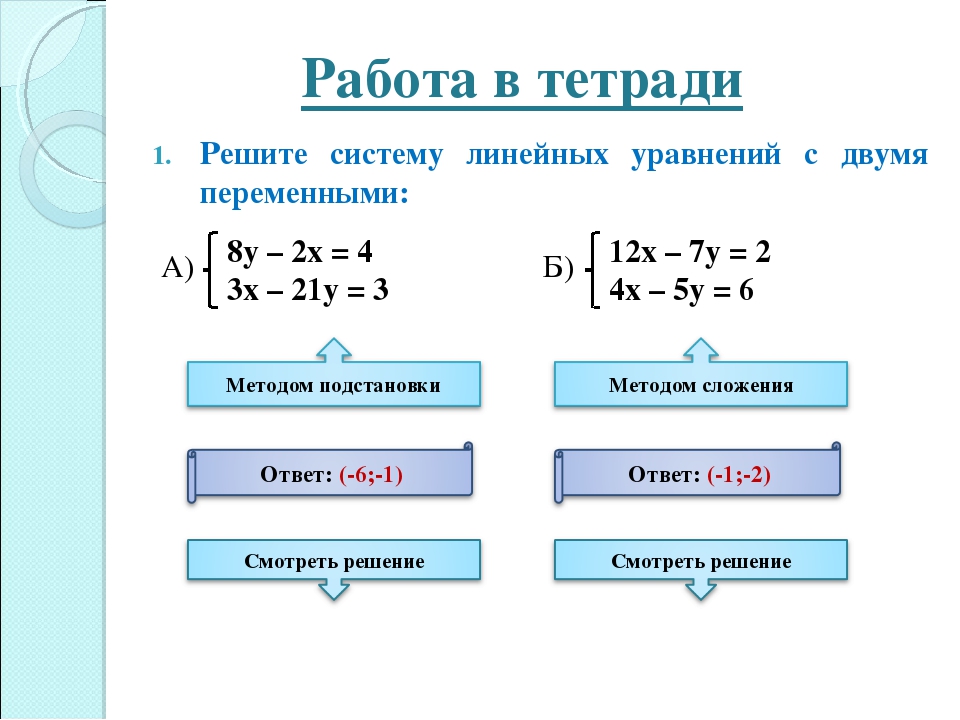 За 11 часов он пройдет (х-2)*11 км.
За 11 часов он пройдет (х-2)*11 км.

 Линейное уравнение представляет собой алгебраическое уравнение, полная
степень многочленов которого равна единице. Существует множество способов решения данных уравнений. Чтобы
решить уравнения данного рода необходимо найти значение переменной. Сделать это можно с помощью простых
правил переноса и несложных математических операций. Если решаемое вами уравнение находится в общем виде, то
все решение сводится к переносу неизвестной в левую сторону, а чисел в правую.
Линейное уравнение представляет собой алгебраическое уравнение, полная
степень многочленов которого равна единице. Существует множество способов решения данных уравнений. Чтобы
решить уравнения данного рода необходимо найти значение переменной. Сделать это можно с помощью простых
правил переноса и несложных математических операций. Если решаемое вами уравнение находится в общем виде, то
все решение сводится к переносу неизвестной в левую сторону, а чисел в правую.
 \)
Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений.
Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились.
Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:
\)
Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений.
Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились.
Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров: 2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ.
2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
 В таком случае говорят, что пара чисел x=8 и y=3 является решением линейного уравнения x-y=5. Еще можно говорить, что пара чисел x=8 и y=3 удовлетворяет линейному уравнению x-y=5.
В таком случае говорят, что пара чисел x=8 и y=3 является решением линейного уравнения x-y=5. Еще можно говорить, что пара чисел x=8 и y=3 удовлетворяет линейному уравнению x-y=5. То есть существует бесконечно много различных двух чисел х и у, которые обращают линейное уравнение в верное тождество.
То есть существует бесконечно много различных двух чисел х и у, которые обращают линейное уравнение в верное тождество. 2 Решение линейных уравнений
2 Решение линейных уравнений 
 2)
2) Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
