Задачи на совместную работу как решать: Задачи на совместную работу. ЕГЭ по математике – Подбор задач на совместную работу и производительность
Конспект урока по математике «Задачи на совместную работу»
5 класс
Открытый урок по математике (ФГОС)
Автор: Турава Наталья Анатольевна,
учитель математики МОУ «Новомичуринская СОШ № 2» Пронского района Рязанской области
Тема: «Задачи на совместную работу»
Тип урока: открытие новых знаний.
Образовательные технологии: технология деятельностного метода.
Основные цели:
сформировать умение решать задачи на совместную работу по формуле и с использованием таблицы в простейших случаях;
повторить и закрепить понятие степени числа, навыки вычисления в дробных выражениях.
Планируемые результаты:
Личностные
— развивать умение слушать; ясно, точно, громко излагать свои мысли в устной и письменной речи;
— развивать креативность мышления, инициативу, находчивость, активность при решении математических задач;
— формулировать представления о математике как способе познания.
Метапредметные: развивать умение видеть математическую задачу в конспекте проблемной ситуации в других дисциплинах, в окружающей жизни; формировать умение работать в группах.
Предметные: развивать умение работать с математическим текстом (анализировать, извлекать необходимою информацию).
Формы работы учащихся: групповая, индивидуальная.
Учебник: Математика, 5 класс Дорофеев Г.В., Петерсон Л.Г. «Математика, 5» — М. : Ювента, 2013.
Оборудование: компьютер, интерактивная доска, доска магнитная, ½ листа ватмана с приклеенными полосками двустороннего скотча.
Демонстрационные материалы: презентация, фрагмент мультфильма,шаги алгоритма, задачи на части(схемы).Приложение
Раздаточный материал: таблицы пустые 4 шт. для каждого ученика, цветные полоски для проведения рефлексии(по три цвета для каждого), маркеры( 1 на стол)
Содержание:
Этап урока
Деятельность учителя
1. Мотивация и самоопределение к учебной деятельности
Посмотрите всё ль в порядке ?
Книжка, ручка и тетрадка?
Все ли правильно сидят ?
Все ли правильно глядят ?
Прозвенел сейчас звонок –
начинается урок !
—Ребята! Сегодняшний урок я предлагаю вам провести в деревне Простоквашино с любимыми героями российского мультфильма.
-Откройте тетради, запишите дату, «Классная работа».
Записывают в тетрадях дату и «Классная работа».
-А начать урок я хочу словами французского философа и математика Рене Декарта:
«Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать»
-Как вы думаете, почему он так сказал? Нам с вами нужно уметь размышлять?
-Потому что простое заучивание приносит меньше пользы, чем то знание, до которого додумываешься сам.
-Правильно. Если бы люди не размышляли, то никогда не сделали великих открытий — не полетели бы в космос, не изобрели бы компьютера и т. д.
-Поэтому нам с вами нужно уметь размышлять.
А вы хотите узнавать новое?
А как считаете,сможете это сделать?
2. Актуализация и фиксирование индивидуального затруднения в пробном действии
-Чтобы узнать что-нибудь новое, надо вспомнить старые знания, которые пригодятся нам для открытия нового знания.
— Угадайте ключевое слово всех наших последних занятий. У меня есть три подсказки:
В словаре С.И. Ожегова о нем написано так:
– это частые прерывистые звуки…;
– это мелкие свинцовые шарики для стрельбы из охотничьего ружья…;
– она может быть правильной или неправильной, обыкновенной или десятичной.
Это слово: ДРОБЬ.
—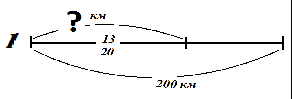
Решим несколько задач на дроби по готовым схемам: (схемы вывешиваю на магнитах на доску)
(остальные работают в тетрадях)
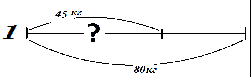
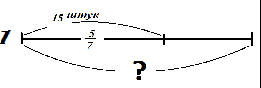
-Теперь вспомним как решать небольшие дробные выражения:(вывешиваю на магнитах на доску)
Далее три человека у доски решают дробные выражения:(остальные работают в тетрадях, проверяют отвечающих у доски)
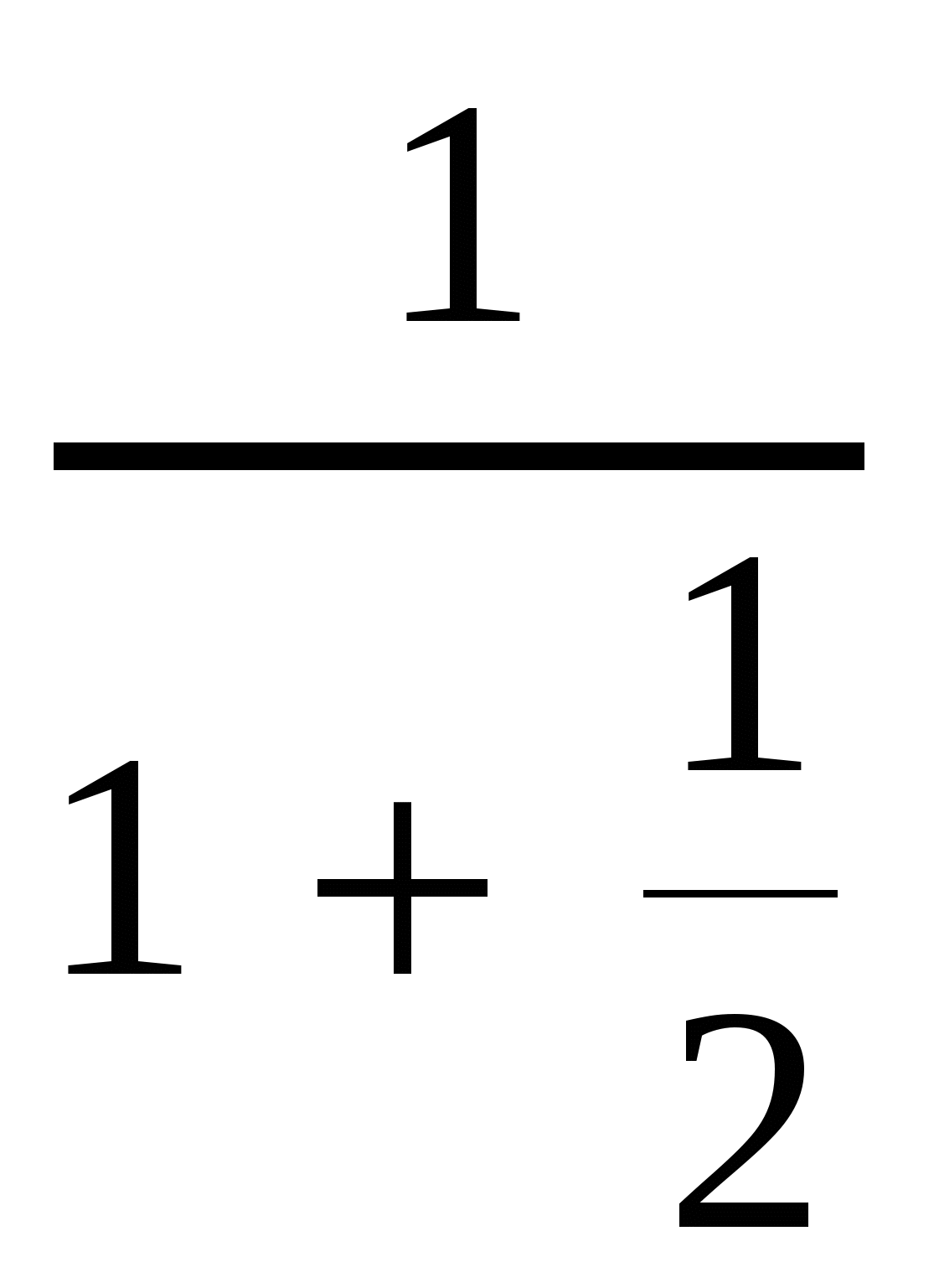
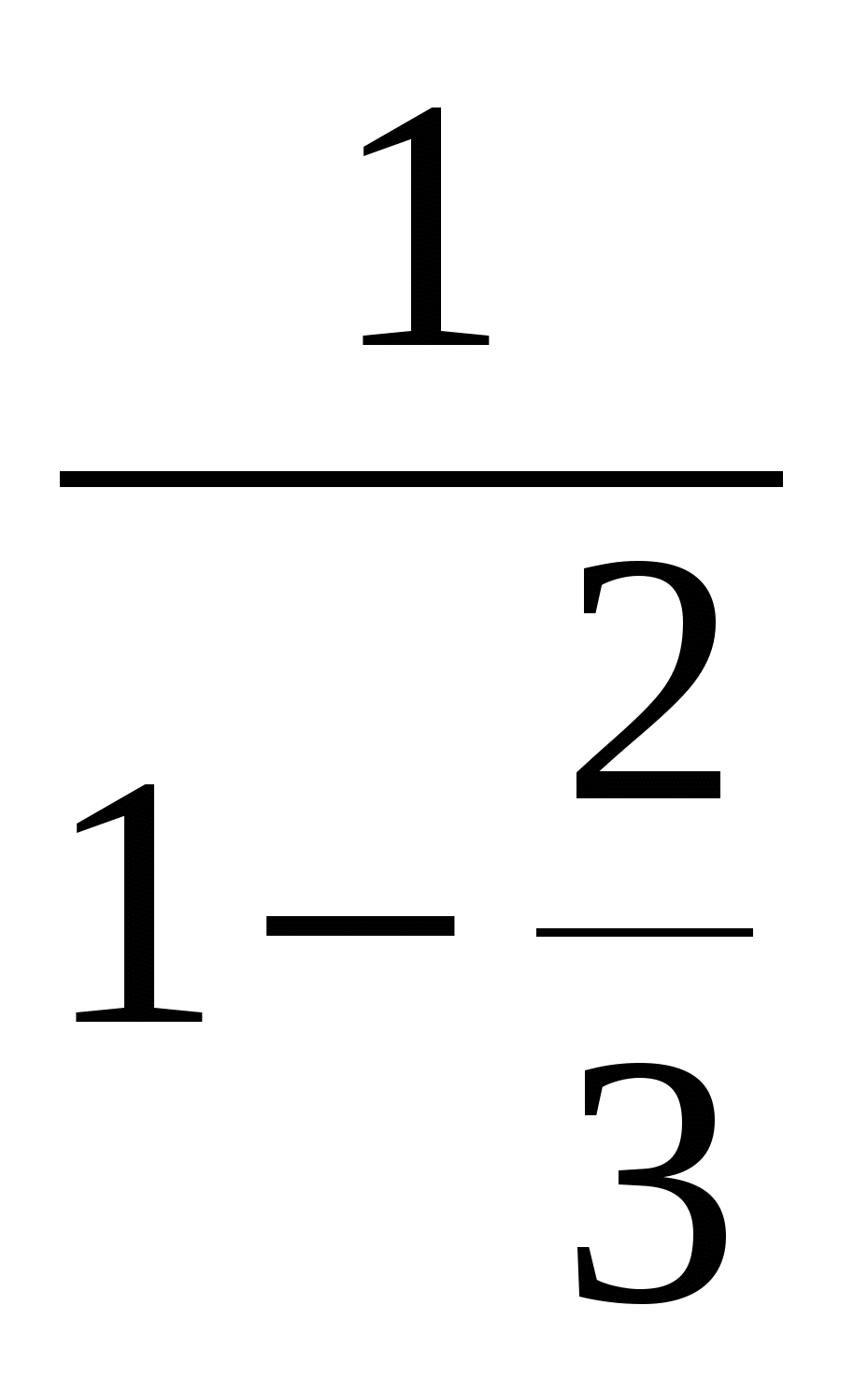
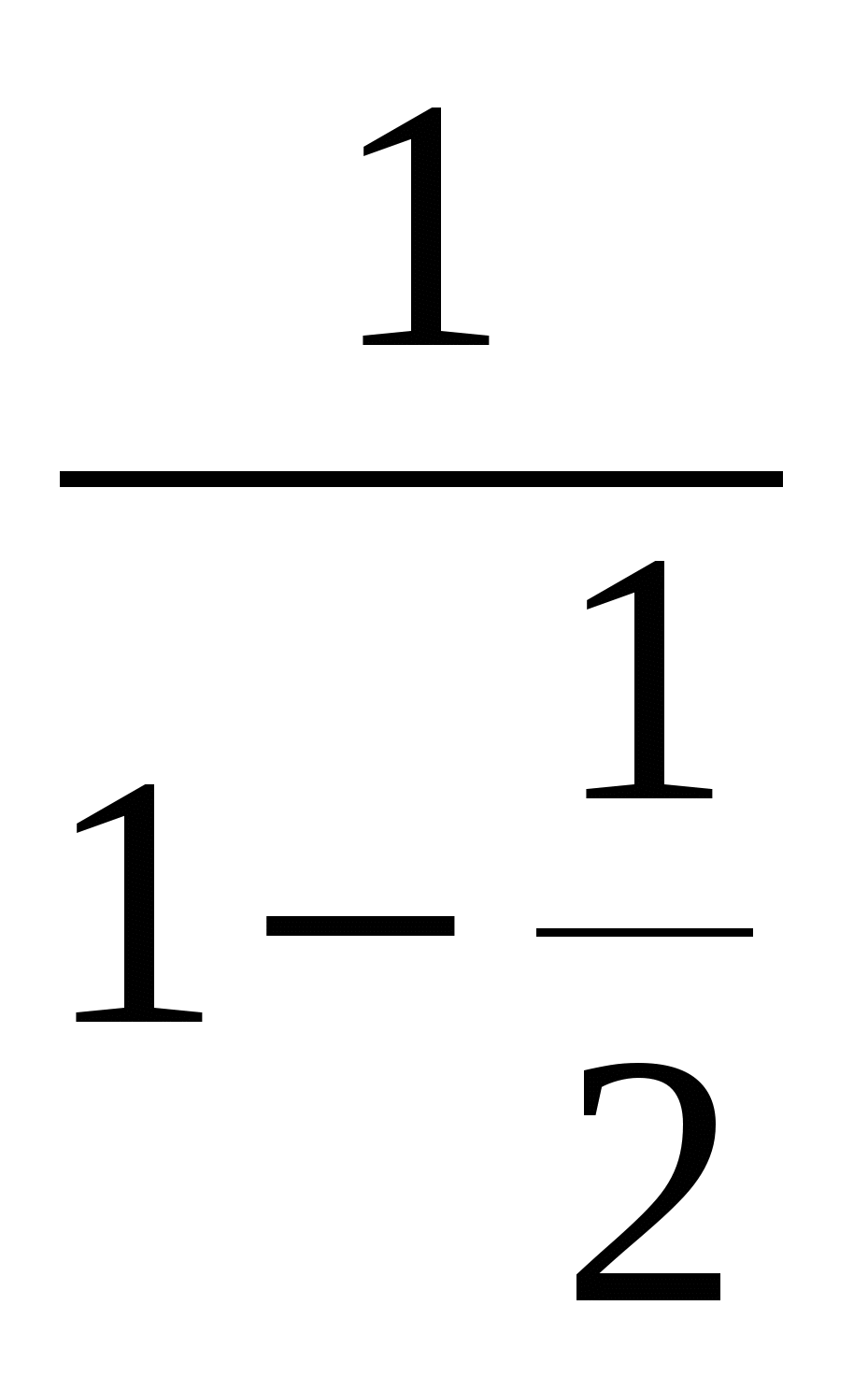
-У вас в домашнем задании была задача на работу :
Героям «Простоквашино» надо заготовить на зиму 90 поленьев дров. Матроскин с д.Фёдором могут выполнить эту работу за 10 часов, а Шарик — за 15 часов. За какое время выполнят эту работу наши герои, если будут работать все вместе?
—Справились? Заполните таблицу на экране. Объясните своё решение.
-Как называются задачи. Где кто-то выполняет некоторые действия, работает?
-Задачи на работу.
-А как назвать задачи,где идёт речь о работе сразу нескольких объектах?
-Задачи на совместную работу.
-Как вы считаете, в жизни встречаются такие ситуации, когда лучше работать вместе, чем по-одному?
-Да. Вместе работа выполняется быстрее, легче,веселее.
-Вот и кот Матроскин утверждает:
(видеофрагмент мультфильма «Совместный труд….»)
-Итак, запишите тему сегодняшнего урока «Задачи на совместную работу».
-Записывают тему урока в тетрадях.
-Если вы так успешно справились с домашней задачей, то может и со следующей справитесь быстро?
Почтальон Печкин может съесть коробку конфет за 2 минуты, Матроскин — за 3 минуты, а Галчонок — за 6 минут. За сколько минут они «уплетут» все конфеты вместе?
-Пытаются решить задачу, используя таблицу.
-Что у вас получилось? (выслушиваю варианты ответов)
3.Выявление места и причины затруднения
-Почему ответы разные? В чём состоит затруднение?
-Мы не знаем объём работы
4.Построение проекта выхода из затруднения
-Тогда сформулируйте цель нашего урока.
Вывести алгоритм решения задач на совместную работу, где неизвестен объём работы.
Научиться решать задачи на совместную работу, где неизвестен объём работы.
5.Реализация построенного проекта
-Действительно, не всегда в задачах на совместную работу известен объём работы, или его невозможно выразить в каких-то единицах измерения. Например,построить дом, сделать домашнее задание, сделать уборку в квартире и т. д.
Как же тогда можно обозначить всю целую выполненную работу?
Её можно обозначить единицей.
А чем тогда выразится производительность?
Частью.
Попробуйте теперь заполнить таблицу к предложенной задаче в пробном действии.
Заполняют таблицу, пробуют решить её.
Выходят к доске. Расставляют шаги алгоритма в правильном порядке.
Физминутка
-Давайте немного отвлечёмся от математики и разомнём свои мышцы.
Выше, выше подтянитесь,
Ну — ка плечи распрямите,
Поднимите, отпустите,
Вправо, влево поверните,
Рук, коленями коснитесь…
И тихонечко садитесь.
6.Первичное закрепление с проговариванием во внешней речи.
-Итак, инструмент для решения таких задач у нас теперь есть. Значит ли, что мы уже умеем их решать?
-Нет. Надо потренироваться подействовать по этому алгоритму.
-Итак, решим следующие задачи, используя алгоритм и готовые пустые таблицы.
Корова сама может съесть стог сена за 3 месяца, а телёнку хватило бы его на 6 месяцев. Хватит ли им на двоих этого стога на два месяца?
Выходят к экрану, заполняют таблицу. Дорешивают задачи.
Дядя Фёдор сам может убрать дом за 12 часов, Матроскин — за 15 часов, а Шарик — за 20 часов.Узнав,что с курорта едут родители, они решили сделать уборку все вместе. Сколько времени у них уйдёт на это?
7.Самостоятельная работа с самопроверкой по эталону.
-Ну что? Научились?
-А как проверить?
—Решить самостоятельно.
-Правильно, следующую задачу вы решаете самостоятельно и затем сами себя проверите, сверившись с эталоном.
Папа может сам вымыть всю посуду за 12 минут, а мама — за 6 минут. За какое время они вымоют посуду, если объединят свои усилия?
Выполняют самостоятельную работу.
Проверяют себя по эталону.
-Молодцы! Почти все справились успешно.
8.Включение в систему знаний и повторение.
-В оставшееся время предлагаю повторить ранее пройденный материал.
№ 579 из учебника.
Дробное выражение, записанное заранее на доске:
(4 5/8 * 3 1/5 + 4 5/8 * 2 4/5) / ( 4 5/8 * 6/7)
Выставляем оценки.
9.Рефлексия учебной деятельности.
-Вспомните цель нашего урока.
-Достигли ли мы её?
-Запишите домашнее задание: № 612, 613; по желанию на отдельную оценку творческое задание «Придумать задачу на совместную работу с героями любимых мультфильмов и сделать к ней рисунок»
-А теперь вспомните весь сегодняшний урок, вспомните, как работали вы, что у вас получилось, что — нет, что было новым, а что просто вспомнили.
-Рефлексию урока предлагаю вам провести необычно.-На экране вы видите облако слов. Выберите из него одно или два слова, которые наиболее точно отражают ваши ощущения от урока.
-Напишите выбранное слово крупно печатными буквами на цветной полоске и прикрепите его на ватман.
Пишут маркерами на цветных полосках выбранные слова и приклеивают в листу ватмана.
-Таким образом у нас получилось «Облако слов» нашего урока.
-Спасибо всем за совместную работу!
Урок «Задачи на совместную работу», ФГОС
Муниципальное бюджетное общеобразовательное учреждение
средняя школа №6
городского округа-город Камышин
Волгоградской области
Урок математики.
«Задачи на совместную работу»
Выполнила: учитель математики
Киселева Г.М.
Апрель, 2017г.
Место урока: первый урок в теме.
Тип урока: урок изучения и первичного закрепления новых знаний.
Цель урока: сформировать у учащихся навыки решения задач на совместную работу; показать значимость данного типа задач в практической деятельности.
Формирование УУД:
Познавательные: умение работать с текстом (анализировать, извлекать нужную информацию), формулировать вопросы, отвечать на них, использовать ранее изученный материал при решении задач.
Регулятивные: постановка целей на каждом этапе урока, формирование навыков самооценки и взаимооценки, отработка навыков действия по плану.
Коммуникативные: совместное решение задач (в парах, группах), анализ полученных результатов.
Ход урока.
Организационный момент (2 мин)
Актуализация опорных знаний (фронтальный опрос с помощью МС) 6 мин
Задание
Трактор вспахал поле за 6 дней. Какая часть поля была вспахана за 1 день, за 3 дня, за 5 дней?
Маляры могут покрасить здание за 2 недели. Какую часть работы они выполнят за 3 дня, за неделю, за 10 дней?
Сергей идет от школы до дома 25 минут. Какую часть пути проходит Коля за 1 минуту, за 6 минут?
Задание.
Разгадайте 2 ребуса и выясните тему сегодняшнего урока.










«Решение задач».
Задание.
Ребята, задачи в математике бывают разные. Какие мы будем решать на сегодняшнем уроке? Чтобы ответить на этот вопрос я Вам предлагаю прочитать следующие задачи и определить, что у них общего.
На птицефабрику привезли корм, которого хватило бы уткам на 6 дней, а гусям – на 3 дня. Рассчитайте, на сколько дней хватит привезенного корма уткам и гусям вместе.
Две бригады построят дорогу в 6 км за 4 дня, первая бригада в одиночку построит дорогу за 6 дней. За сколько дней в одиночку построит дорогу вторая бригада.
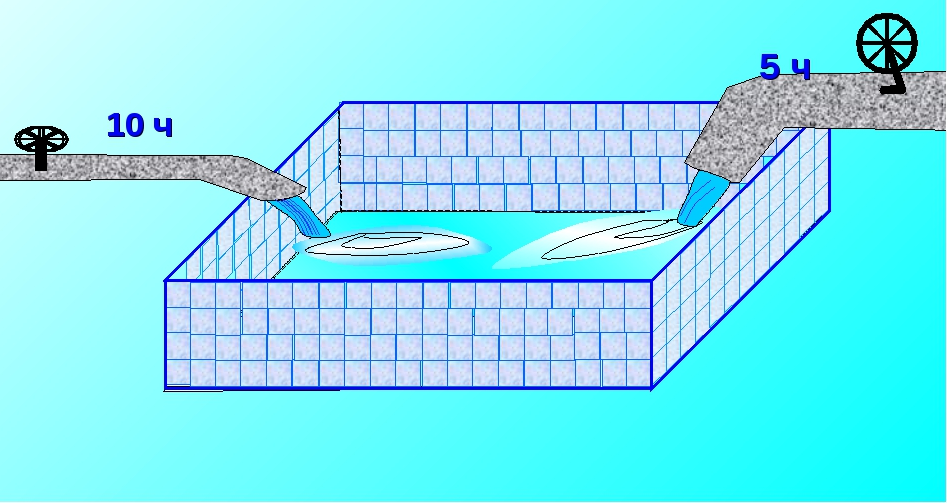
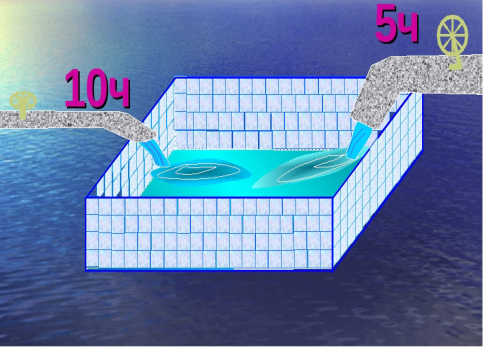
Через первую трубу бассейн можно наполнить за 10 ч, а через вторую за 15ч. Какую часть бассейна наполнят трубы за 1 ч совместной работы. За сколько часов наполнится бассейн, если открыть обе трубы.
Ответ: в этих задачах речь идёт о какой — либо деятельности. Трубы заполняют бассейн, бригады рабочих строят дорогу, животные вместе съедают корм так далее. Деятельность может быть любая.
Формулирование темы, цели и задач урока (2 мин)
Ребята, такие задачи в математике называются задачами на совместную работу.
Какова же цель сегодняшнего урока?
Ответ: Научиться решать задачи на совместную работу. Вывести алгоритм решения такого типа задач.
Изучение нового материала (10мин)
Я предлагаю вам решить следующую задачу: На птицефабрику привезли корм, которого хватило бы уткам на 6 дней, а гусям – на 3 дня. Рассчитайте, на сколько дней хватит привезенного корма уткам и гусям вместе.
Давайте определим, какие величины связаны между собой в этих задачах.
Их всего три.
Первая величина в задачах на работу — время. Это время, за которое выполняется та или иная работа. Измеряется в секундах, минутах, часах, сутках и так далее. Обозначается буквой t.
Вторая величина — объём работы. Сколько сделано деталей, налито воды, вспахано полей и так далее. Измеряется в тех единицах, о которых идёт речь в задаче: деталях, литрах, полях и т.д. Обозначается буквой A или как целое принимается за единицу.
Третья величина — производительность. То есть скорость работы. Обозначается буквой р.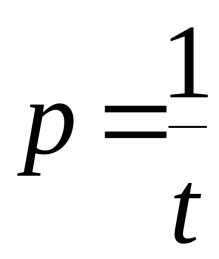
Всю работу («Целое») принимаем за 1,
Производительность — часть работы, выполненная за единицу времени
Какую величину можно найти в задаче?
Ответ: производительность за 1 день уток и гусей.
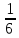 – количество корма, которое съедают утки за день.
– количество корма, которое съедают утки за день.
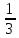 — количество корма, которое съедают гуси за день.
— количество корма, которое съедают гуси за день.
Зная, сколько съедают отдельно за один день утки и за один день гуси, что можем найти?
Ответ: сколько корма в день они съедают вместе.
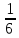 +
+ 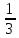 =
= 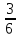 =
= 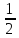 часть корма съедят утки и гуси вместе.
часть корма съедят утки и гуси вместе.
Как узнать на сколько дней хватит привезенного корма уткам и гусям вместе? Как найти число по его дроби?
Ответ: нужно 1 (объем корма) разделить на 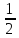 , получаем 2 дня.
, получаем 2 дня.
Ответ: на 2 дня.
Подведение итогов:
Мы составили алгоритм решения задач на совместную работу.
Обратили внимание, что при совместной работе складываются не время работы, а часть работы, которую делают ее участники за единицу времени.
Вся выполняемая работа принимается за 1 – «целое».
Первичное закрепление (10мин)
Учащимся предлагается работа в парах.
Работа с последующей проверкой (с помощью МС)
Через первую трубу бассейн можно наполнить за 10 ч, а через вторую за 15ч. За сколько часов наполнится бассейн, если открыть обе трубы.
Два тракториста вспахали поле за 6 часов совместной работы. Первый тракторист мог бы один выполнить ту же работу за 10 часов. За сколько часов второй тракторист может вспахать поле?
Увидели ли Вы разницу между 1 и 2 задачами?
Возникли ли у вас проблемы с решением 2 задачи?
Давайте обсудим алгоритм ее решения. Учащийся делает записи на доске.
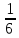 — часть работы, выполняемая трактористами вместе за 1 час.
— часть работы, выполняемая трактористами вместе за 1 час.
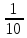 — часть работы, выполняемая 1 трактористом за 1 час.
— часть работы, выполняемая 1 трактористом за 1 час.
Что можно узнать?
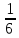 —
— 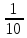 =
= 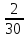 =
= 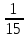 часть работы, выполняемая 2 трактористом за 1 час.
часть работы, выполняемая 2 трактористом за 1 час.

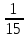 = 15 часов – понадобится 2 трактористу, чтобы вспахать поле. Ответ: 15 часов
= 15 часов – понадобится 2 трактористу, чтобы вспахать поле. Ответ: 15 часов
Физкультминутка (3 мин)
Закрепление полученных знаний (работа в группах) (7 мин)
Ученики могут выбрать сами, задачи какого уровня сложности они будут решать.
1 уровень. Решить № 903 (а) из учебника.
2 уровень.
Крокодил Гена, Чебурашка и старуха Шапокляк решили подготовить площадку, на которой они будут строить дом для друзей. Гена, работая один, может выполнить всю работу за 12 часов, Шапокляк – за 15 часов, а Чебурашка – за 20 часов. Какую часть работы выполнят они вместе за 1 час?
3 уровень.
(Из “Арифметики” Л.Ф. Магницкого.)
Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, в сколько дней жена его отдельно выпьет ту же кадь?
Защита решения (выступает 1 ученик от группы), осуществляем проверку с помощью МС. Анализ выполненной работы (где возникли затруднения? Есть ли вычислительные ошибки? И др.)
Рефлексия (3 мин)
Какие задачи учились решать?
Что было самым трудным?
Продолжите фразу: «Сегодня на уроке я понял, что…»
Продолжите фразу: «Дома мне предстоит…»
Домашнее задание (2 мин)
Лошадь съедает воз сена за месяц, коза — за два, овца – за три месяца. За какое время они вместе съедят воз сена.
Малыш может съесть банку варенья за 30 мин, а Карлсон – в 5 раз быстрее. За сколько времени они съедят такую банку варенья, если начнут со своей обычной скоростью есть ее вместе?
Составить 2 задачи на совместную работу по картинкам.
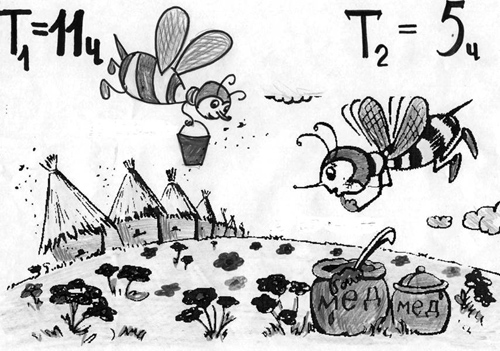
Урок по математике на тему Задачи на совместную работу. 4 класс
Дата:
Тема: Задачи на совместную работу.
Цели: научить решать задачи на совместную работу, составлять обратные задачи; продолжать учить решать задачи на движение; развивать умение выполнять арифметические действия с мерами объема, вычислять, записывая столбиком, сравнивать выражения; прививать интерес к математической деятельности, самостоятельность, взаимопомощь.
Ход урока.
1.Орг.момент.
И вновь «терпенье и труд » придут нам на помощь. Разгадав математическую шараду, вы узнаете, чем мы будем заниматься сегодня на уроке.
Предлог стоит в моем начале.
В конце же – загородный дом.
А в целом мы все решали
И у доски, за столом.
— Правильно, это задача.
2.Актуализация опорных знаний.
№1 стр 112 (на доске).
№1 стр 114 (на доске) устно.
3.Работа по изучению нового материала.
Сегодня мы с вами будем решать разнообразные задачи на совместную работу. Итак, задача №1.
Малыш может съесть 600г. варенья за 6 минут, а Карлсон – в 2 раза быстрее. За какое время они съедят это варенье вместе?
— Сколько варенья съест Малыш за 1 мин.?
600:6=100 (г)
— Сколько варенья съест Карлсон за это же время?
200 х 2=200 (г)
— Сколько же варенья они съедят вместе за 1 мин.?
100+200=300 (г)
— А за какое же время они съедят 600г. варенья?
600:300=2 (мин)
-Итак, мы нашли время за которое Малыш и Карлсон съедят 600г варенья, или иначе говоря выполнят совместную работу.
№2 стр 112.
Мастер- 25 дет за 1 час.
Ученик- 15 дет за 1 час.
Вместе-? Дет за 1 день
1 день= 8 часов.
1) 25+15=40 (дет/ч)- вместе.
2) 40 х 8= 320 (дет/день)- вместе за 1 день.
Ответ: 320 детелей.
Мастер- 25 дет за 1 час.
Ученик- 15 дет за 1 час.
Изготовили- 320 дет.
Работали- ? часов.
1) 25+15=40 (дет)- вместе.
2) 320 : 40= 8 (ч)
Ответ: 8 часов.
За 8 часов- 320 дет.
Мастер- 25 дет/ч
Ученик- ? дет/ч
1) 320:8= 40 (дет)
2) 40 – 25=15 (дет)- ученик
Ответ: 15 деталей.
Правило на стр 112.
4.Формирование умений и навыков.
1.Задача №3 (в) /2 уч-ся работают по карточкам/
Производительность Время Работа
1. одинаковая 3ч ?д. ?
2 одинаковая 4ч ?д. 56д.
5+4=9(ч)
56:7=8(д)
8*3=24(д)
8*4=32 (д)
5. Игра «Поспевай — не зевай»
* Во что превратилась Золушкина карета? / в тыкву/
* Мальвина — брюнетка или блондинка? /она – девочка с голубыми волосами/
* Что просил старик у золотой рыбки, когда выловил ее в первый раз? /ничего/
* Кого водила на веревочке старуха Шапокляк? /крыску Лариску/
* Мерзлая вода? /лед/
6.Решение уравнений сложной структуры
3*а+345=1206 640:(25-х)=80
3*а=1206-345 25-х=640:80
3 а=861 25-х=8
а=287 х=17
7.Работа с мерами объема.
№4 (2 ученика у доски).
8. .Работа с именованными числами
-Отгадайте загадку:
Две сестрицы друг за другом
Пробегают круг за кругом.
Коротышка только раз.
Та, что выше,- каждый час./Стрелки часов/
-Зачем нам нужны часы? /Чтобы измерять короткие промежутки времени/
А знаете ли вы, что одни из первых часов — это водяные часы. Греки называли их « клепсидрой» — похитительницей воды.
Знаменитый философ Платон построил клепсидру. которая в определенный час созывала учеников на занятия. издавая звон. Так появился первый школьный звонок.
/показ клепсидры/
— Назовите единицы времени. Предлагаю поупражняться в сложении и вычитании единиц времени.
№5 стр 113.
17ч28мин+13ч56мин=31ч24мин 2сут4ч+3сут23ч=6ч3ч
№7 Сравни.
9.Домашнее задание. с 113 № 6 (Федотов А №6 (1 столбик).
10.Итог урока
Какие задачи учились решать?
Что было самым легким?
Что было самым трудным?
Продолжите фразу: «Сегодня на уроке я понял, что…”.
Урок задачи на совместную работу
Урок № 134 14.04.2016
Тема урока: «Задачи на совместную работу»
5 класс
Цель урока:
Образовательная: обобщать знания по теме «Задачи на совместную работу»; совершенствовать умения и навыки решения задач на совместную работу методом арифметического действия
Развивающая: способствовать развитию логического мышления, умения применять полученные знания на практике, умение выделять главное, верно использовать аналогию и сравнение; строить логическую цепочку при решении задач; формированию математической речи.
Воспитательная: стимулировать мотивацию и интерес к изучению математики, приучать к эстетическому оформлению записи в тетради, умение слушать и уважать мнение своих товарищей.
Задачи: обобщить знания по решению задач на совместную работу; закрепить навыки решения задач.
Формируемые УУД:
Личностные:
Сформировать ответственное отношение к учению; готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
Метапредметные:
регулятивные
Научиться формулировать и удерживать учебную задачу; выбирать действия в соответствии с поставленной задачей; планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
познавательные
Научиться самостоятельно, выделять и формулировать познавательную цель; использовать общие приёмы решения задач;
коммуникативные
Научиться организовывать учебное сотрудничество и совместную деятельность с учителем и одноклассниками: определять цели, распределять функции и роли участников; взаимодействовать и находить общие способы работы; работать в группе: находить общее решение; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
Предметные:
Научиться работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, обосновывать суждения, проводить классификацию; владеть базовым понятийным аппаратом: иметь представление о числе, дроби.
Тип урока: обобщение и систематизация знаний
Оборудование: компьютер, проектор, презентация, выполненная в программе PowerPoint, карточки с заданиями, оценочные листы.
Ход урока
Готовятся к уроку. Настраиваются на рабочий лад. Записывают число, классная работа.Подписывают оценочные листы
2. Актуализация опорных знаний Ребята, обменяйтесь с соседом тетрадями, возьмите карандаши и будем проверять домашнее задание. При решении домашнего задания, что необходимо было найти?
Что вы делали в первом действии?
Какой ответ у вас получился?
Поставьте плюсики напротив верного действия. Если нет домашнего задания, ставим в оценочный лист 0 баллов,
допущены значительные ошибки – 1 балл;
допущены незначительные ошибки – 2 балла;
нет ошибок – 3 балла.
Обменяйтесь обратно тетрадями и посмотрите на свои ошибки (если они есть).
Скажите мне, пожалуйста, какие числа мы с вами изучаем?
Как вы понимаете, что такое дробь?
Какие операции мы можем производить с дробями?
Хорошо, молодцы. А теперь проверим, как вы это умеете делать. Перед вами лежат сигнальные карточки с буквами «а», «б», «в», на слайдах будут появляться примеры, их необходимо устно решить и поднять карточку с той буквой, которая соответствует правильному ответу.
Назовите число обратное 51
а) 15
б) 1
в)
2. Назовите число обратное
а) 4
б) 14
в)
3. Назовите число обратное
а) 35
б)
в) 5
4. Назовите число обратное
а) 4
б)
в)
5. Назовите число обратное
а) 0
б) нет такого числа
в)
6. Выполните действие
а)
б)
в)
7. Выполните действие
а)
б)
в)
8. Выполните действие
а)
б)
в)
Проверяют домашнюю работу. Выставляют баллы
Рациональные.
Дробь — часть целого числа.
Сравнивать, складывать, вычитать, сокращать, умножать, делить.
Читают задания, решают примеры, поднимают необходимую сигнальную карточку.
.
Ответы:
в
а
б
в
б
в
в
б
3. Мотивация учебной деятельности учащихся. Молодцы! А что еще мы можем делать с помощью дробей?
Мы умеем их решать?
Как вы думаете, какая сегодня будет тема урока?
Скажите, тогда какую цель мы сегодня поставим перед собой?
Что такое производительность? Как ее найти? Давайте решим несколько простых задач.
Отец с сыном красят забор. Если бы забор красил только отец, то ему потребовалось бы 7 часов. А сыну на эту работу требуется 10 часов. Какова производительность каждого и общая производительность?
Кот Матроскин и Шарик решили заготовить дрова на зиму. Если Матроскин будет колоть дрова один, то ему потребуется 11 дней, а Шарику на эту же работу требуется 9 дней. Какова производительность каждого и общая производительность?
Решать задачи на совместную работу.
Да
Задачи на совместную работу
Обобщить и систематизировать знания по теме «Задачи на совместную работу»
Производительность — отношение всей работы ко времени.
Производительность отца — , сына — .
Вместе:
Производительность Матроскина — , Шарика — . Общая: .
4. Обобщение и систематизация знаний
Молодцы! Посмотрите на слайд. Перед вами задача. Скажите, данная задача относится к задачам на совместную работу?
А чем отличается эта задача от всех предыдущих?
Вера и Оля узнали, что у Саши — день рождения. И сразу же стали набирать SMS-ки! Вообще-то, Вера умеет набирать 24 слова за 4 минуты, а Оля — 35 слов за 7 минут. Вера набрала поздравление из 30 тёплых слов, а Оля — из 20. Чьё поздравление Саша получит первым?
А теперь объединитесь в группы, что бы получилось 4 команды. Каждая команда выбирает себе капитана, который будет защищать общее решение у доски.
Каждая группа получает свою задачу, решает ее совместно, записывает краткое условие, решение на листах и поднимает руки.
Задача для 1 группы: Три экскаватора различной мощности могут отрыть котлован, работая отдельно: первый — за 10 дней, второй — за 12 дней, а третий — за 15 дней. За сколько времени они отроют котлован, работая совместно?
Задача для 2 группы: Школа заказала в швейную мастерскую форму для учащихся. Одна швея может выполнить весь заказ за 20 дней, второй для выполнения заказа требуется в 3 раза больше этого времени. За сколько времени выполнит весь заказ две швеи, работая совместно.
Задача для 3 группы: Водоём наполняется двумя трубами за 5 часов, а через одну первую трубу — за 6 часов. Через сколько времени будет наполнен водоём, если открыть только одну вторую трубу?
Задача для 4 группы: К ванне подведены два крана. Через один кран ванна может наполниться за 12 мин, а через другой в 2 раза быстрее. За сколько минут наполнится ванна, если открыть сразу два крана.
После того, как все команды выступили, объявляются командные баллы.
Первая решившая команда — 5 баллов
Вторая – 4 балла;
Третья – 3 балла;
Четвертая – 2 балла.
А так же капитан оценивает вклад каждого участника в решение задачи и выставляет им баллы.
Да, так как набор текста это работа.
Тем, что все исходные данные разные.
ДевочкаКол-во слов
Время (мин.)
SMS (кол.сл.)
Время (мин.)
Вера
24
4
30
?
Оля
35
7
20
?
Решение
Найдем скорости набора текста Веры и Оли. Для этого найдем их производительности.
24:4=6 (слов/мин.) — производительность Веры
35:7=5 (слов/мин.) – производительность Оли
30:6=5(мин.)- время набора сообщения Верой
20:5=4 (мин.) — время набора Олей.
Ответ: сообщение от Оли.
Решают задачи по группам. Записывают решение на листах. Выходят к доске и защищают свое решение. Первая команда, решившая, задачу получает по 2 балла в оценочный лист, остальные за правильное решение по 1 баллу. Так же каждый учащийся выставляет сам себе оценку по 5-ти бальной системе за свое участие в работе команды над задачей.
Выставляют баллы в оценочные листы. Капитан оценивает каждого участника.
5. Физкультминутка
Давайте немного передохнем.
Поднимает руки класс – это «раз».
Повернулась голова – это «два».
Руки вниз, вперед смотри – это «три».
Руки в стороны пошире развернули на «четыре»,
С силой их к плечам прижать – это «пять».
Всем ребятам надо сесть – это «шесть».
Выполняют упражнения, повторяя, за учителем.
.6. Контроль усвоения знаний
Все молодцы! Теперь смотрим внимательно на слайд. Перед вами задачи. Необходимо их решить и выбрать букву соответствующую вашему ответу.
Теперь проверим решение. За правильно решенную задачу получаете 1 балл. Подсчитайте количество баллов и выставьте их в оценочный лист.
1.Саша может прочесть 15 рассказов за 5 дней, а Витя – за 3 дня. Сколько рассказов они вместе прочтут за 7 дней?
а) 120 рассказов
б) 80 рассказов
в) 56 рассказов
г) другой ответ
2.Рабочий может изготовить набор деталей за 17 часов, а ученик – за 34 часа. Какую часть набора деталей они изготовят за час, работая одновременно?
а) 3/34
б)1/51
в) 1/34
г) другой ответ
3.Первая бригада выполнит задание за 10 ч, а вторая – за 15 ч. За сколько часов обе бригады выполнят задание при совместной работе?
а) 4 ч
б) 6 ч
в) 25 ч
г) другой ответ
Решают задачи, выбирают правильный ответ.
Ответы:
1. – в
2. – а
3. – б
Подсчитывают баллы, выставляют их в оценочные листы.
7.Рефлексия.
Ребята, давайте вернемся к цели нашего урока.
Как она звучала?
Как вы думаете, мы ее достигли?
Сделайте вывод о своей работе на уроке, продолжив фразу:
— Мне было интересно…
— Я узнала…
— Мне было сложно…
— У меня остался вопрос…
— Меня удивило…
Обобщить знания по теме «Задачи на совместную работу»; совершенствовать умения и навыки решения задач на совместную работу.
Да.
Отвечают на вопросы.
8. Информация о домашнем задании
Домашнее задание будет на карточках (Приложение 2) по вариантам. Необходимо решить задачу, а так же придумать и оформить свою задачу на совместную работу.
Получают карточки. Записывают домашнее задание.
Приложение 1
Домашнее задание(0-3 балла)
Работа над задачей (группа)
(2-5 баллов)
Личный вклад в работу группы
(0-5 баллов)
Тест
(0-3 балла)
Общее количество
14 – 15 баллов «5»
11 – 13 баллов «4»
7 – 10 баллов «3»
До 7 баллов «2»
Приложение 2.









 Все эти знания помогают ему подобрать качественные семена, правильно их высеять, внести нужное количество удобрений в почву, бороться с вредителями растений. От грамотности человека этой профессии напрямую зависит количество и качество полученного урожая. Часто он занимается еще и подготовкой и организацией самих сельскохозяйственных работ. И, чтобы во всем этом разбираться, качественно выполнять свою работу и получать достойную заработную плату нужно изучать биологию.
Все эти знания помогают ему подобрать качественные семена, правильно их высеять, внести нужное количество удобрений в почву, бороться с вредителями растений. От грамотности человека этой профессии напрямую зависит количество и качество полученного урожая. Часто он занимается еще и подготовкой и организацией самих сельскохозяйственных работ. И, чтобы во всем этом разбираться, качественно выполнять свою работу и получать достойную заработную плату нужно изучать биологию.








 SPEAK ENGLISH. LIVE ENGLISH!В дружеской атмосфере мы научим тебя понимать английский язык и общаться на нём!Записывайся!
SPEAK ENGLISH. LIVE ENGLISH!В дружеской атмосфере мы научим тебя понимать английский язык и общаться на нём!Записывайся!

 Подготовься к ЦТ на 100 баллов!Выпускница курсов Адукар 2019 Яна Никуленкова сдала ЦТ по биологии на 100 баллов и поступила на фармацевтический факультет БГМУ. Записывайся!
Подготовься к ЦТ на 100 баллов!Выпускница курсов Адукар 2019 Яна Никуленкова сдала ЦТ по биологии на 100 баллов и поступила на фармацевтический факультет БГМУ. Записывайся!







 = 3.
= 3. на целое число
на целое число  с остатком (нахождение неполного частного
с остатком (нахождение неполного частного  и остатка
и остатка  , таких, что выполняется равенство:
, таких, что выполняется равенство:  ).
). 
 , где
, где 
 .
. является простым. Доказать, что а) имеет место представление
является простым. Доказать, что а) имеет место представление  для некоторого
для некоторого  ; б)
; б)  .
. . Простое число p может попасть только либо в класс
. Простое число p может попасть только либо в класс  , либо в класс
, либо в класс  . Т.к. числа первого класса делятся на 2, 3, поэтому они составные. Числа третьего класса делятся на 2, числа четвертого класса делятся на 3, числа пятого класса делятся на 2.
. Т.к. числа первого класса делятся на 2, 3, поэтому они составные. Числа третьего класса делятся на 2, числа четвертого класса делятся на 3, числа пятого класса делятся на 2. , т.к. первый множитель делится на 12, а третий на 2. ч.т.д.
, т.к. первый множитель делится на 12, а третий на 2. ч.т.д. последняя цифра любого числа повторяется с периодом 4
последняя цифра любого числа повторяется с периодом 4 для любого натурального числа n.
для любого натурального числа n. .
. .
. .
. .
. сумма делится на 133, т.е.
сумма делится на 133, т.е.  , содержащее не менее трех цифр, делилось на 4, необходимо и достаточно, чтобы делилось на 4 число, образованное двумя последними цифрами числа
, содержащее не менее трех цифр, делилось на 4, необходимо и достаточно, чтобы делилось на 4 число, образованное двумя последними цифрами числа  не делится ни на одно из простых чисел, не превосходящих
не делится ни на одно из простых чисел, не превосходящих  , т.е. на
, т.е. на  , то число –
, то число –  . Проверим, делится ли число 2003 на 2,3,5,7,11,13,17,19,23,29,31,37,41,43. Для проверки деления на 2,3,5,7,11,13 применяем признаки делимости. Деление на 17,19,23,29,31,37,41,43 проверяем при помощи деления уголком. 2003 не делится ни на одно из перечисленных простых чисел
. Проверим, делится ли число 2003 на 2,3,5,7,11,13,17,19,23,29,31,37,41,43. Для проверки деления на 2,3,5,7,11,13 применяем признаки делимости. Деление на 17,19,23,29,31,37,41,43 проверяем при помощи деления уголком. 2003 не делится ни на одно из перечисленных простых чисел  — это все простые числа. Число
— это все простые числа. Число  не делится на
не делится на  , где
, где  — простые числа.
— простые числа.

 . Тогда
. Тогда
![Rendered by QuickLaTeX.com \[Z=297n-8=61k-8=21p-8=45m-8=826f-8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-47264cbb5b836ab110e1e2e315bc9681_l3.png)
![Rendered by QuickLaTeX.com \[297=11\cdot3\cdot9\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a40a7236991fbb212197a691c7ab601d_l3.png)
![Rendered by QuickLaTeX.com \[826=2\cdot7\cdot59\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-96a664e97479a84426f1c982c3e78eba_l3.png)
![Rendered by QuickLaTeX.com \[21=7\cdot3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f021588888626d861f2e7784cd7245d7_l3.png)
![Rendered by QuickLaTeX.com \[45=5\cdot9\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-00b64905cd7007b257ad0635fdd2bc5c_l3.png)
![Rendered by QuickLaTeX.com \[Z=2\cdot7\cdot59\cdot61\cdot11\cdot9\cdot3\cdot5-8=74823202\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-81935a4292543b31512dc3f24e395a90_l3.png)
 .
.![Rendered by QuickLaTeX.com \[S=\frac{2+12}{2}\cdot11=77\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2343e19f8bdc74f8b21e92cb29cd0f91_l3.png)
![Rendered by QuickLaTeX.com \[N=77+78\cdot 42+1+3+6+10=3373\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bd2e7f9db85acd075565ec0627fd1b97_l3.png)
 , если сумма оставшихся цифр равна 1808?
, если сумма оставшихся цифр равна 1808? раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна
раз. Сумма цифр этой части равна 20, следовательно, общая сумма всех цифр числа равна  . Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна
. Раз осталась сумма 1808 – следовательно, сумма вычеркнутых равна  . Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна
. Так как требуется вычеркнуть наибольшее количество цифр, то будем вычеркивать сначала все тройки. Сумма всех троек в числе равна  . Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:
. Теперь, если вычеркнуть все шестерки – это дает еще 2610. Остается вычеркнуть еще какое-то количество восьмерок. Определим, сколько:![Rendered by QuickLaTeX.com \[6892-2610-2610=1672\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9a3471ce36f398825534b9f4d507761b_l3.png)
![Rendered by QuickLaTeX.com \[1672\div 8=209\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ebc3c01c71aef72d3462eb18a86c07d_l3.png)
 . Вторая пара: единицу можем выбрать 73 способами (одна зачеркнута в самом начале), 0 – 111 способами. Следовательно, вторую пару можно выбрать
. Вторая пара: единицу можем выбрать 73 способами (одна зачеркнута в самом начале), 0 – 111 способами. Следовательно, вторую пару можно выбрать  способами.
способами. способов. Итого
способов. Итого  способа.
способа. Как расстояние зависит от времени и скорости?
Как расстояние зависит от времени и скорости? Как решать задачи для 4 класса?
Как решать задачи для 4 класса? В случае опасности заяц может бежать со скоростью 80 км/час
В случае опасности заяц может бежать со скоростью 80 км/час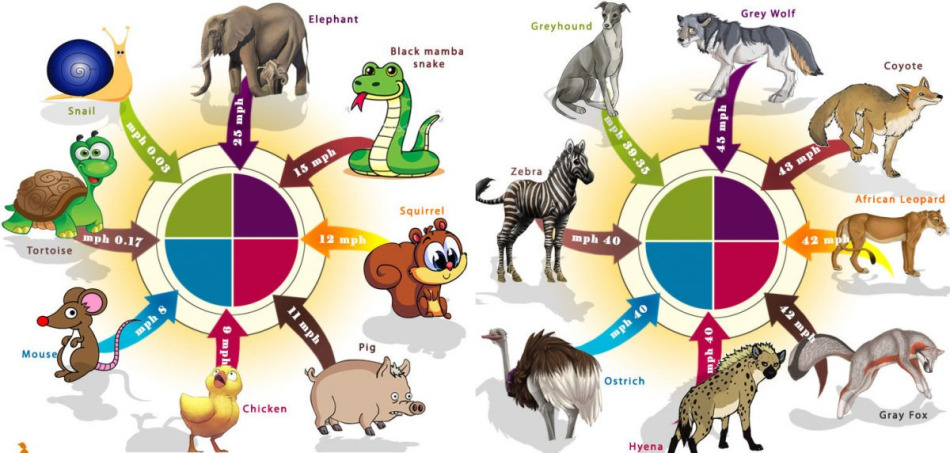 С какой скоростью могут передвигаться разные животные?
С какой скоростью могут передвигаться разные животные?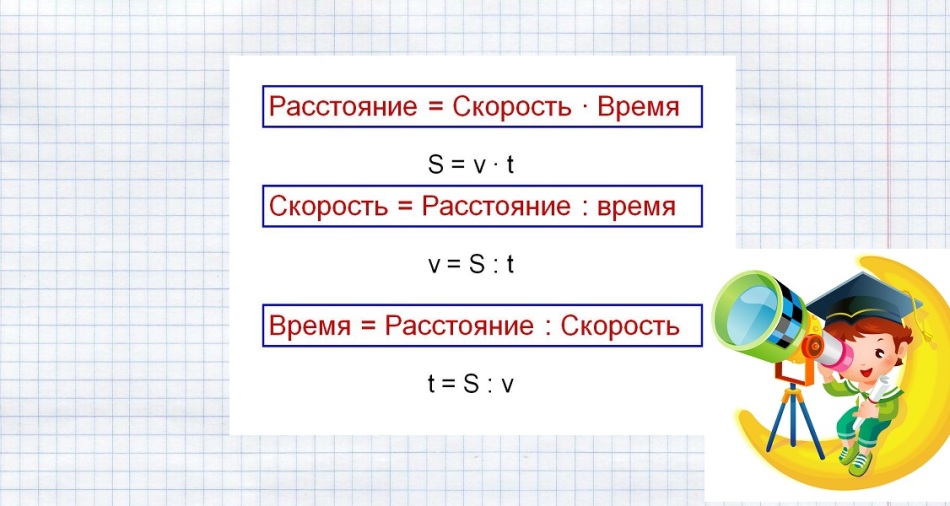 Формулы для решения задач про расстояние, время и скорость
Формулы для решения задач про расстояние, время и скорость Волк может бежать со скоростью 60 км/час
Волк может бежать со скоростью 60 км/час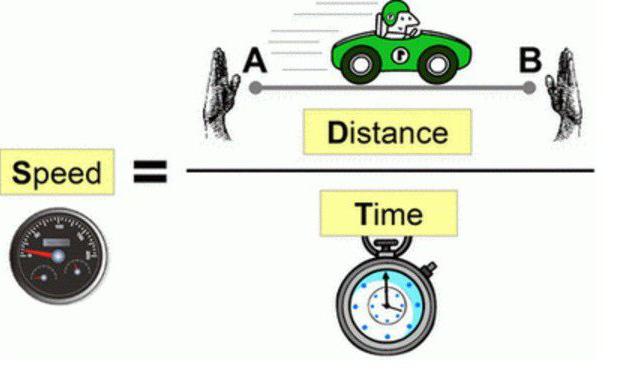


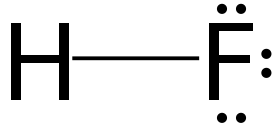
 (
(
 HF в воде. Реактив еще называют фтористоводородной кислотой и плавиковой кислотой. Последнее название связано с тем, что фтороводород получают из содержащего фтор (CaF2) плавикового шпата — очень красивого минерала флюорита, светящегося под ультрафиолетовым излучением или при нагревании.
HF в воде. Реактив еще называют фтористоводородной кислотой и плавиковой кислотой. Последнее название связано с тем, что фтороводород получают из содержащего фтор (CaF2) плавикового шпата — очень красивого минерала флюорита, светящегося под ультрафиолетовым излучением или при нагревании. Плавиковая кислота и ее пары ядовиты. Особенно коварна разбавленная кислота: при попадании на кожу ее брызг человек может вообще ничего не почувствовать, но вещество впитается в кожу и поступит в кровоток. Примерно через сутки проявятся симптомы токсического отравления, отек легких, нарушения работы сердечно-сосудистой системы и ЖКТ, так как соединение образует нерастворимые соли кальция и магния, связывая эти важные для нормального функционирования организма элементы. На коже проявится химический ожог из-за того, что реагент разрушает клетчатку.
Плавиковая кислота и ее пары ядовиты. Особенно коварна разбавленная кислота: при попадании на кожу ее брызг человек может вообще ничего не почувствовать, но вещество впитается в кожу и поступит в кровоток. Примерно через сутки проявятся симптомы токсического отравления, отек легких, нарушения работы сердечно-сосудистой системы и ЖКТ, так как соединение образует нерастворимые соли кальция и магния, связывая эти важные для нормального функционирования организма элементы. На коже проявится химический ожог из-за того, что реагент разрушает клетчатку. фторопластовых) канистрах, контейнерах и кубах. Для больших емкостей используется металлическая обрешетка. Кислоту высокой концентрации допускается перевозить железнодорожным и автомобильным транспортом в железных и стальных цистернах. Температурный режим — не выше +30 °С.
фторопластовых) канистрах, контейнерах и кубах. Для больших емкостей используется металлическая обрешетка. Кислоту высокой концентрации допускается перевозить железнодорожным и автомобильным транспортом в железных и стальных цистернах. Температурный режим — не выше +30 °С.
 (
( (
(
 Медиафайлы на Викискладе
Медиафайлы на Викискладе



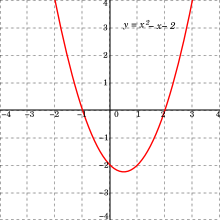 Квадратичный полином с двумя реальными корнями (пересечения х осей) и , следовательно , без каких — либо сложных корней. Некоторые другие квадратичные полиномы имеют свой минимум выше х осей, в этом случае нет никаких действительных корней и два комплексных корня.
Квадратичный полином с двумя реальными корнями (пересечения х осей) и , следовательно , без каких — либо сложных корней. Некоторые другие квадратичные полиномы имеют свой минимум выше х осей, в этом случае нет никаких действительных корней и два комплексных корня. График у = ах 2 + BX + C , где и дискриминант б 2 — 4 переменного тока являются положительными, с
График у = ах 2 + BX + C , где и дискриминант б 2 — 4 переменного тока являются положительными, с Визуализация комплексных корней у = ах 2 + BX + C : парабола поворачивается на 180 ° вокруг своей вершины ( оранжевый ). Ее х -intercepts повернуты на 90 ° вокруг своей средней точки, а декартову плоскость интерпретируются как комплексная плоскость ( зеленый ).
Визуализация комплексных корней у = ах 2 + BX + C : парабола поворачивается на 180 ° вокруг своей вершины ( оранжевый ). Ее х -intercepts повернуты на 90 ° вокруг своей средней точки, а декартову плоскость интерпретируются как комплексная плоскость ( зеленый ). Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда:
Описание слайда: Описание слайда: 13 слайд
Описание слайда: 13 слайд  Описание слайда:
Описание слайда:


 Цели урока:
Цели урока:


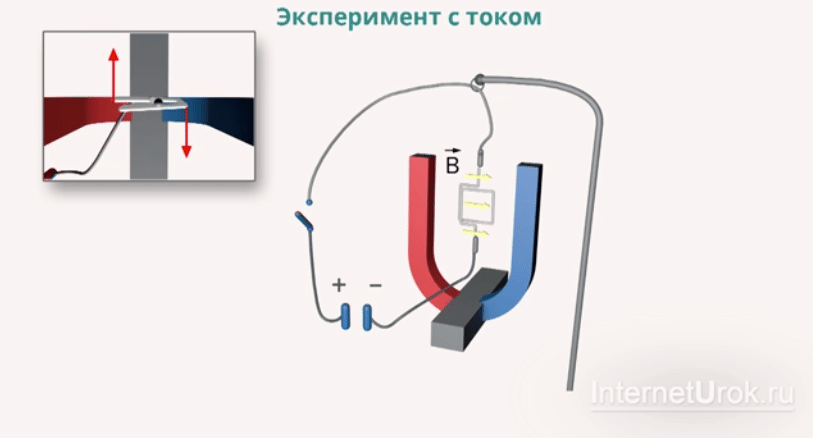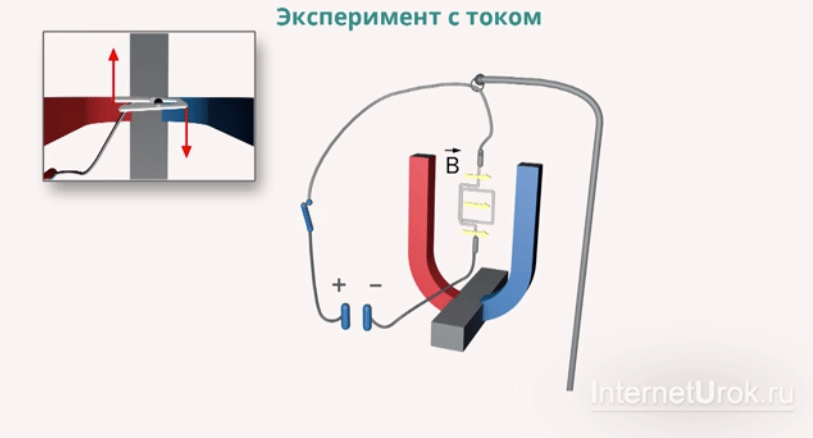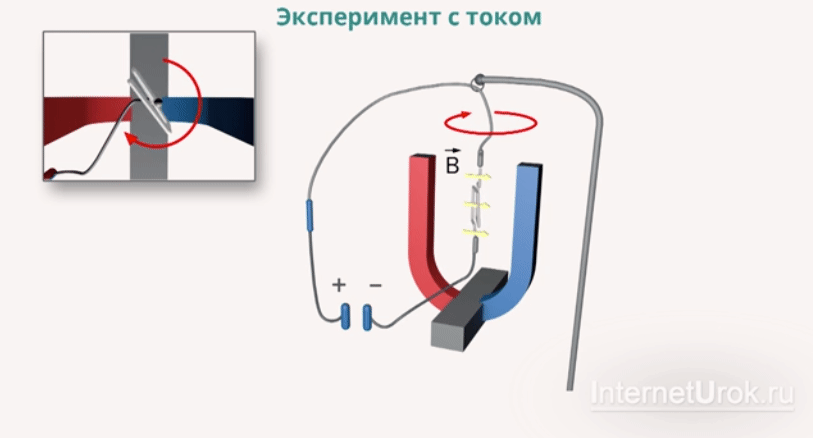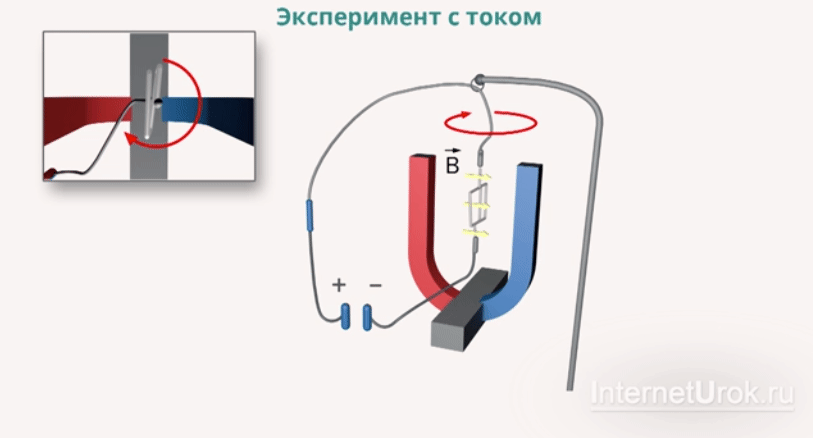
 – индукция магнитного поля
– индукция магнитного поля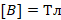
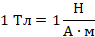
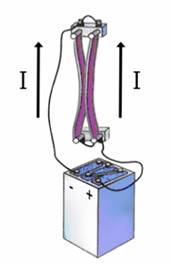
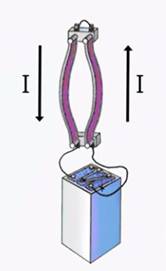
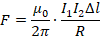








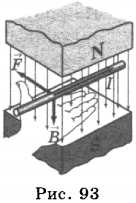
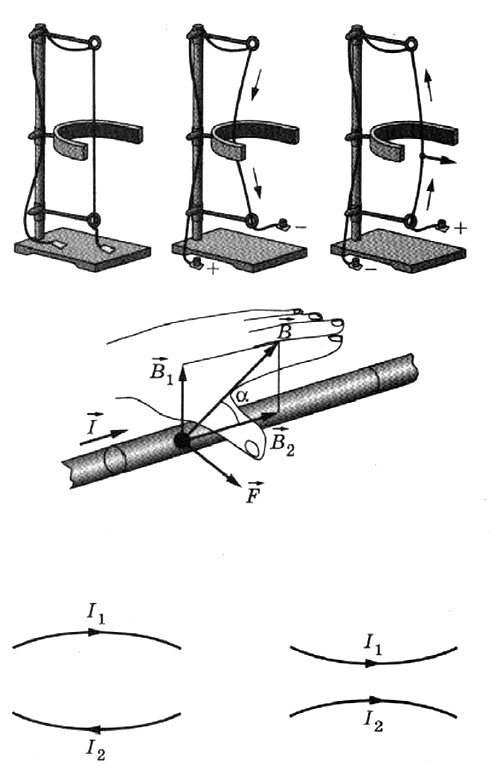
 со стороны магнитного поля зависит от направления электрического тока
со стороны магнитного поля зависит от направления электрического тока 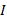 в проводнике и от линий магнитного поля
в проводнике и от линий магнитного поля 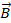

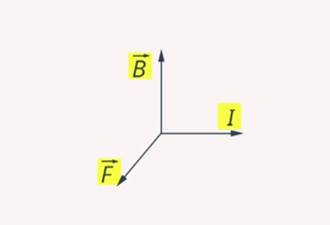
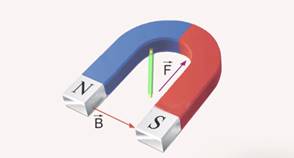
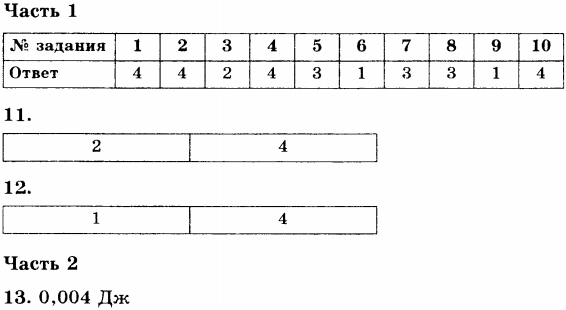
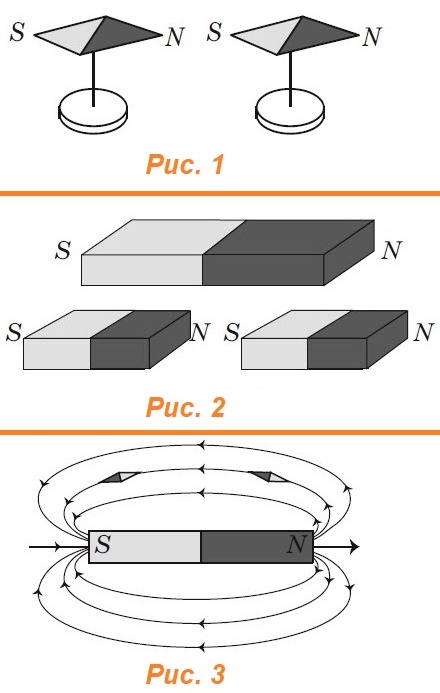
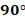 палец левой руки покажет направление действия силы (рис. 17). Сформулированное нами правило называется правилом левой руки.
палец левой руки покажет направление действия силы (рис. 17). Сформулированное нами правило называется правилом левой руки.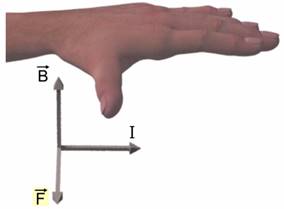

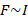
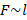
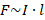
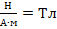 , следовательно, нужно правую часть умножить на модуль магнитной индукции:
, следовательно, нужно правую часть умножить на модуль магнитной индукции: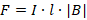
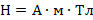

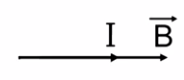
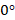
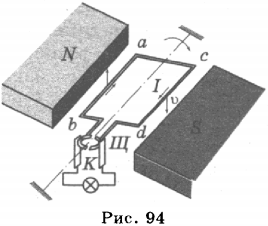
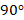 (рис. 22), то сила действия магнитного поля на проводник с током максимальна.
(рис. 22), то сила действия магнитного поля на проводник с током максимальна.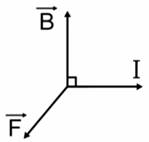
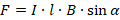
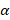 – угол между направлением тока и направлением вектора магнитной индукции:
– угол между направлением тока и направлением вектора магнитной индукции:


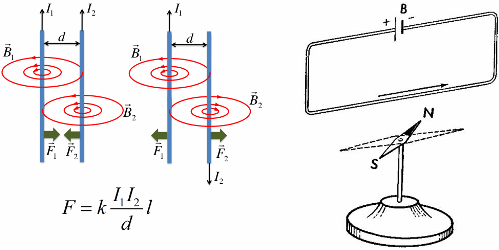






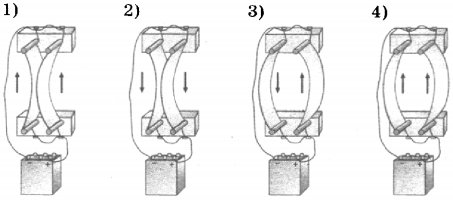



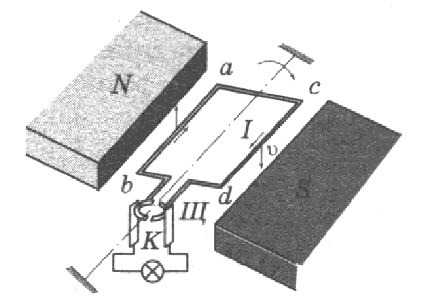

 , гдеB– модуль магнитной
индукции,Fmмаксимальная сила,Iсила
тока, ∆l – длина
проводника.
, гдеB– модуль магнитной
индукции,Fmмаксимальная сила,Iсила
тока, ∆l – длина
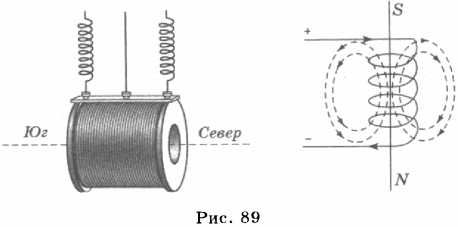
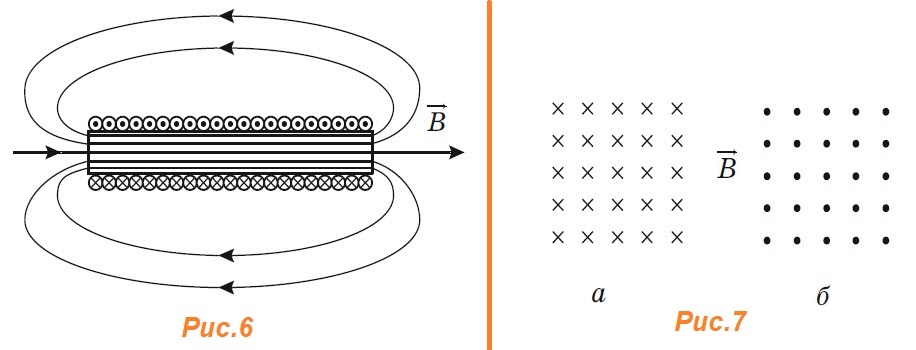
проводника.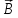 направлен от северного полюса магнита
к южному полюсу.
направлен от северного полюса магнита
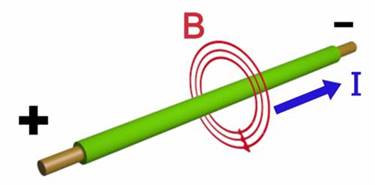
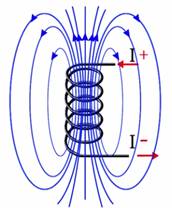
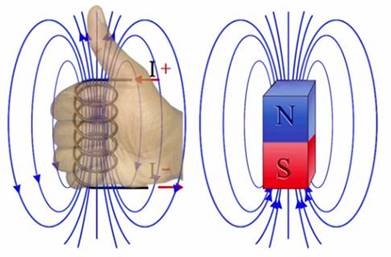
к южному полюсу.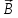 определяют поправилубуравчика:
если направление поступательного
движения буравчика совпадает с
направлением тока в проводнике, то
направление вращения буравчика совпадёт
с направлением вектора
определяют поправилубуравчика:
если направление поступательного
движения буравчика совпадает с
направлением тока в проводнике, то
направление вращения буравчика совпадёт
с направлением вектора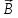 .
.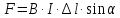 ,
где
,
где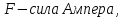
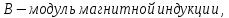
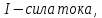
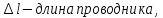
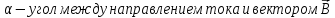 .
.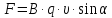 ,
где
,
где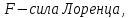
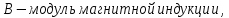
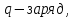
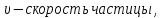
 .
.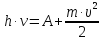 энергия порции света
энергия порции света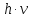 идёт на совершение работы выхода
идёт на совершение работы выхода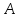 электрона из металла и на сообщение
электрону кинетической энергии
электрона из металла и на сообщение
электрону кинетической энергии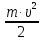 .
.
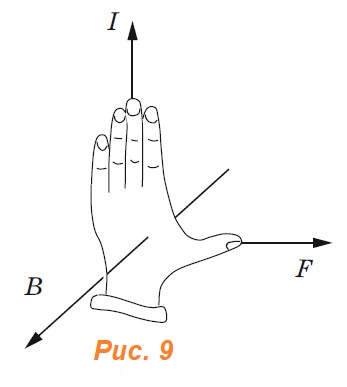 Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.
Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.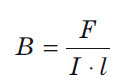 не зависит от свойств проводника и характеризует само магнитное поле.
не зависит от свойств проводника и характеризует само магнитное поле.

 Тесты по русскому языку.Пройти >>
Тесты по русскому языку.Пройти >>