Внутреннюю энергию тела: 500 Internal Server Error
Тепло, теплота и внутренняя энергия тела Текст научной статьи по специальности «Физика»
Научный журнал КубГАУ, №111(07), 2015 года
1
УДК 536.1 UDC 536.1
01.00.00 Физико-математические науки Physics and mathematical sciences
ТЕПЛО, ТЕПЛОТА И ВНУТРЕННЯЯ ЭНЕРГИЯ WARM, WARMTH AND INTERNAL ENERGY OF A ТЕЛА BODY
Александров Борис Леонтьевич Alexandrov Boris Leontievich
д.г.-м..н., профессор Dr.Sci.Geol.-Min., professor
[email protected] [email protected]
Кубанский государственный аграрный университет, Kuban state agrarian University, Krasnodar, Russia Краснодар, Россия
Обсуждается вопрос понятия теплоты и внутренней энергией тела. Дается анализ этих понятий в историческом аспекте и представления автора, основанные на новой фотонной теории строения атома. Анализ исторического аспекта этого вопроса показывает, что понятия тепла, теплоты и внутренней энергии тела долгое время ассоциировалось с понятием теплорода, который может перетекать в веществе. Следующим этапом отождествления понятия теплоты явилась энергия, связанная с движением и работой. В соответствии с этим, Клаузиус обосновал эквивалентность тепла и работы как первое начало теории тепла и ввел понятие внутренней энергии, которую можно увеличить двумя путями — производя над телом работу и подводя к нему тепло. Таким образом, энергия явилась главным объединяющим фактором работы и теплоты. Далее кинетическая теория тепла, как энергия движения молекул, была развита Максвеллом и модель теплорода оказалась помехой в развитии теории тепла. Фактически внутреннюю энергию тела определяют фотоны, вращающиеся вокруг заряженных частиц в атомах по своим орбиталям. Определенные серии фотонов объединяются в отдельные фотонные орбитали, направления вращения фотонов в которых отличаются друг от друга. Таким образом, тело обладает внутренней энергией или внутренней теплотой. Она обусловлена энергией фотонов, вращающихся вокруг электронов на внешней оболочке каждого атома, а также вокруг заряженных частиц — протонов и электронов в ядре атома. Эта внутренняя энергия может увеличиваться при механическом воздействии на тело, приводящее к увеличению результирующей частоты колебаний фотонов вокруг заряженных частиц атомов и эта внутренняя теплота, содержащаяся в теле, может перетекать от тела с большей концентрацией теплоты к телу с меньшей концентрацией теплоты
Фактически внутреннюю энергию тела определяют фотоны, вращающиеся вокруг заряженных частиц в атомах по своим орбиталям. Определенные серии фотонов объединяются в отдельные фотонные орбитали, направления вращения фотонов в которых отличаются друг от друга. Таким образом, тело обладает внутренней энергией или внутренней теплотой. Она обусловлена энергией фотонов, вращающихся вокруг электронов на внешней оболочке каждого атома, а также вокруг заряженных частиц — протонов и электронов в ядре атома. Эта внутренняя энергия может увеличиваться при механическом воздействии на тело, приводящее к увеличению результирующей частоты колебаний фотонов вокруг заряженных частиц атомов и эта внутренняя теплота, содержащаяся в теле, может перетекать от тела с большей концентрацией теплоты к телу с меньшей концентрацией теплоты
The article discusses the question of the concepts of heat and internal energy of a body. The analysis of these concepts in the historical aspect and the views of the author, based on the new photon theory of atomic structure were presented in this study. The analysis of the historical aspect of this question tells that the concepts of heat and internal energy of the body for a long time were associated with the concept of caloric, which can flow in the substance. The next step was the identification of the concept of heat with energy linked with the movement and work. In accordance with this, Clausius proved the equivalence of heat and work as the first principle of the theory of heat and introduced the concept of internal energy, which can be increased in two ways — making work on body, and summing heat to it. Thus, energy was the main uniting factor of work and heat. Then, the kinetic theory of heat, as the energy of motion of molecules, was developed by Maxwell and caloric model turned out to be a hindrance in the development of the theory of heat. In fact, the internal energy of the body is determined photons, rotating around charged particles in atoms in their orbitals. The series of photons are combined into a single photon orbital direction of rotation of the photons, which are different from each other. Thus, the body has an internal energy or internal heat. It is due to the energy of photons, orbiting electrons in the outer shell of each atom, as well as around the charged particles -electrons and protons in the nucleus of an atom. This internal energy may be increased by mechanical action on the body, leading to an increase in resulting oscillation frequency of photons around charged particles of atoms and the internal heat contained in the body can flow of the body with a higher concentration of heat to the body with a lower concentration of heat
The series of photons are combined into a single photon orbital direction of rotation of the photons, which are different from each other. Thus, the body has an internal energy or internal heat. It is due to the energy of photons, orbiting electrons in the outer shell of each atom, as well as around the charged particles -electrons and protons in the nucleus of an atom. This internal energy may be increased by mechanical action on the body, leading to an increase in resulting oscillation frequency of photons around charged particles of atoms and the internal heat contained in the body can flow of the body with a higher concentration of heat to the body with a lower concentration of heat
Ключевые слова: ТЕПЛОТА, РАБОТА, ЭНЕРГИЯ, Keywords: HEAT, WORK, ENERGY, PHOTON
ФОТОН
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
2
Введение
Теория тепла возникла не сразу. Очень долго не могли понять что такое тепло, теплота и какая разница между температурой и теплом. Понятие «тепло», «теплота» и «температура» разделить было очень трудно. И в настоящее время этим понятиям нет ясного определения. Так, в соответствии со словарем русского языка С.И. Ожегова [3], «тепло»- это «нагретое состояние чего-нибудь», а «теплота» означает «теплый» или это «форма движения материи — энергия, образуемая беспорядочным движением частиц тела (молекул, атомов и т.п.)» Поэтому всем вроде бы ясно, что когда нагревают тело, температура его повышается. Когда тепло перетекает от одного тела к другому, температура одного тела падает, а другого — повышается. Тепло во многих случаях ведет себя, как ручей, текущий с горы в долину. Поэтому многие ученые прошлого времени думали, что теплота — это вещество. Они считали ее жидкостью (флюидом), которая может перетекать от одного тела к другому. Этот флюид получил название теплорода. Аналогия между теплом и жидкостью стала еще более убедительной после открытия электрических явлений: электрический ток также течет по проводам, как река, выравнивания потенциал между двумя заряженными телами. Модель теплорода объясняла очень многое и завоевала широкое признание в последней четверти XVIII века. Теплород, казалось, хорошо объяснял свойства тепла. Теория теплового двигателя, построенного Карно, была основана на модели теплорода. Тот факт, что большинство веществ расширяется при нагревании и сжимается при охлаждении, казалось, подтверждал материальную теорию теплоты, потому что теплород занимает место.
Поэтому многие ученые прошлого времени думали, что теплота — это вещество. Они считали ее жидкостью (флюидом), которая может перетекать от одного тела к другому. Этот флюид получил название теплорода. Аналогия между теплом и жидкостью стала еще более убедительной после открытия электрических явлений: электрический ток также течет по проводам, как река, выравнивания потенциал между двумя заряженными телами. Модель теплорода объясняла очень многое и завоевала широкое признание в последней четверти XVIII века. Теплород, казалось, хорошо объяснял свойства тепла. Теория теплового двигателя, построенного Карно, была основана на модели теплорода. Тот факт, что большинство веществ расширяется при нагревании и сжимается при охлаждении, казалось, подтверждал материальную теорию теплоты, потому что теплород занимает место.
Смущало только то обстоятельство, что имеется несколько веществ, которые при нагревании сжимаются, а при охлаждении расширяются. Кроме того, если теплота есть вещество, то в горячем состоянии тело должно весить больше, чем в холодном. Опыт, однако, показывал, что это не так. Таким
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
3
образом, модель теплорода не выдерживала испытаний, когда дело касалось закона сохранения. Рассуждали так: если бы тепло было какой-то жидкостью, то она, протекая, сохранялась бы, ее количество не должно было изменяться. Сколько тепла забрали от нагревателя, столько должен получить и холодильник.
На первый взгляд так оно и есть: охлаждается чайник, нагревается воздух. Но часто бывает совсем не так.
Исторический обзор изменения представлений о теплоте и энергии
Первым, кто обратил на это внимание, был Бенджамен Томсон (граф Румфорд). Наблюдая за сверлением пушечных стволов, он заметил выделение большого количества тепла, — особенно, если сверла были тупые. Это заставило его задуматься, что могло быть источником теплоты. Согласно теории теплорода, теплота могла появиться или из металла, или из окружающего пространства. Но, ни то, ни другое, по мнению Румфорда, не являлось источником теплоты. Чтобы проверить теорию, Румфорд взвесил заготовку ствола до сверления и потом взвесил ствол и стружки после сверления. Оба взвешивания дали одинаковый результат. Единственное решение могло бы состоять в том, что в стружках содержится меньше теплорода, чем в сплошной отливке, и избыток его выделяется при сверлении. Но тогда стружку было бы легче нагреть, чем сплошной металл, у стружек должна была быть меньше теплоемкость, чем у сплошного металла. Но это также не подтвердилось опытом. Он применил для охлаждения ствола воду, но все равно ствол при сверлении нагревался.
Наблюдая за сверлением пушечных стволов, он заметил выделение большого количества тепла, — особенно, если сверла были тупые. Это заставило его задуматься, что могло быть источником теплоты. Согласно теории теплорода, теплота могла появиться или из металла, или из окружающего пространства. Но, ни то, ни другое, по мнению Румфорда, не являлось источником теплоты. Чтобы проверить теорию, Румфорд взвесил заготовку ствола до сверления и потом взвесил ствол и стружки после сверления. Оба взвешивания дали одинаковый результат. Единственное решение могло бы состоять в том, что в стружках содержится меньше теплорода, чем в сплошной отливке, и избыток его выделяется при сверлении. Но тогда стружку было бы легче нагреть, чем сплошной металл, у стружек должна была быть меньше теплоемкость, чем у сплошного металла. Но это также не подтвердилось опытом. Он применил для охлаждения ствола воду, но все равно ствол при сверлении нагревался.
Полученные результаты убедили Румфорда, что теплород, если он действительно существует, не мог прийти ни из металла, ни из окружающего пространства. Все это никак не укладывалось в простую модель перетекающего с места на место теплорода.
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
4
Так как никаких других возможных источников теплоты не было, Румфорд заключил, что теплота получалась как результат работы сверления. Другими словами, он пришел к выводу, что теплота — энергия. Как описано в [8], для дальнейшей проверки гипотезы Румфорда, что теплота — это энергия, современник Румфорда Хемфри Дэви (1778-1829) придумал очень простой решающий опыт. Опыт состоял в трении двух кусков льда друг о друга при температуре ниже температуры плавления этих кусков льда. Оказалось, что при этом лед плавился, и отсюда неизбежно вытекало заключение, что теплота, которая расплавляла лед, получалась из работы на преодоление трения кусков льда. Таким образом, чаша весов склонялась к тому, чтобы связать природу теплоты с движением.
Оказалось, что при этом лед плавился, и отсюда неизбежно вытекало заключение, что теплота, которая расплавляла лед, получалась из работы на преодоление трения кусков льда. Таким образом, чаша весов склонялась к тому, чтобы связать природу теплоты с движением.
Понятие о величине, характеризующей движение и имеющей по современной терминологии размерность «энергии», впервые появилось в механике. Основоположниками здесь являются Галилей (1564-1642), Гюйгенс (1629-1695) и Ньютон (1642-1727). Согласно этим авторам при падении тела массой m с высоты h и ускорении силы тяжести g убыль потенциальной энергии тела (его гравитационной энергии) Д( mgh) равна
mvL
приращению его кинетической энергии ——.
Сформулированный здесь закон сохранения энергии до середины XIX века казался частным случаем, реализующимся в «чистой механике» в отсутствии трения. Да и самого понятия «энергия» не было до начала XIX века, когда оно было введено в механику Юнгом. Р.Клаузиусу (1864) приписывают идею окончательного введения этого термина в физику.
Так что же такое энергия? Ее нельзя увидеть, потрогать или понюхать как какое-нибудь вещество. Она представляет для нас более абстрактное понятие. Поэтому следует попытаться проанализировать
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
5
существующие определения энергии и рассмотреть это понятие с общих позиций, прежде чем углубляться в дальнейшее обсуждение.
Энергия (от греческого energeia — действие, деятельность) — общая количественная мера движения и взаимодействия всех видов материи [6]. Энергия не возникает из ничего и не исчезает, она может только переходить их одной формы в другую. Энергия связывает воедино все явления природы.
Энергия не возникает из ничего и не исчезает, она может только переходить их одной формы в другую. Энергия связывает воедино все явления природы.
Ранее часто вместо энергии говорили «сила», приписывая один и тот же термин величинам разной размерности. Даже Гельмгольц (1874) статью, посвященную закону сохранения энергии, озаглавил «О сохранении силы». Между тем по Ньютону сила — это причина, вызывающая движение, которая, совершая на известном пути работу, сообщает телу энергию. Таким образом, с понятием энергии неразрывно связано другое понятие той же размерности — «работа».
Работа (А), совершаемая системой, обусловлена взаимодействием между системой и внешней средой, в результате которого преодолеваются внешние силы, нарушившие равновесие в системе. Работа определяется суммой произведений действующих на систему сил на соответствующий путь (давление, изменение объема, поверхностного натяжения, изменение поверхности и т.д.)
Таким образом, работа процесса — это энергия, передаваемая одним телом другому при их взаимодействии, не зависящая от температуры этих тел и не связанная с переносом вещества от одного тела к другому [2].
Наиболее затруднительным явилось установление общего закона сохранения энергии, включая действия диссипативных сил, приводящих к рассеянию работы и превращению ее в теплоту.
Р.Клаузиус (1850) первый заговорил об эквиваленте тепла и работы как о первом начале теории тепла и написал уравнение, которого не хватало Карно. Для этого надо было, прежде всего, сказать простую вещь:
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
6
всякое тело имеет внутреннюю энергию.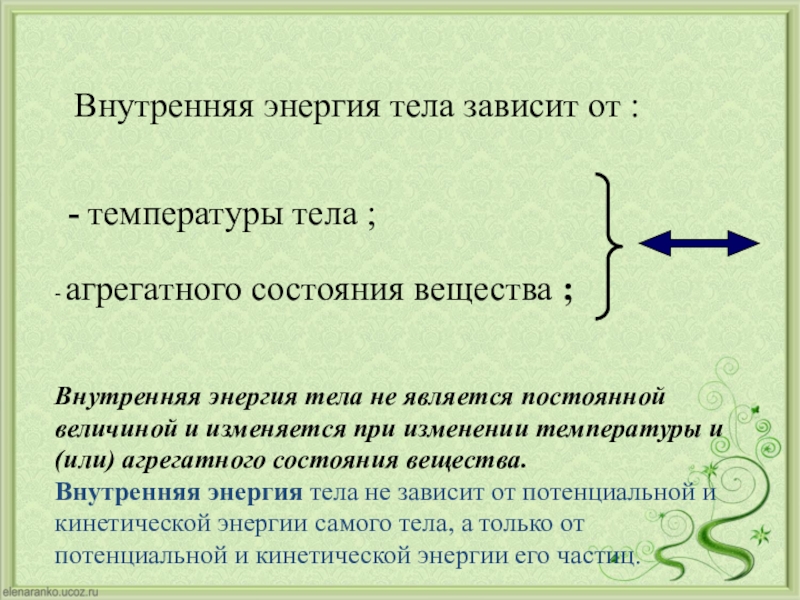 Принято считать [6], что внутренняя энергия равна сумме кинетической энергии хаотического движения молекул относительно центра масс тел и потенциальной энергии взаимодействия молекул друг с другом. Внутреннюю энергию можно увеличить двумя путями — производя над телом работу (АЛ) и подводя к нему тепло (AQ).
Принято считать [6], что внутренняя энергия равна сумме кинетической энергии хаотического движения молекул относительно центра масс тел и потенциальной энергии взаимодействия молекул друг с другом. Внутреннюю энергию можно увеличить двумя путями — производя над телом работу (АЛ) и подводя к нему тепло (AQ).
Смысл этого глубокого утверждения заключен в союзе «и» и описывается простой формулой
AU = AQ + АЛ (1)
Очень важно понимать, что по конечному состоянию системы нельзя никаким образом обнаружить, за счет чего система увеличила свою энергию: за счет тепла или за счет работы. Сам Р.Клаузиус называл U -«теплом, содержащимся в теле», противопоставляя ему Q — «тепло, сообщенное телу». В этом отличии кроется глубокий смысл. Сейчас U называют внутренней энергией (или просто энергией), а AU есть ее приращение.
Таким образом, единственный элемент — энергия — связывает воедино чрезвычайно широкое многообразие явлений, а закон сохранения этого «элемента» не знает исключений ни в макро-, ни в микромире. Энергия, по Ф.Энгельсу, есть мера движения при переходе одной формы движения в другую [9]. Это определение философа дополняет определение физика М.Планка: «Энергия материальной системы в определенном состоянии, взятая по отношению к другому определенному «нулевому» состоянии, имеет однозначное значение» [4]. На основании этого можно говорить о запасе или о «содержании» энергии в системе. Энергия системы однозначно зависит от параметров, характеризующих состояние системы. В случае непрерывной среды или поля вводятся понятия плотности энергии, т.е. энергии в единице объема, и плотности потока энергии, равной произведению плотности энергии на скорость ее перемещения.
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
7
А. Эйнштейн показал, что энергия тела (E) неразрывно связана с его массой т соотношением
Эйнштейн показал, что энергия тела (E) неразрывно связана с его массой т соотношением
E = mc2, (2)
где с — скорость света.
Любое тело обладает энергией. Если масса покоящегося тела m0, то его энергия покоя Е0 = т0с ; эта энергия может переходить в другие виды энергии при превращениях частиц (распадах, ядерных реакциях и так далее). Ю.Г.Белостоцкий [7, стр.15] высказал предположение, что при ускорении материального тела происходит увеличение его собственного гравиполя, причем запас кинетической энергии содержится в гравитационном поле движущегося тела. Это, по его мнению, позволяет определить энергию как процесс превращения вещества в поле. Поэтому
формула E = тс2 характеризует зависимость количества энергии тела от количества превращенного вещества в поле, причем т в этой формуле является полевой массой.
Рассматривая идеальные газы на базе эфирной природы теплоты С.Д.Брусин и Л.Д.Брусин [7, стр.24] отмечают, что количество тепловой энергии Q характеризуется массой эфира «т» и определяется простым
соотношением Q = тс2 (где с — скорость света). Газы представляются состоящими из частичек, сгруппированных в молекулы, и эфира, находящегося как между частичками молекул (молекулярная область), так и между молекулами (межмолекулярная область).
Согласно классической физике энергия любой системы меняется непрерывно и может принимать любые значения. Квантовая теория утверждает, что энергия микрочастиц, движение которых происходит в ограниченном объеме пространства (например, электронов в атоме), принимает дискретный ряд значений. Так, атомы испускают
http://ej. kubagro.ru/2015/07/pdf/38.pdf
kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
8
электромагнитную энергию в виде дискретных порций — световых квантов или фотонов.
Опыт, накопленный при наблюдении множества различных процессов, свидетельствует о том, что хотя энергия может передаваться от одного тела к другому, а также переходить из одной формы в другую, она никогда не создается из ничего и не исчезает.
Подобные наблюдения, подтвержденные количественными измерениями теплоты и работы, лежат в основе первого закона термодинамики.
Ситуация с энергией во многом напоминает ситуацию с веществом — при любом приращении энергии некоторая часть ее всегда превращается в теплоту, которая рассеивается в окружающую среду и, следовательно, не может быть использована для выполнения работы. Так, на практике большая часть энергии, запасенной в угле или бензине, превращается в теплоту. Таким образом, энергия — это способность к выполнению работы, переносу тепла, а работа и теплота являются количественными характеристиками двух форм обмена энергией между системой и окружающей средой, причем работа является макрофизической формой передачи энергии, а теплота микрофизической. Эти превращения, согласно Майеру, осуществляются в определенных эквивалентах соотношениях. Однако, согласно второму закону термодинамики эти формы не равноценны и если в каком-то процессе работа превращается в теплоту (например, посредством трения), то такое превращение ничем не ограниченно, обратное же превращение теплоты в работу ограниченно определенными условиями. В этом и заключается главная «хитрость» природы, путь к пониманию которой оказался столь трудным и долгим [8]. Была еще одна трудность, которую встретила модель теплорода. Если теплород — это род жидкости, которая совершает работу при перетекании от более высокого уровня (от более высокой температуры) к более
Если теплород — это род жидкости, которая совершает работу при перетекании от более высокого уровня (от более высокой температуры) к более
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
9
низкому, то нельзя было понять, что происходит в неоднородно нагретом теле в процессе выравнивания температуры. Куда девается работа, которая должна возникнуть при перетекании теплорода.
Но даже если не обращать внимания на «пропажу» работы, такая картина не смогла объяснить, как передается тепло через вакуум -например, от Солнца к Земле. Говорили о колебаниях эфира, но получить из таких представлений сколько-нибудь убедительную теорию было нельзя. Теория теплорода явно терпела одну неудачу за другой. Согласившись, что теплота есть энергия, естественно было задать вопрос: на что идет эта энергия? Известно, что потенциальная энергия есть энергия положения, а кинетическая — энергия движения. Может ли теплота быть одним из этих видов энергии или быть может, и тем и другим сразу? Мы уже знаем, что вещество построено из молекул, и что если газ или жидкость нагревается, то броуновское движение, как показывают наблюдения, становится более оживленным. Это указывает на усиление движения молекул. Такие наблюдения возможны только в жидкостях и газах, но легко согласиться, что при нагревании, увеличиваются колебания молекул и в твердых телах. Таким образом, экспериментальные наблюдения в сочетании с логическими заключениями привели к выводу, что теплота есть кинетическая энергия молекулярного движения. О том, что теплота связана с движением, говорили многие естествоиспытатели. Писал об этом Декарт. Галилей был одним из первых, кто писал о механической природе тепла. Даниил Бернулли пытался вывести формулу для давления газа. Гук очень ясно говорил о связи между теплотой и движением — колебаниями частиц в нагретом теле. Подобные идеи высказывали Ломоносов, многие философы. Но они не могли превратить эти высказывания в физическую теорию, которую можно проверить на опыте.
Гук очень ясно говорил о связи между теплотой и движением — колебаниями частиц в нагретом теле. Подобные идеи высказывали Ломоносов, многие философы. Но они не могли превратить эти высказывания в физическую теорию, которую можно проверить на опыте.
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
10
Количественная связь энергии с теплотой была установлена в опыте Джеймса Джоуля (1873). Джоуль показал, что, размешивая мешалкой жидкость и нагревая ее таким образом, надо тратить 460 кгс-м (килограмм-сила на метр) работы на каждую большую калорию, полученную жидкостью. Несколько раньше Джоуля эту же величину, но с меньшей точностью (365 кгс-м/ккал) вычислил Роберт Майер, использовав результаты опытов Г ей-Люссака по расширению газов в пустоту.
Дальше всех продвинулся Максвелл. Принято считать, что кинетическая теория тепла, созданная Максвеллом, позволила понять тепловые явления на основе классической механики. В работе Максвелла появилась формула для распределения движущихся частиц по скоростям: формула позволила вычислить постоянные, характеризующие свойства тел, — такие, как теплопроводность и вязкость газа, и установить их зависимость от температуры. Максвелл положил начало статистической физики или кинетической теории газов. Но как отмечает Я.А.Смородинский [5], у Максвелла был предшественник — Ватерсон, первую формулу новой теории тепла которого мало кто заметил. Как описано в [5], в 1845г. в английскую академию наук (Королевское общество) была представлена работа Ватерсона. В ней было показано, что давление газа на стенки сосуда можно объяснить ударами атомов. Хотя сама идея о том, что газ состоит из атомов, была не нова, мало кто принимал всерьез утверждение, что атомы могут свободно двигаться в сосуде от стенки к стенке, а упругие свойства газа можно свести просто к классической механике атомов.
Работа Ватерсона не понравилась членам ученого общества и рецензентом королевского общества была отклонена. Лишь много лет спустя в 1892г. Рэлей нашел ее в архиве и опубликовал в журнале «философские сообщения Королевского общества». То, что было сделано одним человеком и осталось незамеченным, было открыто впоследствии
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
11
лишь в результате работы нескольких ученых, а окончательная формула была написана Максвеллом только в 1859г. Теперь модель не уничтожающейся жидкости — теплорода стала помехой для дальнейшего развития теории тепла и быстро сошла со сцены.
Как видим, происходили удивительные вещи, из вроде бы наивных представлений о теплороде были выведены правильные результаты и разработана гениальная теория тепла Карно. Понятие об атомах, молекулах долго казалось не нужным для теории тепла, но в окончательном результате стало приоритетным. А как же связана теплота и температура с потенциальной энергией молекул тела? Для ответа на этот вопрос Л.Эллиот и У.Уилкокс [8] рассматривают опыты плавления льда и кипения воды. Известно, что для плавления льда надо подвести тепло и при этом во время процесса плавления температура не будет изменяться. Точно так же требуется теплота для того, чтобы воду превратить в пар, и при этом опять температура во время кипения не изменяется. Сегодня общепризнанно, что температура тела есть мера средней кинетической энергии его молекул или температура есть мера нагретости тела. Так как поглощенная теплота при плавлении и кипении не вызывает никакого повышения температуры, а следовательно, и усиления молекулярного движения, то она не должна изменять кинетическую энергию молекул. nst = 100°С, безусловно имеет более высокую кинетическую энергию. Но так как система не выявляет себя нагревом, а кинетическая энергия молекул системы, как принято и сегодня, растет только с увеличением температуры, то и
nst = 100°С, безусловно имеет более высокую кинетическую энергию. Но так как система не выявляет себя нагревом, а кинетическая энергия молекул системы, как принято и сегодня, растет только с увеличением температуры, то и
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
12
делается неверный вывод, что полученное системой тепло затрачивается только на изменение потенциальной энергии. Более того, как можно интерпретировать работу расширения воды при ее охлаждении от +4оС до 0оС в жидком состоянии? При охлаждении выделяется теплота и одновременно совершается работа расширения можно считать за счет убыли внутренней энергии в соответствии с формулой (1) .
Однако при кристаллизации температура не изменяется, т.е. внутренняя энергия должна оставаться постоянной, но происходит увеличение объема, т.е. совершается работа расширения. За счет чего же совершается работа расширения, если одновременно с этим при кристаллизации выделяется теплота кристаллизации? Ответа на этот вопрос в научной литературе нет.
Современное представление сущности теплоты и внутренней
энергии
По нашим представлениям [1], это возможно лишь в том случае, если принять, что внутреннюю энергию в любом теле определяют фотоны, вращающиеся вокруг заряженных частиц в атомах по своим орбитам, причем энергия (е) каждого фотона, в соответствии с формулой Планка (e=hv), пропорциональна его частоте v (где h — постоянная Планка). Определенные серии фотонов объединяются в отдельные фотонные орбитали, направления вращения фотонов в которых отличаются друг от друга. Химическое взаимодействие атомов происходит не просто через валентные электроны атомов, а с учетом внешних фотонных орбиталей вокруг этих электронов. Когда излучаются фотоны внешних орбиталей, то происходит перестройка кристаллической решетки атомов и в целом молекул, например воды, между собой за счет контакта их следующими фотонными орбиталями, направления вращения которых вокруг электронов иное.
Химическое взаимодействие атомов происходит не просто через валентные электроны атомов, а с учетом внешних фотонных орбиталей вокруг этих электронов. Когда излучаются фотоны внешних орбиталей, то происходит перестройка кристаллической решетки атомов и в целом молекул, например воды, между собой за счет контакта их следующими фотонными орбиталями, направления вращения которых вокруг электронов иное.
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
13
Таким образом, тело обладает внутренней энергией или внутренней теплотой. Она обусловлена энергией фотонов, вращающихся вокруг электронов на внешней оболочке каждого атома тела, а также вокруг заряженных частиц — протонов и электронов в ядре атома. Эта внутренняя энергия тела может увеличиваться при механическом воздействии на тело, приводящее к увеличению результирующей частоты колебаний фотонов вокруг заряженных частиц атомов вещества и эта внутренняя теплота, содержащаяся в теле, может перетекать от тела с большей концентрацией теплоты к телу с меньшей концентрацией теплоты или при наличии перепада температур с окружающей средой путем теплового электромагнитного излучения за счет внешних фотонных орбиталей электронов атомов или при ядерных процессах за счет излучения фотонов гамма-квантов, вращающихся вокруг нуклонов в ядрах.
Выводы
1.Энергию любого тела можно подразделить на механическую энергию, включая кинетические энергии поступательного и вращательного движений и потенциальную энергию тела относительно поверхности Земли, и внутреннюю энергию тела или внутреннюю теплоту. Последняя обусловлена энергией фотонов, вращающихся вокруг электронов на внешней оболочке атома, а также вокруг заряженных частиц — протонов и электронов в ядре атома. Внутренняя энергия тела может увеличиваться не только за счет дополнительного поглощения фотонов, но и при механическом воздействии на тело, приводящее к увеличению результирующей частоты колебаний фотонов вокруг заряженных частиц атомов вещества. Таким образом, теплота — это сконцентрированная энергия фотонов, обусловленная как собственной частотой этих фотонов, так и дополнительной частотой за счет механической работы. Последняя приводит к повышению результирующей частоты колебания фотонов и, следовательно, их энергии. Без наличия
Внутренняя энергия тела может увеличиваться не только за счет дополнительного поглощения фотонов, но и при механическом воздействии на тело, приводящее к увеличению результирующей частоты колебаний фотонов вокруг заряженных частиц атомов вещества. Таким образом, теплота — это сконцентрированная энергия фотонов, обусловленная как собственной частотой этих фотонов, так и дополнительной частотой за счет механической работы. Последняя приводит к повышению результирующей частоты колебания фотонов и, следовательно, их энергии. Без наличия
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
14
фотонов в веществе механически невозможно повысить количества теплоты в нем.
2.Роль теплорода в веществе выполняют фотоны, вращающиеся вокруг заряженных частиц в атомах. При наличии перепада концентрации фотонов вокруг внешних валентных электронов, происходит их перераспределение в область более низкой концентрации, т.е. внутренняя энергия тела может перетекать от тела с большей концентрацией теплоты к телу с меньшей концентрацией теплоты.
Литература
1. Александров Б. Л. Роль фотонов в физических и химических явлениях// Б. Л. Александров, М.Б. Родченко, А.Б. Александров. — Краснодар, ГУП «Печатный двор Кубани», 2002- 543 с.
2. Каркапетьянц М.Х. Химическая термодинамика. Изд. 3-е переработанное и дополненное// М.Х. Каркапетьянц,- М.: «Химия», 1975- 584 с.
3. Ожегов С.И. Словарь русского языка. Издание 17-е, стереотипное // С.И. Ожегов.- М.: «Русский язык», 1985 — 797 с.
4. Планк М. Принцип сохранения энергии // М. Планк.- М. — Л.: ГОНТИ, 1938.
Планк М. Принцип сохранения энергии // М. Планк.- М. — Л.: ГОНТИ, 1938.
5. Смородинский Я.А. Температура. Библиотека квант // Я.А. Смородинский. -М.: «Наука», 1981 -160 с.
6. Физический энциклопедический словарь. Главный редактор А.М. Прохоров, М.:, «Советская энциклопедия» 1984.
7. Фундаментальные проблемы естествознания. Международный научный конгресс. 22-27 июня 1998г., Санкт-Петербург, Россия.
8. Эллиот Л. Физика. Перевод с английского под редакцией проф.
А.И.Китайгородского // Л. Эллиот, У. Уилкокс.- Издание третье. М.: «Наука», 1975736 с.
9. Энгельс Ф. Диалектика природы М., «Политиздат» 1965.
References
1. Aleksandrov B.L. Rol’ fotonov v fizicheskih i himicheskih javlenijah// B.L. Aleksandrov, M.B. Rodchenko, A.B. Aleksandrov. — Krasnodar, GUP «Pechatnyj dvor Kubani», 2002- 543 s.
2. Karkapet’janc M.H. Himicheskaja termodinamika. Izd. 3-e pererabotannoe i dopolnennoe// M.H. Karkapet’janc,- M.: «Himija», 1975- 584 s.
3. Ozhegov S.I. Slovar’ russkogo jazyka. Izdanie 17-e, stereotipnoe // S.I. Ozhegov.-M.: «Russkij jazyk», 1985 — 797 s.
4. Plank M. Princip sohranenija jenergii // M. Plank.- M. — L.: GONTI, 1938.
5. Smorodinskij Ja.A. Temperatura. Biblioteka kvant // Ja.A. Smorodinskij. — M.: «Nauka», 1981 -160 s.
6. Fizicheskij jenciklopedicheskij slovar’. Glavnyj redaktor A. M. Prohorov, M.:, «Sovetskaj a j enciklopedij a» 1984.
M. Prohorov, M.:, «Sovetskaj a j enciklopedij a» 1984.
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Научный журнал КубГАУ, №111(07), 2015 года
15
7. Fundamental’nye problemy estestvoznanija. Mezhdunarodnyj nauchnyj kongress. 2227 ijunja 1998g., Sankt-Peterburg, Rossija.
8. Jelliot L. Fizika. Perevod s anglijskogo pod redakciej prof. A.I.Kitajgorodskogo // L. Jelliot, U. Uilkoks.- Izdanie tret’e. M.: «Nauka», 1975-736 s.
9. Jengel’s F. Dialektika prirody M., «Politizdat» 1965.
http://ej.kubagro.ru/2015/07/pdf/38.pdf
Способы изменения внутренней энергии тела
Внутренняя энергия тела не является какой-то постоянной величиной: у одного и того же тела она может изменяться. При повышении температуры тела внутренняя энергия тела увеличивается, так как увеличивается средняя скорость, а значит, и кинетическая энергия, молекул этого тела. С понижением же температуры, наоборот, внутренняя энергия тела уменьшается. Таким образом, внутренняя энергия тела изменяется при изменении скорости движения его молекул. Какими же способами можно увеличить или уменьшить эту скорость? Обратимся к опыту.
На подставке (рис. 181) укреплена тонкостенная латунная трубка, в которую налито немного эфира, трубка плотно закрыта пробкой. Трубку обвивают веревкой и быстро двигают веревку то в одну, то в другую сторону. Через некоторое время эфир закипит и его пар вытолкнет пробку. Этот опыт показывает, что внутренняя энергия эфира, увеличилась: ведь он нагрелся и даже закипел. Увеличение внутренней энергии произошло в результате работы, совершенной при натирании веревкой трубки.
Тела нагреваются также при ударах, разгибании и сгибании, вообще при деформации. Во всех этих случаях за счет совершенной работы увеличивается внутренняя энергия тел.
Итак, внутреннюю энергию тела можно увеличить путем совершения работы над телом. Если работу совершает само тело, то внутренняя энергия его при этом уменьшается. Это можно наблюдать на следующем опыте.
Берут толстостенный стеклянный сосуд, закрытый пробкой. Через специальное отверстие в сосуд накачивают воздух, в котором содержится водяной пар. Через некоторое время пробка выскакивает из сосуда (рис. 182). В тот момент, когда пробка выскакивает, в сосуде появляется туман. Его появление означает, что воздух в сосуде стал холоднее (вспомните, что и на улице туман появляется во время похолодания).
Находящийся в сосуде сжатый воздух, выталкивая пробку, совершает работу. Эту работу он совершает за счет своей внутренней энергии, которая при этом уменьшается. Об уменьшении энергии мы судим по охлаждению воздуха в сосуде.
Внутреннюю энергию тела можно изменить и другим способом.
Известно, что чайник с водой, стоящий на плите, металлическая ложка, опущенная в стакан с горячим чаем, печь, в которой разведен огонь, крыша дома, освещаемая солнцем, нагреваются. Во всех случаях повышается температура тел, а значит, увеличивается и их внутренняя энергия. Как объяснить ее увеличение?
Как, например, нагревается холодная металлическая ложка, опущенная в горячий чай? Сначала скорость и кинетическая энергия молекул горячей воды больше скорости и кинетической энергии частиц холодного металла. В тех местах, где ложка соприкасается с водой, молекулы горячей воды передают часть своей кинетической энергии частицам холодного металла. Поэтому скорость и энергия молекул воды в среднем уменьшается, а скорость и энергия частиц металла увеличивается: температура воды уменьшается, а температура ложки увеличивается — температуры их постепенно выравниваются. С уменьшением кинетической энергии молекул воды уменьшается и внутренняя энергия всей воды, находящейся в стакане, а внутренняя энергия ложки, увеличивается.
С уменьшением кинетической энергии молекул воды уменьшается и внутренняя энергия всей воды, находящейся в стакане, а внутренняя энергия ложки, увеличивается.
Процесс изменения внутренней энергии, при котором над телом не совершается работа, а энергия передается от одних частиц к другим, называют теплопередачей. Итак, внутреннюю энергию тела можно изменить двумя способами: совершением механической работы или теплопередачей.
Когда тело уже нагрето, мы не можем указать, каким из двух способов это было сделано. Так, держа в руках нагретую стальную спицу, мы не можем сказать, каким способом ее нагрели — натирая ее или помещая в пламя.
Вопросы. 1. Приведите примеры, показывающие, что внутренняя энергия тела увеличивается при совершении над телом работы. 2. Опишите опыт, показывающий, что за счет внутренней энергии тело может совершить работу. 3. Приведите примеры увеличения внутренней энергии тела способом теплопередачи. 4. Объясните на основе молекулярного строения вещества теплопередачу. 5. Какими двумя способами можно изменить внутреннюю энергию тела?
Задание.
Положите пятикопеечную, монету на лист фанеры или деревянную доску. Прижмите монету к доске и двигайте ее быстро, то в одну, то в другую сторону. Заметьте, сколько раз надо передвинуть монету, чтобы она стала теплой, горячей. Сделайте вывод о связи между проделанной работой и увеличением внутренней энергии тела.
Способы изменения внутренней энергии | Физика
Внутренняя энергия тела зависит от средней кинетической энергии его молекул, а эта энергия, в свою очередь, зависит от температуры. Поэтому, изменяя температуру тела, мы изменяем и его внутреннюю энергию. При нагревании тела его внутренняя энергия увеличивается, при охлаждении уменьшается.
Проделаем опыт. Укрепим на подставке тонкостенную латунную трубку. Нальем в нее немного эфира и плотно закроем пробкой. Теперь обовьем трубку веревкой и начнем натирать ею трубку, быстро вытягивая веревку то в одну, то в другую сторону. Через некоторое время внутренняя энергия трубки с эфиром возрастет настолько, что эфир закипит и образовавшийся пар вытолкнет пробку (рис. 60).
Через некоторое время внутренняя энергия трубки с эфиром возрастет настолько, что эфир закипит и образовавшийся пар вытолкнет пробку (рис. 60).
Этот опыт показывает, что внутреннюю энергию тела можно изменить путем совершения над телом работы, в частности трением.
Изменяя внутреннюю энергию куска дерева путем трения, наши предки добывали огонь. Температура воспламенения дерева равна 250 °С. Поэтому, чтобы получить огонь, нужно тереть одним куском дерева по другому до тех пор, пока их температура не достигнет этого значения. Легко ли это? Когда таким способом попробовали добыть огонь герои романа Жюля Верна «Таинственный остров», у них ничего не вышло.
«Если бы энергию, которую затратили Наб с Пенкрофом, можно было превратить в тепло, ее, наверное, хватило бы для отопления котла океанского парохода. Но результат их усилий равнялся нулю. Куски дерева, правда, разогрелись, но значительно меньше, чем сами участники этой операции.
После часа работы Пенкроф был весь в поту и с досадой отбросил куски дерева, сказав:
— Не говорите мне, что дикари добывают огонь таким образом! Я скорее поверю, что летом идет снег. Легче, пожалуй, зажечь собственные ладони, потирая их одну о другую».
Причина их неудачи заключалась в том, что огонь следовало добывать не простым трением одного куска дерева о другой, а сверлением дощечки заостренной палочкой (рис. 61). Тогда при определенной сноровке можно за 1 с увеличить температуру в гнезде палочки на 20 °С. А чтобы довести палочку до горения, потребуется всего лишь 250/20=12,5 секунды!
Многие люди и в наше время «добывают» огонь трением — трением спичек о спичечный коробок. Давно ли появились спички? Производство первых (фосфорных) спичек началось в 30-х гг. XIX в. Фосфор загорается при достаточно слабом нагревании — всего до 60 °С. Поэтому, чтобы зажечь фосфорную спичку, достаточно было чиркнуть ею практически о любую поверхность (начиная от ближайшей стены и кончая голенищем сапог). Однако эти спички были очень опасны: они были ядовиты и из-за легкого возгорания часто служили причиной пожара. Безопасные спички (которыми мы пользуемся до сих пор) были изобретены в 1855 г. в Швеции (отсюда их название «шведские спички») Фосфор в этих спичках заменен другими горючими веществами.
Безопасные спички (которыми мы пользуемся до сих пор) были изобретены в 1855 г. в Швеции (отсюда их название «шведские спички») Фосфор в этих спичках заменен другими горючими веществами.
Итак, путем трения можно повысить температуру вещества. Совершая над телом работу (например, ударяя по куску свинца молотком, сгибая и разгибая проволоку, перемещая один предмет по поверхности другого или сжимая газ, находящийся в цилиндре с поршнем), мы увеличиваем его внутреннюю энергию. Если же тело само совершает работу (за счет своей внутренней энергии), то внутренняя энергия тела уменьшается и тело охлаждается.
Пронаблюдаем это на опыте. Возьмем толстостенный стеклянный сосуд и плотно закроем его резиновой пробкой с отверстием. Через это отверстие с помощью насоса начнем накачивать в сосуд воздух. Через некоторое время пробка с шумом вылетит из сосуда, а в самом сосуде появится туман (рис. 62). Появление тумана означает, что воздух в сосуде стал холоднее и, следовательно, его внутренняя энергия уменьшилась. Объясняется это тем, что находившийся в сосуде сжатый воздух, выталкивая пробку, совершил работу за счет уменьшения своей внутренней энергии. Поэтому температура воздуха и понизилась.
Внутреннюю энергию тела можно изменить и без совершения работы. Так, например, ее можно увеличить, нагрев на плите чайник с водой или опустив ложку в стакан с горячим чаем. Нагревается камин, в котором разведен огонь, крыша дома, освещаемая солнцем, и т. д.
Повышение температуры тел во всех этих случаях означает увеличение их внутренней энергии, но это увеличение происходит без совершения работы.
Изменение внутренней энергии тела без совершения работы называется теплообменом. Теплообмен возникает между телами (или частями одного и того же тела), имеющими разную температуру.
Как, например, происходит теплообмен при контакте холодной ложки с горячей водой? Сначала средняя скорость и кинетическая энергия молекул горячей воды превышают среднюю скорость и кинетическую энергию частиц металла, из которого изготовлена ложка. Но в тех местах, где ложка соприкасается с водой, молекулы горячей воды начинают передавать часть своей кинетической энергии частицам ложки, и те начинают двигаться быстрее. Кинетическая энергия молекул воды при этом уменьшается, а кинетическая энергия частиц ложки увеличивается. Вместе с энергией изменяется и температура: вода постепенно остывает, а ложка нагревается. Изменение их температуры происходит до тех пор, пока она и у воды, и у ложки не станет одинаковой.
Но в тех местах, где ложка соприкасается с водой, молекулы горячей воды начинают передавать часть своей кинетической энергии частицам ложки, и те начинают двигаться быстрее. Кинетическая энергия молекул воды при этом уменьшается, а кинетическая энергия частиц ложки увеличивается. Вместе с энергией изменяется и температура: вода постепенно остывает, а ложка нагревается. Изменение их температуры происходит до тех пор, пока она и у воды, и у ложки не станет одинаковой.
Часть внутренней энергии, переданной от одного тела к другому при теплообмене, обозначают буквой Q и называют количеством теплоты.
Q — количество теплоты.
Количество теплоты не следует путать с температурой. Температура измеряется в градусах, а количество теплоты (как и любая другая энергия) — в джоулях.
При контакте тел с разной температурой более горячее тело отдает некоторое количество теплоты, а более холодное тело его получает.
Итак, существуют два способа изменения внутренней энергии: 1) совершение работы и 2) теплообмен. При осуществлении первого из этих способов внутренняя энергия тела изменяется на величину совершенной работы А, а при осуществлении второго из них — на величину, равную количеству переданной теплоты Q.
Интересно, что оба рассмотренных способа могут приводить к совершенно одинаковым результатам. Поэтому по конечному результату невозможно определить, каким именно из этих способов он достигнут. Так, взяв со стола нагретую стальную спицу, мы не сможем сказать, каким способом ее нагрели — путем трения или соприкосновения с горячим телом. В принципе могло быть как то, так и другое.
1. Назовите два способа изменения внутренней энергии тела. 2. Приведите примеры увеличения внутренней энергии тела путем совершения над ним работы. 3. Приведите примеры увеличения и уменьшения внутренней энергии тела в результате теплообмена. 4. Что такое количество теплоты? Как оно обозначается? 5. В каких единицах измеряется количество теплоты? 6. Какими способами можно добыть огонь? 7. Когда началось производство спичек?
Когда началось производство спичек?
Экспериментальное задание. Прижмите монету или кусочек фольги к картону или какой-либо дощечке. Сделав сначала 10, затем 20 и т. д. движений то в одну, то в другую сторону, заметьте, что происходит с температурой тел в процессе трения. Как зависит изменение внутренней энергии тела от величины совершенной работы?
Энергия внутри нас
Способ 1
Теплопередача. Примеров процесса теплопередачи множество — нагревание чайника на плите, оконного подоконника в солнечный день и т.п. Однако никакая работа здесь не совершается.
Изменение внутренней энергии тела без совершения работы называется теплопередачей (или теплообменом). Существует три вида теплопередачи: теплопроводность, конвекция и излучение.
Теплопроводность — это процесс теплообмена между телами (или частями тела) при их непосредственном контакте. Теплопроводность вещества зависит от его агрегатного состояния, пористости и других качеств. Ручки чайников, кастрюль делают из пластмассы, так как она обладает плохой теплопроводностью. Мех животных из-за плохой теплопроводности предохраняет их от охлаждения зимой и перегрева летом.
Конвекция представляет собой теплопередачу нагретыми потоками жидкости или газа от одних участков занимаемого ими объёма в другие. Конвекция невозможна в твёрдых телах. Примеры проявления конвекции: циркуляция воздуха в отапливаемой комнате, центральное водяное отопление, ветры, морские течения и т. д.
Теплообмен при излучении осуществляется на расстоянии посредством электромагнитных волн, которые излучает любое нагретое тело. Так, вся энергия, получаемая Землёй от Солнца, передается путём лучеиспускания. Тепло от костра передаётся человеку путём излучения энергии, так как теплопроводность воздуха мала, а конвекционные потоки направлены вверх.
Механическая работа. Изменение внутренней энергии тела происходит под действием силы трения. Как мы поступаем, когда зимой на улице замерзают руки? Мы трём их, то есть совершаем работу над руками и они нагреваются, а значит, увеличивается их внутренняя энергия.
Внутренняя энергия тела может измениться, если тело деформировать. Например, ударить, надавить, сжать, скрутить, растянуть и т. д. При этом изменяются расстояния между частицами, из которых оно состоит, следовательно, изменяется потенциальная энергия взаимодействия частиц. При неупругих деформациях, кроме того, изменяется температура тела, то есть изменяется скорость отдельных частей тела (следовательно, и кинетическая энергия движения частиц). Например, если кусок алюминиевой проволоки быстро изгибать в одном и том же месте то в одну, то в другую сторону, то это место нагреется.
Способы изменения внутренней энергии | Частная школа. 8 класс
Конспект по физике для 8 класса «Способы изменения внутренней энергии». ВЫ УЗНАЕТЕ: Как можно изменить внутреннюю энергию тела. Что такое теплопередача.
Конспекты по физике Учебник физики Тесты по физике
Способы изменения внутренней энергии
Чтобы понять, каким способом можно изменить внутреннюю энергию, необходимо знать, от чего она зависит. Мы уже знаем, что внутренняя энергия зависит от средней кинетической энергии частиц, составляющих тело, и, следовательно, от его температуры. Значит, для изменения внутренней энергии тела нужно изменить его температуру.
ВНУТРЕННЯЯ ЭНЕРГИЯ И РАБОТА
Совершая работу, мы можем изменить, например, потенциальную энергию тела. Подняв тело над поверхностью земли, мы тем самым увеличили его потенциальную энергию. Совершив работу, можно также изменить и внутреннюю энергию тела.
При трении тела нагреваются. Если потереть одну ладонь о другую, кожа нагреется. Если быстро спуститься по спортивному канату, то кожу на ладонях можно даже обжечь. Нагревание при трении люди использовали в древности для добывания огня. В наше время одним из способов добывания огня является трение спичечной головки о спичечный коробок.
Если потереть одну ладонь о другую, кожа нагреется. Если быстро спуститься по спортивному канату, то кожу на ладонях можно даже обжечь. Нагревание при трении люди использовали в древности для добывания огня. В наше время одним из способов добывания огня является трение спичечной головки о спичечный коробок.
В специализированной физической лаборатории при соблюдении всех мер предосторожности можно провести следующий опыт. На подставке укрепляется тонкостенная латунная трубка. В неё наливается немного эфира, и она закрывается пробкой. Затем трубка обвивается верёвкой. Если быстро натирать трубку верёвкой, то через некоторое время эфир закипит и пар вытолкнет пробку.
Этот опыт показывает, что внутренняя энергия эфира увеличилась, ведь он нагрелся и даже закипел. А причиной изменения внутренней энергии эфира стала наша работа против сил трения.
Именно из-за того, что температура в сосуде понижается, и появляется туман. Как и почему это происходит, мы с вами обсудим немного позднее. Всем, кто открывал бутылки с лимонадом, это явление хорошо знакомо: над горлышком появляется туман.
Увеличить внутреннюю энергию тела можно путём деформации. Если несколько раз ударить молотком по свинцовому шарику, он деформируется и заметно нагреется. Совершённая при этом работа приведёт к изменению взаимного расположения атомов свинца и к изменению характера их движения.
Рассмотрим пример, когда совершённая работа приводит к уменьшению внутренней энергии тела. В стеклянный толстостенный сосуд, закрытый резиновой пробкой, с помощью насоса нагнетается воздух, содержащий водяной пар. Через некоторое время пробка вылетает из сосуда, а в самом сосуде образуется туман, представляющий собой мельчайшие капельки воды.
Накачивая воздух в сосуд, мы совершаем работу. Число молекул в сосуде возрастает, увеличивается частота и сила их ударов, возрастает скорость их движения, и, следовательно, увеличивается внутренняя энергия и температура воздуха в сосуде. Затем сжатый воздух выталкивает пробку, совершая работу. При этом его внутренняя энергия уменьшается, и температура воздуха в сосуде понижается.
ВНУТРЕННЯЯ ЭНЕРГИЯ И ТЕПЛОПЕРЕДАЧА
Внутреннюю энергию тела можно изменить и без совершения механической работы. Например, внутреннюю энергию воды можно увеличить, нагрев на плите чайник. Если поставить горячую кастрюлю на холодную подставку, то с течением времени она остынет. Во всех приведённых примерах внутренняя энергия изменяется, хотя работа при этом не совершается.
Опустим металлическую ложку в стакан с горячей водой. Начальная температура воды выше температуры ложки. Значит, средняя кинетическая энергия молекул воды больше кинетической энергии частиц холодного металла. Молекулы воды, сталкиваясь с атомами металла, передают им часть своей энергии. При этом кинетическая энергия частиц металла увеличивается, а кинетическая энергия молекул воды уменьшается. В результате температура воды уменьшится, а температура ложки увеличится. С течением времени их температуры станут равными.
При непосредственном контакте двух тел с разными температурами происходит передача энергии от тела с более высокой температурой к телу, температура которого изначально была ниже. При этом внутренняя энергия тела с более высокой температурой уменьшается, а внутренняя энергия тела с меньшей температурой увеличивается.
Процесс передачи энергии от более нагретого тела или участков тела к менее нагретым называют теплопередачей или теплообменом.
Когда температуры тел становятся равными, теплопередача прекращается. При этом процесс теплопередачи необратим. Это означает, что невозможен самопроизвольный процесс передачи внутренней энергии от холодного тела к нагретому.
В XVIII в. французскими химиками была выдвинута идея теплорода — некой субстанции, объясняющей явления, связанные с теплотой и теплопередачей. Считалось, что частицы теплорода отталкиваются друг от друга, но притягивают частицы других веществ. Повышение температуры тела связывалось с увеличение количества теплорода, а понижение температуры — с его уменьшением. В середине XIX в. теория теплорода была отвергнута. Ей на смену пришла молекулярно-кинетическая теория строения вещества.
Бенджамин Томпсон (граф Румфорд) (1753 — 1814) Английский физик. В его честь Лондонское королевское общество учредило награду для выдающихся учёных — медаль Румфорда.
В 1798г. Румфорд сделал важное наблюдение: при высверливании канала в пушечном стволе выделяется большое количество тепла. Для более точного исследования он проделал опыт по сверлению канала в цилиндре, выточенном из пушечного металла. В высверленный канал поместили тупое сверло, плотно прижатое к стенкам канала и приводившееся во вращение. Термометр, вставленный в цилиндр, показал, что за 30 мин операции температура повысилась на десятки градусов Цельсия. Румфорд повторил опыт, погрузив цилиндр и сверло в сосуд с водой. В процессе сверления вода нагрелась и спустя 2,5 ч закипела.
Этот опыт Румфорд считал доказательством того, что теплота является формой движения.
Вы смотрели Конспект по физике для 8 класса «Способы изменения внутренней энергии».
Вернуться к Списку конспектов по физике (Оглавление).
Просмотров: 1 799
31. Внутренняя энергия. Теплотехника
Читайте также
Энергия… в воздухе!
Энергия… в воздухе! «Бесполезно было ждать от резины энергии больше, чем она в состоянии накопить», – успокаивал я себя, глядя на предмет моей гордости – авторское свидетельство на изобретение «резиноаккумулятора». Мне удавалось растягивать жгут лишь до известных
Какова же энергия пороха?
Какова же энергия пороха? При выстреле часть энергии, заключенной в заряде пороха, переходит в энергию движения снаряда.Пока заряд еще не зажжен, он обладает скрытой энергией. Ее можно сравнить с энергией высокого уровня воды у шлюзов мельницы, когда они закрыты. Вода
Энергия с горных вершин
Энергия с горных вершин Недавно изобретенный Дедалом тепловой планер (см. «Тепловой планер») — летательный аппарат, использующий разность температур между верхними и нижними слоями атмосферы, — нетрудно преобразовать в более крупномасштабный проект. Значительная
2.2. Энергия для всех
2.2. Энергия для всех Еще раз подчеркну, что я считаю проблему энергии наиболее важной для дальнейшего развития человечества. Все остальные задачи могут быть решены лишь при наличии достаточно мощных и доступных источников энергии. Проблема состоит в том, чтобы обеспечить
Энергия Земли*
Энергия Земли* Земля. По-видимому, Земля есть область человека. Он прикован к ней силою тяжести, отделен от других земель (планет) необозримыми пустынями неба. Ни один человек, ни одно существо не отдалилось еще от Земли, не посетило еще небо, хотя оно и наполнено
Земная энергия*
Земная энергия* Энергию можно выражать в виде работы — в тонно-метрах, в виде теплоты — в тонно-градусах, еще в форме угля или пищи. Притом энергию можно относить к разному времени. Работу (лучше) — к одной секунде. Например, труд работника — 5-10 кг-м/сек, лошадиная сила —
Глава 15 Внутренняя структура электрического потенциального поля
Глава 15 Внутренняя структура электрического потенциального поля Эфир, как и любая физическая среда, существование которой мы можем принять, вместе с Менделеевым, имеет определенные физические свойства. Менделеев писал об упругости данной среды в статье «Попытка
§ 53. Внутренняя и внешняя связь и сигнализация
§ 53. Внутренняя и внешняя связь и сигнализация Внутренняя связь и сигнализация через разветвленные на судне системы обеспечивает быструю и точную передачу приказаний из командных пунктов в исполнительные посты. Кроме того, внутрисудовая связь позволяет передавать
Полная механическая энергия — урок. Физика, 8 класс.
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.
Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.
Eпот+Eкин=const
Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.
Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.
Пример:
При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.
Преобразование энергии отображено на рисунке и в таблице.
Точка нахождения тела | Потенциальная энергия | Кинетическая энергия | Полная механическая энергия |
3) Самая верхняя (h = max) | Eпот = m⋅g⋅h (max) | Eкин = 0 | Eполная = m⋅g⋅h |
2) Средняя (h = средняя) | Eпот = m⋅g⋅h | Eкин = m⋅v22 | Eполная=m⋅v22+m⋅g⋅h |
1) Самая нижняя (h = 0) | Eпот = 0 | Eкин = m⋅v22 (max) | Eполная = m⋅v22 |
Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.
Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:
vmax=2⋅g⋅hmax.
Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:
hmax=vmax22g.
Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.
На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна \(нулю\). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна \(нулю\). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся \(неизменной\) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.
На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.
В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.
Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10 klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)
http://phet.colorado.edu/en/simulation/energy-skate-park
Внутренняя энергия — Простая английская Википедия, бесплатная энциклопедия
В термодинамике внутренней энергии термодинамической системы или тела с четко определенными границами, обозначаемого U или иногда E , является общим кинетической энергии из-за движения молекул (поступательное, вращательное, колебательное) и потенциальной энергии, связанной с колебательной и электрической энергией атомов внутри молекул или кристаллов. Он включает в себя энергию всех химических связей и энергию свободных электронов проводимости в металлах.
Внутренняя энергия — это термодинамический потенциал, и для замкнутой термодинамической системы, поддерживаемой при постоянной энтропии, она будет минимизирована.
Также можно рассчитать внутреннюю энергию электромагнитного излучения или излучения абсолютно черного тела. Это государственная функция системы, огромная величина. Единицей измерения энергии в системе СИ является джоуль, хотя все еще используются другие исторические традиционные единицы, такие как (малая и большая) калорийность тепла. (Калории, указанные на классических этикетках продуктов питания, на самом деле являются килокалориями.)
Внутренняя энергия не включает поступательную или вращательную кинетическую энергию тела в целом . Он также не включает релятивистский эквивалент массы и энергии E = mc 2 . Он исключает любую потенциальную энергию, которую тело может иметь из-за своего местоположения во внешнем гравитационном или электростатическом поле, хотя потенциальная энергия, которую оно имеет в поле из-за индуцированного электрического или магнитного дипольного момента, учитывается, как и энергия деформации твердых тел ( напряжение-деформация).
Принцип равнораспределения энергии в классической статистической механике гласит, что каждая молекулярная степень свободы получает 1/2 кТ энергии, результат, который был изменен, когда квантовая механика объяснила определенные аномалии; например, в наблюдаемых теплоемках кристаллов (когда ч ν> кТ ). Для одноатомного гелия и других благородных газов внутренняя энергия состоит только из поступательной кинетической энергии отдельных атомов. Одноатомные частицы, конечно, не вращаются (разумно) и не вибрируют, и не возбуждаются электронным способом до более высоких энергий, за исключением очень высоких температур.
С точки зрения статистической механики внутренняя энергия равна среднему по ансамблю полной энергии системы.
- Льюис, Гилберт Ньютон; Рэндалл, Мерл: Редакция Питцера, Кеннета С. и Брюера, Лео (1961). Термодинамика (2-е издание). Нью-Йорк, штат Нью-Йорк, США: ISBN компании McGraw-Hill Book Co. 0-07-113809-9 . CS1 maint: несколько имен: список авторов (ссылка)
- Ландау, Л.Д .; Лифшиц, Э.М. (1986). Теория упругости (Курс теоретической физики, том 7) . (Перевод с русского Дж. Б. Сайкса и В. Х. Рейда) (Третье изд.). Бостон, Массачусетс: Баттерворт Хайнеманн. ISBN 0-7506-2633-X .
термодинамика — Тепловая энергия против внутренней энергии?
Сегодня я много думал о том же. Это единственное логическое определение тепла / тепловой энергии, которое я смог получить.
Внутренняя энергия хорошо определена математически (как сумма кинетической и потенциальной энергий частиц, составляющих систему).Выполненная работа математически четко определена. Но тепло, третий член в уравнении 1-го закона, четко не определен.
Итак, можно использовать 1-й закон для математического определения «тепла».
1-й закон термодинамики гласит, что для любой термодинамической системы верно следующее —
дельта E (int) = Q — W
[E (int) = внутренняя энергия системы, Q = тепло, W = работа газа с окружающей средой]
Пусть Вт (вкл.) быть работой, проделанной над термодинамической системой ее окружением.
Итак, ясно, Вт (вкл.) = — Вт
Первый закон теперь можно записать как —
дельта E (int) = Q + W (вкл.)
Внутренняя энергия — это сумма кинетической и потенциальной энергий всех частиц, составляющих термодинамическую систему.
Итак, дельта E (int) = дельта K (sys) + дельта U (sys)
Также, Вт (вкл.) = Дельта K (sys)
[«sys» означает рассматриваемую термодинамическую систему]
Первый закон теперь подразумевает —
дельта K (sys) + дельта U (sys) = Q + дельта K (sys)
подразумевает- Q = дельта U (sys)
Итак, тепла — это не что иное, как изменение потенциальной энергии термодинамической системы.
Тепло — это изменение тепловой энергии.
Итак, тепловая энергия — это чистая потенциальная энергия системы.
, а внутренняя энергия — это чистая потенциальная энергия + чистая кинетическая энергия системы.
Итак, в этом разница.
p.s — У меня были правильные формулы, написанные математическими символами с помощью www.codecogs.com. Не понимаю, почему сработал спам-фильтр. Пришлось их удалить.
Внутренняя энергия и тела разной массы и температуры
Если предположить, что два тела сделаны из одного и того же вещества и все остальные применимые свойства идентичны, тогда да , полная внутренняя энергия тела зависит как от его массы, так и от его температуры — , но масса применяется только в этом путь для тел .
Внутренняя энергия может быть определена как:
сумма различных видов энергии, которой обладают атомы или молекулы вещества
(как определено в Пятом издании Cutnell and Johnson’s Physics)
Обычно это сумма молекулярной кинетической энергии и молекулярной потенциальной энергии (вызванной взаимодействиями между частицами).
Внутренняя энергия зависит от температуры , потому что температура исторически определяется как измерение средней кинетической энергии вещества.Квантовая физика меняет способ выражения термодинамики, но это определение работает нормально. Поскольку внутренняя энергия напрямую зависит от кинетической энергии, более высокая средняя молекулярная кинетическая энергия в веществе приводит к более высокой внутренней энергии в этом веществе.
Внутренняя энергия тела зависит от массы иным образом. Масса — это количество всех частиц в теле. Следовательно, если x частицы имеют определенную полную внутреннюю энергию, 2x частицы имеют более высокую общую энергию, но не более высокую внутреннюю энергию на единицу массы.Внутренняя энергия объекта 2x может быть выше, но если прикоснуться к обоим объектам, они оба почувствуют одно и то же; области (одинаковые на квадратную единицу вашей кожи), которых вы касаетесь, имеют одинаковую внутреннюю энергию. Объекту 2x просто потребуется больше времени, чтобы достичь равновесия рукой.
Если это сбивает с толку, просто представьте, что полная внутренняя энергия тела зависит от массы, но только потому, что каждая единица массы имеет определенную дополнительную внутреннюю энергию.
15.1: Первый закон термодинамики
Если нас интересует, как теплопередача преобразуется в выполнение работы, тогда важен принцип сохранения энергии. Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых передача тепла и выполнение работы являются методами передачи энергии в систему и из нее.
Первый закон термодинамики гласит, что изменение внутренней энергии системы равно чистой теплопередаче в системе за вычетом чистой работы, выполненной системой.В форме уравнения первый закон термодинамики:
\ [\ Delta U = Q — W. \ label {first} \]
Здесь \ (\ Delta U \) — изменение внутренней энергии на \ ( U \) системы. \ (Q \) — это чистое тепло , переданное в систему , то есть \ (Q \) — это сумма всей теплопередачи в систему и из нее. \ (W \) — это чистая работа, выполненная системой , то есть \ (W \) — это сумма всей работы, выполненной в системе или ею.Мы используем следующие соглашения о знаках: если \ (Q \) положительно, то в системе имеется чистый перенос тепла; если \ (W \) положительно, то система выполняет чистую работу. Таким образом, положительное \ (Q \) добавляет энергию системе, а положительное \ (W \) забирает энергию из системы. Таким образом, \ (\ Delta U = Q — W \). Также обратите внимание, что если в систему передается больше тепла, чем проделанной работы, разница сохраняется как внутренняя энергия. Тепловые двигатели — хороший тому пример — в них происходит передача тепла, чтобы они могли выполнять свою работу (рисунок \ (\ PageIndex {2} \)).Теперь мы рассмотрим \ (Q, \, W \) и \ (\ Delta U \) дальше.
Нагрев
Q и работа WТеплопередача \ (Q \) и выполнение работы \ (W \) — два повседневных средства передачи энергии в систему или извлечения энергии из нее. Процессы совершенно разные. Теплообмен, менее организованный процесс, обусловлен разницей температур. Работа — это вполне организованный процесс, в котором действует макроскопическая сила, действующая на расстоянии. Тем не менее тепло и работа могут дать одинаковые результаты.Например, оба могут вызвать повышение температуры. Передача тепла в систему, например, когда Солнце нагревает воздух в велосипедной шине, может повысить ее температуру, и поэтому может работать над системой, например, когда велосипедист нагнетает воздух в шину. Как только произошло повышение температуры, невозможно сказать, было ли оно вызвано теплопередачей или работой. Эта неопределенность — важный момент. Теплообмен и работа — это энергия в пути, и ни одна из них не хранится как таковая в системе.Однако оба могут изменить внутреннюю энергию \ (U \) системы. Внутренняя энергия — это форма энергии, полностью отличная от тепла или работы.
Внутренняя энергия
UМы можем думать о внутренней энергии системы двумя разными, но последовательными способами. Первый — это атомно-молекулярная точка зрения, которая исследует систему в атомном и молекулярном масштабе. Внутренняя энергия \ (U \) системы — это сумма кинетической и потенциальной энергий ее атомов и молекул.Напомним, что кинетическая плюс потенциальная энергия называется механической энергией. Таким образом, внутренняя энергия — это сумма атомной и молекулярной механической энергии. Поскольку невозможно отследить все отдельные атомы и молекулы, мы должны иметь дело со средними значениями и распределениями. Второй способ взглянуть на внутреннюю энергию системы — с точки зрения ее макроскопических характеристик, которые очень похожи на средние атомные и молекулярные значения.
Макроскопически мы определяем изменение внутренней энергии \ (\ Delta U \) как значение, заданное первым законом термодинамики (уравнение \ ref {first}): \ [\ Delta U = Q — W \ nonumber \]
Многие подробные эксперименты подтвердили, что \ (\ Delta U = Q — W \), где \ (\ Delta U \) — это изменение полной кинетической и потенциальной энергии всех атомов и молекул в системе.Экспериментально также было определено, что внутренняя энергия \ (U \) системы зависит только от состояния системы, а не от того, как она достигла этого состояния . Более конкретно, \ (U \) оказывается функцией нескольких макроскопических величин (например, давления, объема и температуры), независимо от прошлой истории, такой как была ли передача тепла или проделанная работа. Эта независимость означает, что, зная состояние системы, мы можем вычислить изменения ее внутренней энергии \ (U \) с помощью нескольких макроскопических переменных.
МАКРОСКОПИЧЕСКИЕ И МИКРОСКОПИЧЕСКИЕ
В термодинамике мы часто используем макроскопическую картину при расчетах поведения системы, в то время как атомная и молекулярная картина дает основные объяснения в терминах средних значений и распределений. Мы еще раз увидим это в следующих разделах этой главы. Например, в теме энтропии расчеты будут производиться с использованием атомно-молекулярного представления.
Чтобы лучше понять, как думать о внутренней энергии системы, давайте рассмотрим систему, переходящую из состояния 1 в состояние 2.Система имеет внутреннюю энергию \ (U_1 \) в Состоянии 1 и внутреннюю энергию \ (U_2 \) в Состоянии 2, независимо от того, как она попала в любое из состояний. Итак, изменение внутренней энергии
\ [\ Delta U = U_2 — U_1 \]
не зависит от причины изменения. Другими словами, \ (\ delta U \) не зависит от пути . Под путем мы подразумеваем способ добраться от начальной точки до конечной точки. Почему важна эта независимость? И \ (Q \), и \ (W \) зависят от от пути , но \ (\ Delta U \) нет (уравнение \ ref {first}).Эта независимость от пути означает, что внутреннюю энергию \ (U \) легче учитывать, чем теплопередачу или проделанную работу.
Пример \ (\ PageIndex {1} \): Расчет изменения внутренней энергии — такое же изменение в \ (U \) производится двумя разными процессами
- Предположим, что теплопередача в систему составляет 40,00 Дж, в то время как система выполняет работу 10,00 Дж. Позже происходит передача тепла из системы на 25,00 Дж, в то время как в системе выполняется 4,00 Дж работы. Каково чистое изменение внутренней энергии системы?
- Каково изменение внутренней энергии системы, когда всего 150.00 Дж теплообмена происходит из (от) системы и 159,00 Дж работы выполняется в системе (рисунок \ (\ PageIndex {3} \))?
Стратегия
В части (а) мы должны сначала найти чистую теплопередачу и чистую работу, выполненную на основе данной информации. Затем первый закон термодинамики (уравнение \ ref {first}).
можно использовать для определения изменения внутренней энергии. В части (b) приведены чистая теплопередача и проделанная работа, поэтому уравнение можно использовать напрямую.
Решение для (а)
Чистая теплопередача — это теплопередача в систему за вычетом теплопередачи из системы, или
\ [\ begin {align *} Q & = 40.00 \, J — 25.00 \, J \\ [5pt] & = 15.00 \, J \ end {align *} \]
Аналогично, общая работа — это работа, выполненная системой за вычетом работы, выполненной в системе, или
\ [\ begin {align *} W & = 10.00 \, J — 4.00 \, J \\ [5pt] & = 6.00 \, J. \ end {align *} \]
Обсуждение на (а)
Неважно, смотрите ли вы на процесс в целом или разбиваете его на этапы, изменение внутренней энергии одинаково.
Решение для (b)
Здесь чистая теплопередача и общая работа даны как \ (Q = -150.00 \, Дж \) и \ (W = -159.00 \, Дж \), так что
\ [\ begin {align *} \ Delta U & = Q — W = -150.00 — (-159.00) \\ [5pt] & = 9.00 \, J. \ end {align *} \]
Обсуждение на (б)
Совершенно другой процесс в части (b) дает такое же изменение внутренней энергии на 9,00 Дж, что и в части (a). Обратите внимание, что изменение системы в обеих частях связано с \ (\ Delta U \), а не с отдельными участвующими \ (Q \) s или \ (W \) s.Система оказывается в том же состоянии как в (a), так и (b). Части (a) и (b) представляют два разных пути, по которым система должна следовать между одними и теми же начальными и конечными точками, и изменение внутренней энергии для каждой из них одинаково — оно не зависит от пути.
Метаболизм человека и первый закон термодинамики
Метаболизм человека — это преобразование пищи в теплообмен, работу и накопленный жир. Метаболизм — интересный пример действия первого закона термодинамики.Теперь мы еще раз посмотрим на эти темы с помощью первого закона термодинамики. Рассматривая тело как интересующую нас систему, мы можем использовать первый закон для изучения теплопередачи, выполнения работы и внутренней энергии в различных видах деятельности, от сна до тяжелых упражнений. Каковы некоторые из основных характеристик теплопередачи, выполнения работы и энергии в организме? Во-первых, температура тела обычно поддерживается постоянной за счет передачи тепла в окружающую среду. Это означает, что \ (Q \) отрицательно. Другой факт: тело обычно работает с внешним миром.Это означает, что \ (W \) положительно. В таких ситуациях тело теряет внутреннюю энергию, поскольку \ (\ Delta U = Q — W \) отрицательно.
Теперь рассмотрим эффекты еды. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии (это неромантичный взгляд на хороший стейк). Организм метаболизирует всю пищу, которую мы потребляем. По сути, метаболизм — это процесс окисления, при котором высвобождается химическая потенциальная энергия пищи. Это означает, что питание осуществляется в форме работы.Энергия пищи указывается в специальной единице, известной как калория. Эта энергия измеряется сжиганием пищи в калориметре, как и определяются единицы.
В химии и биохимии одна калория (обозначается строчной буквой c) определяется как энергия (или передача тепла), необходимая для повышения температуры одного грамма чистой воды на один градус Цельсия. Диетологи и любители веса склонны использовать диетических калорий, которые часто называют калориями (пишется с заглавной буквы ° C).Одна пища Калория — это энергия, необходимая для повышения температуры одного килограмма воды на один градус Цельсия. Это означает, что одна диетическая калория для химика равна одной килокалории, и нужно быть осторожным, чтобы не путать их.
Опять же, рассмотрим внутреннюю энергию, потерянную телом. Эта внутренняя энергия может идти по трем направлениям — на передачу тепла, выполнение работы и накопленный жир (крошечная часть также идет на восстановление и рост клеток). Передача тепла и выполнение работы забирают внутреннюю энергию из тела, а пища возвращает ее.Если вы едите нужное количество пищи, ваша средняя внутренняя энергия остается постоянной. Все, что вы теряете на теплопередачу и выполнение работы, заменяется едой, так что в конечном итоге \ (\ Delta U = 0 \). Если вы постоянно переедаете, то \ (\ Delta U \) всегда положительный результат, и ваше тело сохраняет эту дополнительную внутреннюю энергию в виде жира. Обратное верно, если вы едите слишком мало. Если значение \ (\ Delta U \) отрицательное в течение нескольких дней, то тело метаболизирует собственный жир, чтобы поддерживать температуру тела и выполнять работу, которая забирает у тела энергию.Именно так соблюдение диеты способствует снижению веса.
Жизнь не всегда так проста, как знает любой человек, сидящий на диете. Тело накапливает жир или метаболизирует его только в том случае, если потребление энергии меняется в течение нескольких дней. После того, как вы сели на основную диету, следующая будет менее успешной, потому что ваше тело изменит способ реагирования на низкое потребление энергии. Ваша основная скорость метаболизма (BMR) — это скорость, с которой пища преобразуется в теплообмен и работу, выполняемую, когда организм находится в полном покое. Организм регулирует базальную скорость метаболизма, чтобы частично компенсировать переедание или недоедание.Организм будет снижать скорость метаболизма, а не устранять собственный жир, чтобы заменить потерянную еду. Вы легче простужаетесь и чувствуете себя менее энергичным в результате более низкой скорости метаболизма, и вы не будете терять вес так быстро, как раньше. Упражнения помогают похудеть, потому что они обеспечивают теплоотдачу от вашего тела и работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя. Снижению веса также способствует довольно низкая эффективность тела в преобразовании внутренней энергии в работу, так что потеря внутренней энергии в результате выполнения работы намного больше, чем проделанная работа.Однако следует отметить, что живые системы не находятся в тепловом равновесии.
Тело дает нам отличный показатель того, что многие термодинамические процессы необратимы . Необратимый процесс может идти в одном направлении, но не в обратном, при заданном наборе условий. Например, хотя телесный жир может быть преобразован для выполнения работы и передачи тепла, работа, выполняемая телом, и передача тепла в него не могут быть преобразованы в телесный жир. В противном случае мы могли бы пропустить обед, загорая или спустившись по лестнице.Другой пример необратимого термодинамического процесса — фотосинтез. Этот процесс представляет собой поглощение растениями одной формы энергии — света — и ее преобразование в химическую потенциальную энергию. Оба приложения первого закона термодинамики показаны на рисунке \ (\ PageIndex {4} \). Одним из больших преимуществ законов сохранения, таких как первый закон термодинамики, является то, что они точно описывают начальную и конечную точки сложных процессов, таких как метаболизм и фотосинтез, без учета промежуточных осложнений.
Рисунок \ (\ PageIndex {4} \): (а) Первый закон термодинамики применительно к метаболизму. Тепло, передаваемое телом \ (Q \), и работа, выполняемая телом \ (W \), удаляют внутреннюю энергию, в то время как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую телом.) (Б) Растения преобразуют часть лучистой теплопередачи в солнечном свете в запасенную химическую энергию — процесс, называемый фотосинтезом.Сводка
В таблице представлены термины, относящиеся к первому закону термодинамики.
| Срок | Определение |
|---|---|
| \ (U \) | Внутренняя энергия — сумма кинетической и потенциальной энергий атомов и молекул системы. Можно разделить на множество подкатегорий, таких как тепловая и химическая энергия. Зависит только от состояния системы (например, ее \ (P \), \ (V \) и \ (T \), а не от того, как энергия попала в систему. Изменение внутренней энергии не зависит от пути. |
| \ (Q \) | Тепло — энергия, передаваемая из-за разницы температур. Характеризуется случайным движением молекул. Сильно зависит от пути. Вход \ (Q \) в систему положительный. |
| \ (Вт \) | Работа — энергия, передаваемая силой, перемещающейся на расстояние. Организованный, упорядоченный процесс. Зависит от пути. \ (W \), совершаемое системой (либо против внешней силы, либо для увеличения объема системы), положительно. |
- Первый закон термодинамики задается как \ (\ Delta U = Q — W \), где \ (\ Delta U \) — изменение внутренней энергии системы, \ (Q \) — чистая теплопередача (сумма всей теплопередачи в систему и из нее), а \ (W \) — чистая проделанная работа (сумма всей работы, проделанной в системе или ею).
- И \ (Q \), и \ (W \) — энергия в пути; только \ (\ Delta U \) представляет собой независимую величину, которую можно сохранить.
- Внутренняя энергия \ (U \) системы зависит только от состояния системы, а не от того, как она достигла этого состояния.
- Метаболизм живых организмов и фотосинтез растений — это особые виды передачи тепла, выполнения работы и внутренней энергии систем.
Первый закон термодинамики
Цели обучения
К концу этого раздела вы сможете:
- Определите первый закон термодинамики.
- Опишите, как сохранение энергии соотносится с первым законом термодинамики.
- Укажите примеры первого закона термодинамики, работающие в повседневных ситуациях, включая биологический метаболизм.
- Рассчитать изменения внутренней энергии системы после учета теплопередачи и проделанной работы.
Рис. 1. Этот кипящий чайник представляет энергию в движении. Вода в чайнике превращается в водяной пар, потому что тепло передается от плиты к чайнику. По мере того, как вся система нагревается, работа выполняется — от испарения воды до свиста чайника. (кредит: Джина Гамильтон)
Если нас интересует, как теплопередача преобразуется в выполнение работы, тогда важен принцип сохранения энергии.Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых передача тепла и выполнение работы являются методами передачи энергии в систему и из нее. Первый закон термодинамики гласит, что изменение внутренней энергии системы равно чистой теплопередаче в системе за вычетом чистой работы, выполненной системой. В форме уравнения первый закон термодинамики: Δ U = Q — W .
Здесь Δ U — изменение внутренней энергии U системы. Q — это чистое тепло , переданное в систему , то есть Q — это сумма всей теплопередачи в систему и из нее. W — это чистая работа , выполненная системой , то есть W — это сумма всей работы, выполненной в системе или ею. Мы используем следующие условные обозначения: если значение Q положительно, то в системе имеется чистый теплоперенос; если значение W положительное, значит, система выполняет чистую работу.Таким образом, положительный Q добавляет энергию в систему, а положительный W забирает энергию из системы. Таким образом, Δ U = Q — W . Также обратите внимание, что если в систему передается больше тепла, чем проделанной работы, разница сохраняется как внутренняя энергия. Тепловые двигатели — хороший тому пример — в них происходит передача тепла, чтобы они могли выполнять свою работу. (См. Рис. 2.) Теперь мы рассмотрим Q , W и Δ U далее.
Рисунок 2.Первый закон термодинамики — это принцип сохранения энергии, установленный для системы, в которой тепло и работа являются методами передачи энергии для системы, находящейся в тепловом равновесии. Q представляет собой чистую теплопередачу — это сумма всех теплопередач в систему и из нее. Q положителен для чистой передачи тепла в систему. W — это общий объем работы, проделанной с системой. W является положительным, когда система выполняет больше работы, чем над ней.Изменение внутренней энергии системы Δ U связано с теплом и работой согласно первому закону термодинамики Δ U = Q — W .
Установление связей: закон термодинамики и закон сохранения энергии
Первый закон термодинамики — это закон сохранения энергии, сформулированный в форме, наиболее полезной в термодинамике. Первый закон устанавливает связь между теплопередачей, проделанной работой и изменением внутренней энергии системы.
Нагрев
Q и Работа WТеплопередача ( Q ) и выполнение работы ( W ) — два повседневных средства подачи энергии в систему или отвода энергии из системы. Процессы совершенно разные. Теплообмен, менее организованный процесс, обусловлен разницей температур. Работа — это вполне организованный процесс, в котором действует макроскопическая сила, действующая на расстоянии. Тем не менее, тепло и работа могут дать одинаковые результаты, например, оба могут вызвать повышение температуры.Передача тепла в систему, например, когда Солнце нагревает воздух в велосипедной шине, может повысить ее температуру, и поэтому может работать над системой, например, когда велосипедист нагнетает воздух в шину. Как только произошло повышение температуры, невозможно сказать, было ли оно вызвано теплопередачей или работой. Эта неопределенность — важный момент. Теплообмен и работа — это энергия в пути, и ни одна из них не хранится как таковая в системе. Однако оба могут изменять внутреннюю энергию U системы.Внутренняя энергия — это форма энергии, полностью отличная от тепла или работы.
Внутренняя энергия
UМы можем думать о внутренней энергии системы двумя разными, но последовательными способами. Первый — это атомно-молекулярная точка зрения, которая исследует систему в атомном и молекулярном масштабе. Внутренняя энергия U системы — это сумма кинетической и потенциальной энергий ее атомов и молекул. Напомним, что кинетическая плюс потенциальная энергия называется механической энергией.Таким образом, внутренняя энергия — это сумма атомной и молекулярной механической энергии. Поскольку невозможно отследить все отдельные атомы и молекулы, мы должны иметь дело со средними значениями и распределениями. Второй способ взглянуть на внутреннюю энергию системы — с точки зрения ее макроскопических характеристик, которые очень похожи на средние атомные и молекулярные значения.
Макроскопически мы определяем изменение внутренней энергии Δ U как значение, определяемое первым законом термодинамики: Δ U = Q — W .
Многие подробные эксперименты подтвердили, что Δ U = Q — W , где Δ U — изменение полной кинетической и потенциальной энергии всех атомов и молекул в системе. Также экспериментально было определено, что внутренняя энергия U системы зависит только от состояния системы, а не от того, как она достигла этого состояния . Более конкретно, U , как обнаружено, является функцией нескольких макроскопических величин (например, давления, объема и температуры), независимо от прошлой истории, например от того, была ли проведена теплопередача или проделана работа.Эта независимость означает, что, зная состояние системы, мы можем вычислить изменения ее внутренней энергии U на основе нескольких макроскопических переменных.
Установление соединений: макроскопические и микроскопические
В термодинамике мы часто используем макроскопическую картину при расчетах поведения системы, в то время как атомная и молекулярная картина дает основные объяснения в терминах средних значений и распределений. Мы еще раз увидим это в следующих разделах этой главы.Например, в теме энтропии расчеты будут производиться с использованием атомно-молекулярного представления.
Чтобы лучше понять, как думать о внутренней энергии системы, давайте рассмотрим систему, переходящую из состояния 1 в состояние 2. Система имеет внутреннюю энергию U 1 в состоянии 1 и имеет внутреннюю энергию. энергия U 2 в состоянии 2, независимо от того, как он попал в любое состояние. Таким образом, изменение внутренней энергии Δ U = U 2 — U 1 не зависит от того, что вызвало изменение.Другими словами, Δ U не зависит от пути . Под путем мы подразумеваем способ добраться от начальной точки до конечной точки. Почему важна эта независимость? Обратите внимание, что Δ U = Q — W . И Q , и W зависят от пути , а Δ U — нет. Эта независимость от пути означает, что внутреннюю энергию U легче учитывать, чем теплопередачу или проделанную работу.
Пример 1.Расчет изменения внутренней энергии: одно и то же изменение в
U производится двумя разными процессами- Предположим, что теплопередача в систему составляет 40,00 Дж, в то время как система выполняет работу 10,00 Дж. Позже происходит передача тепла из системы на 25,00 Дж, в то время как в системе выполняется 4,00 Дж работы. Каково чистое изменение внутренней энергии системы?
- Каково изменение внутренней энергии системы, когда в общей сложности 150,00 Дж теплопередачи происходит из (от) системы и 159?00 Дж работы выполнено в системе? (См. Рисунок 3).
Рис. 3. Два разных процесса производят одно и то же изменение в системе. (a) Всего в системе происходит передача тепла 15,00 Дж, в то время как работа потребляет в общей сложности 6,00 Дж. Изменение внутренней энергии составляет ΔU = Q-W = 9,00 Дж. (b) Теплопередача удаляет 150,00 Дж из система во время работы вкладывает в нее 159,00 Дж, увеличивая внутреннюю энергию на 9,00 Дж. Если система начинает работу в одном и том же состоянии в пунктах (а) и (б), она окажется в одном и том же конечном состоянии в любом случае — ее конечное состояние связано с внутренней энергией, а не с тем, как эта энергия была получена.
Стратегия
В части 1 мы должны сначала найти чистую теплопередачу и чистую работу, выполненную на основе данной информации. Тогда первый закон термодинамики (Δ U = Q — W ) может быть использован для определения изменения внутренней энергии. В части (b) приведены чистая теплопередача и проделанная работа, поэтому уравнение можно использовать напрямую.
Решение для Части 1
Чистая теплопередача — это теплопередача в систему за вычетом теплопередачи из системы, или
Q = 40.00 Дж — 25,00 Дж = 15,00 Дж.
Аналогично, общая работа — это работа, выполненная системой за вычетом работы, выполненной в системе, или
Вт = 10,00 Дж — 4,00 Дж = 6,00 Дж
Таким образом, изменение внутренней энергии определяется первым законом термодинамики:
Δ U = Q — W = 15,00 Дж — 6,00 Дж = 9,00 Дж
Мы также можем найти изменение внутренней энергии для каждого из двух шагов. Во-первых, рассмотрим теплопередачу 40,00 Дж в и 10.00 Дж работы, или Δ U 1 = Q 1 — W 1 = 40,00 Дж — 10,00 Дж = 30,00 Дж
Теперь рассмотрим 25,00 Дж теплоотдачи на выходе и 4,00 Дж работы на входе, или
Δ U 2 = Q 2 — W 2 = –25,00 Дж — (- 4,00 Дж) = –21,00 Дж
Общее изменение — это сумма этих двух шагов, или Δ U = Δ U 1 + Δ U 2 = 30.00 Дж + (-21,00 Дж) = 9,00 Дж.
Обсуждение части 1
Неважно, смотрите ли вы на процесс в целом или разбиваете его на этапы, изменение внутренней энергии одинаково.
Решение для Части 2
Здесь чистая теплопередача и общая работа даны непосредственно равными Q = –150,00 Дж и Вт = –159,00 Дж, так что
Δ U = Q — W = –150,00 Дж — (- 159,00 Дж) = 9,00 Дж.
Обсуждение части 2
Совершенно другой процесс в части 2 дает то же 9.Изменение внутренней энергии на 00 Дж, как в части 1. Обратите внимание, что изменение в системе в обеих частях связано с Δ U , а не с отдельными задействованными Q s или W s. Система оказывается в том же состоянии в обеих частях. Части 1 и 2 представляют два разных пути, которыми должна следовать система между одними и теми же начальными и конечными точками, и изменение внутренней энергии для каждой из них одинаково — оно не зависит от пути.
Метаболизм человека и первый закон термодинамики
Метаболизм человека — это преобразование пищи в теплообмен, работу и накопленный жир.Метаболизм — интересный пример действия первого закона термодинамики. Теперь мы еще раз посмотрим на эти темы с помощью первого закона термодинамики. Рассматривая тело как интересующую нас систему, мы можем использовать первый закон для изучения теплопередачи, выполнения работы и внутренней энергии в различных видах деятельности, от сна до тяжелых упражнений. Каковы некоторые из основных характеристик теплопередачи, выполнения работы и энергии в организме? Во-первых, температура тела обычно поддерживается постоянной за счет передачи тепла в окружающую среду.Это означает, что Q отрицательный. Другой факт: тело обычно работает с внешним миром. Это означает, что W положительный. В таких ситуациях тело теряет внутреннюю энергию, поскольку Δ U = Q — W отрицательно.
Теперь рассмотрим эффекты еды. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии (это неромантичный взгляд на хороший стейк). Организм метаболизирует всю пищу, которую мы потребляем.По сути, метаболизм — это процесс окисления, при котором высвобождается химическая потенциальная энергия пищи. Это означает, что питание осуществляется в форме работы. Энергия пищи указывается в специальной единице, известной как калория. Эта энергия измеряется сжиганием пищи в калориметре, как и определяются единицы.
В химии и биохимии одна калория (обозначается строчной буквой c) определяется как энергия (или передача тепла), необходимая для повышения температуры одного грамма чистой воды на один градус Цельсия.Диетологи и любители веса склонны использовать диетических калорий, которые часто называют калориями (пишется с заглавной буквы ° C). Одна пища Калория — это энергия, необходимая для повышения температуры одного килограмма воды на один градус Цельсия. Это означает, что одна диетическая калория для химика равна одной килокалории, и нужно быть осторожным, чтобы не путать их.
Опять же, рассмотрим внутреннюю энергию, потерянную телом. Эта внутренняя энергия может идти по трем направлениям — на передачу тепла, выполнение работы и накопленный жир (крошечная часть также идет на восстановление и рост клеток).Передача тепла и выполнение работы забирают внутреннюю энергию из тела, а пища возвращает ее. Если вы едите нужное количество пищи, ваша средняя внутренняя энергия остается постоянной. Все, что вы теряете на теплопередачу и выполнение работы, заменяется едой, так что в конечном итоге Δ U = 0. Если вы много раз переедаете, то Δ U всегда положительный, и ваше тело сохраняет эту дополнительную внутреннюю энергию в виде жира. Обратное верно, если вы едите слишком мало. Если Δ U будет отрицательным в течение нескольких дней, тогда организм метаболизирует собственный жир, чтобы поддерживать температуру тела и выполнять работу, которая забирает у тела энергию.Именно так соблюдение диеты способствует снижению веса.
Жизнь не всегда так проста, как знает любой человек, сидящий на диете. Тело накапливает жир или метаболизирует его только в том случае, если потребление энергии меняется в течение нескольких дней. После того, как вы сели на основную диету, следующая будет менее успешной, потому что ваше тело изменит способ реагирования на низкое потребление энергии. Ваша основная скорость метаболизма (BMR) — это скорость, с которой пища преобразуется в теплообмен и работу, выполняемую, когда организм находится в полном покое. Организм регулирует базальную скорость метаболизма, чтобы частично компенсировать переедание или недоедание.Организм будет снижать скорость метаболизма, а не устранять собственный жир, чтобы заменить потерянную еду. Вы легче простужаетесь и чувствуете себя менее энергичным в результате более низкой скорости метаболизма, и вы не будете терять вес так быстро, как раньше. Упражнения помогают похудеть, потому что они обеспечивают теплоотдачу от вашего тела и работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя. Снижению веса также способствует довольно низкая эффективность тела в преобразовании внутренней энергии в работу, так что потеря внутренней энергии в результате выполнения работы намного больше, чем проделанная работа.Однако следует отметить, что живые системы не находятся в тепловом равновесии.
Тело дает нам отличный показатель того, что многие термодинамические процессы необратимы . Необратимый процесс может идти в одном направлении, но не в обратном, при заданном наборе условий. Например, хотя телесный жир может быть преобразован для выполнения работы и передачи тепла, работа, выполняемая телом, и передача тепла в него не могут быть преобразованы в телесный жир. В противном случае мы могли бы пропустить обед, загорая или спустившись по лестнице.Другой пример необратимого термодинамического процесса — фотосинтез. Этот процесс представляет собой поглощение растениями одной формы энергии — света — и ее преобразование в химическую потенциальную энергию. Оба применения первого закона термодинамики показаны на рисунке 4. Одно большое преимущество законов сохранения, таких как первый закон термодинамики, состоит в том, что они точно описывают начальную и конечную точки сложных процессов, таких как метаболизм и фотосинтез, без учета осложнения между ними.В таблице 1 представлена сводка терминов, относящихся к первому закону термодинамики.
Рис. 4. (а) Первый закон термодинамики применительно к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, в то время как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую телом.) (Б) Растения преобразуют часть лучистой теплопередачи в солнечном свете в запасенную химическую энергию — процесс, называемый фотосинтезом.
| Таблица 1.Краткое изложение терминов первого закона термодинамики, ΔU = Q — W | |
|---|---|
| Срок | Определение |
| U | Внутренняя энергия — сумма кинетической и потенциальной энергий атомов и молекул системы. Можно разделить на множество подкатегорий, таких как тепловая и химическая энергия. Зависит только от состояния системы (например, P , V и T ), а не от того, как энергия поступает в систему.Изменение внутренней энергии не зависит от пути. |
| Q | Тепло — энергия, передаваемая из-за разницы температур. Характеризуется случайным движением молекул. Сильно зависит от пути. Q вход в систему положительный. |
| Вт | Работа — энергия, передаваемая силой, перемещающейся на расстояние. Организованный, упорядоченный процесс. Зависит от пути. W , выполненный системой (либо против внешней силы, либо для увеличения объема системы), является положительным. |
Сводка раздела
- Первый закон термодинамики задается как Δ U = Q — W , где Δ U — изменение внутренней энергии системы, Q — чистая теплопередача (сумма вся теплопередача в систему и из нее), а W — это чистая проделанная работа (сумма всей работы, проделанной в системе или ею).
- И Q , и W — энергия в пути; только Δ U представляет собой независимую величину, которую можно хранить.
- Внутренняя энергия U системы зависит только от состояния системы, а не от того, как она достигла этого состояния.
- Метаболизм живых организмов и фотосинтез растений — это особые виды передачи тепла, выполнения работы и внутренней энергии систем.
Концептуальные вопросы
- Опишите фотографию чайника в начале этого раздела с точки зрения теплопередачи, проделанной работы и внутренней энергии. Как передается тепло? Какая работа и что делается? Как чайник поддерживает свою внутреннюю энергию?
- Первый закон термодинамики и закон сохранения энергии, как обсуждалось в «Сохранении энергии», явно связаны.Чем они различаются по рассматриваемым видам энергии?
- Теплопередача Q и выполненная работа W — это всегда энергия в пути, тогда как внутренняя энергия U — это энергия, запасенная в системе. Приведите пример каждого типа энергии и конкретно укажите, как он передается или находится в системе.
- Чем отличаются теплопередача и внутренняя энергия? В частности, что можно сохранить как таковое в системе, а что нет?
- Если вы сбежите по лестнице и остановитесь, что произойдет с вашей кинетической энергией и вашей начальной гравитационной потенциальной энергией?
- Объясните, как пищевая энергия (калории) может рассматриваться как молекулярная потенциальная энергия (в соответствии с атомарным и молекулярным определением внутренней энергии).
- Определите тип энергии, передаваемой вашему телу в каждом из следующих случаев: внутренняя энергия, теплопередача или выполнение работы: (а) купание в солнечном свете; (б) употребление пищи; (c) подъем на лифте на более высокий этаж.
Задачи и упражнения
- Как изменится внутренняя энергия автомобиля, если в его бак залить 12 галлонов бензина? Энергетическая ценность бензина составляет 1,3 × 10 8 Дж / галлон. Все остальные факторы, например температура в автомобиле, постоянны.
- Сколько тепла происходит от системы, если ее внутренняя энергия уменьшилась на 150 Дж, пока она выполняла 30,0 Дж работы?
- Система выполняет 1,80 × 10 8 Дж работы, в то время как 7,50 × 10 8 Дж теплопередачи происходит в окружающую среду. Каково изменение внутренней энергии системы при отсутствии других изменений (например, температуры или добавления топлива)?
- Каково изменение внутренней энергии системы, которая выполняет 4,50 × 10 5 Дж работы, пока 3.00 × 10 6 Дж происходит теплопередача в систему, а 8.00 × 10 6 Дж теплопередачи происходит в окружающую среду?
- Предположим, что женщина выполняет 500 Дж работы, и в процессе работы происходит 9500 Дж передачи тепла в окружающую среду. а) Как уменьшается ее внутренняя энергия, если не меняется температура или потребление пищи? (То есть другой передачи энергии нет.) Б) Какова ее эффективность?
- (а) Сколько пищевой энергии человек усвоит в процессе усвоения 35.0 кДж работы при КПД 5,00%? б) Сколько тепла передается в окружающую среду, чтобы поддерживать постоянную температуру?
- (a) Какова средняя скорость метаболизма в ваттах человека, который усваивает 10 500 кДж пищевой энергии за один день? (б) Какое максимальное количество работы в джоулях он может выполнить без расщепления жира, предполагая максимальную эффективность 20,0%? (c) Сравните его производительность с дневной мощностью двигателя 187 Вт (0,250 лошадиных сил).
- (a) На сколько времени хватит энергии в стакане йогурта на 1470 кДж (350 ккал) у женщины, выполняющей работу с мощностью 150 Вт с эффективностью 20?0% (например, при неспешном подъеме по лестнице)? (б) Означает ли время, указанное в части (а), легко потребить больше пищевой энергии, чем вы можете разумно ожидать, работая с упражнениями?
- (a) Женщина, поднимающаяся на памятник Вашингтону, усваивает 6,00 × 10 2 кДж пищевой энергии. Если ее КПД составляет 18,0%, сколько тепла передается в окружающую среду, чтобы поддерживать ее температуру постоянной? (б) Обсудите величину теплопередачи, указанную в (а). Это согласуется с тем, что вы быстро разминаетесь во время тренировки?
Глоссарий
Первый закон термодинамики: гласит, что изменение внутренней энергии системы равно чистой теплопередаче в систему за вычетом чистой работы, выполненной системой
внутренняя энергия: сумма кинетической и потенциальной энергий атомов и молекул системы
метаболизм человека: преобразование пищи в теплообмен, работу и накопленный жир
Избранные решения проблем и упражнения
1.1,6 × 10 9 Дж
3. −9.30 × 10 8 Дж
5. (а) -1,0 × 10 4 Дж, или -2,39 ккал; (б) 5,00%
7. (а) 122 Вт; (б) 2,10 × 10 6 Дж; (c) Работа двигателя составляет 1,61 × 10 7 Дж; таким образом, двигатель производит в 7,67 раз больше работы, чем человек
9. (a) 492 кДж; (б) Такое количество тепла соответствует тому факту, что вы быстро согреваетесь во время тренировки. Поскольку организм неэффективен, выделяемое избыточное тепло должно рассеиваться через потоотделение, дыхание и т. Д.
Первый закон термодинамики
Первый Закон
Первый закон термодинамики гласит, что изменение внутренней энергии системы равно чистой теплопередаче за вычетом чистой работы, выполненной системой.
Цели обучения
Объясните, как чистое переданное тепло и чистая работа, выполняемая в системе, соотносятся с первым законом термодинамики.
Основные выводы
Ключевые моменты
- Первый закон термодинамики — это версия закона сохранения энергии, специально предназначенная для термодинамических систем.
- В форме уравнения первый закон термодинамики выглядит так: [latex] \ Delta \ text {U} = \ text {Q} — \ text {W} [/ latex].
- Тепловые машины — хороший пример применения первого закона; в них происходит передача тепла, так что они могут выполнять работу.
Ключевые термины
- внутренняя энергия : сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно, энергия, необходимая для создания системы, за исключением энергии, необходимой для перемещения ее окружения.
- тепло : энергия, передаваемая от одного тела к другому за счет теплового взаимодействия
- Закон сохранения энергии : Закон, гласящий, что общее количество энергии в любой изолированной системе остается постоянным и не может быть создано или уничтожено, хотя оно может менять форму.
Первый закон термодинамики — это версия закона сохранения энергии, специально предназначенная для термодинамических систем. Обычно его формулируют, утверждая, что изменение внутренней энергии замкнутой системы равно количеству тепла, подаваемого в систему, за вычетом количества работы, выполняемой системой над ее окружением.Закон сохранения энергии можно сформулировать так: энергия изолированной системы постоянна.
Первый закон термодинамики : В этом видео я продолжаю серию обучающих видео по теплофизике и термодинамике. Он рассчитан на бакалавриат, и хотя он в основном нацелен на изучение физики, он должен быть полезен всем, кто изучает первый курс термодинамики, например инженерам и т. Д.
Если нас интересует, как теплопередача превращается в работу, важен принцип сохранения энергии.Первый закон термодинамики применяет принцип сохранения энергии к системам, в которых передача тепла и выполнение работы являются методами передачи энергии в систему и из нее. В форме уравнения первый закон термодинамики равен
.Внутренняя энергия : Первый закон термодинамики — это принцип сохранения энергии, установленный для системы, в которой тепло и работа являются методами передачи энергии для системы, находящейся в тепловом равновесии. Q представляет собой чистую теплопередачу — это сумма всех теплопередач в систему и из нее.Q положительно для чистой передачи тепла в систему. W — это общая работа, проделанная системой и над ней. W положительно, когда система выполняет больше работы, чем над ней. Изменение внутренней энергии системы ΔU связано с теплом и работой в соответствии с первым законом термодинамики ΔU = Q − W.
[латекс] \ Delta \ text {U} = \ text {Q} — \ text {W} [/ latex].
Здесь ΔU — это изменение внутренней энергии U системы, Q — чистое тепло, переданное системе, а W — чистая работа, выполненная системой.Мы используем следующие соглашения о знаках: если Q положительно, то в системе имеется чистый теплообмен; если W положительно, то система выполняет чистую работу. Таким образом, положительный Q добавляет энергию в систему, а положительный W забирает энергию из системы. Таким образом, ΔU = Q − W. Также обратите внимание, что если в систему передается больше тепла, чем проделанной работы, разница сохраняется как внутренняя энергия. Тепловые двигатели — хороший тому пример — в них происходит передача тепла, чтобы они могли выполнять свою работу.
Постоянное давление и объем
Изобарический процесс — это процесс, в котором газ действительно работает при постоянном давлении, а изохорный процесс — это процесс, в котором поддерживается постоянный объем.
Цели обучения
Контрастные изобарические и изохорные процессы
Основные выводы
Ключевые моменты
- Изобарный процесс происходит при постоянном давлении. Поскольку давление постоянно, прилагаемая сила постоянна, а выполненная работа выражается как PΔV.
- Изобарическое расширение газа требует теплопередачи для поддержания постоянного давления.
- Изохорный процесс — это процесс, в котором объем поддерживается постоянным, что означает, что работа, выполняемая системой, будет равна нулю.Единственное изменение будет заключаться в том, что газ приобретает внутреннюю энергию.
Ключевые термины
- внутренняя энергия : сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно, энергия, необходимая для создания системы, за исключением энергии, необходимой для перемещения ее окружения.
Согласно первому закону термодинамики, тепло, передаваемое системе, может быть преобразовано во внутреннюю энергию или использовано для работы с окружающей средой.Процесс, в котором газ воздействует на окружающую среду при постоянном давлении, называется изобарическим процессом, а процесс, в котором поддерживается постоянный объем, называется изохорическим процессом.
Изобарический процесс (постоянное давление)
Изобарный процесс происходит при постоянном давлении. Поскольку давление постоянно, прилагаемая сила постоянна, а выполненная работа выражается как PΔV. Примером может служить подвижный поршень в цилиндре, чтобы давление внутри цилиндра всегда было атмосферным, хотя он изолирован от атмосферы.Другими словами, система динамически связана подвижной границей с резервуаром постоянного давления. Если газ должен расширяться при постоянном давлении, тепло должно передаваться в систему с определенной скоростью. Этот процесс называется изобарическим расширением.
Рис. 1 : Изобарическое расширение газа требует теплопередачи во время расширения, чтобы поддерживать постоянное давление. Поскольку давление постоянно, проделанная работа равна PΔV.
Изохорный процесс (постоянный объем)
Изохорный процесс — это процесс, в котором объем поддерживается постоянным, что означает, что работа, выполняемая системой, будет равна нулю.Отсюда следует, что для простой двухмерной системы любая тепловая энергия, передаваемая системе извне, будет поглощена как внутренняя энергия. Изохорный процесс также известен как изометрический процесс или изоволюметрический процесс. Например, можно поместить в огонь закрытую жестяную банку, содержащую только воздух. В первом приближении баллончик не будет расширяться, и единственное изменение будет заключаться в том, что газ приобретает внутреннюю энергию, о чем свидетельствует повышение его температуры и давления. Математически
[латекс] \ Delta \ text {Q} = \ Delta \ text {U} [/ latex].
Можно сказать, что система динамически изолирована жесткой границей от окружающей среды.
Изотермические процессы
Изотермический процесс — это изменение термодинамической системы, в которой температура остается постоянной.
Цели обучения
Определите типичные системы, в которых происходит изотермический процесс
Основные выводы
Ключевые моменты
- Для идеального газа произведение давления на объем (PV) является постоянным, если газ находится в изотермических условиях.
- Для идеального газа работа, связанная с переходом газа из состояния A в состояние B в результате изотермического процесса, задается как [latex] \ text {W} _ {\ text {A} \ to \ text {B}} = \ text {nRT} \ ln {\ frac {\ text {V} _ \ text {B}} {\ text {V} _ \ text {A}}} [/ latex].
- Для многих систем, если температура поддерживается постоянной, внутренняя энергия системы также остается постоянной. Отсюда следует, что в этом случае Q = -W.
Ключевые термины
- обратимый : Возможность возврата в исходное состояние без потребления свободной энергии и увеличения энтропии. {\ text { V} _ \ text {B}} \ frac {1} {\ text {V}} \ text {dV} = \ text {nRT} \ ln {\ frac {\ text {V} _ \ text {B}} {\ text {V} _ \ text {A}}} [/ latex].
Также стоит отметить, что для многих систем, если температура поддерживается постоянной, внутренняя энергия системы также остается постоянной, и поэтому [latex] \ Delta \ text {U} = 0 [/ latex]. Из первого закона термодинамики следует, что [latex] \ text {Q} = — \ text {W} [/ latex] для того же изотермического процесса.
Адиабатические процессы
Адиабатический процесс — это любой процесс, происходящий без увеличения или уменьшения тепла в системе.
Цели обучения
Оценить среду, в которой обычно происходят изотермические процессы
Основные выводы
Ключевые моменты
- Адиабатические процессы могут возникать, если контейнер системы имеет теплоизолированные стенки или процесс происходит за очень короткое время.
- Для адиабатически расширяющегося идеального одноатомного газа, который действительно воздействует на окружающую среду (W положительно), внутренняя энергия газа должна уменьшаться.
- В некотором смысле изотермический процесс можно рассматривать как противоположную крайность адиабатического процесса. В изотермических процессах теплообмен идет достаточно медленно, чтобы температура системы оставалась постоянной.
Ключевые термины
- Закон Бойля : Наблюдение, согласно которому давление идеального газа обратно пропорционально его объему при постоянной температуре.
- идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и подвергаются упругому столкновению друг с другом и со стенками контейнера.
- обратимый : Возможность возврата в исходное состояние без потребления свободной энергии и увеличения энтропии.
Изотермический процесс — это изменение системы, в которой температура остается постоянной: ΔT = 0. Обычно это происходит, когда система находится в контакте с внешним тепловым резервуаром (термостатом), и изменение происходит достаточно медленно, чтобы позволить система для постоянного регулирования температуры резервуара за счет теплообмена.Напротив, адиабатический процесс — это когда система не обменивается теплом с окружающей средой (Q = 0). (См. Наш атом в «Адиабатическом процессе».) Другими словами, в изотермическом процессе значение ΔT = 0, но Q 0, в то время как в адиабатическом процессе ΔT ≠ 0, но Q = 0.
Идеальный газ в изотермическом процессе
В идеале произведение давления на объем (PV) является постоянным, если газ находится в изотермических условиях. (Исторически это называется законом Бойля.) Однако случаи, когда PV продукта является экспоненциальным членом, не соблюдаются.Значение константы равно nRT, где n — количество моль присутствующего газа, а R — постоянная идеального газа. Другими словами, применяется закон идеального газа PV = nRT. Это означает, что
[латекс] \ text {P} = \ frac {\ text {nRT}} {\ text {V}} = \ frac {\ text {constant}} {\ text {V}} [/ latex]
трюмов. Семейство кривых, порожденных этим уравнением, показано на. Каждая кривая называется изотермой.
Изотермы идеального газа : Несколько изотерм идеального газа на фотоэлектрической диаграмме.{\ text {V} _ \ text {B}} \ text {P} \, \ text {dV} [/ latex].
Для изотермического обратимого процесса этот интеграл равен площади под соответствующей изотермой давление-объем и обозначен синим цветом in для идеального газа. Опять же, применяется P = nRT / V, и если T является постоянным (поскольку это изотермический процесс), мы имеем
Работа, выполненная газом во время расширения : Синяя область представляет «работу», совершаемую газом во время расширения для этого изотермического изменения.
[латекс] \ text {W} _ {\ text {A} \ to \ text {B}} = \ text {nRT} \ int _ {\ text {V} _ \ text {A}} ^ {\ text { V} _ \ text {B}} \ frac {1} {\ text {V}} \ text {dV} = \ text {nRT} \ ln {\ frac {\ text {V} _ \ text {B}} {\ text {V} _ \ text {A}}} [/ latex].
Также стоит отметить, что для многих систем, если температура поддерживается постоянной, внутренняя энергия системы также остается постоянной, и поэтому [latex] \ Delta \ text {U} = 0 [/ latex]. Из первого закона термодинамики следует, что [latex] \ text {Q} = — \ text {W} [/ latex] для того же изотермического процесса.
Метаболизм человека
Первый закон термодинамики объясняет метаболизм человека: преобразование пищи в энергию, которая используется телом для выполнения действий.
Цели обучения
Противоположный катаболизм и анаболизм в отношении энергии
Основные выводы
Ключевые моменты
- Метаболизм человека — сложный процесс. Первый закон термодинамики описывает начало и конец этих процессов.
- Наше тело теряет внутреннюю энергию. Эта внутренняя энергия может идти по трем направлениям — к теплопередаче, выполнению работы и накоплению жира.
- Наш организм представляет собой хороший пример необратимых процессов.Хотя телесный жир может быть преобразован для выполнения работы и передачи тепла, работа, выполняемая телом, и передача тепла в него не могут быть преобразованы в телесный жир.
Ключевые термины
- метаболизм : Полный набор химических реакций, происходящих в живых клетках.
- окисление : реакция, в которой атомы элемента теряют электроны и валентность элемента увеличивается.
- калория : энергия, необходимая для повышения температуры 1 килограмма воды на 1 кельвин.Это эквивалентно 1000 (маленьких) калорий.
Метаболизм человека — это преобразование пищи в энергию, которая затем используется организмом для выполнения действий. Это пример действия первого закона термодинамики. Рассматривая тело как интересующую нас систему, мы можем использовать первый закон для изучения теплопередачи, выполнения работы и внутренней энергии в различных видах деятельности, от сна до тяжелых упражнений. Например, одним из основных факторов в таких действиях является температура тела, обычно поддерживаемая постоянной за счет передачи тепла в окружающую среду, что означает, что Q отрицательно (т.е.е., наше тело теряет тепло). Другой фактор заключается в том, что тело обычно работает с внешним миром, а это означает, что W положительна. Таким образом, в таких ситуациях тело теряет внутреннюю энергию, поскольку ΔU = Q − W отрицательно.
Еда
Теперь рассмотрим эффекты еды. Организм метаболизирует всю пищу, которую мы потребляем. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии. По сути, метаболизм использует процесс окисления, в котором высвобождается химическая потенциальная энергия пищи.Это означает, что питание осуществляется в форме работы. Энергия пищи указывается в специальной единице, известной как калория. Эта энергия измеряется сжиганием пищи в калориметре, как и определяются единицы.
Катаболизм и анаболизм
Катаболизм — это путь, который расщепляет молекулы на более мелкие единицы и производит энергию. Анаболизм — это образование молекул из более мелких единиц. Анаболизм использует энергию, произведенную катаболическим расщеплением вашей пищи, для создания молекул, более полезных для вашего тела.
Внутренняя энергия
Наше тело теряет внутреннюю энергию, и есть три места, куда эта внутренняя энергия может идти — на передачу тепла, выполнение работы и накопленный жир (крошечная часть также идет на восстановление и рост клеток). Как показано на рис. 1, передача тепла и выполнение работы забирают внутреннюю энергию из тела, а затем пища возвращает ее. Если вы едите нужное количество пищи, ваша средняя внутренняя энергия остается постоянной. Все, что вы теряете на теплопередачу и выполнение работы, заменяется едой, так что в конечном итоге ΔU = 0.Если вы постоянно переедаете, то ΔU всегда положительно, и ваше тело сохраняет эту дополнительную внутреннюю энергию в виде жира. Обратное верно, если вы едите слишком мало. Если ΔU отрицательное в течение нескольких дней, тогда организм метаболизирует собственный жир, чтобы поддерживать температуру тела и выполнять работу, которая забирает у тела энергию. Именно так соблюдение диеты способствует снижению веса.
Метаболизм : (а) Первый закон термодинамики применительно к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, в то время как прием пищи заменяет ее.(Прием пищи можно рассматривать как работу, выполняемую организмом.) (Б) Растения преобразуют часть лучистой теплопередачи солнечного света в запасенную химическую энергию, этот процесс называется фотосинтезом.
Метаболизм
Жизнь не всегда так проста, как знает любой человек, сидящий на диете. Тело накапливает жир или метаболизирует его только в том случае, если потребление энергии меняется в течение нескольких дней. После того, как вы сели на основную диету, следующая будет менее успешной, потому что ваше тело изменит способ реагирования на низкое потребление энергии.Ваша основная скорость метаболизма — это скорость, с которой пища преобразуется в теплообмен и работу, выполняемую в то время, когда тело находится в полном покое. Организм регулирует базальную скорость метаболизма, чтобы компенсировать (частично) переедание или недоедание. Организм будет снижать скорость метаболизма, а не устранять собственный жир, чтобы заменить потерянную еду. Вам будет легче охладиться, и вы почувствуете себя менее энергичным в результате более низкой скорости метаболизма, и вы не будете терять вес так быстро, как раньше. Упражнения помогают сбросить вес, потому что они обеспечивают теплоотдачу от вашего тела и работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя.
Необратимость
Тело является прекрасным свидетельством того, что многие термодинамические процессы необратимы. Необратимый процесс может идти в одном направлении, но не в обратном, при заданном наборе условий. Например, хотя телесный жир может быть преобразован для выполнения работы и передачи тепла, работа, выполняемая телом, и передача тепла в него не могут быть преобразованы в телесный жир. В противном случае мы могли бы пропустить обед, загорая или спустившись по лестнице. Другой пример необратимого термодинамического процесса — фотосинтез.Этот процесс представляет собой поглощение растениями одной формы энергии — света — и ее преобразование в химическую потенциальную энергию. Оба применения первого закона термодинамики проиллюстрированы в. Одно большое преимущество таких законов сохранения состоит в том, что они точно описывают начальную и конечную точки сложных процессов (таких как метаболизм и фотосинтез) без учета промежуточных осложнений.
12.2 Первый закон термодинамики: тепловая энергия и работа
Биология: биологическая термодинамика
Мы часто думаем о термодинамике, как о полезной для изобретения или тестирования оборудования, такого как двигатели или паровые турбины.Однако термодинамика также применима к живым системам, таким как наши собственные тела. Это составляет основу биологической термодинамики (рис. 12.7).
Рис. 12.7 (а) Первый закон термодинамики применим к метаболизму. Тепло, передаваемое из тела (Q), и работа, выполняемая телом (W), удаляют внутреннюю энергию, тогда как прием пищи заменяет ее. (Прием пищи можно рассматривать как работу, выполняемую телом.) (Б) Растения преобразуют часть лучистой энергии солнечного света в запасенную химическую энергию — процесс, называемый фотосинтезом .
Сама жизнь зависит от биологической передачи энергии. Посредством фотосинтеза растения поглощают солнечную энергию и используют эту энергию для преобразования углекислого газа и воды в глюкозу и кислород. Фотосинтез принимает одну форму энергии — свет — и преобразует ее в другую форму — химическую потенциальную энергию (глюкозу и другие углеводы).
Метаболизм человека — это преобразование пищи в энергию, выделяемую теплом, работой, выполняемой клетками организма, и накопленным жиром.Метаболизм — интересный пример действия первого закона термодинамики. Прием пищи увеличивает внутреннюю энергию тела за счет добавления химической потенциальной энергии; это неромантичный взгляд на хороший буррито.
Организм усваивает всю пищу, которую мы потребляем. По сути, метаболизм — это процесс окисления, при котором высвобождается химическая потенциальная энергия пищи. Это означает, что питание осуществляется в форме работы. Упражнения помогают вам похудеть, поскольку они обеспечивают передачу энергии от вашего тела как за счет тепла, так и за счет работы, а также повышают уровень метаболизма, даже когда вы находитесь в состоянии покоя.
Биологическая термодинамика также включает изучение трансдукции между клетками и живыми организмами. Трансдукция — это процесс, при котором генетический материал — ДНК — передается от одной клетки к другой. Это часто происходит во время вирусной инфекции (например, гриппа), и именно так вирус распространяется, а именно путем передачи своего генетического материала все большему количеству ранее здоровых клеток. Как только достаточное количество клеток заражается, вы начинаете ощущать воздействие вируса (симптомы гриппа — мышечная слабость, кашель и заложенность носа).
Энергия передается вместе с генетическим материалом и, таким образом, подчиняется первому закону термодинамики. Энергия передается — а не создается и не уничтожается — в процессе. Когда с элементом выполняется работа или тепло передает энергию ячейке, внутренняя энергия ячейки увеличивается. Когда клетка работает или теряет тепло, ее внутренняя энергия уменьшается. Если количество работы, выполняемой ячейкой, такое же, как количество энергии, передаваемой теплом, или количество работы, выполняемой ячейкой, соответствует количеству энергии, передаваемой теплом, чистого изменения внутренней энергии не будет. .
Проверка захвата
Исходя из того, что вы знаете о теплопередаче и о первом законе термодинамики, нужно ли вам есть больше или меньше, чтобы поддерживать постоянный вес в холодную погоду? Объяснить, почему.

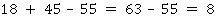
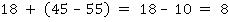
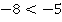
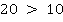 , поэтому
, поэтому  .
.
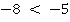 .
.

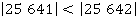
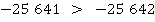
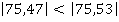
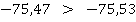
 и
и 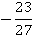
 и
и 
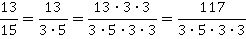


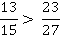

 Можно сделать вывод, что число, находящееся правее больше числа слева.
Можно сделать вывод, что число, находящееся правее больше числа слева. Видно, что число -4 лежит левее нуля, поэтому -4 меньше 0 или запишем математически -4<0.
Видно, что число -4 лежит левее нуля, поэтому -4 меньше 0 или запишем математически -4<0. Число 2 лежит правее числа -3, значит число 2 больше -3 или запишем математически 2>-3.
Число 2 лежит правее числа -3, значит число 2 больше -3 или запишем математически 2>-3. Видно, что число -1 лежит правее числа -4, поэтому -4<-1.
Видно, что число -1 лежит правее числа -4, поэтому -4<-1.















 3 y=x-1+x-3=2x-4 «
3 y=x-1+x-3=2x-4 «








 Плазменная декоративная лампа.
Плазменная декоративная лампа.

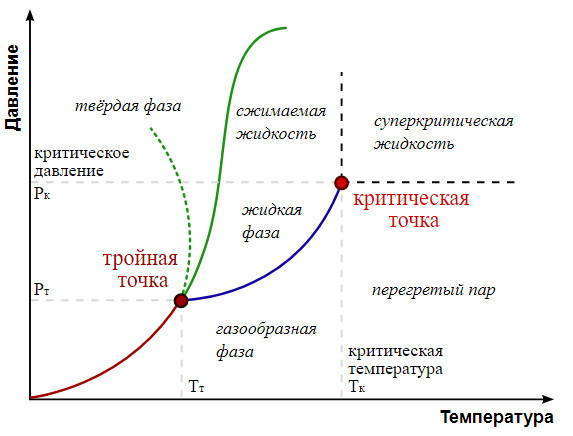
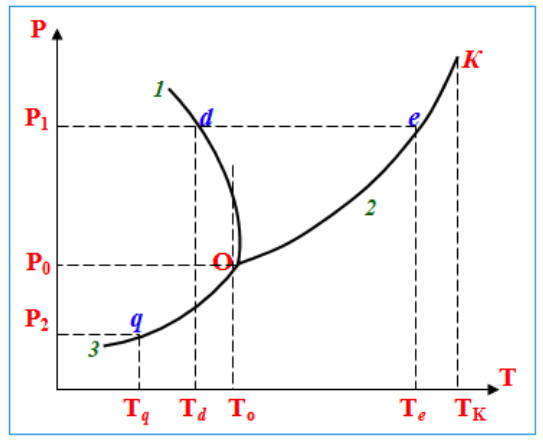
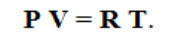

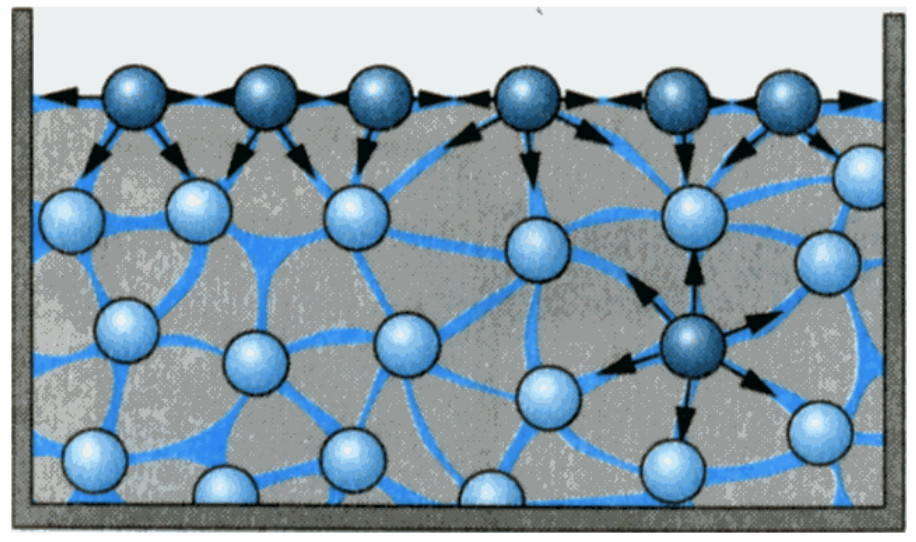
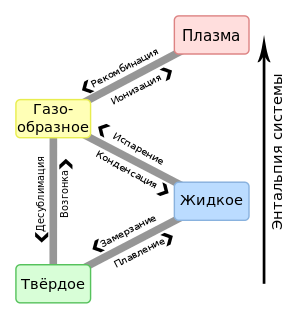
 Кристаллические вещества: атомное разрешение изображения титаната стронция. Яркие атомы — Sr, темнее их Ti.
Кристаллические вещества: атомное разрешение изображения титаната стронция. Яркие атомы — Sr, темнее их Ti. Промежутки между молекулами газа очень большие. Молекулы газа обладают очень слабыми связями. Молекулы в газе могут перемещаться свободно и быстро.
Промежутки между молекулами газа очень большие. Молекулы газа обладают очень слабыми связями. Молекулы в газе могут перемещаться свободно и быстро. Плазменная декоративная лампа.
Плазменная декоративная лампа. Если попадаю в затруднение, то просто изменяю фразу или разбиваю сложное предложение на более простые. Оно и для читателя удобней. Секрет прост — стараться читать книги издания 1960-80-х годов, когда в издательствах корректорами работали настоящие зубры русского языка, а не родственницы главных редакторов, как сейчас.
Если попадаю в затруднение, то просто изменяю фразу или разбиваю сложное предложение на более простые. Оно и для читателя удобней. Секрет прост — стараться читать книги издания 1960-80-х годов, когда в издательствах корректорами работали настоящие зубры русского языка, а не родственницы главных редакторов, как сейчас.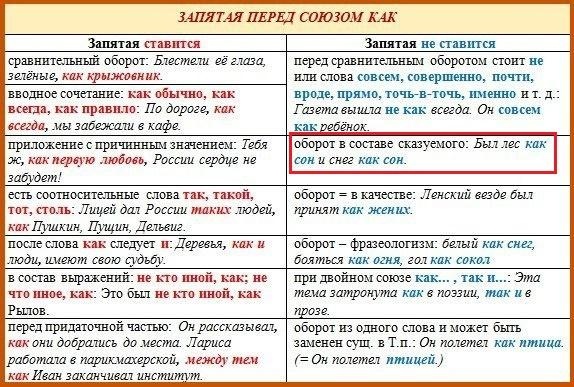

 №4. С тех пор как умерла жена, Герасим пребывал в постоянной печали.
№4. С тех пор как умерла жена, Герасим пребывал в постоянной печали. И тогда уже выбирается слитное или раздельное его применение.
И тогда уже выбирается слитное или раздельное его применение.
 Ему синонимичны следующие фразы: «потому что», «ибо», «затем что», «из-за того что», «оттого что», которыми он может заменяться в контексте. В этой функции он не расчленяется и требует перед собой обязательную постановку запятой. В свою очередь «и» – это простой одиночный союз, который стоит после составного.
Ему синонимичны следующие фразы: «потому что», «ибо», «затем что», «из-за того что», «оттого что», которыми он может заменяться в контексте. В этой функции он не расчленяется и требует перед собой обязательную постановку запятой. В свою очередь «и» – это простой одиночный союз, который стоит после составного.
 Эта последняя запятая часто называется «порядковой» или «Оксфордской». В газетах вы редко ее встретите, однако это не тот знак препинания, которым можно пренебречь в научной литературе.
Эта последняя запятая часто называется «порядковой» или «Оксфордской». В газетах вы редко ее встретите, однако это не тот знак препинания, которым можно пренебречь в научной литературе.


 Но будьте внимательны: вторая запятая ставится после слов автора только в том случае, если они разделяют прямую речь, состоящую из одного предложения, а не из двух. Сравните:
Но будьте внимательны: вторая запятая ставится после слов автора только в том случае, если они разделяют прямую речь, состоящую из одного предложения, а не из двух. Сравните: Например:
Например: Всё чаще вижу запятую перед словом «because», но в школе такого правила у нас не было. Неужели поменялось правило?
Всё чаще вижу запятую перед словом «because», но в школе такого правила у нас не было. Неужели поменялось правило?
 Прогулял физ-ру когда? Однажды!
Прогулял физ-ру когда? Однажды! Придётся переучиваться. «То есть» — это союз, запятая ставится только перед ним. А если в каких-то текстах вы замечали запятую после, то точно по другим причинам. Например, чтобы обособить следующее (вводное) слово или придаточное предложение: «То есть, к сожалению, придётся полностью переписать эссе».
Придётся переучиваться. «То есть» — это союз, запятая ставится только перед ним. А если в каких-то текстах вы замечали запятую после, то точно по другим причинам. Например, чтобы обособить следующее (вводное) слово или придаточное предложение: «То есть, к сожалению, придётся полностью переписать эссе». Правда, иногда всё же допускается авторское выделение запятыми, чтобы подчеркнуть интонационную паузу.
Правда, иногда всё же допускается авторское выделение запятыми, чтобы подчеркнуть интонационную паузу.
 Вот тут-то и усложняется правило запятых. Мы используем запятую перед , начиная с , только если предыдущее предложение отменяется новым предложением.Хорошее практическое правило: если предыдущее предложение содержит отрицательный глагол, используйте запятую.
Вот тут-то и усложняется правило запятых. Мы используем запятую перед , начиная с , только если предыдущее предложение отменяется новым предложением.Хорошее практическое правило: если предыдущее предложение содержит отрицательный глагол, используйте запятую.


 Первый — временный, второй — причинный, третий — причинный, а четвертый — временной.
Первый — временный, второй — причинный, третий — причинный, а четвертый — временной.


 Мы сразу перейдем к делу встречи.
Мы сразу перейдем к делу встречи. Он содержит подлежащее и глагол и образует законченную мысль.
Он содержит подлежащее и глагол и образует законченную мысль. В приведенном выше примере вы можете использовать , следовательно, вместо точки с запятой. Эти статьи напрямую связаны.
В приведенном выше примере вы можете использовать , следовательно, вместо точки с запятой. Эти статьи напрямую связаны.

 Согласно пуристам, нельзя сказать: «Он был отменен из-за дождя», потому что в «из-за» нечего изменять. Это действует как предлог в этом предложении, и пуристы утверждают, что «из-за» является прилагательным; это не должно быть составным предлогом.
Согласно пуристам, нельзя сказать: «Он был отменен из-за дождя», потому что в «из-за» нечего изменять. Это действует как предлог в этом предложении, и пуристы утверждают, что «из-за» является прилагательным; это не должно быть составным предлогом.

 В. Фаулер (и я),
считают, что это вполне приемлемо.
(Библия короля Иакова, великий памятник прекрасного английского стиля, делает это постоянно: все предложения, кроме двух, в ее знаменитой первой главе начинаются
с И!) Одним из следствий этого является то, что предложения, в которых и или , но следует за запятой, могут показаться неудачными при проверке на соединение запятой,
поскольку запятую можно без проблем заменить точкой:
В. Фаулер (и я),
считают, что это вполне приемлемо.
(Библия короля Иакова, великий памятник прекрасного английского стиля, делает это постоянно: все предложения, кроме двух, в ее знаменитой первой главе начинаются
с И!) Одним из следствий этого является то, что предложения, в которых и или , но следует за запятой, могут показаться неудачными при проверке на соединение запятой,
поскольку запятую можно без проблем заменить точкой: Некоторые запятые необходимы для предотвращения неправильного чтения, некоторые вредны, а другие необязательны. С середины двадцатого века эксперты по использованию, такие как Теодор М. Бернштейн, выступали за использование «минимум запятых» (359).Клэр Кервальд Кук предупреждает: «Запятые привлекают внимание к словам. Они заставляют читателей задуматься и обратить внимание. Если вы не хотите такого эффекта, не используйте запятые, которых не требует структура предложения »(125). Другими словами, используйте запятые только тогда, когда они помогают прояснить ваш смысл.
Некоторые запятые необходимы для предотвращения неправильного чтения, некоторые вредны, а другие необязательны. С середины двадцатого века эксперты по использованию, такие как Теодор М. Бернштейн, выступали за использование «минимум запятых» (359).Клэр Кервальд Кук предупреждает: «Запятые привлекают внимание к словам. Они заставляют читателей задуматься и обратить внимание. Если вы не хотите такого эффекта, не используйте запятые, которых не требует структура предложения »(125). Другими словами, используйте запятые только тогда, когда они помогают прояснить ваш смысл.
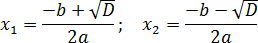

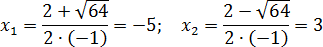
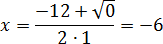

 Другие реакции происходят в любом направлении до тех пор, пока реагенты и продукты находятся в равновесии – точка, в которой нет явных изменений в реагентах или продуктах.
Другие реакции происходят в любом направлении до тех пор, пока реагенты и продукты находятся в равновесии – точка, в которой нет явных изменений в реагентах или продуктах.

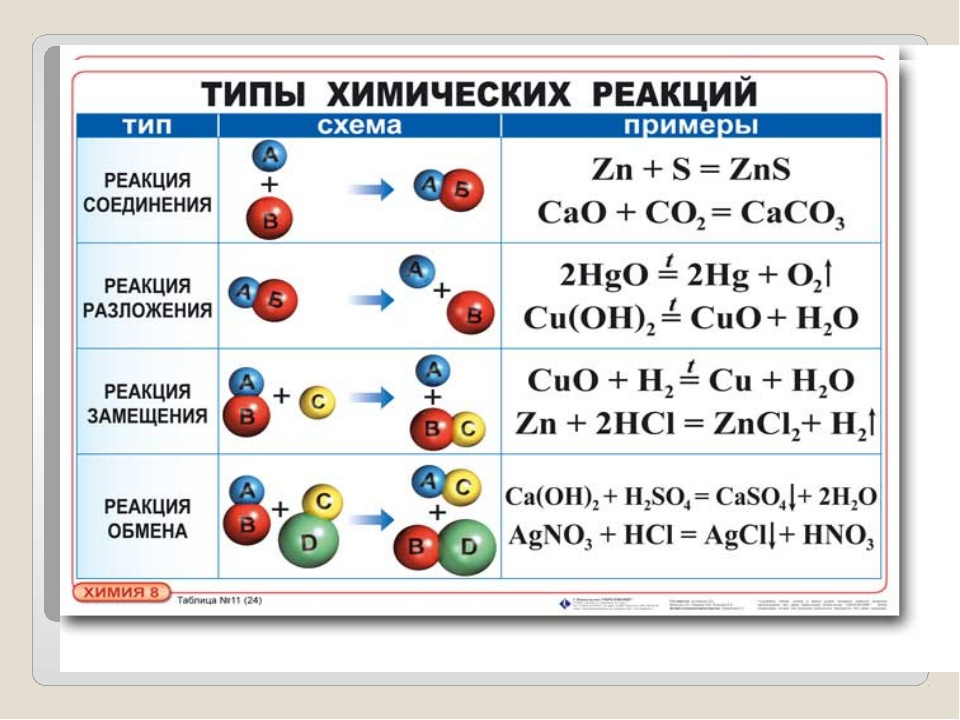


 Обратную реакцию соответственно можно классифицировать как -8R8. Особо отметим тот факт, что для целей классификации, практическая осуществимость конкретной химической реакции не имеет существенного значения.
Обратную реакцию соответственно можно классифицировать как -8R8. Особо отметим тот факт, что для целей классификации, практическая осуществимость конкретной химической реакции не имеет существенного значения.
 Эта химическая реакция выглядит так: 2PbSO4 + 2h3O → PbO2 + Pb + 2h3SO4. Она происходит в процессе зарядки аккумулятора.
Эта химическая реакция выглядит так: 2PbSO4 + 2h3O → PbO2 + Pb + 2h3SO4. Она происходит в процессе зарядки аккумулятора.




 В ходе реакции степени окисления атомов элементов остаются прежними, значит, это превращение относится к реакциям без изменения степеней окисления. Для осуществления такой реакции нам не требуется катализатор, поэтому это будет превращением некаталитическим. При разложении нерастворимого гидроксида меди (II) мы получаем нерастворимый в воде оксид меди (II), поэтому, если мы попробуем провести реакцию между оксидом меди (II) и водой, у нас ничего не выйдет. Значит, реакция разложения гидроксида меди (II) является необратимой. В качестве реагента выступает твердое вещество, а в качестве продуктов – твердый оксид меди (II) и водяной пар, поэтому по фазовому составу такая реакция является гетерогенной. Реакция разложения гидроксида меди (II) начинается при его нагревании, температура превращения составляет около 80 °С. Значит, по виду энергии, инициирующей реакцию, эта реакция является термохимической. Для «запуска» этой реакции требуется нагревание, следовательно, теплота, которую мы подводим извне, будет поглощаться и полученная энергия будет расходоваться на перестройку структуры. Такая реакция относится к эндотермическим.
В ходе реакции степени окисления атомов элементов остаются прежними, значит, это превращение относится к реакциям без изменения степеней окисления. Для осуществления такой реакции нам не требуется катализатор, поэтому это будет превращением некаталитическим. При разложении нерастворимого гидроксида меди (II) мы получаем нерастворимый в воде оксид меди (II), поэтому, если мы попробуем провести реакцию между оксидом меди (II) и водой, у нас ничего не выйдет. Значит, реакция разложения гидроксида меди (II) является необратимой. В качестве реагента выступает твердое вещество, а в качестве продуктов – твердый оксид меди (II) и водяной пар, поэтому по фазовому составу такая реакция является гетерогенной. Реакция разложения гидроксида меди (II) начинается при его нагревании, температура превращения составляет около 80 °С. Значит, по виду энергии, инициирующей реакцию, эта реакция является термохимической. Для «запуска» этой реакции требуется нагревание, следовательно, теплота, которую мы подводим извне, будет поглощаться и полученная энергия будет расходоваться на перестройку структуры. Такая реакция относится к эндотермическим. Это должна быть кальциевая соль уксусной кислоты – ацетат кальция. Ацетат-ион одновалентен, а ион кальция – двухвалентен, следовательно, на каждый ион кальция приходится два ацетат-иона. Его формула (CH3COO)2Ca. Записываем формулу на место пропуска.
Это должна быть кальциевая соль уксусной кислоты – ацетат кальция. Ацетат-ион одновалентен, а ион кальция – двухвалентен, следовательно, на каждый ион кальция приходится два ацетат-иона. Его формула (CH3COO)2Ca. Записываем формулу на место пропуска. У каждой стадии своя скорость и свои требования к температуре, давлению и прочим условиям. В общем, иногда гремучая смесь не гремит. И чтобы понять почему, нужно понять химическую реакцию на всех уровнях мироздания — от отдельных электронов и до заводских реакторов. И для этого придется немного изменить наше восприятие времени.
У каждой стадии своя скорость и свои требования к температуре, давлению и прочим условиям. В общем, иногда гремучая смесь не гремит. И чтобы понять почему, нужно понять химическую реакцию на всех уровнях мироздания — от отдельных электронов и до заводских реакторов. И для этого придется немного изменить наше восприятие времени. Современные ученые могут наблюдать эти явления при помощи особых экспериментальных приемов (фемтосекундная спектроскопия).
Современные ученые могут наблюдать эти явления при помощи особых экспериментальных приемов (фемтосекундная спектроскопия).
 Химия — это попытка классифицировать и лучше понять эти реакции.
Химия — это попытка классифицировать и лучше понять эти реакции. Поскольку в левой части уравнения присутствует только 2 атома азота, к \ (NH_3 \) необходимо добавить коэффициент 2.
Поскольку в левой части уравнения присутствует только 2 атома азота, к \ (NH_3 \) необходимо добавить коэффициент 2. Для определения процентной доходности:
Для определения процентной доходности: ) + H_2SO_4 (вод.) \ Стрелка вправо CaSO_4 (s) + H_2O (l) + CO_2 (g) \ nonumber \]
) + H_2SO_4 (вод.) \ Стрелка вправо CaSO_4 (s) + H_2O (l) + CO_2 (g) \ nonumber \]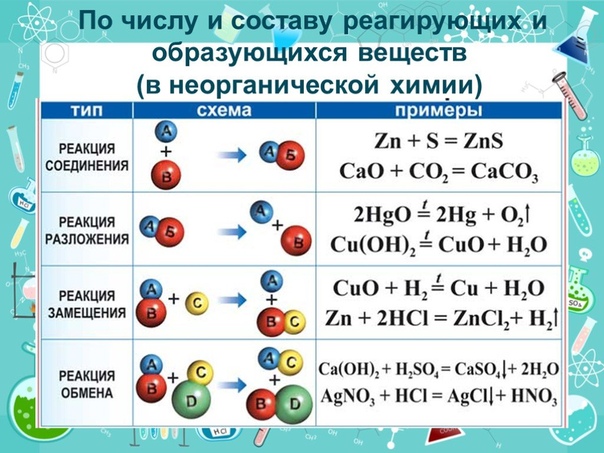 Окисление — это процесс увеличения степени окисления атома, а восстановление — это процесс уменьшения степени окисления атома.Если степени окисления каких-либо элементов в реакции изменяются, реакция является окислительно-восстановительной реакцией. Атом, который подвергается окислению, называется восстановителем, а атом, который подвергается восстановлению, называется окислителем. Примером окислительно-восстановительной реакции является реакция между газообразным водородом и газообразным фтором:
Окисление — это процесс увеличения степени окисления атома, а восстановление — это процесс уменьшения степени окисления атома.Если степени окисления каких-либо элементов в реакции изменяются, реакция является окислительно-восстановительной реакцией. Атом, который подвергается окислению, называется восстановителем, а атом, который подвергается восстановлению, называется окислителем. Примером окислительно-восстановительной реакции является реакция между газообразным водородом и газообразным фтором: Вот коллекция различных примеров, каждый из которых требует кислорода, энергии активации и, конечно же, топлива
Вот коллекция различных примеров, каждый из которых требует кислорода, энергии активации и, конечно же, топлива  ) + KBr (водн.) → AgBr (s) + KNO 3 (водн.)
) + KBr (водн.) → AgBr (s) + KNO 3 (водн.)/beakers-and-cylinders-with-colorful-liquids-98831556-57d2ceb73df78c71b638e6b8.jpg)
 Al окисляется до Al 3+ с помощью Br 2 , который восстанавливается до ионов Br — .Ионный продукт, AlBr 3 , можно наблюдать на часах.
стакан после реакции.
Al окисляется до Al 3+ с помощью Br 2 , который восстанавливается до ионов Br — .Ионный продукт, AlBr 3 , можно наблюдать на часах.
стакан после реакции.


 Три воздушных шара с водородом и один шар
смешанные с водородом и кислородом образуют взрывоопасную смесь
Три воздушных шара с водородом и один шар
смешанные с водородом и кислородом образуют взрывоопасную смесь
 представляет известные факты
представляет известные факты  Когда натрий твердый
Нитрат нагревается, он разлагается с образованием твердого нитрита натрия и газообразного кислорода.
Когда натрий твердый
Нитрат нагревается, он разлагается с образованием твердого нитрита натрия и газообразного кислорода. РЕАКЦИЯ РАЗЛОЖЕНИЯ
РЕАКЦИЯ РАЗЛОЖЕНИЯ




 Когда образуется новое вещество, это изменение называется химическим изменением.
Когда образуется новое вещество, это изменение называется химическим изменением.
 Когда электроны возвращаются вниз, энергия высвобождается в виде света.
Когда электроны возвращаются вниз, энергия высвобождается в виде света.


 Правильно будет сказать, что в этой реакции на каждую молекулу метана приходится две молекулы кислорода.
Правильно будет сказать, что в этой реакции на каждую молекулу метана приходится две молекулы кислорода.


 Используя определение расхода Cidμi / dt = Ji в уравнении (14.18), определяющее соотношение для емкостного элемента C i составляет
Используя определение расхода Cidμi / dt = Ji в уравнении (14.18), определяющее соотношение для емкостного элемента C i составляет