Соляная кислота это что: Соляная кислота: влияние на экологию и здоровье человека. Справка
Соляная кислота: влияние на экологию и здоровье человека. Справка
Получают соляную кислоту растворением в воде хлористого водорода, который синтезируют или непосредственно из водорода и хлора или получают действием серной кислоты на хлорид натрия.
Выпускаемая техническая соляная кислота имеет крепость не менее 31% HCl (синтетическая) и 27,5% HCl (из NaCI). Торговую кислоту называют концентрированной, если она содержит 24% и больше HCl, если содержание HCl меньше, то кислота называется разбавленной.
Соляную кислоту применяют для получения хлоридов различных металлов, органических полупродуктов и синтетических красителей, уксусной кислоты, активированного угля, различных клеев, гидролизного спирта, в гальванопластике. Ее применяют для травления металлов, для очистки различных сосудов, обсадных труб буровых скважин от карбонатов, окислов и др. осадков и загрязнений. В металлургии кислотой обрабатывают руды, в кожевенной промышленности – кожу перед дублением и крашением. Соляную кислоту применяют в текстильной, пищевой промышленности, в медицине и т. д.
Соляную кислоту применяют в текстильной, пищевой промышленности, в медицине и т. д.
Соляная кислота играет важную роль в процессах пищеварения, она является составной частью желудочного сока. Разведенную соляную кислоту назначают внутрь главным образом при заболеваниях, связанных с недостаточной кислотностью желудочного сока.
Транспортируют соляную кислоту в стеклянных бутылях или гуммированных (покрытых слоем резины) металлических сосудах, а также в полиэтиленовой посуде.
Соляная кислота очень опасна для здоровья человека. При попадании на кожу вызывает сильные ожоги. Особенно опасно попадание в глаза.
При попадании соляной кислоты на кожные покрытия ее необходимо немедленно смыть обильной струей воды.
Очень опасны туман и пары хлороводорода, образующиеся при взаимодействии с воздухом концентрированной кислоты. Они раздражают слизистые оболочки и дыхательные пути. Длительная работа в атмосфере HCl вызывает катары дыхательных путей, разрушение зубов, помутнение роговицы глаз, изъязвление слизистой оболочки носа, желудочно-кишечные расстройства.
Острое отравление сопровождается охриплостью голоса, удушьем, насморком, кашлем.
В случае утечки или разлива соляная кислота может нанести существенный ущерб окружающей среде. Во-первых, это приводит к выделению паров вещества в атмосферный воздух в количествах превышающих санитарно-гигиенические нормативы, что может повлечь отравление всего живого, а также появлению кислотных осадков, которые могут привести к изменению химических свойств почвы и воды.
Во-вторых, она может просочиться в грунтовые воды, в результате чего может произойти загрязнение внутренних вод.
Там, где вода в реках и озерах стала довольно кислой (рН менее 5) исчезает рыба. При нарушении трофических цепей сокращается число видов водных животных, водорослей и бактерий.
В городах кислотные осадки ускоряют процессы разрушения сооружений из мрамора и бетона, памятников и скульптур. При попадании на металлы соляная кислота вызывает их коррозию, а, реагируя с такими веществами, как хлорная известь, диоксид марганца, или перманганат калия, образует токсичный газообразный хлор.
В случае разлива соляную кислоту смывают с поверхностей большим количеством воды или щелочного раствора, который нейтрализует кислоту.
Материал подготовлен на основе информации открытых источников
Страница не найдена — Портал Продуктов Группы РСС
Сообщите нам свой адрес электронной почты, чтобы подписаться на рассылку новостного бюллетеня. Предоставление адреса электронной почты является добровольным, но, если Вы этого не сделаете, мы не сможем отправить Вам информационный бюллетень. Администратором Ваших персональных данных является Акционерное Общество PCC Rokita, находящееся в Бжег-Дольном (ул. Сенкевича 4, 56-120 Бжег-Дольный, Польша ). Вы можете связаться с нашим инспектором по защите личных данных по электронной почте: .
Мы обрабатываем Ваши данные для того, чтобы отправить Вам информационный бюллетень — основанием для обработки является реализация нашей законодательно обоснованной заинтересованности или законодательно обоснованная заинтересованность третьей стороны – непосредственный маркетинг наших продуктов / продуктов группы PCC .
Как правило, Ваши данные мы будем обрабатывать до окончания нашего с Вами общения или же до момента, пока Вы не выразите свои возражения, либо если правовые нормы будут обязывать нас продолжать обработку этих данных, либо мы будем сохранять их дольше в случае потенциальных претензий, до истечения срока их хранения, регулируемого законом, в частности Гражданским кодексом.
В любое время Вы имеете право:
- выразить возражение против обработки Ваших данных;
- иметь доступ к Вашим данным и востребовать их копии;
- запросить исправление, ограничение обработки или удаление Ваших данных;
- передать Ваши персональные данные, например другому администратору, за исключением тех случаев, если их обработка регулируется законом и находится в интересах администратора;
- подать жалобу Президенту Управления по защите личных данных.
Получателями Ваших данных могут быть компании, которые поддерживают нас в общении с Вами и помогают нам в ведении веб-сайта, внешние консалтинговые компании (такие как юридические, маркетинговые и бухгалтерские) или внешние специалисты в области IT, включая компанию Группы PCC .
Больше о том, как мы обрабатываем Ваши данные Вы можете узнать из нашего Полиса конфиденциальности.
Соляная кислота — одна из самых сильных кислот, чрезвычайно востребованный реактив
Соляная кислота — неорганическое вещество, одноосновная кислота, одна из самых сильных кислот. Используются также другие названия: хлористый водород, кислота хлороводородная, кислота хлористоводородная.
Свойства
Кислота в чистом виде представляет собой жидкость без цвета и запаха. Техническая кислота обычно содержит примеси, которые придают ей слегка желтоватый оттенок. Соляную кислоту часто называют «дымящей», так как она выделяет пары хлороводорода, вступающие в реакцию с влагой воздуха и образующие кислотный туман.
Очень хорошо растворяется в воде. При комнатной температуре максимально возможное по массе содержание хлороводорода —38%. Кислота концентрации большей 24% считается концентрированной.
Хлористоводородная кислота активно вступает в реакции с металлами, оксидами, гидроксидами, образуя соли — хлориды. HCl взаимодействует с солями более слабых кислот; с сильными окислителями и аммиаком.
HCl взаимодействует с солями более слабых кислот; с сильными окислителями и аммиаком.
Для определения соляной кислоты или хлоридов используют реакцию с нитратом серебра AgNO3, в результате которой выпадает белый творожистый осадок.
Техника безопасности
Вещество очень едкое, разъедает кожу, органические материалы, металлы и их окислы. На воздухе выделяет пары хлороводорода, которые вызывают удушье, ожоги кожи, слизистой глаз и носа, повреждают органы дыхания, разрушают зубы. Соляная кислота относится к веществам 2 степени опасности (высокоопасным), ПДК реактива в воздухе составляет 0,005 мг/л. Работать с хлористым водородом можно только в фильтрующих противогазах и защитной одежде, включая резиновые перчатки, фартук, спецобувь.
При разливе кислоты ее смывают большим количеством воды или нейтрализуют щелочным растворами. Пострадавших от кислоты следует вынести из опасной зоны, промыть кожу и глаза водой или содовым раствором, вызвать врача.
Перевозить и хранить хим реактив допускается в стеклянной, пластиковой таре, а также в металлической таре, покрытой изнутри резиновым слоем. Тара должна герметично закрываться.
Тара должна герметично закрываться.
Получение
В промышленных масштабах соляную кислоту получают из газообразного хлороводорода (HCl). Сам хлороводород производится двумя основными способами:
— экзотермической реакцией хлора и водорода — таким образом получают реактив высокой чистоты, например, для пищевой промышленности и фармацевтики;
— из сопутствующих промышленных газов — кислота на основе такого HCl называется абгазной.
Это любопытно
Именно соляной кислоте природа «поручила» процесс расщепления пищи в организме. Концентрация кислоты в желудке составляет всего 0,4%, но этого оказывается достаточно, чтобы за неделю переварить бритвенное лезвие!
Кислота вырабатывается клетками самого желудка, который защищен от этой агрессивной субстанции слизистой оболочкой. Тем не менее, его поверхность обновляется ежедневно, чтобы восстановить поврежденные участки. Кроме участия в процессе переваривания пищи, кислота выполняет еще и защитную функцию, убивая болезнетворные микроорганизмы, попадающие в организм через желудок.
Применение
— В медицине и фармацевтике — для восстановления кислотности желудочного сока при его недостаточности; при анемии для улучшения всасываемости железосодержащих лекарств.
— В пищепроме это пищевая добавка, регулятор кислотности Е507, а также ингредиент сельтерской (содовой) воды. Используется при изготовлении фруктозы, желатина, лимонной кислоты.
— В химической промышленности — основа для получения хлора, соды, глутамината натрия, хлоридов металлов, например, хлорида цинка, хлорида марганца, хлорида железа; синтеза хлорорганических веществ; катализатор в органических синтезах.
— Больше всего производимой в мире хлористоводородной кислоты расходуется в металлургии для очистки заготовок от окислов. Для этих целей применяется ингибированная техническая кислота, в состав которой введены специальные ингибиторы (замедлители) реакции, благодаря чему реактив растворяет окислы, но не сам металл. Также соляной кислотой травят металлы; очищают их перед лужением, пайкой, гальванированием.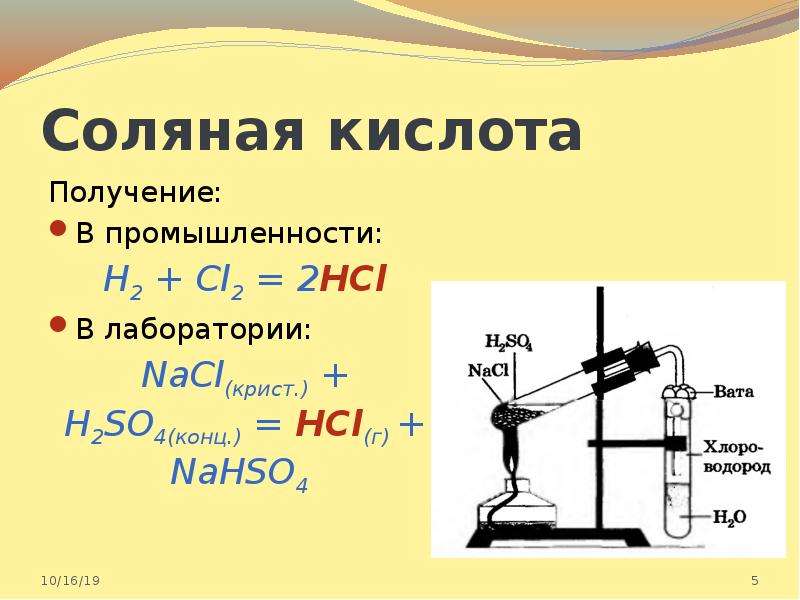
— Обрабатывают кожу перед дублением.
— В добывающей отрасли востребована для очистки буровых скважин от отложений, для обработки руд и горных пластов.
— В лабораторной практике хлористоводородная кислота используется как популярный реактив для аналитических исследований, для очистки сосудов от трудноудаляемых загрязнений.
— Применяется в каучуковой, целлюлозно-бумажной индустрии, в черной металлургии; для очистки котлов, труб, оборудования от сложных отложений, накипи, ржавчины; для очистки керамических и металлических изделий.
Соляная кислота — физические свойства, использование в травлении при цинковании
Соляная кислота – это раствор хлористого водорода в воде. Хлористый водород (HCl) при обычных условиях бесцветный газ со специфическим острым запахом. Однако мы имеем дело с его водными растворами, поэтому остановимся только на них.
Соляная кислота – бесцветный прозрачный раствор с острым запахом хлористого водорода. В присутствии примесей железа, хлора или других веществ кислота имеет желтовато-зеленый цвет. Плотность раствора соляной кислоты зависит от концентрации хлористого водорода в ней; некоторые данные приведены в таблице 6.9.
Плотность раствора соляной кислоты зависит от концентрации хлористого водорода в ней; некоторые данные приведены в таблице 6.9.
Таблица 6.9. Плотность растворов соляной кислоты различной концентрации при 20°С.
|
Содержание HCl |
Плотность d, г/см3 |
Содержание HCl |
Плотность d, г/см3 |
||
|
% |
г/л |
% |
г/л |
||
|
4 |
40,7 |
1,018 |
28 |
319,0 |
1,139 |
|
10 |
104,7 |
1,047 |
30 |
344,8 |
1,149 |
|
16 |
174,2 |
1,078 |
32 |
371,0 |
1,159 |
|
20 |
219,6 |
1,098 |
34 |
397,5 |
1,169 |
|
24 |
268,5 |
1,119 |
36 |
424,4 |
1,179 |
Из этой таблицы видно, что зависимость плотности раствора соляной кислоты от ее концентрации с удовлетворительной для технических расчетов точностью можно описать формулой:
d = 1 + 0,5*(%) / 100
При кипении разбавленных растворов содержание HCl в парах меньше, чем в растворе, а при кипении концентрированных растворов — больше, чем в растворе, что отражено в приведенной на рис. 6.12 диаграмме равновесия. Постоянно кипящая смесь (азеотроп) при атмосферном давлении имеет состав 20,22 % вес. HCl, температуру кипения 108,6°С.
6.12 диаграмме равновесия. Постоянно кипящая смесь (азеотроп) при атмосферном давлении имеет состав 20,22 % вес. HCl, температуру кипения 108,6°С.
Наконец, еще одно важное преимущество соляной кислоты — это практически полная независимость времени ее приобретения от времени года. Как видно из рис. № 6.13, кислота промышленной концентрации (32-36%) замерзает при температурах, практически недостижимых для европейской части России (от -35 до -45°С), в отличие от серной кислоты, которая замерзает при плюсовых температурах, что требует введения операции разогрева цистерн.
Соляная кислота не обладает недостатками, присущими серной кислоте.
Во-первых, хлористое железо обладает повышенной растворимостью в растворе соляной кислоты (рис. 6.14), что позволяет поднять концентрацию хлористого железа в растворе до величины 140 г/л и даже больше; исчезает опасность образования осадка на поверхности.
Работа с соляной кислотой может осуществляться при любой температуре внутри здания (даже при 10°С), и это не вызывает заметных изменений в составе раствора.
Рис. 6.12. Диаграмма равновесия жидкость – пар для системы HCl – H2O.
Рис. 6.13. Диаграмма состояния (плавкости) системы HCl–H2O.
Рис. 6.14. Равновесие в системе HCl – FeCl2.
Наконец, еще очень важное преимущество соляной кислоты — это полная совместимость с флюсом, в котором используются именно хлориды.
Некоторым недостатком соляной кислоты как реактива является высокая летучесть. Нормативами допускается концентрация 5 мг/м3 объема воздуха в цехе. Зависимость упругости паров в равновесном состоянии над кислотой различной процентной концентрации дана в таблице 6.10. В целом при концентрации кислоты в ванне менее 15% масс это условие удовлетворяется. Однако при повышении температур в цехе (то есть в летнее время) возможно превышение этого показателя. Определенную информацию о том, какая концентрация кислоты при конкретной температуре цеха допустима, можно определить из рис. 6.15.
6.15.
Зависимость скорости травления от концентрации и температуры отображена на рис. 6.16.
Недостатки травления обычно вызываются следующим:
- использованием кислоты с большей или меньшей концентрацией, по сравнению с оптимальной;
- малой длительностью травления (ожидаемую длительность травления при разных концентрациях кислоты и железа можно оценить из рис. 6.17;
- пониженной температурой по сравнению с оптимальной;
- отсутствием перемешивания;
- ламинарным движением травильного раствора.
Эти проблемы обычно решаются с помощью конкретных технологических приемов.
Таблица 6.10. Зависимость равновесной концентрации хлористого водорода от концентрации кислоты в ванне.
|
Концентрация кислоты, % |
Концентрация HСl в воздухе, мг/м3 |
Концентрация кислоты, % |
Концентрация HСl в воздухе, мг/м3 |
|
26 |
18 500 (20°C) |
16 |
200 (20°C) |
|
24 |
4 500 (20°C) |
10 |
16 (30°C) |
|
20 |
800 (30°C) |
6 |
3 (30°C) |
Рис. 6.15. Зависимость разрешенной температуры травления от концентрации соляной кислоты в ванне.
6.15. Зависимость разрешенной температуры травления от концентрации соляной кислоты в ванне.
Рис. 6.16. Зависимость скорости травления изделий в соляной кислоте от концентрации и температуры раствора.
Рис. 6.17. Номограмма для расчета продолжительности травления изделий в растворах с различной концентрацией HCl и FeCl2.
Возможно Вас так же заинтересуют следующие статьи: comments powered by HyperCommentsСоляная кислота прекурсор \ Акты, образцы, формы, договоры \ Консультант Плюс
]]>Подборка наиболее важных документов по запросу Соляная кислота прекурсор (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).
Статьи, комментарии, ответы на вопросы: Соляная кислота прекурсор Открыть документ в вашей системе КонсультантПлюс:Статья: Предмет наркопреступлений: подходы к его определению
(Ролик А.
 И.)
И.)(«Lex russica», 2016, N 12)Есть у некоторых исследователей претензии и к самому перечню прекурсоров. Так, А.Я. Кромовой представляется не вполне целесообразным привлечение к уголовной ответственности лиц, ввозящих или вывозящих с территории РФ уксусную кислоту. Уксусная кислота маркируется как пищевая добавка Е260 и широко используется в пищевой промышленности, бытовой кулинарии, а также в консервировании. Ацетон также находит применение в пищевой промышленности и быту, а серная и соляная кислота применяются во всем народном хозяйстве. В связи с изложенным указанный автор предлагает исключить уксусную кислоту, ацетон, серную и соляную кислоты из Списка IV, содержащего перечень прекурсоров . Полагаем, что делать этого не стоит, поскольку при манипуляциях с данными веществами «двойного назначения» преступник четко осознает, что вовлекает их в незаконный оборот именно как прекурсоры с целью совершения наркопреступлений. И наоборот, использование тех же веществ в бытовых целях исключает уголовную ответственность за наркопреступления.
 Открыть документ в вашей системе КонсультантПлюс:
Открыть документ в вашей системе КонсультантПлюс:«Комментарий к Федеральному закону от 8 января 1998 г. N 3-ФЗ «О наркотических средствах и психотропных веществах»
(постатейный)
(Афанасьева О.Р., Бадальянц Э.Ю., Болотин В.С., Грибанов Е.В., Шиян В.И., Щербаков А.Д., Беляев М.А., Вяземская А.А.)
(Подготовлен для системы КонсультантПлюс, 2017)7) регистрация в специальных журналах любых операций с прекурсорами. Постановлением Правительства РФ от 9 июня 2010 г. N 419 утверждены Правила ведения и хранения специальных журналов регистрации операций, связанных с оборотом прекурсоров наркотических средств и психотропных веществ. Ведение соответствующих журналов предусмотрено при осуществлении любых видов деятельности, связанных с оборотом прекурсоров. Все операции, при которых изменяется количество прекурсоров, подлежат занесению в специальный журнал регистрации операций. Данные Правила не распространяются на ведение и хранение журналов в случаях, когда разрешается использование прекурсоров без лицензии в соответствии со ст.
 35 и 36 комментируемого Закона. Также в них установлены упрощенные правила для порядка регистрации операций по отпуску, реализации, приобретению или использованию ряда прекурсоров (диэтилового эфира, ацетона, толуола, соляной кислоты, уксусной кислоты и др.).Нормативные акты: Соляная кислота прекурсор Открыть документ в вашей системе КонсультантПлюс:
35 и 36 комментируемого Закона. Также в них установлены упрощенные правила для порядка регистрации операций по отпуску, реализации, приобретению или использованию ряда прекурсоров (диэтилового эфира, ацетона, толуола, соляной кислоты, уксусной кислоты и др.).Нормативные акты: Соляная кислота прекурсор Открыть документ в вашей системе КонсультантПлюс:Минздравсоцразвития России от 20.12.2006 N 6811-ВС
Приобретение прекурсоров рекомендуем оформлять в день приема отметкой в приходной части журнала регистрации операций (графы 3 — 5). В случае если расход (отпуск, реализация или использование в медицинских и научных целях, в экспертной деятельности) за месяц таких прекурсоров, как перманганат калия, ацетон, серная и соляная кислоты (всех концентраций) не превышает 10 кг, ежедневная отметка в журнале регистрации операций, связанных с оборотом прекурсоров, не производится.
 В графе 14 расходной части журнала отмечается общий расход за месяц, который определяется на основании подтверждающих документов (чековая лента, лабораторно-фасовочный журнал, журнал проведения исследований и др.). Подшивка расходных документов в этом случае не производится.
В графе 14 расходной части журнала отмечается общий расход за месяц, который определяется на основании подтверждающих документов (чековая лента, лабораторно-фасовочный журнал, журнал проведения исследований и др.). Подшивка расходных документов в этом случае не производится.Соляная кислота. Кислородсодержащие кислоты
Соляная кислота HCl
Цистерна с соляной кислотойСоляная кислота — одна из сильных одноосновных кислот и образуется при растворении газа хлороводорода (HCl) в воде, — прозрачная бесцветная жидкость с характерным запахом хлора. Разбавленная соляная кислота (также как и фосфорная) часто применяется для снятия оксидов при пайке металлов.
Иногда газообразное соединение HCl ошибочно называют соляной кислотой. HCl — это газ, который при растворении в воде образует соляную кислоту.
Хлороводород — бесцветный газ с резким удушливым запахом хлора. Он переходит в жидкое состояние при -840C, а при -1120C — переходит в твёрдое состояние.
Он переходит в жидкое состояние при -840C, а при -1120C — переходит в твёрдое состояние.
Хлороводород очень хорошо растворяется в воде. Так при 00C в 1л воды растворяется 500л хлороводорода.
В сухом состоянии газ хлороводород достаточно инертный, но уже может взаимодействовать с некоторыми органическими веществами, например с ацетиленом (газ, который выделяется при опускании карбида в воду).
Химические свойства соляной кислоты
— химическая реакция с металлами:2HCl + Zn =ZnCl2 + H2 — образуется соль (в данном случае прозрачный раствор хлорид цинка) и водород
— химическая реакция с оксидами металлов:
2HCl + CuO = CuCl2 + H2O — образуется соль (в данном случае раствор соли зёленого хлорида меди) и вода
— химическая реакция с основаниями и щелочами (или реакция нейтрализации)
HCl + NaOH = NaCl + H2O — реакция нейтрализации, -образуется соль (в данном случае прозрачный раствор хлорид натрия) и вода.

— химическая реакция с солями (например, c мелом СaCO3):
HCl + СaCO3 = CaCl2 + CO2 + H2O — образуется углекислый газ, вода и прозрачный раствор хлорида кальция CaCl2.
Получение соляной кислоты
Соляную кислоту получают с помощью химической реакции соединения:
H2 + Cl2 = HCl — реакция происходит при повышенной температуре
А также при взаимодействии поваренной соли и концентрированной серной кислотой:
H2SO4 (конц.) + NaCl = NaHSO4 + HCl
В этой реакции, если вещество NaCl — в твёрдом виде, то HCl — это газ хлороводород, который при растворении в воде образует соляную кислоту
Кислородсодержащие кислоты
Соляная кислотаСуществуют сложные химические вещества, по химическому строению сходные с соляной кислотой, но при этом содержащие в молекуле от одного до четырёх атомов кислорода. Эти вещества можно назвать кислородсодержащими кислотами. С повышением числа атомов кислорода увеличивается стойкость кислоты и её окислительная способность.
Эти вещества можно назвать кислородсодержащими кислотами. С повышением числа атомов кислорода увеличивается стойкость кислоты и её окислительная способность.
К кислородсодержащим кислотам слудующие:
- хлорноватистая (HClO),
- хлористая (HClO2),
- хлорноватая (HClO3),
- хлорная (HClO4).
Каждое из этих химических сложных веществ обладает всеми свойствами кислот и способна образовывать соли. Хлорноватистая кислота (HClO) образует гипохлориты, например, соединение NaClO — гипохлорит натрия. Сама хлорноватистая кислота образуется при растворении хлора в холодной воде по химической реакции:
H2O + Cl2 = HCl + HClO,
Как видите, в этой реакции образуется сразу две кислоты — соляная HCl и хлорноватистая HClO. Но последняя — нестойкое химическое соединение и постепенно переходит в соляную кислоту;
Но последняя — нестойкое химическое соединение и постепенно переходит в соляную кислоту;
Хлористая HClO2 образует хлориты, соль NaClO2 — хлорит натрия;
хлорноватая (HClO3) — хлораты, соединение KClO3, — хлорат калия (или бертолетова соль)- кстати, это вещество широко применяется при изготовления спичек.
И наконец самая сильная из известных одноосновных кислот — хлорная (HClO4) — бесцветная, дымящаяся на воздухе, сильно гигроскопичная жидкость, — образует перхлораты, например, KClO4 — перхлорат калия.
Соли, образованные хлорноватистой HClO и хлористой HClO2 кислотами, в свободном состоянии не устойчивы и являются сильными окислителями в водных растворах. А вот соли, образованные хлорноватой HClO3 и хлорной HClO4 кислотами на основании щелочных металлов (например, таrже бертолетова соль KClO3), — достаточно устойчивы и не проявляют окислительных свойств.
Соляная кислота — Medum.ru
Соляная кислота (пищевая добавка Е507) — раствор хлороводорода (HCl) в воде, сильная одноосновная кислота. Бесцветная, прозрачная, едкая жидкость, «дымящаяся» на воздухе (техническая соляная кислота — желтоватого цвета из-за примесей железа, хлора и пр.). В концентрации около 0,5 % присутствует в желудке человека. Соли соляной кислоты называются хлоридами.
Получают абсорбцией хлороводорода водой. Хлористоводородная кислота, получаемая при производстве хлорированных углеводородных инсектицидов, считается непригодной для использования в пищевых продуктах. Примеси: сульфаты.
Пищевая добавка Е507 относится к регуляторам кислотности синтетического происхождения, используется в технологических целях в процессе производства пищевых продуктов.
Историческая справка
Впервые это вещество было обнаружено алхимиками около 800 г.н.э., путём смешивания поваренной соли с серной кислотой, и получила название «купорос». Иоганн Глаубер в ⅩⅦ в. получил соляную кислоту из поваренной соли и серной кислоты. В 1790 году британский химик Гемфри Дэви получил хлороводород из водорода и хлора, таким образом установив его состав. Возникновение промышленного производства соляной кислоты связано с технологией получения карбоната натрия: на первой стадии этого процесса поваренную соль вводили в реакцию с серной кислотой, в результате чего выделялся хлороводород. В 1863 году в Англии был принят закон «Alkali Act», согласно которому запрещалось выбрасывать этот хлороводород в воздух, а необходимо было пропускать его в воду. Это привело к развитию промышленного производства соляной кислоты. Дальнейшее развитие произошло благодаря промышленным методам получения гидроксида натрия и хлора путём электролиза растворов хлорида натрия.
Иоганн Глаубер в ⅩⅦ в. получил соляную кислоту из поваренной соли и серной кислоты. В 1790 году британский химик Гемфри Дэви получил хлороводород из водорода и хлора, таким образом установив его состав. Возникновение промышленного производства соляной кислоты связано с технологией получения карбоната натрия: на первой стадии этого процесса поваренную соль вводили в реакцию с серной кислотой, в результате чего выделялся хлороводород. В 1863 году в Англии был принят закон «Alkali Act», согласно которому запрещалось выбрасывать этот хлороводород в воздух, а необходимо было пропускать его в воду. Это привело к развитию промышленного производства соляной кислоты. Дальнейшее развитие произошло благодаря промышленным методам получения гидроксида натрия и хлора путём электролиза растворов хлорида натрия.
Влияние на организм человека
Контакт с соляной кислотой может привести к негативным последствиям. Из-за того, что это едкое вещество, следует избегать попаданий Е507 на открытые участки кожи и слизистые оболочки, в противном случае может образоваться сильный ожог. Наибольшую опасность кислота представляет для глаз. В момент раскупоривания сосуда с соляной кислотой, мгновенно выделяются пары хлороводорода и образуется туман, вдыхание которых ведёт к сильному раздражению дыхательных путей и слизистых оболочек, удушью. Вступая в реакцию с хлорной известью, перманганатом калия или диоксидом марганцы, Е507 образует очень токсичный и опасный газообразный хлор. Тем не менее, слабые растворы Е507, используемые в пищевой промышленности, человеческому здоровью ничем не грозят.
Наибольшую опасность кислота представляет для глаз. В момент раскупоривания сосуда с соляной кислотой, мгновенно выделяются пары хлороводорода и образуется туман, вдыхание которых ведёт к сильному раздражению дыхательных путей и слизистых оболочек, удушью. Вступая в реакцию с хлорной известью, перманганатом калия или диоксидом марганцы, Е507 образует очень токсичный и опасный газообразный хлор. Тем не менее, слабые растворы Е507, используемые в пищевой промышленности, человеческому здоровью ничем не грозят.
Соляная кислота — входит в состав желудочного сока, поэтому иногда её слабоконцентрированный раствор назначают при недостаточной кислотности желудочного сока.
Применение
Пищевая промышленность
В качестве катализатора гидролиза белков и углеводов.
В производстве инвертного сиропа кислоту используют в виде 25 %-го или 10 %-го раствора. К охлаждённому до 80–90 °C сахарному сиропу добавляют раствор кислоты и выдерживают при этой температуре в течение 60 минут (25 %-й р-р кислоты) или 15–25 минут (10 %-й раствор кислоты) при перемешивании. Расход 25 %-го раствора кислоты составляет 1,1 кг или 0,817 л на 1 т сахара. Количество 10 %-го раствора кислоты в зависимости от качества сахара изменяется в пределах 0,15–0,3 % от массы сахара: при использовании рафинированного сахара достаточно 0,15 %, а для сахарного песка требуется 0,2–0,3 %. Используется для подкисления мелассного сусла в производстве спирта.
Расход 25 %-го раствора кислоты составляет 1,1 кг или 0,817 л на 1 т сахара. Количество 10 %-го раствора кислоты в зависимости от качества сахара изменяется в пределах 0,15–0,3 % от массы сахара: при использовании рафинированного сахара достаточно 0,15 %, а для сахарного песка требуется 0,2–0,3 %. Используется для подкисления мелассного сусла в производстве спирта.
Соляная кислота по ГОСТ 3118-77 «Кислота соляная. Технические условия» внесена в перечень сырья в ГОСТ 12712-80 «Водки и водки особые. Технические условия».
Промышленность
Применяется в гидрометаллургии и гальванопластике (травление, декапирование), для очистки поверхности металлов при пайке и лужении, для получения хлоридов цинка, марганца, железа и других. металлов. В смеси с поверхностно-активными веществами используется для очистки керамических и металлических изделий (тут необходима ингибированная кислота) от загрязнений и дезинфекции.
Медицина
Естественная составная часть желудочного сока человека. В концентрации 0,3–0,5 %, обычно в смеси с ферментом пепсином, назначается внутрь при недостаточной кислотности.
В концентрации 0,3–0,5 %, обычно в смеси с ферментом пепсином, назначается внутрь при недостаточной кислотности.
Кислота соляная
2
Соляная кислота повышает активность катализатора
25 августа 2020 г. — Исследовательская группа разработала процесс синтеза, который резко увеличивает активность катализаторов обессеривания сырой нефти. Возможно, новый процесс можно было бы использовать и для катализаторов …
Секреты жуткой фотографической техники
Октябрь30, 2019 — В 1960-х годах французский художник по имени Жан-Пьер Судр начал экспериментировать с малоизвестным фотографическим процессом XIX века, создавая драматические черно-белые фотографии с неземной вуалью …
Расшифровка механизма: как органические кислоты образуются в атмосфере
12 мая 2021 года — кислотность атмосферы все больше определяется углекислым газом и органическими кислотами, такими как муравьиная кислота. Второе из них влияет на рост облаков и pH дождевой воды. Но химический …
Но химический …
Включение и выключение цвета пористого материала с помощью кислоты
8 февраля 2019 г. — Стабильный изменяющий цвет состав демонстрирует потенциал для электроники, датчиков и газа …
Катализатор превращения биомассы в биотопливо
1 июля 2021 г. — цеолиты — чрезвычайно пористые материалы: десять граммов могут иметь площадь внутренней поверхности размером с футбольное поле. Их полости делают их полезными в катализе химических реакций и, следовательно, в экономии…
«Терминаторский» жидкий металл движется и растягивается в трехмерном пространстве
20 марта 2019 г. — Во франшизе блокбастера «Терминатор» злой робот трансформируется в различные человеческие формы и объекты и просачивается сквозь узкие отверстия благодаря своему «жидкому металлу» …
LED-Ing the Way: чистый и удобный метод окисления пластиковых поверхностей для промышленности
11 июня 2019 г. — Исследовательская группа использовала диоксид хлора для окисления полипропилена. Под облучением светодиодами радикалы ClO2 * атакуют метильные группы полипропилена, превращая их в карбоновую кислоту. C-H …
Под облучением светодиодами радикалы ClO2 * атакуют метильные группы полипропилена, превращая их в карбоновую кислоту. C-H …
Предотвращение разрушения бетонных мостов
19 декабря 2018 г. — В новом исследовании изучается неблагоприятное воздействие адсорбции компонентов природного газа, обнаруженных в окружающей среде, и смесей нескольких таких газов одним из материалов, из которых состоит …
Доставка грузов полимерами
Янв.22 февраля 2021 г. — Разлагаемые полимеры на биологической основе предлагают варианты химической переработки и могут быть инструментом для хранения и высвобождения полезных молекул. Ученые разработали класс полимеров на основе сахара, которые …
Производство водорода с меньшим расходом энергии
22 июня 2021 г. — Теперь подробно описан способ, которым соединение, вдохновленное природой, производит водород. Эти результаты являются основой для энергоэффективного производства водорода как экологически безопасного. ..
..
Соляная кислота — Энциклопедия Нового Света
| Соляная кислота | |
|---|---|
| Общие | |
| Систематическое название | соляная кислота |
| Другие названия | Соляная кислота, Солевой спирт |
| Химическая формула | HCl в воде (H 2 O) |
| Молярная масса | 36.46 г / моль (HCl) |
| Внешний вид | Бесцветный прозрачный до светло-желтая жидкость |
| Номер CAS | [7647-01-0] |
| Недвижимость | |
| Плотность, фаза | 1,18 г / см³, 37% раствор. |
| Растворимость в воде | Полностью смешивается. |
| Точка плавления | −26 ° C (247 K) 38% раствор. |
| Температура кипения | 110 ° С (383 К), 20.2% раствор; 48 ° C (321 K), 38% раствор. |
| Кислотная диссоциация константа p K a | −8,0 |
| Вязкость | 1,9 мПа · с при 25 ° C, 31,5% раствор |
| Опасности | |
| Паспорт безопасности | Внешний паспорт безопасности материала |
| NFPA 704 | 0 3 1 32–38% раствор |
| Основные опасности | Сильно агрессивный. |
| Температура вспышки | Невоспламеняющийся. |
| R / S заявление | R34, R37, S26, S36, S45 |
| Номер RTECS | MW4025000 |
| Страница дополнительных данных | |
| Структура и свойства | n , ε r и т. Д. Д. |
| Термодинамические данные | Фазовое поведение Твердое, жидкое, газовое |
| Спектральные данные | УФ, ИК, ЯМР, МС |
| Родственные соединения | |
| Анионы прочие | HF, HBr, HI |
| Прочие катионы | Н / Д |
| Родственные кислоты | Бромистоводородная кислота Плавиковая кислота Йодистоводородная кислота Серная кислота |
| Если не указано иное, данные приведены для материалов в их стандартном состоянии (при 25 ° C, 100 кПа) Заявление об отказе от ответственности и ссылки в Infobox | |
Химическое соединение соляная кислота (или соляная кислота ) представляет собой водный (водный) раствор газообразного хлористого водорода (HCl).Эта сильная кислота очень агрессивна, и при обращении с ней необходимо соблюдать соответствующие меры безопасности. Это основной компонент желудочной кислоты. Он обычно используется в химических исследовательских лабораториях и на производственных предприятиях. Его применение включает крупномасштабное производство определенных соединений (таких как винилхлорид для поливинилхлоридного (ПВХ) пластика), удаление ржавчины и окалины с металлов, добычу нефти и переработку руды. Меньшие масштабы включают производство желатина и других ингредиентов в продуктах питания, а также обработку кожи.Ежегодно производится около 20 миллионов метрических тонн соляной кислоты.
Это основной компонент желудочной кислоты. Он обычно используется в химических исследовательских лабораториях и на производственных предприятиях. Его применение включает крупномасштабное производство определенных соединений (таких как винилхлорид для поливинилхлоридного (ПВХ) пластика), удаление ржавчины и окалины с металлов, добычу нефти и переработку руды. Меньшие масштабы включают производство желатина и других ингредиентов в продуктах питания, а также обработку кожи.Ежегодно производится около 20 миллионов метрических тонн соляной кислоты.
История
Соляная кислота была впервые обнаружена около 800– гг. г. н. Э. Алхимиком Джабиром ибн Хайяном (Гебер) путем смешивания поваренной соли с купоросом (серной кислотой). Джабир открыл многие важные химические вещества и записал свои открытия в более чем 20 книгах, в которых на протяжении сотен лет содержались его химические знания о соляной кислоте и других основных химических веществах. Изобретение Джабиром растворяющей золото царской водки, состоящей из соляной и азотной кислот, вызвало большой интерес у алхимиков, искавших философский камень.
В средние века соляная кислота была известна европейским алхимикам как спирт соли или acidum salis. Газообразный HCl получил название морской кислый воздух. Старое (досистематическое) название соляная кислота имеет то же происхождение ( соляная кислота означает «относящийся к рассолу или соли»), и это название иногда используется до сих пор. Известное производство было зарегистрировано Базилием Валентином, каноником-алхимиком бенедиктинского монастыря Санкт-Петер в Эрфурте, Германия, в пятнадцатом веке.В семнадцатом веке Иоганн Рудольф Глаубер из Карлштадта-на-Майне, Германия, использовал хлорид натрия и серную кислоту для получения сульфата натрия в процессе Мангейма, выделяя газообразный хлористый водород. Джозеф Пристли из Лидса, Англия, получил чистый хлористый водород в 1772 году, а в 1818 году Хэмфри Дэви из Пензанса, Англия, доказал, что химический состав включает водород и хлор.
Во время промышленной революции в Европе спрос на щелочные вещества, такие как кальцинированная сода, увеличился, и новый промышленный процесс производства соды Николя Леблан (Иссундан, Франция) сделал возможным дешевое крупномасштабное производство.В процессе Леблана соль превращается в кальцинированную соду с использованием серной кислоты, известняка и угля. Хлористый водород выделяется как побочный продукт. До Закона о щелочах 1863 года избыток HCl сбрасывался в воздух. После принятия закона производители кальцинированной соды были обязаны поглощать отработанный газ водой, производя соляную кислоту в промышленных масштабах.
Когда в начале двадцатого века процесс Leblanc был эффективно заменен процессом Solvay без побочного продукта соляной кислоты, соляная кислота уже полностью утвердилась в качестве важного химического вещества во многих областях применения.Коммерческий интерес инициировал другие методы производства, которые все еще используются сегодня, как описано ниже. Сегодня большая часть соляной кислоты производится путем абсорбции хлористого водорода из промышленных органических соединений.
Сегодня большая часть соляной кислоты производится путем абсорбции хлористого водорода из промышленных органических соединений.
Соляная кислота включена в список прекурсоров Таблицы II в соответствии с Конвенцией о борьбе с незаконным оборотом наркотических средств и психотропных веществ 1988 года из-за ее использования в производстве таких наркотиков, как героин, кокаин и метамфетамин.
Химия
Кислотное титрование.
Хлористый водород (HCl) представляет собой монопротоновую кислоту, что означает, что каждая молекула может диссоциировать (ионизировать) только один раз с высвобождением одного иона H + (одного протона). В водной соляной кислоте H + присоединяется к молекуле воды с образованием иона гидроксония, H 3 O + :
- HCl + H 2 O ⇌ H 3 O + + Cl —
Другой образующийся ион — это хлорид-ион Cl —. Поэтому соляную кислоту можно использовать для получения солей, называемых хлоридами , , такими как хлорид натрия. Соляная кислота — сильная кислота, так как полностью диссоциирует в воде.
Поэтому соляную кислоту можно использовать для получения солей, называемых хлоридами , , такими как хлорид натрия. Соляная кислота — сильная кислота, так как полностью диссоциирует в воде.
Монопротоновые кислоты имеют одну константу кислотной диссоциации, K a , которая указывает уровень диссоциации в воде. Для сильной кислоты, такой как HCl, K a больше. Были предприняты теоретические попытки отнести K к к HCl. Когда хлоридные соли, такие как NaCl, добавляются к водной HCl, они практически не влияют на pH, что указывает на то, что Cl — является чрезвычайно слабым сопряженным основанием и что HCl полностью диссоциирует в водном растворе.Для средних и сильных растворов соляной кислоты предположение о том, что молярность H + (единица концентрации) равна молярности HCl, является превосходным и соответствует четырем значащим цифрам.
Из семи распространенных сильных кислот в химии, все они неорганические, соляная кислота является монопротоновой кислотой, которая с наименьшей вероятностью вступает в мешающую окислительно-восстановительную реакцию. Это одна из наименее опасных для обращения сильных кислот; несмотря на свою кислотность, он производит менее реактивные и нетоксичные хлорид-ионы.Растворы соляной кислоты средней концентрации достаточно стабильны, сохраняя свою концентрацию с течением времени. Эти характеристики, а также тот факт, что он доступен в виде чистого реагента, означают, что соляная кислота является отличным подкисляющим реагентом и кислотным титрантом (для определения количества неизвестного количества основания при титровании). Титранты с сильными кислотами полезны, потому что они дают более четкие конечные точки при титровании, что делает титрование более точным. Соляная кислота часто используется в химическом анализе и для переваривания образцов для анализа.Концентрированная соляная кислота растворяет некоторые металлы с образованием окисленных хлоридов металлов и газообразного водорода. Он будет производить хлориды металлов из основных соединений, таких как карбонат кальция или оксид меди (II). Он также используется в качестве простого кислотного катализатора некоторых химических реакций.
Это одна из наименее опасных для обращения сильных кислот; несмотря на свою кислотность, он производит менее реактивные и нетоксичные хлорид-ионы.Растворы соляной кислоты средней концентрации достаточно стабильны, сохраняя свою концентрацию с течением времени. Эти характеристики, а также тот факт, что он доступен в виде чистого реагента, означают, что соляная кислота является отличным подкисляющим реагентом и кислотным титрантом (для определения количества неизвестного количества основания при титровании). Титранты с сильными кислотами полезны, потому что они дают более четкие конечные точки при титровании, что делает титрование более точным. Соляная кислота часто используется в химическом анализе и для переваривания образцов для анализа.Концентрированная соляная кислота растворяет некоторые металлы с образованием окисленных хлоридов металлов и газообразного водорода. Он будет производить хлориды металлов из основных соединений, таких как карбонат кальция или оксид меди (II). Он также используется в качестве простого кислотного катализатора некоторых химических реакций.
Физические свойства
Физические свойства соляной кислоты, такие как точки кипения и плавления, плотность и pH, зависят от концентрации или молярности HCl в растворе кислоты. Они могут варьироваться от значений для воды при 0% HCl до значений для дымящей соляной кислоты при более 40% HCl.
| Конц. (по массе) c: кг HCl / кг | Конц. (вес / объем) c: кг HCl / м 3 | Конц. Baumé | Плотность ρ: кг / л | Молярность M | pH | Вязкость η: мПа · с | Удельная теплота с: кДж / (кг · К) | Пар давление P HCl : Па | точка кипения точка б.п. | точка плавления т.  пл. пл. |
| 10% | 104,80 | 6,6 | 1.048 | 2,87 млн | -0,5 | 1,16 | 3,47 | 0,527 | 103 ° С | -18 ° С |
| 20% | 219.60 | 13 | 1,098 | 6,02 млн | -0,8 | 1,37 | 2,99 | 27,3 | 108 ° С | -59 ° С |
| 30% | 344.70 | 19 | 1,149 | 9,45 млн | -1,0 | 1,70 | 2,60 | 1,410 | 90 ° С | -52 ° С |
| 32% | 370,88 | 20 | 1,159 | 10,17 млн | -1,0 | 1,80 | 2,55 | 3,130 | 84 ° С | -43 ° С |
| 34% | 397,46 | 21 | 1,169 | 10. 90 млн 90 млн | -1,0 | 1,90 | 2,50 | 6 733 | 71 ° С | -36 ° С |
| 36% | 424,44 | 22 | 1,179 | 11,64 млн | -1,1 | 1,99 | 2,46 | 14 100 | 61 ° С | -30 ° С |
| 38% | 451,82 | 23 | 1,189 | 12,39 млн | -1,1 | 2.10 | 2,43 | 28 000 | 48 ° С | -26 ° С |
Соляная кислота как бинарная (двухкомпонентная) смесь HCl и H 2 O имеет азеотроп с постоянным кипением при 20,2 процента HCl и температуре 108,6 ° C (227 ° F). Существует четыре эвтектических точки постоянной кристаллизации для соляной кислоты между кристаллической формой HCl · H 2 O (68 процентов HCl), HCl · 2H 2 O (51 процент HCl), HCl · 3H 2 O (41 процент HCl), HCl · 6H 2 O (25 процентов HCl) и лед (0 процентов HCl). Также существует метастабильная точка эвтектики на уровне 24,8% между льдом и кристаллизацией HCl · 3H 2 O
Также существует метастабильная точка эвтектики на уровне 24,8% между льдом и кристаллизацией HCl · 3H 2 O
Производство
Соляная кислота получается растворением хлористого водорода в воде. Хлористый водород может образовываться разными способами, и, таким образом, существует несколько различных предшественников соляной кислоты. Крупномасштабное производство соляной кислоты почти всегда интегрируется с производством других химических веществ в промышленных масштабах.
Промышленный рынок
Соляная кислота производится в растворах с содержанием HCl до 38% (концентрированная).Химически возможны более высокие концентрации до чуть более 40 процентов, но при этом скорость испарения настолько высока, что при хранении и обращении требуются дополнительные меры предосторожности, такие как давление и низкая температура. Таким образом, массовая продукция промышленного класса составляет от 30 до 34 процентов, что оптимизировано для эффективной транспортировки и ограниченной потери продукта парами HCl. Растворы для бытовых целей, в основном для очистки, обычно составляют от 10 до 12 процентов, при этом настоятельно рекомендуется разбавлять их перед использованием.
Растворы для бытовых целей, в основном для очистки, обычно составляют от 10 до 12 процентов, при этом настоятельно рекомендуется разбавлять их перед использованием.
Основные производители по всему миру включают Dow Chemical с производительностью 2 млн метрических тонн в год (2 млн тонн в год) в пересчете на газ HCl и FMC, Georgia Gulf Corporation, Tosoh Corporation, Akzo Nobel и Tessenderlo с производительностью 0.От 5 до 1,5 млн т / год каждая. Общее мировое производство, в целях сравнения, выраженное в HCl, оценивается в 20 Мт / год, из которых 3 Мт / год — за счет прямого синтеза, а остальная часть — как вторичный продукт в результате органического и аналогичного синтезов. Безусловно, больше всего соляной кислоты потребляется производителем самостоятельно. Объем открытого мирового рынка оценивается в 5 млн т / год.
Приложения
Соляная кислота — сильная неорганическая кислота, которая используется во многих промышленных процессах. Приложение часто определяет необходимое качество продукта.
Регенерация ионообменников
Важным применением высококачественной соляной кислоты является регенерация ионообменных смол. Катионный обмен широко используется для удаления ионов, таких как Na + и Ca 2+ , из водных растворов с получением деминерализованной воды.
- Na + заменяется на H 3 O +
- Ca 2+ заменяется на 2 H 3 O +
Ионообменники и деминерализованная вода используются во всех химических производствах, производстве питьевой воды и многих пищевых отраслях.
Контроль и нейтрализация pH
Соляная кислота часто применяется для регулирования щелочности (pH) растворов.
- OH — + HCl → H 2 O + Cl —
В промышленности, требующей чистоты (пищевая, фармацевтическая, питьевая вода), для контроля pH используется высококачественная соляная кислота. потоков технологической воды. В менее требовательных отраслях промышленности соляной кислоты технического качества достаточно для нейтрализации стоков и очистки бассейнов.
потоков технологической воды. В менее требовательных отраслях промышленности соляной кислоты технического качества достаточно для нейтрализации стоков и очистки бассейнов.
Травление стали
Травление является важным этапом обработки поверхности металла для удаления ржавчины или окалины оксида железа с железа или стали перед последующей обработкой, такой как экструзия, прокатка, гальваника и другие методы. HCl технического качества с концентрацией обычно 18 процентов является наиболее часто используемым травильным агентом для травления марок углеродистой стали.
- Fe 2 O 3 + Fe + 6 HCl → 3 FeCl 2 + 3 H 2 O
Отработанная кислота долгое время повторно использовалась в качестве растворов хлорида железа, но высокие уровни тяжелых металлов в травильном растворе уменьшили эту практику.
Однако в последние годы промышленность травления стали разработала процессы регенерации соляной кислоты, такие как распылительный обжиговой аппарат или процесс регенерации HCl в псевдоожиженном слое, которые позволяют извлекать HCl из отработанного травильного раствора. Самый распространенный процесс регенерации — это процесс пирогидролиза, по следующей формуле:
Самый распространенный процесс регенерации — это процесс пирогидролиза, по следующей формуле:
- 4 FeCl 2 + 4 H 2 O + O 2 → 8 HCl + 2 Fe 2 O 3
За счет рекуперации отработанной кислоты образуется замкнутый кислотный цикл. учредил.Оксид железа, являющийся побочным продуктом процесса регенерации, является ценным побочным продуктом, используемым во множестве вторичных производств.
HCl не является обычным травильным агентом для марок нержавеющей стали.
Производство неорганических соединений
Многочисленные продукты могут быть получены с соляной кислотой в обычных кислотно-основных реакциях, приводящих к неорганическим соединениям. К ним относятся химические вещества для обработки воды, такие как хлорид железа (III) и хлорид полиалюминия (PAC).
- Fe 2 O 3 + 6 HCl → 2 FeCl 3 + 3 H 2 O
Хлорид железа (III) и ПАУ используются в качестве флокулянтов и коагуляторов в сточных водах очистка, производство питьевой воды и производство бумаги.
Другие неорганические соединения, производимые с соляной кислотой, включают хлорид кальция, хлорид никеля (II) для гальваники и хлорид цинка для гальванической промышленности и производства аккумуляторов.
Производство органических соединений
Наибольшее потребление соляной кислоты приходится на производство органических соединений, таких как винилхлорид для ПВХ и MDI и TDI для полиуретана. Часто это внутреннее использование с потреблением соляной кислоты местного производства, которая никогда не попадает на открытый рынок.Другие органические соединения, полученные с помощью соляной кислоты, включают бисфенол А для поликарбоната, активированный уголь и аскорбиновую кислоту, а также многочисленные фармацевтические продукты.
Другие приложения
Соляная кислота является основным химическим веществом, и поэтому она используется в большом количестве небольших применений, таких как обработка кожи, уборка дома и строительство зданий. Кроме того, способ стимулирования добычи нефти заключается в закачке соляной кислоты в породу нефтяной скважины, растворении части породы и создании крупнопористой структуры. Кислотная обработка нефтяных скважин — распространенный процесс в нефтедобывающей промышленности Северного моря.
Кислотная обработка нефтяных скважин — распространенный процесс в нефтедобывающей промышленности Северного моря.
Многие химические реакции с участием соляной кислоты применяются в производстве продуктов питания, пищевых ингредиентов и пищевых добавок. Типичные продукты включают аспартам, фруктозу, лимонную кислоту, лизин, гидролизованный (растительный) белок в качестве пищевого усилителя и при производстве желатина. Пищевая (особо чистая) соляная кислота может применяться при необходимости для конечного продукта.
Физиология и патология
Соляная кислота составляет большую часть желудочного сока, пищеварительной жидкости человека.В сложном процессе и при большой энергетической нагрузке он секретируется париетальными клетками (также известными как оксинтические клетки). Эти клетки содержат обширную секреторную сеть (называемую канальцами), из которой HCl секретируется в просвет желудка. Они являются частью фундальных желез (также известных как кислородные железы) в желудке.
Защитными механизмами, предотвращающими повреждение эпителия пищеварительного тракта соляной кислотой, являются:
- Отрицательные регуляторы его выпуска
- Толстый слой слизи, покрывающий эпителий
- Бикарбонат натрия, секретируемый эпителиальными клетками желудка и поджелудочной железой
- Строение эпителия (плотные контакты)
- Достаточное кровоснабжение
- Простагландины (много разных эффектов: они стимулируют секрецию слизи и бикарбоната, поддерживают целостность эпителиального барьера, обеспечивают адекватное кровоснабжение, стимулируют заживление поврежденной слизистой оболочки)
Когда по разным причинам эти механизмы не работают, изжога или пептический могут развиться язвы.Препараты, называемые ингибиторами протонной помпы, не позволяют организму вырабатывать избыток кислоты в желудке, в то время как антациды нейтрализуют имеющуюся кислоту.
В некоторых случаях в желудке вырабатывается недостаточно соляной кислоты. Эти патологические состояния обозначаются терминами гипохлоргидрия и ахлоргидрия. Потенциально они могут привести к гастроэнтериту.
Эти патологические состояния обозначаются терминами гипохлоргидрия и ахлоргидрия. Потенциально они могут привести к гастроэнтериту.
Химическое оружие
Фосген (COCl 2 ) был обычным боевым химическим веществом, используемым во время Первой мировой войны. Основной эффект фосгена возникает в результате растворения газа в слизистых оболочках глубоко в легких, где он превращается путем гидролиза в угольную кислоту и агрессивная соляная кислота.Последний разрушает альвеолярно-капиллярные мембраны, так что легкое заполняется жидкостью (отек легких).
Соляная кислота также частично ответственна за вредное воздействие горчичного газа или образование пузырей. В присутствии воды, например, на влажной поверхности глаз или легких, горчичный газ распадается с образованием соляной кислоты.
Безопасность
| Этикетки для опасных грузов | |
|---|---|
Соляная кислота в высоких концентрациях образует кислые туманы.И туман, и раствор оказывают разъедающее действие на ткани человека, потенциально повреждая органы дыхания, глаза, кожу и кишечник. При смешивании соляной кислоты с обычными окислителями, такими как отбеливатель (NaClO) или перманганат (KMnO 4 ), образуется токсичный газовый хлор. Чтобы свести к минимуму риски при работе с соляной кислотой, следует принять соответствующие меры предосторожности, в том числе надеть резиновые или ПВХ перчатки, защитные очки и химически стойкую одежду.
Опасность растворов соляной кислоты зависит от концентрации.В следующей таблице приведена классификация растворов соляной кислоты ЕС:
| Концентрация по весу | Классификация | R-фраз |
|---|---|---|
| 10% –25% | Раздражающий ( Xi ) | R36 / 37/38 |
| > 25% | Коррозийный ( C ) | R34 R37 |
См. Также
Список литературы
- Чанг, Раймонд.2006. Химия, 9 изд. Нью-Йорк: McGraw-Hill Science / Engineering / Math. ISBN 0073221031.
- Коттон, Ф. Альберт и Джеффри Уилкинсон. 1980. Продвинутая неорганическая химия, 4-е изд. Нью-Йорк: Вили. ISBN 0471027758.
- Гайтон, Артур К. и Джон Э. Холл. 2000. Учебник медицинской физиологии . Филадельфия: Сондерс. ISBN 072168677X.
- Lide, Дэвид Р., изд. 2005. CRC Handbook of Chemistry and Physics, 86-е изд. Бока-Ратон: CRC Press.ISBN 0849304865.
- McMurry, J., R.C. Фэй. 2004. Химия, 4-е изд. Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall. ISBN 0131402080.
- Перри Р., Д. Грин и Дж. Мэлони. 1984. Справочник инженеров-химиков Перри, 6-е изд. Нью-Йорк: Макгроу-Хилл. ISBN 0070494797.
кредитов
Энциклопедия Нового Света Писатели и редакторы переписали и завершили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних публикаций википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в Энциклопедия Нового Света :
Примечание. Некоторые ограничения могут применяться к использованию отдельных изображений, на которые распространяется отдельная лицензия.
Серная кислота — Энциклопедия Нового Света
| Серная кислота | |
|---|---|
| Общие | |
| Систематическое название | серная кислота |
| Другие названия | Купоросное масло |
| Химическая формула | H 2 SO 4 (водн.) |
| Молярная масса | 98,08 г моль −1 |
| Внешний вид | прозрачная, бесцветная, жидкость без запаха |
| Номер CAS | [7664-93-9] |
| Недвижимость | |
| Плотность и фаза | 1.84 г см −3 , жидкость |
| Растворимость в воде | полностью смешивается (экзотермический) |
| Точка плавления | 10 ° С (283 К) |
| Температура кипения | 338 ° С (611 К) |
| pK a | −3 (оспаривается, см. Обсуждение) 1,99 |
| Вязкость | 26,7 сП в 20 ° C |
| Опасности | |
| Паспорт безопасности | Внешний паспорт безопасности материала |
| Классификация ЕС | Коррозийный ( C ) |
| NFPA 704 | 0 3 2 |
| R-фразы | R35 |
| S-фразы | S1 / 2, S26, S30, S45 |
| Температура вспышки | негорючий |
| Номер RTECS | WS5600000 |
| Страница дополнительных данных | |
| Структура и свойства | n , ε r и т. Д. |
| Термодинамические характеристики | Фазовое поведение Твердое, жидкое, газовое |
| Спектральные данные | УФ, ИК, ЯМР, МС |
| Родственные соединения | |
| Родственные сильные кислоты | Селеновая кислота Соляная кислота Азотная кислота |
| Родственные соединения | Сероводород Сернистая кислота Пероксимоносерная кислота Триоксид серы Олеум |
| Если не указано иное, данные приведены для материалов в их стандартном состоянии (при 25 ° C, 100 кПа) Заявление об отказе от ответственности и ссылки в Infobox | |
Серная кислота (или серная кислота на британском английском языке) — сильная минеральная кислота с химической формулой H 2 SO 4 .Он растворим в воде при всех концентрациях. Когда-то оно было известно как масло купороса , термин, придуманный алхимиком восьмого века Джабиром ибн Хайяном (Гебером), вероятным первооткрывателем этого химического вещества. [1]
Серная кислота имеет множество применений и производится в больших количествах, чем любое другое химическое вещество, кроме воды. Мировое производство в 2001 году составило 165 миллионов тонн при приблизительной стоимости 8 миллиардов долларов. Основные области применения включают переработку руды, производство удобрений, нефтепереработку, очистку сточных вод и химический синтез.Многие белки состоят из серосодержащих аминокислот (таких как цистеин и метионин), которые при метаболизме в организме производят серную кислоту.
История серной кислоты
Открытие серной кислоты приписывают алхимику восьмого века Джабиру ибн Хайяну (Геберу). Позже его изучил врач и алхимик IX века ибн Закария ар-Рази (Расес), который получил это вещество путем сухой перегонки минералов, в том числе гептагидрата сульфата железа (II) (FeSO 4 • 7H 2 O ) и пентагидрат сульфата меди (II) (CuSO 4 • 5H 2 O).При нагревании эти соединения разлагаются на оксид железа (II) и оксид меди (II), соответственно, с выделением воды и триоксида серы. Комбинация воды с триоксидом серы дает разбавленный раствор серной кислоты. Этот метод был популяризирован в Европе благодаря переводам арабских и персидских трактатов и книг европейских алхимиков, в том числе немца XIII века Альберта Магнуса.
Серная кислота была известна средневековым европейским алхимикам как купорос , спирт купороса или просто купорос и другие названия.Слово купорос происходит от латинского vitreus (что означает «стекло») из-за стекловидного вида сульфатных солей, которые также носили название купорос. Соли, которым было дано это название, включали сульфат меди (II) (голубой купорос, или иногда римский купорос), сульфат цинка (белый купорос), сульфат железа (II) (зеленый купорос), сульфат железа (III) (купорос Марса), и сульфат кобальта (II) (красный купорос).
Знаете ли вы?
Серная кислота была известна средневековым европейским алхимикам как «купоросное масло». Диаграмма молекулы серной кислоты Джона Дальтона 1808 года показала, что центральный атом серы связан с тремя атомами кислорода.Купорос широко считался самым важным алхимическим веществом, предназначенным для использования в качестве философского камня. Высокоочищенный купорос использовался в качестве среды для взаимодействия веществ. В основном это было связано с тем, что кислота не реагирует с золотом, что часто является конечной целью алхимических процессов. Важность купороса для алхимии подчеркивается в алхимическом девизе, backronym, [2] Visita Interiora Terrae Rectificando Invenies Occultum Lapidem («Посетите недра земли и исправьте» (т.е. очищение) вы найдете скрытый / секретный камень ‘). [3]
В семнадцатом веке немецко-голландский химик Иоганн Глаубер получил серную кислоту путем сжигания серы вместе с селитрой (нитрат калия, KNO 3 ) в присутствии пара. Когда селитра разлагается, она окисляет серу до SO 3 , которая соединяется с водой с образованием серной кислоты. В 1736 году лондонский фармацевт Джошуа Уорд использовал этот метод, чтобы начать первое крупномасштабное производство серной кислоты.
В 1746 году в Бирмингеме Джон Робак начал производить серную кислоту таким способом в камерах, облицованных свинцом, которые были более прочными, менее дорогими и могли быть больше, чем стеклянные емкости, которые использовались ранее. Этот процесс со свинцовой камерой позволил эффективно индустриализировать производство серной кислоты и, с некоторыми усовершенствованиями, оставался стандартным методом производства в течение почти двух столетий.
Серная кислота Робака состояла всего из 35–40 процентов серной кислоты.Более поздние усовершенствования процесса в свинцовой камере французским химиком Жозефом-Луи Гей-Люссаком и британским химиком Джоном Гловером улучшили этот показатель до 78 процентов. Однако производство некоторых красителей и другие химические процессы требуют более концентрированного продукта, и на протяжении восемнадцатого века это можно было производить только путем сухой перегонки минералов по методике, аналогичной первоначальным алхимическим процессам. Пирит (дисульфид железа, FeS 2 ) нагревали на воздухе с получением сульфата железа (II) (FeSO 4 ), который окисляли при дальнейшем нагревании на воздухе с образованием сульфата железа (III) (Fe 2 (SO 4 ) 3 ).Когда сульфат железа (III) нагревали до 480 ° C, он разлагался до оксида железа (III) и триоксида серы, которые можно было пропустить через воду, чтобы получить серную кислоту в любой концентрации. Стоимость этого процесса не позволила широко использовать концентрированную серную кислоту.
В 1831 году британский торговец уксусом Перегрин Филлипс запатентовал гораздо более экономичный способ производства триоксида серы и концентрированной серной кислоты, теперь известный как контактный процесс. Практически все мировые запасы серной кислоты в настоящее время производятся этим методом.
Серная кислота в различных концентрациях
Хотя можно получить почти 100-процентную серную кислоту, она теряет газообразный триоксид серы (SO 3 ) при температуре кипения с образованием 98,3-процентной кислоты. 98-процентный сорт более стабилен при хранении, что делает его обычной формой для «концентрированной» серной кислоты. Другие концентрации серной кислоты используются для разных целей. Некоторые общие концентрации указаны ниже.
- Десять процентов (pH 1): разбавленная серная кислота для лабораторного использования.
- 33,5 процента (pH 0,5): аккумуляторная кислота (используется в свинцово-кислотных аккумуляторах).
- 62,18 процента (pH около 0,4): камерная или удобрительная кислота.
- 77,67 процентов (pH около 0,25): башня или кислота Гловера.
- 98 процентов (pH около 0,1): концентрированный.
Учитывая, что серная кислота является сильной кислотой, 0,50 молярный (М) раствор этой кислоты имеет pH, близкий к нулю.
Также доступны различные степени чистоты. Техническая чистота H 2 SO 4 нечистая и часто окрашенная, но подходит для внесения удобрений.Чистые сорта, такие как сорт Фармакопеи США (USP), используются для изготовления фармацевтических препаратов и красителей.
При добавлении высоких концентраций SO 3 (г) к серной кислоте образуется H 2 S 2 O 7 . Его называют пиросерной кислотой, дымящей серной кислотой или олеумом. Менее распространенное название — кислота Нордхаузена. Концентрации олеума выражаются либо в процентах SO 3 (называемых процентами олеума), либо в процентах H 2 SO 4 (количество, полученное при добавлении H 2 O).Обычно концентрация олеума составляет 40 процентов (109 процентов H 2 SO 4 ) и 65 процентов олеума (114,6 процентов H 2 SO 4 ). Чистый H 2 S 2 O 7 представляет собой твердое вещество с температурой плавления 36 ° C.
Физические свойства
Безводный H 2 SO 4 представляет собой очень полярную жидкость с диэлектрической проницаемостью около 100. Это свойство возникает из-за того, что она может диссоциировать, протонируя себя, процесс, известный как автопротолиз . [4] Это протонирование происходит в высокой степени, более чем в десять миллиардов раз выше уровня, наблюдаемого в воде. Его можно представить следующим образом:
- 2 H 2 SO 4 → H 3 SO 4 + + HSO 4 —
Этот процесс позволяет протонам быть очень подвижными в H 2 SO 4 . Это также делает серную кислоту отличным растворителем для многих реакций. Фактически, химическое равновесие более сложное, чем показано выше.В состоянии равновесия 100-процентная H 2 SO 4 содержит следующие частицы (цифры в скобках указывают количества в молях на килограмм растворителя):
- HSO 4 — (15,0)
- H 3 SO 4 + (11,3)
- H 3 O + (8,0)
- HS 2 O 7 — (4,4)
- H 2 S 2 O 7 (3,6)
- H 2 O (0.1).
Химические свойства
Реакция с водой
Реакция серной кислоты с водой (называемая реакцией гидратации) выделяет большое количество тепла, поэтому ее называют экзотермической реакцией. Если к концентрированной серной кислоте добавить воду, она может опасно вскипеть и плеваться. Одна из причин такого поведения связана с относительной плотностью двух жидкостей. Вода менее плотная, чем серная кислота, и имеет тенденцию плавать над кислотой.
Для безопасного разбавления кислоты следует всегда добавлять кислоту в воду (небольшими порциями), а не воду в кислоту. [5]
Реакцию лучше всего рассматривать как образование ионов гидроксония, а именно:
- H 2 SO 4 + H 2 O → H 3 O + + HSO 4 —
А затем:
- HSO 4 — + H 2 O → H 3 O + + SO 4 2-
Поскольку гидратация серной кислоты термодинамически благоприятна, [6] Серная кислота является отличным обезвоживающим агентом и используется для приготовления многих сухофруктов.Сродство серной кислоты к воде настолько велико, что она удаляет атомы водорода и кислорода из других соединений. Например, смешивание крахмала (C 6 H 12 O 6 ) n и концентрированной серной кислоты даст элементарный углерод и воду, которая поглощается серной кислотой (которая становится слегка разбавленной):
- (C 6 H 12 O 6 ) n → 6C + 6H 2 O.
Эффект этого можно увидеть, пролив концентрированную серную кислоту на бумагу; крахмал реагирует, давая вид обгоревшего, углерод появляется, как сажа при пожаре.Более драматическая иллюстрация происходит, когда серная кислота добавляется к столовой ложке белого сахара в чашке, когда из чашки выходит высокий жесткий столб черного пористого углерода, сильно пахнущий карамелью.
Другие реакции серной кислоты
В качестве кислоты серная кислота реагирует с большинством оснований с образованием соответствующих сульфатов. Например, сульфат меди (II), знакомая синяя соль меди, используемая для гальваники и в качестве фунгицида, получают реакцией оксида меди (II) с серной кислотой:
- CuO + H 2 SO 4 → CuSO 4 + H 2 O
Серная кислота может использоваться для вытеснения более слабых кислот из их солей.Например, его реакция с ацетатом натрия дает уксусную кислоту:
H 2 SO 4 + CH 3 COONa → NaHSO 4 + CH 3 COOH
Подобным образом реакция серной кислоты с нитратом калия может быть использована для получения азотной кислоты вместе с осадком бисульфата калия. С самой азотной кислотой серная кислота действует как кислота и дегидратирующий агент, образуя ион нитрония NO 2 + , который важен в реакциях нитрования, включающих электрофильное ароматическое замещение.Этот тип реакции, при которой протонирование происходит на атоме кислорода, важен во многих реакциях органической химии, таких как этерификация Фишера и дегидратация спиртов.
Серная кислота реагирует с большинством металлов за одну реакцию замещения с образованием газообразного водорода и сульфата металла. Разбавленный H 2 SO 4 разрушает железо, алюминий, цинк, марганец и никель, но для олова и меди требуется горячая концентрированная кислота. Однако свинец и вольфрам устойчивы к серной кислоте.Реакция с железом типична для большинства этих металлов, но реакция с оловом необычна тем, что дает диоксид серы, а не водород. Эти реакции показаны здесь:
- Fe (тв.) + H 2 SO 4 (водн.) → H 2 (г) + FeSO 4 (водн.)
- Sn (тв.) + 2 H 2 SO 4 (водн.) → SnSO 4 (водн.) + 2 H 2 O (л) + SO 2 (г)
Производство
Серная кислота производится контактным способом из серы, кислорода и воды.
На первом этапе сера сжигается для получения диоксида серы.
- (1) S (s) + O 2 (г) → SO 2 (г)
Затем этот продукт окисляют до триоксида серы с использованием кислорода в присутствии катализатора на основе оксида ванадия (V).
- (2) 2 SO 2 + O 2 (г) → 2 SO 3 (г) (в присутствии V 2 O 5 )
Наконец, триоксид серы обрабатывают с водой (обычно 97-98 процентов H 2 SO 4 , содержащей два-три процента воды) для получения 98-99 процентов серной кислоты.
- (3) SO 3 (г) + H 2 O (л) → H 2 SO 4 (л)
Обратите внимание, что прямое растворение SO 3 в воде нецелесообразно, поскольку реакция сильно экзотермична и образует туман вместо жидкости.
Альтернативный метод заключается в абсорбции SO 3 в H 2 SO 4 с получением олеума (H 2 S 2 O 7 ). Затем олеум разбавляют до серной кислоты.
- (3) H 2 SO 4 (л) + SO 3 → H 2 S 2 O 7 (л)
Олеум реагирует с водой до форма концентрированная H 2 SO 4 .
- (4) H 2 S 2 O 7 (л) + H 2 O (л) → 2 H 2 SO 4 (л)
использует
Серная кислота — очень важный товарный химикат, и действительно, производство серной кислоты в стране является хорошим показателем ее промышленного потенциала. [7] В основном серная кислота (60 процентов от общего количества в мире) используется «мокрым способом» для производства фосфорной кислоты, используемой для производства фосфорных удобрений и тринатрийфосфата для моющих средств. Этот метод предполагает использование фосфоритов, и ежегодно перерабатывается более 100 миллионов метрических тонн. Это сырье, показанное ниже как фторапатит (Ca 5 F (PO 4 ) 3 ) (хотя точный состав может варьироваться), обрабатывают 93-процентной серной кислотой для получения сульфата кальция (CaSO 4 ). , фтороводород (HF) и фосфорная кислота (H 3 PO 4 ).HF удаляют в виде плавиковой кислоты. Общий процесс можно представить следующим образом:
- Ca 5 F (PO 4 ) 3 + 5 H 2 SO 4 + 10 H 2 O → 5 CaSO 4 • 2 H 2 O + HF + 3 H 3 PO 4
Серная кислота используется в больших количествах в производстве чугуна и стали, главным образом в качестве травильной кислоты, используемой для удаления окисления, ржавчины и окалины с листового проката и заготовок перед их продажей в автомобили и белые. товарный бизнес.Использованная кислота часто повторно используется на установке регенерации отработанной кислоты (SAR). Эти установки сжигают отработанную кислоту с природным газом, нефтеперерабатывающим газом, мазутом или другим подходящим источником топлива. В процессе сжигания образуется газообразный диоксид серы (SO 2 ) и триоксид серы (SO 3 ), которые затем используются для производства «новой» серной кислоты. Эти типы заводов являются обычным дополнением к металлургическим заводам, нефтеперерабатывающим заводам и другим местам, где серная кислота потребляется в больших масштабах, поскольку эксплуатация завода SAR намного дешевле, чем покупка товара на открытом рынке.
Сульфат аммония, важное азотное удобрение, чаще всего производится как побочный продукт на коксовых заводах, снабжающих металлургические заводы. Реакция аммиака, образующегося при термическом разложении угля, с отработанной серной кислотой позволяет аммиаку кристаллизоваться. в виде соли (часто коричневой из-за загрязнения железом) и продается в агрохимической промышленности.
Еще одно важное применение серной кислоты — это производство сульфата алюминия, также известного как квасцы для бумагоделателей.Он может реагировать с небольшим количеством мыла на волокнах бумажной массы с образованием гелеобразных карбоксилатов алюминия, которые помогают коагулировать волокна пульпы в твердую поверхность бумаги. Он также используется для производства гидроксида алюминия, который используется на водоочистных станциях для фильтрации примесей, а также для улучшения вкуса воды. Сульфат алюминия получают в результате реакции боксита с серной кислотой:
- Al 2 O 3 + 3 H 2 SO 4 → Al 2 (SO 4 ) 3 + 3 H 2 O
Серная кислота используется для множество других целей в химической промышленности.Например, это обычный кислотный катализатор превращения циклогексаноноксима в капролактам, используемый для производства нейлона. Он используется для производства соляной кислоты из соли по методу Мангейма. Много H 2 SO 4 используется в нефтепереработке, например, в качестве катализатора реакции изобутана с изобутиленом с образованием изооктана, соединения, повышающего октановое число бензина (бензина). Серная кислота также важна при производстве красителей.
Смесь серной кислоты и воды иногда используется в качестве электролита в различных типах свинцово-кислотных аккумуляторов, где она претерпевает обратимую реакцию, при которой свинец и диоксид свинца превращаются в сульфат свинца (II).Серная кислота также является основным ингредиентом некоторых очистителей канализации, используемых для очистки засоров, состоящих из бумаги, ветоши и других материалов, которые трудно растворяются щелочными растворами.
Серная кислота также используется в качестве общего дегидратирующего агента в ее концентрированной форме. См. «Реакция с водой».
Серно-йодный цикл
Серно-йодный цикл — это серия термохимических процессов, используемых для получения водорода. Он состоит из трех химических реакций, чистым реагентом которых является вода, а чистыми продуктами — водород и кислород.
- 2 H 2 SO 4 → 2 SO 2 + 2 H 2 O + O 2 (830 ° C)
- I 2 + SO 2 + 2 H 2 O → 2 HI + H 2 SO 4 (120 ° C)
- 2 HI → I 2 + H 2 (320 ° C)
Соединения серы и йода восстанавливаются и повторно используются, поэтому процесс рассматривается как цикл. Этот процесс эндотермический и должен происходить при высоких температурах, поэтому необходимо подавать энергию в виде тепла.
Серно-йодный цикл был предложен как способ подачи водорода для водородной экономики. Он не требует углеводородов, как современные методы парового риформинга.
В настоящее время серо-йодный цикл исследуется как возможный метод получения водорода, но концентрированная коррозионная кислота при высоких температурах представляет в настоящее время непреодолимую угрозу безопасности, если бы процесс был построен в крупном масштабе.
Экологические аспекты
Серная кислота является составной частью кислотных дождей и образуется в результате атмосферного окисления диоксида серы в присутствии воды, т.е.е. окисление сернистой кислоты. Диоксид серы является основным продуктом при сжигании серы в серосодержащем топливе, таком как уголь или нефть.
Серная кислота образуется естественным путем в результате окисления сульфидных минералов, таких как сульфид железа. Полученная вода может быть очень кислой и называется кислотным дренажем горных пород (ARD). Образовавшаяся кислая вода может растворять металлы, присутствующие в сульфидных рудах, в результате чего получаются ярко окрашенные и токсичные потоки. Окисление пирита сульфида железа молекулярным кислородом дает железо (II), или Fe 2+ :
- FeS 2 + 7/2 O 2 + H 2 O → Fe 2+ + 2 SO 4 2- + 2 H +
Fe 2+ может быть дополнительно окислен до Fe 3+ , в соответствии с:
- Fe 2+ + 1/4 O 2 + H + → Fe 3+ + 1/2 H 2 O
и полученный таким образом Fe 3+ может быть осажден как гидроксид или закись водорода.Уравнение образования гидроксида:
- Fe 3+ + 3 H 2 O → Fe (OH) 3 + 3 H +
Ион железа (III) («трехвалентное железо» в случайной номенклатуре) также может окисляться пирит. Когда происходит окисление пирита железом (III), процесс может стать быстрым, и в результате этого процесса в ARD были измерены значения pH ниже нуля.
ARD может также производить серную кислоту с меньшей скоростью, так что способность нейтрализации кислоты (ANC) водоносного горизонта может нейтрализовать образовавшуюся кислоту.В таких случаях концентрация общего растворенного твердого вещества (TDS) в воде может быть увеличена за счет растворения минералов в результате реакции кислотной нейтрализации с минералами.
Серная кислота образуется в верхних слоях атмосферы Венеры в результате фотохимического воздействия Солнца на двуокись углерода, двуокись серы и водяной пар. Ультрафиолетовые фотоны с длиной волны менее 169 нм могут фотодиссоциировать углекислый газ на окись углерода и атомарный кислород. Атомарный кислород очень реактивен; когда он вступает в реакцию с диоксидом серы, следовым компонентом атмосферы Венеры, в результате образуется триоксид серы, который может соединяться с водяным паром, другим следовым компонентом атмосферы Венеры, с образованием серной кислоты.
- CO 2 → CO + O
- SO 2 + O → SO 3
- SO 3 + H 2 O → H 2 SO 4
В верхних, более холодных частях атмосферы Венеры серная кислота может существовать в виде жидкости, а толстые облака серной кислоты полностью закрывают поверхность планеты. поверхность сверху. Главный облачный слой простирается на 45–70 км над поверхностью планеты, а более тонкие дымки простираются от 30 до 90 км над поверхностью.
Инфракрасные спектры миссии НАСА «Галилео» показывают отчетливые абсорбции на Европе, спутнике Юпитера, которые были приписаны одному или нескольким гидратам серной кислоты. Интерпретация спектров несколько противоречива. Некоторые планетологи предпочитают приписывать спектральные характеристики сульфат-иону, возможно, как части одного или нескольких минералов на поверхности Европы.
Безопасность
Лабораторные опасности
Коррозионные свойства серной кислоты усиливаются ее экзотермической реакцией с водой.Следовательно, ожоги от серной кислоты потенциально более серьезны, чем ожоги от сопоставимых сильных кислот (например, соляной кислоты), поскольку есть дополнительное повреждение тканей из-за обезвоживания и, в частности, из-за тепла, выделяемого при реакции с водой, то есть вторичного термического повреждения. Опасность, очевидно, выше при использовании более концентрированных препаратов серной кислоты, но следует помнить, что даже обычная лабораторная «разбавленная» марка (приблизительно один M, десять процентов) обуглит бумагу из-за обезвоживания, если оставить ее в контакте в течение достаточного времени время.Стандартная процедура оказания первой помощи при попадании кислоты на кожу, как и в случае других коррозионных агентов, заключается в орошении большим количеством воды: мытье следует продолжать в течение достаточного периода времени — по крайней мере, от десяти до пятнадцати минут — для охлаждения тканей. вокруг кислотного ожога и для предотвращения вторичного повреждения. Загрязненную одежду необходимо немедленно снять, а кожу под ней тщательно промыть.
Приготовление разбавленной кислоты также может быть опасным из-за тепла, выделяемого в процессе разбавления.Важно, чтобы концентрированная кислота добавлялась в воду, а не наоборот, чтобы воспользоваться относительно высокой теплоемкостью воды. Добавление воды к концентрированной серной кислоте в лучшем случае приводит к рассеиванию аэрозоля серной кислоты, в худшем — к взрыву. Приготовление растворов с концентрацией более шести M (35 процентов) является наиболее опасным, поскольку выделяемого тепла может быть достаточно для кипячения разбавленной кислоты: эффективное механическое перемешивание и внешнее охлаждение (например.грамм. ледяная ванна).
Промышленные опасности
Хотя серная кислота негорючая, контакт с металлами в случае утечки может привести к выделению газообразного водорода. Распространение кислых аэрозолей и газообразного диоксида серы является дополнительной опасностью пожаров, связанных с серной кислотой. В качестве огнетушащего вещества следует использовать воду , а не из-за риска дальнейшего рассеивания аэрозолей: там, где это возможно, предпочтительна двуокись углерода.
Серная кислота не считается токсичной, за исключением ее очевидной коррозионной опасности, и основными профессиональными рисками являются контакт с кожей, приводящий к ожогам (см. Выше) и вдыхание аэрозолей.Воздействие аэрозолей в высоких концентрациях приводит к немедленному и серьезному раздражению глаз, дыхательных путей и слизистых оболочек: оно быстро прекращается после воздействия, хотя существует риск последующего отека легких, если повреждение тканей было более серьезным. При более низких концентрациях наиболее частым симптомом хронического воздействия аэрозолей серной кислоты является эрозия зубов, обнаруженная практически во всех исследованиях: по состоянию на 1997 год признаки возможного хронического повреждения дыхательных путей неубедительны.В Соединенных Штатах допустимый предел воздействия (PEL) для серной кислоты установлен на уровне 1 мг / м 3 : пределы в других странах аналогичны. Интересно, что поступали сообщения о приеме внутрь серной кислоты, приводящем к дефициту витамина B12 с подострой комбинированной дегенерацией. В таких случаях чаще всего поражается спинной мозг, но зрительные нервы могут демонстрировать демиелинизацию, потерю аксонов и глиоз.
См. Также
Банкноты
- ↑ Амин А. Хайраллах, Обзор вкладов арабского языка в медицину , глава 10 (Бейрут, 1946).
- ↑ Бакроним — это разновидность аббревиатуры, которая начинается с обычного слова и позже интерпретируется как аббревиатура.
- ↑ Упоминается в L’Azoth des Philosophes алхимиком пятнадцатого века Василием Валентином.
- ↑ Н.Н. Гринвуд и А. Эрншоу, Химия элементов, (Оксфорд, Великобритания: Pergamon Press, 1984, ISBN 0080220576), 837-845.
- ↑ Чтобы запомнить это правило, было придумано несколько мнемоник, таких как:
- Всегда делайте то, что вы должны, добавляйте кислоту в воду.Если вы думаете, что ваша жизнь слишком спокойна, добавьте воды в кислоту.
- A.A .: Добавить кислоту.
- Капля кислоты, а не воды.
- ↑ Изменение энтальпии реакции ΔH = -880 килоджоулей / моль.
- ↑ Филип Дж. Шенье, Обзор промышленной химии (Нью-Йорк: Springer, 2002, ISBN 0306472465), 45-57.
Список литературы
- Agamanolis, D.P. «Метаболические и токсические нарушения». В: Прайсон Р. (ред.) Невропатология: объем основ диагностической патологии, серия .Филадельфия: Эльзевьер / Черчилль Ливингстон, 2005.
- Чанг, Раймонд. Химия , 9 изд. Нью-Йорк: McGraw-Hill Science / Engineering / Math, 2006. ISBN 0073221031
- Шенье, Филип Дж. Обзор промышленной химии . Нью-Йорк: Springer, 2002. ISBN 0306472465
- Давенпорт, W.G., и М.Дж. Кинг. Производство серной кислоты: анализ, контроль и оптимизация . Elsevier Science, 2005. ISBN 0080444288
- Гринвуд, Н.Н., и А.Эрншоу. Химия элементов , 2-е изд. Оксфорд, Великобритания; Берлингтон, Массачусетс: Баттерворт-Хайнеманн, Elsevier Science, 1998. ISBN 0750633654.
- Хайраллах, Амин А. Обзор вкладов арабского языка в медицину . Бейрут, 1946.
- Лиде, Дэвид Р. Справочник CRC по химии и физике , 87-е изд. Бока-Ратон, Флорида: CRC Press, 2006. ISBN 0849304873
Внешние ссылки
Все ссылки получены 5 января 2020 г.
кредитов
Энциклопедия Нового Света Писатели и редакторы переписали и завершили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних публикаций википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в Энциклопедия Нового Света :
Примечание. Некоторые ограничения могут применяться к использованию отдельных изображений, на которые распространяется отдельная лицензия.
Соляная кислота | Подкаст | Chemistry World
Мира Сентилингам
На этой неделе кислотное соединение, используемое на протяжении всей истории, в промышленности, а также в нашем организме. Вот Брайан Клегг:
Брайан Клегг
Большинство из нас впервые сталкивается с тремя сильными кислотами — соляной, азотной и серной — когда заходит в химическую лабораторию в школе. Это не те вещества, которые вы найдете в кухонном шкафу дома.Тем не менее, я могу гарантировать, что одно из этих соединений было частью вашей жизни каждый день с самого детства. Потому что соляная кислота играет важную роль в вашем организме.
Эта сильнодействующая кислота, водный раствор хлористого водорода, известна давно. Первые названия кислоты имеют довольно морской привкус, отражающий производство кислоты из поваренной соли. Алхимики назвали бы его «духи соли», в то время как его обычное название до появления современных конвенций было соляной кислотой, где «соляная кислота» была причудливым термином для соленой кислоты.Как сказал один Н. Грю в 1675 году, «Муриатик — это соленость, соединенная с некоторой остротой».
Неизвестно, когда именно была впервые получена соляная кислота. Алхимики имели тенденцию производить смеси, которые вполне могли содержать соляную кислоту, и некоторые предполагали, что Джабир ибн Хайян создал ее еще в девятом веке. В средневековье он наверняка использовался в царской водке, смеси соляной и азотной кислот. Мы действительно знаем, что в одном из газовых экспериментов Джозефа Пристли 1772 года был получен чистый газообразный хлористый водород, и что Хамфри Дэви успешно показал, что это соединение содержит водород и хлор в 1818 году.
Мы склонны довольно свободно называть соляную кислоту HCl, но когда хлористый водород растворяется в воде, положительный ион водорода объединяется с водным H 2 O с образованием гидрокония (H 3 O + ), оставляя отрицательный хлорид-ион. Концентрированная соляная кислота составляет около 38% хлористого водорода.
Первоначально большая часть промышленного хлористого водорода представляла собой отходы, которые выбрасывались в воздух, но к середине девятнадцатого века уровень загрязнения больше не считался приемлемым.К счастью, к этому времени отработанный хлористый водород стал ценным для производства соляной кислоты. Хотя используемые процессы изменились, перейдя от побочного продукта производства карбоната натрия к производству, в основном, наряду с органическими соединениями, соляная кислота по-прежнему в основном представляет собой повторное использование отходов, мармита кислотного мира.
Большая часть промышленного производства соляной кислоты идет на травление и используется в различных химических производственных процессах.Рассматриваемое травление не связано с луком, а является способом удаления поверхностного обесцвечивания стали и других металлов.
В промышленных химических процессах соляная кислота используется для производства молекул, содержащих хлор, для пластмассовых изделий, таких как диохлорэтан и винилхлорид (используется для производства ПВХ). Поскольку большая часть мирового производства хлористого водорода происходит как побочный продукт других химических процессов, соляная кислота часто производится и потребляется на месте, эффективно рециркулируя в процессе, а не когда-либо становится отдельным коммерческим продуктом.
Хотя соляная кислота действительно играет роль в пищевой промышленности, где она используется для контроля pH воды при производстве продуктов питания, она играет гораздо более фундаментальную роль, когда речь идет о потреблении пищи. Ваш желудок содержит значительное количество соляной кислоты и может иметь pH всего 1.
Часть роли этой мощной кислоты — предотвращение инфекции, но ее основная функция — пищеварение. Кислота атакует белки в процессе, известном как денатурирование, что заставляет их распадаться, делая их более легко расщепляемыми ферментами для пищеварения.Возможно, наиболее знакомым примером денатурации является денатурация белков яичного белка при варке, превращаясь из прозрачной жидкости в непрозрачное твердое вещество. Здесь нарушение структуры приводит к образованию запутанной массы денатурированного белка, но в желудке результатом является выполнение первоначальной работы по разрушению, позволяющей ферментам, таким как пепсин, разделять белки на более мелкие фрагменты.
Ваш желудок защищен от содержащейся в нем кислоты толстым слоем слизи, а мощная мышца закрывает верхнюю часть желудка.Но задействованные механизмы иногда могут работать неправильно, в результате чего кислота попадает в пищевод, вызывая ощущение жжения при кислотном рефлюксе, или просто вызывает расстройство желудка.
Хотя сейчас существуют сложные лекарства, которые в первую очередь снижают выработку кислоты, многие из нас по-прежнему прибегают к простой неорганической химической реакции и глотают пару таблеток антацида при заболеваниях желудка. На рынке есть различные лекарства, но многие из них содержат карбонат кальция или магния, что приводит к простой реакции, которая нейтрализует кислоту с образованием хлорида, воды и углекислого газа.
Будь то очистка ржавого металла, производство ПВХ или расщепление белков, соляная кислота — это соединение, которое просто выполняет свою работу. Соляная кислота может быть причиной неудобных ночей, когда мы слишком много ели и страдаем от последствий избытка кислоты в желудке, но это более чем компенсируется ее повседневной ролью в превращении пищи в топливо.
Мира Сентилингам
И поскольку это топливо помогает нам прожить день, я уверен, что мы можем простить несколько бессонных ночей из-за несварения желудка.Это был научный писатель Брайан Клегг с химией, лежащей в основе широко используемого и, возможно, недооцененного соединения — соляной кислоты. Теперь, учитывая то, как мы все любим есть, на следующей неделе мы встретим соединение у источника всей этой пищи.
Дункан Макмиллан
Это, вероятно, недостаточно признанная истина, что мы обязаны своим существованием и поддерживающей нас паутиной жизни пище, производимой светом. У подножия почти каждого древа жизни, от тундры до саванны до коралловых рифов и океанских желобов, всю тяжелую работу выполняет фотосинтезирующий организм.И молекула, которая заставляет это происходить, — хлорофилл.
Мира Сентилингам
И чтобы узнать, как именно хлорофилл использует свет для производства продуктов питания и как это соединение вдохновляло известных художников на протяжении веков благодаря его использованию в определенном духе, присоединяйтесь к Динкану Макмиллану на следующей неделе в презентации Chemistry in its element . А пока спасибо за внимание. Я Мира Сентилингам.
Соляная кислота | Великолепные молекулы
Пару лет назад порт Халл, Великобритания, оказался под облаком соляной кислоты.Пар начал вытекать из трещины в резервуаре для хранения патоки. Никто не пострадал, но несколько человек сообщили о плохом самочувствии. Пожарные всю ночь пытались сдержать облако водяным туманом.
Соляная кислота используется в процессе рафинирования, который превращает сахар в патоку — вероятно, поэтому у торговцев патокой было ее 500 тонн. Но это не то химическое вещество, которое вы хотели бы встретить вне запечатанного контейнера. При вдыхании выделяемый пар представляет серьезную опасность для здоровья.В 1990-х годах грузовик пролил 800 литров соляной кислоты рядом с домами в Луизиане, в результате чего жители жаловались на жжение в глазах и горле и симптомы гриппа. Два года спустя они все еще страдали от стойких последствий.
Пары хлористого водорода также могут попадать в воздух при сжигании пластика или после извержения вулканов. Когда в 1991 году произошло извержение горы Пинатубо на Филиппинах, она выпустила много хлористого водорода. Если бы не тропический шторм, разразившийся сразу после этого, считается, что хлористый водород мог попасть в стратосферу и растворить часть озонового слоя.
Опасность, опасность
Чем опасна соляная кислота? Потому что это сильная кислота. Кислоты называют слабыми или сильными в зависимости от того, насколько легко они «отдают» свои атомы водорода. Соляная кислота образуется при растворении хлористого водорода в воде. В этой ситуации хлористый водород, простая молекула, состоящая из одного положительно заряженного водорода, присоединенного к одному отрицательно заряженному хлору, требует небольшого убеждения, чтобы отделиться друг от друга. Таким образом, весь его водород легко «жертвуется».
Соляная кислота настолько сильна, что может разъедать металл, в чем вы можете убедиться на собственном опыте в школьной химической лаборатории. Большинство студентов естественных наук в какой-то момент возьмут полоску магния и окунут ее в колбу с соляной кислотой. Вы можете видеть, как происходит реакция — пузырьки водорода стекают с поверхности металла, а хлор соединяется с магнием, образуя хлорид магния. С концентрированной соляной кислотой идет бурная реакция, но разбавленные растворы более безопасны для этих экспериментов.То, что разъедает металл, разъедает и кожу.
Вот почему мы не храним соляную кислоту на кухне и не добавляем ее в чипсы, такие как этановая кислота (уксус), которая намного слабее. Однако, как ни странно, мы держим его в животе. Соляная кислота — это кислотная составляющая желудочного сока, химического вещества, которое наш желудок вырабатывает, чтобы помочь нам переваривать пищу.
Крепкий желудок
Желудочная кислота вырабатывается в клетках, называемых париетальными клетками, в слизистой оболочке нашего желудка.Процесс его создания начинается с двуокиси углерода (CO 2 ), которую мы вдыхаем и которая циркулирует в нашем кровотоке. В париетальных клетках этот CO 2 постоянно превращается в угольную кислоту (H 2 CO 3 ) в реакции с водой. Чтобы получить водород для производства соляной кислоты, с каждой молекулы угольной кислоты отрывается один положительно заряженный ион водорода. Париетальные клетки наполнены водородом — его концентрация в миллионы раз выше, чем в соседних кровеносных сосудах.Чтобы получить хлорную часть, происходит кое-что немного сложное. Клетка заменяет оставшийся отрицательно заряженный бикарбонат (HCO 3 ) угольной кислоты на отрицательно заряженный хлор из кровотока. Наконец, H + и Cl — закачиваются в желудок, где они образуют соляную кислоту с pH около 1.
Но если соляная кислота достаточно сильна, чтобы проедать металл и кожу, почему она не проходит через слизистую оболочку вашего желудка? Хороший вопрос.Ответ заключается в том, что желудок защищен слоем липкой слизи, которая действует как барьер между желудочной кислотой в желудке и клетками, выстилающими его. Язвы желудка — это пример повреждения, которое возникает, когда что-то выходит из равновесия, и париетальные клетки сбрасывают слишком много кислоты в желудок.
С другой стороны, недостаточное производство соляной кислоты может привести к дефициту питательных веществ, включая анемию (недостаток железа) из-за неспособности правильно переваривать пищу. Так что, хотя вы не хотите вдыхать пары или окунать в них пальцы, вы все же хотите, чтобы они кружились в животе — только не слишком сильно.
Хейли Беннетт, научный писатель из Великобритании
30 мл соляной кислоты (соляная кислота, духи соли)
Есть вопросы? Обратитесь в службу поддержки клиентов.406-256-0990 или же Живой чат в
- Возраст 14+
- На складе, готово к отправке
- Это нужно быстро? Смотрите варианты доставки в корзине.
Бутылка соляной кислоты на 30 мл представляет собой концентрированный 12-молярный 32–36% раствор. У этого химического вещества есть множество применений! Соляная кислота разъедает и является ядом; пожалуйста, внимательно прочтите предупреждающие надписи. Читать Подробнее
участников My Science Perks зарабатывают не менее $ 0,12 назад на этот товар. Войдите или создайте Бесплатный HST Аккаунт, чтобы начать зарабатывать сегодня
Ограничения на доставку:ОПИСАНИЕ
Бутылка соляной кислоты на 30 мл представляет собой концентрированный 12-молярный 32–36% раствор.
Соляная кислота — бесцветный раствор хлористого водорода (HCl) в воде. Это очень коррозионная кислота, которая используется во многих промышленных целях. Посмотрите ниже, чтобы найти формулу соляной кислоты, плотность соляной кислоты, распространенное использование соляной кислоты и многое другое! Другие названия включают соляную кислоту, духи соли и хлорид гидроксония.
Узнайте больше о кислотах в воде, а также о других кислотах и щелочах. Если вам нужно большее количество, у нас есть 100 мл флаконы с концентрированной соляной кислотой.
| Формула | HCl |
| Вес формулы | 36,461 |
| Форма | Решение |
| Плотность | 1,18 г / мл |
| Молярность | 12 Месяцев |
| Номер CAS | 7647-01-0 |
| Классификация DOT | UN1789, Кислота соляная |
| Код хранения | Белый |
| Срок годности | 24 месяца |
| Альтернативное имя | соляная кислота |
| Обычное использование | Для производства батарей и фейерверков, переработки сахара, производства продуктов питания и многого другого! |
| Опасность | Коррозионные вещества (жидкости и твердые вещества) |
БОЛЬШЕ ИНФОРМАЦИИ
ВКЛАДКА С СОДЕРЖАНИЕМ
ТАБЛИЦА ТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК
- Описание
- UN1789
- Технические характеристики
- СОДЕРЖАНИЕ
Ограничение на доставку: Этот товар доставляется только эконом-классом или UPS на почтовые адреса в 50 штатах США.
Предупреждение: ОПАСНОЕ ХИМИЧЕСКОЕ ВЕЩЕСТВО — Едкая жидкость и яд; внимательно прочтите предупреждающие надписи.
Мы хотим, чтобы этот предмет был живым, когда вы его получите! Следовательно, нам необходимо знать, когда вы будете дома, чтобы получить его (минимизируя воздействие стихии). Пожалуйста, укажите дату доставки, среда — Пятница, это минимум 7 дней с сегодняшнего дня.
Химия / Химия
/ химия /, / химия / химия /
Мы поняли. Наука может быть беспорядочной. Но продукты и услуги Home Science Tools справятся с этим.
Наша продукция долговечна, надежна и доступна по цене, позволяя вам перемещаться из полевых условий в лабораторию и на кухню. Они не подведут, с чем бы они ни боролись.Будь то (чрезмерно) нетерпеливые молодые ученые из года в год или строгие требования, которые возникают раз в жизни.
И если ваш научный запрос идет не так, как ожидалось, вы можете рассчитывать на помощь нашей службы поддержки клиентов. Рассчитывайте на дружеские голоса на другом конце телефона и советы экспертов в вашем почтовом ящике. Они не будут счастливы, пока вы не станете счастливыми.
Нижняя строка? Мы гарантируем, что наши продукты и услуги не испортят ваше научное исследование, каким бы беспорядочным оно ни было.
Вопросы? Свяжитесь с нашей службой поддержки клиентов.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

 Такова традиция. Этому учат в школе. Поэтому эти шесть падежей будем именовать школьными или традиционными.
Такова традиция. Этому учат в школе. Поэтому эти шесть падежей будем именовать школьными или традиционными. Единственное условие, которое следует соблюдать: отправляться в баню надо не раньше, чем через 2–3 месяца после родов. За это время организм молодой мамы полностью восстановится, нормализуется лактация.
Единственное условие, которое следует соблюдать: отправляться в баню надо не раньше, чем через 2–3 месяца после родов. За это время организм молодой мамы полностью восстановится, нормализуется лактация.
 В таблице ниже — все правила посещения бани.
В таблице ниже — все правила посещения бани. Если все прошло хорошо, то в следующий раз можно увеличить время.
Если все прошло хорошо, то в следующий раз можно увеличить время. Наблюдайте за своим самочувствием.
Наблюдайте за своим самочувствием.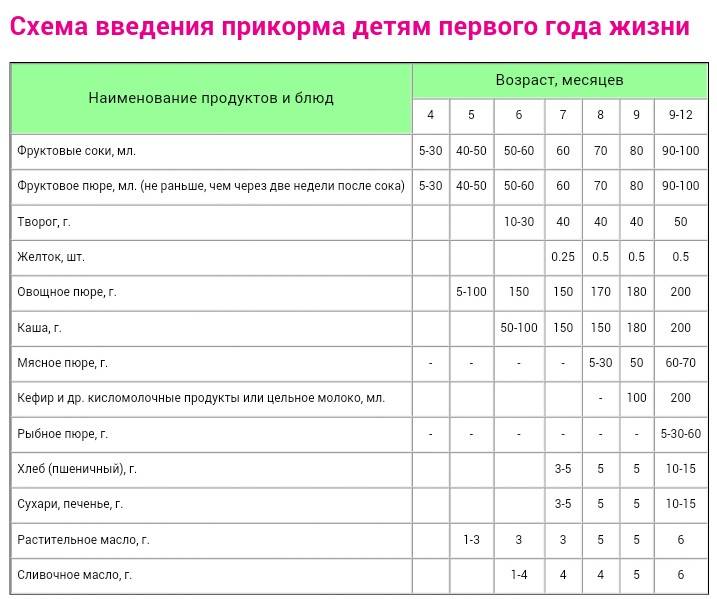 com
com Именно поэтому перегревание опасно для малышей».
Именно поэтому перегревание опасно для малышей».
 Кроме того, активное кровообращение, достигаемое при перепадах температур, способствует выработке молока, поэтому баня даже рекомендуется в тех случаях, когда с этим есть какие-то проблемы.
Кроме того, активное кровообращение, достигаемое при перепадах температур, способствует выработке молока, поэтому баня даже рекомендуется в тех случаях, когда с этим есть какие-то проблемы. Кроме этого, не будет лишним, если вы решите проконсультироваться с вашим наблюдающим врачом, который точно плохого не посоветует.
Кроме этого, не будет лишним, если вы решите проконсультироваться с вашим наблюдающим врачом, который точно плохого не посоветует.
 Некоторые беременные чувствуют себя вполне комфортно под воздействием высоких температур, однако, как говорилось выше, это всё индивидуально и зависит от здоровья не только мамы, но и малыша. Узнайте у врача, можно ли париться при температуре, в вашем случае. Отправляясь в баню, задумайтесь, можно ли кормящим в баню, ведь проблемы могут возникнуть и после беременности.
Некоторые беременные чувствуют себя вполне комфортно под воздействием высоких температур, однако, как говорилось выше, это всё индивидуально и зависит от здоровья не только мамы, но и малыша. Узнайте у врача, можно ли париться при температуре, в вашем случае. Отправляясь в баню, задумайтесь, можно ли кормящим в баню, ведь проблемы могут возникнуть и после беременности.

 Рекомендуем усилить такую ингаляцию, капнув на каменку ароматическим маслом кедра, эвкалипта или лимона. Будьте осторожны, ведь многие масла горят, создавая неприятный запах, поэтому иногда лучше использовать специальные лампы для таких масел.
Рекомендуем усилить такую ингаляцию, капнув на каменку ароматическим маслом кедра, эвкалипта или лимона. Будьте осторожны, ведь многие масла горят, создавая неприятный запах, поэтому иногда лучше использовать специальные лампы для таких масел.
 Посещать баню можно смело, если вы имели большой опыт такого отдыха до родов, ведь организму будет достаточно просто адаптироваться, «вспомнив» условия парной.
Посещать баню можно смело, если вы имели большой опыт такого отдыха до родов, ведь организму будет достаточно просто адаптироваться, «вспомнив» условия парной.
 Если первый заход в парилку увенчался успехом, то вы можете подбавить температуру, однако не стоит снижать бдительность.
Если первый заход в парилку увенчался успехом, то вы можете подбавить температуру, однако не стоит снижать бдительность.
 Ослабевший после родов организм может не перенести высокой температуры, поэтому ходить в баню нужно крайне осторожно.
Ослабевший после родов организм может не перенести высокой температуры, поэтому ходить в баню нужно крайне осторожно.
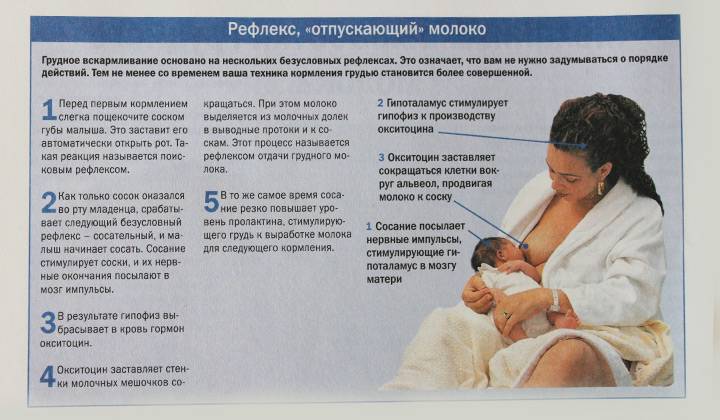
 е. в результате
произведения мы получаем левые части уравнений данной системы. Тогда пользуясь
определением равенства матриц данную систему можно записать в виде
е. в результате
произведения мы получаем левые части уравнений данной системы. Тогда пользуясь
определением равенства матриц данную систему можно записать в виде Однако, матричная запись системы возможна и
в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому
нельзя найти решение системы в виде X = A-1B.
Однако, матричная запись системы возможна и
в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому
нельзя найти решение системы в виде X = A-1B. е.
составленный из коэффициентов при неизвестных,
е.
составленный из коэффициентов при неизвестных,

 Для этого третье уравнение разделим на , умножим на и сложим со вторым.
Тогда будем иметь систему уравнений:
Для этого третье уравнение разделим на , умножим на и сложим со вторым.
Тогда будем иметь систему уравнений:
 Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение.
Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка. е. коэффициенты при неизвестных и свободные члены пропорциональны.
е. коэффициенты при неизвестных и свободные члены пропорциональны. Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
 Проиллюстрируем следующим примером.
Проиллюстрируем следующим примером. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
 Преобразования первоначальных
определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители
при неизвестных
Преобразования первоначальных
определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители
при неизвестных Решения таких систем даёт метод Гаусса.
Решения таких систем даёт метод Гаусса. Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение:
Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение: Решение иррациональных уравнений сводится к переходу от иррационального к рациональному
Решение иррациональных уравнений сводится к переходу от иррационального к рациональному .., ) 0, F ( x, x,…, ) 0, Система уравнений вида где… Fk ( x, x,…, ) 0, F i( x, x,…, ), i,…, k, некоторые многочлены, называется системой рациональных
.., ) 0, F ( x, x,…, ) 0, Система уравнений вида где… Fk ( x, x,…, ) 0, F i( x, x,…, ), i,…, k, некоторые многочлены, называется системой рациональных 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами
0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами Дан граф, на ребрах графа указаны числа, их можно называть «весами» ребер. Расстояние
Дан граф, на ребрах графа указаны числа, их можно называть «весами» ребер. Расстояние Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим. Поляков, 09-6 22 (повышенный уровень, время 7 мин) Тема: динамическое программирование. Что нужно знать: динамическое программирование это способ решения сложных задач путем сведения их к более простым
Поляков, 09-6 22 (повышенный уровень, время 7 мин) Тема: динамическое программирование. Что нужно знать: динамическое программирование это способ решения сложных задач путем сведения их к более простым Ссылочные типы и null. Часто в программах требуется завести большое количество переменных одного и того же типа. Можно, конечно, написать большое количество
Ссылочные типы и null. Часто в программах требуется завести большое количество переменных одного и того же типа. Можно, конечно, написать большое количество Найти общее решение и ФСР однородной системы
$\left\{\begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \\
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \\
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \\
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
\end{array}\right.$
Найти общее решение и ФСР однородной системы
$\left\{\begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \\
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \\
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \\
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
\end{array}\right.$ $$
$$ В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид: Частное решение системы:
Частное решение системы: Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:


 Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
 Установите соответствие между графиком функции и формулойу= х
Установите соответствие между графиком функции и формулойу= х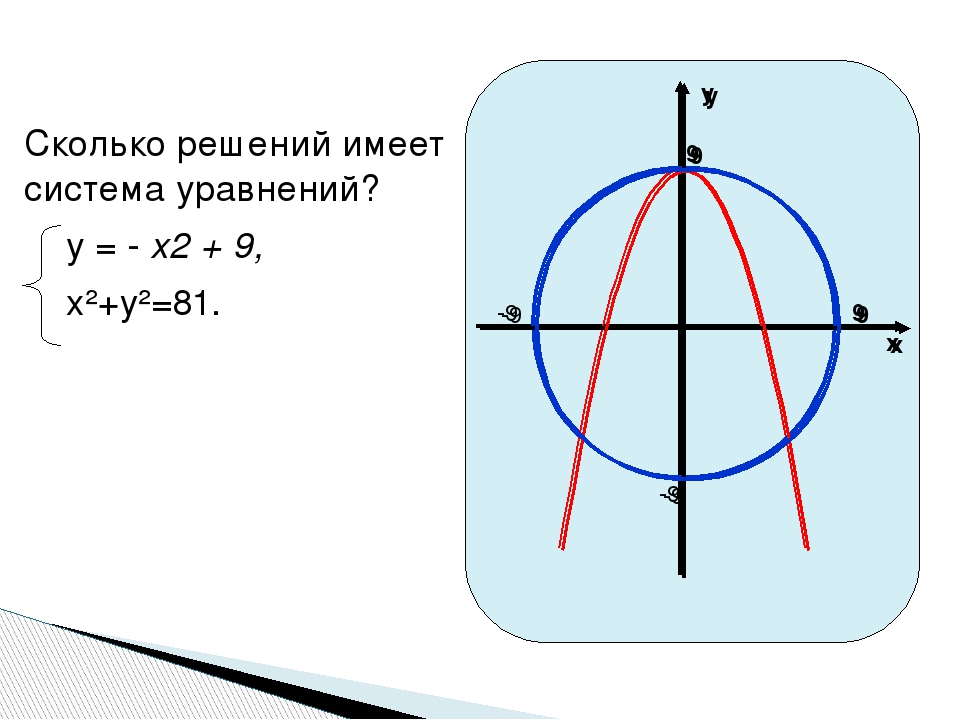 к. графики пересекаются в двух точках ,
к. графики пересекаются в двух точках , 37 (а)
37 (а) Сколько решений имеет система уравнений?2
Сколько решений имеет система уравнений?2
 М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

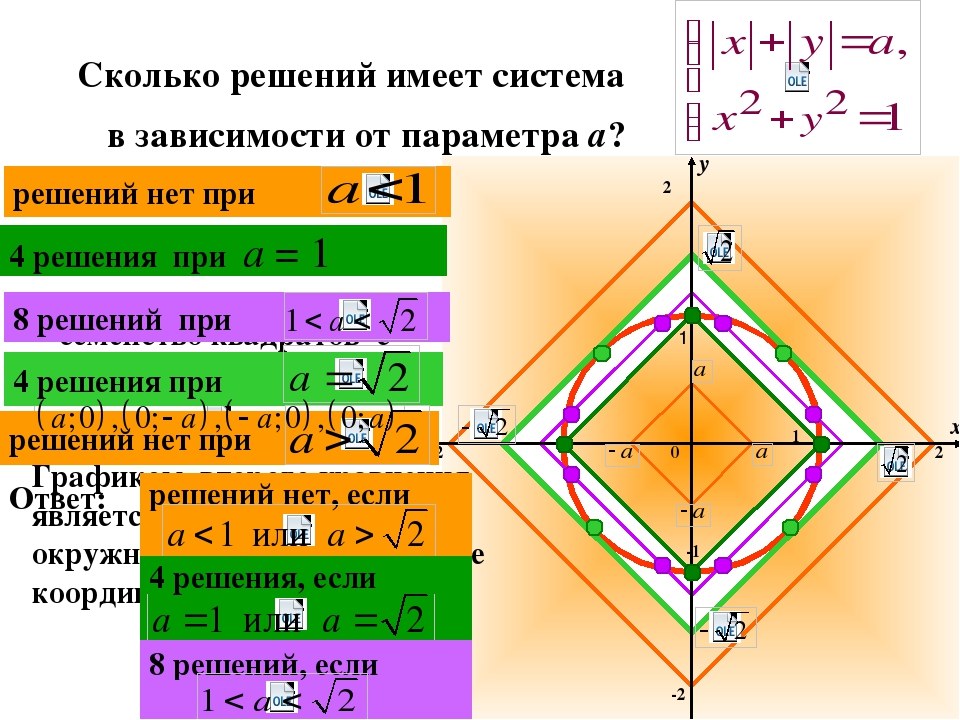 А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.
А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.



 {64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)
{64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)

 Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
 Общая формула членов геометрической прогрессии будет выглядеть так: bn=b1 q(n-1)
Общая формула членов геометрической прогрессии будет выглядеть так: bn=b1 q(n-1)
 8 -1))/(3-1) = 19 680.
8 -1))/(3-1) = 19 680. Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.
Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.
 Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными. Значит, в последовательности натуральных степеней числа 2, для любого натурального n верно равенство bn+1 = bn⋅ 2, то есть q=2.
Значит, в последовательности натуральных степеней числа 2, для любого натурального n верно равенство bn+1 = bn⋅ 2, то есть q=2.



 Серия не имеет суммы.
Серия не имеет суммы. ..
+
1
32768
..
+
1
32768


 ..
если он существует.
..
если он существует.

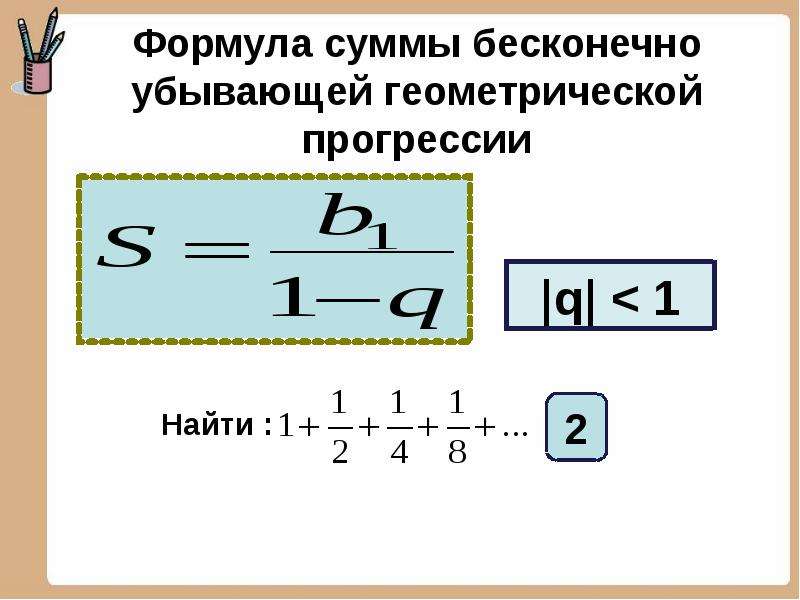 .. = a k ⋅a n-k + 1
.. = a k ⋅a n-k + 1  У первого есть
масштабный коэффициент 1 и общее отношение = 2
У первого есть
масштабный коэффициент 1 и общее отношение = 2  03.2020 18:35 Женский / 30-летний уровень / Средняя школа / Университет / аспирант / Очень /
03.2020 18:35 Женский / 30-летний уровень / Средняя школа / Университет / аспирант / Очень / Кажется, я не могу найти один из таких …
Кажется, я не могу найти один из таких …
 Обычное отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Обычное отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс]. Чередующиеся серии)
Чередующиеся серии) {n}} {1-r}} [/ латекс].
{n}} {1-r}} [/ латекс]. {n}}}} [/ латекс]
{n}}}} [/ латекс] Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которых равна единице.
Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которых равна единице. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
{5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
 Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:

 Еще несколько примеров:
Еще несколько примеров:
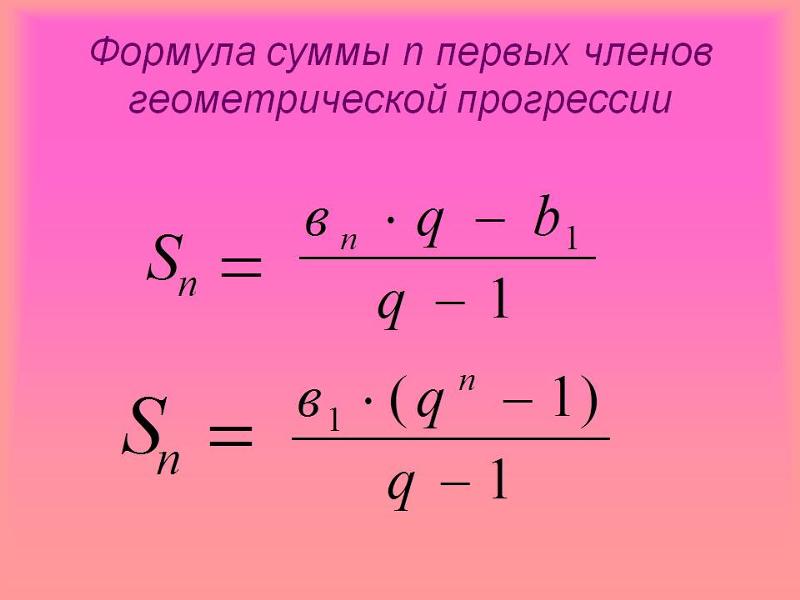
 {3} + \ cdots} [/ latex]
{3} + \ cdots} [/ latex]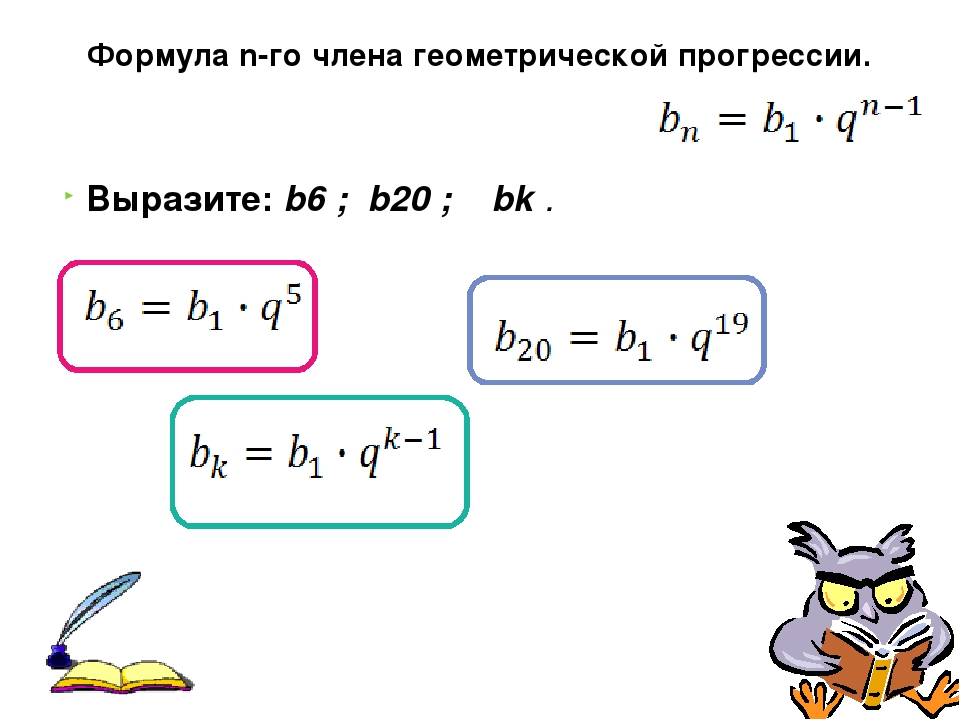 Проще говоря, один из парадоксов Зенона гласит: существует точка A, которая хочет переместиться в другую точку B. Если A перемещается только на половину расстояния между ней и точкой B за один раз, она никогда не доберется туда, потому что вы можете продолжать делить оставшееся пространство пополам навсегда. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной.Теперь мы знаем, что его парадокс не соответствует действительности, о чем свидетельствует сходимость геометрического ряда с [латексом] \ displaystyle {r = \ frac {1} {2}} [/ latex]. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда, чтобы найти сумму пройденных расстояний.
Проще говоря, один из парадоксов Зенона гласит: существует точка A, которая хочет переместиться в другую точку B. Если A перемещается только на половину расстояния между ней и точкой B за один раз, она никогда не доберется туда, потому что вы можете продолжать делить оставшееся пространство пополам навсегда. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной.Теперь мы знаем, что его парадокс не соответствует действительности, о чем свидетельствует сходимость геометрического ряда с [латексом] \ displaystyle {r = \ frac {1} {2}} [/ latex]. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда, чтобы найти сумму пройденных расстояний. {k} [/ латекс]
{k} [/ латекс] Иногда, однако, нас интересует сумма членов бесконечной последовательности, а не сумма только первых [latex] n [/ latex] членов.{\ infty} 2k [/ latex], где верхний предел суммирования равен бесконечности. Поскольку члены не стремятся к нулю, сумма ряда неограниченно увеличивается по мере того, как мы добавляем новые члены. Следовательно, сумма этого бесконечного ряда не определена. Когда сумма не является действительным числом, мы говорим, что ряд расходится на .
Иногда, однако, нас интересует сумма членов бесконечной последовательности, а не сумма только первых [latex] n [/ latex] членов.{\ infty} 2k [/ latex], где верхний предел суммирования равен бесконечности. Поскольку члены не стремятся к нулю, сумма ряда неограниченно увеличивается по мере того, как мы добавляем новые члены. Следовательно, сумма этого бесконечного ряда не определена. Когда сумма не является действительным числом, мы говорим, что ряд расходится на . Ряд геометрический с общим соотношением [латекс] \ frac {2} {3} \ text {.} [/ Latex] Сумма бесконечного ряда определена.
Ряд геометрический с общим соотношением [латекс] \ frac {2} {3} \ text {.} [/ Latex] Сумма бесконечного ряда определена.

 Таким образом, формула, описывающая эту последовательность, имеет вид
Таким образом, формула, описывающая эту последовательность, имеет вид
 Правило гласит: «в корне слова пишется буква «ё». А в суффиксе, окончании прилагательного, существительного и наречия в безударном случае — пишется буква «е», под ударением «о». Получается, что правильно писать чёрный.
Правило гласит: «в корне слова пишется буква «ё». А в суффиксе, окончании прилагательного, существительного и наречия в безударном случае — пишется буква «е», под ударением «о». Получается, что правильно писать чёрный. Выясняется к какой части речи относится слово.
Выясняется к какой части речи относится слово. к. они не изменяются: наречия, деепричастия и проч.
к. они не изменяются: наречия, деепричастия и проч.
 Это слово имеет грамматическую форму женского рода, которое выражено окончанием -а:
Это слово имеет грамматическую форму женского рода, которое выражено окончанием -а: К суффиксу -ян- прилагательного присоединился суффикс -ик- существительного, и так было образовано новое слово. С помощью продуктивного суффикса -ик- также образовались названия других ягод:
К суффиксу -ян- прилагательного присоединился суффикс -ик- существительного, и так было образовано новое слово. С помощью продуктивного суффикса -ик- также образовались названия других ягод:
 Чем больше в тексте тематичных ключевых фраз, тем больше шансов, что он получит высокую оценку.
Чем больше в тексте тематичных ключевых фраз, тем больше шансов, что он получит высокую оценку.
 Нормальное значение — в пределах 5-15%.
Нормальное значение — в пределах 5-15%. — Дипак Чопра
— Дипак Чопра Силован Рамишвили
Силован Рамишвили — Ильф и Петров.
— Ильф и Петров. — Мориц-Готлиб Сафир
— Мориц-Готлиб Сафир — Оскар Уайлд
— Оскар Уайлд — Ильф и Петров
— Ильф и Петров — Станислав Ежи Лец
— Станислав Ежи Лец — Лоренс Питер
— Лоренс Питер  — Уильям Фолкнер
— Уильям Фолкнер  — из Справочника Рантье
— из Справочника Рантье — В. Туровский
— В. Туровский — Закон Бухвальда
— Закон Бухвальда Деньги сравнивают все неравенства. — Федор Достоевский
Деньги сравнивают все неравенства. — Федор Достоевский — Януш Васильковский
— Януш Васильковский — Карл Маркс
— Карл Маркс Качество гарантируется нашими экспертами. Что ты хочешь узнать? Русский язык 5 баллов 1 час назад. Русский язык 5 баллов 5 часов назад. Русский язык 5 баллов 9 часов назад. Запиши название трёх любых жидкостей. Краткий пересказ о изюме. Придумать и записать предложение с одинаковым предлогом и приставкой Русский язык 5 баллов 10 часов назад. Из данных групп слов составь предложения с однородными членами, использую союзы И, А, НО, ДА. Русский язык 15 баллов 10 часов назад. Помогите пожалуйста с заданием дам 29 балов. Русский язык 18 баллов 10 часов назад. Упражнение 10 , 11 , Русский язык 5 баллов 11 часов назад. Борода проверить первую букву о. Отметь крестиком слова, в которых сочетания букв до является частью корня. Бесплатная помощь с домашними заданиями. О нас Карьера Контакт. Общие вопросы Правила Как получить баллы? Скачай iOS-приложение Скачай iOS-приложение. Скачай для Android Скачай для Android.
Качество гарантируется нашими экспертами. Что ты хочешь узнать? Русский язык 5 баллов 1 час назад. Русский язык 5 баллов 5 часов назад. Русский язык 5 баллов 9 часов назад. Запиши название трёх любых жидкостей. Краткий пересказ о изюме. Придумать и записать предложение с одинаковым предлогом и приставкой Русский язык 5 баллов 10 часов назад. Из данных групп слов составь предложения с однородными членами, использую союзы И, А, НО, ДА. Русский язык 15 баллов 10 часов назад. Помогите пожалуйста с заданием дам 29 балов. Русский язык 18 баллов 10 часов назад. Упражнение 10 , 11 , Русский язык 5 баллов 11 часов назад. Борода проверить первую букву о. Отметь крестиком слова, в которых сочетания букв до является частью корня. Бесплатная помощь с домашними заданиями. О нас Карьера Контакт. Общие вопросы Правила Как получить баллы? Скачай iOS-приложение Скачай iOS-приложение. Скачай для Android Скачай для Android.
 Охарактеризуйте смысловые, грамматические, интонационные и пунктуационные признаки обособленных приложений.
Охарактеризуйте смысловые, грамматические, интонационные и пунктуационные признаки обособленных приложений. .поте была особенно молода и внушительно красива.
.поте была особенно молода и внушительно красива. . белого домика захлес.нутого в..ноградниками выходит (на)встречу солнцу древний старец. 3)В священной тиш..не восходит солнце и от к..мней острова поднимается в небо сизый туман насыще(н, нн)ый сла..ким зап..хом золотых цветов. 4) Раздираемое молниями небо дрожало др.. жала и степь то вся вспых..вая синим огнем то погружаясь в холодный тяжелый и тесный мрак страшно суживавший ее. 5) Закова(н, нн)ые в гр..нит волны моря подавле(н, нн)ы громадными тяж..стями ск..льзящ..ми по его хр..бтам. 6) По обеим сторонам к..мина стоят фикусы нищенски бедные листьями. 7) Струйка дыма в..лась в ночном воздух., полном влаг.. и свежеет., моря. 8) Лодка колыхалась на волнах ш..ловливо пл..скавш..хся об ее борта еле двигалась по темному морю а оно играло все резвей и резвей. 9)Тиш..на прерывалась звуками песни дол..тавш..й с реки. 10) Трава сг..баемая ударами ветра и дождя л..жилась на землю.
. белого домика захлес.нутого в..ноградниками выходит (на)встречу солнцу древний старец. 3)В священной тиш..не восходит солнце и от к..мней острова поднимается в небо сизый туман насыще(н, нн)ый сла..ким зап..хом золотых цветов. 4) Раздираемое молниями небо дрожало др.. жала и степь то вся вспых..вая синим огнем то погружаясь в холодный тяжелый и тесный мрак страшно суживавший ее. 5) Закова(н, нн)ые в гр..нит волны моря подавле(н, нн)ы громадными тяж..стями ск..льзящ..ми по его хр..бтам. 6) По обеим сторонам к..мина стоят фикусы нищенски бедные листьями. 7) Струйка дыма в..лась в ночном воздух., полном влаг.. и свежеет., моря. 8) Лодка колыхалась на волнах ш..ловливо пл..скавш..хся об ее борта еле двигалась по темному морю а оно играло все резвей и резвей. 9)Тиш..на прерывалась звуками песни дол..тавш..й с реки. 10) Трава сг..баемая ударами ветра и дождя л..жилась на землю.
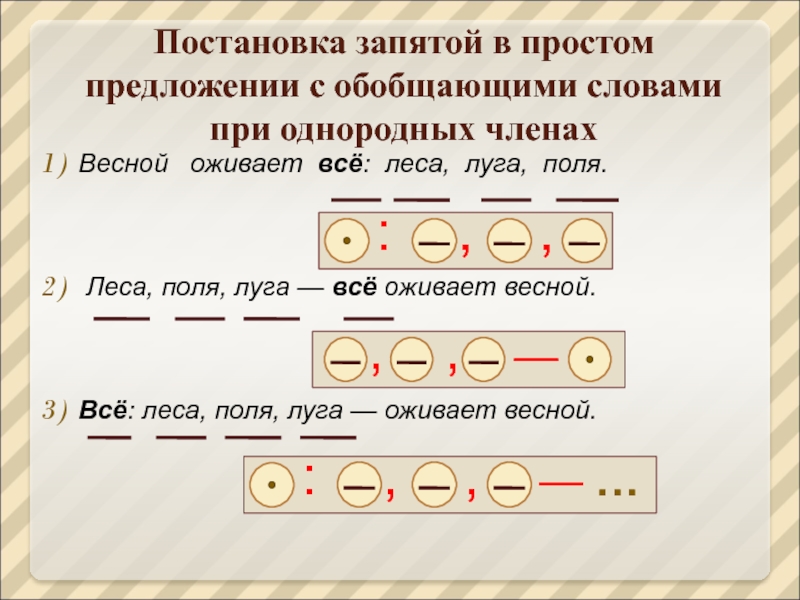
 Москва, столица России, празднует День города.
Москва, столица России, празднует День города. 2) Любимый детский писатель. 3) Надежный друг. 4) Интересный собеседник, 5) Президент совместного предприятия.
2) Любимый детский писатель. 3) Надежный друг. 4) Интересный собеседник, 5) Президент совместного предприятия. (В. Инбер) 2) Анисим, в чёрном сюртуке с красным шнурком вместо галстука, задумался, глядя в одну точку. (А. Чехов) 3) Алёна, с крас¬ными от жары щеками, бегала то в сад, то в дом, то в погреб. (А. Чехов) 4) Рядом с женщиной стоял белобрысый и очень серьёзный мальчик, босой, без шапки. (К. Паустовский) 5) Квадратный, широкогрудый, с огромной кудрявой головой, он явился под вечер. (М. Горький)
(В. Инбер) 2) Анисим, в чёрном сюртуке с красным шнурком вместо галстука, задумался, глядя в одну точку. (А. Чехов) 3) Алёна, с крас¬ными от жары щеками, бегала то в сад, то в дом, то в погреб. (А. Чехов) 4) Рядом с женщиной стоял белобрысый и очень серьёзный мальчик, босой, без шапки. (К. Паустовский) 5) Квадратный, широкогрудый, с огромной кудрявой головой, он явился под вечер. (М. Горький) Островский). 7) Ему казалось, что он был влюблен в кузину и гостью Шумихиной, Анну Федоровну (Чехов).
Островский). 7) Ему казалось, что он был влюблен в кузину и гостью Шумихиной, Анну Федоровну (Чехов).


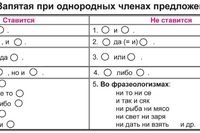 (В.Тренев)
(В.Тренев)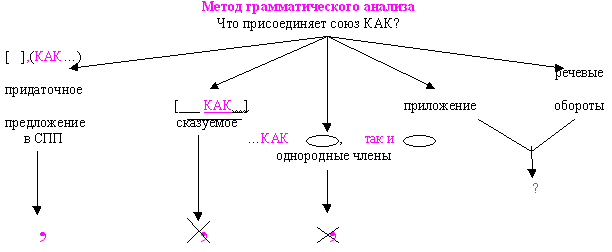 Укажите способ выражения определения в предложении:
Укажите способ выражения определения в предложении: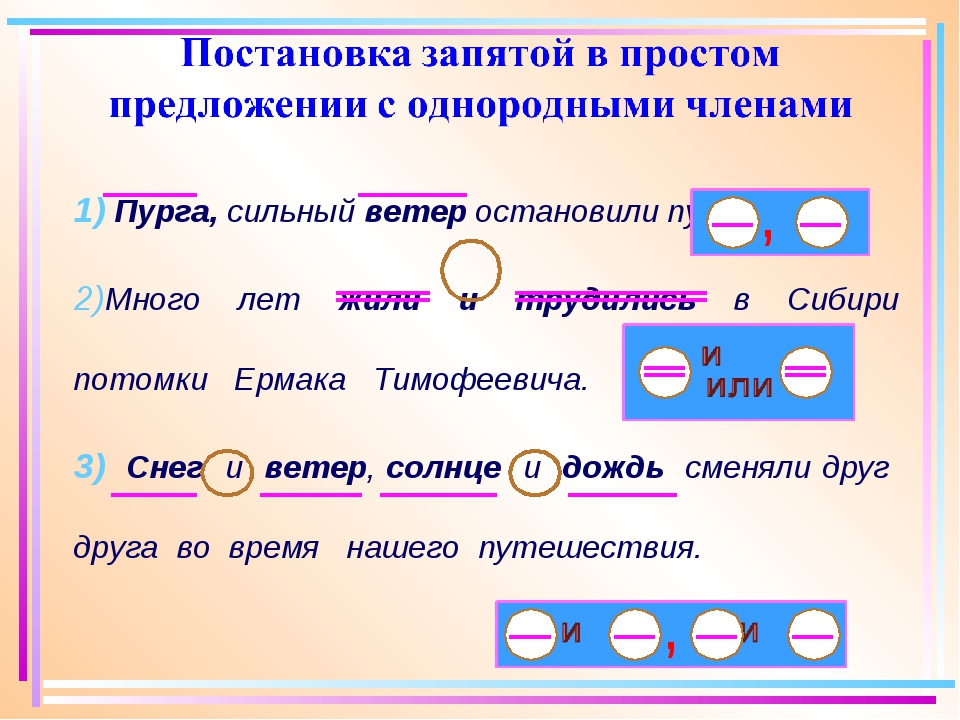 Укажите способ выражения определения в предложении:
Укажите способ выражения определения в предложении: (Л.Князев)
(Л.Князев) Но найдутся и адепты «Общества плоской Земли», для которых это самая что ни на есть истина: Земля — один большой диск, на котором если подпрыгнешь, то приземлишься в то же самое место!
Но найдутся и адепты «Общества плоской Земли», для которых это самая что ни на есть истина: Земля — один большой диск, на котором если подпрыгнешь, то приземлишься в то же самое место!
 Гравитации не существует, а то, что мы принимаем за земное притяжение, является следствием постоянного ускорения движущегося вверх из-за темной энергии диска, который все мы оседлали.
Гравитации не существует, а то, что мы принимаем за земное притяжение, является следствием постоянного ускорения движущегося вверх из-за темной энергии диска, который все мы оседлали.
 Уже из учебника средней школы мы узнаем, что потомство получает половину хромосом от отца и половину — от матери. И никто третий в этот процесс вклиниться не может: таковы законы природы.
Уже из учебника средней школы мы узнаем, что потомство получает половину хромосом от отца и половину — от матери. И никто третий в этот процесс вклиниться не может: таковы законы природы. Уже тогда он развеял миф о телегонии, но эта слишком удобная теория жива для многих и по сей день.
Уже тогда он развеял миф о телегонии, но эта слишком удобная теория жива для многих и по сей день. В 1998 году Российская академия наук в ответ на разгул астрологов, шаманов и оккультистов создала Комиссию по борьбе с лженаукой и призвала академиков активно реагировать на деятельность антинаучных «академий».
В 1998 году Российская академия наук в ответ на разгул астрологов, шаманов и оккультистов создала Комиссию по борьбе с лженаукой и призвала академиков активно реагировать на деятельность антинаучных «академий». Заявление опубликовали на первой полосе The New York Times. Но немногое изменилось с тех пор в восприятии астрологии обывателем.
Заявление опубликовали на первой полосе The New York Times. Но немногое изменилось с тех пор в восприятии астрологии обывателем. Естественно, никакого сходства между временны́ми близнецами найдено не было.
Естественно, никакого сходства между временны́ми близнецами найдено не было. Упражнение 90.
Упражнение 90.

 (Совет от профессионалов: это редко срабатывает.)
(Совет от профессионалов: это редко срабатывает.) Он содержит подлежащее и глагол и образует законченную мысль.
Он содержит подлежащее и глагол и образует законченную мысль.
 Эти статьи напрямую связаны.
Эти статьи напрямую связаны.
 Это включает в себя выбор стиля относительно того, использовать ли оксфордскую запятую в списках из трех или более.
Это включает в себя выбор стиля относительно того, использовать ли оксфордскую запятую в списках из трех или более. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
 Чтобы понять, что такое сложение, мы привели пример 5 + 2 = 7, и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.
Чтобы понять, что такое сложение, мы привели пример 5 + 2 = 7, и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.

 числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс
числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс


 Из 13 вычесть сумму чисел 7 и 3
Из 13 вычесть сумму чисел 7 и 3 Если вы не гений математической мысли, конечно.)
Если вы не гений математической мысли, конечно.) Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений — никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. — это всё состоит из математических выражений. Намёк понятен?)
Да-да! Какую бы задачу мы с вами ни решали (хоть простую, хоть сложную), без математических выражений — никак. Любые формулы, дроби, уравнения, неравенства, синусы, логарифмы, функции, производные, интегралы и т.д. — это всё состоит из математических выражений. Намёк понятен?) Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»
Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»

 д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.)
д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.) ) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.
) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.)
Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.) Непонятно? Поясняю на несложном примере:
Непонятно? Поясняю на несложном примере: Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.
Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички. Почувствуйте разницу, что называется.)
Почувствуйте разницу, что называется.) Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!
Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!


 2$, кроме двух точек с $ x \neq \pm 1 $.
2$, кроме двух точек с $ x \neq \pm 1 $. д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).
д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1). 2 , её свойства и график» ( 7 класс)
2 , её свойства и график» ( 7 класс)
 Дана функция
Дана функция Перенести х из левой части в правую
Перенести х из левой части в правую
 Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде
Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде 3 дают
3 дают 


 Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
 Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю.Чтобы найти точку пересечения y- , мы можем установить x = 0 в уравнении.
Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю.Чтобы найти точку пересечения y- , мы можем установить x = 0 в уравнении. Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и .Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере у нас есть [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Итак, начиная с нашего интервала y (0, 1 ), мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1. Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано на рисунке 2.
Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и .Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере у нас есть [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Итак, начиная с нашего интервала y (0, 1 ), мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1. Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано на рисунке 2.
 Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на –2 единицы «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения и на рисунке 3. От начального значения (0, 5) мы переместимся на 2 единицы вниз и на 3 единицы вправо.Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на –2 единицы «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения и на рисунке 3. От начального значения (0, 5) мы переместимся на 2 единицы вниз и на 3 единицы вправо.Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.  Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Функция также может быть преобразована с помощью отражения, растяжения или сжатия. Обратите внимание на рис. 5, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f на b единиц вверх, если b положительный и | b | единиц вниз, если значение b отрицательное.
Обратите внимание на рис. 5, что добавление значения b к уравнению [латекс] f \ left (x \ right) = x [/ latex] сдвигает график f на b единиц вверх, если b положительный и | b | единиц вниз, если значение b отрицательное.
 4 из 4)
4 из 4)  Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают.
Также, если есть
если в функции больше одного экспоненциального члена, график может выглядеть иначе.
Ниже приведены несколько примеров, чтобы показать вам, как они работают. Больной
присоединяйтесь к набранным мною пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии:
Больной
присоединяйтесь к набранным мною пунктам и убедитесь, что я не забываю рисовать
график в виде кривой линии: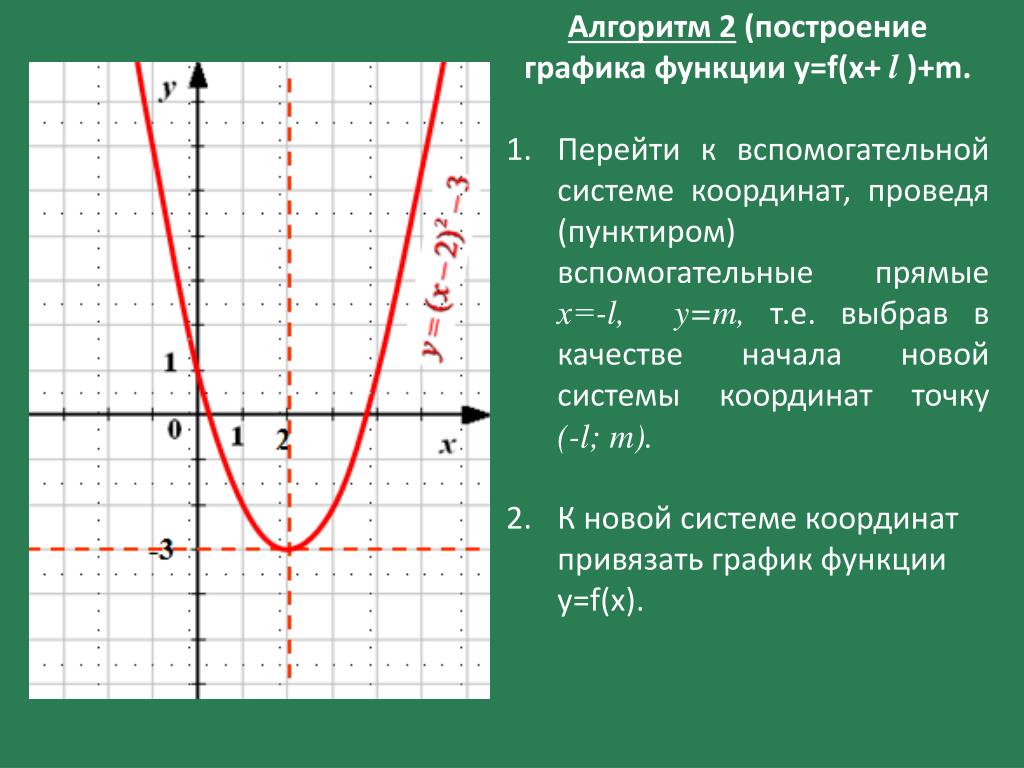 На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением.
На этом этапе в
ваша математическая карьера, скорее всего, вы будете в основном иметь дело
со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно
с его общей формой и поведением. «Графические экспоненциальные функции: примеры». Purplemath .
Доступно по номеру
«Графические экспоненциальные функции: примеры». Purplemath .
Доступно по номеру 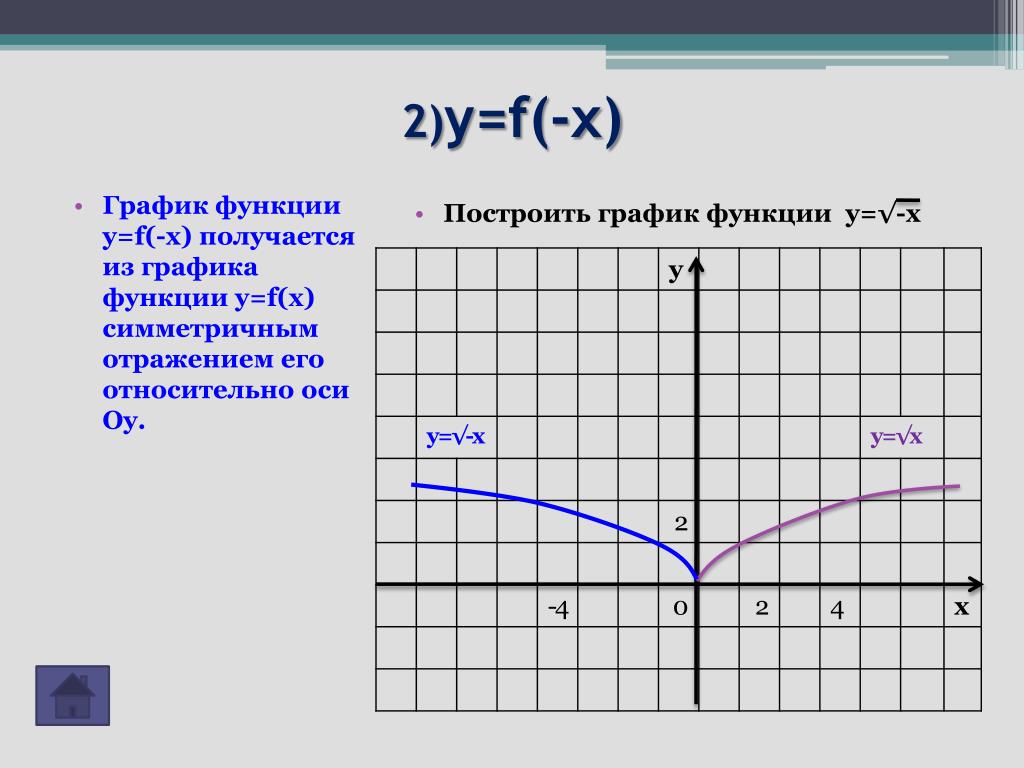 3 здесь
у = х ** 3 # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’) # построить функцию
plt.plot (x, y, ‘g’) # показать сюжет
plt.show ()
3 здесь
у = х ** 3 # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [‘влево’]. set_position (‘центр’)
ax.spines [‘дно’]. set_position (‘центр’)
ax.spines [‘правильно’]. set_color (‘нет’)
ax.spines [‘вверху’]. set_color (‘нет’)
ax.xaxis.set_ticks_position (‘снизу’)
ax.yaxis.set_ticks_position (‘влево’) # построить функцию
plt.plot (x, y, ‘g’) # показать сюжет
plt.show ()  set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
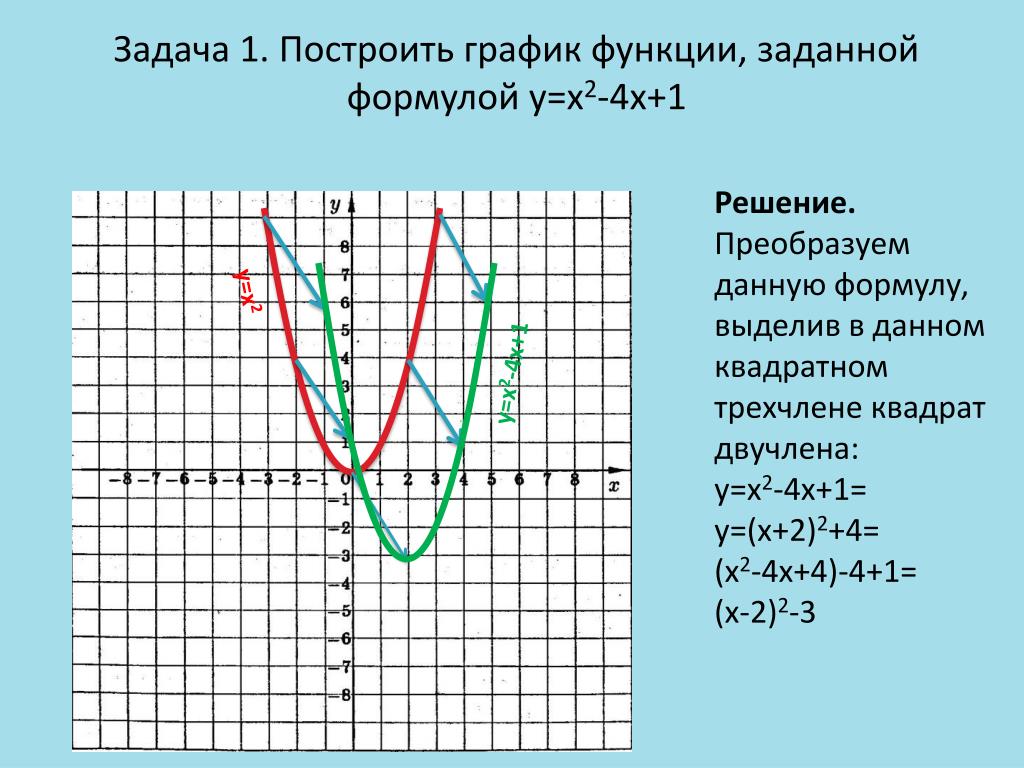 plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')
plt.legend (loc = 'верхний левый')
# показать сюжет
plt.show ()
 Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько точек пересечения по оси x. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции.Вы также можете прокрутить вниз до примера видео ниже.
Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько точек пересечения по оси x. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции.Вы также можете прокрутить вниз до примера видео ниже.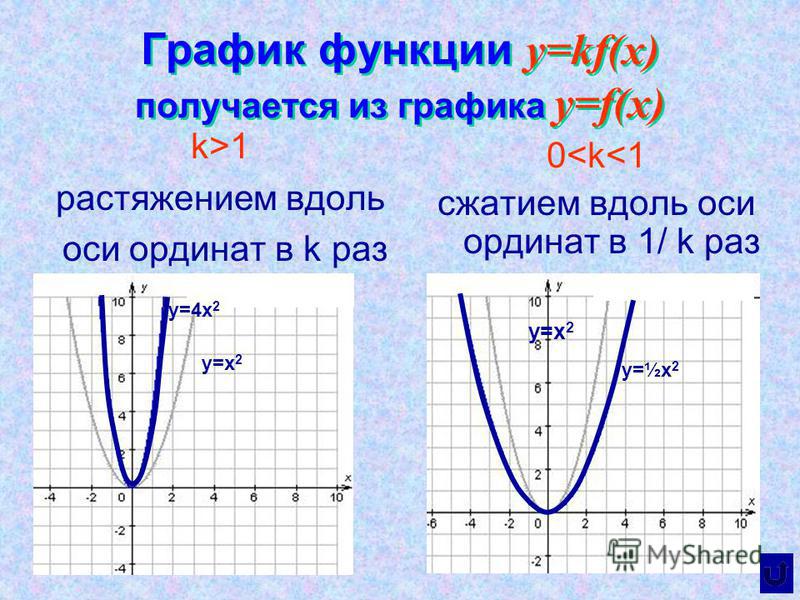


 Это способность
что делает возможным понимание математики. Если бы вы запомнили каждый кусок
математика, представленная вам без связи с другими частями, вы 1) станете
разочарован в математике и 2) не очень понимаю математику.
Это способность
что делает возможным понимание математики. Если бы вы запомнили каждый кусок
математика, представленная вам без связи с другими частями, вы 1) станете
разочарован в математике и 2) не очень понимаю математику.
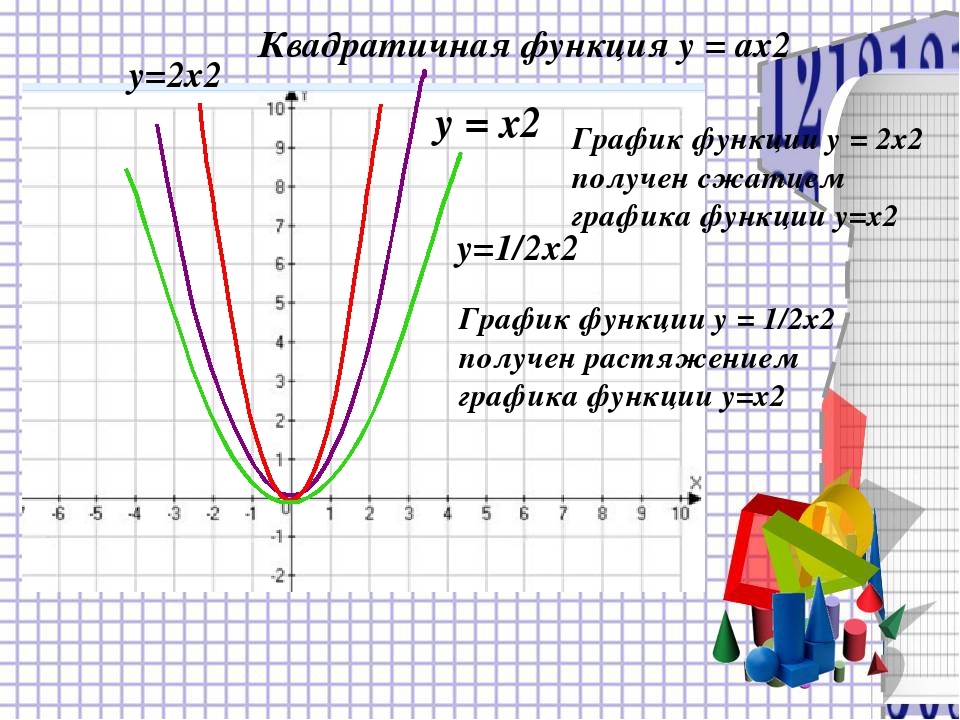 Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.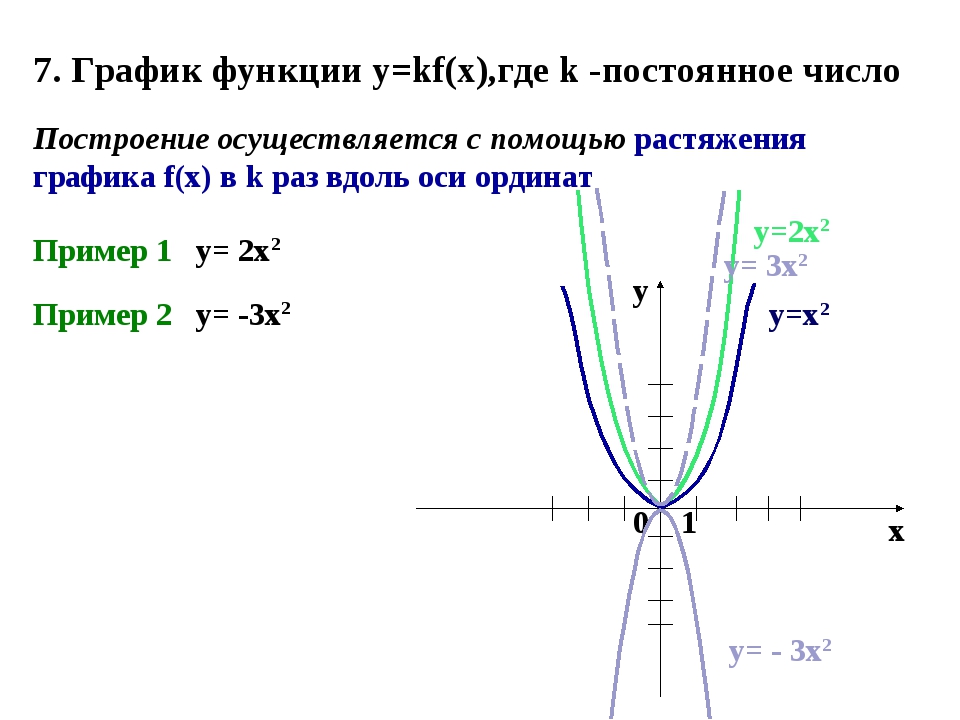
 Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190). множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
 «X минус c» на самом деле означает прибавление c к каждой координате x.
«X минус c» на самом деле означает прибавление c к каждой координате x. Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.
Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Так как там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x.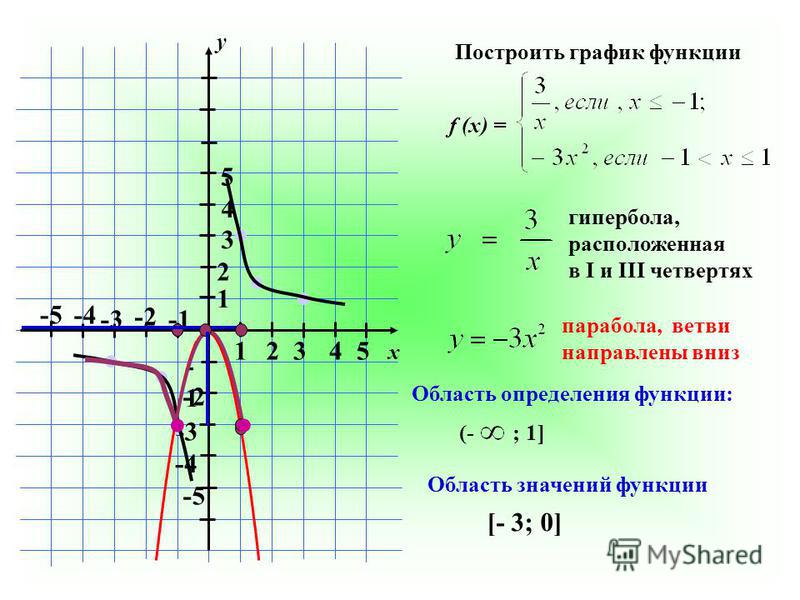
 играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.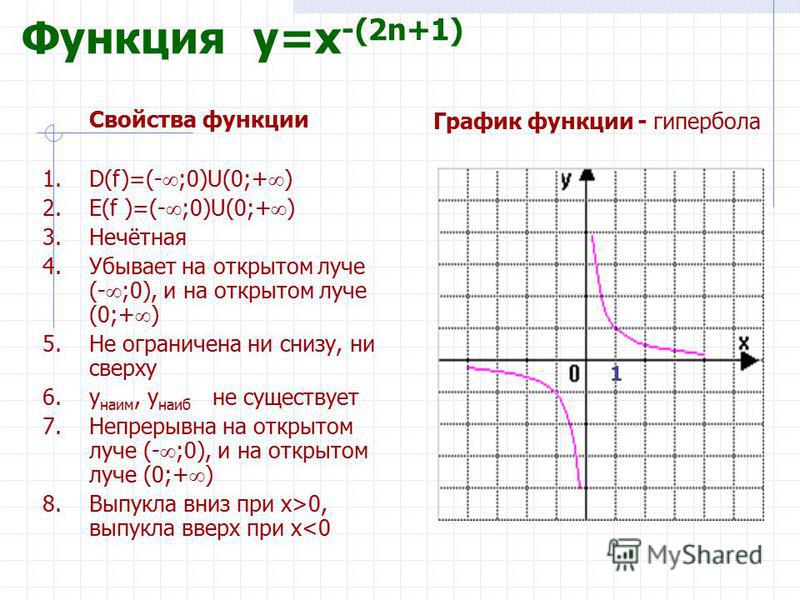
 Разве оба уравнения не являются одинаковыми после упрощения второго? И разве производные каждого из них не одинаковы?
Разве оба уравнения не являются одинаковыми после упрощения второго? И разве производные каждого из них не одинаковы? 2} = \ sqrt {1} = \ pm1
\ end {align}
$
2} = \ sqrt {1} = \ pm1
\ end {align}
$ 2 = 4
$$
вы извлекаете квадратный корень с обеих сторон и в итоге получаете
$$
\ верт х \ верт = 2
$$
и есть два числа, которые находятся на расстоянии два от $ 0 $. Итак, вы получаете
$$
х = \ pm 2.
$$
ОП уже принял ответ, я просто попытался дать более «алгебраическую» точку зрения на смесь.
2 = 4
$$
вы извлекаете квадратный корень с обеих сторон и в итоге получаете
$$
\ верт х \ верт = 2
$$
и есть два числа, которые находятся на расстоянии два от $ 0 $. Итак, вы получаете
$$
х = \ pm 2.
$$
ОП уже принял ответ, я просто попытался дать более «алгебраическую» точку зрения на смесь.
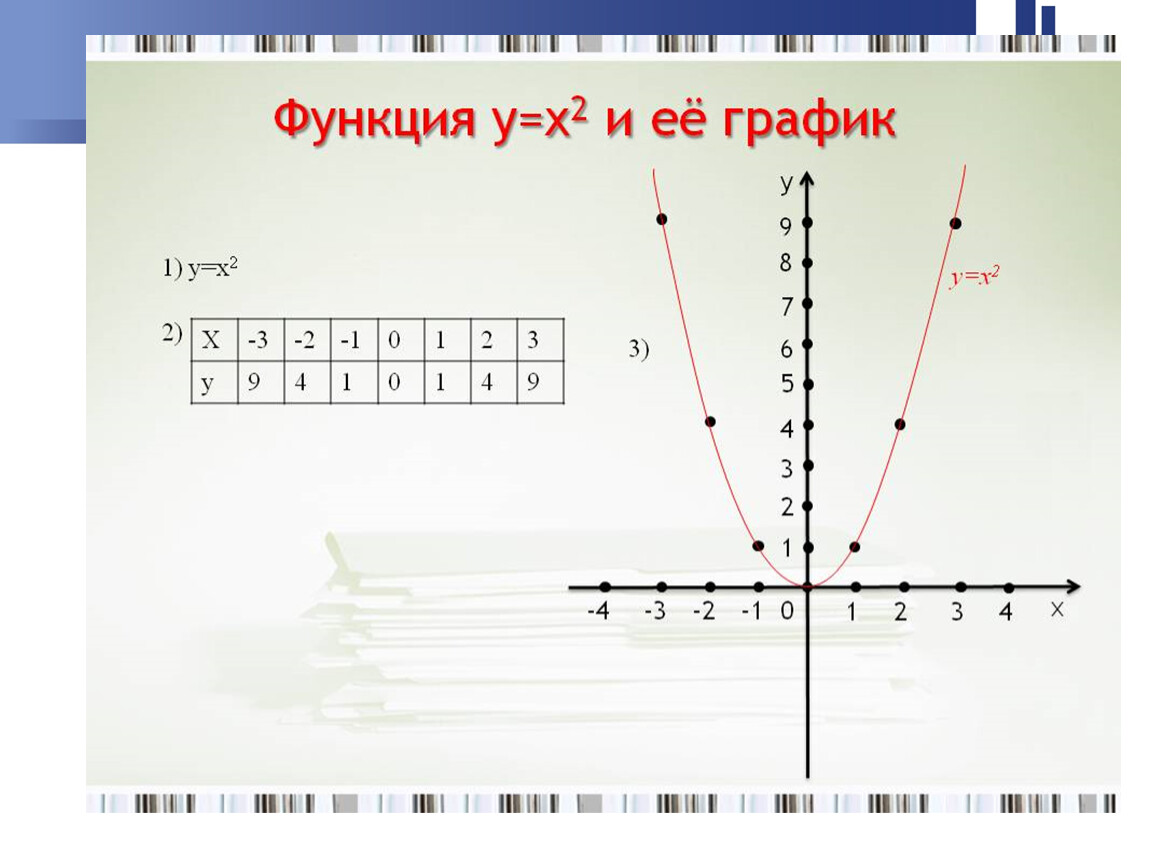 Она называется постоянной функцией, потому что каждому значению x соответствует одно и то же значение y : 3.
Она называется постоянной функцией, потому что каждому значению x соответствует одно и то же значение y : 3.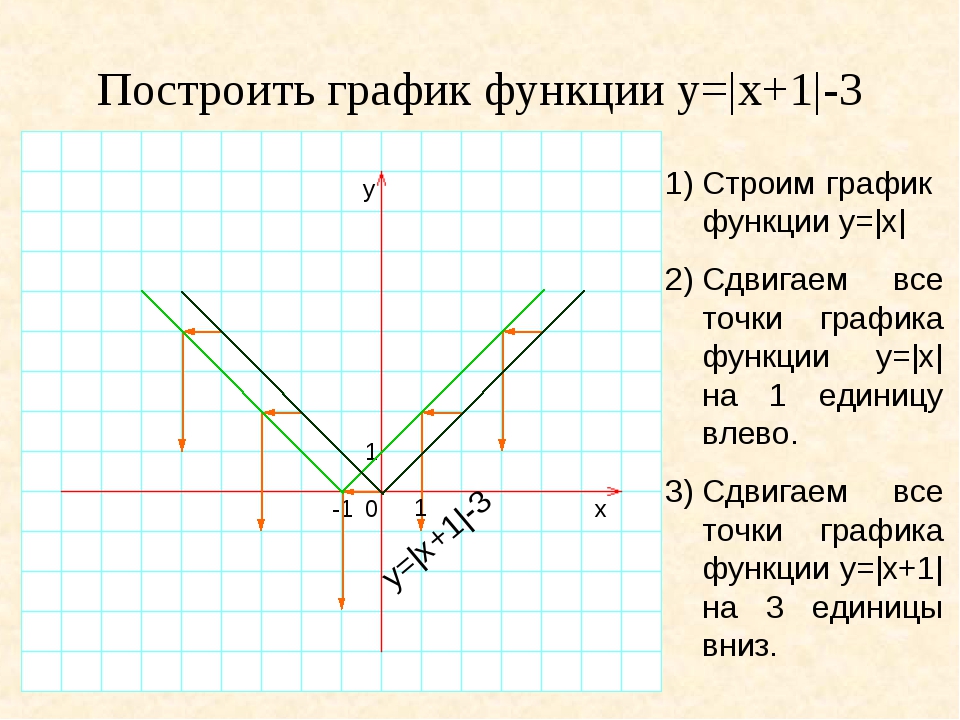 Следовательно, область, в которой «живет» функция, включает каждое действительное число.
Следовательно, область, в которой «живет» функция, включает каждое действительное число.