Разложите на множители формулы: 1. Применение формул сокращённого умножения для разложения многочлена на множители
Ну и что с ним делать будешь? Вроде бы и на \( \displaystyle 3\) что-то делится и на \( \displaystyle 5\), а что-то на \( \displaystyle x\) и на \( \displaystyle y\)
Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?
Тут надо смекалку проявить, а имя этой смекалке – группировка!
Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.
Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.
Не очень понятно все это? Объясню на примере:
В многочлене \( \displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}\) ставим член – \( \displaystyle 3xy\) после члена – \( \displaystyle 5x2y\) получаем:
\( \displaystyle {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}}\)
Группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:
\( \displaystyle ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}})\)А теперь смотрим по отдельности на каждую из двух “кучек”, на которые мы разбили выражение скобками.{2}}-3y)(x-5y)\).
Согласись, уже не такой громоздкий, как был?
Разложение многочлена на множители
Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.
Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.
Предварительные навыкиРазложение многочлена на множители способом вынесения общего множителя за скобки
При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:
6x + 3xy = 3x(2 + y)
В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.
В нашем примере многочлен 6x + 3xy был представлен в виде произведения многочленов 3x и (2 + y). По-другому говорят, что многочлен 6x + 3xy разложен на множители 3x и (2 + y)
Существуют также многочлены, в которых можно вынести за скобки такой общий множитель, который является двучленом. Например, рассмотрим многочлен 5a(x + y) + 7a(x + y). В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки:
Разложение многочлена на множители способом группировки
Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.
Рассмотрим следующий многочлен:
ax + ay + 3x + 3y
Члены ax и ay имеют общий множитель a. Выпишем эти члены и заключим их в скобки:
(ax + ay)
Далее в многочлене ax + ay + 3x + 3y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:
(3x + 3y)
Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»
(ax + ay) + (3x + 3y)
В многочлене (ax + ay) вынесем за скобки общий множитель a, а в многочлене (3x + 3y) вынесем за скобки общий множитель 3. Делать это нужно в исходном выражении:
Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:
Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:
Чтобы проверить правильно ли мы разложили многочлен на множители, выполним умножение (x + y)(a + 3). Если мы всё сделали правильно, то получим многочлен ax + ay + 3x + 3y
(x + y)(a + 3) = ax + ay + 3x + 3y
Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.
Члены 9x и −9y имеют общий множитель 9. А члены ax и −ay имеют общий множитель a. Сгруппируем их с помощью скобок, и объединим с помощью знака «плюс»
(9x − 9y) + (ax − ay)
В первой группе (9x − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y)
Далее вынесем за скобки двучлен (x − y)
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y) = (x − y)(9 + a)
Пример 3. Разложить многочлен ab − 3b + b2 − 3a на множители способом группировки.
Сгруппируем первый член ab с четвёртым членом −3a. А второй член −3b сгруппируем с третьим членом b2. Не забываем, что объединять группы нужно с помощью знака «плюс»
(ab − 3a) + (−3b + b2)
В первой группе вынесем за скобки общий множитель a, во второй группе — общий множитель b
(ab − 3a) + (−3b + b2) = a(b − 3) + b(−3 + b)
Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3)
Теперь вынесем за скобки общий множитель (b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3) = (b − 3)(a + b)
Пример 4. Разложить многочлен x2y + x + xy2 + y + 2xy + 2 на множители способом группировки.
Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:
В первой группе вынесем за скобки общий множитель x, во второй группе — общий множитель y, в третьей группе — общий множитель 2
Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:
Разложение многочлена на множители по формуле квадрата суммы двух выражений
Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.
Вспомним, как выглядит формула квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Поменяем местами левую и правую часть, получим:
a2 + 2ab + b2 = (a + b)2
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)2 представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a2 + 2ab + b2, то мы можем представить его в виде произведения (a + b)(a + b). Иными словами, разложить на множители (a + b) и (a + b).
a2 + 2ab + b2 = (a + b)(a + b)
Пример 1. Разложить на множители многочлен 4x2 + 12xy + 9y2
Чтобы воспользоваться формулой a2 + 2ab + b2 = (a + b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член многочлена 4x2 + 12xy + 9y2 является результатом возведения в квадрат одночлена 2x, поскольку (2x)2 = 4x2. Третий член 9y2 является результатом возведения в квадрат одночлена 3y, поскольку (3y)2 = 9y2, а член 12xy это есть удвоенное произведение членов 2x и 3y, то есть 2 × 2x × 3y = 12xy.
Очевидно, что переменная a в данном случае равна 2x, а переменная b равна 3y
a = 2x
b = 3y
Тогда можно сделать вывод, что когда-то выражение 4x2 + 12xy + 9y2 выглядело в виде квадрата суммы (2x + 3y)2, но в результате применения формулы квадрата суммы оно обратилось в многочлен 4x2 + 12xy + 9y2. Наша задача — вернуть ему былую форму, то есть представить в виде (2x + 3y)2
4x2 + 12xy + 9y2 = (2x + 3y)2
А поскольку (2x + 3y)2 это произведение двух сомножителей, каждый из которых равен многочлену (2x + 3y), то исходный многочлен 4x2 + 12xy + 9y2 можно представить в виде разложения на множители (2x + 3y) и (2x + 3y)
4x2 + 12xy + 9y2 = (2x + 3y)(2x + 3y)
Полностью решение можно записать так:
4x2 + 12xy + 9y2 = (2x)2 + 2 × 2x × 3y + (3y)2 = (2x + 3y)2 = (2x + 3y)(2x + 3y)
Пример 2. Разложить на множители многочлен x2 + 12x + 36
Первый член данного многочлена является результатом возведения в квадрат одночлена x, поскольку x2 = x2, третий член — результатом возведения в квадрат числа 6, поскольку 62 = 36, а член 12x это удвоенное произведение членов x и 6, поскольку 2 × x × 6 = 12x.
Воспользуемся формулой a2 + 2ab + b2 = (a + b)2. Роль переменной a играет одночлен x, а роль переменной b играет одночлен 6. Отсюда:
x2 + 12x + 36 = (x + 6)2
А поскольку (x + 6)2 это произведение двух сомножителей, каждый из которых равен многочлену (x + 6), то исходный многочлен x2 + 12x + 36 можно представить в виде разложения на множители (x + 6) и (x + 6)
x2 + 12x + 36 = (x + 6)(x + 6)
Разложение многочлена на множители по формуле квадрата разности двух выражений
Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.
Формула квадрата разности двух выражений выглядит так:
(a − b)2 = a2 − 2ab + b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − 2ab + b2 = (a − b)2
Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a2 − 2ab + b2 можно разложить на множители (a − b) и (a − b).
a2 − 2ab + b2 = (a − b)(a − b)
Пример 1. Разложить на множители многочлен 9x2 − 12xy + 4y2
Чтобы воспользоваться формулой a2 − 2ab + b2 = (a − b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в квадрат одночлена 3x, поскольку (3x)2 = 9x2. Третий член 4y2является результатом возведения в квадрат одночлена 2y, поскольку (2y)2 = 4y2, а член 12xy это удвоенное произведение членов 3x и 2y, то есть 2 × 3x × 2y = 12xy.
Очевидно, что переменная a в данном случае равна 3x, а переменная b равна 2y
a = 3x
b = 2y
Тогда можно сделать вывод, что когда-то выражение 9x2 − 12xy + 4y2 выглядело в виде квадрата разности (3x − 2y)2, но в результате применения формулы квадрата разности оно обратилось в многочлен 9x2 − 12xy + 4y2. Наша задача — вернуть ему былую форму, то есть представить в виде (3x − 2y)2
9x2 − 12xy + 4y2 = (3x − 2y)2
А поскольку (3x − 2y)2 это произведение двух сомножителей, каждый из которых равен многочлену (3x − 2y), то исходный многочлен 9x2 − 12xy + 4y2 можно представить в виде разложения на множители (3x − 2y) и (3x − 2y)
9x2 − 12xy + 4y2 = (3x − 2y)(3x − 2y)
Полностью решение можно записать так:
9x2 − 12xy + 4y2 = (3x)2 − 2 × 3x × 2y + (2y)2 = (3x − 2y)2 = (3x − 2y)(3x − 2y)
Пример 2. Разложить на множители многочлен x2 − 4x + 4
Воспользуемся формулой квадрата разности двух выражений:
x2 − 4x + 4 = x2 − 2 × x × 2 + 22 = (x − 2)2 = (x − 2)(x − 2)
Разложение многочлена на множители по формуле куба суммы двух выражений
Вспомним, как выглядит формула куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Поменяем местами левую и правую часть, получим:
a3 + 3a2b + 3ab2 + b3 = (a + b)3
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)3 представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a3 + 3a2b +3ab2 + b3, то мы можем представить его в виде произведения (a + b)(a + b)(a + b). Иными словами, разложить на множители (a + b), (a + b) и (a + b).
a3 + 3a2b + 3ab2 + b3 = (a + b)(a + b)(a + b)
Пример 1. Разложить на множители многочлен m3 + 6m2n + 12mn2 + 8n3
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.
Чтобы убедиться, что исходное выражение является кубом суммы двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена m
m3 = m3
Последний член 8n3 является результатом возведения в куб одночлена 2n
(2n)3 = 8n3
Второй член 6m2n является утроенным произведением квадрата первого выражения m и последнего 2n
3 × m2 × 2n = 6m2n
Третий член 12mn2 является утроенным произведением первого выражения m и квадрата последнего выражения 2n
3 × m × (2n)2 = 3 × m × 4n2 = 12mn2
То есть исходный многочлен m3 + 6m2n + 12mn2 + 8n3 по всем параметрам соответствует кубу суммы двух выражений. Переменной a в данном многочлене соответствует m, а переменной b соответствует 2n
a = m
b = 2n
Тогда можно сделать вывод, что когда-то выражение m3 + 6m2n + 12mn2 + 8n3 выглядело в виде куба суммы (m + 2n)3, но в результате применения формулы куба суммы оно обратилось в многочлен m3 + 6m2n + 12mn2 + 8n3. Наша задача — вернуть ему былую форму, то есть представить в виде (m + 2n)3
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)3
А поскольку (m + 2n)3 это произведение трёх сомножителей, каждый из которых равен многочлену (m + 2n), то исходный многочлен m3 + 6m2n + 12mn2 + 8n3 можно представить в виде разложения на множители (m + 2n), (m + 2n) и (m + 2n)
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)(m + 2n)(m + 2n)
Пример 2. Разложить на множители многочлен 125x3 + 75x2 + 15x + 1
Первый член данного многочлена является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Последний член 1 является результатом возведения в куб одночлена 1
13 = 1
Второй член 75x2 является утроенным произведением квадрата первого выражения 5x и последнего 1
3 × (5x)2 × 1 = 3 × 25x2 = 75x2
Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1
3 × 5x × 12 = 15x
Воспользуемся формулой a3 + 3a2b + 3ab2 + b3 = (a + b)3. Роль переменной a играет одночлен 5x, а роль переменной b играет одночлен 1
a = 5x
b = 1
Поэтому,
125x3 + 75x2 + 15x + 1 = (5x + 1)3
А поскольку (5x + 1)3 это произведение трёх сомножителей, каждый из которых равен многочлену (5x + 1), то исходный многочлен 125x3 + 75x2 + 15x + 1 можно представить в виде разложения на множители (5x + 1), (5x + 1) и (5x + 1)
125x3 + 75x2 + 15x + 1 = (5x + 1)(5x + 1)(5x + 1)
Разложение многочлена на множители по формуле куба разности двух выражений
Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.
Вспомним, как выглядит формула куба разности двух выражений:
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Если в этой формуле поменять местами левую и правую часть, то получим:
a3 − 3a2b + 3ab2 − b3 = (a − b)3
Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a3 − 3a2b + 3ab2 − b3 можно разложить на множители (a − b), (a − b) и (a − b).
a3 − 3a2b + 3ab2 − b3 = (a − b)(a − b)(a − b)
Пример 1. Разложить на множители многочлен 64 − 96x + 48x2 − 8x3
Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.
Чтобы убедиться, что исходное выражение является кубом разности двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена 4
43 = 64
Последний член 8x3 является результатом возведения в куб одночлена 2x
(2x)3 = 8x3
Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x
3 × 42 × 2x = 3 × 16 × 2x = 96x
Третий член 48x2 является утроенным произведением первого выражения 4 и квадрата второго выражения 2x
3 × 4 × (2x)2 = 3 × 4 × 4x2 = 48x2
Видим, что исходный многочлен 64 − 96x + 48x2 − 8x3 по всем параметрам соответствует кубу разности двух выражений. Переменной a в данном многочлене соответствует 4, а переменной b соответствует 2x
a = 4
b = 2x
Тогда можно сделать вывод, что когда-то выражение 64 − 96x + 48x2 − 8x3 выглядело в виде куба разности (4 − 2x)3, но в результате применения формулы куба разности оно обратилось в многочлен 64 − 96x + 48x2 − 8x3. Наша задача — вернуть ему былую форму, то есть представить в виде (4 − 2x)3
64 − 96x + 48x2 − 8x3 = (4 − 2x)3
А поскольку (4 − 2x)3 это произведение трёх сомножителей, каждый из которых равен (4 − 2x), то исходный многочлен 64 − 96x + 48x2 − 8x3 можно представить в виде разложения на множители (4 − 2x), (4 − 2x) и (4 − 2x)
64 − 96x + 48x2 − 8x3 = (4 − 2x)(4 − 2x)(4 − 2x)
Пример 2. Разложить на множители многочлен 27 − 135x + 225x2 − 125x3
Первый член данного многочлена является результатом возведения в куб одночлена 3
33 = 27
Последний член 125 является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x
3 × 32 × 5x = 3 × 9 × 5x = 135x
Третий член 225x2 является утроенным произведением первого выражения 3 и квадрата второго выражения 5x
3 × 3 × (5x)2 = 3 × 3 × 25x2 = 225x2
Воспользуемся формулой a3 − 3a2b + 3ab2 − b3 = (a − b)3. Роль переменной a играет одночлен 3, а роль переменной b играет одночлен 5x
a = 3
b = 5x
Поэтому,
27 − 135x + 225x2 − 125x3 = (3 − 5x)3
А поскольку (3 − 5x)3 это произведение трёх сомножителей, каждый из которых равен многочлену (3 − 5x), то исходный многочлен 27 − 135x + 225x2 − 125x3 можно представить в виде разложения на множители (3 − 5x), (3 − 5x) и (3 − 5x)
125x3 + 75x2 + 15x + 1 = (3 − 5x)(3 − 5x)(3 − 5x)
Разложение многочлена на множители по формуле разности квадратов двух выражений
Вспомним, как выглядит формула умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − b2 = (a − b)(a + b)
Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a2 − b2 на множители (a − b) и (a + b).
Пример 1. Разложить на множители многочлен 16x2 − 25y2
Чтобы воспользоваться формулой a2 − b2 = (a − b)(a + b), следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член 16x2 является результатом возведения в квадрат одночлена 4x
(4x)2 = 16x2
Второй член 25y2 является результатом возведения в квадрат одночлена 5y
(5y)2 = 25y2
То есть в данном случае переменной a соответствует одночлен 4x, а переменной b соответствует одночлен 5y
a = 4x
b = 5y
Теперь можно воспользоваться формулой a2 − b2 = (a − b)(a + b). Подставим в неё наши значения a и b
(4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Полностью решение можно записать так:
16x2 − 25y2 = (4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Для проверки можно выполнить умножение (4x − 5y)(4x + 5y). Если мы всё сделали правильно, то должны получить 16x2 − 25y2
(4x − 5y)(4x + 5y) = 16x2 − 20xy + 20xy − 25y2 = 16x2 − 25y2
Пример 2. Разложить на множители многочлен x2 − y2
В данном случае переменной a соответствует x, а переменной b соответствует y. Тогда по формуле квадрата разности имеем:
x2 − y2 = (x − y)(x + y)
Случай как в данном примере является наиболее простым, поскольку здесь сразу видно чему равно a и чему равно b.
Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.
Например, чтобы разложить многочлен 4x4 − 9y6 на множители, нужно исходные члены представить в виде одночленов возведённых в квадрат. Первый член в виде одночлена, возведенного в квадрат, можно записать как (2x2)2, поскольку вычисление этого выражение даёт в результате 4x4
(2x2)2 = 4x4
А член 9y6 в виде одночлена, возведенного в квадрат, можно записать как (3y3)2, поскольку вычисление этого выражение даёт в результате 9y6
(3y3)2 = 9y6
Теперь мы знаем, чему равны a и b. Они равны 2x2 и 3y3 соответственно. Подставим их в формулу a2 − b2 = (a − b)(a + b)
(2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Полностью решение можно записать так:
4x4 − 9y6 = (2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.
Проверим умножением данный пример. У нас должен получиться многочлен 4x4 − 9y6
(2x2 − 3y3)(2x2 + 3y3) = 2x2(2x2 + 3y3) − 3y3(2x2 + 3y3)
= 4x4 + 6x2y3 − 6x2y3 − 9y6 = 4x4 − 9y6
Пример 4. Разложить на множители многочлен 81 − 64
Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:
81 − 64 = 92 − 82 = (9 − 8)(9 + 8)
Разложение многочлена на множители по формуле сумме кубов двух выражений
Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:
(a + b)(a2 − ab + b2) = a3 + b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:
a3 + b3 = (a + b)(a2 − ab + b2)
Эта формула позволяет разложить выражение вида a3 + b3 на множители (a + b) и (a2 − ab + b2).
Пример 1. Разложить на множители многочлен 27x3 + 64y3
Представим члены 27x3 и 64y3 в виде одночленов, возведённых в куб
27x3 + 64y3 = (3x)3 + (4y)3
Теперь воспользуемся формулой суммы кубов. Переменная a в данном случае равна 3x, переменная b равна 4y
27x3 + 64y3 = (3x)3 + (4y)3 = (3x + 4y)((3x)2 − 3x × 4y + (4y)2) =
(3x + 4y)(9x2 − 12xy + 16y2)
Пример 2. Разложить на множители многочлен 125 + 8
Представим члены 125 и 8 в виде одночленов, возведённых в куб:
125 + 8 = 53 + 23
Далее воспользуемся формулой суммы кубов:
125 + 8 = 53 + 23 = (5 + 2)(25 − 10 + 4)
Разложение многочлена на множители по формуле разности кубов двух выражений
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:
(a − b)(a2 + ab + b2) = a3 − b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:
a3 − b3 = (a − b)(a2 + ab + b2)
Эта формула позволяет разложить выражение вида a3 − b3 на множители (a − b) и (a2 + ab + b2).
Пример 1. Разложить на множители многочлен 64x3 − 27y3
Представим члены 64x3 и 27y3 в виде одночленов, возведённых в куб:
64x3 − 27y3 = (4x)3 − (3y)3
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 4x, переменная b равна 3y
64x3 − 27y3 = (4x)3 − (3y)3 = (4x − 3y)((4x)2 + 4x × 3y + (3y)2) =
(4x − 3y)(16x2 + 12xy + 9y2)
Пример 2. Разложить на множители многочлен 64 − 27
Представим члены 64 и 27 в виде одночленов, возведённых в куб:
64 − 27 = 43 − 33 = (4 − 3)(16 + 12 + 9)
Пример 3. Разложить на множители многочлен 125x3 − 1
Представим члены 125x3 и 1 в виде одночленов, возведённых в куб:
125x3 − 1 = (5x)3 − 13
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 5x, переменная b равна 1
125x3 − 1 = (5x)3 − 13 = (5x − 1)((5x)2 + 5x × 1 + 12) =
(5x − 1)(25x2 + 5x + 1)
Разложение многочлена на множители различными способами
К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.
Пример 1. Разложить на множители многочлен ax2 − ay2
В данном многочлене содержится общий множитель a. Вынесем его за скобки:
ax2 − ay2 = a(x2 − y2)
При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:
ax2 − ay2 = a(x2 − y2) = a(x − y)(x + y)
Пример 2. Разложить на множители многочлен 3x2 + 6xy + 3y2
Вынесем за скобки общий множитель 3
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2)
В скобках образовался многочлен, который является квадратом суммы двух выражений, а именно выражений x и y. Тогда этот квадрат суммы можно представить как (x + y)2 и далее записать в виде двух сомножителей, каждый из которых равен (x + y)
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2) = 3(x + y)2 = 3(x + y)(x + y)
Задания для самостоятельного решения
Задание 1. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 2. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 3. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 4. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 5. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 6. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 7. Разложите на множители многочлен:
x2 + 12x + 36
Решение:
x2 + 12x + 36 = x2 + 2 × x × 6 + 62 = (x + 6)2 = (x + 6)(x + 6)
Задание 8. Разложите на множители многочлен:
8xy + y2 + 16x2
Решение:
8xy + y2 + 16x2 = 16x2 + 8xy + y2 = (4x)2 + 2 × 4x × y + y2 = (4x + y)2 = (4x + y)(4x + y)
Задание 9. Разложите на множители многочлен:
Решение:
Задание 10. Разложите на множители многочлен:
Решение:
Задание 11. Разложите на множители многочлен:
Решение:
Задание 12. Разложите на множители многочлен:
Решение:
Задание 13. Разложите на множители многочлен:
Решение:
Задание 14. Разложите на множители многочлен:
Решение:
Задание 15. Разложите на множители многочлен:
Решение:
Задание 16. Разложите на множители многочлен:
Решение:
Задание 17. Разложите на множители многочлен:
Решение:
Задание 18. Разложите на множители многочлен:
Решение:
Задание 19. Разложите на множители многочлен:
Решение:
Задание 20. Разложите на множители многочлен:
Решение:
Задание 21. Разложите на множители многочлен:
Решение:
Задание 22. Разложите на множители многочлен:
Решение:
Задание 23. Разложите на множители многочлен:
Решение:
Задание 24. Разложите на множители многочлен:
Решение:
Задание 25. Разложите на множители многочлен:
Решение:
Задание 26. Разложите на множители многочлен:
Решение:
Задание 27. Разложите на множители многочлен:
Решение:
Задание 28. Разложите на множители многочлен:
Решение:
Задание 29. Разложите на множители многочлен:
Решение:
Задание 30. Разложите на множители многочлен:
Решение:
Задание 31. Разложите на множители многочлен:
Решение:
Задание 32. Разложите на множители многочлен:
Решение:
Задание 33. Разложите на множители многочлен:
Решение:
Задание 34. Разложите на множители многочлен:
Решение:
Задание 35. Разложите на множители многочлен:
Решение:
Задание 36. Разложите на множители многочлен:
Решение:
Задание 37. Разложите на множители многочлен:
Решение:
Задание 38. Разложите на множители многочлен:
Решение:
Задание 39. Разложите на множители многочлен:
Решение:
Задание 40. Разложите на множители многочлен:
Решение:
Задание 41. Разложите на множители многочлен:
Решение:
Задание 42. Разложите на множители многочлен:
Решение:
Задание 43. Разложите на множители многочлен:
Решение:
Задание 44. Разложите на множители многочлен:
Решение:
Задание 45. Разложите на множители многочлен:
Решение:
Задание 46. Разложите на множители многочлен:
Решение:
Задание 47. Разложите на множители многочлен:
Решение:
Задание 48. Разложите на множители многочлен:
Решение:
Задание 49. Разложите на множители многочлен:
Решение:
Задание 50. Разложите на множители многочлен:
Решение:
Задание 51. В следующем выражении вынесите за скобки общий множитель 2a, затем выражение в скобках разложите на множители:
Решение:
Задание 52. В следующем выражении вынесите за скобки общий множитель 4, затем выражение в скобках разложите на множители:
Решение:
Задание 53. В следующем выражении вынесите за скобки общий множитель 2x2y2, затем выражение в скобках разложите на множители:
Решение:
Задание 54. В следующем выражении вынесите за скобки общий множитель 4x3y3, затем выражение в скобках разложите на множители:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Разложение многочленов на множители с помощью формул сокращенного умножения
Примеры
Пример 1.2 = 0 \Rightarrow (x-1-10)(x-1+10) = 0 \Rightarrow \left[ \begin{array}{cc} x_1 = 11 \\ x_2 = -9 \end{array} \right. $$
Ответ: -9; 11
Формулы при разложении на множители
Рассматривая умножение многочленов, мы запомнили несколько формул, а именно: формулы для (a + b)², для (a – b)², для (a + b) (a – b), для (a + b)³ и для (a – b)³.
Если данный многочлен окажется совпадающим с одною из этих формул, то его явится возможным разложить на множители. Напр., многочлен a² – 2ab + b², мы знаем, равен (a – b)² [или (a – b) · (a – b), т. е. удалось a² – 2ab + b² разложить на 2 множителя]; также
Рассмотрим второй из этих примеров. Мы видим, что данный здесь многочлен подходит к формуле, получающейся от возведения в квадрат разности двух чисел (квадрат первого числа, минус произведение двойки на первое число и на второе, плюс квадрат второго числа): x6 есть квадрат первого числа, а, следовательно, само первое число есть x3, квадратом второго числа является последний член данного многочлена, т. е. 1, само второе число есть, следовательно, также 1; произведением двойки на первое число и на второе является член –2x3, ибо 2x3 = 2 · x3 · 1. Поэтому наш многочлен получился от возведения в квадрат разности чисел x3 и 1, т. е. он равен (x3 – 1)2. Рассмотрим еще 4-ый пример. Мы видим, что данный многочлен a2b2 – 25 можно рассматривать, как разность квадратов двух чисел, а именно квадратом первого числа служит a2b2, следовательно, само первое число есть ab, квадратом второго числа является 25, почему само второе число есть 5. Поэтому наш многочлен можно рассматривать получившимся от умножения суммы двух чисел на их разность, т. е.
(ab + 5) (ab – 5).
Иногда случается, что в данном многочлене члены расположены не в том порядке, к которому мы привыкли, напр.
9a2 + b2 + 6ab – мысленно мы можем переставить второй и третий члены, и тогда нам станет ясным, что наш трехчлен = (3a + b)2.
… (переставим мысленно первый и второй члены).
25a6 + 1 – 10x3 = (5x3 – 1)2 и т. п.
Рассмотрим еще многочлен
a2 + 2ab + 4b2.
Мы видим, что первый член его представляет собою квадрат числа a и третий член представляет собою квадрат числа 2b, но второй член не является произведением двойки на первое число и на второе, – такое бы произведение было бы равно 2 · a · 2b = 4ab. Поэтому нельзя применить к этому многочлену формулу квадрата суммы двух чисел. Если бы кто написал, что a2 + 2ab + 4b2 = (a + 2b)2, то это было бы неверно – надо тщательно рассмотреть все члены многочлена, прежде чем применять к нему разложение на множители по формулам.
40. Соединение обоих приемов. Иногда при разложении многочленов на множители приходится комбинировать и прием вынесения общего множителя за скобки и прием применения формул. Вот примеры:
1. 2a3 – 2ab2. Вынесем сначала общего множителя 2a за скобки, – получим 2a (a2 – b2). Множитель a2 – b2, в свою очередь, разлагается по формуле на множители (a + b) и (a – b).
Иногда приходится применять прием разложения по формулам многократно:
1. a4 – b4 = (a2 + b2) (a2 – b2)
Мы видим, что первый множитель a2 + b2 не подходит ни к одной из знакомых формул; мало того, вспоминая особые случаи деления (п. 37), мы установим, что a2 + b2 (сумма квадратов двух чисел) вовсе на множители не раскладывается. Второй из полученных множителей a2 – b2 (разность квадратом двух чисел) разлагается на множители (a + b) и (a – b). Итак,
41. Применение особых случаев деления. На основании п. 37 мы можем сразу написать, что, напр.,
«ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ»
Тема консультации: «ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ.
РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ»
Дидактическая основа
Дидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивают личностные и метапредметные результаты образования, соответствующие ФГОС.Содержание консультации
В соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 7 класса в феврале продолжается работа с четвертой главой «Введение в теорию многочленов». Изучаются три пункта второго параграфа:4.3.2. Разность квадратов;
4.3.3. Куб суммы и разности;
4.3.4. Сумма и разность кубов.
После чего начинается работа с четвертым параграфом «Разложение многочленов на множители», из которого изучаются пункты:
4.4.1. Вынесение общего множителя за скобки;
4.4.2. Способ группировки;
4.4.3. Формулы сокращенного умножения и разложение многочленов.
Основные содержательные цели
- сформировать умение представлять разность квадратов, сумму и разность кубов в виде произведения и наоборот преобразовывать произведения многочленов определенного вида в разность квадратов, сумму и разность кубов с помощью соответствующих формул сокращенного умножения;
- сформировать умение представлять куб суммы и разности в виде многочлена стандартного вида и наоборот преобразовывать многочлен определенного вида в куб суммы или разности с помощью соответствующей формулы сокращенного умножения;
- сформировать умение применять формулы сокращенного умножения для алгебраических преобразований, связанных с умножением, и рационализации вычислений;
- сформировать умение раскладывать многочлены на множители следующими способами: вынесением за скобки общего множителя, способом группировки, с помощью формул сокращенного умножения;
- сформировать умение применять при разложении многочленов на множители различные вспомогательные приемы, такие как, перестановка слагаемых; представление члена многочлена в виде суммы или разности подобных ему членов; прибавление и вычитание одного и того же слагаемого, выделение полного квадрата;
- сформировать умение применять разложение на множители для алгебраических преобразований, решений уравнений и рационализации вычислений.
Тематическое планирование В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по данному учебнику возможно в условиях различных учебных планов образовательных учреждений. Поэтому тематическое планирование по изучению данного курса разработано в двух вариантах на 102 ч и на 136 ч. Вариант планирования, разработанный для 3 часов в неделю, обеспечивает выполнение государственного стандарта знаний, усвоение учебного содержания курса (по темам, обязательным для рассмотрения) и продвижение учащихся в развитии мышления, речи, познавательных интересов. При 4 часах в неделю содержание курса существенно расширяется.
Мы предлагаем Вам скачать тематическое планирование на 3 четверть (3 ч в неделю).
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Центр системно – деятельностной педагогики «Школа 2000…» рекомендует для работы по учебнику математики для 7 класса средней школы Л.Г. Петерсон, Д.Л. Абрарова, Е.В. Чутковой использовать по возможности 4 часа в неделю.
Мы предлагаем Вам скачать тематическое планирование на 3 четверть (4 ч в неделю).
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Методические рекомендации к организации учебного процесса
Глава 4. Введение в теорию многочленов
§ 3. Формулы сокращенного умножения
П. 2. Разность квадратов
1) В данном пункте учащиеся знакомятся с двумя формулами сокращенного умножения – формулой произведения суммы и разности двух выражений и формулой разности квадратов, которые, по сути, являются одинаковыми равенствами, в которых поменяли местами правую и левую части. Традиционно эта формула рассматривалась как одна – формула разности квадратов, что приводило к трудностям, возникающим у учащихся при умножении разности двух выражений на их сумму. Поэтому, чаще всего учителю приходилось регулярно использовать на уроках такой прием, как чтение данной формулы «в обратную сторону». Чтобы раз и навсегда показать учащимся, что любая из формул сокращенного умножения «работает» как справа налево, так и слева направо можно использовать материал данного пункта и специально обратить внимание учащихся на это. Можно пояснить учащимся, что для других «обратных» формул не используют отдельного названия, т.к. звучат их названия менее благозвучно, чем у формулы произведения разности и суммы двух выражений.2) В качестве мотивации к выводу новых формул можно предложить учащимся вычислить
за 30 секунд. После того как они не справятся с этим заданием за указанное время, пояснить, что с помощью формулы сокращенного умножения, открытой сегодня им это легко удастся.
3) Для открытия данных формул учащимся предлагается записать произведение суммы и разности а и b как многочлен стандартного вида. После этого учащимся предлагается обобщить полученное равенство для всех произведений подобного вида и сформулировать правило умножения суммы двух выражений на их разность. Опираясь на полученную формулу, учащиеся формулируют, как можно найти разность квадратов двух выражений (№ 318). Эту работу они могут выполнять самостоятельно в группах или в парах.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 2, а также понятия «сумма» и «разность». Для этого можно использовать задания №№ 316–317.
5) Чтобы показать геометрический смысл данной формулы можно использовать предметные геометрические модели прямоугольника и квадрата, предложенные в учебнике. Необходимо вырезать, прикладывать и перемещать предметные модели либо использовать возможности анимации современной техники. Это поможет учащимся с образным мышлением запомнить данные формулы.
6) Важно показать учащимся применение формул для рационализации вычислений (№№ 322, 337).
7) При 4-часовом планировании рекомендуется отвести больше времени на выполнение заданий более высокого уровня сложности (№№ 340–347).
8) Учащиеся применяют новые формулы для сокращения алгебраических дробей (№ 333), решения уравнений (№ 327, № 336), доказательства утверждений и тождеств (№№ 329, 334, 335). Для формирования умения применять формулы сокращенного умножения в учебнике и другие задания, которые предполагают решение задач с помощью уравнения (№ 339), сравнение значений выражений (№№ 342 – 343) и пр. Учитель выбирает из этих заданий те, которые считает целесообразным выполнить с учащимися.
9) При выполнении заданий на нахождение наибольшего и наименьшего значения выражений (№№ 345 – 346) следует вспомнить с учащимися необходимые свойства. Рекомендуется, после применения формулы произведения суммы выражений на их разность актуализировать, как изменяется разность при изменении ее компонентов. Свойство разности «Если значение уменьшаемого увеличить, то значение разности увеличится» и подобные ему свойства известны учащимся с начальной школы. Кроме того, рекомендуется спросить, какое наименьшее значение может принимать квадрат любого выражения (нуля).
П. 3. Куб суммы и разности
1) В данном пункте учащиеся знакомятся с двумя формулами сокращенного умножения – формулой куба суммы и куба разности.2) Для проблематизации можно предложить учащимся записать выражение
как многочлен стандартного вида, не используя правило умножения многочленов
3) Для открытия формулы куба суммы (разности) учащимся предлагается использовать задание № 377, в котором проедложены шаги по построению новой формулы. Рекомендуется сначала дать возможность учащимся составить план открытия нового знания самостоятельно. Имея опыт, построения формулы квадрата суммы и разности данная задача является для семиклассников посильной задачей.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 3, а также понятия «куб суммы» и «куб разности». Для этого можно использовать задания №№ 374–376.
5) Важно показать учащимся применение формул для рационализации вычислений (№№ 381 – 382).
6) Для формирования умения применять формулы куба суммы и разности в учебнике предлагается целый перечень заданий, которые предполагают доказательство тождеств, нахождение значений выражений, составление и решение уравнений. Учитель выбирает из них те задания, которые считает целесообразным выполнить со своими учениками.
7) После знакомства с формулами куба суммы и куба разности с учащимися следует обобщить, что теперь им известно как возводить двучлен во 2-ю и 3-ю степени и сообщить, что существуют формулы, позволяющие возводить двучлен в более высокую степень. Можно попросить одного из «сильных» учащихся сформулировать идею вывода подобных формул. При 4-часовом планировании (либо в более подготовленных классах) рекомендуется познакомить учащихся с алгоритмом возведения двучлена в n–ю степень (№№ 399 – 400).
П.4. Сумма и разность кубов
1) В данном пункте учащиеся знакомятся с формулами суммы и разности кубов.2) Для проблематизации можно предложить учащимся записать многочлены:
в виде произведения двух многочленов.
3) В связи с особенностями этих формул учащимся вряд ли удастся самостоятельно составить план открытия нового знания, поэтому учащимся предлагается использовать задание № 434, в котором даны шаги по построению новых формул.
4) Чтобы подготовить учащихся к открытию следует актуализировать с ними правило умножения многочленов и понятие степени с показателем 3, а также понятия «сумма кубов» и «разность кубов». Для этого можно использовать задания №№ 432–433.
5) Важно показать учащимся применение формул для рационализации вычислений (№№ 439).
6) Для формирования умения применять формулы суммы и разности кубов в учебнике также как и в других пунктах третьего параграфа предлагается перечень заданий, которые предполагают доказательство тождеств, нахождение значений выражений, составление и решение уравнений с использованием данных формул. Учитель выбирает из них те задания, которые считает целесообразным выполнить со своими учениками.
7) При 4-часовом планировании рекомендуется уделить больше времени на выполнение заданий более высокого уровня сложности (№№ 453–460).
8) При выполнении задания № 459 рекомендуется сначала проанализировать данные равенства, задать, например, следующие вопросы:
- Что записано в левой части равенства? (Произведение многочленов.)
- Что записано в правой части равенства? (Многочлены.)
- Как перейти от произведения многочленов к многочлену? (Перемножить данные многочлены.)
- Как можно рационализировать умножение алгебраических выражений? (Формулы сокращенного умножения помогают при таких преобразованиях.)
- Какие формулы вы здесь сразу видите, подчеркните соответствующие выражения.
Полезным будет показать рациональные способы выполнения данных преобразований, для этого можно воспользоваться заранее заготовленными образцами. Если по какой-либо причине подготовить образцы не удастся можно вызывать к доске не одного, а нескольких учащихся, которые бы параллельно доказывали тождество. После выполнения задания разобрать другие способы, которыми пользовались ученики. Кроме того, можно после того как основная часть класса закончит доказательство, следует поинтересоваться, кто нашел другой, более рациональный способ доказательства. Эти способы демонстрируются с помощью специального технического оборудования либо идея преобразования проговаривается вслух.
Целесообразно на примере а) сравнить два способа доказательства тождеств:
1) приведение левой части к правой, при котором придется применить формулу произведения суммы выражений на их разность и в полученном произведении «увидеть» формулу разности кубов;
2) приведение правой части к левой, при котором в разности шестых степеней можно «увидеть» разность кубов и разложить эту разность на произведение двучлена на трехчлен, а полученный двучлен разложить на сумму и разность по формуле разности квадратов.
Второй способ рекомендуется показать после применения первого. На данном этапе он рассматривается с целью опережающей подготовки учащихся к изучению темы «Разложение на множители с помощью формул сокращенного умножения».
§ 4. Разложение многочлена на множители
П.1 Вынесение общего множителя за скобки
1) В данном пункте учащиеся учатся выносить общий множитель за скобки, они уже имеют опыт простейших преобразований такого рода. Так, для первичного формирования умения приводить подобные слагаемые учащиеся выносили общий множитель за скобки на основании распределительного закона умножения.2) В данном пункте у учащихся формируется понятие разложения многочлена на множители. Нужно отметить, что под разложением на множители понимается разложение на буквенные множители. Так, вынесение за скобки числового множителя не является операцией разложения на множители. Например, представление многочлена 2a + 2ac в виде произведения 2(а + ас) не является разложением на множители, а в виде 2а (1 + с) является. Этот «нюанс» можно обговорить с учащимися при выполнении № 489.
3) Здесь же формируется умение раскладывать на множители путем вынесения общего множителя за скобки. Теперь учащиеся выполняют это преобразование на основании четко сформулированного правила: чтобы вынести за скобки общий множитель с можно в скобках записать многочлен, каждый член которого получен в результате его деления на с. Можно использовать предложенный в учебнике алгоритм вынесения за скобки общего множителя (в более подготовленном классе учащиеся могут построить его самостоятельно – № 493).
4) В связи с тем, что учащиеся уже знакомы с вынесением за скобки общего множителя, для проблематизации можно предложить учащимся сформулировать, что такое «разложение многочлена на буквенные множители».
5) Для построения логики открытия при подготовке к уроку учитель может воспользоваться заданием № 488.
6) Чтобы подготовить учащихся к открытию следует актуализировать с ними распределительное свойство умножения, использование этого свойства для рационализации вычислений. Для этой целей рекомендуется использовать задания №№ 485 – 488.
7) Задание № 497 готовит учащихся к следующему пункту. Часто у учащихся возникает сложность с вынесением за скобки общего множителя, который является многочленом. Чтобы преодолеть это возможное затруднение рекомендуется выполнить это задание с подчеркиванием общего множителя.
8) Задание № 498 показывает применение нового преобразования для решения уравнений. Особо следует подчеркнуть, что без разложения на множители уравнения данного вида учащиеся пока решить не могут.
9) Важно показать учащимся применение правила вынесения общего множителя для рационализации вычислений (№№ 496, 502).
П.2 Способ группировки
1) В данном пункте учащиеся учатся применять еще один способ разложения на множители – способ группировки.2) Для проблематизации можно предложить учащимся разложить на множители многочлен:
Причиной возникшего затруднения будет то, что данные одночлены не имеют общего множителя. Чтобы преодолеть свое затруднения учащиеся должны будут открыть новый способ разложения на множители.
3) Чтобы подготовить учащихся к открытию рекомендуется выполнить задание № 533, в котором учащимся придется переставлять слагаемые местами и группировать произведения, имеющие одинаковые множители, а также № 535. Позже эти идеи помогут семиклассникам построить новый способ самостоятельно.
4) Алгоритм способа группировки, построенный учащимися, может иметь вид:
1) Объединить члены многочлена в группы таким образом, чтобы в каждой группе были общие множители.
2) Найти общий множитель в каждой группе и вынести его.
3) Найти общий множитель в новом многочлене и вынести его.
5) Подготовка, проведенная в предыдущем пункте, дает возможность наряду с простейшими ситуациями использования способа группировки рассмотреть и случаи, которые требуют специальных приемов:
- перестановка слагаемых;
- представление члена многочлена в виде суммы или разности подобных ему членов;
- прибавление и вычитание одного и того же слагаемого.
6) Для проблематизации можно предложить учащимся разложить на множители с использованием способа группировки многочлены:
7) Для организации открытия можно воспользоваться учебником. Учащиеся самостоятельно отбирают и рассматривают примеры 2, 3 и 4 из текста. После работы с текстом учащимся предлагается выполнить задания на пробное действие.
8) Задания №№ 546, 554 показывают применение нового преобразования для решения уравнений. Причем, если раньше указание разложить на множители давалось в задании, то теперь такого указания в тексте задания нет. Анализируя вид уравнения, учащиеся должны понимать, что нужно преобразовать левую часть уравнения в произведение многочленов. Особо следует подчеркнуть, что без разложения на множители уравнения данного вида учащиеся пока решить не могут.
П.3 Формулы сокращенного умножения и разложение многочленов на множители
1) В данном пункте учащиеся учатся раскладывать на множители многочлены с использованием формул сокращенного умножения. Умение использовать формулы, в которых та или иная формула представлена в явном виде, должно быть уже сформировано в предыдущем параграфе. Теперь с учащимися разбираются случаи, когда для применения формулы сокращенного умножения необходимо выполнить предварительное преобразование исходного многочлена.2) Учащиеся учатся видеть в степенях «квадраты» и «кубы», группировать слагаемые для получения нужной формулы, пользуются уже известными приемами: перестановка слагаемых и прибавление и вычитание одного и того же слагаемого.
3) Для этапа актуализации рекомендуется использовать задания №№ 583 – 585, при выполнении которых учащиеся повторят те понятия и способы действий, которые понадобятся им на уроке.
4) № 586 можно использовать для проблематизации. Затруднение, возникшее при выполнении этого задания, потребует новых приемов для применения разложения на множители (либо отбора уже известных приемов для применения в новой ситуации).
5) При изучении данного пункта учащиеся знакомятся с таким приемом, как выделение полного квадрата, который дает возможность применить формулы сокращенного умножения (№ 588 (л–н), № 595(д), № 600 готовят учащихся к этому способу, № 601 требует применения способа). Естественно требовать от каждого ученика умения применять данный способ нельзя. Однако более способные учащиеся должны получить возможность познакомиться с приемом выделения полного квадрата. В восьмом классе этот прием даст возможность вывести формулу для решения квадратных уравнений.
Эталоны
В результате изучения данных пунктов учащиеся знают следующие формулы сокращенного умножения: формулу произведения суммы двух выражений на их разность, формулу разности квадратов; формулы куба суммы и куба разности; формулы суммы и разности кубов и умеют их применять. Учащиеся имеют возможность познакомиться с треугольником Паскаля и соответствующим алгоритмом для возведения двучлена в n–ю степень. Учащиеся знают, что значит разложить многочлен на множители и следующие способы разложения на множители: вынесением за скобки общего множителя, способом группировки, с помощью формул сокращенного умножения и умеют их применять. Учащиеся имеют возможность познакомиться с различными вспомогательными приемами, которые помогают применять вышеперечисленные способы разложения на множители.Методические рекомендации по планированию уроков
При организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствии с зоной ближайшего развития более подготовленных учащихся. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000…». В отличие от уроков, опубликованных нами в предыдущих консультациях, этот урок является примером урока рефлексивного типа. Подробнее с методикой подготовки и проведения уроков такого типа в 7-9 классах основной школы вы можете познакомиться в разделе Модификация технологии деятельности метода обучения на уроках разной целевой направленности в 7–9 классах основной школы нашей вводной консультации.
Урок 60
Тип урока: РТема урока: «Формулы сокращённого умножения»
Автор: Л.А Грушевская
Основные содержательные цели:
1) организовать самоконтроль умения применять формулы сокращённого умножения при выполнении заданий различного характера;
2) тренировать умение решать задачи на движение.
Мы предлагаем Вам cкачать сценарий урока
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Уважаемые коллеги! Предлагаем вам скачать решение некоторых задач на смекалку, которые входят в данные параграфы.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.
Разложение многочленов на множители
Примеры комбинаций вынесения общего множителя, группировки слагаемых и формул сокращенного умножения для разложения многочленов на множители.
1) y3 + 16 – 4y – 4y2 = (y3 – 4y) + (16 — 4y2) = (y3 – 4y) – (4y2 – 16) = y(y2 – 4) – 4(y2 – 4) == (y2 – 4)(y — 4) = (y – 2)(y + 2)(y — 4).
2) (a – b)3 – a + b = (a – b)3 – (a – b) = (a – b)(( a – b)2 – 1) = (a – b)(a2 – 2ab + b2 — 1).
3) x2 – 6xy – 49 + 9y2 = (x2 – 6xy + 9y2) – 49 = (x – 3y)2 – 49 = (x – 3y – 7) (x – 3y +7).
4) c2 + 2c – d2 – 2d = (c2 – d2) + (2c – 2d) = (c – d)(c + d) + 2(c – d) = (c – d)( c + d + 2).
Примеры нестандартных разложений многочленов на множители.
Одно или несколько слагаемых представляется в виде суммы или разности, после чего можно применять группировку или формулы сокращенного умножения.Пример 1. Разложение многочлена на множители y2 – 14y + 40.
y2 – 14y + 40 = y2 – 14y + 49 – 9 = (y2 – 14y + 49) – 9 = (y – 7)2 – 32 = (y – 7 – 3)(y – 7 + 3) = (y – 10)(y – 4).
Пример 2. Разложение многочлена на множители x2 + 7x + 12.
x2 + 7x + 12 = x2 + 3x + 4x + 12 = (x2 + 3x) + (4x + 12) = x(x + 3) + 4(x + 3) = (x + 3)(x + 4).
Пример 3. Разложение многочлена на множители x2 + 8x +7.
x2 + 8x +7 = x2 + 7x + x + 7 = (x2 + 7x) + (x + 7) = x(x + 7) + (x + 7) = (x + 7)(x + 1).
Пример 4. Разложение многочлена x2 + x – 12 на множители.
x2 + x – 12 = x2 + 4x – 3x – 12 = (x2 + 4x) – (3x +12) = x(x + 4) – 3(x + 4) = (x + 4)(x – 3).
Пример 5. Разложение многочлена на множители x2 — 10x + 24.
x2 — 10x + 24 = x2 -2*5 x + 25 – 1 = (x2 — 2*5 x + 25) – 1 = (x – 5)2 – 1 = (x – 5 – 1)(x – 5 + 1) = (x – 6)(x – 4).
Пример 6. Разложение многочлена на множители x2 — 13x + 40.
x2 — 13x + 40 = x2 — 10x – 3x + 25 + 15 = (x2 — 10x + 25) – (3x – 15) = (x – 5)2 – 3(x – 5) =
= (x – 5)(x – 5 – 3) = (x – 5)(x – 8).
Пример 7. Разложим на множители многочлен x2 + 15x + 54.
x2 + 15x + 54 = x2 + (12x + 3x) + (36 + 18) = (x2 + 12x + 36) + (3x + 18) = (x + 6)2 + 3(x + 6) =
= (x + 6)(x + 6 + 3) = (x + 6 )(x + 9).
Пример 8. Разложение многочлена x4 + 3x2 + 4 на множители.
x4 + 3x2 + 4 = x4 + (4x2 – x2) + 4 = (x4 + 4x2 + 4) – x2 = (x2 + 2)2 – x2 = (x2 + 2 – x)( x2 + 2 + x) =
= (x2 – x + 2)( x2 + x + 2).
Пример 9. Разложение многочлена на множители x4 + x2 + 1.
x4 + x2 + 1 = x4 + (2x2 – x2) + 1 = (x4 + 2x2 + 1) – x2 = (x2 + 1)2 – x2 = (x2 + 1 – x)( x2 + 1 + x) =
= (x2 – x + 1)( x2 + x + 1).
Пример 10. Разложение многочлен x4 + 4 на множители. Данный многочлен представляет интересный пример выражения, когда на первый взгляд кажется, что его разложить на множители невозможно. Прибавим к нему 4x2 и вычтем 4x2, чтобы значение выражения не изменилось.
x4 + 4 = x4 + 4 + 4x2 – 4x2 = (x4 + 4x2 + 4) – 4x2 = (x2 + 2)2 – 4x2 = (x2 + 2 – 2x)( x2 + 2 + 2x) =
= (x2 – 2x + 2)( x2 + 2x + 2).
Разложение многочлена на множители: вынесение за скобки, способ группировки, делением
Тестирование онлайн
Разложение многочлена на множители
Представление многочлена в виде произведения нескольких многочленов (или одночленов)
Например,
Вынесение общего множителя за скобки
Необходимо проанализировать каждый член многочлена, найти общую часть (если такая имеется). Например, в выражении каждый член имеет y. Переменную y можно вынести за скобки.
Переменные, входящие в каждый член многочлена выносят за скобки в степенях с наименьшим показателем, который встречается. В примере встречается y2, y5 и y4. Выносим за скобки y2.
Что останется от каждого члена после вынесения общего множителя за скобки? Что записать в скобках? Необходимо каждый член разделить на общий множитель, который выносим за скобки. Например, при вынесении y2 за скобки в нашем примере
Если числовые коэффициенты каждого члена многочлена имеют наибольший общий делитель, то его тоже можно вынести за скобки. В нашем примере НОД(18; 30; 6)=6
Если за скобки выносят множитель «-1» (еще говорят «выносят минус»), то в скобках знак каждого слагаемого меняется на противоположный
Общим множителем могут быть и многочлены. Например, для выражения общим множителем является многочлен
Выносим за скобки, получим
Всегда можно проверить верно ли выполнено вынесение общего множителя за скобки. Для этого необходимо выполнить умножение общего множителя на многочлен в скобках и проверить, что полученное выражение полностью совпадает с первоначальным.
Способ группировки
Если члены многочлена не имеют общего множителя, то следует попытаться разложить его методом группировки.
Для этого надо объединить в группы те члены, которые имеют общие множители, и вынести за скобки общий множитель каждой группы. После этого может оказаться общий множитель многочлен у получившихся групп, который выносят за скобки.
Группировать члены многочлена можно по-разному. Не при всякой группировке удастся разложить многочлен на множители.
Разложение многочлена иногда невозможно известными методами. Тогда разложить многочлен возможно, отыскав один корень и разделив многочлен на многочлен.
Корень многочлена P(x) — это такое число c при котором P(c)=0. Например,
Если многочлен с целыми коэффициентами имеет корни, то их следует искать среди чисел , где m — целый делитель a0, а k — натуральный делитель an
Например,
Если хотя бы один корень найден, остается разделить многочлен на выражение x-c, где c — это корень уравнения.
Например,
Факторинг по алгебре
Факторы
У чисел есть множители:
И выражения (например, x 2 + 4x + 3 ) также имеют множители:
Факторинг
Факторинг (в Великобритании называется « Факторинг ») — это процесс нахождения факторов :
Факторинг: поиск того, что нужно умножить, чтобы получить выражение.
Это похоже на «разбиение» выражения на умножение более простых выражений.
Пример: множитель 2y + 6
У 2y и 6 есть общий множитель 2:
Таким образом, мы можем разложить все выражение на:
2у + 6 = 2 (у + 3)
Таким образом, 2y + 6 было «учтено» в 2 и y + 3
Факторинг также противоположен расширению:
Общий коэффициент
В предыдущем примере мы видели, что 2y и 6 имеют общий множитель 2
Но для правильного выполнения работы нам нужен наивысший общий множитель , включая все переменные
Пример: коэффициент 3y
2 + 12yВо-первых, 3 и 12 имеют общий делитель 3.
Итак, мы могли бы иметь:
3 года 2 + 12 лет = 3 (год 2 + 4 года)
Но мы можем сделать лучше!
3y 2 и 12y также разделяют переменную y.
Вместе, что составляет 3 года:
- 3y 2 — 3y × y
- 12y — это 3y × 4
Таким образом, мы можем разложить все выражение на:
3 года 2 + 12 лет = 3 года (y + 4)
Чек: 3y (y + 4) = 3y × y + 3y × 4 = 3y 2 + 12y
Более сложный факторинг
Факторинг может быть трудным!
До сих пор примеры были простыми, но факторизация может оказаться очень сложной.
Потому что мы должны изобразить то, что мы умножили на , чтобы получить данное нам выражение!
Это все равно, что пытаться найти, какие ингредиенты
пошли на торт, чтобы сделать его таким вкусным.
Это может быть сложно понять!
Опыт помогает
Чем больше опыта, тем проще факторинг.
Пример: Фактор
4x 2 — 9Хммм … похоже, нет общих факторов.
Но знание специальных биномиальных произведений дает нам ключ к разгадке, который называется «разница квадратов». :
Потому что 4x 2 равно (2x) 2 , а 9 равно (3) 2 ,
Итак имеем:
4x 2 — 9 = (2x) 2 — (3) 2
А это можно получить по формуле разности квадратов:
(a + b) (a − b) = a 2 — b 2
Где a — 2x, а b — 3.
Итак, давайте попробуем это сделать:
(2x + 3) (2x − 3) = (2x) 2 — (3) 2 = 4x 2 — 9
Да!
Таким образом, множители 4x 2 — 9 равны (2x + 3) и (2x − 3) :
Ответ: 4x 2 -9 = (2x + 3) (2x − 3)
Как можно этому научиться? Получив много практики и зная «Самобытность»!
Помните эти личности
Вот список общих «Идентификаций» (включая «разность квадратов» , использованную выше).
Об этом стоит помнить, так как они могут облегчить факторинг.
| а 2 — б 2 | = | (а + б) (а-б) |
| a 2 + 2ab + b 2 | = | (а + б) (а + б) |
| a 2 — 2ab + b 2 | = | (а-б) (а-б) |
| a 3 + b 3 | = | (a + b) (a 2 −ab + b 2 ) |
| a 3 — b 3 | = | (a − b) (a 2 + ab + b 2 ) |
| a 3 + 3a 2 b + 3ab 2 + b 3 | = | (а + б) 3 |
| a 3 −3a 2 b + 3ab 2 −b 3 | = | (а-б) 3 |
Подобных гораздо больше, но это самые полезные.
Совет
Обычно лучше всего использовать разложенную форму.
При попытке факторизации выполните следующие действия:
- «Вынести за скобки» любые общие термины
- Посмотрите, подходит ли он какой-либо из идентификационных данных, а также другим, которые вы, возможно, знаете
- Продолжайте, пока вы больше не сможете множить
Существуют также системы компьютерной алгебры (называемые «CAS»), такие как Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce и многие другие, которые хорошо подходят для факторинга.
Другие примеры
Опыт действительно помогает, поэтому вот еще несколько примеров, которые помогут вам на этом пути:
Пример: w
4 — 16Показатель степени 4? Может быть, мы могли бы попробовать показатель степени 2:
w 4 — 16 = (w 2 ) 2 — 4 2
Да, это разница квадратов
w 4 — 16 = (w 2 + 4) (w 2 — 4)
И «(w 2 — 4)» — еще одно отличие квадратов
w 4 -16 = (w 2 + 4) (w + 2) (w -2)
Это все, что я могу (если я не использую мнимые числа)
Пример: 3u
4 — 24uv 3Удалить общий множитель «3u»:
3u 4 — 24uv 3 = 3u (u 3 — 8v 3 )
Тогда разница кубиков:
3u 4 — 24uv 3 = 3u (u 3 — (2v) 3 )
= 3u (u − 2v) (u 2 + 2uv + 4v 2 )
Это все, что я могу.
Пример: z
3 — z 2 — 9z + 9Попробуйте разложить на множители первые два и вторые два по отдельности:
z 2 (z − 1) — 9 (z − 1)
Вау, (z-1) есть на обоих, так что давайте воспользуемся этим:
(z 2 −9) (z − 1)
А z 2 −9 — разность квадратов
(г-3) (г + 3) (г-1)
Это все, что я могу.
А теперь побольше опыта:
Специальный факторинг: суммы и разности кубов и идеальные квадраты
Purplemath
Две другие специальные формулы факторизации, которые вам нужно запомнить, очень похожи друг на друга; это формулы для разложения сумм и разностей кубов.Вот две формулы:
Факторинг суммы кубов:
a 3 + b 3 = ( a + b ) ( a 2 — ab + b 2 )
Фактор разницы кубов:
a 3 — b 3 = ( a — b ) ( a 2 + ab + b 2 )
На более продвинутых курсах вы узнаете, как они пришли к этим формулам.А пока просто запомните их.
MathHelp.com
Чтобы помочь с запоминанием, сначала обратите внимание, что членов в каждой из двух формул факторизации абсолютно одинаковы.Затем обратите внимание, что в каждой формуле есть только один знак «минус». Разница между двумя формулами заключается в расположении одного знака «минус»:
Для разницы кубиков знак «минус» ставится в линейном множителе, a — b ; для суммы кубов знак «минус» стоит в квадратичном множителе, a 2 — ab + b 2 .
Некоторые люди используют мнемонику « SOAP », чтобы отслеживать знаки; буквы обозначают линейный множитель, имеющий «тот же» знак, что и знак в середине исходного выражения, затем квадратичный множитель, начинающийся со «противоположного» знака того, что было в исходном выражении, и, наконец, второй знак внутри квадратичный множитель «всегда положителен».
a 3 ± b 3 = ( a [ Тот же знак ] b ) ( a 2 [ Противоположный знак ] ab [ Всегда Положительный ] b 2 )
Какой бы метод лучше всего ни помог вам сохранить эти формулы, используйте его, потому что вы не должны предполагать, что вам будут даны эти формулы на тесте.Вы должны ожидать, что вам нужно будет их знать.
Примечание. Квадратичная часть каждой формулы куба не учитывает фактор , поэтому не тратьте время на попытки разложить его на множители. Да, a 2 -2 ab + b 2 и a 2 + 2 ab + b 2 коэффициент , но это из-за двойки в середине термины. Квадратичные члены этих формул суммы и разности кубов не содержат , равное «2», и, таким образом, не может множить .
Когда вам дается пара кубиков для факторизации, внимательно примените соответствующее правило. Под «осторожно» я имею в виду «использование круглых скобок для отслеживания всего, особенно отрицательных знаков». Вот несколько типичных проблем:
Это эквивалентно x 3 -2 3 . Со знаком «минус» посередине это разница кубиков. Чтобы провести факторинг, я вставлю x и 2 в формулу разности кубов.Так я получаю:
x 3 — 8 = x 3 -2 3
= ( x -2) ( x 2 + 2 x + 2 2 )
= ( x -2) ( x 2 + 2 x + 4)
Первый член содержит куб 3 и куб x .А как насчет второго срока?
Прежде чем паниковать по поводу отсутствия кажущегося куба, я помню, что 1 можно рассматривать как возведенную в любую степень, которая мне нравится, поскольку 1 для любой степени все еще равна 1. В этом случае мне нужна степень 3, так как это даст мне сумму кубиков. Это означает, что выражение, которое они мне дали, можно выразить как:
Итак, чтобы разложить множители, я подставлю 3 x и 1 в формулу суммы кубов.Это дает мне:
27 x 3 + 1 = (3 x ) 3 + 1 3
= (3 x + 1) ((3 x ) 2 — (3 x ) (1) + 1 2 )
= (3 x + 1) (9 x 2 -3 x + 1)
Во-первых, я отмечаю, что они дали мне бином (двухчленный многочлен) и что степень x в первом члене равна 3, поэтому, даже если я не работал с «суммами и разностями» кубиков »в моем учебнике, я бы заметил, что, возможно, мне следует думать в терминах этих формул.
Глядя на другую переменную, я замечаю, что степень 6 является кубом степени 2, поэтому другая переменная в первом члене также может быть выражена в кубе; а именно, как куб квадрата y .
Второй член — 64, который, как я помню, является кубом 4. (Если бы я не вспомнил или не был уверен, я бы взял свой калькулятор и пробовал вычислять кубики, пока не получил правильное значение. , иначе я бы взял кубический корень из 64.)
Итак, теперь я знаю, что с минусом в середине это разница в два куба; а именно это:
Подставляя подходящую формулу, я получаю:
x 3 y 6 — 64 = ( xy 2 ) 3 — 4 3
= ( xy 2 -4) (( xy 2 ) 2 + ( xy 2 ) (4) + 4 2 )
= ( xy 2 -4) ( x 2 y 4 + 4 xy 2 + 16)
Используя соответствующую формулу, множите 16
x 3 — 250.
Гм … Я знаю, что 16 — это , а не куб чего-либо; на самом деле он равен 2 4 . Как дела?
Что случилось, они ожидают, что я использую то, что я узнал о простом факторинге, чтобы сначала преобразовать это в разность кубов. Да, 16 = 2 4 , но 8 = 2 3 , куб. Я могу получить 8 из 16, разделив на 2.Что будет, если я разделю 250 на 2? Я получаю 125, что является кубом из 5. То, что они мне дали, можно переформулировать как:
Я могу применить формулу разности кубов к тому, что находится в круглых скобках:
2 3 x 3 — 5 3 = (2 x ) 3 — (5) 3
= (2 x -5) ((2 x ) 2 + (2 x ) (5) + (5) 2 )
= (2 x -5) (4 x 2 + 10 x + 25)
Собирая все вместе, я получаю окончательную формулировку:
2 (2 x -5) (4 x 2 + 10 x + 25)
Моей первой реакцией могло бы стать применение формулы разности кубов, поскольку 125 = 5 3 .Но как насчет того знака «минус» впереди?
Поскольку ни одна из приведенных мне формул факторинга не включает «минус» впереди, может быть, я смогу вычесть «минус» …?
— x 3 — 125 = –1 x 3 — 125
Ага! Теперь то, что внутри скобок, — это сумма кубов, кубов, которую я могу разложить на множители. У меня есть сумма куба x и куба 5, поэтому:
x 3 + 5 3 = ( x + 5) (( x ) 2 — ( x ) (5) + (5) 2 )
= ( x + 5) ( x 2 -5 x + 25)
Собирая все вместе, получаем:
–1 ( x + 5) ( x 2 — 5 x + 25)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении суммы кубов.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления .)
URL: https://www.purplemath.com/modules/specfact2.htm
Все о факторах числа
Факторы числа — важная подтема из систем счисления.В этой статье мы обсудим основные факторы числа. Практически каждый конкурсный экзамен состоит из 2-3 вопросов среднего и сложного уровня в зависимости от числа. Принимая это во внимание, мы обсудим расширенное применение этой темы, чтобы дать вам преимущество перед другими кандидатами.
Какие множители у числа?
Множители числа N относятся ко всем числам, которые полностью делят N. Их также называют делителями числа.
Основная формула, связанная с множителями числа:
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. ЗарегистрироватьсяЭто некоторые основные формулы, относящиеся к множителям числа N, так что,
N = p a q b r c
Где p, q и r — простые делители числа n.
a, b и c — неотрицательные степени / показатели
- Количество факторов N = (a + 1) (b + 1) (c + 1)
- Произведение коэффициентов N = N No.факторов / 2
- Сумма факторов: (p 0 + p 1 + … + p a ) (q 0 + q 1 + …. + q b ) (r 0 + r 1 + … + r c ) / (p a -1) (q b -1) (r c -1)
Решенные вопросы по факторам числа:
Пример 1: Рассмотрим число 120. Найдите следующее для n- Сумма факторов
- Количество факторов
- Произведение множителей
- Сумма факторов = [(2 0 +2 1 +2 2 +2 3 ) (3 0 +3 1 ) (5 0 +5 1 ) ] / [(2-1) (3-1) (5-1)] = 45
- Количество факторов = (3 + 1) (1 + 1) (1 + 1) = 16
- Произведение множителей = 120 (16/2) = 120 8
- Количество нечетных множителей
- Число четных множителей
Решение: Разложением на простые множители 84, 84 = 2 2 × 3 1 × 7 1
Общее количество множителей = (2 + 1) (1 + 1) (1 + 1) = 12
- Число нечетных множителей будет всеми возможными комбинациями степеней 3 и 5 (исключая любую степень двойки).Следовательно, количество нечетных множителей = (1 + 1) (1 + 1) = 4
При ручной проверке эти множители равны 1, 3, 7 и 21. - Количество четных множителей = общее количество факторов — нет. четных множителей
= 12 — 4 = 8
Advanced Concepts of Factors числа
Пример 3: Пусть N = 3 15 × 7 43 . Сколько факторов в N 2 меньше N, но не делят N полностью?
Решение: Пусть N = 6, тогда N 2 = 36.
Посредством разложения на простые множители N = 2 × 3 и N 2 = 2 2 × 3 2 . Количество факторов N 2 = 9, которые равны 1, 2, 3, 4, 6, 9, 12, 18, 36. Итак, из них первые пять меньше N, то есть 1, 2, 3, 4 и 6. Но из них 1, 2, 3 и 6 полностью делят 6. Остается 4. Следовательно, нет. факторов, которые меньше N, но не делят N полностью, составляет 1 .
Чтобы прийти к этому по формуле,
- Добавьте 1 к числу множителей N 2 No.факторов = (2 + 1) (2 + 1) = 9; добавив 1, 9 + 1 = 10
- Разделите это на 2, чтобы получить количество пар Количество пар = 10/2 = 5
- Из полученного числа вычтите количество множителей N. Число множителей N = (1 + 1) (1 + 1) = 4; 5-4 = 1, что и есть ответ.
Давайте перейдем к рассматриваемой проблеме, выполнив шаги,
- N 2 = 330 x 786; Количество факторов = (30 + 1) (86 + 1) = 31x 87 = 2697; сложение 1 дает 2698
- Количество пар = 2698/2 = 1349
- №множителей N = (15 + 1) (43 + 1) = 704; Ответ: 1349-704 = 645
Обучение
- Этот вопрос появляется на конкурсных экзаменах каждый год. Следовательно, мы разработали ярлык для данной проблемы. Согласно ему, ответ на такую проблему дает произведение степеней простых чисел N.
- Для вышеупомянутой задачи ответ может быть непосредственно получен как 15 × 43 = 645!
Пример 4: Найдите число положительных целочисленных решений уравнения, x 2 -y 2 = 840?
Решение: Алгебраическое выражение можно записать как x 2 -y 2 = (x + y) (x-y)- Следовательно, чтобы получить решение x и y, нам нужно найти пары, произведение которых равно 840.
- Факторизация на простые числа 840 = 2 3 × 3 × 5 × 7. Итак, количество множителей 840 = (3 + 1) (1 + 1) (1 + 1) (1 + 1) = 32.
- Число пар, которые дадут уникальные положительные интегральные решения для этого уравнения = no. множителей / 2 = 32/2 = 16. Потому что для каждой пары, скажем, 4 x 210, мы получаем уникальные решения для x и y.
Обучение
- x и y будут давать различные целые значения только при условии, что правая часть уравнения является нечетным числом или кратным 4.
Практический вопрос: Сколько натуральных чисел меньше 100 можно записать как разность двух натуральных чисел?
(Подсказка: примените вышеупомянутое обучение, чтобы решить этот вопрос)
Ответ: 75
Факторы числа: ключевые знания
- Некоторые вопросы одного типа от среднего до сложного задаются год за годом на нескольких конкурсных экзаменах.Тщательная практика составления типовых вопросов (как показано в видео) может дать вам большое конкурентное преимущество в управлении временем.
| Как найти общее количество множителей любого числа |
Привет, студенты! Хотите узнать? Как найти общее количество множителей любого числа ? Затем прочтите этот пост Amans Maths Blogs (AMB) , в этой статье вы узнаете о ФОРМУЛЕ ФАКТОРА , которая используется для нахождения числа множителя любого числа .Но прежде вам нужно узнать об основной теореме арифметики . Итак, приступим …
Согласно основной теореме арифметики, каждое положительное целое число может быть выражено как произведение простых чисел уникальным способом. ИЛИ, вы также можете сказать, что число может быть разложено на простые множители только одним способом.
Это означает, что для положительного целого числа N> 1 может быть однозначно записано как,
N = α a × β b × γ c × δ d ×…
где α <β <γ <δ <… - простые числа, а a, b, c, d,… - целые числа, большие или равные 0.Это разложение N также известно как разложение на простые множители N.
Пусть N обозначает число, разложение на простые множители которого
N = p 1 p 2 p 3 …, где p 1, p 2 , p 3, … простые числа.
Предположим, что N также разлагается как N = q 1 q 2 q 3 …, где q 1, q 2, q 3, … другие простые числа.
Тогда p 1 p 2 p 3 … = q 1 q 2 q 3 …,
Теперь p1 делит произведение p 1 p 2 p 3 … и поскольку каждый из множителей этого произведения является простым, q 1 делит один из них p 1 p 2 p 3 …,
Пусть q 1 делит одно из им р 1 .Но p 1 и q 1 простые числа, поэтому p 1 и q 1 равны.
Таким образом, p 1 p 2 p 3 … = q 1 q 2 q 3 …, ⇒ p 2 p 3 … = q 2 q 3 …,
Аналогично q 2 делит одно из них p 2 p 3 …,
Пусть q 2 делит одно из них p 2 . Но p 2 и q 2 простые числа, поэтому p 2 и q 2 равны.
Следовательно, разложение на простые множители p 1 p 2 p 3 … are q 1 q 2 q 3 … то же самое.
Следовательно, N можно разложить на простые множители одним способом.
Пусть N — число, количество множителей которого необходимо вычислить, и его разложение на простые множители равно N = α a × β b × γ c × δ d ×…, где α, β, γ , δ,… простые числа и a, b, c, d,… натуральные числа.
Теперь коэффициенты α a равны 1, α 1 , α 2 , α 3 ,… α a .Общее количество факторов α a равно (a + 1).
Коэффициенты β b равны 1, β 1 , β 2 , β 3 ,… β b . Общее количество факторов β b равно (b + 1).
Аналогично
Общее количество факторов γ c равно (c + 1).
Общее количество факторов δ d равно (d + 1).
Таким образом,
Общее количество факторов N = α a × β b × γ c × δ d ×… равно
(a + 1) (b + 1) (c + 1 ) (d + 1)…
Это общее количество множителей N включает 1 и само число N.
Как найти общее количество множителей числа
Вопрос 1 : Найдите общее число множителей 120.
Решение : простое факторизация 120 составляет 120 = 2 3 × 3 1 × 5 1 .
Таким образом, общее количество множителей 120 равно (3 + 1) (1 + 1) (1 + 1) = 4 × 2 × 2 = 16.
Вопрос 2 : Найдите общее количество множителей 84
Решение : Факторизация на простые множители 84 равна 84 = 2 2 × 3 1 × 7 1 .
Таким образом, общее количество факторов 84 равно (2 + 1) (1 + 1) (1 + 1) = 3 × 2 × 2 = 12.
Вопрос 3 : Каково количество факторов номер 3600?
Решение : Факторизация на простые множители 3600 равна 3600 = 2 4 × 3 2 × 5 2 .
Таким образом, общее количество факторов 3600 равно (4 + 1) (2 + 1) (2 + 1) = 5 × 3 × 3 = 45.
Вопрос 4 : Каково количество факторов номер 504?
Решение : Факторизация на простые множители 504 равна 504 = 2 3 × 3 2 × 7 1 .
Таким образом, общее количество множителей 504 равно (3 + 1) (2 + 1) (1 + 1) = 4 × 3 × 2 = 24.
Вопрос 5 : Найдите общее количество множителей 180 .
Решение : Факторизация на простой множитель 180 равна 180 = 2 2 × 3 2 × 5 1 .
Таким образом, общее количество множителей 180 равно (2 + 1) (2 + 1) (1 + 1) = 3 × 3 × 2 = 18.
Вопрос 6 : Сколько множителей 6480 ?
Решение : Факторизация 6480 на простые множители равна 6480 = 2 4 x 3 4 x 5 1 .
Таким образом, общее количество множителей 6480 равно (4 + 1) (4 + 1) (1 + 1) = 5 × 5 × 2 = 50.
Вопрос 7 : Сколько множителей 420 ?
Решение : Факторизация 420 равна 420 = 2 2 x 3 1 x 5 1 x 7 1 .
Таким образом, общее количество множителей 420 равно (2 + 1) (1 + 1) (1 + 1) (1 + 1) = 3 × 2 × 2 × 2 = 24.
Таблица факторов и кратных
Прочитать : Получить множители и множители от 1 до 100
Прочитать : Как найти множитель любого числа
Прочитать : Как найти число четного множителя любого числа
Прочитать : Как Чтобы найти число нечетных множителей любого числа
Прочтите : Как найти сумму множителей любого числа
Прочтите : Как найти произведение множителей любого числового множителя 36 факторов из 48как найти число множителей данного числакак найти число множителей числакак найти общее число множителей числаколичество вычисляемых множителейколичество множителей из числа множителей из числа множителей из числа множителей на множителичисло функций функцийпроизведение множителей формулы формула множителей
Как разложить на множители полиномы третьей степени
Обновлено 3 декабря 2020 г.
Мишель Брюне
Многочлен третьей степени, также называемый кубическим многочленом, включает в себя по крайней мере один моном или член, кубический или увеличенный в третью степень.2)
при факторизации уравнения с добавлением одного члена в кубе к другому члену в кубе, например, x 3 + 8.
Определите, что представляет собой a в уравнении. В примере x 3 + 8, x представляет a , поскольку x является кубическим корнем из x 3 .
Определите, что представляет собой b в уравнении. В этом примере x 3 +8, b 3 представлено числом 8; таким образом, b представлено числом 2, поскольку 2 является кубическим корнем из 8.3-1
Определите, что представляет собой a в полиноме. В 125 x 3 — 1, 5 x представляет a , поскольку 5 x является кубическим корнем из 125 x 3 . 2 + 6x
Подумайте о моном, который является множителем каждого из членов уравнения.2 + 5x + 6)
Подумайте обо всех множителях 6, последнего члена многочлена. Множители 6 равны 2 × 3 и 1 × 6.
Обратите внимание на центральный член многочлена в скобках — 5 x в данном случае. Выберите множители 6, которые в сумме дают 5, коэффициент при центральном члене. 2 и 3 в сумме дают 5.
Запишите два набора скобок. Поместите x в начале каждой скобки со знаком добавления. Рядом с одним знаком сложения запишите первый выбранный коэффициент (2).Рядом со вторым знаком сложения напишите второй множитель (3). Это должно выглядеть так:
(x + 3) (x + 2)
Запомните исходный общий множитель ( x ), чтобы записать полное решение:
x (x + 3) (x + 2 )
Решите, используя уроки факторинга — Уроки Wyzant
Несколько предыдущих уроков объясняют методы, используемые для факторизации выражений. В этом уроке основное внимание уделяется практическому применению этих методов — решению уравнений.
Зачем решать по факторингу?
Самыми фундаментальными инструментами для решения уравнений являются сложение, вычитание, умножение и деление.Эти методы хорошо работают с уравнениями типа x + 2 = 10-2x и 2 (x — 4) = 0.
Но как насчет уравнений, в которых переменная имеет показатель степени, например x 2 + 3x = 8x — 6? Здесь на помощь приходит факторинг. Мы будем использовать это уравнение в первом примере.
Процесс определения факторинга потребует четырех основных шагов:
- Переместите все члены в одну сторону уравнения, обычно в левую, используя сложение или вычитание.
- Полностью разложите уравнение на множители.
- Установите каждый коэффициент равным нулю и решите.
- Перечислите каждое решение из шага 3 как решение исходного уравнения.
Первый пример
х 2 + 3x = 8x — 6
Шаг 1
Первый шаг — переместить все члены влево, используя сложение и вычитание. Сначала мы вычтем по 8 раз с каждой стороны.
х 2 + 3x — 8x = 8x — 8x — 6
x
2 — 5x = -6
Теперь добавим по 6 с каждой стороны.
х 2 — 5x + 6 = -6 + 6
x
2 — 5x + 6 = 0
Со всеми терминами слева переходим к шагу 2.
Шаг 2
Мы идентифицируем левую как трехчлен и, соответственно, множим ее на множители:
(х — 2) (х — 3) = 0
Теперь у нас есть два фактора: (x — 2) и (x — 3).
Шаг 3
Теперь мы устанавливаем каждый коэффициент равным нулю. Результат — две подзадачи:
х — 2 = 0
и
х — 3 = 0
Решение первой подзадачи x — 2 = 0 дает x = 2.Решение второй подзадачи x — 3 = 0 дает x = 3.
Шаг 4
Последний шаг — объединить два предыдущих решения, x = 2 и x = 3, в одно решение исходной задачи.
х 2 + 3x = 8x — 6
x = 2, 3
Решить по факторингу: почему это работает?
Изучите уравнение ниже:
ab = 0
Если вы позволите a = 3, то логически b должно быть равно 0. Аналогично, если вы положите b = 10, тогда a должно быть равно 0.
Теперь попробуйте позволить быть другим ненулевым числом. Следует заметить, что до тех пор, пока a не равно 0,
b должно быть равно нулю.
Чтобы сформулировать наблюдение в более общем виде: «Если ab = 0, то либо a = 0, либо b = 0.» Это важное свойство нуля, которое мы используем при решении с помощью факторизации.
Когда пример был разложен на (x — 2) (x — 3) = 0, это свойство было применено, чтобы определить, что либо (x — 2) должно быть равно нулю, либо (x — 3) должно быть равно нулю.Таким образом, мы смогли создать два уравнения и определить два решения на основе этого наблюдения.
Второй пример
5x 3 = 45x
Шаг 1
Переместите все члены в левую часть уравнения. Мы делаем это, вычитая по 45x с каждой стороны.
5x 3 — 45x = 45x — 45x
5x
3 — 45x = 0.
Шаг 2
Следующий шаг — полностью разложить на множители левую сторону. Сначала отметим, что два члена слева имеют наибольший общий делитель 5x.
5x (x 2 — 9) = 0
Теперь (x 2 — 9) можно разложить на два квадрата.
5х (х + 3) (х — 3) = 0
У нас осталось три множителя: 5x, (x + 3) и (x — 3). Как объяснено в разделе «Почему это работает?» раздел, по крайней мере, один из трех факторов должен быть равен нулю.
Шаг 3
Создайте три подзадачи, установив каждый коэффициент равным нулю.
1. 5x = 0
2.х + 3 = 0
3. х — 3 = 0
Решение первого уравнения дает x = 0. Решение второго уравнения дает x = -3. И решение третьего уравнения дает x = 3.
Шаг 4
Окончательное решение состоит из решений трех подзадач.
х = -3, 0, 3
Третий пример
3x 4 — 288x 2 — 1200 = 0
Шаги 1 и 2
Все три члена уже находятся в левой части уравнения, поэтому мы можем начать факторизацию.Во-первых, мы выносим за скобки наибольший общий делитель 3.
3 (x 4 — 96x 2 — 400) = 0
Затем факторизуем трехчлен.
3 (x 2 + 4) (x 2 -100) = 0
Наконец, мы множим бином (x 2 — 100) как разность между двумя квадратами.
3 (x 2 + 4) (x + 10) (x — 10) = 0
Шаг 3
Мы продолжаем, устанавливая каждый из четырех факторов равным нулю, в результате чего получаем четыре новых уравнения.
1. 3 = 0
2. x 2 + 4 = 0
3. x + 10 = 0
4. x — 10 = 0
Первое уравнение неверно и не дает решения. Второе уравнение не может быть решено базовыми методами. (x 2 + 4 = 0 на самом деле имеет два решения в виде мнимых чисел, но мы сохраним мнимые числа для другого урока!) Уравнение
3 имеет решение x = -10, а уравнение 4 имеет решение x = 10.
Шаг 4
Теперь мы включаем все найденные нами решения в одно решение исходной проблемы:
х = -10, 10
Это может быть сокращено как
х = ± 10
Решить путем факторинга ресурсов
Калькулятор уравнений — Решить на множитель Практические задачи / Рабочий лист |
Почему мы множим уравнения на множители? — Лучшее объяснение
Что такое алгебра? Изучая переменные ($ x, y, z $), кажется, что они «скрывают» число:
Какое число могло скрываться внутри $ x $? 2, в данном случае.2 $ — это компонент, взаимодействующий сам с собой
После завершения взаимодействия мы должны получить 6. 2 + x $.Желаемое состояние — 6. Новая система:
будет отслеживать разницу между исходной системой и желаемым состоянием. Когда мы счастливее всего? Когда нет разницы:
А! , это , почему мы так заинтересованы в обнулении многочленов! Если у нас есть система и желаемое состояние, мы можем составить новое уравнение, чтобы отследить разницу — и попытаться свести ее к нулю. (Это глубже, чем просто «вычесть 6 с обеих сторон» — мы пытаемся описать ошибку!)
Но.2 + x — 6 $) как связка связанных меньших систем.
Представьте, что вы берете кучу палочек (наша беспорядочная, неорганизованная система) и ставите их так, чтобы они поддерживали друг друга, как вигвам:
/ \
(Это 2-й пример с двумя палками).
Уберите любую палку, и вся конструкция рухнет. Если мы сможем переписать нашу систему:
как серия умножений:
мы засунули палки в «типи». Если Компонент A или Компонент B становится 0, структура разрушается, и в результате мы получаем 0.
Аккуратно! Этот является причиной факторинга камней: мы перестраиваем нашу систему ошибок в хрупкую вигвам, чтобы мы могли сломать ее . Мы найдем то, что устраняет наши ошибки и приводит нашу систему в идеальное состояние.
Помните: мы устраняем ошибку в системе, а не в самой системе.
Факторинг
Научиться «учитывать уравнение» — это процесс организации вашего вигвама. В этом случае:
Если $ x = -3 $, то Компонент А падает.2 + х — 6 $)
Когда error = 0, наша система должна быть в желаемом состоянии. Были сделаны!
Алгебра чертовски полезна:
- Наша система — это траектория, «желаемое состояние» — это цель. По какой траектории попадает в цель?
- Наша система — это наш виджет продаж, «желаемое состояние» — это наша цель по доходу.Какая сумма дохода достигает цели?
- Наша система — это вероятность выигрыша нашей игры, «желаемое состояние» — это результат 50-50 (справедливый). Какие настройки делают игру честной?
Идея «согласования системы с ее желаемым состоянием» — это всего лишь одна из интерпретаций того, почему факторинг полезен. Если есть еще, я бы хотел их услышать!
Приложение
Шпаргалка по процессу:
Еще немного пищи для размышлений:
Умножение часто рассматривается как AND.2 + 1 $ не обнулялись до тех пор, пока не появились мнимые числа.
Счастливая математика.
Другие сообщения в этой серии
- Понимание алгебры: Почему мы множим уравнения на множители?
- Быстрая интуиция для параметрических уравнений
- Интуиция к квадратичной формуле
- Интуиция для формы уклона-пересечения
- Интуиция для графических функций
- Интуиция для многочленов

 Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10: 



 Другими словами:
Другими словами: Еще раз перепишем полученную конструкцию:
Еще раз перепишем полученную конструкцию: е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим: Решение пропорций всегда выполняется с помощью свойства пропорции.
Решение пропорций всегда выполняется с помощью свойства пропорции.
 Найдите отношение x к y.
Найдите отношение x к y.




 Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
 В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
 Умножим каждый член уравнения на х.
Умножим каждый член уравнения на х.

 К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
 Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе.
Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе. 
 Если такая проблема возникает, нужно вернуться к первому пункту.
Если такая проблема возникает, нужно вернуться к первому пункту. 

 При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.
При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны. Для удобства прямой угол обозначается уголком. Вот так:
Для удобства прямой угол обозначается уголком. Вот так:


 Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж. Запишите ребенка на бесплатный пробный урок в онлайн-школу Skysmart и попробуйте сами!
Запишите ребенка на бесплатный пробный урок в онлайн-школу Skysmart и попробуйте сами! С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.



 Для обозначения используется специальный символ – △.
Для обозначения используется специальный символ – △. е. меньше 90°.
е. меньше 90°. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:
Для удобства примем стандартные обозначения сторон – a, b и с. Тогда: Выясните, могут ли они образовать треугольник.
Выясните, могут ли они образовать треугольник.

 ..
.. точка находится (лежит) на прямой, или прямая проходит (проведена) через точку;
точка находится (лежит) на прямой, или прямая проходит (проведена) через точку;
 Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и закончить уравнение реакций онлайн калькулятор. Просто введите задачу в окошко и нажмите
«решить» здесь (например, ионное уравнение онлайн калькулятор).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и закончить уравнение реакций онлайн калькулятор. Просто введите задачу в окошко и нажмите
«решить» здесь (например, ионное уравнение онлайн калькулятор). Дорога шла по крутому берегу Яика. Река еще не замерзала, и ее свинцовые волны грустно чернели в однообразных берегах, покрытых белым снегом. За ними простирались киргизские степи. Я погрузился в размышления, большею частию печальные. Гарнизонная жизнь мало имела для меня привлекательности. Я старался вообразить себе капитана Миронова, моего будущего начальника, и представлял его строгим, сердитым стариком, не знающим ничего, кроме своей службы, и готовым за всякую безделицу сажать меня под арест на хлеб и на воду. Между тем начало смеркаться. Мы ехали довольно скоро. «Далече ли до крепости?» — спросил я у своего ямщика. «Недалече, — отвечал он. — Вон уж видна». Я глядел во все стороны, ожидая увидеть грозные бастионы, башни и вал; но ничего не видал, кроме деревушки, окруженной бревенчатым забором. С одной стороны стояли три или четыре скирда сена, полузанесенные снегом; с другой — скривившаяся мельница, с лубочными крыльями, лениво опущенными. «Где же крепость?» — спросил я с удивлением.
Дорога шла по крутому берегу Яика. Река еще не замерзала, и ее свинцовые волны грустно чернели в однообразных берегах, покрытых белым снегом. За ними простирались киргизские степи. Я погрузился в размышления, большею частию печальные. Гарнизонная жизнь мало имела для меня привлекательности. Я старался вообразить себе капитана Миронова, моего будущего начальника, и представлял его строгим, сердитым стариком, не знающим ничего, кроме своей службы, и готовым за всякую безделицу сажать меня под арест на хлеб и на воду. Между тем начало смеркаться. Мы ехали довольно скоро. «Далече ли до крепости?» — спросил я у своего ямщика. «Недалече, — отвечал он. — Вон уж видна». Я глядел во все стороны, ожидая увидеть грозные бастионы, башни и вал; но ничего не видал, кроме деревушки, окруженной бревенчатым забором. С одной стороны стояли три или четыре скирда сена, полузанесенные снегом; с другой — скривившаяся мельница, с лубочными крыльями, лениво опущенными. «Где же крепость?» — спросил я с удивлением. «Да вот она», — отвечал ямщик, указывая на деревушку, и с этим словом мы в нее въехали.
«Да вот она», — отвечал ямщик, указывая на деревушку, и с этим словом мы в нее въехали. Русский язык, 5 класс.
Русский язык, 5 класс. И/Ы после Ц
И/Ы после Ц

 Такие слова надо запомнить или проверять по словарю.
Такие слова надо запомнить или проверять по словарю. Прочитай правила, рассмотри примеры.
Прочитай правила, рассмотри примеры.
 Единственное, что можно сделать, это найти нужное слово в словаре. Так советуют все учебники. Но словаря может не оказаться под рукой. Значит, такие слова нужно заучивать. Чем больше таких слов ты будешь знать, тем лучше. Постепенно у тебя разовьётся интуиция, и слова с непроверяемыми гласными не будут создавать трудности. Итак, несмотря на кажущуюся глупость, это правило очень полезно!
Единственное, что можно сделать, это найти нужное слово в словаре. Так советуют все учебники. Но словаря может не оказаться под рукой. Значит, такие слова нужно заучивать. Чем больше таких слов ты будешь знать, тем лучше. Постепенно у тебя разовьётся интуиция, и слова с непроверяемыми гласными не будут создавать трудности. Итак, несмотря на кажущуюся глупость, это правило очень полезно! И с легкостью выполнить задание А13.
И с легкостью выполнить задание А13.

 С хорошими результатами будет легче поступить в любой вуз. Данный раздел поможет вам приблизиться к этой цели. Здесь есть всё необходимое для успешной подготовки. Также данный раздел нередко используется учащимися вузов и ссузов.
С хорошими результатами будет легче поступить в любой вуз. Данный раздел поможет вам приблизиться к этой цели. Здесь есть всё необходимое для успешной подготовки. Также данный раздел нередко используется учащимися вузов и ссузов. Изначально эта программа вводилась как эксперимент и уже в первые месяцы тестирования зарекомендовала себя как объективную систему тестирования выпускников. Так что же все-таки представляет из себя этот ЕГЭ?
Изначально эта программа вводилась как эксперимент и уже в первые месяцы тестирования зарекомендовала себя как объективную систему тестирования выпускников. Так что же все-таки представляет из себя этот ЕГЭ? Должен сказать, что квалифицированная подготовка дает свои, далеко не плохие, результаты. Но те, кто уже прошел через это «страшное» испытание, утверждают, что для учеников даже со средними оценками экзамен не должен показаться слишком уж сложным, по крайней мере невыполнимым. Нужно лишь приложить немного усилий, а именно выучить хотя бы самые важные правила, пройденные за весь учебный период, ведь если вы не ленились и хотя бы иногда открывали учебники, то что-то вы должны знать. Очень хорошо помогают различные книжки, предлагающие собственные примеры заданий, примеры их решений и дающие различные рекомендации по сдаче экзамена. Подобной литературой буквально завалены все книжные магазины, причем стоят они очень дешево. Для кого-то, естественно, и этого будет недостаточно. В таких случаях я бы рекомендовал обращаться к своим учителям, большинство из которых готовы помогать бесплатно. Я знаю, что во многих школах учителя предлагают организовывать собственные школьные подготовительные курсы за небольшую плату, а то и вовсе бесплатно.
Должен сказать, что квалифицированная подготовка дает свои, далеко не плохие, результаты. Но те, кто уже прошел через это «страшное» испытание, утверждают, что для учеников даже со средними оценками экзамен не должен показаться слишком уж сложным, по крайней мере невыполнимым. Нужно лишь приложить немного усилий, а именно выучить хотя бы самые важные правила, пройденные за весь учебный период, ведь если вы не ленились и хотя бы иногда открывали учебники, то что-то вы должны знать. Очень хорошо помогают различные книжки, предлагающие собственные примеры заданий, примеры их решений и дающие различные рекомендации по сдаче экзамена. Подобной литературой буквально завалены все книжные магазины, причем стоят они очень дешево. Для кого-то, естественно, и этого будет недостаточно. В таких случаях я бы рекомендовал обращаться к своим учителям, большинство из которых готовы помогать бесплатно. Я знаю, что во многих школах учителя предлагают организовывать собственные школьные подготовительные курсы за небольшую плату, а то и вовсе бесплатно.


 Я целую чистые, святые руки твои!
Я целую чистые, святые руки твои!
 ШОВ
ШОВ


 Видимо, слово ветер словарное и
проверить написание второго гласного надо в орфографическом словаре, ну
и, конечно, запомнить. Ну вот, во втором слоге тоже надо писать букву Е. Ве-те-рок,
ве-тер.
Видимо, слово ветер словарное и
проверить написание второго гласного надо в орфографическом словаре, ну
и, конечно, запомнить. Ну вот, во втором слоге тоже надо писать букву Е. Ве-те-рок,
ве-тер. Что это за слова такие? Сейчас
расскажу.
Что это за слова такие? Сейчас
расскажу.
 Так что не все старославянские слова ушли из
нашего языка.
Так что не все старославянские слова ушли из
нашего языка. Далее предлагается система упражнений на различение гласных и согласных звуков (букв), которые могут смешиваться в устной и письменной речи ребёнка.
Далее предлагается система упражнений на различение гласных и согласных звуков (букв), которые могут смешиваться в устной и письменной речи ребёнка. Канцтовары Brauberg
Канцтовары Brauberg Вот некоторые из моих любимых стратегий обучения швам.
Вот некоторые из моих любимых стратегий обучения швам.
 Выберите слово, которое есть в устном словарном запасе вашего ребенка, например, словесную задачу.
Выберите слово, которое есть в устном словарном запасе вашего ребенка, например, словесную задачу.  С практикой и этими стратегиями ваш ребенок сможет понять суть слова!
С практикой и этими стратегиями ваш ребенок сможет понять суть слова!
 Задача ученика состоит в том, чтобы сначала скопировать слова, а затем написать их независимо, без точек, прорабатывая слово по слогам за раз и проговаривая каждый слог.
Задача ученика состоит в том, чтобы сначала скопировать слова, а затем написать их независимо, без точек, прорабатывая слово по слогам за раз и проговаривая каждый слог. Произношение слов с ударением на правильные слоги поможет вам улучшить разговорный английский, упростит понимание ваших предложений и поможет вам больше походить на носителя языка.
Произношение слов с ударением на правильные слоги поможет вам улучшить разговорный английский, упростит понимание ваших предложений и поможет вам больше походить на носителя языка. В слове всегда есть один или несколько ударных слогов, и это особое ударение помогает словам и предложениям развивать свой собственный ритм.
В слове всегда есть один или несколько ударных слогов, и это особое ударение помогает словам и предложениям развивать свой собственный ритм. Правильное ударение в английском языке имеет решающее значение для быстрого и точного понимания слова.
Правильное ударение в английском языке имеет решающее значение для быстрого и точного понимания слова.
 Так часто бывает со словами, оканчивающимися на «изм».
Так часто бывает со словами, оканчивающимися на «изм».
 Это может привести к забавным недоразумениям и неприятным разговорам!
Это может привести к забавным недоразумениям и неприятным разговорам!
 Его также можно использовать, когда речь идет о представлении теле- или радиопрограммы (т. Е. Быть «ведущим»).
Его также можно использовать, когда речь идет о представлении теле- или радиопрограммы (т. Е. Быть «ведущим»).
 Это означает, что нужно решить, на каких словах сделать ударение как на части предложения в целом. Подчеркнутые слоги могут создавать в предложении отличительный ритмический узор.Вот как образцы ударения в английском языке связаны с ритмом английского языка и помогают создавать «музыку» языка.
Это означает, что нужно решить, на каких словах сделать ударение как на части предложения в целом. Подчеркнутые слоги могут создавать в предложении отличительный ритмический узор.Вот как образцы ударения в английском языке связаны с ритмом английского языка и помогают создавать «музыку» языка. Содержательные слова обычно подчеркнуты.
Содержательные слова обычно подчеркнуты. Это может быть правдой, а может и неправдой — дело в том, что Я, , никогда этого не говорил — сказал кто-то другой.
Это может быть правдой, а может и неправдой — дело в том, что Я, , никогда этого не говорил — сказал кто-то другой.
 Грамматики называют это «шва» или / ə /.
Грамматики называют это «шва» или / ə /. 


 (для поступления весной 2020 г.) или 20 апреля 2020 г. (для поступления осенью). 2020).
(для поступления весной 2020 г.) или 20 апреля 2020 г. (для поступления осенью). 2020). Говоря словами Лысенковой С.Н. –
«опора, схема – опора, опорный лист – это выводы,
которые рождаются в момент объяснения,
оформленные в виде таблиц, карточек, наборного
полотна, чертежа, рисунка». У. Е. Минтоном было
отмечено, что существенные признаки и связи,
зафиксированные в модели (опоре), становятся
наглядными для учащихся тогда, когда эти
признаки, связи были выделены самими детьми в их
собственном действии, т. е. когда они сами
участвовали в создании модели (опоры). В
противном случае можно наблюдать непринятие,
опора не выполняет ту роль, которая на нее
возложена. По мнению Е. А. Мельниковой, «опора –
это зрительный образ, выражающий знание в
предельно абстрактном, концентрированном виде».
Говоря словами Лысенковой С.Н. –
«опора, схема – опора, опорный лист – это выводы,
которые рождаются в момент объяснения,
оформленные в виде таблиц, карточек, наборного
полотна, чертежа, рисунка». У. Е. Минтоном было
отмечено, что существенные признаки и связи,
зафиксированные в модели (опоре), становятся
наглядными для учащихся тогда, когда эти
признаки, связи были выделены самими детьми в их
собственном действии, т. е. когда они сами
участвовали в создании модели (опоры). В
противном случае можно наблюдать непринятие,
опора не выполняет ту роль, которая на нее
возложена. По мнению Е. А. Мельниковой, «опора –
это зрительный образ, выражающий знание в
предельно абстрактном, концентрированном виде». Но все это не
должно быть фоном, наглядностью ради
наглядности. Акцент делается на их
целесообразность и значимость на этапе
«открытия знаний», первичного закрепления,
рефлексии. Ученик должен пропустить через себя
суть явления или знания и опираясь в дальнейшем
на абстрактный образ (алгоритм) продвигаться в
познании, выполнять самоконтроль.
Но все это не
должно быть фоном, наглядностью ради
наглядности. Акцент делается на их
целесообразность и значимость на этапе
«открытия знаний», первичного закрепления,
рефлексии. Ученик должен пропустить через себя
суть явления или знания и опираясь в дальнейшем
на абстрактный образ (алгоритм) продвигаться в
познании, выполнять самоконтроль.
 Карточки
– вопросы крепим магнитами на доске, а
графические обозначения выполняем мелом
(маркером). Можно выполнять эти упражнения,
выкладывая карточки на парте или пленке.
Предлагаю различные виды заданий:
Карточки
– вопросы крепим магнитами на доске, а
графические обозначения выполняем мелом
(маркером). Можно выполнять эти упражнения,
выкладывая карточки на парте или пленке.
Предлагаю различные виды заданий: А. Песняевой о представлении текста в виде
детской пирамидки. Ребята эту идею восприняли на
«ура». После первого (вводного) урока мы отошли от
самой игрушки и заменили ее опорой с
изображением пирамидки. Так как при изучении
темы «Текст» выделяются 3 основные части: начало,
середина и концовка, то ученики предложили
дополнить опору этими сведениями. Эта опора
используется и на уроках риторики при изучении
раздела «Текст».
А. Песняевой о представлении текста в виде
детской пирамидки. Ребята эту идею восприняли на
«ура». После первого (вводного) урока мы отошли от
самой игрушки и заменили ее опорой с
изображением пирамидки. Так как при изучении
темы «Текст» выделяются 3 основные части: начало,
середина и концовка, то ученики предложили
дополнить опору этими сведениями. Эта опора
используется и на уроках риторики при изучении
раздела «Текст». Использую эту опору
так же для обогащения и расширения словарного
запаса учащихся, при составлении загадок,
описании предметов, распространении
предложений, составлении словосочетаний и т. п.
Использую эту опору
так же для обогащения и расширения словарного
запаса учащихся, при составлении загадок,
описании предметов, распространении
предложений, составлении словосочетаний и т. п. Дополняем этой
информацией опору 1 класса, и применяем схему в
дальнейшей работе по теме.
Дополняем этой
информацией опору 1 класса, и применяем схему в
дальнейшей работе по теме.
 д.
д. д.
д. Надеюсь, что мой опыт поможет коллегам в их
стремлении разнообразить школьные будни,
сделать урок продуктивным, интересным и
задействовать всех учащихся как субъектов
процесса собственного обучения.
Надеюсь, что мой опыт поможет коллегам в их
стремлении разнообразить школьные будни,
сделать урок продуктивным, интересным и
задействовать всех учащихся как субъектов
процесса собственного обучения.
 [О, О, О ____ =====] или [O, O, O].
[О, О, О ____ =====] или [O, O, O]. Схема демонстрирует учащимся, что слова следует писать раздельно друг от друга, и можно сосчитать их количество. Систематически практикуясь в их составлении, дети четко уясняют следующую парадигму:
Схема демонстрирует учащимся, что слова следует писать раздельно друг от друга, и можно сосчитать их количество. Систематически практикуясь в их составлении, дети четко уясняют следующую парадигму: Тема не совсем простая. Нужно выработать необходимые навыки, чтобы не совершать ошибок при написании. Схема, как наглядное пособие, способствует закреплению полученных знаний.
Тема не совсем простая. Нужно выработать необходимые навыки, чтобы не совершать ошибок при написании. Схема, как наглядное пособие, способствует закреплению полученных знаний.
 I____ _ I____ ____ __ ____ _ ____.
I____ _ I____ ____ __ ____ _ ____. ру — домашняя школа онлайн.
ру — домашняя школа онлайн. Она помогает разобраться в сути предмета. Например, верно и четко составленная схема позволяет на уроках математики легко и быстро решить любую задачу. Точно также правильно составленная схема предложения помогает увидеть части сложного предложения, отличить сложное предложение от простого с однородными членами и грамотно расставить запятые.
Она помогает разобраться в сути предмета. Например, верно и четко составленная схема позволяет на уроках математики легко и быстро решить любую задачу. Точно также правильно составленная схема предложения помогает увидеть части сложного предложения, отличить сложное предложение от простого с однородными членами и грамотно расставить запятые. Если однородными являются главные члены, то внутри кружка мы рисуем соответствующие линии. Не забудьте поставить запятые между однородными членами. Рассмотрим примеры.
Если однородными являются главные члены, то внутри кружка мы рисуем соответствующие линии. Не забудьте поставить запятые между однородными членами. Рассмотрим примеры. Для этого нужно схему внимательно рассмотреть, определить, какое предложение нужно составить: простое, с однородными членами или сложное. Далее нужно увидеть порядок следования членов предложения, указанных на схеме, а также обратить внимание на знаки препинания.
Для этого нужно схему внимательно рассмотреть, определить, какое предложение нужно составить: простое, с однородными членами или сложное. Далее нужно увидеть порядок следования членов предложения, указанных на схеме, а также обратить внимание на знаки препинания. При составлении схемы сложного предложения каждая часть заключается в отдельные квадратные скобки, между ними ставятся запятые и союзы. После схемы ставится знак препинания, соответствующий концу данного предложения.
При составлении схемы сложного предложения каждая часть заключается в отдельные квадратные скобки, между ними ставятся запятые и союзы. После схемы ставится знак препинания, соответствующий концу данного предложения.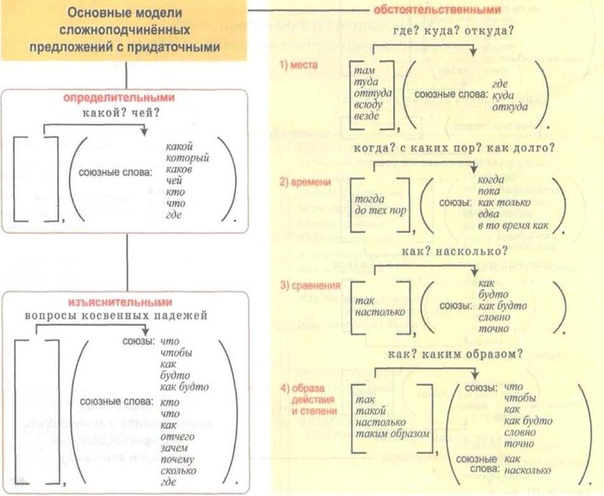
 Отвечает на вопросы «когда?», «как?», «где?», «почему?», «зачем?». Обстоятельство носит такое название, потому что в предложении оно указывает на различные цели, причины, места, время и другое, то есть показывает самые различные обстоятельства, которые указывают на происходящее в предложении. Обстоятельство подчеркивается снизу точкой — тире.
Отвечает на вопросы «когда?», «как?», «где?», «почему?», «зачем?». Обстоятельство носит такое название, потому что в предложении оно указывает на различные цели, причины, места, время и другое, то есть показывает самые различные обстоятельства, которые указывают на происходящее в предложении. Обстоятельство подчеркивается снизу точкой — тире.


