Как правильно готовиться к егэ по биологии: Как подготовиться к ЕГЭ по биологии | Фоксфорд.Медиа
Как подготовиться к ЕГЭ по биологии | Фоксфорд.Медиа
Биология относится к числу сложных предметов для сдачи ЕГЭ. К экзамену нужно усвоить примерно 350 тем, которые в школе изучают на протяжении 6 лет. Дело не только в объёме материала: авторы учебников придерживаются разных точек зрения, например, в вопросах эволюции, а в ЕГЭ требуется определённый ответ.
Чтобы сдать экзамен на 90 и более баллов, нужно глубоко изучать предмет и заниматься самостоятельно несколько раз в неделю. Расскажу, что необходимо учитывать во время подготовки и на самом экзамене.
Коварные синонимы. Трудности у школьников могут возникнуть уже в первом задании, которое оценивается всего в 1 первичный балл. Суть задания: в схему, текст или таблицу нужно вставить пропущенный термин. Проблема в том, что в биологии много синонимов, и не всегда ясно, какой соответствует ответу из базы ЕГЭ.
Ещё один коварный момент — ошибки в написании термина. Хотя распространённые орфографические ошибки не учитываются в ЕГЭ по биологии, термины нужно писать точно. Если верный ответ — «комбинативная», то вариант «комбинационная» компьютер не засчитает.
Пример задания № 1 из демоварианта ЕГЭ 2019 годаУгадать не получится. В вопросах с несколькими вариантами ответов предлагается найти 2 ответа из 5 или 3 из 6. Здесь угадать не получится, нужно знать. Этот тип заданий оценивается в 2 балла.
Нужно учитывать специфику ЕГЭ. На экзамене регулярно встречаются неоднозначные задания на эволюцию, аналогичные и гомологичные органы у животных и растений. Данные современных научных исследований могут быть противоречивыми, поэтому выпускникам необходимо заранее готовиться к «подводным камням» ЕГЭ.
Нужно решить как можно больше вариантов задач и понять логику ответов, которых ждут разработчики КИМов.
Ответы на задания первой части проверяются автоматически: компьютер сравнивает их с верными образцами из базы данных. При получении результатов экзамена можно узнать, в каких заданиях ученик допустил ошибки в работе, но нельзя увидеть эталонный ответ.
Многие боятся заданий второй части, хотя она более предсказуемая. Знаю ребят, которые в прошлом году получили максимум баллов за задания 22–28, а в первой части не добрали десять баллов.
Ответы второй части проверяют люди. С одной стороны, это минус — человеческий фактор, с другой — гораздо больше зависит от ученика, полноты и ясности его ответа.
Лучше писать подробно. Обычно максимальный балл получает ученик, который продемонстрировал свои знания в развёрнутом ответе: не допустил ошибок и упомянул все значимые аспекты. Здесь важно не лениться, принцип «краткость — сестра таланта» в ЕГЭ по биологии неуместен.
Иногда старшеклассники смотрят типовые ответы на задания второй части в интернете. Сайты, которые якобы имеют доступ к базе ответов ЕГЭ, предлагают в качестве образцов лаконичные ответы, в которых главное затрагивается вскользь. Ученики их запоминают и потом пишут по одному слову на каждое утверждение там, где требуется подробный комментарий. В результате выпускники получают меньше баллов, поскольку в развёрнутом ответе было бы легче упомянуть важные тезисы.
Важно писать подробно и при этом без биологических ошибок. Если ученик пишет подробное пояснение, но сомневается в каком-то моменте, лучше его не писать вообще, чем потерять балл за «биологическую неточность».
Не стоит спешить. Торопливость и беглый просмотр заданий тоже вредят экзаменуемым. Школьникам кажется, что они видели вопрос и знают, как писать ответ. Если не вчитываться в формулировки заданий, легко дать ответ не на тот вопрос или неверно истолковать вопрос, не заметив частицу «не», например.
Для решения пригодится математика. Во многих заданиях требуется что-нибудь посчитать, умножить или поделить. Казалось бы, элементарные математические навыки, но из-за них у школьников случаются обидные «проколы». При выполнении расчётных задач лучше не лениться и выполнять вычисления на черновике.
Придётся разобраться с фотосинтезом. В пятом, девятом и одиннадцатом классе ученики совершают одну и ту же ошибку. Все знают, что живые организмы дышат кислородом, но стоит спросить о растениях, отвечают — углекислым газом. Путаница начинается в начальной школе, когда ученики запоминают, что растения поглощают углекислый газ. Верно, они его поглощают в процессе фотосинтеза («воздушного питания»), а дышат кислородом, как и другие организмы.
Нужно быть готовым к синтезу РНК. В задании № 27 в 90% случаев спрашивают про синтез белка. Школьники решают много таких заданий и отлично справляются с ними на ЕГЭ. Однако ученики забывают про оставшиеся 10% заданий, когда в ДНК кодируется не белок, а, например, транспортная РНК. При виде «незнакомого» задания выпускник паникует. Чтобы такого не случилось, нужно помнить про синтез нуклеиновых кислот: все РНК синтезируются на матрице ДНК (процесс транскрипции) — эту тему нужно обязательно повторить.
Пример задания № 27 из демоварианта ЕГЭ 2019 годаЗачем заниматься с преподавателем. Биология развивается быстро, поэтому учебники постоянно устаревают. Когда в ЕГЭ встречается формулировка «По современным данным учёных», стоит задуматься: вопрос про актуальное состояние науки или открытия тридцатилетней давности. Часто верным считается ответ из устаревшего учебника, и школьники, которые хорошо осведомлены о новых открытиях, теряют баллы. Избежать такой обидной ошибки поможет опытный преподаватель, который скажет, что конкретно нужно писать в подобных случаях.
Подготовку лучше всего начинать в десятом классе. Первый год стоит посвятить теоретической подготовке, а в одиннадцатом классе тренироваться выполнять задания и осваивать формат ЕГЭ.
Пособий по биологии много, но все они неидеальны, ведь у каждого автора своя сфера научных интересов. К тому же нельзя шесть лет обучения вложить в одну книжку. Редкий биолог одинаково хорошо разбирается во всех разделах науки, поэтому одним темам в пособии уделяется больше внимания, другим меньше.
Выпускникам рекомендую присмотреться к «Биологии для поступающих в вузы» Габриэля Билича и Валерия Крыжановского. Тем, кто будет проходить дополнительные вступительные испытания по биологии, например, в МГУ — пригодится трёхтомник Г. Билича и В. Крыжановского «Биология. Полный курс». Также стоит обратить внимание на пособия Д.А. Соловкова и Т.А. Шустановой.
Советую полистать книги в магазине и посмотреть, как у разных авторов объясняется самая непонятная школьнику тема. Если материал изложен доходчиво: «О, я понял, наконец, этот метаболизм!» — то можно брать учебник этого автора.
Если какая-то тема никак не даётся, полезно посмотреть короткие обучающие видео в интернете, причём чем больше — тем лучше, и неважно, на каком языке. Мейозы, митозы, метаболизм — всё это наглядно представлено в анимированных видеороликах на ютьюбе.
Если школьник готовится сам, нужно читать пособия, тренироваться решать задания и смотреть в интернете видеоразборы с преподавателями. При должном старании можно подготовиться к экзамену без посторонней помощи и денежных вложений. Однако придётся тратить более шести часов в неделю на изучение материалов и практические задания.
Если школьник готовится к ЕГЭ в группе, то его задача несколько упрощается. Есть возможность обмениваться идеями на занятиях и обсуждать задания в интернете вне уроков: кто-то поделится ссылкой на полезное видео, кто-то — удачным приёмом запоминания информации. Преподаватель научит, как правильно писать ответы на неоднозначные вопросы и подскажет, как распределить время на экзамене с учётом индивидуальных особенностей учеников.
Экзамен длится 3,5 часа и состоит из двух частей:
- часть 1 содержит 21 задание с кратким ответом,
- часть 2 — 7 заданий с развёрнутым ответом.
Лучше спланировать работу заранее: если нужно 30–60 минут на «раскачку», стоит начать с простых заданий. Если пик работоспособности ученика в самом начале экзамена — нужно сперва выполнять более сложные.
В ответах на задания второй части нужно понимать, что работу проверяет живой человек.
Возможно, это уставший преподаватель, который оценил уже сотню работ. Если ответы написаны чисто, грамотно, по пунктам, а не сплошным текстом, проверяющий будет благодарен и, возможно, где-то «не заметит» ошибки. Поэтому утверждения в ответе стоит пронумеровать, а где-то — нарисовать схему в помощь проверяющему.
Чтобы избежать досадных ошибок, необходимо проверить себя и перед тем, как заносить ответы в бланк, и после окончания работы. Старшеклассникам трудно выполнять самопроверку, но это необходимо. Например, ученики иногда пропускают частицу «не» в заданиях: вместо «кому не свойственно определённое поведение» пишут, кому оно свойственно.
1. Для решения заданий на ЕГЭ по биологии нужно проработать много материала, поэтому лучше начинать подготовку за два года: в 10 классе изучить теорию, в 11 — решать задания из демовариантов.
2. Лучше заниматься три раза в неделю по часу, чем один раз по три часа. При регулярном повторении материала информация запоминается прочнее.
3. В ЕГЭ по биологии порой за правильный ответ считаются устаревшие данные или спорная теория. Как следует отвечать в каждом задании, подскажет опытный преподаватель.
4. Учебник нужно подбирать индивидуально, самые трудные темы должны быть изложены понятно.
5. Развёрнутые ответы стоит писать подробно и чётко, чтобы проверяющему не приходилось расшифровывать почерк и было сразу ясно, что школьник имел в виду.
как сдать ЕГЭ по биологии на 100 баллов — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Василий Рогожин,
директор образовательного ЕГЭ-центра «Парамита»,
эксперт ЕГЭ по биологии и химии
В чем, по-вашему, самая большая сложность экзамена по биологии?
Основная сложность экзамена по биологии заключается в большом объеме школьного курса: биология как предмет начинается в школе с 5-6 класса, а до этого ученики изучают биологическую науку в рамках школьных предметов «Окружающий мир» и «Природоведение» в начальной школе. То есть проверке на экзамене подлежат знания по биологии, полученные минимум за шесть лет обучения в школе.
Вторая проблема связана с самой структурой ЕГЭ. Дело в том, что зачастую наличие знаний по предмету еще не гарантирует успешную сдачу экзамена. Писать ЕГЭ на высокие баллы — это отдельная наука. Кроме того, год от года структура экзамена меняется. Так, в 2017 году произошли очередные существенные изменения — в целом, надо признать, в лучшую сторону. Задания стали более объективными, вероятность простого угадывания правильного ответа снижается. Но дело в том, что школьная программа по биологии сегодня основана на знаниях, актуальных для конца XX века. За 30 лет содержание большинства школьных учебников по биологии практически не изменилось, притом что биологическая наука — одна из самых быстро развивающихся сегодня.
И вот получается, что ребенок, который занимается углубленно биологией: по современным научным пособиям, с педагогом, который идет в ногу с наукой и дает актуальные знания, на экзамене сталкивается с серьезной проблемой. Он отвечает на вопросы ЕГЭ с точки зрения современной науки, а в критериях оценивания может быть заложен эталон, который базируется на знаниях 20 или 30-летней давности. В этом случае талантливые выпускники могут пострадать от своих же знаний и получить меньше баллов, чем тот, кто владеет вполне заурядными и не всегда актуальными знаниями. Победители биологических олимпиад, в том числе и Всероссийской олимпиады школьников, редко получают на ЕГЭ 100 баллов. И среди учеников, которые приходят в ЕГЭ-центр «Парамита», таких примеров много.
Какие темы вызывают обычно наибольшую сложность?
Традиционно самые сложные разделы в биологии — те, что являются наименее наглядными. Это молекулярная биология: репликация ДНК, фотосинтез, реакции энергетического обмена, биосинтез белка и т. д. Ребенок не видит в повседневной жизни молекул, из которых построено все живое, — в отличие от животных, растений и собственного тела, которые можно наблюдать каждый день. В случае с молекулами первичный опыт невозможен без специальных методов, которые школьнику, конечно, недоступны. Большинство ошибок в ЕГЭ делают именно в этих темах.
Еще один проблемный раздел — ботаника. Ее изучают в 6-7 классе школы, а к 11 классу многое уже забывается. Усвоить перед экзаменом эту тему с азов очень сложно. Ну и, кроме того, растения очень далеки от нас с эволюционной точки зрения — гораздо дальше, чем, например, животные. Поэтому для растений сложно провести аналогии со строением человеческого тела, у растительного мира много уникальных особенностей.
В каких заданиях чаще делают ошибки или выполняют неправильно? На что стоит обратить особое внимание?
Общая проблема: большинство детей не умеют внимательно читать формулировку задания, не вчитываются, могут пропустить, например, частицу «не» и вместо того, чтобы выбрать нехарактерные особенности строения пресноводной гидры, выбирают, наоборот, характерные. Главное наставление — читать внимательно формулировку задания и, прежде чем ответить, убедиться, что правильно понял то, что от тебя требуется.
Второй общий совет: в заданиях, где есть выбор ответов, прежде чем выбирать из предложенных, попытайтесь ответить на вопрос самостоятельно, а потом уже найти наиболее подходящие или совпадающие варианты. При таком приеме вероятность ошибки резко падает.
В 2016 году в ЕГЭ по биологии было 40 заданий, в этом году количество сократили до 28. А время на выполнение увеличили — с 3 до 3,5 часов. С одной стороны, это хорошо, есть возможность все внимательно проверить. С другой стороны, 3,5 часа умственного напряжения — это непосильная для ребенка нагрузка. Совет: стараться по возможности отвечать на вопросы сразу, уложиться в первые 1,5-2 часа, когда эффективность работы нервной системы будет максимальной.
Что же до заданий, то в 2017 году первая часть — вопросы с № 1 по № 21, где нужно дать краткий ответ или выбрать несколько вариантов из предложенных, были существенно изменены и дополнены заданиями нового формата. В первой части заданий ЕГЭ не осталось вопросов с одновариантным выбором ответа, но появились такие, где надо выбрать, например, два варианта из пяти. И это тоже указано в формулировке вопроса — важно это прочитать и обратить внимание.
Появились в этом году и совершенно уникальные типы вопросов, которых раньше не было:
- № 1 — задание со схемой или таблицей, где пропущен один элемент, который нужно вычислить на основе имеющихся данных и вписать словом. Пример можно посмотреть в демоверсии на сайте ФИПИ.
- № 6 — нужно решить несложную генетическую задачу и записать ответ — соотношение фенотипов или генотипов потомков — в виде последовательности цифр.
- № 9 и № 15 — оригинальные задания, где представлен текст, из которого нужно выбрать предложения, которые соответствуют определенным критериям.
- № 20 — абсолютно новое задание в виде таблицы, где пропущены несколько ячеек. Как и в № 1, здесь нужно найти связь между представленными элементами и вписать недостающие.
- № 21 — работа с графической информацией: графиком или таблицей. Их нужно проанализировать и выбрать из списка утверждений верные, а затем подобрать соответствующие выводы. Верных вариантов в этом задании — два из пяти предложенных.
Какой тип вопросов считается самым сложным? Как по ним лучше тренироваться? Какие вопросы дают больше всего баллов?
Самые сложные вопросы — с № 22 по № 28: те, где требуется развернутый ответ. За них же можно получить максимальное количество баллов — 2 или даже 3 (с № 23 по № 28). Общая проблема тут заключается в том, что современные школьники не умеют литературно излагать свои мысли, а ведь в случае с биологией это тоже имеет значение. Они пропускают в ответах подлежащее или сказуемое, и в результате смысл предложения совершенно теряется. Порой понять, какую мысль хотел донести автор, совершенно невозможно. Совет: перечитывайте то, что вы написали.
Не допускайте биологических ошибок. Даже если ответы на вопрос даны верно, но в описании есть неточности или ошибки, могут снять балл. Третий совет: отвечайте на вопрос как можно более подробно и всесторонне, давайте определение биологическим терминам, даже если в задании это не прописано.
Традиционно сложными заданиями являются: № 27 — задача по цитологии. С ней, по традиции, справляются очень немногие — часто путают типы генов в ДНК, о которых идет речь в задании (белковый, тРНКовый или рРНКовый ген).
№ 28 — генетическая задача. Совет такой: в схеме решения генетической задачи нужно всегда подписывать фенотипы, даже если в задании это не указано.
По каким общедоступным источникам можно готовиться к экзамену?
Во-первых, это материалы, которые представлены на сайте ФИПИ: демоверсии, банк заданий прошлых лет (задания с № 22 по № 28 остались без изменений). На сайте ЕГЭ-центра «Парамита», на странице «Видеоуроки» мы, например, собрали видеоматериалы — короткие ролики по разным темам, в том числе по самым сложным. Это не только полезный, но и интересный для школьника материал. Некоторые видеоролики, в частности по молекулярной биологии и цитологии, выпущены ведущими зарубежными вузами, и, чтобы не возникало трудностей с переводом, закадровый текст мы перевели на русский язык и опубликовали перевод сразу под роликом.
Что касается учебников, то мы готовим слушателей по пособию А.В. Пименова «Биология. Полный курс подготовки к ЕГЭ». В этом пособии довольно кратко, но глубоко изложен весь школьный курс биологии. Язык доступнен даже для тех, у кого уровень знаний минимальный. В учебнике отсутствуют фактические ошибки, поэтому ему можно всецело доверять. Книга была выпущена в 2014 году, и тираж тут же разошелся, поэтому на нашем сайте в разделе «Учебные материалы» можно найти ссылку на электронную версию, а также другие пособия по биологии, которые могут помочь при подготовке к ЕГЭ.
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Как готовиться к ЕГЭ по биологии. Эффективные стратегии подготовки
Статья В.Ю. Ярославцева
1. Курс биологии — это огромное количество фактического материала. Определения, новые понятия, законы и взаимосвязи между явлениями… Как же готовиться к ЕГЭ по биологии?
Известно, что процесс обучения делится на четыре этапа:
• постановка цели,
• действия по ее достижению,
• контроль,
• завершение процесса.
Возьмем понятие «хроматида». Выучить новое понятие – значит легко оперировать им и отвечать на любые вопросы в ЕГЭ, с ним связанные. Это цель.
С действиями – уже сложнее.
Некоторые много раз повторяют само слово, зубрят определение, ничего не представляя, не визуализируя. Они попусту тратят время.
Другие ярко представляют хроматиды, задают много вопросов о том, как они выглядят, где располагаются. Они хотят увидеть образы, раскрывающие смысл понятия. Эта стратегия эффективна в связи с тем, что она визуальная. Ее надо развивать.
О контроле. Как ученик понимает, что он усвоил понятие? — Отвечает на устные вопросы, в любых заданиях и тестах применяет новое знание.
Как завершается процесс освоения понятия? В итоге понятие должно быть логично встроено в систему знаний ученика. В сознании выстраиваются связи нового понятия — с другими, уже известными.
Я показываю ученикам наиболее эффективные стратегии запоминания. Результат — целостная картина и твердое знание предмета.
2. Знаете ли вы, что лучше всего запоминается? Правильно — то, что имеет эмоциональную окраску.
Поэтому на занятиях я организую яркие мозговые штурмы, дискуссии, интересные ситуации. Я выбираю лучшие задачи и задания по биологии, конструирую собственные методики активизации ученика, создаю атмосферу глубокой системной тренировки знаний.
Более того, ученики эмоционально воспринимают то, что они создали сами. Лучше всего запоминаются те таблицы и схемы, которые ученик создал сам. Как же гордятся ученики своими материалами!
Если сложный теоретический материал не только прочитан дома, но и преобразован в таблицу, схему — к нему особое отношение. Такие знания являются понятными, близкими, так как задействована личность ученика.
3. В биологии есть свой язык, своя терминология. Чтобы успешно сдать экзамен, надо уметь говорить с использованием биологических понятий.
К сожалению, в школах мало говорят. А если ученик не говорит — значит, не понимает полностью. Будут сложности с любыми осмысленными ответами, особенно в части «С».
Просто решать тесты — это вообще не подготовка к ЕГЭ, а самообман. Мы ориентированы на самые высокие результаты, поэтому на занятиях учимся аргументировать свое мнение, давать развернутые ответы на вопросы.
4. Как правильно делать домашнее задание?
В моей практике был ученик, который делал уроки и одновременно смотрел футбольные матчи. Такой ученик неосознанно ставил себе цель: «готовиться к ЕГЭ по биологии у телевизора». Эту цель он и осуществлял — пробегал глазами текст, бросал взгляд в телевизор, одновременно мог и поговорить по телефону. Но он был уверен, что делает домашнее задание!
Как же он себя контролировал? — Да никак. «Текст идет к концу, значит, все хорошо». Он завершал процесс, когда заканчивался текст.
Результат был нулевым, потому что стратегия ошибочна.
Цель надо поставить иначе. Сделать ее ясной и детальной. Читать текст в отдельной комнате, где тихо. Более того, читать нужно при полной концентрации — другие источники звука могут быть помехой. После чтения текста по биологии надо отвечать на вопросы, выполнять задания по пособию, работать с компьютерными программами. В реальности учиться можно лучше и быстрее, используя все каналы восприятия информации — зрительный канал, слуховой, а также эмоции.
Ты нашел то, что искал? Поделись с друзьями!
Читаем дальше: ЕГЭ по биологии. Советы репетитора и необходимая литература
Как подготовиться к ЕГЭ по биологии с нуля? С чего начать? Есть ли хорошие видеоуроки?
Окей, вам понадобится: 1. Кодификатор по биологии с сайта фипи. 2. Школьные учебники по биологии за 6-11 класс (мне нравится Пасечник для всего и Билич и Кржановский по анатомии, но сойдут вообще любые, по которым учатся в школах). Школьный учебник — ваш лучший друг, если учите с нуля. В егэ спрашивают все только по школьной программе, так что там не будет ничего лишнего, плюс написано все простым языком.
Когда вы посмотрели кодификатор, выбирайте любую тему и работайте над ней так: читаете в учебнике (лучше в двух разных) — учите это — отрабатываете на тех заданиях егэ, где она встречается — как бонус можете позже повторить ее по сборнику по подготовке к егэ типа Лернера.
В качестве доп материалов есть вот что:
- Сайт ЗЗуброминимум — я начинала готовиться с этого сайта, там 33 коротких конспекта на самые важные темы по биологии, хорошо для совсем начинающих, чтобы начать нарешивать тесты. На самом сайте написано: «Чтобы отвечать на половину вопросов ЕГЭ по биологии, надо зазубрить всего лишь 33 небольших конспекта.» В общем, он как-то придает уверенности.
! На этом же сайте есть очень важный раздел «вопросы, в которых дети чаще всего совершают ошибки». Изучите его внимательно! Я смотрела его незадолго до экзамена и мне _реально_ в егэ попалось несколько вопросов, которые там были разобраны.
http://bio-faq.ru/33ubrominimum.html
Сайт interneturok. Я его использую как дополнение к учебнику, чтобы закрепить материал. Там видео + текстовый конспект + тренажеры + тесты
Плейлист фоксфорда по биологии на ютьюбе. Многие темы очень хорошо разобраны
- Группы вконтакте просто, чтобы мелькали у вас в ленте, там публикуются разные вопросы, хорошо для практики
https://vk.com/ege_biology
https://vk.com/biology_100
https://vk.com/postupivmedclub
Как подготовиться к ЕГЭ по биологии: основные ошибки прошлых лет и сложные задания
ЕГЭ по биологии в 2020 году станет одним из последних экзаменов, он назначен на 20 июля. О типичных ошибках и секретах успешной сдачи итоговой аттестации нам рассказали председатель региональной предметной комиссии по биологии города Москвы, доктор биологических наук, профессор Татьяна Татаренко-Козмина и заместитель председателя, кандидат педагогических наук, доцент Ярославна Скворцова.
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
В чём особенности ЕГЭ по биологии в этом году?
Татьяна Татаренко-Козмина. В 2020 году структура и содержание экзаменационной работы не изменились, экзамен по-прежнему состоит из двух частей и включает в себя 28 заданий. В первой части содержится 21 тестовое задание с выбором правильного ответа, во второй части — семь заданий разного уровня сложности с полным развернутым ответом. Именно они позволяют выпускникам продемонстрировать высокий уровень подготовки по биологии.
Какие ошибки чаще всего допускают ученики на ЕГЭ по биологии?
Ярославна Скворцова. Если говорить о первой части экзамена, то обычно сложности возникают вследствие невнимательности при переносе ответа из черновика в бланк. Особенно можно отметить задание № 20, требующее дополнения недостающей информации в таблице. При этом буквы А, Б, В могут располагаться на разных уровнях таблицы, и при переносе ответа в бланк возникает обидная ошибка: верную цифру ученик ставит не под нужной буквой.
В задании № 1 и № 2 необходимо вписать слово или словосочетание. Очевидно, что биологический термин должен быть написан орфографически верно, иначе он не распознается при проверке и задание будет считаться неверно выполненным.
В задании № 6 ошибки в основном связаны с неправильным прочтением формулировки задания для решения простейшей генетической задачи. Вариантов записи ответа существует множество: соотношение фенотипов или генотипов в порядке возрастания или убывания, число получившихся фенотипов или генотипов, процентное соотношение. При выполнении задания необходимо быть крайне внимательным, подчеркивать ключевые слова и фразы, чтобы не допустить ошибок в записи ответа.
Еще одно задание на внимательность — № 11, на восстановление последовательности. Оно несложное по содержанию, но требует конкретной точки отсчета: либо с наименьшей, либо с наибольшей.
Последнее задание в первой части — № 21 — сложно тем, что нужно анализировать данные графика (или таблицы), а не искать верные или неверные утверждения. Во избежание ошибки необходимо обратить особое внимание на параметры по оси абсцисс (Х) и оси ординат (Y) или на название граф и столбцов в таблице.
Во второй части экзамена, как и в первой, важно внимательно читать формулировку задания до конца, подчеркивая и выделяя важные элементы. Любой ответ на задания второй части, особенно в заданиях № 25 и № 26, требует объяснений, при формулировке которых важно быть кратким и точным. За нее баллы не добавляются, а при наличии ошибок балл будет снижен, так как оценивается вся информация в ответе учащегося.
Не нужно писать ответ по принципу «напишу всё, что знаю»: это не добавит баллов
В задании № 23 важно работать с рисунком и строить ответ на основе информации, представленной на нем. В случае неверно определенного изображения весь ответ может быть оценен в 0 баллов.
В задании № 24 необходимо обратить внимание на название текста и в этом контексте исправлять ошибки, но не более трех предложений: за каждое лишнее исправление снимается балл. Кроме того, лучше переписать верно исправленное предложение целиком в бланк ответа.
При ответе на задания, как в первой, так и второй части, важно быть максимально внимательным, отвечать строго на поставленные вопросы, рассуждать и объяснять свой ответ.
Как эффективнее всего готовиться к ЕГЭ по биологии, чтобы получить высокие баллы?
Татьяна Татаренко-Козьмина. Одним из первых условий в подготовке к экзамену остаются глубокие знания разделов биологии и умение их применить, объясняя то или иное биологическое явление. Необходимы систематические занятия по изучению и запоминанию, повторению пройденного материала. Нужно хорошо знать все разделы школьного курса биологии, объем и содержание которых указаны в кодификаторе к экзамену.
В подготовке к ЕГЭ необходимы регулярные тренировки по выполнению экзаменационных заданий. Для этого существуют сборники тренировочных вариантов, а на сайте ФИПИ размещен открытый банк заданий ЕГЭ. Их нужно не просто просматривать, а вчитываться, обращая внимание на детали задания и поставленные к нему вопросы.
Ярославна Скворцова. Дистанционная работа при правильной организации позволяет планомерно и регулярно готовиться к экзаменам. У выпускника появляется возможность готовиться по собственному плану, у учителя и родителей — отслеживать индивидуальную траекторию подготовки, видеть в режиме реального времени продвижение ученика, его успехи или пробелы. Существующих ресурсов вполне достаточно, чтобы за учителем осталась только корректирующая работа по выявлению и исправлению недочетов.
Много ли выпускников выбирают биологию в качестве предмета по выбору на ЕГЭ?
Татьяна Татаренко-Козьмина. Количество выпускников, выбирающих биологию, за время существования ЕГЭ только в Москве увеличилось почти в два раза (с 5,5 тысячи в 2009 году до более чем 10 тысяч в 2019 году). Это говорит о растущем интересе к предмету. Появляются новые специальности, для освоения которых требуется знание биологии: биотехнолог, IT-генетик, биоинформатик, нанотехнолог биоматериалов, архитектор живых систем, молекулярный диетолог. Сейчас они становятся все более актуальными и востребованными.
Какие рекомендации вы можете дать учителям по подготовке детей к ЕГЭ по биологии?
Татьяна Татаренко-Козьмина. Биология как предмет интересна тем, что она изучает жизнь во всех ее проявлениях, изобилует интересными фактами, событиям из жизни организмов и многочисленными научными открытиями. Поэтому можно смело давать задания на познавательную деятельность, вести с учениками диалог и обсуждать изученный материал.
Работа с учебником, тренировочными заданиями, дискуссии, диалог с учителем в совокупности дают свои положительные результаты при подготовке к экзамену. Разбирая варианты, педагог исправляет ошибки и дает пояснения, обращая особое внимание на критерии оценивания задания.
А какие рекомендации можно дать родителям выпускников?
Ярославна Скворцова. Родители могут помочь в организации самостоятельной подготовки ребенка. Она должна быть равномерной и плановой. Важно соблюдать режим дня. Учителя и различные интернет-ресурсы дают достаточно информации, но итоговый результат во многом зависит от самого выпускника.
Грамотная организация самостоятельного обучения, повторения, разбора трудных вопросов, закрепление материала после изучения, отработка заданий — в этом залог успеха. Доброжелательная и спокойная помощь родителей здесь неоценима.
О подготовке к другим предметам, а также обо всём, что нужно знать о ЕГЭ-2020, читайте в нашей рубрике на сайте или подписывайтесь на рассылку «Пережить ЕГЭ».
Иллюстрация: Shutterstock (GoodStudio)
Как подготовиться к ЕГЭ по биологии — Абитуриент.про
Общие сведения о едином государственном экзамене по биологии
Около 20% выпускников школ ежегодно выбирают этот предмет для сдачи, что делает ЕГЭ по биологии четвертой по популярности дисциплиной. Тест ЕГЭ включает в себя две части, первая состоит из 33 заданий, требующих быстрого анализа вариантов и краткого ответа, представляющего собой цифру или же последовательность цифр. Вторая часть включает в себя 7 заданий с необходимостью развернутого ответа и подробного описания процесса решения поставленной задачи. К 2016 году структура КИМов была значительно оптимизирована: общее количество заданий уменьшилось с 50 до 40 вследствие увеличения числа вопросов, требующих подробного развернутого ответа. Продолжительность экзамена – 180 минут. В 2016 году проходной балл ЕГЭ по биологии равен 37 тестовым баллам (17 первичных баллов из 69 возможных), что означает, что для преодоления минимального порога необходимо справиться с первыми 18 заданиями.
Статисктика биология ЕГЭ
В 2015 году средний тестовый балл ЕГЭ по биологии по данным Рособрнадзора составил 53, 2 балла против 54,1 в 2014 году. Для успешного прохождения процедуры ЕГЭ по биологии необходимо овладеть навыком быстрого принятия решения и анализа существующих данных, содержащихся в самом вопросе.
Результат ЕГЭ по биологии
Грамотное использование собственного времени, а также имеющихся теоретических знаний , полученных при подготовке, позволит справиться с максимумом заданий в короткое время. Несомненно, для сдачи ЕГЭ необходима сильная мотивация и внутренний тезис: четкое понимание того, как этот экзамен повлияет на дальнейшую жизнь, выбор профессии. Полезно будет составить план по тайм-менеджменту и последовательный список мероприятий для подготовки на каждый день, который поможет не отклоняться от плана. После самостоятельного освоения материала стоит вернуться к ранее изученному, сопоставить с новой приобретенной информацией – неоднократное повторение пройденного даже в короткое время поможет закрепить знания.
Онлайн подготовка к ЕГЭ
Если время на подготовку существенно ограничено – имеет смысл обратиться к экспресс- пособиям, а также к онлайн-тестам.
Для ознакомления с теорией дисциплины существует множество сайтов:
• http://onlinebiology.ru — сайт предлагает ознакомиться с видеоуроками по ботанике, зоологии, анатомии, общей биологии, со статьями о разных разделах этой науки, схемами, таблицами и презентациями, которые помогут оперативно составить теоретическое представление о предмете.
• http://examer.ru/ege_po_biologii/2016/- данный сервис поможет укрепить знания и попрактиковаться в решении оригинального теста с возможностью оценивать свой темп прохождения экзамена и возможные пробелы в технике.
• https://ege.yandex.ru/biology/ — очередной портал, позволяющий решить несколько тестов из материалов ЕГЭ прошлых лет.
• http://4ege.ru/biologi/ — данный сайт предлагает множество демонстрационных вариантов ЕГЭ по биологии, а также отдельные задачи по исчерпывающему количеству тем, вопросы о которых могут встретиться в тексте экзамена. Кроме того, на сайте можно найти полезные методические рекомендации.
• http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory — ознакомиться с кодификатором также немаловажно: он содержит перечень минимальных требований к уровню подготовки выпускников, показывает специфику и материалы потенциальных заданий.
Заключение
Выполнение всех рекомендаций, внимание к ним обеспечит наиболее благоприятные условия для быстрой и продуктивной подготовки к экзамену, и в итоге к хорошему результату государственного тестирования.
Как правильно готовиться к ЕГЭ по биологии
Поздравляем! Чтобы поступить в университет, вы решили сдавать такой многогранный и увлекательный предмет, как биология.Это похвально, ведь, скорее всего, вы хотите стать врачом или пойти в науку. Осталось малое — успешно сдать ЕГЭ 2020. Но с этим мы вам поможем. Читайте советы преподавателя биологии Алисы Эдгаровны, и все у вас получится!
ЕГЭ по биологии отличается от ОГЭ увеличенным уровнем сложности. Выпускникам предлагается не только ответить на вопросы из частного цикла (ботаника, зоология, анатомия), но также придется окунуться в мир общей биологии.
Первый вопрос — за что взяться?
Первый ответ — за то, что вам кажется самым простым!
Звучит странно. Вы подумаете: по логике, то, что я знаю, можно повторить «когда-нибудь позже». На деле оказывается, что времени на все, что отложено на «позже», не остается. Поэтому начинаем с самого, на первый взгляд, простого — цикл Ботаники. Начинайте с основ, даже если вы их знаете. Это поможет вам выявить пробелы в самых неожиданных местах =) Ботаника коварна. За напускной простотой скрывается жизненный цикл голосеменных, строение семязачатка и фотосинтез. Пугаться не стоит — просто будьте последовательны!
С началом разобрались. Чем продолжать?
Ответ кроется в том, как вам преподавали биологию в школе. Учитель всегда придерживается учебного плана. Раз вы сдаете ЕГЭ, значит подразумевается, что все, что вы прошли за 7 лет обучения биологии в школе, вы должны знать. Так оно и есть.
Идем по учебникам биологии, начиная с 6-го класса!
1. Ботаника
2. Зоология
3. Анатомия человека
4. Общая биология (куда также входит цитология, генетика, эволюция, экология и т.д.)
В учебниках написано мало, и вам в любом случае понадобится дополнительный материал или помощь репетитора. Но зато оглавление учебника состоит из важных и необходимых тем, которые вы должны знать для успешной сдачи экзамена. На эти темы можно опираться при изучении того или иного блока.
Ну вот, начало положено. Теперь мы знаем, с чего начать подготовку. Осталось подумать и решить, как выстроить план своей работы, чтобы он был максимально эффективным, а вы ничего не забыли. Часто бывает так: мы садимся за подготовку к экзамену в сентябре и заканчиваем готовиться только в июне. Соответственно, то, что было в сентябре, осталось там же…
Как же этого избежать? Вот несколько советов:
1. Повторяйте уже изученное каждый месяц (даже если это очень скучное и унылое занятие).
Теоретическую часть, вызывающую наибольшее количество вопросов, повторяйте каждый определенный промежуток времени (например, раз в месяц). Пусть это будет ритуалом, который вы постараетесь не пропускать. Тогда, к примеру, ответы на вопросы части С (22-26) не застанут вас врасплох на экзамене.
2. Не забывайте про задачи по цитологии и генетике.
Самые распространенные заблуждения по отношению к этим задачам делятся на два типа:
а) я все знаю, решать дополнительные задачи не нужно;
б) я ничего не знаю, решать не буду, лучше сделаю упор на все остальные задания.
И та, и другая тактики заранее обречены на провал!
Для приверженцев первого типа. В этих заданиях каждый новый год встречаются экстраординарные формулировки, что зачастую ставит выпускников в тупик. Бояться этого не нужно — как правило, достаточно знать немного больше теории по данной теме, чтобы не «поплыть». Категорически вредно решать такие задачи «под шаблон» — необходимо понимать механизмы происходящих процессов. Иногда за кажущейся элементарностью задача может оказаться с подвохом.
Необходимо постоянно прорешивать задания из данного блока, даже если визуально они не вызывают у вас проблем.
Для приверженцев второго типа. Опыт показывает, что такое отношение к последним заданиям невольно распространяется и на все остальные. «Что посложнее — лучше не рассматривать вообще, а сделать упор на легкое». Проблема в том, что «легкого» на экзамене — 20%. А это 20 баллов… Маловато.
Соответственно, постепенно, методично, с упорством решаем задания 27 и 28, даже если они не поддаются, а один их вид вызывает тремор в руках. В помощь придут руководства по подготовке к экзамену, репетиторы, обучающие видео (например, видеоуроки и прямые эфиры нашей школы на ютуб-канале). Не стесняйтесь задавать вопросы, не стесняйтесь качества или отсутствия ваших знаний. Не стыдно спросить, стыдно — не хотеть узнать.
3. Не пренебрегайте визуализацией!
Зачастую выпускники делают упор на печатный материал: книжки, статьи, методички. Это нормально, но некоторую информацию легче усваивать с помощью схем, таблиц и рисунков.
Визуальная память — один из самых эффективных и простых инструментов, который поможет усвоить материал. Экзамен по биологии в школе очень сильно отличается от научного представления биологии в целом, он очень сильно упрощает биологию. И это логично, ведь всё важное и нужное в сфере этой науки вы будете изучать в университете. Поэтому на визуальную составляющую материала нужно делать один из основных акцентов.
4. Забудьте про «зубрежку»!
Что значить «зубрить»? Это монотонное повторение материала без понимания его сути. Зубрежка — главный враг биологии, который не может себя оправдать, если вы хотите ПОНИМАТЬ предмет.
Понимание процесса — ключ к отличной сдаче экзамена. В биологии все цепляется друг за друга. Любой необычный вопрос поставит в тупик, даже если вы вызубрили весь курс, но не поняли его смысла.
Как же тогда учить? Прочитайте материал и перескажите его себе, а потом попробуйте объяснить его смысл кому-нибудь, кто вам готов помочь: родители, родственники, друзья, репетитор. Репетитор — самый лучший вариант, т.к. он сможет поправить те места, где вы, возможно, заблуждаетесь.
Ну и напоследок — никогда ничего не бойтесь! Чтобы добиться успеха, необходимо уверенно идти к своей цели, даже если вдруг что-то не получается. Никакой провал не должен останавливать вас. Здесь всё, как в биологии: движение — жизнь, а стояние на месте — эволюционный тупик.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
учебных стратегий по биологии | Сайты Родоса
Сделайте обучение повседневным.
- Повторите исследование в несколько более коротких периодов в разные дни. Изучите материал еженедельно, а не только перед тестами. Оставьте достаточно времени между обучением и самотестированием, чтобы вы не просто проверяли кратковременную память, а повторяли, пока не поймете, что всегда можете сделать их правильно. Задолго до экзамена возьмите часть материала и изучите ее, как если бы экзамен по этой теме был завтра.Наконец, не откладывайте это до ночи перед экзаменом.
- Если ваш профессор предоставляет материалы перед классом (например, план лекции, PowerPoint), возьмите их и используйте их для ведения заметок.
Раскройте заметки в 24-48-часовом цикле. «Нотный массаж»
- После лекции дополняйте или переписывайте свои записи, пока каракули по-прежнему имеют смысл. Делайте это регулярно в рамках официального графика, иначе вы не будете этого делать вообще. Используйте полные предложения; добавляйте метки и примечания к диаграммам, даже если вы думаете, что они уже достаточно ясны; попытайтесь организовать вещи по категориям, чтобы показать отношения.
- Заполните все недостающие отверстия. Используйте других студентов, свой текст и своего профессора.
- По темам, которые вы не совсем понимаете, получите пояснения. Не дожидайтесь окончания экзамена, чтобы понять это понимание. Получи это сейчас. Перед тестом вам нужно учиться с более высоким уровнем понимания.
Учись понимать, а не просто запоминать слова.
- Не перечитывайте свои заметки и баллы PowerPoints. Если все, что вы делаете, это читаете свои заметки, текст и PowerPoint, то вы получите только пассивное знакомство с материалом.
- Пытаясь усвоить материал, сосредоточьтесь на правильном. На вещи, которые ваш профессор считает наиболее важными для предмета и которые с наибольшей вероятностью появятся в викторинах и экзаменах, подчеркивается в лекции и в назначенных чтениях. Изучите это в первую очередь и лучше всего.
- Вы должны попрактиковаться в объяснении материала и применении его в новых ситуациях. Зачем тебе это? Иногда вопросы создают совершенно новые ситуации, которые вам необходимо проанализировать, даже если вы никогда раньше не видели такой ситуации.
- ПРИМЕР: Предположим, например, вы узнали много нового об определенной лесной экосистеме в классе. А затем на экзамене профессор ничего не спрашивает о лесу, а вместо этого помещает вас посреди пустыни, кратко знакомит с некоторыми из его обитателей и задает сложные вопросы об их отношениях друг с другом. Если вы действительно хорошо разбираетесь в данной экосистеме (лесу) — знайте о ее потоке энергии и питательных веществ, адаптивных стратегиях ее обитателей и т. Д.- тогда вы будете лучше подготовлены к тому, чтобы увидеть знакомые закономерности в этой странной новой ситуации (пустыня). Вы заранее знаете, что существует какая-то сеть питания — что в некотором роде она будет похожа на эту в лесу и т. Д. В конечном итоге вы немного поймете экосистему пустыни не потому, что вы ее запомнили это вообще раньше), а скорее потому, что вы так хорошо знаете лесную экосистему, что теперь можете думать не только об этом. Но единственный способ заранее убедиться, что вы действительно хорошо знаете данную систему (лес), — это попрактиковаться в объяснении того, что вы знаете.
Изучите отдельные концепции, прежде чем объединять их вместе.
- Вам необходимо изучить и понять содержание, прежде чем вы сможете перейти на следующий уровень понимания путем интеграции информации.
- Это одна из причин, по которой так важно быстро просматривать свои записи и сразу же отвечать на любые факты и подробные вопросы.
Используйте активные методы обучения.
- Нанесите на карту весь связанный материал.Попытайтесь увидеть, как связаны между собой разрозненные темы лекций. Как концепция или процесс связаны с общей картиной? Как новый материал основывается на содержании предыдущего курса? Как это можно было бы построить позже?
- При объяснении причинных связей важно построить логичную и адекватную цепочку связи между начальной причиной и конечным следствием.
- ПРИМЕР: Например, если вас попросили объяснить, почему убивает угарный газ, вы могли бы ответить: «Потому что он останавливает дыхание.«Этого может быть достаточно для повседневного разговора, но обычно этого недостаточно на экзамене. Слишком много вопросов остается без ответа.« Как углекислый газ подавляет дыхание? »« Почему остановка дыхания приводит к смерти? »В зависимости от некоторых обстоятельств. Курс и уровень детализации, обычно используемый в нем, можно ожидать, что вы предложите ответ, более близкий к следующему: «CO связывается с гемоглобином, подавляя его способность переносить кислород из легких в ткани. Кислород необходим в качестве конечного акцептора электронов в дыхательной системе переноса электронов, которая затем прекращается из-за отсутствия кислорода.Без дыхания АТФ не образуется. А поскольку АТФ является формой энергии, необходимой для многочисленных процессов, требующих энергии, необходимых для жизни, эти процессы прекращаются, и наступает смерть ». Обратите внимание, сколько логических связей между CO и смертью можно с пользой использовать. Некоторые курсы, в зависимости от акцента, могут требуется меньше, чем эти; некоторым может потребоваться больше. Конечно, вам решать, что подходит для вашего курса. Чтобы сформировать привычки и инстинкты предлагать «полные» ответы, станьте более похожими на чумного ребенка кто отвечает на каждое утверждение вопросом: «Почему?» Это очень поможет вашему мышлению.
- Потренируйтесь придумывать вопросы, которые профессор может задать по материалу курса, а также отработайте и уточните ответы на эти вопросы. Экзамены в колледже — не то место, где можно впервые получить обратную связь.
Вам нужно часто проверять себя, чтобы по-настоящему оценить, насколько вы понимаете.
- Проверяя свое понимание, заставляйте себя давать четкие, точные, краткие, но полные объяснения, полностью по памяти.
- Если вы работаете в группе, начните с согласования репрезентативных вопросов, а затем по очереди отвечайте на них, пока другие указывают, какие ответы особенно хороши, а какие требуют улучшения.
- Если вы учитесь в одиночку, запишите те ответы, которые кажутся хорошими, на основе ваших заметок, а затем отложите эти ответы на время и посмотрите, насколько хорошо вы можете воспроизвести их по памяти.
- Сделайте то же самое с любыми диаграммами или рисунками, рассматриваемыми в классе, чтобы убедиться, что вы можете воссоздать их по памяти, со всеми отмеченными ключевыми частями и шагами, а также с указанием их функций и значения. Даже если вам не нужно создавать диаграмму или рисунок на тесте, практика его с нуля поможет вам лучше понять материал.
Щелкните ЗДЕСЬ , чтобы открыть версию для печати.
Взято из «Стратегии изучения биологии» профессора Алана Джаслоу и предложений профессора Терри Хилла по изучению биологии. Щелкните заголовки, чтобы прочитать полные документы.
Узнайте, как изучать биологию
Биология обычно является обязательным курсом как в средней школе, так и на уровне колледжа. В какой-то момент каждый студент должен его сдать.Некоторые студенты считают биологию сложной задачей, но это не обязательно. Как и в случае с математикой и некоторыми другими предметами, изучение биологии представляет собой совокупный процесс. Прежде чем вы сможете понять более сложные биологические концепции и процессы, важно понять основы. Ниже мы рассмотрим проверенные советы и стратегии для улучшения вашей способности изучать биологию.
Приходите на занятия … и приходите подготовленными
Чтение учебника по биологии или копирование заметок одноклассника не компенсирует пропущенный урок.Биология — сложный практический предмет. Он включает изучение биологических систем, требующих объяснений и экспериментов. Биология также является накопительным предметом. То, что вы узнаете в одном классе, создаст строительные блоки для того, что вы узнаете в будущем. Приходите на каждую лекцию, прочитав учебник, выполнив все лабораторные задания и просмотрев свои записи из предыдущей лекции. Вы получите гораздо больше от лекций, если будете подготовлены. Студенты, которые регулярно посещают уроки биологии, успевают намного лучше, чем те, кто этого не делает.
Не играйте в догонялки
«Кэтчуп» может быть приемлемой игрой в истории, домоводстве или социальных науках, но в биологии это не работает. Опять же, процесс изучения биологии является кумулятивным. Каждая новая биологическая концепция, которую вы изучаете, основывается на ранее приобретенных вами знаниях. Большая часть знаний, которые вы приобретете при изучении биологии, вы получите в результате практических экспериментов и исследований в лабораторных условиях. Сделать лабораторию сложно. Составить несколько лабораторий в конце семестра невозможно… и бесплодно. Быть в курсе предмета и вовремя выполнять задания — ключ к изучению биологии.
От общего к частному
Каждый может изучить биологию, но это не всегда легко. Биология не требует столько математики, как физика или астрономия, но все же может быть сложно понять биологические системы и процессы. Один из ключей к эффективному изучению биологии — усвоить общие концепции, прежде чем приступать к конкретным. Например, прежде чем вы сможете понять цикл Кребса, вам необходимо иметь базовое представление о структуре клеток животных.Тщательно изучите каждую новую биологическую концепцию и процесс, прежде чем переходить на следующий уровень.
Воспользуйтесь лабораторным временем
В биологии есть теория, но это еще и практическая наука. Изучать теорию биологии, читая учебник или слушая лекцию, — это одно, а применять биологию на практике в лаборатории — совсем другое. Эксперименты с биологическими системами и процессами в лаборатории — один из самых эффективных способов изучения биологии.То, что вы делаете в лаборатории, останется с вами намного дольше, чем то, что вы прочитаете в книге.
Используйте чертежи и схемы
Биология полна сложных систем и процессов, которые вы должны понимать, запоминать, применять и воспроизводить на экзамене, для своего учителя и, вполне возможно, для своей карьеры. Использование изображений, особенно рисунков и диаграмм, может облегчить понимание и запоминание даже самых сложных биологических процессов. Например, рассмотрим следующее объяснение осмоса, найденное в Википедии:
Осмос — это любой процесс, связанный с чистым перемещением молекул из раствора с более низкой концентрацией через полупроницаемую мембрану в раствор с более высокой концентрацией до тех пор, пока концентрации на каждой стороне мембраны не выровняются.
Довольно легко понять, правда? Тот же самый процесс осмоса поясняется следующей схемой:
Используйте чертежи и схемы для изучения биологии. Это улучшит ваше понимание и запоминание.
Изучите терминологию
Вы бы никогда не подумали о том, чтобы стать врачом и не ожидали бы изучить все части человеческого тела или механика, не зная всех частей автомобиля. То же самое и в биологии.Даже если вы не планируете становиться биологом или не выбрали курс биологии, в котором сейчас находитесь, если вы хотите преуспеть в биологии, вам необходимо (1) обратить внимание на терминологию и (2) узнать его. Чтобы изучать биологию, вы должны понимать слова и термины, используемые для ее объяснения. Встречая незнакомые слова, запишите их, а затем найдите. Когда кажется, что у слов есть приставки или корни, найдите время, чтобы разбить их на части и понять их части.
Читайте эффективно… прочитайте с целью
Чтобы выучить биологию, нужно гораздо больше, чем просто бегать по главам или бегать глазами по страницам в поисках основных моментов. Успешные студенты-биологи атакуют каждое задание по чтению с карандашом в руке и записной книжкой, активно занимаются и читают целенаправленно. Каждый раз, когда вы беретесь за задание по чтению, записывайте в тетрадь важную информацию, включая словарный запас, процессы, концепции и объяснения. Записывание вещей (1) помогает обрабатывать и понимать сложный материал и (2) улучшает удержание.Ваши заметки также помогут вам подготовиться к экзаменам.
Делая заметки во время чтения, запишите следующее:
- Терминология
Заманчиво пропустить незнакомые термины и новую лексику. Сопротивляйтесь этому искушению. Запишите незнакомые термины и словарный запас в тетрадь, а затем найдите их. Это может показаться утомительным (потому что это так), но это необходимая часть изучения биологии. - Концепции
Прочтите подробности, но прочтите, чтобы понять смысл.Прочитав о новой концепции, своими словами запишите в тетрадь краткое изложение концепции. Это улучшит ваше понимание концепции и предоставит вам ценный инструмент для подготовки к экзамену. - Схемы и чертежи
Мы не можем повторить, насколько эффективно использовать диаграммы и рисунки для изучения биологии. То же самое и при чтении текстов по биологии. Рисование картинок и разработка диаграмм для представления и описания процессов и систем, о которых вы читаете в своем учебнике по биологии, улучшат понимание и запоминание.
Научитесь запоминать
Биология является основой многих естественных наук и охватывает множество тем, от осмоса и диффузии до гомеостаза и клеточной биологии до вирусологии и иммунологии. Это действительно одна из самых разнообразных дисциплин, изучаемых в любой средней школе или крупном университете. (Неудивительно, что так много студентов находят изучение биологии временами непосильным.) Таким образом, изучение биологии требует большого количества запоминания, повторения и запоминания информации.Ниже приведены проверенные советы по запоминанию информации при изучении биологии.
- Обучай
Нет лучшего способа убедиться, что вы что-то понимаете, чем научить этому кого-то другого. Обучение биологии другим перемещает информацию из вашей краткосрочной памяти в долговременную. Каждую неделю выделяйте время, чтобы преподавать уроки, которые вы выучили, кому-то другому. - Использовать
Биология полна терминологии и специальной лексики.Лучший способ выучить новую терминологию и запомнить ее — это использовать ее. Каждый раз, когда вы встречаете новый термин или слово, записывайте его, ищите и затем используйте в предложении. Если у вас есть одноклассник, с которым вы можете попрактиковаться, каждую неделю уделяйте некоторое время тому, чтобы повторять вслух и обсуждать новую терминологию, с которой вы столкнулись. - Использовать мнемонические устройства
По какой-то причине человеческий мозг любит отношения и ассоциации, особенно знакомые. Найдите время, чтобы связать сложные или незнакомые биологические термины и словарный запас со знакомыми словами и фразами, и вы запомните их навсегда.Например, чтобы запомнить K ingdom, P hylum, C lass, O rder, F amily, G enus, S pecies (порядок таксономии), вам просто нужно запомнить K ing P hillip C ame O ver F rom G reat S pain. - Флэш-карты
Флэш-карты сегодня так же эффективны для изучения биологии, как и в 1950-х годах.Напишите термины и понятия, которые вы пытаетесь запомнить, на одной стороне карточки 3×5 дюймов, а их определения и описания — на другой стороне. Вы можете изучать биологию с помощью флеш-карточек самостоятельно или с другим одноклассником.
Подготовка к испытаниям
Ниже приведены некоторые из наиболее эффективных методов и стратегий подготовки к экзаменам по биологии.
- Пересмотреть прошлые экзамены
Биология как наука довольно конкретна. Хотя вы можете рассчитывать на то, что вас познакомят с новыми теориями, большинство основных биологических принципов и концепций, которые вы изучите в старшей школе или студенте бакалавриата, уже доказаны.Таким образом, то, что профессора и инструкторы биологии обучают студентов, а затем проверяют на них, не сильно меняется из года в год. Очень эффективный способ подготовиться к экзаменам по биологии — это просмотреть вопросы, найденные на прошлых экзаменах по биологии, которые проводил ваш инструктор.Однако экзамены по биологии могут немного отличаться, поэтому важно не просто запоминать вопросы и ответы. Используйте прошлые экзамены, чтобы определить основные понятия, которые вы, вероятно, встретите на экзамене, и проверить свои знания этих понятий.Прошедшие экзамены также дадут вам представление о том, какие форматы вопросов следует ожидать (например, эссе, множественный выбор, истина / ложь и т. Д.). Просмотрите как можно больше прошлых экзаменов.
- Лаборатории
Просмотрите все свои лабораторные заметки. Если вы тратите время на изучение различных частей животной клетки в лаборатории, есть большая вероятность, что вам потребуется пометить различные структуры животной клетки и объяснить, что они делают. - Лекции
Экзамен проводит ваш инструктор, поэтому обратите особое внимание на то, что он считает наиболее важным и интересным.Каким бы важным ни был ваш учебник, вы лучше сдадите экзамен, вернувшись и просмотрев все, что преподавал вам в классе и во время лабораторных работ. - Назначения
Просмотрите все свои задания на семестр. Ваши задания охватывают темы, которые ваш преподаватель считает наиболее важными. Таким образом, вы можете поспорить, что найдете экзаменационные вопросы, которые исходят непосредственно из заданий, которые вы выполнили в течение семестра.
Прыгнуть обеими ногами
Если вы зашли так далеко, но до сих пор не поняли этого, мы рекомендуем прочитать эту страницу еще раз.Чтобы преуспеть в биологии, нужно прыгать обеими ногами. Ставить одну ногу внутрь и одну наружу не работает. В начале семестра, независимо от ваших основных личных интересов или антипатий, решите, что вы собираетесь отдать биологии все свое сердце. Сделайте это, и вы преуспеете на уроке биологии.
Ресурсы, руководства и учебные пособия, рекомендованные редактором и пользователями, помогут вам изучить биологию и улучшить свои учебные навыки.
Все, что вам НУЖНО ЗНАТЬ, чтобы преуспевать в bioL 101
Так что вы, вероятно, думаете, что вы очень важны, и, учитывая то, как вы себя чувствуете здесь, в Williams, вероятно, так и есть.Однако у каждого есть момент в первом семестре, когда они понимают, что они больше не в Канзасе. Для меня и многих других ученых-энтузиастов и преуспевающих в области медицины этот момент стал первым экзаменом в Bio 101. Это руководство направлено на то, чтобы дать новичкам первого курса биологических факультетов хедз-ап, чтобы они были готовы к строгим требованиям Bio 101, чтобы они могут увлекаться изучением биологии. Он включает в себя советы по изучению от прошлых студентов и комментарии о том, что они хотели бы знать перед первым экзаменом по биологии. Наслаждайтесь и удачи!
Хорошие привычки: обучение в течение семестра
Подготовка к тестам и фактическое изучение материала в Bio 101 и в любом другом занятии, которое вы будете посещать, в этом отношении станет намного проще и приятнее, если вы создадите организованную систему для подхода к лекции и чтению материала в начале семестра.Вот несколько советов от прошлых студентов Bio 101 о том, что помогало им оставаться в курсе дел и избавляться от стресса в течение первого семестра.
1. Делайте хорошие конспекты лекций.
В Bio 101 все важные темы освещаются в лекции. В принципе, если вы хорошо знаете лекционный материал, вы наверняка преуспеете в классе. Это означает, что одна из самых полезных привычек, которую вы можете развить, — это делать подробные, организованные записи в классе.
- Отметить нечеткие понятия на полях
- Просмотрите записи предыдущих лекций за 5 минут до следующего урока и просматривайте заметки за все прошлые недели на выходных
- Цветовой код
- Пишите только на одной стороне страницы
- Номер и титульные листы
- Оставьте много места, не сжимайте все свои заметки в крошечном пространстве
- Иметь систему выделения важных идей по более мелким деталям
- Не вдавайтесь в подробности! Если вы попытаетесь все записать, вы можете упустить что-то важное.К этому нужно привыкнуть, но со временем вы научитесь определять ключевые темы; может помочь сравнение заметок с друзьями после уроков. (Примечание: некоторые технически подкованные люди любят использовать свои mp3-плееры для записи лекций, чтобы они могли сосредоточиться на том, чтобы слушать, а не писать в классе.)
2. Используйте учебник в качестве дополнения к лекционному материалу.
Учебник по Bio 101, к сожалению, излишне сложен. По этой причине многие студенты не читают по назначению, а ждут непосредственно перед экзаменом, чтобы пролистать пять глав.Хотя этот подход может сработать для вас, если вы понимаете весь материал лекции, если вы сбиты с толку или никогда не слышали биографию в старшей школе, чтение учебника может помочь прояснить концепции. Несколько советов по использованию книги:
- Просмотр назначенного чтения перед занятием может быть очень полезным, поскольку он дает вам некоторое представление о том, о чем профессор говорит на лекции, особенно если (как я) вы никогда не проходили AP.
- Делать подробные записи при чтении — вероятно, пустая трата времени.Я делал это в первой половине семестра, и хотя это помогло мне при обучении в середине семестра, это заняло слишком много времени. Создание заметок на полях, подчеркивание или выделение гораздо эффективнее.
- Не зацикливайтесь на незначительных деталях (например, на названии каждого промежуточного звена в цикле Кребса). Обратите внимание на диаграммы, вместо этого большинство студентов сочли их самой полезной частью учебника.
3. Обратитесь за помощью пораньше!
Одна из самых распространенных ошибок первокурсников, которых можно избежать, — это отсутствие помощи до тех пор, пока они безнадежно не справятся.Одна из лучших особенностей Williams — это сотрудничество и взаимодействие между студентами и преподавателями, поэтому воспользуйтесь этим: как только у вас возникнут проблемы, обратитесь за помощью!
- Поговорите со своим проф. профессора здесь могут быть безумно умными и профессиональными в своем классе, но они очень дружелюбны и полезны, когда вы ищете их вне лекций. Не думайте, что вы должны исчерпать все свои ресурсы перед тем, как обратиться к ним, или как будто вам нужен список очень конкретных вопросов (хотя всегда полезно подумать о том, с чем вам нужна помощь в первую очередь).И не просто кивайте и не улыбайтесь, когда вам что-то объясняют — они не сочтут вас глупым, если вы попросите разъяснений. Если вы нервничаете поехать в одиночку, приведите друга. Кроме того, если вы не можете найти рабочее время, напишите своему профессору, чтобы он назначил другое время.
- Посетите ресурсный центр по математике и естествознанию. Если вы не можете встретиться со своим профессором, доступны многие другие ресурсы. Ресурсный центр по математике и естественным наукам открыт с воскресенья по пятницу с 20:00 до полуночи, и в нем работают преподаватели, уже набравшие 101.Просто не забудьте проверить расписание перед поездкой, чтобы убедиться, что на эту ночь будет био-репетитор.
- Напишите своему био-наставнику по электронной почте. Если вы первый год зачислены в Bio 101, вы будете назначены на высшее биологическое образование, чтобы отвечать на вопросы обо всем, что связано с биологией или иным образом. Они смогут дать совет и ответить на все ваши вопросы или, по крайней мере, указать вам на кого-то, кто может.
- Получите помощь от других студентов. Ваши сокурсники часто могут быть вашим лучшим помощником.Используй их!
Обучение: подготовка к экзамену
Разработка хороших стратегий обучения на раннем этапе сэкономит вам много времени и сэкономит нервы в течение следующих четырех лет и позже. Вы можете обнаружить, что то, как вы учились в средней школе, не работает и в колледже, где экзамены проверяют, можете ли вы применить и расширить то, что вы узнали, вместо того, чтобы изрыгать мельчайшие детали. Вот несколько советов по приближению к экзамену:
1. Сформируйте учебную группу.
Учебные группы, если они хорошо структурированы, могут быть наиболее эффективным и экономичным способом проведения обзора.Несколько советов о том, как создать отличную учебную группу:
- Размер: Слишком большие учебные группы склонны дезорганизовываться, и если одни студенты более комфортно разбираются в материале, чем другие, некоторые могут не получить ответы на все свои вопросы. Большинство студентов считают, что лучше всего подходят группы от 2 до 5 друзей.
- Подготовьте: Очень важно просмотреть материал перед тем, как прийти в учебную группу. Это может быть просто беглый просмотр ваших заметок для выявления сбивающих с толку областей, но вы должны составить список вопросов, которые вы хотите передать группе.
- Организуйте: Назначьте каждому человеку определенный раздел (тема, лекция и т. Д.) Для изучения и объяснения группе.
- Групповая динамика: Не позволяйте одному человеку доминировать в разговоре или отвлекаться на другие отвлекающие факторы.
2. Начните учиться раньше.
Просмотрите записи и сделайте учебное пособие. Создайте организованную систему для просмотра ваших заметок. Вот моя личная стратегия:
- План лекционных заметок: Прочтите свои классные заметки и запишите основные идеи в форме плана, включая некоторые конкретные детали, которые, по вашему мнению, вы забудете.Мне нравится составлять эти учебные пособия в конце семестра, чтобы облегчить подготовку к выпускному экзамену. Цветовое кодирование (по теме или важности) также полезно.
- Просмотрите учебник / заметки для чтения: Если вы заметите что-нибудь удивительное или особенно относящееся к лекционному материалу, или найдете полезную схему, сделайте ссылку на нее на полях своего плана лекционных заметок.
- Нарисуйте свои собственные схемы: После изучения конспектов лекции попробуйте связать материал вместе, представив его в виде картинок (не просматривая свои записи.)
3. ПОСЛЕ учебы:
Выполняйте практические задачи и вопросы из учебников.
4. ПОСЛЕ учебы:
Перейти к сеансам просмотра. Приносите вопросы, когда идете на обзорную сессию; иначе это будет пустой тратой времени.
5. Прочие стратегии:
Объяснение материала друзьям — один из лучших способов изучить и определить то, чего вы не знаете (или позвоните своей маме и поразите ее тем, что ей дают ее 40 тысяч долларов в год.)
После теста:
Это еще не конец! Что следует сделать после экзамена:
- Проверьте, ошиблись ли вы.
- Поговорите с профессором, если вы недовольны своей оценкой.
- Сохраните учебное пособие, чтобы использовать его на весь семестр.
Об экзаменах Bio 101:
- Формат: Тесты обычно состоят из вопросов с короткими ответами, в которых вы должны применить свои знания о том, как работают вещи в ячейке, к новым ситуациям в параграфе или меньше.
- Оценка: Частичный зачет предоставляется щедро, и тесты обычно изгибаются на один или два балла. Но не стоит полагаться на это, чтобы получить хорошую оценку! Скорее всего, вам еще нужно учиться, чтобы преуспеть. Не расстраивайтесь, если вы не справитесь с первым тестом или викториной. Многие преподаватели наградят вас за итоговую оценку, если увидят улучшение в течение семестра.
Другие детали:
Никогда не рано думать о лете.У Уильямса потрясающая исследовательская программа на бакалавриате; если вы вообще заинтересованы в исследованиях, подумайте, с каким профессором вы могли бы работать.
Как подготовиться к экзамену по биологии
Экзамены могут показаться запугивающими и утомительными для студентов-биологов. Ключ к преодолению этих препятствий — подготовка. Научившись готовиться к экзаменам по биологии, вы сможете победить свои страхи. Помните, что цель экзамена — продемонстрировать, что вы понимаете концепции и информацию, которой учили.Ниже приведены несколько отличных советов, которые помогут вам научиться готовиться к экзаменам по биологии.
Организуйтесь
Важным ключом к успеху в биологии является организация. Хорошие навыки управления временем помогут вам стать более организованным и тратить меньше времени на подготовку к учебе. Такие элементы, как ежедневники и семестровые календари, помогут вам узнать, что вам нужно делать и когда вам нужно это сделать.
Начать учиться рано
Очень важно заранее начать подготовку к экзаменам по биологии.Я знаю, я знаю, что для некоторых это почти традиция ждать до последней минуты, но ученики, которые умоляют эту тактику, не проявляют себя наилучшим образом, не сохраняют информацию и утомляются.
Просмотр учебника и конспектов лекций
Обязательно ознакомьтесь с конспектами лекций перед экзаменом. Вам следует начать просматривать свои заметки ежедневно. Это гарантирует, что вы постепенно усвоите информацию, и вам не придется зубриться.
Ваш учебник биологии — прекрасный источник для поиска иллюстраций и диаграмм, которые помогут вам визуализировать изучаемые вами концепции.Обязательно перечитайте и просмотрите соответствующие главы и информацию в своем учебнике. Вы должны убедиться, что понимаете все ключевые концепции и темы.
Получите ответы на свои вопросы
Если вы испытываете трудности с пониманием темы или у вас есть вопросы, на которые нет ответа, обсудите их со своим учителем. Вы же не хотите сдавать экзамен с пробелами в знаниях.
Соберитесь с другом или одноклассником и проведите учебную сессию. По очереди задавайте вопросы и отвечайте на них.Запишите свои ответы полными предложениями, чтобы помочь вам организовать и выразить свои мысли.
Если ваш учитель проводит обзорную сессию, обязательно посетите ее. Это поможет определить конкретные темы, которые будут рассмотрены, а также восполнить пробелы в знаниях. Сеансы помощи также являются идеальным местом для получения ответов на свои вопросы.
Quiz Yourself
Чтобы подготовиться к экзамену и узнать, что вы знаете, проведите тест. Вы можете сделать это, используя подготовленные флеш-карты или пройдя пробный тест.Вы также можете использовать онлайн-игры по биологии и викторины. Если ваш учитель проводит обзорную сессию, обязательно присутствуйте на ней. Это поможет определить конкретные темы, которые будут рассмотрены, а также восполнить пробелы в знаниях. Сеансы помощи также являются идеальным местом для получения ответов на свои вопросы.
Relax
Теперь, когда вы выполнили предыдущие шаги, пришло время отдохнуть и расслабиться. Вы должны быть хорошо подготовлены к экзамену по биологии. Лучше всего выспаться в ночь перед экзаменом.Вам не о чем беспокоиться, потому что вы хорошо подготовлены.
Пройдите курс биологии AP
Тем, кто желает пройти вводный курс биологии на уровне колледжа, следует подумать о прохождении курса биологии повышенной сложности. Студенты, зачисленные на курс AP Biology, должны сдать экзамен AP Biology, чтобы получить кредит. Большинство колледжей отдают должное за курсы биологии начального уровня студентам, набравшим на экзамене не менее 3 баллов.
Используйте хорошие учебные пособия
Флэш-карточки по биологии — отличный инструмент для изучения и запоминания ключевых терминов и информации по биологии.Флэш-карты AP Biology — прекрасный ресурс не только для тех, кто изучает AP Biology, но и для студентов-биологов в целом. При сдаче экзамена по биологии AP эти пять лучших книг по биологии AP содержат чрезвычайно полезную информацию, которая обязательно поможет вам получить высокие баллы на экзамене AP по биологии.
Как изучать биологию в колледже
Делайте заметки
Делайте заметки — отличный способ усвоить информацию, которую вы изучаете в классе. Это также позволяет вам просмотреть факты позже.Вам следует попытаться записать все, что ваш инструктор пишет на доске, все, что описано как важно, и любые номера страниц, на которые ссылается ваш инструктор. Не бойтесь просить учителя повторить информацию, если вы думаете, что пропустили что-то важное, или если вам просто неясна концепция.
Некоторые преподаватели позволяют вам записывать лекции, чтобы вы могли их снова прослушать позже. Однако не забудьте спросить перед записью, так как в некоторых школах такая практика запрещена.
Закрепите то, что вы узнали
Хорошая идея — просмотреть свои записи после окончания урока. Это отличный способ убедиться, что вы понимаете все, что было описано.
Вы также можете узнать, есть ли на вашем биологическом факультете кабинет с дополнительными ресурсами, которые вы можете посетить. Создайте учебную группу или посетите своего инструктора в рабочее время, чтобы обсудить предметы, которым вы хотели бы уделять больше времени.
Подготовка к экзаменам
Есть много отличных стратегий для подготовки к экзамену по биологии.Те, которые вы будете использовать, будут зависеть от вашего стиля обучения и от того, как ваш инструктор любит настраивать экзамены. Вы можете ознакомиться с этими предложениями и использовать те, которые подходят вам:
- Make Flashcards : Flashcards — отличный способ быстро накопить в памяти важные термины. Напишите термин, который вам нужно запомнить, с одной стороны, а с другой — краткое определение или картинку.
- Наклейки с рисунками : Распечатайте копии рисунков из учебника и тщательно промаркируйте их.
- Используйте книжку-раскраску : это отличный способ подготовиться к анатомическим тестам. Вы можете найти книжки-раскраски, посвященные анатомии человека, и раскрасить их, чтобы с легкостью практиковать различные части тела.
- Посетите лабораторию : Время открытой лаборатории — отличный способ проверить модели, которые имеют дело с биологической информацией, на которой вы собираетесь тестироваться.
- Нарисуйте рисунок : Если вам трудно вспомнить определенный процесс (например, цикл Кребса), попробуйте нарисовать график, представляющий различные этапы цикла.Вы также можете написать это своими словами, если вам так будет проще.
- Объясните концепцию : Иногда обсуждение биологического процесса помогает вам усвоить его быстрее и эффективнее. Попробуйте объяснить, над чем вы работаете, партнеру по лаборатории или соседу по комнате. Если вам не с кем поработать, повторяйте это вслух, пока не почувствуете, что у вас все получилось.
Обучение онлайн
Вы можете найти онлайн-ресурсы, которые укрепят то, что вы изучаете в классе.Эти учебные пособия включают короткие видео-уроки, в которых подробно рассматриваются концепции биологии, которые вы изучаете. Они также предлагают вам практические викторины и экзамены, которые помогут вам подготовиться к тестам в классе. Приготовьтесь к успеху с этими ресурсами, относящимися к:
5 методов изучения биологии
Мы продолжаем серию «Как учиться…» этим учебным пособием по биологии. Если вы брезгливо относитесь к жидкостям, отвернитесь. Биология — увлекательный предмет, но часто может создавать проблемы для студентов.Если это так, то читайте дальше и узнайте, как улучшить результаты экзамена. Другие предметы, доступные в этой серии: «Как изучать математику» и «Как изучать историю».
Биология изучает жизнь и учит нас о себе и окружающем нас мире. Хорошей отправной точкой при изучении биологии является восхищение совершенством природы и принципами жизни.
С таким мышлением вы готовы применять методы обучения, описанные ниже.
Как изучать биологию: 5 лучших методов обучения # 1 Изучите терминологиюОдна из самых сложных частей изучения биологии — это запоминание множества различных терминов. Если вы хотите понять, что изучаете, вам необходимо сначала ознакомиться со всеми этими терминами. Хороший метод для этого — попытаться разбить сложные слова, чтобы определить их корень .
Настоятельно рекомендуется, чтобы всякий раз, когда вы сталкиваетесь с незнакомыми словами во время изучения биологии, вы должны обратить на них внимание, найти их определение, а затем найти время, чтобы понять его корни.
Зарегистрируйтесь на GoConqr бесплатно, и у вас будет доступ к нашей эксклюзивной группе биологии (и многим другим), где вы можете задавать вопросы и просматривать высококачественные ресурсы, созданные другими учениками и учителями!
# 2 От общего к частномуЧтобы следовать процессу эффективного изучения биологии, вы должны овладеть общими концепциями, прежде чем иметь возможность заниматься конкретными. Например, вам нужно понять, какие факторы идентифицируют млекопитающих, прежде чем начинать факторы, идентифицирующие приматов.
В этом смысле также рекомендуется тщательно изучить процессы, прежде чем переходить на следующий уровень . Чтобы ускорить запоминание различных процессов и их взаимосвязей, интеллектуальные карты являются эффективным образовательным ресурсом для учащихся, поскольку они помогают организовать информацию очень простым и наглядным способом.
# 3 Объять лабораториюПрименяйте теорию биологии на практике, используя лабораторию, когда это возможно, чтобы исследовать свое любопытство.Оказавшись в лаборатории, вы можете проверить свою гипотезу и подтвердить свои теории. Что касается обучения, то действие останется с вами намного дольше, чем действие чтения.
# 4 Использовать чертежиРисунки могут помочь вам понять концепцию и запомнить информацию , которую было бы трудно определить словами. Вам следует привыкнуть к рисованию диаграмм, таких как человеческое сердце, поскольку вас могут попросить создать и обозначить такой рисунок на экзамене по биологии.
# 5 Вопросы прошлых экзаменовПопрактикуйтесь в ответах на прошлые экзаменационные вопросы; прошлые работы, которые должны быть доступны у вашего учителя.Биологические тесты могут сильно различаться, поэтому важно, , знать, как вас будут оценивать, чтобы учиться соответственно . Собираетесь ли вы пройти тест с несколькими вариантами ответов или у вас возникнут вопросы для сочинения по лабораторной работе? Ничего не оставляйте на волю случая. Практика, практика и практика!
Начните с проверки своих знаний по биологии с помощью этой короткой викторины:
Если вы будете следовать этим советам по изучению биологии и сочетать их с позитивным настроем, очень скоро вы можете захотеть стать биологом. Так как насчет этого, биология — ваш любимый предмет?
О блоге GoConqr
Наш блог является частью GoConqr, бесплатной обучающей платформы для создания, обмена и поиска учебных ресурсов, которые помогают учащимся и учителям достигать своих учебных целей.Щелкните здесь, чтобы начать создавать интеллектуальные карты, карточки, заметки, викторины, блок-схемы слайдов и курсы прямо сейчас!
3 «Ключи к успеху»
Коммуникационный персонал
То, как устроено человеческое тело, очаровывает тех, кто склонен к научным предметам. Это стремление понять механизмы жизни и изучить живые организмы часто приводит к курсу биологии.Чтобы добиться успеха, необходимо точно знать, как изучать биологию в колледже. Биология — сложный предмет для освоения, потому что открытия в биологии происходят быстро.
В Кливлендском университете Канзас-Сити (CUKC) повышение квалификации для ускорения темпов изучения биологии в колледже охватывает три области:
Выбирайте правильные учебники
Учебники биологии часто меняются, поэтому вам нужно отметить конкретные издания. Обязательно получите все перечисленные сопроводительные материалы.В большинстве учебников биологии есть ссылки на веб-сайты или ресурсы, которые улучшат ваше обучение. Есть много чего освоить, и эти предметы включают:
- Графики
- Графики
- Анимации
- Тесты
- Области внимания.
Сегодня есть много мест, где можно купить или взять в аренду учебники, но не все варианты одинаковы. Один из проверенных онлайн-вариантов — ecampus.com. Преимущества включают возврат учебника в течение 25 дней, продление или покупку аренды, а также мгновенный доступ к электронным учебникам.
Будьте внимательны в отношении учебного времени
Несмотря на предыдущие успехи в изучении научных дисциплин, сложность университетской биологии может вызывать удивление. Основой того, как изучать биологию в колледже, являются хорошие классные заметки. Если ваш инструктор говорит «это важно», рисует диаграмму или график или упоминает страницы в учебнике, ожидайте, что эти элементы будут частью викторины или теста.
Чтобы понять, что важно, делайте заметки таким образом, чтобы детали были выделены с отступом по определенным темам — не пытайтесь писать полные предложения.После урока потратьте время на более тщательную переработку своих заметок, пока концепции еще свежи. Перед следующим занятием просмотрите записи предыдущего дня, чтобы новые идеи совпадали с имеющимися знаниями.
Имейте смелость задавать вопросы в классе. Записывайте вопросы по мере их поступления, чтобы вы могли систематизировать свои мысли и получать четкие ответы после занятий. Помните: вопросы, которые у вас есть, скорее всего, те же, что и у 10 других одноклассников.
Знать передовой опыт для достижения успеха
Неуспеваемость в колледже чаще всего объясняется плохими привычками в учебе и плохим управлением временем, а не способностями.Часть секрета заключается в том, чтобы потратить правильное количество времени на изучение, но также и усвоение концепций и принципов, а не быстрое запоминание.
Стратегии интеллектуального обучения:
- Планируйте от двух до трех часов занятий на каждый классный час
- Прочтите назначенный текст перед каждым занятием и переписывайте заметки из уроков своими словами
- Используйте карточки с вопросами на одной стороне и ответами на другой для терминов и фраз
- Воспользуйтесь мнемоникой для сложных идей
- Объяснять кому-нибудь концепции и определения
- Присоединяйтесь к учебной группе.Понимание других людей часто дает ответы, которые вы пытаетесь найти.

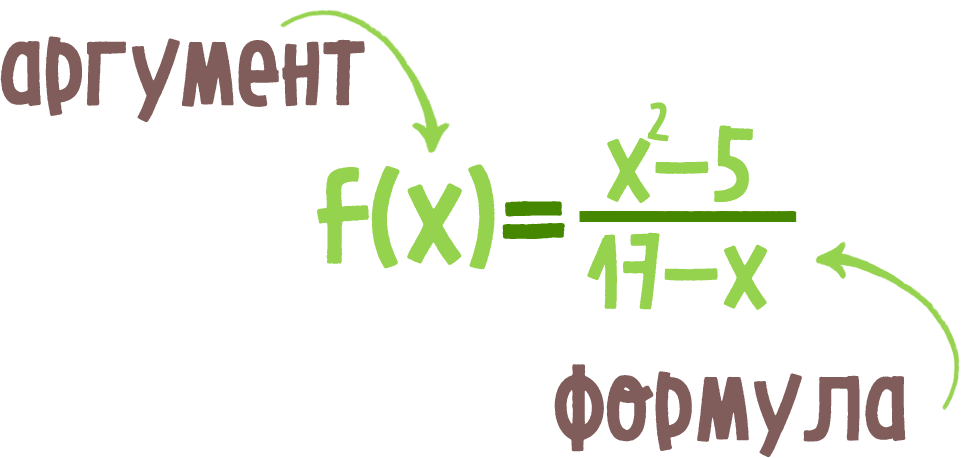
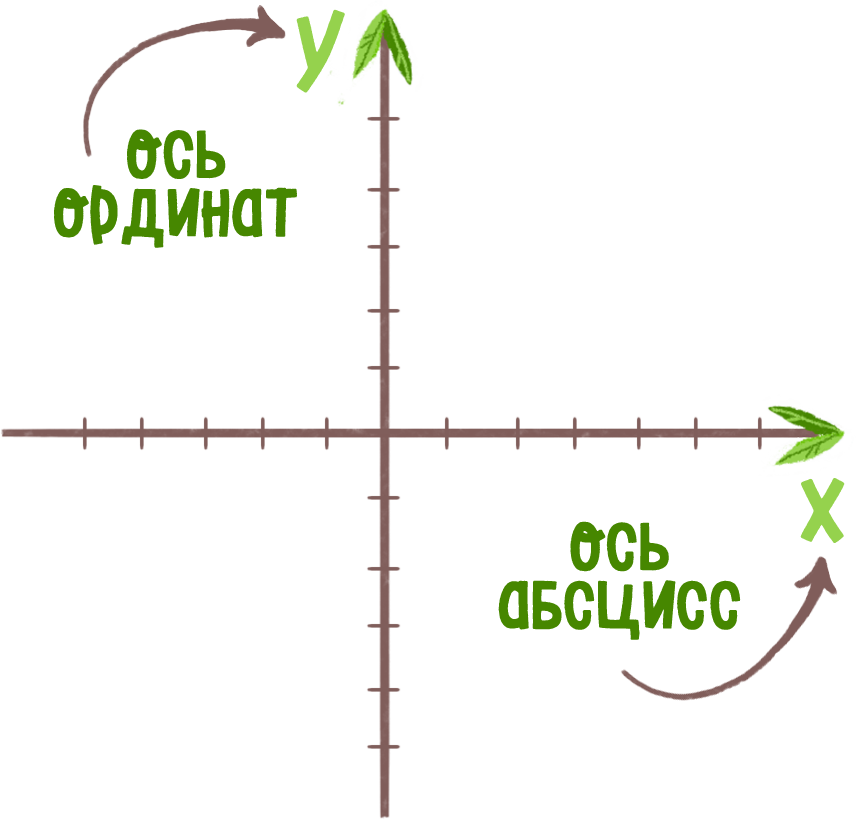
 А
А










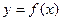 . Этот способ наиболее часто встречается на практике. Так, функция
. Этот способ наиболее часто встречается на практике. Так, функция  задана аналитически.
задана аналитически.

 (при
(при 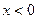 ) и
) и  (при
(при  ).
). , например таблица логарифмов.
, например таблица логарифмов. f(x).
f(x). , если х – рационально,
, если х – рационально,  , если – х иррационально.
, если – х иррационально. , и нечетной, если
, и нечетной, если  . В противном случае функция
. В противном случае функция  является четной, так как
является четной, так как  и
и  — нечетной, так как
— нечетной, так как  и
и  является функцией общего вида, так как
является функцией общего вида, так как  и
и  ,
,  .
. 2. Монотонность. Функция
2. Монотонность. Функция  и
и  . Тогда функция возрастает на промежутке Х, если
. Тогда функция возрастает на промежутке Х, если  , и убывает, если
, и убывает, если 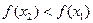 (рис. 4.8).
(рис. 4.8).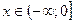 убывает и при
убывает и при  возрастает.
возрастает. для любого
для любого  . В противном случае функция называется неограниченной. Например, функция
. В противном случае функция называется неограниченной. Например, функция  ограничена на всей числовой оси, ибо
ограничена на всей числовой оси, ибо  для любого x
для любого x  R. (рис. 4.9).
R. (рис. 4.9). , если для любых х из области определения функций
, если для любых х из области определения функций  . Например, функция
. Например, функция  , так как для любых значений х
, так как для любых значений х  .
. ) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).
) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).

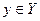 единственноезначение
единственноезначение  . Тогда полученная функция
. Тогда полученная функция  , определенная на множестве Y с областью значений Х, называется обратной.
, определенная на множестве Y с областью значений Х, называется обратной. . Обратную функцию
. Обратную функцию  (аналогично с обозначением обратной величины). Например, для функции y
(аналогично с обозначением обратной величины). Например, для функции y  ax обратной будет функция x
ax обратной будет функция x  .
. Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций 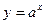 и
и  ).
). есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией
есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией  от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция
от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция  называется сложной функцией (функцией от функции). Например,
называется сложной функцией (функцией от функции). Например, 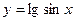 — сложная функция, так как ее можно представить в виде
— сложная функция, так как ее можно представить в виде  , где
, где 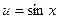 .
. .
. , неразрешенным относительно зависимой переменной. Например,
, неразрешенным относительно зависимой переменной. Например,  . Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например,
. Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например,  — функция задана неявно. Приведем к явному виду:
— функция задана неявно. Приведем к явному виду: 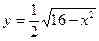 .
.


 в строке формул
в строке формул  .
. чтобы свернуть диалоговое окно, выберите ячейки, на которые вы хотите сослаться, а затем щелкните
чтобы свернуть диалоговое окно, выберите ячейки, на которые вы хотите сослаться, а затем щелкните  чтобы снова развернуть диалоговое окно.
чтобы снова развернуть диалоговое окно.



















































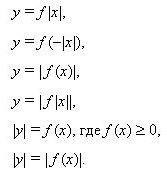
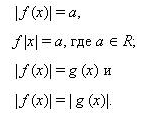
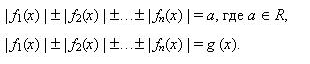

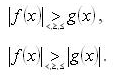
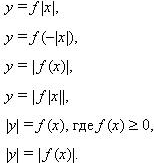

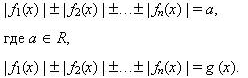

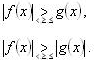
 Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному



 так как выражение под знаком модуля неотрицательно при любых x и y. Или:
так как выражение под знаком модуля неотрицательно при любых x и y. Или:  так так как выражение под модулем неположительно при любых z.
так так как выражение под модулем неположительно при любых z. То есть расстояние от точки −5 до нуля равно 5.
То есть расстояние от точки −5 до нуля равно 5. Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем. . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения
. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения  равно расстоянию между ними на числовой прямой.
равно расстоянию между ними на числовой прямой. (В связи с этим нередко встречается обозначение
(В связи с этим нередко встречается обозначение  длины отрезка AB, то есть расстояния от точки A до точки B.)
длины отрезка AB, то есть расстояния от точки A до точки B.) (расстояние от точки a до точки b равно расстоянию от точки b до точки a).
(расстояние от точки a до точки b равно расстоянию от точки b до точки a). . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
. Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию. Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.
Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля. .
. Ответ: (-11; -3).
Ответ: (-11; -3). Ответ:
Ответ:![(-\infty ;3]\cup [17,+\infty )](/800/600/https/ege-study.ru/wp-content/themes/ege/img/20x.png)
![(-\infty ;3]\cup [17,+\infty )](/800/600/https/ege-study.ru/wp-content/themes/ege/img/21x.png) имеем y = x. Для
имеем y = x. Для ![(-\infty ;3]\cup [17,+\infty )](/800/600/https/ege-study.ru/wp-content/themes/ege/img/22x.png) имеем y = −x. В результате получаем:
имеем y = −x. В результате получаем:![(-\infty ;3]\cup [17,+\infty )](/800/600/https/ege-study.ru/wp-content/themes/ege/img/23x.png) С помощью этого графика также можно решать уравнения и неравенства.
С помощью этого графика также можно решать уравнения и неравенства.![(-\infty ;3]\cup [17,+\infty )](/800/600/https/ege-study.ru/wp-content/themes/ege/img/24x.png) , где – некоторое число или выражение. Не забывайте, что
, где – некоторое число или выражение. Не забывайте, что 
 . Оно равно при
. Оно равно при  и при
и при  , т. е. как раз
, т. е. как раз  .
. при
при  .
. при
при  .
. при
при  .
.





 Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.
Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.


