Тот это местоимение или нет: Недопустимое название — Викисловарь
Указательные местоимения в русском языке
Указательные местоимения в русском языке — это слова, указывающие на предмет, его признак или количество и выделяющие его среди других предметов. Указательные местоимения отвечают на вопросы: какой? каков? сколько?
Что такое указательные местоимения?
По значению и грамматическим признакам все местоимения делятся не несколько разрядов. Поговорим об указательных местоимениях в русском языке. Местоимения этого разряда имеют название в соответствии с той функцией, которую они выполняют. Указательные местоимения выделяют среди однотипных вариантов предметов, признаков и количеств такой предмет, признак или количество, который представляет интерес для говорящего в этой речевой ситуации.
В тот город мы уже не вернемся.
Такой беспорядок царит в комнате!
Столько солнца вокруг!
Указательные местоимения (список)
- этот
- тот
- такой
- таков
- столько.

Добавим в этот список указательных местоимений устарелые синонимы, встречающиеся в литературе:
- экий
- этакий
- сей
- оный
Среди указательных местоимений можно выделить местоимения-прилагательные, указывающие на признак предмета:
- тот
- этот
- такой
- таков
Местоимение «столько» указывает на некоторое количество предметов, поэтому назовем его местоимением-числительным.
Склонение указательных местоимений
Узнаем, как изменяются указательные местоимения, определив, что по грамматической форме местоимения «тот», «такой», «этот» напоминают прилагательные. Эти местоимения склоняются и изменяются по родам и числам, как прилагательные:
- тот человек, та сумка, то сообщение, те дети;
- такой учебник, такая книга, такое озеро, такие дни;
- этот портфель, эта вещь, это дерево, эти новости.

Местоимение-числительное «столько» изменяется только по падежам.
| Падежи | Единственное число | Множественное число | |||
|---|---|---|---|---|---|
| Муж. род | Ср. род | Жен. род | |||
| И. п. | этот тот такой таков | это то такое таково | эта та такая такова | эти те такие таковы свои | столько |
| Р. п. | этого того такого | этой той такой | этих тех таких | стольких | |
| Д. п. | этому тому такому | этой той такой | этим тем таким | стольким | |
В. п. п. | этого (этот) того (тот) такого (такой) | это то такое | эту ту такую | этих (эти) тех (те) таких (такие) | стольких (столько) |
| Т. п. | этим тем таким | этой (этою) той (тою) такой (такою) | этим теми такими | столькими | |
| П. п. | об этом о том о таком | об этой о той о такой | об этих о тех о таких | о стольких | |
Местоимение «каков» напоминает краткую форму прилагательного. Как и краткая форма прилагательного, оно изменяется только по родам и числам:
- каков друг
- какова проблема
- каково предложение
- каковы мосты.

Синтаксическая роль указательных местоимений
В предложении указательные местоимения в одиночку или в сочетании с зависимым словом могут быть подлежащим, составным именным сказуемым, определением или дополнением.
Примеры
Тот вас не поймет.
Этот уже давно ушел, его не догонишь.
Этого человека Федор знал еще в юности.
Узнал все, что ему надо, и был таков.
Какова Устинья, такова и ботвинья.
Он упорно избегал этого.
Местоимение «столько» употребляется в сочетании с существительными в форме родительного падежа единственного или множественного числа. Это синтаксически неделимое сочетание «местоимение + существительное» употребляется в предложении в роли подлежащего или дополнения.
Столько берез выросло здесь с тех пор, как я покинул родное село!
Я не ожидал столько звонков с поздравлениями.
Местоимения «тот», «такой», «столько» участвуют в формировании сложноподчиненных предложений. Они используются в главном предложении в качестве указательных слов.
Виктор до сих пор помнит то место, где он с ребятами ловил раков в детстве.
Была такая непогода, что, как говорят, добрый хозяин собаку не выгонит.
За одну вьюжную ночь выпало столько снега, сколько выпадает за месяц.
Видеоурок
Указательные местоимения в русском языке. Грамматика русского языка с нуля. РКИ» src=»https://www.youtube.com/embed/MRR4aSKdyBA?feature=oembed&wmode=opaque» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Скачать статью: PDFМестоимение / Грамматика — russky.info
Значение и грамматические признаки
Местоимение – это часть речи, которая указывает на предмет, признаки и количества, но не называет их.
- Я, ты, он, она́ – вме́сте це́лая страна́. (= Я, ты, он, она – вместе целая страна.)
- Э́то моя́ кни́га, а э́то твоя́ тетра́дь.
 (= Это моя книга, а это твоя тетрадь.)
(= Это моя книга, а это твоя тетрадь.) - Никто́ не хоте́л выходи́ть на моро́з. (= Никто не хотел выходить на мороз.)
- Навстре́чу мне вы́шло не́сколько люде́й. (= Навстречу мне вышло несколько людей.)
К местоимению можно задать вопросы:
кто?
(= кто?)
что?
(= что?)
какой?
(= какой?)
чей?
(= чей?)
как?
(= как?)
где?
(= где?)
когда?
(= когда?)
и др. Местоимения употребляются вместо имён существительных, прилагательных, числительных или наречий. Большинство местоимений в русском языке изменяется по падежам, многие местоимения изменяются по родам и числам.
Местоимения употребляются вместо имён существительных, прилагательных, числительных или наречий. Большинство местоимений в русском языке изменяется по падежам, многие местоимения изменяются по родам и числам.
- кто? (= кто?) , что? (= что?)
- я (= я) , он (= он) , мы (= мы)
- какой? (= какой?) , чей? (= чей?)
- (этот (= этот) , , наш (= наш)
- как? (= как?) , где? (= где?) , когда? (= когда?)
- так (= так) , там (= там) , тогда (= тогда)
Разряды местоимений
По своему значению и грамматическим признакам местоимения делятся на несколько разрядов:
- личные
- я (= я) , ты (= ты) , он (= он) , она́ (= она) , оно́ (= оно) , мы (= мы) , вы (= вы) , они́ (= они)
- возвратное
- себя́ (= себя)
- вопросительные
- кто (= кто) , что (= что) , како́й (= какой) , чей (= чей) , кото́рый (= который) , како́в (= каков) , ско́лько (= сколько)
- относительные
- кто (= кто) , что (= что) , како́й (= какой) , чей (= чей) , кото́рый (= который) , како́в (= каков) , ско́лько (= сколько)
- неопределённые
- не́кто (= некто) , не́что (= нечто) , не́который (= некоторый) , не́сколько (= несколько) , кое-кто́ (= кое-кто) , кое-что́ (= кое-что) , кто́-либо (= кто-либо) , кто́-нибудь (= кто-нибудь) , кое-како́й (= кое-какой) , како́й-то (= какой-то) , како́й-либо (= какой-либо) , како́й-нибудь (= какой-нибудь) , ско́лько-то (= сколько-то) , ско́лько-нибудь (= сколько-нибудь)
- отрицательные
- никто́ (= никто) , ничто́ (= ничто) , никако́й (= никакой) , ниче́й (= ничей) , не́кого (= некого) , не́чего (= нечего)
- притяжательные
- мой (= мой) , твой (= твой) , ваш (= ваш) , наш (= наш) , свой (= свой) , его́ (= его) , её (= её) , их (= их)
- указательные
- тот (= тот) , э́тот (= этот) , тако́й (= такой) , тако́в (= таков) , сто́лько (= столько)
- определительные
- весь (= весь) , вся́кий (= всякий) , ка́ждый (= каждый) , сам (= сам) , са́мый (= самый) , ино́й (= иной) , друго́й (= другой)
Склонение местоимений
Личные местоимения
я (= я) , ты (= ты) , он (= он) , она́ (= она) , оно́ (= оно) , мы (= мы) , вы (= вы) , они́ (= они)
Личные местоимения имеют формы:
- лица
- числа
- падежа
- рода (только местоимения 3-го лица единственного числа).

| Лицо | Единственное число | Множественное число |
|---|---|---|
| 1 | я (= я) | мы (= мы) |
| 2 | ты (= ты) | вы (= вы) |
| 3 | он (= он) , она (= она) , оно (= оно) | они (= они) |
Местоимения
я
(= я)
и
ты
(= ты)
указывают на участников речи.
Местоимения он (= он) , она (= она) , оно (= оно) , они (= они) указывают на предмет, о котором говорится, говорилось или будет говориться.
Местоимения мы (= мы) и вы (= вы) указывают на говорящего или его собеседника вместе с другими лицами.
| Именительный | |||||||
| Родительный | |||||||
| Дательный | |||||||
| Винительный | |||||||
| Творительный | |||||||
| Предложный | (обо) мне | (о) тебе́ | (о) нём | (о) ней | (о) нас | (о) вас | (о) них |
Местоимения 3-го лица ( он (= он) , она́ (= она) , оно́ (= оно) , они́ (= они) ) после предлогов имеют в начале н:
у него́ (= у него) , к ней (= к ней) , о́коло них (= около них) , к нему́ (= к нему) , за ней (= за ней) , ме́жду ни́ми (= между ними)
У всex личных местоимений формы родительного и винительного падежа совпадают.
Возвратное местоимение
Возвратное местоимение себя́ (= себя) указывает на то лицо, о котором говорят. Это местоимение не имеет формы именительного (nominativ) падежа, а также формы лица, числа и рода.
Именительный Именительный | — |
Родительный Родительный | |
Дательный Дательный | |
Винительный Винительный | |
Творительный Творительный | |
Предложный Предложный | (о) себе́ |
Вопросительные и относительные местоимения
Вопросительные и относительные местоимения:
кто (= кто) , что (= что) , како́й (= какой) , чей (= чей) , кото́рый (= который) , како́в (= каков) , ско́лько (= сколько)
Вопросительные местоимения служат для выражения вопроса.
Относительные местоимения служат для связи частей сложного предложения.
Вопросительные и относительные местоимении кто (= кто) и что (= что) не имеют рода и числа.
Именительный Именительный | |||
Родительный Родительный | |||
Дательный Дательный | |||
Винительный Винительный | ско́лько / ско́льких | ||
Творительный Творительный | |||
Предложный Предложный | (о) ком | (о) чём | (о) ско́льких |
Местоимения
како́й
(= какой)
,
кото́рый
(= который)
,
чей
(= чей)
изменяются по падежам, числам и родам и склоняются как прилагательные. С существительными они согласуются в падеже, числе и роде.
С существительными они согласуются в падеже, числе и роде.
| Местоимения мужского и среднего рода | Местоимения женского рода | Местоимения множественного числа | |
|---|---|---|---|
Именительный Именительный | како́й , чей , како́е , чьё | кака́я , чья | каки́е , чьи |
Родительный Родительный | како́го , чьего́ | како́й , чьей | каки́х , чьих |
Дательный Дательный | како́му , чьему́ | како́й , чьей | каки́м , чьим |
Винительный Винительный | како́й / чей / како́е / чьё | каку́ю , чью | каки́е , чьи , каки́х , чьих |
Творительный Творительный | каки́м , чьим | како́й (-ю) , чьей (-ею) | каки́ми , чьи́ми |
Предложный Предложный | (о) како́м , (о) чьём | (о) како́й , (о) чьей | (о) каки́х , (о) чьих |
| Местоимения мужского и среднего рода | Местоимения женского рода | Местоимения множественного числа | |
|---|---|---|---|
Именительный Именительный | кото́рый , кото́рое | кото́рая | кото́рые |
Родительный Родительный | кото́рого | кото́рой | кото́рых |
Дательный Дательный | кото́рому | кото́рой | кото́рым |
Винительный Винительный | кото́рый , кото́рого | кото́рую | кото́рые / кото́рых |
Творительный Творительный | кото́рым | кото́рой | кото́рыми |
Предложный Предложный | (о) кото́ром | (о) кото́рой | (о) кото́рых |
Неопределённые местоимения
Неопределённые местоимения
не́кто
(= некто)
,
не́что
(= нечто)
,
не́который
(= некоторый)
,
не́сколько
(= несколько)
,
кое-кто́
(= кое-кто)
,
кое-что́
(= кое-что)
,
кто́-либо
(= кто-либо)
,
кто́-нибудь
(= кто-нибудь)
,
кое-како́й
(= кое-какой)
,
како́й-то
(= какой-то)
,
како́й-либо
(= какой-либо)
,
како́й-нибудь
(= какой-нибудь)
,
ско́лько-то
(= сколько-то)
,
ско́лько-нибудь
(= сколько-нибудь)
указывают на неопределённые предметы, признаки, количество. Они образуются посредством присоединения к вопросительным (относительным) местоимениям приставок не- (
кое-что́
(= кое-что)
,
кое-каки́е
(= кое-какие)
) и кое- (
не́кто
(= некто)
,
не́что
(= нечто)
), которая всегда находится под ударением, а также суффиксов -то, -либо, -нибудь (
кто́-то
(= кто-то)
,
кто́-либо
(= кто-либо)
,
кто́-нибудь
(= кто-нибудь)
).
Они образуются посредством присоединения к вопросительным (относительным) местоимениям приставок не- (
кое-что́
(= кое-что)
,
кое-каки́е
(= кое-какие)
) и кое- (
не́кто
(= некто)
,
не́что
(= нечто)
), которая всегда находится под ударением, а также суффиксов -то, -либо, -нибудь (
кто́-то
(= кто-то)
,
кто́-либо
(= кто-либо)
,
кто́-нибудь
(= кто-нибудь)
).
Неопределённые местоимения склоняются по типу местоимений, от которых они образуются (вопросительных и относительных).
Именительный Именительный | кто́-то кто-то | что́-нибудь что-нибудь | не́сколько несколько |
Родительный Родительный | |||
Дательный Дательный | |||
Винительный Винительный | не́сколько / не́скольких | ||
Творительный Творительный | |||
Предложный Предложный | (о) ко́м-то | (о) чём-нибудь | (о) не́скольких |
Примечание
Местоимение
не́кто
(= некто)
имеет только одну форму именительного падежа.
Отрицательные местоимения
Отрицательные местоимения
никто́
(= никто)
,
ничто́
(= ничто)
,
никако́й
(= никакой)
,
ниче́й
(= ничей)
,
не́кого
(= некого)
,
не́чего
(= нечего)
служат для отрицания наличия какого-либо предмета, признака, количества или для усиления отрицательного смысла всего предложения. Они образованы от вопросительных (относительных) местоимений с помощью безударной приставка ни- (
никто́
(= никто)
,
ничто́
(= ничто)
,
никако́й
(= никакой)
,
ниче́й
(= ничей)
) и ударной приставки не- (
не́кого
(= некого)
,
не́чего
(= нечего)
). Местоимения
не́кого
(= некого)
и
не́чего
(= нечего)
не имеют формы именительного падежа.
Местоимения
не́кого
(= некого)
и
не́чего
(= нечего)
не имеют формы именительного падежа.
Отрицательные местоимения изменяются по падежам и числам, а в единственном числе – по родам. Местоимение никто́ (= никто) не изменяется ни по числам, ни по родам.
не́кого некого | не́чего нечего | |||
|---|---|---|---|---|
Именительный Именительный | — | — | ||
Родительный Родительный | ||||
Дательный Дательный | ||||
Винительный Винительный | ||||
Творительный Творительный | ||||
Предложный Предложный |
Притяжательные местоимения
Притяжательные местоимения
мой
(= мой)
,
твой
(= твой)
,
ваш
(= ваш)
,
наш
(= наш)
,
свой
(= свой)
,
его́
(= его)
,
её
(= её)
,
их
(= их)
указывают какому лицу принадлежит предмет.
Притяжательные местоимения мой (= мой) , твой (= твой) , ваш (= ваш) , наш (= наш) , свой (= свой) изменяются как прилагательные по падежам, числам и родам.
| Местоимения мужского и среднего рода | Местоимения женского рода | Местоимения множественного числа | |
|---|---|---|---|
Именительный Именительный | мой (= мой) , ваш (= ваш) , моё (= моё) , ва́ше (= ваше) | моя́ (= моя) , ва́ша (= ваша) | мои́ (= мои) , ва́ши (= ваши) |
Родительный Родительный | моего́ , ва́шего | мое́й , ва́шей | мои́х , ва́ших |
Дательный Дательный | моему́ , ва́шему | мое́й , ва́шей | мои́м , ва́шим |
Винительный Винительный | мой ,
ваш
,
моё ,
ва́ше моего́ , ва́шего | мою́ , ва́шу | мои́ , ва́ши , мои́х , ва́ших |
Творительный Творительный | мои́м , ва́шим | мое́й (-е́ю) , ва́шей (-ею) | мои́ми , ва́шими |
Предложный Предложный | (о) моём , (о) ва́шем | (о) мое́й , (о) ва́шей | (о) мои́х , (о) ва́ших |
Указательные местоимения
Указательные местоимения
тот
(= тот)
,
э́тот
(= этот)
,
тако́й
(= такой)
,
тако́в
(= таков)
,
сто́лько
(= столько)
служат для выделения среди других какого-либо определённого предмета, признака, количества. Указательные местоимения
тот
,
э́тот
,
тако́й
,
сто́лько
изменяются как полные прилагательные по падежам, числам и родам. Местоимение
тако́в
изменяется как краткое прилагательное, т. е. по числам и родам.
Указательные местоимения
тот
,
э́тот
,
тако́й
,
сто́лько
изменяются как полные прилагательные по падежам, числам и родам. Местоимение
тако́в
изменяется как краткое прилагательное, т. е. по числам и родам.
| Местоимения мужского и среднего рода | Местоимения женского рода | Местоимения множественного числа | |
|---|---|---|---|
Именительный Именительный | тако́й , э́тот / тако́е , э́то | така́я , э́та | таки́е , э́ти |
Родительный Родительный | тако́го , э́того | тако́й , э́той | таки́х , э́тих |
Дательный Дательный | тако́му , э́тому | тако́й , э́той | таки́м , э́тим |
Винительный Винительный | тако́й /
э́тот /
тако́е /
э́то тако́го / э́того | таку́ю , э́ту | таки́е ,
э́ти таки́х , э́тих |
Творительный Творительный | таки́м , э́тим | тако́й (-ою) , э́той (-ою) | таки́ми , э́тими |
Предложный Предложный | (о) тако́м , (об) э́том | (о) тако́й , (об) э́той | (о) таки́х , (об) э́тих |
Определительные местоимения
Определительные местоимения
весь
(= весь)
,
вся́кий
(= всякий)
,
ка́ждый
(= каждый)
,
сам
(= сам)
,
са́мый
(= самый)
,
ино́й
(= иной)
,
друго́й
(= другой)
указывают на один предмет из ряда однородных предметов.
Местоимения сам (= сам) , са́мый (= самый) в некоторых формах различаются только ударением.
| Мужской и средний род | Женский род | Множественное число | ||||
|---|---|---|---|---|---|---|
Именительный Именительный | са́мый , са́мое | сам , само́ | ||||
Родительный Родительный | ||||||
Дательный Дательный | ||||||
Винительный Винительный | са́мый ,
са́мое | сам
,
само́ | | | ||
Творительный Творительный | ||||||
Предложный Предложный | (о) са́мом | (о) само́м | (о) са́мой | (о) само́й | (о) са́мых | (о) сами́х |
Местоимение
весь
(= весь)
(
всё
(= всё)
,
вся
(= вся)
,
все
(= все)
) имеет особые формы в творительном падеже единственного числа мужского и среднего рода и во всex формах множественного числа.
| Мужской и средний род | Женский род | Множественное число | |
|---|---|---|---|
Именительный Именительный | весь , всё | ||
Родительный Родительный | |||
Дательный Дательный | |||
Винительный Винительный | весь
,
всё | | |
Творительный Творительный | |||
Предложный Предложный | (обо) всём | (обо) всей | (обо) всех |
Определительные местоимения
тако́в
(= таков)
,
како́в
(= каков)
не склоняются.
Местоимение сам (= сам) указывает на лицо или предмет, который производит действие.
- Я сам расскажу́ о вре́мени и о себе́. (В. В. Маяковский) (= Я сам расскажу о времени и о себе. (В. В. Маяковский))
Местоимение весь (= весь) , вся́кий (= всякий) указывают на полноту охвата, определяют предмет как нечто нераздельное.
- Весь день шёл дождь.
(= Весь день шёл дождь.
 )
) - Все о́чень уста́ли. (= Все очень устали.)
- Всю ночь чита́л рома́н Толсто́го. (= Всю ночь читал роман Толстого.)
Местоимение вся́кий (= всякий) указывает на любой предмет из многих однородных.
- Вся́кое чу́вство име́ет це́ну, лишь пока́ свобо́дно.
 (В. Г. Короленко)
(= Всякое чувство имеет цену, лишь пока свободно. (В. Г. Короленко))
(В. Г. Короленко)
(= Всякое чувство имеет цену, лишь пока свободно. (В. Г. Короленко))
Местоимения са́мый (= самый) , ка́ждый (= каждый) , любо́й (= любой) указывают на выделение единичного предмета или лица из ряда однородных.
- Э́то был он, тот са́мый матро́с! (В. П. Катаев) (= Это был он, тот самый матрос! (В. П. Катаев)) mp3″> Люба́я рабо́та хороша́. (= Любая работа хороша.)
Местоимение са́мый (= самый) может также обозначать высшую степень признака, служить для образования превосходной степени прилагательных.
Указательные местоимения
Указательные местоимения в английском служат для того, чтобы обозначить определенный объект. С их помощью мы описываем предмет и выделяем его из множества других. Кроме того, эти местоимения помогают избегать повторов в речи.
Указательные местоимения имеют различные формы: они изменяются по числу и по расположению предмета относительно говорящего: далеко или близко. Одни и те же формы употребляются как с одушевленными, так и с неодушевленными существительными.
Типичное использование указательных местоимений — в позиции прилагательного. Так они служат для определения предмета. Другой случай — самостоятельное употребление, когда указательное местоимение выступает в качестве самого объекта или ситуации, о которой идет речь.
Формы указательных местоименийВ английском языке указательные местоимения могут различаться по параметру удаленности от говорящего. То есть в английском существуют два местоимения, чтобы сказать, близко или далеко находится предмет. В русском языке тоже есть такая возможность: мы различаем местоимения «этот» / «тот».
Для обозначения предмета, находящегося вблизи от говорящего, используется this (этот). Если же речь идет о более удаленном предмете, употребляется форма that (тот).
This pen is yellow and that pen is green — Эта ручка желтая, а та зеленая.
Оба вида местоимений различаются также по числу: единственное и множественное. Число местоимения совпадает с числом того существительного, к которому оно относится. Множественное число от this — these (эти), а от that образуется форма those (те).
Число местоимения совпадает с числом того существительного, к которому оно относится. Множественное число от this — these (эти), а от that образуется форма those (те).
Look at these kids, they are so beautiful — Посмотри на этих детей, они такие красивые.
No, I’m talking about those pictures that we saw yesterday — Нет, я говорю о тех картинах, которые мы видели вчера.
Таким образом, существует 4 базовых указательных местоимения в английском языке: this (этот), these (эти), that (тот), those (те).
Позиция указательных местоимений в предложенииУказательные местоимения могут употребляться в функции прилагательного: например, «этот стул» (this chair). Поэтому они стоят перед существительным, к которому относятся. Если в словосочетание добавляются определения, то указательное местоимение стоит на первом месте перед всей группой слов:
this wonderful blue chair — этот прекрасный синий стул
Словосочетания с указательным местоимением могут занимать различные позиции в предложении. Вне зависимости от этого любая форма this / these / that / those всегда стоит в начале группы слов.
Вне зависимости от этого любая форма this / these / that / those всегда стоит в начале группы слов.
Указательное местоимение с существительным может стоять в позиции подлежащего:
This / That beautiful postcard reminds me of my vacation in Spain — Эта / Та красивая открытка напоминает мне о моем отпуске в Испании.
These / Those beautiful postcards remind me of my vacation in Spain — Эти / Те красивые открытки напоминают мне о моем отпуске в Испании.
Также словосочетание с указательным местоимением в английском может стоять в позиции дополнения:
Put this / that beautiful postcard in the box — Положи эту / ту красивую открытку в коробку.
Put these / those beautiful postcards in the box — Положи эти /те красивые открытки в коробку.
В словосочетании может стоять только одно указательное местоимение. Кроме того, когда оно используется, употребление артикля становится невозможным. Наличие this / these / that / those обозначает определенный объект, поэтому в таких случаях подразумевается артикль the, и его употребление вместе с указательным местоимением излишне.
Наличие this / these / that / those обозначает определенный объект, поэтому в таких случаях подразумевается артикль the, и его употребление вместе с указательным местоимением излишне.
Неверно: Put the this postcard in the box.
Верно: Put the postcard in the box / Put this postcard in the box — Положи открытку в коробку / Положи эту открытку в коробку.
С неисчисляемыми существительными используются указательные местоимения единственного числа:
This / That furniture would look nice in the big room — Эта / Та мебель будет хорошо смотреться в большой комнате.
Последующее за местоимением существительное может заменяться на слово one (один): this one (это) / that one (то). Такие словосочетания часто используются, чтобы не повторять существительное.
This seat is taken and that one is vacant — Это место занято, а то свободно.
Во множественном числе используется слово ones:
These seats are taken and those ones are vacant — Эти места заняты, а те свободны.
В английском языке указательные местоимения используются также самостоятельно, без существительного, к которому они относятся.
Местоимения this / that могут употребляться в позиции безличного местоимения it. Так они определяют ситуацию, о которой собеседникам уже известно. В этом значении могут использоваться оба варианта местоимений: this и that.
I don’t want to talk about it / this / that — Я не хочу об этом говорить.
Местоимения this / that в таких предложениях часто можно переформулировать как словосочетания с существительными:
I don’t want to talk about this / that situation — Я не хочу говорить об этой ситуации.
Указательные местоимения в английском позволяют избежать повторов в предложении:
Do you know that Mr Smith bought a new car yesterday? Yes, I’ve heard about this — Ты знаешь, что мистер Смит купил вчера новую машину? Да, я слышал об этом (Yes, I’ve heard that Mr Smith bought a new car yesterday).
Самостоятельное употребление может встречаться не только для избежания повторов в предложении, но и как непосредственное указание на предмет:
This / that is my favourite picture — Это моя любимая картина.
Хотя местоимения it / this / that в подобных случаях могут заменять друг друга, небольшое смысловое отличие остается. This / that подчеркивают значение указания, а безличное местоимение it акцентирует внимание на самом объекте и выступает формальным подлежащим для обозначения объекта / ситуации. Сравните предложения:
It is my picture — Это моя картина.
This is my picture — Это моя картина / Вот моя картина.
Местоимение those часто используется в конструкции those who, когда речь идет о некотором множестве людей:
Those who are afraid can stay here — Те, кто боится, могут остаться здесь.
Удаленность во времениУказательные местоимения в английском используются не только для обозначения физического расстояния. Они также могут указывать на удаленность во времени. Сравните словосочетания:
Они также могут указывать на удаленность во времени. Сравните словосочетания:
these days — эти дни
those days — те дни
Местоимения this / these употребляются со словосочетаниями, которые указывают на настоящее или будущее время, а that / those определяют прошедшее время:
This time I won’t do the same mistake — В этот раз я не совершу ту же ошибку.
They lived in New York at that moment — Они жили в Нью-Йорке на тот момент.
She is very busy these days — Она очень занята в последнее время (в эти дни, сейчас).
I remember those days when we used to see each other every weekend — Я помню те дни, когда мы виделись друг с другом каждые выходные.
Это различие между указательными местоимениями в английском языке сохраняется не только в словосочетаниях с показателями времени. Местоимения this / these ассоциируются с тем, что происходит сейчас, а that / those используются с прошедшим временем:
Listen to this, you’ll like it — Послушай это, тебе понравится.
That was nice, what was it? — Здорово, что это было?
Различие this и thatУдаленность местоимения that может пониматься в более широком контексте: как говорящий относится к объекту.
I don’t know what I am doing in this city — Не знаю, что я делаю в этом городе (тот город, в котором человек находится).
I’ve heard lots of stories about that city — Я слышал много историй об этом городе (отстраненность говорящего от объекта).
Различие this / that может передавать разное отношение говорящего. Так, that употребляется в более эмоциональных фразах. Часто это местоимение используется в негативно окрашенных предложениях.
I don’t want to talk to that man — Я с этим человеком не хочу разговаривать.
С местоимением that существуют различные устойчивые словосочетания, закрепившиеся в английском языке:
- and all that — и все прочее
- that’s all right — все в порядке
- that’s all — на этом все
- that’s right — верно
- that’s it — вот именно
- that’s why — вот почему
Не нужно путать указательное местоимение that с союзом that. Они по-разному употребляются. That-местоимение обозначает определенный объект или ситуацию, тогда как союз служит для связи частей предложения.
Они по-разному употребляются. That-местоимение обозначает определенный объект или ситуацию, тогда как союз служит для связи частей предложения.
I’ve already told you that — Я уже говорил тебе это (that — местоимение).
I’ve already told you that he had found a new job — Я тебе уже говорил, что он нашел новую работу (that — союз).
Другие указательные местоименияК указательным местоимениям в английском языке можно отнести не только this / that / these / those. В этом качестве выступают также слова such (такой), the same (тот же самый).
Such отличается от других указательных местоимений тем, что между ним и существительным, к которому он относится, может стоять артикль. Артикль появляется при единственном числе существительного.
It’s such a beautiful day — Сегодня такой прекрасный день.
Во множественном числе артикль стоять не может.
I don’t understand such people — Я не понимаю таких людей.
Слово such также может употребляться самостоятельно:
Such is my opinion — Таково мое мнение.
В конструкции the same определенный артикль употребляется обязательно. После этого указательного местоимения в английском может следовать существительное в единственном или множественном числе.
I always have the same problem — У меня всегда (одна и) та же проблема.
We arrived at the same results — Мы пришли к (одним и) тем же результатам.
The same может использоваться самостоятельно, тогда местоимение занимает позицию наречия и означает «тем же образом, так же»:
If I were you, I would do the same — Будь я на твоем месте, я сделал бы то же самое (поступил так же).
Указательные местоимения в английском языке ‹ engblog.ru
Указательные местоимения в английском языке (demonstrative pronouns / demonstratives) указывают на лицо, предмет, или на их признаки. Указательных местоимений в английском языке несколько.
Указательных местоимений в английском языке несколько.
| Единственное число | Множественное число |
|---|---|
| this – этот, эта, это | these – эти |
| that – тот, та, то | those – те |
| such – такой, подобный | such – такие, подобные |
| the same – тот же самый | the same – те же самые |
| it – это | it – это |
Теперь вы знаете, какие бывают указательные местоимения в английском языке. Далее мы рассмотрим случаи, когда употребляется каждое из них.
Указательные местоимения this и these
This употребляется с существительными в единственном числе, местоимение these – с существительными во множественном числе. Эти местоимения нужно употреблять в следующих случаях:
- Когда мы говорим о людях или вещах, которые расположены рядом с нами.
 Иногда в предложениях с this и these употребляется наречие here (здесь), которое тоже показывает на близость предмета к нам.
Иногда в предложениях с this и these употребляется наречие here (здесь), которое тоже показывает на близость предмета к нам. - Когда ситуация происходит в настоящем или в будущем времени, мы описываем эту ситуацию с помощью this/these.
- Когда мы несколько раз говорим об одном и том же и хотим избежать повтора.
- Когда мы знакомим людей или представляемся в телефонном разговоре.
This table is wooden. – Этот стол деревянный. (стол находится рядом, и мы на него указываем)
These books belong to me. – Эти книги принадлежат мне. (несколько книг находятся рядом со мной)
This girl is here and she is waiting for you. – Эта девушка здесь, и она ждет вас.
We are going to meet this week. – Мы собираемся встретиться на этой неделе.
This month you are making a great progress.
– В этом месяце ты делаешь огромные успехи.
I don’t want to discuss this but I have to. – Я не хочу это обсуждать, но я должен. (подразумевается, что это событие уже называлось ранее, таким образом избегают повторения)
Look at this! He seems to be looking for his money. – Посмотри на это! Кажется, он ищет свои деньги. (местоимение указывает на ситуацию, описанную во втором предложении)
This is the main goal in my life. – Это главная цель в моей жизни.
Jim, these are my brothers, Tom and Carl. – Джим, это мои братья, Том и Карл.
Hello! This is Kate speaking! Can I speak to Mary? – Привет.
Это Кейт. Я могу поговорить с Мэри?
Указательные местоимения that и those
Указательное местоимение that употребляется с существительными в единственном числе, местоимение those – с существительными во множественном. Посмотрим, когда мы можем употреблять указательные местоимения that и those:
- Когда мы говорим о людях или вещах, расположенных далеко от нас. Иногда в предложениях с указательными местоимениями that и those используется наречие there (там).
- Когда мы говорим о ситуации, имевшей место в прошлом.
- Когда мы ссылаемся на какую-либо информацию, которую упоминали ранее, и хотим избежать повтора. Обычно рассказываем о прошедшем действии.
She got married a month ago. That was wonderful! – Она вышла замуж месяц назад. Это было прекрасно!
- Когда мы начинаем разговор по телефону и просим собеседника представиться. Человек на том конце провода находится далеко от нас, поэтому нужно использовать указательное местоимение that.

Good morning! This is Brenda White. Who’s that speaking? – Доброе утро! Это Бренда Уайт! С кем я говорю?
I don’t like this piece of cake. Give me that one, please. – Мне не нравится этот кусок торта. Дай мне тот, пожалуйста. (кусок торта, который понравился говорящему, находится дальше от него)
Those ships are too far. I can’t see their names. – Те корабли слишком далеко. Я не вижу их названий. (указанные корабли находятся на расстоянии от говорящего)
Look at that! There’s a camel.
– Посмотри туда! Вон там верблюд.
That’s my future husband. – То – мой будущий муж.
In those days people didn’t have cars. – В те времена у людей не было машин.
We made only four kilometers that day. – В тот день мы прошли только четыре километра.
На картинке наглядно показано, как работают указательные местоимения this/that и these/those, когда указывают на близость или отдаленность предмета.
Еще предлагаем вам посмотреть видео от преподавателя Alex. Интересно, как эту тему объясняет носитель языка.
Указательные местоимения such, the same, it
К другим указательным местоимениям в английском языке относятся such (такой, подобный), the same (тот же самый) и it (это). Рассмотрим, как их нужно употреблять в речи:
- Когда существительное стоит в единственном числе, то вместе с указательным местоимением such (такой, подобный) используется неопределенный артикль.

It’s such an important decision. – Это такое важное решение.
Если существительное стоит во множественном числе, артикля после местоимения such (такие, подобные) нет.
Don’t do such things! – Не делай таких вещей!
- Указательное местоимение the same (тот же самый / те же самые) всегда употребляется с определенным артиклем. Существительные после the same могут стоять как в форме единственного, так и множественного числа.
- Указательное местоимение it соответствует русскому местоимению «это».
Underline the word with the same meaning, please. – Пожалуйста, подчеркни слово с таким же значением.
He chose the same movies as I did. – Он выбрал те же фильмы, что и я.
– What is it? – Что это?
– It’s my ring.– Это мое кольцо.
Is it your passport? – Это твой паспорт?
Don’t miss it! – Не пропусти это!
Разница между this и it
Многие лингвисты говорят, что особой разницы между it и this нет. Вас поймут в любом случае, если вы скажете This is a cat или It is a cat. Но разница есть, хоть и небольшая.
This is a cat. – ЭТО кошка. (делаем акцент на слове «это», то есть именно это, а не то кошка)
It is a cat. – Это КОШКА. (делаем акцент на слове «кошка», то есть не собака и не морская свинка)
И один маленький нюанс напоследок. Чтобы два раза не повторять одно и то же существительное, вместо него иногда используют слово one. Причем перед этим one также нужно использовать указательное местоимение. Если за указательным местоимением в английском языке не идет прилагательное, то one (ones) можно опустить.
Would you like to buy this hat or that (one)? – Вы бы хотели купить эту шляпку или ту?
А если есть прилагательное, то нужно обязательно сохранить one или ones в предложении.
I don’t want to buy this hat, I will take that blue one. – Я не хочу покупать эту шляпку, я возьму вон ту голубую.
Эта тема тесно связана с другими, которые мы подробно разобрали в следующих статьях:
После ознакомления с ними рекомендуем пройти общий «Тест #2 на употребление местоимений в английском языке».
Для вашего удобства мы собрали все указательные местоимения в одну таблицу. Вы можете ее скачать и использовать для повторения.
↓ Скачать таблицу указательных местоимений (*.pdf, 172 Кб)
Для закрепления темы предлагаем выполнить небольшой тест:
ТестУказательные местоимения в английском
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
the so-called pronouns of identity on JSTOR
AbstractАвтор статьи возвращается к предложению А. Исаченко, сформулированному им в работе 1962-го года Die russische Sprache der Gegenwart, выделять в русском языке класс отождествляющих местоимений. Прежде чем ответить на вопрос о правомерности такого выделения, автор вносит ряд терминологических уточнений и разграничивает термины, с одной стороны, ‘кореферентность’, в основе которой лежит операция идентификации и, с другой, ‘тождество’, ‘сходство’ и ‘аналогия’, опирающиеся на операцию сравнения и предполагающих как сходство, так и различие сопоставляемых объектов. Полагая, что показателем отношения тождества в русском языке является частица ж е , автор анализирует условия ее употребления как с местоимениями, так и с полнозначными словами и показывает, что они различаются целым рядом функциональных особенностей. В заключение автор приводит аргументы за и против предложения А. Исаченко о выделении местоимений тождества в русском языке. The author revisits the proposal put forward by Isačenko in 1962 in Die russische Sprache der Gegenwart stating that it would be useful to identify a specific class of pronouns of identity in Russian. Before answering the question as to the validity of this proposal, the author specifies a number of terms, re-defining the terms ‘coreference’, based on the operation of identification, on the one hand; and, on the other hand, ‘identity’, ‘similarity and ‘analogy’, based on the operation of comparison and involving both similarities and differences of the compared objects. Assuming that the marker of identity relationships in Russian is the particle že, the author analyzes the conditions in which it is used with both pronouns and meaningful words and shows that they present a number of functional differences. In conclusion, the author gives arguments both for and against Isačenko’s proposal calling for a distinction of pronouns of identity in Russian.
Исаченко о выделении местоимений тождества в русском языке. The author revisits the proposal put forward by Isačenko in 1962 in Die russische Sprache der Gegenwart stating that it would be useful to identify a specific class of pronouns of identity in Russian. Before answering the question as to the validity of this proposal, the author specifies a number of terms, re-defining the terms ‘coreference’, based on the operation of identification, on the one hand; and, on the other hand, ‘identity’, ‘similarity and ‘analogy’, based on the operation of comparison and involving both similarities and differences of the compared objects. Assuming that the marker of identity relationships in Russian is the particle že, the author analyzes the conditions in which it is used with both pronouns and meaningful words and shows that they present a number of functional differences. In conclusion, the author gives arguments both for and against Isačenko’s proposal calling for a distinction of pronouns of identity in Russian.
Russian Linguistics is an international forum for all scholars working in the field of Russian linguistics and its manifold diversity, ranging from phonetics and phonology to syntax and the linguistic analysis of texts (text grammar), including both diachronic and synchronic problems. Besides original articles and reviews, Russian Linguistics publishes regular surveys of current scholarly writings from other periodicals. Topics that fall within the scope of the journal include: –Traditional–structuralist as well as generative-transformational and other modern approaches to questions of synchronic and diachronic grammar –Phonetics and phonology, morphology, syntax, pragmatics and semantics of – Russian and Old Russian –Philological problems of Russian and Old Russian texts –Russian grammar in its relation to linguistic universals –History of Russian literary language –Russian dialectology
Publisher Information Springer is one of the leading international scientific publishing companies, publishing over 1,200 journals and more than
3,000 new books annually, covering a wide range of subjects including biomedicine and the life sciences, clinical medicine,
physics, engineering, mathematics, computer sciences, and economics.
Местоимения в английском языке
Местоимение – это часть речи, обозначающая, но не называющая прямо предметы, лица, их свойства и отношения или дающая их временную и пространственную характеристику.
По своему значению местоимения в английском языке делятся на несколько групп. Ниже приведен список этих групп и соответствующих им английских местоимений.
I – я
you – ты, вы
he – он
she – она
it – оно
we – мы
they – они
me – я, мне
him – он
her – она
us – мы
them – они
- Притяжательные
my – мой, моя
your – твой, ваш
his – его
her – ее
its – его, ее, свой
our – наш
their – их
mine – мой
yours – твой
hers – ее
ours – наш
theirs – их
this – этот, эта, это
that – тот, та, то
these – эти
those – те
such – тот, такой
myself – себя, себе
yourself – себя
himself – себя, сам
herself – себя, сама
itself – себя, сам, сама, само
ourselves – себе, себя, собой
yourselves – себя
themselves – себя, себе, сами
each other – друг друга
one another – один другого
- Вопросительные
who – который, кто
what – что, какой
which – который, кто, какой
whose – чей, чьё
whoever – кто бы ни, который бы ни
whatever – что бы ни, (хоть) что-нибудь
whichever – какой угодно, какой бы ни
- Относительные
who – который, кто
whose – чей, чьё
which – который, кто
that – тот, та, то
- Неопределенные
some – кое-кто, некоторые
something – кое-что, нечто, что-нибудь
somebody – кто-нибудь, кто-то
someone – кто-нибудь, кто-то
any – какой-нибудь, что-нибудь
anything – что-нибудь, всё, что угодно
anybody – кто-нибудь, всякий, любой
anyone – кто-нибудь, любой
- Отрицательные
no – никакой
nothing – ничего, ничто
nobody – никто
no one – никто
none – ни один из
neither – ни тот ни другой, ни один, никто
- Разделительные
other – другой, иной
another – ещё один, другой
- Универсальные
all – все, каждый
each – каждый, всякий
both – оба, обе
either – каждый, любой (из двух)
every – каждый, всякий
everything – всё
everybody – каждый
everyone – каждый, всякий человек
Употребление английских местоимений
Местоимение можно употребить вместо только что упомянутого существительного, что поможет избежать излишнего повторения:
Old Jones surprised us again. He has helped to arrest a robber.
He has helped to arrest a robber.
Старик Джонс опять нас удивил. Он помог задержать грабителя.
Также они употребляются, когда лица или предметы, о которых идет речь, уже известны и говорящему, и слушающему:
We have not seen this film, have we?
Мы не видели этого фильма, верно?
Или когда они, наоборот, неизвестны:
Who is that tall man?
Кто тот высокий человек?
Роль английских местоимений в предложении
По роли в предложении английские местоимения можно разделить на:
- местоимения-существительные, которые выполняют синтаксические функции существительного
- местоимения-прилагательные с функциями прилагательных
Некоторые местоимения в зависимости от контекста могут выполнять обе роли:
This is a fast car. (местоимение-существительное, играет роль подлежащего)
Это быстрая машина.
I like this car. (местоимение-прилагательное, играет роль определения)
(местоимение-прилагательное, играет роль определения)
Мне нравится эта машина.
Английские местоимения и артикли
В комбинации с большинством местоимений-прилагательных не нужно использовать артикль, потому что они сами по себе определяют существительное, к которому относятся:
This city is beautiful. (данный конкретный город, равнозначно «The city»)
Этот город красивый.
Any city is beautiful. (любой из городов – равнозначно «A city»)
Любой город – красивый.
Структура английских местоимений
По своему строению местоимения делятся на простые (simple), составные (compound) и сложные (composite).
Простые состоят только из одной морфемы:
I – я
they – они
she – она
we – мы
и т. д.
Составные – из нескольких:
himself – себя, сам
nothing – ничего, ничто
herself – себя, сама
и т. д.
д.
Сложные представляют собой сочетание нескольких слов:
each other – друг друга
one another – один другого
Английские местоимения в детальном рассмотрении:
ТОТ — это… Что такое ТОТ?
ТОТ
та, то, род. того́ [тово], той, того́ [тово] (см. § 69), местоим. указательное [ср. также то (2)]. 1. Указывает на что-н. более отдаленное в пространстве или времени, находящееся не в непосредственной близости, не прямо перед глазами, не в данную минуту; противоп. этот. В каком доме вы живете — в этом или в том? Подай мне вон ту книгу. Тот свет (см. свет (2)). В тот приезд я успел больше сделать, чем в нынешний раз. 2. Употр. в знач. личного местоим. 3 лица, указывая на более отдаленное (в тексте) слово, во избежание смещения с более близко расположенным личным местоимением 3 лица. — Однажды русский генерал из гор к Тифлису проезжал: ребенка пленного он вез. «Тот (ребенок) занемог, не перенес трудов далекого пути.» Лермонтов. 3. Указывает на второй из двух предметов, связанных парным соотношением, на что-н. противоположное непосредственно данному, противолежащее; противоп. этот. На том берегу реки. На той стороне площади. По ту сторону баррикады.
«Тот (ребенок) занемог, не перенес трудов далекого пути.» Лермонтов. 3. Указывает на второй из двух предметов, связанных парным соотношением, на что-н. противоположное непосредственно данному, противолежащее; противоп. этот. На том берегу реки. На той стороне площади. По ту сторону баррикады.4. В главном предложении, в соответствии с относительными словами в начале придаточного, указывает на предмет, определяемый этими словами, или замещает его. «— Скажи, которая Татьяна? – Да та, которая грустна, и молчалива, как Светлана, вошла и села у окна.» Пушкин. «Тот самый человек пустой, кто весь наполнен сам собой.» Лермонтов. «не сдобровать тому, кто мне попадется.» Тургенев. «В те дни, когда мне были новы все впечатленья бытия.» Пушкин. «Смотрел в ту сторону, откуда должна появиться лодка.» Панферов. «Трактирный официант презирает того, кто не дает ему на чай. » Чехов. В то время, как… По той причине, что… (Онегин) «в своей одежде был педант, и то, что мы назвали франт.» Пушкин. «Что дама требует, в том рыцарь не может отказать.» Пушкин. «Чего я опасался, то и случилось.» Пушкин.
» Чехов. В то время, как… По той причине, что… (Онегин) «в своей одежде был педант, и то, что мы назвали франт.» Пушкин. «Что дама требует, в том рыцарь не может отказать.» Пушкин. «Чего я опасался, то и случилось.» Пушкин.
5. Указывает на что-н., уже упоминавшееся в речи, уже известное из предшествующего. «В тот год осенняя погода стояла долго на дворе.» Пушкин. «В ту ночь мороз был нестерпим.» Некрасов. «Натерпелась она в ту пору горя, ваша-то матушка!» Тургенев. «Язык того времени нам сдается натянутым, книжным.» Герцен.
|| То же в знач. сущ. тот, того́, м., та, той, ж., то, того́, «ср. У сильного всегда бессильный виноват; тому в истории мы тьму примеров слышим.» Крылов. «Попадись эта тема другому автору, тот бы ее обделал иначе.» Добролюбов. «Он царя подстрекнет, тот указ подмахнет.» Рылеев. «Он спросил новую бутылку, и только через час ее докончил, затем спросил другую, докончил и ту.» Достоевский. «Мы туда-сюда, спрашиваем кухарку: та ничего не говорит.» Тургенев. — «Он бросился к отцу и горячо поцеловал его. Тот отвечал ему тем же.» Достоевский. За ним ухаживают, а тот-то и внимания не обращает.
«Он царя подстрекнет, тот указ подмахнет.» Рылеев. «Он спросил новую бутылку, и только через час ее докончил, затем спросил другую, докончил и ту.» Достоевский. «Мы туда-сюда, спрашиваем кухарку: та ничего не говорит.» Тургенев. — «Он бросился к отцу и горячо поцеловал его. Тот отвечал ему тем же.» Достоевский. За ним ухаживают, а тот-то и внимания не обращает.6. со словами “самый”, “именно” и без них. Такой, к-рый вполне соответствует потребности, ожиданиям, предположениям, настоящий, нужный. Сел не в тот поезд. Та это книга или опять не та? Та самая. На этот раз та. Именно та. «Вот и ключик тот самый сыскался.» Салтыков-Щедрин. «Федот, да не тот.» Поговорка. «Нет, брат, не на того наскочил!» Тургенев.
7. В знач. сущ. то, того́, мн. нет, ср., при наличии противоположения со словом “это”, указывает на что-н. более отдаленное в пространстве или времени, не непосредственно данное, в противоп. это. То было летом, а это — осенью. То были взрослые, а это дети. То ветер шумел, а это волки воют.
|| Без такого противоположения употр. в знач. это (см. этот в 3 знач.; в разг. речи выходит из употр., сохраняясь лишь в устойчивых сочетаниях). «То было раннею весной.» А.К.Толстой. «То несомненный знак ей был, что едут гости.» Пушкин. «То бурлаки идут бечевой.» Некрасов. «О нет, мой младенец, ослышался ты: то ветер, проснувшись, колы́хнул листы.» Жуковский. «То была минута безумного отчаяния, когда я не мог владеть собою.» Чехов. «То был великолепный апофеоз науки.» Леонов. — «“Твой хор горланит вздор!” – “То правда”, отвечал хозяин с умиленьем.» Крылов. — «Хотите Алексея Ивановича заколоть и желаете, чтоб я при том был свидетелем? Так ли?» Пушкин.
более отдаленное в пространстве или времени, не непосредственно данное, в противоп. это. То было летом, а это — осенью. То были взрослые, а это дети. То ветер шумел, а это волки воют.
|| Без такого противоположения употр. в знач. это (см. этот в 3 знач.; в разг. речи выходит из употр., сохраняясь лишь в устойчивых сочетаниях). «То было раннею весной.» А.К.Толстой. «То несомненный знак ей был, что едут гости.» Пушкин. «То бурлаки идут бечевой.» Некрасов. «О нет, мой младенец, ослышался ты: то ветер, проснувшись, колы́хнул листы.» Жуковский. «То была минута безумного отчаяния, когда я не мог владеть собою.» Чехов. «То был великолепный апофеоз науки.» Леонов. — «“Твой хор горланит вздор!” – “То правда”, отвечал хозяин с умиленьем.» Крылов. — «Хотите Алексея Ивановича заколоть и желаете, чтоб я при том был свидетелем? Так ли?» Пушкин. «А ежели целый век Лазаря петь, то и старуха того не стоит.» Чехов. «Луна светила ярко, хотя незадолго перед тем пробежал легкий дождик.» Тургенев. «Забудут жены про наряды, а их мужья тому и рады.» Мей. «Кузьминское — богатое, а пуще того — грязное, торговое село.» Некрасов. Тем самым удалось предотвратить несчастье. Уж коли на то пошло (ср. пойти в 1 знач.). Мне теперь не до того. «До того ль, голубчик, было!» Крылов. Не в том дело. В том-то и дело.
|| Употр. в составе различных устойчивых сочетаний, из к-рых многие приобрели знач. наречий и сложных союзов (ср. то (1)). В силу того, что. До того, что. Дело в том, что. Вследствие того, что. По мере того, как. После того, как. Перед тем, как. Между тем, как. С тем, чтобы. Для того, чтобы. На то, чтобы. Несмотря на то, что. Вместе с тем. При всем том. Кроме того. К тому же. Тем более, что. Тем не менее. Тем паче. Как бы то ни было.
«А ежели целый век Лазаря петь, то и старуха того не стоит.» Чехов. «Луна светила ярко, хотя незадолго перед тем пробежал легкий дождик.» Тургенев. «Забудут жены про наряды, а их мужья тому и рады.» Мей. «Кузьминское — богатое, а пуще того — грязное, торговое село.» Некрасов. Тем самым удалось предотвратить несчастье. Уж коли на то пошло (ср. пойти в 1 знач.). Мне теперь не до того. «До того ль, голубчик, было!» Крылов. Не в том дело. В том-то и дело.
|| Употр. в составе различных устойчивых сочетаний, из к-рых многие приобрели знач. наречий и сложных союзов (ср. то (1)). В силу того, что. До того, что. Дело в том, что. Вследствие того, что. По мере того, как. После того, как. Перед тем, как. Между тем, как. С тем, чтобы. Для того, чтобы. На то, чтобы. Несмотря на то, что. Вместе с тем. При всем том. Кроме того. К тому же. Тем более, что. Тем не менее. Тем паче. Как бы то ни было. И тому подобное.
|| Указывает на положение, обстоятельство, соответствующее потребностям, ожиданиям, предположениям (ср. 6 знач.). «Эх, братец, всё не то.» Д.Давыдов. «Это не то, нет, нет, это совсем не то!» Достоевский. Вот это — то! 8. В соединении с частицей “же” или без нее указывает одинаковость, тождественность, в знач. не другой какой-н., такой же. «Всё тот же сон! — возможно ль? в третий раз!» Пушкин. «Я всё та же! сказала она решительно.» Гончаров. — «Давно расстались мы с тобою. Быть может, ты теперь не та.» А.Кольцов. «Они (сосны) всё те же; всё тот же их, знакомый уху шорох.» Пушкин. «Теперь, брат, я не тот.» Грибоедов. «Уж точно, стал не тот в короткое ты время.» Грибоедов. В одно и то же время. В ту же минуту. «Тех же щей, да пожиже влей.» Поговорка.(см. щи).
|| То же в знач.
И тому подобное.
|| Указывает на положение, обстоятельство, соответствующее потребностям, ожиданиям, предположениям (ср. 6 знач.). «Эх, братец, всё не то.» Д.Давыдов. «Это не то, нет, нет, это совсем не то!» Достоевский. Вот это — то! 8. В соединении с частицей “же” или без нее указывает одинаковость, тождественность, в знач. не другой какой-н., такой же. «Всё тот же сон! — возможно ль? в третий раз!» Пушкин. «Я всё та же! сказала она решительно.» Гончаров. — «Давно расстались мы с тобою. Быть может, ты теперь не та.» А.Кольцов. «Они (сосны) всё те же; всё тот же их, знакомый уху шорох.» Пушкин. «Теперь, брат, я не тот.» Грибоедов. «Уж точно, стал не тот в короткое ты время.» Грибоедов. В одно и то же время. В ту же минуту. «Тех же щей, да пожиже влей.» Поговорка.(см. щи).
|| То же в знач. то же, что. Коленкор — это тот же миткаль, но отбеленный или окрашенный.
|| То же в знач. сущ. то же, того́ же, мн. нет, ср. (не смешивать с нареч. “тоже”!). «Здоровье без силы то же, что твердость без упругости.» Козьма Прутков. Вечно одно и то же. Он отвечал ему тем же. Того же и вам желаю. 9. В соединении с частицей “же” употр. в знач. такой, о к-ром шла сейчас или идет сейчас речь, упомянутый (разг.). Избегайте табаку, вина, жирной пищи; взять тот же табак — чистый вред! || То же, без предшествующего упоминания, с присоединением еще слова “хотя” или без него, употр. в знач. даже, если хотите, хотя бы (простореч.). Спросите (хоть) того же ребенка, всякий вам скажет. 10. При перечислении противополагается словам: другой, иной, этот (как в знач. прил., так и сущ.). И тот и другой. И тот и этот. Тот или иной (кто-н., всё равно кто). Ни тот, ни другой. Ни тот, ни этот. Не тот, так этот.
то же, что. Коленкор — это тот же миткаль, но отбеленный или окрашенный.
|| То же в знач. сущ. то же, того́ же, мн. нет, ср. (не смешивать с нареч. “тоже”!). «Здоровье без силы то же, что твердость без упругости.» Козьма Прутков. Вечно одно и то же. Он отвечал ему тем же. Того же и вам желаю. 9. В соединении с частицей “же” употр. в знач. такой, о к-ром шла сейчас или идет сейчас речь, упомянутый (разг.). Избегайте табаку, вина, жирной пищи; взять тот же табак — чистый вред! || То же, без предшествующего упоминания, с присоединением еще слова “хотя” или без него, употр. в знач. даже, если хотите, хотя бы (простореч.). Спросите (хоть) того же ребенка, всякий вам скажет. 10. При перечислении противополагается словам: другой, иной, этот (как в знач. прил., так и сущ.). И тот и другой. И тот и этот. Тот или иной (кто-н., всё равно кто). Ни тот, ни другой. Ни тот, ни этот. Не тот, так этот. Не тот, так другой. «Тот пристает, другой, всем дело до меня.» Грибоедов. «Хотел жениться и хотел стать литератором, но не удалось ни то, ни другое.» Чехов. Такой привередливый: того не ест, этого не любит. 11. При повторении употр. в знач. один, другой и т.д. (как в знач. прил., так и сущ.; ср. р. в этом случае не смешивать с союзом “то”!). «Тут, глядя на него, иной качает головой, те шепчутся, а те смеются меж собой.» Крылов. «Тот сватался — успел, а тот дал промах.» Грибоедов. «По делу всяк по своему до полдня вышел из дому; тот путь держал до кузницы, тот шел в село Иваньково.» Некрасов. «Вот, например, вы мне говорите теперь и то, и то…» Тургенев. На него невозможно положиться: того недоделает, то напутает, то забудет.
❖ До того, что — см. до (1). И без того — в достаточной мере и по другим причинам: (это) еще усугубляет (что-н.
Не тот, так другой. «Тот пристает, другой, всем дело до меня.» Грибоедов. «Хотел жениться и хотел стать литератором, но не удалось ни то, ни другое.» Чехов. Такой привередливый: того не ест, этого не любит. 11. При повторении употр. в знач. один, другой и т.д. (как в знач. прил., так и сущ.; ср. р. в этом случае не смешивать с союзом “то”!). «Тут, глядя на него, иной качает головой, те шепчутся, а те смеются меж собой.» Крылов. «Тот сватался — успел, а тот дал промах.» Грибоедов. «По делу всяк по своему до полдня вышел из дому; тот путь держал до кузницы, тот шел в село Иваньково.» Некрасов. «Вот, например, вы мне говорите теперь и то, и то…» Тургенев. На него невозможно положиться: того недоделает, то напутает, то забудет.
❖ До того, что — см. до (1). И без того — в достаточной мере и по другим причинам: (это) еще усугубляет (что-н. ). «Сегодняшний день у меня и без того пропал.» Тургенев. «И без того она, как слышно, неуклюжа, теперь ребра недостает!» Грибоедов. (Да) и то сказать (разг.) — вводит подтверждение сказанному в знач. и в самом деле, и действительно. — «Прекрасной дочерью своей гордится старый Кочубей. И то сказать: в Полтаве нет красавицы, Марии равной.» Пушкин. «У него всегда дел пропасть, да и то сказать, что ему за удовольствие со старухой сидеть?» Л.Толстой. — «Покрал бессовестно, что мог. И то сказать, какая совесть в воре!» Крылов. И тот (та, то, те и т.д.) — в роли вводного слова употр. после (м.б. и не непосредственно) сло́ва, на к-рое указывает, в знач. даже или для усиления уже имеющегося налицо слова “даже” (ср. выше 2 знач.). «Соломин — и тот заметил, что есть две манеры выжидать.» Тургенев. «Есть только устав о кантонистах, да и тот еще надо в архиве отыскивать.» Салтыков-Щедрин.
). «Сегодняшний день у меня и без того пропал.» Тургенев. «И без того она, как слышно, неуклюжа, теперь ребра недостает!» Грибоедов. (Да) и то сказать (разг.) — вводит подтверждение сказанному в знач. и в самом деле, и действительно. — «Прекрасной дочерью своей гордится старый Кочубей. И то сказать: в Полтаве нет красавицы, Марии равной.» Пушкин. «У него всегда дел пропасть, да и то сказать, что ему за удовольствие со старухой сидеть?» Л.Толстой. — «Покрал бессовестно, что мог. И то сказать, какая совесть в воре!» Крылов. И тот (та, то, те и т.д.) — в роли вводного слова употр. после (м.б. и не непосредственно) сло́ва, на к-рое указывает, в знач. даже или для усиления уже имеющегося налицо слова “даже” (ср. выше 2 знач.). «Соломин — и тот заметил, что есть две манеры выжидать.» Тургенев. «Есть только устав о кантонистах, да и тот еще надо в архиве отыскивать.» Салтыков-Щедрин. «Даже расхитители казенного имущества, и те недовольны, что скоро нечего расхищать будет.» Салтыков-Щедрин. «Течь слабая, и та в минуту унята.» Крылов. Не без того — выражение, означающее признание известной степени, доли чего-н. в ком-чем-н. — Опять пьян? – Не без того. Не то (простореч.) — то же, что “не то, что(бы)” во 2 знач. (см. ниже). «Он не то на серебре, на золоте едал.» Грибоедов. «Ему не то чужое взять, а свое бы отдать.» Максим Горький. Не то, что(бы) (разг.) — употр. 1) для уточнения при отрицании возможного предположения или при поправке к сказанному и т.п. «Не то, чтоб очень пьян, но весел бесконечно.» Курочкин. — «Я стал не любить людей. Не то, что не любить, а как-то стали они мне тяжелы.» Достоевский. «Вы не то, чтобы внушали мне доверие; но ваше положение и мое очень схожи.» Тургенев.
«Даже расхитители казенного имущества, и те недовольны, что скоро нечего расхищать будет.» Салтыков-Щедрин. «Течь слабая, и та в минуту унята.» Крылов. Не без того — выражение, означающее признание известной степени, доли чего-н. в ком-чем-н. — Опять пьян? – Не без того. Не то (простореч.) — то же, что “не то, что(бы)” во 2 знач. (см. ниже). «Он не то на серебре, на золоте едал.» Грибоедов. «Ему не то чужое взять, а свое бы отдать.» Максим Горький. Не то, что(бы) (разг.) — употр. 1) для уточнения при отрицании возможного предположения или при поправке к сказанному и т.п. «Не то, чтоб очень пьян, но весел бесконечно.» Курочкин. — «Я стал не любить людей. Не то, что не любить, а как-то стали они мне тяжелы.» Достоевский. «Вы не то, чтобы внушали мне доверие; но ваше положение и мое очень схожи.» Тургенев. «Так вот, матушка…, была история: не то, чтобы притча али сказка какая, а истинное происшествие.» А.Островский. — «Не то, чтоб новизны вводили, — никогда… А придерутся к тому, к сему, а чаще ни к чему, поспорят, пошумят, и… разойдутся.» Грибоедов. «Он дожидался ночи — не то, что с нетерпением, а с любопытством.» Тургенев. «Уж ли с ума сошел? – Не то, чтобы совсем…» Грибоедов. «Он был не то, что развязен, а как-то натурально нахален.» Достоевский. «Он… не то, чтобы уж был совсем в беспамятстве во всё время болезни.» Достоевский. 2) в знач. не только. «Петру не то, что отвечать, — читать эти письма было недосуг.» А.Н.Толстой. Нет того, чтобы (разг.) — см. нет. Ни с того, ни с сего (разг.) — неизвестно почему, без понятного основания или без всякого основания. «Ни с того, ни с сего хлясь меня в ухо.» Лесков. Ни с того, ни с сего рассердился и ушел.
«Так вот, матушка…, была история: не то, чтобы притча али сказка какая, а истинное происшествие.» А.Островский. — «Не то, чтоб новизны вводили, — никогда… А придерутся к тому, к сему, а чаще ни к чему, поспорят, пошумят, и… разойдутся.» Грибоедов. «Он дожидался ночи — не то, что с нетерпением, а с любопытством.» Тургенев. «Уж ли с ума сошел? – Не то, чтобы совсем…» Грибоедов. «Он был не то, что развязен, а как-то натурально нахален.» Достоевский. «Он… не то, чтобы уж был совсем в беспамятстве во всё время болезни.» Достоевский. 2) в знач. не только. «Петру не то, что отвечать, — читать эти письма было недосуг.» А.Н.Толстой. Нет того, чтобы (разг.) — см. нет. Ни с того, ни с сего (разг.) — неизвестно почему, без понятного основания или без всякого основания. «Ни с того, ни с сего хлясь меня в ухо.» Лесков. Ни с того, ни с сего рассердился и ушел. Ни то, ни сё (разг. пренебр.) — о ком-чем-н. неопределенном, не имеющем своего назначения, места в ряду кого-чего-н., никого или ни в чем не удовлетворяющем, а потому негодном, неподходящем, ничтожном. «Ни то, ни сё, ни богу свечка, ни чорту кочерга.» Поговорка. — «Что же он по-вашему такое? – Ни сё, ни то; чорт знает, что такое!» Гоголь. Того (и) гляди — см. глядеть. То ли дело — см. дело. Тому назад — см. назад. То, сё, того́, сего́ и т.д., или то да сё, того́ да сего́ и т.д. (разг. фам.) — выражение, употр. для неопределенного указания на разные дела, обстоятельства, слова́ и т.п., к-рые трудно назвать или нельзя или не стоит называть. «Я, знаете, в дороге издержался: то да сё…» Гоголь. «И столько я о вас слыхал того-сего, что познакомиться давным давно желаю.» Лермонтов. «Ходил в трактир для чаепития, то да сё.» Чехов.
Ни то, ни сё (разг. пренебр.) — о ком-чем-н. неопределенном, не имеющем своего назначения, места в ряду кого-чего-н., никого или ни в чем не удовлетворяющем, а потому негодном, неподходящем, ничтожном. «Ни то, ни сё, ни богу свечка, ни чорту кочерга.» Поговорка. — «Что же он по-вашему такое? – Ни сё, ни то; чорт знает, что такое!» Гоголь. Того (и) гляди — см. глядеть. То ли дело — см. дело. Тому назад — см. назад. То, сё, того́, сего́ и т.д., или то да сё, того́ да сего́ и т.д. (разг. фам.) — выражение, употр. для неопределенного указания на разные дела, обстоятельства, слова́ и т.п., к-рые трудно назвать или нельзя или не стоит называть. «Я, знаете, в дороге издержался: то да сё…» Гоголь. «И столько я о вас слыхал того-сего, что познакомиться давным давно желаю.» Лермонтов. «Ходил в трактир для чаепития, то да сё.» Чехов. Тот-то…, а тот-то… (та-то и т.д.) (разг.) — употр. взамен точного указания лиц в знач.: один…, а другой…, кто-нибудь…, а кто-нибудь… Тот-то пойдет сюда, а тот-то — туда. То-то и тот-то пойдут сюда, а тот-то и тот-то — туда (одни…, а другие…).
Тот-то…, а тот-то… (та-то и т.д.) (разг.) — употр. взамен точного указания лиц в знач.: один…, а другой…, кто-нибудь…, а кто-нибудь… Тот-то пойдет сюда, а тот-то — туда. То-то и тот-то пойдут сюда, а тот-то и тот-то — туда (одни…, а другие…).Толковый словарь Ушакова. Д.Н. Ушаков. 1935-1940.
Что такое местоимение? Типы местоимений и правила
Что такое местоимение?
Местоимения составляют небольшую подкатегорию существительных. Отличительной чертой местоимений является то, что они могут заменять другие существительные. Например, если вы рассказываете историю о своей сестре Саре, эта история станет повторяться, если вы будете повторять «Сара» снова и снова.
Вы можете попытаться смешать это, иногда называя Сару «моей сестрой», но тогда это звучит так, как будто вы имеете в виду двух разных людей.
Вместо этого вы можете использовать местоимения она и ее для обозначения Сары.
Вот совет: Хотите, чтобы ваш текст всегда выглядел великолепно? Grammarly может уберечь вас от орфографических ошибок, грамматических и пунктуационных ошибок и других проблем с написанием на всех ваших любимых веб-сайтах.
Личные местоимения
Есть несколько разных типов местоимений, и некоторые местоимения относятся к более чем одной категории. Она и ее известны как личных местоимений .Другие личные местоимения: I и me , you , he и him , it , we и us , а также они и они . Если вы узнали о местоимениях в школе, вероятно, это те слова, на которых сосредоточился ваш учитель. Мы скоро перейдем к другим типам местоимений.
Предшественники
Местоимения универсальны. Местоимение и может относиться практически ко всему: велосипеду, дереву, фильму, чувству.Вот почему вам нужен антецедент. Антецедент — это существительное или существительная фраза, которую вы упоминаете в начале предложения или рассказа, а затем заменяете местоимением. В приведенных ниже примерах антецедент выделен, а местоимение, которое его заменяет, выделено жирным шрифтом.
В приведенных ниже примерах антецедент выделен, а местоимение, которое его заменяет, выделено жирным шрифтом.
В некоторых случаях антецедент не нужно указывать явно, если контекст полностью ясен. Обычно ясно, к кому относятся местоимения I , me и , к которым относится ваш , в зависимости от того, кто говорит.
Также можно использовать местоимение перед упоминанием антецедента, но старайтесь избегать использования длинных или сложных предложений, потому что это может затруднить понимание предложения.
Относительные местоимения
Относительные местоимения составляют еще один класс местоимений. Они используются для соединения относительных предложений с независимыми предложениями. Часто они вводят дополнительную информацию о чем-то упомянутом в предложении. Относительные местоимения включают , , , , , , , и , .Традиционно — это — люди, а — и — — животные или предметы.
Нужны ли вам запятые с who, which, и that , зависит от того, является ли предложение ограничивающим или неограничивающим.
Кто против кого — подлежащие и объектные местоимения
Теперь, когда мы поговорили об относительных местоимениях, давайте разберемся с тем, которое вызывает наибольшую путаницу: who vs. who . Кто — подлежащее местоимение, например I, he, she, we, и , они . Whom — местоимение объекта, например me, him, her, us и , их . Когда местоимение является объектом глагола или предлога, форма объекта — это та, которую вы хотите. У большинства людей нет особых проблем с объективным падежом личных местоимений, потому что они обычно идут сразу после глагола или предлога, изменяющего его.
А вот сложнее, потому что обычно он стоит перед , глаголом или предлогом, который его изменяет.
Один из способов проверить, нужно ли вам , или , , — это попробовать заменить личное местоимение. Найдите место, где обычно находится личное местоимение, и посмотрите, имеет ли форма субъекта или объекта больше смысла.
Найдите место, где обычно находится личное местоимение, и посмотрите, имеет ли форма субъекта или объекта больше смысла.
С кем / кем вы говорили с по раньше? Вы говорили с он / он раньше?
Мужчина, , которого я никогда раньше не видел , спрашивал о вас. Я видел он / его раньше?
Кому звонит ? Я должен сказать, что она / ее звонит ?
Если местоимение объекта (он или она) звучит правильно, используйте who .Если подлежащее местоимение (он или она) звучит правильно, используйте who .
Прежде чем мы продолжим, есть еще один случай, когда выбор между подлежащими и объектными местоимениями может сбивать с толку. Можете ли вы определить проблему в предложениях ниже?
В каждом из приведенных выше предложений местоимение I должно быть me . Если убрать из предложения другое имя или местоимение, это станет очевидным.
Указательные местоимения
Это , это , эти и те являются указательными местоимениями. Они занимают место существительного или существительной фразы, о которой уже упоминалось.
Они занимают место существительного или существительной фразы, о которой уже упоминалось.
Этот используется для единичных предметов, которые находятся поблизости. Эти используются для нескольких предметов, находящихся поблизости. Расстояние может быть физическим или метафорическим.
Этот используется для отдельных объектов, находящихся далеко. Эти используются для нескольких предметов, которые находятся далеко. Опять же, расстояние может быть физическим или метафорическим.
Неопределенные местоимения
Неопределенные местоимения используются, когда вам нужно указать на человека или вещь, которую не нужно конкретно указывать.Некоторые общие неопределенные местоимения: one, other, none, some, anybody, everybody, и no one .
Когда неопределенные местоимения функционируют как субъекты предложения или придаточного предложения, они обычно принимают глаголы единственного числа.
Возвратные и интенсивные местоимения
Возвратные местоимения оканчиваются на — себя или — себя : себя, себя, себя, себя, себя, себя, себя, себя.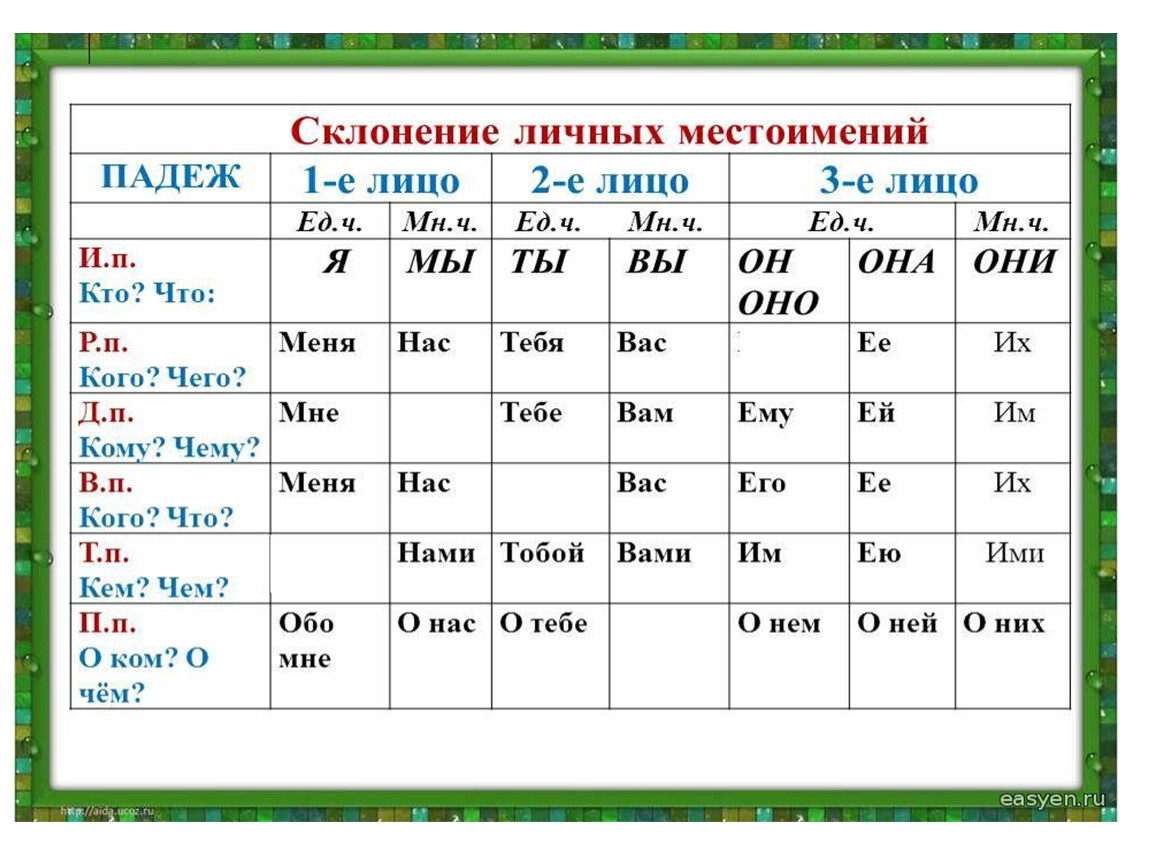
Используйте возвратное местоимение, когда и подлежащее, и объект глагола относятся к одному и тому же человеку или предмету.
Интенсивные местоимения выглядят так же, как возвратные местоимения, но их назначение иное. Интенсивные местоимения добавляют акцента.
«Я построил этот дом» и «Я сам построил этот дом» означают почти одно и то же. Но «я» подчеркивает, что я лично построил дом — я не нанимал кого-то другого, чтобы он делал это за меня. Точно так же: «Вы видели, как Лоретта разлила кофе?» и «Вы сами видели, как Лоретта разлила кофе?» имеют похожие значения. Но «себя» ясно дает понять, что спрашивающий хочет знать, действительно ли вы были свидетелями инцидента или только слышали его описание кем-то другим.
Иногда у людей возникает соблазн использовать self там, где им следует использовать me , потому что это звучит немного красивее. Не попадитесь в эту ловушку! Если вы используете форму местоимения -self , убедитесь, что оно соответствует одному из приведенных выше вариантов использования.
Притяжательные местоимения
Притяжательные местоимения бывают двух видов: ограничивающий и абсолютный. Мой, ваш, его, его, ее, наш, их и , чьи используются, чтобы показать, что что-то принадлежит антецеденту.
Абсолютные притяжательные местоимения: мой, ваш, его, ее, наш, и их . Абсолютные формы могут быть заменены тем, что принадлежит антецеденту.
Некоторые притяжательные местоимения легко спутать с похожими сокращениями. Помните, что притяжательные личные местоимения не содержат апострофов.
Вопросительные местоимения
Вопросительные местоимения используются в вопросах. Вопросительные местоимения: who , what , which и which .
Существует более 100 местоимений. Вот полный список…
Список местоимений, плюс определения для каждого типа местоимения. Прокрутите до конца, чтобы увидеть полный список местоимений.
Что такое местоимение?
Местоимения — одни из самых полезных слов в английском языке. Они используются вместо существительного, чтобы его не называли дважды. Например: Сюзи бросила бумеранг, и он вернулся к ней. В этом предложении «это» — местоимение, представляющее бумеранг, а «ее» — местоимение, относящееся к Сюзи.Без местоимений мы бы сказали, что Сьюзи бросила бумеранг, и бумеранг вернулся к Сюзи. Без местоимений, как бы мы вообще сказали «мы»?
Они используются вместо существительного, чтобы его не называли дважды. Например: Сюзи бросила бумеранг, и он вернулся к ней. В этом предложении «это» — местоимение, представляющее бумеранг, а «ее» — местоимение, относящееся к Сюзи.Без местоимений мы бы сказали, что Сьюзи бросила бумеранг, и бумеранг вернулся к Сюзи. Без местоимений, как бы мы вообще сказали «мы»?
Вот полное определение.
Определение местоимения
В английском языке — часть речи, используемая в качестве замены предшествующего существительного, которое ясно понимается и с которым оно согласуется по личности, числу и полу. Местоимения классифицируются как личные ( я, мы, ты, он, она, оно, они ), указательные ( это, эти, те, те ), родственники ( кто, который, тот , as ), неопределенный ( каждый, все, каждый, любой, один, оба, любой, такой, кто-то ), вопросительный ( who, which, what ), рефлексивный ( я, сама ), притяжательный ( мой, ваш, его, ее, их ). Есть также местоименных прилагательных , иногда называемых притяжательными прилагательными ( мой, ваш, его, ее, наш, их ).
Есть также местоименных прилагательных , иногда называемых притяжательными прилагательными ( мой, ваш, его, ее, наш, их ).
1. Личные местоимения / подлежащие местоимения
Вы уже знаете предметные местоимения, даже если не знали, как они называются. Предметные местоимения используются для замены подлежащего в предложении. Вы также можете увидеть их, называемые «личными» местоимениями, поскольку они обозначают говорящего ( I, me, we, us ), человека, с которым разговаривают ( you ), или человека или предмет, о котором идет речь ( he, она, это, они, он, она, они ).Следующие часто используемые слова являются предметными местоимениями:
- I
- we
- you (единственное и множественное число)
- he
- she
- it
- они
Примеры личных местоимений
I будут оставлены скоро.
Добро пожаловать, .
Она — новый учитель.
Он говорит на трех языках.
Они очень доброжелательные соседи.
2. Объектные местоимения
Объектные местоимения используются как объект глагола или предлога.
- me
- us
- you (единственное и множественное число)
- her
- him
- it
- them
Примеры местоимений объекта
Они предложили me a ride. («Я» является объектом глагола «предложил».)
Это письмо адресовано мне . («Я» — объект предлога «к.»)
Они дали нам бесплатных билетов на шоу. (» Нам «является объектом глагола» дал «)
3. Притяжательные местоимения
Притяжательное местоимение обозначает право собственности и может заменять словосочетания с существительными.
- мое
- наши
- ваши (единственное и множественное число)
- ее
- его
- их
Примеры притяжательных местоимений
Зеленые перчатки мои .
Эта кошка
Эта кошка .
Красный дом — это их .
Притяжательные прилагательные / Pronominal прилагательные
«Pronominal» описывает нечто, напоминающее местоимение, как указание человека, места или предмета, при этом функционируя в основном как другая часть речи. Местоимение прилагательное — это прилагательное, напоминающее местоимение. «Она» в слове «ее машина» — местоименное прилагательное.
4. Возвратные местоимения
Возвратные местоимения могут быть самой простой группой для запоминания, потому что все они имеют одну общую черту: окончание «я» или «я».«Это потому, что возвратные местоимения показывают, как действия вышеупомянутого человека или группы влияют на него или ее (или них).
- я
- себя
- сама
- сам
- сам
- сам
- себя
- сами
Примеры возвратных местоимений
Я купил себе новую машину
Этот человек много думает о себе .
Мы можем обмануть себя .
5. Интенсивные местоимения
Интенсивные и возвратные местоимения — это на самом деле одни и те же слова (заканчивающиеся на «я» или «я»), но они по-разному действуют в предложении. Интенсивные местоимения не только относятся к ранее упомянутому человеку или людям, но они также подчеркивают. Как следует из названия, они усиливаются.
- сам
- сам
- сам
- сам
- сам
- себя
- себя
- себя
Интенсивные примеры местоимений
Я сам был уверен в фактах.
Беда в самой машине .
Повара сами едят после того, как все гости закончили.
6. Неопределенные местоимения
Как следует из слова «неопределенный», эти местоимения не определяют идентичность своих референтов. Они более расплывчаты, чем другие местоимения.
- все
- другой
- любой
- любой
- любой
- что угодно
- оба
- каждый
- либо
- все
- все
- все
- несколько
- никто
- нет
- никто
- ничего
- один
- другой
- другие
- несколько
- какой-то
- кто-то
- кто-то
- оба что-то
- такие 17 были кандидатами.
- что
- что угодно
- которое
- в зависимости от
- кто
- кто угодно
- кто
- кто угодно
- чей
- как
- , что
- что
- независимо от
- которое
- в зависимости от того, что
- кто
- кто угодно
- кто
- кто угодно
- чей
- He
- Это
- Вы
- Я
- Они
- ср
- Кто
- Его
- Их
- Кто угодно
- Любой
- Что-то
- Никто
- Билли, Карен и я играли в покер с друзьями -> Мы, , играли в покер с друзьями.
- Элли любит смотреть фильмы. -> Она любит смотреть фильмы, особенно если они комедии.

- Даниэль пойдет в цирк с Сарой? -> Будет ли он будет там с ей?
- Неопределенные местоимения — те, которые относятся к одному или нескольким неуказанным объектам, существам или местам, таким как кто-то, кто угодно, ничто. Обратите внимание, что в приведенных ниже примерах нет установленной позиции, где неопределенное местоимение будет появляться в предложении.
Примеры неопределенных местоимений:
1. Любой
2. Кто-то
3. Любой
4. Любой
5. Другой
6. Что-то
7. НиктоПримеры неопределенных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.

- Кто-нибудь хотел бы кофе?
- Возьмите как хотите . Джейми взял одно печенье, а Бен — , другое — .
- Кто бы ни владел этим , у него большие проблемы! Я хочу, чтобы кто-нибудь переместил это сейчас .
Неопределенные местоимения также могут использоваться для создания почти абстрактных предложений. Примеры могут включать: это, все, что-то такое и что-то .
- Все не потерялись.
- Такой и есть жизнь.
- Что-то мне подсказывает, что этот плохо кончится.
- Личные местоимения — относящиеся к определенному человеку, вещи или группе; все, кроме вас, имеют разные формы, обозначающие единственное или множественное число.Личные местоимения всегда специфичны и часто используются для замены существительного собственного (чьего-либо имени) или коллективной группы людей или вещей.
 Личные местоимения делятся на две основные группы: одна относится к подлежащему предложения, а другая — к объекту.
Личные местоимения делятся на две основные группы: одна относится к подлежащему предложения, а другая — к объекту.
Первый используется для замены подлежащего в предложении: I, you, he, she, it, we, you and they . Обратите внимание, что you повторяется как you может быть в единственном числе, обращаясь к одному человеку, или во множественном числе, обращаясь к группе людей.Примеры личных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.
- Джек и Дэвид друзья. Они вместе играют в баскетбол.
- I денег больше, чем he
- Мы опоздаем, если вы не поторопитесь.
Вторая группа местоимений заменяет предмет предложения: я, ты, он, она, оно, мы, ты, они . Рассмотрим предложение еще раз:
Мы опоздаем, если вы не поторопитесь.
В приведенном выше примере we является субъектом предложения, но you является объектом. Другие примеры местоимений, заменяющих объект:
- Петр спел песню мне .
- Опоздание на поезд приведет к опозданию us .
Уложила из них плотно в чемодане.
- Возвратные местоимения — те, которым предшествуют наречие, прилагательное, местоимение или существительное, к которым они относятся, и оканчивающиеся на — себя или — сами. Возвратные местоимения используются для обозначения подлежащего или части предложения. В список возвратных местоимений входят: Я, себя, себя, себя, себя, себя, себя, себя.
Примеры возвратных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.- Считайте сами
- Энни должна винить только себя .
Петр и Павел сами испекли лепешек.
- Демонстративные местоимения — те, которые используются для указания на что-то конкретное в предложении. Есть только четыре указательных местоимения — этот, тот, тот, тот , но использование иногда может быть немного сложным. Это и , что — единственное число, тогда как эти и те — множественное число. Как вы, возможно, заметили, может быть некоторое пересечение с неопределенными местоимениями при использовании , и , .
Примеры демонстративных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.- Я предпочитаю , а не .
- Эти красивые, но те принадлежат Дэнни.
- Вы видели , что ?
Хотя это может сбивать с толку, это, то, эти и те иногда могут использоваться как указательные прилагательные. Разница между ними в том, что указательное местоимение заменяет существительное, а указательное прилагательное квалифицирует существительное.
Я предпочитаю это фото . Этих цветов красивых , но эти ваз принадлежат Дэнни. Вы видели, что радуга ?
Должно быть ясно, что this, that, this и те в приведенном выше примере не являются местоимениями, потому что они используются для определения существительного, но не для его замены. Хороший трюк для запоминания разницы заключается в том, что указательное местоимение все равно будет иметь смысл, если после него в предложении следует слово , один или , один .
Я предпочитаю этому (один). Эти (те) красивые. Вы видели , что (один)? Эти (те) принадлежат Дэнни.
- Притяжательные местоимения — обозначающие владение или владение. Примеры включают: мой, его, ее, его, ваш, наш, их, чей. Рассмотрим пример:
Мой указывает на владение, что кошка принадлежит мне. Между прочим, это в предложении не местоимение, а указательное прилагательное, поскольку оно квалифицирует существительное кошка .Вы обнаружите, что притяжательные местоимения часто следуют за фразами, содержащими указательные прилагательные.
Примеры притяжательных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.
- Эти бананы ваши ?
- Это деньги наши .
Это вина их или ваша ?
- Относительные местоимения — те, которые относятся к существительным, упомянутым ранее, вводя прилагательное (относительное) придаточное.Обычно они появляются после существительного, чтобы прояснить предложение или предоставить дополнительную информацию. Примеры включают: кто, который, тот, кто, чей . Рассмотрим следующее предложение:
Мужчина , укравший машину , попал в тюрьму. Относительное местоимение , которое , действует, чтобы отсылать к существительному человек . Он действует, чтобы открыть предложение, идентифицируя мужчину не просто как любого мужчину, а как того, кто украл машину. Примеры относительных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.- Стол , который стоит в коридоре , используется для переписки.
- Автомобиль , который врезался в стену, был синего цвета.
- Это женщина, , ключ которой вы нашли.
- Вопросительные местоимения — вводящие вопрос. Примеры включают: who, who, who, which, what, which. Обычно вопросительное местоимение можно определить по тому факту, что оно часто встречается в начале вопроса.
Примеры вопросительных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.- Кто придет на вечеринку?
- Какой вы предпочитаете?
- Какой вам нужен?
- Чья одежда лежит на полу?
- Кому вы рассказали?
Кого и кого часто путают, и даже носители языка будут их неправильно использовать. Who заменит подлежащее в предложении, а who заменит прямое или косвенное дополнение.Хороший совет для принятия решения о том, что использовать, заключается в том, что вы можете заменить who в предложении личным местоимением, и это все равно будет иметь смысл. Кто придет на вечеринку? Приду на вечеринку . Эта же система не будет работать для Кому вы сказали? Я тебе сказал .
- Взаимные местоимения — выражающие взаимные действия или отношения; то есть друг друга.
В английском языке всего два взаимных местоимения: , и , .Они в основном используются, чтобы остановить ненужное повторение в предложении, но также для того, чтобы укрепить идею о том, что коллективные и взаимные действия происходят более чем с одним человеком или предметом. Джон и Мэри подарили друг другу подарков. Использование друг с другом позволяет нам сделать предложение более эффективным, чем: Джон подарил Мэри подарок, а Мэри — подарок Джону. Страны работали с друг с другом по национальной безопасности. В этом примере друг друга работают, чтобы предположить, что действие работы взаимно совпадает друг с другом более чем в одной стране.Примеры взаимных местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.
- Боксеры ударили друг друга
Пара любит друг друга глубоко
- Интенсивные местоимения — те, которые оканчиваются на — себя или — сами , и которые служат для подчеркивания своего прошлого. Они почти идентичны возвратным местоимениям, но вместо того, чтобы просто возвращаться к предмету предложения, они работают, чтобы усилить действие.Во многих случаях предложение все равно имело бы смысл без интенсивного местоимения.
Интенсивные примеры местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.- сделаю сам .
- Мы сделали этот пирог сами .
- Нация говорит за сама на выборах.
Обратите внимание на то, как интенсивное местоимение подчеркивает утверждение. Предложение все равно было бы технически правильным без интенсивного местоимения, но оно добавляет некоторый важный контекст к его значению.
- Предметные местоимения могут использоваться в начале предложения. Например: мы отлично поработали.
- Предметные местоимения также могут использоваться для переименования предмета. Например: Это она решила, что нам пора на Гавайи.
- Неопределенные местоимения не имеют антецедентов. Они способны стоять самостоятельно. Например: никому не нравится стук ногтей по классной доске.
- Объектные местоимения используются как прямые объекты, косвенные объекты и объекты предлогов. К ним относятся: ты, я, он, она, мы, они и это. Например: Дэвид рассказал ей об ошибке.
- Притяжательные местоимения показывают право собственности. Им не нужны апострофы. Например: Кот вымыл свой
- Ср едем в отпуск.
- Не говорите мне, , что вы, , не можете пойти с us .
- Любой , кто скажет , что это не будет забавным, понятия не имеет, , о чем они говорят.
- Эти — ужасно крутая лестница.
- Мы встретили друг друга в торговом центре.
- Не уверен, , какой из хуже: дождь или снег.
- It — один из лучших итальянских ресторанов в городе.
- Ричард смотрел на самого себя в зеркало.
- Стирка не будет сама .
- Кто-то пролил апельсиновый сок на всю столешницу!
- Это __________ говорит.
- Джон
- He
- Джон
- Am
- Грег такой же умный, как __________.
- Я
- мне
- она
- ср
- Собака прогрызла __________ любимую игрушку.
- это
- это
- его ‘
- его
- Это могло быть __________.
- Джерри
- любой
- лучше
- сложнее
- Терри выше, чем __________ утра.
- Я
- мне
- она
- ср
- B. Это он говорит.
- С.Грег такой же умный, как и она.
- D. Собака жевала любимую игрушку.
- B. Это мог быть кто угодно.
- А. Терри выше меня.
- Это тот, который я оставил в машине. (Здесь говорящий может держать мобильный телефон. Он особенный, и он находится рядом с динамиком.)
- Я возьму их? (В этом примере говорящий может указывать на некоторые тарелки. Они единичные, и они находятся далеко от говорящего.)
- Кто-то, должно быть, видел, как водитель уезжал. («Кто-то» — это не конкретный человек.)
- Мы все в сточной канаве, но некоторые из нас смотрят на звезды. (Драматург Оскар Уайльд) («Все» и «некоторые» не указывают людей.)
- Мне нечего заявить, кроме моей гениальности. (Драматург Оскар Уайльд) (Неопределенное местоимение «ничего» не указывает на вещь. Следует отметить, что неопределенное местоимение «нечто» также не указывает на вещь.)
- Кто тебе сказал? (Ответ на этот вопрос — существительное, представленное вопросительным местоимением «кто».)
- Какая собака выиграла гонку? (Ответ на этот вопрос — существительное, представленное вопросительным местоимением «which.»)
- Мы не можем все быть героями, потому что кто-то должен сидеть на обочине и хлопать, когда они проходят.
- Я купил батарейки, но их не было в комплекте. (Комик Стивен Райт) (Примечание: эта цитата основана на идее, что батарейки никогда не включаются в комплект поставки устройств с электрическим приводом.)
- Билеты наши. (Здесь «наш» представляет собой существительное «билеты» и говорит читателям, что «мы» владеем ими.)
- Должны ли мы следовать его инструкциям или их? (В этом примере «их» представляет существительное «инструкции» и говорит читателям, что «они» владеют ими.)
- Это английская книга Сары. Вы видели ее французскую книгу? (Притяжательный определитель «она» заменяет «Сара». Это доказывает, что притяжательный определитель «она» является типом местоимения.)
- Доктор Адам Сиссонс, , читавший лекции в Кембридже более 12 лет, должен был знать разницу. (Здесь относительное местоимение «who» вводит предложение «который учился в Кембридже 12 лет» и относится к «доктору Адамсу Сиссонсу».)
- Человек , который впервые увидел комету, сообщил о ней как о НЛО. (В этом примере относительное местоимение «who» вводит предложение «кто первым увидел комету» и относится к «человеку».)
- Собака , которая украла мой обед, слоняется снаружи. (Относительное местоимение «который» вводит предложение «украла мой обед» и отсылает к «собаке».»)
- Они нравятся друг другу.
- Они разговаривают друг с другом как с младенцами.
- Собака укусила себя. (Здесь возвратное местоимение «сам» относится к существительному «собака».)
- Вы разговариваете сами с собой? (В этом примере возвратное местоимение «сам» относится к местоимению «ты».»)
- Джон сам печет весь хлеб. (Здесь интенсивное местоимение «сам» относится к существительному «Джон».)
- Кошка сама открыла дверь. (В этом примере интенсивное местоимение «сам» относится к существительному «кошка».)
- Вы не согласны с чем-то на этой странице?
- Вы заметили опечатку?
- Субъективные личные местоимения — это местоимения, которые служат предметом предложения. Если вы изучаете английский как второй язык, помните, что субъективные личные местоимения: I , you , she , he , it , you и они .Например:
- « Я шла прямо на вечеринку».
- « Вы, , опоздали; она, , разозлилась.»
- « Он думал, что ты, , забыл; , мы, , знаем, что ты чуть позади».
- Объективные личные местоимения — это местоимения, которые выступают в качестве объекта предложения. Если вы изучаете английский как второй язык, помните, что объективные личные местоимения: me , you , her , his , it , us , вы и им .Например:
- «Полицейский сказал моему брату и мне притормозить».
- «Он указал на пешеходов и сказал, чтобы они были осторожны, , они ».
- «Полицейский сказал, что есть много быстрых автомобилистов, таких как us ».
- Притяжательные личные местоимения — местоимения, указывающие на владение. Они определяют человека (или несколько человек), которому принадлежит конкретный объект.Если вы изучаете английский как второй язык, помните, что притяжательные личные местоимения — это мое , ваш , ее , его , его , наши и их . Например:
- «Эта книга ваша или его ?»
- «Все книги мои .«
- «Ни в одном доме нет таких книг, как их , даже не наших ».
- « Это платье , которое я надену; то, что — то, что я носил вчера.»
- « Это неправда.»
«Пожалуйста, заплатите за те ».
- « Какой ресторан лучший?»
- « Что он вам сказал?»
- « Кого из пригласить?»
- « Тот, кто добавил счет, сделал ошибку.«
- «Счет , в который включено все наше питание, оказался больше, чем ожидалось».
- «Официант , который нас обслуживал , не умеет складывать».
- « Все заблудились по дороге туда».
- « Кто-то забыл принести карту.»
- «Неудивительно, что появилось несколько «.
- «Она сама испекла торт для ».
- «Сами решили съесть ».
- «Мы слышали, как она сказала:« Им должно быть стыдно за себя »»
- «Я сам нахожу местоимения увлекательными.«
- «Они сами думают, что каждый должен знать о местоимениях».
- «Вы сами должны всем рассказать, насколько хороши местоимения».

Никого нет дома .
Несколько рабочих ушли домой больными.
7. Демонстративные местоимения
Демонстративные местоимения указывают на конкретного человека или предмет.
Примеры демонстративных местоимений
Мне не очень нравятся эти .
Кто такой , что ?
Такие — военное счастье.
8. Вопросительные местоимения
Эта группа местоимений задает вопрос, какой индивидуальный референт или референты подразумеваются в остальной части предложения.
Примеры вопросительных местоимений
04 Кто оставил?Какие из этих ваши?
Сделайте что угодно .
9. Относительные местоимения
Относительные местоимения вводят зависимое предложение и относятся к антецеденту (просто слову или фразе, к которым относится местоимение). Например, , который в ребенок, который носит шляпу или , что в доме, в котором вы живете.
Например, , который в ребенок, который носит шляпу или , что в доме, в котором вы живете.
Примеры относительных местоимений
Автомобиль , который имеет спущенную шину, необходимо буксировать.
Посетитель , пришедший вчера , оставил свой номер телефона.
Сделайте как хотите .
10. Архаические местоимения
Есть несколько местоимений, вышедших из употребления, но часто встречающихся в старых текстах, так что есть шанс, что вы с ними встретитесь. «Тебя» — старое слово, означающее «ты», используемое только при обращении к одному человеку, в то время как «твой» — старое слово для «твоего». «Твое» указывает на то, что принадлежит тебе.
Архаические примеры местоимений
Ты, , не убий.
С этим кольцом я и женился.
Твое имя более ненавистно, чем твое лицо .
К твоему самому быть правдой.
Список всех местоимений
Есть ли какие-то местоимения, которые мы пропустили?
10 типов местоимений с примерами
Сегодня мы много говорим о местоимениях, особенно she / hers , he / him , и, конечно же, старинная болтовня над единственным числом they .Но если вы действительно собираетесь копаться в своих местоимениях, разве вы не должны знать все существующие типы? Мы здесь, чтобы помочь. Определенные типы местоимений тесно связаны друг с другом, и многие слова могут функционировать как несколько разных типов местоимений, в зависимости от того, как они используются.
Что такое местоимение? Местоимение — это «любой член небольшого класса слов, встречающихся во многих языках, которые используются в качестве замены или заменителя существительных и их словосочетаний и имеют очень общие ссылки», например I , you , he , это , это , кто , какой .
Личные местоимения заменяют людей или предметы. Они могут быть в единственном или множественном числе, в зависимости от того, относятся ли они к одному или нескольким существительным. Примеры включают I , me , we и us .
Личные местоимения обычно являются субъектом предложения или объектом в предложении. Каждое личное местоимение имеет разные формы в зависимости от его функции.Например, если писатель имеет в виду себя, он должен использовать I , если он является субъектом предложения, например, « I видел собаку». Если он объект, он должен использовать me , как в «Собака увидела me ».
Знаете ли вы историю использования , и самого в качестве местоимений единственного числа? Узнайте больше и почему они возвращаются сейчас.
Притяжательные местоимения Притяжательные местоимения — личные местоимения, которые также указывают на обладание чем-либо. У них есть формы единственного числа (например, мой ) и множественного числа (например, наш ). Эти местоимения часто появляются перед предметом одержимости, но не всегда. Например, « моя машина» и «это моя машина» указывают, кому принадлежит машина.
У них есть формы единственного числа (например, мой ) и множественного числа (например, наш ). Эти местоимения часто появляются перед предметом одержимости, но не всегда. Например, « моя машина» и «это моя машина» указывают, кому принадлежит машина.
Относительное местоимение начинается с предложения (группа слов, относящихся к существительному). Who , , что , и , где — все относительные местоимения.Они также могут служить другими типами местоимений, в зависимости от предложения. Например, в фразе «Я видел собаку , которая принадлежит вам » относительное местоимение , которое соответствует , является началом предложения , которым вы владеете, , описывающего собаку.
Возвратные местоимения Когда подлежащее выполняет действие над собой, в предложении используется возвратное местоимение после глагола. Возвратные местоимения включают себя , себя , себя, и себя .Примером возвратного местоимения является распространенное выражение «Я ударил себя ногой ».
Возвратные местоимения включают себя , себя , себя, и себя .Примером возвратного местоимения является распространенное выражение «Я ударил себя ногой ».
Интенсивные местоимения похожи на возвратные местоимения, но имеют другую функцию в предложении. Интенсивное местоимение не является необходимой частью предложения и служит только для того, чтобы усилить его антецедент. Например: Я сказал детям, что вы сегодня сами испекете торт . В этом предложении вы сами — это интенсивное местоимение, которое повторяет идею о том, что вы, , делаете торт.(Тогда лучше займитесь этим!)
Неопределенные местоимения Как и личные местоимения, неопределенных местоимений относятся к людям или предметам, но они не имеют отношения к конкретному человеку или предмету. Примеры неопределенных местоимений: , примерно , , любой, , и , все.
Поднимите свою игру по грамматике на новый уровень с вашим личным тренером по грамматике ™! Начни прямо сейчас бесплатно!
Указательные местоименияДемонстрационные местоимения указывают на человека или вещь или видоизменяют их.Есть четыре указательных местоимения: это и , что (для слов единственного числа), и эти и те (для слов множественного числа).
Вопросительные местоименияВопросительные местоимения начинают вопросы. Например, в « Who are you?» Вопросительное местоимение , которое начинает вопрос. Существует пять вопросительных местоимений: who , who и , которые (для вопросов, связанных с людьми), и , которые и what (для вопросов, связанных с вещами).
Говорят, все относительно .
 .. особенно эти 5 местоимений. Узнайте больше о них здесь.
.. особенно эти 5 местоимений. Узнайте больше о них здесь.Что такое местоимение? Типы местоимений и примеры
Что такое местоимение?
Местоимение определяется как слово или фраза, которая используется в качестве замены для существительного или существительной фразы, которая известна как антецедент местоимения.Местоимения — это короткие слова, которые могут делать все то же, что и существительные, и являются одним из строительных блоков предложения. Распространенные местоимения: he, she, you, me, I, we, us, this, them, that . Местоимение может выступать в качестве подлежащего, прямого объекта, косвенного объекта, объекта предлога и т. Д. И заменять любое лицо, место, животное или вещь. Таким образом, кофе становится им, Барбара становится ею, Джереми становится им, команда становится ими, и в предложении Барбара пьет чашку кофе каждый день может стать она пьет чашку кофе каждый день или даже она выпивает каждый день , где это заменит чашкой кофе , а не только кофе .
Без местоимений нам постоянно приходилось бы повторять существительные, и это сделало бы нашу речь и письмо повторяющимися, не говоря уже о громоздкости. Без местоимений, Барбара пьет чашку кофе каждый день , она любит выпить кофе перед ужином будет Барбара пьет чашку кофе каждый день , Барбара любит выпить чашку кофе перед ужином. Использование местоимений помогает строить предложения и делает их более интересными
Примеры местоимений в следующих предложениях выделены жирным шрифтом для облегчения идентификации.
Как уже упоминалось, местоимения обычно используются для замены существительных, однако они также могут заменять определенные наречиями , прилагательными , и другими местоимениями.Практически каждый раз, когда вы обращаетесь к человеку, животному, месту или предмету, вы можете использовать местоимения, чтобы добавить интереса и улучшить свою речь или письмо.
Почти во всех случаях местоимение должно следовать за выражением, называемым антецедентом. По сути, это означает, что местоимение может быть действительно понято только в контексте предшествующей информации о существительном. Например, если мы используем местоимение she в предложении, мы сможем понять его, только если знаем, кто she , таким образом, антецедент, возможно, дающий имя человека, обычно предоставляется первым. .В приведенном выше примере Барбара пьет чашку кофе каждый день , если бы мы никогда не упоминали Барбару или то, что она пьет, было бы неясно, если бы мы сказали, Она пьет это каждый день. Ваш читатель будет сбит с толку и спросит, кто она и что она пьет: вино, воду, лимонад?
.В приведенном выше примере Барбара пьет чашку кофе каждый день , если бы мы никогда не упоминали Барбару или то, что она пьет, было бы неясно, если бы мы сказали, Она пьет это каждый день. Ваш читатель будет сбит с толку и спросит, кто она и что она пьет: вино, воду, лимонад?
После того, как Барбара была упомянута, мы будем использовать местоимения она и ее позже в письме, чтобы перестать повторять собственное имя Barbara и притяжательное имя собственное Barbara .
Барбара пошла в ресторан на ужин с своими (Барбара) друзьями. Она (Барбара) была очень голодна, но ее друзья (Барбара) не прекращали болтать. В конце концов, Барбара решила взять дело в свои руки (Барбара) и она (Барбара) потребовала, чтобы они, (друзья Барбары) прекратили разговаривать.
Представьте себе, как бы читалось это предложение, если бы оно продолжало повторять Барбары и Барбары .Местоимения сделали письмо более плотным и, возможно, более элегантным. Это всего лишь базовый пример использования местоимений, они действуют по-разному, чтобы сделать речь и письмо более ясными и динамичными.
Типы местоимений
Местоимения можно разделить на множество категорий, включая:
Правила местоимений
Есть несколько важных правил использования местоимений. Читая эти правила и примеры в следующем разделе, обратите внимание, как соблюдаются правила местоимений. Скоро вы увидите, что с местоимениями легко работать.
Примеры местоимений
В следующих примерах местоимения выделены курсивом.
Следующие упражнения помогут вам лучше понять, как работают местоимения. Выберите лучший ответ, чтобы завершить каждое предложение.
Ответы
Список местоимений
Читая этот список местоимений, помните, что каждое из этих местоимений — это слово, которое можно использовать вместо существительного. Подумайте, как использовать местоимения из этого списка в предложениях, так как это улучшит ваше понимание.
Я
ср
Я
США
Вы
Она
He
ее
Его
Они
их
Это
То
Какой
Кто
Кого
Чей
В зависимости от того, что
Кто угодно
Кто угодно
Это
Эти
То
те
Кто угодно
Любой
Что-нибудь
каждый
Либо
Каждый
Все
Все
Никто
Ни то, ни другое
Никто
Ничего
Кто-то
Один
Кто-то
Что-то
Немного
Много
Оба
Несколько
Любая
Все
Некоторые
Мост
Нет
Я
себя
Сами
сами
сама
Сам
Сами
Сам
Кто
Что
Какой
Чей
Кого
ПРОНОУН
Местоимения — это слова, заменяющие существительные.
Каждое местоимение должно иметь четкое предшествующий (слово, обозначающее местоимение).
ВИДЫ ПРОНОМИНОВ
А. Личное Местоимения:
ОДИНОЧНЫЙ | МНОЖЕСТВО | |||||
субъективное | цель | притяжательный | субъективное | цель | притяжательный | |
1 ул 918 21 человек | Я | мне | моя, шахта | ср | нас | наша, наши |
2 918 20 ой 918 21 человек | вы | вы | ваш, Ваш | вы | вы | ваш, ваш |
3 рд человек | он она это | ему ее это | его ее, ее это | они | им | их, их |
Личные местоимения имеют следующее Характеристики: |
1.три человека (точки зрения) от 1-го лица
— тот (а) говорит ( я меня мой мой мы нас
наши наши ) Примеры 2. три пола женский ( она
ее ее ) Примеры 3.два числа в единственном числе ( I me
моя шахта ты твоя он ему его
она ее ее это ее ) Примеры 4. три ящика субъективный
( я вы он она это мы они ) Примеры — субъективный случай |
Примеры — притяжательный падеж Примеры — объективный случай ПРИМЕЧАНИЕ: Из-за падежа местоимения форма местоимения меняется вместе с функция в предложении.Перейдите по этой ссылке, чтобы случай местоимения для получения дополнительной информации. |
Б. Демонстративные местоимения:
Демонстративные местоимения также могут использоваться как определители. |
Пример : |
Подай мне тот молоток .( , описывает существительное молоток) |
Демонстративные местоимения также могут использоваться как квалификаторы: |
Пример : |
Она хотела , что много денег? (, ) описывает прилагательное сильно ) |
С . Рефлексивный / Интенсивные местоимения : местоимения «self»
Эти местоимения могут использоваться только для отражения или усилить слово, уже содержащееся в предложении.
Возвратные / интенсивные местоимения НЕ МОГУТ ЗАМЕНИТЬ личные местоимения.
Примеры : |
Я видел сам в зеркало.( Myself — возвратное местоимение, отражающее местоимение I . ) |
Я сделаю это Сам . ( Я — интенсивное местоимение, усиливающее местоимение I . ) |
Примечание: Следующие слова не соответствуют стандартам, и их нельзя использовать :
себя себя сам сам
Д.Неопределенный Местоимения:
Особое число :
один | кто-то | любой | нет один | каждый |
каждый | кто-нибудь | кто угодно | никто | все |
(n) либо | что-то | что угодно | ничего | все |
Примеры : |
Кто-то идет на обед. |
Ни один из нас не верит ни единому слову — говорит Гарри. |
Множественное число :
Примеры : |
Оба ожидаются на аэропорт одновременно. |
Несколько предложили отмена встречи. |
Единственное число с неисчисляемым числом / Множественное число с счетные :
Примеры : |
Немного из грязь стал неотъемлемой частью коврика. |
Некоторые из деревьев были ослаблены штормом. |
Использование неопределенных местоимений апострофы для обозначения притяжательный падеж.
Примеры : |
Авария nobodys вина. |
Как дорожные работы повлияют на на ежедневные поездки на работу? |
Некоторые неопределенные местоимения также могут использоваться в качестве определителей.
один, каждый, либо, ни один, несколько, любой, один, все, оба, несколько, несколько, много, большинство
Обратите внимание на различия : |
У каждого человек есть шанс. |
( Каждый является определителем , описывающим человек. ) |
У каждого есть шанс. |
( Каждый — неопределенное местоимение , заменяющее существительное.) |
Оба юристов пообещали дела хорошо. |
( Оба определитель , описывающий юристов .) |
Оба были в комнате. |
( Оба — неопределенное местоимение , заменяющее существительное.) |
E. Вопросительный Местоимения :
Вопросительные местоимения производят информацию вопросы, требующие более чем положительного или отрицательного ответа.
Примеры : |
Какой вы хотите? |
Кто там ? |
Ф . Родственник Местоимения:
Относительные местоимения вводят относительный (прилагательные) придаточные.
| Примечание: | Используйте who, who, и , на которых нужно сослаться. людям. |
Используйте вместо и вместо для ссылки вещи. |
Типы местоимений
Наша историяТипы местоимений
Термин «местоимение» охватывает множество слов, некоторые из которых не подпадают под стандартное определение местоимения, «слова, заменяющего существительное или именную фразу». Вот краткое описание девяти типов местоимений:Покажи мне инфографику
Понятно? Сделайте быстрый тест. Попробуйте наш тест перетаскивания.Обзор видео
Вот видео, в котором обобщены различные типы местоимений.
Подробнее о различных типах местоимений
Есть девять различных типов местоимений. (Под каждым заголовком есть ссылка на урок и тест на этот тип местоимения.)Указательные местоимения
Указательные местоимения — «это», «то», «эти» и «те». Указательное местоимение представляет собой существительное и сообщает нам, является ли оно единственным или множественным, и находится ли оно близко или далеко (в том числе во времени).Например:| около | далеко | |
|---|---|---|
| единственное число | это | это |
| множественное число | эти | inf000 9284
Подробнее о указательных местоимениях.
Неопределенные местоимения
Неопределенные местоимения относятся к людям или вещам, не будучи конкретными. Это самая большая группа местоимений. Он включает в себя «все», «некоторые», «любые», «несколько», «кто угодно», «никто», «каждый», «оба», «несколько», «любой», «никто», «один» и «никто», которые являются наиболее распространенными. Вот несколько примеров предложений с неопределенными местоимениями:Покажи мне инфографику
Подробнее о неопределенных местоимениях.
Вопросительные местоимения
Вопросительные местоимения — это «что», «который», «кто», «кто» и «чей».»Они используются в вопросах. Хотя они классифицируются как местоимения, не сразу очевидно, как они заменяют существительные. Фактически, ответ на вопрос (который будет существительным) — существительное, представленное вопросительным местоимением. Например, :Покажи мне инфографику
Подробнее о вопросительных местоимениях.
Личные местоимения
Личные местоимения: «Я», «ты», «он», «она», «оно», «мы», «они» и «кто». Чаще всего (но, конечно, не всегда) они заменяют существительные, обозначающие людей. Когда большинство людей думают о местоимениях, на ум приходят личные местоимения. Вот несколько примеров личных местоимений:Покажи мне инфографику
Подробнее о личных местоимениях.
Притяжательные местоимения
Притяжательные местоимения — «мой», «ваш», «его», «ее», «наш» и «их». Притяжательное местоимение представляет существительное и также говорит нам, кому оно принадлежит. Например:Покажи мне инфографику
Подробнее о притяжательных местоимениях и их классификации.
Относительные местоимения
Относительные местоимения — это «который», «тот» и «кто» (включая «кто» и «чей»). Относительное местоимение используется в начале относительного предложения (или прилагательного), которое добавляет дополнительную информацию к предложению. В каждом примере относительное придаточное предложение затенено, а относительное местоимение выделено жирным шрифтом.Покажи мне инфографику
Подробнее об относительных местоимениях.
Подробнее об использовании запятых с «which» и «who».
Взаимные местоимения
Взаимные местоимения — «друг друга» и «друг друга». Взаимные местоимения используются для обозначения взаимных действий или чувств. Например:Покажи мне инфографику
Подробнее о взаимных местоимениях.
Возвратные местоимения
Возвратные местоимения — это «я», «сам», «сама», «сам», «сам», «мы», «себя» и «сами».Возвратное местоимение оканчивается на «-сам» или «-себя» и относится к другому существительному или местоимению в предложении (обычно субъекту предложения). Например:
Покажи мне инфографику
Подробнее о возвратных местоимениях.
Интенсивные (или выразительные) местоимения
Интенсивные местоимения — это «я», «себя», «сама», «сам», «сам», «мы», «себя» и «сами». (Они такие же, как возвратные местоимения, но используются по-разному.)Интенсивное местоимение (иногда называемое «выразительным местоимением») относится к другому существительному или местоимению в предложении, чтобы подчеркнуть его (e.g., чтобы подчеркнуть, что это вещь, выполняющая действие). Например:
Покажи мне инфографику
Подробнее об усиленных местоимениях.
Помогите нам улучшить грамматику Monster
См. Также
Попробуйте наш тест перетаскивания на различных типах местоимений Что такое прилагательные? Что такое наречия? Что такое союзы? Что такое междометия? Что такое предлоги? Что такое глаголы? Что такое существительные? Различные типы существительных Указательные местоимения Неопределенные местоимения Вопросительные местоимения Личные местоимения Притяжательные местоимения Взаимные местоимения Относительные местоимения Возвратные местоимениячастей речи: местоимения | Scribendi
Написано Scribendi
Поймите эту важную часть речи
В вашем английском письме неприятные местоимения причиняют вам боль? Хотите быстро выучить грамматику английского языка? Расслабьтесь — наши профессионалы по редактированию и корректуре ESL готовы помочь вам объяснить эту неприятную часть речи.
Что такое местоимение?
Местоимения используются вместо существительных. Назначение местоимений — избежать повторения и облегчить понимание предложений. Некоторые из наиболее распространенных местоимений, которые нужно помнить при изучении английского как второго языка, — это he , she , it , они и this .
Семь типов местоимений
Существует семь типов местоимений, которые и английский, и английский как второй язык, писатели должны распознавать: личное местоимение, указательное местоимение, вопросительное местоимение, относительное местоимение, неопределенное местоимение, возвратное местоимение и интенсивное местоимение.
1. Личные местоимения
Личные местоимения относятся к определенному человеку или предмету. Их форма меняется, указывая на человека, число, пол или регистр.
2. Указательные местоимения
Демонстративные местоимения указывают на существительное или местоимение и определяют их. Эти и эти относятся к вещам, которые находятся поблизости в пространстве или времени, а , которые и , эти относятся к вещам, которые находятся дальше в пространстве или во времени.Например:
3. Вопросительные местоимения
Вопросительные местоимения используются, чтобы задавать вопросы. Вопросительные местоимения: who , who , which и what .Если вы изучаете английский как второй язык, важно помнить, что , и , используются для обозначения людей, а , используются для обозначения вещей и животных. Кто действует как субъект, а кто действует как объект. Например:
4.Относительные местоимения
Относительные местоимения используются для связывания одной фразы или предложения с другой фразой или предложением. Относительные местоимения: , , , , , , и , . Соединения любой , кто угодно и в зависимости от того, что также являются обычно используемыми относительными местоимениями. Например:
5. Неопределенные местоимения
Неопределенные местоимения относятся к идентифицируемому, но не указанному человеку или предмету. Неопределенное местоимение передает идею всего, любого, ни одного или некоторых. Если вы изучаете английский как второй язык, запомните следующие распространенные неопределенные местоимения: все , еще , любой , любой , любой , , каждый , все , все , все , мало , много никто , 9069 , один , несколько , какой-то , кто-то и кто-то .Например:
6. Возвратные местоимения
Возвратные местоимения относятся к предмету предложения или предложения. Возвратные местоимения, используемые при написании английского: self , self , self , self , сам , self и сами .Например:
7. Интенсивные местоимения
Интенсивные местоимения используются, чтобы подчеркнуть свое предшествующее. Интенсивные местоимения идентичны по форме возвратным местоимениям. Например:
Практика ведет к совершенству при овладении местоимениями
Если у вас все еще возникают проблемы с местоимениями, попробуйте отправить документ нашим английским редакторам. Наши редакторы позаботятся о том, чтобы все ваши местоимения были идеальными.
Источник изображения: StepanPopov / envato.elements.com
Считайте каждое слово. Наймите профессионального редактора.
Об авторе
Штатные редакторы Scribendi работают с писателями со всего мира, чтобы улучшить свои тексты. Они знают, что ни одно произведение не обходится без профессионального редактирования, и им нравится видеть, как хороший текст превращается в отличный.



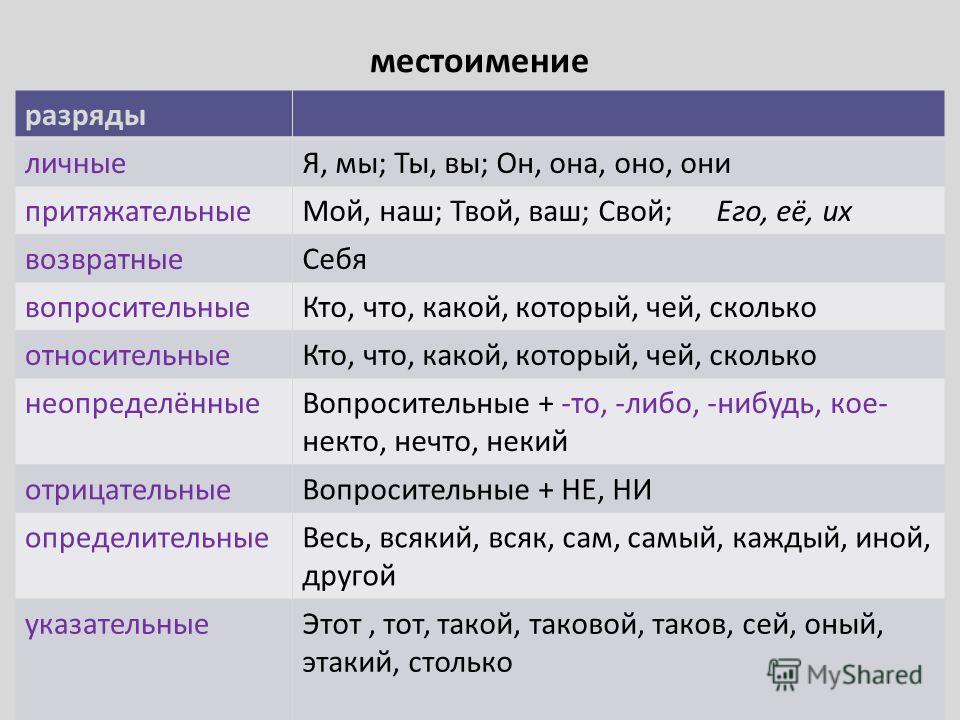
 (= Это моя книга, а это твоя тетрадь.)
(= Это моя книга, а это твоя тетрадь.)
 )
) (В. Г. Короленко)
(= Всякое чувство имеет цену, лишь пока свободно. (В. Г. Короленко))
(В. Г. Короленко)
(= Всякое чувство имеет цену, лишь пока свободно. (В. Г. Короленко)) Иногда в предложениях с this и these употребляется наречие here (здесь), которое тоже показывает на близость предмета к нам.
Иногда в предложениях с this и these употребляется наречие here (здесь), которое тоже показывает на близость предмета к нам. – В этом месяце ты делаешь огромные успехи.
– В этом месяце ты делаешь огромные успехи. Это Кейт. Я могу поговорить с Мэри?
Это Кейт. Я могу поговорить с Мэри? – Посмотри туда! Вон там верблюд.
– Посмотри туда! Вон там верблюд.
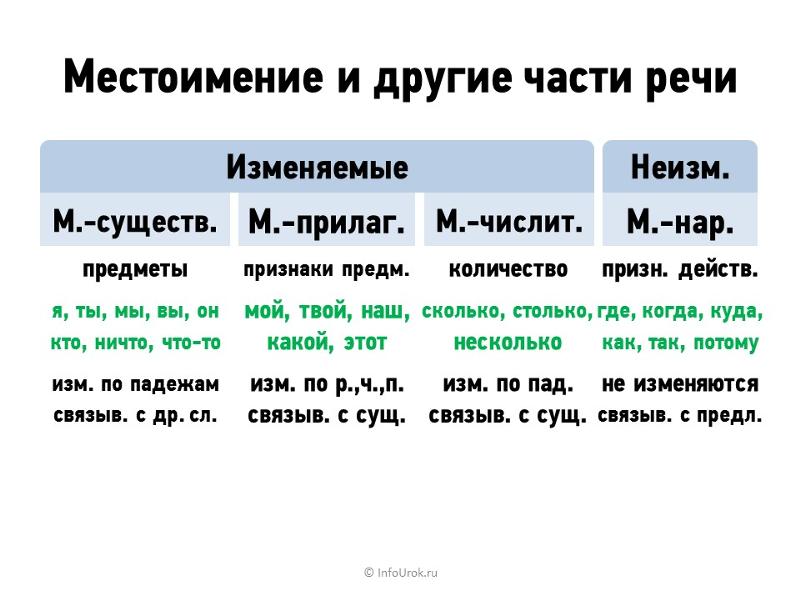
 – Это мое кольцо.
– Это мое кольцо.

 Личные местоимения делятся на две основные группы: одна относится к подлежащему предложения, а другая — к объекту.
Личные местоимения делятся на две основные группы: одна относится к подлежащему предложения, а другая — к объекту. 
 Возьмите 10 одинаковых по размеру желудей, приклейте к ним шляпки термоклеем. Они имеют обыкновение отваливаться. И в центре проколите их насквозь при помощи шила. Проденьте через отверстие проволоку или веревку. Соедините концы в кольцо. Поделка из желудей готова!
Возьмите 10 одинаковых по размеру желудей, приклейте к ним шляпки термоклеем. Они имеют обыкновение отваливаться. И в центре проколите их насквозь при помощи шила. Проденьте через отверстие проволоку или веревку. Соедините концы в кольцо. Поделка из желудей готова! На него приклейте термопистолетом тонкие веточки кустарников или травинки. Над каждой веточкой несколько шляпок желудей и сами желуди. Они будут имитировать цветы и листья. Маленькие шишки, так же пригодятся для этой поделки из шишек и желудей. Установите панно на декоративную подставку для тарелок и украсьте им свой дом.
На него приклейте термопистолетом тонкие веточки кустарников или травинки. Над каждой веточкой несколько шляпок желудей и сами желуди. Они будут имитировать цветы и листья. Маленькие шишки, так же пригодятся для этой поделки из шишек и желудей. Установите панно на декоративную подставку для тарелок и украсьте им свой дом. Пожалуй, возьму на вооружение эту идею с зеркалом.
Пожалуй, возьму на вооружение эту идею с зеркалом. При помощи белой акриловой краски, тонкой кисточки и перманентных маркеров можно нарисовать любой выражение мордочки. Делать можно кого — угодно, даже миньонов!
При помощи белой акриловой краски, тонкой кисточки и перманентных маркеров можно нарисовать любой выражение мордочки. Делать можно кого — угодно, даже миньонов!
 Можно запросто придумать огромное количество разных вещиц, которые будут украшать дом, дачу или сад.
Можно запросто придумать огромное количество разных вещиц, которые будут украшать дом, дачу или сад. Берем небольшую пластиковую бутылку с пробкой. Черным маркером раскрашиваем ее верхнюю часть — это будущая мордочка ежика.
Берем небольшую пластиковую бутылку с пробкой. Черным маркером раскрашиваем ее верхнюю часть — это будущая мордочка ежика.
 Берем вату и вставляем ее между чешуйками шишек.
Берем вату и вставляем ее между чешуйками шишек. В основе поделки лежат два пенопластовых шарика, в которые вставляются и фиксируются клеем шишки.
В основе поделки лежат два пенопластовых шарика, в которые вставляются и фиксируются клеем шишки. Заяц из шишки — готов.
Заяц из шишки — готов. Грецкие орешки склеиваются между собой. Между орешками приклеиваем кусочек красной пушистой проволоки. На верхний орешек приклеиваем глазки — у нас получиться головка. Делаем три таких заготовки. К каждой головке приклеиваем палочку, которую потом вставляем в шишку (обязательно фиксируем на клей). Приклеиваем ножки из грецких орешков, а так же крылышки и хвостик из сухих листиков.
Грецкие орешки склеиваются между собой. Между орешками приклеиваем кусочек красной пушистой проволоки. На верхний орешек приклеиваем глазки — у нас получиться головка. Делаем три таких заготовки. К каждой головке приклеиваем палочку, которую потом вставляем в шишку (обязательно фиксируем на клей). Приклеиваем ножки из грецких орешков, а так же крылышки и хвостик из сухих листиков.
 Для этого прикрепляем к нижним чешуйкам сосновой шишки проволоку.
Для этого прикрепляем к нижним чешуйкам сосновой шишки проволоку. Вы можете сделать венок из шишек, или корзинку, а детям будет интересно сделать фигурку животного. В качестве поделки из шишек на тему осень можно создать топиарий.
Вы можете сделать венок из шишек, или корзинку, а детям будет интересно сделать фигурку животного. В качестве поделки из шишек на тему осень можно создать топиарий.
 Дождитесь высыхания шишки, а затем распустите нить.
Дождитесь высыхания шишки, а затем распустите нить.

 Вырезаем для головы детали из фетра: два кружка разного размера – желтые и голубые. Они должны быть немного больше, чем покупные глазки. Вырезаем оранжевый треугольник – клюв., два овала для крыльев и одна деталь для мордочки из коричневого фетра.
Вырезаем для головы детали из фетра: два кружка разного размера – желтые и голубые. Они должны быть немного больше, чем покупные глазки. Вырезаем оранжевый треугольник – клюв., два овала для крыльев и одна деталь для мордочки из коричневого фетра.
 Пластилин нам потребуется для создания глазок, а фломастер для улыбки.
Пластилин нам потребуется для создания глазок, а фломастер для улыбки. Грецкий орех приклеиваем к туловицу с помощью клея.
Грецкий орех приклеиваем к туловицу с помощью клея. Крона в осеннем варианте топиария состоит из шишек, желудей, листьев, каштанов. В качестве основы для создания кроны используйте пенопластовый шарик, который можно приобрести в рукодельных магазинах.
Крона в осеннем варианте топиария состоит из шишек, желудей, листьев, каштанов. В качестве основы для создания кроны используйте пенопластовый шарик, который можно приобрести в рукодельных магазинах.
 Шишки, желуди и каштаны приклеиваем горячим пистолетом к булавке
Шишки, желуди и каштаны приклеиваем горячим пистолетом к булавке Вспомните, как вы любили собирать каштаны или шишки. Но намного интереснее, если они хранятся в виде красивой поделки, а не просто в коробке насыпью.
Вспомните, как вы любили собирать каштаны или шишки. Но намного интереснее, если они хранятся в виде красивой поделки, а не просто в коробке насыпью.

 Это будут ягодки на полянке.
Это будут ягодки на полянке.
 Они будут играть роль крыльев лебедя.
Они будут играть роль крыльев лебедя. Ведь все знают, что такое шишки, каштаны, желуди.
Ведь все знают, что такое шишки, каштаны, желуди. Повернем вверх и опустим вниз. Она сама по себе очень красива. Я предлагаю в первую очередь использовать именно ее природную красоту. А раз чаще всего мы творим из этого материала зимой, то предлагаю сделать подвес на елку.
Повернем вверх и опустим вниз. Она сама по себе очень красива. Я предлагаю в первую очередь использовать именно ее природную красоту. А раз чаще всего мы творим из этого материала зимой, то предлагаю сделать подвес на елку.
 Остальные части — черным цветом.
Остальные части — черным цветом.

 Ею обматываете каждую шишку и прикручиваете или привязываете к вешалке и соседним шишкам.
Ею обматываете каждую шишку и прикручиваете или привязываете к вешалке и соседним шишкам.

 Они смотрятся достойно и необычно.
Они смотрятся достойно и необычно.
 Дно можно сделать из картона и обклеить шишками.
Дно можно сделать из картона и обклеить шишками.

 Например, Бабу Ягу.
Например, Бабу Ягу.



 Благодаря описанию вы легко смастерите их сами.
Благодаря описанию вы легко смастерите их сами.


 Первым стал рассуждать на эту тему Левкипп, учитель Демокрита.
Первым стал рассуждать на эту тему Левкипп, учитель Демокрита.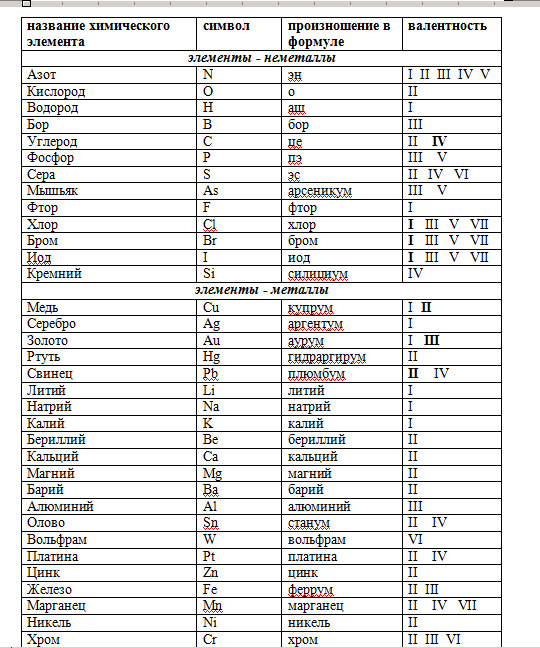
 Изучая составы химических соединений, он установил:
Изучая составы химических соединений, он установил: Он придумал вертикальные столбцы и вставил по семь элементов в каждый. Также ученый определил, что похожие элементы часто попадают в одни и те же горизонтальные ряды.
Он придумал вертикальные столбцы и вставил по семь элементов в каждый. Также ученый определил, что похожие элементы часто попадают в одни и те же горизонтальные ряды.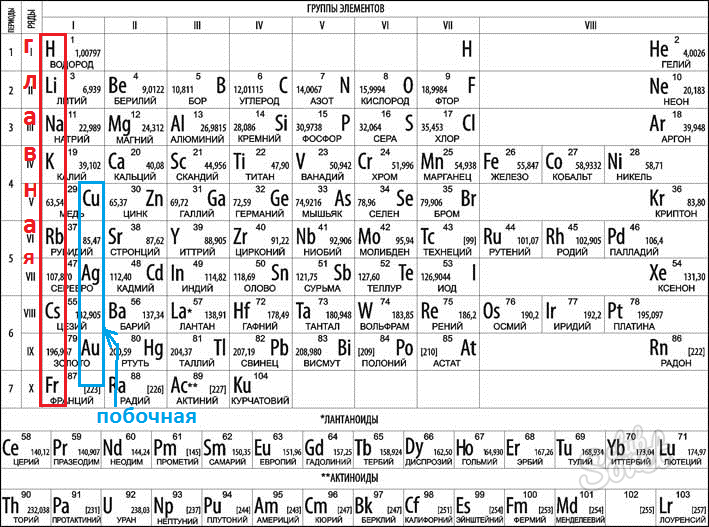 Потом он соотносил это с валентностями в типических соединениях и химическими свойствами элементов.
Потом он соотносил это с валентностями в типических соединениях и химическими свойствами элементов. Слухи породила его революционная научная работа на тему «Рассуждение о соединении спирта с водою», и строго говоря, к алкогольному напитку эта работа имела весьма косвенное отношение – ученый в своей диссертации заложил основы гидратной теории растворов спирта с водой при различных температурах.
Слухи породила его революционная научная работа на тему «Рассуждение о соединении спирта с водою», и строго говоря, к алкогольному напитку эта работа имела весьма косвенное отношение – ученый в своей диссертации заложил основы гидратной теории растворов спирта с водой при различных температурах.
 Молекула
Молекула edu.ru/subject/lesson/2731/main/
edu.ru/subject/lesson/2731/main/ edu.ru/subject/lesson/2684/main/
edu.ru/subject/lesson/2684/main/ edu.ru/subject/lesson/3120/main/
edu.ru/subject/lesson/3120/main/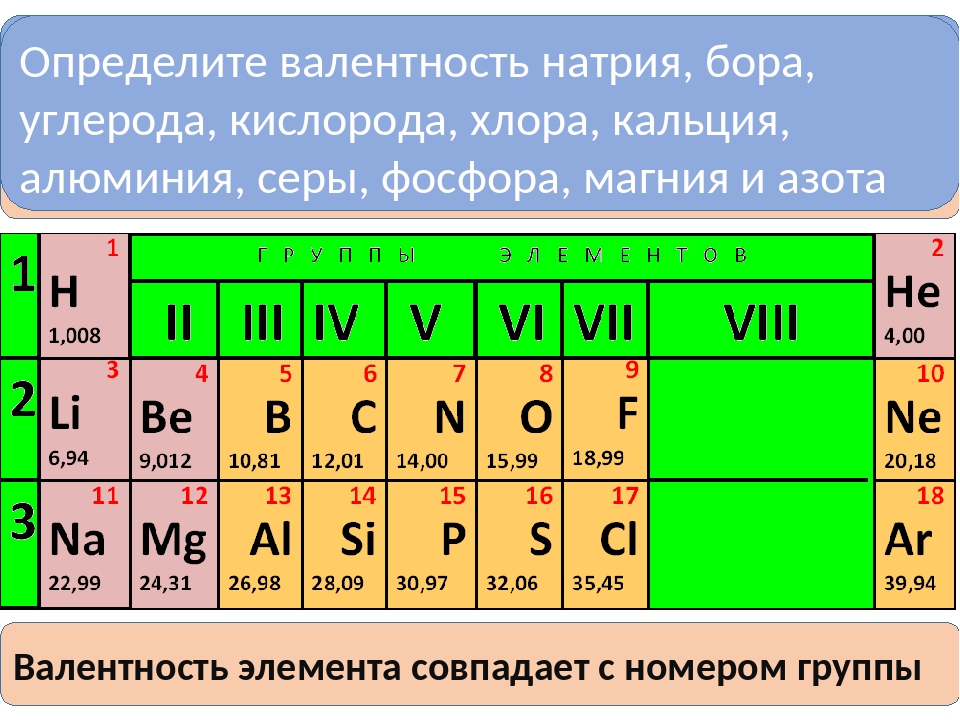 edu.ru/subject/lesson/2050/main/
edu.ru/subject/lesson/2050/main/ Правила определения степеней окисления
Правила определения степеней окисления Молярная масса
Молярная масса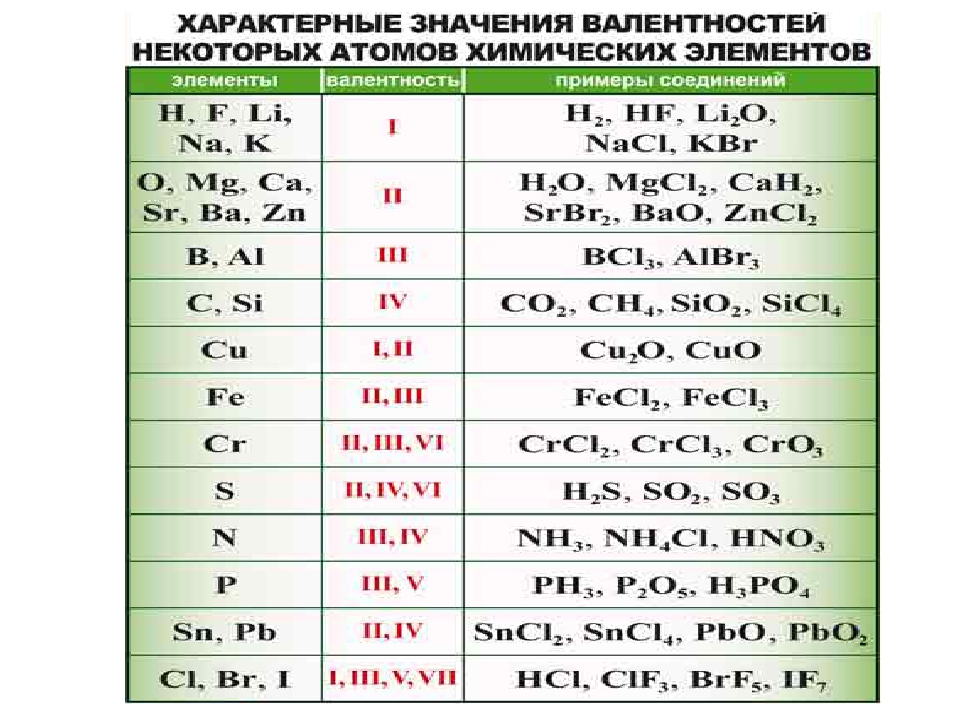 Понятие о химическом равновесии
Понятие о химическом равновесии Галогены в природе. Физические свойства галогенов
Галогены в природе. Физические свойства галогенов Азот в природе. Физические и химические свойства азота
Азот в природе. Физические и химические свойства азота Физические и химические свойства углерода. Аллотропия углерода
Физические и химические свойства углерода. Аллотропия углерода edu.ru/subject/lesson/1607/main/
edu.ru/subject/lesson/1607/main/ И. Менделеева и строение атома. Нахождение в природе. Физические и химические свойства железа
И. Менделеева и строение атома. Нахождение в природе. Физические и химические свойства железа edu.ru/subject/lesson/1609/main/
edu.ru/subject/lesson/1609/main/ youtube.com/watch?time_continue=217&v=3O_1UupZ71E&feature=emb_logo
youtube.com/watch?time_continue=217&v=3O_1UupZ71E&feature=emb_logo


 Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.
Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое. Растения улавливают энергию света от Солнца, и через процесс фотосинтеза преобразуют её в химическую энергию. Эту накопленную энергию можно использовать различными способами. Например, употребление в пищу растительных продуктов обеспечивает наше тело энергией для функционирования, а сжигание древесины или угля (которые представляет собой окаменелые растения) генерирует тепло и электричество. Поэтому, поскольку все изменения материи связаны с изменениями энергии, важно понимать, как энергия переходит из одной формы в другую.
Растения улавливают энергию света от Солнца, и через процесс фотосинтеза преобразуют её в химическую энергию. Эту накопленную энергию можно использовать различными способами. Например, употребление в пищу растительных продуктов обеспечивает наше тело энергией для функционирования, а сжигание древесины или угля (которые представляет собой окаменелые растения) генерирует тепло и электричество. Поэтому, поскольку все изменения материи связаны с изменениями энергии, важно понимать, как энергия переходит из одной формы в другую.  Кинетическая энергия — это энергия, связанная с движением объекта. Например, вода, удерживаемая плотиной, обладает потенциальной энергией из-за ее положения над землей. Когда она течет вниз через генераторы, она приобретает кинетическую энергию, которую можно использовать для производства электроэнергии на гидроэлектростанции.
Кинетическая энергия — это энергия, связанная с движением объекта. Например, вода, удерживаемая плотиной, обладает потенциальной энергией из-за ее положения над землей. Когда она течет вниз через генераторы, она приобретает кинетическую энергию, которую можно использовать для производства электроэнергии на гидроэлектростанции. Например, радиоактивный элемент уран-235 (U235) имеет нестабильное ядро. Чтобы добиться стабильности, оно разделяется на более мелкие, но стабильные элементы и высвобождает накопленную ядерную энергию. Затем эта выделенная энергия может быть использована для производства электроэнергии на атомных электростанциях.
Например, радиоактивный элемент уран-235 (U235) имеет нестабильное ядро. Чтобы добиться стабильности, оно разделяется на более мелкие, но стабильные элементы и высвобождает накопленную ядерную энергию. Затем эта выделенная энергия может быть использована для производства электроэнергии на атомных электростанциях.  Например, пуля, выстреливаемая из пушки, или вода, стекающая по плотине, являются примерами объектов с механической энергией. Электрическая энергия связана с потоком электрических зарядов, как в случае удара молнии во время грозы или обычных электрических цепях и устройствах. Лучистая энергия — это форма кинетической энергии, которая перемещается в виде электромагнитных волн и может быть ощущаться в виде света и тепла. Солнечный свет является примером лучистой энергии.
Например, пуля, выстреливаемая из пушки, или вода, стекающая по плотине, являются примерами объектов с механической энергией. Электрическая энергия связана с потоком электрических зарядов, как в случае удара молнии во время грозы или обычных электрических цепях и устройствах. Лучистая энергия — это форма кинетической энергии, которая перемещается в виде электромагнитных волн и может быть ощущаться в виде света и тепла. Солнечный свет является примером лучистой энергии. Аналогичным образом, если предположить, что химическая реакция или изменение фазы (например, конденсация или замерзание) не происходит, уменьшение тепловой энергии в образце вещества приведет к снижению температуры.
Аналогичным образом, если предположить, что химическая реакция или изменение фазы (например, конденсация или замерзание) не происходит, уменьшение тепловой энергии в образце вещества приведет к снижению температуры. 1: Основы энергии.
1: Основы энергии. В этом случае изменение полной механической энергии тела (системы тел) равно работе внешних сил:
В этом случае изменение полной механической энергии тела (системы тел) равно работе внешних сил: Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .
Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .
 Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.
Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени. Координата тела, движущегося вдоль оси Ox, зависит от времени по закону x(t) = 8,0 − 2,0t + t2, где координата задана в метрах, время — в секундах. Определить изменение кинетической энергии тела с начала третьей до конца четвертой секунды движения. Масса тела составляет 3,0 кг.
Координата тела, движущегося вдоль оси Ox, зависит от времени по закону x(t) = 8,0 − 2,0t + t2, где координата задана в метрах, время — в секундах. Определить изменение кинетической энергии тела с начала третьей до конца четвертой секунды движения. Масса тела составляет 3,0 кг.
 ..
..
 Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени: е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
 Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком: Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
 д.
д. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:

 Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий: Такое же условие выполняется при прохождении верхней точки мертвой петли.
Такое же условие выполняется при прохождении верхней точки мертвой петли.
 Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.
 Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:

 Электрон-вольт используется в атомном и субатомном масштабах.
Электрон-вольт используется в атомном и субатомном масштабах. В системе сантиметр-грамм-секунда единицей энергии является эрг, 10 −7 джоулей, что эквивалентно кинетической энергии летящего комара. В определенных контекстах используются и другие единицы энергии, такие как еще меньшая единица, электрон-вольт, в атомном и субатомном масштабе.
В системе сантиметр-грамм-секунда единицей энергии является эрг, 10 −7 джоулей, что эквивалентно кинетической энергии летящего комара. В определенных контекстах используются и другие единицы энергии, такие как еще меньшая единица, электрон-вольт, в атомном и субатомном масштабе. Объект, который перемещается по поверхности, будет испытывать силу, противоположную его движению. Величина силы зависит от коэффициента кинетического трения между двумя видами материала. Каждая комбинация индивидуальна. Коэффициент кинетического трения обозначается греческой буквой «мю» ( μ ) с нижним индексом « k ». Сила кинетического трения в μ k раз больше нормальной силы, действующей на объект, и выражается в единицах ньютонов (Н).
Объект, который перемещается по поверхности, будет испытывать силу, противоположную его движению. Величина силы зависит от коэффициента кинетического трения между двумя видами материала. Каждая комбинация индивидуальна. Коэффициент кинетического трения обозначается греческой буквой «мю» ( μ ) с нижним индексом « k ». Сила кинетического трения в μ k раз больше нормальной силы, действующей на объект, и выражается в единицах ньютонов (Н). Коробка имеет массу 75,0 кг , и рабочий прилагает вперед усилие в 400,0 Н . Какова величина силы трения и какая результирующая сила перемещает коробку?
Коробка имеет массу 75,0 кг , и рабочий прилагает вперед усилие в 400,0 Н . Какова величина силы трения и какая результирующая сила перемещает коробку? Если мы определим «вперед» как положительное направление, чистая сила составит:
Если мы определим «вперед» как положительное направление, чистая сила составит: Нормальная сила составляет η = mg cosθ , а оставшаяся составляющая силы составляет F = mg sinθ . Используя эту формулу, можно найти величину силы кинетического трения:
Нормальная сила составляет η = mg cosθ , а оставшаяся составляющая силы составляет F = mg sinθ . Используя эту формулу, можно найти величину силы кинетического трения: Две силы, которые следует учитывать, — это сила, направленная вниз по склону, и сила кинетического трения, направленная вверх по холму. Если мы определим положительное направление как спуск по склону, то есть направление движения лыжника, результирующая сила составит:
Две силы, которые следует учитывать, — это сила, направленная вниз по склону, и сила кинетического трения, направленная вверх по холму. Если мы определим положительное направление как спуск по склону, то есть направление движения лыжника, результирующая сила составит: Обратите внимание, что энергия — это скаляр , величина , т.е. она не зависит от направления и всегда положительна. Когда мы удваиваем массу, мы удваиваем энергию; однако, когда мы удваиваем скорость, энергия увеличивается в четыре раза.
Обратите внимание, что энергия — это скаляр , величина , т.е. она не зависит от направления и всегда положительна. Когда мы удваиваем массу, мы удваиваем энергию; однако, когда мы удваиваем скорость, энергия увеличивается в четыре раза. Если объект вдвое тяжелее, потребуется в два раза больше работы, чтобы поднять его на такое же расстояние.Также требуется вдвое больше работы, чтобы поднять один и тот же объект вдвое дальше. Точно так же, чтобы скользить по полу тяжелым предметом, мы должны преодолеть силу трения между предметом и полом. Требуемая работа пропорциональна весу объекта и расстоянию, на которое он перемещается. (Обратите внимание, что если вы несете пианино на спине по коридору, вы на самом деле не делаете никакой реальной работы.)
Если объект вдвое тяжелее, потребуется в два раза больше работы, чтобы поднять его на такое же расстояние.Также требуется вдвое больше работы, чтобы поднять один и тот же объект вдвое дальше. Точно так же, чтобы скользить по полу тяжелым предметом, мы должны преодолеть силу трения между предметом и полом. Требуемая работа пропорциональна весу объекта и расстоянию, на которое он перемещается. (Обратите внимание, что если вы несете пианино на спине по коридору, вы на самом деле не делаете никакой реальной работы.) Если мы уроним объект с полки или отпустим пружину, эта потенциальная энергия снова преобразуется в кинетическую энергию.
Если мы уроним объект с полки или отпустим пружину, эта потенциальная энергия снова преобразуется в кинетическую энергию. Разделив на м и извлекая квадратный корень из обеих частей, получим v 2 = √2 / 2 ∙ v 1 .(Обратите внимание, что v 2 ≠ ½ v 1 .)
Разделив на м и извлекая квадратный корень из обеих частей, получим v 2 = √2 / 2 ∙ v 1 .(Обратите внимание, что v 2 ≠ ½ v 1 .) Сила трения — это сила, сопротивляющаяся движению
когда два объекта соприкасаются. Если вы посмотрите на поверхности всех предметов,
есть крошечные шишки и гребни.Эти микроскопические пики и впадины улавливают
один в другой, когда два объекта движутся мимо друг друга.
Сила трения — это сила, сопротивляющаяся движению
когда два объекта соприкасаются. Если вы посмотрите на поверхности всех предметов,
есть крошечные шишки и гребни.Эти микроскопические пики и впадины улавливают
один в другой, когда два объекта движутся мимо друг друга. Если вы попытаетесь сдвинуть два объекта друг с другом, небольшое количество
силы не приведет к движению. Сила трения больше, чем
приложенная сила.Это статическое трение. Если приложить немного больше силы,
объект «вырывается на свободу» и скользит, хотя вам все равно нужно нанести
сила, чтобы объект скользил. Это кинетическое трение. Вам не нужно
приложить столько силы, чтобы удерживать предмет скольжения, сколько вам нужно изначально
освобождаются от статического трения.
Если вы попытаетесь сдвинуть два объекта друг с другом, небольшое количество
силы не приведет к движению. Сила трения больше, чем
приложенная сила.Это статическое трение. Если приложить немного больше силы,
объект «вырывается на свободу» и скользит, хотя вам все равно нужно нанести
сила, чтобы объект скользил. Это кинетическое трение. Вам не нужно
приложить столько силы, чтобы удерживать предмет скольжения, сколько вам нужно изначально
освобождаются от статического трения. 10
10 Вот почему правило двух секунд («двигайтесь со скоростью, чтобы
две секунды проходят между моментом, когда машина перед вами проезжает ориентир
и момент проезда того же ориентира ») не действует для высоких скоростей;
ваш тормозной путь увеличивается экспоненциально по мере того, как вы едете быстрее.
Вот почему правило двух секунд («двигайтесь со скоростью, чтобы
две секунды проходят между моментом, когда машина перед вами проезжает ориентир
и момент проезда того же ориентира ») не действует для высоких скоростей;
ваш тормозной путь увеличивается экспоненциально по мере того, как вы едете быстрее. Это может быть особенно сложно
если вы собираетесь ударить лося. Другой вариант — прокачка тормоза, которая
имеет эффект чередования использования кинетического и статического трения в качестве
блокировка и разблокировка колес. Это не так эффективно, но проще сделать в
чрезвычайная ситуация.Последний вариант — поручить вашему автомобилю позаботиться о торможении в течение
вы, с помощью антиблокировочной системы тормозов или более сложных средств компьютерного управления.
Антиблокировочная система тормозов делает то же самое, что и вы; прокачать тормоза. Лучшее решение
это, конечно, медленнее ехать.
Это может быть особенно сложно
если вы собираетесь ударить лося. Другой вариант — прокачка тормоза, которая
имеет эффект чередования использования кинетического и статического трения в качестве
блокировка и разблокировка колес. Это не так эффективно, но проще сделать в
чрезвычайная ситуация.Последний вариант — поручить вашему автомобилю позаботиться о торможении в течение
вы, с помощью антиблокировочной системы тормозов или более сложных средств компьютерного управления.
Антиблокировочная система тормозов делает то же самое, что и вы; прокачать тормоза. Лучшее решение
это, конечно, медленнее ехать. Если у шин нет коэффициента трения
достаточно большой, чтобы обеспечить силу, необходимую для бокового движения автомобиля, тогда вы
скользить прямо вперед и съехать с дороги.
Если у шин нет коэффициента трения
достаточно большой, чтобы обеспечить силу, необходимую для бокового движения автомобиля, тогда вы
скользить прямо вперед и съехать с дороги. Но чтобы понять, как они работают, вам сначала нужно понять, что они собой представляют — и определение самой энергии.
Но чтобы понять, как они работают, вам сначала нужно понять, что они собой представляют — и определение самой энергии. Лучше всего это демонстрируется на таком предмете, как лук лучника, в котором накапливается энергия, возникающая при натяжении тетивы. Потенциальная энергия, запасенная при откате, отвечает за энергию, возникающую при высвобождении, которая известна как кинетическая энергия.
Лучше всего это демонстрируется на таком предмете, как лук лучника, в котором накапливается энергия, возникающая при натяжении тетивы. Потенциальная энергия, запасенная при откате, отвечает за энергию, возникающую при высвобождении, которая известна как кинетическая энергия.
 Это измерение является основой кинетической энергии, но не имеет ничего общего с потенциальной энергией. Фактически, скорость является наиболее важной частью уравнения при определении количества кинетической энергии для любого данного объекта, и ее нет в уравнении потенциальной энергии [3] .
Это измерение является основой кинетической энергии, но не имеет ничего общего с потенциальной энергией. Фактически, скорость является наиболее важной частью уравнения при определении количества кинетической энергии для любого данного объекта, и ее нет в уравнении потенциальной энергии [3] .
 Когда резинка растягивается, она заряжается потенциальной энергией; при высвобождении происходит переход к кинетической энергии. Это особенно верно, если резинка транспортирует другой объект, например, камень, брошенный из рогатки. [6]
Когда резинка растягивается, она заряжается потенциальной энергией; при высвобождении происходит переход к кинетической энергии. Это особенно верно, если резинка транспортирует другой объект, например, камень, брошенный из рогатки. [6] 
 Ключевым словом здесь является «хранимая», что означает, что батареи представляют собой форму потенциальной энергии, поэтому вся химическая энергия классифицируется как [ 9 ] . Биотопливо и ископаемое топливо — другие примеры накопленной химической энергии.
Ключевым словом здесь является «хранимая», что означает, что батареи представляют собой форму потенциальной энергии, поэтому вся химическая энергия классифицируется как [ 9 ] . Биотопливо и ископаемое топливо — другие примеры накопленной химической энергии. Звуковая энергия в воздухе, которая создается продольными волнами, которые создают движение в молекулах газа, является кинетической. В твердых телах и жидкостях, которые переносят звук намного дальше, чем через воздух, действует как кинетическая, так и потенциальная энергия. [11 ]
Звуковая энергия в воздухе, которая создается продольными волнами, которые создают движение в молекулах газа, является кинетической. В твердых телах и жидкостях, которые переносят звук намного дальше, чем через воздух, действует как кинетическая, так и потенциальная энергия. [11 ]  Подобно электрону, упомянутому выше, это еще одна форма кинетической энергии, переносимой нефизическим объектом. [13]
Подобно электрону, упомянутому выше, это еще одна форма кинетической энергии, переносимой нефизическим объектом. [13]  Количество накопленной потенциальной гравитационной энергии напрямую зависит от массы объекта и, что более важно, от его высоты над землей. [15]
Количество накопленной потенциальной гравитационной энергии напрямую зависит от массы объекта и, что более важно, от его высоты над землей. [15]  Это энергия, хранящаяся в молекулярных связях, которая является основой химии и химических реакций. Сохраненная потенциальная энергия высвобождается в результате этих химических реакций. [15]
Это энергия, хранящаяся в молекулярных связях, которая является основой химии и химических реакций. Сохраненная потенциальная энергия высвобождается в результате этих химических реакций. [15]  8 м / с2)
8 м / с2) 
 По состоянию на 9 ноября 2020 г.
По состоянию на 9 ноября 2020 г.
 По состоянию на 15 ноября 2020 г.
По состоянию на 15 ноября 2020 г.

 У обоих к хвосту точечной сварки были приварены ребра из листового металла.
Ikessurplus / Wikimedia Commons
У обоих к хвосту точечной сварки были приварены ребра из листового металла.
Ikessurplus / Wikimedia Commons Степени окисления находятся с использованием следующих правил:
Степени окисления находятся с использованием следующих правил: Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10: 



 Другими словами:
Другими словами: Еще раз перепишем полученную конструкцию:
Еще раз перепишем полученную конструкцию: е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим: Решение пропорций всегда выполняется с помощью свойства пропорции.
Решение пропорций всегда выполняется с помощью свойства пропорции.
 Найдите отношение x к y.
Найдите отношение x к y.




 Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
 В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
 Умножим каждый член уравнения на х.
Умножим каждый член уравнения на х.

 К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
 Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе.
Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе. 
 Если такая проблема возникает, нужно вернуться к первому пункту.
Если такая проблема возникает, нужно вернуться к первому пункту. 
