Не с разными частями речи алгоритм: Алгоритм написания НЕ с разными частями речи
Алгоритм написания НЕ с разными частями речи
I. НЕ с существительными, качественными прилагательными и наречиями на –О, -Е
С

 мотрю, употребляется ли слово без НЕ?
мотрю, употребляется ли слово без НЕ?
нет да
Пишу слитно 2. Смотрю, есть ли противопоставление с союзом А или
 слова далеко не, вовсе не, ничуть не, чуть не, отнюдь
слова далеко не, вовсе не, ничуть не, чуть не, отнюдь
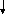
 не, нисколько не?
не, нисколько не?
да нет
пишу раздельно 3. Подбираю к слову синоним
пишу слитно
НО: НЕ пишется раздельно
— С относительными, притяжательными прилагательными, с прил. со значением цвета и наречиями в сравнительной степени:
не кожаный, не синий, не менее
— С наречиями, которые пишутся через дефис:
не по-товарищески
— С краткими прилагательными, которые не употребляются в полной форме:
не рад, не должен, не прав, не виден, не намерен, не расположен, не готов, не согласен
2. НЕ с причастиями
1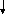
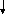 . Смотрю, краткая или полная форма
. Смотрю, краткая или полная форма
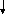
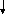 краткая полная
краткая полная
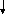
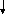
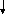
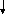 пишу раздельно 2. Смотрю, есть ли противопоставление или зависимые слова
пишу раздельно 2. Смотрю, есть ли противопоставление или зависимые слова
да нет
раздельно слитно
НО: НЕ пишется слитно,
если в качестве пояснительных слов выступают количественные наречия ПОЧТИ, ОТЧАСТИ, ДОВОЛЬНО, ГОРАЗДО, ВПОЛНЕ, ОЧЕНЬ, АБСОЛЮТНО, СОВЕРШЕННО, В ВЫСШЕЙ СТЕПЕНИ и нет других пояснительных слов
3. НЕ с глаголами, деепричастиями
Смотрю, употребляется ли слово без НЕ
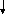
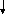
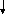
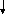 да нет
да нет
пишу раздельно пишу слитно
НО: следует отличать глаголы с приставкой НЕДО-
Если приставка придает глаголу значение неполноты, недостаточности по сравнению с нормой или указывает на постоянное действие:
недорабатывает, недосыпал
«Правописание НЕ с разными частями речи»
Тема урока: Правописание частицы не с разными частями речи
Цели урока:
-Систематизировать знания о написании не с разными частями речи;
-Совершенствовать орфографические навыки написания не с разными частями речи;
-Формировать навык взаимоконтроля и самоконтроля;
-Развивать логическое и критическое мышление, умение отбирать материал, аргументировать свою точку зрения;
-Формировать коммуникативные умения;
-Воспитывать интерес к родному языку.
Оборудование:
-Компьютерная презентация
-Индивидуальные тестовые задания
Ход урока
I.Организационный момент (слайд 1)
II. Определение темы урока и постановка целей.
1.Послушайте стихотворение, определите тему нашего урока, запишите слова и скажите, для чего нужна частица НЕ в данных словах?(слайд 2)
Побывал я однажды в стране,
Где исчезла частица НЕ.
Посмотрел я вокруг с доумением:
Что за лепое положение!
Но кругом было тихо-тихо,
И во всем была разбериха,
И на взрачной клумбе у будки
Голубые цвели забудки.
И погода стояла настная,
И гуляла собака счастная
И, виляя хвостом, уклюже
Пробегала пролазные лужи.
Мне навстречу без всякого страха
Шел умытый, причесанный ряха,
А за ряхой по травке свежей
Шли суразные дотепа и вежа.
А из школы, взявшись за ручки,
Чинным шагом вышли доучки.
И навстречу всем утром рано
Улыбалась царевна Смеяна.
Очень жаль, что только во сне
Есть страна без частицы НЕ.
— Какие слова вы записали? Какова особенность их написания?
( Все слова без не не употребляются, не является приставкой).
-Объясните значение слов «невежа» и «невежда». (слайд 3)
(Невежа— 1.Грубый, неучтивый человек. Невежа тот, кто позволяет себе грубость.
Невежда, невежественный, несведущий, безграмотный, неграмотный, необразованный, неученый, неуч, серый, темный, малограмотный, малокультурный. Невежда он был круглый, ничего не читал.)
2.Сформулируйте задачи нашего урока. ( Для правильного написания слов с частицей НЕ следует повторить правила, составить алгоритм, сводную таблицу. Закрепить полученные знания).
— Прочитайте эпиграф к уроку, объясните смысл этого высказывания. К нему мы еще вернемся в конце нашей работы.
III.Систематизация умений и навыков ( работа над составлением таблицы, алгоритма)
1.Вспомним , чем бывает НЕ в словах. ( Например, в словах стихотворения, эпиграфа).

Правописание не с различными частями речи.
Неряха, нелепый, небрежно
Противопоставление с союзом а
Не друг, а враг
Без не не употребляются
Недоумевающий
Краткое причастие
Не распечатан, не скошена
Без не не употребляются
Нездоровится,
но
Всегда
Не рисует
Не видя
не поздоровится
Можно подобрать синоним
неправдивый=лживый
неправда=ложь
невеселый = грустный
невысоко= низко
Наличие слов далеко не, отнюдь не , вовсе, ничуть не, никогда не
Вовсе не красивое платье
Полное одиночное (нет зависимых слов)
Нерешенный пример,ненаписанное письмо
Противопоставление с союзом а
Не законченная, а только начатая работа
Наличие наречий степени, признака: чрезвычайно, совершенно, абсолютно, почти
Сравнительная степень: не лучше, не умнее
Наличие зависимых слов (входит в причастный оборот)
Еще не скошенная трава
Отрицательные наречия: негде,
некуда
С прил., которые не имеют полной формы: не рад, не должен, не обязан
! Не является частицей и пишется раздельно Слайд 4)
с неопределённым местоимением, если разделено предлогом;
с прилагательными, обозначающими цвет, относительными и притяжательными прилагательными;
с числительными
с местоимениями
с прилагательными и наречиями в сравнительной степени
3.Взаимопроверка
— Эксперты проверяют поочередно составление таблицы у каждой группы и обобщают материал.
4.Самопроверка
-Теперь каждый проверяет свою работу по слайду и дописывает те условия написания, которые пропущены.
5.Построение алгоритма «Правописание НЕ с разными частями речи»
( На основании таблицы выстраиваем алгоритм рассуждения).
Образец рассуждения: (слайд 5)
1.При выборе слитно-раздельного написания не с существительными, прилагательными, наречиями на -о, -е рассуждаем так:
— смотрим, может ли слово употребляться без не. Если не может – пишем слитно: неряха , несуразный, Небрежно.
— если слово может употребляться с не, смотрим, есть ли противопоставление признаков, оценок, или слова далеко не, отнюдь не, вовсе не, ничуть не, чуть не, отнюдь не. Есть одно из указанных условий – пишем не раздельно : не широкий , а узкий пруд; вовсе не интересный рассказ; ничуть не красиво.
— если нет указанних выше условий, подбираем к слову синоним и пишем не слитно: говорил неправду ( ложь), поступил нехорошо ( плохо).
Запомните: не пишется раздельно с относительными, притяжательными прилагательными, с прилагательными со значением цвета, с прилагательными и наречиями в сравнительной степени: не кожаный портфель, не синее небо, не тяжелее, не менее; с наречиями, которые пишутся через дефис: поступил не по — товарищески.
Слитное и раздельное написание НЕ (слайд 6)
АЛГОРИТМ ОПРЕДЕЛЕНИЯ СЛИТНОГО ИЛИ РАЗДЕЛЬНОГО НАПИСАНИЯ НЕ

! Не является частицей и пишется раздельно
с неопределённым местоимением, если разделено предлогом;
с прилагательными, обозначающими цвет, относительными и притяжательными прилагательными;
с числительными
с местоимениями
с наречиями, которые пишутся через дефис ( не по-братски, не по- летнему)
с прилагательными и наречиями в сравнительной степени ( не лучше, не хуже , не красивее, не умнее)
6.Закрепление материала. Работа с текстом. (слайд 7)
(Отпечатанный текст роздан каждому ученику).
-В какой фразе заключена главная мысль текста?
-Как вы ее понимаете?
-Озаглавьте.
-Спишите, раскрыв скобки, обозначив орфограмму «не» с различными частями речи»
-Раскройте главную мысль текста, аргументируйте свой выбор.
-Как бы вы поступили на месте Васи?
Успокоение (не)приходило.(Не) в чем Васе было себя упрекнуть. Это мать,(не)испытывая жалости к старой черепахи, приказала её унести из дома.
Перед Васей (не)ожиданно возникли глаза черепахи, никогда (не) мигающие, мудрые. Вася думал: «(Не) такому уж плохому человеку продал я её. И живет она теперь (не)далеко, а близко». Но вдруг он заплакал.
Это сердце подсказало мальчику (не) ведомую истину: (не) только мир существует для тебя, но и ты для мира.
(Ю.Нагибин «Старая черепаха»)
*Задание. (слайд 8)
Определить, какое слово в каждом ряду «лишнее «. Объяснить. Заменить его таким, которое подходит к данному ряду.
1 (Не)удача,(не)покорный,(не)чего,(не)знает.
2 (Не)приблизившись,(не)слышишь,(не)дотрога, (не)(у)кого
3 Никем (не)тронутый,(не)глубокий, но очень бурный, (не)по-товарищески,(не)убраны
Замените развёрнутое описание одним словом с НЕ (слайд 9)
1.То, чего не было и не бывает в действительности, вымысел, выдумка;
2.Детская игрушка, которую невозможно уложить, Ванька-встанька;
3.Грубый, невоспитанный человек ;
4.Необразованный, малосведущий человек ;
5.Отсутствие удачи, ряд неудач, преследующих кого-то;
6.Неблагоприятные, тяжёлые обстоятельства;
7.Отсутствие свободы, рабство ;
8.Тот, кто не может долго усидеть, пробыть на одном месте;
9.Военный противник, враг .
*ТЕСТ.
1. Не пишется слитно:
а)(не)нарушая режима
б)(не)пересечены линией
в)(не)законченная работа
г)(не)замерзшая река
2.Не пишется раздельно:
а)(не)дорогой, а красивый ситец
б)(не)проснувшийся город
в)(не)был в школе
г)прыгнул (не)высоко, а низко
3.Не пишется слитно:
а)(не)глубокий, а рыбный пруд
б)(не) проснувшийся вовремя
в)долго (не)заживающая рана
г)поступить далеко (не)смело
4.Не пишется слитно:
а)говорить (не)громко, а тихо
б)дорога (не) освещена
в)книга (не)большая, а интересная
-Эксперты проверяют работу и озвучивают результат
* Задания используются как дополнительные.
7.Подведение итогов урока.
— Какую задачу мы с вами решили? ( Систематизировали полученные ранее знания о правописании не с разными частями речи)
-Вспомним случаи слитного и раздельного написания НЕ с разными частями речи.
-Вспомним случаи слитного и раздельного написания НЕ с разными частями речи.
Давайте повторим алгоритм «Написание слов с НЕ».
-Чем является не, когда слово пишется слитно? ( Приставкой )
— Раздельно? ( Частицей)
План-конспект урока по русскому языку (7 класс) на тему: Конспект урока-практикума в 7 классе на тему: «Слитное и раздельное написание НЕ с разными частями речи».
Ибраева Зинаида Михайловна
ГБОУ РМЭ «Новоторъяльская школа- интернат основного общего образования»
Учитель русского языка и литературы
Конспект урока-практикума в 7 классе на тему:
«Слитное и раздельное написание НЕ с разными частями речи».
Цель урока:
— обобщить и систематизировать знания учащихся;
-выработать последовательность действий при выборе слитного и раздельного написания НЕ с разными частями речи;
-развивать логическое мышление и внимание;
-воспитать уважительное отношение друг к другу в процессе парной, коллективной работы.
Оборудование: тесты, схема-алгоритм, таблицы о правописании НЕ с разными частями речи, проектор.
Ход урока
- Вступительное слово учителя.
Учитель. Ребята, сегодня у нас урок-практикум. К слову практикум подберите однокоренные слова: практика, практикант, практиковать, практичный.
Какое определение даётся в словаре Ожегова слову практикум? ( Работа с толковым словарём)
Работа по теме урока.
Тема сегодняшнего урока актуальная и трудная. Почему? Докажите.
Во-первых, НЕ употребляется со всеми самостоятельными частями речи.
Во-вторых, НЕ пишется слитно и раздельно.
Сформулируйте тему нашего урока.
Как можно группировать правила написания НЕ с разными частями речи?
- НЕ с существительными, прилагательными, наречиями.
- НЕ с глаголами, деепричастиями.
- НЕ с причастиями
- НЕ с местоимениям
Работа с таблицей «НЕ с существительными, прилагательными, наречиями »
(ученик рассказывает правила, а другой приводит примеры).
Задание 1: Спишите, раскрывая скобки, обозначая орфограмму.
(Не)везение; проблема (не)простая, а сложная; (не)удачно; (не)внимание, а рассеянность; (не)знакомый автор, (не)здоровье, (не)по-дружески, вовсе (не)интересно. (Взаимопроверка работ и анализ ошибок).
Работа с таблицей «НЕ с глаголами, деепричастиями»
(ученик рассказывает правила, а другой доказывает примерами).
Проверка домашнего задания. Памятка «Как обращаться с учебником».
Задание 2: Выполните творческую работу, вставляя вместо точек нужные глаголы.
- Дело лени ….. .
- Дважды в год лета … .
- Без труда … и рыбку из пруда.
О чём эти пословицы? Объясните их смысл.
Работа с таблицей «НЕ с причастиями»
(ученик рассказывает правила, а другой вместе с классом раскрывает скобки в словарном диктанте).
Задание3. «Конкурс грамотеев»
(Не)скрываемое отчаяние, (не)меркнувшая слава, (не)выразимая печаль, никому (не)признающийся, ни на чём (не)основанная надежда, (не)утверждённый проект, (не)пропускавшие света окно, (не)скрываемое восхищение, окно (не)занавешено шторой. (Определяется победитель).
Работа с таблицей «НЕ, НИ с местоимениями»
(ученик рассказывает правила, а другой с помощью сигнальных карточек проверяет, усвоили ли учащиеся теоретический материал).
Задание 4. Игра «Нарисуй созвездие»
слитно раздельно
(Не)который, (не)с кем, (не)сколько, (не)во что, (не)который, (не)у кого, (ни)к кому, (ни)кто.
Работа с алгоритмом «НЕ с разными частями речи»
Что такое алгоритм? (Работа с толковым словарём)
Задание 5. Комментированный словарный диктант.
(Не)безынтересно, (не)мог, (не)вооружённый знаниями человек, (не)считая, (не)выполненное задание, (не)взрачно, (не)бьющееся стекло, (не)к кому, (не)вкусный, (не)доверие, (не)был, (не)вежливо, а грубо.
Задание 6. Выполнить тест по теме «НЕ с разными частями речи».
- «Чужой» среди «своих».Найди его.
а) (не)здороваясь
б) (не)завлекая
в) (не)навидя
г) (не)чувствуя
- 2. «Чужой» среди «своих».Найди его.
а) (не)надолго
б) (не)крепко
в) (не)закрыто
г) (не)лепо
3. НЕ пишется раздельно.
а) (не)изученный материал
б) (не)забудка
в) ещё (не )продуманный ответ
г) (не)опасное существо
4. Где допущена ошибка?
а) далеко неполный ответ
б) почуять недоброе
в) путь недлинен, а короток
г) не забывший обо мне
5. Выберите правильный вариант.
а) не взгоды
б) конверт не заклеен
в) непришитый воротничок
г) незваный гость
(Проверка с помощью проектора)
1. Чему научились на уроке?
Подводится итог, выставляются оценки учащимся.
Дифференцированное домашнее задание: 1. Написать сочинение на тему: «Частица НЕ».
2. Упражнение 203.
Конспект урока русского языка «Правописание НЕ с разными частями речи»
Конспект урока обобщения по теме:
«Правописание НЕ с разными частями речи»
( 7 класс, по любому учебнику)
Цель урока: формирование обобщенного орфографического навыка на основе обобщения теоретических сведений о правописании НЕ с разными частями речи.
Задачи урока:
1.Обобщить орфографические правила написания не с разными частями речи.
2. Составить обобщающий алгоритм работы над правописанием не с разными частями речи.
3. Формировать обобщенные орфографические умения правописания н и нн в суффиксах разных частей речи на основе системы обобщающих упражнений компетентностно ориентированного характера
Ход урока:
1.Приветствие. Сообщение темы урока и постановка цели.
2.Актуализация знаний теоретического материала.
Беседа по вопросам:
— Какой опознавательный признак является общим для орфограммы – контакт и орфограммы – пробел?
— Какие условия выбора являются основными для слитного или раздельного написания слов с не ?
— Какое общее правило объединяет все виды орфограмм о слитном или раздельном написании слов с не?
3. Систематизация материала и создание обобщающего графа.(Создание таблицы ведется совместно учителем и учениками).
Правописание НЕ с разными частями речи
1)Не употребляется без НЕ2)Образует новое слово или можно подобрать синоним без НЕ
1)Есть противопоставление с союзом а.
2) Есть слова далеко не, вовсе не, с ни и др.
Причастия
1)Не употребляется без НЕ.
2) Нет зависимого слова
1)Есть противопоставление с союзом а.
2) Есть слова далеко не, вовсе не, с ни и др.
3) Есть зависимые слова.
4) Краткая форма
Отрицательные местоимения и наречия
Есть предлог – в три слова
4.Обучение способу применения обобщенного правила.
Составление алгоритма работы над правописанием НЕ с разными частями речи.
1. Определить, употребляется ли слово без НЕ
Да нет – пиши слитно
2. Определи часть речи.
Существ. Прил. Наречие глагол (дееприч.) причаст. Отр.мест
3. есть противопоставление 3.определи
с союзом а, слова с ни, пиши форму слова есть предлог
слова далеко, вовсе, отнюдь раздельно
полная краткая да нет
да нет раздельно
пиши пиши 4. Есть зависимое
раздельно слитно слово или противоп.
с союзом а
да – пиши раздельно нет – слитно
5. Система компетнтностно ориентированных упражнений обобщающего характера
Задание 1.
Стимул:Представьте, что вы учитель.
Задачная формулировка
Объясните ученикам, почему в данных предложениях не пишется слитно с прилагательными и существительными, хотя есть выраженное структурное противопоставление. Переделайте предложения, употребляя такое противопоставление, чтобы не с выделенными словами писалось раздельно.
Источник информации
1)Река была неширокая, но полноводная. 2)Некрасивый, но умный мальчик. 3)Она невысока, но стройна. 4)Недорогой подарок, но приятный был приготовлен к празднику. 5)Неглупый, а скучный разговор.6) Куплен недорогой материал, а красивый.7) Несчастье не сломило старика, а придало ему силы.
Задание 2.
Выберите способ написания НЕ со слова (слитно или раздельно) и вариант написания приставки – частицы с местоимениями и наречиями. Мотивируйте слитное или раздельное написание слов с НЕ с помощью шифра:Слитно:
А- не употребляется без не
Б- возможен подбор синонима
В- отсутствие зависимых слов
Г- наличие показателя интенсивности значения (очень и т.п.)
Д- отсутствие предлога
Раздельно:
а – отрицание
б- противопоставление
в- блок – усилитель отрицания (далеко не и т.п), слова с ни
г- зависимые слова
д- наличие предлога
1 – существительное
2 – прилагательное
3 – наречие на –о,е
4 – причастие (отглагольное прилагательное)
5 – глагол
6 –деепричастие
7-краткое причастие
8- местоимение или наречие
Источник информации
Еще (не)завершенный роман, расставлены (не)давно, здание (не)построено в срок, шел (не)торопясь, дотемна бродил (не)спеша, (не)меньше километра; (не)широкая, но бурная речонка; небо (не)голубое; далеко (не)зрелое яблоко; еще (не)распустившийся цветок; ботинки (не)кожаные; (не)достает теплоты; (не)дочитал книгу; (не)спрашивая ни о чем; вовсе (не)трудная задача; почти (не)отредактированная рукопись; (не)откуда взять; (не)что интересное; (не)по-нашему; (не)каждый; (не)взирая на лица; совершил (не)хороший, а дурной поступок; (не)прочитанная, а лишь просмотренная книга; (не)три дня; глаза были (не)голубые; далеко (не)легкое дело; (не)здоровится; поступил (не)по-товарищески; (не)куда пойти; (не)справедливое решение; очень (не)красивый зонт; (не)легко было в пути; он был (не)весел; читал (не)громко, но выразительно; ситец (не)дорогой, а дешевый; (ни)чем (не)прикрытая голова; (не)убранные поля; (не)подумав; (не)мог заснуть; (не)ясность звука; (не)веселое путешествие; (не)тяжелее; (не)кого спросить.
Задание 3.
Раскройте скобки. Слитное написание обозначайте знаком ∩, раздельное – знаком ∫. Поясните свой выбор.
1. (не)кому позвонить2. (не)богатый помещик
3. (не)приятельская конница
4. (не)навидеть ложь
5.(не)сколько раз
6.(не)громкий, а тихий голос
7.(не)обычайное приключение
8.(не)(у)кого узнать
9.(не)порученное никому дело
10.пирог (не)испечён
11. (не)кошеные луга
12. вес штангистом (не)взят
13. (не)где жить
14. (не)хуже других
15. тут (не)глубоко
16. (не)лепое предположение
17.(не)верить чужим словам
18.(не)закрыв дверь
19. странный (не)знакомец
20. мука (не)просеяна
1. Выпишите из задания слово, которое иллюстрирует правило:
«Неопределённые местоимения с предлогом пишутся в три слова»
2. Выпишите существительное, которое без не не употребляется.
3.Выпишите слово, которое иллюстрирует правило:
«Не с прилагательным пишется слитно, если к нему можно подобрать синоним»
4. Найдите прилагательные – синонимы к слову удивительный, к слову глупый.
6. Подведение итогов урока и выставление оценок.
— При каких условиях пишется не с прилагательными, причастиями, наречиями раздельно, а с глаголами и деепричастиями слитно?
— Какие условия выбора орфограммы самые простые, а какие самые сложные?
7. Домашнее задание.
Составьте правила общения в Интернете на всевозможных чатах, используя частицу НЕ. Например: Не рекомендуется вклиниваться в разговор нескольких людей в чате со своими резкими высказываниями.
Таким образом, вводить компетентностно ориентированные задания обобщающего характера необходимо в уроки, которые дают возможность для обобщения, это могут быть как отдельные этапы урока, так уроки специальной направленности: обобщения и систематизации по орфографии.
«Правописание частицы НЕ с разными частями речи».
Учитель русского языка и литературы: Семина А.А.
Тема урока: Правописание частицы не с разными частями речи
Цели урока:
-Систематизировать знания о написании не с разными частями речи;
-Совершенствовать орфографические навыки написания не с разными частями речи;
-Формировать навык взаимоконтроля и самоконтроля;
-Развивать логическое и критическое мышление, умение отбирать материал, аргументировать свою точку зрения;
-Формировать коммуникативные умения;
-Воспитывать интерес к родному языку.
Оборудование:
-Компьютерная презентация
-Опорный конспект
-Индивидуальные тестовые задания
Форма урока: Урок-обобщение знаний
Обоснование использования ИКТ:
Расширение объема предъявляемой учебной информации;
Разнообразие форм учебной деятельности студентов на уроке;
Повышение интереса к изучению предмета и к учению в целом.
Эпиграф к уроку:
Вам (не)принадлежит то, чего вы не(понимаете).
И.Гете
Ход урока
I.Организационный момент
II. Определение темы урока и постановка целей.
1.Послушайте стихотворение, определите тему нашего урока, запишите слова и скажите, для чего нужна частица НЕ в данных словах?
Побывал я однажды в стране,
Где исчезла частица НЕ.
Посмотрел я вокруг с доумением:
Что за лепое положение!
Но кругом было тихо-тихо,
И во всем была разбериха,
И на взрачной клумбе у будки
Голубые цвели забудки.
И погода стояла настная,
И гуляла собака счастная
И, виляя хвостом, уклюже
Пробегала пролазные лужи.
Мне навстречу без всякого страха
Шел умытый, причесанный ряха,
А за ряхой по травке свежей
Шли суразные дотепа и вежа.
А из школы, взявшись за ручки,
Чинным шагом вышли доучки.
И навстречу всем утром рано
Улыбалась царевна Смеяна.
Очень жаль, что только во сне
Есть страна без частицы НЕ.
— Какие слова вы записали? Какова особенность их написания?
( Все слова без не не употребляются, не является приставкой).
-Объясните значение слов «невежа» и «невежда».
(Невежа— 1.Грубый, неучтивый человек. Невежа тот, кто позволяет себе грубость.
Невежда, невежественный, несведущий, безграмотный, неграмотный, необразованный, неученый, неуч, серый, темный, малограмотный, малокультурный. Невежда он был круглый, ничего не читал.)
2.Сформулируйте задачи нашего урока. ( Для правильного написания слов с частицей НЕ следует повторить правила, составить алгоритм, сводную таблицу. Закрепить полученные знания).
— Прочитайте эпиграф к уроку, объясните смысл этого высказывания. К нему мы еще вернемся в конце нашей работы.
III.Систематизация умений и навыков ( работа над составлением таблицы, алгоритма)
1.Вспомним , чем бывает НЕ в словах. ( Например, в словах стихотворения, эпиграфа).
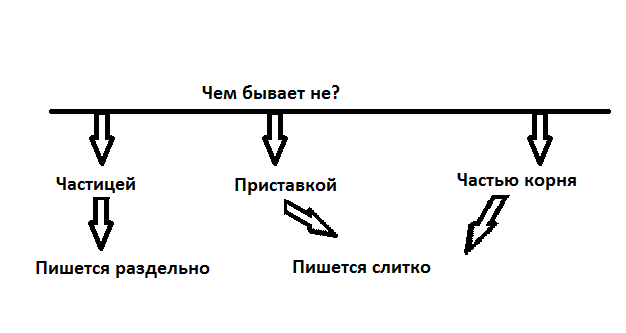
2. Самостоятельная работа студентов
-Я предлагаю вам вспомнить все условия написания «не» с разными частями речи и составить самим таблицу » Правописание не с разными частями речи», которую можно будет использовать для систематизации материала.
-Для этого поделимся на группы, каждая группа составляет свой блок.
1 группа- написание «не» с существительными, прилагательными и наречиями.
2группа-написание «не» с глаголами и деепричастиями
3группа — написание » не» с причастиями
Правописание не с различными частями речи.
Неряха, нелепый, небрежно
Противопоставление с союзом а
Не друг, а враг
Без не не употребляются
Недоумевающий
Краткое причастие
Не распечатан, не скошена
Без не не употребляются
Нездоровится,
но
Всегда
Не рисует
Не видя
не поздоровится
Можно подобрать синоним
неправдивый=лживый
неправда=ложь
невеселый = грустный
невысоко= низко
Наличие слов далеко не, отнюдь не , вовсе, ничуть не, никогда не
Вовсе не красивое платье
Полное одиночное (нет зависимых слов)
Нерешенный пример,ненаписанное письмо
Противопоставление с союзом а
Не законченная, а только начатая работа
Наличие наречий степени, признака: чрезвычайно, совершенно, абсолютно, почти
Сравнительная степень: не лучше, не умнее
Наличие зависимых слов (входит в причастный оборот)
Еще не скошенная трава
Отрицательные наречия: негде,
некуда
С прил., которые не имеют полной формы: не рад, не должен, не обязан
! Не является частицей и пишется раздельно
с неопределённым местоимением, если разделено предлогом;
с прилагательными, обозначающими цвет, относительными и притяжательными прилагательными;
с числительными
с местоимениями
с прилагательными и наречиями в сравнительной степени
3.Взаимопроверка
— Эксперты проверяют поочередно составление таблицы у каждой группы и обобщают материал.
4.Самопроверка
-Теперь каждый проверяет свою работу по слайду и дописывает те условия написания, которые пропущены.
5.Построение алгоритма «Правописание НЕ с разными частями речи»
( На основании таблицы выстраиваем алгоритм рассуждения).
Образец рассуждения:
1.При выборе слитно-раздельного написания не с существительными, прилагательными, наречиями на -о, -е рассуждаем так:
— смотрим, может ли слово употребляться без не. Если не может – пишем слитно: неряха , несуразный, Небрежно.
— если слово может употребляться с не, смотрим, есть ли противопоставление признаков, оценок, или слова далеко не, отнюдь не, вовсе не, ничуть не, чуть не, отнюдь не. Есть одно из указанных условий – пишем не раздельно : не широкий , а узкий пруд; вовсе не интересный рассказ; ничуть не красиво.
— если нет указанних выше условий, подбираем к слову синоним и пишем не слитно: говорил неправду ( ложь), поступил нехорошо ( плохо).
Запомните: не пишется раздельно с относительными, притяжательными прилагательными, с прилагательными со значением цвета, с прилагательными и наречиями в сравнительной степени: не кожаный портфель, не синее небо, не тяжелее, не менее; с наречиями, которые пишутся через дефис: поступил не по — товарищески.
Слитное и раздельное написание НЕ
АЛГОРИТМ ОПРЕДЕЛЕНИЯ СЛИТНОГО ИЛИ РАЗДЕЛЬНОГО НАПИСАНИЯ НЕ

! Не является частицей и пишется раздельно
с неопределённым местоимением, если разделено предлогом;
с прилагательными, обозначающими цвет, относительными и притяжательными прилагательными;
с числительными
с местоимениями
с наречиями, которые пишутся через дефис ( не по-братски, не по- летнему)
с прилагательными и наречиями в сравнительной степени ( не лучше, не хуже , не красивее, не умнее)
6.Закрепление материала. Работа с текстом.
(Отпечатанный текст роздан каждому ученику).
-В какой фразе заключена главная мысль текста?
-Как вы ее понимаете?
-Озаглавьте.
-Спишите, раскрыв скобки, обозначив орфограмму «не» с различными частями речи»
-Раскройте главную мысль текста, аргументируйте свой выбор.
-Как бы вы поступили на месте Васи?
Успокоение (не)приходило.(Не) в чем Васе было себя упрекнуть. Это мать,(не)испытывая жалости к старой черепахи, приказала её унести из дома.
Перед Васей (не)ожиданно возникли глаза черепахи, никогда (не) мигающие, мудрые. Вася думал: «(Не) такому уж плохому человеку продал я её. И живет она теперь (не)далеко, а близко». Но вдруг он заплакал.
Это сердце подсказало мальчику (не) ведомую истину: (не) только мир существует для тебя, но и ты для мира.
(Ю.Нагибин «Старая черепаха»)
-Представьте, что вы учитель. Какие бы вопросы вы задали по изученной теме?
-Составление кластера по теме.
*Задание.
Определить, какое слово в каждом ряду «лишнее «. Объяснить. Заменить его таким, которое подходит к данному ряду.
1 (Не)удача,(не)покорный,(не)чего,(не)знает.
2 (Не)приблизившись,(не)слышишь,(не)дотрога, (не)(у)кого
3 Никем (не)тронутый,(не)глубокий, но очень бурный, (не)по-товарищески,(не)убраны
*ТЕСТ.
1. Не пишется слитно:
а)(не)нарушая режима
б)(не)пересечены линией
в)(не)законченная работа
г)(не)замерзшая река
2.Не пишется раздельно:
а)(не)дорогой, а красивый ситец
б)(не)проснувшийся город
в)(не)был в школе
г)прыгнул (не)высоко, а низко
3.Не пишется слитно:
а)(не)глубокий, а рыбный пруд
б)(не) проснувшийся вовремя
в)долго (не)заживающая рана
г)поступить далеко (не)смело
4.Не пишется слитно:
а)говорить (не)громко, а тихо
б)дорога (не) освещена
в)книга (не)большая, а интересная
-Эксперты проверяют работу и озвучивают результат
* Задания используются как дополнительные.
7.Подведение итогов урока.
— Какую задачу мы с вами решили? ( Систематизировали полученные ранее знания о правописании не с разными частями речи)
-Вспомним случаи слитного и раздельного написания НЕ с разными частями речи.
-Вспомним случаи слитного и раздельного написания НЕ с разными частями речи.
Давайте повторим алгоритм «Написание слов с НЕ».
-Чем является не, когда слово пишется слитно? ( Приставкой )
— Раздельно? ( Частицей)
8.Релаксация
-Слова преподавателя:
С частицей НЕ дружить придется,
На помощь поскорей ее зови,
Она тебе придаст неутомимость,
Непримиримость, неукротимость
И силу нестареющей любви
-Поднимите зеленое яблоко, если вы все усвоили, если вам понравился урок. Желтое — если вам что-то непонятно и вы хотели бы уточнить отдельные моменты.
Красное — если вами материал не усвоен, вы хотели бы повторить все снова.
— Что вы теперь можете сказать по поводу эпиграфа нашего урока?
9. Домашнее задание.
Написать мини- сочинение-рассуждение по пословице «Невежду никакими лекарствами не вылечишь».Объяснить написание частицы не.
-Спасибо за внимание.
Правописание частицы НЕ с разными частями речи
Тема урока: Правописание частицы не с разными частями речи
Цели урока:
-Систематизировать знания о написании не с разными частями речи;
-Совершенствовать орфографические навыки написания не с разными частями речи;
-Формировать навык взаимоконтроля и самоконтроля;
-Развивать логическое и критическое мышление, умение отбирать материал, аргументировать свою точку зрения;
-Формировать коммуникативные умения;
-Воспитывать интерес к родному языку.
Оборудование:
-Компьютерная презентация
-Опорный конспект
-Индивидуальные тестовые задания
Форма урока: Урок-обобщение знаний
Обоснование использования ИКТ:
Расширение объема предъявляемой учебной информации;
Разнообразие форм учебной деятельности студентов на уроке;
Повышение интереса к изучению предмета и к учению в целом.
Эпиграф к уроку:
Вам (не)принадлежит то, чего вы не(понимаете).
И.Гете
Ход урока
I.Организационный момент
II. Определение темы урока и постановка целей.
1.Послушайте стихотворение, определите тему нашего урока, запишите слова и скажите, для чего нужна частица НЕ в данных словах?
Побывал я однажды в стране,
Где исчезла частица НЕ.
Посмотрел я вокруг с доумением:
Что за лепое положение!
Но кругом было тихо-тихо,
И во всем была разбериха,
И на взрачной клумбе у будки
Голубые цвели забудки.
И погода стояла настная,
И гуляла собака счастная
И, виляя хвостом, уклюже
Пробегала пролазные лужи.
Мне навстречу без всякого страха
Шел умытый, причесанный ряха,
А за ряхой по травке свежей
Шли суразные дотепа и вежа.
А из школы, взявшись за ручки,
Чинным шагом вышли доучки.
И навстречу всем утром рано
Улыбалась царевна Смеяна.
Очень жаль, что только во сне
Есть страна без частицы НЕ.
— Какие слова вы записали? Какова особенность их написания?
( Все слова без не не употребляются, не является приставкой).
-Объясните значение слов «невежа» и «невежда».
(Невежа— 1.Грубый, неучтивый человек. Невежа тот, кто позволяет себе грубость.
Невежда, невежественный, несведущий, безграмотный, неграмотный, необразованный, неученый, неуч, серый, темный, малограмотный, малокультурный. Невежда он был круглый, ничего не читал.)
2.Сформулируйте задачи нашего урока. ( Для правильного написания слов с частицей НЕ следует повторить правила, составить алгоритм, сводную таблицу. Закрепить полученные знания).
— Прочитайте эпиграф к уроку, объясните смысл этого высказывания. К нему мы еще вернемся в конце нашей работы.
III.Систематизация умений и навыков ( работа над составлением таблицы, алгоритма)
1.Вспомним , чем бывает НЕ в словах. ( Например, в словах стихотворения, эпиграфа).

2. Самостоятельная работа
-Я предлагаю вам вспомнить все условия написания «не» с разными частями речи и составить самим таблицу » Правописание не с разными частями речи», которую можно будет использовать для систематизации материала.
-Для этого поделимся на группы, каждая группа составляет свой блок.
1 группа- написание «не» с существительными, прилагательными и наречиями.
2группа-написание «не» с глаголами и деепричастиями
3группа — написание » не» с причастиями
Правописание не с различными частями речи.
Неряха, нелепый, небрежно
Противопоставление с союзом а
Не друг, а враг
Без не не употребляются
Недоумевающий
Краткое причастие
Не распечатан, не скошена
Без не не употребляются
Нездоровится,
но
Всегда
Не рисует
Не видя
не поздоровится
Можно подобрать синоним
неправдивый=лживый
неправда=ложь
невеселый = грустный
невысоко= низко
Наличие слов далеко не, отнюдь не , вовсе, ничуть не, никогда не
Вовсе не красивое платье
Полное одиночное (нет зависимых слов)
Нерешенный пример,ненаписанное письмо
Противопоставление с союзом а
Не законченная, а только начатая работа
Наличие наречий степени, признака: чрезвычайно, совершенно, абсолютно, почти
Сравнительная степень: не лучше, не умнее
Наличие зависимых слов (входит в причастный оборот)
Еще не скошенная трава
Отрицательные наречия: негде,
некуда
С прил., которые не имеют полной формы: не рад, не должен, не обязан
! Не является частицей и пишется раздельно
с неопределённым местоимением, если разделено предлогом;
с прилагательными, обозначающими цвет, относительными и притяжательными прилагательными;
с числительными
с местоимениями
с прилагательными и наречиями в сравнительной степени
3.Взаимопроверка
— Эксперты проверяют поочередно составление таблицы у каждой группы и обобщают материал.
4.Самопроверка
-Теперь каждый проверяет свою работу по слайду и дописывает те условия написания, которые пропущены.
5.Построение алгоритма «Правописание НЕ с разными частями речи»
( На основании таблицы выстраиваем алгоритм рассуждения).
Образец рассуждения:
1.При выборе слитно-раздельного написания не с существительными, прилагательными, наречиями на -о, -е рассуждаем так:
— смотрим, может ли слово употребляться без не. Если не может – пишем слитно: неряха , несуразный, Небрежно.
— если слово может употребляться с не, смотрим, есть ли противопоставление признаков, оценок, или слова далеко не, отнюдь не, вовсе не, ничуть не, чуть не, отнюдь не. Есть одно из указанных условий – пишем не раздельно : не широкий , а узкий пруд; вовсе не интересный рассказ; ничуть не красиво.
— если нет указанних выше условий, подбираем к слову синоним и пишем не слитно: говорил неправду ( ложь), поступил нехорошо ( плохо).
Запомните: не пишется раздельно с относительными, притяжательными прилагательными, с прилагательными со значением цвета, с прилагательными и наречиями в сравнительной степени: не кожаный портфель, не синее небо, не тяжелее, не менее; с наречиями, которые пишутся через дефис: поступил не по — товарищески.
Слитное и раздельное написание НЕ
АЛГОРИТМ ОПРЕДЕЛЕНИЯ СЛИТНОГО ИЛИ РАЗДЕЛЬНОГО НАПИСАНИЯ НЕ
! Не является частицей и пишется раздельно
с неопределённым местоимением, если разделено предлогом;
с прилагательными, обозначающими цвет, относительными и притяжательными прилагательными;
с числительными
с местоимениями
с наречиями, которые пишутся через дефис ( не по-братски, не по- летнему)
с прилагательными и наречиями в сравнительной степени ( не лучше, не хуже , не красивее, не умнее)
6.Закрепление материала. Работа с текстом.
(Отпечатанный текст роздан каждому ученику).
-В какой фразе заключена главная мысль текста?
-Как вы ее понимаете?
-Озаглавьте.
-Спишите, раскрыв скобки, обозначив орфограмму «не» с различными частями речи»
-Раскройте главную мысль текста, аргументируйте свой выбор.
-Как бы вы поступили на месте Васи?
Успокоение (не)приходило.(Не) в чем Васе было себя упрекнуть. Это мать,(не)испытывая жалости к старой черепахи, приказала её унести из дома.
Перед Васей (не)ожиданно возникли глаза черепахи, никогда (не) мигающие, мудрые. Вася думал: «(Не) такому уж плохому человеку продал я её. И живет она теперь (не)далеко, а близко». Но вдруг он заплакал.
Это сердце подсказало мальчику (не) ведомую истину: (не) только мир существует для тебя, но и ты для мира.
(Ю.Нагибин «Старая черепаха»)
-Представьте, что вы учитель. Какие бы вопросы вы задали по изученной теме?
-Составление кластера по теме.
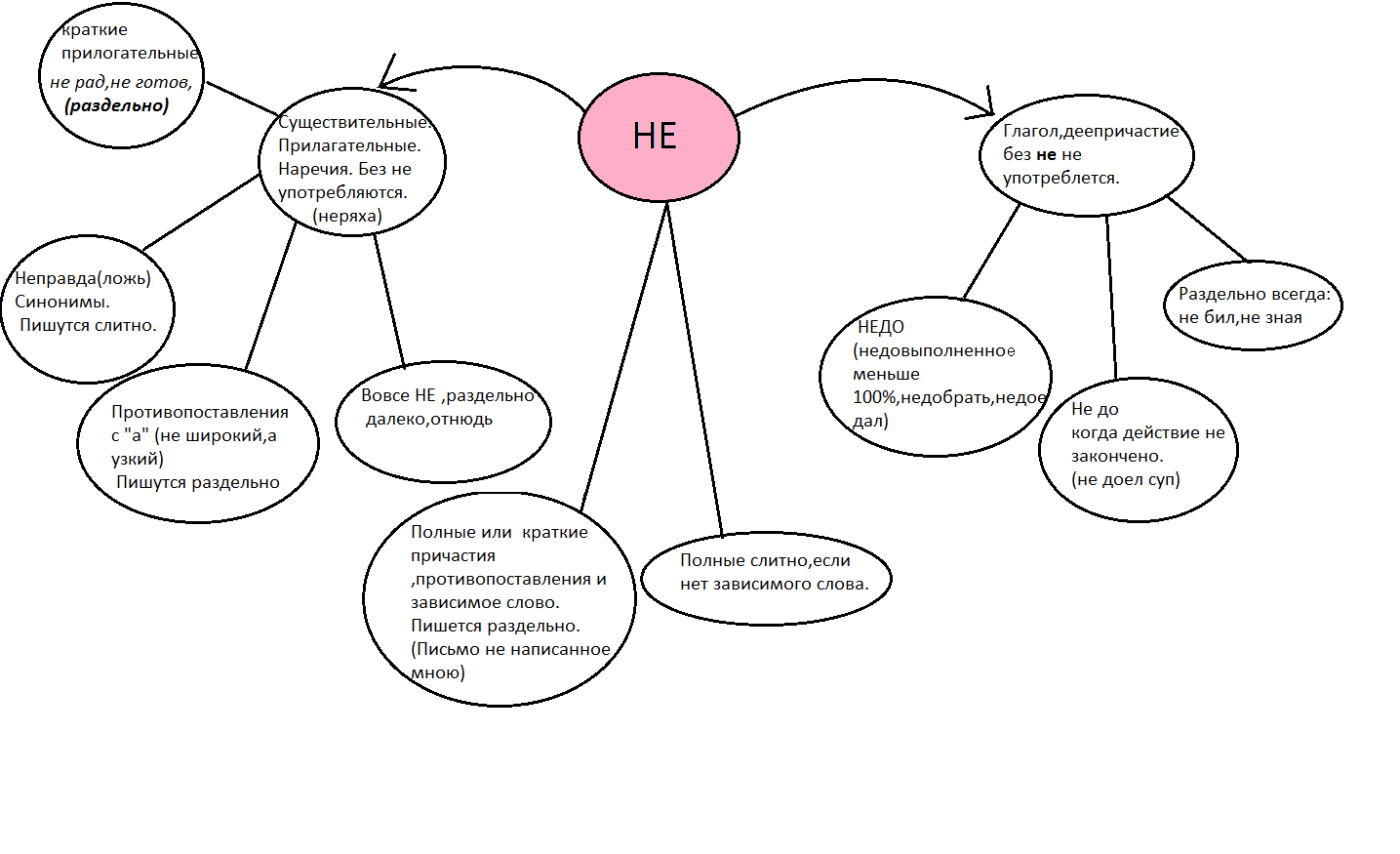
*Задание.
Определить, какое слово в каждом ряду «лишнее «. Объяснить. Заменить его таким, которое подходит к данному ряду.
1 (Не)удача,(не)покорный,(не)чего,(не)знает.
2 (Не)приблизившись,(не)слышишь,(не)дотрога, (не)(у)кого
3 Никем (не)тронутый,(не)глубокий, но очень бурный, (не)по-товарищески,(не)убраны
Глубокое погружение в тегирование частей речи с использованием алгоритма Витерби
Сачин Малхотра
Сачин Малхотра и Дивья Годаял
Источник: https://www.vocal.com/echo-cancellation/viterbi-algorithm-in-speech-enhancement-and-hmm/С возвращением, смотритель !
Если вы забыли проблему, которую мы пытались решить в предыдущей статье, позвольте нам исправить ее для вас.
Итак, вот этот непослушный мальчик Питер, и он будет приставать к своему новому смотрителю, тебе!
Как смотритель, одна из самых важных задач для вас — уложить Питера в постель и убедиться, что он крепко спит.После того, как вы уложили его в постель, вы должны убедиться, что он действительно спит, а не причинить вреда.
Однако вы не можете снова войти в комнату, так как это наверняка разбудит Питера. Все, что вы слышите, — это шумы, которые могут исходить из комнаты.
Либо в комнате тихо , либо из комнаты доносится шум . Это ваши наблюдения.
Все, что у вас есть в качестве смотрителя, это:
- набор наблюдений, который в основном представляет собой последовательность, содержащую шум или тихий во времени и
- Диаграмма состояний, предоставленная мамой Питера, которая случайно быть неврологом, который содержит все различные наборы вероятностей, которые вы можете использовать для решения проблемы, определенной ниже.
Проблема
Учитывая диаграмму состояний и последовательность из N наблюдений во времени, нам нужно сообщить состояние ребенка в текущий момент времени. Математически у нас есть N наблюдений за период времени t0, t1, t2 .... tN . Мы хотим выяснить, будет ли Питер бодрствовать или спать, или, скорее, какое состояние более вероятно в момент времени tN + 1 .
Если что-то из этого кажется вам греческим, прочтите предыдущую статью, чтобы освежить в памяти модель цепи Маркова, скрытые модели Маркова и часть речевых тегов.
Диаграмма состояний, которую мама Питера дала вам перед отъездом.В той предыдущей статье мы вкратце смоделировали проблему тегирования части речи с помощью скрытой марковской модели.
Проблема спит Питер или нет — это всего лишь пример проблемы
.nlp — Часть речевого тегирования с алгоритмом Витерби
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
- Авторизоваться зарегистрироваться
текущее сообщество
Руководств по программированию на Python
Разметка части речи с помощью NLTK
Одним из наиболее мощных аспектов модуля NLTK является тегирование части речи, которое он может сделать за вас. Это означает обозначение слов в предложении как существительных, прилагательных, глаголов и т. Д. Что еще более впечатляюще, он также обозначает время и многое другое. Вот список тегов, их значение и несколько примеров:
Список теговPOS: Координационный союз CC Кардинальная цифра CD Определитель DT ЕХ экзистенциальный там (вроде: «есть»... подумайте об этом как о "существует") FW иностранное слово В союзе предлога / подчинения JJ прилагательное 'большой' JJR прилагательное, сравнительное 'больше' JJS прилагательное, превосходная степень 'самый большой' Маркер списка LS 1) Модальный MD может, будет NN существительное, единственное число 'стол' NNS существительное множественное число 'столы' NNP имя собственное, единственное число 'Harrison' NNPS имя собственное, множественное число - американцы ФДТ предопределитель "все дети" POS притяжательный конечный родитель PRP личное местоимение I, he, she PRP $ притяжательное местоимение my, his, hers РБ наречие очень, тихо, RBR наречие, сравнительно лучше Наречие RBS, превосходная степень лучшего RP частица сдаться ЧТОБЫ пойти «в» магазин.UH междометие errrrrrrrm VB глагол, основная форма взять VBD глагол, прошедшее время взял VBG глагол, герундий / причастие настоящего времени VBN глагол, причастие прошедшего времени принято VBP глагол, петь. настоящее, не 3D дубль VBZ глагол, петь от 3-го лица. настоящее берет WDT wh-определитель, который WP wh-местоимение кто, что WP $ притяжательное местоимение wh, чье WRB wh-abverb где, когда
Как мы можем это использовать? Пока мы это делаем, мы собираемся рассмотреть новый токенизатор предложений, называемый PunktSentenceTokenizer. Этот токенизатор способен к машинному обучению без учителя, поэтому вы можете обучить его любому тексту, который вы используете.Во-первых, давайте избавимся от импорта, который мы собираемся использовать:
импорт НЛТК из nltk.corpus импортировать state_union из nltk.tokenize import PunktSentenceTokenizer
Теперь давайте создадим наши данные для обучения и тестирования:
train_text = state_union.raw ("2005-GWBush.txt")
sample_text = state_union.raw ("2006-GWBush.txt") Одно — это обращение к Государству Союза от 2005 года, а другое — от 2006 года от бывшего президента Джорджа Буша.
Затем мы можем обучить токенизатор Punkt, например:
custom_sent_tokenizer = PunktSentenceTokenizer (train_text)
Затем мы можем токенизировать, используя:
tokenized = custom_sent_tokenizer.tokenize (sample_text)
Теперь мы можем завершить эту часть сценария тегирования речи, создав функцию, которая будет выполнять и отмечать все части речи в предложении следующим образом:
def process_content ():
пытаться:
для i в токенизированном [: 5]:
слова = nltk.word_tokenize (я)
tagged = nltk.pos_tag (слова)
печать (с тегами)
кроме исключения как e:
печать (str (e))
process_content () На выходе должен быть список кортежей, где первый элемент кортежа — это слово, а второй — часть тега речи.Должно получиться так:
[(‘ПРЕЗИДЕНТ’, ‘NNP’), (‘GEORGE’, ‘NNP’), (‘W.’, ‘NNP’), (‘BUSH’, ‘NNP’), («‘S», ‘POS’), (‘АДРЕС’, ‘NNP’), (‘ПЕРЕД’, ‘NNP’), (‘A’, ‘NNP’), (‘СОЕДИНЕНИЕ’, ‘NNP’), (‘СЕССИЯ’, ‘NNP’), (‘OF’, ‘NNP’), (‘THE’, ‘NNP’), (‘КОНГРЕСС’, ‘NNP’), (‘ON’, ‘NNP’), (‘THE’, ‘NNP’), (‘STATE’, ‘NNP’), (‘OF’, ‘NNP’), (‘THE’, ‘NNP’), (‘UNION’, ‘NNP’), (‘Январь’, ‘NNP’), (’31’, ‘CD’), (‘,’, ‘,’), (‘2006’, ‘CD’), (‘THE’, ‘DT’), (‘ПРЕЗИДЕНТ’, ‘NNP’), (‘:’, ‘:’), (‘Спасибо’, ‘NNP’), (‘ты’, ‘PRP’), (‘все’, ‘DT’), (‘.’,’. ‘)] [(‘Мистер’, ‘NNP’), (‘Спикер’, ‘NNP’), (‘,’, ‘,’), (‘Заместитель’, ‘NNP’), (‘Президент’, ‘NNP’ ), (‘Чейни’, ‘NNP’), (‘,’, ‘,’), (‘члены’, ‘NNS’), (‘из’, ‘IN’), (‘Конгресс’, ‘NNP’ ), (‘,’, ‘,’), (‘члены’, ‘NNS’), (‘из’, ‘IN’), (‘the’, ‘DT’), (‘Supreme’, ‘NNP’ ), (‘Суд’, ‘NNP’), (‘и’, ‘CC’), (‘дипломатический’, ‘JJ’), (‘корпус’, ‘NNS’), (‘,’, ‘,’ ), (‘выдающийся’, ‘VBD’), (‘гости’, ‘NNS’), (‘,’, ‘,’), (‘и’, ‘CC’), (‘парень’, ‘JJ’ ), (‘граждане’, ‘NNS’), (‘:’, ‘:’), (‘Сегодня’, ‘NN’), (‘наш’, ‘PRP $’), (‘нация’, ‘NN ‘), (‘ потерянный ‘,’ VBD ‘), (‘ a ‘,’ DT ‘), (‘ любимый ‘,’ VBN ‘), (‘, ‘,’, ‘), (‘ изящный ‘,’ JJ ‘), (‘, ‘,’, ‘), (‘ мужественный ‘,’ JJ ‘), (‘ женщина ‘,’ NN ‘), (‘ кто ‘,’ WP ‘), (‘ названный ‘,’ VBN ‘), (‘ Америка ‘,’ NNP ‘), (‘ к ‘,’ TO ‘), (‘ его ‘,’ PRP $ ‘), (‘ основание ‘,’ NN ‘), (‘ идеалы ‘,’ NNS ‘), (‘ and ‘,’ CC ‘), (‘ снесено ‘,’ VBD ‘), (‘ on ‘,’ IN ‘), (‘ a ‘,’ DT ‘), (‘ благородный ‘,’ JJ ‘), (‘ мечта ‘,’ NN ‘), (‘.’,’. ‘)] [(‘Tonight’, ‘NNP’), (‘мы’, ‘PRP’), (‘are’, ‘VBP’), (‘comforted’, ‘VBN’), (‘by’, ‘IN’) , (‘the’, ‘DT’), (‘надежда’, ‘NN’), (‘of’, ‘IN’), (‘a’, ‘DT’), (‘рад’, ‘NN’) , (‘воссоединение’, ‘NN’), (‘с’, ‘IN’), (‘the’, ‘DT’), (‘муж’, ‘NN’), (‘who’, ‘WP’) , (‘было’, ‘VBD’), (‘занято’, ‘VBN’), (‘так’, ‘RB’), (‘long’, ‘RB’), (‘назад’, ‘RB’) , (‘,’, ‘,’), (‘and’, ‘CC’), (‘мы’, ‘PRP’), (‘are’, ‘VBP’), (‘благодарный’, ‘JJ’) , (‘for’, ‘IN’), (‘the’, ‘DT’), (‘good’, ‘NN’), (‘life’, ‘NN’), (‘of’, ‘IN’) , (‘Коретта’, ‘NNP’), (‘Скотт’, ‘NNP’), (‘Король’, ‘NNP’), (‘.’,’. ‘)] [(‘(‘, ‘NN’), (‘Аплодисменты’, ‘NNP’), (‘.’, ‘.’), (‘)’, ‘:’)] [(‘Президент’, ‘NNP’), (‘Джордж’, ‘NNP’), (‘W.’, ‘NNP’), (‘Bush’, ‘NNP’), (‘реагирует’, ‘VBZ’ ), (‘в’, ‘TO’), (‘аплодисменты’, ‘VB’), (‘во время’, ‘IN’), (‘его’, ‘PRP $’), (‘State’, ‘NNP ‘), (‘ из ‘,’ IN ‘), (‘ the ‘,’ DT ‘), (‘ Union ‘,’ NNP ‘), (‘ Address ‘,’ NNP ‘), (‘ at ‘,’ IN ‘), (‘ the ‘,’ DT ‘), (‘ Capitol ‘,’ NNP ‘), (‘, ‘,’, ‘), (‘ вторник ‘,’ NNP ‘), (‘, ‘,’, ‘), (‘ Ян ‘,’ NNP ‘), (‘. ‘,’. ‘)]
На этом этапе мы можем начать извлекать значение, но нам еще предстоит поработать.Следующая тема, которую мы собираемся затронуть, — это разбиение на фрагменты, при котором мы группируем слова на основе их частей речи в многозначительные группы.
Следующий учебник: фрагменты с помощью NLTK
.
Части речи | Центр письма
Местоимение может заменить существительное или другое местоимение. Вы используете такие местоимения, как «он», «which», «none» и «you», чтобы ваши предложения были менее громоздкими и менее повторяющимися.
Грамматики подразделяют местоимения на несколько типов, включая личное местоимение, указательное местоимение, вопросительное местоимение, неопределенное местоимение, относительное местоимение, возвратное местоимение и интенсивное местоимение.
Личные местоименияЛичное местоимение относится к определенному человеку или предмету и меняет свою форму, чтобы указать лицо, число, пол и падеж.
Субъективные личные местоименияСубъективные личные местоимения указывает на то, что местоимение выступает в качестве подлежащего предложения. Субъективные личные местоимения: «я», «ты», «она», «он», «оно», «мы», «ты», «они».
В следующих предложениях каждое из выделенных слов является субъективным личным местоимением и выступает в качестве подлежащего предложения:
- Я был рад найти проездной на автобусе внизу зеленого ранца.
- Вы, , несомненно, самый странный ребенок , которого я когда-либо встречал.
- Он украл шкуру селки и заставил ее жить с ним.
- Когда она была молодой женщиной, она зарабатывала себе на жизнь, работая шахтером.
- Спустя много лет они вернулись на родину.
- Мы встретимся в библиотеке в 15:30.
- Это стоит на прилавке.
- вы делегаты из Малагавача?
Объективные личные местоимения указывает, что местоимение действует как объект глагола, составного глагола, предлога или инфинитива.Объективные личные местоимения: «я», «ты», «она», «он», «он», «мы», «ты» и «они».
В следующих предложениях каждое из выделенных слов является объективным личным местоимением:
- Симус украл шкуру селки и заставил ее жить с ему .
Объективное личное местоимение «она» является прямым объектом глагола «принудительно», а объективное личное местоимение «он» является объектом предлога «с».
- Прочитав брошюру, Джуди бросила ее в мусорное ведро.
Местоимение «это» является прямым объектом глагола «бросил».
- Взволнованный помощник встал и посмотрел на разгневанного делегаты и сказали: «Наш лидер обратится к you через пять минут».
В этом предложении местоимение «you» является прямым объектом глагола «address».
- Дебора и Роберта встретятся с us в самом новом кафе на рынке.
Здесь предметное личное местоимение «нас» является прямым объектом сложного глагола «встретится».
- Передайте список мне .
Здесь объективное личное местоимение «мне» является объектом предлога «к».
- Я не уверен, что мой контакт свяжется с с вами .
Точно так же в этом примере объективное личное местоимение «ты» является объектом предлога «к».
- Кристофер был удивлен, увидев и на гонках.
Здесь объективное личное местоимение «она» является объектом инфинитивной фразы «видеть».
Притяжательные личные местоименияПритяжательные местоимения указывает на то, что местоимение действует как маркер владения и определяет, кому принадлежит конкретный объект или лицо. притяжательных личных местоимений — это «мой», «ваш», «ее», «его», «его», «наш» и «их». Обратите внимание, что притяжательные личные местоимения очень похожи на притяжательные прилагательные, такие как «мой», «ее» и «их».»
В каждом из следующих предложений выделенное слово является притяжательным личным местоимением:
- Самый маленький подарок — мое .
Здесь притяжательное местоимение« мое »функционирует как предметное дополнение.
- Это твое.
Здесь притяжательное местоимение «твой» функционирует как дополнение подлежащего.
- Его на кухонном столе.
В этом примере притяжательное местоимение «его» выступает в качестве подлежащего приговор.
- Их доставят завтра.
В этом предложении притяжательное местоимение «их» является предметом предложения.
- Наша зеленая на углу.
И здесь притяжательное местоимение «наш» действует как подлежащее.
Демонстративные местоименияДемонстративные местоимения указывает на существительное или местоимение и определяет их. «Это» и «эти» относятся к вещам, которые находятся поблизости либо в пространстве, либо во времени, тогда как «то» и «те» относятся к вещам, находящимся дальше в пространстве или времени.
Указательные местоимения — «это», «то», «эти» и «те». «Это» и «то» используются для обозначения существительных в единственном числе или словосочетаний с существительными, а «эти» и «те» используются для обозначения существительных и фраз во множественном числе. Обратите внимание, что указательные местоимения идентичны указательным прилагательным, хотя, очевидно, вы используете их по-разному. Также важно отметить, что «that» также может использоваться как относительное местоимение.
В следующих предложениях каждое из выделенных слов является указательным местоимением:
- Это не должно продолжаться.
Здесь «это» используется как подлежащее составного глагола «не должен продолжаться».
- Это ничтожно; , что — это дерево, которое я хочу.
В этом примере «это» используется как тема и относится к чему-то близкому к говорящему. Демонстративное местоимение «то» также является подлежащим, но относится к чему-то более далекому от говорящего.
- Три клиента хотели из этих .
Здесь «эти» — прямое дополнение глагола «разыскивается».»
Вопросительные местоименияВопросительные местоимения используются для того, чтобы задавать вопросы. Вопросительные местоимения — это» кто «,» кто «,» который «,» что «, а также составные части, образованные суффиксом» когда-либо «(» кто угодно, » «whomever», «whichever» и «что угодно»). Обратите внимание, что либо «which», либо «what» также может использоваться как вопросительное прилагательное, а «who», «who» или «which» также могут быть используется как относительное местоимение
Вы найдете слова «who», «who» и иногда «which» для обозначения людей, а «which» и «what» — для обозначения вещей и животных.
«Кто» действует как подлежащее глагола, а «кто» действует как объект глагола, предлога или глагола.
Выделенное слово в каждом из следующих предложений является вопросительным местоимением:
- Какой хочет увидеть стоматолога первым?
«Который» является предметом предложения.
- Кто написал роман Rockbound?
Аналогично «кто» является субъектом предложения.
- Кого , по вашему мнению, следует пригласить?
В этом предложении «кого» является объектом глагола «пригласить».«
- К , с кем вы хотите поговорить?
Здесь вопросительное местоимение« кому »является объектом предлога« кому ».
- Кто встретит делегатов на вокзале?
В этом предложении вопросительное местоимение «кто» является подлежащим составного глагола «встретится».
- Кому вы дали бумагу?
В этом примере вопросительное местоимение «кто» является объект предлога «к.
- Что она сказала?
Здесь вопросительное местоимение «что» является прямым объектом глагола «сказать».
Относительные местоименияВы можете использовать относительное местоимение , используется для связи одной фразы или предложение к другой фразе или предложению. Относительные местоимения — это «who», «who», «that» и «which». Составные части «whoever», «whomever» и «whichever» также являются относительными местоимениями.
Вы можете использовать относительные местоимения «who» и «whoever» для обозначения предмета предложения или предложения, а «who» и «whomever» — для обозначения объектов глагола, глагола или предлога.
В каждом из следующих предложений выделенное слово является относительным местоимением.
- Вы можете пригласить кого хотите на вечеринку.
Относительное местоимение «кто угодно» является прямым объектом сложного глагола «может пригласить».
- Кандидат , которого набирает наибольшее количество голосов, не всегда избирается.
В этом предложении относительное местоимение является подлежащим глагола «побеждает» и вводит придаточное предложение «тот, кто получает наибольшее количество голосов.«Это придаточное предложение действует как прилагательное, изменяющее« кандидата ».
- Во время кризиса менеджер просит рабочих , которых считает наиболее эффективными, прибыть на час раньше, чем обычно.
В этом Предложение «кто» является прямым объектом глагола «полагает» и вводит придаточное предложение «кого она считает наиболее эффективным». Это придаточное предложение изменяет существительное «рабочие». придется его заменить.
Здесь «тот, кто» действует как подлежащее глагола «сломал».
- Ящик , который был оставлен в коридоре, теперь перемещен в кладовую.
В этом примере «который» действует как подлежащее составного глагола «был оставлен» и вводит придаточное предложение «которое было оставлено в коридоре». Придаточное предложение действует как прилагательное, изменяющее существительное «ящик».
- Я прочту в зависимости от того, какая из рукописей поступит раньше.
Здесь «в зависимости от того, что» изменяет существительное «рукопись» и вводит придаточное предложение «в зависимости от того, какая рукопись поступит раньше». Придаточное предложение функционирует как прямой объект составного глагола «будет читать».
Неопределенные местоименияНеопределенные местоимения — это местоимение, относящееся к идентифицируемому, но не определенному человеку или предмету. Неопределенное местоимение передает идею всего, любого, ни одного или некоторых.
Самыми распространенными неопределенными местоимениями являются «все», «другой», «любой», «любой», «любой», «что-нибудь», «каждый», «все», «все», «все», «несколько». , «многие», «никто», «никто», «один», «несколько», «некоторые», «кто-то» и «кто-то».»Обратите внимание, что некоторые неопределенные местоимения также могут использоваться как неопределенные прилагательные.
выделено слов в следующих предложениях являются неопределенными местоимениями:
- Многие были приглашены на обед, но пришли только двенадцать.
Здесь «многие» действуют как подлежащее составного глагола «были приглашены».
- Офис был обыскан, и все было брошено на пол.
В этом примере «все» действует как подлежащее был брошен составной глагол «.
- Мы пожертвовали всего , что нашли на чердаке, на распродажу женского приюта в гараже.
В этом предложении «все» является прямым объектом глагола «пожертвовано».
- Хотя они везде искали лишнее копий журнала они нашли нет
Здесь тоже неопределенное местоимение действует как прямой объект: «нет» — это прямой объект «найден».
- Убедитесь, что вы дали каждому копию измененный устав.
В этом примере «каждый» является косвенным объектом глагола «давать», а прямой объект — существительной фразой «копия измененного устава».
- Раздайте регистрационный пакет на каждый .
Здесь «каждый» является объектом предлога «к».
Возвратные местоименияВы можете использовать возвратных местоимений , чтобы вернуться к предмету предложения или предложения.
Возвратные местоимения — это «я», «сам», «сама», «сам», «сам», «мы», «себя» и «себя».«Обратите внимание, что каждое из них также может действовать как интенсивное местоимение.
Каждое из выделенных слов в следующих предложениях является возвратным местоимением:
- Диабетики сами делают инъекций инсулина несколько раз в день.
- Декан часто делает ксерокопирование сама , чтобы секретари могли выполнять более важную работу
- После вечеринки я сам спросил , почему я отправил по факсу приглашения всем в своем офисном здании.
- Ричард обычно не забывал отправлять копию своего электронного письма на номер и сам .
- Хотя хозяин обещал покрасить квартиру, мы в итоге сделали это сами .
Интенсивные местоимения — местоимение, используемое для подчеркивания своего предшествующего. Интенсивные местоимения идентичны по форме возвратным местоимениям.
В выделено слов в следующих предложениях — это интенсивные местоимения:
- Я сам считаю, что инопланетяне должны похитить мою сестру.
- Премьер Сам сказал, что снизит налоги.
- Они сами обещали прийти на вечеринку, хотя выпускной экзамен у них был одновременно.
Написано Хизер МакФадьен
.
 мотрю, употребляется ли слово без НЕ?
мотрю, употребляется ли слово без НЕ?
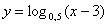
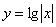
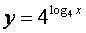
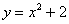 и
и 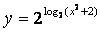
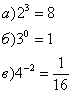
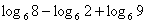
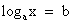 .
.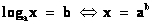
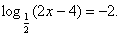
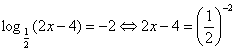 , Отсюда 2х – 4 = 4; х = 4.
, Отсюда 2х – 4 = 4; х = 4.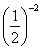 > 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.
> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.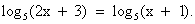
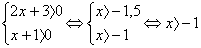
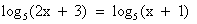 , получим уравнение 2x + 3 = х + 1. Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.
, получим уравнение 2x + 3 = х + 1. Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.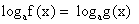

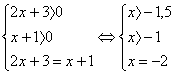
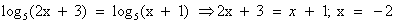 . Сделаем проверку:
. Сделаем проверку: 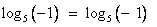 неверно, так как не имеет смысла.
неверно, так как не имеет смысла.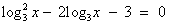 .
.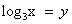 , тогда уравнение примет вид:
, тогда уравнение примет вид: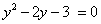 . Дискриминант D > 0. Корни по теореме Виета:
. Дискриминант D > 0. Корни по теореме Виета: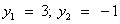 .
.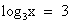 или
или 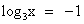 .
.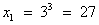 ;
; 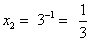 .
.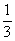
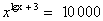 .
.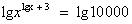 . Применим свойство логарифма степени:
. Применим свойство логарифма степени: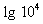
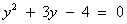 , (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.
, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.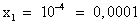 ; lgx = 1,
; lgx = 1,  .
.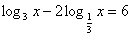
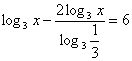 или
или 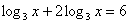 ;
;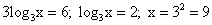 .
.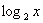 = 3 – x.
= 3 – x.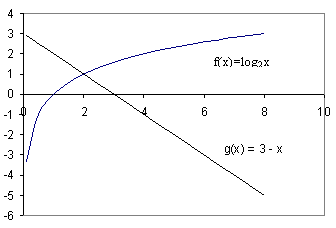
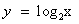 возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение
возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 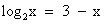 имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как
имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как 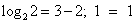 .
.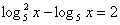
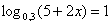
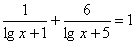
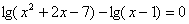
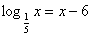
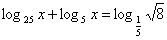
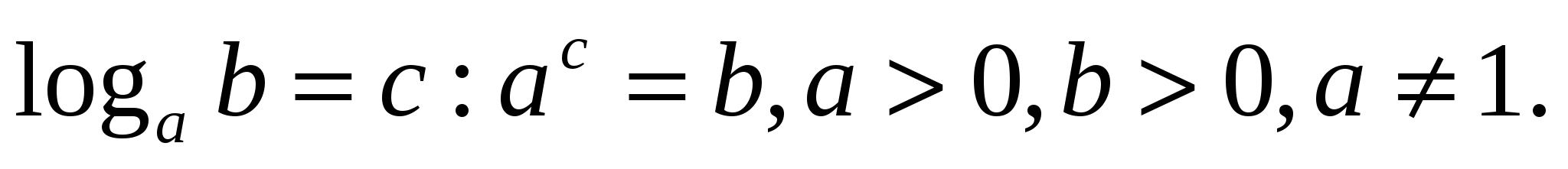
 А сейчас мы рассмотрим пример, в котором в основании логарифма уже не число, а выражение, содержащее переменную. Т. е. уравнение будет иметь вид
А сейчас мы рассмотрим пример, в котором в основании логарифма уже не число, а выражение, содержащее переменную. Т. е. уравнение будет иметь вид 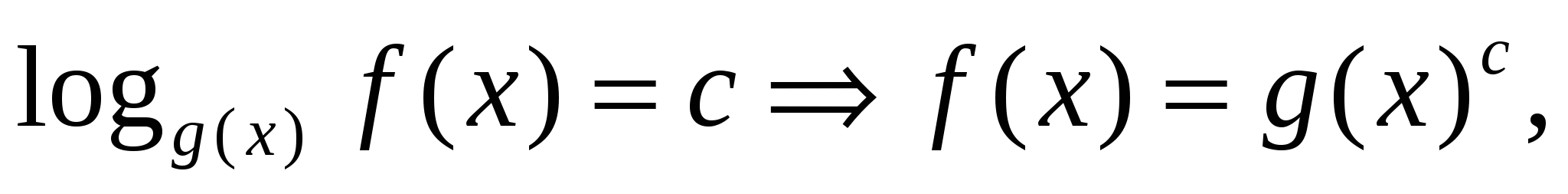 при этом
при этом Хочу отметить особо, что рассуждения НЕ ИЗМЕНИЛИСЬ!
Хочу отметить особо, что рассуждения НЕ ИЗМЕНИЛИСЬ!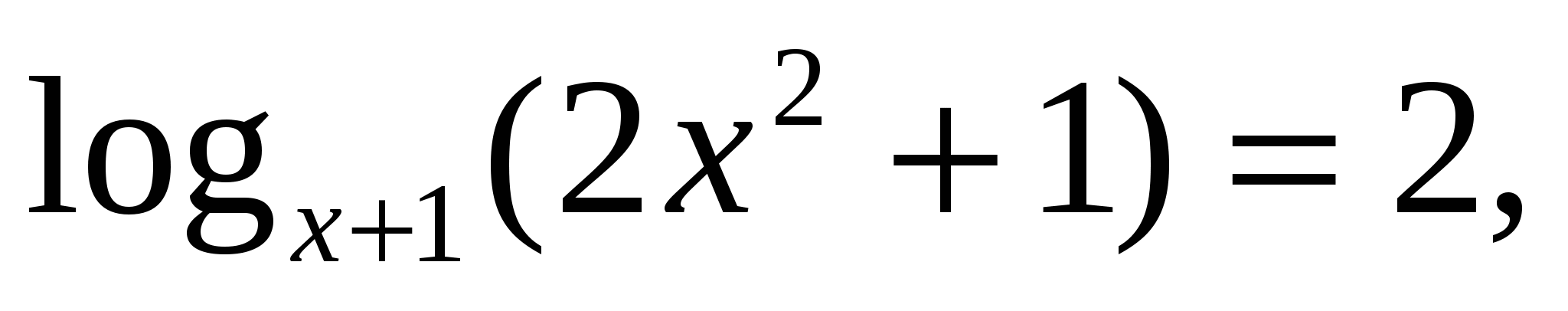
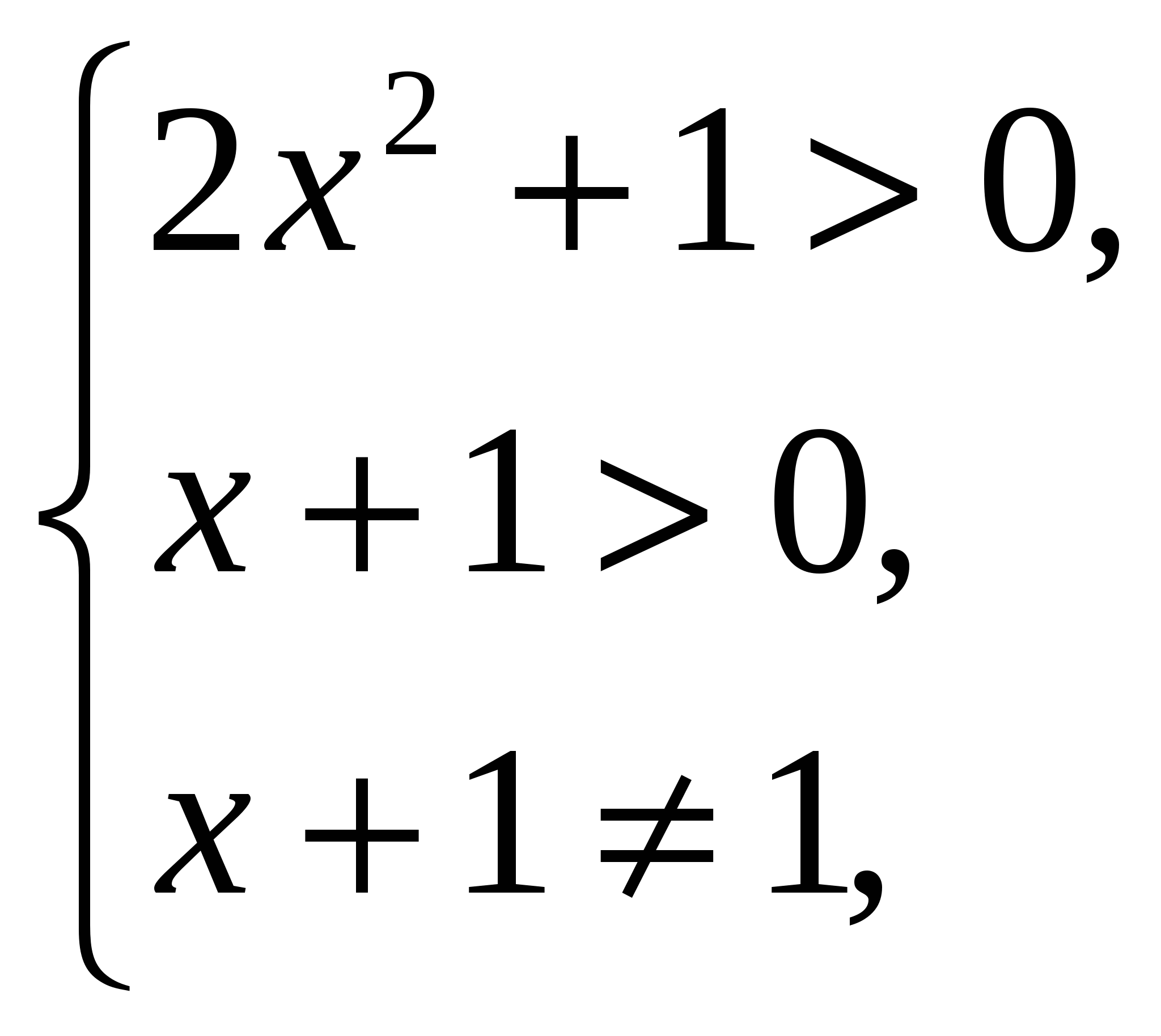

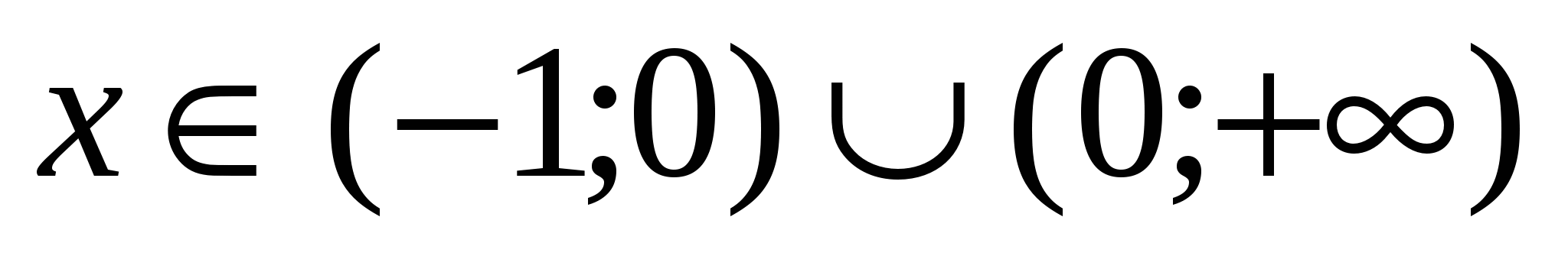 .
.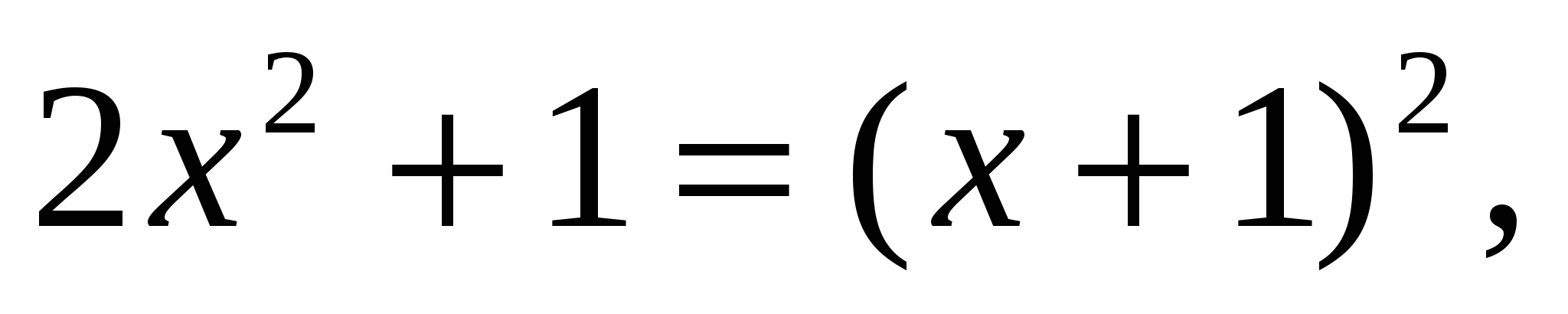
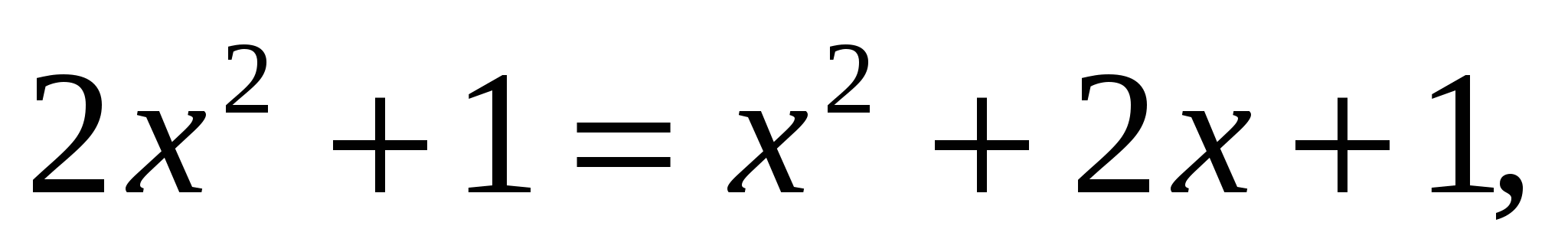
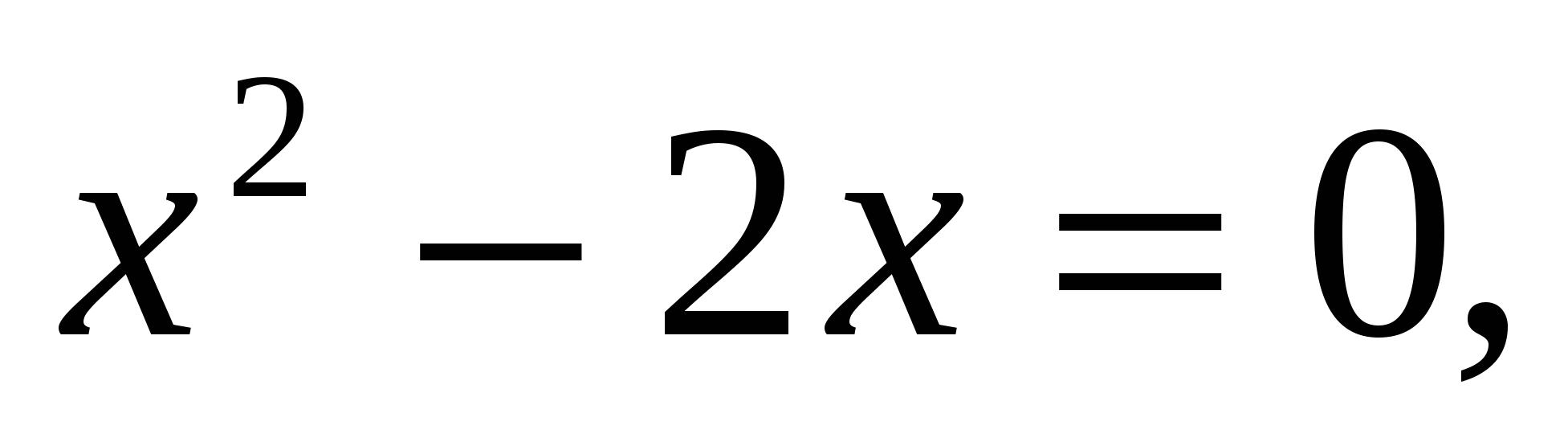
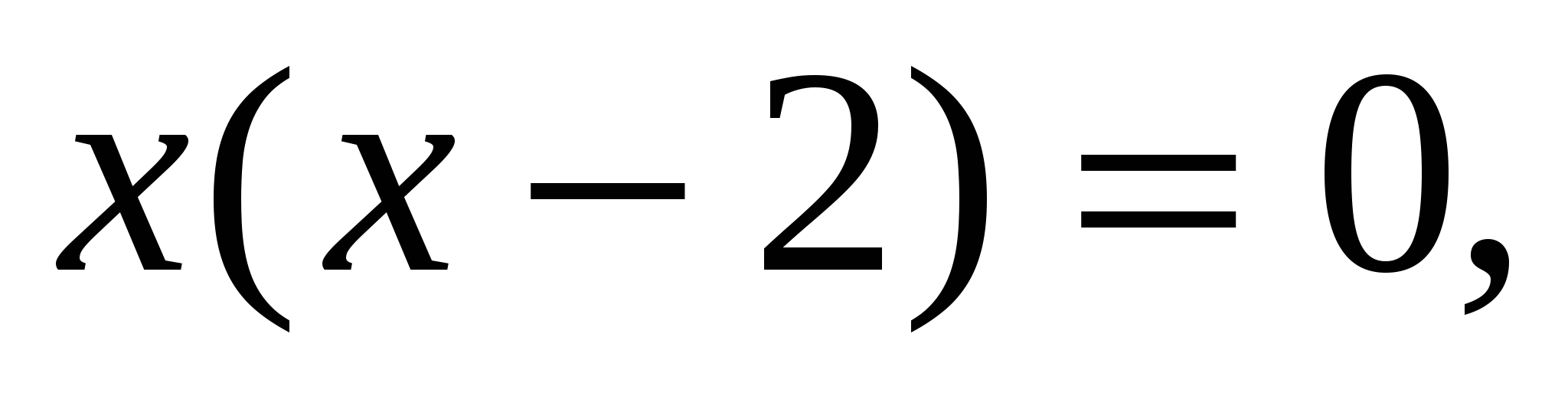
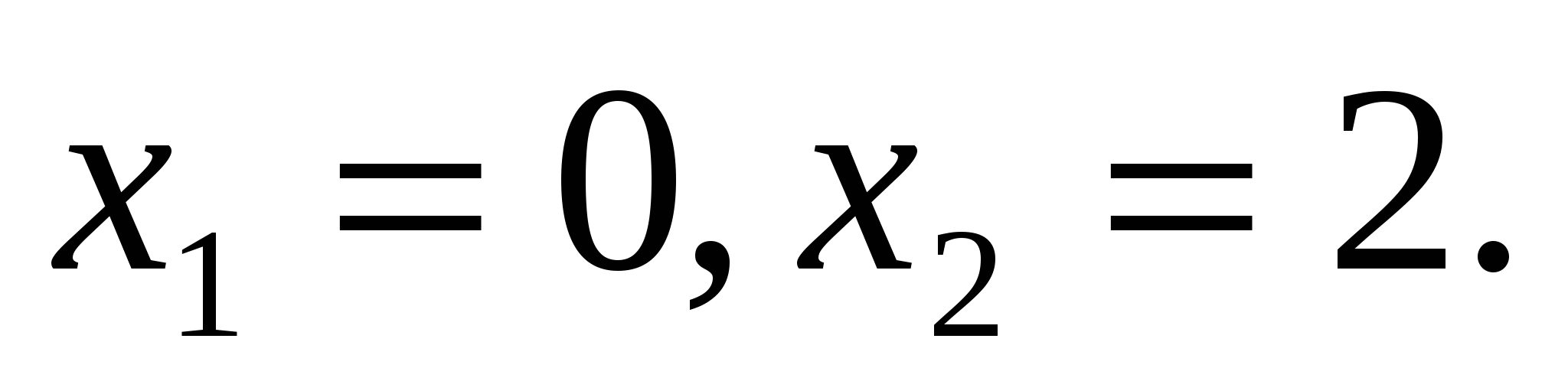

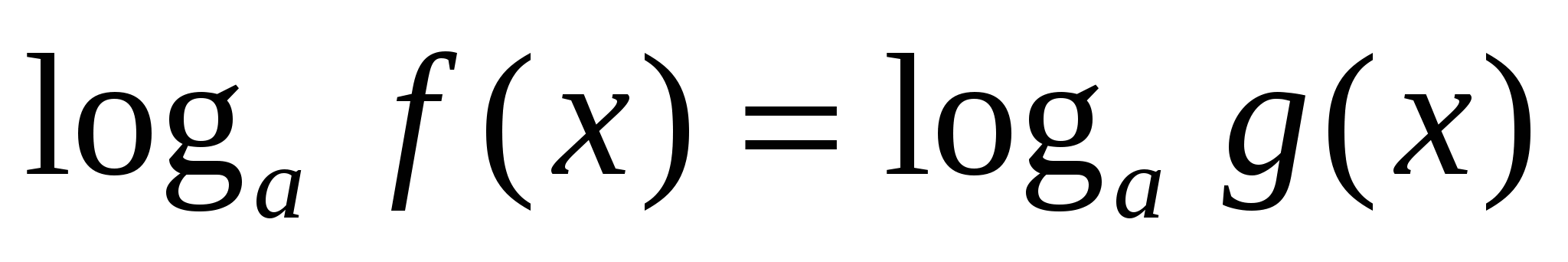
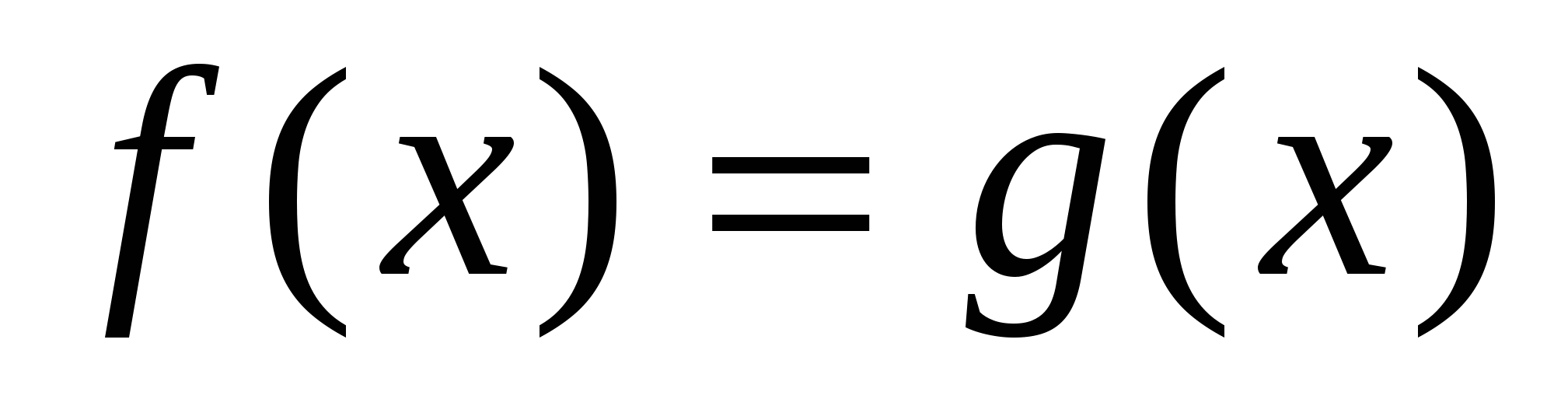 , где
, где 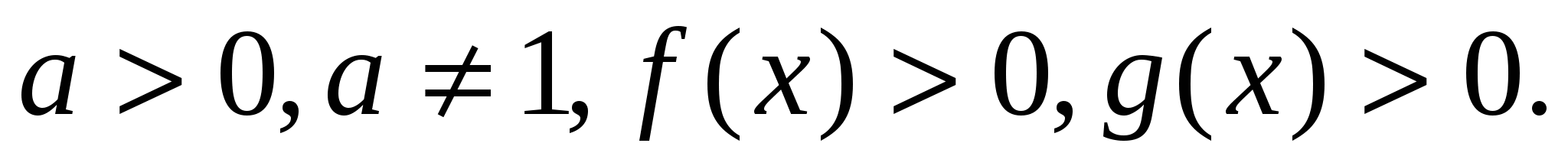
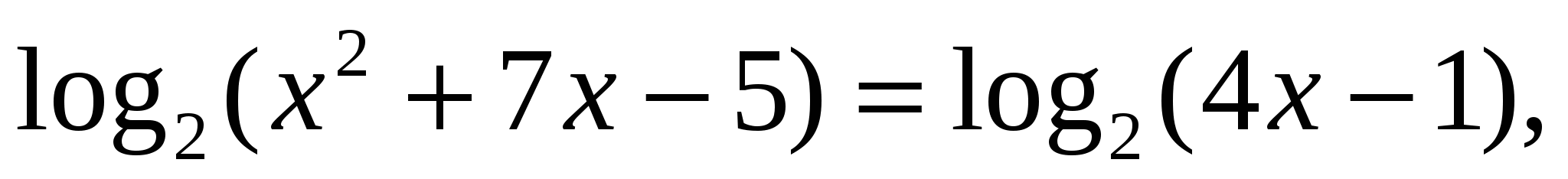
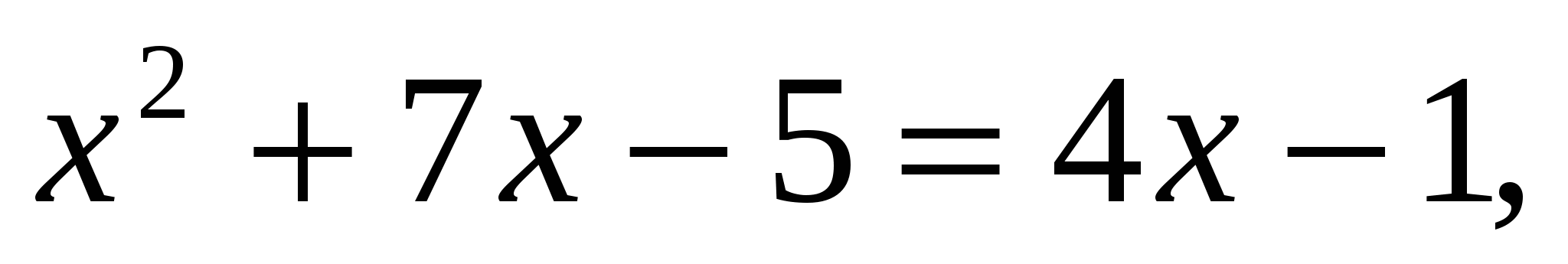
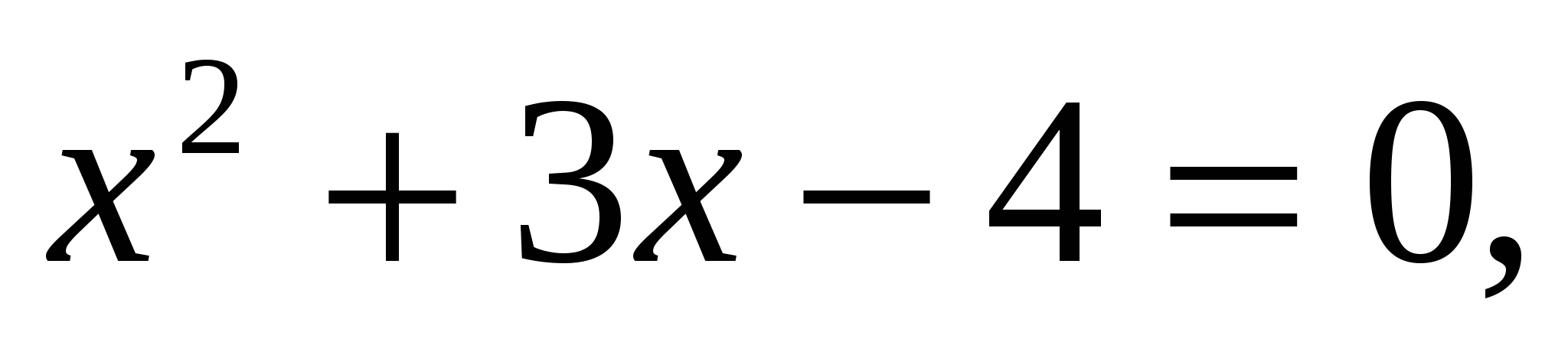
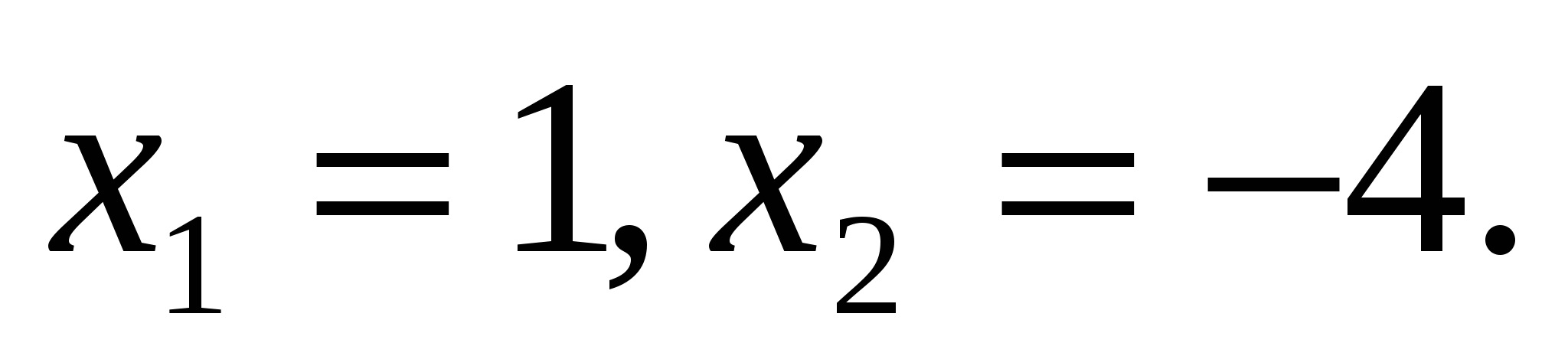
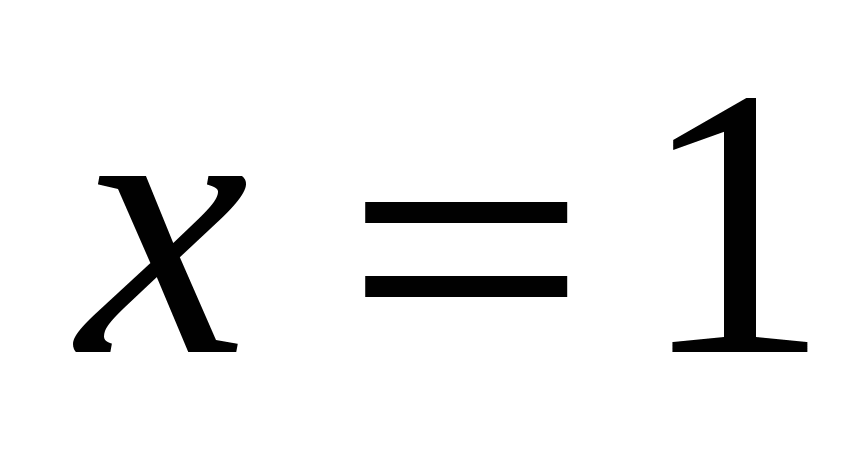
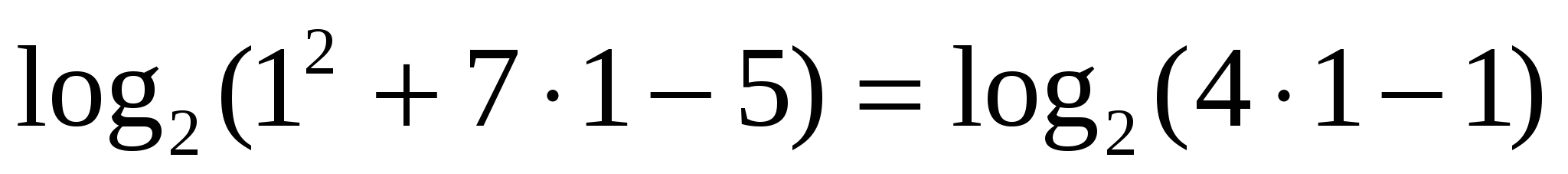
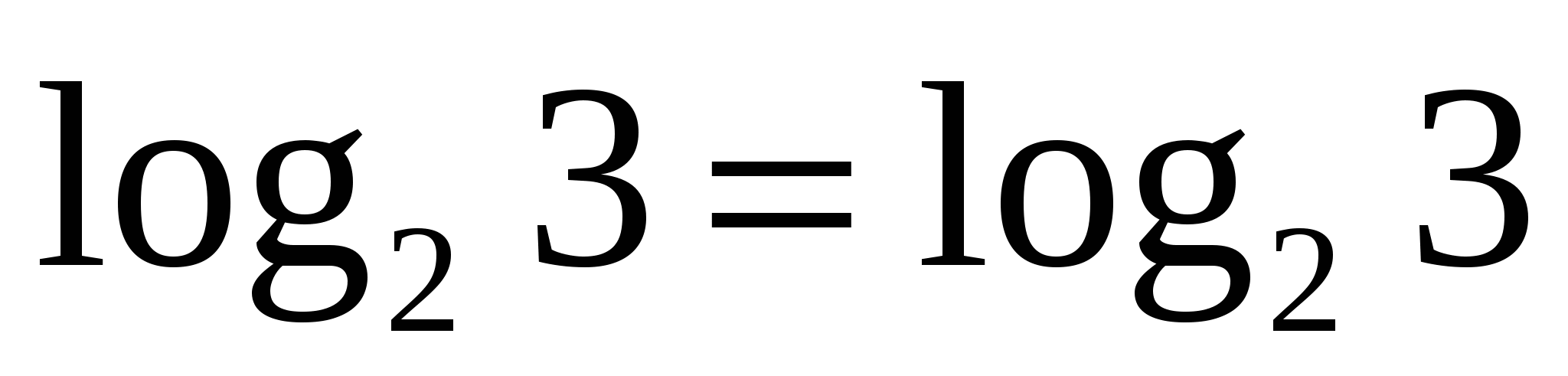 — верно.
— верно.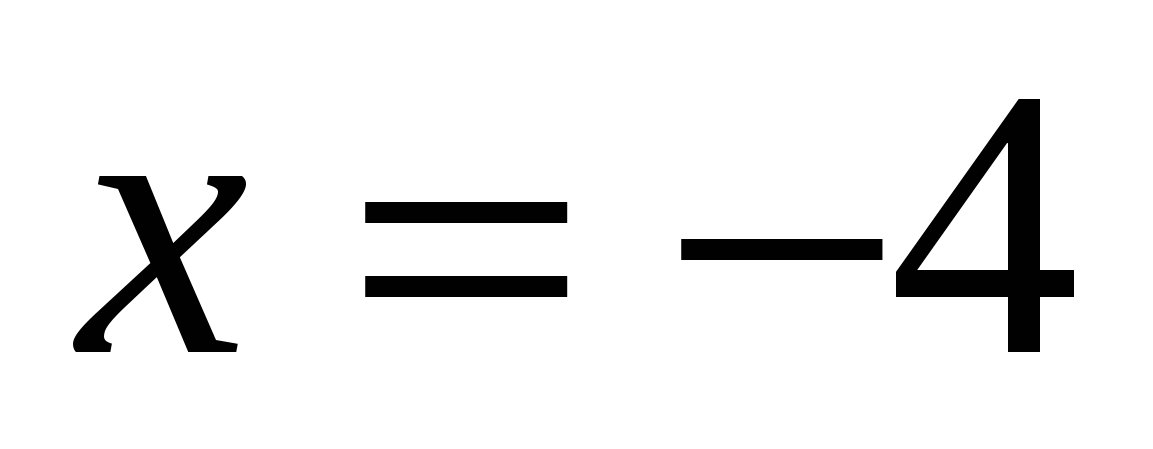
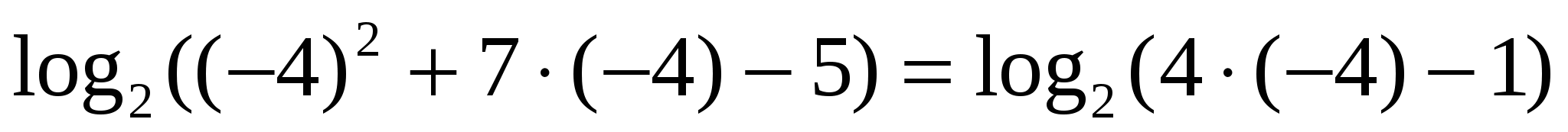
 — не верно.
— не верно.

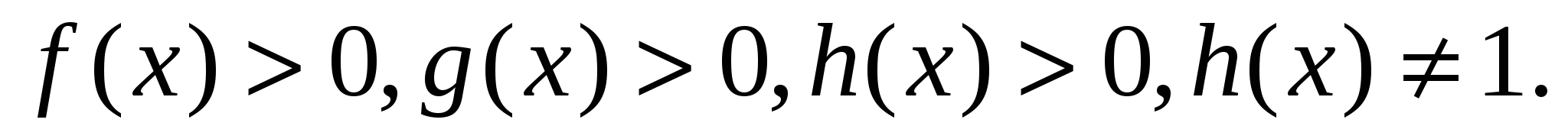
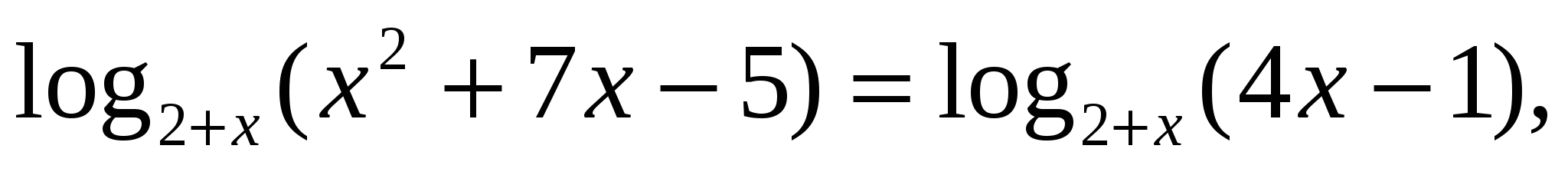
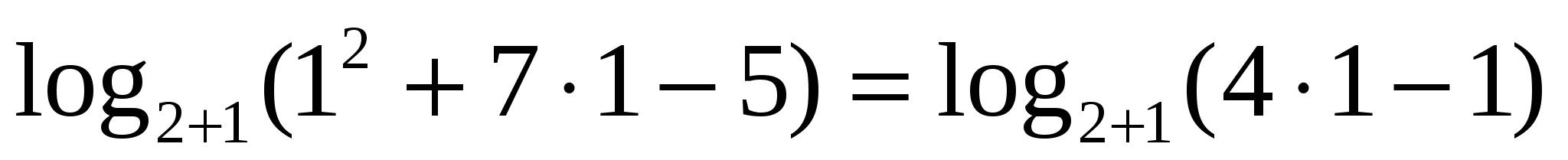
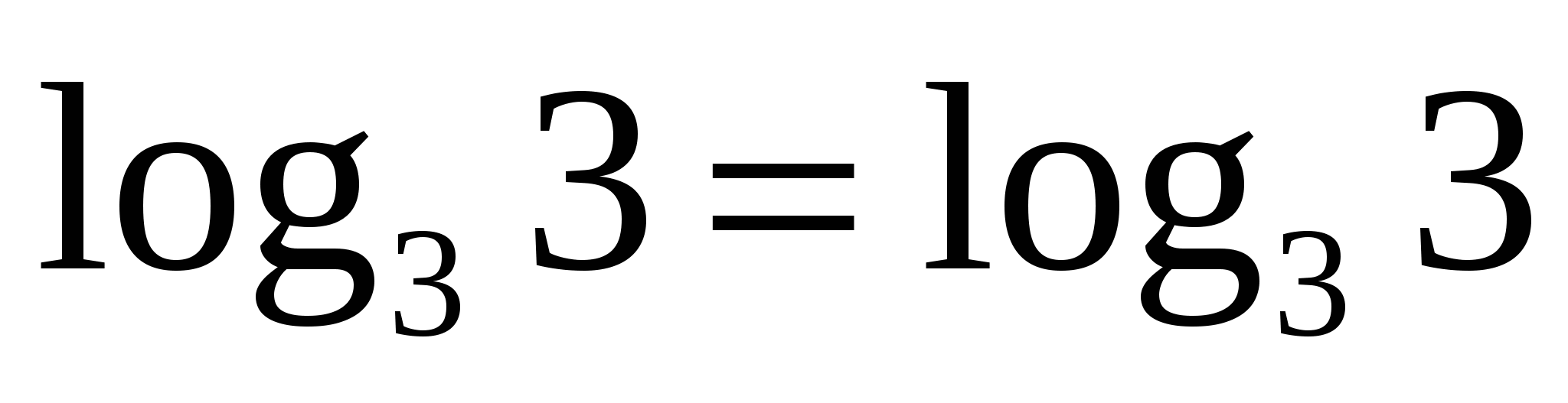
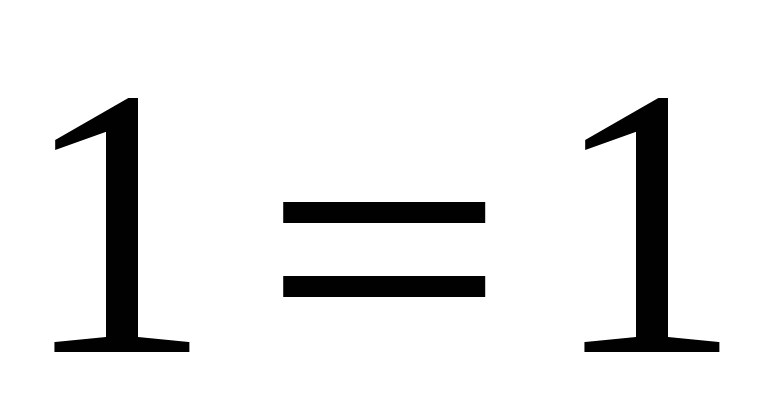 — верно.
— верно.
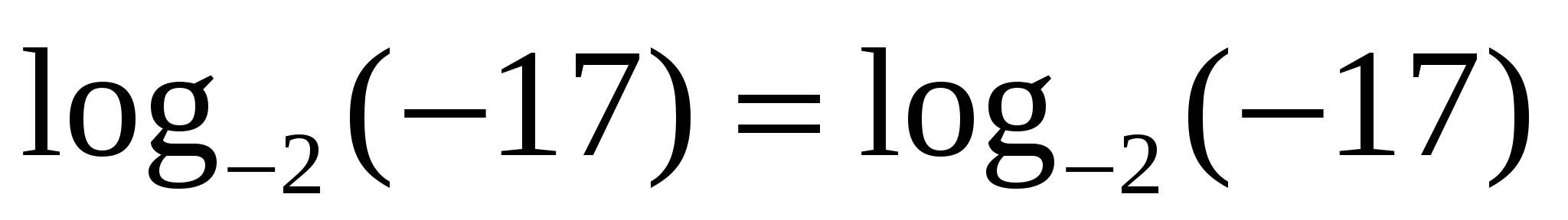 — не верно.
— не верно.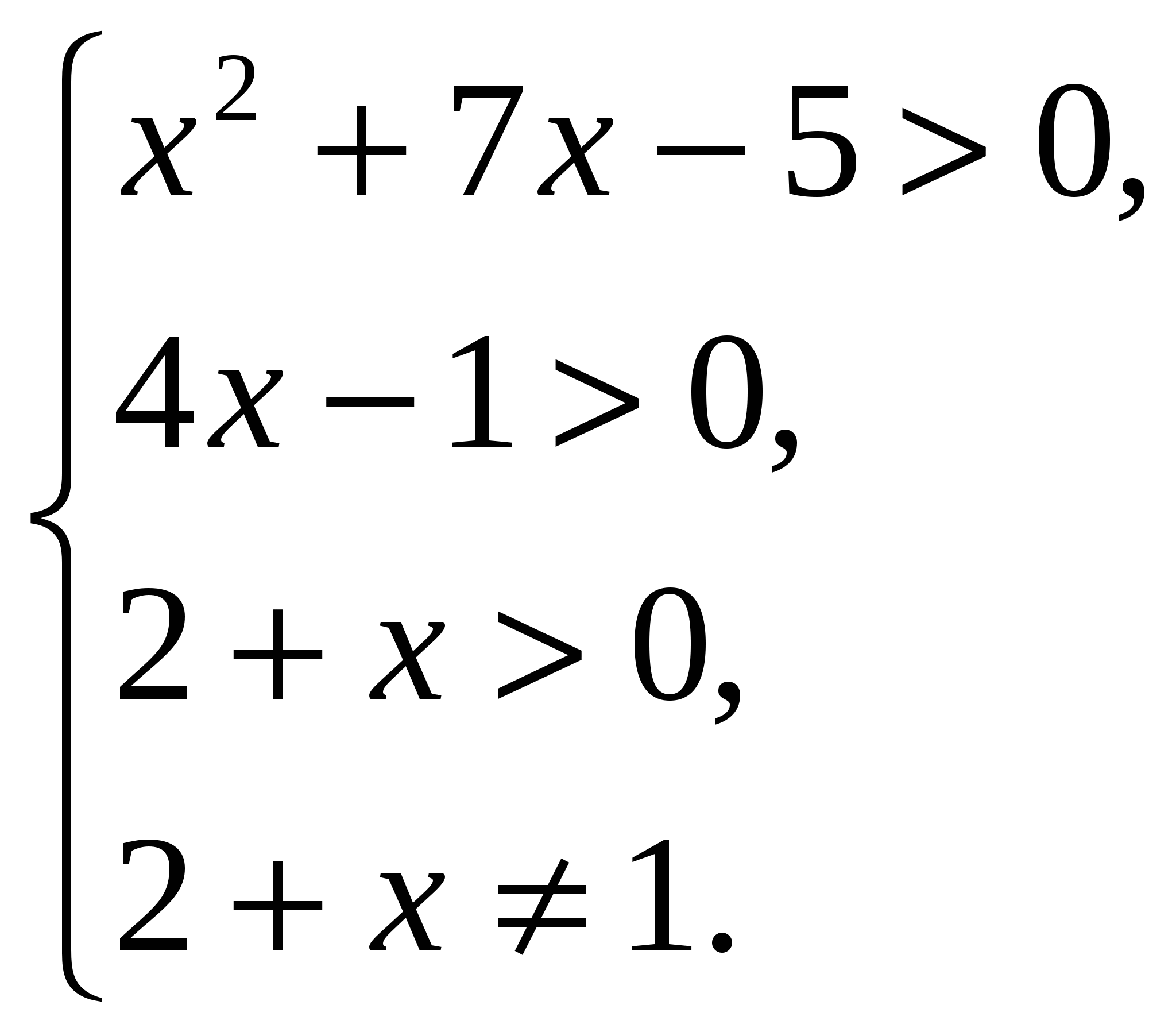


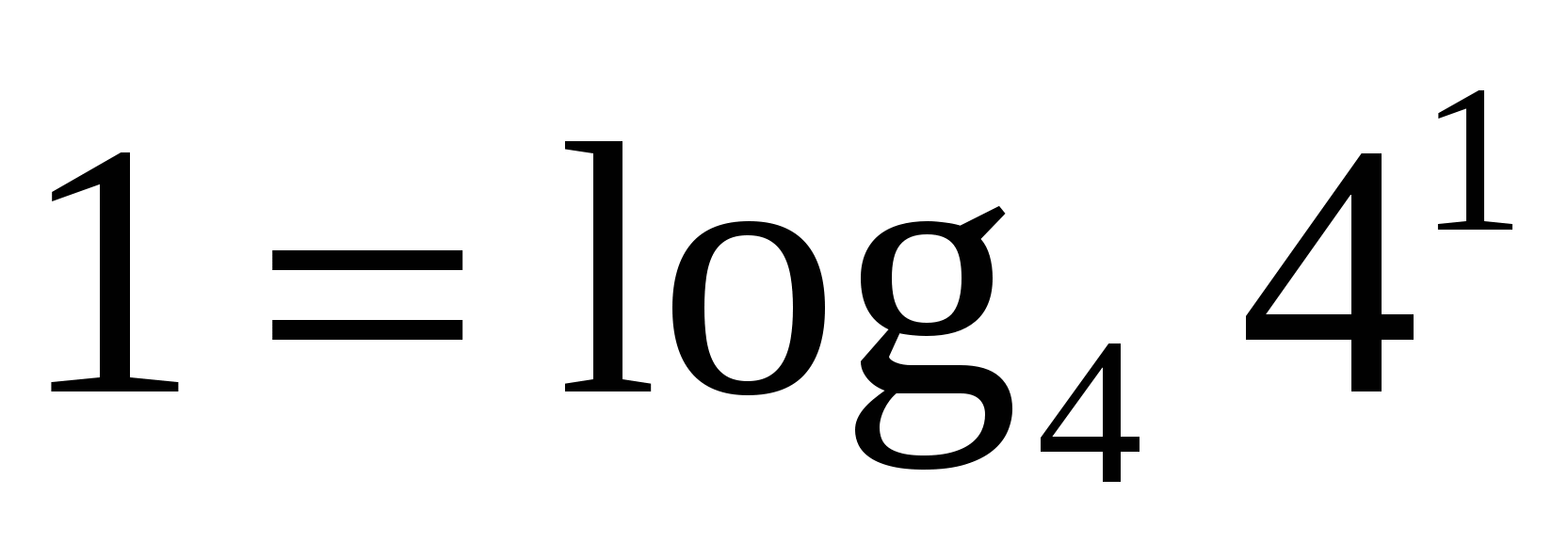 , получим
, получим 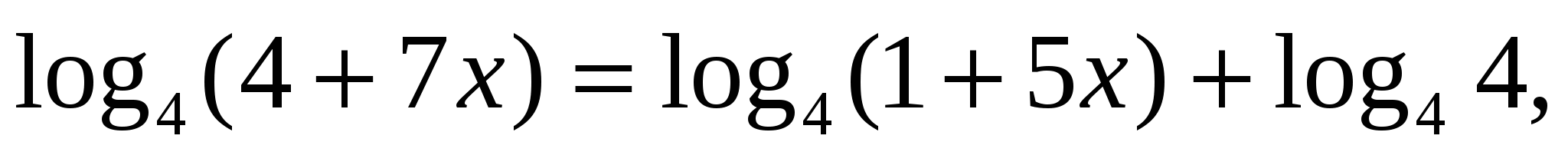
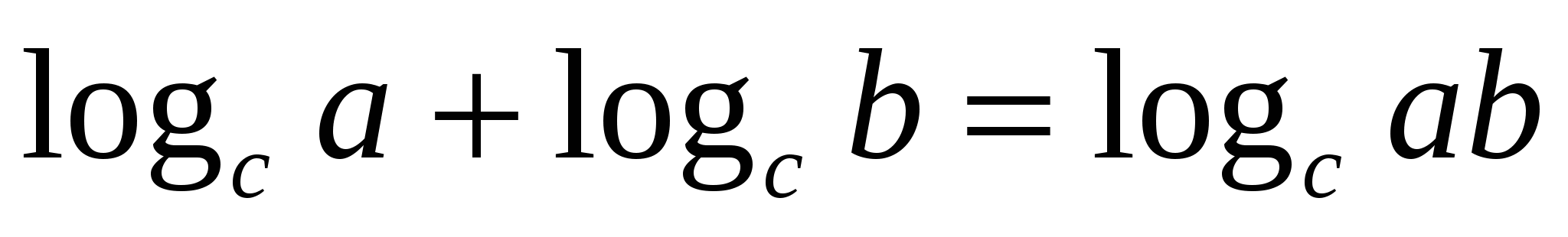 ), получим уравнение
), получим уравнение 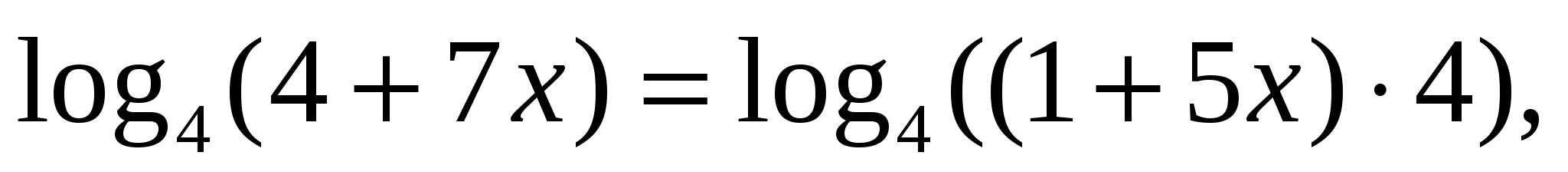 которое в свою очередь замечательно решается методом потенцирования, т. е.
которое в свою очередь замечательно решается методом потенцирования, т. е.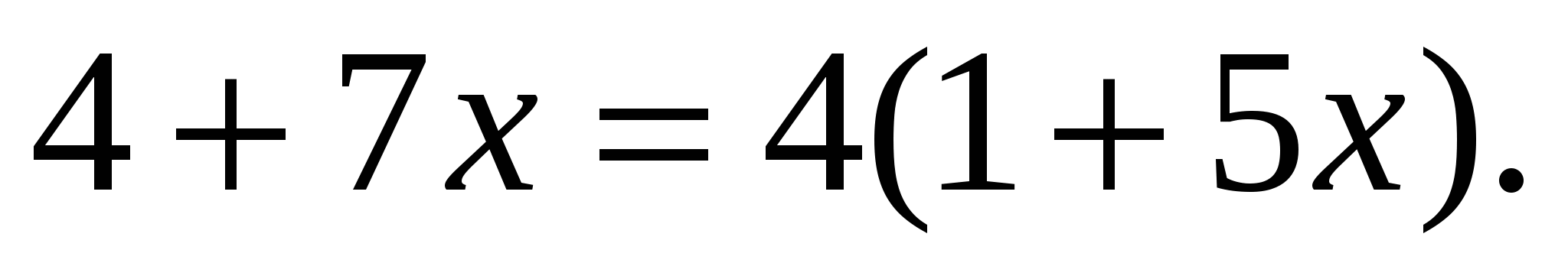 А это линейное уравнение, решив которое, получим
А это линейное уравнение, решив которое, получим 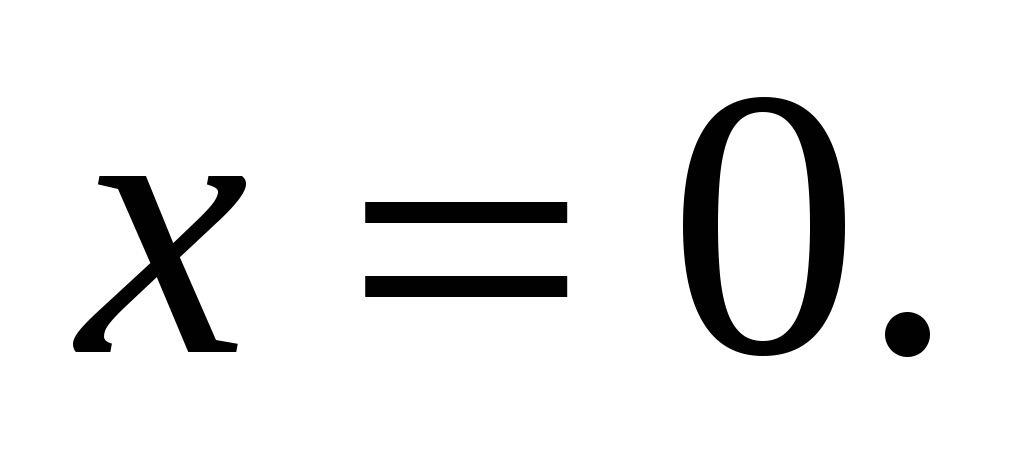
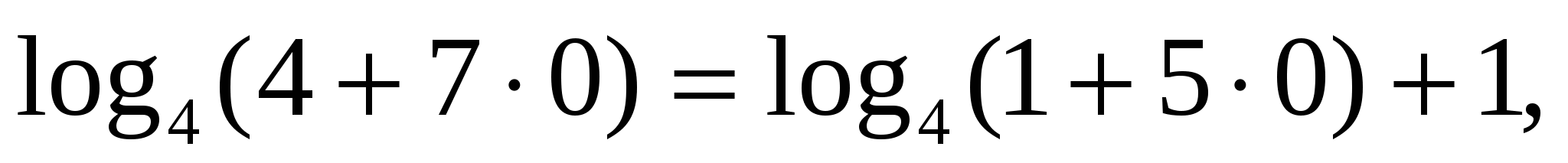
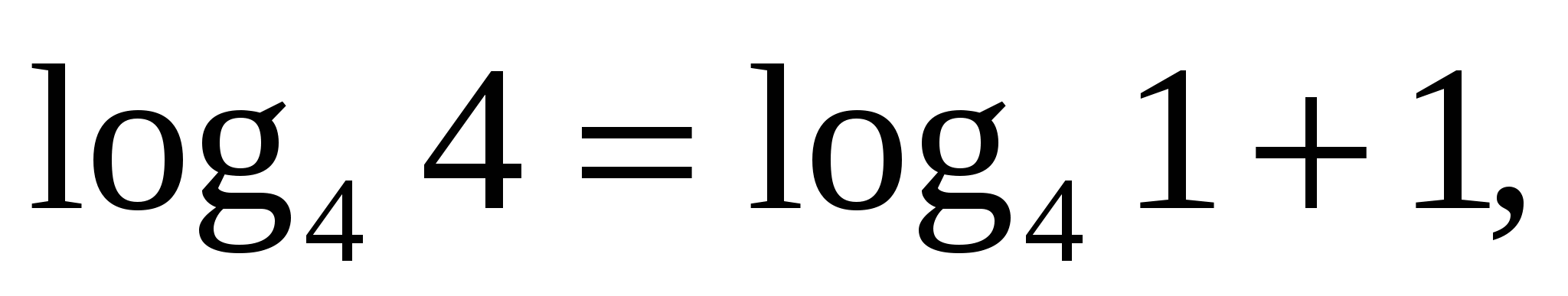
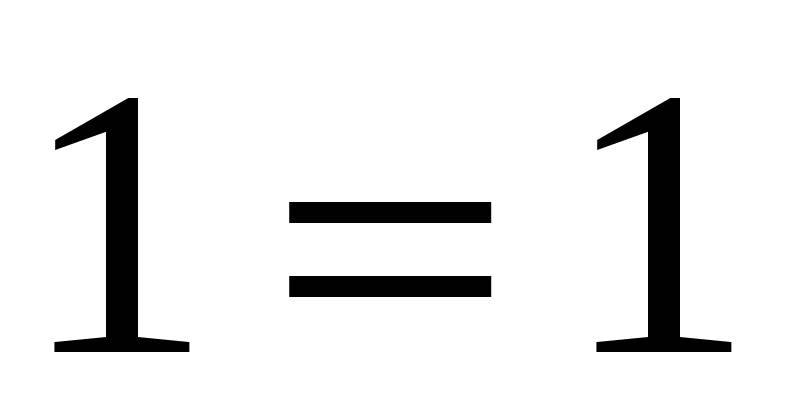 — верно.
— верно.
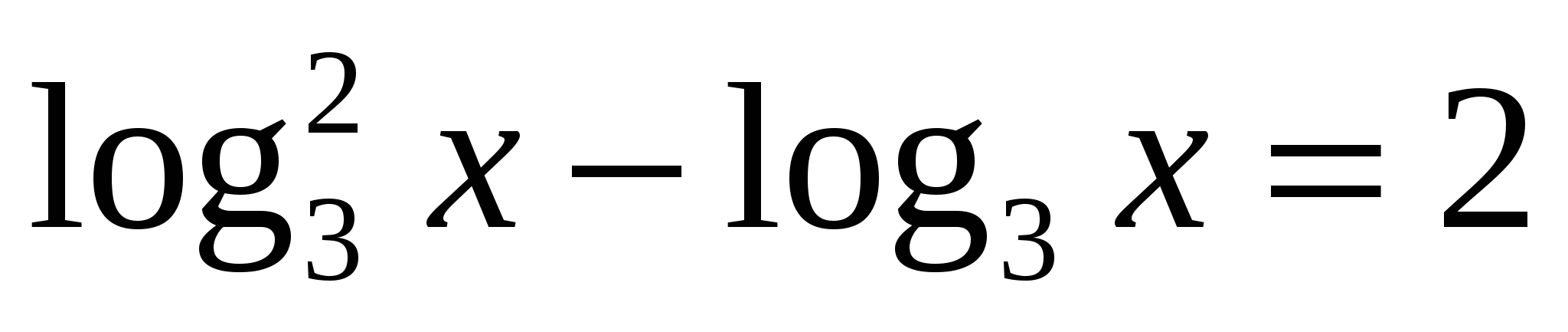 .
.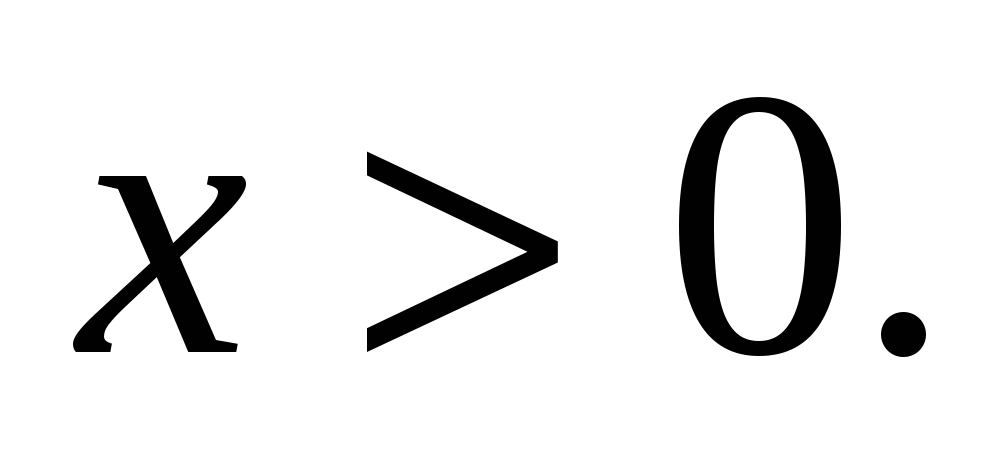
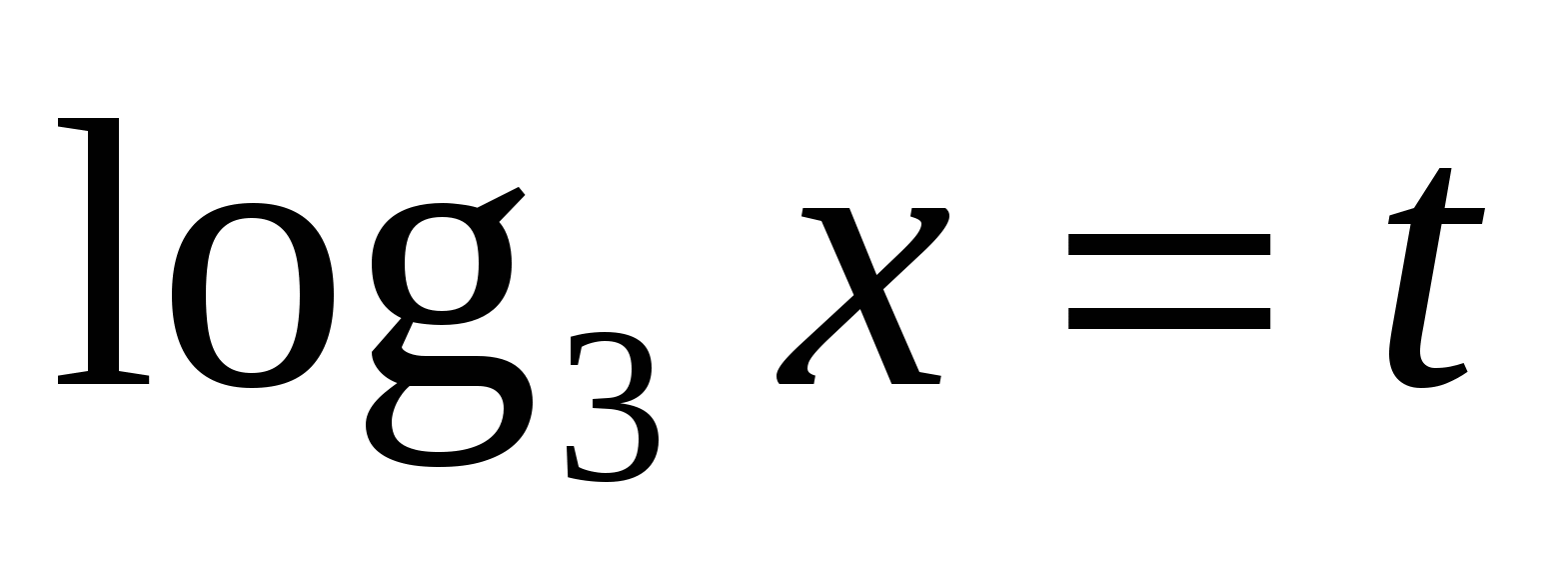 , тогда уравнение примет вид
, тогда уравнение примет вид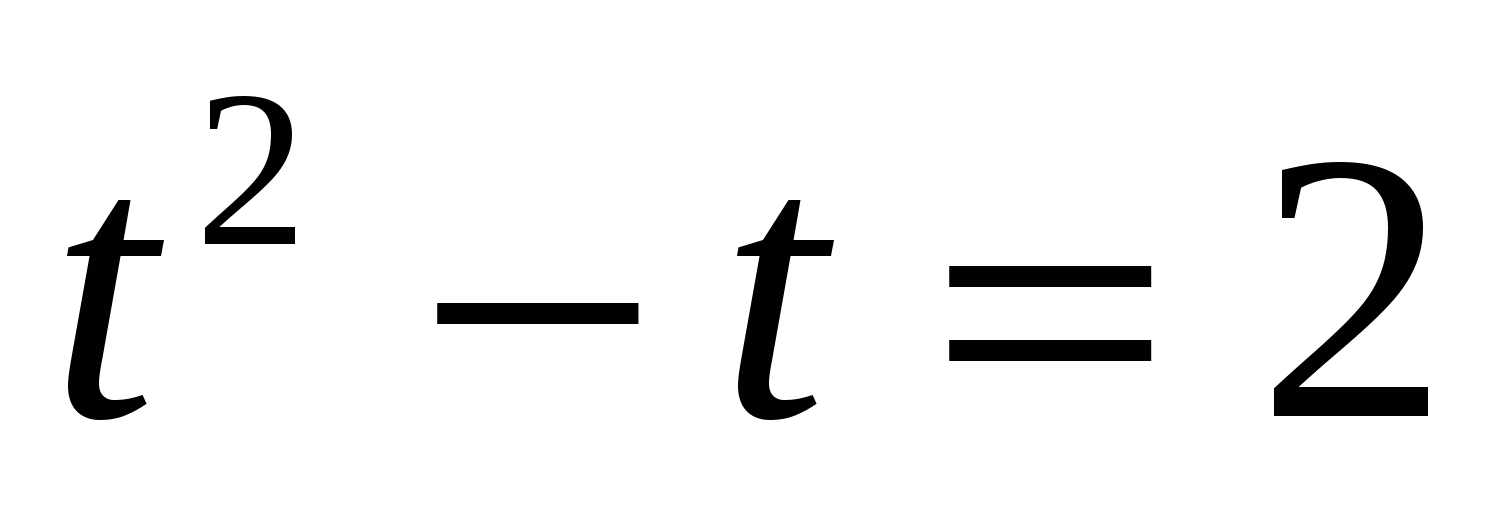 ,
,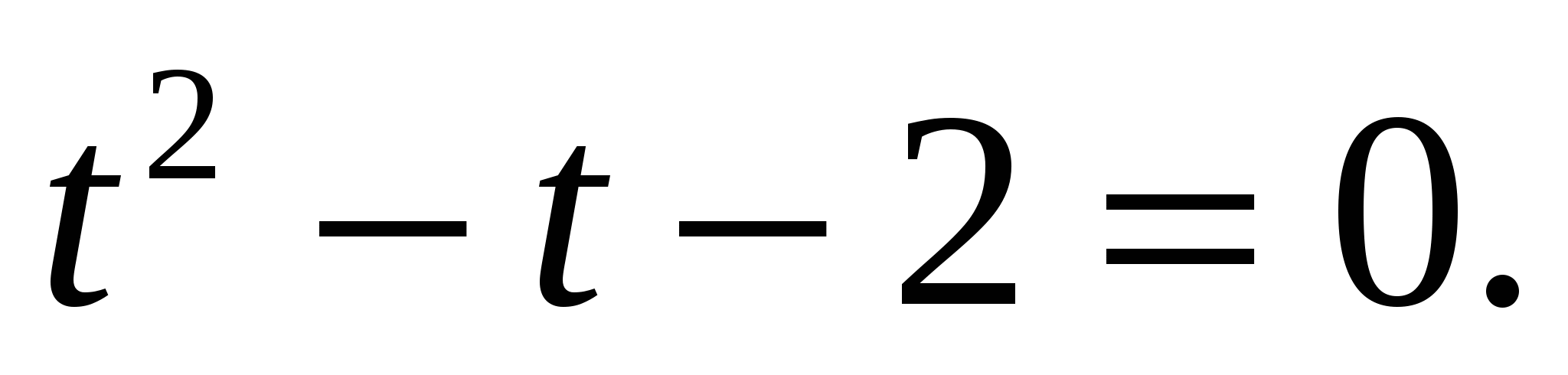

 или
или 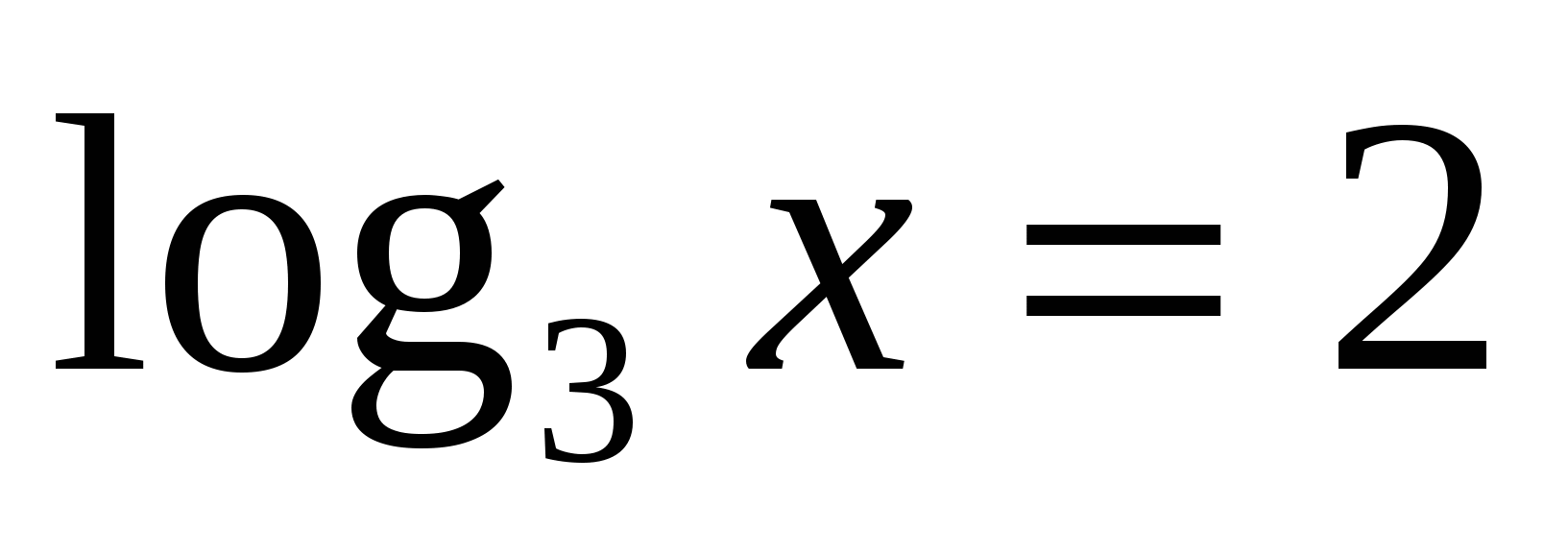 . А это уравнения, которые мы решим, используя определение: 1)
. А это уравнения, которые мы решим, используя определение: 1) 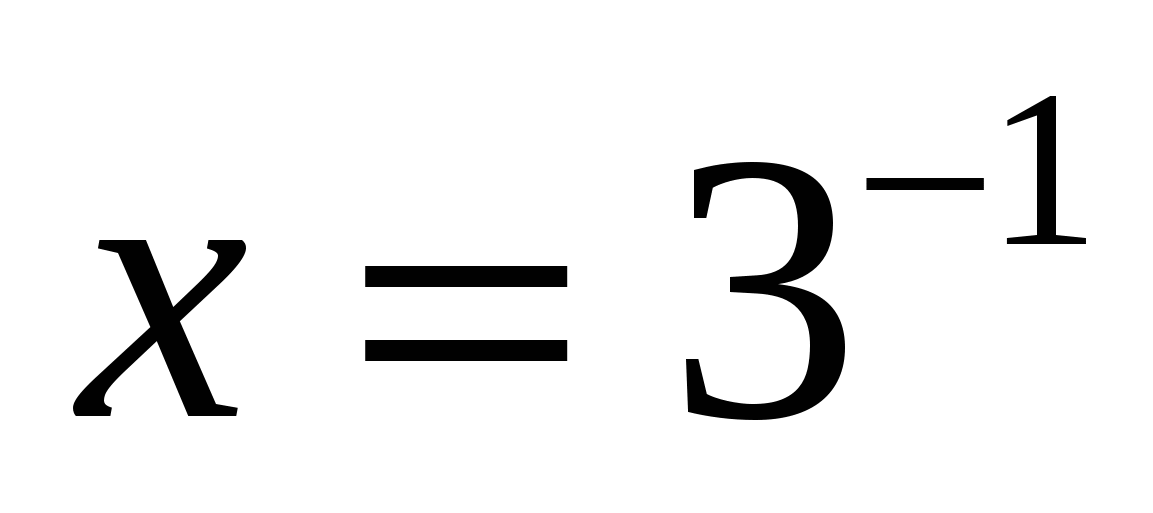
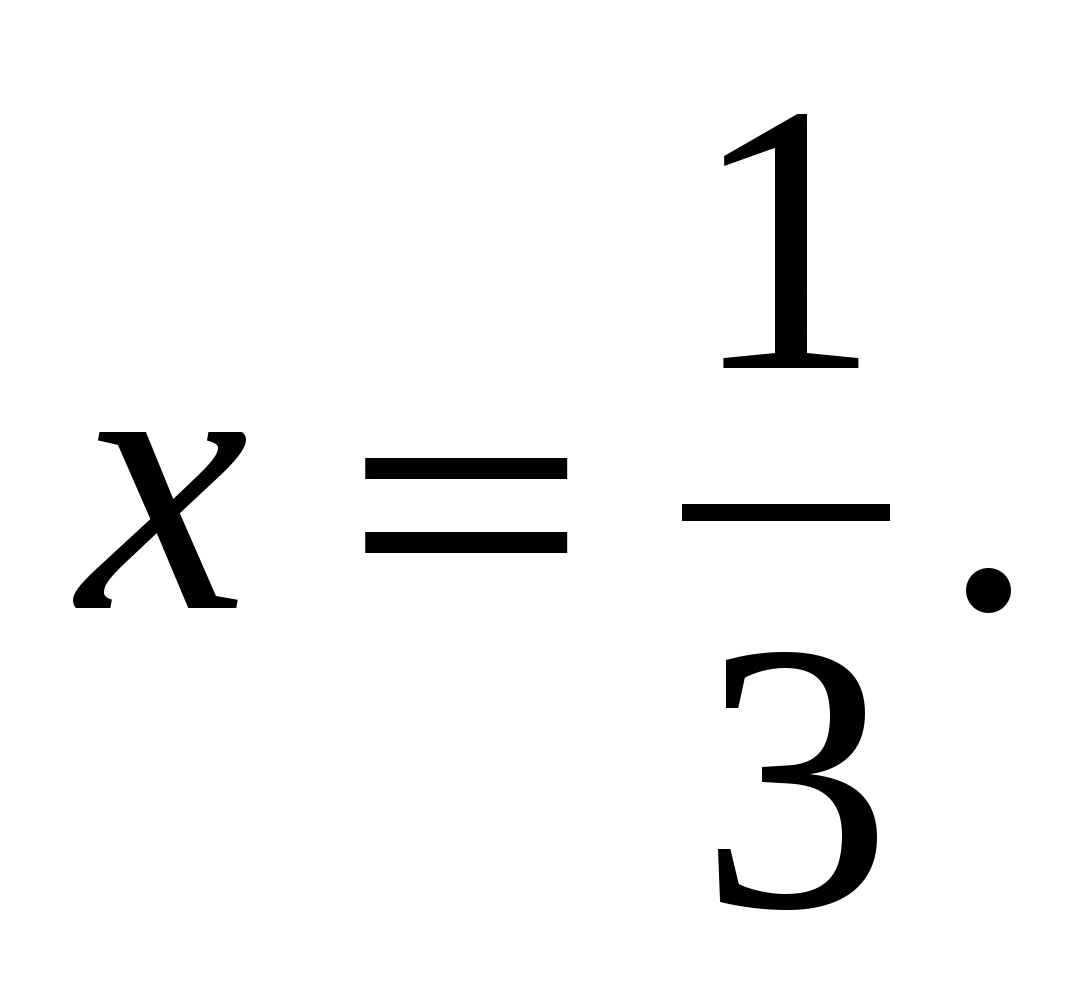
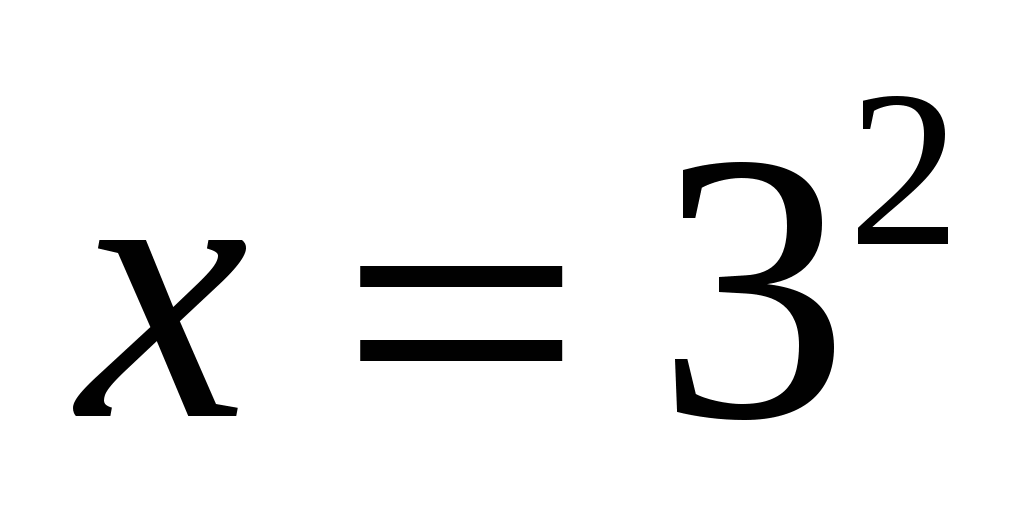
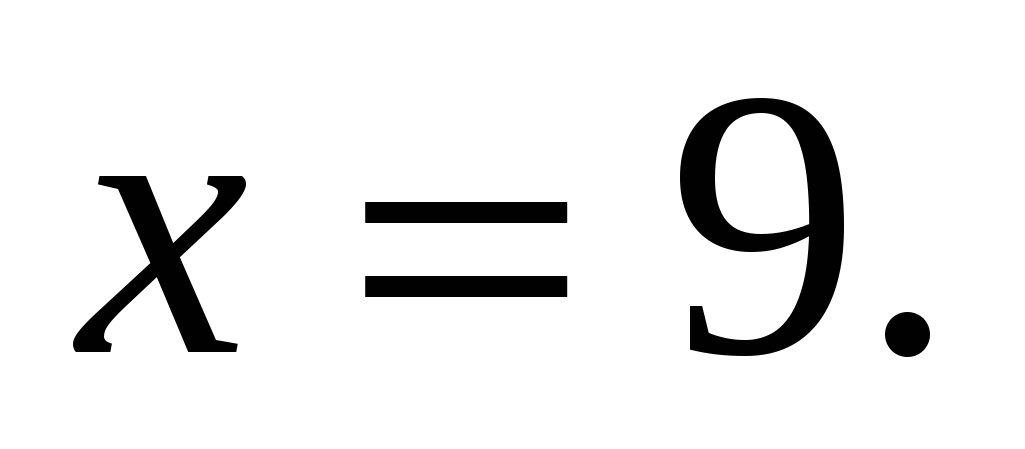
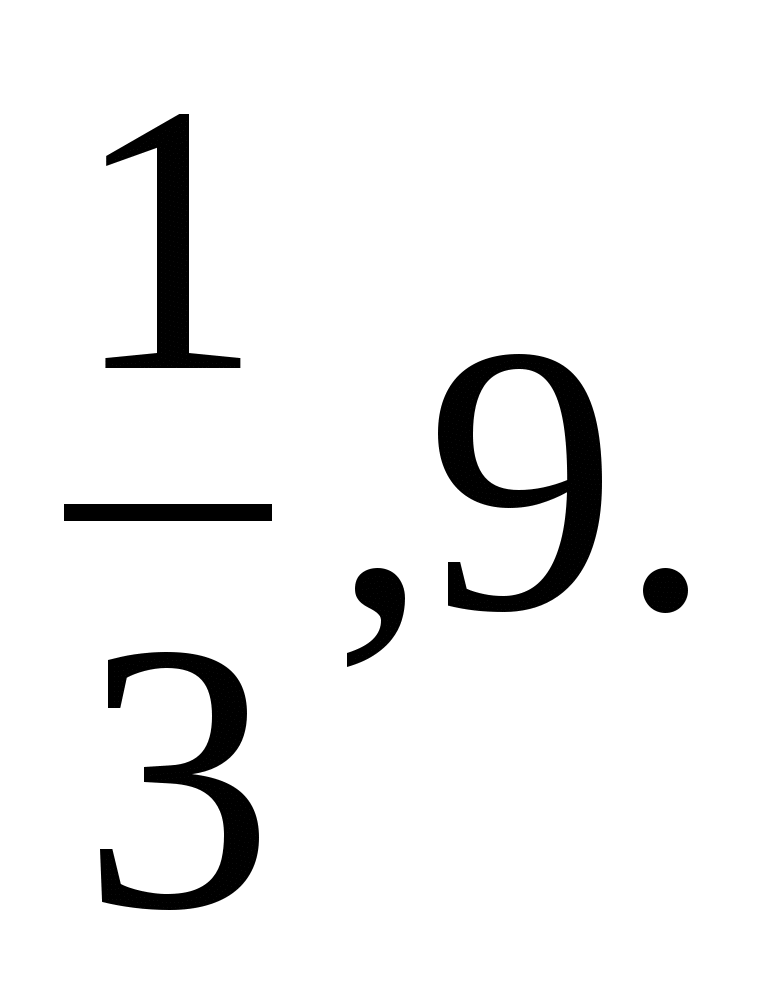

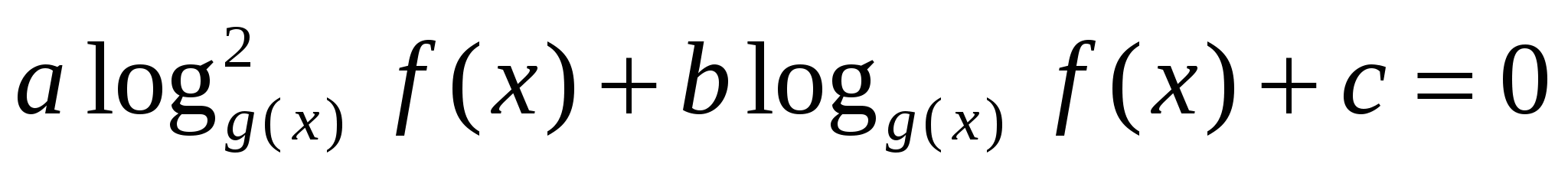 , где
, где 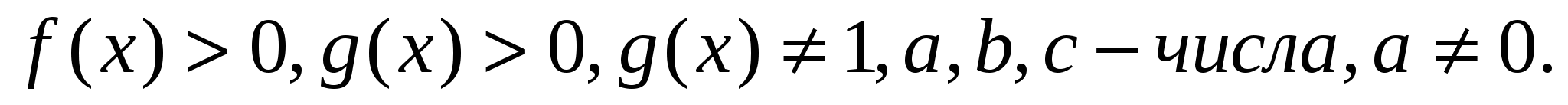
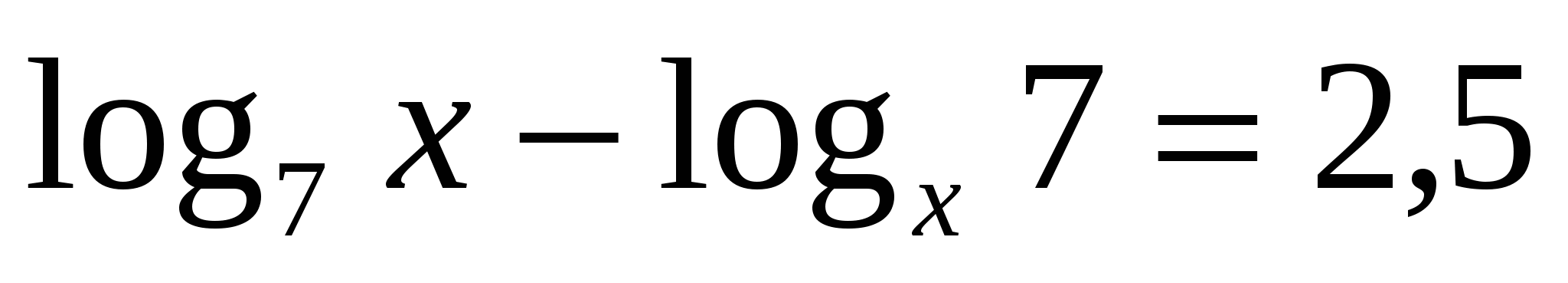 .
.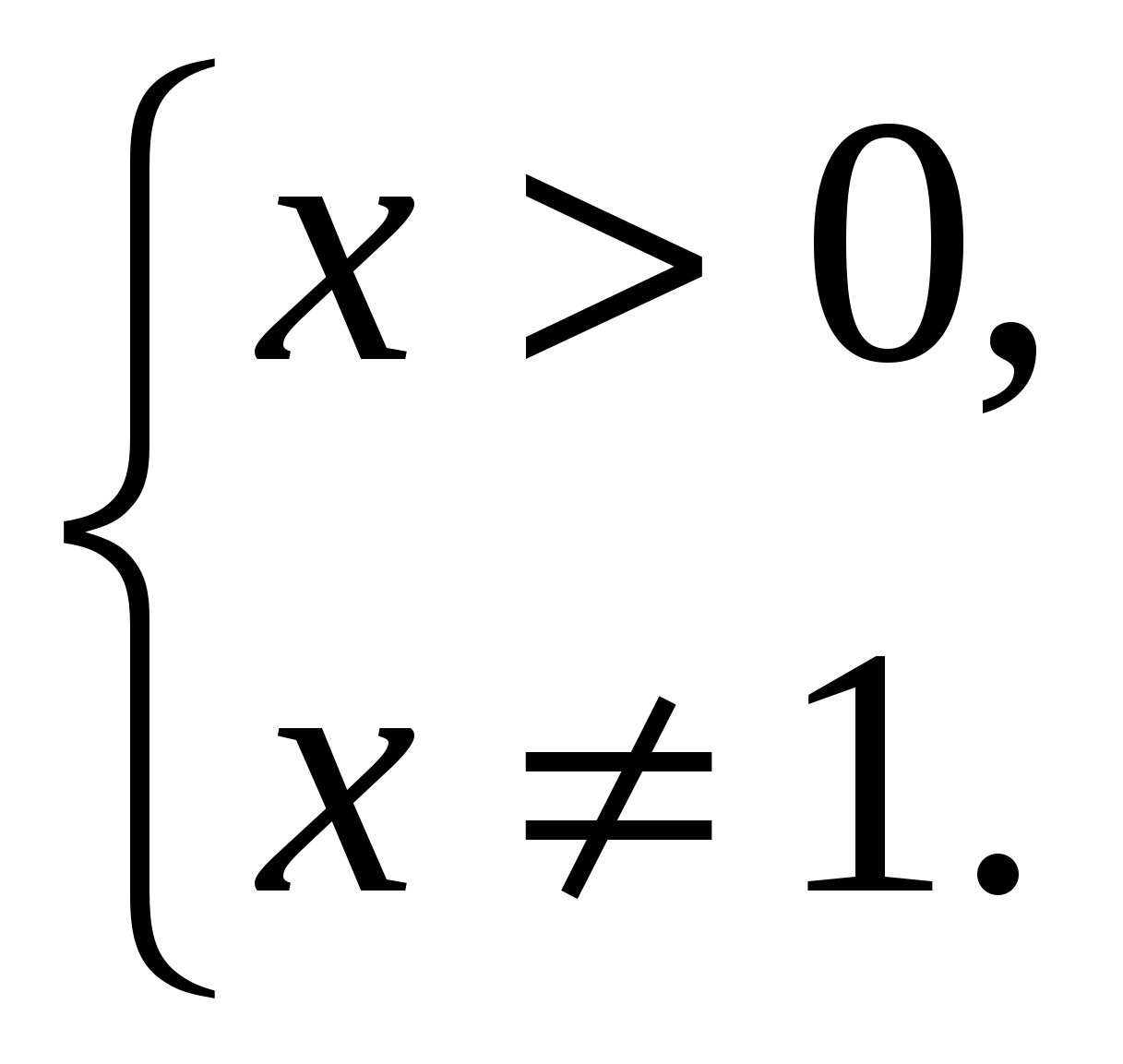
 , получим:
, получим: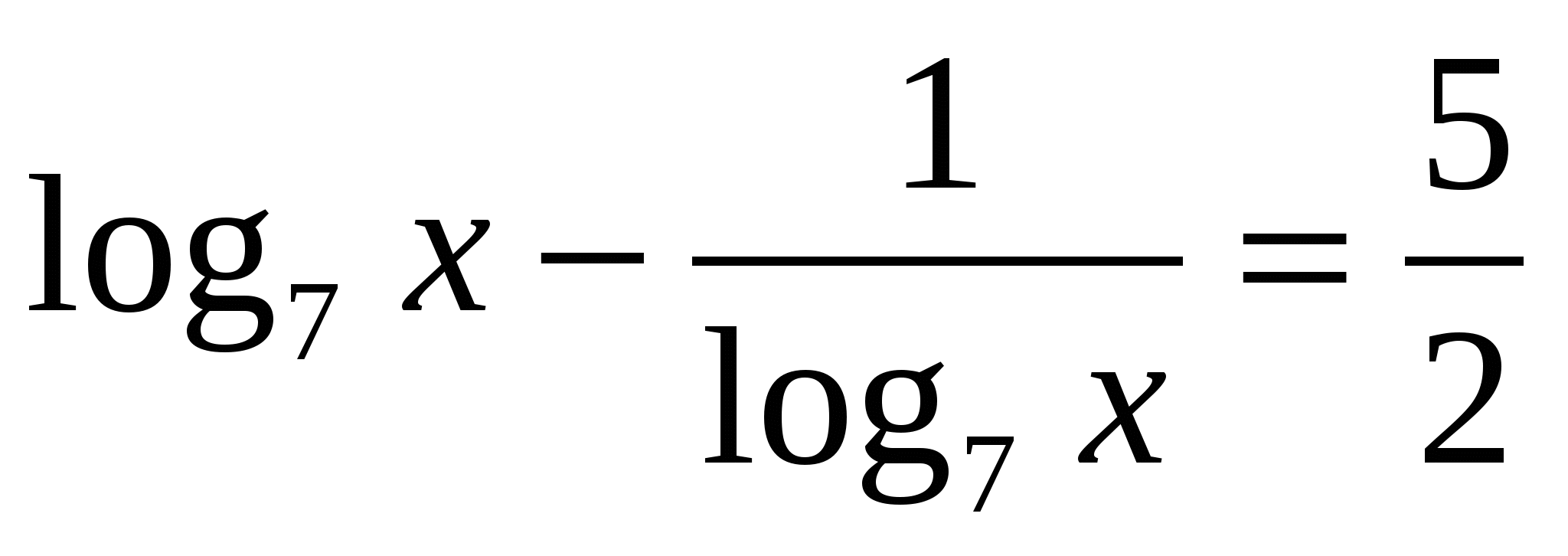 , выполним подстановку
, выполним подстановку 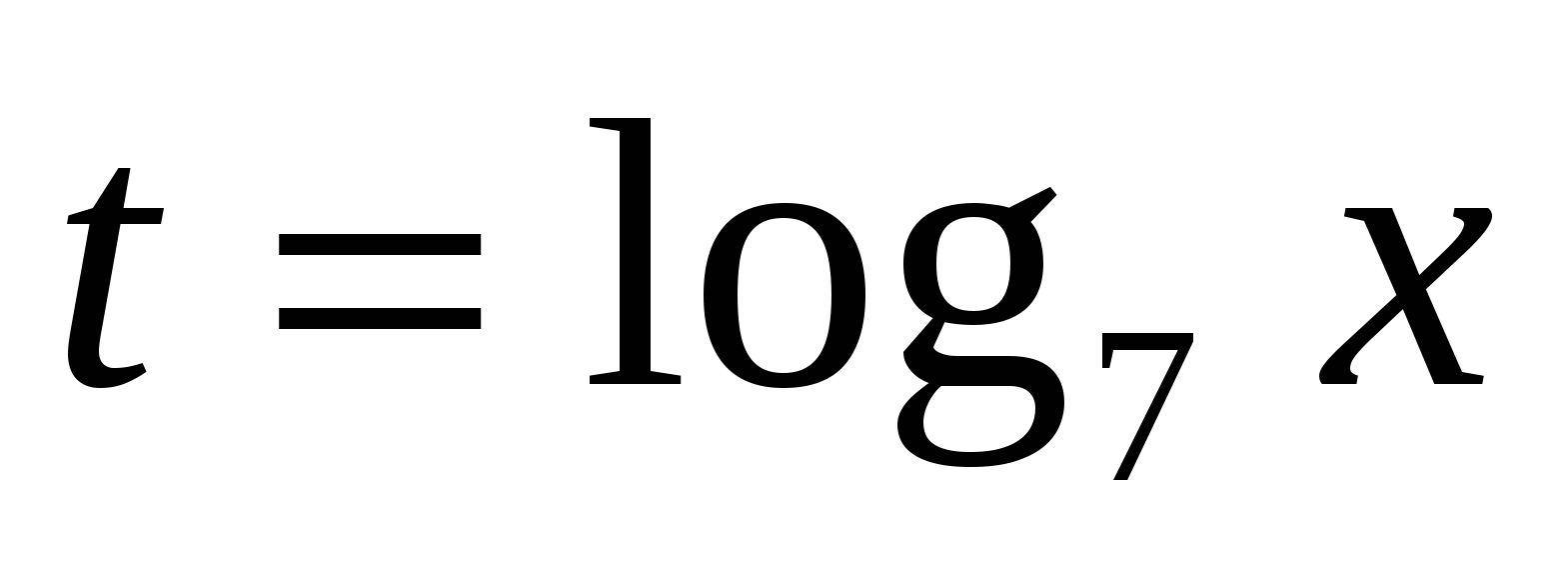 , получим уравнение
, получим уравнение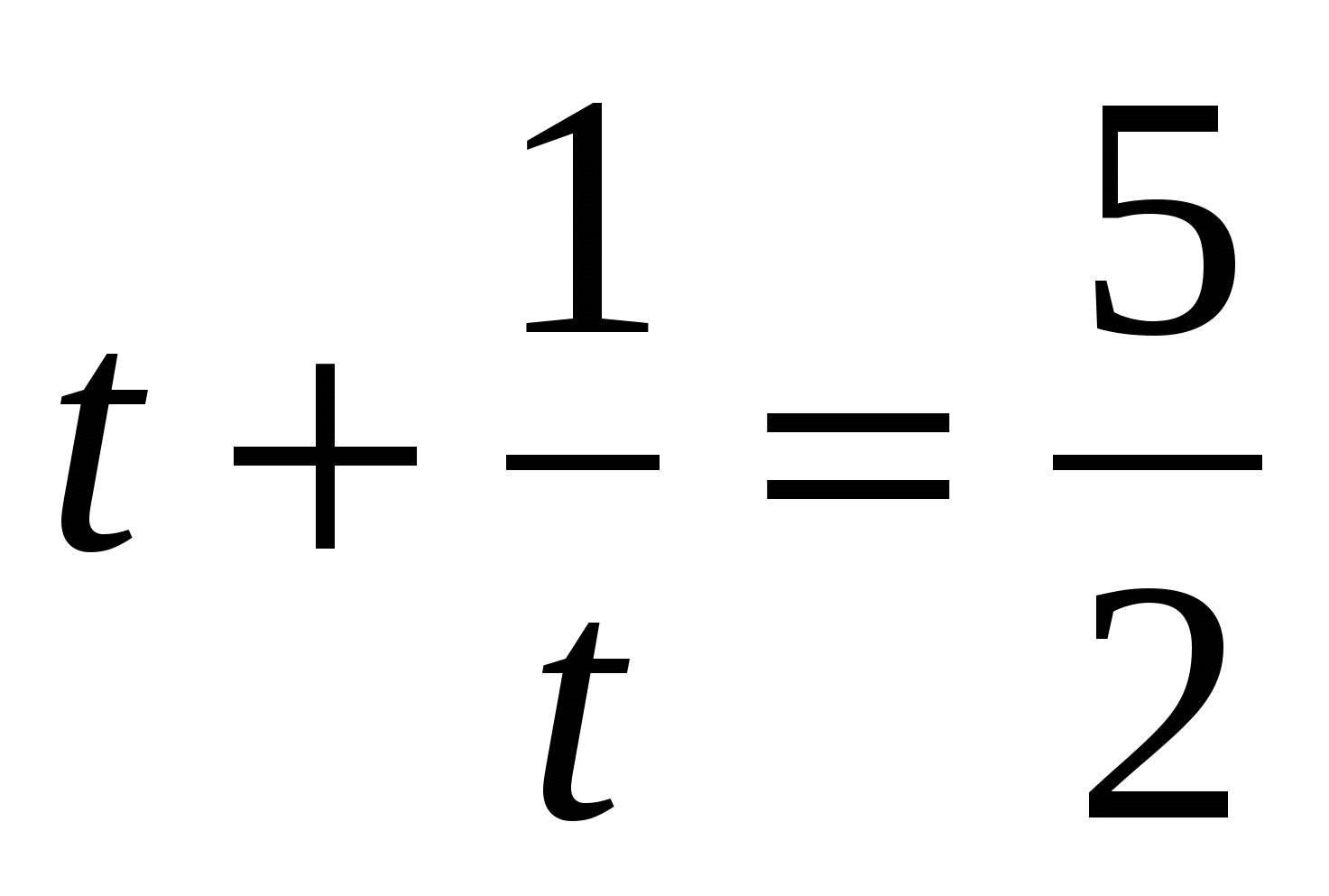 ,
,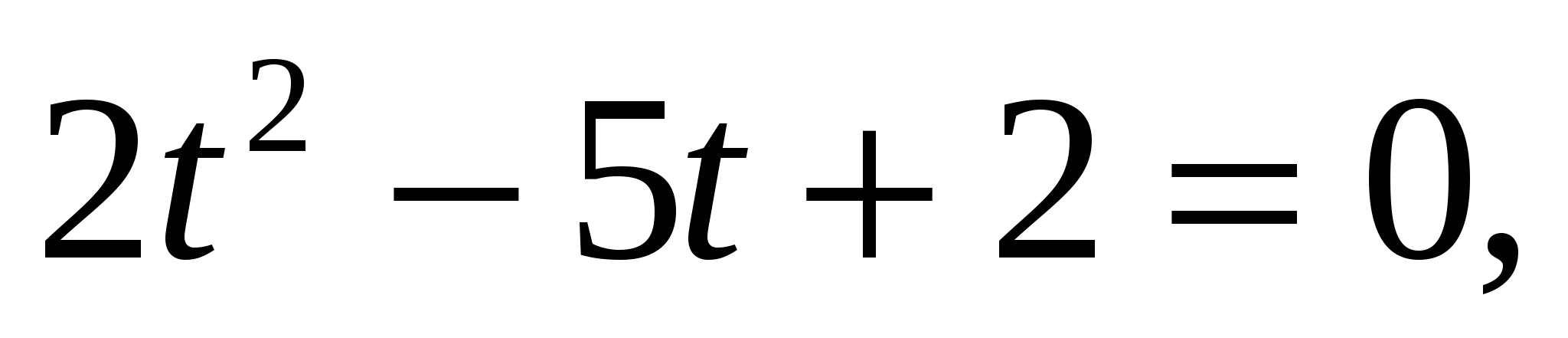
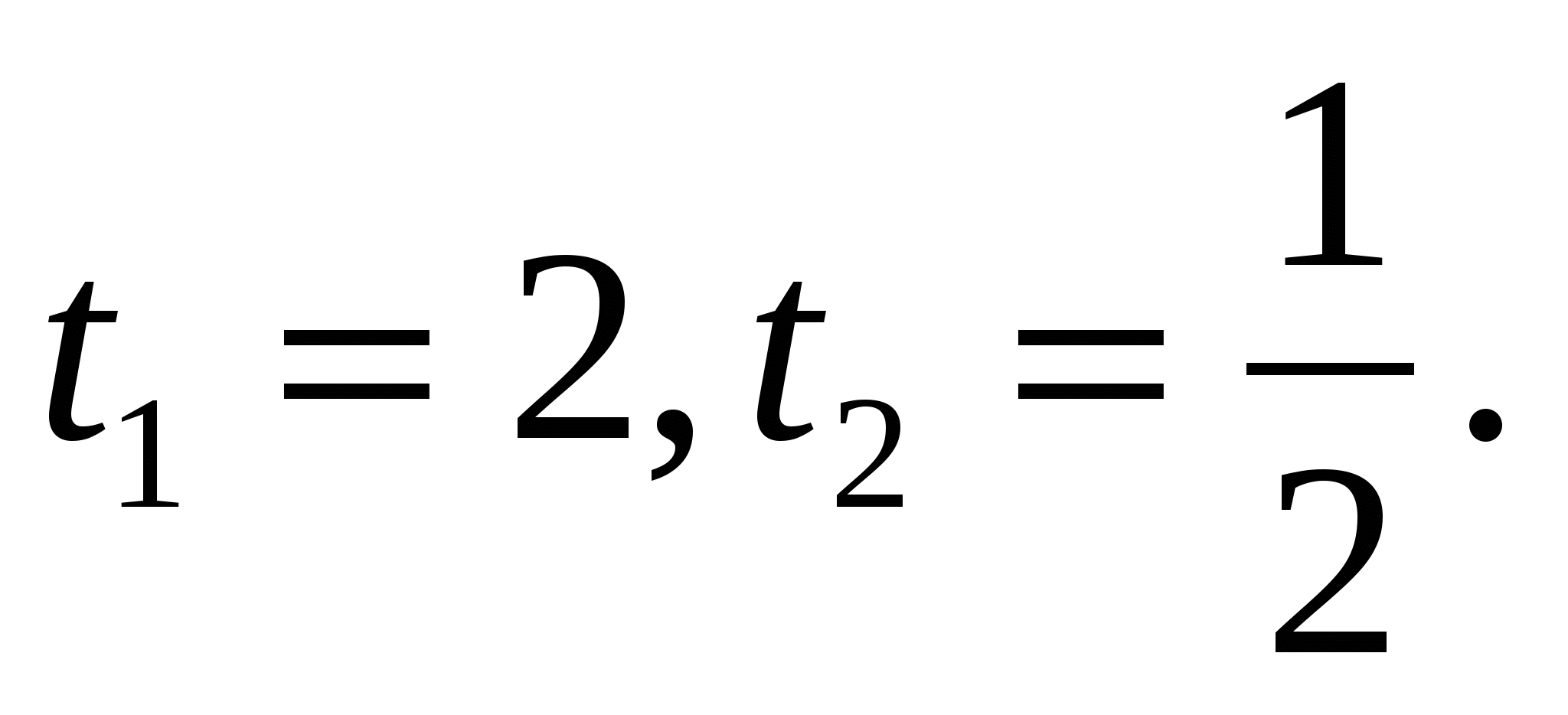
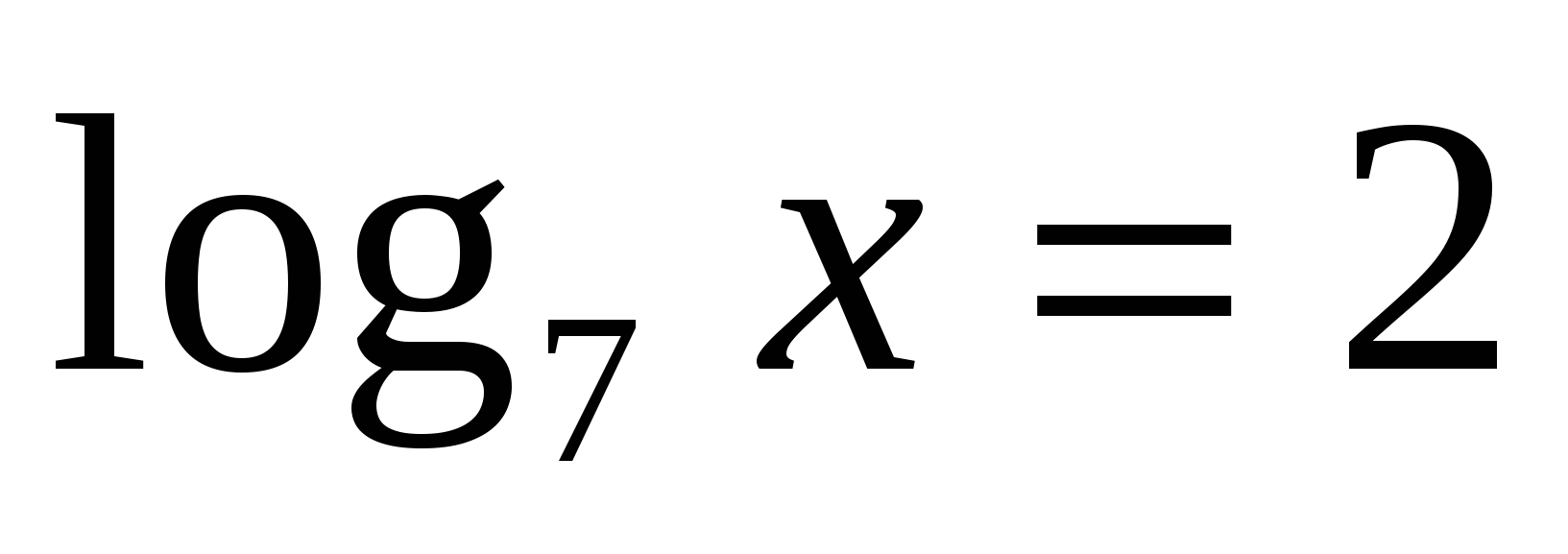 или
или 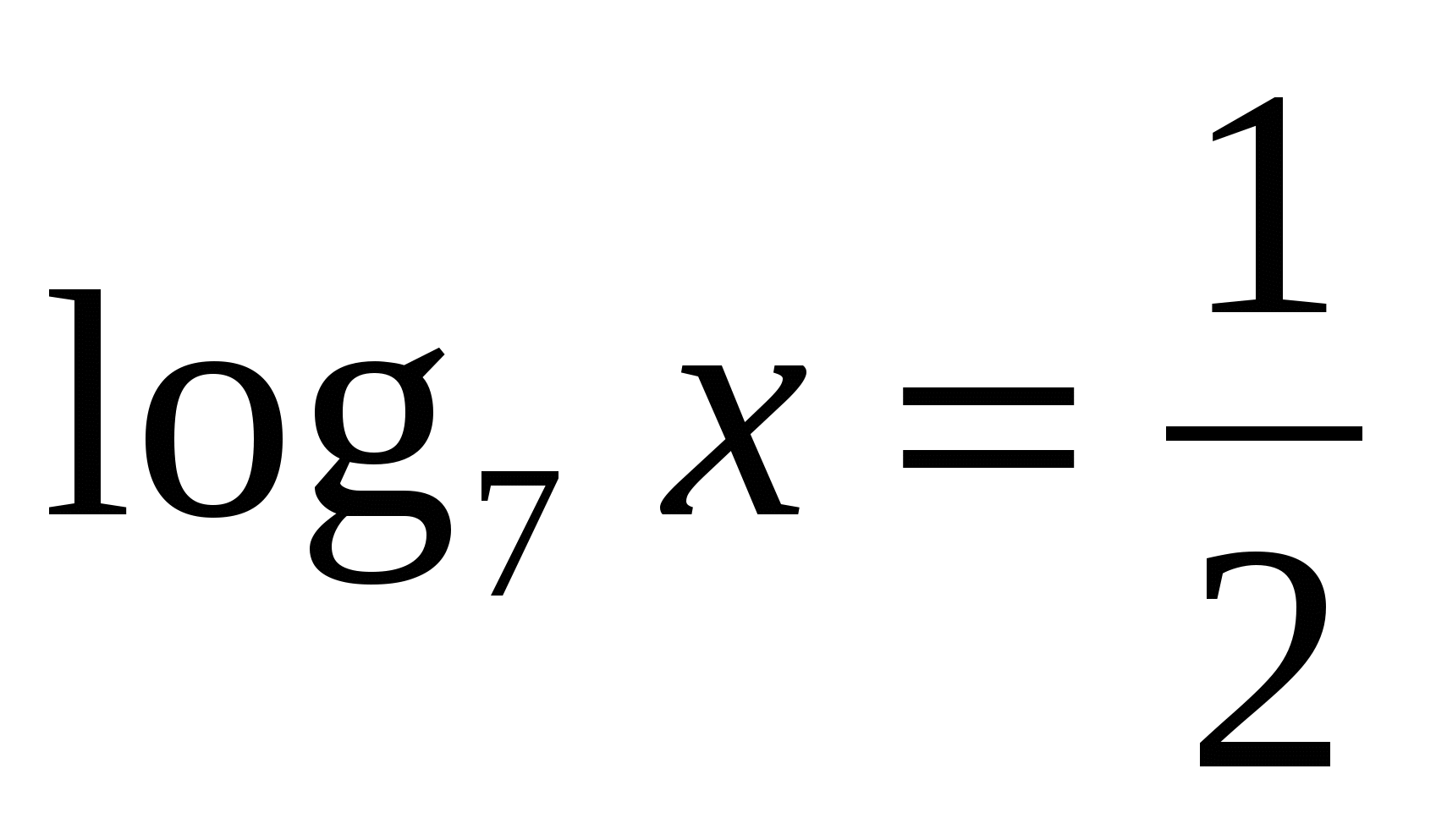 .
.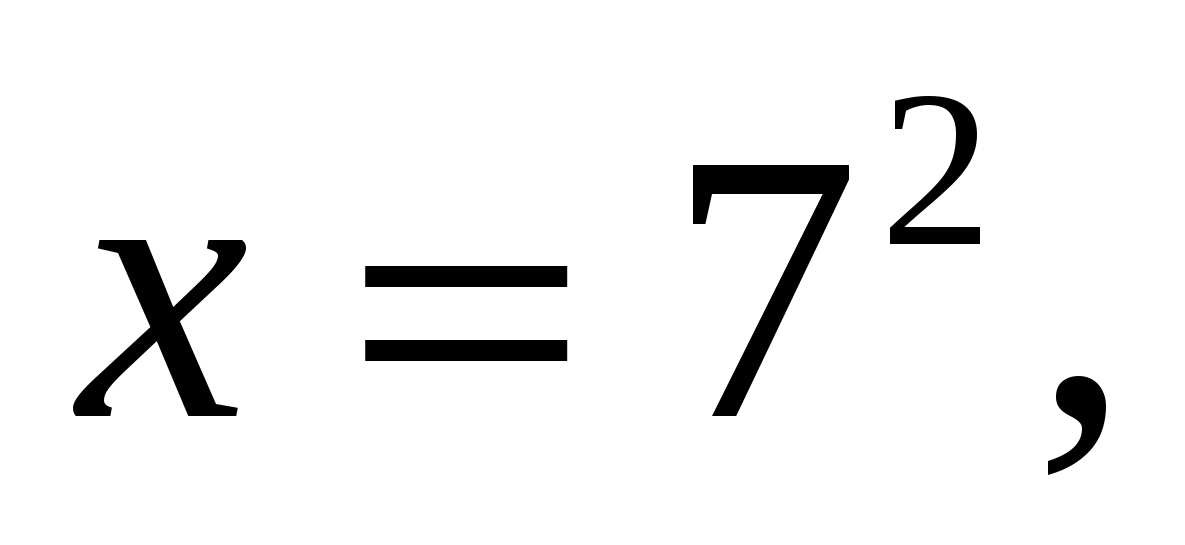
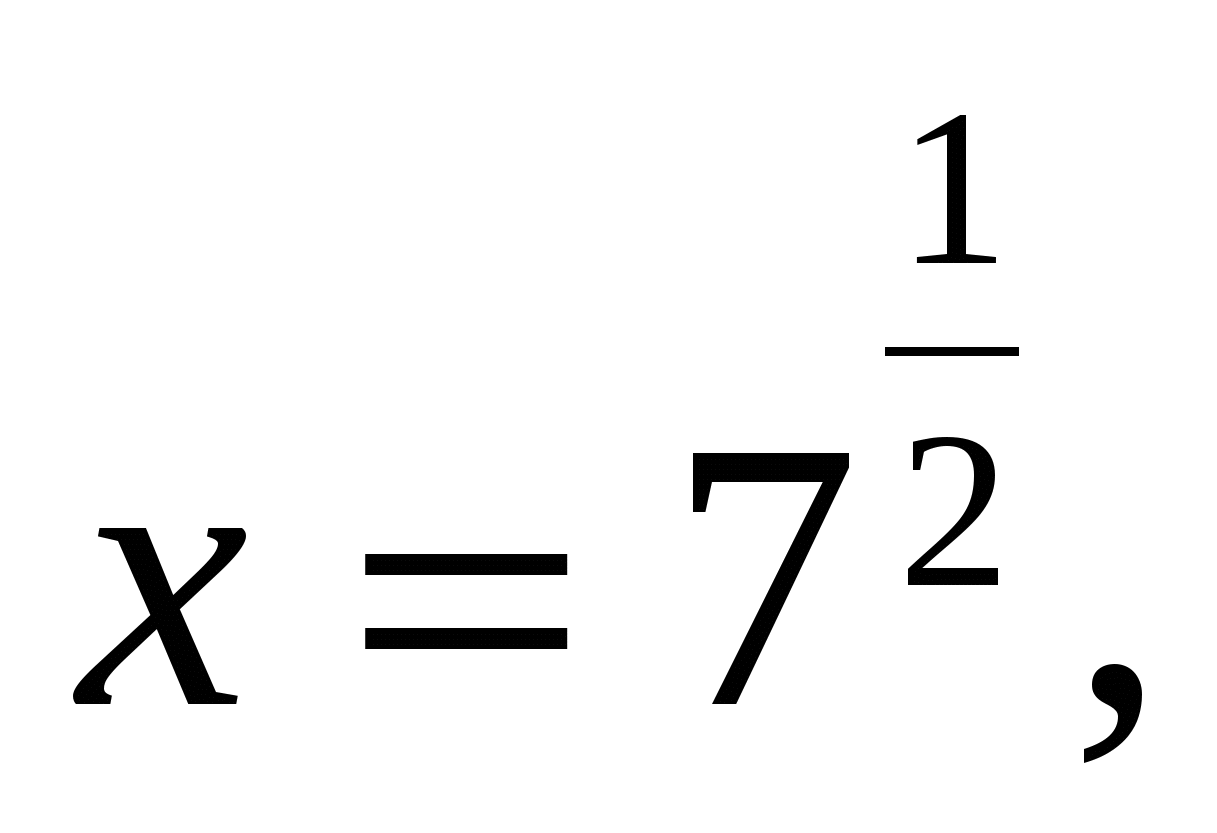
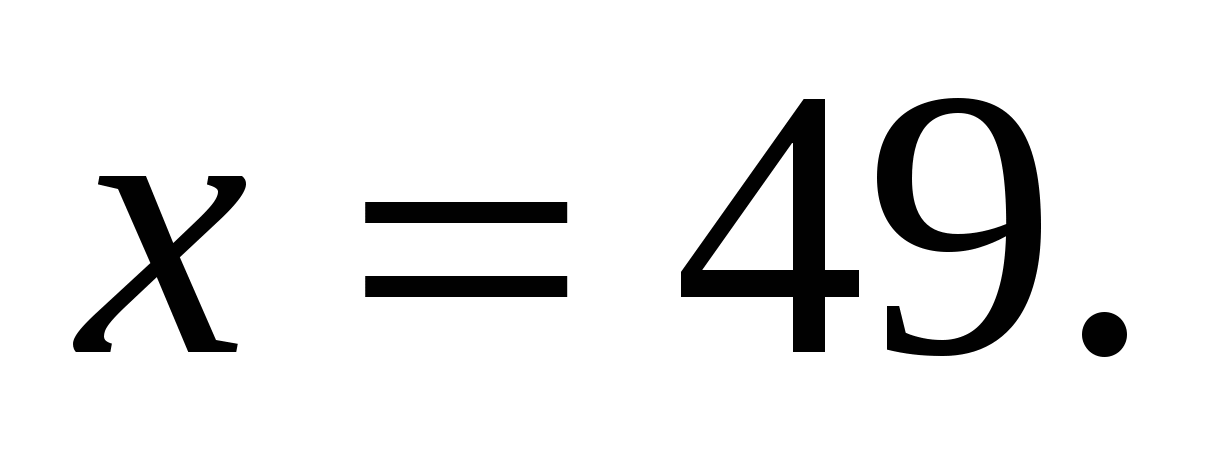
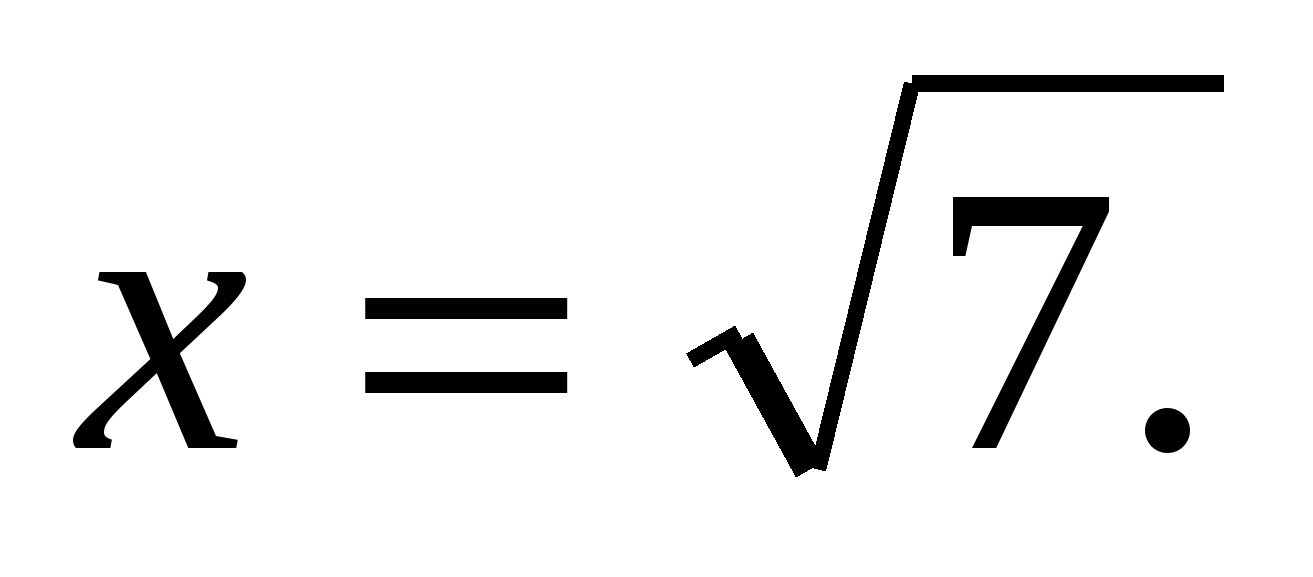
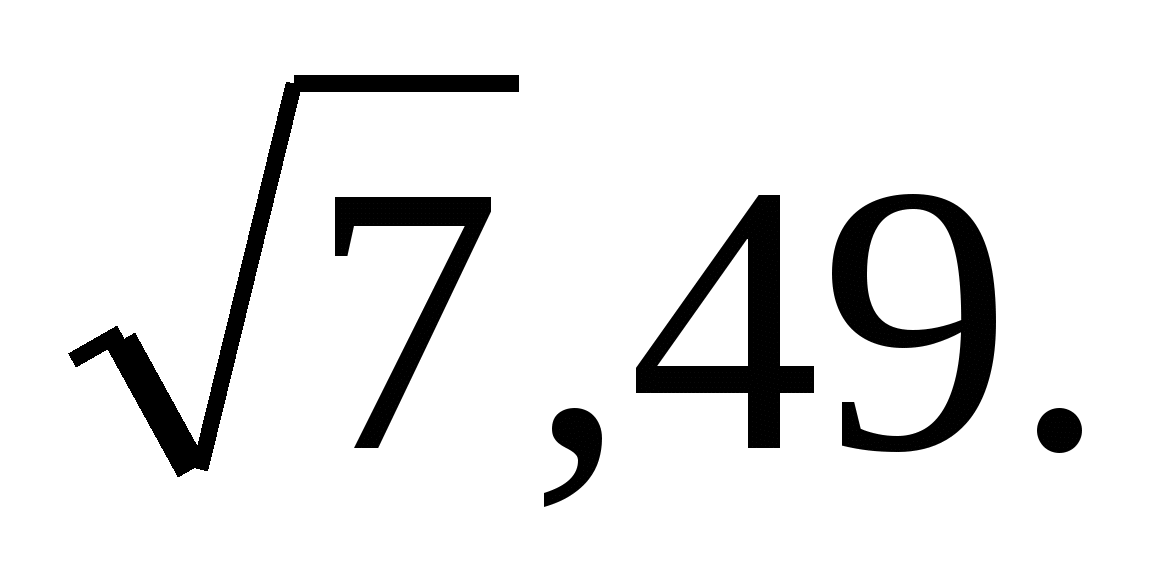

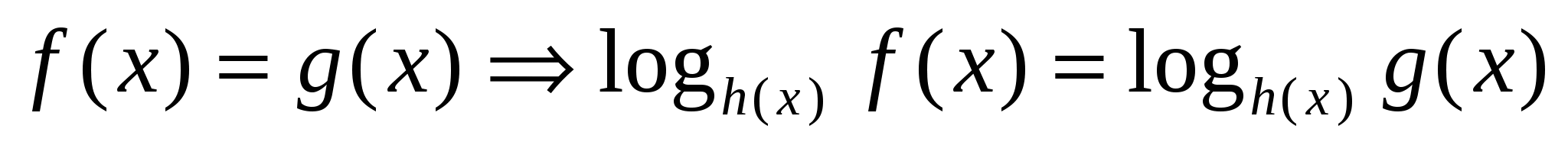 , при этом
, при этом
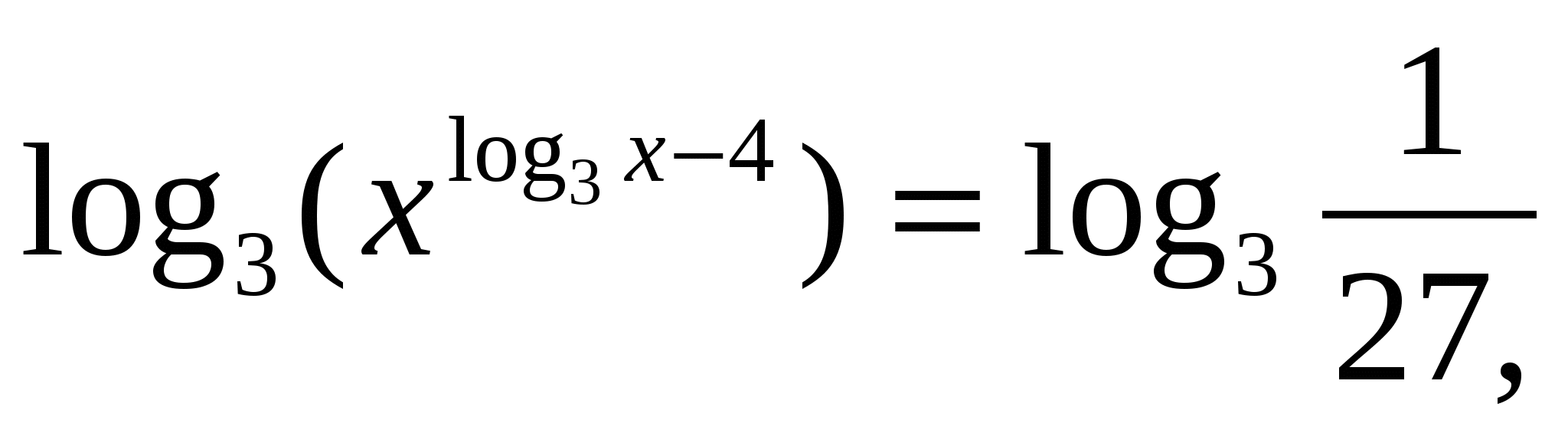 а теперь воспользуемся свойством логарифмов
а теперь воспользуемся свойством логарифмов 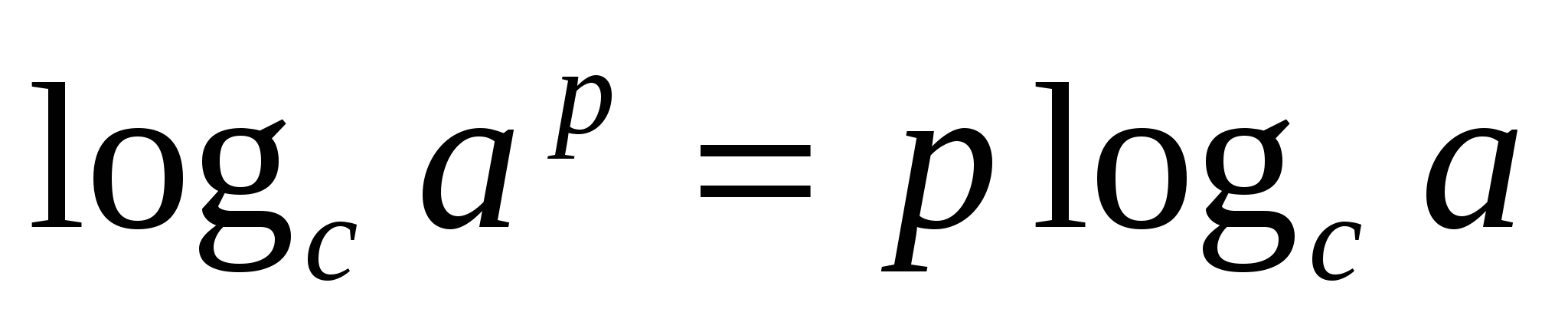 , получим
, получим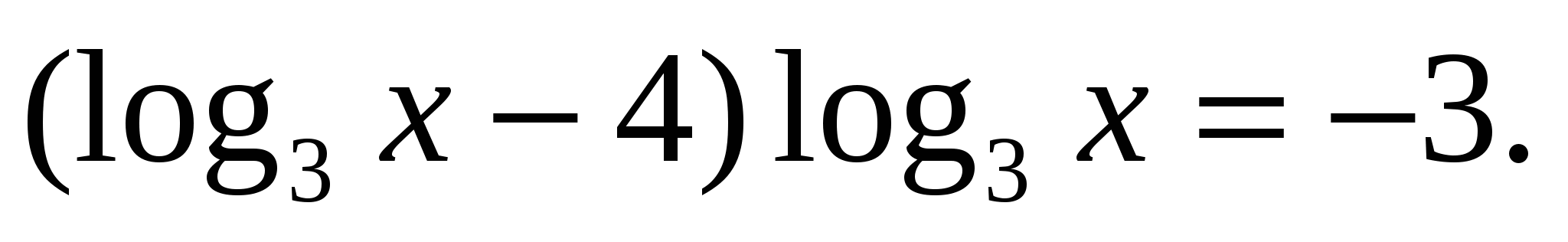
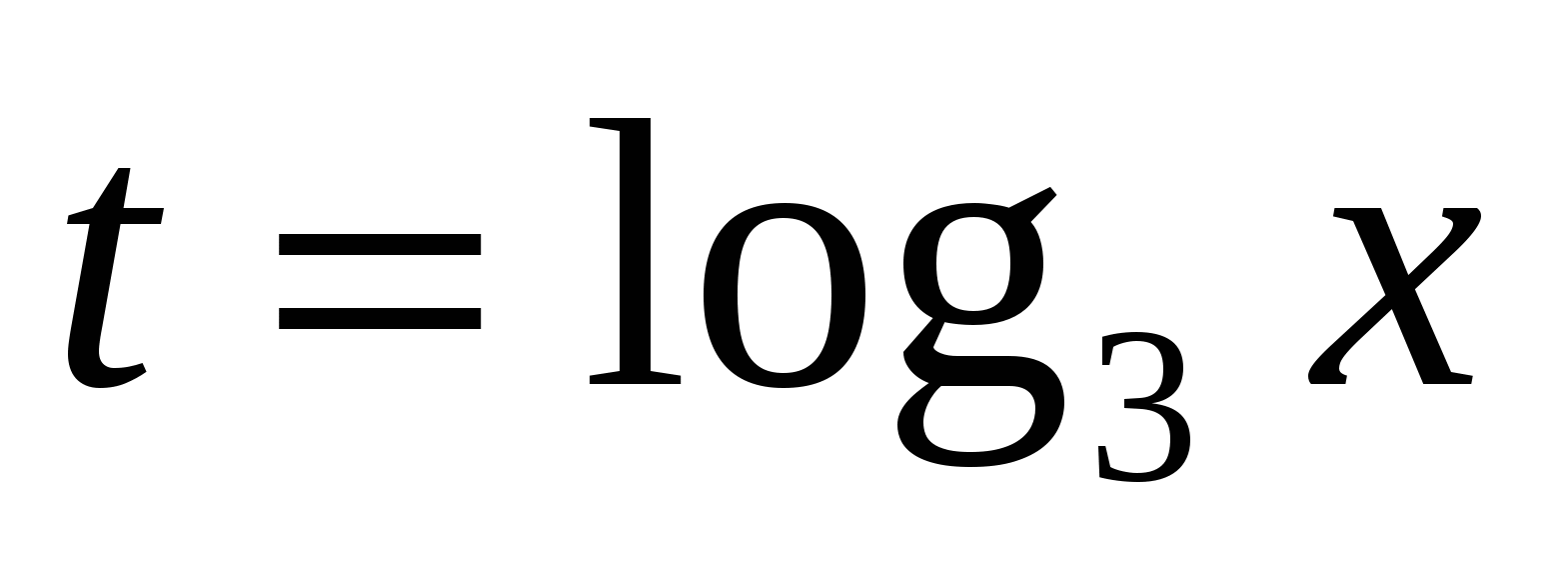 , получим уравнение
, получим уравнение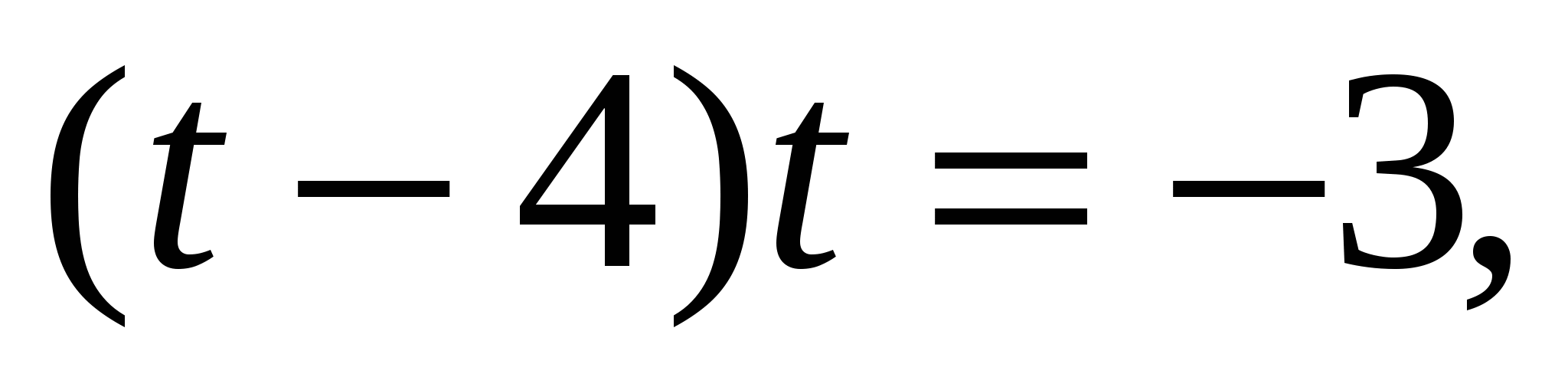
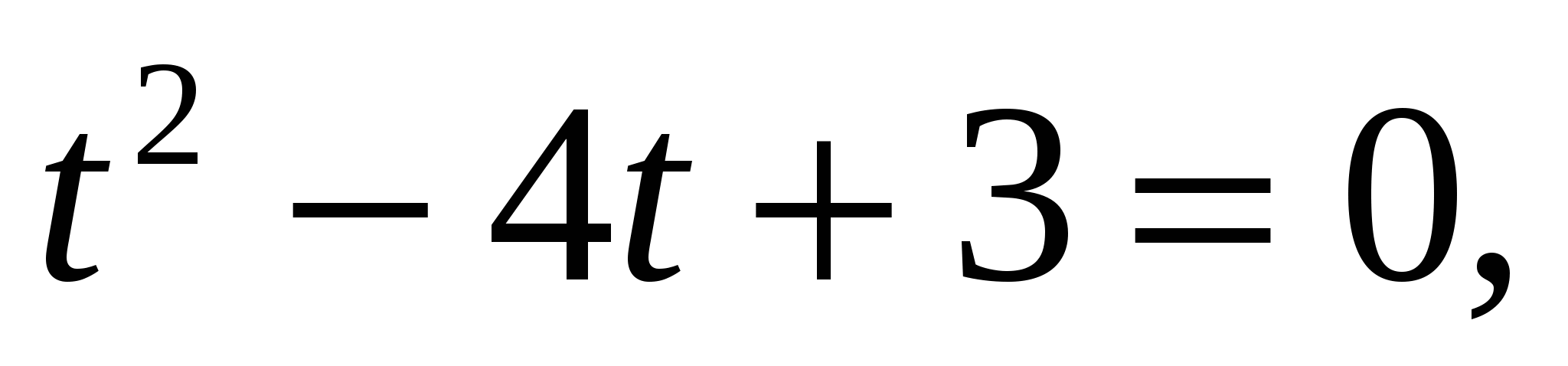
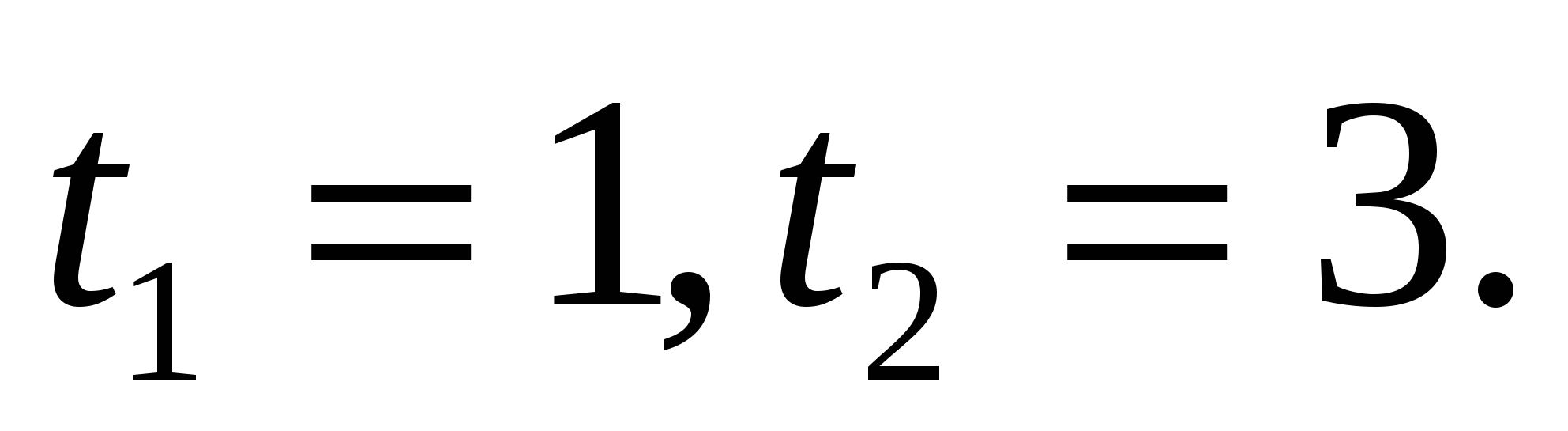
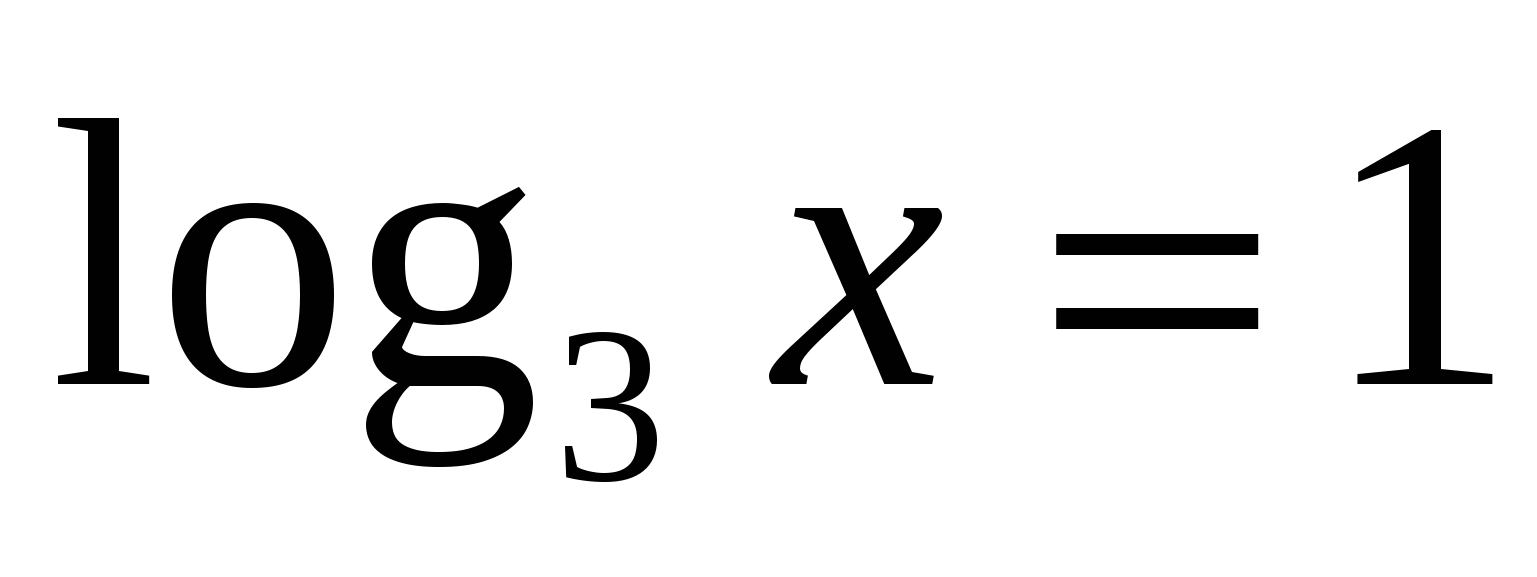 или
или 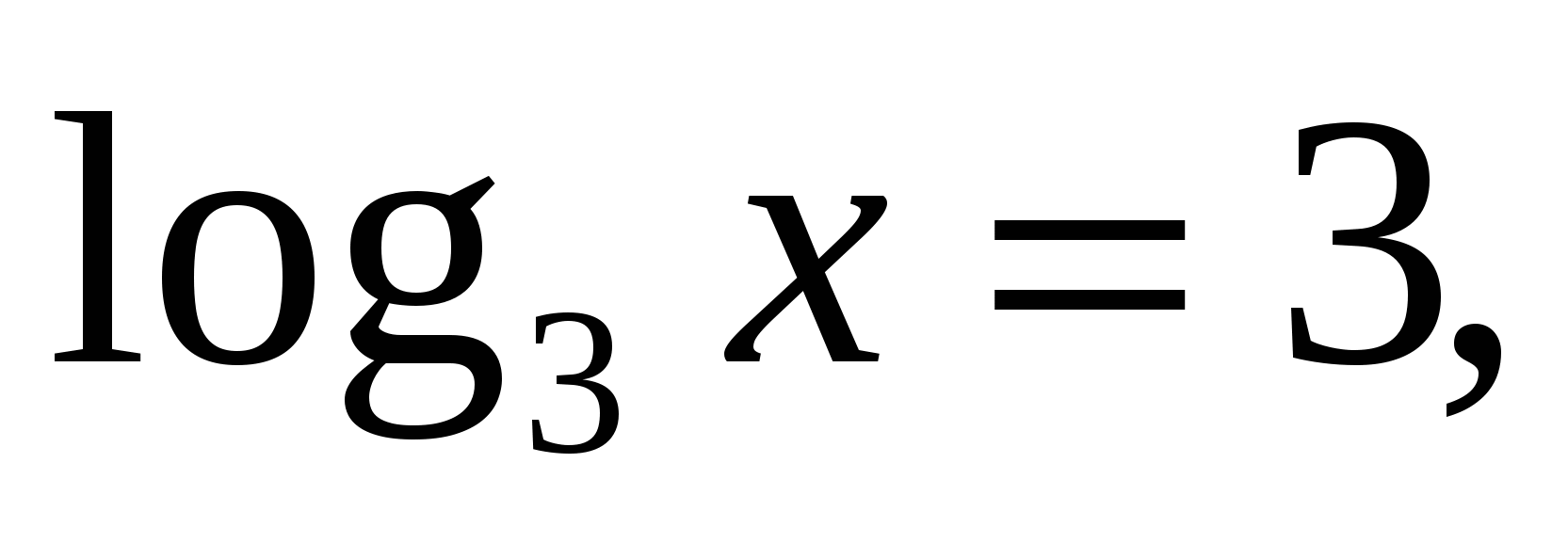 .
.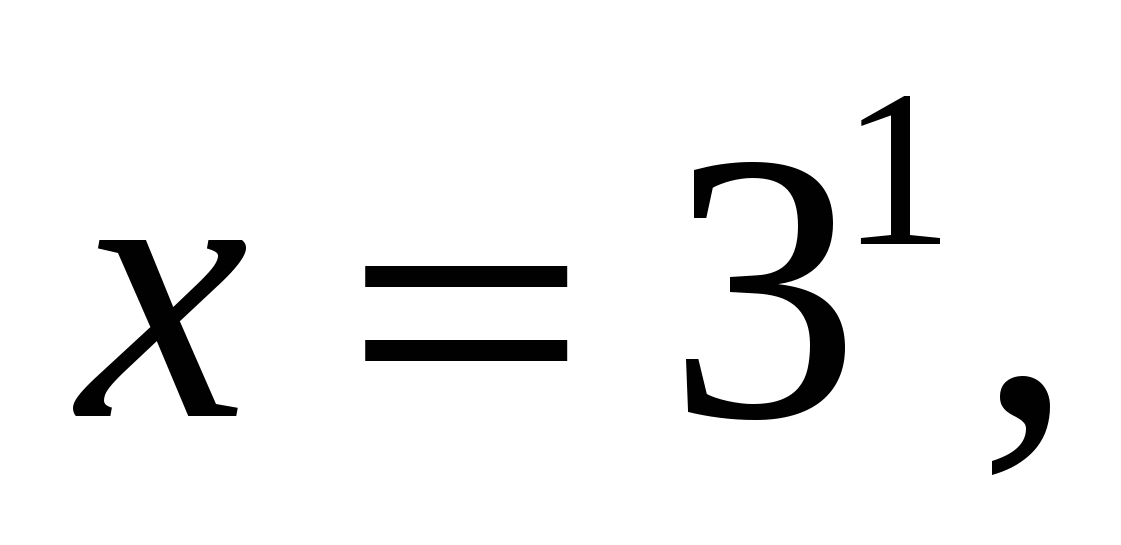
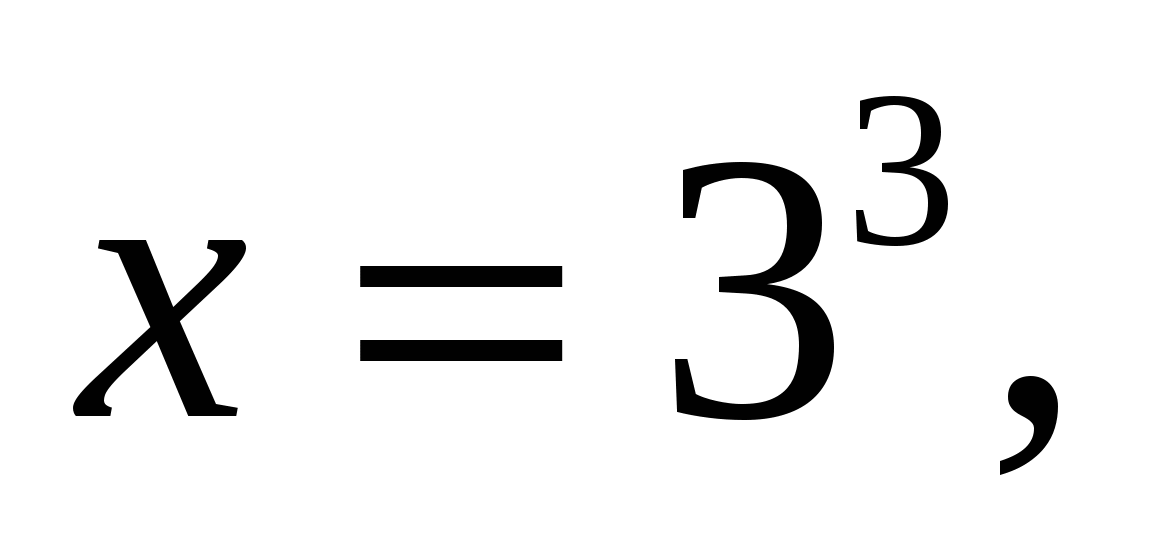
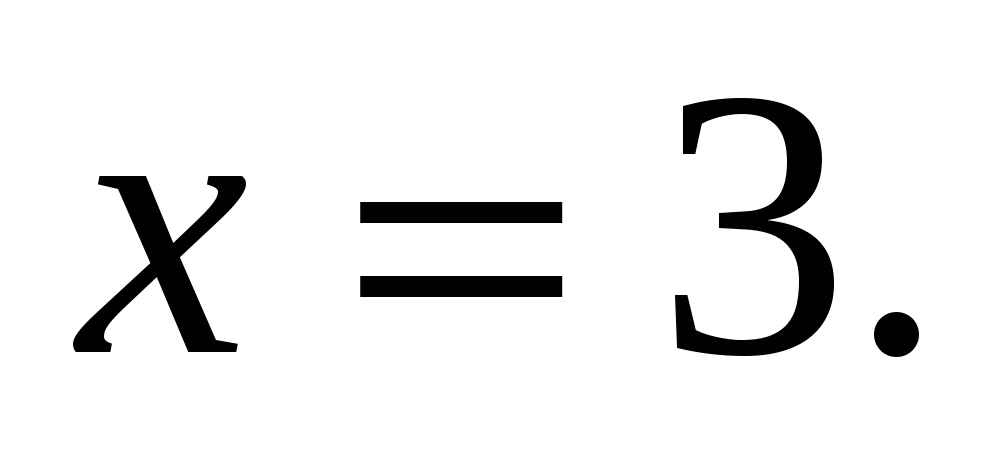
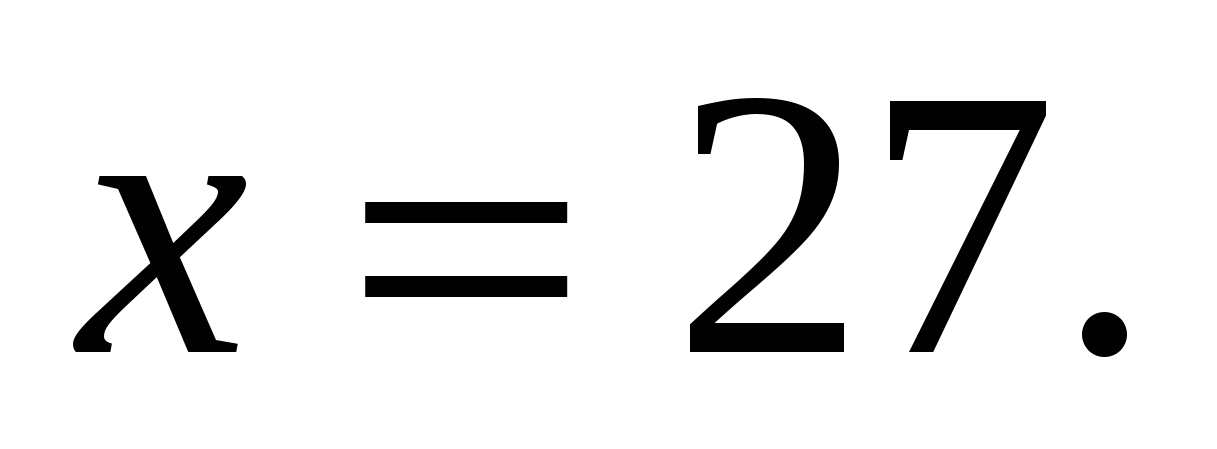

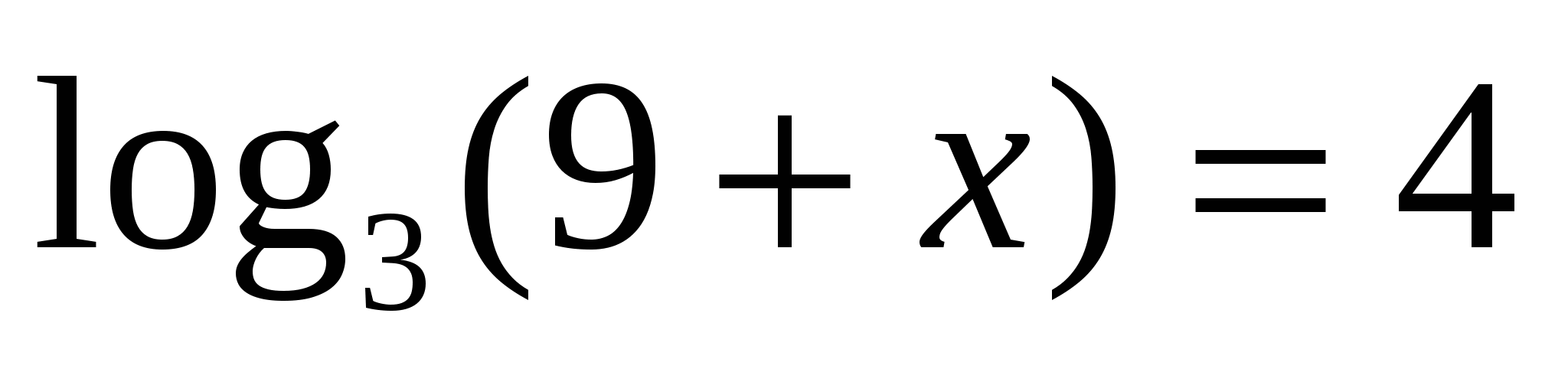

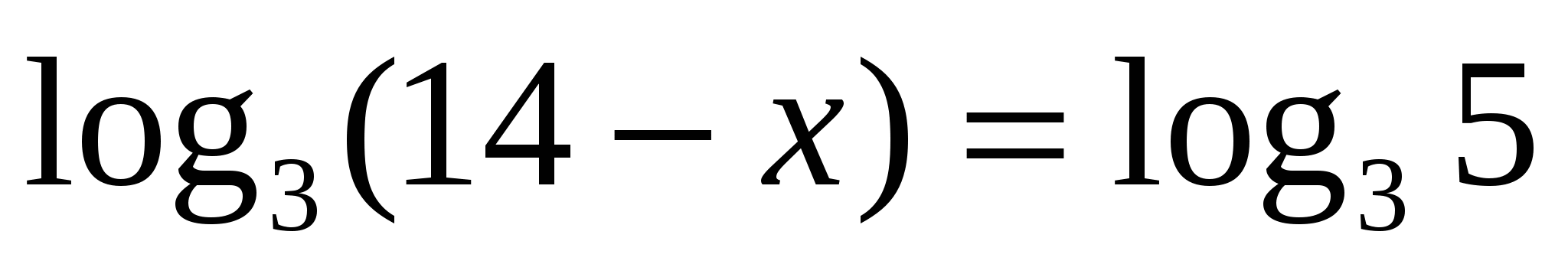
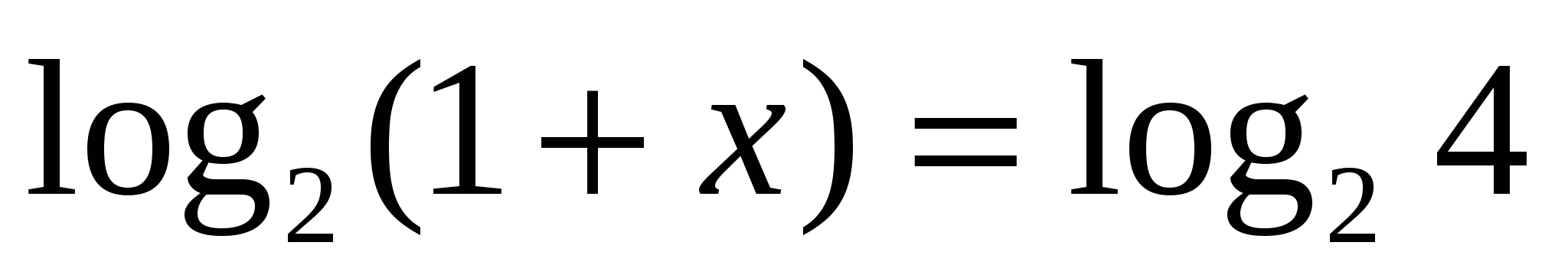
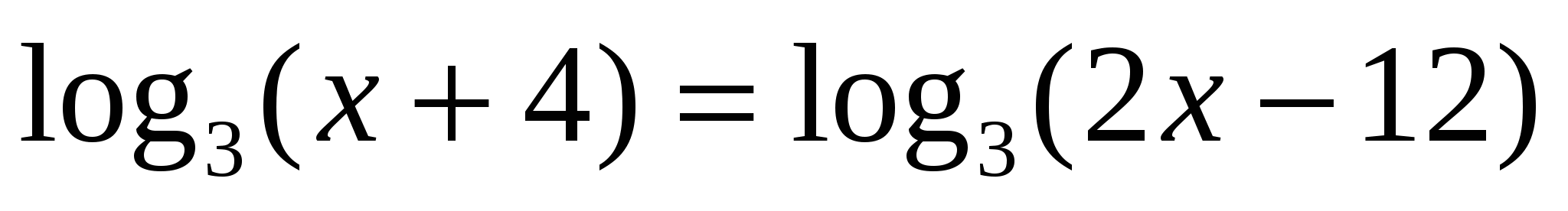

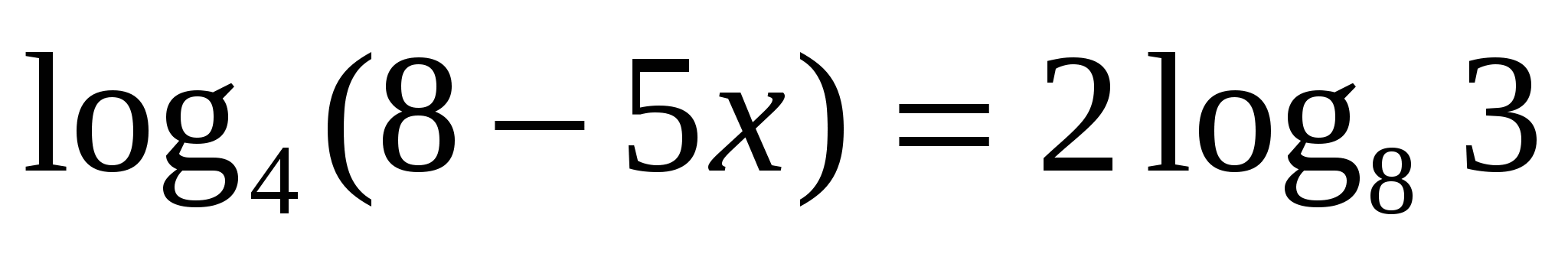
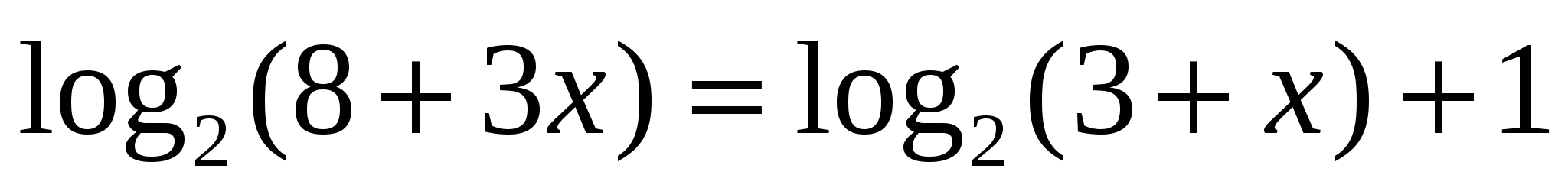
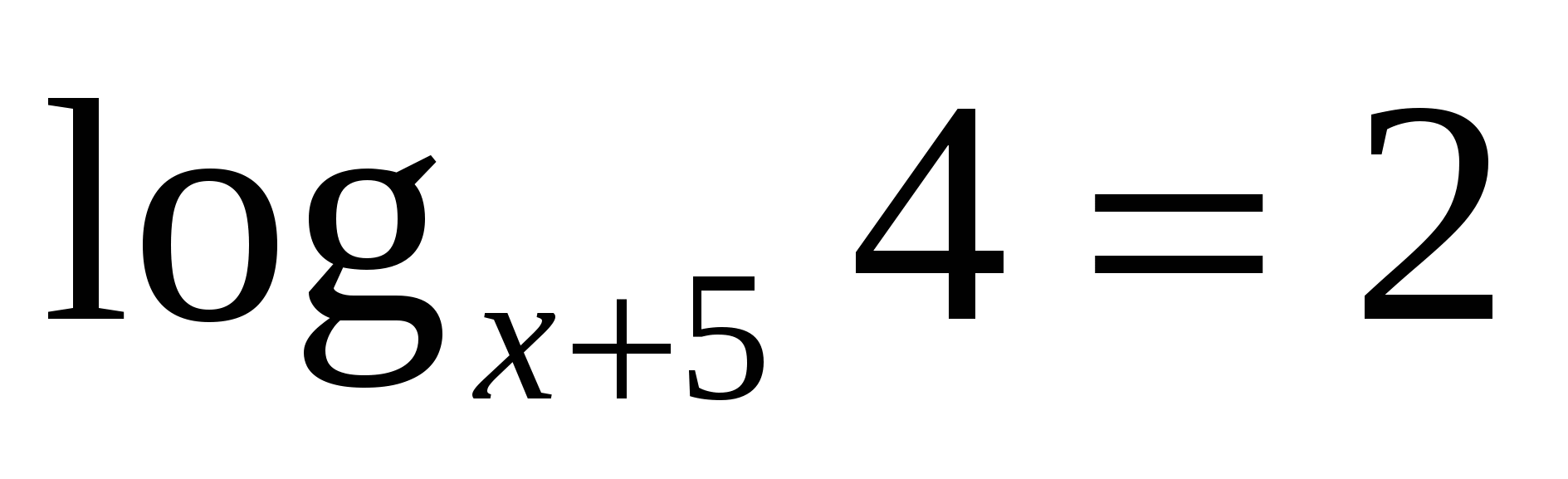
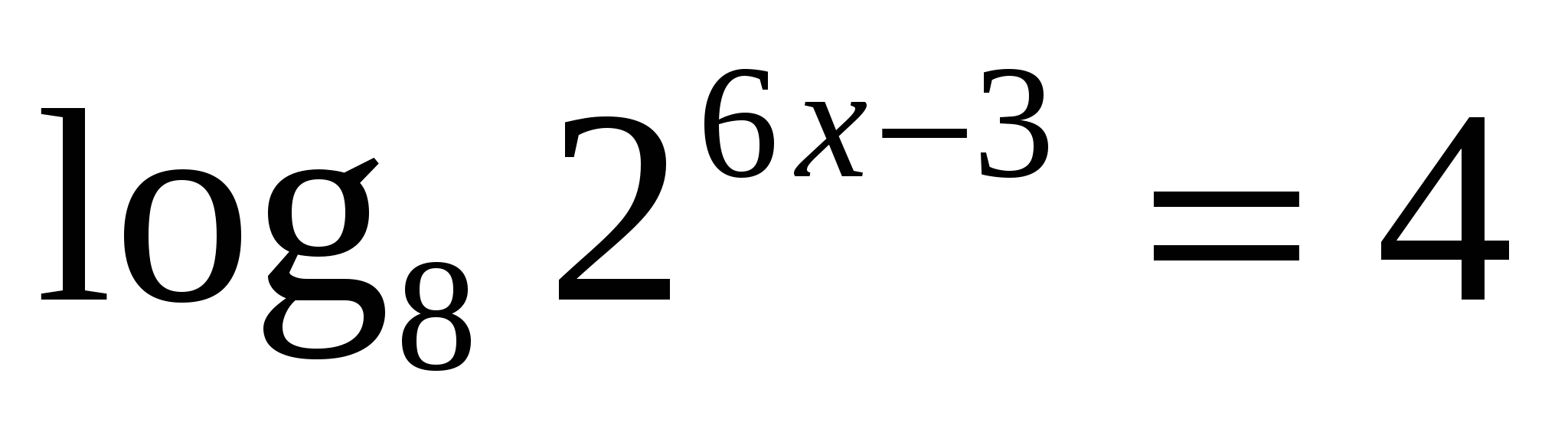
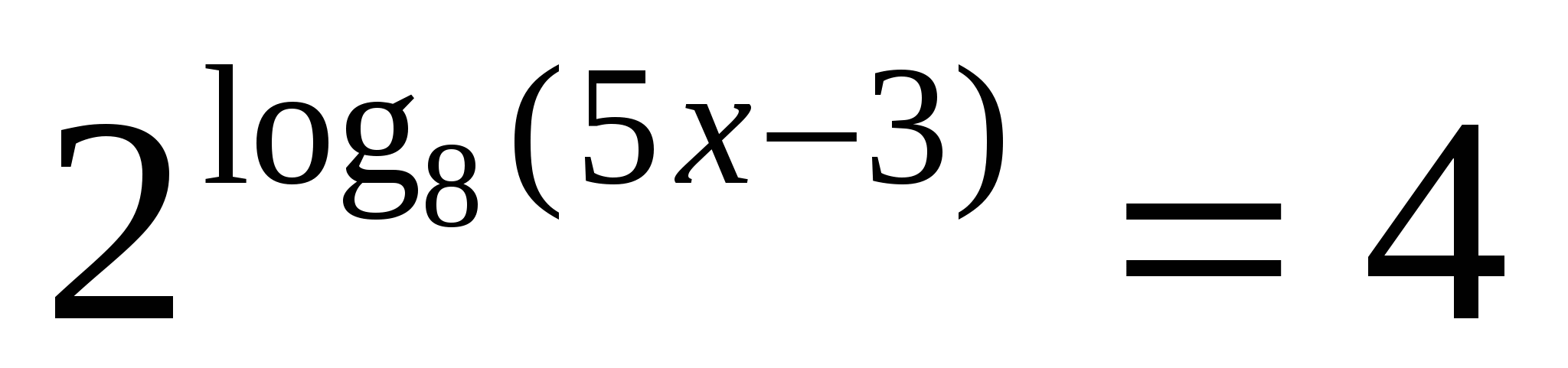

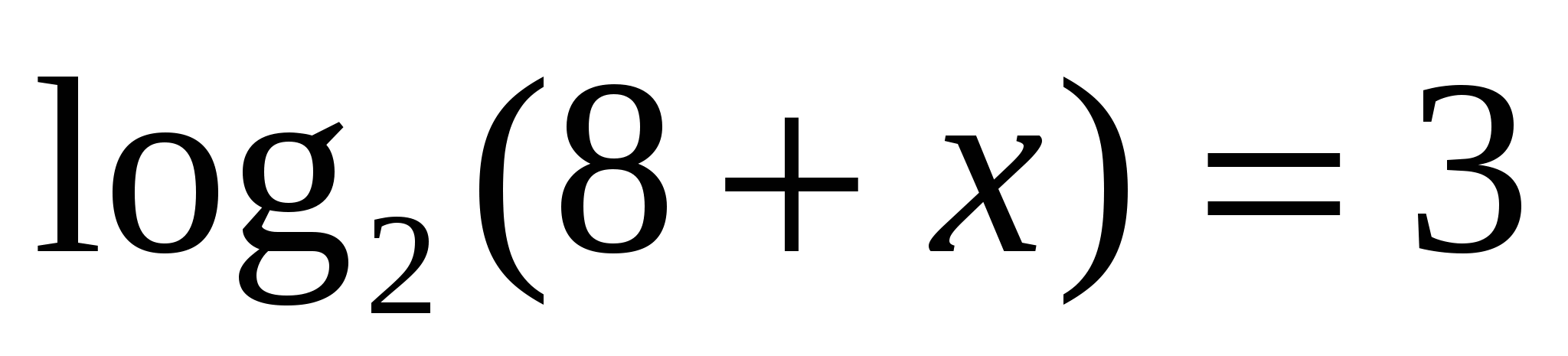
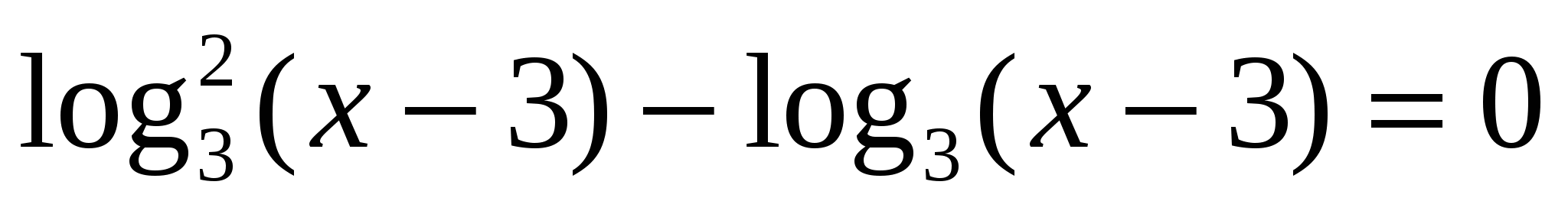
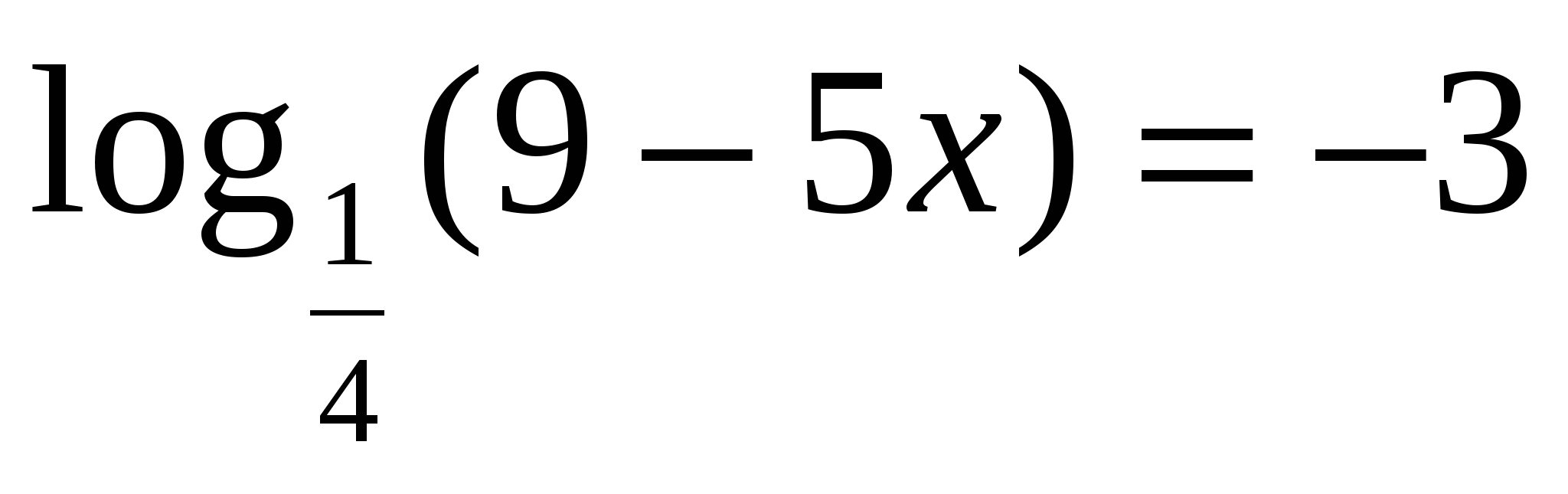
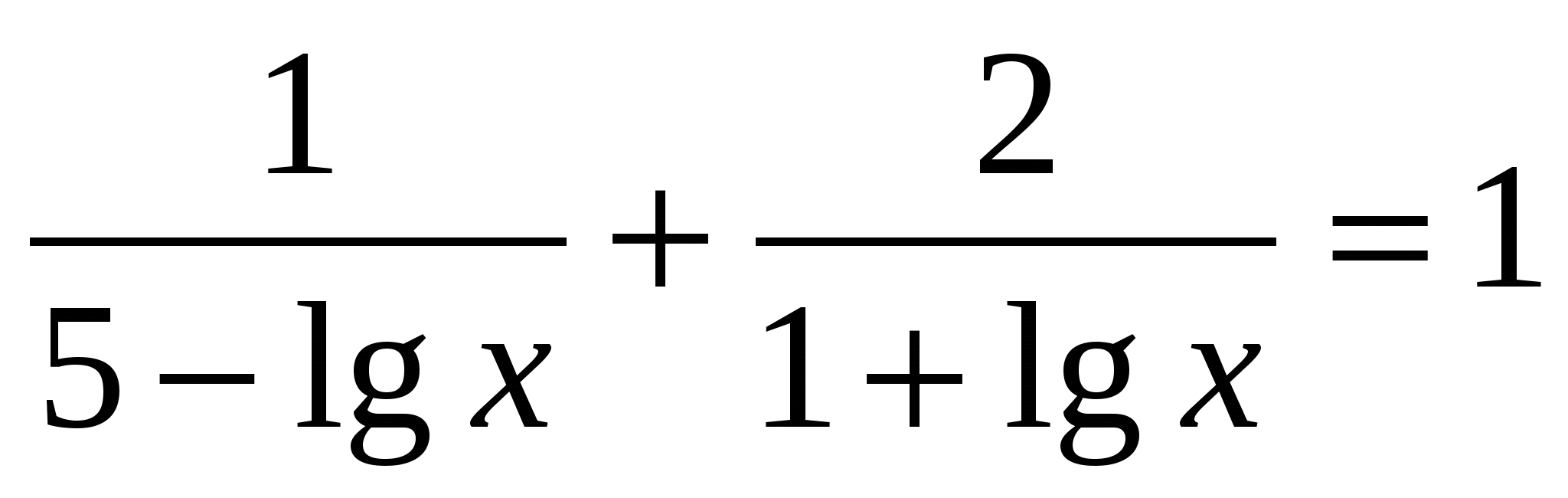
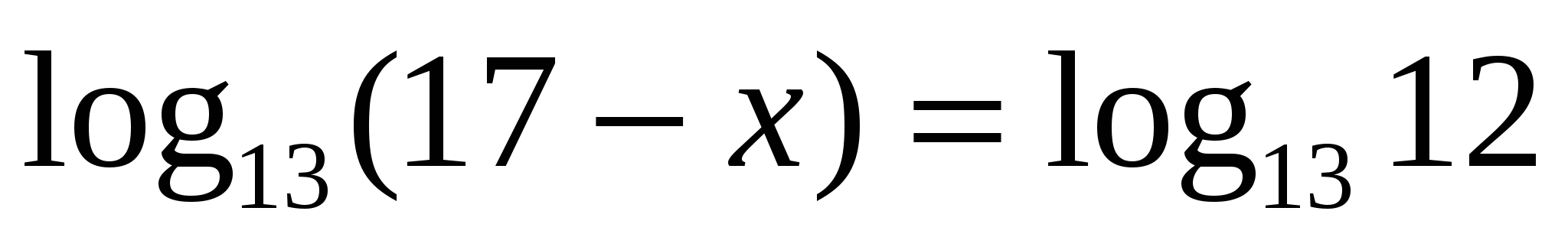
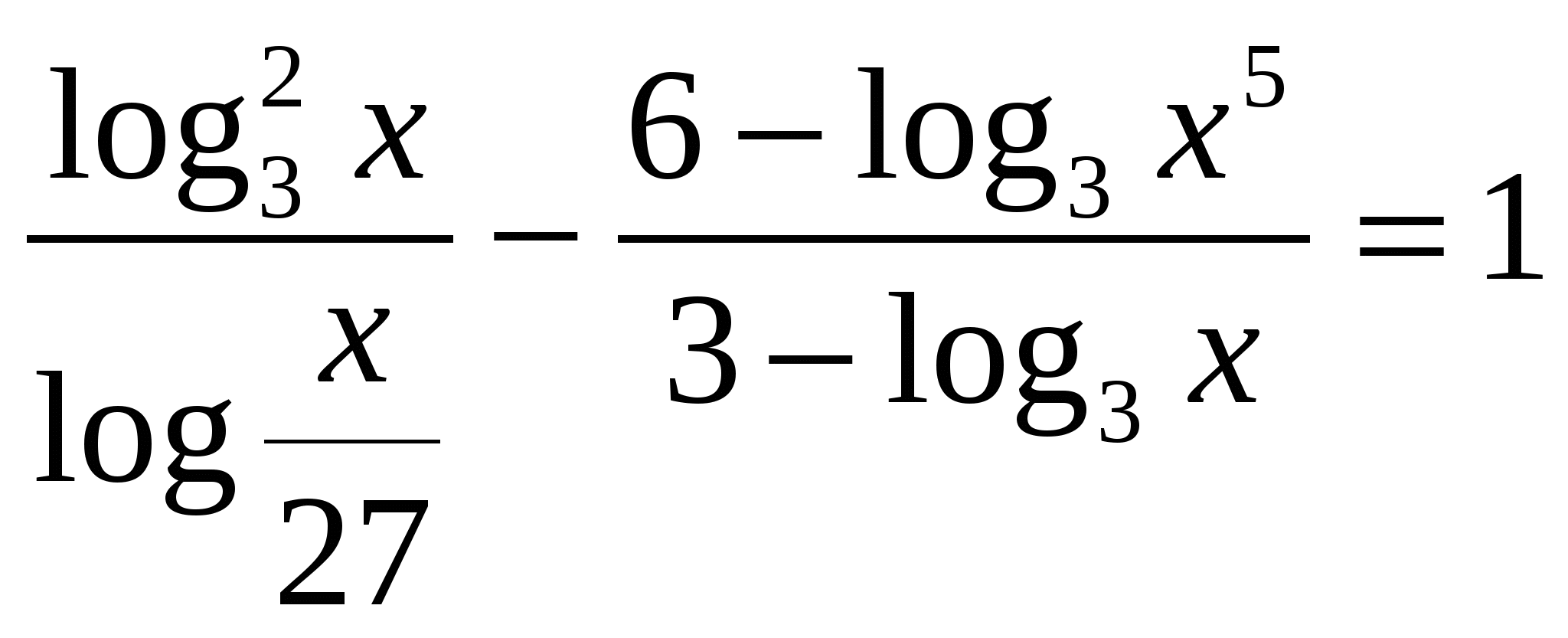
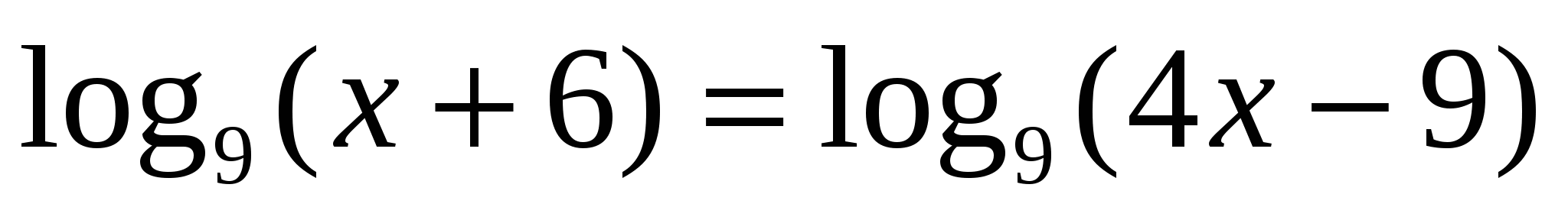
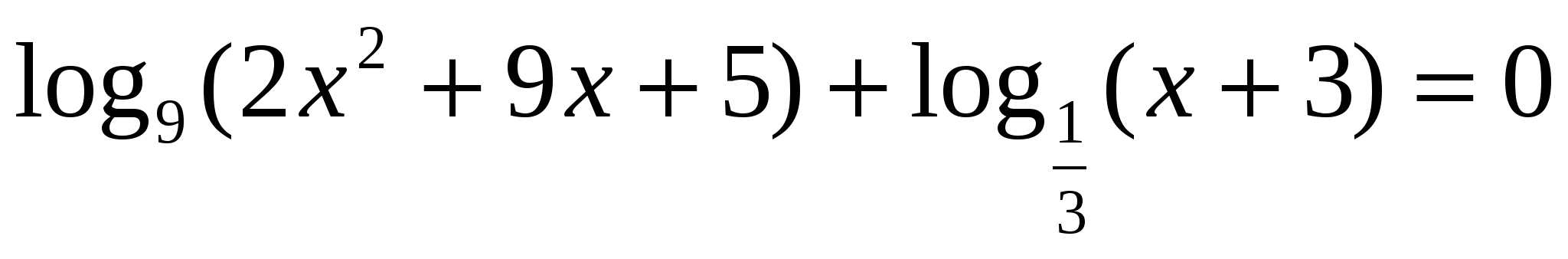
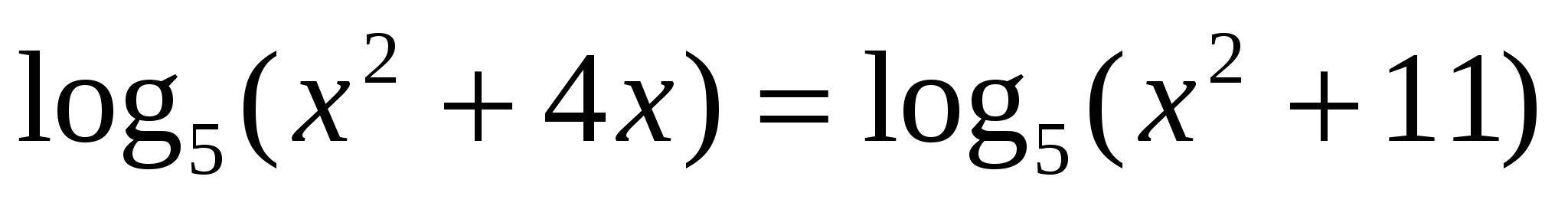
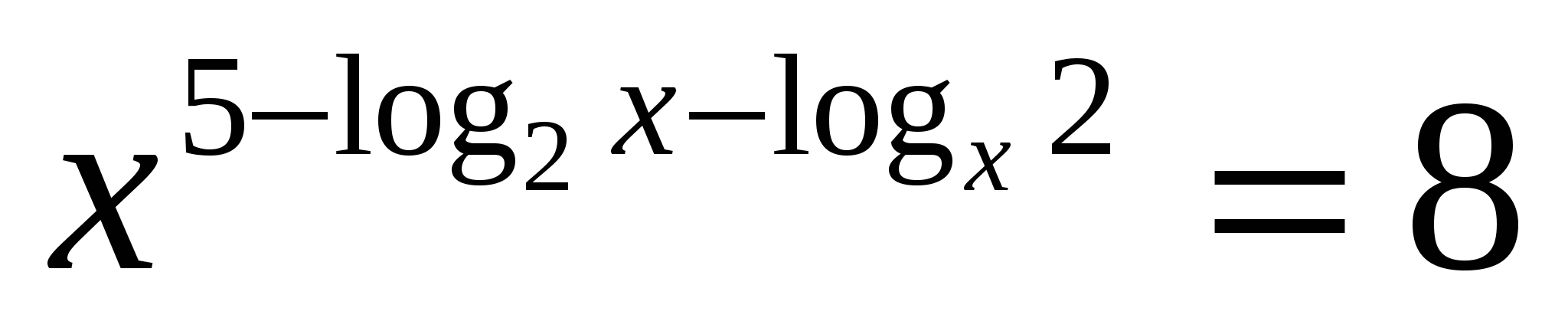
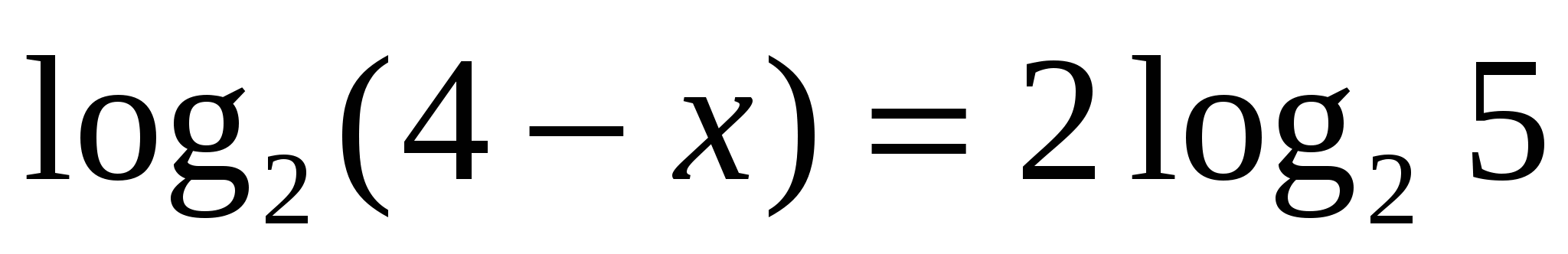
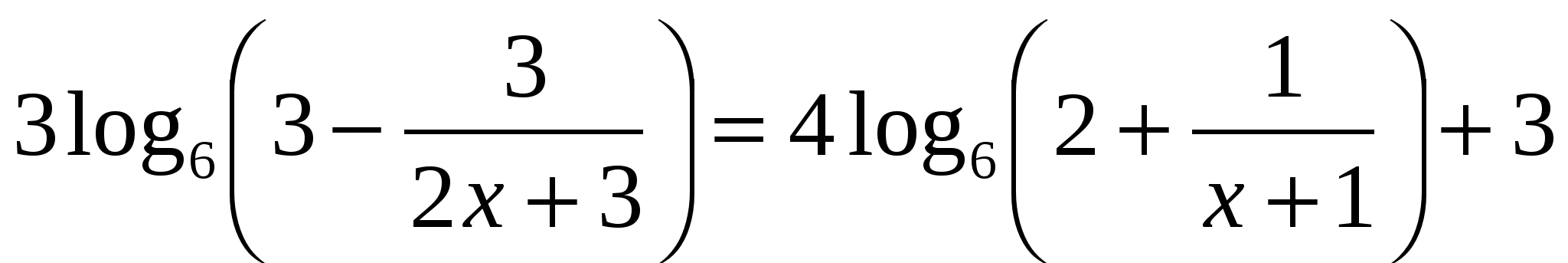
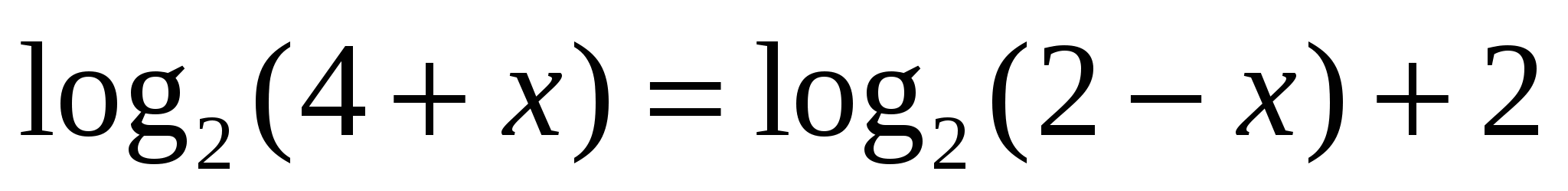
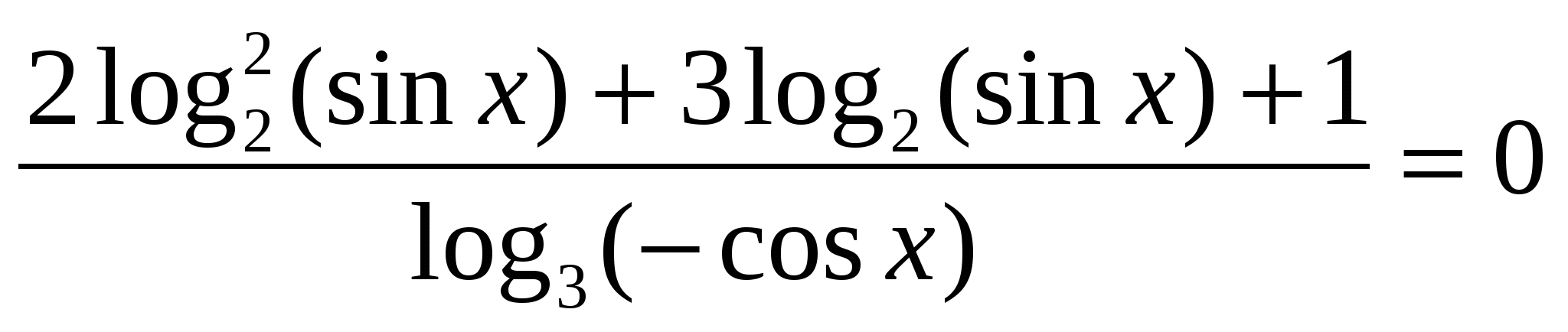
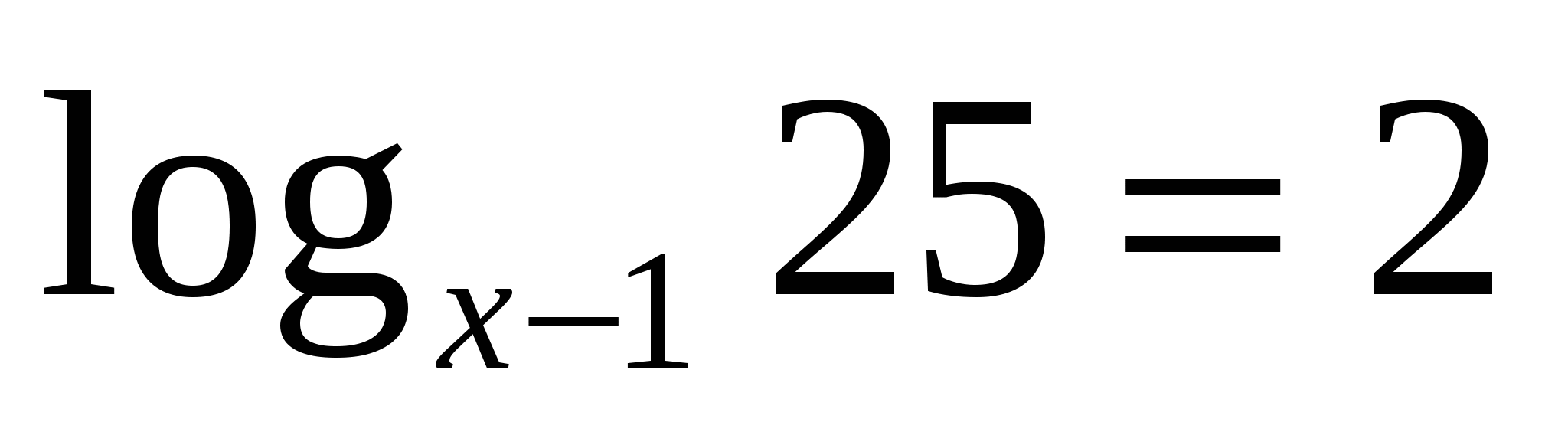
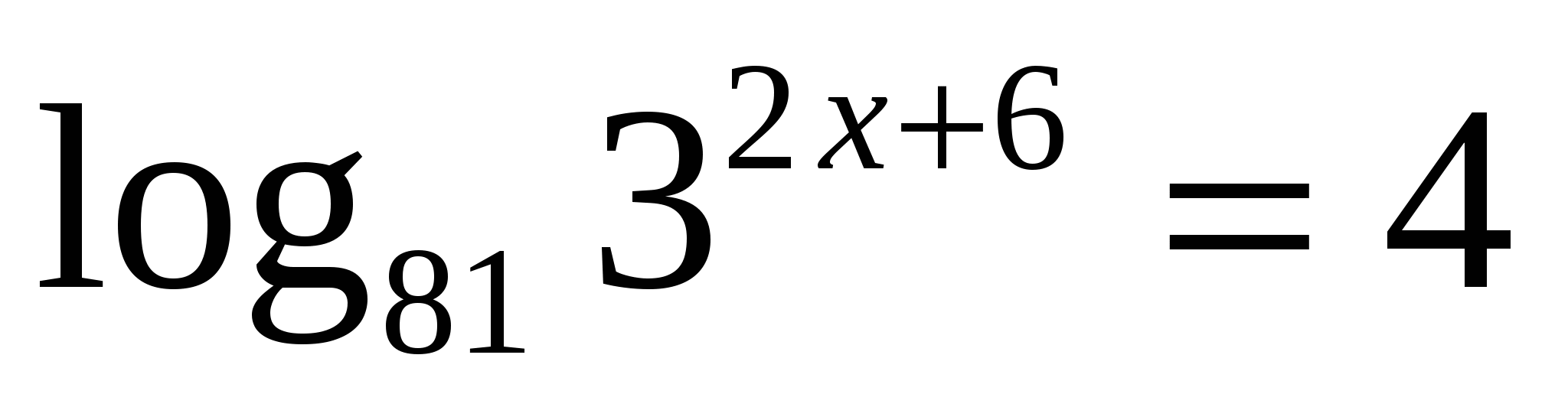
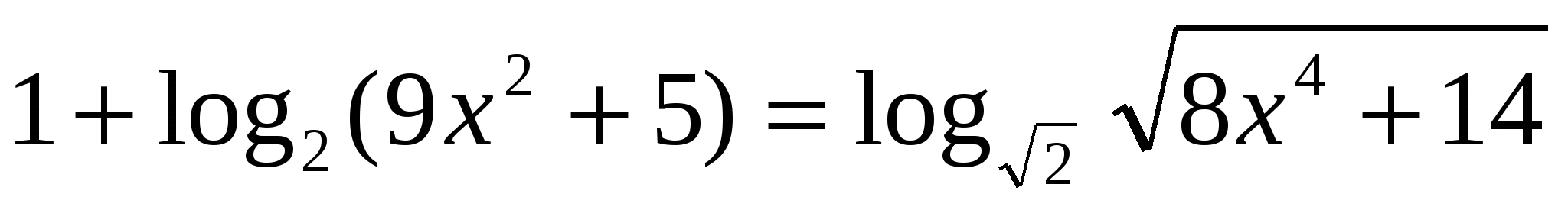 . Найти все корни, принадлежащие отрезку
. Найти все корни, принадлежащие отрезку 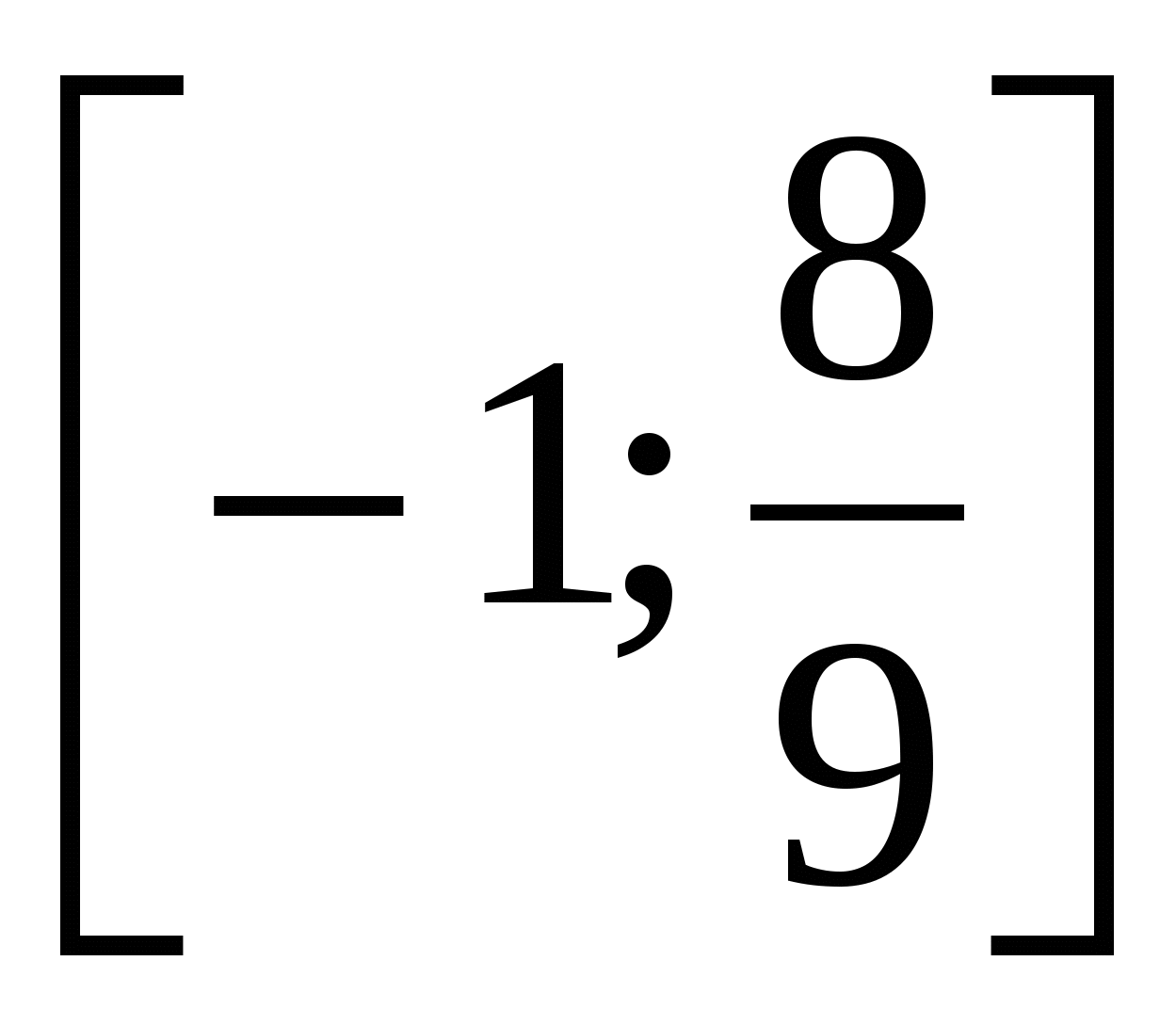 . ЕГЭ, 2013
. ЕГЭ, 2013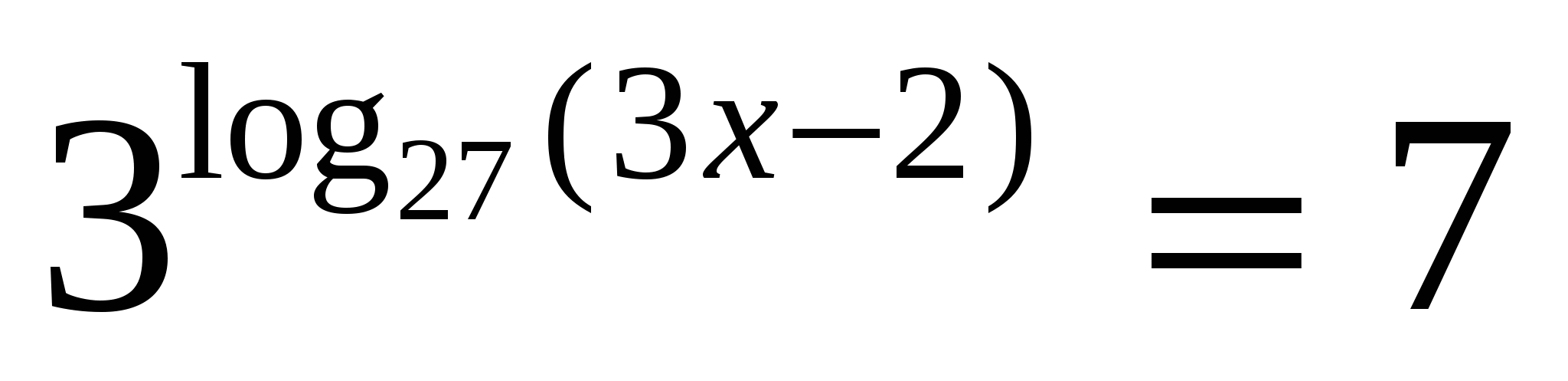
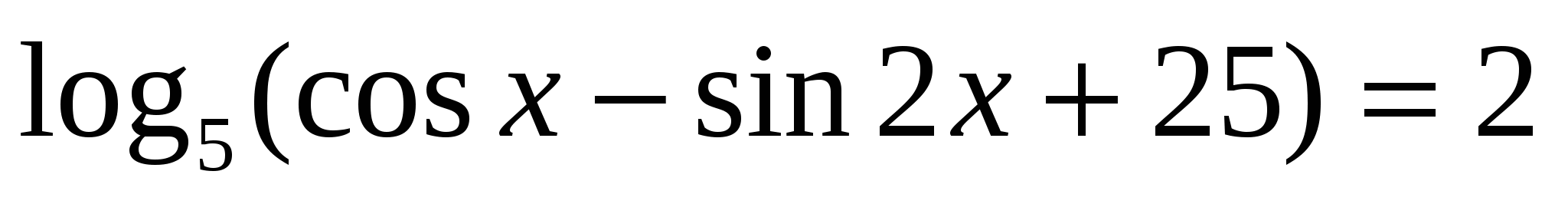 . Найти все корни, принадлежащие отрезку
. Найти все корни, принадлежащие отрезку 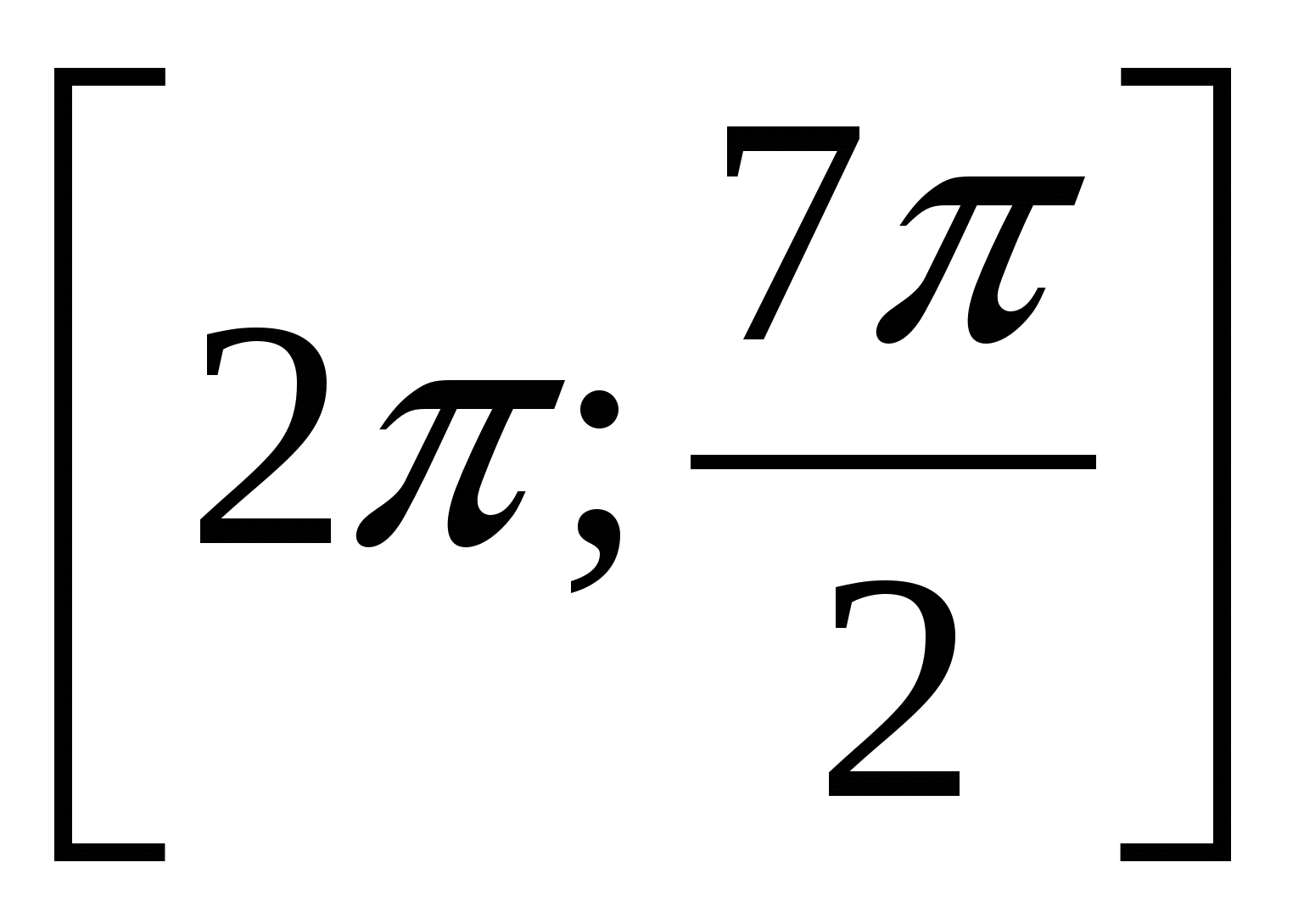 . ЕГЭ, 2012.
. ЕГЭ, 2012.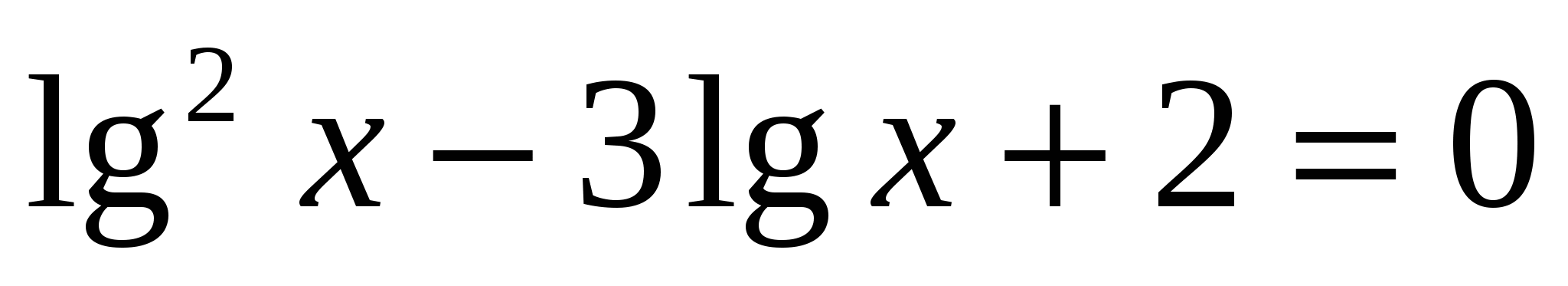
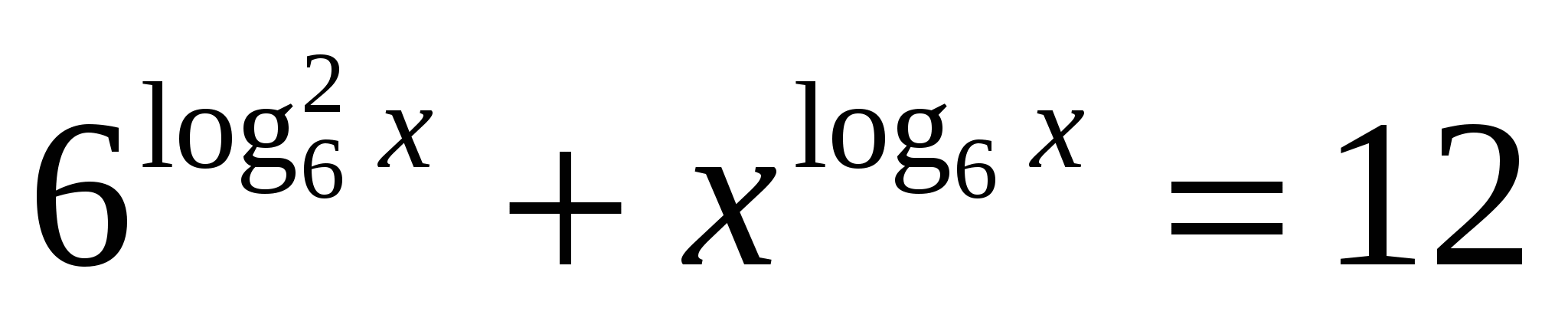
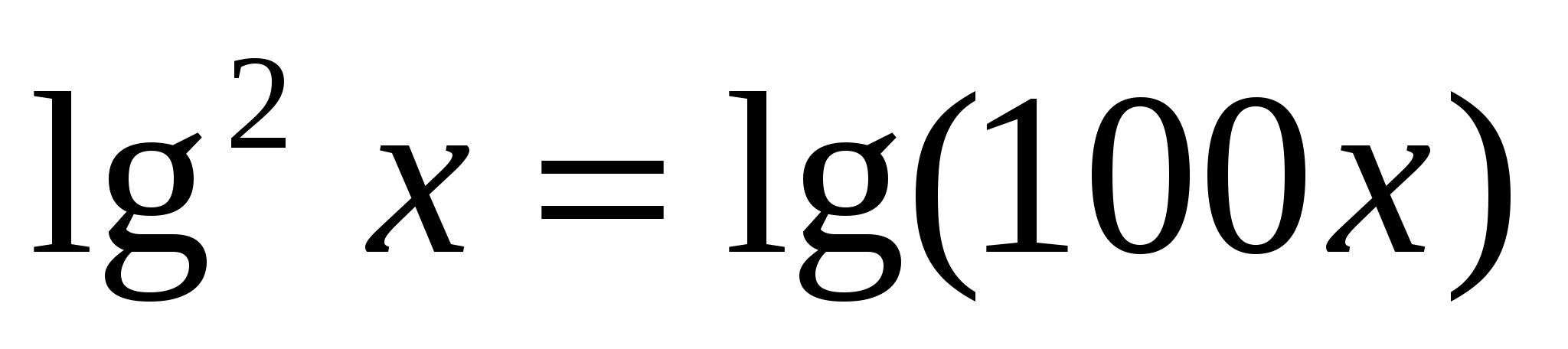
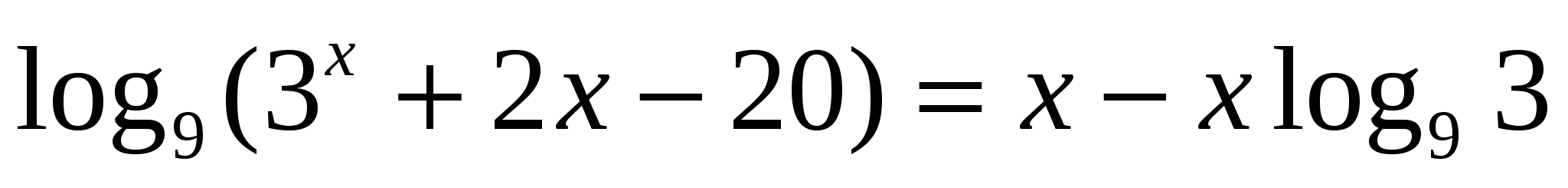
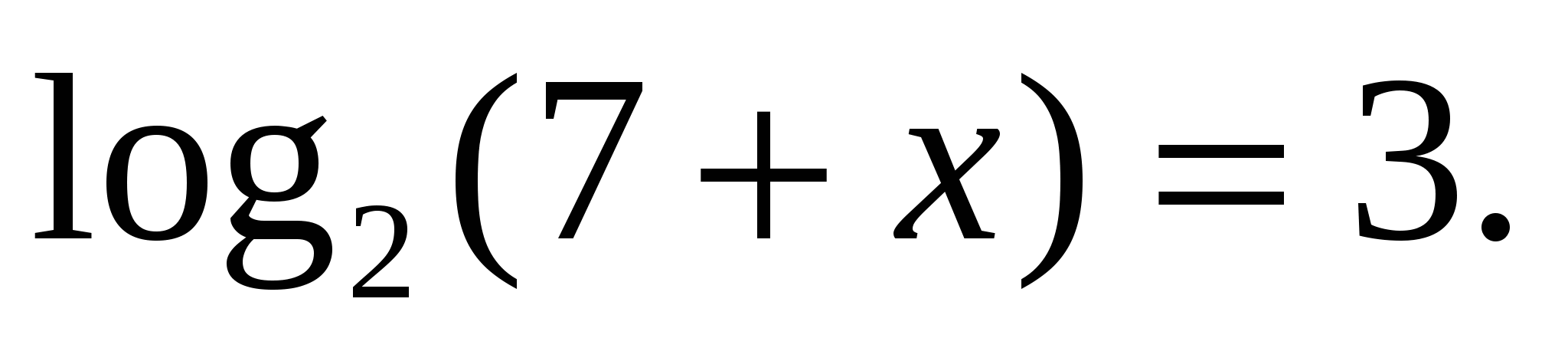 .
.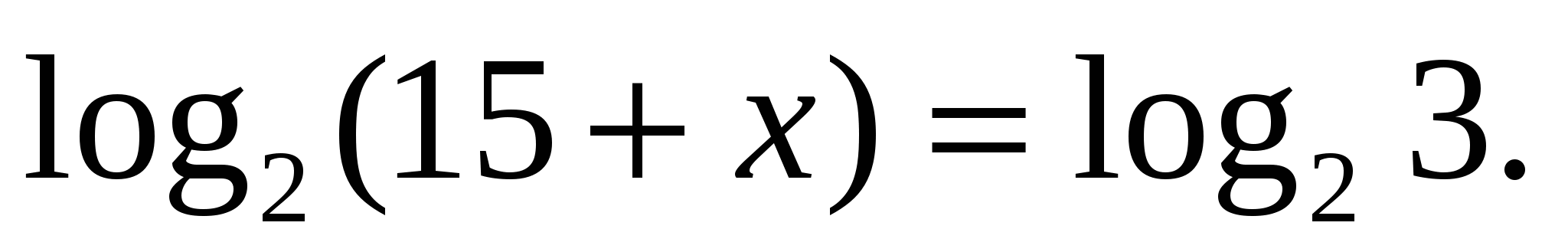 .
.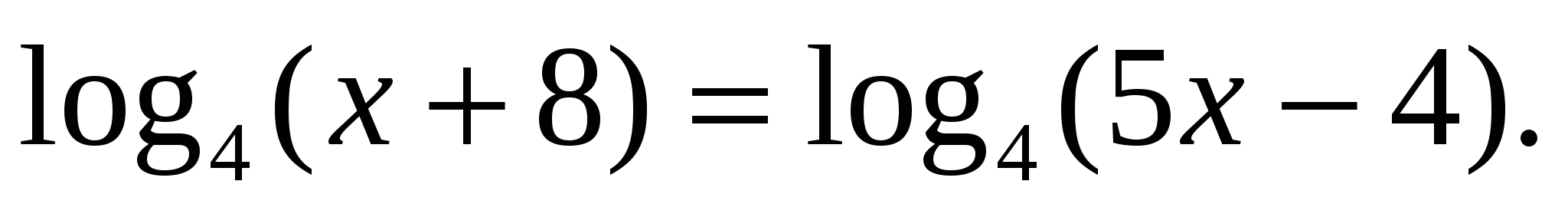 .
.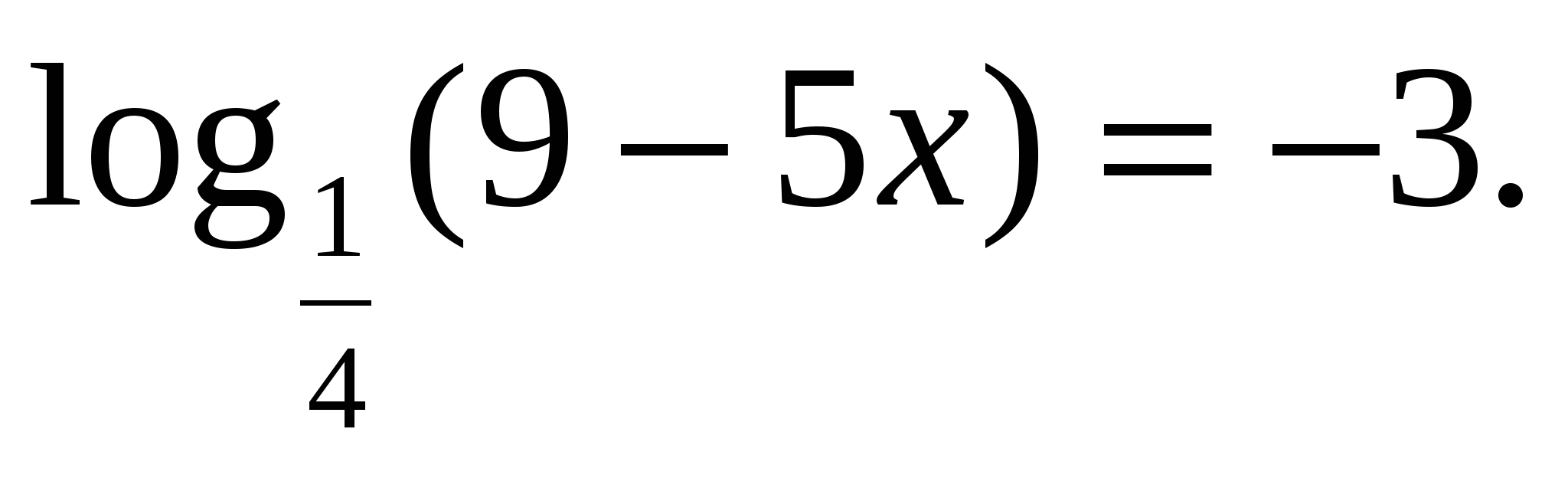 .
.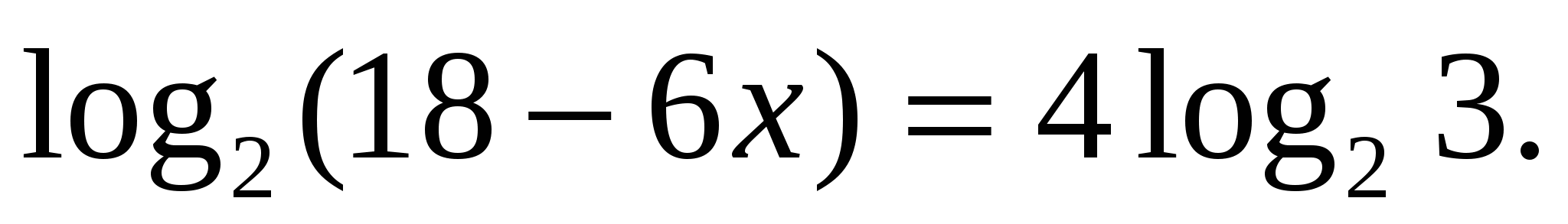 .
.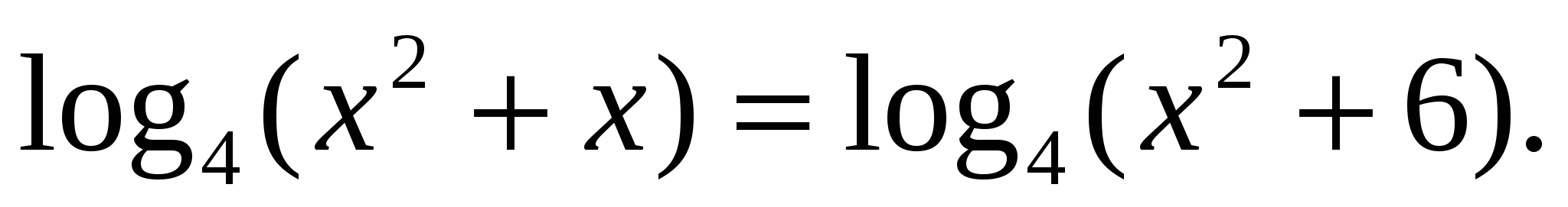 .
. .
.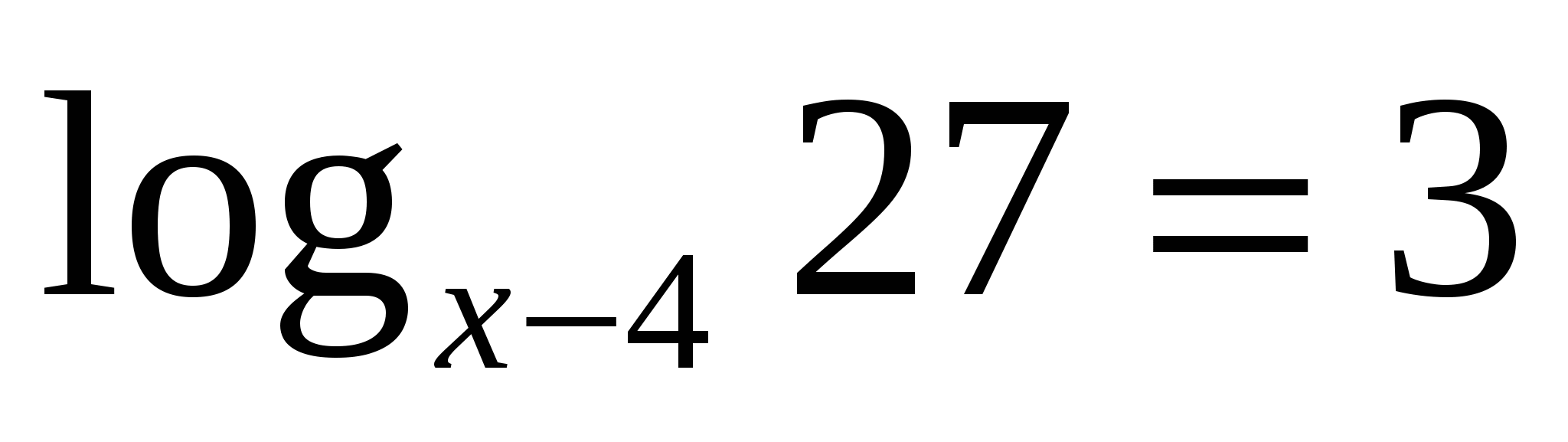 . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
. Если уравнение имеет более одного корня, в ответе укажите меньший из них.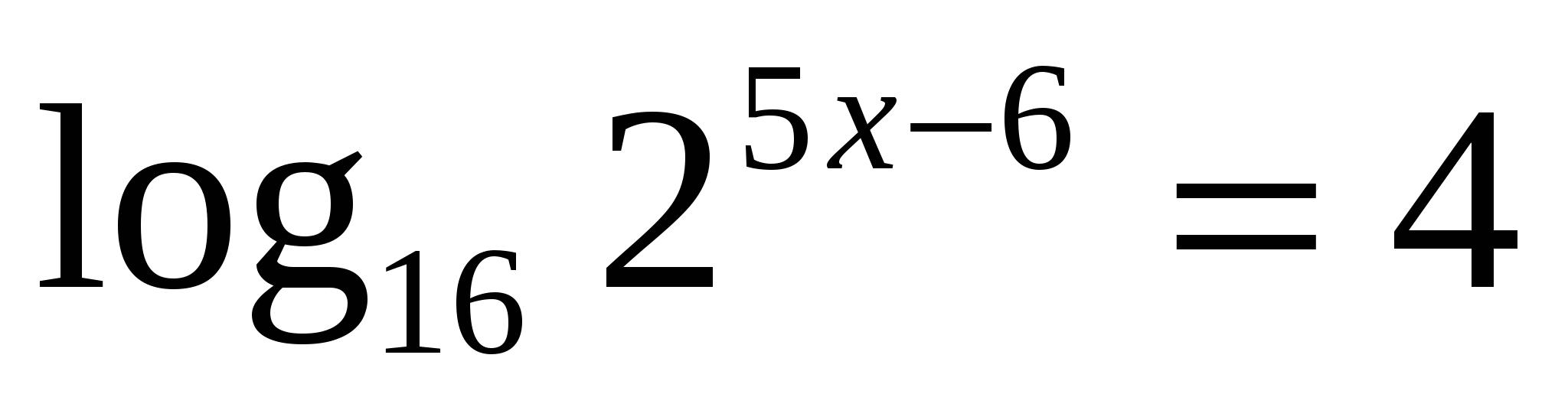 .
.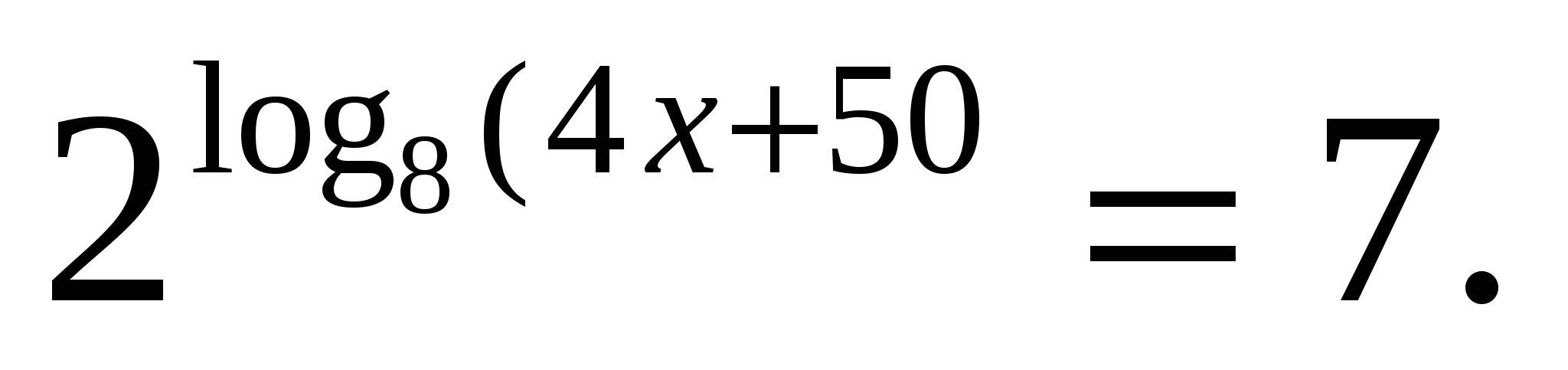
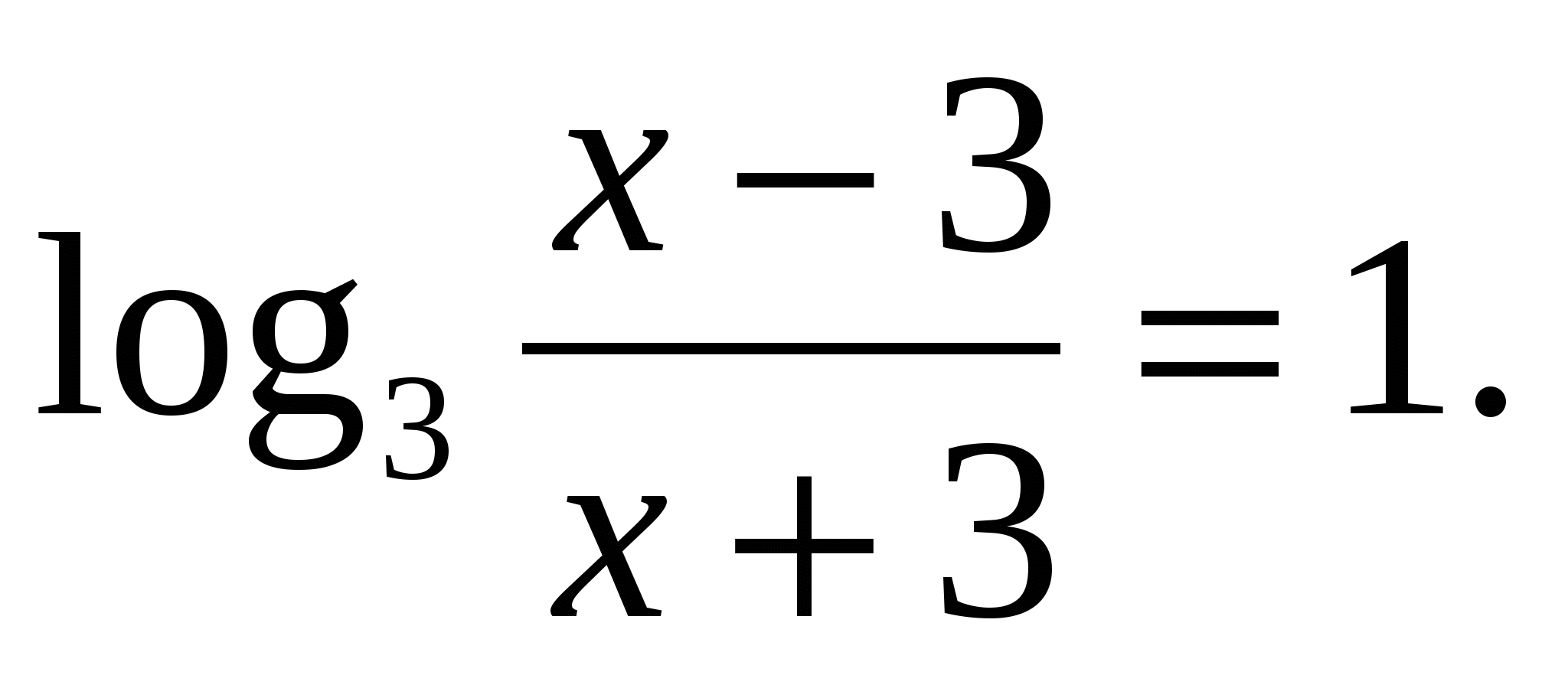
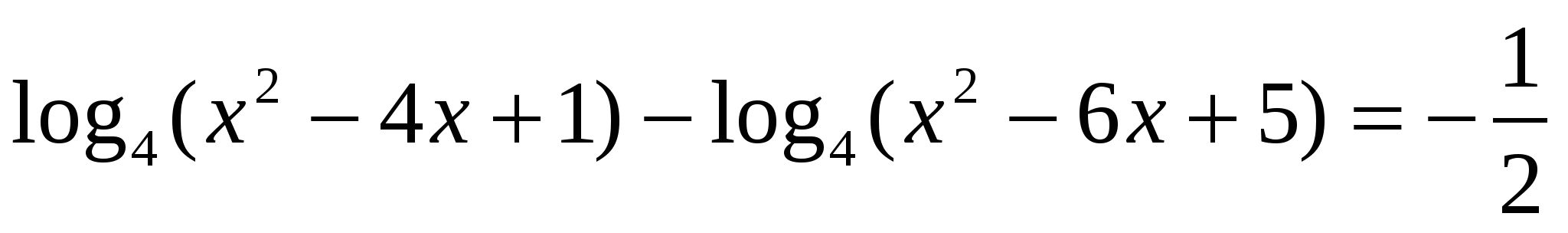 .
.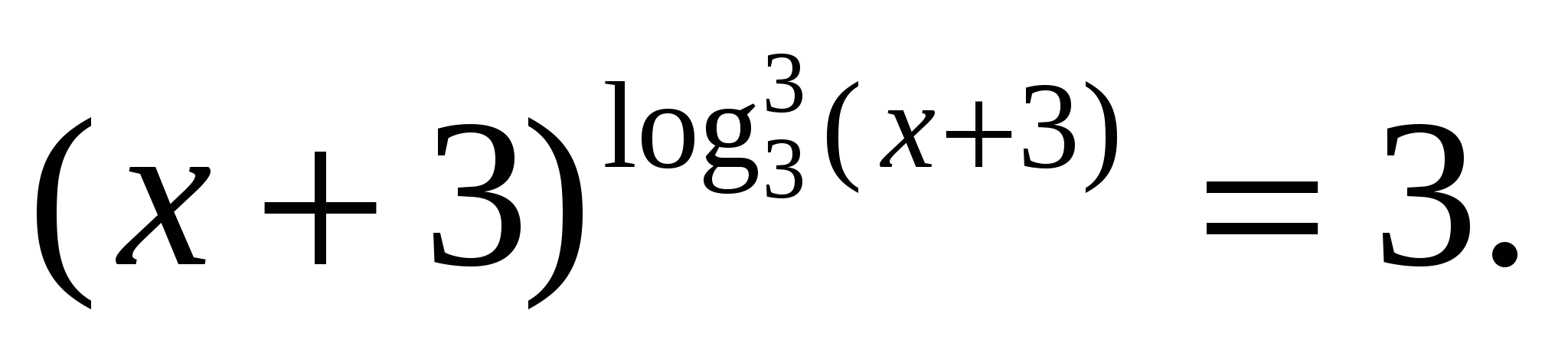 Найти произведение корней.
Найти произведение корней.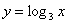
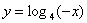
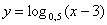
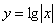
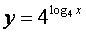
 и
и 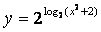
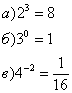
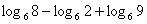
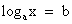 .
.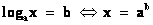
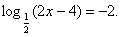
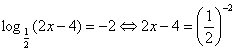 , Отсюда 2х – 4 = 4; х = 4.
, Отсюда 2х – 4 = 4; х = 4.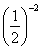 > 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.
> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.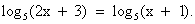
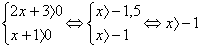
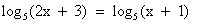 , получим уравнение 2x + 3 = х + 1.
, получим уравнение 2x + 3 = х + 1.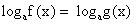

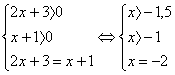
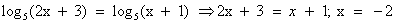 .
.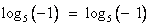 неверно, так как не имеет смысла.
неверно, так как не имеет смысла.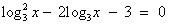 .
.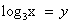 , тогда уравнение примет вид:
, тогда уравнение примет вид: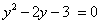 . Дискриминант D > 0. Корни по теореме Виета:
. Дискриминант D > 0. Корни по теореме Виета: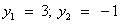 .
.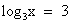 или
или 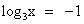 .
.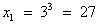 ;
; 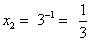 . Ответ: 27;
. Ответ: 27; 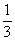
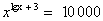 .
.
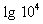
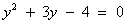 , (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.
, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.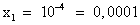 ; lgx = 1,
; lgx = 1, 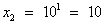 .
.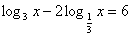
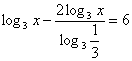 или
или 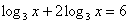 ;
; 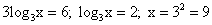 .
.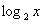 = 3 – x.
= 3 – x.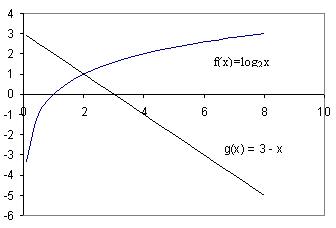
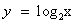 возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение
возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение  имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как
имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как 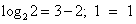 .
.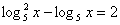

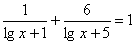
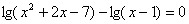
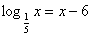
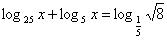
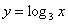
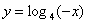
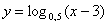
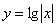
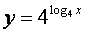
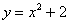 и
и 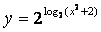
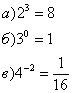
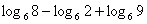
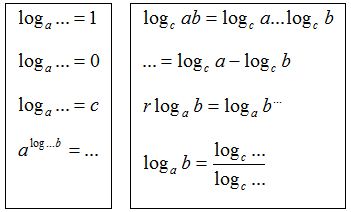
 .
.
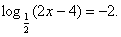
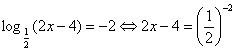 , Отсюда 2х – 4 = 4; х = 4.
, Отсюда 2х – 4 = 4; х = 4.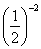 > 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.
> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.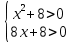
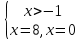

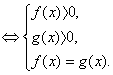
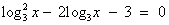 .
.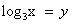 , тогда уравнение примет вид:
, тогда уравнение примет вид: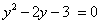 . Дискриминант D > 0. Корни по теореме Виета:
. Дискриминант D > 0. Корни по теореме Виета: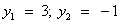 .
.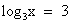 или
или 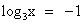 .
.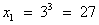 ;
; 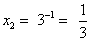 .
.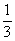
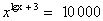 .
.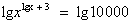 . Применим свойство логарифма степени:
. Применим свойство логарифма степени: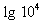
 , (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.
, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.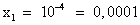 ; lgx = 1,
; lgx = 1,  .
.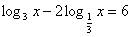
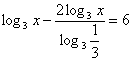 или
или 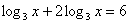 ;
;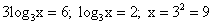 .
.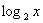 = 3 – x.
= 3 – x.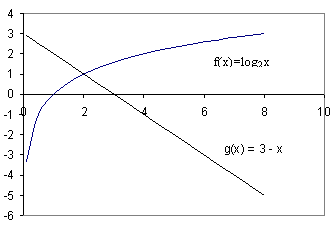
 возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение
возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 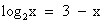 имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как
имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как 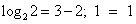 .
.
 – это следует из определения логарифма (под логарифмом не может стоять отрицательное число или 0)
– это следует из определения логарифма (под логарифмом не может стоять отрицательное число или 0) Стоит отметить, что показательная и логарифмическая функции являются взаимно обратными. Поэтому область определения показательной функции совпадает с областью значения логарифмической и наоборот (более подробно о свойствах прямой и обратной функции мы поговорим в теме «Функции»).
Стоит отметить, что показательная и логарифмическая функции являются взаимно обратными. Поэтому область определения показательной функции совпадает с областью значения логарифмической и наоборот (более подробно о свойствах прямой и обратной функции мы поговорим в теме «Функции»).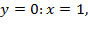 так как логарифм от 1 по любому основанию равен 0 (любое положительное число в 0 степени равно 1). Значит, график логарифмической функции проходит через точку
так как логарифм от 1 по любому основанию равен 0 (любое положительное число в 0 степени равно 1). Значит, график логарифмической функции проходит через точку 
 – не существует, так как 0 не входит в область определения логарифмической функции.
– не существует, так как 0 не входит в область определения логарифмической функции.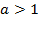 функция монотонно возрастает на всей области определения (обратите внимание на сходство с показательной функцией).
функция монотонно возрастает на всей области определения (обратите внимание на сходство с показательной функцией). функция монотонно убывает на всей области определения.
функция монотонно убывает на всей области определения.
 и монотонно убывает при
и монотонно убывает при 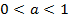 ).
). ):
):  Однако при этом необходимо помнить, что под логарифмом должно стоять положительное число. Таким образом, при решении логарифмических уравнений необходимо учитывать ОДЗ, а именно: проверять, что все подлогарифмические выражения, а также основания логарифмов являются положительными и основания не равны 1.
Однако при этом необходимо помнить, что под логарифмом должно стоять положительное число. Таким образом, при решении логарифмических уравнений необходимо учитывать ОДЗ, а именно: проверять, что все подлогарифмические выражения, а также основания логарифмов являются положительными и основания не равны 1.
 Однако продемонстрированный метод более универсальный.
Однако продемонстрированный метод более универсальный.



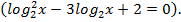
 .
. .
.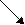 НАНИЯ
НАНИЯ 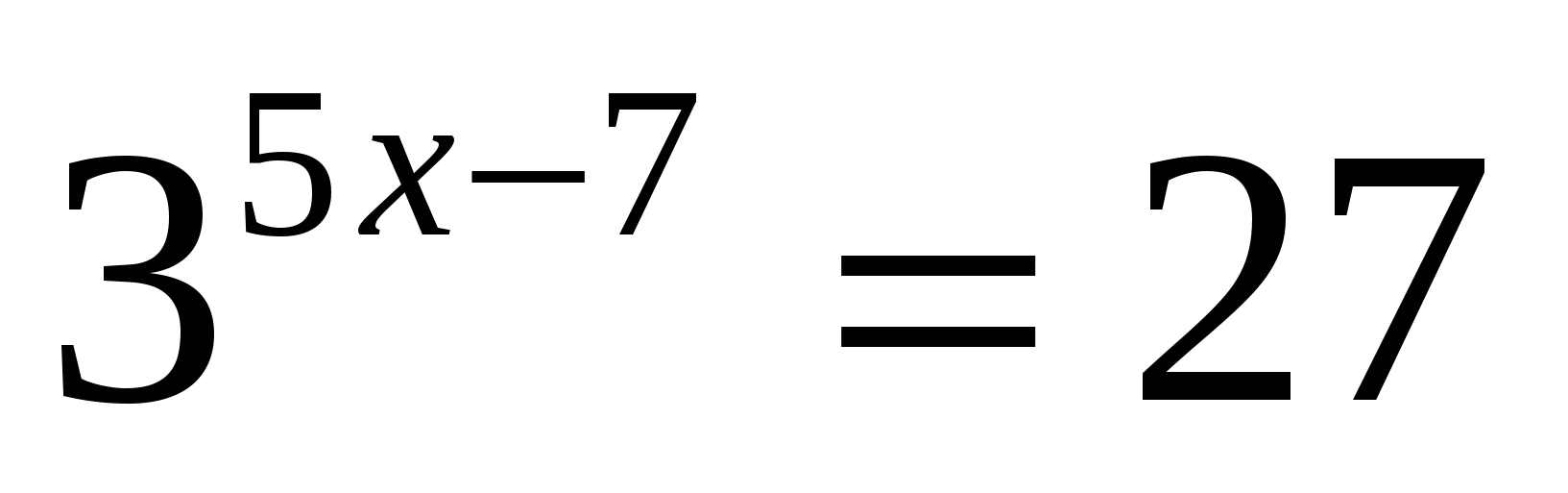

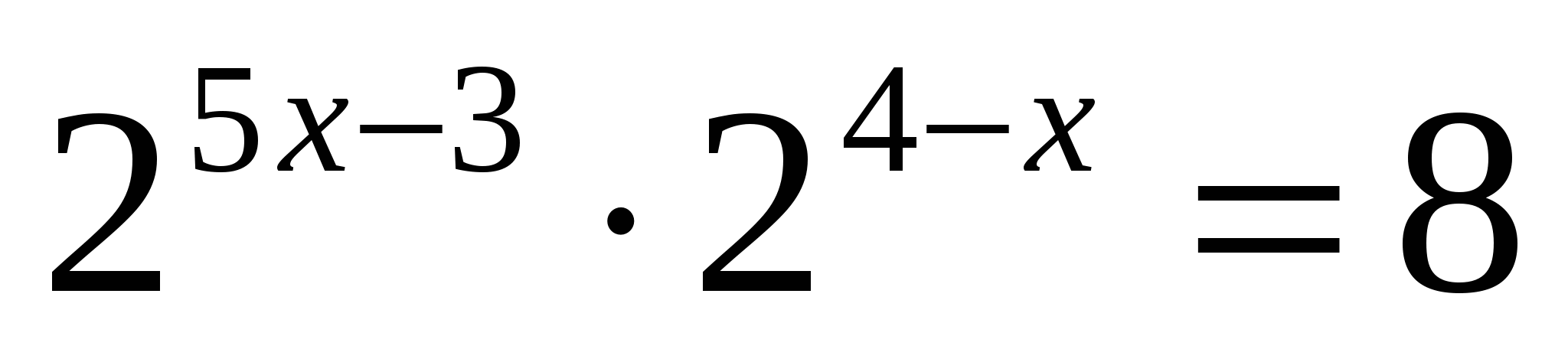
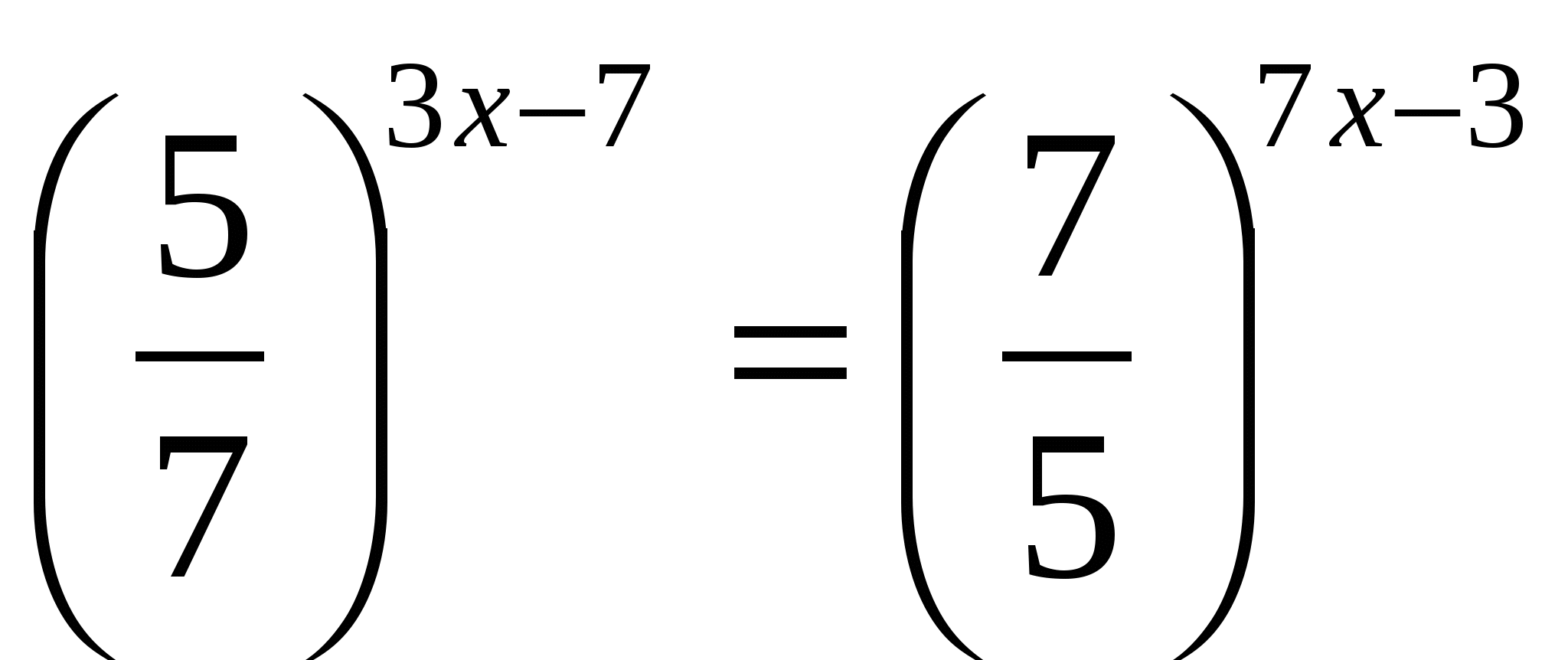

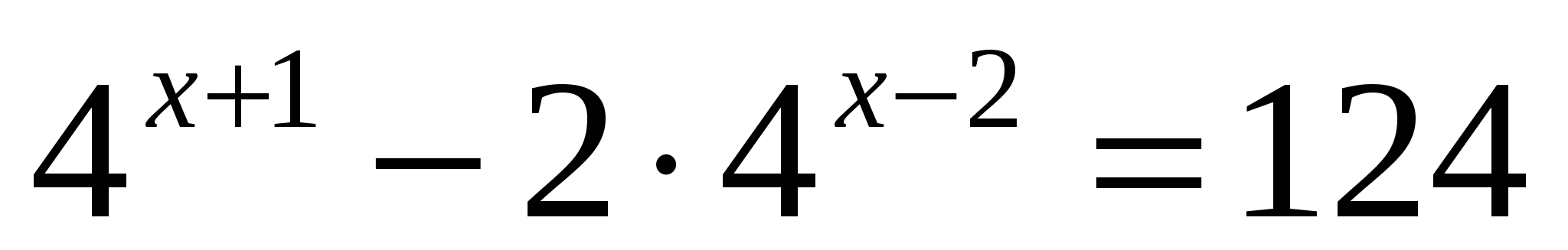
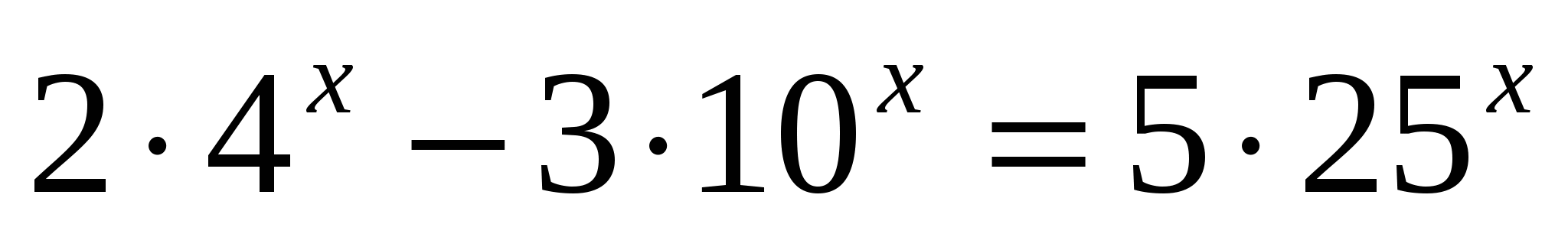
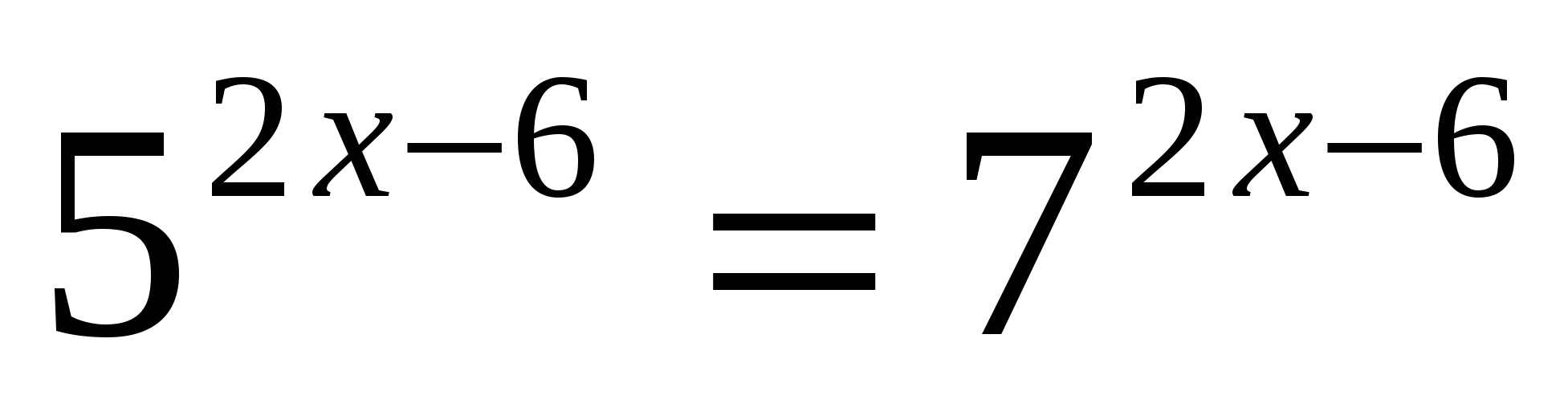
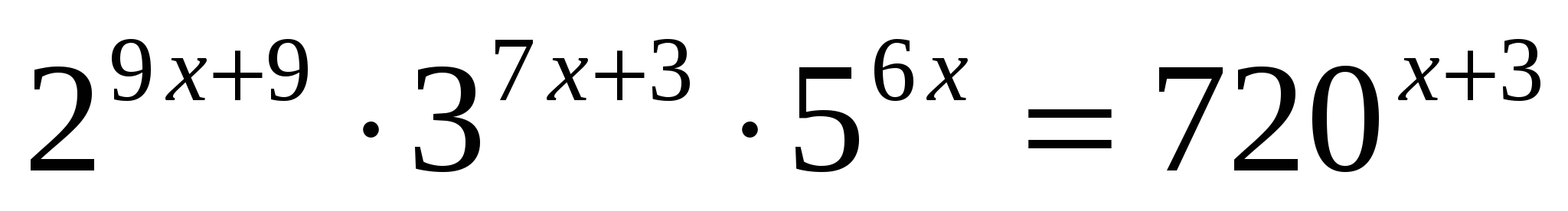
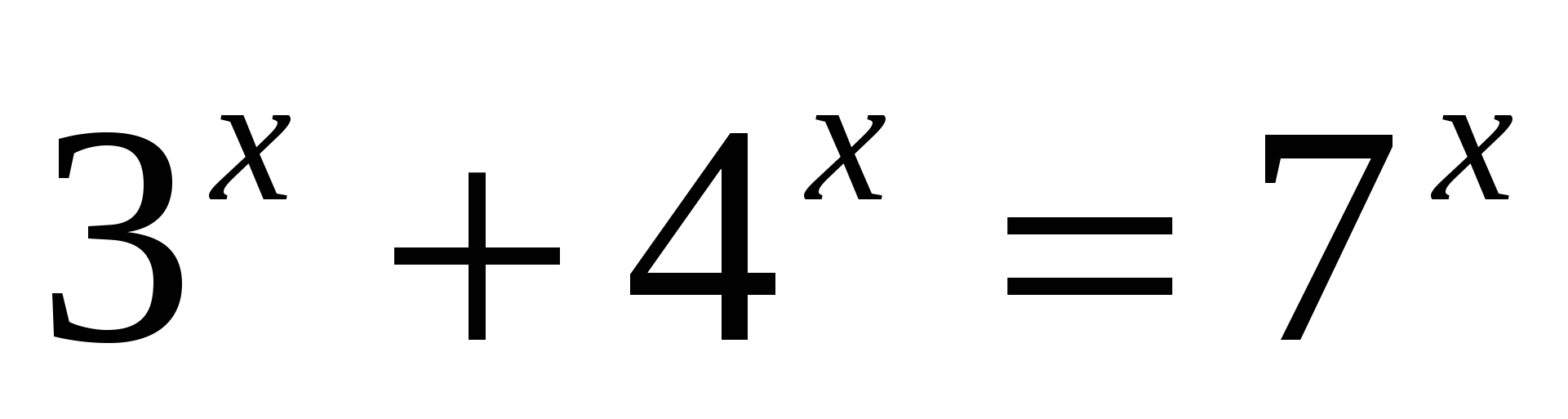
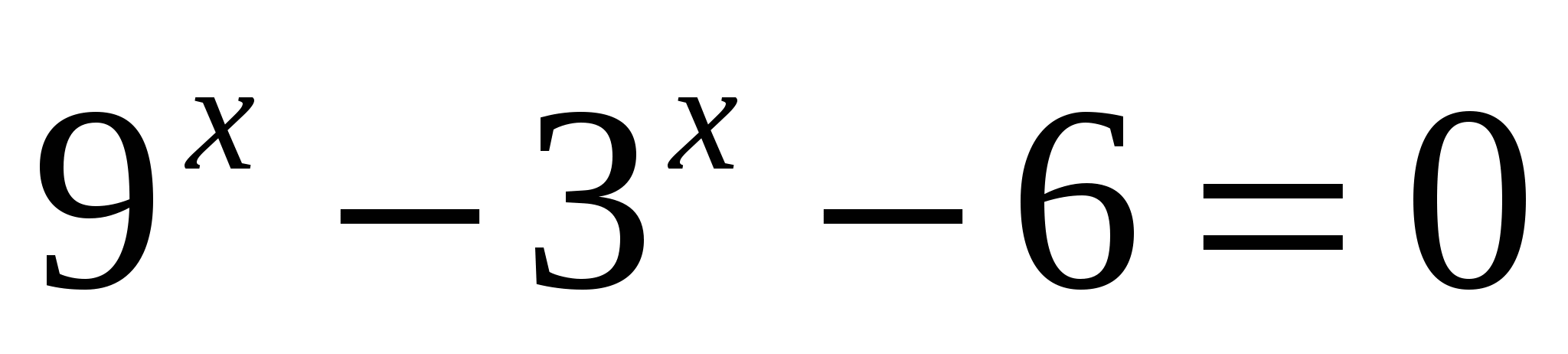
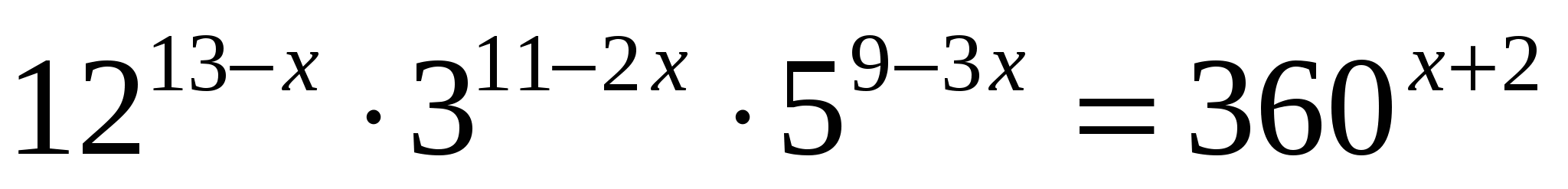
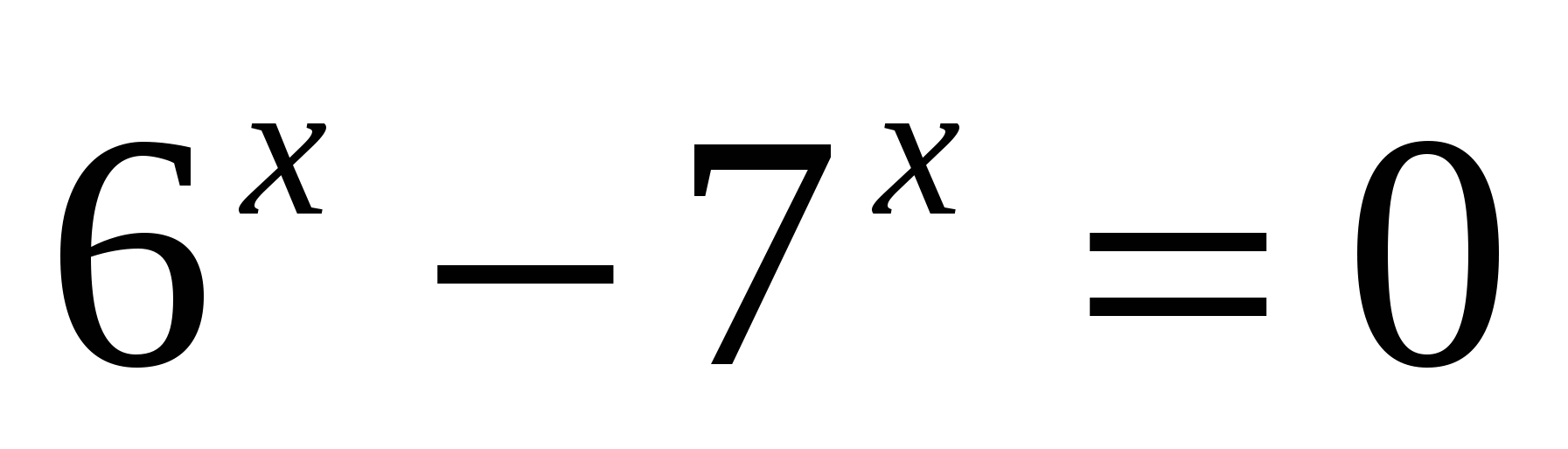
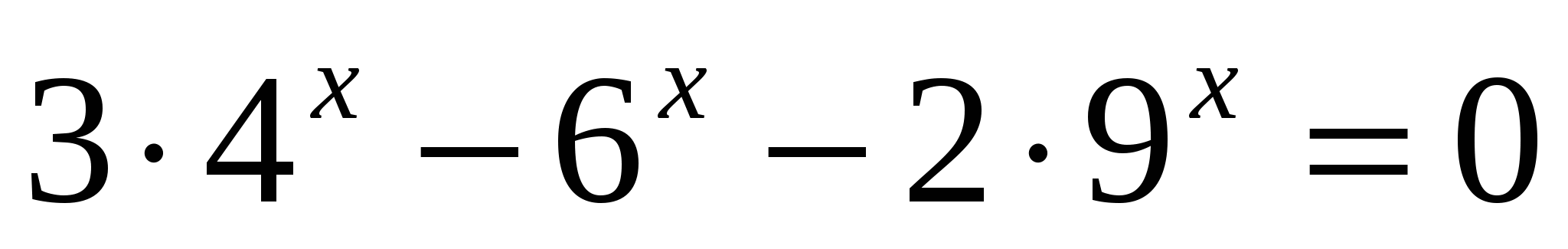
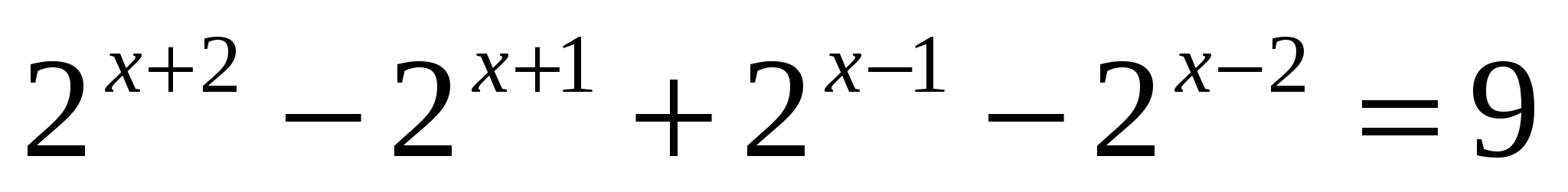
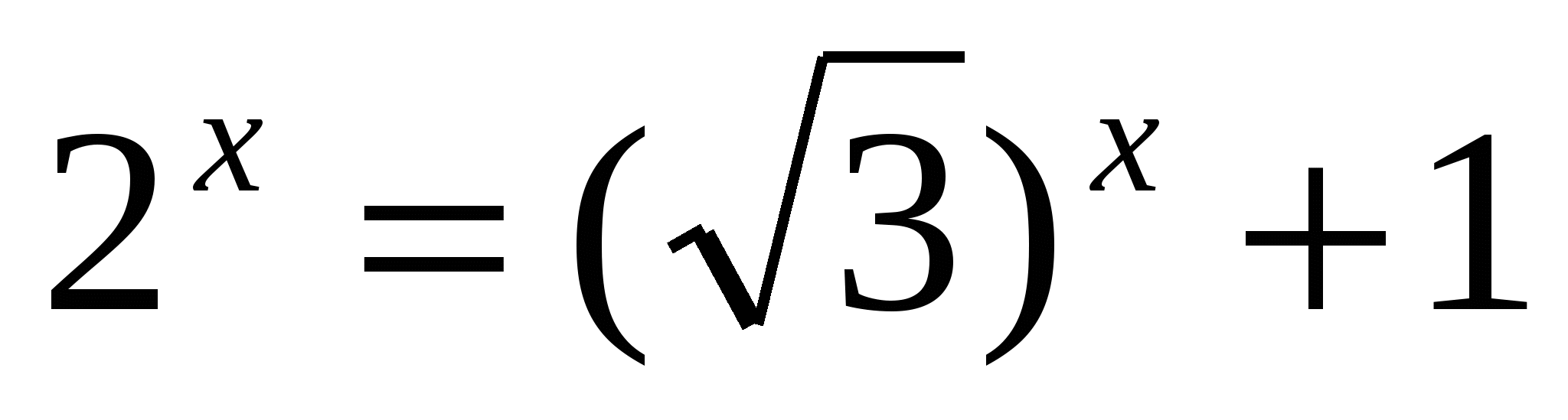
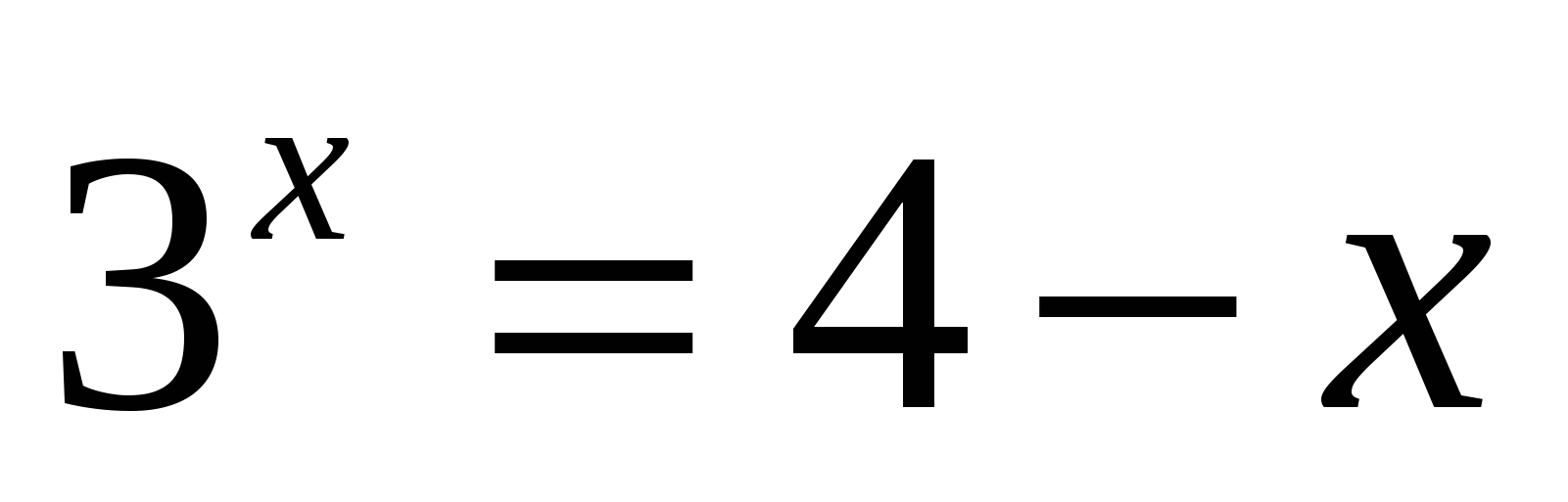
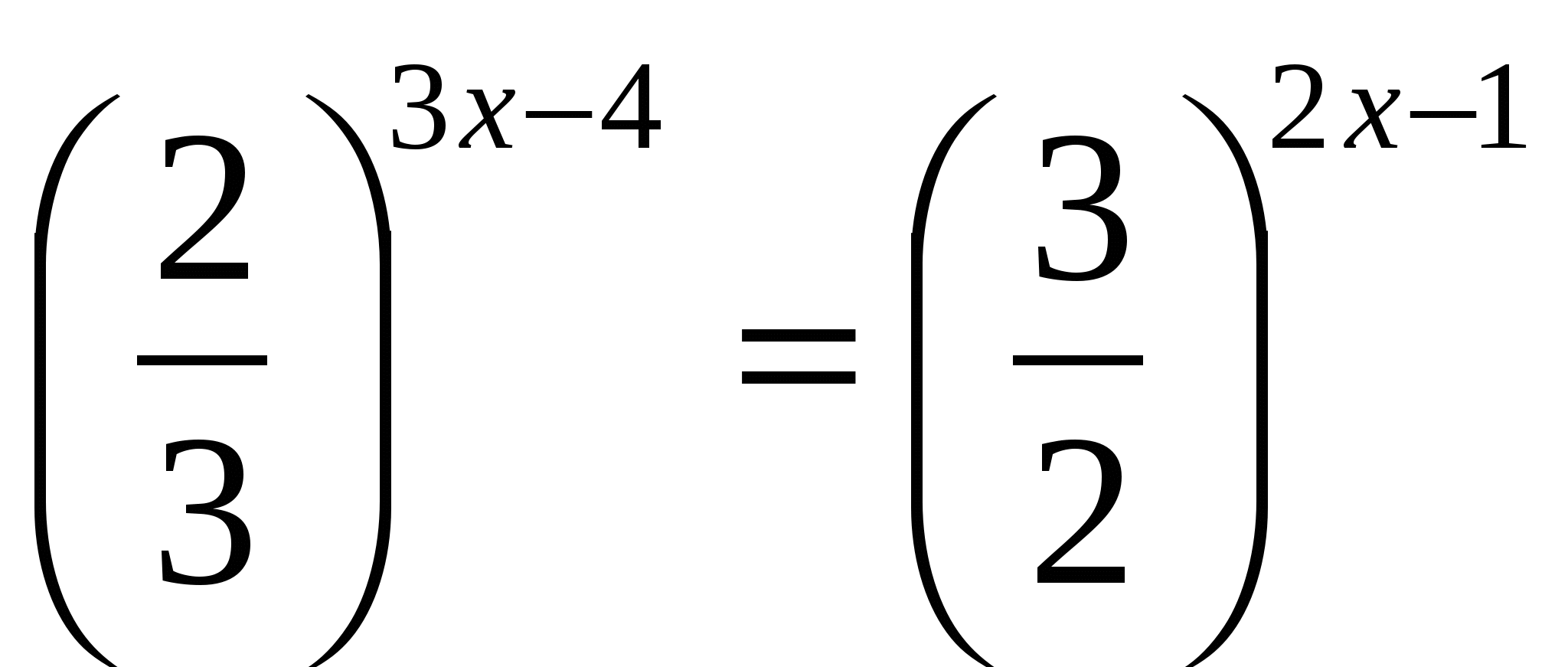

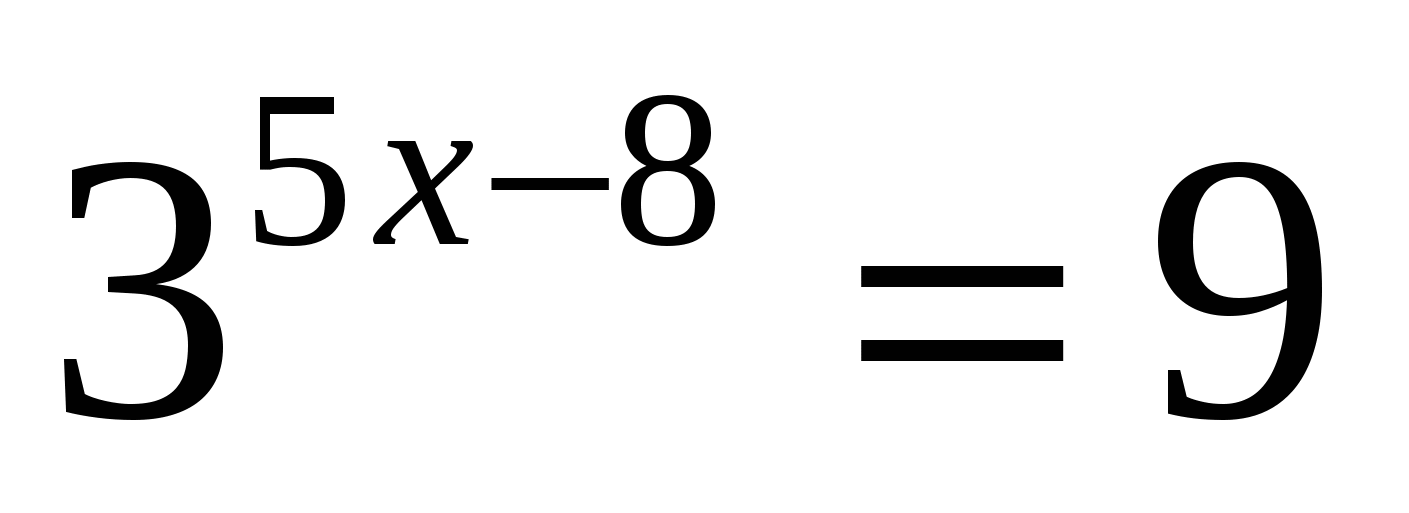
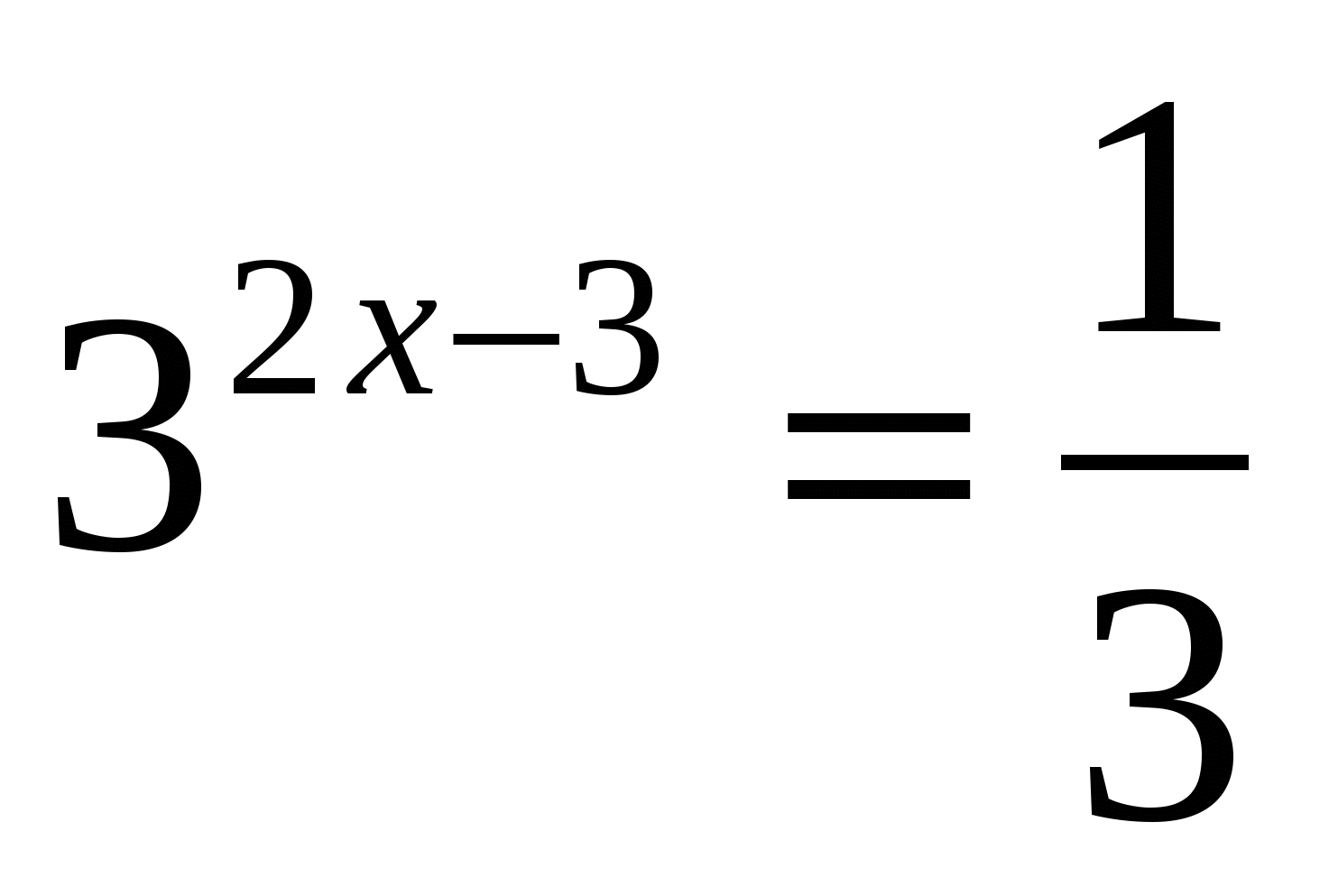 ;
; 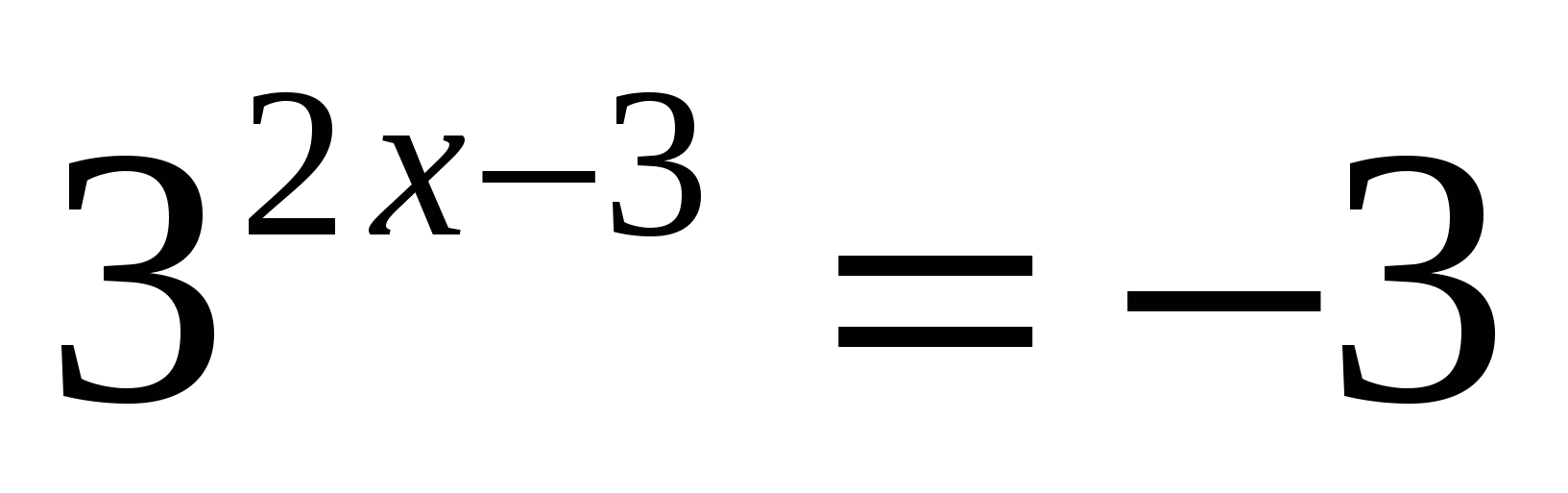 ;
; 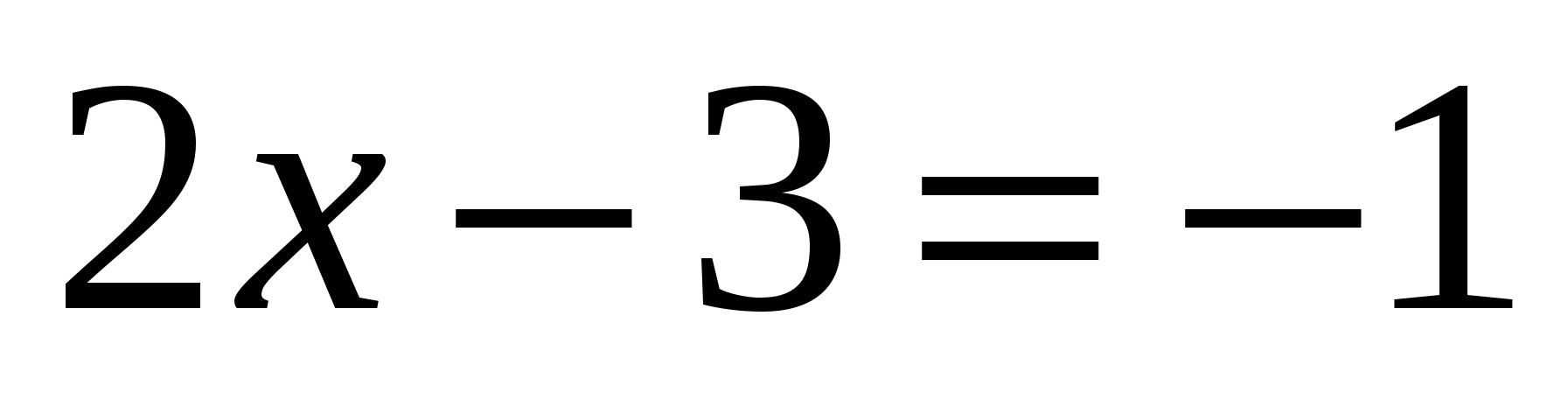 ;
; 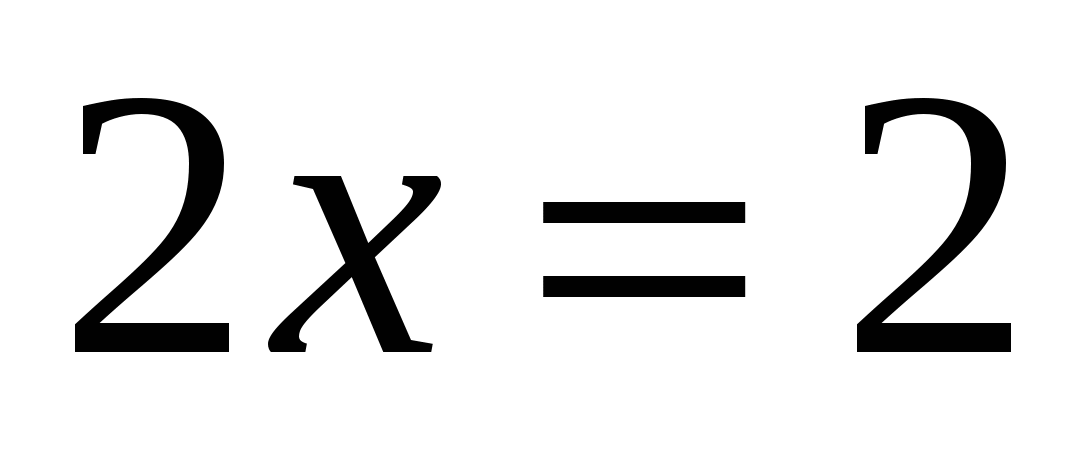 ;
; 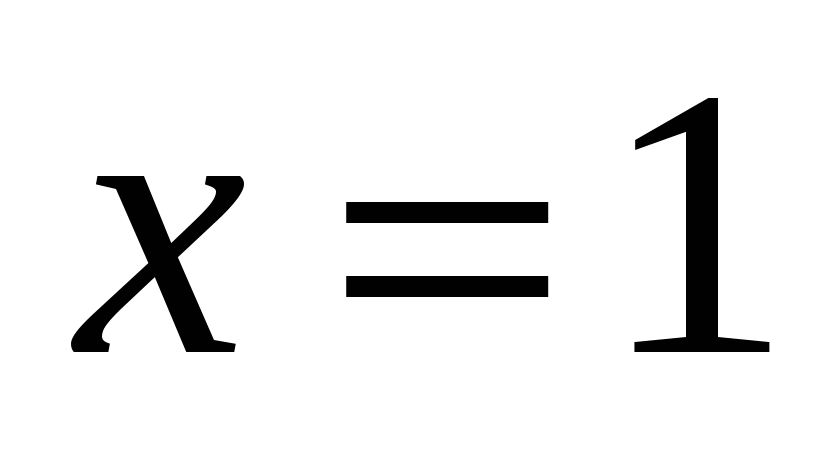
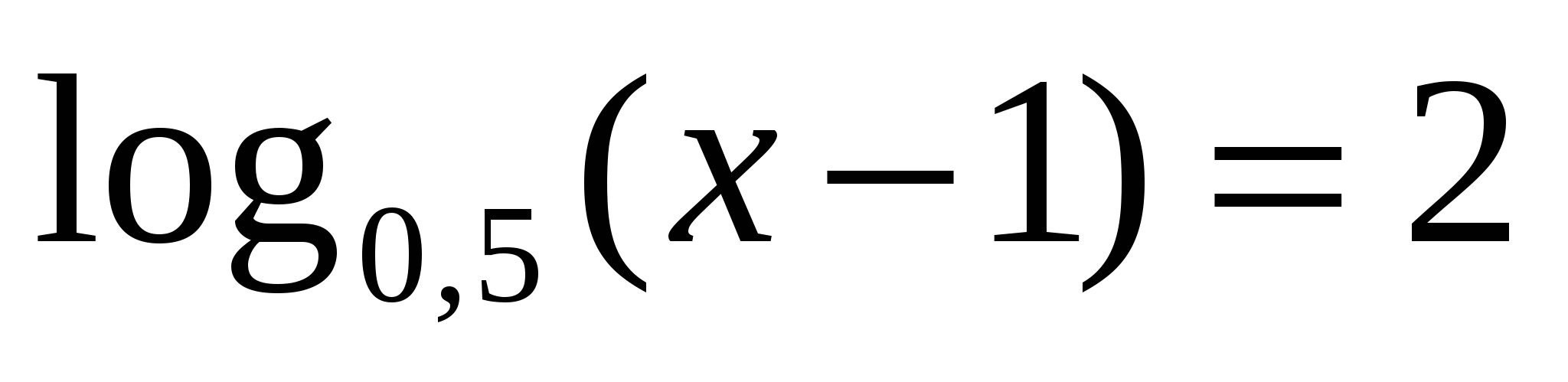
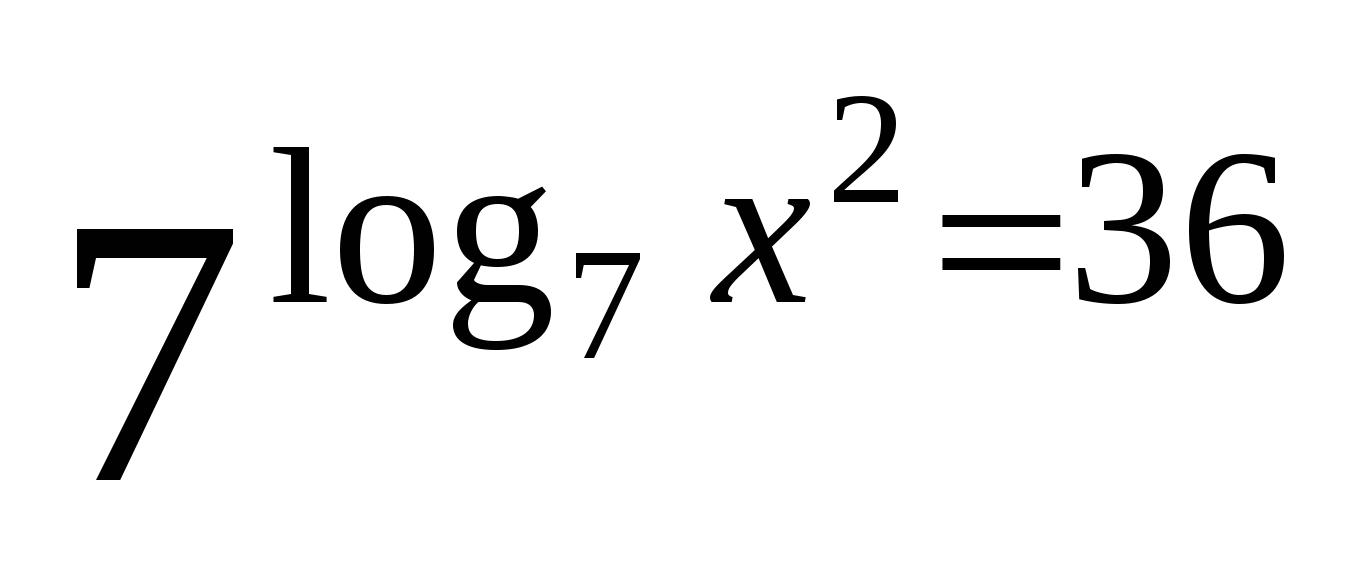
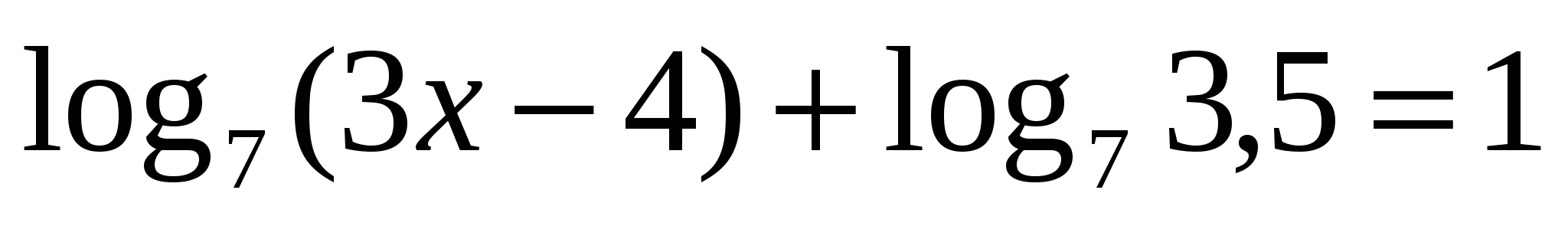
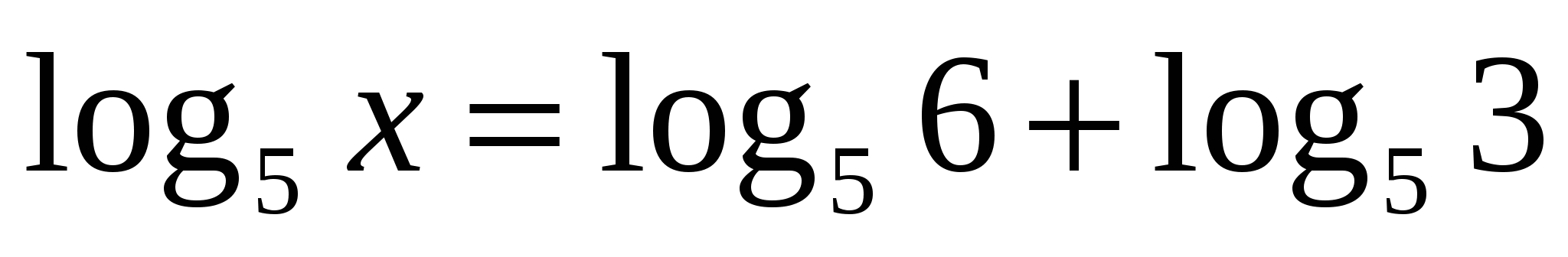
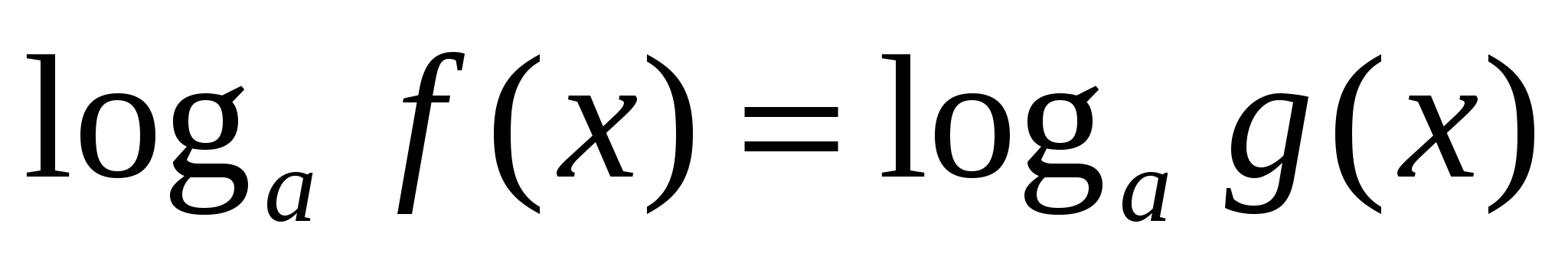 (метод потенцирования)
(метод потенцирования)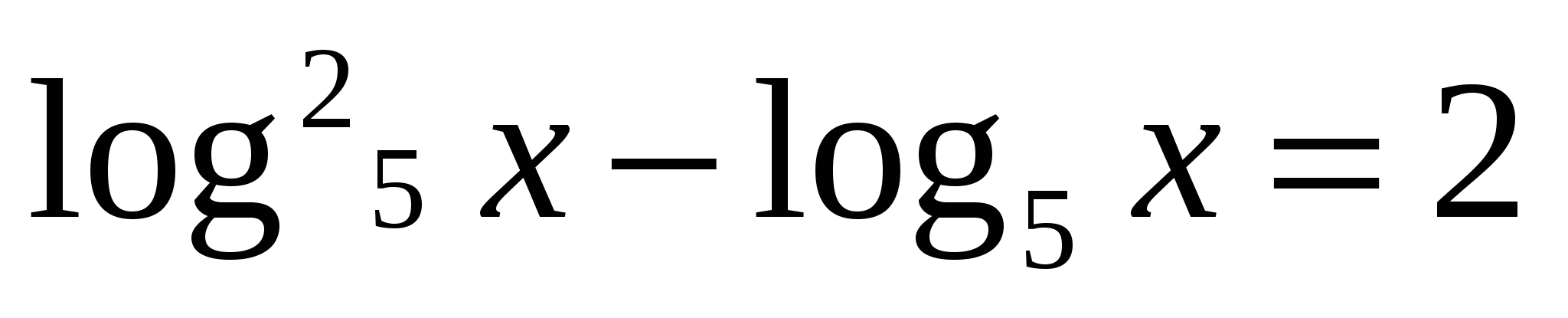
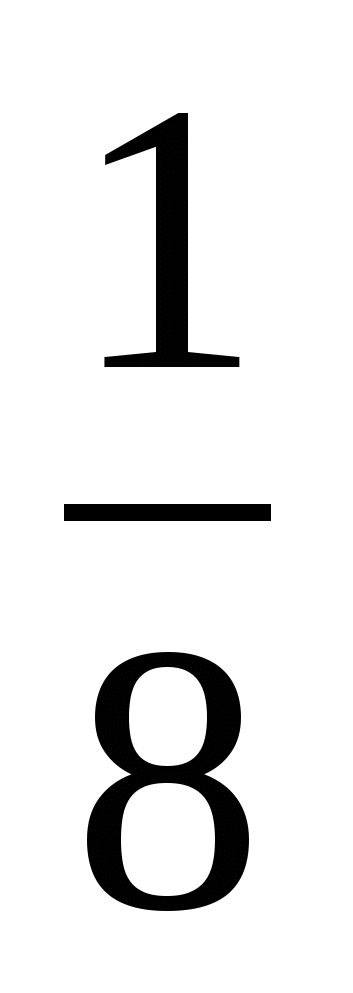
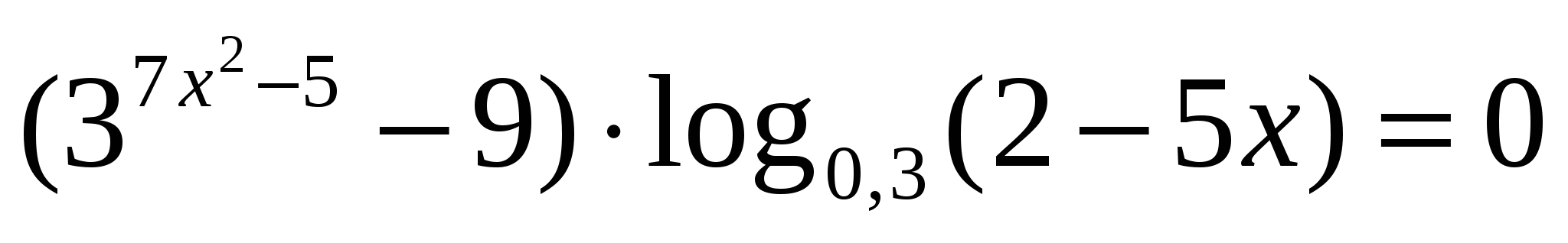
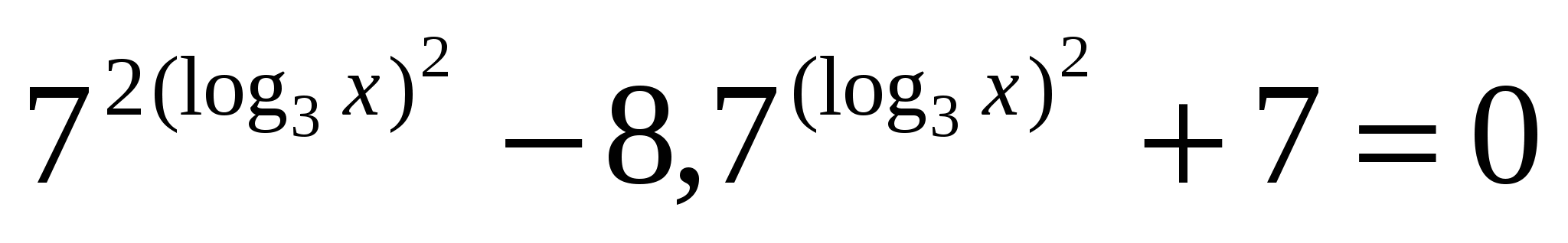
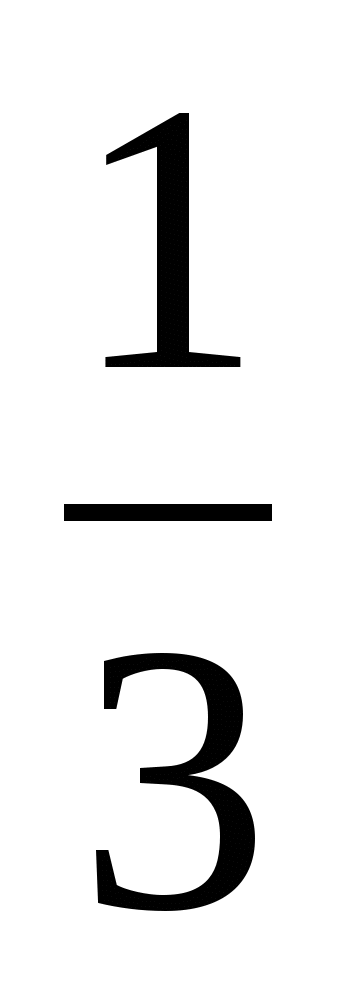 ; 3 произведение = 1
; 3 произведение = 1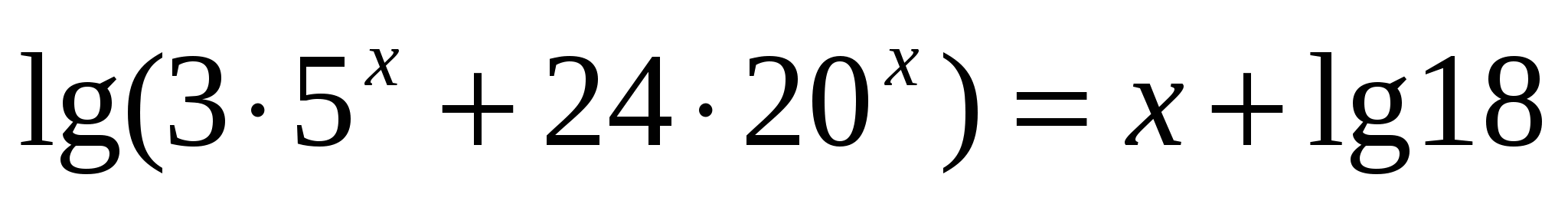
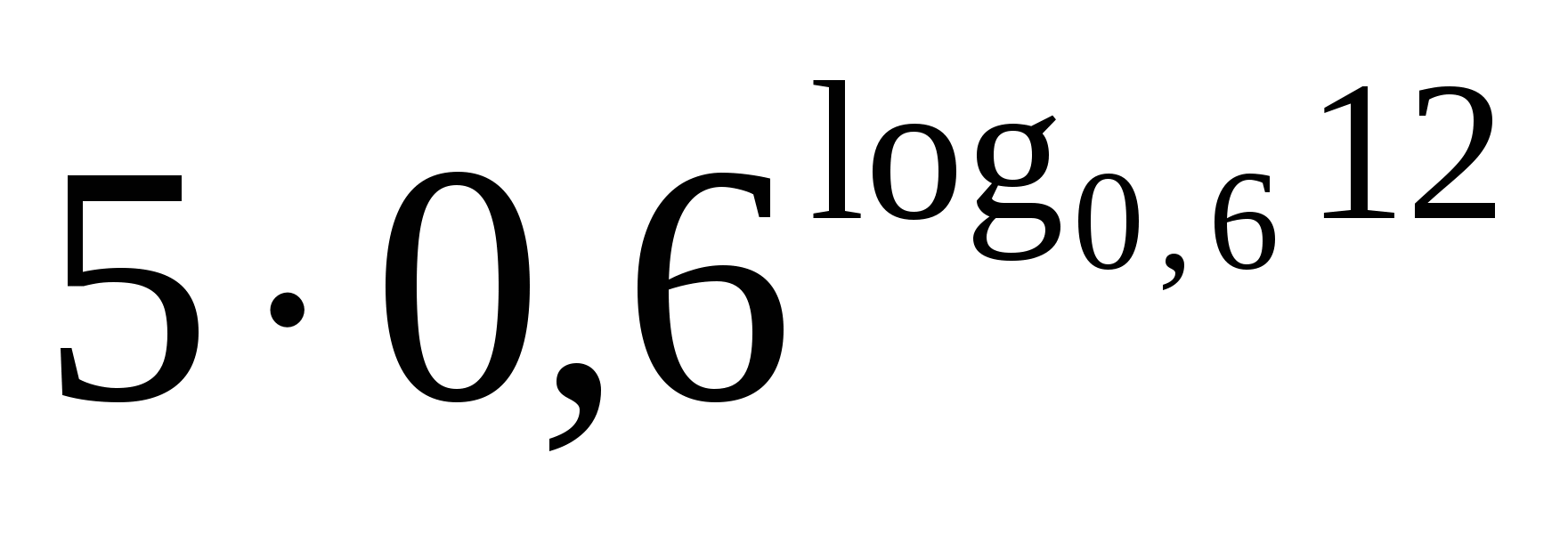
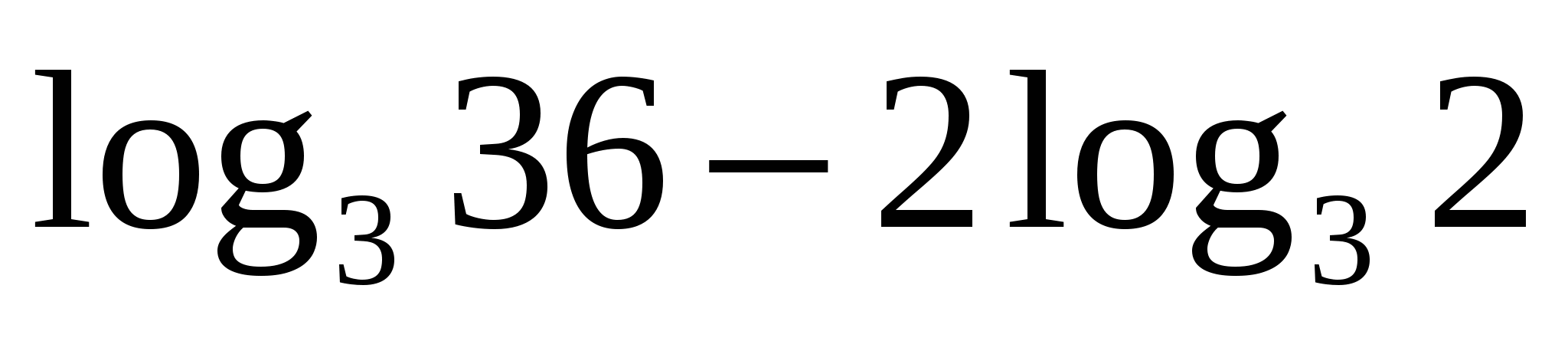
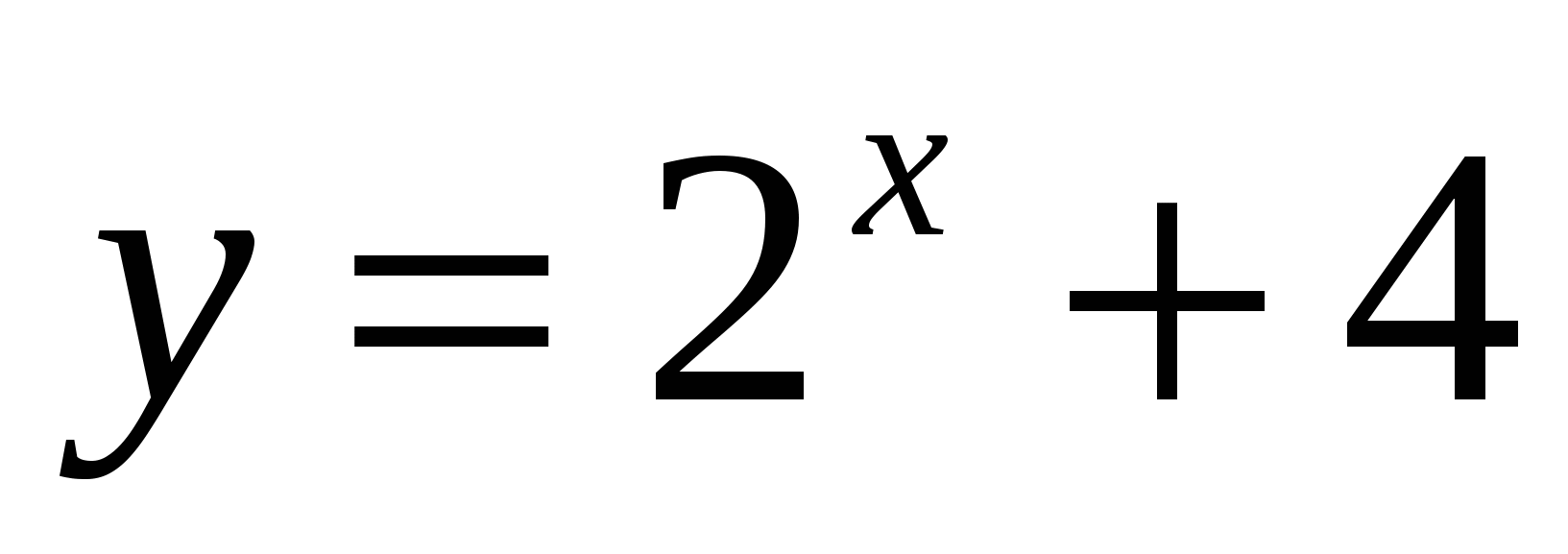
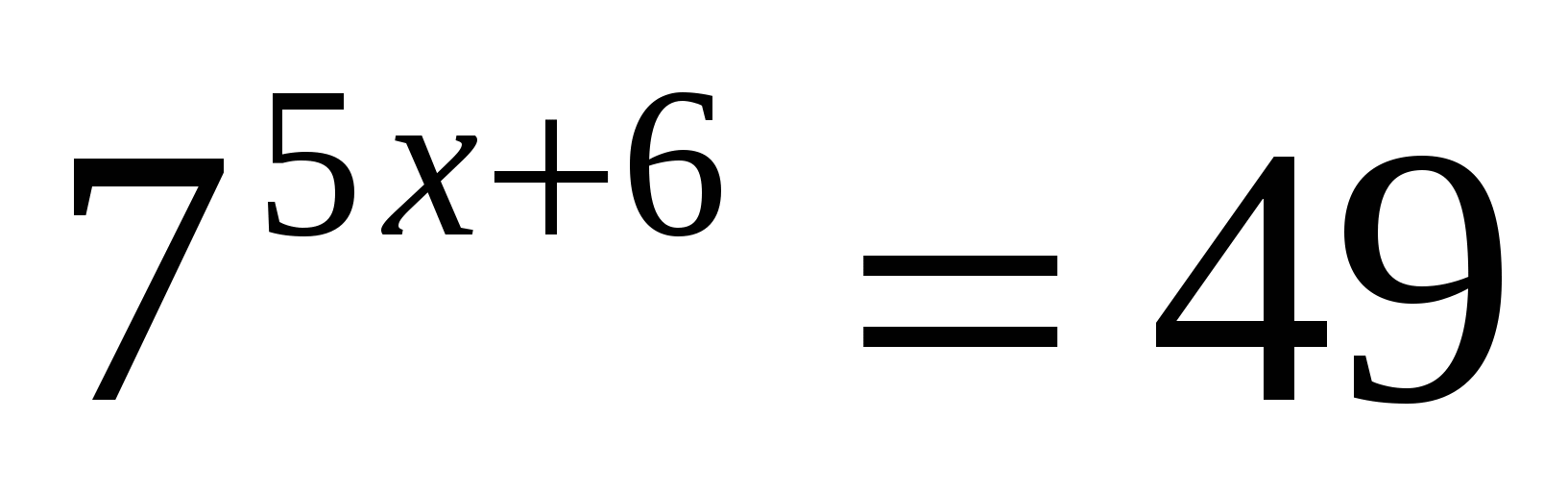

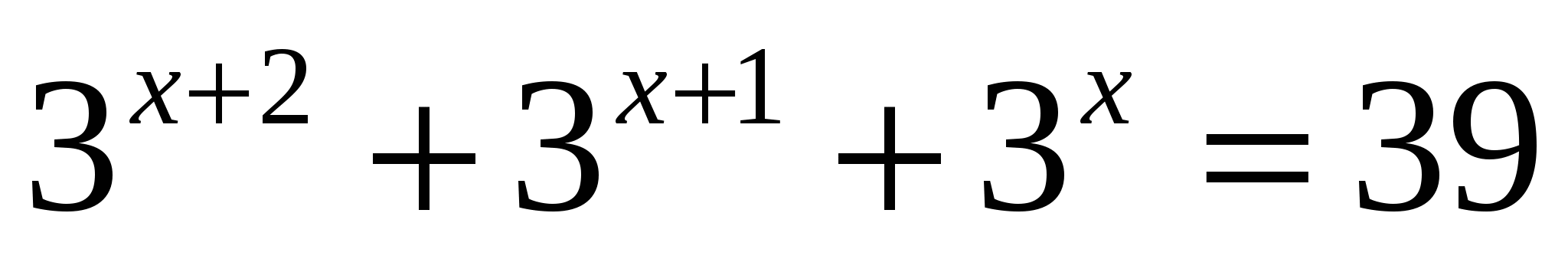
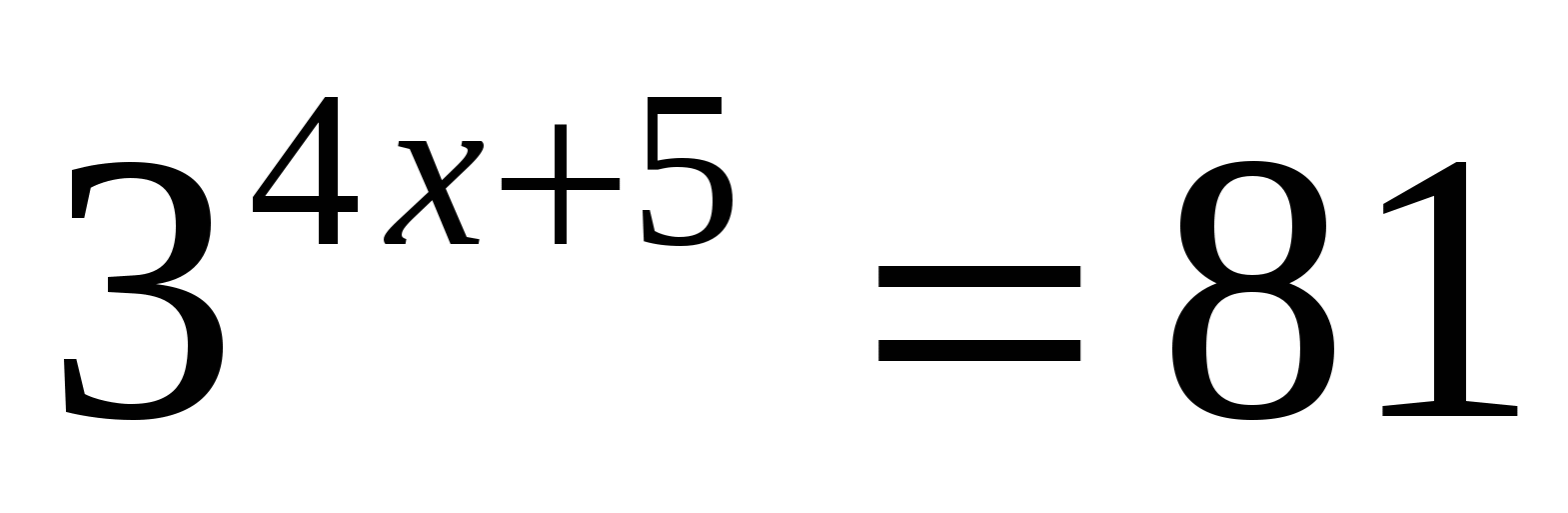
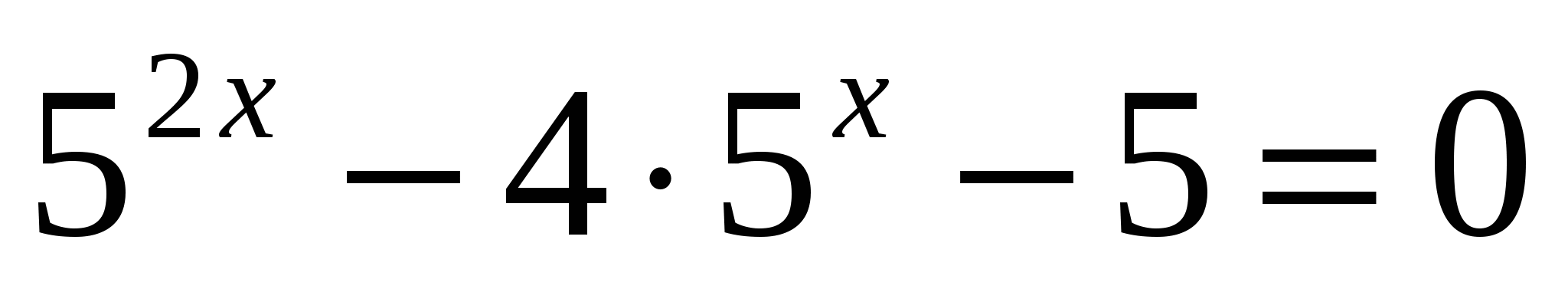
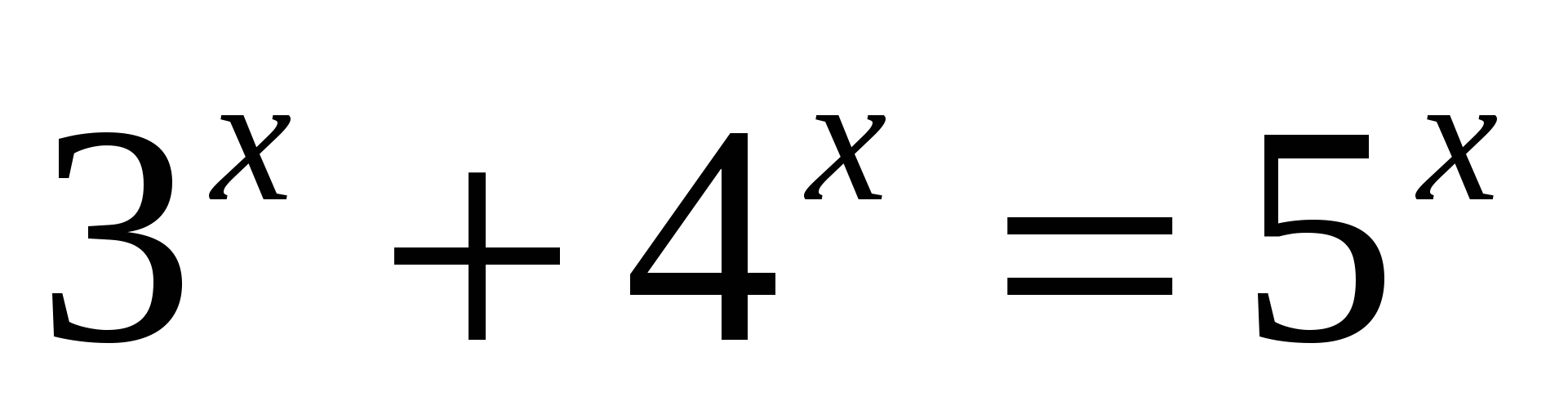
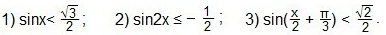
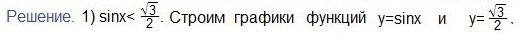

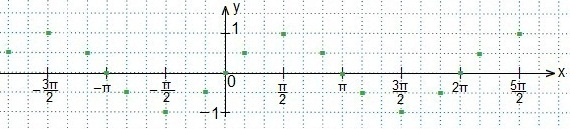
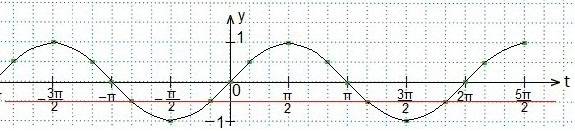
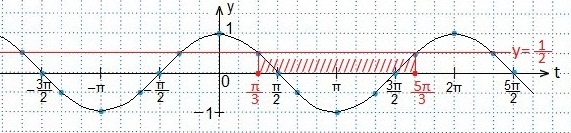
 Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду
Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду Проводим прямую.
Проводим прямую.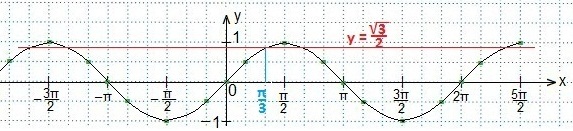
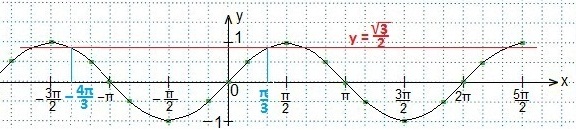


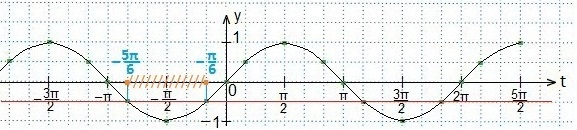
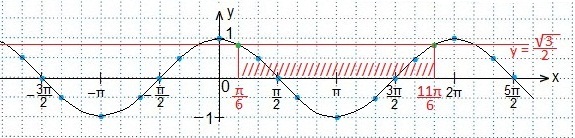
 Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.
Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.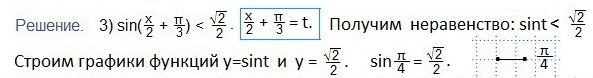
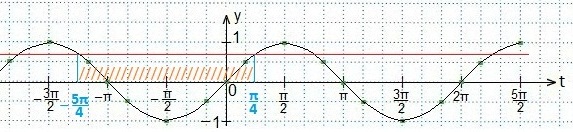
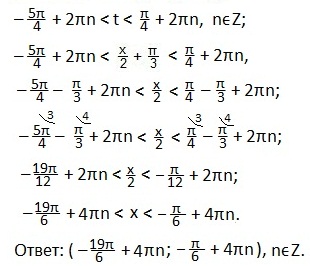 В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместоt подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.
В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместоt подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.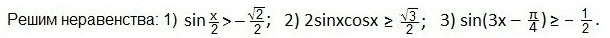
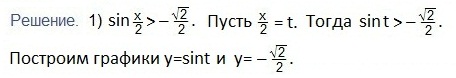
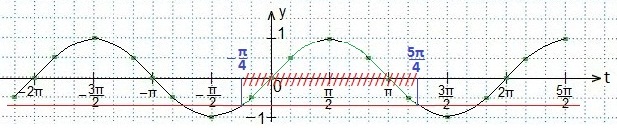
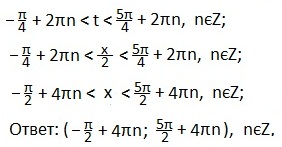

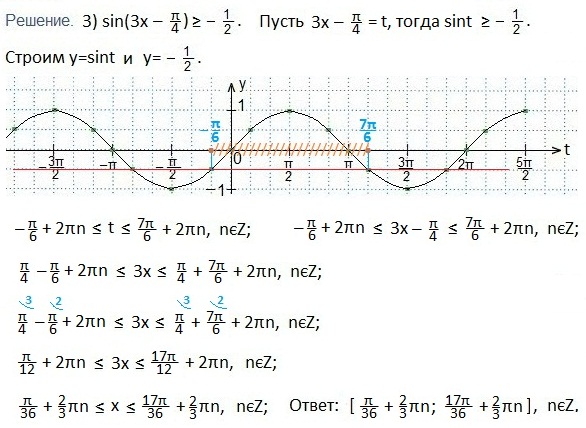
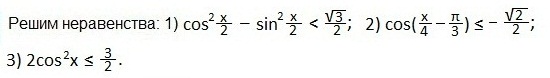
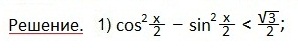

 а также свойствами: графиков четных функций, непрерывностью и периодичностью функции косинуса. Отмечаем точки:
а также свойствами: графиков четных функций, непрерывностью и периодичностью функции косинуса. Отмечаем точки: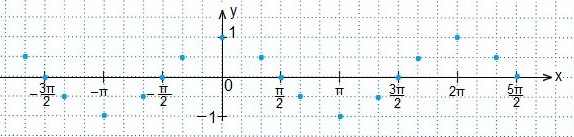
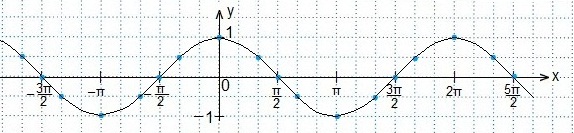

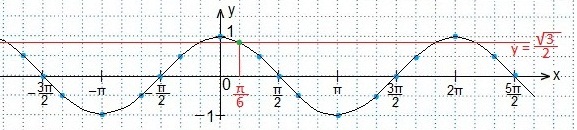
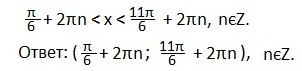


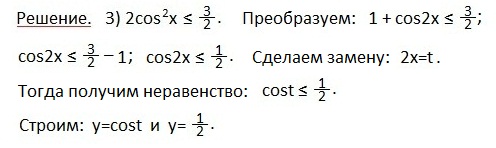
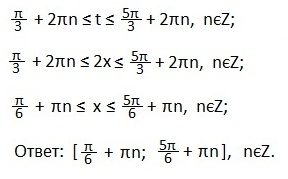


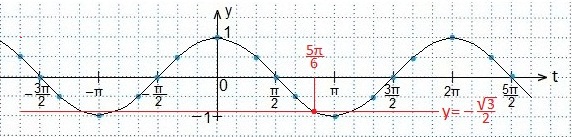
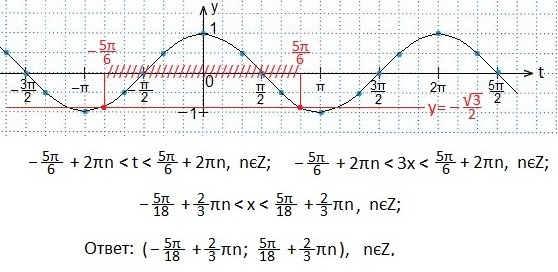
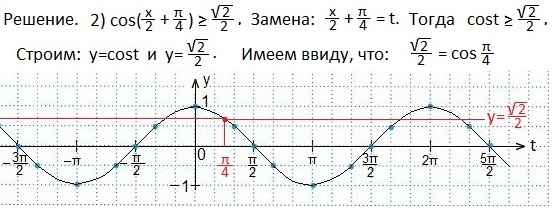
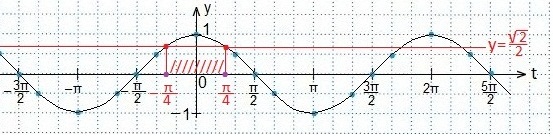
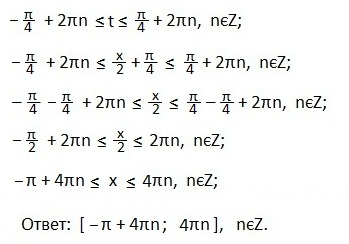


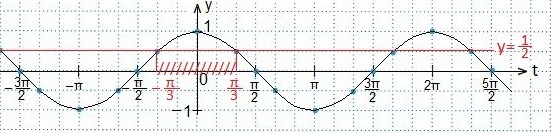

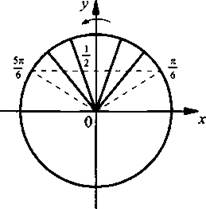
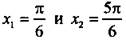 (углы откладываются против часовой стрелки и являются положительными). На рисунке видно, что неравенству sin х > 1/2 удовлетворяют значения
(углы откладываются против часовой стрелки и являются положительными). На рисунке видно, что неравенству sin х > 1/2 удовлетворяют значения  Учтем, что период функции синуса составляет 2π, и получим решение данного неравенства
Учтем, что период функции синуса составляет 2π, и получим решение данного неравенства 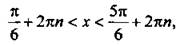 или
или 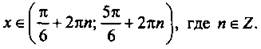
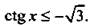
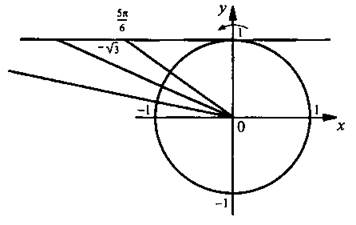
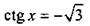 и построим соответствующий угол
и построим соответствующий угол 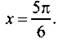 Видно, что неравенству
Видно, что неравенству 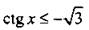 удовлетворяют значения
удовлетворяют значения 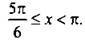 Учитывая период функции котангенса (равный π), получим решение данного неравенства:
Учитывая период функции котангенса (равный π), получим решение данного неравенства: 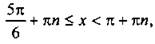 или
или  где n ∈ Z.
где n ∈ Z.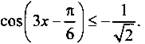
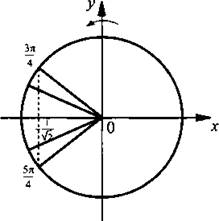
 и получим простейшее тригонометрическое неравенство
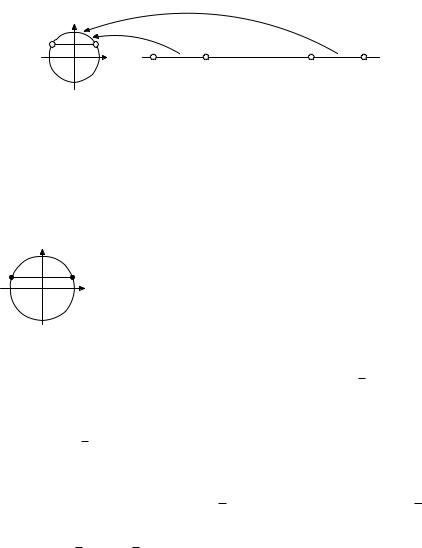
и получим простейшее тригонометрическое неравенство  Решим это неравенство. На единичной окружности по оси абсцисс отложим значение
Решим это неравенство. На единичной окружности по оси абсцисс отложим значение 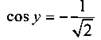 и построим соответствующие углы
и построим соответствующие углы 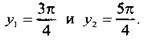 Тогда неравенству
Тогда неравенству 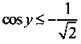 удовлетворяют значения
удовлетворяют значения 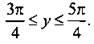 Учтем периодичность функции cos y и получим решения
Учтем периодичность функции cos y и получим решения 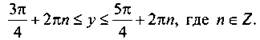
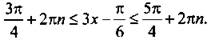 Ко всем частям неравенства прибавим число π/6. Отсюда
Ко всем частям неравенства прибавим число π/6. Отсюда 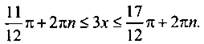 Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим:
Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим:  или
или 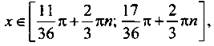 где n ∈ Z.
где n ∈ Z.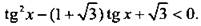
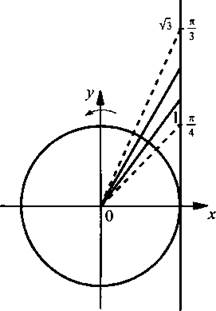
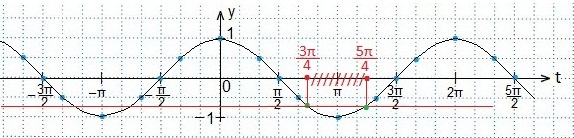
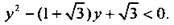 Это неравенство имеет решение
Это неравенство имеет решение 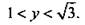 Вернемся к старой неизвестной x и получим двойное неравенство
Вернемся к старой неизвестной x и получим двойное неравенство 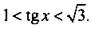 На единичной окружности по оси тангенсов отложим значения 1 и
На единичной окружности по оси тангенсов отложим значения 1 и 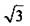 и построим соответствующие углы
и построим соответствующие углы 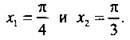 Тригонометрическому неравенству удовлетворяют значения
Тригонометрическому неравенству удовлетворяют значения 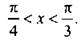 Учтем периодичность функции тангенса и получим решение данного неравенства:
Учтем периодичность функции тангенса и получим решение данного неравенства: 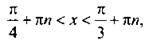 или
или 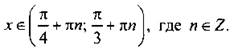
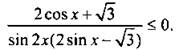
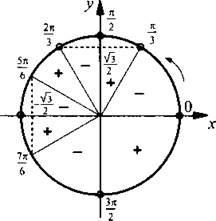
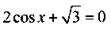 (откуда
(откуда  ) и знаменатель sin 2х = 0 (тогда
) и знаменатель sin 2х = 0 (тогда 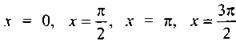 )
) 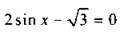 (откуда
(откуда 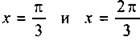 ) дроби. Определим знак этой дроби, например, при х = π/6 и получим:
) дроби. Определим знак этой дроби, например, при х = π/6 и получим:
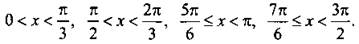 Учитывая, что через 2пn (где n ∈ Z) ситуация повторяется, выпишем решения данного неравенства:
Учитывая, что через 2пn (где n ∈ Z) ситуация повторяется, выпишем решения данного неравенства: 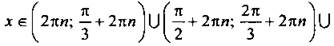
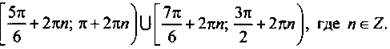
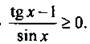
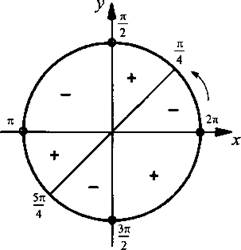
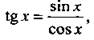 и запишем неравенство в виде
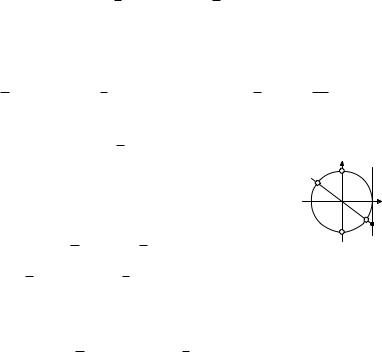
и запишем неравенство в виде 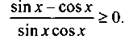 Отметим на единичной окружности значения х, при которых обращается в нуль числитель sin x – cos x = 0 (откуда
Отметим на единичной окружности значения х, при которых обращается в нуль числитель sin x – cos x = 0 (откуда 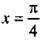 и
и 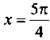 ) и знаменатель sin x cos x = 0 (тогда
) и знаменатель sin x cos x = 0 (тогда 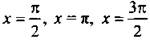 и x = 2π) дроби. Определим знак данной дроби, например, при х = π/3 и получим:
и x = 2π) дроби. Определим знак данной дроби, например, при х = π/3 и получим: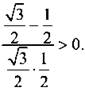
 где n ∈ Z.
где n ∈ Z.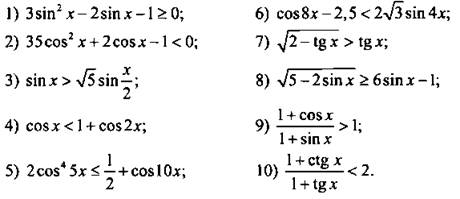
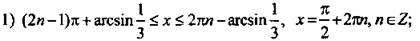

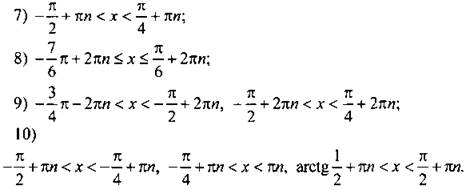



 ..
..

 Это правило применимо к British English, в American English L не удваивается.
Это правило применимо к British English, в American English L не удваивается.
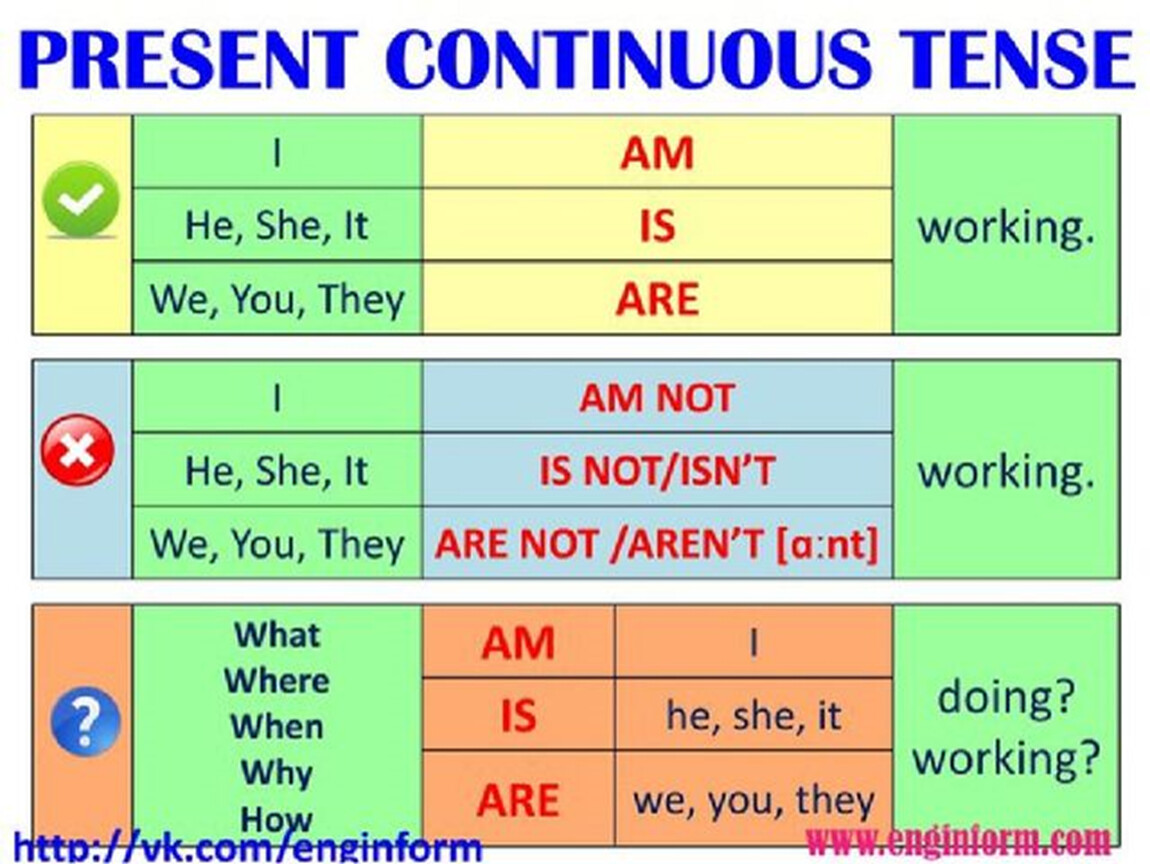
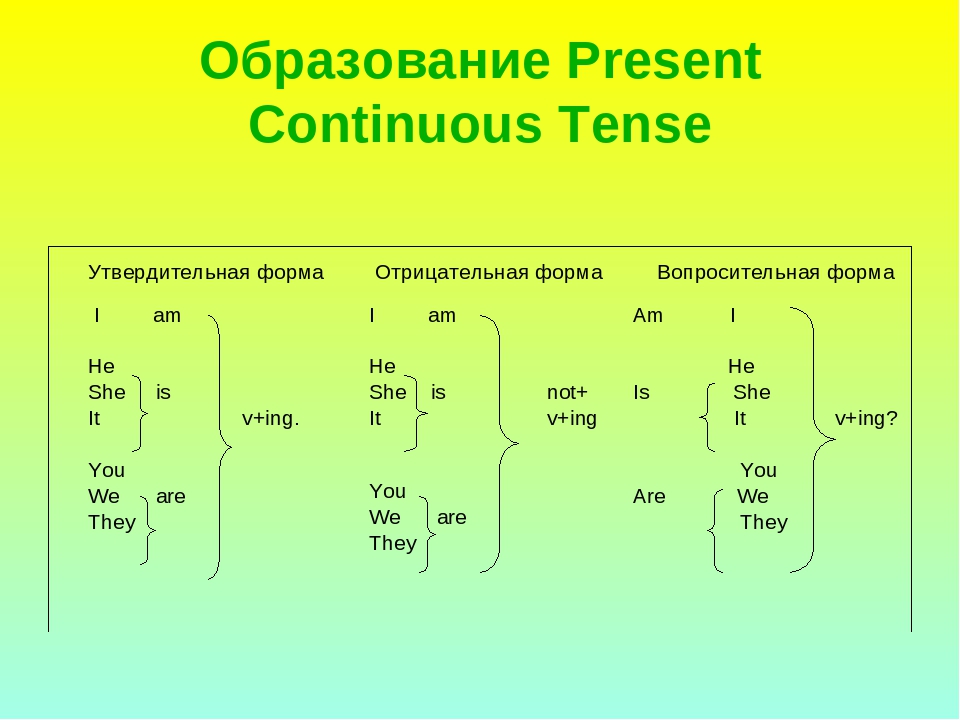
 Временные действия и состояния (Temporary actions and states)
Временные действия и состояния (Temporary actions and states) – В данное время она работает секретарем. (Это непостоянная занятость)
– В данное время она работает секретарем. (Это непостоянная занятость) Smith is leaving tomorrow at 11.00. – Мистер Смит уезжает завтра в 11.00.
Smith is leaving tomorrow at 11.00. – Мистер Смит уезжает завтра в 11.00.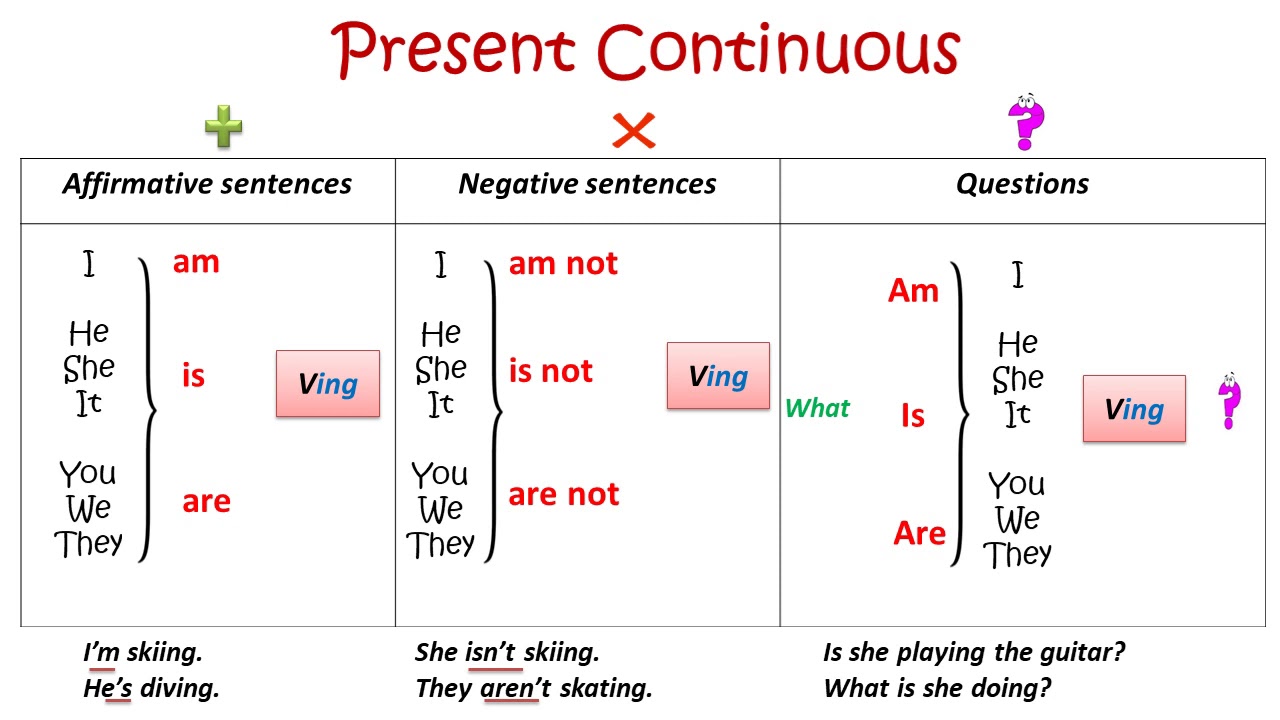 Часто повторяющиеся действия, чтобы передать раздражение или удивление (Annoying or surprising actions)
Часто повторяющиеся действия, чтобы передать раздражение или удивление (Annoying or surprising actions)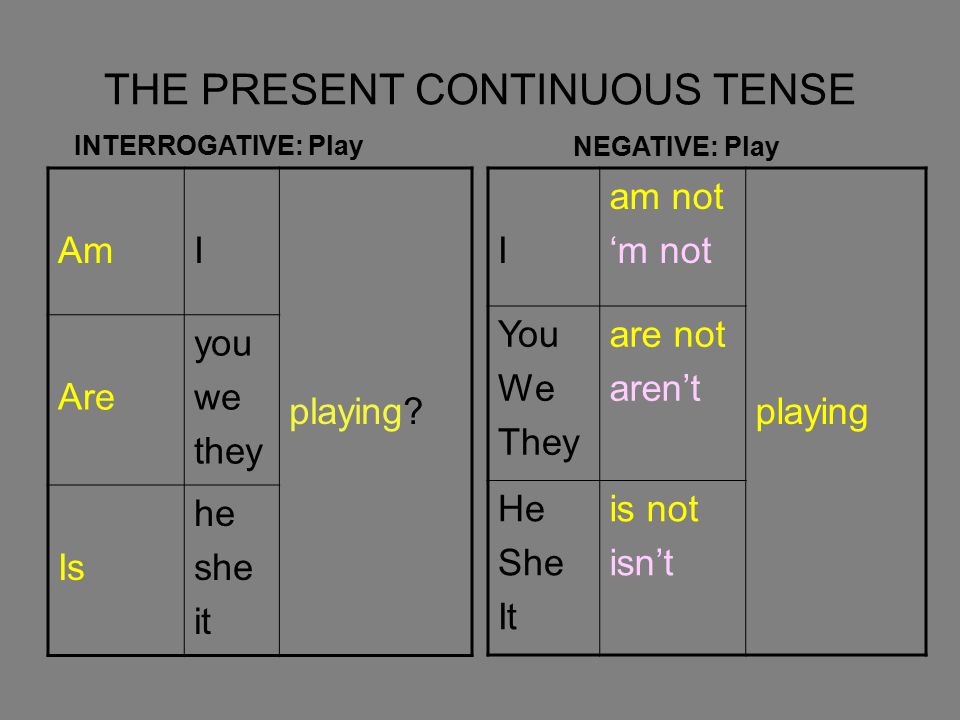
 — Я учу английский.
— Я учу английский. 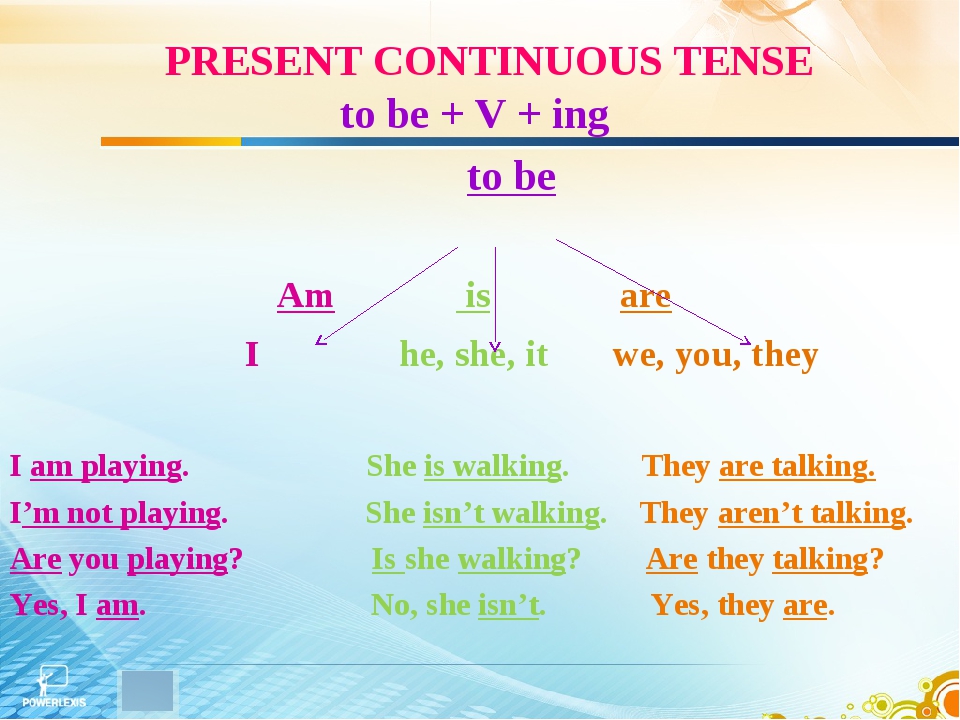 — Мэри всегда оставляет свои носки на полу.
— Мэри всегда оставляет свои носки на полу. Если вы хотите сказать или написать такое слово, скорее всего, все предложение будет в Present Continuous.
Если вы хотите сказать или написать такое слово, скорее всего, все предложение будет в Present Continuous.  По-английски они называются stative verbs. Они выражают мыслительные процессы, чувства — то, что происходит внутри нас.
По-английски они называются stative verbs. Они выражают мыслительные процессы, чувства — то, что происходит внутри нас. 
 — Боб собирается сделать предложение Мэри.
— Боб собирается сделать предложение Мэри.

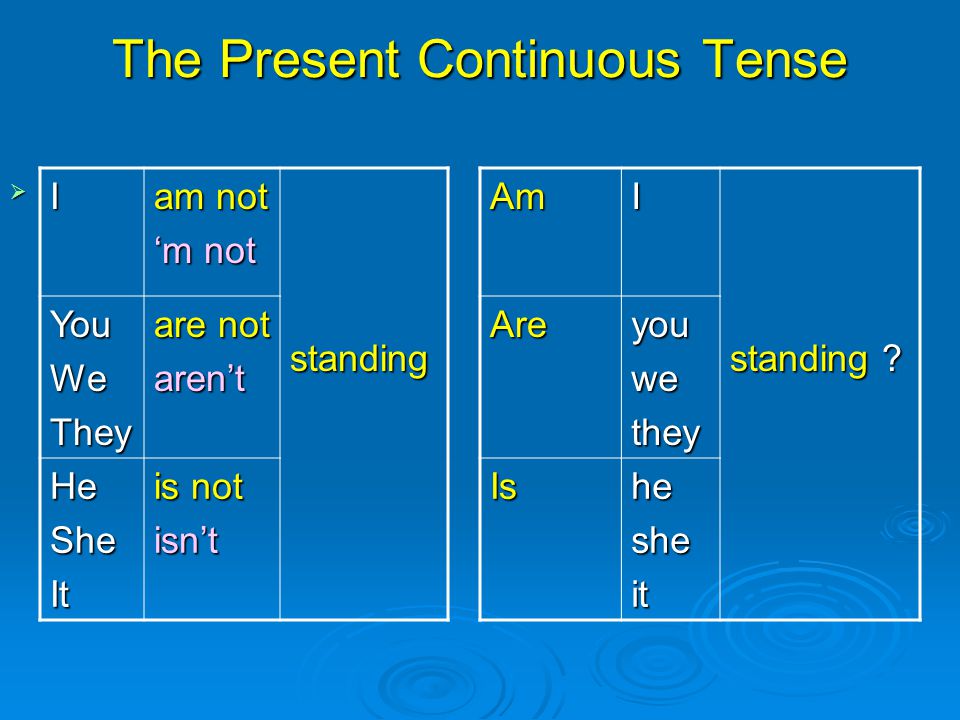 Правила образования -ing форм).
Правила образования -ing форм). п.). В таких предложениях, как правило, есть наречия always, constantly.
п.). В таких предложениях, как правило, есть наречия always, constantly. На этой неделе они едут в Лондон.
На этой неделе они едут в Лондон. В предыдущем уроке мы рассмотрели теорию довольно кратко: знание 4 правил поможет вам не совершить ошибок при выполнении упражнений. В конце урока даны ответы к упражнениям.
В предыдущем уроке мы рассмотрели теорию довольно кратко: знание 4 правил поможет вам не совершить ошибок при выполнении упражнений. В конце урока даны ответы к упражнениям. Напишите глаголы, от которых образованы данные причастия. Переведите их на русский язык.
Напишите глаголы, от которых образованы данные причастия. Переведите их на русский язык.
 Переделайте предложения так, чтобы глаголы стояли в Present Continuous. Каждый раз добавляйте слово подсказку now или at the moment.
Переделайте предложения так, чтобы глаголы стояли в Present Continuous. Каждый раз добавляйте слово подсказку now или at the moment. I am not listening to the radio now.
I am not listening to the radio now.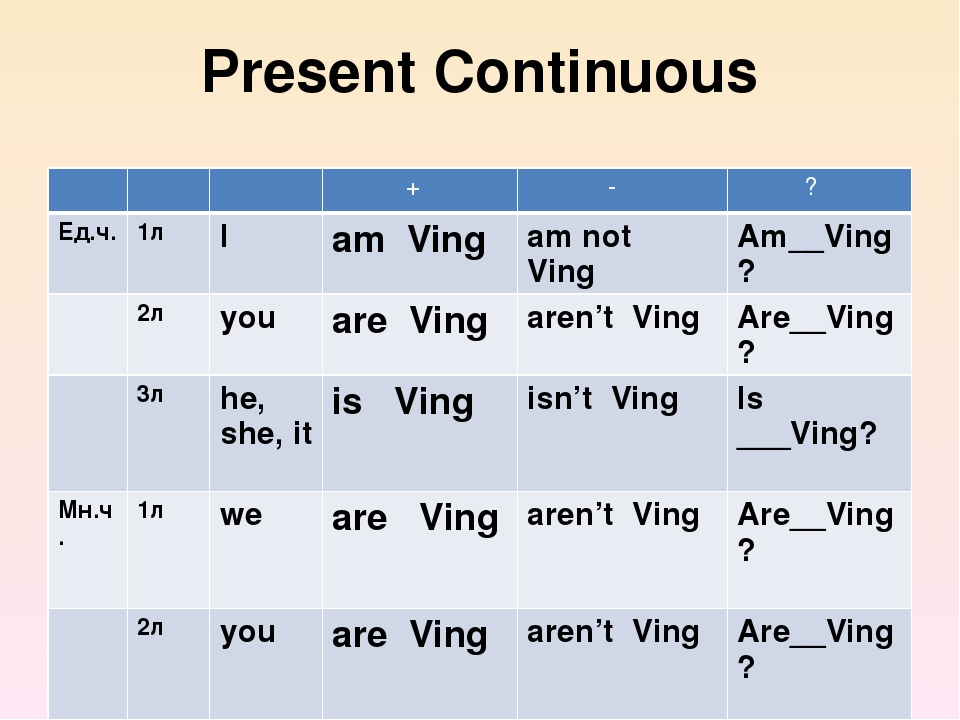 7. Richard and Henry … (not swim) in the river in summer. 8. He … (not have) tea for breakfast. 9. She … (not make) a cake. 10. Kate … (not dance) now.
7. Richard and Henry … (not swim) in the river in summer. 8. He … (not have) tea for breakfast. 9. She … (not make) a cake. 10. Kate … (not dance) now.
 crying/girl/why/is/this
crying/girl/why/is/this
 Опишите картинку. Используйте слова и выражения:
Опишите картинку. Используйте слова и выражения:  За окном
За окном
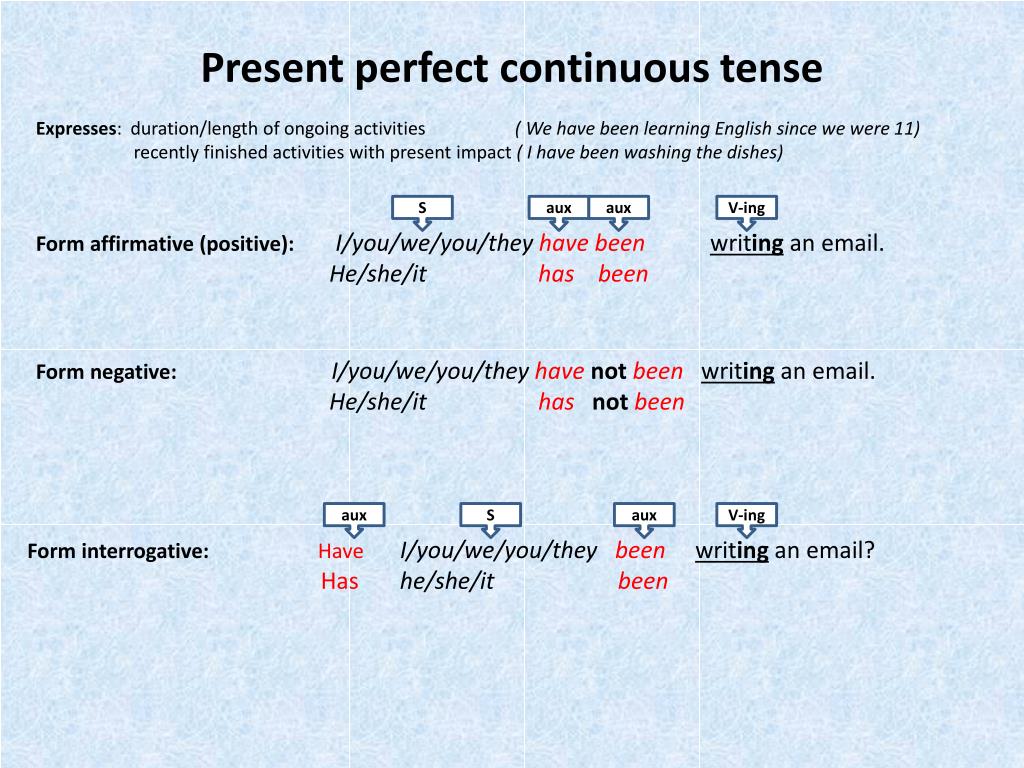



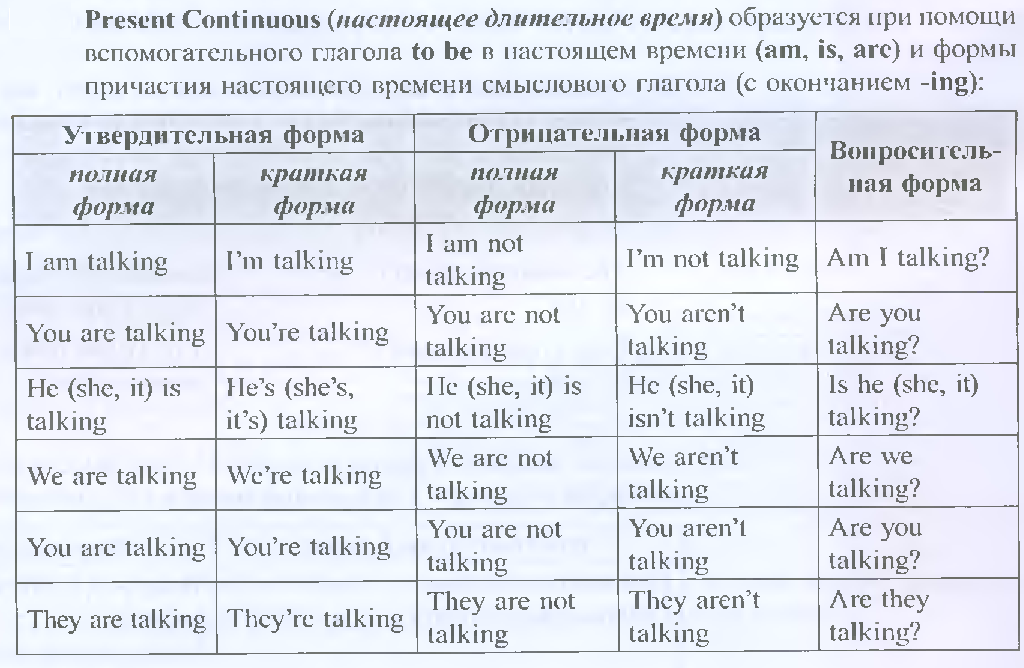 Достаточно просто взять любой глагол в форме инфинитива, убрать предлог to и добавить окончание –ing.
Достаточно просто взять любой глагол в форме инфинитива, убрать предлог to и добавить окончание –ing. В таком случае применяется стандартное правило:
В таком случае применяется стандартное правило:
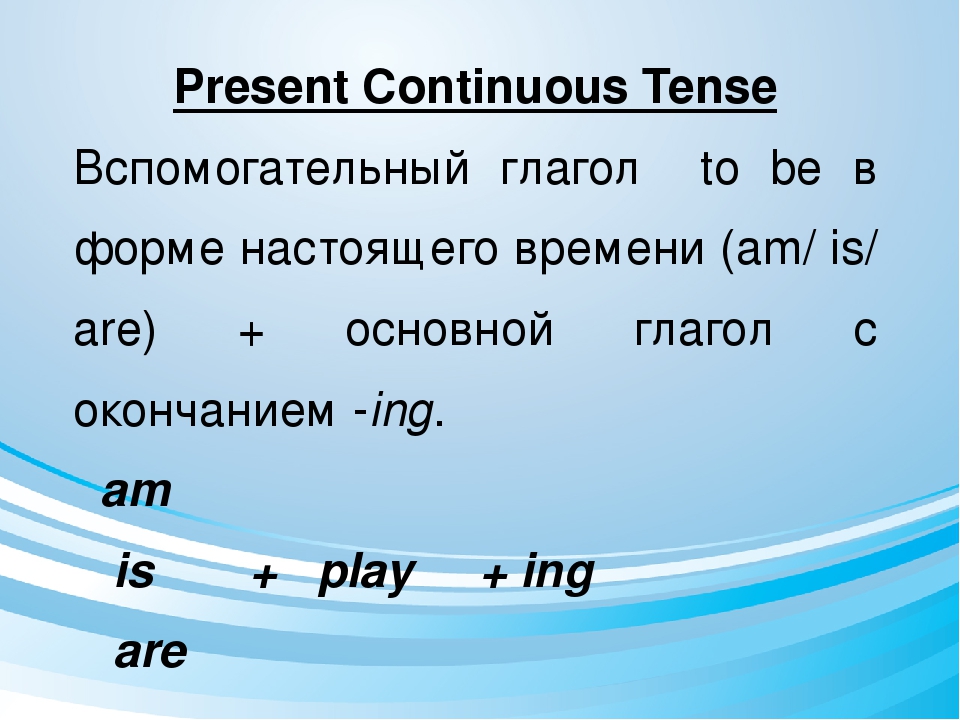 Схема утвердительного предложения:
Схема утвердительного предложения: Он содержит две формы образования, выбор которых зависит от правильности или неправильности английских глаголов.
Он содержит две формы образования, выбор которых зависит от правильности или неправильности английских глаголов.

 / No, it isn’t.
/ No, it isn’t.
 Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!








 Профессия зародилась в XI веке, именно тогда появились сёстры милосердия, которые изначально помогали женщинам, а потом и мужчинам. А в XVII веке в медицинских сёстрах возникла острая необходимость. Именно тогда велись многочисленные войны, было много раненых, которым нужно было оказывать первую помощь и ухаживать после тяжёлых операций.
Профессия зародилась в XI веке, именно тогда появились сёстры милосердия, которые изначально помогали женщинам, а потом и мужчинам. А в XVII веке в медицинских сёстрах возникла острая необходимость. Именно тогда велись многочисленные войны, было много раненых, которым нужно было оказывать первую помощь и ухаживать после тяжёлых операций.  В Российской империи медсёстры появились по инициативе русского хирурга Н. Пирогова во время Севастопольской войны 1854 года. Это были девушки дворянского происхождения.
В Российской империи медсёстры появились по инициативе русского хирурга Н. Пирогова во время Севастопольской войны 1854 года. Это были девушки дворянского происхождения. 

 Моя профессия – медицинская сестра
Моя профессия – медицинская сестра
 Живым примером является сериал «Интерны»
Живым примером является сериал «Интерны» В этом сериале осуждается коррупция и невежество медработников.
В этом сериале осуждается коррупция и невежество медработников. Мы порой забываем, кому обязаны, может быть, не всем, но точно многим
Мы порой забываем, кому обязаны, может быть, не всем, но точно многим Ведь на их руках мы впервые видим мир
Ведь на их руках мы впервые видим мир От их прикосновений мы делаем первый вздох
От их прикосновений мы делаем первый вздох Они всегда борются за нашу жизнь порой сильней чем мы сами
Они всегда борются за нашу жизнь порой сильней чем мы сами Медсестра – это душа, прежде всего. Ярчайший пример тому – Флоренс Найтингейл, англичанка, которая во времена Крымской войны стала основательницей службы сестер милосердия. Она руководила женщинами, оказывающими помощь раненым солдатам. Этой великой женщиной были собраны пожертвования для создания школы медсестер, впоследствии открытой при госпитале Сент -Томас (Лондон). Не случайно россияне отмечают Всемирный день медсестры 12 мая – именно тогда родилась Флоренс. Также эта дата – день создания профессиональной организации сестрами милосердия из разных стран мира.
Медсестра – это душа, прежде всего. Ярчайший пример тому – Флоренс Найтингейл, англичанка, которая во времена Крымской войны стала основательницей службы сестер милосердия. Она руководила женщинами, оказывающими помощь раненым солдатам. Этой великой женщиной были собраны пожертвования для создания школы медсестер, впоследствии открытой при госпитале Сент -Томас (Лондон). Не случайно россияне отмечают Всемирный день медсестры 12 мая – именно тогда родилась Флоренс. Также эта дата – день создания профессиональной организации сестрами милосердия из разных стран мира. Нынешнее общество не возможно представить без медработников. Может и есть плохие врачи, грубые медсестры, но они составляют малую часть от тех людей которые действительно являются Медработниками с большой буквы.
Нынешнее общество не возможно представить без медработников. Может и есть плохие врачи, грубые медсестры, но они составляют малую часть от тех людей которые действительно являются Медработниками с большой буквы. Она находится чуть в тени лечащего врача. На полшага поодаль по своему статусу, но эта дистанция сокращает расстояние между ней и больным. Она медицинская сестра. И в деле выхаживания больного она — главная.
Она находится чуть в тени лечащего врача. На полшага поодаль по своему статусу, но эта дистанция сокращает расстояние между ней и больным. Она медицинская сестра. И в деле выхаживания больного она — главная. Какими же качествами, должна обладать медицинская сестра: Прежде всего — трудолюбием. Чистотой, внешней и внутренней, скромностью. Уметь сочувствовать чужому горю. Медсестра обязана вести себя так, чтобы больной мог довериться ей полностью, не стесняясь любой манипуляции и процедуры. На работе она должна уметь забыть о себе, о своих домашних заботах и проблемах, всегда быть рядом с больным. В процессе излечения, на мой взгляд, одинаково важны все звенья, и если дело врача лечить патологию, то медсестры помочь пациенту психологически справиться с болезнью. Эта профессия на самом деле тяжёлый труд, но когда ты видишь лица счастливых выписывающихся пациентов — это большая радость!
Какими же качествами, должна обладать медицинская сестра: Прежде всего — трудолюбием. Чистотой, внешней и внутренней, скромностью. Уметь сочувствовать чужому горю. Медсестра обязана вести себя так, чтобы больной мог довериться ей полностью, не стесняясь любой манипуляции и процедуры. На работе она должна уметь забыть о себе, о своих домашних заботах и проблемах, всегда быть рядом с больным. В процессе излечения, на мой взгляд, одинаково важны все звенья, и если дело врача лечить патологию, то медсестры помочь пациенту психологически справиться с болезнью. Эта профессия на самом деле тяжёлый труд, но когда ты видишь лица счастливых выписывающихся пациентов — это большая радость! Детские мечты Говорят – мысли материальны, и то человек чаще всего проговаривает о чем мечтает, обязательно сбывается. Каждый раз, видя медсестру или доктора в белоснежном халате, я представляла себя в их образе, в образе медсестры – волшебницы, спасающей людей. Да, мысли материальны, теперь я знаю точно, потому что в скором будущем моя детская мечта сбудется и я стану медицинской сестрой. И пусть я буду не волшебницей из детских грез, но обязательно буду помогать людям!
Детские мечты Говорят – мысли материальны, и то человек чаще всего проговаривает о чем мечтает, обязательно сбывается. Каждый раз, видя медсестру или доктора в белоснежном халате, я представляла себя в их образе, в образе медсестры – волшебницы, спасающей людей. Да, мысли материальны, теперь я знаю точно, потому что в скором будущем моя детская мечта сбудется и я стану медицинской сестрой. И пусть я буду не волшебницей из детских грез, но обязательно буду помогать людям! Почему я хочу выбрать профессию медсестры Во-первых, хочу помогать людям. Когда лежишь в больнице, всегда не хватает тепла, участия, ласковых слов. Медсестра больше с больными, чем врач, и она может утешить больного. Во-вторых, мне самой она пригодится в жизни. Когда у меня будет семья, дети, я смогу оказать им самую элементарную медицинскую помощь. Смогу квалифицированно ухаживать за своими родителями ведь они тоже когда нибудь состарятся. В целом для каждого из нас очень важны специалисты, которые ответственны за нашу с вами жизнь – медики.
Почему я хочу выбрать профессию медсестры Во-первых, хочу помогать людям. Когда лежишь в больнице, всегда не хватает тепла, участия, ласковых слов. Медсестра больше с больными, чем врач, и она может утешить больного. Во-вторых, мне самой она пригодится в жизни. Когда у меня будет семья, дети, я смогу оказать им самую элементарную медицинскую помощь. Смогу квалифицированно ухаживать за своими родителями ведь они тоже когда нибудь состарятся. В целом для каждого из нас очень важны специалисты, которые ответственны за нашу с вами жизнь – медики. Медсестра — это ноги безногого, глаза ослепшего, опора ребенку, источник знаний и уверенность для молодой матери, уста тех, кто слишком слаб или погружен в себя, чтобы говорить. Вирджиния Хендерсон.
Медсестра — это ноги безногого, глаза ослепшего, опора ребенку, источник знаний и уверенность для молодой матери, уста тех, кто слишком слаб или погружен в себя, чтобы говорить. Вирджиния Хендерсон. Нет, наверное, смысла спорить о том, как нужна, важна, прекрасна профессия медсестры. Душевность, эмоциональная культура, способность к восприятию переживаний ближнего, воспитанность в ответственности, искреннее понимание своего долга перед другими людьми, осознание того, что только ты и именно ты можешь и должен помочь заболевшему человеку обрести полноту существования, т. е. стать здоровым – вот нравственные показатели необходимые на мой взгляд, для людей, выбравших эту профессию.
Нет, наверное, смысла спорить о том, как нужна, важна, прекрасна профессия медсестры. Душевность, эмоциональная культура, способность к восприятию переживаний ближнего, воспитанность в ответственности, искреннее понимание своего долга перед другими людьми, осознание того, что только ты и именно ты можешь и должен помочь заболевшему человеку обрести полноту существования, т. е. стать здоровым – вот нравственные показатели необходимые на мой взгляд, для людей, выбравших эту профессию. Без медсестричек невозможно – Без ваших нежных, добрых рук, Что ран касаясь осторожно, Снимают с лиц больных испуг, Вы – воплощение заботы, С любым контакт у вас больным И в воскресенье и в субботы Без ваших полных глаз вниманья, Вы боль разгоните как дым, Без ваших слов приободренья… Все вы – полны очарованья, Своим вниманием сердечным, Все вы – достойны восхищенья! И тех поддержкой, кто без силы, В передвиженьи бесконечном… Как пчелки ловкие снуете, Ах, медсестрички, как вы милы! Кому – укол, кому – попить, Тепло души своей несете, Больных не смея позабыть.
Без медсестричек невозможно – Без ваших нежных, добрых рук, Что ран касаясь осторожно, Снимают с лиц больных испуг, Вы – воплощение заботы, С любым контакт у вас больным И в воскресенье и в субботы Без ваших полных глаз вниманья, Вы боль разгоните как дым, Без ваших слов приободренья… Все вы – полны очарованья, Своим вниманием сердечным, Все вы – достойны восхищенья! И тех поддержкой, кто без силы, В передвиженьи бесконечном… Как пчелки ловкие снуете, Ах, медсестрички, как вы милы! Кому – укол, кому – попить, Тепло души своей несете, Больных не смея позабыть.
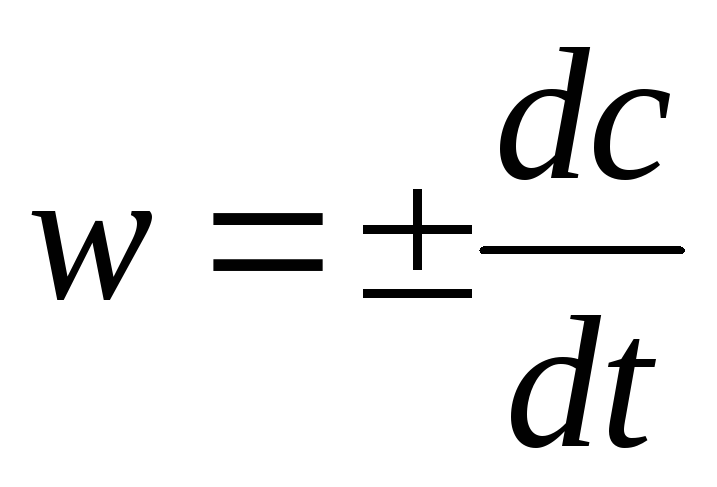 .
.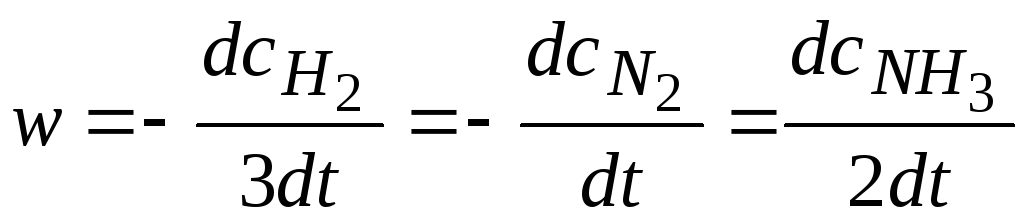 .
.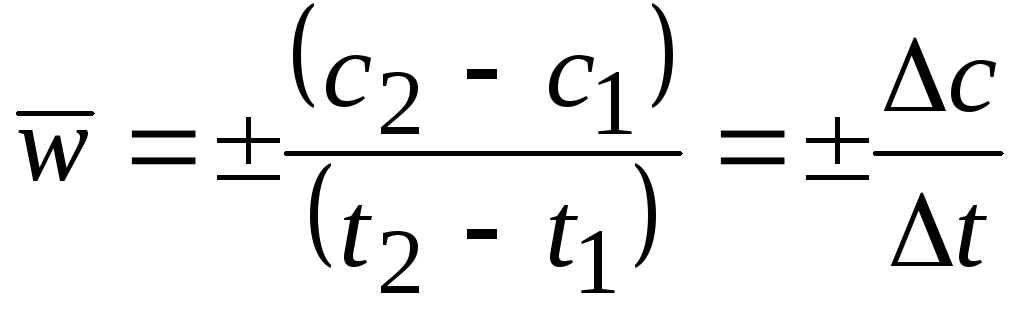 ,
,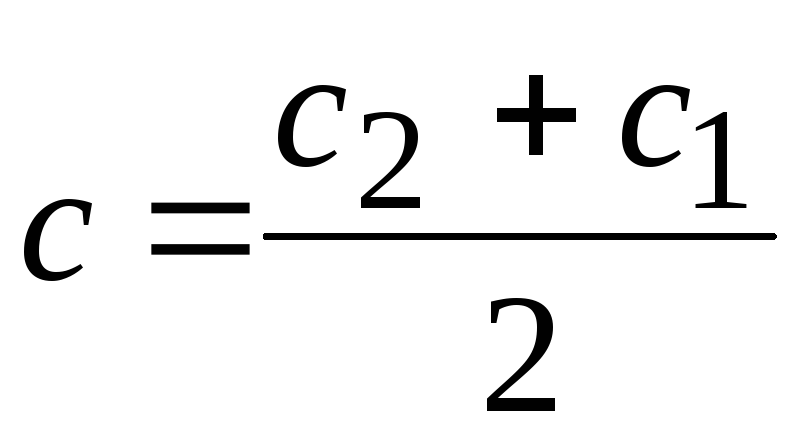
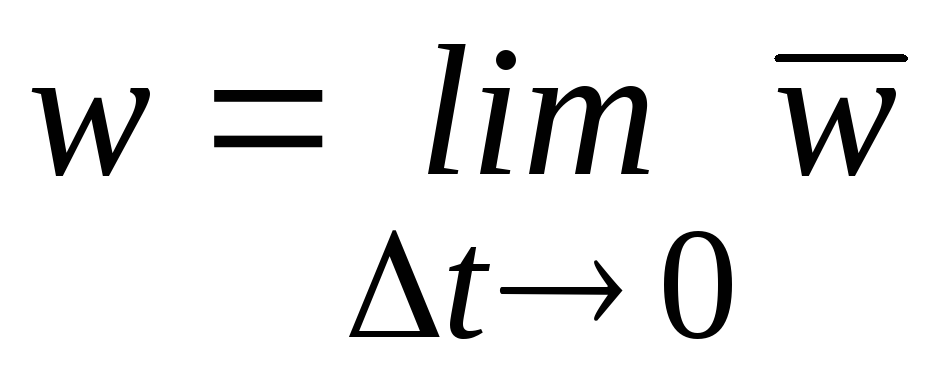 ,
,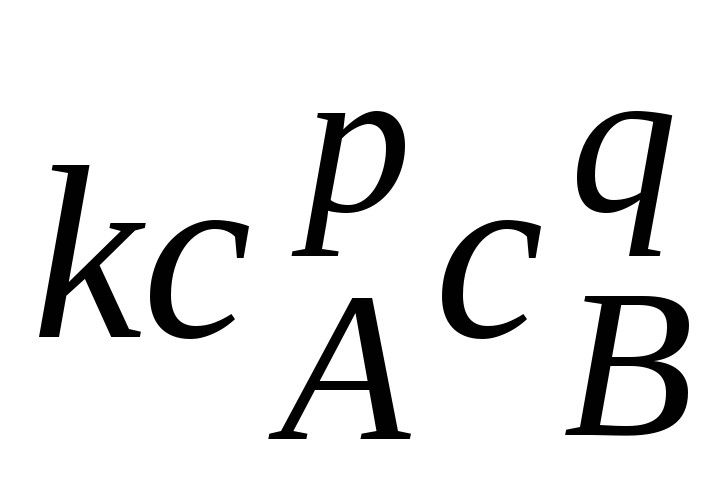
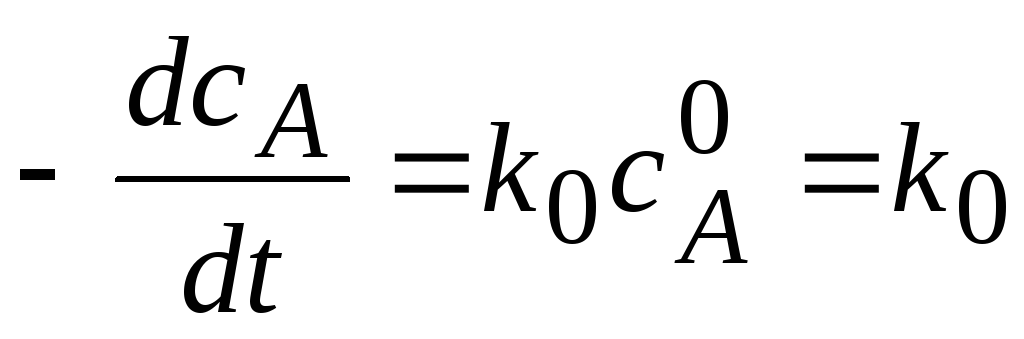 .
или
.
или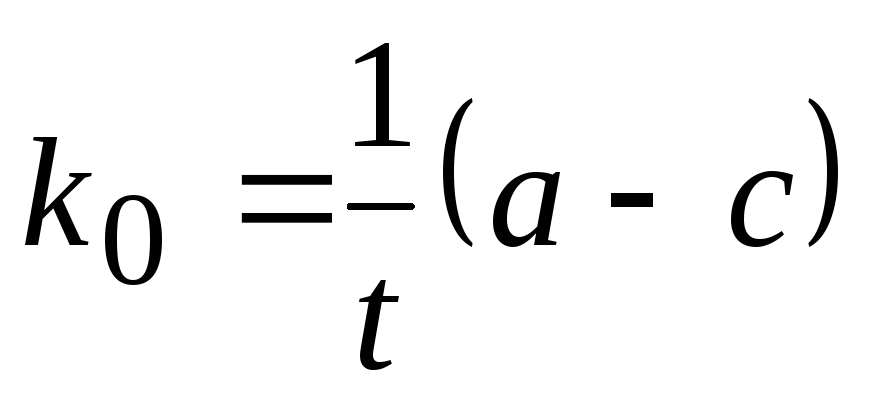 ,
,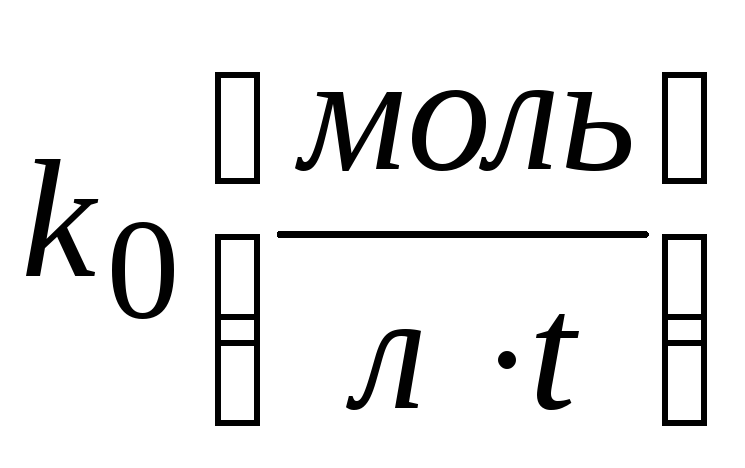 .
.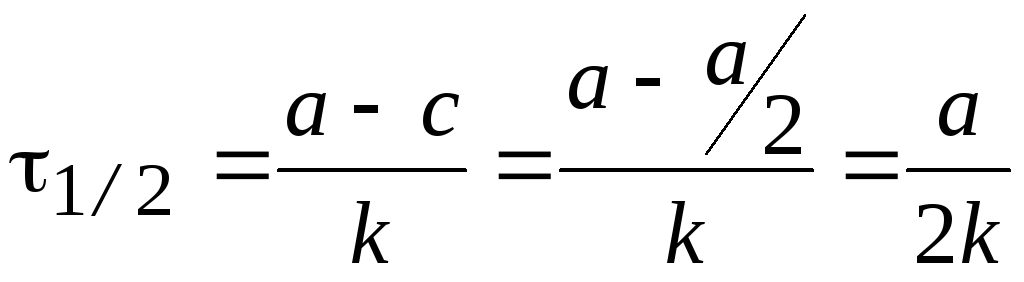 .
.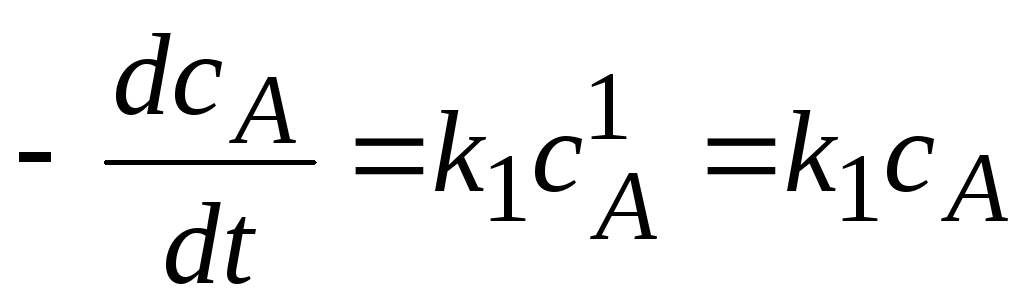 или
или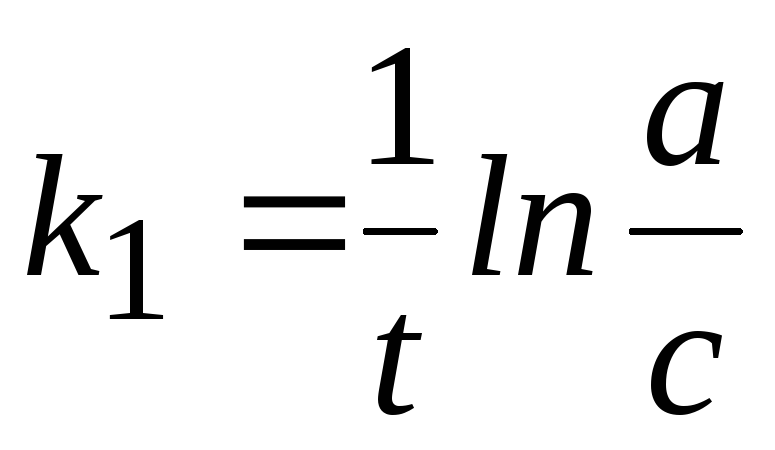 ,
,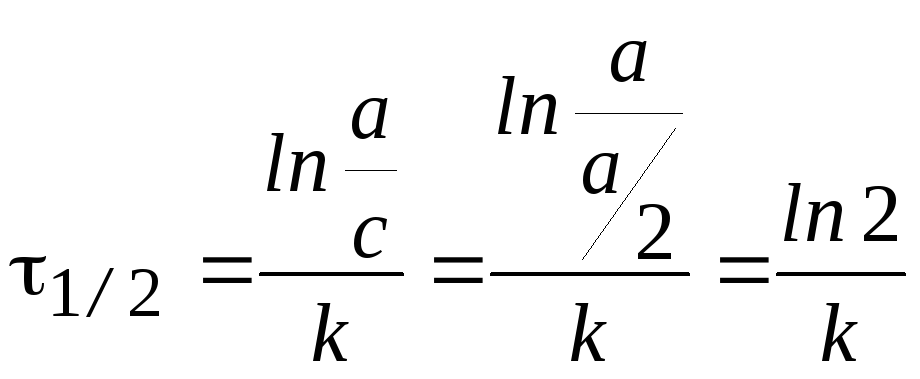 .
.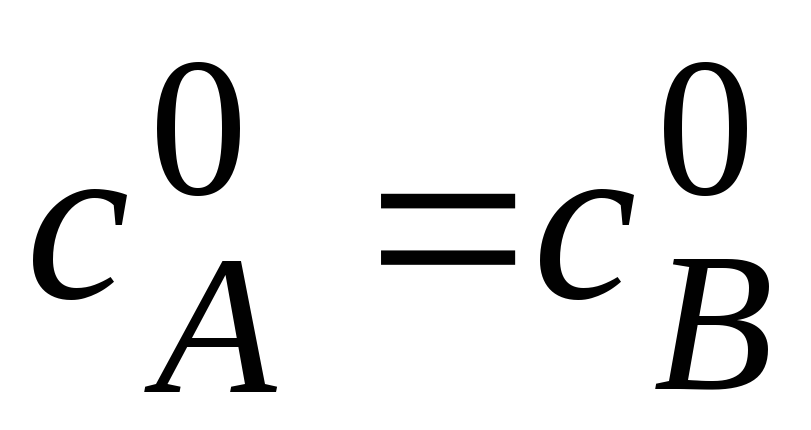 .
.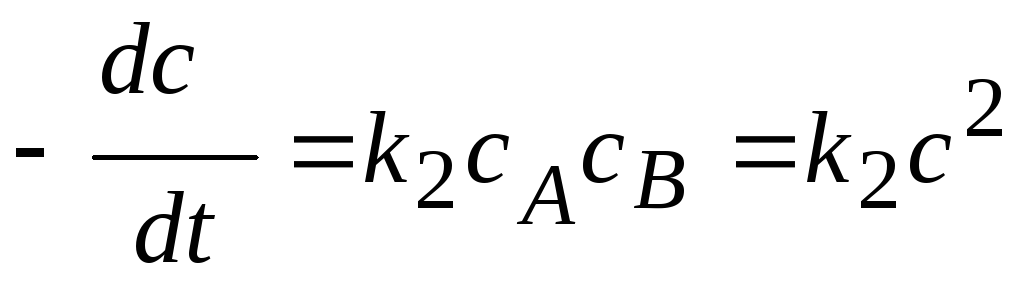 или
или 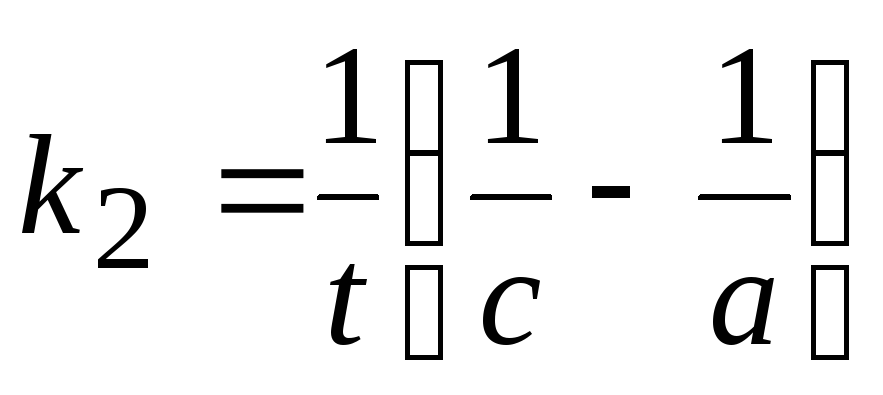 .
.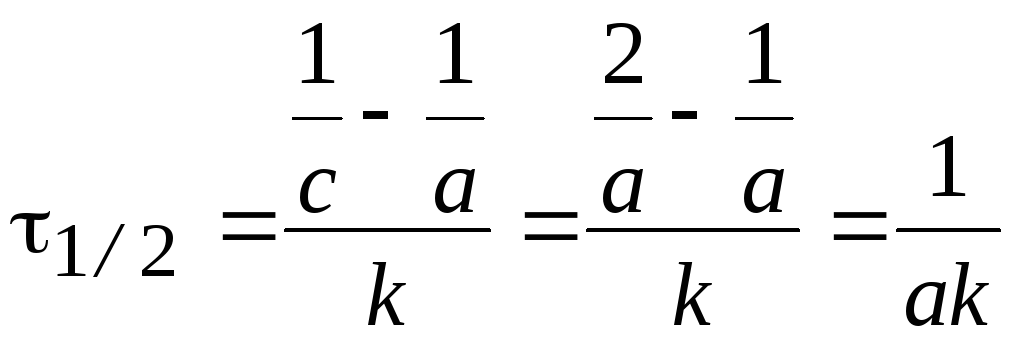 .
.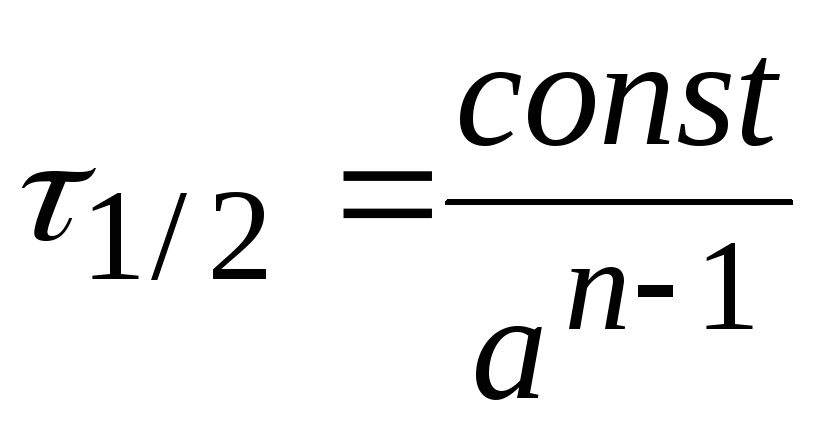 .
.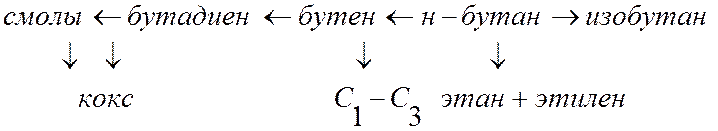
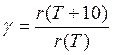 (10)
(10)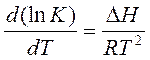 (11)
(11)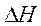 — теплота реакции, которую
представим, как разность двух величин А, имеющих размерность энергии. Тогда (11)
можно записать в виде:
— теплота реакции, которую
представим, как разность двух величин А, имеющих размерность энергии. Тогда (11)
можно записать в виде: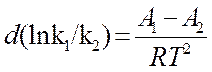 dT (12)
dT (12)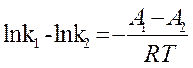 (13) или без индексов:
(13) или без индексов: 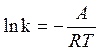 + lnB, откуда
+ lnB, откуда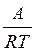 ) (14)
) (14)