Уравнения касательной: Касательная к графику ункции: уравнение касательной
Касательная к графику ункции: уравнение касательной
Рассмотрим следующий рисунок:
На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.
Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.
Касательная к графику функции
Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.
При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной.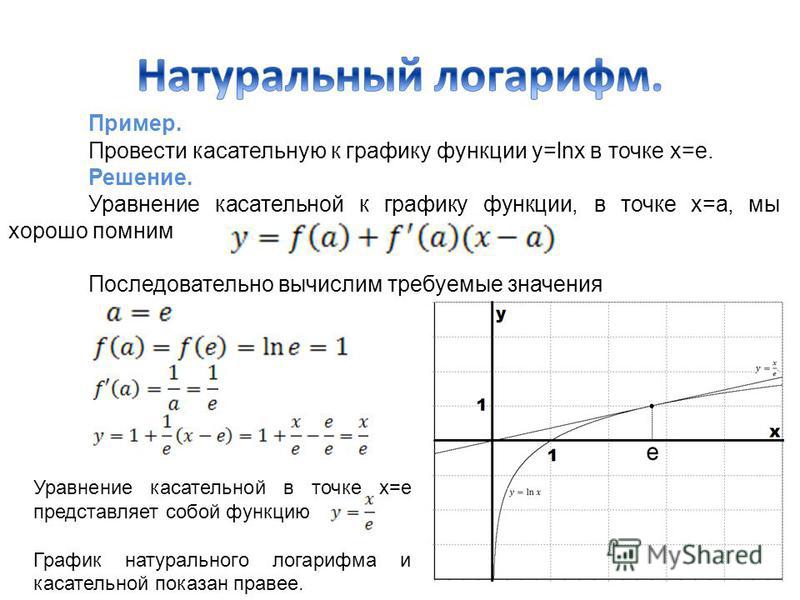 Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).
Уравнение касательной
Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:
y = k*x + b.
Так как у нас угловой коэффициент равен производной f’(x0), то уравнение примет следующий вид: y = f’(x0)*x + b.
Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.
f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) – f’(x0)*x0.
Подставляем полученное значение в уравнение касательной:
y = f’(x0)*x + b = f’(x0)*x + f(x0) – f’(x0)*x0 = f(x0) + f’(x0)*(x — x0).
y = f(x0) + f’(x0)*(x — x0).
Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x3 – 2*x2 + 1 в точке х = 2.
1. х0 = 2.
2. f(x0) = f(2) = 22 — 2*22 + 1 = 1.
3. f’(x) = 3*x2 – 4*x.
4. f’(x0) = f’(2) = 3*22 – 4*2 = 4.
5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x — 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.
Ответ: y = 4*x — 7.
Общая схема составления уравнения касательной к графику функции y = f(x):
1. Определить х0.
2. Вычислить f(x0).
3. Вычислить f’(x)
4. Вычислить f’(x0)
5. Подставить полученные значения в уравнение касательной y= f(x0) + f’(x0)*(x — x0).
Нужна помощь в учебе?
Предыдущая тема: Применения непрерывности: метод интервалов и примеры
Следующая тема:   Критические точки функции: максимумы и минимумы
Уравнение касательной к графику функции
Вопросы занятия:
· рассмотреть касательную к графику функции в точке;
·
вывести
уравнение касательной к графику функции в общем виде.
Материал урока.
Прежде чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.
Итак, мы с вами научились находить производные различных функций. На предыдущих уроках мы говорили, что умение находить производные – помогает в решении разных задач. На сегодняшнем уроке мы разберём, как с помощью производных можно составить уравнение касательной к графику функции и примеры применения производной к приближенным вычислениям.
Давайте сформулируем задачу.
Напомним, что если в некоторой точке к графику функции можно провести касательную, то функция дифференцируема в этой точке и f'(a) существует.
Касательная – это прямая, значит, общее уравнение касательной можно записать в виде y = kx + m. Наша задача сводится к нахождению коэффициентов k и m.
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё один пример.
Пример.
Решая примеры, мы выполняли практически одни и те же действия. Давайте теперь попробуем сформулировать алгоритм составления уравнения касательной к графику функции y = f(x).
Уравнение касательной имеет ещё одно применение: с его помощью можно выполнять приближенные вычисления.
Рассмотрим общий приём.
Рассмотрим это на примере.
Пример.
Рассмотрим ещё один пример.
Пример.
Итак, давайте ещё раз выделим суть теории приближенных вычислений. Сложная кривая в окрестности точки x0 заменяется прямой (касательной к графику функции) и если приращения аргумента не велики, то для каждой функции можно вывести соответствующую формулу, по которой осуществляются приближенные вычисления.
Касательная плоскость и нормаль к явно заданной поверхности.

Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$
Уравнение нормали $$\frac{x-x_0}{F_x'(x_0, y_0, z_0)}=\frac{y-y_0}{F_y'(x_0, y_0, z_0)}=\frac{z-z_0}{F_z'(x_0, y_0, z_0)}.$$
В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.$$
Примеры:
7. 229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=\sin x\cos y$ в точке $(\pi/4, \pi/4, \pi/4).$
229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=\sin x\cos y$ в точке $(\pi/4, \pi/4, \pi/4).$
Решение.
Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.$$
Находим частные производные:
$z’_x=(\sin x\cos y)’_x=\cos x\cos y;$
$z’_x(\pi/4, \pi/4)=\cos \frac{\pi}{4}\cos \frac{\pi}{4}=\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2}=\frac{1}{2};$
$z’_y=(\sin x\cos y)’_y=-\sin x\sin y;$
$z’_y(\pi/4, \pi/4)=-\sin \frac{\pi}{4}\sin \frac{\pi}{4}=-\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2}=-\frac{1}{2};$
Таким образом, уравнение касательной плоскости: $$z-\frac{\pi}{4}=\frac{1}{2}(x-\frac{\pi}{4})-\frac{1}{2}(y-\frac{\pi}{4})\Rightarrow$$ $$\frac{1}{2}x -\frac{1}{2}y-z+\frac{\pi}{4}=0.$$
Уравнение нормали: $$\frac{x-\frac{\pi}{4}}{\frac{1}{2}}=\frac{y-\frac{\pi}{4}}{-\frac{1}{2}}=\frac{z-\frac{\pi}{4}}{-1}. 2-2x+6y=4$ найти уравнение нормали, параллельной прямой $\frac{x+2}{1}=\frac{y}{3}=\frac{z+1}{4}.$
2-2x+6y=4$ найти уравнение нормали, параллельной прямой $\frac{x+2}{1}=\frac{y}{3}=\frac{z+1}{4}.$
Итоговый урок по теме «Уравнение касательной» – Документ 1 – УчМет
Ковалева Елена Ивановна
Учитель 1 категории
МБОУ СОШ№5 г.Рославль, Смоленская область
Учебник Алгебра и начала анализа. 10кл. В 2 ч. (профильный уровень) Мордкович А.Г., Семенов П.В.
ПЛАН-КОНСПЕК УРОКА
Итоговый урок
по теме «Уравнение касательной»
10 класс
Цель урока:
систематизировать и обобщить сведения, полученные учащимися на предыдущем уроке;
расширить представления учащихся о теме;
дополнить и обобщить представления учащихся о применении данной темы в жизни;
познакомить с историей данного вопроса.

9. Задачи:
— обучающие: научиться распознавать сложные функции, знать правила дифференцирования, уметь применять формулу производной сложной функции при решении задач; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером.
-развивающие развивать познавательные интересы через применение информационных технологий.
-воспитательные воспитывать адаптивность к современным условиям обучения.
Тип урока урок закрепления изучаемого материала и выработки практических умений и навыков
Формы работы учащихся самостоятельная, индивидуальная, фронтальная работа.
Необходимое техническое
оборудование компьютер, проектор,
экран, презентация для сопровождения
занятия, раздаточный материал для
учащихся.
I. Организационный момент (0.5 мин.).
II. Постановка целей урока. Мотивация учащихся ( 2 мин). (слайд 1)
III. Обобщение знаний учащихся по теме «Производная. Уравнение касательной»(15 мин)(слайд 2)
Учитель приветствует учащихся и объявляет цель урока и план, используя презентационное сопровождение. Зачитывается эпиграф к уроку.
Учитель. Сегодня на уроке мы обобщим и закрепим идею геометрического смысла производной, сформируем начальное представление о приложениях производной в математике и истории их развития, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями производной; эпиграфом к уроку служат слова французского философа-материалиста Дени Дидро (1713 – 1784) – современника Декарта, Лейбница, личного библиотекаря Екатерины Великой.
«Начинать исследования можно
по-разному… Все равно начало почти
всегда оказывается весьма несовершенной,
нередко безуспешной попыткой. Есть
истины, как страны, наиболее удобный
путь, к которым становится известным
лишь после того, как мы испробуем все
пути. Кому-то приходится, рискуя собой,
сходить с проторенной дороги, чтобы
указать другим правильный путь… На
пути к истине мы почти всегда обречены,
совершать ошибки» (Дени Дидро)
Есть
истины, как страны, наиболее удобный
путь, к которым становится известным
лишь после того, как мы испробуем все
пути. Кому-то приходится, рискуя собой,
сходить с проторенной дороги, чтобы
указать другим правильный путь… На
пути к истине мы почти всегда обречены,
совершать ошибки» (Дени Дидро)
Сегодня мы закрепим материал на тему «Уравнение касательной» решением ключевых или опорных задач, проверим усвоение техники нахождения производной и исследуем связь уравнения касательной с исследованием свойств графика функции , что в дальнейшем нам даст аппарат для построения практически графика любой функции и нахождения ее свойств. Приведет к решению задач на оптимизацию, те нахождения наибольшего и наименьшего значения некоторого конкретного тела, …
Итак, для проверки техники вычисления производной приглашаются учащиеся к компьютерам ( тесты на два варианта)
На местах ребята обсуждают предложенные незавершенные предложения ( слайды 3-4)
1.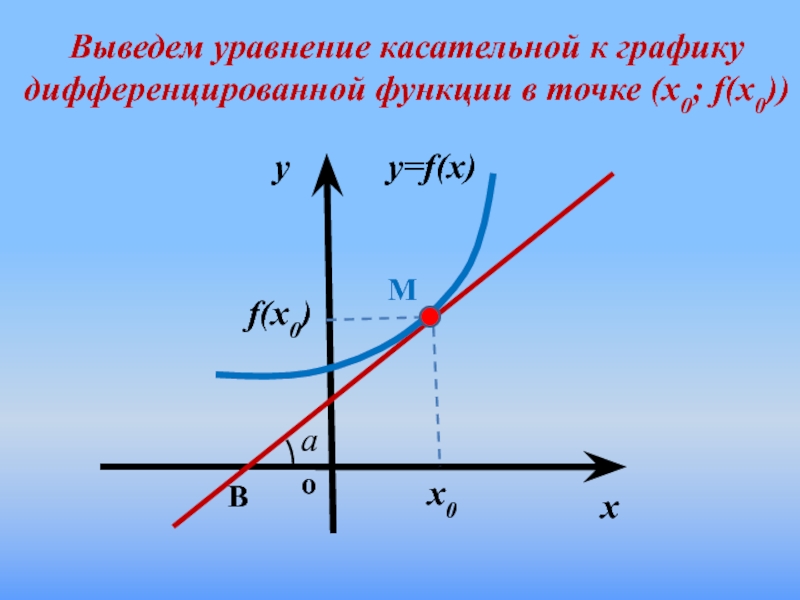 В чем состоит геометрический
смысл производной?
В чем состоит геометрический
смысл производной?
2.В любой ли точке можно построить касательную?
3.Какая функция называется дифференцируемой в точке?
4.Касательная наклонена к под тупым углом к положительному направлению оси Ох ….
5.Кастельная наклонена под острым углом к оси ох…
6.Касательная наклонена под прямым углом к положительному направлению оси Ох…
7.Касательная параллельна оси Ох, следовательно…
8. Что называется секущей для графика функции y=f(x)?
9. Какая прямая называется касательной к графику функции?
10. Какая из отмеченных точек является точкой касания?
11. Записать уравнение касательной к графику функции в заданной точке в общем виде. 12. Чему равен угол наклона касательной к графику функции в заданной точке? 6. Как найти угловой коэффициент касательной?
13. Известно, что угловой коэффициент
касательной к графику функции в точке
с абсциссой хо, равен 0,6. Чему равно
значение производной в этой точке?
Известно, что угловой коэффициент
касательной к графику функции в точке
с абсциссой хо, равен 0,6. Чему равно
значение производной в этой точке?
14. Касательная к графику функции f(x) в точке с абсциссой хо образует с положительным направлением оси ох угол 45о. Найти f/(xo).
Затем обсуждаем решение ключевых задач. (слайд 5)
Задание из предложенных ключевых задач составить свою задачу.
после обсуждения, решенных у доски задач , учащимся предлагается составить алгоритм решения из ключевых задач.
Учитель. Математический анализ,
ядро которого составляют дифференциальное
и интегральное исчисления, — самая тонкая
область всей математики. Раздел
математики, в котором изучаются
производные и их применения к исследованию
функций, называется дифференциальным
исчислением, а раздел математики, в
котором изучается операция интегрирования
функции, то есть восстановления функции
по её производной, называется интегральным
исчислением.
Немного истории ( небольшое сообщение ученицы) (слайды 6-10)
Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия.
Большой вклад в развитие дифференциального исчисления внесли:
Архимед, который задолго до этого решил задачу на построение касательной к спирали, сумел найти максимум функции f(x) = х2 (а — х),
Пьер Ферма (1601 -1665), математическое определение производной, которого было принято всеми математиками, успешно применявшими в своём методе нахождения экстремумов многочленов задачи о построениях касательных к кривым,
Готфрид Вильгельм Лейбниц
(1646 -1716), который установил геометрический
смысл производной, как тангенс угла
наклона касательной. «Штрихи к портрету»
Готфрида Лейбница : в своей работе
«Новый метод максимумов и минимумов»,
используя геометрическое истолкование,
он кратко разъясняет признаки возрастания
и убывания, максимума
и минимума, выпуклости
и вогнутости (следовательно, и
достаточные условия экстремума
для простейшего случая), а также точки
перегиба. Его знаменитая фраза: «Без
настоящих единиц не может быть и
множества». С ним связаны имена
выдающихся личностей, термины и понятия:
Эпоха Просвещения, Петр I,
Россия, Ньютон, рококо, арифмометр,
кратер на Луне, подводная лодка,
«Философский век». Подумайте над этим
дома.
Его знаменитая фраза: «Без
настоящих единиц не может быть и
множества». С ним связаны имена
выдающихся личностей, термины и понятия:
Эпоха Просвещения, Петр I,
Россия, Ньютон, рококо, арифмометр,
кратер на Луне, подводная лодка,
«Философский век». Подумайте над этим
дома.
V I. Решение задач с практическим содержанием ( слайд 11)
Учитель . Обсуждая успехи своего ученика, учитель математики так отозвался о нем: «Он очень мало знает, но у него положительная производная». Все поняли, что хотел сказать учитель: скорость приращения знаний у ученика положительна, а это есть залог того, что его знания возрастут. Подумайте, как вы могли бы охарактеризовать три кривые роста знаний.
Ответ:I -ого знания не растут т.к.
производная в каждой точке прямой равна
нулю, знания II-го растут быстрее, чем
III-го т.к. угол наклона касательных будет
больше, а следовательно и больше
производная, потому что тангенс функция
возрастающая. (слайд 10-анимированный ,
в музыкальном сопровождении)
(слайд 10-анимированный ,
в музыкальном сопровождении)
У вас на столах график некоторой функции, проведите в указанных точках схематично касательные и охарактеризуйте данную функцию у учетом изученного в 10 и 9-ом классах.
А теперь послушайте музыку, которая сейчас помогала исследованию В чем связь? ( слайд12) Почему именно музыку и график функции мы сегодня связываем?
Не всякую музыку можно слушать легко, для восприятия необходимо произвести усилия, вслушаться , представить действие , проникнуться настроением, поймать мысль композитора.
«Здесь мало увидеть,
Здесь нужно всмотреться,
Здесь мало услышать,
Здесь вслушаться нужно,» Н.Рыленков «Все в тающей дымке»
А может быть и с графиком , его надо не только увидеть, но в него надо всмотреться, почувствовать всю гармонию мелодии графика.
Такую мелодию нам предложит
Семченкова Настя( на гитаре попыталась
проиграть мелодию, повторяющую
предложенный график).
А теперь попробуйте сами. Звучит вальс из балета «Лебединое озеро»
П.И.Чайковского.
Учитель. Ребята, а зачем нужно изучать данную тему.
Выберем ответы из левого столбца:
|
|
Нужна ли производная для будущей профессии?
Российский математик 19века
Панфутий Львович Чебышев говорил, что
«особенную важность имеют те методы
науки, которые позволяют решать задачу,
общую для всей практической деятельности
человека, например, как располагать
своими средствами для достижения
наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
Вам предложены задачи из жизни, необходимо применить для решения свойства касательной.
1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста? (слайд13-анимированный –этапы рассуждений)
2.Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м. Из точки Р, расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е(илиА). Какую
высоту h нужно придать
центральной части теплицы , если
желательно, чтобы струя воды( она имеет
форму параболы с вершиной в точке
Р) не достигла крыши теплицы?
Из точки Р, расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е(илиА). Какую
высоту h нужно придать
центральной части теплицы , если
желательно, чтобы струя воды( она имеет
форму параболы с вершиной в точке
Р) не достигла крыши теплицы?
Во многих приложениях встречается
понятие касания кривых между собой.
Кривые называются касающимися ,если
они имеют в этой точке общую касательную.
3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0
4.Покажите, что кривые у=4х2+2х-8 и у=-х3-х+10 касаются в точке А(3;34). Будут ли они касаться в точке В(2;-4)
5. При каких соотношениях парабола ах2+вх+с-0 касается оси Ох?
6. Найдите те значения х, при которых касательные в соответствующих точках параллельны между собой. При каком значении а кривые будут касаться друг друга?
Вам было предложено дома решить не менее творческую задачу: составления алгоритма решения нестандартной задачи , по теме «Уравнение касательной»
Обсуждаем данные алгоритмы.
Как вы уже заметили, что в данных алгоритмах повторяющиеся блоки, перечислите их: составление уравнения касательной в точке; нахождения точки касания по углу наклона касательной к положительному направлению оси Ох, по известному угловому коэффициенту, который может быть известен по условию параллельности прямых ,описанию условия нахождения точек касания
А теперь перейдем к выполнению
практической работы , при выполнении
которой вы должны применить все на
практике. (Приложение1)
(Приложение1)
V. Постановка дифференцированного домашнего задания
Учитель раздает карточки с вариантами заданий (4 варианта) , которые содержат обязательную и необязательную части домашнего задания, делает соответствующие пояснения о том, что результаты будут необходимы на следующем уроке.
VI. Итог урока.
Учитель предлагает обобщить учащимся свои исследования, демонстрирует на слайдах результаты подведения итогов и дальнейший план изучения темы. На экране непрерывно идут титрами новые математические понятия: необходимое условие, достаточное условие, необходимое и достаточное условие.
Учащиеся высказывают свое мнение, подводят общий итог исследованию
Список используемой литературы
Алгебра и начала анализа. 10 класс. В 2 ч. Ч.1. Учебник (профильный уровень) / А.
 Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.
Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений
/А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.; Под ред. А.Н.Колмогорова-
10-е изд.- М..: Просвещение,2000. – стр. 160-166Единый государственный экзамен: Математика: Контрол. измерит. материалы
/Л.О.Денищева, Е.М.Бойченко, Ю.А.Глазков и.др.; М-во образования Рос.
Федерации.- М.: Просвещение, 2003.Производная и её применение: Дидакт. матер, по курсу алгебры и начал анализа
для 10-11 кл.ср.шк./Под ред. М.И.Башмакова — СПб, Свет, 1995.Клайн М. Математика. Утрата определённости: Пер. с англ./ Под ред. С предисл. И
примеч. И.М.Яглома.- М.: Мир, 1984.Степанова М.В. Учебно-исследовательская деятельность школьников в профильном обучении: учебно-методическое пособие для учителя/ Под ред.
 А.П.Тряпининой. –
СПб.: КАРО, 2005.
А.П.Тряпининой. –
СПб.: КАРО, 2005.Маркова В. Что такое исследовательская деятельность школьников / Математика (приложение к 1 сентября), №12, 2007.
Интернет – источники
Музыка «Балет «Лебединое озеро» — Вальс A-dur, акт 1» — (Пётр Ильич Чайковский)http://www.rusmusic.su/instrumental.php
Дени Дидро
http://books.atheism.ru/gallery/Diderot/
Екатерина Великая
http://mail.spb.fio.ru/archive/group15/c3wu3/pagehistory1.htm
Лейбниц
http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%2C_%D0%93%D0%BE%D1%82%D1%84%D1%80%D0%B8%D0%B4_%D0%92%D0%B8%D0%BB%D1%8C%D0%B3%D0%B5%D0%BB%D1%8C%D0%BC
Ньютон
http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA
Архимед
http://ru. wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4
wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4
Лагранж
http://ru.wikipedia.org/wiki/%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%2C_%D0%96%D0%BE%D0%B7%D0%B5%D1%84_%D0%9B%D1%83%D0%B8
Ферма
http://ru.wikipedia.org/wiki/%D0%A4%D0%B5%D1%80%D0%BC%D0%B0%2C_%D0%9F%D1%8C%D0%B5%D1%80
Ньютон
http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA
Приложения к плану-конспекту урока
Итоговый урок по теме «Уравнение касательной»
Приложение 1
Геометрическое приложение производной
1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста?
2. Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м.
Из точки Р , расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е (или А ). Какую
высоту h нужно придать
центральной части теплицы, если
желательно, чтобы струя воды ( она имеет
форму параболы с вершиной в точке Р) не
достигла крыши теплицы?
Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м.
Из точки Р , расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е (или А ). Какую
высоту h нужно придать
центральной части теплицы, если
желательно, чтобы струя воды ( она имеет
форму параболы с вершиной в точке Р) не
достигла крыши теплицы?
C
Р
В D
А Е
Во многих приложениях встречается понятие касания кривых между собой. Кривые называются касающимися , если они имеют в этой точке общую касательную.
3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0
4. Покажите, что кривые у=4х2+2х-8
и у=-х3-х+10 касаются в точке А
(3;34). Будут ли они касаться в точке В
(2;-4)
Покажите, что кривые у=4х2+2х-8
и у=-х3-х+10 касаются в точке А
(3;34). Будут ли они касаться в точке В
(2;-4)
5. При каких соотношениях парабола ах2+вх+с-0 касается оси О х?
Приложение 2
Вариант 2 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3Угловой
коэффициент касательной, проведенной
к параболе A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 |
А5.4 В какой точке касательная, проведенная к графику функции y = x — 2x + 1, параллельна
прямой y = -4(x + 1)? |
А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 450? |
А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108 |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5. |
Вариант 3 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3 Угловой коэффициент касательной,
проведенной к графику функции y =
,в точке (x0, y0) равен
.
Найдите x0, y0. |
А5.4.В каких точках касательная к графику функции образует с осью Ох угол в 450? |
А5.5. При каких значениях x касательная к графику функции y = 2x + 3x — 6x параллельна прямой y = 6x + 1 ? A) -2 и 3 B) 1 и 3 C) -2 и 1 D) 2 и -1 E) -1 и 3 |
А5.6.В точке А(5;0) проведена касательная к графику функции .Найти длину отрезка касательной, заключенного между осями координат. |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5.8. В какой точке нужно провести касательную к графику функции , чтобы она пересекла ось ординат в точке (0;6) ? |
Вариант 4 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3. Угловой коэффициент
касательной, проведенной к параболе A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 |
А5.4. Какая из прямых параллельна касательной
к кривой y = 4 – x
в точке x0 = 2? |
А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 1350? |
А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108 |
А5.7.Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5.8.Касательные, проведенные к графику функции в точках с абсциссами х1 и х2 параллельны. Известно, что х1 =. Найдите отношение |
Приложение 3
Презентация — Уравнение касательной
Слайды и текст этой онлайн презентации
Слайд 1
10 КЛАСС
Уравнение
касательной
ТЕМА УРОКА:
Слайд 2
ЦЕЛИ УРОКА:
1. Уточнить понятие касательной
к графику функции.
2. Вывести уравнение касательной.
3. Создать алгоритм составления уравнения
касательной к графику функции y=f(x).
4. Начать отрабатывать умения и навыки
в составлении уравнения касательной в
различных
математических ситуациях.
Слайд 3
С f(x)=√(3-2x) f'(1)=?
Я f(x)=5/³√(3x+2) f’ (-1/3)=?
Ю f(x)=12/√(3x²+1) f’ (1)=?
Ф f(x)= 4√(3-2x²) f’ (-1)=?
К f(x)=2ctg2x f’ (-π/4)=?
И f(x)=4/(2-cos3x) f’ (- π /6)=?
Л f(x)= tg x f’ (π /6)=?
1 4/3 9 -4 -1 -3 5
РАСШИФРУЙТЕ, КАК ИСААК НЬЮТОН
НАЗВАЛ ПРОИЗВОДНУЮ ФУНКЦИЮ
Слайд 4
ОТВЕТ :
ФЛЮКСИЯ
Слайд 5
Слайд 6
Понятие «производная» возникло в связи
с необходимостью решения ряда задач
физики, механики и математики.
Честь открытия
основных законов
математического
анализа принадлежит
английскому ученому
Ньютону и немецкому
математику Лейбницу.
Лейбниц рассматривал
задачу о проведении
касательной к произвольной
кривой.
Слайд 7
2) y=3/x + 6√x 2) y=3/x + 6√x 2) y=3/x + 6√x
3/x²+3/√ x -3/x²+6/√ x
-3/x²+ 3/√ x
ТЕСТ:
НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ
4) y=x³+4×100 4) y=x³+4×100 4) y=x³+4×100
3x²+400×99 3×3+4×99 x3+4×99
5) y=7tgx+sinx 5) y=7tgx+sinx 5) y=7tgx+sinx
1/cos2x+cosx 7/cos2x+cosx
7/cos2x-cosx
6) y=√x*sinx 6) y=√x*sinx 6) y=√x*sinx
Sinx/(2 √x)+ √x cos x 2sin x cosx
7) y=x/(x2+1) 7) y=x/(x2+1) 7) y=x/(x2+1)
1-x2 x2 +1 (1-x2)/(x2+1) 2
10) y=cos(5x+π/3) 10) y=cos(5x+π/3) 10) y=cos(5x+π/3)
5sin(5x+ π/3)
sin(5x+ π/3)
-5sin(5x+ π/3)
9) y= √ (15-8x) 9) y= √ (15-8x) 9) y= √ (15-8x)
7/ √(15-8x) 3/ √(15-8x) -4/ (√15-8x)
1) y=2x-7 1) y=2x-7 1) y=2x-7
x²-7 2 2x
8) y=(5x+2)9 8) y=(5x+2)9 8) y=(5x+2)9
2(5x+2)8
45(5x+2)8 3(5x+2)8
3) y=cos x+2x 3) y=cos x+2x 3) y=cos x+2x
Sinx+2 -Sinx+2 -Sinx+2x
3) y=cos x+2x 3) y=cos x+2x 3) y=cos x+2x
Sinx+2 -Sinx+2 -Sinx+2x
Слайд 8
ОТВЕТЫ:
1) 2
2) 3
3) 2
4) 1
5) 2
6) 1
7) 3
8) 2
9) 3
10) 3
Слайд 9
ДАВАЙТЕ ОБСУДИМ ПОНЯТИЕ КАСАТЕЛЬНОЙ.
СОГЛАСНЫ ЛИ ВЫ С УТВЕРЖДЕНИЕМ:
»КАСАТЕЛЬНАЯ — ЭТО ПРЯМАЯ,
ИМЕЮЩАЯ С ДАННОЙ КРИВОЙ
ЕДИНСТВЕННУЮ ОБЩУЮ ТОЧКУ»?
1) ДА 2) НЕТ
Слайд 10
Слайд 11
Слайд 12
ПОЧЕМУ УГЛОВОЙ КОЭФФИЦИЕНТ
КАСАТЕЛЬНОЙ РАВЕН ПРОИЗВОДНОЙ?
Слайд 13
АЛГОРИТМ
СОСТАВЛЕНИЯ УРАВНЕНИЯ
КАСАТЕЛЬНОЙ
К ГРАФИКУ ФУНКЦИИ У=f(x)
1. Обозначить абсциссу
точки касания буквой а.
2. Вычислить f(a).
3. Найти f ‘ (x) и вычислить f ‘(a).
4. Подставить найденные числа а, f(a), f ‘(a) в формулу
y = f(a) + f ‘(a) * (x-a)
Слайд 14
ЗАКРЕПЛЕНИЕ
№ 828
Дополнительно:
2. Составить уравнение касательной
к графику функции
f(x)=х2-3х+5 в точке с абсциссой а=-1.
3. Составить уравнение касательной,
проходящей через точку
пересечения касательной графика
функции f(x)=(3-x)/(x+1) с прямой у=1.
4. № 831 (а)
1. Устная работа :
№809.
Слайд 15
ЗАДАНИЯ С ЕГЭ:
(НА ДОМ)
А. КАСАТЕЛЬНАЯ, ПРОВЕДЕННАЯ К ГРАФИКУ ФУНКЦИИ У=Х³-Х В ТОЧКЕ С АБСЦИССОЙ Х=0, ПАРАЛЛЕЛЬНА ПРЯМОЙ:
1) У=7-Х 2) У=Х-7 3) У=2Х-7 4) У=√3*Х+7
А. ДЛЯ ФУНКЦИИ У=4Х-Х² КАСАТЕЛЬНАЯ, ПАРАЛЛЕЛЬНАЯ ОСИ АБСЦИСС, ПРОВЕДЕНА ЧЕРЕЗ ТОЧКУ КАСАНИЯ:
1) (0;0) 2) (4;0) 3) (2;4) 4) (-1;-5)
А. УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ f(x)= 2х²-3х-1,
ПРОВЕДЕННОЙ В ТОЧКЕ С АБСЦИССОЙ Х0=1, ИМЕЕТ ВИД:
1)У=Х-3 2) У=Х-1 3) У=-2Х+3 4) 6У=-11Х-1
А. УРАВНЕНИЕ КАСАТЕЛЬНОЙ, ПРОВЕДЕННОЙ К ГРАФИКУ ФУНКЦИИ
f (х)= 3х²-2х+5 В ТОЧКЕ А(2;13):
1) У=76Х-502 2) У=10Х-7 3) У=10Х+33 4) У=76Х-139
А. НАЙТИ ТАНГЕНС УГЛА НАКЛОНА КАСАТЕЛЬНОЙ, ПРОВЕДЕННОЙ К ГРАФИКУ ФУНКЦИИ У= 3Х²-5Х В ТОЧКЕ С АБСЦИССОЙ Х0=2.
1) 0,83 2) 2 3)3 4) 7
10 класс. Алгебра. Производная. Уравнение касательной к графику функции. — Уравнение касательной к графику функции.
Комментарии преподавателяУравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования. Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую (см. рис.1).
Рис. 1. График функции .
Зафиксируем точку . Если , то значение функции равно . Значит, имеем точку с координатами (.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции в точке с абсциссой , в которой — существует.
Уравнение касательной – это прямая, которая задается формулой
Любая прямая, в том числе и касательная, определяется двумя числами: и . Исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент .
Параметр найдем из условия, что касательная проходит через точку (, то есть .
.
Стало быть .
Запишем уравнение касательной
.
Или, .
Получили уравнение касательной к кривой в точке с абсциссой .
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
2) — угловой коэффициент касательной к графику функции.
3) – произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что – это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
Задача.
К кривой в точке с абсциссой провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
Рис. 2. Касательная к графику функции .
Зафиксируем точку . Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти и точку касания.
— дано.Точка касания: (;.
2) Найти производную в любой точке .
.
3) Найти значение производной в точке с абсциссой .
.
4) Выписать и проанализировать уравнение касательной.
.
Упрощаем и получаем: .
Ответ: .
Задача 1.
Пусть дано уравнение касательной .
Найдите точки пересечения касательной с осями координат.
Если , то . – это первая точка.
Если , то . — вторая точка.
Итак, первая точка – это точка с координатами . Вторая точка – точка пересечения с осью , точка с координатами (см. рис.3).
Рис.3. Точки пересечения касательной к графику функции с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .
Рассмотрим прямоугольный треугольник (Рис. 3). Длина катета равна 1. Длина катета . Длину отрезка из прямоугольного треугольника найдем по теореме Пифагора:
Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .
Рассмотрим пример.
Дана функция . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).
Рис. 4. Касательная к графику функции .
Нахождение точки касания.
1. Точка касания имеет координаты .
2. Найти .
3. Найти
И, последнее действие, – написать уравнение касательной.
4. .
Упростим и получим .
Заметим в точке синусоида и касательная соприкасаются. В районе точки синусоида и прямая почти не различаются.
Итак, мы вывели уравнение касательной. Рассмотрели все элементы этой касательной. Выяснили их смысл. Сформулировали одну из методик нахождения касательных в конкретных функциях, в конкретных точках и решили некоторые сопутствующие задачи.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/uravnenie-kasatelnoy-k-grafiku-funktsii
http://v.5klass.net/zip/457286d0df8865f8084b5db13cbd6e95.zip
http://school.xvatit.com/index.php?title=%D3%F0%E0%E2%ED%E5%ED%E8%E5_%EA%E0%F1%E0%F2%E5%EB%FC%ED%EE%E9_%EA_%E3%F0%E0%F4%E8%EA%F3_%F4%F3%ED%EA%F6%E8%E8
http://itest.kz/lekciya_uglovoj_koehfficzient_kasatelnoj_i_ee_uravnenie_ru
http://www.postupivuz.ru/vopros/12822.htm
Определение формулы касательной к окружности
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Касательная к окружности
Если не использовать понятие производной, и взять объяснение из учебников середины прошлого века, то «Касательная к окружности — это прямая пересекающая окружность в двух совпадающих точках»
Окружность на плоскости может быть представлена в виде нескольких исходных данных
1. В виде координат центра окружности (x0,y0) и её радиуса R.
2. В виде общего уравнения
В виде параметрического вида и в полярных координатах мы рассматривать не будем, так как там формулы тоже на базируются на координатах центра окружности и радиусе.
Наша задача, зная параметры окружности и точку принадлежащую этой окружности вычислить параметры касательной к этой окружности.
Эта задача, является частным решением более общего калькулятор касательная к кривой второго порядка
Итак, если окружность выражена формулой
Уравнение касательной к окружности если нам известны параметры общего уравнения таково:
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в заданной точке.
ВАЖНО: При указании точки, она должна быть обязательно(!!) принадлежать окружности,
и не быть точкой в какой либо стороне. В противном случае, уравнение касательной будет неверным.
Примеры
Вычислить уравнение касательной в точке (13.8, 0) к окружности выраженной формулой
Запишем коэффиценты этой кривой, взглянув на общую формулу
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Второй пример:
Через окружность с центром (8.71, -4) и радиусом 7 проходит касательная и касается в точке (4,-4)
Найти уравнение этой прямой.
Раз у нас заданы радиус и коордианты центтра то уравнение имеет вид
раскроем скобки, получим
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Отрисовав, полученные линии в GeoGebra мы убедимся что расчет произведен верно.
Формально, используя вышеупомянутую программу, касательную можно провести там проще и быстрее. Смотрите где и как проще.
Удачных расчетов!
- Определить формулу окружности по трем точкам >>
Как найти уравнение касательной
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Уравнение касательной к кривой | Дифференциальное исчисление
Нарисуйте график \ (f \) с указанием всех пересечений и точек поворота. {2} — 4x + 3 = 0 \\ (х-3) (х-1) = 0 \\ х = 3 \ текст {или} х = 1 \\ \ text {Shape: «frown»} (a Найдите уравнения касательных к \ (f \) в точке:
- \ (y \) — точка пересечения \ (f \).
- поворотный момент \ (f \).
- точка, где \ (x = \ text {4,25} \).
- \ begin {align *} y _ {\ text {int}}: (0; -3) \\ m _ {\ text {касательная}} = f ‘(x) & = -2x + 4 \\ f ‘(0) & = — 2 (0) + 4 \\ \ поэтому m & = 4 \\ \ text {Касательная} y & = 4x + c \\ \ text {Through} (0; -3) \ поэтому y & = 4x-3 \ end {align *}
- \ begin {align *} \ text {Поворотный момент:} (2; 1) \\ m _ {\ text {касательная}} = f ‘(2) & = -2 (2) + 4 \\ & = 0 \\ \ text {Касательное уравнение} y & = 1 \ end {align *}
- \ begin {align *} \ text {If} x & = \ text {4,25} \\ f (\ text {4,25}) & = — \ text {4,25} ^ {2} +4 (\ text {4,25}) — 3 \\ & = — \ text {4,0625} \\ m _ {\ text {tangent}} \ text {at} x & = \ text {4,25} \\ m & = — 2 (\ text {4,25}) + 4 \\ & = — \ текст {4,5} \\ \ text {Касательная} y & = — \ text {4,5} x + c \\ \ text {Сквозь} (\ text {4,25}; — \ text {4,0625}) \\ — \ text {4,0625} & = — \ text {4,5} (\ text {4,25}) + c \\ \ поэтому c & = \ text {15,0625} \\ y & = — \ text {4,5} x + \ text {15,0625} \ end {align *}
Нарисуйте три касательных выше на вашем графике \ (f \).
Запишите все наблюдения о трех касательных к \ (f \).
Касательная в точке \ (y _ {\ text {int}} \) (синяя линия): градиент положительный, функция в этой точке увеличивается.
Касательная в точке поворота (зеленая линия): градиент равен нулю, касательная — горизонтальная линия, параллельная оси \ (x \).
Касательная в точке \ (x = \ text {4,25} \) (фиолетовая линия): градиент отрицательный, функция в этой точке убывает.
Как найти уравнения касательных и нормальных прямых
Краткий обзор
- Чтобы найти уравнение прямой, вам нужна точка и наклон.2) = 12
$$
Наклон касательной составляет $$ m = 12 $$.
Шаг 3Найдите форму точки с уклоном прямой с уклоном $$ m = 12 $$, проходящей через точку $$ (2,8) $$.
$$ \ begin {align *} y — y_1 & = m (x-x_1) \\ [6pt] у — 8 & = 12 (х-2) \ end {выровнять *} $$
Отвечать$$ y — 8 = 12 (x-2) $$
Для справки, вот график функции и касательная, которую мы только что нашли.2 — х $$. Найдите уравнение касательной с наклоном $$ m = -3 $$.
Шаг 1Найдите производную.
$$ f ‘(x) = 2x -1 $$
Шаг 2Найдите $$ x $$ — значение, где $$ f ‘(x) $$ равно наклону.
$$ \ begin {align *} f ‘(x) & = 2x -1 \\ [6pt] -3 & = 2x -1 \\ [6pt] -2 & = 2x \\ [6pt] х & = -1 \ end {выровнять *} $$
Шаг 3Найдите точку на функции, где $$ x = -1 $$.2 — (-1) = 1 + 1 = 2 $$
Дело в $$ (- 1, 2) $$.
Шаг 4Найдите уравнение прямой, проходящей через точку $$ (- 1,2) $$ с наклоном $$ m = -3 $$.
$$ \ begin {align *} y -y_1 & = m (x-x_1) \\ [6pt] y — 2 & = -3 (x — (-1)) \\ [6pt] у — 2 & = -3 (х + 1) \ end {выровнять *} $$
Отвечать$$ у — 2 = -3 (х + 1) $$
Для справки, вот график функции и касательная, которую мы только что нашли.2 & = 12 \\ [6pt] y & = \ pm \ sqrt {12} \\ [6pt] y & = \ pm \ sqrt {4 \ cdot 3} \\ [6pt] у & = \ pm2 \ sqrt 3 \ end {выровнять *} $$
Поскольку в задаче говорится, что нас интересует $$ y> 0 $$, мы используем $$ y = 2 \ sqrt 3 $$.
Точка касания — $$ (2, 2 \ sqrt 3) $$.
Шаг 2Найдите уравнение для $$ \ frac {dy} {dx} $$.
Поскольку уравнение определено неявно, мы используем неявное дифференцирование.
$$ \ begin {align *} 2x + 2y \, \ frac {dy} {dx} & = 0 \\ [6pt] 2y \, \ frac {dy} {dx} & = -2x \\ [6pt] \ frac {dy} {dx} & = — \ frac {2x} {2y} \\ [6pt] \ frac {dy} {dx} & = — \ frac x y \ end {выровнять *} $$
Шаг 3Найдите наклон касательной в точке касания.
В точке $$ (2,2 \ sqrt 3) $$ наклон касательной составляет
$$ \ begin {align *} \ frac {dy} {dx} \ bigg | _ {(\ blue {2}, \ red {2 \ sqrt 3})} & = — \ frac {\ blue 2} {\ red {2 \ sqrt 3}} \\ [6pt] & = — \ frac 1 {\ sqrt 3} \\ [6pt] & = — \ frac 1 {\ sqrt 3} \ cdot \ blue {\ frac {\ sqrt 3} {\ sqrt 3}} \\ [6pt] & = — \ frac {\ sqrt 3} 3 \ end {выровнять *} $$
Наклон касательной равен $$ m = — \ frac {\ sqrt 3} 3 $$.
Шаг 4Найдите уравнение касательной, проходящей через $$ (2,2 \ sqrt 3) $$ с наклоном $$ m = — \ frac {\ sqrt 3} 3 $$.
В точке $$ (2,2 \ sqrt 3) $$ наклон касательной составляет
$$ \ begin {align *} y — y_1 & = m (x-x_1) \\ [6pt] y — 2 \ sqrt 3 & = — \ frac {\ sqrt 3} 3 (x-2) \ end {выровнять *} $$
ОтвечатьУравнение касательной: $$ y — 2 \ sqrt 3 = — \ frac {\ sqrt 3} 3 (x-2) $$
Для справки график кривой и найденная касательная линия показан ниже.
Нормальные линии
Предположим, у нас есть касательная к функции. Функция и касательная пересекаются в точке касания. Линия, проходящая через ту же точку, которая перпендикулярна касательной, называется нормальной линией .
Напомним, что когда две прямые перпендикулярны, их наклоны обратно пропорциональны.Поскольку наклон касательной равен $$ m = f ‘(x) $$, наклон нормальной линии равен $$ m = — \ frac 1 {f’ (x)} $$.
Пример 4
Предположим, что $$ f (x) = \ cos x $$. Найдите уравнение прямой к функции в $$ x = \ frac \ pi 6 $$.
Шаг 1Найдите точку на функции.
$$ f \ left (\ frac \ pi 6 \ right) = \ cos \ frac \ pi 6 = \ frac {\ sqrt 3} 2 $$
Это $$ \ left (\ frac \ pi 6, \ frac {\ sqrt 3} 2 \ right) $$.
Шаг 2Найдите значение производной в $$ x = \ frac \ pi 6 $$.
$$ f ‘(x) = — \ sin x \ longrightarrow f’ \ left (\ frac \ pi 6 \ right) = — \ sin \ frac \ pi 6 = — \ frac 1 2 $$
Наклон касательной равен $$ m = — \ frac 1 2 $$. Поскольку мы ищем прямую, перпендикулярную касательной, мы хотим использовать $$ m = 2 $$.
Шаг 3Найдите уравнение прямой, проходящей через точку $$ \ left (\ frac \ pi 6, \ frac {\ sqrt 3} 2 \ right) $$ с наклоном $$ m = 2 $$.
$$ \ begin {align *} y -y_1 & = m (x-x_1) \\ [6pt] y — \ frac {\ sqrt 3} 2 & = 2 \ left (x — \ frac \ pi 6 \ right) \ end {выровнять *} $$
ОтвечатьЛиния, нормальная к функции в $$ x = \ frac \ pi 6 $$, это $$ y — \ frac {\ sqrt 3} 2 = 2 \ left (x — \ frac \ pi 6 \ right) $$.
Для справки, вот график функции и нормальной линии, которую мы нашли.
Продолжайте практиковать задачиОшибка: Нажмите «Не робот», затем повторите попытку.
Уравнение касательной линии: проблемы и решения — Matheno.com
В этих задачах всегда указывается, что вы найдете касательную или нормальную (= перпендикулярную) линию в определенной точке функции. Назовем эту точку $ (x_0, y_0) $.Чтобы ответить на эти вопросы, вы почти всегда будете использовать форму линии «точка-уклон». Напомним, что если линия имеет наклон м и и содержит точку $ (x_0, y_0) $, то вы можете записать ее уравнение в виде:
Форма линии «точка-уклон»:
$$ \ bbox [желтый, 5px] {y — y_0 = m (x — x_0)} $$В постановке задачи обычно указывается точка $ (x_0, y_0) $, поэтому на самом деле эти проблемы сводятся к определению наклона м линии — о чем мы поговорим ниже.
Вы будете использовать это уравнение снова и снова; запомните это, если вы этого еще не знаете.
(Это просто вариант определения наклона: $ m = \ dfrac {y — y_0} {x — x_0}.) $
I. Касательная линия к кривой
Очень часто в начале Расчет Вам будет предложено найти уравнение для прямой , касательной к кривой в определенной точке. Мы называем эту точку $ (x_0, y_0) $.
Чтобы найти уравнение линии, вам просто нужно помнить, что касательная линия к кривой имеет наклон, равный производной функции, вычисленной в интересующей точке:
$$ \ bbox [желтый, 5px] {m_ \ text {касательная линия} = f ‘(x_0)} $$
То есть найдите производную функции $ f’ (x) $, а затем вычислите ее как $ x = x_0 $.Это значение, $ f ‘(x_0), $ равно наклону касательной.Следовательно, мы можем записать уравнение для касательной в точке $ (x_0, y_0) $ как
\ [\ bbox [10px, border: 2px сплошной синий] {
\ begin {align *}
y — y_0 & = m_ \ text {касательная} (x — x_0) \\ [8px] y — y_0 & = f ‘(x_0) (x — x_0)
\ end {align *}} \]Если эти уравнения кажутся вам абстрактными, не волнуйтесь. Мы обещаем, что как только вы решите несколько проблем, процесс обретет смысл.
II.Нормальная линия к кривой
Иногда вместо этого вам будет предложено найти прямую нормальную к кривой. Это то же самое, что запросить линию , перпендикулярную кривой.
Вы снова будете использовать форму линии «точка-уклон». Но теперь, чтобы вычислить наклон прямой, вспомним, что наклоны перпендикулярных прямых являются отрицательными величинами, обратными друг другу ($ m_2 = — \ dfrac {1} {m_1} $). Нам нужен наклон линии, перпендикулярной кривой в точке и, следовательно, перпендикулярной касательной к кривой в этой точке:
\ [\ bbox [yellow, 5px] {
\ begin {align *}
m_ \ text {нормальная линия} & = \ frac {-1} {m_ \ text {касательная линия}} \\ [12px] & = \ frac {-1} {f ‘(x_0)}
\ end {align *}} \]
Следовательно, мы можем записать уравнение для нормальной линии в $ (x_0, y_0) $ как\ [\ bbox [10px, граница: сплошной синий 2px] {
\ begin {align *}
y — y_0 & = m_ \ text {нормальная линия} (x — x_0) \\ [8px] y — y_0 & = \ frac {-1} {f ‘(x_0)} (x — x_0)
\ end {align *}} \]
Мы рекомендуем , а не , пытаясь запомнить все приведенные выше формулы.Вместо этого запомните форму линии «точка-наклон», а затем используйте то, что вы знаете о производной, сообщающей вам наклон касательной в данной точке. Проблемы, приведенные ниже, иллюстрируют.Задача 1 иллюстрирует процесс объединения различных фрагментов информации для нахождения уравнения касательной.
Задача 2 требует, чтобы вы нашли фрагменты информации перед тем, как собрать их воедино.
[свернуть]
AC Аппроксимация касательной линии
Подраздел 1.8.1 Касательная линия
Для функции \ (f \), дифференцируемой в точке \ (x = a \ text {,} \), мы знаем, что можем определить наклон касательной к \ (y = f (x) \) в точке \ ((a, f (a)) \) путем вычисления \ (f ‘(a) \ text {.} \) Уравнение результирующей касательной прямой дается в форме точечного уклона как
\ begin {уравнение *} y — f (a) = f ‘(a) (x-a) \ \ \ text {или} \ \ y = f’ (a) (x-a) + f (a) \ text {.} \ end {уравнение *}
Обратите внимание: в этом контексте существует большая разница между \ (f (a) \) и \ (f (x) \).Первая является константой, которая возникает в результате использования заданного фиксированного значения \ (a \ text {,} \), а вторая является общим выражением правила, определяющего функцию. То же самое верно для \ (f ‘(a) \) и \ (f’ (x) \ text {:} \), мы должны тщательно различать эти выражения. Каждый раз, когда мы находим касательную, нам нужно вычислить функцию и ее производную при фиксированном \ (a \) — значении.
На рисунке 1.8.2 мы видим график функции \ (f \) и его касательную линию в точке \ ((a, f (a)) \ text {.} \) Обратите внимание, как при увеличении масштаба мы видим, что локальная линейность \ (f \) более четко выделяется. Функция и касательная к ней почти неотличимы вблизи. Локальную линейность также можно увидеть динамически в java-апплете по адресу http://gvsu.edu/s/6J.
Рисунок 1.8.2. Функция \ (y = f (x) \) и ее касательная линия в точке \ ((a, f (a)) \ text {:} \) слева, на расстоянии и справа, вблизи. Справа мы помечаем функцию касательной линии \ (y = L (x) \) и замечаем, что для \ (x \) около \ (a \ text {,} \) \ (f (x) \ приблизительно L ( х) \ текст {.} \)Подраздел 1.8.2 Локальная линеаризация
Небольшое изменение перспективы и обозначений позволит нам более точно обсудить, как касательная линия приближает \ (f \) около \ (x = a \ text {.} \). Решая для \ (y \ text {, } \) уравнение касательной можно записать как
\ begin {уравнение *} y = f ‘(a) (x-a) + f (a) \ end {уравнение *}
Эта строка сама является функцией \ (x \ text {.} \). Заменяя переменную \ (y \) выражением \ (L (x) \ text {,} \), мы называем
\ begin {уравнение *} L (x) = f ‘(a) (x-a) + f (а) \ end {уравнение *}
локальная линеаризация \ (f \) в точке \ ((a, f (a)) \ text {.} \) В этих обозначениях \ (L (x) \) — не что иное, как новое имя для касательной. Как мы видели выше, для \ (x \), близкого к \ (a \ text {,} \) \ (f (x) \ приблизительно L (x) \ text {.} \)
Пример 1.8.3.
Предположим, что функция \ (y = f (x) \) имеет аппроксимацию касательной, заданную формулой \ (L (x) = 3-2 (x-1) \) в точке \ ((1,3) \ text {,} \), но мы ничего не знаем о функции \ (f \ text {.} \) Чтобы оценить значение \ (f (x) \) для \ (x \) около 1, например \ (f (1.2) \ text {,} \) мы можем использовать тот факт, что \ (f (1.2) \ приблизительно L (1,2) \) и, следовательно,
\ begin {уравнение *} f (1,2) \ приблизительно L (1,2) = 3–2 (1,2–1) = 3–2 (0,2) = 2,6 \ text {.} \ end {уравнение *}
Подчеркнем, что \ (y = L (x) \) — это просто новое имя для функции касательной. Используя это новое обозначение и наше наблюдение, что \ (L (x) \ приблизительно f (x) \) для \ (x \) near \ (a \ text {,} \), мы можем записать
\ begin {уравнение *} f (x) \ приблизительно f (a) + f ‘(a) (x-a) \ \ text {for} \ x \ \ text {near} \ a \ text {.} \ end {уравнение *}
Мероприятие 1.8.2.
Предположим, что известно, что для данной дифференцируемой функции \ (y = g (x) \ text {,} \) ее локальная линеаризация в точке, где \ (a = -1 \) задается выражением \ (L (x) = -2 + 3 (x + 1) \ text {.} \)
Вычислить значения \ (L (-1) \) и \ (L ‘(- 1) \ text {.} \)
Какими должны быть значения \ (g (-1) \) и \ (g ‘(- 1) \ text {?} \) Почему?
Ожидаете ли вы, что значение \ (g (-1.03) \) будет больше или меньше значения \ (g (-1) \ text {?} \) Почему?
Используйте локальную линеаризацию, чтобы оценить значение \ (g (-1.03) \ text {.} \)
Предположим, что вы также знаете, что \ (g » (- 1) = 2 \ text {.} \) Что это говорит вам о графике \ (y = g (x) \) в точке \ (a = -1 \ text {?} \)
Для \ (x \) около \ (- 1 \ text {,} \) нарисуйте график локальной линеаризации \ (y = L (x) \), а также возможный график \ (y = g ( x) \) по осям, указанным на рисунке 1.8.4.
Из действия 1.8.2 мы видим, что локальная линеаризация \ (y = L (x) \) является линейной функцией, которая имеет два важных значения с функцией \ (y = f (x) \), из которой она получена.В частности,
- , поскольку \ (L (x) = f (a) + f ‘(a) (xa) \ text {,} \) следует, что \ (L (a) = f (a) \ text {;} \ ) и
- , поскольку \ (L \) — линейная функция, ее производная — это наклон.
Следовательно, \ (L ‘(x) = f’ (a) \) для каждого значения \ (x \ text {,} \) и, в частности, \ (L ‘(a) = f’ (a) \ text {.} \) Следовательно, мы видим, что \ (L \) — линейная функция, которая имеет то же значение и тот же наклон, что и функция \ (f \) в точке \ ((a, f (a)) \ text {.} \)
Таким образом, если мы знаем линейное приближение \ (y = L (x) \) для функции, мы знаем значение исходной функции и ее наклон в точке касания.Однако остается неизвестным, как выглядит функция \ (f \) в точке касания. По сути, существует четыре возможности, как показано на рисунке 1.8.5.
Рисунок 1.8.5. Четыре возможных графика для нелинейной дифференцируемой функции и то, как она может быть расположена относительно ее касательной в точке.Эти возможные формы являются результатом того факта, что существует три варианта значения второй производной: либо \ (f » (a) \ lt 0 \ text {,} \) \ (f » (a) = 0 \ text {,} \) или \ (f » (a) \ gt 0 \ text {.} \)
- Если \ (f » (a) \ gt 0 \ text {,} \), то мы знаем, что график \ (f \) вогнут вверх, и мы видим первую возможность слева, где касательная линия лежит полностью ниже кривой.
- Если \ (f » (a) \ lt 0 \ text {,} \), то \ (f \) вогнута вниз, а касательная линия проходит над кривой, как показано на втором рисунке.
- Если \ (f » (a) = 0 \) и \ (f » \) изменит знак в \ (x = a \ text {,} \), вогнутость графика изменится, и мы увидим либо третья или четвертая цифра. 2 .
- Пятый вариант (который не очень интересен) может возникнуть, если функция \ (f \) сама по себе линейна, так что \ (f (x) = L (x) \) для всех значений \ (x \ text { .} \)
Возможно, что \ (f » (a) = 0 \), но \ (f » \) не меняет знак в \ (x = a \ text {,} \), и в этом случае график будет выглядеть вроде один из первых двух вариантов.
Графики на рис. 1.8.5 подчеркивают еще одну важную вещь, которую мы можем узнать из вогнутости графика около точки касания: лежит ли касательная линия выше или ниже самой кривой.Это ключевой момент, потому что он сообщает нам, будут ли значения аппроксимации касательной линии слишком большими или слишком маленькими по сравнению с истинным значением \ (f \ text {.} \). Например, в первой ситуации на крайнем левом графике на рис. 1.8.5, где \ (f » (a)> 0 \ text {,} \), поскольку касательная линия опускается ниже кривой, мы знаем, что \ (L (x) \ le f (x) \) для все значения \ (x \) рядом с \ (a \ text {.} \)
Мероприятие 1.8.3.
Это действие касается функции \ (f (x) \), о которой известна следующая информация:
\ (f \) — дифференцируемая функция, определенная для каждого действительного числа \ (x \)
\ (\ Displaystyle f (2) = -1 \)
\ (y = f ‘(x) \) имеет график, показанный на рисунке 1.8,6
Ваша задача — определить как можно больше информации о \ (f \) (особенно около значения \ (a = 2 \)), отвечая на вопросы ниже.
Найдите формулу аппроксимации касательной от \ (L (x) \ text {,} \) до \ (f \) в точке \ ((2, -1) \ text {.} \)
Используйте приближение касательной, чтобы оценить значение \ (f (2.07) \ text {.} \) Покажите свою работу внимательно и ясно.
Нарисуйте график \ (y = f » (x) \) в правой сетке на рис. 1.8.6; обозначьте это соответствующим образом.
Наклон касательной к \ (y = f (x) \) увеличивается, уменьшается или не уменьшается, когда \ (x = 2 \ text {?} \) Объясните.
Нарисуйте возможный график \ (y = f (x) \) рядом с \ (x = 2 \) в левой сетке на рисунке 1.8.6. Включите эскиз \ (y = L (x) \) (находится в части (а)). Объясните, откуда вы знаете, что график \ (y = f (x) \) выглядит так, как будто вы его нарисовали.
Ваша оценка в (b) переоценивает или занижает истинное значение \ (f (2.07) \ text {?} \) Почему?
Идея о том, что дифференцируемая функция выглядит линейной и может быть хорошо аппроксимирована линейной функцией, является важной идеей, которая находит широкое применение в исчислении. Например, аппроксимируя функцию с ее локальной линеаризацией, можно разработать эффективный алгоритм для оценки нулей функции. Локальная линейность также помогает нам лучше понять некоторые сложные ограничения.Например, мы видели, что предел
\ begin {уравнение *} \ lim_ {x \ to 0} \ frac {\ sin (x)} {x} \ end {уравнение *}
является неопределенным, потому что его числитель и знаменатель стремятся к 0. Хотя нет алгебры, которую мы могли бы сделать, чтобы упростить \ (\ frac {\ sin (x)} {x} \ text {,} \), это просто показать, что линеаризация \ (f (x) = \ sin (x) \) в точке \ ((0,0) \) задается выражением \ (L (x) = x \ text {.} \) Следовательно , для значений \ (x \) около 0, \ (\ sin (x) \ приблизительно x \ text {,} \) и, следовательно,
\ begin {уравнение *} \ frac {\ sin (x)} {x} \ приблизительно \ frac {x} {x} = 1 \ text {,} \ end {уравнение *}
, что делает правдоподобным тот факт, что
\ begin {уравнение *} \ lim_ {x \ to 0} \ frac {\ sin (x)} {x} = 1 \ text {. 2 \)), вы можете ожидать, что частные производные могут быть использованы для определения касательной плоскости к графику поверхности \ (z = f (х, у) \).3 \) определяют плоскость, то две касательные к поверхности \ (z = f (x, y) \) в направлениях \ (x \) и \ (y \), описанные на рисунке 2.3.1, содержатся в касательная плоскость в этой точке, , если касательная плоскость существует в этой точке . Существование этих двух касательных линий само по себе не гарантирует существования касательной плоскости. Возможно, что если мы возьмем след поверхности в плоскости \ (x — y = 0 \) (которая составляет угол 45 ° с положительной осью \ (x \)), полученная кривая в этой плоскости может иметь касательную линию, которая не находится в плоскости, определяемой двумя другими касательными линиями, или она может вообще не иметь касательной в этой точке.К счастью, оказывается, что если \ (\ dfrac {∂f} {∂x} \) и \ (\ dfrac {∂f} {∂y} \) существуют в области вокруг точки \ ((a, b) \) и непрерывны в точке \ ((a, b) \), то касательная плоскость к поверхности \ (z = f (x, y) \) будет существовать в точке \ ((a, b, f (a, б)) \). В этом тексте эти условия будут выполняться всегда.
Предположим, что нам нужно уравнение касательной плоскости \ (T \) к поверхности \ (z = f (x, y) \) в точке \ ((a, b, f (a, b)) \) . Пусть \ (L_x \) и \ (L_y \) — касательные линии к следам поверхности в плоскостях \ (y = b \) и \ (x = a \) соответственно (как на рисунке 2.3.2) и предположим, что условия существования \ (T \) выполняются. Тогда уравнение для \ (T \) равно
\ [A (x− a) + B (y− b) + C (z — f (a, b)) = 0 \ label {Eq2.4} \]
, где \ (n = (A, B, C) \) — вектор нормали к плоскости \ (T \). Поскольку \ (T \) содержит линии \ (L_x \) и \ (L_y \), то все, что нам нужно, это векторы \ (v_x \) и \ (v_y \), которые параллельны \ (L_x \ text {и} L_y \) соответственно, а затем пусть \ (n = v_x × v_y \).
Рисунок 2.3.2: Касательная плоскостьПоскольку наклон \ (L_x \) равен \ (\ dfrac {∂f} {∂x} (a, b) \), то вектор \ (v_x = (1,0, \ dfrac {∂f} {∂x} (a, b)) \) параллельно \ (L_x \) (поскольку \ (v_x \) лежит в \ (xz \) — плоскости и лежит на прямой с наклоном \ (\ dfrac {\ dfrac {∂f} {∂x} (a, b)} {1} = \ dfrac {∂f} {∂x} (a, b) \).См. Рисунок 2.3.3). Точно так же вектор \ (v_y = (0,1, \ dfrac {∂f} {∂y} (a, b)) \) параллелен \ (L_y \). Следовательно, вектор
\ [\ textbf {n} = \ mathbf {v_x} × \ mathbf {v_y} = \ begin {vmatrix} \ textbf {i} & \ textbf {j} & \ textbf {k} \\ [4pt] 1 & 0 & \ dfrac {∂f} {∂x} (a, b) \\ [4pt] 0 & 1 & \ dfrac {∂f} {∂y} (a, b) \ end {vmatrix} = — \ dfrac {∂f} {∂x} (a, b) \ textbf {i} — \ dfrac {∂f} {∂y} (a, b) \ textbf {j} + \ textbf {k} \ nonumber \]
нормально к растению \ (T \). Таким образом, уравнение \ (T \) равно
\ [- \ dfrac {∂f} {∂x} (a, b) (xa) — \ dfrac {∂f} {∂y} (a, b) (yb) + zf (a, b) = 0 \ label {Eq2.2 \) имеем \ (\ dfrac {∂f} {∂x} = 2x \) и \ (\ dfrac {∂f} {∂y} = 2y \), поэтому уравнение касательной плоскости в точке \ ((1,2,5) \) равно
\ [\ nonumber 2 (1) (x − 1) +2 (2) (y − 2) — z +5 = 0 \ text {, или} \]
\ [\ nonumber 2x + 4y− z −5 = 0 \]
Аналогичным образом можно показать, что если поверхность определяется неявно уравнением вида \ (F (x, y, z) = 0 \), то касательная плоскость к поверхности в точке \ ( (a, b, c) \) задается уравнением
\ [\ dfrac {∂F} {∂x} (a, b, c) (x− a) + \ dfrac {∂F} {∂y} (a, b, c) (y− b) + \ dfrac {∂F} {∂z} (a, b, c) (z — c) = 0 \ label {Eq2.2 −9 \) имеем \ (\ dfrac {∂F} {∂x} = 2x \), \ (\ dfrac {∂F} {∂y} = 2y \) и \ (\ dfrac {∂F } {∂z} = 2z \), поэтому уравнение касательной плоскости в точке (2,2, −1) равно
\ [\ nonumber 2 (2) (x − 2) +2 (2) (y − 2) +2 (−1) (z +1) = 0 \ text {, или} \]
\ [\ nonumber 2x + 2y− z −9 = 0 \]
Авторы и авторство
Нахождение уравнения прямой, касательной к функции | Ретт Аллен | The Startup
Нет особой причины для этого поста. Я просто собираюсь решить математическую задачу.Почему? Потому что я думаю, это весело. Вот в чем проблема.
Найдите уравнение прямых, которые проходят через точку (-1, -4) и касаются функции f (x) = 3x².
Вот и все. Это проблема. Вот план. Я собираюсь решить эту конкретную проблему, а затем покажу вам отличный способ сделать это с помощью Python (для удовольствия).
Итак, давайте разберемся с вопросом. Во-первых, что это вообще значит? Что ж, будет линия, проходящая через точку (-1, -4) — это ясно.Но это также должно касаться функции. Касательная к функции линия «коснется» ее всего в одной точке. Наклон линии будет равен производной этой функции в точке, которой она касается.
На всякий случай, если вы не помните деривативы, вот краткий обзор.
Хорошо, а теперь набросок, чтобы мы «грокнули» все это. Вот функция, точка (-1, -4) и точка касания (которую мы еще не знаем).
О, обратите внимание, что неизвестная точка функции имеет значение x, равное «x», и значение y, равное f (x).Теперь есть два способа найти наклон этой касательной. Первый способ — просто использовать определение уклона вместе с двумя нашими известными точками. Я собираюсь использовать букву «m» для наклона.
Второй способ найти наклон — использовать производную функции. Я назову производную «f’ (x) ». Мы можем найти производную, используя правило мощности.
Поскольку оба этих метода должны иметь одинаковый наклон, я могу установить их равными друг другу.
Теперь мне просто нужно решить относительно x.Я умножу обе стороны на (x + 4), а затем перенесу все члены в одну сторону.
Используя квадратное уравнение, я получаю ДВА ответа. Это:
Ради удовольствия, позвольте мне построить точки функции, соответствующие этим двум значениям x.
Ага. Выглядит хорошо. Если вы проведете прямую линию из точки (-1, -4), похоже, что она просто коснется функции в обеих этих точках. Теперь нам просто нужно уравнение для этой линии (ну, обеих линий). Здесь я могу использовать формулу угла наклона линии, чтобы получить следующее.Ой, погоди. Во-первых, мне нужно поместить значения x BACK в исходную функцию, чтобы получить значения y этих точек. Кроме того, мне нужно ввести это значение x, чтобы найти наклон. Делая это, СЕЙЧАС я получаю:
Это выглядит безумно, но ТЕХНИЧЕСКИ, это уравнение линии. Я не собираюсь это упрощать. Я должен был выбрать лучшие ценности, чтобы дать более хороший ответ, — но жизнь не всегда хороша (я говорю с вами, 2020 год).
Вы можете сделать то же самое для другого значения x и получить вторую строку.Но теперь по-другому.
Путь Python
Я просто хочу это сделать. Это будет весело. Я не буду вдаваться в подробности программы, поэтому позвольте мне дать вам обзор.
- Сначала я просто построю график функции и точки (точно так же, как график выше, который также был создан на Python).
- Затем я могу переместить точку вдоль кривой функции. Это означает, что у меня будет два очка.
- С этими двумя точками я сделаю две вещи.Сначала вычислите наклон от фиксированной точки до точки на кривой. Во-вторых, найдите производную функции в этой точке (в данном случае я использую числовую производную, если вы не можете найти фактическую производную функции). Вот руководство по числовым производным с помощью Python.
- Поскольку я не смотрю на КАЖДУЮ единственную точку функции (потому что она числовая), я собираюсь искать такие значения x, чтобы разница между наклоном и производной была очень маленькой (но не обязательно нулевой).
- О, мне просто нужно было научиться создавать анимированные графики в VPython — теперь я знаю, как это делать.


 Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.
Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007. А.П.Тряпининой. –
СПб.: КАРО, 2005.
А.П.Тряпининой. –
СПб.: КАРО, 2005. Напишите
уравнение этой касательной.
Напишите
уравнение этой касательной. 8.
8.
 диссертации.
диссертации. 000 евро в год до вычета налогов, после окончания магистратуры — около 43.000 евро в год до вычета налогов (данные на 2018-2019 гг.). Более подробно о зарплатах выпускников немецких вузов можно прочитать здесь.
000 евро в год до вычета налогов, после окончания магистратуры — около 43.000 евро в год до вычета налогов (данные на 2018-2019 гг.). Более подробно о зарплатах выпускников немецких вузов можно прочитать здесь.



 В зависимости от специализации это направление может затрагивать не только транспортную систему, но и возведение недвижимых объектов.
В зависимости от специализации это направление может затрагивать не только транспортную систему, но и возведение недвижимых объектов.



 После окончания вуза Германии можно поехать в любую страну, заняться управлением проектами, заниматься престижным делом.
После окончания вуза Германии можно поехать в любую страну, заняться управлением проектами, заниматься престижным делом.
 На тот момент казалось, что строитель – это, как любят говорить, «вечная профессия». Ведь строители будут нужны всегда.
На тот момент казалось, что строитель – это, как любят говорить, «вечная профессия». Ведь строители будут нужны всегда. Также подкупило, что присваиваемая квалификация не «инженер-строитель», а «инженер-строитель-технолог».
Также подкупило, что присваиваемая квалификация не «инженер-строитель», а «инженер-строитель-технолог».
 Со мной учились замечательные ребята. Прошло почти четыре года после выпуска, а мы до сих пор поддерживаем тесные отношения с большей частью группы. Периодически встречаемся: на День студента или летом во время отпусков. Я очень рад этому, так как в жизни трудно построить такие крепкие дружеские отношения.
Со мной учились замечательные ребята. Прошло почти четыре года после выпуска, а мы до сих пор поддерживаем тесные отношения с большей частью группы. Периодически встречаемся: на День студента или летом во время отпусков. Я очень рад этому, так как в жизни трудно построить такие крепкие дружеские отношения. Так что еще одно место моей работы – автомобиль, в котором я провожу большую часть времени.
Так что еще одно место моей работы – автомобиль, в котором я провожу большую часть времени. Радует, когда люди звонят и говорят: «Мы уже с вами работали, нам все понравилось, давайте еще посотрудничаем…»
Радует, когда люди звонят и говорят: «Мы уже с вами работали, нам все понравилось, давайте еще посотрудничаем…»
 Работая строителем, можно посмотреть мир, например. Некоторые мои коллеги работают в Санкт-Петербурге, Красноярске. Есть один энтузиаст, который сейчас помогает народу Бангладеша строить атомную электростанцию.
Работая строителем, можно посмотреть мир, например. Некоторые мои коллеги работают в Санкт-Петербурге, Красноярске. Есть один энтузиаст, который сейчас помогает народу Бангладеша строить атомную электростанцию. И еще нужно уметь в нужный момент брать ответственность на себя.
И еще нужно уметь в нужный момент брать ответственность на себя.
 Тогда на строителя экзамены сдавать все же потребуется и учиться стоит поступать в один из строительных колледжей или техникумов.
Тогда на строителя экзамены сдавать все же потребуется и учиться стоит поступать в один из строительных колледжей или техникумов.

 Полученные на Едином государственном экзамене баллы не важны, главное – оценки в аттестате. Учиться после 11 класса в ссузе, в среднем, на год меньше.
Полученные на Едином государственном экзамене баллы не важны, главное – оценки в аттестате. Учиться после 11 класса в ссузе, в среднем, на год меньше.



 Вполне предсказуемо, первые вопросы интервью – о причинах этого выбора.
Вполне предсказуемо, первые вопросы интервью – о причинах этого выбора. Просто так совпало.
Просто так совпало.


 Я хожу на дополнительные занятия, проходящие в школе, много времени уделяю и самообразованию. Я хочу все свои усилия приложить физике и сдать ее хорошо.
Я хожу на дополнительные занятия, проходящие в школе, много времени уделяю и самообразованию. Я хочу все свои усилия приложить физике и сдать ее хорошо. Девятый класс я закончила с отличием и получила аттестат особого образца.
Девятый класс я закончила с отличием и получила аттестат особого образца.

 Дополнительную информацию о менеджерах по проектированию см. В профиле менеджеров по архитектуре и проектированию.
Дополнительную информацию о менеджерах по проектированию см. В профиле менеджеров по архитектуре и проектированию.
 Многие задействованные переменные требуют, чтобы они обладали способностью выявлять и оценивать сложные проблемы.Затем они должны иметь возможность использовать свои навыки и обучение для разработки экономичных, безопасных и эффективных решений.
Многие задействованные переменные требуют, чтобы они обладали способностью выявлять и оценивать сложные проблемы.Затем они должны иметь возможность использовать свои навыки и обучение для разработки экономичных, безопасных и эффективных решений.
 После выполнения требований к опыту работы EIT и EI могут сдать второй экзамен, который называется «Принципы и практика проектирования».
После выполнения требований к опыту работы EIT и EI могут сдать второй экзамен, который называется «Принципы и практика проектирования».
 Инженер-строитель специализируется на проектировании и анализе зданий и мостов. Инженер-геолог проектирует и строит туннели, трубопроводы, насыпи и фундаменты. Инженер-эколог анализирует и решает проблемы, связанные с качеством воздуха и воды и управлением отходами и опасными материалами.
Инженер-строитель специализируется на проектировании и анализе зданий и мостов. Инженер-геолог проектирует и строит туннели, трубопроводы, насыпи и фундаменты. Инженер-эколог анализирует и решает проблемы, связанные с качеством воздуха и воды и управлением отходами и опасными материалами.


 Многие профессиональные организации гражданского строительства и NSPE предлагают онлайн-курсы повышения квалификации, иногда бесплатно. Также учитываются выпускные курсы гражданского строительства.
Многие профессиональные организации гражданского строительства и NSPE предлагают онлайн-курсы повышения квалификации, иногда бесплатно. Также учитываются выпускные курсы гражданского строительства. Эти специалисты могут получить сертификаты по следующим специальностям:
Эти специалисты могут получить сертификаты по следующим специальностям:
 .
.









 // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
// И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.


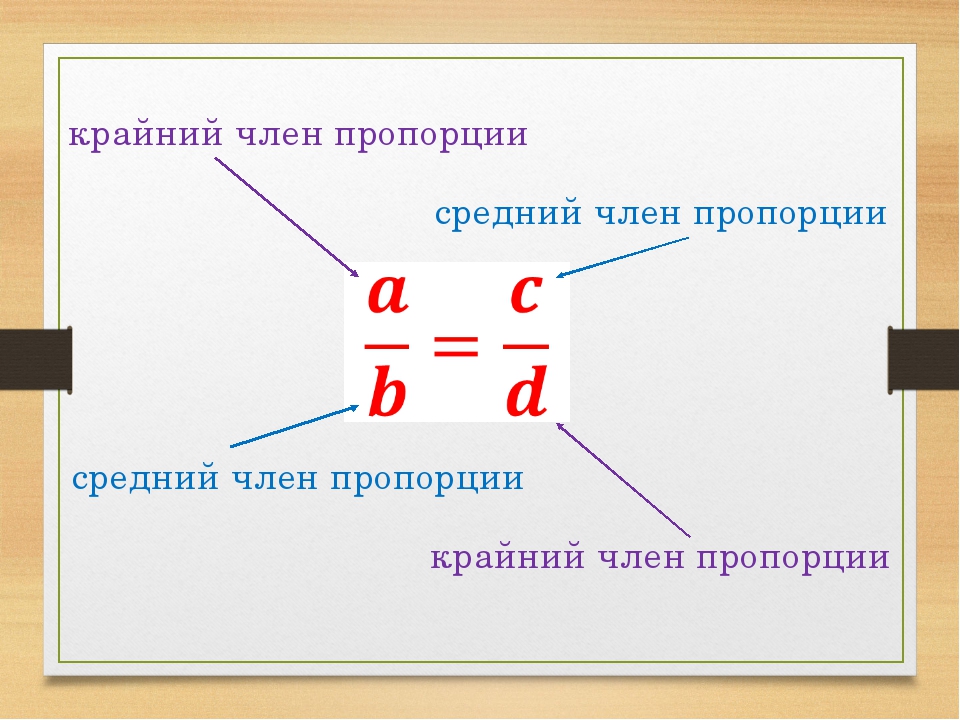 Давайте посмотрим, как же можно найти тот или иной член пропорции, зная значения всех остальных. Для начала, следует усвоить два простых правила:
Давайте посмотрим, как же можно найти тот или иной член пропорции, зная значения всех остальных. Для начала, следует усвоить два простых правила:
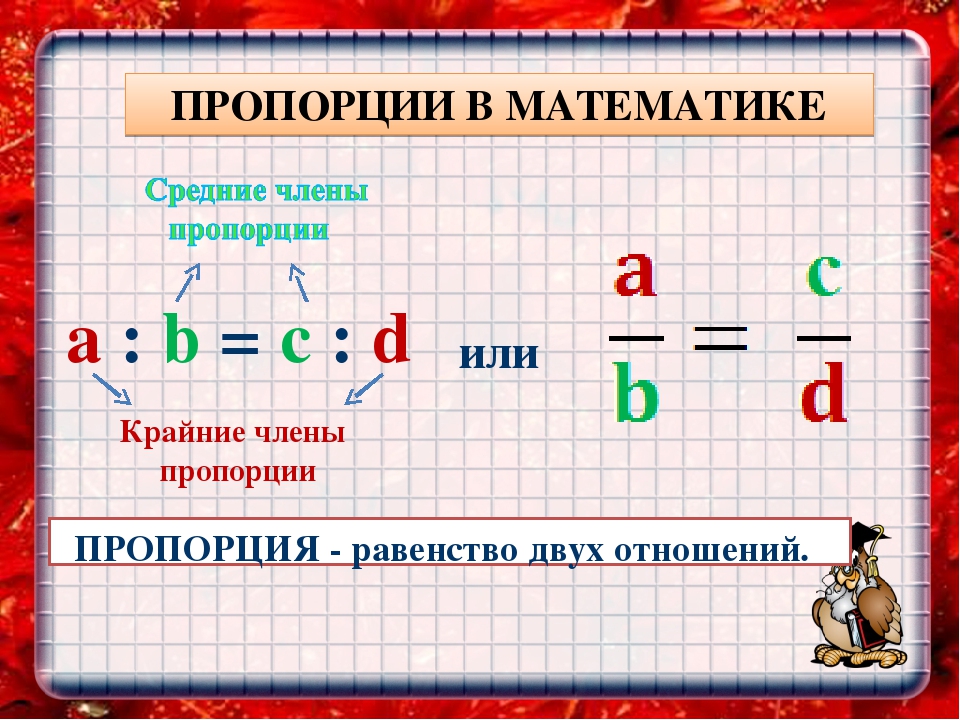 э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.
э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.
И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор. д., известный, как ряд Фибоначчи.
д., известный, как ряд Фибоначчи.
 Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.
Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.
 И здесь мы опять сталкиваемся с закономерность «золотого сечения».
И здесь мы опять сталкиваемся с закономерность «золотого сечения».
 Многие люди сталкиваются с пропорциями. Решать их несложно, но если не знать свойств и правил, можно выполнить неверные вычисления. Специалисты рекомендуют получить теоретические знания, а затем перейти к их практическому применению.
Многие люди сталкиваются с пропорциями. Решать их несложно, но если не знать свойств и правил, можно выполнить неверные вычисления. Специалисты рекомендуют получить теоретические знания, а затем перейти к их практическому применению.
 Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.

 Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения. (½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений: y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается. (½)) / 2a.
(½)) / 2a. Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения.
Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения. Но если величины находятся в геометрической пропорции, произведение её крайних членов равно произведению их средних членов.
Но если величины находятся в геометрической пропорции, произведение её крайних членов равно произведению их средних членов. 

 Но, как правило, необходимо, чтобы эта первая пропорция претерпела ряд трансформаций прежде, чем отчётливо выявится неизвестная величина или утверждение, которое мы хотели доказать. Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.
Но, как правило, необходимо, чтобы эта первая пропорция претерпела ряд трансформаций прежде, чем отчётливо выявится неизвестная величина или утверждение, которое мы хотели доказать. Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.
 4 = 8.6.
4 = 8.6.  Некоторые из утверждений могут быть доказаны более простым способом, возможно, путём умножения крайних и средних членов. Но это не даст ясного понимания природы некоторых изменений в пропорциях.
Некоторые из утверждений могут быть доказаны более простым способом, возможно, путём умножения крайних и средних членов. Но это не даст ясного понимания природы некоторых изменений в пропорциях.
 (Статья. 354, след.)
(Статья. 354, след.) 
 В геометрии на предположение, к которому они принадлежат обычно ссылаются как на «ex aequo«или «ex aequali» (по справедливости). Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.
В геометрии на предположение, к которому они принадлежат обычно ссылаются как на «ex aequo«или «ex aequali» (по справедливости). Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.

 Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим,
Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим, 

 соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны.
соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны. 254, 371,) √a:√b = √c:√d.
254, 371,) √a:√b = √c:√d. 
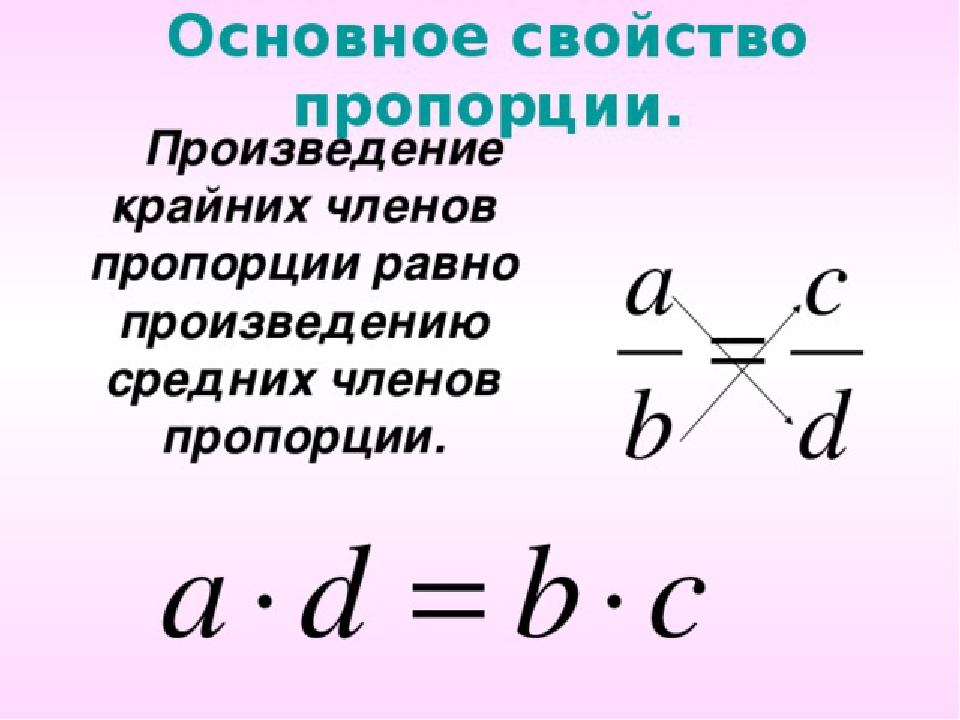 376.
376.  А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент.
А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент. 



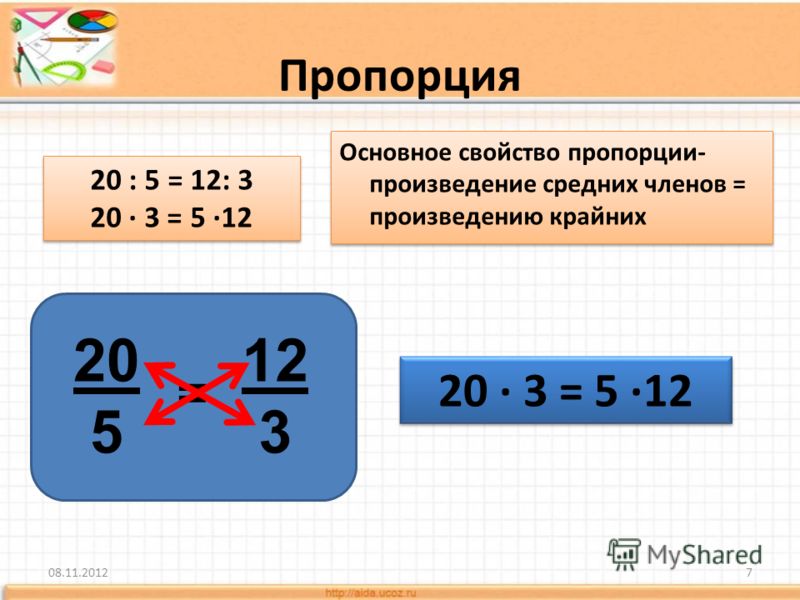 Правило третей может быть очень полезным руководством при создании дизайна.
Правило третей может быть очень полезным руководством при создании дизайна. Это можно записать двумя
способами: как две равные дроби a / b = c / d; или используя двоеточие, a: b = c: d. Следующие
пропорция читается как «двадцать равно двадцати пяти, как четыре — пяти».
Это можно записать двумя
способами: как две равные дроби a / b = c / d; или используя двоеточие, a: b = c: d. Следующие
пропорция читается как «двадцать равно двадцати пяти, как четыре — пяти». длинный.В фильме также использовалась модель здания высотой 30 дюймов. Какого роста
здание кажется в фильме?
длинный.В фильме также использовалась модель здания высотой 30 дюймов. Какого роста
здание кажется в фильме?
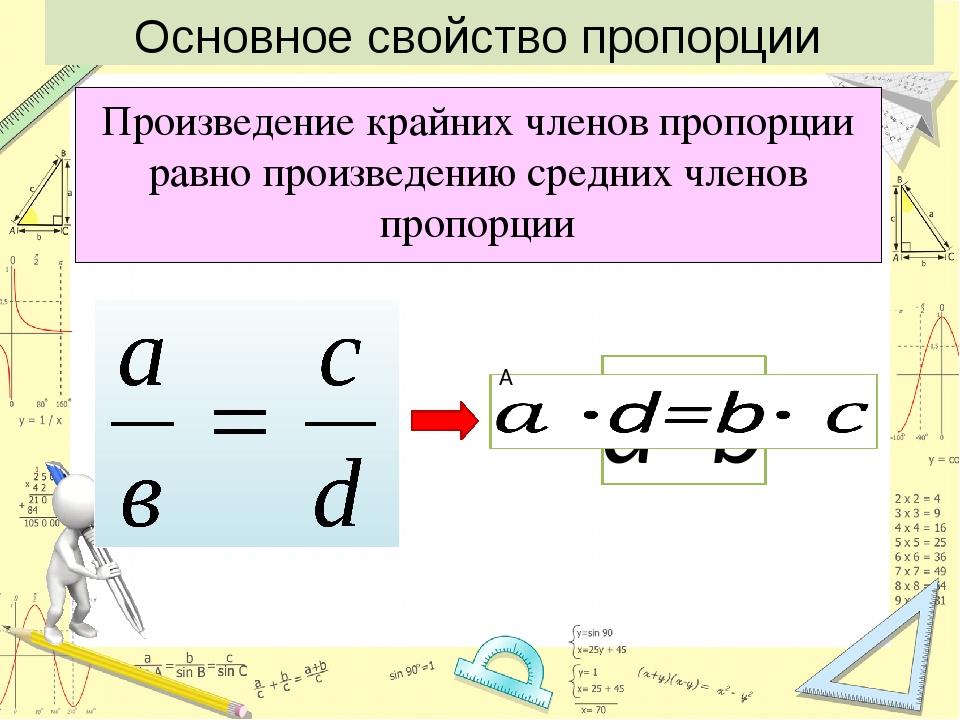 Это одно из тех странных мест, где наука взаимодействует с визуальной эстетикой, философией и смыслом жизни. Может быть.
Это одно из тех странных мест, где наука взаимодействует с визуальной эстетикой, философией и смыслом жизни. Может быть. Я сидел с множеством дизайнеров, которые просто перемещали вещи, пока не почувствовали себя «правильными». Дизайн — это, по сути, коммуникация (я знаю, я знаю, я достаточно разглагольствую об этом, но это не одна из них), но средство коммуникации — это дизайн.Одним из ключевых компонентов средства коммуникации является композиция, а в школе дизайна это то, чему учат как нечто, что вы должны чувствовать, а не создавать логически. Меня это всегда беспокоило.
Я сидел с множеством дизайнеров, которые просто перемещали вещи, пока не почувствовали себя «правильными». Дизайн — это, по сути, коммуникация (я знаю, я знаю, я достаточно разглагольствую об этом, но это не одна из них), но средство коммуникации — это дизайн.Одним из ключевых компонентов средства коммуникации является композиция, а в школе дизайна это то, чему учат как нечто, что вы должны чувствовать, а не создавать логически. Меня это всегда беспокоило. Это математическая формула, наблюдаемая в природе и используемая художниками, архитекторами, дизайнерами и даже музыкантами множеством способов.
Это математическая формула, наблюдаемая в природе и используемая художниками, архитекторами, дизайнерами и даже музыкантами множеством способов.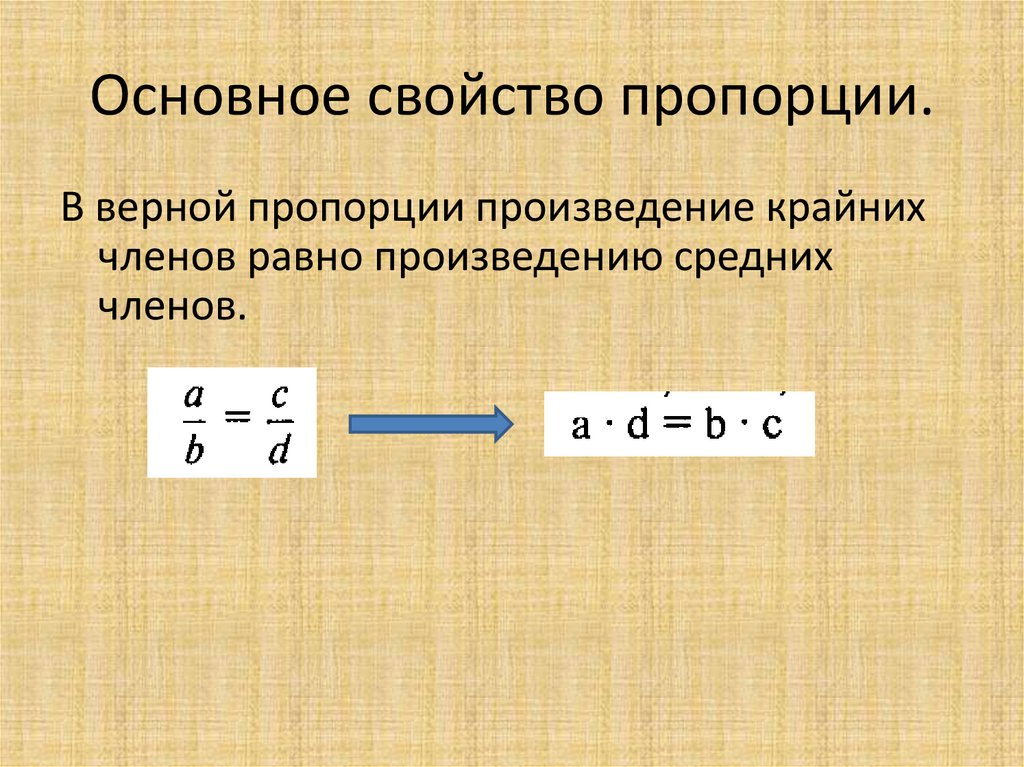 С момента открытия и исследования золотого сечения я могу искренне сказать, что моя эстетика резко улучшилась! Не говоря уже о (благодаря использованию некоторых инструментов, которыми я собираюсь с вами поделиться) о повышении производительности, которое я испытал!
С момента открытия и исследования золотого сечения я могу искренне сказать, что моя эстетика резко улучшилась! Не говоря уже о (благодаря использованию некоторых инструментов, которыми я собираюсь с вами поделиться) о повышении производительности, которое я испытал! Но это всего лишь инструмент, а не правило для композиции. Золотое сечение широко использовалось Леонардо да Винчи. Обратите внимание, как все ключевые измерения комнаты и стола в «Тайной вечере» да Винчи были основаны на золотом сечении, которое в период Возрождения было известно как Божественная пропорция.
Но это всего лишь инструмент, а не правило для композиции. Золотое сечение широко использовалось Леонардо да Винчи. Обратите внимание, как все ключевые измерения комнаты и стола в «Тайной вечере» да Винчи были основаны на золотом сечении, которое в период Возрождения было известно как Божественная пропорция.




 .Эти описания — просто пропорциональные эффекты противостояния, присущего всем вещам.
.Эти описания — просто пропорциональные эффекты противостояния, присущего всем вещам. С помощью линейки и карандаша вы можете быстро разделить весь холст, чтобы создать работоспособную основу для вашей композиции, разработанной с учетом золотого сечения.
С помощью линейки и карандаша вы можете быстро разделить весь холст, чтобы создать работоспособную основу для вашей композиции, разработанной с учетом золотого сечения. По крайней мере, до недавнего времени, не раньше, чем потратить последние трех лет на изучение классических порядков с Тоддом Мердоком — одно исполнение SketchUp за раз.Теперь я знаю, почему мне было так сложно понять правила пропорции. Таких нет. Их не существует. Но есть рекомендации.
По крайней мере, до недавнего времени, не раньше, чем потратить последние трех лет на изучение классических порядков с Тоддом Мердоком — одно исполнение SketchUp за раз.Теперь я знаю, почему мне было так сложно понять правила пропорции. Таких нет. Их не существует. Но есть рекомендации. (Примечание: щелкните любое изображение, чтобы увеличить.)
(Примечание: щелкните любое изображение, чтобы увеличить.) На этот раз я хотел начать с действительно приятного дизайна, и мне нужно было знать, какой ширины и глубины должны быть пилястры, какой высоты должен быть антаблемент, насколько далеко должен выступать карниз. Да, я хотел знать правила. У Бенджамина не было недостатка в правилах. И по какой-то глупой причине я все еще думал, что все они произошли от Парфенона!
На этот раз я хотел начать с действительно приятного дизайна, и мне нужно было знать, какой ширины и глубины должны быть пилястры, какой высоты должен быть антаблемент, насколько далеко должен выступать карниз. Да, я хотел знать правила. У Бенджамина не было недостатка в правилах. И по какой-то глупой причине я все еще думал, что все они произошли от Парфенона! И что еще больше запутало, он описал размер каждой детали лепнины, используя систему, основанную на минутах ( Архитектор, или Практический Дом Карпентер , 1830). Минуты! Какое отношение время имеет к пропорции?
И что еще больше запутало, он описал размер каждой детали лепнины, используя систему, основанную на минутах ( Архитектор, или Практический Дом Карпентер , 1830). Минуты! Какое отношение время имеет к пропорции?
 Ни один из этих примеров не основан на конкретных греческих или римских руинах. Все они зависят от мнения и вкуса отдельного автора. На самом деле, единственное, что их объединяет, это то, что своим подходом они обязаны Витрувию (см. Историю ниже).
Ни один из этих примеров не основан на конкретных греческих или римских руинах. Все они зависят от мнения и вкуса отдельного автора. На самом деле, единственное, что их объединяет, это то, что своим подходом они обязаны Витрувию (см. Историю ниже). 

 э., и он внимательно изучил Парфенон. Он особенно описал мельчайшие отклонения от идеально прямых линий, обнаруженные в стилобате или ступенях, ведущих к храму, в антазисе колонн и в том, что мы сегодня узнаем как слегка изогнутый архитрав, включая изгиб в самих панелях метопа.
э., и он внимательно изучил Парфенон. Он особенно описал мельчайшие отклонения от идеально прямых линий, обнаруженные в стилобате или ступенях, ведущих к храму, в антазисе колонн и в том, что мы сегодня узнаем как слегка изогнутый архитрав, включая изгиб в самих панелях метопа. Альберти основал многие из своих правил пропорции на работе Витрувия, написанной почти полторы тысячи лет назад.
Альберти основал многие из своих правил пропорции на работе Витрувия, написанной почти полторы тысячи лет назад.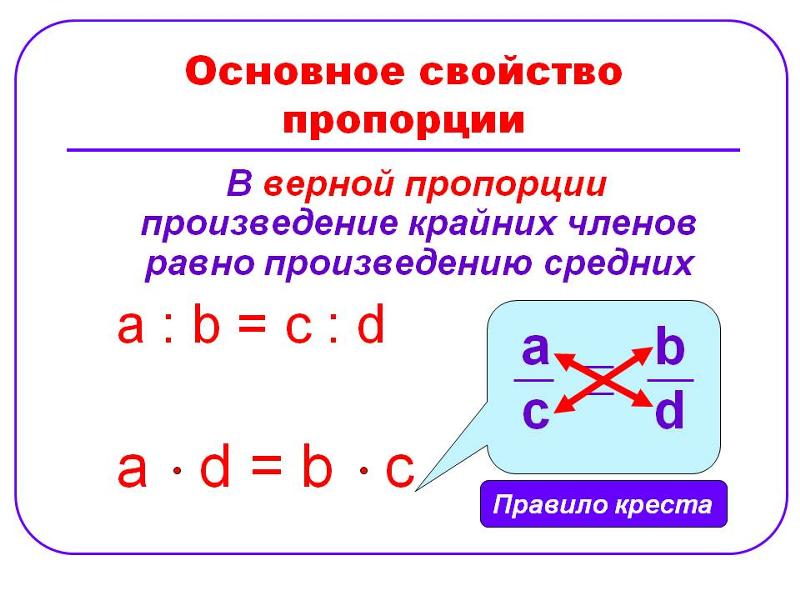 Но именно система Виньолы оказала влияние на большинство авторов архитектуры.
Но именно система Виньолы оказала влияние на большинство авторов архитектуры. Среди этих архитекторов / авторов / иллюстраторов были Джеймс Гиббс (который работал в то же время, что и сэр Кристофер Рен и Иниго Джонс), Авраам Свон и Уильям Чемберс, которые оказали влияние — часто напрямую — на работу Ашера Бенджамина.
Среди этих архитекторов / авторов / иллюстраторов были Джеймс Гиббс (который работал в то же время, что и сэр Кристофер Рен и Иниго Джонс), Авраам Свон и Уильям Чемберс, которые оказали влияние — часто напрямую — на работу Ашера Бенджамина. [v]
[v]
 Большинство авторов никогда не читают фактический исходный материал; большинство авторов просто читают других авторов, которые цитировали исходный материал.Не будьте небрежным исследователем, — сказал он мне, — всегда читайте исходный материал самостоятельно. Возможно, ты единственный, кто это сделает ».
Большинство авторов никогда не читают фактический исходный материал; большинство авторов просто читают других авторов, которые цитировали исходный материал.Не будьте небрежным исследователем, — сказал он мне, — всегда читайте исходный материал самостоятельно. Возможно, ты единственный, кто это сделает ». Во втором абзаце книги «О симметрии» Витрувий даже отмечает пропорциональный размер человеческих стоп: «Длина стопы составляет одну шестую высоты тела; предплечья — одна четвертая; и ширина груди тоже одна четвертая.”
Во втором абзаце книги «О симметрии» Витрувий даже отмечает пропорциональный размер человеческих стоп: «Длина стопы составляет одну шестую высоты тела; предплечья — одна четвертая; и ширина груди тоже одна четвертая.” [Viii]
[Viii] А затем мы рассмотрим Кинг-Конг из всех мифов — отношение золотого прямоугольника к Парфенону.
А затем мы рассмотрим Кинг-Конг из всех мифов — отношение золотого прямоугольника к Парфенону. Далее, обсуждая древнее правило, гласящее, что «в идеальных зданиях разные элементы должны находиться в точном симметричном отношении ко всей общей схеме», Витрувий обсуждает, почему греки остановились на десяти как на «совершенном числе», отчасти потому, что это количество элементов. пальцы рук и ног на человеческом теле, и поскольку оно легко делится, но «как только достигается одиннадцать или двенадцать, числа, будучи чрезмерными, не могут быть идеальными, пока они не дойдут до десяти во второй раз» (стр.73).
Далее, обсуждая древнее правило, гласящее, что «в идеальных зданиях разные элементы должны находиться в точном симметричном отношении ко всей общей схеме», Витрувий обсуждает, почему греки остановились на десяти как на «совершенном числе», отчасти потому, что это количество элементов. пальцы рук и ног на человеческом теле, и поскольку оно легко делится, но «как только достигается одиннадцать или двенадцать, числа, будучи чрезмерными, не могут быть идеальными, пока они не дойдут до десяти во второй раз» (стр.73). выдающееся заблуждение.Чтобы проследить связь между золотым прямоугольником и Парфеноном, я просмотрел все книги по архитектуре, которые попадались мне в руки.
выдающееся заблуждение.Чтобы проследить связь между золотым прямоугольником и Парфеноном, я просмотрел все книги по архитектуре, которые попадались мне в руки.
 Многие из них были известны математикам в древности и в эпоху Возрождения, но нет никаких документальных свидетельств архитектурного интереса до XIX века. … Хотя нет никаких доказательств вечной красоты этой фигуры или ее сознательного использования в какой-либо период, кроме недавнего прошлого, ее характеристики представляют определенный интерес »(стр.116).
Многие из них были известны математикам в древности и в эпоху Возрождения, но нет никаких документальных свидетельств архитектурного интереса до XIX века. … Хотя нет никаких доказательств вечной красоты этой фигуры или ее сознательного использования в какой-либо период, кроме недавнего прошлого, ее характеристики представляют определенный интерес »(стр.116). Он прослеживает мифическую теорию до Луки Пачоли, математика эпохи Возрождения и близкого человека Леонардо да Винчи:
Он прослеживает мифическую теорию до Луки Пачоли, математика эпохи Возрождения и близкого человека Леонардо да Винчи: Однако до XIX века Золотое сечение просто отсутствовало в письменной архитектурной теории.
Однако до XIX века Золотое сечение просто отсутствовало в письменной архитектурной теории. ”
”

 Оберлинский колледж, 1950.
Оберлинский колледж, 1950.
 Это иллюстрирует те же отношения, что и в примере с отрезком линии напротив.
Это иллюстрирует те же отношения, что и в примере с отрезком линии напротив. Здесь используются квадраты размером 1, 1, 2, 3, 5, 8, 13, 21 и 34.
Здесь используются квадраты размером 1, 1, 2, 3, 5, 8, 13, 21 и 34.


 17.)
17.) (Урок 17.) И каждое кратное 2 равно двум третям от того же кратного 3:
(Урок 17.) И каждое кратное 2 равно двум третям от того же кратного 3: Девять умножить на 4 — это 36 «.
Девять умножить на 4 — это 36 «. Это называется Правило трех. Мы можем резюмировать это следующим образом.
Это называется Правило трех. Мы можем резюмировать это следующим образом.



 Хотя его соотношение не соответствует соотношению 1: 1,618, его правильная реализация в композиции даст вам примерно такой же желаемый эффект, но его очень легко представить и реализовать по сравнению с золотым сечением.
Хотя его соотношение не соответствует соотношению 1: 1,618, его правильная реализация в композиции даст вам примерно такой же желаемый эффект, но его очень легко представить и реализовать по сравнению с золотым сечением.  . Яблоки:
. Яблоки: 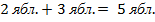 Сантиметры:
Сантиметры: 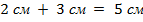 . Даже что-то, про что мы вообще ничего не знаем:
. Даже что-то, про что мы вообще ничего не знаем: 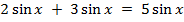 .
.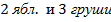 , или
, или 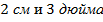 , или
, или 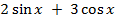 .
.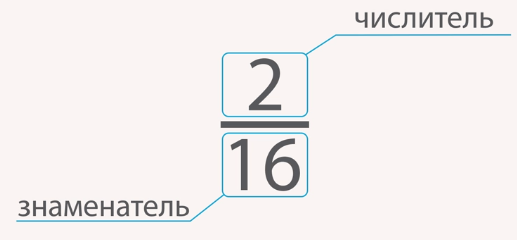
 в дроби
в дроби  ? Пять, так как
? Пять, так как 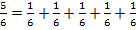 .
.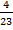 больше, чем
больше, чем 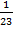 ? В 4 раза. Так как дробь
? В 4 раза. Так как дробь 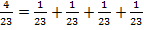 .
.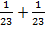 ?
?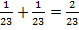 .
.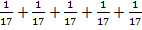 ? Одинаковых слагаемых пять штук.
? Одинаковых слагаемых пять штук.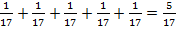 .
.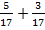 . Сколько всего семнадцатых? Пять и три. Пять и три семнадцатых.
. Сколько всего семнадцатых? Пять и три. Пять и три семнадцатых. 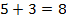 , всего восемь семнадцатых:
, всего восемь семнадцатых: 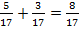 .
.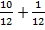 . Сколько всего двенадцатых?
. Сколько всего двенадцатых? 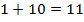
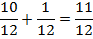
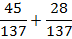
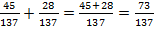 .
.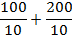
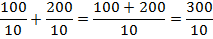
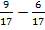 .
.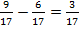 .
.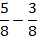
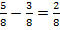 .
.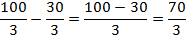
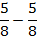
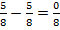 . Но обычно такую запись редко используют. Пишут просто ноль:
. Но обычно такую запись редко используют. Пишут просто ноль: 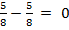 .
.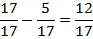
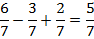
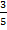 и
и  ? Мы пока не умеем решать такие примеры.
? Мы пока не умеем решать такие примеры.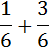
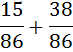
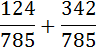
 , а десятичной дроби 4,7 – обыкновенная дробь
, а десятичной дроби 4,7 – обыкновенная дробь  , значит:
, значит:
 , а десятичной дроби 7,368 – обыкновенная дробь
, а десятичной дроби 7,368 – обыкновенная дробь  , значит:
, значит:



 .
. . И далее выполняем уже сложение обыкновенных дробей
. И далее выполняем уже сложение обыкновенных дробей  и
и 
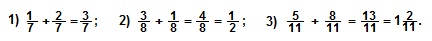

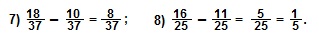
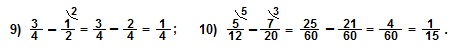
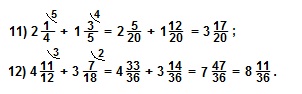 Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.
Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.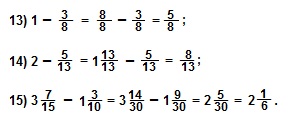 Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.
Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.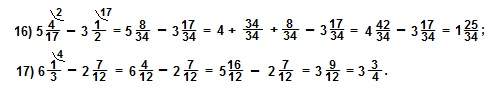
 То есть для сложения или вычитания алгебраических дробей с одинаковыми знаменателями необходимо составить соответствующую алгебраическую сумму числителей, а знаменатель оставить без изменений.
То есть для сложения или вычитания алгебраических дробей с одинаковыми знаменателями необходимо составить соответствующую алгебраическую сумму числителей, а знаменатель оставить без изменений. .
. .
. . Это грубейшая ошибка, поскольку знаменатель остаётся таким же, каким был в исходных дробях.
. Это грубейшая ошибка, поскольку знаменатель остаётся таким же, каким был в исходных дробях. .
. .
.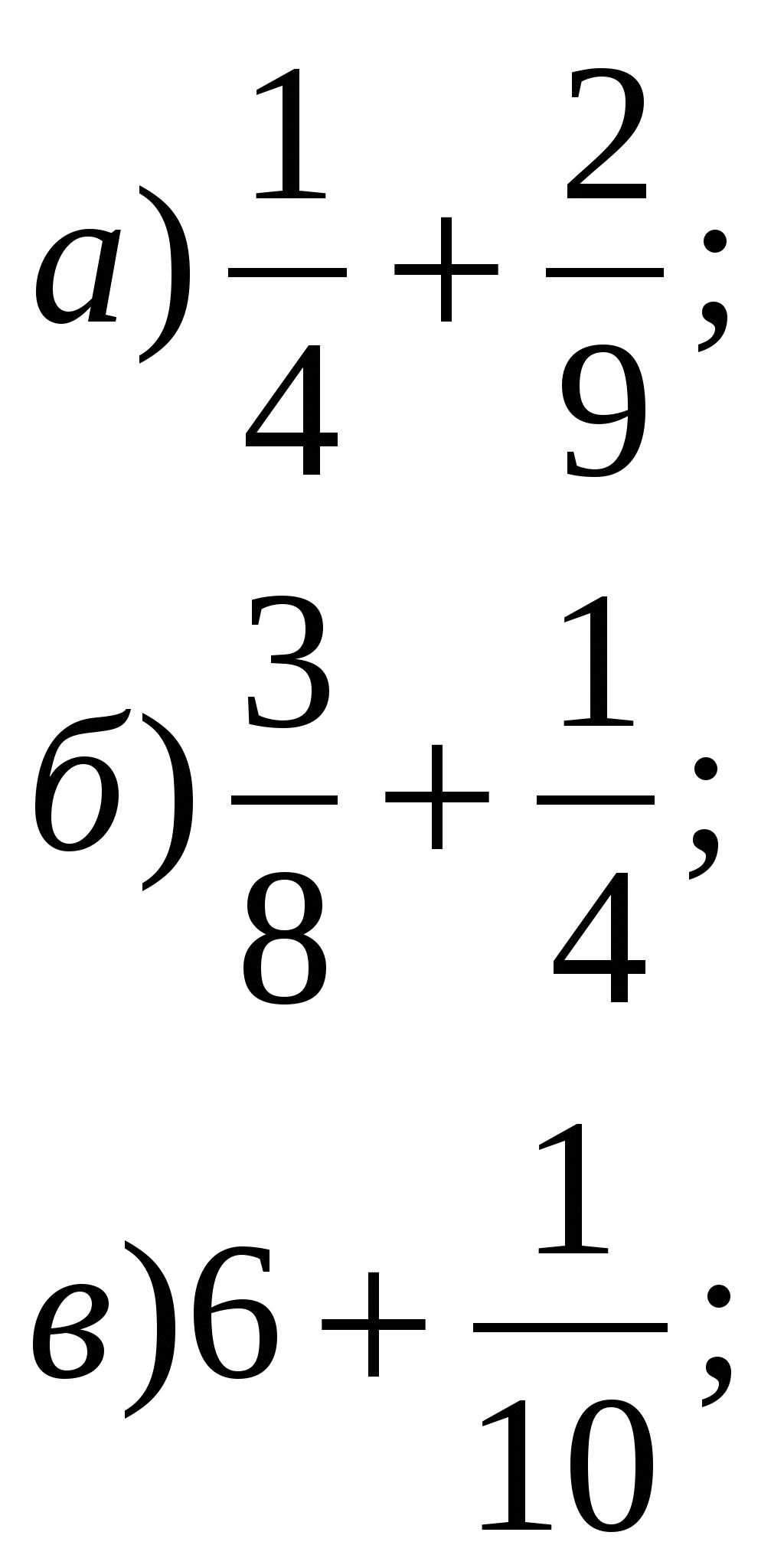
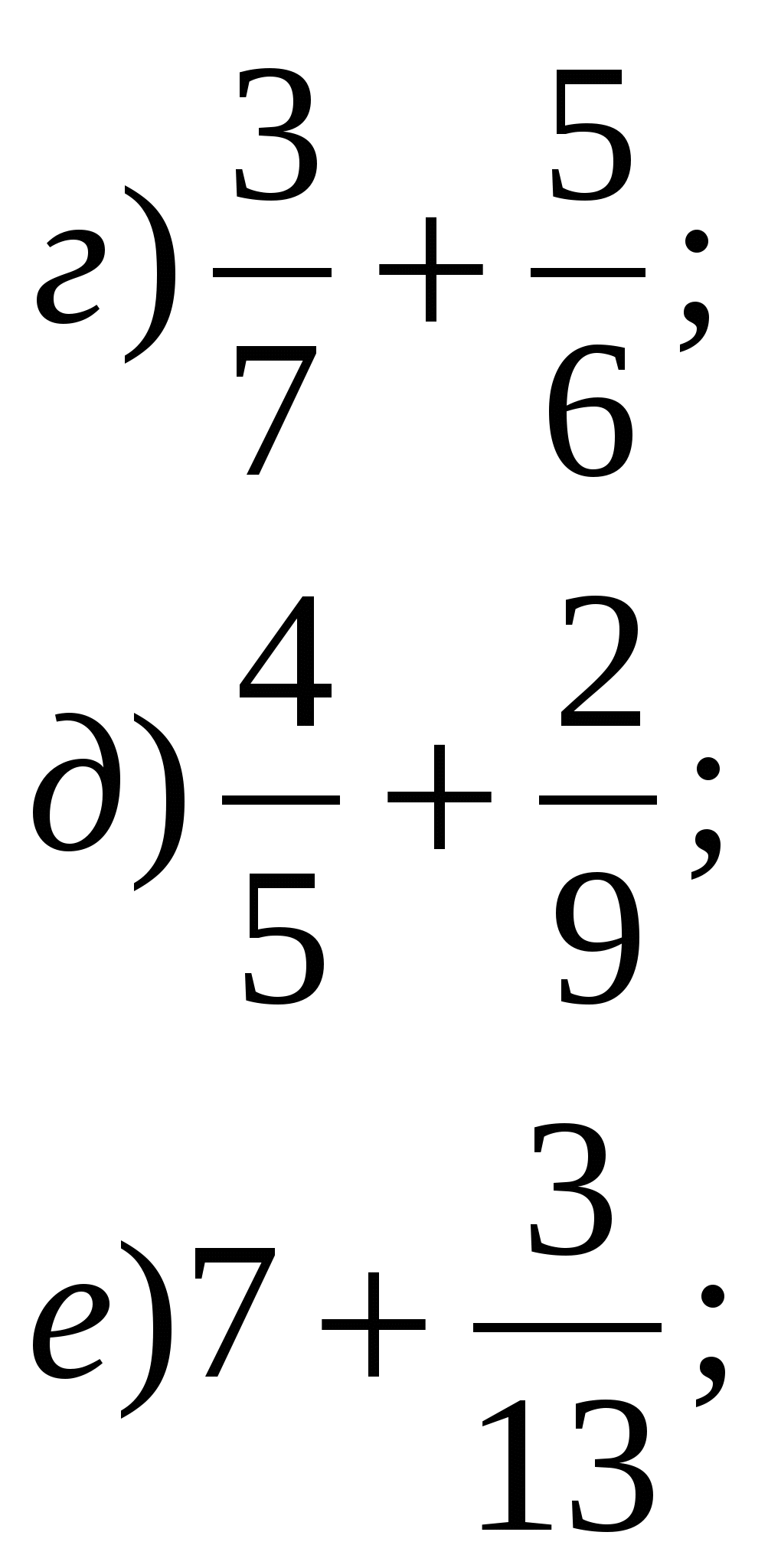
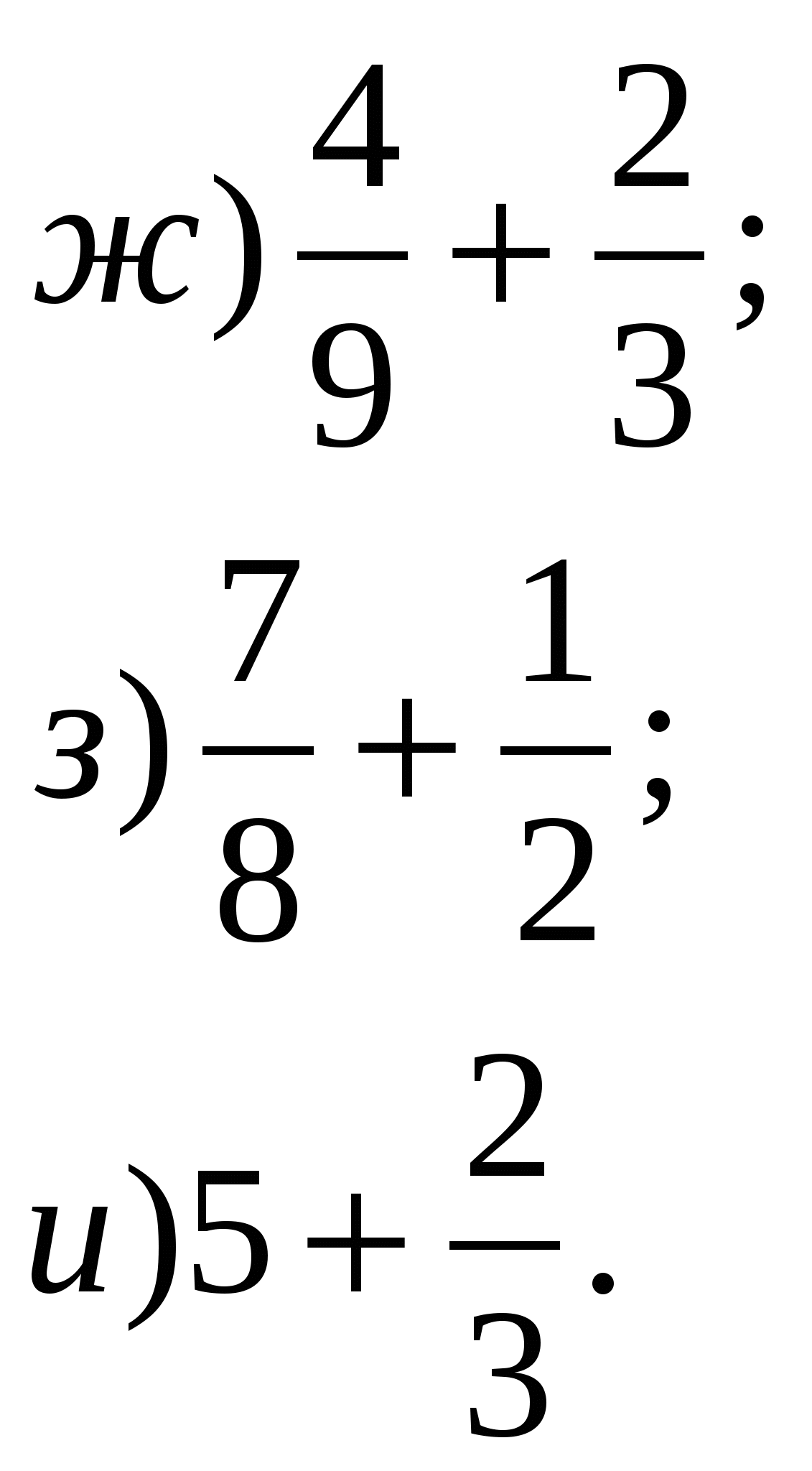
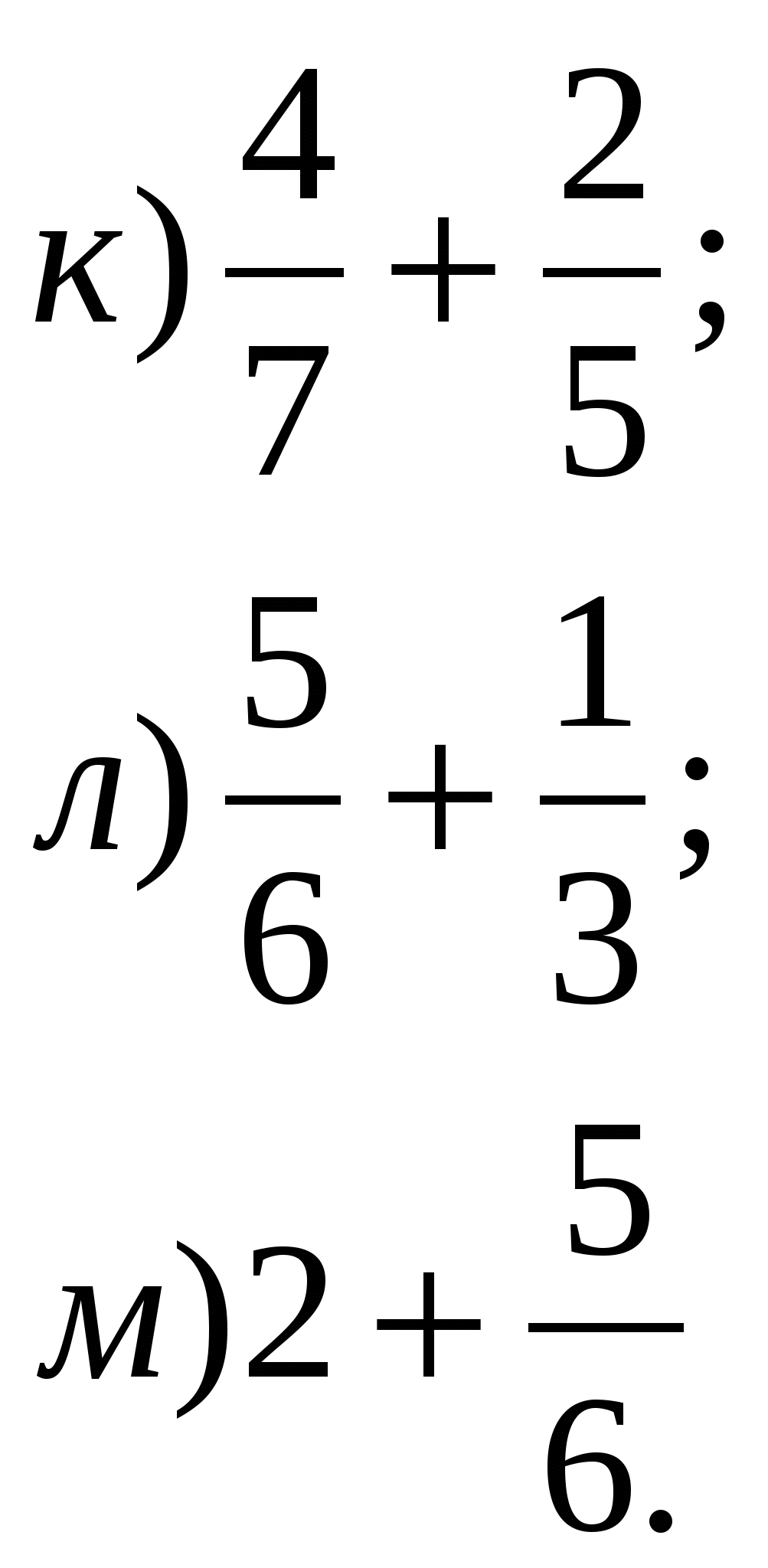
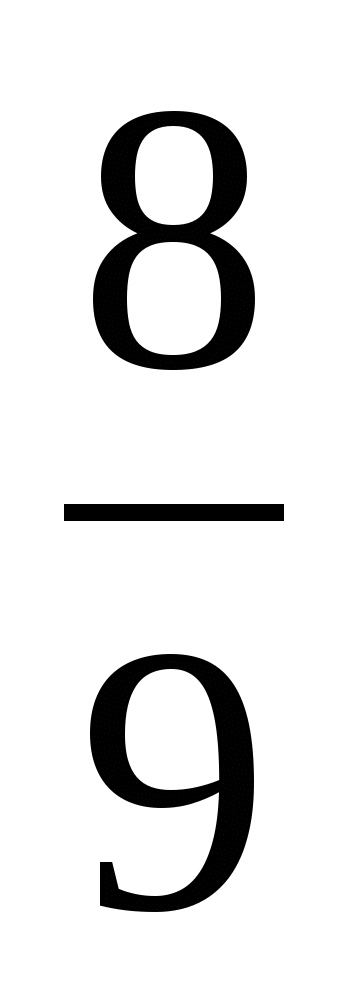 и
и 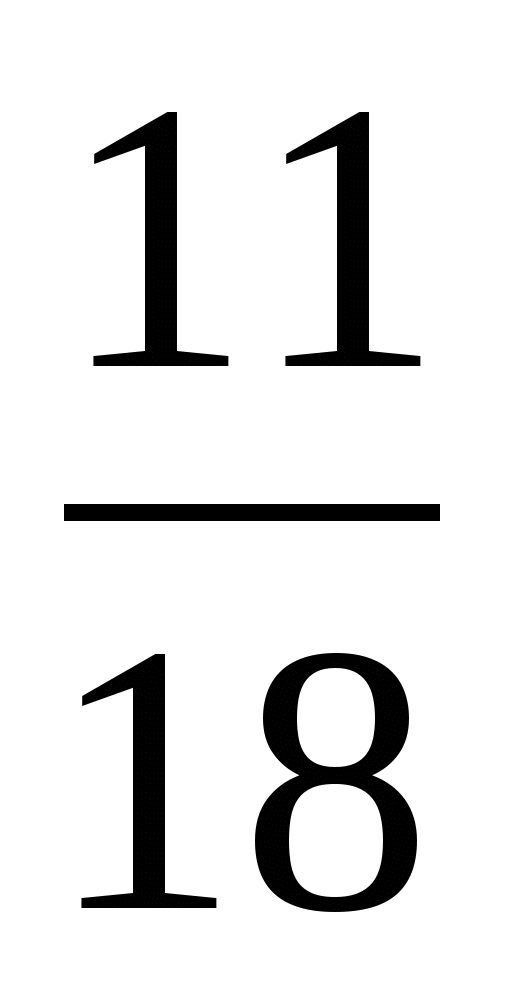 ; б)
; б)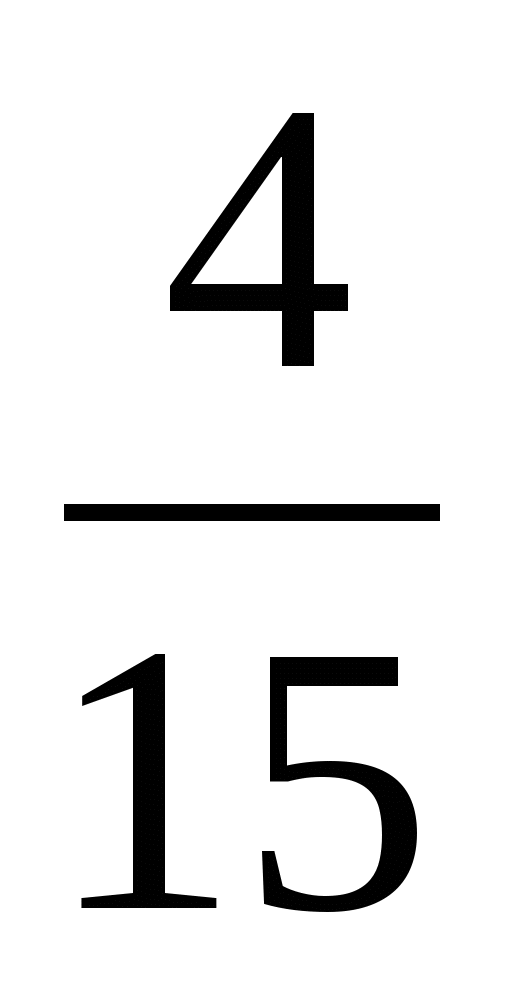 и
и 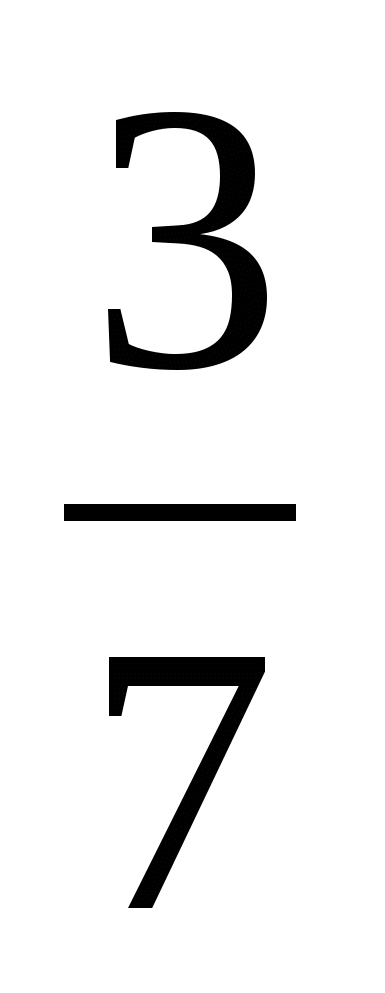 ; в)
; в)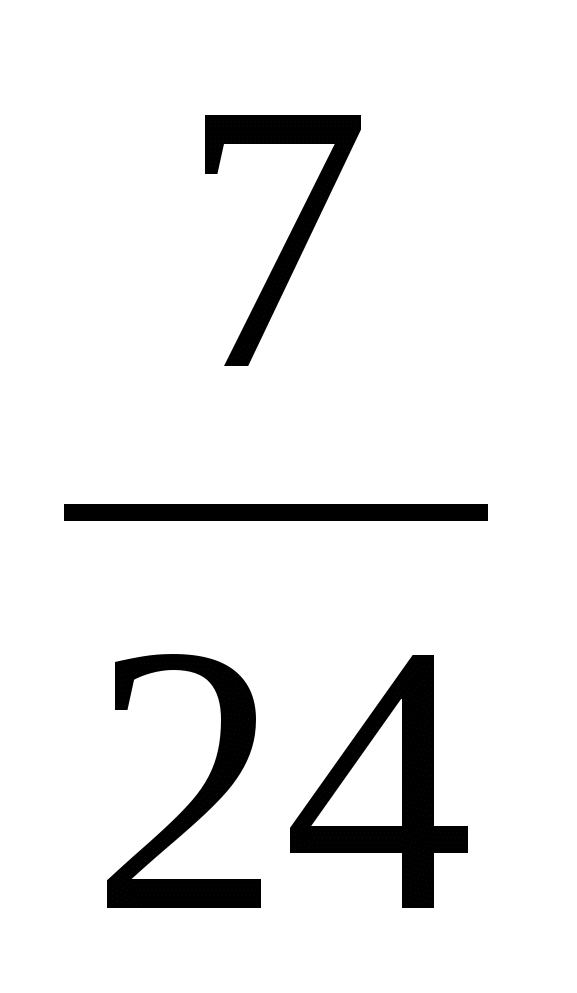 и
и 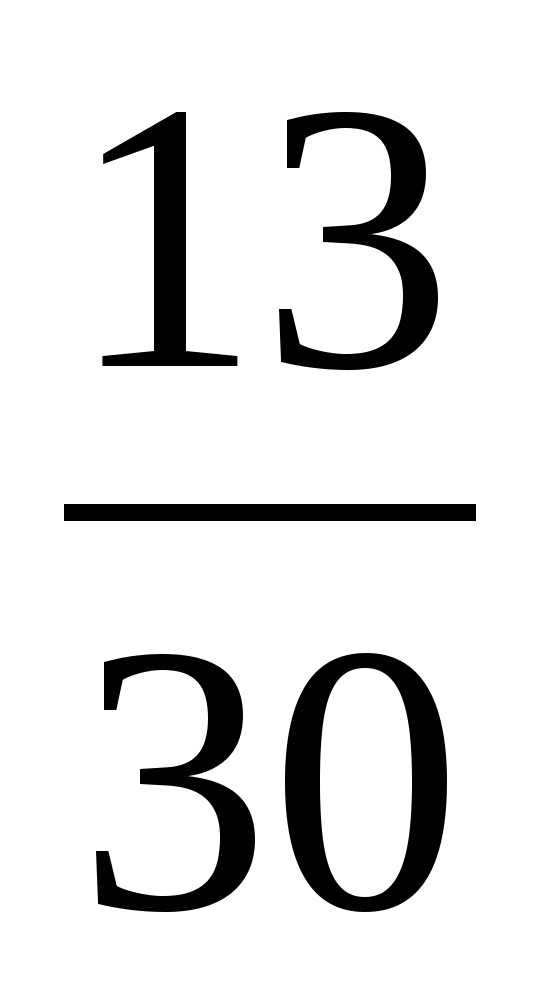 .
.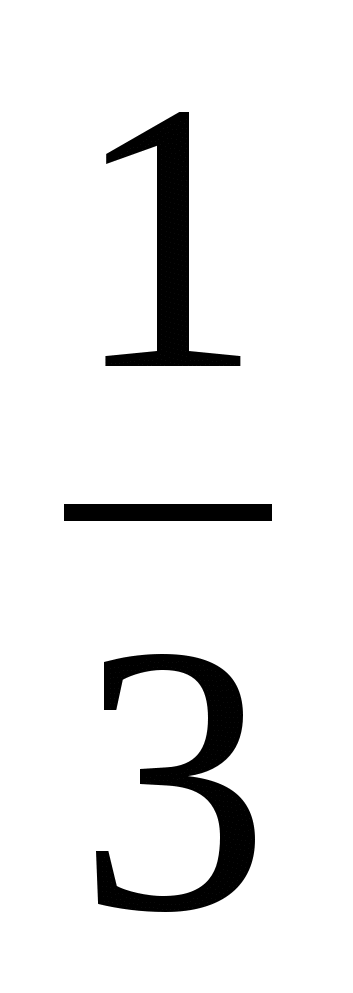 и
и 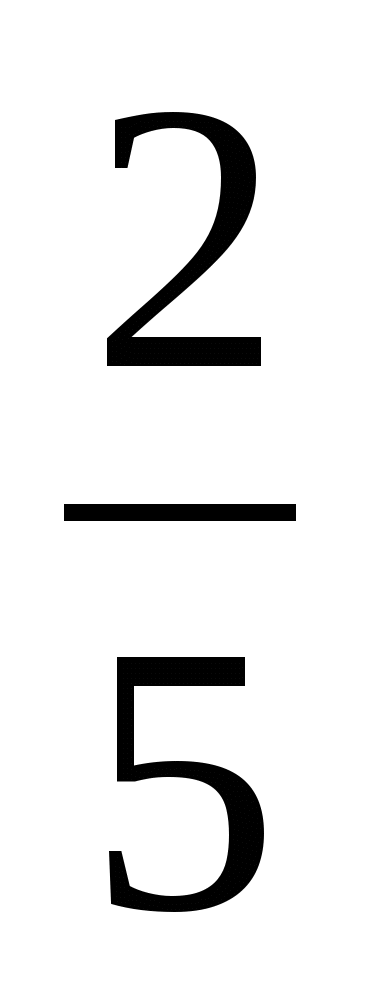 ; б)
; б) 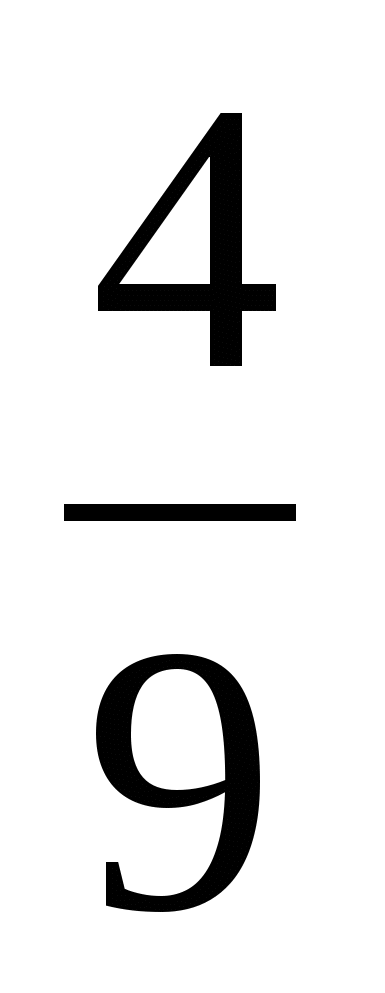 и
и 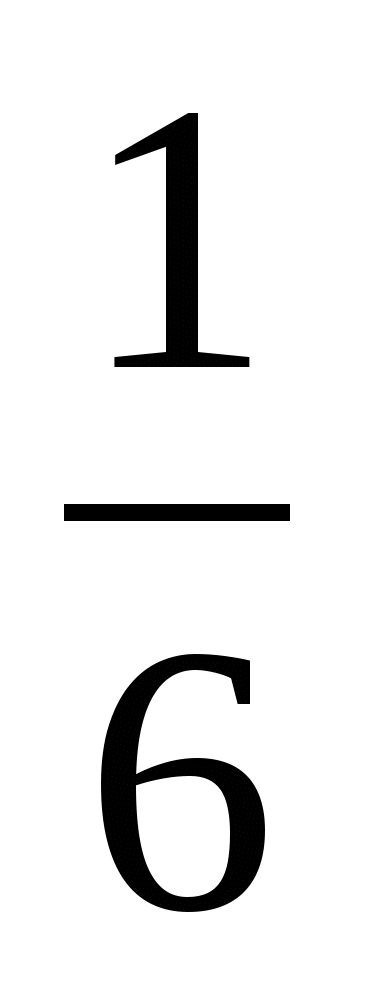 ; в)
; в)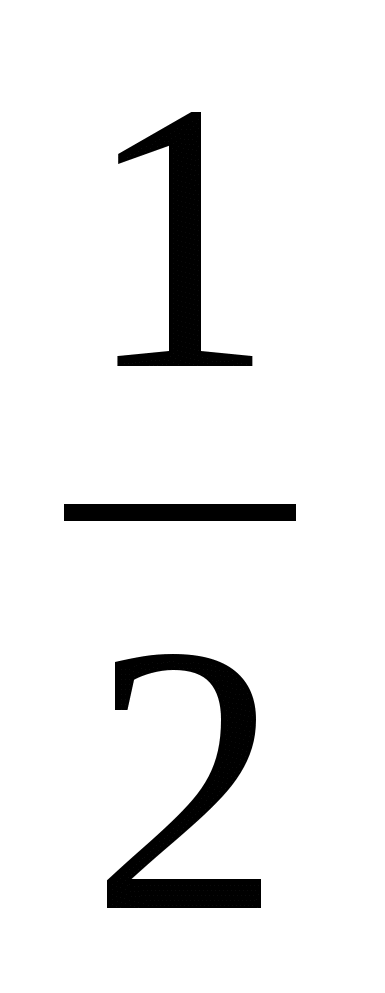 и
и 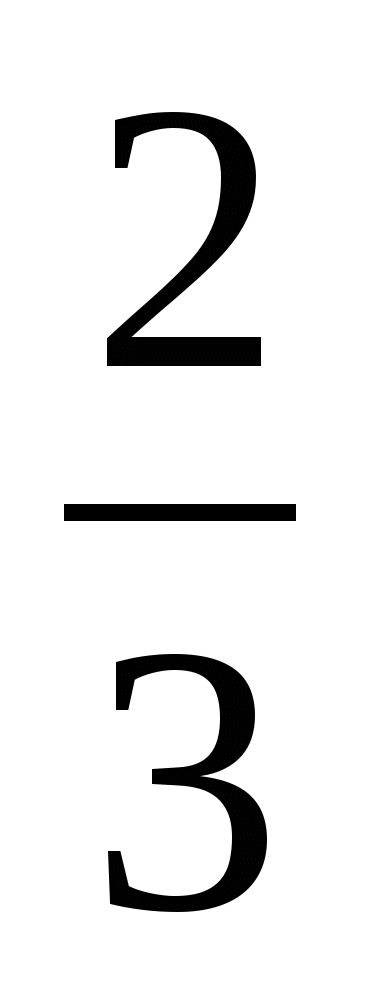 .
.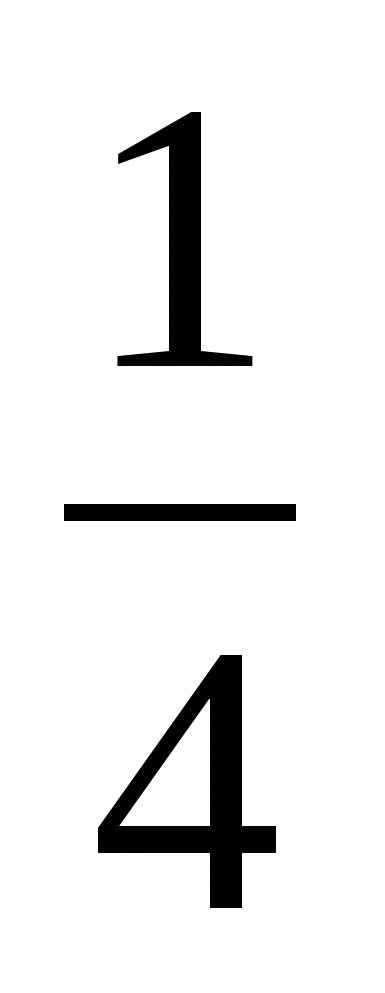 +
+ 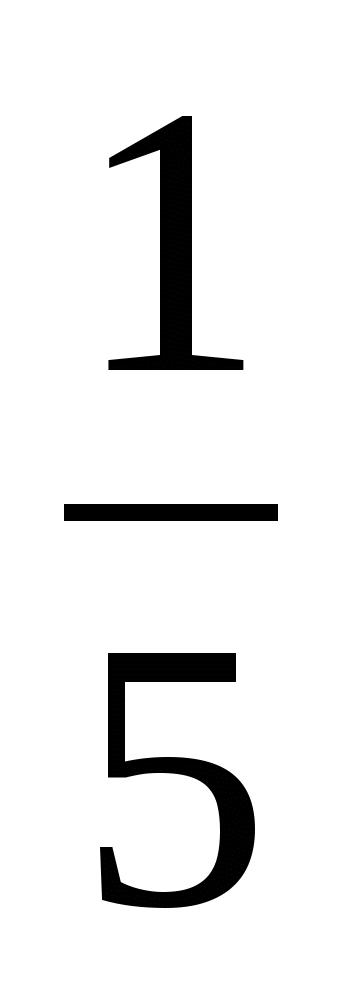 ; б )
; б )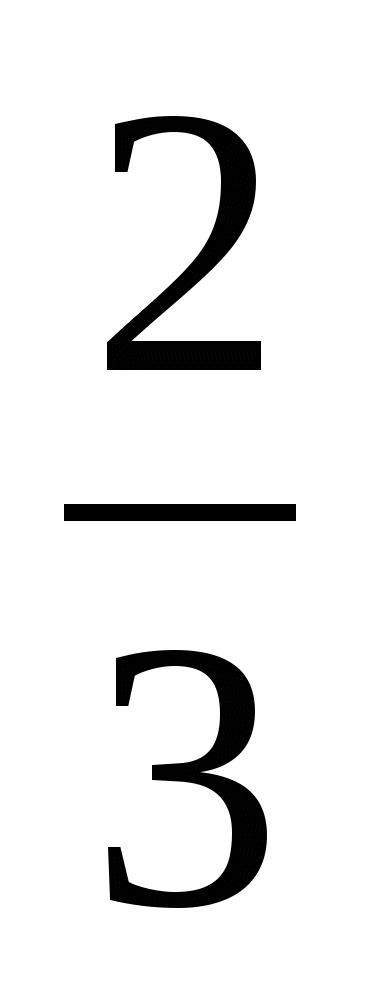 +
+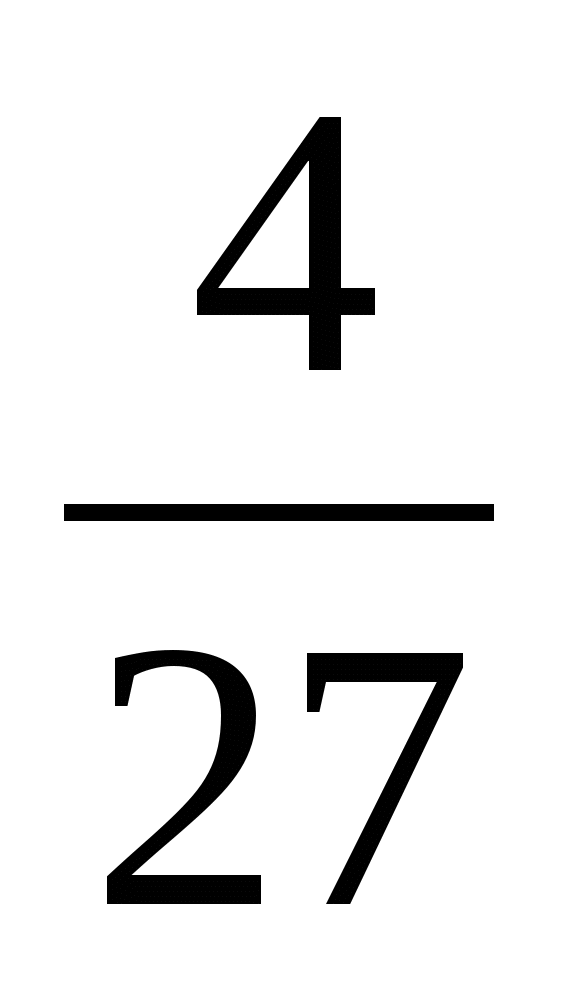 ; в)
; в) 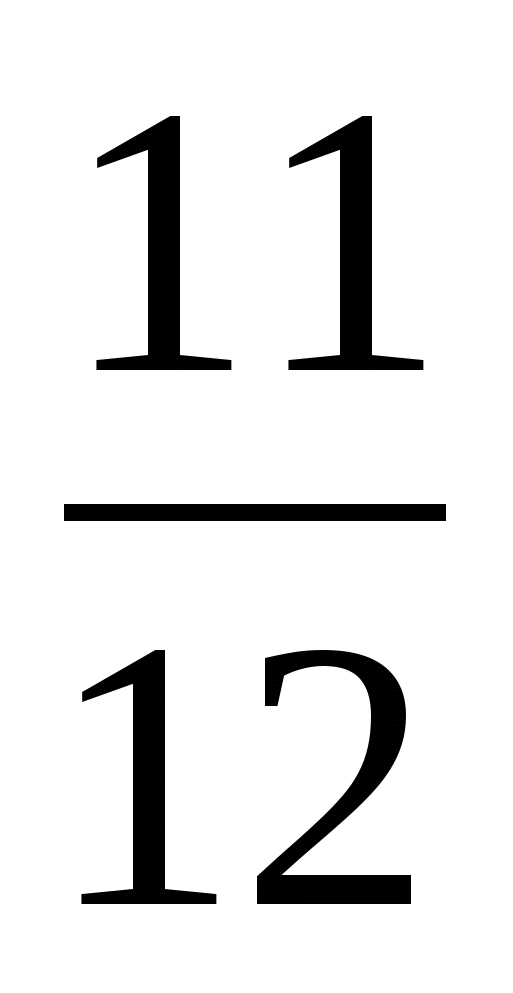 +
+ 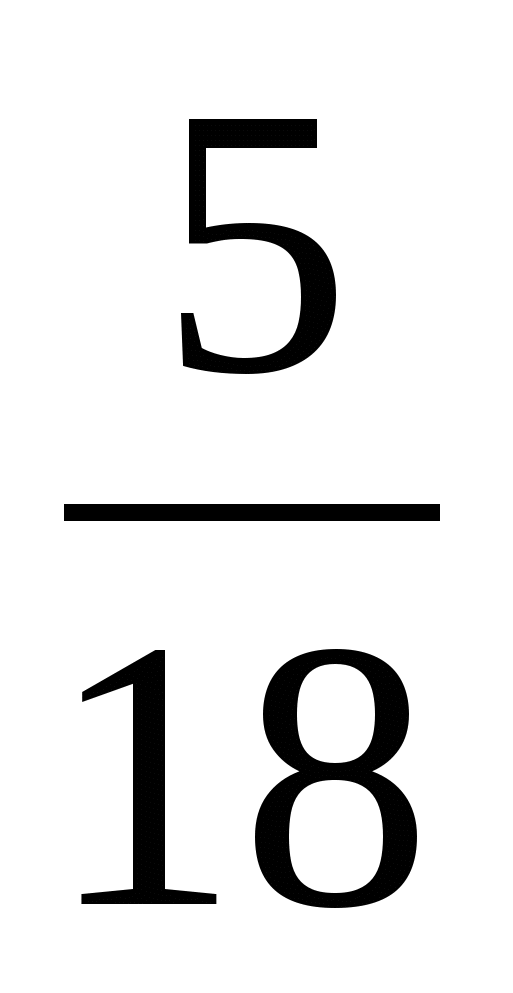 .
.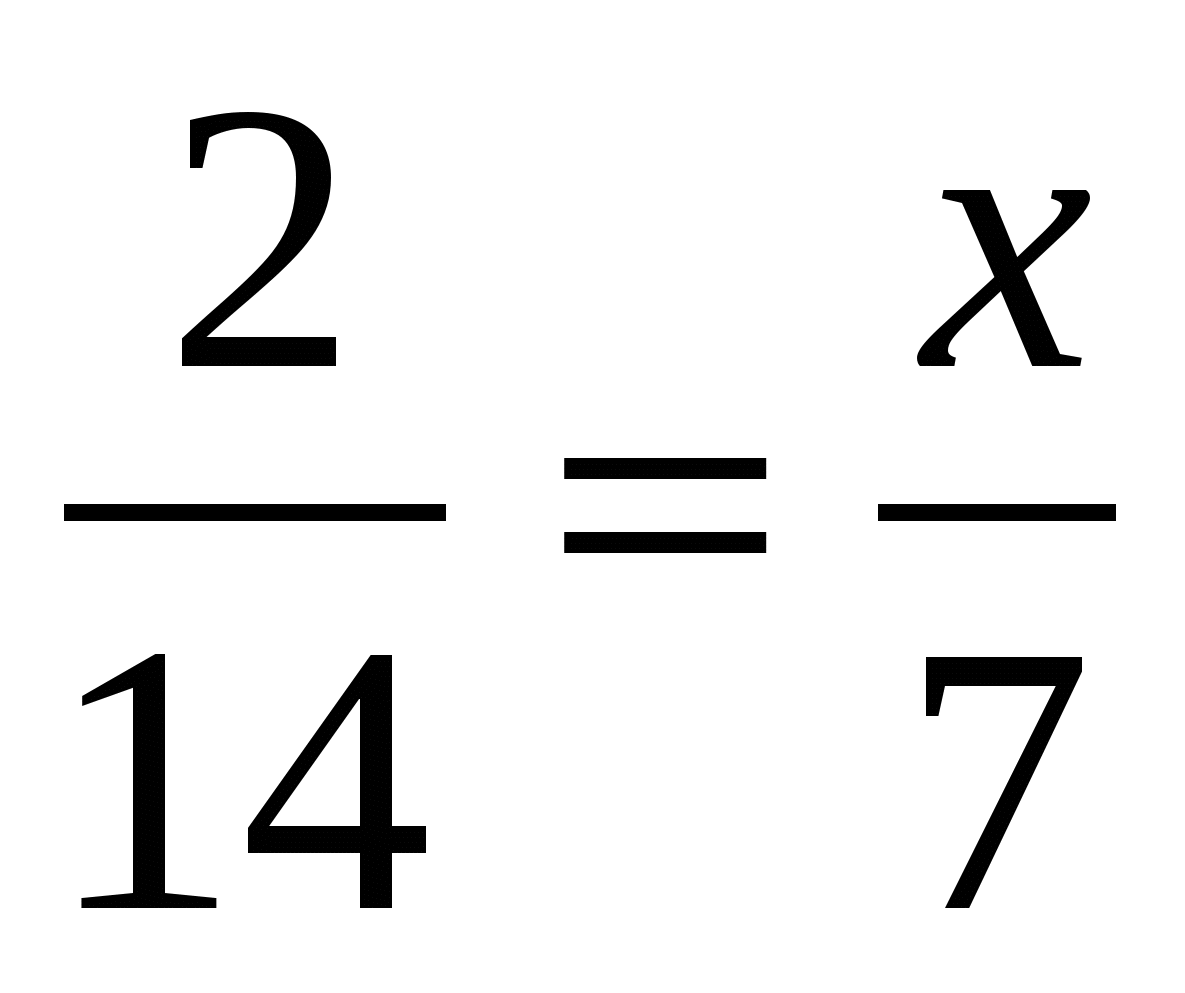 ; б)
; б)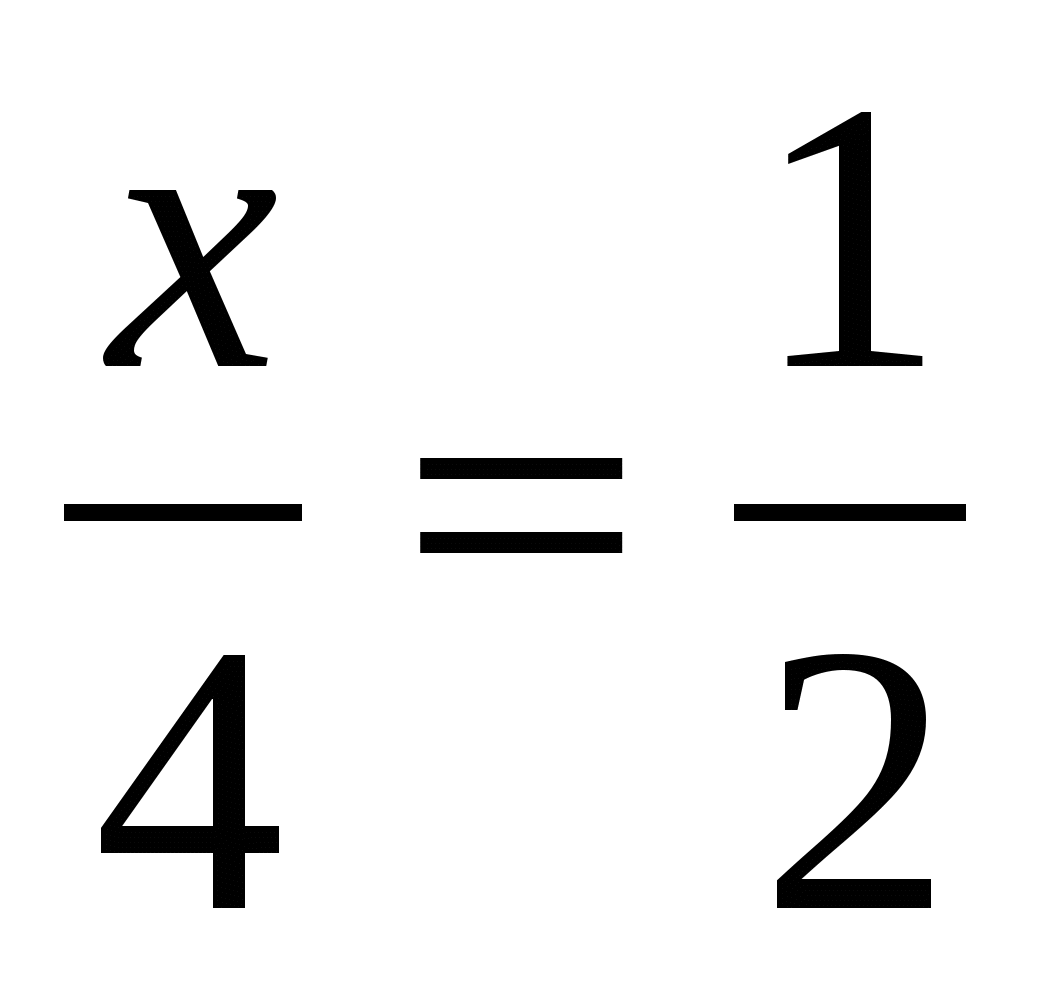 ; в)
; в)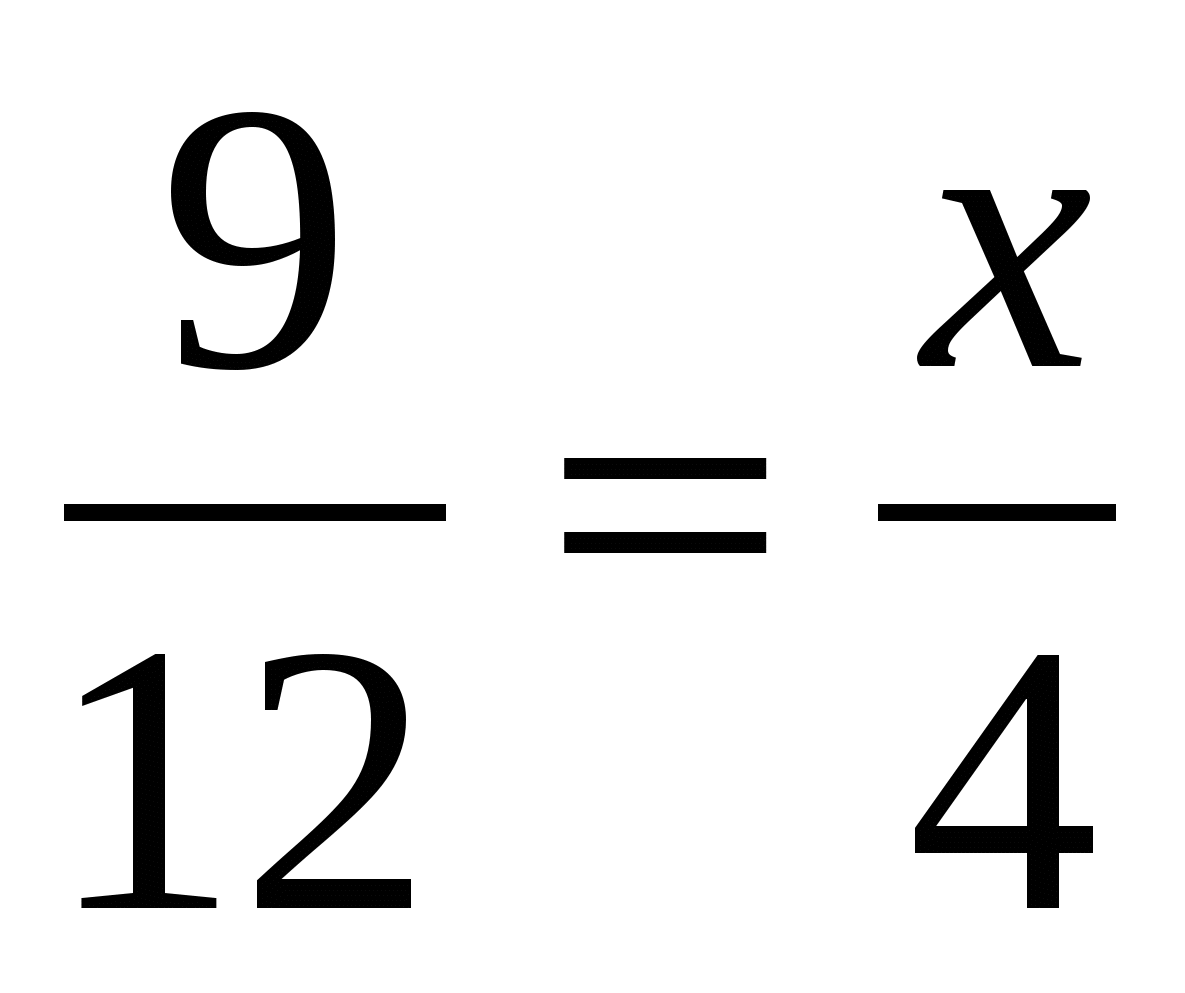 ; г)
; г)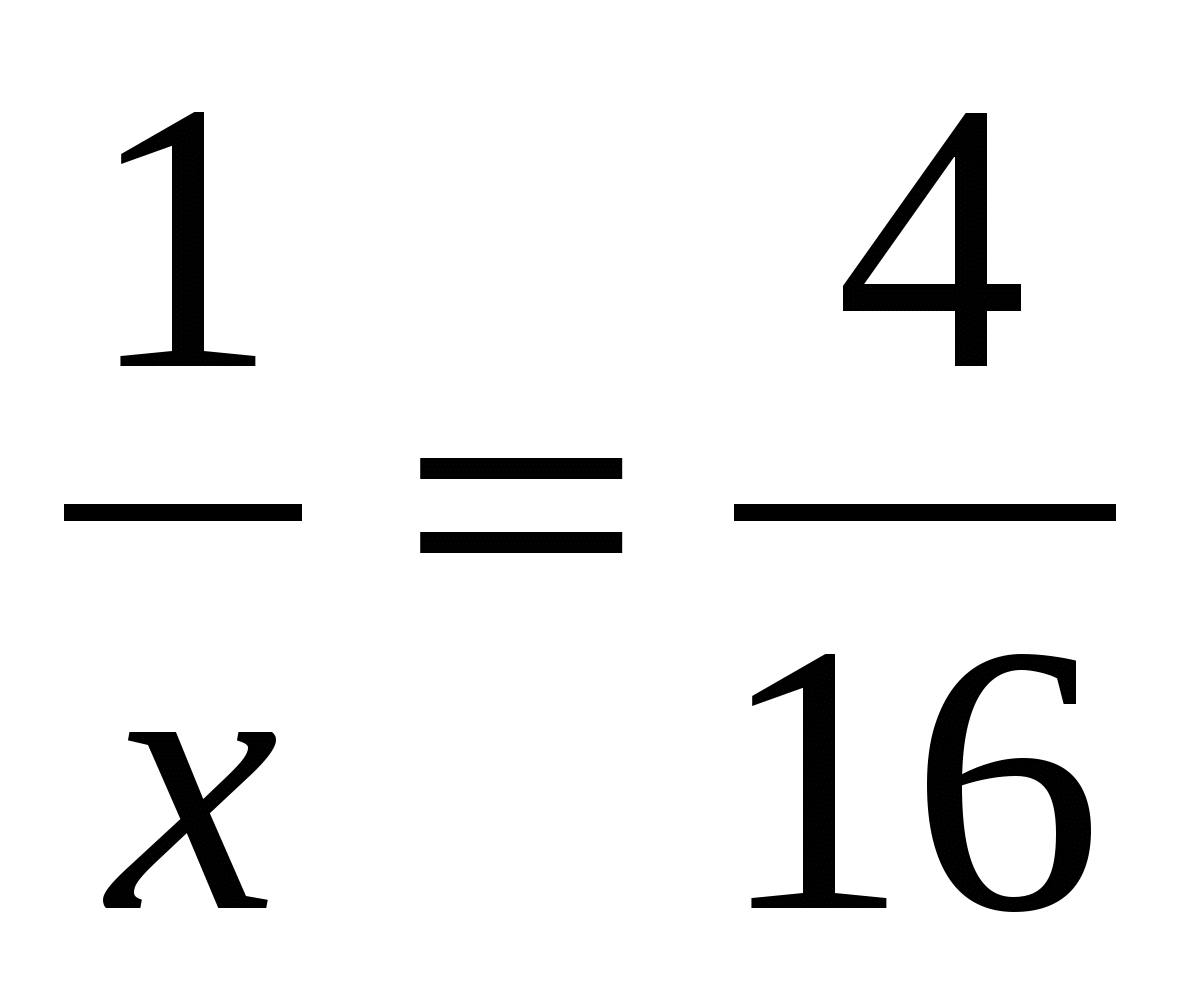 ;
;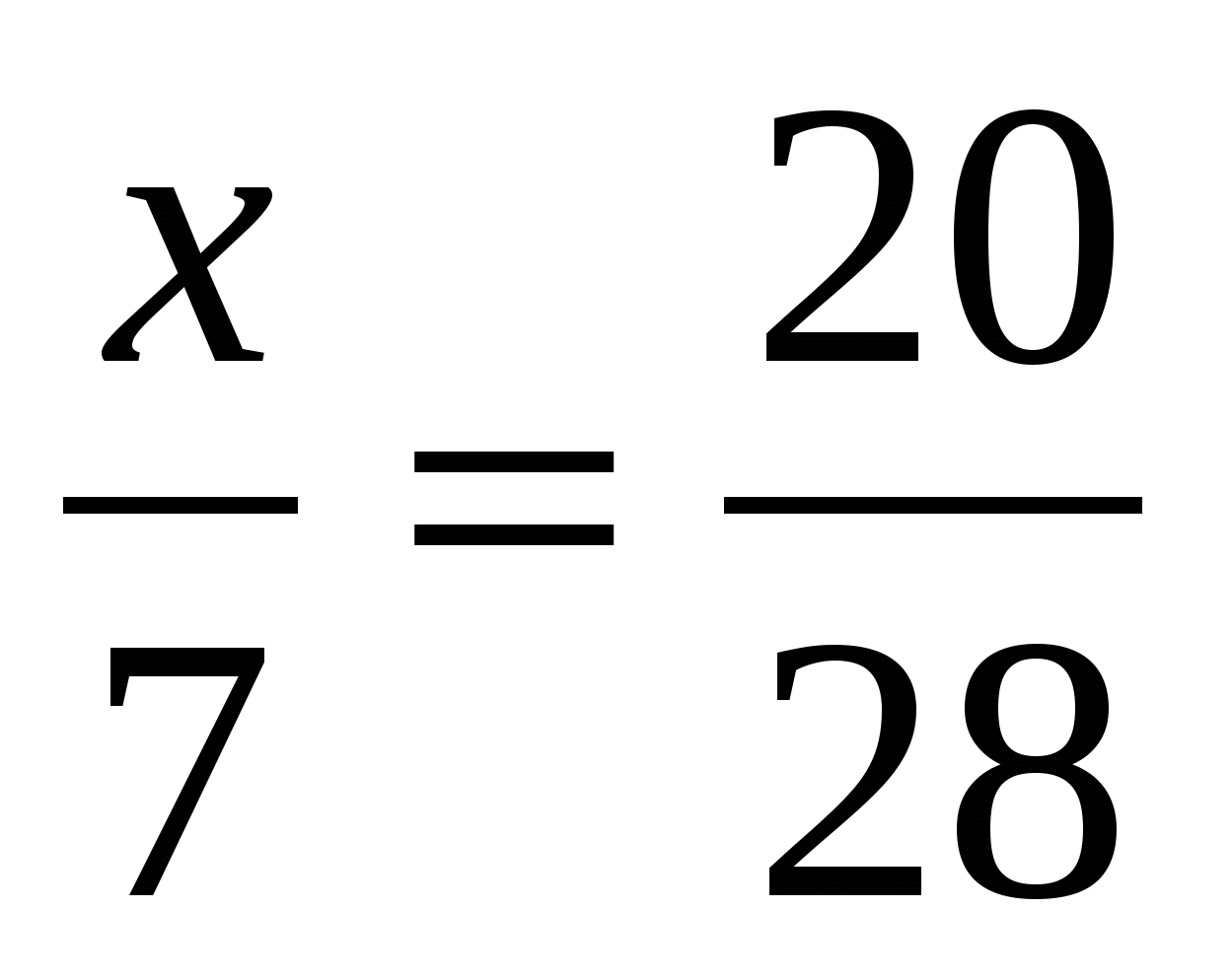 ; е)
; е)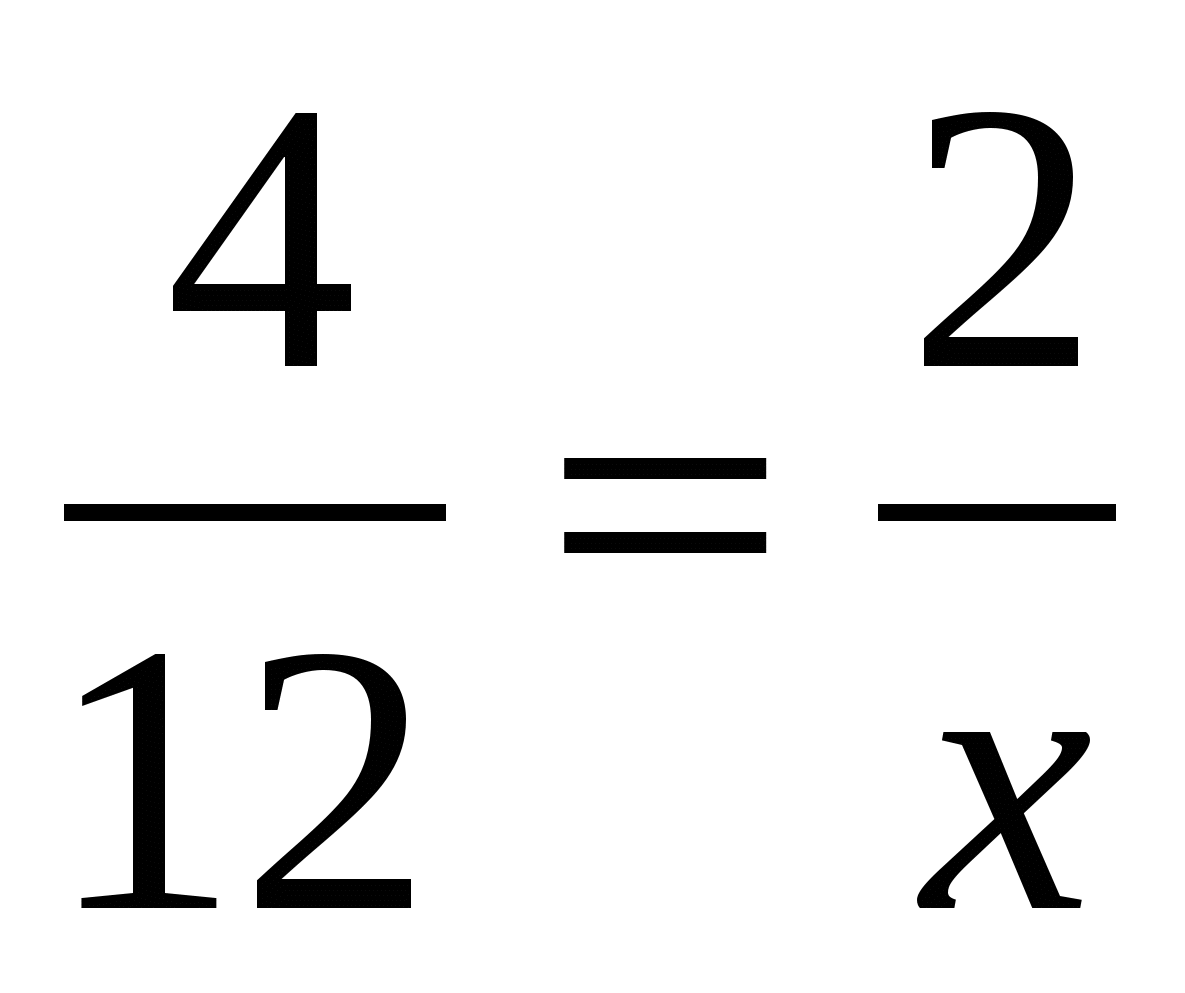 ; ж)
; ж)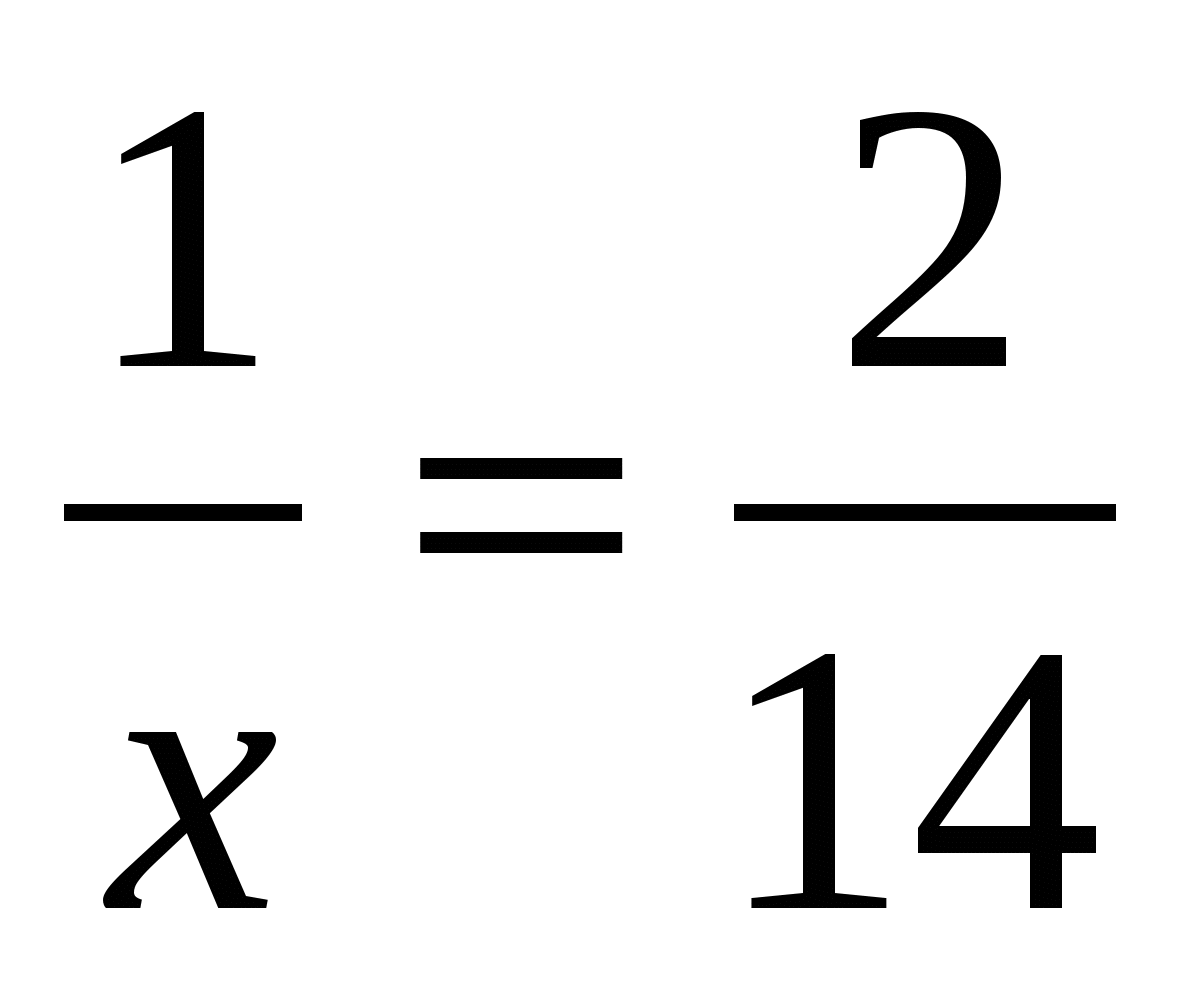 .
.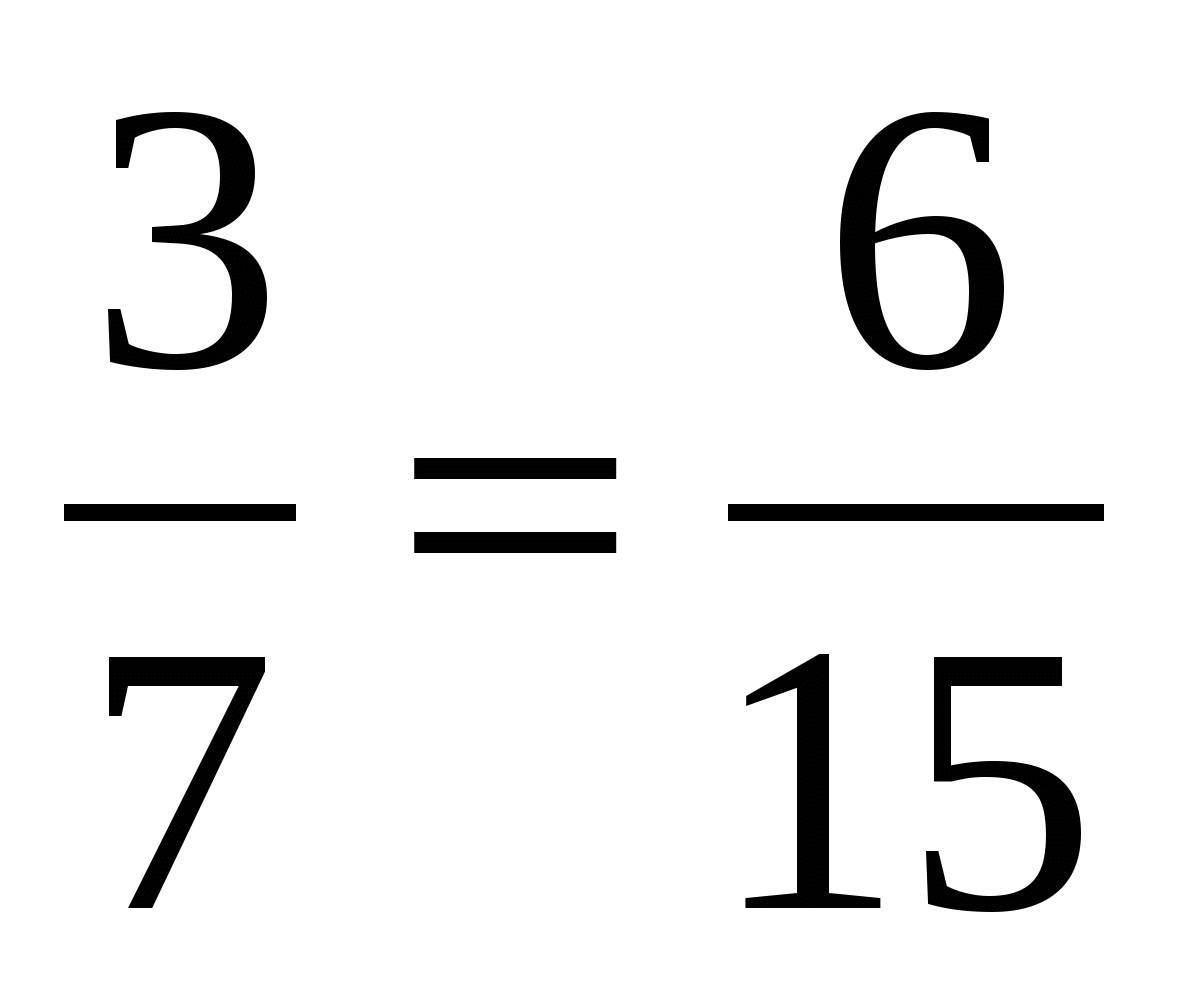 ; б)
; б)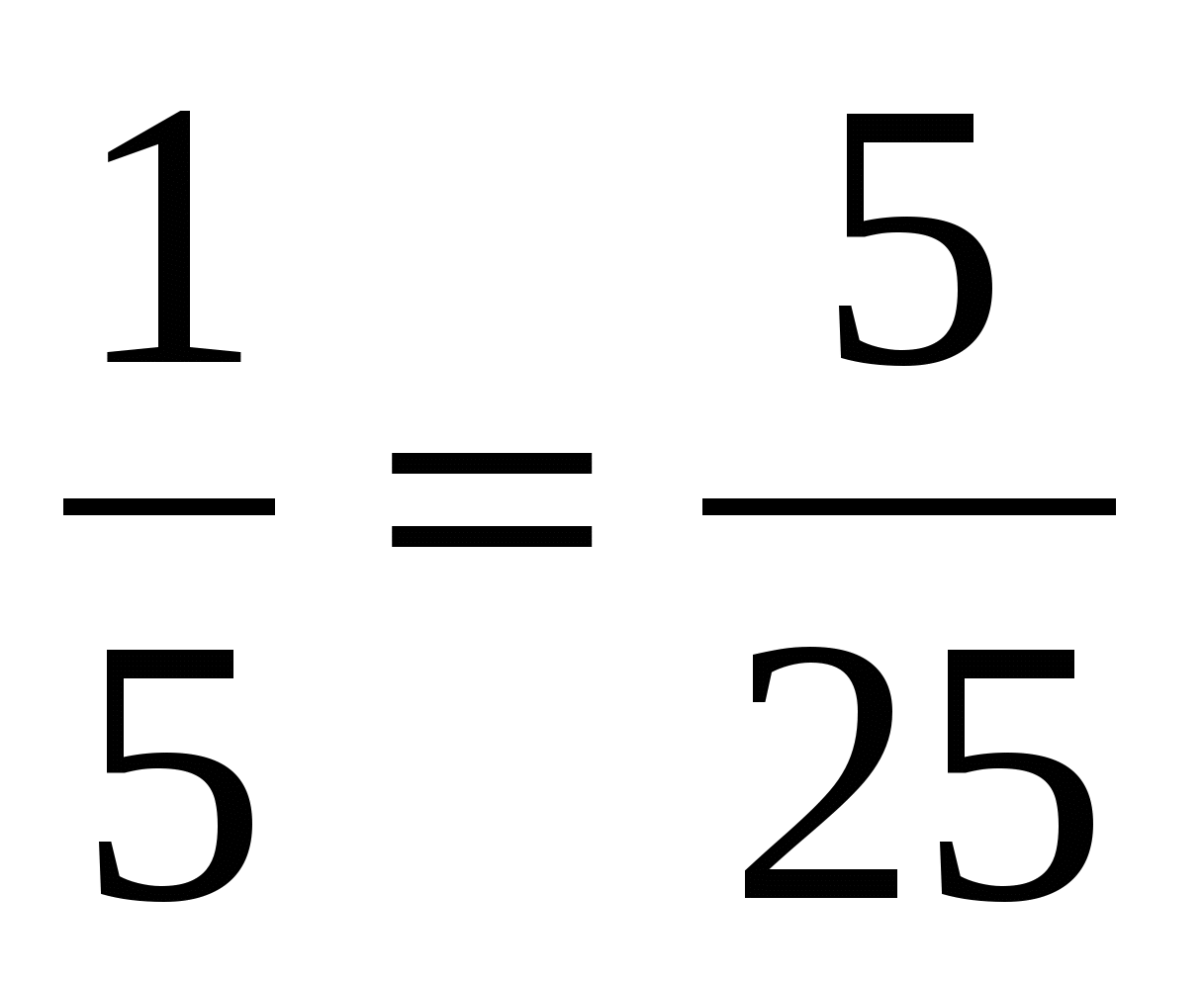 ; в)
; в)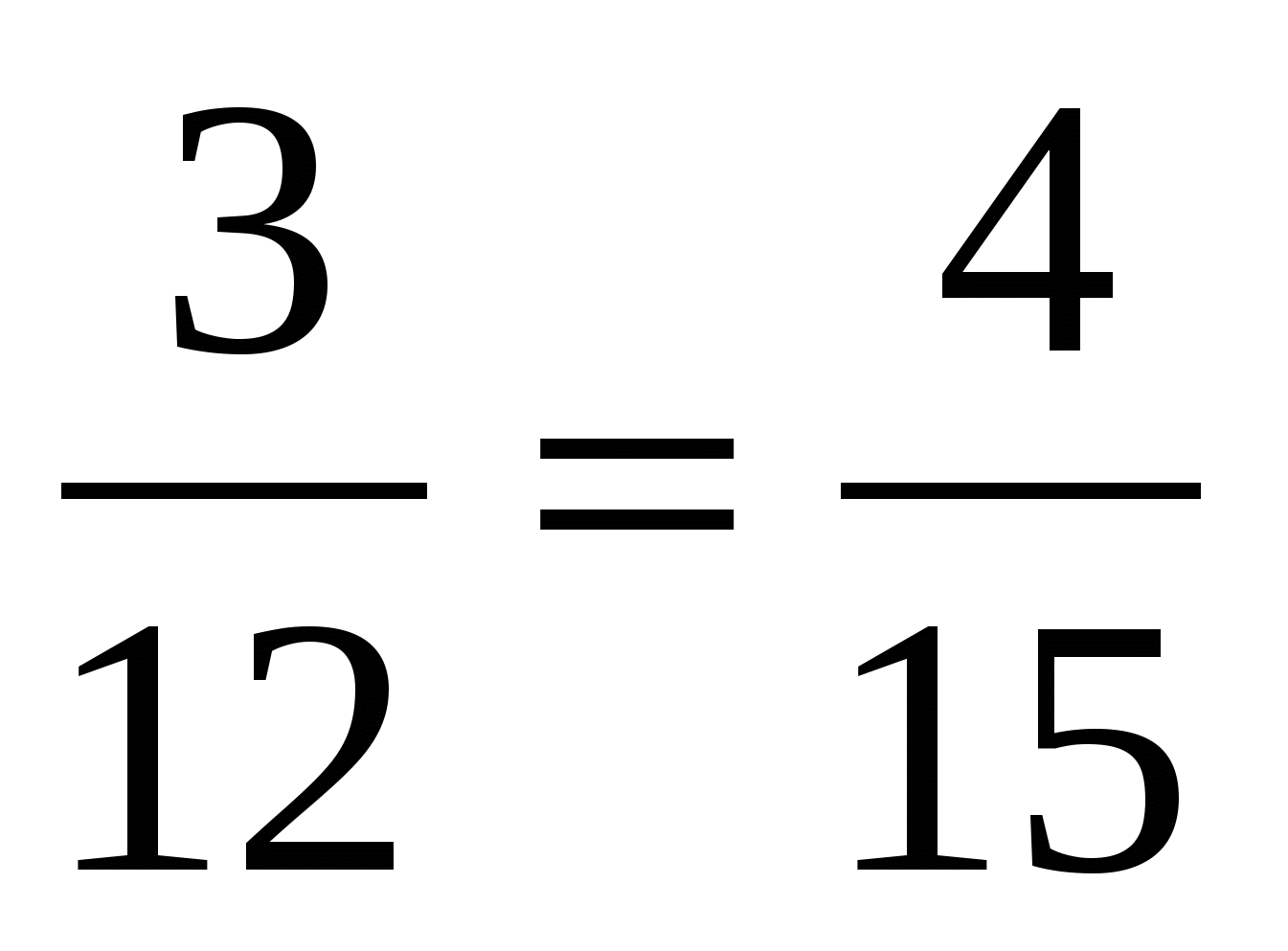 ; г)
; г)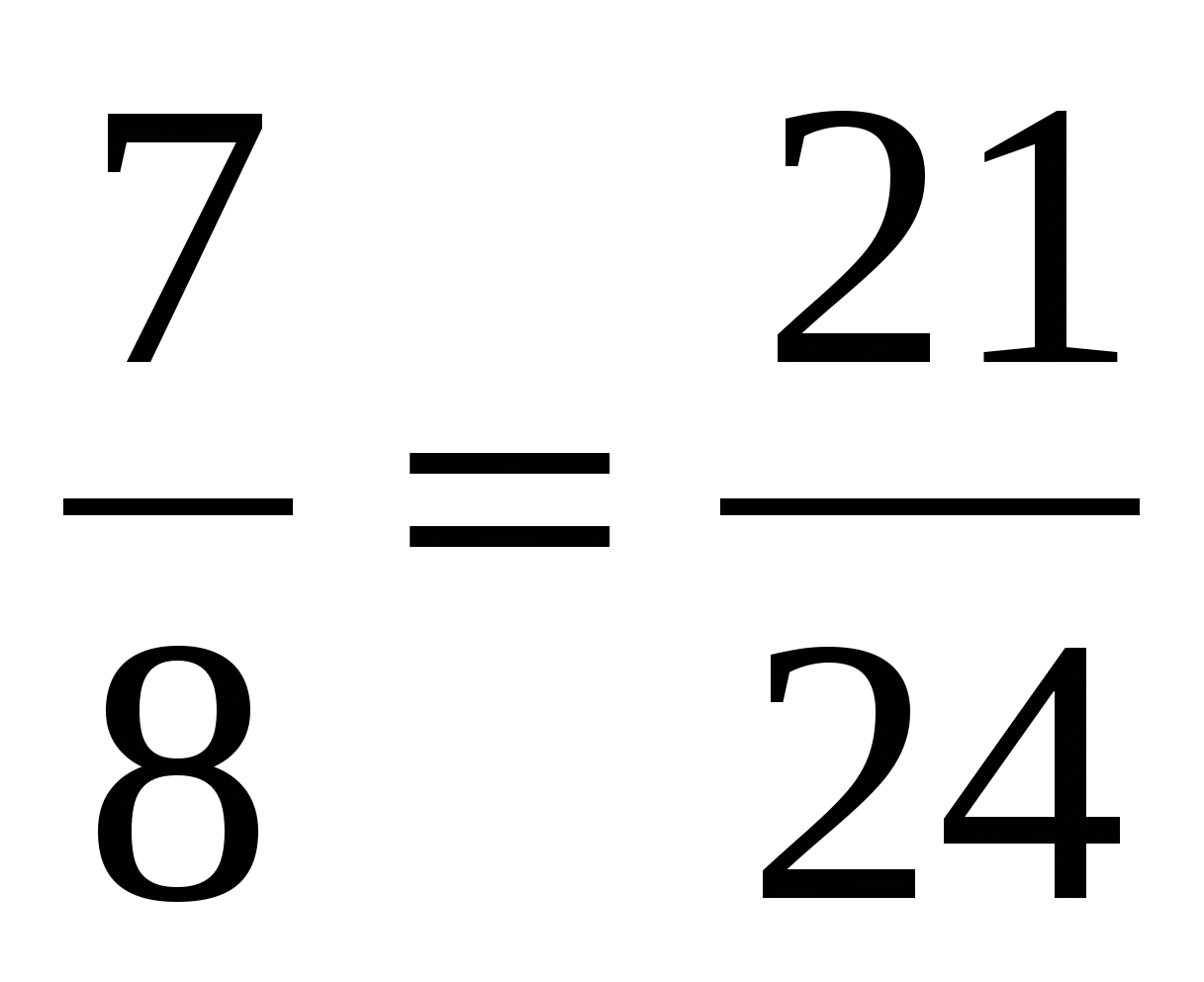 ;
;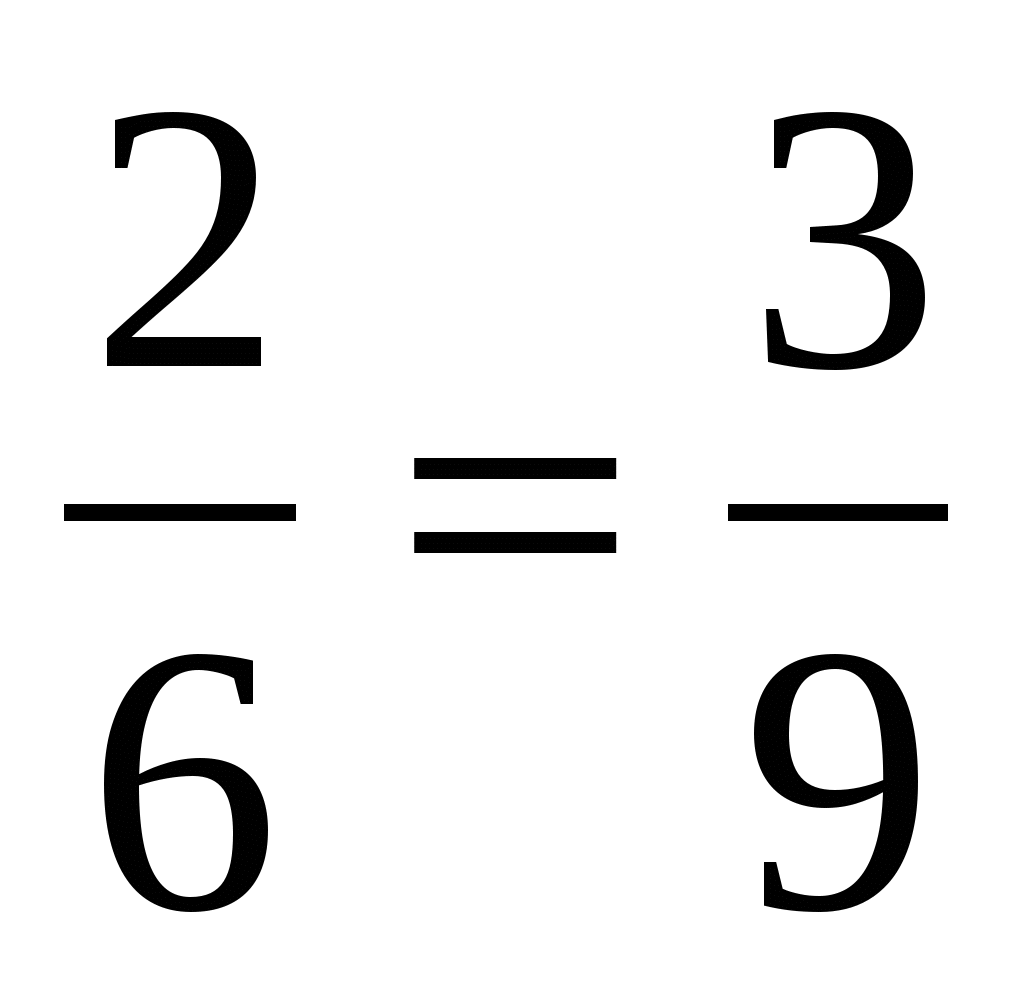 ; е)
; е)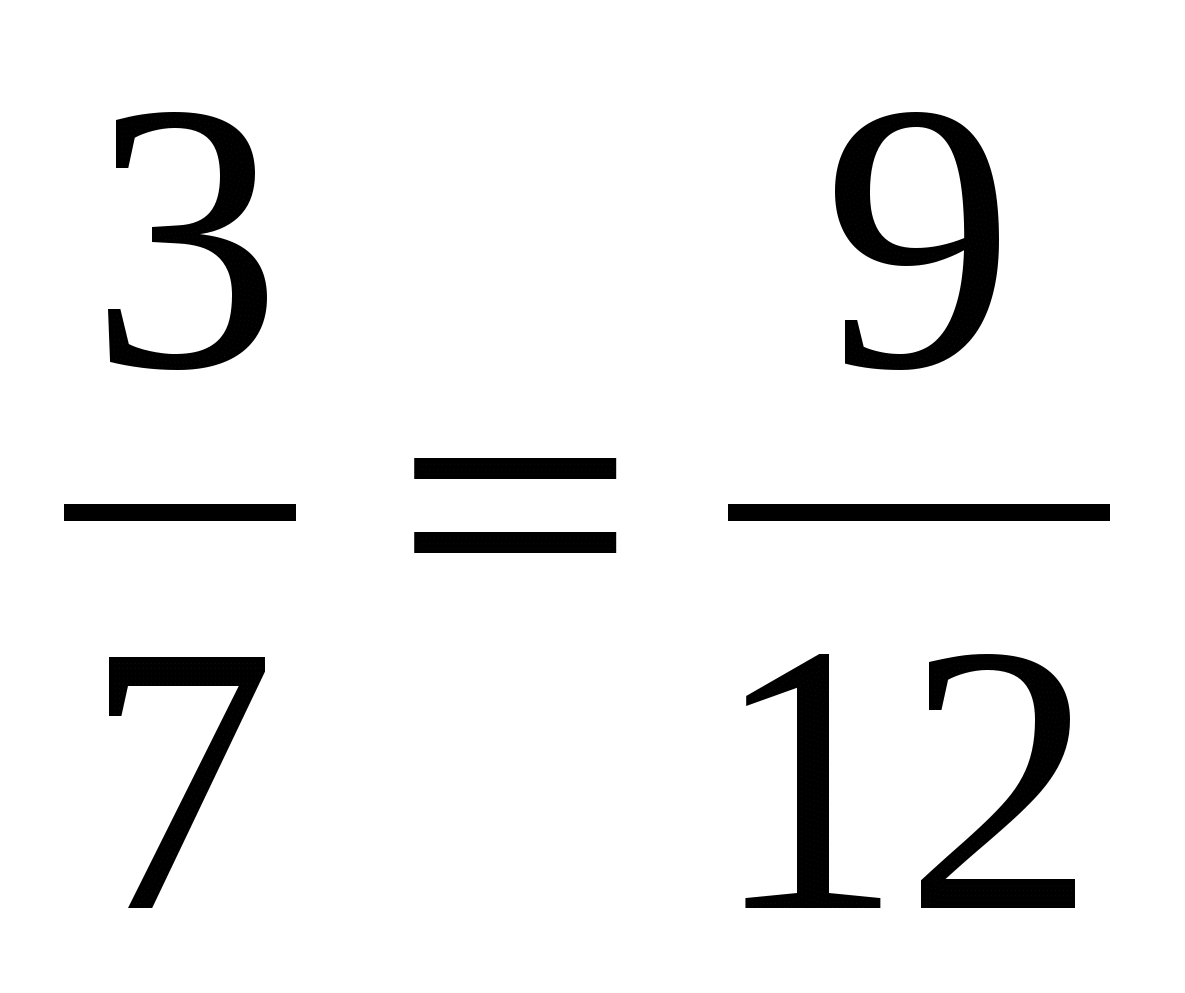 ; ж)
; ж)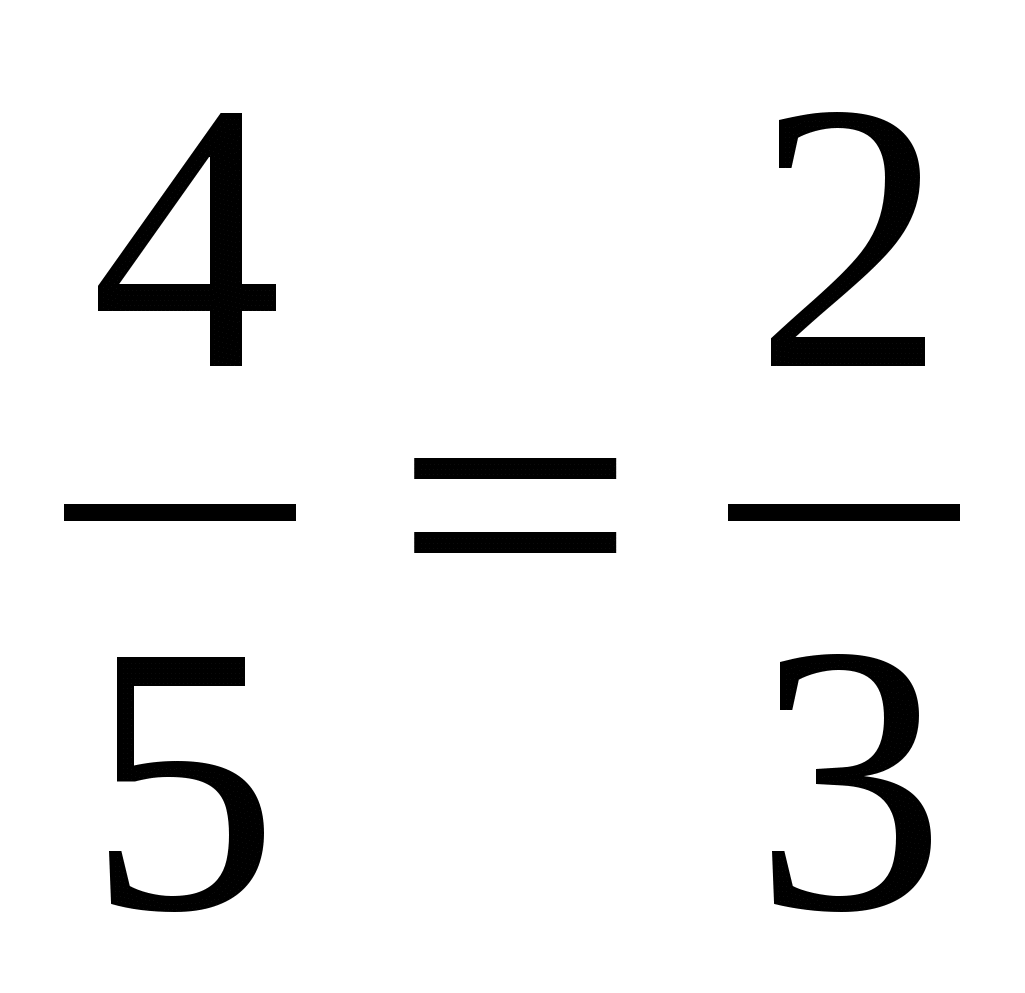 .
.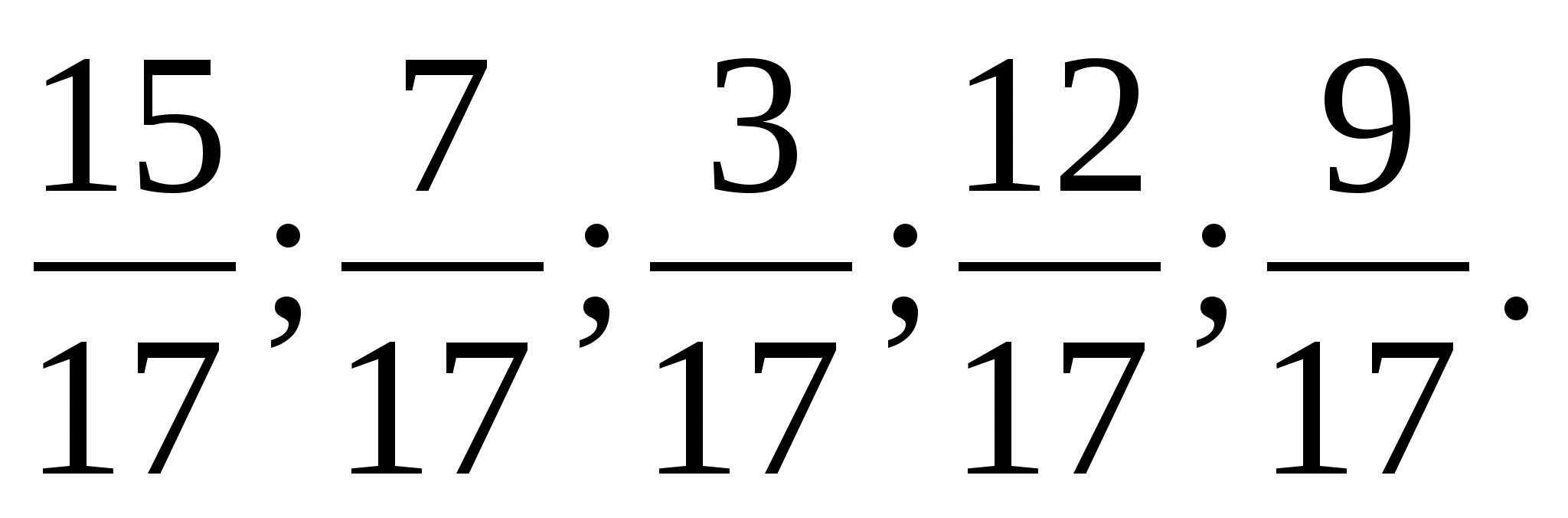
 элемента
элемента

 элемент имеет свою распространенность в природе, S …
элемент имеет свою распространенность в природе, S … Сравнительно невысокая (113 °C) температура плавления серы подтверждала реальность идеи Фраша. В 1890 г. начались испытания, приведшие к успеху.
Сравнительно невысокая (113 °C) температура плавления серы подтверждала реальность идеи Фраша. В 1890 г. начались испытания, приведшие к успеху. Технологические установки для получения серы обычно включают в себя ямы недегазированной серы, ямы дегазации, ямы хранения дегазированной серы, а также налив жидкой серы и склад комовой серы.
Технологические установки для получения серы обычно включают в себя ямы недегазированной серы, ямы дегазации, ямы хранения дегазированной серы, а также налив жидкой серы и склад комовой серы.
 97207100(15)
97207100(15)
 Кафедра Технологии производства машин. Итоговый реферат. «Характеристика химического элемента №16 (Сера)» ММФ-144 Выполнил: Лобзев Е.А. Проверил: Мельнеченко В.Г. Миасс 2001 План. 1.История открытия элемента. 2.Распростронение элемента в природе. 3.Физические свойства. 4.Химические свойства. 5.Получение. 6.Приминение. История открытия элемента. Сера (англ. Sulfur, франц. Sufre, нем. Schwefel) в самородном состоянии, а также в виде сернистых соединений известна с самых древнейших времен. С запахом горящей серы, удушающим действием сернистого газа и отвратительным запахом сероводорода человек познакомился, вероятно, еще в доисторические времена. Именно из-за этих свойств сера использовалась жрецами в составе священных курений при религиозных обрядах. Сера считалась произведением сверхчеловеческих существ из мира духов или подземных богов. Очень давно сера стала применяться в составе различных горючих смесей для военных целей. Уже у Гомера описаны «сернистые испарения», смертельное действие выделений горящей серы.
Кафедра Технологии производства машин. Итоговый реферат. «Характеристика химического элемента №16 (Сера)» ММФ-144 Выполнил: Лобзев Е.А. Проверил: Мельнеченко В.Г. Миасс 2001 План. 1.История открытия элемента. 2.Распростронение элемента в природе. 3.Физические свойства. 4.Химические свойства. 5.Получение. 6.Приминение. История открытия элемента. Сера (англ. Sulfur, франц. Sufre, нем. Schwefel) в самородном состоянии, а также в виде сернистых соединений известна с самых древнейших времен. С запахом горящей серы, удушающим действием сернистого газа и отвратительным запахом сероводорода человек познакомился, вероятно, еще в доисторические времена. Именно из-за этих свойств сера использовалась жрецами в составе священных курений при религиозных обрядах. Сера считалась произведением сверхчеловеческих существ из мира духов или подземных богов. Очень давно сера стала применяться в составе различных горючих смесей для военных целей. Уже у Гомера описаны «сернистые испарения», смертельное действие выделений горящей серы. Сера, вероятно, входила в состав «греческого огня», наводившего ужас на противников. Около VIII в. китайцы стали использовать ее в пиротехнических смесях, в частности, в смеси типа пороха. Горючесть серы, легкость, с которой она соединяется с металлами с образованием сульфидов (например, на поверхности кусков металла), объясняют то, что ее считали «принципом горючести» и обязательной составной частью металлических руд. Пресвитер Теофил (XI в.) описывает способ окислительного обжига сульфидной медной руды, известный, вероятно, еще в древнем Египте. В период арабской алхимии возникла ртутно-серная теория состава металлов, согласно которой сера почиталась обязательной составной частью (отцом) всех металлов. В дальнейшем она стала одним из трех принципов алхимиков, а позднее «принцип горючести» явился основой теории флогистона. Элементарную природу серы установил Лавуазье в своих опытах по сжиганию. С введением пороха в Европе началось развитие добычи природной серы, а также разработка способа получения ее из пиритов; последний был распространен в древней Руси.
Сера, вероятно, входила в состав «греческого огня», наводившего ужас на противников. Около VIII в. китайцы стали использовать ее в пиротехнических смесях, в частности, в смеси типа пороха. Горючесть серы, легкость, с которой она соединяется с металлами с образованием сульфидов (например, на поверхности кусков металла), объясняют то, что ее считали «принципом горючести» и обязательной составной частью металлических руд. Пресвитер Теофил (XI в.) описывает способ окислительного обжига сульфидной медной руды, известный, вероятно, еще в древнем Египте. В период арабской алхимии возникла ртутно-серная теория состава металлов, согласно которой сера почиталась обязательной составной частью (отцом) всех металлов. В дальнейшем она стала одним из трех принципов алхимиков, а позднее «принцип горючести» явился основой теории флогистона. Элементарную природу серы установил Лавуазье в своих опытах по сжиганию. С введением пороха в Европе началось развитие добычи природной серы, а также разработка способа получения ее из пиритов; последний был распространен в древней Руси. Впервые в литературе он описан у Агриколы. Происхождение лат. Sulfur неясно. Полагают, что это название заимствовано от греков. В литературе алхимического периода сера часто фигурирует под различными тайными названиями. У Руланда можно найти, например, названия Zarnec (объяснение «яйца с огнем»), Thucios (живая сера), Terra foetida, spiritus foetens, Scorith, Pater и др. Древнерусское название «сера» употребляется уже очень давно. Под ним подразумевались разные горючие и дурно пахнущие вещества, смолы, физиологические выделения (сера в ушах и пр.). По-видимому, это название происходит от санскритского сirа (светло-желтый). С ним связано слово «серый», т. е. неопределенного цвета, что, в частности, относится к смолам. Второе древнерусское название серы — жупел (сера горючая) — тоже содержит в себе понятие не только горючести, но и дурного запаха. Как объясняют филологи, нем. Schwefel имеет санскритский корень swep (спать, англо- саксонское sweblan — убивать), что, возможно, связано с ядовитыми свойствами сернистого газа.
Впервые в литературе он описан у Агриколы. Происхождение лат. Sulfur неясно. Полагают, что это название заимствовано от греков. В литературе алхимического периода сера часто фигурирует под различными тайными названиями. У Руланда можно найти, например, названия Zarnec (объяснение «яйца с огнем»), Thucios (живая сера), Terra foetida, spiritus foetens, Scorith, Pater и др. Древнерусское название «сера» употребляется уже очень давно. Под ним подразумевались разные горючие и дурно пахнущие вещества, смолы, физиологические выделения (сера в ушах и пр.). По-видимому, это название происходит от санскритского сirа (светло-желтый). С ним связано слово «серый», т. е. неопределенного цвета, что, в частности, относится к смолам. Второе древнерусское название серы — жупел (сера горючая) — тоже содержит в себе понятие не только горючести, но и дурного запаха. Как объясняют филологи, нем. Schwefel имеет санскритский корень swep (спать, англо- саксонское sweblan — убивать), что, возможно, связано с ядовитыми свойствами сернистого газа. (3) Распространение элемента в природе. Сера широко распространена в природе. Она составляет 0,05% массы земной коры. В свободном состоянии (самородная сера) в больших количествах встречается в Италии (острова Сицилия) и США. Месторождения самородной серы имеются в Поволжье, в государствах Средней Азии, в Крыму и других районах. Сера часто встречается в виде соединений с другими элементами. Важнейшими ее природными соединениями являются сульфиды металлов: FeS2 — железный колчедан, или пирит; ZnS — цинковая обманка; PbS — свинцовый блеск; HgS — киноварь и др., а также соли серной кислоты (кристаллогидраты): СаSO4⋅ 2Н2O — гипс, Na2SO4 ⋅ 10h3O — глауберова соль, МgSО4 ⋅ 7h3O — горькая соль и др.(2) Физические свойства. Сера — твердое хрупкое вещество желтого цвета. В воде практически нерастворима, но хорошо растворяется в сероуглероде, анилине и некоторых других растворителях. Плохо проводит теплоту и электричество. Сера образует несколько аллотропных модификаций — сера ромбическая, моноклинная, пластическая.
(3) Распространение элемента в природе. Сера широко распространена в природе. Она составляет 0,05% массы земной коры. В свободном состоянии (самородная сера) в больших количествах встречается в Италии (острова Сицилия) и США. Месторождения самородной серы имеются в Поволжье, в государствах Средней Азии, в Крыму и других районах. Сера часто встречается в виде соединений с другими элементами. Важнейшими ее природными соединениями являются сульфиды металлов: FeS2 — железный колчедан, или пирит; ZnS — цинковая обманка; PbS — свинцовый блеск; HgS — киноварь и др., а также соли серной кислоты (кристаллогидраты): СаSO4⋅ 2Н2O — гипс, Na2SO4 ⋅ 10h3O — глауберова соль, МgSО4 ⋅ 7h3O — горькая соль и др.(2) Физические свойства. Сера — твердое хрупкое вещество желтого цвета. В воде практически нерастворима, но хорошо растворяется в сероуглероде, анилине и некоторых других растворителях. Плохо проводит теплоту и электричество. Сера образует несколько аллотропных модификаций — сера ромбическая, моноклинная, пластическая. Наиболее устойчивой
Наиболее устойчивой Принятое обозначение S (от латинского sulfur).
Принятое обозначение S (от латинского sulfur).

 В процессе реакции с металлами и водородом сера забирает 2 электрона для достижения устойчивого состояния.
В процессе реакции с металлами и водородом сера забирает 2 электрона для достижения устойчивого состояния.
 Сера применяется в металлургии для придания стальным сплавам специальных свойств, ее используют в процессе вулканизации резины, производстве спичек, взрывчатых веществ, пиротехнических изделий, красящих и отбеливающих составов. Огромное промышленное значение имеют производные серы – кислоты, сульфаты и сульфиты.
Сера применяется в металлургии для придания стальным сплавам специальных свойств, ее используют в процессе вулканизации резины, производстве спичек, взрывчатых веществ, пиротехнических изделий, красящих и отбеливающих составов. Огромное промышленное значение имеют производные серы – кислоты, сульфаты и сульфиты.
 При небольшом превышении ПДК, которое допускает не более 0,05 мг/м3 среднесуточной нормы, сернистый ангидрид вызывает першение в горле, обильное слезоотделение, насморк и кашель, появляется головная боль и нарушение координации. Увеличение концентрации вещества ведет к слепоте, химическим ожогам органов дыхания, а в итоге к смерти от удушья.
При небольшом превышении ПДК, которое допускает не более 0,05 мг/м3 среднесуточной нормы, сернистый ангидрид вызывает першение в горле, обильное слезоотделение, насморк и кашель, появляется головная боль и нарушение координации. Увеличение концентрации вещества ведет к слепоте, химическим ожогам органов дыхания, а в итоге к смерти от удушья.

 Оно происходит от
Оно происходит от


 49 г/см 3
49 г/см 3 Все эти реакции относятся к окислительно-восстановительным, в которых свободная сера выступает в роли как окислителя, так и восстановителя, проявляя при этом степени окисления S -2 ← S 0 → S +4 → S +6
Все эти реакции относятся к окислительно-восстановительным, в которых свободная сера выступает в роли как окислителя, так и восстановителя, проявляя при этом степени окисления S -2 ← S 0 → S +4 → S +6 school-collection.edu.ru/dlrstore/3e6b77cf-8fff-882a-d3c3-c50221c6eba9/index.htm
school-collection.edu.ru/dlrstore/3e6b77cf-8fff-882a-d3c3-c50221c6eba9/index.htm большинство этих соединений легко разлагается водой(гидролиз)
большинство этих соединений легко разлагается водой(гидролиз) Составить полуреакции окисления и восстановления
Составить полуреакции окисления и восстановления Серу до сих пор содержат некоторые мази, которыми лечат заболевания кожи. В металлургии.
Серу до сих пор содержат некоторые мази, которыми лечат заболевания кожи. В металлургии. alhimikov.net/element/S.html
alhimikov.net/element/S.html = 113°C;
= 113°C;  Промышленный метод — выплавление из руды с помощью водяного пара.
Промышленный метод — выплавление из руды с помощью водяного пара. И.
Менделеева
И.
Менделеева ..
.. Р. Глаубер во время своего
путешествия внезапно заболел. Он ничего не мог есть, желудок отказывался
принимать пищу. Один из местных жителей направил его к источнику. Как только он
выпил горькую соленую воду, сразу стал есть. Глаубер исследовал эту
воду, из нее выкристаллизовалась соль Na2SO4×10H2O.
Сейчас ее применяют как слабительное в медицине, при окраске хлопчато-
бумажных тканей. Соль также находит применение в производстве стекла
Р. Глаубер во время своего
путешествия внезапно заболел. Он ничего не мог есть, желудок отказывался
принимать пищу. Один из местных жителей направил его к источнику. Как только он
выпил горькую соленую воду, сразу стал есть. Глаубер исследовал эту
воду, из нее выкристаллизовалась соль Na2SO4×10H2O.
Сейчас ее применяют как слабительное в медицине, при окраске хлопчато-
бумажных тканей. Соль также находит применение в производстве стекла С увеличением содержания углерода до 1,2% твердость, прочность и упругость стали увеличиваются, но пластичность и сопротивление удару понижаются, а обрабатываемость ухудшается, ухудшается и свариваемость.
С увеличением содержания углерода до 1,2% твердость, прочность и упругость стали увеличиваются, но пластичность и сопротивление удару понижаются, а обрабатываемость ухудшается, ухудшается и свариваемость. В углеродистой стали допускается серы не более 0,06-0,07%. ( От красноломкости сталь предохраняет марганец, который связывает серу в сульфиды MnS).
В углеродистой стали допускается серы не более 0,06-0,07%. ( От красноломкости сталь предохраняет марганец, который связывает серу в сульфиды MnS).


 065 а.е.м.
065 а.е.м. 36 К (239,38 F)
36 К (239,38 F) 0 E-22 10 6 / м Ом
0 E-22 10 6 / м Ом


































































 Приставочная часть этого слова по- восходит к древнему корню *(а)pо- «кладу, возвращаю обратно», тому же, что в санскритском परतस् /паратас/ «после, за», и в древнегреческом многозначном предлоге απο «от, из, обратно». По-моему, древнейший первообраз, скрытый в этом корне, представляет собой возвращение взятого: «В поте лица твоего будешь есть хлеб, доколе не возвратишься (ἀποστρέψαι /апострепсэ/ «пойдешь обратно») в землю, из которой ты взят, ибо прах ты и в прах возвратишься (ἀπελεύσῃ /апилевси/ «снова ляжешь, вернешься») (Книга Бытия, 3:19). Сочетание основного образа «легкий, невесомый» с приставочным «возвратиться» порождает единое представление о пользе как о возвращении к легкой жизни, облегчении. Стремясь к общей пользе как к облегчению жизни, мы буквально пытаемся устроить себе рай на земле. На бесполезность суетных попыток человека богатеть и наслаждаться, пользуясь плодами своих трудов, указывает еще Ветхий Завет: «Как вышел он нагим из утробы матери своей, таким и отходит, каким пришел, и ничего не возьмет от труда своего, что мог бы он понести в руке своей.
Приставочная часть этого слова по- восходит к древнему корню *(а)pо- «кладу, возвращаю обратно», тому же, что в санскритском परतस् /паратас/ «после, за», и в древнегреческом многозначном предлоге απο «от, из, обратно». По-моему, древнейший первообраз, скрытый в этом корне, представляет собой возвращение взятого: «В поте лица твоего будешь есть хлеб, доколе не возвратишься (ἀποστρέψαι /апострепсэ/ «пойдешь обратно») в землю, из которой ты взят, ибо прах ты и в прах возвратишься (ἀπελεύσῃ /апилевси/ «снова ляжешь, вернешься») (Книга Бытия, 3:19). Сочетание основного образа «легкий, невесомый» с приставочным «возвратиться» порождает единое представление о пользе как о возвращении к легкой жизни, облегчении. Стремясь к общей пользе как к облегчению жизни, мы буквально пытаемся устроить себе рай на земле. На бесполезность суетных попыток человека богатеть и наслаждаться, пользуясь плодами своих трудов, указывает еще Ветхий Завет: «Как вышел он нагим из утробы матери своей, таким и отходит, каким пришел, и ничего не возьмет от труда своего, что мог бы он понести в руке своей. И это тяжкий недуг: каким пришел он, таким и отходит. Какая же польза ему, что он трудился на ветер?» (Екклесиаст, 5:14-15). Согласно Ветхому Завету единственное делание, приносящее пользу, это благотворение, сопровождаемое добрым словом в адрес нуждающегося: «Что есть человек и что польза его? что благо его и что зло его? Число дней человека — много, если сто лет: как капля воды из моря или крупинка песка, так малы лета его в дне вечности. Посему Господь долготерпелив к людям и изливает на них милость Свою. Он видит и знает, что конец их очень бедствен, и потому умножает милости Свои. Милость человека — к ближнему его, а милость Господа — на всякую плоть. Он обличает и вразумляет, и поучает и обращает, как пастырь стадо свое. Он милует принимающих вразумление и усердно обращающихся к закону Его. Сын мой! при благотворениях не делай упреков, и при всяком даре не оскорбляй словами. Роса не охлаждает ли зноя? так слово — лучше, нежели даяние. Поэтому не выше ли доброго даяния слово? а у человека доброжелательного и то и другое» (Книга Иисуса сына Сирахова, 18:7-17).
И это тяжкий недуг: каким пришел он, таким и отходит. Какая же польза ему, что он трудился на ветер?» (Екклесиаст, 5:14-15). Согласно Ветхому Завету единственное делание, приносящее пользу, это благотворение, сопровождаемое добрым словом в адрес нуждающегося: «Что есть человек и что польза его? что благо его и что зло его? Число дней человека — много, если сто лет: как капля воды из моря или крупинка песка, так малы лета его в дне вечности. Посему Господь долготерпелив к людям и изливает на них милость Свою. Он видит и знает, что конец их очень бедствен, и потому умножает милости Свои. Милость человека — к ближнему его, а милость Господа — на всякую плоть. Он обличает и вразумляет, и поучает и обращает, как пастырь стадо свое. Он милует принимающих вразумление и усердно обращающихся к закону Его. Сын мой! при благотворениях не делай упреков, и при всяком даре не оскорбляй словами. Роса не охлаждает ли зноя? так слово — лучше, нежели даяние. Поэтому не выше ли доброго даяния слово? а у человека доброжелательного и то и другое» (Книга Иисуса сына Сирахова, 18:7-17). Согласно Евангелию, единственно настоящую пользу приносят действия, направленные на очищение, хранение и спасение человеческой души для вечной жизни: «Ибо какая польза человеку, если он приобретет весь мир, а душе своей повредит?» (От Марка, 8:36).
Согласно Евангелию, единственно настоящую пользу приносят действия, направленные на очищение, хранение и спасение человеческой души для вечной жизни: «Ибо какая польза человеку, если он приобретет весь мир, а душе своей повредит?» (От Марка, 8:36).


 В культуре овсяный корень известен издавна. В настоящее время ботаниками открыт, изучен и описан 81 вид козлобородника.
В культуре овсяный корень известен издавна. В настоящее время ботаниками открыт, изучен и описан 81 вид козлобородника. Наземную часть растения применяют в виде компрессов как рассасывающее и ранозаживляющее средство при флегмонах, опухолях, гнойных ранах и язвах. Стебли и корни употребляют в пищу.
Наземную часть растения применяют в виде компрессов как рассасывающее и ранозаживляющее средство при флегмонах, опухолях, гнойных ранах и язвах. Стебли и корни употребляют в пищу. Козлобородник хорошо сочетается с любыми овощами и густыми сливочными соусами.
Козлобородник хорошо сочетается с любыми овощами и густыми сливочными соусами. С китайского название растения переводится как «человек-корень», и действительно, корень женьшеня похож на весьма упитанного человечка и длинными-предлинными ногтями. Жутковато! Существует поверье, что чем больше женьшень похож на человека, тем больше полезных свойств имеет женьшень.
С китайского название растения переводится как «человек-корень», и действительно, корень женьшеня похож на весьма упитанного человечка и длинными-предлинными ногтями. Жутковато! Существует поверье, что чем больше женьшень похож на человека, тем больше полезных свойств имеет женьшень. Женьшень активно стимулирует синтез коллагена и эластина кожей, поэтому после применения средств с «корнем жизни» кожа становится более гладкой и мягкой.
Женьшень активно стимулирует синтез коллагена и эластина кожей, поэтому после применения средств с «корнем жизни» кожа становится более гладкой и мягкой. Давайте разберемся что это такое и для чего используют панты в нашей жизни. В чем польза пантов. Панты — неокостенелые рога маралов.
Давайте разберемся что это такое и для чего используют панты в нашей жизни. В чем польза пантов. Панты — неокостенелые рога маралов. Мужчины особенно ценили воздействие пантокрина на организм.
Мужчины особенно ценили воздействие пантокрина на организм. 
 Дерматиты, нейродермиты, псориаз и другие, кроме инфекционных могут значительно уменьшиться.
Дерматиты, нейродермиты, псориаз и другие, кроме инфекционных могут значительно уменьшиться. Они разводятся на маральнике «Алтай» в экологически чистых условиях. Владельцы маральника любят своих животных и не кормят животных стимулирующими добавками в «погоне за длинным рублем». Поэтому вся наша пантопродукция полезна и экологически чиста. Польза пантов не только в своем составе, но и в алтайской природе впитанной маралами.
Они разводятся на маральнике «Алтай» в экологически чистых условиях. Владельцы маральника любят своих животных и не кормят животных стимулирующими добавками в «погоне за длинным рублем». Поэтому вся наша пантопродукция полезна и экологически чиста. Польза пантов не только в своем составе, но и в алтайской природе впитанной маралами. В немецком и датском языке название травы означает «медвежья лапа». Название «борщевик» произошло от слова «борщ» лингвисты предполагают, что в то время это слово означало «что-то зазубренное». Существует версия, согласно которой растение называли «борщ» из-за формы листьев, т. к. в немецком языке Borste означает «щетина». Зелень стали использовать для приготовления пищи, блюдо, в которое его добавляли, стали также называть «борщ». С 18 века под словом «борщ» стали подразумевать суп со свеклой, а борщевик все больше стали забывать.
В немецком и датском языке название травы означает «медвежья лапа». Название «борщевик» произошло от слова «борщ» лингвисты предполагают, что в то время это слово означало «что-то зазубренное». Существует версия, согласно которой растение называли «борщ» из-за формы листьев, т. к. в немецком языке Borste означает «щетина». Зелень стали использовать для приготовления пищи, блюдо, в которое его добавляли, стали также называть «борщ». С 18 века под словом «борщ» стали подразумевать суп со свеклой, а борщевик все больше стали забывать. Долгое время борщевик называли в Польше «местью Сталина». Затем выращивание в масштабах СССР было приостановлено, что никак не сказалось на судьбе самого растения: борщевик начал активно размножатся, превратившись в сорное растение. В связи с тем, что траву долгое время выращивали в качестве силосной культуры, борщевик переселился в дикую природу, его произрастание перестало быть контролированным. Распространение борщевика нарушило экологическое равновесие в ближайших странах Европы, так, например, в Чехии, Германии, Эстонии, Белоруссии были составлены целые программы борьбы с этим опасным растением.
Долгое время борщевик называли в Польше «местью Сталина». Затем выращивание в масштабах СССР было приостановлено, что никак не сказалось на судьбе самого растения: борщевик начал активно размножатся, превратившись в сорное растение. В связи с тем, что траву долгое время выращивали в качестве силосной культуры, борщевик переселился в дикую природу, его произрастание перестало быть контролированным. Распространение борщевика нарушило экологическое равновесие в ближайших странах Европы, так, например, в Чехии, Германии, Эстонии, Белоруссии были составлены целые программы борьбы с этим опасным растением. Дерматит, вызванный борщевиком, проходит в течение 3-6 месяцев, но могут остаться рубцы.
Дерматит, вызванный борщевиком, проходит в течение 3-6 месяцев, но могут остаться рубцы. Также требуется выпить любое противоаллергическое средство, которое есть у вас в аптечке, и постараться не выходить на улицу двое суток, чтобы не получить еще и солнечный ожог, поскольку ожог от сока борщевика делает кожу тела достаточно восприимчивой к солнечному свету.
Также требуется выпить любое противоаллергическое средство, которое есть у вас в аптечке, и постараться не выходить на улицу двое суток, чтобы не получить еще и солнечный ожог, поскольку ожог от сока борщевика делает кожу тела достаточно восприимчивой к солнечному свету.

 В землю высаживают очень плотно газонную траву. На небольших площадях произрастания эффективным будет следующий метод: борщевик накрывают плотной черной пленкой, хорошо прижимают ее к земле. Действенность этого метода обусловлена тем, что земля под пленкой будет очень нагреваться, но солнечные лучи проникнуть под пленку не смогут. Растение в таком случае просто погибнет.
В землю высаживают очень плотно газонную траву. На небольших площадях произрастания эффективным будет следующий метод: борщевик накрывают плотной черной пленкой, хорошо прижимают ее к земле. Действенность этого метода обусловлена тем, что земля под пленкой будет очень нагреваться, но солнечные лучи проникнуть под пленку не смогут. Растение в таком случае просто погибнет. Растение быстро распространилось по всей Европе. Этот вид также считается очень опасным.
Растение быстро распространилось по всей Европе. Этот вид также считается очень опасным. Листья часто сушили, но перед этим тщательно вымачивали для того, чтобы удалить эфирное масло и кумарины. Из растения получали сахар, из которого потом гнали водку.
Листья часто сушили, но перед этим тщательно вымачивали для того, чтобы удалить эфирное масло и кумарины. Из растения получали сахар, из которого потом гнали водку. Отвар корней применят при кожных болезнях, которые сопровождаются зудом. Листья при наружном применении хорошо помогают при ревматизме.
Отвар корней применят при кожных болезнях, которые сопровождаются зудом. Листья при наружном применении хорошо помогают при ревматизме. Двумястами миллилитрами девяностопроцентного спирта залить чайную ложечку измельченного корня борщевика и оставить настаиваться на пять часов. При появлении зубной боли полоскать настоем ротовую полость. Также, чтобы снять сильную боль в зубе, понадобится примерно десять граммов сушеных листочков борщевика залить полным стаканом спирта. Жидкость перелить в герметичную емкость и убрать в неосвещаемое помещение на четырнадцать суток. Спиртово-травяной настойкой следует полоскать только больной зуб при возникновении сильной боли.
Двумястами миллилитрами девяностопроцентного спирта залить чайную ложечку измельченного корня борщевика и оставить настаиваться на пять часов. При появлении зубной боли полоскать настоем ротовую полость. Также, чтобы снять сильную боль в зубе, понадобится примерно десять граммов сушеных листочков борщевика залить полным стаканом спирта. Жидкость перелить в герметичную емкость и убрать в неосвещаемое помещение на четырнадцать суток. Спиртово-травяной настойкой следует полоскать только больной зуб при возникновении сильной боли. Необходимо четырьмястами миллилитрами охлажденной кипяченой водички залить приблизительно тридцать граммов высушенной травы борщевика и дать настояться около полутора часов. Далее настой требуется профильтровать. Ежедневно один раз в день необходимо выпивать не больше пятидесяти миллилитров настоя за пятнадцать минут до еды.
Необходимо четырьмястами миллилитрами охлажденной кипяченой водички залить приблизительно тридцать граммов высушенной травы борщевика и дать настояться около полутора часов. Далее настой требуется профильтровать. Ежедневно один раз в день необходимо выпивать не больше пятидесяти миллилитров настоя за пятнадцать минут до еды. Чтобы болезнь отступила, необходимо выпивать по четыре чайные ложечки отвара не менее четырех раз в день за четверть часа до того, как начнете употреблять пищу.
Чтобы болезнь отступила, необходимо выпивать по четыре чайные ложечки отвара не менее четырех раз в день за четверть часа до того, как начнете употреблять пищу. Как уже было сказано, сок этого растения вызывает сильные дерматиты, которые лечат продолжительное время. Также избыток кумаринов в организме может привести к развитию витилиго.
Как уже было сказано, сок этого растения вызывает сильные дерматиты, которые лечат продолжительное время. Также избыток кумаринов в организме может привести к развитию витилиго.
 Определение словаря
Определение словаря «После сегодняшнего подкаста li , вы больше не будете чувствовать lig ed, чтобы искать слова с lig , li и ly в них!
«После сегодняшнего подкаста li , вы больше не будете чувствовать lig ed, чтобы искать слова с lig , li и ly в них!

 Когда вы знаете корни словарного запаса, который мы используем в повседневной речи прямо сейчас, вы делаете шаг вперед в понимании словарного запаса, которого у других людей может не быть. Это не только поможет вам в школе по всем направлениям (области науки известны своей греческой и латинской терминологией), но и знание греческих и латинских корней поможет вам в основных стандартизированных тестах, таких как PSAT, ACT, SAT и даже LSAT и GRE.
Когда вы знаете корни словарного запаса, который мы используем в повседневной речи прямо сейчас, вы делаете шаг вперед в понимании словарного запаса, которого у других людей может не быть. Это не только поможет вам в школе по всем направлениям (области науки известны своей греческой и латинской терминологией), но и знание греческих и латинских корней поможет вам в основных стандартизированных тестах, таких как PSAT, ACT, SAT и даже LSAT и GRE. Знание одного корня может мгновенно увеличить ваш словарный запас.
Знание одного корня может мгновенно увеличить ваш словарный запас.
 Если бы вы не знали корень, вы бы даже не догадывались.
Если бы вы не знали корень, вы бы даже не догадывались.



 Некоторые грибы также защищают деревья от болезней и вредителей, передаваемых через почву, производя соединения антибиотиков, стимулируя другие полезные микроорганизмы в корневой зоне, активируя гены защиты растений, побеждая вредные грибы и действуя как броня вокруг хрупких корней.
Некоторые грибы также защищают деревья от болезней и вредителей, передаваемых через почву, производя соединения антибиотиков, стимулируя другие полезные микроорганизмы в корневой зоне, активируя гены защиты растений, побеждая вредные грибы и действуя как броня вокруг хрупких корней. Эти процессы также могут помочь улучшить структуру почвы, продвигая почвенные агрегаты. Улучшенная структура почвы может уменьшить эрозию, увеличить проникновение воды и способствовать росту других полезных форм жизни, обитающих в почве.
Эти процессы также могут помочь улучшить структуру почвы, продвигая почвенные агрегаты. Улучшенная структура почвы может уменьшить эрозию, увеличить проникновение воды и способствовать росту других полезных форм жизни, обитающих в почве. (Фото любезно предоставлено Лесной службой Северной Дакоты)
(Фото любезно предоставлено Лесной службой Северной Дакоты)  Покупка деревьев, уже колонизированных грибами, или нанесение грибов на корни саженцев с использованием инокулянта во время посадки — наиболее эффективные способы заселения корней деревьев хорошими грибами.
Покупка деревьев, уже колонизированных грибами, или нанесение грибов на корни саженцев с использованием инокулянта во время посадки — наиболее эффективные способы заселения корней деревьев хорошими грибами. Этот пух не тревожит, пока сеянцы выглядят здоровыми. (Фото любезно предоставлено Mycorrhizal Applications, Inc.)
Этот пух не тревожит, пока сеянцы выглядят здоровыми. (Фото любезно предоставлено Mycorrhizal Applications, Inc.) 
 ”
” «Это один из самых многообещающих способов развития знания слов», — сказал он. «Любой, кто когда-либо изучал латынь в старшей школе, видит, как сильно она влияет на английский, и может помочь пополнить словарный запас».
«Это один из самых многообещающих способов развития знания слов», — сказал он. «Любой, кто когда-либо изучал латынь в старшей школе, видит, как сильно она влияет на английский, и может помочь пополнить словарный запас». «Я не думаю, что [ученики] видят в этом« я изучаю латынь », — сказал Крис Шмидт, талантливый педагог с 3-5 классов из округа Банкомб в Северной Каролине.Он использует программу Caesar’s English для обучения словарю с греческими и латинскими корнями. «Они видят в этом больше загадку. «Это то, что я пытаюсь понять. Здесь код, и я пытаюсь его взломать ».
«Я не думаю, что [ученики] видят в этом« я изучаю латынь », — сказал Крис Шмидт, талантливый педагог с 3-5 классов из округа Банкомб в Северной Каролине.Он использует программу Caesar’s English для обучения словарю с греческими и латинскими корнями. «Они видят в этом больше загадку. «Это то, что я пытаюсь понять. Здесь код, и я пытаюсь его взломать ». Но часто нет однозначного правильного ответа. Например, учащиеся могут увидеть слова «предварительная готовка», «предварительный нагрев», «предварительная смесь» и «предварительное тестирование». Один студент может сказать, что предварительный тест — это другое дело, потому что он не имеет отношения к кулинарии.Другой может выбрать готовую смесь, потому что она единственная с окончанием -ed.
Но часто нет однозначного правильного ответа. Например, учащиеся могут увидеть слова «предварительная готовка», «предварительный нагрев», «предварительная смесь» и «предварительное тестирование». Один студент может сказать, что предварительный тест — это другое дело, потому что он не имеет отношения к кулинарии.Другой может выбрать готовую смесь, потому что она единственная с окончанием -ed. Затем Ульрих попросил студентов составлять свои собственные слова, используя приставки, суффиксы и корни, которые они выучили.
Затем Ульрих попросил студентов составлять свои собственные слова, используя приставки, суффиксы и корни, которые они выучили.
 Но некоторые преподаватели говорят, что подход к построению словарного запаса полезен даже для учащихся, которые только начинают читать.
Но некоторые преподаватели говорят, что подход к построению словарного запаса полезен даже для учащихся, которые только начинают читать.
 Оригинальный пост читайте здесь.
Оригинальный пост читайте здесь.  » и так далее.
» и так далее.
 Например, слово «руководство» происходит от латинского корня «человек», что означает «рука». Однако похожее по звучанию слово «манна» происходит от древнеанглийского «manna», означающего «предоставленная провиденциальной субстанцией», восходящего к еврейскому корню «man-», означающему «вещество, исходящее из дерева тамариск». Это означает, что незнакомому слову очень легко придать совершенно неверное значение.
Например, слово «руководство» происходит от латинского корня «человек», что означает «рука». Однако похожее по звучанию слово «манна» происходит от древнеанглийского «manna», означающего «предоставленная провиденциальной субстанцией», восходящего к еврейскому корню «man-», означающему «вещество, исходящее из дерева тамариск». Это означает, что незнакомому слову очень легко придать совершенно неверное значение. Вам нужно не только распознавать определенные слова, но и точно понимать, как их использовать. По сути, вам необходимо увеличить свой функциональный словарный запас — количество слов, которые вы уверенно и правильно используете в предложении.
Вам нужно не только распознавать определенные слова, но и точно понимать, как их использовать. По сути, вам необходимо увеличить свой функциональный словарный запас — количество слов, которые вы уверенно и правильно используете в предложении. Есть некоторая выгода в том, чтобы посвятить небольшое количество времени изучению словарного запаса изучению некоторых основных корней, префиксов и суффиксов. Они могут дать некоторые подсказки, если вы в конечном итоге произнесете несколько действительно незнакомых слов в день теста GRE, и сделают любое предположение, которое вы делаете, немного более образованным.Таким образом, вы можете подумать о создании нескольких (например, 50) карточек с корневыми словами GRE, которые станут небольшим подмножеством вашей более обширной словарной стратегии, ориентированной на слова.
Есть некоторая выгода в том, чтобы посвятить небольшое количество времени изучению словарного запаса изучению некоторых основных корней, префиксов и суффиксов. Они могут дать некоторые подсказки, если вы в конечном итоге произнесете несколько действительно незнакомых слов в день теста GRE, и сделают любое предположение, которое вы делаете, немного более образованным.Таким образом, вы можете подумать о создании нескольких (например, 50) карточек с корневыми словами GRE, которые станут небольшим подмножеством вашей более обширной словарной стратегии, ориентированной на слова. Это потому, что все они имеют греческий корень «путь», означающий чувство или эмоцию. Но вам не обязательно знать конкретный корень или его происхождение, чтобы понять тот факт, что слова со словом «путь» часто имеют отношение к аффектам и эмоциям.
Это потому, что все они имеют греческий корень «путь», означающий чувство или эмоцию. Но вам не обязательно знать конкретный корень или его происхождение, чтобы понять тот факт, что слова со словом «путь» часто имеют отношение к аффектам и эмоциям. Этот список был составлен путем изучения того, какие корни неоднократно появлялись в официальных материалах подготовки GRE.
Этот список был составлен путем изучения того, какие корни неоднократно появлялись в официальных материалах подготовки GRE.
 Обзор
Обзор
