Самая соль: новые виды наркотиков привлекли все группы населения | Статьи
Российские социологи зафиксировали появление в обществе наркотиков «выходного дня» и новой схемы их «контролируемого» потребления. Эти данные приводят ученые сектора социологии девиантного поведения Федерального научно-исследовательского социологического центра РАН. В результате действия новой схемы у людей растягивается период приобретения зависимости. Есть риск, что через десятилетие мы можем получить население, вовлеченное в потребление наркотиков во всех возрастных группах, говорят социологи. Результаты исследования социологов подтверждает официальная статистика МВД. Эксперты Минздрава напоминают, что «контролируемое» потребление наркотиков — это миф.
Дешевый кайфСогласно официальному ответу МВД на запрос «Известий», в последние годы отмечается трансформация российского нелегального наркорынка в сторону вытеснения наркотиков растительного происхождения синтетическими. Это связано с их относительной дешевизной, доступностью и возможностью изготовления в условиях подпольных нарколабораторий.
С 2011 года удельный вес «синтетики» в общей массе изымаемых наркотических средств постепенно увеличивался. В 2017 году эта доля достигла 26,1%.
При этом, как писали «Известия, в прошлом году заболеваемость наркоманией в России достигла исторического минимума — 11,1 нового случая на 100 тыс. населения. Всего на учете, по данным на 2017 год, состояло 259,5 тыс. больных наркоманией, зафиксировал Минздрав. Это минимальный показатель с 2003-го. Тогда в стране числилось 326,6 тыс. «официальных» наркоманов.
Фото: РИА Новости/Александр Вильф
Некоторые специалисты стали говорить о стабилизации наркоситуации, другие же отказывались признать позитивные изменения, наблюдая за постепенно разворачивающейся новой схемой «контролируемого» потребления наркотиков. Это означает, что потребители не становятся зависимыми за недели и месяцы. Они могут годами использовать наркотик по выходным дням. Однако, по словам специалистов, такое потребление только растягивает период вовлечения в сильную зависимость.
Они могут годами использовать наркотик по выходным дням. Однако, по словам специалистов, такое потребление только растягивает период вовлечения в сильную зависимость.
Исследование сектора девиантного поведения Института социологии РАН, поддержанное грантом РФФИ, показывает, что на сегодняшний день наркоситуация в России представляет собой состояние сжатой пружины: через несколько лет общество может быть втянуто в наркопотребление во всех возрастных группах и социальных статусах. Даже пожилые люди сейчас нередко употребляют наркотики.
Аптечная наркомания и ставка на синтетику В старших возрастных группах (после 50 лет) выявлена незначительная доля женщин-потребительниц, для которых характерна «аптечная наркомания». По словам старшего научного сотрудника Федерального научно-исследовательского социологического центра РАН Виктории Брюно, это связано с привычкой у пожилых людей к ежедневному употреблению лекарств.
— Нередко всё начинается с того, что пожилая женщина с молодости привыкла снимать головную боль лекарством. Постепенно она увеличивает его дозу, а потом начинает использовать для этого каннабиноиды, — говорит эксперт.
Главная проблема современной наркотизации заключается в том, что рынок заполонили новые — синтетические наркотики. Эти наркотики, часто называемые «легкими» или «тихими», порождают идеологию «безопасного наркопотребления».
Фото: ТАСС/DPA/Frank May
По данным социологов, если в 2007 году «новые наркотики» употребляли лишь в 19 субъектах, то в 2018 году зафиксировано их систематическое использование практически во всех регионах. Ассортимент химических стимуляторов расширяется, и некоторые наркосодержащие препараты, еще не попавшие в запрещенные списки, продаются под видом лекарственных. Также большое распространение получили так называемые дизайнерские наркотики, формула вещества которых меняется для того, чтобы избежать выявления разработанными методами. Сейчас можно говорить уже о четырех поколениях «дизайнерских» наркотиков, которые доступны в России. Особую опасность представляет совместное употребление «новых» наркотических веществ с «традиционными» наркотиками, а также с алкоголем.
Сейчас можно говорить уже о четырех поколениях «дизайнерских» наркотиков, которые доступны в России. Особую опасность представляет совместное употребление «новых» наркотических веществ с «традиционными» наркотиками, а также с алкоголем.
Анализ первых проб наркотика позволил выделить и значимые поколенческие различия. Ранние (до 16 лет) пробы характерны только для двух возрастных групп: 30–39 лет и 24–29 лет. В младшей возрастной группе (18–23 года на момент опроса) и в старшей (40–55) респонденты значительно реже приобретали первый наркотический опыт в таком раннем возрасте. Очень поздние первые пробы (после 30 лет) характерны только для тех, кому сейчас 50–55 лет.
Семейные тоже «в строю»Проведенный учеными мониторинг интернет-ресурсов показал, что в рамку новой модели потребления активно включены люди в возрасте 30–40 лет, семейные, образованные, профессиональные, с высоким уровнем доходов, с устоявшимся кругом интересов — хорошо социально адаптированные.
Фото: ИЗВЕСТИЯ/Павел Бедняков
Причины распространенности наркотиков новой волны ученые видят в установлении более тесных связей между странами, новых возможностях приготовления наркотиков из аптечных средств, расширении рынка психоактивных средств в связи с распространенностью даркнета и росте «серого поля» потребителей. В этой группе находятся те люди, которые не попадают в поле зрения ни правоохранительных органов, ни медиков и имеют иные личностные характеристики и ценностные ориентации, нежели потребители наркотиков конца ХХ века.
Проблема больных и врачейПо словам руководителя сектора социологии девиантного поведения Маргариты Поздняковой, в настоящее время наркоситуация требует особых форм социального контроля и обязательного участия специалистов различных областей знания.
Фото: РИА Новости/Алексей Сухоруков
— Исследование показало, что, к сожалению, в научном сообществе и СМИ проблему наркотиков до сих пор презентуют прежде всего как проблему «больных» и «врачей». При таком подходе снимается ответственность с потребителя наркотиков: индивид не несет ответственности за свою болезнь вследствие того, что он находится в рабской зависимости от психоактивного вещества. То есть сам факт зависимости и делает его больным. Такой подход играет как позитивную, так и негативную роль, однако он упускает из виду личность потребителя как субъекта собственной воли, отказывая ему в способности самостоятельно принимать решения, управлять своей жизнью и соответственно контролировать употребление, — подчеркивает эксперт.
При таком подходе снимается ответственность с потребителя наркотиков: индивид не несет ответственности за свою болезнь вследствие того, что он находится в рабской зависимости от психоактивного вещества. То есть сам факт зависимости и делает его больным. Такой подход играет как позитивную, так и негативную роль, однако он упускает из виду личность потребителя как субъекта собственной воли, отказывая ему в способности самостоятельно принимать решения, управлять своей жизнью и соответственно контролировать употребление, — подчеркивает эксперт.
Социолог отмечает, что в среде отечественных медиков, и в первую очередь наркологов, существует общее недоверие к феномену «контролируемого» потребления.
Минздрав предупреждаетДоктор медицинских наук, директор Национального научного центра наркологии — филиала ФГБУ «ФМИЦПН им. В.П. Сербского» Минздрава Татьяна Клименко опровергает возможность «контролируемого потребления».
— Это миф, который строится на основе опросов, проводимых социологами. Любой наркоман или алкоголик мечтает достичь контролируемого поведения. На начальных стадиях это получается. Но через некоторое время мы наблюдаем обычное течение болезни, — утверждает эксперт.
Татьяна Клименко подтверждает, что медики также фиксируют изменение структуры потребления наркотиков и связано это прежде всего с выходом на рынок новых наркотиков — солей и спайсов.
— Мы не наблюдаем активного потребления наркотиков лицами пожилого возраста. Основными потребителями остаются всё же молодежь и люди среднего возраста, — подчеркивает эксперт.
Недооцененная опасностьВсе эти данные говорят о том, что социологи правильно «ухватили» саму суть изменений в схеме потребления наркотических средств. По их мнению, общество недооценивает опасность, связанную с вовлечением в употребление наркотиков всех групп населения.
Фото: РИА Новости/Павел Бедняков
В Федеральном научно-исследовательском социологическом центре РАН уверены, что для изменения создавшейся ситуации нужно детально разработать методы профилактики для каждой возрастной группы в отдельности. Также они надеются на повышение научной обоснованности предложений, которые будут внесены в новый документ Стратегии государственной антинаркотической политики Российской Федерации.
Также они надеются на повышение научной обоснованности предложений, которые будут внесены в новый документ Стратегии государственной антинаркотической политики Российской Федерации.
ЧИТАЙТЕ ТАКЖЕ
Что такое синтетические наркотики, как они встраиваются в культуру и как понять, что близкому человеку нужна помощь?
Употребление наркотических средств серьёзно вредит здоровью. Наркотики запрещены законом – хранение и сбыт караются лишением свободы сроком до 15 лет. В том случае, если наркотик распространяется в организациях образования, закон предусматривает лишение свободы на 20 лет или даже пожизненно (см. 1-4 ч. статьи 297 УК РК).
Бытие требует от человека почти невозможного: внимания к ближайшему.
«Дело Хайдеггера»
Под синтетикой
«Знаешь, ты будто бы превращаешься в один огромный клитор, – говорит Елена (имя изменено), – каждая мысль прекрасна, звуки, запахи. Не хочется ни есть, ни пить, ни заниматься сексом». Собеседница informburo.kz не «сидит» на синтетике, но иногда принимает. Считает, что чем реже, тем лучше: при повышении частоты употребления впечатления, по её словам, притупляются с каждым разом.
Раздобыть «концентрированное счастье» в крупных городах Казахстана не так сложно, как хотелось бы. В клубах и на «вписках», у проверенных друзей.
«Связанные с трипом воспоминания, пусть и отрывочные, настолько прекрасны, – продолжает Елена, – что вот если человек, которого ты не очень хотел видеть и вообще на дух не переносишь, напишет тебе что-то типа «у меня есть мдмашечка», ты, скорее всего, его увидишь. Соблазн просто огромный».
Соблазн просто огромный».
Читайте также: Как определить, употребляет ли ваш ребёнок наркотики, и как быть, если это так?
В основном в Казахстане встречается две группы «синтетики»: JWH (синтетический канабиноид) и МДПВ (метилендиоксипировалерон). Мефедрон – это эйфоретик, созданный на основе стимулятора нервной системы амфетамина и алкалоида катинона. МДПВ, его более распространённый в Казахстане аналог – психоактивное вещество со стимулирующими свойствами, действует как ингибитор обратного захвата дофамина и норадреналина. Но на самом деле веществ, которые поступают в страну, огромное разнообразие.
По словам Ольги Агаповой (Фонд «Свободные люди»), огромное количество синтетических наркотиков, из-за того что формулы постоянно меняются, до 1 января 2019 года не попадало под запрет. Все знают, что вещество наркотическое, но оно не запрещено, его нет в таблице запрещённых веществ, и человеку, который его распространяет, вменить ничего невозможно. К тому моменту, как выходил новый закон с обновлённой таблицей, а это почти год, на рынке уже появлялись сотни других формул.
Это химическое соединение, и изменить формулу в лабораторных условиях – процесс несложный.
Как действует «синтетика»?
Синтетические наркотики повышают активность, чувствительность, улучшают настроение, снимают напряжение, повышают эмпатию, будят жажду действий, раскрывают коммуникативность. Эффект начинает проявляться в течение 25-45 минут после принятия. Его длительность зависит от особенностей организма. Если вещество принимается на голодный желудок, то эффект длится три-четыре часа.
«В одиночестве нельзя принимать, должен быть кто-то, кто проконтролирует, чтобы ты не сделал какую-нибудь жуть, – говорит Елена. – Да и вообще под этим делом очень хочется не быть одному. Хочется трогать кого-то, совсем без сексуального подтекста. Разговаривать, делиться открытиями. Ты сидишь, смотришь на человека и говоришь: расслабь, расслабь челюсть».
Разговаривать, делиться открытиями. Ты сидишь, смотришь на человека и говоришь: расслабь, расслабь челюсть».
Синтетические наркотики непредсказуемо действуют на тело. Так, к примеру, в зависимости от дозы разные мышцы (чаще всего челюсть) могут сжиматься и разжиматься бесконтрольно.
«Как действует «синтетика?» – говорит Ольга Агапова. – Ключевое слово – непредсказуемо. Это и есть их основная опасность. Одно и то же вещество в одной и той же дозе у одного вызовет наркотическое опьянение, а у другого передозировку. Они безумно токсичны. Что в итоге? Либо суицид, либо приобретённый психиатрический диагноз на всю жизнь».
Если «приход» зависит от особенностей организма, от психологического состояния, душевного равновесия и может быть так, что никакого счастья человек не испытает (минимум – ничего, максимум – депрессия), то «отходят» практически все одинаково – очень тяжело.
«На следующий день ты п**ц жрёшь кактусы, как в «Магазинчике Бо», – делится Елена. – Серотонин кончился, химической возможности счастья в тебе больше нет. Дня два ходишь в полной депрессии».
Как понять, что близкому человеку нужна помощь?
Постоянно расширенные зрачки, сухость во рту (человек всё время хочет пить), учащение пульса, холодные руки, потеря аппетита и раздражительность – это главные признаки употребления синтетических наркотиков. Если вы замечаете что-то подобное в поведении близкого человека (ребёнка, друга, супруга/супруги), стоит немедленно обратиться на горячую линию реабилитационного центра для наркозависимых в вашем городе либо в Единую телефонную консультативную службу доверия по вопросам наркомании и кризисным состояниям по номеру 8 800 080 3515.
Как выглядит «синтетика» и как распространяется?
Синтетические наркотики получают в искусственных условиях. МДПВ и мефедрон выглядят или как порошок, похожий на соль, или выпускаются в таблетках. В качестве примеси к ним может быть добавлен кофеин или ацетаминофен (парацетамол). Употребляют синтетические наркотики не только перорально (пьют), но и нюхают, колют в вены и даже принимают ректально.
Употребляют синтетические наркотики не только перорально (пьют), но и нюхают, колют в вены и даже принимают ректально.
Согласно результатам опроса, проведённого в 2011 году в Великобритании, каждый 25-й молодой человек признался, что годом ранее, в 2010 году, хотя бы раз принимал мефедрон. Аудитория в почти 300 тысяч человек сделала этот наркотик третьим после марихуаны и кокаина по популярности среди людей от 16 до 35 лет в Британии. Он продавался под видом пищевой добавки или соли для ванн, а стоила порция 20-25 фунтов (9-12 тысяч тенге по текущему курсу).
Читайте также: Как в Казахстане лечат от наркозависимости?
В 2019 году в Казахстане грамм «соли» обойдётся в 20-25 тысяч, а таблетку можно купить примерно за 12 тысяч, как договоришься.
По словам другого собеседника informburo.kz, Айдара (имя изменено), существуют закрытые Telergam-чаты и группы в «ВКонтакте» где по-прежнему можно «раздобыть», однако он в них не состоит, не причастен к продаже и не может помочь в поиске. Паблик «ВКонтакте» под названием «Империя стаффа», о котором мы писали в 2016 году, найти уже нельзя, но подобных много. То есть найти продавца теоретически несложно, однако невозможно встретиться с ним лично.
По словам Ольги Агаповой, новые технологии полностью изменили систему продаж наркотических средств: «Сейчас все вещества продаются бесконтактным методом, то есть продавец и покупатель друг друга не видят и друг с другом не встречаются. Общение идёт через мессенджеры, оплата через анонимную платежную систему. Забирают товар через «закладку». Кто, где и когда будет делать «закладку», выявить сложно. Чтобы отследить, кто её придёт забирать, нужно знать, где она лежит. В качестве закладчиков вербуют несовершеннолетних, потому что с них спрос меньше. Предметно инструктируют (опять же через мессенджеры), как вести себя в той или иной ситуации».
В интернете тот же мефедрон стал доступен в 2007-м, три года оставался легальным в России и Европе. В 2010 году был запрещён в России и других странах СНГ, а также в Великобритании и ещё в 27 странах ЕС.
В 2010 году был запрещён в России и других странах СНГ, а также в Великобритании и ещё в 27 странах ЕС.
Поводом для запрета в ЕС послужили 40 смертей от передозировки.
В Англии «синтетику» запретили, когда к власти пришла Консервативная партия Великобритании. Тогда был принят ряд решительных законодательных мер по борьбе с наркотиками, а с 2010-го до 2017-го количество смертей среди потребителей героина/морфина выросло на 30% и на 200% – среди потребителей кокаина. Общий рост смертности от употребления наркотиков составил 37% за 17 лет, в 2017-м достигнув рекордного для Европы уровня: было зарегистрировано 3756 смертей.
Сначала считалось, что мефедрон и его аналоги не вызывают зависимости, но стойкое привыкание может появиться уже после второй дозы, при этом вне зависимости от того, насколько вторая отделена по времени от первой. Ломка – острое желание новой дозы также наступает довольно быстро, человек начинает испытывать психологические мучения, стресс. Возможны приступы истерики и провалы в памяти.
Состав многих синтетических наркотиков остаётся загадкой для учёных, так как в широкий оборот они вошли сравнительно недавно, и поэтому процесс диагностирования и определения путей лечения зависимости затруднён. Что успели выяснить: оказывая сильное воздействие на нервную систему, препарат быстро вызывает зависимость, от которой сложно (почти невозможно) избавиться самостоятельно.
Со временем происходит деградация личности, утрачиваются когнитивные способности, останавливается интеллектуальное развитие.
«Последствия страшные. В перспективе после длительного употребления у всех синтетических наркоманов наблюдается значительный откат по интеллекту и приобретённый психиатрический диагноз, – говорит Ольга Агапова. – Их и сейчас специалисты классифицируют как пациентов с двойным диагнозом: первый – наркологический, второй – психиатрический. И порой психиатрический диагноз остаётся на всю жизнь, то есть человек всю оставшуюся жизнь будет жить на психокорректорах. К последствиям приема также относят и суицидальность. Ведь неспроста с появлением синтетических наркотиков резко выросла статистика по подростковым и молодёжным суицидам».
И порой психиатрический диагноз остаётся на всю жизнь, то есть человек всю оставшуюся жизнь будет жить на психокорректорах. К последствиям приема также относят и суицидальность. Ведь неспроста с появлением синтетических наркотиков резко выросла статистика по подростковым и молодёжным суицидам».
Однако согласно доступным данным официальной статистики в Казахстане идёт уменьшение суицидов среди молодых людей в возрасте от 14 до 28 лет – с 970 в 2015-м году до 818 в 2017-м.
Читайте также: Список запрещённых в Казахстане наркотиков расширится
Зачем люди вообще принимают наркотики?
Мы живём в обществе потребления, говорит социолог Александра Дмитриева, и любое потребление, в том числе и потребление наркотиков, исходя из соответствующей теории, нормально. Неинъекционные наркотики, нерегулярное употребление которых не видно со стороны, формируют стили поведения, становятся своего рода социальным ориентиром в пространстве. «Если я здесь, то не там; с этими, а не с теми».
Это работает примерно как религиозная принадлежность.
Важно понимать, что проблема чрезмерного потребления распространяется на все сферы жизни. И разумное, осознанное потребление, гипотетически, может относиться и к наркотикам. Но в этой сфере сложнее найти ту грань, за которой начинаются проблемы. Сложнее признать и заговорить о проблемах, ведь вести диалог о проблемах «такого рода» в «приличном обществе» не принято.
Вместо работы с людьми, которые по тем или иным причинам стали принимать наркотики, другие люди и общественные институты, в том числе и государство, немедленно их клеймят. И речь прежде всего об общественном восприятии, здравоохранение и закон на время оставим за скобками. Хотя даже лечение, по крайней мере на постсоветском пространстве, устроено как наказание.
У Мишеля Фуко есть мысль о том, что власть не только репрессивна, но и продуктивна: она производит субъекты, называя их определённым именем и давая им определённые характеристики. Больницы и поликлиники создают пациентов, суды и тюрьмы – преступников, подобную аналогию можно провести и с наркоманами. Очевидно, наркоманы появляются не как феномен, а как отдельная социальная группа – с медикализацией общества, распространением врачебного и научного знания и с интенсификацией государственного управления человеческими жизнями (последнее явление Фуко называет биополитикой). А если наркоман – часть общества, то невозможно сделать вид, что его не существует.
Больницы и поликлиники создают пациентов, суды и тюрьмы – преступников, подобную аналогию можно провести и с наркоманами. Очевидно, наркоманы появляются не как феномен, а как отдельная социальная группа – с медикализацией общества, распространением врачебного и научного знания и с интенсификацией государственного управления человеческими жизнями (последнее явление Фуко называет биополитикой). А если наркоман – часть общества, то невозможно сделать вид, что его не существует.
«Вопрос, который в таком случае можно поставить, следующий: «Кто такой наркоман и когда, при каких условиях он возникает?» – рассуждает социолог Алексей Блохин. – И здесь уже стоит подумать о том, как определяются наркотики. В разное время в список наркотиков включаются, например, никотин, алкоголь и кофеин, и, хотя это кажется странным из 21-го века, в Мекке, Оттоманской империи и Западной Европе предпринимались попытки запретить кофе. В качестве обоснования запрета приводились и аргументы, связанные с негативным влиянием напитка на здоровье. Более известные истории связаны с запретами или ограничениями на курение и потребление алкогольных напитков. Возможно, само появление термина «наркоман» связано с необходимостью как-то обозначить феномен, выделить его, скорее всего, с целью приведения в норму, борьбы с ним, стигматизации».
Есть сформированная таким образом общественная декларация: наркотики – это плохо, потому что все так сказали. Но если все так сказали и все так думают, то почему наркотики продолжают существовать?
Роберт Джонсон, американский блюзмен
В статье «Наркотики и популярная культура» культуролог Эндрю Блейк упоминает своеобразный миф о Фаусте (только героиновом): Роберт Джонсон, популярный блюзовый музыкант (он входит в «Клуб 27»), якобы однажды встретил дьявола на перекрёстке где-то в Миссисипи, продал ему душу и стал играть лучше всех на свете. И подобного рода легенды о чудесном воздействии героина на творчество выходят далеко за пределы США. Блейк считал, что британские музыканты употребляли этот наркотик в надежде сравняться с гениальными афроамериканцами. Но в культуру наркотики попадают не сразу. Так, многие наркотики, включая никотин и алкоголь, использовались в лечебных практиках (в том числе, как бы парадоксально это ни звучало, в борьбе с наркотиками, вспомним морфий и ЛСД).
Блейк считал, что британские музыканты употребляли этот наркотик в надежде сравняться с гениальными афроамериканцами. Но в культуру наркотики попадают не сразу. Так, многие наркотики, включая никотин и алкоголь, использовались в лечебных практиках (в том числе, как бы парадоксально это ни звучало, в борьбе с наркотиками, вспомним морфий и ЛСД).
«Кроме того, наркотические вещества являлись и являются составной частью многих религий и социальных практик, – продолжает Алексей Блохин. – Централизованная борьба с наркотиками в западноевропейских странах начинается, по всей видимости, в 19-м веке, и в каждом случае вопросы, кого считать наркоманом, а кого нет, что считать наркотиком, а что медицинским препаратом или пагубной привычкой, определяются сложившейся в данный момент и в данное время конъюнктурой отношений между разными видами знания и власти – основными факторами здесь, скорее всего, являются медицина и государство, но не стоит забывать и о религии, традиции и экономической системе».
Читайте также: Депрессия: почему она возникает и как нужно лечиться?
Экономический аспект нужно рассмотреть отдельно. Система сбыта наркотиков формируется культурой, отражает культуру и социальные модели и формирует некоторые общественные институты.
«Очевидно, что географическое распространение растений, из которых производятся наркотические вещества, определяет жизнь этих сообществ: вспомним про наркотрафик в Центральной Америке и разные маршруты транспортировки наркотиков из Афганистана в Европу; в странах, где производятся наркотики и/или через которые проходят маршруты наркотрафика, «наркоэкономика» создает рабочие места, альтернативные виды занятости, повышает уровень преступности (так, в Гондурасе, через который проходит большинство кокаина, идущего в США, самый высокий в мире уровень убийств). Здесь наркотики действуют как любой другой колониальный товар (какао-бобы, сахарный песок, хлопок и т. п.), и тогда не столько наркотики определяют форму и содержание социальных отношений, сколько наследие европейского империализма и неравные экономические отношения между глобальным севером и глобальным югом», – говорит Алексей Блохин.
Кроме того, наркотики – это часть популярной культуры и для некоторых они становятся своего рода окном эффективности культур, в которых мы живём. В 20-30-х годах прошлого века был популярен кокаин, во время и после войны началась эпоха героина, в 50-х пальму первенства перехватили барбитураты и ЛСД, в 80-90-х – экстази и опять кокаин. Сегодняшнее окно эффективности культуры – вещества, которые увеличивают продуктивность и улучшают когнитивные способности. Такие как мефедрон или МДПВ.
Алексей Блохин уточняет, что из бывшей столицы огромной колониальной империи довольно сложно на самом деле говорить о культуре глобального юга, глобального севера и особенностях их культур, однако можно рассмотреть феномен включения наркотиков в западную культуру, некоторые особенности которой перенимает культура СНГ.
«Вспомним Вудсток, битников. Часто в этом дискурсе возникает интересная сцепка протестной культуры и духовного освобождения; наркотики, какое-то время в 60-70-х точно, ассоциировались с духовным ростом, осознанием себя, выходом из западной системы ценностей, а также протестом против официальной культуры и политики. Как говорил Фуко: власть создаёт в том числе и субъектов, протестующих против неё; запрет на наркотики мог стать одним из факторов расцвета культуры, которая относилась к ним положительно».
Олдос Хаксли считал, что наркотики, на которых общество «сидит» в определённое время, соответствуют нуждам и потребностям культуры. Они как бы восполняют то, чего больше всего не хватает тому или иному поколению. Конечно, уносят жизни, разрушают семьи и судьбы, но если человек голоден (здесь имеется в виду голод экзистенциальный), то он пойдёт на всё, чтобы поесть. Наркотики, «закреплённые» за эпохой, действуют как отражение самых глубоких переживаний и тайных желаний человека, как иллюзорная возможность реализовать потребности эпохи, которые не могут быть реализованы в силу недостаточных личных качеств или экономической ситуации.
Существует теория, что Дали написал многие свои картины под воздействием «веществ»
Жажда метафизических духовных переживаний, свободы от неопределённости и страха перед завтрашним днём (вполне физического страха, потому что мировую экономику шатает туда-сюда вот уже десять лет), потребность в чувстве исключительности, в веселье, и чтобы это всё было быстро и в одном флаконе – вот как формируется страсть к наркотикам.
Это тайная дверь, за которой смысл. Так кажется. На самом деле смысла там никакого нет.
«В реабилитационные центры не обращался, – говорит Айдар. – Не чувствую, что проблема есть, точнее, даже если есть, я пока могу её решить самостоятельно. В обществе всегда это будет. Хочется попробовать то, что запрещено, а если понадобится помощь, обратиться за ней будет страшно – суд, срок, да и отношение к тебе в принципе изменится. Такой замкнутый круг, орден Феникса. Каждый второй мой знакомый в Алматы хоть раз в жизни что-то пробовал, главное, знаешь, не переходить границы, но вот где именно эти границы, чёрт его знает…».
Для чего нужно говорить про наркотики?
«Врага» нужно знать в лицо. Так, согласно статистике реабилитационных центров, более 60% обращений – синтетические наркотики. 25% – аптечные и 15% – опиоды. И если героин это «старая школа», люди, которые стали употреблять ещё в 90-х и чудом выжили, то средний возраст «аптечного» наркомана – 14 лет, а к 18 они «переходят в другую лигу» и пробуют «синтетику». При этом проблема практически не обсуждается в обществе.
«Иногда на консультациях родители, зная только, что «наркотики – это героин», склонны обесценивать проблему, преуменьшать. Типа: «Он же не наркоман, он же не колется, а только курит». Руководствуясь принципом «из двух зол», всегда хочется сказать: лучше бы он кололся. У него хотя бы было бы больше шансов…» – говорит Ольга Агапова.
В октябре 2018 года CADAP (Программа предотвращения распространения наркотиков в Центральной Азии) проводила в Алматы региональное экспертное совещание по теме «Новые психоактивные вещества: правовые и практические вызовы». Собирались эксперты из Бельгии, Нидерландов, Польши, Чехии, Германии, Эстонии, Финляндии, Венгрии и стран Центральной Азии и все они озвучивали одни и те же проблемы: наркокриминал всегда на шаг впереди.
Собирались эксперты из Бельгии, Нидерландов, Польши, Чехии, Германии, Эстонии, Финляндии, Венгрии и стран Центральной Азии и все они озвучивали одни и те же проблемы: наркокриминал всегда на шаг впереди.
Наркодилеры используют неповоротливость государства (новый закон, принятый в РК буквально на днях, должен существенно помочь в «войне»), неосведомлённость групп риска и их родных и близких, так как в «цивилизованном обществе» вообще стараются не говорить об этом. В заключении о смерти 18-летнего подростка никто не напишет «спрыгнул с крыши под воздействием неустановленного вещества», непременно найдут более социально приемлемую причину.
Но вместо того, чтобы замалчивать проблему, можно начинать решать её цивилизованным путем. Так, Глобальная комиссия по наркополитике выпустила седьмой по счёту доклад о проблеме наркотиков в мире и отношении общества к наркозависимым, который предлагает начать конструктивный диалог. Например, не разбрасываться словом «наркоман» и ввести в широкий оборот понятие наркофобия.
Что со статистикой?
“На учёте сейчас состоят 23,5 тысячи наркопотребителей, из них 124 – несовершеннолетние, 1 735 – женщины. За пять лет выявлено свыше 19 тысяч наркопреступлений, из них 13 тысяч связано со сбытом, свыше 1300 – с контрабандой. Из незаконного оборота изъято более 185 тонн различных наркотиков», – сказал в октябре 2018 года Иван Добрышин, представитель департамента по борьбе с наркобизнесом и контролю за оборотом наркотиков МВД РК на II Региональной конференции по наркополитике в Центральной Азии.
В 2016 году, согласно данным МВД, количество наркозависимых, состоящих на учёте в Казахстане, составляло 31 тысячу человек. То есть за пять лет оно сократилось на 25%, а с 2011-го по 2016-й – на 37%. По состоянию на декабрь 2005 года, также согласно официальным данным, число наркоманов в РК составляло 52 тысячи человек, почти на 10% меньше, чем в 2004 году (в 2004 было около 57 тысяч человек). Значит, за 14 лет количество наркоманов, состоящих на учёте, сократилось в 2 раза – с 57 до 23 тысяч человек.
Однако, по словам Ольги Агаповой, знак равенства между «состоящими на учёте» и реальным количеством наркозависимых проводить нельзя. Чаще всего близкие предпочитают решать проблему анонимно и конфиденциально.
Для сравнения: в России на 2017 год это число составляет 800 тысяч человек, тогда как в 2006-м было 350 тысяч.
Соль – белая смерть — Сахалин и Курилы — SKR.SU
Особенно это выражение подходит не к привычной для нас поваренной соли, а к страшному наркотику.
Не для ванн
Как только его не называют: «антиеж», «скорость», «шалфей», «эйфория». Но чаще всего в нашей стране его маскируют под обычную соль для ванн. Именно поэтому абсолютно новый вид наркотика еще называют просто – «соль». Тем, кто более-менее знаком со школьным курсом химии, будет понятно – к хлориду натрия «антиеж» не имеет никакого отношения.
Медики, ученые и наркополицейские обозначают его как JWH. Таким мудреным названием наркотик обязан своему создателю – американскому химику Джону Хаффману. Тогда синтетический дурман был придуман, чтобы облегчать страдания онкобольных. Но хорошая идея со временем видоизменилась до неузнаваемости, а изобретение стало приносить исключительно вред.
Некоторые синтетические наркотики запретили еще в 2010 году. Но расторопные псевдо-ученые пошли дальше – меняя главную химическую формулу, они научились производить все новые и новые виды синтетики.
По данным заместителя начальника оперативной службы УФСКН России по Сахалинской области Виталия Котенева, существует синтезированный аналог каннабиса (конопли, гашиша и проч.). Как нетрудно догадаться, при его изготовлении растения не используются вовсе. Также удалось придумать наркотики, которые являются химическими братьями-близнецами других, не менее опасных веществ.
Современная действительность такова: совсем крохотный химический заводик вполне может производить синтетические наркотики в промышленных масштабах. Чем сегодня и занимается Китай. Наркотические вещества оттуда наводнили Урал, Сибирь и наш Дальний Восток. Сахалин, к сожалению, исключением не стал.
Сахалин, к сожалению, исключением не стал.
Первые случаи синтетической наркомании в России были зафиксированы в конце нулевых. В нашей области эта зараза появилась примерно в это же время.
– Когда на Сахалине был популярен героин, наркоман искал того, кто смог бы запрещенное вещество доставить на остров с материка. Теперь же синтетику запросто можно заказать в Интернете, – объяснил В. Котенев.
Вы спросите: где полиция, куда смотрит наркоконтроль? К сожалению, не все так просто для правоохранителей, как просто для сегодняшнего наркомана. Сайтов, где можно разжиться кайфом, пруд пруди. «Почта России» доставляет посылки по стране, не имея возможности проверить каждый сверток. А за сутки в регион прибывает около 5 тыс. отправлений, и прошерстить каждое на наличие грамма порошка – нереально.
Кроме того, на территории области работают еще и частные курьерские службы, которым и вовсе не выгодно терять клиентов, отказывая в услуге.
Наркоторговцы придумывают все новые способы, как безнаказанно травить людей. Схема проста – потенциальный покупатель заказывает в Интернете наркотик, оплачивает товар тут же в «виртуальном кошельке», после чего получает эсэмэс с инструкцией – где в его городе спрятан заветный сверток.
Тем не менее полиция на месте не сидит. С начала этого года удалось изъять 7 тыс. разовых доз синтетического наркотика (около 1,5 кг). О популярности, которую набирает химия, красноречиво говорят цифры: из 230 изъятий самых разных запрещенных веществ в 130 случаях это был JWH.
Проклинаю тот день
Эксперты в глобальной сети, предостерегая тех, кто только думает познакомиться с «солью», утверждают, что все синтетические наркотики можно разделить на четыре основные группы: психостимуляторы, галлюциногены, наркотические анальгетики и депрессанты. Разумеется, на пакетике с порошком без вкуса и запаха подпольный производитель не указывает, к какому виду относится данная синтетика. Так же, как и то, какой именно наркотик вы держите в руке (помните, выше мы говорили, что вариантов убийственной «соли» сейчас много). Поэтому сложно предугадать, какой орган у вас откажет после употребления запрещенной химии.
Поэтому сложно предугадать, какой орган у вас откажет после употребления запрещенной химии.
А в том, что организм даст, мягко скажем, сбой, можете не сомневаться.
Там же, в Интернете, где и приобретается наркотик, можно легко найти отзывы счастливых и не очень покупателей. Те, что познакомились с «солью» недавно, в восторге от ее воздействия. Однако их эйфория очень быстро сходит на нет. Вот выдержка из комментария того, кто, скорее всего, недавно с упоением описывал, какая же это классная штука – «соль для ванн»: «Я проклинаю тот день, когда узнал о порошках. Похудел, осунулся, заикаться стал, башка не варит, и хочется одного – нюхнуть, нюхнуть, нюхнуть. В трезвом состоянии мир серый… Все это, мне кажется, ведет к неизбежной инвалидности… Но самое главное – это депрессия… Употребляю его почти каждый день, меньше месяца… Задумайтесь: 3–5 часов кайфа вам вернутся тремя сутками апатии, агонии и тяжелейшей депрессии».
Автору этих пронизывающих строк, разумеется, виднее. Тем не менее наркологи говорят, что действие синтетики может ощущаться не часами, а сутками. Все дело в том, что химические компоненты, попадая в организм, не метаболизируются, то есть, говоря человеческим языком, не разрушаются и слишком медленно выводятся. Более того, существуют «соли», которые и вовсе не выводятся из организма человека.
У несчастного, принявшего наркотик, активность начинает зашкаливать, возникает эйфория, чувство собственного могущества, силы или сверхспособностей. Спать такой «сверхчеловек» не может совершенно. Именно поэтому синтетика особенно популярна среди так называемых клабберов – тусовщиков, отжигающих на дискотеках ночи напролет. Этот факт подтверждает и то, что в ходе регулярных рейдов по сахалинским ночным клубам островные наркополицейские чаще изымают именно JWH. И в крови у посетителей «ночника» обнаруживается он же.
«Соль» способна усиливать и сексуальные ощущения. Синтетика как бы одалживает удовольствие. Но процент по займу настолько велик, что расплатиться с ним уже нет никаких шансов. Рядовые радости жизни наркоману кажутся скучными и невыразительными.
Рядовые радости жизни наркоману кажутся скучными и невыразительными.
Как рассказал врач амбулаторного приема Сахалинского областного наркологического диспансера Виктор Витюк, привозят таких клиентов к ним на освидетельствование в последнее время нередко.
– Синтетические наркотики легко употреблять, – рассказал Виктор Анатольевич, – смеси едят, запивая водой, втирают в слизистые, нюхают, курят. Также легко их и приобрести, заказав по Интернету. И стоят они намного дешевле большинства запрещенных веществ. Именно поэтому их популярность набирает обороты.
Зависимость у больного формируется уже после первого приема порошка. Хоть раз попробовавшему «соль» хочется повторять приемы вновь и вновь.
Бессонница может продолжаться до трех суток, а в периоды «марафона» – до двух недель. Все это, как правило, перемежается галлюцинациями.
Еще одна опасность заключается в том, что синтетические наркотические вещества здорово влияют на процессы в мозге, отвечающие за движения, память, формирование эмоций, болевую чувствительность, а также вегетативные функции организма. Выжигаются клетки иммунной и репродуктивной систем. Особенно жестко нарушается интеллект.
Салонный дурак
Далеко не сразу можно почувствовать зависимость от «соли». Особенностью синтетического наркомана является и то, что он напрочь теряет способность критически оценивать себя и свое состояние. Одним словом, наркоманом себя зависимый не считает до последнего. А устойчивую тягу объясняет лишь желанием испытать нечто новое.
При отказе от «соли» человек чувствует сильнейшую ломку, которая выражается не только в психических нарушениях, но и в физических недомоганиях. Нередки высыпания на коже, тошнота, мышечные спазмы, тик. Не заживают обычные царапины и ссадины. Этот букет можно дополнить острой сердечной недостаточностью, аритмией, гипертонией, инфарктом миокарда.
Некоторые синтетические наркотики провоцируют панические атаки. Когда действие вещества заканчивается, человеку становится страшно.
– В прошлом году был бум на таких зависимых, – вспоминает сотрудник островного наркоконтроля В. Котенев, – кого ни задержим, все паникуют. Им кажется, что кто-то их преследует, наблюдает за ними.
Наркологи отмечают, что наркоманы действительно склонны страдать параноидальными синдромами. Они ищут скрытые угрозы, им всюду мерещится заговор, в темноте пугают шевелящиеся тени, в голове образовываются сумасшедшие логические цепочки.
Человек путает слова, не может сформулировать предложение. Иногда же, наоборот, его просто распирает от желания поговорить, и он выплескивает на окружающих весь свой восторг или же, наоборот, негодование.
Состояние наркомана начинает напоминать синдром, который психиатры называют «салонный дурак». Этот термин, по всей видимости, произошел от тех недалеких завсегдатаев светских салонов, что тусовались на всех мыслимых и немыслимых приемах и званых ужинах, прослыв непроходимыми тупицами и терроризируя всех беседами на тему «куда катится этот мир».
Специфических методов лечения зависимости от синтетических наркотиков еще не изобрели. В нашем областном наркологическом диспансере таких больных прокапывают, что помогает снять некоторые симптомы отравления.
По данным В. Витюка, чаще в наркологию по подозрению в употреблении «соли» попадают молодые парни-сахалинцы в возрасте от 20 до 35 лет.
– Те, кого к нам привезла полиция, искренне жалеют о случившемся и держат обещание впредь синтетику не употреблять, – делится Виктор Анатольевич, – и обещание, как правило, сдерживают. Об этом говорят результаты анализов, которые мы заставляем их сдавать регулярно после инцидента. Кстати, часто задержанные жалуются на то, что порошок им втайне подсыпали в коктейль в ночном клубе. Может, конечно, они так пытаются оправдать себя, но, как говорится, нет дыма без огня. Советуем нашим читателям быть внимательнее.
Наша справка
Химическая структура «соли» разрешает легко изменять ее главную формулу. После некоего вмешательства – вуаля! – наркотик не соответствует по своему составу официально запрещенным веществам. А поэтому юридически он становится легальным. Но если вы решили подзаработать на продаже таких якобы разрешенных наркотиков, не обольщайтесь.
А поэтому юридически он становится легальным. Но если вы решили подзаработать на продаже таких якобы разрешенных наркотиков, не обольщайтесь.
По данным УФСКН России по Сахалинской области, в начале распространения и мутаций «соли», с установлением запретов, действительно, были сложности – ведомства и законодатели не всегда поспевали за ушлыми химиками. Теперь же система отлажена. Как только в организме выявляется тот или иной абсолютно не известный доселе ни науке, ни полиции наркотик, его тут же вносят в список запрещенных веществ, за сбыт или потребление которого светит срок.
Самый свежий такой запрет вступил в силу 23 июля. С этого дня вещество хеналин официально стало являться наркотиком.
Соль пищевая. Термины и определения – РТС-тендер
1 РАЗРАБОТАН Федеральным государственным бюджетным научным учреждением «Всероссийский научно-исследовательский институт пищевых добавок» (ФГБНУ ВНИИПД) и Публичным акционерным обществом «Соль Руси» (ПАО «Соль Руси»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 154 «Пищевые добавки, ароматизаторы, соль пищевая»
4 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомления и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www. gost.ru)
gost.ru)
Установленные в настоящем стандарте термины расположены в порядке, отражающем систему понятий, используемых в сфере добычи, производства и применения пищевой соли.
Для каждого понятия установлен один стандартизованный термин.
Приведенные определения можно при необходимости изменять, вводя в них производные признаки, раскрывая значения используемых в них терминов, указывая объекты, входящие в объем определяемого понятия. Изменения не должны нарушать объем и содержание понятий, определенных в настоящем стандарте.
В стандарте приведены эквиваленты стандартизованных терминов на английском языке.
Стандартизованные термины набраны полужирным шрифтом.
Настоящий стандарт устанавливает термины и определения понятий в сфере добычи, производства и применения пищевой соли.
Термины, установленные настоящим стандартом, рекомендуются для использования при проведении работ по стандартизации, во всех видах документации и научно-технической литературы, касающихся указанной сферы деятельности.
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 51574-2000 Соль поваренная пищевая. Технические условия
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
| |
1 пищевая соль: Кристаллический продукт, содержащий не менее 97,0% хлорида натрия, используемый в качестве ингредиента в пище, представляющий собой кристаллы, гранулы, чешуйки или хлопья, зерна или куски.
Примечания
1 В составе пищевой соли могут присутствовать другие естественные компоненты в зависимости от происхождения и способа производства соли.
2 Помимо основной функции пищевая соль может быть использована в качестве носителя пищевых добавок, вкусоароматических веществ и обогащающих элементов.
3 Мелкокристаллическая пищевая соль, предназначенная для посола пищи во время ее употребления, в обиходе называется столовой.
4 Синоним пищевой соли «поваренная соль» в силу своей архаичности далее использовать в нормативных документах не рекомендуется.
| food grade salt |
2 каменная соль: Природная неочищенная соль, получаемая из подземных кристаллических масс, залегающих в толще горных пород, содержащая не менее 97,0% хлорида натрия, примеси неорганических и органических веществ.
Примечание — Каменная соль добывается шахтным или карьерным способом.
| rock salt
|
3 каменная соль очищенная: Хлорид натрия промытый, отбеленный и очищенный от всех возможных примесей и элементов. | refined salt
|
4 каменная соль отбеленная: Кристаллический хлорид натрия, прошедший стадию отбелки с помощью механической обработки.
| bleached rock salt |
5 рассол: Концентрированный раствор хлорида натрия.
| brine
|
6 сырой рассол: Рассол, добываемый из скважин путем подземного выщелачивания пластов соли, с массовой концентрацией хлорида натрия не менее 300 г/дм.
| raw brine
|
7 очищенный рассол: Рассол, прошедший химическую очистку, с массовой концентрацией хлорида натрия не менее 290 г/дм.
| purified brine |
8 шлам от очистки рассола: Очищенный и маточный рассолы, смешанные с химически осажденным мелом и гидроксидом магния.
| brine sludge
|
9 маточный рассол: Рассол, получаемый в процессе вываривания соли из очищенного рассола с массовой концентрацией хлорида натрия не менее 150 г/дм.
| mother brine |
10 естественный рассол: Раствор соли, образующийся в результате проникновения грунтовых вод и размывания подземного пласта.
| natural brine
|
11 искусственный рассол: Раствор соли, получаемый подземным выщелачиванием соли водой, специально подаваемой в зону расположения соляного пласта через скважины, или путем растворения в бассейнах добытой твердой соли.
| artificial brine |
12 озерные рассолы: Концентрированные растворы соли, образующиеся в безсульфатных и сульфатных озерах и лиманах хлоридного типа при естественном испарении воды под действием солнечного тепла.
| lake brines |
13 выварочная соль: Соль, получаемая в результате вываривания искусственных или естественных рассолов, представляющая собой кристаллический сыпучий продукт, с массовой концентрацией хлорида натрия не менее 99,7%.
| pan salt
|
14 самосадочная соль: Соль, кристаллизующаяся из рапы озер и лиманов в результате естественного испарения воды под действием солнечного тепла.
| solar evaporated salt
|
15 гранатка: Слой рыхлой, рассыпчатой самосадочной соли в озерах в виде несцементированных крупных и слабосцементированных кристаллов, загрязненных илом.
Примечание — Гранатка образуется в озерах, где соляная масса целиком пропитана рапой.
| |
16 новосадка: Новый слой самосадочной соли, кристаллизующейся над старым слоем в самосадочных озерах после разбавления рапы.
| |
17 обогащенная необработанная соль: Соль, освобожденная от примесей в процессе промывки в соляном растворе либо при выдерживании ее в буграх соли.
| enriched crude salt |
18 обогащенная соль: Пищевая соль, содержащая помимо хлорида натрия регулируемое количество минералов и микроэлементов.
Примечание — В качестве микроэлементов обогащенная соль может содержать фтор или йод.
| enriched salt
|
19 старосадка: Слой самосадочной соли, кристаллизующейся над гранаткой.
| |
20 садочная соль: Соль, кристаллизующаяся из рапы искусственно созданных соляных озер и бассейнов.
| evaporated salt
|
21 : Насыщенный рассол в хлоридных, сульфатных и карбонатных озерах, лиманах и бассейнах.
| leach brine |
22 дендритная соль: Кристаллы хлорида натрия в виде трехмерных дендритов с объемным весом от 0,7 до 0,8 г/см, выделяемые из концентрированных растворов хорошо растворимых в воде хлоридов.
| dendritic salt |
23 морская соль: Пищевая соль, получаемая из морской воды путем ее отвода в специальные бассейны для дальнейшего испарения и концентрирования естественным путем, содержащая не менее 95,0% хлорида натрия.
Примечания
1 Наличие в морской воде микроэлементов и примесей может придавать морской соли разные цветовые оттенки.
2 Неочищенная морская соль представляет собой мелкие кристаллы серого цвета.
3 Очищенная морская соль, прошедшая рекристаллизацию и сушку, содержит не менее 97,0% хлорида натрия и представляет собой мелкокристаллический продукт белого цвета.
| sea salt |
24 чешуйчатая соль: Пищевая морская соль, представляющая собой тонкие чешуйки и хлопья, достигающие размера 1 см в ширину, имеющие белый цвет и насыщенный вкус.
| flake salt
|
25 йодированная соль: Пищевая соль с добавлением йодсодержащих соединений: йодида или йодата калия или натрия.
| iodised salt
|
26 фторированная соль: Пищевая соль с добавлением фтористого калия из расчета содержания фтора не более 0,025%.
| fluoridated salt
|
27 лечебно-профилактическая соль: Пищевая соль с пониженным содержанием хлорида натрия, обогащенная калием и магнием.
| curative and prophylactic salt |
28 ароматизированная соль: Пищевая соль с добавлением различных ароматизаторов и добавок.
| flavoured salt |
29 завершающая соль: Пищевая соль, используемая для посола и декорирования готовых блюд.
Примечание — Виды завершающей пищевой соли приведены в справочном приложении Б к настоящему стандарту.
| finishing salt
|
30 посолочная смесь: Комплексная пищевая добавка на основе пищевой соли с добавлением нитрита натрия не более 0,9%, используемая в качестве стабилизатора окраски и консерванта при производстве мясопродуктов.
| curing salt
|
31 солезаменитель: Смесь ингредиентов, являющаяся альтернативой пищевой соли, содержащая в составе хлорида натрия не более 50,0%, солей калия и магния не более 30,0%, микроэлементы и фитокомпозиции, составленные из натуральных пряных трав и специй.
| salt substitute
|
32 солезаменитель «Органическая ламинария в порошке»: Гранулированный продукт морской водоросли «ламинария», содержащий в составе небольшое количество хлорида натрия.
Примечание — Служит источником йода и придает продукту острый и солоноватый вкус с привкусом рыбы и морской капусты. | kelp powder
|
| |
33 цвет соли: Окрас кристаллов соли в измельченном состоянии.
Примечание — Окрас кристаллов добываемой соли зависит от природы, содержания примесей, степени очистки.
| salt colour
|
34 вкус соли: Ощущение солености при помещении соли на язык.
Примечание — Разные виды соли различаются по степени солености.
| salt taste
|
35 запах соли: Свойство, придаваемое соли присутствующими в ней добавками, например йода, различных примесей, минералов и водорослей.
Примечание — Пищевая соль без добавок запахом не обладает.
| salt odour
|
36 слеживаемость: Способность измельченной соли терять свойства сыпучести и образовывать комки разной степени прочности.
| caking capacity
|
37 гигроскопичность: Свойство соли впитывать влагу.
| water absorbing capacity
|
38 гранулометрический состав: Техническая характеристика, обеспечивающая качество продукта, представляющая собой номер помола и размер кристаллов соли.
| particle size distribution
|
39 мелкокристаллическая соль: Пищевая соль с преимущественным размером кристаллов не более 0,8 мм.
| fine-grained salt |
40 крупнокристаллическая соль: Пищевая соль с размером кристаллов более 3 мм.
| coarse salt
|
41 сорт соли: Техническая характеристика, определяющая качество соли по степени очистки и гранулометрическому составу.
Примечание — В соответствии с ГОСТ Р 51574-2000 пищевая соль классифицируется на сорта: экстра, высший, первый и второй.
| salt grade
|
42 экстра: Сорт очищенной соли, содержащей не менее 99,7% хлорида натрия, кристаллов, имеющих размеры не более 0,8 мм — не менее 75,0%, свыше 0,8 до 1,2 мм — не более 25,0%.
Примечание — Соль «Экстра» содержит антислеживающий агент в установленном количестве.
| extra
|
43 помол: Характеристика степени крупности соли по размеру кристаллов, гранул, зерен.
Примечание — В соответствии с ГОСТ Р 51574-2000 пищевая соль классифицируется по гранулометрическому составу на помолы: N 0, N 1, N 2 и N 3. | particle size
|
| |
44 галургия: Отрасль химической технологии, изучающая способы получения и переработки растворимых природных солей.
| halurgy
|
45 залежи растворимых солей: Растворимые минералы, встречающиеся в земной коре и на ее поверхности в виде твердых отложений и растворов.
| deposits of soluble salts
|
46 солончаки: Тип почв, характеризующийся наличием в верхних горизонтах легкорастворимых солей в количествах от 1,0 до 15,0%, выделяемых в виде мелкокристаллических скоплений ярко-белого или ярко-бурого цвета.
| saline soils |
47 возгоны соли: Выделение кристаллической соли из лавы вулканов.
| salt sublimates
|
48 солевые пласты: Подземные соленосные отложения протяженностью несколько километров и толщиной несколько сотен метров, имеющие плотное компактное строение, сопровождаемые залежами ангидритовых, гипсовых и других пород.
Примечание — Солевые отложения могут иметь формы: пластов, пластово-линзообразные, линзообразные, куполо- и штокообразные и гнездообразные в виде мелких линз и блоков.
| salt beds |
49 галит: Минерал каменной соли NaCI, представляющий собой твердые кристаллические образования, имеющие форму октаэдра или ромбического додекаэдра плотностью 2,16 г/см при 20°С и температуру плавления 800,8°С.
Примечания
1 Чистый галит — бесцветный со стеклянным блеском.
2 Примеси окрашивают его в разные цвета.
| halite |
50 солеварение: Добыча пищевой соли вываркой ее из рассолов.
Примечание — Старинные варницы соли известны в Древней Руси как чренные солеварни.
| salt making
|
51 подземный способ разработки: Механизированный и буровзрывной способ выемки соли из галерей или камер шахт соляного пласта.
| underground mining
|
52 подземное выщелачивание: Извлечение сырого рассола из пластов соли на поверхность через буровые скважины или колодцы.
| underground leaching
|
53 прямоточный режим выщелачивания: Режим извлечения из скважины рассола, при котором воду подают по внутренней трубе, а рассол выдавливается по наружной.
| co-current leaching
|
54 противоточный режим выщелачивания: Режим извлечения из скважины рассола, при котором воду подают по наружной трубе, а рассол поднимается по внутренней трубе.
| counter-current leaching
|
55 комбинированный приточно-прямоточный режим выщелачивания: Режим извлечения рассола из скважины, при котором чередуется размыв слоя соли прямотоком с промывкой противотоком.
| combined cocurrent and counter-current leaching |
56 способ выщелачивания гидроврубом: Способ, при котором растворение солевого пласта происходит по окружности камеры плоской цилиндрической формы.
| leaching by hydraulic cut
|
57 ступенчатое выщелачивание: Способ, при котором периодически повышается уровень подвода воды к пласту и производится ступенчатое растворение соли.
| stages leaching
|
58 бассейный способ добычи соли: Способ, при котором ненасыщенная рапа из естественного источника накачивается в искусственные бассейны, где в результате принудительного концентрирования происходит садка соли.
Примечание — Рапа последовательно проходит отстаивание и концентрирование в подготовительных и запасных бассейнах, а затем направляется в садочные бассейны.
| ponds for salt extraction
|
59 ломка соли: Разламывание пласта садочной соли вручную на куски после откачивания рапы из бассейна.
Примечание — Куски выломанной соли собирают на берегу бассейна в бугры трапецеидальной формы высотой от 3 до 4 м для стекания маточного рассола.
| salt breakage
|
60 измельчение соли: Дробление кусков соли на вальцовых солемельницах, дезинтеграторах или жерновах и других дробильных устройствах.
| salt crushing
|
61 промывка: Стадия производственного цикла переработки пищевой соли, в процессе которой соль теряет все посторонние включения, выпадающие в осадок.
| salt washing
|
62 выпаривание соли: Процесс концентрирования растворов хлорида натрия путем удаления растворителя в виде паров.
| salt extraction by evaporation
|
63 вываривание: Процесс концентрирования и выделения соли путем вываривания солевого раствора в вакуум-аппаратах.
| salt extraction by boiling |
64 чрен: Аппарат для выпаривания соли в заводских условиях, обогреваемый топочными газами, представляющий собой открытый прямоугольный резервуар.
| salt pan |
65 обогащение каменной соли: Повышение концентрации основного вещества — дробленого хлорида натрия и снижение содержания примесей.
Примечание — Обогащение каменной соли позволяет получать осветленную пищевую соль с содержанием примесей не более 0,05%.
| rock salt treatment |
66 азотирование хлорида натрия: Технологический процесс химико-термической обработки, при котором хлорид натрия насыщают азотом в специальной азотирующей среде.
| nitrided sodium chloride |
67 очистка рассола: Удаление нежелательных примесей из сырого рассола.
| brine purification
|
68 содовый способ очистки рассола: Освобождение сырого рассола от кальциевых и частично магниевых солей путем обработки его кальцинированной содой.
| salt brine purification by soda |
69 известково-содовый способ очистки рассола: Освобождение сырого рассола от кальциевых и частично магниевых солей путем обработки его кальцинированной содой и известью.
| salt brine purification by lime and soda |
70 известково-сульфатно-содовый способ очистки рассола: Освобождение сырого рассола от кальциевых и магниевых солей в две стадии с помощью введения в рассол сульфата натрия и извести.
Примечания
1 На первой стадии проводится удаление растворимых солей кальция и магния.
2 На второй стадии проводится карбонизация рассола двуокисью углерода и введением в него соды.
| salt brine purification by lime, sulfate and soda |
71 центрифугирование промытой соли: Удаление воды из соли до остаточной влажности от 2,5 до 4,0% с помощью гидроэкстрактора непрерывного действия.
| salt centrifugal drying
|
72 сушка соли: Отделение влаги в специальных аппаратах с температурой греющей среды от 180 до 300°С и до остаточной влажности не более 1,0%.
| salt drying
|
73 грохочение: Операция просеивания соли разного гранулометрического состава, полученной после помола и сушки, на вибрационных ситах соответствующей мощности и калибровки.
| screen sizing
|
74 вымораживание соли: Способ добычи соли из концентрированных рассолов, заключающийся в кристаллизации соли при охлаждении рапы с вымерзанием сначала дигидрата, а затем криогидрата при температуре -21,2°С.
Примечания
1 При повышении температуры дигидрата после его извлечения из рапы выше 0,15°С происходит разложение дигидрата с переходом в чистую соль.
2 Вымораживание соли зимой может производиться в таких же бассейнах, как садка соли летом.
3 Метод искусственного вымораживания при наличии дешевой электроэнергии может оказаться выгодным для получения соли сорта «Экстра», особенно из морской воды.
| freezing out salt
|
75 высаливание: Способ получения соли из рассолов с помощью растворов хлористого магния или хлористого кальция путем смешивания и разделения выпавших кристаллов солей и последующей сушкой NaCI.
| salting out
|
76 брикетирование соли: Изготовление из соляной пыли и соли первого помола методом прессования брикетов соли для пищевых и кормовых целей.
| salt briquetting |
77 предотвращение слеживаемости соли: Понижение гигроскопичности соли за счет уменьшения размера частиц и применения антислеживающих агентов, препятствующих перекристаллизации соли в местах контакта частиц и схватыванию ее в сплошной конгломерат или плотные комки.
| prevention of salt caking
|
78 йодирование пищевой соли: Процесс включения в состав пищевой соли йодида или йодата калия и/или натрия с целью ее обогащения йодом.
Примечания
1 Массовая доля йода (40±15) мкг/г — в соответствии с ГОСТ Р 51574-2000.
2 Йодирование осуществляется мокрым или сухим способом.
| salt iodisation
|
79 мокрый способ йодирования соли: Способ, при котором производят добавление в соль раствора йодида или йодата калия и/или натрия, обеспечивающий равномерное распределение йода в продукте.
| salt iodisation by spray mixing
|
80 сухой способ йодирования соли: Способ смешения соли с концентратом йодида или йодата калия и/или натрия в аппаратах непрерывного действия.
Примечания
1 Влажность концентрата должна быть не более 0,1%.
2 Смешение производится в шнековых и барабанных смесителях.
| salt iodisation by dry mixing |
81 способ открытой добычи соли: Разработка соляного пласта, верхний горизонт которого находится на поверхности Земли или залегает на небольшой глубине. | salt open mining |
| |
А.1 молдонская морская соль: Чешуйчатая соль с крупными кристаллами, достигающими размера 1 см в ширину, имеющая белый цвет и насыщенный вкус.
Примечание — Добывается в акватории южного побережья Англии.
| maldon sea salt
|
А.2 флер де сель: Морская соль, представляющая собой тонкие ломкие кристаллы белого и сероватого цвета благодаря присутствию частичек глины и водорослей в местах ее сбора, обладающая ароматом и влажной хрустящей структурой.
Примечание — Добывается вручную на западе Франции, в Португалии, на Майорке, Мадагаскаре.
| fleur de sel
|
А.3 красная гавайская соль: Морская соль, содержащая пыль вулканической красной глины Alaea, включающей йод, магний, железо, минералы и микроэлементы, окрашивающие соль в розовый или кораллово-красный цвет.
| hawaiian pink Alaea sea salt
|
А.4 черная гавайская соль: Морская соль, содержащая более 80 минералов и микроэлементов, которые из-за примесей вулканической лавы окрашивают ее в черный цвет.
Примечание — Добывается методом естественного выпаривания воды под действием солнечного тепла.
| hawaiian black sea salt
|
А.5 крымская розовая морская соль: Морская соль, добываемая методом комплексной переработки морской рапы крымских морских заливов, лиманов или озер.
| сrimean pink sea salt |
А.6 сицилийская соль: Соль, добываемая в мелководных загонах, заполненных морской водой, где происходит естественное выпаривание под воздействием тепла и сильных ветров, содержащая хлорид натрия, йод, фтор, магний и калий, обладающая нежным вкусом и ароматом.
Примечание — Добывается в лиманах Средиземного моря.
| sicilian sea salt
|
А.7 кипрская черная морская соль: Смесь чешуйчатой соли с малым количеством активного угля, придающего соли темный блеск вулканического стекла и отчетливый насыщенный привкус угля.
Примечание — Добывается на соляных лагунах из морской воды Кипрского моря.
| cyprus black sea salt
|
А.8 трюфельная соль: Смесь морской соли с кусочками черного или белого трюфеля, обладающая насыщенным вкусом, используемая в качестве приправы к яичнице, мясу, соевому сыру и макаронам.
Примечание — Трюфельная соль производится в Хорватии.
| truffle salt |
А.9 австралийская розовая соль: Соль, добываемая из соленых подземных вод, богатых красными водорослями, окрашивающими ее в нежный розово-абрикосовый цвет и придающими ей мягкий вкус.
Примечание — Добывается в подземных озерах.
| australian rose salt
|
А.10 розовая гималайская соль: Минеральная соль крупного или мелкого помола, содержащая около 5,0% примесей, 84 минерала и микроэлемента, окрашивающих ее в нежный розовый цвет.
Примечание — Добывается из вулканических отложений Гималаев.
| himalayan rose salt
|
А.11 боливийская розовая соль: Столовая соль вулканического происхождения, содержащая минералы с высоким содержанием железа, предназначенная для заправки салатов, мясных блюд, морепродуктов, соусов, рассолов и маринадов.
Примечание — Добывается в Боливии из вулканических отложений.
| bolivian pink salt |
А.12 черная гималайская соль: Природная вулканическая каменная соль, образовавшаяся в период формирования Гималайских гор и высыхания древних морей, имеющая вкус сваренного вкрутую яйца и сероводородный запах.
| himalayan black salt
|
А.13 черная соль «Кала Намак»: Природная неочищенная соль, добываемая из пород вулканического происхождения в соляных шахтах Северной Индии и Пакистана, содержащая соединения железа и серы, обладающая характерным сероводородным запахом и кисловатым вкусом.
| Kala Namak black salt
|
А.14 персидская голубая соль: Каменная соль, добываемая в соляных рудниках Ирана, содержащая минеральные вещества, представляющая собой крупные прозрачные с голубоватым оттенком кристаллы. | persian blue salt
|
| |
Б.1 цветная соль: Природная пищевая соль, окрашенная в зависимости от места происхождения или способа получения, представляющая собой крупные хлопья или зерна.
| naturally tinted salt
|
Б.2 крашеная европейская соль: Природная пищевая соль, окрашенная красителем из чернильного мешка морской каракатицы, используемая для декорирования блюд.
| european tinted salt |
Б.3 копченая соль: Морская соль, прошедшая процесс копчения на дровяном огне, имеющая характерный копченый запах, представляющая собой крупные кристаллы от светло-серого до темно-коричневого цвета.
| smoked salt
|
Б.4 копченая ольховая соль: Пищевая соль, прошедшая процесс копчения на ольховых дровах, обладающая оригинальным ароматом копчения.
Примечание — Ольховую копченую соль можно использовать отдельно или в смеси с другими специями для завершения блюда из макарон, салатов.
| alderwood smoked salt |
Б.5 копченая яблоневая соль: Пищевая соль, прошедшая процесс копчения на яблоневых дровах, обладающая сладким пикантным вкусом.
| applewood smoked salt
|
Б.6 запеченная соль: Пищевая соль, обжариваемая на огне в «емкости», придающей аромат конечному продукту.
| roasted salt |
Б.7 бамбуковая корейская соль: Пищевая соль, помещенная в бамбуковый стебель, запечатанный с обеих сторон желтой глиной, жареная над сосновой смолой и предназначенная для завершения блюд из мяса и овощей.
| korean bamboo salt
|
Б.8 сельдерейная соль: Смесь свежего или сушеного сельдерея с хлоридом натрия массовой долей не более 75,0%.
| celery salt
|
Б.9 чесночная соль: Смесь сушеного чеснока с хлоридом натрия массовой долей не более 75,0%.
| garlic salt
|
Б.10 луковая соль: Смесь сухого порошкового лука с хлоридом натрия массовой долей не более 75,0%.
| onion salt
|
Б.11 морская соль в виде икринок и жемчужин: Соль, образующаяся по краям лиманов, получаемая путем перемешивания рассола с образованием полых сфер. | caviar and pearl sea salt |
| |
азотирование хлорида натрия
| 66 |
брикетирование соли
| 76 |
вкус соли
| 34 |
возгоны соли
| 47 |
вываривание
| 63 |
вымораживание соли
| 74 |
выпаривание соли
| 62 |
высаливание
| 76 |
выщелачивание подземное
| 52 |
выщелачивание ступенчатое
| 57 |
галит
| 49 |
галургия
| 44 |
гигроскопичность
| 37 |
гранатка
| 14 |
грохочение
| 73 |
залежи растворимых солей
| 45 |
запах соли
| 35 |
измельчение соли
| 60 |
йодирование пищевой соли
| 78 |
ломка соли
| 59 |
новосадка
| 15 |
обогащение каменной соли
| 65 |
очистка рассола
| 67 |
пласты солевые
| 48 |
помол
| 43 |
предотвращение слеживаемости соли
| 77 |
промывка
| 61 |
| 21 |
рассол
| 5 |
рассол естественный
| 11 |
рассол искусственный
| 10 |
рассол маточный
| 9 |
рассол очищенный
| 7 |
рассол сырой
| 6 |
рассолы озерные
| 12 |
режим выщелачивания противоточный
| 54 |
режим выщелачивания приточно-прямоточный комбинированный
| 55 |
режим выщелачивания прямоточный
| 53 |
слеживаемость
| 36 |
смесь посолочная
| 30 |
солеварение
| 50 |
солезаменитель
| 31 |
солезаменитель «Органическая ламинария в порошке»
| 32 |
солончаки
| 46 |
соль австралийская розовая
| А.9 |
соль ароматизированная
| 28 |
соль боливийская розовая
| А.11 |
соль выварочная
| 13 |
соль гавайская красная
| A.3 |
соль гавайская черная
| А.4 |
соль гималайская розовая
| А.10 |
соль гималайская черная
| А.12 |
соль дендритная
| 22 |
соль европейская крашеная
| Б.2 |
соль завершающая
| 29 |
соль запеченная
| Б.6 |
соль йодированная
| 25 |
соль «Кала Намак» черная
| А.13 |
соль каменная
| 2 |
соль каменная отбеленная
| 4 |
соль каменная очищенная
| 3 |
соль кипрская черная морская
| А.7 |
соль крымская розовая морская
| А.5 |
соль копченая
| Б.3 |
соль копченая ольховая
| Б.4 |
соль копченая яблоневая
| Б.5 |
соль корейская бамбуковая
| Б.7 |
соль крупнокристаллическая
| 40 |
соль лечебно-профилактическая
| 27 |
соль луковая
| Б.10 |
соль мелкокристаллическая
| 39 |
соль молдонская морская
| А.1 |
соль морская
| 23 |
соль морская в виде икринок и жемчужин
| Б.11 |
соль обогащенная
| 18 |
соль обогащенная необработанная
| 17 |
соль персидская голубая
| А.14 |
соль пищевая
| 1 |
соль садочная
| 20 |
соль самосадочная
| 14 |
соль сельдерейная
| Б.8 |
соль сицилийская
| А.6 |
соль трюфельная
| А.8 |
соль фторированная
| 26 |
соль цветная
| Б.1 |
соль чесночная
| Б.9 |
соль чешуйчатая
| 24 |
сорт соли
| 41 |
состав гранулометрический
| 38 |
способ выщелачивания гидроврубом
| 56 |
способ добычи соли бассейный
| 58 |
способ йодирования соли мокрый
| 79 |
способ йодирования соли сухой
| 80 |
способ открытой добычи соли
| 81 |
способ очистки рассола известково-содовый
| 69 |
способ очистки рассола известково-сульфатно-содовый
| 70 |
способ очистки рассола содовый
| 68 |
способ разработки подземный
| 51 |
старосадка
| 19 |
сушка соли
| 72 |
флер де сель
| А.2 |
цвет соли
| 33 |
центрифугирование промытой поваренной соли
| 71 |
чрен
| 64 |
шлам от очистки рассола
| 8 |
экстра | 42 |
| |
alderwood smoked salt
| Б.4 |
applewood smoked salt
| Б.5 |
artificial brine
| 10 |
australian rose salt
| A.9 |
bleached rock salt
| 4 |
bolivian pink salt
| A.11 |
brine
| 5 |
brine purification
| 67 |
brine sludge
| 8 |
caking capacity
| 36 |
caviar and pearl sea salt
| Б.11 |
celery salt
| Б.8 |
coarse salt
| 40 |
co-current leaching
| 53 |
combined co-current and counter-current leaching
| 55 |
counter-current leaching
| 54 |
crimean pink sea salt
| A.5 |
curative and prophylactic salt
| 27 |
curing salt
| 30 |
cyprus black sea salt
| A.7 |
dendritic salt
| 22 |
deposits of soluble salts
| 45 |
enriched crude salt
| 17 |
enriched salt
| 18 |
european tinted salt
| Б.2 |
evaporated salt
| 20 |
extra
| 42 |
fine-grained salt
| 39 |
finishing salt
| 29 |
flake salt
| 24 |
flavoured salt
| 28 |
Fleur de sel
| A.2 |
fluoridated salt
| 26 |
food grade salt
| 1 |
freezing out salt
| 74 |
garlic salt
| Б.9 |
halite
| 49 |
halurgy
| 44 |
hawaiian black sea salt
| A.4 |
hawaiian pink Alaea sea salt
| A.3 |
himalayan black salt
| A.12 |
himalayan rose salt
| A.10 |
underground mining
| 51 |
iodised salt
| 25 |
Kala Namak black salt
| A.13 |
kelp powder
| 32 |
korean bamboo salt
| Б.7 |
lake brines
| 12 |
leach brine
| 21 |
leaching by hydraulic cut
| 56 |
maldon sea salt
| A.1 |
mother brine
| 9 |
natural brine
| 11 |
naturally tinted salt
| Б.1 |
nitrided sodium chloride
| 66 |
onion salt
| Б.10 |
pan salt
| 13 |
particle size
| 43 |
particle size distribution
| 38 |
persian blue salt
| A.14 |
ponds for salt extraction
| 58 |
prevention of salt caking
| 77 |
purified brine
| 7 |
raw brine
| 6 |
refined salt
| 3 |
roasted salt
| Б.6 |
rock salt
| 2 |
rock salt treatment
| 65 |
saline soils
| 46 |
salt beds
| 48 |
salt breakage
| 59 |
salt briquetting
| 76 |
salt brine purification by lime and soda
| 69 |
salt brine purification by lime, sulfate and soda
| 70 |
salt brine purification by soda
| 68 |
salt centrifugal drying
| 71 |
salt colour
| 33 |
salt crushing
| 60 |
salt drying
| 72 |
salt extraction by boiling
| 63 |
salt extraction by evaporation
| 62 |
salt grade
| 41 |
salt iodisation
| 78 |
salt iodisation by dry mixing
| 80 |
salt iodisation by spray mixing
| 79 |
salt making
| 50 |
salt odour
| 35 |
salt open mining
| 81 |
salt pan
| 64 |
salt sublimates
| 47 |
salt substitute
| 31 |
salt taste
| 34 |
salt washing
| 61 |
salting out
| 75 |
screen sizing
| 73 |
sea salt
| 22 |
sicilian sea salt
| A.6 |
smoked salt
| Б.3 |
solar evaporated salt
| 14 |
stages leaching
| 57 |
truffle salt
| A.8 |
underground leaching
| 52 |
water absorbing capacity | 37 |
| | |
УДК 663.05:006.354 | ОКС 01.040.67 | Н 00 |
| 67.220.20
| |
Ключевые слова: соль пищевая, садочная соль, самосадочная соль, выщелачивание солевого пласта, йодированная соль, сорт соли |
Электронный текст документа
подготовлен АО «Кодекс» и сверен по:
официальное издание
М.: Стандартинформ, 2018
Про соль с точки зрения химика / Хабр
На самом деле этот пост был подготовлен еще в апреле 2014 года, я не смог тогда его опубликовать. Являлся вторым в ожидавшейся серии. Можете глянуть первый. На эту тему писать меня сподвигло желание внести немного ясности в представления о некоторых химических аспектах нашего бытия. Пользуясь тем, что химия — наука, не слишком популярная в массах, нам иногда рекламщики и пресса выдают такие перлы, что у меня не хватает слов для описания эмоций. Так что попробуем слегка рассеять туман, ну и чтоб это было интересно и актуально для наших условий. Недавно встретил похожую переводную публикацию, тоже про соль. Серьёзную и хорошо сделанную, правда, слегка не о нашей действительности.
Итак — про соль
Так в Африке ею и торгуют. Толщина кусков, вероятно определяется толщиной пласта. Слабенькие пласты.
Солить или не солить. А зачем вообще соль, может лучше без неё? Заменитель соли? Ценная соль с минералами и розового цвета — а зачем козе баян? Рекламные посты — хороший способ приготовить лапшу на уши.
Итак, продолжим наши игры. Сегодня начнем, в меру сил и способностей, прояснять ряд кухонных вопросов, ведь химия — это не только скучные строчки в учебнике. Химия окружает нас и даже, варится внутри нас, это также новые материалы и технологии, окружающие нас. Да, микросхему не сделаешь, без химически сверхчистого и однородного кристалла кремния или другого полупроводника.
Вопросы, что есть и как готовить, что, где содержится ядовитого — любимая тема интернет-изданий. Если всё это прочитать, а ещё, не дай Бог, всему этому поверить, в голове точно шарики за ролики зайдут. Постараемся не спеша, разобраться в сегодняшней теме.
Соль и соль, что с неё взять… Ага! Пищевая добавка, эта Ваша соль. Ядовитая. Смертельная доза для среднего человека 200 грамм. Соль настолько искажает вкус продуктов, что мы начинаем их есть в количествах, больших достаточных. Про невкусность продуктов без соли — проверяйте, не боюсь. Избыток соли повышает артериальное давление и кислотность, он вообще вреден, как и избыток еды вообще. Просто беда. Вроде правда. Но это не 100% правды, даже в очень чёрном, есть немножко белого и наоборот. А, казалось бы, натуральный продукт, да еще и древний — в основном, мы едим соль из древних морских отложений, так что современных технологических загрязнений и радиации (современной, созданной человеком) там быть не может. Почему-то об этом забывают говорить в рекламе. А чего её рекламировать — самый дешёвый продукт.
Солевой пласт. Видны слои отлагавшейся в древности соли
Соль бывает каменная — это дроблёный пласт древнего высохшего моря, в нём попадаются древние песчинки, и есть примеси естественных морских солей калия, кальция, магния. Эти-то примеси и оказывают благотворное влияние на жёсткость квашеных огурцов.
Выварочная или соль Экстра, это соль, очищенная перекристаллизацией, и от примесей, и от песчинок.
А вот так добывают каменную соль. Толщина пласта, не то что в Африке
Ещё туда добавляют немного соединений йода — такая соль может попахивать йодом, но сильно злобствовать на этот счёт не надо, йод предохраняет от ряда серьёзных проблем со здоровьем. Когда их нет, мы их склонны недооценивать, а случись они у нас, страдали бы потом всю жизнь. Так что терпим благосклонно. Причём я-то живу у моря, на побережье с йодом лучше, но ем и не жужжу.
Теперь вопрос — а если мы вообще не будем употреблять соль в пищу? Если питаться продуктами совсем без соли, да при большой нагрузке, да еще при жаре — можно даже умереть. От нехватки соли. Соль выводится с потом, тот самый хлористый натрий(и не только). Тепловой удар, если кто с ним сталкивался, это и есть нарушение водно-солевого обмена.
Тут мы немного поговорим как используется соль в организме, потому что, важность соли для организма не только в её участии в образовании из неё соляной кислоты для переваривания пищи. Это, как в той истории про боксёра, у которого спросили, зачем ему голова. — «А ещё, я в неё ем» — был ответ. Соль в растворе, состоит большей частью, из ионов натрия и хлора, и используется нашим организмом в механизме передачи нервных импульсов — сигналов, идущих от клетки к клетке. Это значит, что любые движения нашего тела и органов, происходят не без участия соли. Как это работает: — Понятно, что в теле проводов нет, поэтому клетки обходятся своими отростками — иногда довольно длинными, их называют аксонами и дендритами. Но важно не это, важно то что клетке надо передать сигнал действия другой клетке. Это делается электрическим путем.
А электрический потенциал участок клетки получает за счет разности концентраций калия и натрия. По принципу действия, это похоже на действие батарейки — ионы туда — сюда, и вот уже есть ток. Для того, что бы этот механизм работал, в клетке поддерживается повышенная концентрация ионов калия, а снаружи, в межклеточном пространстве, больше натрия. Когда надо передать сигнал действия, клетка в этом месте меняет соотношение калий-натрий(открываются каналы, пропускающие внутрь натрий или другие каналы, пропускающие калий наружу). Понятно, что соотношение концентраций натрия-калия должно выдерживаться очень точно — если оно нарушается, нарушается передача импульсов. Жизнь останавливается. Отсюда мы можем понять, почему кардиологи, так носятся с этим калием -он очень, очень важен— сердце самый важный мускульный орган и если в нем проблемы с импульсами -плохо всему организму.
Так же из соли, наш желудок приготавливает соляную кислоту, которой и переваривает пищу. Избыток кислоты приводит к изжоге, различным воспалениям, вплоть до язвы. Недостаток — не позволяет нормально переваривать пищу.
Так что опять — всё хорошо в меру, соль тоже.
При жаре, большой физической нагрузке, вместе с потом, выводится значительное количество соли. Именно соли, живой организм старается удерживать соли калия. При этом могут возникнуть нарушения баланса натрий/калий — тепловой удар.
Некогда в Германии судили медсестру — массовую убийцу. На деле она убивала безнадёжных больных, вероятно из жалости. Инъекцией хлористого калия, как сообщали в прессе. Равновесие нарушалось и…
Так что, давайте поговорим о модных и дорогих разновидностях соли: — морской и гималайской. Их пропагандируют как полезную альтернативу обычной «белой смерти». Понятную и верную информацию очень трудно выудить среди рекламных публикаций. Ложь, незнание, передергивание — в итоге, умудряются так объяснить вопрос, что и у меня — человека с хорошим химическим образованием, голова кругом идет. Сначала я попытался выяснить состав продажной морской соли: — 97-98.5% хлористый натрий, остальное, как сказано: « 1,5-3 % — это извлеченные из морской воды полезные макро- и микроэлементы (калий, кальций, магний, йод и др.).» Причем сайт даже ничего не скрывает — заголовок — «развод по-русски»
Морская соль — модный аксессуар
Может, это я такой без чувства юмора, а там тонкий стёб?.. Нууу, очень тонкий.
Господи, прошу дай мне терпения! «Извлеченные из морской воды полезные макро и микро элементы…»никто их не извлекал. В мелкой луже происходит выпаривание морской воды, в таких условиях начинает выпадать в первую очередь соль, чем мельче лужа и жестче (то есть быстрее процесс) выпаривание, тем больше примесей из морской воды захватывают кристаллы соли. Выпавшие на дно кристаллы сгребают в зависимости от технологии — чем-нибудь. Это и есть продукт. Оставшийся рассол сливают — в нем осталось мало соли и много солей калия и магния- а они горькие. Поэтому получается, что в зависимости от момента сгребания кристаллов может очень сильно меняться состав соли.
А вот так добывают морскую соль
Состав океанской воды, взял из Википедии. В океанской воде(я взял данные по ней, хотя они и не сильно различаются по морям — но океанская вода, она основа) -почти 78% натрий хлористый, сиречь — соль. Остальные примеси — ионы магния — 3,7% (если считать по чистому магнию), кальция — 1,2% (то же), калия 1,1%, в форме хлоридов, сульфатов и даже бромидов. Остальное до суммы 100%- придется на сульфат, хлорид и бромид — ионы, связанные с этими кальцием, магнием и калием — мы ведь считаем их, по чистым ионам. Естественно, содержатся и почти все остальные элементы, но уже вовсе, в ничтожных количествах. Не без труда, удалось найти более подробные данные по составу пищевой морской соли: — кальций — не больше 0,5 %, калий 0,2%, магний — 0,1% Как видим, гораздо беднее состава морской воды. Попробуем посчитать, какую долю минеральных веществ мы получим из «морской соли». Будем считать, что съедаем 10 грамм соли в день -это вообще-то многовато, ведь есть соль в хлебе, колбасе и т.д. Получилось что в 10 граммах «морской соли» -содержится 3% рекомендованной дневной нормы (RPN) магния, 6% — кальция, и 1,1 процента калия. Впрочем, состав такой соли может меняться в разы от партии к партии, что тоже не воодушевляет. По йоду морская соль в 40 раз беднее йодированной — технология такая, часть улетучивается, йод — он такой, да его туда и не добавляют, сколько есть, столько есть. В йодированную соль, добавляют более стойкое соединение йода — йодат калия (он не так выветривается), и то, за год, взаимодействуя с кислородом и углекислотой воздуха, йод испаряется почти полностью. Так что рассматривать морскую соль как источник минералов неправильно. Немного развлечёмся, почитаем дальше про соль, а я покомментирую. Очень восхитило выражение «путем вакуумного выпаривания рассола практически все полезные соединения разрушаются – в такой соли остается 99,9 % NaCl. Такую соль называю «белой смертью», потребление которой следует строго ограничивать» Как понять — хлорид калия или сульфат магния разрушатся от выпаривания? Это же не витамины, которые превратятся во что-нибудь менее ценное, простым солям разрушаться дальше некуда, причём от вакуумного выпаривания. К слову — самый щадящий способ, температура-то процесса — градусов 30, в отсутствие кислорода воздуха. Даже витамины не разрушаются. Только я лично, сомневаюсь, что такую дорогую технологию будут применять для приготовления просто очищенной соли. Не зачем. Может писавший имеет в виду те 2% примесей, которые отделяются при очистке? Да, они полезны, но с питьевой водой мы их получаем гораздо больше. Итак, в очищенной соли, действительно 99,9% натрия хлористого. Нам говорят, что это называют «белой смертью». Значит морскую соль, в которой натрия хлористого на 2-3% меньше, надо называть «на 98% белой смертью». Рекламщик не знает того, что учёные доказали еще 250 лет назад — вещества не исчезают и не появляются ниоткуда (Ещё солнце наше М.В.Ломоносов занимался). А ещё, он утверждает, что из-за двух — трёх процентов примесей, остальные 97-98% стали мёдом. На лицо попытка сделать бочку мёда из… э-э-э — доступных веществ и ложки мёда. В реальности, вред уменьшился лишь на два-три процента, да и то, при условии, что Вы не станете солить больше, чтобы компенсировать недосол. На практике, примеси магния и кальция могут заметно повлиять на жесткость огурцов при квашении и варёных овощей при варке — из-за содержания солей магния и кальция, правда доля магния и кальция из водопроводной воды, в масштабах нашего потребления велика. Кстати, мощные осмотические (мембранной технологии) системы очистки воды могут существенно снизить содержание этих важных элементов в питьевой воде. Это надо просто учитывать в своём рационе, чтоб потом не случилось неприятностей типа частых переломов костей и быстрого разрушения зубов. И крохи из морской соли тут не помогут. Молочные продукты, минеральная вода и т. д. Верный сигнализатор малого содержания кальция/магния в воде — отсутствие накипи в чайнике.
Продолжим — крупные крупинки соли приятны на вид, и медленно растворяются, потому приятны на вкус. А вот ещё, посмотрим рекламный фрагмент, — вообще достойно «занесения в анал к историкам»:- «Во-первых, находящаяся в недрах Земли соль, подвергается воздействию высоких давлений и температур, становится пластичной и благодаря этому выходит на поверхность Земли, создавая огромные пики. Что происходит с 1,5-3% элементов в это время? Большая часть из них распадается…» У-у-у, атомы распадаются от давления, силен мужик, руками рельсы рвёт. Температуры высокие. Явно перепутал высохшее древнее море с кимберлитовой трубкой, где рождались алмазы. И где у нас такие огромные пики соли в Украине? А в Саксонии? А в Белоруссии? Древнее море было большим, испарялось медленно, потому разделение получилось очень хорошим, примесей немного, но это как где. Да, земная поверхность двигалась, изгибалась, но важно что верхние слои не пропустили вниз воду, а то соль вымыло бы. В Саксонии, больше 150 лет назад, когда начинали разведку соляных пластов, хотели даже остановить работы, потому что верхние слои были богаты сульфатами калия, магния, а соли было мало. Это теперь калийные соли — очень ценятся. Тогда было не так. Только когда пробурились поглубже, пошла хорошая соль и люди поняли какая ценность там лежит.
Ах да! Ещё одно свойство соли с примесями — она заметно сильнее слёживается.
Следующим пунктом поговорим про розовую гималайскую соль — нашел, вроде бы, честный пост про неё. Подземная каменная соль, окрашенная слегка солями железа — ну было в том древнем море много железа, не страшно. И тут- фанфары! — «По разным данным, гималайская соль содержит от 82 до 92 микроэлементов, в то время, когда в обыкновенной поваренной их всего — 2.» Какие 92 микроэлемента, последний не искусственный элемент — уран, номер 92. Отнимем инертные газы, их 6 и технеций, его совсем нет в природе, он искусственно получен, потому так и называется. Почему инертные газы — а они ни с чем не реагируют в природе, вот и не удержаться им в соли. Да и зачем они нам, если они никак не воздействуют на организм. На самом деле, при больших давлениях этих газов, немного влияют на ту самую передачу импульсов, и получается нечто вроде опьянения. Но где соль, а где 10 атмосфер ксенона. Итак, получилось 85, считая с полонием и другими менее опасными ядами. Нашел я выписку этих анализов. Вот ведь, не поленились анализы делать на элементы, которых в природе почти нет. Реально нашли около 30 элементов, остальные цифры показывают, что содержание ниже чувствительности применявшегося метода или его нет в природе, так как не стоек. Причем чувствительность хорошая -1 миллиграмм на тонну. Впрочем и в морской воде, и в нас, всё это тоже найдётся. Всё дело в точности анализа. Охмуреж. Делается вывод что нашли, хотя опыт показал, что не нашли. Где логика? Да и с микроэлементами не так — в энциклопедии дается такое определение микроэлементов: «химические элементы, необходимые живым организмам для обеспечения нормальной жизнедеятельности». Их не так много — штук 15, до 30. Так что на самом деле — соль как соль, правда красивая и кристаллики приятные.
Розовая гималайская соль — гламурненькая
Так что кушайте ту соль, какая нравится, но помните — это просто соль. Морская и каменная — с примесями магния, кальция, калия, что иногда неплохо. Соль очищенная, мелкая — хорошо сыплется. Главное, не драматизируйте вопрос выбора — хорошее настроение, очень важный фактор нашего самочувствия.
Но есть другие варианты замены соли — соль где сильно снижено содержание хлорида натрия. Заменой на что-нибудь другое. Это уже в случае, когда явно нельзя, но очень хочется. Это уже с медиками и конкретно. Я встречался только с одним из них — солью в которой 30% соли и 70% хлористого калия. Конечно, вкус сильно отличается — если лизнуть, то даже жгучий, но для сердечно-сосудистой системы калий очень нужен, так что это вполне себе вариант, кому актуально. Я немного использую. Но не увлекайтесь! Избыток калия тоже может быть опасен! В случае проблем с почками.
Соль с содержанием хлористого калия 70%Выводы: Какая соль вам нравится, такую и кушайте. Замена на морскую соль — ничего не решит. Просто солите меньше. Йодированную не избегайте. Каменная — хороша для засолки огурцов, да и вообще неплоха. Морская и Гималайская — красиво смотрятся в солонке.
Классическая соль. Главное — не пересаливать.
В заключение добавлю, что есть еще такое интересное применение соли и шахт остающихся от её выработки — лечение астмы и других заболеваний лёгких. Глубоко под землю не добирается пыльца растений, бактерии и всякая пыль, там сухо. В солевой шахте, в воздухе находятся, в основном, мелкие частицы соли. Специалисты расскажут подробнее, но лечение пребыванием в соляных выработках, уже давно известно и отзывы о нём были самые положительные.
В белорусских соляных шахтах. Дети подземелья 8).
Прошу заметить — то что я рассказываю, это не запрет и не приказание как жить. Это значит, что сейчас считается, что так делать лучше, а я постарался в этом разобраться и донести это до Вас. В конце концов, ведь не все мы делаем зарядку, хотя это и полезно?
Если этот пост понравился, есть ещё про сахара/углеводы: Про сахар. Какие бывают сахара. Про кленовый сахар и сахар ли он? Что общего у омара, тарантула, ёлки, гриба, мёда и ракеты «Кассам». Ставим химический опыт по превращению крахмала… Как блеснуть эрудицией. Фруктоза — польза и вред, две стороны вопроса. Кто виноват в том, что от молока болит живот. Как получается, что кислое варенье меньше засахаривается. Из чего делают сахар. Про тростниковый сахар — едим ради его вкуса.
Соль – необходимость или «белая смерть»?
Сколько соли нужно нашему организму и чем опасно злоупотребление этой приправой
Соль необходима для организма человека. Однако сегодня ее нередко называют «белой смертью». Насколько справедливо такое мнение?
Для начала ответим на простой вопрос: можно ли обойтись без добавления в пищу соли? Ведь, как говорит русская пословица, «без соли и хлеб не естся». Оказывается, дело не только во вкусовой ценности этого продукта. Пищевая соль содержит не менее 97% хлорида натрия. А наш организм не может самостоятельно вырабатывать натрий. Суточная потребность взрослого человека в этом элементе – 1,3-1,6 грамма. Такое количество содержится в 3-4 граммах столовой соли – это примерно половина чайной ложки. У детей норма потребления зависит от возраста.
ВАЖНО ЗНАТЬ!
Натрий – важный биологически активный элемент, без которого невозможна нормальная работа организма человека. Он участвует в процессах клеточного обмена, поддерживает водно-солевой баланс, регулирует деятельность нервной системы. В организме человека обычно содержится от 70 до 110 г натрия. Из них треть – в костях, две трети – в жидкости, мышечной и нервной тканях. Недостаток и избыток натрия негативно отражается на работе многих органов и систем.
Сбалансированное содержание натрия в организме зависит от правильной работы почек. При регулярном употреблении соленой пищи натрий накапливается в организме и восполняет его недостаток, который возникает в ряде случаев.. При больших физических нагрузках, вызывающих повышенное потоотделение, при диарее и рвоте, ожогах или обморожениях, а также при таких заболеваниях, как, например, болезнь Аддисона, из организма выводится большое количество натрия. Его дефицит возникает и при приеме мочегонных препаратов.
Напротив, перенасыщение натрием становится причиной потери таких жизненно важных элементов, как калий, магний и кальций, и одновременно увеличивает количество жидкости в организме, что ведет к патологиям сердечно-сосудистой системы изаболеваниям почек.
Поэтому эксперты рекомендуют сократить ежедневное употребление соли максимум до 5 грамм и избегать продуктов с повышенным содержанием этого вещества.
Там, где соль выступает в качестве усилителя вкуса и консерванта. Есть переизбыток натрия. Поэтому лучше использовать продукты с природным содержанием соли, например, морскую рыбу, водоросли, мидии, сельдерей, яйца, свеклу, укроп, луке-поре и т. д.
Содержание натрия в некоторых продуктах питания
|
Название продукта
|
Количество Na (г) в 100 г продукта
|
Процент средней суточной потребности
|
|
Соль поваренная
|
38,7
|
2419%
|
|
Бульонный кубик
|
24,0
|
1500%
|
|
Соевый соус
|
5,6
|
352%
|
|
Сельдь среднесоленая
|
5,4
|
336%
|
|
Рыба вяленая
|
4,7
|
292%
|
|
Молоко сухое
|
2,3
|
143%
|
|
Колбаса салями
|
2,0
|
126%
|
|
Сыр рокфор
|
1,8
|
113%
|
|
Сыр пармезан
|
1,7
|
106%
|
|
Оливки зеленые маринованные
|
1,6
|
97%
|
|
Перец сладкий консервированный
|
1,4
|
86%
|
|
Сыр плавленый «Колбасный»
|
1,3
|
81%
|
|
Фаст фуд, булочка с ветчиной
|
1,3
|
79%
|
|
Огурцы квашенные
|
1,2
|
76%
|
|
Брынза из коровьего молока
|
1,2
|
75%
|
|
Сухой завтрак
|
1,1
|
67%
|
|
Крекеры пшеничные
|
0,9
|
57%
|
|
Капуста квашеная
|
0,8
|
50%
|
|
Детское питание – крекеры овощные
|
0,6
|
36%
|
|
Креветка
|
0,5
|
34%
|
|
Морская капуста
|
0,5
|
33%
|
|
Майонез «Провансаль»
|
0,5
|
32%
|
На этикетке продуктов питания может быть указано содержание как соли, так и натрия. Чтобы понять, сколько натрия в продукте – нужно указанное количество соли разделить на 2,5. И наоборот.
ВАЖНО ЗНАТЬ!
Контролируйте содержание соли в вашем рационе питания. Это не так сложно, как может показаться. Покупайте меньше готовых продуктов, больше готовьте сами. Приправляйте пищу перцем, чесноком, сухими травами и специями, в составе которых нет соли.
По материалам с сайта «ЗДОРОВОЕ ПИТАНИЕ» (https://здоровое-питание.рф)
Спайсы соли и другие новые психоактивные вещества – кто виноват и что делать?
Новый закон
12 декабря Госдума приняла в первом чтении законопроект, вносящий коррективы в контроль над оборотом так называемых «новых психоактивных веществ», а именно, позволяющий ФСКН самостоятельно формировать реестр новых потенциально опасных психоактивных веществ и вносить туда вещества, не внесенные в Постоянный список, утверждаемый правительством РФ. Второе чтение состоится после зимних каникул.
В связи с рассмотрением этого законопроекта, в СМИ поднялась новая информационная волна по поводу «спайсов», меня пригласили выступить на некоем ток-шоу на Первом канале и высказать свои соображения по этому поводу. Как у человека, не смотрящего телевизор, у меня сложилась некая иллюзия, что я действительно смогу там сказать хотя бы два связных слова о современной мировой наркополитике в отношении этих веществ. Я провела подготовку, прочитала ряд материалов, поговорила с несколькими коллегами— экспертами по наркополитике, которые занимаются этим вопросом в других странах и попыталась разобраться своим не юридическим мозгом в том, насколько вредна новая инициатива ФСКН (поскольку от них всегда ожидаешь нового подвоха). На передаче мне не удалось сказать ни слова – среди ора многочисленных депутатов о грядущей гибели нации и шокирующей моде подростков впадать в острые психопатические припадки, воплей разгоряченных женщин «всех сажать!», «всех лечить принудительно!» и урагане возгласов о том, что нашу страну хотят в очередной раз уничтожить, конечно же, бесполезно было бы встревать для того, чтобы изложить более-менее уравновешенную позицию, основанную на изучении материалов и общении с настоящими экспертами в этой области. Поэтому конспект своих находок и соображений я излагаю в письменном виде для тех, кому, как и мне, интересно более глубоко разобраться в этом вопросе.
Что такое новые психоактивные вещества и откуда они взялись?
С термином «новые психоактивные вещества» (НПВ, novelpsychoactivesubstances) сегодня уже знакомы даже люди, не особо интересующиеся наркотиками и наркополитикой, хотя им они чаще известны под названием «спайсы», «соли» – это вещества, которые стремительной кометой ворвались на мировой наркорынок в середине 2000-х, как легальная альтернатива запрещенным психоактивам. Существует несколько основных классов НПВ, в соответствии с теми веществами, действие которых они воспроизводят: синтетические каннабиноиды (например, «спайсы»), стимуляторы (воспроизводят действие кокаина, амфетаминов и MDMA, к ним относятся, например,мефедрон и т.п., получившие название «соли», так как одно время продавались под видом солей для ванн). Третий разряд НПВ — галлюциногены/диссоциативы — сюда входят синтетики, воспроизводящие эффект известных галлюциногенов, но также в этот разряд относят вещества, которые до недавнего времени оставались легальными, например, шалфей предсказателей и даже кетамин (в некоторых странах).
Формулы прародителей различных новых веществ появлялись в совершенно легальных научных лабораториях, например, первый известный синтетический каннабиноид был разработан ученым Джоном Уильямом Хаффманом (не путать с Альбертом Хоффманом!) и получил название в честь трех первых букв имени ученого — JWH. Исследование синтетических каннабиноидов доктор Хаффман начал еще в середине 1980-х годов, когда он вёл разработку каннабиноидных составляющих, которые могли бы помочь в изучении рассеянного склероза, ВИЧ и химиотерапии. В течение 20 лет после этого Хаффман разработал более 450 синтетических каннабиноидов. В середине 2000-х два каннабиноида начали открыто продаваться в Германии под названием Spice и K-2 – считается, что их формулы были опубликованы в одной из научных статей и затем использованы предприимчивыми химиками для производства альтернативной синтетической марихуаны. Известный галлюциноген 25I-NBOMe – кузен ЛСД – был синтезирован в 2003 году Ральфом Хеймом в Свободном университете Берлина в рамках его диссертации по теме синтеза и фармакологии агонистов серотониновых рецепторов. С мефедроном (синтетический катинон, «соли») история еще более интересная – по сообщению Европейского центра мониторинга наркотиков и наркозависимости (EMCDDA), впервые упоминание формулы мефедрона было задокументировано в научном журнале аж в 1929 году, однако она оставалась в тени до 2003 года, когда была опубликована подпольным химиком, работающим под псевдонимом Кинетик, на ныне почившем сайте TheHive (форум людей, интересующихся синтезом, химией, биологией и легальными аспектами веществ). Буквально за несколько лет ранний мефедрон или, как его ласково называли, «мяу-мяу», в силу своих свойств приятного стимулятора-эмпатогена, приобрел огромную популярность в Европе, например в Британии в 2009 году он был признан четвертым по популярности веществом после каннабиса, кокаина и экстази.
Сначала все эти вещества назывались «дизайнерские наркотики», или «legalhighs» – легальный кайф, но вскоре это название потеряло свой смысл, так как законодатели разных стран стали предпринимать попытки взять вещества под контроль. Кроме «спайсов», официальный термин НПВ включает любые новые вещества, которые мимируют действие нелегальных веществ (каннабис, МДМА, амфетамины и т.д.) и либо все еще легальны, либо недавно были запрещены.
Закон и контроль
Наверное, ни для кого не удивительно, что первой реакцией правительств разных стран, узнавших о распространении новых, не запрещенных, но и не разрешенных законом психоактивных веществ, стал не поиск новых подходов к регулированию НПВ с опорой на данные научных и медицинских исследований, с максимальной эффективностью и снижением риска для потребителей, а попытки во что бы то ни стало их запретить. Все законодательные нормативы относительно НПВ исходили из предпосылки об их вреде, и законодатели не удосуживали себя тщательным взвешиванием pro и contra запрета этих веществ – достаточно было того, что они обладают психоактивным воздействием и возможными негативными последствиями (последнее, кстати, касается множества веществ, в том числе фармакологических, продуктов питания и т.д.). Ни одно из решений даже наиболее прогрессивных правительств мира о запрете НПВ не было основано на научной оценке возможных последствий этого запрета, в том числе оценке того, как он повлияет на уровень употребления и связанные с ним вредные последствия (анализ подходов к регулированию можно посмотреть в коротком докладе европейской исследовательской группы по изучению наркополитики Alice RAP).
Первые запреты НПВ начались в конце 2000-х. Так, в 2008 году в Израиле и вскоре в Швеции был запрещен мефедрон, который к тому времени достаточно широко распространился в мире. В 2010 году он был признан нелегальным во всем Европейском Союзе. В 2010 году Агентство по контролю за наркотиками США предложило внести JWH-018 и четыре связанных с ним компонента в Список запрещенных препаратов и уже в марте 2011 года они были запрещены в США. В Великобритании с 2011 года действует временный реестр веществ (Temporaryclassdrugsorder), предполагающий временный запрет на новые вещества и санкции за производство, импорт и сбыт (но не хранение) внесенных в него веществ – запрет налагается на 1 год, и за это время вещество должно быть изучено и вынесено решение о его постоянном запрете или легальном регулировании. За два года временному запрету подверглось около 75 НПВ.
В Швеции полиция и таможенная служба имеют право изымать вещества, не входящие в списки наркотиков, если есть подозрения, что данные вещества имеют отношение к нелегальному обороту наркотиков. По решению прокурора изъятые вещества могут быть уничтожены. Интересно, что шведы частенько выступают на международных конференциях, рассказывая о своих успехах в борьбе со спайсами, за что подвергаются критике со стороны международных экспертов – ведь успех этот измеряется в количестве изъятых или вновь запрещенных веществ, а не уровнем их потребления.
Правительство Австралии пошло по другому пути и осуществило обширный запрет веществ только на основе их химической структуры. Данный запрет делает нелегальными многие вещества ещё до их создания. Федеральный Закон об аналогах, подлежащих контролю, а также законодательные акты отдельных штатов, например Нового Южного Уэльса, используют принцип, при котором под запрет попадают миллионы несуществующих химических соединений. С другой стороны, закон не распространяется на вещества, которые не имеют структурного сходства с запрещёнными наркотиками, даже если они производят схожие эффекты.
В сентябре 2013 года Евросоюз принял новые правила об ускоренном изъятии вредных НПВ из оборота. В соответствии с этими правилами, в случае подозрения на вредное воздействие продукта, он может быть немедленно изъят из продажи еще до завершения полной оценки рисков, занимающей два года. Была предложена градационная система, в соответствии с которой в отношении веществ, несущих «низкий риск», не будут предприниматься никакие действия, в то время как продукты «среднего риска» будут подвергаться частичным ограничениям распространения на рынке, а продукты «высокого риска» полному запрету распространения. И только «наиболее опасные» вещества, представляющие серьезный риск для здоровья потребителей, будут запрещены уголовным законодательством наряду с ныне нелегальными веществами. Вообще, подходы к регулированию НПВ можно разделить на несколько типов: защита потребителей, фарма-регулирование и применение закона о нелегальных веществах.
Эффективность запрета
Очень скоро стало понятно, что НПВ представляют собой новый и ранее не виданный вызов мировой системе контроля над наркотиками, так как новые формулы различных веществ появлялись почти молниеносно, не успевали вносить в списки запрещенных веществ что-то одно, как его место уже занимало несколько новых препаратов – сходных по действию, но отличающихся по формуле, а следовательно, совершенно легальных. Война с наркотиками вышла на новый виток крушительного поражения, так как в борьбе со спайсами и другими НПВ отразилась вся её суть – попытки запретить какие-то вещества порождали новые, чаще всего более опасные вещества и средства их распространения. Как объяснил мне эксперт британской организации TransformСтив Роллз, первый запрет коснулся около десятка веществ «первого поколения» НПВ, на месте которых появилось два десятка веществ «второго поколения», запрет которых в свою очередь привел к появлению сотни новых веществ и т.д.
На таблице Европейского центра мониторинга наркотиков и наркозависимости видно, как возрастало количество различных видов НПВ в Европе, начиная с тех лет, когда их начали запрещать: по данным EMCDDA, в 2009 появилось 24 новых вещества, в 2010 – 41; в 2011 – 49; в 2012– 73.
В последнем Всемирном докладе о наркотиках Управление ООН по наркотикам и преступности признает: новые вещества появляются на наркорынке с неиссякаемой регулярностью, и международная система контроля над наркотиками провисает под скоростью и изобретательностью этого процесса. Так, к концу 2013 года было зарегистрировано 348 НПВ, что намного превышает число всех запрещенных наркотиков, находящихся в обороте за последние 50 лет (234 вещества).
Вместе с появлением новых видов веществ начали кардинально меняться и технологии их продажи. Основной площадкой оборота наркотиков и прекурсоров стал интернет, в том числе те его слои, которые не доступны для обычных средств интернет-поиска и правоохранительных органов в силу анонимности и защищенности пользователей (так называемая «теневая сеть») . Веб-торговля веществами начала набирать новые обороты, результатом чего стало создание огромных веб-наркорынков, такие как SilkRoad и Agora. Правоохранительные меры борьбы с нелегальными веб-рынками давали точно такие же результаты, как борьба с наркотиками – закрытие одного ресурса приводило к появлению гораздо больших по объему рынков – по сути, закрытие крупных рынков, таких как SilkRoad, играло на руку конкурирующим рынкам и позволяло им разрастаться. Например, рынок Agora за год после закрытия SilkRoad предлагал на несколько тысяч больше продуктов, чем SilkRoad за год до этого (вот статья Wired про это), а также множество новых рынков, которым закрытие SilkRoad пошло только на руку. Сам основатель SilkRoad Ужасный Пират Робертс называет этот процесс «эффектом гидры» – на месте отрубленной головы у нее вырастает три новые. После ликвидации SilkRoad было установлено, что совокупные доходы, полученные за время существования этого сайта (от двух до пяти лет) составили около 1,2 млрд. долларов США. В своем Всемирном докладе о наркотиках 2014 УНП ООН подчеркивает, что веб-рынок для новых психоактивных веществ, а также для высококачественного каннабиса, героина, метилендиоксиметамфетамина (МДМА) и кокаина представляет собой новую масштабную проблему контроля за оборотом наркотиков. Конечно, сетевой наркорынок не ограничивается крупными конгломератами вроде SilkRoad. И оптовая, и розничная торговля веществами в целом перемещаются на веб-платформы, становясь всё эффективней, анонимней и мобильней.
Новый тип взаимодействия между производителями, продавцами и покупателями веществ значительно упростил и процесс разработки новых веществ. Сегодня произвести свой новый легальный наркотик не очень сложно и под силу даже рядовому любителю. Чтобы проверить это утверждение, британский журналист Майк Пауэр провел расследование – не имея специальных познаний в области химии, за два месяца ему удалось сделать мимическую формулу амфетамина, почитаемого его любимыми писателями и музыкантами. По словам Майка в отчете об эксперименте, опубликованном в TheGuardian, для производства своего вещества понадобилась лишь пара десятков звонков в Шанхай, новый аккаунт в почте Gmail, банковский трансфер, почтовый ящик, зарегистрированный на ненастоящее имя, и несколько имейлов для связи с лицами с веб-форумов, предоставивших ему варианты синтеза и модификации, а также контакты с дружественной лабораторией в Шанхае. Интереснейшую статью Майка в переводе Алексея Ковалева можно прочитать на Бихае. Основной вывод статьи, к которому сейчас приходит всё больше право— и здравоохранителей, достаточно очевиден: в эпоху интернета контролировать рынок наркотиков старыми способами просто невозможно. Новые запреты порождают новые вещества. Ужесточение контроля над НПВ увеличивает объемы их производства и продажи, при этом стоимость их растет, а качество резко падает.
Появление все большего количества новых веществ привело к серьезным проблемам не только для правоохранителей, но и для системы здравоохранения – по мере наращивания гонки с законом значительно росли риски для потребителей. Чем больше запрещали веществ, тем больше появлялось новых, снижалась информация о них и возрастали риски их употребления. По данным доклада британского Королевского колледжа психиатров, опубликованного в этом году, на наркосцене Великобритании каждую неделю появляется новое психоактивное вещество, и британские наркосервисы совершенно не готовы к подобной ситуации. Когда люди обращаются к специалистам за лечением или консультацией, те зачастую просто не знают, что сказать.
Огромный риск здравоохранения состоит в том, что люди нередко вообще не знают, что именно содержится в веществе, которое они покупают. Кроме этого, увеличивается риск выпуска партий веществ с ошибочной формулой. Так, в своем интервью журналу DrinkandDrugsNews один из ведущих экспертов по НПВ, британский химик-аналитик Джон Рамзей указывает на высокую вероятность подобных ошибок и приводит известную историю вещества MPTP, которое было произведено по ошибке, при производстве синтетического опиоида MPPP, и приводило к необратимым симптомам, аналогичным болезни Паркинсона у всех, кто его употребил (сюжет с МPTP был использован Уильямом Гибсоном в романе «Нейромант»). С подобными искажениями формул могут быть связаны случаи острой интоксикации веществами.
Хлорид натрия-NaCl-соль Земли
Октябрь 2003 г.
«Пожалуйста, передайте хлорид натрия». Это еще один способ попросить соль для печеного картофеля в следующий раз, когда вы сядете вместе с семьей за ужином. Хлорид натрия, обычная поваренная соль, также известен как минерал галит. На диаграмме справа показано, как атомы натрия и хлора плотно упаковываются вместе, образуя кубообразные единицы соединения NaCl.Кристаллы поваренной соли имитируют эту структуру — они имеют форму маленьких кубиков. Вы можете убедиться в этом сами, рассмотрев несколько крупинок соли через увеличительную линзу или микроскоп.
Соляная шахта более 1000 футов
ниже Детройта
Откуда берется поваренная соль? (Пожалуйста, не говорите супермаркет.) Галит, хлорид натрия, естественным образом встречается в огромных геологических отложениях солевых минералов, оставшихся от медленного испарения древней морской воды. (Вы удивлены? Вы когда-нибудь ощущали вкус морской воды во рту на пляже?) Эти месторождения добываются для получения различных солей, в том числе хлорида натрия, достаточного для наполнения многих, многих солонок!
Что в имени?
NaCl — химическое короткое
рука (или формула) для хлорида натрия.Это просто
, чтобы узнать, откуда берется «Cl» (хлор, да), но как же, спросите вы, «Na» представляет натрий?
Ответ: «На»
означает «натрий»,
Латинское слово для натрия.
NaCl абсолютно необходим для жизни на Земле. Это необходимый ингредиент в рационе людей и животных. А хлорид натрия имеет буквально тысячи применений! Одно из таких применений — служить источником хлора для химического производства. Почему, спросите вы? И вот почему: хлор известен как «химическое вещество рабочей лошадки». Он играет ключевую роль в производстве тысяч товаров, от которых мы зависим каждый день, в том числе волейбольных мячей, компьютеров, автомобилей, химикатов для бассейнов, лекарств и косметики (см.
Дерево продукта хлора).Это лишь небольшая часть многих предметов, которые производятся с использованием хлора.
Как вы думаете, как освободить хлор из этих плотно упакованных кристаллов NaCl? Электричество — это инструмент, используемый для электрохимического расщепления NaCl, высвобождая Cl для его многочисленных химических применений. Инженеры-химики проектируют системы, позволяющие создавать пузырьки газообразного хлора из соленой, электрифицированной воды.Газ улавливается и охлаждается настолько, что превращается в жидкость.
Весь процесс очень крутой (но небезопасно пытаться дома). Средний американец потребляет около 7 фунтов хлорида натрия в год и более 500 фунтов в течение жизни! Сложите это вместе с использованием всех продуктов, изготовленных с использованием хлора, и я думаю, вы согласитесь, что NaCl является важным соединением!
Пожалуйста, передайте галит!
Дополнительные вопросы:
- Найдите натрий и хлор в Периодической таблице элементов.Каковы их атомные номера? Какую информацию мы можем получить из атомного номера элемента?
- NaCl известен как ионное соединение. Что это обозначает?
- Хлор известен как двухатомная молекула. Объясните, что это значит. (Подсказка: «ди» означает «два».)
Идеи научных проектов:
- Галофиты — это растения, приспособившиеся к жизни в среде с высоким содержанием соли. Назовите некоторые из этих сред и опишите некоторые из найденных там галофитов.Как они приспособились к «соленому» существованию? Что происходит с обычными растениями, если их поливать соленой водой?
- Узнайте химические соединения и названия минералов для некоторых других солей, которые образуются в результате медленного испарения древней морской воды (кроме хлорида натрия). Для чего они нужны?
Чтобы просмотреть список предыдущих функций «Хлорное соединение месяца», щелкните
здесь.
Химические или научные наименования обычных веществ
Химические или научные названия используются для точного описания состава вещества. Даже в этом случае вы редко просите кого-нибудь передать хлорид натрия за обеденным столом. Важно помнить, что общие названия неточны и меняются от одного места к другому. Поэтому не предполагайте, что вы знаете химический состав вещества на основе его общего названия. Это список архаичных химических названий и общепринятых названий химикатов с их современными названиями или названиями, эквивалентными ИЮПАК.Вас также может заинтересовать список распространенных химических веществ и их местонахождение.
Общие химические названия
| Общее название | Химическое название |
| ацетон | диметилкетон; 2-пропанон (обычно известный как ацетон) |
| кислый сульфат калия | бисульфат калия |
| кислота сахарная | щавелевая кислота |
| Кокей | азотная кислота |
| летучие алкали | гидроксид аммония |
| спирт зерновой | спирт этиловый |
| серный спирт | сероуглерод |
| спирт, дерево | спирт метиловый |
| квасцы | алюминия сульфат калия |
| глинозем | оксид алюминия |
| антихлор | тиосульфат натрия |
| антифриз | этиленгликоль |
| сурьма черная | трисульфид сурьмы |
| цветение сурьмы | трехокись сурьмы |
| взгляд сурьмы | трисульфид сурьмы |
| сурьма красная (киноварь) | оксисульфид сурьмы |
| аммиак водный | водный раствор гидроксида аммония |
| Аква Фортис | азотная кислота |
| царская водка | кислота солянокислая |
| аммиак ароматический | аммиак в спирте |
| мышьяковистое стекло | триоксид мышьяка |
| азурит | Минеральная форма основного карбоната меди |
| асбест | силикат магния |
| аспирин | ацетилсалициловая кислота |
| пищевая сода | бикарбонат натрия |
| банановое масло (искусственное) | изоамилацетат |
| барий белый | сульфат бария |
| бензол | бензол |
| бикарбонат соды | гидрокарбонат натрия или бикарбонат натрия |
| бихлорид ртути | хлорид ртути |
| бихром | дихромат калия |
| соль горькая | сульфат магния |
| ясень черный | сырая форма карбоната натрия |
| черный оксид меди | оксид меди |
| черный свинец | графит (углерод) |
| Блан-фикс | сульфат бария |
| обесцвечивающий порошок | известь хлорированная; гипохлорит кальция |
| медь синяя | сульфат меди (кристаллы) |
| синий провод | сульфат свинца |
| голубые соли | сульфат никеля |
| синий камень | сульфат меди (кристаллы) |
| купорос голубой | сульфат меди |
| голубой камень | сульфат меди |
| костяная зола | неочищенный фосфат кальция |
| кость черный | неочищенный древесный уголь |
| борная кислота | борная кислота |
| бура | борат натрия; тетраборат натрия |
| синий бремен | карбонат меди основной |
| сера | сера |
| квасцы обожженные | калия сульфат алюминия безводный |
| Известь негашеная | оксид кальция |
| охра жженая | оксид железа |
| руда обожженная | оксид железа |
| рассол | водный раствор натрия хлорида |
| масло сурьмяное | треххлористая сурьма |
| масло жестяное | олова безводный |
| масло цинковое | хлорид цинка |
| каломель | хлорид ртути; хлорид ртути |
| карболовая кислота | фенол |
| углекислый газ | двуокись углерода |
| каустическая известь | гидроксид кальция |
| едкий калий | гидроксид калия |
| каустическая сода | натрия гидроксид |
| мел | карбонат кальция |
| Селитра Чили | натрия нитрат |
| Чили нитра | натрия нитрат |
| Красный китайский | основной хромат свинца |
| Китайский белый | оксид цинка |
| хлорид соды | гипохлорит натрия |
| извести хлористая | гипохлорит кальция |
| квасцы хромовые | хромовый сульфат калия |
| хром зеленый | оксид хрома |
| хром желтый | Хромат свинца (VI) |
| хромовая кислота | триоксид хрома |
| копер | сульфат железа |
| сублимат коррозионный | хлорид ртути (II) |
| корунд (рубин, сапфир) | в основном оксид алюминия |
| Винный камень | битартрат калия |
| порошок крокуса | оксид железа |
| Кристалл карбонат | карбонат натрия |
| дехлор | тиофосфат натрия |
| алмаз | кристалл углерода |
| наждак | нечистый оксид алюминия |
| соли Эпсома | сульфат магния |
| этанол | спирт этиловый |
| Фарина | крахмал |
| ферро-прусский | феррицианид калия |
| железо | утюг |
| Флорес Мартис | ангидрид железа (III) хлорид |
| плавиковый шпат | фторид кальция природный |
| фиксированный белый | сульфат бария |
| Цветки серы | сера |
| «цветы из любого металла» | оксид металла |
| формалин | водный раствор формальдегида |
| Французский мел | природный силикат магния |
| Французский вергидрис | основной ацетат меди |
| галенит | сульфид свинца природный |
| Глауберова соль | натрия сульфат |
| зеленый вердитер | карбонат меди основной |
| купорос зеленый | кристаллов сульфата железа |
| гипс | сульфат кальция природный |
| твердое масло | Масло льняное вареное |
| тяжелый лонжерон | сульфат бария |
| синильная кислота | цианид водорода |
| гипо (фотография) | раствор тиосульфата натрия |
| Индийский красный | оксид железа |
| Изингласс | агар-агар желатин |
| румяна ювелирных | оксид железа |
| убитые духи | хлорид цинка |
| черная лампа | неочищенная форма углерода; древесный уголь |
| веселящий газ | закись азота |
| перекись свинца | диоксид свинца |
| Двуокись свинца | оксид свинца |
| лайм | оксид кальция |
| известь гашеная | гидроксид кальция |
| известковая вода | водный раствор гидроксида кальция |
| щелок аммиак | раствор гидроксида аммония |
| горит | оксид свинца |
| лунная каустика | Нитрат серебра |
| печень серная | насыщенный калий |
| щелочь или содовая щелочь | натрия гидроксид |
| магнезия | оксид магния |
| марганец черный | диоксид марганца |
| мрамор | в основном карбонат кальция |
| оксид ртути, черный | оксид ртути |
| метанол | спирт метиловый |
| метилированные спирты | спирт метиловый |
| известковое молоко | гидроксид кальция |
| молоко магния | гидроксид магния |
| молоко серное | Сера осажденная |
| «муриат» из металла | хлорид металла |
| соляная кислота | соляная кислота |
| натрон | карбонат натрия |
| нитра | нитрат калия |
| кислота Нордхаузена | дымящая серная кислота |
| масло марс | расплывающийся безводный хлорид железа (III) |
| Купоросное масло | серная кислота |
| грушаное масло (искусственное) | метилсалицилат |
| ортофосфорная кислота | фосфорная кислота |
| Синий Париж | ферроцианид железа |
| Париж зеленый | ацетоарсенит меди |
| Париж белый | карбонат кальция порошковый |
| грушевое масло (искусственное) | изоамилацетат |
| жемчужно-ясеневый | карбонат калия |
| перманентный белый | сульфат бария |
| гипс Париж | сульфат кальция |
| свинец | графит |
| калий | карбонат калия |
| потасса | гидроксид калия |
| мел осажденный | карбонат кальция |
| Синильная кислота | цианистый водород |
| пиротехника | пирофосфат тетранатрия |
| Известь негашеная | оксид кальция |
| ртуть | ртуть |
| красный свинец | тетраоксид свинца |
| красный щелок | раствор ацетата алюминия |
| Пруссат калий красный | ферроцианид калия |
| пруссат содовый красный | ферроцианид натрия |
| Рошельская соль | калия тартрат натрия |
| каменная соль | натрия хлорид |
| румяна, ювелирные | оксид железа |
| медицинский спирт | изопропиловый спирт |
| нашатырный спирт | хлорид аммония |
| содовая соляная | карбонат натрия |
| соль поваренная | натрия хлорид |
| соль лимона | биноксалат калия |
| винный камень | карбонат калия |
| селитра | нитрат калия |
| кремнезем | диоксид кремния |
| гашеная известь | гидроксид кальция |
| кальцинированная сода | карбонат натрия |
| содовая селитра | натрия нитрат |
| содовый щелок | натрия гидроксид |
| растворимое стекло | силикат натрия |
| кислая вода | разбавленная серная кислота |
| дух хартсхорна | раствор гидроксида аммония |
| соляной спирт | соляная кислота |
| винный спирт | спирт этиловый |
| спирты азотистого эфира | этилнитрат |
| сахар столовый | сахароза |
| сахар свинцовый | ацетат свинца |
| серный эфир | этиловый эфир |
| тальк или тальк | силикат магния |
| кристаллы олова | Хлорид олова |
| трона | карбонат натрия натуральный |
| негашеная известь | оксид кальция |
| Венецианский красный | оксид железа |
| вердигр | основной ацетат меди |
| Венская лайм | карбонат кальция |
| уксус | нечистая разбавленная уксусная кислота |
| витамин C | аскорбиновая кислота |
| купорос | серная кислота |
| сода стиральная | карбонат натрия |
| стакан для воды | силикат натрия |
| каустик белый | натрия гидроксид |
| белый свинец | карбонат свинца основной |
| купорос белый | кристаллы сульфата цинка |
| пруссат калийный | ферроцианид калия |
| пруссат содовый желтый | ферроцианид натрия |
| купорос цинковый | сульфат цинка |
| цинк-белый | оксид цинка |
Смотри:
Выращивание кристаллов сульфата меди
Что такое каменная соль?
Галит, более известный как каменная соль, представляет собой минерал, образованный из хлорида натрия.Его химическая формула — NaCl, и это также включает другие разновидности соли, такие как поваренная соль и поваренная соль. Промышленное название галита — каменная соль.
Он образует изометрические кристаллы и обычно бесцветный или белый, но может быть и других цветов в зависимости от количества и типа содержащихся в нем примесей. Соль встречается в пластах осадочных минералов эвапоритов. Это вызвано высыханием крупных озер и морей. Глубина этих соляных пластов может достигать сотен метров.
Кристаллы галита образуются очень быстро в некоторых быстро испаряющихся озерах. Англия была покрыта внутренними морями более 200 миллионов лет назад, что помогло создать слои соли, которые добываются сегодня. Когда очень высокие температуры в этом районе испаряли воду очень медленно, они оставляли большие солевые отложения под землей. В Великобритании, когда вода испарилась и начали образовываться кристаллы соли, они приобрели свой коричневатый цвет из-за песка, принесенного из восточных пустынь. Однако из-за других геологических факторов цвет каменной соли иногда может меняться от прозрачного, до розового, до темно-коричневого.
Большая часть каменной соли, используемой для грунтования дорог в Великобритании, поступает из шахт древних подземных соляных месторождений в Кливленде, графстве Антрим и Винсфорд. Уинсфорд находится в Чешире, а четыре из окружающих его городов — Мидлвич, Нантвич, Нортвич и Лэфтвич — исторически связаны с производством соли. «Wich» (или иногда «wych») в их названии часто ассоциируется с соляными источниками или колодцами.
Соляная ассоциация, занимающаяся торговлей производителями соли, оценивает, что соляные шахты Великобритании имеют около 225 км (140 миль) туннелей.Если вы думали, что запасы соли в ближайшее время будут исчерпаны, вы будете удивлены, узнав, что доказанные запасы соли в Великобритании обширны, с расчетной мощностью 500 лет при текущих темпах добычи.
Основное отличие каменной соли от обычной поваренной соли — это размер и цвет. Каменная соль образует очень большие массивные кристаллы, в отличие от мелких кристаллов, которые можно увидеть в поваренной соли. Как и поваренная соль, каменная соль также содержит ряд микроэлементов, которые могут влиять на ее химическое поведение.Большой размер кристаллов каменной соли означает, что ее обычно не используют в кулинарии, так как она слишком долго растворяется.
Есть и другие различия между двумя наиболее распространенными типами соли. Отложения каменной соли обычно представляют собой остатки внутренних морей, испарившихся тысячи или миллионы лет назад. Напротив, поваренная соль поступает почти исключительно из прудов-испарителей, которые удаляют соль из морской воды.
Соль: применение, эффекты и источники
Соль нужна каждому для поддержания баланса жидкости и функционирования мышц и нервов.Но мы слышали, что слишком много соли вредно для нас. Так сколько нам нужно?
Человеческое тело регулирует количество натрия в нем. Если уровень слишком высок, мы испытываем жажду и пьем, а почки ускоряют процесс избавления от него.
Слишком много натрия связано с камнями в почках, высоким кровяным давлением и сердечно-сосудистыми заболеваниями.
Слишком мало натрия может привести к гипонатриемии и симптомам головокружения, спутанности сознания, мышечных подергиваний и судорог.
Большинство американцев потребляют слишком много соли и натрия из-за большого количества обработанных, ресторанных и полуфабрикатов.Насколько далеко мы должны зайти в отказе от соли?
То, что мы называем солью, на самом деле хлорид натрия. Это 40 процентов натрия, а остальное — хлор.
Краткие сведения о соли
- Организму нужна соль, но слишком много или слишком мало соли может вызвать проблемы.
- Натрий составляет 40 процентов соли. Если на этикетке продукта указан натрий вместо соли, умножьте ответ на 2,5, чтобы получить точное представление о содержании соли.
- Большинство американцев потребляют слишком много соли, и 75 процентов ее скрыто в обработанных и упакованных продуктах.
- Американская кардиологическая ассоциация (AHA) рекомендует максимальное потребление не более 2,3 грамма (г) или 2300 миллиграммов (мг) натрия в день, или около 1 чайной ложки, а лучше не более 1500 мг.
Поделиться на Pinterest Натрий, который получают из соли, может помочь поддерживать определенные функции, но слишком большое его количество может быть вредным. Соль содержит 40 процентов натрия. На каждые 10 граммов соли, которую мы съедаем, приходится 4 грамма натрия.
Слово «соль» происходит от латинского слова «сал», означающего соль. Когда-то он был ценным товаром и использовался в качестве валюты для торговли.Английское слово «зарплата» происходит от слова «соль».
Соль издавна использовалась для ароматизации и консервирования пищевых продуктов. Он также использовался при дублении, окрашивании и отбеливании, а также в производстве керамики, мыла и хлора. Сегодня он широко используется в химической промышленности.
Обычно его подают на столе или на кухне в виде сыпучей поваренной соли, каменной соли, морской соли или кошерной соли. Высокий уровень соли или натрия скрывается в повседневных продуктах, от фаст-фуда до замороженной курицы.
Организм использует натрий для поддержания уровня жидкости. Баланс жидкости и натрия необходим для здоровья сердца, печени и почек. Он регулирует уровень жидкости в крови и предотвращает низкое кровяное давление.
Слишком мало соли
Низкий уровень натрия может возникнуть, если в организме слишком много жидкости, например, из-за задержки жидкости. В этом случае назначают диуретики, чтобы уменьшить задержку жидкости.
К другим причинам низкого содержания натрия в организме относятся:
- Болезнь Аддисона
- закупорка тонкой кишки
- диарея и рвота
- недостаточная активность щитовидной железы
- сердечная недостаточность
- употребление слишком большого количества воды
- ожоги
Если уровень натрия в крови падает, это влияет на мозговую деятельность.Человек может чувствовать себя вялым и вялым. Они могут испытывать мышечные подергивания, за которыми следуют судороги, потеря сознания, кома и смерть. Если уровень натрия падает быстро, это может произойти очень быстро.
У пожилых людей симптомы могут быть тяжелыми.
Одно исследование показало, что когда крысам не давали натрия, они избегали занятий, которые им обычно нравились. Таким образом, исследователи предположили, что натрий может действовать как антидепрессант.
Слишком много соли
Избыточное потребление натрия связано с проблемами со здоровьем, такими как остеопороз, заболевание почек и гипертония, или высокое кровяное давление, что может привести к сердечно-сосудистым заболеваниям и инсульту.
Американская кардиологическая ассоциация (AHA) объясняет, что когда в крови слишком много натрия, он «втягивает больше воды в кровоток». По мере увеличения объема крови сердцу становится все труднее перекачивать ее по телу. Со временем это может привести к растяжению стенок кровеносных сосудов, что сделает их более восприимчивыми к повреждениям.
Высокое кровяное давление также способствует накоплению бляшек в артериях, что, среди прочего, увеличивает риск инсульта и сердечных заболеваний.
AHA призывает людей потреблять больше калия при одновременном снижении потребления натрия. Считается, что калий уменьшает негативное воздействие натрия.
Было также показано, что натрий чрезмерно стимулирует иммунную систему, что предполагает связь с аутоиммунными заболеваниями, такими как волчанка, рассеянный склероз, аллергия и другие состояния.
Исследователи обнаружили, что дети, употребляющие соленую пищу, чаще употребляют с ней сладкие напитки. Комбинация может увеличить риск ожирения.
Поделиться на PinterestЗакуски с высоким содержанием соли содержат 75 процентов диетической соли. Стремитесь сократить употребление соленых и обработанных продуктов.
Соль и натрий встречаются в естественных условиях растворенными в морской воде или в виде кристаллического твердого вещества в каменной соли.
Соль, которую мы едим сегодня, в основном поступает из переработанных продуктов и полуфабрикатов в нашем рационе, но некоторые натуральные и необработанные продукты также содержат соль или натрий. Он естественным образом содержится в мясе, морепродуктах, яйцах, некоторых овощах и молочных продуктах.
Шесть самых соленых блюд в США (U.S.), согласно AHA, являются:
- хлеба и булочек
- колбас и колбас
- пиццы
- суп
- бутербродов
- птицы
Морская соль, каменная соль и кошерная соль содержат около 40 процентов натрия по весу. Они могут содержать дополнительный калий и другие минералы, но в небольших количествах. Все виды соли следует употреблять в умеренных количествах.
Сколько соли?
Средний американец в настоящее время съедает более 3400 миллиграммов (мг) или 3.4 грамма натрия каждый день. Соль на 40 процентов состоит из натрия, то есть около 8 500 мг или 8,5 г соли.
AHA и Всемирная организация здравоохранения рекомендуют не превышать суточное потребление натрия 1500 мг, или 1,5 г в день, или чуть более половины чайной ложки поваренной соли.
Людям с высоким кровяным давлением, диабетом или сердечно-сосудистыми заболеваниями следует проявлять особую бдительность и следить за тем, чтобы их потребление не превышало порогового значения в 1 500 мг.
Как выглядит 1500 мг натрия?
- одно яйцо: до 140 мг
- 230 г свежего молока: около 50 мг
- 200 г простого йогурта: 40 мг
- 200 г натурального обезжиренного йогурта: 76 мг
- 50 г сырой сельдерей: 140 мг
- 60 г вареный шпинат: 120 мг
В других овощах мало натрия, но в консервированных овощах содержится больше соли и гораздо больше натрия.
Диетологи призывают людей не добавлять дополнительную соль в пищу, потому что уже добавлено достаточно соли, если она обработана или упакована.
Младенцам в возрасте до одного года нельзя давать соль, потому что их почки еще не созрели.
Трудно измерить, сколько соли мы потребляем, поскольку она скрыта во многих продуктах питания. Более 75 процентов соли, потребляемой американцами, поступает не из солонки.
Важно проверять информацию о пищевой ценности обработанных пищевых продуктов, чтобы узнать, какие из них содержат большое и низкое содержание соли или натрия, и в чем разница между солью и натрием.
Соль на 40 процентов состоит из натрия, поэтому, если на этикетке пищевой ценности указан натрий вместо соли, вы должны умножить количество на 2,5, чтобы получить эквивалентное содержание соли. Если в 100 г пищи содержится 1 г натрия, содержание соли в этой пище будет 2,5 г.
Однако это может быть ненужным шагом, поскольку в рекомендациях по охране здоровья в качестве справочного материала используются миллиграммы натрия, а не соли.
Насколько низко «низко»?
Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США (FDA) рекомендует людям внимательно ознакомиться с заявлениями о низком содержании соли на упаковке.
Если порция содержит 1,400 мг (1,4 г) или меньше натрия на порцию, содержание соли и натрия классифицируется как «низкое».
Пища с высоким содержанием натрия — это пища, которая содержит более 20 процентов рекомендуемой суточной дозы или более 480 мг (0,48 г) на порцию.
Если пища не содержит соли или натрия, например, она может содержать до 5 мг (0,005 г) натрия на порцию. Такие термины, как «легкий» или «пониженный» натрий, не обязательно означают мало соли, но меньше соли, чем в обычном продукте на порцию.
Врачи рекомендуют избегать продуктов с высоким содержанием соли и, по возможности, выбирать продукты без добавления соли. Вы получите много соли из свежего мяса, овощей и молочных продуктов.
Странные науки: Типы солей в морской воде
Странные науки: Типы солей в морской воде | manoa.hawaii.edu/ExploringOurFluidEarth
Версия для печати
Основные дисциплинарные идеи NGSS:
Морская соль состоит из множества различных солей.Эти соли имеют разный химический состав и свойства. Если морская вода испаряется с поверхности с небольшим изгибом, разные типы соли выглядят как отдельные кольца из-за их различной растворимости.
По мере испарения морской воды соленость оставшегося раствора увеличивается. Различные соли становятся нерастворимыми при разной солености. Когда соль становится нерастворимой, она выпадает из раствора и образует кристаллы.SF На рис. 2.1 показаны некоторые из солевых колец, образовавшихся при испарении морской воды из часового стекла. Внешнее кольцо, которое первым выпало в осадок из раствора, в основном состоит из карбоната кальция (CaCO 3 ). Карбонаты — наименее растворимые соли в морской воде. Внутреннее кольцо в основном состоит из солей калия (KCl) и магния (MgCl 2 ), которые хорошо растворимы.
SF В таблице 2.1 подробно описана растворимость каждой из основных солей, которые выпадают в осадок из морской воды и показаны в кольцах SF на рис.2.1. Вкус этих солей зависит от их химического состава.
SF Таблица 2.1. Растворимость солевых соединений в морской воде.| Соединение соли | Изображение | Растворимость | Вкус |
|---|
CaCO 3
(карбонат кальция) | | Нерастворим при испарении 50%
(≈70 частей на миллион) | Мел |
CaSO 4 · H 2 O
(гипс) | | Нерастворим при испарении 80%
(≈100 частей на миллион) | Мел |
NaCl
(хлорид натрия или галит) | | Нерастворим при испарении 90%
(≈130 частей на миллион) | Соленый |
KCl и MgCl 2
(соли калия и магния) | | Нерастворим при испарении> 95%
(> 150 частей на миллион) | Соленый |
Exploring Our Fluid Earth, продукт Группы исследований и разработок учебных программ (CRDG) Педагогического колледжа.Гавайский университет, 2011 г. Этот документ можно свободно воспроизводить и распространять в некоммерческих образовательных целях.
Соль — Энциклопедия Нового Света
- О химических свойствах соли см. Хлорид натрия; для химического термина см соль (химия).
- Для использования в других целях, см Соль (значения).
Соль в основном представляет собой хлорид натрия (NaCl). Эта солонка также содержит зерна риса, которые обеспечивают физическое возбуждение и предотвращают слеживание соли.
Соль — это минерал, состоящий в основном из хлорида натрия, который обычно употребляется в пищу людьми.Существуют разные формы соли: неочищенная соль (например, морская соль), очищенная соль (поваренная соль) и йодированная соль. Это твердое кристаллическое вещество белого, бледно-розового или светло-серого цвета, обычно получаемое из морской воды или каменных отложений. Натуральная морская соль, помимо хлорида натрия, содержит жизненно важные микроэлементы. Пищевая каменная соль может быть слегка сероватой из-за содержания минералов.
Натрий и хлор, два компонента соли, необходимы для выживания всех живых существ, включая человека, но их не нужно употреблять в виде соли, поскольку они находятся вместе в очень концентрированной форме.Было обнаружено, что некоторые изолированные культуры, такие как яномами в Южной Америке, потребляют мало соли. [1] Соль участвует в регулировании содержания воды (баланса жидкости) в организме. Солевой аромат — один из основных вкусов. Тяга к соли может быть вызвана недостатком микроэлементов, а также недостатком самого хлорида натрия.
Чрезмерное потребление соли может увеличить риск проблем со здоровьем, включая высокое кровяное давление. При приготовлении пищи соль используется в качестве консерванта и приправы.
Рассол из соленой скважины доводится до чистой соли в Цзигуне, Китай
Определение
Соль в химии определяется как продукт, образующийся в результате реакции нейтрализации кислот и оснований. Соли — это ионные соединения, состоящие из катионов (положительно заряженных ионов) и анионов (отрицательных ионов), поэтому продукт является электрически нейтральным (без чистого заряда). Эти составляющие ионы могут быть неорганическими, такими как хлорид (Cl —), а также органическими, такими как ацетат (CH 3 COO —) и одноатомными ионами, такими как фторид (F —), а также многоатомными. ионы, такие как сульфат (SO 4 2-).
Есть несколько разновидностей солей. Соли, которые производят ионы гидроксида при растворении в воде, представляют собой основных солей и солей, которые производят ионы гидроксония в воде кислотных солей. Нейтральные соли — это соли, которые не являются ни кислотными, ни основными солями. Цвиттерионы содержат анионный центр и катионный центр в одной и той же молекуле, но не считаются солями. Примеры включают аминокислоты, многие метаболиты, пептиды и белки.
Когда соли растворяются в воде, они называются электролитами и способны проводить электричество — свойство, присущее расплавленным солям.Смеси многих различных ионов в растворах — например, в цитоплазме клеток, в крови, моче, растительных соках и минеральных водах — обычно не образуют определенных солей после испарения воды. Поэтому их солесодержание дано для соответствующих ионов.
Внешний вид
Поваренная соль и перец горошком.
Цвет
Соли могут быть прозрачными (хлорид натрия), непрозрачными и даже металлическими и блестящими (дисульфид железа). Во многих случаях кажущаяся непрозрачность или прозрачность связаны только с разницей в размерах отдельных монокристаллов.Поскольку свет отражается от фазовых границ, более крупные кристаллы имеют тенденцию быть прозрачными, в то время как поликристаллические агрегаты выглядят как белые порошки. Конечно, некоторые соли по своей природе непрозрачны.
Соли существуют в полном ассортименте различных цветов. Примеры:
желтый (хромат натрия),
апельсин (дихромат калия),
красный (сульфид ртути),
лиловый (гексагидрат хлорида кобальта),
синий (пентагидрат сульфата меди, гексацианоферрат железа),
зеленый (оксид никеля),
бесцветный (сульфат магния),
белый и
черный (диоксид марганца).Большинство минералов и неорганических пигментов, а также многие синтетические органические красители являются солями.
Вкус
Различные соли могут вызывать все пять основных вкусов, например, соленый (хлорид натрия), сладкий (диацетат свинца; но при проглатывании вызывает отравление свинцом), кислый (битартрат калия), горький (сульфат магния) и умами или острый ( глутамат натрия).
Запах
Соли сильных кислот и сильных оснований («сильные соли») нелетучие и не имеют запаха, в то время как соли слабых кислот или слабых оснований («слабые соли») могут пахнуть после конъюгированной кислоты (напр.грамм. ацетаты, такие как уксусная кислота (уксус), и цианиды, такие как цианистый водород (миндаль), или сопряженное основание (например, соли аммония, такие как аммиак) составляющих ионов. Это медленное частичное разложение обычно ускоряется присутствием воды, поскольку гидролиз составляет другую половину уравнения обратимой реакции образования слабых солей.
Номенклатура
Химический состав морской соли
Название соли начинается с названия катиона (например, натрия или аммония ), за которым следует название аниона (например, натрия или аммония ).g., хлорид или ацетат ). Соли часто упоминаются только по названию катиона (например, натриевая соль или аммониевая соль ) или по имени аниона (например, хлорид или ацетат ).
Формация
Соли образуются в результате химической реакции между:
Соли также могут образовываться, если растворы различных солей смешиваются, их ионы рекомбинируют, а новая соль нерастворима и выпадает в осадок (см .: равновесие растворимости).
Солеобразующие ионы
Солеобразующие катионы обыкновенные включают:
Обычные солеобразующие анионы (и названия исходных кислот в скобках) включают:
История использования поваренной соли
Консервирующие свойства соли были основой цивилизации. Он устранял зависимость от сезонной доступности пищи, позволял путешествовать на большие расстояния и был жизненно важной пищевой добавкой. Однако, поскольку соль (NaCl) было трудно достать, на протяжении всей истории она стала очень ценным предметом торговли.До 1900-х годов соль была одним из главных двигателей национальной экономики и войн. Соль часто облагалась налогом; Исследования показали, что такая практика существовала еще в ХХ веке, г. до н. э. в Китае.
Первые регистры использования соли были составлены около 4000 г. до н. Э. г. в Египте, а затем в Греции и Риме. Соль была очень ценной и использовалась для консервирования и ароматизации продуктов. В Древнем Риме соль использовалась в качестве валюты. Латинское слово salarium , означающее оплату солью, является корнем слова «зарплата».»К несчастью для тех, кому платили солью, он был легко разрушен дождем и другими погодными условиями. Платежи римским рабочим и солдатам производились солью. [2]
Финикийцы датируют свидетельства сбора твердой соли из моря Они также экспортировали его другим цивилизациям. В результате увеличения поставок соли из моря стоимость соли обесценилась. Используемый метод сбора урожая заключался в затоплении равнин морской водой, а затем оставлении равнин высыхать. После того, как вода высохла , оставшаяся соль была собрана и продана.
В Малийской империи торговцы в Тимбукту XII века — воротах в пустыню Сахара и резиденции ученых — ценили соль (NaCl) настолько, чтобы покупать ее на вес золота; Эта торговля привела к легендам о невероятно богатом городе Тимбукту и подпитывала инфляцию в Европе, которая импортировала соль. [3]
Во время протестов в Индии Мохандас Ганди совершил знаменитый соляной марш, чтобы бросить вызов британской монополии на соль.
В религии
У древних, как и у нас, «соль» (солнце) и «сал» (соль) считались необходимыми для поддержания жизни.
В Библии 35 упоминаний (стихов) о соли (версия короля Якова), наиболее известной из которых, вероятно, является история жены Лота, которая превратилась в соляной столб, когда она ослушалась ангелов и оглянулась на нечестивых. город Содом (Бытие 19:26). В Нагорной проповеди Иисус также назвал своих последователей «солью земли». Апостол Павел также призывал христиан «пусть ваш разговор всегда будет благодатным, приправленным солью» (Колоссянам 4: 6), чтобы, когда другие спрашивают об их верованиях, ответ христианина вызывает «жажду» узнать больше о Христе.Соль является обязательной в обряде Тридентской мессы. Соль используется в третьем пункте (который включает в себя экзорцизм) кельтского освящения (см. Галликанский обряд), который используется при освящении церкви. Соль можно добавлять в воду «там, где это принято» в римско-католическом обряде святой воды. Самое раннее библейское упоминание о соли, по-видимому, относится к разрушению Содома и Гоморры (Бытие, XIX, 24-26), когда царь Авимелех разрушил город Сихем, что, как считается, произошло в тринадцатом веке в году до нашей эры.В году н. Э. Он, как говорят, «посыпал его солью», и эта фраза выражает полноту его разорения. (Судьи ix. 45.)
В исконной японской религии синто соль используется для ритуального очищения людей и мест, например, в борьбе сумо.
В ацтекской мифологии Хуикстоциуатль была богиней плодородия, правившей соленой и соленой водой.
Формы соли
Соль нерафинированная
Различные природные соли имеют разную минеральность, что придает каждой из них уникальный вкус.Fleur de sel, натуральная морская соль, собранная вручную, обладает уникальным вкусом, который варьируется от региона к региону.
Некоторые утверждают, что нерафинированная морская соль более полезна, чем рафинированная. [4] Однако полностью сырая морская соль горькая из-за соединений магния и кальция, поэтому ее редко едят. Другие люди думают, что сырая морская и каменная соли не содержат достаточного количества солей йода для предотвращения йододефицитных заболеваний, таких как гипотиреоз. [5]
Соль рафинированная
Рафинированная соль, которая в настоящее время наиболее широко используется, в основном представляет собой хлорид натрия.Пищевая соль составляет лишь небольшую часть производства соли в промышленно развитых странах (3% в Европе [6] ), хотя во всем мире на пищевые продукты приходится 17,5% производства соли [7] . Большинство из них продается для промышленного использования, от производства целлюлозы и бумаги до окрашивания тканей и тканей, производства мыла и моющих средств, и имеет большую коммерческую ценность.
Соляные курганы в Боливии. Соль собирают традиционным способом.
Производство и использование соли — одно из старейших предприятий химической промышленности. [8] Соль также получают путем испарения морской воды, обычно в неглубоких бассейнах, нагретых солнечным светом; [9] Полученная таким образом соль раньше называлась заливной солью, а теперь ее часто называют морской солью или солнечной солью. Рафинированную соль также получают из каменной соли: минеральные отложения с высоким содержанием соли. Эти отложения каменной соли образовались в результате испарения древних соленых озер. [10] Эти месторождения можно добывать традиционным способом или путем закачки воды. Закачиваемая вода растворяет соль, и рассол можно перекачивать на поверхность, где собирается соль.
После получения сырой соли ее очищают и улучшают характеристики хранения и обращения с ней. Очистка обычно включает перекристаллизацию. При перекристаллизации рассол обрабатывают химическими веществами, которые осаждают большинство примесей (в основном соли магния и кальция). [11] Затем используются несколько стадий испарения для сбора чистых кристаллов хлорида натрия, которые сушат в печи.
С 1950-х годов в рассол обычно добавляли следы гексацианоферрата натрия II, который действует как антислеживающий агент, способствуя образованию кристаллов неправильной формы. [12] Другие агенты против слеживания (и йодид калия для йодированной соли) могут быть добавлены после кристаллизации. Эти вещества представляют собой гигроскопичные химические вещества, которые поглощают влагу, предотвращая слипание кристаллов соли. Некоторые используемые противослеживающие агенты представляют собой трикальцийфосфат, карбонаты кальция или магния, соли жирных кислот (кислотные соли), оксид магния, диоксид кремния, силикат кальция, алюмосиликат натрия и алюмосиликат алюминия. Высказывались опасения относительно возможных токсических эффектов алюминия в последних двух соединениях, однако и Европейский Союз, и Управление по контролю за продуктами и лекарствами США (FDA) разрешают их использование. [13] Очищенная соль готова для упаковки и распределения.
Соль поваренная
Пакетики соли на одну порцию
Поваренная соль — это очищенная соль, 99% хлорида натрия. [14] [15] Обычно содержит вещества, придающие ему сыпучесть (антислеживатели), такие как силикоалюминат натрия или карбонат магния. Обычно в солонки кладут несколько зерен сырого риса, чтобы впитать лишнюю влагу, когда средств против слеживания недостаточно.
Соль йодированная
Йодированная соль (BrE: йодированная соль ), поваренная соль, смешанная с незначительным количеством йодида натрия, йодата или иногда йодида калия, используется для снижения вероятности дефицита йода у людей. Дефицит йода обычно приводит к проблемам со щитовидной железой, особенно к эндемическому зобу. Эндемический зоб — это заболевание, характеризующееся опухолью щитовидной железы, которая обычно приводит к выпячиванию на шее. Хотя для предотвращения зоба в диете требуется лишь небольшое количество йода, Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США рекомендует (21 CFR 101.9 (c) (8) (iv)) 150 микрограммов йода в день как для мужчин, так и для женщин, и есть много мест по всему миру, где естественный уровень йода в почве низкий, а йод не усваивается овощами. .
Сегодня йодированная соль более распространена в США, Австралии и Новой Зеландии, чем в Великобритании.
Поваренная соль также часто йодируется — небольшое количество йодида калия (в США) или йодата калия (в ЕС) добавляется в качестве важной пищевой добавки. Поваренная соль в основном используется в кулинарии и в качестве столовой приправы.Йодированная поваренная соль значительно снизила уровень йодной недостаточности в странах, где она используется. [16] Йод важен для предотвращения недостаточной выработки гормонов щитовидной железы (гипотиреоз), которые могут вызывать зоб, кретинизм у детей и микседему у взрослых.
Соль фторированная
В некоторых европейских странах, где фторирование питьевой воды не практикуется, доступна фторированная поваренная соль. Во Франции 35 процентов продаваемой поваренной соли содержат фторид натрия или калия. [17] Еще одна добавка, особенно важная для беременных, — фолиевая кислота (витамин B), придающая поваренной соли желтый цвет.
Приправы соленые
Во многих азиатских культурах поваренная соль традиционно не используется в качестве приправы. [18] Однако такие приправы, как соевый соус, рыбный соус и устричный соус, как правило, имеют высокое содержание соли и выполняют почти ту же роль, что и столовая приправа, обеспечивающая соль, которую поваренная соль служит в западных культурах.
Влияние потребления соли на здоровье
Натрий — один из основных электролитов в организме.Все три электролита (натрий, калий и кальций) доступны в виде нерафинированной соли, как и другие жизненно важные минералы, необходимые для оптимального функционирования организма. Слишком много или слишком мало соли в рационе может привести к мышечным спазмам, головокружению или даже нарушению электролитного баланса, что может вызвать серьезные, даже фатальные, неврологические проблемы. [19] Употребление слишком большого количества воды с недостаточным потреблением соли подвергает человека риску отравления водой. Соль даже иногда используется как лечебное средство, например, при лечении дизавтономии. [20]
Риск людей заболеть из-за слишком низкого или слишком высокого потребления соли варьируется в зависимости от биохимической индивидуальности. Некоторые утверждали, что, хотя риски употребления слишком большого количества соли реальны, риски для большинства людей преувеличены или что исследования, проведенные по потреблению соли, можно интерпретировать по-разному. [21] [22]
Избыточное потребление соли связано с:
- астма, вызванная физической нагрузкой. [23] С другой стороны, другой источник утверждает: «… мы до сих пор не знаем, способствует ли соль развитию астмы. Если есть связь, значит, она очень слабая…». [24]
- изжога [25] .
- Остеопороз: один отчет показывает, что диета с высоким содержанием соли действительно снижает плотность костей у девочек. [26] . Тем не менее, «несмотря на то, что высокое потребление соли было связано с пагубным воздействием на здоровье костей, данных для окончательных выводов недостаточно». ( [27] , p3)
- Рак желудка (рак желудка) связан с высоким уровнем натрия, «но доказательства, как правило, не относятся к продуктам, обычно потребляемым в Великобритании.»( [28] ) Однако в Японии потребление соли выше. [29]
- гипертония (высокое кровяное давление): «С 1994 года данные о связи между потреблением соли с пищей и кровяным давлением увеличились. Данные были согласованы в различных исследуемых популяциях и во всем возрастном диапазоне взрослых». ( [30] ). «Директор по здравоохранению [главный врач] Англии в своем годовом отчете (DH, 2001) подчеркнул, что у людей с высоким кровяным давлением вероятность развития сердечных заболеваний и инсульта в три раза выше, а вероятность смерти от этих заболеваний в два раза выше, чем у те с нормальным уровнем.»( [31] ). Одно исследование показало, что низкий уровень натрия в моче связан с повышенным риском инфаркта миокарда у леченных гипертоников [32] .
- Гипертрофия левого желудочка (увеличение сердца): «Данные свидетельствуют о том, что высокое потребление соли вызывает гипертрофию левого желудочка, сильный фактор риска сердечно-сосудистых заболеваний, независимо от влияния артериального давления». ( [33] ) «… накапливаются доказательства того, что высокое потребление соли предсказывает гипертрофию левого желудочка.»( [34] ) Чрезмерное потребление соли (натрия) в сочетании с недостаточным потреблением воды может вызвать гипернатриемию. Это может усугубить заболевание почек. [35]
- отек (BE: отек): для лечения отеков было предложено уменьшение потребления соли (BE: отек) (задержка жидкости). [36]
- язвы двенадцатиперстной кишки и желудка [37]
Крупномасштабное исследование, проведенное Нэнси Кук и соавт. показывает, что у людей с [38] артериальным давлением, которые значительно снизили количество соли в своем рационе, снизились шансы на развитие сердечно-сосудистых заболеваний на 25 процентов в течение следующих 10-15 лет.Их риск смерти от сердечно-сосудистых заболеваний снизился на 20 процентов. [39] [40]
Рекомендуемая доза
Морская соль и перец горошком.
Соляная мельница для морской соли.
В этом разделе обобщается потребление соли, рекомендованное учреждениями здравоохранения различных стран. Рекомендации обычно похожи. Обратите внимание, что цели для населения в целом имеют тенденцию быть прагматичными (что достижимо), в то время как рекомендации для отдельного человека идеальны (что лучше для здоровья).Например, в Великобритании цель для населения — «съедать не более 6 г в день», а для человека — 4 г.
Потребление может быть выражено по-разному в виде соли или натрия и в различных единицах.
- 1 г натрия = 1000 мг натрия = 42 ммоль натрия = 2,5 г соли
Соединенное Королевство : В 2003 году Научный консультативный комитет Великобритании по питанию (SACN) рекомендовал для типичного взрослого человека рекомендуемую норму потребления питательных веществ. составляет 4 г соли в день (1,6 г или 70 ммоль натрия).Однако среднее потребление натрия взрослым в два с половиной раза превышает референсное потребление натрия. «Хотя точных данных о детях нет, консервативные оценки показывают, что в пересчете на массу тела среднее потребление соли детьми выше, чем у взрослых». SACN нацелен на достижимое целевое снижение среднего потребления соли до 6 г в день (2,4 г или 100 ммоль натрия) — это примерно эквивалентно чайной ложке соли. Рекомендации SACN для детей:
- 0–6 месяцев: менее 1 г / день
- 7–12 месяцев: 1 г / день
- 1-3 года: 2 г / день
- 4–6 лет: 3 г / день
- 7–10 лет: 5 г / день
- 11–14 лет: 6 г / день
SACN заявляет: «Целевое потребление соли, установленное для взрослых и детей, не является идеальным или оптимальным уровнем потребления, но представляет собой достижимые цели для населения.« [41]
Республика Ирландия : Управление по безопасности пищевых продуктов Ирландии поддерживает цели Соединенного Королевства», подчеркивая, что рекомендуемая суточная норма 1,6 г натрия (4 г соли) должна лечь в основу рекомендаций, предназначенных для отдельных лиц: отличается от целевого показателя здоровья населения, предполагающего среднее потребление соли 6 г в день »( [42] ).
Канада : Министерство здравоохранения Канады рекомендует адекватное потребление (AI) и верхний предел (UL) с точки зрения натрия .
- 0–6 месяцев: 0.12 г / день (AI)
- 7–12 месяцев: 0,37 г / день (AI)
- 1-3 года: 1 г / день (AI) 1,5 г / день (UL)
- 4–8 лет: 1,2 / день (AI) 1,9 г / день (UL)
- 9–13 лет: 1,5 г / день (AI) 2,2 г / день (UL)
- 14–50 лет: 1,5 г / день (AI) 2,3 г / день (UL)
- 51–70 лет: 1,3 г / день (AI) 2,3 г / день (UL)
- 70 лет и старше: 1,2 г / день (AI) 2,3 г / день (UL) [43]
Новая Зеландия
- Достаточное потребление (AI) 0.46 — 0,92 г натрия = 1,2 — 2,3 г соли
- Верхний предел (UL)) 2,3 г натрия = 5,8 г соли
Австралия : Рекомендуемая доза с пищей (RDI) составляет 0,92–2,3 г натрия в день (= 2,3–5,8 г соли) [44]
США : Само Управление по санитарному надзору за качеством пищевых продуктов и медикаментов не дает рекомендации [45] , но отсылает читателей к Диетические рекомендации для американцев 2005 . Они предполагают, что граждане США должны потреблять менее 2300 мг натрия (= 2.3 г натрия = 5,8 г соли) в сутки. [46]
Маркировка
Великобритания: Агентство по пищевым стандартам определяет уровень соли в пищевых продуктах следующим образом: «Высокий — более 1,5 г соли на 100 г (или 0,6 г натрия). Низкий — 0,3 г соли или менее на 100 г (или 0,1 г натрия). Если количество соли на 100 г находится между этими цифрами, значит, это средний уровень соли ». В Великобритании продукты, производимые некоторыми супермаркетами и производителями, имеют на передней части упаковки цвета «светофора»: красный (высокий), янтарный (средний) или зеленый (низкий). [47]
США: Руководство FDA по маркировке пищевых продуктов определяет, может ли продукт быть помечен как «свободный», «с низким содержанием» или «с пониженным / меньшим содержанием натрия». Когда о продукте питания делаются другие заявления о пользе для здоровья (например, с низким содержанием жира, калорий и т. Д.), Требуется заявление о раскрытии информации, если продукт превышает 480 мг натрия на «порцию». [48]
Кампании
В 2004 году Британское агентство по пищевым стандартам начало кампанию в области общественного здравоохранения под названием «Соль — следите за ней», которая рекомендует употреблять не более 6 г соли в день; В нем присутствует персонаж по имени Сид Слизень, который подвергся критике со стороны Ассоциации производителей соли (SMA). [49] Управление по стандартам рекламы не поддержало жалобу SMA в своем решении. [50] .
Исследовательский институт Мензиса в Тасмании, Австралия, поддерживает веб-сайт [51] , посвященный информированию людей о потенциальных проблемах соленой диеты.
Заменители соли
Потребление соли можно уменьшить, просто уменьшив количество соленой пищи в рационе, не прибегая к заменителям соли. Заменители соли имеют вкус, похожий на поваренную соль, и содержат в основном хлорид калия, который увеличивает потребление калия.Избыточное потребление калия может вызвать гиперкалиемию. Различные заболевания и лекарства могут снизить выведение калия организмом, тем самым увеличивая риск гиперкалиемии. Если у вас почечная недостаточность, сердечная недостаточность или диабет, обратитесь за медицинской помощью, прежде чем использовать заменитель соли. Производитель LoSalt выпустил консультативное заявление [52] о том, что люди, принимающие следующие рецептурные препараты, не должны использовать заменители соли: амилорид, триамтерен, Dytac, спиронолактон, альдактон, эплеренон и Inspra.
Производственные тенденции
Соль получают путем испарения морской воды или рассола из других источников, таких как рассольные скважины и соленые озера, а также путем добычи каменной соли , называемой галитом. В 2002 году общее мировое производство оценивалось в 210 миллионов метрических тонн, в первую пятерку производителей входили США (40,3 миллиона метрических тонн), Китай (32,9), Германия (17,7), Индия (14,5) и Канада (12,3). . [53] Обратите внимание, что эти цифры относятся не только к поваренной соли, но и к хлориду натрия в целом.
См. Также
Судно загружает соль с терминала.
- Электролит
- Галогенид
- Натрия хлорид
- Соль морская
- История соли
- Fleur de sel
- Лечение (консервирование)
- Кислотная соль
- Щелочные соли
- Соль пищевая
- Ионные связи
- Кошерная соль
- Натрон
- Старый соляной путь
- Соль дорожная
- Засоление земли — это преднамеренное массовое использование соли для того, чтобы сделать почву непригодной для возделывания и, таким образом, препятствовать обитанию.
- Натрий
- Соль поваренная
- Цвиттерион
- Соленость
- гипертония
Примечания
- ↑ Индейцы яномами в исследовании INTERSALT. Проверено 28 июля 2007 года.
- ↑ Дэвид Блох, Экономика NaCl: Соль заставила мир вращаться. www.salt.org . Проверено 28 июля 2007 года.
- ↑ Дженис Макдональд. Совершите путешествие в Тимбукту. CNN News. Проверено 28 июля 2007 г.
- ↑ Сьюзан Диринг.Морская соль полезна и производится в Колиме! Проверено 28 июля 2007 года.
- ↑ Йод в не йодированной морской соли. Институт соли . Проверено 28 июля 2007 года.
- ↑ Соль и ее применение. Европейская ассоциация производителей соли . Проверено 28 июля 2007 года.
- ↑ Производство соли в Азии быстро увеличивалось с 2003 года. Roskill Information Services . Проверено 28 июля 2007 года.
- ↑ Археология Salt.org . Проверено 28 июля 2007 года.
- ↑ ЗАДАНИЕ ТРЕТЬЕ — ВОДНЫЙ ЦИКЛ Nauticus — Weather Curriculum . Проверено 28 июля 2007 года.
- ↑ Что такое соль ?. Ассоциация производителей соли Великобритании . Проверено 28 июля 2007 года.
- ↑ О соли: Производство. Ассоциация производителей соли . Проверено 30 июля 2007 года.
- ↑ Соль и химическая революция: 8 Производство соли в 20 веке. Ассоциация производителей соли . Проверено 30 июля 2007 года.
- ↑ Дэниэлс Берджесс, Вилелла Дэниэлс и Мейсон, Эйприл С. Что это за химические вещества в моей пище? Университет Пердью, Кооперативная служба распространения знаний . Проверено 30 июля 2007 года.
- ↑ Анализ питания столовой соли Tesco от Tesco Stores Ltd (Великобритания) показывает 38,9% натрия по весу, что соответствует 98,9% хлорида натрия.
- ↑ Солевые продукты — Столовая соль. WA Запасы соли . Проверено 30 июля 2007 года.
- ↑ Йодированная соль Институт соли .Проверено 30 июля 2007 года.
- ↑ [1] Оценка рисков для здоровья от несоблюдения параметров питьевой воды
значения. AFSSA . Проверено 30 июля 2007 года.
- ↑ Мэтью Амстер-Бертон. 2001. Соль Юго-Восточной Азии. Сиэтл Таймс . Проверено 30 июля 2007 года.
- ↑ Соль. Австралия: канал «Лучшее здоровье» (Австралия, Виктория) . Проверено 30 июля 2007 года.
- ↑ Dysautonomia. Медицинский информационный центр клиники Кливленда .Проверено 30 июля 2007 года.
- ↑ Соль и другие раны. Почему файлы, статья . Проверено 30 июля 2007 года.
- ↑ Гэри Таубс. 1998. (Политическая) наука о соли, Science 281 (14 августа 1998 г.) (5379): 898 — 907. Проверено 30 июля 2007 г.
- ↑ Трейси Джеймс. 2003. Астма, вызванная физическими упражнениями, более четко связана с диетой с высоким содержанием соли. Домашние страницы IU . Проверено 30 июля 2007 года.
- ↑ Д-р Триша Макнейр, «Ухудшает ли употребление соли астму?» BBC Health .Проверено 30 июля 2007 года.
- ↑ Исследование добавляет соли к подозреваемым триггерам изжоги Все . Проверено 30 июля 2007 года.
- ↑ Высокосолевая диета снижает плотность костей у девочек. Food Navigator . Проверено 30 июля 2007 года.
- ↑ Соль и здоровье. Научно-консультативный комитет по питанию (SACN) . Проверено 30 июля 2007 года.
- ↑ Там же, 18
- ↑ Соль повышает «риск рака желудка». BBC News . Проверено 30 июля 2007 года.
- ↑ САКН, 3
- ↑ Там же, 14
- ↑ Майкл Х. Олдерман, Шанта Мадхаван, Хиллель Коэн, Жан Э. Сили и Джон Х. Лараг, 1992. Низкий уровень натрия в моче ассоциируется с повышенным риском инфаркта миокарда у леченных гипертоников Гипертония 25 (1995): 1144 -1152. Проверено 30 июля 2007 года.
- ↑ SACN 3
- ↑ Соль и здоровье: Обзор научных данных и рекомендаций для государственной политики в Ирландии Управление по безопасности пищевых продуктов Ирландии .Проверено 30 июля 2007 года.
- ↑ унция
- ↑ Задержка жидкости Австралия: Better Health Channel (Австралия, Виктория) . Проверено 30 июля 2007 года.
- ↑ Связь высокосолевой диеты с риском развития язвы. BBC . Проверено 30 июля 2007 года.
- ↑ [http://www.vaughns-1-pagers.com/medicine/blood-pressure.htm График артериального давления
]. Вонз . Проверено 30 июля 2007 года.
- ↑ Режущая соль «снижает риск сердечного приступа». BBC News . Проверено 30 июля 2007 года.
- ↑ Употребление меньшего количества соли может предотвратить сердечно-сосудистые заболевания Eurikalert . Проверено 30 июля 2007 года.
- ↑ SACN
- ↑ фсай, 16
- ↑ Рекомендуемая диета (ищите натрий) Health Canada . Проверено 2 августа 2007 года.
- ↑ Salt Better Health Channel (Австралия, Виктория) . Проверено 2 августа 2007 года.
- ↑ Немного споров вызывает диетическую соль Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США .Проверено 2 августа 2007 года.
- ↑ «Натрий и калий» Министерство здравоохранения и социальных служб (HHS) и Министерство сельского хозяйства (USDA) . Проверено 2 августа 2007 года.
- ↑ Что такое этикетки Агентство пищевых стандартов . Проверено 2 августа 2007 года.
- ↑ Руководство по маркировке пищевых продуктов — Приложение A Управление по санитарному надзору за качеством пищевых продуктов и медикаментов . Проверено 2 августа 2007 года.
- ↑ Новая соляная кампания под ударом Пресс-релиз Ассоциации производителей соли .Проверено 2 августа 2007 года.
- ↑ Судебные решения по вещательной рекламе: 20 апреля 2005 г. Управление по стандартам в области рекламы . Проверено 2 августа 2007 года.
- ↑ Salt Matters Исследовательский институт Мензиса . Проверено 2 августа 2007 года.
- ↑ Информационное сообщение LoSalt . Проверено 2 августа 2007 года.
- ↑ Сьюзен Р. Фельдман. Натрия хлорид. John Wiley & Sons, Inc., опубликовано в Интернете 2005 . Хлорид натрия Кирк-Отмер Энциклопедия химической технологии .Проверено 2 августа 2007 года.
Список литературы
- Курланский, Марк. 2002. Соль: Всемирная история. Нью-Йорк, Нью-Йорк: Уолкер Паблишинг Компани. ISBN 0142001619.
- __________. и С. Д. Шиндлер. 2006. История соли. Нью-Йорк, Нью-Йорк: G.P. Сыновья Патнэма. ISBN 0399239987 — детская книга о соли.
- Ласло, Пьер. 2002. Соль: зерно жизни. Искусство и традиции стола. Нью-Йорк, Нью-Йорк: издательство Колумбийского университета, 2001.ISBN 0060084685.
- Великобритания: Министерство здравоохранения, Диетические справочные значения пищевой энергии и питательных веществ для Великобритании: Отчет Группы по DRV Комитета по медицинским аспектам пищевой политики. Канцелярия.
Внешние ссылки
Все ссылки получены 31 августа 2019 г.
Кредиты
Энциклопедия Нового Света Писатели и редакторы переписали и завершили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних публикаций википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в Энциклопедия Нового Света :
Примечание. Некоторые ограничения могут применяться к использованию отдельных изображений, на которые распространяется отдельная лицензия.
Свойства соли — The Salt Association
Соль — химическое соединение с рядом интересных свойств:
- Кристаллы или белый кристаллический порошок.
- Прозрачный и бесцветный в кристаллической форме, похожий на лед.
- Кристаллизуется в изометрической системе, обычно в форме кубов.
- Растворим в воде (35,6 г / 100 г при 0 ° C и 39,2 г / 100 г при 100 °).
- Слабо растворим в спирте, но не растворим в концентрированной соляной кислоте.
- Плавится при 801 ° C и начинает испаряться при температурах чуть выше этой точки кипения 1413 ° C.
- Твердость 2,5 по шкале твердости MOH.
- Удельный вес 2,165.
- Негорючие — низкая токсичность.
- Гигроскопичен — впитывает влагу из влажной атмосферы с относительной влажностью выше 75% — ниже этого она высыхает.
В натуральном виде соль часто содержит следы хлорида магния, сульфата магния, бромида магния и других.Эти примеси могут окрашивать прозрачные кристаллы в желтый, красный, синий или фиолетовый цвет.
Химикаты из соли
При пропускании электрического тока через крепкий раствор соли в воде происходит электролиз и образуются три продукта:
- Хлор (Cl 2 )
- Гидроксид натрия (NaOH)
- Водород (H 2 ).

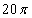 рад/с. Найдите число оборотов за 10 минут.
рад/с. Найдите число оборотов за 10 минут.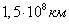
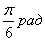 . Определить линейную скорость (м/с) шарика, если его период 0,5с,
. Определить линейную скорость (м/с) шарика, если его период 0,5с, 
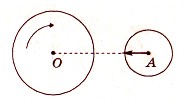
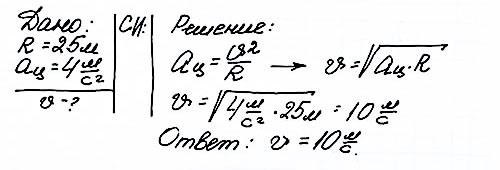
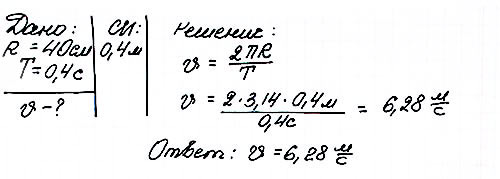


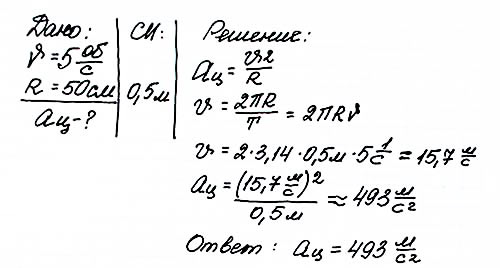
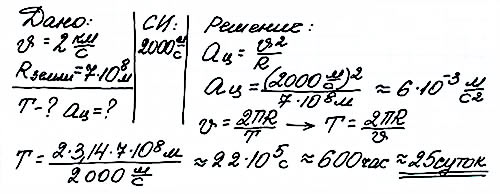
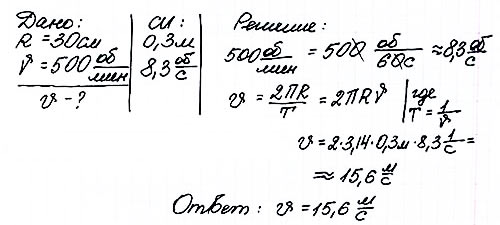

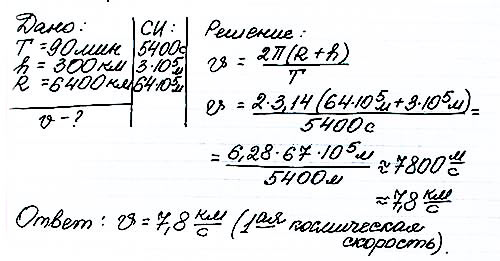



 , если бы Земля вращалась вокруг Солнца в противоположном направлении? Ответ дать в сутках, округлив до целых. Считать, что сейчас год длится ровно
, если бы Земля вращалась вокруг Солнца в противоположном направлении? Ответ дать в сутках, округлив до целых. Считать, что сейчас год длится ровно  дней.
дней. вокруг Солнца
вокруг Солнца  год). Рассмотрим точку
год). Рассмотрим точку  на экваторе Земли, которая в свою очередь вращается вокруг земной оси с угловой скоростью
на экваторе Земли, которая в свою очередь вращается вокруг земной оси с угловой скоростью  . Назовем земными сутками интервал времени между двумя последовательными положениями Солнца, например, в зените.
. Назовем земными сутками интервал времени между двумя последовательными положениями Солнца, например, в зените. . Угол, на который сместилась Земля относительно Солнца, будет равен
. Угол, на который сместилась Земля относительно Солнца, будет равен  . В этом случае длительность суток будет
. В этом случае длительность суток будет![Rendered by QuickLaTeX.com \[\frac{T}{N_2}=\frac{2\pi-\frac{2\pi}{N_2}}{\omega}.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8f9281875897c14dd7584f4d83295dda_l3.png)

![Rendered by QuickLaTeX.com \[\frac{T}{N_1}=\frac{2\pi+\frac{2\pi}{N_1}}{\omega}.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2bb7cade95bf9b13e041392ca7167ab1_l3.png)
![Rendered by QuickLaTeX.com \[\frac{N_2}{N_1}=\frac{2\pi+\frac{2\pi}{N_1}}{2\pi-\frac{2\pi}{N_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-32748289be48332bc050a6609fdb4d9e_l3.png)
![Rendered by QuickLaTeX.com \[2\pi N_2-2\pi=2\pi N_1+2\pi\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5fe93d0dbb9f0be493de16b1c28a791c_l3.png)
 , то есть число дней в «длинном» году станет 367.
, то есть число дней в «длинном» году станет 367. см/с, а скорость точки
см/с, а скорость точки  , находящейся на
, находящейся на  см ближе к оси диска, равна
см ближе к оси диска, равна  см/с. Определите период вращения диска. Ответ дать в секундах. Округлить до сотых.
см/с. Определите период вращения диска. Ответ дать в секундах. Округлить до сотых. . Тогда можно записать линейные скорости точек через угловую скорость и радиусы:
. Тогда можно записать линейные скорости точек через угловую скорость и радиусы:![Rendered by QuickLaTeX.com \[\upsilon _1=\omega(L+x)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6005a9ea532d209f880895a3e8c117e2_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon _2=\omega x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1e13619217be935d0e8a7fa9f7b0ffa8_l3.png)
 . Подставив период
. Подставив период  , получаем
, получаем![Rendered by QuickLaTeX.com \[T=\frac{2\pi L}{ \upsilon _1-\upsilon _2}=6,28 c.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-066cac533dafb5196ccb2bd70f3cdb13_l3.png)
 м, в вертикальной плоскости с частотой
м, в вертикальной плоскости с частотой  Гц. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх? Ответ дать в метрах, округлив до десятых. Ускорение свободного падения
Гц. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх? Ответ дать в метрах, округлив до десятых. Ускорение свободного падения  м/c
м/c .
.![Rendered by QuickLaTeX.com \[V_0=\frac{2\pi \cdot l}{T}=2\pi \cdot l\cdot \nu\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-199b51d1015cf665c3b9bc56e547f505_l3.png)
![Rendered by QuickLaTeX.com \[H=\frac{\upsilon^2-\upsilon_0^2}{-2g}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2080be9d8c82016b5746b9412470da4c_l3.png)
 получаем
получаем![Rendered by QuickLaTeX.com \[H=\frac{\upsilon_0^2}{2g}=\frac{2\pi^2\cdot \nu^2\cdot l^2}{g}\approx 4,4.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-612d302669a33b8af405dd1310d4b660_l3.png)
 об/мин. После выключения вращение происходит равнозамедленно, причём вентилятор делает до остановки
об/мин. После выключения вращение происходит равнозамедленно, причём вентилятор делает до остановки  оборотов. Сколько времени прошло с момента выключения вентилятора до полной его остановки? Ответ дать в секундах, округлив до целых.
оборотов. Сколько времени прошло с момента выключения вентилятора до полной его остановки? Ответ дать в секундах, округлив до целых.![Rendered by QuickLaTeX.com \[\upsilon_{cp}=\frac{N}{t}.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e0bbb6ef0033d93d5fd5bd608b6a0e46_l3.png)
 – начальная скорость,
– начальная скорость,  – конечная скорость)
– конечная скорость)![Rendered by QuickLaTeX.com \[\upsilon_{cp}=\frac{\upsilon_1+\upsilon_2}{2}=\frac{\upsilon_0}{2},\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-97f92562453934712183530c7a78eafb_l3.png)
 , получим, что
, получим, что![Rendered by QuickLaTeX.com \[t=\frac{2N}{\upsilon_0}=10\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9ac82bc9738c683f7b50913eff227f35_l3.png)
 м друг от друга. Ближайший к центру виража самолет движется по окружности
м друг от друга. Ближайший к центру виража самолет движется по окружности  м. Средний самолет движется со скоростью
м. Средний самолет движется со скоростью  км/ч. Найти ускорение самолета, летящего по внешней траектории. Ответ дать в м/c
км/ч. Найти ускорение самолета, летящего по внешней траектории. Ответ дать в м/c , округлив до целых.
, округлив до целых.![Rendered by QuickLaTeX.com \[\omega=\frac{\upsilon^2}{R+s}.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-28e34c385e644dd1d28603566607949c_l3.png)
![Rendered by QuickLaTeX.com \[a=\omega^2(R+2s)=\frac{\upsilon^2(R+2s)}{(R+2s)^2}=15.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-274a1fc29d17e775ef81231f4bd4383a_l3.png)



![Период и частота Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности. Единица измерения периода - секунда Частота вращения n – число полных оборотов в единицу времени. Единица измерения частоты [n ] = с -1 = Гц.](/800/600/https/fsd.multiurok.ru/html/2017/12/11/s_5a2ecd8e0eeeb/img3.jpg)











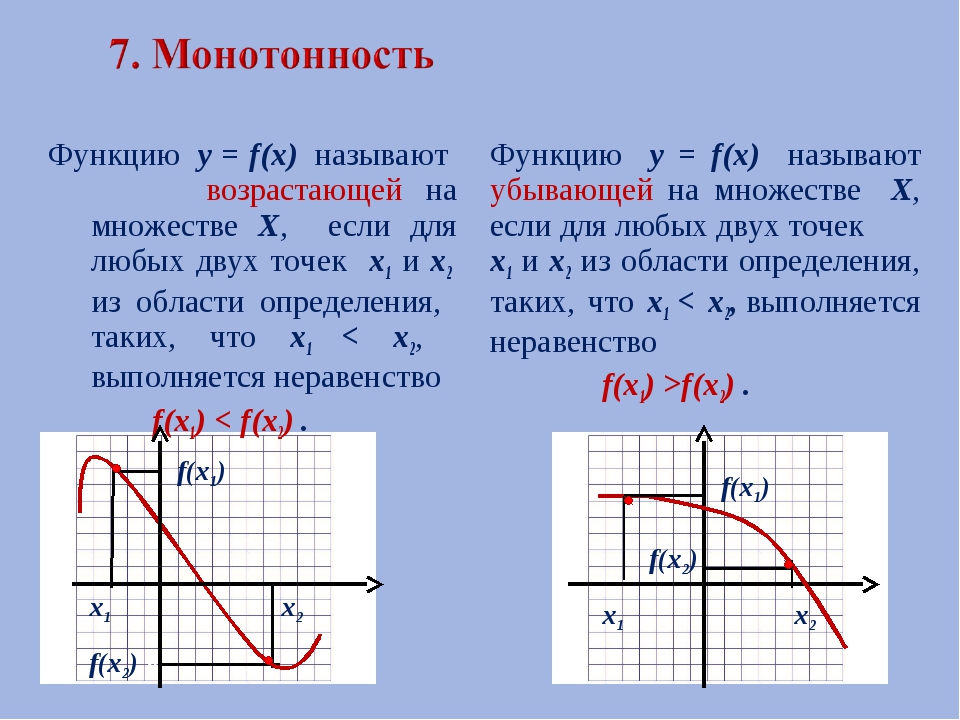
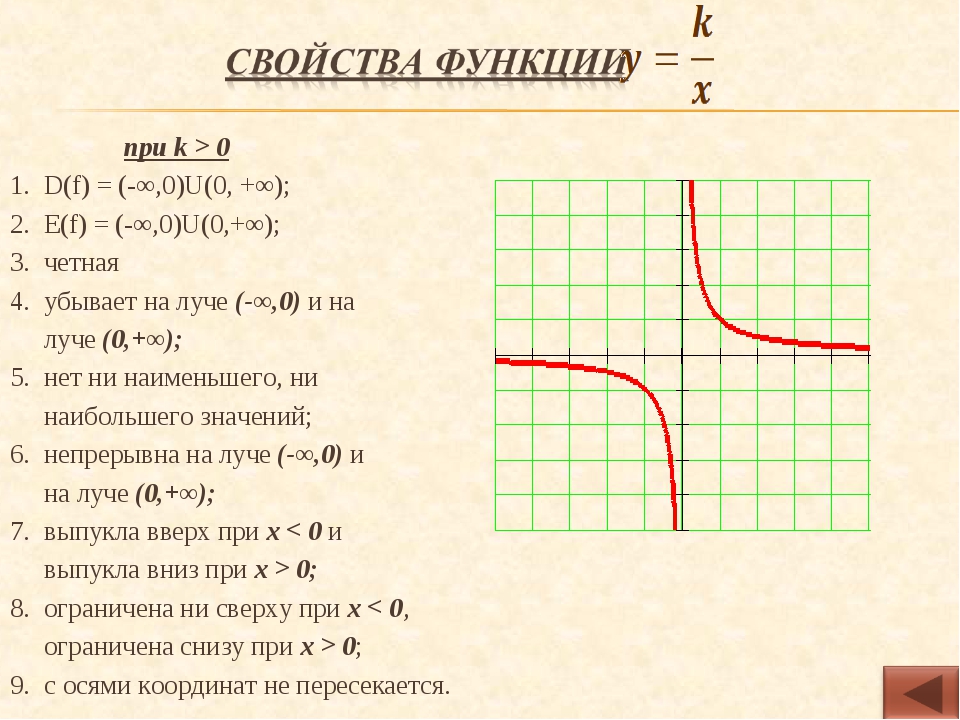 Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.
Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.

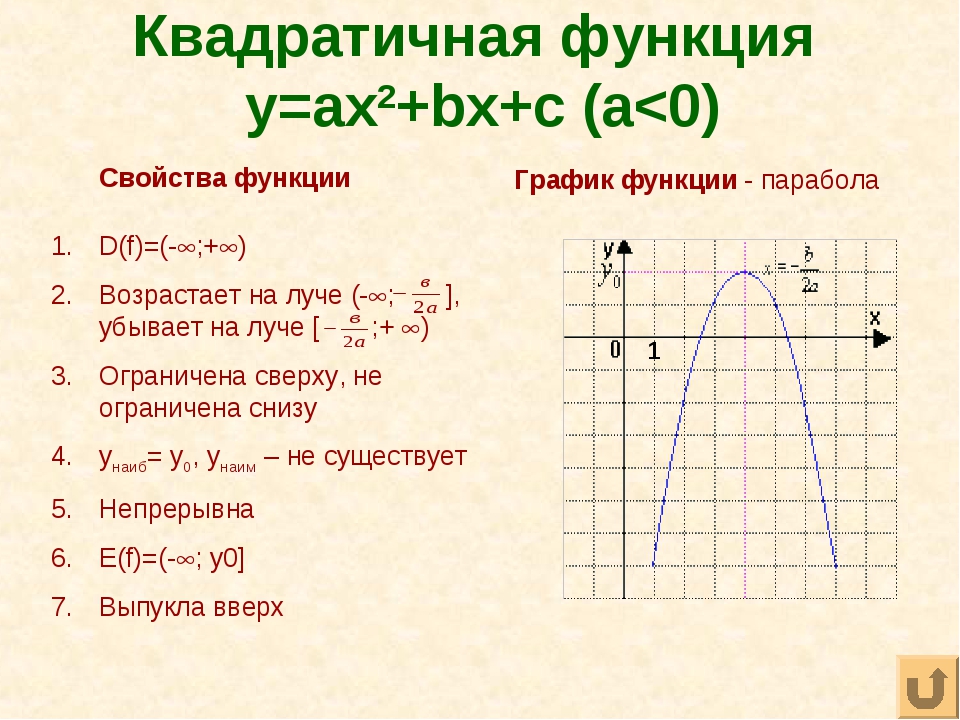
 Карточки 8
вариантов (Приложение №1).
Карточки 8
вариантов (Приложение №1). Постройте
график функции, если известно, что она а)
чётная б) нечётная
Постройте
график функции, если известно, что она а)
чётная б) нечётная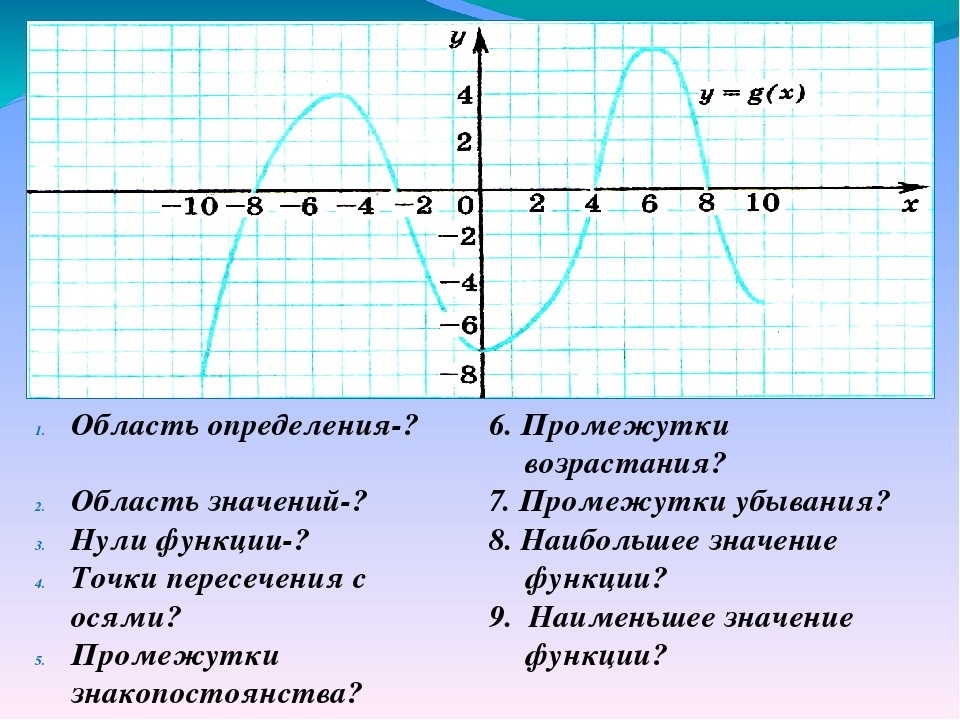

 ..10 Основные свойства функций…11 Четность и нечетность…11 Периодичность…12 Нули функции…12 Монотонность (возрастание, убывание)…13 Экстремумы (максимумы
..10 Основные свойства функций…11 Четность и нечетность…11 Периодичность…12 Нули функции…12 Монотонность (возрастание, убывание)…13 Экстремумы (максимумы Изучение математики на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений,
Изучение математики на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений, 1) Область определения. ( f ) R.
1) Область определения. ( f ) R. Находим область определения функции D( f.. Определяем точки разрыва функции.. Находим
Находим область определения функции D( f.. Определяем точки разрыва функции.. Находим Елабуга
Елабуга Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации. В школьном курсе изучается немало функций.
Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации. В школьном курсе изучается немало функций. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
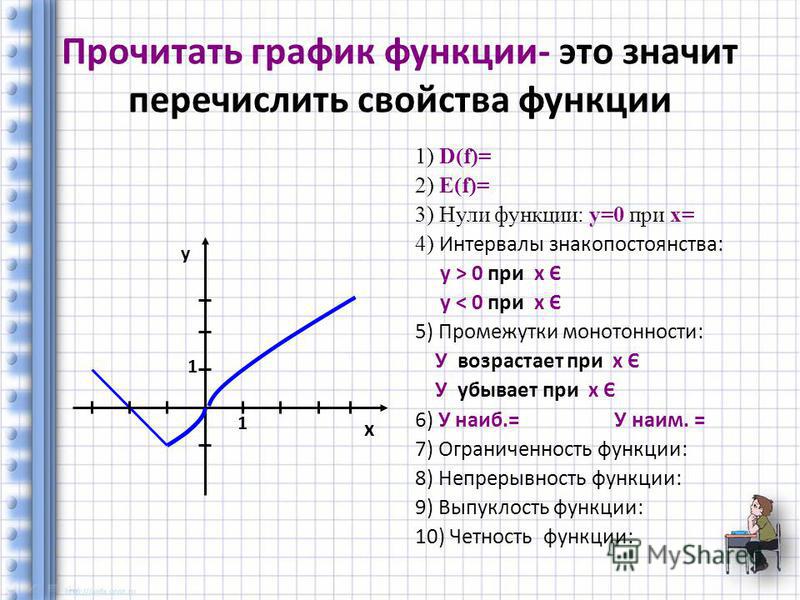

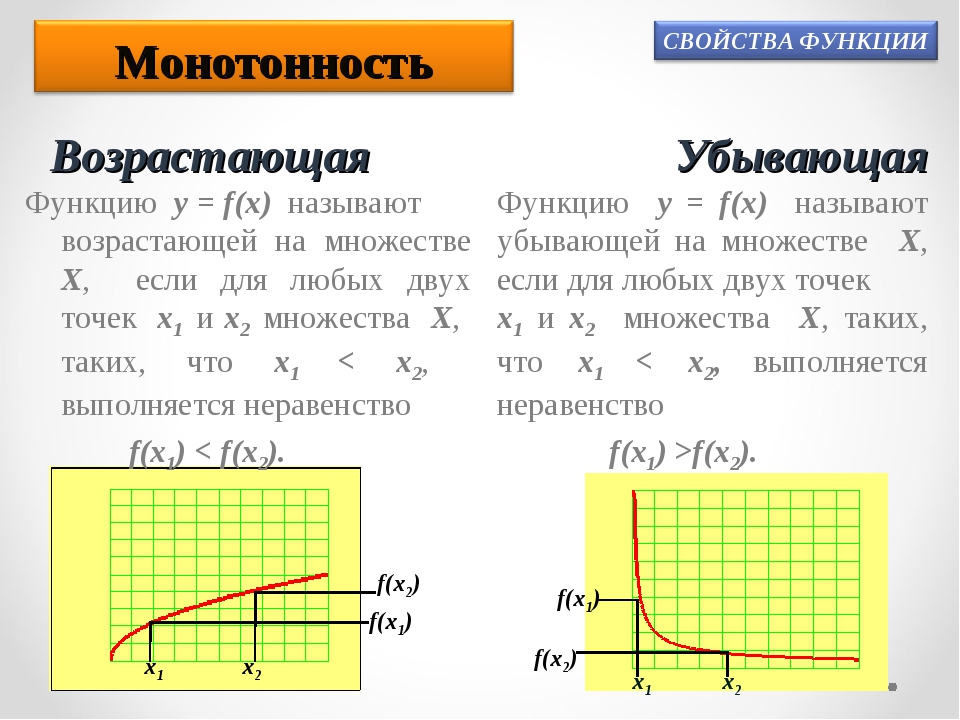 График четной функции симметричен относительно оси ординат.
График четной функции симметричен относительно оси ординат.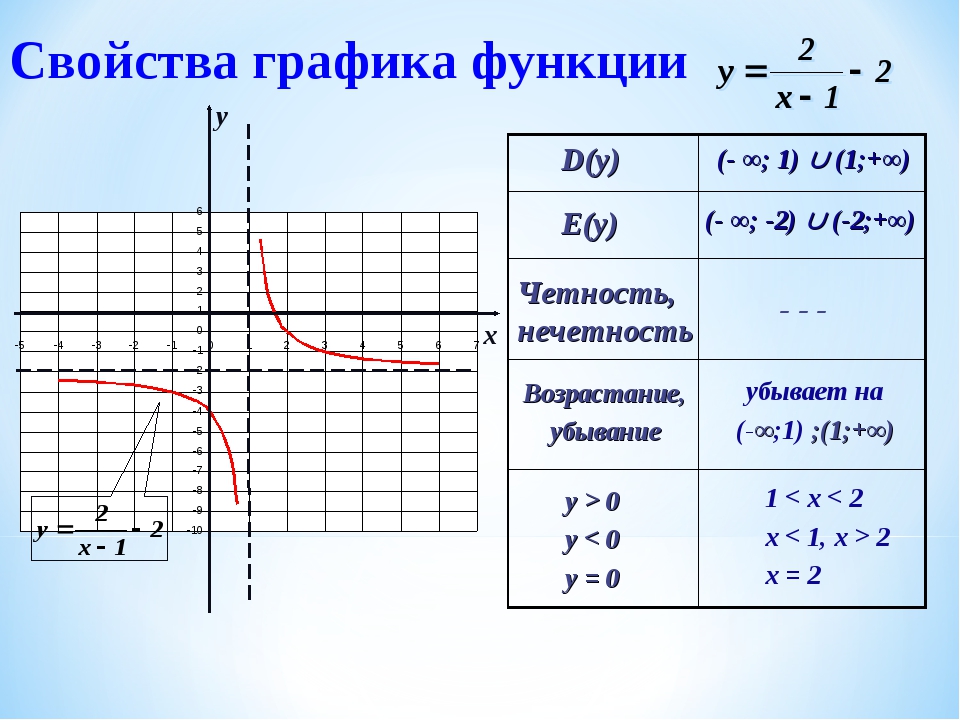 1А Функция, ее свойства и график
1А Функция, ее свойства и график
 Приходят к единому мнению по спорным вопросам. При необходимости получают консультацию учителя. Необходимо выполнить задание
Приходят к единому мнению по спорным вопросам. При необходимости получают консультацию учителя. Необходимо выполнить задание

 Докажем сначала, что:
Докажем сначала, что: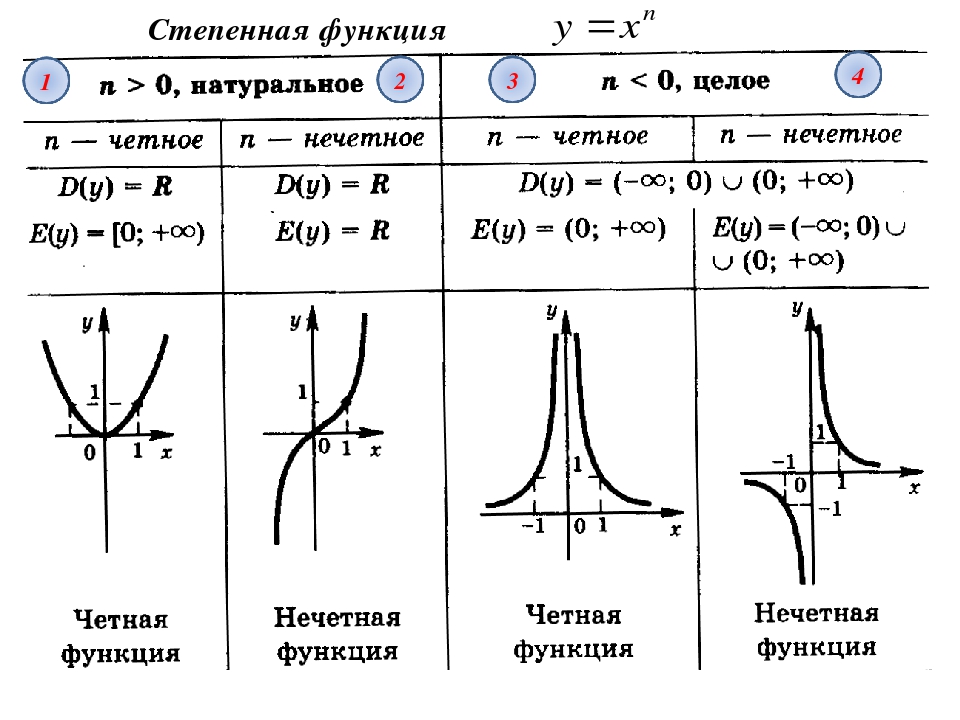 График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).
График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).

 Мы называем это тройным нулем или нулем с кратностью 3.
Мы называем это тройным нулем или нулем с кратностью 3. Это единственный ноль кратности 1.
Это единственный ноль кратности 1. Посмотрите на график полиномиальной функции в (рисунок).На графике есть три поворотные точки.
Посмотрите на график полиномиальной функции в (рисунок).На графике есть три поворотные точки. Если функция является четной функцией, ее график симметричен относительно оси, то есть
Если функция является четной функцией, ее график симметричен относительно оси, то есть 
 Поскольку полиномиальная функция, записанная в факторизованной форме, будет иметь перехват x , где каждый множитель равен нулю, мы можем сформировать функцию, которая будет проходить через набор перехватов x , введя соответствующий набор факторов.
Поскольку полиномиальная функция, записанная в факторизованной форме, будет иметь перехват x , где каждый множитель равен нулю, мы можем сформировать функцию, которая будет проходить через набор перехватов x , введя соответствующий набор факторов. В этих случаях мы говорим, что поворотная точка — это глобальный максимум или глобальный минимум. Они также называются абсолютным максимальным и абсолютным минимальным значениями функции.
В этих случаях мы говорим, что поворотная точка — это глобальный максимум или глобальный минимум. Они также называются абсолютным максимальным и абсолютным минимальным значениями функции. 23.
23. 


 Это также верно для g (-2) и g (2). Вы правильно угадали; g (x) — функция, не имеющая взаимно однозначного соответствия.
Это также верно для g (-2) и g (2). Вы правильно угадали; g (x) — функция, не имеющая взаимно однозначного соответствия. Давайте начнем с последнего!
Давайте начнем с последнего! Как же тогда это сделать?
Как же тогда это сделать?
 Уже одно это скажет нам, что функция не является взаимно однозначной.
Уже одно это скажет нам, что функция не является взаимно однозначной.


 Вот некоторые из тех, которые мы можем использовать для построения графиков:
Вот некоторые из тех, которые мы можем использовать для построения графиков:



 Экстремумы можно разделить на глобальные и локальные. Как следует из названий,
глобальный максимум — это максимальное значение функции
достигает, в то время как глобальный минимум — это минимальное значение, достигаемое функцией. Если функция
ограничен и имеет область, состоящую из всей действительной прямой, глобальный максимум равен
самый высокий пик и глобальный минимум — самая низкая долина.
Экстремумы можно разделить на глобальные и локальные. Как следует из названий,
глобальный максимум — это максимальное значение функции
достигает, в то время как глобальный минимум — это минимальное значение, достигаемое функцией. Если функция
ограничен и имеет область, состоящую из всей действительной прямой, глобальный максимум равен
самый высокий пик и глобальный минимум — самая низкая долина.

 )
) 2-9`, которое, как мы понимаем, можно записать как `(x + 3) (x-3)`. Таким образом, наши значения для `x` не могут включать` -3` (из первой скобки) или `3` (из второй).
2-9`, которое, как мы понимаем, можно записать как `(x + 3) (x-3)`. Таким образом, наши значения для `x` не могут включать` -3` (из первой скобки) или `3` (из второй).
 2 + 4` для
`x> 2`
2 + 4` для
`x> 2` 082`»
082`» е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Точно так же, когда мы приближаемся к \ (x = 0 \), функция снова сохраняет тот же знак, что и \ (x \), но начинает становиться довольно большим.Вот набросок этого графика.
Точно так же, когда мы приближаемся к \ (x = 0 \), функция снова сохраняет тот же знак, что и \ (x \), но начинает становиться довольно большим.Вот набросок этого графика. Поскольку в самой оси нет ничего особенного, мы будем использовать тот факт, что ось \ (x \) на самом деле является линией, заданной \ (y = 0 \), а ось \ (y \) — действительно строка, заданная \ (x = 0 \).
Поскольку в самой оси нет ничего особенного, мы будем использовать тот факт, что ось \ (x \) на самом деле является линией, заданной \ (y = 0 \), а ось \ (y \) — действительно строка, заданная \ (x = 0 \). Помните, что \ (y \) — точка пересечения задается как \ (\ left ({0, f \ left (0 \ right)} \ right) \), и мы находим \ (x \) — точки пересечения, устанавливая числитель равен нулю и решает.
Помните, что \ (y \) — точка пересечения задается как \ (\ left ({0, f \ left (0 \ right)} \ right) \), и мы находим \ (x \) — точки пересечения, устанавливая числитель равен нулю и решает. 1) Нули синуса:
1) Нули синуса:
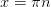
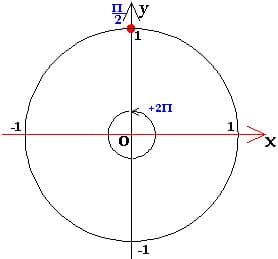
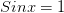
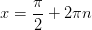
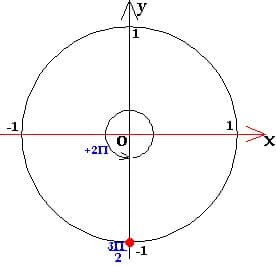

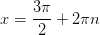

 Возможно это вовсе не акне новорожденных , а аллергия. Симптомы могут быть схожи и поэтому в данной ситуации лучше обратиться к педиатру и дерматологу, так как только они смогут отличить эти кожные высыпания у детей.
Возможно это вовсе не акне новорожденных , а аллергия. Симптомы могут быть схожи и поэтому в данной ситуации лучше обратиться к педиатру и дерматологу, так как только они смогут отличить эти кожные высыпания у детей.
 К аллергическим заболеваниям, затрагивающим кожу у младенцев, можно отнести: атопический дерматит, острую крапивницу и отек Квинке. Острая крапивница крайне редка у младенцев- это острая аллергическая реакция в виде своеобразных высыпаний по типу волдырей (как при ожоге от крапивы, отсюда и название), которые внезапно появляются на коже и так же внезапно исчезают не оставляя после себя никакого следа, обычно не существуют на коже дольше суток и сопровождаются выраженным зудом, что проявляется в общем беспокойстве ребенка. Причиной, чаще всего, служат пищевые белки(например, коровьего молока), вирусные инфекции, укусы насекомых и лекарственные препараты (например, антибиотики). В тяжелых случаях может сопровождаться отеком и покраснением мягких тканей лица, шеи, гортани, рук, ног, гениталий или брюшной полости — отеком Квинке, который требует незамедлительной врачебной помощи.
К аллергическим заболеваниям, затрагивающим кожу у младенцев, можно отнести: атопический дерматит, острую крапивницу и отек Квинке. Острая крапивница крайне редка у младенцев- это острая аллергическая реакция в виде своеобразных высыпаний по типу волдырей (как при ожоге от крапивы, отсюда и название), которые внезапно появляются на коже и так же внезапно исчезают не оставляя после себя никакого следа, обычно не существуют на коже дольше суток и сопровождаются выраженным зудом, что проявляется в общем беспокойстве ребенка. Причиной, чаще всего, служат пищевые белки(например, коровьего молока), вирусные инфекции, укусы насекомых и лекарственные препараты (например, антибиотики). В тяжелых случаях может сопровождаться отеком и покраснением мягких тканей лица, шеи, гортани, рук, ног, гениталий или брюшной полости — отеком Квинке, который требует незамедлительной врачебной помощи.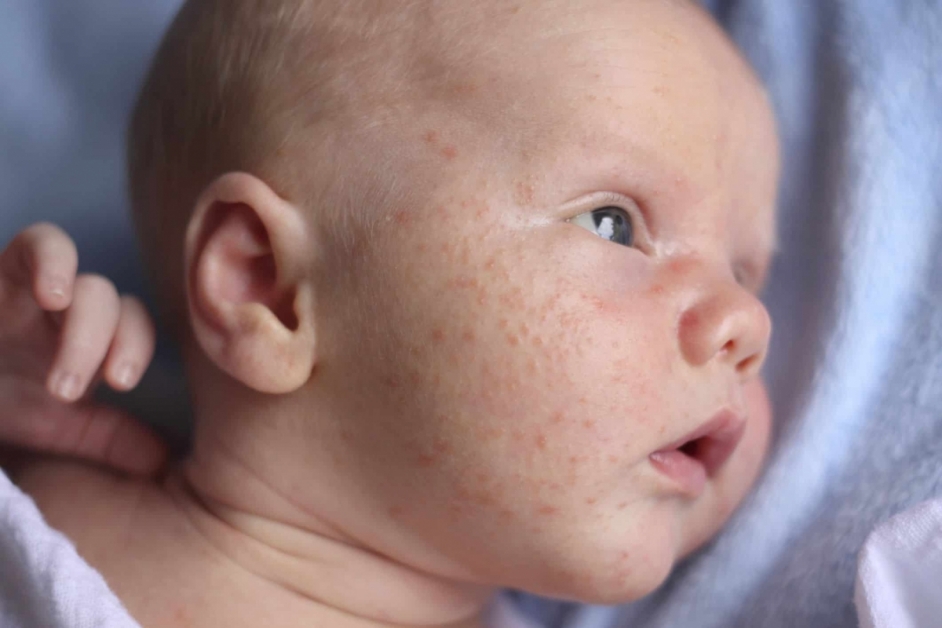

 Далеко не все прыщики у детей нуждаются в нем, многие проходят самостоятельно.
Далеко не все прыщики у детей нуждаются в нем, многие проходят самостоятельно. Также аллергию может повлечь за собой стиральный порошок, стоит использовать только специальные его виды. Наконец, аллергенами становятся шерсть животных, пыльца растений и так далее. Типичный признак аллергии – это шелушения, корочки и мелкая сыпь на красных пятнах. Малыша с аллергической реакцией нужно непременно показать врачу.
Также аллергию может повлечь за собой стиральный порошок, стоит использовать только специальные его виды. Наконец, аллергенами становятся шерсть животных, пыльца растений и так далее. Типичный признак аллергии – это шелушения, корочки и мелкая сыпь на красных пятнах. Малыша с аллергической реакцией нужно непременно показать врачу. И, как уже говорилось, нельзя выдавливать прыщи любых видов у детей.
И, как уже говорилось, нельзя выдавливать прыщи любых видов у детей. Поэтому детская рыхлая кожа так подвержена аллергическим реакциям.
Поэтому детская рыхлая кожа так подвержена аллергическим реакциям.
 Если появляется отечность или краснота кожи вокруг пупка, то необходимо обратиться к педиатру.
Если появляется отечность или краснота кожи вокруг пупка, то необходимо обратиться к педиатру.
 Масло не раздражает глазки малыша, не щиплет и малышу комфортно.
Масло не раздражает глазки малыша, не щиплет и малышу комфортно. А если не соблюдать надлежащий уход, то вероятно присоединение инфекции в местах опрелостей.
А если не соблюдать надлежащий уход, то вероятно присоединение инфекции в местах опрелостей.

 д.). У детей после года отмечаются высыпания на введение таких продуктов в питание, как конфеты, шоколад, пирожные, кексы и другие кулинарные продукты промышленного производства, содержащие большое количество красителей и консервантов, часто вызывающих аллергические проявления на коже, даже у взрослых. Учитывая незрелость ферментативных систем пищеварительного тракта у детей раннего возраста, незрелость иммунной системы, данные продукты не рекомендуется вводить в рацион детям до 3 летнего возраста.
д.). У детей после года отмечаются высыпания на введение таких продуктов в питание, как конфеты, шоколад, пирожные, кексы и другие кулинарные продукты промышленного производства, содержащие большое количество красителей и консервантов, часто вызывающих аллергические проявления на коже, даже у взрослых. Учитывая незрелость ферментативных систем пищеварительного тракта у детей раннего возраста, незрелость иммунной системы, данные продукты не рекомендуется вводить в рацион детям до 3 летнего возраста.
 Обычно возникает в жаркую погоду, при перегревании ребенка из-за лихорадки, высокой температуры воздуха или чрезмерного укутывания.
Обычно возникает в жаркую погоду, при перегревании ребенка из-за лихорадки, высокой температуры воздуха или чрезмерного укутывания.
 Геморрагические высыпания имеют вид пятен красного или темного цвета (синячков), не исчезающих при надавливании. При наличии геморрагической сыпи необходима консультация врача-педиатра, врача-гематолога и проведение дополнительных методов исследования.
Геморрагические высыпания имеют вид пятен красного или темного цвета (синячков), не исчезающих при надавливании. При наличии геморрагической сыпи необходима консультация врача-педиатра, врача-гематолога и проведение дополнительных методов исследования.
 Не стоит впадать в крайности. Достаточно всего лишь ориентироваться в основных видах и причинах сыпи, чтобы принять верное решение.
Не стоит впадать в крайности. Достаточно всего лишь ориентироваться в основных видах и причинах сыпи, чтобы принять верное решение.
 Часть из них не требует лечения и проходит самостоятельно, а часть угрожает здоровью и жизни ребенка. Поэтому, правильным будет, если родители проконсультируются с врачом и не будут заниматься самолечением.
Часть из них не требует лечения и проходит самостоятельно, а часть угрожает здоровью и жизни ребенка. Поэтому, правильным будет, если родители проконсультируются с врачом и не будут заниматься самолечением.
 К таким заболеваниям относится скарлатина, при которой ярко-красные прыщики появляются на сгибательных поверхностях конечностей и реже – на теле и на лице, кроме носогубного треугольника. Повышается температура тела, шелушится кожа ладоней и стоп, появляется покраснение слизистой глотки и малиновый цвет языка.
К таким заболеваниям относится скарлатина, при которой ярко-красные прыщики появляются на сгибательных поверхностях конечностей и реже – на теле и на лице, кроме носогубного треугольника. Повышается температура тела, шелушится кожа ладоней и стоп, появляется покраснение слизистой глотки и малиновый цвет языка. Считается, что прыщи у новорожденных появляются из-за того, что во время беременности от матери к ребенку передаются гормоны. В любом случае прыщи новорожденного совершенно безвредны и пройдут самостоятельно, без лечения.
Считается, что прыщи у новорожденных появляются из-за того, что во время беременности от матери к ребенку передаются гормоны. В любом случае прыщи новорожденного совершенно безвредны и пройдут самостоятельно, без лечения. Милии выглядят как крошечные белые бугорки на коже, похожие на пустулы, но без воспаления.
Милии выглядят как крошечные белые бугорки на коже, похожие на пустулы, но без воспаления. Не используйте мыло для лица ребенка и не трите его. Слишком частое или слишком сильное очищение вызовет раздражение нежной кожи вашего ребенка.
Не используйте мыло для лица ребенка и не трите его. Слишком частое или слишком сильное очищение вызовет раздражение нежной кожи вашего ребенка. Детские прыщи также называют неонатальными прыщами и являются обычным явлением — им заболевают примерно 3 из 10 младенцев. Эксперты не совсем уверены, что вызывает прыщи у ребенка, но это может быть связано с одной из следующих причин:
Детские прыщи также называют неонатальными прыщами и являются обычным явлением — им заболевают примерно 3 из 10 младенцев. Эксперты не совсем уверены, что вызывает прыщи у ребенка, но это может быть связано с одной из следующих причин: Врач может назначить лечебный крем или другое лечение. Но не используйте безрецептурные кремы или лекарства без предварительной консультации с лечащим врачом, так как они могут повредить нежную кожу вашего ребенка.
Врач может назначить лечебный крем или другое лечение. Но не используйте безрецептурные кремы или лекарства без предварительной консультации с лечащим врачом, так как они могут повредить нежную кожу вашего ребенка. Чтобы облегчить этот стресс, специалисты Mustela собрали 11 советов по избавлению от детских прыщей.
Чтобы облегчить этот стресс, специалисты Mustela собрали 11 советов по избавлению от детских прыщей.
 Они возникают, когда мертвые клетки кожи попадают в крошечные карманы кожи и могут появиться в течение нескольких недель после рождения. Милии не связаны с детскими прыщами и не требуют лечения — они обычно возникают и проходят сами по себе.
Они возникают, когда мертвые клетки кожи попадают в крошечные карманы кожи и могут появиться в течение нескольких недель после рождения. Милии не связаны с детскими прыщами и не требуют лечения — они обычно возникают и проходят сами по себе. Кроме того, подумайте, срыгивает ли ваш малыш, что, как мы знаем, распространено среди младенцев.Если ваш ребенок постоянно срыгивает смесью — даже если каждый раз совсем немного — это может привести к высыпанию.
Кроме того, подумайте, срыгивает ли ваш малыш, что, как мы знаем, распространено среди младенцев.Если ваш ребенок постоянно срыгивает смесью — даже если каждый раз совсем немного — это может привести к высыпанию. Для лечения упорных детских прыщей педиатр может назначить лечебный крем или мазь, которые помогут вылечить это заболевание.
Для лечения упорных детских прыщей педиатр может назначить лечебный крем или мазь, которые помогут вылечить это заболевание. Одевайте ребенка в сверхмягкую одежду и держите его кожу подальше от шерсти и других грубых волокон.
Одевайте ребенка в сверхмягкую одежду и держите его кожу подальше от шерсти и других грубых волокон. Таким образом, мицеллы способны вытягивать загрязнения, не раздражая чувствительную кожу.
Таким образом, мицеллы способны вытягивать загрязнения, не раздражая чувствительную кожу. А если у вас есть домашние животные, будьте особенно внимательны к содержанию окружающей среды вашего ребенка в чистоте, потому что перхоть может вызвать аллергическую реакцию на склонной к акне коже.
А если у вас есть домашние животные, будьте особенно внимательны к содержанию окружающей среды вашего ребенка в чистоте, потому что перхоть может вызвать аллергическую реакцию на склонной к акне коже. Эти пижамы также уменьшат желание вашего малыша выщипывать прыщи. Вы почувствуете облегчение, узнав, что ваш малыш одет из гипоаллергенного материала, не содержащего парабенов и феноксиэтанола и сделанного из 100% натуральных ингредиентов.
Эти пижамы также уменьшат желание вашего малыша выщипывать прыщи. Вы почувствуете облегчение, узнав, что ваш малыш одет из гипоаллергенного материала, не содержащего парабенов и феноксиэтанола и сделанного из 100% натуральных ингредиентов. Всегда избегайте всего, что может вызвать раздражение нежной кожи вашего малыша, включая агрессивные средства по уходу за кожей, одежду, продукты питания и другие предметы в их окружении. И постарайтесь проявить терпение в отношении прыщей вашего ребенка. Следуйте советам из этой статьи и помните, что прыщи, скорее всего, нисколько не беспокоят вашего малыша, поэтому постарайтесь не позволять им беспокоить вас!
Всегда избегайте всего, что может вызвать раздражение нежной кожи вашего малыша, включая агрессивные средства по уходу за кожей, одежду, продукты питания и другие предметы в их окружении. И постарайтесь проявить терпение в отношении прыщей вашего ребенка. Следуйте советам из этой статьи и помните, что прыщи, скорее всего, нисколько не беспокоят вашего малыша, поэтому постарайтесь не позволять им беспокоить вас!

 Люди, достаточно взрослые, чтобы заботиться о том, как они выглядят, могут попросить их удалить.
Люди, достаточно взрослые, чтобы заботиться о том, как они выглядят, могут попросить их удалить. Если неясно, являются ли кисты милиями или каким-либо другим типом кожного заболевания, может быть полезна биопсия кожи. Это тест, в ходе которого снимается небольшой кусочек кожи и исследуется под микроскопом.
Если неясно, являются ли кисты милиями или каким-либо другим типом кожного заболевания, может быть полезна биопсия кожи. Это тест, в ходе которого снимается небольшой кусочек кожи и исследуется под микроскопом. Вы можете повысить свои шансы избежать вторичных милиумов, в частности, если примете меры по защите своей кожи. Избегайте чрезмерного пребывания на солнце, избегайте использования густых кремов / мазей для лица и отшелушивания — вот вещи, которые помогут.
Вы можете повысить свои шансы избежать вторичных милиумов, в частности, если примете меры по защите своей кожи. Избегайте чрезмерного пребывания на солнце, избегайте использования густых кремов / мазей для лица и отшелушивания — вот вещи, которые помогут.
 Несколько водяных пузырей или прыщей, сгруппированных в группу. Они похожи на герпес (волдыри от лихорадки), которые появляются у взрослых на губах. Через несколько дней они покрываются коркой.
Несколько водяных пузырей или прыщей, сгруппированных в группу. Они похожи на герпес (волдыри от лихорадки), которые появляются у взрослых на губах. Через несколько дней они покрываются коркой.
 Они могут возникать где угодно на поверхности тела, кроме ладоней и подошв.
Они могут возникать где угодно на поверхности тела, кроме ладоней и подошв.

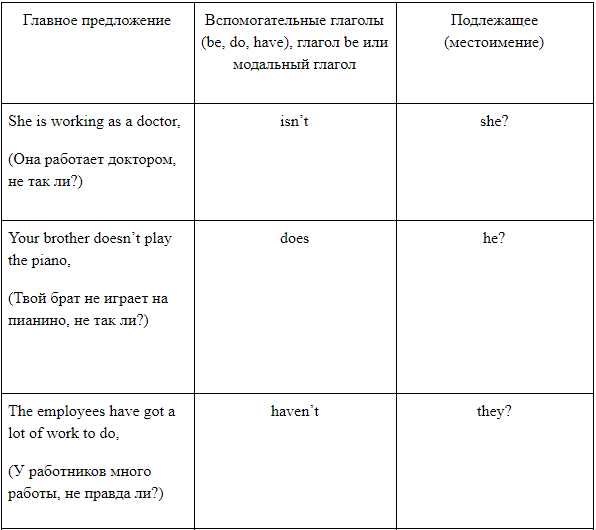
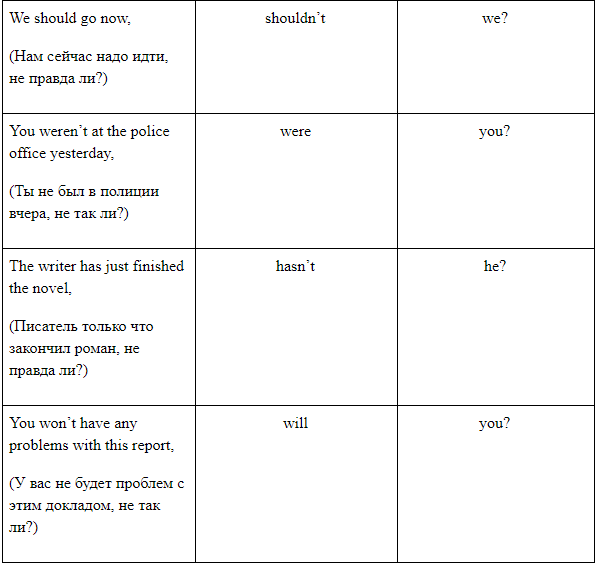


 Они могут годами использовать наркотик по выходным дням. Однако, по словам специалистов, такое потребление только растягивает период вовлечения в сильную зависимость.
Они могут годами использовать наркотик по выходным дням. Однако, по словам специалистов, такое потребление только растягивает период вовлечения в сильную зависимость. Сейчас можно говорить уже о четырех поколениях «дизайнерских» наркотиков, которые доступны в России. Особую опасность представляет совместное употребление «новых» наркотических веществ с «традиционными» наркотиками, а также с алкоголем.
Сейчас можно говорить уже о четырех поколениях «дизайнерских» наркотиков, которые доступны в России. Особую опасность представляет совместное употребление «новых» наркотических веществ с «традиционными» наркотиками, а также с алкоголем. При таком подходе снимается ответственность с потребителя наркотиков: индивид не несет ответственности за свою болезнь вследствие того, что он находится в рабской зависимости от психоактивного вещества. То есть сам факт зависимости и делает его больным. Такой подход играет как позитивную, так и негативную роль, однако он упускает из виду личность потребителя как субъекта собственной воли, отказывая ему в способности самостоятельно принимать решения, управлять своей жизнью и соответственно контролировать употребление, — подчеркивает эксперт.
При таком подходе снимается ответственность с потребителя наркотиков: индивид не несет ответственности за свою болезнь вследствие того, что он находится в рабской зависимости от психоактивного вещества. То есть сам факт зависимости и делает его больным. Такой подход играет как позитивную, так и негативную роль, однако он упускает из виду личность потребителя как субъекта собственной воли, отказывая ему в способности самостоятельно принимать решения, управлять своей жизнью и соответственно контролировать употребление, — подчеркивает эксперт. Также они надеются на повышение научной обоснованности предложений, которые будут внесены в новый документ Стратегии государственной антинаркотической политики Российской Федерации.
Также они надеются на повышение научной обоснованности предложений, которые будут внесены в новый документ Стратегии государственной антинаркотической политики Российской Федерации. Соблазн просто огромный».
Соблазн просто огромный».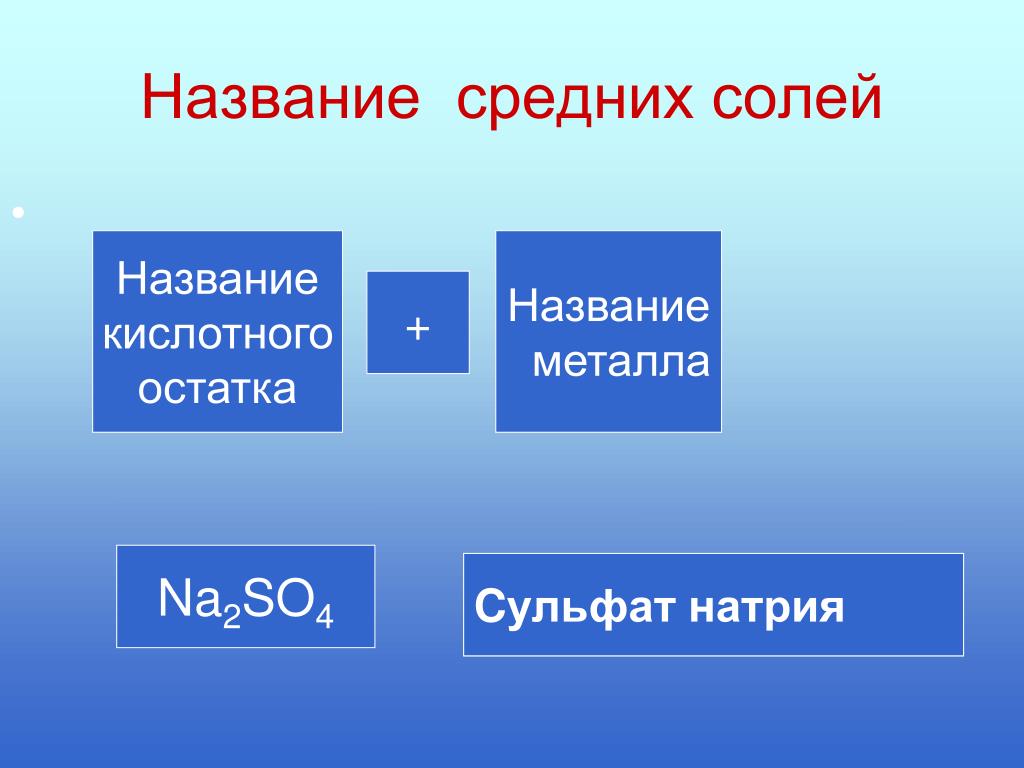 Разговаривать, делиться открытиями. Ты сидишь, смотришь на человека и говоришь: расслабь, расслабь челюсть».
Разговаривать, делиться открытиями. Ты сидишь, смотришь на человека и говоришь: расслабь, расслабь челюсть».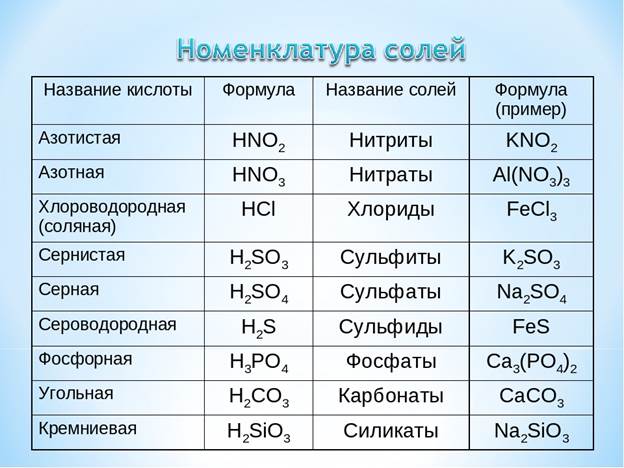 Употребляют синтетические наркотики не только перорально (пьют), но и нюхают, колют в вены и даже принимают ректально.
Употребляют синтетические наркотики не только перорально (пьют), но и нюхают, колют в вены и даже принимают ректально. В 2010 году был запрещён в России и других странах СНГ, а также в Великобритании и ещё в 27 странах ЕС.
В 2010 году был запрещён в России и других странах СНГ, а также в Великобритании и ещё в 27 странах ЕС. И порой психиатрический диагноз остаётся на всю жизнь, то есть человек всю оставшуюся жизнь будет жить на психокорректорах. К последствиям приема также относят и суицидальность. Ведь неспроста с появлением синтетических наркотиков резко выросла статистика по подростковым и молодёжным суицидам».
И порой психиатрический диагноз остаётся на всю жизнь, то есть человек всю оставшуюся жизнь будет жить на психокорректорах. К последствиям приема также относят и суицидальность. Ведь неспроста с появлением синтетических наркотиков резко выросла статистика по подростковым и молодёжным суицидам». Больницы и поликлиники создают пациентов, суды и тюрьмы – преступников, подобную аналогию можно провести и с наркоманами. Очевидно, наркоманы появляются не как феномен, а как отдельная социальная группа – с медикализацией общества, распространением врачебного и научного знания и с интенсификацией государственного управления человеческими жизнями (последнее явление Фуко называет биополитикой). А если наркоман – часть общества, то невозможно сделать вид, что его не существует.
Больницы и поликлиники создают пациентов, суды и тюрьмы – преступников, подобную аналогию можно провести и с наркоманами. Очевидно, наркоманы появляются не как феномен, а как отдельная социальная группа – с медикализацией общества, распространением врачебного и научного знания и с интенсификацией государственного управления человеческими жизнями (последнее явление Фуко называет биополитикой). А если наркоман – часть общества, то невозможно сделать вид, что его не существует. Блейк считал, что британские музыканты употребляли этот наркотик в надежде сравняться с гениальными афроамериканцами. Но в культуру наркотики попадают не сразу. Так, многие наркотики, включая никотин и алкоголь, использовались в лечебных практиках (в том числе, как бы парадоксально это ни звучало, в борьбе с наркотиками, вспомним морфий и ЛСД).
Блейк считал, что британские музыканты употребляли этот наркотик в надежде сравняться с гениальными афроамериканцами. Но в культуру наркотики попадают не сразу. Так, многие наркотики, включая никотин и алкоголь, использовались в лечебных практиках (в том числе, как бы парадоксально это ни звучало, в борьбе с наркотиками, вспомним морфий и ЛСД)..PNG)

 Собирались эксперты из Бельгии, Нидерландов, Польши, Чехии, Германии, Эстонии, Финляндии, Венгрии и стран Центральной Азии и все они озвучивали одни и те же проблемы: наркокриминал всегда на шаг впереди.
Собирались эксперты из Бельгии, Нидерландов, Польши, Чехии, Германии, Эстонии, Финляндии, Венгрии и стран Центральной Азии и все они озвучивали одни и те же проблемы: наркокриминал всегда на шаг впереди.
 Сахалин, к сожалению, исключением не стал.
Сахалин, к сожалению, исключением не стал. Поэтому сложно предугадать, какой орган у вас откажет после употребления запрещенной химии.
Поэтому сложно предугадать, какой орган у вас откажет после употребления запрещенной химии. Рядовые радости жизни наркоману кажутся скучными и невыразительными.
Рядовые радости жизни наркоману кажутся скучными и невыразительными.
 А поэтому юридически он становится легальным. Но если вы решили подзаработать на продаже таких якобы разрешенных наркотиков, не обольщайтесь.
А поэтому юридически он становится легальным. Но если вы решили подзаработать на продаже таких якобы разрешенных наркотиков, не обольщайтесь. gost.ru)
gost.ru) Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.




 ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
 Эта функция очень похожа на sin Икс с доменом как набор действительных чисел и диапазоном как интервал [-1, 1]. Эта функция периодическая с периодом (в отличие от периода 2ᴫ функции sin Икс). Грех 2Икс может быть расширен тождеством Sin 2Икс = 2 греха Икспотому чтоИкс слишком.
Эта функция очень похожа на sin Икс с доменом как набор действительных чисел и диапазоном как интервал [-1, 1]. Эта функция периодическая с периодом (в отличие от периода 2ᴫ функции sin Икс). Грех 2Икс может быть расширен тождеством Sin 2Икс = 2 греха Икспотому чтоИкс слишком.

 Графики y = a sin x и y = a cos x
Графики y = a sin x и y = a cos x
 Мы узнаем больше о периоде в следующем разделе Графики y = a sin bx.
Мы узнаем больше о периоде в следующем разделе Графики y = a sin bx. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности.
Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности. См. Рисунок 3.
См. Рисунок 3.

 Кроме того, обратите внимание на пример, что
Кроме того, обратите внимание на пример, что (x) = \ sin (x− \ frac {π} {4}) \\ [/ latex], который сдвигается вправо на единицы [latex] \ frac {π} {4} \\ [/ latex].
(x) = \ sin (x− \ frac {π} {4}) \\ [/ latex], который сдвигается вправо на единицы [latex] \ frac {π} {4} \\ [/ latex]. Если значение C отрицательное, сдвиг влево.
Если значение C отрицательное, сдвиг влево. См. Рисунок 14.
См. Рисунок 14. Таким образом, наша функция становится
Таким образом, наша функция становится
 Константа 3 вызывает растяжение значений y функции в 3 раза по вертикали, что мы можем видеть на графике на рисунке 22.
Константа 3 вызывает растяжение значений y функции в 3 раза по вертикали, что мы можем видеть на графике на рисунке 22.

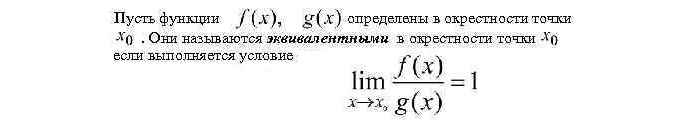
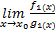
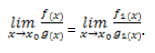
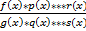
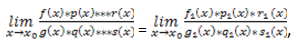
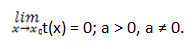
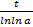
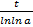 + 0(t)
+ 0(t)
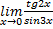
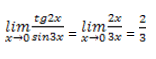
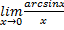
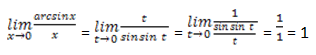

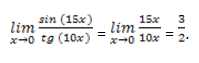
 )
)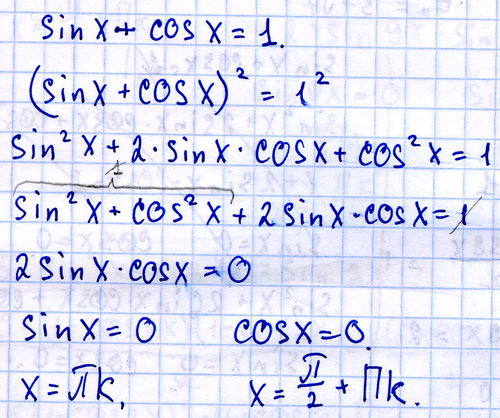 )
) )
) )
) )
)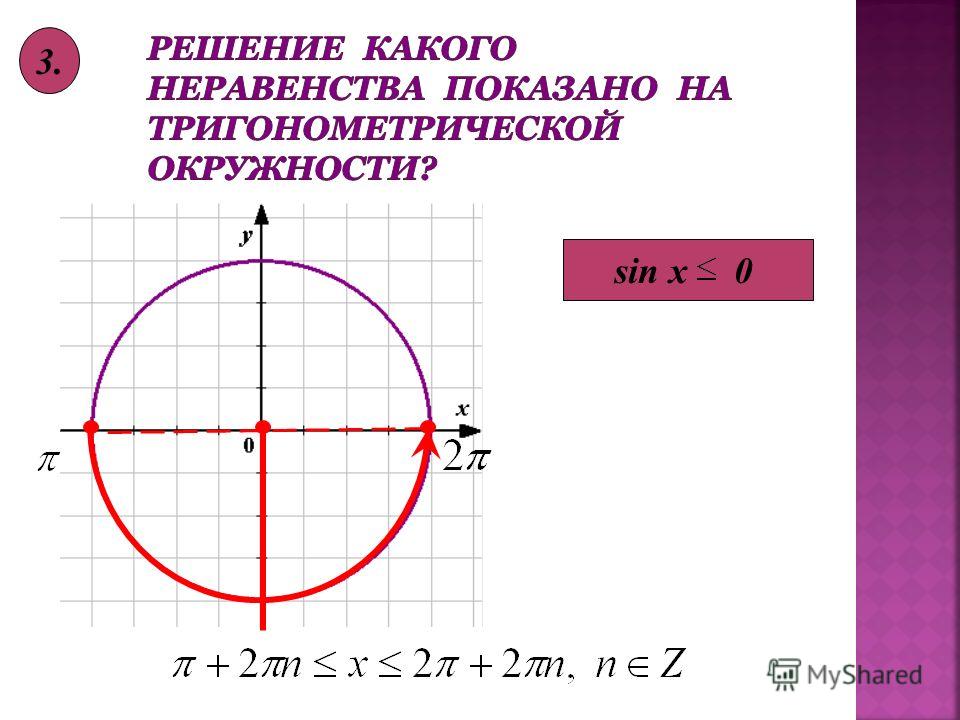

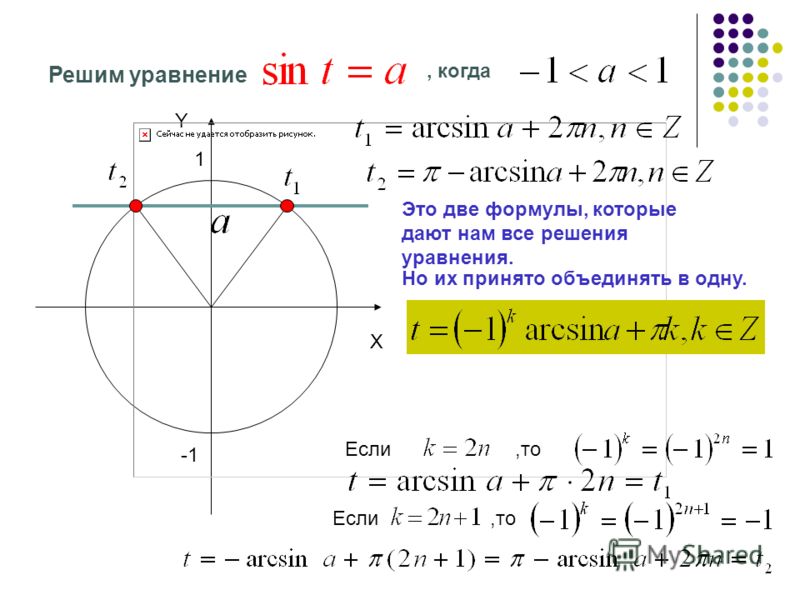

 (πR², где R=1).
(πR², где R=1).


 е. красная линия, всегда находится между синей и светло-голубой линиями.
е. красная линия, всегда находится между синей и светло-голубой линиями. 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`. – Режим доступа: http://ege.fipi.ru/
– Режим доступа: http://ege.fipi.ru/
 Необходимые понятия и примеры нахождения
Необходимые понятия и примеры нахождения
 08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1.62y(4)=44-5·43+6·42=32
08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1.62y(4)=44-5·43+6·42=32 Теперь определим, как ведет себя функция в заданных границах:
Теперь определим, как ведет себя функция в заданных границах:

 Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.
Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.
 Изобразим ход нашего решения на графике.
Изобразим ход нашего решения на графике.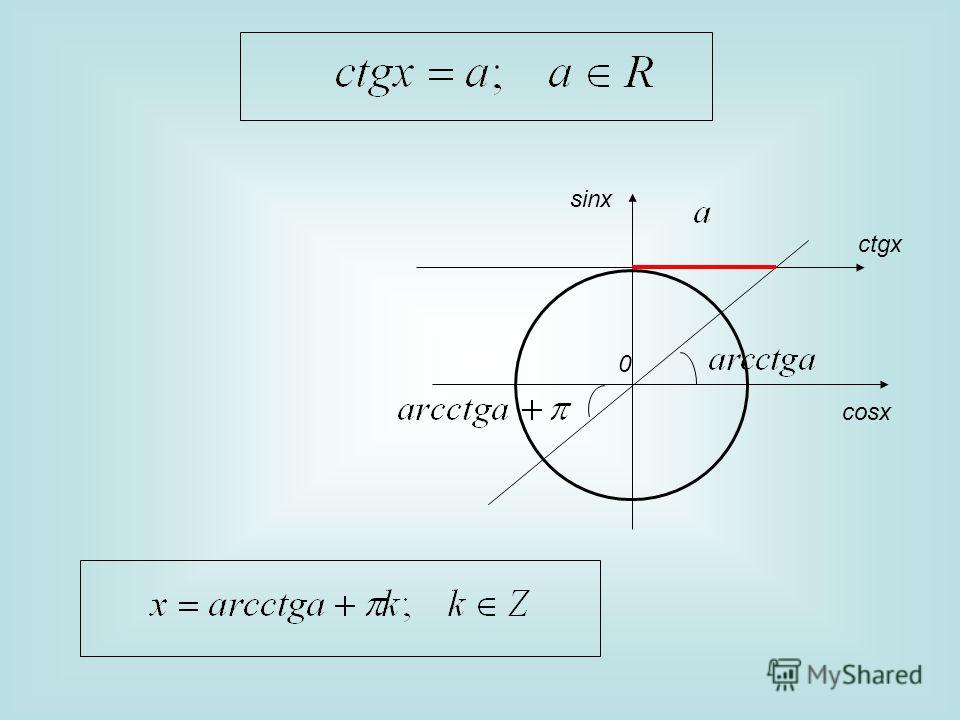
 .
. 2} \ dx $$
2} \ dx $$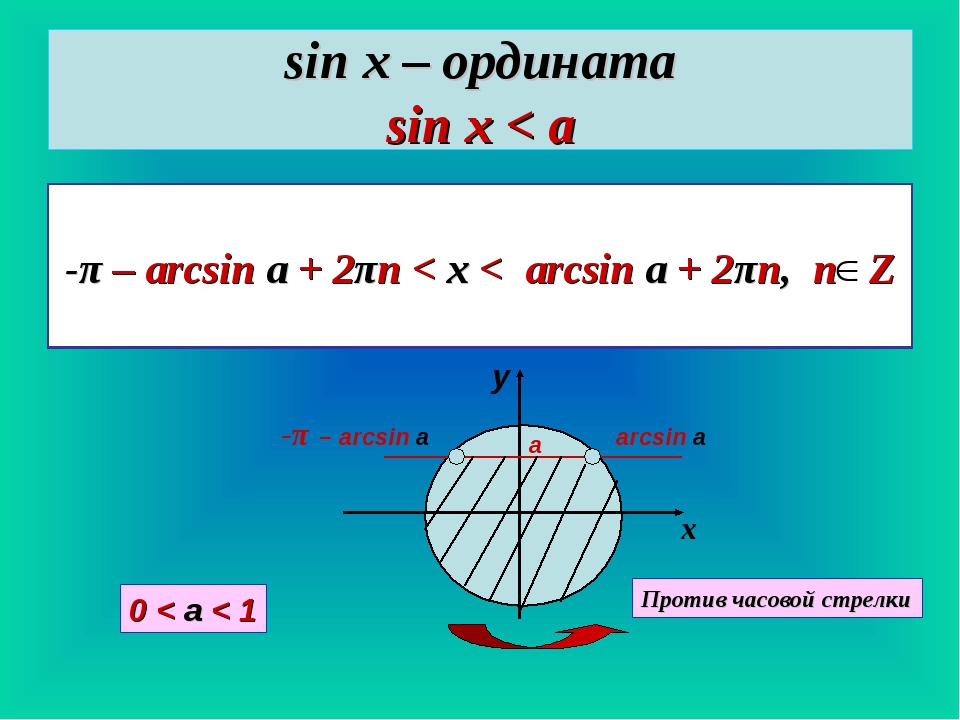 Регистрация займет всего минуту.
Регистрация займет всего минуту.


 Затем, поскольку x и -x оба приближаются к 0, когда x приближается к 0 справа,
так должен x sin (1 / x).
Затем, поскольку x и -x оба приближаются к 0, когда x приближается к 0 справа,
так должен x sin (1 / x).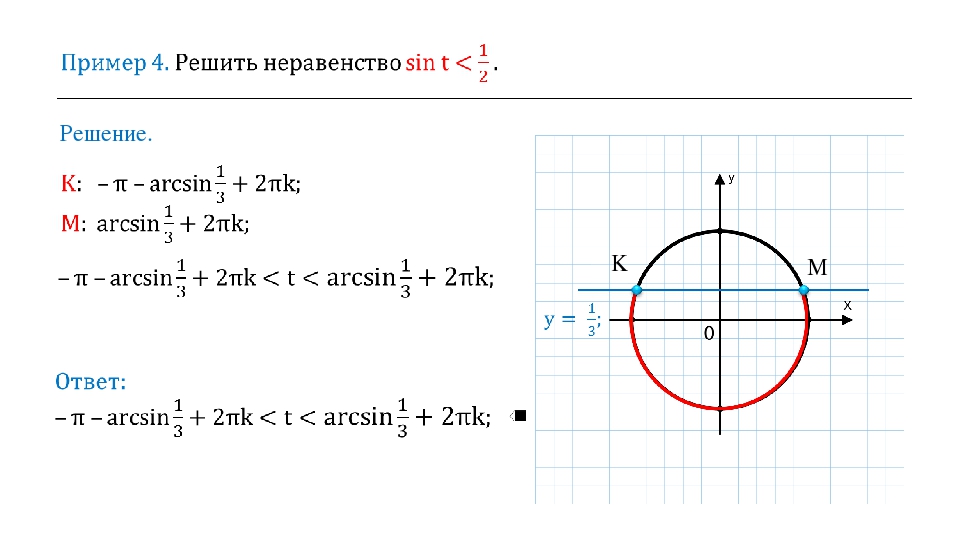 Следовательно, первый шаг в оценке этого выражения — сказать, что если y = sin -1 (1/2), то sin y = 1/2. Эта простая тригонометрическая функция имеет бесконечное количество решений:
Следовательно, первый шаг в оценке этого выражения — сказать, что если y = sin -1 (1/2), то sin y = 1/2. Эта простая тригонометрическая функция имеет бесконечное количество решений:




 3pt {\ xi \ in \ left ({a, b} \ right).} \]
3pt {\ xi \ in \ left ({a, b} \ right).} \] 2}}}.2} — z — 1 = 0, \; \; \;} \ Rightarrow
2}}}.2} — z — 1 = 0, \; \; \;} \ Rightarrow 