Рисунки в акварели: Акварель рисунки Акварель поэтапно видео Акварель для начинающих Акварель рисунки простые Рисунок маяк акварелью Ри…
Рисунки цветов акварелью: очень вдохновляющая подборка!
Что может быть прекраснее цветов? Пожалуй, только красивая женщина. 🙂
Или женщина, рисующая цветы. Акварелью. 🙂
Вот вам целая охапка букетов от прекрасной половины человечества, от студенток курса «Цветы в акварели». Наслаждайтесь красотой и ловите весеннее настроение!
Рисунки цветов акварелью
Как женщины похожи на цветы!
Меня порою это удивляет.
Они не могут жить без красоты.
А красота нас в жизни вдохновляет!
Цветы цветут повсюду для всех, кто только хочет их видеть.
Цветы не решают всех проблем. Но они — хорошее начало.
Сколько бы мы ни говорили о пустоте жизни, иногда достаточно лишь одного цветка, чтобы нас разубедить.
Протягивая руки к звездам, люди часто забывают о цветах под ногами.
Цветы — стихи природы!
Конечно, я мог бы обойтись и без цветов, но они помогают мне сохранить уважение к самому себе, ибо доказывают, что я не скован по рукам и ногам будничными заботами. Они свидетельство моей свободы.
/Рабиндранат Тагор/
У Феи – глазки изумрудные,
Всё на траву она глядит.
У ней наряды дивно-чудные,
Опал, топаз и хризолит.
Есть жемчуга из света лунного,
Каких не видел взор ничей.
Есть поясок покроя струнного
Из ярких солнечных лучей.
Ещё есть платье подвенечное
Да колокольчик полевой,
Сулил ей счастье бесконечное,
Звонил в цветок свой голубой.
Росинка с грёзой серебристою
Зажглась алмазным огоньком.
А ландыш свечкою душистою
Горел на свадьбе с светляком.
/Константин Бальмонт/
В мире цветов тепло и прохладно,
Целый букет ароматов и звуков…
Каждый цветок — он по-своему нарядный…
В форме изысканных праздничных кубков.
В мире цветов я желала б остаться,
Стать героиней рассказов и сказок,
Чтоб красотой каждый день любоваться,
Слиться с гармонией цвета и красок.
/Лариса Кузьминская/
Чтобы жить, нужно солнце, свобода и маленький цветок. /Ганс К. Андерсен/
Тюльпаны и нарциссы – оранжево-золотистая буря весны. /Эрих Мария Ремарк/
Поистине, искусство заключено в природе; кто умеет обнаружить его, тот владеет им. /Альбрехт Дюрер/
Розы прививают любовь к природе, а шипы — уважение. /Антон Лигов/
Запах — душа цветка. /Жюль Верн/
Творчество больших художников — это всегда прекрасный сад и с цветами, и с репейником, а не красивый парк с утрамбованными дорожками. /Александр Блок/
Радость необходима для творчества. /Эдвард Григ/
В творчестве нельзя скрыться, нельзя играть. /Рената Литвинова/
Творчество заразительно. Передай другому! /Альберт Эйнштейн/
Для усердия и искусства нет ничего невыполнимого. /Джонсон Сэмюэл/
Мне нравится быть женщиной за двадцать:
Смеяться, увлекаться, ошибаться,
Влюбляться до безумия навеки
И видеть друга в каждом человеке.
О звуках Мендельсоновского марша
Мечтать. И чтоб мужчина был постарше…
Надеяться стать светочем Вселенной,
Чтоб замер мир передо мной смиренно!
Мне нравится быть женщиной за тридцать:
Сиять огранкой и собой гордиться,
Любить со страстью и душой и телом,
Желанной быть, раскованной, умелой.
Семью хранить, как свечечку, в ладошках,
Слыть умницей, но взбалмошной немножко.
И чувствовать: я- светоч во Вселенной,
Мир замирает предо мной смиренно!
Мне нравится быть женщиной за тридцать:
Сиять огранкой и собой гордиться,
Любить со страстью и душой и телом,
Желанной быть, раскованной, умелой.
Семью хранить, как свечечку, в ладошках,
Слыть умницей, но взбалмошной немножко.
И чувствовать: я- светоч во Вселенной,
Мир замирает предо мной смиренно!
Мне нравится быть женщиной за сорок:
Быть мудрой и прекрасной , как богиня,
Не ведающей злобы и гордыни,
При этом знать: Я — светоч во вселенной
И замер мир передо мной смиренно!
Мне нравится быть женщиной! И точка! Любить и жизни заполнять листочки
За двадцать, тридцать, сорок иль полсотни…
Не важно, просто женщиною будьте! Любите мудро, нежно, безраздельно…
Дарите, принимайте беспредельно!
Но помните, вы светоч во вселенной, Весь мир у ваших ног лежит смиренно!
/Автор неизвестен/
Как украшают женщину цветы!
Любую, даже самую красивую.
Её глаза, как луч из темноты,
Вдруг заблестят, с неведомою силою.
И ей не важен повод и размах.
Ромашки ль это на листе бумажном,
Иль эдельвейс, разысканный в горах.
Для женщины совсем не это важно.
Чужой букет — пленяет красотой.
От дочки роза — мама расцветает.
А от него — хоть лютик полевой…
И сердце с нежным стоном замирает.
/Рина Любимая/
Чем бы вы ни занимались в жизни, делайте это всем своим сердцем. /Конфуций/
Кто испытал наслаждение творчества, для того уже все другие наслаждения не существуют. /Антон Чехов/
Чувство меры в искусстве — все. /Анатоль Франс/
Чтобы рисовать, вы должны закрыть глаза и начать петь. /Пабло Пикассо/
Пока человек способен видеть красоту, он не стареет. /Франц Кафка/
Дарите женщинам цветы. Не только в праздники, —
Как водится, а средь забот и суеты
Дарите женщинам цветы – невестам, жёнам, юным модницам.
Дарите женщинам цветы, чтоб жизнь ещё светлей казалась.
Чтоб будни были не пусты,
Дарите женщинам цветы. Как много значит эта малость!
Как много значит эта малость!
Дарите женщинам цветы. И годы их не будут старить…
Среди забот и суеты
Дарите женщинам цветы, Как нам они улыбки дарят.
/Дементьев Андрей/
Больше материалов по теме «рисунки цветов акварелью»:
рисунки акварелью — Blog — Ghenadie Sontu Fine Art
Основное различие прозрачных и кроющих техник, например, акварели и гуаши заключается в том, что гуашь теряет свои качества при недостаточной укрывистости красочного слоя, а акварель, наоборот, по настоящему работает только при той степени прозрачности, когда через красочные слои просвечивает бумага. Белая бумага имеет наибольший коффициент отражения солнечных лучей, чем усиливает яркость положенной на нее прозрачной краски, создавая ей «подсветку». Гуашь имеет мучнистую основу, содержащую каолин (качественную белую глину), мел или белый пигмент, что и определило противоположную акварели технику нанесения красок. В технике гуаши наносимый слой краски для передачи яркости цветового тона, должен быть достаточно толстым и кроющим, а такой метод не позволяет использовать цвет имприматуры или подкладки, а осветление тона и блики передаются, как и в темперной и масляной живописи белилами.
Субъективные цветовые предпочтения прослеживаются не только в выборе и сочетании цветов, но и в величине цветовых пятен, характере и ориентации мазков. В популярном у нас двадцатичетырехцветном наборе завода «Невская Палитра», например, наибольшей прозрачностью обладает голубая ФЦ, кобальт синий – наименьшей, а ультрамарин занимает промежуточное положение. Таким образом, при лессировках, многослойной акварели, предпочтение стоит отдать голубой. Среди представленных зелёных красок – изумрудной зеленой. Из трех красных можно посоветовать краплак. Желтые кадмии не достаточно прозрачны, желтый полупрозрачен, а лимонный и оранжевый наиболее укрывисты. Но только собственным опытным путем, смешивая краски и изучая, какие сочетания дают грязь, а какие – необходимые цвета, отсутствующие в наборе, можно создать свою палитру, постепенно расширяя её ассортимент. Некоторые великие художники – акварелисты достигали тонкой изысканности цвета и многообразия оттенков, пользуясь крайне ограниченной палитрой. Томас Гиртин, например, пользовался всего пятью красками, последовательно накладывая их одну на другую и передавая тонкие градации цветового тона.
Некоторые великие художники – акварелисты достигали тонкой изысканности цвета и многообразия оттенков, пользуясь крайне ограниченной палитрой. Томас Гиртин, например, пользовался всего пятью красками, последовательно накладывая их одну на другую и передавая тонкие градации цветового тона.
Техника рисунка акварельными карандашами. Выбираем акварельные карандаши.
| Вероятно, многие не раз подмечали красивые плавные переходы цветов в работах, выполненных техникой акварельной живописи. Насыщенно яркие или, наоборот, нежно пастельные акварельные рисунки притягивают взгляд и позволяют почувствовать эмоции, вложенные художником в свою работу. И далеко не всегда в основе достижения такого эффекта лежит использование традиционных акварельных красок. Прогресс не стоит на месте, и сейчас акварель можно встретить в совершенно другой форме — в виде акварельных карандашей с богатой палитрой цветов и оттенков, которые совершенно не уступают привычной «водяной» краске и позволяют работать в различных техниках. |
В арсенале художников акварельные карандаши появились относительно недавно и уже завоевали свою аудиторию среди любителей рисования акварелью.
По своему внешнему виду акварельные карандаши очень похожи на обычные цветные карандаши, но спектр их применения гораздо шире. Внутри деревянной внешней оболочки прячется яркая сердцевина из спрессованной по специальной технологии акварели, которая и проявляется при рисовании. Бывают, однако, и «монолитные» карандаши, полностью состоящие из красящей основы, и похожие больше на мелки.
|
Несмотря на свою похожесть, братья-близнецы цветных грифельных карандашей имеют ряд своих индивидуальных особенностей, на которые стоит обратить внимание. Отличия акварельных и цветных карандашей. Как выбрать акварельные карандаши. Поскольку цветные и акварельные карандаши очень похожи, при покупке стоит обращать внимание на специальные пометки на упаковке или на самих карандашах, если они приобретаются поодиночке. |
В отличие от наборов с обычными цветными карандашами, на упаковках с акварельными часто изображают кисть, размывающую карандашный рисунок. Уже этого достаточно, чтобы убедиться, что эти карандаши — акварельные. Помимо этого на упаковке всегда присутствует надпись, подтверждающая родство карандашей с акварельными красками. Это могут быть любые слова и словосочетания со словом «water» (вода), например: Watercolour, Water Color Pencils, Water-soluble, а так же с основой «aqua» (что тоже переводится как вода): Aquarelle Coloured Pencils, Aquarell, Aquacolor.
|
На такие же надписи стоит обратить внимание при выборе отдельных от набора карандашей. Обозначение обязательно будет написано на самом инструменте. Если надпись отсутствует, то на карандаш может быть нанесен небольшой рисунок в виде капли или кисточки. |
Несмотря на то, что акварельные карандаши, равно как и цветные, не имеют показателя жесткости-мягкости, их твердость может варьироваться от производителя к производителю. При выборе нужно учитывать, что мягкая сердцевина размывается гораздо лучше, не оставляя и намека на штрихи и линии, тогда как более твердый грифель рискует не размыться полностью. Однако это не является минусом, и может как раз помочь художнику получить желаемый результат: штрихи, просвечивающие через краску, станут интересным художественным эффектом.
|
Таким образом, при выборе акварельных карандашей решайте, что хотите видеть в конечном итоге, и приступайте к выбору материалов для творчества! Разнообразие акварельных карандашей. Несмотря на свою непродолжительную историю существования, акварельные карандаши обзавелись приличным спектром выбора производителей, выпускающих материалы самого разного качества и в различной ценовой категории. В продаже можно встретить наборы акварельных карандашей от 6 до 72 цветов в комплекте. Коробочка может быть выполнена из картона, пластика, металла или дерева. Некоторые производители вкладывают в упаковку кисть. |
Самыми известными фирмами-производителями, выпускающими наборы акварельных карандашей, являются: FABER-CASTELL, DERWENT, KOH-I-NOOR, STABILO, LYRA, GIOTTO, CRETACOLOR, MARCO и другие.
Так уж повелось, что в случае с акварельными карандашами цена говорит за качество. Поэтому, выбирая дешевый комплект карандашей, приготовьтесь, что цветной грифель будет хуже или бледнее размываться, в сравнении с более дорогими собратьями. Впрочем, если вы ищете более твердые акварельные карандаши с яркой сухой линией и несильной степенью размытия — это ваш вариант.
Акварельные карандаши не имеют возрастного ограничения, подходят для любого возраста, и при этом неважно, занимаетесь ли вы живописью профессионально или «для себя».
|
Техника работы акварельными карандашами. Существует несколько способов работы с акварельными карандашами. Давайте вкратце рассмотрим каждый из них. |
Техника 1 Как и в случае с обычной акварелью, можно сначала нарисовать контур рисунка простым карандашом, а можно рисовать сразу акварельным. В этой технике рисунок должен быть полностью закрашен цветом, прорабатываются все детали и оттенки, а полутона и переходные цвета получаются уже при размытии.
В этой технике рисунок должен быть полностью закрашен цветом, прорабатываются все детали и оттенки, а полутона и переходные цвета получаются уже при размытии.
После того, как карандашная основа рисунка готова, можно приступить к размытию акварельных карандашей водой. Размывать рисунок следует от более светлых к более темным тонам, чтобы не получилось «грязи» на изображении. Мазки лучше делать по форме предмета — тогда рисунок получится более живой. Например, нарисовав яблоко, не размывайте его сверху вниз, а двигайтесь полукругом, добиваясь более объемной формы.
Техника 2 Такая техника носит название «по-сырому». Перед тем, как приступить к рисованию, попробуйте смочить бумагу водой. Соприкасаясь с мокрой поверхностью, акварельный карандаш будет давать мягкую широкую линию, украшая работу интересными эффектами.
|
Техника 3 Акварельные карандаши можно использовать и как обычную акварель: намочите карандаш водой и возьмите с его грифеля краску кончиком кисти, а затем нанесите на бумагу. Еще можно накрошить при помощи ножа или резака для бумаги немного грифеля и развести водой. Получится жидкая акварель, которой удобно заливать большие плоскости рисунка, например, фон. А еще такой акварельной водой можно заправить специальную кисть с резервуаром для краски. Кисть очень удобна и проста в использовании, особенно для людей, которые увлекаются рисованием акварелью. |
Техника 4 Намочите карандаши водой и рисуйте по сухой бумаге. Это даст очень яркие и насыщенные цвета.
Техника 5 Даже самые твердые акварельные карандаши все равно мягче обычных цветных карандашей, поэтому многие любят использовать такие карандаши вместо их цветных собратьев. Акварельные карандаши в качестве цветных дают яркие и плотные цвета, что делает их очень хорошим творческим инструментом как для детей, так и для взрослых.
|
Хитрости работы акварельными карандашами! Какую бы технику рисунка вы ни выбрали, всегда можно сделать более насыщенные акценты на некоторых участках. |
Еще можно поэкспериментировать и добиться интересных и несложных в исполнении эффектов. Например, попробуйте посыпать смоченный водой фон порошком из раскрошенного грифеля акварельного карандаша.
|
Или посыпьте солью уже покрашенный, но еще влажный рисунок. Соль втянет часть краски вокруг себя, создавая необычный эффект россыпи цветов, звезд или подобия снежинок. Чем крупнее соль, тем больше и фактурнее будут «цветочки». Акварельные карандаши расширяют привычное представление об акварельной живописи, при этом не нарушая традиции. Подобный вид творчества, безусловно, придется по нраву как детям, так и взрослым и позволит создавать поистине необычные, яркие и запоминающиеся картины. |
Если данная статья оказалось полезной для вас, пожалуйста, оцените ее (вверху страницы). Спасибо!
Посетители этой страницы чаще всего выбирают в интернет-магазине:
Акварель и рисунки на стене в современной гостиной
Акварель на стене в гостиной — это оригинально, стильно и точно привлечет внимание. Оформление внутреннего пространства – один из важных моментов при проведении обустройства квартиры. От того, насколько грамотно выполнена эта работа, будет зависеть самочувствие и настроение жильцов, поэтому подходить к данной проблеме следует внимательно. В настоящее время все большее распространение получают необычные техники декора помещений, одним из которых является акварельная роспись стен.
Читайте также: фрески и картины в интерьере гостиной.
Роспись стен акварелью в гостиной
Акварель, как изобразительное средство, появилась еще в древние времена, однако долгое время ей не уделялось должного внимания. Считалось, что такой материал может использоваться только для набросков и черновых эскизов. Намного позднее некоторые художники стали обращаться к этой технике, создавая шедевры, отличающиеся легкостью и свежестью изображений. Сегодня техника акварели наряду с картинами так же нашла новое применение – роспись на стенах. При этом можно получать как абстрактные мотивы и узоры, так и восхитительные изображения цветов, пейзажи, или просто плавные цветовые переходы.
Акварельная техника позволяет получить как светлые и легкие оттенки, так и насыщенные тона, плавные переходы, воздушную атмосферу. При этом таким способом можно декорировать стену как самостоятельно, так и прибегнуть к помощи профессионалов.
Акварельный рисунок за диваном: пастельные тона и розово-голубой градиентПодобный вид дизайна позволит скрыть имеющиеся недостатки, подчеркнуть необходимые акценты и создавать необходимую атмосферу в жилье.
Самостоятельная роспись стен акварелью
При желании акварельной росписью можно заняться самостоятельно, даже без наличия навыков рисования. В этом случае можно выполнить следующие приемы:
- градиентную растяжку цвета по стенам по горизонтали, или вертикали от самого темного оттенка цвета до самого светлого. Можно использовать несколько цветов, добившись плавного перехода из одного в другой;
- как вариант, иногда выполняется окраска стены двумя гармонично сочетающимися между собой оттенками, а потом они смешиваются по границе. При этом смешение выполняется не плавно, а наоборот – чтобы оставить небрежными мазками живописные разводы и полосы;
- чтобы получить абстрактный мотив на стене можно воспользоваться одним цветом краски, желательно более сдержанного оттенка.
 Для этого снизу проводится полоса, потом ее края размываются водой до получения разводов. Потом наносится следующая полоса повыше и снова размывается. Таким образом, можно получить красивые разводы на стене, наводящие на определенные размышления и притягивающие взгляд;
Для этого снизу проводится полоса, потом ее края размываются водой до получения разводов. Потом наносится следующая полоса повыше и снова размывается. Таким образом, можно получить красивые разводы на стене, наводящие на определенные размышления и притягивающие взгляд; - для создания абстрактной росписи можно использовать и несколько цветов краски. Главное – не переусердствовать с палитрой, иначе может получиться слишком кричаще и ярко, что будет утомлять глаз. Что касается техники исполнения, можно проводить произвольные линии кистями, наносить пятна, смешивать их между собой, разбрызгивать краску, выполнять размывку.
Как нанести рисунок на стены в гостиной
Стоит отметить, что не каждый осмелится приступать к оформлению стены в технике акварели самостоятельно. В этом случае можно обратиться за помощью к профессиональным художникам и дизайнерам, которые смогут создать на стене самый настоящий шедевр на требуемую тему.
Кроме того, некоторую трудность может представлять уход за стеной, или ее частью, которая расписана акварелью, так как данная краска является водорастворимой и может смазаться. Чтобы этого не произошло, необходимо готовую расписанную область на стене обработать специальным прозрачным лаком, который покроет защитной пленкой изображение. В результате украшенная таким образом стена будет радовать долгое время жильцов, оживляя интерьер квартиры.
Читайте также: 20 способов украсить стены в гостиной.
Фото гостиных с акварельным рисунком на стене
Восточный колорит: роспись стены в гостиной под мозаику в турецком стилеНеобычная идея для любителей восточного колорита — вовсе не обязательно воссоздавать мозаику из стекла, вы вполне можете просто нарисовать ее на стене. А если воспользоваться готовым трафаретом — то вполне можно сделать и своими руками. Впрочем, без чертежных навыков не обойтись, если вы собираетесь расписать большой участок комнаты.
Также с помощью акварели или любых других красок вы можете превратить скучную гостиную в стильный богемный интерьер — подобный яркий абстрактный рисунок сможет нарисовать на стене любой, главное, подобрать краски, которые сочетаются между собой. Ну и не забывать, что пестрых элементов в комнате не должно быть много, иначе вам и самому будет не слишком уютно там находиться.
Облака и небо на рассвете — рисунок за диваном на стенеАкварель может быть не только абстрактной, вы вполне можете нарисовать ваш любый пейзаж. Не обязательно что-то сложно, можно взять небо на рассвете или на закате или просто попробовать нарисовать белые облака на голубом фоне — в гостиной смотрится очень эффектно. Хотя подойдет и для любой другой комнаты.
Роспись белых стен в гостиной акварелью — желтый и зеленый — легко раскрасить своими рукамиА вот если художник из вас так себе и ничего сложного вы нарисовать просто не сможете — этот прием как раз для вас. Все просто. Красим стены в гостиной в белый цвет или используем такие же обои под покраску, и просто раскрашиваем акварелью два угла в комнате, создавая абстрактный силуэт без какой-либо симметрии.
Необычный яркий рисунок на стене — цветной акцент в строгой серой гостинойС помощью яркого рисунка на свободной стене в этой комнате вы также можете превратить скучный интерьер во что-то более оригинальное. Например, если уж вы сделали серую гостиную, то в ней не обойтись без каких-то ярких деталей. Без них комната выглядит слишком уныло. Впрочем, этот оттенок всегда стоит использовать с умом. Вот почитайте про серый цвет в интерьере гостиной — мы уже писали про это отдельную статью.
Березовый лес — роспись стен в светлой гостинойЕще одна идея для пейзажей в данной комнате — это стволы деревьев. Думаю, нарисовать березу так, чтобы ее нельзя было ни с чем перепутать, под силу каждому. Постарайтесь создать перспективу, в этом случае будет казаться, что ваш лес уходит «вглубь» за стены помещения, что позволит еще и визуально увеличить пространство в небольшой гостиной.
А уж если вы умеете рисовать — почему бы не добавить какой-то нестандартный акварельный рисунок? Это может быть девушка в очках, как на фотографии выше, животные или птицы, цветы и растения, дома и города — все, что вам взбредет в голову. А если сами вы не готовы к такому, почему бы не позвать в гости знакомого художника или просто пригласить дизайнера?
Простая акварельная техника для росписи стены — подойдет для любой гостинойА вот просто раскрасить стену в голубой или какой-то еще цвет, не забыв про расплывающиеся края, переходы и оттенки, брызги краски и другие эффекты, которые легко получить с помощью акварели — это для тех, у кого руки слишком «кривые» для того, чтобы реализовать что-то более сложное.
Мрачноватый, но необычный рисунок красками — крылья на стене в гостинойВпрочем, и любители готического стиля вполне могут придумать что-то для своей гостиной. Например, вот такие черные крылья на стене или силуэт падшего ангела. Хотя такой рисунок больше подходит для комнаты подростка, но кто сказал, что мы не остаемся подростками внутри даже тогда, когда приходит время менять паспорт?
Акварельный рисунок в рамке над камином — сочетается с подушками и шторамиНе обязательно красить стены для того, чтобы украсить рисунком комнату — вы можете нарисовать его на холсте и поставить в рамке на каминную полку или туалетный столик. А для большего эффекта — можно сочетать его с диванными подушками, шторами и другим текстилем.
Листья растений — настенный рисунок в зелено-голубых тонах для стены гостинойМаленькая хитрость: сначала купите шторы и подушки, а потом просто перенесите узор с них на холст.
Комнатные растения способны украсить любое помещение, но все они требуют за собой ухода — поливать, не забывать про удобрения, солнечный свет, влажность и так далее. Искусственные цветы — это как-то пошло. А вот акварельный рисунок на стене — в самый раз. Причем можно нарисовать не только существующие растения, но и что-то сказочное и волшебное, чего и на свете нет.
Причем можно нарисовать не только существующие растения, но и что-то сказочное и волшебное, чего и на свете нет.
А лично мне больше по душе лес и горы — пейзаж, на который можно вживую любоваться вечно. Но на опушке днями и ночами стоять не будешь, да и рассвет — это слишком мимолетно. А вот перенести этот ошеломляющий вид на стену в своей гостиной — это действительно идея, заслуживающая внимания. А что бы вы нарисовали на стене в вашей гостиной?
Понравилась статья? Поделись в соцсетях!
Легкие рисунки красками. Archive for the ‘Акварель. Рисование акварелью’ Category
Попробуйте положить на бумагу насыщенный мазок краски. Пока он не высох, добавьте в него мазок другого цвета. Последний мазок краски будет перетекать в предыдущую краску, тем самым создавая пятно цвета, с неровными краями.
Однако подобный эффект получается не на всякой бумаге. Чем более впитывающая способность и зернистость бумаги, тем меньше по ней растекается краска. И наоборот: на плотной и гладкой бумаге растекание будет максимальным. С приобретением некоторого опыта, пользоваться данным приемом станет проще. Удастся контролировать рассекание краски на листе.
Даже этот не сложный прием на начальных стадиях может не дать ожидаемого результата. В случае неудачи, можно просто смыть краску и начать заново. Этот прием широко применим в практике профессиональных художников, как для рисования больших объектов (вода и небо), так и для локальных участков картины (лепестки цветов).
Эффекты, создаваемые подтеками краски, практически невозможно воссоздать с помощью кисти. В этом их уникальность. Например, чтобы добиться эффекта отражения на водной глади, можно добавить сильно разбавленную краску или воду на нанесенную ранее и уже подсохшую краску. Свежая краска начнет растекаться, тем самым образуя размытые края, подобно отражению в воде подернутому рябью. Правда потребуется некоторый опыт, чтобы суметь точно определить, подсохла ли краска на первом слое.
Правда потребуется некоторый опыт, чтобы суметь точно определить, подсохла ли краска на первом слое.
Инвентарь
Кисти
Кисть для акварели должна удовлетворять следующим требованиям:
1. хорошо впитывать и удерживать воду;
2 .быть гибкой;
3. легко принимать прежнюю форму после мазка;
4. при нанесении длинных или точечных мазков ее волоски не должны топорщиться.
В отличии от других видов кистей, у акварельных кистей короткие ручки.
Широкая плоская кисть (1), довольно жесткая. Она позволяет снимать или вытирать краску и очень облегчает работу.
Кисть для размывки (3) — довольно большая круглая мягкая кисть, позволяющая обрабатывать большие участки, например, фон. Никакая кисть не способна также хорошо принимать различные формы и удерживать нужное количество краски и воды и не пересыхать.
Рабочие кисти — их размер зависит от особенностей техники. Плоская кисть из синтетики (2), малая круглая кисть из синтетики (4), малая круглая кисть из волоса колонка (5).
Бумага
Бумага для рисования акварелью не должна расслаиваться, когда вы стираете краску, коробиться, краса по ней не должна стекать.
Бумага должна быть белой. Если вы хотите использовать разнообразную цветовую гамму, то с белой бумагой работать будет проще. На тонированной бумаге цвета могут измениться непредсказуемым образом.
Бумага должна быть проклеенной. Это значит, что вода будет впитываться сравнительно медленно. Кроме того, быстрое и сильное впитывание воды приводит к излишнему высветлению положенной на бумагу краски. Акварельная бумага, продаваемая в пачках по несколько листов формата А3, страдает обычно и желтизной, и плохой проклеенностью.
Бумага должна быть достаточно толстой
Зернистость — это как бы степень гладкости бумаги:
1. мелкозернистая бумага очень гладкая.
 Такая бумага используется для работ, предполагающих тщательную передачу деталей. На такой бумаге мазок почти не встречает препятствий.
Такая бумага используется для работ, предполагающих тщательную передачу деталей. На такой бумаге мазок почти не встречает препятствий.2. среднезернистая бумага. Этой бумагой пользуются чаще всего. Она пригодна для любых работ. Альбомы для акварели чаще всего изготавливаются именно из этой бумаги.
3. крупнозернистая бумага имеет слегка шероховатую поверхность. Обладает отчетливой фактурой. Используется, как правило, для специальных работ. Для такой бумаги характерна большая плотность, очень часто именно такую бумагу изготавливают вручную.
Самая распространенная бумага для акварели имеет среднюю зернистость и плотность 250г/м²
Тонкой бумагой или бумагой без зернистости пользоваться нельзя, т.к. такая бумага плохо впитывает и коробится при намокании
Краски
Купили школьные акварельные краски? Это тоже вариант, но лучше взять профессиональные краски для художников.
Более-менее подойдут «краски медвые акварельные» производства Санкт-Петербург
Акварельные краски выпускаются в пластиковых ванночках и в тюбиках .
Краски в ванночках требуют немного больше усилий при подготовке к работе: нужно капнуть по капельке воды с кисточки в ванночку, чтобы краски немного размокли. Пользоваться такими красками удобнее, т.к. они разводятся прямо в ванночке и после окончания рисования там и остаются. На начальных стадиях рекомендуется использовать краски в ванночках.
Краски в тюбиках рекомендуются тем, кто уже имеет некоторый опыт работы с акварелью. Художник самостоятельно формирует набор красок, руководствуясь собственными потребностями. Готовый набор в тюбиках с дюжиной красок можно рекомендовать художникам-любителям.
Количество красок в наборе
В наборах может быть от 12 до 36 красок, однако далеко не все из них будут использованы. Большое количество красок в наборе иметь совершенно не обязательно, более того, это просто неудобно.
 Желательно перепробовать все возможные комбинации красок, чтобы знать, какие сочетания дают грязь, а какие — необычные цвета, отсутствующие в наборе.
Желательно перепробовать все возможные комбинации красок, чтобы знать, какие сочетания дают грязь, а какие — необычные цвета, отсутствующие в наборе.Выбираются для работы не более десяти наиболее употребимых красок.Чаще всего, это голубая, кадмий желтый, красный и оранжевый, охры, умбра, изумрудно-зеленая, нейтральная черная.
Вообще краски делятся на две группы — теплые и холодные. К теплым относятся желтые, оранжевые, красные, коричневые, то есть все краски, которые в основе своей содержат то или иное количество красного или желтого цвета. К группе холодных — голубые, синие, зеленые, фиолетовые, если в них преобладают холодновато-синие оттенки. Зеленые, фиолетовые, серые и черные цвета могут быть как холодными, так и теплыми в зависимости от особенностей колера и влияния окружения.Цвета синий, желтый, красный — основные, остальные, полученные путем смешения, считаются производными — теплыми или холодными в зависимости от состава красок. Даже такие нейтральные цвета, как серый и черный, содержат бесчисленное множество нюансов, которые подчас трудно определить по качеству цвета. Если взять группу теплых цветов, например красных, и сравнить между собой по теплохолодности, то заметно, что и в этой группе по отношению друг к другу есть цвета холоднее и теплее.
Для начинающих рекомендуется взять: жёлтый, красный, синий и чёрный цвет, каждого в 2 оттенках холодном и тёплом. Все остальные цвета получать путём смешивания имеющихся.
Конечно, акварелью рисовать намного сложнее, чем, например, гуашью или масляными красками. Но можно попробовать сделать небольшие прозрачные и нежные работы, убедиться, что рисовать красками не так уж страшно, а наоборот, необычайно приятно.
Акварельные мазки обычно делают прозрачными, не используя белый цвет. Исходят из того, что самой белой частью композиции является цвет листа бумаги.
Акварельные работы почти невозможно исправить, поэтому старайтесь все сделать с первого раза. Начинать надо с самых простых композиций и потихоньку переходить к более сложным работам.
Попробуйте сначала просто смешать несколько красок и посмотреть, как они естественно перетекают друг в друга.
Намочите небольшой кусочек листа бумаги водой (только не создавайте луж, бумага должна быть влажной) и проведите по влажной поверхности кисточкой с краской. Набирайте на кисточку краски небольшое количество, излишки снимите о край стаканчика с водой.
Рисуйте кончиком кисти, не давите сильно на нее, легонько, воздушно.
Попробовали? Краска должна красиво растечься, рядом сделайте еще мазок другой краской и посмотрите, как они затекают друг на друга. Не затирайте, не смешивайте на одном месте больше трех цветов – получите грязные разводы.
Теперь приступим к нашим цветам.
Нарисуем сначала карандашом набросок цветов.
Сделаем фон. Аккуратно, стараясь не сушить краски (то есть не давайте мазкам сильно подсохнуть, чтобы границы между ними не были заметными и резкими) прорисуем задний план. Все мазки должны перетекать друг в друга, следов «карандашной раскраски» видно не должно. Используйте светло-зеленую краску, желтую и охру.
Как научиться рисовать акварелью с нуля?Акварельная живопись одна из самых сложных в мире, но в то же время, является самой нежной, хрупкой и привлекательной для начинающих художников. Что же в ней такого особенного? Весь секрет в прозрачности линий, благодаря которым видны даже самые незначительные цветовые переходы. Водянистость рисунка, которая придаёт ему объем. Но как постичь это не простое искусство? Как научиться рисовать акварелью с нуля? Перед тем, как приступить к рисованию, нам необходимо выбрать вспомогательные материалы. Художественная школа для взрослых и детей на своих курсах предлагает профессиональное обучение рисованию в любых техниках, но научиться можно и самому. Рассмотрим в статье моменты, которые помогут нам в этом.
На какой бумаге и какими кистями рисовать акварелью?
1. Бумага. Лучше сразу приобрести акварельную, она стоит не дорого (около 40р. блокнот). Её отличие от обычной в плотной текстуре листов. Такая бумага не будет разбухать от воды и коробиться.
блокнот). Её отличие от обычной в плотной текстуре листов. Такая бумага не будет разбухать от воды и коробиться.
2. Кисти. В магазине для рисования для начала берём две кисти. Маленькую и большую. Шерсть белки хорошо подходит для акварельных красок.
3. Палитра. Выбор палитры не принципиален, выбираем любую. Некоторые художники заменяют палитру на небольшое стекло, оно практично в использовании, его удобно мыть.
4. Краски. Детские медовые краски с добавлением лимона и прочего — сразу откладываем в сторону. Они нам не понадобятся. В магазине для художников берем любые профессиональные краски. Откройте их и посмотрите на цвета, они должны вам понравится. Не обязательно брать самые дорогие, это не принципиально.
Как научиться правильно рисовать акварелью начинающим поэтапно?
Как красиво рисовать акварелью? Для того, чтобы наши акварельные рисунки получались качественными, необходимо освоить несколько базовых приёмов.
1.Равномерная заливка. На бумаге проведите квадрат или прямоугольник. Лучше выбрать цвет потемнее, на нём будет лучше видно. Наберите его на кисть и протяните с одного угла к другому. Наберите краску снова. Проведите следующую полосу так, чтобы она перекрывала стык предыдущий. Если первая полоса полностью не перетекает во вторую, то наклоните лист бумаги. Набирайте краску и продолжайте рисовать полосы, сохраняя однородный оттенок. Промойте кисть в воде и выжмите. Темные полосы разровняйте с помощью кисти. Дайте рисунку высохнуть. Если у вас получился прямоугольник равномерно залитые краской, у вас всё получилось.
2.Зависимость оттенка краски от количества воды. Наберем краску на кисть и проведем первую линию, затем опустим кисть в воду и проведем вторую через 1 см от неё. Продолжим обмакивать кисть в воду и проводить линии до тех пор, пока они не станут максимально прозрачными. Это упражнение помогает почувствовать, сколько воды необходимо добавлять, чтобы получить желаемый оттенок.
3.Градиент. Цель этого упражнения получить однородный переход от тёмного тона к светлому. Наберите кистью краску и проведите вертикальную линию, после чего обмакните кисть в воду и проведите вторую так, чтобы она немного заходила за первую и краска начала перетекать. Снова повторяем тоже самое, добавляя воды. Добиваемся полного перехода цвета. Последнюю полосу проведите просто водой. Просушите кисть и проведите валик краски снизу заливки.
Наберите кистью краску и проведите вертикальную линию, после чего обмакните кисть в воду и проведите вторую так, чтобы она немного заходила за первую и краска начала перетекать. Снова повторяем тоже самое, добавляя воды. Добиваемся полного перехода цвета. Последнюю полосу проведите просто водой. Просушите кисть и проведите валик краски снизу заливки.
Учимся рисовать акварелью поэтапно с помощью различных техник для начинающих
Как начать рисовать акварелью? Необхдимо постичь основы искусства. Это определенные упражнения, выполняя которые, вы освоите первые азы рисования акварельными красками.
1. Мокрым по мокрому. Намочите водой небольшой кусочек бумаги. Лист должен быть равномерно пропитан водой. А теперь возьмите краски на кисть и проведите по мокрому месту. Понаблюдайте, как растекается краска. Попрактикуйтесь, добавляя больше или меньше краски на лист бумаги. Это вам очень пригодится.
2. Перетекание из цвета в цвет. Сначала водой нарисуем любые фигуры. Берем на кисть, к примеру, синий цвет и наносим на фигуру. Добавляем немного бордового и желтого. Вы должны добиться плавного перехода от одного цвета к другому. Если этого не происходит, добавьте немного воды.
3. Наложение слоёв. Нарисуем фон, как в первом упражнении. Немного подождем, дадим ему высохнуть полностью. Рисуем на фоне пару кругов разных цветов и даём высохнуть. На кругах рисуем третий слой.
4. Приём с использованием пищевой соли. Рисуем фон и засыпаем сверху немного обычной столовой соли. Ждём. Кристаллы соли понемногу впитывают в себя краску и становятся похожи на звёзды. Заметнее всего эффект проявляется в темных областях.
5. Облака с помощью салфетки. Заливаем фон и пока краска еще влажная, начинает прикладывать салфетку, придавая форму. Таким образом, у нас получается текстура, напоминающая облака. Эту технику можно использовать для исправления ошибок, которые возникают у вас в процессе рисования. Просто промокните лишнюю краску.
6. Брызги. Набираем краску на кисть и проводим пальцем по кисти над бумагой или капаем, образуя неравномерные брызги по всей поверхности. Стол лучше застелить тканью, чтобы избежать загрязнений.
Набираем краску на кисть и проводим пальцем по кисти над бумагой или капаем, образуя неравномерные брызги по всей поверхности. Стол лучше застелить тканью, чтобы избежать загрязнений.
10 распространенных ошибок начинающих художников
1. Любите себя. Очень многие художники начинают себя ругать и излишне критиковать свои картины. Этого делать не нужно. Нарисовали что-то — похвалите себя. Всё что вы делаете -это только для вас и для реализации ваших творческих потребностей. Чем больше вы будете получать удовольствия от процесса рисования, тем лучше у вас будет получатся.
2. Используйте удобные материалы. Качественные кисти, бумага и краску. Тогда процесс рисования будет приносить вам только удовольствие.
3. Копируйте сюжеты известных художников. Они будут служить вам основой ваших знаний.
4. Показывайте ваши картины всем вашим друзьям,близким и знакомым. Подарите свою картину. Собирайте вокруг себя единомышленников, которые будут поддерживать вас.
5. Теплые и холодные краски. Используйте больше холодных оттенков вдалеке и теплых вблизи. Так вы покажите воздушную перспективу в своей картине.
6. Не красьте одной краской весь фон. Меняйте тон, смешивайте краски, создавайте на вашей картине колорит. Сделали два-три мазка одним цветом, добавьте другой. Чем больше оттенков вы будете использовать, тем интереснее будет ваша картина.
7. Дайте картине возможность подсохнуть. Так вы сделаете её более проработанной и глубокой.
8. Показывайте объем вблизи. Наносите больше краски на ближние предметы с помощью мастихина. Делайте их объемными.
9. Чем больше вы смешаете красок, тем более живописной будет ваша картина. Подмешивайте полутона.
10. Оформляйте картины багетом. Он придаёт картине дополнительный объём.
Если Вы хотите смотреть видео уроки рисования гуашью для начинающих, то на нашем сайте Вы их найдете. Мы собрали здесь большое количество обучающих роликов с ютуб на тему рисования именно этим типом краски. Вы бесплатно можете получить информацию не прибегнув к регистрации. Мы сделали для Вас новую рубрику с хобби, которая очень полезен для того, чтобы развивать в себе творческий талант. Это будет полезно и взрослым и детям. Вы можете пользоваться красками для рисования рисунков, картин, баннеров и многого другого. Вы сможете легко научиться рисовать гуашью в быстрые сроки и бесплатно. Наши видео уроки помогут Вам очень просто рисовать шедевры. Данное хобби позволяет успокоиться, набраться сил, поразмыслить. Важно понимать, что это требует усидчивости и большого желания развиваться постоянно.
Вы бесплатно можете получить информацию не прибегнув к регистрации. Мы сделали для Вас новую рубрику с хобби, которая очень полезен для того, чтобы развивать в себе творческий талант. Это будет полезно и взрослым и детям. Вы можете пользоваться красками для рисования рисунков, картин, баннеров и многого другого. Вы сможете легко научиться рисовать гуашью в быстрые сроки и бесплатно. Наши видео уроки помогут Вам очень просто рисовать шедевры. Данное хобби позволяет успокоиться, набраться сил, поразмыслить. Важно понимать, что это требует усидчивости и большого желания развиваться постоянно.
Многим будет полезно смотреть онлайн мастер-классы с обучением рисованию гуашью для новичков в хорошем качестве на русском языке. Мы собрали здесь самую качественную коллекцию с уроками, которые позволят Вам обучиться рисованию красками гуашью. Вы научитесь правильно держать кисточку и наносить краску на полотно. Рисование гуашью отличается от рисования другими красками. Тут необходимо знать некоторые секреты, именно они позволят стать Вам начинающим художником. Все необходимые знания Вы найдете у нас. Люди, которые любят визуально получать информацию могут пользоваться нашим ресурсом с большим удовольствием. Теперь наш сайт стал еще больше. Рисуем картины гуашью с видео уроками для начинающих поэтапно. Получите ИЗО обучение в домашних условиях от лучших специалистов. Учимся писать рисунки гуашью с помощью мастер классов для детей и взрослых. Все, что Вы найдете здесь, абсолютно бесплатно. Здесь Вы узнаете как нарисовать гуашью красивые картины, интересные рисунки и многое другое. У нас Вы научитесь красить.
Для людей, кто хочет узнать и про другие виды рисования, те могут посетить рубрику про общее рисование . Там есть разное, начиная от гелевых ручек, заканчивается линерами, губками, мелом. Там тоже по-своему увлекательно.
Если Вы хотите смотреть онлайн поэтапное обучение рисование гуашью, то наши видео уроки помогут Вам. Здесь много обучающих роликов с ютуб. И ребенку и взрослому будет легко и понятно начать обучаться у нас. Если Вы впервые взяли в руку кисть, или уже имеете какой-то опыт, всё равно заходите к нам. Мы собрали самое лучшее, чтобы Вам было легко пройти обучение как начинающему художнику.
Если Вы впервые взяли в руку кисть, или уже имеете какой-то опыт, всё равно заходите к нам. Мы собрали самое лучшее, чтобы Вам было легко пройти обучение как начинающему художнику.
В школе учат на изо разному, но там нет большого уклона по определенному стилю. Мы же предлагаем Вам более детально и глубоко уйти в рисование. У Вас обязательно получится научиться создать шедевр. Если Вы хотите создать рисунок гуашью, но не знаете как, то заходите к нам на мастер класс.
Видео уроки живописи гуашью для начинающих на русском языке здесь Вы можете смотреть онлайн. В огромном количестве и без регистрации Вам ждут ролики про рисование. Если Вы новичок, то Вы сможете научится рисовать гуашью простые рисунки поэтапно и пошагово. Здесь Вы узнаете о разных способах, технике, секретах рисования. Такой большой коллекции, наверное, нет ни у одного русско-язычного сайта.
Здесь пошаговые видео уроки по рисованию гуашью для начинающих Вы сможете смотреть онлайн. Мастер классы для начинающих на русском языке помогут всем в обучении. Вам потребуется мало времени, чтобы создать свой первый красивый рисунок. Пейзажи, портреты, натюрморты, животных и многое другое Вы найдете у нас.
Красивые рисунки гуашью Вы можете научиться рисовать с помощью онлайн видео уроков для детей и взрослых. Мы подготовили большой список обучалок. Обучающие ролики помогут Вам легко и быстро научиться рисовать используя краски гуашь и нужные кисточки. Для обучения Вам требуется интернет и большое желание. Уверен, что Вам у нас будет увлекательно.
Акварель и рисунок
Графическая коллекция ККХМ им. Коваленко начала складываться еще при жизни ее основателя.
Хотя Федор Акимович не собирал графику столь планомерно, как живопись, но уже в то время были сделаны первые приобретения рисунков и акварелей таких признанных мастеров как А. А. Иванов, П. П. Соколов, И. И. Шишкин, А. Н. Бенуа, и некоторых других художников. Активное пополнение графической коллекции происходило в первые десятилетия ХХ века, когда из Государственной Третьяковской галереи, Московского музейного фонда в музей поступили работы В. М. Васнецова, В. Е. Маковского, В. В. Верещагина, Е. Е. Лансере и др.
А. Иванов, П. П. Соколов, И. И. Шишкин, А. Н. Бенуа, и некоторых других художников. Активное пополнение графической коллекции происходило в первые десятилетия ХХ века, когда из Государственной Третьяковской галереи, Московского музейного фонда в музей поступили работы В. М. Васнецова, В. Е. Маковского, В. В. Верещагина, Е. Е. Лансере и др.
Безусловным украшением музейного собрания являются два графических листа А. О. Орловского – «Автопортрет» (1806) и «Монголы» (1808). Художник бурного темперамента, романтик по натуре, Орловский в «Автопортрете» показал мятежные и страстные порывы души художника.
Несомненный интерес представляет эскиз А. А. Иванова «Рождение Христа». Библейская тема занимает особое место в творчестве художника. Рисунок отличается живостью и энергией жестов и движений персонажей. В компоновке фигур на листе чувствуется умение работать над большой многофигурной композицией.
Графика художников-реалистов второй половины XIX в. Представлена И.И. Шишкиным. И. И. Шишкин — один из крупнейших, и едва ли не самый популярный среди русских пейзажистов. Шишкин знал русскую природу “ученым образом” и любил ее со всей силой своей неповторимой натуры. Карандашные рисунки И. И. Шишкина «Дорога в лесу», «Сосны», «Облако» и др. выполнены с непосредственностью и свободой; живым движением карандаша в них отобрано и передано в немногих линиях и пятнах главное из всего многообразия натуры.
Рисунок — тщательно проработанный, несущий в себе отпечаток раздумий художника над образом получил самостоятельное художественное значение. В эскизе М. А. Врубеля к его программному произведению «Демон» в полной мере раскрывается своеобразие мастера – особого рода кристаллический рисунок, мерцающий темными тонами мирового сумрака. Особый интерес представляют находящийся в музее набросок к картине Ф. А. Малявина «Вихрь», «Сошествие во ад» (1902) — эскиз росписи В. М. Васнецова для Георгиевской церкви в Гусь-Хрустальном, версальские акварели Александра Бенуа, крымские акварели Максимилиана Волошина.
Своеобразный стиль Н. К. Рериха — «Идолы» (1908), обозначается уже в ранних его работах — ясность линий и лаконизм, чистота цвета и музыкальность, великая простота выражения и правдивость. Рисунок построен на глубоком знании исторического материала, передает ощущение духа языческой Руси.
В области портретного жанра особый интерес вызывает жанр детского портрета. Акварель З. Е. Серебряковой «Мальчик в кресле» относится к тому периоду, когда художница писала акварельные и карандашные портреты своих детей, соседских и крестьянских ребят, и только начинала формировать свой собственный стиль детского портрета.
Рядом со знаковыми именами русского искусства – работы незаслуженно забытых художников прошлого, виртуозно владеющих техникой акварели. Неброская прелесть родной природы воплотилась в лирических акварелях председателя Общества акварелистов — Альберта Бенуа. Для художника характерна живая наблюдательность и чувство искреннего восхищения красотой русского пейзажа. Основной темой К. Я. Крыжицкого стал лирический пейзаж. Большинство акварелей художника появлялось на выставках Общества русских акварелистов, деятельным членом которого он был с момента его основания.
Коллекция Краснодарского художественного музея им. Ф.А. Коваленко позволяет получить представление о развитии графического искусства начала XIX – первой половины XX веков, демонстрирует своеобразие акварели и рисунка как самоценных форм существования искусства.
Очень легкие рисунки акварелью. Приемы и техники работы акварельными красками
Сегодня хочу представить Вам не совсем обычный мастер-класс. Т.е. диптих, который мы будем рисовать вполне обычен, необычным будет процесс. Хочу в этом мастер-классе порассуждать и показать, о том, как по разному будет вестись работа над картиной, как выбирается путь, и как сложно сделать действительно Мастер-класс.
Хороших мастер-классов действительно очень мало, и не потому что мало художников, которые могут объяснить доходчиво и описать процесс своей работы, а потому что, часто, сама работа над картиной часто является не предсказуемым процессом)).
Т.е. мастер-класс, на мой взгляд, должен быть как бы инструкцией — четкой и понятной, пошаговым таким путеводителем! Но часто, когда начинаешь просматривать видео или поэтапные фото, понимаешь, что некоторые вещи ты просто не в состоянии объяснить))
Сначала я хотела сделать мастер-класс, только по второй картинке, где черешенка рассыпана, там все лаконично и прозрачно! Но потом решила запечатлеть весь процесс как есть и еще попробовать объяснить начинающим художникам, что не всегда все просто и гладко. И этих моментов не стоит бояться. Итак приступим!
Нам понадобится:
1. Акварельные краски — у меня Ленинград 24 цвета.
2. Бумага для акварели, любая, лучше плотностью больше чем 260 г\м
3. Маскирующая жидкость (можно обойтись без нее)
4. Белый акрил или гуашь.
4. Простой карандаш не сильно мягкий, Н или 2Н, ластик.
5. Планшет или лист фанеры, на который мы будем крепить лист.
6. Палитра (пластиковая или керамическая) и кусочек бумаги, такой же на которой мы будем рисовать, что бы пробовать наши цвета.
7. Фото с которого мы будем рисовать
Итак начинаем…
Сразу небольшое отступление. если отталкиваться от академического обучения, правил ведения работы, то нужно идти от общего у частному. Т.е. работая в любой технике, мы должны отталкиваться от пятен общих предметов и постепенно уточнять и уточнять, и накладывать более насыщенные слои.
Но! В акварели имеет место такой момент как смена воды. Нужно или буквально ежеминутно бгать менять воду, так как тут имеют место яркие ягоды и грязная вода может сильно им навредить. Или обставиться кучей емкостей с водой и пользоваться для разных предметов разным стаканчиком.
Я предпочитаю работать с двумя емкостями для воды, одна для смывания краски с кисти, вторая для мытья кисти (вторая баночка долго остается чистой) и работать по типу прорисовки отдельных цветов (оттенков) и потом обобщать картину.
В данной работе я пользовалась прямо несколькими методами, разными. Искала, как мне удобней вести работу.
Искала, как мне удобней вести работу.
Сначала я попробовала сделать несколько ягод и чуть чуть фона вокруг них, что бы в целом понять, какой я хочу видеть картину, реалистичной или акварельно-легкой…
На данном этапе я не пользовалась маскирующей жидкостью, и еще не знала, буду ли я ее использовать)). Но поняла, что хочу создать, четкую, реалистичную картинку. Теперь я нанесла маскирующую жидкость тонким слоем на белые блики и продолжила дальше.
Я сделала первый слой ягод, всех. Для светлых я использовала Кадмий желтый и алую, а для темных краплак с капелькой фиолетового.
Поменяла воду! Разбавленной водичкой голубой краской немного прошлась по кувшинчику и тарелочке.
Немного поработаем с листиками. Смесь зеленого и ультрамарина. Сначала я закрыла листики полностью сильно разбавленной смесью краски. Потом сделала еще два слоя, оставляя прожилочки и более плотный цвет в тени. Между слоями все должно просохнуть.
Смесью фиолетовой и сепии я немного сделела тень на тарелочке, что бы подчеркнуть игру света и тени.
Теперь у меня на палитре 5 смесей красок — первые две для двух видов ягод, третья для листиков, четвертая для кувшинчика и тарелочки и пятая сепия с фиолетовой для теней и фона.
Я полусухой кистью наношу движения по фактуре дерева. И тонкой кистью делаю разделение между досками.
Продолжаю тень на тарелочке, с добавление голубого. Должны получиться такие разводы, напоминающие облезлую краску.
Дальше работаю и с фоном и с ягодами, там, где уже есть фон, так проще и понятнее уловить распределение света и тени на рисунке и позволяет видеть сразу все предметы едино, и не один из них не будет выпадать из картины.
После высыхания наношу еще и тени на листик и рисую веточки черешни, все той же смесью сепии и фиолетового в разных пропорциях разбавленной водой.
Маскирующую жидкость я снимаю не со всей картины сразу, а по мере необходимости, после прорисовки ягод определенных. что бы завершить их доработку, так как блики не везде прямо белые, гдето они с синевой или розовинкой. Тут уже вступает в работу ваша наблюдательность!
что бы завершить их доработку, так как блики не везде прямо белые, гдето они с синевой или розовинкой. Тут уже вступает в работу ваша наблюдательность!
Так же уделяю внимание кувшинчику, прокладываю слой голубой краски, тени, нашей темной смесью, снимаю с нее маскировочную жидкость.
Продолжаю работу и над ягодами и над кувшинчиком и тарелочкой. Довожу их до готовности, внимательно смотрю где свет а где тень. После высыхания делаю мелкие дефекты, при помощи нашей теневой смеси и белого акрила.
Делаю падающую тень на поверхность от тарелочки и от ягод НА тарелочке.
По предыдущему алгоритму прорабатываю листик, который лежит на ягодах.
Фон тоже уточняется по пути, по мере уточнения «главных героев» натюрморта.
Двигаемся дальше по ягодам и по фону, не зависаем над одним предметом. Уточняем уже нарисованные детали тоже. По мере проработки дальше, иногда прямо хочется «влезть» и что то подправить)). Часто от этого нужно воздержаться. что бы не заметно для себя не выделить лишнего. Натюрморт должен смотреться весь в одном ключе!
Осталось проработать мелкие детали, веточки ягод. Еще раз внимательно посмотреть на картину. Может стоит оставить ее на день два и вообще убрать с глаз. Потом достать и посмотреть свежим взглядом, свериться с референсом, послушать свои ощущения. Что то уточнить. Поставить подпись и снимать уже скотч!
Завтра будем рисовать вторую часть нашего диптиха! До встречи!
Оригинал МК находится на моем сайте
Для работы акварелью, предлагаю Вам ознакомиться с различными методами и техническими приемами. Работать акварелью проще, чем маслом, но ошибки исправлять сложнее. Однако это не значит, что нельзя корректировать акварельные работы. А знание терминов помогут Вам в дальнейшем изучении техник работ с акварелью.
Ополоснуть кисть
Чтобы удалить краску с кисти слегка постучите ею по дну ёмкости с водой. Это позволит вымыть большую часть краски. Если Вы только что работали с темным цветом и Вам необходимо набрать на кисть более светлый, сильнее постучите кистью. Затем промойте кисть в ёмкости с чистой водой.
Это позволит вымыть большую часть краски. Если Вы только что работали с темным цветом и Вам необходимо набрать на кисть более светлый, сильнее постучите кистью. Затем промойте кисть в ёмкости с чистой водой.
Набрать полную кисть
Проведите чистой кистью по разведённой краске, а затем поднимите её. Вы поймёте, что кисть полная, если с её кончика будет стекать избыток краски. Удалите избыток краски, проведя одним только кончиком по ободку ёмкости.
Набрать кисть
Сделайте так же, как описано выше, но удалите лишнюю краску с кисти, проведя несколько раз по ободку ёмкости.
Промокнуть или промакивание
Другой способ удалить лишнюю краску или влагу с кисти, это провести ею по свернутому бумажному полотенцу. Этим термином также описывается удаление лишней влаги или краски с рисунка.
Слегка промокнуть
Прикоснитесь один раз кончиком кисти к ткани или бумажному полотенцу. Это позволит удалить часть лишней акварели или влаги с кисти. Этим термином также описывается степень нажима бумажным полотенцем (салфеткой) при удалении краски или влаги с рисунка.
Полностью удалить влагу
Шаг 1.
Прикоснитесь одной стороной кисти к бумажному полотенцу.
Шаг 2.
Переверните кисть и прикоснитесь другой стороной кисти к бумажному полотенцу, тем самым, удаляя всю влагу.
Снятие, соскабливание и промакивание
Иногда при рисовании необходимо удалить акварельную краску с бумаги. Возможно, цвет или тон являются слишком темными, или была допущена ошибка, или была закрашена область, на которой Вы не собирались рисовать.
Я покажу три простых способа как удалить краску: чистой влажной кистью, соскабливанием жесткой кистью и промакиванием тканью.
Как удалять акварельную краску
Используется эта техника для удаления влажной, слегка увлажнённой или сухой акварели.
Вам понадобятся: чистая сырая кисть и чистая влажная ткань.
Снятие краски, используя плоскую сторону кисти. Снятие краски, используя кончик кисти.
Как снять краску, используя плоскую сторону кисти
Чистой сырой кистью, сделайте несколько мазков в той области, где Вы хотите снять слой краски. Вытрите кисть о влажную ткань. Повторите мазки ещё раз. Если Вы хотите удалить больше краски, то ополосните кисть и промокните её о ткань. Вытрите краску с кисти о ткань. Повторите ещё раз при необходимости.
Как снять краску кончиком кисти
Если Вы хотите снять узкие линии, сформируйте кончик кисти пальцами. Используя короткие мазки кисти, снимите линию краски, затем протрите кисть на влажной ткани.
Как соскабливать краску
Эта техника применяется для удаления краски, которая уже высохла. Вам понадобятся кисть с жесткой щетиной и сухая ткань.
Соскабливание кончиком кисти. Соскабливание плоской стороной кисти.
Как соскабливать краску кончиком кисти
Увлажните кисть и слегка постучите ею несколько раз по бортику ёмкости с водой. Кончиком кисти, слегка вычистите область непрерывными мазками. Сухой тканью удалите лишнюю краску с вычищаемой области. Удалите краску из кисти, ударяя ею по дну ёмкости с водой. Если Вам необходимо удалить больше краски, то повторите предыдущие шаги.
Как соскабливать краску плоской стороной кисти
Применяется тот же метод что и при соскабливании кончиком кисти, но только используя плоскую сторону кисти. Можно удалять краску непрерывными перекрывающими друг друга нисходящими мазками, или перекрывающими друг друга мазками из стороны в сторону. Для достижения наилучшего результата, удаляйте краску только в одном направлении, иначе краска будет попадать назад в область, которую Вы уже очистили.
Для того, чтобы удалить краску на сильно закрашенной области, её лучше промокнуть бумажным полотенцем, а не тканью.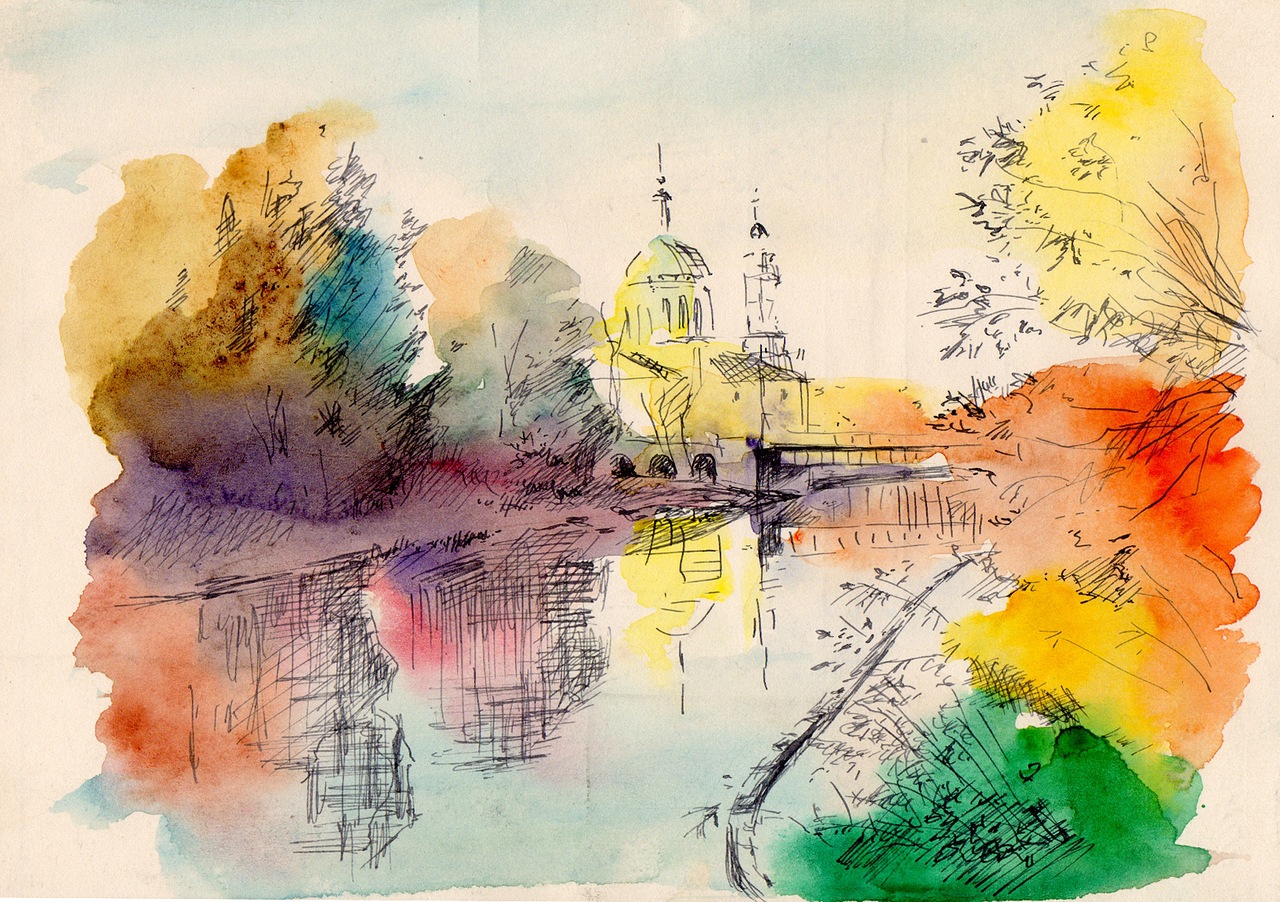 Ткань оставит следы нитей на окружающей области.
Ткань оставит следы нитей на окружающей области.
Как промокнуть краску тканью
Промокнуть краску тканью – простой способ осветлить закрашенную область; этим способом можно добавить текстуру рисунку. То, насколько сильно снимается краска, зависит от влажности размывки и степени давления ткани на бумагу.
На примерах ниже, в верхнем ряду квадратов показаны результаты, когда промокнули тканью по мокрой размывке. В нижнем ряду показаны результаты, когда промокнули тканью по влажной размывке.
Возьмите сухую ткань и сомните её рукой. Это изменит жесткость ткани. Если Вы промакиваете краску, создавая текстуру, то сомните ее ещё больше.
Прижмите ткань к влажной области, чтобы промокнуть некоторое количество краски. Как Вы можете видеть из примера выше, достаточное давление на размывку может значительно осветлить краску.
Сухая кисть, по-сырому и соль
Техника сухой кисти
Как художникам, нам нравится изучать различные и креативные способы создания текстур на наших рисунках. Я представлю следующие методы: сухая кисть, по-сырому и создание текстуры при помощи соли. Освоим эти методы постепенно, руководствуясь примерами.
Техника сухой кисти
Сухая кисть – универсальная и креативная техника, которая наносит на бумагу больше пигмента, чем воды. Эта техника лучше всего подходит к фактурной акварельной бумаге холодного прессования или бумаге с крупнозернистой текстурой.
Пример сухой кисти
На иллюстрации крупным планом показано как применялась техника сухой кисти при создании эффекта структуры дерева на скворечнике и на старом заборе.
Применение техники сухой кисти
Наберите краску на кисть, а затем промокните кисть на бумажном полотенце. Слегка проведите кистью по поверхности бумаги, используя только боковую сторону щетины. Для того, чтобы усилить контрастность, просушите рисунок и повторите процесс нанесения краски снова.
Для достижения лучших результатов, используйте качественную круглую кисть с маленьким кончиком. При помощи такой кисти можно провести линию, едва прикоснувшись поверхности бумаги.
Техника по-сырому
По-сырому, другая универсальная и популярная техника, где краска наносится на увлажнённую поверхность. Эта замечательная техника применяется для создания эффекта мягкого размытого фона на картине.
Примеры техники по-сырому
Сухой
Влажный
На иллюстрации крупным планом показан плавный переход от тёмного цвета к более светлому. Показана текстура, которую можно создать при помощи этой техники.
Применение техники по-сырому
Нанесите чистую воду на поверхность, которую будете закрашивать. Когда блеск воды исчезнет, начните её закрашивать. Поверх краски можно добавить воды, чтобы усилить эффект.
Для достижения хороших результатов применяйте однотонные цвета. Прежде чем нанести новый цвет, дождитесь, пока пропадёт влажный блеск предыдущего цвета. Иначе поверхность будет слишком влажной и цвета не создадут желаемого эффекта.
Цвета будут немного светлее, если они наносятся на влажную поверхность. Прежде чем использовать краску, можно проверить её тон на небольших кусочках бумаги.
Техника соли
Техника соли – интересный и креативный способ добавления различных структур на рисунке. Столовая соль даст небольшой и компактный узор, а при использовании морской соли узор будет большим и красивым.
Пример техники соли
На иллюстрации крупным планом справа показан увеличенный рисунок с замечательной структурой, которая была сделана при помощи соли.
Применение техники соли
Во-первых, закрасьте область, на которой Вы хотели бы применить соль. Когда блеск воды почти прекратился, возьмите щепотку соли и немного насыпьте на закрашенную область. Просушите бумагу, но НЕ ОСТАВЛЯЙТЕ СОЛЬ НА ПОВЕРХНОСТИ БУМАГИ! Как только область с солью полностью высохнет, аккуратно сметите соль бумажным полотенцем.
Я думаю, что главный секрет применения соли – выбор времени и степени влажности бумаги. Тёплая и сухая окружающая среда может заставить краску сохнуть слишком быстро, не оставляя времени для растворения соли. При высокой влажности может быть противоположный эффект и Вы будете ждать очень долго.
Губка, градуированная размывка и брызги
Продолжим знакомство с техниками и эффектами. Здесь представлено использование губки, рисование градуированной размывки и использование брызг на картинах. У каждой из техник есть краткая инструкция, примеры и иллюстрации.
Техника применения губки
Применение губки – действительно забавный и простой способ придать легкость и воздушность листве и деревьям.
Пример техники
На крупном плане справа можно увидеть, насколько великолепен эффект техники при создании иллюзии листвы деревьев.
Использование губки
Подготовьте морскую губку, погружая её в чистую воду и отжимая. Прокатайте губку несколько раз в бумажных полотенцах, пока она не станет просто влажной. Осмотрите губку и найдите на ней область, которую Вы хотите использовать. Опустите губку в краску. Слегка прикоснитесь губкой к бумаге там, где Вы хотели бы сделать текстуру. Когда нанесёте краску, промокните губку на влажных бумажных полотенцах. Повторите эту процедуру несколько раз, чтобы окончательно удалить краску. Теперь опустите губку в следующую краску и повторите процесс. Для достижения наилучших результатов, начинайте со светлых цветов и заканчивайте темными.
Самой популярной губкой для этой техники является “морская губка”, которую можно найти в некоторых магазинах. Я тоже пользуюсь морской губкой.
Если Вы не можете найти морскую губку, то можете использовать бытовую губку.
Бытовая губка
Как подготовить бытовую губку
Ножницами разрежьте новую сухую губку на квадраты 2″ x 2″. Промойте квадраты несколько раз, чтобы удалить загрязнения после производства губки изготовителем. Затем сожмите, и скатайте квадраты в бумажном полотенце. Пальцами закруглите один из углов квадрата, отрывая маленькие кусочки губки. Когда закончите, окуните губку этим углом в краску и слегка прикоснитесь им к обрезку акварельной бумаги, чтобы посмотреть на полученный отпечаток. Продолжайте удалять кусочки, пока Вам не понравится результат.
Затем сожмите, и скатайте квадраты в бумажном полотенце. Пальцами закруглите один из углов квадрата, отрывая маленькие кусочки губки. Когда закончите, окуните губку этим углом в краску и слегка прикоснитесь им к обрезку акварельной бумаги, чтобы посмотреть на полученный отпечаток. Продолжайте удалять кусочки, пока Вам не понравится результат.
Техника градуированной размывки
Градуированная размывка – превосходная техника для передачи на рисунке неба. При рисовании бесконечного неба Вы начинаете с глубокого синего цвета. При приближении неба к линии горизонта, его оттенок становится светлее. Вы можете создать этот эффект при помощи техники градиентной размывки.
Пример градуированной размывки
На иллюстрации крупным планом показано использование обратного метода при рисовании неба. Вы можете видеть, как небо меняет цвет от темно-синего до более светлого при приближении к горизонту.
Применение техники градуированной размывки
Начните также, как если бы Вы рисовали цветную контролируемую размывку. Нанесите на бумагу краску от одного края бумаги до другого. Затем наберите на кисть каплю чистой воды и быстро смешайте её с краской на бумаге. Размывайте краску каплей воды от одного края бумаги до другого. Снова наберите на кисть чистую воду и быстро смешайте её полученным цветом. Продолжайте закрашивать, таким образом, весь рисунок. Вытрите лишнюю воду с кисти и рисунка.
Применение техники переменной градуированной размывки
Разведите два оттенка на палитре два оттенка краски небесного цвета, делая один светлее, а другой темнее. Начните градуированную размывку с капли чистой воды. Затем, наберите на кисть светлый оттенок и закрашивайте рисунок, пока не достигнете другой стороны. Хорошо промойте кисть. Снова наберите на кисть светлый оттенок и закрашивайте рисунок каплей краски, пока не достигаете другой стороны. Хорошо промойте кисть. Повторяйте эту процедуру, пока не нарисовали достаточный участок неба со светлым оттенком. Затем также начинайте наносить темный оттенок. Когда Вы закончите, вытрите лишнюю краску. Оставьте свой рисунок под некоторым углом и продолжайте вытирать лишнюю краску, пока не пропадет блеск.
Затем также начинайте наносить темный оттенок. Когда Вы закончите, вытрите лишнюю краску. Оставьте свой рисунок под некоторым углом и продолжайте вытирать лишнюю краску, пока не пропадет блеск.
Пример обратной градуированной размывки
Оба эти метода сделаны на наклонной поверхности. Когда используете метод обратной градуированной размывки, переверните рисунок так, чтобы верх неба был ближе к Вам.
Техника брызг
Техника брызг – великолепная техника для создания эффекта глубины и текстуры. Вы можете использовать или акварельную кисть или зубную щетку. Они дают один и тот же эффект, но с разными результатами.
Пример техники брызг
На крупном плане можно увидеть, как техника брызг придала двойное ощущение глубины и текстуры вдоль краев лепестка.
Применение техники брызг
Разведите на палитре краску со средним темным оттенком. Коснитесь краски всей щетиной зубной щетки. Поднимите зубную щетку и держите ее перевернутой вверх щетиной над необходимой областью рисунка. Теперь медленно проведите большим пальцем вдоль щетины до конца. Этот процесс можно повторить несколько раз, прежде чем снова набрать краску. Направляйте брызги, поворачивая зубную щетку.
Для достижения лучших результатов, используйте средний темный оттенок краски. Более светлые оттенки не будут создавать хорошего эффекта. Можете придать видимость размытия, брызгая на влажную поверхность.
Брызги могут случайно попасть на те области, где они не нужны. Для того чтобы этого не допустить, рисунок необходимо закрыть бумажными полотенцами.
Акварельные термины – продолжение
Рисуя и изучая эти термины и техники, Вы будете одновременно развивать свои навыки. Скоро простое “Набрать полную кисть”, станет привычкой.
Сайзинг
Сайзинг – похожее на клей вещество, которое наносится изготовителем на одну или обе стороны акварельной бумаги. Оно позволяет замедлить полное впитывание акварели и воды, и предотвращает любое нежелательное их распространение. Что в свою очередь позволит Вам что-либо дорисовать и достигнуть при этом глубоких и богатых цветов с ровными краями.
Что в свою очередь позволит Вам что-либо дорисовать и достигнуть при этом глубоких и богатых цветов с ровными краями.
Так как сайзинг невидим для глаза, нельзя точно определить, было ли его слишком много или мало, и был ли он равномерно распределен по поверхности бумаги, особенно после того, как он был высушен. Могут появиться белые пятна и шероховатость, которые потом трудно исправить.
Акварельная капля
Слово капля, которое я использую в обучающих программах и проектах, относится к акварельной капле – непрерывному горизонтальному объему капелек акварели или воды, растянутым через определенную область на листе бумаги. Лист бумаги при этом должен иметь некоторый угол наклона относительно горизонтальной поверхности.
Контролируемая размывка
Контролируемая размывка – аккуратное и ровное нанесение акварели (как в плоской поверхностной размывке или в градуированной), покрывающей большую или маленькую область. С протяженной горизонтальной акварельной каплей необходимо работать на наклонной поверхности.
Неконтролируемая размывка
Этим термином описывается, более выразительный и менее управляемый способ нанесения акварели или воды на бумагу. Краска при этом наносится плоской кистью разнообразными мазками по сухой или влажной поверхности бумаги.
Переход
Это слово описывает влажный переход от одного цвета акварели к другому.
Блеск/Мокрый блеск
“Мокрый блеск” – термин, описывающий метод или методы не позволяющие высохнуть только что закрашенной области рисунка. Они должны поддерживать блеск некоторое время. Блеск характеризуется ярким отблеском, который вызывает вода при отражении освещения. Интенсивность блеска говорит о степени влажности акварели на бумаге.
На главной фотографии показан блеск на недавно закрашенной области рисунка; на фотографии ниже та же самая область с блеском, который уже почти пропал.
Общие проблемы размывки
Итак, Вы прочитали все шаги к уроку «Как рисовать контролируемую размывку», нарисовали несколько прямоугольников и подготовили краску. Затем нарисовали акварельную размывку следуя инструкции, но все-равно она выглядит неправильно. Возникают вопросы: «Что послужило причиной тех или иных полос?» и «Почему там получилась большая клякса около границы прямоугольника?».
Затем нарисовали акварельную размывку следуя инструкции, но все-равно она выглядит неправильно. Возникают вопросы: «Что послужило причиной тех или иных полос?» и «Почему там получилась большая клякса около границы прямоугольника?».
Эти проблемы возникают у всех, особенно в начале освоения этой техники. Хорошая новость – есть советы по устранению этих и многих других проблем. Ниже представлены рисунки, показывающие некоторые самые распространенные акварельные проблемы размывки.
Общие проблемы размывки и советы по их устранению
Проблемы
1. Акварельной капли не было, поэтому верх быстро высох.
2. Слишком сильно надавили на кисть, создавая более светлый оттенок и неравномерное наложение краски.
3. За один раз была закрашена вся область прямоугольника и краска на размывке высохла слишком быстро.
4. Излишки краски не были удалены в конце размывки и оставили на бумаге эффект пузырьков.
5. Акварельная капля была слишком маленькой и уже подсохла. После добавления краски, цвет стал более насыщенный, создавая эффект пузырьков.
6. Акварельная капля закончилась и, после создания новой, получился эффект пузырьков.
7. Размывка хорошо была доведена до конца. Кисть ополоснули, но не слишком тщательно промокнули от влаги прежде, чем вытереть остатки краски.
Советы по устранению
1. Перед началом закрашивания области создайте акварельную каплю.
2. Попытайтесь при рисовании не надавливать кистью на поверхность бумаги слишком сильно. Применяйте легкие аккуратные мазки.
3. Сократите расстояние между мазками и чаще набирайте краску на кисть.
4. Не забудьте удалить лишнюю краску, когда закончите размывку.
5. Удостоверьтесь, что акварельной капли введено достаточное количество и область выше неё остается сырой.
6. Набирайте краску на кисть чаще для поддержания достаточного объема акварельной капли.
7. Нет никакой необходимости ополоскивать кисть в конце размывки. Достаточно хорошо промокнуть кисть перед удалением остатков краски.
Если Вы только начинаете свой путь в акварельной живописи, курс Вам подскажет правильное отношение к технике и даст несколько бесценных примеров, которые могут стать основой в постижении мастерства.
Если Вы учитесь в художественной школе или на курсах, Вы найдете в моих видео-уроках решение многих технических и художественных задач, встающих перед Вами в процессе обучения.
Если Вы пишете акварелью уже давно , мои приемы могут обогатить Вашу технику, подытожить опыт и подвести к новой ступени мастерства, освободив и раскрепостив Вашу кисть.
Рисование — один из самых любимых видов детского творчества. Дети берут в руки кисть очень рано, в 1-2 года, и с удовольствием переносят свою фантазию на бумагу. Становясь старше, они нечто уже рисуют конкретное, стремясь к максимальному сходству с оригиналом.
Обычно первой краской, с которой знакомится малыш, является акварель или гуашь. Они различны по своим свойствам, и, прежде чем начать обучение своего ребенка рисованию, родителям следует ознакомиться с особенностями этих красок. К примеру, акварельные краски отличаются от других своей прозрачностью и легкостью, которую они придают художественным работам. Именно поэтому рисовать акварелью, как правило, гораздо сложнее: все недоработки сразу становятся видны на рисунке.
Как выбрать акварель?Чтобы купить качественные краски, обратите внимание на следующие моменты.
- Акварель бывает сухой, в кюветах и в тюбиках. Выбирайте краску с учетом возраста и навыков ребенка. Например, краску в тюбиках легче смешивать, но у неопытного художника ее расход слишком велик. Для дошкольников удобны краски в кюветах, только обязательно научите ребенка мыть кисть перед каждым набором нового цвета.
- Стандартный «школьный» набор акварели подойдет для рисования на любительском уровне. Если же ваш ребенок ставит перед собой цель серьезно учиться изобразительному искусству, купите ему профессиональные краски. Их качество гораздо выше, и они не отобьют у ребенка охоту к искусству из-за рисунка, испорченного «поплывшей» или слишком тусклой краской.

- Не думайте, что чем больше оттенков акварели в наборе, тем лучше. На самом деле используется максимум десять цветов, которые, смешиваясь между собой, дают многочисленные оттенки, и наличие дополнительных цветов на палитре, которые редко используются, является попросту неудобным.
Также не забудьте о кисточках для акварели: они должны быть мягкими (пони, белка) и хорошего качества. Возьмите кисти разных размеров: большие пригодятся для покрытия краской больших площадей, например, для рисования фона, кисти средних размеров — для основной работы, а самые тонкие и заостренные — для прорисовки мелких деталей.
Бумага тоже играет важную роль в рисовании. Если хотите, чтобы рисунки получались живыми и яркими, а лист не коробился, используйте специальную бумагу для акварели. Она более плотная, чем обычные альбомные листы, имеет специфический рельеф и хорошо впитывает влагу. Бумага для акварели бывает как белой, так и цветной.
Как красиво и правильно рисовать акварелью?
Чтобы научиться рисовать, нужно освоить на практике различные техники акварельной живописи. Вот основные моменты обучения, о которых следует знать.
1. Изначально бумагу для акварели следует смочить и натянуть, прикрепив кнопками к планшету, чтобы она не коробилась в процессе рисования.
2. Как разводить акварель? Смешайте на палитре небольшое количество краски с водой. Если цвет более интенсивный, чем нужно, добавляйте понемногу воды до достижения нужной прозрачности. Имейте в виду, что после высыхания акварель заметно светлеет.
3. Как смешивать акварель? Для этого нужно знать основы цветовой грамоты: три основных цвета образуют три дополнительных, которые, в свою очередь, также смешиваются в оттенки. Объясните ребенку, что если он смешает красную краску с синей, то получит фиолетовый цвет, и т.п.
4. Какие существуют техники акварели?
5. Как стереть акварель с бумаги? Это легко сделать, пока краска еще не высохла: отожмите кисть, чтобы она была почти сухой, и, макая ее в пятно краски, которое нужно стереть, постепенно «вымакайте» его. Стереть высохшую акварель гораздо сложнее, и делать это следует чуть влажной кистью. Действуйте аккуратно, чтобы не повредить бумагу. Работа с акварелью подразумевает минимум ошибок именно потому, что неправильные мазки сложно стереть. Кроме того, помните, что белой акварели не бывает, поэтому те места на рисунке, которые должны остаться белыми, изначально не следует закрашивать.
Стереть высохшую акварель гораздо сложнее, и делать это следует чуть влажной кистью. Действуйте аккуратно, чтобы не повредить бумагу. Работа с акварелью подразумевает минимум ошибок именно потому, что неправильные мазки сложно стереть. Кроме того, помните, что белой акварели не бывает, поэтому те места на рисунке, которые должны остаться белыми, изначально не следует закрашивать.
Я буду писАть про свой личный опыт обучения акварели, про свои ошибки и удачи.
Первое, что необходимо почувствовать, начиная — это то, что акварель — водорастворимая краска . Да, мы все это знаем: акварель растворяется водой, акварель любит воду и тому подобные прописные истины, навязшие в зубах. Но у большинства это абстрактное знание, не ставшее личным опытом. И связь акварели и воды необходимо почувствовать. Так как одна из ошибок начинающих учиться — рисовать акварелью, как гуашью или акрилом, набирая краску прямо из кюветы. То есть рисунок получается корпусным и непрозрачным. Это ошибка. Акварель — прозрачна! И эта прозрачнось достигается именно водой.
Самый лучший помощник на этом начальном этапе: собственный опыт. Берем бумагу, краски-кисти, банку с водой и начинаем пачкать бумагу. Нанося краску на мокрую бумагу, на сухую, организуя подтеки и кляксы, позволяя цвету жить своей жизнью на бумаге, а краскам — смешиваться самостоятельно. В конце у вас будет пачка испорченных пятнистых листов и бесценный опыт.
Бумага для акварели, что выбрать?
И мы плавно переходим (или перетекаем, раз вода??) к следующему этапу. К выбору акварельной бумаги . Акварель-то воду любит, а вот бумага — нет. Она коробится, идет волнами. И вместо рисунка получается фигня; у меня, по крайней мере.
Поэтому плотная специальная бумага для акварели — наше всё!! Я бы не стала заострять на этом внимание, если бы не встречала в интернете акварельные рисунки, нарисованные на обычной бумаге для принтера, тонкой, плотностью 80 г/кв. м. Так делать не надо. Плотность бумаги для начинающих — 200 г/кв.м. Хотя бывает бумага плотностью и 600г/кв.м. Да и сама я пробовала рисовать на ватмане. Не на акварельном, а на обычном. Результаты не очень..
м. Так делать не надо. Плотность бумаги для начинающих — 200 г/кв.м. Хотя бывает бумага плотностью и 600г/кв.м. Да и сама я пробовала рисовать на ватмане. Не на акварельном, а на обычном. Результаты не очень..
Я больше всего люблю тип акварельной бумаги с ярко выраженной шершавой поверхностью , холодного прессования. А более гладкую, с тиснением «холст» или «яичная скорлупа» люблю меньше. Опять же «опыт — сын ошибок трудных». Поэтому — покупаем разные типы бумаги в пределах ценовой доступности и пробуем. Выбирая наиболее комфортную.
Хотя вот еще что, два дополнения: бумага для акварели бывает не только белой! У меня лежит купленная склейка кремовой. Интересно будет ее опробовать. И по фирмам: из российских наиболее приемлимой является Гознак. Прочую акварельную бумагу российских производителей даже в руки брать страшно, не то что на ней рисовать.
Какими акварельными красками рисовать?
Имхо, самое главное в акварели — хорошая бумага. А краски и кисти вторичны. Хотя многие со мной не согласятся. А уж профессиональные аквалеристы точно закидают тапками..
Я учусь рисовать акварелью, и у меня есть три типа красок : детские акварельные краски, художественные краски в кюветах, и художественные краски в тюбиках. Далее — о каждых из них поподробнее. Хотя совсем уж сногсшибающей разницы я между ними не вижу. Опыта мало и практики, конечно.
Акварельные краски фирмы ГаммаЭти акварельные краски называются «Пчелка», в моем наборе 12 цветов. Среди них нет охры, но зато есть белый.. Черная и ультрамарин почти уже закончились. Коробка компактная, планирую ее отмыть и использовать для выдавливания акварели из тюбиков. Нормальные краски.
Акварельные краски фирмы Луч24 цвета в наборе, охра есть, но и белый цвет тоже есть. Огромный минус этой акварели: кюветы расположены слишком близко друг к другу. Неудобно большой кистью набирать краску. Купила их только потому что помнила из прошлой жизни их прозрачные и чистые цвета. Так было много лет назад. Сейчас цвета этой акварели более глухие. Больше не куплю.
Купила их только потому что помнила из прошлой жизни их прозрачные и чистые цвета. Так было много лет назад. Сейчас цвета этой акварели более глухие. Больше не куплю.
У меня старый-престарый набор акварели «Санкт-Петербург» . Аж по ТО-003-92. Качество соответствует ГОСТ 11481-75, чтобы это не означало.. В пластиковой коробке. 24 цвета в кюветах, почти закончившиеся и высохшие. Но рисовать ими можно. Сейчас вижу в продаже какие-то варианты с названиями «Ленинград», «Ладога» или «Белые Ночи»..
Акварельные краски в тюбикахИли более мне нравящийся термин: акварель в тубах . Давно хотела попробовать такие краски, постоянно читая про тюбики в иностранных самоучителях по акварели. И вот они у меня есть! В двух вариантах. Первый: набор «Белые Ночи» от Завода Художественных Красок «Невская Палитра», 12 цветов в тюбиках по 10 мл. И эта краска оказалась более жидкой, чем я ожидала! Я-то ждада консистенции масляных красок, но они гораздо более жидкие ..
И еще у меня есть 5 цветов фирмы «Cotman», заказанные поштучно. По 8 мл в тубе. Есть повторяющиеся цвета с «Белыми Ночами», поэтому позже сделаю сравнительный тест тех и других. Посмотрим, будет интересно посмотреть, как поведут себя те и другие.
Какие кисти для акварели выбрать?
Классический вариант акварельных кистей : белка или колонок. Но я пробовала и синтетику, и щетину, и китайские кисти для суми-е. И даже водяную кисточку с резервуаром для воды, о которой позже поподробнее. Какие лучше — не знаю. Зависит от площади листа и поставленной задачи.
А некоторые вообще без кистей обходятся!! Попробовать обязательно!
Палитра для смешивания акварельных красок
У меня простая плоская пластиковая палитра на восемь ячеек, пока мне хватает. А потом буду думать. Главное правило, как я поняла: палитра должна быть белой ! А будет ли это пластик, керамическая плитка или фарфоровое блюдце — не важно.
Так чем же рисовать, скажите?
Чем же рисовать , что из огромного множества товаров в художественном магазине выбрать? Я поняла: теми материалами, которыми вам рисовать удобнее всего. Потом можно экспериментировать, пробуя непривычные краски, кисти и бумагу. Но на начальном этапе обучения акварели правильнее всего выбрать наиболее комфортные материалы.
Уточняю: все вышевысказанное: мой личный опыт двухмесячного периода рисования акварелью . Вполне допускаю, что через полгода мое мнение по поводу того, чем же рисовать, будет иным. Тогда я напишу новый обзор бумаги, красок и кистей..
Copyright 2008-2016. Я надеюсь, материалы этого сайта доставят радость и помогут вам.
Акварельные краски — одни из самых любимых художниками. Во-первых, акварель имеет массу различных техник, а во-вторых, с ее помощью можно создать красивый рисунок, даже если вы не умеете рисовать вовсе.
Эти техники помогут новичкам обучиться рисованию, а профессионалам — освежить их в памяти и найти вдохновение и идеи.
1. Рисование с помощью плоской кисти
Шаг 1
Нарисуйте квадрат или прямоугольник, чтобы отметить начало и конец слоя.
Выберите более темный оттенок (его легче увидеть) и, начиная с верхнего левого угла, коснитесь кистью бумаги и нежно проведите прямую линию вплоть до верхнего правого угла.
Но: левшам стоит рисовать от правого угла к левому.
Шаг 2
Еще раз наполните кисть краской.
Начните следующий штрих с нижнего края первого, постарайтесь перекрыть скопление краски, которое образовалось снизу первого штриха.
Подсказка 1 : если скопление краски в первом штрихе не перетекло полностью во второй, то увеличьте угол наклона своего мольберта, чтобы помочь краске свободно течь.
Подсказка 2 : увеличивая угол наклона, вы также увеличиваете шансы получить неуправляемые потоки краски. Поэтому старайтесь работать быстрее или имейте под рукой что-то вроде тряпки или губки, чтобы быстро убрать капли.
Шаг 3
Повторите предыдущий шаг, так же стараясь перекрывать скопление краски в верхнем штрихе.
Подсказка 3 : вы можете использовать плоский край кисти, чтобы «обрезать» начало слоя и сделать его ровным.
Подсказка 4 : если вы хотите сделать ровнее конечный край слоя, то в конце штриха приостановитесь и проведите кистью вверх, а затем вниз так, как вы бы это сделали с начальным краем.
Подсказка 5 : если штрих получается прерывистым, то немедленно наполните кисть краской и заново проведите его.
Шаг 4
Повторяйте предыдущие шаги до самого конца. Старайтесь придерживаться одинакового тона краски.
Подсказка 6 : вы не поверите, насколько может различаться поведение кистей, красок и бумаги разных брендов. Обычно, более дорогие и популярные бренды облегчают вашу работу, предоставляя высокое качество продуктов.
Подсказка 7 : если ваши штрихи прерываются, даже если кисть полна краски, то вы используете слишком плотную бумагу, или же бумага имеет слишком грубую текстуру. Если вам попалась такая бумага, то побрызгайте на нее водой, промокните чистой губкой и дайте высохнуть. Так вы сделаете поверхность более восприимчивой для вашей краски.
Шаг 5
Промойте кисть и выжмите все остатки воды из нее. Аккуратно подберите кистью сгустки краски, оставшиеся снизу последнего штриха, но не забирайте слишком много краски, или вы обесцветите ваш рисунок.
Для создания более выраженной текстуры вашего рисунка, оставьте его сохнуть под углом. Так краска обретет более интересный вид.
Градиент
Шаг 1
Нарисуйте квадрат или прямоугольник. Затем окуните вашу кисть в более темный оттенок краски (смешивать стоит на палитре) и аккуратно проведите кистью штрих.
Шаг 2
Вытрите кисть губкой или бумажным полотенцем и снова окуните ее в более светлый оттенок.
Затем проведите новый штрих, перекрывая нижнюю часть предыдущего. Заметьте, что левая часть слоя уже слилась с предыдущим штрихом. Позвольте гравитации сделать свое дело.
Шаг 3
Снова промойте кисть и вытрите ее. А затем вновь наполните кисть краской и сделайте еще один штрих. Повторяйте этот процесс до самого конца.
Подсказка 1 : если штрих прерывается или не ложится так гладко, как хотелось бы, быстро еще раз наполните кисть краской и повторите слой.
Шаг 4
Промойте кисть чистой водой, вытрите ее и подберите все остатки краски.
Подсказка 2 : пробуйте использовать эту технику, работая с разными цветами и создавая интересные переходы.
Акварельная глазурь
Шаг 1
Эта техника требует импровизации и фантазии. На примере будем рисовать импровизированный ландшафт.
Сначала рисуем небо и реку голубой краской. Краску разделим небольшим количеством воды, это у нас будет водопад.
Шаг 2
Рисуем облака темно-розового цвета и начинаем рисовать гору желтым цветом. Также желтым цветом мы обозначим нижнюю часть рисунка.
На примере используются светлые и прозрачные тона, чтобы вы могли увидеть, как слои взаимодействуют.
Шаг 3
Смешав кобальтовый синий и ультрамариновый синий, мы нарисуем горизонт горы и оттеним маленький желтый склон.
Подсказка 1: позволяйте каждому слою высохнуть. Вы можете использовать фен, чтобы ускорить этот процесс. Держите его на расстоянии не менее 25-30 см, включите холодный режим и настройте фен на самый легкий поток воздуха. Никакого пара и горячего воздуха!
Шаг 4
Чтобы оттенить и добавить интересных цветов, используем оранжевый цвет. С его помощью мы создадим берега на переднем плане и оттеним небо.
Подсказка 2: если у вас образовались капельки лишней краски, промойте и вытрите кисть, как вы делали это в предыдущих техниках, и подберите ею капли.
Шаг 5
Обратите внимание, что на изображениях показаны разные кисти для рисования. Вы можете использовать те, что есть у вас в наличии.
Возьмем темно-синий цвет и оттеним им верхушку горы, изменяя давление на кисть и проворачивая ее, чтобы создать интересную текстуру.
Шаг 6
Используя тот же синий цвет, поиграем с водопадом, нарисовав несколько кругов. Иногда визуальные клише становятся вашими друзьями.
Промоем кисть и наберем желтый цвет, им мы добавим визуальных деталей нашим берегам.
Шаг 7
После того, как краска высохла, оттеним пузырьки в водопаде оттенком фиолетового цвета. Так мы сделаем их интереснее.
Шаг 8
Нам нужно связать некоторые элементы и добавить деревья. На примере мы использовали круглые шаблоны для крон, но вы можете рисовать как вам угодно.
Шаг 9
Коричневым цветом мы изобразим стволы деревьев. Также с помощью синего мы еще немного оттеним воду и небо. Затем, используя розовый, голубой и зеленый, изобразим траву на переднем плане.
Шаг 10
Используем смесь розового и красного, чтобы добавить финальные детали. Деревья у нас теперь плодоносят, и несколько плодов лежит под ними.
Если вы присмотритесь, вы увидите, как каждый слой взаимодействует друг с другом. Более темный оттенок имеет большую силу, но когда цвета перекрывают друг друга, то они создают интересное и красивое сочетание.
«Мокрая» техника
Шаг 1
Намочите бумагу водой
Шаг 2
Промокните чистой губкой бумагу, убрав излишки воды. Старайтесь достичь равномерного распределения влаги по бумаге, у вас должен получиться атласный эффект.
Если бумага блестит, то значит, что она слишком мокрая, промокните ее еще раз.
Шаг 3
Мы снова будем рисовать ландшафт. Начнем, конечно же, с неба. Используя данную технику, проще рисовать сначала фон, переходя потом к объектам первого плана.
Используя данную технику, проще рисовать сначала фон, переходя потом к объектам первого плана.
Шаг 4
Продолжаем рисовать небо до тех пор, пока оно нам не начнет нравиться. Штрихи будут расплываться, создавая интересный эффект.
Шаг 5
Теперь приступим к траве на первом плане. Используя зеленый цвет, сделаем несколько широких штрихов, оставив место для камней.
По мере высыхания бумаги, штрихи расплываются все меньше.
Шаг 6
Добавим формы. Для этого используем различные оттенки зеленого и нарисуем деревья на горизонте.
Шаг 7
Добавив деревья, давайте постараемся прибавить им фактуру. Для этого используйте более темный оттенок зеленого, чтобы расставить акценты.
Шаг 8
Добавим камни, используя серый цвет. Мы заполнили этим цветом пробелы на переднем плане, оставив немного просветов.
Старайтесь использовать либо темные, либо холодные оттенки. Использование и темных, и холодных оттенков создаст визуальный диссонанс.
Шаг 9
Расставим акценты, чтобы разнообразить рисунок. Используя багровый оттенок, изобразим несколько флористических элементов на переднем плане. Позвольте багровому растечься так, как ему хочется. Затем, используя сухую кисть, уберите цвет из средины пятен.
Шаг 10
Затем капните чистой водой в центр этих пятен, чтобы позволить им смешаться с травой.
Самое сложное в этой технике — знать, когда остановиться. Переусердствовав с размытиями и цветами, вы получите грязный рисунок.
Данная техника дает немного странный, но интересный результат. Рисунок, выполненный в этой технике, имеет гипнотизирующий эффект.
Рисунок сухой кистью
Шаг 1
Думаем, название техники говорит само за себя. Нам нужно будет набирать краску на кисть, промакивать ее от лишней жидкости бумажным полотенцем или губкой, а уж потом рисовать.
Для начала сделаем набросок карандашом. После этого грубо обозначим небо, водя кистью по поверхности бумаги.
Шаг 2
Нарисуем зеленым цветом деревья на линии горизонта, очертив то, что потом станет нашим озером.
Затем, смешав лиловый с голубым, нарисуем первый слой ствола дерева.
Шаг 3
Дайте рисунку подсохнуть и добавьте некоторые элементы: отражение дерева в озере и поток воды.
Смешав зеленый и голубой, оттеним берег на фоновой части изображения и снова дадим рисунку высохнуть.
Шаг 4
Смешаем интенсивный синий цвет с ультрамарином и нарисуем слой на стволе дерева, чтобы создать тени и текстуру коры.
Шаг 5
Затем, используя оттенки оранжевого, изобразим осенний пейзаж, закрасив фоновые деревья.
Шаг 6
Закончив с предыдущим шагом, светло-оранжевым оттенком изобразим отражение деревьев в воде.
Еще, смешав серый с голубым, расставим темные акценты на деревьях.
Также добавим деревья и с другой стороны горизонта. Обозначим формы деревьев оранжевым цветом.
Шаг 7
Займемся водой. Используем темно-зеленый и коричневый, чтобы достичь нужного цвета. И волнообразными движениями нарисуем воду в озере.
Шаг 8
Рисуя озеро, меняйте давление на кисть, чтобы прибавить фактуру.
Подсказка: если кисть слишком мокрая, краска будет выглядеть плоско. Высушите кисть, чтобы сделать цвета интенсивнее.
Шаг 9
Добавим немного травы под деревом, используя тот же цвет, что и для травы на фоне.
Шаг 10
Добавим несколько деталей на передний план.
Также немного затемним озеро, добавив синий оттенок. А еще оттеним этим же цветом и небо.
Убираем влагу
Эта техника потребует несколько губок. Она подходит для изображения облаков, мягкого света. А еще ею можно контролировать поведение красок.
А еще ею можно контролировать поведение красок.
Губки
Лучше всего подойдут спонжи для макияжа. Они хорошо впитывают и дают интересный эффект.
Старайтесь не тереть губкой бумагу, а если вы это и делаете, то делайте это очень осторожно, чтобы не повредить бумагу.
Бумажные полотенца
С их помощью вы можете создать более четкие высветления. Но бумажные полотенца очень быстро впитывают огромное количество краски. Поэтому свежую краску они могут впитать полностью.
Бумажные полотенца могут пригодиться, если вы сделали ошибку. Тогда вы сможете быстро убрать краску.
Сухая кисть
Вы можете использовать сухую кисть, чтобы создать рисунок в данной технике. Для этого хорошенько промойте и выжмите кисть. С ее помощью вы сможете создать четкие линии.
Другие способы:
- Вы можете брызнуть водой туда, откуда нужно убрать краску, а затем впитать ее губкой.
- Используйте различные ткани, чтобы придать текстуру
- Можно использовать пальцы или другие части тела. Кожа тоже может впитывать влагу.
Обесцвечивание высохшей краски
Кисти для акварельной краски
Используйте чистую воду и тряпочку, намочите нужные участки, аккуратно потрите рисунок и сухой кистью уберите влагу. Этот метод позволяет контролировать области, которые вы осветляете.
Кисти для масляной или акриловой краски
Жесткая щетина позволяет быстро соскрести краску с нужной области. Но стоит заметить, что этот метод может повредить бумагу, поэтому контролируйте себя.
Здесь так же, как и в первом методе, нужно сначала смочить область, а потом обработать кистью.
Спрей и полотенце
Возьмите пульверизатор и побрызгайте на нужную область, а потом приложите к ней бумажное полотенце. Такой метод оставляет большие светлые пятна и придает интересный эффект.
Наждачная бумага
Очень редко используется, так как ею можно повредить бумагу. Лучше всего ее использовать в конце для придания текстуры. Для этого метода вам не понадобится вода, просто потрите рисунок в нужном месте.
Лезвия и ножи
Можно использовать для высветления небольших областей и создания четких линий. Этот метод тоже очень рискованный, так как может повредить бумагу.
Губки
Также можно использовать губки. Намочите нужную область и высушите ее губкой.
Рисунок акварелью и пером
Рисование пером и тушью с последующим добавлением акварельных мазков — это быстрый и удобный способ оживить ваши рисунки. Рисунок акварелью и пером представляет собой идеальное сочетание четких четких линий, контрастирующих с жидкими водянистыми оттенками цвета.
Это также быстрый и удобный способ рисования, акварель и чернила очень быстро сохнут, и вы можете носить их с собой, если хотите опробовать эти методы для городского или ландшафтного эскиза.
Возможно, вас также заинтересует:
Рисование живых рисунков чернилами India
Рисование живых рисунков акриловыми и акварельными карандашами
Альтернатива бумаге Yupo: гелевая среда на обычной бумаге.
Вот как можно рисовать акварелью и рисовать пером:
Начните с создания контура вашего рисунка. Здесь я использую рисунки, которые сделал на уроке рисования в живую. Поскольку я работаю в классе с бумагой большого размера в английской системе единиц, я просто распечатал изображение своего оригинального рисунка (слева) и нарисовал его на акварельной бумаге (справа).
Я являюсь партнером Blick Art Materials и получаю небольшую компенсацию за продажи. Это никоим образом не влияет на стоимость заказа покупателя, но помогает мне сохранять содержание этого блога бесплатным.
Набор для создания эскизов SpeedballЭтот набор пера и наконечника для каллиграфии дает вам все необходимые инструменты для создания прекрасных произведений искусства. Идеально подходит для рисования, штриховки, литографии и мелких деталей.В комплект входят два пластиковых держателя для ручек и шесть перьев. |
Вы можете начать с рисования от руки. Я рекомендую вам делать это вместо того, чтобы обводить рисунок, чтобы сохранить непосредственность и свежий вид оригинала. Это нормально, если рисунок не является точной копией или если пропорции не совсем точны.
Для рисования можно использовать перо для окунания.
Смешайте немного индийских чернил с водой, чтобы получить средний серый цвет, который немного мягче, чем черный для вашего рисунка с помощью пера.
Я являюсь партнером Blick Art Materials и получаю небольшую компенсацию за продажи. Это никоим образом не влияет на стоимость заказа покупателя, но помогает мне сохранять содержание этого блога бесплатным.
Затем вы можете смешать несколько акварельных мазков, цвета, которые вы будете использовать, не обязательно должны быть реалистичными. На самом деле сами цвета не так важны, как их тональные значения.
Есть несколько методов, которые вы можете попробовать: Вы можете начать с рисования светлых тонов, а затем нарисовать более темные цвета.или вы можете рисовать от верха фигуры к низу и позволить цветам смешаться мокрым с влажным, что я и сделал в этом случае, начиная с темно-фиолетовой смывки для волос.
Вы также можете использовать 2 цвета для волос и позволить им смешать мокрые с мокрыми.
Продолжайте рисовать акварельными красками мокрое в мокрое, позволяя цветам перетекать друг в друга и оставляя некоторые участки светлых тонов неокрашенными.
Я являюсь партнером Blick Art Materials и получаю небольшую компенсацию за продажи.Это никоим образом не влияет на стоимость заказа покупателя, но помогает мне сохранять содержание этого блога бесплатным.
Ярка Санкт-Петербург Профессиональные акварельные краскиТа же палитра традиционных цветов, которую великие мастера использовали столетие назад. Заливка жидкостью означает, что полувлажные сковороды мгновенно реагируют на влажную щетку. 24 кастрюли в пластиковом кейсе. Также индивидуальные кастрюли. — Мастер-сет |
Вы можете смягчить некоторые края, закрасив их кистью, наполненной простой водой.
Это позволит избежать резкости всех краев и добавит разнообразия краев вашему эскизу.
Продолжайте закрашивать всю фигуру.
Другой способ, который вы можете попробовать, — сначала нанести легкие мазки и подождать, пока они высохнут. Затем нарисуйте еще один слой в нескольких более темных областях.
Рисуем первый светлый слой.
А затем закрашиваем вторым слоем несколько более темных областей.
Вот несколько примеров рисунков акварелью и пером:
абстрактных акварелей, которые вы просто не можете пропустить!
Blog Home20 марта 2020 г.
Обожаемый за его непревзойденные качества — уникальную прозрачность, непостоянство и яркость — акварельное искусство долго не получало признания или славы, присущей таким техникам, как живопись маслом.Хотя его история восходит к самому раннему палеолитическому искусству, его современное использование было изгнано на самые окраины области искусства, принижено как техника, подходящая только для эскизов или хобби-рисования. Однако абстрактная акварель должна была изменить это! Печально известные Василий Кандинский, Пол Клее, Джорджия О’Киф и Артур Дав — все использовали акварельную живопись, чтобы выразить свой собственный голос, сделав ее техникой, одновременно актуальной и уважительной. Большие атмосферные акварельные полотна Марка Ротко или интимные абстрактные акварельные пейзажи Джона Марина излучали двусмысленность и беспорядочный характер акварельного искусства, его прозрачную и тонкую сущность, а также его внутреннее аксиологическое измерение.Семь самых увлекательных акварельных работ, которые нельзя пропустить — ждем ниже!
Питер Сориано — Колби 10
Сориано, который, по его собственным словам, скульптор, больше не занимающийся скульптурой, широко известен своими крупномасштабными настенными росписями, напоминающими граффити. Colby 10 является частью его первоначальных рисунков для Постоянного обслуживания — крупнейшего настенного рисунка Сориано на сегодняшний день, заказанного Музеем Колби — и чертежа его культовой настенной росписи. Это произведение из смешанной техники с его замечательными акварельными сегментами выполнено на сложенной в несколько раз бумаге, которая приобретает скульптурный характер.В «Колби 10» Сориано применяет множество техник, чтобы собрать и упорядочить свой визуальный опыт в предварительной картине, стиль, созданный так, чтобы выглядеть непринужденно и незавершенно. Colby 10 полон смысла и полон наблюдений, что делает общую конструкцию забавно сложной и заумной. Сориано — французско-американский художник-абстракционист, родившийся на Филиппинах, живущий в Нью-Йорке и Пенобскоте, штат Мэн. Он известен своими смелыми росписями на стенах, окрашенными аэрозольной краской, и своими более интимными работами на бумаге.
Питер Сориано — Colby 10, 2015. Бумага, аэрозольная краска, карандаш, тушь, акварель. 94 х 125,5 см.
Лаура Ньюман — Рамки
Рамки, наряду со Свупом и Свервом, являются частью незавершенных картин на бумаге Васли ручной работы, которую Ньюман обнаружил во время путешествия по Индии. Вдохновленная необъятностью открытого неба, видимого из окна ее студии, и сопоставлением его с ограниченностью городского пейзажа, Фреймс разъясняет переплетение свободы и всех окружающих ограничений — как пространственных, так и метафорических.Ее геометрические очертания пространства и эфемерные цветовые поля подчеркиваются одновременным использованием акварели и акрила, которые выражают горизонт интерпретации ее атмосферных образов. Ньюман — американский художник-абстракционист, создающий яркие, динамичные картины, в которых гармонично сочетаются жестикуляция, резкие геометрические пространственные композиции и многослойные архитектурные композиции. Ньюман родился в Кливленде, штат Огайо, в настоящее время живет и работает в Бруклине, штат Нью-Йорк.
Лаура Ньюман — Оправы, 2016.Бумага Васли ручной работы, акрил, акварель. 56 х 38 см.
Мелисса Мейер — Яддо B
Абстрактная экспрессионистка в третьем поколении, Мейер хорошо разбирается в большом разнообразии техник и ее разнообразное творчество охватывает акварели, картины маслом, рисунки, гравюры и крупномасштабные заказы. Ее лирическое и тонкое выражение воплощено в полупрозрачных акварелях или разбавленных масляных красках, раскрывающих неуверенную, тревожную и самоуничтожающуюся реальность. Яддо Би раскрывает свои грациозные прикосновения и нежные мазки, подчеркивающие ее визуальный словарный запас, на который сильно влияют цвет и линия.Мейер наносит акварельные краски на ацетатные листы и пропускает их через пресс, часто перенося несколько слоев на бумагу, создавая резкий визуальный диссонанс. Мейер — американский художник-абстракционист и гравер. Ее энергичные, красочные композиции выражают эмоции и преходящую суть действительности. Она живет и работает в Нью-Йорке.
Мелисса Мейер — Яддо Б., 2005. Акварель на 100% тряпичной бумаге для горячего прессования. 50,8 x 81,2 см.
Holly Miller — Голубые водные точки
Это интуитивно понятное и игривое произведение создано с помощью акварели и ниток; нанося краску кистью, проведите иглой и нитью с повторением рисунка.Необычный выбор Миллер нити перекликается с ее непреходящим увлечением тактильными и скульптурными свойствами и убедительностью интерпретации средства, которое в своей простоте и неприхотливости сочетает рисунок, живопись и скульптуру. Голубые водные точки заключают в себе дихотомию присутствия / отсутствия и совершенства / несовершенства, поскольку физичность проколотых отверстий и монохроматических мазков кисти контрастирует с смелым и тонким, иллюзией и реальностью. Миллер — американский художник-абстракционист, чьи картины стремятся объединить оптическое и тактильное через язык абстракции.Она живет и работает в Бруклине, штат Нью-Йорк.
Холли Миллер — Голубые водные точки, 2005. Бумага, акварель, нитки. 22,9 х 30,5 см.
Kim Uchiyama — Chord
Chord — это заманчивое акварельное произведение на бумаге Arches, которое отражает исключительный талант Учиямы передавать свою эмоциональную сущность и глубоко личные мысли с помощью цвета. Ее путешествие начинается с первоначального оттенка на чистой поверхности, и по мере того, как она продолжает их наносить, она приближается к линейному горизонтальному узору из уникальных слоев.Ее выбор акварелей отражает саму природу таинственного света, излучаемого ее картинами. Она использует насыщенные цвета, чтобы подчеркнуть достаточность и самореференциальную силу своих цветов, поскольку каждая полоса сама по себе несет в себе свое значение. Учияма — американский художник-абстракционист, чьи работы используют цвет для создания света и формы, которые активируют метафизический потенциал живописного пространства. Она живет и работает в Нью-Йорке.
Ким Учияма — Аккорд, 2018.Бумага Arches, акварель. 40,6 х 30,5 см.
Фиероза Доорсен — Без названия (Ид. 1297)
Голубая акварельная краска преобладает над Без названия (Ид. 1297) (пере) определяя все визуальные элементы диалектики отношений Доорсена. Она искусно противопоставляет структуру интуиции, исследуя точки соприкосновения органического и геометрического, организованного и случайного. Она действует как посредник между своими материалами и узорами, формами и цветами, которые они раскрывают, используя обветренные листы бумаги, чтобы подчеркнуть ее растворяющееся «я», глубоко погруженное в ее картины.Без названия (Id. 1297), поскольку большая часть ее работ колеблется между загадочным смыслом, открытым для созерцания и зрительской интерпретации, и понятным кодом, который, однако, неубедителен. Зритель остается с чувством неуверенности, поскольку ее визуальный словарь изобилует двусмысленностью. Доорсен — английский художник-абстракционист, которая разработала свой собственный язык с акцентом на узоры и цветные формы. Живет и работает в Лондоне.
Фиероза Дорсен — Без названия (ид.1297), 2017. Бумага, акварель. 19 х 27 см.
Джессика Сноу — Fling 3
Серия Fling демонстрирует яркость и четкую артикуляцию работ Сноу с уникальными жестами в ее исследовании форм. Fling 3 очаровательно исследует пересечение рационального и эмоционального, сочетая игривые формы с яркими цветами, органичными линиями жестов, геометрическими и линейными формами. Она применяет полную палитру с непонятным диссонансом и соответствием оттенков, определяющих форму и излучающих свет.Интуитивный подход Сноу, при котором мазки инстинктивно исчезают, а слои становятся неразличимыми, передает ее легкий и плавный характер. Сноу — американский художник-абстракционист, чьи картины и рисунки отличаются красочной игривой геометрией. Она живет в Сан-Франциско.
Джессика Сноу — Fling 3, 2015. Бумага, акварель. 36,9 х 25,4 см.
Featured image: Melissa Meyer — Yaddo B, 2005, вид установки.
Автор Йована Вукович
Уроки акварельного искусства — Happy Family Art
Я не всегда любил акварель так сильно, как сегодня. По мере того, как я все больше и больше практиковался и узнавал больше, я начал ценить эту удивительную универсальную среду. С акварелью можно сделать так много всего. Я не могу дождаться, чтобы узнать больше и стать лучше. Вот несколько бесплатных уроков акварельного искусства, которые я сделал для вас. Я надеюсь, они тебе нравятся.
*** Эта страница содержит партнерские ссылки.***
Давайте сначала поговорим о некоторых основных принадлежностях для рисования. Мои любимые акварели для себя и для обучения детей — это полувлажные акварели на медовой основе, которые я покупаю в русском книжном магазине в Бруклине. Однако я нашел те, которые действительно близки к Amazon, так что проверьте их: АКВАРЕЛЬНЫЕ КРАСКИ . Недавно я попробовала еще одну акварельную краску, которая мне очень понравилась: АКВАРЕЛЬНЫЕ КРАСКИ KOI FIELD. Для бумаги существует широкий выбор.В детских классах я часто обращаюсь к бумаге Strathmore, например, THIS ONE , они бывают разных размеров и отлично подходят для детей. Лично я предпочитаю более плотную бумагу, которая пропускает больше воды и плохо гнется. Для меня это обычно означает, что мне нужно пойти в магазин и потрогать бумагу перед покупкой. То же самое я делаю с кистями для своих картин. Для детей, а часто и для себя, мне нравятся эти ЩЕТКИ . Часто, когда я провожу урок рисования, мы заканчиваем тем, что используем черные перманентные маркеры. ЭТИ мне нравятся. Они не бегают, когда их касается вода, и у них нет того ужасного запаха, который так часто сопровождает перманентные маркеры.
Уроки акварельного искусства:
Акварельные картины в негативном космосе
Эти картины исследуют негативное пространство, цветовую ценность и атмосферную перспективу с использованием акварельной краски и контактной бумаги. Иногда мне нужен урок, который исследует концепцию в увлекательной игровой форме, длится ровно один час и не переносится на следующую неделю, так что это именно то, что было.
Веселое пространство, галактика и инопланетная пейзажная живопись акварелью
Эти картины позволили мне исследовать различные акварельные техники, одновременно прекрасно проводя время. Мне очень понравилось их делать, поэтому я хотел поделиться пошаговым процессом с другими. Надеюсь, вам будет так же весело рисовать их, как и мне.
Картина ромашки
Учебник по рисованию ромашек в технике негативной акварели. Я нашел этот процесс очень приятным и увлекательным.Здесь вы найдете мой пошаговый процесс рисования ромашек, а затем переноса этого рисунка на акварельную бумагу, а затем пошаговый процесс их раскрашивания!
3D Акварельные аквариумные рыбки
Этот трехмерный аквариум, полный рыбок, было интересно сделать и собрать в трехмерный коллаж. Объединение цветного резиста, теплых и холодных цветов, узоров и фактур, а также элементов перспективы в одном уроке.
Самодельные акварельные краски
Мы сделали эти замечательные акварельные краски ручной работы.Было так весело! Были бурлящие химические реакции, создание наших собственных уникальных цветов, смешивание вещей и забавная раскраска. Детям и мне очень понравилось! Мы также делали чернила из старых маркеров и медицинского спирта.
Акварельные кувшинки
Водяные лилии писали многие замечательные художники. Я решил сделать этот быстрый урок, как рисовать водяные лилии, и раскрасить его акварельной краской. Сначала я рисовала маркерами для разных цветов, а потом раскрашивала, попутно делая много фотографий!
Акварельная живопись сакуры
В этом уроке у меня есть два разных способа нарисовать цветы сакуры акварелью.Первый проще и быстрее, второй несложный, хотя и требует времени и усилий. Я также сделала инструкции, как нарисовать цветущую вишню маркером.
Урок «Веселая роспись по искусству»
Это отличный урок для совместной работы группы детей. Это было так весело делать, и это вызвало много смеха. Дети работали вместе, используя маркеры, акварельные краски и акварельные карандаши, чтобы создать эту подводную сцену.
Урок рисования зданий акварелью
Поначалу эта картина может показаться устрашающей, но если вы будете просто следовать простым указаниям, результат вас удивит.Он состоит из простых форм, а мелкие детали делают его красивым! Написана акварелью, немного акрила и туши.
Crayon Resist Fall Leaves Art Lesson
Знаете ли вы, что когда вы рисуете белым мелком, сильно нажимаете на бумагу, а затем закрашиваете ее акварелью, белый цвет мелка проступает? Это такой простой и веселый арт-проект. Забавно наблюдать, как загораются лица детей, когда они видят, как сквозь бумагу просвечивает белый карандаш.
От наскальных рисунков к модернистам: история акварельной живописи
Акварельная живопись — это отличительная среда, объединяющая миры живописи и рисунка, чтобы создать уникальную форму искусства.Краски состоят из пигментов, взвешенных в водорастворимой среде, и могут наноситься на все, от бумаги до холста, от дерева до тканей. Что делает акварельную живопись такой уникальной, так это ее неумолимая природа; линии, цвета и формы должны быть применены безупречно с первого раза, так как любая попытка закрасить просто делает весь эффект нечетким. Акварель доминировала в азиатском искусстве и остается до сих пор, но она также заняла видное место в истории западного искусства.Ранние примеры акварельной живописи
Вам нужно отправиться в далекое прошлое, чтобы найти корни акварельной живописи, к тому времени, когда доисторические люди в эпоху палеолита красили стены своих пещер смесью охры, древесного угля и других природных пигментов. .Акварели также писались на папирусе и использовались в формах египетского искусства. В Азии традиционная китайская живопись акварелью развивалась около 4000 г. до н.э., в первую очередь как декоративная среда, а к I веку нашей эры утвердилось искусство росписи религиозных фресок. К 4 веку пейзажная акварель в Азии утвердилась как самостоятельный вид искусства.Успехи акварельной живописи в 15-м и 16-м веках
Акварельная живопись возникла в Европе в период Возрождения с достижениями в производстве бумаги.В то время как ранние европейские художники готовили свои собственные акварельные смеси для настенной росписи фресками, вскоре они были применены к бумаге. С увеличением доступности синтетических пигментов гравер и художник эпохи Возрождения Альбрехт Дюрер (1471–1528) разработал новые методы работы с акварельными красками, подчеркнув светящиеся, прозрачные эффекты, которые они предлагали, и вдохновив других художников на эксперименты. Эту тенденцию подхватил Ганс Бол (1534–1593), основавший важную школу акварельной живописи в Германии в рамках эпохи Дюрера эпохи Возрождения.Однако, несмотря на эти усилия, среда оставалась в значительной степени изолированной для подготовительных набросков, за исключением школ ботаники и иллюстрации дикой природы, где ее поразительный эффект мог придать естественный вид естественным предметам. Акварельные краски также были популярны для создания карт и считались особенно эффективными для визуализации топографии местности.Английское движение акварели и его влияние на современное искусство
Акварельная живопись действительно утвердилась в западном искусстве в 18 веке, особенно в Англии, где Пол Сэндби (1730–1809), английский картограф, стал художником (и одним из основатели Королевской академии) использовал столь популярные акварельные краски при создании карт для своих пейзажных картин.Именно в это время акварельная живопись утвердилась как серьезное и выразительное художественное средство. Возглавлял это движение J.M.W. Тернер (1775–1851), технический новатор и художник-романтик, который экспериментировал с доступными синтетическими минеральными пигментами. Вдохновленный работами акварелиста Томаса Гиртина, который первым использовал его для создания широкоформатных, романтических или живописных пейзажей, Тернер исследовал как выразительную природу, так и технические аспекты этого материала. К середине 1800-х годов английское художественное общество стало свидетелем создания Общества художников-акварелистов (1804 г.) и Общества новых акварелей (1832 г.).Уникальные световые эффекты и более свободная манера письма, созданная английской школой акварельной живописи, привлекли внимание ранних импрессионистов и повлияли на их творчество. В XIX и XX веках акварель стала средством, используемым многими выдающимися художниками. Конечно, Джон Джеймс Одюбон особенно использовал акварель для документирования своих объектов дикой природы, но и другие художники, известные другими средствами, такими как масляная живопись, также работали с акварелью. Американский художник Уинслоу Гомер использовал акварельные краски, чтобы исследовать красоту мира природы.Поль Сезанн использовал технику перекрытия акварельных мазков в некоторых своих натюрмортах, в то время как Винсент Ван Гог использовал акварельные техники для создания замечательных форм искусства. Немецкий художник-абстракционист Василий Кандинский и швейцарский модернист Пауль Клее — известные акварелисты 20-го века, что свидетельствует о том, что и в современную эпоху акварель ценится художниками независимо от их национальности и движения.
В 21 веке художники использовали преимущества этого уникального средства для создания ярких произведений искусства.Прежде всего, акварель универсальна, предлагая поочередно богатые, яркие тона или мягкие, успокаивающие формы. Взгляните на акварельные картины, представленные в онлайн-галереях Agora, и вы увидите универсальность и красоту, которые может предложить акварель.
Эта статья написана для ARTmine Лорой Монро.
акварельных проектов, которые нравятся детям — 60+ занятий акварелью для детей
Вот множество техник акварели для детей, включая соленые акварельные краски, методы сопротивления акварели и печать.В этой коллекции более 60 акварельных проектов, которые понравятся детям!
Акварельные краски — один из любимых материалов для творчества в нашей семье.
Мы использовали их для всего: от рисования до печати, рисования акварелью и мультимедийных арт-проектов, а также для различных научных экспериментов и окрашивания различных предметов.
Детские акварельные краскиЧто касается самих акварельных красок, мы в первую очередь используем жидкие акварельные краски (которые мы, , любим, любим, любим ) и палитры акварельных красок.Но мы также используем несколько других вариантов акварели, в том числе и самодельные!
Акварельные проекты, которые любят дети — наши фавориты!Вот более 60 акварельных техник и идей, которые дети и семьи могут изучить вместе.
Любимые акварельные проектыРоспись солью и мраморность кремом для бритья — два самых любимых вида искусства, которыми мы любим заниматься акварелью.
Еще больше интересных акварельных проектов, которые нравятся детямРисование каракулями и раскрашивание легко, абстрактно и задумчиво.Рисовать выдуванием — это глупо и весело.
Эксперименты с разными техникамиПоэкспериментируйте с различными техниками и эффектами акварели… Попробуйте рисовать акварелью солью, клеем или медицинским спиртом!
Резист для акварели
Акварельный резист — традиционный фаворит, и есть много способов сделать это!
Точечный рисунок акварельюТочки и круги можно нарисовать ватными палочками, ватными шариками и нарисовать водой с последующим добавлением цвета.
Графика акварельюАкварель на удивление хорошо подходит для художественных проектов печати. Помимо мраморности крема для бритья (показано выше), вот еще несколько идей для печати с использованием акварельных красок.
Витраж с акварельюЗнаете ли вы, что акварелью и маслом можно придать бумаге вид витража ?!
Использование акварельных мелков и карандашейЖидкие акварельные краски и палитры красок — не единственные материалы, которые можно использовать для акварельной «живописи».Попробуйте рисовать акварельными мелками или карандашами, а затем нанести кистью на воду для создания эффекта краски.
Хотите больше акварельных проектов, которые нравятся детям? Нажмите, чтобы увидеть The Artful Parent Архив для всей категории!
А если вы ищете конкретное мероприятие, используйте поле поиска на правой боковой панели сайта.
Прикрепите его для последующего использования
31 простая идея для рисования акварелью для начинающих
Вот список из 31 простой простой идеи рисования акварелью, которую стоит попробовать для начинающих. Некоторые из них более простые, чем другие — но я думаю, что на каком бы уровне вы ни находились, вы все равно можете попробовать многие из этих картин на себе.
Акварель — это смелость и расслабленность!
Пусть цвета текут естественно — никакие картины не будут выглядеть одинаково из-за природы рисования акварелью. Так что получайте удовольствие и не беспокойтесь об ошибках.
** Эта запись в блоге является обновленной версией моей предыдущей, посвященной идеям акварельного искусства. Я хотел разместить больше оригинальных постов в этом блоге.Надеюсь, вы понимаете эти изменения.
ЦВЕТНЫЕ НАКОНЕЧНИКИ:
- Для чистых краев используйте малярную ленту или промывочную ленту .
- Создавайте красивый фон из акварели и для переднего плана или создавайте фигуры, используйте ручку, маркер или акриловую краску для более точного управления.
- Убедитесь, что ваша кисть влажная при создании градаций или эффектов «мокрый по мокрому». Работайте быстро, пока акварельная краска не высохла.
- Звезды можно создать с помощью белой ручки или разбрызгивания белой акриловой или гуашевой краски (проведите щетиной по бумаге, чтобы создать брызги).
Этот сайт является участником программы Amazon Services LLC Associates, партнерской рекламной программы, разработанной для предоставления сайтам средств для получения рекламных сборов за счет рекламы и ссылок на Amazon.com
1. Shooting Stars
2. Линии электропередач
3. Космическое пространство
4. Птицы
5. Горы
6. Качели
7. Струнные светильники
8.Горизонт города
9. Верхушки деревьев
10. Тропа
11. Палатка
12. Лодка
13. Кактус
14. Лес
15. Цветы
16. Колесо обозрения
17. Туман
18. Дерево
19. Красная луна
20. Кит
21. Уличный фонарь
22. Пальмовое дерево
23. Зонтик
24358
.Осенние листья25. Кот
26. Дом
27. Ночное небо
28. Закат
29. Дверь
30. Трава
31. Одуванчики 9
Сообщений:
40 простых вещей для рисования для начинающих художников
60 простых вещей для рисования
35 милых и простых идей для рисования животных
25 милых и простых рисунков для рисования
Спасибо, что заглянули! Надеюсь, вы нашли несколько акварельных картин, которые хотели бы попробовать сами.
Не забывайте просто получать удовольствие и получать удовольствие от процесса! Акварель — такая веселая и увлекательная краска, которую стоит попробовать!
Поделись любовью!
- Поделиться
- Pin
12 Советы по рисованию акварелью
Картина акварелью
Ни один другой живописный материал не является таким уникальным, как акварель. Акварельные картины безошибочны. Жидкие цвета танцуют на поверхности, когда вода вытягивает пигмент, создавая нежные картины.При желании цвета можно накладывать друг на друга, что обеспечивает контролируемую сложность. Или цвета могут быть применены смело, широкими свободными мазками, подразумевая предмет, а не описывая его полностью.
Этот уникальный носитель имеет ряд проблем. Многие считают, что акварель трудно контролировать, и если ваш первый опыт рисования был с непрозрачной средой (масло, акрил или темпера), процесс рисования акварелью может показаться «вспять».
Мои самые лучшие советы по рисованию акварелью…
# 1 — Используйте качественные краски
Качество имеет значение. Материалы, которые вы используете, сильно влияют на ожидаемые результаты. Многие художники решают покупать более дешевые бренды, чтобы «посмотреть, нравится ли им это», прежде чем тратить еще несколько долларов на более качественные краски. Хотя это хороший подход к некоторым материалам, акварель — другое дело. Есть широкий спектр качества.
Использование материалов более низкого качества неизбежно ведет к снижению качества результатов.Низкое качество результатов часто приводит к разочарованию. Разумно потратить немного больше на краски более высокого качества, чтобы дать вашему опыту работы с акварелью «шанс».
Новичкам рекомендую акварельные краски Winsor & Newton Cotman. Они доступны в наборах для торта (или сковороды) или в виде трубок. Цвета тюбиков дают художнику большую насыщенность цвета, а наборы для тортов легче путешествовать.
# 2 — Используйте правильную бумагу
Поверхность, на которую наносится акварель, чрезвычайно важна.Поверхности должны быть водопоглощающими и выдерживать многократные стирки цвета. Это означает, что соответствующие бумага и поверхности обычно тяжелее.
Вес бумаги относится к весу одной пачки бумаги (500 листов). Чем тяжелее бумага, тем лучше она подходит для акварельных аппликаций. Я рекомендую использовать бумагу не менее 140 фунтов (300 г). Обычно вы можете найти эту информацию четко обозначенной на первой странице блокнота.
Также доступны отдельные листы бумаги с водяными знаками.Хотя некоторые спорят, какая сторона бумаги лучше всего подходит, я обнаружил, что это действительно личный выбор, и любая из сторон даст качественные результаты.
Бумага для акварели бывает холодной, горячей и грубой. Эти обозначения относятся к процессу изготовления бумаги. Бумага холодного отжима прессуется на холодных цилиндрах. Бумага горячего пресса прессуется на горячих цилиндрах. Грубая бумага прессуется без использования цилиндров.
Процесс влияет на текстуру или зубец бумаги.Бумага для горячего прессования гладкая, а бумага для холодного прессования имеет четко очерченный зуб. Шероховатая бумага, как следует из названия, имеет самую прочную текстуру.
Если использовать неподходящую бумагу, может произойти коробление. Хотя многие производители выпускают бумагу с пометкой «акварельная бумага», использование этой бумаги не гарантирует, что бумага не будет изгибаться. Лучший показатель — это вес бумаги. Бумага, изображенная ниже, помечена как «акварельная бумага», но при нанесении акварели изгибается.Как видите, вес бумаги составляет всего 108,1 фунта. (160 г).
Подробнее о бумаге для акварели можно прочитать здесь.
# 3 — Растяните акварельную бумагу
Бумагу для акварели можно растянуть, чтобы она лучше впитывала цветные пятна. Растягивание бумаги обеспечивает натянутую поверхность. Бумаги большего размера можно замочить в ванне с водой и наклеить на твердый картон, пока они влажные. Для приклеивания бумаги можно использовать скобки или толстую ленту. По мере высыхания бумага слегка усаживается, создавая подходящую поверхность для рисования.
Бумагу меньшего размера можно просто приклеить к доске с помощью малярной ленты или бумажной ленты, а затем слегка промыть водой.
# 4 — Легко рисовать
Обычно делают набросок композиции до начала рисования. В то время как некоторые художники не против видеть графитовые следы на картине, другие предпочитают, чтобы они были полностью покрыты акварельными аппликациями.
Чтобы гарантировать, что графитовые следы скрыты, слегка нарисуйте карандашом HB.Избегайте затенения и сосредоточьтесь на разработке контурных линий. Более мягкие карандаши (2B, 4B и т. Д.) Могут создавать слишком темные линии, а более твердые карандаши (2H, 4H и т. Д.) Могут создавать бороздки на поверхности бумаги.
Графитовые аппликации можно аккуратно приподнять с помощью ластика перед началом покраски. Но после того, как была добавлена акварель, удалить графитовые следы с поверхности практически невозможно.
(Изображение вверху из серии «Акварельный пейзаж»)
# 5 — Используйте правую щетку
Кисти для рисования акварелью разнообразны, и нет четких правил, какие кисти вам следует использовать.Однако обычно предпочтительны щетки с более мягкой щетиной. Я предпочитаю использовать синтетические кисти, мягкие, но достаточно упругие, чтобы обеспечить контроль. Мой личный фаворит — акварельные кисти Grumbacher Golden Edge.
Эксперименты часто приводят к поиску правильной кисти, которая соответствует вашему стилю, но синтетические кисти — хорошее место для начала. Они недорогие по сравнению со многими щетками из натурального волоса, такими как соболь.
Более жесткие кисти, такие как свиная щетина, обычно предназначены для текстурных эффектов и не используются для общего применения.
Более подробную информацию о кистях можно найти здесь.
# 6 — Ослабить вверх
Поскольку средством для нанесения пигмента является вода, цвета будут естественным образом перетекать и образовывать интересные формы. Часто лучше не бороться с этим, а вместо этого использовать это. Полное описание предметов не требуется. Формы цвета и значения могут быть применены свободно, подразумевая предмет.
Позвольте краске «делать то, что она хочет» на участках и рассыпать ваши аппликации.Хотя акварель можно использовать с большим контролем, она часто становится наиболее привлекательной, когда используется неаккуратно.
(Изображение вверху из Модуля 8 «Мастерской акварели»)
# 7 — Ограничьте свою палитру
Как и в случае с любой другой живописью или рисунком, следует учитывать теорию цвета. Хотя может возникнуть соблазн использовать каждый доступный вам цвет, часто лучше ограничить свою палитру. Ищите предметы, у которых уже есть определенные цветовые отношения (т. Е.дополнительные, аналогичные и т. д.) или упростить наблюдаемые цвета.
Когда ваша палитра упрощена, картина часто получается гармоничной и эстетически успешной.
(Изображение вверху из Модуля 6 «Мастерской акварели»)
# 8 — Промывка слоев
При рисовании акварелью можно получить более темные оттенки и постепенно более интенсивные цвета с помощью нескольких применений цвета. Если дать каждому слою краски высохнуть перед нанесением дополнительных смывок, получится эффект глазури.Поскольку цвета, расположенные ниже, по-прежнему видны в самых популярных приложениях, достигается сложность цвета.
Обычно более темные оттенки развиваются по мере прорисовки. Более светлые значения разрабатываются с минимальным количеством применений, поскольку белый цвет бумаги влияет на результирующее значение.
Хотя цвета можно смешивать на палитре перед нанесением, оптическое смешивание цветов также возможно. Один из примеров — наложение полупрозрачного синего слоя поверх полупрозрачного красного.Полученный цвет будет фиолетовым, так как красный и синий оптически смешиваются.
(Изображение вверху из Модуля 13 «Мастерской акварели»)
# 9 — Используйте маскирующую жидкость
Маскирующая жидкость — это жидкий материал, обычно на основе латекса. Его можно наносить кистью, чтобы защитить участки картины от вымытых аппликаций. Поскольку белый цвет бумаги так важен в акварельной живописи, маскирующая жидкость становится важным инструментом.
После высыхания маскирующую жидкость можно легко удалить, потерев ее пальцем или удалив ластиком. Маскирующая жидкость имеет неприятную привычку портить кисти, поэтому рекомендуется использовать старую кисть при нанесении ее на поверхность.
(Изображение вверху из простого акварельного пейзажа)
# 10 — Создать полный диапазон значений
Ценность, пожалуй, самый важный элемент искусства. Значение относится к темноте или яркости цвета.Это то, как мы видим и понимаем свет, форму и текстуру в плоской работе.
Создание полного диапазона значений означает, что мы должны включить в картину полный спектр темных и светлых тонов. В случае цветной раскраски это означает, что мы должны обязательно использовать более темные значения цветов, а также более светлые версии.
Распространенная ошибка начинающих акварелистов — писать легко, не имея полной ценности. Если это применимо к вам, обязательно сдвиньте более темную сторону шкалы значений, чтобы убедиться, что вы включаете самые темные значения, присутствующие на вашем объекте или в сцене.
(Изображение вверху из раздела Как нарисовать глаз акварелью)
# 11 — Знайте, когда остановиться
Одна из самых больших проблем, с которой сталкивается художник, — это знать, когда остановиться. Мы часто оказываемся в «художественном потоке», где творить так весело, что мы не хотим, чтобы это заканчивалось. Но если мы будем слишком много работать, результат может показаться переутомленным.
К сожалению, акварелью легко переутомиться, и особенно важно знать, когда остановиться.Узнать, когда работа закончена, — дело тонкое, и на него нет простого ответа. Однако, если вы задаетесь вопросом: «Что еще я могу сделать?», То картина, скорее всего, закончена, и пора отложить кисть. Помните, что зрителю не нужно объяснять каждую деталь.
(Изображение выше из Как нарисовать птицу акварелью)
# 12 — Практика, практика, практика
Развитие навыков требует практики. Живопись — это просто навык, который может развить любой желающий.Следует признать, что это означает терпеливую практику.

 И если в наборах отличие видно сразу невооруженным глазом, то к карандашам следует присмотреться повнимательнее.
И если в наборах отличие видно сразу невооруженным глазом, то к карандашам следует присмотреться повнимательнее.
 Для этого просто смочите карандаш водой и пройдитесь чистым цветом там, где хотите его усилить.
Для этого просто смочите карандаш водой и пройдитесь чистым цветом там, где хотите его усилить.  Для этого снизу проводится полоса, потом ее края размываются водой до получения разводов. Потом наносится следующая полоса повыше и снова размывается. Таким образом, можно получить красивые разводы на стене, наводящие на определенные размышления и притягивающие взгляд;
Для этого снизу проводится полоса, потом ее края размываются водой до получения разводов. Потом наносится следующая полоса повыше и снова размывается. Таким образом, можно получить красивые разводы на стене, наводящие на определенные размышления и притягивающие взгляд; Такая бумага используется для работ, предполагающих тщательную передачу деталей. На такой бумаге мазок почти не встречает препятствий.
Такая бумага используется для работ, предполагающих тщательную передачу деталей. На такой бумаге мазок почти не встречает препятствий.


 Китай (КНР)
Китай (КНР) Индия
Индия США
США Индонезия
Индонезия Пакистан
Пакистан Бразилия
Бразилия Нигерия
Нигерия Бангладеш
Бангладеш Россия
Россия Япония
Япония Мексика
Мексика Филиппины
Филиппины Египет
Египет Эфиопия
Эфиопия Вьетнам
Вьетнам Турция
Турция Германия
Германия Иран
Иран Демократическая Республика Конго
Демократическая Республика Конго Южная Африка (Южно-Африканская Республика)
Южная Африка (Южно-Африканская Республика) Таиланд
Таиланд Франция
Франция Великобритания
Великобритания Италия
Италия Танзания
Танзания Англия
Англия Аргентина
Аргентина Мьянма
Мьянма Южная Корея (Республика Корея)
Южная Корея (Республика Корея) Кения
Кения Колумбия
Колумбия Йемен
Йемен Испания
Испания Уганда
Уганда Мадагаскар
Мадагаскар Нигер
Нигер Саудовская Аравия
Саудовская Аравия Украина
Украина Алжир
Алжир Малайзия
Малайзия Судан
Судан Непал
Непал Перу
Перу Ирак
Ирак Кот-д’Ивуар
Кот-д’Ивуар Польша
Польша Мали
Мали Буркина-Фасо
Буркина-Фасо Афганистан
Афганистан Канада
Канада Марокко
Марокко Замбия
Замбия Узбекистан
Узбекистан Венесуэла
Венесуэла Малави
Малави Камерун
Камерун Ангола
Ангола Гана
Гана Мозамбик
Мозамбик Северная Корея (КНДР)
Северная Корея (КНДР) Сирия
Сирия Шри-Ланка
Шри-Ланка Австралия
Австралия Зимбабве
Зимбабве Гватемала
Гватемала Камбоджа
Камбоджа Бурунди
Бурунди Чад
Чад Гвинея
Гвинея Южный Судан
Южный Судан Сенегал
Сенегал Румыния
Румыния Чили
Чили Казахстан
Казахстан Боливия
Боливия Нидерланды
Нидерланды Эквадор
Эквадор Руанда
Руанда Бельгия
Бельгия Куба
Куба Тунис
Тунис Греция
Греция Доминиканская Республика
Доминиканская Республика Чехия
Чехия Португалия
Португалия Бенин
Бенин Сомали
Сомали Швеция
Швеция Гаити
Гаити Венгрия
Венгрия Азербайджан
Азербайджан Объединённые Арабские Эмираты (ОАЭ)
Объединённые Арабские Эмираты (ОАЭ) Белоруссия
Белоруссия Таджикистан
Таджикистан Израиль
Израиль Австрия
Австрия Гондурас
Гондурас Швейцария
Швейцария Папуа — Новая Гвинея
Папуа — Новая Гвинея Того
Того Иордания
Иордания Сербия
Сербия Парагвай
Парагвай Болгария
Болгария Лаос
Лаос Сьерра-Леоне
Сьерра-Леоне Ливия
Ливия Никарагуа
Никарагуа Сальвадор
Сальвадор Киргизия
Киргизия Ливан
Ливан Туркмения
Туркмения Дания
Дания Финляндия
Финляндия Сингапур
Сингапур Словакия
Словакия Норвегия
Норвегия Эритрея
Эритрея Центральная Африка (Центральноафриканская Республика)
Центральная Африка (Центральноафриканская Республика) Новая Зеландия
Новая Зеландия Коста-Рика
Коста-Рика Республика Конго
Республика Конго Либерия
Либерия Ирландия
Ирландия Хорватия
Хорватия Оман
Оман Кувейт
Кувейт Панама
Панама Грузия
Грузия Мавритания
Мавритания Молдавия
Молдавия Босния и Герцеговина
Босния и Герцеговина Уругвай
Уругвай Монголия
Монголия Армения
Армения Ямайка
Ямайка Албания
Албания Литва
Литва Намибия
Намибия Ботсвана
Ботсвана Катар
Катар Лесото
Лесото Македония
Македония Словения
Словения  Гамбия
Гамбия Габон
Габон Латвия
Латвия Гвинея-Бисау
Гвинея-Бисау Бахрейн
Бахрейн Свазиленд
Свазиленд Тринидад и Тобаго
Тринидад и Тобаго Эстония
Эстония Экваториальная Гвинея
Экваториальная Гвинея Маврикий
Маврикий Восточный Тимор
Восточный Тимор Джибути
Джибути Фиджи
Фиджи Кипр
Кипр Коморы
Коморы Гайана
Гайана Бутан
Бутан Черногория
Черногория Соломоновы Острова
Соломоновы Острова Люксембург
Люксембург Суринам
Суринам Кабо-Верде
Кабо-Верде Мальта
Мальта Бруней
Бруней Багамы
Багамы Белиз
Белиз Мальдивы
Мальдивы Исландия
Исландия Барбадос
Барбадос Вануату
Вануату Самоа
Самоа Сан-Томе и Принсипи
Сан-Томе и Принсипи Сент-Люсия
Сент-Люсия Кирибати
Кирибати Сент-Винсент и Гренадины
Сент-Винсент и Гренадины Гренада
Гренада Тонга
Тонга Микронезия (Федеративные Штаты Микронезии)
Микронезия (Федеративные Штаты Микронезии) Сейшельские Острова
Сейшельские Острова Антигуа и Барбуда
Антигуа и Барбуда Андорра
Андорра Доминика
Доминика Сент-Китс и Невис
Сент-Китс и Невис Маршалловы Острова
Маршалловы Острова Монако
Монако Лихтенштейн
Лихтенштейн Сан-Марино
Сан-Марино Палау
Палау Науру
Науру Тувалу
Тувалу











 Чунцин — город с самым большим населением в мире
Чунцин — город с самым большим населением в мире Несильно отстает и Микко Рантанен, чья результативная серия достигла девяти встреч.
Несильно отстает и Микко Рантанен, чья результативная серия достигла девяти встреч.

 В итоге им это не помешало победить, но неужели такое возможно снова?
В итоге им это не помешало победить, но неужели такое возможно снова?

 Самое большое отечественное представительство было в 1994-м году на матче «Рейнджерс» — «Ванкувер» (3:2): Павел Буре, Алексей Ковалев, Сергей Немчинов и Сергей Зубов. Причем Немчинов, как и позже Сергей Брылин, дважды участвовал в подобных встречах.
Самое большое отечественное представительство было в 1994-м году на матче «Рейнджерс» — «Ванкувер» (3:2): Павел Буре, Алексей Ковалев, Сергей Немчинов и Сергей Зубов. Причем Немчинов, как и позже Сергей Брылин, дважды участвовал в подобных встречах. М. Лавров. В своей речи он подчеркнул, что в этом году форум открывает цикл обсуждений в сфере бюджетной системы страны с экспертным сообществом и общественностью. Рассматриваемые вопросы на форуме должны помочь в определении стратегических задач страны в бюджетной политике, формировании адекватных инструментов для надстройки бюджетной системы в национальные проекты.
М. Лавров. В своей речи он подчеркнул, что в этом году форум открывает цикл обсуждений в сфере бюджетной системы страны с экспертным сообществом и общественностью. Рассматриваемые вопросы на форуме должны помочь в определении стратегических задач страны в бюджетной политике, формировании адекватных инструментов для надстройки бюджетной системы в национальные проекты. Результаты обследования позволили смоделировать, какой вклад в снижение или увеличение численности малоимущих вносит каждый из компонентов методики – состав домохозяйства, величина используемой «линии бедности» и другие критерии нуждаемости.
Результаты обследования позволили смоделировать, какой вклад в снижение или увеличение численности малоимущих вносит каждый из компонентов методики – состав домохозяйства, величина используемой «линии бедности» и другие критерии нуждаемости. Вот так:
Вот так:

 Переменную c можно умножить на каждое слагаемое в скобках:
Переменную c можно умножить на каждое слагаемое в скобках: Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?
Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?


 Остановимся на ключевых моментах.
Остановимся на ключевых моментах. Помимо получения питания, ребенок находит и успокоение у маминой груди. Поэтому не рекомендуется кормить ребенка «по режиму»-например, раз в 3 часа или ограничивать его время пребывания у груди-например, кормить не более 15 минут. Решающее значение для успешной лактации имеют ночные кормления – благодаря им уровень пролактина поддерживается на необходимом уровне.
Помимо получения питания, ребенок находит и успокоение у маминой груди. Поэтому не рекомендуется кормить ребенка «по режиму»-например, раз в 3 часа или ограничивать его время пребывания у груди-например, кормить не более 15 минут. Решающее значение для успешной лактации имеют ночные кормления – благодаря им уровень пролактина поддерживается на необходимом уровне.
 При недостаточном питании новорожденного ребенка желтуха может быть более интенсивной и длительной в связи со сгущением желчи. (источник-НАЦИОНАЛЬНАЯ ПРОГРАММА ОПТИМИЗАЦИИ ВСКАРМЛИВАНИЯ ДЕТЕЙ ПЕРВОГО ГОДА ЖИЗНИ В РОССИЙСКОЙ ФЕДЕРАЦИИ, стр.17).
При недостаточном питании новорожденного ребенка желтуха может быть более интенсивной и длительной в связи со сгущением желчи. (источник-НАЦИОНАЛЬНАЯ ПРОГРАММА ОПТИМИЗАЦИИ ВСКАРМЛИВАНИЯ ДЕТЕЙ ПЕРВОГО ГОДА ЖИЗНИ В РОССИЙСКОЙ ФЕДЕРАЦИИ, стр.17).
 В больших количествах не стоит употреблять цельное молоко, красные овощи и фрукты, экзотические фрукты. Воду, чай употреблять по жажде.
В больших количествах не стоит употреблять цельное молоко, красные овощи и фрукты, экзотические фрукты. Воду, чай употреблять по жажде.
 Поддерживать Siri новый пульт, скорее всего, не будет. А нужен ли голосовой ассистент телевизору?
Поддерживать Siri новый пульт, скорее всего, не будет. А нужен ли голосовой ассистент телевизору? Этот онлайн-решебник был разработан вовсе не для того, чтобы школьник просто списывал верные ответы в чистовик, как многие взрослые думают, а для того, чтобы облегчить образовательный процесс. К сожалению, с каждым годом рабочая программа становится все сложнее. Полностью освоить материал по всем предметам не получится без качественного ГДЗ издательства «Народная асвета».
Этот онлайн-решебник был разработан вовсе не для того, чтобы школьник просто списывал верные ответы в чистовик, как многие взрослые думают, а для того, чтобы облегчить образовательный процесс. К сожалению, с каждым годом рабочая программа становится все сложнее. Полностью освоить материал по всем предметам не получится без качественного ГДЗ издательства «Народная асвета». К тому же посещение круглосуточное, то есть подсмотреть конкретный результат можно в любое удобное для пользователя время.
К тому же посещение круглосуточное, то есть подсмотреть конкретный результат можно в любое удобное для пользователя время. Никаких пакетов или подписок, платите только за необходимое время.
Никаких пакетов или подписок, платите только за необходимое время. ..
.. & nbsp
& nbsp ..]
..] ..]
..] ..]
марки должны быть t w o — седьмая ( 2 /7 ) марки.
..]
марки должны быть t w o — седьмая ( 2 /7 ) марки.
 ..]
возможности вращения вокруг bl ue s y седьмых .
..]
возможности вращения вокруг bl ue s y седьмых .

 ..]
..] Наконец, они сами делят фигуры на равные части и показывают данную дробь.
Наконец, они сами делят фигуры на равные части и показывают данную дробь.
 Напишите дроби,
и прочтите их вслух.
Напишите дроби,
и прочтите их вслух. фракции.
фракции.
 1 =
1 =
 Разделите фигуру на три равные части.
Разделите фигуру на три равные части.
 4: Сложение и вычитание дробей
4: Сложение и вычитание дробей И, в конце концов, они правы!
И, в конце концов, они правы! Мы утверждаем, что
Мы утверждаем, что
 Если вы можете сразу увидеть знаменатель (или подумать о более быстром методе, который всегда работает), дерзайте!
Если вы можете сразу увидеть знаменатель (или подумать о более быстром методе, который всегда работает), дерзайте!
 Если знаменатели не совпадают, потребуется немного больше работы. В частности, одна или обе дроби должны быть алгебраически скорректированы для создания общих знаменателей .
Если знаменатели не совпадают, потребуется немного больше работы. В частности, одна или обе дроби должны быть алгебраически скорректированы для создания общих знаменателей .

 называется абсцисса (то есть координата по оси
называется абсцисса (то есть координата по оси  ) точки на единичной окружности, соответствующей повороту на данный угол
) точки на единичной окружности, соответствующей повороту на данный угол  ) точки на единичной окружности, соответствующей повороту на данный угол
) точки на единичной окружности, соответствующей повороту на данный угол 
 , которые соответствуют точкам окружности, ордината которых равна
, которые соответствуют точкам окружности, ордината которых равна  .
.
 и
и радиан:
радиан:
 радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой
радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой  (или
(или  ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении,
). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, ,
,  ,
,  — множество целых чисел (1)
— множество целых чисел (1) , где
, где 
 ( то есть четное
( то есть четное  ( то есть нечетное
( то есть нечетное 
 — это абсцисса точки единичной окружности, полученной поворотом на угол
— это абсцисса точки единичной окружности, полученной поворотом на угол 
 и
и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
 ,
,  ,
,  .
.


 и
и  :
:
 радиан друг от друга, то мы можем записать решение таким образом:
радиан друг от друга, то мы можем записать решение таким образом: ,
, 

 единичной окружности параллельно оси
единичной окружности параллельно оси 
 и
и  радиан:
радиан:





























 , поэтому получим:
, поэтому получим: . Разделим обе части равенства на 3:
. Разделим обе части равенства на 3:


 , поэтому получим:
, поэтому получим:
 , для этого сначала перенесем
, для этого сначала перенесем  вправо с противоположным знаком:
вправо с противоположным знаком:


 знак не меняется, поскольку k может принимать любые целые значения.
знак не меняется, поскольку k может принимать любые целые значения.
 Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений

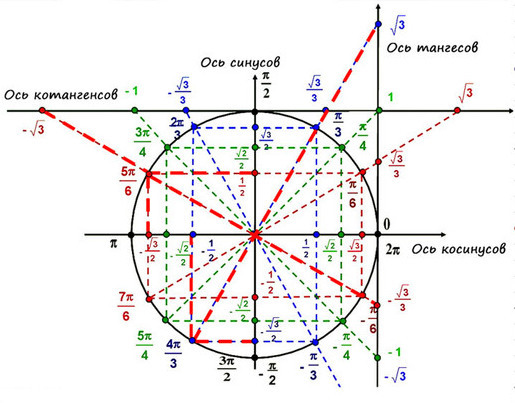
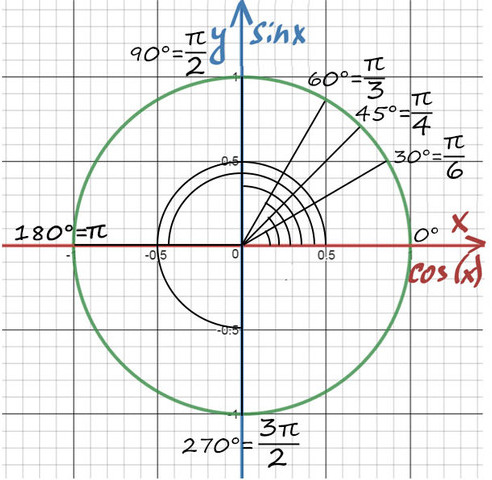
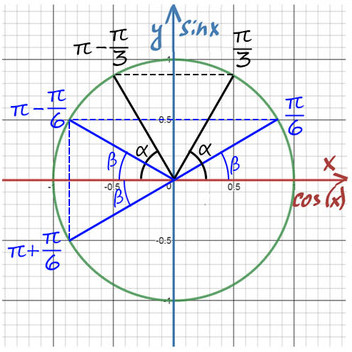
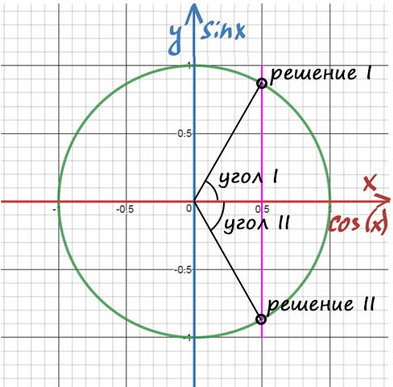
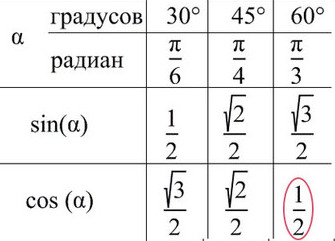

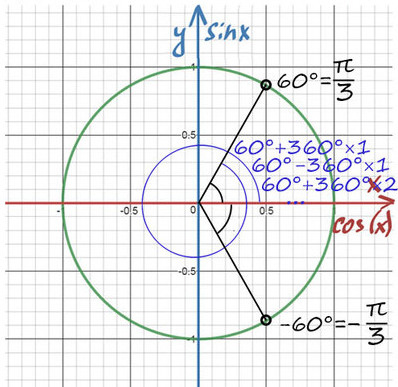

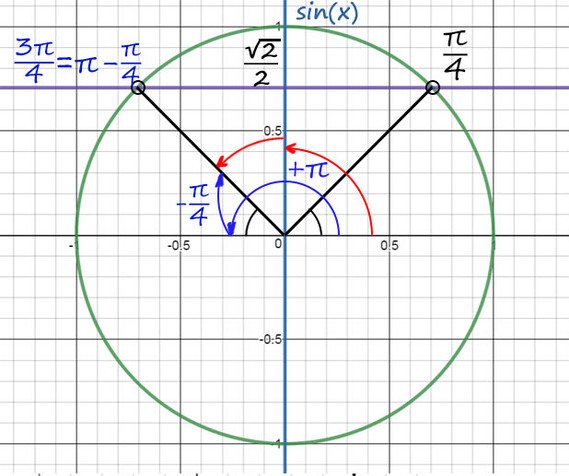







 Вы обратили внимание, решая тригонометрическое неравенство с тангенсом, – мы не включаем в ответ точки
Вы обратили внимание, решая тригонометрическое неравенство с тангенсом, – мы не включаем в ответ точки 














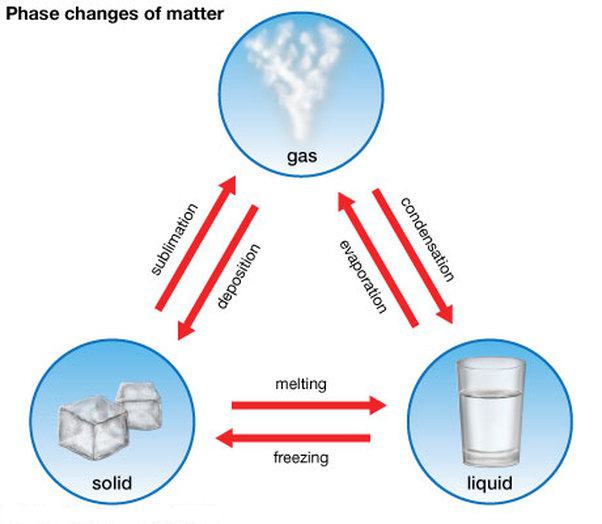


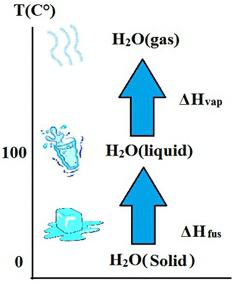
 (1.1)
(1.1)
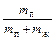 , (1.4)
, (1.4)

 Тесты по русскому языку.Пройти >>
Тесты по русскому языку.Пройти >>
 6
6
 При любом значении r1, не совпадающем с r прямая линия, заданная уравнением
При любом значении r1, не совпадающем с r прямая линия, заданная уравнением

 {«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.
{«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.

 Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a. [+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.
[+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.
 Значит мы может полагать, что коэффициент bу обоих графиков равен 4.
Значит мы может полагать, что коэффициент bу обоих графиков равен 4.

 Здесь k = 1.
Здесь k = 1. Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Как следует из названия, главным слагаемым является ax 2 . То есть а не должно равняться нулю, остальные коэффициенты (b и с ) нулю равняться могут.
Как следует из названия, главным слагаемым является ax 2 . То есть а не должно равняться нулю, остальные коэффициенты (b и с ) нулю равняться могут.

 Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2: Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.

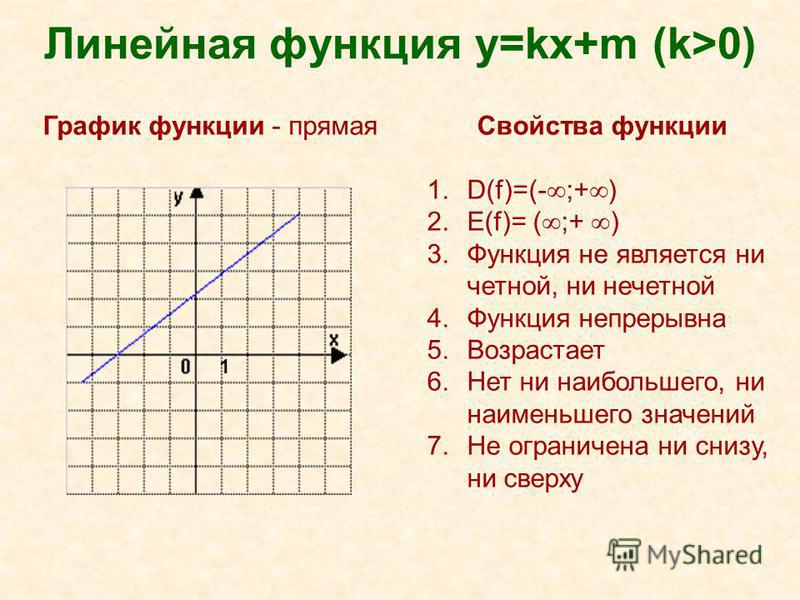
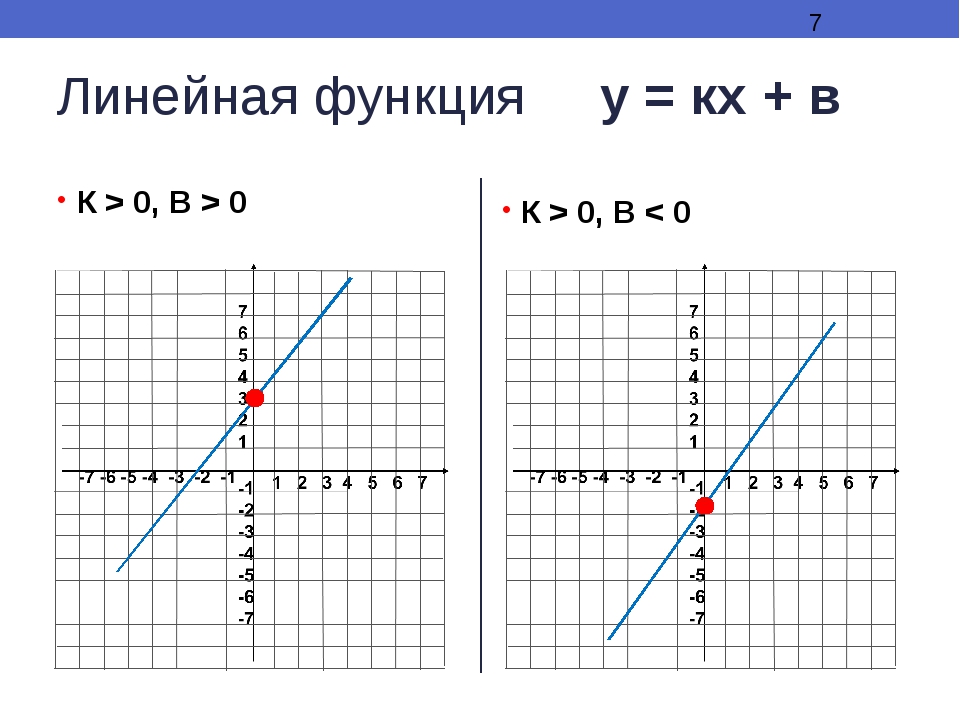 Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.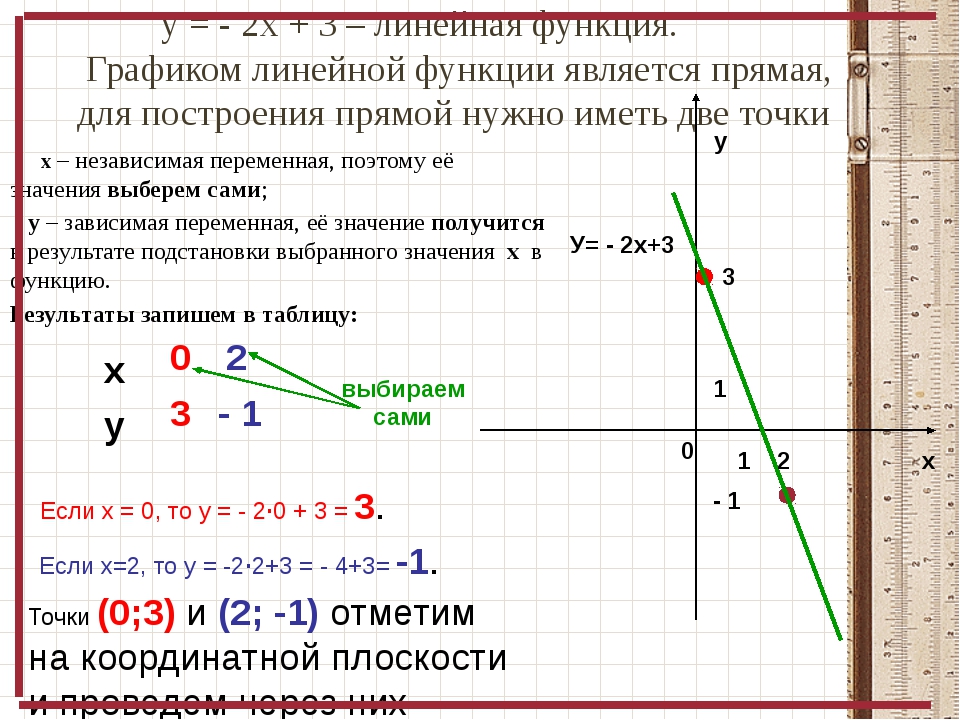 Условие перепендикулярности двух прямых:
Условие перепендикулярности двух прямых: 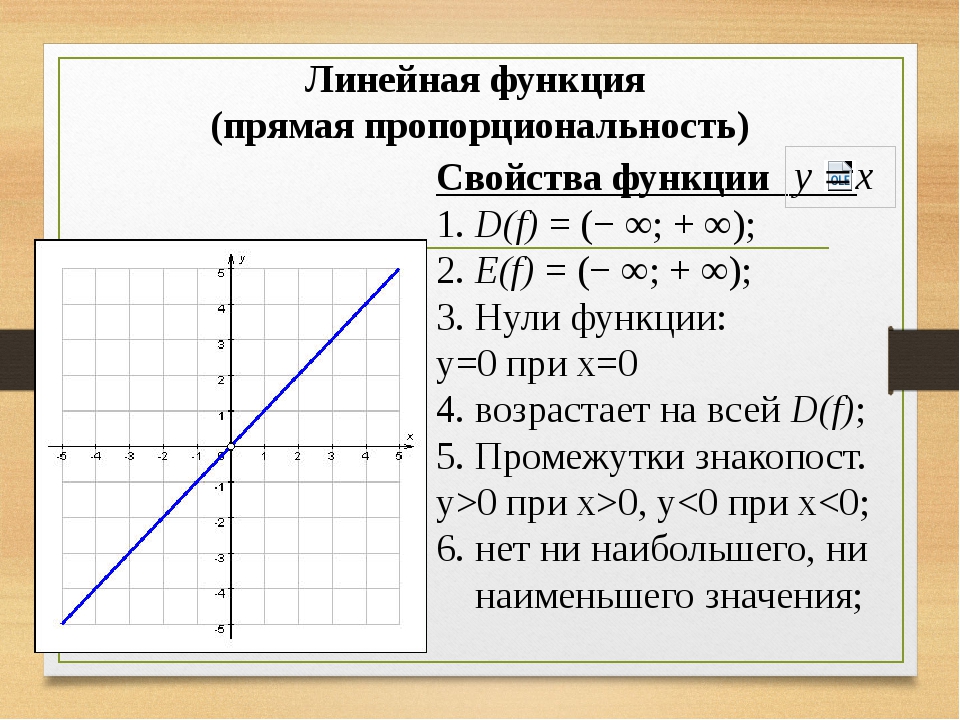
 Ниже приведена таблица, которая наглядно это иллюстрирует.
Ниже приведена таблица, которая наглядно это иллюстрирует. 2 $, дающая площадь квадрата как функцию длины его стороны, не является линейной, потому что ее график содержит точки $ (1,1) $, $ (2,4) $ и (3,9) $, которые не находятся на прямой линии .
2 $, дающая площадь квадрата как функцию длины его стороны, не является линейной, потому что ее график содержит точки $ (1,1) $, $ (2,4) $ и (3,9) $, которые не находятся на прямой линии .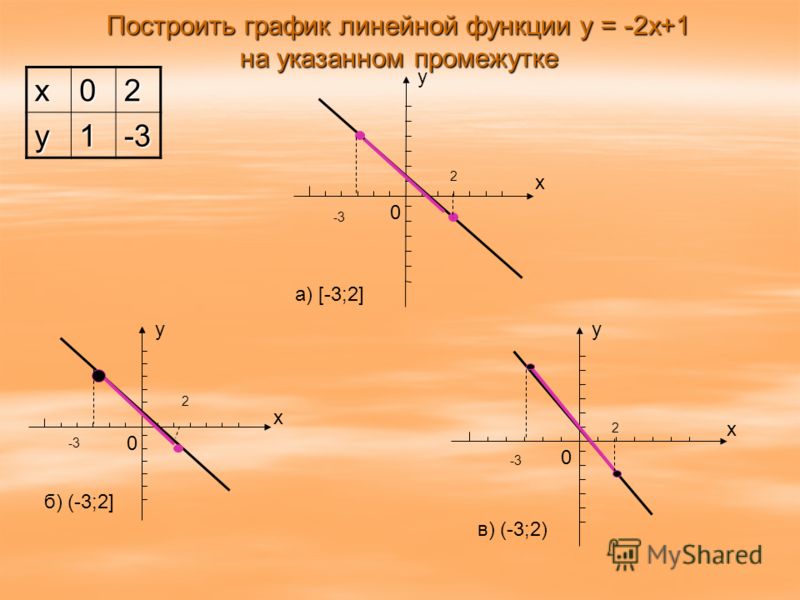 Итак, $ | BP | / | AP | = | CQ | / | AQ | $, что означает наличие масштабного фактора $ k = | AQ | / | AP | = | CQ | / | BP | $, так что расширение с центром $ A $ и масштабным фактором $ k $ переводит $ P $ в $ Q $, а вертикальный отрезок $ BP $ переводит в вертикальный отрезок на основе $ Q $ той же длины, что и $ CQ $. Это означает, что это должно занять от $ B $ до $ C $.
Итак, $ | BP | / | AP | = | CQ | / | AQ | $, что означает наличие масштабного фактора $ k = | AQ | / | AP | = | CQ | / | BP | $, так что расширение с центром $ A $ и масштабным фактором $ k $ переводит $ P $ в $ Q $, а вертикальный отрезок $ BP $ переводит в вертикальный отрезок на основе $ Q $ той же длины, что и $ CQ $. Это означает, что это должно занять от $ B $ до $ C $.
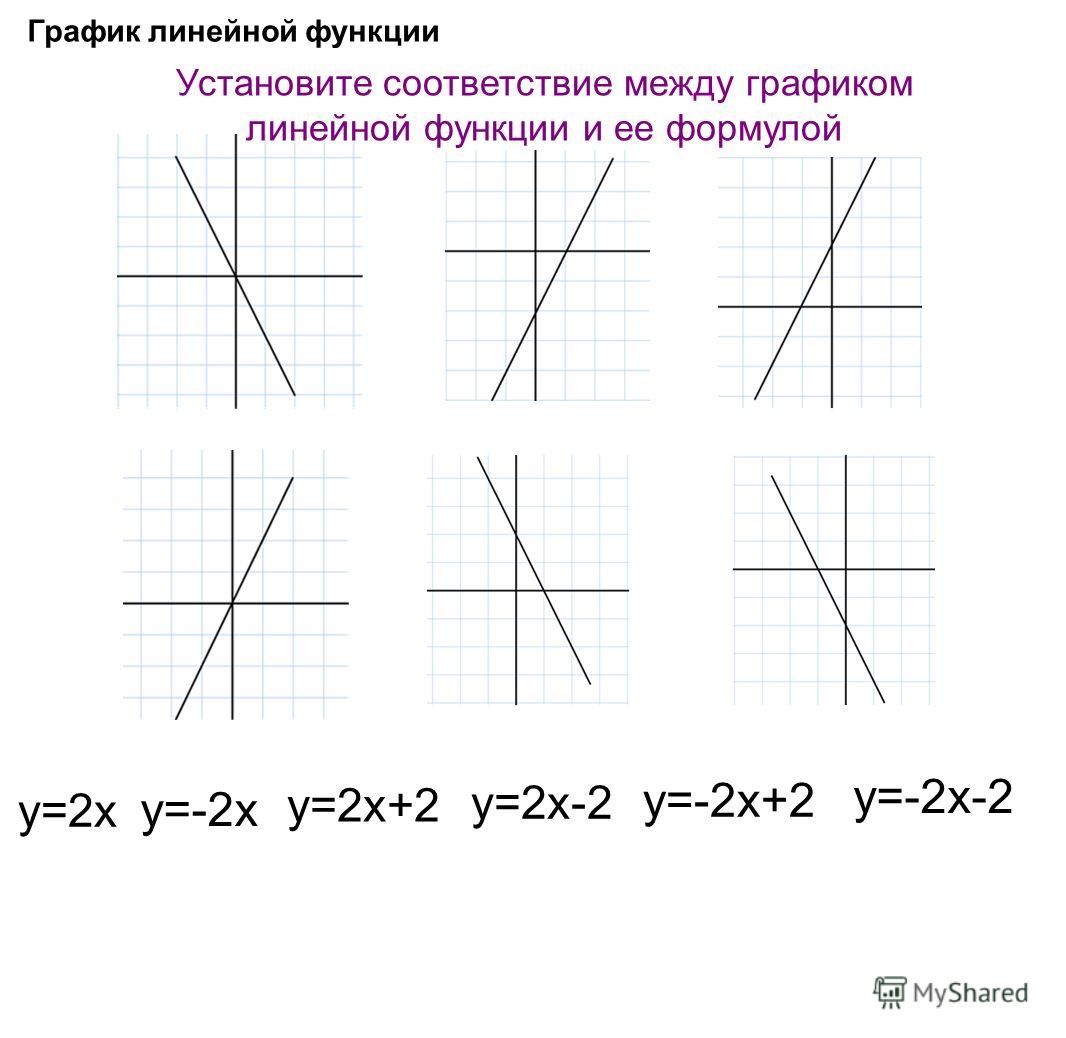 А что насчет этого:
А что насчет этого:
 а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:
а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:
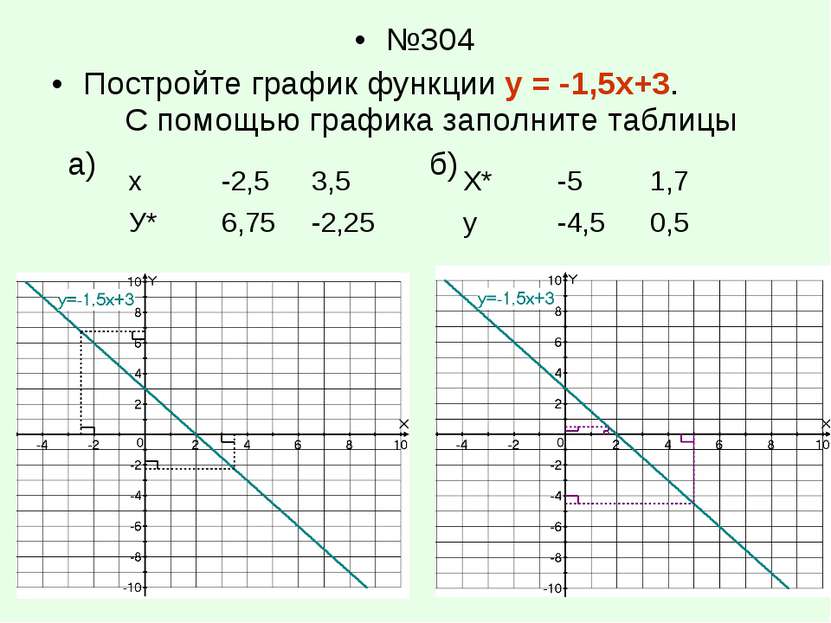
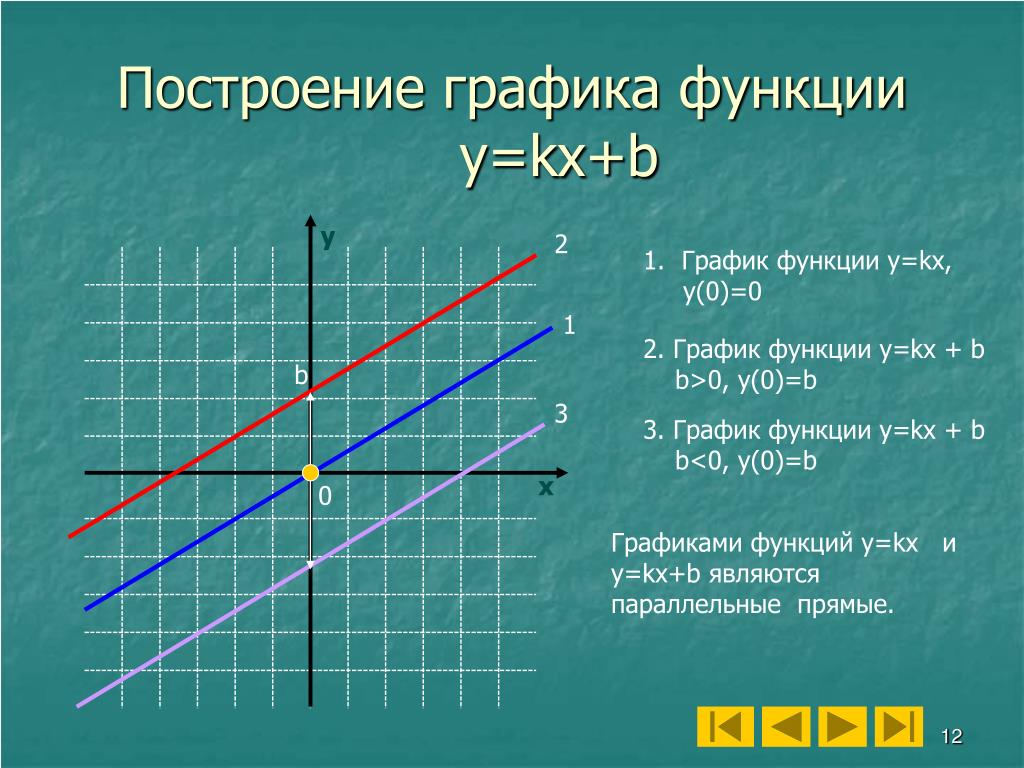 Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение:
Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение: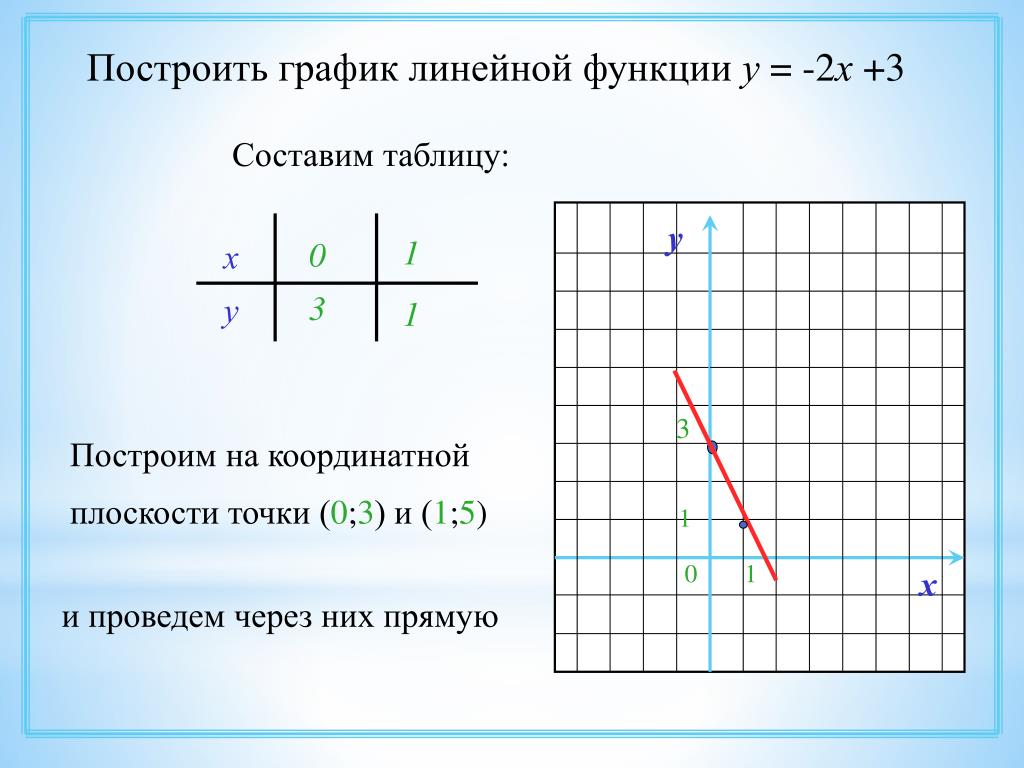 Неизвестный b может быть исключен путем вычитания уравнений:
Неизвестный b может быть исключен путем вычитания уравнений: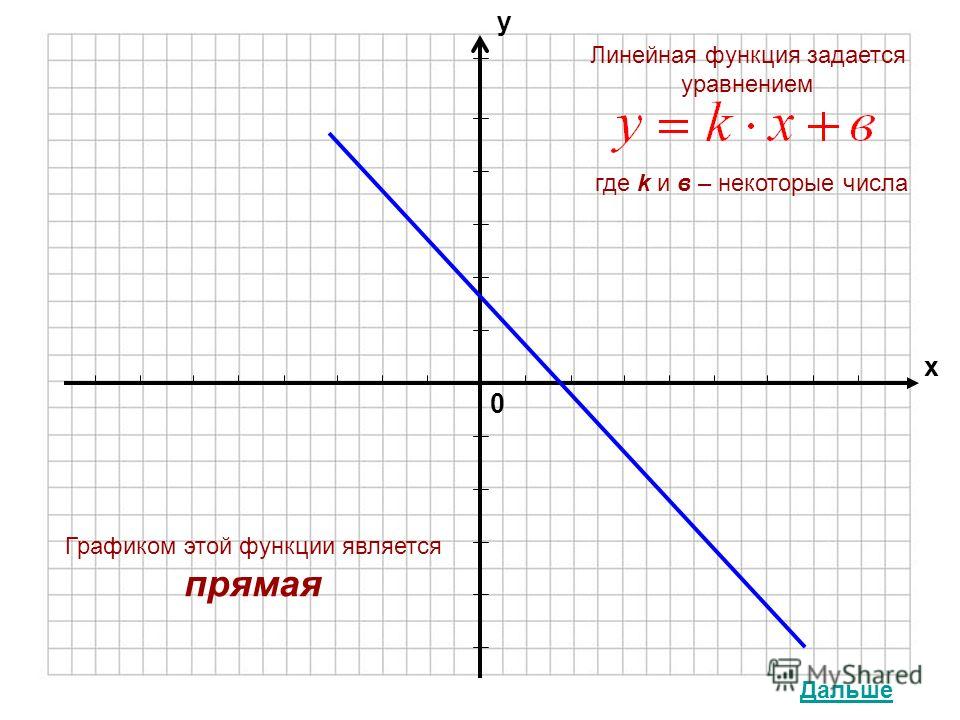 Это гарантирует, что его обратная функция тоже должна быть функцией. Возможно, вы знакомы с тестом горизонтальной линии, который гарантирует, что он будет иметь инверсию всякий раз, когда ни одна горизонтальная линия не пересекает или пересекает график более одного раза.
Это гарантирует, что его обратная функция тоже должна быть функцией. Возможно, вы знакомы с тестом горизонтальной линии, который гарантирует, что он будет иметь инверсию всякий раз, когда ни одна горизонтальная линия не пересекает или пересекает график более одного раза.

 Однако важно помнить, что не каждая точка на линии, которую описывает уравнение, обязательно будет решением проблемы, которую описывает уравнение. Например, проблема может не иметь смысла для отрицательных чисел (скажем, если независимая переменная — это время) или очень больших чисел (скажем, чисел больше 100, если зависимая переменная — это оценка в классе).
Однако важно помнить, что не каждая точка на линии, которую описывает уравнение, обязательно будет решением проблемы, которую описывает уравнение. Например, проблема может не иметь смысла для отрицательных чисел (скажем, если независимая переменная — это время) или очень больших чисел (скажем, чисел больше 100, если зависимая переменная — это оценка в классе).


 Однако в данных можно найти линии тренда, которые образуют грубую версию линейной зависимости. Например, вы можете посмотреть на ежедневные продажи мороженого и дневную высокую температуру как на две действующие переменные на графике и найти грубую линейную зависимость между ними.
Однако в данных можно найти линии тренда, которые образуют грубую версию линейной зависимости. Например, вы можете посмотреть на ежедневные продажи мороженого и дневную высокую температуру как на две действующие переменные на графике и найти грубую линейную зависимость между ними.