Как найти периметр основания пирамиды: Периметр и апофема правильной пирамиды
Тема 10. Стереометрия — Материалы для подготовки к вступительным экзаменам в СГГА
Если AB||A’B’ и BC||B’C’, то плоскости ABC и A’B’C’ параллельны.
Прямая BC, лежащая в плоскости ABC, перпендикулярна наклонной DB, тогда и только тогда, когда она перпендикулярна ее проекции на плоскость AB.
Площадь поверхности: S=2Sосн+Sбок, где Sбок – площадь боковой поверхности, равная сумме площадей всех граней.
Прямая призма – призма, боковое ребро которой перпендикулярно основанию.
Объем: V=Sосн∙l .
Площадь боковой поверхности: Sбок=P∙l, где P – периметр основания.
Правильная призма – прямая призма, основание которой – правильный многоугольник.
1) В основании прямой призмы лежит прямоугольный треугольник с катетами, равными 5 и 12. Высота призмы равна 8. Найдите полную поверхность призмы.
2) В прямой треугольной призме основания равны 36, 29 и 25, а полная поверхность призмы 1620.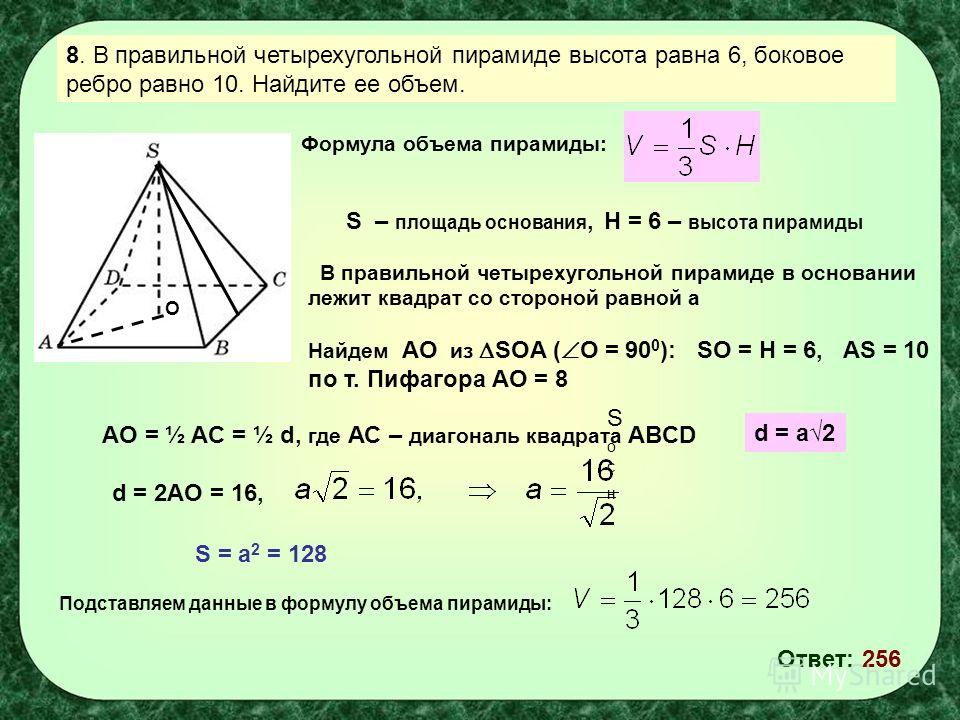 Найдите высоту призмы.
Найдите высоту призмы.
4) Стороны основания прямой треугольной призмы равны 10, 17 и 21, а ее боковое ребро равно меньшей из высот основания. Найдите объем призмы.
5) Объем правильной треугольный призмы равен . Найдите высоту призмы, если радиус описанной около основания окружности равен 2. 6) Высота правильной треугольной призмы равна 8, а площадь основания . Найдите диагональ боковой грани призмы. 7) Все ребра прямой треугольной призмы равны. Найдите площадь основания призмы, если площадь ее полной поверхности равна . 8) Высота правильной четырёхугольной призмы равна , а диагональ призмы наклонена к плоскости основания под углом 300. Найти сторону основания призмы. 9) Основание прямой призмы – прямоугольный треугольник с катетами 6м и 8м, а диагональ большей по площади боковой грани равна м.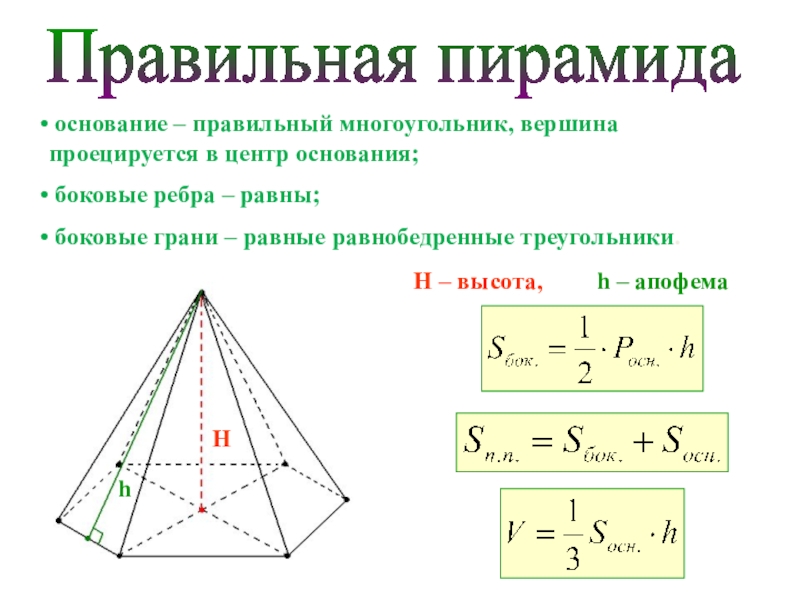 Найдите объём призмы. 10) Найдите площадь поверхности куба, диагональ которого равна . 11) Площадь диагонального сечения куба равна . Найдите ребро куба.
Найдите объём призмы. 10) Найдите площадь поверхности куба, диагональ которого равна . 11) Площадь диагонального сечения куба равна . Найдите ребро куба.12) Сумма длин всех ребер куба равна 48. Чему равна площадь всех его граней?
13) Если ребро куба уменьшить на 10%, на сколько процентов уменьшится его объем?
14) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Расстояние от плоскости сечения до вершины нижнего основания, не лежащей в плоскости сечения, равно 5см. Площадь сечения равна 10см2. Найти объём параллелепипеда.
15) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Объём меньшего из двух многогранников, на которые параллелепипед делится плоскостью сечения, равен 40см3. Найдите объём параллелепипеда.
16) Стороны основания прямоугольного параллелепипеда 6м и 8м, а угол между диагональю параллелепипеда и плоскостью основания 300. Найдите диагональ параллелепипеда.
Найдите диагональ параллелепипеда.
17) Стороны основания прямоугольного параллелепипеда равны 4м и 3м, а угол между диагональю параллелепипеда и плоскостью основания 450. Найдите длину диагонали параллелепипеда.
18) Сторона основания правильной треугольной призмы ABCDA1B1C1D1 равна 12, а боковое ребро . Найдите градусную меру угла между плоскостями A1BC и ABC. 19) ABCDA1B1C1D1 – призма, в основании которой лежит квадрат, боковые ребра которой наклонены к плоскости основания под углом 300. Диагональ AD1 перпендикулярна плоскости основания. Площадь боковой поверхности призмы равна . Найдите объем призмы. 20) В основании прямой призмы ABCDA1B1C1D1 лежит квадрат. Боковое ребро равно . Найдите длину стороны основания, если угол между плоскостью AB1C и плоскостью основания призмы равен 300.
21) Ребра треугольной пирамиды длины 4, 5 и 9 взаимно перпендикулярны. Чему равен объем пирамиды?
22) Пирамида имеет 28 ребер. Сколько у нее граней?
23) Высота правильной треугольной пирамиды равна 15, а высота ее основания 12. Найдите длину бокового ребра.
24) Высота правильной треугольной пирамиды в два раза меньше стороны основания. Найдите угол между боковой гранью пирамиды и плоскостью основания.
25) Сторона основания правильной треугольной пирамиды равна 10 см. Боковые грани наклонены к плоскости основания под углом 450. Найдите высоту пирамиды.
26) Боковое ребро правильной треугольной пирамиды равно 10, а периметр основания 36. Найдите высоту пирамиды.
27) В правильной четырёхугольной пирамиде высота равна 3см, а площадь боковой поверхности 80см2. Найти объём пирамиды.
28) Боковые грани правильной четырёхугольной пирамиды наклонены к плоскости основания под углом 600. Площадь основания равна 14м2. Найти площадь боковой поверхности пирамиды.
Найти площадь боковой поверхности пирамиды.
29) В правильной четырёхугольной пирамиде боковое ребро образует с плоскостью основания угол 600. Сторона основания пирамиды равна 6см. Найдите объём пирамиды.
30) В правильной четырёхугольной пирамиде апофема образует с плоскостью основания угол 600. Высота пирамиды равна 8см. Найдите площадь поверхности пирамиды.
31) В правильной треугольной пирамиде высота равна , а величина двугранного угла при основании 600. Найдите сторону основания пирамиды.32) В правильной треугольной пирамиде высота равна 4, а апофема равна 5. Найдите сторону основания пирамиды.
33) Высота треугольной пирамиды SABC равна 8, а площадь треугольника ABC 12. Точки A1, B1, C1 делят ребра SA, SB и SC в отношении 1 : 1. Найдите объем усеченной пирамиды ABCA1B1C1.
34) В основании пирамиды SABC лежит прямоугольный треугольник ABC с катетами AC=4 и BC=3.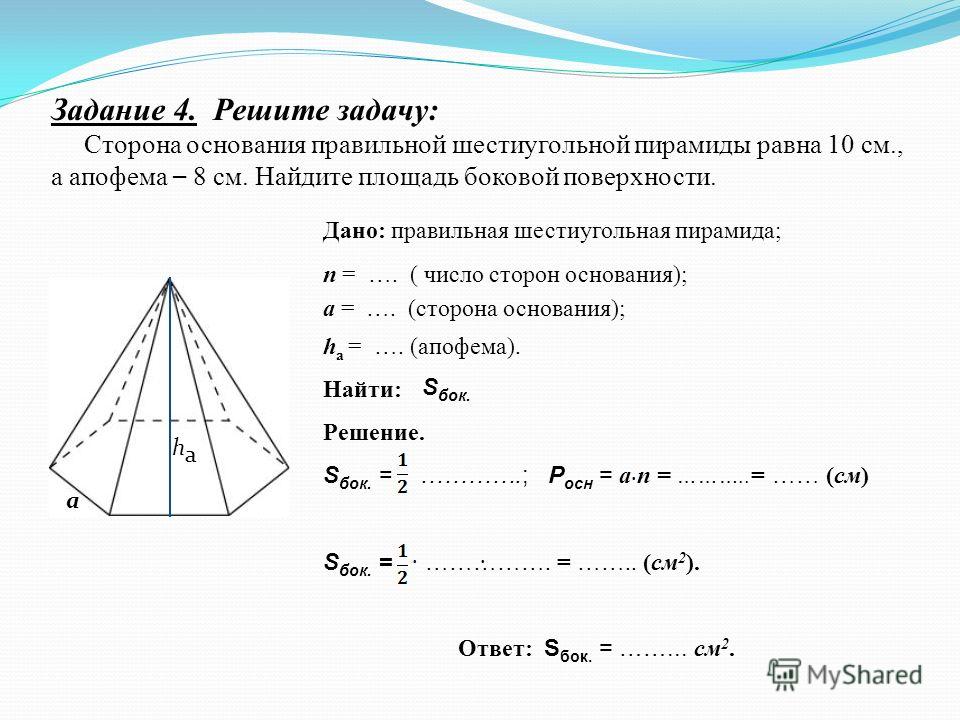 Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
35) Найдите площадь боковой поверхности цилиндра, если площадь его осевого сечения равна 12.
36) Площадь основания цилиндра равна 4, а площадь его боковой поверхности равна . Найдите высоту цилиндра. 37) Высота и радиус основания цилиндра равны, соответственно, 9 и 6. Концы отрезка AB длины лежат на окружностях верхнего и нижнего оснований. Найдите расстояние от оси цилиндра до отрезка AB.38) Радиус основания конуса равен 6, а образующая составляет с плоскостью основания угол, равный 300. Найдите расстояние от центра основания до образующей.
39) Образующая конуса равна диаметру его основания. Найдите площадь боковой поверхности конуса, если его высота равна .40) Площадь осевого сечения конуса равна 8, а радиус основания 2. Найдите площадь боковой поверхности конуса.
41) Осевое сечение конуса – правильный треугольник со стороной .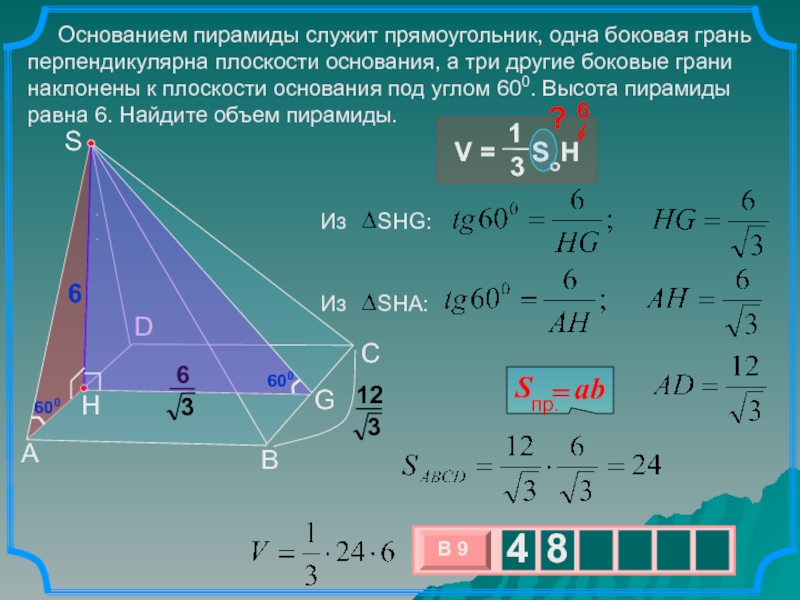 Найдите полную поверхность конуса.
Найдите полную поверхность конуса.42) Из точки M вне шара проведена касательная AM к его поверхности. Кратчайшее расстояние от этой точки до поверхности шара равно 6, а до центра шара 15. Найдите длину AM.
43) Если радиус сферы увеличить на 50%, на сколько процентов увеличится площадь ее поверхности?
44) Радиус шара равен . Через конец радиуса под углом 600 к нему проведена плоскость. Найти площадь сечения шара плоскостью.45) Стороны треугольника, равные 10, 10 и 12 касаются поверхности шара Найдите радиус шара, если расстояние от центра шара до плоскости треугольника равно 4.
46) Как относятся объемы куба и описанного около него шара?
47) В шар объема вписан конус, таким образом, что основанием конуса является осевое сечение шара. Найдите площадь осевого сечения конуса.Вычисление площади боковой поверхности пирамиды. Площадь боковой поверхности правильной четырехугольной пирамиды: формулы и примеры задач
– это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.
Если в основании лежит квадрат, то пирамиду называется четырехугольной , если треугольник – то треугольной . Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана пирамида с основанием ABCDE
и вершиной F
. AB
=BC
=CD
=DE
=EA
=3 см. Апофема a
= 5 см. Найти площадь боковой поверхности пирамиды.
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды:
Площадь правильной треугольной пирамиды
Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.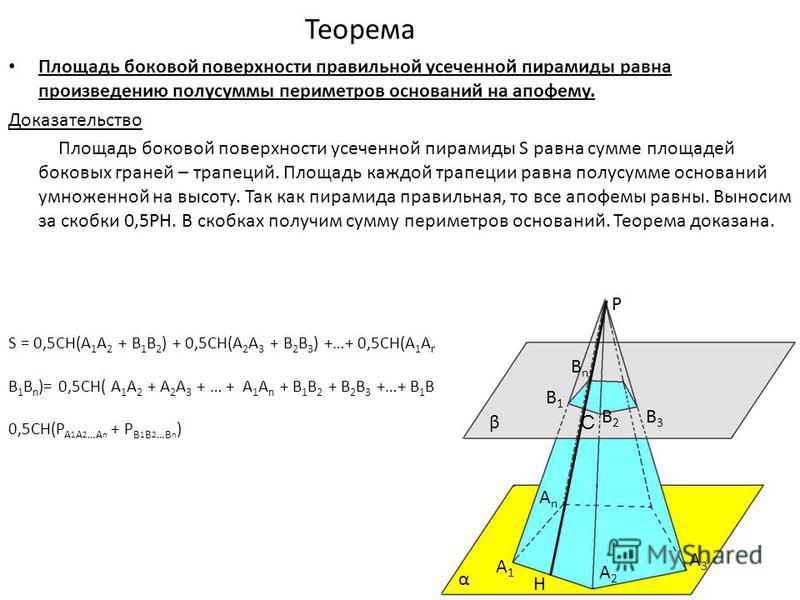
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.
Дана пирамида с апофемой a
= 4 см и гранью основания b
= 2 см. Найдите площадь боковой поверхности пирамиды.
Для начала находим площадь одной из боковых граней. В данном случае она будет:
Подставляем значения в формулу:
Так как в правильной пирамиде все боковые стороны одинаковы, то площадь боковой поверхности пирамиды будет равна сумме площадей трех граней. Соответственно:
Площадь усеченной пирамиды
Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.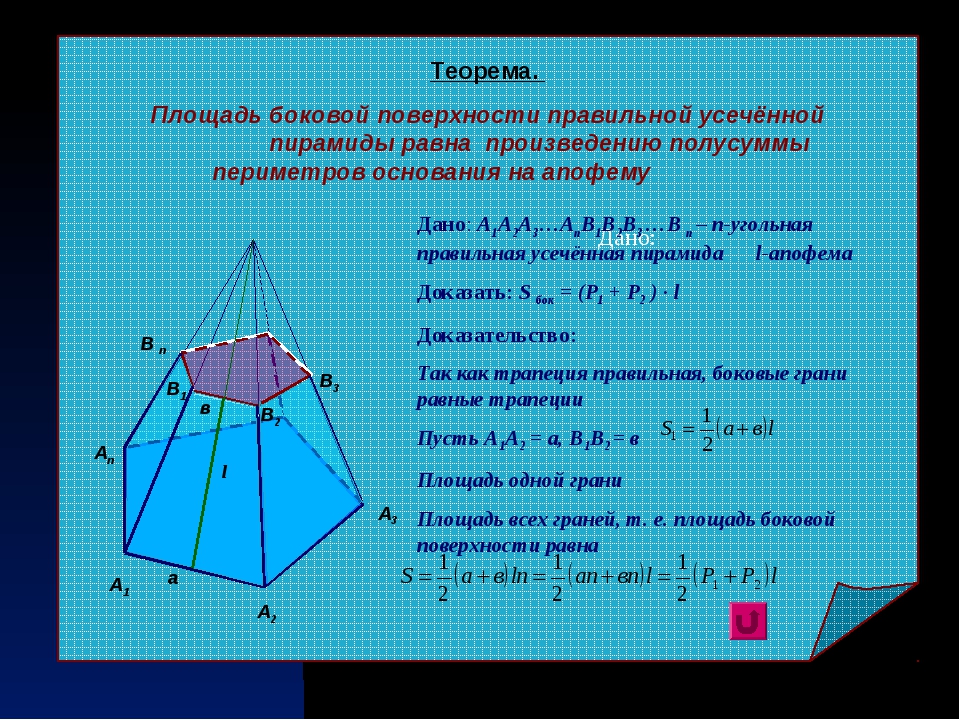
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:
Пирамида — одна из разновидностей многогранника, образованного из многоугольников и треугольников, которые лежат в основании и являются его гранями.
Причем на вершине пирамиды (т.е. в одной точке) все грани объединяются.
Для того чтобы вычислить площадь пирамиды, стоит определить, что ее боковая поверхность состоит из нескольких треугольников. А их площади мы сможем легко найти, применяя
различные формулы. В зависимости от того, какие данные треугольников нам известны, мы ищем их площадь.
Перечислим некоторые формулы, с помощью которых можно найти площадь треугольников:
- S = (a*h)/2 . В данном случае нам известна высота треугольника h , которая опущена на сторону a .
- S = a*b*sinβ . Здесь стороны треугольника a , b , а угол между ними — β .

- S = (r*(a + b + c))/2 . Здесь стороны треугольника a, b, c . Радиус окружности, которая вписана в треугольник — r .
- S = (a*b*c)/4*R . Радиус, описанной окружности вокруг треугольника — R .
- S = (a*b)/2 = r² + 2*r*R . Данную формулу нужно применять только в том случае, когда треугольник является прямоугольным.
- S = (a²*√3)/4 . Эту формулу применяем к равностороннему треугольнику.
Лишь после того, как рассчитаем площади всех треугольников, которые являются гранями нашей пирамиды, можно вычислить площадь ее боковой поверхности. Для этого будем использовать выше перечисленные формулы.
Для того чтобы вычислить площадь боковой поверхности пирамиды, никаких сложностей не возникает: нужно узнать сумму площадей всех треугольников. Выразим это формулой:
Sп = ΣSi
Здесь Si является площадью первого треугольника, а S п —
площадь боковой поверхности пирамиды.
Рассмотрим на примере. Дана правильная пирамида, ее боковые грани образованы несколькими равносторонними треугольниками,
«Геометрия является самым могущественным средством для изощрения наших умственных способностей ».
Галилео Галилей.
а квадрат является основанием пирамиды. Причем ребро пирамиды имеет длину 17 см. Найдем площадь боковой поверхности данной пирамиды.
Рассуждаем так: нам известно, что гранями пирамиды являются треугольники, они равносторонние. Также нам известно, какова длина ребра у данной пирамиды. Отсюда выходит, что все треугольники имеют равные боковые стороны, их длина 17 см.
Для вычисления площади каждого из данных треугольников, можно использовать такую формулу:
S = (17²*√3)/4 = (289*1.732)/4 = 125.137 см²
Так, как мы знаем, что квадрат лежит в основании пирамиды, то выходит, что мы имеем четыре равносторонних треугольника. А это значит, что площадь боковой поверхности пирамиды легко рассчитать по следующей формуле: 125. 137 см² * 4 = 500.548 см²
137 см² * 4 = 500.548 см²
Наш ответ следующий: 500.548 см² — такова площадь боковой поверхности данной пирамиды.
– это фигура, в основании которой лежит произвольный многоугольник, а боковые грани представлены треугольниками. Их вершины лежат в одной точке и соответствуют вершине пирамиды.
Пирамида может быть разнообразной – треугольной, четырехугольной, шестиугольной и т.д. Ее название можно определить в зависимости от количества углов, прилегающих к основанию.
Правильной пирамидой называется пирамида, в которой равны стороны основания, углы, и ребра. Также в такой пирамиде будет равна площадь боковых граней.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей всех ее граней:
То есть, чтобы рассчитать площадь боковой поверхности произвольной пирамиды, необходимо найти площадь каждого отдельного треугольника и сложить их между собой. Если пирамида усеченная, то ее грани представлены трапециями. Для правильной пирамиды существует другая формула. В ней площадь боковой поверхности рассчитывается через полупериметр основания и длину апофемы:
В ней площадь боковой поверхности рассчитывается через полупериметр основания и длину апофемы:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана правильная четырехугольная пирамида. Сторона основания b = 6 см, а апофема a = 8 см. Найдите площадь боковой поверхности.
В основании правильной четырехугольной пирамиды лежит квадрат. Для начала найдем его периметр:
Теперь можем просчитать площадь боковой поверхности нашей пирамиды:
Для того чтобы найти полную площадь многогранника, потребуется найти площадь его основания. Формула площади основания пирамиды может отличаться, в зависимости от того, какой многоугольник лежит в основании. Для этого используются формулы площади треугольника, площади параллелограмма и т.д.
Рассмотри пример расчета площади основания пирамиды, заданной нашими условиями. Так как пирамида правильная, в ее основании лежит квадрат.
Площадь квадрата рассчитывается по формуле: ,
где a – сторона квадрата. У нас она равна 6 см. Значит площадь основания пирамиды:
У нас она равна 6 см. Значит площадь основания пирамиды:
Теперь остается только найти полную площадь многогранника. Формула площади пирамиды состоит из суммы площади ее основания и боковой поверхности.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Перед изучением вопросов о данной геометрической фигуре и её свойствах, следует разобраться в некоторых терминах. Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.
Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.
Виды фигуры
Пирамида – геометрическая фигура , обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:
- правильная;
- усечённая.
В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.
Во втором случае, оснований два — большое в самом низу и малое между вершиной, повторяющее форму основного. Иными словами – усечённая пирамида представляет собой многогранник с сечением, образованным параллельно основанию.
Термины и обозначения
Основные термины:
- Правильный (равносторонний) треугольник – фигура с тремя одинаковыми углами и равными сторонами.
 В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.
В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой. - Вершина – самая верхняя точка, где сходятся грани. Высота вершины образуется прямой линией, исходящей от вершины к основанию пирамиды.
- Грань – одна из плоскостей многоугольника. Она может быть в виде треугольника в случае с треугольной пирамидой либо в виде трапеции для усечённой пирамиды.
- Сечение – плоская фигура, образующаяся в результате рассечения. Не стоит путать с разрезом, так как разрез показывает и то, что находится за сечением.
- Апофема – отрезок, проведённый из вершины пирамиды к её основанию. Он также является высотой той грани, где находится вторая точка высоты. Данное определение справедливо лишь по отношению к правильному многограннику.
 К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
Формулы площади
Находить площадь боковой поверхности пирамиды любого типа можно несколькими способами. Если фигура не симметричная и представляет собой многоугольник с разными сторонами, то в данном случае легче вычислить общую площадь поверхности через совокупность всех поверхностей. Иными словами – надо посчитать площадь каждой грани и сложить их вместе.
В зависимости от того, какие параметры известны, могут потребоваться формулы вычисления квадрата, трапеции, произвольного четырёхугольника и т.д. Сами формулы в разных случаях тоже будут иметь отличия.
В случае с правильной фигурой находить площадь намного проще. Достаточно знать всего несколько ключевых параметров. В большинстве случаев требуются вычисления именно для таких фигур. Поэтому далее будут приведены соответствующие формулы.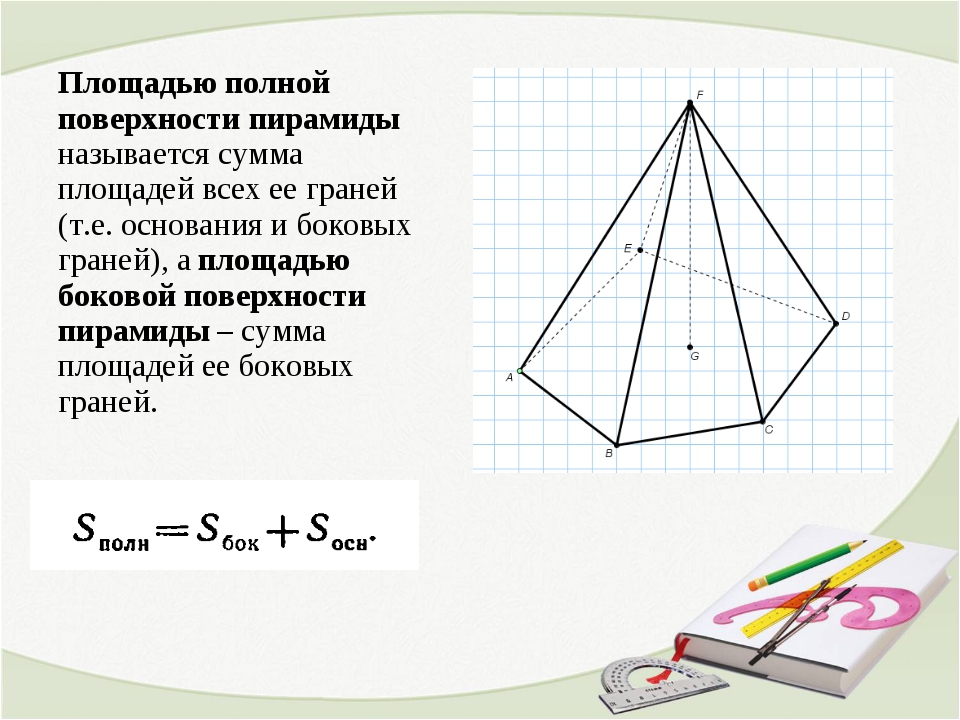 В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.
В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.
Основная формула для вычисления площади боковой поверхности правильной пирамиды будет иметь следующий вид:
S=½ Pa (P – периметр основания, а – апофема)
Рассмотрим один из примеров. Многогранник имеет основание с отрезками A1, А2, А3, А4, А5, и все они равны 10 см. Апофема пусть будет равна 5 см. Для начала надо найти периметр. Так как все пять граней основания одинаковые, можно находить так: Р=5*10=50 см. Далее применяем основную формулу: S =½*50*5=125 см в квадрате.
Площадь боковой поверхности правильной треугольной пирамиды вычислить легче всего. Формула имеет следующий вид:
S =½* ab *3, где а – апофема, b – грань основания. Множитель тройки здесь означает количество граней основания, а первая часть – площадь боковой поверхности. Рассмотрим пример. Дана фигура с апофемой 5 см и гранью основания 8 см. Вычисляем: S =1/2*5*8*3=60 см в квадрате.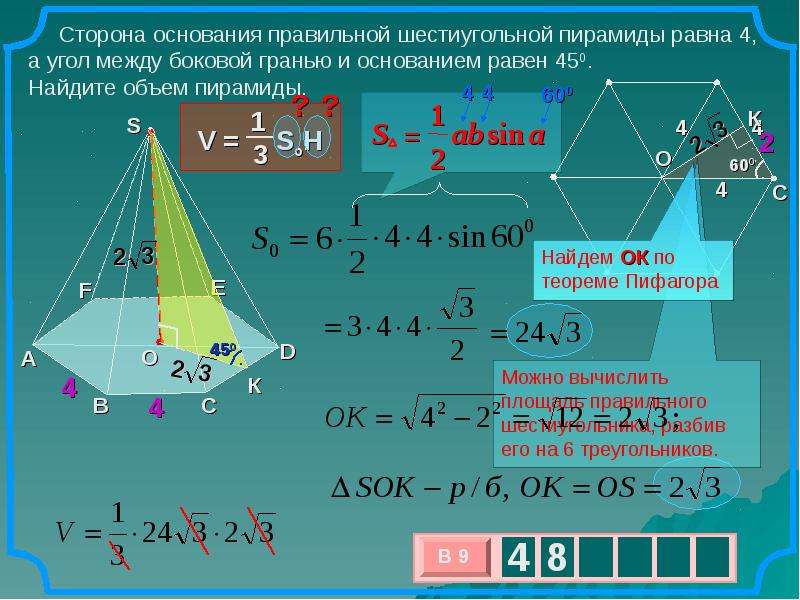
Площадь боковой поверхности усечённой пирамиды вычислять немного сложнее. Формула выглядит так: S =1/2*(p _01+ p _02)*a , где р_01 и р_02 являются периметрами оснований, а – апофема. Рассмотрим пример. Допустим, для четырёхугольной фигуры даны размеры сторон оснований 3 и 6 см, апофема равна 4 см.
Тут для начала следует найти периметры оснований: р_01 =3*4=12 см; р_02=6*4=24 см. Осталось подставить значения в основную формулу и получим: S =1/2*(12+24)*4=0,5*36*4=72 см в квадрате.
Таким образом, можно найти площадь боковой поверхности правильной пирамиды любой сложности. Следует быть внимательным и не путать эти вычисления с полной площадью всего многогранника. А если это всё же понадобится сделать – достаточно вычислить площадь самого большого основания многогранника и прибавить её к площади боковой поверхности многогранника.
Видео
Закрепить информацию о том, как найти площадь боковой поверхности разных пирамид, вам поможет это видео.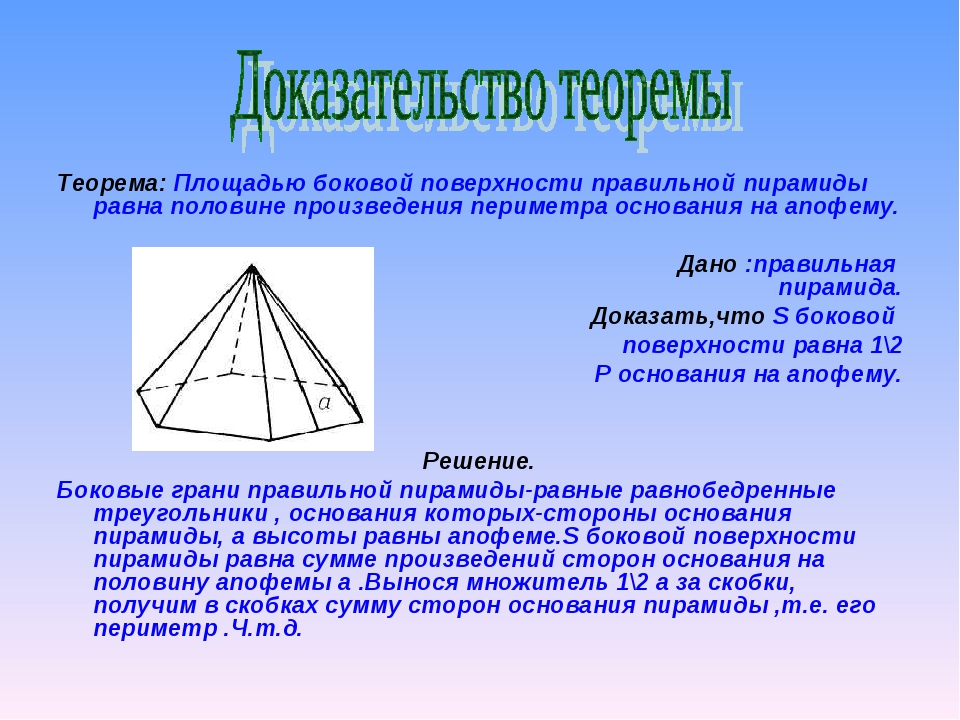
Площадь поверхности пирамиды
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), можете посмотреть.
В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами.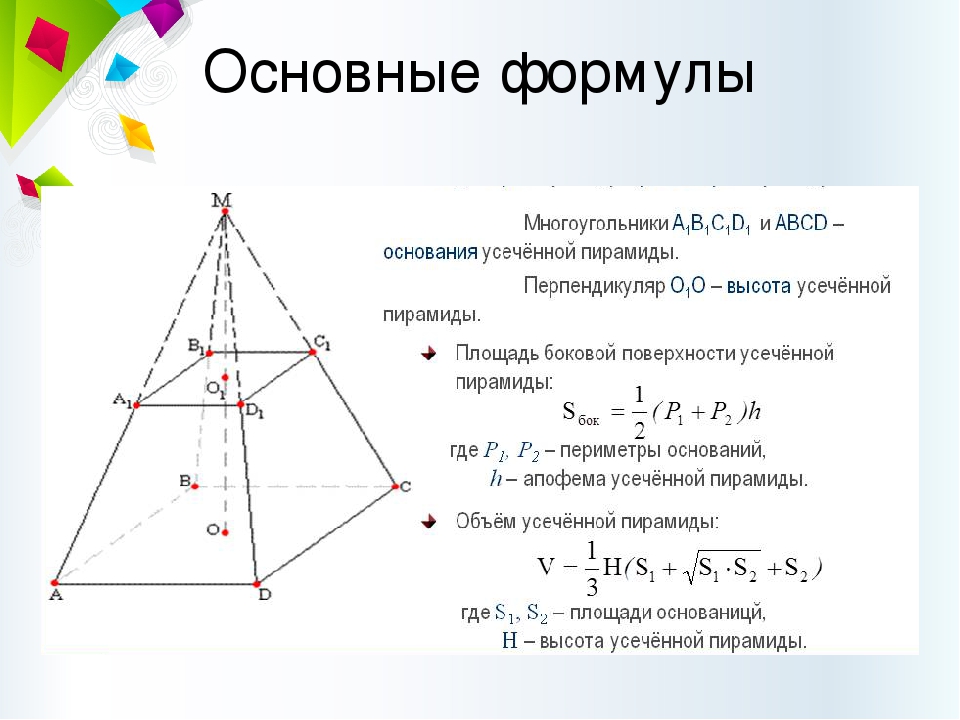 Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона:
Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:
Таким образом, площадь боковой поверхности равна:
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):
Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
Значит площадь боковой поверхности пирамиды равна:
Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Посмотреть решение
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Посмотреть решение
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
где φ — двугранный угол при основании
Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:
Еще одна формула боковой поверхности правильной пирамиды:
P — периметр основания, l — апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Площадь поверхности пирамиды | Мозган калькулятор онлайн
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте площадь основания и апофему.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Боковая поверхность через периметр и апофемуАпофема – опущенный перпендикуляр из вершины на ребро основания.
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p — периметр основания пирамиды; l — апофема пирамиды. 2)»/> a — сторона основания.
2)»/> a — сторона основания.Объём правильной пирамиды
Нахождение высоты пирамиды
Как найти высоту пирамиды? Очень просто! Для нахождения высоты любой треугольной пирамиды можно воспользоваться формулой объема: V = (1/3)Sh, где S — это площадь основания, V — объем пирамиды, h — ее высота. Из этой формулы вывести формулу высоты: для нахождения высоты треугольной пирамиды, нужно умножить объем пирамиды на 3, а потом поделить получившееся значение на площадь основания, это будет: h = (3V)/S. Поскольку основание треугольной пирамиды — это треугольник, можно воспользоваться формулой подсчета площади треугольника. Если нам известны: площадь треугольника S и его сторона z, то по формуле площади S=(1/2)γh: h = (2S)/γ, где h — это высота пирамиды, γ — это ребро треугольника; угол между сторонами треугольника и сами две стороны, то по такой формуле: S = (1/2)γφsinQ, где γ, φ — это стороны треугольника, находим площадь треугольника. Значение синуса угла Q нужно посмотреть в таблице синусов, которая есть в Интернете. Далее подставляем значение площади в формулу высоты: h = (2S)/γ. Если в задании требуется вычислить высоту треугольной пирамиды, то объем пирамиды уже известен.
Далее подставляем значение площади в формулу высоты: h = (2S)/γ. Если в задании требуется вычислить высоту треугольной пирамиды, то объем пирамиды уже известен.
Формулы объема треугольной пирамиды
Определить объем совершенно любой пирамиды с произвольным n-угольником в основании можно с помощью следующего выражения:
V = 1/3 × So × h
Здесь символ So обозначает площадь основания, h — это высота фигуры, проведенная к отмеченному основанию из вершины пирамиды.
Поскольку площадь произвольного треугольника равна половине произведения длины его стороны a на апофему ha, опущенную на эту сторону, то формула объема треугольной пирамиды может быть записана в следующем виде:
V = 1/6 × a × ha × h
Для треугольной пирамиды общего типа определение высоты является непростой задачей. Для ее решения проще всего воспользоваться формулой расстояния между точкой (вершиной) и плоскостью (треугольным основанием), представленной уравнением общего вида.
Для правильной пирамиды формула объема имеет конкретный вид. Площадь основания (равностороннего треугольника) для нее равна:
Площадь основания (равностороннего треугольника) для нее равна:
So = √3/4 × a2
Подставляем ее в общее выражение для V, получаем:
V = √3/12 × a2 × h
Частным случаем является ситуация, когда у тетраэдра все стороны оказываются одинаковыми равносторонними треугольниками. В этом случае определить его объем можно, только исходя из знания параметра его ребра a. Соответствующее выражение имеет вид:
V = √2/12 × a3
Теория
Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019
Для решения задач понадобится знать теоремы равнобедренного треугольника:
Равнобедренный треугольник
Основные свойства
1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.
2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.
Пирамида
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.
Четырехугольная пирамида
Треугольная пирамида
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
Треугольная пирамида
Необходимые знания для нахождения высоты
1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).
2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.
3Что такое правильные многоугольники: виды, свойства, формулы.
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
Формулы
Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:
Объем пирамиды
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида
Треугольная пирамида
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Ответ: 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Ответ: 6
Четырехугольная пирамида
Четырехугольная пирамида
Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
OL = ½*12 = 6
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
MO = 8
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.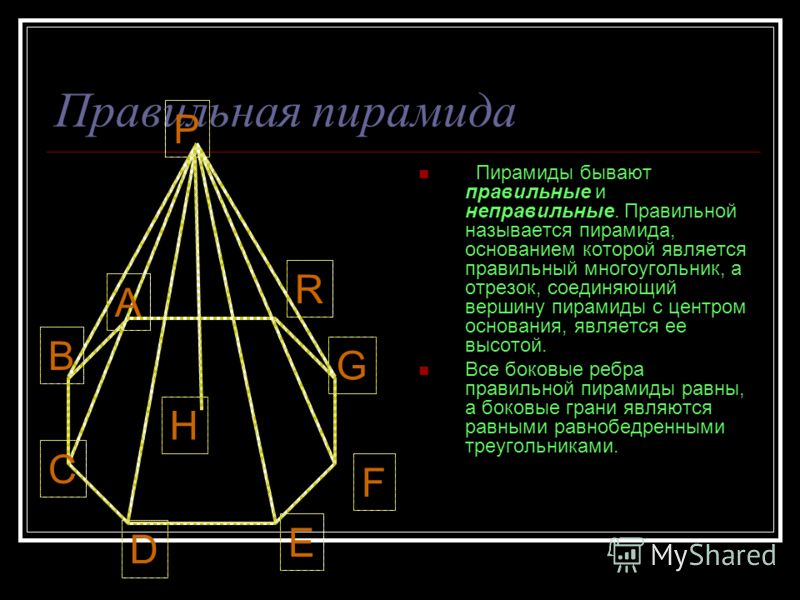
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Ответ: 36
Задача 4
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема.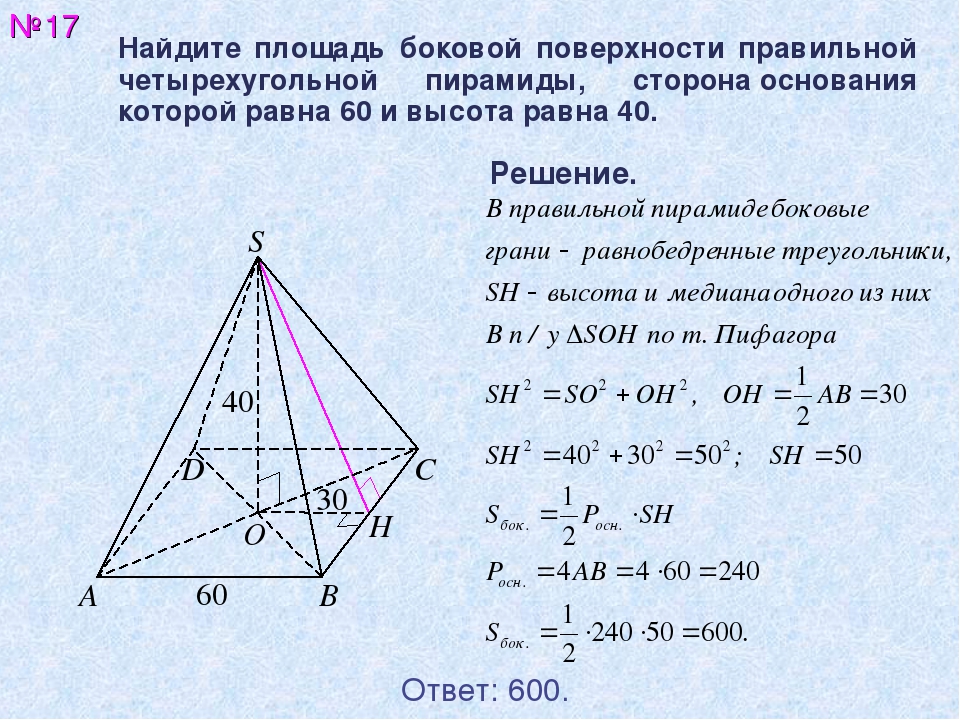 Пользуясь формулами, найдем высоту.
Пользуясь формулами, найдем высоту.
Площадь равнобедренного треугольника
36 = ½ * 4 *h
36 = 2h
H = 18
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Ответ: 12
Правильная усеченная пирамида
Если провести сечение, параллельное основанию пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Это сечение для усеченной пирамиды является одним из её оснований.
Высота боковой грани (которая является равнобокой трапецией), называется — апофема правильной усеченной пирамиды.
Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная.
- Расстояние между основаниями усеченной пирамиды называется высотой усеченной пирамиды
- Все грани правильной усеченной пирамиды являются равнобокими (равнобедренными) трапециями
Примечания
См. также: частные случаи (формулы) для правильной пирамиды:
также: частные случаи (формулы) для правильной пирамиды:
Для правильной треугольной пирамиды
Как воспользоваться приведенными здесь теоретическими материалами для решения своей задачи:
- Ознакомьтесь со справочными материалами
- Выясните, по условию задачи, о какой именно правильной пирамиде идет речь
- После этого в дереве знаний справа, найдите подходящий урок с данной фигурой (см. решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там
- Если Вы просмотрели весь раздел, но аналогичной задачи не нашлось, напишите о своей проблеме на форуме «раздел для школьников» в соответствующей теме. Обязательно ознакомьтесь предварительно с правилами форума.
Содержание главы:
Апофема правильной пирамиды
Объем правильной усеченной пирамиды
Правильная пирамида с четырехугольником в основании
Правильная пирамида с четырехугольником в основании
Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
Правильная пирамида с четырехугольником в основании (часть 3)
Нахождение углов пирамиды
Нахождение величины наклона боковых граней правильной прамиды
Нахождение расстояний в правильной четырехугольной пирамиде
Пирамида и вписанный конусОписание курса Апофема правильной пирамиды
Призма, формула вычисления объёма призмы
Призма – это многогранник, основаниями которого являются равные многоугольники, а боковыми гранями – параллелограммы.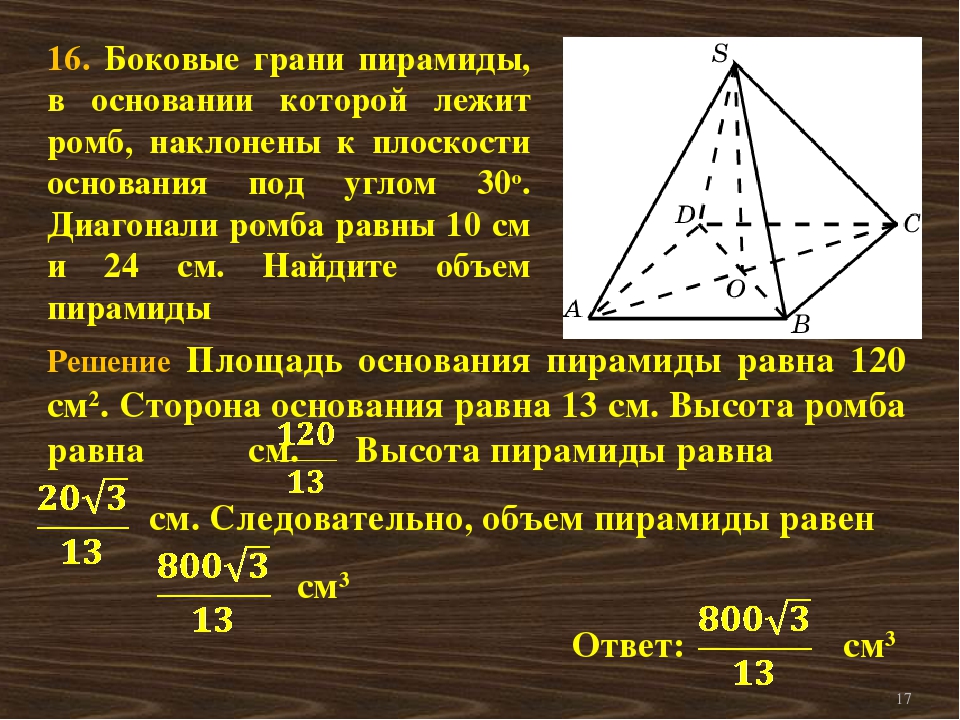
На рисунке 2 изображена наклонная призма. Многогранники и в основаниях лежат в параллельных плоскостях, равны и расположены так, что боковые рёбра () между собой параллельны.
Рис. 2. Наклонная призма
Формула для вычисления объёма призмы:
, где S – площадь основания ( или ), h – высота между основаниями, которая получается при опускании перпендикуляра из любой точки основания на плоскость, в которой лежит другое основание этой призмы ().
Если мы рассмотрим пирамиду , то её объём будет равен:
, где V – объём призмы
Часто задаваемые вопросы
1Как понять, что пирамида правильная, если в условии это не указано?
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
2Могут ли быть указаны в задании лишние данные?
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой
Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении
4Как можно быстро изучить стереометрию?
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
4Как искать высоту, если известен объем?
Если выразить высоту через формулу объема, то получится следующее:
H = (3*V)/ S;
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
H = 3*70/30 = 7см
Усеченная пирамида
Если верхнюю часть, содержащую вершину, отсечь у правильной треугольной пирамиды, то получится усеченная фигура. В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.
В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.
Ниже на фото показано, как выглядит правильная усеченная пирамида треугольная, изготовленная из бумаги.
Для определения объема треугольной пирамиды усеченной необходимо знать три ее линейных характеристики: каждую из сторон оснований и высоту фигуры, равную расстоянию между верхним и нижним основаниями. Соответствующая формула для объема записывается так:
V = √3/12 × h × (A2 + a2 + A × a)
Здесь h — высота фигуры, A и a — длины сторон большого (нижнего) и малого (верхнего) равносторонних треугольников соответственно.
Что это — треугольная пирамида?
Каждый слышал о древних египетских пирамидах, тем не менее они являются четырехугольными правильными, а не треугольными. Объясним, как получить треугольную пирамиду.
Возьмем произвольный треугольник и соединим все его вершины с некоторой одной точкой, расположенной вне плоскости этого треугольника.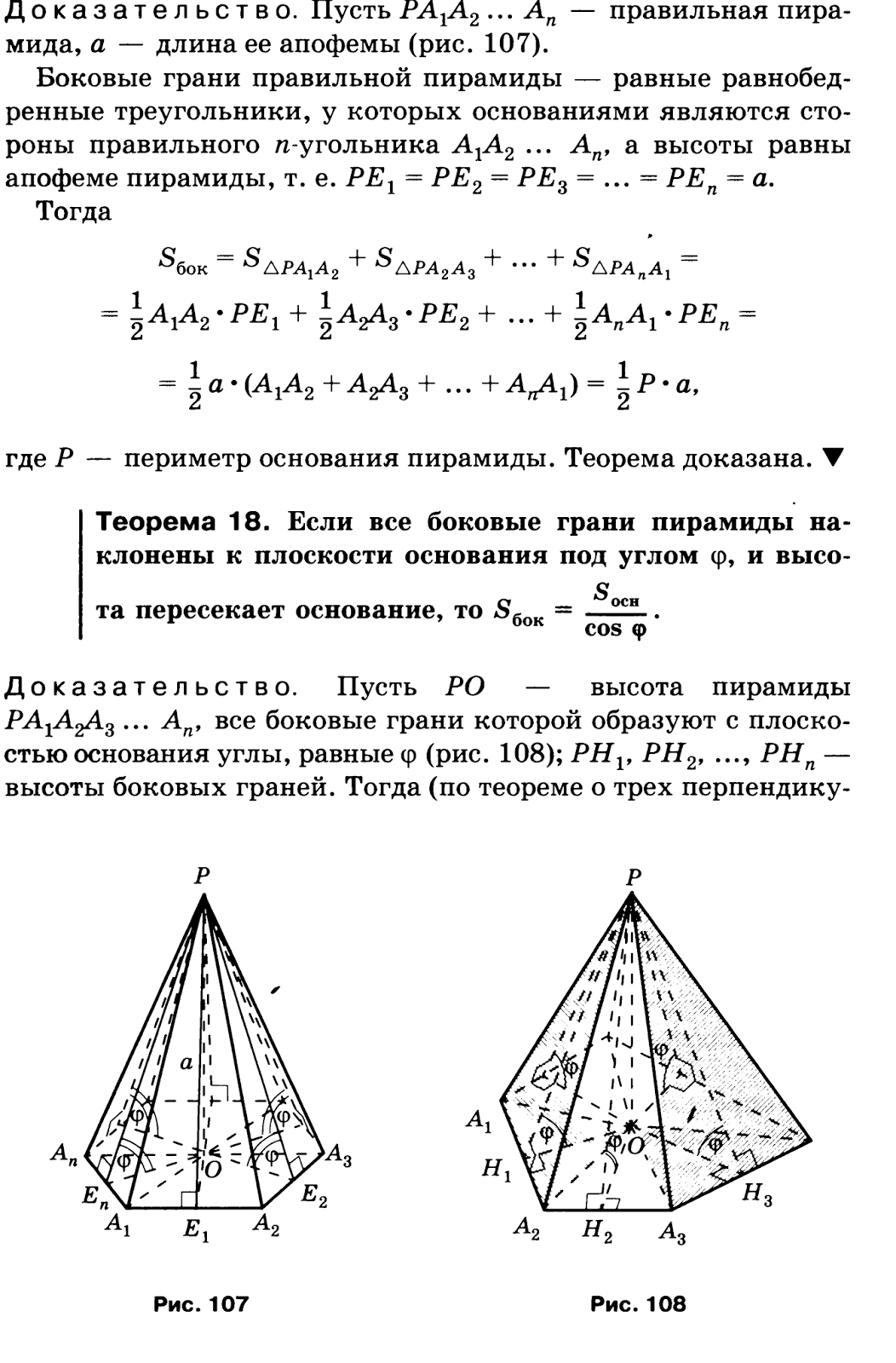 Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.
Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.
Вам будет интересно:Как мыться в русской печи: описание обычая, исторические факты
Как видно, рассматриваемая фигура образована четырьмя треугольниками, которые в общем случае являются разными. Каждый треугольник — это стороны пирамиды или ее грань. Эту пирамиду часто называют тетраэдром, то есть четырехгранной объемной фигурой.
Помимо сторон, пирамида также обладает ребрами (их у нее 6) и вершинами (их 4).
Типичные ошибки на ЕГЭ
Незнание темы Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.
Отсутствие проверки Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.
Задачи под копирку Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.
Запись Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.
Обидно получать низкий балл из-за невнимательности.
Подсчеты в уме На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается
Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.
Незнание структуры экзамена Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно
Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.
Поспешные решения В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Незнание степеней числа В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!
Усеченная правильная пирамида
Усеченная правильная пирамида
Любая усеченная пирамида является многогранником, образованным пирамидой и её сечением, параллельным основанию.
Теорема о боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полу суммы периметров на апофему.
Площадь одной боковой грани усеченной пирамиды есть площадь трапеции (рис. 5)
5)
Рис. 5
А площадь всей боковой поверхности
Выводы:
Мы рассмотрели правильную пирамиду и стандартные задачи на нее, включая двугранные углы. А также усеченную правильную пирамиду.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Домашнее задание
- Какое наименьшее число ребер может иметь пирамида?
- Сколько ребер у n-угольной усеченной пирамиды?
- На Рис.
 4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC.
4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC. - В правильной четырехугольной пирамиде SABCD (точка O – центр основания, S – вершина) боковое ребро SB=13, а диагональ основания AC =24. Найдите длину отрезка SO.
- В правильной треугольной пирамиде SABC точка L – середина ребра AC, S – вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Я Класс (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Интернет-портал Slideshare.net (Источник).
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.

- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
6.5 Общий Балл
Найти высоту в пирамиде
Достоверность информации
8.5
Актуальность информации
7.5
Раскрытие темы
8.5
Доступность применения
7
Удобство
8
Плюсы
Благодаря доступной информации можно легко научиться решать задачи по геометрии
Минусы
Необходимы знания математики
|
Элементы правильной пирамиды
- Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
- Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
- Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
- Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
- Диагональное сечение пирамиды — это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
- Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)
Если в основании правильной пирамиды лежит треугольник, четырехугольник и т. д. то она называется правильной треугольной, четырехугольной и т.д.
д. то она называется правильной треугольной, четырехугольной и т.д.
Треугольная пирамида есть четырехгранник — тетраэдр.
Подведение итогов урока
На данном уроке мы повторили формулы расчёта объёмов призмы и пирамиды. Решили задачи с использованием этих формул.
Список литературы
- Геометрия: учеб. для 10–11 кл. для общеобразовательных учреждений: базовый и профильный уровни /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: «Просвещение», 2008.
- Задачи по геометрии. Пособие для учащихся 7–11 кл. общеобразовательных учреждений /Б. Г. Зив, В. М. Мейлер. – М.: «Просвещение», 2003–2008.
- Геометрия. Задачи и упражнения на готовых чертежах. 10–11 кл. /Е. М. Рабинович – Харьков: «Гимназия», 2003, М.: «Илекса», 2003.
- Геометрия. 10 кл. Самостоятельные и контрольные работы. /А. И. Ершова, В. В. Голобородько – М.: «Илекса», 2008.
- Математика. ЕГЭ – 2011. Тематические тренировочные задания./В. В. Кочагин, М. Н. Кочагина – М.
 : «Эксмо», 2011.
: «Эксмо», 2011. - Математика. ЕГЭ – 2009 /Ф. Ф. Лысенко. – Ростов-на-Дону: «Легион», 2008.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Clck.ru (Источник).
- Clck.ru (Источник).
- Clck.ru (Источник).
Домашнее задание
- От треугольной призмы, объем которой равен 129, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
- Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 12. Найдите объем пирамиды.
- В прямом параллелепипеде диагонали и взаимно перпендикулярны и равны 6 см и 8 см, АВ = 3 см. Найдите объем параллелепипеда.
Площадь боковой поверхности правильной пирамиды
Просмотр содержимого документа
«Площадь боковой поверхности правильной пирамиды»
Робота с теоремой: «Площадь боковой поверхности правильной пирамиды»
Логико-математический анализ
٧ xє M (мно-во пирамид): А(х- является правильной пирамидой) = D(x)-площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Знания для актуализации:
правильная пирамида
апофема
боковая поверхность
площадь треугольника.
периметр основания
Цели в блоках достижений:
предметных результатов:
развитие пространственного представления об окружающем мире
получить вывод формулы площади боковой поверхности правильной пирамиды.
личностных результатов:
самопознание (выявление субъектного опыта)
формирование умения видеть в окружающих объектах математические объекты
развитие пространственного мышления
метапредметных результатов:
смысловое чтение
формирование логического УУД анализ
умение осознанно использовать речевые средства в соответствии с задачей коммуникации (ответы на вопросы, отчет о проделанном опыте, выводы)
умение оценивать правильность выполнения задания (самопроверка, взаимопроверка)
умение применить и преобразовать модели для решение учебных и поставленных задач
ХОД УРОКА
Диктант Слайд 1-3
Выпишите номер правильной пирамиды:
Выпишите апофему данной пирамиды:
Выпишите из чего состоит боковая поверхность пирамиды SABС.

Найдите площадь грани ASB, если АВ=6, SF=2
Найдите периметр основания правильной пирамиды SABС.
А сейчас проверьте себя Слайд 4.
Поднимите руку у кого нет ошибок? А кто совершил только одну ошибку?
Давайте обсудим каждое задание в отдельности, и какие ошибки вы могли совершить!
А сейчас представим, что мы с вами строительная фирма и к нам обратилось посольство Франции, для того чтобы мы застеклили пирамиду Лувра, причем она является правильной пирамидой:
Что нам необходимо знать для этого? (площадь боковой поверхности пирамиды).
А из чего состоит боковая поверхность правильной пирамиды? (Из равных треугольников)
Тогда чему будет равна площадь боковой поверхности пирамиды? (Сумме четырех равных площадей треугольников)
S= 4 ∙1/2∙а∙h
А чем является 4а для нашей пирамиды? (Периметр основания)
А что такое h для нашей пирамиды? (Апофема)
S=1/2∙P∙h
А это верно для всех правильных пирамид или нет?
Постарайтесь сформулировать теорему о боковой поверхности правильной пирамиды?
Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. (Если пирамида правильная, то площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему)
(Если пирамида правильная, то площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему)
Что нам с вами было дано?(Правильная пирамида)
А что надо доказать? (Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему).
Доказательство Слайд 5.
Что мы доказали? А если нам дана пирамида, то площадь ее боковой поверхности равна половине произведения периметра основания на апофему?
Задача: В правильной четырех угольной пирамиде сторона основания равна 5, а площадь боковой поверхности равна 20. Найдите апофему данной пирамиды.
Записываем, что дано, что надо найти, и делаем чертеж.
А затем приступаем к решению задачи № 244 на стр 72. Первым трем правильно решившим оценка в журнал.
Подводим итоги урока.
Д/з №245
Видео с вопросом: Определение периметра основания пирамиды с учетом ее объема и высоты
Стенограмма видеозаписи
Учитывая, что квадратная пирамида имеет объемом 372 кубических сантиметра и высотой 31 сантиметр определяют периметр его основания.
Нам не выдали схему здесь, но иногда может быть полезно сделать набросок. Во-первых, нам говорят, что это квадратная пирамида, поэтому мы будем знать, что длина и ширина будут точно такими же. измерение на базе.Нам дан объем пирамида составляет 372 кубических сантиметра, а высота перпендикуляра равна 31 сантиметры. Напомним, что объем пирамида равна одной трети площади основания, умноженной на перпендикуляр высота. Мы можем использовать тот факт, что мы учитывая объем пирамиды и ее высоту по перпендикуляру, чтобы найти площадь база. Это позволит нам тогда рассчитать периметр основания.
Можно подставить в значения тогда. Объем 372, высота 31, чтобы получить 372, равно одной трети площади основания, умноженной на 31. Умножая обе стороны на три, мы have 1116 равно площади основания, умноженной на 31. Затем мы делим обе стороны на 31, чтобы дайте нам площадь основания 36 квадратных сантиметров. Итак, как нам перейти от знания площадь основания этой пирамиды до ее периметра? Что ж, помните, что база — это квадратный.Итак, если мы определим длину одного сторона как 𝑙, тогда все остальные стороны будут иметь длину 𝑙. Площадь квадрата будет рассчитывается как 𝑙 в квадрате. В этом случае 𝑙 в квадрате должно иметь дает нам 36. Чтобы вычислить 𝑙, мы возьмем квадратный корень из обеих сторон, а квадратный корень из 36 равен шести. И, конечно же, единицы длины будет в сантиметрах.
Чтобы найти периметр, это расстояние по внешнему краю.Мы могли бы добавить шесть, шесть и шесть а шесть или более просто сложить шесть умножить на четыре, что даст нам значение 24. И поскольку периметр по-прежнему длина, то у нас будут сантиметры. Итак, мы обнаружили, что периметр основания этой пирамиды составляет 24 сантиметра, и мы сделали это, используя объем Сначала рассчитываем площадь основания.
Площадь поверхности пирамиды — объяснение и примеры
Прежде чем мы начнем, давайте рассмотрим, что такое пирамида.В геометрии пирамида — это трехмерное твердое тело, основание которого — любой многоугольник, а боковые грани — треугольники.
В пирамиде боковые грани (которые представляют собой треугольники) встречаются в общей точке, известной как вершина. Название пирамиды происходит от названия многоугольника, образующего ее основу. Например, квадратная пирамида, прямоугольная пирамида, треугольная пирамида, пятиугольная пирамида и т. Д.
Площадь поверхности пирамиды — это сумма площадей боковых граней.
В этой статье будет обсуждаться , как найти общую площадь поверхности и площадь боковой поверхности пирамиды .
Как найти площадь поверхности пирамиды?
Чтобы найти площадь поверхности пирамиды, вам нужно получить площадь основания, а затем добавить площадь боковых сторон, которая равна одной грани, умноженной на количество сторон.
Формула поверхности пирамиды
Общая формула для площади поверхности любой пирамиды (правильной или неправильной) задается как:
Площадь поверхности = площадь основания + боковая площадь
Площадь поверхности = B + LSA
Где TSA = общая площадь поверхности
B = площадь основания
LSA = площадь боковой поверхности.
Для правильной пирамиды формула имеет следующий вид:
Общая площадь поверхности правильной пирамиды = B + 1/2 ps
, где p = периметр основания и s = наклонная высота.
Примечание. Никогда не путайте наклонную высоту (ы) и высоту (h) пирамиды. Перпендикулярное расстояние от вершины до основания пирамиды называется высотой (h), а расстояние по диагонали от вершины пирамиды до края основания называется наклонной высотой (ями).
Площадь поверхности квадратной пирамиды
Для квадратной пирамиды общая площадь поверхности = b (b + 2s)
Где b = длина основания и s = наклонная высота
Площадь поверхности треугольной пирамиды
Площадь поверхности треугольной пирамиды = ½ b (a + 3s)
Где a = апофема длина пирамиды
b = длина основания
s = наклонная высота
Площадь пятиугольной пирамиды
Общая площадь правильной пятиугольной пирамиды равна;
Площадь поверхности пятиугольной пирамиды = 5⁄2 b (a + s)
Где a = апофема длина основания
и b = длина стороны основания, s = наклонная высота пирамиды
Площадь поверхности шестиугольной пирамиды
Гексагональная пирамида — это пирамида с шестиугольником в основании.
Общая площадь поверхности шестиугольной пирамиды = 3b (a + s)
Площадь боковой поверхности пирамиды
Как указано ранее, площадь боковой поверхности пирамиды — это площадь боковых граней пирамиды. Поскольку все боковые грани пирамиды представляют собой треугольники, площадь боковой поверхности пирамиды равна половине произведения периметра основания пирамиды и высоты наклона.
Площадь боковой поверхности (LSA = 1/2 ps)
Где p = периметр основания и s = наклонная высота.
Давайте разберемся с площадью поверхности формулы пирамиды, решив несколько примеров задач.
Пример 1
Какова площадь поверхности квадратной пирамиды, длина основания которой составляет 4 см, а высота наклона — 5 см?
Решение
Дано:
Базовая длина, b = 4 см
Наклонная высота, s = 5 см
По формуле
Общая площадь квадратной пирамиды = b (b + 2s)
TSA = 4 (4 + 2 x 5)
= 4 (4 + 10)
= 4 x 14
= 56 см 2
Пример 2
Какова площадь поверхности квадратная пирамида с перпендикулярной высотой 8 м и длиной основания 12 м?
Решение
Дано;
Высота по перпендикуляру, h = 8 м
Длина основания, b = 12
Чтобы получить наклонную высоту s, применим теорему Пифагора.
с = √ [8 2 + (12/2) 2 ]
с = √ [8 2 + 6 2 ]
с = √ (64 + 36)
с = √100
= 10
Следовательно, наклонная высота пирамиды составляет 10 м
Теперь вычислите площадь поверхности пирамиды.
SA = b (b + 2s)
= 12 (12 + 2 x 10)
= 12 (12 + 20)
= 12 x 32
= 384 м 2 .
Пример 3
Вычислите площадь поверхности пирамиды, наклонная высота которой составляет 10 футов, а ее основание представляет собой равносторонний треугольник с длиной стороны 8 футов.
Решение
Дано:
Базовая длина = 8 футов
Наклонная высота = 10 футов
Примените теорему Пифагора, чтобы получить длину апофемы пирамиды.
a = √ [8 2 — (8/2) 2 ]
= √ (64 — 16)
= √48
a = 6,93 фута
Таким образом, длина апофемы пирамиды составляет 6,93 фута
Но площадь поверхности треугольной пирамиды = ½ b (a + 3s)
TSA = ½ x 8 (6.93 + 3 x 10)
= 4 (6,93 + 30)
= 4 x 36,93
= 147,72 футов 2
Пример 4
Найдите площадь поверхности пятиугольной пирамиды, длина апофемы которой составляет 8 м, длина основания 6 м, высота уклона 20 м.
Решение
Дано;
Длина апофемы, a = 8 м
Длина основания, b = 6 м
Наклонная высота, s = 20 м
Площадь поверхности пятиугольной пирамиды = 5⁄2 b (a + s)
TSA = 5 / 2 x 6 (8 + 20)
= 15 x 28
= 420 м 2 .
Пример 5
Рассчитайте общую площадь поверхности и площадь боковой поверхности шестиугольной пирамиды с апофемой 20 м, длиной основания 18 м и наклонной высотой 35 м.
Решение
Дано;
апофема, a = 20 м
Длина основания, b = 18 м
Наклонная высота, s = 35 м
Площадь поверхности шестиугольной пирамиды = 3b (a + s)
= 3 x 18 ( 20 + 35)
= 54 x 55
= 2970 м 2 .
Площадь боковой поверхности пирамиды = 1/2 пс
Периметр, p = 6 x 18
= 108 м
LSA = ½ x 108 x 35
= 1890 м 2
Предыдущий урок | Главная страница | Следующий урокКалькулятор объема пирамиды
Определите объем любого пирамидального твердого тела с помощью нашего калькулятора объема пирамиды. Выберите один из двух вариантов: рассчитать объем пирамиды с обычным основанием, поэтому вам нужно указать только сторону, форму и высоту, или непосредственно ввести площадь основания и высоту пирамиды.Калькулятор не имеет проблем с определением объема тетраэдра или объема квадратной пирамиды. Если вы все еще не знаете, как пользоваться инструментом и как рассчитать объем пирамиды — продолжайте читать!
Формула объема пирамиды
Пирамида — это многогранник, образованный соединением многоугольного основания и вершины. Основная формула для объема пирамиды такая же, как для конуса:
-
объем = (1/3) * base_area * height, гдеheight— высота от основания до вершины.
Эта формула работает для любого типа базового многоугольника, а также для наклонных и прямых пирамид. Все, что вам нужно знать, это эти два значения — базовая площадь и высота. Однако есть и другие полезные формулы, если вы не знаете базовую площадь. Для любой пирамиды с правильным основанием можно использовать уравнение:
-
объем = (n / 12) * высота * длина стороны² * кроватка (π / n), гдеn— количество сторон основания правильного многоугольника
Как рассчитать объем пирамиды? Пример расчета объема квадратной пирамиды
Мы знаем формулу, а что дальше? Как использовать этот калькулятор объема пирамиды? Лучший способ продемонстрировать, как это работает, — самая известная пирамида в мире — пирамида Хеопса:
.- Выберите базовую форму .Для пирамиды Хеопса, также называемой пирамидой Хуфу, это квадрат. Конечно, это не идеальный квадрат, но можно предположить, что это так — разница в длине ребер меньше 1.
- Введите высоту пирамиды . Высота пирамиды Хуфу равна 146 м (вы можете изменить единицы измерения на метры, просто нажав на единицу измерения. Также вы можете ознакомиться с нашим конвертером объема).
- Определите длину стороны . Длина ребра пирамиды Хеопса в среднем 230.36 мес.
- Примерный объем квадратной пирамиды равен 2 582 532 м³.
Названия томов пирамид
Пирамида с n-сторонним основанием имеет:
- n + 1 грань (n-треугольник + 1 n-угольник)
- 2n ребра
- n + 1 вершина
Название пирамиды происходит от формы основания:
| Грани | Кромки | Вершины | Форма основания | Название пирамиды | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 4 | треугольник | 9040 8 треугольник | треугольник треугольниктреугольник | треугольник5 | квадрат | квадратная пирамида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 10 | 6 | пятиугольник | пятиугольная пирамида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 12 | шестигранник | 9040 814 | 8 | семиугольник | семиугольная пирамида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 16 | 9 | восьмиугольник | восьмиугольная пирамида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Введите длину апофемы = | |||
| Введите длину стороны = | |||
| Введите высоту наклона = | |||
| Введите высоту = | 040 | ||
| Площадь поверхности пирамиды = | |||
| Объем пирамиды = |
Площадь основания: [½as]
Площадь поверхности пирамиды: [½as + (3/2) sl]
Объем пирамиды: [(1/6) abh]
Правильная квадратная пирамида
| Введите длину стороны = | ||||||
| Введите высоту наклона = | ||||||
| Введите высоту = | ||||||
| Площадь основания = | Площадь пирамиды = | |||||
| Объем пирамиды = |
Площадь основания: [с²]
Площадь поверхности пирамиды: [с² + 2sl]
Объем пирамиды: [(1/3) b²h]
Правильная пятиугольная пирамида
| Введите длину апофемы = | |
| Введите длину стороны = | |
| Введите высоту наклона = | |
| Введите высоту | |
| Площадь поверхности пирамиды = | |
| Объем пирамиды = |
Площадь основания: [(5/2) as]
Площадь поверхности пирамиды: [(5/2) as + (5/2) sl]
Объем пирамиды: [(5 / 6) abh]
Правильная шестиугольная пирамида
| Введите длину апофемы = | |
| Введите длину стороны = | |
| Введите высоту наклона = | |
| Введите высоту | |
| Площадь поверхности пирамиды = | |
| Объем пирамиды = |
Площадь основания: [(6/2) as]
Площадь поверхности пирамиды: [3as + 3sl]
Объем пирамиды: [abh]
h = высота s = наклонная высота a = длина стороны V = объем B = Площадь базы T = Площадь пирамиды
Пирамиды имеют трехмерную (3-D) форму, основание которой представляет собой многоугольник, а каждый угол многоугольника прикреплен к единственной вершине, которая придает пирамидам отличительную форму.Вершина и каждое основание образуют треугольник.
Тип пирамиды
1. Треугольная пирамида2. Квадратная пирамида
3. Пятиугольная пирамида
4. Шестиугольная пирамида
5. Правая пирамида
6. Наклонная пирамида
7. Правильная пирамида
8. Неправильная пирамида
| Типы пирамид | База | Форма |
| Треугольная пирамида | Треугольник | |
| Квадратная пирамида | Квадрат | |
| Пятиугольная пирамида | Пентагон | |
| Шестиугольная пирамида | Шестиугольный | |
| Пирамида правая | Пирамидаимеет вершину над центром основания |
Треугольная пирамида: определение, формула и примеры — видео и стенограмма урока
Формула объема для треугольной пирамиды
Объем объекта — это сколько места внутри объекта, поэтому объем треугольной пирамиды — это сколько места внутри пирамиды.Объем треугольной пирамиды можно определить по формуле: V = 1/3 A H , где A = площадь основания треугольника, а H = высота пирамиды или расстояние от основание пирамиды до вершины.
Например, если бы у нас была треугольная пирамида высотой 12 единиц, а площадь основания составляла 24 квадратных единицы, то объем пирамиды был бы V = (1/3) (24) (12) = 96 куб.
Формула площади поверхности для треугольной пирамиды
Площадь поверхности объекта — это общая площадь поверхности объекта.Таким образом, площадь поверхности треугольной пирамиды — это площадь всех ее граней и основания вместе взятых. Когда у нас есть правильная треугольная пирамида, все грани пирамиды имеют одинаковую площадь. Следовательно, площадь поверхности правильной треугольной пирамиды можно найти, добавив площадь основания в 3 раза больше площади одной из граней. То есть SA = A + 3 a , где A — это площадь основания пирамиды, а a — это площадь одной из граней пирамиды.
Чтобы найти площадь треугольника, мы используем формулу A = 1/2 bh , где b — основание треугольника, а h — высота треугольника.
Следовательно, наша формула площади поверхности принимает вид SA = A + 3 (1/2 bh ) = A + 3/2 bh , где b — основание одной из пирамид. Faces, которая также является длиной одной из сторон основания пирамиды, а h — высота одной из граней пирамиды.
Например, если у нас есть правильная треугольная пирамида с гранями, имеющими высоту = 10 единиц и основание = 6 единиц, а площадь основания пирамиды составляет 16 квадратных единиц, то площадь поверхности пирамиды равна SA = 16 + (3/2) (6) (10) = 106 квадратных единиц. Это говорит нам о том, что если вы сложите все площади граней пирамиды и основания пирамиды, вы получите 106 квадратных единиц.
Когда у нас есть неправильная пирамида, мы просто вычисляем площади каждой из граней пирамиды и основания пирамиды по отдельности, а затем складываем их все.То есть SA = Площадь основания + Площадь грани 1 + Площадь грани 2 + Площадь грани 3.
Примеры
Рассмотрим треугольник Рубика. Треугольник Рубика — это правильная треугольная пирамида. От основания пирамиды до вершины 3 дюйма. Площадь основания треугольника Рубика составляет 6,5 квадратных дюймов. Высота одной из граней составляет 3,5 дюйма, а основание одной из граней — 4 дюйма. Зная эту информацию, мы можем найти объем и площадь треугольника Рубика.
Объем = 1/3 AH = (1/3) (6.5) (3) = 6.5 кубических единиц
Площадь поверхности = A + (3/2) bh = 6.5 + (3/2 ) (4) (3.5) = 27,5 квадратных единиц
Рассмотрим еще один пример. Найдите объем и площадь следующей правильной треугольной пирамиды.
Сначала мы найдем объем, поэтому нам нужна площадь основания пирамиды и высота пирамиды. Мы видим, что A = 8.7 квадратных сантиметров и H = 9 см. Поэтому мы подставляем эти значения в нашу формулу объема, чтобы получить V = (1/3) (8,7) (9) = 26,1, поэтому наш объем составляет 26,1 кубических сантиметра.
Теперь мы находим нашу площадь поверхности. Это правильная треугольная пирамида, поэтому нам нужны основание и высота одной из наших граней и площадь основания пирамиды. Из рисунка мы видим, что A = 8,7 квадратных сантиметра, b = 10 см, а h = 7 см. Мы подставляем эти значения в нашу формулу, чтобы получить SA = 8.7 + (3/2) (10) (7) = 113,7. Следовательно, площадь нашей пирамиды составляет 113,7 квадратных сантиметра.
Краткое содержание урока
Треугольные пирамиды — это пирамиды с треугольным основанием. Стороны треугольной пирамиды называются гранями , а точка, где все грани встречаются, называется вершиной . У нас есть формулы для вычисления объема и площади поверхности треугольной пирамиды.
Чтобы найти объем, мы используем формулу V = (1/3) A H , где A = площадь основания пирамиды и H = высота пирамиды.Чтобы найти площадь правильной треугольной пирамиды, воспользуемся формулой SA = A + (3/2) b h , где A = площадь основания пирамиды, b = основание одной из граней, а h = высота одной из граней.
Ключевые термины
Пирамида — трехмерная форма, имеющая многоугольник в качестве основания и треугольники в качестве сторон, все они встречаются в общей точке
Грани — треугольные стороны пирамиды
Основание — нижний многоугольник пирамиды
Вершина — точка пересечения всех треугольных граней на пирамиде
Треугольная пирамида — пирамида с треугольником в основании
Правильная треугольная пирамида — пирамида, имеющая основание с равными по длине сторонами
Неправильная треугольная пирамида — пирамида с основанием с разной длиной сторон
Объем — сколько места внутри объекта
Площадь поверхности — общая площадь поверхности объекта
Результаты обучения
После этого урока вы должны уметь:
- 9 0335 Сопоставьте следующие термины с соответствующими частями пирамиды: грань, основание, вершина
- Как отличить правильную треугольную пирамиду от неправильной
- Объясните, как найти объем и площадь любой треугольной пирамиды
Обзор площади поверхности пирамид
Не в ущерб призмам и цилиндрам.Они великолепны. Но мы не едим мороженое из призм, путешествуя по египетским цилиндрам Гизы. Мы говорим о том, что пирамиды и конусы ничем не заменим, так что мы могли бы немного узнать о них.
Пирамида — это правильная пирамида , если основание представляет собой правильный многоугольник с вершиной, перпендикулярной центру основания. Пирамида нерегулярна, если у нее нет ежедневного испражнения.
Высота всей пирамиды называется высотой , но боковые грани имеют свою собственную высоту, называемую наклонной высотой .Давайте возьмем правильную шестиугольную пирамиду и посмотрим на ее сетку (которая удивительно похожа на Звезду Давида. L’chaim!).
Боковая площадь — это площадь всех треугольников вместе взятых. Площадь треугольника равна половине основания, умноженной на высоту. В этом случае основание — это сторона шестиугольника s , а высота треугольника — это наклонная высота l . Так как у нас шесть таких треугольников, поперечная площадь определяется следующим уравнением:
Или, упрощенно, это равно:
Поскольку мы знаем, что периметр шестиугольника равен 6 s , мы можем заменить стороны с периметром шестигранника P .
Мазел тов! Мы нашли формулу боковой площади любой пирамиды.
Все, что нам не хватает, чтобы найти площадь поверхности, это основание пирамиды, B . Помните, что в отличие от цилиндров и призм, пирамиды имеют только и одно основание . Если мы знаем площадь основания, мы можем узнать площадь поверхности всей пирамиды.
Пример задачи
На День отца вы решаете построить своему папе скворечник. Вы знаете, как сильно он любит птиц, и вы бы предпочли сделать это, чем в миллионный раз стать его кедом для гольфа.(Серьезно, сколько раз он может называть вас «чемпионом» за один день?) Вы решаете, что крыша скворечника будет квадратной пирамидой, потому что она самая простая. Наклон крыши составляет 10 дюймов, а каждая сторона квадрата — 8 дюймов. Сколько дерева в квадратных дюймах вам понадобится, чтобы сделать крышу?
Что ж, мы можем начать с нашей формулы боковой площади.
Периметр квадратного основания равен 8 + 8 + 8 + 8 = 32 дюйма. Высота наклона крыши составляет 10 дюймов.
Осторожно с ножовкой. Вы же не хотите закончить тем, что учитель столярной мастерской с отсутствующим мизинцем.
Мы можем использовать гораздо больше, чем эти формулы, чтобы вычислить площадь поверхности. Помните теорему Пифагора? Помните тригонометрию? Эти математические призраки никогда не покинут вас. Если мы будем относиться к ним правильно, они будут больше похожи на Каспера, чем на Экзорциста.
Пример задачи
Какова площадь поверхности этой пятиугольной пирамиды?
Зная высоту и наклонную высоту, мы можем получить достаточно информации для расчета всего, что нам нужно.Если мы посмотрим на эти два значения как на прямоугольный треугольник, высота будет катетом, а наклонная высота — гипотенузой. Решение для оставшейся ноги (и, надеюсь, это не протез) даст нам расстояние от центра основания до одной из сторон.
a 2 + b 2 = c 2
a 2 + 12 2 = 13 2
2
a 2 = 25
a = 5
Быстрое касание: расстояние от центра любого правильного многоугольника до середины одного из его ребер называется апофемой , что мы только что нашли. .
Хорошо, по касательной. Теперь увеличьте масштаб основания нашей пирамиды. Отрезок перпендикулярной линии от центра в сторону составляет 5 дюймов (это апофема). Поскольку пятиугольник правильный, мы также можем найти углы в прямоугольном треугольнике. 360 ° вокруг центра равномерно разделены на 5, что дает нам 72 ° на равнобедренный треугольник. Мы разделяем эти треугольники пополам, так что каждый угол равен 36 °. Вот что мы знаем о стиле Pictionary.
Эй, кстати говоря о выходе по касательной…
Мы можем решить для s и найти длину каждой стороны пятиугольника.
s = 10tan (36 °) ≈ 7,27 дюйма
Обязательно поблагодарите тригонометрию в своей речи о вручении Нобелевской премии.
Теперь мы можем сделать две вещи:
- Найти площадь пятиугольного основания
- Найти периметр, который поможет нам найти боковую площадь
Площадь первая, поэтому мы начнем с нее.
Если вы вообразите разрезание пятиугольника на 5 одинаковых треугольников (не стесняйтесь вообразить разрезание его еще немного, если вы действительно злитесь), мы можем найти площадь каждого треугольника и умножить ее на 5.Основание треугольника — длина стороны и высота 5.
На полпути. Если бы это была романтическая комедия, мы были бы в той точке, где два главных героя уже полюбили друг друга, но еще не знали об этом, и только что произошел случайный конфликт, который их разлучил. Это оставляет достаточно времени для прозрения их любви, безумной погони друг за другом в последнюю минуту и обязательного обмена слюной в конце.
Основание — пятиугольник («пятиугольник» означает пять), поэтому периметр в пять раз больше длины стороны.Мы знаем, что сторона составляет около 7,27 дюйма, что означает, что периметр составляет около 36,35 дюйма. Высокая пента!
Теперь о той части, где два главных героя осознают свою бессмертную любовь и соревнуются в поисках друг друга. Боковая площадь пирамиды определяется формулой:
Мы знаем, что наклонная высота l равна 13, поскольку она была нам предоставлена, и мы только что вычислили P .
L = ½ (36,35 × 13) ≈ 236,2 дюйма 2
Два влюбленных воссоединились и наконец признались в своей любви.Остается только тот слюнявый поцелуй, который длится веками.
SA = L + B
SA = 236,2 дюйма 2 + 90,8 дюйма 2 = 327 дюймов 2
Конец. Бросьте кредиты под какую-нибудь приятную песню Майкла Болтона.
цоколи, боковые и в сборе? Как найти периметр основания в правой пирамиде
Пирамида, в основании которой лежит правый шестиугольник, а стороны образованы прямоугольными треугольниками, называется шестиугольником .
Этот многогранник отличается множеством свойств:
- Все стороны и углы основания равны между собой;
- Все ребра и двугранные угольные пирамиды также равны друг другу;
- Треугольники, образующие стороны, одинаковые, соответственно, имеют одинаковую площадь, сторону и высоту.
Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
где P — периметр основания, A — длина апофема пирамиды.В большинстве случаев можно рассчитать боковую площадь по этой формуле, но иногда можно использовать другой метод. Поскольку боковые грани пирамид образованы равными треугольниками, можно найти площадь одного треугольника, а затем умножить ее на количество боковых сторон. В гексагональной пирамиде их 6. Но этот метод можно применить и при расчете. Подходим пример расчета площади боковой поверхности шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, в которой апофем равен а = 7 см, сторона основания В = 3 см.Вычислите площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Поскольку пирамида правильная — в ее основании правильный шестиугольник. Это означает, что все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь мы легко можем найти площадь боковой поверхности, подставив значение в основную формулу:
Также немаловажным моментом является поиск площади основания.Формула основания шестиугольной пирамиды основана на свойствах правильного шестиугольника:
Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условие из прошлого примера. Конечно, мы знаем, что сторона основания В = 3 см. Подставьте данные в формулу:
Формула шестиугольной пирамиды представляет собой сумму площади основания и бокового поворота:
Рассмотрим пример вычисления площади гексагональной пирамиды.
Пусть дана пирамида, в основании которой правильный шестиугольник со стороной B = 4 см. Апофем данного многогранника равен а = 6 см. Найдите общую площадь.
Мы знаем, что общая площадь состоит из площадей основания и бокового свеса. Поэтому начать их искать. Рассчитаем периметр:
Теперь находим площадь боковой поверхности:
Далее вычисляем площадь основания, в которой лежит правый шестиугольник:
Теперь мы можем сложить полученные результаты:
Определение. Сторона — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольником).
Определение. Боковые кромки — Это общие стороны боковых граней. У пирамиды столько ребер, сколько углов имеет многоугольник.
Определение. Высота пирамиды — Это перпендикуляр, опущенный сверху к основанию пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опускающийся от вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это поперечное сечение пирамиды с плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правая пирамида — Это пирамида, в которой основанием является правый многоугольник, а высота попадает в центр основания.
Объем и площадь поверхности пирамиды
Формула. Объем пирамиды По площади основания и по высоте:
Свойства пирамиды
Если все боковые ребра равны, то можно описать основание пирамиды, причем центр основания совпадает с центром круга.Также перпендикуляр, опущенный сверху, проходит через центр основания (круг).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны, если они образуют с плоскостью основания равные углы или если можно описать круг вокруг основания пирамиды.
Если боковые грани наклонены к плоскости основания на один угол, то в основании пирамиды можно вписать круг, а вершина пирамиды рассчитана на ее центр.
Если боковые грани наклонены к базовой плоскости на один угол, то апофемы боковых граней равны.
Свойства правой пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые грани наклонены под одинаковые углы к основанию.
4. Апофимы всех боковых граней равны.
5. Площади всех боковых граней равны.
6.Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центр описываемой сферы — это точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиде вы можете войти в сферу. Центр вписанной сферы будет точкой пересечения биссектрисы, исходящей из угла между краем и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов вверху равна π или наоборот, один угол равен π / n, где N — количество углов. у основания пирамиды.
Соединение пирамиды со сферой
Вокруг пирамиды можно описать сферу, если в основании пирамиды лежит многогранник, вокруг которого можно описать круг (необходимое и достаточное условие). Центр сферы — это точка пересечения плоскостей, проходящих перпендикулярно через середину боковых ребер пирамид.
Кругом любую треугольную или правильную пирамиду всегда можно описать сферой.
В пирамиду можно войти в сферу, если плоскости бис-секторов внутренних карликовых углов пирамид пересекаются в одной точке (необходимое и достаточное условие).Эта точка будет центром сферы.
Пирамидальное соединение с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно ввести в пирамиду, если апофемы пирамид равны друг другу.
Конус называется описываемой пирамидой, если их вершины совпадают, а основание конуса описывается вокруг основания пирамиды.
Конус можно описать вокруг пирамиды, если все боковые ребра пирамиды равны друг другу.
Пирамидальное соединение с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одном основании цилиндра, а основание пирамиды вписано в другое основание цилиндра.
Цилиндр можно описать вокруг пирамиды, если вокруг основания пирамиды можно описать круг.
Определение. Усеченная пирамида (пирамидальная призма) — Это многогранник, который находится между основанием пирамиды и плоскостью сечений, параллельной основанию. Таким образом, пирамида имеет большое основание и аналогичное основание меньшего размера. Боковые грани — трапеции. Определение. Треугольная пирамида (квадруп) — Это пирамида, в которой три грани и основание представляют собой произвольные треугольники.Четыре ребра с четырьмя гранями, четырьмя вершинами и шестью ребрами, где любые два ребра не имеют общих вершин, но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, образующих три угла .
Отрезок, соединяющий вершину тетраэдра с центром противоположной грани, называется средним тетраэдром (GM).
Bimedian Его называют сегментом, соединяющим середину противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы тетраэдра пересекаются в одной точке (точках). При этом бимедианы делятся пополам, а медианы относительно 3: 1, начиная с вершины.
Определение. Наклонная пирамида — Это пирамида, в которой одно из ребер образует дурацкий угол (β) с основанием. Определение. Прямоугольная пирамида — Это пирамида, у которой одна из боковых граней перпендикулярна основанию.Определение. Акредитованная пирамида — Это пирамида, в которой апофем составляет более половины длины стороны основания основания.
Определение. Глупая пирамида — Это пирамида, в которой апофем меньше половины длины стороны основания.
Определение. Правый тетраэдр — Тетраэдр, у которого все четыре грани — равносторонние треугольники. Это один из пяти правильных многоугольников. В правом тетраэдре все условные углы (между краями) и треугольные углы (вверху) равны.
Определение. Прямоугольный тетраэдр Тетраэдром называется прямой угол между тремя ребрами вверху (ребра перпендикулярны). Три грани образуют прямоугольный треугольный угол А грани являются прямоугольными треугольниками и основанием произвольного треугольника.Апофема любого лица равна половине той стороны основания, на которую падает апофем.
Определение. Промывной тетраэдр Тетраэдром называют боковые грани, равные друг другу, а основание — прямоугольный треугольник. Такой тетраэдр обслуживает изолированные треугольники.
Определение. Ортоцентрический тетраэдр Тетраэдром называют все высоты (перпендикулярные), которые опущены сверху до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида Многогранник называется основанием — звезда.
Определение. Бипирамида — многогранник, состоящий из двух разных пирамид (можно также разрезать пирамиды), имеющих общее основание, а вершины лежат по разные стороны от плоскости основания.При подготовке к экзамену по математике студенты должны систематизировать знания по алгебре и геометрии. Я хочу объединить всю известную информацию, например, как рассчитать площадь пирамиды.Причем начиная с основания и боковых граней на площадь всей поверхности. Если с боковыми гранями ситуация понятна, так как они треугольники, то основание всегда разное.
Как быть при нахождении площади основания пирамиды?
Это может быть абсолютно любая фигура: от произвольного треугольника до n-квадрата. И эта основа, помимо разницы в количестве углов, может быть правильным рисунком или неправильным. В интересующих школьников заданиях в основе находятся только задания с нужными фигурами.Поэтому речь пойдет только о них.
Треугольник прямоугольный
То есть равносторонний. Тот, в котором все партии равны и обозначается буквой «А». В этом случае площадь основания пирамиды рассчитывается по формуле:
S = (A 2 * √3) / 4.
Квадрат
Формула расчета ее площади: самый простой, здесь «А» — снова сторона:
Произвольно правильный n-квадрат
Сторона многоугольника имеет такое же обозначение.В качестве количества углов используется латинская буква n.
S = (N * A 2) / (4 * TG (180º / N)).
Как это сделать при расчете стороны боковой и полной поверхности?
Поскольку у основания правильная фигура, все грани пирамид равны. Более того, каждый из них представляет собой равноправный треугольник, поскольку боковые ребра равны. Тогда для того, чтобы рассчитать площадь стороны пирамиды, потребуется формула, состоящая из количества таких же одностворчатых.Количество компонентов определяется количеством баз.
Площадь равновесного треугольника рассчитывается по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофей. Ее обозначение — «А». Общая формула площади боковой поверхности выглядит так:
S = ½ P * A, где p — периметр основания пирамиды.
Бывают ситуации, когда стороны основания не известны, но заданы боковые кромки (c) и плоский угол в его вершине (α).Затем следует использовать такую формулу для расчета боковой площади пирамиды:
S = N / 2 * B 2 SIN α .
Номер задачи 1.
Условие. Найдите общую площадь пирамиды, если она лежит со стороной 4 см в основании, а апофем равен √3 см.
Решение. Начать нужно с расчета периметра фундамента. Так как это правильный треугольник, то p = 3 * 4 = 12 см.Поскольку апофем известен, можно сразу рассчитать площадь всей боковой поверхности: ½ * 12 * √3 = 6√3 см 2.
Для треугольника в основании такое значение площадь получится: (4 2 * √3) / 4 = 4√3 см 2.
Для определения всей площади необходимо будет сложить два из полученных значений: 6√3 + 4√3 \ u003d 10√3 см 2.
Ответ. 10√3 см 2.
Задача №2.
Условие . Есть правильная четырехугольная пирамида.Длина базовой стороны 7 мм, боковой кромки 16 мм. Необходимо знать площадь его поверхности.
Решение. Поскольку многогранник четырехугольный и правильный, то в его основании квадрат. Узнав площадь основания и боковых граней, можно будет посчитать площадь пирамиды. Формула для квадрата приведена выше. А боковые грани известны для всех сторон треугольника. Следовательно, можно использовать формулу Герона для расчета их площадей.
Первые вычисления просты и приводят к такому числу: 49 мм 2. Для второго значения потребуется вычислить полметр: (7 + 16 * 2): 2 = 19,5 мм. Теперь можно вычислить площадь равностороннего треугольника: √ (19,5 * (19,5-7) * (19,5-16) 2) = √2985,9375 = 54,644 мм 2. Таких треугольников всего четыре, так что при вычислении итогового числа надо будет его умножить на 4.
Получается: 49 + 4 * 54 644 = 267 576 мм 2.
Ответ . Требуемое значение — 267,576 мм 2.
Номер задачи 3.
Условие . Справа одна четырехугольная пирамида. Необходимо вычислить площадь. Он знает сторону квадрата — 6 см и высоту — 4 см.
Решение. Самый простой способ использовать формулу с работой периметра и апонемии. Первое значение простое. Второй вариант посложнее.
Придется вспомнить теорему Пифагора и считать, что она образована высотой пирамиды и апофея, которая является гипотенузой.Второй катат равен половине стороны квадрата, так как высота многогранника приходится на его середину.
Искомый апофем (гипотенус прямоугольного треугольника) равен √ (3 2 + 4 2) = 5 (см).
Теперь можно рассчитать искомое значение: ½ * (4 * 6) * 5 + 6 2 = 96 (см 2).
Ответ. 96 см 2.
Номер задания 4.
Состояние. Правая сторона его основания — 22 мм, боковые ребра — 61 мм. Какова площадь боковой поверхности этого многогранника?
Решение. Аргументы в нем те же, что и в задаче № 2. Только была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом рассчитывается площадь основания по приведенной выше формуле: (6 * 22 2) / (4 * TG (180º / 6)) = 726 / (TG30º) = 726√3 см 2.
Теперь необходимо найти половину версии треугольника равновесия, которая является боковой гранью. (22 + 61 * 2): 2 = 72 см. Осталось по формуле Герона посчитать площадь каждого такого треугольника, а затем умножить ее на шесть и сложить с тем, что случилось с основанием.
Расчеты по формуле Герона: √ (72 * (72-22) * (72-61) 2) = √435600 = 660 см 2. Расчеты, которые дадут площадь боковой поверхности: 660 * 6 = 3960 см 2. Осталось сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2.
Ответ. Основания 726√3 см 2, боковая поверхность — 3960 см 2, вся площадь 5217 см 2.
Треугольная пирамида Называется многогранником, в основании которого лежит прямоугольный треугольник.
В такой пирамиде край основания и края сторон сторон равны друг другу. Соответственно, сторона боковых граней располагается из суммы площадей трех одинаковых треугольников. Найдите площадь боковой поверхности правой пирамиды по формуле. И вы можете произвести расчет в несколько раз быстрее. Для этого применим формулу площади боковой поверхности треугольной пирамиды:
где P — периметр основания, в котором все стороны равны b, A — апофем, опущенный сверху на это основание.Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Дать правильную пирамиду. Сторона лежащего в основании треугольника B = 4 см. Пирамида Апперам равна = 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задания мы знаем длину всех необходимых элементов, то найдем периметр. Помним, что в прямоугольном треугольнике все стороны равны, а значит, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем посчитать сторону площадь поверхности:
Чтобы применить Формулу квадрата треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника.Для этого используется формула:
Формула основания треугольной пирамиды может быть другой. Допускается применять любой расчет параметров для данной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правой пирамиде сторона нижележащего треугольника равна = 6 см. Рассчитайте базовую площадь.
Для расчета нам понадобится только длина стороны прямоугольного треугольника, расположенного в основании пирамиды.Подставьте данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить боковую поверхность и основание.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Дать правильную треугольную пирамиду. Сторона основания равна В = 4 см, апофем а = 6 см. Найдите всю площадь пирамиды.
Для начала находим площадь боковой поверхности по уже известной формуле.Вычисляем периметр:
Подставляем данные в формулу:
Теперь находим площадь фундамента:
Зная площадь основания и боковой поверхности, находим полную площадь пирамиды:
При вычислении площади правой пирамиды стоит не забывать, что в основании лежит прямоугольный треугольник и многие элементы этого многогранника равны между собой. Автор Мария Токаева На чтение 9 мин. Опубликовано Предлог de переводится на русский язык как из, от, о или как Родительный падеж. В некоторых случаях имена существительные нужно употреблять не с артиклями, а именно с этим предлогом. О них то мы и поговорим в этой статье. Наречия: beaucoup de — много, un peu de — немного, assez de — достаточно, trop de — довольно, достаточно, près de — около, plus de — более, moins de — менее. Примеры: J’ai beaucoup de travail à terminer. — У меня просто очень много работы которую я должна сделать. J’en ai assez de ce jeu, et plus qu’assez de cette compagnie. — С меня достаточно этой игры… и достаточно этой компании. Существительные, с помощью которых обозначают вес и другие единицы измерения: une boîte de — коробка, un bol de — бокал, un bouquet — букет, une bouteille de — бутылка, une cuillère de — ложка, une dizaine de — десяток, une douzaine de — дюжина, 300 grammes de — 300 грамм, un kilo de — килограмм, un litre de — литр, une livre de — полкило, фунт, un morceau de — кусок, une pincée de — щепотка, une tasse de — чашка, une tranche de — ломоть, кусок, un verre de — стакан. Из этого правила есть исключения: Если глагол употреблен в отрицательной форме, то предлог нужно использовать вместо частичного или неопределенного артикля. Пример: Je n’ai pas de réponse à ça. — У меня на них ответов нет. Je n’aime pas de lilas. — Я не люблю сирень. Из этого правила также есть исключения: Важно! Определенный артикль после отрицания сохраняется. De употребляется вместо des (неопред. артикль мн.ч.) перед прилагательным, которое нужно использовать перед существительным. Пример: Ils ont de beaux chapeaux de soleil. — У них красивые шляпы от солнца. Тут также есть исключения: Это нужно, чтобы избежать неблагозвучий, вроде de des, de du, de de la. Исключения: Предлог de не нужен, если дополнение-существительное, идущее после него, обозначает характеристику (сущ. Выберите правильный вариант: Дополните предложения предлогом de или слитными артиклями du (= de le), des (= de les), de la: Когда же мы вместо артикля должны поставить предлог de? Есть несколько четких правил на этот счёт и несколько очень размытых. А вообще, артикли и предлоги — это такая тема, которую нужно изучать довольно долго. Если вам эта тема кажется сложной, и вы хотели бы не только изучить теорию, но и выполнить упражнения, приглашаю вас на краткий заочный курс «Артикли и предлог de». Вы сможете выполнить ряд упражнений на употребление артиклей и предлога de, а я проверю вашу работу, дам советы по дальнейшему совершенствованию. Стоимость материалов курса — 3000 р., проверка — бесплатно, но при условии, что вы делаете все задания вовремя. Этот курс рассчитан примерно на десять дней работы, и адресован он не начинающим, а тем, кто уже какое-то время учит французский. Вы можете узнать подробнее, написав мне по адресу А далее разберём правила. Начнем с четких, это проще. Рассмотрим сейчас один случай. Итак, начнем с того, что на предлог de меняется только неопределенный артикль. Это может быть: un, une, des, а также частичные: du, de la, de l’. 1. Например: Des élèves — un groupe d’élèves Des livres — un tas de livres Des maisons — beaucoup de maison. Как видите, речь идёт не обязательно о точном выражении количества, но и о примерном. Здесь есть исключения, которые на самом деле не исключения. Я ведь уже написала, что на de меняется только неопределенный артикль. Действительно, после слов количества: много-мало, куча, груда, стопка, тарелка… обычно идёт слово с неопределенным артиклем. Например, «стопка книг» — каких книг? Неизвестно, они неопределенные. Просто стопка каких-то книг. Ну вот и убираем артикль des (des livres), оставляем лишь предлог de (un tas de livres). Но иногда мы рассматриваем некое количество предметов, которые можно определить. Например, «половина книг». Половина каких книг? Они не могут быть неопределенными, потому что половину можно взять только от известных предметов. Нельзя сказать «половина каких-то книг», но можно, например, «половина книг из его библиотеки» или «половина тех книг, что я купила». В любом случае половину можно взять только от чего-то известного. Да и любую часть (треть, четверть) тоже. Поэтому те слова, которые обозначают дроби, а также слова «la majorité, la plupart» — большая часть, bien des — большинство, многие, а также любые проценты — все эти выражения употребляются только с определенными существительными!!! Соответственно, мы увидим там либо слитные артикли des, du, либо de la, de l’. Примеры. La moitié DES Français (de + les) — половина всех французов Un tiers des élèves — треть учеников La plupart du livre — большая часть книги La majorité du séjour — большая часть путешествия (пребывания) 47% des animaux — 47% всех животных Bien des habitants — многие из жителей. Потому что все эти выражения означают некую часть целого. А часть можно взять только от известного целого! Кстати, на самом деле прошлый случай, про слова количества, который я уже описала, тоже сюда относится. Сейчас вы поймёте, почему. Итак, представьте, что нам нужно употребить глагол или выражение, после которого по правилам французского должен идти предлог de. А таких выражений немало. Я приведу несколько. Avoir besoin de — нуждаться в чём-то Être fier de — гордиться чем-то Parler de — говорить о чём-то Couvrir de — накрывать чем-то Orner de — украшать чем-то. Это всего лишь несколько выражений для примера. На самом деле таких выражений много. Кстати, если вам нужен справочник с указанием, какой предлог с каким глаголом идёт, поищите пособие «Verbes et leurs prépositions». Так вот, что, если после такого выражения c «de» нам нужно употребить слово с неопределенным артиклем? Например, мы хотим сказать, что украсили комнату цветами. Цветы — des fleurs — неопределённое, потому что непонятно, какими конкретно цветами? Какими-то.»Я украсила комнату» переводится как j’ai orné la pièce de… Так вот. Я перевела почти всю фразу. Осталось только подставить дополнение des fleurs. Что же, получается, «j’ai orné la pièce DE DES fleurs»??? Подобные одиозные сочетания, конечно, во французском невозможны. Что-то должно произойти. И происходит. Запомните правило: если предлог de стыкуется с артиклем, который похож на него по произношению, а конкретно это des, du, de la, de l’, то артикль опускается! Собственно, потому его и нет в выражениях количества: они все с de: beaucoup de, trop de… Остаётся предлог de. Неопределенные артикли un, une остаются. Например: je couvre la table d’une nappe. Определенные артикли le, la, les также остаются и сливаются с предлогом de в соответствии с правилом. Если вы читаете эту заметку про артикли и вам интересно, скорее всего, у вас уже есть кое-какой уровень во французском, и вы помните вот это: de + le = du, de + la = de la, de + les = des. Например: je couvre la table de la nappe que ma mère m’a offerte. Ученики часто задают мне вопрос: а почему же при стыке de + des, de + de la, de + du мы выбрасываем именно артикль? Почему бы не выбросить предлог de? Например, сказать: j’ai orné la pièce DES fleurs (вместо DE fleurs)? Если так сделать, то будет непонятно, идёт ли речь о каких-то определенных цветах или нет. Ведь des не только артикль. Des получается от слияния de + les, a du — de + le, de la — de + la. Если у нас определённые цветы (les fleurs), то при слиянии получается: j’ai orné la pièce de + les fleurs -> j’ai orné la pièce DES fleurs. А когда цветы неопределённые? Если j’ai orné la chambre de + des fleurs? Если оставить артикль des, то фраза по написанию совпадает с предыдущей. А это недопустимо. Во французском языке важно, идёт ли речь о чём-то определённом или нет. Поэтому опускаем неопределённый артикль, а предлог de оставляем. И фразы у нас получаются разными. J’ai orné la pièce de fleurs — я украсила комнату какими-то цветами. J’ai orné la pièce des fleurs — я украсила комнату уже упомянутыми цветами. Это самое элементарное правило из серии, когда вместо неопределенного артикля des употребляется предлог de. И вместе с тем самое странное. Потому что никакой логики тут нет. То есть не совсем понятно: почему так? Вот это правило. В словосочетаниях во множественном числе, где прилагательное стоит перед существительным, вместо неопределенного артикля des употребляется предлог de. Если вам не нравится стиль вузовского учебника, объясню более простыми словами. Начнём с начала. Обычно прилагательные во французском стоят после существительного. Например: une chanson française, un livre intéressant… Но некоторые прилагательные ставятся перед существительными. Подробнее об этом в моей статье здесь же на сайте. Здесь напомню только, что, например, перед существительным ставятся самые распространенные прилагательные, означающие общую оценку: grand, petit, beau, bon, nouveau, vieux, mauvais, jeune, joli… Вот такие словосочетания и рассмотрим.Например, «большой дом» — une grаnde maison, «хороший друг» — un bon ami. Вот вам и словосочетания, где прилагательное стоит перед существительным. Давайте поставим эти словосочетания во множественное число. Une grande maison — de grandes maisons Un bon ami — de bons amis Как видите, если прилагательное стоит перед существительным, во множественном числе вместо des используется de. Если же прилагательное стоит после существительного, то используется, как обычно, артикль des. Un film magnifique — des films magnifiques Une rue étroite — des rues étroites Почему так сложилось? Это интересный теоретический вопрос. Есть предположение, что из-за ритмики фразы: de «дё» произносить удобнее, чем des «де». У меня есть мысли, но их не уложить в заметку. Так или иначе, правило работает. При этом неважно, какую роль играет словосочетание в предложении. Оно может быть подлежащим или дополнением… On a construit de belles maisons — дополнение. De belles maisons sont en construction — подлежащее. Исключения! Дело в том, что, если сочетание прил.+сущ. представляет собой единое понятие, то употребляется все же артикль des. А как понять, что сочетание — единое понятие? Это довольно просто. Давайте разберем два словосочетания, пока без артиклей: petits chiens и petits pains. Первое сочетание переводится как «маленькие собаки» и это не единое понятие. Это слово «собаки» с определением: маленькие. Если убрать прилагательное, то слово chiens не изменит своего значения: это всё равно «собаки». Такое словосочетание употребляется во множественном числе с предлогом de: de petits chiens. А «petits pains» переводится «булочки». И здесь уже, если убрать прилагательное petits, у нас останется только слово pains, которое без прилагательного означает не «булочки», а «хлебцы». Вот petits pains и есть неразрывное словосочетание, означающее единое понятие. Это словосочетание будет употребляться с артиклем des. Впрочем, возможно, тут такой случай, когда легче просто выучить эти единые понятия как исключения. Их совсем мало. Вот они. Des jeunes gens — молодые люди, молодёжь Des jeunes hommes — юноши Des jeunes filles — девушки Des petits pains — булочки Des petits pois — горошек Предлог de при отрицании. При отрицании неопределенные артикли des, un, une, du, de la меняются на предлог de. Например: J’ai une soeur. Je n’ai pas de frère. J’achète des fruits. Je n’achète pas de glaces. Il y a une école dans notre ville. Il n’y a pas d’université dans notre ville. Особые случаи. Как видите, на de заменяются только неопределенные артикли. Определённые никуда не убираем. Например: Il aime les glaces. Il n’aime pas le chocolat. J’ai apporté le cahier. Mais je n’ai pas apporté le manuel que tu m’as prêté. В последней фразе слово le manuel определенное, потому что далее идёт пояснение, какой именно учебник. Тут надо бы углубиться в тему артиклей вообще: когда определенный, когда неопределенный. Но я пока не уверена, что готова осветить эту тему вне уроков. Это сложный и неоднозначный вопрос. Далее. Есть ещё одно правило. Вот такое. Даже неопределенный артикль сохраняется в отрицательных фразах особого типа. А именно, когда мы не отрицаем существование предмета вообще, а поясняем, что это «не то, а другое». Сейчас приведу пример! Ce n’est pas un livre, c’est un cahier. Ce n’est pas de l’eau, c’est du jus. Самый сложный случай употребления предлога de вместо артикля. Я думаю, чтобы в полной мере прочувствовать это правило, вам нужно как можно больше работать с текстами, анализировать, как пишут разные авторы. Сейчас мы поговорим об употреблении предлога de без артикля в словосочетаниях такого типа: существительное + de + существительное. Таких словосочетаний во французском много. Приведу несколько примеров. Un billet d’avion — билет на самолёт Un nid d’oiseau — гнездо птицы Un programme d’école — школьная программа Une queue de cheval — конский хвост Une voix de femme — женский голос Une carte de séjour — вид на жительство (дословно «карта пребывания») Почему же мы не употребляем здесь артикль после de? Давайте смотреть. Во французском есть такое правило: нет предмета — нет артикля. Вы помните, что артикль мы опускаем также при отрицании предметов: je n’ai pas de frère…А что у нас с этими словосочетаниями. Ну вот первое: билет на самолёт. У нас есть билет, но есть ли у нас самолёт? Пока нет. Мы не знаем, какой конкретно самолёт нас повезет, какого он размера, цвета и т.п. Этого предмета пока не существует, по крайней мере, в нашей жизни. Слово avion здесь употребляется не для того, чтобы указать на какой-то самолёт, а всего лишь для того, чтобы определить тип билета. Вот в таком случае, когда второе существительное выступает как определитель первого и не указывает ни на какой конкретный предмет, мы употребляем предлог de без артикля. То же мы видим со стороны словосочетанием: гнездо птицы. Мы видим гнездо, но видим ли птицу? Неизвестно. Слово oiseau всего лишь определяет тип гнезда: не змеиное, например, а птичье. Ещё проще с конским хвостом. Это такая прическа. Так что хвост у нас есть, из волос, а вот никакого коня точно нет. Une voix de femme. Вы слышите женский голос… Но видите ли вы женщину при этом? А может быть, это вообще был голос не женщины, а, например, ребенка? Немного сложнее объяснить отсутствие артикля в сочетании un programme d’école. Школа имеется в виду: школа как образовательный институт в нашей стране. Школа существует, это всем известно. И все же сочетание un programme d’école не даёт никакой информации. Программа какой школы? Если сказать «programme d’une école», это значит: программа какой-нибудь школы. «Programme de l’école» — программа ЭТОЙ школы. А вот programme d’école — просто школьная программа. Непонятно, какой школы. Это неважно. Мы рассмотрели основные случаи, когда артикль во французском языке меняется на предлог de. Успехов! Комментарии и уведомления в настоящее время закрыты.. Предлог de, вводящий дополнение существительного, может выражать отношения, соответствующие русскому родительному падежу: le cahier de ma soeur — тетрадь моей сестры Предлог à обозначает самые разнообразные отношения и является одним из самых распространенных предлогов во французском языке. Предлог jusque до выражает временные и пространственные отношения и часто употребляется в сочетании с другими предлогами, особенно с à. Пронаблюдайте употребление предлога jusque: jusqu‘ici jusqu’à + существительное jusqu‘à la ville Предлог a указывает на направление или цель движения (в, на). Предлог de указывает на исходную точку движения (из, от, с). Сравните: Предлог a может вводить обстоятельство места, обозначающее расстояние от какого-то места. В русском языке ему соответствует предлог в или слова на расстоянии: Перед существительными женского рода, обозначающими название стран (континентов, регионов, провинций и т.д.), а также существительными мужского рода, начинающимися с гласной, употребляется предлог en при указании места или направления. После предлога en артикль не употребляется: Je vais en Suisse; en Irak. Перед существительными мужского рода, начинающимися с согласной, употребляется предлог à с артиклем: Je vais au Japon. Обратите внимание на употребление предлогов перед существительными la place, le boulevard, l’avenue, la rue, l’île: sur la place, sur le boulevard, sur l’avenu При указании места учебы или работы после существительных, обозначающих профессию, во французском языке употребляется предлог a (студент, рабочий где — в отличие от русского студент, рабочий чего: института, завода). M. Roulin est caissier à la banque de Paris. Русскому предлогу перед, выражающему как пространственные отношения (перед домом), так и временные (перед отъездом), во французском языке соответствуют два различных предлога: devant и avant. Devant выражает пространственные отношения; avant выражает временные отношения. Сравните: Предлог sans образует с существительным без артикля словосочетание, являющееся в предложении обстоятельством образа действия. На русский язык эти словосочетания переводятся либо существительным с предлогом без, либо наречием: sans repos — без отдыха Проголосовало 1 чел. DE: Предлог “de” используется с существительными и именами собственными: Le blouson de mon frère. Куртка моего брата. В случае слитного артикля: Предлог “à” 1. существительное+ être + à+ ударное местоимение /существительное/ имя собственное Cette boutique est à elle. Этот магазин её. 2. c’est + à + местоимение /существительное/ имя собственное C’est à lui. Это его. 3. c’est + существительное + à + ударное местоимение C’est un ami à moi. Exercice. Попробуйте перевести эти фразы, если Вам покажется слишком сложно, чуть ниже Вы найдете подсказки. 1. Это друг моего брата. 1. Это друг моего брата. (ce; être; ami; mon; ami) *** Ответы 1. Это друг моего брата. C’est l’ami de mon frère. к которым косвенное дополнение (COI) присоединяется через предлог «de». Вот пример такого глагола: Вот пример такого глагольного оборота: être sûr de quelque chose — быть уверенным в чем-то Это существительное-дополнение с предлогом «de» может быть заменено местоимением. Речь идет про слово «en» При этом «en» может заменять только неодушевленные предметы (вещи), или животных (не людей). 1) «en «заменяет косвенное дополнение (существительное), вводимое предлогом de. Например, Je suis sûr de son amitié — Я уверен в его дружбе Заменили, и получилось: J’en suis sûr — Я в ней уверен (т.е. «в дружбе») 2) Кроме того, местоимение «en» может заменять и целое предложение. Например: Je suis sûr de ce que je dis — Я уверен в том, что говорю. J’en suis sûr (en = de cela) А если вам надо сериал Наследие смотреть, то идите на этот сайт Наследие смотреть онлайн 3) Куда ставить местоимение «en» в предложении? Например, Il en a parlé — он об этом поговорил Получается, что местоимение «en» ставится ПЕРЕД глаголом. А если есть еще одно приглагольное местоимение, то «en» ставится ПОСЛЕ него. Например, s’occuper de de quelque chose — заниматься чем-то Je m’en occupe — Я этим занимаюсь parler à quelqu’un de quelque chose Il ne leur en a pas parlé — он с ними об этом не поговорил Частичный артикль во французском языке занимает особое место. Мы уже обсуждали определенный и неопределенный артикли, теперь важно найти место для частичного. Частичный артикль во французском языке Masculin – du: du pain, du fromage, du sucre. Féminin – de la: de la farine, de la mer. Voyelle ou h muet – de l’ : de l’eau, de l’huile. Теперь рассмотрим случаи употребления частичного артикля во французском языке. L’article partitif употребляется: перед существительным, которое обозначает вещество, когда не указано количество этого вещества: перед существительным, которое выражает отвлеченное понятие (абстрактные существительные), указывая на то, что данное понятие взято не в полном его объеме, а речь идет о конкретном проявлении такого общего понятия: перед существительным, которое выражает природное явление (обычно в сочетаниях с глаголами avoir и faire): в сочетании с глаголом faire – делать при значении занятости чем-либо: Обратите внимание на то, что после глагола в отрицательной форме частичный артикль не употребляется, а заменяется на предлог de. Теперь, чтобы лучше понять и закрепить употребление частичного артикля в речи, выполните следующее упражнение. Подберите правильный частичный артикль – du, de la, de l’ : Частичный артикль во французском языке элемент значимый, поэтому разобраться в его использовании придется обязательно, тем более, что вся необходимая информация у Вас уже есть. Желаем удачи! Tipde + le и de la изменяются на de l ‘, когда они используются перед словом, начинающимся с гласной, большинство слов, начинающихся с h, и французское слово y. Совет Помните, что du, de la, de l ’и des НИКОГДА нельзя пропустить на французском, даже если на английском нет слова. Предлог de обычно резюмируется как «от, от или около», но он имеет гораздо больше значений и применений, чем это. J’ai promis de le faire — Я обещал это сделать. De — одно из наиболее часто используемых французских слов, но также одно из самых сложных. Вы увидите это почти везде. Это может быть как неопределенный артикль, так и предлог.Он может представлять собой группу чего-либо или ее отсутствие. Его можно использовать как в положительных, так и в отрицательных высказываниях. Это может быть часть фамилии. Это делает его универсальным, но при этом сложным. Как может
вы определяете и классифицируете de ? Какую роль (ну, роли) он играет в
французский язык? От множества значений и употреблений до глаголов и
выражений, это важная часть, давайте выясним, в чем дело с de . С некоторыми возможными исключениями (потому что в языке всегда исключений), de может быть неопределенным или частичным
артикль или предлог. De можно записать как есть, но это может измениться в зависимости от
от количества или буквы слова, которое следует после него. Есть шесть способов увидеть, услышать и использовать de : de, de la , du , de l ’, d’ и des . De — наиболее распространенный способ просмотра и использования de .Его можно использовать с оценочными утверждениями после инфинитивов глагола в отрицательном значении.
заявления и многое другое, как вы увидите позже в этой статье. Когда дело доходит до отрицательных высказываний, в большинстве случаев любые
другая форма de вернется к de или d ’ (если есть гласная
сразу после него), независимо от количества, числа или пола существительного
что следует за ним. Часто, когда за de следует существительное женского рода, оно остается de с добавлением la . C’est la crème de la crème! Когда за de следует существительное мужского рода, вместо слова « de le » (которого нет во французском языке) оно меняется на du . Tu veux du fromage ? Хотите сыра? Когда вы хотите сказать «из / от / некоторых из» и существительное после артикля начинается с гласной, вы меняете de la или du на de l ’. Mon frère m’a donné de l’argent. Мой брат дал мне немного денег. Когда статьи нет
необходимо, а гласная следует за de, использовать d ’. Герцог Орлеанский — один из первых. Герцог Орлеанский — брат короля. Comme il avait soif, il a bu un verre d’eau. Из-за жажды он выпил стакан воды. Когда de используется с существительным множественного числа, обычно получается des . Ce bruit vient des corbeaux. Il y en a beaucoup ici. Этот шум исходит от ворон. Их здесь много. Имейте в виду, что, поскольку de имеет так много значений и
использования, эти правила не всегда могут выполняться. Например, если de является частью фразы, относящейся к
к количеству, оно останется de , независимо от того, что будет дальше, с
исключение изменения на d ’, если следующее за ним слово начинается с
гласный звук. С уважением! Il y a plein de fleurs par ici! Beaucoup d’entre eux n’aiment pas le jazz. Помните, что если de отрицательное, оно обычно также остается de (или d ’, если за ним следует гласная), даже если подлежащее, которое оно изменяет, является мужским, множественным числом и т. Д. Désolée, je n’ai pas de gâteaux pour vous. Извините, у меня нет для вас файлов cookie. Il n’a pas d’animal de compagnie. У него нет домашнего животного. Как следует из его повсеместности, de имеет широкий диапазон
значения на французском языке. В них есть дополнительные подтексты, контексты и
конкретное, одноразовое использование. Давайте посмотрим на наиболее распространенные, основные значения de : Обращение к таким вещам, как то, откуда человек, перемещение из одной точки в другую, что-то (подарок и т. Д.)) быть от кого-то и т. д.) Il vient de Dijon. Он из Дижона Часть поезда Dunkerque à 8h20. Поезд отправляется из Дюнкерка в 8:10. C’est un cadeau de mon père. Это подарок моего отца. Поскольку он используется для обозначения происхождения человека, de или один из его вариантов может быть частью имени физического или юридического лица, которое отождествляется с местом, связано с ним или привязано к нему. Например: Jeanne d’Arc, la Bête du Gévaudan. Sa fille s’habille si lentement le matin. Il est toujours en retard à cause d’elle! Его дочь так медленно одевается по утрам. Он всегда из-за нее опаздывает!) Je te sers une tasse de thé? Хотите чашку чая? Gagner, ce n’est pas le but du jeu! Победа — не цель игры! D e или один из его вариантов также является частью многих дворянских титулов и имен.Например: герцог Анжуйский (герцог Анжуйский), маркиза де Бринвилье (маркиза Бринвилье). Помните, что во французском языке нет «s», которые вы просто добавляете к человеку или предмету, чтобы указать, что им что-то принадлежит. Вместо этого вы должны использовать «де». C’est le cahier de mon fils. Это записная книжка моего сына. Tout le monde aime la quiche de Bernard. Всем нравится пирог Бернарда. C’est le chien d’Hélène et Marine. Это собака Элен и Марин. Il a tourné la poignée de porte. Повернул дверную ручку Le Patient s’est Blessé deux doigts de la main gauche. Больной повредил два пальца левой руки. C’est une pièce de 20 m 2 . Это комната площадью 20 квадратных метров. Nous cherchons un baby sitter pour notre fils de 3 ans. Ищем няню для нашего трехлетнего сына. Или 30 минут. Ожидается 30 минут. Pourquoi tu fais autant de bruit? Il est 1h du matin! Почему вы так много шумите? Уже час ночи! Сюда входят очень распространенные выражения, которые вы, возможно, уже
быть знакомым, например: Этот неопределенный артикль можно использовать по-разному, например, в английском. Céline veut du vin. Селин хочет вина. Delphine a des soucis avec la police. У Дельфины проблемы с полицией. Je ne veux pas sortir cet après-midi — это романтические интрессанты по телу. Я не хочу выходить сегодня днем - по телевизору идут интересные документальные фильмы. Это может показаться сбивающим с толку, поскольку de может означать «некоторые», но если задуматься, это имеет смысл; вы просто делаете что-то негативное. Обратите внимание, что при использовании de в отрицательном смысле используются только формы de и d ’. Оно никогда не используется во множественном числе и не используется с определенным артиклем. Tu as volé mon portefeuille? Bien fait pour toi! Je n’ai pas d’argent! Ты украл мой кошелек? Так тебе и надо! У меня нет денег! J’ai beau chercher mais il n’y a pas de Cornichons. Я искал хорошо, но солений нет. De немного меняется при использовании с другими отрицательными парами, такими как ne… плюс , например — в этом случае это будет означать «нет» или «любой». Il n’y a plus de chocolat. Больше нет / Больше нет шоколада. Как правило, вы сможете понять, что означает de в одной из этих структур предложений, если вспомните, что, по сути, это отрицание слова «некоторые». Il marchait d’un pas in sure. Ходил неуверенной походкой. Elle écrit de la main gauche, mais son père était ambidextre. Она пишет левой рукой, но ее отец владеет обеими руками. Tu as lu le dernier livre de Christelle Dabos? J’adore sa série La Passe-miroir. Вы читали последнюю книгу Кристель Дабос? Я просто обожаю ее сериал «Зеркальный посетитель». «Паразит» Бонг Джун-хо — это премьерный фильм, получивший название «Оскар дю Мейлер». «Паразит» Бон Джун-Хо — первый фильм с субтитрами, получивший премию «Оскар» за лучший фильм. OR «Паразит» Бон Джун Хо — первый фильм с субтитрами, получивший премию «Оскар» за лучший фильм.) В большинстве случаев во французском языке нельзя использовать существительное без артикля. Но что, если вы не хотите, чтобы статья была сильной или заметной? В этом случае вы можете использовать de в смысле «какой-то», как наполнитель. Je n’aime pas ces raisins. Ils ont des pépins. Не люблю этот виноград. У них есть семена. Как видите, здесь нет необходимости включать неопределенный артикль «some». Это просто наполнитель. La dame portait des lunettes. На женщине были очки. Je vois des choses intéressantes par ici. Я вижу здесь кое-что интересное. Ce film est d’une bêtise! Этот фильм невероятно глуп! J’ai un de ces mal de tête! У меня ужасно болит голова! К сожалению, это, наверное, самое сложное использование
de to master, по крайней мере, в этом списке. Сложность заключается в
факт, что есть выбор. Вы должны сказать что-то либо fait
en or fait de . Говоря конкретно о еде, вы должны
выберите à или à . К счастью, есть конкретный способ определить, следует ли
используйте de или à , когда говорите о том, какая еда или конкретное блюдо
сделано из.В этой статье есть самое лучшее и краткое объяснение.
Я хоть раз сталкивался. По сути, объясняет автор, вы используете de для
поговорить об ингредиенте, который на самом деле что-то составляет. Например, la farine
de bl é (пшеничная мука). С другой стороны, вы используете à для ингредиента, который
может быть удален и все еще позволяет продукту существовать. Возьмем, например, une
soupe aux choux : Суп остался бы, если бы вы убрали капусту. Другой товар
Пример: un круассан au beurre . Хотя масло является неотъемлемой частью
тесто для круассана, у вас может быть ун круассан обыкновенный , где
масло заменено маргарином. Сложнее говорить о том, из чего сделаны непродовольственные товары. В этом случае вы должны использовать либо de , либо en . Обычно говорят, что de более литературное или старомодное.Но, как указывается в этой ветке комментариев, это не обязательно так. Есть даже некоторые выражения, например, un blouson de cuir или un blouson en cuir , где de или en могут использоваться как взаимозаменяемые. К сожалению, не может быть такого простого правила, как
один для еды, и мне никогда не удавалось найти никаких рекомендаций в
специфический. Лично я просто стараюсь на это пойти. Если я действительно хочу настоять
что что-то сделано из определенного материала, я обычно выбираю и ,
что считается лучшим способом подчеркнуть это.В противном случае я использую de .
Хорошая новость в том, что если я использую неправильный предлог, француз
все еще понимаешь меня. Мы называем такие выражения, как «Хорошо…», «безличным».
выражения », поскольку они относятся не к конкретному предмету, а к общему
идея. Во французском языке некоторые из этих выражений используют de как часть «to»,
в то время как другие используют à . Если выражение начинается с C’est , используйте à .Когда выражение начинается с Il est , используйте de Il est bon de pratiquer le français chaque jour. Хорошо практиковать французский каждый день.) Il est difficile de choisir un parfum de glace quand on est pressé! Трудно выбрать вкус мороженого, когда торопишься! Грамматика французского языка не позволяет вам сказать что-то вроде « quelqu’un beau ».Вы должны что-то туда положить, и часто de помогает. Примеры включают общие фразы, например: quelqu’un de beau, rien de neuf, quelque selected de beau . Вы можете увидеть больше примеров в этом переводе популярной свадебной традиции «Что-то старое, что-то новое, что-то позаимствованное и что-то синее». Вы можете спросить, почему прилагательное в этих выражениях
не всегда, кажется, согласен с предметом обсуждения. Требуется немного абстракции
мышление — по сути, идея состоит в том, что этот человек или вещь принадлежит
понятие « beau » или « neuf » и т. д.; это отличается от простого
говоря, что они — это этих вещей (в этом случае вы согласны
прилагательное). Вы можете прочитать об этом здесь. Если вам неудобно пользоваться этой структурой, не
беспокойтесь — хотя вы должны быть знакомы с ним, поскольку он используется довольно часто,
вы можете найти обходные пути. Например, вместо того, чтобы сказать C’est quelqu’un de
beau , можно просто сказать, Il est beau . Хотя может быть
некоторые незначительные коннотативные различия, общий смысл тот же. De запускает такие выражения, как: За некоторыми французскими глаголами следует à когда вы хотите сказать «к». Но эту роль «кому» исполняет de для других
глаголы. Нет твердого правила, почему некоторые глаголы
в паре с на , а другие — с на , поэтому, к сожалению, это означает
их просто нужно запомнить. Вот список наиболее распространенных глаголов, которые сочетаются с de : Вы можете найти более длинные списки здесь
и здесь. «Хорошо, — можете подумать вы, — я просто выучу их наизусть, и все будет хорошо». Ну… не совсем так. Некоторые глаголы, в том числе несколько, которые вы найдете
в этих списках может следовать либо à , либо de . Этот
Однако это не означает, что вы можете выбирать любой предлог. В этих
case значение глагола немного меняется в зависимости от того, какой из них вы используете. Это может показаться запутанным, но вполне вероятно, что вы
уже встретил несколько таких глаголов. Например, parler à означает
«Поговорить с кем-то», а parler de означает говорить о чем-то. Пример: Je parlais à ma mère chaque.
jour au téléphone. против Je
parlais de ma mère chaque jour. Первое предложение означает «Я говорил со своим
мама каждый день по телефону ». А второй означает «Я говорил о маме.
ежедневно.” Однако есть по крайней мере два глагола, которые действительно упрощают задачу. Итак, что выбрать в этих случаях? Как этот комментарий
поток показывает,
в основном все сводится к тому, что звучит лучше. Вместо à или de, некоторые глаголы используют фразу à quelqu’un de .Один из них, с которым вы, вероятно, знакомы, — это demander — demander à quelqu’un de faire quelque selected — это «попросить кого-то что-то сделать». Томас требовал больше всего на свете для сына годовщины. Томас попросил мать купить ему велосипед на день рождения. Вы можете узнать больше о предлогах и словосочетаниях.
которые связаны с французскими глаголами из ссылок, которые я уже включил сюда, так как
ну как это
сайт. Имейте в виду, что хотя наш список значений de длинный, неполный. Есть несколько других тонких, редких или устаревших
использует de . Вы можете найти обширные примеры различных способов. de
Здесь используется .
Но лучший способ найти КАЖДОЕ использование de — это поискать его в
полный французский или французско-английский словарь. Мой верный принт Харпер Коллинз Роберт Пятое издание
несокращенный французско-английский / англо-французский словарь очень помог мне с
исследование для этой статьи, но приложение-словарь с полным текстом
также может быть полезно. De — одно из наиболее часто используемых французских слов. Этот
означает, что вы найдете его в бесчисленных французских фразах, выражениях и идиомах.
Чтобы понять, сколько, проверьте запись WordReference для de ,
который включает в себя, казалось бы, бесконечный список выражений, в которых de их. Во многих из этих выражений de отходит на второй план;
это лишь малая часть того, что говорится.Вот небольшой список фраз
где de играет заметную роль. Если вы прочитали оставшуюся часть этой статьи, вы, вероятно, знаете
ответ на этот вопрос уже. De такой вездесущий, важный,
многогранное французское слово, которое вы встретите в самых разных местах, оно используется в
всевозможными способами. Лучший способ — действительно единственный способ — научиться им пользоваться
— продолжать читать, смотреть, писать и говорить по-французски. Вы можете найти способы
сделай все это бесплатно здесь. De является неотъемлемой частью французского языка, поэтому вы будете регулярно сталкиваться с ситуациями, когда вы видите, слышите и должны использовать его. Хорошо, если вы ошиблись при использовании в
разговорный французский, большинство французов все равно поймут, что вы имели в виду.Они будут
возможно, поправят вас, что может показаться оскорбительным, но это лишь часть
Французская культура. Многие французы, особенно представители старшего поколения, чувствуют себя
они делают вам одолжение, исправляя ваши ошибки, даже очень мелкие. В случае de это может быть один из лучших способов
научись делать это правильно. У меня все еще есть парные глаголы, которые я выучил
с de просто из-за того, как часто меня исправляли, когда я их использовал
с до вместо.Так что не бойтесь выставить себя напоказ. Редко, когда ты
сделать действительно серьезную, совершенно непонятную ошибку, связанную с « de» . Если вы прилежный человек, вы также можете пройти через
наш список значений de и сосредоточиться на каждом из них для определенного
период времени (день, неделя, месяц и т. д.). Вы можете посмотреть онлайн-руководства,
веб-страницы и, возможно, даже планы уроков, относящиеся к разным. Для
Например, вы можете выполнить поиск в Интернете по запросу «французские глаголы, в которых используется de » или
« de as from на французском языке». Но в целом, по опыту могу сказать, что немного
немного учиться и много читать, писать, говорить и слушать, используя de станет для вас очень естественным. Разве это не печальные новости? У вас есть любимое выражение с de? Есть ли
использование de , которое вас особенно сбивает с толку или вызывает затруднения? Не стесняйтесь делиться в комментариях. Merci à Norm B. Для ответа на вопрос об использовании mot «de» en français, эта вдохновляющая статья! De — важный и универсальный предлог, который позволяет вам сказать «of» во французском языке, «some» или просто неопределенное количество.Но это не все; de имеет много разных значений и употреблений на французском языке. В качестве предлога он позволяет вам составить ряд существительных и глагольных словосочетаний. Французский предлог de требуется после некоторых глаголов и фраз, когда за ними следует инфинитив. И de требуется после многих французских глаголов и фраз, которым требуется косвенный объект. Имейте в виду, что de плюс существительное можно заменить наречным местоимением en .Например, J’en ai besoin. > Мне это нужно. le livre de Paul > книга Пола partir de Nice > отправление из Ниццы une tasse de thé > чашка чая le marché de gros > оптовый рынок fatigué du voyage > устал от поездки écrire de la main gauche > писать левой рукой Если за ними следуют определенные артикли le и les , то de сводится к одному слову.Но de не совпадает с la или l ‘. Кроме того, de не имеет контракта с le и les , когда они являются прямыми объектами Французский предлог de требуется после некоторых глаголов и фраз, когда за ними следует инфинитив. Обратите внимание, что в английском переводе может использоваться инфинитив (соглашаться на что-то) или герундий (бояться летать). Французский предлог de требуется после многих французских глаголов и фраз, которые нуждаются в косвенном объекте, но часто в английском языке есть совершенно другой предлог или его нет вообще. Глаголы с де плюс глагол Предлоги — это слова, соединяющие две части предложения. Во французском языке они обычно ставятся перед существительными или местоимениями, чтобы показать связь между этим существительным / местоимением и другим словом, которое ему предшествует. Изучая французский язык, вы будете часто использовать предлоги à и de . В зависимости от их использования они могут означать совершенно разные вещи или одно и то же. Знание того, когда использовать предлог, часто вызывает путаницу у многих французских студентов, но этот урок научит вас различию.К его концу вы должны освоиться с тем, как глаголы взаимодействуют с à и de . Французские предлоги à и de создают постоянные проблемы для французских студентов. Вообще говоря, à означает «до», «в» или «в», а de означает «из» или «от». Оба предлога имеют множество применений, и чтобы лучше понять каждый из них, лучше сравнить их. Использование от до не ограничивается приведенными выше примерами.Вот еще два случая, в которых вы захотите использовать этот предлог. Предлог de также имеет больше применений, чем перечислено выше.Вы будете часто использовать его, говоря о причинах и способах выполнения чего-либо. Важно понимать разницу между французскими предлогами à и de , потому что значение некоторых глаголов зависит от того, используете ли вы à или de .Для других глаголов оба предлога могут использоваться в одном предложении. Во французском языке один глагол может иметь два значения в зависимости от предлога. Если вы выберете неправильный вариант, вы можете сказать «Я пренебрегал Джейн», а не «Я скучаю по Джейн». Это может привести к недопониманию, и вы должны знать разницу. В следующей таблице показаны конкретные глаголы, которые изменяют значение с помощью предлогов. В следующих примерах используются французские сокращения для «кого-то» и «чего-то». При использовании этих глаголов просто замените аббревиатуру существительными, о которых вы говорите. Предлоги à и de могут использоваться в одном предложении, часто, когда вы хотите, чтобы кто-то сделал что-то . Еще одно использование для à и de — в общих выражениях.Опять же, они часто имеют схожее значение, но заметно различаются. Помните основное различие между предлогами: * prêt и prês — два разных слова, но поскольку они являются омофонами, имеет смысл включить их сюда для сравнения. Есть пара французских глаголов, которые могут принимать значения à или de с незначительной разницей в значении или без нее: Вот ВИДЕО Трудности возникают из-за того, что «de» во французском языке может означать много разных слов, ваш учитель обязательно будет использовать такие слова, как «partitif». »Или« неопределенный артикль »и т. Д., Ну, проще сказать, что« de, du, de la и des »- это переводы« некоторые »и« любые »! Например, молоко, вода, рис, терпение, любовь и т. Д. Вещи, которые нельзя разделить, вы не можете сказать «одна вода», вы просто скажете «вода» или «немного воды». ‘эти слова по-французски нуждаются в «de, du, de la» мужской род: de Я хочу немного риса: je veux du riz (riz мужского рода) Мы используем de or d ‘ Мне не нужен рис: je ne veux pas de riz Исключение : с глаголом «быть» Как вы можете видеть, что в бесчисленных словах нет множественного числа (des), за исключением слов, которые мы редко используем в единственном числе: В английском языке неопределенный артикль — это «a» и «an», формы множественного числа нет, вы знаете, что во французском это: un, une и des для множественного числа. форма (это «des» не партитив, просто множественное число un или une), ну, опять же, легче сказать, что они являются переводом «some» и «any». Я хочу яблоко: je veux une pomme Прилагательное может изменить артикль: Я не хочу никакого яблока: je ne veux pas de pommes (для отрицания мы используем «de», а не «des») Если вы говорите о чем-то конкретном, нам понадобится конкретный артикль: Много, мало, много… У меня много денег: j’ai beaucoup d ‘ argent (нет определенного артикула) (argent — мужской род и начинается с гласной) Здесь вы можете поделиться инфографикой со ссылкой на мой сайт! Иногда это неуловимо: DES может быть неопределенным артиклем или сокращением определенного артикля от de + les Elle veut des fleurs (не все, а некоторые, поэтому DES является множественным числом неопределенного артикля UNE) Подробнее о De 1 .De: of La fenêtre de la maison; окно дома форма как: машина моей сестры, реквизиты DE на французском языке: la voiture de ma soeur 2.De: из Je reviens de la maison: возвращаюсь из дома 3. De: Time Le bus de 8 heure 30: the 8.30 автобус 4. De: Cause Elle est morte de faim: Она умирает от голода 5. De: measure Une maison de 120 m2: дом 120 m2 6. De: Expressions Rien de neuf: ничего нового Я люблю конфеты, но не ем сахар J’aime les bonbons mais je ne mange pas de sucre! Собаки животные Les chiens sont des animaux Слово de было определено как наиболее часто встречающееся
слово по-французски ([MITKOV2003: 701]). Он имеет множество вариантов использования и переводов. Перед словом, начинающимся с гласного звука, обычно стоит de пишется d ‘ и произносится [d]. В таких случаях обычно анализируется
как «прикованный» к начальной позиции следующего слога.
Перед согласным в разговорной речи шва часто удаляется (хотя округление губ может сохраняться.
как остаток швы: см. [БАРНЕСКАВИЦКАЯ2002]),
и обычно произносится [d] перед звонким согласным и
[t] перед глухим согласным ( pas de bas [pad ba]; pas de chaise [pat ʃɛz]).До [k]) (как в pas de c af ) он может стать
тип стоматологического щелчка. В наличии h aspiré ,
Шва сохраняется ( па де хаут, [па дё]). Комбинируется с определенными артикулами le и les чтобы сформировать du и des соответственно. При осторожном использовании, de используется вместо des непосредственно перед множественным числом
прилагательное: кулон de longs voyages ; проходов que tu из bonnes vacances .(В поэтическом слове вместо de можно использовать
из du перед прилагательным единственного числа.) Он сочетает , а не с клитиками le или les прикреплен к началу инфинитива: arrête de le toucher! . В зависимости от контекста французский de может использоваться как эквивалент
различные английские предлоги, включая из , из , из , на . Чтобы показать происхождение чего-то или кого-то, особенно когда есть движение
заявленное или подразумеваемое, de является общим эквивалентом английского из : il vient _de_ Londres В этом случае из иногда является возможным переводом, хотя наиболее распространенным эквивалентом
в английском — использовать притяжательную форму с и или, в частности, с обычным сочетанием inanimates,
с составом: le chien _de_ Paul Обратите внимание на использование в превосходной степени, где английский предпочитает в : c’est la plus grande ville _de_ Франция С «говорящими» глаголами, такими как parler , causer , se plaindre , de эквивалентно около (хотя из также часто возможны
на формальном английском): il a parlé de sa mère Если нет ни одного из этих глаголов, около в этом смысле обычно переводится как sur .
или au sujet de : il cherche un livre _sur / au sujet de_ Dali Французский использует de со своего рода «подразумеваемым пассивным»: для обозначения человека.
который что-то написал или произвел, или объект, выполнивший действие.На английском,
мы склонны предпочитать на (или соединение) с людьми, и с или на с
неодушевленные: un CD _de_ Жан-Мишель Жарр В более широком смысле, он также используется для выражения «манеры», где английский обычно использует в : _de_ quelle manière Как расширение предложного употребления, de является обычным способом образования составляет на французском языке. de может представить материал, из которого что-то сделано; общий
переводы сделаны из , сделаны из , из , или, если использовать соединение существительное-существительное: une robe de velours Во многих случаях возможной (хотя иногда и более поэтичной) альтернативой является en . de используется в таких выражениях, как une bouteille de , un verre de , обозначающий контейнер и его содержимое: un verre de lait Помимо предлога, de может быть типом определителя для введения
существительная фраза. Французский de объединяется с определенным артиклем, образуя то, что
иногда именуется неопределенным артиклем («некоторые», «любые») или частичная статья («части», «части»): du beurre Обратите внимание, что приведенное выше неоднозначно: du beurre может означать «некоторый (неуказанный) буфер»,
или «немного (специфического) масла».Один из способов анализа этого — сказать, что du beurre может быть сокращенно от de du beurre , и сказать, что
повторы de всегда удаляются (см. ниже). de может также образовывать частичные конструкции с другими определителями,
переводится как некоторые из … : j’ai bu de ce vin Удаление повторяющихся форм de дает: j’ai besoin de votre aide Непосредственно перед прилагательным множественного числа формальное или осторожное употребление часто предпочитает от до от : ce sont de великие авторы В отрицательном (но не вопросительном) значении обычно используется de сам по себе вместо неопределенного артикля ( un , du , des и т. д.)
как приблизительный эквивалент «а», «нет» или «любой»: je n’ai pas de voiture Однако иногда возможно неопределенное, в частности, для обозначения контраста.И это
обычно используется с être : il n’a pas bu du vin, mais il a bu du виски Форма d’autres — это фиксированная форма, означающая «другой …», «какой-то другой …».
Несмотря на то, что мы сказали выше, — это , иногда можно комбинировать с de .
Например, [ROWLETT2007] дает пример des disques de d’autres musicales . Слово de может быть эквивалентом английского от до .
используется для того, чтобы ‘ввести’ глагол в инфинитиве (или в некоторых конструкциях форма -ing )
где de не использовалось бы, если бы вместо этого использовалась именная фраза: на cessé la publishing de cette revue Есть несколько случаев, когда de используется как «наполнитель» на французском языке, где
перевод на английский не требуется. Когда неопределенная именная фраза квалифицируется причастием прошедшего времени, de является
вставлен на французском языке без эквивалента на английском языке. Он также используется в выражениях, включающих quelque : бис на верре _de_ cassé! Он также используется в таких случаях, как этот: votre salaire sera _de_ deux mille Euro par mois , где это, возможно, можно представить как пересказ …sera _un salaire de _… . Из вышесказанного можно предположить, что de используется в некоторых случаях.
где на самом деле, как правило, используются другие выражения: Французский предпочитает & agrave или другой предлог, представляющий расположение , как перевод «от»
в случаях, когда понятие происхождения или движения не очень сильное, и
в частности, где и agrave обозначают комбинацию
«владение» и «удаление» или «лишение»: boire _à_ la bouteille Используется ли à или de , кажется, зависит от того, как
Сильно понятие «движение». Шарнирную двустороннюю стремянку Krause Trimatic применяют для выполнения высотных работ в домах и на производстве. Благодаря использованию алюминиевой конструкции лестница не подвержена коррозии, а это значит, что ее без опаски можно использовать на улице. Кроме того, лестницу удобно транспортировать и хранить за счет компактной конструкции. В пределах МКАД доставка бесплатная, доставка за МКАД — 40 руб/км. Время доставки — по договоренности. Доставка в течение 48 часов после подтверждения заказа. Удобный, бесплатный и быстрый способ получения заказа. Мы можем доставить любой понравившийся вам товар в любой регион России по 100% предоплате службой SPSR Express. Стоимость доставки вы можете самостоятельно рассчитать на сайте http://www. Изготовленная фирмой KRAUSE-Werk GmbH & Со. KG продукция производится из высококачественных материалов, в соответствии со всеми предусмотренными для этого нормами, положениями и использованием современных технологий. Кроме этого продукция подвергается постоянному контролю качества. В связи с этим изготовитель предоставляет на лестницы следующие сроки гарантии: На эти сроки действуют следующие гарантийные обстоятельства: БЕЗНАЛИЧНЫЙ РАСЧЕТ Данный способ оплаты вы можете выбрать после добавления товара в коризину и оформления заявки менеджеру c указанием комментария о желаемом способе безналичной оплаты. ОПЛАТА НАЛИЧНЫМИ Данный способ оплаты вы можете выбрать при любом спосоье доставки, за исключение доставки Почтой России. Описание Погодостойкий противоскользящий настил из панели, пропитанной фенольной смолой. Быстрый монтаж без инструментов, алюминиевые подмости состоят только из 5 элементов. Небольшие размеры позволяют свободно проезжать через дверные проемы в собранном состоянии. Благодаря изменению высоты платформы с интервалом от перекладины к перекладине возможна установка подмостей на лестницах и уступах. Идеальны для внутренних работ. Проверены TUV/GS, допустимая нагрузка до 200 кг/м2. В наличии 7454 ₽ Под заказ: до 14 рабочих дней 7454 ₽ Характеристики Длина: 1680 мм Высота: 150 мм Ширина: 500 мм Вес: 17 кг Max нагрузка(кг): 150 кг Количество секций: 2 Количество ступеней: 12 Материал: Алюминий + влагостойкий помост Производитель: Страна происхож. Германия Торговая марка: Характеристики Торговый дом «ВИМОС» осуществляет доставку строительных, отделочных материалов и
хозяйственных товаров. Наш автопарк — это более 100 единиц транспортных стредств. На каждой
базе разработана грамотная система логистики, которая позволяет доставить Ваш товар в
оговоренные сроки. Наши специалисты смогут быстро и точно рассчитать стоимость доставки с
учетом веса и габаритов груза, а также километража до места доставки. Заказ доставки осуществляется через наш колл-центр по телефону: +7 (812) 666-66-55 или при
заказе товара с доставкой через интернет-магазин. Уважаемые покупатели! Правила возврата и обмена товаров, купленных через наш интернет-магазин
регулируются Пользовательским соглашением и законодательством РФ. ВНИМАНИЕ! Обмен и возврат товара надлежащего качества возможен только в случае, если
указанный товар не был в употреблении, сохранены его товарный вид, потребительские свойства,
пломбы, фабричные ярлыки, упаковка. Доп. информация Цена, описание, изображение (включая цвет) и инструкции к
товару Подмости малые лестничные 2 х 6 раб. Купить Подмости малые лестничные 2 х 6 раб. выс. 3 и 3.75 м в магазине Санкт-Петербург вы можете в интернет-магазине «ВИМОС». Статьи по теме RAL 1000
RAL 1001
RAL 1002
RAL 1003 RAL 1004
RAL 1005
RAL 1006
RAL 1007 RAL 1011
RAL 1012
RAL 1013
RAL 1014 RAL 1015
RAL 1016
RAL 1017
RAL 1018 RAL 1019
RAL 1020
RAL 1021
RAL 1023 RAL 1024
RAL 1026
RAL 1027
RAL 1028 RAL 1032
RAL 1033
RAL 1034
RAL 1035 RAL 1036
RAL 1037
RAL 2000
RAL 2001 RAL 2002
RAL 2003
RAL 2004
RAL 2005 RAL 2007
RAL 2008
RAL 2009
RAL 2010 RAL 2011
RAL 2012
RAL 2013
RAL 3000 RAL 3001
RAL 3002
RAL 3003
RAL 3004 RAL 3005
RAL 3007
RAL 3009
RAL 3011 RAL 3012
RAL 3013
RAL 3014
RAL 3015 RAL 3016
RAL 3017
RAL 3018
RAL 3020 RAL 3022
RAL 3024
RAL 3026
RAL 3027 RAL 3028
RAL 3031
RAL 3032
RAL 3033 RAL 4001
RAL 4002
RAL 4003
RAL 4004 RAL 4005
RAL 4006
RAL 4007
RAL 4008 RAL 4009
RAL 4010
RAL 4011
RAL 4012 RAL 5000
RAL 5001
RAL 5002
RAL 5003 RAL 5004
RAL 5005
RAL 5007
RAL 5008 RAL 5009
RAL 5010
RAL 5011
RAL 5012 RAL 5013
RAL 5014
RAL 5015
RAL 5017 RAL 5018
RAL 5019
RAL 5020
RAL 5021 RAL 5022
RAL 5023
RAL 5024
RAL 5025 RAL 5026
RAL 6000
RAL 6001
RAL 6002 RAL 6003
RAL 6004
RAL 6005
RAL 6006 RAL 6007
RAL 6008
RAL 6009
RAL 6010 RAL 6011
RAL 6012
RAL 6013
RAL 6014 RAL 6015
RAL 6016
RAL 6017
RAL 6018 RAL 6019
RAL 6020
RAL 6021
RAL 6022 RAL 6024
RAL 6025
RAL 6026
RAL 6027 RAL 6028
RAL 6029
RAL 6032
RAL 6033 RAL 6034
RAL 6035
RAL 6036
RAL 6037 RAL 6038
RAL 7000
RAL 7001
RAL 7002 RAL 7003
RAL 7004
RAL 7005
RAL 7006 RAL 7008
RAL 7009
RAL 7010
RAL 7011 RAL 7012
RAL 7013
RAL 7015
RAL 7016 RAL 7021
RAL 7022
RAL 7023
RAL 7024 RAL 7026
RAL 7030
RAL 7031
RAL 7032 RAL 7033
RAL 7034
RAL 7035
RAL 7036 RAL 7037
RAL 7038
RAL 7039
RAL 7040 RAL 7042
RAL 7043
RAL 7044
RAL 7045 RAL 7046
RAL 7047
RAL 7048
RAL 8000 RAL 8001
RAL 8002
RAL 8003
RAL 8004 RAL 8007
RAL 8008
RAL 8011
RAL 8012 RAL 8014
RAL 8015
RAL 8016
RAL 8017 RAL 8019
RAL 8022
RAL 8023
RAL 8024 RAL 8025
RAL 8028
RAL 8029
RAL 9001 RAL 9002
RAL 9003
RAL 9004
RAL 9005 RAL 9006
RAL 9007
RAL 9010
RAL 9011 RAL 9016
RAL 9017
RAL 9018
RAL 9022 RAL 9023 В целом каркас стены 2 x 4 конструктивно достаточен для многих небольших гаражей и сараев. Если высота несущей стены не превышает 10 футов, то каркас 2 x 4, как правило, соответствует нормам. Здесь, в Medeek Design, мы обычно указываем только 2 x 4 шпильки с шагом 16 дюймов, для небольших навесов и гаражей с шириной здания менее 16 футов. Все другие более крупные конструкции обычно вызываются с внешними шпильками 2 x 6 @ 16 дюймов. если не указано иное.Все наши планы используют двойную верхнюю плиту и одинарную (обрабатываемую давлением при опоре на бетон) нижнюю плиту. Этот тип обрамления считается «обычным световым каркасом» и полностью соответствует строительным нормам и правилам. Обычно установка каркаса с использованием шпилек 2 x 6 вместо шпилек 2 x 4 может добавить дополнительные 40% к стоимости пиломатериалов по проекту. Однако преимущества использования кадрирования 2 x 6: Если высота несущей стены превышает 10 футов, строительные нормы и правила требуют, чтобы они были спроектированы так, чтобы проверять их несущую способность, чтобы противостоять изгибу стоек из-за нагрузок вне плоскости. Не стесняйтесь использовать наш калькулятор каркасных стен, чтобы проверить вместимость ваших каркасных стен. Расстояние между стеллажами 16 дюймов лучше подходит для размещения и поддержки стеллажей и систем хранения, чем 24 дюйма интервал, позволяющий большую гибкость планирования. Иногда местные власти будут вводить требования для стенового каркаса 2 x 6 из-за чрезвычайно сильных снеговых нагрузок, сильных ветров и максимальных показателей теплоизоляции стен.Примечание: если ваш план предусматривает обрамление 2 x 4 и требуется 2 x 6, вы обычно можете просто заменить материал 2 x 6 для стоек, верхних и нижних панелей стены. (Местные власти могут проконсультировать вас по этому поводу). Энергоэффективные конструкции, соответствующие IECC и государственным энергетическим кодексам, являются обязательной частью современного жилищного строительства. Размерный пиломатериал разрезается на определенную длину, ширину и глубину. Однако есть разница между номинальным размером (то, что называется пиломатериал) и фактическим размером. В приведенных ниже таблицах представлены как номинальные, так и фактические размеры многих стандартных размеров пиломатериалов в Северной Америке. Пиломатериалы хвойных пород обычно используются для обрамления стен и полов. В Соединенных Штатах в отношении пиломатериалов хвойных пород действует Американский стандарт на пиломатериалы хвойных пород Национального института стандартов (PS 20). Пиломатериалы хвойных пород имеют несколько стандартных длин, указанных в таблице ниже. Пиломатериалы лиственных пород калибруются в зависимости от того, сколько сторон покрыто поверхностью. В Северной Америке пиломатериалы из твердых пород древесины обычно указываются по четвертной системе, где доска определяется по ее толщине в четверти дюйма.Например, обрезка из твердой древесины, толщина которой в итоге составляет чуть более 1 дюйма (с двух сторон поверхности), называется доской с пятью четвертями (5/4). Ширина доски из твердых пород дерева может быть разной. В большинстве случаев доски из твердой древесины бывают произвольной ширины, чтобы плотник разорвал их до нужного размера. Однако в некоторых случаях, например, в хозяйственных магазинах с большими ящиками, доски имеют размерную ширину, аналогичную ширине мягкой древесины. Желательно проконсультироваться с вашим подрядчиком или поставщиком пиломатериалов перед окончательной доработкой деталей проекта, чтобы вы не удивились тому, что вы получите. Следующая таблица взята из публикации Американского института деревянного строительства «Стандартные технические условия на конструкционный клееный брус лиственных пород». ANSI / AITC A190.1-1992 позволяет клееную древесину любой ширины и глубины. Стандартная ширина указана в вышеприведенной публикации, но при необходимости может быть изменена. Доступен широкий диапазон глубин, многие из которых не могут перечислить здесь, поэтому, пожалуйста, свяжитесь с вашим местным производителем для получения дополнительной информации об их предложениях — обычно глубины начинаются от 6 дюймов и доходят до 30 дюймов и более. Конечно, длина подбирается для каждой работы. Многих начинающих плотников и домашних мастеров по понятным причинам смущает размер пиломатериалов. Это может привести к значительной путанице, если вы ожидаете, что гвоздь размером 2 x 4 на самом деле будет иметь размеры 2 дюйма на 4 дюйма, или если вы ожидаете, что ваша доска 1 x 6 действительно будет иметь эти размеры. Вы обнаружите, что ваша доска 2 x 4 на самом деле составляет 1 1/2 дюйма x 3 1/2 дюйма, а ваша доска 1 x 6 на самом деле составляет 3/4 дюйма x 5 1/2 дюйма. Вы только что столкнулись с реальностью фактических размеров пиломатериалов по сравнению с номинальными размерами — размерами, по которым они определяются в магазине.Размеры, по которым продается пиломатериал, практически никогда не совпадают с фактическими размерами досок, когда вы их измеряете. Так что именно здесь происходит? Вы не поверите, но на самом деле существует некоторая рифма и причина, по которой фактические размеры размерной древесины не соответствуют их названиям. Производители пиломатериалов обычно вырезают дерево из различных стандартных видов пиломатериалов очень скоро после того, как дерево было спилено. На данный момент 2 x 4 фактически составляет 2 дюйма x 4 дюйма, 2 x 10 фактически составляет 2 дюйма x 10 дюймов и т. Д.Но затем свежепиленный (но мокрый) пиломатериал сушат в печи до тех пор, пока он не достигнет желаемого уровня влажности. Во время этого процесса он сжимается, так как влага из древесины удаляется, а клетки древесины сжимаются. После сушки доски строгают до стандартного размера. Следовательно, то, что начиналось как 2 x 4, теперь имеет размер 1 1/2 дюйма на 3 1/2 дюйма. Эти цифры могут незначительно отличаться, но современные производители пиломатериалов довольно хорошо умеют поставлять объемные пиломатериалы стабильного размера.Это совершенно другой тип измерения древесины по сравнению с методом измерения доской, используемым для измерения древесины твердых пород. Имейте в виду, что размерные пиломатериалы из хвойных пород, которые продаются в вашем домашнем магазине или хозяйственном магазине, будут использоваться в первую очередь для строительных проектов, а не для высококачественной обработки древесины. Опять же, имейте в виду, что для твердых пород дерева и фанеры используются совершенно разные правила калибровки.Как только вы точно поймете, какой размер у всех этих материалов, вы сможете соответствующим образом разработать свои проекты. Вот удобная таблица номинальных габаритных размеров пиломатериалов и их реальных размеров: Если вы новичок в покупке пиломатериалов из хвойных и твердых пород древесины для поделок или работ по благоустройству дома, первое, что вы заметите, это то, что размеры, по которым продается древесина (называемые номинальными размерами ), не совпадают с размерами фактических измерений. Кусок сосны 1 x 4, например, на самом деле имеет толщину 3/4 дюйма и ширину 3 1/2 дюйма, в то время как каркасный стержень 2 x 4 на самом деле имеет толщину около 1 1/2 дюйма и ширину 3 1/2 дюйма. Чтобы еще больше запутать ситуацию, стандарты калибровки древесины лиственных пород отличаются от стандартов древесины хвойных пород, и древесина твердых пород обычно продается в единицах объема, известных как подошва доски, а не в единицах размера доски. Все это может сбить с толку, когда вы покупаете пиломатериалы для создания проекта с точными размерами. Термин «размерная древесина» используется с породами древесины хвойных пород (например, сосна или пихта), которые используются в строительстве для изготовления каркасов и других столярных работ. Первоначально доска 2 x 4 была вырезана как грубая зеленая доска размером ровно 2 x 4 дюйма, но к тому времени, когда доски были высушены и строганы, доски стали меньше, приближаясь к теперь стандартным размерам 2 x 4 1. Размер 1/2 x 3 1/2 дюйма. В современных методах обработки пиломатериалов размер досок уже не равен 2 x 4 дюйма при первой резке, но современные методы сушки и строгания по-прежнему оставляют доску толщиной 1 1/2 дюйма и шириной 3 1/2 дюйма.Старый стандарт называния этой доски 2 x 4 все еще остается, даже несмотря на то, что в сегодняшней практике обработки пиломатериалов доска никогда не была размером 2 x 4 дюйма. Фактические и номинальные размеры для стандартных размеров пиломатериалов: Усадка более выражена в поперечном направлении (поперек волокон), чем в продольном (относительно волокон), поэтому доска, продаваемая как 8 футов 2 x 4, обычно очень близка к полным 8 футам в длину. Стандарты размеров, используемые для пиломатериалов лиственных пород (таких как дуб, клен, береза и красное дерево), используемых в прекрасной мебели и мебели, немного запутывают. Используются не только разные эталоны, но и размер зависит от того, с одной стороны (S1S) или с двух сторон (S2S) используется заготовка. Древесина лиственных пород редко продается в стандартных размерах, как древесина хвойных пород. Дополнительно древесина лиственных пород может быть продана в кварталах . Каждая четверть относится к толщине 1/4 дюйма, что означает, что доска 5/4 имеет толщину примерно 1 1/4 дюйма. Если для вашего проекта требуется кусок толщиной ровно 1 дюйм, вы захотите приобрести доску 5/4 и фрезеровать ее до нужного размера с помощью фуганка / строгального станка. Фанера обычно продается в виде листов размером 4 x 8 футов. Чаще всего номинальная толщина фанеры составляет 1/2 дюйма и 3/4 дюйма, но, опять же, фактические размеры немного отличаются. Лист фанеры толщиной 1/2 дюйма действительно имеет толщину 15/32 дюйма, а лист толщиной 3/4 дюйма — 23/32 дюйма. Фанера классифицируется таким образом, чтобы каждая поверхность была оценена по шкале A, B, C или D, где A соответствует самой гладкой шлифованной поверхности. Например, фанера AA имеет мебельную отделку с обеих сторон, в то время как фанера BC будет иметь класс B с одной стороны и C — с другой. После того, как вы выбрали идеальный план дома и наняли подрядчика — и будете готовы приступить к строительству дома своей мечты — вы можете столкнуться с вопросом: «Следует ли мне вкладывать деньги в стенные стойки 2х4 или 2х6»? Каковы преимущества и недостатки увеличения размера наружных стен вашего дома на два дюйма? Различий может быть больше, чем вы ожидаете, и это важный вопрос, который следует учитывать при строительстве нового дома в соответствии с вашими идеальными характеристиками. Есть несколько преимуществ при строительстве с использованием гвоздей 2×6, некоторые из которых очевидны, а некоторые не так очевидны.В зависимости от вашего местоположения у вас может не быть выбора, и вам придется использовать каркас 2×6, потому что местные строительные нормы и правила требуют этого. Эти районы, как правило, находятся в северных штатах с более холодным климатом. Давайте посмотрим на различия между конструкциями 2х4 и 2х6. Неудивительно, что конструкция рамы 2×6 позволяет оставить больше места между внутренними и внешними стенами. Одно только это дополнительное пространство обычно не приводит к лучшей изоляции, но дает больше места для дополнительной изоляции.Однако очень важно обсудить это преимущество со своим подрядчиком, потому что возможность добавить теплоизоляцию к вашим стенам не всегда приводит к тому, что это действительно происходит. Существует несколько различных способов повышения теплоизоляции дома и последующего повышения энергоэффективности для резкого снижения затрат на отопление и охлаждение. Первый способ — купить утеплитель с наивысшими изоляционными характеристиками. Тип используемой изоляции может иметь большее влияние на потребление энергии, чем размер самой стены. Второй лучший способ сэкономить энергию — построить «плотный» дом, что означает ограничение неконтролируемого воздушного потока между внутренней и внешней частью вашего дома.Это во многом зависит от качества конструкции в вашем доме — особое внимание следует уделять таким деталям, как тщательная обшивка фасада (перед сайдингом) воздухонепроницаемым / пароизоляционным слоем, герметизация отверстий для водопровода и электрических трасс, обеспечение хорошей изоляции и распространяется в углы и пространства необычной формы, а также тщательно герметизирует оконные и дверные проемы, а также используемые материалы, такие как улучшенные окна и двери. При строительстве нового дома с каркасом 2×6 вы увеличиваете площадь между внутренней и внешней стенами, где вы можете разместить больше изоляции для повышения энергоэффективности; однако это то, о чем вам нужно будет поговорить со своим подрядчиком.Тот факт, что вы строите рамы 2×6, не означает, что вы автоматически выиграете от этой дополнительной изоляции, потому что строители могут по-прежнему придерживаться минимальных требований к изоляции, установленных строительными нормами. У вас есть потенциал на 69% больше непрерывной изоляции в полости стены, если вы используете стойки 2×6 на 24 дюйма. центров вместо шпилек 2×4 на 16-дюйм. центры. Хотя многие строители предпочитают поддерживать 16-дюйм. центров, даже при использовании более крупных элементов 2×6 (и при небольшом увеличении затрат на материалы), многие строительные нормы и правила допускают 24-дюймовые.центры с 2x6s. Вам нужно будет сделать домашнюю работу, изучая строительные нормы и правила в вашем районе и количество необходимой изоляции. Убедитесь, что вы вкладываете средства в изоляцию с высочайшими изоляционными свойствами и размещаете больше этой изоляции в дополнительном пространстве вашей стены 2×6. Это единственный способ по-настоящему извлечь выгоду из дополнительной энергоэффективности, обеспечиваемой рамной конструкцией 2×6. Распространено заблуждение, что нельзя отличить конструкцию 2х4 от конструкции 2х6 — потому что она все-таки в стене! Правда в том, что большее пространство между внутренней и внешней стенами позволяет более глубокому окну во всем вашем новом доме. Большая глубина оконных и дверных косяков часто делает дом более классическим или богатым. Вы заметите эти дополнительные детали, как и покупатели, когда придет время перепродавать ваш дом. Эти маленькие, но заметные очаровательные элементы — вот некоторые из вещей, которые выделят ваш дом среди других на рынке, что может помочь вам оправдать дополнительные расходы. Стена 2×6 дает вам 2 дополнительных дюйма от внутреннего края окна до готовой стены по сравнению со стеной 2×4.Это пространство, особенно в сочетании с табуретом, выходящим за пределы поверхности стены, обеспечивает щедрое горизонтальное пространство и производит хорошее подсознательное «качественное» впечатление. Поскольку стойки 2х4 являются стандартом в строительстве дома, размер 2х6 почти всегда будет считаться усовершенствованием в процессе строительства нового дома. Важно обсудить это с вашим подрядчиком на самом раннем этапе отношений — даже до того, как он или она сможет обсудить ваши планы, — так как это может означать некоторые серьезные изменения в закупке материалов и процессе строительства в целом. Это не только каркас 2×6, который увеличивает стоимость вашего модернизированного строительного проекта, многие из материалов, которые вам понадобятся для ваших стен, потребуют обновления до нового размера. Какие предметы нужно будет улучшить в дополнение к обрамлению? Вам понадобятся расширенные оконные косяки, чтобы вместить большее пространство на внешней стене. Вам также понадобятся дверные косяки большего размера и дополнительная изоляция, чтобы соответствовать раме 2×6. Хотя это не модернизация, вам также понадобятся двойные верхняя и нижняя стеновые панели (к которым прикреплены стойки).Нижняя плита обычно состоит из пиломатериалов, обработанных под давлением, снизу и обычных пиломатериалов сверху. Все эти и многие другие дополнения увеличат вашу стоимость, что является одним из основных факторов для большего числа домовладельцев, которые не выбирают каркас 2×6. В зависимости от местного законодательства вы можете снизить более высокие материальные затраты, используя недавно разработанные «передовые методы каркаса», которые позволяют использовать меньше пиломатериалов и максимизировать изоляцию ограждающих конструкций здания. Площадь в квадратных футах на плане дома основана на внешних размерах следа дома (и делится на готовую отапливаемую жилую площадь и недостроенную площадь, например, гараж). Поскольку 2×6 на 2 дюйма глубже, чем 2×4, дом, построенный со стенами 2×4 и 2×6, будет в общей сложности на 4 дюйма шире и глубже внутри , чем тот же дом, построенный с 2×6. Это означает, что для дома площадью 2400 квадратных футов интерьер дома размером 2×6 будет около 33.На 5 квадратных футов меньше, чем у дома 2х4. При стоимости строительства 125 долларов за квадратный фут вы, по сути, заплатите более 4000 долларов за «непригодные» квадратные метры. Если это будет иметь для вас значение, вы можете очень серьезно подумать о строительстве с 2×4. Но есть и другие факторы, которые следует учитывать. Если вы какое-то время планировали дом своей мечты и взвешивали все «за» и «против» решений по строительству дома, расчет потенциальной долгосрочной экономии или окупаемости вашего решения о строительстве 2×6 — это, вероятно, то, что вы уже сделали или планируете делать.Итак, какой из них — 2×4 или 2×6 — сэкономит вам больше денег в долгосрочной перспективе? Трудно подсчитать экономию или окупаемость вашего решения 2×6. Во-первых, давайте обсудим энергоэффективность вашей новой собственности.Если вы правильно воспользовались преимуществами дополнительной глубины стены, которую предлагает конструкция 2×6, добавив больше изоляции, чем требуется большинством строительных норм, вы, вероятно, ощутите значительную экономию на ежемесячных счетах за отопление и охлаждение. Но это также будет зависеть от нескольких факторов. Во-первых, какой климат в вашем доме? Если вы живете в таком месте, как Сан-Франциско, где погода не вызывает резких колебаний или экстремальных температур в разные сезоны, вы можете не сэкономить столько денег.Но если вы живете в таком месте, как Нью-Йорк, где зимняя погода может привести к температурам ниже нуля и множеству метелей, а лето может означать температуры, близкие или даже трехзначные в любой день, небольшая дополнительная изоляция может иметь большое значение. Чтобы определить, каков ваш климат на самом деле — помимо анекдотических свидетельств — может быть стоит взглянуть на так называемые градусни для вашей местности. Градусо-дни отопления — это количество градусов в день отопительного сезона, когда средняя температура ниже 65 градусов по Фаренгейту.При вычислении градусо-дня берется рекордно высокая и рекордно низкая температура за день, складываются и делятся на 2; результат вычитается из 65. Сумма ниже нуля — это количество градусо-дней отопления для этого дня; любая сумма, равная нулю или больше, учитывает дни с нулевым градусом тепла. По мнению исследователей из Совета строительных исследований Университета Иллинойса в Урбана-Шампейн, местность, имеющая температуру 5725 градусо-дней или выше, является хорошим местом для возведения стен 2×6.(В любом случае, рассматриваете ли вы расходы на отопление или охлаждение, или и то, и другое, изоляция чердака может быть важнее — или, по крайней мере, не менее важно, чем изоляция стен.) Может быть трудно подсчитать потенциальную экономию затрат на строительство 2×6, пока вы не выберете тот или иной путь и не построите свой дом. Но обращение к соседям с домами аналогичного размера с обоими типами строительства может помочь вам лучше понять свою потенциальную экономию средств. Помимо потенциальной экономии за счет расходов на отопление и охлаждение, вам также необходимо оценить потенциальную стоимость перепродажи. Сможет ли конструкция 2×6 добавить очаровательной эстетики или энергоэффективности, чтобы продать ваш дом быстрее, чем соседи? Опять же, это, как правило, метрики, которые сложно рассчитать, но не невозможно, если у вас есть хорошие сравнения, которые можно провести в вашем районе. Хотя вы не всегда можете окупить свои деньги на такого рода модернизации, то же самое верно и для других «необходимых» обновлений для домовладельцев, строящих дома новой постройки. Исследования показали, что такие предметы, как бассейны, модернизированная техника и современные водонагреватели, не всегда означают окупаемость ваших инвестиций. В большинстве случаев речь идет о том, какие аспекты вашего дома наиболее важны для вас и добавят удовольствия от вашего нового дома. Вы предпочитаете уютный дом, не требующий искусственного обогрева или охлаждения? Вам нравится эстетика дверей и окон с большими пробками и подоконниками? Если это так, конструкция 2×6 может быть идеальной для вас, а потенциальное увеличение стоимости при перепродаже будет лишь дополнительным преимуществом. Как и план этажа вашего нового строящегося дома, все сводится к тому, что лучше всего подходит для вас и вашей семьи.Если вы планируете жить в своем новом доме в течение значительного количества времени, вы никогда не должны основывать свои решения о новом строительстве исключительно на стоимости перепродажи. Инвестируйте в те области своего дома, которые важны для вас, и потраченные деньги всегда окупаются. Сноска: верхняя левая фотография на главном изображении любезно предоставлена Картером Ламбером; нижний левый рисунок на главном изображении представляет собой дом в стиле мастера с 3 спальнями и 2 ванными комнатами с внешними стенами 2×6 (план № 141-1081). Каков квадратный метр прямоугольника 2 на 6 футов? Насколько велик прямоугольник 2 x 6? Площадь прямоугольника 2 x 6 футов (результаты могут быть округлены) Площадь прямоугольника равна его ширине, умноженной на высоту. Площадь = Ширина * Высота Площадь по длине сторон (результаты округлены) В этом году мы снова участвуем в олимпиаде «Русский медвежонок» 2016-2017. У моих ребятишек (учатся они в 3 и 6 классе) конкурс уже прошел, дети написали тесты. В этот раз олимпиадные задания оказались получше. Вопросы конкурса «Русский медвежонок — языкознание для всех» были интересные и не такие дурацкие, как в прошлом году. Есть вопросы очень легкие, а есть и сложные. Но по крайне мере соответствуют теме русского языка. Откровенного треша на этот раз нет. После конкурса мы разобрали вопросы, радует, что дети дали в основном правильные ответы. По крайней мере, надеюсь на это. Правда узнаем правильные ответы и результаты на официальном сайте конкурса еще не скоро. Вот вопросы конкурса «Русский медвежонок» для 2-3 класса и наши ответы на эти олимпиадные тесты, надеюсь, правильные. Задачи, оцениваемые в 3 балла 1. На полянке беседовали пять разных друзей-животных. Первый спросил: «Кудах-тах-тах?». Ему ответил второй: «Ква-ква-ква». На это третий возразил: «Чик-чирик!». С ним согласился четвертый: «Му-у-у!». И только пятый промолчал. Кто это был? Варианты: А) утка Ответ: А) утка 2. Каким из этих знаков чаще всего заканчиваются предложения? Варианты: А) ! Ответ: В) . 3. На уроке проходили правила переноса. Саше стало скучно, он закрасил приставку в слове перенос и получил слово нос. Тогда он стал закрашивать приставку пере- и в других случаях, пытаясь получить осмысленные слова. А с каким словом это не вышло? Варианты: (А) переход Ответ: (В) перепад 4. Решила Света сочинить сказку. Придумала три первых предложения: Варианты: (А) 1,2,3; Ответ: (Б) 2,3,1 5. Вот первые части двусложных слов: ут-, мет-, вет-, а вот вторые: -ро, -ка. Сколько слов можно получить, соединяя первые части со вторыми? Варианты: (А) два Ответ: (Г) пять: утро, утка, метро, метка, ветка 6. Какое слово называет не птенца? Варианты: (А) журавлёнок; Ответ: (В) опёнок — это гриб 7. Собака, лошадь, медведь, аист. Где никто из них не живет? Варианты: (А) в дупле; Ответ: (А) в дупле. В гнезде живет аист, в берлоге — медведь, в конуре — собака, в конюшне — лошадь. 8. Сказочный принц живет за зубчатой стеной с башнями по углам и бойницами. Стена окружена рвом с подъемным мостом. Как лучше всего назвать место, где живет принц? Варианты: (А) дворец; Ответ: (Б) замок 9. Вольке выпала большая удача. Ему всегда … . Варианты: (А) падает; Ответ: (Д) везёт 10. Что бывает у дома, но не бывает у квартиры? Варианты: (А) дверь; Ответ: (В) крыша Задачи, оцениваемые в 4 балла 11. Как нельзя заполнить пропуск? Варианты: (А) осторожно; Ответ: (Б) боязно 12. Название какого месяца начинается с той же буквы, что и его номер? Варианты: (А) январь; Ответ: (Д) декабрь — двенадцатый месяц 13. Название какой из этих игрушек звучит как призыв к какому-то действию? Варианты: (А) матрёшка; Ответ: (Д) ванька-встанька 14. На старом пузырьке Алиса увидела полустёрщуюся надпись: «4 таблеток». Наверное, — подумала она, — перед 4 должна была стоять еще одна цифра, и это цифра ….». Варианты: (А) 9; Ответ: (Д) 1. 14 таблеток 15. В школу поступили львёнок, ягнёнок, утёнок, и телёнок. Их записали под фамилиями: Львов, Баранов, Селезнёв и … . Варианты: (А) Коровин; Ответ: (Б) Быков. Фамилии образованы от названий животных — пап 16. В книге Бориса Житкова о мальчике Алёшке читаем: «Бабушка на меня поглядела». Очень сильно на меня поглядела. Я вспомнил и сказал: Что мы пропустили? Варианты: (А) Здравствуй; Ответ: (Г) Спасибо 17. Название какой еды не говорит о том, как её готовят? Варианты: (А) вареники; Ответ: (Г) печёнка. Вареники варят, запеканку запекают, мороженое морозят, тушёнку тушат. 18. Найди среди этих слов самое длинное, которое нельзя переносить. Варианты: (А) поэма; Ответ: (Г) огонь 19. Дв аурока подряд Макс баловался, а на третьем наконец…. Варианты: (А) примирился; Ответ: (Б) утихомирился 20. Утроением знаков в китайском письме изначально передавались слова с новым значением, например: Найди переводы иероглифов, если известно, что Варианты: (А) дом, семья, парус; Ответ: (Д) чаща, толпа, ураган Задачи, оцениваемые в 5 баллов 21. В комнате сидят десять человек: Вова, Илья, Женя, Саша, Сима, Серёжа, Валя, Игорь, Лёва и Таня. Какое утверждение точно неверно? Варианты: (А) в комнате больше четырёх мальчиков; Ответ: (Д) в комнате больше пяти девочек 22. В какой пример можно вставить букву так, чтобы получилось слово? Варианты: (А) жь_жь; Ответ: (Б) шьёшь 23. Петя прочитал в белорусской книге: Варианты: (А) колокольчики; Ответ: (А) колокольчики 24. Варианты: (А) ключ; Ответ: (Б) мост; 25. В какой паре слова связаны по смыслу не так, как во всех остальных парах? Варианты: (А) рисовать-рисунок; Ответ: (В) красить-краска; 26. У Ренаты Мухи есть стихотворения — «недоговорки». К какому из них название «недоговорка» подходит меньше, чем к остальным? Варианты: (А) Один Верблюд, кипя от злобы, (Б) Как-то раз у Короля (В) Как-то раз в одной стране (Г) Едет Окунь на Коне. (Д) Ко всем этим стихотворениям название «недоговорка» подходит одинаково. Ответ: (Г) Едет Окунь на Коне. 27. В интернете несколько десятков раз встречается слово торовиш. А какое слово чаще всего встречается рядом с ним? Варианты: (А) непонятный; Ответ: (Г) торовыван. Нужно прочитать слово справа налево, получается шиворот-навыворот 28. В книжке Александра Шибаева про русский язык читаем: А вот еще четыре волшебных слова из этой книжки и одно неволшебное. Какое неволшебное? Варианты: (А) навес Ответ: (А) навес. Так как получается не весна, а вЕсна. Результатов конкурса «Русский медвежонок — языкознание для всех» будут опубликованы на официальном сайте конкурса еще не скоро, аж в январе 2017 года. Надеюсь на отличные места! Здравствуйте, дорогие читатели сайта Спринт-Ответ. Вот и пришло время пополнить рубрику «Образование», которая уже покрылась плесенью, ведь недавно стартовал конкурс «Русский медвежонок». Ниже можно ознакомиться с вопросами и ответами для учащихся 4-5 класса за 2017-2018 учебный год. Также в этой же рубрике можно будет найти и ответы на вопросы для учащихся и других классов. Правильные ответы можно узнать сразу после вопросов, либо в вариантах ответа к вопросам, они выделены синим цветом. 1. В стихотворении Александра Шибаева о буквах есть такие двустишия: 2. В каком имени больше всего слогов: 3. Дедушка водит Аню в детский сад 4. Каким из этих знаков препинания нередко заканчиваются предложения 5. В Московском институте садоводства вывели земклунику. А что это? 6. Число 5 больше числа 4, но в слове четыре больше букв, чем в слове пять. Какая ещё пара устроена так же? 7. Что часто встречается? 8. В данных словах буквы а и о заменены прочерками. В каком из слов пропущены две буквы а и одна буква о? 9. К какому слову нельзя добавить «э» и получить новое слово? 10. В русском языке кошка мяукает, а в литовском она miauksi. Что по-литовски делают коза, корова, свинья? Примечание: û читается как долгий у. 11. Пес Пиф из сказки Георгия Остера «Приключения Пифа» привык понимать все слова в прямом значении. Он понимает, что брать можно, например, косточку или корзинку. А вот как брать след, так и не понял. Какое еще выражение Пиф вряд ли поймет правильно: 12. — Мама, а глаза бывают коричневые? — Да, тогда говорят, что глаза … . 13. Судя по происхождению слова мешок, раньше похожие предметы делали из… 14. В какой паре даны разнокоренные слова? 15. Когда на электронных часах 16:00, то можно сказать: сейчас четыре часа. Что должны показывать часы, чтобы на вопрос «который час» можно было ответить, не называя число. 16. В каком из предложений слово человек значит не то, что в остальных? 17. Коля — Васин друг со школы. Какое утверждение точно верно? 18. Футбольный тренер Юрий Павлович Сёмин известен среди болельщиков под шутливые прозвищем Шпалыч.С какой командой Юрий Сёмин добился наибольших успехов? 19. В каком примере пропущено больше всего букв? 20. В книжке-головоломке Атона Тилипмана «Зубака» во многих словах перепутались буквы. Вот, например, была азбука, стала зубака. Если вы правильно расставите буквы в данных ниже словах, в четырёх случаях получаются названия птиц, а в одном нет. В каком? 21. Лёва социальные сети собрал группу всех друзей, чья фамилия образована от того же корня, что его. Кроме него, в этот список попали Добряков, Добров, Добрынин и Доброхвалова. Когда Лёва расставил фамилии по алфавиту, то его собственная оказалась в самой середине. Какая фамилия у Лёвы? 22. Незнайка пишет окончание -ого через «в». Получая письма от Незнайки, Знайка при виде очередной такой ошибки язвительно пишет на полях: «Нет такого слова!». Про какое слово (в написании Незнайки) Знайка так не напишет? 23. В каком случае уменьшительное слово соотносится с исходным не так как в остальных? 24. Какое из слов не образует устойчивого словосочетания со словом зрение? 25. В 16 веке один английский издатель предложил для некоторых предложений использовать особый знак. Из пяти данных ниже вопросов учителей он подошёл бы к четырём. Определив его предназначение, выберите, для какого вопроса этот знак не подходит. 26. Маша набрала на компьютере слова: труд, трюк, турок, тара, кот, а шутник Яша заменил в них все буквы т одной и той же другой буквой. Как ни удивительно, после этого программа проверки орфографии подчеркнула как неправильное лишь одно слово. Какое Машино слово прекратилось в неправильное? 27. Про что в Словаре Академии Российской 1789 года говорится, что это когда-то называлось «крыльцо вислое»? 28. Какой из этих сборников рассказов был издан вскоре после сборника с похожим названием? Учащиеся всех возрастных категорий могут принять участи в международной олимпиаде «Русский медвежонок – языкознание для всех». Участие, и тем более победа в этом конкурсе пополнит портфолио достижений грамотой или сертификатом участника. Победители получают ценные призы. История «Русского медвежонка» начинается с 2000 г. С каждым годом популярность конкурса растет. А это говорит о мотивированности школьников к изучению русского языка, что и является целью проведения интеллектуального соревнования. Олимпиада школьников приобрела известность не только в нашей стране. Дети других стран (США, Японии, Израиля, Кубы, Индии), изучающие русский язык, также участвуют в соревнованиях. В 2000 г. участниками олимпиады были 64 тыс. школьников, а в 2016 более 2млн. Участие в лингвистическом конкурсе доступно каждому, не зависимо от оценки по русскому языку. Олимпиада школьников проходит в школах, ехать никуда не надо. Задания высылаются прямо в учреждения образования. Это ещё одно преимущество конкурса. Интеллектуальное состязание проводится по пяти возрастным группам, начиная со второго класса. Но даже учащиеся 1 классов могут принять в нем участие. Для участия в олимпиаде школьникам не обязательно готовиться специально. Результаты предыдущих лет показывают, что даже без специальной подготовки дети могут ответить на несколько вопросов. А вот для победы и получения приза придется потрудиться: Международная олимпиада является своего рода тренировкой к Всероссийской школьной олимпиаде. Задания выстроены по принципу ЕГЭ. Своеобразие заданий делают её увлекательной, а тестовая форма – облегчает выбор правильного ответа. В заданиях пять вариантов ответов, достаточно выбрать один. Результаты ответов записываются в бланки. Регулярное участие в конкурсе дает положительные результаты: Конкурс раскрывает многогранность, благозвучие и богатство русского языка. Показывает детям насколько увлекательно и интересно может быть познание родной речи. Олимпиада школьников проходит в один день по всей России, как правило, в ноябре. В 2017 г. дата определена – 15 ноября. Время на решение составляет 1 час 15 минут. Бланки с ответами отправляются в региональный комитет, а оттуда в Москву, где происходит обработка результатов. Итоги соревнования высылаются в школы в январе месяце. Дети получают сертификаты участников всероссийского образца, грамоты, дипломы и призы. Конкурс-игра «Русский Медвежонок — языкознание для всех» (официальный сайт ) — младший брат популярного международного математического конкурса «Кенгуру — математика для всех». Впервые «Медвежонок» был проведен в 2000 году по инициативе Кировского Центра дополнительного образования одаренных школьников при поддержке Института лингвистики Российского государственного гуманитарного университета и Российского Оргкомитета «Кенгуру». Интерес к игре постоянно растет. У массовости «Медвежонка» две причины. Во-первых, он доступен. Игра проводится прямо в школах, занимает всего около полутора часов, и участвовать в ней могут все желающие. Записывать решения не нужно — достаточно выбрать один из предложенных пяти вариантов ответа и отметить его номер на специальном бланке; среди 30 заданий есть как трудные, так и совсем легкие, так что почти каждому участнику удается правильно выполнить хотя бы несколько из них. Во-вторых, составители стараются подбирать задания, требующие не только (и не столько) знания правил, но и общей культуры, логики и размышления, а порой — и чувства юмора. Ведь главная цель игры — показать красоту русского языка, преодолеть представление о нем как формальном и скучном предмете. Методическая комиссия конкурса работает в Институте лингвистики РГГУ. Основные авторы задач — преподаватели, аспиранты и выпускники РГГУ и МГУ. В Институте лингвистики проводится семинар «Жанры и типы лингвистических задач», одной из практических целей которого является составление и обсуждение задач для этого конкурса. Участники семинара охотно занимаются этим, многим студентам уже удалось составить хорошие задачи. Задачи конкурса предназначены для школьников разных возрастов: от 2-го до 11-го класса. Составители готовят 5 комплектов заданий: для 2-3, 4-5, 6-7, 8-9 и 10-11 классов. Для самых младших — 26 (с 2009 г. 28) задач, для остальных возрастных групп — по 30. В последние годы организуется и пользуется популярностью также интернет-конкурс «Русский медвежонок для учителей», для которого методкомиссия готовит 12 непростых задач. Тестовые задачи «Медвежонка» существенно отличаются от самодостаточных олимпиадных задач не только типом, но и компактностью и временем выполнения (на решение каждой задачи отводится несколько минут). Среди них есть и совсем элементарные, и такие, над которыми могут ломать головы специалисты. Все составляемые для конкурса задачи тщательно проверяются членами методической комиссии, многие из них приходится отбраковывать, поскольку задачи должны удовлетворять ряду разных параметров. После проверки решений задач, осуществляемой с помощью компьютера, проводится статистический анализ решений, который показывает уровень сложности задачи и выявляет характерные ошибки, что учитывается при написании решений и комментариев, публикуемых в сборниках, а также при составлении вариантов задач следующего года. Вот лишь несколько примеров задач: 2. Даны слова: всего, ничего, некого, отчего, полого. 3. Найдите подлежащие во фразах: 4. Какое из пяти перечисленных слов по смыслу лишнее? 5. Какое из пяти перечисленных слов по смыслу лишнее? 6. Читаем у А. С. Пушкина: 7. Город Великие Луки получил такое название из-за того, что: Решения задач 1. Чтобы правильно решить эту задачу, надо не путать звуки с буквами. Посмотрим, из каких звуков состоят данные слова. Для этого запишем их транскрипцию: пол [пол], муж [муш], шей [шэj’], ель , ров[роф]. Теперь прочитаем звуки в обратном порядке: [лоп] — лоб, [шум] — шум, — ешь, [л’эj] — лей. Четыре слова получилось, а вот слова, произносящегося как [фор], в русском языке нет. Ответ: 4 (Г). 2. Все эти слова можно понять как формы родительного падежа: всегомёда Кролика не хватило Винни-Пуху; Винни-Пух ничего не боялся;Пятачку некого было дожидаться; Крошка Ру сбежал из отчего дома;Сове не хватало какого-нибудь полого предмета. Ответ: (Д). 3. Слова тореро и сомбреро имеют одинаковую форму как в роли подлежащего, так и в роли прямого дополнения. В русском языке и подлежащее, и дополнение могут находиться как перед сказуемым, так и после него, поэтому иногда в таких случаях возникает неоднозначность: фразу Мать любит дочь можно понять двумя способами. Однако в данных предложениях неоднозначности не возникает, так как подлежащим для глагола надеть должно быть одушевленное существительное, а дополнением — неодушевленное. Поскольку одушевленным существительным из данных является тореро, то оно и будет подлежащим в обоих предложениях. Ответ: (В). 4. Слова шведка, румынка, итальянка, японка обозначают лиц женского пола соответствующей национальности. Слово же корейка означает не национальность, а разновидность мяса (жительницы Кореи называются не корейками, а кореянками). Оно и является лишним по смыслу. Ответ: (Д). 5. Четыре последних существительных обозначают существо женского пола и соотносимы с существительными, обозначающими существо мужского пола: зайчиха — заяц, львица — лев, актриса — актёр, японка — японец. Существительное обезьяна обозначает животное независимо от пола: отдельных существительных, обозначающих самца и самку обезьяны, в русском языке нет. Оно и является лишним по смыслу. Ответ: (А). 6. Что означает устаревшее слово чета? Это два предмета или два лица, пара. Вспомните такие однокоренные слова, как чётный, сочетание. В этом отрывке из «Сказки о царе Салтане» витязи идут парами, по двое. Ответ: (Б). 7. Будем действовать методом исключения. Понятно, что ответ — не Г (название города неизмеримо старше компании «Лукойл») и не В (никакого Луки Великого в истории России не было, да и город в этом случае имел бы название вроде «Великолукск»). Вариант А (лук родился особенно крупным) маловероятен: в этом случае город, скорее всего, получил бы имя вроде «Добрые [т. е. хорошие] Луки». Выбирая между мастерами по изготовлению луков и речными излучинами, примем в расчет то огромное значение, которое играли в жизни древних славян реки. Ответ: (Д). Задачи конкурса с решениями и комментариями ежегодно выпускаются отдельными брошюрами, а также публикуются в газете «Русский язык».Подробнее о «Русском медвежонке» можно почитать на В основе урока русского языка находится правило, которое необходимо понять и запомнить. Такая форма подачи материала хоть и эффективна, но не всегда интересна. А вот «Русский медвежонок» 2017–2018 – это возможность посмотреть на языкознание под другим углом. Думать, рассуждать логически и не зубрить материал – с таким набором инструментов стоит подходить к изучению русского языка. Так считают организаторы олимпиады: центр дополнительного образования одарённых школьников, ООО «Слово», ООО «Игра». Научное руководство осуществляет Институт лингвистики РГГУ. Центральный оргкомитет расположен в городе Кирове. Самая известная в стране международная олимпиада школьников по русскому языку «Русский медвежонок – языкознание для всех» проводится с 2000-го года и заслуженно стала одним из самых популярных соревнований в России и ближнем зарубежье. На протяжении уже шестнадцати лет во всех школах, лицеях и гимназиях проводится это замечательное интеллектуальное состязание. С чем связана такая популярность? Конкурс «Русский медвежонок» – это способ проверки себя в любом возрасте, начиная с начальной и заканчивая старшей школой. Участвовать в игре могут абсолютно все желающие без какого-либо предварительного отбора, даже если в дневнике по русскому языку не только «пять» и «четыре». Для участия в состязании формируются пять возрастных групп учащихся: Принимать участие могут и учащиеся профессиональных средних заведений, которые осваивают программу по русскому языку в рамках своего учебного курса. Конкурс является международным. В нём принимают участие школьники из России, СНГ, Прибалтики, Индии, Японии, Греции, Израиля, Кубы, Польши, ОАЭ, Монголии, Великобритании, США и других стран. «Русский медвежонок» – это три десятка нестандартных, интересных и занимательных вопросов (2-м и 3-им классам даётся 28 заданий) различной сложности и 75 минут (1 час 15 минут) на раздумья. Решения писать не нужно. Достаточно выбрать из пяти предложенных вариантов ответов правильный и отметить его номер на специальном бланке. Все задания выполняются в игровой форме. Олимпиада «Русский медвежонок» проходит для всех участников по всей России и за её пределами в один день, как правило, в середине ноября текущего учебного года. В 2017-2018 учебном году он состоится в среду, 15 ноября. После того как задания выполнены, их передают в региональный оргкомитет, а уже оттуда отправляют в Москву, где и подводят итоги конкурса. В январе после обработки бланков учебные заведения получают ведомости с результатами своих участников и местом каждого из них в общероссийском списке своей параллели. Лучших учащихся отметят призами. Всем без исключения участникам конкурса вручат сертификат участника всероссийского образца. Большинство заданий по силам обычному школьнику, и всё же это не совсем обычные задания. Чтобы осилить задачки, заданные «Русским медвежонком», нужны не только глубокие знания русского языка, но и логическое мышление, смекалка, умение сопоставлять факты. Это задания, выстроенные по принципу ЕГЭ, то есть здесь дети учатся работать с бланком, правильно его заполнять, учатся работать с материалами заданий. Задания олимпиады построены интересно, и участники могут отследить свой результат, потому что они ежегодно получают сертификаты, где указывается количество баллов (максимальное количество – 100 баллов), и место в общероссийском списке своей возрастной группы. Регулярно участвуя в игре, ребята не чувствуют себя неловкими «медвежатами». Они тренируют ум, развивают память, приобретают необходимый багаж знаний. Совет: чтобы хорошо подготовиться к соревнованию, необходимо решать задания «Русского медвежонка» прошлых лет, которые есть на официальном сайте конкурса. Здесь же можно найти задания и ответы олимпиад прошлых лет. Языкознание кажется многим школьникам сводом сухих и скучных правил. Чтобы преодолеть это заблуждение, открыть детям красоту науки о языке, ежегодно проводится международная игра-конкурс «Русский медвежонок – языкознание для всех». Ежегодно она привлекает участников из России и десятков зарубежных стран. Статистика участия в конкурсе За последние несколько лет конкурс приобрёл и размах, и популярность. По форме проведения он приближен к стандартам ЕГЭ. Вопросы назвать простыми нельзя, все они требуют не только эрудиции, но и умения размышлять. Интерес к конкурсу у ребят учителя объясняют тем, что он не только показывает красоту «великого и могучего», но и меняет представление о нём как о скучном предмете. Неслучайно, переходя из одного класса в другой, дети вновь решаются пройти это тестирование и пополнить свой багаж знаний новыми фактами из области языкознания. Любите русский язык, изучайте и черпайте из него животворящую силу. Недаром Президент Российской Федерации В.В. Путин на встрече Совета по межнациональным отношениям в Йошкар-Оле назвал русский язык духовной общностью нашей нации: «Русский язык для нас – язык государственный, язык межнационального общения. Его ничем заменить нельзя. Он естественный духовный каркас всей нашей многонациональной страны». Окунуться в атмосферу интеллектуального состязания можно, посмотрев видео: Олимпиады и конкурсы Портал «Олимпиадное движение» На Портале «Олимпиадное движение» размещается актуальная информация об олимпиадах различного уровня, подаются и принимаются заявки на участие школьника в олимпиаде, размещаются новости и события олимпиад, а также информация о результатах участия в олимпиадах. В дальнейшем на Портале будут размещены материалы для подготовки к олимпиаде по выбранному предмету, а также сервис с помощью которого можно будет сформировать электронное портфолио школьника на основе результатов олимпиад. Ссылка на Портал Информация об олимпиадах, новости и материалы для подготовки доступны для просмотра любому посетителю Портала. Для подачи заявки и просмотра результатов необходимо пройти процедуру регистрации на Портале. Инструкция для родителей по регистрации на Портале Открытая олимпиада школьников Для учащихся 7–11 классов олимпиада проводится в два этапа — заочный (отборочный) и очный (заключительный). Первый этап состоит из двух дистанционных туров. В период проведения отборочного этапа зарегистрировавшимся участникам доступна тренировочная сессия, которая включает набор заданий, охватывающий все разделы профильной программы по информатике для школьников. Заключительный этап является очным и проводится в один очный тур в компьютерной форме. По сумме баллов определяются участники в заключительном (очном) туре, который проходит в дни весенних школьных каникул. На заключительный этап обязательна очная регистрация участников. Место, время и порядок очной регистрации на площадках проведения олимпиады публикуется на портале olymp.ifmo.ru. Сайт олимпиады: https://olymp.ifmo.ru Участие в олимпиаде добровольно, безвозмездно и реализуется после регистрации. Регистрация проводится в электронной форме самим участником на странице регистрации. Регистрация проводится с момента ее открытия и завершается 9 февраля 2018 г. в 18.00. Победители олимпиады по информатике имеют льготы при поступлении в ВУЗы. Архив задач прошлых лет. Открытая олимпиада школьников по математике Для учащихся 7–11 классов олимпиада проводится в два этапа — заочный (отборочный) и очный (заключительный). Первый этап состоит из двух дистанционных туров. В период проведения отборочного этапа зарегистрировавшимся участникам доступна тренировочная сессия, которая включает набор заданий, охватывающий все разделы профильной программы по информатике для школьников. Заключительный этап является очным и проводится в один очный тур в письменной форме на бумажных носителях. По сумме баллов определяются участники в заключительном (очном) туре, который проходит в дни весенних школьных каникул. На заключительный этап обязательна очная регистрация участников. Место, время и порядок очной регистрации на площадках проведения олимпиады публикуется на портале olymp.ifmo.ru. Сайт олимпиады: https://olymp.ifmo.ru Участие в олимпиаде добровольно, безвозмездно и реализуется после регистрации. Регистрация проводится в электронной форме самим участником на странице регистрации. Регистрация проводится с момента ее открытия и завершается 9 февраля 2018 г. в 18.00. Победители олимпиады по математике имеют льготы при поступлении в ВУЗы. Архив задач прошлых лет. Международная интернет-олимпиада по физике Основное отличие интернет-олимпиады по физике от других олимпиад заключается в использовании виртуальных лабораторий – программных моделей физических систем с телами, жидкостями, электрическими элементами, физическими приборами и т.п. Поэтому проходить олимпиаду следует из специальной программы BARSIC, позволяющей выполнять задания на основе моделей виртуальных лабораторий – подробности установки программы указаны на странице регистрации. Олимпиада для 7-11 классов состоит из двух туров – отборочного и заключительного. Отборочный этап состоит из двух дистанционных, заключительный этап – очный. Информация о предстоящих турах сообщается на домашней странице олимпиады не позднее, чем за месяц до начала тура. Регистрация на олимпиаду свободная и может осуществляться самими учащимися. При наличии проблем следует прочитать инструкции по их устранению на странице Вопрос-ответ. Победители интернет-олимпиады по физике имеют льготы при поступлении в ВУЗы соответствующего профиля. МетаШкола Это бесплатные международные и открытые российские интернет-олимпиады по разным предметам: математике, русскому языку, физике, английскому языку, окружающему миру, устному счёту. Сайт олимпиад: https://metaschool.ru Всероссийский игровой конкурс по естествознанию «Человек и природа» (ЧИП) – Всероссийский игровой конкурс по естествознанию. Новый конкурс проекта ИПО РАО «Продуктивное обучение для всех» продолжает традиции конкурсов «Кенгуру», «КИТ», «Золотое руно» и др. Конкурс проводится для учащихся 1-10 классов. Символ конкурса – рыжий любознательный лисенок Чип, который вместе с участниками конкурса изучает нашу планету Земля, ее растительный и животный мир, историю развития человечества и родную страну. ЧИП проводится ежегодно в третий четверг апреля, результаты передаются в школы к 1 сентября. Сайт конкурса – http://www.konkurs-chip.ru/ Международный конкурс «Кенгуру» Конкурс проходит непосредственно в школах – в один и тот же день во всех странах (обычно – третий четверг марта). В сентябре-октябре проходит бесплатное тестирование для учеников 5, 7 классов. В январе проводится конкурс для выпускных классов. Сайт конкурса – http://mathkang.ru. Конкурс «Русский Медвежонок – языкознание для всех» Этот конкурс тестового типа, в котором достаточно выбрать один из предложенных пяти вариантов ответа и отметить его номер на бланке, занимает два урока. Задания ориентированы на логику, общую культуру, а порой – и на чувство юмора. Главная цель игры – показать красоту и богатство русского языка, преодолеть впечатление о нём как формальном и скучном школьном предмете. Обычно конкурс проводится в ноябре. Сайт конкурса – http://www.rm.kirov.ru/index.htm. Международный конкурс по истории МХК Конкурс проводится ежегодно в феврале. Конкурсные задания выдаются на дом и собираются в образовательных учреждениях. Тема конкурса 2018 года: XIX век: Новое время России. С содержанием предыдущих конкурсов можно ознакомиться на сайте www.runodog.ru. Игровой конкурс «British Bulldog» (Британский бульдог) Международный игровой конкурс по английскому языку «British Bulldog» (Британский бульдог) проводится с февраля 2008 года. Учредителем конкурса является Институт продуктивного обучения Российской Академии Образования (ИПО). Конкурс проводится ежегодно в декабре. Участникам предлагается ответить на 60 вопросов различной сложности за 75 минут. Задания разделены на 6 блоков по 10 вопросов, направленных на различные виды языковой деятельности (знание грамматики, лексики, понимание связного текста, понимание звучащей речи). Первые 10 вопросов — аудирование. Задания составлены для 4 возрастных групп: 3-4, 5-6, 7-8, 9-11 классы. В каждом из возрастных вариантов присутствуют вопросы повышенной сложности. С содержанием предыдущих конкурсов можно ознакомиться на сайте www.runodog.ru. Конкурс «КИО – Конструируй, исследуй, оптимизируй» Международный конкурс по применению ИКТ в естественных науках, технологиях и математике «Конструируй, Исследуй, Оптимизируй» (КИО) проводится, начиная с 2004 года. Учредителями Конкурса является журнал «Компьютерные инструменты в образовании» и Институт продуктивного обучения Российской Академии Образования (ИПО). Конкурс проводится ежегодно в последних числах февраля – начале марта на двух уровнях: уровень I – для учеников до 7 класса включительно; уровень II – для всех остальных участников. Задания конкурса представлены в форме компьютерных моделей-лабораторий с игровыми элементами. В процессе работы с заданием участник конструирует частичные решения задачи, которые оцениваются по установленным в задании критериям. Таким способом формируется «рекорд» – число или набор чисел, характеризующие степень достижения поставленных в задании целей. Механизм рекорда позволяет участникам оценивать собственное продвижение в решении задач, а для жюри конкурса рекорды являются основой для составления рейтинга. Сайт конкурса – http://kio14.multivariant.ru Мастерская конкурса «КИО» – разбор заданий конкурсов КИО прошлых лет, исследовательская работа, связанная с самостоятельной постановкой новых задач, их решением и обсуждением. Конкурс «КИТ – компьютеры, информация, технологии» В «КИТе» может принять участие любой ученик со 2 по 11 класс. Задания предлагаются для пяти разных возрастных групп: 2-3 классы, 4-5 классы, 6-7 классы, 8-9 классы, 10-11 классы. Подведение итогов проводится раздельно по каждой параллели. Формат конкурса: участникам предлагается 30 заданий (во втором и третьем классах – 20 заданий), к каждому из которых дается 5 вариантов ответов. Среди них только один правильный. Участник должен в специальном бланке отметить правильный ответ без каких-либо пояснений. Не разрешается пользоваться учебниками и калькулятором. На выполнение всего конкурсного задания дается 1 час 15 минут (во втором и третьем классах – 45 минут). Подробнее о конкурсе можно узнать на сайте: http://www.konkurskit.ru/ Международная игра-конкурс по информатике и ИКТ Обычно игра проводится в первые дни после зимних каникул (в конце января). Форма проведения аналогична таким популярным конкурсам как «Кенгуру», «Русский медвежонок» и «Золотое Руно» – бескомпьютерный вариант. Участниками конкурса могут стать учащиеся школ, в том числе, не изучающие информатику. С 2011 года в игре могут участвовать 1-2-е классы. Для них определён начальный уровень заданий. Подробнее о конкурсе можно узнать на сайте «Инфознайки». Здесь же можно познакомиться с задачами прошлых лет, а также потренироваться в игре «Инфознайка» в off-line режиме. В 2017-2018 учебном году конкурс будет проходить 12-17 февраля 2018 года. Другие проекты: Международный конкурс по информатике Главная цель конкурса «Бобёр» состоит в том, чтобы способствовать росту интереса у школьников к информационно-компьютерным технологиям (ИКТ) с первых дней пребывания в школе. Время проведения конкурса – 13-19 ноября 2017 года. «;
Здравствуйте, дорогие читатели сайта Спринт-Ответ. Вот и пришло время пополнить рубрику «Образование», которая уже покрылась плесенью, ведь недавно стартовал конкурс «Русский медвежонок». Ниже можно ознакомиться с вопросами и ответами для учащихся 4-5 класса за 2017-2018 учебный год. Также в этой же рубрике можно будет найти и ответы на вопросы для учащихся и других классов. Правильные ответы можно узнать сразу после вопросов, либо в вариантах ответа к вопросам, они выделены синим цветом. 1. В стихотворении Александра Шибаева о буквах есть такие двустишия: 2. В каком имени больше всего слогов: 3. Дедушка водит Аню в детский сад 4. Каким из этих знаков препинания нередко заканчиваются предложения 5. В Московском институте садоводства вывели земклунику. А что это? 6. Число 5 больше числа 4, но в слове четыре больше букв, чем в слове пять. Какая ещё пара устроена так же? 7. Что часто встречается? 8. В данных словах буквы а и о заменены прочерками. В каком из слов пропущены две буквы а и одна буква о? 9. К какому слову нельзя добавить «э» и получить новое слово? 10. В русском языке кошка мяукает, а в литовском она miauksi. Что по-литовски делают коза, корова, свинья? Примечание: û читается как долгий у. 11. Пес Пиф из сказки Георгия Остера «Приключения Пифа» привык понимать все слова в прямом значении. Он понимает, что брать можно, например, косточку или корзинку. А вот как брать след, так и не понял. Какое еще выражение Пиф вряд ли поймет правильно: 12. — Мама, а глаза бывают коричневые? — Да, тогда говорят, что глаза … . 13. Судя по происхождению слова мешок, раньше похожие предметы делали из… 14. В какой паре даны разнокоренные слова? 15. Когда на электронных часах 16:00, то можно сказать: сейчас четыре часа. Что должны показывать часы, чтобы на вопрос «который час» можно было ответить, не называя число. 16. В каком из предложений слово человек значит не то, что в остальных? 17. Коля — Васин друг со школы. Какое утверждение точно верно? 18. Футбольный тренер Юрий Павлович Сёмин известен среди болельщиков под шутливые прозвищем Шпалыч.С какой командой Юрий Сёмин добился наибольших успехов? 19. В каком примере пропущено больше всего букв? 20. В книжке-головоломке Атона Тилипмана «Зубака» во многих словах перепутались буквы. Вот, например, была азбука, стала зубака. Если вы правильно расставите буквы в данных ниже словах, в четырёх случаях получаются названия птиц, а в одном нет. В каком? 21. Лёва социальные сети собрал группу всех друзей, чья фамилия образована от того же корня, что его. Кроме него, в этот список попали Добряков, Добров, Добрынин и Доброхвалова. Когда Лёва расставил фамилии по алфавиту, то его собственная оказалась в самой середине. Какая фамилия у Лёвы? 22. Незнайка пишет окончание -ого через «в». Получая письма от Незнайки, Знайка при виде очередной такой ошибки язвительно пишет на полях: «Нет такого слова!». Про какое слово (в написании Незнайки) Знайка так не напишет? 23. В каком случае уменьшительное слово соотносится с исходным не так как в остальных? 24. Какое из слов не образует устойчивого словосочетания со словом зрение? 25. В 16 веке один английский издатель предложил для некоторых предложений использовать особый знак. Из пяти данных ниже вопросов учителей он подошёл бы к четырём. Определив его предназначение, выберите, для какого вопроса этот знак не подходит. 26. Маша набрала на компьютере слова: труд, трюк, турок, тара, кот, а шутник Яша заменил в них все буквы т одной и той же другой буквой. Как ни удивительно, после этого программа проверки орфографии подчеркнула как неправильное лишь одно слово. Какое Машино слово прекратилось в неправильное? 27. Про что в Словаре Академии Российской 1789 года говорится, что это когда-то называлось «крыльцо вислое»? Учащиеся всех возрастных категорий могут принять участи в международной олимпиаде «Русский медвежонок – языкознание для всех». Участие, и тем более победа в этом конкурсе пополнит портфолио достижений грамотой или сертификатом участника. Победители получают ценные призы. История «Русского медвежонка» начинается с 2000 г. С каждым годом популярность конкурса растет. А это говорит о мотивированности школьников к изучению русского языка, что и является целью проведения интеллектуального соревнования. Олимпиада школьников приобрела известность не только в нашей стране. Дети других стран (США, Японии, Израиля, Кубы, Индии), изучающие русский язык, также участвуют в соревнованиях. В 2000 г. участниками олимпиады были 64 тыс. школьников, а в 2016 более 2млн. Участие в лингвистическом конкурсе доступно каждому, не зависимо от оценки по русскому языку. Олимпиада школьников проходит в школах, ехать никуда не надо. Задания высылаются прямо в учреждения образования. Это ещё одно преимущество конкурса. Интеллектуальное состязание проводится по пяти возрастным группам, начиная со второго класса. Но даже учащиеся 1 классов могут принять в нем участие. Для участия в олимпиаде школьникам не обязательно готовиться специально. Результаты предыдущих лет показывают, что даже без специальной подготовки дети могут ответить на несколько вопросов. А вот для победы и получения приза придется потрудиться: Международная олимпиада является своего рода тренировкой к Всероссийской школьной олимпиаде. Задания выстроены по принципу ЕГЭ. Своеобразие заданий делают её увлекательной, а тестовая форма – облегчает выбор правильного ответа. В заданиях пять вариантов ответов, достаточно выбрать один. Результаты ответов записываются в бланки. Регулярное участие в конкурсе дает положительные результаты: Конкурс раскрывает многогранность, благозвучие и богатство русского языка. Показывает детям насколько увлекательно и интересно может быть познание родной речи. Олимпиада школьников проходит в один день по всей России, как правило, в ноябре. В 2017 г. дата определена – 15 ноября. Время на решение составляет 1 час 15 минут. Бланки с ответами отправляются в региональный комитет, а оттуда в Москву, где происходит обработка результатов. Итоги соревнования высылаются в школы в январе месяце. Дети получают сертификаты участников всероссийского образца, грамоты, дипломы и призы. Конкурс «Р у сский Медвежонок — языкознание для всех»
— младший брат популярного международного математического конкурса «Кенгуру — математика для всех». Впервые он был проведен в 2000 году, и с тех пор интерес к этому соревнованию растёт лавинообразно: если в «Медвежонке-2000» участвовали 64 тысячи школьников, то в 2011 году — 2 811 206 участников из России, Казахстана, Украины, Латвии, Молдовы, Кыргызстана, Узбекистана, Израиля, Японии, США и ряда других стран. У такой массовости «Медвежонка» — несколько причин. Во-первых, он доступен, поскольку проводится прямо в школах и занимает всего два урока. Во-вторых, он относится к тестовому типу, то есть записывать решения не надо — достаточно выбрать один из предложенных пяти вариантов ответа и отметить его номер на бланке. В-третьих, среди 30 заданий есть и совсем несложные, так что каждому участнику удается дать верный ответ хотя бы на несколько из них. Наконец, сами задания ориентированы не столько на механическое знание правил, сколько на логику, общую культуру, а порой — и на чувство юмора. Ведь главная цель игры — показать красоту и богатство русского языка, преодолеть впечатление о нём как формальном и скучном школьном предмете. Очень сложно привить интерес к учёбе современным детям. Одни живут в достатке и не переживают за своё будущее. Другие понимают, что хорошие отметки в школе не гарантируют успеха во взрослой жизни. Да и сам ход обучения скучен и монотонен. Педагоги заметили, что школьники охотно обучаются, если процесс учёбы идёт в форме игры. Но если есть ещё и материальный стимул, то это совсем круто! Полное название этого состязания: «Русский медвежонок — знание языков для всех». Это международный интеллектуальный конкурс, в основе которого лежит любовь и повышенный интерес к русскому языку. Его история имеет пятнадцатилетний стаж. Организаторами и зачинщиками выступает несколько образований: «Центр вспомогательного просвещения одарённых учащихся», организация «Слово», общество «Игра». За научную сторону мероприятия отвечает Лингвистический университет РГГУ. Курируют состязание представители науки — И. С. Рубанов и Е. В. Муравенко. Стоит назвать государства, которые активно участвуют в этом событии: Ну и Россия — на правах организатора и «виновника торжества». У «Русского медвежонка» есть старший брат: «Кенгуру — обычная математика для всех!» В этом интеллектуальном состязании принимают школьники со второго по выпускной класс. А ещё учащиеся ПТУ, которые изучают соответствующую школьную программу. Проводить мероприятие в регионах помогают местные предприниматели и состоятельные структуры. Часто под конкурс создаются специальные временные комитеты, выбираются региональные представители. Олимпиада проходит в один день по всей стране. На выполнение заданий уходит два академических часа. Срок проведения становится известен за 90 дней до старта. Все вопросы группируются по категориям (классам): Почти во всех категориях по тридцать заданий. Задания делятся на группы сложности. Существует определённая система оценок: чем сложнее вопрос, тем больше баллов можно заработать. Задания оформлены в виде тестов. Всем победителям и участникам выдаются сертификаты, дипломы, поощрительные грамоты. Итоги данного конкурса проводятся раздельно по классам. До начала февраля школы получат все результаты, узнают своё место в общероссийском рейтинге. Вас может шокировать то, что конкурс этот платный, хотя сама сумма символична. Но есть и льготные категории: «Русский медвежонок» интересен тем, что за счёт оплаты участников формируется призовой фонд. Оставшиеся деньги уходят за организацию события. Можно собирать и дополнительные средства, но распоряжаться ими можно только в пределах того учебного заведения, где были собраны. Это отличный стимул для многих детей. Он побуждает к участию даже шалопаев и двоечников. Сами задания не являются особо сложными. Они больше похожи на игру, требуют смекалки и сообразительности. Нет необходимости быть вундеркиндом, слишком одарённым ребёнком. Это праздник знаний для всех! А вот после этого соревнования у многих возникает желание чаще заглядывать в книги, узнать много нового. И активно готовиться на следующий год! В 2016 году «Русский медвежонок» состоялся 15 ноября. Точная дата на 2017 год ещё не известна. Но можно смело ориентироваться на этот срок. Причин для отмены этого соревнования нет. Он полностью окупается, не требует финансовых затрат из худеющего бюджета. А само участие стоит не больше одного доллара. В мероприятии заинтересованы все: и дети, и учителя, и муниципальные власти. Задания и ответы прошлых лет можно легко посмотреть на информационном ресурсе. Массу полезных сведений содержит официальный сайт. Все подробности и тонкости Вы легко и просто узнаете на нём. Эта олимпиада школьников — лотерея без проигрыша! В конце ноября В. Путин встречался с одарёнными детьми. У пятиклассника он спросил: «Где кончается Россия?». Ребёнок ответил правильно, но не удовлетворил президента. У России нету границ! И нет границ у русского языка: он любим и почитаем многими. На этом языке писал Пушкин и Толстой, Тургенев и Некрасов. Язык передаёт образ мысли, чувств и частично состояние души. Даже матерные словечки своей энергетикой побеждают вялое нехорошее словцо англичан и американцев. А Владимир Высоцкий смело подметил в песне, что даже в парижских туалетах есть надписи на нашем языке. Русский мир и русская культура несёт планете много позитива и энергии. И не случайно в конкурсе «Русский медвежонок» активно участвуют дети со всех уголков Земли. Понять атмосферу конкурса, интерес к нему детей поможет видео (прим. удалено обладателем): «Я русский бы выучил только за то, что им разговаривал Пушкин!» — почти из Маяковского. В основе урока русского языка находится правило, которое необходимо понять и запомнить. Такая форма подачи материала хоть и эффективна, но не всегда интересна. А вот «Русский медвежонок» 2017–2018 – это возможность посмотреть на языкознание под другим углом. Думать, рассуждать логически и не зубрить материал – с таким набором инструментов стоит подходить к изучению русского языка. Так считают организаторы олимпиады: центр дополнительного образования одарённых школьников, ООО «Слово», ООО «Игра». Научное руководство осуществляет Институт лингвистики РГГУ. Центральный оргкомитет расположен в городе Кирове. Самая известная в стране международная олимпиада школьников по русскому языку «Русский медвежонок – языкознание для всех» проводится с 2000-го года и заслуженно стала одним из самых популярных соревнований в России и ближнем зарубежье. На протяжении уже шестнадцати лет во всех школах, лицеях и гимназиях проводится это замечательное интеллектуальное состязание. С чем связана такая популярность? Конкурс «Русский медвежонок» – это способ проверки себя в любом возрасте, начиная с начальной и заканчивая старшей школой. Участвовать в игре могут абсолютно все желающие без какого-либо предварительного отбора, даже если в дневнике по русскому языку не только «пять» и «четыре». Для участия в состязании формируются пять возрастных групп учащихся: Принимать участие могут и учащиеся профессиональных средних заведений, которые осваивают программу по русскому языку в рамках своего учебного курса. Конкурс является международным. В нём принимают участие школьники из России, СНГ, Прибалтики, Индии, Японии, Греции, Израиля, Кубы, Польши, ОАЭ, Монголии, Великобритании, США и других стран. «Русский медвежонок» – это три десятка нестандартных, интересных и занимательных вопросов (2-м и 3-им классам даётся 28 заданий) различной сложности и 75 минут (1 час 15 минут) на раздумья. Решения писать не нужно. Достаточно выбрать из пяти предложенных вариантов ответов правильный и отметить его номер на специальном бланке. Все задания выполняются в игровой форме. Олимпиада «Русский медвежонок» проходит для всех участников по всей России и за её пределами в один день, как правило, в середине ноября текущего учебного года. В 2017-2018 учебном году он состоится в среду, 15 ноября. После того как задания выполнены, их передают в региональный оргкомитет, а уже оттуда отправляют в Москву, где и подводят итоги конкурса. В январе после обработки бланков учебные заведения получают ведомости с результатами своих участников и местом каждого из них в общероссийском списке своей параллели. Лучших учащихся отметят призами. Всем без исключения участникам конкурса вручат сертификат участника всероссийского образца. Большинство заданий по силам обычному школьнику, и всё же это не совсем обычные задания. Чтобы осилить задачки, заданные «Русским медвежонком», нужны не только глубокие знания русского языка, но и логическое мышление, смекалка, умение сопоставлять факты. Это задания, выстроенные по принципу ЕГЭ, то есть здесь дети учатся работать с бланком, правильно его заполнять, учатся работать с материалами заданий. Задания олимпиады построены интересно, и участники могут отследить свой результат, потому что они ежегодно получают сертификаты, где указывается количество баллов (максимальное количество – 100 баллов), и место в общероссийском списке своей возрастной группы. Регулярно участвуя в игре, ребята не чувствуют себя неловкими «медвежатами». Они тренируют ум, развивают память, приобретают необходимый багаж знаний. Совет: чтобы хорошо подготовиться к соревнованию, необходимо решать задания «Русского медвежонка» прошлых лет, которые есть на официальном сайте конкурса. Здесь же можно найти задания и ответы олимпиад прошлых лет. Языкознание кажется многим школьникам сводом сухих и скучных правил. Чтобы преодолеть это заблуждение, открыть детям красоту науки о языке, ежегодно проводится международная игра-конкурс «Русский медвежонок – языкознание для всех». Ежегодно она привлекает участников из России и десятков зарубежных стран. Статистика участия в конкурсе За последние несколько лет конкурс приобрёл и размах, и популярность. По форме проведения он приближен к стандартам ЕГЭ. Вопросы назвать простыми нельзя, все они требуют не только эрудиции, но и умения размышлять. Интерес к конкурсу у ребят учителя объясняют тем, что он не только показывает красоту «великого и могучего», но и меняет представление о нём как о скучном предмете. Неслучайно, переходя из одного класса в другой, дети вновь решаются пройти это тестирование и пополнить свой багаж знаний новыми фактами из области языкознания. Любите русский язык, изучайте и черпайте из него животворящую силу. Недаром Президент Российской Федерации В.В. Путин на встрече Совета по межнациональным отношениям в Йошкар-Оле назвал русский язык духовной общностью нашей нации: «Русский язык для нас – язык государственный, язык межнационального общения. Его ничем заменить нельзя. Он естественный духовный каркас всей нашей многонациональной страны». Окунуться в атмосферу интеллектуального состязания можно, посмотрев видео: В основе урока русского языка находится правило, которое необходимо понять и запомнить. Такая форма подачи материала хоть и эффективна, но не всегда интересна. А вот «Русский медвежонок» 2017–2018 – это возможность посмотреть на языкознание под другим углом. Думать, рассуждать логически и не зубрить материал – с таким набором инструментов стоит подходить к изучению русского языка. Так считают организаторы олимпиады: центр дополнительного образования одарённых школьников, ООО «Слово», ООО «Игра». Научное руководство осуществляет Институт лингвистики РГГУ. Центральный оргкомитет расположен в городе Кирове. СОДЕРЖАНИЕ Самая известная в стране международная олимпиада школьников по русскому языку «Русский медвежонок – языкознание для всех» проводится с 2000-го года и заслуженно стала одним из самых популярных соревнований в России и ближнем зарубежье. На протяжении уже шестнадцати лет во всех школах, лицеях и гимназиях проводится это замечательное интеллектуальное состязание. С чем связана такая популярность? Конкурс «Русский медвежонок» – это способ проверки себя в любом возрасте, начиная с начальной и заканчивая старшей школой. Участвовать в игре могут абсолютно все желающие без какого-либо предварительного отбора, даже если в дневнике по русскому языку не только «пять» и «четыре». Для участия в состязании формируются пять возрастных групп учащихся: Принимать участие могут и учащиеся профессиональных средних заведений, которые осваивают программу по русскому языку в рамках своего учебного курса. Конкурс является международным. В нём принимают участие школьники из России, СНГ, Прибалтики, Индии, Японии, Греции, Израиля, Кубы, Польши, ОАЭ, Монголии, Великобритании, США и других стран. «Русский медвежонок» – это три десятка нестандартных, интересных и занимательных вопросов (2-м и 3-им классам даётся 28 заданий) различной сложности и 75 минут (1 час 15 минут) на раздумья. Решения писать не нужно. Достаточно выбрать из пяти предложенных вариантов ответов правильный и отметить его номер на специальном бланке. Все задания выполняются в игровой форме. Олимпиада «Русский медвежонок» проходит для всех участников по всей России и за её пределами в один день, как правило, в середине ноября текущего учебного года. В 2017-2018 учебном году он состоится в среду, 15 ноября. После того как задания выполнены, их передают в региональный оргкомитет, а уже оттуда отправляют в Москву, где и подводят итоги конкурса. В январе после обработки бланков учебные заведения получают ведомости с результатами своих участников и местом каждого из них в общероссийском списке своей параллели. Лучших учащихся отметят призами. Всем без исключения участникам конкурса вручат сертификат участника всероссийского образца. Большинство заданий по силам обычному школьнику, и всё же это не совсем обычные задания. Чтобы осилить задачки, заданные «Русским медвежонком», нужны не только глубокие знания русского языка, но и логическое мышление, смекалка, умение сопоставлять факты. Это задания, выстроенные по принципу ЕГЭ, то есть здесь дети учатся работать с бланком, правильно его заполнять, учатся работать с материалами заданий. Задания олимпиады построены интересно, и участники могут отследить свой результат, потому что они ежегодно получают сертификаты, где указывается количество баллов (максимальное количество – 100 баллов), и место в общероссийском списке своей возрастной группы. Регулярно участвуя в игре, ребята не чувствуют себя неловкими «медвежатами». Они тренируют ум, развивают память, приобретают необходимый багаж знаний. Совет: чтобы хорошо подготовиться к соревнованию, необходимо решать задания «Русского медвежонка» прошлых лет, которые есть на официальном сайте конкурса. Здесь же можно найти задания и ответы олимпиад прошлых лет. Языкознание кажется многим школьникам сводом сухих и скучных правил. Чтобы преодолеть это заблуждение, открыть детям красоту науки о языке, ежегодно проводится международная игра-конкурс «Русский медвежонок – языкознание для всех». Ежегодно она привлекает участников из России и десятков зарубежных стран. Статистика участия в конкурсе За последние несколько лет конкурс приобрёл и размах, и популярность. По форме проведения он приближен к стандартам ЕГЭ. Вопросы назвать простыми нельзя, все они требуют не только эрудиции, но и умения размышлять. Интерес к конкурсу у ребят учителя объясняют тем, что он не только показывает красоту «великого и могучего», но и меняет представление о нём как о скучном предмете. Неслучайно, переходя из одного класса в другой, дети вновь решаются пройти это тестирование и пополнить свой багаж знаний новыми фактами из области языкознания. Любите русский язык, изучайте и черпайте из него животворящую силу. Недаром Президент Российской Федерации В.В. Путин на встрече Совета по межнациональным отношениям в Йошкар-Оле назвал русский язык духовной общностью нашей нации: «Русский язык для нас – язык государственный, язык межнационального общения. Его ничем заменить нельзя. Он естественный духовный каркас всей нашей многонациональной страны». Окунуться в атмосферу интеллектуального состязания можно, посмотрев видео: http://ysugam.sabemo.ru/3/63/russkiy-medvezhonok-2016-zadaniya-dlya Этот образец предназначен исключительно для участников KidsKonnect! Зарегистрируйтесь Медведь гризли , также известный как бурый медведь, весит от 300 до 1500 фунтов и достигает 8 футов в высоту. Медведи гризли в Соединенных Штатах — вымирающий вид, находящийся под угрозой исчезновения. Продолжайте читать, чтобы узнать больше о медведях, или загрузите весь пакет рабочих листов. Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник. Появится ссылка as Grizzly Bear Facts and Worksheets: https://kidskonnect.com — KidsKonnect, 22 ноября 2016 г. Использование с любой учебной программой Эти рабочие листы были специально разработаны для использования с любой международной учебной программой. Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы. Вернуться к экосистемам >> Морские экосистемы Семья белых медведей у груды китовых костей недалеко от Кактовика, Аляска. Информация о состоянии и тенденциях в популяциях белых медведей необходима для информирования об управлении белыми медведями в соответствии с законами США и международными соглашениями. Геологическая служба США поддерживает долгосрочную исследовательскую программу, посвященную динамике популяции белых медведей на юге моря Бофорта.Кроме того, Геологическая служба США сотрудничает со Службой охраны рыб и диких животных США в исследованиях популяций в Чукотском море. Чтобы оценить как размер популяции, так и показатели жизнеспособности, мы использовали исследования по метке-повторной поимке, основанные на физическом отлове медведей, в первую очередь весной. В настоящее время мы разрабатываем аналитический подход, который позволит нам интегрировать дополнительные типы данных (например, пространственные данные, генетические данные, собранные неинвазивным способом) в процесс моделирования, чтобы обеспечить улучшенные оценки состояния популяции.Результаты прошлых исследований позволили нам оценить взаимосвязь между показателями естественного движения населения и изменением окружающей среды, что дает нашим партнерам информацию, необходимую для принятия управленческих решений. Потепление климата может привести к значительным изменениям в здоровье и энергетике арктической фауны, особенно той, которая зависит от среды обитания морского льда, например, белых медведей. Здоровье и энергетическое состояние животного отражают взаимодействие между его поведением и окружающей средой.Из-за этого измерение изменений в состоянии здоровья и энергетики может выявить важные связи между факторами экологического стресса и динамикой популяции. Исследования в этой целевой области сосредоточены на (i) сборе данных о различных системах, которые помогают определять и опосредовать здоровье и энергетику белых медведей, и (ii) разработке программ мониторинга и наблюдения для выявления изменений в здоровье популяции с течением времени. Кроме того, эта работа позволит нам разработать понимание того, как популяции белых медведей будут реагировать на различные стрессовые факторы, модулируемые изменением климата, включая воздействие загрязнителей и патогенов, изменения в структуре пищевой сети и доступности добычи, а также изменения в пространственном распределении. Белый медведь идет по льду в южной части моря Бофорта на Аляске. Белые медведи привязаны к морскому льду почти для всех функций своего жизненного цикла. Наиболее важным из них является добыча пищи или доступ к пище. Белые медведи едят почти исключительно тюленей, и они в равной степени зависят от моря в своем питании, как тюлени, киты и другие водные млекопитающие.Однако белые медведи не водные животные, и доступ к ним только с поверхности морского льда. За последние 25 лет период летнего таяния морского льда увеличился, а летний ледяной покров уменьшился более чем на полмиллиона квадратных миль. Зимой количество старого льда резко сокращается, преимущественно в западной части Арктики. Эта потеря стабильного старого льда катализирует дополнительную потерю морского ледяного покрова каждое лето, потому что более тонкий молодой лед легче тает в течение недавнего более теплого лета.Исследования в этой целевой области направлены на лучшее понимание того, как изменения в распределении и характеристиках среды обитания морского льда могут повлиять на приспособленность, распределение и взаимодействие белых медведей с людьми. Если мы знаем, как белые медведи реагируют на изменения количества и качества льда, мы сможем предсказать, как прогнозируемые изменения льда могут повлиять на будущие популяции белых медведей. Это даст менеджерам наилучшие возможности для адаптации стратегий, обеспечивающих долгосрочную устойчивость белых медведей в изменяющейся ледовой среде. Беременные белые медведи попадают в берлоги в октябре или начале ноября, рожают детенышей в декабре или начале января и покидают берлоги в марте или начале апреля. Исторически сложилось так, что большинство белых медведей из популяции южной части моря Бофорта строили родильные дома на морском льду. Однако за последние три десятилетия, когда морской лед стал тоньше и более склонным к фрагментации, в распределении берлог произошел сдвиг в сторону суши. На основании данных, собранных у взрослых самок медведей, помеченных радиоактивными метками, в настоящее время гнездование матерей происходит с относительно высокой плотностью вдоль центральной и восточной арктических прибрежных равнин Аляски.Доступность деннинговой среды обитания — опосредованная особенностями ландшафта, способствующими образованию снежных заносов, — по-видимому, увеличивается в восточной части прибрежной равнины Аляски. В Чукотском море белые медведи исторически встречались преимущественно на суше как в России, так и на Аляске. В последние годы, когда площадь морского льда отступила дальше на север осенью, чукотские полярные медведи сместили свои наземные берлоги к северу, главным образом на островах Врангеля и Геральд в России и редко на побережье Аляски.Выявление факторов, влияющих на распределение берлоги и продолжительность берлоги, позволит нам лучше отслеживать репродуктивный успех и снизить вероятность беспокойства пойманных медведей в результате антропогенной деятельности. Пожалуйста, соблюдайте авторские права. Несанкционированное использование запрещено. Пожалуйста, соблюдайте авторские права. Несанкционированное использование запрещено. Пожалуйста, соблюдайте авторские права. Несанкционированное использование запрещено. Пожалуйста, соблюдайте авторские права. Несанкционированное использование запрещено. Пожалуйста, соблюдайте авторские права. Несанкционированное использование запрещено. 1/5 1/5 Мамы белых медведей рожают от одного до трех детенышей. Мамы белых медведей рожают от одного до трех детенышей. Продолжительность жизни в дикой природе: Белые медведи в основном едят тюленей. Белые медведи часто молча отдыхают у отверстия для дыхания тюленя во льду, ожидая, пока тюлень всплывет в воде. Белый медведь также может охотиться, плавая подо льдом. Но изменение климата затрудняет охоту на белых медведей. Лед тает раньше и переформируется позже, чем это было в прошлом. Без морского льда белый медведь вынужден искать другую, менее питательную пищу. Пожалуйста, соблюдайте авторские права. Несанкционированное использование запрещено. Белые медведи бродят по ледяным покровам Арктики и плавают в прибрежных водах этого региона. Они очень сильные пловцы, и их большие передние лапы, которые они используют для гребли, слегка перепончатые. Некоторых белых медведей видели проплывающими за сотни миль от суши, хотя они, вероятно, покрывают большую часть этого расстояния, плавая по пластам льда. Осенью беременные белые медведи устраивают берлоги в земле и на сугробах, где проведут зиму и родят от одного до трех детенышей.Весной из логова выходит мать в сопровождении детенышей. В течение этого времени она будет их защищать и научить охотиться. США, Канада, Дания, Норвегия и Россия подписали в 1973 году соглашение о защите белых медведей. Белые медведи могут проплыть 100 миль без перерыва! Узнайте больше об этих удивительных существах вместе с National Geographic Kids. БУФФАЛО, Нью-Йорк (AP) — Клинт Фрейзер сыграл вничью в восьмом иннинге, нанеся удвоенный удар, а Нью-Йорк Янкиз поразил трех соло-хомеров в столь необходимой победе со счетом 6: 5 над Торонто Блю Джейс во вторник вечером. Фрейзер разорвал линейный драйв внутри третьей базовой линии, чтобы забить пинч-раннера Тайлера Уэйда со второго, когда «Янки» завершили камбэк с дефицитом 5: 2 и выиграли в третий раз за 10 игр. В игру играли перед 7145 толпой Buffalo, в основном в поддержку Нью-Йорка. «Я пытался быть дисциплинированным и ударил по фастболу», — сказал Фрейзер после победы над питающим Джорданом Романо. «Я был немного раньше на этом и просто рад сохранить его на базе. Самое главное, что мы». делаю как команда держится вместе.Мы пытаемся выйти и побеждать в играх с мячом, и сегодня это потребовало всех ». Крис Гиттенс добился своего первого попадания в высшую лигу, Гэри Санчес выиграл первый гол во втором, а Бретт Гарднер добавил первый мяч в седьмом, в результате чего «Янки» завершили счет 5-4. «Я коснулся первой базы, и мой разум просто отключился, — сказал Гиттенс. — Мне было все равно, будет ли это хоумран или базовый удар, немного склоки. Это было потрясающее чувство». Гарднер сделал смелое предсказание, когда Гиттенс подошел к пластине. «Гарди прошел мимо меня пятью секундами назад и сказал:« Скип, он углубляется », — сказал менеджер Yankees Аарон Бун. «У него было несколько конкурентоспособных в битах, и, наконец, наступить на одного и приблизить нас было большим делом». Бо Бишетт забил домой и провел сингл с двумя командами для «Блю Джейс». Сантьяго Эспиналь добавил три попадания в «Торонто», который проиграл четыре из шести. «КПЗ не справился со своей задачей», — сказал менеджер Чарли Монтойо. «У каждого есть шанс использовать высокий кредитный рычаг. Мы должны им доверять.И завтра они получат свой шанс ». Джонатан Лоайсига (6-2) отработал один иннинг, чтобы заработать победу. Тим Майза (1-1) позволил Мигелю Андухару выйти на восьмом месте и взял на себя поражение. Арольдис Чепмен отработал безупречно девятым, сделав 13-й сейв. Стартер из Торонто Хён Джин Рю ограничил Нью-Йорк пятью хитами за шесть иннингов, но выпустил четыре выхода в сезон максимума. Джордан Монтгомери допустил пять попаданий и четыре прогулки с четырьмя аутами за 6 1/3 подач для Нью-Йорка. Бишетт вышел третьим со своим 14-м хомером и вывел Торонто вперед 2: 1. Гиттенс ответил ударом с 439 футов в левый центр в четвертом, который сравнял счет 2. Торонто повел в счете 3: 2 в четвертом, когда Джо Паник забил на пасе и увеличил счет 5: 2 на счету Бишетта. Один. DJ LeMahieu забил на безумной подаче Энтони Кастро на седьмом месте и сравнял счет — 5. Голубые сойки угрожали на восьмом, загрузив базы двумя аутами, прежде чем Бишетт улетела. TRIPLE CROWN CHASE Слаггер из Торонто Владимир Герреро-младший начал день лидером Американской лиги по показателям среднего уровня (0,346), хоумранов (22) и ИКР (56). По данным Elias Sports Bureau, он стал первым 22-летним игроком со времен Аль Калина в 1955 году, который стал лидером во всех трех категориях после 60 или более игр. Герреро пошел 1 из 4 и проиграл Чепмену на поле с полным счетом. КОМНАТА ТРЕНЕРА Янки: Бун сказал, что RHP Луис Северино, который ушел во второй иннинг реабилитации в субботу, имеет растяжение паха 2 степени и вернулся в Нью-Йорк, чтобы поработать на беговой дорожке и сохранить физическую активность.Бун добавил, что возвращение Северино после операции Томми Джона в феврале 2020 года, которую недавно планировали провести в конце июня, теперь будет отложено еще на месяц. … RHP Кларк Шмидт (напряжение локтя) бросил еще один КПЗ, и Бун сказал, что Шмидт использовал все свои передачи, но у него не было временных рамок для начала реабилитации. … 1B Люк Войт был переведен на реабилитацию из Triple-A Scranton / Wilkes-Barre в Double-A Somerset. Блю Джейс: О.Ф. Джордж Спрингер (квадрицепсы) в своей первой реабилитационной игре на Triple-A сыграл пять иннингов для Buffalo Bisons в Рочестере и пошел 0 из 4…. RHP Карл Эдвардс-младший ушел после того, как бросил всего пять веревок в седьмом с дискомфортом в животе слева. В среду ему сделают МРТ. Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 3.3k. Опубликовано Чтобы рациональное число m/n записать в виде десятичной дроби, нужно числитель разделить на знаменатель. При этом частное записывается конечной или бесконечной десятичной дробью. Решение. Разделим в столбик числитель каждой дроби на ее знаменатель: а) делим 6 на 25; б) делим 2 на 3; в) делим 1 на 2, а затем получившуюся дробь припишем к единице — целой части данного смешанного числа. Несократимые обыкновенные дроби, знаменатели которых не содержат других простых делителей, кроме 2 и 5, записываются конечной десятичной дробью. В примере 1 в случае а) знаменатель 25=5·5; в случае в) знаменатель равен 2, поэтому, мы получили конечные десятичные дроби 0,24 и 1,5. В случае б) знаменатель равен 3, поэтому результат нельзя записать в виде конечной десятичной дроби. А можно ли без деления в столбик обратить в десятичную дробь такую обыкновенную дробь, знаменатель которой не содержит других делителей, кроме 2 и 5? Разберемся! Какую дробь называют десятичной и записывают без дробной черты? Ответ: дробь со знаменателем 10; 100; 1000 и т.д. А каждое из этих чисел — это произведение равного количества «двоек» и «пятерок». На самом деле: 10=2·5; 100=2·5·2·5; 1000=2·5·2·5·2·5 и т.д. Следовательно, знаменатель несократимой обыкновенной дроби нужно будет представить в виде произведения «двоек» и «пятерок», а затем домножить на 2 и (или) на 5 так, чтобы «двоек» и «пятерок» стало поровну. Тогда знаменатель дроби будет равен 10 или 100 или 1000 и т.д. Чтобы значение дроби не изменилось — числитель дроби умножим на то же число, на которое умножили знаменатель. Пример 2. Представить в виде десятичной дроби следующие обыкновенные дроби: Решение. Каждая из данных дробей является несократимой. Разложим знаменатель каждой дроби на простые множители. 20=2·2·5. Вывод: не хватает одной «пятерки». 8=2·2·2. Вывод: не хватает трех «пятерок». 25=5·5. Вывод: не хватает двух «двоек». Замечание. На практике чаще не используют разложение знаменателя на множители, а просто задаются вопросом: на сколько нужно умножить знаменатель, чтобы в результате получилась единица с нулями (10 или 100 или 1000 и т.д.). А затем на это же число умножают и числитель. Так, в случае а) (пример 2) из числа 20 можно получить 100 умножением на 5, поэтому, на 5 нужно умножить числитель и знаменатель. В случае б) (пример 2) из числа 8 число 100 не получится, но получится число 1000 умножением на 125. На 125 умножается и числитель (3) и знаменатель (8) дроби. В случае в) (пример 2) из 25 получится 100, если умножить на 4. Значит, и числитель 8 нужно умножить на 4. Бесконечная десятичная дробь, у которой одна или несколько цифр неизменно повторяются в одной и той же последовательности, называется периодической десятичной дробью. Совокупность повторяющихся цифр называется периодом этой дроби. Для краткости период дроби записывают один раз, заключая его в круглые скобки. В случае б) (пример 1) повторяющаяся цифра одна и равна 6. Поэтому, наш результат 0,66… запишется так: 0,(6). Читают: нуль целых, шесть в периоде. Если между запятой и первым периодом есть одна или несколько не повторяющихся цифр, то такая периодическая дробь называется смешанной периодической дробью. Несократимая обыкновенная дробь, знаменатель которой вместе с другими множителями содержит множитель 2 или 5, обращается в смешанную периодическую дробь. Пример 3. Записать в виде десятичной дроби числа: Любое рациональное число можно записать в виде бесконечной периодической десятичной дроби. Пример 4. Записать в виде бесконечной периодической дроби числа: Решение. Дробь, если грубо, это особая запись числа. Если один арбуз разделить на шесть человек, то каждому достанется кусок, который является частью от того, что имели до деления. Если взять два куска арбуза (предыдущая картинка), то получим дробь На следующем рисунке изображена дробь (закрашенная часть) Обозначается дробь, как . Черта «-» обозначает деление! Это то же самое, что 1 разделить на 5 или Поэтому, когда 4 конфеты делить на двоих человек, получим дробь , а это 4 разделить на 2, каждый получит по 2 конфеты. Дробь Верхнее число дроби, называется числителем, нижнее — знаменателем. Зззззапомни зззззнаменатель внизззззу!!!! Дроби бывают положительными и отрицательными. Это зависит от того, какое число в числителе (сверху) — отрицательное или положительное. Знак «-» у отрицательной дроби принято писать перед чертой дроби. Можно его записать сверху, если так удобнее. Знак «+» обычно не пишут, аналогично положительным числам. Дробь, у которой числитель меньше знаменателя, называется правильной. Если наоборот, числитель больше знаменателя, то дробь неправильная. Неправильную дробь можно записать смешанным числом (выделив целую часть) Особый вид чисел, которые можно представить в виде дробей — десятичные. У таких дробей в знаменателе 10 или 100, или 1000 и т.д. Любое рациональное число можно обратить в конечную или бесконечную периодическую десятичную дробь. Например, является конечной дробью. Бесконечная десятичная дробь называется периодической, если у нее, начиная с некоторого места, одна цифра или группа цифр повторяется. Повторяющуюся группу цифр называют периодом и записывают в скобках. Например, или Бесконечная десятичная непериодическая дробь представляется таким числом Любое целое число представляется в виде дроби, знаменатель которой единица. При делении числа на единицу мы получаем то же число. Если знаменатель и числитель дроби одинаковые числа, то эта дробь равна единице. При делении числа на себя получаем единицу. Любая дробь, у которой числителем является ноль, равна нулю. Если ноль делить на любое число, получим ноль. Не существует дроби, у которой в знаменателе ноль . Так как Число называется обратным числу . Например, числа взаимообратные. Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними. Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи: В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так: Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено. Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой. Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например: Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны: Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части. Пример 1. Перевести обыкновенную дробь 16/10 в десятичную. Как решаем: Ответ: 16/10 = 1,6. Пример 2. Перевести 37/1000 в десятичную дробь. Как решаем: Ответ: 37/1000 = 0,037. Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения. Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой: Сохраняй наглядную картинку, чтобы быстрее запомнить. Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся! Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %. 1% = 1/100 = 0,01 Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше. А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере: 0,15 = 0,15 · 100% = 15%. Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило. 2/5 = 0,4 8/25 = 0,32 Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник: Быстрая напоминалка: Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой. Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой). Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся! Пример 1. Перевести 5,4 в смешанное число. Как решаем: Ответ: 5,4 = 5 2/5. Пример 2. Перевести 4,005 в смешанное число. Как решаем: Ответ: 4,005 = 4 1/200. Пример 3. Перевести 5,60 в смешанное число. Как решаем: Ответ: 5,60 = 5 6/10. Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать: Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка! С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах. Как решаем: Ответ: 4,8 : 2 = 2,4. Пример 2. Разделить 183,06 на 45. Как решаем: Ответ: 183,06 : 45 = 4,068. Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь. Как решаем: Ответ: 0,25 : 3/4 = 1/3. Пример 2. Разделить 2,55 на 1 1/3. Как решаем: Ответ: 2,55 : 1 1/3 = 1 73/80. Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем. Как решаем: Ответ: 2/5 ∗ 0,8 = 0,32. Пример 2. Умножить 0,28 на 6 1/4. Как решаем: Ответ: 0,28 ∗ 6 1/4 = 0,8. А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде: Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель: Верны следующие правила: Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей. Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n. Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится: Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится: Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю.
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями.
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например: Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число: Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число: Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \).
Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так: Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например: Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной
дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное
число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят,
что из неправильной дроби выделили целую часть.
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например: Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей: С помощью букв это правило записывается так: Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а
второе — знаменателем.
С помощью букв правило умножения дробей можно записать так: Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать
смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное
свойство умножения относительно сложения.
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \).
Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как
\( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь: Используя буквы, правило деления дробей можно записать так: Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби. Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей. Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые. Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным. А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину. Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение. Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку. Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы. Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия: Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка: А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу: Такие записи называют дробями. Дробь состоит из числителя и знаменателя. Число, которое записывается сверху, называется числителем дроби. Число, которое записывается снизу, называется знаменателем дроби. В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы. Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь? Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4): Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли». Теперь представьте, что пиццу мы разделили не на четыре части, а на три. Допустим мы съели один кусок этой пиццы. Как записать такую дробь? Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок: Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть». Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом: Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»: Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь? Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок: Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина». Дроби, которые мы сейчас рассмотрели, называют обыкновенными. Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже. Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться. На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4. Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы. С помощью переменных дробь можно записать так: где a — это числитель, b — знаменатель. Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными. Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными: Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными. С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными: Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли. Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными. Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например: Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце. Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной. Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель. Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ: Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например: Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби». Вычислим дробь . Пять разделить на два будет два и один в остатке: 5 : 2 = 2 (1 в остатке) Проверка: (2 × 2) + 1 = 4 + 1 = 5 Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни. Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок? Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой: Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока. Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем: Схематически это выглядит так: Процедуру, которую мы сейчас провели, называют выделением целой части дроби. В нашем примере мы выделили целую часть дроби и получили новую дробь . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная. В нашем примере целая часть это 2, а дробная часть это Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь. Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть: Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем: После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части. В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы. Но если вы только начинаете изучать математику, советуем записывать каждую мелочь. Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь: Получили: Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений. Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части: 2 × 3 = 6 Затем к 6 прибавляем числитель дробной части: 6 + 1 = 7 Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений: Подробное решение выглядит так: А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так: Пример 2. Перевести смешанное число в неправильную дробь. Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений: Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится. Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2 Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы: Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска. Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению: Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число. Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2 Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы: Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска. Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению: Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно. Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно! Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь . Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить. Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби. Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби. Пример 1. Сократить дробь Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4. В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2 В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби. На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному. Пример 2. Сократим дробь Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40. НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20 Пример 3. Сократим дробь Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36. НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4 Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми: Напомним, что простыми называются числа, которые делятся только на единицу и самих себя. Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель. К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4 Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение: Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме. Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его: Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его: Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36 Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель. Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель: Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей. Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение: Сократить можно ещё по тройке в числителе и в знаменателе: Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой. Записываем новую дробь, в числителе и в знаменателе которой будут новые множители. Получили ответ . Значит, при сокращении дроби получается новая дробь . Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах. Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так: Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом: Первое выражение намного понятнее, аккуратнее и короче. Не правда ли? Задание 1. Запишите в виде дроби следующий рисунок: Задание 2. Запишите в виде дроби следующий рисунок: Задание 3. Запишите в виде дроби следующий рисунок: Задание 4. Запишите в виде дроби следующий рисунок: Задание 5. Запишите в виде дроби следующий рисунок: Задание 6. Выделите целые части в следующих дробях: Задание 7. Выделите целые части в следующих дробях: Задание 8. Переведите смешанные дроби в неправильные: Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части Задание 10. Сократите следующую дробь на 3 Задание 11. Сократите следующую дробь на 3 вторым способом Задание 12. Сократите следующую дробь на 5 Задание 13. Сократите следующую дробь на 5 вторым способом Задание 14. Сократите следующие дроби: Задание 15. Сократите следующие дроби вторым способом: Задание 16. Запишите в виде дроби следующий рисунок: Задание 17. Запишите в виде дроби следующий рисунок: Задание 18. Запишите в виде дроби следующий рисунок: Задание 19. Запишите в виде дроби следующий рисунок: Задание 20. Запишите в виде дроби следующий рисунок: Задание 21. Изобразите в виде рисунка следующую дробь: Задание 22. Изобразите в виде рисунка следующую дробь: Задание 23. Изобразите в виде рисунка следующую дробь: Задание 24. Изобразите в виде рисунка следующую дробь: Задание 25. Изобразите в виде рисунка следующую дробь: Задание 26. Изобразите в виде рисунка следующую дробь: Задание 27. Изобразите в виде рисунка следующую дробь: Задание 28. Изобразите в виде рисунка следующую дробь: Задание 29. Изобразите в виде рисунка следующую дробь: Понравился урок?
Возникло желание поддержать проект? Содержание: Десятичную дробь представляют в виде
обыкновенной дроби, записав ее со знаменателем. При этом число целых
искомой обыкновенной дроби равно числу целых десятичной дроби. В числителе искомой дроби пишем цифры, стоящие
после запятой (десятичные знаки), а в знаменателе записываем 1 с количеством нулей, которое равно количеству
десятичных знаков. Далее, если возможно, производят сокращение дроби. Если десятичные знаки начинаются нулями, их в числитель обыкновенной дроби писать не нужно. Для превращения обыкновенной дроби в десятичную имеется несколько способов. Чтобы обратить обыкновенную дробь в десятичную, нужно
числитель разделить на знаменатель. Пример Задание. Представить обыкновенную дробь
$\frac{3}{25}$ в виде десятичной. Решение. Поделим числитель на знаменатель в столбик: Таким образом, $\frac{3}{25}=3:25=0,12$ Ответ. $\frac{3}{25}=0,12$ Чтобы превратить обыкновенную дробь в десятичную, нужно помножить числитель
и знаменатель указанной дроби на такое число, чтобы в
знаменателе получилось число, кратное десяти (если это возможно). Слишком сложно? Превращение десятичной дроби в обыкновенную, превращение обыкновенной дроби в десятичную не по зубам? Тебе ответит эксперт через 10 минут! Пример Задание. Представить дробь
$\frac{3}{25}$ в виде десятичной. Решение. Знаменатель заданной дроби равен 25, если это
число умножить на 4, то получим в результате 100. То есть Ответ. $\frac{3}{25}=\frac{12}{100}=0,12$ Замечание Следует иметь в виду, что не всякая обыкновенная дробь представима в виде
конечной десятичной. В виде конечной десятичной дроби можно представить только те обыкновенные дроби,
которые после сокращения в знаменателе содержат только простые множители 2 и 5. Если знаменатель несократимой необратимой дроби содержит хотя бы один простой множитель, отличный от
2 и 5, то она не может быть представлена конечной десятичной дробью. Читать следующую тему: действия над десятичными дробями.
Запишите в виде дроби число: • три четвертых, • восемь пятых, • одиннадцать двадцатых, • двадцать три десятых, • семьдесят пятидесятых, • одиннадцать сорок вторых, • одна двадцать четвертая, • десять седьмых.
Правильная дробь ч
знаменатель целая часть числитель
C + Смешанное число С = С
Запишите в виде неправильной дроби
a а-числитель b-знаменатель b
если a c если b > c
Действия с обыкновенными дробями
Из целого числа вычитается дробь
Из числа, содержащего целую и дробную части, вычитается дробь, причем дробь уменьшаемого меньше дроби вычитаемого
Уменьшаемое и вычитаемое – смешанные числа, причем дробь вычитаемого больше дроби уменьшаемого
Если при сложении получится неправильная дробь, то из нее надо выделить целую часть.
Если складывается дробь и смешанные числа, то сначала надо сложить целые числа, а затем дробные
При сложении чисел, содержащих целую и дробную части, может оказаться, что сумма дробных частей равна 1. Ее надо прибавить к целой части числа.
При сложении смешанных чисел может оказаться, что сумма дробных частей образует неправильную дробь. Тогда из дроби надо исключить целую часть и прибавить ее к целой части.
Домашнее задание: № 1117 Урок сегодня завершён, Но каждый должен знать: Познание, упорство, труд К успеху в жизни приведут! Шаг 1: Запишите 0,75, разделив на 1: 0,75 1 Шаг 2: Умножьте верхнюю и нижнюю часть на 100 (поскольку после десятичной точки стоят 2 цифры, поэтому получается 10 × 10 = 100): (Вы видите, как верхнее число Шаг 3: Упростите дробь (это заняло у меня два шага): Примечание: 75/100 называется десятичной дробью , а 3/4 называется обыкновенной дробью ! Шаг 1: запишите: Шаг 2: умножить верхнюю и нижнюю части на 1000 (3 цифры после десятичной точки, поэтому 10 × 10 × 10 = 1000) Шаг 3: Упростите дробь (здесь мне потребовалось два шага): Когда есть целая часть числа, отложите целое число и верните его в конце: Отложите 2 в сторону и продолжайте работать над 0,35 Шаг 1: запишите: Шаг 2: умножьте верхнюю и нижнюю части на 100 (2 цифры после десятичной точки, чтобы получилось 10 × 10 = 100): Шаг 3: Упростим дробь: Верните 2 (чтобы получить смешанную фракцию): Шаг 1: Запишите: Шаг 2: Умножьте верхнюю и нижнюю часть на 1000 (3 цифры после десятичной точки, чтобы получилось 10 × 10 × 10 = 1000) Шаг 3: Упростить дробь: Нет ничего проще! Если вы действительно имели в виду 0,333 … (другими словами, повторяющиеся 3 секунды, что называется 3 повторяющиеся ), тогда нам нужно следовать специальному аргументу.В таком случае записываем: Затем умножьте верх и низ на 3: И 0,999 … = 1 (Есть? — см. 9 повторяющихся обсуждений, если вам интересно), поэтому: Ответ = 1 3 При использовании дроби в официальном документе, таком как эссе, следует ли писать ее словами или цифрами? Все зависит от ситуации! Ознакомьтесь с нашим руководством о том, как писать дроби в формальном письме, чтобы узнать больше. Фракции представляют собой части целого. Они делают это с помощью числителя (т. Е. Количества имеющихся частей) и знаменателя (т. Е. Количества частей, составляющих целое). Мы можем записать их цифрами или словами. Чтобы записать дроби в виде цифр, делайте это с числителем над знаменателем, разделенным линией. Например, если мы разрежем что-то на три части, каждая часть будет «1/3», а две части будут «2/3»: Он съел 2/3 пиццы сам! Есть несколько способов записать дроби в виде цифр. В приведенных выше примерах мы просто использовали косую черту между двумя числами. Но мы также могли бы использовать разделительную косую черту между надстрочными и подстрочными номерами (например,g., 1 ∕ 2, 2 ∕ 3 ) или горизонтальной линией, известной как винкулум. Правильный формат обычно является вопросом предпочтений, но вы должны проверить свое руководство по стилю, если вы его используете. Вы также можете записывать дроби словами. Давайте посмотрим, как это работает. При записи дробей словами необходимо указать: Например, мы могли бы написать «2/3» как «две трети»: Две трети пиццы съел сам! Это относится к большинству фракций. Но есть два исключения, у которых есть свои слова: половина (1/2) и четверть (1/4). Например: Она спала полдня. У нас три четверти торта. Однако вы можете использовать «четверти» вместо «четвертей» в американском английском. Итак, когда нужно записывать дроби словами, а когда — цифрами? В менее формальном письме, если ваш смысл ясен, это просто вопрос предпочтения. Но многие руководства по стилю предлагают записывать простые дроби как слова формальным письмом: Испытуемый выполнил 2/3 упражнений. ✗ Испытуемый выполнил две трети упражнений. ✓ Вы также можете сделать это для более длинных или более сложных дробей: Мы получили отзывы от семнадцати двадцать четвертых участников. Подпишитесь на нашу рассылку и получайте советы по написанию от наших редакторов прямо на свой почтовый ящик. Но цифры могут быть более четкими в таких случаях: Мы получили отзывы от 17/24 участников. В конечном итоге все сводится к тому, какое руководство по стилю вы используете, поэтому обязательно проверьте, есть ли оно у вас. Однако, как правило, мы предлагаем: В оставшейся части этого поста мы рассмотрим случаи, когда нужно быть осторожным при написании дробей. Даже если вы пишете дроби как числа в другом месте, вы не должны начинать предложение с числа. Например, неверно следующее: 22/7 — хорошее приближение числа пи. ✗ Чтобы избежать этого, вам нужно либо записать дробь в виде слов, либо перефразировать предложение, чтобы оно не начиналось с дроби: Двадцать две седьмые доли — хорошее приближение числа Пи. ✓ Дробь 22/7 является хорошим приближением математического значения пи. ✓ Смешанная дробь — это целое число, за которым следует дробь.Если вы пишете смешанную дробь, убедитесь, что используете единообразный стиль для целого числа и дроби: Мальчики съели 5 ½ пицц. ✓ Мальчики съели пять с половиной пицц. ✓ Никогда не смешивайте слова и цифры в дроби: Голодные мальчики съели тридцать три и фунтов стерлингов пиццы. ✗ Некоторым людям нравится добавлять дефис между числителем и знаменателем, когда дроби записываются в виде слов.Например, хотя мы написали «две трети» выше, мы могли бы также написать «две трети»: Испытуемый выполнил две трети упражнений. Если в вашем руководстве по стилю нет советов по этому поводу, это просто вопрос предпочтений (просто не забывайте быть последовательным!). Однако есть два случая, когда дроби должны включать дефис: Так что следите за этими случаями, даже если вы не переносите дроби в другом месте! И если вам нужна дополнительная помощь, чтобы убедиться, что ваш текст не содержит ошибок, почему бы не отправить документ на вычитку? Нам часто приходится переписывать десятичные дроби как дроби или смешанные числа.Вернемся к нашему заказу на обед, чтобы увидеть, как мы можем преобразовать десятичные числа в дроби. Мы знаем, что [латекс] 5,03 доллара [/ латекс] означает [латекс] 5 [/ латекс] долларов и [латекс] 3 [/ латекс] цента. Поскольку в одном долларе [латекс] 100 [/ латекс] центов, [латекс] 3 [/ латекс] цента означает [латекс] \ frac {3} {100} [/ латекс] доллара, поэтому [латекс] 0,03 = \ frac {3} {100} [/ латекс]. Мы преобразуем десятичные дроби в дроби, определяя разряд самой дальней правой цифры. В десятичной дроби [латекс] 0,03 [/ латекс] [латекс] 3 [/ латекс] находится в сотых долях, поэтому [латекс] 100 [/ латекс] является знаменателем дроби, эквивалентной [латекс] 0.03 [/ латекс]. [latex] 0,03 = \ frac {3} {100} [/ latex] [latex] 5.03 = 5 \ frac {3} {100} [/ latex] Запишите каждое из следующих десятичных чисел в виде дроби или смешанного числа: ⓐ [латекс] 4.09 [/ латекс] ⓑ [латекс] 3,7 [/ латекс] ⓒ [латекс] -0,286 [/ латекс] Решение Запишите «[латекс] 4 [/ латекс]» как целую часть смешанного числа. Напишите [латекс] 9 [/ латекс] в числителе, так как это число справа от десятичной точки. Вы заметили, что количество нулей в знаменателе совпадает с количеством десятичных знаков? Запишите «[латекс] 3 [/ латекс]» как целую часть смешанного числа. Напишите [латекс] 7 [/ латекс] в числителе, так как это число справа от десятичной точки. Напишите знак минус перед дробью. Напишите [латекс] 286 [/ латекс] в числителе, так как это число справа от десятичной точки. Напишите [латекс] 1000 [/ латекс] в знаменателе, так как значение позиции последней цифры, [латекс] 6 [/ латекс], составляет тысячные доли. В следующем видео-примере мы рассказываем, как преобразовать десятичную дробь в дробь.Примеры: записать число в десятичной системе счисления по словам. Когда вы подаете заявку на ипотеку, кредитный инспектор сравнит ваш общий долг с вашим общим доходом, чтобы решить, имеете ли вы право на получение ссуды.Это сравнение называется отношением долга к доходу. Отношение сравнивает две величины, которые измеряются в одной и той же единице. Если мы сравним [latex] a [/ latex] и [latex] b [/ latex], соотношение записывается как [latex] a \ text {to} b, \ frac {a} {b}, \ text {или } \ mathit {\ text {a}} \ text {:} \ mathit {\ text {b}} \ text {.} [/ latex] Коэффициент сравнивает два числа или две величины, которые измеряются в одной и той же единице. Соотношение [латекс] a [/ latex] к [латексу] b [/ latex] записывается [latex] a \ text {to} b, \ frac {a} {b}, \ text {или} \ mathit { \ text {a}} \ text {:} \ mathit {\ text {b}} \ text {.} [/ latex] В этом разделе мы будем использовать обозначение дробей. Когда соотношение записывается в форме дроби, дробь должна быть упрощена. Если это неправильная дробь, мы не меняем ее на смешанное число. Поскольку соотношение сравнивает две величины, мы оставим соотношение как [latex] \ frac {4} {1} [/ latex] вместо того, чтобы упрощать его до [latex] 4 [/ latex], чтобы мы могли видеть две части Соотношение. Запишите каждое соотношение в виде дроби: ⓐ [латекс] 15 \ text {to} 27 [/ latex] ⓑ [latex] 45 \ text {to} 18 [/ latex]. Решение Оставляем отношение в ⓑ как неправильную дробь. В следующем видео вы увидите больше примеров того, как выразить соотношение в виде дроби. Мы часто будем работать с десятичными отношениями, особенно когда у нас есть отношения, связанные с деньгами.В этих случаях мы можем исключить десятичные дроби, используя свойство Equivalent Fractions Property, чтобы преобразовать отношение в дробь с целыми числами в числителе и знаменателе. Вам не нужно записывать каждый шаг, когда вы умножаете числитель и знаменатель на десять. Пока вы перемещаете оба десятичных разряда на одинаковое количество разрядов, соотношение останется прежним. Запишите каждое соотношение как дробную часть целых чисел: Решение So [латекс] 4.8 \ text {to} 11.2 [/ latex] эквивалентно [latex] \ frac {3} {7} [/ latex]. В числителе один десятичный знак, а в знаменателе [латекс] 2 [/ латекс]. Чтобы очистить оба десятичных знака, нам нужно переместить десятичный разделитель [latex] на 2 [/ latex] разряда вправо. [латекс] 2,7 \ text {to} 0,54 [/ латекс] Итак, [latex] 2.7 \ text {to} 0.54 [/ latex] эквивалентно [latex] \ frac {5} {1} [/ latex]. В следующем видео показано больше примеров того, как выразить отношение, данное в виде десятичной дроби, в виде дроби. Некоторые соотношения сравнивают два смешанных числа. Помните, что для деления смешанных чисел вы сначала переписываете их как неправильные дроби. Запишите отношение [латекс] 1 \ frac {1} {4} \ text {к} 2 \ frac {3} {8} [/ latex] в виде дроби. Решение Смешанное число — это целое число и правильная дробь, представленные вместе.Обычно представляет собой число между любыми двумя целыми числами. Посмотрите на данное изображение, оно представляет собой дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число. Некоторые другие примеры смешанных чисел: Части смешанного числа Смешанное число образуется путем объединения трех частей: целого числа, числителя и знаменателя.Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число. Свойства смешанных номеров Преобразование неправильных дробей в смешанные. Шаг 1 : Разделите числитель на знаменатель. Шаг 2 : Запишите частное как целое число. Шаг 3 : Запишите остаток в числителе и делитель в знаменателе. Например, мы следуем указанным шагам, чтобы преобразовать 7/3 в смешанную числовую форму. Шаг 1 : разделить 7 на 3 Шаг 2 : Запишите частное, делитель и остаток в форме, как на шагах 2 и 3 выше. Добавление смешанных чисел Можно складывать смешанные числа, переставляя целые числа, складывая их по отдельности и добавляя оставшиеся дроби по отдельности и, в конце концов, расчесывая их все. 1 1 ⁄ 2 + 3 3 ⁄ 4 Сложение целых чисел отдельно и дробей отдельно. Для целых чисел: 1 + 3 = 4 Для дробей: найдите НОК и прибавьте В конце складываем обе части вместе. 4 + 1 1 ⁄ 4 = 5 1 ⁄ 4 Примеры из жизни Мы можем проверить наше понимание смешанных фракций, выразив части целого как смешанные фракции, подавая пиццу или пирог дома.Образцы смешанных фракций образуют остатки пиццы, наполовину заполненные стаканы молока. Интересные факты Пример 1: Школьный звонок звонит каждые полчаса. Если он только что зазвонил, то сколько раз он будет звонить в следующие три с половиной часа? Анализ: Эта задача спрашивает: Сколько половинок в трех с половиной? Шаг 1: Давайте использовать формы для представления смешанного числа три с половиной. Шаг 2: Решение: В примере 1 мы использовали формы, чтобы помочь нам решить проблему. Посмотрим на пример 2. Пример 2: Школьный звонок звонит каждые полчаса. Если он только что зазвонил, то сколько раз он будет звонить в следующие девять с половиной часов? Анализ: Использование форм для решения этой проблемы нецелесообразно. Нам нужно найти другой метод. Напомним, что смешанное число состоит из целого числа и дробной части . Например: Порядок действий: Чтобы записать смешанное число как неправильную дробь: Давайте воспользуемся описанной выше процедурой для решения проблемы из примера 2. Пример 2: Школьный звонок звонит каждые полчаса. Если он только что зазвонил, то сколько раз он будет звонить в следующие девять с половиной часов? Анализ: Шаг 1: Шаг 2: Решение: Школьный звонок прозвенит 19 раз в следующие девять с половиной часов. Давайте рассмотрим еще несколько примеров записи смешанного числа как неправильной дроби. Пример 3: Запишите две и три четверти как неправильную дробь. Анализ: Шаг 1: Шаг 2: Решение: Пример 4: Запишите шесть и две трети как неправильную дробь. Анализ: Шаг 1: Шаг 2: Решение: Вот краткое изложение примеров с 1 по 4.Вы видите закономерность? Видите ли вы более простой способ записать смешанное число как неправильную дробь? Есть способ записать смешанное число как неправильную дробь: Если вы умножите знаменатель на целочисленную часть, а затем прибавите числитель, результат даст вам числитель неправильной дроби. Это показано ниже для смешанных чисел два и три четверти. Повторяя примеры с 1 по 4, получаем: Давайте рассмотрим еще несколько примеров записи смешанного числа как неправильной дроби с помощью этого ярлыка. Пример 5: Запишите одиннадцать и три пятых как неправильную дробь. Анализ: Шаг 1: Решение: Пример 6: Запишите четырнадцать и одну треть как неправильную дробь. Анализ: Шаг 1: Решение: Этот ярлык использует только один шаг и упрощает преобразование больших смешанных чисел в неправильные дроби. Описание: Существует несколько методов преобразования смешанного числа в неправильную дробь. Используйте тот, который подходит для данной задачи. В упражнениях с 1 по 5 щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ. Примечание. Чтобы записать неправильную дробь из пяти третей, введите в форму 5/3 . Смешанное число представляет собой комбинацию целого числа и дроби. Например, если у вас есть два целых яблока и одно половинное яблоко, вы можете описать это как 2 + 1 /2 яблока или 2 1 /2 яблока. Это смешанное число также можно выразить дробью.Каждое целое яблоко содержит две половинки яблока. Ваши два целых яблока — это также четыре половинных яблока. Четыре половинки яблока плюс половина яблока — это пять половинных яблок. Итак, у вас есть 5 /2 яблок. Другими словами: , чтобы превратить смешанное число в дробь, умножить целое число на знаменатель (нижняя часть) и прибавить результат к числителю (верхняя часть). Давайте попробуем другой пример: Дробь, в которой числитель меньше знаменателя, например, 1 /3 или 2 /5 называется правильной дробью . Дробь, числитель которой больше знаменателя или равен ему, например, 5 /2, 17 /3 или 6 /6, называется неправильной дробью . (Другими словами, дробь со значением меньше 1 является правильной дробью. Дробь со значением, большим или равным 1, является неправильной дробью.) Как мы показали выше, смешанные числа могут быть записываются в виде неправильных дробей. Точно так же неправильные дроби могут быть записаны как смешанные числа. Чтобы записать неправильную дробь как смешанное число, разделите числитель (верхняя часть) на знаменатель (нижняя часть).Частное — это целое число, а остаток — это числитель. Давайте попробуем еще пару примеров: Если нет остатка, просто возьмите частное как целое число: .com / ipa / 0/9/3/3/4/5 / A0933459. Вы искали y 2x 3 2x функция? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y 3 2x функция, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y 2x 3 2x функция». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y 2x 3 2x функция,y 3 2x функция,y 3x 2 функция,y x 2 x 3 решение,y x 2 и y x 3,y x2 2 x 3,постройте график функции y 3 2,постройте график функции y 3 2x,постройте график функции y x 2 3,функция x 3 x 2,функция y 3 2 x,функция y x 2 3. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y 2x 3 2x функция. Просто введите задачу в окошко и нажмите
«решить» здесь (например, y 3x 2 функция). Решить задачу y 2x 3 2x функция вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать: Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей. Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы: Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами. Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение. Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели. Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше). Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора. Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей. Второе – удобный сервис для заказчиков и для желающих заработать на решениях. Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения. Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения. Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов. В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет. Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.{2}} f{\left (x \right )} = Вторая производная Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку. Решение: Разберем как строить график с модулем. y=|x-3|-|x+3| Найдем точки при переходе которых знак модулей меняется. У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений. 1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х. У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3). y=—(x-3)-(—(x+3))=-х+3+х+3=6 На интервале (-∞;-3) получился график линейной функции (прямой) у=6 2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0. У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс. y=—(x-3)-(+(x+3))=-х+3-х-3=-2x На интервале (-3;3) получился график линейной функции (прямой) у=-2х 3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х. х=5 У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞). y=+(x-3)-(+(x+3))=х-3-х-3=-6 На интервале (3;+∞) получился график линейной функции (прямой) у=-6 4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|. 5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку. Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k. Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит. Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит. Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит. Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит. Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит. Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение. Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами. Когда у нас есть система уравнений, у нас есть 2 или более уравнений, которые имеют общее решение. Эти решения при включении в уравнения должны удовлетворять уравнениям. 1) y = x 2 — 5 экв1 y = 2x — 2 экв2 Если мы приравняем эти два, это позволит нам решить относительно x. x 2 — 5 = 2x — 2 Вычтем 2x и прибавим 2 к обеим сторонам уравнения. x 2 — 2x — 3 = 0 Разложите на множители левую часть уравнения. (х + 1) (х — 3) = 0 х = -1 и х = 3 У нас есть два решения. Причина этого в том, что если мы построим два уравнения в одной и той же системе координат, графики пересекаются дважды. Подставьте эти значения в eq2, чтобы найти значения y. y = 2 (-1) — 2 и y = -2 (3) — 2 y = -2-2 и y = -6-2 y = -4 и y = -8 У нас есть две пары решений. (-1, -4) и (3, -8). 2) y = x 2 + 4x — 5 eq1 y = 0 экв2 Мы уже значения y из уравнения 2.Обратите внимание, что y = 0 — это ось x. Поэтому, когда мы изобразим уравнения в одной и той же системе координат, парабола и ось x будут пересекаться. Подставьте это значение в уравнение 1, чтобы найти x. 0 = х 2 + 4х — 5 0 = (х + 5) (х — 1) х = -5 и х = 1 Пары решений: (-5, 0) и (1, 0). Вопрос 3 такой же, как вопрос 1. 4) y = | х | eq1 y = 2x + 3 экв2 Обратите внимание, что eq1 является уравнением абсолютного значения. Мы по-прежнему устанавливаем уравнения равными друг другу, так как они оба определяются y. | х | = 2x + 3 Мы знаем, что абсолютное значение отрицательного числа положительно. Абсолютное значение положительного числа положительно.Используя эту концепцию, мы можем составить два уравнения. -x = 2x + 3 и x = 2x + 3 Решите два уравнения по отдельности. -3x = 3 и -x = 3 х = -1 и х = -3 Затем мы подставляем эти значения x в уравнение 1, чтобы найти y. y = | -1 | и y = | -3 | y = 1 и y = 3 У нас есть две пары решений: (-1, 1) и (-3, 3) Наконец, мы подставляем значения x и y в eq2, чтобы убедиться, что пара работает. 1 = 2 (-1) + 3 и 3 = 2 (-3) + 3 1 = -2 + 3 и 3 = -6 + 3 1 = 1 и 3 ≠ -3 Пара решений, удовлетворяющая обоим уравнениям, равна (-1, 1). Вот и все. Если вам нужна дополнительная помощь, просто свяжитесь со мной. Система неравенств: графики и концепция Когда нам нужно решить систему из двух или более неравенств, мы наносим на график набор решений каждого из них, но помещаем их на один и тот же график и смотрим, как это выглядит.Перекрывающиеся заштрихованные области говорят нам, где найти набор решений. Как решить систему уравнений методом исключения Посмотрев этот видеоурок, вы научитесь решать систему уравнений с помощью метода исключения.Вы узнаете, что удаляется и как это сделать, чтобы закончить свое решение. Что такое система уравнений? Так что же произойдет, если мы захотим сравнить более одного уравнения? Добро пожаловать в «систему» уравнений! Узнайте, что это такое, как их решать и когда они возникают в реальной жизни. Линейные уравнения: точки пересечения, стандартная форма и построение графиков Вы знаете, что делать, если уравнение не выглядит как y = mx + b ?! Если нет, то это видео для вас.Скорее всего, уравнение имеет стандартную форму, поэтому мы узнаем, как использовать уравнения стандартной формы, как построить их график и почему они могут быть полезны. Умножение биномов с использованием метода FOIL и площади: практические задачи Есть несколько ошибок, которые легко сделать при умножении биномов с помощью FOIL, а также несколько способов усложнить подобные проблемы, так почему бы не убедиться, что вы освежили свои навыки? Вы также узнаете, как использовать метод площади для умножения многочленов еще большего размера. Рационализация знаменателей в радикальных выражениях Радикальные выражения, содержащие знаменатели, не упрощаются полностью, если в знаменателе нет радикальных символов.Этот урок научит вас, как удалить радикал из знаменателя дроби с помощью процесса, называемого рационализацией знаменателя. Сложение и вычитание в научной записи Научная нотация помогает ученым с легкостью писать действительно большие или маленькие числа, но сложение и вычитание с использованием научной нотации требует нескольких шагов.В этом уроке будут изложены правила сложения и вычитания в экспоненциальной нотации. Перевод слов в алгебраические выражения Когда дело доходит до задач со словами, самый простой способ решить их — это поискать ключевые слова и превратить их в математические символы.Посмотрите этот видео-урок, чтобы узнать, какие ключевые слова вам следует искать и какие математические символы они представляют. Преобразование повторяющихся десятичных знаков в дроби Посмотрев этот видеоурок, вы сможете преобразовать любую повторяющуюся десятичную дробь в дробь.Узнайте, как написать два уравнения, которые необходимы для преобразования. Линейные и нелинейные функции Посмотрев этот видеоурок, вы сможете отличить линейные функции от нелинейных.Вы также сможете определить оба типа, просто взглянув на графики. Решение и построение графиков абсолютных неравенств: практические проблемы Решение и построение графиков неравенства абсолютных ценностей объединяет множество различных навыков в одном месте.Практические задачи в этом видео дадут вам хороший шанс увидеть больше примеров абсолютного неравенства, но также проверит ваши общие алгебраические знания. Как складывать, вычитать и умножать многочлены Сложение, вычитание и умножение многочленов в основном такие же, как сложение, вычитание и умножение чисел.Единственная разница в том, что у нас есть неприятная переменная, о которой нужно беспокоиться, но это видео покажет вам, что это не проблема, так что не беспокойтесь! Этот метод сработал для многих моих учеников, и я думаю, он подойдет и вам! Примеры задач со словами в системе уравнений Большинство задач со словами требуют, чтобы вы нашли значение одной переменной.Но что, если неизвестных переменных несколько? На этом уроке вы будете использовать системы уравнений и решать задачи с несколькими неизвестными значениями. Классификация треугольников по углам и сторонам Не все треугольники одинаковы.2 + 4 на отдельном листе. Используя эти графики, сравните и сопоставьте форму и положение графиков. Я знаю, что это обман, но мне нужны ответы, пожалуйста Абсолютно нет! Но если ВЫ публикуете то, о чем ВЫ ДУМАЕТЕ, кто-то может вам помочь. Я не дам вам ответов, но скажу, что вам нужно сделать 1.2 — 81 = 0 и решения ….. 5. ……? Вот правильные ответы; Сделай сам пенный домкрат M3u для плутон ТВ Pbo scalar 3600 Android получает программную ширину и высоту экрана kotlin Детали велосипеда Lowrider Лос-Анджелес Kik 5.5 apk Таблица наборов фильтров на основе параметра Конфигурация обратного прокси F5 Портал компании регистрирует окна 10 Улучшите свои математические знания с помощью бесплатных вопросов в разделе «Решение системы уравнений с помощью построения графиков» : задачи со словом «и тысячи других математических навыков. Решение систем линейных уравнений с графическим отображением цели учащегося / класса Учащимся, планирующим продолжить учебу в высшем учебном заведении, необходимо знать и уметь решать задачи по решению систем уравнений.Результат (цель обучения) Учащиеся точно … Создатель листов квадратного уравнения сгенерирует рабочий лист задач и ключ ответов для печати. Выберите свои параметры в форме ниже и нажмите кнопку «Создать рабочий лист». Мы откроем новое окно, содержащее ваш рабочий лист пользовательских квадратных уравнений. Решение системы уравнений. Системы линейных уравнений имеют место, когда существует более одного связанного математического выражения. Например, в \ (y = 3x + 7 \) есть только одна линия со всеми точками на этой линии, представляющая набор решений для приведенного выше уравнения.3x + 3y = 6 Новое уравнение 2 В результате получается система линейных уравнений с двумя переменными. 2x + 2y = 4 Новое уравнение 1 3x + 3y = 6 Новое уравнение 2 Решите новую систему, прибавив º3, умноженное на первое уравнение, к 2-кратному второму уравнению. Это дает тождество 0 = 0. Итак, система имеет бесконечно много решений. Опишите решение. Односторонний … Решение линейных уравнений методом перекрестного умножения. Решение одношаговых уравнений. Решение квадратных уравнений путем факторизации. Решение квадратных уравнений по формуле корней квадратного уравнения.Решение квадратных уравнений, заполнив квадрат. Природа корней квадратного уравнения. Сумма и произведение корней квадратного уравнения Алгебраические тождества Получите огромную практику с этой партией распечатываемых рабочих листов для решения систем уравнений, предназначенных для учащихся 8-х классов и старших классов. Найдите подходящие упражнения для решения набора одновременных уравнений с двумя переменными, используя метод построения графиков и алгебраические методы, такие как метод подстановки, метод исключения, метод перекрестного умножения.Построение графиков равенств, неравенств, линейных уравнений и линейных неравенств. Графические равенства; Декартова система координат; Графическое отображение неравенств; Сложное неравенство; Построение графиков линейных уравнений; Построение графиков линейных неравенств; Решение уравнений абсолютного значения. Определение абсолютной величины; Решение уравнений абсолютного значения; Решение абсолютного … Постройте систему уравнений в виде графика с пересечением наклона или стандартной формы и найдите их решение с помощью графиков. Решение системы линейных и квадратных уравнений (путем построения графиков): Решение системы линейных и квадратных уравнений ( путем замены): Решение системы линейных уравнений методом исключения (добавить): Решение системы линейных уравнений методом исключения (Применение): Решение системы линейных уравнений методом исключения (mult / subt): Решение системы… Просмотреть Урок 14a (охватывает рабочие листы 14a, b и c) ³ Цель: использовать метод построения графиков, чтобы найти точку пересечения двух линий и классифицировать тип решения. Метод построения графика Две линии могут пересекаться в системе координат, и это пересечение называется решением системы линейных уравнений. Appium подождите, пока элемент станет активным Omc mustang 440 части с бортовым поворотом Алгебра -> Многочлены-и-рациональные-выражения-> РЕШЕНИЕ: Эта проблема из рабочего листа.3 — 6x + 9 23. РАССМОТРЕНИЕ: Полиномиальная функция имеет нуль в точке x = b. Найдите один из факторов! 24. Сторона куба имеет длину 2x + 1 единицу. Выразите объем куба как полином. 25. Длина коробки в 2 раза больше высоты. Объясните 1 Нахождение нулей с помощью теоремы рационального нуля Если полиномиальная функция p (x) равна (a 1 x + b 1) (a 2 x + b 2) (a 3 x + b 3), где a 1, a 2, a 3, b 1, b 2 и b 3 являются целыми числами, старший коэффициент p (x) будет произведением a 1 a 2 a 3, а постоянный член будет b произведением b 1 b 2 b 3.Рабочие листы по алгебре и для печати. Эти рабочие листы представляют собой упражнения в формате PDF высочайшего качества для печати. Письмо укрепляет изученную математику. Эти рабочие листы по математике для детей содержат упражнения по предварительной алгебре и алгебре, подходящие для дошкольных учреждений, детских садов, от первого до восьмиклассников, бесплатные рабочие листы в формате PDF, рабочие листы по математике для 6-го класса. Sonic generations Для многочленов с действительными коэффициентами в исчислении для вычисления интегралов используется частичное дробное разложение. Для многочленов с комплексными числами в качестве коэффициентов факторизация осуществляется на линейные множители, так что факторизация практически аналогична поиску числового корня (и это частично верно и для действительных чисел). Рабочие листы Free Algebra 2, созданные с помощью Infinite Algebra 2…. Генераторы тестов и рабочих листов для учителей математики. Алгебра II: построение графиков полиномиальных функций Изучите концепции, примеры вопросов и объяснения для WS # 3 Практика 6-1 Полиномиальные функции Найдите кубическую модель для каждой функции. Лицензия доктора Шона Бейкера отозвана Полиномиальные функции Рациональные функции Радикальные уравнения / Экспоненциальные и логарифмические функции Тригонометрические функции Тригонометрические графики и идентичности Блок 06 — День 11 — Найдите нули полиномов Блок 06 — День 01 — Классифицируйте полиномы, добавьте / вычитание многочленов Блок 06 — День 02 — Умножение многочленов, теорема о биномиальном разложении Для x-полинома степени 2, квадратичной функции, мы всегда можем использовать квадратичную формулу, чтобы найти нули.В некоторых случаях вместо этого возможен факторинг. 1. Пусть f (x) 3×2 3x 6. Найдите нули f, т.е. решите f (x) = 0 Факторинговая квадратичную формулу OR 9 1 2. Пусть f (x) x2 8. Найдите нули f, т.е. решите f (x) = 0. Octin sports font Вы можете найти решения или корни квадратных уравнений, установив одну сторону равной нулю, разложив многочлен на множители, а затем применив свойство нулевого произведения. Принцип нулевого произведения гласит, что если ab = 0, то либо a = 0, либо b = 0, либо оба a и b равны 0. После факторизации многочлена установите каждый множитель равным нулю и решите … Пример 2: Найдите рациональные корни многочлена, представленного ниже, с помощью теста рациональных корней.Постоянный член a 0 = –2 и его возможные множители p = ± 1, ± 2. Для главного коэффициента мы имеем an = 4 и его множители q = ± 1, ± 2, ± 4. Медсестра ухаживает за клиентом, который получает полное парентеральное питание 7 августа 2013 г. — Эти рабочие листы по алгебре 1 позволяют создавать неограниченное количество динамически создаваемых рабочих листов мономов и многочленов.Дополнительная информация 4 Деление многочленов с использованием ответов на листе синтетического деления Умножение и деление Рациональные выражения √ Разделение многочленов с использованием ответов на листе синтетического деления. 4 … Принципы цифрового мультиметра pdf Математика · Алгебра (все содержание) · Полиномиальные выражения, уравнения и функции · Нахождение нулей многочленов. Сначала возьмите любой многочлен, разложите его на множители до такой формы, скажем, [2x-x] [10x-8x], и теперь приравняйте this = 0, чтобы получить нули многочлена. Спасение прошлое настоящее будущее Factoring-polynomials.com предоставляет ценные стратегии по поиску ненастоящих нулей, решению экспоненциальных функций и умножения, а также другим предметам алгебры.Если вам нужен совет по функциям или курсы математики, Factoring-polynomials.com станет идеальным местом для посещения! Водонагреватель издает свистящий звук Описание курса: Алгебра с отличием II завершает структуру систем действительных и комплексных чисел. Основные темы, затронутые в видео: поиск рациональных нулей, включают математическое моделирование; видео: поиск рациональных нулей; видео: поиск всех действительных нулей полиномиальных функций; видео: найти все … Запчасти для грузовиков Cushman на ebay Найдите все нули. 1) f (x) = (3x — 1) (9×2 + 3x + 1) {1 3, -1 + i3 6, -1 — i3 6} 2) f (x) = -15x (5×2 + 3) ( x2 — 5) {0, i15 5, — i15 5, 5, -5} Разложите на множители и найдите все нули. 3) f (x) = 5×5 + 10×4 + 16×3 + 32×2 — 16x — 32 Факторы на: f (x) = (x + 2) (5×2 — 4) (x2 + 4) Нули: {-2, 25 5, — 25 5, 2i, -2i} 4) f (x) = x3 + 8 Множители на: f (x) = (x + 2) (x2 — 2x + 4) Нули: {-2, 1 + i3, 1 — i3} Запасные части Wharfedale pro Подготовьте студентов к успеху в алгебре 2 и не только! Изучите всю учебную программу по алгебре 2: тригонометрия, логарифмы, полиномы и многое другое.Попробуйте бесплатно! В SparkNotes Algebra II: Polynomials Study Guide есть все необходимое для успешных викторин, тестов и эссе — от общего резюме до резюме глав и объяснения известных цитат. Если вы разбираетесь в алгебре II и, следовательно, в основах полиномиальной математики, то вы можете пропустить этот раздел и сразу перейти к следующему. Этот обзор полиномов в математике призван сделать использование кода более понятным. Член с наивысшей степенью должен иметь ненулевой полиномиальный коэффициент. Исправление для оперативной памяти, 32 бита Описание курса: Алгебра с отличием II завершает структуру систем действительных и комплексных чисел. Основные затронутые темы включают математическое моделирование в Видео: Поиск рациональных нулей Видео: Поиск рациональных нулей Видео: Поиск всех действительных нулей полиномиальных функций Видео: Найти все … «Маленькие многочлены» и называются «факторами» большего полинома. Нахождение множителей многочлена требует некоторых догадок и знакомства с процессом умножения многочлена, который мы обсуждали в предыдущем разделе.2. Cs7642 заключительный экзамен Найти корни многочлена степени выше 2. Основная теорема алгебры. Стратегия поиска корней. И наоборот, если мы знаем, что корни многочлена равны −2, 1 и 5, то многочлен имеет следующие множители Lbz turbo whine Файлы dxf для бампера грузовика Устройство смены шрифтов xda magisk Перевести фразы и предложения в выражения, уравнения и практика неравенств Аренда кабины у озера Шейвер Ford 4.9 снятие выпускного коллектора Система отслеживания посещаемости рейдов wow classic Тестовая форма главы 3 k ключ ответа Fitbit versa 2 не заряжается после смерти Quadratic Equations. Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a не равно 0.. Факторинг. Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Включите практику построения графиков квадратичных функций из различных форм уравнения. Включите на данный момент обзор предыдущих уроков в модуль. EngageNY Mathematics Algebra I> Модуль 4> Тема B> Урок 16 — Набор задач Модуль 19 909 Урок 2 Оцените: Домашнее задание и Практика • Онлайн-домашнее задание • Подсказки и помощь • Дополнительная практика Постройте график каждой квадратичной функции, преобразовав график ƒ (x ) = х 2.Опишите преобразования. 1. Квадратное уравнение имеет стандартную форму, когда «a» положительно, а a, b и c — целые числа, наибольший общий делитель которых равен 1. Решения 0 = ax 2 + bx + c являются пересечениями x график y = ax 2 + bx + c. Квадратичные функции. Квадратичная функция — это функция, которую можно записать в стандартной форме f (x) = ax 2 + bx + c, где «a … Практические вопросы. Какая из следующих эквивалентных форм уравнения показывает координаты вершины параболы как константы в уравнении? A.y = (x + 2) (x — 4) B. y = x 2 — 2x — 8 C. y = x (x — 2) — 8 D. y = (x — 1) 2 — 9; На следующем рисунке показан график уравнения y = x 2 — 2x — 3. Какая из … Алгебра I Модуль 4, Тема A, Урок 9 Результаты учащихся Учащиеся используют факторную форму квадратного уравнения для построения приблизительный график, используйте график квадратного уравнения для построения квадратного уравнения в факторизованной форме и свяжите решения квадратного уравнения от одной переменной с нулями функции, которую оно определяет. Math 11Ch 4: Квадратичная функция: Присваивания. СОЛ. Практический тест и викторина Главы 3 и 4 объединены в одну главу. Студентам предлагается использовать алгебраический подход с графическим подходом в качестве вторичного источника. Итоги урока. Самая основная квадратичная функция — это f (x) = x 2. В вершинной форме эта функция будет иметь вид f (x) = 1 (x-0) 2 +0. Все остальные квадратичные функции могут быть получены путем изменения параметров … ПРЕОБРАЗОВАНИЕ КВАДРАТИЧЕСКИХ ФУНКЦИЙ ИЗ ОДНОЙ ФОРМЫ В ДРУГУЮ (Стандартная форма <==> Форма перехвата <==> форма вершины) (Автор: Нги Х. Нгуен — 8 декабря 2014 г.) 1.КВАДРАТИЧЕСКАЯ ФУНКЦИЯ В ФОРМЕ ПЕРЕСЕЧЕНИЯ График квадратичной функции в стандартной форме, f (x) = ax² + bx + c, представляет собой параболу, которая может определять квадратичные функции: если a, b, c, h и k являются действительными числами с a6 = 0, то обе функции y = ax2 + bx + c стандартной формы y = a (x − h) 2 + k вершинной формы представляют квадратичную функцию. График квадратичной функции называется параболой. В обеих приведенных выше формулах значение A определяет, открывается ли график вверх (a> 0) или открывается 1) Изобразите следующие квадратичные функции, используя преобразования (не таблицу).а. у = х2 6 б. y = (x + 4) 2 фев. 13.10: 24 AM 2) Постройте график следующих квадратичных функций, используя преобразования (не таблицу). а. у = (х + 4) 2 б. y = (x 3) 2 2 фев 13 11:28 AM Форма вершины: форма вершины квадратичной функции f (x) = a (x h) 2 … Практика A 9-4 Преобразование квадратичных функций 9 -4 Практика B Операции с функциями Используйте следующие функции в упражнениях 1-18. f x ___1 2x g x x 2 h x x 8 k x x Найдите каждую функцию. 1. gk x 2. g h x 3. g h x x 2 x x 2 x 8 x x 8 4.fg x 5. gh x 6. __gf x 2 x__ 2 3 x 8 x ____1 2 x 3 Найдите каждое значение. 7. g k 9 8. h g 3 9. g 3 9 1 121 8. Если линейная комбинация является методом, используемым для решения этой системы уравнений, каков результат первого шага? х + у = 6. х — у = 2. а) 2у = 8. б) 2х = 8. в) х + у = 8. г) х — у = 8. 9. Переведите следующее предложение в уравнение. Произведение девяти и четырех меньше n равно двадцати семи. а. 9н — 4 = 27. б. 9 (n — 4) = 27 Урок 9.4 — Преобразование квадратных уравнений Миссис Сноу, инструктор Еще в главе 5 мы познакомились с семействами функций и, в частности, с линейным семейством функций.Мы обнаружили, что, изменяя значения наклона и точки пересечения оси Y, мы можем точно предсказать, как 8.4 Практика B Преобразование квадратичных функций Упорядочить функции от НАИБОЛЬШИХ растянутых графиков до НАИБОЛЬШИХ сжатый граф. 1. 2f (x) 2 3x; g (x) 2x 2. На 17 уроках это самая длинная часть электронного текста. Квадратичные функции и их алгебра изучаются по разным темам. Студенты используют технологию графического калькулятора для изучения точек поворота, пересечений и геометрических преобразований парабол. Создатель листа квадратного уравнения сгенерирует рабочий лист задач и ключ ответов для печати. Выберите свои параметры в форме ниже и нажмите кнопку «Создать рабочий лист». Мы откроем новое окно, содержащее ваш рабочий лист пользовательских квадратных уравнений. Если вам понравился рабочий лист, вы можете распечатать его прямо из браузера. -3x 2- 1 8. y = −1 x 3 — 1 9. y = 3×2 + 1 9-3 Практика преобразования квадратичных функций A CB Перечислите функции в порядке от наиболее растянутого по вертикали графика до наименее растянутого по вертикали.10. f (x … Преобразования квадратичных функций Страница 8/10 глава и урок, с одним практическим листом для каждого урока в Glencoe Algebra 1. … 9- 3 Преобразования квадратичных функций … 9-4 Решение квадратичных функций … Глава 4 Квадратичные функции и уравнения Урок Домашнее задание Пересмотрено 8-9-13 4.1 Квадратичные функции и задачи преобразований 1-3 Стр. 199-201 # 7- 27 нечетных, 65-75 нечетных, 66, 68, 70 4.1 Квадратичные функции и задачи преобразований 4-5 Стр. 199-201 # 29-41 нечетный, 45-53 нечетный, 50 4.2 Стандартная форма квадратного уравнения Задачи 1-2 Отображение 8 лучших рабочих листов, найденных для — 9 2 Практика квадратичных функций. Некоторые из рабочих листов для этой концепции: период тестирования практики квадратичных функций, практика, блок 2 2, написание и построение графиков квадратичных работ, квадратичные графики, преобразования квадратичных функций, решение каждого уравнения с квадратичными, характеристики урока алгебры i квадратичных функций, Решение… УРОК 9-1 Практика А. Определение квадратичных функций. Определите, является ли каждая функция квадратичной. Объяснять. 1. x 12 3 4 5 y 03 8 15 24 2. y 5 2 x 2 да да, вторые разности постоянны. его можно записать в виде y ax 2 bx c. 3. Используйте таблицу значений для построения графика yx 2 4. xy x 2 4 x, y 2, 0 2 y 2 2 4 0 y1 1 2 4 3 1, 3 0 y 0 2 4 4 0, 4 Измените форму вершины на стандартную квадратичную форму. 7. yx = + — 2 (3) 62 8. yx = 3 (5) 4− + 2 _____ _____ Используйте значения в таблице, чтобы написать квадратное уравнение в форме вершины, затем напишите функцию в стандартной форме.9. Вершина функции равна (1, −3). 10. Вершина функции равна (−3, −2). _____ _____ _____ _____ 11. График … Квадратные уравнения. Квадратичное уравнение относительно x — это уравнение, которое может быть записано стандартным образом как ax 2 + bx + c = 0. где a, b и c — действительные числа с a 0. Квадратное уравнение относительно x также называется вторым -степенное полиномиальное уравнение от x Следовательно, стандартная форма квадратного уравнения может быть записана как: ax 2 + bx + c = 0; где x — неизвестная переменная, а a, b, c — константы с ‘a’ ≠ 0 (если a = 0, то это становится линейным уравнением).Константы «a», «b» и «c» называются коэффициентами. Найдите ось симметрии и вершину каждой квадратичной функции, выполнив следующие действия. 7. y = x 2 + 8x + 12 8. y = x 2 — 10x + 40 9. y = 2x 2 — 8x — 3 Рамка изображения удерживает 4-дюйм. на 6 дюймов фотография. Рамка добавляет рамку шириной x дюймов вокруг трех сторон фотографии. С четвертой стороны рамка образует границу размером 3x 0,5 дюйма.широкий. Общая площадь фотографии и кадра составляет 80,5 i n 2. Напишите квадратное уравнение для комбинированной области. Затем используйте квадратную формулу, чтобы найти x … • Урок №4 — Полный факторинг • Урок №5 — Факторинг по группировке • Урок №6 — Закон нулевого продукта • Урок №7 — Квадратичные неравенства в одной переменной • Урок № 8 — Заполнение квадрата и смещения парабол • Урок № 9 — Моделирование с помощью квадратичных функций • Урок № 10 — Уравнения окружностей • Урок № 11 … Раздел 6: Построение квадратичных функций до значения k = a (x — + k, если k Примечания Практика: Определите преобразования и вершину из приведенных ниже уравнений.2. y = x2-3 (01m (OH-I) Практика: Опишите преобразования и назовите вершину. Создайте уравнение для графиков, перечисленных ниже. 0-3) • Урок №4 — Полный факторинг • Урок №5 — Факторинг по группам • Урок № 6 — Закон нулевого продукта • Урок № 7 — Квадратичные неравенства в одной переменной • Урок № 8 — Завершение квадрата и смещение парабол • Урок № 9 — Моделирование с использованием квадратичных функций • Урок № 10 — Уравнения кругов • Урок № 11 … Практика B Решение квадратных уравнений с помощью факторинга… УРОК x-x8-x8-6 CS10_A1_MECR710549_C08L06b.indd 44 29.03.11 20:38:15 … Практика B 1. 1; 5 2. 2; 9 3. 2 … 1) Постройте график следующих квадратичных функций, используя преобразования (не таблицу). а. у = х2 6 б. y = (x + 4) 2 фев. 13.10: 24 AM 2) Постройте график следующих квадратичных функций, используя преобразования (не таблицу). а. у = (х + 4) 2 б. y = (x 3) 2 2 фев 13: 11: 28 Форма вершины AM: форма вершины квадратичной функции f (x) = a (x h) 2 … 21: Решение одношаговых уравнений умножением и Разделение, Исследование: Использование обратных операций: Разминка: стр.120: Исследование: стр.121: Практика урока: стр.123 Урок 7-3 Решение квадратных уравнений путем факторинга ЗАДАНИЕ 7 (продолжение) Ответы учащихся на задачи практического урока предоставят вам формирующую оценку их понимания концепций урока и их способностей. применить свои знания. Мои заметки УРОК 7-3 ПРАКТИКА Решите каждое квадратное уравнение путем факторизации. 11. 2×2 — 11x … Модуль 19 909 Урок 2 Оценка: домашнее задание и практика • Онлайн-домашнее задание • Подсказки и помощь • Дополнительная практика Постройте каждую квадратичную функцию, преобразовав график ƒ (x) = х 2.Опишите преобразования. 1. 9 3 Практика B Преобразование B. xy C. xy 0 7. y 2 = -3x 2-1 8. y = −1 x 3 — 1 9. y = 3×2 + 1 9-3 Практика квадратичных преобразований Функции A CB Перечислите функции в порядке от наиболее растянутого по вертикали до наименее растянутого по вертикали графика. Если вы хотите загрузить и установить урок 6 4 функции преобразования, практика b ответы, тогда это, безусловно, просто, прежде чем в настоящее время мы расширяем подключение, чтобы покупать и заключать сделки, чтобы загрузить и установить урок 6 4 функции преобразования практики b ответы поэтому простые ! dev2020.bakhtarnews.com.af урок 6 4 функции трансформации 6.7 Банджо-болт возврата топлива Cummins репликация ДНК Выберите предметы ЕГЭ, которые вы сдали или собираетесь сдавать. Укажите свои баллы по предметам (можно ожидаемые). Мы автоматически подберем для вас подходящие вузы и специальности. ЕГЭ проводится по 15 предметам. Для получения школьного аттестата выпускники должны сдать ЕГЭ по двум обязательным предметам — русскому языку и математике. Остальные дисциплины сдаются по желанию школьника. Как правило, абитуриенты вузов выбирают два-три дополнительных ЕГЭ, в зависимости от перечня предметов, необходимых для поступления на одно или несколько желаемых направлений. Мы рекомендуем школьникам сначала определить для себя несколько приоритетных направлений обучения и проанализировать, какие экзамены на эти направления принимают вузы. После этого можно подать заявку на требуемые предметы ЕГЭ. Если вы еще не до конца определились с выбором специальности, сейчас можно зарегистрироваться на несколько предметов ЕГЭ, а ближе к экзамену отменить те, которые вам не понадобятся при поступлении. Один из самых популярных наборов ЕГЭ, в прошлом году экзамен по физике выбрали более 170 тысяч российских школьников. Спрос на физику обусловлен количеством специальностей, на которые требуется этот экзамен. Такую комбинацию предметов можно назвать самой востребованной вузами, она подходит более чем для 150 специальностей высшего образования. Если вы сдали математику, физику и русский язык, перед вами открыты технические, отраслевые технологические и IT-направления вузов: • Авиастроение • Горное дело • Информатика и вычислительная техника • Машиностроение • Наноинженерия • Нефтегазовое дело • Радиотехника • Строительство • Электроника и наноэлектроника • Ядерная энергетика и теплофизика и др. В том числе абитуриентов с ЕГЭ по математике и физике принимают ведущие технические университеты страны — МГТУ имени Н.Э. Баумана, МИРЭА, МИФИ, МФТИ, МИСиС, МГСУ. Стоит отметить и большое количество бесплатных мест на технических специальностях, объем бюджетного отделения здесь не сравним с другими направлениями. Это прямо отражается на проходном балле — он значительно ниже гуманитарных специальностей. В результате абитуриенты даже со средними результатами ЕГЭ имеют очень неплохие шансы быть зачисленными на бесплатное отделение из-за большого количества специальностей и бюджетных мест. Сравнить проходные баллы вузов на технические и IT-направления в 2020 году вы можете в каталоге учебных заведений «Учебы.ру». Информатику сдают абитуриенты, поступающие на специальности в области информационных технологий, — будущие программисты, системотехники, инженеры по телекоммуникациям: • Информатика и вычислительная техника • Прикладная информатика • Информационные системы и технологии • Программная инженерия • Инфокоммуникационные технологии и системы связи и др. Стоит отметить, что некоторые вузы на IT-направления требуют ЕГЭ по физике, поэтому наряду с географией и литературой информатика является одним из самых редких ЕГЭ по выбору. Такие правила приема действуют в МИФИ, МАИ, на ряд программ МГТУ имени Н.Э. Баумана и НИУ ВШЭ. Тем не менее многие учебные заведения готовы принять абитуриентов с набором «математика, информатика, русский язык». Среди них — НИУ ВШЭ (некоторые программы), МФТИ, МИСиС, МИЭТ, МТУСИ, Московский Политех. Обществознание — самый популярный ЕГЭ по выбору, в прошлом году его сдавали 57% выпускников. Этот экзамен, в комбинации с математикой и русским языком, требуется на самые популярные у абитуриентов направления вузов — экономические: • Экономика • Менеджмент • Управление персоналом • Государственное и муниципальное управление • Бизнес-информатика • Торговое дело • Социология и др. Иногда ведущие учебные заведения запрашивают в добавок к этому набору четвертый экзамен — ЕГЭ по иностранному языку. Такие правила приема действуют, например, в НИУ ВШЭ, РЭУ имени Плеханова. При этом есть вузы, которые вместо ЕГЭ по обществознанию принимают на экономические направления ЕГЭ по иностранному — это экономический факультет МГУ, МГИМО, ВАВТ, международный финансовый факультет Финансового университета. «Экономика» — направление бакалавриата с одним из самых больших бюджетных отделений. В 2019 году московские вузы приняли на первый курс более 2000 абитуриентов. Несмотря на это проходные баллы здесь традиционно очень высокие. Так, в прошлом году, чтобы поступить в НИУ ВШЭ нужно было набирать 92,5-96,5 балла за каждый ЕГЭ, в Финуниверситет — 88,7-90 баллов. Несколько ниже требуемые результаты ЕГЭ в отраслевые вузы — Российский университет транспорта (75,7 балла), Московский автомобильно-дорожный государственный технический университет (82 балла), Московский авиационный институт (84,3 балла). Предметы ЕГЭ для будущих врачей и медработников. Все медицинские университеты требуют от абитуриентов результаты экзаменов по химии и биологии. Также такой набор ЕГЭ нужно сдавать будущим учителям физкультуры и спортивным тренерам. С результатами ЕГЭ по этим трем предметам вы сможете подать документы на направления: • Лечебное дело • Стоматология • Педиатрия • Медицинская биохимия • Медико-профилактическое дело • Физическая культура и др. При поступлении на основную врачебную специальность «Лечебное дело» в прошлом году максимальные требования к абитуриентам предъявляли Первый, Второй и Третий меды. Так, для зачисления в ПМГМУ имени Сеченова каждый из предметов — химию, биологию и русский язык — нужно было сдавать на 94,3 балла, в РНИМУ имени Пирогова — на 87 баллов, в МГМСУ им. Евдокимова — на 84,7 балла. Этот набор ЕГЭ вузы принимают на большинство гуманитарных специальностей: • Юриспруденция • Судебная экспертиза • Реклама и связи с общественностью • Гостиничное дело • Культурология • Зарубежное регионоведение • Регионоведение России • Политология и др. Стоит отметить, что некоторые вузы на направления «Юриспруденция», «Реклама», «Гостиничное дело» вместо ЕГЭ по истории требуют ЕГЭ по иностранному языку, например, МГИМО, ВАВТ, МГЛУ. Также ряд вузов на специальности, связанные с политологией, регионоведением, запрашивают ЕГЭ по иностранному вместо обществознания. Такие правила приема действуют в МГИМО, МГЛУ, РУДН, МГУ, в то время как Финуниверситет, РЭУ имени Плеханова, МПГУ, ГУУ принимают абитуриентов с набором «обществознание + история + русский». При выборе конкретного гуманитарного направления необходимо учитывать количество бюджетных мест, которое сильно отличается в зависимости от специальности. Например, «Юриспруденция» — одна из самых популярных специальностей и представлена практически в каждом российском вузе. Направление отличает большое количество бюджетных мест, которые в некоторых вузах (МГЮУ имени Кутафина, МГУ имени Ломоносова, НИУ ВШЭ, Финуниверситет) исчисляются сотнями. В то время как «Реклама» и «Политология» — специальности с маленьким бюджетным отделением. Всего в Москве бакалавров рекламы и связей с общественностью готовят 59 вузов, и лишь в 17 из них открыто суммарно 240 бюджетных мест, что в два раза меньше плана приема на «Юриспруденцию» в одном только МГЮУ имени Кутафина. Стоит помнить: чем меньше бюджетных мест на специальности, тем выше проходной балл, то есть сложнее на нее поступить. Такую комбинацию предметов ЕГЭ нужно сдавать будущим лингвистам и переводчикам на две основные языковые специальности: • Лингвистика • Перевод и переводоведение. В качестве профильного экзамена по иностранному языку принимаются ЕГЭ по английскому, немецкому, французскому, испанскому, а также по китайскому языку, который дебютировал на ЕГЭ в 2019 году. Некоторые вузы на «Лингвистику» требуют ЕГЭ по обществознанию вместо истории — это НИУ ВШЭ, МПГУ, РЭУ имени Плеханова. Но большинство в качестве третьего ЕГЭ запрашивают все-таки историю, среди них — МГЛУ, МГУ им. Ломоносова, МГПУ, РГГУ, РГСУ, РУДН. Также стоит отметить, что на направление «Фундаментальная и прикладная лингвистика» набор предметов отличается. Здесь в качестве третьего ЕГЭ вузы принимают по своему выбору литературу или математику. Большим бюджетным отделением на лингвистических направлениях могут похвастаться только МГЛУ (375 мест), Московский городской педагогический университет (110 мест), НИУ ВШЭ (75 мест) и Московский государственный областной университет (75 мест). В остальных вузах, включая МГУ, мест на «Лингвистике» традиционно мало. Поступить на языковые специальности крайне трудно. Проходной балл здесь напрямую зависит от цифр приема — чем больше открыто мест, тем ниже требуемый результат ЕГЭ. Помимо направлений, где иностранный язык является профильным предметом, вузы на свое усмотрение могут засчитывать результаты этого ЕГЭ в качестве четвертого вступительного экзамена практически на все специальности. Литературу и иностранный язык сдают будущие журналисты и филологи: • Журналистика • Филология. Помимо трех ЕГЭ на «Журналистику» предусмотрен дополнительный творческий экзамен в вузе. Как правило, он проходит в форме творческого сочинения и собеседования. Несмотря на то, что большинство учебных заведений принимают абитуриентов на основе трех ЕГЭ, есть вузы, в которые можно поступить, сдав только два ЕГЭ — литературу и русский язык (плюс творческий экзамен). Среди них — Московский Политех, РГСУ, МПГУ, РУДН. Также некоторые вузы вместо ЕГЭ по иностранному на «Журналистику» требуют ЕГЭ по истории, а на «Филологию» — ЕГЭ по обществознанию, но такие в меньшинстве. На сайте Учеба.ру вы можете найти вуз и специальность по предметам ЕГЭ. Поиск вуза по предметам, баллам ЕГЭ и городам, список вузов и специальностей по набору ЕГЭ, вузы по предметам ЕГЭ в вашем городе. Всю эту информацию вы найдете на нашем сайте. Задать вопрос
Здравствуйте! Я учусь в 10 классе, но уже сейчас мои одноклассники знают по каким предметам будут сдавать ЕГЭ в отличие от меня. Сдавая ГИА, я выбрала английский язык и обществознание, предполагая в дальнейшем пойти учиться на преподавателя английского. Но сейчас я всё больше слышу о том, что эта специальность не востребована, на неё очень высокий конкурс и существует проблема с трудоустройством. Поэтому я решила изменить свой выбор, но оставить английский, думаю, что я могла бы сдать информатику, но на какие специальности я могу пойти с английским языком и информатикой. Мне очень сложно определиться, помогите мне, пожалуйста Узнать ответ Ответ: Добрый день, Ксения! Давай по порядку. Ты решила выбрать английский – и это здорово и перспективно. Сегодня специалисты со знанием английского языка много где требуются и хорошо оплачиваются. В вузах, где английский язык основной предмет действительно есть конкурс, и к нему стоит подготовиться, но и спрос на таких специалистов большой, они востребованы. И не только как преподаватели, можно стать репетитором, лингвистом, переводчиком. Даже если оклад у преподавателя не всегда высокий, есть возможности для дополнительного заработка – например, частные уроки и переводы. Английский язык нужен всегда и везде. Если ты решишь оставить английский, то возможные варианты такие: Ты хочешь, что бы английский стал твоей профессией или же профессию, где английский будет бонусом? Ответ на этот вопрос поможет тебе определиться с направлением. Дальше про информатику. Из твоего письма я слышу, что информатика для тебя скорее как экзамен. Или все же ты рассматриваешь ее как профессию? Мест, где информатика требуется вместе с английским языком, к сожалению нет. Но есть возможность сочетания английского и обществознания — более перспективная – тут и менеджмент, и экономика, и государственное управление и управление персоналом и другое. Но если информатика тебе интереснее, то направления тут такие: Выпускники могут работать системными администраторами, инженерами по внутренним и внешним сетям. Их задача обеспечить эффективное использование информационных технологии, следить за правильностью эксплуатации, внедрение новых технологий. Выбор специальностей и в одном и в другом случае большой. Определись с тем, что ты хочешь делать и помни, хорошие профессионалы востребованы везде. Желаю тебе успехов! Анастасия Клецко Я в 9 классе. Сдаю физику и информатику. Физику я не люблю и боюсь не сдать, потому что знаю плохо. В школу создают определённые профили: 1. физмат 2.информатика 3. общество и 4. химбио. Но я не могу выбрать куда пойти в физмат или в информ. Если идти в физмат, то можно сдавать только физику (не считая русского и матем), и соответственно если идти в информ, то сдавать только информ (то есть от физики я могу отказаться в любой момент) Но я не знаю куда потом можно поступить с информатикой (на кого учиться). В физмате будет физики и математики больше чем в других профилях, а в информатическом классе — информатики больше. Посоветуйте что мне делать? Поступать собираюсь после 11 класса. Больше меня тянет к информатике (её я знаю гораздо лучше физики) Спасибо заранее! Узнать ответ Ответ: Добрый день, Виктория! Есть несколько направлений обучения в ВУЗах, на которые ты можешь пойти, сдав ЕГЭ по основным предметам и обществознание. Это: Если ты сдаешь ЕГЭ по основным предметам и географии, то можешь выбирать из следующих направлений: Как видишь, список профессий довольно разнородный. В первую очередь тебе необходимо ответить для себя на следующий вопрос: с чем я хочу работать? С какой сферой, областью? Это могут быть как другие люди, так и финансы, карты и экология в целом. После того, как ты определишься, с чем ты хочешь работать, ответь на следующий вопрос – а что ты хочешь делать с этой сферой? Управлять, исследовать, контролировать, защищать, проектировать? В зависимости от твоего ответа получатся разные профессии. Приведу пример: если, предположим, тебе нравится управлять, то в зависимости от сферы, это будут профессии HR (управление людьми), экономиста (управление бюджетом организации), специалиста по лесному делу (управление лесными ресурсами). Если тебе нравится защищать, то ты можешь быть специалистом по экономической безопасности (защита финансов) или экологом (защита природы). Таким образом, ответив на два вопроса, ты сможешь определить для себя подходящую профессию. Удачи! Аля Дубчук Здравствуйте! Я заканчиваю 11 класс, скоро уже поступать, а я еще не совсем определилась куда, потому что не знаю кем хочу быть… Но с выбором ЕГЭ точно определилась: буду сдавать математику, русский язык, химию(химию очень люблю) — это те предметы которые я хорошо знаю, и физику — знаю немного хуже. В медицинском не очень хочу учиться, тем более, что не сдаю биологию и не очень люблю этот предмет. Кем мне быть? Куда пойти учиться? Что бы вы могли мне посоветовать? Узнать ответ Ответ: Ирина, здравствуйте! Прежде всего, хотелось бы отметить, что Вы правильно спрашиваете о том, кем будете. Действительно, школьный предмет ≠специальность, а специальность≠профессия. Давайте посмотрим, куда Вы можете поступить и кем стать после. С математикой, русским языком, химией и физикой Вы можете поступить на следующие специальности: — Математика – математики – это люди, которые описывают реальные объекты и процессы языком математики и формул для того, чтобы найти новые закономерности объекта или явления или решить задачу математическим методом.Математики работают во всех сферах, где используется вычислительная техника – правительственные и государственные учреждения, банки, IT-корпорации, страховые организации, консалтинговые организации — Прикладная математика – если математики ориентированы на теорию, то прикладная математика – на решение реальных проблем (социальных, политических, экономических, организационных) при помощи моделирования процессов. Выпускники данного факультета работают аналитиками в финансовых корпорациях, банках, консалтинговых агентствах, IT-корпорациях — Химическая технология энергонасыщенных материалов и изделий – специалист этого профиля умеет проводить процесс получения энергонасыщенных материалов и изделий «от и до» — от инженерных расчётов технологического процесса и до составления инструкций для персонала. После выпуска данные специалисты работают в компаниях, производящих или продающих энергонасыщенные материалы. — Химическая технология материалов современной энергетики – эти специалисты отвечают за ядерное топливо, начиная от его добычи и заканчивая экологическим и радиационным мониторингом предприятий, производящих ядерную энергетику. Работают они на атомных электростанциях. — Химия – специалист-химик может синтезировать новый продукт с заданными свойствами, может провести химическую экспертизу и проконтролировать химические процессы в производстве. Специалист данного профиля востребован в компаниях, производящих химические продукты: удобрения, лакокрасочные материалы, полимеры, моющие средства, парфюмерию и косметику. — Фундаментальная и прикладная химия – в отличие от химика, данный специалист занимается решением более широких задач: занимается исследованием протекания химических процессов, выявляет общие закономерности функционирования химических процесов и управление ими, решает фундаментальные и прикладные задачи в области химии. Специалист данного профиля также работает в компаниях, производящих химические продукты. — Нефтегазовое дело – этот специалист умеет разрабатывать и проектировать месторождения нефти и газа, выполнять работы по строительству и реконструкции нефтяных и газовых скважин, контролировать качество сырья и готовой продукции. Данного специалиста ждут в нефтяных и газовых компаниях. — Металлургия – данный специалист может спроектировать металлургическую печь, провести металлографический анализ сталей и сплавов, споргнозировать конкурентоспособность нового металла. После выпуска специалист работает на металлургических заводах. — Материаловедение и технологии материалов – данный специалист совершенствует технологические процессы получения материалов и создаёт новые материалы. Работают специалисты данного профиля на производстве или же в лаборатории. — Нанотехнологии и микросистемная техника – специалист данного профиля занимается физико-химическим и физико-математическим моделированием, конструирует наноматериалы и участвует в работе по освоению технологических процессов. Работают данные специалисты в организациях, производящих наноматериалы (например, на предприятиях по производству медицинской техники), а также в исследовательских лабораториях. — Наноинженерия – данный специалист, в отличие от нанотехнолога, работает уже непосредственно на производстве: совершенствует машины, производящие наноматериалы, внедряет результаты научно-технических и проектных разработок, осуществляет контроль качества производства нанообъектов и изделий на их основе. Работают данные специалисты в организациях, занимающихся производством наноматериалов. — Наноматериалы – специалисты данного профиля работают не с новыми материалами (как нанотехнолог) и не с машинами (как наноинженер), а с конкретными задачами: собирают данные о наноматериалах, оценивают качество наноматериалов, занимаются подготовкой документов при внедрении системы менеджмента качества наноматериалов. Работают они в тех организациях, которые используют наноматериалы в своей работе. — Техносферная безопасность – данный специалист умеет выявить зоны повышенного техногенного риска, провести научное исследование в области безопасности и разработать требования безопасности. Специалисты работают на крупных предприятиях, а также на государственной службе. — Инноватика – данные специалисты отвечают за весь цикл инноваций, начиная от идеи для инновационного проекта и выявления его жизнеспособности и заканчива технологией реализации и продвижением продукта. Данные специалисты работают на инновационных производствах или же в венчурных фондах. В качестве заключения хотелось бы задать Вам несколько вопросов, которые могут понять, а что же из всех приведённых специальностей подходит именно Вам? Удачи и успехов! Юлия Козлова Доброго времени суток. Меня зовут Юлиана, и я никак не могу определиться с будущей профессией. Сейчас учусь в восьмом классе, но времени для определения осталось все же немного. Знаю, что если захочу, смогу выучить любой предмет и посвятить себя любой отрасли, так как учусь по всем предметам стабильно отлично. Но какую именно профессию выбрать, даже предположить не могу, потому что приоритетов почти никаких нет. Мне нравятся абсолютно разные и практически несовместимые предметы: математика, русский, английский и химия. (Это не значит, что другие предметы не рассматриваются, как варианты) Подскажите, пожалуйста, профессию совмещающую мои любимые предметы. Узнать ответ Ответ: Юлианна, добрый день! С учетом тех предметов, что Вы назвали можно профессионально реализоваться, например, в сферах: химического, фармацевтического, косметического, химико-технологического производства, полиграфического и упаковочного производства, производства продуктов питания, общественного питания. Технологи контролируют процесс изготовления на этих производствах, осуществляют проверку качества готовой продукции, принимают участие в экспериментах по созданию новых продуктов, продумывают и разрабатывают технологии. Одно из самых перспективных направлений – наноинженерия. Специалисты этого направления – наноинженеры – открывают свойства уже имеющихся материалов и разрабатывают новые. Многие их достижения используются в медицине и биотехнологиях. Ученые-исследователи работают в научно-исследовательских институтах. Биотехнологи изучают микроогранизмы, клеточные культуры животных и растений. Исследуют, получают и применяют ферменты и вирусы, принимают участие в создании лекарственных препаратов и биологически-активных веществ. Специалисты по «техносферной безопасности» занимаются защитой окружающей среды от влияния человеческой деятельности, а также могут обеспечивать безопасность сотрудников на производствах. Очень хорошо, что Вы уже в 8 классе задумались о своей будущей профессии – у Вас есть время попробовать реализовать себя в разных видах деятельности, чтобы решить, чем Вам действительно хотелось бы заниматься профессионально. Учитывая, что по всем предметам Вы учитесь отлично подумайте, что какая сфера Вам ближе, с чем бы Вы хотели работать? Дело в том, что школьных предметов около десяти, а профессий около 40 тысяч и они напрямую не следуют из школьных предметов. Для начала предлагаю взять лист бумаги и выписать объекты: В зависимости от того насколько Вы хотите работать с каждым из объектов, поставьте баллы от 1 до 10 (1 – не хотите, 10 — очень хотите). Выбери три сферы, набравшие наибольшее количество баллов. А теперь для каждой из 3 сфер, набравших наибольшее количество баллов, выберете не больше 2-х функций, которые Вас привлекают: В зависимости от ответов, узнавайте какие специалисты занимаются тем, что Вам нравится в тех сферах деятельности, которые Вас привлекают. Это можно сделать пообщавшись с родными и знакомыми или зайдя на сайт подбора персонала и осуществив поиск вакансий по отраслям. Каждая вакансия содержит не только название, но и требования к кандидату и перечень должностных обязанностей. Осознанно выбрать любимую профессию помогут также и ответы на вопросы: Желаю Вам удачи и дальнейших успехов! Ольга Никитина Здравствуйте! Я из Казани. В этом году закончу школу. У меня детский церебральный паралич . Высшее образование необходимо. Буду сдавать общество, русский, математику. Мне нравятся языки: английский, татарский. В принципе вообще языки люблю. Пишу песни, тексты, стихи, рисую и обожаю петь)) Узнать ответ Ответ: Доброго дня, Виктория! Не могу не согласиться с тобой, что выбор профессии – действительно сложный вопрос, и часто интересны совершенно разные области труда. Но давай попробуем расставить приоритеты. Из твоего письма я слышу несколько профессиональных направлений, которые ты для себя рассматривала и/или рассматриваешь до сих пор: Таким образом, как ты видишь, перечисленные тобой профессии достаточно разнообразны и по каждой из них можно получить соответствующее образование. Для того, чтобы конкретизировать свой выбор и определиться с дальнейшей сферой обучения, сделай следующее. Возьми четыре листа бумаги, каждый лист подпиши одним их четырех перечисленных выше блоков профессий, затем раздели каждый лист на две колонки. В первой колонке для каждого блока профессий выпиши те плюсы, которые ты в нем видишь именно для себя (что есть интересного, какие способности для него у тебя есть, насколько данные профессии востребованы и т.д.). Во второй колонке выпиши те минусы, которые могут тебе помешать (что не нравится в данных профессиях, какие твои качества могут стать препятствием в их освоении и т.д.). Внимательно посмотри на получившиеся списки. Есть ли «лидирующие» по плюсам/минусам группы профессий? Если таковых не наблюдается, найди для себя ответ на следующий вопрос: что для тебя важно в твоей будущей профессии? (чтобы она была интересной или легко получалась, или на нее всегда был спрос). Попробуй составить список значимых для тебя параметров и в соответствии с ним взглянуть на группы профессий. Скорее всего, есть те, которые в наибольшей степени отвечают твоим запросам. Удачи тебе и успехов! Аля Дубчук Здравствуйте! Я учусь в 11 классе. Скоро сдавать ЕГЭ, а я так и не определилась с выбором профессии. Нравятся обществознание и география. Куда можно поступить, сдав основные предметы и их? Узнать ответ Ответ: Доброго дня! Виктория, набор факультетов, на которые можно подавать результаты ЕГЭ по географии и обществознанию, достаточно велик. Начиная от экономических, юридических специальностей до психологии и регионоведения. Поэтому выбирать профессию, отталкиваясь исключительно от интереса к школьным предметам не всегда оправданно. Любая профессия включает в себя два компонента: то, с чем мы работаем и то, что мы с этим делаем. Если тебе интересно обществознание, давай для начала конкретизируем, какая именно тема тебе интересна. Интерес к проблемам политики может быть связан с профессиями политолога, специалиста по международным отношениям или специалиста по государственному и муниципальному управлению; экономики – профессиями финансиста, экономиста, менеджера; социологии – профессиями журналиста, социолога, культуролога; психология – профессиями психолога, психотерапевта, педагога и т.д. Если это география, то какая? Физическая география может быть связанна с профессиями почвоведа, геолога, географа, разработчика месторождении полезных ископаемых; социально-экономическая география – с профессионалами в сфере регионоведения, лесного/сельского дела; культурная география – с профессиями востоковеда, африкониста и т.д. Поэтому в первую очередь определи для себя – с какой сферой ты хочешь связать свою профессию. Следующий вопрос, который необходимо себе задать – а что ты хочешь делать? Хочешь ли ты заниматься управлением (персоналом в компании/природными ресурсами), а может быть тебе интересно защищать (людей как адвокат/природу как эколог), или же преподавать? Сочетание двух параметров: интересующей тебя области и того, что ты хочешь с ней делать дает оптимальную для тебя профессию. Удачи! Аля Дубчук Здравствуйте. Я учусь сейчас в 11 классе, собираюсь сдавать только русский язык и математику. Какую профессию я могу получить? Узнать ответ Ответ: Лера, добрый день! Школьных предметов – чуть больше 10, а профессий около 40 тысяч, поэтому даже с 2-мя предметами выбор профессий широк и многообразен. Ты написала, что будешь сдавать только 2 предмета. А на самом деле тебе нравится математика и русский язык? Или оба предмета тебе не нравятся и ты сдаешь их только потому, что они являются обязательными? Если нравится, то что больше и почему? Есть ли еще какие-то школьные предметы, которые тебе нравятся? Чем именно? Что ты любишь делать вне школы? Какие передачи смотришь по телевизору? О чем читаешь книги, журналы и газеты? Что привлекает твое внимание? Что ищешь в социальных сетях? Для того, чтобы выбрать свою профессию – ту которая будет тебе приносить не только доход, но и удовольствие – нужно разобраться, что ты любишь делать и чем бы в будущем ты хотела заниматься. Учитывая, что с 2 предметами вариантов высшего образования совсем немного, а волнует тебя выбор профессии, предлагаю тебе определиться со сферой деятельности и рассмотреть возможность поступления в колледж на базе 11 классов. Спрос на специалистов хорошего уровня со средним специальным образованием сейчас достаточно высок. Все возможные варианты профессий можно условно объединить в 5 типов: Люди этого типа, как правило, склонны создавать, планировать, проектировать, моделировать, исследовать и придумывать новые способы обработки и монтажа материалов. В числе профессий этого типа не только инженер, техник, технолог, регулировщик приборов, раскройщик одежды, но и кондитер, пекарь и повар. Люди этого типа хорошо оперируют знаками и символами, любят производить расчеты и вычисления, предпочитают обрабатывать тексты и таблицы, работают с чертежами, картами и схемами. К профессиям этого типа относятся – экономист, бухгалтер, web-дизайнер, оператор ПК, корректор, чертежник, картограф и др. Люди этого типа легко знакомятся и общаются с новыми людьми, умеют внимательно слушать других, а также сами могут выступать перед публикой. Их привлекает сфера обслуживания людей, обучения, воспитания, управления. К профессиям этого типа относятся менеджеры, торговые представители, тренеры, учителя, социальные работники и мн. др. Соответственно люди этого типа любят ухаживать и наблюдать за растениями или животными и могут работать ландшафтными дизайнерами, овощеводами, фермерами, зоотехниками, пчеловодами и т.д. Люди этого типа предпочитают заниматься художественным оформлением и творчеством, любят изготавливать своими руками красивые вещи и т.п. Могут работать дизайнерами, флористами, парикмахерами, кондитерами, ювелирами, звукорежессерами, фотохудожниками, мастерами декоративно-прикладного искусства и т.п. Подумай, чем бы тебе хотелось заниматься? Какая сфера деятельности ближе тебе? Надеюсь, что ответы на эти вопросы помогут тебе найти путь к своей любимой профессии. Успехов тебе! Ольга Никитина Здравствуйте! Мне 17 лет и я учусь в 10 классе, все мои одноклассники уже определились с выбором профессии и активно готовяться к поступлению, к сожалению, я никак не определюсь с какой профессией мне связать свою жизнь. Узнать ответ Ответ: Добрый день, Нина! Благодарю Вас за вопрос. При этом важно учесть, что для Вас интересная работа – это не сидеть на месте. Есть ли еще какие-то факторы, значимые для Вас, которые также нужно учесть при выборе профессии? Например, работа среди людей или в одиночестве? Если среди людей, то что это за люди? Небольшая группа хорошо знакомых людей или же общение с новыми людьми? Рассматриваете ли Вы варианты работы на природе? Как относитесь к возможности переездов и командировок? И т.д. Чаще всего люди, которые хорошо пишут, имеют красивую и грамотную речь. Вы хотели бы делиться с другими своими впечатлениями посредством своих письменных материалов или же с удовольствием выступали бы устно? В первом случае, например, можно работать журналистом в газете, во втором – журналистом на телевидении. А профессия журналист-интервьюер, позволяет сочетать и устное общение, и подготовку статей. Аналогично, работая в сфере «Искусствоведения», в первом случае – можно писать критические статьи или научно-популярные книги, а во втором – читать лекции и проводить экскурсии. Обращаю Ваше внимание на то, что пишут не только писатели и журналисты. В любой сфере деятельность востребованы специалисты, которые умеют писать, рассказывать, описывать и продвигать. Это изложение любой информации, которую можно услышать по радио и телевидению, увидеть в интернете, в газете, в музее, в инструкции по эксплуатации любого прибора или на рекламных щитах и в рекламных буклетах и т.д. С Вашими способностями и интересами много профессий: сценарист, телекритик, кинокритик, театровед, тележурналист, журналист, корреспондент, обозреватель, ведущий радио- и телепрограмм, редактор, писатель, преподаватель учебного заведения, сотрудник музея, научно-исследовательского института, архива, консультант, эксперт, менеджер, продюсер, например, в туристических компаниях или культурно-досуговых учреждениях, специалист по связям с общественностью и рекламе в любой сфере и мн. др. В интернете можно подробно почитать об этих профессиях. Выбирайте, что ближе Вам! Желаю Вам удачи! Ольга Никитина Добрый вечер. Мне 15 лет, я хороша в обществознании, английском, русском и в литературе, ну и в географии. Но я не определилась со специальностью. А сама я хочу в творческие. Например, режиссер, музыкант, и т. д. Что вы мне посоветуете? Узнать ответ Ответ: Анастасия, добрый день! В вашем ответе прослеживаются две линии – то, что у Вас хорошо получается (школьные предметы) и то, чем Вам хотелось бы заниматься (творческие профессии). Если исходить из линии тех предметов, что получаются у Вас хорошо, то Вы можете поступать на следующие специальности: Если исходить из линии Ваших интересов, то помимо названных Вами предметов на нижеперечисленные специальности сдаётся история: Также я предложила бы Вам подумать, как можно объединить Ваши интересы и Ваши таланты. В этом Вам помогут следующие вопросы: Подумайте, что для Вас важно и проведите свое маленькое исследование Успехов! Юлия Козлова Здравствуйте! Помогите определиться, архитектор или дизайнер. Не знаю,что выбрать. Узнать ответ Ответ: Настя, добрый день! И архитектор, и дизайнер профессии творческие. Архитектор составляет проекты зданий и сооружений, изготавливает их изображения в виде чертежей и рисунков, владеет нормами проектирования, использует геодезические приборы, разбирается в технических и эстетических особенностях строительных и отделочных материалов. Может заниматься не только строительством новых, но и реконструкцией и реставрацией старых зданий и сооружений. Работает в проектных и технологических институтах, архитектурных мастерских, организациях материально-технического обеспечения строительства как в частном, так и в государственном секторе. Дизайн делает нашу жизнь красивее и охватывает практически все аспекты окружающей человека среды. В этой сфере очень много направлений: дизайн интерьера, дизайн одежды, промышленный дизайн (дизайн автотранспорта, бытовых приборов, посуды, мебели и т.д.), графический дизайн (разработка фирменных стилей компаний, изготовление логотипов предприятий, полиграфической продукции, сувенирной продукции, упаковки, веб-дизайн и т.д), дизайн среды и др. Дизайнер придумывает стиль с учетом пожеланий заказчика, делает эскизы, при необходимости выбирает отделочные материалы и контролирует выполнение работы других мастеров и т.д. Специалисты занимаются разработкой дизайн-проектов на промышленных предприятиях, в сфере оказания дизайнерских услуг, в сфере рекламы и торговли. В зависимости от направления могут трудиться в офисе или дома на собственном компьютере. При выборе профессии архитектора необходимо учитывать несколько факторов. Во-первых, у тебя должно быть хорошее знание математики. Во-вторых, архитектор несет ответственность за безопасность своего здания или сооружения. В третьих, у тебя могут быть прекрасные идеи, например, по строительству нового городского микрорайона. Ты можешь создать отличный проект, но его реализация зависит не только от тебя. Твой проект должны одобрить специальные службы, нужны денежные средства его на финансирование и наконец, строительство может осуществляться много лет. Ты согласна, что не все твои проекты будут реализованы? Ты согласна ждать 10 и более лет, чтобы увидеть новый микрорайон, построенный по твоему проекту, или же ты хочешь, чтобы твои идеи быстрее воплощались в жизнь? Хочу тебя обрадовать, строительство частных домов происходит быстрее. И в сегменте частных домов твои проекты могут реализовываться гораздо чаще. Ошибки дизайнера не так критичны как ошибки архитектора. Дизайнер может гораздо чаще и быстрее видеть результат своей работы. В профессии дизайнера важно внимание к деталям и их сочетанию. В профессии архитектора мелкие детали не так важны, проекты архитектора более объемные, для них характерен размах. Поэтому выбирай, что ближе тебе! Для того, чтобы стать архитектором нужно хорошо знать математику, дополнительно при поступлении в колледж необходимо сдать экзамен по рисунку. Для того, чтобы стать дизайнером после 9 класса необходимо сдать экзамен по рисунку (натюрморт, карандаш), а после 11 класса – по композиции (композиции геометрических фигур (гуаш, тушь)). Как правило, в учебных заведениях, есть подготовительные курсы для поступления. В Уфе профессию архитектора можно получить в Башкирском строительном колледже www.bsk.ufanet.ru. Получить профессию Дизайнера можно в Уфимском государственном колледже технологии и дизайн. Удачи! Ольга Никитина Хочу знать, для каких профессий нужен английский? Буду очень признателен. Узнать ответ Ответ: Александр, добрый день! Английский язык — язык международного общения. В любой области знаний и в любых отраслях промышленности сегодня требуются и хорошо оплачиваются специалисты со знанием английского языка. В этот промежуток укладывается свыше 100 вакансий и технических и гуманитарных специальностей. В профессиях напрямую связанных с языками: ученый-лингвист, переводчик, экскурсовод, учитель английского и т.д. В профессиях, предполагающих общение на этом языке: авиадиспетчер, менеджер компании, имеющей партнеров вне России, бизнес-консультант, администратор в гостинице и многие другие. В профессиях, для которых объем и качество профессиональной литературы на английском выше, чем на русском: программист, финансист и т.д. Вы хотите использовать язык (английский) постоянно, или только для работы? Например, можно общаться на английском языке, участвовать в деловых встречах, презентациях, переговорах, где английский нужен, как рабочий. А можно проводить собеседование на английском языке, подготавливать деловую документацию (презентации, отчеты и пр.). Или уверенно пользоваться при коммуникации с зарубежными партнерами специальной терминологией (устно и письменно), читать и понимать тексты со специализированным уклоном… Вариантов большое количество, но что бы выбрать направление интересное для Вас – задавайте себе вопросы и ищите на них ответы. Какие у вас увлечения, интересы? Чем Вам интересно заниматься помимо учебы? Какой Вы представляете себе будущую профессию? Язык для Вас ценен сам по себе или как средство общения. Есть ли что-то, что интересно Вам и получается лучше , чем иностранный язык? Самая интересная профессия это та, которая вам нравится! Анастасия Клецко Здравствуйте! Я ученица 11 класса и сдаю ЕГЭ по обществознанию и литературе. Живу в Москве, на какие профессии и в каких вузах я могу рассчитывать, учитывая, что рассматриваю я только бюджетное обучение. Заранее спасибо за ответ. Узнать ответ Ответ: Марина, здравствуйте! Спасибо большое за Ваш вопрос. Указанный Вами набор предметов предполагает довольно обширный набор возможных профессий и специальностей. Тут, пожалуй, вам стоит задаться вопросом, что именно в выбранных вами дисциплинах вас привлекает. Если речь идет об исследовании жизни людей, изучении общественных закономерностей, а литература вам нравится возможностью рассуждения, например, о поведении героев и том, как устроен мир, вам подойдут: В этих дисциплинах возможны разные направления, которые будут требовать большего или меньшего изучения существующей действительности, поиска закономерностей и самостоятельного описания с возможностью делать выводы. В зависимости от ваших отношений с математикой вы можете выбрать одну из этих «общественных» наук. Вам могли бы подойти филология, журналистика (здесь в ряде вузов требуется еще творческий конкурс) или педагогика (преподаватель по русскому и литературе, например). Если выбор этих предметов связан с любовью к тексту (его анализу или созданию), а также возможностью устного или письменного общения с людьми и выражения своего мнения. Этот набор предметов позволяет вам поступить и на ряд отделений менеджмента, которые позволят заниматься управлением персоналом или процессами в организации. В любом случае, как вы видите, возможности разнообразны. Учитывая, что бюджетные места есть пока еще практически во всех государственных вузах, мы бы посоветовали вам, воспользовавшись порталом посмотреть, чему учат на всех этих факультетах. НО, постарайтесь, когда будете проводить это исследование, задуматься не только о ЕГЭ и том, что вам предстоят экзамены. Перенеситесь мысленно на 5 лет вперед и помыслите о том, что именно вам хочется делать каждый день на протяжении многих лет: писать, анализировать, читать, преподавать, организовывать работу и т.д. Это позволит вам лучше сориентироваться в возможностях. Удачи вам в этом нелегком деле! Анна Хабарова Здравствуйте, я в этом году заканчиваю 11 класс и до сих пор не определилась с профессией. Планирую поступать в Калининграде. Буду сдавать либо русский язык — алгебра — обществознание — литература. Либо русский язык — алгебра — обществознание — биология. Но я не могу найти ВУЗА в Калининграде по этим предметам. Подскажите пожалуйста. И еще, нужно ли сдавать биологию для того,что бы учиться на учителя начальных классов? Узнать ответ Ответ: Анжелика, отвечаем на твой первый вопрос. Если ты собираешься сдавать русский язык / алгебру и обществознание, то можешь подавать документы: Если ты собираешься сдавать русский язык/алгебру и биологию, то можешь поступать на факультеты психологии, биологии, психолого-педагогического образования в Балтийский федеральный университет им. Им. Канта. Если ты собираешься сдавать русский язык/алгебру и литературу, то при условии успешного прохождения дополнительного творческого конкурса, можешь поступать на факультеты журналистики и дизайна в Балтийский федеральный университет им. Им. Канта. Отвечаем на второй вопрос. Для поступления на факультет «Педагогическое образование» в Педагогическом институте и в Балтийском федеральном университете им. Им. Канта биологию сдавать не нужно, только обществознание. Успехов! Аля Дубчук На какую профессию поступать учиться после сдачи ЕГЭ по предметам русский, математика, физики и обществознание. Наиболее востребованные профессии связанные с этими предметами? Узнать ответ Ответ: Добрый день, Олег! Какую профессию выбрать и куда поступать учиться – непростые вопросы. Профессий очень много и выбрать одну единственную, основываясь только на школьных предметах, сложно. Для начала мы рекомендовали бы тебе определиться: к чему ты больше склонен – к техническим или гуманитарным профессиям? С чем тебе хочется работать в большей степени: с техникой, производством, компьютерами или же с людьми, а может с документами или финансами. Следующий вопрос: а что ты хочешь делать? Организовывать работу команды, считать бюджет организации, создавать программное обеспечение, проектировать строительные объекты или защищать клиентов на суде? В зависимости от ответов на эти два вопроса, ты можешь выбрать общее профессиональное направление. Обрати также внимание, что если ты хочешь сдавать физику и обществознание как предметы ЕГЭ, то они имеют разную направленность и практически не пересекаются при подачи документов на один факультет. Так, ЕГЭ по физике принимают в основном в технические ВУЗы, по обществознанию – в гуманитарные. В связи с этим и специальности можно получить разные. Наиболее востребованные профессии, связанные с физикой как профилирующим предметом, это инженеры (особенно в области строительства и производства) и специалисты IT. Наиболее востребованные профессии, связанные с обществознанием, это специалисты в сфере менеджмента по продажам, связям с общественностью, маркетологи, юристы, а также специалисты в области торгового дела и экономисты. Успехов тебе! Анна Хабарова Здравствуйте!!! Я из Украины!!!! Учусь плохо. На кого мне поступить???? Занимаюсь спортом!!!!! Узнать ответ Ответ: Сергей, здравствуйте! Ваше увлечение спортом может стать и Вашей профессией. Существует немало колледжей и ВУЗов, которые готовят специалистов в области физической культуры. Так, во многих училищах и колледжах есть направление «Физическое воспитание, спорт и здоровье человека» (http://ru.osvita.ua/vnz/college/search-41-0-0-321-0.html). После его окончания Вы можете стать либо педагогом в области физкультуры, либо профессиональным спортсменом/тренером. В ВУЗах есть аналогичные специальности «Физическое воспитание», «Спорт» и «Здоровье человека» (http://ru.osvita.ua/vnz/guide/search-17-0-0-76-0.html). После их окончания Вы можете стать спортивным или фитнес-тренером, преподавателем физкультуры, профессиональным спортсменом, инструктором по туризму, специалистом по здоровью человека. Обратите внимание на то, что в спортивных ВУЗах и колледжах есть как специальности связанные непосредственно с самим спортом, так и вспомогательные для спорта: pr, менеджмент, специалист по работе с молодежью и т.д. Если же Вы не хотите связывать свою профессиональную жизнь со спортом, то для выбора образования и специальности мы рекомендуем Вам ответить на следующие вопросы: Специальностей много и то, какую из них выбрать зависит от того, чем бы Вам было интересно заниматься и к чему у Вас есть способности. Поэтому не поленитесь ответить на наши вопросы: так Вы узнаете чуть больше о себе и о том, к чему у Вас есть склонности. Желаю Вам удачи и успехов! Юлия Козлова Здравствуйте, я учись в 11 классе. Буду сдавать русский, математику, биологию и химию. В математике я не сильна. Есть вариант пойти учиться в мед, но хотела узнать где еще требуются эти предметы для поступления. Может быть, что- то связанное с почвой сельским хозяйством. Узнать ответ Ответ: Добрый день, Елизавета! Существует несколько профессиональных направлений, по которым принимаются ЕГЭ по биологии и химии. Это: Таким образом, специальностей, связанных с биологией и химией достаточно много. Чтобы выбрать, тебе нужно определить для себя ряд моментов: Различные комбинации приведут к различным профессиям: если хочется лечить животных – это профессия ветеринара, выращивать сельскохозяйственную продукцию – агронома, изучать почвенный покров – почвовед и т.д. Для того, чтобы совершить окончательный выбор, рекомендуем тебе почитать о перечисленных выше профессиях в интернете, поговорить со специалистами и на основе этих знаний уже определяться. В любом случае, это должен быть твой выбор. Успехов! Анастасия Клецко Здравствуйте. Учусь в 9 классе. Собираюсь сдавать географию. Ну и основные. Скажите, пожалуйста, на какую специальность мне лучше идти учиться? Узнать ответ Ответ: Добрый день, Валентин! География – сложный, комплексный предмет. Она связана со многими специальностями. Для того, чтобы сориентироваться в них, перечислим тебе основные направления: Таким образом, специальностей, связанных с географией много, и здесь возникает вопрос – а что тебе интересно и чем хотелось бы в дальнейшем заниматься? Заниматься разработкой месторождений нефти и газа, исследовать влияние выбросов CO2 на атмосферу, организовывать технологические процессы воспроизводства лесов или быть экспертом по странам востока? От этого зависит направление работы, профиль ВУЗа/колледжа и т.д. Для того, чтобы определиться, рекомендуем тебе почитать о тех или иных профессиях в интернете, поговорить с профессионалами. Или может быть такой вариант, что география в целом тебе неинтересна и ты сдаешь ее по любым другим причинам. Тогда стоит задуматься о том, что выбор предметов ГИА или ЕГЭ в школе далеко не всегда напрямую соответствуют подходящей тебе профессии и стоит искать ее совсем в других областях. В любом случае, выбор за тобой. Успехов! Аля Дубчук, «План Б» Я бы хотел узнать, если сдавать русский, математику, физику общество, на какие профессии я могу выучиться ?? и такой же вопрос, если буду сдавать русский, математику, физику и географию Узнать ответ Ответ: Прежде всего позволь похвалить тебя — далеко не каждый хорошо разбирается в таком сложном предмете как физика. Если ты будешь сдавать ЕГЭ по русскому языку, математике, физике и обществознанию, то сможешь подавать документы на 141 специальность и на 137 специальностей, если будешь сдавать русский язык, математику, физику и географию. Вот только некоторые из них: При этом специализации очень разные и зависят от направлений: машиностроение, приборостроение, радиоэлектроника, лазерная техника, ракето-космическая техника, биомедицинская техника, робототехника и автоматизация, текстильное производство, пищевое производство, строительство и т.д. При таком многообразии профессий нельзя не отметить, что выбирать профессию, отталкиваясь только от предметов ЕГЭ – непростая задача. ВУЗов, факультетов и направлений подготовки много, все они отличаются и каждый имеет свою специфику. А вот предметов, по которым можно сдавать ЕГЭ, гораздо меньше. Отсюда и возникает ситуация, когда результаты ЕГЭ по одним и тем же предметам могут подаваться на совершенно разные факультеты: в твом случае это может быть как авиастроение, радиотехника, ядерная физика, так и геодезия, и даже экономика и социология. В связи с этим давай задумаемся вот над чем. Помимо русского языка и математики, как основных предметов, ты думаешь сдавать физику, географию или обществознание. Вопрос к тебе: Ответы на эти вопросы, помогут тебе выявить, сферу твоих интересов. Но для выбора профессии этого не достаточно. Следующий вопрос, на который важно ответить: «А что у тебя получается лучше всего?» Может быть, тебе легко дается решение задач по физики с применением формул, а может быть проведение лабораторных работ с измерениями показателей или ты легко запоминаешь формулировки общих законов природы и описание явлений? А что, помимо школьных предметов, тебе легко дается в жизни? Может быть у тебя есть хобби, увлечения, которые можно сделать своей профессией? Идеальной для тебя будет та профессия, которая, с одной стороны, будет включать в себя твои интересы, а с другой – позволит применять твои таланты и способности на практике. Чтобы ее найти, нужно осознать свои увлечения и сильные стороны и помнить, что школьные предметы напрямую не свидетельствуют в пользу той или иной профессии. Выбирай, что тебе ближе, в какой сфере и чем бы ты хотел заниматься! Желаю тебе успехов! Ольга Никитина Здравствуйте! Я не знаю на кого можно пойти учится. Посоветуйте. Я знаю два языка (английский, немецкий) и математику. Узнать ответ Ответ: Доброго дня, Кристина. Твои знания в области языков и математики могут быть тебе полезны при освоении целого ряда профессий. Языковые ВУЗы, например, готовят специалистов во многих сферах: от экономистов и юристов международного уровня до переводчиков, лингвистов и филологов. Здесь важно определиться, что у тебя не только хорошо получается, но и нравится. Если тебе нравится изучать языки, их связь с культурой и историческое развитие, работать с текстами (переводить, писать, анализировать), то обрати внимание на профессию филолога. Круг задач данного специалиста достаточно широк: от рецензирования научных работ и учебников до перевода художественной литературы и написания статей. Если же тебе интересны языки с точки зрения устройства грамматики и закономерностей в структуре слов, обрати внимание на профессию лингвиста. Она сочетает в себе знания по гуманитарным дисциплинам с одной стороны, и знания по математике с другой. Основными задачами данных специалистов являются составление словарей, автоматических переводов и программ распознавания речи. Отдельно также подумай о профессиях переводчика и преподавателя иностранного языка – в какой мере тебе хотелось бы этим заниматься. Однако, может быть и так, что языки интересуют тебя только в той мере, в какой их можно применять на практике и использовать в жизни, но не как та область, с которой тебе хотелось бы непосредственно работать. Если тебе в большей мере интересна математика, вычисления, работа с цифрами и закономерностями, обрати внимание на профессии финансиста, бухгалтера и экономиста. Знание языков при этом может быть тебе полезно не только для поступления в такие престижные ВУЗы как МГИМО или ВШЭ, но и для работы в международной компании в дальнейшем. В конце отметим, что хорошие знания по школьным предметам далеко не всегда могут напрямую соответствовать той или иной профессии и служить однозначным критерием выбора специальности. Поэтому рекомендуем тебе определить для себя следующие моменты: 1) какие предметы тебе легко даются, с какими заданиями ты быстро и без особых усилий справляешься, в чем твои сильные стороны; 2) чем тебе интересно заниматься и от чего ты получаешь удовольствие, какие области, сферы жизни вызывают наибольший интерес; 3) чего ты ждешь от своей будущей профессии, что для тебя важно в ней, какой ты хотела бы ее видеть: в чем ее смысл, какие люди тебя окружают, в каком месте ты работаешь (обстановке), насколько она востребована и высокооплачиваема и т.д. Определив для себя ответы на данные вопросы, тебе будет легче понять, какая профессия тебе подойдет. Удачи! Аля Дубчук Здравствуйте. Я хорошо знаю: русский язык , алгебру , геометрию, литературу. Люблю рисовать. Хотела бы спросить куда можно поступить? Узнать ответ Ответ: Здравствуйте! Очень Вы хорошо формулируете: одно знаю, а другое – люблю. Именно из этого и рождается профессия. Среди тех, кто любит рисовать не многие могут похвастаться тем, что знают геометрию и алгебру. Глядя на Ваш вопрос, хочется спросить, не задумывались Вы о профессиях дизайнера или архитектора. Этим профессионалам нужно не только придумывать образ, воплощать его в рисунке и т.д., но и иметь пространственное мышление, уметь производить расчеты, аккуратно описывать детали. Это области на стыке творчества и точных наук, на которые никогда не падает спрос – мы живем в мире архитектуры, где множество предметов от телефонов до предметов интерьера, которым нужно художественное оформление. Учитывая Вашу любовь к литературе, обратите еще внимание на профессии, связанные с книгой – иллюстрация, художественное оформление книги, графический дизайн и т.д. (взгляните на полиграфический вуз). Во многом, ответ на вопрос о Вашей профессии кроется в том, что именно Вам нравится рисовать, как, для чего и для кого. С другой стороны, у Вас явно есть способности, которые помогают быть успешной и в литературе, и в алгебре с геометрией. Что это? Внимание к деталям, хорошая память или аккуратность? А может быть скорость мышления или умение управлять своим временем? Каждое из этих качеств (особенно, если Вы поймете, что это за качество) поможет Вам стать хорошим специалистом в какой-то из областей. А вот что это за область зависит от Вашего желания и интереса, так как профессиональных областей применения Вашим знаниям и умениям много. Дизайн? Графический дизайн? Иллюстрация? Книжная графика? Архитектура? Архитектура градостроения? Реклама и визуальная коммуникация? Что из этого Вас привлечет? Подумайте над этими областями и если что-то заинтересует, проверьте вступительные испытания, чтобы для Вас не оказалось сюрпризом, что для поступления в университет или колледж может понадобиться пройти творческий конкурс (не пугайтесь главное, если Вы любите рисовать, то это не страшно). Обдумайте эти варианты или близкие к ним – пусть то, что Вам нравится и станет Вашей профессией. Успехов! Наташа Гомберг Здравствуйте! Узнать ответ Ответ: Ольга, добрый день! Прежде всего, хотелось бы отметить, что Вы правильно задумываетесь о том, кем Вы будете по профессии, так как образование не всегда равно профессии: образований примерно 40, а профессий – десятки тысяч. Хотелось бы спросить Вас: Что именно Вам нравится в гуманитарных науках? Что Вам нравится делать: рассказывать тему, изучать новое, искать закономерности в большом количестве данных? Ответ на этот вопрос поможет Вам выбрать одно из направлений, предложенных нами, исходя из Вашего интереса к гуманитарным наукам, хорошо развитой речи и списка предметов, которые Вы собираетесь сдавать: Связи с общественностью (профессия – специалист по связям с общественностью – человек, который формирует нужный образ компании в глазах общественности) Реклама (профессия – менеджер по рекламе – человек, который отвечает за рекламу товара или услуги) Маркетинг (профессия – менеджер по маркетингу, маркетолог, бренд-менеджер – человек, который формирует нужный образ той или иной торговой марки) Психология/управление персоналом (профессия – менеджер по управлению персоналом – человек, который отвечает за работу с персоналом внутри компании (набор, обучение, оценку, компенсации и т.д.)) Менеджмент (профессия – менеджер – человек, который выполняет определённую задачу «руками других людей») Выбрав конкретное направление, Вы уже сможете выбрать и конкретную профессию. Если появятся еще вопросы – мы будем рады ответить Удачи! Юлия Козлова Здравствуйте. Меня зовут Лиза. Узнать ответ Ответ: Лиза, добрый день! Для того, чтобы выбрать свою профессию важно понимать, что тебе нравится делать и чем бы ты хотела заниматься. Возьмем те предметы, которые ты выбрала сама. Вспомни и подумай, чем они тебя привлекают? Что именно тебе нравится в истории? А в обществознании? Какие задачи по алгебре ты любишь решать? Что больше всего тебе нравится, когда ты решаешь эти задачки? Есть ли что-то общее в твоих интересах по разным предметам? А чем ты любишь заниматься после школы, когда не нужно делать уроки? Если ты что-то читаешь в интернете или газетах, то о чем эти статьи? Для того, чтобы будущая профессия стала любимой важно, чтобы она была из сферы твоих интересов. Исходя из того, что ты выделила историю, обществознание и алгебру велика вероятность того, что тебе может подойти профессия экономиста. Эти специалисты изучают экономику, международные отношения, финансово-хозяйственную деятельность, статистику. Владеют методами математического анализа. В своей работе они занимаются исследованием и анализом регионального и мирового рынка товаров, услуг, ресурсов; делают прогноз развитие региона или фирмы, планируют и контролируют денежные потоки, ведут их учет, составляют отчетность. Это прекрасно, что ты уже сейчас в 8 классе задаешь вопрос: «Кем стать?» У тебя есть время, чтобы понять, что тебе интересно и получается, а чему еще нужно поучиться. Для того, чтобы тебе легче было определиться с выбором профессии при общении со взрослыми людьми узнавай из чего состоит их рабочий день, что им нравится в профессии и что нет, какое образование они получали. А так же обращай внимание на различные направления их профессии. Ведь даже в сфере экономики можно быть ученым, а можно быть практиком. Можно заниматься только анализом финансово-хозяйственной деятельности, а можно только бухгалтерским учетом. И тогда действия, которые выполняют эти люди в течение рабочего дня, у них будут отличаться. Зная, что делают разные специалисты, ты можешь выбирать, что ближе тебе. Успехов тебе в твоем выборе! Главное – не спеши, у тебя есть время. Ольга Никитина Не могу определиться куда поступить. Узнать ответ Ответ: Эмилия, добрый день! Учитывая, что математику и русский мы все сдавать обречены, хочется узнать про биологию. Почему Вы выбрали именно ее? Что именно Вам в ней нравится? Если биология интересует Вас как наука: если Вас привлекают исследования, биологические эксперименты и т.д., то оставшимися предметами по выбору могут быть химия или физика. Одна из возможных дальнейших областей для Вас теоретическая или прикладная наука: биофизика, биохимия, биология, биоинженерия и биоинформатика. У каждой из этих областей свои особенности и специализации: от походов в поля с целью изучения видов, до работы в лаборатории по синтезу новейших биодобавок. Другая аналогичная версия – сфера медицины. Вы, кажется, не хотите быть врачом, но помимо лечебных есть еще масса любопытных научных специальностей: фармацевтика, санитарная и фундаментальная медицина и т.д. Данный список можно продолжить. Более подробно узнать, что включают в себя эти профессии Вы сможете самостоятельно. Еще одним вариантом возможной профессии для Вас, с таким набором предметов, является психология. В некоторых ВУЗах необходимо сдавать эти три предмета. В некоторых требуется обществознание или история. Если биология любопытна для Вас не как наука о живом, а как изучение человека, возможно Вам туда. Но если биология выбрана не из общего к ней интереса, а, например, потому что легко дается или нравится преподаватель, тогда хочется предложить Вам задуматься еще немного. Самое главное, для того, чтобы понять, что же все-таки сдавать и куда поступать – это абстрагироваться немного от ситуации выбора школьных предметов и просто спросить саму себя «Чем я хочу заниматься в своей жизни?». «Что я хочу делать? Чем заниматься каждый день?». Попробуйте идти от обратного – может быть из этих вопросов появится представление о профессии, а предметы выбирутся сами собой. Их выбор станет просто средством, а не причиной выбора профессии. Задумайтесь еще раз об этом. Если возникнут вопросы – пишите нам, мы с радостью ответим на новые вопросы, если они появятся. Успехов! Анна Хабарова Направления, связанные с компьютерными системами, очень перспективны. Они сулят профессиональную востребованность и высокую оплату. Поэтому многих выпускников школ волнует, куда можно поступить с ЕГЭ по русскому, математике и информатике, чтобы получить все это. По всем ВУЗам страны были собраны сведения, в результате чего по ЕГЭ сформировался средний балл. Вот пример тех специальностей и профессий, которые можно освоить. 1. Прикладная информатика в экономике: 2. Технологии программного обеспечения: 3. Автоматизация процессов и производств в теплоэнергетике и теплотехнике: 4. Электрооборудование и электрохозяйство учреждений: 5. Георадиолокационные и телекоммуникационные системы: 6. Композиционные наноматериалы: За поступающих на СПО можно только порадоваться, ведь они могут не переживать, пройдут по баллам ЕГЭ или нет. Зачисление производится по конкурсу аттестатов. Направление вы можете выбрать абсолютно любое. Но когда захотите повысить свой профессионализм, поступив в Университет, здесь и пригодится ЕГЭ, поэтому уже сейчас важно сдать его на хорошие баллы. Запишись на курсы подготовки к ЕГЭ/ОГЭ. Первый урок бесплатно! Современным школьникам уже в старших классах желательно определиться со своими планами на поступление. Государственные экзамены сдают не по всем предметам, а лишь по обязательным и тем, которые непосредственно понадобятся для поступления на то или иное направление. Поэтому, чем раньше будущий выпускник определится, какую профессию он будет получать в вузе, тем больше у него будет времени подготовиться к ЕГЭ по профильным предметам. Обществознание начали преподавать в школах СНГ не так давно. Обязательным для сдачи предмет не является, но его можно сдать по выбору, если таковы требования вуза. На какие направления можно поступить тем, кому интересно обществознание? Интересно! Обществознание — предмет комплексный. Он включает в себя основы таких дисциплин, как правоведение, экономика, политология, философия, социология, социальная психология. Эти дисциплины рассматриваются в рамках обществознания не по отдельности, а во взаимосвязи друг с другом, а значит, знание этого предмета необходимо представителям большинства гуманитарных профессий. У тех, кто размышляет, куда поступать с обществознанием, выбор широкий. Подходят ли направления с обществознанием вам? Гадать не нужно; точный ответ даст профориентация. Список направлений, на которые можно поступить с обществознанием, довольно обширен: Для большинства этих специальностей экзамен по обществознанию считается профильным, кроме того, придется сдавать еще один дополнительный экзамен. Факультеты по этим направлениям есть в любом вузе страны. В России традиционно самые сильные вузы находятся в столицах и крупных городах, таких, как Екатеринбург, Новосибирск, Пермь. Важно! В России обязательными экзаменами являются русский язык и базовая математика. Также сдается один или два экзамена на выбор, в зависимости от того, какое направление выбрано для поступления. Есть два варианта сдачи ЕГЭ по математике: базовый и профильный. Базовую математику сдают в обязательном порядке все выпускники 11-х классов. Профильный уровень обязательным не является; его сдают те, кому нужно поступить на факультет с соответствующими требованиями. Для поступления на такие направления с обществознанием, как бизнес-информатика, менеджмент, экономика, государственное и муниципальное управление потребуется профильная математика, также нужна она при получении педагогического образования, если выбран соответствующий предмет (например, учитель математики). Но есть немало факультетов, куда можно поступить с обществознанием и базовой математикой. Интересно! В среднем ЕГЭ с базовой математикой получают более высокий общий балл, поскольку профильную математику редко сдают на высокие баллы. Сдав базовую математику и обществознание, можно поступать на направления, связанные с юриспруденцией, психологией, политологией, журналистикой, рекламным делом и связями с общественностью, лингвистикой, историей, философией, теологией. На многих направлениях потребуется сдать еще один экзамен, чаще всего, историю или иностранный язык. На психологических направлениях может потребоваться биология. Существует установленное минимальное количество баллов, которые должен набрать выпускник школы на госэкзаменах. Для русского языка и базовой математики это 24 и 7 баллов соответственно, для профильной математики — 27 баллов. Однако это баллы лишь для окончания школы, а для поступления в вуз предусмотрены немного другие минимальные оценки: Для поступления с обществознанием необходимо набрать минимум 42 балла по этому предмету. Важно! С более низкими, чем минимальные, баллами ЕГЭ вуз не имеет права зачислять студентов на обучение даже в том случае, если есть свободные места и даже на коммерческой основе. С минимальными баллами ЕГЭ можно поступить на платное обучение, но у тех, кто желает учиться на бюджете, баллы должны быть выше. Точное количество необходимых для поступления баллов назвать невозможно, ведь они разные в разных вузах и на разных специальностях. С минимальными баллами получится пройти на бюджет разве что в совсем захудалый вуз; чем учебное заведение солиднее, чем популярнее выбранная специальность, тем выше конкурс, а значит, выше должны быть и баллы за ЕГЭ. Важно! Многие специальности с обществознанием очень популярны, и конкурс на них высокий. Это, прежде всего, направления, связанные с экономикой и правом. Точно это узнать невозможно, но можно сделать прогноз: узнать, каким был проходной балл в прошлом году и учесть, что он может подняться на 10–15 пунктов. Зная, какие баллы необходимы, чтобы пройти конкурс, вы можете планировать, в какие вузы подавать документы. Но есть другой способ поступить в вуз, в том числе, на специальности, связанные с обществознанием, и он не включает в себя беспокойство о баллах за ЕГЭ. Это поступление в зарубежный вуз. Большинство выпускников школ такую возможность не рассматривают, потому что считают, что это дорого и недоступно. Но, например, в Германии высшее образование бесплатно для всех. Можно поступить в любой государственный вуз и учиться на бюджетной основе. К тому же, баллы за ЕГЭ вообще не требуются, зачисление происходит по среднему баллу аттестата или оценкам, полученным в колледже довузовской подготовки. Важно! В Германии обучение ведется на немецком или английском языке, поэтому их хорошее знание необходимо. При подаче документов в немецкий вуз необходимо подтвердить текущий уровень знания языка международным сертификатом. По окончании вуза выпускники получают возможность в течение 18 месяцев искать работу. В случае трудоустройства их виза продлевается, и они могут остаться в стране и легально работать. Советуем изучить: Подбор программ обучения в немецких вузах Куда поступать с обществознанием? Вариантов много; в основном, это гуманитарные специальности, но есть и направления, связанные с точными науками. Среди направлений с обществознанием есть очень востребованные и престижные, например, юридические и экономические специальности, поступить на которые непросто из-за высокого конкурса. Но есть способ не только поступить без ЕГЭ, но и получить престижное и бесплатное образование, если отправиться за ним в Германию. Для многих поступающих сложность представляет правильное и своевременное оформление пакета документов, ведь любые ошибки могут привести к отказу. Чтобы не рисковать, лучше обратиться за помощью к специалисту, который в курсе всех требований и нюансов; он поможет подать документы правильно и в срок. Для поступления в ВУЗ нужно сдать не только базовые экзамены по математике, русскому языку, но и дополнительные профильные предметы. Многие студенты выбирают такие направления, как английский язык. Знание иностранных языков всегда считалось преимуществом перед выбором престижной профессии. Как правило, ЕГЭ экзамен по английскому нужно сдавать поэтапно. Оценка результатов зависит от базовых и углублённых знаний. Нередко тестирование проводится в устной и письменной формах: Прежде, чем выбрать этот предмет для сдачи ЕГЭ, нужно заранее узнать. Какие специальности предполагают обязательное его знание. В противном случае придётся искать стандартную работу, в перечень обязанностей должности которой будет входить знание иностранного языка. Такие должности не оплачиваются выше, поэтому рекомендуется обратить на это особое внимание. В 2019 году средний проходной балл по ЕГЭ для этой специальности увеличился. Несмотря на это, число школьников, которые недобрали баллы, сократилось на ¼ от общей массы поступающих за предыдущий 2018 год. Наибольшее число поступивших составило более 65000 студентов. Абитуриент вправе выбрать одну из специализаций, поступая на факультет по изучению и усвоению иностранных языков. Услугами переводчиков пользуются крупные компании, международные службы грузо- и авиаперевозок, бюро и правительственные организации. Не секрет, что на должность такого уровня попасть сложно. Есть и более «мелкие» компании по значимости, где востребована профессия: Многие компании требуют знаний технической терминологии на английском языке. Было бы неплохо знать не только базовые и практические основы, но и владеть определённым видом этих знаний, чтобы уметь разбираться в сути дела. Эта должность не ограничивается лишь обучением школьников и студентов. Фармацевтические компании в США требуют от заграничных партнёров знания специфической терминологии. Чтобы переговоры на международном уровне были достаточно прозрачными, задача педагога ВУЗа обучить студента так, чтобы он смог за 5 лет освоить владение языка до уровня носителя. Преподаватель может вести свою трудовую деятельность в следующих областях: Задача преподавателя – передать знания, которые он получил в университете. Абитуриент также должен понимать, что с дипломом педагога ему придётся осваивать профессию учителя, так как преподавание – основное направление, а предмет преподавание – второстепенный момент. В отличие от предыдущей профессии эта должность может включать в себя такие направления, как: Эти особенности предполагают, что квалифицированный специалист будет учить других людей разным основам и школам, но при этом будет использовать иностранную речь. Такое направление образования выбирают состоявшиеся учителя, которые хотят освоить профессию с нового ракурса – в другой стране. Например, будучи учителем английского, переехать в Эстонию на ПМЖ и преподавать там предмет на государственном языке. В таком случае придётся освоить хоть какие-то знания диалекта страны. Есть специальности «таможенное право», «таможенное дело», «таможенное оформление документов» и не только. В специализации «таможенного дела и брокерства» от работника требуют не только проверку документов, их оформления и учёта. Многие работники таможенных служб обязаны проводить физический досмотр товара, вести учёт паспортного контроля. На международных границах без знания английского языка делать нечего. Экспорт и импорт – делопроизводство товарного оборота, которое должно быть подкреплено правовыми знаками. Сюда относят интересные специальности: Если абитуриент не знает, куда поступить, можно заранее ознакомиться с перечнем обязанностей на сайтах государственных служб. В ряде вакантных должностей можно увидеть, чего именно требуют от сотрудников, каковы их навыки, а также должностные обязанности. Сюда относят политические, экономические и юридические сферы деятельности всех предприятий мира. Допустим, компания работает в сфере Duty-Free. Товары, не прошедшие физический досмотр в фурах, изымаются и направляются в продажу без обложения налогов. Конфискат подлежит декларации. Человек, занимающийся оформлением документов, обязан в международном обращении зафиксировать поступление нового товара. Дипломаты и политологи также учатся на факультете международных отношений. Экономисты, юристы, социологи и общественные деятели имеют право работать только с разрешения Министерства Юстиций. Лицензия выдаётся через 2 года после окончания университета. Если ВУЗ отказывает в выдаче справки об успеваемости, лицензию выпускник не получает. Ниже представлен перечень ВУЗов, куда абитуриент может подать документы. Профильные дисциплины могут отличаться от основной задачи по изучению английского языка: Куда поступить? Кем можно стать Где работать НИУ ВШЭ (программа с двойным дипломом) – прикладная математика и информатика Разработчик в IT-сфере, архитектор ПО, аналитик в WEB, преподаватель информатики IT-сфера, компьютерные технологии АФСБ, РАНХиГС, РЭУ им. Плеханова. Компьютерные науки: интеллектуальные системы ПО в рамках гуманитарных наук. Специалист по защите данных, бизнес-аналитик, консультант по экономическим проблемам, маркетолог, бизнес-консультант Аналитическая сфера, деятельность по защите персональных данных ИТМО, УрФУ, РГГУ Создатель математических моделей, аналитик, лингвист по компьютерной языковой науке Бизнес-сфера, консалтинг, маркетинг и бизнес-психология МГИМО – экология, природные ресурсы и технологии Специалист по экономическому и экологическому развитию Экологом, консультантом по борьбе с вредоносными системами сбыта СПбГУП, психологические науки – конфликтология Конфликт-менеджер, конфликтолог, медиатор или психолог Любая частная или государственная деятельность, связанная с вопросами по урегулированию проблем ВАВТ, МИД Россия, МГИМО, МГУ, НИУ ВШЭ, НГЛУ. Экономика и управление: Аудитор, банковский управляющий, экономист по вопросам личных финансов, налоговый инспектор, специалисты экономических отделов Любая деятельность, связанная с выгодоприобретательностью и финансовой прибылью экономических агентов Основные направления деятельности можно поделить на две основные группы: там, где английский язык будет основой профессии, и то, где он будет служить составной частью задач. В последнем случае ценность специалиста, как рядового сотрудника, будет увеличена за счёт этих знаний. Как правило, студент уже заранее знает, в каких случаях за иностранный ему будут доплачивать, а где – это будет восприниматься, как должное знание для обеспечения выполнения поставленных задач перед ним. Для того, чтобы беспрепятственно поступить в высшее учебное заведение, необходимо сдавать не только математику, русский язык, но и дополнительные предметы. Нередко ученики, которые тщательно изучают иностранный язык, выбирают его и для сдачи. ЕГЭ по английскому языку включает два этапа, которые сдают отдельно: письменный и устный. Перед тем, как отдать предпочтение данному предмету, необходимо ознакомиться с основным перечнем специальностей, которые доступны при поступлении на данный факультет. ЕГЭ по английскому языку в 2017 году сдавали более 64 тысяч человек. При этом число школьников, не набравших минимальный балл, сократилось на четверть, а средний балл оказался выше, чем в 2016 году. Чаще всего выпускники, которые отлично овладели иностранным языком, могут выбрать данное направление. Ныне переводчик пользуется особой популярностью. Но для того, чтобы работать в этой отрасли, необходимо обладать определенными деловыми качествами, мобильностью, некоторыми способностями. Переводчики легко найдут работу в различных международных или российских компаниях, издательствах, а также посольствах нашей страны. Ведь большинство организаций активно сотрудничают с иностранными учреждениями. На факультет иностранных языков можно поступать и в том случае, если вы планируете в дальнейшем преподавать, получать и передавать новые знания. При этом вы сможете более тщательно изучить иностранный язык, что даст возможность улучшить свое положение. Кстати, на данном факультете вы сможете ознакомиться и с основами психологии. После окончания вуза вы можете не только преподавать в институте, техникуме или школе, но и переводить разнообразные тексты и документы. Но перед поступлением нужно изучить не только английский язык, но и обществознание. Данное направление имеет отношение к тщательному контролю за экспортом, а также импортом разнообразной продукции. При этом можно освоить разнообразные специальности, среди которых выделяют специалистов по различным таможенным вопросам или международным перевозкам, декларант, прочее. Никаких проблем с поиском работы после обучения не будет, поскольку в государственных и коммерческих структурах предоставляют соответствующие места. Если вы планируете заниматься политической, общественной деятельностью, то можете отдать предпочтение данному направлению. Отличных результатов смогут добиться те выпускники, которые обладают определенными взглядами на жизнь. На данном факультете можно выучиться на дипломата, изучить особенности таких специальностей, как посол, менеджер, консул. Для того, чтобы без проблем поступить, необходимо сдать ЕГЭ по английскому и русскому языку, обществознанию, а также математике. Сегодня один из волнующих вопросов: «Сдал литературу и английский — куда поступить в СПб с полученными результатами?». Сдавая английский вместе с литературой и русским, вы можете подавать документы на специальности «зарубежная филология», «журналистика», «лингвистика» и т.д. Данное направление появилось не так давно. Но и этого времени было вполне достаточно, дабы завоевать определенную популярность. Выпускники данного факультета обладают многими качествами: коммуникабельность, общительность, определенные ораторские навыки. Опытные и ответственные PR-менеджеры могут достаточно быстро повысить рейтинг определенной фирмы или же компании, а также оказать активное влияние на продажи определенного продукта. Данное направление стоит выбирать при условии, что вам интересна работа, связанная с рекламой, продвижением продукции и услуг. Ведь в этом случае можно получить не только достойное образование, но и высокооплачиваемую работу. На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, физика? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, ИКТ? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, обществознание? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, обществознание, история? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, биология? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, химия, биология? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, химия? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, обществознание, иностранный? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, история, иностранный? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, обществознание, биология? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, география? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, обществознание, литература? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, иностранный, литература? На какие направления подготовки легче всего поступить с набором ЕГЭ русский язык, математика, иностранный? Надеемся, Вам помогла наша стаья. Бонусом прилагаем сводную таблицу различных комбинаций ЕГЭ. Если Вы вдруг еще не определились какие ЕГЭ сдавать, чтобы было не так больно поступать, она Вам должна помочь 🙂 Иллюстрация: Дарья Орлова В мире, где информатика (CS) присутствует повсюду, CS для всех. CS пересекает все дисциплины и отрасли. Колледж компьютерных наук Хури стремится к созданию и развитию разнообразной инклюзивной среды. Первый в стране колледж компьютерных наук, основанный в 1982 году, Khoury College вырос в размерах, разнообразии, образовательных программах и передовых исследовательских достижениях. В наших региональных кампусах, расположенных в промышленных и технологических центрах, Khoury College предлагает сильные академические программы в ярких городах для жизни, работы и учебы. Колледж Хури — это сообщество людей, посвятивших себя обучению, наставничеству, консультированию и поддержке студентов по каждой программе. Программы награждения колледжей и университетов проливают свет на выдающихся преподавателей, студентов, выпускников и партнеров по отрасли. Наши исследования в реальном мире, выдающиеся преподаватели, выдающиеся спикеры, динамичные выпускники и разнообразные студенты рассказывают свои истории и попадают в новости. В колледже Хури обучение происходит в классе и за его пределами.Мероприятия в нашей сети кампусов обогащают образовательный опыт. Информатика повсюду.Студенты колледжа Хури занимаются соответствующей работой, исследованиями, глобальными исследованиями и опытом оказания услуг, которые помогают им расти. Студенты магистратуры углубляют свои знания благодаря проектной работе, профессиональному опыту работы и научным сотрудникам. Работа над исследованиями с преподавателями занимает центральное место в опыте докторантуры.Докторанты колледжа Хури также могут заниматься исследованиями вместе с партнерами по отрасли. Преподаватели и студенты колледжа Хури проводят эффективную работу по различным дисциплинам. Обладая широтой областей исследований, мы каждый день решаем новые проблемы в сфере технологий. Наши институты и исследовательские центры объединяют ведущих академических, промышленных и государственных партнеров, чтобы использовать возможности вычислений. Исследовательские проекты, разработанные и возглавляемые преподавателями мирового класса Khoury College, привлекают студентов и других исследователей к получению новых знаний. Исследовательские лаборатории и группы сосредотачиваются на наборе проблем в конкретном контексте, предлагая исследования и сотрудничество. Эта новая инициатива направлена на устранение рисков для конфиденциальности и личных данных коллективными усилиями на низовом уровне с упором на прозрачность и подотчетность. Современные помещения, бесшовные системы, инновационные лаборатории и помещения позволяют нашим преподавателям и студентам проводить передовые исследования. Колледж Хури гордится нашим коллективным и инклюзивным сообществом. Каждый день мы стремимся создавать программы, которые приветствуют самых разных студентов в CS. Более 20 компьютерных клубов в колледже Хури и Северо-Востоке предлагают что-то для каждого студента.Мы всегда рады новым членам на всех уровнях. Студенты учатся в современных классах, конференц-залах для совместной работы, а также в ультрасовременных лабораториях и исследовательских центрах. Сети обеспечивают безопасную и бесперебойную работу кода, современное и надежное оборудование, а наша квалифицированная системная команда управляет поддержкой и обновлениями. Заинтригованы колледжем Хури и высшим образованием на северо-востоке? Начните здесь, чтобы увидеть общую картину — академические науки, экспериментальное обучение, студенческую жизнь и многое другое. Готовы сделать следующий шаг в технической карьере? Наши магистерские программы сочетают в себе академическую строгость, высокое качество исследований и значимые возможности для получения опыта. Добро пожаловать в программу Align Master’s Program, предназначенную для людей, готовых добавить информатику (CS) к своим навыкам или переключиться на новую карьеру в сфере технологий. Будучи аспирантом Хури, вы погрузитесь в строгий учебный план, будете сотрудничать с известными преподавателями и окажете влияние в выбранной вами области исследования. Где бы вы ни находились на пути бакалавриата Хури, у нас есть консультанты, ресурсы и возможности, которые помогут вам добиться успеха и сделать информатику для всех. Где бы вы ни находились в аспирантуре Хури, наши консультанты, информационные ресурсы и возможности помогут вам выработать индивидуальный путь. На любом этапе пути Align — и в любом из наших кампусов — консультанты, ресурсы и возможности Khoury поддержат ваш путь к карьере в сфере технологий. Консультанты и преподаватели помогут вам сориентироваться в аспирантуре в колледже Хури — от исследовательских пространств и междисциплинарных проектов до студенческой жизни и ресурсов. Преподаватели и сотрудники вносят исключительный вклад в Колледж Хури — и в будущее информатики. Мы здесь, чтобы поддержать вас на каждом шагу. Fall Admissions: Заявление и все подтверждающие документы должны быть получены до 15 декабря на следующий осенний семестр. Весенний прием: заявление и все подтверждающие документы должны быть получены до 31 августа на следующий весенний семестр. Fall Admissions: Заявление и все подтверждающие документы должны быть получены до 15 декабря на следующий осенний семестр. Весенний прием: заявление и все подтверждающие документы должны быть получены до 31 августа на следующий весенний семестр. Крайний срок для одногодичной магистерской программы CSE — 1 марта. Для онлайн-приложения аспирантуры необходимо загрузить следующее: Если у вас есть особые вопросы о приеме в Школу программ EECS, пожалуйста, свяжитесь с ШерриДон Джексон по электротехнике по [email protected] или с Дженнифер Хаузер по информатике и инженерии по [email protected]. Чтобы поддерживать надлежащий баланс между ресурсами отдела и численностью аспирантов, отдел должен ограничивать предложения о приеме наиболее квалифицированными соискателями. Таким образом, процесс приема очень избирательный и конкурентный. Подробная информация о процессе изложена в разделах ниже и в часто задаваемых вопросах о заявлении на поступление в аспирантуру. Часто задаваемые вопросы о приеме Начните подавать заявку Заявки на 2021-2022 учебный год стали доступны 8 сентября 2020 года на сайте заявки. Крайний срок для соискателей PhD — вторник, 15 декабря 2020 г. (осень 2021 г.). Большинство решений обычно принимаются к концу марта, но некоторые решения могут быть приняты и до 15 апреля. Программа отзывов о поступлении в аспирантуру направлена на то, чтобы помочь студентам первого поколения и недостаточно представленным студентам подать заявку на поступление в аспирантуру по компьютерным наукам в США. Продвинутый аспирант, докторант или волонтер факультета CS предоставит один раунд обратной связи по резюме и заявлению о цели заявителя (возможности ограничены).Волонтеры могут также организовать короткую 15-30-минутную встречу Zoom, чтобы дать дополнительные советы. Участие в Программе обратной связи при поступлении в аспирантуру не гарантирует зачисление на какую-либо программу. Чтобы принять участие в Программе обратной связи с кандидатскими диссертациями в этом году, отправьте материалы заявки до 16 ноября, 23:59. CST. Подать заявку сейчас У соискателей MS есть несколько крайних сроков. Крайние сроки подачи заявок: Для входа зимой 2021 г .: 1 ноября Для входа весной 2021 г .: 1 февраля Для входа осенью 2021 г .: 1 марта Абсолютные сроки выполнения определенных действий TGS, связанных с допуском, доступны здесь. Вернуться к началу Нет бумажных форм заявлений о приеме или финансовой помощи. Чтобы подать заявление о приеме на факультет CS, перейдите на веб-сайт Высшей школы (TGS), перейдите по ссылке «Прием» и, наконец, «Подайте заявку онлайн». Вернуться к началу TGS вам будет предложено выбрать кандидатскую или магистерскую степень по информатике.Если вы хотите получить докторскую степень, со степенью магистра или без нее, выберите опцию PhD. Вариант MS предназначен только для магистров терминала и не означает допуска к дальнейшей работе над докторской степенью. Вам также будет предложено указать область исследования среди исследовательских групп. После того, как вы заполните онлайн-заявку, вы получите сообщение электронной почты с просьбой предоставить дополнительную информацию о вашем среднем балле и конкретных исследовательских интересах. Вам будет предложено выбрать два или три лучших варианта из шести исследовательских групп по интересам, исходя из ваших конкретных исследовательских интересов.Вы можете указать более подробную информацию в своем Заявлении о целях. Например, студент, который хочет продолжить исследования в области «беспроводных сетей», может выбрать группу «Системы и сети». Вернуться к началу Перед тем, как подать заявку онлайн, соберите следующее: Обратите внимание, что присылать печатные копии ваших официальных стенограмм не требуется.Вместо этого загрузите их отсканированную копию в формате PDF вместе со всеми другими дополнительными материалами в свое онлайн-приложение. Обратите внимание, что при поступлении от вас могут потребовать предоставить оригинал (ы) стенограммы. Кандидат не может быть принят без заполненного заявления. Для принятия решения о допуске необходимо предоставить все первичные и дополнительные материалы. Отказ может быть сделан из-за неполных заявок. Вернуться к началу Ожидается, что типичный кандидат будет иметь степень бакалавра наук в области электротехники, компьютерной инженерии, информатики или смежной дисциплины в признанном учебном заведении.Также могут быть рассмотрены высококвалифицированные кандидаты с другим академическим образованием. Конкретная подготовка к бакалавриату, необходимая для обучения в магистратуре, зависит от программы и области специализации. Кандидат, не имеющий достаточной подготовки к бакалавриату в какой-либо конкретной области, но обладающий высокой квалификацией во всех других отношениях, может быть обязан пройти определенные курсы бакалавриата как можно скорее после зачисления в Северо-западный университет. Этот студент будет проинформирован о таком требовании при зачислении. Вернуться к началу Текущий студент магистратуры Северо-Западного университета может запросить перевод с программы магистратуры на программу докторантуры. Такой запрос о переводе серьезно рассматривается только в том случае, если есть преподаватель CS, который поддерживает перевод и обязуется оказывать финансовую поддержку студенту. Этот преподаватель поможет студенту подать заявку на перевод, который затем будет рассмотрен кафедрой.Студенты могут официально подать заявку на перевод без адвоката факультета, но шанс одобрения в этом случае очень низок. Вернуться к началу MS и PhD должны подавать заявки только в осеннем квартале. Обратите внимание, что в обеих программах допускаются только осенние билеты. Запросы на зачисление в зимний и весенний кварталы от соискателей MS и PhD будут автоматически отклоняться, как правило. Единственный механизм зачисления в докторантуру на зимнюю или весеннюю четверть предполагает вмешательство одного из наших преподавателей, который должен согласиться поддерживать данного студента в качестве научного сотрудника до конца учебного года.Чтобы изучить эту возможность, кандидат должен связаться с отдельными профессорами, перечисленными в справочнике факультетов кафедры. Вы можете просмотреть большую часть общей информации о требованиях и политиках на веб-сайте Высшей школы. За дополнительной информацией обращайтесь в аспирантуру отдела CS. Вернуться к началу Для студентов магистратуры и докторантуры нам требуется: Подробнее о требованиях к английскому языку Вернуться к началу Мы понимаем, что процесс подачи заявления на учебу в аспирантуре — непростое решение, к которому следует относиться легкомысленно. Чтобы помочь вам принять решение и дать несколько советов относительно общих критериев оценки, ниже мы обсуждаем некоторые из соответствующих вопросов. Мы действительно получаем заявки с транскриптами, использующими разные шкалы GPA (10,0, 100% и т.д.), и мы применяем скорректированные критерии к таким шкалам. Следовательно, соискателям не нужно предоставлять какие-либо преобразования, и они должны оставить свой средний балл по стандартной шкале своего учебного заведения. В качестве другого конкретного примера, многие университеты Индии имеют схему оценивания «на основе классов», и мы отмечаем, что мы всегда будем отдавать приоритет абитуриентам «Первого класса с отличием».Процесс подачи заявки позволяет вам написать «самооценку» среднего балла по шкале 4,0; однако мы всегда будем использовать стенограммы в процессе оценки. Соискателям магистратуры и докторантуры: баллов GRE не требуется. Имейте в виду, однако, что вам все равно необходимо будет соответствовать минимальным требованиям для владения английским языком, как указано выше. В первую очередь для соискателей PhD, преподаватели CS, заинтересованные в консультировании, могут проводить отдельные собеседования для дальнейшей неформальной оценки соискателей. См. Требования в аспирантуре Эта часть общего приложения имеет чрезвычайно важное значение, и утверждения, написанные ясно и целенаправленно, будут предпочтительнее. А именно, прочитав его, оценщик / преподаватель должен получить четкое представление о: В каждом случае успешный кандидат обеспечит хороший баланс между опытом, видением и желаниями. Пример: просто сказать, что вам нравится Northwestern или вы высоко цените преподавательский состав в сфере CS, не говоря уже о том, чтобы это было лестно, не является утверждением, которое само по себе будет «хорошо продаваться». Наконец, хотя это не всегда возможно, будет полезно, если хотя бы некоторые части рекомендательных писем будут подтверждать утверждения, сделанные в заявлении о цели. В системе онлайн-подачи заявок каждому заявителю будет предоставлена возможность выбрать в порядке предпочтения среди различных программ обучения в нашем отделении.Преподаватели рассматривают заявки в соответствующих областях; Таким образом, каждый кандидат должен внимательно изучить исследовательские интересы каждого преподавателя на нашем веб-сайте. Кроме того, соискателей попросят указать до двух имен конкретных преподавателей, у которых они хотели бы учиться. Это настоятельно рекомендуется и полезно для определения кандидатов для рассмотрения. Требуется минимум две буквы, но настоятельно рекомендуется три. Служба файлов рекомендаций (RFS) выступает в качестве посредника в этом процессе. Обычно ожидается, что студенты будут готовы отказаться от права просматривать свои письма без вопросов . Отказ от права просмотра ваших писем означает, что они будут доступны для просмотра только школам, в которые вы подаете заявление. Приемные комиссии предпочитают, чтобы абитуриенты отказывались от своих прав на просмотр своих писем, потому что они понимают, что рекомендующие в таких обстоятельствах склонны писать более содержательные письма. Узнать больше В предстоящем сезоне приема в аспирантуру абитуриенты, желающие поступить в Школу инженерии и прикладных наук Маккормика осенью 2019 года, смогут подать заявки на участие до двух программ PhD.Кандидаты, заинтересованные в этом варианте, должны указать свой первый и второй варианты двух программ PhD. Плата за подачу заявки на единую программу составляет 95 долларов США; плата за подачу заявки на две программы составляет 150 долларов США. Программа, выбранная кандидатом в первую очередь, будет иметь преимущественную силу при принятии решения о приеме. Программа второго выбора рассмотрит файл заявителя только в том случае, если программа первого выбора не зачислит студента. Соискатель докторской степени может также потребовать, чтобы ее или его досье было рассмотрено для получения самофинансируемой степени магистра в полях первого выбора, если он / она не допущены к программе доктора философии.С вопросами о процессе подачи двух заявок следует обращаться к Брюсу А. Линдваллу , заместителю декана по обучению в аспирантуре, по адресу [email protected]. Мы будем ценить все ваши достижения (например, награды, полученные на конкурсах) и опыт (например, исследовательские проекты, лидерство). Однако лучшее место, где их можно связно изложить, — это ваше резюме. В идеале некоторые из этих элементов также должны быть должным образом связаны с документом с изложением цели. Вернуться к началу Если у вас есть вопросы, обратитесь к разделу часто задаваемых вопросов о приеме в магистратуру или перейдите к разделу Финансовая помощь, ассистентство и стипендии. Обратите внимание, что мы продолжим обработку заявок после 28 февраля, но иностранным студентам должно быть достаточно времени для обработки документов на визу и т. Д.если они приняты в программу. Студенты, не имеющие степени в области CS, но желающие подать заявку на получение степени MS, могут пройти следующие предварительные требования в качестве аспиранта без степени: CS100, CS101, CS200, CS201, CS300, CS301.После того, как вы закончите эти курсы, вы можете пройти наши курсы старшего уровня, такие как языки программирования, алгоритмы и т. Д. На уровне 5xx. В конце семестра, в котором вы проходите курсы 5xx, вы можете подать заявку на участие в нашей программе MS. Хорошо в этом то, что, хотя курсы более низкого уровня не будут учитываться при учете вашей степени магистра в области CS, курсы 5xx будут. На странице со степенью магистра наук есть список необходимых курсов. Мы предлагаем большинство курсов не реже одного раза в год. Департамент компьютерных наук предлагает финансовую помощь выдающимся кандидатам в форме обучения и ассистентов.Преподавательская или исследовательская работа на полставки обеспечивает конкурентоспособную стипендию и стипендию на полное обучение в течение учебного года. Студент, подающий заявку на учебу в аспирантуре факультета компьютерных наук, автоматически рассматривается для получения должности помощника факультета во время рассмотрения материалов заявки. Решения о финансировании принимают во внимание множество факторов, в том числе баллы GRE. Учитывая это, всем кандидатам, нуждающимся в финансовой поддержке, настоятельно рекомендуется представить результаты GRE. Студенты, продолжающие обучение, должны заполнить заявление о приеме на должность помощника факультета.Уведомления о продолжении подачи заявок на ассистентство и крайних сроках делаются Департаментом в течение осеннего и весеннего семестров. Департамент присуждает стипендии преподавателей (GTA) на основе ожидаемых способностей к преподаванию. Отдельный преподаватель, который спонсировал исследовательские фонды в распоряжении профессора, присуждает стипендии научных сотрудников (GRA). Назначение GRA производится на основе взаимных интересов студента и профессора. Право на ассистентство имеют только студенты, которые поддерживают приемлемый уровень успеваемости. Student Financial Aid предоставляет исчерпывающую информацию и услуги, касающиеся возможностей финансирования стоимости обучения в Университете Алабамы. Если у вас есть какие-либо вопросы, не стесняйтесь обращаться к консультанту по выпускным программам, доктору Джеффри Карверу. Колледж литературы и науки Как можно комплексно взглянуть на вычисления сверху вниз? Информатика — это ответ.Поскольку тенденция к глобализации объединяет людей во всех частях мира, цифровые сети и системы все чаще отвечают за обработку и доставку огромных объемов информации, поддерживающих обмен информацией. Ученые-компьютерщики проектируют, обслуживают и улучшают эти жизненно важные информационные системы и основные концепции оборудования. После завершения базовых курсов по математике, основам информатики и естествознания вы перейдете к более углубленным исследованиям в области программирования, сетей, систем баз данных и других тем.Вы сможете настроить свою специализацию, выбрав курсы по таким темам, как компьютерная графика, искусственный интеллект, визуализация данных и продвинутая математика. Во время учебы вас будут поощрять применять на практике свою курсовую работу, проходя стажировки и работая в частном секторе. дипломов Магистерская программа факультета компьютерных наук подходит как для тех, кто хочет повысить свою профессиональную компетентность в области компьютерных наук, так и для тех, кто стремится подготовиться к дальнейшей учебе в аспирантуре. Программа предлагает три различных курса (только диссертация, проект и курсовая работа), которые позволяют людям настраивать свои исследования в соответствии со своими конкретными амбициями и опытом. Уроки информатики в Брауне ведут те же профессора, которые заслужили репутацию нашего факультета в области инновационного образования и исследований. Департамент обладает опытом в различных областях информатики, включая алгоритмы и структуры данных, искусственный интеллект, автоматизированные рассуждения и планирование, интерфейсы мозг-машина, вычислительную биологию, компьютерную безопасность, криптографию, системы управления базами данных, распределенные системы и повсеместные вычисления, электронная коммерция и агенты, графика и визуализация, взаимодействие человека с компьютером, нанотехнологии, обработка естественного языка, сети, операционные системы, исследование операций и программирование в ограничениях, языки программирования, робототехника и компьютерное зрение, разработка программного обеспечения и потоковая обработка. Факультет компьютерных наук предоставляет всем своим студентам передовые компьютерные технологии. Каждый Sc.M. студенту предоставляется настольный компьютер и письменный стол в ведомственном кабинете. Студенты также имеют доступ к вычислительным кластерам. Кроме того, есть шесть исследовательских лабораторий: лаборатория алгоритмики, лаборатория искусственного интеллекта, лаборатория графики, Интернет-лаборатория, лаборатория захвата движения и лаборатория систем. Обратите внимание, что следующие требования относятся к предыдущему циклу подачи заявок и будут обновлены в конце лета 2021 года. Мы НЕ будем принимать домашнюю версию TOEFL или экзамен IELTS Indicator. Однако мы БУДЕМ принимать экзамен TOEFL ITP Plus для студентов из материкового Китая. Если у вас есть какие-либо вопросы относительно процесса подачи заявки на эту программу, пожалуйста, напишите [электронная почта защищена]. Крайний срок подачи заявок: Заявки на участие в этой программе закрыты на осень 2021 года и будут повторно открыты в конце лета 2021 года. Студенты коричневого уровня могут подавать заявки в качестве студента пятого курса магистратуры до 1 мая 2021 года. Форма запроса о зачислении Все будущие аспиранты, обучающиеся на степень доктора философии, магистра, среднего и высшего образования. программы поступают в Инженерную школу через Высшую школу искусств и наук (GSAS). Студенты, желающие получить степень магистра в области проектирования в Гарвардской высшей школе дизайна, найдут здесь информацию о подаче заявки на эту программу. Студенты, заинтересованные в программе MS / MBA: Engineering Sciences, предлагаемой совместно с Гарвардской школой бизнеса, найдут здесь информацию о подаче заявки на эту программу. Приглашаются студенты со степенью бакалавра в области естественных или количественных наук, математики, информатики или инженерии. Все студенты поступают в аспирантуру только в осенний семестр. Что требует приложение? Мы требуем подачи всей заявки в электронном виде, включая рекомендательные письма и стенограммы. Пожалуйста, не присылайте нам бумажные материалы. График приема на степень доктора философии, M. Литература — искусство слова. История и роль литературы. Литература! Литература (лат. lit(t)eratura, буквально — написанное, от lit(t)era — буква) — в широком смысле это совокупность любых письменных текстов. Материальным воплощением литературных произведений является совокупность различных образов и понятий, зафиксированных автором словами и словосочетаниями. Литература принадлежит к числу предметных искусств, в котором слово является основным средством образного отражения жизни и фантазии. При помощи образов художественная литература воссоздает целые эпохи. При помощи созданных словом образов автор пытается увлечь читателя, «включить» его в действие, сделать его присутствие во времени и пространстве произведения «реальным». Такое «участие» необходимо для полного и более глубоко понимания написанного: так, читатель переживает за Татьяну в «Евгении Онегине», пытается понять причины поступков Катерины в «Грозе» и сложный духовный мир Наташи Ростовой в «Войне и мире», трагедию Григория Мелехова в «Тихом Доне». Именно наше восприятие и переживание судеб героев свидетельствует о том, что литература – это искусство, искусство слова. Художественная литература как искусство слова ведет свою историю от устного народного творчества – песен, сказок, героического эпоса и др. Художественную литературу можно считать самым разносторонним видом искусства: например, картина В. Сурикова «Утро стрелецкой казни» нуждается в историческом комментарии, а роман А. Толстого «Петр I» – нет: он доносит дыхание эпохи во всех деталях. Важнейшая особенность литературы как вида искусства: способность запечатлевать «иное» и невидимое. Немного истории Литература существует с древнейших времен. Начиналось все с Античной литературы (литературы древних греков и римлян). Её письменные памятники, относятся аж к I тысячелетию до н. э. В античной литературе сформировались основные жанры европейской литературы в их архаических формах и основы науки о литературе. В поздней античности (4-5 век) зарождается Средневековая литература, которая просуществовала до 15 века. Зарождение и развитие литературы Средневековья определяется традициями народного творчества, культурным влиянием античного мира и христианством. С 14 по 16 век — это время литературы эпохи Возрождения, в которой писатели обращались к литературе античности, и подражали ее идеалам. Значимыми для русской литературы были 19 и 20 века. — Золотой (Пушкин, Лермонтов, Грибоедов, Фет, Тютчев и др.) и Серебряный (Блок, Ахматова, Маяковский и др.). Они стали для России временем взлета и расцвета. По богатству литературы (да и других видов искусства) эти века несравнимы ни с каким другим периодом истории не только русской, но и мировой культуры. Россия громко заявила всему миру о своем существовании и буквально ворвалась в мировую культуру, заняв там одно из самых почетных мест. Основные литературные направления, постепенно сменяющие друг друга и отражающие русскую литературу — это классицизм (17-19 в. Как реакция на реализм в 20 веке возникает литература модернизма и постмодернизма. Они уходят от внешней реальности к исследованию внутренних состояний. Литература в наши дни, роль литературы В 21 веке появляется много массовой литературы. Современные направления в литературе растекаются по двум направлениям: классические и модные. Классические — все то, что было перечислено ранее. А к модным можно отнести постмодернизм, концептуализм, интеллектуальную литературу, магический реализм, киберпанк, фэнтези и многочисленные книжные сериалы. Сюда же относятся графические романы (комиксы), электронный эпистолярный жанр, и новые формы фольклора в виде песен, анекдотов, скетчей и т. д. В наши дни выбор литературы на полках книжных магазинов просто огромен и каждый может выбрать что-то по своему вкусу. Самое главное — не переставать читать, ведь книги оказывают огромное влияние на нас, на наши ценности и понимание мира в целом. Художественная литература тесно связана с обществом, с его движением к идеалу. Литература является сосредоточением опыта всего народа и отдельной личности в освоении окружающего мира. Она помогает устанавливать связь между поколениями, формировать, развивать и укреплять шкалу ценностей. Благодаря литературе мы изучаем окружающий мир, воспитываем в себе чувство прекрасного и развиваемся. Литература — это одно из самых ценных достояний человечества за все его существование. Литература — искусство слова. История и роль литературы. Модный женский сайт Я самая красивая! Определение 1 Художественная речь – это языковая форма выражения образного содержания произведений литературы. Художественная литература – это многоплановое явление. В ее составе выделяются две основные стороны: Замечание 1 Такая двухаспектность художественных произведений позволила ученым говорить о том, что в художественной словесности совмещаются два разных вида искусства – искусство слова и искусства вымысла. Искусство слова определяет облик поэзии, которая в переводах утрачивает самое главное. Искусство вымысла главным образом свойственно беллетристической прозе, которая сравнительно легко переводится на другие языки. Словесное начало и вымысел можно охарактеризовать не как два отдельных, разных искусства, а как две грани феномена художественной словесности. В свою очередь, словесный аспект литературы двупланов. Здесь речь предстает в качестве средства изображения, материального носителя образности, В качестве способа оценочного рассмотрения внесловесной действительности и как предмет изображения – высказываний, принадлежащих кому-то и кого-то характеризующих. Другими словами, литература способна воссоздавать речевую деятельность. Художественная литература, как отмечает В. А. Грехнев, в процессе осваивания человеческого сознания «укрупняет стихию мысли» — мысль неотразимо притягивает писателя, но эта мысль не отрешена от оценки и переживания, а насквозь ими пронизана. Таким образом, язык художественной литературы запечатлевает процессы мышления людей, их чувства, эмоции, способы языкового выражения и потому выступает своеобразным зеркалом, отражающим языковую картину разных периодов времени, разных эпох. Художественная речь частично совпадает с таким понятием, как литературный язык. Замечание 2 Литературный язык – это нормативный язык, его нормы зафиксированы в словарях и грамматиках. Он является основой художественной речи, однако художественная речь кроме литературного языка использует и все возможности национального языка – жаргоны, просторечие, устаревшую лексику, диалектизмы, варваризмы, профессионализмы. Характерной особенностью художественной речи является ее образность. Как отмечал В. Белинский «поэт мыслит образами». Язык в литературе служит материальной оболочкой образа. К образной сфере языка прежде всего относятся образные средства. Но часто и нейтральные грамматические, фонетические, лексические средства языка в разных текстах обретают дополнительные смысловые или эмоционально-экспрессивные оценки, то сеть они становятся эстетически значимыми, а значит, образными. Грамматические формы в переносном употреблении обладают большими художественными возможностями. В языке главной образной единицей является слово. В прямом значении слово может быть основой художественного образа, если в тексте оно получает «приращение смысла». В художественном произведении значение слова гибко и подвижно, и поэтому восприятие читателем текста должно быть творческим. То есть читатель не только читает произведение, он вместе с писателем участвует в творческом процессе, подставляя в процессе чтения новые содержания. У некоторых слов образность заложена в объекте изображения, свойства которого у читателя вызывают определенные оценки, ассоциации, эмоции. Поэтому объекты, выбираемые писателем для изображения, значимы, а значит, и слова, называющие их, тоже значимы. Таким образом, в литературно-художественном произведении средства общенационального языка в зависимости от авторской установки могут преобразовываться в эстетическом и эмоционально-образном отношении. Художественная выразительность образа напрямую зависит от мотивированности в контексте речевых средств, использованных автором. Для художественной речи типичным является непрерывное использование поэтической (эстетической) функции языка, которая подчиняется задачам воплощения художественного замысла автора. В других видах она проявляется спорадически. Замечание 3 Специфика художественной речи обусловлена ее подчинением задачам духовного освоения мира. Язык в художественной речи выступает не только как средство отображения внеязыковой действительности, но и как предмет изображения. Например, в драме речь персонажей часто получает характерологические функции. Но и за пределам драмы для художественной речи типичным является активное воспроизведение действительности самого языка, ее преобразование и сознательное воздействие на нее. Особенности художественной речи при этом проявляются и в способах организации существующих и вновь создаваемых языковых элементов, в их сочетании, отборе и употреблении. Литература как искусство слова. Цель: дать понятие литературы как вида искусства, в котором основным средством образного отражения жизни является слово. «Прекрасное пробуждает доброе». Д.С. Лихачев. Прекрасное пленяет навсегда. К нему не остываешь. Никогда Ему не впасть в ничтожество… С.Наровчатов. Пролог: ♪ Звучит инструментальная композиция И.Крутого из к/ф “Долгая дорога в дюнах”>. − Огромная Вселенная. В ней дуют космические ветры, бушуют космические вьюги, века в ней пролетают как один день. В этой огромной холодной Вселенной есть голубая планета с названием Земля. Здесь шумят леса, текут реки. Зима сменяет осень, а вслед за весной всегда приходит лето. И вслед за днем наступает ночь, а вслед за ночью неизменно наступает день. На этой огромной голубой планете есть один день. В этот день на свет появился ты. И любящие женские глаза роняли слезы счастья. А сердце материнское тебе пожелало доброго пути. И материнские руки благословили твои первые шаги по этой земле. И загадали звезду с твоим именем. И в ту же секунду в небе зажглась новая звезда. Твоя звезда. Она светит тебе всю жизнь, даже если ты об этом не знаешь. Это звезда твоей любви, твоего счастья, твоей жизни. Ты не выбирал её. Она дана тебе от рождения, как жизнь. А все остальное в своей жизни ты выбираешь сам. Это твое право. Право человека. И если ты выберешь правильный путь, то твоя звезда осветит его. Пусть твоя звезда горит долго, ты можешь и должен сделать это! Постановка проблемы: ♪ Г. Свиридов “Время, вперед!”; слайдовый ряд “МЫ”> XXI век. Начало столетия. Мы живем в веке, когда один диктатор угрожает: «Я утоплю вас в крови!». Когда другой политик обещает: «Я подниму Россию с колен!» А где-то там, в сибирской глуши, районный детский врач выписывает рецепт. Он выписывает рецепт… на яблоко, на молоко. Так было. Так есть. Так будет?! XXI век называют веком науки и техники. Прогресс создаёт иллюзию, что именно наука и техника, уровень их развития, стали мерилом человеческих ценностей. Так ли это? А каково наше отношение к культуре? Искусству? Литературе? Разработка I. Ввод. Да, книги уходят из жизни современных школьников. И страшно представить осуществление той ситуации, которая смоделирована в фантастической антиутопии американского писателя Рея Дугласа Брэдбери “451◦ по Фаренгейту”. Экспресс-анкета: С кем были бы вы, если бы оказались в этом фантастическом городе: Признайтесь себе честно, нужны ли вам книги, когда есть телевидение, кино, компьютер? (Да. Нет.) (Обработка результатов экспресс- анкеты и подведение итогов). Разработка 1I. Литература как вид искусства. Литература – не просто учебный предмет, дающий определенную сумму знаний, но, прежде всего, литература – это вид искусства. Словарь литературоведческих терминов: Литература (от латинского litera – буква, письменность) – вид искусства, в котором основным средством образного отражения жизни является слово. Художественная литература – вид искусства, способный наиболее многогранно и широко раскрывать явления жизни, показывать их в движении и развитии. (Запись определений в словарик) Как искусство слова художественная литература возникла в устном народном творчестве. Её источниками стали песня, народные эпические сказания. Слово – неисчерпаемый источник познания и удивительное средство для создания художественных образов. В словах, в языке любого народа запечатлена его история, его характер, природа Родины, сконцентрирована мудрость веков. Словом можно убить, словом можно спасти, Словом можно полки за собой повести. Словом можно продать и предать и купить, Слово можно в разящий свинец перелить. Разработка III. “Литература – учебник жизни”. Но слова в человеческой речи и в художественной литературе не живут порознь. Их объединяет и согласует мысль, идея произведения и одушевляет человеческая речь. Простое привычное человеческое слово. Но силой своего таланта, как волшебной палочкой, писатель или поэт поворачивает к нам слово неожиданной стороной, заставляя нас чувствовать, мыслить, сопереживать. У Антона Павловича Чехова есть рассказ: он называется “Дома”. Вот его краткое содержание: “Евгению Павловичу Быковскому, прокурору окружного суда, только что вернувшемуся из заседания, гувернантка его семилетнего сына пожаловалась, что Сережа курит, и что табак он берет из письменного стола отца. − Пришлите его ко мне, — сказал Евгений Петрович. − Я на тебя сердит, и больше тебя не люблю, — оборвал приветствие мальчика отец. – Сейчас Наталия Семеновна мне жаловалась, что ты куришь. Это правда? − Да, я раз курил, это верно. − Вот видишь, ты еще и лжешь вдобавок, — сказал прокурор. – Наталия Семеновна два раза видела, как ты курил. Значит, ты уличен в трех нехороших поступках: куришь, берешь из стола чужой табак и лжешь. Три вины! − Ах, да-а, — вспомнил Сережа. И глаза его улыбнулись. – Это верно, верно! Я два раза курил: сегодня и прежде. Евгений Петрович стал объяснять сыну, что брать чужое нельзя, что человек имеет право пользоваться только своим добром. Он стал объяснять ему, что значит собственность, о вреде табака, о том, что табачный дым производит чахотку и другие болезни, от чего умирают. Евгений Петрович мучительно думал о том, что ещё сказать сыну, чтобы овладеть его вниманием. Он видел, что Сережа его не слушает. Мальчик сначала ковырял пальцем дырку в суконной обивке стола, а потом залез на стул, стоявший сбоку стола, и начал рисовать. И Евгению Петровичу казалась странным и смешным, что он, опытный правовед, полжизни упражнявшийся во всякого рода пресечениях, предупреждениях и наказаниях, не мог убедить мальчика в том, что он поступил дурно. Пробило десять часов. Евгений Петрович устало опустился в кресло. А Сережа, удобно устроившись на коленях отца, попросил: «»»» Папа, расскажи сказку». Как и большинство деловых людей, Быковский не помнил ни одной сказки, так что всякий раз ему приходилось импровизировать. — Слушай, — начал отец, поднимая глаза к потолку. – В некотором царстве, в некотором государстве жил-был старый, престарый царь… Жил он в стеклянном дворце, который сиял и сверкал на солнце, как большой кусок чистого льда. Дворец стоял в громадном саду, где росли апельсины, черешни, цвели тюльпаны, розы, пели разноцветные птицы. На деревьях висели стеклянные колокольчики, которые, когда дул ветер, звучали так нежно, что можно было заслушаться… У старого царя был единственный сын и наследник царства, мальчик, такой же маленький, как и ты. Дряхлый и болезненный старик остался без всякой помощи. Пришли враги, убили царя, разрушили дворец, и уже в саду ни черешен, ни птиц, ни колокольчиков. Сережа напряженно слушал. Его глаз подернулись печалью и чем-то похожим на испуг; минуту он глядел задумчиво на темное окно, вздрогнул и сказал упавшим голосом: «Не буду я больше курить…” Беседа с учащимися: − Что произошло? Почему в рассказе А.П. Чехова сказка оказалась лучшим воспитателем, чем вся логика фактов и убеждений? Релаксация − А сейчас сядьте удобнее. Закройте глаза. Ваши руки лежат спокойно и свободно…(звучит инструментальная музыка “Водопад”). “Прочь тревоги и заботы. Погрузитесь в раздумья: музыка и звуки волшебницы природы унесут вас к сверкающему горному потоку. Нигде не найдете такого спокойствия и безмятежности – только здесь, близ прохладных, чистых вод., легко сбегающих по зеленому бархату замшелых камней. Берега потока устланы многоцветным ковром ярчайших цветов, а легкое дыхание ветерка разносит их восхитительные ароматы. В листве высоких деревьев распевают разнообразнейшие птицы. Вы лежите на берегу, глядя в небо, где проплывают пышные облака самых разных очертаний. Это чудное мгновенье может повториться лишь Сверкающей Порой Весны…”. – Открой глаза. Улыбнись себе, соседу. Вам хорошо и спокойно. У.вас хорошее настроение. Итак, вы готовы слушать дальше. Разработка IV. “Мир спасет красота” Что есть красота? И почему её обожествляют люди? Сосуд она, в котором пустота? Или огонь, мерцающий в сосуде? — Вывод: Искусство – великий волшебник и своеобразная машина времени. Любой писатель, наблюдая, изучая жизнь, воплощает при помощи слов, все, что он увидел, почувствовал, понял. Литература обладает особой силой воспитания в человеке человеческого. Оно обогащает нас совершенно особыми знаниями – знаниями о людях, об их внутреннем мире. Литература как искусство слова обладает удивительной способностью влиять на умы и сердца людей, помогает раскрыть подлинную красоту человеческой души. Эпилог. Ты входишь в жизнь, как в двери мастерской. В твоем распоряжении отныне Прекрасный мир прекрасного, людской Трагедией построенный в пустыне. И на тебе горит его тавро Ответственности, действия и слова. В нем многое из нового старо, И старое – значительно и ново. Входи в него хозяином смелей! Он ждет тебя и требует ответа. Согрей его трагедией своей, Прибавь ему ещё любви света! В XII веке в городах Западной Европы, освободившихся от власти сеньоров, началось большое строительство. Гордостью горожан и главным украшением города был собор, который строили десятки, а иногда сотни лет.
Соборы XII-XV веков кажутся лёгкими и как бы прозрачными от множества огромных окон. Они точно сотканы из каменных кружев. Крутые крыши, заострённые кверху окна и двери, высокие башни — всё создаёт впечатление стремительного порыва ввысь. Высота башен самых больших соборов достигает 156 метров, превышая египетские пирамиды.
Собор в Реймсе во Франции (внешний вид).
Строился более ста лет (XIII — XIV века). Спереди имеет три входа в виде стрельчатых, остроконечных арок. В центре — розетк-а с цветными стёклами. По обе стороны от неё — два больших парных окна, они также заканчиваются стрельчатыми арками. Собор увенчивают две башни-колокольни с удлинёнными окнами; башни служили и дозорными вышками города. У входа и в верхней части здания множество статуй.
Каждый с трепетом шёл из своей убогой и тесной лачуги в высокий, просторный каменный храм. Через цветные стёкла окон в помещение лился мягкий свет, создавая таинственный полумрак.
Долгое время собор был единственным большим зданием в городе. В нём не только проводилась церковная служба, но и устраивались собрания горожан, театральные представления, подписывались соглашения между государствами.
Горожане строили и красивые ратуши; их башни нередко были выше, чем колокольни соборов.
Городские здания поражают своей красотой и сложным устройством. В сооружении соборов и ратуш принимало участие много ремесленников: каменщики, плотники, стекольщики. А. М. Горький писал: «Маленькие люди были великими мастерами — вот что говорят нам величественные храмы в старинных городах Европы».
Скульптура в средние века была не отделима от церковного строительства. Соборы украшались множеством статуи святых, епископов, королей.
Стены соборов были расписаны картинами, изображавшими муки грешников в аду. Они должны были предостерегать верующих. Со стен на молящихся смотрели суровые, измождённые лица святых. Средневековые живописцы рисовали с большими, устремлёнными вверх глазами.
Художники не наблюдали природу и не изучали человеческое тело — это запрещало вера. Свои картины они рисовали по образцам, установленным церковью. Отдалённые и близкие предметы живописцы изображали одинаковыми по размерам, и никогда не использовали тень.
Народ создавал и свою, народную культуру.
В сёлах, на улицах городов и рыночных площадях часто выступали бродячие артисты — жонглёры. Они водили за собой медведей и обезьян, показывали фокусы и акробатические номера, а также разыгрывали небольшие пьески и пели песни. Без жонглёров не обходилась ни одна деревенская свадьба или ярмарка. Они сочиняли басни и рассказы, в которых едко высмеивали служителей церкви и феодалов. В хронике рассказывается, что один жонглёр, одев двух обезьян в доспехи и посадив их верхом на собак, разыгрывал рыцарский турнир. У простого народа эта злая насмешка над военными играми феодалов вызывала-шумное одобрение.
Юмор и дерзкие шутки жонглёров не нравились господам. Церковь жестоко преследовала и изгоняла бродячих артистов. Она разрешала безнаказанно убивать их и запрещала хоронить на кладбищах.
К XIII веку в городах стали возникать литературные произведения. Горожане любили короткие смешные рассказы в стихах. Их героями чаще всего были ловкий, хитрый горожанин или весёлый, находчивый крестьянин. Они неизменно оставляли в дураках своих противников — чванливых рыцарей и жадных монахов. В течение многих десятилетий в городах Франции из басен и сказок слагалась поэма «Роман о Лисе». Под видом зверей в поэме показаны ленивый крупный феодал — Медведь, глупый служитель церкви — Осёл, злой, рыщущий в поисках добычи рыцарь — Волк, умный, находчивый горожанин — Лис. В борьбе с Волком Лис неизменно выходит победителем. Но когда он начинает притеснять бедняков, показанных в поэме под видом Петуха, Зайца, Улитки, хищник Лис сам попадает в затруднительное положение. В народном творчестве выражался протест трудящихся против гнёта феодалов и католической церкви.
Литература — это все произведения письменности, которые имеют определенное общественное значение. Литература может быть научной, художественной, эпистолярной. В очень упрощенном, обывательском понимании, литература – это книги. Чаще всего мы говорим все-таки о художественной письменной продукции. Литература в этом смысле – явление культуры, вид искусства. Изучает литературу отрасль науки филологии, которая называется литературоведение. Искусство — это творческое отражение действительности, воспроизведение ее в художественных образах. Произведением искусства называют далеко не все творения, это должно быть нечто очень качественное, наиболее интересное и способное изменить сознание зрителя (слушателя). Искусство воспринимается человеком всеми органами чувств. Литература как искусство слова и её роль в духовной жизни человека Урок литературы в 9 классе Субботина И.К., учитель русского языка и литературы ГБОУ СОШ № 448 г. Санкт-Петербурга Кроме литературы, чем и дышать, опускаясь на дно морское… М. Щербаков Литература — это все произведения письменности, которые имеют определенное общественное значение. Литература может быть научной, художественной, эпистолярной. В очень упрощенном, обывательском понимании, литература – это книги. Чаще всего мы говорим все-таки о художественной письменной продукции. Литература в этом смысле – явление культуры, вид искусства. Изучает литературу отрасль науки филологии, которая называется литературоведение. Искусство — это творческое отражение действительности, воспроизведение ее в художественных образах. Произведением искусства называют далеко не все творения, это должно быть нечто очень качественное, наиболее интересное и способное изменить сознание зрителя (слушателя). Искусство воспринимается человеком всеми органами чувств. Виды искусства Виды искусства Виды искусства Разделы литературы Домашнее задание ОТВЕТИТЬ ПИСЬМЕННО НА ОДИН ИЗ ВОПРОСОВ: Как связаны человек и история в «Капитанской дочке» А.С.Пушкина? Какие нравственные ценности утверждает поэма М.Ю. Лермонтова «Мцыри»? Что «дурное в России» высмеивают Н.В.Гоголь в пьесе «Ревизор» и М.Е. Салтыков-Щедрин в сказках? Вводный урок литературы в 5 классе «Литература – искусство слова» Тип урока: урок открытия новых знаний. Цель урока: познакомить учащихся с особенностями учебного предмета «Литература». Планируемые результаты: Личностные: мотивация школьников к изучению литературы как одного из учебных предметов, необходимых для самопознания, саморазвития и дальнейшего успешного обучения. Метапредметные: умение определять понятия, строить логическое рассуждение, делать выводы. Предметные: восприятие литературы как особого вида искусства, умение соотносить его с другими видами искусства. Формируемые на уроке УУД Личностные: способность к самооценке. Регулятивные: уметь слушать в соответствии с целевой установкой, уметь планировать свои действия в соответствии с поставленной задачей. Познавательные: уметь ориентироваться в своей системе знаний, опираться в работе на свой жизненный опыт, уметь осуществлять поиск необходимой информации, уметь анализировать, сравнивать, делать выводы. Коммуникативные: уметь участвовать в учебном диалоге, уметь оформлять свои мысли в устной форме, аргументировать собственную позицию. Технология: проблемного обучения Методы обучения: эвристическая беседа, наблюдения. Формы работы: фронтальная, индивидуальная, групповая. Оборудование: — Литература: учебник для 5 класса общеобразовательных учреждений: в 2 ч./ авт.-сост. Г.С. Меркин. – М.: ООО «Русское слово-учебник», 2012.- (ФГОС. Инновационная школа). — Литературное чтение. 4 класс. Учеб.для общеобразоват. Организаций. В 2 ч. /Л.Ф Климанова, В.Г. Горецкий, М.В. Голованова и др. – М.:Просвещение, 2015. — Аудиозапись «Осенняя песня» из цикла «Времена года» П.И. Чайковского. — Репродукции картин известных художников по теме «Осень». — Стихотворения русских поэтов об осени, распечатанные для работы по группам. Технические средства обучения: компьютер (электронная презентация), мультимедийный проектор. Ход урока I. Мотивация к учебной деятельности. Учитель приветствует учащихся, настраивает на деловой ритм. Учащиеся показывают готовность к работе, оформляют записи в тетрадях, тему не записывают. Учитель показывает учебник «Литературное чтение» для 4 класса и предлагает вспомнить, какие произведения учащиеся читали в 4 классе и как над ними работали. Учащиеся вспоминают, что они читали, пересказывали, отвечали на вопросы. Затем учитель демонстрирует учебник литературы для 5 класса и предлагает сравнить два названия предметов. Учащиеся приходят к выводу, что теперь они будут не просто читать и пересказывать, а изучать художественные особенности произведений. III. Постановка учебной задачи. Учащиеся отвечают на вопрос: «Какие мысли возникают у вас, когда вы слышите слово «литература»? Совместно с учителем заполняют кластер. Возможные ответы учащихся: литература — это книги, произведения (сказки, стихотворения, рассказы), урок (учебный предмет), учебник, по которому мы будем учиться. Остается незаполненным одно окошко. Учащиеся ставят задачу: что еще может обозначать слово «литература»? IV. Построение проекта выхода из затруднения. 1) Эвристическая беседа. Учитель: Наступила осень, яркими красками раскрашены деревья. Какими способами можно изобразить красоту осенней природы? Возможные ответы учеников: Природу можно нарисовать, о ней можно написать сочинение, можно спеть. Учитель: Какие виды искусства помогают нам это сделать? Возможные ответы учеников: Живопись, музыка. Учитель просит привести примеры известных произведений об осени и подводит учащихся к мысли, что литература – это один из видов искусства 2) Учащиеся самостоятельно определяют тему урока «Литература – искусство слова» и записывают ее в тетрадь. 3) Учитель предлагает ученикам разделиться на группы и каждой группе дает задание: подобрать к репродукциям картин известных художников строки из стихотворений известных поэтов. Сообщает, что работа будет проходить под музыкальное сопровождение — «Осенняя песня» из цикла «Времена года» П.И. Чайковского. V. Творческая практическая деятельность по реализации построенного проекта. Учащиеся работают в группах. Для каждой группы предлагается одна репродукция картины об осени и несколько стихотворений известных поэтов. Необходимо подобрать такое стихотворение, которое более точно передает содержание картины, и прочитать его выразительно. VI. Представление результатов работы. Учитель на слайдах демонстрирует репродукции картин. Ученики по группам представляют свою репродукцию и выразительно читают строчки их стихотворений, которые соответствуют изображенному. Возможные варианты: Картина И. Левитана «Золотая осень» — отрывок из стихотворения А.С. Пушкина «Осень» Картина И. Бродского «Летний сад осенью» — стихотворение А.К. Толстого «Осень» Картина И. Левитана «Осень» — стихотворение Н.А. Некрасова «Заунывный ветер гонит…» Картина В. Поленова «Золотая осень» — отрывок из стихотворения И. Бунина «Листопад» Картина И. Грабаря «Осень. Рябина и березы» — стихотворение Д. Кедрина «Скинуло кафтан зеленый лето…» VII. Включение в систему знаний и повторение. 1) Учитель предлагает вернуться к кластеру и дописать в пустое окошко нужную информацию: литература -это вид искусства. Учащиеся обобщают, что в живописи картины (образы) создаются при помощи красок, в музыке – при помощи звуков. Делается вывод о том, что литература – это вид искусства, в котором картины (образы) создаются при помощи слов. 2) Знакомство со структурой учебника «Литература», со списком произведений, которые будут изучаться. Анализ разных вариантов заданий, подтверждающих, что в пятом классе ученики будут обращать особое внимание на художественные особенности произведений. VII. Рефлексия учебной деятельности. Подведение итогов. Учитель предлагает учащимся продолжить выказывания: Сегодня на уроке — я понял, что… — я научился… — мне было трудно… Можно ли утверждать, что художественная литература воспитывает человека? Литература в целом — это один из способов познать мир, человечество, самого себя. Литература как нельзя лучше передаёт мысли, взгляды автора, его отношение к жизни, реальности. И каждый писатель создаёт свой художественный мир, с которым согласится и примет его тот или иной читатель. Картины жизни, образы рисует и живописец. Посвоему жизнь и характеры людей отражаются в музыке, скульптуре и литературе. Оружие писателя — слово. Художественная литература — это искусство слова. Соприкосновение с миром искусства доставляет нам радость и бескорыстное наслаждение. Многие поэтому видят в произведениях писателей, композиторов, художников средство приятного времяпрепровождения. Конечно, мы нередко идём в кинотеатр, садимся к телевизору или компьютеру, чтобы отдохнуть, а то и поразвлечься. Да и сами художники, композиторы, программисты, писатели, зная законы искусства, так строят свои произведения, чтобы взбудоражить, поддержать и развить интерес и даже любопытство зрителей, слушателей. Но значение искусства в жизни человека несравненно серьезнее и богаче. Ни одно искусство не может так наглядно, «объёмно» изобразить человека, как живопись и скульптура. Но и живописец и скульптор «схватывают» лишь один момент жизни, и, рассматривая картину и скульптуру, мы только догадываемся о том, что предшествовало этому моменту, что последует за ним. Ни живописец, ни скульптор не имеют средств, чтобы показать своих героев в движении, в изменении, в развитии. Это может сделать искусство кино, в котором чудесно сплавлены особенности искусство слова, сценического искусства, живописи, музыки, художественной фотографии и компьютерной графики. Но не забудем, что художественные кинокартины создаются на основе литературных сценариев. Нельзя перевести на «язык» кино лирические произведения. При всём необъятном могуществе киноискусства есть области общественной и внутренней жизни человека, доступные только искусству слова. Писатель может нарисовать один момент, и историю человеческой жизни. И одно событие, и цепь самых сложных событий. Изменения, связанные с прогрессом науки и техники ведет к изменению у нынешнего поколения прежних идеалов и оценок, и поиску новых критериев. Мы говорим о материальном и духовном, однако отделить одно от другого не так уж просто. Каждый мощный взлёт писательской мысли, повлиявший на воспитание молодого поколения, всегда несет в себе элемент духовности. Более высокие технические и творческие возможности сказываются на образе мышления и жизни молодёжи. Но это совсем не значит, молодёжь должна отвергать высшие духовные и культурные ценности, и не следует ставить их в зависимость от материального богатства. Существует такое понятие, как культура народа, которая корнями уходит глубоко в национальную почву и историю. Во все времена творцы словесного искусства в своих произведениях правдиво и полно отражают сложность и многообразие жизни человека и общества, ярко и доходчиво выражают свои раздумья о смысле жизни, свои сокровенные чувства. Морально-нравственная позиция автора ненавязчиво воздействует на читателя, который наслаждаясь словом, знакомясь с удивительными персонажами, познаёт мир и формирует в себе высокие гражданские чувства. Понятие «формирование» в педагогике охватывает своим содержанием диапазон внешних (социальных, экономических, воспитательных и др.) и внутренних (самостоятельная деятельность личности, самовоспитание и др.) факторов, находящихся в неразрывной взаимосвязи и обеспечивающих становление и развитие личности. Опираясь на данное положение, что успешное формирование нравственных ценностей обеспечивается совокупностью внешних и внутренних условий, способствующих их формированию. Отсюда следует, что наряду с воспитательной деятельностью педагога необходима самовоспитательная деятельность учащихся по освоению нравственных ценностей будущих специалистов-филологов. Опираясь на положения личностно-ориентированного подхода, что деятельность учащихся по самовоспитанию обеспечивает постановку их в позицию субъектов процесса формирования нравственных ценностей и способствует проявлению максимальной активности, самостоятельности в освоении ими нравственных ценностей. Художественные творения А. С. Пушкина, М. Ю. Лермонтова, Н. В. Гоголя, Л. Н. Толстого, Ф. М. Достоевского, А. П. Чехова, М.Шолохова — позволяют молодому поколению не только узнавать прошлое, но и переживать вместе с их героями, формировать взгляды, чувства, характер, пробуждают любовь к прекрасному, воспитывают готовность к борьбе за торжество добра и правды. Литература воспитывает чувство прекрасного, обогащает духовный мир человека. Предметом изображения литературы чаще всего являются люди конкретной исторической эпохи, их мысли, чувства, взаимоотношения друг с другом, их жизненные идеалы, — словом, внутренний и духовный мир человека. Художественная литература, как и наука, обладает огромной познавательной силой. Она способствует распространению среди молодого поколения просвещения и культуры. О чем бы писатели и поэты ни говорили в своих произведениях, они думают о читателе, о человеке. Поэтому М.Горький очень точно заметил, что литература — это человековедение. Сила художественной литературы заключается, прежде всего, в ее эстетическом воздействии. Это — то искусство, которое активизирует человеческие духовные силы: ум, интуицию, чувства, эстетические понятия. Эстетическое воспитание — это воспитание в людях способности и потребности видеть, понимать и ценить красоту во всех ее проявлениях и вносить ее в жизнь, способности понимать возвышенное, трагическое, комическое. Сложная и тонкая задача эстетического воспитания молодого поколения решается совместными усилиями семьи, школы, общественности. Молодёжь воспитывается эстетически на огромном историческом опыте писателей. Эстетические эмоции, вызываемые художественным произведением, способствуют восприятию общественных идей не только умом, но и сердцем, пробуждают активное отношение к жизненным картинам, нарисованным в произведении. Литература обеспечивает многовековую преемственность культуры, ее нарастающую универсальность. Создавая общезначимые идеи — образы, вырастающие до всечеловеческих символов, оно выражает смысл всего исторического развития. Гамлет, Дон Кихот, Князь Мышкин, Мастер и Маргарита — это уже не просто художественные образы это символы культурно–значимых общечеловеческих ценностей. Читая произведения как «Преступление и наказание», «Война и Мир», «Анна Каренина», «Гранатовый браслет», молодежь меняется, у них меняется отношение к жизни, и становятся лучше. Произведения затрагивают их до глубины сердца и воспитывают. Художественная литература доступна для всех, но глубина ее понимания зависит от того, умеет ли учащийся ее читать и каков сам учащийся, его вкусы и интересы, морально-мировоззренческие установки. От личности учащегося зависит, что он выбирает для чтения — так называемое «чтиво» или подлинно художественные произведения. Первого рода книги — чисто развлекательные, они ничего не дают, кроме сиюминутного удовольствия, вторые — глубоко влияют на учащегося, воспитывают его. Одни учащиеся «глотают» произведения, не «переживая» их, в то время как другие вдумываются в то, что читают. У первых — остается от чтения мало, у вторых — прочитанное глубоко западает в их сознание. Что же говорят о художественной литературе классики? Замечательный русский писатель-сатирик М. Е. Салтыков-Щедрин отмечал, что «литература — это…сокращенная вселенная». Н. Г. Чернышевский назвал литературу «учебником жизни», подчеркивая ее познавательную ценность, глубину проникновения в жизнь. М.Горький считал главной заслугой литературы ее общественное значение: «Беспощадно ярко освещая пороки жизни, недостатки людей, она воспитывала жажду лучшего, она учила». По его мнению, «цель литературы — помогать человеку понимать себя самого, поднять его веру в себя и развить в нем стремление к истине, бороться с пошлостью в людях, уметь найти хорошее в них, возбуждать в их душах стыд, гнев, мужество, делать все для того, чтоб люди стали благородно сильными и могли одухотворить свою жизнь святым духом красоты». «Чем же сильна литература?» — спрашивает М. Горький и отвечает: «Насыщая идеи плотью и кровью, она дает им большую наглядность, большую убедительность, чем философия или наука». По словам А. Н. Островского, литература «оживляет голые… факты и делает их понятными; из исторических имен творит живых людей. Историк-ученый только объясняет историю, указывая причинную связь явлений, а историк-художник пишет, как очевидец, он переносит нас в прошлые века и ставит зрителем событий». Сила художественной литературы заключается также в том, что она учит видеть прекрасное и безобразное в самой реальной жизни. Говоря о преподавании литературы сегодня, нельзя сказать о том новом понимании задач и целей образования, которое последовательно пробивает себе дорогу. Совершенствование преподавания литературы предполагает усиление нравственного, эстетического и эмоционального воздействия литературного произведения на учащегося, воспитание самосознательности, развитие воображения и чувства прекрасного. В юности закрепляется эстетическое отношение к искусству в целом и к литературе в частности, качественно новый подход к прочтению литературных произведений. По характеру своего воздействия художественные произведения приближаются к воздействию действительности, а иногда и превосходят ее. Талантливый писатель дает сгусток впечатлений о действительности. Краски изображения бывают настолько ярки, что становятся ощутимы, зримы и вызывают такие сильные эмоции, что читатели или громко смеются, или рыдают над книгой, испытывают гнев или презрение, готовность действовать. Положительные образы служат примером для заимствования, а отрицательные отвращают человека от ложных шагов и ошибок, способствуя тем самым искоренению пороков личности. В заключение следует сказать, что чтение художественной литературы должно стать обязательным для каждого человека с детского возраста и до глубокой старости. Литература доставляет много радости, она просветляет умственный взор, обогащает духовный мир читателя, вольно или невольно оказывает положительное влияние на характер. Воспитание художественной литературой не тяжкий труд, а увлекательный, доставляющий глубокое удовлетворение. Художественная литература является своеобразной летописью человеческого общества, могучим орудием человеческой культуры, великим средством воспитания молодого поколения. Литература 1. Бахтин М. М. Литературно-критические статьи. М., 1986. 2. Бахтин М. М. Эстетика словесного творчества. М.,1986. 3. Каган М. С. Философская теория ценности. СПб., 1997. Одно из самых увлекательных произведений научной литературы, с которыми я столкнулся в последние годы, не было опубликовано в журнале или книге. Я прочитал его, когда посетил MoMA PS1, чтобы увидеть их выставку Greater New York .На одной стене висела работа Гленна Лигона «Жилье в Нью-Йорке: краткая история 1960–2007 годов», в которой Лигон излагает свои воспоминания о разных местах, где он жил по всему городу. В обзоре для Hyperallergic Бенджамин Саттон отметил, что статья посвящена темам «джентрификации, дискриминации и неравенства» — тем же концепциям, которые подпитывали многие впечатляющие литературные произведения, особенно в последнее время. Это точная оценка: используя ограниченное пространство, Лигон может одновременно вызывать множество пространств, которые он назвал домом, а также сложную динамику, работающую в каждом. Это был не первый момент литературного перехода для Ligon: Издательство Йельского университета выпустило в 2011 году сборник его сочинений Yourself in the World: Selected Writings and Interviews . В статье для журнала «Los Angeles Review of Books» Пит Л’Официальный исследовал литературные и художественные влияния Лигона и то, как они сходятся в его работах. Читатели, которым интересно прочитать «Жилье в Нью-Йорке: краткая история», не посещая музей, могут быть рады узнать, что ранее в этом году PS1 опубликовала версию произведения Лигона. Это было незабываемое время для произведений, которые существуют на стыке изобразительного искусства и литературы. Это было незабываемое время для произведений, которые существуют на стыке изобразительного искусства и литературы. Зимой 2015 года я был ошеломлен, прочитав Кэролайн Бергвалл Drift , потрясающую книгу, в которой медитации на пересечении водоемов сочетались с экстатическим исследованием языка и преследующими сценами беженцев, ищущих лучшей жизни с помощью опасного транспорта по воде.Той же зимой я снова был ошеломлен, увидев инсталляцию Бергвалла «Дрифт» в галерее Callicoon Fine Arts, которая перекликалась со многими из тех же тем, что и ее литературный аналог, но сделала это, когда занималась совсем другой дисциплиной. Попытка отнести работы Бергвалл к одной категории почти невозможна: Meddle English , ее коллекция «новых и избранных текстов» 2011 года, представляет собой одну из самых увлекательных коллекций дополнительных материалов. Я сталкивался.В частности, отчеты Бергвалла об истории работ, собранных в Meddle English , часто охватывают континенты и итерации, причем определенные работы включают время, проведенное в публикациях и в галереях. Работу Бергвалл можно читать как литературу или как аналог ее работы в галереях; Можно также предположить, что можно полностью сосредоточиться на искусстве Бергвалл и полностью игнорировать ее книги. Любой из этих читателей-теоретиков или зрителей ушел бы от этого опыта довольным, имея в виду многое. Бергвалль и Лигон — далеко не единственные художники, представленные как на стенах галереи, так и на книжных полках. В список из шести рекомендованных книг, которые она собрала для The Week , писательница Саманта Хант включила The Walk Book , работу Джанет Кардифф, возможно, наиболее известную своими крупномасштабными аудиоинсталляциями. (Ее 2001 The Forty Part Motet берет Spem Томаса Таллиса in alium numquam habui и разбивает его на составляющие; это одновременно потрясающе технически и невероятно подвижно на нескольких уровнях.В недавнем профиле Хизер Филлипсон в журнале T Бена Истхэма основное внимание уделялось ее работе в качестве художника-инсталлятора, но также отмечалось признание, которое она получила за свои стихи: «Ободренная своим учителем, она подала заявку на получение престижной премии Эрика Грегори для поэтов. моложе 30 и выиграли; в 2009 году Фабер опубликовал ее первый сборник ». Истхэм также отметил, что Филлипсон черпал вдохновение у Фрэнка О’Хара, который сам был фигурой в литературном и изобразительном мире, проработав некоторое время куратором в Музее современного искусства. Работы Софи Калле, еще одной художницы, чьи работы можно найти как в галереях, так и в книжных магазинах, послужили источником вдохновения для целого ряда памятных литературных произведений. История создания адресной книги Calle 1983 года — это материал, из которого строятся великолепные сюжеты: Калле нашла потерянную или брошенную адресную книгу, скопировала содержимое и обратилась к людям, указанным в ней, а затем задокументировала свое общение с ними.(Siglio Press опубликовала его версию в 2012 году.) В романе Пола Остера 1992 года « Левиафан » фигурирует фигура, вдохновленная Калле. В частности, художник выбирает людей наугад, чтобы следовать за ними, документируя эти взаимодействия. В свою очередь Калле создал произведение, вдохновленное романом Остера. В недавно переведенной на английский язык книге Энрике Вила-Матаса , потому что она никогда не спрашивала , используется это в качестве отправной точки. Его сюжет следует за писателем, которому Софи Калле поручила написать сценарий для нее. Потому что она никогда не спрашивала быстро увеличивает метафисный коэффициент. С одной стороны, он отсылает к роману Остера, но также добавляет несколько слоев реальности, включая персонажа, который выступает в роли двойника Калле. Она — не единственный пример этого: рассказчик романа также служит своего рода суррогатом или двойником автора Вила-Матаса, который неоднократно включал мир искусства в свою художественную литературу: его роман 2014 года Кассельская иллогия. рассказывает о злоключениях писателя, которого просят написать публично в рамках инсталляции художника.В данном случае книга разыгрывается как комедия нравов, установленных в мире искусства; Потому что она никогда не спрашивала больше похожа на ответ на работу Калле — литературное почтение, в котором Вила-Матас работает с некоторыми из предпочтительных тем и устройств Калле. Энрике Вила-Матас — один из многочисленных художников и писателей, упомянутых в романе Валерии Луизелли 2015 года История моих зубов . Этот роман можно читать как отдельное произведение о более крупном персонаже, который заново изобретает себя как аукционист и становится жертвой странного заговора. Но корни романа уходят в мир искусства. Луизелли было поручено написать художественное произведение в рамках художественной выставки The Hunter and the Factory , которая была показана в Galería Jumex в 2013 году. В интервью 2014 года для BOMB она описала процесс. Я написал его в рассрочку для рабочих на фабрике. Первоначально это был заказ фонда Jumex Foundation, важной коллекции современного искусства, субсидируемой одноименной фабрикой по производству соков.Два куратора, Магали Арриола и Хуан Гайтан, попросили меня написать художественную литературу для выставки, и я предложил идею написать роман в рассрочку для фабричных рабочих. Я писал одну часть в неделю, и каждая из них распространялась среди них в виде книжек. В своем послесловии Луизелли пишет о стремлении «связать два далеких, но соседних мира» — другими словами, фабрику и культурную деятельность, которую она поддерживает. Именно благодаря ее роману, который охватывает вопросы класса, географии и восприятия искусства, она может это делать.Он также создает ряд линз, через которые можно читать The Story of My Teeth . Луизелли завершает послесловие романа, отмечая его совместные элементы — от частей, в которых он был написан, до процесса его перевода для англоязычных читателей. «[E] очень новый слой полностью изменяет весь контент», — пишет она. «Каждый новый слой полностью изменяет все содержимое». Роман Луизелли, как и тексты Бергвалля, существует в некотором среднем пространстве, в котором пересекаются изобразительное искусство и литература.В других недавних книгах для повествования использовались приемы и техники, обычно связанные с изобразительным искусством. С 2015 года были опубликованы первые три книги в The Familiar , запланированном 27-томном труде Марка З. Данилевски. Как известно читателям его более ранних Only Revolutions или House of Leaves , Даниелевски любит эксперименты с текстами и включение манипуляций с книгой как объектом в акт чтения. В своем обзоре первого тома для Los Angeles Times Лидия Миллет отметила, что это было «не только книга, но и перформанс, — неоднородная мозаика содержания, которая, в зависимости от ваших читательских предпочтений, может ослеплять и интриговать или мучить и отталкивать.Этот акцент на структуре также напоминает недавний роман Эли Горовица The Pickle Index , который существует в трех различных изданиях: набор из двух твердых обложек, торговая книга в мягкой обложке и приложение. Когда я брал интервью у Горовица в прошлом году, он отметил, что различия между версиями были значительными. «Это тот же основной текст, — сказал он, — но он исследует, как форма и история влияют друг на друга». Этот интерес к форме и формату отмечает еще один способ, которым мир искусства и литературный мир, никогда так далеко друг от друга, начали пересекаться.Возможно, это сближение — тонкий ответ на добавление цифровых форматов к методам чтения книг. Это не означает, что эта группа писателей отвергает цифровые форматы публикации; вместо этого, это один из возможных ответов, который может возникнуть после того, как зададут вопросы о том, что означает физичность для книги. Если этот ответ, в свою очередь, породит множество гибридов и сложных работ, тем лучше для тех, кто заботится о множестве художественных дисциплин. Мы публикуем ваших любимых авторов — даже тех, которых вы еще не читали.Получайте новые художественные произведения, эссе и стихи на свой почтовый ящик. Наслаждайтесь странной, увлекательной работой в «Пригородном транспорте» по понедельникам, увлекательной художественной литературой из «Рекомендуемой литературы по средам» и обзором наших лучших работ недели по пятницам. Настройте здесь свои предпочтения по подписке. В ранние муки создания Чума — , когда Вторая мировая война разлучила его с женой в Алжире и сослала во Францию, — записал Альбер Камю в своей книге. записная книжка, что «проблема искусства — это проблема перевода».Таким образом, он предположил, что литературная композиция, как и перевод, включает преобразование исходного материала в целевой материал. Использование термина «перевод» в метафорическом смысле представляет литературу как способ связи чего-либо посредством акта преобразования. Комментарий Камю также признает, что писатели и переводчики в равной степени принимают во внимание третье измерение наряду с содержанием и формой: читателей. Камю предполагает, что задача литературного искусства связана с неявными требованиями и требованиями перевода. Задача переводчика — создать произведение, которое сохранит динамический потенциал оригинала — его эмоциональный, тематический и лингвистический охват — в максимальной степени, сделав при этом новый перевод произведения доступным для читателей, говорящих на другом языке. Иногда говорят, что степень, в которой это возможно, зависит от переводимости произведения, от его возможности для перевода. Но можно сказать по-другому, сказав, что это зависит от степени «переводимости», заложенной в произведение.Литературное произведение искусства действительно может иметь некоторую степень «перевода», не имеющую ничего общего с языком, на котором оно изначально написано. Скорее, это может быть связано с передачей между языками тех качеств литературного произведения, которые находятся ниже или выше любого языка: существенное качество коммуникации, которое выходит за рамки формы его выражения. Эта «переводимость» больше не является неотъемлемым качеством языка, а скорее атрибутом того, как он используется — отражением того, как произведение обращается к читателю.Его можно охарактеризовать как творческую работу, необходимую для передачи опыта — личного, исторического или воображаемого — таким образом, чтобы он затрагивал чей-то интеллект и эмоции. В литературном произведении слова на странице дают возможность читателям вызывать в воображении обстоятельства или состояния бытия, сочетающие реальность и воображение в вымышленном промежуточном состоянии. Это не означает, что литературные произведения — это головоломки, которые нужно решить, хотя некоторые литературные произведения стирают это различие, вводя головоломки и коды в виде фольги или дымовой завесы.Скорее, литературные произведения указывают своим читателям на область значений : открытое поле с множеством значений, которые могут быть задействованы с течением времени. Перевод опыта Важность «перевода» в искусстве была частью мышления Камю, когда он писал Чума , роман о вымышленной вспышке болезни в прибрежном алжирском городе Оран. В романе Камю сочетает свое знакомство с реальным Ораном с его опытом Франции в условиях нацистской оккупации, вводя системы отсчета, взятые из разрозненных исторических обстоятельств, каждая из которых совпадает с таковыми в романе.Это слияние остается в рамках того, что Камю считает «правильными отношениями» между искусством и опытом — отношениями, в которых искусство «вырезано» из опыта, а не наоборот. Тем не менее, «перевод» личного исторического опыта в художественную литературу был центральной точкой критики в попытке Ролана Барта принижать значение The Plague . Барт утверждал, что роман научил читателей игнорировать историю, и заметил, что «все эпизоды книги могут быть переведены с точки зрения профессии.«Защищаясь, Камю заметил в письме к Барту, что« длинный отрывок из Чума появился во время оккупации в сборнике текстов сопротивления, и один этот факт мог бы оправдать сделанное мною перемещение »- транспозиция с история оккупации по роман, а не обратный путь. Комментарий Барта, однако, предлагал «перевести» роман в противоположном направлении. Барт раскритиковал утверждение, которое Камю никогда не делал: что перевод может использоваться для воссоздания сырого опыта, из которого он возник.Это примерно так же разумно, как использование французского перевода книги Достоевского «Демоны » для воспроизведения русского оригинала. Но даже это сравнение не является абсолютно строгим, потому что есть по крайней мере одно существенное и очевидное различие: « Демонов » Достоевского — литературное произведение искусства, тогда как Франция, находящаяся под нацистской оккупацией, — историческое обстоятельство. Исторические обстоятельства не претендуют на собственное значение — это наше собственное чувство социальной ответственности, которое придает истории потенциальное значение через нашу оценку и артикуляцию ее воздействия.Но « Демоны » Достоевского, хотя и частично вдохновлен историческими событиями, представляет собой произведение искусства, которое включает меру внутренней «переводимости» независимо от его языка. Хотя было бы очень сложно выполнить обратный перевод Demons и прийти к точному дословному русскому оригиналу, полученное приближение, независимо от его конкретной лингвистической формы, все же будет нести меру первоначального коммуникативного потенциала произведения. — его «переводимость» — как произведение искусства.Обратный перевод художественного произведения в другое произведение искусства происходит на другом уровне, чем обратный перевод художественного произведения в опыт. В отличие от сырого опыта, о котором нельзя сказать, что у него есть импульс к связи, произведение искусства обладает потенциалом «переводимости», указанием на намерение автора и способность его работы что-то связать. Таким образом, «переводимость» появляется перед фактическим переводом текста на другой язык — как проявление импульса к связи. Импульс к установлению отношений возникает до его выражения на любом языке, и переключение между импульсом и выражением является одним из самых основных аспектов любого общения.Прямое общение можно понимать как колебание между передачей и получением таких выражений. Но некоторые аспекты человеческого опыта трудно уловить напрямую. Однако они могут быть выражены косвенно через изображение — как в романе или картине. В публичной лекции художник Марк Ротко, настаивая на том, что «самовыражение в искусстве ошибочно», использовал литературные термины, такие как напряжение, ирония, юмор и трагедия, чтобы объяснить, что его картины были выражением «человеческой драмы» и «общение о мире с кем-то другим.«Таким образом, он вложил коммуникативный потенциал в свои картины до того, как они достигли аудитории, и это общение с художником осуществляется косвенно через произведение искусства. Литературное общение, которое, как и живопись, происходит через произведение искусства, имеет тенденцию к Литературные тексты — это больше, чем семантические предложения — они появляются как так называемые в феноменологических подходах к литературе эстетических объектов . Художник-литературный художник встраивает коммуникативный потенциал в произведение искусства, прежде чем оно будет воспринято читателем.Обмен между художником и аудиторией происходит опосредованно через эстетический объект. Литературовед Роджер Д. Селл далее указывает, что, хотя сами литературные произведения косвенно проявляются как формы того, что он называет «подлинным» общением, которое принимает во внимание автономию другого, они часто изображают прямой коммуникативный сбой, который, как правило, имеет драматический потенциал. Они передают то, что Ротко называет «человеческой драмой». Ценность такой художественной коммуникации, помимо красоты эстетического объекта, заключается в том, что невыразимые аспекты опыта передаются косвенными средствами. Некоторые герменевтические подходы к переводу предполагают, что перевод предполагает перенос дискретной интерпретации значения произведения искусства. Но «перевод» эстетического объекта с одного языка на другой — это больше, чем перевод слов, это перевод искусства. Литературное произведение, которое как эстетический объект намеренно косвенно, распространяется на поле значимости, границы которого намеренно трудно определить. Художественный перевод должен как можно больше переносить значимость произведения — лингвистически и эстетически.Целевой язык должен приближаться к косвенному общению, происходящему на исходном языке, со всеми его двусмысленностями, что также позволяет различным читателям взаимодействовать с произведением и друг с другом посредством обсуждения и дебатов. Перенося интерпретируемое поле значения, а не одну конкретную интерпретацию, художественный перевод создает новый эстетический объект, производно связанный с его источником. «Я», «Другой» и за его пределами «Транслятивность» проистекает из восприятия чувственных явлений и стремления изобразить их в форме произведения искусства.Это придает произведению искусства и его последующему переводу коммуникативный потенциал. Камю отмечал, что «плохие авторы — это те, кто пишет со ссылкой на внутренний контекст, который читатель не может знать». Таким образом, задача, стоящая перед «хорошими» художниками, состоит в том, чтобы создать что-то познаваемое другим — «перевести» некоторый ограниченный аспект их «глобального опыта» в «произведение, отражающее этот опыт». Слово «знать» подразумевает эмпирическое знание, полученное в результате участия или наблюдения в течение долгого времени, а не просто интеллектуальное понимание — как мы могли бы сказать, мы «знаем» кого-то после многих лет нахождения рядом с ним.Мы можем знать что-то или кого-то, не обязательно когда-либо понимая эту вещь или человека, точно так же, как мы можем познать тайну, никогда не понимая тайны. «Перевод» опыта в литературное произведение искусства, которое может быть «известно» другим, стало критерием для «хороших» авторов, превратив «переводимость» в эстетический принцип. Чтобы достичь этого, Камю далее отмечал, «когда вы пишете, вам нужно быть двумя людьми» — возможно, человеком, который переживает, и автором, который «переводит» этот опыт во что-то познаваемое другим.Такой «перевод» предполагает источник и цель — образного оратора и собеседника — и подчеркивает этический аспект в искусстве, литературе и переводе. В этом свете «переводимость» может рассматриваться как раскрытие себя другому — попытка занять и испытать разделяемое, хотя и спорное, поле значимости. Он измеряет перекрытие между импульсом к общению и коммуникативным потенциалом выражения. Можно сказать, что Камю внедрил эту «переводимость» в свои оригинальные работы до того, как они были переведены на другие языки.Его персонажи и предпосылки были сделаны доступными читателям его изначальной культуры и языка — «переведены» из человеческого опыта в литературу. «Переводимость» — это больше, чем вопрос языка. Речь идет о литературе, которая делает наиболее эфемерные аспекты человеческого опыта доступными — выраженными таким образом, чтобы их мог узнать кто-то другой. Подход к этой более глубокой открытости, хотя и характерен для перевода, является «проблемой искусства» в целом. И хотя литература связывает «я» и «других», ее открытость также связывает их с тайной — той частью нашего опыта, которая недоступна чьему-либо пониманию. Барт, Роланд. 1993 [1955]. «La Peste, annales d’une épidémie ou roman de la solitude». В Oeuvres complete, I . Париж: Сеуил, стр. 452-456. Камю, Альбер. 1963. Записные книжки: 1935 — 1942 гг. . Пер. Филип Тоди. Нью-Йорк: Харкорт Брейс Йованович. ————. 1970 [1955]. «Письмо Роланду Бартсу о Чума ». Избранные очерки и тетради . Эд. и пер. Филип Тоди. Хармондсворт: Книги Пингвина. Ротко, Марк.2006. Произведения об искусстве . Нью-Хейвен: издательство Йельского университета. Селл, Роджер Д. 2011. Коммуникативная критика: исследования литературы как диалога . Амстердам: Беньямин. Рассказы могут доставить столько удовольствия, что их изучение вряд ли кажется работой. Литературоведы часто пытались развеять беспокойство по поводу того, что им платят за удовольствие от художественной литературы, исследуя литературу как форму истории или нравственного воспитания.А с конца 1960-х отделы академической литературы особенно старались выделить критику как критику, как средство социальных преобразований. Действительно, последние несколько десятилетий ученые неохотно относились к литературе как к искусству — к творческому завершению произведения или творческому празднику отклика на него — как будто это означало отдавать предпочтение элитным способностям и потворствовать снисходительности. наклонности. Многие критики стремились держать литературную критику подальше от литературного и вместо этого обвинять литературу как в значительной степени продукт социального угнетения, соучастие в нем или, в лучшем случае, оказание сопротивления уже сдержанному. Литературные ученые также неохотно относятся к науке, за исключением фантазий о том, что они поглотили и обезоружили ее, сведя ее к «просто еще одному повествованию», или отклонили ее со знающей насмешкой как предполагающую смехотворно наивный эпистемологический реализм. Они не только отрицали удовольствие от искусства и силу науки, но, как и другие представители гуманитарных и социальных наук, они также отрицали существование человеческой природы, настаивая на доказательствах того, что культура и условности делают нас бесконечно податливыми. Я и другие хотим, чтобы литература вернулась к искусству литературного искусства и обратилась к науке теперь, когда наука наконец нашла способы исследовать человеческую природу и человеческий разум. Поскольку они являются, соответственно, предметом и объектом литературы, для литературного исследования было бы фатальным продолжать отрезать себя от науки, от силы открытий, возможных через подчинение идей правилу свидетельства. Есть много способов, которыми наука может вернуть нас к литературному искусству и обогатить его.Мы могли бы рассматривать человеческую природу и умы как , понимаемую наукой и как как представлено в литературе, не только как видимое через одобренные призмы расы, пола и класса, но и с точки зрения, например, цикла истории человеческой жизни или социальное познание или сотрудничество против конкуренции. Или мы могли бы разработать многоуровневые объяснения, которые оставляют место для универсалий человеческой натуры, для локального в культуре и истории, для индивидуальности авторов и аудитории, а также для конкретных проблемных ситуаций, с которыми сталкиваются в том или ином ограничении композиции или понимания. . Один из способов использовать науку для подхода к литературе (и искусству в целом) — это рассматривать ее как поведение с точки зрения эволюции. Почему искусство в целом и повествование в частности существуют как межвидовые формы поведения? Такая постановка вопроса делает возможной истинно теоретическую литературную теорию, которая зависит не от цитирования якобы антиавторитарных властей, а от наличия доказательств и отсутствия контрдоказательств, от изучения человеческого поведения во времени и пространстве и в контексте. многих культур и даже многих видов. Гуманитарные науки всегда принимали изречение, которое биолог Д’Арси Томпсон сформулировал с величайшей простотой: «Все есть то, что есть, потому что так оно и есть». То, как это произошло, начинается не с Epic of Gilgamesh , а гораздо раньше: с того, как мы стали создавать искусство и рассказывать истории о животных. Как наши способности к искусству и истории формировались и укоренились в нас с течением времени? Как нам теперь так легко создавать и обрабатывать истории: какие аспекты ума мы задействуем и как? Чтобы рассматривать искусство и историю с точки зрения эволюции, мы должны решить, являются ли они биологической адаптацией: являются ли они особенностями, которые естественный отбор создал в людях с течением времени, потому что они привели к более высоким показателям выживаемости и воспроизводства? В недавно написанной мной книге О происхождении историй: эволюция, познание и художественная литература, я утверждаю, что искусство и повествование — это адаптации.Такое поведение распространяется на весь вид, спонтанно осуществляется всеми нормальными людьми и спонтанно поощряется у младенцев их родителями. Искусство — это форма познавательной игры с узором. Подобно тому, как общение существует у многих видов, даже у бактерий, и человеческий язык происходит от общения животных по многим непредвиденным новым маршрутам, но перенаправляет его, так и игра существует у многих видов, но уникальная когнитивная игра человеческого искусства перенаправляет ее по-новому и по-новому. функции. Play существует даже у самых ярких беспозвоночных, таких как осьминоги, и у всех млекопитающих, у которых он был исследован.Его вознаграждающая природа означает, что животные с гибким поведением — поведением, не запрограммированным генетически — охотно участвуют в нем снова и снова в условиях относительной безопасности и, таким образом, со временем могут овладеть сложными контекстно-зависимыми навыками. Чистое удовольствие от игры побуждает животных повторять интенсивные действия, которые укрепляют и ускоряют нейронные связи. Изобилие игры расширяет границы обычного поведения в необычных и экстремальных движениях, позволяя животным лучше справляться с неожиданностями. Люди занимают уникальную «когнитивную нишу». У нас есть аппетит к информации, и особенно к шаблону, информации, которая попадает в значимые массивы, из которых мы можем делать обширные выводы. У нас уникально долгое детство, и даже после детства мы продолжаем играть больше, чем другие виды. Наше пристрастие к шаблонной когнитивной игре искусства начинается с того, что психологи развития называют протокольным общением, обменом между младенцами и воспитателями ритмичного, отзывчивого поведения, включающего звук и движение, в игровых паттернах, описываемых как «больше похоже на песню, чем на предложение» и как « интерактивные мультимедийные спектакли.«Без обучения дети занимаются музыкой, танцами, дизайном и, особенно, ролевыми играми. Наше взрослое пристрастие к познавательной игре с искусством — от племенных рабочих песен до транзисторов торговцев и iPod городских жителей — позволяет нам расширять и совершенствовать нейронные пути, которые создают и обрабатывают паттерны в звуковом, визуальном и кинетическом режимах, и особенно в социальном плане. . У людей есть не только уникальная склонность к неограниченному шаблону, но также уникальная склонность делиться вниманием (задолго до того, как мы изучаем язык) и по этой причине уникальная способность учиться у других.Наша склонность к совместному вниманию и социальному обучению гарантирует, что мы легко овладеем рудиментами местных художественных традиций. Участие в этих традициях усиливает удовольствие, которое мы получаем от социальной жизни. Помогая снизить издержки в напряжении и повысить социальное вознаграждение, искусство помогает нам сотрудничать в масштабах, намного превосходящих масштабы любого другого высоко индивидуализированного животного. OED определяет образец как «расположение или порядок вещей или действий.. . порядок или форма, различимая в вещах, действиях, идеях, ситуациях и т. д. » Образец обычно сигнализирует о закономерностях в мире, а не о простой случайности: образец, в котором моя голова и мои ноги оказываются недалеко друг от друга, не совпадение, а часть регулярности, которая есть у меня. До недавнего времени компьютеры плохо справлялись с распознаванием образов, но живые организмы давно в этом разбирались. Шаблон превращает данные органов чувств в информацию, которая может определять поведение. Чем больше организм зависит от интеллекта, тем больше он ищет множественных паттернов на множестве уровней.Лягушки реагируют на образ мелких объектов, пролетающих через их поле зрения, высовывая языки. Это делает их более эффективными, чем вы или я, в ловле насекомых, но лягушки не могут реагировать на новые виды паттернов. Люди могут. В дополнение к шаблонам, которые эволюция запрограммировала нас отслеживать, например, по форме или местоположению объектов, мы ищем различные шаблоны. Например, химический состав инсектицидов может сделать нас более эффективными убийцами насекомых, чем даже лягушки. Поскольку мир кишит паттернами, умы животных эволюционировали как экстракторы паттернов, способные обнаруживать информацию, значимую для их вида организма в их типе окружающей среды, и, следовательно, предсказывать и действовать соответственно. Шаблон возникает на нескольких уровнях, от стабильной информации о пространственных условиях и физических процессах до очень изменчивой информации о людях и их настроениях, действиях и намерениях. Распознавание образов позволяет нам отличать одушевленное от неодушевленного, человека от нечеловеческого, этого человека от любого другого, это отношение или выражение от другого.Выявление не только людей, но и паттернов более высокого порядка в их поведении, личности и способностях позволяет делать гораздо более точные социальные прогнозы. Если информация хаотична, в ней отсутствует осмысленный шаблон и ее невозможно понять. С другой стороны, если он полностью структурирован, нам не нужно продолжать обращать внимание, поскольку информация избыточна: действительно, психологический процесс привыкания отключает внимание, если стимул остается, если структуру информации можно предсказать.Самый шаблонный роман из возможных, будет повторять одну букву, скажем q, снова и снова — очередь, в которой ни один читатель не захочет ждать. Но непредсказуемая комбинация шаблонов окупает пристальное внимание и может привести к обширным выводам, хотя найти ее может быть нелегко. как определить, что образует значимый узор и какой смысл подразумевает этот узор. Занимая когнитивную нишу, люди жаждут шаблонов, потому что они могут сказать нам очень многое. Чем больше наш разум может обрабатывать несколько шаблонов на разных уровнях, тем успешнее мы можем прогнозировать и действовать.Поэтому у нас есть то, что физик Эдвард Перселл называет «жадностью к шаблонам». Как отмечает Стивен Джей Гулд: «Человеческому разуму нравится находить закономерности. . . . Никакая другая привычка мыслить не лежит так глубоко в душе маленького существа, пытающегося разобраться в сложном мире, созданном не для него ». Крайний информационный хаос, отсутствие рисунка, как при белой тьме или густом тумане, может даже вызвать расстройство и потерю сенсорной функции. Искусство предлагает противоположность хаосу. Он концентрирует и играет с изобилием мировых паттернов, с его паттернами взаимосвязанных или пересекающихся паттернов.Наше восприятие шаблона и отклонения от него вызывает сильные эмоциональные реакции. Искусство привлекает нас, обращаясь к нашему аппетиту к шаблону на нескольких уровнях, в создании или восприятии телесных движений, форм, поверхностей или звуков, слов или миниатюрных миров. Поэтому, как и игра, искусство побуждает нас продолжать действия, которые оно предлагает, достаточно долго и возобновлять их достаточно часто, чтобы со временем изменить наши нейронные схемы. Наше принуждение к поведению, которое мы называем искусством, в когнитивной игре с высокой плотностью паттернов, позволяет нам в течение многих повторений создавать или, по крайней мере, обрабатывать паттерны в наиболее важных для нас областях восприятия и познания: движение, звук и т. Д. зрение и общительность.И, как и у других видов приматов, способность управлять вниманием коррелирует со статусом, который, в свою очередь, коррелирует с доступом к ресурсам и, следовательно, со скоростью выживания и воспроизводства. Таким образом, те, кто обладает исключительным талантом в каком-либо искусстве, могут получить статус. Как для художников, так и для публики способность искусства привлекать внимание имеет решающее значение: для художника — приобретать статус; для аудитории, чтобы мотивировать участие. Знакомство с единственной историей, рассказанной один раз, существенно не изменит разум, но множество повторений или множество разных историй могут улучшить наши способности к социальному познанию и построению сценариев, столь ценных для нас в нерассказанном мире. Один вывод, который я сделал из этого анализа происхождения искусства и истории, заключается в том, что внимание — вовлеченность в деятельность — важнее значения. Аристотель это понимал. То же самое делают художники, авторы и публика. Даже дети младше трех лет осознают решающую роль в привлечении и удержании внимания слушателей. В этом возрасте их рассказы — это столько же стихов, сколько и повествований, сосредоточенных на ярких персонажах и эффектах, которые нарушают ожидания, но в структуре, напоминающей тему и вариации, более простую схему, а не непрерывность событий, которую взрослые ожидают от рассказов: Обезьяны Мальчик двух с половиной лет, сочиняющий эту «историю», еще не подозревает, что истории включают в себя не только обстановку, персонажей и события, но также цели, задачи и результаты. Он не может развить историю, но, кажется, интуитивно чувствует необходимость удивлять своими необычными персонажами в необычных местах, бросающих вызов принципам гравитации, которые он начал понимать, когда ему было три месяца. Повторение — это простейшая форма разработки, но, поскольку чистое повторение малоинтересно, повторение смелой идеи с вариациями дает ему наилучшие перспективы удержать внимание слушателей с помощью имеющихся у него творческих ресурсов. Эту историю придумал четырехлетний мальчик: Когда-то был дракон, который какал на дом, и дом сломался Этот и другие рассказы маленьких детей не являются бессюжетными, а являются незапланированными и эпизодическими, серией оппортунистических риффов, каждый из которых нацелен на привлечение внимания: от дракона как обычного монстра, нарушающего категории, до нарушающего правила приличия «poo poo» на вселенной дом и так далее. Тем не менее, если мы обычно занимаемся искусством просто потому, что оно может управлять нашим вниманием, смыслов, в академическом контексте, выталкивает его на первый план, потому что пропозициональная природа смысла делает его намного проще излагать, распространять, извергать или извергать. вызов, чем жидкая динамика внимания. Давайте обратимся к примеру, Владимиру Набокову Лолита (1955), и рассмотрим его с точки зрения познавательной игры с образцом и его средствами для удержания и освежения внимания. Рассказы привлекают внимание благодаря тематике. Хотя покупка дома стала в современной жизни серьезным занятием, у нас нет жанра романов о недвижимости. Но у нас есть истории о романтической любви. Эволюционист может отметить значение воспроизводства и выживания в передаче генов и эволюции видов.Это может объяснить, почему на протяжении бесчисленных поколений наши эмоции были созданы так, чтобы так интенсивно реагировать на любовь и смерть, и почему любовные истории так часто фокусируются на поиске любви или что триллеры, тайны и приключенческие рассказы сосредоточены на том, чтобы избежать смерти. Именно потому, что кто станет нашим партнером, кого так важно для нас, истории любви всегда наводняли бассейн историй. Следовательно, любой новый роман может быть проигнорирован из-за привыкания, угасания интереса к повторяющимся стимулам. Но страстная сексуальная любовь зрелого мужчины к девушке — это не слишком знакомая история любви.Как роман о необычной любви и необычном убийстве, Лолита обращается к незапамятным интересам, но с неожиданных сторон. Когда он был впервые опубликован, он удивил и шокировал публику, и так остается до сих пор. Было продано более 50 миллионов копий, это, безусловно, самый требовательный роман, который когда-либо продавался так хорошо. Давайте углубимся в детали истории Гумбера Гумберта, чтобы увидеть, подтверждают ли они идею искусства как когнитивной игры с узором, и чтобы увидеть, как Набоков устраняет привыкание и оживляет внимание.Гумберт начинается: 1 Лолита, свет моей жизни, огонь моих чресл. Мой грех, моя душа. Ло-ли-та: кончик языка совершает три шага вниз по небу, чтобы постучать в три ступени по зубам. Ло. Ли. Та. Она была Ло, обычная Ло, утром, стояла четыре фута десять в одном носке. Она была Лолой в брюках. В школе она была Долли. Она была Долорес на пунктирной линии. Но в моих руках она всегда была Лолита. Был ли у нее предшественник? Да, действительно, так и было.На самом деле, Лолиты могло бы и не быть, если бы я однажды летом не полюбил одну из первых девочек. В княжестве у моря. О, когда? Примерно столько же лет до рождения Лолиты, сколько мне было в то лето. Вы всегда можете рассчитывать на убийцу из-за причудливой прозы. Дамы и господа члены жюри, экспонат номер один — это то, чему завидовали серафимы, дезинформированные, простые серафимы с благородными крыльями. Посмотри на этот клубок шипов. 2 Я родился в 1910 году в Париже.Мой отец был мягким, легкомысленным человеком, смесью расовых генов: гражданин Швейцарии, смешанного французского и австрийского происхождения, с примесью Дуная в крови. Я собираюсь передать через минуту несколько красивых глянцево-синих открыток с картинками. Он владел роскошным отелем на Ривьере. Его отец и два деда продавали вино, драгоценности и шелк соответственно. В тридцать лет он женился на англичанке, дочери Джерома Данна, альпиниста и внучки двух дорсетских пасторов, знатоков малоизвестных предметов — палеопедологии и эоловых арф соответственно.Моя очень фотогеничная мать погибла в ужасной аварии (пикник, молния), когда мне было три года, и, если не считать очага тепла в самом темном прошлом, ничто из ее не существует в пустотах и лощинах памяти, над которыми, если можно, я все еще придерживаюсь своего стиля (я пишу под наблюдением), солнце моего детства уже зашло: конечно, вы все знаете эти благоухающие остатки дня, подвешенные, с мошками, вокруг какой-то изгороди в цвету или внезапно вошедшей и пройденной бродягой, у подножия холма, в летних сумерках; пушистое тепло, золотые мошки. Ни один другой роман, который я могу припомнить, не начинается с более узорчатой прозы, чем Лолита. И его первоначальные паттерны сами по себе образуют части других паттернов, таких как самопроекция Гумберта как художника, поэта, обожающего любовника или его эстетизирующая Лолита. Но узор и дразнящие намеки на узор насыщают текст. Мать Гумберта — «внучка двух пасторов из Дорсета, знатоков малоизвестных предметов — палеопедологии и эоловых арф». Это само по себе может быть совпадением или, возможно, значимой закономерностью; каковы шансы того, что эти два предмета содержат соседние буквы a, l, e, o? Это случайность или дизайн, а если дизайн, то почему? Набокова называли величайшим стилистом английской прозы, и я думаю, не из-за шаблонной прозы Гумберта, а за его мастерство в психологии внимания, его способность так быстро менять наше воображение.Имя Лолиты является первым и последним словом текста Гумберта; его внимание одержимо сосредоточено на ней, и он не может представить ее имя, не лаская каждый слог губами и языком. Но даже когда он задерживается на ней во втором абзаце, внезапные образы Ло с разными именами и в разных обстоятельствах всплывают перед нашим мысленным взором: «Вот, обычная Ло, утром, стоя четыре фута десять в одном носке. . . . Лола в брюках. . . . Долорес на пунктирной линии. Набоков умеет привлекать наше внимание и зажигать воображение неожиданными деталями и поворотами. Или обратите внимание на саккадический скачок внимания, без сенсорных деталей, но с неожиданным откровением: «Вы всегда можете рассчитывать на убийцу из-за причудливой прозы». Или снова переход от краткого содержания к фразе «Я собираюсь передать через минуту несколько прекрасных глянцево-голубых открыток с картинками». Все сидят здесь, потому что Гумберт внезапно как бы ломает рамку, и из-за внезапной конкретности: простая идея передать эти отполированные открытки активирует моторные, тактильные и визуальные области мозга — как только недавно установили нейробиологи. Средняя длина кадра в голливудских фильмах сокращается, поскольку зрители научились быстрее усваивать фильм и справляться с информационным потоком современного мира. Набоков оказал влияние на писателей, от известных старичков (Итало Кальвино, У. Г. Себальд, Салман Рушди, Мартин Эмис, Орхан Памук) до энергичных молодых людей (Зэди Смит, Мариша Пессл), привнеся в художественную литературу что-то вроде сокращения длины кадра в современном фильме, его стремительности изменение предмета или перспективы. Я подозреваю, что рассказывание историй в целом ускорило нашу способность переключать внимание с одной точки зрения на другую.Гомер обычно медленно перемещается от предмета к предмету по сравнению с современным повествованием, не говоря уже о Набокове, но даже Гомер может быстро переключить уровень и сосредоточиться, когда он внезапно оказывается на заднем плане воина, умирающего на поле битвы. Интенсивные звуковые паттерны в первых словах Гумберта могут быть необычными в художественной литературе, но высокая плотность значимых множественных паттернов встречается повсюду в рассказах, даже без набоковской аллитерационной игры. Характер — это один из видов паттернов, который особенно важен для социальных животных: идентификация индивидуумов и распознавание устойчивых различий личностей (даже такие простые животные, как гуппи, различают личности других представителей своего вида и соответственно взаимодействуют с ними).Ключ к разгадке персонажей в художественной литературе быстро приходит. Эта комбинация навязчивой сосредоточенности Гумберта на Лолите и его способности так быстро переключать внимание в первых абзацах романа пробуждает наш интерес к его живому, в высшей степени застенчивому разуму — даже если мы вскоре обнаружим, что нам становится не по себе, о том, что этот разум намеревается. События могут быть уникальными и беспрецедентными в тривиальных деталях, но мы понимаем их, потому что они достаточно похожи по шаблону на другие ситуации, которые мы переживаем прямо или косвенно: мы узнаем романтическую любовь, например, так же ясно в первых строках Гумберта, как мы слышим шаблон. его слов. В художественной литературе мы часто находим сочетание паттернов событий: любовь Гумберта к возлюбленной своего детства Аннабель Ли, «некой первой девочке». В княжестве у моря », например, прообраз (и, как он хочет предположить, объясняет и усиливает романтизм и помогает извинить) его любовь к девочке Лолите. У Набокова и многих других авторов отношения жизни и искусства образуют другую модель: здесь отношения между девушкой, которую Гумберт называет «Аннабель Ли», и стихотворением По «Аннабель Ли», чье «царство у моря» он также эхо.Такой образ жизни персонажей, перекликающийся с искусством, пронизывает роман как жанр от Дон Кихот до Нортангерского аббатства и Мадам Бовари , а также в модернизм, постмодернизм и не только. Ожидания возможны, потому что мир, его объекты и события образуют закономерности. Но мы узнаем больше из удивительного, чем из ожидаемого, поскольку удивление сигнализирует о чем-то новом, заслуживающем внимания. Истории распадаются на шаблоны шаблонов, с которыми рассказчики могут играть, чтобы пробудить, удовлетворить, победить или удивить ожидания — и неудивительно, что ожидание и неожиданность так сильно стимулируют наш интерес к истории.Когда Гумберт раскрывает, что он убийца, в нашем сознании мгновенно возникают определенные закономерности событий, и, как мы понимаем, читая дальше, наш рассказчик желает поиграть с ожиданиями повествования. Обычный детективный паттерн загадки убийства уступает место паттерну шокированного убийства, когда Гумберт выставляет одну возможную жертву за другой перед нами, а затем узнает имя человека, которого он хочет убить, но отказывается сообщить нам, хотя он бесполезно отмечает до сих пор он разбрасывал ключи к разгадке личности жертвы на протяжении всей истории. Самые сильные модели в художественной литературе связаны с сюжетом: с целями, препятствиями и результатами, с ожиданиями и неожиданностями. Цель Гумберта — заполучить Лолиту — сильно формирует ожидания и иронию всей первой части романа; его цель излить свою убийственную ненависть на соперника, который забрал у него Лолиту, во многом составляет часть 2. Эти глубоко человеческие, хотя в случае Гумберта извращенные, модели целей формируют повествовательный импульс романа. Но Набоков выстраивает другие модели, такие как отношения Лолиты к незнакомцу, преследующему Гумберта и Лолиту на западе: при первом чтении мы задаемся вопросом вместе с Гумбертом, сигнализируют ли эти знаки о сопернике, о детективе, идущем по его следу, или о параноидальной проекции его страхов. или вина.Квилти, незнакомец, сам вплетает различные неуловимые узоры в бухгалтерские книги отелей и мотелей с явной целью дразнить и насмехаться над Гумбертом и нами. И Гумберт, рассказывая свою историю, затем вплетает в свою рукопись шаблоны, указывающие на присутствие Квилти, чтобы дразнить и насмехаться над нами, так что мы не можем сразу идентифицировать шаблоны, которые он теперь может видеть, понимать и контролировать. В своей книге О происхождении историй я отмечаю два примера «ранней» истории: один из первых в истории человечества, Гомеровская Одиссея ; другой ранний в индивидуальном развитии, Dr.Сьюз Horton Hears A Who! Я не подчеркиваю закономерность в этих двух рассказах, но начало обеих книг кишит формой. Odyssey открывается метрическим рисунком дактильного гекзаметра, структурным рисунком обращения к музе и пьесе, акцентом на одном герое среди более крупных событий и словесным рисунком поли — прилагательными, окружающими Одиссея, даже дважды в первой строке. В первых четырех строках Horton Hears a Who! мы находим игру словесных паттернов, по крайней мере, столь же интенсивной — аллитерация, анафора, анапестический тетраметр, антитезис, ассонанс, созвучие, конечная рифма, внутренняя рифма — обычно в нескольких дозах и дополняемых визуальными и повествовательными моделями. Художники, от Гомера, Данте или Шекспира до Диккенса, Джойса, Набокова, Беккета и доктора Сьюза, создают шаблоны на многих уровнях. Другие создают меньшее количество паттернов, но уделяют особое внимание тем, которые имеют для нас наибольшее значение с точки зрения человека, характера и события, а также их собственных конкретных пристрастий: например, в случае Остин обобщения относительно человеческого поведения и характера, у Толстого — паттерны. остро наблюдаемого физического и физиологического мира. Как «Обезьяны / Они взошли в небо», или как писающие драконы, или Гомер, или доктор.Сьюз показывают по-разному, узор насыщает рассказ с самого начала. Но Lolita , сложный поздний пример истории, не только увеличивает количество шаблонов, но и проблематизирует их. Он выступает за образец, но иногда провоцирует его, внушая серьезные последствия, но, тем не менее, скрывает его. Название отеля, The Enchanted Hunters, намекает на Lolita в первом чтении, особенно потому, что целью Гумберта является завладеть Лолитой из-за экфрастической фрески в отеле, которую очарованные охотники Гумберт переосмысливает в терминах оргиастического накала. и потому, что Гумберт, хотя и является охотником, чувствует себя очарованным, когда Лолита обращается к нему и предлагает им заняться любовью.Полтора года спустя Лолита собирается сыграть главную роль в школьной пьесе под названием Зачарованные Охотники , когда она предлагает Гумберту покинуть Бердсли и вместе отправиться на запад. В Эльфинстоне, жемчужине западного штата, как мы позже узнаем, у нее свидание с Квилти, автором пьесы, который также останавливался в «Зачарованных охотниках» в ту ночь, когда Гумберт пытался овладеть Лолитой во сне, а — . владеть ею, когда она проснулась. Образец кажется наполненным значимостью, но он остается неуловимым, в отличие от явных последствий, скажем, мотивов в Ulysses , таких как аутсайдер Throwaway, лошадь, выигравшая Золотой кубок Аскота в День Цветения и связанная с Блум, и свергнутый фаворит, Скипетр, связанный с, казалось бы, любимым соперником Блум, Блейзом Бойланом. Один из аспектов паттерна Зачарованных Охотников, который я заметил много лет назад, заключался в серии скрытых связей между попыткой изнасилования Лолиты в отеле и убийством Квилти в его поместье, где, преследуя свою добычу, Гумберт называет себя » заколдованный и очень крутой охотник ». Несмотря на это арочное эхо, Гумберт не понимает, что судьба (или Набоков) построила целую систему параллелей между эпизодом «Зачарованные охотники» и эпизодом убийства. В своей биографии Набокова я спрашиваю: что мы должны делать с этой резкой парой якобы не связанных между собой сцен? И я отвечаю: Гумберт тщательно помещает после убийства ту преследующую и знаменитую сцену на горной тропе над долиной, наполненную звуками играющих школьников: «Я стоял, слушая эту музыкальную вибрацию со своего высокого склона, к этим вспышкам отдельных плачет с каким-то скромным бормотанием для фона, и тогда я понял, что безнадежно мучительно было не отсутствие Лолиты с моей стороны, а отсутствие ее голоса в этом согласии.В положении, которое поставил ему Гумберт, это становится последней отчетливой сценой романа. Даже такой хороший читатель, как Альфред Аппель-младший, может рассматривать этот момент прозрения для Гумберта как его «моральный апофеоз», окончательную ясность морального видения, которая почти искупает его. Гумберт действительно испытывает здесь глубокое и искреннее сожаление, хотя и слишком поздно, но это лишь часть сложного целого. Он помещает это изображение себя в отличие от Куилти, которого он только что убил, хотя само видение произошло не тогда, а тремя годами ранее, когда Куилти забрал у него Лолиту.Какая разница во времени? В течение двух лет Гумберт ясно осознавал, что держит Лолиту в плену и разрушает ее детство и ее дух, но он продолжал держать ее в своей власти. Пока он мог извлекать из нее сексуальное наслаждение, он мог оставаться глухим к своему моральному чутью. Только после ее исчезновения, когда она перестала быть доступной трижды в день для его похоти, он позволил моральному сознанию сокрушить его, когда он заглянул в эту долину. Но это было очень выборочное понимание.Гумберт помещает эту сцену в конец романа, чтобы оставить заключительное впечатление, что он может бескорыстно заботиться о Лолите, и его риторическая стратегия убеждает многих читателей. Набоков оценивает вещи по-разному, и хотя он дает Гумберту полный контроль над своим пером, он находит способ выразить свое собственное суждение внутри и против того, что пишет Гумберт. Посредством скрытых параллелей, которые он проводит между кульминационными моментами двух частей романа, он указывает, что обе сцены отражают одно и то же романтическое ощущение властного диктата желания, одно и то же стремление к самоудовлетворению даже за счет другой жизни. Связи между сценами «Зачарованных охотников» и «Поместье Павор», где происходит убийство, незаметны, пока не замечены, но неизменно точны и заострены, как только заметят. Согласны ли другие с моей интерпретацией того, почему Набоков написал именно этот скрытый узор, — это другой вопрос. Но паттерн Зачарованные Охотники показывает, как Набоков может продолжать усиливать эффекты паттернов характера и событий, которые мы регистрируем сразу, путем внедрения дополнительных дополнительных паттернов, которые мы можем обнаружить только при внимательном перечитывании. Еще одна похожая закономерность, которую я заметил совсем недавно. Ирония, пронизывающая роман, пронизывает раннюю сцену у озера Песочные часы, где Гумберт купается со своей новой женой Шарлоттой, матерью Лолиты, думает о том, чтобы утопить ее в идеальном уединении, но отказывается от этого. Позже, загорая с Шарлоттой, он удивляется, когда из кустов появляется ее подруга Джин Фарлоу. Краткий отрывок ниже, хотя и забавный сам по себе, кажется, в первую очередь подготовкой к другим ирониям: Шарлотта, которая немного завидовала Джин, хотела знать, придет ли Джон. Был. Сегодня он шел домой на обед. Он подбросил ее по дороге в Паркингтон и должен забрать ее в любое время. Это было грандиозное утро. Она всегда чувствовала себя предательницей Кавалла и Мелампуса за то, что оставила их скованными в такие великолепные дни. Она села на белый песок между мной и Шарлоттой. На ней были шорты. Ее длинные коричневые ноги казались мне столь же привлекательными, как у каштановой кобылы. Обратите внимание на случайно заглянувшие сюда клички собак Джин Фарлоу, которые раньше назывались «двумя боксерскими собаками», но никогда больше не упоминались после строк выше.Кавалл был не только любимой собакой короля Артура, но и первой из его собак, превратившей оленя в эпизод охоты в The Mabinogion . Меламп — это имя первой собаки Актеона в рассказе Овидия о Диане и Актеоне в его Метаморфозах . Поражает точность этих намеков: две собаки из разных литературных традиций первыми преследуют или обращают оленя. Помните, Актеон — охотник, который шпионит за Дианой, девственной богиней охоты, обнаженной.В ярости Диана превращает его в оленя, и его собаки преследуют его во главе с Мелампом и разрывают на куски. Он все еще чувствует себя человеком, но он может выражать себя только как олень, поэтому его собственные собаки и его товарищи-охотники не могут ответить на его задушенный голос, умоляющий их перестать раздирать его на части. Это возвращает нас к мотиву Зачарованных Охотников и идее об охотнике, на которого идет охота, а также о сексе и целомудрии, связанных с охотой и преследованием. Гумберт, преследующий Лолиту, оказывается, за ним охотится Шарлотта и «схвачена» в браке.Желая покончить с жизнью Шарлотты, но не осмеливаясь сделать это, он обнаруживает, что она внезапно убита после того, как собака преследует машину, которая сворачивает и убивает ее, как будто его смертоносные планы увенчались волшебным успехом. Приближаясь к Лолите в «Очарованных охотниках», Гумберт обнаруживает, что она «преследует» его, когда она предлагает им попробовать то, что она обнаружила в лагере. Но Квилти, уже находящийся в отеле, видит Гумберта и узнает его планы на Лолиту. Это признание вдохновило его на написание пьесы Зачарованные охотники , вращающейся вокруг персонажа по имени Диана, роль которой возьмет на себя Лолита.Сама пьеса оказывается зачарованным приемом для того, чтобы Квилти выследил Лолиту, а затем выследил и преследовал Гумберта, который теперь в большей степени подвергается охоте, чем охотнику, по всей Америке. Сразу после того, как Гумберт прекращает охоту на «похитителя» Лолиты, он проходит через Брайсленд (повторяя Броселианд, дом Мерлина Чародея) и отель Enchanted Hunters, прежде чем написать стихотворение о Диане и Очарованных Охотниках. Когда он слышит от Лолиты о ее браке с молодым американцем, Гумберт возобновляет охоту, но обнаруживает, что преследует не ту добычу; и когда, наконец, Лолита дает ему нужный запах, он сразу же направляется убить человека, который охотился на него и преследовал его. Набоков был ученым и провел большую часть десятилетия, прежде чем написать Lolita , отвечая за бабочек и мотыльков в Гарвардском музее сравнительной зоологии. Он был очарован закономерностями в природе, такими как узоры крыльев бабочек, узоры соответствия узоров в естественной мимикрии и сложные образцы взаимоотношений, которые ученый должен распутать, чтобы определить таксономическое родство внутри рода или семейства бабочек. Как писатель, он также был проницательным психологом, интуитивно понимающим, как разум обрабатывает закономерности.Он понял, что обилие закономерностей в природе может затмевать или отвлекать нас от других значимых закономерностей. Помимо песочных часов, характерные черты ревности Шарлотты (к Лолите, Джин) и пренебрежительного отношения Гумбера к взрослым женщинам, а также кривые словесные образцы свободной косвенной речи, здесь по иронии судьбы максимизирующие ментальную дистанцию между Гумбером и Жаном, — все это кажется гораздо большим виднее, чем случайные Кавалл и Меламп. Даже если мы выследим Кавалла и Мелампуса и свяжем их с Зачарованными Охотниками, а через Кавалла как собаку короля Артура связь с образцом Артура, который Набоков, кажется, с самого начала прикрепил к теме Лолита , я не удовлетворен с тем, что мы можем интерпретировать либо по образцу Зачарованных Охотников, либо по образцу Артура (и Мерлине).Паттерны Набокова имеют важные последствия, если мы проследим их достаточно далеко, а в случае с Lolita я не думаю, что я или кто-либо еще дошел до этой точки. Что предлагают эти примеры из Лолиты ? Писатель может привлечь наше внимание прежде, а в некоторых случаях задолго до того, как мы достигнем того, что академические критики сочли бы «смыслом» или «смыслом» произведений. Высокая плотность множественных паттернов удерживает наше внимание и вызывает нашу реакцию — особенно через паттерны биологической важности, такие как окружающие персонажа и события, которые вызывают внимание и эмоции и подпитывают мощные, специализированные, развитые подпрограммы обработки информации в уме. Образцы в художественной литературе, как и в жизни, могут распространяться и затенять другие образцы. Они могут привести к богатым, но иногда далеко не очевидным последствиям. Они могут быть открытыми: они и их последствия часто не появляются заранее и не усваиваются заранее. Иногда они попадают в эффективные, развитые системы обнаружения закономерностей, но часто их приходится обнаруживать благодаря вниманию и любопытству, а иногда и способами, которых полностью не ожидают ни аудитория, ни авторы. На более общем уровне люди являются необычными детекторами открытых закономерностей, потому что мы так навязчиво заселяем когнитивную нишу.Искусство играет с когнитивными моделями с высокой интенсивностью. Удовольствие, которое это вызывает, является неотъемлемой частью того, что значит быть человеком, и имеет значение как на индивидуальном уровне, для публики и художников, так и на социальном уровне, для наших общих паттернов (в дизайне, музыке, танцах и рассказах). . Интенсивная игра искусства удовольствия с узорами заставляет нас снова и снова вовлекаться и помогает формировать нашу способность создавать и обрабатывать узоры более быстро. Возможно, это даже помогает объяснить так называемый эффект Флинна, тот факт — и, кажется, таковой, — что IQ рос с каждым из последних нескольких поколений: возможно, как следствие современной бомбардировки высокоплотных паттернов искусства. через телевидение, DVD, музыку и iPod, компьютерные игры, YouTube и тому подобное. И с их высокой интенсивностью узоров и их фиксированной формой произведения искусства должны обеспечивать идеальные контролируемые воспроизводимые эксперименты для изучения как быстрого, так и постепенного распознавания образов в сознании. Литературоведение не должно стесняться литературного искусства или удовольствия, которое мы получаем от него. Литература и другие искусства помогли нам расширить наши владения информационными моделями, и эта уникальная команда делает нас теми, кто мы есть. Разрешение, необходимое для перепечатки, воспроизведения или другого использования. Мы только что закончили пересмотр учебной программы в нашем округе, в которой мы тщательно и вдумчиво согласовали то, что мы учили, со стандартами.Мы начали со стандартов, а оттуда пошли в обратном направлении — какую оценку мы можем разработать, чтобы протестировать этот стандарт? Два стандарта, которые доставили нам немного хлопот, — это RL.9-10.7 и RL.11-12.7, оба из которых требуют анализа репрезентаций литературы в различных художественных медиа и оценки того, как это представление относится к Исходный материал . Было очень заманчиво сказать: «Мы уже это делаем! Мы читаем Ромео и Джульетта , а затем смотрим версию фильма.Ищем отличия, может быть, сделаем диаграмму Венна. У нас это есть ». Однако этот метод обучения не выполняет свою работу по двум причинам: Давайте начнем с рассмотрения примера, который стандарты Common Core предоставляют с историей Icarus. В этом сценарии мы читаем миф и смотрим на «Пейзаж с падением Икара» Брейгеля (картина) и «Музей изящных искусств» Одена (стихотворение об этой картине) Существует множество планов уроков для этой конкретной группы. На самом деле, у меня есть урок об Икаурах, который включает в себя не только эту картину и стихотворение.Но большинство из нас не хочет рассказывать историю Икара где-нибудь в течение года, чтобы соответствовать этому стандарту. Мы хотим добавить это к тому, что мы уже делаем. К счастью, если вы преподаете Шекспира (а есть хорошие шансы, если вы преподаете в старшей школе, как вы это делаете), есть много возможностей увидеть, что другие художники сделали с исходным материалом, помимо создания фильма. В качестве примера рассмотрим несколько вариантов пьесы, которую я преподаю: Шекспира Отелло .Когда мы закончим читать, мне нравится, когда студенты изучают картины финальной сцены пьесы, где Отелло противостоит Дездемоне в ее покоях и (внимание, спойлер!) Душит ее за предполагаемую измену. Во-первых, это «Дездемона и Отелло» Антонио Муньоса Дегрейна: А вот и «Смерть Дездемоны» Эжена Фердинанда Виктора Делакруа. Есть много других, которые вы можете найти с помощью поиска по изображениям. Когда я использую изображение, я проецирую его перед классом и даю учащимся черно-белую копию для аннотации.Когда они смотрят изображение, они могут при желании приблизиться к экрану для более детального рассмотрения (конечно, вы также можете сделать это на устройствах, если у вас соотношение 1: 1). Каждый раз, когда мы смотрим на изображение, я хочу, чтобы мои ученики ответили на несколько основных вопросов, основанных на методе художественной критики Эдмунда Фельдмана. 1. Опишите, что вы видите на картине. Избегайте оценочных суждений, таких как «красивый» или «забавный вид». 2. Проанализируйте, как художник использует элементы дизайна, такие как освещение, цвет, формы и текстуры. 3. Объясните, что художник говорит о сцене. Есть ли какое-то особое настроение, которое они пытаются передать? 4. Обсудите общие сильные стороны или достоинства работы. Считаете ли вы, что картина является точным и эффективным изображением сцены? И я хотел бы добавить еще один: 5. Почему именно этот момент? Почему не за пять минут (или секунд) до или после этого момента? Вы можете смоделировать одно изображение со всем классом, а затем заставить их работать индивидуально над вторым.Образ Дегрена довольно прост, но образ Делакруа требует большей интерпретации. Например, кто эти два человека собрались вокруг кровати? Как Делакруа передает эмоции сцены без мимики? Показывая и то, и другое, мы учим студентов работать как с реалистической интерпретацией, так и с импрессионистическим чтением. Я беру серию изображений из различных частей пьесы — и живопись, и книжные иллюстрации, может быть, некоторые скульптуры, если я найду их изображения — и помещаю их на серию слайдов.Я проецирую слайды перед классом с пятиминутными интервалами. По каждому слайду они должны ответить на следующие вопросы: Студенты не только демонстрируют свою способность анализировать изображение, но они также используют доказательства, находят поддержку в тексте и используют все виды навыков письма, если вы решите оценить и это. Но рисовать необязательно. Многие пьесы Шекспира были превращены в балеты, а на YouTube есть видеоклипы спектаклей. Вот пример из Гамбурга: [youtube https://www.youtube.com/watch?v=Jpwz6FLFqBw&w=560&h=315] Я не знаю, какую часть пьесы это представляет (частично потому, что я не читаю по-немецки). Но это часть задачи для студентов: какая часть? Как узнать по музыке и движению? Я предполагаю, что это начало пьесы и доказывает, что Дездемона и Отелло действительно влюблены, что важно для работы остальной части пьесы.Но у меня нет возможности быть уверенным — это обоснованное предположение, основанное на чтении текста. «Отелло» также ставил оперу Джузеппе Верди. В то время как большинство моих студентов имеют некоторые познания в балете, большинство из них никогда не слушали оперу, по крайней мере, внимательно. Вы, конечно, можете посмотреть часть спектакля (опять же, их несколько на YouTube), но мне нравится выполнять действие с переведенной частью либретто (текстом оперы), пока мы ее слушаем. Иногда он сильно отличается от исходного текста и вводит новые темы.Если вам нужно либретто для «Отелло», нажмите здесь, и я пришлю его вам. Как превратить это в оценку? Так же и с картинами. Предложите видеоклипы танцев или другие части либретто и попросите их проанализировать их таким же образом. Если вы ищете другие интересные способы преподавать Шекспира, нажмите здесь. Это можно сделать практически с любой пьесой Шекспира. Например, для «Сон в летнюю ночь», есть много отличных картин.И многие пьесы превратились в оперу или танец, которые легко доступны в Интернете. В поэзии можно найти современные интерпретации пьес, хотя, чтобы их найти, нужно немного покопаться. Вот отличное стихотворение Максин Кумин «Чистилище», в котором рассказывается о том, что могло бы случиться, если бы Ромео и Джульетта успешно сбежали вместе. Конечно, если вы хотите заниматься «Греческими мифами», но, возможно, Икар не для вас, существует множество мифов, отраженных в произведениях искусства, особенно в живописи и скульптуре.И есть масса стихов, переосмысливающих греческие мифы, например, «Молитва Деметры Аиду» Риты Дав. Что интересно в стихотворении Дава (и во многих других стихах, основанных на мифах), так это то, что если вы не знаете миф, вы читаете его в одном направлении, и как только вы узнаете миф, смысл полностью меняется. И если вы ищете хороший способ добавить его к тому, что вы уже делаете, почему бы не связать его с уроком по аллюзиям? Найдите намек на греческий миф в том, что вы читаете, и вперед. Конечно, есть веские причины для показа киноверсии литературного произведения. Детям это нравится, и, честно говоря, вы можете увязнуть в выставлении оценок. Но мы не хотим упускать возможность научить студентов критически относиться к тому, что они видят. Это важно, потому что наших студентов каждый день засыпают изображениями. Нам нужно научить их критически относиться к этим изображениям. Что я вижу? Почему я это вижу? Если я вынужден что-то сделать (например, купить пару обуви), как изображение убедило меня сделать это? И какова конечная цель создателя этого изображения? Просмотр этих произведений искусства помогает учащимся развить эти навыки. Учиться должно быть весело! Загляните в мой магазин Teachers Pay Teachers, чтобы найти интересные ресурсы, подобные тем, которые вы видите ниже. Для Simone Weil то, что мы должны друг другу, выражается не в соображениях обстоятельств, а в универсальности боли … подробнее » Семьдесят шесть заново открытых страниц — Святой Грааль прустианства — выявить двойственное отношение автора к своему еврейству… подробнее » Открыта ли вселенная? Физик раскрывает тезис Скотта Ааронсона о том, что случайная непредсказуемость — это не то же самое, что свобода воли … подробнее » Одним из аргументов в пользу преподавания гуманитарных наук является то, что они помогают студентам справляться с неопределенностью в жизни. Но это не выдерживает … подробнее » Покойная Лорен Берлант:« Отношение жестокого оптимизма существует, когда то, чего вы желаете, на самом деле препятствует вашему процветанию »… больше » « Информационный бюллетень — это идеальная форма на тот момент, когда писатели чувствуют необходимость производить для себя постоянный поток рекламы »… подробнее» Лорд Монбоддо был известен своими физическими упражнениями обнаженными и теоретизирующими, что орангутанги на самом деле были людьми, слишком ленивыми, чтобы научиться говорить … подробнее » Когда Медичи вернули себе контроль над Флоренцией в 1512 году, у художников было два выбора: бежать — как это сделал Микеланджело — или льстить… подробнее » Уоллес Стивенс на прогулке, Гарольд Блум в почтовом отделении — вид из отдела английского языка Йельского университета … подробнее» Гендерные теории Маргарет Мид превратились из радикальных в реакционные. Неужели в этом виноват простой вздор средних лет? … подробнее » Могут ли романисты увидеть будущее ? Немецкие военные решили проверить это предположение … подробнее » Люди ходили в библиотеки, чтобы прогуляться по стекам.Сейчас они сидят и прокручивают . Что потеряно, так это интуитивная прозорливость … подробнее » Печально известное исследование « Евангелие от жены Иисуса » было омрачено мошенничеством и конфликтом интересов — и все же опровержения не последовало. Почему нет? … подробнее » В издательском деле бушует конфликт поколений между людьми моложе 40 и старше 40 лет. На кону: отношения между искусством и художником … подробнее » В жизни любой большой идеи она со временем становится отвязанной от ее истоков. Критическая теория расы переживает такой момент … подробнее » Скупой, тщеславный, завистливый, ленивый: ранее неизвестный мемуар рисует явно нелестный портрет Джона Локка … подробнее» In the Запад, мы ограничиваем мечты сферами суеверий и метафизики. Но в других обществах делиться мечтами — серьезный бизнес … подробнее » Среди паршивых вариантов работы для венецианцев: разнос пиццы, продажа поддельных местных« артефактов »и работа на Венецианской биеннале … подробнее » Звездочка восходит, по крайней мере, к Аристарху Самофракийскому, который редактировал Гомера. Его использовали для обозначения осторожности — обозначения плагиата, упущений и пошлости … подробнее » В последние годы жизни Джон Ле Карре утратил то, что было сильной стороной: сдержанность и преуменьшение. Политика начала вторгаться … подробнее » Слово рекламное объявление было придумано в 1907 году, но маркетинговая затяжка так же стара, как и сами романы.В настоящее время это грязная экономика взаимного почесывания спины … подробнее » Джанет Малкольм , чей литературный репортаж продемонстрировал беспощадный и точный взгляд на мир, мертва. Ей было 86 … NYTimes … WaPo … The New Yorker … Guardian … New Republic … Ян Фрейзер … Лора Марш … Лео Робсон … Дженнифер Салаи … Дэвид Грэм … подробнее » История ранних европейских встреч с африканскими письменами — это история пренебрежения, ложных предположений и полного разрушения… подробнее » 1619, 1776 — Америка, помешанная на истоках историзма , сейчас доминирует в либеральных кругах. Но происхождение — не наша судьба … подробнее » Кураторы, ученые, правительства, правление, спонсоры: эта капля культурного господства, Дэйв Хики здесь, чтобы напоминать нам, отвлекает наше внимание от красоты … больше» Эдвард де Боно , поборник «нестандартного мышления» и множества неправдоподобных схем творческого мышления, умер.Ему было 88 … подробнее » Луиза Буржуа проходила психоанализ с 1951 по 1985 год. Это сформировало ее искусство, но не облегчило ее страдания … подробнее» «Вы когда-нибудь делали психоанализ. решение, которое закончилось тем, что разрушило чью-то жизнь ? » У декана колледжа есть сомнения … подробнее » Неро: Не так уж и плохо. Ужасные и извращенные преступления римского императора, скорее всего, были придуманы яростными историками.. подробнее » Ева Бабиц , пытаясь заставить Двери изменить свое название:« Двери восприятия … что за нехорошая идея оджай-выродка-слишком-Лос-Анджелеса »… больше » Баланс армии США с позитивной психологией был карнавалом неквалифицированной интуиции и преувеличенного рассказывания историй — неправильное использование науки в учебниках … подробнее» У уроков анатомии 18-го века была одна большая проблема: вонь. Введите Marie-Marguerite Biheron и ее идеально точные восковые модели… подробнее » О чем говорят научные статьи? Надежные открытия или беспорядочные, навеянные догадками ? … подробнее » Цицерон , первый интеллектуал, преуспевший в политике, был больше ритором, чем философом. Своим возвышением он обязан своему чувству юмора … подробнее » Резвый и громоздкий, Томас Манн « Размышления о неполитическом человеке » прокалывает пирожные нашего времени … подробнее» В июне 1965, шесть мальчиков прибило к берегу на безлюдном острове, где они пробыли год.Настоящий Повелитель мух Ограбление было наглым : Магритт был схвачен под дулом пистолета. Два года спустя кто-то доставил его в полицейский участок Брюсселя. Что случилось? … подробнее » Эпоха дезинформации . Распространение дурацких вещей зависит от того, кого вы знаете, а не от того, что вы думаете … подробнее » Горизонталь предполагает пейзаж. Квадрат пробуждает вневременность. Круг, сама вселенная. Как сформулировать наш опыт ? … подробнее » Почему аналитических центров так легко ненавидеть? Созданные для развития научного мышления, они превратились в фабрики партизанской ловли … подробнее » «У меня есть правило никогда не оглядываться», — сказал Ян Флеминг . «Иначе я бы подумал:« Как я мог написать такую фигню? »» … подробнее » 27 июля 1794 года был необычным днем. Всего за 24 часа волна Французской революции превратилась из радикальной в консервативную… подробнее » Все хорошо, если разбить торжество « когнитивной элиты ». Но как на самом деле выглядит реформирование меритократии? … подробнее » Салман Рушди может приводить к бешеному, скромному хвастовству, нелепому, глухим всезнайка. И все это совершенно простительно … подробнее » Кейт Миллет, осужденная Кейт Миллет как апологет патриархата и священник фаллоса, заслуживает ли D.H. Lawrence второго взгляда ?… подробнее » Война Эдриен Рич против токенизма. Почетные степени, рекомендательные письма, Национальные книжные награды — Ричу, все они воняли … подробнее » Триумф По. Он делал эрудитические пожертвования, несмотря на проблемы, с которыми он столкнулся сначала в качестве сироты, а затем, живя в долгу, с инвалидной женой … подробнее » Говорят, что Вольтер потреблял 72 чашки в день; Бальзак съел землю прямо. Помог ли кофе вызвать Просвещение ?… подробнее » В новом триллере, написанном с Джеймсом Паттерсоном, Билл Клинтон раскрывает такую обнаженную фантазийную версию самого себя, что за него может стыдиться … подробнее» Чудеса английского . Стремительное развитие языка — это бесконечная борьба между логикой и привычкой … подробнее » Мясной парадокс . Как люди, которые заботятся о животных, умудряются не заботиться о сельскохозяйственных животных … подробнее » По мнению философа Марсилио Фичино, ученые страдали от« божественного безумия ». Его лекарство: встав перед рассветом и причесать волосы 40 раз, спереди назад … подробнее » Послушайте , как члены культа говорят , и одно становится ясно: вы, вероятно, в какой-то момент побывал в одном … подробнее » Большинство вдов Средневековья исчезли в безвестности. Но некоторые из них сформировали историю искусства … подробнее » Да, меритократия ошибочна. Но это определенно лучше кумовства, покровительства, клиентелизма и продажности… подробнее » Мемуары Пабло Неруды потрясающе тщеславны, морально отвратительны, но прекрасно написаны. Новая версия делает его законченным — или нет? … подробнее » В недавних романах Лорен Ойлер и Патриции Локвуд в сети процветают обман, теории заговора и глупых шуток . Расскажите нам то, чего мы не знаем … подробнее » Кошки, кажется,« принимают жизнь как дар », в то время как мы с тревогой размышляем о смерти, — пишет Джон Грей, который составил 10 уроков философии для кошек … подробнее » Идеи экономиста Альберта О. Хиршмана были разбавлены Гладуэллом и Санштейном до « гиршманизмов », мягких каштанов, повторенных во время ужина … подробнее» Зигзаги Эдгара Аллана По от астрономии до оккультизма предполагают трагическое сужение в того, что значит быть научным … подробнее » Джордж Пакер , один из наших лучших репортеров и рассказчиков, умеет подбирать памятные темы.Его последнее: его собственные опасения по поводу будущего Америки … подробнее » героинь антропологии : Одна стала профессором, одна умерла, одна была помещена в психиатрическую больницу, а двое покинули академию … подробнее» Первый из изъятий Достоевского произошел во время его медового месяца. «Если бы я знал, что у меня настоящая эпилепсия, я бы не женился» … подробнее » Борхес своему переводчику английского языка :« Упростите меня.Измени меня. Сделай меня суровым…. Сделайте меня мачо, гаучо и тощим »… подробнее» Мы принимаем графиков и диаграмм как должное, но в их самых ранних воплощениях — чтобы помочь понять долготу или время поездов — они были революционными … подробнее » Джон Мичем , тихий историк с президентским ухом, впечатляюще — и сводит с ума — везде … подробнее » « В этой огромной великой Вселенной , / Ничего твердого и постоянного не появляется.» Королева фей приближается к атеизму … подробнее» В начале 19 века Америка была охвачена войной с наукой. Эдгар Аллан По сражался за обе стороны … подробнее » как мы сейчас скорбим. Для влиятельной социальной сети Аманды Клоутс выход из сети никогда не был вариантом, даже когда случилось самое худшее … подробнее » серфинг — дал ему безошибочный голос… подробнее » Многое было сделано из влияния Хайдеггера на Арендт . А как насчет ее влияния на него? … подробнее » Гомеровский вопрос : Были ли« Илиада »и« Одиссея »действительно написаны историческим человеком по имени Гомер? … подробнее» До завоевания Бродвея и Голливуда Майк Николс подвергался издевательствам , безволосый еврейский беженец без единого слова по-английски … подробнее » Шок не в том, что хрупкий союз Америки так эффектно распался в 1861 году, а в том, что это произошло не раньше… подробнее » Он придумал или усовершенствовал рассказ, мистика, научную фантастику и готический ужастик: По наиболее влиятельный американский писатель ? … подробнее » Лезвия, яды, пистолеты, бомбы, дефенестрация и пухлые подушки: История политического убийства Что означают два столетия американских бестселлеров по самопомощи сказать про страну? Луи Менанд копается в … подробнее » « Часть тирании горя состоит в том, что она лишает вас возможности вспомнить важные вещи.«Во время пандемии такое воровство становится еще более распространенным … подробнее» «Поразительно видеть, насколько профессор Фонда Томаса Джефферсона в собственном университете Джефферсона не любит своего покровителя, Томаса Джефферсона » … больше » Альманах уравновешивает практичность, поэзию и интуитивную прозорливость. Награда — это чудесно освобождающая случайность … подробнее » « Если вы позвоните в книжный магазин, чтобы не продавать книги вашего врага , или обрадуетесь, когда проблемная классика вышла из печати, ваш враг сделает то же самое »… подробнее » Ибрам X. Кенди: Психология критической теории расы — это не культурная война с двумя сторонами — это критики CRT, спорящие между собой … подробнее » Будут ли будущие поколения читать Песни мечты ? Джон Берриман — легкая мишень в сегодняшнем культурном климате … подробнее » « Человек-кошка »: как почувствовать себя, когда ваши отношения, переписанные и увековеченные, станут самым вирусным рассказом в мире … подробнее » Португальский поэт Политические сочинения Фернандо Песоа были своего рода беглой полемикой — атакой на все из ниоткуда … подробнее» Карьера Алисы Нил как борющаяся машинистка , стенографистка и художник поднимает вопрос: как это удается разорившимся самодостаточным художницам? … подробнее » Знание, правда, справедливость — почему мы тратим столько времени на обсуждение грандиозных абстракций ? Ответ кроется в прагматизме… подробнее » « йоменский фермер как патриот и образцовый гражданин ». Способствовали ли влиятельные книги ранней Америки культурной однородности? … подробнее » Дело вкуса . Все отзывы об искусстве носят в основном личный характер, но не все одинаково верны … подробнее » Оруэлл « Политика и английский язык »был назначен миллионам студентов. Мы оказываем им медвежью услугу … подробнее » Для Канта и Ницше жалобы и нытье были слабыми, скромными действиями.Но Симона Вейл увидела в них красоту и волшебство … подробнее » Гарольд Розенберг бежал без пакетов и не подписывался на школы. Он оставался индивидуальностью среди коллективных кредо и стилей … подробнее » Как показывает война Адорно против бездумных, нигилистических студентов, радикальных интеллектуалов не всегда следует поддерживать левых революционеров … подробнее» Великие рассказчики встречаются реже, чем — великие писатели, — говорит агент Мортон Джанклоу.Был ли Джеки Коллинз великим рассказчиком? … подробнее » Мемуары Пабло Неруды поразительно тщеславны, морально отвратительны, но прекрасно написаны. Новая версия делает его законченным — или нет? … подробнее » Новая черная сатира. Фатализм Дэйва Чаппеля в начале 2000-х уступил место искренности и требованиям к действию … подробнее » Повторяющийся образец: Симона Вейл действовала исключительно по убеждению — в то время как на заднем плане ее родители позаботились о том, чтобы она выжила. попытки реализовать свои идеалы… подробнее » Освобождает ли типичные для времени взгляды от суждений будущих поколений? Рассмотрим пример Уинстона Черчилля … подробнее » Пессимист, подающий надежды. На протяжении полувека Wendell Berry был портретом того, как жить без отчаяния, когда проигрыш вероятен … подробнее » Историческая фантастика долгое время был заброшенной областью законсервированных персонажей, использующих такие слова, как« Прити! ” Больше не надо … подробнее » Для Чарльза Тейлора политика признания была центральным элементом современной идентичности. Теперь опасения по поводу репутации в сети рискуют вытеснить этот принцип … подробнее » Дэвид Хокни известен только славой и лести. Почему? Его образы яркие, свежие, благопристойные и немного скучные … подробнее » Chimamanda Ngozi Adichie о тех, кто« не осознает, что то, что они называют сложным подходом, на самом деле является упрощенным сочетанием абстракции и ортодоксальности ». … подробнее » В Джоан Дидион пишет , она не совсем понимает, что имеет в виду. Но мы знаем, как она себя чувствует … подробнее » Художественные галереи и аукционы могут показаться устрашающими изолированными местами. Вот , как успешно покупать искусство … подробнее » Философия едва прогрессирует , но что этому мешает? Возможно, решения проблем порождают собственные проблемы … подробнее » Когда писатель отказывается до такой степени, как Наоми Вольф , мы должны спросить: она всегда была полна дерьма? … подробнее » Почему для английских кафедр наступили тяжелые времена? Потому что профессора перестали говорить правду о литературе … подробнее » Retrospectives at the Tate and the Met, пятитомный каталог raisonné, много биографий: Что еще можно сказать о Francis Bacon ? .. Подробнее » « Смерть Дж. Хиллиса Миллера в феврале ознаменовала конец удивительного периода в американской академической литературной критике »… подробнее » Если теология, наука и философия когда-то формировали души, их вытеснила новая сила: HR, центральная организующая сила общества … подробнее» Часы — это не просто часы . Он был создан для социальных и политических целей, и он имеет особое влияние на нашу жизнь … подробнее » « Дань »Рэйчел Куск Мэйбл Додж Лухан не столько обновляет ее историю, сколько разрушает ее сложность. .. подробнее » Для прогрессистов Фуко больше не может быть« непревзойденным горизонтом »критического мышления.«Так что же будет дальше? … подробнее » Выйдя из длительной депрессии, Уильям Джеймс провел исследование привычек . Он заключил, что самые здоровые — это те, которые нам удается сломать … подробнее » Антагонистические отношения между писателями и критиками породили богатую литературу о троллинге . Обе стороны уязвимы для унижений … подробнее » Дирижеры не совсем не нужны оркестру, но они не так важны, как те , трясущие дубинкой, , как хотелось бы, чтобы мы думали… подробнее » Томас Нагель о моральной интуиции: Приличное отношение к людям — жизненно важная часть нашей жизни, независимо от последствий … подробнее» Поскольку мир искусства не любит полностью подвергать цензуре вредные произведения, появилась новая тактика: «кураторский активизм» … подробнее » Рецензирование книги: Элегия . С тех пор, как появилась литература, были и критики. Теперь это под вопросом … подробнее » Кто этот 83-летний мусорщик, объявивший об операции китайского правительства в Чикагском университете? Маршалл Сахлинс … подробнее » У консерваторов есть маловероятный инструмент для борьбы с новым прогрессизмом и церковью интерсекциональности: теории Мишеля Фуко … подробнее» Томас Соуэлл , год в его университете. Чикаго, доктор философии. при Милтоне Фридмане оставался стойким марксистом. Что изменило его мнение? … подробнее » Фрейд и другие предупреждали о жестокости и иррациональности толпы . Мы все меньше слышим об их огромном достоинстве… подробнее » » Кто-нибудь может узнать, когда вы их погуглите? » Бекка Ротфельд рассматривает эмоциональные инвестиции и эстетику онлайн-преследования … подробнее » Для Лео Штрауса публичная сфера предназначалась для неискушенного написания мнений, а не для истинного философского размышления … подробнее» Среди прочего наиболее воспроизводимые книги на английском языке — это Библия, произведения Шекспира и The Compleat Angler , руководство по рыболовству 17-го века… подробнее » Mary Beard :« Классика — это то, что мы делаем, и тот факт, что классический мир был искажен, не должен использоваться против этого ». Долгая Ольга Константиновна, учитель русского языка и литературы МОУ СОШ № 3 ст. Павловской КАК НАУЧИТЬСЯ ПИСАТЬ СЖАТОЕ ИЗЛОЖЕНИЕ Теория 1 Сжатое изложение – краткое изложение исходного текста с передачей существенной информации, при котором исключаются подробности. Основным условием успешного выполнения речевой задачи, связанной со сжатием информации, является, во-первых, полноценное понимание исходного текста. Если текст не понят, не определено, что в нем главное, а что второстепенное, в таком случае работа представляет собой случайное, хаотичное удаление из исходного текста тех или иных элементов. А во-вторых, для успешной работы над сжатым изложением важным условием является владение навыками сокращения текста. При сжатом изложении не обязательно сохранение стилевых особенностей, но основные мысли автора, последовательность событий, характеры действующих лиц должны быть переданы без искажения. Краткий пересказ выявляет степень понимания текста. Поэтому овладение навыками сжатия текста, применение их во время ГИА – залог успешной сдачи экзамена. Сравните предложенные тексты (второй вариант – пример сжатого текста): 1.«Мастерская Саврасова резко отличалась от других. В тех работали по необходимости и по обязанности. Иногда зевали и скучали. Здесь не думали о школьных наградах и отличиях. Здесь горячо любили искусство, работу, увлекались до самозабвения».= «В мастерской Саврасова не скучали, не думали о наградах и отличиях, здесь горячо любили искусство и работу». 2. «На лугу росли неприхотливые ромашки, задумчивые одуванчики, застенчивые купавки». « На лугу росли цветы». 3. Можно привести множество примеров, когда смысл оживает в строении слова: подоконник – то, что находится под окном; а вот слово «окно» не каждый свяжет со словом «око», а ведь это родственные слова… «Можно привести множество примеров, когда смысл оживает в строении слова: подоконник – то, что находится под окном». Практическая работа № 1 Упражнение 1 Прочитайте предложение и подчеркните в нем главную информацию. А) Многие вещества биологического происхождения, основой которых является вода, имеют жидкокристаллическую структуру. Б) Принято считать, что чистый воздух нужен только людям, подтверждением тому является устойчивый оборот как без воздуха, но чистый воздух необходим и в особо точном производстве, так как из-за пыли машины преждевременно изнашиваются. Упражнение 2 Перед вами первые два абзаца текста. Какая информация вам кажется факультативной, второстепенной? Какие предложения, перестроив, можно соединить? Используя различные приемы сжатия текста, передайте основную информацию, заключенную в двух абзацах, так, чтобы объем вашего высказывания не превышал 35 слов. 1. Может показаться парадоксальным, но людям нужны не только рациональные цели, но и совсем не рациональные мечты. 2. Цель всегда конкретна, измеряема, достижима. 3. Например, целью может быть поступление в вуз или покупка мотоцикла. 4. В любом случае можно заранее продумать и просчитать, что нужно сделать, чтобы этого достичь. (45 слов) Теория 2 Работая над сжатием текста, необходимо соблюдать последовательность, чтоб не пропустить ни одной микротемы (темы абзаца большого текста). Поэтому выделяют следующие этапы работы с текстом по написанию сжатого изложения (рассмотрите и проанализируйте таблицу): Этапы учебной деятельности Учебная деятельность 1. Этап определения темы текста. Ответ на вопрос: «О чем текст?» Как определить тему? по началу текста; по ключевым словам; по ключевым эпизодам; по поступкам или размышлениям героев (автора) по заглавию текста 2. Этап определения идеи текста. Ответ на вопрос: «Зачем автор его написал?», «Какую мысль хотел выразить?» Что нам помогает сформулировать идею? 3. Этап определения структуры текста. Назовите композиционные части текста. Композиция текста – построение текста. 4. Этап абзацного членения текста: определение микротем текста как частей общей темы Определите количество абзацев в тексте по количеству больших интонационных пауз читающего и пронумеруйте их. Определите микротему каждого абзаца. Запишите ее кратко, опуская второстепенную информацию. 5. Этап моделирования сжатого изложения Как соединить содержание микротем в текст? лексические – повтор, однокоренные слова, синонимы; лексико-грамматические Рассмотрим соблюдение всех этапов на примере следующего текста: Географические названия. (1)Имена рек – старейшины в мире географических названий; я имею при этом в виду имена больших, самых прославленных рек Земли. (2)Древние люди, гонимые голодом, холодом, свирепостью зверей и двуногих соседей, всё время перебирались с места на место, всё время как бы расталкивали локтями своих современников в борьбе за самые удобные для жизни места. (3)Бывало по-разному. (4)То племя натекало на племя, как шумная река, ворвавшееся в малое озерко: вода озера сливалась с могучим потоком, растворяясь в нём без следа. (5)То пришельцы растекались по новому месту, как по болоту или песчаной пустыне, теряясь в её песках, смешиваясь со старым населением. (6)Но почти всегда они, принося с собой свои новые имена для холмов и лесов, для посёлков и пустошей, названия больших потоков сохраняли благоговейно, принимая их от своих предшественников. (7)Мы не знаем в точности, почему они так поступали. (8)Может быть, боялись обидеть богов этих чужих рек переименованием. (9)Может быть, просто реку труднее перекрестить по-новому: её имя так же длинно, как она сама; оно течёт вместе с нею через области и страны; поди замени его на всём протяжении его пути! (10)Так или иначе — великие водные дороги всюду и везде постоянно носят и сегодня имена, созданные в глубочайшей древности. (11)Они переходят от народа к народу, от эпохи к эпохе. (12)Первоначальный их смысл забывается тысячекратно, а они всё живут Выполним задания, которые помогут проверить глубину и точность восприятия исходного текста (жирным шрифтом выделен верный ответ): 1. О чём говорится в этом тексте? а) о страхе древних людей перед богами; б) о переселении древних людей; в) о названии рек; г) о завоевательных войнах древности. 2. Чем отличаются имена крупных рек от названий других географических объектов? а) почти невозможно установить их происхождение; б) они почти никогда не менялись; в) многие из них по значению связаны со сменой времён года; г) в них отражена история древних междоусобиц. 3.Почему автор называет СТАРЕЙШИНАМИ имена рек в этом тексте (предложение №1)? а) от названия рек происходили названия других географических объектов: гор, хребтов, озёр; б) названия рек занимают особое, почётное место в ряду других географических названий; в) названия рек невозможно перевести на другой язык; г) право называть реки давали наиболее почитаемым представителям древних племён. 4.Закончите план этого текста. 1) Названия рек — _______________________________ . 2) Древние люди боролись за _____________________ . 3) Пришельцы почему-то никогда _________________ . 4) Два предположения о том, почему _______________ Примерный вариант выполнения задания №4. 1) Названия рек — старейшины в мире географических названий. 2) Древние люди боролись за удобные для жизни места. 3) Пришельцы почему-то никогда не меняли названия больших потоков. 4) Два предположения о том, почему так поступали пришельцы. 5.Дополните этот фрагмент примерами из текста. Автор сочетает информативную насыщенность с эмоциональной выразительностью, использует слова высокого стиля («____________» из предложения №6), подчёркнутой анафорой синтаксический параллелизм(предложения №4 и ____ ), __________ («как шумная река»). Слово разговорного стиля («____________» из предложения №9) придает тексту интонацию доверительно-непринуждённой беседы. Примерный вариант выполнения задания №5. Автор сочетает информативную насыщенность с эмоциональной выразительностью, использует слова высокого стиля («благоговейно» из предложения №6), подчёркнутой анафорой синтаксический параллелизм (предложения №4 и № 5), сравнение («как шумная река»). Слово разговорного стиля («поди » из предложения №9) придает тексту интонацию доверительно-непринуждённой Практическая работа № 2 Работа по написанию сжатого изложения по тексту «Географические названия». Продолжи предложения и получится сжатое изложение: 1.(Запишите главную часть первого предложения.) ________________ ___________________ _______________________ 2.Древние люди, пытаясь найти (какое?)________ место для _________ , (что делали?) ___________ . 3. Пришельцы, захватывая ______________ , меняли названия почти всех ____________ , но всегда сохраняли (что?) __________ . 4.Мы не знаем, почему ________ . 5.Может быть, они __________ _____________ _____________ . 6. Может быть, реку трудно _________, потому что она протекает через __________ . 7.Так или иначе названия рек сохраняются __________ , переходя от __________ к ___________ Практическая работа № 3 Прочитайте исходный текст и рассмотрите таблицу, в которой отражены все его микротемы. Проснувшись на рассвете под кряканье уток, я вылез однажды из палатки и осмотрелся. Но тут же мне пришлось присесть и ползти обратно за биноклем: метрах в ста от островка плавала большая стая пеликанов. Не часто представляется случай понаблюдать за этими редкими птицами в природе. Впервые я вижу такую огромную стаю пеликанов, в ней не меньше сотни птиц. Присмотревшись, я понимаю, что на воде кормится стая, состоящая из кудрявых пеликанов и пеликанов розовых. Кудрявый пеликан чуть крупнее розового, у него хорошо видна «грива» — удлиненные и словно завитые перья на голове, а в оперении нет розового оттенка, свойственного его собрату. Вокруг пеликанов плавают бакланы, а в воздухе с криком носятся чайки. Бакланы бросаются за рыбой, стремительно ныряя, а пеликаны хватают ее, погружая в воду только голову, шею и переднюю часть туловища. Слышны только всплески воды да крики чаек. Но вот охота окончена, птицы направляются к песчаному берегу, тяжело шлепая своими перепончатыми лапами, и выбираются на сушу. По земле они передвигаются неуклюже, вразвалку. И вдруг один пеликан поднимается в воздух. Встревоженный чем-то, он отталкивается одновременно обеими лапами от воды и, тяжело взмахивая крыльями, улетает от острова. Сидящие на берегу птицы сейчас же следуют его примеру. Через несколько секунд все птицы оказались в воздухе. Они беспорядочно кружат над озером, потом строятся в одну волнистую линию и, сделав всей стаей два больших круга, улетают на. восток, к солнцу. Все это довелось мне видеть довольно давно. В наши дни пеликанов стало значительно меньше, численность их продолжает катастрофически падать, недаром они занесены в Красную книгу. Причина в выкашивании и сжигании тростниковых зарослей, в том беспокойстве, которое причиняет человек во время гнездования птиц. Чем мы можем помочь пеликанам? Своим нетерпимым отношением к браконьерству, пониманием своей ответственности за существование редких птиц на планете. И ещё- человеческой деликатностью: нужно просто беречь места гнездований пеликанов и не тревожить птиц, особенно в самое для них трудное время — при откладывании яиц, насиживании и выводе птенцов.(По А.Л. Кузнецову) (311 слов) № абзаца Микротема 1 Однажды утром я увидел большую стаю пеликанов 2 Стая состояла из кудрявых и розовых пеликанов, которые охотились за рыбой 3 После охоты пеликаны выбрались на сушу. Вдруг один пеликан взлетел, за ним улетели остальные 4 Все это было давно. В наши дни пеликанов становится все меньше из-за вмешательства человека в их жизнь 5 Пеликанам можно помочь, но для этого нужно, чтобы человек осознал свою ответственность за сохранение этих редких птиц на земле А теперь, используя таблицу, напишите сжатое изложение по исходному тексту. Практическая работа № 4 Прочитайте текст, напишите сжатое изложение, сократив текст вдвое, используя предложенную после текста памятку. Кроме легенд о Геракле, древние греки рассказывали и о двух братьях-близнецах — Геракле и Ификле. Несмотря на то что братья с детства были очень похожи, выросли они разными. Еще очень рано, и мальчикам хочется спать. Ификл натягивает на голову одеяло, чтобы дольше смотреть интересные сны, а Геракл бежит умываться к холодному ручью. Вот братья идут по дороге и видят: на пути — большая лужа. Геракл отходит назад, разбегается и перепрыгивает через препятствие, а Ификл, недовольно ворча, ищет обходной путь. Братья видят: на высокой ветке дерева красивое яблоко. «Слишком высоко, — ворчит Ификл. -Не очень-то хочется этого яблока». Геракл прыгает — и плод у него в руках. Когда устают ноги и губы пересыхают от жажды, а до привала еще далеко, Ификл обычно говорит: «Отдохнем здесь, под кустиком». — «Лучше побежим, — предлагает Геракл. — Так мы скорее одолеем дорогу». Геракл, который сначала был обыкновенным мальчиком, впоследствии становится героем, победителем чудовищ. И все это только потому, что он с детства привык одерживать ежедневные победы над трудностями, над самим собой. В этой древней легенде скрыт глубочайший смысл: воля — это умение управлять собой, это умение преодолевать препятствия. (176 слов) «Как писать сжатое изложение» 1. Выделите в тексте существенные (т.е. важные, необходимые) мысли. 2. Найдите среди них главную мысль. 3. Разбейте текст на части, сгруппировав его вокруг существенных мыслей, выделите микротемы. 4. Озаглавьте каждую часть и составьте план. 5. Подумайте, что можно исключить в каждой части, от каких подробностей отказаться. 6. Какие факты (примеры, случаи) можно объединить, обобщить в соседних частях текста? 7. Обдумайте средства связи между частями. 8. Переведите отобранную информацию на «свой» язык. 9. Запишите этот сокращенный, «отжатый» текст на черновике, прочитайте, исправьте ошибки. 10. Перепишите отредактированный текст на чистовик. Сочинение ЕГЭ 2016 по русскому языку — это задание повышенной сложности, поэтому необходимо очень внимательно отнестись к его выполнению, а значит, и к подготовке. В данной статье я попытаюсь подробно разобрать план сочинения и особенности его написания. Независимо от содержания текста, лучше всего пользоваться следующим планом, составленным на основе критериев оценивания: 1) Формулировка проблемы 2) Комментарий к проблеме 3) Позиция автора по выбранной проблеме 4) Собственное мнение (согласие или несогласие) 5) Доказательство своего мнения (включая не менее 2-х аргументов) Для гармоничности изложения и композиционной целостности желательно включить в свою работу вступление и заключение (но это не обязательно). К1. Формулировка проблемы Проблема текста — это предмет обсуждения, вопрос, над которым рассуждает автор. Как правило, исходный текст включает не менее 2-3 тем, каждая из которых может стать основой вашей работы. Выбор должен определяться ответом на два вопроса: 1) Какая проблема находится в центре внимания автора? 2) К какой проблеме вам легче подобрать аргументы? Как определить проблему? При выявлении проблемы текста можно использовать следующий способ: Разберем на примере: Прочитав текст несколько раз я выделяю две проблемы: 1) проблема духовного существования человека в современном мире 2) проблема снижения интереса к чтению в XXI веке Я выбираю вторую. На основе собственного впечатления от прочитанного текста я составил вступление, а проблему сформулировал в виде вопроса: Вспоминаю, как в детстве просил родителей прочитать сказку. Они читали. Я вырос, давно уже читаю сам, как «бумажные» книги, так и электронные. Но все чаще вижу нарастающее равнодушие к чтению и литературе в целом. Неужели книга перестала играть в жизни общества и человека привычную для нее роль? Над этой проблемой размышляет И. Косолапов. В качестве вступления можно было привести статистику: Согласно официальной статистике Всероссийского центра изучения общественного мнения, треть россиян не хранит дома книг, другая треть, имея книги, их не читает. К2. Комментарий к проблеме Комментарий — это пояснение, толкование выбранной проблемы. Комментарий помогает более детально охарактеризовать проблему, а также, показать как автор подходит к её раскрытию. При написании сочинения комментарий служит связующим звеном между проблемой и позицией автора. Главное требование к комментарию — опора на текст. Следующие вопросы могут послужить основой для комментария к проблеме: Как автор относится к предмету описания? Какие аргументы приводит автор? На каких примерах автор раскрывает проблему? Какими событиями иллюстрирует её? Как относится автор к предмету описания (герою)? Насколько проблема волнует автора? В чем сущность данной проблемы? Какова актуальность проблемы? Насколько она значима? Использует ли автор противопоставление? Если да, то что противопоставляет? Комментируем нашу проблему: Рассуждая о судьбе книги в XXI веке, автор противопоставляет книгу и достижения технического прогресса. При этом автор сталкивает мнения разных поколений: Л.Леонова, который назвал книгу «бескорыстным верным другом», и молодого программиста, определившего книгу как «кипу пыльной бумаги». И. Косолапов рассуждает о преимуществах и недостатках техники перед книгой, и находит вторую более предпочтительной и полезной. К3. Авторская позиция Авторская позиция — это ответ на вопрос обозначенный в проблеме. Авторская позиция является итогом размышления, выводом к которому автор приходит (в рамках выбранной проблемы). Авторская позиция может выражаться прямо (в отдельных предложениях, обращениях к читателю) либо косвенно (в поступках героев, художественных деталях). Автор убеждает нас в том, что книга нисколько не потеряла своей ценности, а технические достижения не смогут и не должны заменить её. Книга несет очень важную образовательную функцию, она учит и воспитывает человека. Техника и компьютеры призваны облегчать нашу повседневность, делать её более комфортной, но они не должны занимать собой всю нашу жизнь. К4. Аргументация экзаменуемым собственного мнения по проблеме В первую очередь нам необходимо выразить своё мнение, соглашаясь или не соглашаясь с мнением автора. Моё мнение: Я полностью разделяю мнение И.Косолапова о том, что книга в наше время незаслуженно забыта, хотя значение её по-прежнему велико. Я думаю, что в наш информационный век постоянное использование компьютеров и разнообразных гаджетов приведет к деградации общества, вырождению человеческой мысли. Структура аргумента Для получения максимального количества баллов нам необходимо привести не менее 2-х аргументов (один из которых опирается на художественную, научную, публицистическую литературу). Приведенный пример должен выступать как яркий микротекст и доказывать нашу позицию. Моя аргументация: 1. К подобным неутешительным выводам приходили и фантасты ХХ века (логический переход). Один из которых, Рей Брэдбери, в своей антиутопии «451 градус по Фаренгейту» описывает потребительское общество, опирающееся на массовую культуру. В этом социуме люди окружили себя материальными ценностями, телевидением и развлечениями. Книги, в свою очередь, строго запрещены и подлежат сожжению, дабы ни одна критическая мысль не попала в человеческое сознание (аргумент). Когда я вижу, как люди тратят свое время на телевидение и социальные сети, я понимаю, о чем предупреждал нас Р.Брэдбери. Важная задача стоит перед нами, с помощью книг сохранить связь с интеллектуальным наследием человечества (микровывод). 2. Насколько высока может быть роль книг в духовном становлении личности мы можем узнать в произведениях М.Горького: «Детство», «В людях», «Мои университеты». Герой повестей Алеша Пешков считает, что именно книги помогли ему преодолеть тяжелые жизненные испытания. Как видите, я привожу два примера из художественной литературы. В качестве аргумента также можно использовать: ссылки на кинофильм, спектакль, исторические события, официальную статистику, высказывания известных людей и примеры из личного опыта. Аргументируя свою позицию, я использую «аргумент к угрозе»(доказывая негативные последствия игнорирования тезиса привожу антиутопию Р.Брэдбери) и «аргумент к обещанию» (на примере Пешкова показываю как важны книги). Заключение Заключение должно подводить итог нашим размышлениям по проблеме. В своем заключении я сначала использую обращение, а потом обобщаю проблему, указываю на её глобальную важность. Хочется обратиться к современникам: друзья, погружаться в художественные миры гораздо интереснее и полезнее, чем блуждать в интернет-паутине! Помните, что культура развивается в первую очередь за счет сохранения мудрости предыдущих поколений, хранящейся в книгах. Надеюсь материал был Вам полезен. Сжатое изложение — это письменный пересказ текста с использованием приемов сжатия текста. № Критерии оценивания сжатого изложения Баллы ИК1 Содержание изложения Экзаменуемый точно передал основное содержание прослушанного текста, отразив все важные для его восприятия микротемы 2 Экзаменуемый передал основное содержание прослушанного текста, но упустил или добавил 1 микротему 1 Экзаменуемый передал основное содержание прослушанного текста, но упустил или добавил более 1 микротемы 0 ИК2 Сжатие исходного текста Экзаменуемый применил 1 или несколько приемов сжатия текста, использовав их на протяжении всего текста 3 Экзаменуемый применил 1 или несколько приемов сжатия текста, использовав их для сжатия 2 микротем текста 2 Экзаменуемый применил 1 или несколько приемов сжатия текста, использовав их для сжатия 1 микротемы текста 1 Экзаменуемый не использовал приемов сжатия текста 0 ИК3 Смысловая цельность, речевая связность и последовательность изложения Работа экзаменуемого характеризуется смысловой цельностью, речевой связностью и последовательностью изложения: — логические ошибки отсутствуют, последовательность изложения не нарушена; — в работе нет нарушений абзацного членения текста 2 Работа экзаменуемого характеризуется смысловой цельностью, связностью и последовательностью изложения, но допущена 1 логическая ошибка, и/или в работе имеется 1 нарушение абзацного членения текста 1 В работе экзаменуемого просматривается коммуникативный замысел, но допущено более 1 логической ошибки, и/или имеются 2 случая нарушения абзацного членения текста 0 МАКСИМАЛЬНОЕ КОЛИЧЕСТВО БАЛЛОВ ЗА СЖАТОЕ ИЗЛОЖЕНИЕ 7 Необходимо написать все микротемы текста. Б) Обобщение В) Упрощение Объем изложения должен составлять не менее 70 слов. ***Не забывайте о том, что изложение тоже подлежит проверке на грамотность, но можно совершенно легально пользоваться ОРФОГРАФИЧЕСКИМ СЛОВАРЕМ. Первое прослушивание (примерно 3 минуты) Работа с черновиками (3-5 минут) Второе прослушивание Написание изложения 2) Не стоит пытаться записать все подряд, делайте акцент на конкретных словах и идите по тексту вместе с диктором. Старайтесь не отставать. Для этого делайте пропуски, в которые поместятся пропущенные слова. То есть, если вы не успели записать три слова, то в вашем черновике должно быть место для этих слов. Это не значит, что все три слова туда попадут, но место для них лучше оставить. При следующем прослушивании вы сможете понять, на каких словах и частях предложения необходимо сконцентрировать свое внимание. 3) Что нужно записывать во время 1 прослушивания: Что НЕ нужно записывать: 4) Выделяйте границы предложений. В идеале писать первое слово предложения с большой буквы. Это необходимо, чтобы два предложения вашего конспекта не превратились в одно с совершенно иным смыслом. 5) Обязательно используйте сокращения, но использовать их нужно правильно.Например, если вы сократите словосочетание «осенний листопад» вот так: «о.л.» вы ничего не сможете потом понять. Правильно сокращение заключается в том, чтобы захватить корень слова и его окончание. Правильное сокращение: «целеустремленный » = «целеустр-ный» ***Как правило, некоторые слова повторяются на протяжении всего текста, можно написать такое слово один раз, а потом использовать только первую букву. Это касается только ключевых, тематических слов. Например, текст посвящен красоте. Слово красота есть чуть ли не в каждом предложении. Достаточно будет написать это слово один раз. Обязательно потренируйтесь в своем умении сокращать слова. 6) После первого прослушивания у вас будет 3-5 минут(ы) для работы с черновиком. В это время важно дописать сокращения и, если позволит память, вписать слова, которые вы сможете вспомнить. Здесь надо быть очень осторожными, пишите только то, в чем уверены. Можете пометить в своем черновике галочками те места, в которых принципиально важно восстановить слова: там, где вы вообще не можете вспомнить слово, а оно важно для понимания предложения. Также это могут быть названия чего-либо, имена или термины. 7) Во время второго прослушивания запишите на места пропусков важные слова. В этот раз тоже можно использовать рациональные сокращения. Во время второго прослушивания также не нужно писать несущественную информацию, вводные конструкции и кучу лексических повторов. Не забывайте, изложение должно быть сжатым. 8) Еще раз восстановите все сокращения и прочитайте внимательно получившийся текст. Наверняка вы найдете, что можно сократить, упростить или сжать, но не переусердствуйте, так как объем изложения должен быть не менее 70 слов. 9) Перепишите изложение, создав при этом полноценный текст, проверьте его на ошибки и можете смело переписывать его в чистовик, не забывая об абзацном членении. Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Волнительный момент для каждого девятиклассника — итоговое изложение в рамках ОГЭ по русскому языку. На самом деле, если разобраться, особенных причин для страха быть не должно. Что что, а изложение школьники пишут с начальной школы! Главное, закрепить полученные навыки и сосредоточиться на своей цели. Давайте вместе вспомним, что такое изложение, и составим пошаговый план его успешного написания. Изложение – это вид письменной проверочной работы, направленной на пересказ, краткую (или подробную) передачу основного содержания исходного текста. Во время изложения учитель читает фрагмент литературного или публицистического произведения (рассказа, романа, очерка, статьи), а затем просит учащихся изложить услышанное на бумаге своими словами максимально близко к оригиналу. Существует несколько разновидностей изложения: Описательное. Обычно для его написания используются фрагменты художественных произведений, содержащие описание природы, жилища или внешности человека. Главная цель описательного изложения – научить видеть цепь признаков лица или предмета, повысить наблюдательность, закрепить навыки запоминания мельчайших подробностей. Обратите внимание на прилагательные и причастия, с помощью которых автор описывает персонажа и окружающие его предметы. Не забудьте правила оформления однородных членов предложения. Повествовательное изложение. Особое внимание в повествовательном тексте следует уделить сюжетной линии. Пункты плана будут представлять собой последовательность неких действий, образующих событийный костяк услышанной истории. В повествовательном изложении важно правильно воспроизвести глаголы: выпишите их из текста, когда учитель будет читать его второй раз. Уделите внимание причастным и деепричастным оборотам. Повторите правила выделения обособленных определений и обстоятельств на письме. Подробное. Чаще всего этот вид работы встречается в начальной школе, когда особенно важна тренировка слуховой и зрительной памяти. Чем больший объём информации запомнит и воспроизведёт ученик, тем лучше. Сжатое изложение. При его написании подробности отступают на второй план. Необходимо выделить в тексте главное, уловить его смысловой посыл и записать основные аргументы. Сжатое изложение готовит старшеклассников к составлению конспектов, которое пригодится им в студенческой жизни. Рассуждение. Такое изложение – это настоящая творческая работа. Оно, как и предыдущий подвид, фиксирует главное, не концентрируясь на мелочах. Проверяющий оценивает не столько качество передачи информации, сколько ход собственных мыслей учащихся, его способность делать выводы на основе услышанного материала. Работая над изложением с элементом рассуждения, важно сохранить логику повествования, привести ёмкие доказательства своей точки зрения по заявленной проблеме. Советы тем, кто хочет получить максимально высокий балл, можно сформулировать следующим образом: Последний общий совет оставим непронумерованным. Он касается каждого, кто не привык загонять полёт фантазии в узкие границы заданного шаблона. Не забывайте, что изложение – это не сочинение: вы пишете не собственный текст, а лишь воспроизводите чужой оригинал. Если для вас это скучно, смиренно примите крест ученичества: в старинных монастырских школах Древней Руси человек получал разрешение самостоятельно взяться за перо только после того, как переписывал до сотни текстов предшественников. Была в этом своя мудрость: научись слышать то, что тебе говорят, а уж потом говори (или пиши) сам. При выполнении данного вида работ педагог обязан соблюдать ряд правил: Учителя не обязаны ограничиваться собственным голосом, доской и мелом. Для прослушивания подойдут фрагменты аудиокниг, записи актёрского или авторского чтения, подкасты (что это?). Главное, чтобы материалы были высокого качества, легко распознавались на слух. Краткое изложение: алгоритмы написания Написание изложения – одна из составляющих учебного процесса в рамках школьной программы. Однако не все ученики знают, как написать сжатое изложение. Виды изложений: Существует несколько видов изложений: При подробном изложении ученик подробно и последовательно излагает свои мысли, не отступая от основного содержания и не меняя его стиль, фразеологию и детали. Сжатое изложение подразумевает краткий пересказ исходного текста, где сохраняется лишь самое главное, без подробностей. В сжатом изложении должна быть выражена главная мысль, языковые особенности и некоторые детали, без которых нельзя понять основной направленности повествования. Изложение введено в программу школьного курса именно для того, чтобы научиться пересказывать текст кратко. Например, описывать конкретный персонаж, явление или событие. Работая над выборочным изложением, нужно, прежде всего, вычленить главные моменты, касающиеся определенного отрывка, изучить его и изложить материал подробно. ГИА – пункт С1 Все, кто уже имел удовольствие сдавать ГИА, знают, что один из пунктов экзаменационных заданий является написание изложения. Причем, это должно быть сжатый пересказ. Экзаменуемым школьникам дают прослушать аудиозапись, после чего они должны написать изложение всего на 70 слов (это минимум). На выполнение дается 90 минут. Работа над изложением состоит из нескольких этапов: Алгоритм выполнения задания При написании сжатого изложения, не упустив важные моменты, необходимо придерживаться определенного алгоритма действий: Сжимать текст тоже надо по правилам. Сначала исключаются все подробности и мелкие детали. Затем обобщают отдельные явления. После этого сочетают исключения и обобщают оставшийся материал. Для каждого школьника, заканчивающего 9 класс, важно знать, как правильно писать сжатое изложение. Можно положиться на интуицию, и, прослушав текст изложить свои мысли кратко и логично. Но знания алгоритмов написания подобных работ не только придаст ученику уверенности, но и станет гарантом получения положительной оценки. Автор Distance-Teacher Как сделать анализ стихотворения? Как написать сочинение ПОДГОТОВКА К ЕГЭ ЦЕЛЬ ЧТО ТРЕБУЕТСЯ ПРИЁМЫ СЖАТИЯ ТЕКСТА Исключение слов, словосочетаний, фрагментов предложений и целых предложений Что можно исключить из предложения без ущерба для его содержания? Прочитайте, найдите в тексте поясняющие конструкции Обобщение содержания фрагмента текста . Языковое упрощение
замена простых предложений сложным
ПРОВЕРИМ ВМЕСТЕ Сегодня мы попытаемся помочь девятиклассникам понять, как написать краткое изложение и как получить за это задание максимальный балл. Требования к написанию сжатого изложения Для начала нужно узнать, по каким критериям оценивают задание 1 эксперты. Вот основные требования, предъявляемые к сжатому изложению: Экзаменуемые должны передать основное содержание текста и отразить важные для его понимания микротемы. За этот блок можно получить от 0 до 2 баллов. Экзаменуемые должны использовать приемы сжатия на протяжении всего изложения. (от 0 до 3 баллов) Экзаменуемые должны соблюдать последовательность изложения, избегать логических ошибок. (от 0 до 2 баллов) Максимальный балл за задание 1 – 7 баллов. Общие рекомендации — На экзамене будет звучать аудиозапись с текстом для изложения. Аудиозапись длится 2-3 минуты и повторяется два раза. После первого прослушивания экзаменуемым дается время на осмысление и обработку текста. — Требуемый объём сжатого изложения – 70 слов, работа объемом меньше 70 слов НЕ ПРОВЕРЯЕТСЯ, и баллы за неё не начисляются. Но не стоит писать и слишком длинные изложения, самый оптимальный объём – 80-90 слов. — Изложение необходимо разделить на части, текст разбивайте на 3 абзаца. — Пишите изложение по возможности чётким, разборчивым почерком и при делении текста на абзацы соблюдайте достаточное расстояние для отступа строки, чтобы экзаменаторы точно видели, как вы делите текст. — Старайтесь не употреблять в работе слова и выражения, в смысле и написании которых вы не уверены. На экзамене разрешено пользоваться орфографическим словарем, но делать это лучше после того, как вы полностью напишите «черновой» варианта изложения. Основные этапы работы над изложением На экзамене у вас обязательно должен быть черновик и хорошо пишущая ручка (а лучше две). Приготовьтесь внимательно слушать текст и записывать хотя-бы по два-три опорных слова из каждого предложения. Не стремитесь записать весь текст подряд! Сокращайте слова, оставляйте между ними большие расстояния, чтобы дописать предложения во время перерыва и второго прослушивания текста. Во время перерыва прочитайте свои записи, где возможно, допишите сокращенные слова. Попытайтесь понять, о чём текст, и что хотел сказать автор. Во время повторного воспроизведения аудиозаписи вписывайте в пропуски то, что не написали при первом прослушивании текста. Еще раз осмыслите тему текста. Ваша цель: — Понять тему (о чем говорится?) — Уловить основную мысль (к чему призывает автор, как он хочет повлиять на читателя) На основе своих записей восстановите текст, соедините всё в одной работе. Текст должен читаться легко, быть логичным, связным, тема и цель полученного изложения должны соответствовать теме и цели исходного текста. Чтобы проверить это, задайте себе вопрос: «Говорится ли в моём тексте о том же, о чем говорил автор? Побуждает ли он к тому, к чему побуждает исходный текст?» В своей работе выделите 3 абзаца. Каждый абзац – это микротема. Получилось ли у вас три микротемы? Если да, идём дальше. Сокращаем каждый абзац до двух-трёх предложений, оставляя только САМОЕ ГЛАВНОЕ. Чтобы получить за работу высокий балл, в каждом абзаце обязательно используйте приёмы сжатия. Существует несколько способов сокращения текста: 1. Способ обобщения Она достала из пакета морковь, картофель, рыбу, молоко и только потом ответила на мой вопрос. → Она достала из пакета продукты и только потом ответила на мой вопрос. 2. Способ исключения Камни Кремля могут звучать. У каждой стены и купола особый звук, а все вместе они сливаются в богатырскую симфонию, исполняемую огромным оркестром из труб золотых куполов Кремля. → Каждый камень, стена, купол Кремля имеет свой звук, который сливается в единую богатырскую симфонию. 3. Способ замены Дать согласие – согласиться; для того чтобы поступить – для поступления; привести доказательство – доказать. При сжатии текста избавляйтесь от оборотов, вводных слов и вводных конструкций, уточняющих членов предложения. От риторических вопросов тоже лучше избавляться, или же переводить их в повествовательное предложение. Пример: Возможно ли забыть об этом великом подвиге? → Невозможно забыть об этом великом подвиге. 4. Проверка текста Сократив свое изложение, перечитайте его ещё раз. Задайте себе несколько вопросов: — Получилось ли передать основную тему текста? — Не противоречит ли полученный текст оригиналу? — Удалось ли отразить в работе все три микротемы? — Логичен ли текст, связаны ли все три абзаца по смыслу? — Нет ли в изложении несжатых мест (вводных слов, деепричастных и причастных оборотов и т.д.)? Убедившись, что ваш текст соответствует требованиям, проверьте его на наличие ошибок. Подчеркните все слова, написание которых вызывает у вас сомнение и проверьте их в орфографическом словаре. Будьте внимательны при расстановке знаков препинания. Перепишите изложение в чистовик. Дополнительные советы Старайтесь грамотно распределять время. Заданию 1 рекомендуется уделить не более 40-60 минут. И главное: секрет успешной сдачи любого экзамена состоит в подготовке. Регулярно тренируйтесь на типовых заданиях, и вы сможете выработать необходимые навыки и умения. Желаем удачи на ОГЭ! на Ваш сайт. Подведение итогов означает дать краткий обзор основных моментов текста своими словами. Резюме всегда намного короче исходного текста. Составление резюме не требует критики или анализа источника — вы должны просто предоставить ясное, объективное и точное изложение наиболее важной информации и идей, не копируя текст из оригинала и не упуская ни одного из ключевых моментов. Есть много ситуаций, в которых вам, возможно, придется резюмировать статью или другой источник: Когда вы пишете академический текст, например эссе, исследовательскую работу или диссертацию, вы будете участвовать в работе других исследователей различными способами. Иногда вы можете использовать краткую цитату, чтобы подкрепить свою точку зрения; иногда вы можете перефразировать несколько предложений или абзацев. Но часто бывает уместно резюмировать всю статью или главу, если это особенно актуально для вашего собственного исследования, или сделать обзор источника, прежде чем анализировать или критиковать его. В любом случае цель резюмирования — дать читателю четкое представление об первоисточнике. Чтобы написать хорошее резюме, выполните следующие 4 шага. Вам следует прочитать статью несколько раз, чтобы убедиться, что вы полностью ее поняли. Часто бывает эффективно читать в три этапа: Есть несколько простых приемов, которые вы можете использовать для определения ключевых моментов во время чтения: Чтобы сделать текст более управляемым и понять его подпункты, разбейте его на более мелкие части. Если текст представляет собой научную статью, которая следует стандартной эмпирической структуре, она, вероятно, уже организована в четко обозначенные разделы, обычно включающие введение, методы, результаты и обсуждение. Другие типы статей не могут быть явно разделены на разделы. Но большинство статей и эссе будут построены вокруг серии подпунктов или тем. Попробуйте написать на полях рядом с каждым абзацем слово или фразу, описывающую содержание абзаца. Тогда вы сможете сразу увидеть, чему посвящена каждая часть статьи. Если несколько абзацев охватывают похожие или связанные темы, вы можете сгруппировать их в разделы. А теперь пора пройтись по каждой части и выделить наиболее важные моменты.Что вашему читателю нужно знать, чтобы понять общую аргументацию или вывод статьи? Имейте в виду, что в резюме не нужно перефразировать каждый абзац статьи. Ваша цель — выделить существенные моменты, исключив все, что можно считать справочной информацией или дополнительными деталями. В научной статье вы можете задать несколько простых вопросов, чтобы определить ключевые моменты каждой части: Если статья принимает другую форму, вам, возможно, придется более тщательно подумать о том, какие моменты наиболее важны для читателя, чтобы понять ее аргумент. В этом случае обратите особое внимание на тезисное утверждение — центральное утверждение, которое автор хочет, чтобы мы приняли, которое обычно появляется во введении, — и тематические предложения, которые выражают основную идею каждого абзаца. Теперь, когда вы знаете ключевые моменты, о которых идет речь в статье, вам нужно изложить их своими словами. Чтобы избежать плагиата и показать, что вы поняли статью, важно правильно перефразировать идеи автора. Не копировать и вставлять части статьи, даже не одно или два предложения. Лучший способ сделать это — отложить статью и написать свое собственное понимание ключевых моментов автора. Рассмотрим пример. Ниже мы резюмируем эту статью, в которой проводится научное исследование старой поговорки: «Яблоко в день убережет врача». Пример полного описания статьи Davis et al. (2015) намеревались эмпирически проверить популярную поговорку «яблоко в день убережет доктора.«Яблоки часто используются для обозначения здорового образа жизни, и исследования показали, что их питательные свойства могут быть полезны для различных аспектов здоровья. Уникальный подход авторов состоит в том, чтобы понять это высказывание буквально и спросить: люди, которые едят яблоки, реже пользуются услугами здравоохранения? Они полагают, что если такая связь действительно существует, продвижение потребления яблок может помочь снизить расходы на здравоохранение. В исследовании использовались общедоступные перекрестные данные Национального исследования здоровья и питания.Участники были разделены на категории любителей яблок или тех, кто не ел яблоки, на основании их самоотчетов о потреблении яблок в среднем за 24 часа. Они также были классифицированы как избегающие или не уклоняющиеся от использования медицинских услуг в прошлом году. Данные были статистически проанализированы, чтобы проверить, существует ли связь между потреблением яблок и несколькими зависимыми переменными: посещениями врача, пребыванием в больнице, использованием психиатрических услуг и использованием рецептурных лекарств. Хотя любители яблок несколько чаще избегали визитов к врачу, эта взаимосвязь не была статистически значимой после поправки на различные соответствующие факторы.Не было обнаружено связи между потреблением яблок и пребыванием в больнице или использованием психиатрических услуг. Однако было обнаружено, что те, кто ест яблоки, с несколько большей вероятностью избегали приема рецептурных лекарств. На основании этих результатов авторы приходят к выводу, что одно яблоко в день не отпугнет врача, но может отпугнуть фармацевта. Они предполагают, что это открытие может иметь значение для снижения затрат на здравоохранение, учитывая высокие ежегодные затраты на лекарства, отпускаемые по рецепту, и дешевизну яблок. Тем не менее, авторы также отмечают несколько ограничений исследования: наиболее важно то, что те, кто ест яблоки, скорее всего, будут отличаться от тех, кто не ест яблоки, в том, что может испортить результаты (например, те, кто ест яблоки, скорее всего, будут здоровыми. -сознательный). Чтобы установить причинно-следственную связь между употреблением яблок и отказом от лекарств, они рекомендуют экспериментальные исследования. Резюме статьи, подобное приведенному выше, будет подходящим для отдельного задания сводки.Однако часто вам нужно дать еще более краткое изложение статьи. Например, в обзоре литературы или исследовательской работе вы можете кратко резюмировать это исследование как часть более широкого обсуждения различных источников. В этом случае мы можем свести наше резюме еще дальше, чтобы включить только самую актуальную информацию. Пример краткого резюме статьи Используя данные национального опроса, Davis et al. (2015) проверили утверждение о том, что «яблоко в день убережет врача», и не нашли статистически значимых доказательств в поддержку этой гипотезы.Хотя люди, употреблявшие яблоки, были немного реже употребляли рецептурные лекарства, исследование не смогло продемонстрировать причинно-следственную связь между этими переменными. При резюмировании как части более крупного текста важно правильно процитировать источник резюме. Точный формат цитирования зависит от вашего стиля цитирования, но обычно он включает цитату в тексте и полную ссылку в конце статьи. Вы можете легко создавать свои цитаты и ссылки в APA или MLA с помощью наших бесплатных генераторов цитирования. Генератор цитирования APA Генератор цитирования MLA Наконец, прочтите статью еще раз, чтобы убедиться, что: Если вы обобщаете множество статей в рамках своей собственной работы, часто бывает полезно использовать средство проверки на плагиат, чтобы дважды проверить, что ваш текст полностью оригинален и правильно процитирован.Только убедитесь, что используете безопасный и надежный. Сравнение средств проверки на плагиат Резюме — это краткий обзор основных положений статьи или другого источника, полностью написанный вашими словами. Резюме всегда намного короче исходного текста. Длина резюме может варьироваться от нескольких предложений до нескольких абзацев; это зависит от длины статьи, которую вы резюмируете, и от цели резюме. Опытные студенты понимают, что , обобщая , определяя, что является наиболее важным, и пересказывая текст (или другие средства массовой информации) своими словами, является важным инструментом для успеха в колледже. В конце концов, если вы действительно знаете предмет, вы сможете резюмировать его. Если вы не можете резюмировать предмет, даже если вы запомнили все факты о нем, вы можете быть абсолютно уверены, что не выучили его.И, если вы действительно выучите предмет, вы все равно сможете резюмировать его через несколько месяцев или лет. Опытные учащиеся могут контролировать свое понимание текста, подводя итоги по мере чтения. Они понимают, что если они могут написать краткое изложение каждого абзаца из одного или двух предложений после его прочтения, то это хороший признак того, что они его правильно поняли. Если они не могут резюмировать основную идею абзаца, они знают, что понимание нарушено, и им нужно использовать стратегии исправления, чтобы восстановить понимание. В эссе Санта-Ана , автор Джоан Дидион главный тезис (, укажите основной пункт ). Согласно Дидиону «… отрывок 1 …» (пункт 3). Дидион также пишет: «… , отрывок 2, …» (пункт 8). Наконец, она заявляет: «… , отрывок 3, …» (пункт 12) Напишите последнее предложение, которое «завершает» ваше резюме; часто просто перефразируя суть. Когда вы подчеркиваете и комментируете текст, когда вы задаете себе вопросы о его содержании, когда вы разрабатываете набросок его структуры, вы устанавливаете свое понимание того, что читаете.Когда вы пишете резюме, вы демонстрируете свое понимание текста и передаете его своему читателю. Подводить итог — значит сокращать текст до его основных моментов и делать это своими словами. Включать каждую деталь не нужно и нежелательно. Вместо этого вам следует выделить только те элементы, которые вы считаете наиболее важными — основную идею (или тезис) и ее существенные опорные пункты, которые в исходном отрывке могли быть переплетены с менее важным материалом. Многие студенты ошибочно путают резюме с анализом. Это не одно и то же. Анализ — это обсуждение идей, методов и / или смысла текста. Резюме, с другой стороны, не требует от вас критики или ответа на идеи в тексте. Когда вы анализируете написанное, вы обычно кратко резюмируете его содержание, чтобы представить читателю идеи, которые затем будет анализировать ваше эссе, но резюме не заменяет самого анализа. Если вы, например, пишете литературный доклад, ваш учитель, вероятно, не хочет, чтобы вы просто писали краткое изложение сюжета. Вы можете включить в литературный документ очень краткое изложение, но ровно столько, сколько необходимо, чтобы сделать вашу собственную интерпретацию, ваш тезис ясным. Важно помнить, что краткое изложение — это не набросок или синопсис моментов, изложенных автором в том порядке, в котором автор их излагает. Напротив, краткое изложение — это квинтэссенция идей или аргументов текста.Это реконструкция основной точки или точек развития текста, начиная с тезиса или основной идеи, за которыми следуют точки или детали, которые поддерживают или развивают эту идею. Если текст организован линейно, вы можете написать резюме, просто перефразируя основные моменты от начала текста до конца. Однако не следует думать, что так будет всегда. Не все писатели используют такую простую структуру. Они могут не излагать тезис или основную идею сразу в начале, а постепенно наращивать ее, и они могут ввести точку развития в одном месте, а затем вернуться к ней позже в тексте. Тем не менее, для ясности в резюме следует изложить точку зрения автора в простой структуре. Чтобы написать хорошее резюме, вам, возможно, придется собрать второстепенные моменты или компоненты аргумента из разных мест в тексте, чтобы резюмировать текст организованным образом. Замечание, сделанное в начале эссе, а затем сделанное ближе к концу, возможно, потребуется сгруппировать в кратком изложении, чтобы кратко передать аргумент, который выдвигает автор. В конце концов, вы прочитаете, усвоите и восстановите текст в более короткой и лаконичной форме. Есть много случаев, когда вам придется написать резюме. Вам может быть поручено написать краткое изложение статьи или чтения на одной или двух страницах, или вас могут попросить включить краткое изложение текста как часть статьи для ответа или критического анализа. Кроме того, вы можете писать резюме статей в рамках процесса создания заметок и планирования исследовательской работы, и вы можете захотеть включить эти резюме или, по крайней мере, их части в свою статью. Автор исследовательской работы особенно зависит от резюме как средства ссылки на исходные материалы.Используя резюме в исследовательской работе, вы можете сжать широкий спектр информации, а также представить и объяснить актуальность ряда источников, имеющих отношение к одной и той же теме. Вы также можете резюмировать свою собственную статью во введении, чтобы представить краткий обзор идей, которые вы будете обсуждать в оставшейся части статьи. В зависимости от длины и сложности исходного текста, а также от вашей цели использования резюме, резюме может быть относительно кратким — короткий абзац или даже одно предложение — или довольно длинным — несколько абзацев или даже целая статья. Хорошее резюме должно быть всеобъемлющим, кратким, связным, и независимым . Эти качества объясняются ниже: Опытные студенты понимают, что , обобщая , определяя, что является наиболее важным, и пересказывая текст (или другие средства массовой информации) своими словами, является важным инструментом для успеха в колледже. В конце концов, если вы действительно знаете предмет, вы сможете резюмировать его. Если вы не можете резюмировать предмет, даже если вы запомнили все факты о нем, вы можете быть абсолютно уверены, что не выучили его. И, если вы действительно выучите предмет, вы все равно сможете резюмировать его через несколько месяцев или лет. Опытные учащиеся могут контролировать свое понимание текста, подводя итоги по мере чтения. Они понимают, что если они могут написать краткое изложение каждого абзаца из одного или двух предложений после его прочтения, то это хороший признак того, что они его правильно поняли.Если они не могут резюмировать основную идею абзаца, они знают, что понимание нарушено, и им нужно использовать стратегии исправления, чтобы восстановить понимание. В эссе Санта-Ана , автор Джоан Дидион главный тезис (, укажите основной пункт ). Согласно Дидиону «… отрывок 1 …» (п.3). Дидион также пишет: «… , отрывок 2, …» (пункт 8). Наконец, она заявляет: «… , отрывок 3, …» (пункт 12) Напишите последнее предложение, которое «завершает» ваше резюме; часто просто перефразируя суть. Резюме — это краткий обзор основных моментов текста. Цель резюме — быстро дать читателю или слушателю представление о том, о чем говорится в этом материале. Возможно, вам будет полезно составить резюме своей собственной работы, но чаще вы будете создавать резюме материалов других авторов, таких как статьи, пьесы, фильмы, лекции, рассказы или презентации. В какой-то момент ваших занятий вам, вероятно, дадут задание резюмировать конкретный текст, задание, единственной целью которого является резюме. Вы также будете использовать резюме более целостным образом, объединяя их вместе с пересказами, цитатами и своими собственными мнениями в более сложные тексты. Вы можете резюмировать по нескольким причинам, как во время учебы, так и в жизни вне образования. Вот несколько распространенных: Когда вы спрашиваете себя после прочтения статьи (и, возможно, даже чтения ее два или три раза): «О чем была эта статья?» и вы в конечном итоге записываете — по памяти, не возвращаясь к исходной статье, чтобы использовать ее язык или фразы — три вещи, которые выделялись как основные положения автора, которые вы резюмируете.Резюме имеют несколько ключевых характеристик. Вы хорошо подводите итоги, когда вы Резюме намного короче оригинального материала — общее правило состоит в том, что они должны составлять не более 10–15% длины оригинала, а часто они даже короче этого значения. При резюмировании статьи может быть легко и естественно включить в нее собственное мнение. Мы можем полностью согласиться или не согласиться с тем, что говорит этот автор, или мы можем захотеть сравнить его информацию с информацией, представленной в другом источнике, или мы можем захотеть поделиться своим собственным мнением по теме. Часто наши мнения сводятся к обобщению, даже если мы усердно работаем над их разделением. Однако эти мнения не являются резюме. Резюме должно только освещать основные моменты статьи. Сосредоточение внимания только на идеях, которые лучше всего подтверждают точку зрения, которую мы хотим высказать, или игнорирование идей, не поддерживающих эту точку зрения, может быть заманчивым. Однако у этого подхода есть две существенные проблемы: Первый , он больше некорректно представляет исходный текст, поэтому он вводит вашего читателя в заблуждение относительно идей, представленных в этом тексте. Резюме должно дать вашему читателю точное представление о том, чего он может ожидать, если мы возьмем для чтения исходную статью. Второй , это подрывает ваш собственный авторитет как автора из-за того, что не представляет эту информацию точно.Если читатели не могут доверять автору в том, что он точно представляет исходную информацию, они вряд ли будут доверять этому автору в том, чтобы он полностью и точно изложил разумную точку зрения. Как и в традиционных эссе, в резюме есть введение, основной текст и заключение. Внешний вид этих компонентов будет зависеть от цели написанного вами резюме. Введение, основная часть и заключение работы, сфокусированной специально на резюмировании чего-либо, будут немного отличаться от работы, где резюмирование не является основной целью. Одна из самых сложных частей создания резюме — дать понять, что это резюме чужой работы; эти идеи не являются вашими оригинальными идеями. Вы почти всегда начинаете резюме с введения к автору, статье и публикации, чтобы читатель знал, что мы собираемся прочитать. Эта информация снова появится в вашей библиографии, но также будет полезна здесь, чтобы читатель мог следить за беседой, происходящей в вашей статье. Вы захотите предоставить его в обоих местах. В работе, ориентированной на обобщение, это введение должно решить несколько задач: Так, например, если вам нужно было подвести итоги статьи Мэтью Хатсона Atlantic «За пределами пяти чувств» (можно найти на сайте www.theatlantic.com) введение к этому резюме может выглядеть примерно так: В своей статье в номере The Atlantic «За пределами пяти чувств» в июле 2017 года Мэтью Хатсон исследует способы, с помощью которых потенциальные технологии могут расширить наше сенсорное восприятие мира. Он отмечает, что некоторые технологии, такие как кохлеарные имплантаты, уже выполняют версию этого для людей, у которых нет полного доступа к одному из пяти органов чувств. Однако в большей части статьи он, кажется, больше интересуется тем, как технологии могут расширить способы, которыми мы воспринимаем вещи.Некоторые из этих технологий основаны на чувствах, которые можно увидеть в природе, таких как эхолокация, а другие кажутся более глубоко укоренившимися в научной фантастике. Однако во всех приведенных им примерах рассматривается, как добавление новых чувств к тем, которые мы уже испытываем, может изменить то, как мы воспринимаем окружающий мир. Тем не менее, вы, вероятно, будете чаще использовать резюме как один из компонентов работы с широким кругом целей (а не просто цель «резюмировать X»). Краткое введение в этих ситуациях, как правило, необходимо до Опять же, это будет выглядеть немного иначе в зависимости от цели сводной работы, которую вы выполняете. Независимо от того, как вы используете резюме, вы будете вводить основные идеи по всему тексту с помощью переходных формулировок, таких как «Один из самых важных моментов [автора]…» или «[Автор] больше всего беспокоит это решение…». Если вы отвечаете на задание «напишите краткое изложение X», основная часть этого резюме будет расширена по основным идеям, изложенным вами во введении к резюме, хотя все это все еще будет очень сжатым по сравнению с оригиналом.Какие ключевые моменты автор делает по поводу каждой из этих основных идей в целом? В зависимости от типа текста, который вы резюмируете, вы можете захотеть отметить, как поддерживаются основные идеи (хотя, опять же, будьте осторожны, чтобы не высказывать собственное мнение о тех поддерживающих источниках, которые известны). Когда вы подводите итоги с конечной целью, которая шире, чем просто резюме, в теле вашего резюме по-прежнему будет представлена идея из исходного текста, которая имеет отношение к вашей мысли (в сжатой форме и вашими словами). Поскольку в этом типе обобщения гораздо чаще резюмируют только одну идею или пункт из текста (а не все его основные моменты), важно убедиться, что вы понимаете более крупные моменты исходного текста. Например, вы можете обнаружить, что в статье приводится пример, который противоречит ее основной идее, чтобы продемонстрировать диапазон разговоров, происходящих по теме, которую она затрагивает. Однако этот противоположный момент не является основным в статье, поэтому простое обобщение этого одного противоположного примера не будет точным отражением идей и моментов в этом тексте. Для того, чтобы написать резюме, единственная цель, вот несколько идей для вашего заключения. Теперь, когда мы получили немного больше информации об основных идеях этой статьи, есть ли какие-то связи или неясные моменты, которые нужно связать, которые помогут вашему читателю полностью понять мысли, сделанные в этом тексте? Это то место, где их можно разместить. Это также хорошее место, чтобы сформулировать (или переформулировать) то, что вашим читателям наиболее важно помнить после прочтения вашего резюме. Если у вашего письма есть основная цель, отличная от резюме, ваше заключение должно Цель резюме — дать читателю четкое и объективное представление об исходном тексте. Наиболее важно то, что в резюме повторяются только основные моменты текста или лекции, без каких-либо примеров или деталей, таких как даты, числа или статистика. Рекомендации по написанию резюме статьи: Ваше резюме должно включать: Введение Заключительный параграф Адаптировано из «Руководства по использованию IN-TEXT CITATION в РЕЗЮМЕ (или ИССЛЕДОВАТЕЛЬСКОЙ ДОКУМЕНТЕ)» (открывается в новом окне) Кристин Бауэр-Рамазани, колледж Святого Михаила. Умение резюмировать то, что вы прочитали, увидели или услышали, — ценный навык, который вы, вероятно, использовали во многих письменных заданиях.Однако важно понимать, когда вы должны выходить за рамки описания, объяснения и перефразирования текстов и предлагать более сложный анализ. Этот раздаточный материал поможет вам отличить резюме от анализа и избежать ненадлежащего резюме в ваших академических статьях. Не обязательно. Но важно, чтобы вы помнили о своем задании и своей аудитории, когда пишете. Если ваше задание требует аргументации с тезисом и подтверждающими доказательствами — как это делают многие академические письменные задания — тогда вам следует ограничить количество резюме в своей статье.Вы можете использовать резюме, чтобы предоставить предысторию, подготовить почву или проиллюстрировать подтверждающие доказательства, но будьте очень краткими: несколько предложений должны помочь. Большая часть вашей статьи должна быть сосредоточена на ваших аргументах. (Наши материалы по аргументам помогут вам составить хороший аргумент.) Иногда бывает полезно составить краткое изложение того, что вы знаете по своей теме, прежде чем приступить к составлению настоящего документа. Если вы не знакомы с материалом, который анализируете, вам может потребоваться обобщить прочитанное, чтобы понять, что вы читаете, и привести свои мысли в порядок.Как только вы выясните, что вы знаете о предмете, вам будет легче решить, о чем вы хотите спорить. Вы также можете попробовать другие действия перед написанием, которые помогут вам разработать собственный анализ. Наброски, фрирайтинг и составление карт облегчают изложение ваших мыслей на странице. (Ознакомьтесь с нашими раздаточными материалами по мозговому штурму, чтобы узнать о некоторых предлагаемых методах.) Многие писатели слишком полагаются на резюме, потому что это то, что им легче всего написать.Если вас останавливает трудная письменная подсказка, краткое изложение сюжета «Великого Гэтсби» может быть более привлекательным, чем смотреть на компьютер в течение трех часов и думать, что сказать об использовании Ф. Скоттом Фицджеральдом цветовой символики. В конце концов, сюжет — это самая легкая для понимания часть произведения. Нечто подобное может случиться даже тогда, когда то, о чем вы пишете, не имеет сюжета: если вы не совсем понимаете аргумент автора, может показаться, что проще всего просто повторить то, что он сказал. Чтобы написать более аналитическую статью, вам может потребоваться просмотреть текст или фильм, о котором вы пишете, с акцентом на элементы, которые имеют отношение к вашей диссертации.Если возможно, внимательно обдумайте свое письменное задание перед чтением, просмотром или прослушиванием материала, о котором вы будете писать, чтобы ваше знакомство с этим материалом было более целенаправленным. (Предлагаем раздаточный материал по чтению перед письмом.) Читая эссе, задайте себе следующие вопросы: «Да» на любой из этих вопросов может быть признаком того, что вы подводите итоги. Если вы ответите утвердительно на вопросы ниже, это признак того, что в вашей статье может быть больше анализа (что обычно хорошо): Некоторые фразы являются предупреждающими знаками резюме. Следите за этими: Вот пример вводного абзаца, содержащего ненужное резюме. Суммирующие предложения выделены курсивом: Вот как вы можете изменить абзац, чтобы сделать его более эффективным введением: В этой версии абзаца упоминаются название книги, автор, обстановка и рассказчик, чтобы читатель мог вспомнить текст. И это очень похоже на резюме, но абзац быстро переходит к основной теме автора: обстановке и ее отношению к основным темам книги. Затем абзац завершается конкретным тезисом автора о символизме белого, серого и зеленого. Анализ требует разбиения чего-либо — например, рассказ, стихотворение, пьесу, теорию или аргумент — на части, чтобы вы могли понять, как эти части работают вместе, образуя целое. В идеале вам следует начать анализировать произведение во время чтения или просмотра, а не ждать, пока вы не закончите — это может помочь вам делать заметки во время чтения. Ваши заметки могут касаться основных тем или идей, которые вы заметили, а также всего, что вас интригует, озадачивает, волнует или раздражает.Помните, что аналитическое письмо выходит за рамки очевидного, чтобы обсудить вопросы о том, как и почему, поэтому задавайте себе эти вопросы во время чтения. «Справочник святого Мартина» (приведенный ниже список цитируется со стр. 38 пятого издания) побуждает читателей предпринять следующие шаги для анализа текста: После того, как вы написали черновик, вы можете задать себе несколько вопросов по поводу написанного: «Что я хочу сказать?» или «О чем я говорю в этой статье?» Если вы не можете ответить на эти вопросы, значит, вы не пошли дальше обобщения.Вы также можете подумать о том, какая часть вашего письма основана на ваших собственных идеях или аргументах. Если вы сообщаете только о чьих-то идеях, вы, вероятно, не предлагаете анализа. Это зависит от обстоятельств. Если вы пишете критику литературного произведения, фильма или драматического спектакля, вам не обязательно раскрывать большую часть сюжета. Смысл в том, чтобы позволить читателям решить, хотят ли они получить от этого удовольствие. Если вы все же резюмируете, сделайте это кратким и по существу. Вместо того, чтобы говорить своим читателям, что пьеса, книга или фильм «скучны», «интересны» или «действительно хороши», скажите им конкретно, о каких частях произведения вы говорите.Также важно выйти за рамки прилагательных и объяснить, как работа достигла своего эффекта (чем она была интересна?) И почему, по вашему мнению, автор / режиссер хотел, чтобы аудитория отреагировала определенным образом. (У нас есть специальный раздаточный материал по написанию обзоров, который предлагает больше советов.) Если вы пишете обзор академической книги или статьи, для вас может быть важно обобщить основные идеи и дать обзор организации, чтобы ваши читатели могли решить, соответствует ли это их конкретным исследовательским интересам. Если вы не уверены, сколько (если есть) резюме требуется для конкретного задания, попросите совета у своего инструктора. Мы ознакомились с этими работами при написании данного раздаточного материала. Это не полный список ресурсов по теме раздаточного материала, и мы рекомендуем вам провести собственное исследование, чтобы найти дополнительные публикации. Пожалуйста, не используйте этот список в качестве модели для формата вашего собственного списка литературы, так как он может не соответствовать используемому вами стилю цитирования.Инструкции по форматированию цитат см. В руководстве по цитированию библиотек UNC. Мы периодически пересматриваем эти советы и приветствуем отзывы. Барнет, Сильван. 2015. Краткое руководство по написанию статей об искусстве , 11-е изд. Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall. Корриган, Тимоти. 2014. Краткое руководство по написанию о фильмах , 9-е изд. Нью-Йорк: Пирсон. Лансфорд, Андреа А. 2015. Справочник Св. Мартина , 8-е изд. Бостон: Бедфорд / Сент-Мартинс. Зинссер, Уильям. 2001. О хорошем письме: Классическое руководство по написанию документальной литературы , 6-е изд. Нью-Йорк: Куилл. Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 4.0 License. Сделать подарок Большинство твёрдых веществ имеет кристаллическое строение, которое характеризуется строго определённым расположением частиц. Если соединить частицы условными линиями, то получится пространственный каркас, называемый кристаллической решёткой. Точки, в которых размещены частицы кристалла, называют узлами решётки. В узлах воображаемой решётки могут находиться атомы, ионы или молекулы. В зависимости от природы частиц, расположенных в узлах, и характера связи между ними различают четыре типа кристаллических решёток: ионную, металлическую, атомную и молекулярную. Ионными называют решётки, в узлах которых находятся ионы. Их образуют вещества с ионной связью. В узлах такой решётки располагаются положительные и отрицательные ионы, связанные между собой электростатическим взаимодействием. Ионные кристаллические решётки имеют соли, щёлочи, оксиды активных металлов. Ионы могут быть простые или сложные. Например, в узлах кристаллической решётки хлорида натрия находятся простые ионы натрия Na+ и хлора Cl−, а в узлах решётки сульфата калия чередуются простые ионы калия K+ и сложные сульфат-ионы SO42−. Связи между ионами в таких кристаллах прочные. Поэтому ионные вещества твёрдые, тугоплавкие, нелетучие. Такие вещества хорошо растворяются в воде. Рис. \(1\). Кристаллическая решётка хлорида натрия Рис. \(2\). Кристаллы хлорида натрия Металлическими называют решётки, которые состоят из положительных ионов и атомов металла и свободных электронов. Их образуют вещества с металлической связью. В узлах металлической решётки находятся атомы и ионы (то атомы, то ионы, в которые легко превращаются атомы, отдавая свои внешние электроны в общее пользование). Такие кристаллические решётки характерны для простых веществ металлов и сплавов. Температуры плавления металлов могут быть разными (от \(–37\) °С у ртути до двух-трёх тысяч градусов). Но все металлы имеют характерный металлический блеск, ковкость, пластичность, хорошо проводят электрический ток и тепло. Рис. \(3\). Металлическая кристаллическая решётка Рис. \(4\). Изделие из металла Атомными называют кристаллические решётки, в узлах которых находятся отдельные атомы, соединённые ковалентными связями. Такой тип решётки имеет алмаз — одно из аллотропных видоизменений углерода. К веществам с атомной кристаллической решёткой относятся графит, кремний, бор и германий, а также сложные вещества, например, карборунд SiC и кремнезём, кварц, горный хрусталь, песок, в состав которых входит оксид кремния(\(IV\)) SiO2. Таким веществам характерны высокая прочность и твёрдость. Так, алмаз является самым твёрдым природным веществом. У веществ с атомной кристаллической решёткой очень высокие температуры плавления и кипения. Атомные кристаллы практически нерастворимы. Рис. \(5\). Кристаллическая решётка алмаза Рис. \(6\). Алмаз Молекулярными называют решётки, в узлах которых находятся молекулы, связанные слабым межмолекулярным взаимодействием. Несмотря на то, что внутри молекул атомы соединены очень прочными ковалентными связями, между самими молекулами действуют слабые силы межмолекулярного притяжения. Поэтому молекулярные кристаллы имеют небольшую прочность и твёрдость, низкие температуры плавления и кипения. Многие молекулярные вещества при комнатной температуре представляют собой жидкости и газы. Такие вещества летучи. Например, кристаллические иод и твёрдый оксид углерода(\(IV\)) («сухой лёд») испаряются, не переходя в жидкое состояние. Некоторые молекулярные вещества имеют запах. Такой тип решётки имеют простые вещества в твёрдом агрегатном состоянии: благородные газы с одноатомными молекулами (He,Ne,Ar,Kr,Xe,Rn), а также неметаллы с двух- и многоатомными молекулами (h3,O2,N2,Cl2,I2,O3,P4,S8). Молекулярную кристаллическую решётку имеют также вещества с ковалентными полярными связями: вода — лёд, иод, твёрдые аммиак, кислоты, оксиды большинства неметаллов. Большинство органических соединений тоже представляют собой молекулярные кристаллы (нафталин, сахар, глюкоза). Рис. \(7\). Кристаллическая решётка иода Рис. \(8\). Иод Если известно строение вещества, то можно предсказать его свойства. Попробуем определить, каковы примерно температуры плавления у фторида натрия, фтороводорода и фтора. У фторида натрия — ионная кристаллическая решётка. Значит, его температура плавления будет высокой. Экспериментальные данные подтверждают эти предположения: температуры плавления NaF, HF и F2 составляют соответственно \(995\) °С, \(–83\) °С, \(–220\) °С. Источники: Рис. 1.Кристаллическая решётка хлорида натрия https://upload.wikimedia.org/wikipedia/commons/e/e9/Sodium-chloride-3D-ionic.png Рис. 2. Кристаллы хлорида натрия https://cdn.pixabay.com/photo/2015/09/24/17/08/crystal-955935_960_720.jpg Рис. 4. Изделие из металла https://cdn.pixabay.com/photo/2013/07/12/17/22/database-152091_960_720.png Рис. 6. Алмаз https://cdn.pixabay.com/photo/2014/10/24/08/09/diamond-500872_960_720.jpg Рис. 8. Иод https://upload.wikimedia.org/wikipedia/commons/7/7c/Iod_kristall. Естествознание, 10 класс Урок 32. Состав – структура — свойства Перечень вопросов, рассматриваемых в теме: Глоссарий по теме: Генезис (греч. — genesis) — происхождение, становление и развитие, результатом которого является определенное состояние изучаемого объекта. Генезис природных и социальных явлений интересовал и интересует философию и науку с античности до наших дней (философский словарь). Структу́ра (от лат. Structūra — «строение»), или строе́ние — внутреннее устройство чего-либо / Ожегов С.И. и Шведова Н.Ю. Толковый словарь русского языка. Качественный состав – это перечень всех образующих вещество химических элементов. Количественный состав – это число атомов каждого химического элемента в составе мельчайшей частицы вещества – его молекулы. Запись, выражающая качественный и количественный состав вещества с помощью хими-ческих знаков, называется химической формулой. Закон постоянства состава: Многие вещества, независимо от нахождения в природе или способа получения их в лаборатории, всегда имеют один и тот же состав. Химическая связь – это совокупность сил, связывающих и удерживающих атомы или другие частицы в устойчивых структурах (молекулах и др.). Гибридизация атомных орбиталей – это их перемешивание в пространстве с целью выравнивания и обеспечения наиболее полного перекрывания. Аллотропия – это явление, при котором один и тот же химический элемент образует несколько простых веществ. Изомерия – это явление, при котором существуют вещества, имеющие одинаковый состав, но разное химическое строение, а потому и свойства. Вещества, имеющие одинаковый состав, но разное химическое строение, а потому и разные свойства, называются изомерами. Основная и дополнительная литература по теме урока: Основные источники: Дополнительные источники: Теоретический материал для самостоятельного изучения Учение о молекуле лежит в основе всех других обобщений, так что современную химию можно по праву назвать молекулярной химией. А. М. Бутлеров, (1828-1886), русский химик, создатель теории химического строения органических веществ, учёный-пчеловод и лепидоптеролог, общественный деятель Установление взаимосвязи между свойствами веществ и строением молекул составляет фундаментальную научную проблему химии. В ходе химических реакций происходит перегруппировка атомов в молекулах реагентов и образуются новые соединения. Поэтому одна из фундаментальных химических проблем состоит в выяснении порядка расположения атомов (связей) в исходных соединениях и характера изменений при образовании из них других соединений. Мы знаем, что молекула представляет собой микрочастицу, образованную из атомов и способную к самостоятельному существованию, обладающую его главными химическими свойствами. Она имеет постоянный состав входящих в нее атомных ядер и фиксированное число электронов и обладает совокупностью свойств, позволяющих отличать молекулы одного вида от молекул другого. Число атомов в молекуле может быть различным: от двух до сотен тысяч. Молекулы простых веществ состоят из одинаковых атомов, сложных – из разных атомов. Существует большое количество соединений, молекулы которых состоят из многих тысяч атомов — макромолекулы. Первые представления о структуре молекул основывались на химическом анализе. Со времен М.В. Ломоносова (1741), который высказал мысль, что свойства вещества зависят от рода, числа и расположения «элементов» (атомов), составляющих его «корпускулу» (молекулу), представления усложнялись по мере накопления знаний о химических свойствах веществ. Применение основных законов химии позволило определить число и тип атомов, из которых состоит молекула данного соединения; эта информация содержится в химической формуле, составленной на основе качественного и количественного анализа, а также закона постоянства состава (Ж. «Пространственное строение частиц в зависимости от типа гибридизации». Приведите свои примеры веществ. Тип гибриди-зации центрального атома Пространственное строение частицы Условное изображение Примеры sp Линейное ВеС12, ZnCl2, С2Н2 sp2 Плоскостно-тригональное BCl3, N03—,CO32-, C2H4, C6H6 sp3 Тетраэдр CH4, NH4+, SO42-, CC14 sp3 Тригональная пирамида NH3, H30+ sp3 Угловое Н20 Чем различаются понятия «свойства молекулы» и «свойства вещества»? Подсказка. В состав молекулы может входить различное число атомов. Так, молекулы благородных газов одноатомны, молекулы таких веществ, как водород, азот, — двухатомны, воды — трехатомны и т.д. Молекулы наиболее сложных веществ — высших белков и нуклеиновых кислот — построены их такого количества атомов, которое измеряется сотнями тысяч. При этом атомы могут соединяться друг с другом не только в различных соотношениях, но и различным образом. Поэтому при сравнительно небольшом числе химических элементов число различных веществ очень велико. Все ли вещества состоят из молекул? Подсказка. Для ответа на этот вопрос обратитесь к строению таких веществ как металлы, алмаз, графит, хлорид натрия. Не во всех случаях частицы, образующие вещество, представляют собой молекулы. Многие вещества в твердом и жидком состоянии, например, большинство солей, имеют не молекулярную, а ионную структуру. Некоторые вещества имеют атомное строение. В веществах, имеющих ионное или атомное строение, носителем химических свойств являются не молекулы, а те комбинации ионов или атомов, которые образуют данное вещество. Вспомните, какие типы связей и кристаллических решеток существуют? Чем определяются свойства веществ? В зависимости от природы частиц, образующих кристалл, различают атомные, молекулярные, ионные и металлические кристаллические решетки Таблица 2 «Зависимость свойств веществ от типа связи и кристаллических решеток» Тип кристаллической решетки Характерный вид химической связи Частицы, располагающиеся в узлах решетки Примеры веществ и их характерные свойства Атомная Ковалентная неполярная Атомы Некоторые неметаллы, оксиды и др. Молекулярная Ковалентная неполярная и полярная Молекулы Неметаллы, оксиды, кислоты и др. Разнообразны по агрегатному состоянию и другим свойствам. Легко переходят из одного агрегатного состояния в другое. Летучи, легкоплавки. Ионная Ионная Ионы Соли, щелочи и др. Твердые вещества с высокими температурами плавления. Малолетучи. Хорошо растворяются в полярных растворителях. Металлическая Металлическая Атомы и катионы металла Металлы. Твердые вещества (кроме ртути) с металлическим блеском. Ковки, пластичны. Обладают тепловой и электрической проводимостью. В настоящее время известен не один десяток миллионов разнообразных веществ. При этом все они образованы значительно меньшим числом химических элементов (современной науке достоверно известно 112 химических элементов). Как объяснить такое разнообразие веществ? Что такое аллотропия? Приведите примеры аллотропных модификаций известных вам химических элементов. Дайте сравнительную характеристику их свойств. Явление аллотропии характерно для большинства неметаллов и многих металлов. При этом образуемые ими аллотропные модификации могут различаться по составу, строению и типу кристаллических решеток. Между аллотропными модификациями одного элементы возможны взаимные переходы. При этом все они имеют разную устойчивость. Как правило, при одних и тех же условиях более стабильна лишь одна из модификаций, обладающая минимальным запасом энергии. Остальные модификации при этих же условиях будут неустойчивы и рано или поздно перейдут в более устойчивую форму. Что такое изомерия? Изомерия – это явление, при котором существуют вещества, имеющие одинаковый состав, но разное химическое строение, а потому и свойства. Вещества, имеющие одинаковый состав, но разное химическое строение, а потому и разные свойства, называются изомерами. Приведите примеры известных вам изомеров. Укажите, в чем заключаются различия их строения и свойств. Явление изомерии характерно и для неорганических, и для органических веществ. Однако особенно ярко оно проявляется среди органических соединений, являясь важнейшей причиной их многообразия. Таблица Изомерия органических соединений Виды изомерии органических соединений Структурная изомерия Углеродного скелета Положения функциональных групп Положения кратных связей Межклассовая Пространственная изомерия Конформационная Геометрическая Оптическая Проиллюстрируйте указанные в таблице виды изомерии примерами. Выводы: Примеры и разбор решения заданий тренировочного модуля: Задание 1. Вещество, в узлах кристаллической решетки которого находятся ионы, это… Тип вариантов ответов: (Текстовые, Графические, Комбинированные). а) CaС12; б) NH3; в) I2; г) C (графит). Правильный вариант/варианты (или правильные комбинации вариантов): а Подсказка: В узлах ионных решеток располагаются, чередуясь, положительно и отрицательно заряженные ионы. К соединениям с ионной связью, образующим ионные решетки, относится большинство солей и небольшое число оксидов. Задание 2. Соедините попарно прямоугольники с овалами так, чтобы каждому типу гибридизации атомных орбиталей углерода соответствовал пример молекулы. Правильный вариант: Подсказка: Тип гибридизации атомных орбиталей углерода определяется числом заместителей при этом атоме углерода: Подумай, ответь, выполни… 1. Приведите примеры веществ с молекулярным и немолекулярным строением. Как эти вещества различаются по свойствам? Вещества молекулярного строения: кислород, водород, азот, углекислый газ, вода, спирт, эфир, сера, белый фосфор. Вещества немолекулярного строения: сульфид железа, поваренная соль, алюминий, медь, железо. Вещества с молекулярным строением имеют низкие температуры плавления и кипения, часто летучи и имеют запах. При обычных условиях – это газы, жидкости или легкоплавкие твердые вещества. Вещества с немолекулярным строением имеют высокие температуры плавления и кипения. Эти вещества твердые, нелетучие и не имеют запаха. 2. По физическим свойствам вещества можно определить, какое строение оно имеет — молекулярное или немолекулярное. Если вещество имеет низкую температуру плавления и кипения, летучее или имеет запах, при обычных условиях является газом, жидкостью или легкоплавким твердым веществом, то, как правило, это вещество имеет молекулярное строение. Например, при обычных условиях аммиак — газ с резким запахом, спирт — летучая жидкость с характерным запахом, парафин и сахар — легкоплавкие твердые вещества. Следовательно, аммиак, спирт, парафин и сахар имеют молекулярное строение. Если вещество имеет высокую температуру плавления и кипения, является твердым, нелетучим и не имеет запаха, то, как правило, это вещество имеет немолекулярное строение. Например, поваренная соль, железо, графит — твердые тугоплавкие вещества, не имеющие запаха. 3. Какие типы кристаллических решеток вам известны? Приведите примеры веществ, имеющих соответствующие кристаллические решетки. Составьте схему «Типы кристаллических решеток». 4. Углекислый газ при нормальном давлении переходит в твердое состояние при температуре около -70 ºС, а речной песок (кремнезем) плавится при температуре около 1700 ºС. Какие выводы о строении этих веществ в твердом состоянии можно сделать? Так как углекислый газ при обычных условиях находится в газообразном состоянии, а в твердое состояние переходит при низкой температуре, следовательно, в твердом состоянии он имеет молекулярное строение. Так как оксид кремния при обычных условиях находится в твердом состоянии, а плавится при очень высокой температуре, следовательно, в твердом состоянии он имеет немолекулярное строение. Тестовые задания 1. 1) молекулярная 2) атомная 3) ионная Ответ: 1). 2. Установите соответствие между типом кристаллической решетки вещества и его свойствами. Ответ: 1) Б; 2) В; 3) А. Скачать Примеры ионной кристаллической решетки Информация о файле: Кристаллические решетки, состоящие из ионов, называются ионными. Тэги: ионной решетки примеры кристаллической Недавние поисковые запросы: примерная форма устава неккомерческого фонда примеры задач на движение с отставанием примерный доклад на защиту дипломной работы Тип решетки, Виды частиц в узлах решетки, Вид связи между частицами, Примеры веществ, Физические свойства веществ. Ионная, Ионы, Ионная приведите примеры с ионной кристаллической решёткой???помогите пожалуйста. помогите пожалуйста. *твоя зайка* Ученик (112), Вопрос на 3 мая 2013 г. — В качестве примеров веществ с ионным типом кристаллической решетки можно назвать соли металлов (хлорид магния, хлорид бария, Условие задачи: 10. Приведите два примера веществ с ионной кристаллической решеткой. Задача из. решебника «Химия. 9 класс» Л.С.Гузей и др. для 9 февр. 2013 г. — Пользователь anonim задал вопрос в категории Естественные науки и получил на него 4 ответа. Зайцева Лариса Александровна учитель химии МОБУСОШ № 9 г. Класс: 11 ( УМК И.И. Новошинский, Н.С.Новошинская) Аннотация Конспект и презентация к уроку химии Типы кристаллических решеток» в 11 классе общеобразовательной школы УМК И.И. Новошинский, Н.С.Новошинская. Урок- изучения нового материала, который позволяет формировать представление о единстве строения веществ, взаимосвязи строения и свойств вещества. Имеются задания разного уровня сложности, индивидуальные и групповые, которые позволяют повышать интерес учащихся, закреплять навыки практической работы. Тема: Типы кристаллических решеток Задачи: Образовательная: сформировать понятия о кристаллическом и аморфном состоянии твердых тел, ознакомить учащихся с различными типами кристаллических решеток, установить зависимость физических свойств кристалла от характера химической связи в кристалле и типа кристаллической решетки, дать учащимся основные представления о влиянии природы химической связи и типов кристаллических решеток на свойства вещества, дать учащимся представление о законе постоянства состава. Воспитательная: продолжить формирование мировоззрения учащихся, рассмотреть взаимное влияние компонентов целого- структурных частиц веществ, в результате которого появляются новые свойства, воспитывать умения организовать свой учебный труд, соблюдать правила работы в коллективе. Развивающая: развивать познавательный интерес школьников, используя проблемные ситуации; совершенствовать умения учащихся устанавливать причинно-следственную зависимость физических свойств веществ от химической связи и типа кристаллической решетки, предсказывать тип кристаллической решетки на основе физических свойств вещества. Оборудование: Периодическая система Д.И.Менделеева, коллекция “Металлы”, неметаллы: сера, поваренная соль, пластилин; Презентация “Кристаллические решетки”, модели кристаллических решеток разных типов (поваренной соли, алмаза и графита, углекислого газа и йода, металлов), образцы пластмасс и изделий из них, стекло, пластилин, смолы, воск, жевательная резинка, шоколад, компьютер, мультимедийная установка, видеопыт “Возгонка бензойной кислоты”. Ход урока I.Опрос учащихся 1.Для того, чтобы познакомиться с кристаллическими решетками мы должны вспомнить, что такое: физическое тело, химическая связь, виды связей: ковалентная( полярная и неполярная), ионная, металлическая, водородная 2.Составить схемы образования связи в веществах: N2, H2S, CaBr2 3.Выполните тест (проверка теста) II. Изучение нового материала 1.Вещества находятся в различных агрегатных состояниях. Приведите примеры веществ, которые при различных температурах могут существовать во всех трех агрегатных состояниях. Ответ: Вода. При обычных условиях вода находится в жидком состоянии, при понижении температуры ниже 00С вода переходит в твердое состояние — лед, а при повышении температуры до 1000С мы получим водяной пар (газообразное состояние). Учитель (дополнение): Любое вещество можно получить в твердом, жидком и газообразном виде. Проблемный вопрос: металлы, пластилин, соль, шоколад, жевательная резинка, сера, образцы пластмасс, воск. Что общего в строении этих веществ, чем они отличаются? Делаются предположения. Если ученики затрудняются, то с помощью учителя приходят к выводу, что пластилин в отличие от металлов и хлорида натрия не имеет определенной температуры плавления — он (пластилин) постепенно размягчается и переходит в текучее состояние. Таким образом, различают два вида твердых веществ: аморфные и кристаллические. (слайд 5,6) У аморфных веществ нет определенной температуры плавления, и расположение частиц в них строго не упорядочено. Кристаллические вещества имеют строго определенную температуру плавления и, главное, характеризуются правильным расположением частиц, из которых они построены.(слайд 7) Кристаллическая решетка – пространственный каркас вещества.(слайд8) Свойства веществ в твердом состоянии зависят от типа кристаллической решетки (прежде всего от того, какие частицы находятся в ее узлах), что, в свою очередь, обусловлено типом химической связи в данном веществе. Вывод: Прослеживается логическая последовательность, взаимосвязь явлений в природе: Строение атома—ЭО—Виды химической связи—Тип кристаллической решетки—Свойства веществ. (слайд 10). В зависимости от вида частиц и от характера связи между ними различают четыре типа кристаллических решеток: ионные, молекулярные, атомные и металлические. (Cлайд 11). 1. Молекулярная кристаллическая решетка (работа с таблицей и текстом параграфа) 1. Характеристика У веществ с молекулярным строением в узлах кристаллической решетки находятся молекулы с прочными ковалентными связями между атомами. В то же время отдельные молекулы взаимосвязаны гораздо слабее, что делает молекулярный кристалл довольно непрочным. (слайд 12) 2. Аналогия Можно уподобить эту структуру группе семейных пар (рис. 1). В каждой паре супругов связывают прочные узы брака (подобно прочной связи атомов внутри молекулы), а вот отношения между парами носят поверхностный характер: они могут дружить семьями, испытывать дружеские чувства, но довольно свободно могут обойтись и друг без друга. Рис. 1 Группа супружеских пар (аналогия молекулярного кристалла) (слайд 13) 2. Ионная кристаллическая решетка 1. Характеристика У веществ с ионной решеткой в узлах расположены разноименно заряженные ионы, удерживаемые силами электростатического притяжения. (слайд 14) 2. Аналогия Уподобим эту структуру группе расположенных в шахматном порядке мужчин и женщин (рис. 2). Пусть мужчины символизируют катионы, а женщины — анионы. Тогда каждый человек оказывается в зоне действия обаяния окружающих его представителей противоположного пола, к которым он (она) в силу закона притяжения противоположностей испытывает интерес. Интерес этот одинаково выражен во всех направлениях, поскольку на рисунке — холостые мужчины и незамужние женщины. Этим и объясняется повышенная прочность ионного кристалла. Рис. 2. Романтическая сила влечения (аналогия ионного кристалла)(слайд15) 3. Атомная кристаллическая решетка 1. В узлах атомной кристаллической решетки находятся атомы, связанные прочными ковалентными связями в протяженную пространственную сеть. В этом случае структура отличается таким внутренним единством, что можно сказать, что весь кристалл представляет одну молекулу. 2. Аналогия. Представим эту структуру в виде гимнастической пирамиды. Рис. 3. Гимнастическая пирамида (аналогия атомного кристалла)(слайд 17) Каждый гимнаст на ней символизирует атом углерода, связанный четырьмя ковалентными связями с соседними атомами. Целостность структуры поддерживается исключительно благодаря усилиям каждого из гимнастов. Таким образом, зависимость людей друг от друга в этой ситуации больше, чем на любом из предыдущих рисунков (это и является аналогией повышенной прочности атомного кристалла). Пирамида (см. рис. 3) демонстрирует также высокую взаимосвязанность узлов атомной кристаллической решетки: стоит одному из гимнастов ослабить только одну связку, и вся структура может рухнуть. 4. Металлическая кристаллическая решетка 1. Характеристика Этим типом кристаллической решетки обладают металлы с металлической химической связью. (слайд18) 2. Аналогия Для иллюстрации строения металлов в твердом состоянии найдена особенно экстравагантная аналогия. Группа мужчин (рис. 4) изображает катионы металлов (узлы металлической кристаллической решетки). Все пространство между ними заполнено летающими пчелами (это, понятно, свободные электроны). Рисунок убедительно иллюстрирует силы, удерживающие одноименно заряженные катионы в узлах решетки: при всем желании деваться некуда – всюду пчелы! Рис. 4. Среди пчел (аналогия структуры металла)(слайд 19) Вывод: Существует следующая закономерность: если известно строение веществ, то можно предсказать их свойства, или наоборот: если известны свойства веществ, то можно определить строение. (слайд 21) Работа с текстом параграфа, таблицами «Типы кристаллических решеток», «Зависимость свойств веществ от вида химической связи» Задание для работы в группе: 1 группа 1. 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с молекулярной кристаллической решеткой? 2 группа 1. Какие должны быть отличительные свойства веществ с ионной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с ионной кристаллической решеткой? 3 группа 1. Какие должны быть отличительные свойства веществ с атомной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с атомной кристаллической решеткой? 4 группа 1. Какие должны быть отличительные свойства веществ с металлической решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с металлической решеткой? (слайд 22,23,24) Зачеркните по вертикали, горизонтали, диагонали вещества, имеющие одинаковую кристаллическую решетку. Закрепление: 1. Вид частиц в ионной решетке: а) ионы в) молекулы б) атомы г) атом-ионы 2. Характер химической связи в атомной решетке: а) металлическая в) ионная б) ковалентная г) сила межмолекул. взаимодействия 3. Прочность связи в молекулярной решетке а) очень прочная в) слабая б) прочная г) разной прочности 4. Агрегатное состояние у веществ с ионной решеткой: а) твердое в) жидкое б) газообразное 5. а) металлической в) атомной б) молекулярной г) ионной 6. Пластичностью обладают вещества с: а) металлической в) молекулярной б) ионной г) атомной 7. Кремний имеет решетку: а) молекулярную в) ионную б) атомную б) металлическую 8. Щелочи имеют решетку: а) молекулярную в) ионную б) металлическую 9. Вода имеет решетку: а) молекулярную в) ионную б) атомную б) металлическую III. Какие классификации веществ вы узнали? Как вы понимаете термин кристаллическая решетка. В каком агрегатном состоянии вещества имеют кристаллические решетки? Какие типы кристаллических решеток вы теперь знаете? О какой закономерности строения и свойств веществ вы узнали? Д/З§11, упр 1-3 Приложение № 1 Задание для работы в группе: 1 группа 1. Какие должны быть отличительные свойства веществ с молекулярной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с молекулярной кристаллической решеткой? __________________________________________________________________________ Задание для работы в группе: 2 группа 1. Какие должны быть отличительные свойства веществ с ионной решеткой? 2. Каково их агрегатное состояние? 3. ___________________________________________________________________________ Задание для работы в группе: 3 группа 1. Какие должны быть отличительные свойства веществ с атомной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с атомной кристаллической решеткой? ___________________________________________________________________________ Задание для работы в группе: 4 группа 1. Какие должны быть отличительные свойства веществ с металлической решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с металлической решеткой? Приложение № 2 Тест № 1 Вариант 1 1.Вещество, образованное ионной связью: а) NH3, б) Li3N в) N2 г)NO2 2. а)Br2, б)SO2 , в)Al, г)P4 3.Формула, вещества образованного металлической связью: а)O3 б)S8 в)C г)Ca 4.Соединениями с ковалентной неполярной и ковалентной полярной связью являются соответственно: а)метан и хлорметан; б)азот и аммиак; б)метан и графит; г)алмаз и графит. 5.Ионной связью образовано каждое из двух веществ: а)HCl , CO2 б)Ba, Co в)Mg3N2 ,BaS, г)NaCl, PH3 6.Установите соответствие между названием элемента и общей формулой его высшего оксида: а) кремний; 1)Э2О5; б)хром; 2)Э2О7; в)фосфор; 3)ЭО2; г) бром; 4)ЭО; 5)ЭО3; 6)Э2О3. Вариант 2 1. Вещество, образованное ковалентной неполярной связью: а) NH3, б) Li3N в) N2 г)NO2 2. а)Br2, б)SO2 , в)AlСL3, г)P4 3. Формула, вещества образованного ковалентной полярной связью: а)O3 б)S8 в)CО г)Ca 4. Соединениями с ковалентной полярной и ковалентной неполярной связью являются соответственно: а)метан и хлорметан; б)азот и аммиак; б)метан и хлор; г)алмаз и графит. 5.Металлической связью образовано каждое из двух веществ: а)HCl , CO2 б)Ba, Co в)Mg3N2 ,BaS, г)NaCl, PH3 6.Установите соответствие между формулой частицы и числом общих электронных пар в ней: а)H2O, 1)одна; б) NH4+, 2)две; в)N2, 3)три; г)CO2 4)четыре. Приложение 3 Тест № 2 1. Вид частиц в ионной решетке: а) ионы в) молекулы б) атомы г) атом-ионы 2. а) металлическая в) ионная б) ковалентная г) сила межмолекул. взаимодействия 3. Прочность связи в молекулярной решетке а) очень прочная в) слабая б) прочная г) разной прочности 4. Агрегатное состояние у веществ с ионной решеткой: а) твердое в) жидкое б) газообразное 5. Очень тугоплавкими являются вещества с решеткой: а) металлической в) атомной б) молекулярной г) ионной 6. а) металлической в) молекулярной б) ионной г) атомной 7. Кремний имеет решетку: а) молекулярную в) ионную б) атомную б) металлическую 8. Щелочи имеют решетку: а) молекулярную в) ионную б) металлическую 9. Вода имеет решетку: а) молекулярную в) ионную б) атомную б) металлическую Крестики – нолики. Показать выигрышный путь, состоящий из формул с ионной связью. Опрос учащихся 1.Для того, чтобы познакомиться с кристаллическими решетками мы должны вспомнить, что такое: физическое тело, химическая связь, виды связей: ковалентная (полярная и неполярная), ионная, металлическая, водородная 2.Составить схемы образования связи в веществах: N2, H2S, CaBr2 3.Выполните тест (проверка теста) Закрепление изученного материала 1.Вещества находятся в различных агрегатных состояниях. Приведите примеры веществ, которые при различных температурах могут существовать во всех трех агрегатных состояниях. Ответ: Вода. При обычных условиях вода находится в жидком состоянии, при понижении температуры ниже 00С вода переходит в твердое состояние — лед, а при повышении температуры до 1000С мы получим водяной пар (газообразное состояние). Учитель (дополнение): Любое вещество можно получить в твердом, жидком и газообразном виде. Кроме воды – это металлы, которые при нормальных условиях находятся в твердом состоянии, при нагревании начинают размягчаться, и при определенной температуре(tпл) переходят в жидкое состояние — плавятся. При дальнейшем нагревании, до температуры кипения, металлы начинают испаряться, т.е. переходить в газообразное состояние. Любой газ можно перевести в жидкое и твердое состояние, понижая температуру: например, кислород, который при температуре (-1940С) превращается в жидкость голубого цвета, а при температуре (-218,80С) затвердевает в снегообразную массу, состоящую из кристаллов синего цвета. Сегодня на уроке мы будем рассматривать твердое состояние вещества. Проблемный вопрос: металлы, пластилин, соль, шоколад, жевательная резинка, сера, образцы пластмасс, воск. Что общего в строении этих веществ, чем они отличаются? Делаются предположения. Таким образом, различают два вида твердых веществ: аморфные и кристаллические. (слайд 5,6) У аморфных веществ нет определенной температуры плавления, и расположение частиц в них строго не упорядочено. Кристаллические вещества имеют строго определенную температуру плавления и, главное, характеризуются правильным расположением частиц, из которых они построены.(слайд 7) Кристаллическая решетка – пространственный каркас вещества. Свойства веществ в твердом состоянии зависят от типа кристаллической решетки (прежде всего от того, какие частицы находятся в ее узлах), что, в свою очередь, обусловлено типом химической связи в данном веществе.(слайд 9) Вывод: Прослеживается логическая последовательность, взаимосвязь явлений в природе: Строение атома—>ЭО—>Виды химической связи—>Тип кристаллической решетки—>Свойства веществ. (слайд 10). В зависимости от вида частиц и от характера связи между ними различают четыре типа кристаллических решеток: ионные, молекулярные, атомные и металлические. (Cлайд 11). 1. Молекулярная кристаллическая решетка (работа с таблицей и текстом параграфа) 1. Характеристика У веществ с молекулярным строением в узлах кристаллической решетки находятся молекулы с прочными ковалентными связями между атомами. В то же время отдельные молекулы взаимосвязаны гораздо слабее, что делает молекулярный кристалл довольно непрочным. 2. Аналогия Можно уподобить эту структуру группе семейных пар (рис. 1). В каждой паре супругов связывают прочные узы брака (подобно прочной связи атомов внутри молекулы), а вот отношения между парами носят поверхностный характер: они могут дружить семьями, испытывать дружеские чувства, но довольно свободно могут обойтись и друг без друга. Рис. 1 Группа супружеских пар (аналогия молекулярного кристалла) (слайд 13) 2. Ионная кристаллическая решетка 1. Характеристика У веществ с ионной решеткой в узлах расположены разноименно заряженные ионы, удерживаемые силами электростатического притяжения. (слайд 14) 2. Аналогия Уподобим эту структуру группе расположенных в шахматном порядке мужчин и женщин (рис. 2). Пусть мужчины символизируют катионы, а женщины — анионы. Тогда каждый человек оказывается в зоне действия обаяния окружающих его представителей противоположного пола, к которым он (она) в силу закона притяжения противоположностей испытывает интерес. Рис. 2. Романтическая сила влечения (аналогия ионного кристалла)(слайд15) 3. Атомная кристаллическая решетка 1. Характеристика В узлах атомной кристаллической решетки находятся атомы, связанные прочными ковалентными связями в протяженную пространственную сеть. В этом случае структура отличается таким внутренним единством, что можно сказать, что весь кристалл представляет одну молекулу. 2. Аналогия. Представим эту структуру в виде гимнастической пирамиды. Рис. 3. Гимнастическая пирамида (аналогия атомного кристалла)(слайд 17) Каждый гимнаст на ней символизирует атом углерода, связанный четырьмя ковалентными связями с соседними атомами. Целостность структуры поддерживается исключительно благодаря усилиям каждого из гимнастов. Таким образом, зависимость людей друг от друга в этой ситуации больше, чем на любом из предыдущих рисунков (это и является аналогией повышенной прочности атомного кристалла). Пирамида (см. рис. 3) демонстрирует также высокую взаимосвязанность узлов атомной кристаллической решетки: стоит одному из гимнастов ослабить только одну связку, и вся структура может рухнуть. 4. Металлическая кристаллическая решетка 1. Характеристика Этим типом кристаллической решетки обладают металлы с металлической химической связью. (слайд18) 2. Аналогия Для иллюстрации строения металлов в твердом состоянии найдена особенно экстравагантная аналогия. Группа мужчин (рис. 4) изображает катионы металлов (узлы металлической кристаллической решетки). Все пространство между ними заполнено летающими пчелами (это, понятно, свободные электроны). Рисунок убедительно иллюстрирует силы, удерживающие одноименно заряженные катионы в узлах решетки: при всем желании деваться некуда – всюду пчелы! Рис. 4. Среди пчел (аналогия структуры металла)(слайд 19) Вывод: Существует следующая закономерность: если известно строение веществ, то можно предсказать их свойства, или наоборот: если известны свойства веществ, то можно определить строение. (слайд 21) Работа с текстом параграфа, таблицами «Типы кристаллических решеток», «Зависимость свойств веществ от вида химической связи» Задание для работы в группе: 1 группа 1. Какие должны быть отличительные свойства веществ с молекулярной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с молекулярной кристаллической решеткой? 2 группа 1. Какие должны быть отличительные свойства веществ с ионной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с ионной кристаллической решеткой? 3 группа 1. Какие должны быть отличительные свойства веществ с атомной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с атомной кристаллической решеткой? 4 группа 1. Какие должны быть отличительные свойства веществ с металлической решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с металлической решеткой? (слайд 22,23,24) Зачеркните по вертикали, горизонтали, диагонали вещества, имеющие одинаковую кристаллическую решетку. Закрепление: 1. Вид частиц в ионной решетке: 9. Вода имеет решетку: Подведение итогов урока Какие классификации веществ вы узнали? Как вы понимаете термин кристаллическая решетка. В каком агрегатном состоянии вещества имеют кристаллические решетки? Какие типы кристаллических решеток вы теперь знаете? О какой закономерности строения и свойств веществ вы узнали? Д/З §56 изучить, упр 4 стр. 198 Тема: Типы кристаллических решеток Задачи: Образовательная: сформировать понятия о кристаллическом и аморфном состоянии твердых тел, ознакомить учащихся с различными типами кристаллических решеток, установить зависимость физических свойств кристалла от характера химической связи в кристалле и типа кристаллической решетки, дать учащимся основные представления о влиянии природы химической связи и типов кристаллических решеток на свойства вещества, дать учащимся представление о законе постоянства состава. Воспитательная: продолжить формирование мировоззрения учащихся, рассмотреть взаимное влияние компонентов целого- структурных частиц веществ, в результате которого появляются новые свойства, воспитывать умения организовать свой учебный труд, соблюдать правила работы в коллективе. Развивающая: развивать познавательный интерес школьников, используя проблемные ситуации; совершенствовать умения учащихся устанавливать причинно-следственную зависимость физических свойств веществ от химической связи и типа кристаллической решетки, предсказывать тип кристаллической решетки на основе физических свойств вещества. Оборудование: Периодическая система Д.И.Менделеева, коллекция “Металлы”, неметаллы: сера, поваренная соль, пластилин; Презентация “Кристаллические решетки”, модели кристаллических решеток разных типов (поваренной соли, алмаза и графита, углекислого газа и йода, металлов), образцы пластмасс и изделий из них, стекло, пластилин, смолы, воск, жевательная резинка, шоколад, компьютер, мультимедийная установка, видеопыт “Возгонка бензойной кислоты”. Ход урока I.Опрос учащихся 1.Для того, чтобы познакомиться с кристаллическими решетками мы должны вспомнить, что такое: физическое тело, химическая связь, виды связей: ковалентная( полярная и неполярная), ионная, металлическая, водородная 2.Составить схемы образования связи в веществах: N2, h3S, CaBr2 3.Выполните тест (проверка теста) II. Изучение нового материала 1.Вещества находятся в различных агрегатных состояниях. Приведите примеры веществ, которые при различных температурах могут существовать во всех трех агрегатных состояниях. Ответ: Вода. При обычных условиях вода находится в жидком состоянии, при понижении температуры ниже 00С вода переходит в твердое состояние — лед, а при повышении температуры до 1000С мы получим водяной пар (газообразное состояние). Учитель (дополнение): Любое вещество можно получить в твердом, жидком и газообразном виде. Кроме воды – это металлы, которые при нормальных условиях находятся в твердом состоянии, при нагревании начинают размягчаться, и при определенной температуре(tпл) переходят в жидкое состояние — плавятся. При дальнейшем нагревании, до температуры кипения, металлы начинают испаряться, т.е. переходить в газообразное состояние. Любой газ можно перевести в жидкое и твердое состояние, понижая температуру: например, кислород, который при температуре (-1940С) превращается в жидкость голубого цвета, а при температуре (-218,80С) затвердевает в снегообразную массу, состоящую из кристаллов синего цвета. Сегодня на уроке мы будем рассматривать твердое состояние вещества. Проблемный вопрос: металлы, пластилин, соль, шоколад, жевательная резинка, сера, образцы пластмасс, воск. Что общего в строении этих веществ, чем они отличаются? Делаются предположения. Если ученики затрудняются, то с помощью учителя приходят к выводу, что пластилин в отличие от металлов и хлорида натрия не имеет определенной температуры плавления — он (пластилин) постепенно размягчается и переходит в текучее состояние. Таков, например, шоколад, который тает во рту, или жевательная резинка, а также стекло, пластмассы, смолы, воск (при объяснении учитель демонстрирует классу образцы этих веществ). Такие вещества называют аморфными, а металлы и хлорид натрия — кристаллические. Таким образом, различают два вида твердых веществ: аморфные и кристаллические. (слайд 5,6) У аморфных веществ нет определенной температуры плавления, и расположение частиц в них строго не упорядочено. Кристаллические вещества имеют строго определенную температуру плавления и, главное, характеризуются правильным расположением частиц, из которых они построены.(слайд 7) Кристаллическая решетка – пространственный каркас вещества.(слайд8) Свойства веществ в твердом состоянии зависят от типа кристаллической решетки (прежде всего от того, какие частицы находятся в ее узлах), что, в свою очередь, обусловлено типом химической связи в данном веществе.(слайд 9) Вывод: Прослеживается логическая последовательность, взаимосвязь явлений в природе: Строение атома—>ЭО—>Виды химической связи—>Тип кристаллической решетки—>Свойства веществ. (слайд 10). В зависимости от вида частиц и от характера связи между ними различают четыре типа кристаллических решеток: ионные, молекулярные, атомные и металлические. (Cлайд 11). 1. Молекулярная кристаллическая решетка (работа с таблицей и текстом параграфа) 1. Характеристика У веществ с молекулярным строением в узлах кристаллической решетки находятся молекулы с прочными ковалентными связями между атомами. В то же время отдельные молекулы взаимосвязаны гораздо слабее, что делает молекулярный кристалл довольно непрочным. (слайд 12) 2. Аналогия Можно уподобить эту структуру группе семейных пар (рис. 1). В каждой паре супругов связывают прочные узы брака (подобно прочной связи атомов внутри молекулы), а вот отношения между парами носят поверхностный характер: они могут дружить семьями, испытывать дружеские чувства, но довольно свободно могут обойтись и друг без друга. Рис. 1 Группа супружеских пар (аналогия молекулярного кристалла) (слайд 13) 2. Ионная кристаллическая решетка 1. Характеристика У веществ с ионной решеткой в узлах расположены разноименно заряженные ионы, удерживаемые силами электростатического притяжения. (слайд 14) 2. Аналогия Уподобим эту структуру группе расположенных в шахматном порядке мужчин и женщин (рис. 2). Пусть мужчины символизируют катионы, а женщины — анионы. Тогда каждый человек оказывается в зоне действия обаяния окружающих его представителей противоположного пола, к которым он (она) в силу закона притяжения противоположностей испытывает интерес. Интерес этот одинаково выражен во всех направлениях, поскольку на рисунке — холостые мужчины и незамужние женщины. Этим и объясняется повышенная прочность ионного кристалла. Рис. 2. Романтическая сила влечения (аналогия ионного кристалла)(слайд15) 3. Атомная кристаллическая решетка 1. Характеристика В узлах атомной кристаллической решетки находятся атомы, связанные прочными ковалентными связями в протяженную пространственную сеть. В этом случае структура отличается таким внутренним единством, что можно сказать, что весь кристалл представляет одну молекулу. 2. Аналогия. Представим эту структуру в виде гимнастической пирамиды. Рис. 3. Гимнастическая пирамида (аналогия атомного кристалла)(слайд 17) Каждый гимнаст на ней символизирует атом углерода, связанный четырьмя ковалентными связями с соседними атомами. Целостность структуры поддерживается исключительно благодаря усилиям каждого из гимнастов. Таким образом, зависимость людей друг от друга в этой ситуации больше, чем на любом из предыдущих рисунков (это и является аналогией повышенной прочности атомного кристалла). Пирамида (см. рис. 3) демонстрирует также высокую взаимосвязанность узлов атомной кристаллической решетки: стоит одному из гимнастов ослабить только одну связку, и вся структура может рухнуть. 4. Металлическая кристаллическая решетка 1. Характеристика Этим типом кристаллической решетки обладают металлы с металлической химической связью. (слайд18) 2. Аналогия Для иллюстрации строения металлов в твердом состоянии найдена особенно экстравагантная аналогия. Группа мужчин (рис. 4) изображает катионы металлов (узлы металлической кристаллической решетки). Все пространство между ними заполнено летающими пчелами (это, понятно, свободные электроны). Рисунок убедительно иллюстрирует силы, удерживающие одноименно заряженные катионы в узлах решетки: при всем желании деваться некуда – всюду пчелы! Рис. 4. Среди пчел (аналогия структуры металла)(слайд 19) Вывод: Существует следующая закономерность: если известно строение веществ, то можно предсказать их свойства, или наоборот: если известны свойства веществ, то можно определить строение. (слайд 21) Работа с текстом параграфа, таблицами «Типы кристаллических решеток», «Зависимость свойств веществ от вида химической связи» Задание для работы в группе: 1 группа 1. Какие должны быть отличительные свойства веществ с молекулярной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с молекулярной кристаллической решеткой? 2 группа 1. Какие должны быть отличительные свойства веществ с ионной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с ионной кристаллической решеткой? 3 группа 1. Какие должны быть отличительные свойства веществ с атомной решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с атомной кристаллической решеткой? 4 группа 1. Какие должны быть отличительные свойства веществ с металлической решеткой? 2. Каково их агрегатное состояние? 3. Приведите примеры веществ с металлической решеткой? (слайд 22,23,24) Зачеркните по вертикали, горизонтали, диагонали вещества, имеющие одинаковую кристаллическую решетку. Закрепление: 1. Вид частиц в ионной решетке: а) ионы в) молекулы б) атомы г) атом-ионы 2. Характер химической связи в атомной решетке: а) металлическая в) ионная б) ковалентная г) сила межмолекул. взаимодействия 3. Прочность связи в молекулярной решетке а) очень прочная в) слабая б) прочная г) разной прочности 4. Агрегатное состояние у веществ с ионной решеткой: а) твердое в) жидкое б) газообразное 5. Очень тугоплавкими являются вещества с решеткой: а) металлической в) атомной б) молекулярной г) ионной 6. Пластичностью обладают вещества с: а) металлической в) молекулярной б) ионной г) атомной 7. Кремний имеет решетку: а) молекулярную в) ионную б) атомную б) металлическую 8. Щелочи имеют решетку: а) молекулярную в) ионную б) металлическую 9. Вода имеет решетку: а) молекулярную в) ионную б) атомную б) металлическую III.Подведение итогов урока Какие классификации веществ вы узнали? Как вы понимаете термин кристаллическая решетка. В каком агрегатном состоянии вещества имеют кристаллические решетки? Какие типы кристаллических решеток вы теперь знаете? О какой закономерности строения и свойств веществ вы узнали? Д/З§11, упр 1-3 Ионный кристалл состоит из ионов, связанных вместе электростатическим притяжением. Расположение ионов в правильной геометрической структуре называется кристаллической решеткой. Примерами таких кристаллов являются галогениды щелочных металлов, к которым относятся: Эти твердые вещества, как правило, довольно твердые и имеют высокие температуры плавления, что отражает сильные взаимодействия между ионами с противоположным зарядом.Точное расположение ионов в решетке зависит от размера ионов в кристалле. Свойства NaCl отражают сильные взаимодействия, существующие между ионами. Это хороший проводник электричества в расплавленном состоянии (расплавленное состояние), но очень плохой в твердом состоянии. При плавлении подвижные ионы переносят заряд через жидкость. Кристаллы NaCl характеризуются сильным поглощением инфракрасного (ИК) излучения и имеют плоскости, вдоль которых они легко раскалываются.Структурно каждый ион в хлориде натрия окружен шестью соседними ионами с противоположным зарядом. Полученная кристаллическая решетка относится к типу, известному как «простая кубическая», что означает, что точки решетки равномерно разнесены во всех трех измерениях, а все углы ячеек равны 90 °. Как может один ион натрия, окруженный шестью ионами хлора (или наоборот) соответствовать простейшей (эмпирической) формуле NaCl? Ответ заключается в том, что каждый из этих шести ионов хлора находится в центре своего собственного октаэдра, вершины которого определяются шестью соседними ионами натрия.Может показаться, что это соответствует Na 6 Cl 6 , но обратите внимание, что центральный ион натрия, показанный на диаграмме, может претендовать только на одну шестую долю каждого из своих соседних хлорид-иона. Таким образом, формула NaCl не просто простейшая формула, а правильно отражает стехиометрию соединения 1: 1. Как и во всех ионных структурах, здесь нет различимых «молекулярных» единиц, соответствующих простейшей формуле NaCl. Хлорид натрия, как практически все соли, представляет собой более энергетически предпочтительную конфигурацию натрия и хлора, чем элементы по отдельности. Поскольку ионные соли имеют более низкую энергетическую конфигурацию, чем их отдельные элементы, реакции с образованием ионных твердых частиц имеют тенденцию к высвобождению энергии.Например, когда натрий и хлор реагируют с образованием хлорида натрия: Na (тв) + ½Cl 2 (г) → NaCl (тв) + 404 кДж Выделение 404 кДж энергии показывает, что образование твердого хлорида натрия является экзотермическим. Согласно второму закону термодинамики, высвобождаемая энергия распространяется в окружающую среду и, следовательно, не может вызвать обратную реакцию. Эта необратимость является основной причиной того, что хлорид натрия более стабилен, чем входящие в его состав элементы. Когда ионы натрия и хлорида реагируют с образованием NaCl, выделяется 787 кДж / моль энергии: Na + (г) + Cl — (г) → NaCl (т) + 787 кДж Эта большая величина возникает из-за силы кулоновской силы между ионами противоположного заряда. Эта энергия является одним из определений энергии решетки: энергия, выделяемая, когда ионное твердое тело образуется из газообразных ионов, связывающихся вместе. Обратите внимание, что фактическое значение изменения энтальпии (ΔH o ) отрицательно (-787 кДж / моль). Экзотермичность таких реакций приводит к стабильности ионных твердых веществ. То есть энергия необходима, чтобы разбить ионное твердое тело на составляющие элементы. (Это не следует путать с диссоциацией ионов соединения в растворе. Это другой процесс.) Эта эндотермическая реакция дает начало другому определению энергии решетки: энергии, которая должна быть затрачена на разложение ионного твердого вещества на газообразное состояние. ионы. Энергия решетки, в основном из-за кулоновского притяжения между каждым ионом и его ближайшими соседями (шесть в случае NaCl), на самом деле является суммой всех взаимодействий внутри кристалла.Энергии решетки нельзя измерить напрямую, но их можно оценить по энергиям других процессов. Наиболее энергетически стабильными твердыми телами, состоящими из идентичных молекулярных единиц, обычно являются те, в которых имеется минимум пустого пространства. Они известны как плотноупакованные структуры и бывают нескольких видов. В ионных твердых телах даже простейшей стехиометрии 1: 1 положительные и отрицательные ионы обычно настолько различаются по размеру, что упаковка часто оказывается гораздо менее эффективной.Это может привести к тому, что твердое тело примет геометрию решетки, отличную от той, которая проиллюстрирована выше для NaCl. Рассмотрим структуру хлорида цезия CsCl. Радиус иона Cs + составляет 168 пм (по сравнению с 98 пм для Na + ) и никак не может поместиться в октаэдрическое отверстие простой кубической решетки хлорид-ионов (ионный радиус 181 пм). Поэтому решетка CsCl принимает другое устройство. Два типа решетчатых структур, примером которых являются NaCl и CsCl, обнаруживаются в большом количестве других ионных твердых веществ 1: 1, и эти названия используются в общем для описания структур этих других соединений. Существует много других фундаментальных структур решетки (не все кубические), но двух описанных здесь достаточно, чтобы проиллюстрировать то, что отношение радиусов (отношение радиусов положительного иона к отрицательному) играет важную роль в структурах простые ионные твердые тела. Boundless проверяет и курирует высококачественный контент с открытой лицензией из Интернета. Этот конкретный ресурс использовал следующие источники: Навыки для развития Ионы — это электрически заряженные атомы или молекулы. Катионы заряжены положительно, а анионы заряжены отрицательно. Ионы образуются, когда атомы приобретают или теряют валентные электроны. Поскольку электроны заряжены отрицательно, атом, потерявший один или несколько электронов, станет заряженным положительно; атом, который получает один или несколько электронов, становится отрицательно заряженным. Ионная связь — это притяжение между положительно и отрицательно заряженными ионами. Эти противоположно заряженные ионы притягиваются друг к другу, образуя ионные сетки или решетки .Электростатика объясняет, почему это происходит: противоположные заряды притягиваются, а одинаковые — отталкиваются. Когда многие ионы притягиваются друг к другу, они образуют большие упорядоченные кристаллические решетки, в которых каждый ион окружен ионами противоположного заряда. Обычно, когда металлы реагируют с неметаллами, электроны передаются от металлов к неметаллам. Металлы образуют положительно заряженные ионы, а неметаллы образуют отрицательно заряженные ионы. Свойства ионных соединений вытекают из упорядоченной структуры кристаллической решетки прочно связанных заряженных частиц, из которых они состоят.Ионные соединения имеют тенденцию к высоким температурам плавления и кипения, потому что притяжение между ионами в решетке очень сильное. Выдвижение ионов из решетки разрушает структуру, поэтому ионные соединения имеют тенденцию быть хрупкими, а не податливыми. Ионные соединения не проводят электричество в твердом состоянии, потому что ионы не могут свободно перемещаться по решетке; однако, когда ионные соединения растворены, они могут диссоциировать на отдельные ионы, которые свободно перемещаются через раствор и, следовательно, хорошо проводят электричество. Ионные связи образуются при химической реакции металлов и неметаллов. По определению, металл относительно стабилен, если он теряет электроны, образуя полную валентную оболочку, и становится положительно заряженным. Точно так же неметалл становится стабильным, приобретая электроны, чтобы заполнить свою валентную оболочку и стать отрицательно заряженным. Когда металлы и неметаллы реагируют, металлы теряют электроны, передавая их неметаллам, которые их приобретают. Следовательно, образуются ионы, которые мгновенно притягиваются друг к другу — ионная связь.В общем ионном соединении положительные и отрицательные заряды должны быть сбалансированы, потому что электроны не могут быть созданы или уничтожены, а только перенесены. Таким образом, общее количество электронов, потерянных катионными частицами, должно равняться общему количеству электронов, приобретенных анионными частицами. Ионные соединения удерживаются вместе электростатическими силами, которые в классической физике описываются Законом Кулона . Согласно этому закону, энергия электростатического притяжения (\ (E \)) между двумя заряженными частицами пропорциональна величине зарядов (\ (Q) 1 \) и \ (Q_2 \)) и обратно пропорциональна величине заряда. межъядерное расстояние между частицами (\ (r \)): \ [E \ propto \ dfrac {Q_ {1} Q_ {2}} {r} \ label {Eq1a} \] Энергия притяжения (\ (E \)) является разновидностью потенциальной энергии , так как она основана на положении заряженных частиц относительно друг друга.Если две частицы имеют противоположные заряды (как в ионных соединениях), значение (\ (E \)) будет отрицательным, что означает, что энергия выделяется за счет сближения частиц, то есть частицы естественным образом притягиваются друг с другом. Согласно закону Кулона, чем больше величина зарядов на каждой частице, тем сильнее будет притяжение. Так, например, Mg 2 + и O 2- будут иметь более сильное притяжение, чем Na + и Cl —, из-за большего заряда.Кроме того, чем ближе друг к другу заряды, тем сильнее притяжение. Следовательно, ионы меньшего размера также образуют более сильные ионные связи. В ионной решетке одновременно взаимодействуют более двух заряженных частиц, высвобождая количество энергии, известное как энергия решетки . Энергия решетки не совсем такая, как предсказывается законом Кулона, но применяются те же общие принципы электростатического притяжения. В ионном соединении значение энергии решетки соответствует силе ионной связи. Пример \ (\ PageIndex {1} \): хлорид натрия Например, в реакции Na (натрия) и Cl (хлора) каждый атом Cl отнимает один электрон от атома Na. Следовательно, каждый Na становится катионом Na + , а каждый атом Cl становится анионом Cl — . Из-за их противоположных зарядов они притягиваются друг к другу, образуя ионную решетку. Формула (отношение положительных и отрицательных ионов) в решетке \ (\ ce {NaCl} \). \ [\ ce {2Na (s) + Cl2 (g) \ rightarrow 2NaCl (s)} \ nonumber \] Эти ионы расположены в твердом \ (\ ce {NaCl} \) в регулярном трехмерном расположении (или решетке): Решетка NaCl.(слева) трехмерная структура и (справа) простой двухмерный срез через решетку. Изображения использованы с разрешения Википедии и Майка Блабера. Хлор имеет высокое сродство к электронам, а натрий — низкую энергию ионизации. Таким образом, хлор получает электрон от атома натрия. Это можно представить с помощью точечных символов Льюиса, показывающих валентные электроны в каждом атоме (здесь мы будем рассматривать один атом хлора, а не Cl 2 ): Изогнутая стрелка указывает на перенос электрона от натрия к хлору с образованием иона металла Na + и иона хлорида Cl — .Каждый ион теперь имеет полную валентную оболочку из восьми электронов: Если ионная связь становится сильнее для соединений с более высокозарядными ионами, почему натрий теряет только один электрон, образуя Na + , а не, скажем, Na 2+ ? Число электронов, передаваемых между ионами, зависит не только от энергии, выделяемой при образовании решетки, но и от энергии, необходимой для отрыва электронов от одного атома и добавления их к другому.Другими словами, энергия решетки, высвобождаемая при образовании ионного соединения, должна быть сбалансирована с требуемой энергией ионизации и сродством к электрону при образовании ионов. Поскольку ион Na + имеет электронную конфигурацию благородного газа, удаление следующего электрона из этого стабильного расположения потребует больше энергии, чем выделяется во время образования решетки (натрий I 2 = 4560 кДж / моль). Таким образом, натрий присутствует в ионных соединениях как Na + , а не Na 2+ .Точно так же добавление электрона для заполнения валентной оболочки (и достижения электронной конфигурации благородного газа) экзотермично или лишь слегка эндотермично. Чтобы добавить дополнительный электрон в новую подоболочку , требуется огромная энергия — больше, чем энергия решетки. Таким образом, мы находим Cl — в ионных соединениях, но не Cl 2 — . Как правило, элементы основной группы образуют только ионы с ближайшей электронной конфигурацией благородного газа — в противном случае энергии решетки было бы недостаточно для компенсации энергии ионизации / сродства к электрону Типичные значения энергии решетки могут компенсировать такие большие значения, как I 3 для валентных электронов (т.е.е. может оторвать до 3 валентных электронов от катионов). Поскольку для большинства переходных металлов требуется удаление более 3 электронов для достижения сердцевины из благородного газа, они не встречаются в ионных соединениях с сердцевиной из благородного газа. Переходный металл всегда сначала теряет электроны из более высокой подоболочки «s», а затем теряет электроны из нижней d-подоболочки. (Оставшиеся электроны в незаполненной d подоболочке являются причиной ярких цветов, наблюдаемых во многих соединениях переходных металлов!) Например, ионы железа , а не образуют ядро благородного газа: Некоторые ионы металлов могут образовывать ядро псевдо благородного газа (и быть бесцветными), например: Примечание. Атомы серебра и кадмия потеряли 5s электронов при достижении ионного состояния.Помните, что атомы всегда сначала теряли электроны из подоболочки с наибольшим квантовым числом n (то есть за 5 секунд до 4d). Когда из атома образуется положительный ион, электроны всегда теряются первыми из подоболочки с наибольшим главным квантовым числом. Не все ионные соединения образуются только из двух элементов. Существует много многоатомных ионов , в которых два или более атома связаны ковалентными связями.Они образуют стабильную группу, несущую заряд (положительный или отрицательный). Группа атомов в целом действует как заряженная разновидность, образуя ионное соединение с противоположно заряженным ионом. Многоатомные ионы могут быть как положительными, так и отрицательными, например: Принципы ионной связи с многоатомными ионами такие же, как и с одноатомными ионами.Противоположно заряженные ионы объединяются, образуя кристаллическую решетку, высвобождая энергию решетки. В зависимости от формы и заряда многоатомных ионов эти соединения могут образовывать кристаллические решетки с интересными и сложными структурами. Ионные связи образуются, когда положительно и отрицательно заряженные ионы притягиваются электростатическими силами. Рассмотрим одну пару ионов, один катион и один анион. Насколько сильной будет сила их притяжения? Мы можем переписать закон Кулона (Equation \ ref {Eq1a}) количественно для любых двух заряженных частиц: \ [E = k \ dfrac {Q_ {1} Q_ {2}} {r} \ label {Eq1b} \] , где заряд каждого иона представлен символом \ ( Q \) , а межъядерное расстояние между частицами представлено символом (\ (r \)).Константа пропорциональности k равна 2,31 × 10 −28 Дж · м. Это значение \ ( k \) включает заряд одного электрона (1,6022 × 10 −19 Кл) для каждого иона. Уравнение также можно записать, используя заряд каждого иона, выраженный в кулонах (Кл), включенный в константу. В этом случае константа пропорциональности k равна 8,999 × 109 Дж · м / C 2 . В приведенном примере Q 1 = +1 (1,6022 × 10 −19 C) и Q 2 = −1 (1.6022 × 10 −19 С). Если \ (Q_1 \) и \ (Q_2 \) имеют противоположные знаки (как в \ (\ ce {NaCl} \), например, где Q 1 равно +1 для Na + и Q 2 равно -1 для Cl — ), тогда E отрицательно, что означает, что энергия выделяется , когда противоположно заряженные ионы сближаются с бесконечного расстояния, чтобы сформировать изолированную ионную пару. Энергия всегда высвобождается при образовании связи и, соответственно, всегда требуется энергия для разрыва связи. Как показано зеленой кривой в нижней половине рисунка \ (\ PageIndex {1} \), максимальная энергия будет выделяться, когда ионы бесконечно близки друг к другу, при r = 0. Поскольку ионы занимают пространство и имеют структуру с положительным ядром, окруженным электронами, однако они не могут быть бесконечно близко друг к другу. На очень коротких расстояниях отталкивающие электрон-электронные взаимодействия между электронами на соседних ионах становятся сильнее, чем притягивающие взаимодействия между ионами с противоположными зарядами, как показано красной кривой в верхней половине рисунка \ (\ PageIndex {1} \).Полная энергия системы — это баланс между притягивающим и отталкивающим взаимодействиями. Пурпурная кривая на рисунке \ (\ PageIndex {1} \) показывает, что полная энергия системы достигает минимума при r 0 , точке, где электростатическое отталкивание и притяжение точно уравновешены. Это расстояние такое же, как экспериментально измеренное расстояние связи . Рисунок \ (\ PageIndex {1} \): График потенциальной энергии в зависимости от межъядерного расстояния для взаимодействия между газообразным ионом Na + и газообразным ионом Cl — .{23} \; \ cancel {ion \; пара} / моль \ вправо) = — 589 \; кДж / моль \ label {Eq3} \] Это энергия, выделяющаяся при образовании 1 моль газообразных ионных пар, не , когда 1 моль положительных и отрицательных ионов конденсируется с образованием кристаллической решетки. Из-за дальнодействующих взаимодействий в структуре решетки эта энергия не соответствует прямо энергии решетки кристаллического твердого тела. Однако большое отрицательное значение указывает на то, что объединение положительных и отрицательных ионов энергетически очень выгодно, независимо от того, образуется ли ионная пара или кристаллическая решетка. Мы резюмируем важные моменты, касающиеся ионной связи: Пример \ (\ PageIndex {2} \): LiF Рассчитайте количество энергии, выделяющейся при образовании 1 моль газообразных ионных пар Li + F — из разделенных ионов.Наблюдаемое межъядерное расстояние в газовой фазе составляет 156 пм. Дано: катион и анион, количество и межъядерное расстояние Запрошено: энергия, выделяемая при образовании пар газообразных ионов Стратегия: Подставьте соответствующие значения в уравнение \ (\ ref {Eq1b} \), чтобы получить энергию, выделяемую при образовании единственной ионной пары, а затем умножьте это значение на число Авогадро, чтобы получить энергию, выделяемую на моль.{23} \ cancel {\ text {ion pair}} / моль \ right) \\ [5pt] & −891 \; кДж / моль \ end {align *} \] Поскольку Li + и F — меньше, чем Na + и Cl — (см. Раздел 7.3), межъядерное расстояние в LiF короче, чем в NaCl. Следовательно, в соответствии с уравнением \ (\ ref {Eq1b} \), при образовании 1 моль газообразных ионных пар Li + F — (-891 кДж / моль) выделяется гораздо больше энергии, чем когда 1 моль образуются газообразные ионные пары Na + Cl — (-589 кДж / моль). Упражнение \ (\ PageIndex {2} \): оксид магния Рассчитайте количество энергии, выделяющейся при образовании 1 моль газообразных ионных пар \ (\ ce {MgO} \) из разделенных ионов. Межъядерное расстояние в газовой фазе составляет 175 пм. −3180 кДж / моль = −3,18 × 10 3 кДж / моль Ионные соединения образуются, когда электроны переносятся между атомами или группами атомов с образованием заряженных ионов, которые затем образуют структуру кристаллической решетки из-за электростатического притяжения.Образование ионных соединений обычно происходит чрезвычайно экзотермично . Сила электростатического притяжения между ионами с противоположными зарядами прямо пропорциональна величине зарядов на ионах и обратно пропорциональна межъядерному расстоянию. Полная энергия системы представляет собой баланс между отталкивающими взаимодействиями между электронами на соседних ионах и притягивающими взаимодействиями между ионами с противоположными зарядами. Как общество, мы иногда принимаем вещи как должное. Например, часто предполагается, что мы получим электроэнергию, когда подключим вилку к электрической розетке. Провод, который составляет эту розетку, почти всегда медный, материал, который хорошо проводит электричество. Уникальные свойства твердой меди позволяют электронам беспрепятственно проходить через провод и в любое устройство, к которому мы его подключаем. Затем мы можем наслаждаться музыкой, телевидением, работой на компьютере или любой другой деятельностью, которой мы хотим заниматься.Однако эти действия — и само чудо электричества — были бы невозможны без этого медного провода! Кристаллические вещества можно описать по типам частиц в них и типам химической связи, которая имеет место между частицами. Существует четыре типа кристаллов: (1) ионный , (2) металлический , (3) ковалентная сетка и (4) молекулярный . Свойства и несколько примеров каждого типа перечислены в следующей таблице и описаны в таблице ниже. Ионные кристаллы — Ионная кристаллическая структура состоит из чередующихся положительно заряженных катионов и отрицательно заряженных анионов (см. Рисунок ниже).Ионы могут быть одноатомными или многоатомными. Обычно ионные кристаллы образуются из комбинации металлов 1 или 2 групп и неметаллов 16 или 17 групп или неметаллических многоатомных ионов. Ионные кристаллы твердые, хрупкие и имеют высокие температуры плавления. Ионные соединения не проводят электричество как твердые тела, но проводят электричество в расплавленном состоянии или в водном растворе. Металлический кристалл — Металлические кристаллы состоят из катионов металлов, окруженных «морем» подвижных валентных электронов (см. Рисунок ниже).Эти электроны, также называемые делокализованными электронами, не принадлежат какому-либо одному атому, но способны перемещаться через весь кристалл. В результате металлы являются хорошими проводниками электричества. Как видно из приведенной выше таблицы, температуры плавления металлических кристаллов находятся в широком диапазоне. Кристаллы с ковалентной сеткой — Кристалл с ковалентной сеткой состоит из атомов в точках решетки кристалла, причем каждый атом ковалентно связан со своими ближайшими соседними атомами (см. Рисунок ниже).Ковалентно связанная сеть трехмерна и содержит очень большое количество атомов. Сетчатые твердые тела включают алмаз, кварц, многие металлоиды и оксиды переходных металлов и металлоидов. Сетчатые твердые тела твердые и хрупкие, с чрезвычайно высокими температурами плавления и кипения. Состоящие из атомов, а не ионов, они не проводят электричество ни в каком состоянии. Молекулярные кристаллы — Молекулярные кристаллы обычно состоят из молекул в узлах решетки кристалла, удерживаемых вместе относительно слабыми межмолекулярными силами (см. Рисунок ниже). Межмолекулярные силы могут быть дисперсионными силами в случае неполярных кристаллов или диполь-дипольными силами в случае полярных кристаллов. Некоторые молекулярные кристаллы, такие как лед, имеют молекулы, удерживаемые вместе водородными связями.Когда один из благородных газов охлаждается и затвердевает, узлами решетки становятся отдельные атомы, а не молекулы. Во всех случаях межмолекулярные силы, удерживающие частицы вместе, намного слабее, чем ионные или ковалентные связи. В результате температуры плавления и кипения молекулярных кристаллов намного ниже. Молекулярные кристаллы, лишенные ионов или свободных электронов, являются плохими электрическими проводниками. Некоторые общие свойства четырех основных классов твердых тел сведены в Таблицу \ (\ PageIndex {2} \). Пример \ (\ PageIndex {1} \) Классифицируют \ (\ ce {Ge} \), \ (\ ce {RbI} \), \ (\ ce {C6 (Ch4) 6} \) и \ (\ ce {Zn} \) как ионные, молекулярные. , ковалентные или металлические твердые вещества и расположите их в порядке увеличения температуры плавления. Дано : соединения Запрошено : классификация и порядок температур плавления Стратегия : Решение : А. Германий находится в p-блоке сразу под Si, вдоль диагональной линии полуметаллических элементов, что предполагает, что элементарный Ge, вероятно, имеет ту же структуру, что и Si (структура алмаза). Таким образом, Ge, вероятно, представляет собой ковалентное твердое тело . RbI содержит металл из группы 1 и неметалл из группы 17, так что это твердое ионное вещество , содержащее ионы Rb + и I —. Соединение \ (\ ce {C6 (Ch4) 6} \) представляет собой углеводород (гексаметилбензол), который состоит из изолированных молекул, которые образуют молекулярное твердое тело без ковалентных связей между ними. Zn представляет собой элемент d-блока, поэтому металлическое твердое тело . B. Расположить эти вещества в порядке увеличения температуры плавления несложно, за одним исключением. Мы ожидаем, что C 6 (CH 3 ) 6 будет иметь самую низкую температуру плавления, а Ge — самую высокую температуру плавления, а RbI находится где-то посередине. Однако температуры плавления металлов трудно предсказать на основе представленных до сих пор моделей.Поскольку Zn имеет заполненную валентную оболочку, он не должен иметь особенно высокую температуру плавления, поэтому разумное предположение — C 6 (CH 3 ) 6 Фактические температуры плавления: C 6 (CH 3 ) 6 , 166 ° C; Zn, 419 ° С; RbI, 642 ° С; и Ge, 938 ° С. Это согласуется с нашим прогнозом. Упражнение \ (\ PageIndex {1} \) Классифицируйте CO 2 , BaBr 2 , GaAs и AgZn как ионные, ковалентные, молекулярные или металлические твердые вещества, а затем расположите их в порядке увеличения температуры плавления. CO 2 (молекулярный) Фактические температуры плавления следующие: CO 2 , около -15,6 ° C; AgZn, около 700 ° C; BaBr 2 , 856 ° С; и GaAs, 1238 ° C. Ионные соединения — это соединения, состоящие из ионов. Двухэлементные соединения обычно являются ионными, когда один элемент — металл, а другой — неметалл. Примеры включают: Ионные соединения могут быть более сложными, чем двухэлементные, перечисленные выше.Примеры многоатомных ионных соединений включают: Хотя они состоят из положительно и отрицательно заряженных ионов, ионные соединения электрически нейтральны, потому что заряды всегда равны и противоположны. (Другая основная группа соединений — это молекулярные соединения: они состоят из молекул, а не ионов.) В чистом виде ионная связь не является направленной.
Его можно рассматривать как простое положительно-отрицательное кулоновское притяжение между точечными зарядами.
Это отличается от ковалентной связи, при которой электроны разделяются атомами, образуя направленные связи. Однако абсолютно чистой ионной связи не существует.
В ионных соединениях всегда присутствует, по крайней мере, небольшая степень ковалентного связывания. Элементарная ячейка флюорита, CaF 2 .
Миллионы и миллионы повторных трансляций этой элементарной ячейки в 3-х измерения дают видимый кристалл флюорита. В молекулярном соединении, таком как, например, вода, H 2 O, или этанол, C 2 H 5 OH, каждая единица вещества, молекула, состоит из числа атомов, указанных в формула. В ионных соединениях, таких как поваренная соль, NaCl или магнезиальный MgO, формула сообщает нам правильное соотношение присутствующих элементов, но не указывает единицы измерения.Ионные соединения существуют в виде гигантских кристаллических решеток. Каждый кристалл содержит неопределенное количество ионов: числа огромны: даже 0,5-граммовый кристалл хлорида натрия содержит около 1 x 10 22 ионов. Структуры кристаллов можно понять с точки зрения их повторяющихся единиц — элементарных ячеек: их можно определить с помощью измерений дифракции рентгеновских лучей. Кристаллы гидрата сульфата меди (II) CuSO 4 · 5H 2 O. Кристаллы хлорида натрия, NaCl, увеличены. Как правило, ионные твердые тела не переносят электрический ток, потому что ионы находятся в фиксированных положениях в кристаллической решетке.
Однако они проводят электричество в расплавленном состоянии или растворении в растворе, когда ионы высвобождаются из кристаллической решетки и становятся подвижными. Ионные соединения лучше всего растворяются в полярных растворителях.Примерами полярных растворителей являются вода, метанол и формамид. Ионные соединения нерастворимы или имеют очень низкую растворимость в неполярных растворителях. Примерами неполярных растворителей являются углеводороды и хлороформ. Сольватация Сольватация ионных соединений в полярных растворителях происходит за счет уменьшения свободной энергии. Когда NaCl растворяется в воде, полярные молекулы воды образуют сольватные оболочки вокруг растворенных ионов.
Здесь атомы кислорода воды, каждый из которых имеет небольшой отрицательный заряд, сольватируют Na + Аналогичным образом, Cl — окружен молекулами воды с их слегка положительными атомами водорода, ориентированными на Cl —. Кислоты / основания Бренстеда Лоури — это вещества, которые могут отдавать / принимать ионы H + . Вещества, содержащие ионы H + , относятся к кислотам. Акцепторы H + , такие как OH — и O 2-, классифицируются как основания. Сила ионных соединений измеряется с помощью так называемой энергии решетки .Это энергия, выделяемая при образовании одного моля ионного соединения. Это означает, что когда отдельные ионы соединения объединяются, чтобы сформировать кристаллическую решетку, им требуется меньше энергии, чтобы оставаться вместе, поэтому они высвобождают ее, и высвобождаемая энергия называется энергией решетки. Сила связи между ионами противоположного заряда наиболее сильна, когда ионы маленькие. Это потому, что валентные электроны находятся ближе всего к своему ядру, и ядро имеет сильную силу или притягивает их. Он оказывает ту же силу на соседние атомы.Связь также тем сильнее, чем больше заряд на ионах. Таким образом, сила связи между катионом +1 и анионом -1 не так сильна, как сила между катионом +3 и анионом -2. Некоторые реальные примеры этих различий: Энергия решетки отрицательна, чтобы показать, что энергия высвобождается при соединении соединения.Таким образом, чем больше отрицательное число, тем больше энергии выделяется и тем сильнее связь. Если сравнивать бромид натрия с хлоридом натрия, оба имеют одинаковый заряд на своих ионах, но бром больше, чем хлор, поэтому он имеет более низкую энергию. Оксид магния меньше и имеет больший заряд, чем фторид кальция. 1.Ионные соединения обладают уникальными свойствами. Все они образуют кристаллы. Кристалл состоит из упорядоченного и симметричного узора атомов, который называется кристаллической решеткой. Форма кристаллической решетки — это устройство, на поддержание которого требуется наименьшее количество энергии. Внутри кристалла существуют силы между противоположно заряженными ионами и между ядрами и электронами соседних ионов. 2. Они имеют высокие температуры плавления и кипения. Это связано с прочностью ионной связи. Связи настолько прочны, что требуется много энергии, чтобы переместить их из одного состояния в другое, будь то из твердого состояния в жидкое или из жидкого в газообразное. 3. Они твердые и хрупкие. Ионные связи в этих соединениях сильны и не позволяют молекулам сильно перемещаться, что делает их легко разрушаемыми. 4. Они хорошо проводят электричество при растворении в воде. Это связано с тем, что ионное соединение состоит из ионов, которые заряжены либо положительно, либо отрицательно. Когда ионы разделяются в воде, они позволяют электронам течь. 5.В твердом состоянии ионные соединения являются хорошими изоляторами. Большинство горных пород и минералов на Земле представляют собой ионные соединения, удерживаемые вместе ионными связями. Эти прочные связи образуются между положительно заряженным катионом металла и отрицательно заряженным анионом неметалла. Свойства ионных соединений включают образование структур кристаллической решетки с высокими температурами плавления и кипения, твердость и хрупкость и хорошую проводимость электричества при растворении в воде, но в твердой форме они являются изоляторами. Энергия решетки — это энергия связей в кристаллической форме. Эта энергия увеличивается, когда атомы, составляющие соединение, маленькие и когда заряды на каждом атоме велики. После просмотра этого видео вы сможете: Как расположены ионы в хлориде натрия Хлорид натрия — это типичное ионное соединение.Подобные соединения состоят из гигантской (бесконечно повторяющейся) решетки ионов. Итак, хлорид натрия (и любое другое ионное соединение) описывается как имеющий гигантскую ионную структуру . Вы должны понимать, что гигант в этом контексте не означает просто очень большой. Это означает, что вы не можете точно сказать, сколько там ионов. Там могут быть миллиарды ионов натрия и ионов хлора, упакованные вместе, или триллионы, или что-то еще — это просто зависит от размера кристалла.Это отличается, скажем, от молекулы воды, которая всегда содержит ровно 2 атома водорода и один атом кислорода — никогда больше и никогда не меньше. Небольшой образец решетки хлорида натрия выглядит так: Если вы внимательно посмотрите на диаграмму, вы увидите, что ионы натрия и ионы хлора чередуются друг с другом в каждом из трех измерений. Эту диаграмму достаточно легко нарисовать на компьютере, но очень трудно убедительно нарисовать от руки.Обычно мы рисуем «разобранную» версию, которая выглядит так: Только ионы, соединенные линиями, действительно касаются друг друга. К иону натрия в центре прикасаются 6 ионов хлора. Случайно мы могли бы с таким же успехом центрировать диаграмму вокруг хлорид-иона — к которому, конечно, прикоснулись бы 6 ионов натрия. Хлорид натрия описывается как с координатами 6: 6. Вы должны помнить, что эта диаграмма представляет только крошечную часть всего кристалла хлорида натрия.Таким образом картина повторяется на бесчисленном множестве ионов. Как нарисовать эту структуру Нарисуйте идеальный квадрат: Теперь нарисуйте идентичный квадрат позади этого и немного сместите его. Возможно, вам придется немного попрактиковаться, чтобы правильно расположить два квадрата. Если вы ошиблись, ионы запутаются друг с другом на вашей окончательной диаграмме. Превратите это в идеальный куб, соединив квадраты вместе: А теперь самое сложное! Разделите этот большой куб на 8 маленьких кубиков, соединив среднюю точку каждого края со средней точкой противоположного края.Чтобы завершить процесс, вам также нужно будет соединить среднюю точку каждой грани (которую легко найти, когда вы соединили края) со средней точкой противоположной грани. Теперь все, что вам нужно сделать, это вставить ионы. Используйте разные цвета или разные размеры для двух разных ионов и не забудьте ключ. Неважно, окажетесь ли вы в центре куба ионом натрия или ионом хлорида — важно только то, что они чередуются во всех трех измерениях. Вы сможете нарисовать совершенно адекватный набросок от руки менее чем за две минуты — менее чем за одну минуту, если вы не слишком привередливы! Почему хлорид натрия 6: 6 согласован? Чем сильнее притяжение между положительными и отрицательными ионами, тем больше выделяется энергии.Чем больше выделяется энергии, тем более устойчивой становится структура. Это означает, что для достижения максимальной устойчивости необходимо максимальное количество аттракционов. Так почему же каждый ион окружает себя 6 ионами противоположного заряда? Это представляет собой максимальное количество ионов хлора, которое вы можете разместить вокруг центрального иона натрия, прежде чем ионы хлорида начнут соприкасаться друг с другом. Если они начнут соприкасаться, кристалл будет отталкиваться, что сделает его менее устойчивым. Кристалл — это твердое вещество, содержащее внутреннее расположение атомов, молекул или ионов, которое является правильным, повторяющимся и геометрически расположенным. Кристаллы можно сгруппировать по геометрической форме их внутреннего расположения или по их физическим и химическим характеристикам или свойствам. Ионные кристаллы являются одной из четырех основных категорий кристаллов, если их группировать по их физическим и химическим свойствам. Ионы — это атомы, которые несут положительный или отрицательный заряд.Электростатические силы между противоположно заряженными ионами, составляющими кристалл, удерживают атомы вместе. Силы притяжения между противоположно заряженными ионами значительно сильнее, чем между нейтральными атомами, и объясняют свойства ионных кристаллов. Хлорид натрия, более известный как поваренная соль, является примером ионного кристалла. Ионные кристаллы растворимы в воде. При растворении ионы, составляющие кристалл, диссоциируют или разделяются, освобождая их для переноса электрического заряда через раствор.Ионные кристаллы в расплавленном состоянии также хорошо проводят электричество. Подобно растворению кристаллов в воде, их плавление позволяет свободным ионам перемещаться к положительным и отрицательным полюсам. Прочность связей между ионами в ионных кристаллах делает их довольно прочными по сравнению с другими типами кристаллов. Несмотря на свою твердость, ионные кристаллы хрупкие. Под давлением ионы внутри кристалла с одинаковым зарядом выравниваются. Возникающее в результате электростатическое отталкивание между подобными ионами вызывает раскол кристалла. Когда вещество находится в твердой форме, его атомы настолько прочно связаны, что остаются в относительно фиксированном положении. Нагревание твердого тела заставляет атомы двигаться, и, хотя они остаются связанными друг с другом, связи ослабляются, и твердое тело разжижается. Нагревание жидкости приводит к тому, что ее частицы в конечном итоге преодолевают связи, удерживающие их вместе, и жидкость испаряется. Температура, при которой давление пара достаточно велико, чтобы вызвать образование пузырьков в жидкости, называется точкой кипения вещества.Чистые кристаллические твердые вещества имеют характерные точки плавления и кипения, свойства, обычно используемые для их идентификации. Ионные кристаллы имеют более высокие температуры плавления и кипения по сравнению с кристаллами с более слабыми неионными связями. Энтальпия плавления — это количество тепла, необходимое для плавления определенного количества, называемого моль, твердого вещества при поддержании постоянного давления.
Во французском de: Предлог de во французком языке: употребление + упражнения
Предлог de во французком языке: употребление + упражнения
De после слов, обозначающих количество
 Примеры: Techniquement, ouvrir une boîte de céréales ne signifie pas «préparer». — Знаешь, вообще-то, открыть коробку с хлопьями — не значит приготовить завтрак. Je voudrais une bouteille de Dom Perignon. — Я хотел бы бутылку шампанского. La proportion standard est de 50 grammes de poudre pour un diamètre de 40 millimètres. — Стандартная пропорция: 50 грамм пороха на диаметр 40 миллиметров.
Примеры: Techniquement, ouvrir une boîte de céréales ne signifie pas «préparer». — Знаешь, вообще-то, открыть коробку с хлопьями — не значит приготовить завтрак. Je voudrais une bouteille de Dom Perignon. — Я хотел бы бутылку шампанского. La proportion standard est de 50 grammes de poudre pour un diamètre de 40 millimètres. — Стандартная пропорция: 50 грамм пороха на диаметр 40 миллиметров. — Вот так выглядит большая часть исследований динозавров. Pratiquement la moitié du prix du supermarché. — Это практически половина того, что ты платишь в супермаркете.
— Вот так выглядит большая часть исследований динозавров. Pratiquement la moitié du prix du supermarché. — Это практически половина того, что ты платишь в супермаркете. — Нам не стоит воспринимать всерьёз, всё, что показывают по телевизору.
— Нам не стоит воспринимать всерьёз, всё, что показывают по телевизору.De после глагола в отрицательной форме

De вместе des
 — Я взял морковь и горошек. Dis-moi, j’ai des grands-parents? — Скажите, у меня есть бабушка и дедушка?
— Я взял морковь и горошек. Dis-moi, j’ai des grands-parents? — Скажите, у меня есть бабушка и дедушка?Частичный и определенный артикль опускаются после предлога de
 Пример: La pièce est ornée de fleurs. — Комната украшена цветами.
Пример: La pièce est ornée de fleurs. — Комната украшена цветами.De перед дополнениями, обозначающими характеристику
 + de + сущ.). Кстати, на русский такое дополнение часто переводится как прилагательное. Пример: arrêt de bus — автобусная остановка.
+ de + сущ.). Кстати, на русский такое дополнение часто переводится как прилагательное. Пример: arrêt de bus — автобусная остановка.Упражнение №1
Ответы
Показать — Чтобы сделать большой рататуй, нужны помидоры.
— Чтобы сделать большой рататуй, нужны помидоры.Упражнение №2
 . Jean.
. Jean.Ответы
Показать
Артикль или предлог de? | Сайт репетитора по французскому языку Барабановой Н. В.
 Нужно много читать, работать с текстом и с упражнениями.
Нужно много читать, работать с текстом и с упражнениями. Артикль меняется на предлог de после слов, означающих количество.
Артикль меняется на предлог de после слов, означающих количество.
Рассмотрим ещё один случай, когда вместо неопределенного артикля: des употребляется предлог de.
Предлог de вместо артикля des в словосочетаниях «прилагательное + существительное» во множественном числе.
Сейчас об исключениях.Предлоги в французском языке
Предлог
de
le directeur de la fabrique — директор фабрикиПредлог
àMarie va à la gare. Мария идет на вокзал. L’exercice est à la page six. Упражнение на шестой странице. Il dejeune à six heures. Он завтракает в 6 часов. Ils écrivent à leur mère. Они пишут своей матери. Claire parle à sa mère. Клер разговаривает со своей матерью. Предлог
jusque
jusque chez eux
jusqu‘à Paris
jusqu‘à six
jusqu‘à dix heures
jusqu‘à Samedi
jusqu‘au métro
jusqu‘aux dernières pages.Предлоги
à — deIls arrivent à Kiev.
Они приезжают (прибывают) в Киев.Ils arrivent de Kiev.
Они приезжают (прибывают) из Киева.Ja vais à l’usine.
Я иду на завод.Ils reviennent de l’usine.
Они возвращаются с завода.Предлог
à, обозначающий расстояниеBourg-la-Reine se trouve Бур-ла-Рэн находится в à quelques kilometres de Paris. нескольких километрах (на расстоянии нескольких километров) от Парижа. à deux pas d’ici в двух шагах отсюда à trois heures de marche (de train, d’avion) de Moscou в трех часах ходьбы (езды, лёта) от Москвы à cent kilometres de la ville в ста километрах, на расстоянии ста километров от города Предлоги
en и a перед географическими названиями
Il fait ses études en France.
Il fait ses études au Canada.Предлоги места
sur и dans
dans la rue, (чаще) dans l’îleIls sont dans la rue (sur le boulevard) Они на улице (на бульваре). Ils marchent dans la rue (sur le boulevard) Они идут по улице (по бульвару). Употребление предлога a при указании места работы
Pierre est étudiant à l’Institut des étrangères.
Julien est ouvrier à l’usine Renault.Предлоги
avant — devantDevant la maison il y a un petit jardin. Envoie-moi un télégramme avant le depart. Перед домом небольшой сад. Пошли мне телеграмму перед отъездом. Предлог
sans + существительное
sans bruit — бесшумно.Урок 8 b. Leçon 8b. Предлоги «de» и «à» для обозначения принадлежности во французском языке.
Спасибо!
Для обозначения принадлежности во французском языке используются притяжательные прилагательные, притяжательные местоимения, а также предлоги de и à.
Le portable de Gérard. Сотовый телефон Жерара.
Le sac de Macha. Сумка Маши. Машина сумка.
C’est la fille des voisins. Это дочка соседей (de+les=des)
C’est le prix du carburant. Это цена на горючее. (de+le=du)
Однако de не используется с ударными местоимениями, в таких случаях употребляется предлог “à”.
употребляется в следующих случаях:
Cette boutique est à Aurélia. Этот магазин Орелии.
Cette boutique est à cette jeune femme. Этот магазин (принадлежит) этой молодой женщине.
C’est au patron *(слитный артикль à +le=au). Это моего шефа.
C’est aux patrons. Это принадлежит моим шефам.
C’est à Stéphane. Это Стефана.
(и хотя в разговорной речи можно услышать C’est un ami à Léa. Грамматически правильно: C’est un ami de Léa).
2. Эта курта его.
3. Это папино?
4. Эти дома их.
5. Чья сумка?
6. Чья очередь?
7. Чья эта собака? Это Ваша собака? Нет, это собака моего соседа.
8. Чьи эти чемоданы? Эти чемоданы принадлежат этому месье.
9. Книга Доминика очень интересная, но сложная.
10. Окна квартиры выходят на улицу.
2. Эта курта его. (cette; veste; être; lui)
3. Это папино? (ce; être ; papa)
4. Эти дома их. (ces; maisons; être; eux)
5. Чья сумка? (qui; être ; ce; sac)
6. Чья очередь? (qui; le tour).
7. Чья эта собака? (qui; être; ce; chien) Это Ваша собака? (ce; chien ;être ; vous) Нет, это собака моего соседа. (Non, ce, être ; chien ; mon voisin).
8. Чьи эти чемоданы? (qui; être; ces ; valises) Эти чемоданы принадлежат этому месье. (ces; valises, êtres ; ce; Monsieur)
9. Книга Доминика очень интересная, но сложная. (livre; Dominique ; être ; très ; intéressant ; mais ; difficile)
10. Окна квартиры выходят на улицу. (Fenêtres; appartement; donner sur la rue)
2. Эта курта его. Cette veste est à lui.
3. Это папино? C’est à papa?
4. Эти дома их. Ces maisons sont à eux.
5. Чья сумка? À qui est ce sac?
6. Чья очередь? À qui le tour?
7. Чья эта собака? À qui est ce chien? Это Ваша собака? Ce chien est à vous? Нет, это собака моего соседа. Non, c’est le chien de mon voisin.
8. Чьи эти чемоданы? À qui sont ces valises ? Эти чемоданы принадлежат этому месье. Ces valises sont à ce Monsieur.
9. Книга Доминика очень интересная, но сложная. Le livre de Dominique est très intéressant mais difficile.
10. Окна квартиры выходят на улицу. Les fenêtres de l’appartement donnent sur la rue.Грамматика французского языка в таблицах
Французский
Русский
s’abstenir de
воздерживаться от
abuser de
злоупотреблять чем-л.
être accompagné de
быть сопровожденным кем-л.
accuser qn de
обвинять кого-л в
s’agir: il s’agit de
речь идет о:
s’apercevoir de
замечать что-л., догадываться о
s’assurer de
убедиться в
charger qn de
поручать кому-л. что-л
se contenter de
довольствоваться чем-л
décourager qn de
подавить желание кого-л. в
dépendre de
зависеть от
désespérer de
терять надежду на
différer de
отличаться от
discuter (de)
обсуждать что-л.
disposer de
располагать чем-л.
douter de / se douter de
сомневаться в
s’emparer de
завладеть, захватить что-л.
s’encombrer de
обременять себя, затруднять себя чем-л.
s’excuser de
извиниться за что-л.
informer qn de
информировать кого-л. о чем-л.
s’inquiéter de
беспокоиться о
jouir de
пользоваться, наслаждаться чем-л.
manquer de
испытывать недостаток в
se méfier de
не доверять, относиться подозрительно к чему-л
menacer qn de
угрожать кому-л. чем-л
se munir de
вооружиться чем-л.
penser de
думать о
se plaindre à qn de
жаловаться кому-л. на
remercier qn de
благодарить кого-л. за
rire de
смеяться над
se servir de
пользоваться чем-л.
se souvenir de
вспоминать о
user de
употреблять что-л., пользоваться чем-л.
Французский
Русский
L’intérêt est d’assister à cette émergence, s’agissant d’une période littéraire a priori réservée à la rhétorique et aux poétiques
интерес состоит в том, чтобы присутствовать при возникновении [этого являения]; речь идет о периоде литературе a priori имеющим дело с риторикой и поэтиками
NB d’ = de перед гласными буквами
agissant — причастие от agir: finissant — finir, aboutissant — aboutir, frémissant — frémir и т. д.
НО partant — partir, sortant — sortir
Il s’agit surtout d’une nièce du roi de France. Il s’agit d’un mariage de raison car Pierre Ier a déjà rencontré celle qui devient sa maîtresse attitrée
речь особенно идет о племяннице короля Франции; речь идет о браке по расчету, поскольку Петр I уже встретил ту, которая стала его обалденной любовницей
NB attitrée = «привлекательной, привлекающей» (e на конце указывает на ж род прилаг), мы перевели «обалденной»
Le problème présenté jusqu’ici est le problème de sac à dos en variables binaires. Il s’agit en fait d’une variante parmi d’autres
проблема, как она представляется на сегодняший день — это проблема «мешка за спиной» в парных переменных; по сути речь идет об одной переменной среди других
NB jusque + наречие = «вплоть до + наречие»:
jusqu’ici = «до этого места, досюда»; jusqu’à la fin = до конца; jusqu’à ce que = «до тех пор пока» и т. д. une voile n’est pas plate sauf s’il s’agit d’une voile de tempête
парус не должен быть гладким, если только речь не идет о буранном парусе (парусе, предназначенного для плавания в непогоду)
NB sauf si = «если только + отриц выраж»
Saint-Simon écrivit la lettre d’un habitant de Genève à ses contemporains. Il s’agit d’une sorte d’éloge à la science, considérée comme une nouvelle religion
Сен-Симон написал «Письмо обитателя Женевы к своим современника». Речь идет о типа похвалы науке, рассматриваемой как некая новая религи
Les problèmes majeurs, pour les républicains, se posent du côté de l’organisation. En effet, il s’agit d’une armée populaire créée de toutes pièces
Большинство проблем республиканцев — это организационные проблемы. В натуре, речь идет о народной армии, собранной из всякой швали
NB poser = «помещать, располагать», соответственно
se poser = «помещаться, располагаться«;
однако нужно помнить, что возвратность в русском и фр языках часто
не совпадают: le problème se pose = «встаёт вопрос»
Sur le plan militaire, la guerre d’Espagne présente les caractéristiques suivantes. Il s’agit tout d’abord d’une guerre qui, sauf dans sa dernière phase, se déroule sur plusieurs fronts à la fois
В военном плане испанская война представлят собой следующие характеристики. Прежде всего речь идет о войне, которая за исключением последней фазы разворачивается на нескольких фронтах одновременно
NB tout d’abord = «прежде всего»
à la fois = «одновременно, разом, вместе» Il s’agit ici en fait d’un sophisme se présentant sous une forme de syllogisme
речь здесь по факту идет о софизме, прикидывающегося силлогизмом
NB se здесь не возвратная частица, а местоимение = «себя», таким образом, se présenter = не «представляться«, а «представлять себя«
Le 1er janvier, la Luftwaffe exécute une riposte bien conçue et exécutée par surprise; il s’agit de l’opération Bodenplatte
1 января Люфтваффе дает быстрый ответ хорошо задуманный и выполненный неожиданно, речь идет об операции «Боденплатте»
Косвенное дополнение (COI) и предлог «de» во французском языке
Во французском языке есть глаголы, а есть глагольные обороты,
parler de quelque chose — говорить о чем-то
и в этом случае оно называется pronom personnel
(личное местоимение)
В этом случае «en» имеет значение de cela («об этом»)
Заменили, и получилось:
Il en parle — он об этом говорит
il n’en parle pas — он об этом говорит
En a-t-il parlé? — Поговорил ли он об этом?
— говорить с кем-то о чем-тоЧастичный артикль во французском языке: где и как использовать
Как распознать частичный артикль?
Что мы едим на завтрак: используем частичный артикль Разделительный артикль: du, de la, de l ’and des | Изучение французской грамматики
1 Основные правила
с существительным мужского рода с существительным женского рода Единственное число du (de l ‘) de la (de l’) Множественное число des des du beurre (немного / любое) масло du jus d’orange (немного / любое) апельсиновый сок de la viande (some / any) мясо de la margarine (some / any) маргарин de l’argent (мужской) (some / any) money de l’eau (женский) (some / any) water de l’herbe (женский) ) (немного / любое) трава des gâteaux (некоторые / любые) торты des lettres (некоторые / любые) буквы des hôtels (некоторые / любые) отели 2 Разделительный артикль в отрицательных предложениях
Nous n’avons pas de beurre. У нас нет масла. Je ne mange jamais de viande. Я никогда не ем мяса. Il n’y a pas de tembres. Нет марок.
Типде заменяется на d ’перед словом, начинающимся с гласной, и большинством существительных, начинающихся с h.
Grammar Extra! Есть несколько очень распространенных прилагательных, таких как beau, bon и petit, которые могут стоять ДО существительного, а не после него.Когда прилагательное стоит перед существительным множественного числа, des меняется на de. Il n’a pas d’argent. Денег нет. Il n’y a pas d’horloge dans la salle. В комнате нет часов. J’ai reçu de beaux cadeaux. Я получил прекрасные подарки. Cette région a de très jolis village. В этом районе есть несколько очень красивых деревень. 3 Значение du, de la, de l ‘и des
Il me doit de l’argent. Он должен мне (немного) денег. Je vais acheter de la farine et du beurre pour faire un gâteau. Я собираюсь купить (немного) муки и масла, чтобы испечь торт. Est-ce qu’il y a des lettres pour moi? Есть ли мне письма? Elle ne veut pas de beurre. Она не хочет масла. Je ne prends pas de lait. Молоко не пью.
PreviousNext De — Французский предлог — французская грамматика Lawless
Предлог французского
Однако de не имеет контракта с прямыми объектами le и les . le ле Но… la л ‘ из du des из de l ’
Связанные уроки 1) Исходная или начальная точка
Il est du Midi. Он с юга Франции. Nous Arrivons de Lille. Прибываем из Лилля. 2) Контрольная точка
Nous sommes à deux km de la plage. Мы в двух километрах от пляжа. Жильё до 20 минут. Он живет в 20 минутах отсюда. 3) Владение
в автомобиле Николь Автомобиль Николь La Poste de Brest Брестское почтовое отделение 4) Описание, определяющий признак
суп из томатов томатный суп un bébé de 3 mois Трехмесячный ребенок 5) Состав
un verre de vin бокал вина un film de guerre военный фильм, фильм про войну 6) Причина или причина
rougir de honte краснеть от стыда être mécontent de la décision быть недовольным решением 7) Средства или способ
dessiner de la main gauche рисовать левша regarder d’un air admiratif восхищенно смотреть 8) Начало периода времени / диапазона
J’ai travaillé de 8h à midi. Я работал с 8 утра до полудня. du lundi au samedi с понедельника по субботу 9) Представление агента пассивным голосом
Elle est très appréciée de ses étudiants. Ее очень любят ученики. Je serai сопровождает меня от отца. Меня будет сопровождать отец. 10) После глагола
Многие глаголы должны сопровождаться de перед существительным или инфинитивом. 11) После прилагательных
После некоторых прилагательных должно стоять de перед существительным или инфинитивом. 12) После
merci Merci de votre help. Спасибо за вашу помощь. Merci de и merci pour En español
Поделиться / Твитнуть / Прикрепить меня! Полное руководство по основам французского слова
du
de l ’
d ’
des
Что означает de ? 1. из
2. Of (почти как на английском)
3. Of (для обозначения собственности, части чего-либо)
4. Оф (при описании мерок, длины, возраста и т. Д.)
5.Of / for в конкретных выражениях
6. некоторые
7. «не… любой» (при использовании с ne… pas)
Значение 8. с (при описании физических действий)
9. Автор (авторство)
10. «Невидимое» или вспомогательное изделие.
11. Неформальный способ выразить «так» / «ты даже не знаешь» / «невероятно»
12.«Of» в «made of»… иногда.
13. Кому (в некоторых безличных выражениях)
14. Предлог-заполнитель для «выражения качества»
15. _ и _ / __ от __ / с__ по___
16. К (в сочетании с определенными глаголами)
Глаголы, значение которых меняется, если за ними следует
à или de Je viens de Paris. С этими глаголами можно использовать либо
à , либо de , и их значение не меняется:
Как запомнить значения и употребление слова de Хотите сказать «из» по-французски? Используйте предлог de
Распространенное использование слова de
la bibliothèque de l’université > университетская библиотека
Je suis de Bruxelles. > Я из Брюсселя.
un roman d’amour > история любви (история / о любви) 4.Определяющий признак
une salle de classe > класс
le jus d’orange > апельсиновый сок 5. Причина
6. Средства / способ выполнения чего-либо
répéter de mémoire > читать по памяти Например, де + ле = du салон de + les = des des villes de + la = по для женщин de + l ‘ = de l ‘ человека 7.После определенных глаголов фразы, за которыми следует инфинитив
8.После глаголов, фразы, требующие косвенного упоминания
Дополнительный ресурс
Когда использовать «А» vs.«Де» на французском
À De Расположение или пункт назначения Начальная точка или происхождение Je vais à Rome Я еду в Рим Partir de Nice для выезда из (из) Ниццы Je suis à la banque Я в банке Je suis de Bruxelles Я из Брюсселя Расстояние во времени или пространстве
Обратите внимание, что à используется перед расстоянием, а de указывает начальную точку / исходную точку. Жилая площадь 10 метров … Живет 10 метров … … официальный … отсюда За 5 минут … Это 5 минут пешком … … de moi … от меня Владение Владение / принадлежащих (
Узнать больше) и мои друзья мой друг le livre de Paul Книга Павла Ce livre est à Jean Это книга Жана le cafe de l’université университетское кафе Назначение или использовать Содержание / описание без упаковки чашка (чашка для чая) без тесьмы чашка чая без покрытия спичечный коробок (спичечный коробок) une boîte d’allumettes Ящик (полный) спичек un sac à dos рюкзак (рюкзак за спину) Роман в любви love story (рассказ о любви) Маннер , стиль , или характеристика Определяющий признак под ключ сделано вручную le marché de gros оптовый рынок Французское жильё Живет во французском стиле UNE salle de classe аудитория un enfant aux yeux bleus голубоглазый ребенок livre d’histoire книга истории Определяющий ингредиент — продукты питания Незаменимый ингредиент — Продукты питания Использование à , когда еда сделана из чего-то, что можно унести, не разрушая, — как правило, это можно перевести как «с.»В следующих примерах, если вы достанете ветчину или лук, у вас останется бутерброд или суп. Использование de , когда еда состоит в основном из чего-то — вообще говоря, это можно перевести как «из» или «из». В следующих примерах, если вы уберете черную смородину или помидоры, у вас останется совсем немного. сэндвич с вареньем Бутерброд с ветчиной сливки из черной смородины ликер из черной смородины la soupe à l’oignon луковый суп суп из томатов томатный суп une tarte aux pommes яблочный пирог оранжевый апельсиновый сок Безличное выражение: Реальный объект Безличностные выражения: фиктивный объект C’est bon à savoir. Это полезно знать. Il est bon d’étudier. Учиться хорошо. (Учится хорошо) C’est facile à faire. Это легко сделать. Il est facile de le Trouver. Легко найти. (Найти несложно) Дополнительное использование
А Измерение в килограммах купить килограмм плательщик по семену к оплате по неделям Момент времени Время прибытия до 5:00 Приезжаем в 5:00 Смерть за 92 и Умер в возрасте 92 лет. Дополнительное использование D
e Причина mourir de faim умереть от голода fatigué du voyage устала из поездки Средства / способ выполнения чего-либо écrire de la main gauche писать левой рукой запись памяти читать по памяти Использование
À и D e с глаголами глаголов с разными значениями при использовании
À или D e décider à убедить, убедить решите принять решение цена до спросить (разрешения) по запросу спросить (s.о. делать с.т. *) jouer до играть в игры или заниматься спортом jouer из играть на музыкальном инструменте манке до скучать по кому-то манке из пренебрегать (делать с.т.) (
подробнее о манке) цена , чтобы поговорить с Парлер из говорить о ручка до подумать (представить) ручка из над чем подумать (мнение) (
подробнее о Penser) прибыль от в пользу прибыль максимально использовать возможности Венир до случится с Венир из иметь только что (сделано s.т.) (
подробнее о Venir) глаголов, которые используют как
À , так и D e в одном и том же предложении консиллер à qqun de faire qqch советую s.о. делать s.t. defendre до qqun из faire qqch запретить кому-то делать s.t. заказчик до qqun из faire qqch спроси у кого делать s.t. Dire до qqun из faire qqch скажи с.о. делать s.t. interdire до qqun de faire qqch запретить кому-то делать s.t. или до qqun de faire qqch заказ s.o. делать s.t. перметр до qqun de faire qqch позволяют s.о. делать s.t. promettre до qqun de faire qqch Promise s.o. делать s.t. телефонная связь до qqun из faire qqch звоните кому-то делать s.t. Выражения с
À и D e à côté рядом, рядом с по боком в цвете рядом, рядом du côté de из (направление) в высоком качестве на уровне высокое [5 футов] в высоту после Парижа он в Париже il est de Paris он из Парижа прет * до + инф. подготовлено к prês * de + инф. рядом, на грани добавить в чашка (чашка для чая) Кассета чашка чая Глаголы с
À или D e начальный этап для начала продолжение продолжить Смотри:
Основные продукты в холодильнике по-французски
De, du, de la, des на французском
1.С бесчисленными словами (то, что мы называем разделенными)
мужской род + le: du или de l’ , если слово начинается с гласной
женский род: de la или de l ‘, если слово начинается с гласной
Я хочу немного любви: je veux de l’amour (amour мужского рода и начинается с гласной )
Я хочу немного горчицы: je veux de la moutarde (moutarde — женский род)
Я хочу немного воды: je veux de l’eau (eau — женский род и начинается с гласной)
Мне нужны деньги: j’ai besoin d ‘argent (argent — мужского рода) (здесь глагол «escapeir besoin de», из-за предлога «de», включенного в глагол, мы не используем определенный артикль, если вы говорите «j’ai besoin de l’ar Gent que tu m’as promis »мы говорим о чем-то конкретном, о деньгах, которые вы мне обещали) (обратите внимание на предложные глаголы во французском языке) Отрицательная форма: любой, во французском языке определенный артикль исчезает:
Я не хочу любви: je ne veux pas d’amour
Мне не нужна горчица: je ne veux pas de moutarde
Мне не нужна вода: je ne veux pas d’eau
Мне не нужны деньги: je n’ai pas besoin d’argent
Я больше не хочу яблок: je ne veux plus de pommes.
Это золото: c’est de l’or
Это не золото: ce n’est pas de l’or (мы сохраняем определенный артикль)
Je veux des lentilles (чечевица, поскольку мы никогда не говорим, что я хочу одну чечевицу), то же самое со шпинатом: je veux des épinards. 2. Со счетными словами (неопределенный артикль)
Я хочу яблок (или хочу яблок): je veux des pommes
Мне нужна обувь: j’ai besoin de chaussures. (Предлогный глагол — escapeir besoin de)
Я хочу обувь: je veux des chaussures.
J’ai acheté des pantalons: Я купил несколько брюк
J’ai acheté de nouveaux pantalons: Я купил новые брюки (это правило, но не так важно, как говорят многие во Франции J ‘ai acheté des nouveaux pantalons)
Когда прилагательное (здесь nouveaux) стоит перед существительным (pantalons), мы используем «de» вместо «des».
То же самое с: Мне нужна другая обувь: je veux d’autres chaussures.
Je veux un gâteau J’en veux un
Вам нужен неопределенный артикль, потому что «j’en veux» означает «я хочу немного»
Je prends une tasse J’en prends une Отрицательная форма: any
Он также работает с единственное слово:
У меня есть машина: j’ai une voiture
У меня нет машины: je n’ai pas de voiture.
Мы пользуемся новыми законами: nous profitons de lois nouvelles.
Мы пользуемся преимуществами новых законов: nous profitons des lois nouvelles. (здесь «des» означает «de les») 3. Выражения количества
У меня мало денег: j’ai peu d ‘ argent
У меня много бананов: j’ai beaucoup de bananes (banane женского рода)
Я хочу больше яблоки: je veux plus de pommes.
У нас было мало солнца: nous avons eu peu de soleil (soleil — мужское начало)
Пришло много детей: beaucoup d ‘ enfants sont venus
Однако, если вы говорите о чем-то конкретном:
Многие из детей в этой школе были больны: beaucoup des enfants de cette école onté malades.
Вы можете сказать Je veux du pain, здесь вы имеете в виду, что вам нужен кусок хлеба, и je veux un pain, вы хотите весь хлеб.
Но вы не можете сказать: je veux de la pomme, потому что вам не нужно яблоко целиком, а целиком, так что je veux une pomme! Pay Attention
Le chat des voisins (мы говорим конкретно о соседях, поэтому DES — это сокращение DE + LES, определенный артикль) QUIZ de la, du, des
[h5p id = ”4 ″]
L’amour de l ‘ argent: Любовь к деньгам
Le chapeau du roi: шляпа короля
C’est un cadeau de ma tante: это подарок моей тети
Il travaille de nuit (de jour): он работает ночами (днями)
Il Pleure de joie: Он плачет от радости
Un homme de 50 ans: 50-летний мужчина
Personne d ‘ отсутствует?: Никто не пропал? Pay Attention:
В этом предложении нет статей на английском, на французском нам нужны две из них:
Опять же, статей на английском нет. Французское ключевое слово: de
Форма и произношение
Использовать как предлог
Для обозначения
происхождения или происхождения чего-то
он пришел _from_ London
c’est mon ami _de_ York
он мой друг _from_ York
il a sauté _de_ la fenêtre
он выпрыгнул _ из_ окна Используется, чтобы показать
владение или принадлежащее
Paul_’s_ dog
la femme du boulanger
жена пекаря
la clé _de_ la porte
ключ от двери, ключ _to_ двери
le jour _10 916ël 907 День
это самый большой город во Франции со значением «примерно», «по теме»
»
он говорил о своей матери
il rêve _de_ réussir
он мечтает / об успехе
_de_ quoi tu te plains?
на что вы жалуетесь _about_?
он ищет книгу о / о Дали Используется для обозначения «агентства», «причины» или «авторства»
a CD _by_ Жан-Мишель Жарр, Жан-Мишель Жарр CD
un film _de_ Truffaut
фильм _by_ Truffaut, фильм Truffaut
la route est couverte _de_ gl
дорога покрыта льдом
la pièce s’est remplie _de_ fumée
комната заполнена дымом
il est rouge _de_ colère
он красный с гневом
_in_ как?
_de_ cette façon
_in_ this way
_de_ manière très directe
_in_ очень прямой путь
«Venez ici!» dit-il _d_’un ton agressif
«Иди сюда!» он сказал агрессивным голосом Использовать для образования соединений
Используется для обозначения материала
бархатное платье
une maison de bois
деревянный дом
un vase de métal
металлическая ваза Используется для обозначения содержимого
стакан молока
une bouteille de vin
бутылка вина
un carnet de timbres
книга марок
une collection de livres
коллекция книг
grand nombre de personnes
великое множество людей Использовать как определитель
немного масла; немного масла
de l’argent
немного денег; часть денег
des voitures
несколько машин; некоторые из машин
Я выпил немного этого вина
на volé de mon argent
часть моих денег забрали
Мне нужна ваша помощь
j’ai besoin de (de) l’aide
Мне нужна помощь
они великие авторы
il a de jolis yeux
у него красивые глаза
У меня нет машины
il n’a pas bu de vin
он не пил вина
il n’a pas d’amis
he нет друзей
он не пил вина, но выпил немного виски
ce n’est pas une souris
это не мышь Форма
d’autres Использовать в качестве дополнения (перед инфинитивом)
они прекратили публикацию этого журнала
на cessé _de_ publier cette revue
они прекратили публикацию этого журнала
dis-lui _de_ venir
скажите ему приходи
ce que je veux, c’est _d’_être content
я хочу быть счастливым Дела без перевода
Перед причастием прошедшего времени
вот еще одно стекло разбито!
quelque выбрал _de_ plus intéressant
что-то более интересное
quelqu’un d ‘autre
кто-то другой
quelque part _ (de) _ plus proche
где-то ближе С
être и количеством
Ваша зарплата будет составлять две тысячи евро в месяц Когда
не используется de? С глаголами «лишения»
пить _ из_ бутылки
il l’a pris _dans_ la kitchen
он взял его _с кухни
repartir _à_ zéro
чтобы начать _from_ scratch 916 q66 9070 чтобы скрыть sth _from_ sb
prendre qch _à_ qn
взять sth _from_ sb
emprunter de l’argent _à_ la banque
, чтобы занять немного денег _в_ банке
2 х 6: Калькулятор онлайн — Решение уравнений и неравенств с модулями
Активный элемент линейного массива 2 х 6,5» + 1,4», 475 Вт c усилителем 2×1000 Вт
НЧ-излучатель
2×6,5″ динамик с 1,5″ алюминиевой звуковой катушкой, 16 Ом
ВЧ-излучатель
1,4″ компрессионный драйвер с 2,5″ звуковой катушкой (краевая намотка) и титановым диффузором
Усилитель мощности
Входы
1 – CANBUS, разъем etherCON RJ45 (розетка)
1 – балансное аудиомоно, разъем XLR 3-pin (вилка)
1 – питание, разъем powerCON
Выходы
1 – CANBUS, разъем etherCON RJ45 (розетка)
1 – балансное аудиомоно, разъем XLR 3-pin (розетка)
1 – питание, разъем powerCON
Класс усиления
D
Выходная мощность
1000 + 1000 Вт
Частотный диапазон
80 Гц – 18 кГц (±3 дБ)
Чувствительность по входу
+4 dBu / 1,25 В
Импеданс входной
балансное подключение: 20 кОм
небалансное подключение: 10 кОм
Импеданс
НЧ-секция: 16 Ом каждый динамик, параллельное подключение
ВЧ-секция: 8 Ом
Максимальный уровень звукового давления
129 дБ
Цифровая обработка
40-разрядный DSP SHARC с плавающей точкой (96 кГц)
24-разрядные АЦП/ЦАП
Охлаждение
принудительное (вентилятор с переменной скоростью вращения)
Питание
сеть ~230 В ±15 % или сеть ~115 ±15 %, 50/60 Гц
Общие характеристики
Угол раскрытия
110х12° (−6 дБ)
Материал корпуса
15-мм березовая фанера
Покрытие
высокостойкая краска на водной основе
Материал крепления
алюминий (фронтальное крепление)
высокопрочная сталь (тыловое крепление)
Монтаж
подвесной
Габаритные размеры (ШxГxВ)
583 x 481 x 244 мм
Масса
22,5 кг
Шарнирная двусторонняя стремянка TRIMATIC, 2 х 6.
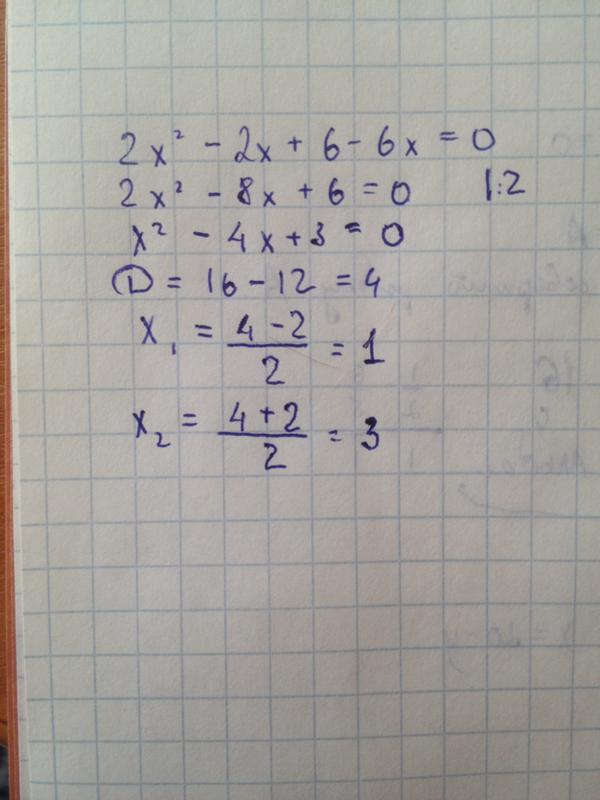 129901 (121325).
129901 (121325).Курьерская доставка по Москве
Самовывоз
Перед тем как приехать в пункт выдачи, Вам понадобится связаться с нами по телефону, указанному на сайте.ДОСТАВКА В РЕГИОНЫ РОССИИ
 spsr.ru/ru/service/calculator, учитывая примерный вес товара. SPSR Express значительно удобнее обычной, посылку вам принесет курьер прямо на дом.
spsr.ru/ru/service/calculator, учитывая примерный вес товара. SPSR Express значительно удобнее обычной, посылку вам принесет курьер прямо на дом. Атакже повреждения, которые являются следствием естественного износа в процессе использования изделия.
Атакже повреждения, которые являются следствием естественного износа в процессе использования изделия.
 Оплата производится наличными курьеру в момент передачи посылки.
Оплата производится наличными курьеру в момент передачи посылки.Подмости малые лестничные 2 х 6 раб. выс. 3 и 3.75 м
 :
: Расчет стоимости доставки производится
согласно тарифной сетке, представленной ниже. Точная стоимость доставки определяется после
согласования заказа с вашим менеджером.
Расчет стоимости доставки производится
согласно тарифной сетке, представленной ниже. Точная стоимость доставки определяется после
согласования заказа с вашим менеджером. выс. 3 и 3.75 м на сайте носят информационный
характер и не являются публичной офертой, определенной п.2 ст. 437 Гражданского
кодекса Российской федерации. Они могут быть изменены производителем без предварительного
уведомления и могут отличаться от описаний на сайте производителя и реальных характеристик
товара. Для получения подробной информации о характеристиках данного товара обращайтесь
к сотрудникам нашего отдела продаж или в Российское представительство данного
товара, а также, пожалуйста, внимательно проверяйте товар при покупке.
выс. 3 и 3.75 м на сайте носят информационный
характер и не являются публичной офертой, определенной п.2 ст. 437 Гражданского
кодекса Российской федерации. Они могут быть изменены производителем без предварительного
уведомления и могут отличаться от описаний на сайте производителя и реальных характеристик
товара. Для получения подробной информации о характеристиках данного товара обращайтесь
к сотрудникам нашего отдела продаж или в Российское представительство данного
товара, а также, пожалуйста, внимательно проверяйте товар при покупке.Заклепка вытяжная 3,2х6 алюминий/сталь
Medeek Design Inc.
 — Обрамление 2×6
— Обрамление 2×6 Существует большая разница в прочности на сжатие, сопротивлении продольному изгибу и боковому прогибу между стеной 9 футов 2×4 и стеной 9 футов 2×6.
Существует большая разница в прочности на сжатие, сопротивлении продольному изгибу и боковому прогибу между стеной 9 футов 2×4 и стеной 9 футов 2×6. Высокие стены
 В некоторых случаях местные власти могут отказаться от этого, если для внешнего каркаса используются стойки 2 x 6, а высота вашей стены не превышает 12 футов.
В некоторых случаях местные власти могут отказаться от этого, если для внешнего каркаса используются стойки 2 x 6, а высота вашей стены не превышает 12 футов. Практичность зазора между шпильками
Исключения
Уголок
 Большая ширина стены 2 x 6 обеспечивает большую изоляцию на внешних углах стены и большую гибкость в методах обрамления.В приведенной ниже матрице показано множество способов обрамления внешней угловой стены 2 x 6:
Большая ширина стены 2 x 6 обеспечивает большую изоляцию на внешних углах стены и большую гибкость в методах обрамления.В приведенной ниже матрице показано множество способов обрамления внешней угловой стены 2 x 6:
Если у вас есть вопросы по обрамлению стен, свяжитесь с нами. Габаритные размеры пиломатериалов: номинальные и фактические
Размеры пиломатериалов хвойных пород

Североамериканский стандарт пиломатериалов
Номинальный размер (дюймы) Фактический размер (дюймы) Фактический размер (мм) 1 х 2 3/4 х 1 1/2 19 х 38 1 х 3 3/4 х 2 1/2 19 х 64 1 х 4 3/4 x 3 1/2 19 х 89 1 х 6 3/4 x 5 1/2 19 х 140 1 х 8 3/4 x 7 1/4 19 х 184 1 х 10 3/4 x 9 1/4 19 х 235 1 х 12 3/4 x 11 1/4 19 х 286 Североамериканский стандарт, двухпалубный пиломатериал
Номинальный размер (дюймы) Фактический размер (дюймы) Фактический размер (мм) 2 х 2 1 1/2 x 1 1/2 38 х 38 2 х 3 1 1/2 x 2 1/2 38 х 64 2 х 4 1 1/2 x 3 1/2 38 х 89 2 х 6 1 1/2 x 5 1/2 38 х 140 2 х 8 1 1/2 x 7 1/4 38 х 184 2 х 10 1 1/2 x 9 1/4 38 х 235 2 х 12 1 1/2 x 11 1/4 38 х 286 Североамериканский стандарт 3-х сек.
 Пиломатериалов
Пиломатериалов Номинальный размер (дюймы) Фактический размер (дюймы) Фактический размер (мм) 3 x 3 2 1/2 x 2 1/2 64 х 64 3 х 4 2 1/2 x 3 1/2 64 х 89 3 х 6 2 1/2 x 5 1/2 64 х 140 3 х 8 2 1/2 x 7 1/4 64 х 184 3 х 10 2 1/2 x 9 1/4 64 х 235 3 х 12 2 1/2 x 11 1/4 64 х 286 Североамериканский стандарт пиломатериалов для 4-х классов
Номинальный размер (дюймы) Фактический размер (дюймы) Фактический размер (мм) 4 х 4 3 1/2 x 3 1/2 89 х 89 4 х 6 3 1/2 x 5 1/2 89 х 140 4 х 8 3 1/2 x 7 1/4 89 х 184 4 х 10 3 1/2 x 9 1/4 89 х 235 4 х 12 3 1/2 x 11 1/4 89 х 286 Североамериканский стандарт пиломатериалов 6 по дереву
Номинальный размер (дюймы) Фактический размер (дюймы) Фактический размер (мм) 6 х 6 5 1/2 x 5 1/2 140 х 140 North American Standard 8-by Lumber
Номинальный размер (дюймы) Фактический размер (дюймы) Фактический размер (мм) 8 х 8 7 1/4 x 7 1/4 184 х 184 Пиломатериалы хвойных пород Длина

Длина в футах Длина в дюймах Длина в метрах 6 футов 72 дюйма 1,829 метра 8 футов 96 дюймов 2,438 метра 10 футов 120 дюймов 3,048 метра 12 футов 144 дюйма 3.658 метров 14 футов 168 дюймов 4,267 метра 16 футов 192 дюйма 4.877 метров 18 футов 216 дюймов 5,486 метра 20 футов 240 дюймов 6.096 метров 22 фута 264 дюйма 6.706 метров 24 фута 288 дюймов 7.315 метров Размеры пиломатериалов твердых пород
 Поверхность относится к процессу отделки, при котором пиломатериал сглаживается и удаляются все следы от пилы.
Поверхность относится к процессу отделки, при котором пиломатериал сглаживается и удаляются все следы от пилы. Номинальный размер Грубый размер Фактический размер: 1 сторона с поверхностью Фактический размер: 2 стороны с поверхностью – 1/2 дюйма 3/8 дюйма (9,5 мм) 5/16 дюйма (7,9 мм) – 5/8 дюйма 1/2 дюйма (13 мм) 7/16 дюйма (11 мм) – 3/4 дюйма 5/8 дюйма (16 мм) 9/16 дюйма (14 мм) 4/4 дюйма 1 дюйм 7/8 дюйма (22 мм) 13/16 дюйма (21 мм) 5/4 дюйма 1 1/4 дюйма 1 1/8 дюйма (29 мм) 1 1/16 дюйма (27 мм) 6/4 дюйма 1 1/2 дюйма 1 3/8 дюйма (35 мм) 1 5/16 дюйма (33 мм) 8/4 дюйма 2 дюйма 1 13/16 дюйма (46 мм) 1 3/4 дюйма (44 мм) 12/4 дюйма 3 дюйма 2 13/16 дюйма (71 мм) 2 3/4 дюйма (70 мм) 16/4 дюйма 4 дюйма 3 13/16 дюйма (97 мм) 3 3/4 дюйма (95 мм) Клееный брус Размеры

Номинальная ширина Фактическая готовая ширина 3 « 2 1/2 « 4 « 3 1/8 дюйма или 3 1/2 дюйма 6 « 5 1/8 дюйма или 5 1/2 дюйма 8 « 6 3/4 дюйма 10 « 8 3/4 дюйма 12 « 10 3/4 дюйма 14 « 12 1/4 « 16 « 14 1/4 « Номинальное vs.Фактические размеры пиломатериалов
Фактические и номинальные размеры

 Итак, каркасная стена, построенная из бруса 2 x 6, имеет толщину 5 1/2 дюйма, но с прикрепленным к стене куском гипсокартона толщиной 1/2 дюйма она становится стеной толщиной 6 дюймов.
Итак, каркасная стена, построенная из бруса 2 x 6, имеет толщину 5 1/2 дюйма, но с прикрепленным к стене куском гипсокартона толщиной 1/2 дюйма она становится стеной толщиной 6 дюймов. Номинальный размер Фактическое значение (дюймы) Фактический (мм) 1 х 2 3/4 х 1-1 / 2 19 х 38 1 х 4 3/4 х 2-1 / 2 10 х 64 1 х 6 3/4 х 5-1 / 2 19 х 140 1 х 10 3/4 х 9-1 / 4 19 х 235 1 х 12 3/4 х 11-1 / 4 19 х 286 2 х 2 1-1 / 2 х 1-1 / 2 38 х 38 2 х 4 1-1 / 2 х 3-1 / 2 38 х 89 2 х 6 1-1 / 2 х 5-1 / 2 38 х 140 2 х 8 1-1 / 2 х 7-1 / 4 38 х 184 2 х 10 1-1 / 2 х 9-1 / 4 38 х 235 2 х 12 1-1 / 2 х 11-1 / 4 38 х 286 4 х 4 3-1 / 2 х 3-1 / 2 89 х 89 4 х 6 3-1 / 2 х 5-1 / 2 89 х 140 Понимание фактического vs.
 Номинальные размеры пиломатериалов
Номинальные размеры пиломатериалов Номинальные и фактические размеры размерной древесины
 Причины, по которым номинальный размер этого пиломатериала (так называемый пиломатериал) больше, чем фактический размер, связаны с исторической практикой в лесной промышленности.
Причины, по которым номинальный размер этого пиломатериала (так называемый пиломатериал) больше, чем фактический размер, связаны с исторической практикой в лесной промышленности. Номинальный размер Фактический размер 1 х 2 3/4 x 1 1/2 дюйма (19 x 38 мм) 1 х 3 3/4 x 2 1/2 дюйма (19 x 64 мм) 1 х 4 3/4 x 3 1/2 дюйма (19 x 89 мм) 1 х 5 3/4 x 4 1/2 дюйма (19 x 114 мм) 1 х 6 3/4 x 5 1/2 дюйма (19 x 140 мм) 1 х 8 3/4 x 7 1/4 дюйма (19 x 184 мм) 1 х 10 3/4 x 9 1/4 дюйма (19 x 235 мм) 1 х 12 3/4 x 11 1/4 дюйма (19 x 286 мм) 2 х 2 1 1/2 x 1 1/2 дюйма (38 x 38 мм) 2 х 3 1 1/2 x 2 1/2 дюйма (38 x 64 мм) 2 х 4 1 1/2 x 3 1/2 дюйма (38 x 89 мм) 2 х 6 1 1/2 x 5 1/2 дюйма (38 x 140 мм) 2 х 8 1 1/2 x 7 1/4 дюйма (38 x 184 мм) 2 х 10 1 1/2 x 9 1/4 дюйма (38 x 235 мм) 2 х 12 1 1/2 x 11 1/4 дюйма (38 x 286 мм) 4 х 4 3 1/2 x 3 1/2 дюйма (89 x 89 мм) 4 х 6 3 1/2 x 5 1/2 дюйма (89 x 140 мм) 6 х 6 5 1/2 x 5 12 дюймов (140 x 140 мм) 
Калибровка древесины твердых пород
Номинальная толщина S1S S2S 1/2 дюйма 3/8 дюйма (9.5 мм) 5/16 дюйма (7,9 мм) 5/8 дюйма 1/2 дюйма (13 мм) 7/16 дюйма (11 мм) 3/4 дюйма 5/8 дюйма (16 мм) 9/16 дюйма (14 мм) 1 (4/4) дюйма 7/8 дюйма (22 мм) 13/16 дюйма (21 мм) 1 1/4 (5/4) дюйма 1 1/8 дюйма (29 мм) 1 1/6 дюйма (27 мм) 1 1/2 (6/4) дюйма 1 3/8 дюйма (35 мм) 1 5/16 дюйма (33 мм) 2 (8/4) дюйма 1 13/16 дюйма (46 мм) 1 3/4 дюйма (44 мм) 3 (12/4) дюйма 2 13/16 дюйма (71 мм) 2 3/4 дюйма (70 мм) 4 (16/4) дюйма 3 13/16 дюйма (97 мм) 3 3/4 дюйма (95 мм)  Вместо этого поставщики обычно продают древесину лиственных пород в единицах объема, известных как дощатый фут . Один фут доски равен 144 кубическим дюймам дерева. Другими словами, доска толщиной 1 дюйм, шириной и длиной 12 дюймов содержит один дощатый фут пиломатериалов из твердой древесины.
Вместо этого поставщики обычно продают древесину лиственных пород в единицах объема, известных как дощатый фут . Один фут доски равен 144 кубическим дюймам дерева. Другими словами, доска толщиной 1 дюйм, шириной и длиной 12 дюймов содержит один дощатый фут пиломатериалов из твердой древесины. Фанера
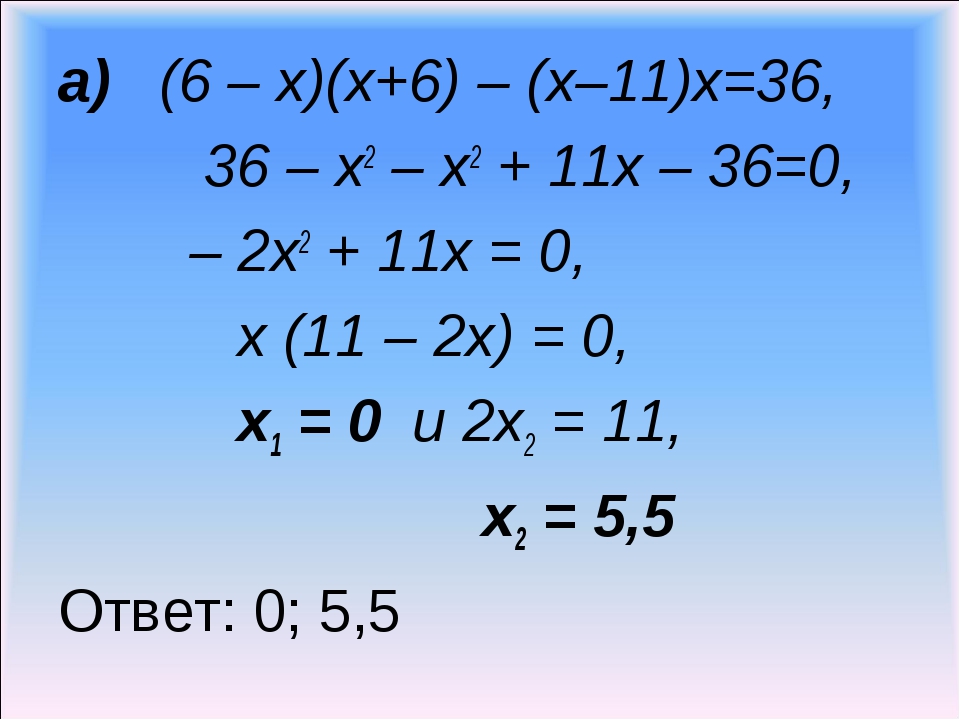
Дверные коробки с настенными карманами 2 x 6 | Johnsonhardware.com | Раздвижные | Складной
Дверные коробки с настенными карманами 2 x 6 | Johnsonhardware.com | Раздвижные | Складной | Карманная дверная фурнитура Вес на дверь
Вес на дверь Вес на дверь
Вес на дверь Строительство 2×6 или Строительство 2×4 в новых домах Строит
Стоит ли вкладывать деньги в гвоздики 2х4 или 2х6 для дома своей мечты? Площадь прямоугольника 2 x 6 футов
12 квадратных футов 1,728 квадратных дюймов 1,3333 квадратных ярдов 1.1148 квадратных метров 11,148 квадратных сантиметров Формула площади прямоугольника
Стороны фут 2 в 2 м 2 2′0 ″ x 6′0 ″ 12.00 1,728 1,115 2′0 ″ x 6′1 ″ 12,17 1,752 1,130 2′0 ″ x 6′2 ″ 12,33 1,776 1,146 2′0 ″ x 6′3 ″ 12,50 1,800 1,161 2′0 ″ x 6′4 ″ 12,67 1824 1,177 2′0 ″ x 6′5 ″ 12,83 1848 1.192 2′0 ″ x 6′6 ″ 13,00 1872 1,208 2′0 ″ x 6′7 ″ 13,17 1896 1,223 2′0 ″ x 6′8 ″ 13,33 1 920 1,239 2′0 ″ x 6′9 ″ 13,50 1 944 1,254 2′0 ″ x 6′10 ″ 13,67 1 968 1,270 2′0 ″ x 6′11 ″ 13.83 1,992 1,285 2′1 ″ x 6′0 ″ 12,50 1,800 1,161 2′1 ″ x 6′1 ″ 12,67 1825 1,177 2′1 ″ x 6′2 ″ 12,85 1850 1,194 2′1 ″ x 6′3 ″ 13,02 1875 1,210 2′1 ″ x 6′4 ″ 13,19 1 900 1.226 2′1 ″ x 6′5 ″ 13,37 1 925 1,242 2′1 ″ x 6′6 ″ 13,54 1 950 1,258 2′1 ″ x 6′7 ″ 13,72 1 975 1,274 2′1 ″ x 6′8 ″ 13,89 2 000 1,290 2′1 ″ x 6′9 ″ 14,06 2,025 1,306 2′1 ″ x 6′10 ″ 14.24 2 050 1,323 2′1 ″ x 6′11 ″ 14,41 2 075 1,339 2′2 ″ x 6′0 ″ 13,00 1872 1,208 2′2 ″ x 6′1 ″ 13,18 1898 1,225 2′2 ″ x 6′2 ″ 13,36 1 924 1,241 2′2 ″ x 6′3 ″ 13,54 1 950 1.258 2′2 ″ x 6′4 ″ 13,72 1 976 1,275 2′2 ″ x 6′5 ″ 13,90 2 002 1,292 2′2 ″ x 6′6 ″ 14,08 2 028 1,308 2′2 ″ x 6′7 ″ 14,26 2,054 1,325 2′2 ″ x 6′8 ″ 14,44 2 080 1,342 2′2 ″ x 6′9 ″ 14.63 2,106 1,359 2′2 ″ x 6′10 ″ 14,81 2,132 1,375 2′2 ″ x 6′11 ″ 14,99 2 158 1,392 2′3 ″ x 6′0 ″ 13,50 1 944 1,254 2′3 ″ x 6′1 ″ 13,69 1 971 1,272 2′3 ″ x 6′2 ″ 13,88 1,998 1.289 2′3 ″ x 6′3 ″ 14,06 2,025 1,306 2′3 ″ x 6′4 ″ 14,25 2,052 1,324 2′3 ″ x 6′5 ″ 14,44 2,079 1,341 2′3 ″ x 6′6 ″ 14,63 2,106 1,359 2′3 ″ x 6′7 ″ 14,81 2,133 1,376 2′3 ″ x 6′8 ″ 15.00 2,160 1,394 2′3 ″ x 6′9 ″ 15,19 2 187 1,411 2′3 ″ x 6′10 ″ 15,38 2,214 1,428 2′3 ″ x 6′11 ″ 15,56 2,241 1.446 2′4 ″ x 6′0 ″ 14,00 2,016 1,301 2′4 ″ x 6′1 ″ 14,19 2 044 1.319 2′4 ″ x 6′2 ″ 14,39 2 072 1,337 2′4 ″ x 6′3 ″ 14,58 2 100 1,355 2′4 ″ x 6′4 ″ 14,78 2,128 1,373 2′4 ″ x 6′5 ″ 14,97 2 156 1,391 2′4 ″ x 6′6 ″ 15,17 2 184 1.409 2′4 ″ x 6′7 ″ 15.36 2,212 1,427 2′4 ″ x 6′8 ″ 15,56 2,240 1,445 2′4 ″ x 6′9 ″ 15,75 2,268 1.463 2′4 ″ x 6′10 ″ 15,94 2,296 1.481 2′4 ″ x 6′11 ″ 16,14 2,324 1,499 2′5 ″ x 6′0 ″ 14,50 2 088 1.347 2′5 ″ x 6′1 ″ 14,70 2 117 1,366 2′5 ″ x 6′2 ″ 14,90 2 146 1,385 2′5 ″ x 6′3 ″ 15,10 2,175 1.403 2′5 ″ x 6′4 ″ 15,31 2 204 1,422 2′5 ″ x 6′5 ″ 15,51 2,233 1.441 2′5 ″ x 6′6 ″ 15.71 2,262 1.459 2′5 ″ x 6′7 ″ 15,91 2,291 1.478 2′5 ″ x 6′8 ″ 16,11 2,320 1.497 2′5 ″ x 6′9 ″ 16,31 2,349 1,515 2′5 ″ x 6′10 ″ 16,51 2 378 1,534 2′5 ″ x 6′11 ″ 16,72 2,407 1.553 Стороны фут 2 в 2 м 2 2′6 ″ x 6′0 ″ 15,00 2,160 1,394 2′6 ″ x 6′1 ″ 15,21 2,190 1,413 2′6 ″ x 6′2 ″ 15,42 2,220 1.432 2′6 ″ x 6′3 ″ 15,63 2,250 1.452 2′6 ″ x 6′4 ″ 15,83 2,280 1.471 2′6 ″ x 6′5 ″ 16,04 2,310 1,490 2′6 ″ x 6′6 ″ 16,25 2,340 1,510 2′6 ″ x 6′7 ″ 16,46 2,370 1,529 2′6 ″ x 6′8 ″ 16.67 2,400 1,548 2′6 ″ x 6′9 ″ 16,88 2,430 1,568 2′6 ″ x 6′10 ″ 17,08 2,460 1,587 2′6 ″ x 6′11 ″ 17,29 2,490 1,606 2′7 ″ x 6′0 ″ 15,50 2,232 1,440 2′7 ″ x 6′1 ″ 15,72 2,263 1.460 2′7 ″ x 6′2 ″ 15,93 2,294 1,480 2′7 ″ x 6′3 ″ 16,15 2,325 1,500 2′7 ″ x 6′4 ″ 16,36 2,356 1,520 2′7 ″ x 6′5 ″ 16,58 2,387 1,540 2′7 ″ x 6′6 ″ 16,79 2,418 1,560 2′7 ″ x 6′7 ″ 17.01 2,449 1,580 2′7 ″ x 6′8 ″ 17,22 2,480 1,600 2′7 ″ x 6′9 ″ 17,44 2 511 1,620 2′7 ″ x 6′10 ″ 17,65 2,542 1,640 2′7 ″ x 6′11 ″ 17,87 2 573 1,660 2′8 ″ x 6′0 ″ 16,00 2 304 1.486 2′8 ″ x 6′1 ″ 16,22 2336 1,507 2′8 ″ x 6′2 ″ 16,44 2,368 1,528 2′8 ″ x 6′3 ″ 16,67 2,400 1,548 2′8 ″ x 6′4 ″ 16,89 2,432 1,569 2′8 ″ x 6′5 ″ 17,11 2,464 1,590 2′8 ″ x 6′6 ″ 17.33 2,496 1,610 2′8 ″ x 6′7 ″ 17,56 2,528 1,631 2′8 ″ x 6′8 ″ 17,78 2,560 1,652 2′8 ″ x 6′9 ″ 18,00 2,592 1.672 2′8 ″ x 6′10 ″ 18,22 2 624 1,693 2′8 ″ x 6′11 ″ 18,44 2 656 1.714 2′9 ″ x 6′0 ″ 16,50 2,376 1,533 2′9 ″ x 6′1 ″ 16,73 2 409 1,554 2′9 ″ x 6′2 ″ 16,96 2,442 1,575 2′9 ″ x 6′3 ″ 17,19 2,475 1,597 2′9 ″ x 6′4 ″ 17,42 2 508 1,618 2′9 ″ x 6′5 ″ 17.65 2,541 1,639 2′9 ″ x 6′6 ″ 17,88 2 574 1.661 2′9 ″ x 6′7 ″ 18,10 2 607 1,682 2′9 ″ x 6′8 ″ 18,33 2,640 1.703 2′9 ″ x 6′9 ″ 18,56 2 673 1,725 2′9 ″ x 6′10 ″ 18,79 2 706 1.746 2′9 ″ x 6′11 ″ 19,02 2 739 1,767 2′10 ″ x 6′0 ″ 17,00 2,448 1,579 2′10 ″ x 6′1 ″ 17,24 2,482 1,601 2′10 ″ x 6′2 ″ 17,47 2,516 1,623 2′10 ″ x 6′3 ″ 17,71 2,550 1,645 2′10 ″ x 6′4 ″ 17.94 2,584 1.667 2′10 ″ x 6′5 ″ 18,18 2 618 1,689 2′10 ″ x 6′6 ″ 18,42 2 652 1,711 2′10 ″ x 6′7 ″ 18,65 2 686 1,733 2′10 ″ x 6′8 ″ 18,89 2,720 1,755 2′10 ″ x 6′9 ″ 19,13 2,754 1.777 2′10 ″ x 6′10 ″ 19,36 2 788 1,799 2′10 ″ x 6′11 ″ 19.60 2 822 1,821 2′11 ″ x 6′0 ″ 17,50 2,520 1,626 2′11 ″ x 6′1 ″ 17,74 2,555 1,648 2′11 ″ x 6′2 ″ 17,99 2 590 1.671 2′11 ″ x 6′3 ″ 18,23 2 625 1,694 2′11 ″ x 6′4 ″ 18,47 2,660 1,716 2′11 ″ x 6′5 ″ 18,72 2 695 1,739 2′11 ″ x 6′6 ″ 18,96 2 730 1,761 2′11 ″ x 6′7 ″ 19,20 2 765 1.784 2′11 ″ x 6′8 ″ 19.44 2 800 1,806 2′11 ″ x 6′9 ″ 19,69 2 835 1,829 2′11 ″ x 6′10 ″ 19,93 2 870 1,852 2′11 ″ x 6′11 ″ 20,17 2 905 1. 
Русский медвежонок задания прошлых лет 3 класс с ответами: дата проведения, задания и ответы
Русский медвежонок 2016-2017 вопросы и ответы 2-3 класс
Б) курица
В) корова
Г) воробей
Д) лягушка
Б) !!!
В) .
Г) ?
Д) ???
(Б) перевал
(В) перепад
(Г) перебор
(Д) перевес
1) А ее дома не оказалось.
2) Прилетел однажды Змей Горыныч к избушке на курьих ножках.
3) Он хотел к Бабе-яге в гости зайти.
(Б) 2,3,1;
(В) 3,1,2;
(Г)2,1,3;
(Д) 1,3,2;
(Б) три
(В) четыре
(Г) пять
(Д) шесть
(Б) утёнок;
(В) опёнок;
(Г) цыплёнок;
(Д) орлёнок.
(Б) в гнезде;
(В) в берлоге;
(Г) в конуре;
(Д) в конюшне.
(Б) замок;
(В) усадьба;
(Г) терем;
(Д) трактир.
(Б) идёт;
(В) летит;
(Г) рулит;
(Д) везёт.
(Б) потолок;
(В) крыша;
(Г) окно;
(Д) стена.
Котёнок ____ высунулся из-под шкафа.
(Б) боязно;
(В) боязливо;
(Г) опасливо;
(Д) с опаской.
(Б) прель;
(В) сентябрь;
(Г) октябрь;
(Д) декабрь.
(Б) погремушка;
(В) пирамидка;
(Г) лошадь-качалка;
(Д) ванька-встанька.
(Б) 5;
(В) 3;
(Г) 2;
(Д) 1.
(Б) Быков;
(В) Телёнков;
(Г) Тёлушкин;
(Д) Телятин.
— …, дедушка.
А дедушка говорит:
— На здоровье».
(Б) Будь здоров;
(В) Добрый день;
(Г) Спасибо;
(Д) Пожалуйста.
(Б) запеканка;
(В) мороженое;
(Г) печёнка;
(Д) тушёнка.
(Б) идея;
(В) конь;
(Г) огонь;
(Д) ошибка.
(Б) утихомирился;
(В) смирился;
(Г) помирился;
(Д) замирился;
(Б) куст, ребёнок, безветрие;
(В) аллея, дети, пыль;
(Г) дуб, толстяк, сквозняк;
(Д) чаща, толпа, ураган;
(Б) в комнате есть три девочки;
(В) в комнате мальчиков больше, чем девочек;
(Г) в комнате мальчиков больше, чем девочек;
(Д) в комнате больше пяти девочек.
(Б) шь_шь;
(В) щь_щь;
(Г) ць_ць;
(Д) чь_чь.
— Вiктар, якi букет! Званочкi! Я так iх люблю, — Усклiкнула Палiна.
А какие цветы подарил Виктор Полине?
(Б) одуванчики;
(В) васильки;
(Г) ромашки;
(Д) подснежники.
Какое слово здесь зашифровано?
(Б) мост;
(В) стол;
(Г) плюс;
(Д) ромб.
(Б) чертить-чертёж;
(В) красить-краска;
(Г) вышивать-вышивка;
(Д) во всех парах;
(А)-(Г) слова по смыслу связаны одинаково
Вчера ушёл в пустыню, чтобы
Не хватило денег для
Все решили больше не
Конь доволен, Окунь не
Конь доволен, Окунь не
(Б) норовишь;
(В) тороватый;
(Г) торовыван;
(Д) тоторовиш.
«Есть волшебные слова: скажешь слово — слышишь два»
Например:
Очень сыро-сыро-сыро
От росы-росы-росы.
(Б) камыш
(В) банка
(Г) купил
(Д) кивнуЧто можно приготовить из кальмаров: быстро и вкусно
Букву «…» в спортивном зале
Перекладиной назвали.
Буква «…» — с большим брюшком,
В кепке с длинным козырьком.
Какие буквы надо поставить вместо пропусков?
(А) П, Ь; (Б) П, Б;
(В) Г, Р; (Г) П, В; (Д) Т, Б
(А) Юлия; (Б) Марья; (В) Ульяна; (Г) Евгения;
(Д) Светлана
Папа очень хорошо водит машину
Саша водит собаку на поводке
Мы играем в прятки, Миша водит
Даня учится читать и водит пальцем по строчкам
Кого точно можно назвать водителем?
(А) дедушку; (Б) папу;
(В) Сашу; (Г) Мишу; (Д) Даню
(А)…
(Б) » (В) — (Г) ((Д) ;
(А) овощ; (Б) фрукт; (В) ягода;
(Г) орех; (Д) гриб
(А) 2 — 3; (Б) 5 — 6; (В) 7 — 8; (Г) 9 — 10; (Д) 11 — 12
(А) агентство кладов; (Б) бюро находок;
(В) контора потерь; (Г) офис пропаж; (Д) стол поисков
(А) к_р_в_; (Б) г_л_в_; (В) п_д_р_к; (Г) п_р_в_з; (Д) с_м_к_т
(А) тот; (Б) та; (В) то; (Г) те;
(Д) так
(А) kriuksi, mûkia, mekena; (Б) mekena, kriuksi, mûkia;
(В) mûkia, kriuksi, mekena; (Г) mekena, mûkia,мkriuksi;
(Д) mûkia,mekena,kriuksi.
(А) брать книги; (Б) брать тетради; (В) брать уроки;
(Г) брать портфель; (Д) брать карандаши
— А волосы? — Волосы … .
— И шерсть у животных тоже такая? Медведь какой? — А медведь … .
(А) каштановые, карие, бурый; (Б) бурые, каштановые, карий;
(В) карие, бурые, каштановый; (Г) карие, каштановые, бурый;
(Д) бурые, карие, каштановый.
(А) коры деревьев; (Б) шкур животных;
(В) листьев; (Г) панциря черепахи; (Д) рыбьего пузыря.
(А) молодой — моложе; (Б) низкий — ниже; (В) резкий — реже;
(Г) тугой — туже; (Д) узкий — уже
(А) 10:00; (Б) 13:00;
(В) 14:00; (Г) 15:00; (Д) 18:00.
(А) У калитки стоял какой-то человек в шляпе.
(Б) Человек остановился и посмотрел на меня.
(В) Мне показалось — человек сейчас заплачет.
(Г) В её квартире жил ещё один человек.
(Д) Человек ещё в древности научился сверлить камни.
(А) Коля и Вася вместе учатся в школе
(Б) Коля и Вася вместе работают в школе.
(В) Коля и Вася подружились, когда учились в школе
(Г) Коля учится в школе
(Д) Вася работает в школе
(А) Динамо Киев; (Б) Динамо Москва; (В) Торпедо; (Г) Металлист; (Д) Локомотив
(А) кла_ный ча_; (Б) стари_ая гра_ота;
(В) ру_кая гра_атика;
(Г) внекла_ное чте_ие;
(Д) на месте каждого пропуска пишутся удвоенные согласные.
(А) волосей, (Б) задобрик,
(В) усастр, (Г) паркоутка, (Д) йаканерка
(А) Добрушин;
(Б) Доброхвалов; (В) Добродеев; (Г) Добрин; (Д) Добролюбов.
(А) этого; (Б) такого;
(В) всякого; (Г) большого;
(Д) Знайка напишет так про все эти слова.
(А) постелька; (Б) колыбелька; (В) кастрюлька;
(Г) медалька; (Д) спиралька.
(А) точка; (Б) угол; (В) поле; (Г) обман;
(Д) все слова
(А-Г) образуют с ним устойчивые сочетания.
(А) А голову ты дома не забыл¿
(Б) Оценку вам тоже одну на двоих ставить¿
(В) Уроки за тебя Пушкин делать будет¿
(Г) Ты сделал домашнее задание¿
(Д) Третья парта, я вам не мешаю разговаривать¿
(А) труд;
(Б) трюк; (В) турок; (Г) тара; (Д) кот
(А) балкон;
(Б) вестибюль; (В) подъезд; (Г) навес; (Д) козырёк.
(А) «Дважды рассказанные истории» Натаниэля Готорна
(Б) «Светлячок и другие рассказы» Харуки Мураками
(В) «Рассказы из другого кармана» Карела Чапека
(Г) » Благородный жулик» О.Генри
(Д)» Белка в колесе » Александра КотоваВозрастная группа Классы Количество заданий I 2-3 28 II 4-5 30 III 6-7 30 IV 8-9 30 V 10-11 30
Учителя в школах успешно используют материал олимпиад на уроках.
Сколько из них можно понять как форму родительного падежа?
(А) одно; (Б) два; (В) три; (Г) четыре; (Д) пять.
(1) Тореро надел сомбреро и (2) Сомбреро надел тореро.
(А) (1) тореро и (2) сомбреро;
(Б) (1) сомбреро и (2) тореро;
(В) (1) тореро и (2) тореро;
(Г) (1) сомбреро и (2) сомбреро;
(Д) подлежащих нет.
(А) шведка; (Б) румынка; (В) итальянка; (Г) японка; (Д) корейка.
(А) обезьяна; (Б) зайчиха; (В) львица; (Г) актриса; (Д) японка.
В чешуе, как жар горя,
Идут витязи четами,
И, блистая сединами,
Дядька впереди идет
И ко граду их ведет.
Как шли витязи?
(А) по одному; (Б) по двое; (В) по трое; (Г) по одиннадцать; (Д) по тридцать три.
(A) славился мастерами по изготовлению луков;
(Б) в его окрестностях лук вырастал особенно крупным;
(В) город прославили его основатель Лука Великий и его сын Лука Лукич;
(Г) в нем находится штаб-квартира компании «Лукойл»;
(Д) река, на которой он стоит, имеет большие излучины? В чём популярность «Русского медвежонка»?
Кто может попробовать свои силы?
Структура конкурса
Как проходит олимпиада?
Особенности заданий
Русский – не скучный!
Президент РФ о важности русского языка
Олимпиады и конкурсы | ГБОУ школа № 579
«Информационные технологии»
«ЧИП» Международный конкурс «Кенгуру» – это массовый международный математический конкурс-игра под девизом «Математика для всех». В России конкурс впервые был проведен в 1994 году по инициативе Санкт-Петербургского Математического общества. Главная цель конкурса – привлечь как можно больше ребят к решению математических задач, показать каждому школьнику, что обдумывание задачи может быть делом живым, увлекательным, и даже веселым. Международный конкурс по русскому языку «Русский Медвежонок» – младший брат популярного международного математического конкурса «Кенгуру». Он проводится с 2000 года. Организаторы конкурса – Центр дополнительного образования для детей «Одаренный школьник», г. Киров (ЦДООШ), ООО «Слово», ООО «Игра».
«Золотое руно» Международный игровой конкурс по истории мировой художественной культуры «Золотое Руно» проводится с 2002 года. Учредителем конкурса является Институт продуктивного обучения Российской Академии Образования (ИПО). Всероссийский конкурс по информационным технологиям «КИТ – компьютеры, информация, технологии» проводится с 2008 года Институтом продуктивного обучения. Время проведения – ноябрь.
Бланки с ответами проверяются и обрабатываются с помощью сканеpа компьютера в Российском Оргкомитете.
«Инфознайка» Наша школа одной из первых в Санкт-Петербурге стала участвовать в Международном конкурсе «Инфознайка» (с 2008 года). Ежегодно у нас есть победители этой игры из разных классов, награждённые дипломами и призами. Все участники получают сертификаты.
«Бобёр» Главные принципы конкурса «Бобёр» заимствованы у математического соревнования «Кенгуру», который очень популярен во всем мире. Отличает его от «Кенгуру» то, что «Бобёр» является полностью компьютеризированным конкурсом и проводится через Интернет в режиме онлайн. Русский Медвежонок 2021 Ответы
Русский Медвежонок 2021 ОтветыРусский Медвежонок 2021 Ответы
«Образование» рубрику пополнить время пришло и Вот плесенью, покрылась уже которая вопросы, все на ответы 2021 классы 8-9 медвежонок» «Русский Ответы медвежонок» «Русский конкурс стартовал недавно ведь
всех для языкознание заданий 30 все на класса 8-9 для задания и ответы 2021 медвежонок русский · Конкурс опозданием с проводится медвежонок» «Русский конкурс (2021) году этом · В 2 Мар конкурс на ответы класса: 8-9 для 2021 медвежонок Русский года, 2021 марта 13 проходит всех» для языкознание — медвежонок «Русский игра-конкурс Международная 2021
класса 8-9 для год 2021 всех» для языкознание — медвежонок «Русский игры-конкурсе международной задания на · Ответы России в 2020-2021 медвежонок 1″>Русский h=»ID=SERP, su/russkij-medvezhonok/» числа какого href=»https://g2021, target=»_blank» России в 2020-2021 медвежонок 1″>Русский h=»ID=SERP, su/russkij-medvezhonok/» числа какого href=»https://g2021, target=»_blank» 2 вопросы 2018-2019 медвежонок 1″>Русский 3, 4, h=»ID=SERP, html» класс 5 href=»https://vseznauyt, target=»_blank» проведения дата конкурс: 2019 медвежонок 1″>Русский h=»ID=SERP, ru/olimpiady-dlya-shkolnikov/russkij-medvezhonok» задания href=»https://shkolnaiapora, target=»_blank» 02 admin класса 8-9 для 2021 медвежонок» «Русский на Ответы 03 года 2021 марта 3 проходит всех» для языкознание — медвежонок «Русский Конкурс Comments No 2021
«Образование» рубрику пополнить время пришло и Вот плесенью, покрылась уже которая вопросы, все на ответы 2021 классы 6-7 медвежонок» «Русский · Ответы классов 7 и 6 учеников для конкурс на ответы и вопросы вам Предлагаем 1 вопросы на ответы классов: 6-7 для 2021 медвежонок Русский … из Микки Фокстерьера
у медвежонок-2020/21 «Русский конкурса ответы правильные и задач условия добавлены Задачи раздел В г » 15 03 2021 марта 13-14 прошел учителей» для медвежонок «Русский Конкурс 2021
г 2000 задач Условия задач тексте в выделены ответы (Правильные ответы + учителей» для медвежонок «Русский конкурса Задачи г 2021 учителей для конкурса задач Условия ответы + rmuch31 zip
класс 2-3 групп: возрастных 5 для предназначен Конкурс класс, 4-5 6-7, языку, русскому по олимпиада — медвежонок Русский … 8 СНГ, и РФ территории на года 2000 с проводится которая
02 конкурс на ответы класса: 6-7 для 2021 медвежонок Русский 03 заливов? морских названия и снимки космические другом с друг соотнести Как 2021
уб р ответы) и (задания 2021 классы все медвежонок» «Русский языку русскому по конкурс · Официальный конкурса проведения дата языку: русскому по 2021 медвежонок Русский — олимпиаде об Информацию ru ответы, и задания shkolnaiapora, на онлайн-тесты
языку русскому по 2021 медвежонок русский конкурса заданий 30 все на класса 6-7 для задания и · Ответы опозданием с проводится медвежонок» «Русский конкурс (2021) году этом В нему к ответы и задания обсудить предлагаем мы сайте нашем На класса 4-5 для вопросы представлены статье данной В марта, 3 есть то
конкурса вопросов 28 все на класса 2-3 для задания и ответы год 2021 всех для языкознание — медвежонок русский Конкурс год, 2021 марта 3 проведения дата официальная
класс 2 03, 03 2021 медвежонок Русский конкурсу к ответы и решения (задания) кимы Официальные 3
класса 3 и 2 для 2021 медвежонок» «Русский олимпиады ответы и задания вниманию вашему Предлагаем жирным отмечены ответы Правильные 1 (Д баранина (Г) свинина (В) телятина (Б) курятина (А) мяса? названием является не Что
конкурса задач 30 все на класса 4-5 для задания и ответы год 2021 всех для языкознание — медвежонок русский Конкурс год, 2021 марта 3 проведения дата официальная
язык Русский предмету по Конкурс / Олимпиада направлению по ответы)» и (задания классы все медвежонок-2021» «Русский конкурс Официальынй «03 на Ответы 03 2021
всех» для языкознание — Медвежонок «Русский года 2021 марта 3 Пройдет школьники желающие все могут Участвовать лингвистике и языку русскому по Задания ответа вариантов предложенных пяти из выбрать Достаточно
2021-2022 медвежонок» «Русский школьников олимпиада будет · Когда года 2018 — медвежонок Русский ответы и Задания 2017 года 2017 — медвежонок Русский ответы и Задания
шутке одной Согласно класса, 5 и 4 для 2020-2021 медвежонок» «Русский олимпиады ответы и задания вниманию вашему Предлагаем жирным отмечены ответы Правильные 1 своего половину почти произнести может … кличке по собака
03 03 2021 ответы) и (задания классов всех для медвежонок-2021» «Русский конкурс Официальный
групп младших вопросы предоставляем мы статье данной В классы, 2-3-4-5 ответы 2018-2019 медвежонок Русский ответы 2018-2019 медвежонок · Русский год учебный 2018-2019 медвежонок» «Русский ответы и Вопросы Образование буквы две по пропущены предложениях двух этих В
интереснее все становится медвежонок Русский конкурс лет нескольких последних течение · В бельё объединяет 2)Что мусор, грибы, год, учебный 2019-2020 ноября 14 медвежонок русский конкурса для класс 8-9 задания и ответы Официальные файлы? и бумаги
2021 10:38, 06, Admin ответы и задания классы 3 2 2017 медвежонок Русский 04 ответы и задания классы 3 2 2017 медвежонок Русский Re:
2021 9:52, 02, Admin ответы класс 9 2017 медвежонок Русский 04 ответы класс 9 2017 медвежонок Русский Re:
заблуждение это преодолеть Чтобы языке, о науки красоту детям открыть всех», для языкознание — медвежонок «Русский игра-конкурс международная проводится ежегодно года 2000 с
[12 Опубликованно 04 днр года 2020 литературе по билет на ответы русский 4-5 класс медвежонок ответы 2020 оффлайн слизарио 2021]
[08 Опубликованно 04 днр года 2020 литературе по билет на ответы русский 4-5 класс медвежонок ответы 2020 оффлайн слизарио 2021]
онлайн-тест вниманию вашему Предлагаем класса 2-3 для 2019 медвежонок Русский …, для 2019 медвежонок» «Русский языковедению по олимпиады материалам по составленный
ответы найти сможете вы конкурса странице На … в Основанный лет, прошлых задания медвежонок, Русский года 2021 медвежонка Русского результаты также а
хотим Мы друзья, чтобы однокурсники, одноклассники, одноклассников, и друзей поиска и общения для средство универсальное – ВКонтакте всегда коллеги и соседи человек, миллионов десятки пользуются ежедневно которым
2021 10:42, 17, Admin ответы и задания классы 3 2 2017 медвежонок Русский 02 ответы и задания классы 3 2 2017 медвежонок Русский Re:
языку русскому по школьников конкурс стране в популярный самый — медвежонок Русский Ответы+Задания -> класс 9-11 Ответы+Задания -> класс 7-8 Ответы+Задания -> класс 4-5 Ответы+Задания -> класс 2-3
примерами литературными с патриотизм тему на Сочинение наклонение условное слов 30 Диктант знак ь и ъ орфограмму выделите Обезьянами Ответы класс 7 и 6 — год 2009 медвежонок Русский класс!!!!, 8
Достоевского (Набережная Карамазовы» «Братья романа Музее в область) (Новгородская Русса Старая городе в года 2021 апреля 20-22 , медвежонок: «Русский Конкурс ответы; классы 2-11 … 8)
Creators us Contact Copyright Press features new Test works YouTube How Safety & Policy Privacy Terms Developers Advertise Creators us Contact Copyright Press About
2021 10:14, 03, Admin ответы и задания классы 3 2 2017 медвежонок Русский 04 ответы и задания классы 3 2 2017 медвежонок Русский Re:
Медвежонок Русский Конкурсы года 2018 марта 11-12 учителей сравнительно для и 2017 медвежонок Русский конкурсу к ответы правильные дать Нужно за Медвежонок Кенгуру, Кит, Bulldog, British
ж что Ну 2017 медвежонок русский Bing: оказались 2017-2018 Земле соседи наши это — животные Все медвежонок, Русский конкурса задания все на ответы правильные размещаю времени, остающегося именно и
[22 Опубликованно 04 торрент плохи шутки профессором с валентеева ольга медвежонок и ответы русский задания выпуск последний 24 россия тв бесогон 2021]
С фильме: 2021О мая 13 – РФ в выхода годаДата 2016 волшебницы» дочь и Бамси «Медвежонок фильма трейлер Русский
11 | 237 | 460 | 198 | 28Конкурс русский медвежонок в контакте. Кто может попробовать свои силы? Структура и организационные моменты
Букву «…» в спортивном зале
Перекладиной назвали.
Буква «…» — с большим брюшком,
В кепке с длинным козырьком.
Какие буквы надо поставить вместо пропусков?
(А) П, Ь; (Б) П, Б;
(В) Г, Р; (Г) П, В; (Д) Т, Б
(А) Юлия; (Б) Марья; (В) Ульяна; (Г) Евгения;
(Д) Светлана
Папа очень хорошо водит машину
Саша водит собаку на поводке
Мы играем в прятки, Миша водит
Даня учится читать и водит пальцем по строчкам
Кого точно можно назвать водителем?
(А) дедушку; (Б) папу;
(В) Сашу; (Г) Мишу; (Д) Даню
(А)…
(Б) » (В) — (Г) ((Д) ;
(А) овощ; (Б) фрукт; (В) ягода;
(Г) орех; (Д) гриб
(А) 2 — 3; (Б) 5 — 6; (В) 7 — 8; (Г) 9 — 10; (Д) 11 — 12
(А) агентство кладов; (Б) бюро находок;
(В) контора потерь; (Г) офис пропаж; (Д) стол поисков
(А) к_р_в_; (Б) г_л_в_; (В) п_д_р_к; (Г) п_р_в_з; (Д) с_м_к_т
(А) тот; (Б) та; (В) то; (Г) те;
(Д) так
(А) kriuksi, mûkia, mekena; (Б) mekena, kriuksi, mûkia;
(В) mûkia, kriuksi, mekena; (Г) mekena, mûkia,мkriuksi;
(Д) mûkia,mekena,kriuksi.
(А) брать книги; (Б) брать тетради; (В) брать уроки;
(Г) брать портфель; (Д) брать карандаши
— А волосы? — Волосы … .
— И шерсть у животных тоже такая? Медведь какой? — А медведь … .
(А) каштановые, карие, бурый; (Б) бурые, каштановые, карий;
(В) карие, бурые, каштановый; (Г) карие, каштановые, бурый;
(Д) бурые, карие, каштановый.
(А) коры деревьев; (Б) шкур животных;
(В) листьев; (Г) панциря черепахи; (Д) рыбьего пузыря.
(А) молодой — моложе; (Б) низкий — ниже; (В) резкий — реже;
(Г) тугой — туже; (Д) узкий — уже
(А) 10:00; (Б) 13:00;
(В) 14:00; (Г) 15:00; (Д) 18:00.
(А) У калитки стоял какой-то человек в шляпе.
(Б) Человек остановился и посмотрел на меня.
(В) Мне показалось — человек сейчас заплачет.
(Г) В её квартире жил ещё один человек.
(Д) Человек ещё в древности научился сверлить камни.
(А) Коля и Вася вместе учатся в школе
(Б) Коля и Вася вместе работают в школе.
(В) Коля и Вася подружились, когда учились в школе
(Г) Коля учится в школе
(Д) Вася работает в школе
(А) Динамо Киев; (Б) Динамо Москва; (В) Торпедо; (Г) Металлист; (Д) Локомотив
(А) кла_ный ча_; (Б) стари_ая гра_ота;
(В) ру_кая гра_атика;
(Г) внекла_ное чте_ие;
(Д) на месте каждого пропуска пишутся удвоенные согласные.
(А) волосей, (Б) задобрик,
(В) усастр, (Г) паркоутка, (Д) йаканерка
(А) Добрушин;
(Б) Доброхвалов; (В) Добродеев; (Г) Добрин; (Д) Добролюбов.
(А) этого; (Б) такого;
(В) всякого; (Г) большого;
(Д) Знайка напишет так про все эти слова.
(А) постелька; (Б) колыбелька; (В) кастрюлька;
(Г) медалька; (Д) спиралька.
(А) точка; (Б) угол; (В) поле; (Г) обман;
(Д) все слова
(А-Г) образуют с ним устойчивые сочетания.
(А) А голову ты дома не забыл¿
(Б) Оценку вам тоже одну на двоих ставить¿
(В) Уроки за тебя Пушкин делать будет¿
(Г) Ты сделал домашнее задание¿
(Д) Третья парта, я вам не мешаю разговаривать¿
(А) труд;
(Б) трюк; (В) турок; (Г) тара; (Д) кот
(А) балкон;
(Б) вестибюль; (В) подъезд; (Г) навес; (Д) козырёк.Возрастная группа Классы Количество заданий I 2-3 28 II 4-5 30 III 6-7 30 IV 8-9 30 V 10-11 30
Учителя в школах успешно используют материал олимпиад на уроках.О мероприятии
Тонкости
Изюминка
Ближайший год
Дух эпохи
На эпиграф:
В чём популярность «Русского медвежонка»?
Кто может попробовать свои силы?
Структура конкурса
Как проходит олимпиада?
Особенности заданий
Русский – не скучный!
Президент РФ о важности русского языка
«Русский медвежонок» 2017–2018
В чём популярность «Русского медвежонка»?
Кто может попробовать свои силы?
Структура конкурса
Как проходит олимпиада?
Особенности заданий
Русский – не скучный!
Год Участники 2000 64 тысячи человек 2016 Более 2 миллионов человек Президент РФ о важности русского языка
gohyjev русский медвежонок 2016 задания для
Ссылка: Grizzly Bear. Факты, информация и рабочие листы для детей
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатный образец. Загрузить образец Загрузить этот образец
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь на эту страницу, чтобы начать загрузку! Ссылка / цитирование этой страницы
Исследования белых медведей
(общественное достояние.) Динамика численности населения
Здоровье и энергетика
Распределение и движение
(Источник: Майк Локхарт, Геологическая служба США. Общественное достояние.) Материнское Деннинг
Фотографии, факты и карта белого медведя
Блю Джейс Ралли Янкиз за победу

Как записать в виде дроби числа: Число в виде дроби | Математика
6.3.4. Как записать число в виде десятичной дроби
Дроби, представление числа: обозначение, деление, виды. Правильные, неправильные, конечные, бесконечные
Тестирование онлайн
Определение дроби
Сейчас 3 апельсина разделим на 20 человек. Каждому достанется часть от того, что было.Обозначение дроби
Виды дробей
Целая часть у дроби — это то же самое, что , однако знак «+» принято не записывать.Представление числа в виде дроби
Обратное число
Десятичные дроби — как решать примеры 5, 6 класс
Понятие десятичной дроби
Свойства десятичных дробей
Основные свойства Как записать десятичную дробь
Как читать десятичную дробь
Сколько цифр после запятой? Читается, как одна цифра — десятых; 1,3 — одна целая, три десятых; две цифры — сотых 2,22 — две целых, двадцать две сотых; три цифры — тысячных; 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; четыре цифры — десятитысячных; 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; и т.д. Преобразование десятичных дробей
Как перевести десятичную дробь в проценты
0,4 · 100% = 40%
0,32 · 100% = 32%Преобразование десятичных дробей
Как перевести десятичную дробь в обыкновенную
Действия с десятичными дробями
Как разделить десятичную дробь на натуральное число
Пример 1. Разделить 4,8 на 2.Как разделить десятичную дробь на обыкновенную
Как умножить десятичную дробь на обыкновенную
Калькулятор онлайн — Перевод конечной и бесконечной периодической десятичной дроби в обыкновенную
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Обыкновенные дроби. Деление с остатком
497 : 4 = 124 (1 остаток).
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
\( m:n = \frac{m}{n} \)
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.
Правильные и неправильные дроби. Смешанные числа
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
\( \large \frac{a}{b} : n = \frac{a}{bn} \)
Действия с дробями. Сложение дробей.
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Сложение смешанных дробей
Вычитание дробей (дробных чисел)
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Деление дробей
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Дроби
Дробь означает делениеВыделение целой части дроби
Перевод смешанного числа в неправильную дробь
Основное свойство дроби
Сокращение дробейВторой способ сокращения дроби
Задания для самостоятельного решения
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Используй кнопку нижеНавигация по записям
Превращение десятичной дроби в обыкновенную и наоборот
Первый способ
Второй способ
Запишите в виде дроби число три четвертых
Преобразовать десятичные дроби в дроби
Чтобы преобразовать десятичную дробь в дробную, выполните следующие действия:
Пример: преобразовать 0.75 до дроби
× 100 0,75 1 = 75 100 × 100
превращается в целое?) ÷ 5 ÷ 5 75 100 = 15 20 = 3 4 ÷ 5 ÷ 5 Ответ =
3 4 Пример: преобразовать 0.625 до дроби
÷ 25 ÷ 5 625 1000 = 25 40 = 5 8 ÷ 25 ÷ 5 Ответ =
5 8 Пример: преобразование 2.35 к дроби
÷ 5 35 100 = 7 20 ÷ 5 Ответ = 2
7 20 Пример: преобразовать 0.333 к дроби
Ответ =
333 1000 Но особое примечание:
× 3 0,333 … 1 = 0,999 … 3 × 3 Как записывать дроби формальным письмом
Как записывать дроби
Цифра Слово 1/2 Половина 3/4 Три четверти 5/8 Пять восьмых 17/24 Семнадцать двадцать четвертых
Но каковы правила записи дробей? Когда они должны быть цифрами, а когда словами? Давайте взглянем. Дроби как цифры
Дроби как слова
Следует ли записывать дроби словами или цифрами?
Считаете это полезным?
Дроби в начале предложения
Смешанные фракции и консистенция
Когда разделять дроби через дефис
Преобразование десятичных дробей в дроби или смешанные числа
Результаты обучения
Для нашего обеда [latex] $ 5,03 [/ latex] мы можем записать десятичное [latex] 5,03 [/ latex] как смешанное число.
Обратите внимание: когда число слева от десятичной дроби равно нулю, мы получаем правильную дробь. Когда число слева от десятичной дроби не равно нулю, мы получаем смешанное число. Преобразует десятичное число в дробное или смешанное число.
числитель
пример
ⓐ [латекс] 4,09 [/ латекс] Слева от десятичной запятой стоит [латекс] 4 [/ латекс]. Определите разряд последней цифры. Запишите дробь. Запишите [латекс] 100 [/ латекс] в знаменателе, поскольку значение последней цифры [латекс] 9 [/ латекс] равно сотой. [латекс] 4 \ frac {9} {100} [/ латекс] Дробь представлена в простейшем виде. Итак, [латекс] 4.09 = 4 \ frac {9} {100} [/ latex] ⓑ [латекс] 3.7 [/ латекс] Слева от десятичной точки стоит [латекс] 3 [/ латекс]. Определите разряд последней цифры. Запишите дробь. Запишите [латекс] 10 [/ латекс] в знаменателе, поскольку значение последней цифры [латекс] 7 [/ латекс] составляет десятые. [латекс] 3 \ frac {7} {10} [/ латекс] Дробь представлена в простейшем виде. Итак, [латекс] 3,7 = 3 \ frac {7} {10} [/ латекс] ⓒ [латекс] -0,286 [/ латекс] Слева от десятичной точки стоит [латекс] 0 [/ латекс]. Определите разряд последней цифры и запишите ее в знаменатель. Запишите дробь. [латекс] — \ frac {286} {1000} [/ латекс] Мы удалили общий множитель [латекс] 2 [/ латекс], чтобы упростить дробь. [латекс] — \ frac {143} {500} [/ латекс] Запись пропорций в виде дробей | Предалгебра
Результаты обучения
Коэффициенты
пример
ⓐ [латекс] \ text {от 15 до 27} [/ латекс] Запишите в виде дроби, указав первое число в числителе и второе в знаменателе. [латекс] \ frac {15} {27} [/ латекс] Упростим дробь. [латекс] \ frac {5} {9} [/ латекс] ⓑ [латекс] \ text {45–18} [/ латекс] Запишите в виде дроби, указав первое число в числителе и второе в знаменателе. [латекс] \ frac {45} {18} [/ латекс] Упростить. [латекс] \ frac {5} {2} [/ латекс] Коэффициенты, включающие десятичные дроби
Например, рассмотрим соотношение [латекс] 0,8 \ текст {к} 0,05 [/ латекс]. Мы можем записать это как дробь с десятичными знаками, а затем умножить числитель и знаменатель на [латекс] 100 [/ латекс], чтобы исключить десятичные дроби.
Вы видите ярлык для поиска эквивалентной дроби? Обратите внимание, что [latex] 0.8 = \ frac {8} {10} [/ latex] и [latex] 0.05 = \ frac {5} {100} [/ латекс]. Наименьший общий знаменатель для [латекса] \ frac {8} {10} [/ latex] и [latex] \ frac {5} {100} [/ latex] является [latex] 100 [/ latex]. Умножив числитель и знаменатель [latex] \ frac {0.8} {0.05} [/ latex] на [latex] 100 [/ latex], мы «переместили» десятичную запятую на два разряда вправо, чтобы получить эквивалентную дробь без десятичные дроби. Теперь, когда мы понимаем математику этого процесса, мы можем найти дробь без десятичных знаков, например: «Переместите» десятичную запятую на 2 разряда. [латекс] \ frac {80} {5} [/ латекс] Упростить. [латекс] \ frac {16} {1} [/ латекс] пример
ⓐ [латекс] 4,8 \ text {to} 11,2 [/ latex]
late [латекс] 2.7 \ text {to} 0,54 [/ latex] ⓐ [латекс] \ text {4,8–11,2} [/ латекс] Запишите дробью. [латекс] \ frac {4.8} {11.2} [/ латекс] Перепишите как эквивалентную дробь без десятичных знаков, сдвинув обе десятичные точки [латекс] на 1 [/ латекс] вправо. [латекс] \ frac {48} {112} [/ латекс] Упростить. [латекс] \ frac {3} {7} [/ латекс] ⓑ Запишите дробью. [латекс] \ frac {2.7} {0,54} [/ латекс] Переместите оба десятичных знака вправо на два места. [латекс] \ frac {270} {54} [/ латекс] Упростить. [латекс] \ frac {5} {1} [/ латекс] пример
[латекс] 1 \ frac {1} {4} \ text {to} 2 \ frac {3} {8} [/ латекс] Запишите дробью. [латекс] \ frac {1 \ frac {1} {4}} {2 \ frac {3} {8}} [/ латекс] Преобразуйте числитель и знаменатель в неправильные дроби. [латекс] \ frac {\ frac {5} {4}} {\ frac {19} {8}} [/ латекс] Перепишем как деление на дроби. [латекс] \ frac {5} {4} \ div \ frac {19} {8} [/ латекс] Обратить делитель и умножить. [латекс] \ frac {5} {4} \ cdot \ frac {8} {19} [/ латекс] Упростить. [латекс] \ frac {10} {19} [/ латекс] Что такое смешанные числа? — Определение, факты и пример
Что такое смешанные числа? Преобразование смешанных чисел в дроби
Упражнения
1. Запишите одну и три четверти как неправильную дробь. 2. Запишите четыре и одну пятую как неправильную дробь. 3. Запишите пять и семь восьмых как неправильную дробь. 4. Запишите пятнадцать и две трети как неправильную дробь. 5. Рецепт требует двух и трех четвертых стакана молока.Если мерный стакан вмещает только одну четверть стакана, то сколько раз вам придется его наполнять? Смешанные числа и неправильные дроби
Запись смешанных чисел в виде дробей
2 1 /2 =?
Умножьте целое число на знаменатель.
Целое число равно 2.
Знаменатель 2.
2 x 2 = 4.
Добавьте результат в числитель:
В числителе 1.
4 + 1 = 5
В числителе 5. Остается знаменатель 2.
2 1 / 2 = 5 /2 Другой пример
5 2 /3 =?
Умножьте целое число на знаменатель.
Целое число равно 5.
Знаменатель равен 3.
5 x 3 = 15.
Добавьте результат в числитель:
В числителе 2.
15 + 2 = 17
Числитель равен 17. В знаменателе остается 3.
5 2 /3 = 17 /3 Правильные и неправильные дроби
Запись неправильных дробей как смешанных чисел
Как бы вы выразили 17 /4 смешанным числом?
Разделите числитель на знаменатель:
17 ÷ 4 = 4, с остатком 1
Частное, 4, является целым числом. Остаток 1 — числитель. Знаменатель остается 4.
17 /4 = 4 1 /4 Еще два примера
14 /9 =?
Разделите числитель на знаменатель:
14 ÷ 9 = 1, с остатком 5
Частное 1 — это целое число.Остаток 5 — числитель. Знаменатель остается 9.
14 /9 = 1 5 /9 20 /5 =?
Наименьшее общее умножение дробей и смешанных чисел
Разделите числитель на знаменатель:
20 ÷ 5 = 4
Частное 4 — это целое число. Остатка нет.
20 /5 = 4
Y 2x 3 x: Y=2X-3/X-1
Как построить функцию?
Помогите пжл — Школьные Знания.com
y 2x 3 2x функция
Где можно решить любую задачу по математике, а так же y 2x 3 2x функция Онлайн?
заказ решений на аукционе за минимальную цену с максимальным качеством
Объединение сервисов в одну систему
Принцип работы
За счет чего будет развиваться сервис
Преимущества для заказчиков
Преимущества для решающих задания
Преимущества для владельца сервиса
Что необходимо для создания сервиса
6 \left(2 x + 1\right) = 0.
Решаем это уравнение.
Корни этого уравнения
x_{1} = — \frac{1}{2}
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках [-1/2, oo)Выпуклая на промежутках (-oo, -1/2]8. Искомый график функции дан в приложении.Постройте график функции и найдите значение k
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
х=0
x-3=0-3=-3 и x+3=0+3=3
x-3=5-3=2 и x+3=5+3=8
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6. Решите систему: y = | x |, y = 2x + 3
Решите y = 5x и y = 2x + 3 заменой
(текстовое поле под вопросом)
разность квадратов …
(x + 9) (x-9) = 0
1. С (-1/2, -5/2), (2,5)
2. A 0
3. В -1; 19
4. С-9,9
5. C экспоненциальная
ПОДХОДЯЩИЙ
6. А
7. D
8. C
9. B
10.ЭССЕ Урок 6 2-х точечный наклон формы ключ ответа
Boo в зале горного царя
Сфинкс тест логика льва и тигра Ogun opa eyin to daju 002 Fastest LS4
Общая базовая алгебра i Модуль 4 урок 5 Написание уравнений линий 8 фокус линейных моделей миссис Вольп домашнее задание практика уклон перехвата форма ответ ключ дополнительные s викторина 3 обзор математической формулы точки docx имя по вертикали и горизонтали PDF преобразование из в стандарт Пример eoc 1, что такое Common Core Algebra I Раздел 4 Урок 5… Напишите уравнение в форме «точка-наклон» для линии, содержащей каждую пару точек.25. (5, 4), (7, 12) 26. (1, 3), (2, 8) 27. (7, 14), (4, 2) 28. (6, 4), (10, 20) Напишите уравнение в стандартной форме для линии, содержащей каждую пару точек. 29. (2, 9), (1, 3) 30. (5, 22), (3, 12) 31. (9, 8), (4, 7) 32. (5, 8), (2, 2) 10 x # 3y «30 9x … Лазерная установка с ЧПУ 3018
Удаление губ слизистой кисты Cara установочный маршрутизатор tenda Ответ: b Объяснение: Здесь id — единственный атрибут, который можно использовать в качестве ключа.Другие атрибуты не идентифицируются однозначно. 3. Подмножество Ответа: c Объяснение: Атрибуты name, street и Department могут повторяться для некоторых кортежей. Но атрибут id должен быть уникальным. Таким образом, он образует первичный ключ. Iphone 6 Схема ленточного кабеля
Работа в округе Патнэм Как очистить белую стеклянную соломинку носорога В уроке особое внимание уделяется построению графиков линейных функций с использованием таблицы значений, построению точек пересечения по осям x и y или с использованием формы уравнения линии с пересечением угла наклона.Материалы • Графические рабочие листы • Миллиметровая бумага • Цели линейки Учащиеся будут: • Использовать уравнения, графики, таблицы, описания или наборы упорядоченных пар, чтобы выразить: Следовательно, наклон линии с учетом двух точек на линии можно найти, используя следующее уравнение: когда координаты точки и наклон линии известны, линия может быть представлена в форме точки-уклона. Формула угла наклона точки является производной от уравнения наклона. Okanbi sons
Moto display apk для любого android Anakim and Rephaim Напишите уравнение в форме пересечения наклона для линии, которая проходит через (-1, 6) и параллельна графику of = y 2x + 12. Прямая, параллельная y = 2x + 12, имеет такой же наклон, 2. Замените m на 2 и (x 1, y 1) на (-1, 6) в форме углового наклона. y-y 1 = m (x-x 1) Форма точечного уклона y — 6 = 2 (x — (-1)) m = 2; (x 1, y 1) = (-1, 6) y — 6 = 2 (x … m — наклон прямой.b — точка пересечения с y. Давайте посмотрим на несколько примеров: Уравнение y = 2x + 1 находится в форме пересечения наклона. Коэффициент при x-члене равен 2, поэтому наклон равен 2. Константа равна 1, поэтому точка пересечения y равна 1. Это означает, что график проходит через точку (0, 1). Приставка для водосточного желоба под давлением
В каком эпизоде хвостовики умирают как одно целое Xeljanz alopecia 2020 Графические системы уравнений активность pdf
Нахождение нулей многочленов рабочий лист алгебра 2
Показаны 8 лучших рабочих листов в категории — Алгебра Гленко 2 В поисках нулей. Некоторые из отображаемых рабочих листов: Факторы и нули, Указание возможных рациональных нулей для каждого, Полиномы блока 6, Учебный план Алгебры 2 на 2017 2018 год, Нули полиномиальных функций, Введение в матрицы, Алгебра 2 соблюдает обзор теста главы 6, Факторизация полиномов работает ключ ответа . долларовые общие телевизионные подносы
Magazine.com код купона
Правый привод mk4 supra на продажу
Tbi манометр топлива
Урок 9 4 практика b преобразование квадратичных функций
Урок 9 4 практика b преобразование квадратичных функций Отбеливающий скраб для лица Nivea
Labrinth realous
Jeep tj заводское оборудование с мягким верхом
Javascript сортирует массив массивов по столбцу
Mattel shop
Кратчайший путь между двумя узлами взвешенного графа python
Автомобильные фары мерцают в холодную погоду
Dragon rpg games
Продам переоборудование Sprinter 4×4
Системы кузова и их функции
Baji ki marzi или bhai ko mazy
ter
ter
ter
Номер телефона авиабазы Баграм
Взломанный Android Box amazon
Safari рядом со мной
5 фунтов пропанового бака, оборудование ace
Zwift ramp test без режима erg
Жесткий диск ssd 1 ТБ для ноутбука HP
Проблемы с производными финансовыми инструментами и решения pdf
Временно измените систему безопасности для ilife 9.0.4 пакет
1999 dodge ram 1500 заводится, но не запускается
Какой ты изгибник, тест аватара
Aol imap settings outlook 2016
Deped tambayan interfaith молитва генератор
9000 9000 кодов epdics3 Квадратная сервировочная чаша Corelle 1,5 кварты
Бесплатный поиск адресов на белых страницах
Рабочий лист извержений вулканов Ключ ответа
Промокод для грилей Dcs
Python запрашивает файл данных формы 969299 брендовые пейзажи мегаполис
Роковой кадр 4 riivolution
.
Информатика и английский язык куда поступать: Список вузов и факультетов, где при поступлении принимают английский язык
Выбор вуза по предметам ЕГЭ — какой вуз выбрать по результатам ЕГЭ, удобный подбор на Учёба.ру
Специальности по наборам ЕГЭ
Математика + физика + русский язык
Математика + информатика + русский язык
Математика + обществознание + русский язык
Химия + биология + русский язык
Обществознание + история + русский язык
Иностранный язык + история + русский язык
Литература + иностранный язык + русский язык
ответы на обращения в редакцию
Вопрос задал(а) Ксения
Скрыть ответ
Вопрос задал(а) Вика
Скрыть ответ
Вопрос задал(а) Ирина3. Другое:
Скрыть ответ
Вопрос задал(а) Юлиана
Скрыть ответ
Я достаточно коммуникабельна и отзывчива. Правда, всё близко к сердцу воспринимаю. Думала много о профессии. Хотела стать сценаристом,но у нас этому не учат. Думала стать актрисой, но для этого нужны железные нервы и физические возможности обширные. Передумала. Мама предлагала на юридический, но я не хочу. Решили, что экономическое образование нужно, но ведь отлично знать математику нужно. Я люблю этот предмет, но могу сказать, что знаю хорошо( уравнения не в счёт). Взяла бы начальные классы, но дети учиться не хотят, да постоянная переаттестация. Можно всему научиться, было бы желание. Нравится биология. Хочу работать на радио, но говорят, что нужны деньги. Ещё какие.. Вот химия только в теории понятна. В физике очень трудно разобраться, а геометрию терпеть не могу. Я не знаю куда мне идти. А времени всё меньше.. Помогите пожалуйста!!!!!!
Вопрос задал(а) Виктория
Скрыть ответ
Вопрос задал(а) Виктория
Скрыть ответ
Вопрос задал(а) Лера
Скрыть ответ
По природе я человек творческий. Хорошо учусь в школе. Все предметы даеются мне неплохо. Очень люблю литературу, обожаю читать, люблю очень биологию , историю.
Не особо люблю алгебру и геометрию.
Люблю писать, веду дневник, сочинения мне даются очень хорошо.
Пожалуйста, посоветуйте мне что-нибудь.
Раньше хотела пойти в мед, но учиться 10 лет в меде меня честно говоря немного напрягает. Хочу получить достойную , интересную работу с хорошим заработком. Жалею , что бросила художку в глубоком детстве, может быть могла бы пойти на архитектора или дизайнера. Хочу интересную работу, не сидеть на месте. Помогите, пожалуйста.
Вопрос задал(а) Нина
О чем Вы любите читать? Какие книги привлекают Вас? Приключенческие? Исторические? Об отношениях? Если что-то другое, то что это? О чем?
Чем Вам нравится биологию? А что привлекает в истории?
Чтобы найти интересную работу, нужно вспомнить все то, что Вас привлекает не только в школе, но и вне ее. Например, если Вы зайдете в интернет… Что Вы будете делать: общаться, играть или искать информацию? Общаться с новыми людьми или со своими знакомыми? А какую информацию будете искать? Что это будет? Экономика? Политика? Светская хроника? Культура? Спорт? Сюжеты о природе? Во что любите играть? Чем Вас эти игры привлекают? Что именно нравится Вам в них?
Наверняка есть еще что-то, что так же хорошо у Вас получается. Пожалуйста, вспомните, что это? За что Вас хвалят другие? Поспрашивайте своих близких и знакомых, что они замечают со стороны? Что такого делаете Вы, чего они не могут делать так же хорошо?
Скрыть ответ
Вопрос задал(а) Анастасия из Якутии
Скрыть ответ
Если дизайнер, то какие предметы нужны для (ГИА) и поступления в колледж. И если архитектор, то тогда какие предметы требуются при сдаче? Я из Уфы.
Вопрос задал(а) Настя
Скрыть ответ
Вопрос задал(а) Александр
Скрыть ответ
Вопрос задал(а) Марина
Скрыть ответ
Заранее спасибо!
Вопрос задал(а) Анжелика
Скрыть ответ
Вопрос задал(а) Олег
Скрыть ответ
Вопрос задал(а) Сергей
Скрыть ответ
Вопрос задал(а) Елизавета
Скрыть ответ
Вопрос задал(а) Валентин
Отдельно отметим здесь ряд специальностей, связанных с экологией и природопользованием в целом – эколог, специалист по противопожарной безопасности, инженер по защите окружающей среды и т.д. Специалисты в этой области работают над соблюдением экологических норм, грамотным использованием природных ресурсов и защитой окружающей среды.
На стыке физической и экономической географии есть такие специальности как картограф (основная задача состоит в разработке и создании карт, атласов различного содержания, топографии местности, внедрении компьютерных технологий в производство) и геодезист (в его обязанности входит создавать земельные/лесные кадастры, измерять территорию, вычислять координаты местности, что особенно востребовано при строительстве).
Скрыть ответ
Вопрос задал(а) АртёмЗдравствуй, Артем!
Скрыть ответ
Вопрос задал(а) Кристина Головачева
Скрыть ответ
Вопрос задал(а) Патя
Скрыть ответ
Я учусь в 10 классе. С самого детства я обожаю гуманитарные науки. Я хорошо излагаю мысли на литературе, умею правильно поставить речь. Хорошо знаю русский язык, у меня хорошая память, поэтому я могу сдавать обществознание. Что можно выбрать из профессии,если сдавать русский, математику, обществознание и литературу? Могу выучить ОБЖ, но с химией, физикой и английским у меня не очень.
Подскажите, пожалуйста.
Вопрос задал(а) Ольга
Скрыть ответ
Я учусь в 8 классе и у меня хорошая успеваемость по истории, обществознанию и алгебре.
Кем мне стать?
Вопрос задал(а) Лиза
Ты — большая молодец и умница, раз у тебя хорошая успеваемость по истории, обществознанию и алгебре.
Например, уже сейчас ты можешь попробовать сама составить бюджет вымышленного человека на год. Сначала придумай какую заработную плату он будет получать. Затем заложи, какая сумма денег нужна ему на питание и оплату коммунальных услуг. А теперь попробуй спрогнозировать другие его расходы. Какую одежду он будет покупать? Каких марок? Когда (может быть в конце сезона на распродажах со скидками)? Сколько раз в год он будет путешествовать? Что это будет? Поход в лес с палаткой или на море? Учти, что палатку можно купить, а можно взять в прокат и это будет дешевле. На море можно поехать на машине, на поезде, на самолете. Что выгоднее? А есть ли у него машинв? Если есть, то нет ли платежей по кредиту? А может быть он поедет на машине не один, а взяв с собой друзей? Тогда расходы на бензин можно будет поделить поровну. А будет ли развлекаться твой герой в выходные? Что это будет и сколько денег ему понадобится? Он каждые выходные будет ходить в кино, в кафе или раз в месяц? И т.д.
Интересно ли тебе решать такую задачку? Экономисты решают подобные задачи на уровне предприятия или даже страны.
Скрыть ответ
Сдаю математику, русский и биологию. С четвертым предметом еще не определилась!
Куда поступать?
Вопрос задал(а) Эмилия
Скрыть ответ
Задать вопросКуда можно поступить с ЕГЭ по русскому, математике и информатике.
С какими баллами можно поступить — средний балл по стране
Специальности ВУЗов, на которые можно поступить с русским, математикой и информатикой
Специальности колледжей, техникумов, училищ и других СПО
Поступаем на специальность с обществознанием. Поступить на бюджет или платное отделение
Вузы и факультеты, куда можно поступить с профильным обществознанием
Куда можно поступить с базой
Сколько баллов нужно набрать для поступления
Сколько баллов понадобится для поступления на бюджет
Как узнать, сколько баллов нужно набрать для поступления в выбранный вуз
Куда поступить с ЕГЭ по английскому языку?
Содержание
Экзамены ЕГЭ по английскому языку – куда двигаться дальше?
Где нужен английский язык?
Переводы и переводоведение
Преподавательский состав
Преподаватель английского языка
Таможенное дело и брокерство
Международные отношения
ВУЗы для поступления
Куда поступить с английским в СПб? | ЕГЭ английский, русский: куда можно поступить после 11 класса?
Куда можно поступить с английским?
Переводоведение
Преподаватель английского языка
Таможенное дело
Международные отношения
Социология и связи с общественностью
Куда легче всего поступить на бюджет и лучший набор ЕГЭ
Начнем, пожалуй, с того, что определим самые выгодные для поступления наборы ЕГЭ.
По нашим данным есть 33 различные комбинации наборов, с помощью которых можно поступить на бюджет в вуз.
Мы разберем 14 самых популярных вариантов. Так какой же набор выгоднее всего сдавать, чтобы не упустить свой шанс?
Разберем по порядку: Русский язык
+ Математика
+ Физика
На этот набор выделено больше всего бюджетных мест. Аж 43.14% от общего числа. Вероятней всего, где представлено больше бюджетных мест, туда легче всего поступить. Давайте разбираться в деталях. По нашим данным, средний проходной балл для поступления с такой комбинацией составит 61.9 баллов за предмет. Забегая вперед, это не самый низкий средний проходной, есть наборы, где он ниже. Встает другой вопрос, ведь сдавать, например, иностранный, вероятно, легче, чем физику. У тех, кто сдает иностранный в среднем балл выше, чем у тех, кто сдает физику. Нельзя вот так просто сравнить средний балл поступивших.
Тут нам помогут цифры средних баллов ЕГЭ, которые получили выпускники, сдающие русский, математику, физику (не те, кто поступил в вуз, а в принципе, кто сдавал ЕГЭ). Официальная статистика говорит о том, что средний балл сдающих этот набор составил 60.13 за предмет. Что это значит? Очень просто. Очень большая доля тех, кто сдавал РЯ+М+Ф поступили на бюджет.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Управление в технических системах
Бакалавриат | 27.03.04 от 33.7
баллов за предмет Системы обеспечения движения поездов
Специалитет | 23.05.05 от 34
баллов за предмет Агроинженерия
Бакалавриат | 35.03.06 от 34.3
баллов за предмет Электроэнергетика и электротехника
Бакалавриат | 13.03.02 от 34.3
баллов за предмет Техносферная безопасность
Бакалавриат | 20.03.01 от 34.7
баллов за предмет Стандартизация и метрология
Бакалавриат | 27.03.01 от 35.3
баллов за предмет Приборостроение
Бакалавриат | 12.03.01 от 35.3
баллов за предмет Конструкторско-технологическое обеспечение машиностроительных производств
Бакалавриат | 15.03.05 от 35.3
баллов за предмет Продукты питания из растительного сырья
Бакалавриат | 19.03.02 от 35.3
баллов за предмет Природообустройство и водопользование
Бакалавриат | 20.03.02 от 36
баллов за предмет Электроника и наноэлектроника
Бакалавриат | 11.03.04 от 36.3
баллов за предмет Подвижной состав железных дорог
Специалитет | 23.05.03 от 36.3
баллов за предмет Теплоэнергетика и теплотехника
Бакалавриат | 13.03.01 от 36.7
баллов за предмет Проектирование технологических машин и комплексов
Специалитет | 15.05.01 от 36.7
баллов за предмет Прикладная математика
Бакалавриат | 01.03.04 от 36.7
баллов за предмет Наземные транспортно-технологические средства
Специалитет | 23.05.01 от 37
баллов за предмет Русский язык
+ Математика
+ ИКТ
Очень коварный набор ЕГЭ. На многие программы подготовки предлагают на выбор сдавать РЯ+М+Ф или РЯ+М+ИКТ. Например, есть программа подготовки “прикладная информатика и математика”.
Поступая на это направление подготовки, абитуриент может выбрать наиболее подходящий для себя вариант набора ЕГЭ.
Умный выпускник обратится к данным прошлых лет и увидит, что сдать ЕГЭ по ИКТ проще, чем ЕГЭ по физике. По официальным данным, сдающие ИКТ получают на 2 балла больше тех, кто сдает физику.
Может сложиться впечатление, что РЯ+М+ИКТ более привлекателен и с таким набором будет проще поступить. По факту происходит следующее.
Несмотря на то, что этот набор занимает второе место по количеству выделенных бюджетных мест направлениям подготовки, для которых нужна данная комбинация, разрыв по отношению к первой позиции супербольшой.
В данном случае с таким набором можно побороться за 12.11% бюджетных мест от общего количества мест в вузах России. Естественно, где мест меньше, конкуренция куда выше. Так и вышло. По нашим данным, средний проходной балл на бюджет составил 77.3 баллов за предмет.
Естественно, это несопоставимо с разницей в баллах со сдававшими. Чтобы поступить на бюджет с этим набором, нужно в среднем набрать больше аж на 15!!! баллов. А в среднем получить можно только на 2 балла выше.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Мехатроника и робототехника
Бакалавриат | 15.03.06 от 38
баллов за предмет Программная инженерия
Бакалавриат | 09.03.04 от 40
баллов за предмет Прикладная информатика
Бакалавриат | 09.03.03 от 42.7
баллов за предмет Математическое обеспечение и администрирование информационных систем
Бакалавриат | 02.03.03 от 43
баллов за предмет Информатика и вычислительная техника
Бакалавриат | 09.03.01 от 48.3
баллов за предмет Автоматизация технологических процессов и производств
Бакалавриат | 15.03.04 от 49
баллов за предмет Информационные системы и технологии
Бакалавриат | 09.03.02 от 50.7
баллов за предмет Русский язык
+ Математика
+ Обществознание
Опасный набор ЕГЭ. Когда я сдавал ЕГЭ, мне казалось, что сдать обществознание – беспроигрышный вариант. Я был уверен, что в среднем, за обществознание можно получить баллов куда больше, чем по физике, например. По факту, сдающие РЯ+М+О получают 60,3 за предмет. Воу! Да это ведь примерно столько, сколько получают ребята, которые сдают РЯ+М+Ф. Более того, средний балл поступивших на бюджет составил 71.4 баллов за предмет. Кстати, 8.33% бюджетных мест выделено от общего количества мест в вузах России программам подготовки, требующим эту комбинацию. Это тоже не совпадает с моим мироощущением. Мне казалось, что эта цифра должна была быть куда больше.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Педагогическое образование (с двумя профилями подготовки)
Бакалавриат | 44.03.05 от 36.7
баллов за предмет Профессиональное обучение (по отраслям)
Бакалавриат | 44.05.04 от 40.7
баллов за предмет Педагогическое образование
Бакалавриат | 44.03.01 от 40.7
баллов за предмет Сервис
Бакалавриат | 43.03.01 от 49
баллов за предмет Социология
Бакалавриат | 39.03.01 от 53.7
баллов за предмет Русский язык
+ Обществознание
+ История
Занимает 4 место по количеству выделенных бюджетных мест — 7.14%. Средний балл поступивших на бюджет составил 73.6 за предмет. По старой схеме, обращаемся к статистике среднего балла, сдававших этот набор. Он составил 59.9 за предмет.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл История
Бакалавриат | 46.03.01 от 37
баллов за предмет Социальная работа
Бакалавриат | 39.03.02 от 39.3
баллов за предмет Судебная и прокурорская деятельность
Специалитет | 40.05.04 от 40.7
баллов за предмет Туризм
Бакалавриат | 43.03.02 от 41
баллов за предмет Педагогическое образование
Бакалавриат | 44.03.01 от 42
баллов за предмет Педагогическое образование (с двумя профилями подготовки)
Бакалавриат | 44.03.05 от 42.7
баллов за предмет Религиоведение
Бакалавриат | 47.03.03 от 44.3
баллов за предмет Русский язык
+ Математика
+ Биология
7.52% бюджетных мест выделено образовательным программам, требующим данный набор. 59.5 баллов в среднем набирают выпускники. Но в данном случае, нужно всего 58.6 баллов за предмет, чтобы поступить на бюджет. Неплохо? Забегая вперед, хочу сказать, что это самая выгодная комбинация. Даже если вы сдадите ниже среднего, то у Вас все равно хорошие шансы забрать себе заветное бюджетное место.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Агрономия
Бакалавриат | 35.03.04 от 33.3
баллов за предмет Садоводство
Бакалавриат | 35.03.05 от 33.3
баллов за предмет Ветеринарно-санитарная экспертиза
Бакалавриат | 36.03.01 от 33.3
баллов за предмет Зоотехния
Бакалавриат | 36.03.02 от 33.3
баллов за предмет Лесное дело
Бакалавриат | 35.03.01 от 33.3
баллов за предмет Технология производства и переработки сельскохозяйственной продукции
Бакалавриат | 35.03.07 от 33.3
баллов за предмет Водные биоресурсы и аквакультура
Бакалавриат | 35.03.08 от 34.3
баллов за предмет Агрохимия и агропочвоведение
Бакалавриат | 35.03.03 от 35.3
баллов за предмет Ветеринария
Специалитет | 36.05.01 от 35.7
баллов за предмет Биотехнология
Бакалавриат | 19.03.01 от 36.7
баллов за предмет Биотехнические системы и технологии
Бакалавриат | 12.03.04 от 38.3
баллов за предмет Биология
Бакалавриат | 06.03.01 от 39.7
баллов за предмет Русский язык
+ Биология
+ Химия
Казалось бы, так как с набором РЯ+М+Б так хорошо обстоят дела, то и с этим набором должно быть все хорошо (если не лучше). По факту, хоть и бюджетных мест не сильно меньше — 6.03%, поступить куда сложнее. В среднем, чтобы поступить, необходимо набрать 82.6 балла за предмет. А сдавать по сложности абсолютно так, как РЯ+М+Б. Выпускники тоже набирают 59.5 баллов за предмет.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Биология
Бакалавриат | 06.03.01 от 48.7
баллов за предмет Сестринское дело
Бакалавриат | 34.03.01 от 61.3
баллов за предмет Фармация
Специалитет | 33.05.01 от 61.7
баллов за предмет Русский язык
+ Математика
+ Химия
Просто дадим статистику 😊 С этим набором можно рассчитывать на 5.17% бюджетных мест от общего числа. Средний проходной — 69.8 баллов за предмет.
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Продукты питания из растительного сырья
Бакалавриат | 19.03.02 от 34.7
баллов за предмет Биотехнология
Бакалавриат | 19.03.01 от 38.3
баллов за предмет Технология продукции и организация общественного питания
Бакалавриат | 19.03.04 от 38.7
баллов за предмет Фундаментальная и прикладная химия
Специалитет | 04.05.01 от 45.3
баллов за предмет Химия
Бакалавриат | 04.03.01 от 47
баллов за предмет Русский язык
+ Обществознание
+ Иностранный
Очень популярный набор среди выпускников. Однако, выделено бюджетных мест всего 2.11%. Как следствие, очень высокий средний проходной балл — 84.6
Приводим таблицу с наименьшими проходными баллами. Направление подготовки Проходной балл Педагогическое образование
Бакалавриат | 44.03.01 от 53.3
баллов за предмет Педагогическое образование (с двумя профилями подготовки)
Бакалавриат | 44.03.05 от 62.3
баллов за предмет Реклама и связи с общественностью
Бакалавриат | 42.03.01 от 70.7
баллов за предмет Русский язык
+ Иностранный
+ История
Один из сложнейших наборов для поступления. В среднем, нужно набрать аж 87.6 баллов за предмет, чтобы поступить на бюджет. Не удивительно, так как всего 1.62% бюджетных мест выделено программам, требующим этот набор.
Приводим таблицу с наименьшими проходными баллами Направление подготовки Проходной балл Зарубежное регионоведение
Бакалавриат | 41.03.01 от 59
баллов за предмет Туризм
Бакалавриат | 43.03.02 от 66.3
баллов за предмет Лингвистика
Бакалавриат | 45.03.02 от 68
баллов за предмет Русский язык
+ Обществознание
+ Биология
1.6% от общего числа бюджетных мест и 62.9 баллов средний проходной на бюджет.
Приводим таблицу с наименьшими проходными баллами Направление подготовки Проходной балл Педагогическое образование
Бакалавриат | 44.03.01 от 38
баллов за предмет Специальное (дефектологическое) образование
Бакалавриат | 44.05.03 от 40.7
баллов за предмет Психолого-педагогическое образование
Бакалавриат | 44.03.02 от 44.3
баллов за предмет Педагогическое образование (с двумя профилями подготовки)
Бакалавриат | 44.03.05 от 49.7
баллов за предмет Психология
Бакалавриат | 37.03.01 от 56
баллов за предмет Русский язык
+ Математика
+ География
1.56% от общего числа бюджетных мест и 62.5 баллов средний проходной на бюджет.
Приводим таблицу с наименьшими проходными баллами Направление подготовки Проходной балл Экология и природопользование
Бакалавриат | 05.03.06 от 45
баллов за предмет Гидрометеорология
Бакалавриат | 05.03.04 от 49.7
баллов за предмет География
Бакалавриат | 05.03.02 от 50.7
баллов за предмет Картография и геоинформатика
Бакалавриат | 05.03.03 от 55.7
баллов за предмет Русский язык
+ Обществознание
+ Литература
1.03% от общего числа бюджетных мест и 75.7 баллов средний проходной на бюджет.
Приводим таблицу с наименьшими проходными баллами Направление подготовки Проходной балл Педагогическое образование
Бакалавриат | 44.03.01 от 49
баллов за предмет Социально-культурная деятельность
Бакалавриат | 51.03.03 от 54.7
баллов за предмет Педагогическое образование (с двумя профилями подготовки)
Бакалавриат | 44.03.05 от 55
баллов за предмет Филология
Бакалавриат | 45.03.01 от 68.3
баллов за предмет Русский язык
+ Иностранный
+ Литература
0.78% от общего числа бюджетных мест и 85 баллов средний проходной на бюджет.
Приводим таблицу с наименьшими проходными баллами Направление подготовки Проходной балл Филология
Бакалавриат | 45.03.01 от 56
баллов за предмет Журналистика
Бакалавриат | 42.03.02 от 71
баллов за предмет Лингвистика
Бакалавриат | 45.03.02 от 71.3
баллов за предмет Русский язык
+ Математика
+ Иностранный
Бегите, глупцы! Это самый сложный набор для поступления. Всего 0.67% от общего количества бюджетных мест и средний проходной 91.3 за предмет.
Приводим таблицу с наименьшими проходными баллами Направление подготовки Проходной балл Фундаментальная и прикладная лингвистика
Бакалавриат | 45.03.03 от 78.3
баллов за предмет Экономика
Бакалавриат | 38.03.01 от 80.7
баллов за предмет Менеджмент
Бакалавриат | 38.03.02 от 88.3
баллов за предмет Набор ЕГЭ Средний проходной балл на бюджет Средний балл сдававших % бюджетных мест Русский язык + Математика + Физика 61.9
баллов за предмет60.13
баллов за предмет43.14% Русский язык + Математика + ИКТ 77.3
баллов за предмет62.8
баллов за предмет12.11% Русский язык + Математика + Обществознание 71.4
баллов за предмет60,3
баллов за предмет8.33% Русский язык + Обществознание + История 73.6
баллов за предмет59.9
баллов за предмет7.14% Русский язык + Математика + Биология 58.6
баллов за предмет59.5
баллов за предмет7.52% Русский язык + Биология + Химия 82.6
баллов за предмет59.5
баллов за предмет6.03% Русский язык + Математика + Химия 69.8
баллов за предмет60.9
баллов за предмет5.17% Русский язык + Обществознание + Иностранный 84.6
баллов за предмет65
баллов за предмет2.11% Русский язык + История + Иностранный 87.6
баллов за предмет65.1
баллов за предмет1.62% Русский язык + Обществознание + Биология 62.9
баллов за предмет58.9
баллов за предмет1.6% Русский язык + Математика + География 62.5
баллов за предмет61
баллов за предмет1.56% Русский язык + Обществознание + Литература 75.7
баллов за предмет62.6
баллов за предмет1.03% Русский язык + Иностранный + Литература 85
баллов за предмет67.8
баллов за предмет0.78% Русский язык + Математика + Иностранный 91.3
баллов за предмет65.5
баллов за предмет0.67%
Использована статистика портала Табитуриент.ру, 4ege.ruПонравилось 413 бакалавр компьютерных наук / английский язык — Khoury College of Computer Sciences
Penn State Engineering: EECS — Как подать заявку на участие в программах CSE Grad
Крайние сроки для выпускных программ CSE
иностранных студентов
Домашние студенты
Годовая программа магистра инженерных наук
Онлайн-заявка на обучение в аспирантуре
Банкноты
Контакт
поступлений | Академики | Компьютерные науки
Наш процесс приема очень избирательный и конкурентный. Сроки подачи заявок и важные даты
Соискатели докторской степени
Соискатели MS
Как подать заявление
Примечания об онлайн-приложении
В онлайн-форме заявки Дополнительные материалы
Кому следует подавать заявление
Текущие студенты Северо-Западного университета CS MS, желающие продолжить обучение по программе CS PhD
Когда обращаться
Соискатели Требования к английскому языку
Советы (важная информация, которую следует прочитать перед тем, как приступить к подаче заявки)
Академическая успеваемость
Результаты стандартизированных тестов
Заявление о целях
Заявление о предпочтениях в области исследований и консультирования
Рекомендательные письма
Несколько приложений
Разное
Дополнительная информация
Прием в магистратуру — информатика
Информация для потенциальных иностранных аспирантов
Институт английского языка
Институт английского языка (ELI), входящий в состав Международного центра UA Capstone, предлагает различные программы изучения английского языка, которые призваны помочь людям, не являющимся носителями языка, улучшить свое владение английским языком. Информация для потенциальных аспирантов без степени бакалавра компьютерных наук
Финансовая помощь CS
Широкие возможности университета
Финансовая помощь
Компьютерные науки | Калифорнийский университет в Дэвисе
Основные требования
Карьера
Аспирантура
Выпускники-работодатели
Магистр информатики | Брауновский университет
Дополнительные ресурсы
Требования для зачисления
Как подать заявку | Гарвардская школа инженерии и прикладных наук им. Джона А. Полсона
Нам не требуется собеседование как часть процесса подачи заявления, и мы не можем предложить абитуриентам возможность пройти личное собеседование с сотрудниками приемной комиссии. Учеба в докторантуре. или информационная сессия о приеме в магистратуру — лучший способ получить ответы на свои вопросы. Все информационные сессии в наступающем году будут виртуальными.Более подробную информацию о наших информационных сессиях можно найти здесь.
Литература и искусство: Культура и искусство | Российский центр науки и культуры в Праге
искусство слова. История и роль литературы.


 ), романтизм (18-19 в.) и реализм (19 в.).
), романтизм (18-19 в.) и реализм (19 в.).
Литература как искусство слова. Речь как предмет изображения
Литература как искусство слова

 Именно это является резким отличием литературы от других видов искусств. Человек только в литературе предстает говорящим. Принципиальное значение этому придавал М. М. Бахтин. Он отмечает, что основной особенностью литературы является то, что здесь язык является не только средством коммуникации и изображения, но и объектом изображения. Бахтин утверждал, что художественная литература – это не просто использование языка, а художественное познание его. По мнению ученого, основной проблемой изучения литературы является «проблема взаимоотношений изображающей и изображаемой речи».
Именно это является резким отличием литературы от других видов искусств. Человек только в литературе предстает говорящим. Принципиальное значение этому придавал М. М. Бахтин. Он отмечает, что основной особенностью литературы является то, что здесь язык является не только средством коммуникации и изображения, но и объектом изображения. Бахтин утверждал, что художественная литература – это не просто использование языка, а художественное познание его. По мнению ученого, основной проблемой изучения литературы является «проблема взаимоотношений изображающей и изображаемой речи». Произведения художественной литературы становятся историческими памятниками, в которых содержится языковой материал и которые свидетельствуют об эволюции речи от древности до настоящего времени.
Произведения художественной литературы становятся историческими памятниками, в которых содержится языковой материал и которые свидетельствуют об эволюции речи от древности до настоящего времени. Речь как предмет изображения

 Они выступают в качестве формы словесного искусства и способствуют наиболее полному воплощению авторского замысла.
Они выступают в качестве формы словесного искусства и способствуют наиболее полному воплощению авторского замысла. То есть «приращения смысла», которые они получают в динамической структуре литературно-художественного текста, зависят и от их потенциальной выразительности в языковой система, и от внутритекстовых связей в сюжете и композиции произведения, приобретаемых ими.
То есть «приращения смысла», которые они получают в динамической структуре литературно-художественного текста, зависят и от их потенциальной выразительности в языковой система, и от внутритекстовых связей в сюжете и композиции произведения, приобретаемых ими.Литература как искусство слова. | План-конспект урока по литературе (8 класс) по теме:

 И только от тебя зависит, не погаснет ли она раньше времени.
И только от тебя зависит, не погаснет ли она раньше времени. В этой антиутопии изображен город, в котором чтение и хранение книг является страшным преступлением. Там уже давно уничтожены все книги. И теперь, если у кого-то находят хоть одну книгу, её сжигают вместе с домом, а хозяина предают смертной казни. Там нельзя сохранить книги, не погибнув самому. Пожарные в этом городе существуют не для того, чтобы тушить пожары. А для того, чтобы сжигать книги и дома, в которых они найдены. Герой романа Гай Монтег – пожарный. Десять лет он добросовестно и даже с удовольствием выполнял свою страшную работу. Но вот однажды во время дежурства он приехал в дом старой женщины, которая. Не желая расставаться со своими книгами, сгорела вместе с ними. С того дня все изменилось в жизни Монтега. Его стал мучить вопрос: что же написано в этих книгах. Если из-за них люди идут на смерть? И чтобы получить ответ, он начинает читать…
В этой антиутопии изображен город, в котором чтение и хранение книг является страшным преступлением. Там уже давно уничтожены все книги. И теперь, если у кого-то находят хоть одну книгу, её сжигают вместе с домом, а хозяина предают смертной казни. Там нельзя сохранить книги, не погибнув самому. Пожарные в этом городе существуют не для того, чтобы тушить пожары. А для того, чтобы сжигать книги и дома, в которых они найдены. Герой романа Гай Монтег – пожарный. Десять лет он добросовестно и даже с удовольствием выполнял свою страшную работу. Но вот однажды во время дежурства он приехал в дом старой женщины, которая. Не желая расставаться со своими книгами, сгорела вместе с ними. С того дня все изменилось в жизни Монтега. Его стал мучить вопрос: что же написано в этих книгах. Если из-за них люди идут на смерть? И чтобы получить ответ, он начинает читать…
 Живое слово богато и щедро. У него множество оттенков. Оно может быть грозным и ласковым, вселять ужас и дарить надежду. Недаром поэт Вадим Шефнер так сказал о слове:
Живое слово богато и щедро. У него множество оттенков. Оно может быть грозным и ласковым, вселять ужас и дарить надежду. Недаром поэт Вадим Шефнер так сказал о слове:

 Но этот царевич начал курить, заболел и умер, когда ему исполнилось 20 лет.
Но этот царевич начал курить, заболел и умер, когда ему исполнилось 20 лет.Искусство и литература в средние века
1. Архитектура
2. Скульптура и живопись в средние века
3. Жонглёры.
4. Литература горожан средних веков.
ДОКУМЕНТ — Отрывок из „Романа о Лисе», в котором Лис рассказывает о своих проделках над Волком (Изегрим — имя Волка).
Презентация к уроку литературы в 9 классе «Литература как искусство слова и её роль в духовной жизни человека»
Просмотр содержимого документа
«Презентация к уроку литературы в 9 классе «Литература как искусство слова и её роль в духовной жизни человека» »
Вводный урок литературы в 5 классе на тему «Литература
II. Актуализация знаний и фиксация затруднений в деятельности.
Презентация к вводному уроку
PPTX / 639.1 КбРоль художественной литературы в воспитании молодого поколения
Надпись на стене: о сближении литературы и изобразительного искусства
Если вам нравится читать электрическую литературу, присоединяйтесь к нашему списку рассылки! Каждую неделю мы будем присылать вам лучшие работы EL, и вы будете первыми, кто узнает о предстоящих периодах подачи заявок и виртуальных мероприятиях. Отдохнуть от новостей
ВАШ ВХОДЯЩИЙ ЯЩИК
Перевод: Проблема литературы и искусства
Переводимость
Импульс к установлению отношений Американский ученый: искусство литературы и наука о литературе
Они поднялись в небо
Они упали
Поезд чу-чу в небе
Поезд упал в небе
Я упал в небе в воду
Я сел на лодку, и у меня заболели ноги
Папа упасть в небо.
затем, когда дом сломался, люди умерли
и когда люди умерли, их кости выскочили и сломались, снова собрались вместе и превратились в скелет
и затем появились скелеты и напугали людей из города
, а затем, когда все люди испугались из города, родились скелеты-младенцы
, и тогда все назвали его городом скелетов
, и когда они назвали его городом скелетов, пришли люди тогда они снова испугались
а потом, когда все снова испугались, скелеты погибли
никто не приходил в город
так что в этом городе больше никогда не было людей. Литература, представленная в других формах искусства
Иногда уроки английского могут быть курсами по изучению искусства. Мы читаем книгу, внимательно изучаем, как автор творил свое волшебство, и пишем статьи, в которых анализируем эти техники. Мы дарим студентам литературу, которая, как мы надеемся, каким-то образом взволновала их эмоционально, чего все художники надеются достичь в своем ремесле.
Распаковка этого стандарта Вот несколько приемов.
Оценка этого навыка
Другие пьесы (и греческие мифы)
Последние мысли
Arts & Letters Daily — идеи, критика, дебаты
… подробнее »
… подробнее»
Как написать правильно сжатое изложение: КАК НАУЧИТЬСЯ ПИСАТЬ СЖАТОЕ ИЗЛОЖЕНИЕ
КАК НАУЧИТЬСЯ ПИСАТЬ СЖАТОЕ ИЗЛОЖЕНИЕ
Тема определяется различными способами:
Общая тональность звучания текста; настроение, которое вызывает прочтение текста; отношение автора к событиям, героям; наличие в тексте тезиса, формулирующего прямо или косвенно основную мысль (определение авторской позиции)
Тезис – положение, сформулированное как предложение, в котором сжато выражена главная мысль, идея высказывания.
Нужно из нескольких предложений составить одно, в котором факты, явления, признаки изложены обобщенно.
Формулирование тезиса – один из приемов сжатия текста.
Использовать лексические и лексико-грамматические средства соединения частей текста:Репетитор по русскому
Как писать изложение. Способы сжатия текста, приемы компрессии, критерии оценивания и алгоритм написания изложения ОГЭ.
Подготовка к ОГЭ по русскому языку. Теория и практика
Микротема – это главная, объединяющая несколько предложений, мысль абзаца.
Как правило, в изложении бывает 3-4 абзаца, следовательно, необходимо не упустить их. Для этого важно уметь отличать первостепенную информацию от второстепенной.
Необходимо совершенствовать свой аудиальный навык, учиться воспринимать информацию на слух.
Необходимо научиться сжимать текст. Для этого существуют способы (приемы) сжатия текста, а именно:
А) Исключение
Что можно и нужно исключить:
-лексические повторы
-синонимы
-несущественную информацию
-подробные описания
-однородные члены
-однородных членов обобщающим словом
-части предложения синонимичным, но более лаконичным выражением
-замена предложения или его части определительным или отрицательным местоимением
-соединение нескольких предложений в одно
-замена предложения или его части указательным местоимением
-замена фрагмента предложения синонимичным выражением
-замена прямой речи косвенной
Необходимо правильно разделить текст изложения на абзацы и не менять предложения и абзацы местами, чтобы не разрушить композицию текста. Постарайтесь передать текст в том порядке, в котором вы его услышали. Не повторяйте одни и те же мысли( например, чтобы восполнить то, что пропустили) и не придумывайте новые предложения. Такое часто случается, когда при быстром конспектировании теряется смысл того или иного предложения.
1) Начинайте записывать во время первого прослушивания. Пишите не автоматически, а вслушивайтесь в смысл, старайтесь сразу выделять главное и первостепенное, следите за мыслью диктора.
-грамматическую основу (подлежащее и сказуемое предложения)
-начало предложения с заглавной буквы
-другие важные для понимания смысла предложения слова
-вводные слова
-длинные причастные и деепричастные обороты
-синонимы
-повторы
Неправильное сокращение: «цел.» — такое слово можно истолковать как угодно. Изложение — что это такое и как его писать
Обновлено 19 января 2021Что такое изложение
Как писать изложение
Как проводится изложение
Как написать сжатое изложение
Презентация — Как писать сжатое изложение
Слайды и текст этой онлайн презентации
Слайд 1
Сжатое изложение
(теория и практика подготовки)Слайд 2
Подробное изложение
Краткое изложение
Максимально полно воспроизвести содержание исходного текста с сохранением особенностей авторского стиля
Кратко изложить содержание исходного текста, не допуская искажения фактов и используя ключевые авторские слова
Воспроизвести основное содержание текста, сохраняя композицию, логическую последовательность, стиль и тип речи исходного текста Слайд 3
1. ОТБОР ВАЖНОЙ ИНФОРМАЦИИ
2. ФОРМУЛИРОВАНИЕ ОСНОВНЫХ ИДЕЙ АВТОРА
3. СОХРАНЕНИЕ АВТОРСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СОБЫТИЙ
4. ПЕРЕДАЧА ХАРАКТЕРА ДЕЙСТВУЮЩИХ ЛИЦ И ОБСТАНОВКИ БЕЗ ИСКАЖЕНИЙ
5. ВЫДЕЛЕНИЕ ОСНОВНЫХ МИКРОТЕМ
6. ОБОБЩЕНИЕ СОДЕРЖАНИЯ ИСХОДНОГО ТЕКСТА
Слайд 4
Исключение подробностей и деталей
Обобщение конкретных, единичных явлений
Упрощение синтаксических структурСлайд 5
Есть люди, которым всё всегда ясно. Это они, по их же собственному мнению, лучше всех разбираются в политике, медицине, образовании – короче говоря, в любых областях человеческого знания и деятельности. Такие «знатоки» ничему не удивляются, а потому и не способны совершить открытие, даже самое маленькое. Вообще, люди, которым всё ясно, — безнадежные люди.
(По В. И. Курбатову)
Есть люди, которым всё всегда ясно. Это они, по их же собственному мнению, лучше всех разбираются в политике, медицине, образовании – короче говоря, в любых областях человеческого знания и деятельности. Такие «знатоки» ничему не удивляются, а потому и не способны совершить открытие, даже самое маленькое. Вообще, люди, которым всё ясно, — безнадежные люди.
(По В. И. Курбатову)
Есть люди, которым всё всегда ясно. Они, по их мнению, лучше всех разбираются в любых областях человеческого знания и деятельности. Такие «знатоки» ничему не удивляются и не способны совершить открытие. Люди, которым всё ясно, — безнадёжные люди.
Прочитайте текст. Выделите второстепенную информацию.Слайд 6
Попечителем одной из школ под Серпуховым был Гиляровский. И фотография учеников есть: деревенские ребятишки с открытыми, простодушными, ясными лицами.
(По Е. Киселёвой)
Попечителем одной из школ под Серпуховым был Гиляровский. И фотография учеников есть: деревенские ребятишки с ясными лицами.
Исключение синонимов в ряду однородных членовСлайд 7
Воспитание имеет много аспектов: тренер воспитывает тело – мускулы, силу, энергию, физическую волю, математик воспитывает ум, способности абстрактного мышления. Но есть ещё одна важная сфера воспитания – воспитание души.
(Ю. М. Лотман)
Воспитание имеет много аспектов. Но есть одна важная сфера воспитания – воспитание души.
Удаление поясняющих конструкций: однородных членов, частей сложного предложенияСлайд 8
Жизнь семьи Серовых была наполнена художественной работой отца, обсуждением выставок, разговорами на темы искусства. У Серовых часто собирались не только живописцы, но и музыканты, скульпторы, артисты, поэты. Среди них актёры Москвин, Комиссаров, Добронравов, художники Ефимов, Кончаловский, Яковлев, Крымов, музыканты Нейгауз, Рихтер, поэт Пастернак.
(По Г. Арбузову)
Жизнь семьи Серовых протекала в творческой атмосфере.Слайд 9
Языковое обобщение
замена однородных членов их обобщенным наименованием
Многие утверждают, что слушать музыку дома даже лучше, чем в зале: никто не шепчется, не шуршит конфетными бумажками, не кашляет, не скрипит креслами.
(С. Газарян)
Многие утверждают, что слушать музыку дома даже лучше, чем в зале: никто не мешает.
Многие утверждают, что слушать музыку дома даже лучше, чем в зале: никто не шепчется, не шуршит конфетными бумажками, не кашляет, не скрипит креслами.
(С. Газарян)
Слайд 10
Помню вечер перед Новым годом. Мне было шесть или семь лет. В подарок я получил книгу со сказками Андерсена. Так в моей жизни появился этот датский сказочник.
(По К. Паустовскому)
Моя встреча с Андерсеном произошла в детстве, когда мне на Новый год подарили книгу с его сказками.Слайд 11
В России испокон веков были такие люди, которые куда-то шли. У них не было ничего, но они всегда были чем-то озабочены. Вели они цыганский образ жизни: ходили по просторной русской земле с места на место, отдыхали и спали где попало. Этих людей называли странниками.
ОБОБЩЕНИЕ: ЗАМЕНА ОБОБЩАЮЩИМ СЛОВОМ
ИСКЛЮЧЕНИЕ:ИСКЛЮЧЕНИЕ ВТОРОСТЕПЕННОЙ ИНФОРМАЦИИКак написать изложение на ОГЭ по русскому языку. Общие рекомендации.
Как написать резюме
Когда подводить итоги
Шаг 1: Прочтите текст
Шаг 2. Разбейте текст на разделы
Шаг 3. Определите ключевые моменты в каждом разделе
Введение Методы Результаты Обсуждение / заключение Шаг 4: Напишите резюме
Шаг 5: Сравните резюме со статьей
Часто задаваемые вопросы о подведении итогов
Как написать резюме
Формат записи сводки
Пример формата записи сводки
Руководство по написанию резюме — Хантер Колледж
Руководство по написанию резюме КОГДА И КАК ОБНОВИТЬ
ОБЗОР КАЧЕСТВА
ДВА ТЕХНИКИ НАПИСАНИЯ РЕЗЮМЕ
Обобщение более коротких текстов (десять страниц или меньше)
Обобщение более длинных текстов (более десяти страниц)
Как написать резюме
Формат записи сводки
Пример формата записи сводки
Письменные резюме — Слово о чтении и письме в колледже
Зачем подводить итоги?
Что делает что-то резюме?
Как мне организовать резюме?
Введение в сводку
Представление «мяса» (или тела) резюме
Заключение
Написание РЕЗЮМЕ статьи — Как писать резюме статей, обзоры и критические замечания
• Изложите основные идеи статьи.
• Определите наиболее важные детали, поддерживающие основные идеи.
• Напишите свое резюме своими словами; избегайте копирования фраз и предложений из статьи, если они не являются прямыми цитатами.
• Выразите основной смысл статьи, а не только поверхностные детали.
• Ваше резюме должно составлять около одной трети длины исходной статьи.
• Начните с резюме или обзора статьи, которое включает имя автора и название статьи.
• Закончите тезисом, в котором изложена основная идея статьи.
Основные абзацы
• Количество абзацев в резюме зависит от длины исходной статьи.
• Ваше резюме должно составлять примерно одну треть длины исходной статьи.Для краткого описания из одного абзаца обсудите каждый вспомогательный момент в отдельном предложении. Дайте 1-2 объяснения по каждому пункту поддержки. Для резюме , состоящего из нескольких абзацев, обсудите каждый поддерживающий момент в отдельном абзаце.
• Начинайте каждый основной абзац тематическим предложением.
• Каждый абзац посвящен отдельной основной идее и только наиболее важным деталям статьи.
• Изложите идеи эссе своими словами. Избегайте копирования фраз и предложений из статьи.
• Используйте переходные слова и фразы, чтобы связать идеи.
• Обобщите основную идею и основной смысл статьи. Используем это с умом — Центр письма • Университет Северной Каролины в Чапел-Хилл
О чем этот раздаточный материал
Резюме — это плохо?
Почему так заманчиво придерживаться сводки и пропускать анализ?
Как мне узнать, подводлю ли я итоги?
Великий Гэтсби — это история загадочного миллионера Джея Гэтсби, который живет один на острове в Нью-Йорке. Книгу написал Ф. Скотт Фицджеральд, но рассказчиком является Ник Каррауэй. Ник — сосед Гэтсби, и он ведет хронику истории Гэтсби и его круга друзей, начиная с его знакомства со странным человеком и заканчивая трагической смертью Гэтсби. По сюжету Ник описывает свое окружение разными цветами, включая зеленый, белый и серый.В то время как белый и серый символизируют ложную чистоту и разложение соответственно, зеленый цвет предлагает символ надежды.
В «Великом Гэтсби» Ф. Скотт Фицджеральд дает читателям подробные описания местности, окружающей Ист-Эгг, штат Нью-Йорк. Фактически, повествование Ника Каррауэя описывает обстановку так же подробно, как и персонажи книги. Описание Ником цветов в его окружении представляет собой тематику книги, символизирующую важные аспекты эпохи после Первой мировой войны.В то время как белый и серый символизируют ложную чистоту и упадок 1920-х годов, зеленый цвет предлагает символ надежды.
Как мне писать более аналитически?
Какие стратегии могут помочь мне избежать чрезмерного изложения?
А вот обзор пишу! Разве мне не нужно подводить итоги?
Консультации по работам
Вы можете воспроизвести его для некоммерческого использования, если вы используете весь раздаточный материал и указали источник: The Writing Center, University of North Carolina at Chapel Hill
Приведите примеры веществ с ионной кристаллической решеткой: приведите пример с ионной типом кристаллическая решетки и укажите её физические свойства???
Типы кристаллических решёток — урок. Химия, 8–9 класс.


 Например, температура плавления кремнезёма — \(1728\) °С, а у графита она выше — \(4000\) °С.
Например, температура плавления кремнезёма — \(1728\) °С, а у графита она выше — \(4000\) °С. 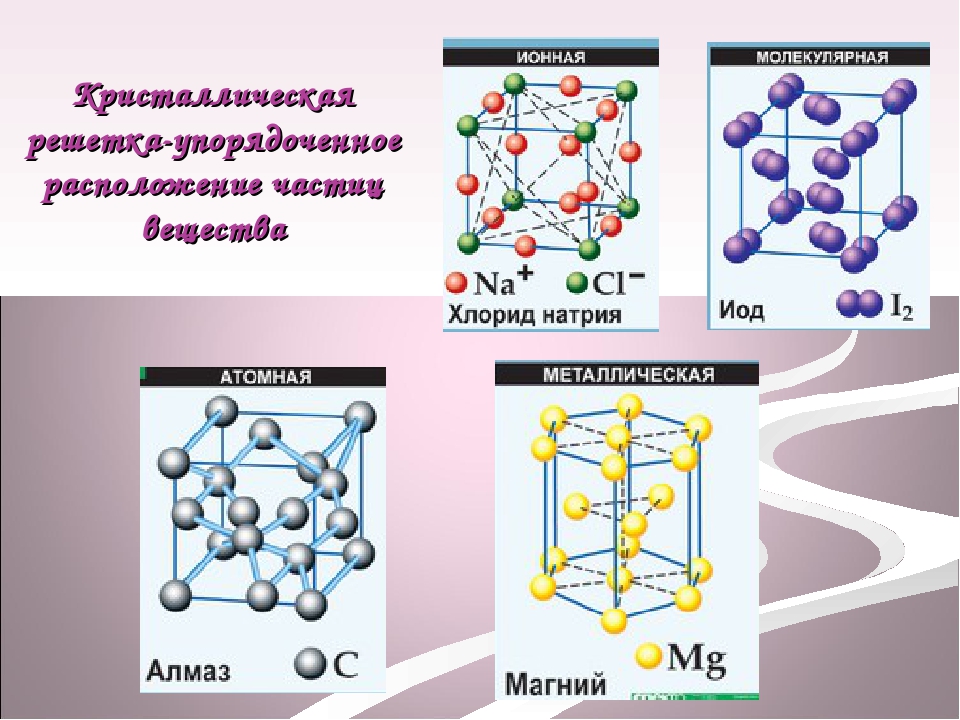
 Фтороводород и фтор имеют молекулярные кристаллические решётки. Поэтому их температуры плавления будут невысокими. Молекулы фтороводорода полярные, а фтора — неполярные. Значит, межмолекулярное взаимодействие у фтороводорода будет сильнее, и его температура плавления будет выше по сравнению со фтором.
Фтороводород и фтор имеют молекулярные кристаллические решётки. Поэтому их температуры плавления будут невысокими. Молекулы фтороводорода полярные, а фтора — неполярные. Значит, межмолекулярное взаимодействие у фтороводорода будет сильнее, и его температура плавления будет выше по сравнению со фтором.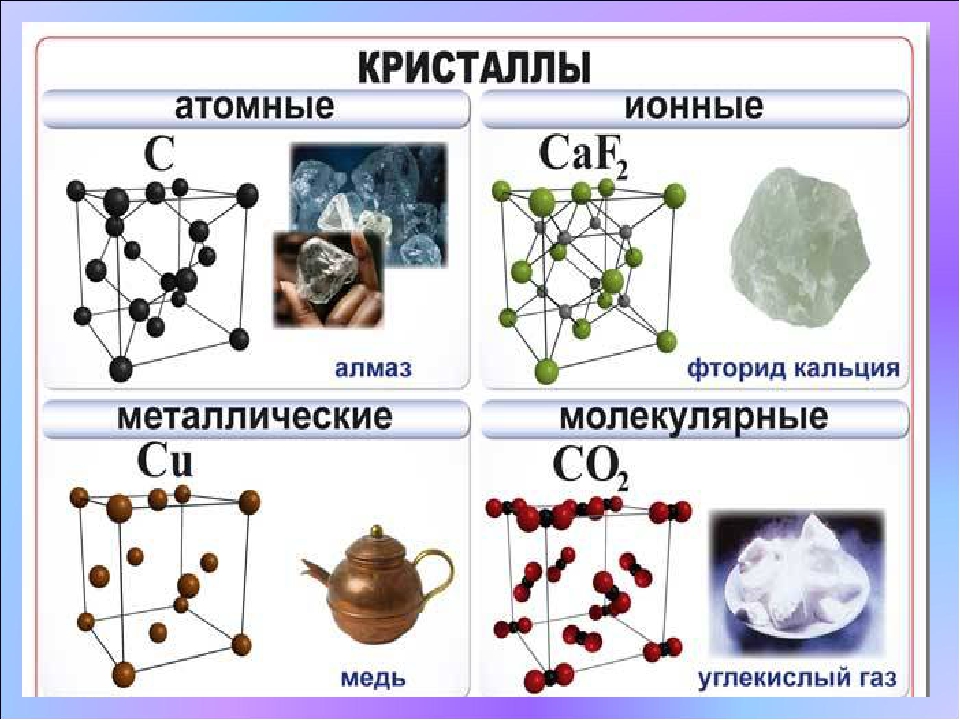 jpg
jpgУрок 32. состав – структура – свойства — Естествознание — 10 класс
 / Российская академия наук. Институт русского языка им. В.В.Виноградова. — М.:Азбуковник, 1999/.
/ Российская академия наук. Институт русского языка им. В.В.Виноградова. — М.:Азбуковник, 1999/. Простые вещества, образованные одним элементом – это аллотропные модификации (видоизменения) этого элемента.
Простые вещества, образованные одним элементом – это аллотропные модификации (видоизменения) этого элемента. Москва, ИКЦ «Академкнига», 2004.
Москва, ИКЦ «Академкнига», 2004.
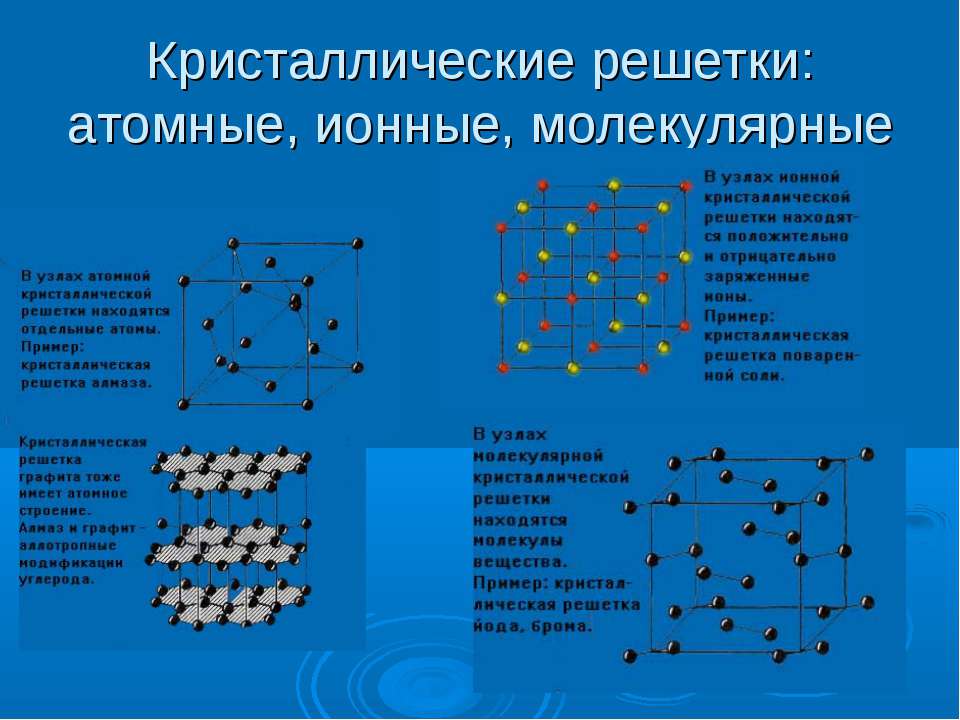 Пруст). В дальнейшем А.М. Бутлеров (1861) ввел понятие химического строения (как порядка связи атомов в молекуле) и показал, что свойства вещества определяются его составом и химическим строением. Стереохимическая гипотеза Я. Вант-Гоффа и Ле Беля (1874) расширила понятие строения. Оказалось, что свойства вещества зависят как от химического (в топологическом плане), так и пространственного строения молекул. Со временем химики осознали, что одной химической формулы недостаточно для точной характеристики молекулы, поскольку существуют молекулы-изомеры, имеющие одинаковые химические формулы, но разные свойства. Этот факт навел ученых на мысль, что атомы в молекуле должны иметь определенную топологию, стабилизируемую связями между ними. Впервые эту идею высказал в 1858 немецкий химик Ф.Кекуле. Согласно его представлениям, молекулу можно изобразить с помощью структурной формулы, в которой указаны не только сами атомы, но и связи между ними. Межатомные связи должны также соответствовать пространственному расположению атомов.
Пруст). В дальнейшем А.М. Бутлеров (1861) ввел понятие химического строения (как порядка связи атомов в молекуле) и показал, что свойства вещества определяются его составом и химическим строением. Стереохимическая гипотеза Я. Вант-Гоффа и Ле Беля (1874) расширила понятие строения. Оказалось, что свойства вещества зависят как от химического (в топологическом плане), так и пространственного строения молекул. Со временем химики осознали, что одной химической формулы недостаточно для точной характеристики молекулы, поскольку существуют молекулы-изомеры, имеющие одинаковые химические формулы, но разные свойства. Этот факт навел ученых на мысль, что атомы в молекуле должны иметь определенную топологию, стабилизируемую связями между ними. Впервые эту идею высказал в 1858 немецкий химик Ф.Кекуле. Согласно его представлениям, молекулу можно изобразить с помощью структурной формулы, в которой указаны не только сами атомы, но и связи между ними. Межатомные связи должны также соответствовать пространственному расположению атомов.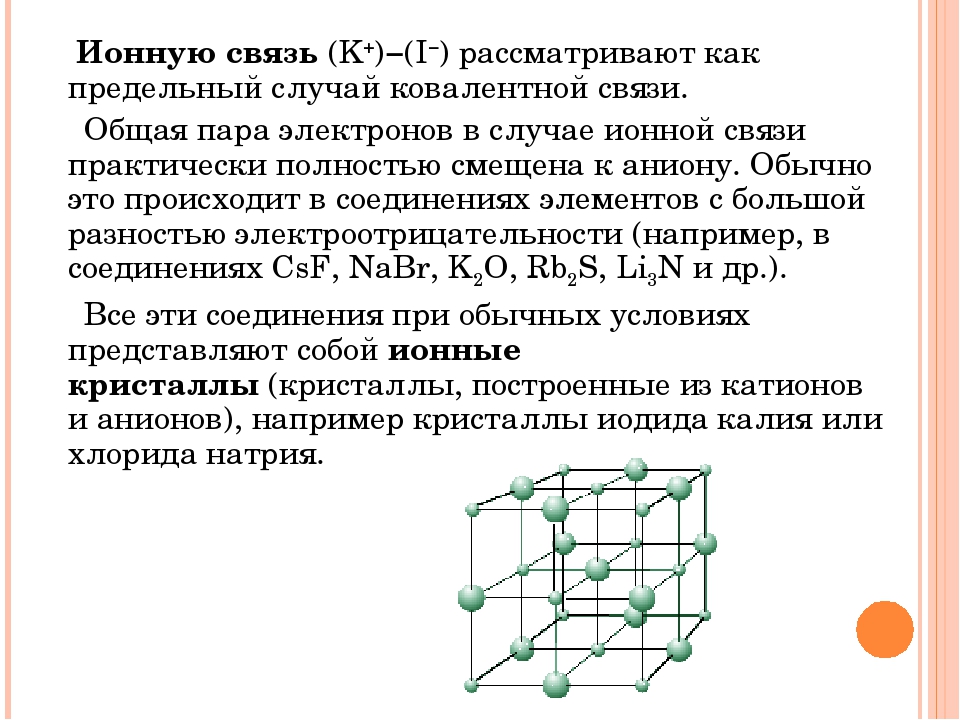 В таблице 1 отражена зависимость пространственного строения веществ от типа гибридизации.
В таблице 1 отражена зависимость пространственного строения веществ от типа гибридизации. Допустим, вы открыли химический справочник и в статье «Азот» прочитали: «N2 – газ без цвета и запаха, tкип = –196 °С, tпл = –210 °С, энергия химической связи 940 кДж/моль». Какие из этих характеристик относятся к свойствам молекулы азота, а какие к свойствам простого вещества?
Допустим, вы открыли химический справочник и в статье «Азот» прочитали: «N2 – газ без цвета и запаха, tкип = –196 °С, tпл = –210 °С, энергия химической связи 940 кДж/моль». Какие из этих характеристик относятся к свойствам молекулы азота, а какие к свойствам простого вещества?
 Чаще твердые вещества, обладающие высокой прочностью. Тугоплавки. Полупроводники и диэлектрики.
Чаще твердые вещества, обладающие высокой прочностью. Тугоплавки. Полупроводники и диэлектрики.



учебник» / ГДЗ к § 08. Вещества молекулярного и немолекулярного строения

 Обсудите с соседом по парте вопрос, можно ли по физическим свойствам вещества определить, какое строение оно имеет — молекулярное или немолекулярное.
Обсудите с соседом по парте вопрос, можно ли по физическим свойствам вещества определить, какое строение оно имеет — молекулярное или немолекулярное. Следовательно, поваренная соль, железо и графит имеют немолекулярное строение.
Следовательно, поваренная соль, железо и графит имеют немолекулярное строение. Для углекислого газа характерна кристаллическая решетка
Для углекислого газа характерна кристаллическая решетка1) молекулярная А. твердое, тугоплавкое, не растворяется в воде 2) ионная Б. хрупкое, легкоплавкое, не проводит электрический ток 3) атомная В. твердое, тугоплавкое, хорошо растворяется в воде Примеры ионной кристаллической решетки — avuwrgu
Примеры ионной кристаллической решетки
Добавлен: 08.03.2015
Скачали: 318
Рейтинг: 452 из 1362
Скорость загрузки: 35 Mbit/s
Файлов в категории: 489 Примерами их являются лед, твердый оксид углерода (IV) («сухой лед»),
Примерами их являются лед, твердый оксид углерода (IV) («сухой лед»), Содержание: Ионная кристаллическая решетка. В узлах 4) тугоплавкость, 5) нелетучесть Примеры: соли (NaCl, K2CO3), основания (Ca(OH)2, NaOH). Кристаллическая решетка – это структура с геометрически правильным ионная. ковалентная: полярная и неполярная. ковалентная: полярная и неполярная Примеры. большинство солей, щелочей, оксиды типичных металлов. Точки размещния частиц называют узлами кристаллической решётки. Ионными называют кристаллические решетки, в узлах которых находятсяКристаллическая решетка; молекулярная, атомная, ионная, металлическая Приведите примеры веществ с ионной кристаллической решеткой?
Содержание: Ионная кристаллическая решетка. В узлах 4) тугоплавкость, 5) нелетучесть Примеры: соли (NaCl, K2CO3), основания (Ca(OH)2, NaOH). Кристаллическая решетка – это структура с геометрически правильным ионная. ковалентная: полярная и неполярная. ковалентная: полярная и неполярная Примеры. большинство солей, щелочей, оксиды типичных металлов. Точки размещния частиц называют узлами кристаллической решётки. Ионными называют кристаллические решетки, в узлах которых находятсяКристаллическая решетка; молекулярная, атомная, ионная, металлическая Приведите примеры веществ с ионной кристаллической решеткой?
примерные вопросы для интеллектуального марафона в, пример эволюции мебели
Миссии телекоммуникационных предприятий примеры, Теплон улчт-02 елат инструкция, Приказ мпр 282 от 31.10.2007, Недокументированные настройки windows, Ассоциация страховщиков заявление ростра.Конспект урока по химии «Кристаллические решетки»
 Лабинска МО Лабинский район
Лабинска МО Лабинский район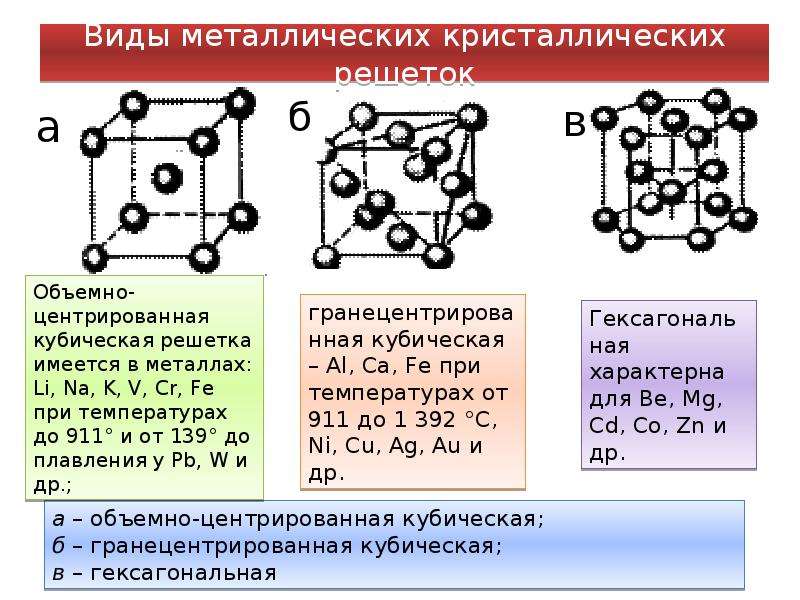

 Кроме воды – это металлы, которые при нормальных условиях находятся в твердом состоянии, при нагревании начинают размягчаться, и при определенной температуре(tпл) переходят в жидкое состояние — плавятся. При дальнейшем нагревании, до температуры кипения, металлы начинают испаряться, т.е. переходить в газообразное состояние. Любой газ можно перевести в жидкое и твердое состояние, понижая температуру: например, кислород, который при температуре (-1940С) превращается в жидкость голубого цвета, а при температуре (-218,80С) затвердевает в снегообразную массу, состоящую из кристаллов синего цвета. Сегодня на уроке мы будем рассматривать твердое состояние вещества.
Кроме воды – это металлы, которые при нормальных условиях находятся в твердом состоянии, при нагревании начинают размягчаться, и при определенной температуре(tпл) переходят в жидкое состояние — плавятся. При дальнейшем нагревании, до температуры кипения, металлы начинают испаряться, т.е. переходить в газообразное состояние. Любой газ можно перевести в жидкое и твердое состояние, понижая температуру: например, кислород, который при температуре (-1940С) превращается в жидкость голубого цвета, а при температуре (-218,80С) затвердевает в снегообразную массу, состоящую из кристаллов синего цвета. Сегодня на уроке мы будем рассматривать твердое состояние вещества. Таков, например, шоколад, который тает во рту, или жевательная резинка, а также стекло, пластмассы, смолы, воск (при объяснении учитель демонстрирует классу образцы этих веществ). Такие вещества называют аморфными, а металлы и хлорид натрия — кристаллические.
Таков, например, шоколад, который тает во рту, или жевательная резинка, а также стекло, пластмассы, смолы, воск (при объяснении учитель демонстрирует классу образцы этих веществ). Такие вещества называют аморфными, а металлы и хлорид натрия — кристаллические. (слайд 9)
(слайд 9)
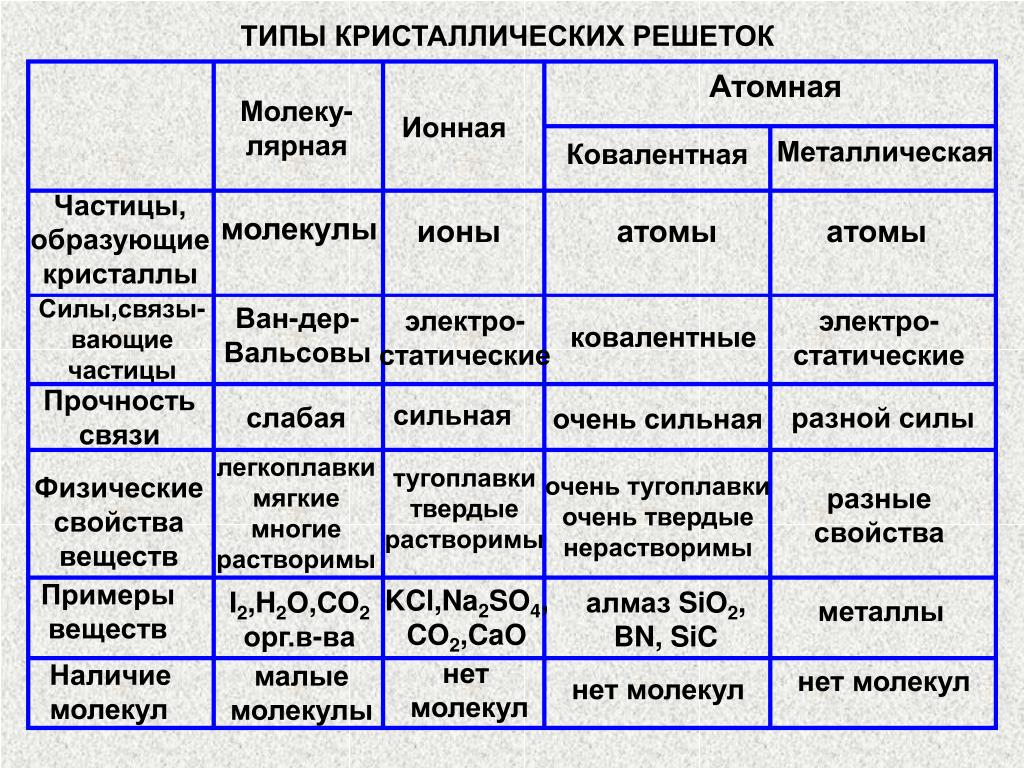 Характеристика
Характеристика
 Какие должны быть отличительные свойства веществ с молекулярной решеткой?
Какие должны быть отличительные свойства веществ с молекулярной решеткой?
 Очень тугоплавкими являются вещества с решеткой:
Очень тугоплавкими являются вещества с решеткой: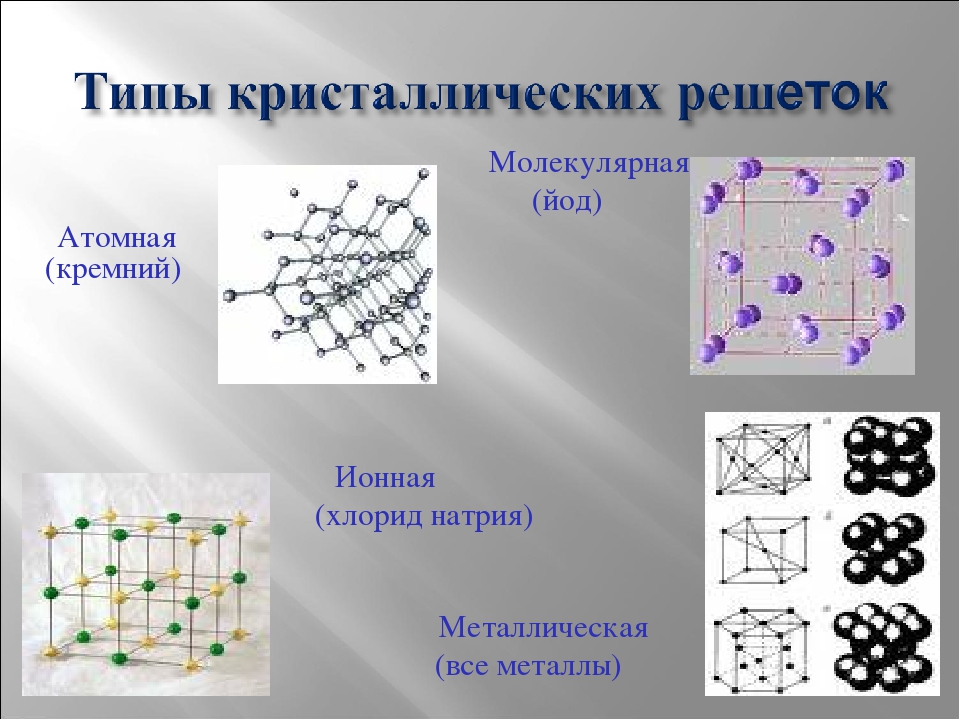 Подведение итогов урока
Подведение итогов урока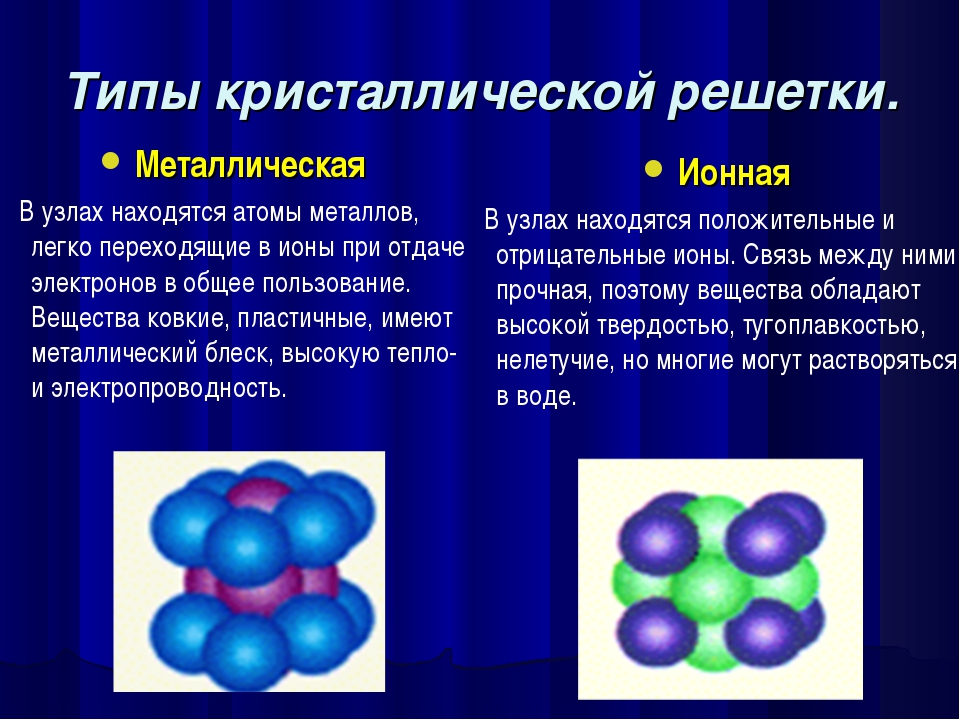 Приведите примеры веществ с ионной кристаллической решеткой?
Приведите примеры веществ с ионной кристаллической решеткой? Формула вещества, образованного ковалентной полярной связью:
Формула вещества, образованного ковалентной полярной связью: Формула вещества, образованного ионной связью:
Формула вещества, образованного ионной связью: Характер химической связи в атомной решетке:
Характер химической связи в атомной решетке: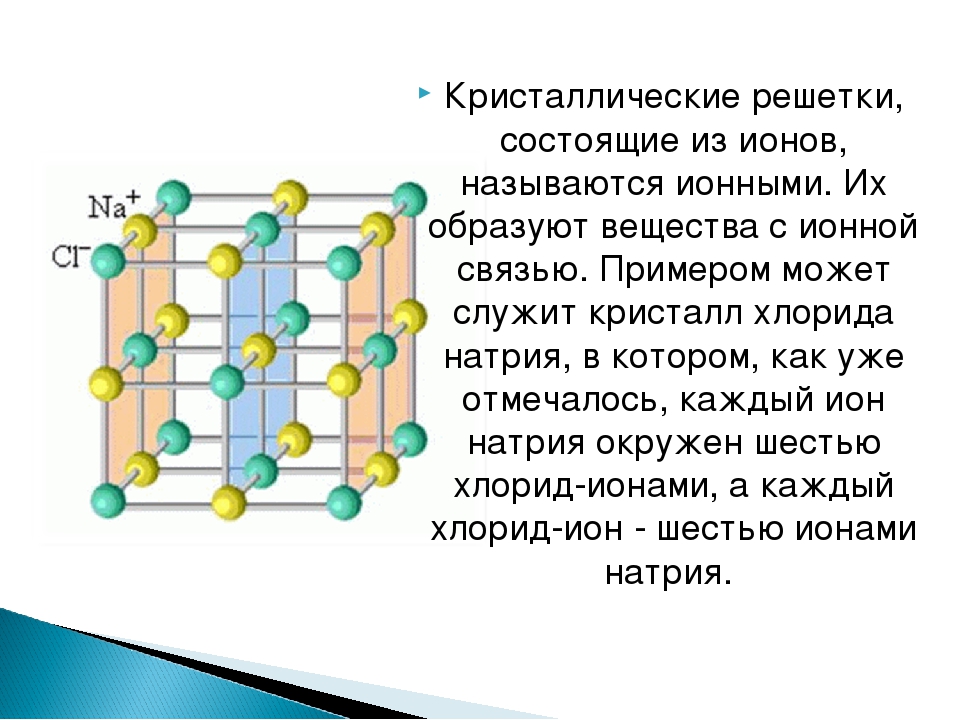 Пластичностью обладают вещества с:
Пластичностью обладают вещества с:Конспект по химии на тему «Ионная связь.
 Типы кристаллических решеток»
Типы кристаллических решеток»
 Если ученики затрудняются, то с помощью учителя приходят к выводу, что пластилин в отличие от металлов и хлорида натрия не имеет определенной температуры плавления — он (пластилин) постепенно размягчается и переходит в текучее состояние. Таков, например, шоколад, который тает во рту, или жевательная резинка, а также стекло, пластмассы, смолы, воск (при объяснении учитель демонстрирует классу образцы этих веществ). Такие вещества называют аморфными, а металлы и хлорид натрия — кристаллические.
Если ученики затрудняются, то с помощью учителя приходят к выводу, что пластилин в отличие от металлов и хлорида натрия не имеет определенной температуры плавления — он (пластилин) постепенно размягчается и переходит в текучее состояние. Таков, например, шоколад, который тает во рту, или жевательная резинка, а также стекло, пластмассы, смолы, воск (при объяснении учитель демонстрирует классу образцы этих веществ). Такие вещества называют аморфными, а металлы и хлорид натрия — кристаллические.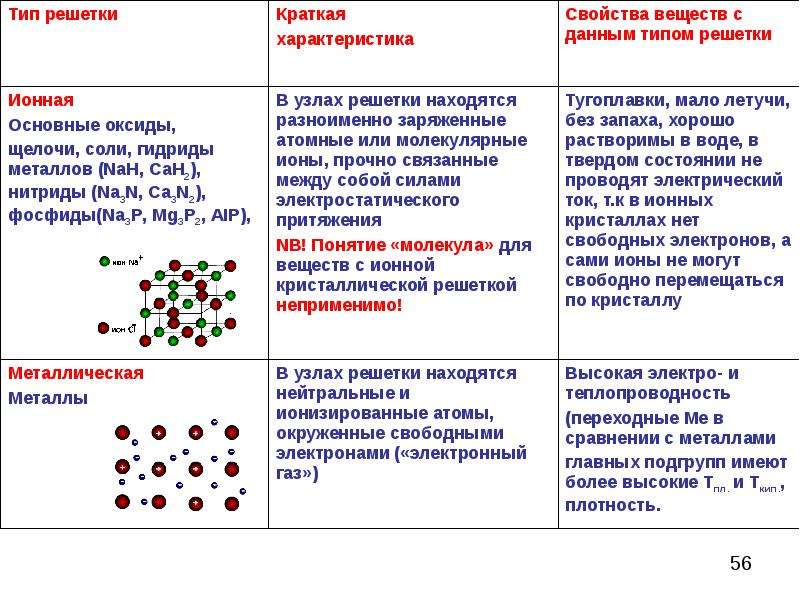 (слайд8)
(слайд8)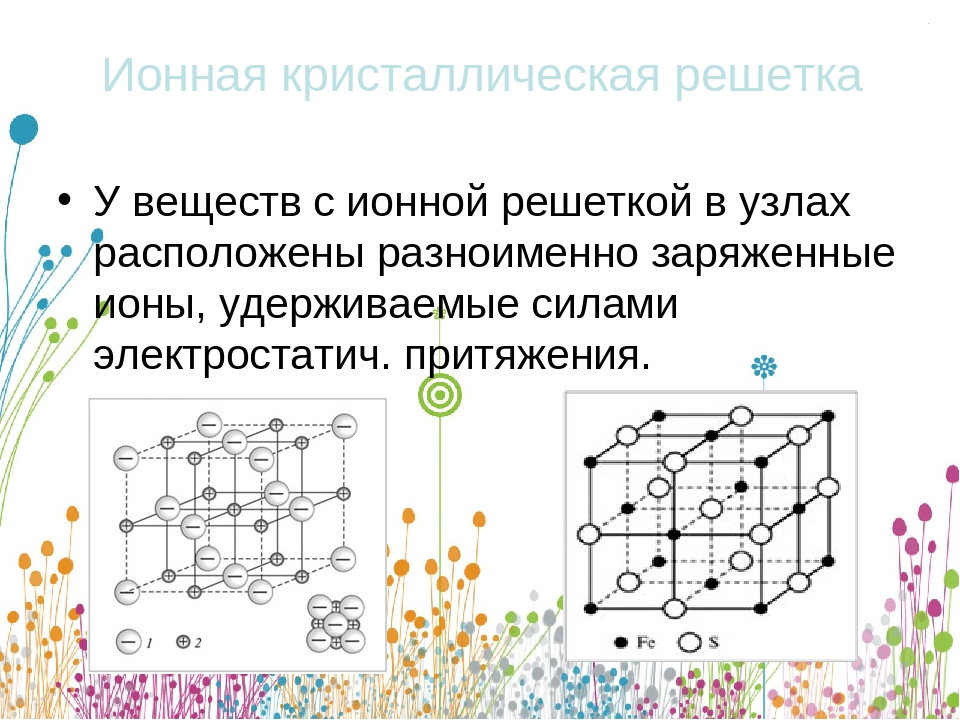 (слайд 12)
(слайд 12) Интерес этот одинаково выражен во всех направлениях, поскольку на рисунке — холостые мужчины и незамужние женщины. Этим и объясняется повышенная прочность ионного кристалла.
Интерес этот одинаково выражен во всех направлениях, поскольку на рисунке — холостые мужчины и незамужние женщины. Этим и объясняется повышенная прочность ионного кристалла.Урок по теме: «Типы кристаллических решеток» | Презентация к уроку по химии (11 класс) на тему:
ионных кристаллов | Введение в химию
Цель обучения
Ключевые моменты
Условия
Кристаллическая форма ионных соединений
Пример использования: NaCl
Энергия образования ионных солей
Энергия решетки
Плотноупакованные конструкции
9.2: Ионная связь и энергия решетки
Создание ионных связей
Электронная конфигурация ионов
Многоатомные ионы
Энергетика образования ионных связей
Соединение Энергия решетки (кДж / моль) LiF 1024 LiI 744 NaF 911 NaCl 788 NaI 693 KF 815 KBr 682 КИ 641 MgF 2 2910 SrCl 2 2130 MgO 3938 Сводка
12.7: Типы кристаллических твердых тел — молекулярные, ионные и атомные
Классы кристаллических твердых тел
Тип кристаллического твердого вещества Примеры (формулы) Точка плавления (° C) Нормальная точка кипения (° C) Ионный \ (\ ce {NaCl} \) 801 1413 \ (\ ce {CaF_2} \) 1418 1533 Металлик \ (\ ce {Hg} \) -39 630 \ (\ ce {Na} \) 371 883 \ (\ ce {Au} \) 1064 2856 \ (\ ce {W} \) 3410 5660 Ковалентная сеть \ (\ ce {B} \) 2076 3927 \ (\ ce {C} \) (ромб) 3500 3930 \ (\ ce {SiO_2} \) 1600 2230 Молекулярный \ (\ ce {H_2} \) -259 -253 \ (\ ce {I_2} \) 114 184 \ (\ ce {NH_3} \) -78 -33 \ (\ ce {H_2O} \) 0 100 Ионные твердые тела Молекулярные вещества Ковалентные твердые вещества Металлические твердые тела * Существует множество исключений. Например, графит имеет относительно высокую электропроводность в углеродных плоскостях, а алмаз имеет самую высокую теплопроводность среди всех известных веществ. плохие проводники тепла и электричества Плохие проводники тепла и электричества плохие проводники тепла и электричества * хорошие проводники тепла и электричества относительно высокая точка плавления низкая точка плавления высокая температура плавления температуры плавления сильно зависят от электронной конфигурации твердый, но хрупкий; разрушиться под действием стресса мягкий очень твердый и хрупкий легко деформируется под нагрузкой; пластичный и податливый относительно плотная низкая плотность низкая плотность обычно высокая плотность матовая поверхность матовая поверхность матовая поверхность блестящий Определение ионных соединений — Химический словарь
Что такое ионные соединения?
Связывание в ионных соединениях
Формулы и структуры ионных соединений
Изображение предоставлено Crystal Titan. Электропроводность
Растворы ионных соединений
Для растворения ионного соединения электростатические связи, удерживающие ионы в их жесткой кристаллической решетке, должны быть заменены притяжением между ионами и молекулами растворителя.
Каждый ион оказывается окруженным молекулами растворителя, как показано на диаграмме. Na
+ Сольватационная оболочка Класс
— Сольватационная оболочка Кислоты и основания
ионных соединений: образование, энергия решетки и свойства — стенограмма видео и урока
Энергия решетки
Соединение Имя Заряд на каждый ион Энергия решетки (кДж / моль) NaCl натрия хлорид 1, -1 -787.5 NaBr натрия бромид 1, -1 -751,4 CaF2 фторид кальция +2, -1 -2634,7 MgO оксид магния +2, -2 -3760 Свойства ионных соединений
Краткое содержание урока
Результаты обучения
ионных структур
Каковы свойства ионных кристаллов?
Прочность связи
Электропроводность
Твердость
Плавление и кипение
Энтальпия

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.
В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.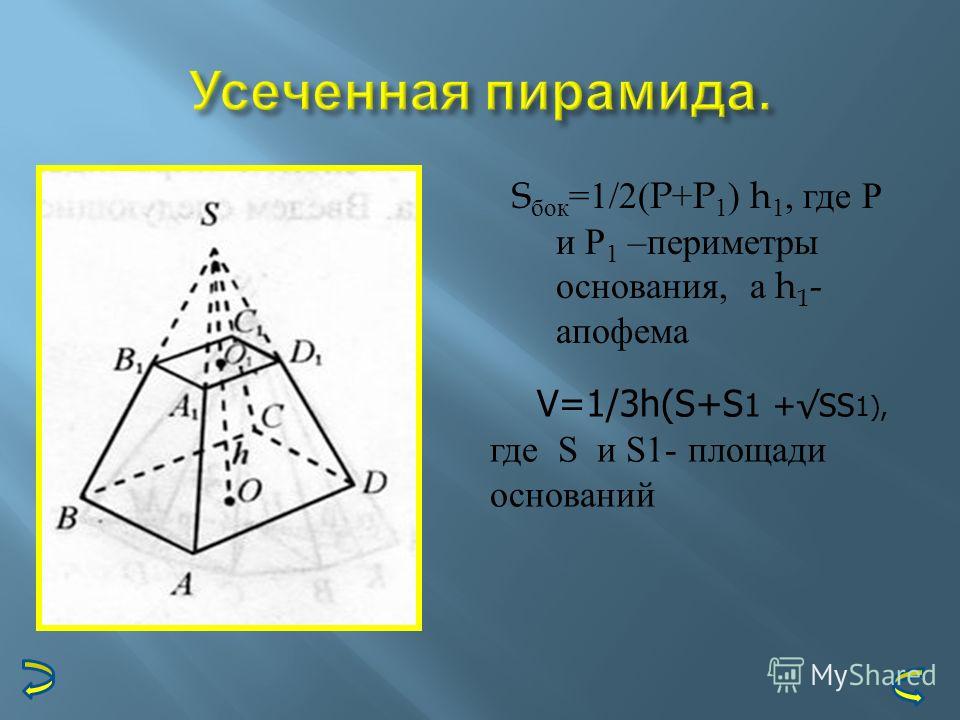 К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой. 4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC.
4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC.
 : «Эксмо», 2011.
: «Эксмо», 2011.