Собачка аквагрим фото: Как нарисовать собаку на лице, лице ребенка? Как сделать аквагрим?
Аквагрим для детей: фото, идеи и инструкции
Аквагрим для детейГрим для детейНеподражаемое и удивительное дополнение к любому карнавальному, детскому новогоднему костюму или веселая часть детского праздника – это аквагрим для детей.
Воспользовавшись специальными красками на водной основе, кисточками и потратив всего лишь несколько минут, вы сможете подарить своему ребенку настоящую волшебную сказку. Малыш, как по волшебству превратится в сказочную принцессу или красавицу-бабочку, пирата или человека паука, кота или тигра, медвежонка или милого зайчика.
Маленькие дети не только любят преображаться в любимых сказочных персонажей, но и наблюдать за тем, как происходит волшебство нанесения аквагрима.
Новостной портал «Vtemu.by» в этой статье подготовил для Вас несколько простых в исполнении идей по нанесению грима для детей. Вы можете использовать аквагрим, грим или декоративную косметику. Главное условие, обязательно проверьте реакцию кожи ребенка на грим или декоративную косметику, ведь не редки случаи аллергических реакций на компоненты красок.
В случае использования вами акваграма риск аллергических реакций практически исключен, поэтому его можно смело наносить на лицо ребенка склонного к аллергическим реакциям. В состав аквагрима входят краски на водной основе, которые безопасны для чувствительной кожи ребенка. Аквагрим быстро сохнет, не растекается, легко смывается водой при умывании, а при попадании на одежду отлично стирается. И при всем при этом, аквагрим имеет яркие насыщенные цвета, которые так нравятся детишкам.
Грим Хэллоу КиттиАквагрим наносится на кожу при помощи тонких кисточек или маленьких губок. Используя разные цвета можно создать на лице у ребенка удивительной красоты произведения, которые будут достойны самого удивительного и волшебного маскарада и карнавала.
Итак, вооружитесь яркими красками и умением рисовать!
Грим медведяДля мальчиков подойдут следующие образы: тигр, пират, человек-паук, собачка, медвежонок, зайчонок и др.
Грим зайцаДля девочек подойдут следующие образы: бабочка, зайчик, кошечка, божья коровка, Хэллоу Китти, пчелка и др.
Перед нанесением грима на лицо, обязательно поинтересуйтесь о том, чего бы хотел ребенок. Ни в коем случае не настаивайте на образе, который совсем не нравится малышу. Этим вы можете не только испортить ребенку настроение, но даже напугать его.
Грим собакиГрим бабочкаГрим льваГрим ведьмыГрим Человека-ПаукаГрим кошкиРисунки на лице для детей и взрослых: идеи и фото
Грим для детей будет очень к месту при создании новогоднего костюма для ребенка. Новогодний костюм плюс удачно подобранный грим – это залог отличного новогоднего образа!
Грим на Коляду. Как разукрасить лицо на колядки?
Новогодний аквагрим. Аквагрим своими руками к Новому году
Звериный аквагрим: перевоплощаемся в животных
Уверены, вас ждут веселые выходные, ведь мы собрали для вас самые креативные идеи для детского звериного аквагрима. Перевоплощаемся!
www.pinterest.com
Сразу видно, в этой семье любят молоко. Чьи бы дети мычали, лишь бы маме не мешали. А колокольчики на шею — в обязательном порядке, чтобы слышать, где что натворили и куда пошли.
uk.pinterest.com
Я у мамы обезьянка. Маленькая, любимая, самая лучшая. А это невинное выражение мордочки вовсе не гарантирует тишину и порядок в доме. Можно же немного пошалить, правда?
psalmbook.wix.com
Нет, я не грущу. Я просто примеряю новый образ. Больше никаких драк с братишкой и сестренкой, никаких разбросанных игрушек. Честно-честно! По крайней мере, пока я панда.
paintedparty.com
Р-ррр… Я злой голодный волчонок. Где моя котлетка?
media-cache-ec0.pinimg.com
Стоя спать не очень удобно, а в остальном я даже немного завидую жирафам.
paintedparty.com
Догоню — и съем! Берегись!
ansiktsmalning.com
Сделаешь что-то не по-моему — покажу когти, а может еще и зубки. Они у меня ого-го!
daizydesign.comЧего я весь такой серьезный? А нечего будить так рано. Не хочу открывать глазки, буду досматривать сон.
scary-pictures.feedio.net
Я не просто еж, я еж, который не спит зимой. Да-да! Кстати, неправда все это про яблоки. Ежи их не любят, а вот я не прочь похрустеть.
Как нарисовать собачку: аквагрим
www.bolshoyvopros.ru
Нарисуйте на лице малыша забавную мордочку собачки — и радости и счастья хватит на весь день! Как это сделать? Очень просто, главное для начала убедиться в отсутствии аллергии на краски (этот текст обязательно нужно сделать перед нанесением аквагрима на все лицо). Если при контакте красок с кожей нет покраснений, ничего не чешется и не шелушится, приступайте к мейкапу.
www.bolshoyvopros.ru
Если будете делать рисунок на все лицо, нанесите основу — ровный тон. И только потом приступайте к прорисовке деталей и обводке. Можно придать лохматость штрихами, сделать ушки торчком, большие круглые глазки по линии век, пятна, реснички, усы, высунутый язычок и тд.
www.bolshoyvopros.ru
Очень аккуратно рисуйте в области глаз. Лучше немного не доходить до нижнего века.
www.bolshoyvopros.ru
Самым юным моделям лучше всего раскрасить только часть лица, область глаз постарайтесь вообще не трогать.
Окрас может быть самым разным, в зависимости от породы и от наличия красок. Можно даже нарисовать на личике ребенка мордашку любимого мопса.
www.bolshoyvopros.ru
Важен творческий подход и смелость. Если что-то не получится с первого раза, можно смыть и переделать.
Аквагрим на лице ребенка — это не только праздничный антураж или образ для фотосессии. Побалуйте малышей и в будни. Веселых вам выходных в кругу семьи.
Делитесь в комментариях своими фотографиями, показывайте, какой аквагрим у ваших детишек.
Идеи для рисунков 🥝 краски для аквагрима, как нарисовать кошку
У детей нашего времени есть много интересных развлечений, например, очень популярным считается детский аквагрим. Такая разновидность боди-арта безопасна из-за хорошего состава красок и очень популярна на детских мероприятиях. Киска и зайчик для маленького ребенка, белка, тигр и лиса – для деток чуть постарше: практически любой рисунок на лице родители могут сделать сами пошагово, техника аквагрима доступна даже для начинающих, но необходимо знать главные правила нанесения красок и тонкости этой техники.
Содержание материала
Рисунки на лице
Многие родители путают акваграфию с аквагримом. Но это абсолютно разные вещи. Делают рисунки с помощью аквагрима для детишек на новогодние праздники, утренники и другие мероприятия. Краска имеет уникальный состав на водной основе, поэтому не вызывает аллергической реакции и не загрязняет поры на коже.
Помимо этого, состав очень эластичен, не разваливается и не сыпется. Качественная краска всегда быстро высыхает и не пачкает в процессе работы. Фейс-арт для детишек очень приятен, ведь рисунки долгое время не теряют своего окраса и легко смываются при помощи воды с мылом.
Перед началом работы с аквагримом в домашних условиях, необходимо приобрести все нужные материалы и инструменты для грима. Цена на эти специальные краски небольшая. Их можно приобрести в интернете или в обычном магазине, где есть отдел товаров, предназначенный для творчества.
Чтобы наносить аквагрим на лицо детям и взрослым, потребуется следующее:
- Разные краски.
- Спонжик.
- Губка и специальная кисточка из хорошего материала.
- Мелки.
Перед украшением лица своего милого ребенка, нужно учесть следующие противопоказания:
- Возраст до трех лет.
- Индивидуальная непереносимость каких-либо компонентов краски.
- Царапины и ранки на лице (ведь можно занести инфекцию).
- Болезни кожи.
Если вы думаете, что стоит нарисовать на лице, то вначале спросите мнение ребенка и не забывайте учитывать возраст и пол ребенка.
Девочкам в большинстве случаев импонируют изображения цветков, мордочек кошечек или лисичек, образы волшебных фей, принцесс или королев.
Мальчикам обычно больше нравится грим супермена, пирата, волка или человека-паука. Не создавайте чересчур жуткий образ, ведь вы можете испугать своего ребенка. До начала нанесения краски, необходимо провести по лицу ребенка сухой кисточкой, чтобы он начал привыкать к новым ощущениям.
Галерея: аквагрим для девочек и мальчиков (25 фото)
Как правильно нанести аквагрим на лицо, мастер-класс
Разберем все поэтапно:
- Основу необходимо нанести от линии роста волос с помощью губки или спонжика. Нужно уделить большое внимание носогубным складкам, областям возле глаз, бровям.
- При помощи специальной кисточки обрабатываем веки малышам.
- Брови создаем с помощью карандаша.
- Все делаем по порядку, сначала наносим краску на щечки и губы, а потом на подбородок.
- Прорисовываем контуры и другие незначительные детали.
Новогодний аквагрим своими руками
Одним из самых приятных праздников для всех детей является Новый год. На утренники в честь этого торжества часто зовут мастеров фейс-арта, которые за небольшие деньги, возьмут и быстро разрисуют всех присутствующих детишек в сказочных героев или милых животных.
У большинства профессионалов своего дела, всегда при себе имеется каталог с фотографиями, где можно выбрать для ребенка образ.
Если же вы хотите сделать аквагрим для ребенка самостоятельно, то нарисовать можно: королеву, принцессу, фею, пингвина, морозный узор, снеговика и т. д.
Аквагрим кошка, мастер-класс.
Чтобы свою малышку превратить в милую кошечку, необходимые специальные краски, кисточки, спонжик, вода и ватные палочки. Описание работы по созданию кошки:
- При помощи спонжика наносим белую основу (брови, подбородок, переносица).
- Берем розовую краску и изображаем над бровями ушки.
- С помощью тонкой кисти создаем черный контур ушей.
- Потом рисуем носик и усы.
- Создаем розовые шерстинки на щечках и подбородке.
Аквагрим бабочка
Одним из распространенных образов для всех девушек считаются красивые бабочки. Но перед началом рисования, стоит спросить мнение вашего ребенка, каждая девочка по-своему уникальна и ей может не понравиться это изображение. Если ребенок готов, то следуйте простой инструкции, как изобразить на лице бабочку:
- Сделать основу с помощью белого грима (начать со лба и скул).
- Создать контур крыльев, черным цветом используя тонкую кисть.
- Нарисовать еще один контур более яркого цвета толстой кисточкой.
- Прибавить фантазийные узоры разных красочных цветов.
- На носике ребенка изобразить тело бабочки с усиками.
- Добавить ярких полосок на теле бабочки.
- Прибавить блесток к общему рисунку.
Аквагрим тигр
Такой рисунок подходит для детей разного возраста. Аквагрим тигренка смотрится довольно эффектно на любом празднике. Для создания этого рисунка потребуются оранжевые, черные и белые краски, кисти различного диаметра, спонжик.
Описание работы:
- Вначале берем белую краску для аквагрима, рисуем нос и щечки нашего тигренка.
- Изображаем верхнее веко, потом контур лица и подбородок.
- Ровным слоем наносим краску оранжевого цвета на остальную поверхность лица ребенка.
- С помощью черной краски рисуем следующие детали: усы, полоски, нос, рот.
Аквагрим собачка и аквагрим лиса
Этих животных рисуют для милых малышей, которые любят побыть забавными зверьками. Описание работы к рисунку собаки и кошки. Все делается примерно так же, как и в других случаях, только добавляют к основному изображению шерстку или бандану.
Заключение
Существует много интересных и необычных рисунков, кто-то даже рискует и изображает аквагрим зомби. Запомните самое главное, это ваше творчество, и рисунок выбирать только вам и вашим детям. Если у вас что-то не получается, вы всегда можете изучить дополнительные уроки или попробовать сделать что-нибудь простое.
Другие виды росписи и рисования
Аквагрим для девочек простой. Примеры работ аквагрим,фото аквагрима.
Как изобразить на лице и руке бабочку с помощью аквагрима? Новогодний аквагрим с бабочкой.
Одним из самых популярных развлечений на праздниках и увеселительных мероприятиях для детей сегодня стал аквагрим. Он используется, как дополнительный элемент игры, развлекательной программы или представления. Все дети просто в восторге от такого внимания к себе и от того, как видоизменяется их внешность в считанные минуты благодаря опытной кисти мастера. Но использовать столь интересный вид искусства можно не только по праздникам. Сделать аквагрим своему ребенку можно и самостоятельно.
Как ребенку раскрасить лицо в виде бабочки: варианты, фото
Одним из самых излюбленных рисунков в виде аквагрима на лице для девочек (и не только) является изображение бабочки.
Бабочку можно нарисовать на все лицо или разместить небольшого мотылька только на какой-то части лица — щечки, лоб.
Точно так же можно изобразить рисунок лишь на одной части лица — правой или левой. При этом, можно нарисовать только половину бабочки или ее целиком с поднятыми вверх крыльями.
Если изображать бабочку на все лицо, то нос малыша в данном случае будет выступать в роли тельца бабочки, а ее крылышки будут расположены на лбу и щеках крохи.
Как нарисовать на лице ребенка бабочку аквагрим поэтапно?
Для того чтобы начать разрисовывать детское личико, нужно запастить определенным набором предметов:
- Специальные гипоаллергенные краски на водной основе
- Кисточки — 2 шт. (тонкая и толстая)
- Спонжик
- Губка
- Специальные мелки или карандаши
Перед началом работы желательно провести пробный тест на наличие аллергической реакции у крохи — выполнить ее можно на небольшом участке кожи руки или ноги. Если после нанесения краски в течение получаса у ребенка не было обнаружено никакой реакции, можно приступать к нанесению аквагрима.
Как сделать аквагрим бабочка ребенку на лице?
Алгоритм действий:
- На лоб и щечки наносим белую основу с помощью губки или спонжа (глаза можно оставить не закрашенными, а можно затушевать и их поверхность).
- Тонкой кисточкой обрисовываем контур будущей бабочки — верхние крылышки располагаются над бровями крохи, а нижние опускаются под глазками на щеки.
- На носике изображаем частично или целиком тельце бабочки.
- Головку насекомого с усиками располагаем на лбу или между бровями малышки.
- Толстой кисточкой с темной яркой краской прорисовываем еще один контур бабочки.
- На усмотрение ребенка или согласно с собственным воображением прорисовываем на теле бабочки различные узоры и линии.
- Если есть желание и возможность, украшаем весь рисунок блестками, стразиками или камушками.
Как нарисовать бабочку аквагрим на щеке, руке пошагово?
Как нарисовать аквагрим в виде бабочки на щеке?
Пользуясь подсказками предыдущего пункта, можно изобразить на одной части лица лишь половинку бабочки.
Таким же образом можно изобразить и всю бабочку, только в меньших размерах на одной из щечек.
Чтобы сделать аквагрим в виде бабочки на руке, необходимо также сделать фон любого цвета (желательно светлых тонов), прорисовать контур мотылька, а затем изобразить на его крылышках различные орнаменты и элементы.
Как разрисовать ребенку лицо в виде бабочки на Новый год?
Новогодняя бабочка — аквагрим
Новогодняя бабочка выполняется точно так же, как и обычная бабочка.
Единственным отступлением в данном случае могут стать более нежные, новогодние цвета контура и рисунков на теле насекомого.
К примеру, контур может быть уже не черным, а синим или зеленым.
Вне крыльев бабочки или даже на них можно отобразить небольшие элементы новогодней тематики (снежинки, снеговички, снежки, елочка, елочные игрушки, олени, Дед Мороз и т.д.).
Новогоднюю бабочку просто необходимо украсить блестками и камнями.
Как сделать аквагрим бабочка на Новый год?
Фото рисунков бабочек для детского аквагрима
Что такое аквагрим? Это специальные краски для лица и тела на водной основе. Они легко смываются и легко наносятся, а их гипоаллергенность позволяет их использовать даже для детских мордашек.
Но кроме функции чисто эстетической, аквагрим несет в себе и практическую функцию: ребенку будет куда проще вжиться в образ своего героя, что уменьшит и физическую, и психологическую нагрузку.
Прежде чем приступать к гримированию, запомните несколько простых правил для начинающих гримеров:
- Не заставляйте ребенка гримироваться, если он этого не хочет: не всем детям нравится прикосновение кисти к телу.
- Прежде чем рисовать, поводите малышу по лицу сухой кисточкой, так процесс рисования не станет для ребенка неожиданностью.
- Не предлагайте ребенку рисунок, который нравится вам. Ведь грим носить придется не вам, а ему.
- Не рисуйте дольше десяти минут. Конечно, вы захотите создать настоящий шедевр, однако дети не могут долго сидеть неподвижно (куда уж нам с многолетним опытом школы, университета и домашних компьютерных посиделок), и им быстро это надоест. Если вы видите, что ребенок устал, отпустите его свободно побегать или подышать, ведь некоторые дети даже дышать боятся, пока на них рисуют.
- Держите перед собой небольшое зеркало, чтобы ребенок видел, что же такое интересное происходит у него на лице.
- Обязательно говорите с чадом о чем-нибудь интересном во время рисования.
Теперь перейдем собственно к технике выполнения и материалам:
Материалы:
1. Краски.
2. Кисточки. Нужны 2 кисти — №1 и № 5-6.
3. Спонж или губка.
4. Ватные диски, палочки, салфетки.
Ход работы
Начинаем, конечно же, с основы. Это общий элемент для рисования различных животных.
Основа
Наносим широкой кистью белую краску на участки между носом и верхней губой. Красим кончик носа черной кистью, затем рисуем полоску до верхней губы, обводим её и закругляем вверх. У нас получились щечки! На них можем нанести точечки и усики. Переносицу окрашиваем в белый цвет и чуть-чуть растушевываем, чтобы не было резких границ.
Базовая основа готова, теперь мы можем нарисовать несколько зверят со своими отличительными особенностями.
Кошечка
Для нее подойдет любой цвет (в нашем случае — голубой). Наносим краску на лицо по контуру, не захватывая глаз, рисуем ушки над бровями. Теперь нарисуем красный язычок на нижней губе, а черным подчеркнем шерсть и ушки. Глаза не были захвачены специально, т.к. у некоторых детей эта область тела очень чувствительна и на нее наносить краску не стоит.
Зайчонок
Какая самая главная отличительная черта зайца? Правильно, зубы.Поэтому нарисуем их на нижней губе. Нарисуем белый прямоугольник. Чёрным цветом обозначаем зубы, нанесем контур в форме бабочки (где ее «крылышки» будут ушами зайки) и закрасим (все, кроме щечек). Нарисуем шерстку с помощью черной краски и тонкой кисточки. Теперь покроем щечки белой краской и немного растушуем спонжем.
Вы можете и сами додумывать характерные черты зверей: к примеру, у мышки — серый цвет, маленькие зубки и маленький язычок, рысь будет похожа на кошечку, только оранжевая, и на ушах будут кисточки и т.д.
Видео по данной тематике:
А в этих видео вы увидите еще несколько мастер-классов и схем, с помощью которых вы сможете сделать любой праздник незабываемым для вашего ребенка.
Образ сурового пирата:
Гроза всех злодеев — человек-паук (он же спайдермен):
Вот такой вот замечательный кролик:
Стиль а-ля индийская принцесса:
Красивая бабочка:
Простой способ нарисовать на лице тигриную морду:
Очевидно, если вы впервые будете изображать рисунки на лицах у детей, вам стоит заранее подготовить несколько образов. Интернет является прекрасным источником для поиска простейших образов, которые могут быть особенно полезны, если вы только что начали практиковаться в рисунках на лице. Начиная от кошечек и собачек и кончая любимыми супергероями — вы сможете найти нужные вам образы.
Основы рисования на лице
Первое, что вам нужно сделать, когда вы собираетесь рисовать на лице у ребенка (хотя было бы хорошо, если бы вы сначала потренировались, прежде чем показывать общественности свои таланты), это представить то, как должно в результате выглядеть лицо ребенка. Вот почему было бы хорошо заранее распечатать образ, прежде чем вы начнете рисовать. Вы можете использовать обычные кисти для нанесения краски для лица, но было бы лучше, если бы вы использовали губки вместо кисточек для нанесения краски на большие области, например, когда вы наносите на лицо основной слой краски. Лучше использовать губку, потому что таким образом вы сможете покрыть большую часть лица быстрее, и вам не придется беспокоиться о том, чтобы отстирывать эти губки, потому как они совершенно недорогие. К тому же губка позволит вам нанести краску более равномерно, что предотвратит появление разводов. Неважно, используете ли вы кисть или губку, вам стоит наносить краску тонким слоем; а если краски будет слишком много, она потрескается или потеряет свой блеск.
Ваш первый опыт рисования на лице
Прежде чем начать рисовать на лице в первый раз, вам нужно распечатать понравившиеся вам образы и ограничиться теми, которые вы уже пробовали. Позвольте детям самим выбрать себе образы, которые бы им хотелось, чтобы вы нарисовали. Будем надеяться, что ограниченное количество образов, представленных детям, обрадует их и спасет вас от того, что дети будут просить нарисовать неизвестных вам героев.
Более продвинутые рисунки на лице
После того, как вы овладеете основами, вы сможете попробовать развивать новые навыки создания более сложных образов. Одним из самых больших испытаний может стать отказ от основных рисунков и предложение детям придумать самим то, что они хотят видеть на своем лице. Вы будете удивлены и восхищены их запросами, и в то же самое время вы будете поражены своими новыми способностями рисования на лицах!
Итак, поговорим об аквагриме
Аквагрим (Face Painting) — это творческие рисунки, которые наносят на лицо и тело специальной краской. Дети очень часто фантазируют и представляют себя принцессами, отважными принцами, бабочками, волшебниками, и многими другими сказочными персонажами! Аквагрим- своеобразный элемент костюма. Он не только привлекает внимание к действию, но и показывает характер персонажа, для возможность погрузиться в свой сказочный, волшебный мир. Аквагрим абсолютно безвреден для кожи, он легко наносится и также легко смывается водой и мылом
Как просто и легко задать новое настроение, образ, помочь детям и взрослым стать сказочными героями. Всего-то немного грима на лице. Этим занимаются профессионалы, но можно попробовать и любителям. Главное — хорошее настроение и творческий задор.
Грим . Советы начинающим
И в драматических, и в музыкальных постановках, и просто на веселом празднике грим помогает забыть о реальности и с головой окунуться в фантастический мир. Ну в самом деле, что за Дракула без мертвенной бледности лица и окровавленных клыков? А Клоун разве будет смешным без красного носа и нарисованной улыбки?
Основные принадлежности
Грим можно приобрести в универмаге, магазине игрушек, но лучше покупать его в специализированных театральных магазинах. Правда, там он дороже, но зато реже вызывает аллергическую реакцию. Предпочтительнее составы на водной основе, чем на жировой, так как их легче смыть с лица и инструментов. Вам необходимо иметь: бесцветную пудру, карандаши, губную помаду, порошкообразные тени для век и румяна, краски для лица различных оттенков, тазик с водой, чистые полотенца (как для вытирания кистей и наведения порядка, так и для защиты одежды), 1-2 тонких кисточки, большую кисть, пуховку, две-три губки, ленту, чтобы убирать волосы со лба, блеск, пудру с блестками, вазелин, вату или ватные палочки, салфетки, кусок мыла, «Деттол» или подобное дезинфицирующее средство.
Правила гигиены
Некоторые виды грима и краски для лица, особенно красного цвета, содержат сильнодействующие пигменты. Прежде чем наносить их на лицо, проведите местную аллергическую пробу кожи ребенка. Если на участке кожи возникло покраснение или появился зуд, прекратите пользоваться средством, тщательно смойте и смажьте воспаленное место успокаивающим кремом или лосьоном, Но даже если аллергическая реакция не возникла, неплохо нанести под грим защитный слой крема. Имейте наготове мыльную воду с несколькими каплями «Деттола», чтобы мыть кисти и другие приспособления для грима. Можно замачивать принадлежности для нанесения грима в мыльном растворе. Делая грим нескольким детям, обязательно дезинфицируйте инструменты, переходя от одного ребенка к другому. Если вы используете грим на жировой основе, вам понадобятся синтетические губки, которые после применения нужно кипятить.
Нанесение грима
Если вы замыслили нечто амбициозное — скажем, характерный или сказочный персонаж, — нарисуйте сначала эскиз на листе бумаги. Так вы облегчите себе работу и снизите шансы на ошибку. Полезно также начинать гримировать по возможности с верхней части лица. Тогда вы сможете прикасаться к коже ребенка, не опасаясь размазать уже сделанное. Затушевывание бровей: если у вас достаточно времени, можно, прежде чем приступать к гриму, затушевать брови. Это позволит вам расширить поле деятельности, включив в него область бровей. Можно получать разнообразные выражения лица, просто меняя форму бровей. Смочите край куска мыла водой и намыльте им брови, водя по одним волоскам вверх, по другим вниз. Это изменяет линию бровей, волоски плотно прижимаются к коже. Дайте им несколько секунд просохнуть. Нанесите теперь на брови основу под макияж с помощью пальца или губки. Нанесите пуховкой слой прессованной пудры, вдавливая ее в кремообразную основу. Нанесение основы: с помощью губки, начиная от центра лба, нанесите основу, водя губкой в поперечном направлении и в направлении вниз по обеим сторонам лица и на подбородке. Попросите ребенка взглянуть на потолок, чтобы можно было нанести основу под глазами. Если основа легла неровно, нанесите второй слой, на этот раз скорее похлопывающими, чем поглаживающими движениями, чтобы не повредить нижний слой. Тени для век: мягкой кистью нанесите порошкообразные тени выбранного вами оттенка. Попросите ребенка закрыть при этом глаза, Брови: нарисуйте желаемую форму мягким карандашом или тонкой кистью. Румяна: наносите румяна на щеки большой пушистой кистью или ватным тампоном. Начните вблизи линии роста волос и продвигайтесь вперед, растушевывая румяна к носу. Для достижения большего драматизма можно использовать пудру с блеском, Губная помада: наносите помаду ватной палочкой (используйте ее только один раз и выбрасывайте) или маленькой кисточкой. Контур: если грим состоит из нескольких цветов, нанесите их контуры на лице тонкой кисточкой или мягким карандашом. Тогда грим разных цветов не будет размазываться и приобретать неопрятный вид. Блестки: если вы хотите украсить лицо блестками, смажьте немного этот участок вазелином, а затем наклейте на него блестки по задуманной вами схеме. Избегайте наносить блестки вблизи глаз.
Снятие грима
Грим на водной основе легко смывается мягким мылом и водой. Грим на основе кремов и масел смывается с помощью специальных средств. Чтобы удалить блестки с лица, отрежьте кусочек скотча, наложите на блестки. Слегка надавите и снимите. Блестки прилипнут к скотчу.
Описание примера аквагрима
Собачка .
- На кончике носа (на самом выступающем месте) поставить точку. Через эту точку провести горизонтальную линию, начиная с крыльев носа. Носик ниже проведенной линии закрасить темным цветом (черным или коричневым).
- Провести прямые вертикальные линии от бровей до проведенной ранее горизонтали. Крылья носа тонировать более темным оттенком, получившуюся полосу посередине носа — более светлым.
- По впадинке над верхней губой провести линию. Верхнюю губу закрасить темным карандашом. Если губы полные, предварительно покрыть тональным кремом, а уже потом проводить тонкую линию.
- Область над верхней губой закрасить белым. Нарисовать усики и точки.
- Вокруг глаза, захватывая небольшую область над бровью и часть щеки нарисовать «пятно» и закрасить его белым (или, наоборот, темным) цветом.
Т.к. театральный раздобыть не всегда есть возможность, то можно, к примеру, обойтись простым косметическими карандашом и купить коричневые и белые тени без блесток и перламутра.
Совет. Если придется гримироваться при помощи простых теней для век, предварительно нанесите на лицо крем или тональную основу, т.к. тени осыпаются.
Образ Снежинки , Зимушки, Снежной королевы, Змеи, Звездочки и т.п. можно эффектно подчеркнуть при помощи украшений для тела. Самый простой (но не самый дешевый) способ — наклеить на лицо специальные хрустальные татуировки Сваровски (Swarovski Crystal Tattoo). Они легко наносятся, не смываются водой и держатся на теле до двух недель. В магазинах сейчас можно увидеть широкий ассортимент узоров из страз с плоским дном, обработанным специальным клеем, чувствительным к теплу и давлению для легкого нанесения на кожу.
Не столь элегантный, зато вполне доступный по цене вариант — использовать обычные блестки (пайетки) или самостоятельно вырезанные из упаковочной бумаги кружки, треугольнчики, звездочки. Приклеить их на кожу можно при помощи обычного меда!
Лицо Снегурочки и руки покройте очень светлым тональным кремом и припудрите всё лицо белыми тенями с блёстками. Эффектно смотрятся белые ресницы и брови. Нанесите на ресницы обычную бесцветную тушь-гель для бровей, и пока не высохла, покройте ресницы белыми перламутровыми тенями для век. Выделите глаза голубой подводкой, причём обведите сильно и нижнее веко. Используйте нежно-розовую помаду с сильным блеском для губ. Такая Снегурочка в вашем исполнении удивит даже искушённых театралов.
Вдохновившись нашей подборкой, вы легко сможете превратить любимую мордашку ребенка в забавного зверька или мультяшного героя. Даже если последний раз кисточку в руках вы держали на уроке рисования!
Практически ни один детский праздник или развлекательное мероприятие не обходится теперь без гримеров. Стоит одному ребенку увидеть другого с необычным рисунком на лице — и начинается: «Мам-пап! Я тоже хочу!». Поэтому очередь к заветным столикам с баночками — такой же привычный атрибут детского досуга, как батуты и сахарная вата. А это удовольствие, надо сказать, не из дешевых. Особенно если вас ждет целая череда новогодних елок и увеселительных активностей на каникулах.
Почему бы вам самим не попробовать освоить эту живописную процедуру? Так вам удастся не только сэкономить, но и получить удовольствие от творчества. Потратившись разок на краски, вы можете сколько угодно радовать ребенка новыми образами. Кроме того, такие рисунки отлично дополнят соответствующий карнавальный костюм. Сделать аквагрим для детей своими руками не так уж и сложно. Взгляните на эти идеи рисунков на лице для начинающих и попробуйте себя в новой роли художника!
Используя только белый и черный цвета, вы без труда нарисуете традиционного зимнего персонажа. Нанесите сначала белые кружочки снеговика: голову снеговика в шляпе или ведерке — на лбу ребенка, продолжая очертания вокруг глаз и на носу. А затем обведите полученную фигуру черной краской, поставив пятнышки глаз, рта и пуговиц. Капелька оранжевой вам понадобится для морковки-носа. Дополнительно на лице вы можете дорисовать .
Этот герой тоже не вызовет у вас особых затруднений. Черной краской прорисуйте сначала контуры летучей мыши вокруг глаз-крыльев и закрасьте. Нос ребенка и часть лба станут туловищем и головой . Не забудьте изобразить восходящую над головой, которая символизирует любимое время суток героя. Для живости черкните белой краской по краям.
Образ панды продолжает наш ряд черно-белых рисунков. Закрасьте почти все лицо белым гримом, оставив места вокруг глаз. Ну и все, образ практически готов. Только дорисуйте черным цветом уши, нос, губы и пятна глаз, обозначив контуры мордашки. Завершающий штрих — зеленая веточка бамбука во рту.
Главная часть образа — белая мордочка . Глаза ребенка станут ее глазками, а ушки — над его бровями. Вам остается только обвести черным контуры и усики, а также нарисовать розовый бантик мультяшной героини и желтый кружок носика.
Нарисуйте белки глаз птички над бровями ребенка, а когда они подсохнут, обведите черной краской, добавьте зрачки и черточки бровок. Между глазами разместите желтый ромбик клюва. Все остальное пространство на лбу закрасьте красным полукругом, из которого получится голова персонажа.
Двух цветов вам вполне хватит и для того, чтобы непоседа превратился в яркую . Нарисуйте желтую маску вокруг глаз в виде больших очков. А затем доведите дело до конца, обработав фон черной краской: стрелочки глаз, носик, лоб и антенны усиков.
Нанесите белый фон от половины лба до верхней губы. Черной краской обведите его, дорисовав с задорным хохолком. Закрасьте желтым гримом нос ребенка в виде треугольного клюва. Розовые румяна дополнят образ антарктической птицы.
Ну и какой праздник без любимого ! Наверняка каждый мальчишка хоть раз примерял эту роль на себя. На создание образа у вас уйдет буквально пара минут. Закрасьте пол-лица красным цветом в форме овала. А затем прочертите черные нити паутинки. Нанесите местами белые блики — и вы смело можете гордиться своим художеством.для девочки , так и для мальчика. Подготовьте основу, закрасив центральную часть лица белым цветом. Обозначьте при этом контуры щек и ушей. Дайте фону подсохнуть и завершите рисунок черной краской, нарисовав очертания мордашки, пятна, брови, нос, усы и рот. Контуры не нужно делать ровными: нанесите их штрихами, похожими на шерстку. Последний шаг — красный высунутый язычок.
Если вы можете нарисовать «палку, палку, огуречик» — значит, изобразить божьей коровки над глазами ребенка вам тоже вполне под силу. Красным цветом пройдитесь и по губам, а черным обведите раскрашенное по контуру, добавив кружок головы насекомого, пятна и усики. Белой краской дорисуйте глазки, улыбку и блики на крылышках.
Несмотря на то, что — прислужники злодеев, эти забавные и трогательные персонажи покорили сердца многих зрителей по всему миру. На лбу ребенка нарисуйте желтую голову мультяшки, оставив не закрашенными глазницы, а над бровями — пальчики героя. Раскрасьте белки и зрачки, добавьте белозубую улыбку и подчеркните все черным контуром, не забыв про волосики.
Нанесите розовый фон вокруг глаз ребенка, старясь придать ему очертания крыльев. Круглую головку насекомого с усиками нарисуйте на лбу, а вытянутое тельце — на детском носу. Такой же черной краской окантуйте наложенный грим, штрихами подчеркивая воздушность и узоры на крылышках.
Обведите все черным цветом, в том числе и контур рта, а нос закрасьте полностью, обозначив ноздри. Штрихами прочертите шерсть. Финальную точку в вашем художестве пусть поставит сам ребенок — изобразит улыбку!
Передо мной лицо, которого я раньше никогда не видела, чаще всего это лицо ребенка, еще чаще девочки. Люблю рисовать аквагрим на лице детям и на это есть весомые причины. Аквагрим на детскую кожу ложится ровно, потому что кожа нежная и гладкая, из-за этого легко рисовать. А еще, дети очень благодарные и настоящие ценители аквагрима. Они стараются сидеть ровно и с замиранием сердца ждут, когда посмотрят в зеркало, чтобы испытать яркие эмоции от сказочного перевоплощения. Моя красочная мобильная студия наполнена множеством разнообразных баночек с красками и блестками, кистями, которых превеликое множество. Готовясь к росписи, я вроде волшебника, открывающего свой сундук со сказками и начинаю воплощать идеи для аквагрима.
Рисунки для аквагрима для детей бывают разными, все зависит от мастерства художника аквагримера. А что нужно чтобы рисовать аквагрим рисунки красиво, так чтобы носитель данного творчества на своем лице был счастлив, и хозяин рисунка доволен своей работой?В первую очередь, конечно художественное образование, но и наличие этих знаний не дает полной уверенности, что аквагрим будет красивым. Рисунки на лице для детей требуют опыта мастера аквагримера, потому как рисовать на лице и на бумаге, совсем не одно и тоже. Рисовать аквагрим на лице, не так-то просто как кажется, потому что рука находится на весу, а опоры нет, нужно изрядно изловчится, чтобы оперятся о щеку ребенка не мешая не ему, не себе. Рисунки аквагримом требуют тонких и послушных линий, а если модель не усидчивая, что бывает частенько, то нарисовать что-то ровное сложно. Поэтому художник гример это еще и психолог, который во время рисования общается с неусидчивой особой, чтобы хоть на немного обездвижить ее. Аква грим требует постоянной тренировки на себе на детях, на всем, чтобы получить красивые аквагрим картинки.
Справившись с собой и со своими руками, понимаешь, что это только пол пути, и твои рисунки на лицах детей аквагрим, требуют еще и качественных материалов. Все не так если кисть старая, и плохая, если краски блеклые и плохо ложатся, а еще ужаснее, если краски вызывают реакцию на коже. Опыт гримера складывается еще из того, какие краски для аквагрима он использует. Я пробовала рисовать разным гримом, и выбрала свой аквагрим, который известен во всем мире своей безопасностью для кожи, имеет сертификат качества, и конечно неповторимые сочные цвета. В интернете много фото аквагрима для детей и чаще всего фото аквагрима повторяются, все рисуют, одно и тоже. Не все, есть и непосредственные аквагримеры, но их мало. Очень важно, быть оригиналом в своем деле, наитии свой супер стиль, это и есть искусство рисовать на лице. Аквагрим фото несет нам не только информацию о рисунке, но и о самом человеке, которого разрисовали аквагримом. Аквагрим на лице должен украшать и прятать недостатки, чтобы ребенок избавлялся от каких –то комплексов, ведь аквагрим на лице это, своего рода арт- терапия и для художника и для мадели. Гримм на лице может привлечь к себе так необходимое внимание взрослых, сделает лучше и подарит уверенность в себе. Рассматривая аквагрим картинки, мы многое можем понять о настроение мастера и его переживаниях. Аквагрим на лице своими руками можно и нужно делать, это полезно и тренируют образное мышление, моторику, вкус, чувство цвета и композиции. Оцените мои работы по аквагриму, фото грима, рисунки аквагрим.
Мы немножко пошалим — изучаем аквагрим!
Фото: Константин НАГОВИЦЫН
Аквагрим – рисунок на лице специальными красками. Дети его просто обожают – в этом мы убедились сами, пригласив в наш пресс-центр визажиста, парикмахера и мастера по гриму Людмилу Романенкову.
А в следующую среду у нас пройдет мастер-класс по декупажу! Приходите в наш пресс-центр 8 октября в 17.00 по адресу: проспект Октябрьский, 4, кабинет 4.
Напомним, в прошлый раз мы учились вязать!
Фото: Константин НАГОВИЦЫН
Ребята облепили столы с картинками, споря, кому кем стать – собачкой, котенком или зайцем. А мы тем временем выбирали, кто из детворы станет нашей моделью.
Фото: Константин НАГОВИЦЫН
Доверить нам свое лицо согласилась девочка по имени Алина. Она решила, что ее непременно нужно превратить в щенка. Ну что же, попробуем!
Фото: Константин НАГОВИЦЫН
— Краски для аквагрима отличаются от акварельных,- рассказала Людмила Романенкова. – Они гипоаллергенные. Лицо ребенка должно быть чистым, а вода для красок – теплой.
Краски эти продаются в магазинах, много цветов покупать не нужно. Основные – синий, красный и желтый при смешивании дадут любые цвета.
Фото: Константин НАГОВИЦЫН
Кисточки должны быть натуральными и мягкими. Кстати, толстой колонковой кистью можно рисовать и тонкие контуры – у нее острый кончик.
Фото: Константин НАГОВИЦЫН
Начинаем! Для начала наносим основу – у щенка белые уши и мордочка. Если рука дрогнула, все можно легко исправить сухой кистью или ватным диском. Рисовать на детском лице, да еще и без опоры мне пришлось впервые, но все получилось с первого раза.
Фото: Константин НАГОВИЦЫН
Затем основу обводим по контуру черной краской – это подчеркнет рисунок. Чтобы ничего не испортить, краска должна быть правильной консистенции – не течь и не капать, а предыдущий слой успеть высохнуть. Это был очень ответственный момент, и он нам удался.
Фото: Константин НАГОВИЦЫН
Щенячий язык рисуется точно таким же образом.
Фото: Константин НАГОВИЦЫН
Осталось нарисовать черное пятно на глазу. Так как дети будут бегать и потеть, лучше не закрашивать область вокруг глаз, чтоб туда не попала краска.
Алина в восторге!
Аквагрим для детей фото для девочек поэтапно
Многообразие рисунков для детского аквагрима поражает, но какие из них самые популярные? Смотрите нашу подборку и выбирайте вариант, который понравится вашему ребенку. Вы ведь помните о том, что весь материал для детского аквагрима должен быть гипоаллергенным?
Варианты модного детского аквагрима
…цветочная радуга
© Instagram @dariaaquagrum_ekaterina
…единороги
© Instagram @hilariabaldwin
© Instagram @aquagrim.sveta.si
…если с папой на футбол
© Instagram @anna__faceart
. хитрый лисенок
© Instagram @karina_face_art
…а я — котенок
© Instagram @vseobovsem.les
Фея цветов
© Instagram @larisa.sobol
…яркокрылая бабочка
© Instagram @akvagrimart
Мальчикам понравится черепашка-ниндзя
© Instagram @yulia_owlz
…и Человек-паук
© Instagram @emerald_face_painting
А это аквагрим для мальчишек, которые мечтают стать космонавтами
© Instagram @fizzbubblefaceandbodyart
Как вам такой тигренок?
© Instagram @vaznieludi
А панда?
© Instagram @unicorngang_facepaint
Варианты аквагрима для девочек — птичка-царевна.
© Instagram @akvagrim_bodyart_spb
. и павлин
© Instagram @asyadgrim
Расскажите, какие рисунки вам понравились?
Развлекательные мероприятия или детские праздники сейчас не обходятся без гримёров. Кисточки и баночки с красками — это привычный атрибут таких вечеринок. Изучив инструкцию, будет нетрудно нарисовать мультяшного героя или забавного зверька на лице малыша. Особенно ярко смотрится аквагрим для девочек. Это возможность не только получить удовольствие от самой процедуры, но и шанс сэкономить деньги, потому что этот вид творчества не из дешёвых.
Детский аквагрим
Детский праздник пройдёт в более весёлой атмосфере, если на лице малыша создать образ любимого героя или животного. Его можно сделать и маминой косметикой, но такой аквагрим будет нестойким. Потрясающим будет не только сам результат, но и сам процесс доставит много радости. Это рецепт отличного настроения на любом детском мероприятии.
Безопасность творчества
Для аквагрима производят специальные краски, которые можно приобрести в специализированных магазинах. Они предназначены не только для росписи лица, но и для тела в целом. Прекрасно смотрится аквагрим на руке или на ноге малыша.
Основа материала содержит только натуральное сырьё и может продаваться как в баночках, так и в тюбиках. Выбирать краски можно поштучно или целым набором. У таких красок есть преимущества:
- Пятна от них легко отстираются от одежды.
- Они практичны в использовании и почти не пачкаются.
- Грим удаляется с тела при помощи обычного мыла и воды.
Несмотря на натуральный состав красок, у них есть один недостаток: они могут вызывать аллергические кожные высыпания. Это случается редко, но чтобы избежать такой неприятности, родителям следует придерживаться инструкции по использованию аквагрима.
Не следует наносить грим детям младше 3-х лет. Перед нанесением акваколора его следует протестировать. Лучше это сделать на тыльной стороне ладошки. Малыш должен не смывать краску в течение получаса. Если кожа не покраснеет в этом месте, то можно приступать к процедуре.
Необходимые материалы
Если решение порадовать ребёнка аквагримом принято, то следует позаботиться о необходимых материалах. В некоторых случаях будут отличия, которые зависят от подобранного рисунка. Но основной список необходимых инструментов следующий:
- краски;
- кисточки;
- губки;
- вата и ватные палочки;
- небольшое полотенце и салфетки.
Краски необходимо брать на водной основе. Они выпускаются в виде карандашей и просто красок.
От карандашей стоит отказаться, так как ими рисовать сложнее и нужно иметь уже определённый навык, в то время как рисование красками осилит и новичок. При выборе кисти следует отдать предпочтение толстой, но с тоненьким кончиком.
Пошаговый мастер-класс
После того как принято решение, изображение какого героя или животного будет нарисовано на лице, необходимо обзавестись трафаретом этого рисунка. Сделать аквагрим в домашних условиях можно, используя популярные схемы. Рисунок подбирается в зависимости от того, кому наносят изображение. Аквагрим для мальчиков всегда мужественный, а иногда и устрашающий. Самые популярные рисунки для парней:
- леопард или тигрёнок;
- пират;
- бэтмен;
- динозавр;
- человек-паук;
- заяц;
- кот;
- собака;
- волк;
- зомби;
- железный дровосек;
- вампир;
- медведь;
- черепашки ниндзя.
В первую очередь нужно выбрать материалы и схемы, чтобы сделать аквагрим для детей. Мастер-класс по рисованию тигра включает в себя следующие шаги:
- Взять оранжевую краску для тона и раскрасить всё лицо малыша, кроме места под носом и в области бровей, для которых нужна белая краска.
- При помощи чёрного цвета проводятся горизонтальные линии на лбу, щеках и от внутренней линии глаз.
- В области лица, окрашенной в белый цвет, наносится изображение усиков, ресниц и клыков чёрной краской. Мордочка тигра готова.
Очень популярен Бэтмен среди мальчиков. Такой рисунок выполнить достаточно легко:
- Понадобится чёрная краска для прорисовывания контура крыльев вокруг глаз, который потом закрашивается.
- Туловище героя — это нос и часть лба, окрашенные чёрным цветом.
- На верхней части лба изображается полукруг луны жёлтой краской.
- Заключительный этап — нанесение белого контура.
Аквагрим для девочек подразумевает рисунки нежные и красочные. Выбор юных леди:
- Хелло Китти;
- пчёлка Майя;
- принцесса или Золушка;
- кошечка;
- белочка;
- новогодняя снежинка;
- бабочка;
- забавная обезьянка;
- мышка.
Если малышка выбрала аквагрим «бабочка «, то следует сделать следующие шаги:
- Яркая основа накладывается вокруг глаз в виде крыльев. Цвет подходит фиолетовый, голубой, жёлтый или розовый.
- Нос ребёнка — это тело бабочки, а головка с усиками рисуется между бровями.
- Любой тёмной краской наносится контур, крылья выделяются широкими штрихами.
- Дополнительно используются стразы и блёстки.
Аквагрим для начинающих включает в себя совсем простые рисунки. Это может быть собачка, кошка, зайчик, лисичка, белка, лев, дракон или время года, например, осень. Достаточно взять один урок и можно уже порадовать ребёнка своим творчеством.
Девочки очень любят яркий макияж, поэтому предпочитают красивые цветы, узоры или образ Литл Пони. Радуга, яркое сердечко и блестящие звёзды приведут современную модницу в восторг.
Идея грима зависит от фантазии ребёнка и креативности его родителей. Если вечеринка тематическая, то подойдёт и аквагрим для взрослых. Папа и мама могут выступить в роли котика и киски. Это доставит огромное удовольствие младшему поколению и внесёт изюминку в праздничную вечеринку.
Современным детям доступно много развлечений, например, очень популярным является детский аквагрим. Этот вид боди-арта безопасен из-за особого состава красок и очень востребован на детских праздниках. Большинство рисунков на лице родители могут сделать самостоятельно, но нужно знать правила нанесения красок и особенности этой техники.
Рисунки на лице
Некоторые родители путают акваграфию с аквагримом. Однако это две разные технологии. Делают рисунки аквагримом для детей на новогодние праздники, дни рождения и прочие мероприятия. Краска используется с особым безопасным составом на водной основе, поэтому не вызывает аллергии и не забивается в поры на коже. Кроме того, состав очень эластичен, не трескается при высыхании. Качественная краска должна быстро высыхать и не пачкать в процессе работы аквагримера. Фейс-арт для детей популярен: рисунки длительное время не теряют своего вида и легко смываются водой с мылом.
Прежде чем приступать к этой процедуре в домашних условиях, нужно купить все материалы и инструменты для аквагрима. Цена на краски и наборы приемлемая. Можно все купить в интернет-магазине или супермаркете, где есть специальный отдел товаров для творчества. Чтобы делать рисунки на лице для детей и взрослых, понадобится следующее:
- краски разных цветов;
- спонж;
- губка;
- кисточки из натурального материала;
- карандаши или мелки.
Техника аквагримирования является простой даже для начинающих. Однако прежде чем разрисовать лицо любимого малыша, стоит учитывать следующие противопоказания:
- возраст до 3 лет;
- индивидуальная непереносимость;
- царапины, повреждения на лице;
- кожные заболевания.
Что можно нарисовать на лице, зависит от возраста и пола ребенка. Девочкам, как правило, нравятся изображения цветков, мордочек котят или лисичек, образы фей, снежинок или принцесс. Мальчишкам же больше подойдет грим супермена, пирата, волка или человека-паука. В любом случае, нужно учитывать пожелания ребенка и наносить то изображение, которое нравится ему самому. Важно учитывать возраст малыша и не делать слишком страшным образ, чтобы не испугать свое чадо. До начала процедуры рекомендуется провести по лицу ребенка сухой кисточкой, чтобы он привык к новым ощущениям.
Как рисовать на лице детям красками? Ниже описаны основные этапы и правила для начинающих:
- Основу нужно наносить от линии роста волос с помощью губки или спонжа. Особое внимание уделяют носогубным складкам, области вокруг глаз, бровям.
- С помощью широкой кисточки обрабатывают веки.
- Брови рисуют специальным карандашом.
- Наносят рисунок поэтапно: на щечки, губы, подбородок ребенка.
- Прорабатывают контуры и мелкие детали.
Аквагрим на Хэллоуин
Одним из специфичных праздников, который последние годы активно празднуют взрослые и дети, является Хэллоуин. Образ в этот день обязательно должен быть особенным, поэтому макияж для детей, превращающий их в зомби, вампиров, ведьм и вурдалаков будет очень уместным. Однако грим малыша должен отличаться от взрослого. Краску стоит проверить на аллергены, а сама картинка не должна быть слишком пугающей.
Аквагрим для девочек
Маленьким модницам в любом возрасте важно быть самыми красивыми. Рисунки на лице для девочек стоит выбирать с учетом события. Это могут быть:
Аквагрим для мальчиков
Выбирая образ для мальчика, стоит учитывать его возраст. Если ребенок маленький, то загримировать его лучше под безобидного мультяшного персонажа, котенка, ежика или другое милое животное. Рекомендуется спросить самого малыша, кем он хочет быть. Рисунки на лице для мальчиков школьного возраста могут быть в виде образов супергероев, пиратов, кощеев, черепашек ниндзя, драконов.
Аквагрим на Новый год
Одним из самых долгожданных праздников для всех ребят является Новый год. На утренники по этому поводу часто приглашают мастеров фейс-арта, которые недорого и быстро разрисуют всех присутствующих в сказочных героев или милых зверят. У профессионалов всегда с собой каталог с фото, где можно выбрать для себя образ. Если же новогодний аквагрим для детей родители решат сделать самостоятельно, то изобразить можно:
- снежинки;
- принцессу;
- фею;
- пингвина;
- снеговика;
- морозный узор;
- снежную королеву.
Аквагрим Кошка
Чтобы своего ребенка превратить в забавную кошечку, нужны специальные краски, кисточки, спонж, вода и ватные палочки. Ниже представлена инструкция с фото, как нарисовать кошку на лице:
- Спонжем наносят белую основу (межбровье, подбородок, переносица).
- Розовой краской рисуют над бровями ушки.
- Тонкой кистью делают черный контур ушей.
- Рисуют нос и усы.
- Добавляют розовые шерстинки на щеках и подбородке.
Аквагрим Бабочка
Одним из популярных образов для девчонок всех возрастов являются красивые бабочки. Однако прежде чем нарисовать малышке такую картинку, стоит показать ей фотографии образцов, ведь не все девочки захотят такой аквагрим. Если модель готова, то придерживайтесь следующей инструкции, как нарисовать на лице бабочку:
- Нанести основу белым гримом (лоб, скулы).
- Нарисовать контур крыльев черным цветом с помощью тонкой кисточки.
- Сделать еще один контур более яркого оттенка кисточкой большего диаметра.
- Добавить фантазийные узоры ярких цветов.
- На носу ребенка нарисовать тело бабочки с усиками.
- Добавить красочных полосочек по телу бабочки.
- При желании можно добавить блестки.
Аквагрим на детский праздник в Москве
Мы думаем, что каждый современный родитель знает, что такое аквагрим. Приятная процедура необычной росписи относится к популярному искусству боди-арта. Узоры, которые рисуются с помощью безвредных для кожи красок на водной основе, вызовут умиление у всех собравшихся на мероприятии.
Начните подготовку к торжеству уже сегодня и не забудьте включить в программу вечера услугу аквагрима для детей от нашей арт-студии. У нас нет каталога с эскизами рисунков, по одной простой причине – аквагрим мастер «услышит» юную особу и изобразит на его личике любую маску. Детский аквагрим сделает Ваш праздник ярким и задаст всем приподнятое настроение.
Профессиональный аквагрим на детский праздник: быстро, красиво, необычно
Талантливый мастер кисти, предоставляющий свои услуги от агентства «Detsky-prazdnik.ru», оформит милое детское личико с использованием мелких страз на липкой основе, которые значительно увеличивают зрительный эффект. Наш художник по аквагриму применяет тематические «штуки», чтобы максимально точно выполнить образ того или иного известного персонажа.
От карапузов потребуется только побыть до 10 минут в состоянии полного спокойствия, чтобы гример смог четкими линиями нарисовать малышу усы, выразительно обвести глаза и превратить мальчика или девочку в забавную зверушку. Родителям необходимо будет заказать на праздник хорошего фотографа, чтобы запечатлеть на память своих маленьких принцесс и отважных супергероев.
Аквагример на День рождения ребенка: разнообразие масок ничем не ограничено
Каждый кроха постоянно представляет себя каким-то любимым персонажем. Услуги аквагримера в Москве сделают мечты непосед красочной реальностью. Волшебное перевоплощение состоится молниеносно! Как только в зале появится наш добродушный художник по аквагриму, вокруг него соберется вся детвора, чтобы с умилением наблюдать за «рождением» образов.
Ребята получат то, о чем давно мечтали и примерят именно ту маску, которую сами пожелают, а в их числе:
- Бабочки и цветочки;
- Собачки и котики;
- Рыбки и насекомые;
- Принцессы и феи;
- Индейцы и пираты;
- Сказочные и мультяшные персонажи.
Стойкий «макияж», который не растекается, будет гордо «носиться» весь день и умывать такую красоту перед сном будет очень жалко. Но мама и папам не нужно переживать – специальные краски хорошего качества, поэтому не раздражают нежную кожу ребенка и не вызывают аллергии при прямом контакте.
Детский аквагрим и карнавальный костюм – идеальное решение при создании образа
Буквально пять-десять минут работы кистью (в зависимости от сложности) – и красочный рисунок сияет на счастливом лице ребенка! Выездной аквагрим, который мы предоставляем на мероприятиях в Москве и Московской области, будет уместен независимо от тематики торжества. Вашему имениннику и его друзьям такое развлечение придется по душе на 100%.
Когда на личиках появляется такая невероятная красота, любознательные почемучки пребывают в состоянии абсолютной радости. А если еще подобрать костюм, тогда по залу будут носиться настоящие тигры, супер агенты или Микки Маусы. Прогрессивное художественное развлечение является ярким дополнением к основному интерактивному представлению.
Аквагрим на День рождения для детей: минимум усилий, максимум удовольствия
Быстрое нанесение аквагрима нисколько не утомит Вашего сорванца или юную леди. Мы устраиваем подобные росписи независимо от места проведения праздника. Вы можете без проблем заказать услуги аквагримера (стоимость рассчитана за 1 час работы) как к себе домой, так и непосредственно на выездное мероприятие. Вот увидите, как засияют глаза карапузов счастьем, когда на их лицах появятся шикарные разрисовки.
Для этого необходимо совсем немного – пригласить в гости профессионального аквагримера. Восторг от разноцветных мордочек задаст хороший праздничный тон торжеству. Мы готовы приятно удивлять Ваше чадо уже сегодня и в их памяти встреча с «Detsky-prazdnik.ru» останется надолго, как нечто безгранично прекрасное.
Отмечайте праздники в разноцветных красках!
Наши фантазийные «художества» будут прекрасно смотреться на лицах Ваших родимых кровинок. Детишки смогут, наблюдая за движениями кисти опытного мастера аквагрима, научиться правильно наносить акварельную краску на открытые участки тела, а также узнают, в какими способами это делается. Позитивные эмоции захлестнут юную аудиторию через край и это не просто слова. Палитра цветовых решений имеется в наличии в полном комплекте, поэтому рисунки получаются насыщенными.
Аквагрим мастер работает кистью аккуратно, поэтому не надо волноваться, что у ребенка запачкается нарядная одежда. Сам же художник аквагример на праздник пожалует в забавном костюме, чтобы быстро наладить контакт с детворой. Специалист своего дела будет весело шутить со своими новыми знакомыми, импровизировать в общении. Цена услуги аквагрима не должна у Вас вызвать вопросов, потому как мы работаем не на стоимость, а на качество. Сумма за час данной услуги указана в соответствующем разделе сайта.
Перевоплощаемся с аквагримом до неузнаваемости и веселимся от души!
Пара легких взмахов кисточкой – и появилось чудное творение! Востребованные маленькими клиентами услуги добавят к основной программе желаемую искорку веселья и позитивного настроения. Вы можете также позажигать вместе со своими детишками, а наш художник по аквагриму проявит импровизацию и для взрослых.
Фейс-арт не знает возрастных ограничений, и поэтому мы устроим маски-шоу по полной семейной программе. Никто в зале не останется равнодушным к такому феерическому размаху вечеринки. Обращайтесь в наше агентство и ни на секунду не пожалеете о своем выборе!
Заказать29 удивительных идей рисования лица для детей, которые вы можете сделать
Ищете ли вы занятие в дождливый день, что-нибудь, чтобы сделать вечеринку незабываемой, или какие-нибудь идеи для вашего следующего школьного мероприятия по сбору средств, раскраска лица — это ответ. Невозможно превзойти молчаливую, нетерпеливую очередь раскрашенных лиц возбужденных человечков, ожидающих превращения в персонажей из их воображения, или тот момент, когда вы поворачиваете к ним зеркало, и появляется маленькое радужное личико, благоговейно смотрящее на себя .
И не паникуйте, что аквагрим предназначен только для художников. С помощью качественных красок для лица (мы любим Snazaroo — как и родители, ванны, стиральные машины и одежду), нескольких кистей и губок, вы тоже можете создавать краски для лица, чтобы удивлять, вдохновлять и развлекать.
Наш главный совет для художников-любителей: помните, что вы стремитесь к общему эффекту, а не к деталям. Никто не смотрит вблизи, и самый резкий критик — это вы сами. Дети гораздо более подготовлены к тому, чтобы смотреть дальше любых шатких линий и теряться в своих трансформациях.Так что будьте уверены, получайте удовольствие и черпайте вдохновение из этих популярных идей раскраски лиц для детей.
Грубо говоря, эти рисунки усложняются по мере продвижения, поэтому, если вы новичок в рисовании лица, начните с самого начала, прежде чем пытаться реализовать более сложные идеи.
1. Трафареты для рисования лица — для мальчиков
Нет ничего проще для новичков в раскраске лица, чем трафареты для раскрашивания лица. Просто нанесите на губку краску и нанесите мазок.Для классических фаворитов, таких как гоночные автомобили, рыцари и ракеты, набор трафаретов Snazaroo для мальчиков отлично подходит как для мальчиков, так и для девочек.
2. Трафареты для рисования лица — для девочек
Если ваш ребенок хочет больше макияжа принцессы или рисунков, таких как русалки или короны, то набор трафаретов для рисования лица Fantasy от Snazaroo будет таким же простым.
3. Раскрашивание лица бабочки
Супер популярный, вы можете настроить раскраску бабочки в соответствии с любимыми цветами ребенка.Относительно просто, сначала нанесите губкой примерно цветные крылья, а затем сделайте дизайн впечатляющим с помощью черных очертаний бабочек. Не забудьте немного блесток!
4. Рисование лица человека-паука
Позвольте маленьким супергероям произвести огромное впечатление с помощью простого дизайна лица Человека-паука. Просто, но эффективно. Совет: сначала сделайте белые глаза.
5. Раскраска лица тигра
По какой-то причине, известной только детям младше 8 лет, тигр является невероятно популярным средством для раскрашивания лица на ярмарках, вечеринках и мероприятиях.Некоторые рисунки с изображением лица тигра могут заставить художника дрожать в сапогах. Этот простой дизайн рисования лица тигра может быть выполнен самым любителем рисования лица.
6. Лицо «Холодное сердце и снежинки»
Если на кресле для рисования есть дети младше 7 лет, убедитесь, что у вас есть много сине-белой краски для лица и много блесток! Этот будет пользоваться большим спросом, но мы упрощаем его доставку.
7. Камуфляжная раскраска лица солдата
Выгляди как профессионал, делая самую простую раскраску для лица.Превратите готовых новобранцев в боевых солдат с помощью этой техники раскраски лица камуфляжного солдата. Вам понадобятся 3 губки и несколько хороших мутных, грязных цветов. Вы не ошибетесь с этим.
8. Цветочная роспись лица
Просто, но потрясающе. Все, что вам нужно для создания лучших цветочных узоров, — это качественная кисть для рисования лица. Используйте форму кисти сбоку, чтобы создать лепестки. Потрясающий дизайн в мгновение ока: цветы особенно хороши для самых маленьких людей, которым сложно сидеть на месте.
9. Раскрашивание лица зомби
Будь то Хэллоуин или мероприятие, на котором вы пытаетесь соблазнить старших мальчиков поиграть в раскрашивание лиц, образ зомби вам подойдет. Полные крови и ужаса, но легко воспроизводимые, вы еще дадите волю их воображению.
10. Раскраска лица пиратов Ахой
Привет, раскройте сундук с сокровищами для раскрашивания лиц с этим пиратским дизайном.Нет банданы? Просто раскрасьте одну! Это будет пиратская жизнь для всех, у кого будет хороший йо-хо-хо.
11. Раскрашивание морды кошки
Некоторые рисунки раскраски кошачьей мордочки оставляют вас немного более взъерошенными, чем у среднего представителя семейства кошачьих. Этот дизайн обманчиво прост, но он понравится вашему маленькому любителю кошек.
12. Раскрашивание морды щенка
Если они не просят котят, будьте уверены, вам будут предложены щенки. Сложный дизайн, позволяющий хорошо выглядеть, при этом язык не портится, но оставьте это напоследок или вообще отбросьте, и у вас будет очень преданная собака.
13. Раскраска лица динозавра
Рев для динозавра! Чтобы произвести впечатление юрского периода на самых увлеченных палеонтологов, проявите хитрость с раскрашенным лицом динозавра с впечатляющими чешуями и рогами.
14. Рисование лица Hello Kitty
Hello Kitty, полюбившаяся своей милой внешностью и лентой для волос, является популярным выбором для раскрашивания лица и ее легко воспроизвести. Не беспокойтесь о том, чтобы получить идеальный белый цвет — помните, на расстоянии это не имеет значения.
15. Cheeky Designs Face Painting
Если вы не слишком уверены в том, что включаете все лицо, решением вашей проблемы может быть просто нанесение рисунка на область щек. Таким образом, вы можете просмотреть изображение выбранного мотива или персонажа на своем телефоне и не беспокоиться о том, как интегрировать его в бровь, два глаза и нос.
16. Раскрашивание лица черепах-ниндзя
Будь их любимый Леонадо или Донателло, мгновенно приготовьте из них их любимую черепаху-ниндзя.Просто убедитесь, что у вас под рукой достаточно зеленой краски для лица!
17. Закатный рай Face Painting
Если у вас есть любитель дельфинов, но мысль о дизайне дельфинов пугает вас, или вы просто хотите отпраздновать лето стильно, этот невероятно эффективный дизайн легко реализовать без особых навыков. Начните с верхней части лица и нанесите губкой цвета заката и моря вниз, а затем закончите черной деталью.
18. Раскраска лица принцессы
Самый простой способ преобразить любую начинающую принцессу — сделать акцент на короне и блестках.Помимо блеска краски для лица, драгоценные камни краски для лица придают этим рисункам вау-фактор.
19. Рисование лица феи
Посыпьте волшебной пылью и дайте своим малышам летать с красивым рисунком раскрашенного лица феи.
20. Раскраска лица радуги
А вот и солнце, прекрасный круглый год дизайн, который мгновенно дарит счастье и улыбки.
21. Раскраска лица миньона
Ваши усилия не будут подлыми, но вы будете в пользу, когда научитесь рисовать раскраску лица миньона.
22. Хэллоуин Рисование лица пауков
Впечатляюще простой, с небольшим вниманием к этому рисунку раскраски лица паука Хэллоуина. Определите любимый цвет ребенка и используйте его как основу, прежде чем рисовать паутину и пауков. Именно белые штрихи в конце действительно оживляют.
23. Раскраска лиц футболиста
Заставьте эти беспокойные ноги постоять несколько минут, пока вы выполняете их страсть к футболу с помощью этой футбольной раскраски лица.
24. Раскрашивание лица клоуна
Девочки и Мальчики вызовут улыбку на всех лицах этим сказочным и забавным дизайном клоуна. Убедитесь, что белая основа намочена губкой и высохла, прежде чем красить цветные элементы.
25. Раскраска лица Бэтмена
Поскольку Бэтмен так популярен, как никогда, этот дизайн гарантирует, что вы станете героем Готэм-сити. Воспользуйтесь нашим советом и сначала нарисуйте желтый контур, используя нос как центральную точку для хвоста летучей мыши.Затем заполните черный цвет кистью.
26. Рисование лица змеи
Некоторые дети могут быть закоренелыми покупателями, и невозможно уклониться от того, чтобы дать им их любимого персонажа. Другой дизайн, который поддается настройке цвета, позвольте их воображению скользить, когда вы создаете эту краску для лица змеи.
27. Картина лица акулы
Дети от природы игривы, и поэтому они просто обожают интерактивные рисунки с краской на лице, позволяющие их воображению разыграться.Картина лица акулы, в которой для усиления эффекта используется собственный рот ребенка, получит большой отклик.
28. Сердца и лица
Иногда вашим маленьким клиентам нужно немного вдохновения, когда дело доходит до выбора дизайна для раскрашивания лица. Дайте им идею красивого дизайна, основанного на сердечках, и их сердце будет биться за вас.
29. Просто раскрашивание лица девушки
Девочки постарше иногда просто обожают превращение обыденного в зрелищное, и твердой рукой вы можете создать дизайн, который развеет тревогу до-подросткового возраста.Работайте от центра и думайте о симметрии!
Какой бы дизайн для раскрашивания лица ни нравился вашим детям, ознакомьтесь с подборкой sitters.co.uk. Имея огромный опыт общения с маленькими людьми в вашей жизни, мы знаем, что они любят. Так что возьмите губку и кисть и проявите творческий подход, преобразив не только лицо, но и воображение. Повеселись!
Мы уверены, что ваши дети заслуживают самого лучшего ухода. Вот почему наша местная сеть няни лично проверяется и выбирается нашей семьей для вашей семьи www.sitters.co.uk.
портретов питомцев: холст для домашних животных адмирала
Хайди О.
Во время пандемии я работала из дома, и эти ребята были моими коллегами. Теперь я вернулся в свой офис, и мои коллеги по офису скучали по этим ребятам — так что теперь они отображаются в моем офисе. Неплохо для группы спасателей. Эти картинки делают мой день каждый день! Все (88+) должны были зайти, чтобы увидеть их. Спасибо — весь процесс прошел отлично!
Никита И.
Чтобы добраться туда, потребовалось некоторое время, но изображение потрясающее, и я обязательно куплю еще несколько своих других домашних животных
Ноа Р.
10/10 чудо-подруге это понравилось! Отличная идея для подарка Мне тоже она очень нравится! Думаю, Джилл это тоже нравится!
Rich W.
Наш питомец прошел, но моей жене понравилась фотография!
Тодд Р.
Всем нравится !! Отлично смотрится в нашем домашнем офисе !!
шейла гр.
У меня не было отличной фотографии Лося без кого-то другого, поэтому я прислал только это.Удивительно, как хорошо вам удалось отделить его от моей головы и плеча, как в оригинале. Это круто.
Дженнифер М.
Нам это очень нравится! Однозначно уже рекомендовано друзьям!
Найджел Г.
Как только мы получили изображение, общий эффект принял полную форму. Выражение лица Сэмвайса на фото действительно ожило. Это отличный способ отпраздновать 19-летие жизни старого скряги! Теперь он занимает почетное место на стене.Следующая его младшая сестра!
Роберт О.
Лучшее фото моей собаки получилось так идеально 10/10 отличная работа
Джо М.
Было здорово, что теперь подарить еще одну мою собаку!
Джефф С.
Мой кот Симба в роли адмирала Ее Величества «капитана Туна». Я буду дорожить этим до смерти !!!
Эд Х.
Я получил это, чтобы помнить моего мальчика и заставлять всех улыбаться, как всегда. Получилось идеально, и всей моей семье просто нравится то, что вы сделали для нас с этим холстом.Мы настоятельно рекомендуем вас всем, кто любит своих питомцев так же, как мы. Процесс был легким, обратная связь была быстрой, а конечный результат был идеальным. Большое спасибо!
Памела Д.
Купила это для моего друга, который недавно потерял любимого питомца. Не могу дождаться, чтобы отдать ей это. Это прекрасно.
Шарлотта Х.
Компания очень отзывчива — они дают вам возможность просмотреть портрет и предоставить обратную связь о любых изменениях, которые вы можете пожелать.Вторая версия, которую они прислали, была на высоте — отличный сервис и очень быстрая доставка!
Серина С.
Я сделала одну из моей мамы, собачки Дюк. Я подарил ее ей на день рождения, и всем, включая ее, он очень понравился !! Наш дуки еще никогда не выглядел таким красивым!
Джимми П.
Я купил это для своего мужа (Джимми), ему это очень понравилось! Тай очень молодец
Кортни Дж.
Нам нравится наше фото!
Джефф Дж.
Портрет получился великолепным, не могу дождаться, чтобы подарить его жене на День матери.
Саша М.
Великолепно. Это все.
Эбби П.
Лучшую подругу моей сестры 15 лет недавно пришлось усыпить. Я хотел сделать для нее что-то особенное. Я видел их раньше и знал, что это будет идеальный подарок. Я выбрал Адмирала, потому что его звали Наполеон. Когда она открыла его, это была идеальная смесь слез и смеха с любящими словами «Наполеон как Наполеон»! Отличный подарок любому любителю животных!
Джоанн Ф.
Они обе вышли очень хорошо.Я был приятно удивлен. Оба питомца перешли на радужный мост, и портреты, основанные на присланных мною фотографиях, имеют характер, который подходит им обоим. Отличная работа! Спасибо!
Дэвид У.
Получил и очень нравится … Сейчас выбираю рамку.
SIMON C.
Очень приятно, спасибо
Tracy M.
Отличное обслуживание. Так быстро прибыть. Замечательный портрет !!
Alex C.
Обожаю! Так взволнован, чтобы поставить это в рамку и повесить на стенуУ Каша сейчас летняя стрижка, но его портрет — зимняя лохань!
Michelle C.
Я купила это на день рождения мамы, и ей это очень понравилось! Вы, ребята, проделали замечательную работу, создав этот портрет. Это действительно сделало мою маму такой счастливой.
Маркос К.
Именно то, что я хотел, большое спасибо
Дафне В.
Не могу быть счастливее! Он отлично поймал нашего щенка! Заказ было легко оформить и быстро получить.
Анита Х.
Это мой третий заказ и подарок другу! Получилось потрясающе !!!!
Сидней С.
Так великолепно запечатлела нашего красавца!
Майкл С.
Я использовал Crown and Paw несколько раз для подарков семье и друзьям и наконец получил один для себя и своей собаки Вито! Команда Crown and Paw позволила мне внести несколько изменений в мой холст и была очень понимающей, гибкой и терпеливой. Идеальный способ почтить память лучшего друга человека!
Patrick C.
Я купил это, потому что подумал, что продукты были восхитительными, но, к сожалению, они горьковато-сладкие.Любимая собака моей девушки недавно скончалась, и я почувствовал, что подарок от меня поможет переживать горе, не говоря уже о том, чтобы пара посмеялась. Я показал ей это, и хотя она действительно плакала, она была вне себя от радости, что ее собака могла быть увековечена таким стоическим, легендарным образом, как изображенный портрет адмирала. Спасибо, что приносите владельцам такие замечательные товары!
Kodiak T.
Вот такая потрясающая штука! Действительно подчеркивает красоту кодиса Абсолютно люблю эту картину! Так здорово, однозначно рекомендую!
Тори П.
Мне это очень нравится! Это заставляет всех, кто видит это, смеяться и улыбаться. Я повесил его в своем офисе и ЛЮБЛЮ !!
Майк Д.
Нашему псу, Джо Пеши, нравится его новый холст Admiral! Спасибо за сверхбыструю доставку. Возможно, нам просто придется заказать еще несколько тем!
Памела Д.
Такая классная концепция! Не могу дождаться, чтобы сделать сюрприз дочери на день рождения!
Терри Г.
Обожаю наш портрет! И это произошло намного быстрее, чем указанные 2-3 недели!
Элла Д.
На месте !! Купил это как подарок кому-то, кому это очень понравилось, просто потрясающе. Большое спасибо.
Владимир С.
Абсолютно идеально!
Альберт Р.
Получил это в подарок жене, и ей это очень понравилось. Отличное качество холста
Александра С.
Получила сегодня портрет нашей любимой Рокси. Просто люби это. Прекрасная работа. Спасибо
Christa H.
Это была ОТЛИЧНАЯ покупка! Отличная компания, отличный продукт.Купил бы снова в мгновение ока!
Cherri W.
Получил 2 фото. По одной из наших смешанных собачек для моего муженька в качестве сюрприза ко Дню святого Валентина. Он любил их!
Корал Д.
Очень мило. Молодец
Боб Б.
Совершенно фантастическая работа. Папа остался очень доволен подарком на день рождения! Большое спасибо за быстрый и простой в использовании сервис!
Кайла К.
Мой питомец недавно скончался. Я хотел сделать для него что-нибудь забавное в память о горе нашей семьи.Это такой особенный холст для нас. Полностью стоит своих денег. Спасибо вам, ребята, за справедливое отношение к меху.
Лиза К.
Это так мило !!!!
Jennifer S.
Это были лучшие $ когда-либо потраченные! Качество холста, зависание на спине, то, как голова и тело без стыков выглядят так, как будто это одна картина, а не две вместе взятые … Я не могу достаточно восторженно относиться к этому! Я настоятельно рекомендую это всем родителям домашних животных!
Greg W.
Фантастическая идея и исполнение.Смешно, мило и круто ** одновременно. Скоро буду покупать снова. # гений
Брайан Ф.
Получилось даже лучше, чем ожидалось. Отличные работы — мы их любим !!!!
эшли с.
Качество намного лучше, чем я ожидал. Очень признателен за возможность просмотреть его до того, как он был завершен.
Кэти Б.
Такая милая фотография моего французского бульдога каш
Мария Д.
Я заказала этот портрет нашей собаки Арчи на день рождения моего парня! Он был так взволнован.Это идеально! Теперь мы зовем его «Адмирал Арчи»
Никола Р.
Моя 80-летняя мать сказала, что это лучший подарок, который у нее когда-либо был
Эмили Б.
Нам очень нравится наш портрет адмирала! Получилось отлично.
Катерина С.
Картинка говорит сама за себя! Они раздавили этот портрет! От заказа до получения по почте — все прошло гладко и легко. Обязательно буду заказывать еще раз в Crown and Paw!
Элисон Т.
Получилось отлично, и процесс был таким простым! Он собака моей мамы, и это будет идеальный подарок на день рождения; ей определенно понравится!
Rhonda S.
Это наша вторая подарочная покупка, и получатели очень довольны! Спасибо ❤️
Анастасия П.
Отличный подарок нашим пушистым друзьям и нашей семье. Красивое дополнение к нашей галерее. Прекрасная работа.
Бриджит П.
Адмирал Оушен самый милый!
Райан Т.
Прекрасное фото нашего питомца, который только что прошел. Гордо висит в доме
Екатерина Александровна
Спасибо! Какой прекрасный способ запомнить его!
Марианна Л.
Отличная идея для подарка. Супер мило. Хорошее качество. Жаль, что я не заказал немного больше. В следующий раз.
Кристофер Б.
Мне это так нравится !!! Я так счастлив, и мой Бруно выглядит таким красивым!
Кристина К.
Купила для брата и его кота. Это мурррф!
Джек К.
Получил одну из моих собак Дэйва для семьи на Рождество, и это хороший смех
Дарлин Л.
Я хотела получить уникальный подарок на день рождения моего мужа, и я думала, что этот портрет одной из наших кошек будет самым лучшим. прекрасный выбор. Процесс был действительно легким и увлекательным. Мой муж был приятно удивлен, и мы планируем приобрести дополнительные изделия, чтобы продемонстрировать других наших кошек. Спасибо Crown & Paw за невероятный подарок !!
Erika B.
Детали потрясающие! Было очень весело заказать это с моими детьми, поскольку мы украшаем игровую площадку для собак.
Celia P.
Отличная идея для подарка! Сервис от команды был отличным, и нам очень понравился конечный результат. Лучшие оценки!
Мэри Энн М.
Купил для друга, и я был поражен, насколько красивой получилась картинка!
Грег С.
Картина была потрясающая, и моему другу она понравилась.
Михаил Ю.
Отличный сервис во всех отношениях. Доволен товаром и проблем с доставкой нет.
Келли С.
Я бы с удовольствием прислал фотографию Молсона с его портретом, но это скорее великий памятник.Я подарила это мужу, и нам это очень нравится. Это отличный способ вспомнить прекрасный день. Это вызывает улыбку на нашем лице и в сердце. Спасибо
Jobie W.
Купил этот портрет для брата морского пехотинца и его жены. У их щенка только что диагностировали рак поджелудочной железы. Они были абсолютно легкомысленны и впечатлены качеством, как и я. 5 звезд
Megan R.
Портреты идеальны и являются центром внимания нашего дома <3
Marianne J.
Очень красивое маленькое произведение искусства Портрет был подарком моим родителям, и им это НРАВИТСЯ. Моя мама так смеялась, что чуть не намочила штаны, портрет уже висит на лучшем месте на стене. Спасибо за очень любезное обслуживание. С наилучшими пожеланиями от Марианны / Дания
Табита О.
Это собака моего шурина, и я подумал, что он и его жена оценят небольшую глупую радость. Они звали меня смеясь и в слезах от веселья. Так что спасибо вам всем за счастье, которое вы распространяете.
Дебби Т.
Была на седьмом небе от счастья, это оказалось
Гэри С.
Удивительный рождественский подарок, получился лучше, чем ожидалось. Обслуживание клиентов было очень полезным.
Jeremia H.
Потребовалось 5 недель, чтобы сделать заказ и подготовить его к отправке, но мне очень нравится готовый продукт!
Saleena J.
Получил это в подарок другу. Не могу дождаться, чтобы отдать ей это! Получилось намного лучше, чем я ожидал! Не могу дождаться, чтобы получить их еще! Благодарю вас!
Сара С.
Доставка заняла немного больше времени, чем ожидалось. Сама картинка отличная! Прекрасный подарок.
Allie F.
Наш щенок скончался до того, как получил посылку, поэтому было прекрасно снова увидеть его счастливое лицо. Огромное спасибо.
Люба Л.
Хаос был частью моей жизни долгое время, когда я достиг дна, я отдал его моему лучшему другу, который очень заботился о нем. Это очень много значит для него, так что спасибо вам, ребята. Я бы порекомендовал вас всем, кого знаю.Luba-❤️
ANSEL O.
Моей маме очень понравился рождественский подарок. Она думала, что это сделано очень хорошо и продуманно!
Kelly W.
Мне очень понравились портреты! Они были подарком моему партнеру, и он тоже их любил. Большое спасибо!
Роберт А.
Отличное качество. Отличное время ответа от их компании. Именно то, что я заказал!
Джо Г.
Хорошие впечатления во всем, кроме упаковки. Совершенно ужасная упаковка и упаковка.
Patricia T.
Наша невестка подарила нам одну из ваших фотографий на Рождество, она нам так понравилась, что у нас есть еще одна, которую мы хотели повесить в офисе моего мужа. Люблю это Люблю Люби
Саманта С.
Обожаю! Я надеялся подарить его сестре на Рождество, но он появился только на этой неделе, поэтому я был немного разочарован тем, сколько времени это заняло. Хорошая новость в том, что на следующей неделе у нее день рождения, так что все обошлось! Это супер весело, и я не могу дождаться, когда она это увидит! Спасибо! Ваше здоровье, Сэм
Бетани Л.
Куплен в подарок брату и его девушке. Им это нравится, и они повесили это над своим камином!
Andrew W.
Прошло около 6 недель с момента заказа до момента получения в Дублине. Это было во время напряженного рождественского периода и с covid. Я был очень доволен результатом, и картинка потрясающая!
Lily W.
Мне это очень нравится, моя собака так избалована, я купила ее на Рождество в подарок отцу, и она висит у него в офисе.Нам всем это нравится. Очень рекомендую сделать это людям с домашними животными.
Jessica W.
Я купила это для своей сестры на Рождество, и ей это очень понравилось. Вблизи изображение выглядит нечетким, но вдали выглядит потрясающе. Получилось действительно красиво.
Christianna M.
Этот портрет — именно то, что мы искали! Я рада, что мы заблаговременно утвердили портрет! Это действительно помогло.
Учебное пособие по рисованию милой и легкой морды собаки: шаг за шагом
Быть профессиональным рисовальщиком лица не всегда означает, насколько развиты ваши художественные навыки.Мы видели десятки художников по холстам, чьи попытки рисовать лица выглядели… хм, скажем так, «им было много возможностей для улучшения». 😅
Быть профессиональным рисовальщиком означает, что вы можете легко удовлетворить запросы ребенка с помощью быстрого, сбалансированного и впечатляющего дизайна.
Говоря, что вы уже знаете из нашего блога «10 лучших дизайнов рисования лица, которые необходимо изучить», что дизайн раскраски мордочки щенка находится в верхней части этого списка.
Таким образом, Рози Либерман, одна из наших недавних выпускников и новый инструктор школы подготовки, создала этот потрясающий учебник по рисованию мордочки собаки, чтобы помочь вам, новичкам, освоить его и добавить в свое меню.
Погрузимся! 👇
Материалы:
- Белый на основе глицерина (я использовал Kryolan)
- Glitter Gold 066 от FAB (в качестве альтернативы используйте любое золото на основе глицерина)
- DFX essential brown
- DFX Essential black 9060 Shimmer by FAB
- Лепестковые губки x 2
- Желтые губки DFX (с закругленными краями) x 2
- Loew Cornell 795 Round no. 3 кисть
Не знаете, где взять лучшие инструменты для рисования лица? Ознакомьтесь с рекомендациями наших экспертов здесь.
Шаг 1: Сначала создайте область морды, чтобы начать рисовать мордочку вашей собаки.
Я начал с того, что намазал квадратную морду белым цветом, переходящий на лоб. Затем я покрыл глаза и область под глазами золотом.
Затем я немного смешал белый и золотой на лбу с помощью губки с золотым наполнителем (без добавления краски).
Совет: Заостренный конец лепестковой губки идеальной формы для заполнения промежутка между мордочкой и глазом.
Шаг 2: Определите форму лица
Я создал форму головы из узкой коричневой полосы, используя закругленный кончик губки.
Я убедился, что верхняя и нижняя половины головы встречаются во внешних углах глаза, а верхняя часть головы имеет слегка коническую форму.
Используя губку, предварительно окрашенную в золотой цвет, я затем смешал коричневый и золотой.
Наконечник: Использование золота на основе глицерина упрощает смешивание.Узнайте больше о типах красок и о том, что лучше всего подходит для чего, в нашем Руководстве для начинающих. 😍
Шаг 3: Создайте уши
Для каждого уха я начал с создания 2 параллельных линий равной длины, чтобы отметить внутренний и внешний края уха. Это было сделано путем перетаскивания губкой коричневой краски.
Затем я соединил две линии сверху и сделал внешнюю линию шире, чтобы представить перевернутое ухо.
Совет: Попробуйте сделать линию внутреннего уха под углом 45 градусов от горизонтали, чтобы собака выглядела счастливой и расслабленной, а не удивленной (что происходит, когда уши слишком вертикальны!).
Шаг 4: Добавьте немного цвета.
Я протер розовым губкой внутреннюю часть ушей рисунка раскраски мордочки собаки, а затем довольно сухой губкой добавил несколько черных пятен для интереса.
В качестве альтернативы вы можете использовать черный на основе глицерина или черный металлик для пятен. Они не такие темные, и их легче наносить губкой, чем воско-черным.
Шаг 5: Набросайте дизайн
Затем я обрисовал в общих чертах все детали, начиная с морды, потом ушей и, наконец, шерсти.
Не устраивает ваша линия? Примите участие в семинаре «Улучшите свою линию за 3 дня»! Это бесплатно!
Шаг 6: Раскраска морды собаки extas
Чтобы добавить интереса и плавности рисунку раскраски морды собаки, я решил нанести несколько черных пятен на фокальные точки щек (направляя их вниз к рту) и на лоб (направлен к центральной фокусной точке).
Так как брови в этом дизайне покрыты краской, я увеличил область вокруг глаз изогнутыми линиями и бровями, идущими от внешней к внутренней фокусным точкам глаза.
Совет: Чтобы легко рисовать точки различной формы, приложите кончик хорошо загруженной кисти к коже, затем сильно надавите. Изменение веса дает пятна разной формы.
Шаг 7: Добавляем блики
Чтобы по-настоящему выделить собаку, я, наконец, добавил белые блики в области, которые будут отражать наиболее естественный свет в солнечный день.
Дополнительные пояснения:
ПРЕДСТАВЛЯЙТЕ… все, что выходит из-под вашей кисти, заставляет ваших клиентов восклицать «ВАУ!»
… именно в этот момент, когда «ребенок начинает улыбаться и не отдаст зеркало, вот что делает меня счастливым!»
Пройдите курс в Международной школе рисования лиц и станьте профессиональным рисовальщиком, не выходя из собственного дома.
Вам понравилось это руководство? Нажмите « ПОДЕЛИТЬСЯ », и пусть ваши коллеги по рисованию лица узнают об этом! 👇👇👇
Как нарисовать портрет пожилой собаки — Советы и хитрости
Портрет пожилой собаки имеет несколько уникальных проблем. Но эти милые пожилые лица так приятно рисовать по разным причинам.
При рисовании портретов пожилых людей нужно учитывать, как раскрашивать морщины, седину и меняющиеся черты лица. Когда вы рисуете портрет пожилой собаки, наличие плана рисования белого меха на их морде, а также меняющейся кожи на носу может сделать ваш портрет успешным.
Если вы предпочитаете смотреть видео о том, как рисовать собак, у меня скоро выйдет одно, демонстрирующее, как рисовать этого немецкого короткошерстного пойнта по кличке Герцог. Ссылка на видео появится ниже, но до премьеры я буду держать на своем месте портрет мопса. Зайдите в ближайшее время. Я работаю над этим! А пока продолжайте читать.
Подготовка к рисованию портрета пожилой собаки
Этот портрет герцога был заказан в качестве подарка на день рождения одному из его преданных людей. Герцог — главный специалист по морали в Braden Heidner Lowe & Associates, поэтому я чувствовал давление, создаваемое такой высокопоставленной деловой собакой. Мне дали несколько изображений Герцога для работы, и мы выбрали образ, в котором его личность, казалось, просвечивала больше всего.
Изображение ниже является последней справочной фотографией.Я изменил размер исходной фотографии пропорционально, чтобы она поместилась на холсте размером 16 ″ x20 ″, и добавил простую сетку. Я не всегда использую сетку, но для более быстрого перемещения я использую ее, чтобы сохранить точные пропорции на раннем этапе.
Мне казалось, что все идет хорошо, пока я не нарисовал набросок винным углем на холсте. Хотя композиция отлично смотрелась на экране моего компьютера, когда я нарисовал ее в натуральную величину на холсте, голова Дюка выглядела слишком большой. Ниже первый набросок.Я посидел с ним в течение дня, чтобы посмотреть, что я чувствую по этому поводу. На следующий день это все еще беспокоило меня, поэтому я вытер уголь и решил начать все сначала.
Раннее исправление ошибок
На эталонной фотографии выше вы можете увидеть, где я изменил изображение сверху и снизу. Я удлинил ноги Герцога и увеличил изображение в верхней части фотографии после того, как решил изменить размер Герцога для картины.
Когда я пишу портреты на большом холсте, таком как 16 ″ x20 ″, я обычно предпочитаю, чтобы размер головы был как можно ближе к реальному размеру.Ничего страшного, если он немного больше, но я могу сказать, что этот первый рисунок был слишком большим. Бывают случаи, когда на огромном холсте можно было сделать намного больше реального, и это не кажется странным. Я нарисовал такую картину со своей собакой Эдди, которую вы можете увидеть в конце этой статьи.
Голова герцога слишком велика на холсте. Похоже, мне придется начинать все сначала.
Однако по какой-то причине, когда размер холста приближает портрет к реальному размеру, возникает чувство дискомфорта из-за слишком большой головы.Я не знаю, есть ли для этого причина или нет, но если я выясню это, я дам вам знать.
Возможно, я просто хотел запечатлеть личность Герцога, но портрет все же должен был вписаться в семейный дом и иметь немного более формальный вид. Так как я был только на стадии наброска, начать все заново не составляло большого труда. Если бы я продолжил и закончил с портретом наполовину, у меня были бы большие проблемы. Если вы заметили ошибку на ранней стадии, лучше сразу исправить ее.
Примечание о размерах холста
Если бы я рисовал крошечную собачку, такую как чихуахуа, я бы, вероятно, начал с холста меньшего размера, такого как 8 ″ x10 ″ или 9 ″ x12 ″, и также держал бы голову близко к натуральному. Однако чихуахуа, вероятно, предпочли бы, чтобы их рисовали в соответствии с размером их личности на холсте шириной не менее 36 дюймов. Это было бы вполне приемлемо и сделало бы заявление больше, чем жизнь, которое может полюбиться человеку чихуахуа. Важно работать с вашим клиентом, чтобы он хорошо понимал, в каком направлении движется картина.
Искусство эмоционально, и иногда его трудно выразить словами. Несколько быстрых разговоров по телефону или по электронной почте могут иметь решающее значение.
Второй набросок выглядит намного лучше, и с тонированным холстом будет легче работать.
Тонированный холст против. Белый холст
Так как я начал с наброска, я решил тонировать холст, смешав черный цвет слоновой кости с желтой охрой и разбавив его Gamsol. Я нанесла легкую стирку на холст и дала ему высохнуть.Я снова добавил сетку и быстро набросал Дьюка углем. Причина тонирования холста заключается в том, чтобы яркий белый цвет холста не привносил слишком много контраста к цветам, когда я их блокирую. Тонированный холст может помочь в более точном сопоставлении значений. Это также не так страшно, как рисовать на ярко-белом холсте.
Если вы не хотите использовать сетку, вы можете нарисовать от руки. Я бы рекомендовал использовать пропорциональный делитель для проверки размеров, если вы можете распечатать ссылку на фактический размер.Это полезно для начинающих художников, и я покажу, как я использовал фактический размер отпечатка, когда рисовал белую немецкую овчарку по имени Дева. Что касается Герцога, его эталонная фотография была на моем iPad, поэтому сетка была намного полезнее, поскольку эталон был другого размера, чем холст.
Многие художники не используют уголь и рисуют в своих картинах краской, разбавленной Gamsol. Я делал это много раз для своих картин, но обычно обязательно использую сетки, когда выполняю работу в сжатые сроки.Это просто экономит время в долгосрочной перспективе.
Обзор малярных материалов
Не стесняйтесь пропустить следующие несколько абзацев, если не хотите просматривать материалы, которые я использовал.
Я использовал довольно ограниченную палитру для этой картины старшей собаки, но все же использовал большинство цветов на фотографии ниже. Вводный набор красок от Gamblin великолепен, так как их выгоднее покупать, чем в отдельных тюбиках. Я по-прежнему буду включать в текст ссылки на Amazon для отдельных цветов, если вы хотите их проверить.Я использовала натянутый хлопковый холст, грунтованный левкасом. Лучше выбрать холст более высокого качества, чем дешевый холст студенческого класса. Льняные панели с масляной грунтовкой — моя любимая поверхность для рисования, но они не доступны в больших размерах и намного дороже.
Я в основном использовал черный цвет слоновой кости, жженую умбру, желтую охру и красный свет вместе с теплым белым от M. Graham для этого портрета старшей собаки. В конце картины я также использовал титановый белила Windsor Newton (не показан).Его использовали для рисования шерсти вокруг мордочки и глаз, а также для более ярких отражений в глазах.
Уайт-спирит Gamsol использовался для разбавления краски, особенно для тонирования холста, а позже я использовал гель Gamblin без растворителей, чтобы придать краске консистенцию.
Какой тип мольберта следует использовать?
Мольберт, который я использовал, представляет собой простой настольный мольберт. У меня есть гигантский мольберт художника, но я всегда бьюсь по нему ногами, пока рисую. Это очень раздражает. С настольным мольбертом я могу сидеть на табурете для рисования, подставив ноги под стол и не преграждая путь.Единственная проблема с этим мольбертом заключается в том, что, как я обнаружил, прикрепление к столешнице светильника для рисования может опрокинуть его. Это можно исправить с помощью пары 5 фунтов. веса, которые я добавляю к задней части мольберта, когда он стоит на столе.
Этот мольберт на Amazon очень похож на тот, который я использую, и на нем можно разместить холсты большего размера. Если вы не прикрепите к нему фонарь, у вас не должно возникнуть проблем с его опрокидыванием вперед.
Что такое палка Мала?
Несколько человек спросили меня, что за палку я использовал в своих видеороликах.На мой взгляд, махловая палочка — это палочка-выручалочка для художника. Это помогает стабилизировать вашу руку, чтобы вы могли быть более точными при рисовании. Я очень рекомендую его использовать. Палка у меня не изящная, но она помогает. Это похоже на Amazon, если вам интересно. Вы также можете сделать свою собственную, если у вас будет возможность. Некоторые люди вместо этого используют трости или клюшки для гольфа. Я хотел бы убедиться, что все, что вы используете, будет легким.
Хватит материалов и подготовки, пора красить!
Блокировка в темных областях на портрете старшей собаки
Если вы прошли какой-либо из моих других уроков рисования, я начну звучать как побитая пластинка.Я всегда начинаю рисовать, сначала блокируя темные области. Ниже вы можете увидеть, где я взял жженую умбру, смешанную с небольшим количеством черного цвета слоновой кости, и нарисовал углем набросок. Уголь легко стереть, поэтому, если вы не хотите потерять рисунок, лучше быстро закрасить его. Вам не обязательно использовать такую толстую кисть, как у меня. Если вы хотите, чтобы ваш рисунок был более точным, используйте кисть меньшего размера и разбавьте краску небольшим количеством Gamsol.
Начнем с темных участков и закрасим эскиз.
Я обычно работаю довольно быстро на этом этапе и использую кисть большего размера, чтобы нарисовать краску как можно быстрее. Делайте то, что вам удобно.
В дополнение к рисованию углем я также заблокировал самые темные области. Я все время щурился. Прищурившись, вы сможете увидеть более крупные формы и не вдаваться в детали.
На этом этапе я не проявлял особой осторожности. Это будет позже, когда я перейду к деталям.
Обозначение бликов на морде
Обычно на этом этапе я не использовал бы какие-либо блики, но после того, как я добавил немного красновато-коричневого меха с помощью каштанового красного и жженой умбры, я добавил теплый белый цвет на мордочку.
При рисовании портрета взрослой собаки может быть большой контраст между белым / серым мехом на морде и более темным мехом. Я добавил несколько более светлых тонов, чтобы помочь мне понять и определить свой диапазон значений. Я также знал, что это милое лицо будет в центре внимания, поэтому я хотел убедиться, что морда не станет слишком яркой слишком рано.
На изображении выше камера видит область морды ярче, чем то, что я нарисовал. Когда вы рисуете белый мех, вы хотите начать с более темных серых тонов, чтобы вы могли наращивать слои и создавать объем.
Белый мех на лице Герцога — одна из черт, делающих его похожим на Герцога, и ключ к созданию подобия. Быстро добавив немного этого более светлого цвета, я понял, что снимаю его правильно. Опять же, вот где важно прищуриться, чтобы увидеть, совпадают ли значения.
Добавление средних тонов к портрету старшей собаки
Ниже я начал добавлять средние красноватые тона на лицо. Я был очень осторожен, чтобы не добавить слишком много теплого белого цвета к моей смеси красно-коричневого и жженой умбры.Слишком много белого в краске может стать серьезной проблемой. Это все равно, что добавить в рецепт слишком много соли. Трудно вернуться.
Вот почему я держу свои картины на темной стороне и увеличиваю ее до светлых областей. Вы всегда можете добавить больше белого, если он слишком темный, но обратное не так. Сохранение темной стороны делает картину более драматичной. Больше драматизма — больше эмоций, а это то, чего вы хотите, рисуя любимую собаку.
Строительная форма
Ниже я очень слабо заблокирован остальной частью тела Дюка, стараясь быть консервативным с светлыми тонами.Я добавил немного желтой охры, чтобы осветлить некоторые области и добавить тепла, не загрязняя темные участки слишком белым.
Я начал думать об источнике света для портрета. На контрольной фотографии свет падал сверху и первым попадал в его лицо, что делало эту область самой яркой. Свет, падающий на остальную часть его тела, будет менее ярким. Затем я представил его в темной комнате и светящим на него светом. Эффект прожектора на сцене вызывает много эмоций и драматизма, поэтому я позаимствовал эту идею, когда писал «Герцога».
Блокировка цвета в глазах
Я люблю рисовать глаза и обычно не могу с собой поделать, чтобы сразу их закрасить. Я немного сдержался в глазах Герцога. Характер его глаз уже присутствовал, поэтому я знал, что они отлично подойдут.
На изображении выше у меня уже было немного черного, чтобы обозначить зрачок и структуру глаза. На этом этапе я добавил к ирису немного жженой умбры и желтой охры. Возможно, я добавил немного теплого белого, чтобы немного осветлить радужную оболочку.
Умышленное создание некоторых областей в мягком фокусе
Уши у собак могут стать несколько сложными, если на них слишком много внимания. Я обнаружил, что указание складок в ушах просто несколькими мазками кисти — лучший подход. Уши Герцога в основном темные с небольшими бликами. Я хотел, чтобы более четкие части картины были в центре лица, а остальная часть картины была более мягкой и немного абстрактной. Это делает композицию более интересной.Это также помогает глазам зрителя вернуться в фокус картины после прохождения абстрактных мазков.
Эта тонкая игра между мягким фокусом и более резким фокусом создает движение. А небольшое движение на картине вызывает больше эмоций. Ведь в слове «эмоция» есть слово «движение».
Добавление фона
Пора было заблокировать в фоне. Обычно я стараюсь создать фон на ранней стадии, но поскольку холст был окрашен в довольно темный цвет, это было не так критично.
УDuke много красных тонов в мехе, поэтому я знал, что хочу использовать зеленую сторону в качестве дополнительного цвета фона. Я начал с серовато-зеленого ниже, но ближе к концу картины я решил сделать этот цвет намного богаче. Однако это была хорошая отправная точка.
Начальная деталь лица для пожилой собаки
Вы также можете увидеть на изображении выше, что я начал добавлять детали лица. На данный момент это довольно грубо, но я начинаю определять направление шерсти.Я также пытался решить, какой уровень детализации я собираюсь использовать для Duke.
В моих прошлых портретах собак я был немного более абстрактным с моими мазками кисти для меха. Когда у вас есть правильные значения, глазу не нужно видеть все сложные детали, чтобы понять картину в целом.
В случае с герцогом я решил остановиться подробнее, так как белый мех на его лице был ключевым определяющим фактором на этом этапе его жизни. Это была большая картина, поэтому зрителю было бы легче рассмотреть детали, чем смотреть на картину гораздо меньшего размера.
Добавляем немного волшебства в глаза
На изображении ниже вы можете видеть, что глаза имеют немного больше жизни, чем на предыдущем изображении. Для этого радужная оболочка слегка сливается с зрачком и краем глаз. Я также добавил немного золотого сияния в радужную оболочку с помощью теплой белой и желтой охры. Для глаз важно иметь тень под веком, когда источник света идет сверху. Я также немного осветил блики, но еще немного подправлю их, прежде чем картина будет закончена.
Мне нравятся эти глаза и его маленькие седые волосы такие милые!
Создание носа и морды
Вторая по важности часть создания сходства с Герцогом — правильная пропорция его носа и морды. Его голова находится под необычным углом, и получить правильный ракурс было непросто.
Когда я нарисовал более светлые красноватые тона на носу, он продолжал казаться мне странным. В этот момент я знал, что, возможно, испытал проклятие художника и мне нужно было ненадолго отойти от картины.После перерыва я обязательно прищурился, переводя взгляд между картиной и исходной фотографией. Все выглядело так, как будто все совпало, поэтому я продолжал.
Я сосредоточился на приведении моих ценностей в соответствие и старался игнорировать то, что происходило в моей голове. Иногда рациональная часть мозга не участвует в творческом процессе.
Изменение фона и добавление деталей лица
Ниже вы можете увидеть, где я решил, что зеленый фон должен быть богаче.Раньше он был слишком серым, и я подумал, что из-за этого картина выглядит немного плоской. Из-за того, что зеленый стал более насыщенным, красный в пальто Герцога выглядел очень красиво. Вы должны полюбить хорошую дополнительную цветовую схему.
Углубление фона имело большое значение.
Я также сделал зеленый темнее по краям, создав виньетку. Это делает центр картины ярким и добавляет глубины.
Я также добавил намного больше деталей лица с помощью тонкой кисти.На это уходит довольно много времени, но было очень приятно заполучить туда все седые волосы его маленького старичка. Мне нравятся собачьи мордашки постарше, и чем больше деталей я добавлял герцогу, тем больше мне казалось, что он находится в одной комнате со мной.
По меху на шее и тиканью на ногах видно, насколько абстрактными я оставил эти штрихи. Опять же, это было сделано для того, чтобы взгляд снова возвращался к фокусной точке, а также продолжал создавать иллюзию глубины.
Проблемы с носом на портрете пожилой собаки
Я нарисовал много собачьих носов, и у каждой есть свои уникальные проблемы, но по большей части я считаю, что их довольно легко нарисовать.Поэтому я был немного удивлен, обнаружив, что трачу МНОГО времени на то, чтобы поправить этот нос.
Поначалу меня поставили в тупик из-за этого носа, но я знал, что это сработает.
То, что я понял, отличалось от носа Дьюка, так это то, что это был старый нос. Кожа на носу пожилой собаки сильно отличается от носа молодой собаки. На нем есть обесцвечивание и отметины, указывающие на возраст собаки. Как только я понял это, я начал приближаться к носу, как когда я рисую кожу пожилого человека.
Более светлые носы, такие как у Дюка, также должны иметь красноватый оттенок или румянец. Было немного сложно сбалансировать красный и серо-коричневый цвета. Результатом носа очень доволен. На расстоянии он читается правильно, но не идеален для фотографий. В конце концов, я хотел, чтобы это выглядело как картина маслом.
Последние штрихи к портрету старшей собаки
Ниже представлена законченная картина Герцога. Как видите, я потратил некоторое время на добавление растительности на его лице и усов.
Я также восстановил темные области, которые нуждались в усилении. Бирка на воротнике Герцога нарисована очень просто. Это всего лишь несколько темно-серых мазков с добавлением пяти ярких бликов. Меня никогда не перестает удивлять, на что способны пара удачно нанесенных мазков.
Герцог Брейден, офицер морального духа и отличный мальчик.
Подпись к картине
Я только что закончил писать статью о подписании картин и, посмотрев фотографии Дюка, испугался, что забыл поставить подпись на лицевой стороне.Он был подписан, но его действительно трудно увидеть на изображении выше. Я использовал более темный цвет, чтобы слиться с фоном. Фотография слишком хорошо скрывает подпись в левом нижнем углу. Это там. Я обещаю.
Каждый раз, когда вы заканчиваете картину, не забудьте подписать ее. Я говорю все о том, почему так важно поставить свою подпись здесь, в этой статье.
Спасибо, Сэнди, Грег и Герцог!
Одна из лучших вещей в создании портретов для людей — это встретиться с ними лично и услышать историю о том, как их собака вошла в их жизнь.Я убежден, что некоторые собаки выбирают себе людей. Герцог не был исключением. Сэнди и Грег — совершенно замечательных человек, и Дюк нашел их через отца Грега, который забрал его.
Герцогу очень повезло, что в его жизни так много людей, которые его любят. Быть старшим офицером по морали в BHL — это большая работа, но, насколько я слышал, он чрезвычайно популярен и выполняет свою работу лучше, чем когда-либо мог бы любой человек. Удачи, герцог!
Надеюсь, вам понравился этот урок о том, как рисовать старшую собаку
Спасибо, что заглянули и узнали, как нарисовать портрет пожилой собаки.Я люблю делиться тем, над чем работаю. Если вас интересуют другие советы и руководства для художников, вы можете ознакомиться с некоторыми из них:
8 советов по покраске черного меха — традиционное и цифровое
Зачем красить вверх ногами? 15 полезных советов по рисованию
Цветочная живопись импрессионистов ПЛЮС Как рисовать серебро и ткань
сообщить об этом объявленииПортретная живопись питомца: смотри, как я рисую мопса
Три быстрых совета, как рисовать портреты собак
Йоханн Манги, «Джорджи», 2012 г., льняное полотно, масло, 6 x 6 дюймов.Недавно Йоханна Манги, одна из лучших в мире художников-собак, провела день в нашей студии, где записала подробное видео о том, как рисовать портреты собак, шаг за шагом. Рисовать и раскрашивать собак может быть интересно — мы так любим своих собак, — но есть рынок и для комиссионных работ. Когда вы овладеете искусством рисования портретов собак, подумайте о возможностях. Для начала возьмите мастер-класс, например, изучите книгу Йоханн «Изобразительное искусство рисования портретов собак» (доступно здесь).А пока ознакомьтесь с этими быстрыми советами, чтобы начать работу.
Йоханн Манги, «Чарли с ветром», 2017, масло, 18 x 14 дюймов.3 быстрых совета по рисованию портретов собак
Автор Johanne Mangi
Я все время слышу: «Я не знаю, с чего начать!»
«Как красить мех?»
«Почему мои рисунки животных выглядят неправильно?»
Если вы думаете, что эти заявления были сделаны новыми, неопытными художниками, подумайте еще раз. Это были настоящие высказывания опытных мастеров живописи.В мехе есть что-то, что сбивает с толку даже самого уверенного художника.
Йоханн Манги, «Пенни», 2017, масло, 10 x 8 дюймовЯ дам вам несколько быстрых советов , которые направят вас в правильном направлении, когда дело доходит до изучения , как рисовать портреты собак :
1. Под всем этим мехом скрывается дорожная карта. Скелетная структура. Вам просто нужно его искать.
2. ЭТО ПРОСТО КРАСКА! Верно. Легко надеть, легко снять. Если этот первый мазок не сработал, избавьтесь от него и повторите попытку!
3. БОЛЬШИЕ ЩЕТКИ! Людям нравятся их крошечные кисточки. Поверьте, вы не получите желаемого эффекта. Подойдет только большая кисть.
Я гарантирую, что если вы последуете этим простым шагам, вы сразу же станете лучше. Удачи! ~ Йоханн Манги
Посмотреть превью нового учебного DVD Джоанн «Искусство рисования портретов собак» можно здесь:
Дополнительные портреты собак от Йоханны Манги:
Плоскошерстный ретривер PennyStreet Singer Понравилось? Нажмите здесь, чтобы подписаться на PleinAir Today,
от издателей журнала PleinAir .
Захвати свое существо: советы по рисованию портретов питомцев
Домашние животные делают нашу жизнь лучше. Они привносят любовь и живость в нашу повседневную жизнь; они уважаемые члены наших семей. Портреты домашних животных — прекрасный способ отпраздновать этих любимых пушистых, пернатых, пушистых или чешуйчатых друзей в нарисованной форме.
Рисование портрета домашнего животного может показаться сложным, но эти советы по рисованию портретов домашних животных помогут упростить процесс. От определения идеальной композиции и настройки тона до растушевки краски — мы проведем вас через весь процесс, чтобы вы в кратчайшие сроки нарисовали портреты домашних животных.
Перед покраской:
Портрет кошки через Craftsy member pastelart 3252519
Познакомьтесь с домашним животным
Примечание автора: Я расскажу вам небольшой анекдот, чтобы проиллюстрировать важность улавливания сущности домашнего животного. Однажды мне поручили написать портрет бульдога, и, когда я подал эскизы, мне разочарованным голосом сказали, что я упустил «сущность» собаки. Ну… у меня было одно эталонное фото, и я никогда не встречал собаку.Что мне было делать?
Этот анекдот иллюстрирует важный момент: подобно рисованию портретов людей, рисование домашнего животного — это не просто получение реалистичного изображения камерой. Речь идет о том, чтобы уловить сущность и личность существа.
Дело в том, что невозможно передать истинную личность питомца без достаточного количества информации. Если вы рисуете своего собственного питомца, вы уже имеете хорошее представление о его телосложении. Если вы рисуете для кого-то другого, у вас может не быть возможности познакомиться с домашним животным, но вы потратите некоторое время на то, чтобы владелец домашнего животного говорил о нем или о ней.Узнайте о его личности, манерах и любых важных или примечательных качествах.
Получите достаточно справочного материала
Фото через CakeSpy
Если вы будете создавать свой портрет по эталонным фотографиям, убедитесь, что у вас есть много фотографий с разных ракурсов и с разными типами света. Не соглашайтесь только на одну эталонную фотографию, так как на ней, скорее всего, не будет информации, которая может стать важной в процессе рисования, например, как свет падает на шерсть питомца или цвет глаз питомца при солнечном свете.Либо запросите, либо сделайте свои собственные фотографии, чтобы продемонстрировать любые отметки или позиции, которые могут иметь отношение к вашему портрету.
Знакомство с домашним животным в контексте может помочь в создании портрета. Знание его любимых игрушек или мест может помочь вам выбрать сцену или, по крайней мере, помочь вам выбрать цветовую схему. Также будут полезны фотографии с любимыми игрушками, настройками или аксессуарами.
Сделать эскизы
Рисунок кошки, сделанный мастером-инструктором Пэтом Уивером
Сделайте множество набросков, прежде чем выбрать окончательную композицию для своего портрета.Использование газетной бумаги или более дешевой бумаги поможет вам разогреться и даст возможность поэкспериментировать с разными взглядами, прежде чем продолжить. Создавая наброски, вы сможете определить ракурс и композицию окончательного портрета.
Выберите композицию, которая подходит питомцу
Портреты домашних животных не обязательно должны быть серьезными или полностью фотореалистичными. Они могут проявлять юмор и прихоти, как на портрете, показанном выше, на котором изображена озорная черная собака, едущая на одноколесном велосипеде перед гробницей Гранта на Манхэттене (да, действительно).Выбор обстановки и композиции, которые подходят как питомцу, так и владельцу, сделает портрет драгоценным и особенным, помимо простого изображения сходства.
Заранее настройте рабочее место
Как и в случае с любым другим портретом, вам нужно, чтобы ваше рабочее пространство было настроено так, чтобы вам не приходилось делать паузы в процессе рисования. Соберите кисти, холст или рабочую поверхность и все принадлежности, которые вам понадобятся в процессе рисования. Заранее подготовив рабочее место, вы сможете сосредоточиться на картине.
Как только вы начнете рисовать:
Сделать подмалевок
Если вы работаете акриловыми или масляными красками, создание подмалевка может быть чрезвычайно полезным при создании портрета домашнего животного. Так же, как рисование портрета человека, подмалевок может добавить объемности вашему портрету питомца. Контрастный цвет может выглядеть странно на холсте, но позже он сделает вашу готовую вещь более реалистичной. Блупринт, курс Классический автопортрет очень детализирован в процессе подмалевка.
Создайте идеальную палитру
Портрет питомца через Ремесленника Микки Арнольда
Как и рисование телесных тонов, получение идеального цвета меха, чешуи или перьев не зависит от смешивания одного простого цвета. Будь то собака, кошка, черепаха или питон, вы можете увидеть вариации и оттенки цвета лица и тела питомца. Таким образом, даже собака, которая кажется вполне белой, может иметь желтый или серый оттенок, тогда как черная кошка может иметь красноватый оттенок на солнце.Оцените эти оттенки и создайте палитру, отражающую эти тонкие оттенки.
Покраска слоями
Подобно человеческому портрету, вы можете добиться успеха в многослойной работе над портретом питомца. Создание базового слоя для захвата основных цветов и форм лица и тела с последующим уточнением для добавления текстуры и деталей поможет вам получить объемный, реалистичный окончательный портрет.
Оттачивайте свои навыки рисования портретов домашних животных с помощью курса Bluprint Pet Portraits .Присоединяйтесь к известному художнику-животному Пэту Уиверу и узнайте, как легко фотографировать, рисовать и рисовать своего питомца. От сбора справочных материалов до нанесения краски на бумагу или холст — вы будете на правильном пути к созданию идеального портрета питомца.
Вы когда-нибудь рисовали портрет питомца?
Раскраска лица для вечеринок — 30 идей раскраски лица для детей
Объявление
Раскраска лица — отличное занятие, которое стоит попробовать, особенно для детей.Гуляете ли вы по сезонной ярмарке в своем городе, тематическому парку или карнавалу, там обязательно будет стенд для рисования лица. Если ваш ребенок устраивает вечеринку, вы можете попробовать научиться раскрашивать лица для вечеринок. Таким образом вы сможете придать изысканный вид всем детям на вечеринке. Ниже мы собрали 30 детских рисунков на лице, чтобы помочь вам найти отличные идеи! Если вас интересуют идеи рисования лица и макияжа, обязательно ознакомьтесь с нашей коллекцией!
1.Капитан Америка — Раскраска для вечеринок
Если ваш ребенок является поклонником кинематографической вселенной Marvel и всех ее супергероев, то ему понравится эта идея рисования лица! Нарисуйте им на лбу символ Капитана Америки. Затем нарисуйте два крыла на месте бровей, добавив немного белых блесток кое-где. Эта идея раскраски лица идеально подходит для поклонников чуда!
2. Милый жираф — Любимые идеи животных
Жирафы — очень милые животные с длинными шеями и длинными языками! Если жирафы — любимое животное вашего ребенка, почему бы не нарисовать жирафа у них на морде? Нарисуйте это животное сбоку от лица ребенка, как если бы жираф тоже смотрел боком.Дело в том, чтобы его рот находился там, где на самом деле находится рот ребенка. Таким образом, всякий раз, когда ребенок высовывает язык, это будет выглядеть так, как будто жираф высовывает его!
3. Красивая птица — блестит и искрится
Еще одна фантастическая идея нарисовать лицо вашего ребенка — это птичка! Убедитесь, что он красочный и яркий, используя набор различных цветов, чтобы он выглядел экзотично. Вы также можете покрыть птицу несколькими слоями блесток или блесток, чтобы придать ей дополнительное сияние красоты.
4. Радужный пони — идеи рисования лиц для детей
Радуга — это сочетание цветов, которое очень нравится детям. Так что не забудьте использовать его в краске для лица! Нарисуйте пони на лице, которое покрыто множеством полос. Вместо того, чтобы раскрашивать полосы простым черным, делая их похожими на зебру, раскрасьте полосы в спектр радуги!
5. Удивительный дракон — свирепый и пламенный
Драконы — мифологические существа, которых считали огнедышащими крылатыми змеями.Эти вымышленные звери стали популярными в современной культуре. Если ваш ребенок любит драконов, почему бы не создать их лицо, похожее на точную копию дракона? Не забудьте про рога и попробуйте создать на лице ребенка небольшие пятна, изображающие чешую дракона. Это будет отличная идея макияжа, подходящего к детскому карнавальному костюму.
6. Цветущая красота — Раскраска для вечеринок
Вот красивая идея раскраски лица, которая понравится девочкам! Нарисуйте розовые цветы им на лбу, создав великолепный образ! Он будет напоминать цветочную корону.Естественно, вы также можете добавить несколько цветов разного цвета, в зависимости от ваших предпочтений!
7. Радужная рыба — с пузырьками
Ваш ребенок любит обитателей морских глубин или рек и озер нашей планеты? Почему бы не нарисовать симпатичную радужную рыбку сбоку у них на лице? Вы даже можете добавить несколько пузырьков, плавающих ко лбу ребенка.
8. Счастливая черепаха — Раскраска для детей
Черепахи — такие милые животные. Нарисуйте черепаху сбоку на лице ребенка, убедившись, что рот находится на том же месте, что и рот ребенка.Таким образом, всякий раз, когда ребенок открывает рот, чтобы что-то сказать, это будет выглядеть так, как будто говорит черепаха.
9. Цыпленок — учимся летать
Вот еще одна супер милая идея! Нарисуйте цыпленка на лице ребенка, рисуя большую часть его тела на носу. Затем пусть его крылья хлопают над бровями. Используйте желтый цвет для тела цыпленка и оранжевый для его клюва и лап.
10. Цветы над радугой — Великолепная раскраска лиц для вечеринок
Вот изысканный образ, который понравится любой маленькой девочке! Покройте части вокруг глаз сверкающими цветами радуги.Убедитесь, что вы используете много блесток для дополнительного свечения! Затем нарисуйте множество маленьких белых цветов по всей радуге. Это будет похоже на волшебный сад цветов!
11. Ящерица и муха — Зеленая изобилие
Ящерицы — милые животные, особенно когда дело доходит до быстрой раскраски лица! Их также очень легко создать, вам понадобятся две овальные формы и вьющийся хвост. Высовывай язык изо рта ящерицы и прикрепи к нему муху, как будто ящерица только что поймала свой обед! Посадите эту ящерицу на одну из бровей вашего ребенка, чтобы получить фантастический вид!
12.Красивая бабочка с радужными крыльями
Бабочки — красивые и эффектные животные. Эти порхающие насекомые всегда очаровывают детей. Используйте их как вдохновение для раскрашивания лица и нарисуйте два радужных крылышка на лице ребенка и вокруг его глаз. Вы также можете нарисовать цветок у них на лбу для дополнительного эффекта.
13. Скользящая змея — Раскраска лица для детей
Если ваш ребенок обожает змей любого вида и размера, почему бы не использовать этих скользких животных в качестве идеи для раскраски лица? На лбу малыша можно нарисовать голову змеи.Естественно, не забудьте и о раздвоенном язычке закуски!
14. Радужный единорог — настоящая классика
Идея классической раскраски лица основана на использовании единорога в качестве вдохновения! Все дети обязательно полюбят это волшебное животное. Нарисуйте единорога сбоку на лице ребенка, используя белый цвет в качестве основного цвета меха. Используйте цвета радуги для гривы для особого и потрясающего эффекта!
15. Черепаха-ниндзя-подросток-мутант — Идеи быстрого рисования лица
Ваш ребенок любит смотреть черепашек-ниндзя? Если это так, убедитесь, что на них нарисована морда одной из своих любимых черепах! В зависимости от того, кто их любимый персонаж, выберите цвет маски, так как у каждой черепахи ниндзя маска разного цвета.Это будет потрясающе смотреться для детского костюма на Хэллоуин.
16. Милый щенок — легко и просто
Собаки — любимые животные малышей! Если вашему ребенку очень нравятся щенки и собаки, почему бы не использовать лучшего друга человека в качестве вдохновения? Нарисуйте «пушистое» кольцо вокруг одного глаза вашего ребенка, а также воссоздайте нос и рот собаки с высунутым в сторону языком. Когда все будет готово, ваш ребенок будет действительно похож на собаку!
17. Поцелуй лягушки — Прикольная раскраска лиц для детей
Существует множество сказок о лягушках, которые на самом деле являются принцами.Как только вы поцелуете эту лягушку, она снова превратится в принца! Хотя мы не верим в эти детские сказки, мы все же можем почерпнуть несколько идей из этих милых историй! Нарисуйте лягушку вокруг рта и подбородка вашего малыша. Вы даже можете сделать губы лягушки губами ребенка, сделав раскраску на лице забавной!
18. Кролик с морковкой
Вот еще одна из множества очаровательных идей раскраски для лица для детей! Превратите своего ребенка в лицо кролика. Нарисуйте морковку, торчащую изо рта, на лицо! Не забудьте нарисовать кончик носа бледно-розовым! Эта идея раскраски лица подойдет любому малышу, который любит животных!
19.Радужный клоун — Happy Face Painting для вечеринок
Классическая идея раскраски лица — это раскраска клоуна! Но вместо того, чтобы придерживаться традиционной раскраски лица клоуна, сделайте это веселым и веселым для вашего ребенка! Оставьте нос и рот красными. Затем нарисуйте радуги над их глазами, добавив типичные брови клоуна в качестве последнего штриха. Это будет эффектно смотреться на любом ребенке, который любит шутить!
20. Полосатая зебра — Раскрашивание лица для детей
Зебры — необычные и уникальные животные с изысканным набором полос! Если ваш ребенок обожает этих животных, обязательно используйте их бело-черный узор в качестве вдохновения для рисования их мордочки! Вы даже можете воссоздать голову зебры на их лице!
21.Розовый фламинго — Brilliant Birds
Фламинго — блестящие птицы, известные своим ярким розовым цветом! Если ваш ребенок любит этот цвет и этих птиц, обязательно используйте фламинго в качестве вдохновения для рисования их лица! Нарисуйте фламинго над одним из их глаз, как если бы он отдыхал. Несколько перьев, струящихся внизу, — тоже фантастическая идея!
22. Очаровательная собака — Раскрашивание лица для детей
Вот еще одна идея рисования лица щенка, которая обязательно понравится вашему ребенку! Нарисуйте всю мордочку щенка на лице вашего ребенка, включая высунутый язык и пушистые ушки.Вы можете даже прикрепить лук к одному из ушей собаки.
23. Уникальный образ клоуна — тающая радуга
Вот еще один классный клоунский образ для детей! Покрыв лицо белым цветом, добавив красочный нос и губы, нарисуйте тающую радугу в верхней части головы. Это поднимет взгляд клоуна на совершенно новый уровень, придав ему новую интерпретацию!
24. Волшебный единорог — Звезды и цветы
Как мы упоминали ранее, единороги супер модны во всех смыслах! Так что имело бы смысл использовать их только как идею для раскраски лица! На лбу малыша нарисуйте рог, уши и гриву единорога.Вы можете дополнительно украсить это изображение распускающимися по бокам цветами и сияющими звездами над рогом единорога.
25. Величественная бабочка — Раскраска лиц для вечеринок
Нет ничего лучше замысловатых деталей крыльев бабочки. Воссоздайте крылья бабочки на лице вашего ребенка. Это одна из многих очень красивых и уникальных идей краски для лица, которая будет эффектно смотреться на любой вечеринке! Используйте теплые цвета, например желтый и оранжевый, для крыльев бабочки, и не забудьте добавить немного блеска на кончики крыльев!
26.Повсюду пауки — страшный вид
Вы готовитесь к Хэллоуину в этом году? Убедитесь, что у вашего ребенка жуткий наряд или хотя бы страшная краска для лица! Почему бы не нарисовать формы пауков по всему лицу для супер-крутого вида? Вы даже можете использовать временные татуировки вместо краски для лица, чтобы получить весь этот жуткий образ.
27. Шмель — Излишняя привлекательность
Если вы ищете чего-то более милого, почему бы не использовать шмеля в качестве вдохновения для рисования лица вашего ребенка? Просто нарисуйте изображение шмеля на одной стороне лица ребенка, а за ним следуют следы пятен.Вы также можете добавить несколько изображений цветов вокруг шмеля, так как они вписываются в общую картину.
28. Краска для лица Минни Маус — Раскрашивание лица для вечеринок
Ваш ребенок большой поклонник фильмов Диснея и особенно любит Минни Маус? Если да, не забудьте использовать Минни в качестве вдохновения для рисования лица вашего ребенка. Нарисуйте ей ушки над бровями ребенка и не забудьте добавить фирменный бантик Минни Маус к рисунку краски для лица. Эта краска для лица Минни Маус — идеальный образ для тематической вечеринки Диснея или в качестве макияжа к карнавальным костюмам для младенцев!
29.Вспышка — еще одна идея супергероя
Ваш ребенок любит фильмы о супергероях и сериалы? Если это так, убедитесь, что вы добавили элемент супергероя на краску лица! Например, если ваш ребенок любит Флэш, почему бы не использовать маску этого супергероя как немного вдохновения? Если ваш ребенок собирается на вечеринку в стиле супергероев, то эта маска-краска для лица подойдет вам идеально!
30. Потрясающий петух — Раскрашивание лица для детей
Это животное, из которого вы можете нарисовать особую краску для лица! Петух! Вы можете нарисовать петуха только на одной стороне лица ребенка.Петуха тоже нужно раскрасить сбоку. Используйте красный цвет для петушиных гребешков и прутьев, белый для перьев и желтый для клюва. Этот детский рисунок петуха будет смотреться потрясающе!
Мы надеемся, что эта коллекция из 30 идей раскраски лиц для вечеринок помогла вам найти вдохновение! Для других идей, касающихся детей, таких как идеи детской комнаты или подарки на день рождения для детей, просто посетите наш сайт!
Объявление
.
 Какое расстояние будет между ними через \(2\) часа?
Какое расстояние будет между ними через \(2\) часа?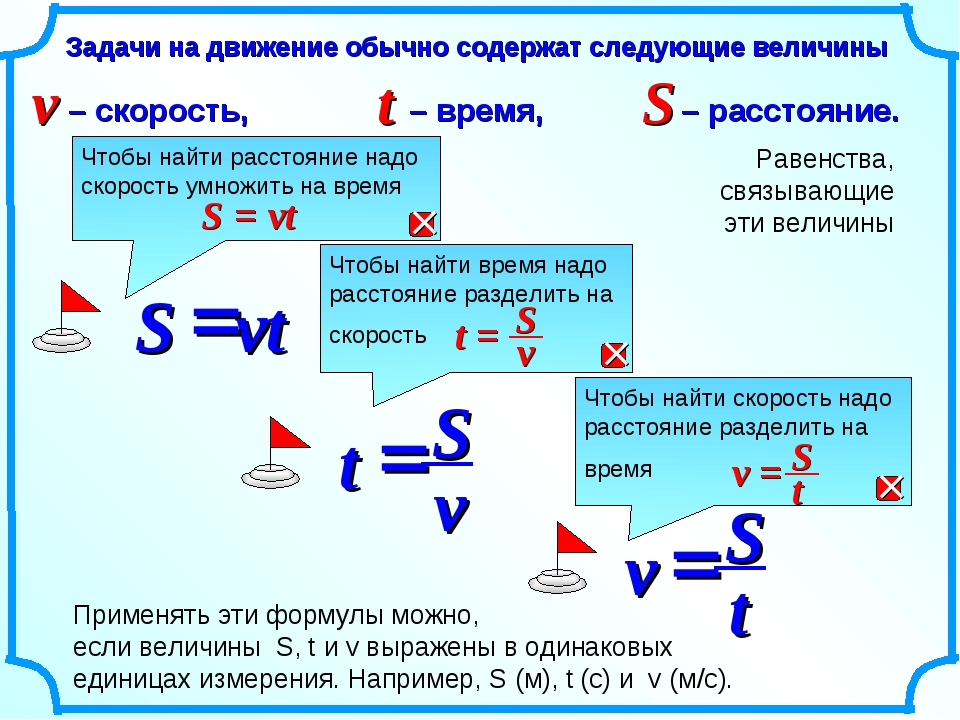 В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.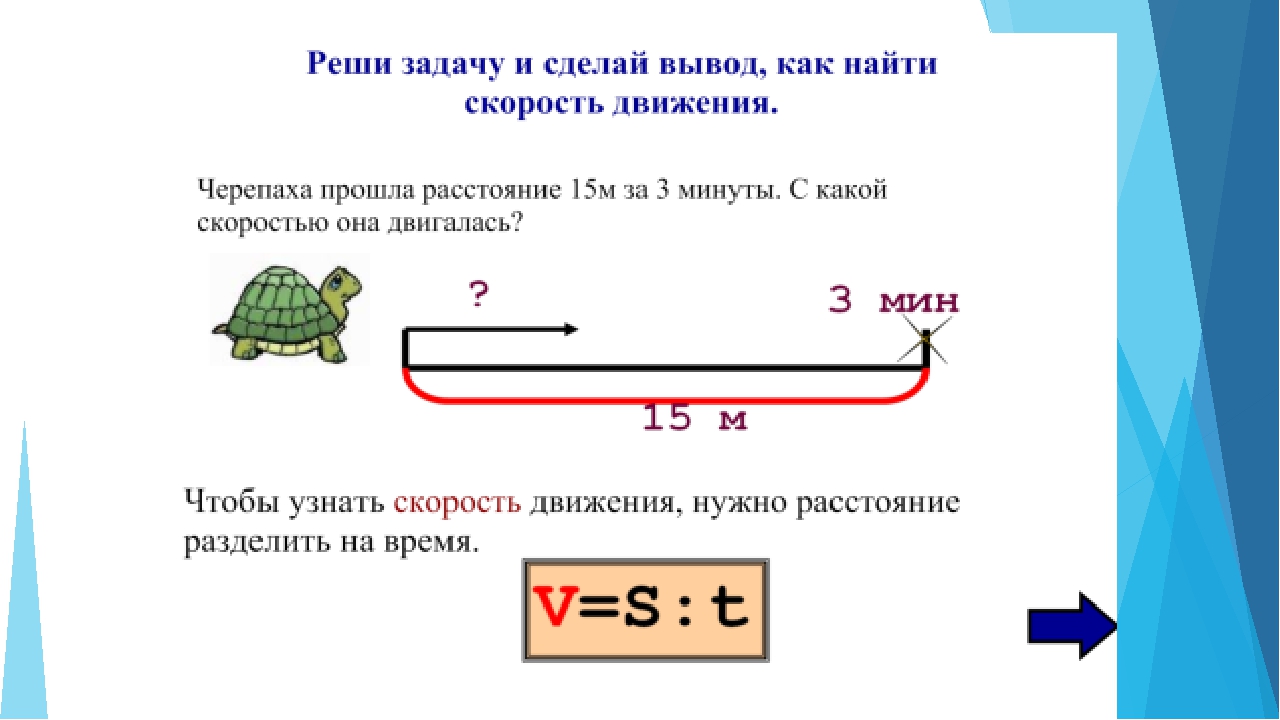 Люблю математику, потому что она логична и красива, она приносит удовольствие и развивает ум, ее нельзя переписать, например, как историю. Хочу, чтобы дети не боялись ее и полюбили, как я. Когда у ребенка начинает получаться, он становится счастливее. Сделать счастливее ваших детей — это моя главная задача!
Люблю математику, потому что она логична и красива, она приносит удовольствие и развивает ум, ее нельзя переписать, например, как историю. Хочу, чтобы дети не боялись ее и полюбили, как я. Когда у ребенка начинает получаться, он становится счастливее. Сделать счастливее ваших детей — это моя главная задача! А.С. Пушкина
А.С. Пушкина Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях!
Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях! Учитель первой категории. Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. Объясняю доступно, ясно, легко. Учитываю личность, характер ученика. К нахожу индивидуальный подход.
Учитель первой категории. Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. Объясняю доступно, ясно, легко. Учитываю личность, характер ученика. К нахожу индивидуальный подход.
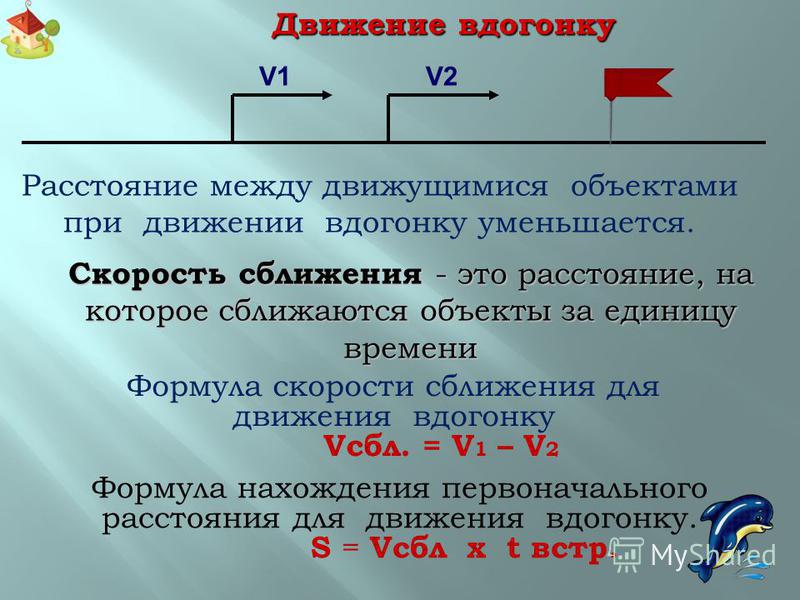


 {2}}-25 \right)\)
{2}}-25 \right)\) Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S. 
 Тогда мы получим время, за которое мы доедем до спортивной секции:
Тогда мы получим время, за которое мы доедем до спортивной секции: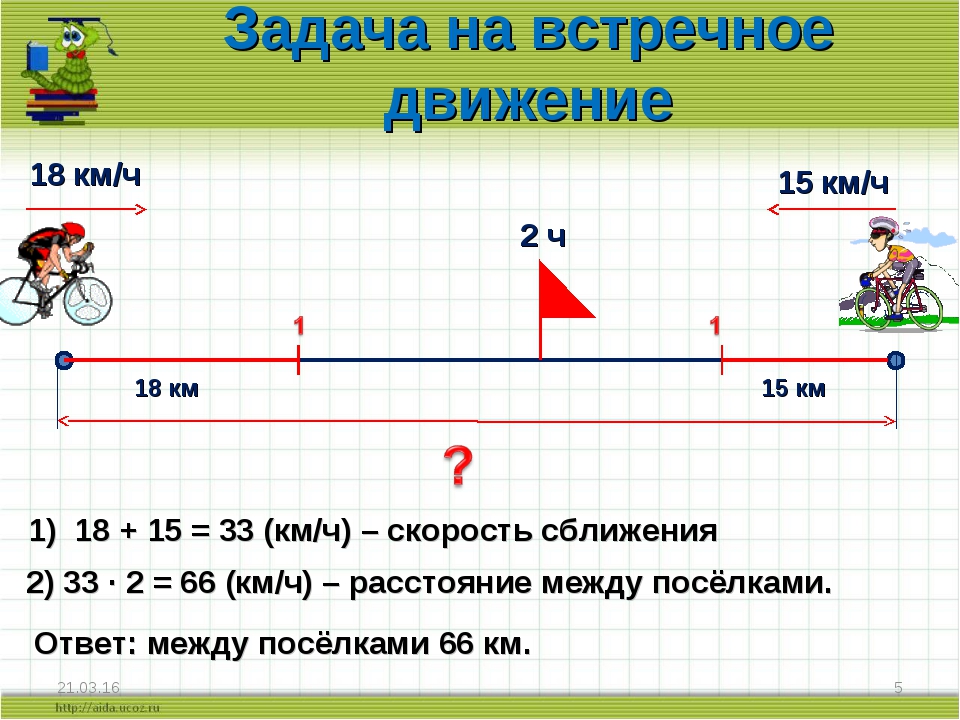 Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Школьник дошёл до этой школы за 8 минут. Какова была его скорость? Тогда мы получим время, за которое мы дойдём до спортивной секции:
Тогда мы получим время, за которое мы дойдём до спортивной секции: Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
 В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
 За три минуты он пройдёт в три раза больше, то есть 255 метров:
За три минуты он пройдёт в три раза больше, то есть 255 метров: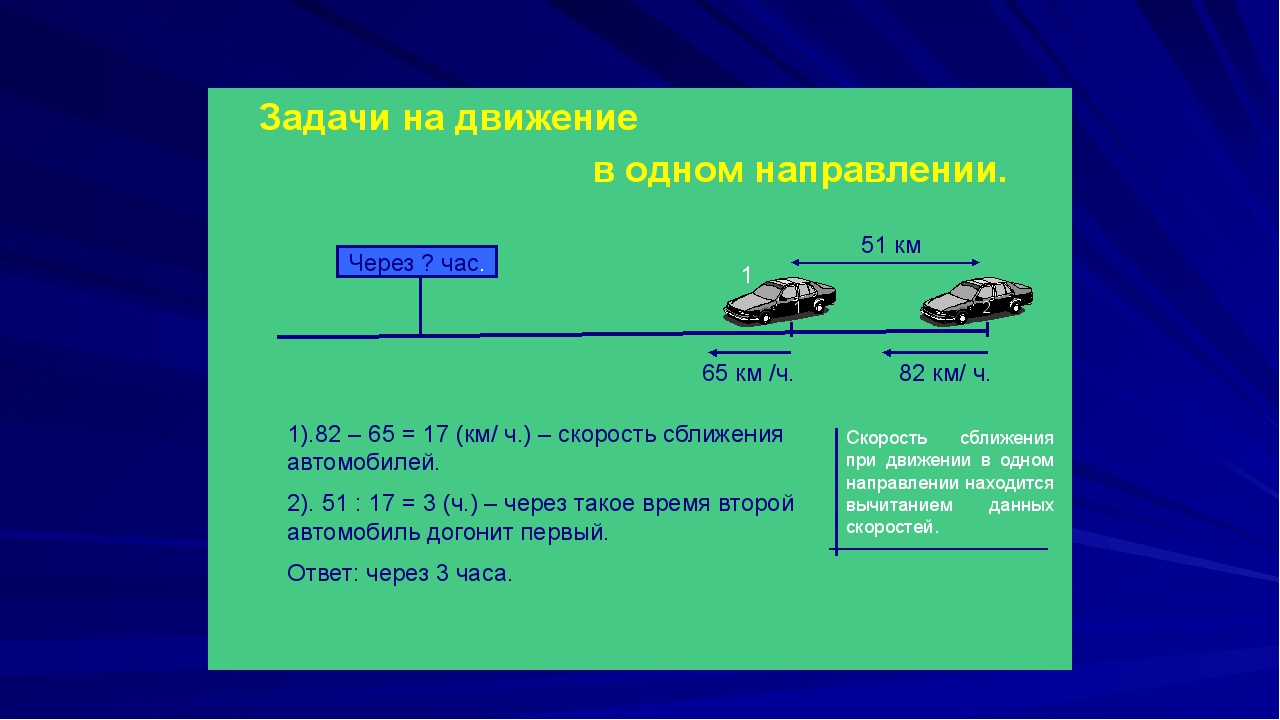 Это был наш ответ на первый вопрос задачи:
Это был наш ответ на первый вопрос задачи:
 Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?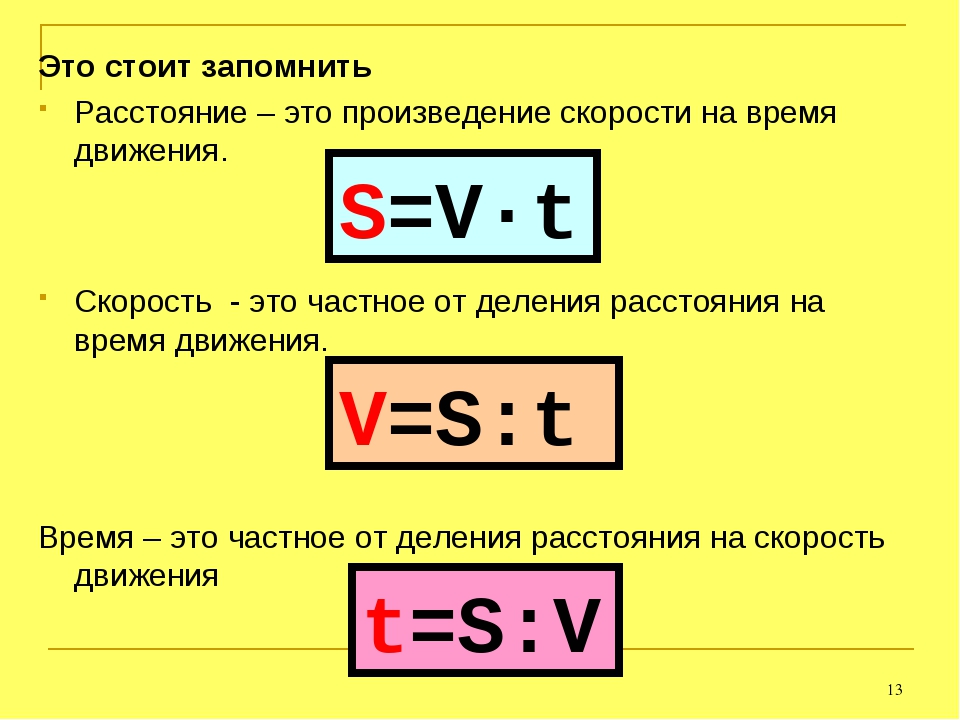 Главное — знать к ним подход.
Главное — знать к ним подход. А в школе в этот момент они «проходят» первообразные и интегралы 🙂
А в школе в этот момент они «проходят» первообразные и интегралы 🙂 Из этой формулы можно выразить скорость или время .
Из этой формулы можно выразить скорость или время .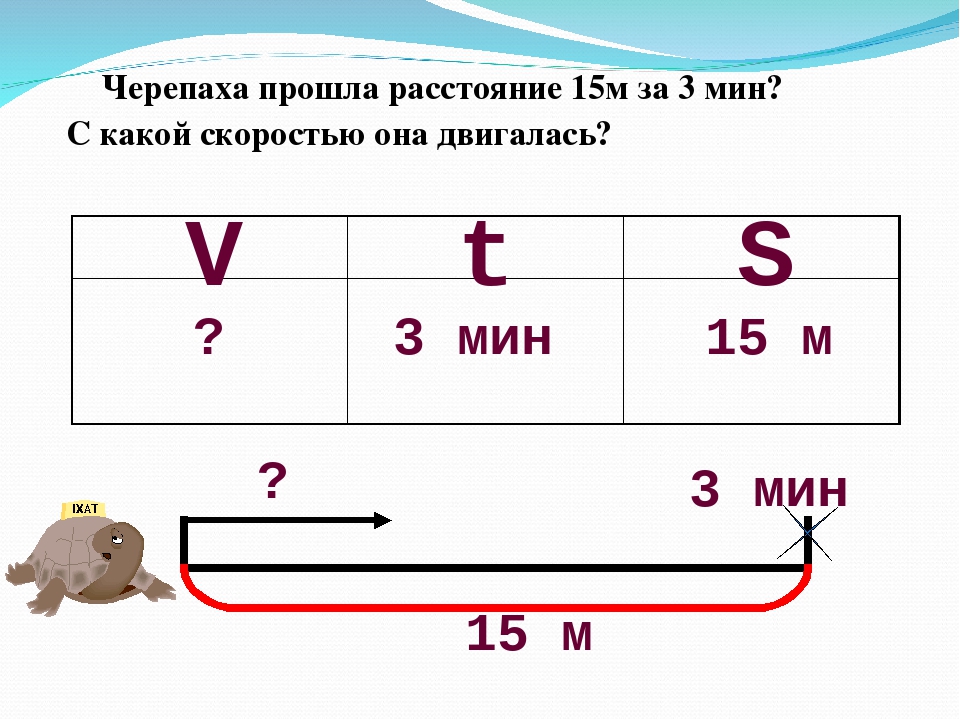
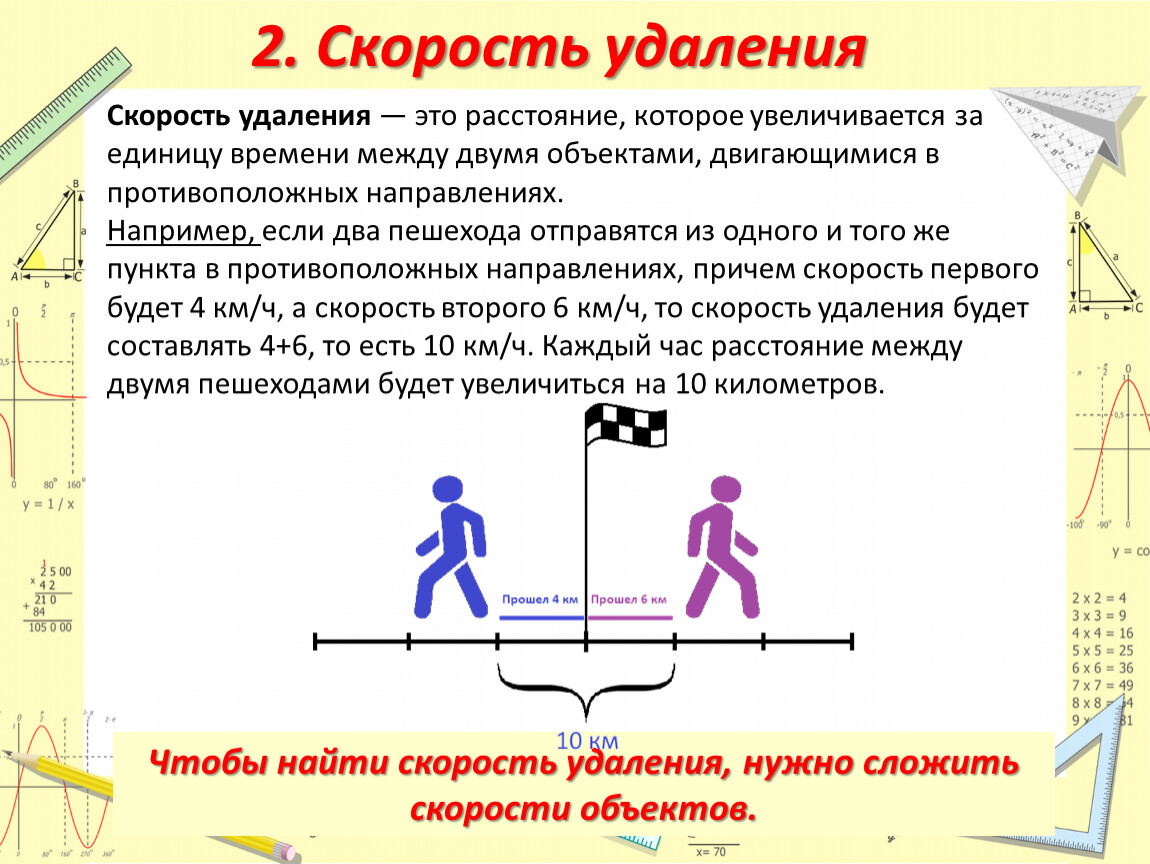 Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!


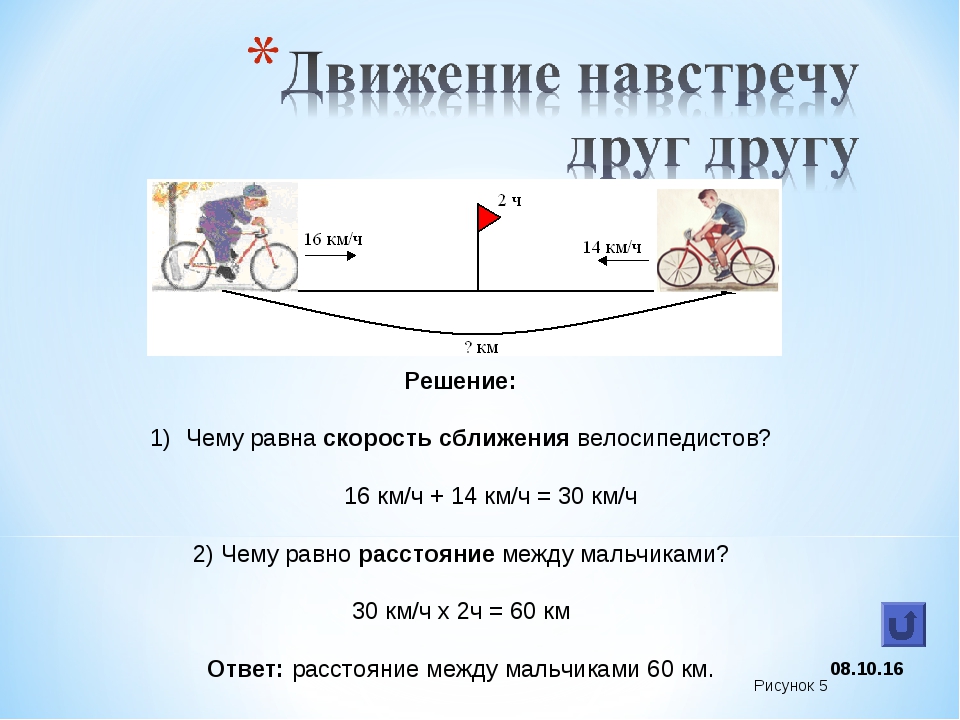
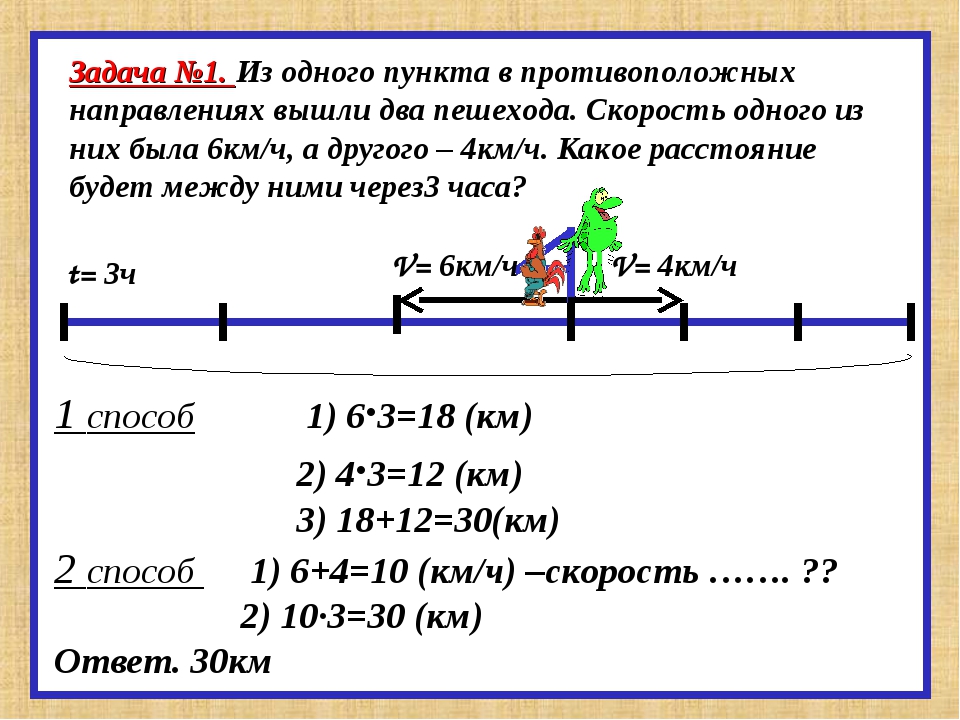 Расстояния — и туда, и обратно — равны км.
Расстояния — и туда, и обратно — равны км.
 Получим:
Получим: Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?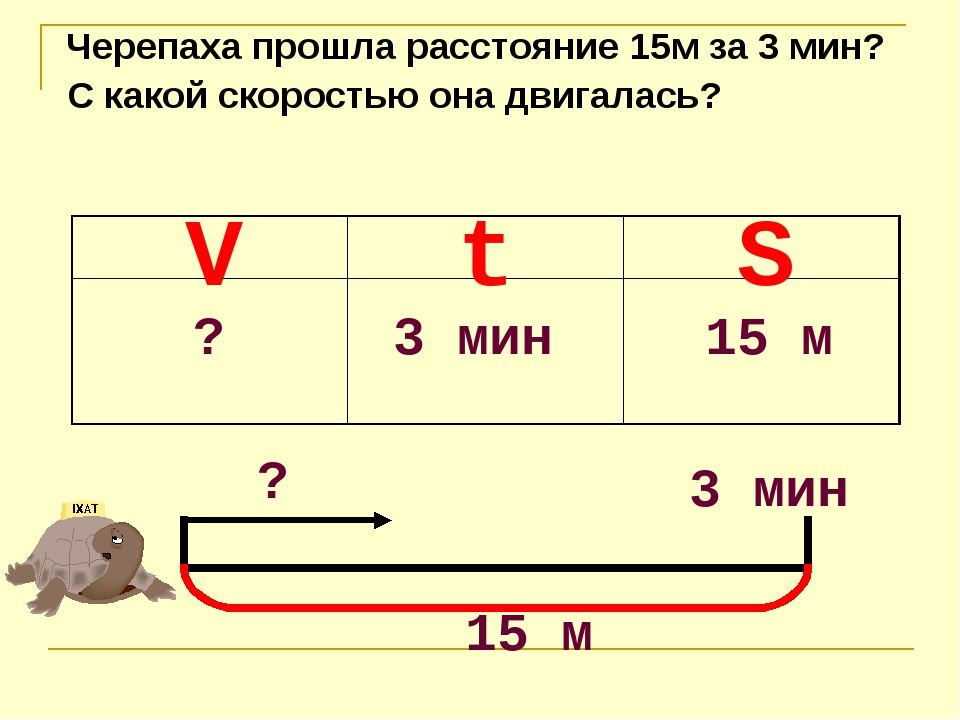
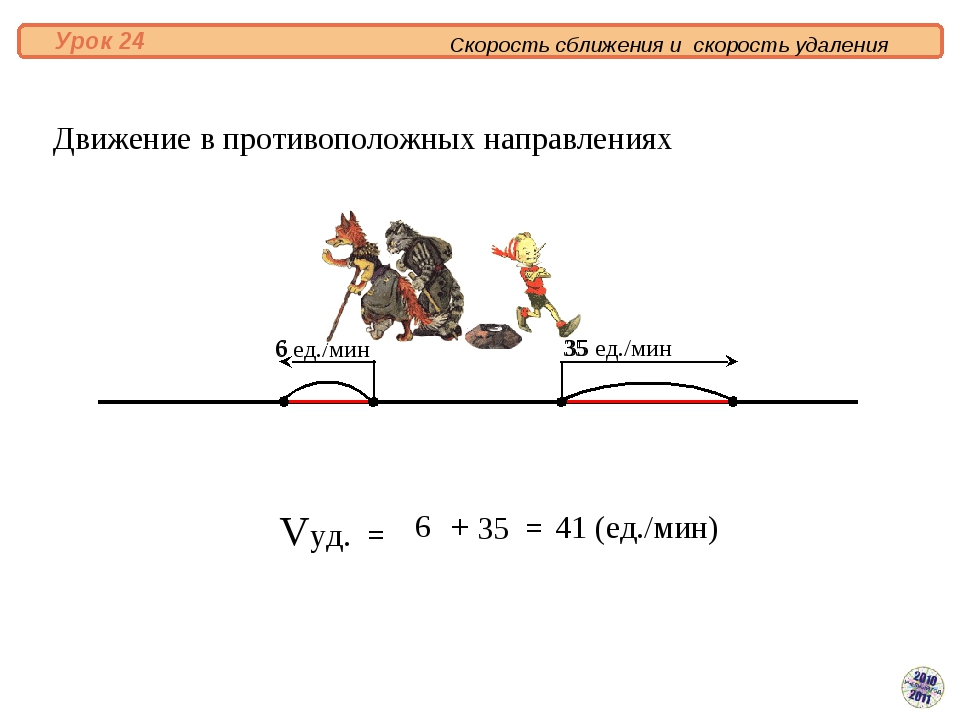

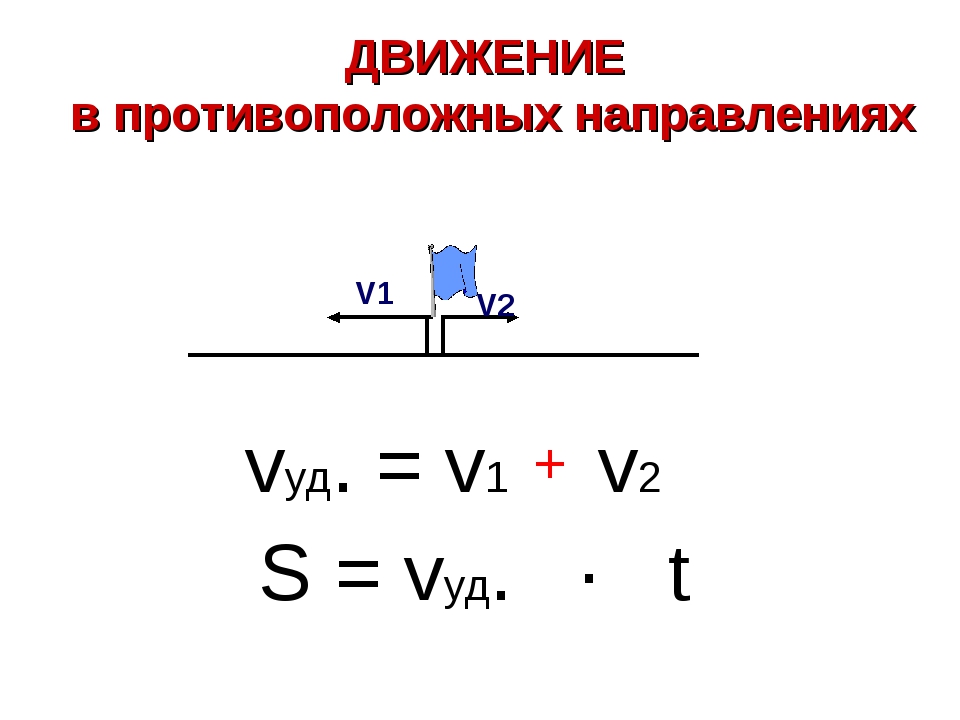
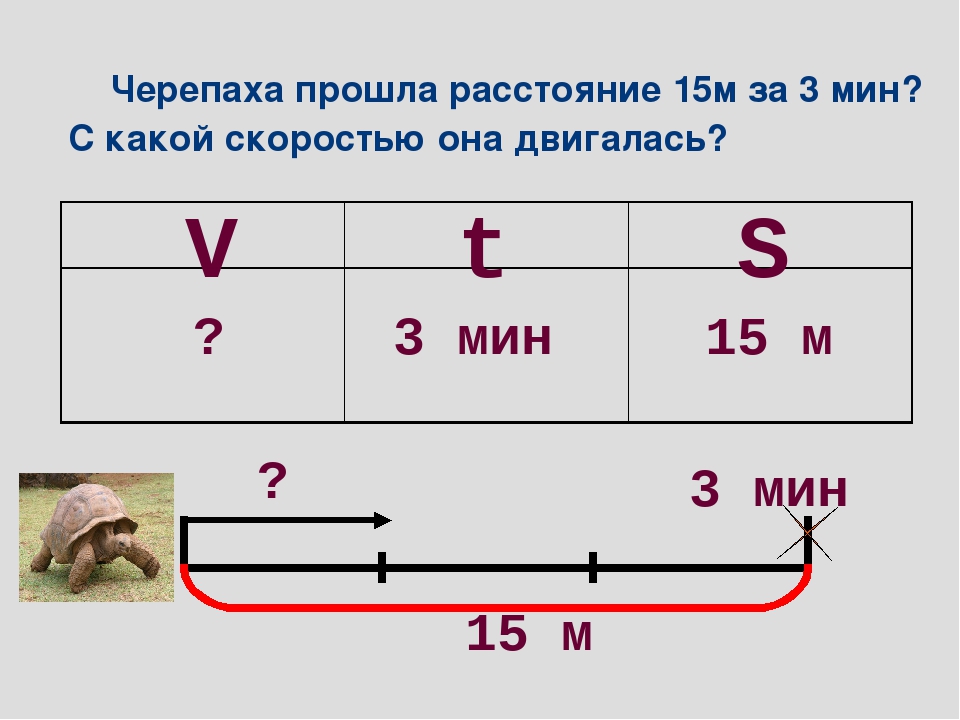 А что такое скорость сближения?
А что такое скорость сближения?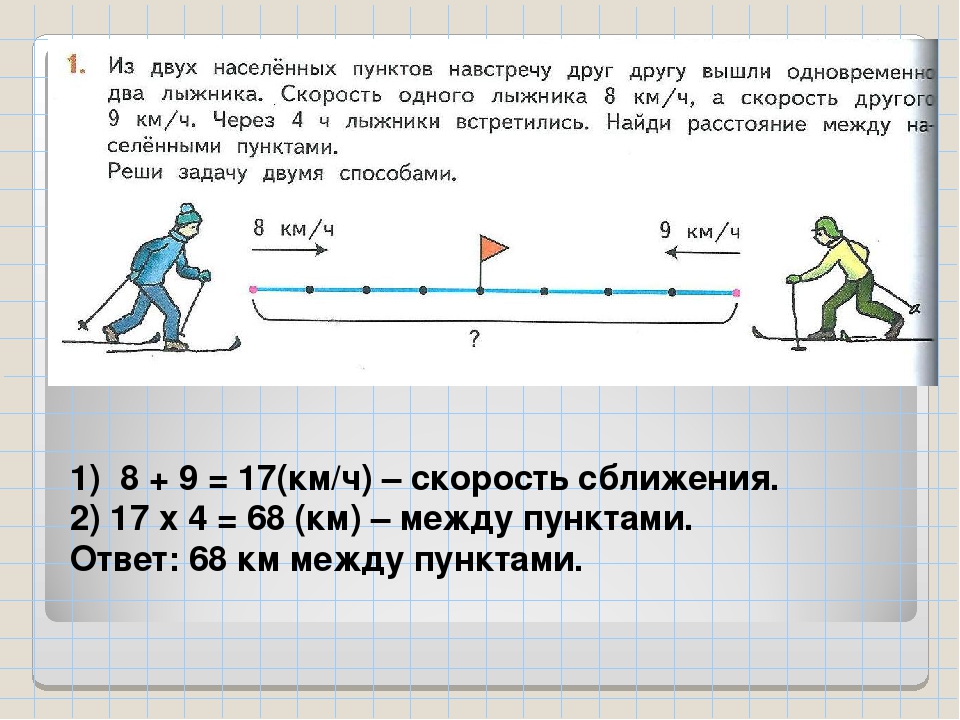
 Мы ведь знаем его скорость и время, которое он был
в пути. Чтобы узнать расстояние, мы скорость умножаем на время.
Мы ведь знаем его скорость и время, которое он был
в пути. Чтобы узнать расстояние, мы скорость умножаем на время.
 Как направлено центростремительное ускорение?
Как направлено центростремительное ускорение?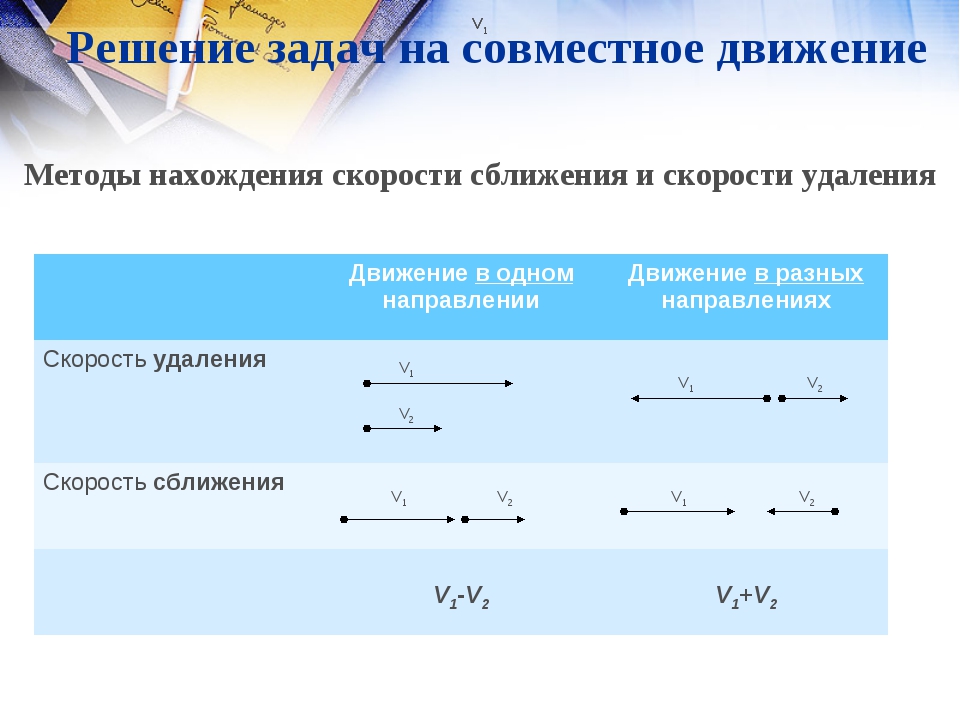 Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности. Какова линейная скорость тела?
Какова линейная скорость тела?
 2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.




 К тому же, достаточно часто отечественных медиков приглашают работать за границу, где им обычно предлагают выгодные условия труда и очень хорошую зарплату.
К тому же, достаточно часто отечественных медиков приглашают работать за границу, где им обычно предлагают выгодные условия труда и очень хорошую зарплату.
 /ТАСС/. Приемная кампания началась в колледжи Москвы, в этом году вырос спрос на медицинское направление. Об этом сообщила журналистам заместитель мэра столицы по вопросам социального развития Анастасия Ракова.
/ТАСС/. Приемная кампания началась в колледжи Москвы, в этом году вырос спрос на медицинское направление. Об этом сообщила журналистам заместитель мэра столицы по вопросам социального развития Анастасия Ракова. заявлений. Самой востребованной за первый месяц стала специальность «Сестринское дело» — на нее заявление подали почти 15 тыс. человек.
заявлений. Самой востребованной за первый месяц стала специальность «Сестринское дело» — на нее заявление подали почти 15 тыс. человек.

 Пациенты медицинских учреждений Республики Татарстан получают медицинский уход от бойцов студенческих медицинских отрядов. Слаженная работа и поддержка регионального Министерства здравоохранения и Министерства по делам молодежи обеспечила реализацию перспективного проекта – Окружной студенческий медицинский отряд «Доктор Зай», который был реализован второй раз в г. Заинск, на базе Заинской центральной районной больницы. В трудовом проекте приняли участие бойцы студенческих медицинских отрядов из 8 субъектов Приволжского федерального округа, которые работали в качестве младшего и среднего медицинского персонала.
Пациенты медицинских учреждений Республики Татарстан получают медицинский уход от бойцов студенческих медицинских отрядов. Слаженная работа и поддержка регионального Министерства здравоохранения и Министерства по делам молодежи обеспечила реализацию перспективного проекта – Окружной студенческий медицинский отряд «Доктор Зай», который был реализован второй раз в г. Заинск, на базе Заинской центральной районной больницы. В трудовом проекте приняли участие бойцы студенческих медицинских отрядов из 8 субъектов Приволжского федерального округа, которые работали в качестве младшего и среднего медицинского персонала. N 432 «Об особенностях реализации базовой программы обязательного медицинского страхования в условиях возникновения угрозы распространения заболеваний, вызванных новой коронавирусной инфекцией».
N 432 «Об особенностях реализации базовой программы обязательного медицинского страхования в условиях возникновения угрозы распространения заболеваний, вызванных новой коронавирусной инфекцией». 07.2019 №17-8/3065416-31880, подписанного заместителем директора Департамента Л.Е. Беляевой, срок действия учетной формы №057-у не урегулирован действующими нормативными актами.
07.2019 №17-8/3065416-31880, подписанного заместителем директора Департамента Л.Е. Беляевой, срок действия учетной формы №057-у не урегулирован действующими нормативными актами.

 Заявителем могут быть представлены документы (при наличии), подтверждающие доводы заявителя, либо их копии.
Заявителем могут быть представлены документы (при наличии), подтверждающие доводы заявителя, либо их копии.
 , д. 1, e‑mail:
, д. 1, e‑mail:  spb.ru.
spb.ru. ул., 19, Санкт‑Петербург, 197101, e‑mail:
ул., 19, Санкт‑Петербург, 197101, e‑mail: 
 (Подтверждено в апреле 2012 г.)
(Подтверждено в апреле 2012 г.) Частично они могут достичь этой цели, обеспечив лидерство в местных, региональных и государственных системах неотложной помощи и неотложной медицинской помощи посредством своего участия в обеспечении медицинского руководства, обучении поставщиков услуг, улучшении качества и защите законодательства.(Октябрь 2006 г.)
Частично они могут достичь этой цели, обеспечив лидерство в местных, региональных и государственных системах неотложной помощи и неотложной медицинской помощи посредством своего участия в обеспечении медицинского руководства, обучении поставщиков услуг, улучшении качества и защите законодательства.(Октябрь 2006 г.) (По состоянию на ноябрь 2013 г.)
(По состоянию на ноябрь 2013 г.) и сообщество EMS в целом.В нем также обсуждаются рекомендации по образованию, производительности и опыту медицинского директора, чтобы обеспечить качество, безопасность и рентабельность ухода за пациентами. (Декабрь 2002 г.)
и сообщество EMS в целом.В нем также обсуждаются рекомендации по образованию, производительности и опыту медицинского директора, чтобы обеспечить качество, безопасность и рентабельность ухода за пациентами. (Декабрь 2002 г.) Предполагается, что медицинский директор скорой помощи штата обеспечивает медицинские аспекты руководства, надзора, координации, доступа к передовым методам, управления качеством системы и исследованиями, чтобы обеспечить наилучшее возможное функционирование скорой помощи для пациентов.(2008)
Предполагается, что медицинский директор скорой помощи штата обеспечивает медицинские аспекты руководства, надзора, координации, доступа к передовым методам, управления качеством системы и исследованиями, чтобы обеспечить наилучшее возможное функционирование скорой помощи для пациентов.(2008) руководящих принципов (EBG) и проекта национального модельного процесса EBG (Приложение A) для разработки, внедрения и оценки руководящих принципов EMS.
руководящих принципов (EBG) и проекта национального модельного процесса EBG (Приложение A) для разработки, внедрения и оценки руководящих принципов EMS. В этой публикации НАБДД подробно описывает прогресс (Приложение A) проекта с сообществом EMS. (Январь 2013 г.)
В этой публикации НАБДД подробно описывает прогресс (Приложение A) проекта с сообществом EMS. (Январь 2013 г.) ) Центры были выбраны в качестве базовых станций, потому что они соответствовали двум основным критериям: каждый из них обозначен как специализированный педиатрический центр, и каждый из них обеспечивает круглосуточное обслуживание лечащих врачей педиатрической службы неотложной медицинской помощи (PEM), имеющих право на прием или на борт. Две педиатрические базовые станции также служат консультационными центрами для государственных больниц.
) Центры были выбраны в качестве базовых станций, потому что они соответствовали двум основным критериям: каждый из них обозначен как специализированный педиатрический центр, и каждый из них обеспечивает круглосуточное обслуживание лечащих врачей педиатрической службы неотложной медицинской помощи (PEM), имеющих право на прием или на борт. Две педиатрические базовые станции также служат консультационными центрами для государственных больниц. Изменения протокола происходят ежегодно 1 июля. Все люди, использующие радиосвязь базовой станции (скорая помощь, врачи и медсестры), должны пройти курс обновления протокола лично, в Интернете или на DVD.Медицинское руководство в режиме онлайн для детей может быть предоставлено одновременно как базовой педиатрической станцией, так и одной из местных базовых станций или ближайшим травматологическим центром для взрослых — все они следуют одним и тем же протоколам.
Изменения протокола происходят ежегодно 1 июля. Все люди, использующие радиосвязь базовой станции (скорая помощь, врачи и медсестры), должны пройти курс обновления протокола лично, в Интернете или на DVD.Медицинское руководство в режиме онлайн для детей может быть предоставлено одновременно как базовой педиатрической станцией, так и одной из местных базовых станций или ближайшим травматологическим центром для взрослых — все они следуют одним и тем же протоколам.
 Это руководство предоставит обзор медицинского направления для агентств скорой медицинской помощи в Айдахо и послужит введением в эту важную роль в сфере здравоохранения. (2012)
Это руководство предоставит обзор медицинского направления для агентств скорой медицинской помощи в Айдахо и послужит введением в эту важную роль в сфере здравоохранения. (2012) Этот раздел веб-сайта Департамента здравоохранения штата Нью-Йорк помогает агентствам скорой медицинской помощи и медицинским директорам врачей понять направление лечения пациентов любого возраста.Он определяет роли и обязанности службы, медицинского директора службы, Регионального совета скорой помощи и Регионального консультативного комитета по неотложной медицинской помощи (REMAC) в отношении этой темы. (Март 2011 г.)
Этот раздел веб-сайта Департамента здравоохранения штата Нью-Йорк помогает агентствам скорой медицинской помощи и медицинским директорам врачей понять направление лечения пациентов любого возраста.Он определяет роли и обязанности службы, медицинского директора службы, Регионального совета скорой помощи и Регионального консультативного комитета по неотложной медицинской помощи (REMAC) в отношении этой темы. (Март 2011 г.) Система медицинского управления EMS состоит из следующих компонентов: государственный медицинский директор, региональные медицинские директора, государственный комитет по интенсивной терапии, онлайн-система медицинского управления, региональные медицинские командные центры и разработка сферы деятельности. (По состоянию на ноябрь 2013 г.)
Система медицинского управления EMS состоит из следующих компонентов: государственный медицинский директор, региональные медицинские директора, государственный комитет по интенсивной терапии, онлайн-система медицинского управления, региональные медицинские командные центры и разработка сферы деятельности. (По состоянию на ноябрь 2013 г.) Только глубоко, раздувая рёбра, вздохнул, когда почувствовал подпруги (И. Бунин. Последнее свидание).
Только глубоко, раздувая рёбра, вздохнул, когда почувствовал подпруги (И. Бунин. Последнее свидание). Потом она обернулась к другой сестре, Татьяне Аркадьевне, около которой возилась на полу модистка, подмётывая на живую нитку низ голубой юбки (А. Куприн. Тапёр).
Потом она обернулась к другой сестре, Татьяне Аркадьевне, около которой возилась на полу модистка, подмётывая на живую нитку низ голубой юбки (А. Куприн. Тапёр). Куприн. В цирке)
Куприн. В цирке) Бунин. Солнечный удар)
Бунин. Солнечный удар) Антонимы. Омонимы
Правописание -Н- и -НН- в различных частях речи
Правописание личных окончаний глаголов и суффиксов причастий
Знаки препинания в сложном предложении с разными видами связи
Знаки препинания в простом осложненном предложении
Правописание НЕ и НИ
Как писать сочинения
Правописание корней
Слитное и раздельное написание НЕ с различными частями речи
Грамматические нормы (синтаксические нормы)
Слитное, дефисное, раздельное написание слов различных частей речи
Пунктуация в простом и сложном предложениях
Правописание суффиксов различных частей речи (кроме -Н-/-НН-)
Знаки препинания в предложениях со словами и конструкциями, грамматически не связанными с членами предложения
Лексическое значение слова
Знаки препинания в сложноподчиненном предложении
Анализ средств выразительности
Пунктуационный анализ
Информационная обработка текстов различных стилей и жанров
Средства связи предложений в тексте
Часть С.
Антонимы. Омонимы
Правописание -Н- и -НН- в различных частях речи
Правописание личных окончаний глаголов и суффиксов причастий
Знаки препинания в сложном предложении с разными видами связи
Знаки препинания в простом осложненном предложении
Правописание НЕ и НИ
Как писать сочинения
Правописание корней
Слитное и раздельное написание НЕ с различными частями речи
Грамматические нормы (синтаксические нормы)
Слитное, дефисное, раздельное написание слов различных частей речи
Пунктуация в простом и сложном предложениях
Правописание суффиксов различных частей речи (кроме -Н-/-НН-)
Знаки препинания в предложениях со словами и конструкциями, грамматически не связанными с членами предложения
Лексическое значение слова
Знаки препинания в сложноподчиненном предложении
Анализ средств выразительности
Пунктуационный анализ
Информационная обработка текстов различных стилей и жанров
Средства связи предложений в тексте
Часть С. Информационная обработка текстов различных стилей и жанров. Создание текстов различных стилей и функционально-смысловых типов речи
Лексическое значение слова (часть Б)
Текст как речевое произведение. Смысловая и композиционная целостность текста
Стили и функционально-смысловые типы речи
Фразеологические обороты
Средства связи предложений в тексте
Группы слов по происхождению и употреблению
Информационная обработка текстов различных стилей и жанров. Создание текстов различных стилей и функционально-смысловых типов речи
Лексическое значение слова (часть Б)
Текст как речевое произведение. Смысловая и композиционная целостность текста
Стили и функционально-смысловые типы речи
Фразеологические обороты
Средства связи предложений в тексте
Группы слов по происхождению и употреблению
 Он хотел еще раз увидеть Ольгу, увидеть ее глаза и каштановые волосы.
Он хотел еще раз увидеть Ольгу, увидеть ее глаза и каштановые волосы. Пригрело лучами солнца.
Пригрело лучами солнца.
 Выявление языковых приёмов связи предложений в текстеТема. Работа с текстом. Выявление языковых приёмов
Выявление языковых приёмов связи предложений в текстеТема. Работа с текстом. Выявление языковых приёмов Каждое следующее предложение строится на базе предыдущего.
Каждое следующее предложение строится на базе предыдущего.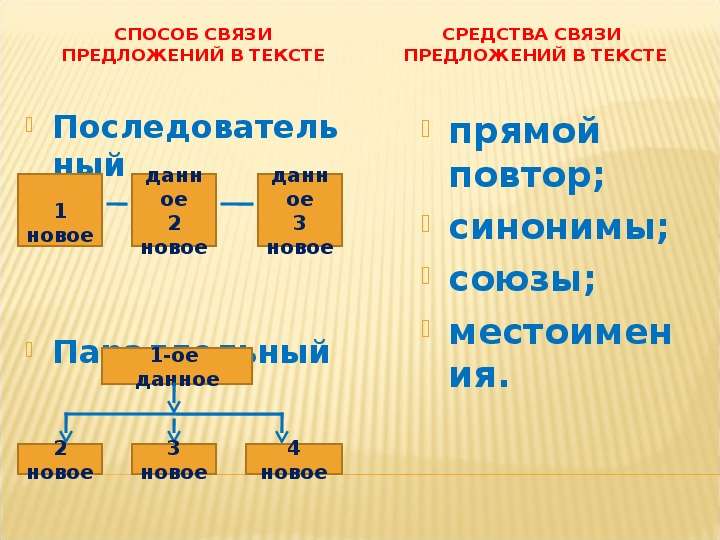 В лесах попадались большие луговины и глухие озёра с огромными старыми соснами по берегам. Сосны всё время тихонько шумели. (Ю.Казаков)
В лесах попадались большие луговины и глухие озёра с огромными старыми соснами по берегам. Сосны всё время тихонько шумели. (Ю.Казаков)
 Подруг у неё не было: изо всех девиц, посещавших дом Страховых, она не сошлась ни с одной.)
Подруг у неё не было: изо всех девиц, посещавших дом Страховых, она не сошлась ни с одной.)  (В самом конце 80-х годов в нём запретили ловить рыбу. Не для того, чтобы сберечь её стадо, дать нагуляться молоди… А потому, что выловленная рыба стала опасной для человека.)
(В самом конце 80-х годов в нём запретили ловить рыбу. Не для того, чтобы сберечь её стадо, дать нагуляться молоди… А потому, что выловленная рыба стала опасной для человека.)  Лёд в ледниках содержит мало примесей, при таянии из него получается самая чистая вода. Поэтому сейчас её всё чаще используют в лечебных целях.
Лёд в ледниках содержит мало примесей, при таянии из него получается самая чистая вода. Поэтому сейчас её всё чаще используют в лечебных целях.  Для объединения предложений в грамотный и понятный текст авторы применяют два ее вида — цепную и параллельную. Первый случай подразумевает связь новых предложений со старыми, образуя звенья одной цепи. Во параллельном случае кажется, будто конструкции не имеют связи, однако они все же выстроены вокруг единого общего тезиса. Правило использования каждого из случаев следует разобрать подробнее.
Для объединения предложений в грамотный и понятный текст авторы применяют два ее вида — цепную и параллельную. Первый случай подразумевает связь новых предложений со старыми, образуя звенья одной цепи. Во параллельном случае кажется, будто конструкции не имеют связи, однако они все же выстроены вокруг единого общего тезиса. Правило использования каждого из случаев следует разобрать подробнее.
 Этот повтор позволяет связывать оба высказывания и постепенно развивать мысль.
Этот повтор позволяет связывать оба высказывания и постепенно развивать мысль.
 В конструкции должны повторяться некоторые элементы предшествующего предложения: На веточке дикой яблони сидела стая синиц. Увидев меня, синицы встревоженно зачирикали.
В конструкции должны повторяться некоторые элементы предшествующего предложения: На веточке дикой яблони сидела стая синиц. Увидев меня, синицы встревоженно зачирикали. Деревня начала просыпаться. Послышались голоса людей и лай собак. Уличные фонари погасли и открылись магазины.
Деревня начала просыпаться. Послышались голоса людей и лай собак. Уличные фонари погасли и открылись магазины.
 По утрам он хочет есть и будит весь дом. Не пройдет и дня, чтобы он не погонял кур по двору и нашего энергичного кота Бориса. Однако я его все равно очень люблю.
По утрам он хочет есть и будит весь дом. Не пройдет и дня, чтобы он не погонял кур по двору и нашего энергичного кота Бориса. Однако я его все равно очень люблю.
 К примеру, для описания местности или помещения выбирается централизованная связь, а о том, что случилось за день — цепная.
К примеру, для описания местности или помещения выбирается централизованная связь, а о том, что случилось за день — цепная.
 Мороженое таяло и текло по руке.
Мороженое таяло и текло по руке.
 Ударили сильные морозы. Деревья покрылись белоснежным снегом.
Ударили сильные морозы. Деревья покрылись белоснежным снегом.
 Никогда не забыть, как она чуть не попрощалась с жизнью.
Никогда не забыть, как она чуть не попрощалась с жизнью.
 Это больше зависит от целей произведения и его стиля.
Это больше зависит от целей произведения и его стиля.

 Стара-Загора, 226А
Стара-Загора, 226А Основной целью данного направления является: раскрытие творческих способностей обучающихся, нравственное и художественно-эстетическое развитие личности ребёнка. Художественная направленность включает следующие группы программ: исполнительство на струнных, народных, духовых, клавишных, ударных инструментах, оркестры и ансамбли, сольный вокал, хоровое пение, эстрадно-джазовое творчество, театральное творчество, цирковое искусство, хореографическое искусство, художественное слово, литературное творчество, изобразительное искусство, декоративно-прикладное творчество, дизайн.
Основной целью данного направления является: раскрытие творческих способностей обучающихся, нравственное и художественно-эстетическое развитие личности ребёнка. Художественная направленность включает следующие группы программ: исполнительство на струнных, народных, духовых, клавишных, ударных инструментах, оркестры и ансамбли, сольный вокал, хоровое пение, эстрадно-джазовое творчество, театральное творчество, цирковое искусство, хореографическое искусство, художественное слово, литературное творчество, изобразительное искусство, декоративно-прикладное творчество, дизайн. ), производственные технологии (радиоэлектроника, технический дизайн, эргономика и др.), мультимедиа и IT-технологии (технологии киноискусства, фототехнологии, программирование и WEB- дизайн и др.), техническое творчество и инновационное предпринимательство (инновационные бизнес технологии, проектная деятельность, исследовательская деятельность).
), производственные технологии (радиоэлектроника, технический дизайн, эргономика и др.), мультимедиа и IT-технологии (технологии киноискусства, фототехнологии, программирование и WEB- дизайн и др.), техническое творчество и инновационное предпринимательство (инновационные бизнес технологии, проектная деятельность, исследовательская деятельность). Эколого-биологическая направленность включает следующие группы программ: основы и углубленное изучение экологии и биологии (общая экология, современные экологические проблемы, ботаника и др.), прикладные эколого-биологические программы (аквариумистика, охрана природы, растениеводство и др.).
Эколого-биологическая направленность включает следующие группы программ: основы и углубленное изучение экологии и биологии (общая экология, современные экологические проблемы, ботаника и др.), прикладные эколого-биологические программы (аквариумистика, охрана природы, растениеводство и др.). А для этого важно сформировать опыт проживания в социальной системе, очертить профессиональные перспективы. Образовательные программы данной направленности охватывают широкий возрастной диапазон и многофункциональны по своему назначению.
А для этого важно сформировать опыт проживания в социальной системе, очертить профессиональные перспективы. Образовательные программы данной направленности охватывают широкий возрастной диапазон и многофункциональны по своему назначению. Физкультурно-спортивная направленность включает следующие группы программ: спортивная подготовка (спортивная акробатика, бадминтон, гандбол, художественная гимнастика, плавание, хоккей, футбол, шашки, фехтование, различные виды борьбы и другие виды спорта), общая физическая подготовка и лечебная физкультура (фитнес-аэробика, йога, лечебная физкультура, ритмическая гимнастика и др.)
Физкультурно-спортивная направленность включает следующие группы программ: спортивная подготовка (спортивная акробатика, бадминтон, гандбол, художественная гимнастика, плавание, хоккей, футбол, шашки, фехтование, различные виды борьбы и другие виды спорта), общая физическая подготовка и лечебная физкультура (фитнес-аэробика, йога, лечебная физкультура, ритмическая гимнастика и др.) гр УУ
гр УУ  5А, кабинет № 104
5А, кабинет № 104
 ..
..
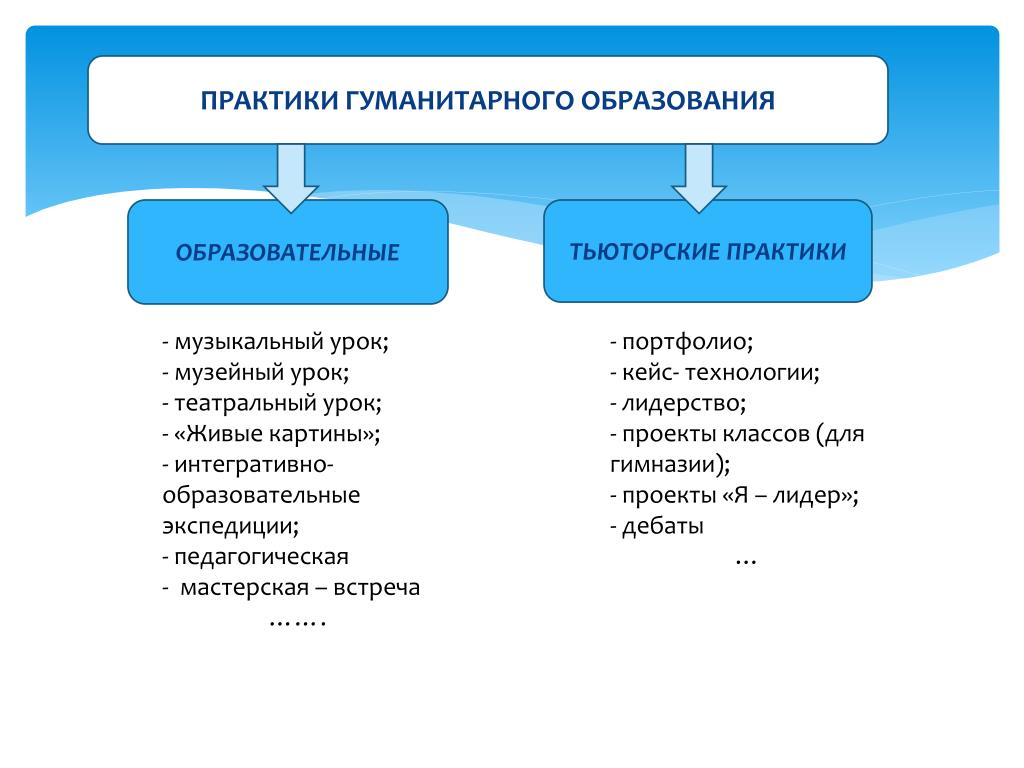 В сентябре 2011 года на Городском слете ЮИД ребята заняли I место в конкурсе «КВН» и VI место в конкурсе «Стенгазета». В городском Финале детско-юношеских соревнований юных инспекторов движения «Безопасное колесо-2012», команда учащихся объединения в упорной борьбе завоевала III место! В Финале регионального этапа Всероссийского конкурса юных инспекторов движения «Безопасное колесо-2013», «Безопасное колесо — 2014», «Безопасное колесо -2015», «Безопасное колесо — 2016» — снова призовые место!
В сентябре 2011 года на Городском слете ЮИД ребята заняли I место в конкурсе «КВН» и VI место в конкурсе «Стенгазета». В городском Финале детско-юношеских соревнований юных инспекторов движения «Безопасное колесо-2012», команда учащихся объединения в упорной борьбе завоевала III место! В Финале регионального этапа Всероссийского конкурса юных инспекторов движения «Безопасное колесо-2013», «Безопасное колесо — 2014», «Безопасное колесо -2015», «Безопасное колесо — 2016» — снова призовые место!

 Детство — время активного социального «развертывания» растущего человека и освоения им социокультурных достижений и ценностей, период пробы и самоопределения в постоянно расширяющихся и усложняющихся контактах. Ждем Вас в нашем кружке «Мастерская творческих дел» — встречи проходят на площадке № 1 нашей школы.
Детство — время активного социального «развертывания» растущего человека и освоения им социокультурных достижений и ценностей, период пробы и самоопределения в постоянно расширяющихся и усложняющихся контактах. Ждем Вас в нашем кружке «Мастерская творческих дел» — встречи проходят на площадке № 1 нашей школы.
 Правомерным можно считать мнение В.Л.
Кургузова о том, что гуманитарная среда (ГС) – это сознательно
сформированная гуманитарная направленность учебных программ и
конкретных дисциплин, представляющих единство материальных и духовных
факторов, способствующих формированию личности [5,21]. Кроме того,
как отмечает Л.Е. Сараскина, ГС – это образовательное
пространство, в котором используются активные методы обучения,
способствующие усвоению концепции целеполагания и формирования
механизмов ее активной реализации [7,152]. Также, Р.М. Петрунева
определяет ГС как совокупность «организационных структур,
педагогических технологий и административных действий по созданию
условий для реализации задач гуманитаризации образования»
[6,13].
Правомерным можно считать мнение В.Л.
Кургузова о том, что гуманитарная среда (ГС) – это сознательно
сформированная гуманитарная направленность учебных программ и
конкретных дисциплин, представляющих единство материальных и духовных
факторов, способствующих формированию личности [5,21]. Кроме того,
как отмечает Л.Е. Сараскина, ГС – это образовательное
пространство, в котором используются активные методы обучения,
способствующие усвоению концепции целеполагания и формирования
механизмов ее активной реализации [7,152]. Также, Р.М. Петрунева
определяет ГС как совокупность «организационных структур,
педагогических технологий и административных действий по созданию
условий для реализации задач гуманитаризации образования»
[6,13].
 Данные условия, по словам Л.
Г. Викторовой и Л. В. Петровой, предполагают использование
исторического опыта, культурных традиций, достижений мировой науки и
техники [2,11], что, на наш взгляд, должно быть отражено при
построении содержания обучения и организации образовательного
процесса в технических вузах.
Данные условия, по словам Л.
Г. Викторовой и Л. В. Петровой, предполагают использование
исторического опыта, культурных традиций, достижений мировой науки и
техники [2,11], что, на наш взгляд, должно быть отражено при
построении содержания обучения и организации образовательного
процесса в технических вузах. Их основной задачей
является создание комфортной атмосферы для получения знаний, развития
умений и навыков, формирования различных качеств личности будущих
специалистов.
Их основной задачей
является создание комфортной атмосферы для получения знаний, развития
умений и навыков, формирования различных качеств личности будущих
специалистов.

 С нашей точки зрения, данная классификация не
полностью отражает структуру ГС вуза и не раскрывает её особенности.
Её автор рассматривает составляющие ГС только с позиции формирования
качеств личности, необходимых современному специалисту, забывая о
том, что понятие ГС гораздо шире, так как включает в себя бóльшее
количество элементов, функционирующих как единое целое.
С нашей точки зрения, данная классификация не
полностью отражает структуру ГС вуза и не раскрывает её особенности.
Её автор рассматривает составляющие ГС только с позиции формирования
качеств личности, необходимых современному специалисту, забывая о
том, что понятие ГС гораздо шире, так как включает в себя бóльшее
количество элементов, функционирующих как единое целое.

 3. Приведите пример трех физических явлений и напишите их признаки.
3. Приведите пример трех физических явлений и напишите их признаки.
 Известно, что марганец в организме ускоряет образование антител, нейтрализующих вредное воздействие чужеродных белков. Так, внутривенным вливанием соли, содержащей марганец, удается спасти человека, укушенного каракуртом — ядовитейшим из среднеазиатских пауков. Установите формулу соли марганца по следующим данным: m(K) : m(Mn) : m(O) = 32 : 55 : 64. Задание 6
Требования к оформлению и решению задач по химии
Заполните таблицу по примеру:
Явление Вид явления (химическое или физическое) Объяснение
Испарение воды Физическое Т.к. в ходе данного явления не происходит образования новых химических веществ, а изменяется только агрегатное состояние вещества. Явление Вид явления (химическое или физическое) Объяснение
Выпаривание воды из раствора соли
Засахаривание варенья
Распространение запаха духов
Горение свечи
Пожелтение листьев осенью
Фотосинтез Задание 7
Требования к оформлению и решению задач по химии
Опишите химические явления по плану:
А) условия начала реакции;
Б) условия течения реакции;
В) признаки реакции.
Известно, что марганец в организме ускоряет образование антител, нейтрализующих вредное воздействие чужеродных белков. Так, внутривенным вливанием соли, содержащей марганец, удается спасти человека, укушенного каракуртом — ядовитейшим из среднеазиатских пауков. Установите формулу соли марганца по следующим данным: m(K) : m(Mn) : m(O) = 32 : 55 : 64. Задание 6
Требования к оформлению и решению задач по химии
Заполните таблицу по примеру:
Явление Вид явления (химическое или физическое) Объяснение
Испарение воды Физическое Т.к. в ходе данного явления не происходит образования новых химических веществ, а изменяется только агрегатное состояние вещества. Явление Вид явления (химическое или физическое) Объяснение
Выпаривание воды из раствора соли
Засахаривание варенья
Распространение запаха духов
Горение свечи
Пожелтение листьев осенью
Фотосинтез Задание 7
Требования к оформлению и решению задач по химии
Опишите химические явления по плану:
А) условия начала реакции;
Б) условия течения реакции;
В) признаки реакции. Химическое явление Условия начала реакции Условия течения реакции Признаки реакции
Горение древесины
Разложение воды под действием электрического тока
Реакция железа с соляной кислотой
Взаимодействие уксуса с содой Задание 8
Укажите, на каких явлениях — физических или химических — основаны известные методы разделения и очистки веществ.
Метод разделения и очистки веществ Выпаривание Отстаивание Дистилляция Фильтрование Кристаллизация
На каком явлении основан Задание 9
Требования к оформлению и решению задач по химии
При хранении на воздухе серы и молока появляется запах, тогда как у свежих этих веществ его практически нет. Предположите для каждого случая, какие вещества — более простые, чем исходное, или более сложные — образуются. Поясните свой выбор. Атомы золота и серебра отличаются:
• тем, что имеют разные размеры
• наличием ядра и электронов
• цветом
• наличием электрического заряда Молекулы азота сходны с молекулами аммиака _______. • температурой плавления
• тем, что состоят из ядра и электронов
• своим составом
• способностью существовать самостоятельно Можно сказать:
• молекула железа
• атом парафина
• атом водорода
• молекула сахара Молекулу можно охарактеризовать: — температурой плавления
— количественным составом
Выбери общие характеристики для 1 молекулы азота и 1 г азота:
• температура кипения
• вкус
• взаимодействие с теми же веществами
• состав Установи соответствие между частицами и их характеристиками: 1.
Химическое явление Условия начала реакции Условия течения реакции Признаки реакции
Горение древесины
Разложение воды под действием электрического тока
Реакция железа с соляной кислотой
Взаимодействие уксуса с содой Задание 8
Укажите, на каких явлениях — физических или химических — основаны известные методы разделения и очистки веществ.
Метод разделения и очистки веществ Выпаривание Отстаивание Дистилляция Фильтрование Кристаллизация
На каком явлении основан Задание 9
Требования к оформлению и решению задач по химии
При хранении на воздухе серы и молока появляется запах, тогда как у свежих этих веществ его практически нет. Предположите для каждого случая, какие вещества — более простые, чем исходное, или более сложные — образуются. Поясните свой выбор. Атомы золота и серебра отличаются:
• тем, что имеют разные размеры
• наличием ядра и электронов
• цветом
• наличием электрического заряда Молекулы азота сходны с молекулами аммиака _______. • температурой плавления
• тем, что состоят из ядра и электронов
• своим составом
• способностью существовать самостоятельно Можно сказать:
• молекула железа
• атом парафина
• атом водорода
• молекула сахара Молекулу можно охарактеризовать: — температурой плавления
— количественным составом
Выбери общие характеристики для 1 молекулы азота и 1 г азота:
• температура кипения
• вкус
• взаимодействие с теми же веществами
• состав Установи соответствие между частицами и их характеристиками: 1. Атомы А. сохраняются без изменений в химических процессах
2. Молекулы Б. известно 118 видов таких частиц
В. мельчайшие час
Атомы А. сохраняются без изменений в химических процессах
2. Молекулы Б. известно 118 видов таких частиц
В. мельчайшие час

 Представьте себя на минуту конструктором мощной ракеты, способной выводить на орбиту космические корабли и другие полезные грузы.
Представьте себя на минуту конструктором мощной ракеты, способной выводить на орбиту космические корабли и другие полезные грузы. В энергетике с помощью теплот сгорания топлива рассчитывают выработку тепловой энергии.
В энергетике с помощью теплот сгорания топлива рассчитывают выработку тепловой энергии.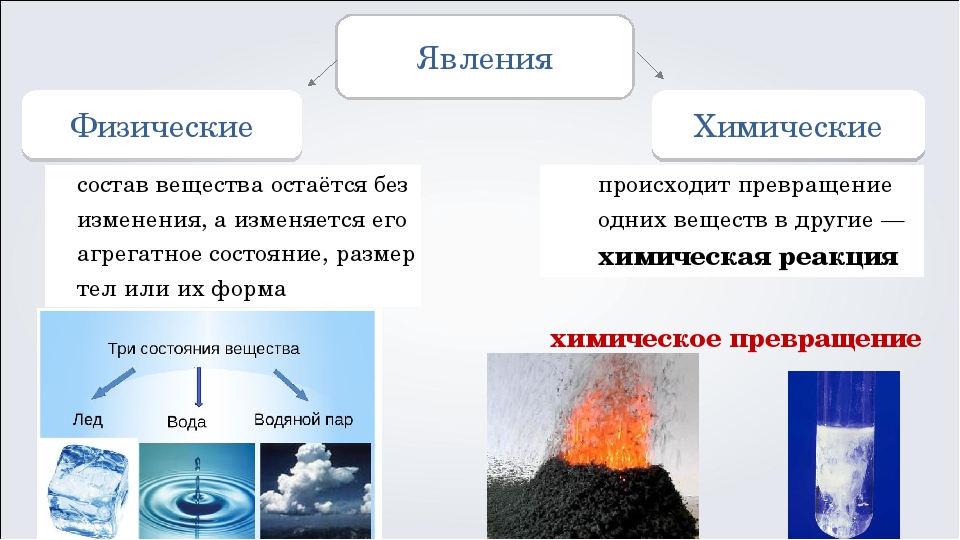 Эта информация меня очень заинтересовала, и я решил для себя разобраться в чем разница между этими понятиями. Возможно, именно эта тема повлияла на то, что я начал изучать химию и поступил на химический факультет. Как бы там ни было, эти явления стали для меня одним из самых больших открытий.
Эта информация меня очень заинтересовала, и я решил для себя разобраться в чем разница между этими понятиями. Возможно, именно эта тема повлияла на то, что я начал изучать химию и поступил на химический факультет. Как бы там ни было, эти явления стали для меня одним из самых больших открытий. Таким образом изменяется структурная формула вещества, количество и разновидность атомов элемента. Если на мгновение забыть, что алхимия невозможна, тогда химическое явление можно назвать алхимией, ведь одно вещество превращается в другое. Примером химического явления может быть горение любого вещества, ведь при горении соединение окисляется кислородом. Дерево или целлюлоза с формулой (C6h20O5)n горит, образовывая углекислый газ (СО2) и воду (Н2О). Таким образом, наше исходное вещество целлюлоза поменяло свою структурную формулу, а значит это — химическое явление. Для химических явлений характерно:
Таким образом изменяется структурная формула вещества, количество и разновидность атомов элемента. Если на мгновение забыть, что алхимия невозможна, тогда химическое явление можно назвать алхимией, ведь одно вещество превращается в другое. Примером химического явления может быть горение любого вещества, ведь при горении соединение окисляется кислородом. Дерево или целлюлоза с формулой (C6h20O5)n горит, образовывая углекислый газ (СО2) и воду (Н2О). Таким образом, наше исходное вещество целлюлоза поменяло свою структурную формулу, а значит это — химическое явление. Для химических явлений характерно: Наш ножик из стального цвета станет коричневым, а это один из признаков химического явления.
Наш ножик из стального цвета станет коричневым, а это один из признаков химического явления. Алюминия, цинка, ацетона, извести, мыла, аспирина, полиэтилена и многих других веществ в природе не существует.
Алюминия, цинка, ацетона, извести, мыла, аспирина, полиэтилена и многих других веществ в природе не существует. Например, запасы топливных ископаемых в природе на исходе.
Например, запасы топливных ископаемых в природе на исходе. Бытовое (тривиальное) название такого вещества «сухой лед». Такое название дано этому веществу из-за того, что «сухой лед» превращается в углекислый газ без плавления, то есть, без перехода в жидкое агрегатное состояние, которое присутствует, например, у воды.
Бытовое (тривиальное) название такого вещества «сухой лед». Такое название дано этому веществу из-за того, что «сухой лед» превращается в углекислый газ без плавления, то есть, без перехода в жидкое агрегатное состояние, которое присутствует, например, у воды. Вода замерзает и превращается в лед при температуре 0°С, а закипает и превращается в пар при температуре +100°С. Данные явления относятся к физическим, так как вода не превратилась в другие вещества, происходит только изменение агрегатного состояния. Данные температуры замерзания и кипения – это физические свойства, характерные именно для воды.
Вода замерзает и превращается в лед при температуре 0°С, а закипает и превращается в пар при температуре +100°С. Данные явления относятся к физическим, так как вода не превратилась в другие вещества, происходит только изменение агрегатного состояния. Данные температуры замерзания и кипения – это физические свойства, характерные именно для воды. Такие физические свойства как цвет, запах, вкус, форма кристаллов, можно определить визуально, с помощью органов чувств, а плотность, электропроводность, температуру плавления и кипения определяют измерением. Сведения о физических свойствах многих веществ собраны в специальной литературе, например, в справочниках. Физические свойства вещества зависят от его агрегатного состояния. Например, плотность льда, воды и водяного пара различна.
Такие физические свойства как цвет, запах, вкус, форма кристаллов, можно определить визуально, с помощью органов чувств, а плотность, электропроводность, температуру плавления и кипения определяют измерением. Сведения о физических свойствах многих веществ собраны в специальной литературе, например, в справочниках. Физические свойства вещества зависят от его агрегатного состояния. Например, плотность льда, воды и водяного пара различна. Если рассмотреть образец поваренной соли под увеличительным стеклом, можно заметить, что соль состоит из множества мельчайших кристаллов. В соляных месторождениях можно встретить и весьма крупные кристаллы. Кристаллы – твердые тела, имеющие форму правильных многогранников Кристаллы могут иметь различную форму и размер. Кристаллы некоторых веществ, таких как поваренная соль – хрупкие, их легко разрушить. Существуют кристаллы довольно твердые. Например, одним из самых твердых минералов считается алмаз. Если рассматривать кристаллы поваренной соли под микроскопом, можно заметить, что все они имеют похожее строение. Если же рассмотреть, например, частицы стекла, то все они будут иметь различное строение – такие вещества называют аморфными. К аморфным веществам относят стекло, крахмал, янтарь, пчелиный воск. Аморфные вещества – вещества, не имеющие кристаллического строения
Если рассмотреть образец поваренной соли под увеличительным стеклом, можно заметить, что соль состоит из множества мельчайших кристаллов. В соляных месторождениях можно встретить и весьма крупные кристаллы. Кристаллы – твердые тела, имеющие форму правильных многогранников Кристаллы могут иметь различную форму и размер. Кристаллы некоторых веществ, таких как поваренная соль – хрупкие, их легко разрушить. Существуют кристаллы довольно твердые. Например, одним из самых твердых минералов считается алмаз. Если рассматривать кристаллы поваренной соли под микроскопом, можно заметить, что все они имеют похожее строение. Если же рассмотреть, например, частицы стекла, то все они будут иметь различное строение – такие вещества называют аморфными. К аморфным веществам относят стекло, крахмал, янтарь, пчелиный воск. Аморфные вещества – вещества, не имеющие кристаллического строения Химическая реакция.
Химическая реакция. В нашем организме непрерывно происходят превращения множества веществ, вещества реагируют друг с другом, образуя продукты реакции. Таким образом, в химической реакции всегда есть реагирующие вещества, и вещества, образовавшиеся в результате реакции.
В нашем организме непрерывно происходят превращения множества веществ, вещества реагируют друг с другом, образуя продукты реакции. Таким образом, в химической реакции всегда есть реагирующие вещества, и вещества, образовавшиеся в результате реакции. К таким признакам можно отнести изменение окраски веществ, выделение газа, образование осадка, выделение тепла, излучение света.
К таким признакам можно отнести изменение окраски веществ, выделение газа, образование осадка, выделение тепла, излучение света. Напомним, что в терминах энергетических переменных движущей силой диффузии является не градиент концентрации, а градиент химического потенциала. Для примера рассмотрим случай простой реакции А г В, протекающей в идеальном растворе при наличии одномерной ди( к )узии компонентов в направлении оси ох. Диффузионный поток каждого компонента определяется законом Фика [c.131]
Напомним, что в терминах энергетических переменных движущей силой диффузии является не градиент концентрации, а градиент химического потенциала. Для примера рассмотрим случай простой реакции А г В, протекающей в идеальном растворе при наличии одномерной ди( к )узии компонентов в направлении оси ох. Диффузионный поток каждого компонента определяется законом Фика [c.131]  Его изучали и изучают многие исследователи, так как возникновение индуцированных реакций слулСущность явления состоит в том, что некоторые окислительно-восстановительные реакции не протекают или протекают медленно. Предположим, что в растворе имеются вещества А и С, скорость реакции между которыми равна нулю. [c.374]
Его изучали и изучают многие исследователи, так как возникновение индуцированных реакций слулСущность явления состоит в том, что некоторые окислительно-восстановительные реакции не протекают или протекают медленно. Предположим, что в растворе имеются вещества А и С, скорость реакции между которыми равна нулю. [c.374] Им было дано объяснение этому явлению. Согласно Н. А. Шилову, химическая индукция объясняется тем, что сопряженные реакции протекают через общие активные промежуточные вещества. [c.234]
Им было дано объяснение этому явлению. Согласно Н. А. Шилову, химическая индукция объясняется тем, что сопряженные реакции протекают через общие активные промежуточные вещества. [c.234]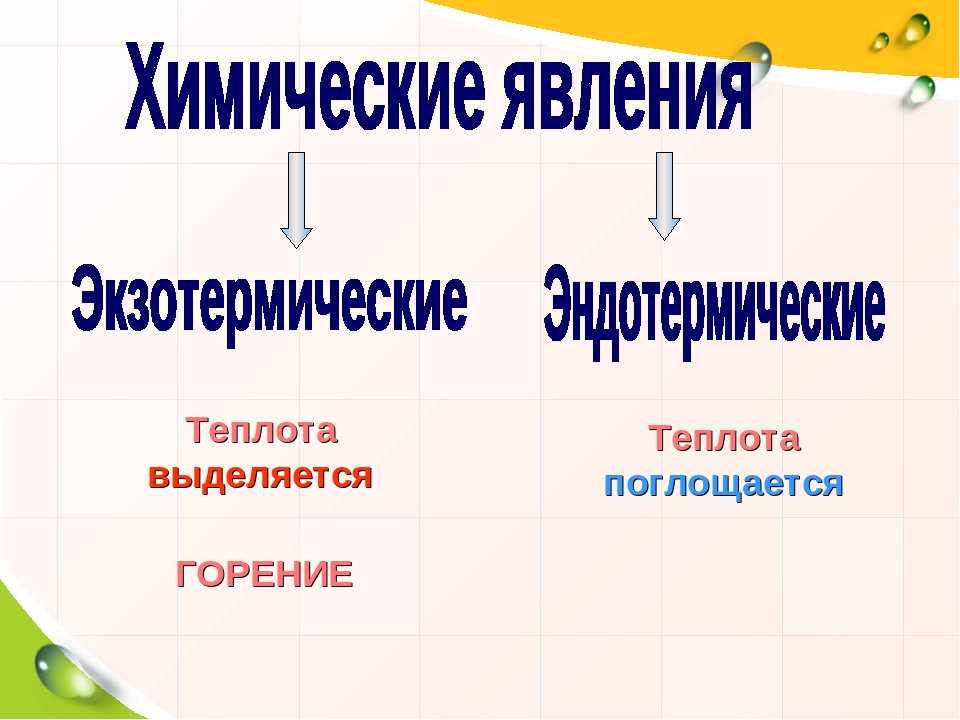 Адсорбция газов на поверхности твердых тел охватывает как явления чисто физической адсорбции, близкой к процессам физической конденсации пара в жидкость, так и явления химической адсорбции. [c.377]
Адсорбция газов на поверхности твердых тел охватывает как явления чисто физической адсорбции, близкой к процессам физической конденсации пара в жидкость, так и явления химической адсорбции. [c.377] п.). [c.310]
п.). [c.310]