Концентрированная соляная кислота: Кислота соляная — производство и применение
Кислоты в лаборатории — правила работы c кислотами в обзорной статье Глювекс
Кислоты часто используются в большинстве химических лабораторий. Прежде чем покупать, хранить, использовать и утилизировать кислоты, важно изучить их свойства, риски и правила работы с кислотами в лаборатории.
Свойства
|
Кислотность |
Химическая формула |
Молекулярный вес по формуле соединения |
Удельная плотность |
Концентрированная кислота |
|
|
Массовая доля кислоты (в %) |
Молярность |
||||
|
Уксусная кислота |
HC2h4O2 |
60,05 |
1,05 |
99,8 |
17,4 |
|
Соляная кислота |
HCL |
36,46 |
1,19 |
37,2 |
12,1 |
|
Азотная кислота |
HNO3 |
63,02 |
1,42 |
69,5 |
15,8 |
|
Фосфорная кислота |
h4PO4 |
98,00 |
1,70 |
86 |
14,8 |
|
Серная кислота |
h3SO4 |
98,08 |
1,84 |
96 |
18,0 |
Меры предосторожности
Концентрированные кислоты оказывают сильное разъедающее воздействие на все ткани организма, в особенности на глаза и кожу. Концентрированные кислоты очень токсичны из-за своей чрезвычайно высокой коррозионной активности. Соляная и уксусная кислоты также токсичны при вдыхании. Другие факторы риска перечислены в этом обзоре. При работе с концентрированными кислотами в лаборатории или растворами всегда носите закрытые очки для защиты от агрессивных жидкостей, химически стойкие перчатки и химически стойкий фартук. Пожалуйста, ознакомьтесь с действующими паспортами безопасности материалов, чтобы узнать подробную информацию о технике безопасности, правилах обращения и утилизации.
Концентрированные кислоты очень токсичны из-за своей чрезвычайно высокой коррозионной активности. Соляная и уксусная кислоты также токсичны при вдыхании. Другие факторы риска перечислены в этом обзоре. При работе с концентрированными кислотами в лаборатории или растворами всегда носите закрытые очки для защиты от агрессивных жидкостей, химически стойкие перчатки и химически стойкий фартук. Пожалуйста, ознакомьтесь с действующими паспортами безопасности материалов, чтобы узнать подробную информацию о технике безопасности, правилах обращения и утилизации.
Покупка
Покупайте, по возможности, разбавленные кислоты для лаборатории. По сравнению с концентрированными кислотами, разбавленные кислотные растворы проще и безопаснее в использовании, хранении и обращении. При работе с растворами вы не потеряете драгоценное время на подготовку.
Покупайте кислоту всегда в небольших количествах. В этом случае кислота не испортится раньше времени, а сам процесс хранения и обработки станет более безопасным и легким. Разлив кислоты в количестве 100 мл ликвидировать намного легче, чем в объеме 2,5 л.
Разлив кислоты в количестве 100 мл ликвидировать намного легче, чем в объеме 2,5 л.
Всегда покупайте концентрированные кислоты в стеклянных бутылках с защитным ПВХ-покрытием. При падении такие бутылки не разобьются, а кислота из них не выльется. ПВХ создает своеобразную пластиковую защитную оболочку, что значительно уменьшает риск разлива и повреждения. ПВХ-покрытие может со временем обесцвечиваться, особенно если подвергается воздействию паров соляной кислоты. Это изменение цвета не влияет на ПВХ-покрытие или качество кислоты внутри бутылки.
Условия хранения
Храните все кислоты в специальном шкафу для сильнодействующих веществ или кислот. Самые лучшие шкафы для хранения кислот в лаборатории изготавливают из дерева, потому что металлические шкафы быстро корродируют под воздействием кислотных паров. Деревянные шкафы обеспечивают безопасное и надежное хранение кислот на протяжении многих лет. Шкаф должен находиться в закрываемом на ключ складе химических реагентов. В противном случае сам шкаф должен закрываться на замок.
В противном случае сам шкаф должен закрываться на замок.
Разрешается хранить кислоты и основания все вместе в одном шкафу для агрессивных веществ. При этом на бутылках может образоваться налет из хлорида аммония под воздействием паров соляной кислоты и аммиака. Промойте шкаф и бутылки при помощи тринатрийфосфата или другого сильного растворителя, чтобы удалить белую пленку.
Если у вас нет специального шкафа для хранения кислот, храните концентрированную кислоту в кубических контейнерах. Такие кубы обеспечивают надежное хранение кислот в лаборатории за счет дополнительной защитной оболочки.
Прежде чем поместить подготовленные растворы кислот на хранение, промаркируйте их с указанием как минимум следующей информации: название кислоты, концентрация кислоты, предупреждение об опасности или о вредном воздействии на организм человека, дата.
Техника безопасности при работе с кислотами
Всегда закрывайте бутылки с концентрированной кислотой крышками с соответствующей цветовой маркировкой. Никогда не используйте эти крышки на других бутылках. Цветовая маркировка является дополнительной мерой безопасности и позволяет идентифицировать концентрированные кислоты в тех случаях, когда этикетка была удалена или повреждена.
Никогда не используйте эти крышки на других бутылках. Цветовая маркировка является дополнительной мерой безопасности и позволяет идентифицировать концентрированные кислоты в тех случаях, когда этикетка была удалена или повреждена.
Если при работе с кислотой в лаборатории крышка на бутылке треснула или потеряла изначальный цвет, замените крышку на новую с соответствующей цветовой маркировкой.
Учитывая то, что концентрированная соляная кислота постоянно испаряется, при хранении следует предусмотреть отвод возникающих паров. Эти пары являются главным виновником повреждений на вашем складе химических реагентов, вызванных коррозией. Хранение соляной кислоты в деревянном шкафу для кислот является обязательным требованием. Пары соляной кислоты быстро разъедают металлические шкафы.
Азотная кислота является сильным окислителем. Концентрированную азотную кислоту следует хранить в отдельном непроницаемом для жидкостей отсеке внутри шкафа для кислот. Если смешать азотную кислоту с горючим органическим соединением, например, уксусной кислотой, то тепла, образовавшегося от реакций окисления и нейтрализации, будет достаточно для воспламенения этого соединения. Азотная кислота также способна медленно разрушать красную пластиковую крышку бутылки. Азотная кислота может также со временем желтеть вследствие выделения диоксида азота под действием света.
Азотная кислота также способна медленно разрушать красную пластиковую крышку бутылки. Азотная кислота может также со временем желтеть вследствие выделения диоксида азота под действием света.
Ледяная уксусная кислота является горючей жидкостью. Ледяную уксусную кислоту следует хранить в шкафу для кислот, в месте, защищенном от возможного контакта с азотной кислотой. Ледяная уксусная кислота замерзает при температуре +16,6 ° C. Кислота может кристаллизоваться на холодном складе. Если это произошло, дайте бутылке нагреться до температуры окружающей среды (+25 °C).
Концентрированная серная кислота является сильным обезвоживающим агентом. Сильной способностью поглощать воду объясняется и обугливание многих органических веществ, например, сахара, древесины, бумаги, при действии на них концентрированной серной кислоты. Если серная кислота приобрела коричневый цвет, значит, скорее всего, она была загрязнена органическими веществами и больше уже не является чистой.
Концентрированная фосфорная кислота имеет температуру плавления, близкую к температуре окружающей среды, и также может кристаллизоваться на холодном складе. Фосфорная кислота гигроскопична и имеет свойство впитывать влагу из воздуха. Храните емкости с фосфорной кислотой плотно закрытыми.
Фосфорная кислота гигроскопична и имеет свойство впитывать влагу из воздуха. Храните емкости с фосфорной кислотой плотно закрытыми.
Транспортировка
Вторичная защитная оболочка имеет решающее значение для предотвращения крупных разливов или аварий при транспортировке кислот. Храните кислоты в бутылках с ПВХ-покрытием или на небьющихся держателях для бутылок.
Возьмите себе за правило проверять наличие трещин на бутылке с кислотой, прежде чем прикасаться к ней или брать ее. Проверьте также, не пролилась ли кислота на ручку или бутылку.
Носите 2,5-литровые бутылки с кислотой, взявшись одной рукой за дно бутылки, а другой рукой обхватив горлышко или углубление для пальцев. В этом случае вы будете держать бутылку ближе к телу, и опасность разбить или повредить бутылку при контакте с острыми предметами, например, при ударе об угол стола, будет снижена.
При транспортировке кислот из одной лаборатории в другую или из кладовой (склада) в лабораторию, следует использовать пластиковые или резиновые защитные держатели для бутылок.
Если вы используете тележку для перевозки опасных химических веществ (например, кислот), поместите совместимые химические вещества во вторичный защитный контейнер, изготовленный из небьющихся материалов, например, в пластиковый лоток. Тележка должна иметь защитное ограждение, чтобы не допустить соскальзывания пластиковых лотков или бутылок.
Если опасные химические вещества перемещаются с одного этажа на другой, используйте, по возможности, лифт. И даже несмотря на то, что несчастные случаи в лифтах происходят редко, соблюдайте необходимую предосторожность. Если утечка материала в лифте все же произойдет, последствия для пассажиров, находящихся в кабине лифта, могут оказаться весьма плачевными.
Подготовка раствора
- Добавьте необходимое количество кислоты — примерно 2/3 от заданного количества дистиллированной или деионизированной воды.
- Всегда добавляйте кислоту в воду! Работая с кислотами в лаборатории, никогда не добавляйте воду в концентрированные кислоты.
 Кислота может начать разбрызгиваться с выделением кислотных паров.
Кислота может начать разбрызгиваться с выделением кислотных паров. - Всегда используйте посуду из боросиликатного стекла.
- Перемешайте раствор.
- Как только раствор остынет до температуры окружающей среды, разбавьте его водой до нужного объема.
- Используйте мерную лабораторную колбу, чтобы точно определить необходимое количество.
- При разбавлении серной кислоты, поместите боросиликатный стакан или колбу в ледяную ванну. Не забывайте о том, что разбавление серной кислоты всегда сопровождается выделением большого количества тепла. Пластиковые контейнеры под воздействием тепла могут расплавиться, а стеклянная посуда, изготовленная не из боросиликатного стекла, может треснуть.
Использование и дозирование кислот
Перед каждым использованием любого опасного материала в лаборатории следует внимательно ознакомиться с паспортом безопасности материала.
Разливайте кислоты из небольших бутылок, чтобы ограничить возможные утечки и испарения.
При дозировании кислот, используйте лабораторные коврики и/или пластиковые лотки для сбора случайно пролившейся кислоты.
Дозирование кислот, особенно соляной, азотной и уксусной, производите в функционирующем вытяжном шкафу.
В процессе лабораторных работ установите бутылку с кислотой на центральную площадку дозирования и поставьте градуированный цилиндр или контрольную пробирку в зону дозирования. Это поможет минимизировать разливы и несчастные случаи, а также ограничить количество кислоты, возвращаемой обратно на лабораторный стенд.
Вылейте необходимое для эксперимента количество кислоты из бутылки с реактивом. Запрещается помещать химические вещества обратно в бутылку с реактивом.
Держите наготове материалы для ликвидации разливов кислот при работе с ними.
Кислоты являются химически агрессивными веществами и разъедают большинство тканей, в результате чего на одежде образуются небольшие дырки. Этот процесс происходит не сразу, а в течение нескольких часов и может не проявляться до тех пор, пока одежда не будет постирана. При работе с кислотами всегда носите химически стойкий фартук или лабораторный халат.
При работе с кислотами всегда носите химически стойкий фартук или лабораторный халат.
Средства индивидуальной защиты и инструкции по технике безопасности
Перчатки из нитрильного каучука устойчивы к воздействию кислот и являются оптимальным средством защиты при работе с концентрированными кислотами. Однако любые полимерные или виниловые перчатки способны обеспечить некоторую защиту от случайных брызг, небольших разливов, которые могут возникнуть при использовании или дозировании кислот.
Средства для аварийного промывания глаз должны быть доступны в любом кабинете или лаборатории, в которых проводятся работы с кислотами или растворами кислот. Средство для аварийного промывания глаз должно обеспечивать промывку обоих глаз и подачу чистой питьевой воды как минимум в течение 15-20 минут.
При работе с кислотами в лаборатории или кислотными растворами следует носить закрытые очки для защиты от агрессивных жидкостей. Защитные очки не являются надлежащим средством индивидуальной защиты.
Следует обеспечить надлежащую вентиляцию при работе с соляной, азотной или уксусной кислотами.
Прежде чем работать с кислотами или кислотными растворами, убедитесь в наличии подходящих материалов и средств для ликвидации разливов (песок, абсорбент и нейтрализующий агент).
Меры по оказанию первой помощи
- Всегда обращайтесь за профессиональной медицинской помощью, если вы подверглись воздействию любого опасного химического вещества, особенно концентрированных кислот в лаборатории.
- При любом химическом воздействии на ткани тела или глаза лучше всего немедленно промыть их водой.
- Если кислота попала в глаза, промывайте глаза в течение как минимум 15-20 минут, воспользовавшись средством аварийного промывания глаз. Держите веки открытыми, чтобы тщательно промыть глаза.
- Если кислота попала на открытые участки кожи, промывайте их водой не менее 15-20 минут.
- Если брызги кислоты попали на одежду, сразу же снимите ее, не допуская проникновение кислоты через одежду и контакта с кожей.
 Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов.
Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов. - При попадании кислоты в желудок, первое, что нужно предпринять, — это попытаться разбавить кислоту в желудке и предотвратить дальнейшие травмы, вызванные рвотой. Если пострадавший находится в сознании, немедленно попросите его прополоскать рот водой. Попросите пострадавшего выпить одну или две чашки воды или молока. Можно также дать пострадавшему антациды, т. е. препараты для нейтрализации желудочной кислоты. Не вызывайте рвоту, не пытайтесь нейтрализовать кислоту сильным основанием и не давайте пострадавшему бикарбонат натрия или газированные напитки. Позвоните в скорую помощь и следуйте их указаниям.
Комплексное оснащение химических лабораторий
Компания Gluvex выполняет проектирование и комплексное оснащение химических лабораторий всеми видами качественного лабораторного оборудования. Возможно расширение функционала текущих отделений или организация новых. Гарантируется полное соответствие всем нормативно-правовым актам страны клиента и международным стандартам GLP, ISO/IEC 17025, ISO 15189, ISO 7218-2015 и другим.
Возможно расширение функционала текущих отделений или организация новых. Гарантируется полное соответствие всем нормативно-правовым актам страны клиента и международным стандартам GLP, ISO/IEC 17025, ISO 15189, ISO 7218-2015 и другим.
Ваши преимущества с Gluvex:
- Грамотная разработка проектной документации.
- Тесное сотрудничество с клиентом и его подрядчиками.
- Создание лабораторий «под ключ».
- Возможность интеграции в существующую среду.
- Оснащение ведущим европейским оборудованием.
- Доставка в любой регион РФ.
- Установка, наладка и калибровка всех устройств.
- Оптимизация под бюджет клиента без потери качества.
- Последовательное обучение персонала.
- Гарантия и фирменный сервис.
- Расходные материалы всегда в наличии.
- Быстрая поставка запасных частей.
- Своевременные консультации и техническая поддержка.
Специалисты Gluvex уверенно решают задачи любой сложности.Свяжитесь с нами по телефону +7 (499) 270-16-62 и убедитесь в этом!
Соляная кислота (хлористоводородная кислота) – водный раствор хлористого водорода HCl, представляет собой прозрачную бесцветную жидкость с острым запахом хлористого водорода.
Соляная кислота (хлористоводородная кислота) – водный раствор хлористого водорода HCl, представляет собой прозрачную бесцветную жидкость с острым запахом хлористого водорода.
Техническая кислота имеет желтовато-зеленый цвет из-за примесей хлора и солей железа. Максимальная концентрация соляной кислоты около 36% HCl, такой раствор имеет плотность 1,18 г/см3. Концентрированная кислота на воздухе «дымит», так как выделяющийся газообразный HCl образует с водяным паром мельчайшие капельки соляной кислоты.
Максимальная концентрация соляной кислоты около 36% HCl, такой раствор имеет плотность 1,18 г/см3. Концентрированная кислота на воздухе «дымит», так как выделяющийся газообразный HCl образует с водяным паром мельчайшие капельки соляной кислоты.
⠀
Соляная кислота не горюча, не взрывоопасна. Она является одной из самых сильных кислот, растворяет все металлы. Получают соляную кислоту растворением в воде хлористого водорода, который синтезируют или непосредственно из водорода и хлора или получают действием серной кислоты на хлорид натрия.
⠀
Выпускаемая техническая соляная кислота имеет крепость не менее 31% HCl (синтетическая) и 27,5% HCl (из NaCI). Торговую кислоту называют концентрированной, если она содержит 24% и больше HCl, если содержание HCl меньше, то кислота называется разбавленной.
⠀
Соляную кислоту применяют для получения хлоридов различных металлов, органических полупродуктов и синтетических красителей, уксусной кислоты, активированного угля, различных клеев, гидролизного спирта, в гальванопластике. Ее применяют для травления металлов, для очистки различных сосудов, обсадных труб буровых скважин от карбонатов, окислов и др. осадков и загрязнений. В металлургии кислотой обрабатывают руды, в кожевенной промышленности – кожу перед дублением и крашением. Соляную кислоту применяют в текстильной, пищевой промышленности, в медицине и т.д. Транспортируют соляную кислоту в стеклянных бутылях или гуммированных металлических сосудах, а также в полиэтиленовой посуде.
Ее применяют для травления металлов, для очистки различных сосудов, обсадных труб буровых скважин от карбонатов, окислов и др. осадков и загрязнений. В металлургии кислотой обрабатывают руды, в кожевенной промышленности – кожу перед дублением и крашением. Соляную кислоту применяют в текстильной, пищевой промышленности, в медицине и т.д. Транспортируют соляную кислоту в стеклянных бутылях или гуммированных металлических сосудах, а также в полиэтиленовой посуде.
Наши контакты:
Приемная: +998781479090
Отдел маркетинга: +998781474004
Email: office@ukie.uz
Email: marketing@ukie.uz
Опыты по химии. Соляная кислота
Чтобы поделиться, нажимайте
Получение соляной кислоты (практическая работа)
Соляная кислота HCl получается при растворении газа хлороводорода воде.
Хлороводород можно получить действием концентрированной серной кислоты на поваренную соль.
NaCl + H2SO4 = HCl ↑ + Na2HSO4
Направим поток хлороводорода в пробирку с водой. Этот газ легко растворяется в воде: до 450 объемов хлороводорода — в одном объеме воды. В пробирке образуется соляная кислота – раствор хлороводорода в воде.
Этот газ легко растворяется в воде: до 450 объемов хлороводорода — в одном объеме воды. В пробирке образуется соляная кислота – раствор хлороводорода в воде.
Оборудование: пробирка, штатив для пробирок, пробирка с газоотводной трубкой, штатив, химические стаканы, воронка.
Техника безопасности. Соблюдать правила работы с нагревательными приборами. Необходима особая осторожность при работе с концентрированной серной кислотой. Недопустимо попадание выделяющегося хлороводорода в дыхательные пути. Опыт следует проводить под тягой.
Постановка опыта – Елена Махиненко, текст – к.п.н. Павел Беспалов.
Химические свойства соляной кислоты (практическая работа)
Соляная кислота это раствор хлороводорода в воде. Чтобы получить кислоту, получим хлороводород взаимодействием растворов поваренной соли и серной кислоты.
NaCl + H2SO4 = HCl + Na2HSO4.
Растворим хлороводород в воде, получится кислота. Соляная кислота – сильная кислота с типичными для кислот свойствами. Соляная кислота взаимодействует с основаниями с образованием солей и воды. В стакане со щелочью при добавлении соляной кислоты происходит реакция нейтрализации ‑ цвет индикатора изменяется, указывая на появление нейтральной среды.
HCl + NaOH = NaCl+ H2O
Проведем качественную реакцию на хлорид-ион – реакцию с нитратом серебра.
Образуется нерастворимая соль – хлорид серебра.
HCl + AgNO3 = AgCl ↓ + HNO3
Соляная кислота взаимодействует с активными металлами: Когда цинк попадает в раствор соляной кислоты – начинается бурное выделение водорода.
2HCl + Zn = ZnCl2 + H2 ↑
Мы убедились в том, что соляная кислота реагирует с металлами, основаниями, солями.
Оборудование: спиртовка, шпатель, пробирка, штатив для пробирок, пробирка с газоотводной трубкой, штатив, химические стаканы, воронка.
Техника безопасности. Следует соблюдать правила работы с растворами кислот и щелочей. Избегать попадания кислот, щелочей, нитрата серебра на кожу и слизистые оболочки.
Постановка опыта – Елена Махиненко, текст – к.п.н. Павел Беспалов.
Растворение хлороводорода в воде
Как хранить кислоту❓ Серную, соляную, азотную ⚗️ Материалы сосуда и пробки
Однажды для целей экспериментов с гальваникой и паяльными флюсами в домашних условиях были закуплены три вида кислот: соляная, серная, азотная. Все концентрированные, химически чистые. Все они были в одинаковых небольших пластиковых флакончиках миллилитров на 100. Позже выяснилось, что материал этих флаконов — полиэтилен высокой плотности (PEHD). Казалось, что раз в таких ёмкостях эти кислоты продают, то и хранить их можно таким же образом сколь угодно долго. Тем более, что в интернейтах этих ваших всяких пишут, что полиэтилен и полипропилен химически стойки к кислотам. Но… жизнь показала, где тут крабы зимуют:
Коричневый флакон слева на фото хранил в себе соляную кислоту (чда) 2 года. Флакон справа — для сравнения, таким матово-белым он был изначально. Кроме того, весь это флакон снаружи покрылся росой, пахнущей соляной кислотой, и вообще вонь распространялась вокруг, из-за чего этот (и другой, с азотной кислотой) забытый было уже флакон и был обнаружен.
Оказалось, что соляная кислота просачивается через полиэтилен (PE) и полипропилен (PP), причём целиком (т. е. вся молекула HCL проходит), поэтому долгосрочно (более года) в такой таре хранить её нельзя. Кислота была перелита в стеклянную тару, но с полиэтиленовой крышкой. Через два года:
В общем-то, капелек кислоты на поверхности крышки не наблюдается, но запах снаружи есть. Т. е. теперь проблема в подборе материала крышки-пробки. Кто-то в Сети написал, что достаточно пробки из мягкой резины… пробуем:
Хрен-то с два — это фото сделано уже через неделю. Активно испаряющаяся кислота сконденсировалась у пробки и явно реагирует с ней, судя по пузырькам и тёмно-жёлтому цвету. Часть пробки, побывавшая внутри, бодро изменила цвет:
Неполучи… лося. Походу хранить её можно только в стеклянной колбе со стеклянной плотно притёртой пробкой:
Но такой в наличии нет… Не совсем понятно, каким образом стеклянная пробка может герметично закрыть отверстие. Наверное, её нужно ещё смазывать таким веществом, с которым данная кислота реагирует с образованием в итоге такого другого вещества, которое плотно-непроницаемо заполнит промежуток между пробкой и горлышком. Какую смазку для какой кислоты лучше использовать — тема отдельного исследования.
Наверное, её нужно ещё смазывать таким веществом, с которым данная кислота реагирует с образованием в итоге такого другого вещества, которое плотно-непроницаемо заполнит промежуток между пробкой и горлышком. Какую смазку для какой кислоты лучше использовать — тема отдельного исследования.
С серной кислотой никаких проблем не возникло. Её продают в магазинах типа «Автозапчасти» в 6-литровых полипропиленовых (PP) канистрах (аккумуляторный электролит), из этого же материала сделаны корпуса автомобильных аккумуляторов, и храниться в таких ёмкостях данная кислота может десятилетиями. Она почти не испаряется, поэтому не пахнет, даже если её кипятить (а если кипятить, то испаряется вода, концентрация кислоты повышается, температура её кипения возрастает и испарительные способности при комнатной температуре падают совсем до нуля). Так что с хранением серной кислоты проблем нет, лишь бы не разлить её и не испачкаться ею. Соответственно, хранить серную кислоту лучше как раз не в стеклянной (бьющейся) таре, а в PP (правда сильно концентрированную советуют хранить всё-таки в стекле с PP-пробкой, т. к. полипропилен со временем этой кислотой обугливается).
к. полипропилен со временем этой кислотой обугливается).
А вот с азотной кислотой совсем всё плохо получилось. Хотя цвет флакона со временем не изменился, эта кислота тоже просочилась через PEHD и воняла, и это испарение её вредно для здоровья. Провёл эксперимент: положил флакон во внешнюю бочку, в которую напихал бумажки. Через некоторое время все бумажки в бочке стали влажными и покоричневели. Интернет нам говорит по этому поводу, что хранить азотную кислоту можно только в стеклянном сосуде, со стеклянной пробкой. За неимением таковой тары, пришлось сей флакон выбросить (азотную кислоту, предварительно разбавив, можно вылить в землю, там с неё получится много разных азотных удобрений, которые очень любят все растения).
Профессиональное хранение
Но давайте разберёмся, в чём советуют хранить эти кислоты в промышленности (помимо стекла). Вот что гласят инструкции от производителей химреактивов по этому поводу.
Серная кислота
- Может перевозиться в бочках и цистернах из коррозионно-стойкой стали марки 06ХН28МДТ.
 На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается.
На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается. - Полиэтилен высокой плотности (PEHD), полипропилен (PP), тефлон (он же polytetrafluoroethylene = PTFE, он же фторопласт-4).
На практике концентрированная серная кислота приводит к коричневению (обугливанию изнутри) PEHD и PP, что, по всей видимости, портит её чистоту. Но зато она через эти пластики не проникает. Тефлон… надо проверять, да и дороговат он. Серная кислота аккумуляторной концентрации (1.27-1.28 г/см3) может в PP-канистре храниться многие годы, канистра не коричневеет, количество кислоты не уменьшается (если, конечно, крышка нормально-плотно завинчена).
Соляная кислота
- В стальных гуммированных (покрытых изнутри резиной) бочках и цистернах.
- UPVC (Unplasticized Polyvinyl Chloride — непластифицированный поливинилхлорид, нПВХ), упрочнённый (снаружи) оболочкой из пропитанного эпоксидной смолой стекловолокна.
- Полиэтилен высокой плотности, HDPE.

- Полипропилен, PP, упрочнённый пропитанным эпоксидной смолой стекловолокном.
Как показал опыт и эксперименты, все эти промышленные методы хранения годятся только для непродолжительного хранения или транспортировки («в бочках и цистернах»). Сохранить в течение многих лет соляную кислоту, наверное, получится только в стеклянной таре со стеклянной же пробкой (и непонятно какой смазкой: кто-то использует силиконовое масло).
Через фторопласт (= тефлон, PTFE) соляная кислота просачивается, также как и через PP/PEHD, и оный тоже коричневеет.
Азотная кислота
- Концентрации более 92% — в алюминиевых бочках и цистернах. Алюминий либо чистый, либо сплав, не содержащий меди. А также из нержавеющих сталей марок (импортных) 304L и DIN 1.4361.
- Концентрация 60-70% — в бочках и цистернах из коррозионно-стойкой российской стали марки Х18Н9Т, импортные — 304L, 316L, 321.
- Оказывается даже обычная стеклянная тара не годится для хранения особо чистой азотной кислоты (имеет место быть реакция и кислота загрязняется) — нужно кварцевое стекло или окварцованное изнутри силикатное бутылочное стекло (внутренняя поверхность химически обрабатывается в течение 6-12 часов кипящей 70%-ной азотной кислотой с последующим прокаливанием при температуре 400-500°С в течение 3 ч).
- Поливинилхлорид (PVC). Точнее нПВХ — непластифицированный поливинилхлорид, в котором нет пластификаторов. Укреплённый стекловолокном, пропитанным полиэфирной/эпоксидной смолой.
- Поливинилиденфторид (PVDF).
- Этиленхлортрифторэтилен (ECTFE).
- Тефлон (он же политетрафторэтилен = PTFE — polytetrafluoroethylene, он же фторопласт-4).
Банальные ПВХ, фторопласт, алюминий — вот в чём, оказывается, надо хранить азотную кислоту. В тефлоновых контейнерах ещё (бывают такие, но они маленькие и почти непрозрачны). Или тогда уж проще купить стеклянный флакон с тефлоновой пробкой. И совсем уж просто и дёшево — тефлоновую пробку. Или самому вырезать нужной формы и диаметра на токарном станке из PTFE-стержня.
Что используют в лабах
Помимо стеклянных бутылок со стеклянными пробками, на случайных фотках различных лабораторий наиболее часто наблюдаются вот такие бутыли:
Установлено, что эти красные (иногда серые) пробки сделаны из полипропилена.
Также продают разноцветные крышки для разных кислот (видимо, сделаны из разных материалов; точнее, наверное, прокладка в них из подходящего материала):
По [ссылке] с картинки — КУПИТЬ их
Ещё бывают стеклянные бутылки, обтянутые полиэтиленовой оболочкой:По [ссылке] продают КИСЛОТЫ в этих бутылках
Если такая бутылка упадёт и разобьётся, то вся кислота останется внутри PE-мешка.Такие дела… А как храните кислоты вы?
Свойства алюминия
Свойства алюминия
Отличительные особенности алюминия — высокая электропроводимость, теплопроводность, коррозионная стойкость, малая плотность и отличная обрабатываемость давлением в холодном состоянии. **Физические свойства алюминия [2-6]**Плотность (99,996% А1), г/см3, при температуре: |
|
| 20 °С | 2,6989 |
| 1000 °С | 2,289 |
Температура, °С: |
|
| плавления | 660 |
| кипения | ~2452 |
Теплота кДж/моль: |
|
| плавления | 10,55 |
| испарения | 291,4 |
Давление пара, Па, при температуре: |
|
| 660 °С | 0,266 |
| 1123 °С | 13 3 |
| 1279 °С | 133 |
Удельная теплоемкость, Дж/(кг*К), при температуре: |
|
| 20 °С | 929,46 |
| 100 °С | 931,98 |
| Коэффициент линейного расширения при температуре 20-100 °С, К-1 | 24,58*10-6 |
Теплопроводность, Вт/( м*К), при температуре: |
|
| 20 °С | 217 |
| 190 °С | 343 |
| Электропроводность по отношению к меди при температуре 20 °С | 65,5% |
| Удельное электросопротивление, мк*Ом*м | 0.0265 |
| Температурный коэффициент электросопротивления | 0,042 |
Динамическая вязкость (99,85% А1), Н*с/м2, при температуре: |
|
| 800 °С | 2*10-3 |
| 1123 °С | 1,540-3 |
| 1279 °С | 1,3*10-3 |
Модуль нормальной упругости Е, МПа, при температуре: |
|
| 180 °С | 7,8*104 |
| 20 °С | 7,1*104 |
| 100 °С | 7,0*104 |
| 200 °С | 6,6*104 |
| 400 °С | 5,6*104 |
| 500 °С | 5,0*104 |
| 600 °С | 4,4*104 |
| Модуль сдвига при температуре 20 °С | 2,7*104 МПа |
| Магнитная характеристика алюминия | Слабо парамагнитен |
Временное сопротивление разрыву σв,МПА: |
|
| в отожженном состоянии | 50 |
| в деформированном (холоднокатаном) состоянии | 115 |
Предел текучести s 0,2 : |
|
| в отожженном состоянии | 50-80 |
| в деформированном состоянии | 120 |
Предел усталости (500*10 6 циклов),σ -1: |
|
| в отожженном состоянии | 40 |
| в деформированном состоянии | 50 |
Предел ползучести, при температуре: |
|
| 15 °С | 50 |
| 100 °С | 27 |
| 200 °С | 7 |
Предел прочности при срезе,σ ср: |
|
| в отожженном состоянии | 60 |
| в деформированном состоянии | 100 |
Относительное удлинение,δ: |
|
| в отожженном состоянии | 30-40% |
| в деформированном состоянии | 5-10% |
Относительное сужение, ψ: |
|
| в отожженном состоянии | 70-90% |
| в деформированном состоянии | 50-60% |
| Ударная вязкость при температуре 20 °С aм | 140 |
Твердость по Бринеллю, НВ: |
|
| в отожженном состоянии | 25 |
| в литом состоянии | 20 |
| в деформированном состоянии | 30-35 |
| Состояние | Содержание Аl, % | Предел прочности при растяжении σв2МПа | Предел текучести при растяжении σ.00,2, МПа | Относительное удлинение δ, % | Твердость по Бринеллю, НВ |
| Литой в землю | 99,996 | 50 | — | 45 | 13-15 |
| Литой в землю | 99,5 | 75 | — | 29 | 20 |
| Литой в землю | 99.0 | 85 | — | 20 | 25 |
| Литой в кокиль | 99,0 | 90 | — | 25 | 25 |
| Деформированный и отожженный | 99.0 | 90 | 30 | 30 | 25 |
| Деформированный | 99,0 | 140 | 100 | 12 | 32 |
| Литой в землю | 98,0 | 90 | 35 | 12,5 | 28 |
| Температура | °С |
| литья горячей обработки отжига отпуска Линейная усадка, % Допускаемая деформация (холодная и горячая), % Начало рекристаллизации, °С Жидкотекучесть, мм. |
690-710 350-450 370-400 150 2,7 75-90 150 317 |
Насосы Lutz для кислот | ЕТ-Сервис
Для перекачки высококонцентрированной серной кислоты особенно хорошо подходят насосы из сплавов нержавеющей стали, так как они образуют пассивный слой, защищающий от коррозии. В этом материальном исполнении можем предложить:
Перекачивать высоко агрессивную разбавленную серную кислоту лучше всего насосами из фторопласта (PVDF).
Lutz может предложить различные по конструкции насосы из этого материала. В зависимости от задачи перекачивания вы можете выбрать:
Для дозирования серной кислоты в большой концентрации свыше 40% подходят дозирующие насосы LUTZ-JESCO с корпусом из нержавеющей стали, а в малой концентрации можно выбрать любой насос, исходя из задачи.
Скрыть
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Концентрат соляной кислоты | 38282
Концентрат соляной кислоты | 38282 | Honeywell Research ChemicalsПохоже, в вашем браузере отключен JavaScript. Для максимального удобства работы на нашем сайте обязательно включите Javascript в своем браузере.
Мы используем выбранное вами местоположение, чтобы персонализировать контент на нашем веб-сайте и предоставлять вам актуальную информацию о ценах на продукты и их наличии.
{{еще}}{{{title.snippet}}} ({{total_results}})
{{/если}} {{else ifEq this.searchTypeValCheck «product»}} {{#if cas_number_all.snippet}} {{#ifEq cas_number_all.snippet «НЕ ПРИМЕНИМО»}}{{{имя.сниппет}}} | {{{short_description.snippet}}} ({{total_results}})
{{еще}}{{{name.snippet}}} | {{{short_description.snippet}}} | {{{cas_number_all.snippet}}} ({{total_results}})
{{/ ifEq}} {{еще}}{{{name.snippet}}} | {{{short_description.snippet}}} ({{total_results}})
{{/если}} {{/ ifEq}} {{иначе ifEq this.multiSearchCheck false}} {{#ifEq this.searchTypeValCheck «aem»}} {{#if resource_type.snippet}}{{{dc_title.snippet}}}
{{еще}}{{{title.snippet}}}
{{/если}} {{else ifEq this.searchTypeValCheck «product»}} {{#if cas_number_all.snippet}} {{#ifEq cas_number_all.snippet «НЕ ПРИМЕНИМО»}}{{{name.snippet}}} | {{{short_description.snippet}}}
{{еще}}{{{имя.сниппет}}} | {{{short_description.snippet}}} | {{{cas_number_all.snippet}}}
{{/ ifEq}} {{еще}}{{{name.snippet}}} | {{{short_description.snippet}}}
{{/если}} {{/ ifEq}} {{/ ifEq}} {{/каждый}}Из-за бездействия вы выйдете из системы через 0: 0.
для 1 л стандартного раствора, 1.0 M HCl (1.0 N)
Синоним (ы)Раствор соляной кислоты; Раствор хлористого водорода
XВойдите, чтобы просмотреть цены и доступность для конкретного аккаунта.
Цены, указанные в каталоге, не включают действующие налоги.
Войдите в систему или создайте учетную запись
Общая информация:- Лидирующий в отрасли более 65 лет
- Honeywell теперь поставляет неорганические реагенты премиум-класса Fluka ™ по всему миру — с гарантированной консистенцией, чистотой и точностью
| Бренд Fluka | Код UNSPSC 12352301 | Номера CAS (все) | Линейная формула HCl | Номер MDL |
| Молярный246 г / моль | Синонимы Раствор соляной кислоты; Раствор хлороводорода |
Технические характеристики
| Свойство | Значение | |
|---|---|---|
| Фактор | 0,998-1,002 | |
| BAM / EMPA | ||
| TraceabletoNISTSRM | эффективный |
Свойства
| Свойство | Значение | Значение | |
|---|---|---|---|
| Температура самовоспламенения | / | Температура кипения | 10092 |
| Не горюч. (1.013 гПа) | |||
| Сертификация | Отслеживается до SRM от NIST | ||
| Цвет | Бесцветный | ||
| Коррозионная активность | Коррозионно по отношению к металлам | ||
| Плотность | 1,010 г / см3 (20 ° C) | ||
| Температура воспламенения | Неприменимо | ||
| Форма | Жидкость | ||
| Марка | Объемный концентрат | ||
| Несовместимые материалы | Этиленимин, аммиак, хлорсульфоновая кислота, серная кислота, сильные окислители основания, уксусный ангидрид, амины, металлы | ||
| Нижний предел взрываемости | Неприменимо | ||
| Точка плавления / диапазон | 0 ° C | ||
| Коэффициент распределения | Нет данных | ||
| Растворимость в воде | Полностью смешивается | ||
| Верхний предел взрываемости | Неприменимо | ||
| Давление пара | Аналогично воде | ||
| Вязкость | Нет данных | ||
| Значение pH | 1 | ||
| Температура хранения | Окружающая среда |
Информация по технике безопасности
соляная кислота на продажу | Купить водные растворы | 36-38%, 10%, 5%, 7%, 15%, 20%, 25%, 28%, 37%, 0.1N, 1.0M, 1N, 1 молярный | Формула HCl | «Соляная кислота» | Для промышленного и фармацевтического использования | Опасная коррозионная жидкость
Купить концентрированную соляную кислоту для очистки, дезинфицирующего средства, плавательных бассейнов, травления, очистки воды, регулирования pH, уничтожения вирусов и бактерий, домов, канализации, удаления ржавчины, очистки унитаза, извлечения золота, камней, очистки цемента и бетона, средства от сорняков, Батареи, Медицина, Стоматология, Пищеварение, Больницы, Контроль pH питьевой воды, Пищевая и фармацевтическая промышленность, Продукты питания и косметика [Бесцветный водный раствор газообразного хлористого водорода]
Продажа 10% раствора соляной кислоты
Соляная кислота, 10% (об. / Об.) Водный раствор Краткое описание продукта
Формула HCl | pH -0.5 | «Соляная кислота» | CAS # 7647-01-0 | Исследования карбоната кальция в горных породах | Для плавательных бассейнов, травления, водоподготовки, регулирования pH | Кислый раствор газообразного хлористого водорода, растворенный в воде
30% раствор соляной кислоты для продажи онлайн | Лабораторный класс
37% раствор соляной кислоты (36-38%) для продажи через Интернет | Реагент ACS
5% раствор соляной кислоты для продажи на сайте LabAlley.com
5% раствор соляной кислоты Краткое описание продукта
5% водный раствор соляной кислоты | Формула HCl | Бутылки 125 мл, 500 мл и 1 литр | Для уничтожения вирусов и бактерий, Косметика, Медицина, Бассейны, Средства для чистки унитазов, Бытовая чистка и стоки | Для контроля pH питьевой воды, продуктов питания и фармацевтики | CAS # 7647-01-0 | «Кислота соляная»
7% раствор соляной кислоты для продажи на сайте LabAlley.com
7% соляная кислота Краткое описание продукта
Купить 7% раствор соляной кислоты | 16 унций | 1 галлон | Бутылки 500 мл и 4 литра | Формула HCl | CAS # 7647-01-0 | «Соляная кислота» | SDS | Для бассейнов, чистки, дренажа, батарей, медицины, дома, восстановления золота, удаления ржавчины, чистящего цемента
Технический раствор соляной кислоты 15% (об. / Об.) Для продажи в Интернете на LabAlley.com
- Купите бутылку на 16 унций (500 мл) с 15% раствором соляной кислоты
Раствор соляной кислоты 15% Краткое описание продукта
Купить раствор соляной кислоты 15% об. / Об. | 16 унций | Бутылка 500 мл | Продажа онлайн | Аналитический реагент (AR) | Технический класс | Формула HCl | «Соляная кислота» | CAS # 7647-01-0 | Для бассейнов, медицины, фармацевтики, очистки, водостока, батарей, медицины, стоматологии, больниц, домов
Дополнительные продукты с концентрированной соляной кислотой для продажи через Интернет в LabAlley.com
Купите соляную кислоту онлайн (HCl) оптом здесь или по телефону: 512-668-9918
Если у вас есть вопросы о заказе концентрированной соляной кислоты онлайн здесь, на LabAlley.com, или вы хотите разместить заказ, позвоните по телефону 512-668-9918 или напишите по адресу customerservice@laballey.com, чтобы поговорить со специалистом по соляной кислоте. Чтобы запросить паспорт безопасности или паспорт безопасности для соляной кислоты, обратитесь в Lab Alley. Купите азотную кислоту здесь.
Соляная кислота (Часть I) — Периодическая таблица видео [YouTube Video]
Использование соляной кислоты
- Соляная кислота для бассейнов
- Соляная кислота для уничтожения вирусов, бактерий и грибков
- Соляная кислота для очистки
- Соляная кислота от изжоги
- Соляная кислота для удаления ржавчины
- Соляная кислота для стоков
- Соляная кислота, используемая в батареях
- Соляная кислота, используемая в медицине
- Соляная кислота, используемая в плавательных бассейнах
- Соляная кислота, используемая в стоматологии
- Соляная кислота, используемая в пищеварении
- Соляная кислота, используемая в больницах
- Использование соляной кислоты в домашних условиях
Химические свойства и структура соляной кислоты
- Температура плавления соляной кислоты: зависит от концентрации
- соляная кислота Молекулярный вес: 36.46 г / моль
- Соляная кислота Температура кипения: в зависимости от концентрации
- Соляная кислота Молекулярная формула: HCI
- Соляная кислота pH
- Безопасность и опасности соляной кислоты
- Концентрированная соляная кислота (36,5-38%) представляет собой жидкость от бесцветной до желтоватой с острым запахом.
- Соляная кислота 37% Цена: 30 мл, 500 мл, 1 литр, 2,4 литра, 4 литра, бочка 55 галлонов
- Соляная кислота Синонимы: хлористый водород, 7647-01-0, соляная кислота, спирты соли, хлорид гидроксония, хлороводородная кислота, хлороводородная кислота
- Структура соляной кислоты: показатель преломления (n), диэлектрическая проницаемость (εr)
- Плотность соляной кислоты: удельный вес (плотность относительно плотности воды) раствора соляной кислоты составляет 1.18 г / мл.
- Заряд соляной кислоты: когда HCl растворяется в воде, образуются ионы H и Cl. Водород теряет электрон (становится ионом с зарядом +1), а хлор приобретает электрон (становится ионом с зарядом -1).
- Соляная кислота ChemSpider ID: 307
- Соляная кислота, точка кипения 37%
- Кислота соляная Номер ООН: 1789
- Соляная кислота Номер ЕС: 231-595-7
- Соляная кислота Регистрационный номер CAS: 7647-01-0
- Соляная кислота PubChem CID: 313
- соляная кислота продается онлайн в США на сайте LabAlley.com
- Факты химической безопасности соляной кислоты
- Соляная кислота на коже: соляная кислота — опасная жидкость, которую необходимо использовать с осторожностью. Сама кислота вызывает коррозию, а ее концентрированные формы выделяют кислые туманы, которые также опасны. Если кислота или туман попадут на кожу, глаза или внутренние органы, повреждение может быть необратимым или даже смертельным в тяжелых случаях. Прочтите больше советов по безопасности здесь.
- Гидрохлористая кислота используется для извлечения золота, добычи золота, тестирования продуктов из золота и его аффинажа
- Использует: ингредиент в бытовых чистящих средствах, растворяет металлы, ингредиент в смеси царской водки, титрование, очищающее золото и удаление ржавчины.
- Другое применение соляной кислоты: соляная кислота также используется в производстве батарей, фотовспышек и фейерверков.Его даже используют для обработки сахара и изготовления желатина. Соляная кислота, как и хлорид натрия в прошлом месяце, является еще одним химическим веществом «рабочей лошадки», потому что он невероятно полезен во многих отношениях. Соляная кислота является предпочтительной кислотой при титровании для определения количества оснований.
- Соляная кислота часто используется в химическом анализе для подготовки («переваривания») проб для анализа. Концентрированная соляная кислота растворяет многие металлы и образует окисленные хлориды металлов и газообразный водород.Подробнее читайте здесь.
- Соляная кислота отправляется FedEx и LTL в США
- Купите соляную кислоту здесь
- Купите азотную кислоту здесь
Как безопасно добавить соляную кислоту в бассейн | Процедуры Orenda [YouTube Video]
Обзор линейки продуктов соляной кислоты
Купить соляную кислоту | Бутылка 16 унций (500 мл) | 33 унции (1 литр) | Бутылка 1 галлон | Формула HCl | Для продажи онлайн в США | ACS Reagent Grade 37% соляная кислота для продажи | Продукты соляной кислоты: 0.1%, 0,5%, 1%, 5%, 7%, 10%, 15% степени аналитического реагента (AR), 20% степени аналитической степени (AR), 25% степени аналитического реагента (AR), 28%, 30%, 37%, 0,1N, 1N, 1: 1, 5N, 12N, 3M, 6M, 1 молярная, 5% соляная кислота в денатурированном спирте | Использует | SDS / MSDS | Информация о безопасности и опасностях
О соляной кислоте
Соляная кислота также известна как соляная кислота. Это простейшая кислотная система на основе хлора, содержащая воду. Соляную кислоту получают путем растворения хлористого водорода в воде и множестве других химических веществ.Бесцветный и неорганический. Химическая формула HCl: h3O, номер CAS 7647-01-0. Соляная кислота имеет характерный запах и очень кислая. Он реагирует с основными соединениями и растворяет многие металлы. Он естественным образом вырабатывается в пищеварительной системе большинства животных и людей.
Соляная кислота была открыта в 800 г. н.э., исторически в Европе она называлась acidum salis, духами соли и хлорида гидроксония. Название «соляная кислота» было придумано французским химиком Жозефом Луи Гей-Люссаком в 1814 году.
Можно ли купить соляную кислоту?
Соляная кислота доступна практически в любом хозяйственном магазине или магазине товаров для бассейнов. Он продается в виде раствора в воде примерно половинной крепости (по соображениям безопасности) под торговым названием «соляная кислота». Иногда соляная кислота не очень чистая. Подробнее читайте здесь.
Какова молярность 37% соляной кислоты?
Таким образом, дымящаяся / концентрированная 37% HCl составляет 12 моль (= M = моль / л). Подробнее читайте здесь.
Для чего используется соляная кислота?
Соляная кислота также используется в производстве батарей, фотовспышек и фейерверков. Его даже используют для обработки сахара и изготовления желатина. Соляная кислота, как и хлорид натрия в прошлом месяце, является еще одним химическим веществом «рабочей лошадки», потому что он невероятно полезен во многих отношениях. Подробнее читайте здесь.
Состав соляной кислоты
Химическое соединение соляная кислота представляет собой водный (водный) раствор газообразного хлористого водорода (HCl).Молекула хлористого водорода HCl представляет собой простую двухатомную молекулу, состоящую из атома водорода H и атома хлора Cl, соединенных ковалентной одинарной связью. Подробнее читайте здесь.
Соляная кислота для пищеварения
Соляная кислота способствует перевариванию белков, поставляя H +, который активирует пепсиноген, предшественник пепсина. Пепсиноген секретируется главными клетками желудочных желез тела и антрального отдела желудка. Подробнее читайте здесь.
Может ли соляная кислота повредить вам?
Соляная кислота — опасная жидкость, которую необходимо использовать с осторожностью.Сама кислота вызывает коррозию, а ее концентрированные формы выделяют кислые туманы, которые также опасны. Если кислота или туман попадут на кожу, глаза или внутренние органы, повреждение может быть необратимым или даже смертельным в тяжелых случаях. Подробнее читайте здесь.
Соляная кислота для лечения рака
КТ-опосредованная чрескожная инъекция соляной кислоты показала хорошие деструктивные эффекты; он будет использоваться в качестве нового минимально инвазивного лечения для чрескожного лечения рака печени вместо уксусной кислоты и безводного спирта с его безопасностью, управляемостью и отсутствием ядовитых эффектов.Подробнее читайте здесь.
Соляная кислота от изжоги
Соляная кислота (HCl) — важный желудочный секрет, который позволяет организму расщеплять белки, активировать важные ферменты и гормоны и защищать от чрезмерного роста бактерий в кишечнике. Симптомы пониженной кислотности желудка включают, среди прочего, изжогу, расстройство желудка и вздутие живота. Подробнее читайте здесь.
Использование соляной кислоты
Соляная кислота полезна по-разному.Он используется в производстве органических соединений и поливинилхлорида для пластмасс. В быту его часто используют в качестве средства для удаления накипи. Он предназначен для удаления накипи с котлов и водонагревателей. В пищевой промышленности он используется в качестве пищевой добавки и для производства желатина. Он также используется в кожевенной промышленности. Соляная кислота используется рабочими в ювелирных магазинах для очистки золота.
Соляная кислота обычно используется в химическом анализе для подготовки проб. Это сильная кислота и реагент.Это также предпочтительная кислота при титровании для определения количества оснований. Существует множество промышленных применений соляной кислоты, например, для рафинирования металлов. В индустрии травления стали используется соляная кислота для удаления ржавчины или окалины оксида железа с железа или стали.
Соляная кислота на коже
При использовании соляной кислоты необходимо использовать средства индивидуальной защиты. Но если он попал на кожу, немедленно промойте водой. Это нужно делать не менее 15 минут, снимите загрязненную одежду.При попадании в глаза или проглатывании немедленно обратитесь за медицинской помощью.
Соляная кислота 37% для кожи
HCl — очень коррозионная, сильная кислота и может быть прозрачной / бесцветной или светло-желтой жидкостью. Из-за его коррозионных свойств EPA классифицировало HCl с концентрацией 37% и выше как токсичное вещество. Этой коррозии подвержены слизистые оболочки, кожа и глаза. Подробнее читайте здесь.
Безопасность и опасности соляной кислоты
В концентрированной жидкой форме соляная кислота может вызывать повреждения и является очень коррозийной.Это опасная жидкость, с которой следует обращаться осторожно. Химические ожоги — распространенная угроза безопасности. По данным Национальной медицинской библиотеки США, попадание в глаза может вызвать повреждение глаз и даже слепоту. При обращении с соляной кислотой необходимо надевать защитные средства.
Соляная кислота и азотная кислота для извлечения и переработки золота
Для извлечения и очистки золота многие клиенты Lab Alley используют кислотный метод «царская водка». Царская водка представляет собой смесь азотной и соляной кислот, оптимально в молярном соотношении 1: 3.Чтобы приготовить и очистить царскую водку, смешайте три (3) части соляной кислоты с одной (1) частью азотной кислоты в стеклянной посуде. Чтобы узнать, как использовать царскую водку для очистки золота, щелкните здесь. Царская водка используется для удаления с подложек благородных металлов, таких как платина, золото и палладий.
Делайте покупки в Интернет-магазине Lab Alley для широкого спектра обычных кислот, используемых в химии и повседневной жизни, включая азотную кислоту, борную кислоту, угольную кислоту, соляную кислоту, плавиковую кислоту, винную кислоту, серную кислоту, соляную кислоту, лимонную кислоту, фосфорную кислоту. , Щавелевая кислота, абсорбционная кислота и уксусная кислота на https: // www.laballey.com/collections/acids.
Приобретайте химикаты для извлечения золота и химикаты для аффинажа золота в Интернете по адресу LabAlley.com/pages/Buy-Gold-Recovery-Chemicals.
Соляная кислота и соляная кислота
Некоторые люди задаются вопросом, совпадает ли соляная кислота с соляной кислотой. Когда вы ищете средство для снижения pH воды в бассейне, вы идете в магазин и покупаете емкость с соляной кислотой. Вместо этого вы, вероятно, будете брезгливо относиться к соляной кислоте в вашем бассейне, особенно если вы собираетесь плавать, но на самом деле это, по сути, то, что вы делаете.
Хлористый водород отличается от соляной кислоты и соляной кислоты. Это бесцветный едкий ядовитый газ, который дымится во влажном воздухе и выделяет соляную кислоту при растворении в воде. Соляная кислота — сильная коррозионная кислота. Он также известен как духи соли или acidum salis. «Мюриатический» означает «относящийся к рассолу или соли».
Соляная кислота — одно из названий соляной кислоты, и это было самое распространенное название, пока французский химик Жозеф Луи Гей-Люссак не ввел термин соляная кислота в начале 19 века.Современные химики проводят различие между соляной и соляной кислотами по концентрации и чистоте. У них обоих химическая формула HCl.
Хранение соляной кислоты
Соляную кислоту нельзя хранить в металлических контейнерах, но пластиковые контейнеры, изготовленные из поливинилхлорида, являются отличным вариантом. Его следует хранить в прохладном, хорошо проветриваемом помещении, вдали от источников влаги. Держите контейнер плотно закрытым и держите его подальше от несовместимых материалов.
Информация о соляной кислоте из PubChem
Соляная кислота составляет большую часть желудочного сока, пищеварительной жидкости человека.В сложном процессе и при большой энергетической нагрузке он секретируется париетальными клетками (также известными как оксинтические клетки). Эти клетки содержат обширную секреторную сеть (называемую канальцами), из которой HCl секретируется в просвет желудка. Они являются частью эпителиальных фундальных желез (также известных как кислородные железы) в желудке. Химическое соединение соляная кислота представляет собой водный (на водной основе) раствор газообразного хлористого водорода (HCl). Это сильная кислота, главный компонент желудочного сока, широко применяемая в промышленности.При обращении с соляной кислотой необходимо соблюдать соответствующие меры безопасности, поскольку это очень коррозионная жидкость. Соляная кислота, или соляная кислота по своему историческому, но все еще иногда используемому названию, была важным и часто используемым химическим веществом с ранней истории и была обнаружена алхимиком Джабиром ибн Хайяном около 800 года. Хлористый водород, также известный под названием HCl, это очень едкий и токсичный бесцветный газ, образующий белые пары при контакте с влажностью. Эти пары состоят из соляной кислоты, которая образуется при растворении хлористого водорода в воде.Молекула хлористого водорода HCl представляет собой простую двухатомную молекулу, состоящую из атома водорода H и атома хлора Cl, соединенных ковалентной одинарной связью. Поскольку атом хлора гораздо более электроотрицателен, чем атом водорода, ковалентная связь между атомами довольно полярна. Хлористый водород образует агрессивную соляную кислоту при контакте с тканями тела. Вдыхание паров может вызвать кашель, удушье, воспаление носа, горла и верхних дыхательных путей, а в тяжелых случаях — отек легких, недостаточность системы кровообращения и смерть.Контакт с кожей может вызвать покраснение, боль и серьезные ожоги кожи. Хлористый водород может вызвать серьезные ожоги глаз и необратимые повреждения глаз. Раствор соляной кислоты представляет собой бесцветную водянистую жидкость с резким раздражающим запахом. Состоит из хлористого водорода, газа, растворенного в воде. Тонет и смешивается с водой. Выделяет раздражающий пар. При комнатной температуре хлористый водород представляет собой едкий негорючий газ от бесцветного до слегка желтоватого цвета, который тяжелее воздуха и имеет сильный раздражающий запах.При контакте с воздухом хлористый водород образует плотные белые коррозионные пары. Хлороводород может выделяться из вулканов. Хлористый водород находит множество применений, включая очистку, травление, гальванику металлов, дубление кожи, а также очистку и производство широкого спектра продуктов. Хлористый водород может образовываться при горении многих пластмасс. При контакте с водой образует соляную кислоту. И хлористый водород, и соляная кислота вызывают коррозию. Подробнее читайте здесь.
Информация о соляной кислоте из Википедии
Соляная кислота или соляная кислота — бесцветная неорганическая химическая система с формулой HCl.Соляная кислота имеет характерный резкий запах. Он классифицируется как сильно кислый и может поражать кожу в широком диапазоне состава, поскольку хлористый водород полностью диссоциирует в водном растворе.
Соляная кислота — это простейшая кислотная система на основе хлора, содержащая воду. Это раствор хлористого водорода и воды, а также множества других химических веществ, включая ионы гидроксония и хлорида. Это естественный компонент желудочной кислоты, вырабатываемой пищеварительной системой большинства видов животных, включая человека.
Соляная кислота — важный химический реагент и промышленный химикат, используемый при производстве поливинилхлорида для пластмасс. В домашних условиях разбавленная соляная кислота часто используется в качестве средства для удаления накипи. В пищевой промышленности соляная кислота используется в качестве пищевой добавки и при производстве желатина. Соляная кислота также используется при обработке кожи.
Соляная кислота была открыта алхимиком Джабиром ибн Хайяном около 800 года нашей эры. Его исторически называли acidum salis и спиртами соли, потому что он был произведен из каменной соли и «зеленого купороса» (сульфата железа (II)) (Базилием Валентином в 15 веке), а затем из химически подобной поваренной соли и серной кислоты ( Иоганна Рудольфа Глаубера в 17 веке).Свободная соляная кислота была впервые официально описана в 16 веке Либавиусом. Позже его использовали в своих научных исследованиях химики, такие как Глаубер, Пристли и Дэви. Если не находится под давлением или не охладиться, соляная кислота превратится в газ, если в ней будет около 60% или меньше воды. Соляная кислота также известна как хлорид гидроксония, в отличие от ее безводного родителя, известного как хлористый водород или сухая HCl.
коррозионных характеристик сплавов на основе никеля в высококонцентрированной соляной кислоте | NACE CORROSION
ABSTRACT
Никелевые сплавы, особенно семейство никель (Ni) -хром (Cr) -молибден (Mo), обладают отличной стойкостью к соляной кислоте.Целью данной статьи является изучение коррозионных характеристик различных сплавов на основе Ni при высоких концентрациях HCl кислот ниже точки кипения. В данной работе исследуется коррозионная стойкость сплавов на основе никеля C-276 (UNS N10276), C-22 (UNS N06022), C-2000 (UNS N06200), Hybrid-BC1 (UNS N10362) и B-3 (UNS N10675). ) в отожженном в мельнице состоянии исследовали в высококонцентрированных (25-37 мас.%) растворах HCl. На основании имеющихся данных была предпринята попытка построить диаграммы изокоррозии 10 млн / год (0.25 мм / год) и 20 млн / год (0,5 мм / год) для выбранных сплавов в диапазоне от 25 до 35 мас.% HCl.
Кроме того, скорости коррозии вышеупомянутых сплавов, подвергнутых термообработке (760 ° C / 15 мин / охлаждение на воздухе), были изучены с помощью методов погружения и электрохимического линейного поляризационного сопротивления (LPR) и сравнивались со скоростями коррозии, полученными на заводе. отожженное состояние.
Это исследование показывает, что термообработанные сплавы показывают относительно более высокую скорость коррозии при воздействии более концентрированных растворов HCl при более высоких температурах.
ВВЕДЕНИЕ
Соляная кислота (HCl) — бесцветная жидкость, очень коррозионная по своей природе и считается сильной минеральной кислотой. HCl является монопротонным, что означает, что он имеет высокий уровень диссоциации в воде, что создает переизбыток ионов H + в растворе. Избыток ионов H + означает, что он имеет очень низкий уровень pH 0-1. Это указывает на то, что это очень коррозионное вещество, и только некоторые материалы устойчивы. Большинство обычно используемых металлов и их сплавов подвергаются обширному общему и / или локальному коррозионному воздействию в HCl.Далее агрессивность раствора резко меняется в зависимости от концентрации и температуры.
HCl используется во многих областях, от добычи металлов и хлоридов до кислотной обработки нефтяных скважин. Основные области применения включают травление стали, химическую очистку, химическую обработку, восстановление руды, переработку пищевых продуктов и синтез винилхлорида и алкилхлорида. 1
| Свойство | Значение |
|---|---|
| Класс опасности | 8 |
| Группа упаковки | III |
| UN ID | UN178916 |
ВОДОРОДНАЯ КИСЛОТА И ХЛОРИД ВОДОРОДА
Соляная кислота Хлористый водород | ||
Х.ч. конц. HCl содержит HCl | ||
Концентрированная кислота выделяет HCl при т.кип. 110 ° C, т.пл. -24 ° C, т.кип. -85 ° C, т.пл. -114 ° C Смешивается с водой | ||
Резкий раздражающий запах Резкий раздражающий запах | ||
1,27 (воздух = 1,0) | ||
LD 50 перорально (кролик) 900 мг / кг LC 50 ингалято (крыса) 3124 ppm (1 ч) PEL (OSHA) 5 ppm (7 мг / м 3 ; потолок) ПДК (ACGIH) 5 частей на миллион (7,5 мг / м 3 ; потолок) | Сильно агрессивный; вызывает сильные ожоги при попадании в глаза и на кожу, а также при вдыхании газа. | Соляная кислота и газообразный хлористый водород являются очень едкими веществами, которые могут вызвать серьезные ожоги при контакте с тканями тела. Водная кислота и газ — сильные раздражители глаз и слезоточивые средства. Попадание концентрированной соляной кислоты или концентрированных паров HCl в глаза может привести к серьезным травмам, что приведет к необратимому ухудшению зрения и возможной слепоте, а контакт с кожей приведет к тяжелым ожогам. Проглатывание может вызвать серьезные ожоги полости рта, горла и желудочно-кишечного тракта и привести к летальному исходу.Вдыхание газообразного хлористого водорода может вызвать сильное раздражение и травму верхних дыхательных путей и легких, а воздействие высоких концентраций может вызвать смерть. Считается, что газ HCl обладает адекватными предупреждающими свойствами. Не было обнаружено, что хлористый водород является канцерогенным и не проявляет токсичности для репродуктивной системы или развития человека. |
Негорючие, но при контакте с металлами может образовываться легковоспламеняющийся газообразный водород. | ||
Соляная кислота и хлористый водород бурно реагируют со многими металлами с образованием легковоспламеняющегося газообразного водорода, который может взорваться.Реакция с окислителями, такими как перманганаты, хлораты, хлориты и гипохлориты, может привести к образованию хлора или брома. | ||
С соляной кислотой следует обращаться в лаборатории в соответствии с «основными принципами осторожности», описанными в главе 5.C. При работе с этой кислотой следует использовать защитные очки и резиновые перчатки, а контейнеры с HCl следует хранить в хорошо вентилируемом месте, изолированном от несовместимых металлов. Ни в коем случае нельзя добавлять воду в HCl, поскольку это может привести к разбрызгиванию; всегда добавляйте кислоту в воду.Емкости с соляной кислотой следует хранить во вторичных пластиковых лотках, чтобы избежать коррозии металлических полок для хранения из-за капель или разливов. С газообразным хлористым водородом следует обращаться в лаборатории, используя «основные разумные методы», описанные в главе 5.C, дополненные процедурами, описанными в главе 5.H для работы со сжатыми газами. Баллоны с хлороводородом следует хранить в прохладном, сухом месте, отдельно от щелочных металлов и других несовместимых веществ. | ||
При попадании на кожу снять загрязненную одежду и немедленно промыть проточной водой не менее 15 мин. В случае попадания в глаза немедленно промыть большим количеством воды не менее 15 минут, удерживая веки открытыми. Обратитесь за медицинской помощью. В случае проглатывания не вызывать рвоту. Дайте большое количество воды или молока и доставьте в медицинское учреждение. В случае вдыхания вынести на свежий воздух и обратиться за медицинской помощью. Тщательно нейтрализуйте пролитую соляную кислоту подходящим средством, например порошкообразным бикарбонатом натрия, затем разбавьте абсорбирующим материалом, поместите в соответствующий контейнер и утилизируйте должным образом. Разбавление водой перед нанесением твердого адсорбента может быть эффективным средством уменьшения воздействия паров хлористого водорода. В случае большого разлива или выброса в замкнутом пространстве может потребоваться защита органов дыхания. Утечки газообразного HCl проявляются в образовании плотных белых паров при контакте с атмосферой.Небольшие утечки можно обнаружить, подержав открытый контейнер с концентрированным гидроксидом аммония рядом с местом предполагаемой утечки; густые белые пары подтверждают наличие утечки. В случае случайного выброса газообразного хлористого водорода, например, из протекающего баллона или связанного с ним устройства, эвакуируйте зону и устраните источник утечки, если это можно сделать безопасно. Переместите баллон в вытяжной шкаф или в удаленное место, если его нельзя отключить. Может потребоваться полная защита органов дыхания и защитная одежда для борьбы с выбросом хлористого водорода. | ||
Во многих местах соляная кислота или остатки разлива могут быть сброшены в канализацию после соответствующего разбавления и нейтрализации. В противном случае соляную кислоту и отходы, содержащие это вещество, следует поместить в соответствующий контейнер, четко помеченный, и обращаться с ними в соответствии с инструкциями по утилизации отходов вашего учреждения. Избыток хлористого водорода в баллонах следует вернуть производителю. | ||
Информация в этом LCSS была собрана комитетом Национального исследовательского совета по литературным источникам и материалам Паспорта безопасности и считается точным по состоянию на июль 1994 года.Это резюме предназначено для использования обученным лабораторным персоналом. в сочетании с отчетом NRC Prudent Практика в лаборатории: обращение с химическими веществами и их утилизация . Этот LCSS представляет собой краткую краткое изложение информации по безопасности, которое должно быть достаточным для большинства лабораторное использование указанного вещества, но в некоторых случаях может рекомендуется ознакомиться с более подробными ссылками. Эта информация не следует использовать в качестве руководства для внелабораторного использования этого химический. Copyright 1995 Национальная академия наук.Все права защищены. | ||
Производство соляной кислоты | KBR
Работа с кислотой требует современных технологий. Наши индивидуальные установки для обработки кислот и отходов производства соляной кислоты удовлетворяют особым требованиям, сочетая самые современные технологии с проверенными материалами.
KBR предлагает полный спектр обработки и обработки соляной кислотой (HCl), начиная от простой перегонки над ректификацией до экстрактивной ректификации и ректификации с двойным давлением, для достижения любой чистоты и концентрации во всем диапазоне вплоть до почти полного отсутствия воды, 100% сухой газ.Кроме того, предлагается противоположная абсорбция сухого газообразного HCl для достижения желаемой более низкой концентрации HCl.
«Что касается обработки соляной кислоты, мы специализируемся на обработке кислот и потоков отходов, что обеспечивает экономические и экологические преимущества».
Мы предлагаем технологические решения и технологии для концентрирования побочного продукта HCl от химического процесса, такого как фосгенирование, для рециркуляции или продажи третьим сторонам, для концентрирования разбавленных потоков HCl из вентиляционных скрубберов и удаления HCl из сточных вод по соображениям производительности или защиты окружающей среды.Мы также разрабатываем новые приложения нашей технологии и управляем лабораторией с пилотными установками, которые позволяют нам разрабатывать и масштабировать такие новые приложения очень надежно и эффективно для наших клиентов.
Мы проектируем малогабаритные установки, на которых восстанавливается всего несколько сотен килограммов кислоты в час, вплоть до установок мирового масштаба.
Предварительное концентрирование
Предварительное концентрирование используется для обработки сырой соляной кислоты с низким содержанием HCl для достижения концентрации HCl до 24% по весу. Воду удаляют ректификацией, а азеотроп вода / соляная кислота удаляют в нижнем потоке.В зависимости от рабочего давления азеотропная концентрация HCl составляет от 18 до 24 мас.%. Летучие и нелетучие примеси также удаляются из потока HCl во время предварительного концентрирования.
Средняя концентрация
Соляная кислота с концентрацией 30–35 мас.% Может быть произведена из любой разбавленной сырой соляной кислоты. При экстракционной ректификации слабая соляная кислота смешивается с экстракционным агентом и подается в ректификационную колонну. Вода абсорбируется экстрагирующим агентом, и летучесть потока соляной кислоты увеличивается.В верхней части колонны очищают соляную кислоту средней концентрации. Разбавленный экстракционный агент собирается в отстойнике, повторно концентрируется во внешнем испарителе и подается обратно в колонну. CaCl2, MgCl2 или h3SO4 могут использоваться в качестве экстрактивных агентов для удаления воды. Процесс двойного давления также доступен для производства соляной кислоты средней концентрации. На первом этапе предварительно сконцентрированная кислота с содержанием HCl 22–24 мас.% Разделяется на головной продукт с примерно 30–35 мас.% HCl и азеотропную кислоту отстойного продукта с использованием ректификации под давлением.На втором этапе азеотропная кислота восстанавливается путем испарения воды в условиях вакуума до 22–24 мас.% HCl, а затем возвращается на первую стадию. В качестве альтернативы азеотропная кислота может быть повторно усилена с помощью концентрированного газообразного HCl.
Высокая концентрация
Чтобы производить газообразный HCl с высокой концентрацией до 100% по весу HCl, можно применять ту же конфигурацию процесса для средней концентрации, изменяя при этом рабочие условия.
Очистка
Отработанные соляные кислоты различного происхождения, содержащие органические и неорганические примеси, могут быть извлечены и очищены с использованием технологии KBR PLINKE.
СОП: Разбавление концентрированной соляной кислоты
Решить переменные, которые нужно изменить и измерить в честных тестах, и наблюдать, измерить и записать данные с точностью, используя цифровые технологии, в зависимости от ситуации Решить переменные, которые необходимо изменить и измерить в честных тестах, и наблюдать, измерить и записать данные с точностью, используя цифровые технологии в зависимости от ситуации Навыки — Планирование и проведение — Участвовать в исследованиях и делать наблюдения с помощью органов чувств — Общение — Обмен наблюдениями и идеями — Задавать вопросы и предсказывать — Ставить вопросы о знакомых объектах и событиях и отвечать на них — Обработка и анализ данных и информации — Участвуйте в обсуждениях наблюдений и представляйте идеи-Наука как человеческое усилие — Природа и развитие науки — Наука включает в себя наблюдение, постановку вопросов и описание изменений в объектах и событиях-Наука Понимание — Физические науки — Способ движения объектов зависит от множества факторов, включая их размер и форму — Биологические науки- — У живых существ есть базовые потребности, включая пищу и воду — Науки о Земле и космосе — Ежедневные и сезонные изменения в нашей окружающей среде влияют на повседневную жизнь — Химические науки — Объекты сделаны из материалов, которые обладают наблюдаемыми свойствами1-Понимание науки — Биологические науки — Живые существа имеют множество внешних характеристик — Живые существа живут в разных местах, где их потребности удовлетворяются — Химические науки — Повседневные материалы можно физически изменять различными способами — Физические Науки — Свет и звук производятся различными источниками и могут быть восприняты — Науки о Земле и космосе — Наблюдаемые изменения происходят в небе и ландшафте — Наука как деятельность человека — Природа и развитие науки — — Наука включает в себя наблюдение, постановку вопросов и описание изменений в объектах и событиях — Использование и влияние науки — Люди используют науку в своей повседневной жизни, в том числе при заботе об окружающей среде и живых существах — Навыки исследования науки — Вопросы и прогнозы Инг — Ставьте вопросы и отвечайте на вопросы, а также делайте прогнозы относительно знакомых объектов и событий — Планирование и проведение — Участвуйте в управляемых исследованиях, чтобы исследовать и отвечать на вопросы, используя неформальные измерения для сбора и записи наблюдений, используя при необходимости цифровые технологии- —Участвовать в контролируемых исследованиях, чтобы изучить и ответить на вопросы, используя неформальные измерения для сбора и записи наблюдений, используя при необходимости цифровые технологии — Обработка и анализ данных и информации — Использование ряда методов для сортировки информации, включая чертежи и предоставленные таблицы и посредством обсуждения сравнивать наблюдения с прогнозами — использовать ряд методов для сортировки информации, включая рисунки и предоставленные таблицы, а также путем обсуждения сравнивать наблюдения с прогнозами — оценка — сравнивать наблюдения с наблюдениями других — общение— -Представлять и передавать наблюдения и идеи различными способами 2-Понимание науки — Биологические науки — — Живые существа растут, изменяются и имеют потомство, похожее на самих себя — Химические науки — Различные материалы можно комбинировать для определенной цели — Физические науки — Толчок или притяжение влияет на то, как объект движется или меняет форму — Науки о Земле и космосе — Ресурсы Земли используются различными способами — Наука как деятельность человека — Природа и развитие науки — Наука включает в себя наблюдение, постановку вопросов и описание изменений в объектах и событиях — Использование науки и ее влияние — Люди используют науку в своей повседневной жизни, в том числе при заботе об окружающей среде и живых существах. Навыки исследования науки — Задавать вопросы и делать прогнозы — Ставить вопросы и отвечать на них, а также делать прогнозы относительно знакомых объектов и события — Обработка и анализ данных и информации — Используйте ряд методов для сортировки информации, включая рисунки и предоставленные таблицы, а также путем обсуждения, сравнивайте наблюдения с прогнозами — Используйте ряд методов для сортировки информации, в том числе dr обзоров и предоставленных таблиц, а также в ходе обсуждения сравните наблюдения с прогнозами — Планирование и проведение — Участвуйте в управляемых исследованиях, чтобы исследовать и отвечать на вопросы, используя неофициальные измерения для сбора и записи наблюдений, при необходимости используя цифровые технологии — Участвуйте в управляемых исследованиях исследовать и отвечать на вопросы, используя неформальные измерения для сбора и записи наблюдений, используя при необходимости цифровые технологии — Оценка — Сравнение наблюдений с наблюдениями других — Общение — Представлять и передавать наблюдения и идеи различными способами3-Наука Понимание — Биологические науки — Живые существа можно сгруппировать на основе наблюдаемых характеристик и отличить от неживых существ — Физические науки — Тепло может производиться разными способами и может переходить от одного объекта к другому — Химические науки — Изменение состояния между твердым и жидким телом может быть вызвано добавлением или удалением тепла — Науки о Земле и космосе — Ea Вращение rth вокруг своей оси вызывает регулярные изменения, в том числе дневные и ночные — Наука как человеческое усилие — Использование и влияние науки — Научные знания помогают людям понять эффект своих действий — Природа и развитие науки — Наука включает в себя прогнозирование и описание закономерностей и взаимосвязей — Навыки исследования науки — Опрос и прогнозирование — Под руководством вы определяйте вопросы в знакомых контекстах, которые можно исследовать с научной точки зрения, и делать прогнозы на основе предшествующих знаний — Обработка и анализ данных и информации — —Сравните результаты с прогнозами, предлагая возможные причины выводов — Используйте ряд методов, включая таблицы и простые столбчатые диаграммы, для представления данных и выявления закономерностей и тенденций — Планирование и проведение — Рассмотрите элементы объективных тестов и использовать формальные измерения и цифровые технологии по мере необходимости для точного проведения и записи наблюдений — Планируйте и проводите научные исследования под руководством найти ответы на вопросы, учитывая безопасное использование соответствующих материалов и оборудования — Оценка — Обдумайте исследования, в том числе, был ли тест справедливым или нет — Общение — Представляйте и сообщайте наблюдения, идеи и результаты, используя формальные и неформальные формы Представления4-Понимание науки — Биологические науки — Живые существа зависят друг от друга и окружающей среды, чтобы выжить — У живых существ есть жизненные циклы — Химические науки — Природные и обработанные материалы имеют ряд физических свойств, которые могут влиять их использование — Науки о Земле и космосе — Поверхность Земли изменяется с течением времени в результате естественных процессов и деятельности человека — Физические науки — Силы могут быть применены одним объектом к другому посредством прямого контакта или с расстояния — Наука как человеческое усилие — Использование и влияние науки — Научные знания помогают людям понять эффект своих действий — Природа и развитие науки — Наука включает в себя предсказания и описание закономерности и взаимосвязи — Навыки исследования науки — Обработка и анализ данных и информации — Сравнение результатов с прогнозами, указание возможных причин для выводов — Использование ряда методов, включая таблицы и простые столбчатые диаграммы, для представления данных и выявления закономерностей и тенденции — Опрос и прогнозирование — Под руководством выявляйте вопросы в знакомых контекстах, которые можно исследовать с научной точки зрения, и делать прогнозы на основе предшествующих знаний — Планирование и проведение — Рассмотрение элементов честных тестов и использование формальных измерений и цифровых технологий по мере необходимости, точно производить и записывать наблюдения — Под руководством, планировать и проводить научные исследования, чтобы найти ответы на вопросы, учитывая безопасное использование соответствующих материалов и оборудования — Оценка — Обдумайте исследования, в том числе, было ли испытание справедливо или нет — Общение — Представлять и сообщать наблюдения, идеи и выводы, используя формальные и неформальные представления5-Sci Понимание — Биологические науки — У живых существ есть структурные особенности и приспособления, которые помогают им выживать в окружающей среде — Химические науки — Твердые тела, жидкости и газы имеют разные наблюдаемые свойства и ведут себя по-разному — Земля и Космос Науки — Земля является частью системы планет, вращающихся вокруг звезды (Солнца) — Физические науки — Свет от источника образует тени и может поглощаться, отражаться и преломляться — Наука как человеческое усилие — Использование и влияние науки — Научные знания используются для решения проблем и информирования людей и решений сообщества — Научное понимание, открытия и изобретения используются для решения проблем, которые непосредственно влияют на жизнь людей — Природа и развитие науки — -Важный вклад в развитие науки внесли люди, принадлежащие к разным культурам — Наука включает проверку предсказаний путем сбора данных и использования доказательств для разработки объяснений событий и явлений и т. Д. отражает исторический и культурный вклад — Навыки исследования науки — Планирование и проведение — Решите, какую переменную следует изменить и измерить с помощью объективных тестов, и точно наблюдать, измерять и записывать данные, используя при необходимости цифровые технологии — Определить, спланировать и применить элементы научных исследований для ответов на вопросы и решения проблем с безопасным использованием оборудования и материалов и выявления потенциальных рисков — Определение, планирование и применение элементов научных исследований для ответа на вопросы и решения проблем с безопасным использованием оборудования и материалов и выявления потенциальных рисков — Обработка и анализ данных и информации — Сравнение данных с прогнозами и использование в качестве доказательства при разработке объяснений — Создание и использование ряда представлений, включая таблицы и графики, для представления и описания наблюдений, закономерностей или взаимосвязей в данных с использованием цифровых технологий при необходимости — Оценка — Обдумайте и предложите улучшения в научных исследованиях tions — Общение — Передача идей, объяснений и процессов с использованием научных представлений различными способами, включая мультимодальные тексты — Вопросы и прогнозы — Под руководством задавайте уточняющие вопросы и делайте прогнозы относительно научных исследований6-Понимание науки — Биологические науки — Физические условия окружающей среды влияют на рост и выживание живых существ — Химические науки — Изменения материалов могут быть обратимыми или необратимыми — Физические науки — Электрическая энергия может передаваться и преобразуется в электрические цепи и может генерироваться из ряда источников — Электроэнергия может передаваться и преобразовываться в электрических цепях и может вырабатываться из ряда источников — Науки о Земле и космосе — Внезапные геологические изменения и экстремальные погодные явления могут повлиять на поверхность Земли — Наука как человеческое усилие — Использование и влияние науки — Научные знания используются для решения проблем и информирования людей и решения сообщества — Научное понимание, открытия и изобретения используются для решения проблем, которые напрямую влияют на жизнь людей — Природа и развитие науки — Важный вклад в развитие науки внесли люди, принадлежащие к разным культурам — Наука включает в себя проверку предсказаний путем сбора данных и использования доказательств для разработки объяснений событий и явлений и отражает исторический и культурный вклад. — Навыки исследования науки — Оценка — Обдумывайте и предлагайте улучшения в научных исследованиях — Планирование и проведение — — Решите, какая переменная должна быть изменена и измерена в честных тестах, и точно наблюдать, измерять и записывать данные, используя при необходимости цифровые технологии — Выявлять, планировать и применять элементы научных исследований для ответа на вопросы и решения проблем с использованием оборудования и материалов безопасно и выявить потенциальные риски — Определить, спланировать и применить элементы научных исследований для реагирования Решайте вопросы и решайте проблемы, используя оборудование и материалы безопасно и выявляя потенциальные риски — Общение — Передача идей, объяснений и процессов с использованием научных представлений различными способами, включая мультимодальные тексты — Обработка и анализ данных и информации — -Сравнить данные с прогнозами и использовать их в качестве доказательств при разработке объяснений — Построить и использовать ряд представлений, включая таблицы и графики, для представления и описания наблюдений, закономерностей или взаимосвязей в данных с использованием цифровых технологий в зависимости от обстоятельств — Опрос и прогнозирование- — Под руководством задавайте уточняющие вопросы и делайте прогнозы относительно научных исследований7 — Понимание науки — Биологические науки — Взаимодействия между организмами, включая последствия деятельности человека, могут быть представлены пищевыми цепями и пищевыми цепями — Классификация помогает организовать разнообразная группа организмов — Химические науки — Смеси, включая растворы, содержат комбинацию p Вещества, которые можно разделить с помощью ряда методов — Физические науки — Изменение движения объекта вызвано несбалансированными силами, в том числе гравитационным притяжением Земли, действующими на объект — Гравитация Земли притягивает объекты к центру Земля — Науки о Земле и космосе — Некоторые ресурсы Земли являются возобновляемыми, включая воду, циркулирующую в окружающей среде, но другие невозобновляемые — Вода является важным ресурсом, который циркулирует в окружающей среде — Предсказуемые явления на Земля, включая времена года и затмения, вызваны относительным положением Солнца, Земли и Луны — Наука как человеческое усилие — Природа и развитие науки — Научное знание изменило представление людей о мире и усовершенствовано как становятся доступными новые данные — Научные знания могут развиваться посредством сотрудничества между научными дисциплинами и вклада людей из разных культур — Использование науки и влияние — Люди нас Понимание науки и навыки в своей профессии, и они повлияли на развитие практики в областях человеческой деятельности — Люди используют понимание и навыки из разных научных дисциплин в своей профессии — Решения современных проблем, которые обнаруживаются с помощью науки и технологии могут влиять на другие области общества и могут включать этические соображения — Навыки исследования в области науки — Задавать вопросы и прогнозировать — Выявлять вопросы и проблемы, которые можно исследовать с научной точки зрения, и делать прогнозы на основе научных знаний — Обработка и анализ данных и информации — Обобщайте данные, полученные из собственных исследований учащихся и из вторичных источников, и используйте научное понимание для выявления взаимосвязей и делайте выводы на основе доказательств — Создавайте и используйте ряд представлений, включая графики, ключи и модели для представления и анализа закономерностей или взаимосвязи в данных с использованием цифровых технологий в зависимости от ситуации — Оценка — Размышляйте о науке Научные исследования, включая оценку качества собранных данных и выявление улучшений — Использование научных знаний и результатов исследований для оценки заявлений, основанных на доказательствах — Планирование и проведение — Измерение и контроль переменных, выбор оборудования, подходящего для задачи и собирать данные с точностью — Совместно и индивидуально планировать и проводить ряд типов исследований, включая полевые работы и эксперименты, обеспечивая соблюдение правил безопасности и этических норм — Общение — Обмен идеями, выводами и основанными на фактах решениями проблем с использованием научных язык и представления с использованием цифровых технологий в зависимости от ситуации8-Понимание науки — Биологические науки — Многоклеточные организмы содержат системы органов, которые выполняют специализированные функции, которые позволяют им выживать и воспроизводиться — Клетки являются основными единицами живых существ и имеют специализированные структуры и функции — Химические науки — Свойства различных состояния материи можно объяснить с точки зрения движения и расположения частиц — Различия между элементами, соединениями и смесями можно описать на уровне частиц — Химические изменения включают вещества, вступающие в реакцию с образованием новых веществ — Физические науки — -Энергия проявляется в различных формах, включая движение (кинетическая энергия), тепло и потенциальная энергия, а преобразования и передачи энергии вызывают изменения внутри систем — Науки о Земле и космосе — Осадочные, магматические и метаморфические породы содержат минералы и образуются в результате процессов, которые происходят на Земле в различных временных масштабах — Наука как человеческое усилие — Природа и развитие науки — Научное знание изменило понимание мира людьми и уточняется по мере появления новых данных — Научное знание может развиваться посредством сотрудничества через научные дисциплины и вклад людей из разных культур — Использование и влияние науки — Люди используют понимание и навыки ls из разных научных дисциплин в своей профессии — Решения современных проблем, которые обнаруживаются с помощью науки и техники, могут повлиять на другие области общества и могут включать этические соображения — Люди используют научные знания и навыки в своей профессии, и эти повлияли на развитие практики в областях человеческой деятельности — Навыки проведения научных исследований — Планирование и проведение — Совместно и индивидуально планировать и проводить ряд типов исследований, включая полевые работы и эксперименты, обеспечивая соблюдение правил безопасности и этических норм — В ходе честных испытаний измеряйте и контролируйте переменные и выбирайте оборудование для сбора данных с точностью, соответствующей задаче — Измеряйте и управляйте переменными, выбирайте оборудование, соответствующее задаче, и собирайте данные с точностью — Обработка и анализ данных и информации — -Создать и использовать ряд представлений, включая графики, ключи и модели для представления и анализа закономерностей или отношений в d ata, используя при необходимости цифровые технологии — Обобщайте данные, полученные из собственных исследований учащихся и из вторичных источников, и используйте научное понимание для выявления взаимосвязей и делайте выводы на основе доказательств — Общение — Обмен идеями, выводами и решениями, основанными на фактах к проблемам с использованием научного языка и представлений с использованием цифровых технологий по мере необходимости — Опрос и прогнозирование — Определение вопросов и проблем, которые можно исследовать с научной точки зрения, и делать прогнозы на основе научных знаний — Оценка — Использование научных знаний и результатов исследований для оценивать утверждения, основанные на доказательствах — Обдумывать научные исследования, включая оценку качества собранных данных и выявление улучшений9-Понимание науки — Науки о Земле и космосе — Теория тектоники плит объясняет глобальные закономерности геологической активности и движения континентов —Биологические науки — Экосистемы состоят из сообществ интерд независимые организмы и абиотические компоненты окружающей среды; материя и энергия проходят через эти системы — Многоклеточные организмы полагаются на скоординированные и взаимозависимые внутренние системы, чтобы реагировать на изменения в окружающей их среде — Химические науки — Химические реакции, включая горение и реакции кислот, важны как в неживые и живые системы и включают передачу энергии — Химические реакции включают перегруппировку атомов с образованием новых веществ; во время химической реакции масса не создается и не разрушается — Вся материя состоит из атомов, которые состоят из протонов, нейтронов и электронов; естественная радиоактивность возникает в результате распада ядер в атомах — Физические науки — Передача энергии через различные среды может быть объяснена с помощью моделей волн и частиц — Наука как человеческое усилие — Природа и развитие науки — Научное понимание, в том числе модели и теории, оспариваются и со временем уточняются в процессе обзора научным сообществом — Прогресс в научном понимании часто зависит от технологических достижений и часто связан с научными открытиями — Использование и влияние науки — Люди использовать научные знания, чтобы оценить, принимают ли они утверждения, объяснения или прогнозы, а достижения в науке могут повлиять на жизнь людей, в том числе создать новые возможности для карьерного роста — Ценности и потребности современного общества могут повлиять на направленность научных исследований — Люди используют научные знания для оценки того, принимают ли они утверждения, объяснения или прогнозы, а достижения науки могут повлиять на жизнь людей, в том числе Создание новых возможностей для карьерного роста — Навыки проведения научных исследований — Планирование и проведение — Выбор и использование соответствующего оборудования, включая цифровые технологии, для систематического и точного сбора и записи данных — Планирование, выбор и использование соответствующих типов исследований, включая полевые работы и лабораторные эксперименты для сбора надежных данных; оценивать риски и решать этические проблемы, связанные с этими методами — Обмен информацией — Обмен научными идеями и информацией для конкретной цели, включая построение доказательных аргументов и использование соответствующего научного языка, условностей и представлений — Обработка и анализ данных и информации — —Анализ закономерностей и тенденций в данных, включая описание взаимосвязей между переменными и выявление несоответствий — Использование знаний о научных концепциях, чтобы делать выводы, согласующиеся с доказательствами — Вопросы и прогнозы — Формулировать вопросы или гипотезы, которые можно исследовать с научной точки зрения — Оценка — Оценить выводы, включая определение источников неопределенности и возможных альтернативных объяснений, и описать конкретные способы повышения качества данных — Критически проанализировать достоверность информации в первичных и вторичных источниках и оценить подходы, используемые для решать проблемы10-Понимание науки — Физические науки ences — Движение объектов можно описать и спрогнозировать с помощью законов физики — Сохранение энергии в системе можно объяснить описанием передачи и преобразований энергии — Науки о Земле и космосе — Глобальные системы, включая углерод цикла, полагаться на взаимодействия с участием биосферы, литосферы, гидросферы и атмосферы — Вселенная содержит особенности, включая галактики, звезды и солнечные системы, и теорию Большого взрыва можно использовать для объяснения происхождения Вселенной — Химические науки — Атомная структура и свойства элементов используются для организации их в Периодической таблице — Различные типы химических реакций используются для производства ряда продуктов и могут происходить с разной скоростью — Биологические науки — Передача наследственных характеристик от поколения к поколению включает ДНК и гены. Теория эволюции путем естественного отбора объясняет разнообразие живых существ и поддерживается рядом научных данных. человеческое усилие — Использование и влияние науки — Люди используют научные знания, чтобы оценить, принимают ли они утверждения, объяснения или прогнозы, а достижения науки могут повлиять на жизнь людей, включая создание новых карьерных возможностей — Люди используют научные знания для оценить, принимают ли они утверждения, объяснения или прогнозы, и могут ли достижения в науке влиять на жизнь людей, в том числе создавать новые возможности для карьерного роста — Ценности и потребности современного общества могут влиять на направленность научных исследований — Природа и развитие науки — -Научное понимание, включая модели и теории, является спорным и со временем уточняется в процессе обзора научным сообществом — Достижения в научном понимании часто зависят от технологических достижений и часто связаны с научными открытиями -Навыки исследования науки — Общение — передача научных идей и информации для определенной цели, включая сбор доказательств. -основанные аргументы и использование соответствующего научного языка, условностей и представлений — Планирование и проведение — Планировать, выбирать и использовать соответствующие типы исследований, включая полевые работы и лабораторные эксперименты, для сбора надежных данных; оценивать риски и решать этические проблемы, связанные с этими методами — Выбирать и использовать соответствующее оборудование, включая цифровые технологии, для систематического и точного сбора и записи данных — Обработка и анализ данных и информации — Использовать знания научных концепций, чтобы делать выводы которые согласуются с доказательствами — Анализировать закономерности и тенденции в данных, включая описание взаимосвязей между переменными и выявление несоответствий — Ставить под сомнение и прогнозировать — Формулировать вопросы или гипотезы, которые можно исследовать с научной точки зрения — Оценка — Критически анализировать достоверность информации в первичных и вторичных источниках и оценка подходов, используемых для решения проблем — Оценка выводов, включая определение источников неопределенности и возможных альтернативных объяснений, и описание конкретных способов повышения качества данных —Химические науки — Науки о Земле и космосе — Физические науки ces-Наука как человеческое усилие — Использование и влияние науки — Природа и развитие науки — Навыки исследования науки — Коммуникация — Планирование и проведение — Обработка и анализ данных и информации — Опрос и прогнозирование — Оценка
.
 Кислота может начать разбрызгиваться с выделением кислотных паров.
Кислота может начать разбрызгиваться с выделением кислотных паров. Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов.
Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов. Свяжитесь с нами по телефону +7 (499) 270-16-62 и убедитесь в этом!
Свяжитесь с нами по телефону +7 (499) 270-16-62 и убедитесь в этом! На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается.
На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается.


 Одиночные знаки препинания отделяют члены предложения и предложения друг от друга. Например:
Одиночные знаки препинания отделяют члены предложения и предложения друг от друга. Например:



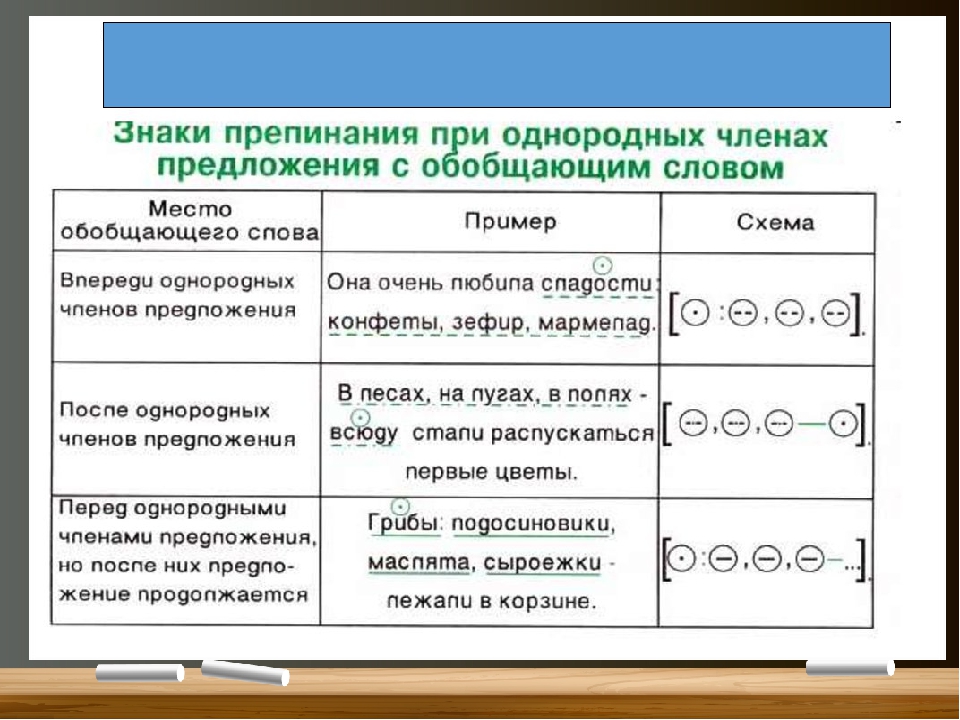 В каком ряду все слова согласно литературной норме имеют ударение на втором слоге, независимо от их лексического значения?
В каком ряду все слова согласно литературной норме имеют ударение на втором слоге, независимо от их лексического значения? Выполните задания B3-B5.
Выполните задания B3-B5.
 в употреблении их врагов). — Укр. демагог, бел. дэмагог, польск. demagog, чешек. demagog, словацк. demagog, болг. демаго́г.
в употреблении их врагов). — Укр. демагог, бел. дэмагог, польск. demagog, чешек. demagog, словацк. demagog, болг. демаго́г. Выпишите непроизводное прилагательное, образуйте от него отвлечённое (абстрактное) существительное.
Выпишите непроизводное прилагательное, образуйте от него отвлечённое (абстрактное) существительное.
 4
4 Термин «пунктуация» произошел от средневекового латинского слова « pūnctuātiōn », что означает маркировку или знаки.
Термин «пунктуация» произошел от средневекового латинского слова « pūnctuātiōn », что означает маркировку или знаки. ( Придирчивые цитаты , Блер Шевчук)
( Придирчивые цитаты , Блер Шевчук)

 Использование точки указывает на конец мысли. Точку также можно использовать как паузу после мысли.
Использование точки указывает на конец мысли. Точку также можно использовать как паузу после мысли.
 У каждого есть конкретная цель, и все они достаточно распространены, и мы полагаемся на них каждый день. Вот почему мы включаем их в руководство «6 распространенных типов знаков препинания», где вы можете узнать больше о каждом из них.
У каждого есть конкретная цель, и все они достаточно распространены, и мы полагаемся на них каждый день. Вот почему мы включаем их в руководство «6 распространенных типов знаков препинания», где вы можете узнать больше о каждом из них. У него также есть несколько специальных применений: он может заменить вопросительный знак, когда имеется в виду ирония или подчеркнутый тон, например, Как ты мог! Вам может быть интересно, используется ли этот знак препинания по-разному в формальном и неформальном (т.е., текстовые сообщения) написание. Ответ положительный! (Или да !!!)
У него также есть несколько специальных применений: он может заменить вопросительный знак, когда имеется в виду ирония или подчеркнутый тон, например, Как ты мог! Вам может быть интересно, используется ли этот знак препинания по-разному в формальном и неформальном (т.е., текстовые сообщения) написание. Ответ положительный! (Или да !!!) Запятые также используются в диалогах и ставятся перед цитатой после вступительной фразы, например, Она тихо сказала: «Я люблю тебя».
Запятые также используются в диалогах и ставятся перед цитатой после вступительной фразы, например, Она тихо сказала: «Я люблю тебя». 
 Они также могут сами соединять слова. Например, во фразе современные технологии мы ставим дефис до , чтобы обозначить, что эти три слова следует читать как одно понятие.Вы не поверите, но использование дефиса со временем сильно изменилось — такие слова, как завтра , когда-то переносились через дефис ( завтра ).
Они также могут сами соединять слова. Например, во фразе современные технологии мы ставим дефис до , чтобы обозначить, что эти три слова следует читать как одно понятие.Вы не поверите, но использование дефиса со временем сильно изменилось — такие слова, как завтра , когда-то переносились через дефис ( завтра ). Этот знак удобен для писателей, поскольку предлагает способ выделить слово или предложение для выделения. Или он может сигнализировать о прерывании (подробнее об этом читайте в нашей статье о прерывании предложений!) Или об усилении идеи. Но не верьте нам на слово — прочтите об этом здесь!
Этот знак удобен для писателей, поскольку предлагает способ выделить слово или предложение для выделения. Или он может сигнализировать о прерывании (подробнее об этом читайте в нашей статье о прерывании предложений!) Или об усилении идеи. Но не верьте нам на слово — прочтите об этом здесь! Многие из этих знаков также появляются в информатике и программировании, где они выполняют уникальные роли. Наше руководство по скобкам и скобкам объясняет разницу между этими часто путающими знаками.
Многие из этих знаков также появляются в информатике и программировании, где они выполняют уникальные роли. Наше руководство по скобкам и скобкам объясняет разницу между этими часто путающими знаками.
 Апостроф также может указывать на владение. Помимо этого обычного использования, апостроф также сопровождает отдельные буквы и цифры, обозначающие десятилетия.(Апостроф также создает некоторые острые проблемы: это День ветеранов или День ветеранов?)
Апостроф также может указывать на владение. Помимо этого обычного использования, апостроф также сопровождает отдельные буквы и цифры, обозначающие десятилетия.(Апостроф также создает некоторые острые проблемы: это День ветеранов или День ветеранов?) Существует хорошо известная история, которую обычно приписывают Олдосу Хаксли, 5 , о том, что 100 обезьян, набирающих случайным образом в течение достаточно долгого времени, в конечном итоге (благодаря чистой случайности и статистике) напечатали все произведения Шекспира.В большинстве случаев обезьяна набирает полную чушь, но иногда она набирает Hamlet . Конечно, Гамлет будет появляться снова и снова из этого «тумана» печати (как и « Sound and the Fury » Фолкнера, и колонка мисс Мэннерс из газеты прошлых выходных и т. Д.), Но подавляющее преобладание будет совершенно бессмысленно.
Существует хорошо известная история, которую обычно приписывают Олдосу Хаксли, 5 , о том, что 100 обезьян, набирающих случайным образом в течение достаточно долгого времени, в конечном итоге (благодаря чистой случайности и статистике) напечатали все произведения Шекспира.В большинстве случаев обезьяна набирает полную чушь, но иногда она набирает Hamlet . Конечно, Гамлет будет появляться снова и снова из этого «тумана» печати (как и « Sound and the Fury » Фолкнера, и колонка мисс Мэннерс из газеты прошлых выходных и т. Д.), Но подавляющее преобладание будет совершенно бессмысленно. Мы знаем, что пробелы встречаются довольно часто, что большая часть строк между пробелами (словами) встречается в относительно небольшом словаре, что слова «Гамлет» и «Офелия» встречаются с некоторой относительной частотой и т.д. Разве эта полная чушь несет в себе больше информации, чем слова великого автора.
Мы знаем, что пробелы встречаются довольно часто, что большая часть строк между пробелами (словами) встречается в относительно небольшом словаре, что слова «Гамлет» и «Офелия» встречаются с некоторой относительной частотой и т.д. Разве эта полная чушь несет в себе больше информации, чем слова великого автора.
 Но у союзников были веские причины предполагать, что определенное кодовое имя было именем определенного корабля, который они знали. Поэтому они отправили сообщение с низким уровнем шифрования, в котором упоминалось кое-что интересное об этом корабле. Они прислушивались к немецкому трафику, и, как и предполагалось, эта информация была отправлена при упоминании этого корабля под его кодовым названием. Это, конечно, подтвердило правильность прогноза. Таким образом, даже несмотря на то, что считалось весьма вероятным, что у союзников было правильное кодовое имя, и, следовательно, весьма вероятно, что оно появится в немецкой передаче, похоже, что оно все же содержало важную информацию, когда это было.
Но у союзников были веские причины предполагать, что определенное кодовое имя было именем определенного корабля, который они знали. Поэтому они отправили сообщение с низким уровнем шифрования, в котором упоминалось кое-что интересное об этом корабле. Они прислушивались к немецкому трафику, и, как и предполагалось, эта информация была отправлена при упоминании этого корабля под его кодовым названием. Это, конечно, подтвердило правильность прогноза. Таким образом, даже несмотря на то, что считалось весьма вероятным, что у союзников было правильное кодовое имя, и, следовательно, весьма вероятно, что оно появится в немецкой передаче, похоже, что оно все же содержало важную информацию, когда это было. Стандартное представление состоит в том, что риск события является продуктом вероятности и стоимости последствий, и те из нас, кто рационально использует это понятие на ежедневной основе, имея очень приблизительное представление как о вероятности, так и о стоимости. данного события.
Стандартное представление состоит в том, что риск события является продуктом вероятности и стоимости последствий, и те из нас, кто рационально использует это понятие на ежедневной основе, имея очень приблизительное представление как о вероятности, так и о стоимости. данного события. Писатели разработали его так, чтобы люди знали, когда нужно сделать паузу, остановиться или сделать что-то другое, когда они говорят. Это не было частью литературы, потому что у большинства людей не было даже доступа к печатным работам. Но в настоящее время, поскольку все читают, а печатная литература доступна для всех, мы используем знаки препинания в письменной форме, чтобы предложения читались так же, как мы говорим. Знание того, как, когда и зачем использовать знаки препинания, теперь является стандартной частью письма на английском языке.
Писатели разработали его так, чтобы люди знали, когда нужно сделать паузу, остановиться или сделать что-то другое, когда они говорят. Это не было частью литературы, потому что у большинства людей не было даже доступа к печатным работам. Но в настоящее время, поскольку все читают, а печатная литература доступна для всех, мы используем знаки препинания в письменной форме, чтобы предложения читались так же, как мы говорим. Знание того, как, когда и зачем использовать знаки препинания, теперь является стандартной частью письма на английском языке.
 Действительно, любое предложение может заканчиваться точкой (если это не вопрос), но это не всегда означает, что это лучшая оценка.Однако точка является стандартной отметкой в конце предложения:
Действительно, любое предложение может заканчиваться точкой (если это не вопрос), но это не всегда означает, что это лучшая оценка.Однако точка является стандартной отметкой в конце предложения: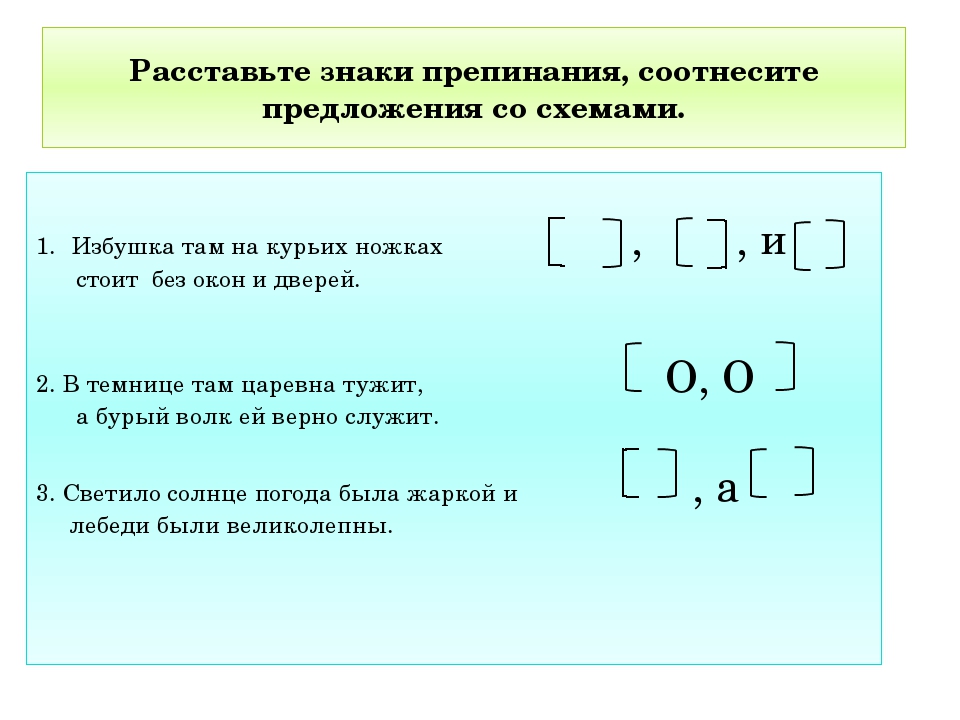

 ПРАВИЛЬНО
ПРАВИЛЬНО 


 если информация в круглых скобках идет в конце предложения, знак конца выходит за скобки; и б. запятые обычно ставятся после скобок.
если информация в круглых скобках идет в конце предложения, знак конца выходит за скобки; и б. запятые обычно ставятся после скобок. Итак, вы можете увидеть, насколько простая запятая может повлиять на смысл предложения.
Итак, вы можете увидеть, насколько простая запятая может повлиять на смысл предложения. Некоторые знаки препинания используются интуитивно, в то время как другие часто используются неправильно и требуют изучения. Мы создали полное руководство, чтобы научить вас основам использования 12 наиболее распространенных знаков препинания.
Некоторые знаки препинания используются интуитивно, в то время как другие часто используются неправильно и требуют изучения. Мы создали полное руководство, чтобы научить вас основам использования 12 наиболее распространенных знаков препинания.
 Использование нескольких восклицательных знаков недопустимо в литературе и в профессиональной среде, но совершенно нормально в неформальном письме.
Использование нескольких восклицательных знаков недопустимо в литературе и в профессиональной среде, но совершенно нормально в неформальном письме. ] росту считался между Пигмеями великаном. Из этого вы можете судить, какие это были маленькие человечки. Приятно было бы посмотреть на маленькие города Пигмеев, где улицы были шириною в пять или шесть четвертей, мостовые из крошечных камешков, а самый большой дом не больше беличьей клетки. Дворец пигмейского короля был очень велик – выше даже нашего стула! Стоял он посредине такой обширной площади, что ее, может быть, не закрыть бы и заслонкой из кухонной печи. Главный пигмейский храм был величиною с детский комод, и Пигмеи смотрели с гордостью на это величественное здание. Вообще Пигмеи были очень искусные строители и строили свои дома почти так же, как птички вьют свои гнезда: из соломы, перьев, яичных скорлупок и других не слишком тяжелых материалов. Все это скреплялось вместо извести вишневым клеем, и когда такое величественное здание высыхало на солнце, то карлики находили его и красивым и удобным.
] росту считался между Пигмеями великаном. Из этого вы можете судить, какие это были маленькие человечки. Приятно было бы посмотреть на маленькие города Пигмеев, где улицы были шириною в пять или шесть четвертей, мостовые из крошечных камешков, а самый большой дом не больше беличьей клетки. Дворец пигмейского короля был очень велик – выше даже нашего стула! Стоял он посредине такой обширной площади, что ее, может быть, не закрыть бы и заслонкой из кухонной печи. Главный пигмейский храм был величиною с детский комод, и Пигмеи смотрели с гордостью на это величественное здание. Вообще Пигмеи были очень искусные строители и строили свои дома почти так же, как птички вьют свои гнезда: из соломы, перьев, яичных скорлупок и других не слишком тяжелых материалов. Все это скреплялось вместо извести вишневым клеем, и когда такое величественное здание высыхало на солнце, то карлики находили его и красивым и удобным. О жизни христианской (1990)]
О жизни христианской (1990)]
 Прочитайте предложение дважды в разных вариантах. Правильным будет тот, который обеспечивает легкое прочтение и быстрое понимание текста.
Прочитайте предложение дважды в разных вариантах. Правильным будет тот, который обеспечивает легкое прочтение и быстрое понимание текста. Примеры:
Примеры:

 В контексте оно зависит от глагола и обозначает обстоятельство, при котором совершается действие:
В контексте оно зависит от глагола и обозначает обстоятельство, при котором совершается действие:

 Спасибо заранее.
Спасибо заранее. Но зависит от того, отдельное это у вас предложение или часть сложного.
Но зависит от того, отдельное это у вас предложение или часть сложного. Ничего не поделать, время идет. Кроме того, тенденции к подобному решению даже у Розенталя уже просвечивали: у него не ставится запятая, если вводное внутри обособления, в начале или в конце предложения.
Ничего не поделать, время идет. Кроме того, тенденции к подобному решению даже у Розенталя уже просвечивали: у него не ставится запятая, если вводное внутри обособления, в начале или в конце предложения.


 В этих случаях слово по значению близко к вводному и поэтому тоже выделяется запятыми.
В этих случаях слово по значению близко к вводному и поэтому тоже выделяется запятыми. Поэтому соединительный «и» вызывает немало сомнений – нет единого правила, как для союзов «а», «но». В каких-то случаях запятая перед «и» нужна, в каких-то ее постановка неверна. Чтобы не запутаться, нужно запомнить несколько пунктуационных правил.
Поэтому соединительный «и» вызывает немало сомнений – нет единого правила, как для союзов «а», «но». В каких-то случаях запятая перед «и» нужна, в каких-то ее постановка неверна. Чтобы не запутаться, нужно запомнить несколько пунктуационных правил. «И я увидел друга на набережной, и он меня заметил».
«И я увидел друга на набережной, и он меня заметил».



 С. Тургенев).
С. Тургенев).

 Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.
Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.


 Решение. Находим определитель системы:
Решение. Находим определитель системы: Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
 Это называется
Это называется
 е. подстановку в первое
е. подстановку в первое Запишем новую эквивалентную систему с учетом расширенной матрицыx 2 y 2z 3
Запишем новую эквивалентную систему с учетом расширенной матрицыx 2 y 2z 3

 Симметричными могут быть лишь квадратные матрицы.
Симметричными могут быть лишь квадратные матрицы.

 е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.