Тремор ног у грудничка: подбородок у грудничка и руки, Комаровский и дрожание конечностей, симптомы неврологии – У грудничка трясется подбородок, ручки или ножки: причины тремора
У грудничка трясется подбородок, ручки или ножки: причины тремора
Бдительность и тревожность многих мамочек порой зашкаливает. Когда молодые родители замечают, что у их грудного ребенка почему-то трясется подбородок, появляется тремор рук и ног, их охватывает паника. Есть ли реальный повод для волнения?
Что такое тремор
Каждый человек при определенных обстоятельствах замечал за собой, что у него трясутся конечности. Чаще всего это происходит от сильного волнения. В результате переохлаждения возникает тремор рук, ног, дрожит нижняя челюсть, а при плаче – подбородок, нижняя губа.


Почему у грудных детей нередко трясется ножка, дрожат ручки? Подергивание мышц является результатом чрезмерной нагрузки, перенапряжения нервной системы.
Дрожание рук и ног, головы, нижней челюсти, губ, которое начинается в результате внешних воздействий (холода) или же при плаче, не является патологическим состоянием, если оно исчезает, когда устранен внешний раздражитель.
Тремор у новорожденного ребенка
Как правило, до трехмесячного возраста нервная система младенца является несовершенной, в результате чего можно наблюдать, как у него дергается ножка, трясутся ручки, а при плаче зачастую дрожит подбородок, нижняя губа, челюсть. Следует сразу отметить, что если эти симптомы быстро исчезают после того, как малыш успокоился, то повода для волнения нет.
Тремор головы может свидетельствовать об определенных неврологических расстройствах, при которых требуется соответствующее лечение у невролога или невропатолога.


Причины тремора у грудничков:
- Физиологическая незрелость нервной системы малыша.
- Недоношенная беременность.
- Осложнения в процессе родов, такие как стремительные роды или затяжные.
- Осложнения, возникшие в течение беременности: гипертонус матки, гипоксия плода, пр.
- Стресс, который испытывает мама во время вынашивания ребенка, ее переживания, страхи. Все это способно повлиять на уязвимую нервную систему малыша.
Как правило, лечение не требуется, если:
- Тремор рук, ног, подбородка наблюдается у малыша до достижения им трехмесячного возраста.
- Подбородок дрожит во время плача ребенка.
Когда бить тревогу
Родителей малыша должно насторожить, если:
- У ребенка трясутся не только ручки, подбородок, но и наблюдается судорожное дрожание всего тела.
- Тремор головы.
- Ручки и ноги ребенка дрожат без видимых причин.
- Общее состояние малыша вызывает тревогу: он вялый, плаксивый, плохо спит.
- По мере взросления ребенка тремор рук, ног не проходит, становится более выраженным.


Заметив данные симптомы, стоит поспешить к доктору, который, осмотрев малыша, сможет объяснить, почему присутствует тремор.
Не стоит волноваться
Дети растут не по дням, а по часам. Каждый день в их развитии заметны изменения. Многие симптомы малыш просто «перерастает». Нервная система дозревает, и, соответственно, остаются позади тремор, срыгивания и прочие неприятности.
Чтобы сохранить свои нервы, родителям нужно помнить, что тема дрожащих конечностей у новорожденного с большей долей вероятности не является проблемой, если:
- У ребенка трясется подбородок в возрасте до трех месяцев.
- Малыш быстро успокаивается, и дрожь тут же исчезает.
- На фоне дрожания руки ног, подбородка не наблюдается нарушения общего состояния крохи.
- Отсутствуют прочие неврологические симптомы.
- Подбородок, нижняя губа дрожат во время плача.
Что делать
Как правило, лечение тремора у детей до 3 месяцев не требуется, однако необходимо:
- Наблюдать за состоянием малыша.
- Проанализировать, какие факторы являются причиной того, что у ребенка трясутся ручки, подбородок, нижняя губа, челюсть.
- Определить наличие или отсутствие других осложнений в самочувствии крохи, например, нарушения сна, плаксивости, легкой возбудимости, дрожания конечностей и тела без видимых причин и т. п.


- Поставить в известность лечащего педиатра или же семейную медсестру о том, что у малыша дрожат ручки или ноги, требовать, чтобы малыш был осмотрен соответствующими специалистами.
- Создать в доме атмосферу спокойствия и доброжелательности, так как психологический микроклимат в семье существенным образом влияет на здоровье детей.
- Полезными также будут массажи, теплые ванночки, при условии, что малыш воспринимает их с удовольствием.
Лечение тремора у грудных детей проводит невропатолог. Только опытный специалист может назначить необходимые препараты, контролировать и при необходимости корректировать лечение крохи.
И все же
Когда речь идет о развитии малыша, всегда лучше лишний раз перестраховаться, ведь упущенное время может существенно осложнить лечение возможного недуга.
Если трясущаяся при плаче губа или подбородок не вызывают серьезных опасений, то вот тремор ног, рук, который не проходит по мере взросления ребенка, должен как минимум насторожить родителей и послужить поводом обратиться к специалисту. При необходимости будет назначено соответствующее лечение.
трясутся руки, ноги, подбородок и голова у грудничка
Тремор является абсолютно нормальным явлением для только что родившихся крох. В некоторых случаях он говорит о заболеваниях. Симптом может просто свидетельствовать об эмоциях, позитивные эмоциональные состояния вызывают дрожание мышц.

Малыш плачет, руки трясутся
Говорить этот признак может и о коликах в животе, усталости.
Тремор у новорожденных (причины и последствия здесь невероятно разнообразны) нередко возникает в ответ на любой стрессогенный фактор. Например, некоторые дети реагируют на купание.
Важно! Если у ребенка в ответ на купание начинают трястись ручки и ножки, это не значит, что можно отказаться от гигиенических процедур.
Определение понятия
Тремор – симптом, выраженный в подергивании мышц, подбородка или головы. Бывает и тремор ног у новорожденных. Дрожь нередко несимметрична. Например, могут дрожать части тела по отдельности: одна ножка или подбородок сам по себе.

Новорожденный кроха
Мышечная дрожь очень часто возникает до первого месяца. Это адаптационный период, во время которого нужно оберегать кроху от любых стрессов. В том числе нельзя закалять карапуза с использованием воздушных ванн, делать массаж, поскольку все эти непонятные для грудного малыша операции вызывают у него беспокойство.
Важно! Необходимо наблюдать за ребенком. Есть более пугливые дети, есть и такие, которых даже резкий громкий звук не потревожит. Следовательно, подход нужно менять. Не нужно оберегать смелого малыша от любого негативного, по мнению взрослого, фактора, иначе он может стать пугливым.
По истечению месяца можно увеличивать количество процедур.
До 3 месяцев трясущиеся ручки и ножки – норма. Дело в том, что нейроны еще не полностью покрыты миелиновой оболочкой, задача которой – ускорить прохождение нервных сигналов.
Тремор головы у грудничка
У новорожденных или младенцев постарше нередко трясется голова в процессе кормления или засыпания. Если ребенок себя чувствует хорошо, других симптомов нет, повода для беспокойства тоже нет.

Взрослый ухаживает за ребенком
Это состояние считается потенциально опасным, рекомендуется пойти к врачу, чтобы убедиться в том, что у крохи нет каких-то угрожающих болезней. Если есть сомнения относительно здоровья чада, можно сделать ЭЭГ.
Тремор рук у грудничка или новорожденного
Тремор конечностей у новорожденных в большинстве случаев не указывает на какие-то проблемы со здоровьем.
Тремор подбородка или губ
Тремор подбородка или губ у новорожденных вызывается теми же причинами, что и рук, ног или головы. Как правило, поводов для беспокойства родителей нет.
Рекомендация. Некоторые люди пишут «триммер подбородка у новорожденных». Правильно писать слово «тремор».
Причины тремора у новорожденных
Почему у грудничка могут трястись мышцы? Тремор у новорожденных может быть вызван целым рядом состояний, как физиологических, так и патологических.
Естественные
К физиологическим причинам относятся:
- Недостаточно развитая нервная система у грудничка. В частности, не до конца сформированы отделы мозга, отвечающие за осуществление движений.
- Слишком интенсивная выработка норадреналина. Это также вызвано недостаточной сформированностью нервной системы. Кроме этого, состояние провоцируется сильными эмоциями, а также неприспособленностью надпочечников к жизни новорожденного за пределами материнской утробы.
- Слишком длительные негативные эмоции, плач. В такой ситуации начинает трястись нижняя губа.
Физиологических причин значительно меньше, чем у болезней, но они покрывают большую часть случаев.
Патологические
Тремор у младенцев может провоцироваться болезнями, которые появлялись в критические периоды развития: 1, 3, 9,12-е месяцы. Если в этот период возникают любые болезни, сопровождающиеся тремором конечностей, головы или подбородка, важно сразу же обратиться к доктору. Также этот признак может быть вызван следующими причинами:
- Травмы в ходе беременности, родов.
- Чрезмерно высокий уровень норадреналина «в положении». Провоцируется нервами матери, когда она вынашивает ребенка. Если дрожь вызвана этой причиной, то она может продолжаться до года и позже.
- Кислородное голодание плода.
- Инфекционные заболевания, которые мать перенесла во время вынашивания плода. Опасность представляет даже грипп.
- Трудные или чрезмерно быстрые роды.
- Гипоксия после рождения.
- Наркотическая ломка (вызвана тем, что беременная женщина принимала запрещенные вещества). Также тремор может наблюдаться при похмелье. Если мать во внутриутробном периоде часто принимала алкогольные напитки, у младенца может сформироваться зависимость. Одно из проявлений алкогольного абстинентного синдрома – интенсивный тремор.
- Повышенное содержание в организме кальция, сахара, магния.
- Перинатальная энцефалопатия.
Также причиной может быть заражение крови. Кроме этого, родственники довольно часто путают этот симптом с судорогами. Очевидно, что разобраться в таком большом количестве причин родитель самостоятельно не может (за исключением некоторых). Поэтому нельзя заниматься самолечением, необходимо обращаться к доктору.
Когда проходит тремор у грудничков
О том, что дрожь у новорожденных имеет естественные причины, свидетельствует ее проявление в возрасте до 3 (в крайних случаях шести) месяцев. Также длительность не может быть слишком большой – не более 30 секунд.
Последствия
Последствия тремора зависят от основного заболевания. Если это нормальное явление, то он проходит сам собой. Если дрожь вызвана перинатальной энцефалопатией, могут возникать тяжелые устойчивые неврологические нарушения.
Чем помочь ребенку
Если причиной является заболевание, то надо обратиться к доктору. Если симптом является следствием стресса, то достаточно расслабляющих мероприятий.
Массаж
Можно выполнять релаксирующий массаж два раза в день. Перед этим нужно посоветоваться со специалистом. Освоить технику несложно, без предварительного обучения массажи запрещаются.
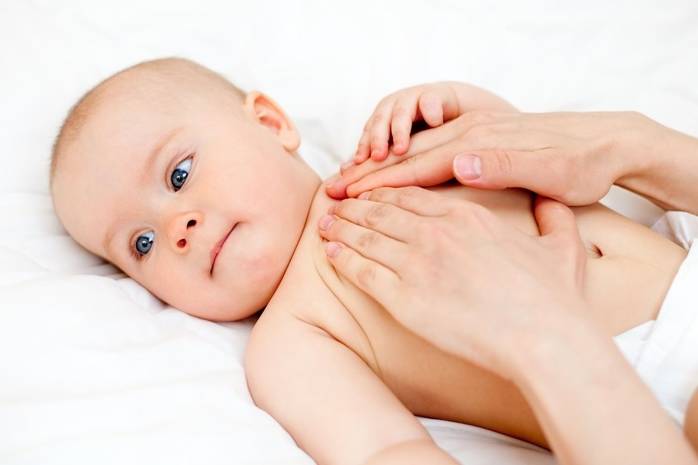
Массаж малышу с тремором
Упражнения
Также можно делать специальные упражнения, направленные на расслабление мышц.
Спокойная обстановка
Создание благоприятного эмоционального климата положительно сказывается на развитии ребенка. Поэтому родители не должны ссориться, конфликтные ситуации решать спокойно, учитывая интересы друг друга.
Важно помнить! Малыш заражается эмоциональным состоянием родителей.
Прогулка
Это одно из самых важных дел, которые родитель должен совершать для здоровья малыша. Прогулка помогает избавиться от стресса и начать познавать мир.
Если тремор вызван патологией
Насторожить родителя должны следующие признаки:
- Синхронный тремор головы, подбородка, ручек и ножек. По отдельности они могут трястись, вместе – нежелательно.
- Длительность более 30 секунд. Если продолжительность небольшая, речь идет о незначительных возрастных нарушениях функционирования нервной системы. При продолжительности больше 30 секунд может идти речь о повышенной судорожной активности или других проблемах со здоровьем.
- Синюшность кожных покровов.
- Ребенок продолжает спать и дрожать, хотя уже достиг шестимесячного возраста.
- Сложные роды.
Когда обращаться к врачу
Если появляется один из описанных выше симптомов, и одномоментно трясутся руки у грудничка (голова, губа, подбородок), необходимо вовремя обращаться к специалисту. Вообще нужно постоянно посещать педиатра, который оперативно может решать проблемы, которые возникают по ходу развития крохи.
Понятно, что это такое тремор конечностей у новорожденных. Обычно это явление не является поводом для тревог у родственников. Необходимо следить, чтобы оно хорошо переносилось грудничком. О том, что мышечная дрожь является естественным физиологическим явлением у новорожденного, говорит и доктор Комаровский.
Видео
дрожание конечностей и бодбородка. Советы Комаровского
Тремор у новорожденных малышей проявляется в основном подергиванием подбородка и верхних конечностей. Его можно считать аналогичным проявлением мышечного гипертонуса, который является главным признаком не созревшей нервной системы крохи. Тремор у грудничков проявляется в основном из-за перевозбудимости нервной системы, когда малыш кричит, плачет, а также, когда он хочет есть, или его кто-то испугал. Еще родители могут заметить, что у ребенка во время сна двигаются глазные яблоки. Обычно это происходит в фазе сна, которая называется быстрой.
Тремор у новорожденных – не редкое явление, оно имеет место быть практически у 50% всех появившихся на свет детей. С первого дня жизни и до 4 месяцев признаки тремора считаются нормальным явлением, но если они не исчезли по истечении этого срока, то нужно присмотреться к малышу. Возможно, стоит уже в этот момент получить консультацию врача. А вот если ручки и подбородок не перестали дрожать и после года, то это уже явный сигнал о проблемах со здоровьем ребенка. Чтобы понять, когда тремор является доброкачественным специфическим состоянием нервной системы, а когда серьезной проблемой, предлагаем ознакомиться с данной статьей.
Детская нервная система хорошо поддается «регулировке». Поэтому, чем раньше вы заметите проблему и получите квалифицированную помощь, тем больше шансов нормализовать состояние ЦНС и восстановить ее.
Что больше всего затрагивает непроизвольное дрожание у детей
Если посмотреть на статистику, то можно сделать однозначный вывод — зачастую практически у всех малышей присутствует тремор головы. Именно это говорит о неокончательной зрелости нервной системы малыша. Когда у малыша трясутся руки или ноги, а также губы и подбородок, то это уже является следствием недоношенности.

Родители также должны понимать, что подобные явления возникают не у каждого крохи. Поэтому не стоит сразу паниковать, в ожидании своего малыша.
Тремор у детей: основные причины
Как уже было сказано выше, виновником может стать несформированность нервной системы. Но привести к дрожанию могут и прочие факторы, такие, как преждевременные роды и гипоксия плода.
Несформировавшаяся нервная система ребенка
После появления на свет у детей еще нет сформировавшейся координации движений, а их нервная система не достигла нужного этапа зрелости. Именно это чаще всего вызывает тремор подбородка у грудничка, а также и дрожание конечностей. Бурный всплеск эмоций, который повышает в организме уровень норадреналина, также способствует появлению дрожания ручек и ножек крохи. Увеличивает шансы развития данного явления и гипертонус мышц.
Гипоксия плода
Довольно частой проблемой стала и гипоксия плода, которая способна развиться как внутриутробно, так и в момент родов. Нехватка кислорода, особенно продолжительная, отрицательно сказывается на работе головного мозга. Развитию гипоксии способствует ряд факторов:
- Нарушения функциональной деятельности плаценты.
- Инфекция, развившаяся внутриутробно.
- Повышенный тонус матки, когда маме ставят угрозу выкидыша.
- Кровотечения во время вынашивания.
- Многоводие.
Все эти факторы ограничивают поступление кислорода ко всем клеткам организма, включая и головной мозг, что также влияет на развитие нервной системы. Помимо этого кислородное голодание может быть вызвано и особенностями родовой деятельности (стремительные роды и слабые схватки), и обвитием плода пуповиной, и отслоением плаценты.
Преждевременные роды
 Тремор подбородка у новорожденных, появившихся на свет раньше положенного срока, также возникает из-за несформированности нервной системы, поскольку кроха был лишен продолжения внутриутробного развития. Поэтому ЦНС недоношенного малыша продолжает формироваться уже вне нахождения крохи в утробе, и это сложно назвать оптимальными для данного процесса условиями. Как бы внимательно и заботливо не относилась к младенцу мама, обеспечить ему ту атмосферу, которая была у нее в животе, она не в состоянии. Поэтому можно смело говорить о том, что тремор конечностей у малышей в любом случае зависит от зрелости нервной системы.
Тремор подбородка у новорожденных, появившихся на свет раньше положенного срока, также возникает из-за несформированности нервной системы, поскольку кроха был лишен продолжения внутриутробного развития. Поэтому ЦНС недоношенного малыша продолжает формироваться уже вне нахождения крохи в утробе, и это сложно назвать оптимальными для данного процесса условиями. Как бы внимательно и заботливо не относилась к младенцу мама, обеспечить ему ту атмосферу, которая была у нее в животе, она не в состоянии. Поэтому можно смело говорить о том, что тремор конечностей у малышей в любом случае зависит от зрелости нервной системы.
Целенаправленное лечение и его необходимость
Исходя из тех данных, которыми обладают врачи, можно говорить о том, что опасение вызывает тремор, сохраняющийся на протяжении 4 месяцев. При этом дрожание распространяется на ноги и головку малыша, и мама точно знает, что ребенка трясет не в какие-то определенные моменты (голод, испуг и т.д.). Родители должны понимать, что подобное явление может быть «звоночком» следующих проблем:
- Гипомагнеимия.
- Повышение уровня сахара в крови.
- Внутричерепное кровоизлияние.
- Наркотическая ломка или абстинентный синдром.
- Гипоксия-ишемия головного мозга.
- Повышенное внутричерепное давление.
- Низкое содержание кальция в крови.
- Сепсис.
В этих случаях врач обязательно назначит вам полное обследование и соответствующее лечение.
В чем заключается лечение
Если у ребенка трясутся ручки, ножки или голова, то лечение должно быть направлено не только на восстановление состояния нервной системы, но и на здоровье в целом. Именно поэтому мама должна строго соблюдать предписания невролога и придерживаться всех рекомендаций. Чаще всего назначают такие медикаментозные препараты, как Глицин, Аспаркам и пр. Но выявить точную причину дрожания конечностей и назначить лекарства может только детский невролог. Поэтому заниматься самолечением опасно.
А вот процедуры, которые обязательно назначают малышам, страдающим тремором, выполнять просто необходимо. В первую очередь – это массаж, гимнастика и плавание.
Массажные мероприятия при треморе
В домашних условиях сделать массаж ребенку достаточно просто, и с этим справится любая мама. Главное, сочетать массаж с постоянными разговорами с малышом. Из главных движений массажа можно выделить разминание, поглаживание, растирание и вибрацию. Обычно пример того, как вам следует делать массаж, показывает сам врач. Но вы можете посмотреть и специальное видео, находящееся чуть ниже.
А пока хочется сказать о том, что во время сеанса ваш малыш должен чувствовать себя максимально комфортно, ведь все ваши действия направлены именно на укрепление нервной система ребенка. Поэтому стоит запомнить некоторые правила:
- Хорошо проветрите помещение.
- Перед массажем обязательно снимите с себя кольца и браслеты, чтобы не оцарапать кроху. Также не лишним будет состричь ногти.
- Потрите свои ладони друг об друга и разомните кисти.
- Массаж нужно делать только тогда, когда ребенок активен и находится в хорошем расположении духа.
- Если в процессе настроение ребенка ухудшается, то остановите сеанс. Малыш должен успокоиться и снова стать веселым.
- Не несите кроху на массаж в поликлинику. Уж лучше наймите массажиста и познакомьте его с ребенком, чтобы он смог привыкнуть к чужому человеку. В идеале делать массаж лучше самостоятельно в привычной для малыша атмосфере.
- Ребенка не должно ни что раздражать. Громкая музыка, яркий свет и прочие внешние факторы лучше устранить до начала сеанса массажа.
- Будьте общительны и ласковы с ребенком. Песенки, стишки и забавные прибаутки – лучшие сопровождающие любой процедуры.
- Делайте массаж за полчаса до водных процедур. Так вы сможете обеспечить малыша еще большим «релаксом».
Плавание и гимнастика
Если вы еще не решились отдать малыша на плавание для грудничков, то вы можете проводить водные процедуры в домашних условиях. Если у ребенка тремор конечностей, то ему будет крайне полезно плавать, даже находясь у вас на руках. Пусть малыш вдоволь наиграется ручками и ножками, а водичка в ванной будет максимально комфортно температуры.
Гимнастика для малыша также полезна. Имеется ряд упражнений, которые вы также можете проводить с малышом дома.
- Обхватите стопу малыша одной рукой, а другой постучите ему по внешней стороне ноги. Это упражнение называется «молоточек», и повторяется на обеих ногах поочередно.
- Погладьте ручки и ножки малыша. Возьмите кроху за руку и слегка потряхивая ее опускайтесь от плеча к запястью. Это упражнение нужно проводить на ножках и ручках поочередно.
- Разомните ягодички малыша. Для этого положите кроху на животик и просто слегка постучите кулочками по его попе.
Помните, что тремор – это вполне естественное явление, которое не должно вызывать у вас паники. Но вы должны ежедневно наблюдать за малышом. Дети до года продолжают развиваться, поэтому нужно не упустить момент, когда вы, совместно со специалистом, сможете внести какие-либо коррективы. Врачи отмечают несколько критических периодов в жизни малыша. Это 1, 3, 9 и 12 месяц. Именно в это время нервные окончания становятся очень чувствительными, а любое отклонение может стать причиной патологий. Поэтому от вашего внимания и участия зависит будущее здоровье вашего крохи.
Тремор подбородка и конечностей у новорожденного / Mama66.ru
При появлении на свет ребёнка многие его органы функционируют неполноценно. Поэтому такое явление, как тремор у новорождённых считается абсолютно нормальным. Но лишь до определённого момента.


Педиатры советуют мамочкам следить за дрожанием подбородка и конечностей у младенца, но не впадать в панику при малейшем их колебании. Также родителям, чтобы успокоить себя, стоит изучить соответствующую информацию и понимать, когда тремор у новорождённого – это норма, а когда – отклонение.
Как это выглядит
Тремор конечностей и подбородка у малышей, возникающий зачастую во время плача, связан с уравновешивающим возбуждением нервной системы, помогающим стабилизировать состояние организма. Подёргивания, обычно возникающие на фоне стресса, имеют мелкую амплитуду и совершаются через очень краткие промежутки времени.
Можно сказать, что тремор подбородка и ног у новорождённого – это побочный эффект повышенного тонуса мышц. Так что первые три месяца жизни ребёнка мелкие подёргивания являются абсолютной нормой. Кроме того, такая картина напрямую связана с незрелостью нервной системы грудничка.
Также тремор у новорождённых может наблюдаться во время фазы быстрого сна. Выглядит это так – ручки и ножки ребёнка интенсивно вздрагивают, глазки под полуприкрытыми веками часто двигаются.
Спустя неделю после появления на свет приступы тремора постепенно начинают исчезать, проявляясь только при сильном испуге или надрывном крике. Если конечности или подбородок ребёнка дрожат даже в расслабленном состоянии, нужно проконсультироваться с врачом.
Варианты нормы: что провоцирует тремор у новорождённых
Если вы заметили непроизвольное дрожание подбородка или ножек у своего малыша, можете смело списывать их на незрелость нервной системы или надпочечников. И в первом, и во втором случае при перевозбуждении или дискомфорте организм реагирует выбросом адреналина, который провоцирует тремор. Под дискомфортом подразумевается недовольство крохи, возникшее при одевании, кормлении, купании. Например, если вода в ванночке некомфортной – слишком высокой или низкой – температуры, ребёнок может расплакаться, а его подбородок при этом будет дрожать.


Также нередко возникает тремор подбородка и конечностей у новорождённых, появившихся раньше срока. У недоношенных детей периферическая и центральная нервные системы ещё более незрелые, чем у доношенных. И хотя они продолжают развиваться вне утробы, стресс, который получил ребенок при преждевременном появлении на свет, может давать о себе знать в виде подёргиваний ручек и ножек.
Кроме того, если во время родов имела место гипоксия плода, скорее всего, до трёх месяцев у ребёнка будет проявляться тремор. Нормой такое состояние считается при плаче или перевозбуждении. Но если дрожание конечностей возникает непроизвольно, и продолжается по достижении ребёнком трёхмесячного возраста, это серьёзный повод для посещения невропатолога.
Когда тремор является патологией
Тремор у новорождённых, возникающий без видимых причин, может быть свидетельством некоторых заболеваний. В любом случае, если вы заметили подозрительные симптомы, будет нелишне проконсультироваться у невропатолога и по совету врача обследовать ребёнка.
Иногда тремор подбородка у новорождённого охватывает всю голову. Если это единичное явление, объясняющееся плачем, причин для беспокойства нет. Но если дрожание головки, сопровождающееся гипертонусом мышц шеи, повторяется вновь и вновь, речь может идти о серьёзном неврологическом недуге. Непроизвольные подёргивания головы могут возникнуть на фоне сепсиса, внутричерепных кровоизлияний, гипоксически-ишемической энцефалопатии, гипокальциемии, гипергликемии, гипомагнезиемии, наркотического абстинентного синдрома.
Тремор подбородка, по большому счёту, считается нормой. Но если он продолжается после трёх месяцев, а также сопровождается мышечной дистонией, частыми срыгиваниями, отсутствием сна и перевозбуждённостью, всё же стоит обратиться к врачу.
Непроизвольные сокращения конечностей после выхода из периода новорождённости, возникающие беспричинно, должны насторожить родителей. Например, дрожание ручек может быть признаком нарушения работы щитовидной железы. Особенно если тремору сопутствует бессонница, усиленное потоотделение, расстройство кишечника и колики. При появлении таких симптомов стоит показать ребёнка эндокринологу.


Иногда тремор ног у новорожденных мамы путают с судорогами, возникающими при гипертонусе. Определить разницу между этими симптомами может только врач. Так что не стоит пренебрегать регулярными осмотрами у педиатра. К тому же тремор может быть связан с повышенным внутричерепным давлением или кровоизлиянием, а также неправильным строением стопы или голени. Иногда подёргивания нижних конечностей возникают после травмы.
Что делать родителям
В первую очередь мамочкам стоит усвоить, что предпринимать какие-либо активные действия без разрешения врача нельзя. От неумелого массажа состояние ребёнка может только ухудшиться.
Для начала прислушайтесь к доктору. Если он советует какие-либо лекарства – не противьтесь. Они назначаются в сложных случаях и призваны улучшить поступление кислорода к клеткам. К таким препаратам относятся «Мидокалм», «Пантогам», «Глицин» и пр.
Кроме того, если подёргивания головы и конечностей является симптомом заболевания нервной или эндокринной систем, то лечить нужно причину, а не следствие. В таком случае без медикаментов не обойтись.
Но чаще всего с тремором можно справиться более лёгкими методами. К таковым относятся: расслабляющие ванночки с травами, лечебный массаж и, главное, создание вокруг ребёнка спокойной атмосферы.
Необходимо по максимуму избавить ребёнка от всех стрессовых ситуаций. От кормления, купания, одевания, естественно, никуда не деться, но вот убрать посторонние шумы, обеспечить малышу приятное, не режущее глаз, освещение и доброжелательную атмосферу, под силу всем родителям.
Программа с участием эксперта: неврологические проблемы у малышей до года
Советуем почитать: Родничок у новорождённых: что о нём нужно знать родителям?
причины и последствия тремора рук, ног, подбородка
Тремор у новорожденных проявляется подрагиванием подбородка, конечностей, и наблюдается почти у всех детей. Незначительный тремор в момент эмоционального напряжения расценивается специалистами в качестве варианта нормы, и не требует врачебного вмешательства. При отсутствии патологий исчезновение тремора наблюдается в течение первых трех месяцев жизни. Однако при появлении этого симптома в более позднем возрасте рекомендуется обратиться к врачу для исключения возможных заболеваний.
 Чаще тремор у младенцев является результатом эмоционального возбуждения.
Чаще тремор у младенцев является результатом эмоционального возбуждения.Причины тремора
Тремор у новорожденных характеризуется общими проявлениями, но факторы, способствующие его возникновению, могут быть разными:
- Незрелость нервной системы. Причины, провоцирующие дрожание конечностей, могут быть разными, но самой распространенной называют незрелость нервной системы. В этом случае в результате эмоционального возбуждения возможен тремор конечностей или подбородка. Этот вариант является нормой, и не требует лечения.
- Гипоксия. Кислородное голодание может быть результатом стремительных либо затяжных родов, внутриутробной инфекции, обвития пуповиной. Недостаток кислорода замедляет развитие ребенка, из-за чего тремор может исчезнуть позже обычного возраста.
- Недоношенность. Особенно часто тремор наблюдается у детей, появившихся на свет раньше срока. Дрожание конечной и подбородка в данном случает также может быть результатом незрелости нервных центров.
Если факторы, результатом которых является тремор подбородка, носят физиологичный характер, вероятность негативных последствий минимальна.
Чтобы исключить возможные заболевания, родителям новорожденного важно обратиться к врачу при появлении характерного подрагивания конечностей. При наличии патологий последствия тремора могут быть необратимыми.
Заболевания и патологии
В ряде случаев тремор рук, ног, подбородка может говорить о наличии у ребенка ряда заболеваний и патологий:
- дефицит в организме кальция, магния или иных веществ, необходимых организму;
- нарушения функционирования органов пищеварительного тракта;
- увеличение показателей внутричерепного давления;
- заболевания инфекционной этиологии;
- тремор губ и конечностей может быть следствием поражения мозжечка.
Тремор расценивается специалистами в качестве патологии, требующей лечения в том случае, если дрожание конечностей наблюдается после того, как ребенку исполниться четыре – пять месяцев.
Последствия тремора
 При правильном подходе негативные последствия тремора минимальны.
При правильном подходе негативные последствия тремора минимальны.Важно знать, чем опасен тремор. Если дрожание носит физиологический характер и полностью исчезает к четырем месяцам жизни ребенка, негативные последствия маловероятны.
Патологический тремор является более опасным, и может говорить о поражениях головного мозга. Отсутствие лечения в таких случаях может привести к ДЦП или тяжелым двигательным нарушениям. Существует несколько признаков патологического тремора:
- дрожь охватывает не только конечности, но и все тело ребенка;
- дрожь наблюдается не только при плаче или иной форме эмоционального возбуждения, но также во сне, при нахождении ребенка в спокойном состоянии;
- тремор наблюдается у ребенка, возраст которого составляет более пяти месяцев;
- наблюдается дрожание только одной конечности;
- тремор ног или рук сопровождается изменением цвета кожных покровов, нарушением дыхания.
При появлении любого из тревожных признаков ребенка важно немедленно показать специалисту. Своевременная диагностика и лечение помогут предупредить возможные последствия.
Категорически недопустимо давать ребенку какие-либо препараты или добавки, обладающие успокаивающим или иным действием. Бесконтрольное использование препаратов может усугубить состояние грудничка.
Лечение тремора
Подбирать методы, как лечить тремор у новорожденных, требуется только после постановки диагноза. Выбор препаратов осуществляется с учетом имеющегося заболевания, возраста ребенка. При отсутствии патологий рекомендуется задействовать общие способы, которые помогут устранить дрожание конечностей:
- Обязательны регулярные прогулки на свежем воздухе не менее двух раз в день.
- Полезно купать ребенка в ванной с теплыми травяными отварами. Отлично подойдет отвар ромашки, мяты, душицы.
- Ежедневно нужно делать грудничку расслабляющий массаж. Тонкостям его выполнения можно обучиться у педиатра или практикующего массажиста.
- Важен покой и благоприятная обстановка в семье. Требуется исключить ситуации, провоцирующие стресс у ребенка.
Соблюдение приведенных рекомендаций улучшает кровоснабжение органов и тканей малыша, нормализуя их состояние и стимулируя созревание нервной системы. Важно также периодически показывать ребенка врачу, который, если возникнет такая необходимость, подберет щадящие лекарственные препараты, способствующие достижению эффекта расслабления.
Также рекомендуем почитать: пиодермия у детей
Тремор у новорожденных, неврология у новорожденных
Тремор у новорожденных – это разного рода мышечные подергивания, наблюдающиеся у детей с самого рождения. Чаще всего говорят о треморе конечностей или подбородка. Может быть и тремор головы – но это уже признак довольно серьезных неврологических проблем, а дрожание ручек или подбородка при крике, плаче до трех месяцев патологией не считается.
Тремор у новорожденных возникает из- за незрелости нервных центров, отвечающих за движение в головном мозге и избыточного содержания норадреналина в крови ребенка при проявлениях эмоций. А избыток этот возникает, опять же, вследствие незрелости мозгового слоя надпочечников, вырабатывающих норадреналин.
Существуют так называемые критические периоды развития нервной системы ребенка первого года жизни, в которые она наиболее уязвима для того, чтобы наступил какой-то сбой в нормальном развитии. Это первый, третий, девятый и двенадцатый месяцы жизни ребенка – именно в эти периоды желательно посещать детского невролога.
Если приступы «дрожания» остаются дольше, а они могут наблюдаться и в год, и позже – значит, есть или было повреждение нервной системы ребенка – во время беременности или в родах. Причин этому может быть много – даже стрессы мамы в процессе беременности имеют значение, ведь в ее крови частенько «зашкаливал» тот же самый норадреналин, только выражалось это не в подергиваниях мышц, а в других эмоциональных реакциях. И такое же наводнение гормонов переживал малыш, что могло привести к разбалансировке как центральной нервной, так и эндокринной системы. Гипоксия плода во время беременности и в процессе родов, а причин у нее очень много, также способствует нарушениям деятельности головного мозга. Гипоксия может быть и при нарушениях функции плаценты, при кровотечениях и угрозах выкидыша, при многоводии и внутриутробных инфекциях. В родах может быть и слабость родовой деятельности и стремительные роды, обвитие пуповиной и отслойка плаценты – вариантов много. Все они приводят к нарушению поступления кислорода к головному мозгу и в последующем проявляются, как тремор у новорожденных.
Недоношенные дети часто страдают тремором конечностей, подбородка, губ, поскольку их центральная и периферическая нервная система изначально незрелые, а созревание вне материнского организма даже при отличном и правильном уходе – это не совсем то.
Поэтому тремор у новорожденных, хоть и считается до трех месяцев не требующим коррекции, должен навести родителей на мысль, что такое «слабое звено» у ребенка есть и оно требует пристального наблюдения. Нервная система новорожденного – очень податливое и динамичное образование, и при правильном и своевременном лечение она прекрасно восстанавливается, приходит в норму, укрепляется – и через некоторое время малыш может быть совершенно здоров.
Кроме наблюдения детского невролога и выполнения его назначений малышу, подверженному тремору, обязательно показан расслабляющий массаж и лечебная гимнастика, проводить которую, хотя бы на первом году жизни, должен опытный специалист, хорошо раннее плавание в специальном бассейне, спокойная, ровная и доброжелательная обстановка в семье.
Тремор у грудничков — Груднички(дети)
Причины тремора у малышей
У новорожденных нередко можно заметить мелкое подергивание конечностей и подбородка. Подобные мышечные сокращения наблюдаются у 50% детей в течение первых недель жизни. Они возникают впоследствии сильного эмоционального возбуждения во время: интенсивного плача, сильного испуга, фазы быстрого сна. Нервная система новорожденного незрелая, поэтому он излишне возбудим, и совершает некоторые неуправляемые движения. Такой тремор считается нормой, но в любом случае педиатр должен о нем знать.
Частый по интенсивности и мелкий по амплитуде тремор, сопровождающий плачь, является физиологической особенностью нервной системы ребенка. Так организм компенсирует возбуждение и стабилизирует состояние.
Частые и мелкие подрагивания естественны для не окрепшей нервной системы. Но если они не проходят к 3 месяцам и появляются без причины, то необходимо подумать о нарушениях функций нервной системы.
Есть еще одна причина возникновения тремора – высокое содержание норадреналина в крови новорожденных. Этот мозговой гормон надпочечников отвечает на передачу нервных импульсов в мозг. Именно большая концентрация норадреналина в крови провоцирует резкое сокращение мышц во время сильного эмоционального напряжения.
Спровоцировать тремор могут различные факторы, мешающие нормальному развитию грудничка до и после рождения. Негативно сказываются на формировании центральной нервной системы переживания, стрессы беременной женщины, плохая экологическая обстановка. После рождения тремор возникает на фоне плохих бытовых и психологических условий.
Тремор головы у грудничка
Тремор у грудничка обычно проявляется на подбородке и конечностях. В редких случаях дрожание затрагивает всю голову.
Тремор головы может быть абсолютно безопасным явлением первых месяцев жизни. Но чаще он служит сигналом, говорящим о серьезном неврологическом заболевании. Особенно опасно оставлять малыша без медицинской помощи, если проявления тремора носят интенсивный характер, возникают без причины и не ослабевают долгое время.
Причиной развития тремора головы у грудничка может стать: наркотический абстинентный синдром, гипоксически-ишемическая энцефалопатия, гипокальциемия, гипергликемия, гипомагнезиемия, сепсис, внутричерепные кровоизлияния.
Тремор подбородка у грудничка
Не стоит пугаться мелкой и частой дрожи подбородка новорожденного, если он эмоционально возбужден. Тремор вызван незрелостью нервного центра головного мозга. Но если приступы чересчур интенсивны и растянуты по времени и, кроме того, дрожать конечности и голова, то медицинская помощь необходима в срочном порядке.
Также дрожание подбородка, сопровождающееся частыми срыгиваниями, беспокойством, нарушением сна, является признаками мышечной дистонии.
Тремор рук у грудничка
Тремор рук также безобиден, как и подрагивание подбородка. Но только до определенного времени, после 3 месяцев непроизводное мелкое сокращение мышц не считается нормой и требует лечения.
Дополнительные симптомы должны насторожить молодую маму. Например, тремор рук в сочетании с бессонницей, повышенным потоотделением, поносами и болями в животе – это, скорее всего, признак нарушений работы щитовидной железы. Точный диагноз выяснится после посещения эндокринолога и прохождения всех необходимых исследований.
Тремор ног у грудничка
Тремор ног у грудничка отмечается реже, чем сокращение мышц подбородка и рук. Но это все тот же неопасный проходящий признак незрелости организма малыша. Часто тремор ног появляется у недоношенных детей, перенесших гипоксию и травму при родах.
Но если ноги дрожат очень сильно и тремор не прекращается к 3 месяцам, то помочь сможет только врач. Прекрасно помогает лечебный массаж, гимнастика и плавание, все, что укрепляет мышцы ног и нервную систему. Если тремор появился впервые нужно убедиться, что это не судороги.
В редких случаях непроизвольные сокращение мышц вызваны неправильным строением отдельных частей ноги, травмой.
Иногда сопутствующие тремору ног симптомы способны рассказать о более серьезном заболевании. Диагностировать болезнь и назначить лечение должен квалифицированный специалист.
Лечение тремора у грудничков
Не требует лечения тремор, возникающий исключительно при испуге, плаче, быстром сне. Но если он не уменьшается и не проходит к 3 месяцам нужно обратиться к неврологу. Особенно важна консультация врача при беспричинном и усиливающемся треморе.
Серьезные неврологические нарушения требуют медикаментозной коррекции, а в остальных случаях назначается лечебный массаж, специальная гимнастика, плавание в бассейне, соблюдение рационального режима дня.
Психическое равновесие окружающих грудничка людей и неукоснительное выполнение всех рекомендаций врача гарантируют полное излечение, за исключением детей, находящихся в крайне тяжелом состоянии.
Похожие статьи:
Плавание для грудничков
Грудничок запрокидывает голову
Массаж для грудничков
Холодные ручки у грудничка
Дистония у грудничка






 Реконструкция внешнего вида
Реконструкция внешнего вида
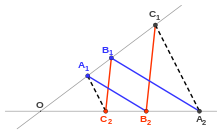 Закон Паппа: якщо червоні прямі паралельні і сині прямі паралельні, то пунктирні чорні прямі повинні бути паралельні.
Закон Паппа: якщо червоні прямі паралельні і сині прямі паралельні, то пунктирні чорні прямі повинні бути паралельні.
 Про паралельні прямі (Постулат 5): Якщо пряма, що перетинає дві інші прямі, утворює внутрішні односторонні кути, які менші, ніж два прямі кути, то ці дві прямі перетнуться як завгодно далеко з тієї сторони, де кути (давньогрецькою:Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ’ ἄπειρον συμπίπτειν, ἐφ’ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες).
Про паралельні прямі (Постулат 5): Якщо пряма, що перетинає дві інші прямі, утворює внутрішні односторонні кути, які менші, ніж два прямі кути, то ці дві прямі перетнуться як завгодно далеко з тієї сторони, де кути (давньогрецькою:Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ’ ἄπειρον συμπίπτειν, ἐφ’ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες). Одне з доведень із «Елементів» Евкліда: враховуючи лінійний сегмент, існує рівносторонній трикутник, який включає сегмент як одну з його сторін. Конструктивне доведення: рівносторонній трикутник ΑΒΓ зроблений шляхом нанесення кругів Δ і Ε, центрованих по точкам А і В, і взяття одного перетину кругів як третьої вершини трикутника.
Одне з доведень із «Елементів» Евкліда: враховуючи лінійний сегмент, існує рівносторонній трикутник, який включає сегмент як одну з його сторін. Конструктивне доведення: рівносторонній трикутник ΑΒΓ зроблений шляхом нанесення кругів Δ і Ε, центрованих по точкам А і В, і взяття одного перетину кругів як третьої вершини трикутника. Приклад конгруентності: дві фігури ліворуч є конгруентними, а третя — подібною до них. Остання фігура не конгруентна з ними. Конгруентність змінює деякі властивості, такі як місце розташування та орієнтація, але залишають інші незмінними, наприклад, відстані та кути. Останні властивості називаються інваріантами, і їх вивчення є сутністю геометрії.
Приклад конгруентності: дві фігури ліворуч є конгруентними, а третя — подібною до них. Остання фігура не конгруентна з ними. Конгруентність змінює деякі властивості, такі як місце розташування та орієнтація, але залишають інші незмінними, наприклад, відстані та кути. Останні властивості називаються інваріантами, і їх вивчення є сутністю геометрії.
 Конгруентність трикутників визначається шляхом визначення двох сторін і кута між ними (SAS), двома кутами та сторони між ними (ASA) або двома кутами та відповідною суміжною стороною ( AAS). Проте, якщо вказати дві сторони та сусідній кут (SSA), можна отримати два різні можливі трикутники, якщо вказаний кут не є прямим.
Конгруентність трикутників визначається шляхом визначення двох сторін і кута між ними (SAS), двома кутами та сторони між ними (ASA) або двома кутами та відповідною суміжною стороною ( AAS). Проте, якщо вказати дві сторони та сусідній кут (SSA), можна отримати два різні можливі трикутники, якщо вказаний кут не є прямим.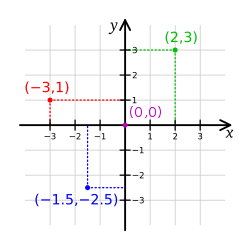 Ілюстрація декартової системи координат. Чотири відмічені точки позначені їх координатами: (2,3) зеленим, (−3,1) червоним, (−1.5,−2.5) синім, і початок координат (0,0) пурпуровим.
Ілюстрація декартової системи координат. Чотири відмічені точки позначені їх координатами: (2,3) зеленим, (−3,1) червоним, (−1.5,−2.5) синім, і початок координат (0,0) пурпуровим.
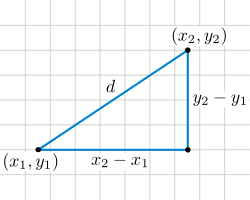 Формула відстані на площині слідує із теореми Піфагора.
Формула відстані на площині слідує із теореми Піфагора.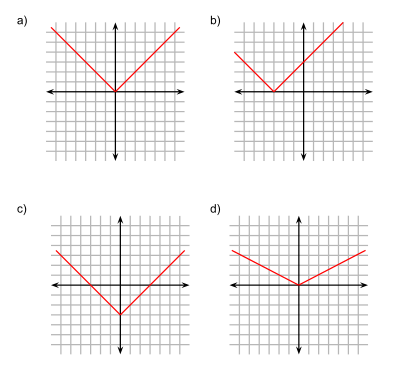 a) y = f(x) = |x| b) y = f(x+3) c) y = f(x)-3 d) y = 1/2 f(x)
a) y = f(x) = |x| b) y = f(x+3) c) y = f(x)-3 d) y = 1/2 f(x)
 Отрезок AB (выделен красным)
Отрезок AB (выделен красным)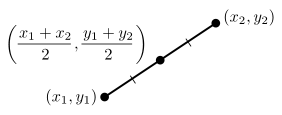 Средняя точка отрезка с вершинами (x1, y1) и (x2, y2)
Средняя точка отрезка с вершинами (x1, y1) и (x2, y2) Построение с помощью циркуля и линейки
Построение с помощью циркуля и линейки Построение с помощью одного циркуля
Построение с помощью одного циркуля
 Загрузка…
Загрузка…
 Графики четырёх функций вида y=ax{\displaystyle y=a^{x}}, a{\displaystyle a} указано рядом с графиком функции
Графики четырёх функций вида y=ax{\displaystyle y=a^{x}}, a{\displaystyle a} указано рядом с графиком функции


 Кровянистые выделения
Кровянистые выделения Либи́до
Либи́до
 График базальной температуры.
График базальной температуры.
 Здоровое питание
Здоровое питание






















 Загрузка…
Загрузка…












 : —————-
: —————- 36. От двух железнодорожных станций навстречу друг другу одновременно отправились два поезда и встретились через 4 часа. Скорость одного поезда 75 км/ч, а второго — 60 км/ч. Какое расстояние прошёл до встречи каждый поезд? Чему равно расстояние между станциями?
36. От двух железнодорожных станций навстречу друг другу одновременно отправились два поезда и встретились через 4 часа. Скорость одного поезда 75 км/ч, а второго — 60 км/ч. Какое расстояние прошёл до встречи каждый поезд? Чему равно расстояние между станциями? 38. Из двух ульев навстречу друг другу одновременно вылетели 2 пчелы. Первая пролетела до встречи 14 м со скоростью 7 м/с. Скорость второй пчелы 6 м/с. Какое расстояние до встречи пролетела вторая пчела?
38. Из двух ульев навстречу друг другу одновременно вылетели 2 пчелы. Первая пролетела до встречи 14 м со скоростью 7 м/с. Скорость второй пчелы 6 м/с. Какое расстояние до встречи пролетела вторая пчела?
 41. Из двух посёлков навстречу друг другу одновременно отправились велосипедист и пешеход. Скорость велосипедиста 16 км/ч, пешехода — 4 км/ч. Расстояние между посёлками 24 км. На каком расстоянии друг от друга будут велосипедист и пешеход через 1 час?
41. Из двух посёлков навстречу друг другу одновременно отправились велосипедист и пешеход. Скорость велосипедиста 16 км/ч, пешехода — 4 км/ч. Расстояние между посёлками 24 км. На каком расстоянии друг от друга будут велосипедист и пешеход через 1 час? 43. Из посёлков, расстояние между которыми х км, одновременно выехали навстречу друг другу два велосипедиста. Скорость одного велосипедиста 18 км/ч, другого — 17 км/ч. Через сколько часов они встретятся?
43. Из посёлков, расстояние между которыми х км, одновременно выехали навстречу друг другу два велосипедиста. Скорость одного велосипедиста 18 км/ч, другого — 17 км/ч. Через сколько часов они встретятся? 46. С разных концов беговой дорожки одновременно навстречу друг другу выбежали два спортсмена. Один спортсмен бежал со скоростью х м/с и до встречи пробежал т метров, а второй бежал со скоростью у м/с. Какое расстояние-до встречи пробежал второй спортсмен? Запиши решение задачи выражением.
46. С разных концов беговой дорожки одновременно навстречу друг другу выбежали два спортсмена. Один спортсмен бежал со скоростью х м/с и до встречи пробежал т метров, а второй бежал со скоростью у м/с. Какое расстояние-до встречи пробежал второй спортсмен? Запиши решение задачи выражением. 48. Из города одновременно в противоположных направлениях отправились два автобуса. Скорость одного 55 км/ч, второго — 63 км/ч. На каком расстоянии они будут друг от друга через 3 часа?
48. Из города одновременно в противоположных направлениях отправились два автобуса. Скорость одного 55 км/ч, второго — 63 км/ч. На каком расстоянии они будут друг от друга через 3 часа? 50. Из спортивного лагеря в противоположных направлениях одновременно вышли две туристические группы. Скорость движения одной группы б км/ч, а второй — на 1 км/ч меньше, На каком расстоянии друг от друга будут группы через 4 часа?
50. Из спортивного лагеря в противоположных направлениях одновременно вышли две туристические группы. Скорость движения одной группы б км/ч, а второй — на 1 км/ч меньше, На каком расстоянии друг от друга будут группы через 4 часа? 52. От пристани одновременно в противоположных направлениях отошли два теплохода, скорости которых были равны 40 км/ч и 35 км/ч. Найди расстояние между теплоходами через 3 часа.
52. От пристани одновременно в противоположных направлениях отошли два теплохода, скорости которых были равны 40 км/ч и 35 км/ч. Найди расстояние между теплоходами через 3 часа. 54. Из двух пунктов, расстояние между которыми 10 км, одновременно в противоположных направлениях выехали два велосипедиста. Скорость одного велосипедиста 19 км/ч, а другого — на 3 км/ч меньше. Найди расстояние между велосипедистами через 2 часа.
54. Из двух пунктов, расстояние между которыми 10 км, одновременно в противоположных направлениях выехали два велосипедиста. Скорость одного велосипедиста 19 км/ч, а другого — на 3 км/ч меньше. Найди расстояние между велосипедистами через 2 часа. 56. От лыжной базы одновременно в противоположных направлениях вышли два лыжника. Скорость одного лыжника 13 км/ч, второго — 14 км/ч. Какое расстояние преодолел каждый лыжник, когда расстояние между ними стало 54 км?
56. От лыжной базы одновременно в противоположных направлениях вышли два лыжника. Скорость одного лыжника 13 км/ч, второго — 14 км/ч. Какое расстояние преодолел каждый лыжник, когда расстояние между ними стало 54 км?