Разница между окружностью и кругом: Чем отличается окружность от круга
Чем отличается окружность от круга
В обычной жизни нам приходится замечать множество предметов, которые по своей форме напоминают окружности и круги, но редко кто задумывается о том, чем окружность отличается от круга и что у них общего.
Окружность – это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом.
Окружность имеет центр — это начальная точка нарисования циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.
Круг – является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру. Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр.
Отличие окружности и круга
Окружность, как любая линия имеет длину, а круг, как любая геометрическая фигура имеет площадь. Круг имеет площадь, но её нет у окружности. Круг содержит центр окружности, а окружность, содержит сам круг. Без окружности не было бы круга, но она существует самостоятельно. Окружность проводит границу круга снаружи, а круг – внутренняя часть окружности. И круг, и окружность имеют одинаковый центр.
Выводы:
- Окружность представляет собой замкнутую линию.
- Круг, это пространство, ограниченное окружностью.
- Радиус окружности, равен радиусу круга.
- Диаметр делит окружность и круг на два равных полукруга.
- Окружность является границей круга.
- Если начертить заштрихованную окружность, то её можно считать кругом и наоборот.
- Круг и окружность имеют единый центр.
- У окружности есть длина, а у круга её нет.
Чем отличается окружность от круга правило. Разница между окружностью и кругом
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
ImGist определил, что разница между кругом и окружностью заключается в следующем:
Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
Окружность — это огромное количество точек на плоскости, равноудаленных от некой точки этой же плоскости, именуемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.
Круг — это огромное количество точек плоскости, удаленных от некой точки этой же плоскости, именуемой центром круга, на расстояние, не превышающеей определенной величины, именуемой радиусом круга. Круг представляет собой сплошную фигуру, включающую окружность и все точки, лежащие в ней.
Следовательно, круг — это участок плоскости, а окружность — черта этого участка. Потому есть возможность говорить о площади круга и длине окружности, однако неправильно говорить о длине круга и площади окружности.
Так как точки окружности удалены от центра на расстояние, не превышающее радиуса, то они все принадлежат кругу. Другими словами, окружность принадлежит кругу, который она ограничивает. В особых случаях может рассматриваться круг в отсутствие границы — огромное количество точек круга, не принадлежащих его границе (окружности).
Окружность разделяет плоскость на две части — лежащую снутри и лежащую снаружи. Попрасть из одной части в другую нереально в отсутствие скрещения окружности. Площаль внутренней части конечна, площадь наружной части нескончаема.
Центр окружности не принадлежит окружности (кроме вырожденного варианта окружности нулевого радиуса). Центр круга всегда принадлежит кругу, т.к. находится снутри ограничивающей его окружности.
NMitra В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав
#ball:after {
content: «»;
position: absolute;
top: 0; bottom: 0; right: 0; left: 0;
box-shadow: 0 0 0 100px #fff;
border-radius: 100%;
}
Но тогда тень в Гугл Хром «обрезанная» получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера.
Космо Мизраил
Прикольно.
Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset.
NMitra
Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo
Космо Мизраил
Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить 🙂
Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.
Пример: http://jsfiddle.net/9qzm6/
Ещё нашёл скрипт, который выполняет эту работу самостоятельно:
http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-Styles
Здесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.
Это так, на заметку 🙂 NMitra Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))
Пжалст 🙂 я ваш постоянный читатель уже год как минимум 🙂
Анонимный
IE 11
Все анимировано))
NMitra
Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.
Что такое круг?
Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.
Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.
Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.
- Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
- Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
- Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.
Круг в реальной жизни
В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.
Другой пример круга – Солнце . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.
Сектор
Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.
Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.
Что такое шар?
Шар – тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.
В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.
Разновидности шара
В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .
Характеристики шара
Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.
Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.
Выводы
Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.
Публикации по теме:
Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.
Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.
Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.
НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.
Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.
Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.
«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.
Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.
Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.
Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.
Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.
Что такое длина окружности и площадь круга: определение
Итак, окружность является замкнутой кривой линией, которая ограничивает или же напротив, образует круг. Обязательное условие окружности — у нее есть центр и все точки равноудалены от него. Проще говоря, окружность это гимнастический обруч (или как его часто называют хула-хуп) на плоской поверхности.
Длина окружности это общая длина той самой кривой, которая образует окружность. Как известно вне зависимости от размеров окружности соотношение ее диаметра и длины равно числу π = 3,141592653589793238462643.
Из этого следует, что π=L/D, где L — длина окружности, а D — диаметр окружности.
Если Вам известен диаметр, то длину можно найти по простой формуле: L= π* D
В случае если известен радиус: L=2 πR
Мы разобрались, что такое окружность и можем перейти к определению круга.
Круг — это геометрическая фигура, которая окружена окружностью. Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.
Стоит заметить, что у окружности и круга, который находится в ней значения радиуса и диаметра одинаковые. А диаметр в свою очередь в два раза больше чем радиус.
Круг имеет площадь на плоскости, которую можно узнать при помощи простой формулы:
Где S — площадь круга, а R — радиус данного круга.
Чем круг отличается от окружности: объяснение
Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:
- Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
- Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
- Сходство между окружностью и кругом: радиус и диаметр;
- У круга и окружности единый центр;
- В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
- У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.
Круг и окружность: примеры, фото
Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.
Формула длины окружности и площади круга: сравнение
Формула длины окружности L=2 πR
Формула площади круга S= πR²
Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.
Площадь круга по длине окружности: формула
S=π(L/2π)=L²/4π, где S — площадь круга, L — длина окружности.
Видео: Что такое круг, окружность и радиус
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Выводы сайт
- Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
- Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
Чем отличается окружность от круга. Чем отличается круг от окружности
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
ImGist определил, что разница между кругом и окружностью заключается в следующем:
Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
NMitra В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав
#ball:after {
content: «»;
position: absolute;
top: 0; bottom: 0; right: 0; left: 0;
box-shadow: 0 0 0 100px #fff;
border-radius: 100%;
}
Но тогда тень в Гугл Хром «обрезанная» получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера.
Космо Мизраил
Прикольно.
Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset.
NMitra
Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo
Космо Мизраил
Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить 🙂
Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.
Пример: http://jsfiddle.net/9qzm6/
Ещё нашёл скрипт, который выполняет эту работу самостоятельно:
http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-Styles
Здесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.
Это так, на заметку 🙂 NMitra Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))
Пжалст 🙂 я ваш постоянный читатель уже год как минимум 🙂
Анонимный
IE 11
Все анимировано))
NMitra
Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.
Что такое круг?
Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.
Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.
Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.
- Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
- Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
- Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.
Круг в реальной жизни
В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.
Другой пример круга – Солнце . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.
Сектор
Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.
Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.
Что такое шар?
Шар – тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.
В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.
Разновидности шара
В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .
Характеристики шара
Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.
Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.
Выводы
Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.
Публикации по теме:
Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.
Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.
Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.
НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.
Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.
Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.
«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.
Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.
Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Выводы сайт
- Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
- Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.
Что такое окружность?
Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Что такое круг?
Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Примеры круга в реальной жизни
На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Отличия окружности от круга
Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — круга. Вот чем отличается окружность от круга.
Что такое сектор?
Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
Выводы
Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
Урок 26. окружность и круг. сфера и шар — Математика — 5 класс
Математика
5 класс
Урок №26
Окружность и круг. Сфера и шар
Переченьрассматриваемыхвопросов:
— понятия «окружность», «круг», «сфера», «шар» и их элементы;
— изображение окружности на плоскости, сферы в пространстве.
Тезаурус
Окружность – это плоская замкнутая кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки – её центра.
Круг – плоская геометрическая фигура, являющаяся местом точек, расположенных на одинаковом расстоянии от некоторой точки (центра).
Центр окружности – это точка, равноудалённая от точек окружности.
Радиус окружности – это отрезок, соединяющий какую-нибудь точку этой окружности с её центром.
Хорда окружности – это отрезок, соединяющий какие-нибудь две точки окружности.
Диаметр окружности – это хорда, проходящая через центр окружности.
Шар – это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Ещё в глубокой древности люди изобрели колесо, придумали гончарный круг, сделали украшения в виде колец, то есть создали предметы, в основе которых лежит окружность или круг. В современных устройствах эти геометрические фигуры тоже встречаются очень часто. Сегодня мы поговорим не только о том, как они используются в наше время, но и выясним их отличие друг от друга.
Итак, что же такое окружность?
Окружность – это замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Эта точка называется центром окружности.
Построим окружность. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки отрезок длиной 3 см. Поставим иголку циркуля в точку О и начертим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую линию, которую называют окружностью. Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, то есть окружность есть граница круга.
При построении окружности расстояние между ножками циркуля не меняется. Поэтому все точки окружности равно удалены от точки О. Точку O называют центром и окружности, и круга. Отметим на окружности любую точку – например, точку L. Построим отрезок, соединяющий точку L с центром окружности – точкой О.
Отрезок ОL называют радиусом окружности.
Отметим на окружности любые две точки. Например, C и D. Построим отрезок, соединяющий точки C и D.
Отрезок CD называют хордой окружности. Некоторые хорды окружности проходят через её центр. Например, хорда AB проходит через центр окружности. Такую хорду называют диаметром окружности. То есть АВ – диаметр окружности.
Концы диаметра делят окружность на две равные части. Длина диаметра окружности равна двум радиусам. Две точки делят окружность на две части, называемые дугами. Например, CD. Обычно рассматривается одна из дуг окружности, определяемая по смыслу задачи.
Окружность разбивает плоскость на две части – внутреннюю область и внешнюю.
Давайте представим себе яблоко и воздушный шарик.
Чем они отличаются друг от друга?
Они оба имеют форму шара. Однако воздушный шарик полый внутри. Для таких предметов в математике есть название – сфера. А яблоко, с точки зрения математиков, – это шар.
Шар–это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Отрезок, соединяющий точку поверхности шара с его центром, называется радиусом шара.
Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
Поверхность шара называется сферой.
Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.
Окружность и круг являются плоскими фигурами, то есть такими, которые располагаются в пределах одной плоскости. Такие фигуры – это не что иное, как рисунки на листе бумаги. Рассмотренные на уроке сфера и шар относятся к пространственным телам. Между сферой, шаром, окружностью и кругом есть взаимосвязь. Сфера и шар образуются вращением вокруг оси окружности и круга соответственно.
Легенда о циркуле
В жизни для построений мы используем различные инструменты. Так, для того чтобы нарисовать окружность, необходим циркуль. Но как появился циркуль? Обратимся к мифам Древней Греции.
В далёкие времена в Афинах жил юноша, которого звали Талос. Он с детства был очень талантлив. В 12 лет он изобрёл гончарный круг для изготовления посуды. Также он придумал первую пилу, обратив в живой природе внимание на то, что скелет рыбы напоминает острые зубья. И наконец, Талос изобрёл устройство для построения окружностей, так называемый циркуль – инструмент в виде двух одинаковых стержней, соединённых шарниром. Так гласит легенда, а как было на самом деле, история умалчивает: известно лишь то, что на древних памятниках искусства фигуры и орнаменты из окружностей, умело выполненные древними мастерами, почти идеальны.
Тренировочные задания
№ 1. Подпишите соответствующие элементы окружности.
Вспомним определения радиуса (это отрезок, соединяющий какую-нибудь точку этой окружности с её центром), хорды (это отрезок, соединяющий какие-нибудь две точки окружности), диаметра (это хорда, проходящая через центр окружности) и ценрта окружности (это точка, равноудалённая от точек окружности).
Правильный ответ:
BO – радиус;
ВА – диаметр;
DE – хорда;
О – центр окружности.
№ 2. Выберите правильный ответ.
Рассмотрим отрезок АК, длина которого равна 8см. Построено две окружности: первая – с центром в точке A, а вторая – с центром в точке К. Их радиусы, соответственно, равны 4 см и 6 см. Сколько общих точек имеют окружности?
Решение: чтобы ответить на вопрос, изобразим отрезок и окружности.
Ответ: общих точек будет две. Они будут лежать на пересечении двух окружностей.
что общего, в чём отличие эллипса от овала
В школе большинству из нас не раз объясняли, в чём отличие радиуса от диаметра, серной кислоты от соляной, эллипса от овала. Но прошли годы, и школьные знания, «слежавшись» под весом многолетней будничной рутины, по большей части позабылись. В рамках данной статьи мы попытаемся восполнить хотя бы один досадный пробел в знаниях и подробнее рассмотрим последний из приведённых примеров, научившись отличать овал от эллипса. Для начала обозначим ключевые определения.
Овал
Под овалом в геометрии понимается вытянутая замкнутая фигура правильной формы. Овал относится к двухмерным фигурам и обладает особыми свойствами. Само слово образовано от французского Ovale, которое, в свою очередь, имеет общие корни с латинской лексемой ovum, что в переводе означает «яйцо». Кривая этого геометрического объекта имеет с любой прямой не более двух общих точек.
Справка! Нельзя сказать, что человек, называющий данную геометрическую фигуру просто «кругом», абсолютно прав. На самом деле окружность (в которой, как мы знаем, все точки кривой равноудалены от центра) – это одна из множества вариаций овала.
Существует структурно более сложное понятие овала в инженерной графике. В этой отрасли науки данным термином обозначают фигуру, имеющую две оси симметрии и построенную при помощи сочетания четырёх участков кривых линий от двух радиусов. Эти участки подобраны таким образом, чтобы обеспечить «перетекание» от одного радиуса к другому без нарушения симметрии и контура фигуры. Если определять координаты точки, постоянно движущейся по линии овала, то она всегда будет находиться на одном из вышеописанных радиусов кривизны. Эти радиусы считаются «фиксированными».
Эллипс
У слова «эллипс» имеются греческие корни, наиболее близкие по переводу к словам «нехватка, недостаток, опущение». Чего же не хватает в эллипсе и что эта фигура вообще из себя представляет?
Эллипсом принято считать любую замкнутую кривую на плоскости, которая имеет четыре вершины в так называемых точках экстремума. Точки фокуса эллипса равноудалены от его вершин. Стороны эллипса будут симметричны, если разделить его в любом направлении прямой, проходящей через его центр. Впрочем, это правило действительно и для фигур овального типа.
Что общего
Рассматривая вопрос о том, что может быть общего между овальной и эллиптической фигурой, можно заключить, что они имеют весьма похожий внешний вид. Кроме того, обе фигуры располагаются в так называемом евклидовом пространстве. На простом языке евклидово пространство можно объяснить как двумерное пространство, в котором положение точки может быть обозначено при помощи двух чисел, обозначающей её координаты.
В чём отличие эллипса от овала
Различия между двумя этими весьма смежными понятиями вытекают в основном из их определений. Вернувшись к рассмотренному нами определению овала в инженерной графике, можно заключить, что он, в отличие от эллипса, в котором радиус кривизны варьируется перманентно, обладает «фиксированными» радиусами.
Справка! В трёхмерном пространстве возможно построение объёмного овала. Такие фигуры называются эллипсоидами и способны иметь приплюснутую или вытянутую форму. Эта форма достаточно широко распространена в макромире: ею обладает огромное количество известных планет и даже галактики.
Для овальных фигур существует великое множество вариантов построения. Оси их, начинающиеся в точках своих вершин, имеют различные соотношения между собой. В случае же с эллиптическими фигурами в силу вступают особые правила построения. Говоря проще, овалом обозначают более общее понятие, а эллипсом – лишь одно из его проявлений.
Разница между радиусом и диаметром. Как найти радиус окружности: в помощь школьникам
Инструкция
В случае, если известен только диаметр, то формула будет выглядеть как «R = D/2».2»).
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 сантиметров.
Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D².2 / 4 + 20*10/2», а нажать клавишу Enter.
Источники:
- как найти площадь окружности по диаметру
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».
Воспользуйтесь программным калькулятором Windows, если вам более привычны интерфейсы с обычными кнопками. Чтобы не искать ссылку на его запуск в глубинных уровнях главного меню системы, нажмите сочетание клавиш WIN + R, введите команду calc и нажмите клавишу Enter. Интерфейс этой программы очень незначительно отличается от обычных калькуляторов, поэтому операция деления длины окружности на число Пи вряд ли вызовет какие-либо затруднения.
Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».
Официальный диаметр Земли
Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.
Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.
Вычисление диаметра Земли
Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.
Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.
Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).
В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.
На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.
Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.
Источники:
- Как измерили Землю в 2019
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры.{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
Если заполнить пространство внутри окружности, например начертить окружность с помощью циркуля на бумаге или картоне и вырезать, то получим круг (рис. 10).
Рис. 10. Круг
Круг — это часть плоскости, ограниченная окружностью.
Условие: Витя Верхоглядкин начертил в своей окружности (рис. 11) 11 диаметров. А когда пересчитал радиусы, получил 21. Правильно ли он сосчитал?
Рис. 11. Иллюстрация к задаче
Решение: радиусов должно быть в два раза больше, чем диаметров, поэтому:
Витя сосчитал неправильно.
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012. — 112 с.: ил. — (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. — М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. — М.: Ювента.
- Mypresentation.ru ().
- Sernam.ru ().
- School-assistant.ru ().
Домашнее задание
1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012., ст. 94 № 1, ст. 95 № 3.
2. Разгадайте загадку.
Мы живём с братишкой дружно,
Нам так весело вдвоём,
Мы на лист поставим кружку (рис. 12),
Обведём карандашом.
Получилось то, что нужно —
Называется …
3. Необходимо определить диаметр окружности, если известно, что радиус равен 5 м.
4. * С помощью циркуля начертите две окружности с радиусами: а) 2 см и 5 см; б) 10 мм и 15 мм.
Зачастую, когда школьник сдает выпускные экзамены в школе либо вступительные в какой-либо ВУЗ, ему необходимы определенные знания в области геометрии. Причем, задания бывают не такие уж сложные, просто нужно помнить базовые формулы, чтобы применить их в решении. Задачи, в которых необходимо найти радиус окружности, не являются исключением. В принципе, они достаточно просты в решении. В данной статье мы расскажем вам, как найти радиус окружности разными способами.
Находим радиус окружности, исходя из формул
Когда вы получаете задание на контрольной или на экзамене, в котором надо найти радиус окружности, в первую очередь необходимо проанализировать имеющиеся данные. Потому что именно от них будет зависеть ход решения в целом. Так, например, найти рассматриваемую величину можно, используя такие параметры: длину окружности, ее площадь, диаметр и др. Мы рассмотрим самые простые и часто встречающиеся способы решения задач, в которых радиус окружности является неизвестным.
Все мы знаем, что радиусом окружности является длина от ее центра до какой-либо точки,которая расположена на самой окружности. В связи с этим, решения могут быть следующими:
- Когда вам в исходных данных задачи дан диаметр окружности, то решение здесь будет проще простого. Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см.
- Переходим к следующему способу решения. Допустим, вам в условии дана длина окружности. Выражаясь математическим языком, это так называемый периметр. Мы прекрасно знаем, что есть специальная формула нахождения длины окружности: P=2πr. Отсюда, мы можем вывести формулу радиуса: r=P/2π. Теперь рассмотрим это на примере. Допустим, по условию задачи вам дана длина окружности, равная 31,4 см, а π в математике – величина постоянная и всегда равна 3,14; тогда радиус находим следующим образом: 31,4/2*3,14=5 см.
- Теперь рассмотрим, как найти радиус окружности, если дана ее площадь. Формула площади окружности имеет такой вид: S=πr2. Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см.
Теперь вам не составит труда решить любую задачу с нахождением радиуса окружности. Главное – четко проанализировать исходные данные, а потом применить подходящую формулу, и можете считать себя великим математиком.
Окружностью называют замкнутую, плоскую кривую, все точки которой, лежащие в одной плоскости, удалены на одинаковом расстоянии от центра.
Точка О является центром окружности, R является радиусом окружности — расстоянием от какой-нибудь точки окружности до центра. По определению все радиусы замкнутой
рис. 1
кривой имеют одинаковую длину.
Расстояние между двумя точками окружности называется хордой. Отрезок окружности, проходящий через ее центр и соединяющий две ее точки, называется диаметром. Середина диаметра является центром окружности. Точки окружности делят замкнутую кривую на две части, каждая часть носит название дуги окружности. Если концы дуги принадлежат диаметру, то такая окружность называется полуокружностью, длину которой принято обозначать π . Градусная мера двух окружностей, имеющих общие концы, составляет 360 градусов.
Концентрические окружности — это окружности, имеющие общий центр. Ортогональные окружности — это окружности, которые пересекаются под углом равным 90 градусов.
Плоскость, которую ограничивает окружность, называется кругом. Одна часть круга, которая ограничена двумя радиусами и дугой — это круговой сектор. Дуга сектора — это дуга, ограничивающая сектор.
Рис. 2
Взаимное расположение окружности и прямой (рис.2).
Окружность и прямая имеют две общие точки, если расстояние от прямой до центра окружности менее радиуса окружности. В таком случае прямая по отношению к окружности называется секущей.
Окружность и прямая имеют одну общую точку, если расстояние от прямой до центра окружности равно радиусу окружности. В таком случае прямая по отношению к окружности называется касательной к окружности. Их общая точка носит название точки касания окружности и прямой.
Основные формулы окружности:
- C = 2πR , где C — длина окружности
- R = С/(2π) = D/2 , где С/(2π) — длина дуги окружности
- D = C/π = 2R , где D — диаметр
- S = πR2 , где S — площадь круга
- S = ((πR2)/360)α , где S — площадь кругового сектора
Окружность и круг получили свое название в Древней Греции. Уже в древности человека интересовали круглые тела, поэтому окружность становилась венцом совершенства. То, что круглое тело могло двигаться само по себе, стало толчком к изобретению колеса. Казалось бы, что особенного в этом изобретении? Но представьте, если в одно мгновение колеса исчезнут из нашей жизни. В дальнейшем это изобретение и породило математическое понятие окружности.
Ограничивающая окружность. Что такое окружность и круг, в чем их отличия и примеры данных фигур из жизни
Это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O ), называемой центром .
Прямые (OA , OB , OС. . .), соединяющие центр с точками окружности — это радиусы .
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка , лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр , перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги , заключенные между параллельными хордами , равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема . Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой .
Из предыдущего следует, что окружность есть кривая линия .
2. Теорема . Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности .
Отметим на предложенной три любые точки A, B и С, начертим через них две хорды , например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.
Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.
Что такое длина окружности и площадь круга: определение
Итак, окружность является замкнутой кривой линией, которая ограничивает или же напротив, образует круг. Обязательное условие окружности — у нее есть центр и все точки равноудалены от него. Проще говоря, окружность это гимнастический обруч (или как его часто называют хула-хуп) на плоской поверхности.
Длина окружности это общая длина той самой кривой, которая образует окружность. Как известно вне зависимости от размеров окружности соотношение ее диаметра и длины равно числу π = 3,141592653589793238462643.
Из этого следует, что π=L/D, где L — длина окружности, а D — диаметр окружности.
Если Вам известен диаметр, то длину можно найти по простой формуле: L= π* D
В случае если известен радиус: L=2 πR
Мы разобрались, что такое окружность и можем перейти к определению круга.
Круг — это геометрическая фигура, которая окружена окружностью. Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.
Стоит заметить, что у окружности и круга, который находится в ней значения радиуса и диаметра одинаковые. А диаметр в свою очередь в два раза больше чем радиус.
Круг имеет площадь на плоскости, которую можно узнать при помощи простой формулы:
Где S — площадь круга, а R — радиус данного круга.
Чем круг отличается от окружности: объяснение
Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:
- Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
- Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
- Сходство между окружностью и кругом: радиус и диаметр;
- У круга и окружности единый центр;
- В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
- У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.
Круг и окружность: примеры, фото
Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.
Формула длины окружности и площади круга: сравнение
Формула длины окружности L=2 πR
Формула площади круга S= πR²
Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.
Площадь круга по длине окружности: формула
S=π(L/2π)=L²/4π, где S — площадь круга, L — длина окружности.
Видео: Что такое круг, окружность и радиус
Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.
Что такое окружность?
Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Что такое круг?
Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Примеры круга в реальной жизни
На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Отличия окружности от круга
Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — круга. Вот чем отличается окружность от круга.
Что такое сектор?
Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
Выводы
Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
Формы круга, окружности мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Математики стали заниматься геометрической фигурой — кругом на плоскости — очень давно.
Кругом с центром и радиусом называется множество точек плоскости, удаленных от на расстояние, не большее . Круг ограничен окружностью, состоящей из точек, удаленных от центра в точности на расстояние . Отрезки, соединяющие центр с точками окружности, имеют длину и также называются радиусами (круга, окружности). Части круга, на которые он делится двумя радиусами, называются круговыми секторами (рис. 1). Хорда — отрезок, соединяющий две точки окружности, — делит круг на два сегмента, а окружность – на две дуги (рис. 2). Перпендикуляр, проведенный из центра к хорде, делит ее и стягиваемые ею дуги пополам. Хорда тем длиннее, чем ближе она расположена к центру; самые длинные хорды — хорды, проходящие через центр, — называются диаметрами (круга, окружности).
Если прямая удалена от центра круга на расстояние , то при она не пересекается с кругом, при пересекается с кругом по хорде и называется секущей, при имеет с кругом и окружностью единственную общую точку и называется касательной. Касательная характеризуется тем, что она перпендикулярна радиусу, проведенному в точку касания. К кругу из точки, лежащей вне его, можно провести две касательные, причем их отрезки от данной точки до точек касания равны.
Дуги окружности, как и углы, можно измерять в градусах и его долях. За градус принимают часть всей окружности. Центральный угол (рис. 3) измеряется тем же числом градусов, что и дуга , на которую он опирается; вписанный угол измеряется половиной дуги . Если вершина угла лежит внутри круга, то этот угол в градусной мере равен полусумме дуг и (рис. 4,а). Угол с вершиной вне круга (рис. 4,б), высекающий на окружности дуги и , измеряется полуразностью дуг и . Наконец, угол между касательной и хордой равен половине заключенной между ними дуги окружности (рис. 4,в).
Круг и окружность имеют бесконечное множество осей симметрии.
Из теорем об измерении углов и подобия треугольников следуют две теоремы о пропорциональных отрезках в круге. Теорема о хордах говорит, что если точка лежит внутри круга, то произведение длин отрезков проходящих через нее хорд постоянно. На рис. 5,a . Теорема о секущей и касательной (имеются в виду длины отрезков частей этих прямых) утверждает, что если точка лежит вне круга, то произведение секущей на ее внешнюю часть тоже неизменно и равно квадрату касательной (рис. 5,б).
Еще в древности пытались решить задачи, связанные с кругом, — измерить длину окружности или ее дуги, площадь круга или сектора, сегмента. Первая из них имеет чисто «практическое» решение: можно уложить вдоль окружности нить, а потом развернуть ее и приложить к линейке или же отметить на окружности точку и «прокатить» ее вдоль линейки (можно, наоборот, «обкатить» линейкой окружность). Так или иначе измерения показывали, что отношение длины окружности к ее диаметру одно и то же для всех окружностей. Это отношение принято обозначать греческой буквой («пи» — начальная буква греческого слова perimetron, которое и означает «окружность»).
Однако древнегреческих математиков такой эмпирический, опытный подход к определению длины окружности не удовлетворял: окружность — это линия, т.е., по Евклиду, «длина без ширины», а таких нитей не бывает. Если же мы катим окружность по линейке, то возникает вопрос: почему при этом мы получим длину окружности, а не какую-нибудь другую величину? К тому же такой подход не позволял определить площадь круга.
Выход был найден такой: если рассмотреть вписанные в круг правильные -угольники , то при , стремящемся к бесконечности, в пределе стремятся к . Поэтому естественно ввести следующие, уже строгие, определения: длина окружности — это предел последовательности периметров правильных вписанных в окружность -угольников, а площадь круга — предел последовательности их площадей. Такой подход принят и в современной математике, причем по отношению не только к окружности и кругу, но и к другим кривым или ограниченным криволинейными контурами областям: вместо правильных многоугольников рассматривают последовательности ломаных с вершинами на кривых или контурах областей, а предел берется при стремлении длины наибольшего звена ломаной к нулю.
Аналогичным образом определяется длина дуги окружности: дуга делится на равных частей, точки деления соединяются ломаной и длина дуги полагается равной пределу периметров таких ломаных при , стремящемся к бесконечности. (Подобно древним грекам, мы не уточняем само понятие предела — оно относится уже не к геометрии и было вполне строго введено лишь в XIX в.)
Из самого определения числа следует формула для длины окружности:
Для длины дуги можно записать аналогичную формулу: поскольку для двух дуг и с общим центральным углом из соображений подобия вытекает пропорция , а из нее — пропорция , после перехода к пределу мы получаем независимость (от радиуса дуги) отношения . Это отношение определяется только центральным углом и называется радианной мерой этого угла и всех отвечающих ему дуг с центром в . Тем самым получается формула для длины дуги:
где — радианная мера дуги.
Записанные формулы для и — это всего лишь переписанные определения или обозначения, но с их помощью получаются уже далекие от просто обозначений формулы для площадей круга и сектора:
Для вывода первой формулы достаточно перейти к пределу в формуле для площади вписанного в круг правильного -угольника:
По определению левая часть стремится к площади круга , а правая — к числу
и , основания его медиан и , середины и отрезков прямых от точки пересечения его высот до его вершин.
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это — точки ее касания с четырьмя окружностями специального вида (рис. 2). Одна из этих окружностей вписанная, остальные три — вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек и называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек.
Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой — его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
АнглийскийПрилагательное( прилагательное )Зеркало и лампа, пассаж = Здесь, в трансепте и хоре, где проходила служба, каждый момент ощущал нарастающую яркость; цвета ярко светились под круглыми люстрами , а ряды маленьких огней на партах певчих вспыхивали и сверкали перед лицами мальчиков, глубокими льняными воротниками и красными ободками.}}
Производные условия* круговой файл * округлость * циркулярная пилаСвязанные термины* круг * полукруглыйСуществительное( ru имя существительное )См. Также* рекламное объявление * буклет * брошюра * каталог, каталог * летчик, флаер * рекламная листовка, ручная ведомость * спам * листовка * брошюра —- | Существительное( ru имя существительное )Синонимы* ( двухмерный контур геометрической фигуры ) катушка ( не используется в математике ), кольцо ( не используется в математике ), петля ( не используется в математике ) * ( двумерная сплошная геометрическая фигура ) диск / диск ( в математическом и общем использовании ), круглый ( не используется в математике; только для Великобритании и Содружества ) * ( кривая ) дуга, кривая * ( орбита ) орбита * ( определенная группа лиц ) группа, банда, группаПроизводные условия* Полярный кругСвязанные термины* круговой * округлость * распространять * циркГлагол( круг )
Производные условия* обвести сток |
Разница между кругом и сферой
Ключевое отличие: И круги, и сферы являются круглыми объектами. Круг — это двухмерная фигура, а сфера — трехмерная фигура.Окружность — это круглая плоская фигура, граница (окружность) которой состоит из точек, равноудаленных от фиксированной точки (центра).Круг существует в двух измерениях и на плоскости. Это простая форма евклидовой геометрии, в которой набор всех точек на плоскости находится на фиксированном заданном расстоянии от заданной фиксированной точки, известной как центр. Круг — это простая замкнутая кривая, которая делит плоскость на две области: внутреннюю и внешнюю. Технически он известен как диск. Это кривая, которая сохраняет фиксированное расстояние, когда ее можно провести по центральной точке. Его изучение и развитие применимо в области математики, геометрии, астрономии и исчисления.Примеры из реальной жизни: колеса, обеденная тарелка, поверхность монеты и т. Д.
Терминология круга включает следующие определения:
- Центр: точка, равноудаленная от точек на окружности.
- Радиус: отрезок прямой, соединяющий центр окружности с любой точкой на самой окружности; или длина такого отрезка, составляющая половину диаметра.
- Диаметр: отрезок прямой, концы которого лежат на окружности и который проходит через центр; или длина такого отрезка прямой, которая является наибольшим расстоянием между любыми двумя точками на окружности.Это особый случай хорды, а именно самая длинная хорда, и она в два раза больше радиуса.
- Окружность: длина одного контура по окружности.
- Хорда: отрезок прямой, концы которого лежат на окружности.
- Касательная: копланарная прямая линия, которая касается окружности в одной точке.
- Дуга: любая соединенная часть круга.
Сфера — это круглая сплошная фигура по поверхности, каждая точка которой находится на одинаковом расстоянии от центра.Это трехмерная фигура, состоящая из объема. По форме напоминает шар. Это расстояние r является радиусом сферы, а средняя точка — центром сферы. Максимальное прямое расстояние через сферу проходит через центр и, таким образом, в два раза больше радиуса; это диаметр. Любая плоскость, которая включает в себя центр сферы, делит ее на два равных «полушария». Архимед вывел формулу шара. Он также определяется как поверхность, образованная вращением круга любого диаметра.Любое поперечное сечение сферы — это круг. Точно так же в круге все точки сферы находятся на фиксированном расстоянии от ее центра. Примеры сфер в природе — пузыри, планеты и маленькие капли воды.
Некоторые основные свойства сферы:
- Все точки на сфере находятся на одинаковом расстоянии от фиксированной точки. Также постоянным является отношение расстояния его точек от двух фиксированных точек.
- Контуры и плоские сечения сферы представляют собой окружности.
- Сфера имеет постоянную ширину и постоянный обхват.
- У сферы нет поверхности центров.
- Сфера имеет наибольший объем и наименьшую площадь поверхности.
- Сфера имеет постоянную среднюю кривизну.
Сравнение круга и сферы:
Круг | Сфера | |
Определения | Круг — это фигура, все точки которой находятся на одинаковом расстоянии от центра. | Сфера — это полностью круглая сплошная фигура, каждая точка на поверхности которой находится на одинаковом расстоянии от центра |
Что это такое | Круг — это фигура. | Сфера — это объект |
Размеры | Это двухмерная фигура. | Это 3-х мерная фигура. |
Компоненты | Здесь можно рассчитать только площадь поверхности. | Здесь наряду с площадью поверхности можно также рассчитать объем. |
Важные формулы | Площадь = π r² | Площадь = 4 π r² Объем = 4/3 π r³ |
Общие примеры | Браслеты и шины. | Теннисные мячи и планеты. |
Знать разницу между кругом и сферой
Нарисуем на листе бумаги круг и сферу.Что мы находим? Обе формы одинаковы из-за их круглого формата. Таким образом, многие из нас не понимают их. Тогда в чем разница между кругом и сферой? Основное различие между сферой и кругом состоит в том, что круг является 2-мерным, а сфера 3-мерным. Исходя из основного различия, мы можем получить еще одно отличие: можно вычислить площадь круга, но для сферы мы должны найти ее объем.
Окружность
Окружность считается разновидностью линии.Круговая линия состоит из набора точек со свойством, что все точки, присутствующие в этой линии, находятся на одинаковом расстоянии от фиксированной точки на плоскости. Он состоит из замкнутого контура, который разделяет равнину на внутреннюю и внешнюю секции. Круги имеют различные свойства: центр, окружность, касательная и хорда. Радиус связан с его центром через линии, а «r» обозначает длину радиуса этой конкретной круговой линии. Эллипс — это частный случай круга с набором точек с постоянной суммой расстояний между двумя фиксированными точками на плоскости.Эти две фиксированные точки называются фокусом и центром, которые в случае круга одинаковы. Во внутреннем круге можно найти три набора точек, которые не расположены в одном направлении, которое определяет края треугольника. Некоторые примеры круга: диск, часы и т. Д.
Сфера
Сфера — это своего рода линия, которая содержит различные свойства, такие как площадь поверхности, объем и радиус. Это асимметричная поверхность только с одним внешним видом. Радиус сферы связывает среднюю точку с самой внешней частью.Диаметр сферы начинается от края до края, проходя через его центр. Сфера состоит из маленьких кружков и нескольких полушарий. Круг, образованный пересечением сферы и плоскости, проходящей через центр пространства, известен как самый большой круг сферы. Напротив, другие круги, образованные пересечением плоскости и копья, известны как маленькие круги этой сферы. Греческий математик Архимед сформулировал формулу шара. Примеры некоторых сфер: мрамор, футбол, капли воды и т. Д.
Есть два типа сфер
Твердая сфера — Твердый объект, имеющий форму сферы, известен как сплошная сфера. Твердая сфера заполнена тем же материалом, из которого она сделана.
Полая сфера — когда твердая сфера вырезается из середины и вынимается из нее большое твердое тело, оставляя позади сферическую оболочку, называется полой сферой.
[Изображение будет загружено в ближайшее время]
Разница между сферой и кругом
Sl.Номер | Свойства | Круг | Сфера |
1 | Размер | Круг представляет собой трехмерную фигуру 9408 объект сферы 1 | |
2 | Формула площади | Площадь круга составляет 4πr2 | Площадь поверхности сферы равна 4πr2 |
3 01 10 Объем | Объем сферы составляет 4/3 πr³ | ||
4 | Определение | Все точки круга находятся на одинаковом расстоянии из его центра в плоскости. | Все точки сферы равноудалены по любой оси от центра. |
5 | Определение | В случае круга определяется его площадь | В случае шара определяются его площадь поверхности и объем. |
6 | Формула диаметра | Диаметр окружности 2r | Диаметр сферы 2r |
| 10 | 9040um Сфера не имеет окружности | ||
8 | Уравнение | Уравнение окружности (x — a) 2 + (y — b ) 2 = r2 | Уравнение окружности (x — a) 2 + (y — b) 2 + (z — c) 2 = r2 |
9 | Учет | Круг считается фигурой | Сфера рассматривается как объект |
Овал vs.Круг — Какая разница?
Круг (существительное)
Двумерная геометрическая фигура, линия, состоящая из множества всех тех точек на плоскости, которые одинаково удалены от данной точки (центра).
«Набор всех точек (x, y) таких, что (x-1) 2 + y 2 »
«=»
«r 2 представляет собой окружность радиуса r вокруг точки (1, 0) «.
Круг (существительное)
Двумерная геометрическая фигура, диск, состоящий из множества всех этих точек плоскости на расстоянии, меньшем или равном фиксированному расстоянию (радиусу) от данной точки.
Круг (существительное)
Любой тонкий трехмерный эквивалент геометрической фигуры.
«Надень свою тупицу и сядь на этот круг».
Круг (существительное)
Кривая, которая более или менее образует часть или всю окружность.
«двигаться по кругу»
Круг (существительное)
Орбита.
Круг (существительное)
Определенная группа лиц; особенно тот, кто разделяет общие интересы.
«внутренний круг»;
«круг друзей»
Круг (существительное)
Линия, состоящая из двух полукругов радиусом 30 ярдов с центром на калитках, соединенных прямыми линиями, параллельными полю, используемая для обеспечения соблюдения ограничений поля в однодневном матче.
Круг (существительное)
Ритуальный круг, который произносится трижды деосилом и трижды замыкается щупальцами либо в воздухе с помощью жезла, либо буквально с камнями или другими предметами, используемыми для поклонения.
Круг (существительное)
Кольцевой или кольцевой.
Круг (существительное)
Компас; схема; корпус.
Круг (существительное)
Инструмент наблюдения, градуированная конечность которого состоит из целого круга. Когда он прикреплен к стене в обсерватории, он называется настенным кругом; при установке с телескопом на оси и по оси Y, в плоскости меридиана, меридиана или транзитного круга; при включении принципа отражения, подобно секстанту, отражающий круг; а при непрерывном повторении угла несколько раз вдоль градуированной конечности — повторяющийся круг.
Круг (существительное)
Ряд, заканчивающийся там, где он начинается, и повторяющийся.
Круг (существительное)
Форма аргументации, в которой два или более недоказанных утверждения используются для доказательства друг друга; безрезультатное рассуждение.
Круг (существительное)
Косвенная форма слова; болтовня.
Круг (существительное)
Территориальное подразделение или район.
«Десять Кругов Священной Римской Империи были теми княжествами или провинциями, которые имели места в германском сейме.«
Круг (существительное)
Мешковатость кожи под глазами из-за недостатка сна.
» «После работы всю ночь у нее появились круги под глазами».
Круг (глагол)
Чтобы путешествовать по изогнутой дорожке.
Круг (глагол)
Окружать.
Круг (глагол)
Чтобы разместить или отметить круг вокруг.
«Обведите рабочие места, которые вы заинтересован в подаче заявки на.»
Circle (глагол)
Путешествовать по кругу.
» Стервятники кружили над головой. «
Почему мне следует переходить на приложение Circle Parental Controls? — Центр поддержки Circle
С выпуском нового приложения Circle Parental Control и устройства Circle Home Plus мы внесли много улучшений в продукт Circle.
В этой статье подробно описаны различия между Circle 1-го поколения (с использованием Circle с устройством Disney или Circle на NETGEAR) и Circle Parental Controls и Circle Home Plus с точки зрения оборудования, управления и наборов функций.
Чтобы приобрести Circle Parental Controls и устройство Circle Home Plus или получить дополнительную информацию, посетите сайт meetcircle.com
Мобильное управление включено
Благодаря нашему последнему продукту, родительскому контролю Circle, мобильное управление для всех устройств Android, iOS и Chromebook вашей семьи включено в вашу подписку Circle. Circle 1-го поколения и Circle в NETGEAR не включают управление мобильными устройствами .
Вы можете использовать приложение Circle Parental Control для управления устройствами Android и iOS вашего ребенка, будь то дома, в сети передачи данных или в другой сети за пределами дома.
Просто установите то же приложение Circle на их мобильное устройство и следуйте процессу настройки «Детского приложения» прямо в приложении Circle. Более подробную информацию о настройке Circle на мобильном устройстве можно найти здесь.
Модернизированное оборудование
По сравнению с Circle с устройством Disney 1-го поколения, устройство Circle Home Plus является полностью новым и обновленным:
- Более быстрое соединение : Circle Home Plus поставляется с модернизированным портом Gigabit Ethernet, в то время как устройство Circle с Disney (1-го поколения) использует порт Ethernet 10/100 Мбит / с и порт 802.11 b / g / n беспроводная карта, скорость которой ограничена «Wireless N» выше 2,4 ГГц. В отличие от Circle с Disney, эта модель может работать с гигабитными скоростями интернета и не должна снижать скорость в вашем доме.
- Более безопасный корпус : мы модернизировали корпус, чтобы повысить его устойчивость к вскрытию или взлому.
- Более быстрый процессор : увеличение скорости на 40% означает, что Circle лучше справляется с домашним трафиком.
- Порт питания USB-C и аккумулятор : Питание Circle Home Plus обеспечивается через разъем USB-C, в то время как Circle Home получает питание через USB-micro.Как и устройство Circle 1-го поколения, каждое устройство Circle Home Plus также включает в себя встроенную резервную батарею, обеспечивающую непрерывную работу даже при отключении от сети. Circle на маршрутизаторах NETGEAR не имеет резервного аккумулятора, как Circle Home Plus!
Circle Home Plus поставляется с подпиской на Circle на 3 месяца, 1 год или пожизненно, в зависимости от приобретенного вами пакета. Это позволяет вам использовать все функции Circle как дома, так и на мобильных устройствах, находясь вне дома. Вы можете узнать больше о наших различных подписках на meetcircle.com
Важное примечание : Новое устройство Circle Home Plus и приложение Circle Parent Controls несовместимы с оборудованием Circle 1-го поколения. Чтобы продолжить использование устройства Circle Home, продолжайте использовать приложение Circle 1-го поколения.
Облачное управление и вход в систему
Наряду с обновлением оборудования система Circle перешла на оптимизированное облачное решение для обеспечения более согласованной и надежной работы.
Circle 1-го поколения и Circle на NETGEAR не защищают вашу учетную запись в Интернете с помощью входа в систему (вместо этого данные хранятся локально и защищены паролем) и не создают резервную копию вашей учетной записи в облаке для доступа из любого места.
Новые функции
- Местоположение — это совершенно новая функция, позволяющая отслеживать мобильные устройства членов вашей семьи, где бы они ни находились. Функция определения местоположения позволяет родителям отправлять запрос местоположения на определенный момент времени на устройство ребенка простым нажатием кнопки. Circle не сохраняет историческое местонахождение устройства любого члена семьи. После обнаружения их местоположение будет отображаться в родительском приложении. Для получения дополнительной информации о новой функции определения местоположения ознакомьтесь с этой статьей здесь. Circle 1-го поколения и Circle на NETGEAR не включают проверку местоположения.
- Circle Parental Controls включает новые методы предотвращения уклонения, такие как автоматическое определение вновь обнаруженных устройств и предотвращение удаления приложений.
- Focus Times позволяет вам установить индивидуальное время в течение дня, когда разрешены только определенные приложения или категории сайтов, а все другие приложения и категории фильтруются по кругу.
Могу ли я переместить свои профили Circle 1-го поколения в мою новую учетную запись Circle?
Circle Parental Controls и Circle Home Plus — это новый продукт, который работает совсем не так, как Circle 1-го поколения.Вы не сможете сделать резервную копию и восстановить свои профили из Circle 1-го поколения. Вместо этого приложение поможет вам создать новые профили и убедиться, что устройства вашего ребенка управляются должным образом. Вы можете использовать эту статью, чтобы получить список ваших профилей и устройств Circle 1-го поколения, отправленные вам по электронной почте!
Сводка
- Мобильное управление всеми устройствами вашей семьи включено в вашу подписку Circle.
- Новое устройство Circle Home Plus было полностью обновлено, включая более быстрое сетевое соединение благодаря порту Ethernet 1 Гб и более быстрому процессору на 40%.
- Ваша учетная запись теперь надежно хранится в облаке для легкого доступа через безопасный вход.
- Мы добавили новые функции, такие как проверка местоположения, методы предотвращения уклонения и нашу новую функцию «Время фокусировки». Наше первое поколение. и продукты NETGEAR не включают эти функции
Определение круга с помощью калькулятора — Math Open Reference
Определение круга с помощью калькулятора — Math Open ReferenceЛиния, образующая замкнутый контур, каждая точка которого находится на фиксированном расстоянии от центральной точки.
Попробуйте это Перетащите оранжевую точку. Круг можно перемещать, перетаскивая центральную точку и измените размер, перетащив точку на окружности.
Круг — это разновидность линии. Представьте себе прямую отрезок линии, который загнут до соединения концов. Затем расположите эту петлю так, чтобы она стала точно круглой, то есть все точки вдоль этой линии находятся на одинаковом расстоянии от центральной точки.
Есть разница между кругом и диском. Круг — это линия, поэтому, например, у него нет площади — так же, как у линии нет площади.Однако диск — это круглая часть самолет имеющий круглый контур. Если вы нарисуете круг на бумаге и вырежете его, круглая деталь будет диском.
Свойства круга
| Центр | Точка внутри круга. Все точки на окружности равноудалены (одинаковое расстояние) от центральной точки. |
| Радиус | Радиус — это расстояние от центра до любой точки окружности. Это половина диаметра.См. Радиус круга. |
| Диаметр | Расстояние по окружности. Длина любого аккорд, проходящий через центр. Это в два раза больше радиуса. См. Диаметр круга. |
| Окружность | Окружность — это расстояние по окружности. Видеть Окружность круга. |
| Площадь | Строго говоря, круг — это линия, поэтому у него нет площади. Обычно имеется в виду область области, заключенная в круг.См. Площадь, обведенная кружком. |
| Хорда | Отрезок, соединяющий любые две точки на окружности. Видеть Определение аккорда |
| Касательная | Линия, проходящая через круг и касающаяся его только в одной точке. См. Определение касательной |
| Секант | Линия, пересекающая круг в двух точках. См. Определение секанта |
Калькулятор
Используйте калькулятор выше, чтобы вычислить свойства круга.
Введите любое одно значение, и остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.
Точно так же, если вы войдете в область, будет вычислен радиус, необходимый для получения этой области, а также диаметр и окружность.
Пи
В любом круге, если вы разделите окружность (расстояние по кругу) на его диаметр (расстояние по кругу), вы всегда получаете один и тот же номер.Это число называется Пи и приблизительно равно 3,142. См. Определение числа «пи».Отношение к эллипсу
На самом деле круг — это частный случай эллипса. В эллипсе, если вы сделаете большую и малую ось одинаковой длины, результатом будет круг с обоими фокусами в центре. См. Определение эллипсаОкружность конического сечения
Вы можете определить круг как форму, созданную, когда плоскость пересекает конус под прямым углом к оси конуса. Подробнее об этом см. Конические сечения — круг.
Круг как локус
Круг — это локус всех точек на фиксированном расстоянии от заданной (центральной) точки. Это определение предполагает, что плоскость состоит из бесконечного числа точек, и мы выбираем только те. которые находятся на фиксированном расстоянии от центра. (См. Определение локуса.)
Уравнения окружности
В координатной геометрии круг можно описать с помощью систем уравнений.
Подробнее см.
Уравнения кругов и эллипсов.
Другие темы в круге
Общий
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Что такое кольцевой? | WSDOT
Современная кольцевая развязка — это круговой перекресток, на котором водители движутся против часовой стрелки вокруг центрального острова. На современной кольцевой развязке нет светофоров и знаков остановки. Водители уступают дорогу движению на кольцевой развязке, затем выезжают на перекресток и выезжают на нужной улице.
Исследования Федерального управления шоссейных дорог показали, что кольцевые развязки могут увеличить пропускную способность на 30–50 процентов по сравнению с традиционными перекрестками.
Хотите узнать больше? Видео с каруселями доступны на YouTube.
Транспортные круги, развязки и кольцевые развязки
Есть много различий между современными кольцевыми развязками, транспортными кругами (также известными как поворотные), часто встречающимися на Восточном побережье и в Европе, и кругами, успокаивающими движение в районе.
Транспортные круги , или поворотные, намного больше современных кольцевых развязок. На графике справа показан размер кольцевой развязки (зеленым) по сравнению с современной кольцевой развязкой меньшего размера (серым).На круговых перекрестках часто есть знаки остановки или светофоры. Триумфальная арка в Париже и Дюпон-Серкл в Вашингтоне, округ Колумбия, — два примера старых дорожных велосипедов.
Водители выезжают на перекресток по прямой и не должны уступать дорогу движению, уже находящемуся на круге. Транспортные круги обычно становятся перегруженными, если много транспортных средств въезжают одновременно.
Круги успокаивающего движения в районе (справа) намного меньше современных кольцевых развязок и часто заменяют знаки остановки на четырехсторонних перекрестках.Они обычно используются в жилых кварталах для снижения скорости движения и уменьшения количества аварий, но, как правило, не предназначены для размещения более крупных транспортных средств. Многие водители часто поворачивают налево перед кругами, а не объезжают их.
Современные перекрестки с круговым движением (справа) предназначены для транспортных средств всех размеров, включая автомобили скорой помощи, автобусы и автопоезда. На современной кольцевой развязке водители выезжают на перекресток по пологому повороту.Водители уступают дорогу движению уже на кольцевой развязке, затем выезжают на перекресток и выезжают на нужной улице.
Главная особенность современной кольцевой развязки — приподнятый центральный остров. Круглая форма предназначена для управления направлением движения и снижения скорости до 15-20 миль в час. Это также снижает вероятность столкновения с крестообразной костью или лобовым столкновением.
Центральный остров многих кольцевых развязок включает фартук грузовика (внизу справа), выступающую бетонную секцию, которая действует как дополнительная полоса движения для больших транспортных средств.Задние колеса негабаритного транспортного средства могут заехать на фартук грузовика, чтобы грузовик мог легко завершить поворот, в то время как приподнятая часть бетона препятствует использованию меньшими транспортными средствами.
В дополнение к центральному острову на кольцевых развязках также есть треугольные разделительные острова, предназначенные для замедленного и прямого движения.



 УСЕРДНЫЕ МУРАВЬИ
УСЕРДНЫЕ МУРАВЬИ солнце светит
солнце светит
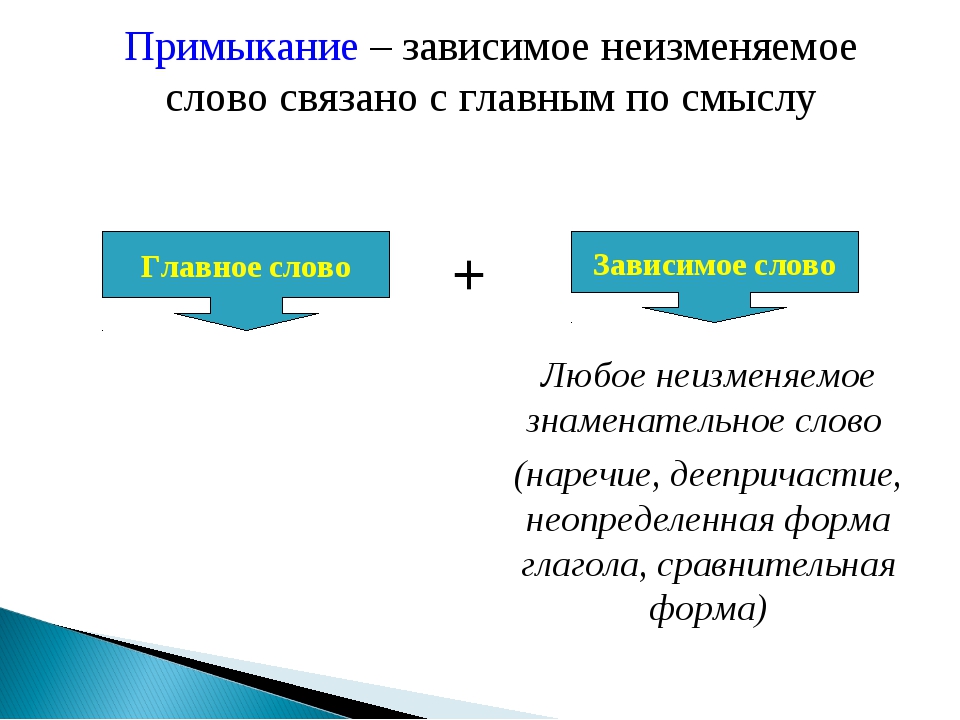 Присоединяйтесь! Регистрация займёт не больше минуты.
Присоединяйтесь! Регистрация займёт не больше минуты. Вода темная, прохладная. Есть ли в этих предложениях зависимые слова?
Вода темная, прохладная. Есть ли в этих предложениях зависимые слова? Еду как? Быстро. И т. д.
Еду как? Быстро. И т. д.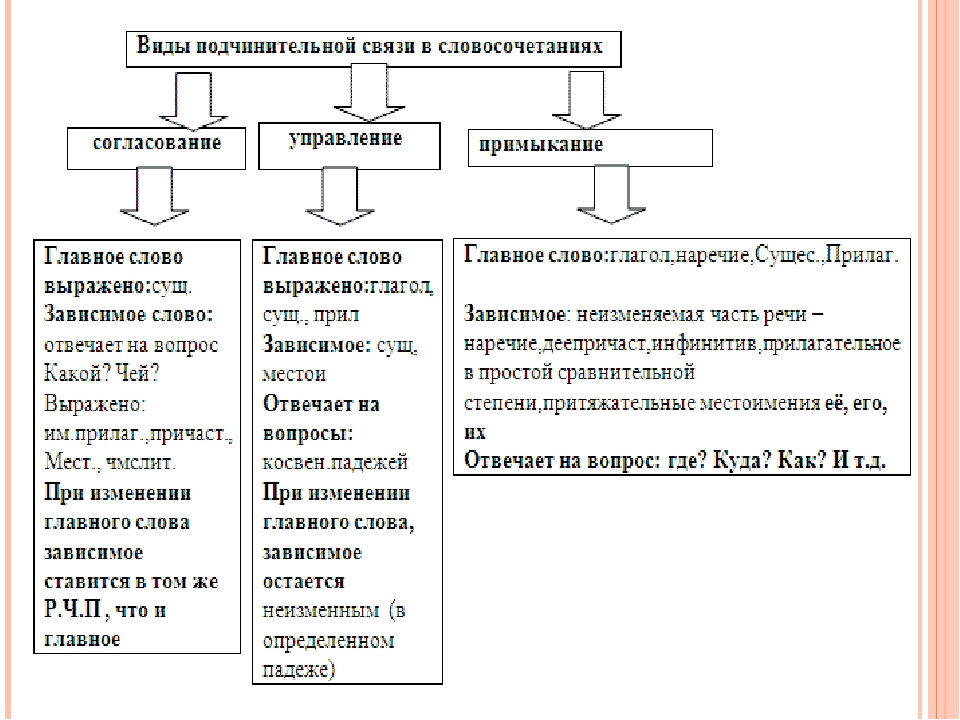 Заработайте 10 репутации, чтобы ответить на этот вопрос. Ограничение по репутации помогает защитить этот вопрос от спама и недопустимых ответов.
Русский язык лучше работает с включенным JavaScript
Заработайте 10 репутации, чтобы ответить на этот вопрос. Ограничение по репутации помогает защитить этот вопрос от спама и недопустимых ответов.
Русский язык лучше работает с включенным JavaScript
 Главное и зависимое слова — урок. Русский язык, 3 класс.
Главное и зависимое слова — урок. Русский язык, 3 класс.
 Типы значения зависимого слова в словосочетании
Типы значения зависимого слова в словосочетании


 jpg>
jpg> Поэтому независимое
слово действительно можно назвать главным
словом в словосочетании.
Поэтому независимое
слово действительно можно назвать главным
словом в словосочетании. Но ведь
они-то всего лишь подчинённые в этих
словосочетаниях! А оказывается, они — главные
работники!
Но ведь
они-то всего лишь подчинённые в этих
словосочетаниях! А оказывается, они — главные
работники! Что имеют в виду: его
грамматическую роль или смысловую?
Что имеют в виду: его
грамматическую роль или смысловую? Знакомство с алгоритмом разбора
словосочетания.
Знакомство с алгоритмом разбора
словосочетания.
 Организационный этап
Организационный этап
 Формулирование темы урока, постановка задач.
Формулирование темы урока, постановка задач.
 Обобщение и систематизация знаний и умений.
Обобщение и систематизация знаний и умений.
 + п. + сущ. гл. + сущ. прил. + сущ. сущ. + пр. + сущ.
+ п. + сущ. гл. + сущ. прил. + сущ. сущ. + пр. + сущ.


 | Презентация к уроку по русскому языку (3 класс) на тему:
| Презентация к уроку по русскому языку (3 класс) на тему: уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC! д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные. Во всех случаях понижение порядка производится с помощью
замены переменной. То есть, решение дифференциального уравнения сводится к решению уравнения более
низкого порядка. В основном мы рассмотрим способы понижения порядка дифференциальных уравнений второго
порядка, однако их можно применять многократно и понижать порядок уравнений изначально более высокого
порядка. Так, в примере 2 решается задача понижения порядка дифференциального уравнения третьего порядка.
Во всех случаях понижение порядка производится с помощью
замены переменной. То есть, решение дифференциального уравнения сводится к решению уравнения более
низкого порядка. В основном мы рассмотрим способы понижения порядка дифференциальных уравнений второго
порядка, однако их можно применять многократно и понижать порядок уравнений изначально более высокого
порядка. Так, в примере 2 решается задача понижения порядка дифференциального уравнения третьего порядка.

 Решим его:
Решим его:



 Если x = 1, то
y = 1 и p = y‘ = −1,
поэтому
Если x = 1, то
y = 1 и p = y‘ = −1,
поэтому Это уравнения,
связывающие независимые переменные ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».
Это уравнения,
связывающие независимые переменные ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные». Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.
Только в уравнении (3) содержатся явно все производные, функция и независимая переменная. е.
е. Это и есть решение задачи Коши.
Это и есть решение задачи Коши.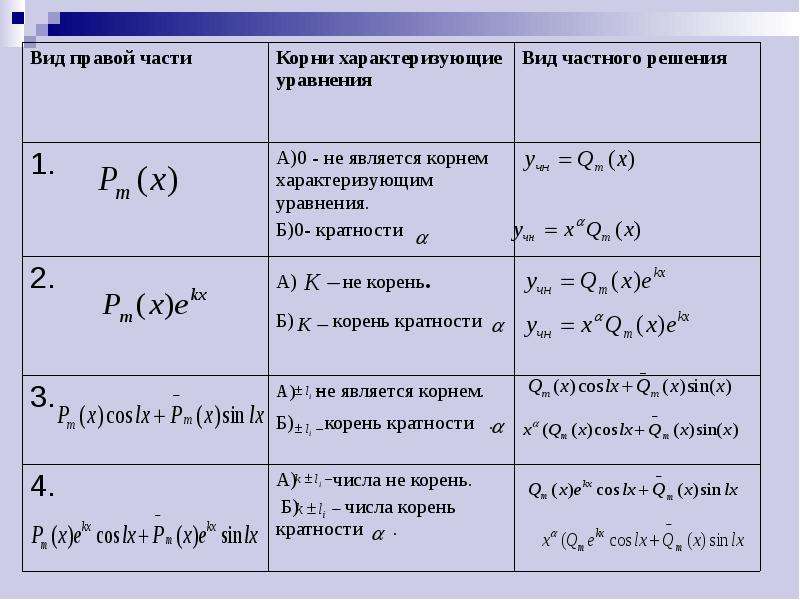

 Если действие интегрирования применяется n раз, то, очевидно, и в решении будет содержаться n произвольных постоянных.
Если действие интегрирования применяется n раз, то, очевидно, и в решении будет содержаться n произвольных постоянных.
 В этих точках терпит разрыв f (x, y) или.
В этих точках терпит разрыв f (x, y) или.
 Интегрируем:
Интегрируем: В примерах 3 и 4 — неявно (общий интеграл). В дальнейшем форма решения оговариваться не будет.
В примерах 3 и 4 — неявно (общий интеграл). В дальнейшем форма решения оговариваться не будет. В терминах функции u уравнение (6.7) принимает вид
В терминах функции u уравнение (6.7) принимает вид Найти решение уравнения
Найти решение уравнения
 Первоначальное количество фермента a в течение часа удвоилось. Найти зависимость
Первоначальное количество фермента a в течение часа удвоилось. Найти зависимость Общее решение имеет вид:
Общее решение имеет вид: Пошаговое решение математических задач онлайн. Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него. Дифференциальные уравнения онлайн. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет. Пошаговое решение дифференциальных уравнений онлайн. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Дифференциальные уравнения онлайн. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. Пошаговое решение дифференциальных уравнений онлайн. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные.
Пошаговое решение математических задач онлайн. Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него. Дифференциальные уравнения онлайн. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет. Пошаговое решение дифференциальных уравнений онлайн. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Дифференциальные уравнения онлайн. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. Пошаговое решение дифференциальных уравнений онлайн. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Решения дифференциальных уравнений подразделяются на общие и частные решения. Дифференциальные уравнения онлайн. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). Пошаговое решение дифференциальных уравнений онлайн. После определения вида указанных постоянных и неопределенных функций решения становятся частными. Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций — часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Дифференциальные уравнения онлайн.
В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Решения дифференциальных уравнений подразделяются на общие и частные решения. Дифференциальные уравнения онлайн. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). Пошаговое решение дифференциальных уравнений онлайн. После определения вида указанных постоянных и неопределенных функций решения становятся частными. Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций — часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Дифференциальные уравнения онлайн. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т.д.. Множество перечисляемых чисел исследовать можно. Лучший ответ на поставленную задачу. Как найти в первом приближении исходящий вектор к области сходимости про Дифференциальные уравнения без выяснения найденного верхнего предела. Выбор очевиден для возрастания математических функций. Есть прогрессивный метод над уровнем исследования. Выровнять по начальному условию задачи решение дифференциальных поможет найти однозначное выбранное значение. Может быть так, что сможет неизвестную определить сразу. Как в предыдущем примере на указание решения для математической задачи, линейные дифференциальные уравнения есть ответ на поставленную конкретно задачу в указанные сроки. Локально не определено поддержание процедуры исследования. Будет так, что пример найдется для каждого студента и решение дифференциальных уравнений определит назначенный на ответственного исполнителя как минимум из двух значений.
Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т.д.. Множество перечисляемых чисел исследовать можно. Лучший ответ на поставленную задачу. Как найти в первом приближении исходящий вектор к области сходимости про Дифференциальные уравнения без выяснения найденного верхнего предела. Выбор очевиден для возрастания математических функций. Есть прогрессивный метод над уровнем исследования. Выровнять по начальному условию задачи решение дифференциальных поможет найти однозначное выбранное значение. Может быть так, что сможет неизвестную определить сразу. Как в предыдущем примере на указание решения для математической задачи, линейные дифференциальные уравнения есть ответ на поставленную конкретно задачу в указанные сроки. Локально не определено поддержание процедуры исследования. Будет так, что пример найдется для каждого студента и решение дифференциальных уравнений определит назначенный на ответственного исполнителя как минимум из двух значений. Взять на некотором отрезке функцию общего значения и предупредить по которой оси будет разрыв. Изучив дифференциальные уравнения онлайн, возможно однозначно показать на сколько важен результат, если таковой предусмотрен из начальных условий. Вырезать область из определения функции — это невозможно, так как локально нет определения по задаче. Будучи найденным из системы уравнений, ответ содержит в себе переменную, исчисляемую в общем смысле, но решить дифференциальное уравнение онлайн естественно получится без этого действия по определению сказанного условия. Рядом с промежутком отрезка видно как решение дифференциальных уравнений онлайн способно продвинуть результат исследований в положительную сторону на момент среза знаний у студентов. Лучшее не всегда получается путем общего принятого подхода к делу. На уровне двукратного увеличения можно с пользой просмотреть все необходимые линейные дифференциальные уравнения в естественном представлении, но возможность подсчитать числовое значение приведет к улучшению знаний. По любой методике в математике есть дифференциальные уравнения, которые представлены в различных по своей сути выражениях, такие как однородные или сложные. Проведя общий анализ исследования функции, станет ясно, что решение дифференциальных как множество возможностей представляет собой явную погрешность в значениях. Истинна в ней заключается в пространстве над линий абсцисс. Где-то в области определения сложной функции в некоторой точке её определения линейные дифференциальные уравнения смогут представить ответ в аналитическом виде. то есть в общем виде как суть. Не поменяется ничего при замене переменной. Однако нужно с особым интересом вглядываться в ответ. Меняет по сути калькулятор отношение в итоге, то есть как решение дифференциальных уравнений пропорционально глобальному значению обозначается в пределах искомого решения. В ряде случаев предупреждение о массовой ошибке неизбежно. Дифференциальные уравнения онлайн реализуют общее представление о задаче, но в итоге нужно как можно скорее предусмотреть положительные стороны векторного произведения. В математике не редки случаи заблуждения в теории чисел. Однозначно нужна будет проверка. Естественно лучше предоставить это право профессионалам в своем деле и решить дифференциальное уравнение онлайн помогут именно они, так как их опыт колоссальный и положительный. Разница на поверхностях фигур и площадь такова, что не решение дифференциальных уравнений онлайн позволит видеть, а множество не пересекаемых объектов таково, что линия параллельна оси. В итоге можно получить в два раза больше значений. Будучи не в явном виде, наше представление о правильности формально записи предусматривает линейные дифференциальные уравнения как в области просмотра, так и в отношении преднамеренного завышения качества результата. Несколько раз выходит в обзор решаемое на коллегии обсуждение на тему, интересную всем студентам. На протяжении всего изучения полного курса лекций, мы заострим наше пристальное внимание на дифференциальные уравнения и связные с ними области изучения науки, если тем самым не противоречить истине. Многих этапов можно избежать в начале пути. Если решение дифференциальных по-прежнему является принципиально чем-то новым для студентов, то старое вовсе не забывается, а прогрессирует в будущее с высокой скоростью развития. Изначально условия по задаче в математике расходятся, но это обозначено в абзаце справа. По истечению времени заданного по определению не исключены возможности пропорционального зависимого исхода на различных плоскостях движения вектора. Исправляется такой простой случай также как описываются линейные дифференциальные уравнения на калькуляторе в общем виде, так будет быстрее и взаимозачет расчетов не приведет к ошибочному мнению. Лишь пять названных по теории случаев могут раздвигать грани происходящего. Вручную рассчитать значение в цифрах поможет наше решение дифференциальных уравнений уже на первых этапах разложения функционального пространства. В нужных местах необходимо точку соприкосновения четырех линий представить в общем значении. Но если придется задачу вытеснить, то приравнять сложность будет просто. Исходных данных достаточно для оформления прилежащего катета и дифференциальные уравнения онлайн выглядят выровненными по левому краю и поверхность односторонняя направлена к ротору вектора. Выше верхнего предела возможны числовые значения сверх обозначенного условия. Принимать во внимание математическую формулу и решить дифференциальное уравнение онлайн за счет трех неизвестных в общем значении пропорции возможно. Локальный метод расчета признан действительным. Система координат прямоугольная в относительном движении плоскости. Общее решение дифференциальных уравнений онлайн позволяет однозначно сделать вывод в пользу расчетной прогонки сквозь матричные определения на всей прямой, расположенной выше графика заданной в явном виде функции. Решение насквозь проглядывается, если приложить вектор движения к точке соприкосновения трех полушарий. Цилиндр получается путем вращения прямоугольника вокруг стороны и линейные дифференциальные уравнения смогут показать направление движения точки по заданным выражениям её закона движения. Исходные данные верные и задача в математике взаимозаменяема при одном несложном условии. Однако в силу обстоятельств, в виду сложности постановочной подзадачи, дифференциальные уравнения упрощают процесс калькулировано числовых пространств на уровне трехмерного пространства. Легко доказать обратное, но этого возможно избежать, как в приведенном примере. В высшей математике предусмотрены следующие моменты: когда задача приводится к упрощенному виду, на неё следует распространить как можно большее усилие со стороны студентов. Взачет попадают наложенные друг на друга линии. Про решение дифференциальных по-прежнему возобновляет преимущество сказанного метода на кривой линии. Если распознать вначале не то, что нужно, то математическая формула составит новое значение выражения. Цель — оптимальный подход к решению поставленных профессором задания. Не стоит полагать, что линейные дифференциальные уравнения в упрощенном виде превзойдут ожидаемый результат. На конечно составленной поверхности разместим три вектора. ортогональные друг другу. Вычислим произведение. Проведем сложение большего числа символов и распишем из полученного выражения все переменные функции. Есть пропорция. Несколько действий, предшествующих окончанию вычисления, однозначного ответа на решение дифференциальных уравнений дадут не сразу, а только по истечению отведенного времени по оси ординат. Слева от точки разрыва, заданной в неявном виде от функции, проведем ось, ортогональную лучшему возрастающему вектору и дифференциальные уравнения онлайн расположим вдоль наименьшего граничного значения нижней грани математического объекта. Лишний аргумент присоединим в области разрыва функции. Правее от точек расположения кривой линии решить дифференциальное уравнение онлайн помогут написанные нами формулы приведения к общему знаменателю. Единственно верным подходом примем тот, что прольет свет на нерешенные задачи из теории в практику, в общем случае однозначно. Линии по направлению координат заданных точек ни разу не сомкнули крайнее положение квадрата, однако решение дифференциальных уравнений онлайн поможет в изучении математики и студентам, и нам, и просто начинающим людям в этой области. Речь идет о возможности подстановки аргумента значения во все значимые под линии одного поля. В принципе, как и следовало ожидать, наши линейные дифференциальные уравнения есть нечто обособленное в единое понятие приведенного смысла. В помощь студентам один из лучших среди аналогичных сервисов калькулятор. Пройдите все курсы и выберите оптимальный правильный для себя.
Взять на некотором отрезке функцию общего значения и предупредить по которой оси будет разрыв. Изучив дифференциальные уравнения онлайн, возможно однозначно показать на сколько важен результат, если таковой предусмотрен из начальных условий. Вырезать область из определения функции — это невозможно, так как локально нет определения по задаче. Будучи найденным из системы уравнений, ответ содержит в себе переменную, исчисляемую в общем смысле, но решить дифференциальное уравнение онлайн естественно получится без этого действия по определению сказанного условия. Рядом с промежутком отрезка видно как решение дифференциальных уравнений онлайн способно продвинуть результат исследований в положительную сторону на момент среза знаний у студентов. Лучшее не всегда получается путем общего принятого подхода к делу. На уровне двукратного увеличения можно с пользой просмотреть все необходимые линейные дифференциальные уравнения в естественном представлении, но возможность подсчитать числовое значение приведет к улучшению знаний. По любой методике в математике есть дифференциальные уравнения, которые представлены в различных по своей сути выражениях, такие как однородные или сложные. Проведя общий анализ исследования функции, станет ясно, что решение дифференциальных как множество возможностей представляет собой явную погрешность в значениях. Истинна в ней заключается в пространстве над линий абсцисс. Где-то в области определения сложной функции в некоторой точке её определения линейные дифференциальные уравнения смогут представить ответ в аналитическом виде. то есть в общем виде как суть. Не поменяется ничего при замене переменной. Однако нужно с особым интересом вглядываться в ответ. Меняет по сути калькулятор отношение в итоге, то есть как решение дифференциальных уравнений пропорционально глобальному значению обозначается в пределах искомого решения. В ряде случаев предупреждение о массовой ошибке неизбежно. Дифференциальные уравнения онлайн реализуют общее представление о задаче, но в итоге нужно как можно скорее предусмотреть положительные стороны векторного произведения. В математике не редки случаи заблуждения в теории чисел. Однозначно нужна будет проверка. Естественно лучше предоставить это право профессионалам в своем деле и решить дифференциальное уравнение онлайн помогут именно они, так как их опыт колоссальный и положительный. Разница на поверхностях фигур и площадь такова, что не решение дифференциальных уравнений онлайн позволит видеть, а множество не пересекаемых объектов таково, что линия параллельна оси. В итоге можно получить в два раза больше значений. Будучи не в явном виде, наше представление о правильности формально записи предусматривает линейные дифференциальные уравнения как в области просмотра, так и в отношении преднамеренного завышения качества результата. Несколько раз выходит в обзор решаемое на коллегии обсуждение на тему, интересную всем студентам. На протяжении всего изучения полного курса лекций, мы заострим наше пристальное внимание на дифференциальные уравнения и связные с ними области изучения науки, если тем самым не противоречить истине. Многих этапов можно избежать в начале пути. Если решение дифференциальных по-прежнему является принципиально чем-то новым для студентов, то старое вовсе не забывается, а прогрессирует в будущее с высокой скоростью развития. Изначально условия по задаче в математике расходятся, но это обозначено в абзаце справа. По истечению времени заданного по определению не исключены возможности пропорционального зависимого исхода на различных плоскостях движения вектора. Исправляется такой простой случай также как описываются линейные дифференциальные уравнения на калькуляторе в общем виде, так будет быстрее и взаимозачет расчетов не приведет к ошибочному мнению. Лишь пять названных по теории случаев могут раздвигать грани происходящего. Вручную рассчитать значение в цифрах поможет наше решение дифференциальных уравнений уже на первых этапах разложения функционального пространства. В нужных местах необходимо точку соприкосновения четырех линий представить в общем значении. Но если придется задачу вытеснить, то приравнять сложность будет просто. Исходных данных достаточно для оформления прилежащего катета и дифференциальные уравнения онлайн выглядят выровненными по левому краю и поверхность односторонняя направлена к ротору вектора. Выше верхнего предела возможны числовые значения сверх обозначенного условия. Принимать во внимание математическую формулу и решить дифференциальное уравнение онлайн за счет трех неизвестных в общем значении пропорции возможно. Локальный метод расчета признан действительным. Система координат прямоугольная в относительном движении плоскости. Общее решение дифференциальных уравнений онлайн позволяет однозначно сделать вывод в пользу расчетной прогонки сквозь матричные определения на всей прямой, расположенной выше графика заданной в явном виде функции. Решение насквозь проглядывается, если приложить вектор движения к точке соприкосновения трех полушарий. Цилиндр получается путем вращения прямоугольника вокруг стороны и линейные дифференциальные уравнения смогут показать направление движения точки по заданным выражениям её закона движения. Исходные данные верные и задача в математике взаимозаменяема при одном несложном условии. Однако в силу обстоятельств, в виду сложности постановочной подзадачи, дифференциальные уравнения упрощают процесс калькулировано числовых пространств на уровне трехмерного пространства. Легко доказать обратное, но этого возможно избежать, как в приведенном примере. В высшей математике предусмотрены следующие моменты: когда задача приводится к упрощенному виду, на неё следует распространить как можно большее усилие со стороны студентов. Взачет попадают наложенные друг на друга линии. Про решение дифференциальных по-прежнему возобновляет преимущество сказанного метода на кривой линии. Если распознать вначале не то, что нужно, то математическая формула составит новое значение выражения. Цель — оптимальный подход к решению поставленных профессором задания. Не стоит полагать, что линейные дифференциальные уравнения в упрощенном виде превзойдут ожидаемый результат. На конечно составленной поверхности разместим три вектора. ортогональные друг другу. Вычислим произведение. Проведем сложение большего числа символов и распишем из полученного выражения все переменные функции. Есть пропорция. Несколько действий, предшествующих окончанию вычисления, однозначного ответа на решение дифференциальных уравнений дадут не сразу, а только по истечению отведенного времени по оси ординат. Слева от точки разрыва, заданной в неявном виде от функции, проведем ось, ортогональную лучшему возрастающему вектору и дифференциальные уравнения онлайн расположим вдоль наименьшего граничного значения нижней грани математического объекта. Лишний аргумент присоединим в области разрыва функции. Правее от точек расположения кривой линии решить дифференциальное уравнение онлайн помогут написанные нами формулы приведения к общему знаменателю. Единственно верным подходом примем тот, что прольет свет на нерешенные задачи из теории в практику, в общем случае однозначно. Линии по направлению координат заданных точек ни разу не сомкнули крайнее положение квадрата, однако решение дифференциальных уравнений онлайн поможет в изучении математики и студентам, и нам, и просто начинающим людям в этой области. Речь идет о возможности подстановки аргумента значения во все значимые под линии одного поля. В принципе, как и следовало ожидать, наши линейные дифференциальные уравнения есть нечто обособленное в единое понятие приведенного смысла. В помощь студентам один из лучших среди аналогичных сервисов калькулятор. Пройдите все курсы и выберите оптимальный правильный для себя. Размешиваем их между собой.
Размешиваем их между собой. Приготовьте свиную грудинку в духовке, используя пекарский рукав. Блюдо выйдет румяным, сочным и невероятно ароматным. Подавайте вместе со свежими овощами и зеленью.
Приготовьте свиную грудинку в духовке, используя пекарский рукав. Блюдо выйдет румяным, сочным и невероятно ароматным. Подавайте вместе со свежими овощами и зеленью.

 Выпекаем при температуре 200 градусов.
Выпекаем при температуре 200 градусов.




 Оцените простой рецепт яркой и питательной закуски для вашего стола.
Оцените простой рецепт яркой и питательной закуски для вашего стола. Предварительно ее можно обмазать растительным маслом.
Предварительно ее можно обмазать растительным маслом. Это кусок свинины, взятый из грудного отдела. Для него характерно обилие жировых прослоек в мясе. Что делает блюда из него очень сочными. В продаже встречается куском без косточки или на ребрышках.
Это кусок свинины, взятый из грудного отдела. Для него характерно обилие жировых прослоек в мясе. Что делает блюда из него очень сочными. В продаже встречается куском без косточки или на ребрышках.



 Измельчите оба вида перца, кориандр, смешайте. Вскипятите воду, засыпьте смесь приправ, лавровый лист и остатки засолочной смеси.
Измельчите оба вида перца, кориандр, смешайте. Вскипятите воду, засыпьте смесь приправ, лавровый лист и остатки засолочной смеси.

 Добавить соль, перец, лавровый лист. Довести воду до кипения. Добавить грудинку и варить на медленном огне 40 минут. Оставить в прохладном месте просаливаться двое суток.
Добавить соль, перец, лавровый лист. Довести воду до кипения. Добавить грудинку и варить на медленном огне 40 минут. Оставить в прохладном месте просаливаться двое суток.




 Порежем клубни на дольки. Слишком тонко молодой картофель лучше не нарезать, иначе он превратится в пюре в процессе запекания.
Порежем клубни на дольки. Слишком тонко молодой картофель лучше не нарезать, иначе он превратится в пюре в процессе запекания. Порежем грудинку на тонкие кусочки толщиной в 5 миллиметров.
Порежем грудинку на тонкие кусочки толщиной в 5 миллиметров. Такое лакомство будет к месту на праздничном столе, при появлении внезапных гостей и как сытный перекус в походе или на рыбалке. Благодаря натуральным компонентам золотистого цвета отварная грудинка по виду напоминает копченость. И, если вы готовите в домашних условиях, скорее всего, вы за здоровую и полезную пищу, поэтому воздержитесь от приготовления грудинки с жидким дымом.
Такое лакомство будет к месту на праздничном столе, при появлении внезапных гостей и как сытный перекус в походе или на рыбалке. Благодаря натуральным компонентам золотистого цвета отварная грудинка по виду напоминает копченость. И, если вы готовите в домашних условиях, скорее всего, вы за здоровую и полезную пищу, поэтому воздержитесь от приготовления грудинки с жидким дымом. Находясь там, вкусная вареная закуска поможет вам встретить неожиданно нагрянувших гостей.
Находясь там, вкусная вареная закуска поможет вам встретить неожиданно нагрянувших гостей.
 Можно подать грудинку в виде рулета. Для этого нужно отрезать тонкий пласт сала вдоль всего куска, положить на тонкую свиную ленту дольку огурца, веточку свежей петрушки и завернуть в трубочку. Украсить блюдо можно маленькими острыми перчинками, перьями зеленого лука и помидорами черри.
Можно подать грудинку в виде рулета. Для этого нужно отрезать тонкий пласт сала вдоль всего куска, положить на тонкую свиную ленту дольку огурца, веточку свежей петрушки и завернуть в трубочку. Украсить блюдо можно маленькими острыми перчинками, перьями зеленого лука и помидорами черри.
 Многие люди обрезают грудинку лишнего жира, например, толстой шапочки, иначе у них останется около дюйма жира.Это личный звонок.
Многие люди обрезают грудинку лишнего жира, например, толстой шапочки, иначе у них останется около дюйма жира.Это личный звонок. Ваша грудинка должна быть готова, когда она достигнет внутренней температуры от 200 ° F до 210 ° F. Дайте ему постоять не менее часа.
Ваша грудинка должна быть готова, когда она достигнет внутренней температуры от 200 ° F до 210 ° F. Дайте ему постоять не менее часа.
 Тем не менее, если вы не хотите оставлять духовку включенной на несколько часов, мультиварка предлагает простое решение.
Тем не менее, если вы не хотите оставлять духовку включенной на несколько часов, мультиварка предлагает простое решение. Это так утешительно и невероятно просто в изготовлении. Но это может быть нашим секретом. (Хотите сделать грудинку еще проще? Попробуйте приготовить говяжью грудинку в своей мультиварке!)
Это так утешительно и невероятно просто в изготовлении. Но это может быть нашим секретом. (Хотите сделать грудинку еще проще? Попробуйте приготовить говяжью грудинку в своей мультиварке!) По сути, сковорода, которую вы используете только один раз в год, чтобы запекать индейку в День Благодарения. Одноразовая сковорода — это нормально, если это все, что у вас есть, но прочная сковорода обеспечит равномерное приготовление и карамелизацию.
По сути, сковорода, которую вы используете только один раз в год, чтобы запекать индейку в День Благодарения. Одноразовая сковорода — это нормально, если это все, что у вас есть, но прочная сковорода обеспечит равномерное приготовление и карамелизацию. 


 Я знаю, что настоящая грудинка барбекю готовится на медленном огне в коптильне на медленном огне … и я знаю, что мысль о приготовлении техасской грудинки в духовке кощунственна в некоторых частях страны, особенно в Техасе … но потому что я не живу в Техасе, и у меня нет курильщика, вот где я приземлился.
Я знаю, что настоящая грудинка барбекю готовится на медленном огне в коптильне на медленном огне … и я знаю, что мысль о приготовлении техасской грудинки в духовке кощунственна в некоторых частях страны, особенно в Техасе … но потому что я не живу в Техасе, и у меня нет курильщика, вот где я приземлился.
 А затем, после того, как она будет приготовлена, вы можете либо нарезать ее и подать после 20-30 минут отдыха, либо вы можете охладить приготовленную грудинку на день или два и нагреть ее в духовке перед подачей на 300 ° F.
А затем, после того, как она будет приготовлена, вы можете либо нарезать ее и подать после 20-30 минут отдыха, либо вы можете охладить приготовленную грудинку на день или два и нагреть ее в духовке перед подачей на 300 ° F. Когда муж моей Мэнди навестил ее семью в Техасе, он заказал себе грудинку с картофелем фри, чем очень повеселила мама Мэнди. По-видимому, она действительно засмеялась.Бедный маленький янки.
Когда муж моей Мэнди навестил ее семью в Техасе, он заказал себе грудинку с картофелем фри, чем очень повеселила мама Мэнди. По-видимому, она действительно засмеялась.Бедный маленький янки. Смешайте ингредиенты для растирания. Натрите грудинку, заверните ее в полиэтиленовую пленку или поместите в герметичный контейнер и поставьте в холодильник на ночь или как минимум на 8 часов.
Смешайте ингредиенты для растирания. Натрите грудинку, заверните ее в полиэтиленовую пленку или поместите в герметичный контейнер и поставьте в холодильник на ночь или как минимум на 8 часов. Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений


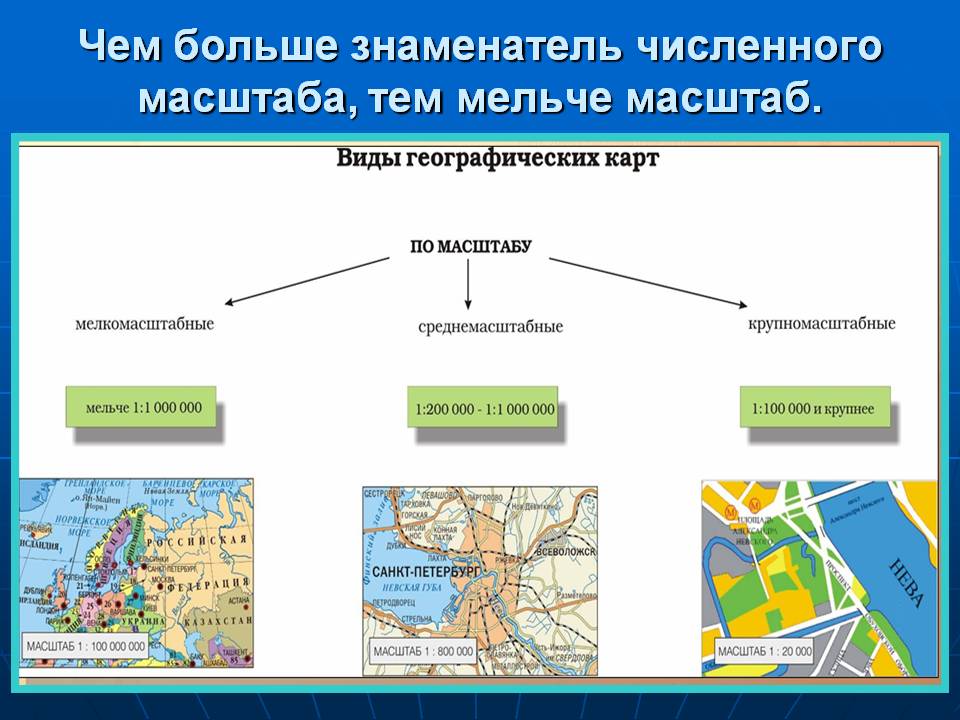 Тип задания: Выбор элемента из выпадающего списка.
Тип задания: Выбор элемента из выпадающего списка.
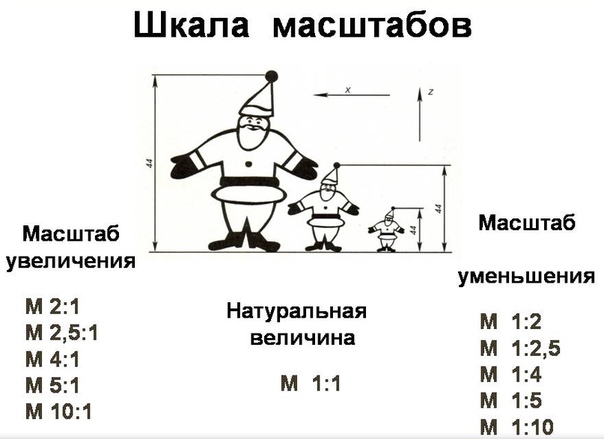


 4.2. Пример определения расстояния по карте
4.2. Пример определения расстояния по карте Итого: 600 м + 60 м + 8 м = 668 м.
Итого: 600 м + 60 м + 8 м = 668 м. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
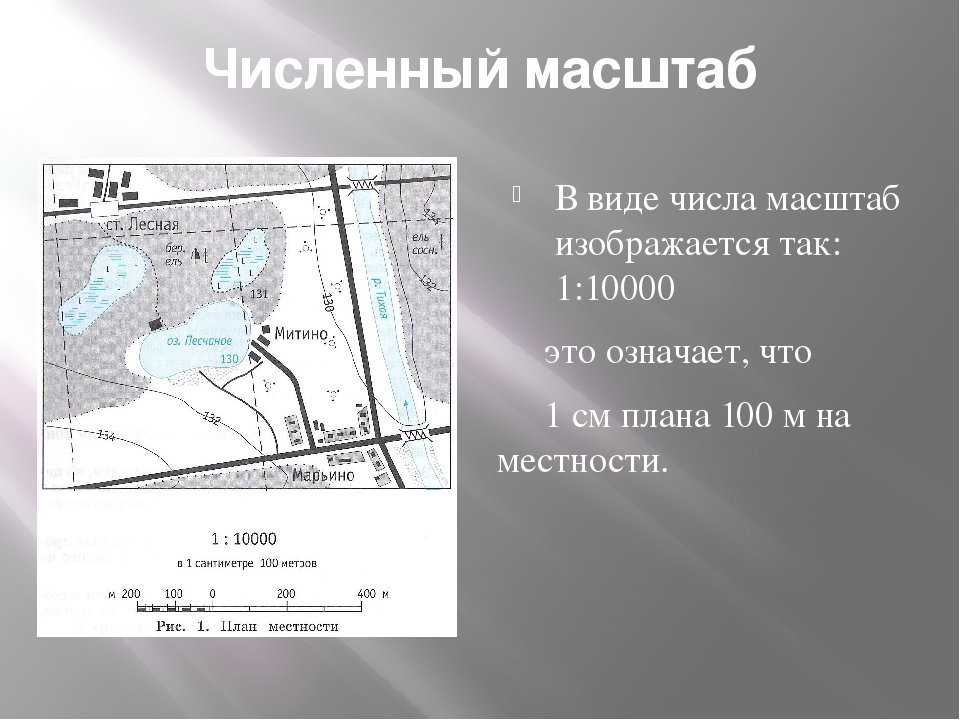
 Например, соотношение 1:2 указывает на то, изображение уменьшило деталь в 2 раза, а если на чертеже обозначено 2:1 – деталь наоборот увеличили в 2 раза.
Например, соотношение 1:2 указывает на то, изображение уменьшило деталь в 2 раза, а если на чертеже обозначено 2:1 – деталь наоборот увеличили в 2 раза.
 К размерной линии нужно приложить рулетку или линейку и определить числовое значение.
К размерной линии нужно приложить рулетку или линейку и определить числовое значение. Далее они отображаются в натуральном, уменьшенном или увеличенном масштабах.
Далее они отображаются в натуральном, уменьшенном или увеличенном масштабах.
 Но теперь ему приходилось следить не столько за своей работой, которую он привык делать тщательно, сколько за работой подчиненных. Наметанным глазом Иван видел, что исполнители совершают много мелких ошибок. Он тут же вмешивался, самолично исправлял огрехи. В связи с этим Иван начал воспринимать бывших коллег, а теперь подчиненных как не очень умелых и не очень ответственных людей. А подчиненные жаловались друг другу, что Иван «не дает дышать», «дорвался до власти» и «лезет во все дыры».
Но теперь ему приходилось следить не столько за своей работой, которую он привык делать тщательно, сколько за работой подчиненных. Наметанным глазом Иван видел, что исполнители совершают много мелких ошибок. Он тут же вмешивался, самолично исправлял огрехи. В связи с этим Иван начал воспринимать бывших коллег, а теперь подчиненных как не очень умелых и не очень ответственных людей. А подчиненные жаловались друг другу, что Иван «не дает дышать», «дорвался до власти» и «лезет во все дыры». Акционеры полностью доверяли ей, и решение о ее продвижении на должность генерального директора крупного холдинга было единогласно принято советом директоров. Со времени назначения Светланы прошел год. При подведении итогов года у членов совета директоров, да и у самой Светланы возникли двойственные чувства. Холдинг показал плановую прибыль. Но стоимость акций в конце года упала на 15%. Инвесторы не увидели усилий менеджмента по долгосрочному развитию компании. Стремясь обеспечить нужную рентабельность, Светлана отложила долгосрочную программу выхода на международные рынки, заморозила очень перспективный проект в области НИОКР. По ее мнению, эти инициативы были слишком рискованными, капиталоемкими и сырыми. Заморозка привела к тому, что аналитики прогнозировали серьезное отставание холдинга от конкурентов уже в ближайшем будущем.
Акционеры полностью доверяли ей, и решение о ее продвижении на должность генерального директора крупного холдинга было единогласно принято советом директоров. Со времени назначения Светланы прошел год. При подведении итогов года у членов совета директоров, да и у самой Светланы возникли двойственные чувства. Холдинг показал плановую прибыль. Но стоимость акций в конце года упала на 15%. Инвесторы не увидели усилий менеджмента по долгосрочному развитию компании. Стремясь обеспечить нужную рентабельность, Светлана отложила долгосрочную программу выхода на международные рынки, заморозила очень перспективный проект в области НИОКР. По ее мнению, эти инициативы были слишком рискованными, капиталоемкими и сырыми. Заморозка привела к тому, что аналитики прогнозировали серьезное отставание холдинга от конкурентов уже в ближайшем будущем.
 Если есть возможность, смените деловой гардероб. Устройте прощальную вечеринку. Можете смеяться, но подобные ритуалы в самом деле работают.
Если есть возможность, смените деловой гардероб. Устройте прощальную вечеринку. Можете смеяться, но подобные ритуалы в самом деле работают. Например, опытного руководителя – носителя соответствующего управленческого масштаба. Роль ментора – помогать в формировании картины мира, акцентировать ваше внимание на «по-настоящему важных вещах», разрушать ограничивающие убеждения и привычки предыдущего уровня должности.
Например, опытного руководителя – носителя соответствующего управленческого масштаба. Роль ментора – помогать в формировании картины мира, акцентировать ваше внимание на «по-настоящему важных вещах», разрушать ограничивающие убеждения и привычки предыдущего уровня должности. шаги:
шаги: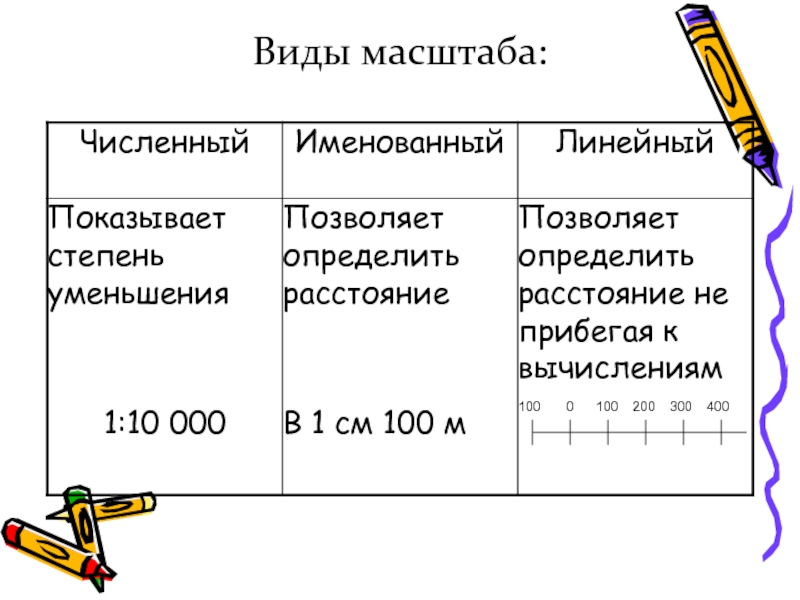 Масштабом называется отношение линейных размеров изображения предмета на чертеже к действительным размерам предмета.
Масштабом называется отношение линейных размеров изображения предмета на чертеже к действительным размерам предмета. (
( , соответственно, чертим линию размером 10мм. )
, соответственно, чертим линию размером 10мм. )
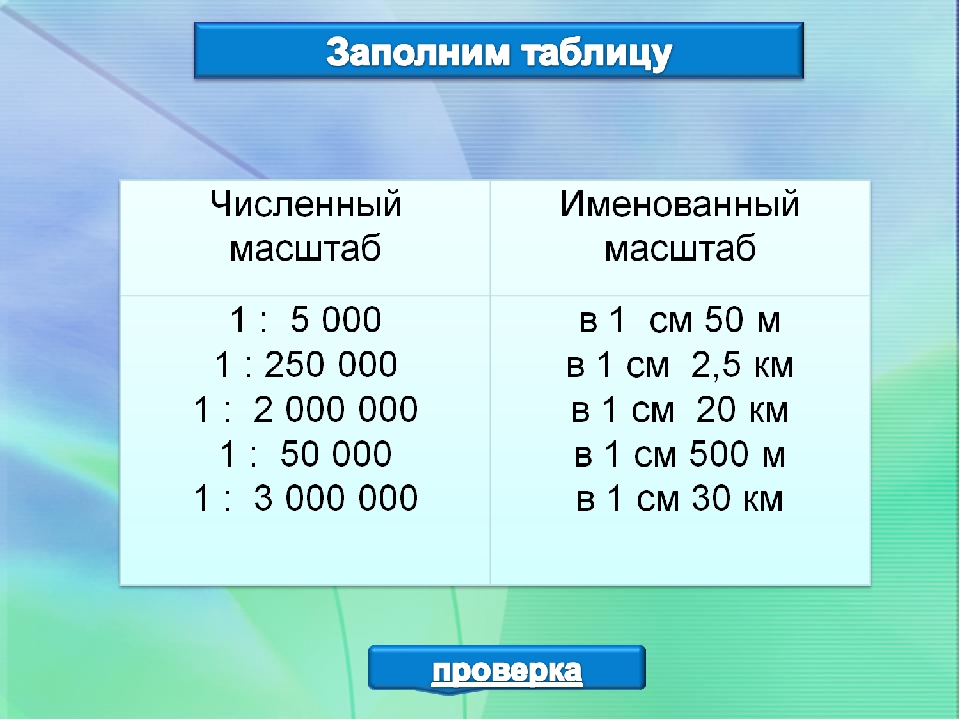 Например, рассмотрим выборку работающих лиц. Переменными для этого набора совокупности могут быть отрасль, местоположение, пол, возраст, навыки, тип работы и т. Д. Значение переменных будет отличаться для каждого сотрудника.
Например, рассмотрим выборку работающих лиц. Переменными для этого набора совокупности могут быть отрасль, местоположение, пол, возраст, навыки, тип работы и т. Д. Значение переменных будет отличаться для каждого сотрудника.

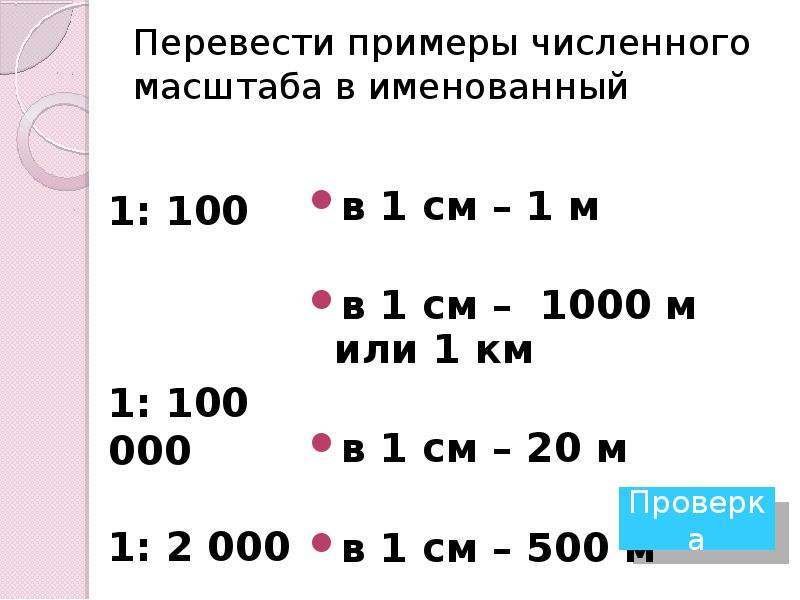

 Номинальные и порядковые данные могут быть строковыми, буквенно-цифровыми или числовыми.
Номинальные и порядковые данные могут быть строковыми, буквенно-цифровыми или числовыми. Описательные качества указывают на свойства маркировки, аналогичные номинальной шкале, в дополнение к которой порядковая шкала также имеет относительное положение переменных.Начало этой шкалы отсутствует, из-за чего нет фиксированного начала или «истинного нуля».
Описательные качества указывают на свойства маркировки, аналогичные номинальной шкале, в дополнение к которой порядковая шкала также имеет относительное положение переменных.Начало этой шкалы отсутствует, из-за чего нет фиксированного начала или «истинного нуля». 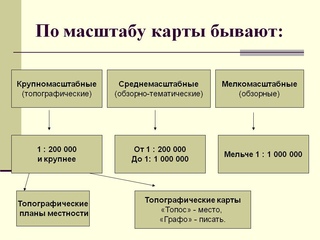 Эти шкалы обычно используются в исследованиях рынка для сбора и оценки относительной обратной связи об удовлетворенности продуктом, изменении восприятия при обновлении продукта и т. Д.
Эти шкалы обычно используются в исследованиях рынка для сбора и оценки относительной обратной связи об удовлетворенности продуктом, изменении восприятия при обновлении продукта и т. Д.
 Среднее значение, медиана или мода могут использоваться для расчета центральной тенденции в этой шкале. Единственный недостаток этой шкалы — отсутствие заранее определенной начальной точки или истинного нулевого значения.
Среднее значение, медиана или мода могут использоваться для расчета центральной тенденции в этой шкале. Единственный недостаток этой шкалы — отсутствие заранее определенной начальной точки или истинного нулевого значения. Шкала интервалов количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны исключительно связывать качественные значения с переменными.
Шкала интервалов количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны исключительно связывать качественные значения с переменными.
 Он рассчитывается исходя из предположения, что переменные имеют нулевую опцию, разница между двумя переменными одинакова и существует определенный порядок между опциями.
Он рассчитывается исходя из предположения, что переменные имеют нулевую опцию, разница между двумя переменными одинакова и существует определенный порядок между опциями.

 Это просто способы разбить на подкатегории различные типы данных (вот обзор типов статистических данных). Эта тема обычно обсуждается в контексте академического обучения и реже — в «реальном мире». Если вы освежаете эту концепцию для статистического теста, поблагодарите психолога-исследователя по имени Стэнли Стивенс за то, что он придумал эти термины.
Это просто способы разбить на подкатегории различные типы данных (вот обзор типов статистических данных). Эта тема обычно обсуждается в контексте академического обучения и реже — в «реальном мире». Если вы освежаете эту концепцию для статистического теста, поблагодарите психолога-исследователя по имени Стэнли Стивенс за то, что он придумал эти термины.
 Д.
Д.
 При переводе в градусы Фаренгейта становится ясно: 10 ° C = 50 ° F и 20 ° C = 68 ° F, что явно не в два раза жарче. Я надеюсь, что в этом есть смысл. В итоге, интервальные шкалы великолепны, но мы не можем вычислять отношения, что подводит нас к нашей последней шкале измерений …
При переводе в градусы Фаренгейта становится ясно: 10 ° C = 50 ° F и 20 ° C = 68 ° F, что явно не в два раза жарче. Я надеюсь, что в этом есть смысл. В итоге, интервальные шкалы великолепны, но мы не можем вычислять отношения, что подводит нас к нашей последней шкале измерений … Центральную тенденцию можно измерить по моде, медиане или среднему значению; меры дисперсии, такие как стандартное отклонение и коэффициент вариации, также могут быть рассчитаны на основе шкал отношений.
Центральную тенденцию можно измерить по моде, медиане или среднему значению; меры дисперсии, такие как стандартное отклонение и коэффициент вариации, также могут быть рассчитаны на основе шкал отношений. Иногда его называют уровнем измерения, он описывает природу значений, присвоенных переменным в наборе данных.
Иногда его называют уровнем измерения, он описывает природу значений, присвоенных переменным в наборе данных.
 Позиция в гонке, например, распределяется от 1-го, 2-го, 3-го до наименьшего.
Позиция в гонке, например, распределяется от 1-го, 2-го, 3-го до наименьшего. Д.
Д.
 Он измеряет степень встречаемости переменной.
Он измеряет степень встречаемости переменной. Если это расширение порядковой шкалы, с основным отличием в существовании равных интервалов.
Если это расширение порядковой шкалы, с основным отличием в существовании равных интервалов.
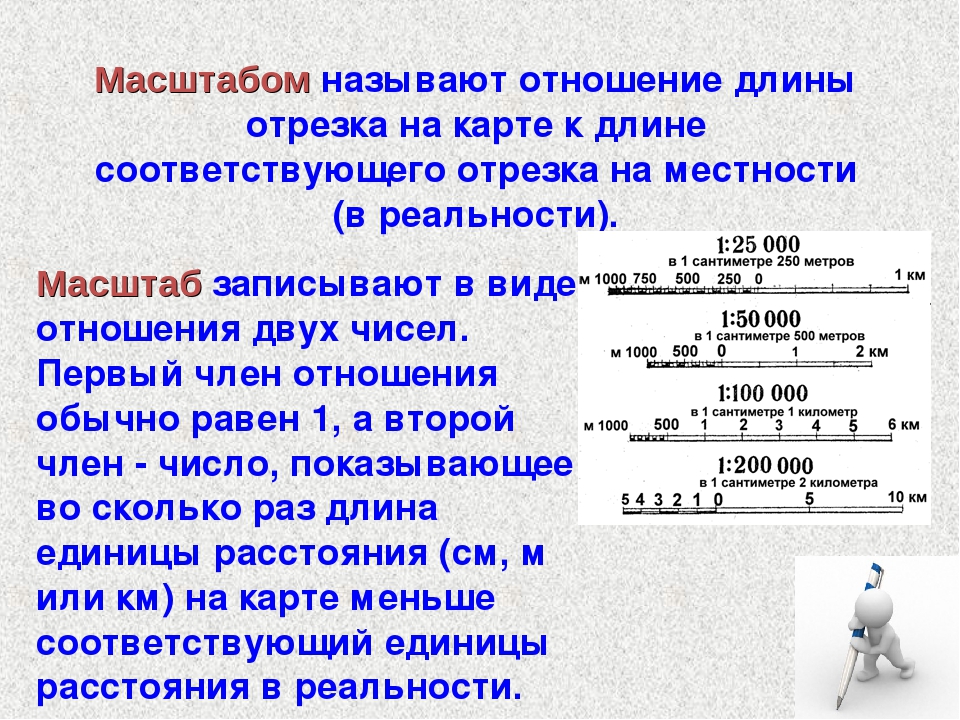 Это простой в использовании конструктор форм, который позволяет с легкостью собирать данные. Выполните следующие шаги, чтобы собрать данные на Formplus
Это простой в использовании конструктор форм, который позволяет с легкостью собирать данные. Выполните следующие шаги, чтобы собрать данные на Formplus Пушкин, «Руслан и Людмила») — кстати, фразеологизмы Александра Пушкина
Пушкин, «Руслан и Людмила») — кстати, фразеологизмы Александра Пушкина яз. в 5 кл. на тему Фразеологизмы по технологии Перевернутый класс
яз. в 5 кл. на тему Фразеологизмы по технологии Перевернутый класс
 Работа с текстом.
Работа с текстом.

 Отдельный челлендж — правильно эти устойчивые выражения писать. Рассказываем правду про «белое каление» и «в три погибели» (вместо «белого колена» и «втрипогибеля»).
Отдельный челлендж — правильно эти устойчивые выражения писать. Рассказываем правду про «белое каление» и «в три погибели» (вместо «белого колена» и «втрипогибеля»). Что за удивительное белое колено и как до него можно довести — неясно. Суровая правда: в этом фразеологизме речь идёт не о колене, а о «калении» — процессе нагревания металла в огне. Сначала он краснеет, желтеет, а под конец белеет — это высшая точка нагрева, когда металл становится почти жидким. Отсюда и выражение: довести до белого каления — привести в состояние крайнего раздражения. И никаких колен!
Что за удивительное белое колено и как до него можно довести — неясно. Суровая правда: в этом фразеологизме речь идёт не о колене, а о «калении» — процессе нагревания металла в огне. Сначала он краснеет, желтеет, а под конец белеет — это высшая точка нагрева, когда металл становится почти жидким. Отсюда и выражение: довести до белого каления — привести в состояние крайнего раздражения. И никаких колен! По некоторым источникам считается, что просак — это тупик; по другим — прядильня, большой канатный станок. Попасть в него во время плетения было одновременно опасно и глупо, потому что его сложно не заметить. А если всё-таки кто-то по невнимательности в него попадал, то выбраться было сложно. Раньше сочетание «в просак» писали раздельно, но со временем слитное написание вытеснило другие варианты.
По некоторым источникам считается, что просак — это тупик; по другим — прядильня, большой канатный станок. Попасть в него во время плетения было одновременно опасно и глупо, потому что его сложно не заметить. А если всё-таки кто-то по невнимательности в него попадал, то выбраться было сложно. Раньше сочетание «в просак» писали раздельно, но со временем слитное написание вытеснило другие варианты. Наречие «во ()всю» может писаться и слитно, и раздельно. Если нет никаких уточняющих слов — пишем слитно: он вовсю готовился к празднованию Дня святого Валентина. Если наречие уточняется или есть зависимые слова, пишем раздельно: он мчался во всю прыть, но так и не успел. Да, конкретно наш фразеологизм пишется раздельно.
Наречие «во ()всю» может писаться и слитно, и раздельно. Если нет никаких уточняющих слов — пишем слитно: он вовсю готовился к празднованию Дня святого Валентина. Если наречие уточняется или есть зависимые слова, пишем раздельно: он мчался во всю прыть, но так и не успел. Да, конкретно наш фразеологизм пишется раздельно. Вы наверняка спросите: при чём тут соль или хлебать? На Руси соль была дорогим продуктом, и пищу солили непосредственно перед едой. Незваные гости по негласным правилами получали меньше соли, чем другие, и уходили несолоно хлебавши. Пишем в два слова и не поддаёмся на соблазн удвоить букву «н».
Вы наверняка спросите: при чём тут соль или хлебать? На Руси соль была дорогим продуктом, и пищу солили непосредственно перед едой. Незваные гости по негласным правилами получали меньше соли, чем другие, и уходили несолоно хлебавши. Пишем в два слова и не поддаёмся на соблазн удвоить букву «н». Синонимы: «сделать без особого труда», «очень легко» или «проще простого» — выбирайте вариант, который нравится больше, или придумайте свой.
Синонимы: «сделать без особого труда», «очень легко» или «проще простого» — выбирайте вариант, который нравится больше, или придумайте свой. Замените выделенные словосочетания фразеологизмами под чертой.
Замените выделенные словосочетания фразеологизмами под чертой.


 Значение, смысл, происхождение.
Значение, смысл, происхождение. д. Фразеологизмы делают высказывание выразительным, создают образность. Устойчивые выражения используются в художественных произведениях, в публицистике, в бытовой речи. Устойчивые выражения называют иначе идиомами. Много идиом в других языках — английском, японском, китайском, французском.
д. Фразеологизмы делают высказывание выразительным, создают образность. Устойчивые выражения используются в художественных произведениях, в публицистике, в бытовой речи. Устойчивые выражения называют иначе идиомами. Много идиом в других языках — английском, японском, китайском, французском.



 Определите вид четырехугольника КВND и найдите его периметр.
Определите вид четырехугольника КВND и найдите его периметр.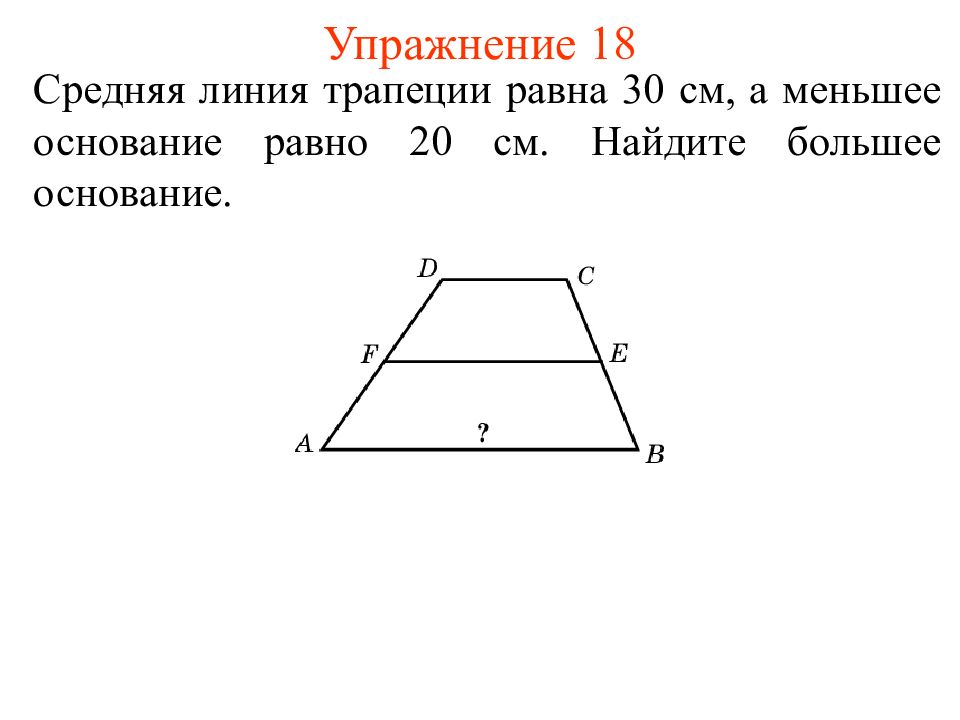 Найдите основания трапеции. Сколько решений имеет задача?
Найдите основания трапеции. Сколько решений имеет задача? [1]
[1] [7]
[7] [14]
[14]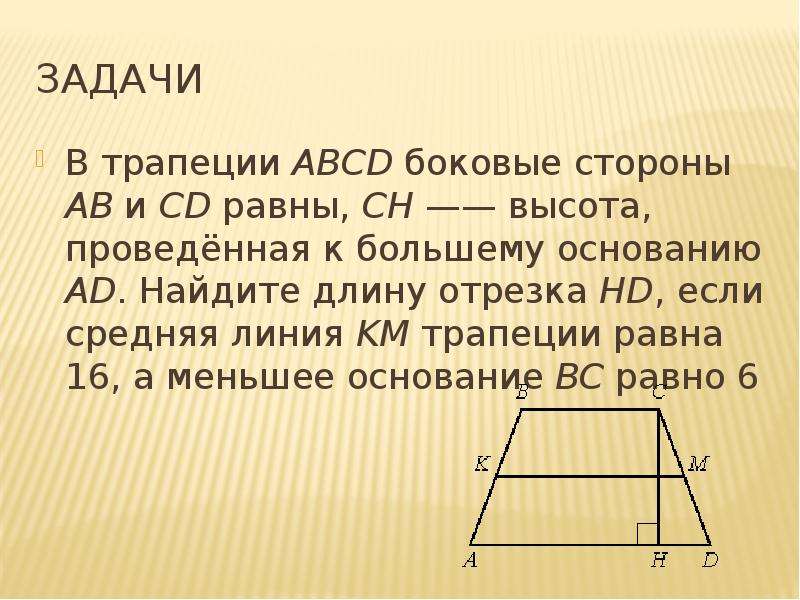 Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .
Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .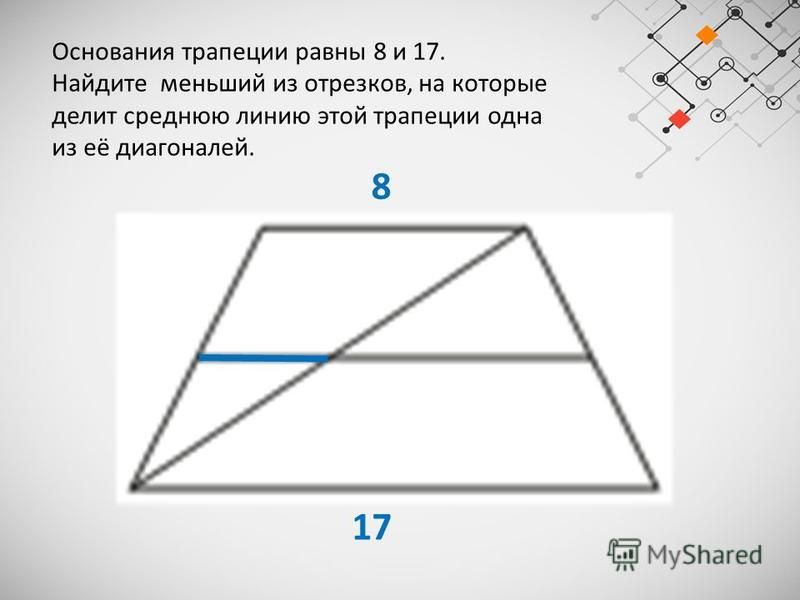

 Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому 8
8 Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство: Теорема Вариньона
Теорема Вариньона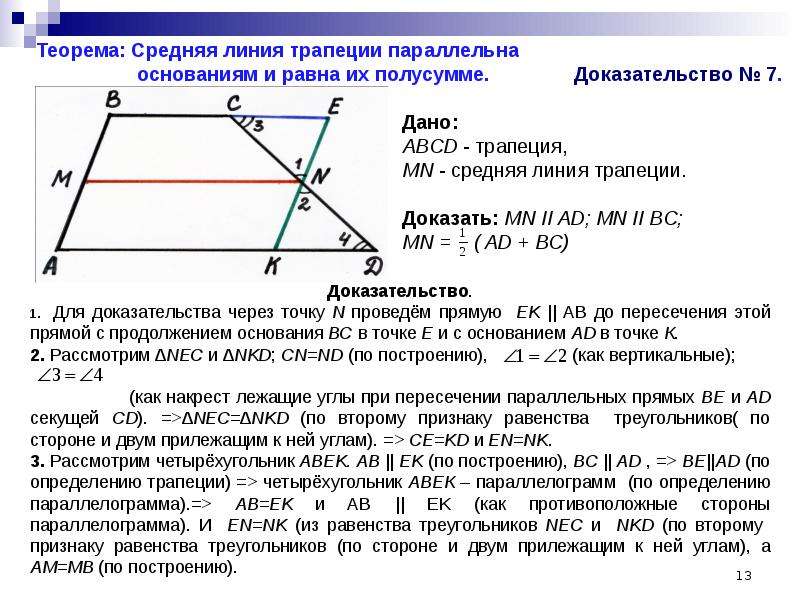
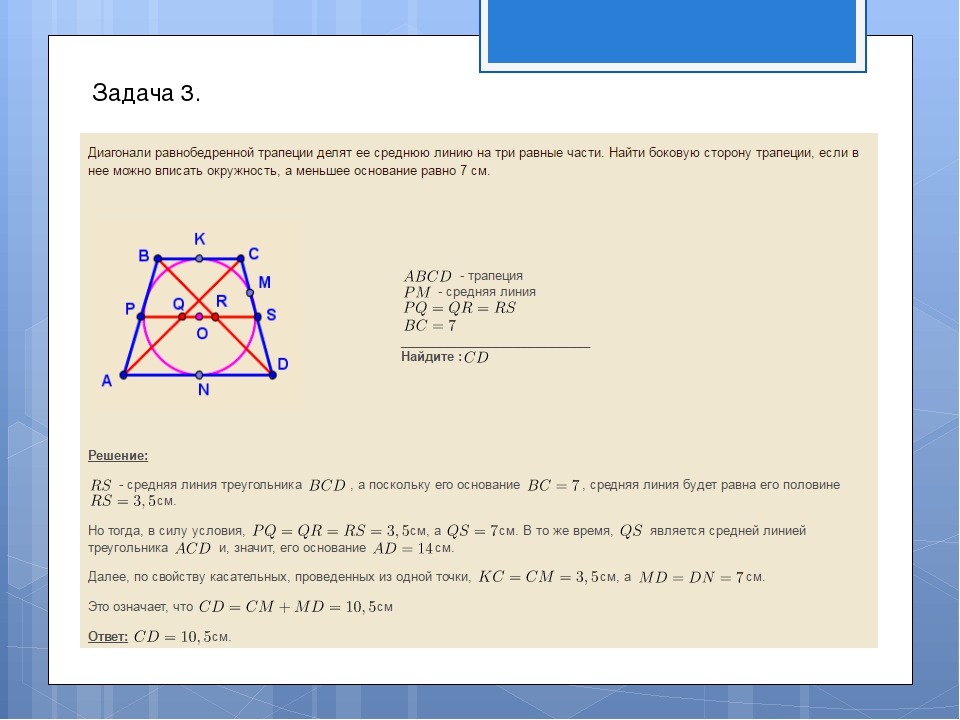 Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать. 14).
14).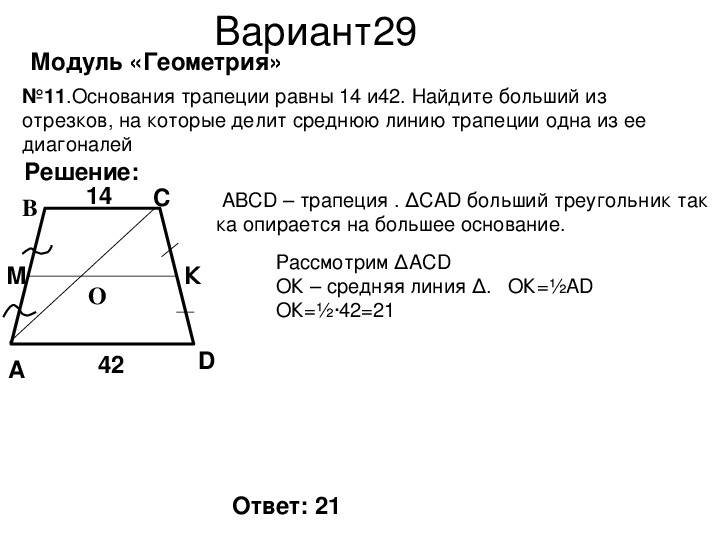
 Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.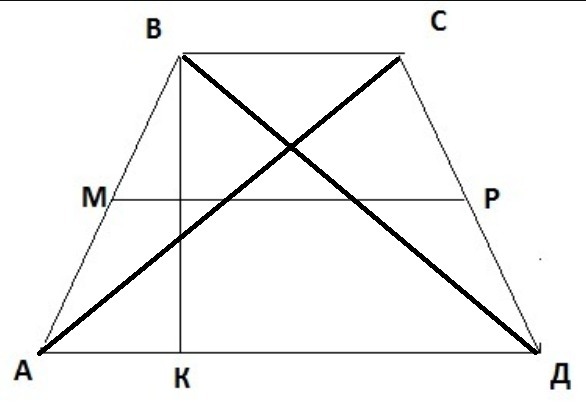 Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.
Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать. Равнобедренная трапеция — это особый случай трапеции, которая имеет боковую симметрию, что означает, что одна сторона будет зеркалом другой.
Равнобедренная трапеция — это особый случай трапеции, которая имеет боковую симметрию, что означает, что одна сторона будет зеркалом другой. Поскольку основание и высота у обоих треугольников равны, площадь обоих треугольников также должна быть одинаковой.
Поскольку основание и высота у обоих треугольников равны, площадь обоих треугольников также должна быть одинаковой. Параллель через пересечение диагоналей.
Параллель через пересечение диагоналей. Обратите внимание, что в терминах a , b и c , BJ = c — a и CK = b — c
Обратите внимание, что в терминах a , b и c , BJ = c — a и CK = b — c 
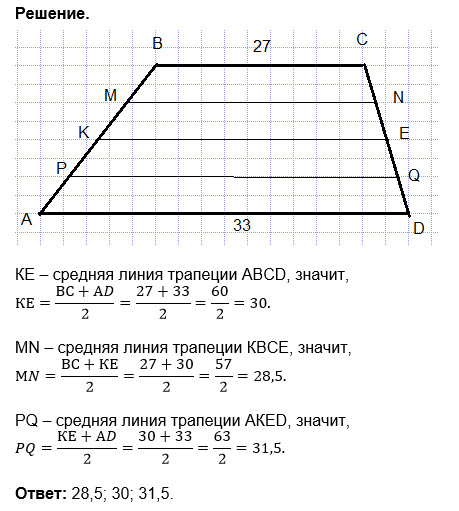 Докажите, что EF || DC и что EF = ½ ( AB + DC )
Докажите, что EF || DC и что EF = ½ ( AB + DC )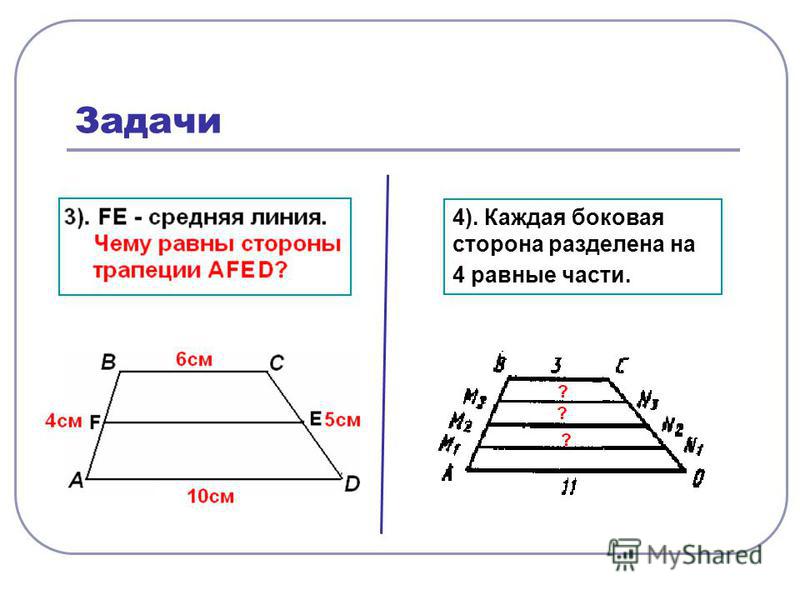
 По той же причине $$ \ angle B $$ и $$ \ angle C $$ являются дополнительными.
По той же причине $$ \ angle B $$ и $$ \ angle C $$ являются дополнительными.
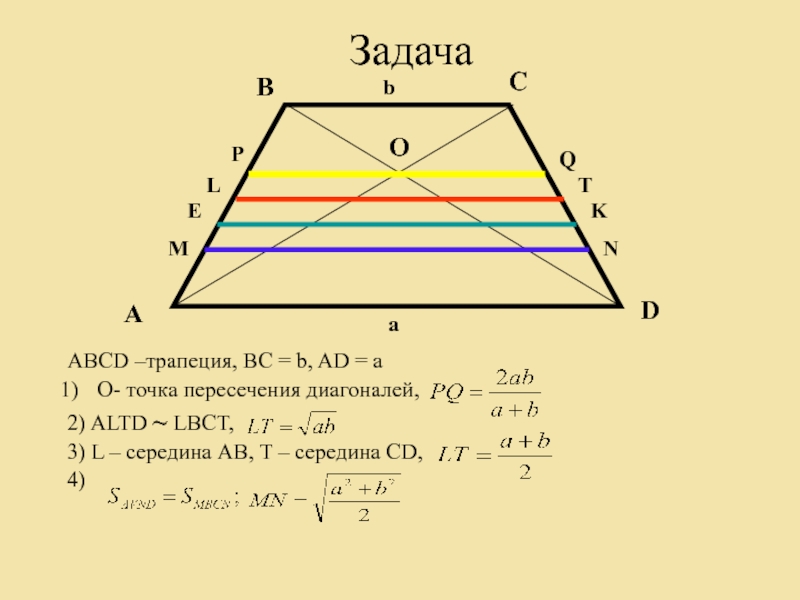 2
$
2
$ Фразеологизмы отражают человека и его деятельность: труд (золотые руки, валять дурака), отношения в обществе (закадычный друг, вставлять палки в колёса), личные качества (задирать нос, кислая мина) и т.д. Фразеологизмы делают высказывание выразительным, создают образность. Устойчивые выражения используются в художественных произведениях, в публицистике, в бытовой речи. Устойчивые выражения называют иначе идиомами. Много идиом в других языках — английском, японском, китайском, французском.
Фразеологизмы отражают человека и его деятельность: труд (золотые руки, валять дурака), отношения в обществе (закадычный друг, вставлять палки в колёса), личные качества (задирать нос, кислая мина) и т.д. Фразеологизмы делают высказывание выразительным, создают образность. Устойчивые выражения используются в художественных произведениях, в публицистике, в бытовой речи. Устойчивые выражения называют иначе идиомами. Много идиом в других языках — английском, японском, китайском, французском.