Модуль х минус х: Решите уравнение (|-x|)=7 ((модуль от минус х |) равно 7)
Модуль
Модулем положительного числа называют само это число; модулем отрицательного числа называют число, ему противоположное; модуль нуля равен нулю.
\(|a|=\begin{cases} a, \;\; если \; a>0 \\ 0, \; если\;\; a=0\\ -a,\; если \;\; a<0 \end{cases}\)
Второе название модуля – «абсолютное значение действительного числа».
Фактически модуль делает всё, что находится внутри него положительным. Поэтому чтобы правильно его раскрыть, необходимо сначала выяснить знак выражения внутри него:
— если подмодульное выражение положительно, модуль просто убирается. При этом само выражение не меняется.
— если же оно отрицательно, то при снятии модуля перед подмодульным выражением надо добавить знак «минус», чтобы сделать его положительным.
Об этом правиле нужно помнить при работе с более сложными выражениями или выражениями, содержащими переменные. 4+1\)
4+1\)
Пример. Вычислить значение выражения \(|7-x|-|x+3|\), при \(x>12\).
Решение: При любом \(x\) большем \(12\), первое подмодульное выражение будет отрицательно, а второе – положительно. Соответственно, первый модуль будет раскрываться с минусом, а второй – с плюсом (значит перед ним останется минус, который стоял перед ним до раскрытия):
\(|7-x|-|x+3|=-(7-x)-(x+3)=-7+x-x-3=-10\)
Ответ: \(-10\)
Геометрическое определение модуля
\(|a|\) — это расстояние от \(0\) до числа \(a\) на числовой оси
Пример. Чему равен \(|5|\) и \(|-5|\)?
Представим числовую ось и отметим на ней точки \(5\) и \(-5\). Какое будет расстояние от нуля до этих точек? Очевидно \(5\).
Значит ответ: \(|5|=5\), \(|-5|=5\).
Так как модуль это расстояние, а расстояние не может выражаться отрицательным числом, то он всегда положителен.
Понимать легче второе определение, но практике удобнее использовать первое.
Решение простейших уравнений с модулем
Уравнения вида \(|f|=g\) решается с помощью перехода к совокупности \( \left[ \begin{gathered}f= g\\ f=-g\end{gathered}\right.\) , при условии, что \(g≥0\).
Сначала об условии \(g≥0\). Откуда оно берется? Из определения модуля, ведь модуль всегда неотрицателен (то есть, положителен или равен нулю). Поэтому условие \(g≥0\) обязательно. Иначе уравнение не будет иметь решения.
Теперь о совокупности. Почему уравнение распадается на два? Давайте, к примеру, рассмотрим уравнение \(|x|=3\). Какое число под модулем будет равно \(3\)? Конечно \(3\) и \(-3\), потому что \(|3|=3\), \(|-3|=3\). Корни уравнения \(|x|=3\): \(3\) и \(-3\). Логично? Логично! В общем виде получается, что подмодульное выражение \(f\) должно быть равно \(g\) и \(-g\). Иначе равенство не получится.
Пример.
 Решить уравнение:
Решить уравнение:|
\(|x-1|=3x\) |
Найдем ограничения уравнения. Запишем его немного правее от основного решения |
|
|
\(3x≥0\) |
Когда ограничение записано — можно со спокойной душой решать уравнение. Избавимся от модуля и перейдем к совокупности уравнений |
|
|
\( \left[ \begin{gathered}x-1=3x\\ x-1=-3x\end{gathered}\right.\) |
Перед нами 2 линейных уравнения. Решаем их с помощью известного заклинания: «иксы влево, числа вправо» |
|
|
\( \left[ \begin{gathered}x-3x=1\\ x+3x=1\end{gathered}\right. |
Приведем подобные слагаемые |
|
|
\( \left[ \begin{gathered}-2x=1\\ 4x=1\end{gathered}\right.\) |
|
Поделим первое уравнение на \(-2\), второе на \(4\). |
|
\( \left[ \begin{gathered} x=-\frac{1}{2}\\ x=\frac{1}{4}\end{gathered}\right.\) |
|
Корень \(-\)\(\frac{1}{2}\) – не подходит, т.к. \(x≥0\). Остается корень \(\frac{1}{4}\), его и запишем в ответ |
Ответ: \(\frac{1}{4}\)
Решение простейших неравенств с модулем
Неравенство вида \(|f|< c\) решается с помощью перехода к двойному неравенству \( -c< f< c\) , при условии, что \(c>0\).
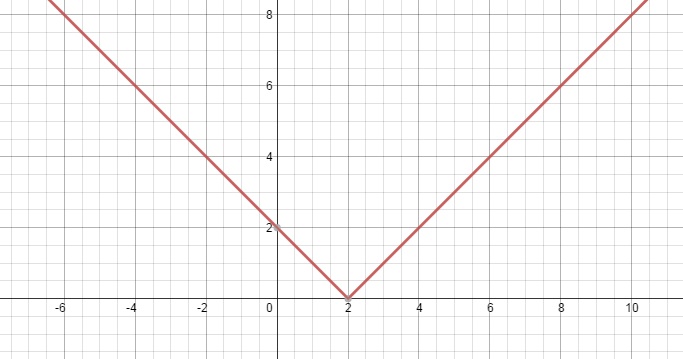
Начнем опять с условия. Почему \(c>0\)? Потому что, иначе неравенство не будет иметь решения. Здесь все также как в уравнениях. В самом деле, когда, например, модуль икса меньше \(-7\)? Никогда!
Теперь разберем неравенство \(|x|<3\). Какие иксы нам подойдут? Все от \(-3\) до \(3\). Иначе говоря, икс должен лежать между \(-3\) и \(3\). Это утверждение можно записать вот так \(-3< x <3\) либо системой \(\begin{cases}x<3\\x > -3\end{cases}\). В любом случае ответ будет \(xϵ (-3;3)\).
Неравенство вида \(|f|>c\) решается с помощью перехода к совокупности неравенств \( \left[ \begin{gathered} f>c\\ f< -c\end{gathered}\right.\), при условии, что \(c≥0\).
А здесь почему \(c≥0\)? Потому что иначе решать нечего: если \(c\) отрицательно, то модуль абсолютно любого икса нам подойдет. И значит ответ, икс – любое число.
Теперь о переходе. Рассмотрим неравенство \(|x|>3\). Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
|
\(|3x-7|≤8\) |
\(|3x-11|≥11\) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(-8≤3x-7≤8\) \(|+7\) |
\( \left[ \begin{gathered}3x-11≥11\\ 3x-11≤-11\end{gathered}\right.\) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(-1≤3x≤15\) |
\( \left[ \begin{gathered}3x≥22\\ 3x≤0\end{gathered}\right.\) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(-\frac{1}{3}≤x≤5\) |
\( \left[ \begin{gathered}x≥\frac{22}{3}\\ x≤0\end{gathered}\right. Задача 1. Построить графики функций y=|x| y=|x-1|. y=|x| Построим графики: y=|x-1| Это была простенькая задачка. Теперь то, что многих приводит в ужас. Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|. Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11. Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся. Вот ссылка, которая поможет вам проверить ваши построения: Общие сведения об уравненияхУравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач. С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии. В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно. Предварительные навыкиЧто такое уравнение?Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство. Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5. А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x, значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство. Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части. Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет Говорят, что число 2 является корнем или решением уравнения 3 + x = 5 Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство. Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет. Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы. Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части. Выразить одно через другоеИзучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также. Рассмотрим следующее выражение: 8 + 2 Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10 8 + 2 = 10 Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8. Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8: 2 = 10 − 8 Мы выразили число 2 из равенства 8 + 2 = 10. Как видно из примера, ничего сложного в этом нет. При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении. Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8. Данное равенство можно прочесть так: 2 есть 10 − 8 То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Число 2 есть разность числа 10 и числа 8 или Число 2 есть разница между числом 10 и числом 8. Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий. Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние: 8 + 2 = 10 Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2 8 = 10 − 2 Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние: 8 + 2 = 10 В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно: 10 = 8 + 2 Пример 2. Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить: 8 = 6 + 2 Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние: 8 − 2 = 6 Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6 2 = 8 − 6 Пример 3. Рассмотрим равенство 3 × 2 = 6 Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2 Вернем получившееся равенство в первоначальное состояние: 3 × 2 = 6 Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3 Пример 4. Рассмотрим равенство Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5 15 = 3 × 5 Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние: Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3 Правила нахождения неизвестныхРассмотрим несколько правил нахождения неизвестных. Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2. В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой. Чтобы выразить число 2, мы поступили следующим образом: 2 = 10 − 8 То есть из суммы 10 вычли слагаемое 8. Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x 8 + x = 10 В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10, а переменная x берет на себя роль так называемого неизвестного слагаемого Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10. Для нахождения неизвестного слагаемого предусмотрено следующее правило: Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10. Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8 2 = 10 − 8 А сейчас, чтобы найти неизвестное слагаемое x, мы должны из суммы 10 вычесть известное слагаемое 8: x = 10 − 8 Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x x = 2 Мы решили уравнение. Значение переменной x равно 2. Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно: В результате получается верное числовое равенство. Значит уравнение решено правильно. Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8. x + 2 = 10 В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. x = 10 − 2 x = 8 Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8. В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность Чтобы выразить число 8, мы поступили следующим образом: 8 = 6 + 2 То есть сложили разность 6 и вычитаемое 2. Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x x − 2 = 6 В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого Для нахождения неизвестного уменьшаемого предусмотрено следующее правило: Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6. А сейчас, чтобы найти неизвестное уменьшаемое x, мы должны к разности 6 прибавить вычитаемое 2 x = 6 + 2 Если вычислить правую часть, то можно узнать чему равна переменная x x = 8 Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x 8 − x = 6 В этом случае переменная x берет на себя роль неизвестного вычитаемого Для нахождения неизвестного вычитаемого предусмотрено следующее правило: Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6. А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6 x = 8 − 6 Вычисляем правую часть и находим значение x x = 2 Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3. В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение Чтобы выразить число 3 мы поступили следующим образом: То есть разделили произведение 6 на множитель 2. Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x x × 2 = 6 В этом случае переменная x берет на себя роль неизвестного множимого. Для нахождения неизвестного множимого предусмотрено следующее правило: Чтобы найти неизвестное множимое, нужно произведение разделить на множитель. Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6. Произведение 6 мы разделили на множитель 2. А сейчас для нахождения неизвестного множимого x, нужно произведение 6 разделить на множитель 2. Вычисление правой части позволяет нам найти значение переменной x x = 3 Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель: Чтобы найти неизвестный множитель, нужно произведение разделить на множимое. Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6. Тогда для получения числа 2 мы разделили произведение 6 на множимое 3. А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3. Вычисление правой части равенства позволяет узнать чему равно x x = 2 Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя: Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель. Например, решим уравнение 9 × x = 18. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9 Отсюда . Решим уравнение x × 3 = 27. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3 Отсюда . Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное. Чтобы выразить число 15 мы поступили следующим образом: 15 = 3 × 5 То есть умножили частное 3 на делитель 5. Теперь представим, что в равенстве вместо числа 15 располагается переменная x В этом случае переменная x берет на себя роль неизвестного делимого. Для нахождения неизвестного делимого предусмотрено следующее правило: Чтобы найти неизвестное делимое, нужно частное умножить на делитель. Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5. А сейчас, чтобы найти неизвестное делимое x, нужно частное 3 умножить на делитель 5 x = 3 × 5 Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x. x = 15 Теперь представим, что в равенстве вместо числа 5 располагается переменная x. В этом случае переменная x берет на себя роль неизвестного делителя. Для нахождения неизвестного делителя предусмотрено следующее правило: Чтобы найти неизвестный делитель, нужно делимое разделить на частное. Что мы и сделали, когда выражали число 5 из равенства . А сейчас, чтобы найти неизвестный делитель x, нужно делимое 15 разделить на частное 3 Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x. x = 5 Итак, для нахождения неизвестных мы изучили следующие правила:
КомпонентыКомпонентами мы будем называть числа и переменные, входящие в равенство Так, компонентами сложения являются слагаемые и сумма Компонентами вычитания являются уменьшаемое, вычитаемое и разность Компонентами умножения являются множимое, множитель и произведение Компонентами деления являются делимое, делитель и частное В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть. Пример 1. Найти корень уравнения 45 + x = 60 45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. x = 60 − 45 Вычислим правую часть, получим значение x равное 15 x = 15 Значит корень уравнения 45 + x = 60 равен 15. Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить. Пример 2. Решить уравнение Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма. При этом слагаемое 2x содержит переменную x. После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое: Теперь применяем правило нахождения неизвестного слагаемого. Вычислим правую часть получившегося уравнения: Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение При этом переменная x является не просто множителем, а неизвестным множителем Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое: Вычислим правую часть, получим значение переменной x Для проверки найденный корень отправим в исходное уравнение и подставим вместо x Получили верное числовое равенство. Значит уравнение решено правильно. Пример 3. Решить уравнение 3x + 9x + 16x = 56 Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить. Приведем подобные слагаемые в левой части данного уравнения: Имеем дело с компонентами умножения. Отсюда x равен 2 Равносильные уравненияВ предыдущем примере при решении уравнения 3x + 9x + 16x = 56, мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56. Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают. Уравнения называют равносильными, если их корни совпадают. Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2. Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56, а затем в уравнение 28x = 56, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Согласно порядку действий, в первую очередь выполняется умножение: Подставим корень 2 во второе уравнение 28x = 56 Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными. Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56, которое проще решать. Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает. Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному. и аналогично: Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному. Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число. Пример 1. Решить уравнение Вычтем из обеих частей уравнения число 10 Приведем подобные слагаемые в обеих частях: Получили уравнение 5x = 10. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 10 разделить на известный сомножитель 5. Отсюда . Вернемся к исходному уравнению и подставим вместо x найденное значение 2 Получили верное числовое равенство. Решая уравнение мы вычли из обеих частей уравнения число 10. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2 Пример 2. Решить уравнение 4(x + 3) = 16 Раскроем скобки в левой части равенства: Вычтем из обеих частей уравнения число 12 Приведем подобные слагаемые в обеих частях уравнения: В левой части останется 4x, а в правой части число 4
Получили уравнение 4x = 4. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 4 разделить на известный сомножитель 4 Отсюда Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно. Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12. Пример 3. Решить уравнение Раскроем скобки в левой части равенства: Прибавим к обеим частям уравнения число 8 Приведем подобные слагаемые в обеих частях уравнения: В левой части останется 2x, а в правой части число 9 В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5 Получили верное числовое равенство. Значит уравнение решено правильно. Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5 Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному. То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений. Рассмотрим следующее уравнение: Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство Получается верное равенство. Значит число 2 действительно является корнем уравнения . Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки. Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный: Получилось уравнение 12 = 9x − 3x. Приведем подобные слагаемые в правой части данного уравнения: Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Отсюда x = 2. Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными. На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число. Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x. Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием. Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12. В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом: Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения. Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число. Пример 1. Решить уравнение При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение. В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8: Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8 Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения: В результате останется простейшее уравнение Ну и нетрудно догадаться, что корень этого уравнения равен 4 Вернемся к исходному уравнению и подставим вместо x найденное значение 4 Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись: От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом: Пример 2. Решить уравнение Умнóжим обе части уравнения на 15 В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5 Перепишем то, что у нас осталось: Раскроем скобки в правой части уравнения: Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак: Приведем подобные слагаемые в обеих частях, получим Имеем дело с компонентами умножения. Отсюда Вернемся к исходному уравнению и подставим вместо x найденное значение 5 Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15. Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x. Корень этого уравнения, как и уравнения равен 5. Значит эти уравнения равносильны. Пример 3. Решить уравнение Умнóжим обе части уравнения на 3 В левой части можно сократить две тройки, а правая часть будет равна 18 Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель: Отсюда Вернемся к исходному уравнению и подставим вместо x найденное значение 9 Получается верное числовое равенство. Пример 4. Решить уравнение Умнóжим обе части уравнения на 6 В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель: Сократим в обеих частях уравнениях то, что можно сократить: Перепишем то, что у нас осталось: Раскроем скобки в обеих частях уравнения: Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x, сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой: Приведем подобные слагаемые в обеих частях: Теперь найдем значение переменной x. Для этого разделим произведение 28 на известный сомножитель 7 Отсюда x = 4. Вернемся к исходному уравнению и подставим вместо x найденное значение 4 Получилось верное числовое равенство. Значит уравнение решено правильно. Пример 5. Решить уравнение Раскроем скобки в обеих частях уравнения там, где это можно: Умнóжим обе части уравнения на 15 Раскроем скобки в обеих частях уравнения: Сократим в обеих частях уравнения, то что можно сократить: Перепишем то, что у нас осталось: Раскроем скобки там, где это можно: Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные: Приведем подобные слагаемые в обеих частях уравнения: Найдём значение x В получившемся ответе можно выделить целую часть: Вернемся к исходному уравнению и подставим вместо x найденное значение Получается довольно громоздкое выражение. Воспользуемся переменными. Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B Найдем значение выражения, находящегося в переменной А. Значение переменной А равно . Теперь найдем значение переменной B. То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно Видим, что значение переменной B, как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно. Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить. Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42. Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Подставим найденное значение 2 вместо x в исходное уравнение: Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое: Выполним сокращение в каждом слагаемом: Перепишем то, что у нас осталось: Решим это уравнение, пользуясь известными тождественными преобразованиями: Получили корень 2. Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны. Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14, нам потребовалось разделить произведение 14 на известный сомножитель 7. Этим методом мы тоже будем пользоваться часто. Умножение на минус единицуЕсли обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному. Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1. Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать. Рассмотрим уравнение . Чему равен корень этого уравнения? Прибавим к обеим частям уравнения число 5 Приведем подобные слагаемые: А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . То есть минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом: Имеем дело с компонентами умножения. Чтобы найти х, нужно произведение −5 разделить на известный сомножитель −1. или разделить обе части уравнения на −1, что еще проще Итак, корень уравнения равен 5. Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице Получилось верное числовое равенство. Значит уравнение решено верно. Теперь попробуем умножить обе части уравнения на минус единицу: После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10 Корень этого уравнения, как и уравнения равен 5 Значит уравнения и равносильны. Пример 2. Решить уравнение В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1. Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками. Так, умножение уравнения на −1 можно записать подробно следующим образом: либо можно просто поменять знаки всех компонентов: Получится то же самое, но разница будет в том, что мы сэкономим себе время. Итак, умножив обе части уравнения на −1, мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3 Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали. Пример 3. Решить уравнение Умнóжим обе части уравнения на −1. Тогда все компоненты поменяют свои знаки на противоположные: Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые: Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые: Приравнивание к нулюНедавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному. А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего. В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Приведем подобные слагаемые в левой части: Прибавим к обеим частям 77, и разделим обе части на 7 Альтернатива правилам нахождения неизвестныхОчевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных. К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2 Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5 Уравнения вида мы решали выражая неизвестное слагаемое: Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак: Далее разделить обе части на 2 В левой части уравнения сократятся две двойки. Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее: В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения: Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме. Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится. Когда корней несколькоУравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9. В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9), которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй). То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю. x = 0 или x + 9 = 0 Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0. Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0. Несложно догадаться, что корень этого уравнения равен −9. Проверка показывает, что корень верный: −9 + 9 = 0 Пример 2. Решить уравнение Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2). А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2)). Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули: Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю: Когда корней бесконечно многоУравнение может иметь бесконечно много корней. Пример 1. Решить уравнение Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14. Это равенство будет получаться при любом x Пример 2. Решить уравнение Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x Когда корней нетСлучается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x, левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид Пусть Пример 2. Раскроем скобки в левой части равенства: Приведем подобные слагаемые: Видим, что левая часть не равна правой части. И так будет при любом значении y. Например, пусть y = 3. Буквенные уравненияУравнение может содержать не только числа с переменными, но и буквы. Например, формула нахождения скорости является буквенным уравнением: Данное уравнение описывает скорость движения тела при равноускоренном движении. Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s. Умнóжим обе части уравнения на t В правой части переменные t сократим на t и перепишем то, что у нас осталось: В получившемся уравнении левую и правую часть поменяем местами: У нас получилась формула нахождения расстояния, которую мы изучали ранее. Попробуем из уравнения определить время. Для этого нужно выразить переменную t. Умнóжим обе части уравнения на t В правой части переменные t сократим на t и перепишем то, что у нас осталось: В получившемся уравнении v × t = s обе части разделим на v В левой части переменные v сократим на v и перепишем то, что у нас осталось: У нас получилась формула определения времени, которую мы изучали ранее. Предположим, что скорость поезда равна 50 км/ч v = 50 км/ч А расстояние равно 100 км s = 100 км Тогда буквенное уравнение примет следующий вид Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t. Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t либо можно воспользоваться тождественными преобразованиями. Затем разделить обе части на 50 Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x Вычтем из обеих частей уравнения a Разделим обе части уравнения на b Теперь, если нам попадется уравнение вида a + bx = c, то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться. Решим уравнение 2 + 4x = 10. Оно похоже на буквенное уравнение a + bx = c. Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения: Видим, что второе решение намного проще и короче. Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0), поскольку деление на ноль на допускается. Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x Раскроем скобки в обеих частях уравнения Воспользуемся переносом слагаемых. Параметры, содержащие переменную x, сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой. В левой части вынесем за скобки множитель x Разделим обе части на выражение a − b В левой части числитель и знаменатель можно сократить на a − b. Так окончательно выразится переменная x Теперь, если нам попадется уравнение вида a(x − c) = b(x + d), то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Допустим нам дано уравнение 4(x − 3) = 2(x + 4). Оно похоже на уравнение a(x − c) = b(x + d). Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения: Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d. Это позволит нам не ошибиться при подстановке: Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0). Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю. Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d). В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части: Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x Приведем левую часть уравнения к общему знаменателю: Умнóжим обе части на a В левой части x вынесем за скобки Разделим обе части на выражение (1 − a) Линейные уравнения с одним неизвестнымРассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным. Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой». Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2(x + 3) = 16. Давайте решим его. Раскроем скобки в левой части уравнения, получим 2x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x, разделим произведение 10 на известный сомножитель 2. Отсюда x = 5. Уравнение 2(x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10, для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный». Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b. Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x. Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю. Если в линейном уравнении a = 0 и b = 0, то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0. При любом значении x левая часть будет равна правой части. Если в линейном уравнении a = 0 и b ≠ 0, то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5. Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти. Если в линейном уравнении a ≠ 0, и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3, и b равно какому-нибудь числу, скажем числу 6, то уравнение примет вид . Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0. Это то же самое уравнение, что и ax = b, но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0. Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде. В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным. Задания для самостоятельного решенияЗадание 1. Используя метод переноса слагаемого, решите следующее уравнение: Задание 2. Используя метод прибавления (или вычитания) числа к обеим частям, решите следующее уравнение: Задание 3. Решите уравнение: Задание 4. Решите уравнение: Задание 5. Решите уравнение: Задание 6. Решите уравнение: Задание 7. Решите уравнение: Задание 8. Решите уравнение: Задание 9. Решите уравнение: Задание 10. Решите уравнение: Задание 11. Решите уравнение: Задание 12. Решите уравнение: Задание 13. Решите уравнение: Задание 14. Решите уравнение: Задание 15. Решите уравнение: Задание 16. Решите уравнение: Задание 17. Решите уравнение: Задание 18. Решите уравнение: Задание 19. Решите уравнение: Задание 20. Решите уравнение: Задание 21. Решите уравнение: Задание 22. Решите уравнение: Задание 23. Решите уравнение: Задание 24. Решите уравнение: Задание 25. Решите уравнение: Задание 26. Решите уравнение: Задание 27. Решите уравнение: Задание 28. Решите уравнение: Задание 29. Решите уравнение: Задание 30. Решите уравнение: Задание 31. Решите уравнение: Задание 32. В следующем буквенном уравнении выразите переменную x: Задание 33. В следующем буквенном уравнении выразите переменную x: Задание 34. В следующем буквенном уравнении выразите переменную x: Задание 35. В следующем буквенном уравнении выразите переменную x: Задание 36. В следующем буквенном уравнении выразите переменную y: Задание 37. В следующем буквенном уравнении выразите переменную z: Понравился урок?
Возникло желание поддержать проект? Навигация по записямНатуральный логарифм, функция ln xПриведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел. Определение
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x. Исходя из определения, основанием натурального логарифма является число е: График натурального логарифма ln xГрафик функции y = ln x. График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x. Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения. При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ). При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция xa с положительным показателем степени a растет быстрее логарифма. Свойства натурального логарифмаОбласть определения, множество значений, экстремумы, возрастание, убываниеНатуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Значения ln x ln 1 = 0 Основные формулы натуральных логарифмов Формулы, вытекающие из определения обратной функции: Основное свойство логарифмов и его следствияФормула замены основания Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания: Обратная функцияОбратной для натурального логарифма является экспонента. Если , то Если , то . Производная ln x Производная натурального логарифма: Интеграл Интеграл вычисляется интегрированием по частям: Выражения через комплексные числа Рассмотрим функцию комплексной переменной z: Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией. Разложение в степенной ряд При имеет место разложение: Использованная литература: Автор: Олег Одинцов. Опубликовано: Изменено: Примеры вычисления полей в Python—ArcGIS ProВвод значений с клавиатуры – не единственный способ редактирования значений в таблице. В некоторых случаях вам может потребоваться выполнить математические вычисления для получения значения поля отдельной записи или даже всех записей. Можно выполнять как простые, так и сложные вычисления над всеми либо только выбранными записями. Кроме того, в полях атрибутивных таблиц можно вычислить длину, периметр и прочие геометрические свойства. В разделах ниже приводятся примеры использования калькулятора поля. Вычисления выполняются с помощью Python, SQL и Arcade. Этот раздел описывает примеры скриптов Python для Вычисления поля. Более подробно о выражениях Arcade, см. Руководство ArcGIS Arcade. Более подробно о выражениях SQL можно узнать в разделе Вычисление поля.
Простые вычисленияРяд вычислений можно производить, используя только короткое выражение. Примеры простых строчекСтроки поддерживаются несколькими строковыми функциями Python, в том числе capitalize, rstrip и replace. Сделать заглавной первую букву текста в поле CITY_NAME. Убрать все пробелы на концах строк в поле CITY_NAME . Заменить написание «california» на «California» в поле STATE_NAME. Доступ к символам в текстовом поле осуществляется путем индексации и разделения в Python. Индексация возвращает символы в индексном местоположении; разделение – группу символов. В следующей таблице предположим, что это строковое поле !fieldname! со значением «abcde».
Python также поддерживает форматирование строк с использованием метода format(). Скомбинировать поля FieldA и FieldB, разделенные двоеточием. Простые математические примерыPython предоставляет инструменты для обработки чисел. Python также поддерживает ряд числовых и математических функций, в том числе, math, cmath, decimal, random, itertools, functools и operator.
Вычислить объем сферы по заданному полю с радиусами. Прежние версии:В ArcGIS Pro используется Python 3, а в ArcGIS Desktop – Python 2. В Python 2 используются математические целые числа, то есть деление двух целочисленных значений всегда дает в результате целочисленное значение (3 / 2 = 1). В Python 3 при делении целочисленных значений результат будет числом с плавающей точкой (3 / 2 = 1.5). Встроенные функции PythonPython содержит ряд встроенных функций, включая max, min, round и sum. Вычисление максимального значения для каждой записи в списке полей. Вычисление суммы для каждой записи в списке полей. Использование блоков кодаС помощью выражений Python и параметра Блок кода вы можете сделать следующее:
Прежние версии:В ArcGIS Desktop инструмент Вычислить поле поддерживает типы выражений VB, PYTHON и PYTHON_9.3. Тип выражения VB, поддерживаемый в некоторых продуктах, не поддерживается в 64-битных продуктах, и в том числе в ArcGIS Pro. Ключевые слова PYTHON и PYTHON_9.3 все еще поддерживаются в ArcGIS Pro для сохранения обратной совместимости, но не указываются в списке выбора. Скрипты Python, использующие ключевые слова, продолжат работать корректно. Единственное различие между типом выражения Python 3 и устаревшим ключевым словом PYTHON_9.3 заключается в том, что Python 3 возвращает значения в полях данных как объекты Python datetime. Тип выражения Python 3 не связан с версией Python, установленной с ArcGIS Pro. Это просто исторически связанное с Python стороннее ключевое слово (после PYTHON и PYTHON_9.3). Функции Python задаются с помощью ключевого слова def, за которым идет имя функции и ее входные аргументы. Можно написать функцию Python, которая будет принимать любое число входных аргументов (в т.ч. их может и не быть). Значение возвращается из функции с помощью выражения return. Имя функции остаётся на ваш выбор (не используйте пробелы и не начинайте с цифр). Если функция с выражением return не возвращает значения, будет возвращено None. Помните, что отступы являются частью синтаксиса Python. Для определения каждого логического уровня используются четыре пробела. Приводите в соответствие начало и конец каждого блока, и будьте последовательны. Примеры кода – mathДля использования всех приведенных ниже математических примеров используйте тип выражения Python 3. Округлить значения поля до двух десятичных знаков. Используйте модуль math для конвертации метров в футы. Конвертация возводит в степень 2 и умножает на площадь. Вычисления полей с использованием логики PythonЛогические структуры могут быть включены в блок кода через выражения if, else и elif. Классифицировать на основании значений поля. Примеры кода – геометрияПомимо следующих примеров кода см. раздел Преобразование геометрических единиц, расположенный ниже, для получения дополнительной информации о преобразовании геометрических единиц. Вычислить площадь объекта. Вычислить максимальную x-координату объекта. Вычислить количество вершин объекта. Для точечного класса пространственных объектов сдвинуть x-координату каждой точки на 100. Информация о единицах измерения геометрииСвойства площади и длины в поле геометрии можно изменить с помощью типов единиц, обозначаемых знаком @.
Если данные хранятся в географической системе координат и поддерживаются линейные единицы (например, футы), вычисления длин будут конвертированы по геодезическому алгоритму. Внимание:Преобразование единиц площади в географическую систему координат даёт сомнительные результаты, так как десятичные градусы в разных частях глобуса имеют разную длину. Вычислить длину пространственного объекта в ярдах. Вычислить длину пространственного объекта в акрах. Геодезическая площадь и длина также может быть вычислена с помощью свойств geodesicArea и geodesicLength, с помощью символа @, следующего за ключевым словом единицы измерения. Вычисление геодезической длины пространственного объекта в ярдах. Вычисление геодезической площади пространственного объекта в акрах. Примеры кода – датыДату и время можно вычислить с помощью модулей datetime и time. Вычислить текущую дату. Вычислить текущие дату и время. Вычислить дату как 31 декабря 2000. Вычислить количество дней между текущей датой и значением в поле. Вычислить дату, прибавив 100 дней к значению даты в поле. Вычислить строку, представляющую дату, используя метод ctime в модуле datetime. В примере создается строка в формате: ‘Mon Feb 22 10:15:00 2021’. Вычислить день недели (например, воскресенье) для значения даты в поле. Вычислить отформатированную строку из поля даты, используя метод strftime модуля datetime и строку явного формата. В примере создается строка в формате: ’02/22/2021, 10:15:00′. Примеры кода – текстСтроковые вычисления могут выполняться с использованием различных шаблонов кодирования Python. Вернуть три самых правых символа. Заменить все вхождения заглавной буквы P на прописную p. Конкатенировать два поля, разделив их пробелом. Конвертация в нужный регистрВ этих примерах показаны различные способы конвертации слов таким образом, чтобы каждое слово начиналось с большой буквы, а остальные буквы были прописными. Регулярные выраженияМодуль Python re содержит операции сопоставления регулярных выражений, которые используются для сопоставления сложных примеров и правил замещения для строк. Замена St или St. перед новым словом в конце строки словом Street. Накопительные и последовательные вычисленияНакопительные и последовательные вычисления могут выполняться с использованием глобальных переменных. Вычислить последовательные идентификаторы ID или порядковые номера на основании интервала. Вычислить накопительные значения числового поля. Вычислить процентное приращение числового поля. Случайные значенияСлучайные значения можно получить с помощью модуля random. Используйте пакет numpy для вычисления случайных значений с плавающей точкой от 0.0 до 1.0. Используйте модуль random случайных чисел для вычисления случайных целочисленных значений от 0 до 10. Вычисление значений nullВ выражении Python пустые значения (null) можно вычислить, используя Python None. Следующее вычисление будет работать, только если поле может содержать нулевые значения. Используйте Python None для вычисления пустых значений. Связанные разделыОтзыв по этому разделу? Доказательства свойств модуля☰ Существуют следующие свойства модуля действительных чисел: 1) |a + b| ≤ |a| + |b|; 2) |ab| = |a| × |b|; 3) , a ≠ 0; 4) |a – b| ≥ |a| – |b|. Проведем доказательства, рассматривая различные случаи значений a и b. Доказательство 1) |a + b| ≤ |a| + |b|: Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b. Из этого следует, что |a + b| = |a| + |b|. Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a|. Выражение же |a| + |b| равно сумме абсолютных значений a и b, что больше, чем b – a. Поэтому |a + b| < |a| + |b|. Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b|, что также меньше суммы модулей |a| + |b|. Если a и b – отрицательные числа, то получим |–a – b|. Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b|). Но уже было доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|. Доказательство 2) |ab| = |a| × |b|: Доказательство 3) , a ≠ 0: Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/a. Если a – отрицательное число, то имеем . Взятие модуля в обоих выражениях приведет к делению единицы на абсолютное значение a. Значит эти выражения равны друг другу. Доказательство 4) |a – b| ≥ |a| – |b|: Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b|, потому что можно не брать модули вообще и тогда с двух сторон получим a – b. Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b|, что больше, чем |a| – |b|. Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b|, что больше, чем |a| – |b|. ASUS ROG Strix XG43UQ: 43-дюймовый монитор для игровых консолейКонсольное направление — совсем новое для игровых мониторов, но в нем уже появляются очень интересные модели. Как, например, ASUS ROG Strix XG43UQ — с поддержкой режима [email protected] и технологии AMD FreeSync Premium Pro. от 52 299 грн Предложений: 6
ДизайнПри диагонали экрана в 43 дюйма ASUS XG43UQ выглядит скорее как некрупный телевизор: если его использовать как монитор для ПК, то он займет собой большую часть типичного компьютерного стола. Но при этом в его внешнем виде явно прослеживаются элементы дизайна, характерные для игровой линейки ASUS – ROG (Republic of Gamers). Дисплей обрамлен рельефной рамкой средней ширины (~14 мм сверху и по бокам и ~23 мм — снизу) из черного матового пластика, стоит он на металлической V-образной подставке с широко расставленными «ногами». Подставка позволяет регулировать лишь угол наклона экрана (-5..10°) — изменения высоты экрана над уровнем стола или его поворотов влево-вправо здесь нет. Подставка опирается на столешницу тремя дисками с прорезиненным низом, так что монитор сдвинуть с места оказывается очень нелегко (в том числе и благодаря его массе — целых 15 кг). При желании ASUS ROG Strix XG43UQ можно повесить на стену — ножка у него съемная, а на тыльной стороне есть VESA-совместимое крепление (100х100). Тыльная панель — из белого матового пластика, с рядом вентиляционных отверстий в верхней части и большим рельефным лого ROG справа. Разъемы разделены на две «группы», как это часто бывает в телевизорах: одна из них ориентирована вбок, другая — вниз. Первая предназначена для быстрого подключения устройств, здесь можно найти два порта HDMI 2.0, USB-концентратор на два порта USB 3.0 и два мини-джека — для наушников и микрофона. Вторая спрятана за декоративной крышкой, что предполагает более редкий доступ к разъемам; тут находятся два порта HDMI 2.1, один DisplayPort 1.4, разъем питания и порт micro-USB для подключения отдельного модуля, который высвечивает на поверхности стола логотип ROG.
МенюДля навигации по меню используется джойстик и три аппаратные кнопки, расположенные на боковой панели в правом нижнем углу, сразу над кнопкой питания. В основном меню первый пункт — игровой раздел Gaming: тут находятся видеорежимы GameVisual, управление овердрайвом и AMD FreeSync, высветление теней ShadowBoost, включение технологии повышения четкости EMLB и т.д. Далее идут два пункта настройки графики — Image и Color (яркость, контрастность, HDR, гамма, насыщенность, цветовая температура), после них — пункт с ручным выбором видеовхода. В разделе Lighting Effect — управление RGB-подсветкой и активация Aura Sync (синхронизация подсветки с другими устройствами ASUS), в MyFavorite можно переназначить «горячие клавиши» (по умолчанию им присвоены переключение видеовходов и вызов меню GameVisual). И в последнем разделе, System Setup, находятся системные настройки вроде параметров работы экранного меню, поведения индикатора активности, включения технологии DSC, вывода информации о текущем видеорежиме, сброса всех настроек на заводские установки и т.д.
ФункциональностьВ ASUS ROG Strix XG43UQ используется 10-битная 43-дюймовая VA-панель с разрешением 4K. Плотность пикселей составляет ~112,5 PPI, размер точки — 0,2451 мм. Если использовать его как очень большой компьютерный монитор и сидеть за ним на типичном расстоянии от экрана в полметра или чуть больше, при большом желании увидеть отдельные точки можно, хоть и с трудом; но уже с расстояния в метр разглядеть их получится только у игроков с очень острым зрением. Максимальная частота обновления экрана при подключении по DisplayPort составляет 144 Гц при разрешении 4K – причем благодаря технологии Display Stream Compression этого удается достичь при использовании одного входа DP 1.4 и без применения ухудшающей качество изображения цветовой субдескритизации. Впрочем, этот режим будет востребован только у компьютерных игроков, зато консольные геймеры наверняка оценят поддержку [email protected] Гц при подключении по HDMI 2.1 – именно этот режим востребован в консолях текущего поколения от Sony и Microsoft. Хоть игр с его поддержкой пока и не очень много, тем не менее, оценить все преимущества высокой частоты обновления при 4K-разрешении на консоли PlayStation 5 можно в таких проектах, как, например, ремастер обеих частей Nioh, Destiny 2, Borderlands 3 или Call of Duty: Black Ops Cold War. ASUS ROG Strix XG43UQ поддерживает технологию AMD FreeSync Premium Pro, которая согласовывает частоту обновления экрана с выводом кадров в игре, устраняя расслоение изображения в динамичных сценах и сохраняя при этом максимальную частоту обновления. Premium Pro – самая «продвинутая» версия AMD FreeSync, и для ее полноценной поддержки дисплей должен обладать рядом дополнительных характеристик (частота обновления не ниже 120 Гц при разрешении не ниже Full HD, полноценная поддержка HDR-режима, низкая задержка ввода как в SDR, так и в HDR, а также работоспособность FreeSync на низких частотах обновления). Яркость в этом мониторе регулируется с помощью изменения силы тока, ШИМ не применяется на всем диапазоне яркости, так что мерцания подсветки у него нет. В то время как обычные телевизоры не могут похвастаться высокой отзывчивостью — задержка ввода в десятки миллисекунд у них обычное дело, ASUS ROG Strix XG43UQ в этом плане демонстрирует результаты на уровне хорошего игрового десктопного монитора. При использовании овердрайва и технологии повышения четкости в динамике Extreme Low Motion Blur (ELMB) заявленное время отклика этого монитора составляет 1 мс (MPRT). Впрочем, один типичный «телевизионный» атрибут у этого монитора все-таки есть — пульт ДУ; учитывая, что ASUS ROG Strix XG43UQ в первую очередь ориентирован на консольный гейминг и, соответственно, стоять он скорее всего будет на месте телевизора в гостиной, пульт ДУ окажется явно не лишним.
Качество изображения ASUS ROG Strix XG43UQВ мониторе используется полуматовое покрытие экрана, которое почти полностью устраняет паразитные блики и отражения, при этом минимально страдает от кристаллического эффекта (легкая зернистость на однотонных участках изображения, заметная на обычных матовых дисплеях). Равномерность черного очень хорошая, каких-то заметных светлых пятен на черном фоне разглядеть не получается; глубина черного цвета, благодаря использованию VA-панели, также оказывается просто отличной: увидеть легкое свечение в темном помещении можно, лишь значительно подняв яркость экрана. Glow-эффект у ASUS ROG Strix XG43UQ также минимален, при отклонении в сторону свечение черных участков изображения практически отсутствует. Углы обзора весьма хороши как для VA-панели: при отклонении в сторону несколько снижается насыщенность цветов, появляется умеренный теплый оттенок, а черный фон становится светлее, из-за чего темная картинка «сереет», а контрастные сцены становятся менее насыщенными — в целом, типичное поведение экрана, изготовленного по этой технологии. Минимальная яркость довольно высокая: в зависимости от режима, она составляет 85-95 кд/м²; в полной темноте этот экран будет ощущаться довольно ярким даже в комнате со слабым освещением. Максимальная яркость в обычном режиме составляет 840 кд/м² (что интересно, заявленная в технических характеристиках оказывается ниже — «всего» 750 кд/м²), в HDR поднимается еще выше – вплоть до 1000 кд/м². Этот результат, наряду с остальными характеристиками панели, позволил монитору получить сертификацию VESA DisplayHDR1000. Статическая контрастность, в зависимости от видеорежима и настроек яркости, может достигать 3600:1, что является очень хорошим результатом даже по меркам VA-панелей. Дисплей обладает расширенным цветовым охватом, покрывающим 92% пространства DCI-P3 (84% Adobe RGB и 125% sRGB), благодаря чему он выдает очень яркие, насыщенные цвета. В меню GameVisual представлен почти десяток различных видеорежимов, как типичных для десктопных мониторов (Кино, Пейзаж, sRGB), так и предназначенных для различных игровых жанров (гонки, RTS/RPG, FPS, MOBA). Все они отличаются различными графическими установками, и в большинстве из них оказываются заблокированы те или иные параметры в экранном меню. Полный доступ к ручным регулировкам (и при этом максимально универсальные настройки по умолчанию) предлагает пользовательский режим — именно его мы бы и рекомендовали использовать как основной, особенно если вы планируете подстраивать под себя не только яркость. В нем экран демонстрирует полный цветовой охват, значение гаммы в настройках мы бы рекомендовали устанавливать в 2,5 (по результатам измерений в этом случае получается практически идеальное соответствие стандартному значению 2,2) или, если захочется чуть высветлить тени и проявить «прячущуюся» там информацию — в 2,2 (реальное значение при этом оказывается чуть ниже, 2,1). Режим «Пользовательский»: Цветовая температура при изменении яркости меняется очень слабо: при выборе пользовательского значения в соответствующем параметре от 5700K на минимальной яркости и до 6100K — на максимальной; если изображение при этом будет казаться чересчур теплым, лучше переключиться в режим Warm, в котором температура почти идеально соответствует стандартной, 6500K. Установки Normal и Cool выдают заметно более холодную температуру (7900K и 10100K, соответственно). Равномерность подсветки, как для экрана такой диагонали, оказывается достаточно хорошей: верхняя и нижняя части дисплея показывают на 8-13% меньшую яркость, чем центральная зона. А вот с равномерностью цветовой температуры ситуация несколько хуже: перепад между правой частью экрана и нижним левым углом оказывается в районе 10%. В режиме sRGB цветовой охват сужается до 91% sRGB (68% Adobe RGB, 70% DCI-P3). Кроме того, ASUS ROG Strix XG43UQ проходит заводскую калибровку режима sRGB, так что среднее значение deltaE в нем оказывается меньше единицы: это отличный результат, с такими характеристиками этот монитор вполне можно использовать не только для игр, но и для работы с графикой. Тут же стоит отметить, что в пользовательском режиме точность цветопередачи также очень высока и почти не отличается от этого. Режим sRGB: Плюсы: Отличное качество изображения; быстрая и отзывчивая панель; VESA DisplayHDR1000; AMD FreeSync Premium Pro; поддержка [email protected] Гц по HDMI 2.1 и [email protected] Гц по DisplayPort 1.4Минусы: Стоимость Вывод: ASUS ROG Strix XG43UQ — «консольный» игровой монитор в формате телевизора. Он демонстрирует отличное качество изображения и минимальную задержку ввода, на уровне десктопных игровых моделей, а поддержка видеорежима [email protected] Гц при подключении по HDMI 2.1 делает его отличным выбором для работы в связке с консолями Sony PlayStation 5 и Microsoft Xbox Series X. Единственное, что при желании можно записать ему в «минусы» — это высокую стоимость.Технические характеристики
Решение более простых абсолютных уравнений | PurplemathPurplemathКогда мы берем абсолютное значение числа, мы всегда получаем положительное число (или ноль). Независимо от того, был ли вход положительным или отрицательным (или нулевым), выход всегда положительный (или нулевой). Например, | 3 | = 3 и | –3 | = 3 тоже. Это свойство — положительное и отрицательное превращение в положительное — делает решение абсолютных уравнений немного сложным.Но как только вы усвоите «трюк», они не так уж и плохи. Начнем с простого: MathHelp.comЯ уже решил эту проблему в своем обсуждении выше: Значит, x должно быть равно 3 или равно –3. Но как мне решить эту проблему, если я, , не знаю ответа? Я буду использовать свойство положительного / отрицательного абсолютного значения, чтобы разделить уравнение на два случая, и я буду использовать тот факт, что знак «минус» в отрицательном случае означает «противоположный знак», а не «отрицательное число». Например, если у меня x = –6, то «- x » означает «противоположность x » или, в данном случае, — (- 6) = +6, положительное число.Знак «минус» в «- x » просто указывает на то, что я меняю знак на x . Это означает, что , а не , означает отрицательное число. Это различие очень важно! Каким бы ни было значение x , взятие абсолютного значения x делает его положительным. Поскольку значение x изначально могло быть положительным, а может быть отрицательным, я должен признать этот факт, когда удаляю столбцы абсолютного значения.Я делаю это, разбивая уравнение на два случая. Для этого упражнения это следующие случаи: а. Если значение x было неотрицательным (то есть, если оно было положительным или нулевым) для начала, то я могу вывести это значение из столбцов абсолютного значения, не меняя его знака, давая мне уравнение x = 3. г. Если значение x изначально было отрицательным, то я могу вывести это значение из столбцов абсолютного значения, изменив знак на x , получив уравнение — x = 3, которое решает как х = –3. Тогда мое решение — Кстати, мы можем проверить это решение графически. Когда мы пытаемся решить уравнение абсолютных значений | x | = 3, мы, по сути, приравниваем два линейных уравнения друг другу и находим, где они пересекаются. Например: Выше я построил график y 1 = | x | (синяя линия, которая выглядит как «V») и y 2 = 3 (зеленая горизонтальная линия).Эти два графика пересекаются при x = –3 и x = +3 (две красные точки). Если вы хотите проверить свои ответы на тесте (перед тем, как сдать его), может быть полезно подключить каждую сторону исходного уравнения абсолютного значения в ваш калькулятор как их собственные функции; затем спросите у калькулятора точки пересечения. Конечно, любое решение также можно проверить, вставив его обратно в исходное упражнение и подтвердив, что левая часть (LHS) уравнения упрощается до того же значения, что и правая часть (RHS). уравнение.Вот мой чек для приведенного выше уравнения: Если вы когда-нибудь сомневаетесь в своем решении уравнения, попробуйте построить график или попробуйте снова вставить свое решение в исходный вопрос. Проверяю свою работу всегда нормально! Шаг выше, где уравнение абсолютного значения было переформулировано в двух формах, одна со знаком «плюс», а другая со знаком «минус», дает нам удобный способ упростить ситуацию: когда мы изолировали абсолютное значение и перейти к снятию стержней, мы можем разделить уравнение на два случая; мы обозначим эти случаи, поставив «минус» на противоположной стороне уравнения (для одного случая) и «плюс» на противоположной стороне (для другого).Вот как это работает:
Абсолютное значение выделено в левой части уравнения, поэтому я уже настроил его, чтобы разделить уравнение на два случая. Чтобы очистить столбцы абсолютного значения, я должен разделить уравнение на два возможных случая, по одному для каждого случая, если содержимое столбцов абсолютного значения (то есть, если «аргумент» абсолютного значения) отрицательное, и если он неотрицательный (то есть положительный или нулевой).Для этого я создаю два новых уравнения, единственное различие между которыми — это знак в правой части. Сначала сделаю «минусовый» случай: x + 2 = –7 x + 2 = –7 x = –9 Теперь я займусь неотрицательным случаем, когда я могу просто опустить столбцы и решить: Теперь мне нужно проверить свои решения.Я сделаю это, вставив их обратно в исходное уравнение, поскольку оценщик не видит, как я проверяю графики на моем графическом калькуляторе. Оба решения проверяют, поэтому мой ответ:
Во-первых, я выделю часть уравнения, относящуюся к абсолютным значениям; то есть, я получу само выражение абсолютного значения с одной стороны от знака «равно», а все остальное — с другой стороны: | 2 x — 3 | — 4 = 3 | 2 x — 3 | = 7 Теперь я очищу столбцы абсолютных значений, разделив уравнение на два случая, по одному для каждого знака аргумента.Сначала сделаю отрицательный случай: 2 x — 3 = –7 2 x = –4 x = –2 А затем сделаю неотрицательный случай: 2 x — 3 = 7 2 x = 10 х = 5 Это упражнение не говорит мне о проверке, поэтому я не буду.(Но, если бы я хотел, я мог бы вставить «abs (2X – 3) –4» и «3» в свой калькулятор (как Y1 и Y2, соответственно), и увидеть, что точки пересечения были на моем x -значения.) Мой ответ: URL: https://www.purplemath.com/modules/solveabs.htm неравенств | Безграничная алгебраВведение в неравенствоНеравенства используются для демонстрации отношений между числами или выражениями. Цели обученияОбъясните, что представляет собой неравенство и как оно используется Основные выводыКлючевые моменты
Ключевые термины
В математике неравенства используются для сравнения относительного размера значений.Их можно использовать для сравнения целых чисел, переменных и различных других алгебраических выражений. Ниже приводится описание различных типов неравенств. Строгое неравенствоСтрогое неравенство — это отношение между двумя значениями, когда они различны. Точно так же, как в уравнениях используется знак равенства =, чтобы показать, что два значения равны, в неравенствах используются знаки, чтобы показать, что два значения не равны, и для описания их взаимосвязи. Символы строгого неравенства: [latex] <[/ latex] и [latex]> [/ latex]. Строгие неравенства отличаются от обозначения [latex] a \ neq b [/ latex], что означает, что a не равно [latex] b [/ latex]. Символ [latex] \ neq [/ latex] не говорит о том, что одно значение больше другого или даже о том, что их можно сравнить по размеру. В двух типах строгих неравенств [latex] a [/ latex] не равно [latex] b [/ latex]. Для сравнения размеров значений существует два типа отношений:
Значение этих символов можно легко запомнить, заметив, что «большая» сторона символа неравенства (открытая сторона) обращена к большему числу. «Меньшая» сторона символа (точка) обращена к меньшему числу. Указанные выше отношения можно показать на числовой прямой. Вспомните, что значения на числовой строке увеличиваются по мере продвижения вправо.Следовательно, следующее представляет отношение [латекс] a [/ латекс] меньше, чем [латекс] b [/ латекс]:
[латекс] a[latex] a [/ latex] находится слева от [latex] b [/ latex] в этой числовой строке. и следующее демонстрирует, что [латекс] a [/ latex] больше, чем [latex] b [/ latex]:
[латекс] a> b [/ латекс][latex] a [/ latex] находится справа от [latex] b [/ latex] в этой числовой строке. В целом обратите внимание, что:
Другое неравенствоВ отличие от строгого неравенства, существует два типа отношений неравенства, которые не являются строгими:
Неравенства с переменнымиВ дополнение к отображению взаимосвязей между целыми числами, неравенства могут использоваться для отображения взаимосвязей между переменными и целыми числами. Например, рассмотрим [латекс] x> 5 [/ латекс]. Это будет читаться как «[latex] x [/ latex] больше 5 ″ и означает, что неизвестная переменная [latex] x [/ latex] может иметь любое значение больше 5, но не 5 сама по себе.Для визуализации этого см. Числовую строку ниже:
[латекс] x> 5 [/ латекс]Обратите внимание, что кружок над цифрой 5 не заполнен, что означает, что 5 не входит в возможные значения [latex] x [/ latex]. В качестве другого примера рассмотрим [латекс] x \ leq 3 [/ латекс]. Это будет читаться как «[latex] x [/ latex] меньше или равно 3 ″ и указывает, что неизвестная переменная [latex] x [/ latex] может иметь значение 3 или любое значение меньше 3. Для визуализации это, см. числовую строку ниже:
[латекс] x \ leq 3 [/ латекс]Обратите внимание, что кружок над цифрой 3 закрашен, что означает, что 3 входит в возможные значения [latex] x [/ latex]. Неравенства демонстрируются раскрашиванием стрелки в соответствующем диапазоне числовой линии, чтобы указать возможные значения [latex] x [/ latex]. Обратите внимание, что открытый кружок используется, если неравенство строгое (т. Е. Для неравенств, использующих [latex]> [/ latex] или [latex] <[/ latex]), а закрашенный кружок используется, если неравенство не является строгим ( т.е. для неравенств, использующих [latex] \ geq [/ latex] или [latex] \ leq [/ latex]). Решение проблем с неравенствомНапомним, что уравнения могут использоваться для демонстрации равенства математических выражений, включающих различные операции (например: [latex] x + 5 = 9 [/ latex]).Точно так же неравенства можно использовать для демонстрации взаимосвязи между различными выражениями. Например, рассмотрим следующие неравенства:
Каждое из них представляет связь между двумя разными выражениями. Одно из полезных применений неравенств, подобных этому, — в задачах, связанных с максимальными или минимальными значениями. Пример 1У Джареда есть лодка, максимальная масса которой составляет 2500 фунтов. Он хочет взять на лодку как можно больше друзей и предполагает, что он и его друзья в среднем весят 160 фунтов. Сколько людей могут одновременно кататься на его лодке? Эту проблему можно смоделировать с помощью следующего неравенства: [латекс] 160n \ leq 2500 [/ латекс] где [latex] n [/ latex] — это количество людей, которые Джаред может взять на лодку. Чтобы понять, почему это так, рассмотрим левую часть неравенства.Он представляет собой общий вес [латексных] n [/ латексных] людей весом 160 фунтов каждый. Неравенство гласит, что общий вес Джареда и его друзей должен быть на меньше или равен максимальному весу 2500, что является пределом веса лодки. Есть шаги, которые можно выполнить, чтобы решить такое неравенство. На данный момент важно просто понять значение таких утверждений и случаев, в которых они могут быть применимы. Правила разрешения неравенствАрифметические операции могут использоваться для решения неравенств для всех возможных значений переменной. Цели обученияРешите неравенства, используя правила работы с ними Основные выводыКлючевые моменты
Ключевые термины
Операции с неравенствамиКогда вы выполняете алгебраические операции с неравенствами, важно проводить точно такие же операции с обеих сторон, чтобы сохранить истинность утверждения. Каждая арифметическая операция подчиняется определенным правилам: Сложение и вычитаниеЛюбое значение [латекс] c [/ латекс] может быть добавлено или вычтено из обеих сторон неравенства. То есть для любых действительных чисел [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс]:
Пока одна и та же стоимость добавляется или вычитается с обеих сторон, результирующее неравенство остается верным. Например, рассмотрим следующее неравенство: [латекс] 12 <15 [/ латекс] Давайте применим описанные выше правила, вычтя 3 с обеих сторон: [латекс] \ begin {align} 12 — 3 & <15 - 3 \\ 9 & <12 \ end {align} [/ latex] Это утверждение все еще верно. Умножение и делениеВ свойствах, связанных с умножением и делением, указано, что для любых действительных чисел [latex] a [/ latex], [latex] b [/ latex] и ненулевое [latex] c [/ latex]: Если [latex] c [/ latex] положительное значение, то умножение или деление на [latex] c [/ latex] не меняет неравенства:
Если [latex] c [/ latex] отрицательно, то умножение или деление на [latex] c [/ latex] меняет неравенство:
Обратите внимание, что умножение или деление неравенства на отрицательное число изменяет направление неравенства. Другими словами, символ больше становится символом меньше, и наоборот. Чтобы увидеть применение этих правил, рассмотрим следующее неравенство: [латекс] 5> -3 [/ латекс] Умножение обеих сторон на 3 дает: [латекс] \ begin {align} 5 (3) &> -3 (3) \\ 15 &> -9 \ end {align} [/ latex] Мы видим, что это верное утверждение, потому что 15 больше 9. Теперь умножьте то же неравенство на -3 (не забудьте изменить направление символа, потому что мы умножаем на отрицательное число): [латекс] \ begin {align} 5 (-3) & <-3 (-3) \\ -15 & <9 \ end {align} [/ latex] Это утверждение также верно. Это демонстрирует, насколько важно изменить направление символа «больше» или «меньше» при умножении или делении на отрицательное число. Устранение неравенствРешение неравенства, которое включает переменную, дает все возможные значения, которые может принимать переменная, которые делают неравенство истинным.Решение неравенства означает преобразование его таким образом, чтобы переменная находилась с одной стороны символа, а число или выражение — с другой. Часто для преобразования неравенства таким образом требуется несколько операций. Сложение и вычитаниеЧтобы увидеть, как правила сложения и вычитания применяются к решению неравенств, примите во внимание следующее: [латекс] x — 8 \ leq 17 [/ латекс] Сначала выделите [латекс] x [/ латекс]: [латекс] \ begin {align} x — 8 + 8 & \ leq 17 + 8 \\ x & \ leq 25 \ end {align} [/ latex] Следовательно, [латекс] x \ leq 25 [/ latex] является решением [латекса] x — 8 \ leq 17 [/ latex].Другими словами, [latex] x — 8 \ leq 17 [/ latex] истинно для любого значения [latex] x [/ latex], которое меньше или равно 25. Умножение и делениеЧтобы увидеть, как применяются правила умножения и деления, рассмотрим следующее неравенство: [латекс] 2x> 8 [/ латекс] Делим обе стороны на 2, получаем: [латекс] \ begin {align} \ dfrac {2x} {2} &> \ dfrac {8} {2} \\ x &> \ dfrac {8} {2} \\ x &> 4 \ end {align } [/ латекс] Таким образом, выражение [latex] x> 4 [/ latex] является решением для [latex] 2x> 8 [/ latex].Другими словами, [latex] 2x> 8 [/ latex] верно для любого значения [latex] x [/ latex] больше 4. Теперь рассмотрим другое неравенство: [латекс] — \ dfrac {y} {3} \ leq 7 [/ латекс] Из-за отрицательного знака мы должны умножить его на отрицательное число, чтобы найти [латекс] y [/ latex]. Это означает, что мы также должны изменить направление символа: [латекс] \ begin {align} \ displaystyle -3 \ left (- \ frac {y} {3} \ right) & \ geq -3 (7) \\ y & \ geq -3 (7) \\ y & \ geq -21 \ end {align} [/ латекс] Следовательно, решение [latex] — \ frac {y} {3} \ leq 7 [/ latex] — это [latex] y \ geq -21 [/ latex].Таким образом, данное утверждение верно для любого значения [latex] y [/ latex], большего или равного [latex] -21 [/ latex]. ПримерРешите следующее неравенство: [латекс] 3л — 17 \ geq 19 [/ латекс] Сначала прибавьте 17 к обеим сторонам: [латекс] \ begin {align} 3y — 17 + 17 & \ geq 19 + 17 \\ 3y & \ geq 36 \ end {align} [/ latex] Затем разделите обе стороны на 3: [латекс] \ begin {align} \ dfrac {3y} {3} & \ geq \ dfrac {36} {3} \\ y & \ geq \ dfrac {36} {3} \\ y & \ geq 12 \ конец {align} [/ latex] Особые соображенияОбратите внимание, что было бы проблематично, если бы мы попытались умножить или разделить обе части неравенства на неизвестную переменную.Если какая-либо переменная [latex] x [/ latex] неизвестна, мы не можем определить, имеет ли она положительное или отрицательное значение. Поскольку правила умножения или деления положительных и отрицательных чисел различаются, мы не можем следовать этому же правилу при умножении или делении неравенств на переменные. Однако переменные можно складывать или вычитать с обеих сторон неравенства. Сложные неравенстваСоставное неравенство включает в себя три выражения, а не два, но также может быть решено, чтобы найти возможные значения переменной. Цели обученияРешите сложное неравенство, уравновесив все три компонента неравенства Основные выводыКлючевые моменты
Ключевые термины
Определение сложных неравенствСложное неравенство имеет следующий вид: [латекс] a На самом деле здесь есть два утверждения. Первый оператор [латекс] a Составное неравенство [латекс] a Рассмотрим [латекс] 4 Указанное выше неравенство по числовой прямой. Аналогичным образом рассмотрим [латекс] -2 Указанное выше неравенство по числовой прямой. Теперь рассмотрим [латекс] 1 Утверждение [латекс] 1 Чтобы найти возможные значения [latex] x [/ latex], нам нужно получить [latex] x [/ latex] отдельно: [латекс] 1 — 6 [латекс] -5 Следовательно, мы находим, что если [latex] x [/ latex] — любое число строго между -5 и 2, утверждение [latex] 1 Решите [латекс] -3 <\ dfrac {-2x-7} {5} <7 [/ latex]. Умножьте каждую часть, чтобы удалить знаменатель из среднего выражения: [латекс] -3 \ cdot (5) <\ dfrac {-2x-7} {5} \ cdot (5) <7 \ cdot (5) [/ латекс] [латекс] -15 <-2x-7 <35 [/ латекс] Изолировать [латекс] х [/ латекс] в середине неравенства: [латекс] — 15 + 7 <-2x -7 + 7 <35 + 7 [/ латекс] [латекс] — 8 <-2x <42 [/ латекс] Теперь разделите каждую часть на -2 (и не забудьте изменить направление символа неравенства!): [латекс] \ displaystyle \ frac {-8} {- 2}> \ frac {-2x} {- 2}> \ frac {42} {- 2} [/ латекс] [латекс] 4> x> -21 [/ латекс] Наконец, принято (хотя и не обязательно) писать неравенство так, чтобы стрелки неравенства указывали влево (т.е., чтобы числа шли от наименьшего к наибольшему): [латекс] -21 Неравенства с абсолютными значениями можно решить, рассматривая абсолютное значение как расстояние от 0 до числа на числовой прямой. Решите неравенства с абсолютным значением Рассмотрим следующее неравенство, которое включает абсолютное значение: [латекс] | x | <10 [/ латекс] Зная, что решение [latex] \ left | x \ right | = 10 [/ latex] равно [latex] x = ± 10 [/ latex], многие студенты отвечают на этот вопрос [latex] x <± 10 [/ latex ].Однако это неверно. Вот два разных, но оба совершенно правильных подхода к решению этой проблемы. Какие номера работают? То есть, для каких чисел [латекс] \ left | x \ right | <10 [/ latex] верное утверждение? Давай попробуем. 4 работы. -4 тоже. 13 не работает. Как насчет -13? Нет: Если [латекс] x = -13 [/ латекс], то [латекс] \ left | x \ right | = 13 [/ latex], что не менее 10. Играя с числами таким образом, вы сможете убедить себя, что работающие числа должны быть где-то между -10 и 10.Это один из подходов к поиску ответа. Другой способ — представить абсолютное значение как расстояние от 0. [latex] \ left | 5 \ right | [/ latex] и [latex] \ left | -5 \ right | [/ latex] равны 5, потому что оба числа — 5 от 0. В данном случае [латекс] \ left | x \ right | <10 [/ latex] означает «расстояние между [latex] x [/ latex] и 0 меньше 10». Другими словами, вы находитесь в пределах 10 единиц от нуля в любом направлении.Еще раз делаем вывод, что ответ должен быть между -10 и 10. Этот ответ можно визуализировать в числовой строке, как показано ниже, в которой выделены все числа, абсолютное значение которых меньше 10. Решение для [латекса] \ left | x \ right | <10 [/ latex]: Все числа, абсолютное значение которых меньше 10. Нет необходимости использовать оба этих метода; используйте тот метод, который вам легче понять. К более сложным задачам абсолютного значения следует подходить так же, как к уравнениям с абсолютными значениями: алгебраически выделить абсолютное значение, а затем алгебраически решить для [латекс] x [/ латекс]. Например, рассмотрим следующее неравенство: [латекс] \ влево | 2x \ вправо | + 3> 8 [/ латекс] Трудно сразу представить себе значение этого абсолютного значения, не говоря уже о самом значении [latex] x [/ latex]. Необходимо сначала выделить неравенство: [латекс] \ begin {align} \ left | 2x \ right | + 3 — 3 &> 8 — 3 \\ \ left | 2x \ right | &> 8 \ end {align} [/ латекс] А теперь подумайте о числовой прямой. В этих терминах это утверждение означает, что выражение [latex] 2x [/ latex] должно находиться более чем в 8 разрядах от 0.Следовательно, оно должно быть больше 8 или меньше -8. Выражая это неравенствами, имеем: [латекс] 2x> 8 [/ латекс] или [латекс] 2x <-8 [/ латекс] Теперь у нас есть 2 отдельных неравенства. Если каждая из них решается отдельно для [latex] x [/ latex], мы увидим полный диапазон возможных значений [latex] x [/ latex]. Рассмотрим их самостоятельно. Первый: [латекс] \ begin {align} 2x &> 8 \\ \ dfrac {2x} {2} &> \ dfrac {8} {2} \\ x &> 4 \ end {align} [/ latex] Секунда: [латекс] \ begin {align} 2x & <-8 \\ \ dfrac {2x} {2} & <\ dfrac {-8} {2} \\ x & <-4 \ end {align} [/ latex ] Теперь у нас есть два диапазона решений исходного неравенства абсолютных значений: [латекс] x> 4 [/ латекс] и [латекс] x <-4 [/ латекс] Это также может быть визуально отображено в числовой строке: Решение для [латекса] \ left | 2x \ right | + 3> 8 [/ latex]: Решение — любое значение [latex] x [/ latex] меньше -4 или больше 4. Решите следующее неравенство: [латекс] \ влево | x-2 \ вправо | + 10> 7 [/ латекс] Во-первых, алгебраически выделите абсолютное значение: [латекс] \ begin {align} \ left | x-2 \ right | + 10-10 &> 7-10 \\ \ left | x-2 \ right | &> — 3 \ end {align} [/ латекс] А теперь подумайте: абсолютное значение выражения больше –3. Чему могло быть равно выражение? 2 работы. –2 тоже работает. И 0. И 7. И –10. Абсолютные значения всегда положительны, поэтому абсолютное значение чего-либо больше –3! Поэтому все числа работают. Функция модуля дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения. В этом мини-уроке мы узнаем об определении модульной функции, вычислении модуля для чисел, переменных и многочленов, а также о решаемых примерах и вопросах о модульной функции. Попробуйте калькулятор функции mod, чтобы найти модуль числа!
Модуль функции, который также называется абсолютным значением функции, дает величину и абсолютное значение числа независимо от того, положительное или отрицательное число.Он всегда дает неотрицательное значение любого числа или переменной. Представляется как \ (\ begin {align} y = | x | \ end {align} \) или \ (\ begin {align} f (x) = | x | \ end {align} \) , где \ (\ begin {align} f: R \ rightarrow R \ end {align} \) и \ (\ begin {align} x \ in R \ end {align} \) \ (\ begin {align} | x | \ end {align} \) — это модуль \ (\ begin {align} x \ end {align} \), где \ (\ begin {align} x \ end { align} \) — неотрицательное число. Если \ (\ begin {align} x \ end {align} \) положительное значение, то \ (\ begin {align} f (x) \ end {align} \) будет иметь то же значение \ (\ begin {align } х \ конец {выравнивание} \).Если \ (\ begin {align} x \ end {align} \) отрицательно, то \ (\ begin {align} f (x) \ end {align} \) будет величиной \ (\ begin {align} х \ конец {выравнивание} \). Подводя итог вышеприведенным строкам, Это означает, что если значение \ (\ begin {align} x \ end {align} \) больше или равно 0, то функция модуля принимает фактическое значение, но если \ (\ begin {align} x \ end {align} \) меньше 0, тогда функция берет минус фактического значения ‘x’. Шаги по вычислению функций модуля приведены ниже. , если \ (\ begin {align} x = -3 \ end {align} \), то \ (\ begin {align} y = f (x) = f (-3) = — (-3) = 3 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) меньше 0 , если \ (\ begin {align} x = 4 \ end {align} \), то \ (\ begin {align} y = f (x) = f (4) = 4 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) больше 0 , если \ (\ begin {align} x = 0 \ end {align} \), то \ (\ begin {align} y = f (x) = f (0) = 0 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) равно 0 Подводя итог, можно сказать, что модуль отрицательного числа и положительного числа — это одно и то же число. Теперь давайте посмотрим, как построить график для функции модуля и найти ее домен и диапазон. Рассмотрим x как переменную, принимающую значения от -5 до 5 При вычислении модуля упругости для положительных значений ‘x’ линия на графике имеет вид ‘y = x’ , а для отрицательных значений «x» линия на графике имеет вид «y = -x». 2} \ end {align} \) Есть несколько других неотрицательных выражений, которые перечислены ниже.{2n} \ end {align} \) где \ (\ begin {align} n \ in Z \ end {align} \) \ (\ begin {align} y = 1 — sin \: x; y = 1 — cos \: x \: as \: sin \: x ≤1 \: и \: cos \: x ≤1 \ end { align} \) Signum функция определяется как математическая функция, которая дает знак действительного числа. Сигнум-функция выражается следующим образом. График сигнум-функции выглядит следующим образом. Комплексное число — это число, имеющее форму \ (\ begin {align} a + bi \ end {align} \), где ‘a’ и ‘b’ — действительные числа, а ‘i’ — мнимая единица.2} \ end {align} \) Функция модуля всегда возвращает неотрицательное число для всех действительных значений «x». Также некорректно приравнивать функцию модуля к отрицательному числу. \ (\ begin {align} | f (x) | = a; \: a> 0⇒f (x) = ± a \\ | f (x) | = a; \: a = 0⇒f (x ) = 0 \\ | f (x) | = a; a <0 \ end {align} \) Случай 1: (Если a> 0) Неравенство отрицательного числа \ (\ begin {align} | f (x) | Неравенство для положительного числа \ (\ begin {align} | f (x) |> a; a> 0 \ Rightarrow -a Случай 2: (Если <0) \ (\ begin {align} | f (x) | \ (\ begin {align} | f (x) |> a; a <0 \ Rightarrow \ end {align} \) - это действительно для всех реальных значений f (x). Если x, y — действительные переменные, то \ (\ begin {align} | -x | = | x | \ end {align} \) \ (\ begin {align} | x − y | = 0⇔x = y \ end {align} \) \ (\ begin {align} | x + y | ≤ | x | + | y | \ end {align} \) \ (\ begin {align} | x − y | ≥ || x | — | y || \ end {align} \) \ (\ begin {align} | xy | = | x | \ times | y | \ end {align} \) \ (\ begin {align} | \ dfrac {x} {y} | = \ dfrac {| x |} {| y |}; | y | \ neq 0 \ end {align} \) Теперь давайте рассмотрим некоторые решенные вопросы о модульных функциях, чтобы лучше понять их. Найдите модуль x для Раствор а) х = -4 \ (\ begin {align} | x | = | -4 | = — (-4) = 4 \ end {align} \) б) х = 6 \ (\ begin {align} | x | = | 6 | = 6 \ end {align} \) Для x = -4, \ (\ begin {align} | -4 | = 4 \ end {align} \) и для x = 6 \ (\ begin {align} | 6 | = 6 \ end {align} \) Решить \ (\ begin {align} | x + 3 | = 8 \ end {align} \) Раствор Сформируем два уравнения следующим образом. Корпус 1: Значение функции модуля отрицательное. \ (\ begin {align} | x + 3 | = 8 \ end {align} \) \ (\ begin {align} — | x + 3 | = 8 \ end {align} \) \ (\ begin {align} x + 3 = -8 \ end {align} \) \ (\ begin {align} x = -8 — 3 \ end {align} \) \ (\ begin {align} x = -11 \ end {align} \) Корпус 2: Значение функции модуля положительное. \ (\ begin {align} | x + 3 | = 8 \ end {align} \) \ (\ begin {align} x + 3 = 8 \ end {align} \) \ (\ begin {align} x = 8 — 3 \ end {align} \) \ (\ begin {align} x = 5 \ end {align} \) Следовательно, возможные значения x в модульной функции: \ (\ begin {align} x = 5, -11 \ end {align} \) Нарисуйте график для \ (\ begin {align} y = | x +2 | \ end {align} \) Раствор Согласно определению функции модуля, у нас есть \ (\ begin {align} y = | x + 2 | = x + 2, если \: x \ geq 1 \\ — 2 — x, если \: x <1 \ end {align} \) Изобразим таблицу с положительными и отрицательными значениями ‘x’. Построение графика с различными значениями \ (\ begin {align} x \ end {align} \) и \ (\ begin {align} -x \ end {align} \) мы получаем график для модуля функция, как показано ниже, Решить \ (\ begin {align} | 2x — 4 | = 5 — x \ end {align} \) Раствор Согласно определению функции модуля имеем В зависимости от функции модуля могут быть две возможности. Корпус 1: \ (\ begin {align} — | 2x — 4 | = 5 — x \ end {align} \) \ (\ begin {align} 2x — 4 = — (5 — x) \ end {align} \) \ (\ begin {align} 2x — 4 = -5 + x \ end {align} \) \ (\ begin {align} 2x — x & = -5 + 4 \\ x & = -1 \ end {align} \) Корпус 2: \ (\ begin {align} | 2x — 4 | = 5 — x \\ 2x — 4 = 5 — x \\ 2x + x = 5 + 4 \\ 3x = 9 \ x = 3 \ end {align} \)
Урок был посвящен увлекательной концепции модульной функции, ее области и диапазона.Надеюсь, вам понравилось их изучать. Просматривая решенные примеры и решая неэффективные вопросы, вы получите больше знаний по предмету. Вы также можете попробовать калькулятор функции модуля, чтобы проверить модуль числа. В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению. Уравнение, которое дает модуль или величину данного числа, называется уравнением модуля. Обозначается как y = | x |. Модуль означает определение положительного или отрицательного числа. Применение модуля к неотрицательному и отрицательному числу всегда приводит к одному и тому же числу. Взяв отрицательные значения, такие как (-1, -2, -3), и положительные значения, такие как (1,2,3), в соответствии с данным уравнением модуля, мы можем нарисовать функцию модуля. Функция модуля используется для определения величины положительного или отрицательного числа. Модуль положительного числа положительный. Модуль отрицательного числа получается игнорированием знака минус. Таким образом, модуль всегда положителен. Производная функции модуля равна x / | x |. Диапазон функции модуля — это набор всех неотрицательных чисел или просто (0, бесконечность). | x | всегда положительный, независимо от того, начали ли мы с + x или -x. | y | всегда положительный, независимо от того, начали ли мы с + y или -y. Сложив или вычтя их без абсолютных значений, вы получите один из четырех возможных результатов: (+ x) + (+ y) или (+ x) + (-y) или (-x) + (+ y) или (-x) + (-y) Поскольку оба имеют одинаковый знак (xy> 0), это первое утверждение всегда верно, оно верно даже для x> y во втором утверждении.Но второе утверждение, | x | — | y | = | x — y | тогда xy <0 кажется ложным. Сначала разберемся со сложением … Мы будем использовать x = 3 и y = 10 для наших примеров: Оба отрицательные: -3 + (-10) = -13. Оба положительных: 3 + 10 = 13. Итак, пока оба числа имеют одинаковый знак (именно это означает xy> 0), ответ будет ± 13. Как только вы поместите это в абсолютное значение, оба результата будут положительными 13 и | x | + | y | = | x + y | Значение | -3 | + | -10 | = 3 + 10 = 13 (отдельные значения абс.) И | (-3) + (-10) | = | -13 | = 13 (объединены в один абс) (13 = 13, так что работает) | x | + | y | = | х + у | если оба числа имеют одинаковый знак (xy> 0) Здесь оба числа положительные: | 3 | + | 10 | = 3 + 10 = 13 и | 3 + 10 | = | 13 | = 13 (13 = 13 так работает) С другой стороны, если одно положительное, а другое отрицательное, вы, по сути, вычитаете. Например -3 + 10 = 7 или 3 + (-10) = -7 С разными знаками вы получите +7 или -7 в зависимости от порядка вычитания. Если вы поместите любой из этих результатов в абсолютное значение, вы получите ПОЛОЖИТЕЛЬНЫЙ 7. Все четыре случая с вычитанием, когда x Оба положительных: | 3 | — | 10 | = 3 — 10 = -7 и вместе внутри | 3-10 | = | -7 | = 7 (-7 ≠ 7 так не получится!) Оба отрицательных: | -3 | — | -10 | = 3 — 10 = -7 и вместе внутри | -3 — (-10) | = | 7 | = 7 (-7 ≠ 7 так не получится!) Различных знаков (xy <0): Негатив «3» и положительный «10»: | -3 | — | 10 | = 3 — 10 = -7 и вместе внутри | -3 — 10 | = | -13 | = 13 (-7 ≠ 13 так не получится!) «10» негр и «3» поз: | 3 | — | -10 | = 3 — 10 = -7 и вместе внутри | 3 — (-10) | = | 3 + 10 | = 13 (-7 ≠ 13 так не получится!) Второй, | x | — | y | = | x — y | когда xy <0, не работает ни в одном из четырех случаев, пока x (примечание: | x | — | y | может дать отрицательный результат (когда | x | <| y |), а | x - y | всегда будет положительным) Но если мы потребуем, чтобы x> y, так что теперь x = 10 и y = 3, мы имеем это: Обе позиции: | 10 | — | 3 | = 10 — 3 = 7 и | 10 — 3 | = | 7 | = 7 (7 = 7 так работает) Оба негатива: | -10 | — | -3 | = 10 — 3 = 7 и | -10 — (-3) | = | -10 + 3 | = | -7 | = 7 (7 = 7 так работает) «10» отрицательных и «3» положительных: | -10 | — | 3 | = 10 — 3 = 7 и | -10 — (+3) | = | -13 | = 13 (7 ≠ 13, так что НЕ РАБОТАЕТ!) Положения «10» и отрицательные «3»: | 10 | — | — = 3 | = 10 — 3 = 7 и | 10 — (-3) | = | 10 + 3 | = | 13 | = 13 (7 ≠ 13, так что НЕ РАБОТАЕТ!) Итак, вторая формулировка исходной задачи, вероятно, должна содержать xy> 0 AND x> y. Я нашел это в Интернете — истинное утверждение: | x-y |> | x | — | y | для xy <0. Это НЕРАВЕНСТВО истинно, УРАВНЕНИЕ во второй строке неверно. Раздел неравенств QuickMath позволяет решить практически любое неравенство или систему неравенств в одной переменной.В большинстве случаев можно найти точные решения. Даже когда это невозможно, QuickMath может дать вам приблизительные решения практически с любым требуемым уровнем точности.
Кроме того, вы можете построить регионы, удовлетворяющие одному или нескольким неравенствам по двум переменным, четко видя, где происходят пересечения этих регионов. Вот несколько примеров неравенства: 2 х — 9> 0 х 2 — 3 х + 5 <= 0 | 5x — 1 | <> 5 х 3 + 1 <= 0 Команду Решить можно использовать для решения одного неравенства для одного
неизвестно на основной странице решения
или для одновременного решения системы многих неравенств в одном неизвестном на странице расширенного решения.2–5 <0 Другими словами, QuickMath попытается найти решения, удовлетворяющие сразу обоим неравенствам.
Перейти на страницу решения
Команда Plot из раздела Graphs построит график любого неравенства, связанного с
две переменные. Чтобы построить область, удовлетворяющую единственному неравенству
с участием x и y, перейдите к основному
страница построения неравенства, где вы можете ввести неравенство и указать
верхний и нижний пределы x и y, по которым вы хотите построить график
для.Продвинутый
Страница построения неравенства позволяет построить объединение или пересечение
до 8 регионов на одном графике. Вы можете контролировать такие вещи, как
или не показывать оси, где оси должны быть расположены и какой аспект
соотношение сюжета должно быть. Кроме того, у вас есть возможность показать каждый
отдельный регион самостоятельно. Уравнение говорит, что два выражения равны, а неравенство говорит
что одно выражение больше, больше или равно, меньше или
меньше или равно другому.Как и в случае с уравнениями, значение переменной для
что неравенство истинно, является решением неравенства, а множество всех
таких решений является множество решений неравенства. Два неравенства с
одинаковое множество решений являются эквивалентными неравенствами. Неравенства решаются с помощью
следующие свойства неравенства. СВОЙСТВА НЕРАВЕНСТВА Для действительных чисел a, b и c: (a) (Одно и то же число может быть добавлено к обеим сторонам неравенства без изменения
набор решений.) (Обе части неравенства можно умножить на одно и то же положительное число
без изменения набора раствора.) ПРИМЕЧАНИЕ Поскольку деление определяется в терминах умножения, слово
«умноженный» может быть заменен на «разделенный» на части (b) и (c) свойств
неравенства. Обратите особое внимание на часть (c): если обе стороны неравенства
умноженное на отрицательное число, направление символа неравенства должно быть
наоборот. Например, начиная с истинного утверждения — 3 <5 и умножая
обе стороны на положительное число 2 дают все еще верное заявление. С другой стороны, начиная с — 3 <5 и
умножение обеих сторон на отрицательное число -2 дает истинный результат только в том случае, если
направление символа неравенства меняется на обратное. При умножении или делении обеих сторон неравенства на минус
числа, мы должны изменить направление символа неравенства, чтобы получить
эквивалентное неравенство. ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично
линейное уравнение. Линейное неравенство по одной переменной — это неравенство, которое можно записать в виде
форма Пример 1 Теперь умножьте обе стороны на -1/3. (Мы также можем разделить на -3.) Поскольку -1/3 <
0, поменяйте направление символа неравенства на противоположное. Исходному неравенству удовлетворяет любое действительное число меньше 4.
множество решений можно записать как {x | x <4}. График множества решений показан на
Фигура 2.6, где скобки используются, чтобы показать, что 4 само по себе не принадлежит
к набору решений. Пример 2 Отныне решения всех неравенств будут записываться с интервалом
обозначение. Решить -2 <5 + 3m <20. Решение показано на Рисунке 2.8 Квадратичное неравенство — это неравенство, которое можно записать в виде Мы обсудим квадратичные неравенства в следующем разделе.
Перейти на страницу графика неравенств
CO-6: Применяйте основные концепции вероятности, случайной вариации и обычно используемых статистических распределений вероятностей. ЛО 6.22: Примените выборочное распределение выборочного среднего, как указано в Центральной предельной теореме (при необходимости). В частности, уметь идентифицировать необычные образцы из данной популяции. До сих пор мы обсуждали поведение статистической p-шляпы, доли выборки, относительно параметра p, доли генеральной совокупности (когда интересующая переменная является категориальной). Теперь мы переходим к исследованию поведения статистической шкалы x, выборочного среднего, по отношению к параметру μ (mu), генеральному среднему (когда интересующая переменная является количественной). Начнем с примера. Вес при рождении регистрируется для всех младенцев в городе. Средний вес при рождении составляет 3500 граммов, µ = mu = 3500 г. Если мы собираем множество случайных выборок по 9 младенцев за раз, как, по вашему мнению, будут вести себя выборочные средства? Здесь мы снова работаем со случайной величиной, поскольку случайные выборки будут иметь средства, которые непредсказуемо изменяются в краткосрочном периоде, но демонстрируют закономерности в долгосрочном периоде. Основываясь на нашей интуиции и на том, что мы узнали о поведении пропорций выборки, мы могли бы ожидать следующего относительно распределения выборочных средних: Центр : Некоторые средние образцы будут на низком уровне — скажем, 3000 граммов или около того — в то время как другие будут на высоком уровне, скажем, на 4000 граммов или около того.При повторной выборке мы можем ожидать, что случайные выборки будут иметь среднее значение в 3500 г. Другими словами, среднее значение выборки будет µ (мю), так же как среднее значение пропорции образца было p. Распространение : для больших выборок можно ожидать, что средние значения выборки не будут слишком сильно отклоняться от среднего значения генеральной совокупности, равного 3500. Выборка означает, что ниже 3000 или выше 4000 может вызвать удивление. Для меньших выборок мы были бы менее удивлены средними значениями выборки, которые немного варьируются от 3500.Другими словами, мы можем ожидать большей изменчивости средних значений выборки для меньших выборок. Таким образом, размер выборки снова будет играть роль в распределении показателей выборки, как мы наблюдали в отношении пропорций выборки. Форма : средние значения выборки, близкие к 3500, будут наиболее распространенными, а средние значения выборки, далеко от 3500 в любом направлении, постепенно менее вероятны. Другими словами, форма распределения средств выборки должна выпуклость в середине и сужение на концах, придавая ей некоторую нормальную форму.Это, опять же, то, что мы увидели, когда посмотрели на образцы пропорций. Комментарий: Давайте посмотрим на симуляцию: Результаты, полученные нами в ходе моделирования, неудивительны. Продвинутая теория вероятностей подтверждает это, утверждая следующее: Если повторяющиеся случайные выборки заданного размера n взяты из совокупности значений для количественной переменной, где среднее значение генеральной совокупности равно μ (мю), а стандартное отклонение генеральной совокупности равно σ (сигма), тогда среднее всех средних значений выборки (x -бар) — среднее значение μ (мю). Что касается разброса всех выборочных средних, теория определяет поведение гораздо точнее, чем утверждение, что для больших выборок разброс меньше. Фактически, стандартное отклонение всех средних значений выборки напрямую связано с размером выборки n, как указано ниже. Поскольку квадратный корень из размера выборки n появляется в знаменателе, стандартное отклонение действительно уменьшается с увеличением размера выборки. Давайте сравним и сопоставим то, что мы теперь знаем о выборочных распределениях для выборочных средних и выборочных пропорций. Теперь мы исследуем форму выборочного распределения выборочных средних. Когда мы обсуждали выборочное распределение пропорций выборки, мы сказали, что это распределение является приблизительно нормальным, если np ≥ 10 и n (1 — p) ≥ 10. Другими словами, у нас были рекомендации, основанные на размере выборки для определения условий в что мы могли бы использовать вычисления нормальной вероятности для пропорций выборки. Когда распределение выборочных средних станет примерно нормальным? Это зависит от размера выборки? Кажется разумным, что совокупность с нормальным распределением будет иметь выборочные средние, которые нормально распределены даже для очень маленьких выборок.Мы видели это в предыдущем моделировании с выборками размером 10. Что произойдет, если распределение переменной в генеральной совокупности сильно искажено? Имеют ли выборочные средства также искаженное распределение? Если мы возьмем действительно большие выборки, станут ли средние выборки распределенными более нормально? В следующем моделировании мы исследуем эти вопросы. Подводя итог, можно сказать, что распределение выборочных средних будет приблизительно нормальным, пока размер выборки достаточно велик.Это открытие, вероятно, является самым важным результатом, представленным на вводных курсах статистики. Формально она сформулирована как Центральная предельная теорема . Мы будем снова и снова полагаться на Центральную предельную теорему, чтобы производить вычисления нормальной вероятности, когда мы используем выборочные средства для того, чтобы делать выводы о среднем по генеральной совокупности. Теперь мы знаем, что можем сделать это, даже если распределение населения ненормальное. Какой большой размер выборки нам нужен, чтобы предположить, что выборочные средние будут нормально распределены? Что ж, это действительно зависит от распределения населения, как мы видели в моделировании.Общее практическое правило состоит в том, что выборки размером 30 или более будут иметь довольно нормальное распределение независимо от формы распределения переменной в генеральной совокупности. Комментарий: Прежде чем приступить к работе с примерами, давайте сравним и сопоставим то, что мы теперь знаем о выборочных распределениях для выборочных средних и выборочных пропорций. Размер домохозяйства в США составляет в среднем 2,6 человека и стандартное отклонение 1,4 человека. Должно быть ясно, что это распределение искажено вправо, поскольку наименьшее возможное значение — это домохозяйство из 1 человека, но самые большие домохозяйства действительно могут быть очень большими. (a) Какова вероятность того, что в случайно выбранном домохозяйстве более 3 человек? Здесь не следует использовать нормальное приближение, поскольку распределение размеров домохозяйств будет значительно смещено вправо. У нас недостаточно информации для решения этой проблемы. (b) Какова вероятность того, что средний размер случайной выборки из 10 домохозяйств больше трех? По любым меркам 10 — это небольшой размер выборки.Центральная предельная теорема не гарантирует, что среднее значение выборки, полученное из искаженной совокупности, будет приблизительно нормальным, если размер выборки не велик. (c) Какова вероятность того, что средний размер случайной выборки из 100 домохозяйств больше трех? Теперь мы можем применить центральную предельную теорему: даже несмотря на то, что распределение размера домохозяйства X искажено, распределение среднего размера домохозяйства по выборке (x-столбец) приблизительно нормально для большого размера выборки, такого как 100.Его среднее значение совпадает со средним значением генеральной совокупности, 2,6, а его стандартное отклонение — это стандартное отклонение генеральной совокупности, деленное на квадратный корень из размера выборки: Найти мы стандартизируем от 3 до z-значения, вычитая среднее значение и деля результат на стандартное отклонение (среднего по выборке). Затем мы можем найти вероятность с помощью стандартного обычного калькулятора или таблицы. Домохозяйства, состоящие из более чем 3 человек, конечно, довольно распространены, но было бы крайне необычно, если бы средний размер выборки из 100 домохозяйств был бы больше 3. Цель следующего упражнения — дать инструкции по нахождению выборочного распределения выборочного среднего (x-bar) и использовать его, чтобы узнать о вероятности получения определенных значений x-bar. math / -inf math / abs math / acos math / acosh math / asin math / asinh math / atan math / atan2 math / atanh math / cbrt math / ceil math / cos math / cosh math / e math / erf math / erfc math / exp math / exp2 math / expm1 math / floor math / gamma math / hypot math / inf math / int-max math / int-min math / int32-max math / int32-min math / log math / log10 math / log1p math / log2 math / nan math / next math / pi math / pow math / random math / rng math / rng-buffer math / rng-int math / rng-uniform math / round math / seedrandom math / sin math / sinh math / sqrt math / tan math / tanh math / trunc Звонкие согласные — это звуки, которые состоят из голоса и шума. Выясним, что такое звонкие согласные звуки в русском языке. Рассмотрим, как образуются звонкие согласные звуки, какими они бывают и чем отличаются от глухих согласных. Наша речь состоит из законченных по смыслу и интонационно отрезков, которые называются предложениями. Каждое предложение строится из отдельных слов, а слова в свою очередь состоят из звуков. Звук является минимальной единицей речи, как слово и предложение. Звуки по своему качеству бывают разные. Те звуки, в образовании которых участвует только голос, так и называются — гласные. Это звуки [а], [о], [у], [э], [и], [ы], которые произносятся открытым голосом. Остальные звуки нашей речи являются шумными. Но шумят они по-разному. Те звуки, которые произносятся с участием голоса и шума, являются звонкими. При их образовании воздух проходит через голосовые связки на выдохе и заставляет их дрожать, вибрировать. Эту вибрацию голосовых связок можно ощутить, если положить руки на горло. Если заткнуть уши, то при произношении звонких согласных возникает звон в ушах. При произношении глухих согласных, которые состоят только из шума, такого колебания голосовых связок и звона в ушах не ощущается. Определение Звонкие согласные — это шумные звуки речи, в образовании которых шум преобладает над голосом. В фонетике русского языка насчитывается 20 звонких звуков, которые в письменной речи обозначаются 11 буквами: Большинство букв, обозначающих звонкие согласные, находятся в начале алфавита. Как видим, многие звонкие согласные образуют пары по признаку мягкости/твёрдости. Все звонкие согласные различаются по признаку мягкости/твердости, кроме всегда твёрдого звонкого согласного [ж] и всегда мягкого (палатального) звука [й’]. Произношение мягкого и твёрдого согласного различается положением языка. При образовании мягкого согласного средняя спинка языка выгибается к нёбу говорящего. Мягкость и твёрдость звонких согласных зависит от их фонетической позиции в слове. Если после них находятся гласные [а], [о], [у], [э], [ы], то согласные произносятся твёрдо. Если же после согласных пишутся буквы «е», «ё», «и» ,»ю», «я», «ь», то при произношении слов звонкие согласные звучат мягко: У перечисленных звонких согласных имеются парные глухие согласные. Глухие согласные образуют пару с подобными им звонкими согласными. Только в их образовании почти нет голоса, а преобладает шум. В русском языке, кроме рассмотренных парных согласных, существуют непарные звонкие согласные, которые произносятся с большей долей голоса, чем шума. Их называют термином «сонорные», который восходит к греческому слову sonorus, что значит «звучный». Как становится ясно из их названия, сонорные согласные в силу своей природы не имеют пары по признаку звонкости/глухости. Эту группу согласных составляют 9 звуков, обозначенных в письменной речи буквами: Сонорные звуки, кроме [й’], составляют пары между собой по признаку твёрдости/мягкости. Понаблюдаем: Они не меняют своего качества звучания и не зависят от фонетической позиции в слове. Остальные звонкие согласные подвержены влиянию глухих согласных. Их качество меняется в зависимости от местонахождения в слове. Рассмотрим эти фонетические процессы подробнее. Звонкие согласные, если стоят в конце слова, находятся в слабой фонетической позиции и подвергаются оглушению. При произношении они заменяются парными им глухими согласными: Если звонкий согласный находится перед глухим, то аналогично для него это слабая фонетическая позиция. Звонкий подвергается воздействию глухого согласного и уподобляется ему, то есть меняет свое качество и звучит приглушённо. Происходит ассимиляция звонкого согласного звука (лат. assimilatio — «уподобление», «сопоставление») по признаку глухости/звонкости. Понаблюдаем: Согласные звуки самостоятельно не образуют фонетический слог, а только в паре с гласными звуками. В русском языке различаем звонкие (с участием тона — звука) и глухие (только с шумом) согласные. Влияние последующего согласного на качество предыдущего называется регрессивной ассимиляцией, это, например, оглушение или озвончение согласных в русском языке.водъм ], с городом [з горъдъм] Укажите, какие из этих букв обозначают звонкие, а какие глухие звуки. Назовите к ним соответствующие парные звуки. /в/, /ж/, /ч/, /т/, /м/, /р/, /с/, /б/, /к/, /х/, /ц/ Слушайте и пишите слоги Перепишите в транскрипции Сегóдня я пойдý с дрýгом в парк.гзáл тóч’нъ] Ключ Урок был подготовлен с использованием следующей литературы: [1]Оливериус, З. Фонетика русского языка. Praha : SPN, 1978. 164 c.
[2]Брызгунова, Е. А. Звуки и интонации русской речи. Москва : Русский язык, 1977. 279 с.
[1]Бархударова, Е. Л. – Панков, Ф. И. По-русски с хорошим произношением. Практический курс звучащей речи. Москва : Русский язык,
2008. 192 с. ISBN 978- 5-88337-160-7.
[2]Одинцова, И. В. Звуки. Ритмика. Интонация. Москва : Наука, 2008. 368 с. ISBN 978- 5-02-002762-6.
[3]Лизалова, Л. И. Упражнения по фонетике современного русского языка. Брно : МУ, 1991. 78 с.
Звонкие и глухие согласные: Парные Звонкие Глухие Б П В Ф Г К Д Т Ж Ш З С Непарные Л, М, Н, Р, Й (сонорные) Х, Ц, Ч, Щ Твердые и мягкие согласные: Парные Перед А, О, У, Ы, Э – твердые. Твердые Мягкие бук б б‘ бег вал в в‘ висок год г г‘ гид дом д д‘ день зал з з‘ земля кора к к‘ кит лом л л‘ лиса мак м м‘ мера нос н н‘ нёс парк п п‘ пир рубль р р‘ рис сом с с‘ сено тон т т‘ тень фон ф ф‘ фен халва х х‘ химия Непарные ж, ш, ц ч, щ, й В русском языке 21 согласная буква и 36 согласных звуков. Согласные буквы и соответствующие им согласные звуки: Согласные звуки делятся на звонкие и глухие, твёрдые и мягкие. Они бывают парные и непарные. Всего 36 различных комбинаций согласных по парности-непарности твёрдых и мягких, глухих и звонких: глухих — 16 (8 мягких и 8 твёрдых), звонких — 20 (10 мягких и 10 твёрдых). Согласные бывают твёрдыми и мягкими. Они делятся на парные и непарные. Парные твёрдые и парные мягкие согласные помогают нам различать слова. Сравните: конь [кон’] — кон [кон], лук [лук] — люк [л’ук]. Для понимания объясним «на пальцах». Если согласная буква в разных словах означает либо мягкий, либо твёрдый звук, то звук относится к парным. Например, в слове кот буква к обозначает твёрдый звук [к], в слове кит буква к обозначает мягкий звук [к’]. Получаем: [к]-[к’] образуют пару по твёрдости-мягкости. Нельзя относить к паре звуки для разных согласных, например [в] и [к’] не составляют пару по твёрдости-мягкости, но составляет пара [в]-[в’]. Если согласный звук всегда твёрдый либо всегда мягкий, то он относится к непарным согласным. Например, звук [ж] всегда твёрдый. В русском языке нет слов, где бы он был мягким [ж’]. Так как не бывает пары [ж]-[ж’], то он относится к непарным. Согласные звуки бывают звонкие и глухие. Благодаря звонким и глухим согласным мы различаем слова. Сравните: шар — жар, кол — гол, дом — том. Глухие согласные произносятся почти с прикрытым ртом, при их произнесении голосовые связки не работают. Для звонких согласных нужно больше воздуха, работают голосовые связки. Некоторые согласные звуки имеют схожее звучание по способу произношения, но произносятся с разной тональностью — глухо или звонко. Такие звуки объединяются в пары и образуют группу парных согласных. Соответственно, парные согласные — это пара из глухой и звонкой согласной. Сонорные — звонкие непарные согласные звуки. Сонорных звуков 9: [й’], [л], [л’], [м], [м’], [н], [н’], [р], [р’]. Шипящие согласные звуки (4): [ж], [ч’], [ш], [щ’]. Согласные звуки (мягкие и твёрдые, глухие и звонкие) делятся на парные и непарные. Выше в таблицах показано деление. Обобщим всё схемой: Чтобы уметь делать фонетический разбор, помимо согласных звуков нужно знать гласные звуки и правила фонетики. Слова с буквой ё обязательно пишите через ё. Фонетические разборы слов «все» и «всё» будут разными! Русский язык. 2 класс. Урок 56. Как отличить звонкие согласные звуки от глухих? Цель: Задача: На уроке мы узнаем: мы научимся: мы сможем: Тезаурус Звонкие согласные звуки – это звуки, в образовании которых участвуют и голос, и шум. Глухие согласные звуки – это звуки, которые создаются только одним шумом, без участия голоса. Парные по звонкости-глухости согласные звуки – это звуки, которые могут озвончаться или оглушаться в зависимости от положения в слове. Основная и дополнительная литература по теме урока Канакина В. П., Горецкий В. Г. Русский язык. Учебник. 2 класс. В 2 ч. Ч. 2. — М.: Просвещение, 2018. – С. 16 – 19. Канакина В. П. Русский язык. Рабочая тетрадь. 2 класс. В 2 ч. Ч. 2. — М.: Просвещение, 2018. – С. 10-18. Канакина В.П., Щеголёва Г.С. Русский язык. 2 класс. Контрольные работы. В 2 ч. Ч. 2. – М.: Просвещение, 2018. — С. 35 — 40. Канакина В. П. Русский язык. 2 класс. Тетрадь учебных достижений. – М.: Просвещение, 2017. – С. 46 — 47. Канакина В. П. Русский язык. Раздаточный материал. Пособие для учащихся. 2 класс. – М.: Просвещение, 2018. — С. 36. Тихомирова Е.М. Тренажёр по русскому языку к учебнику В.П. Канакиной, В. Г. Горецкого «Русский язык. 2 класс. В 2 ч.» ФГОС (к новому учебнику) – М.: Издательство «Экзамен», 2018. — С.55-60. Тихомирова Е.М. Тесты по русскому языку. 2 класс. В 2 ч. Ч. 2: к учебнику В.П. Канакиной, В. Г. Горецкого «Русский язык. 2 класс. В 2 ч. Ч. 1.» ФГОС (к новому учебнику) – М.: Издательство «Экзамен», 2017. — С. 14 — 21. Русский язык: предварительный контроль: текущий контроль: итоговый контроль: 2 класс: учебное пособие для общеобразовательных организаций / О. Е. Курлыгина, О. О. Харченко. – М.: Просвещение: УчЛит, 2018. — С. 60-63. Открытые электронные ресурсы по теме урока Канакина В. П. и др. Русский язык. 2 класс. Электронное приложение. — М.: Просвещение, 2011. Ссылка для скачивания: http://catalog.prosv.ru/attachment/ca950bac-d794-11e0-acba-001018890642.iso Теоретический материал для самостоятельного изучения. Мир наполнен разнообразными звуками. Звучат вода и солнце, звучит лес, тишина тоже звучит. И человек тоже живёт со звуками. Только звуки, издаваемые человеком, за многие тысячелетия выстроились в определённом порядке и стали словами. По мнению учёных, в русском языке всего 42 звука. Различаются они тем, как работает наш речевой аппарат при их произнесении. Следует заметить, что у него есть несколько «инструментов», которые помогают нам произносить звуки по-разному. Это губы, зубы, язык, нёбо, голосовые связки. От действий каждого «инструмента» зависит, каким будет произносимый звук. В произношении многих звуков принимают участие голосовые связки. Все гласные звуки образуются только с участием голоса. Однако для произношения чуть больше половины согласных звуков нужен голос. Из 36 согласных звуков русского языка, без голоса произносятся 16, а вот для того, чтобы услышать оставшиеся 22 звука, голосовые связки необходимы. Конечно, согласные звуки, которые произносятся с голосом, звучат ярче и звонче, чем другие согласные звуки. Поэтому их и назвали «звонкими согласными звуками». А вот другие согласные звуки, в образовании которых голос участия не принимает, назвали «глухими». Значит, чтобы определить тип согласного звука – звонкий или глухой – достаточно узнать, участвуют ли голосовые связки в образовании этого звука. Но как распознать это? А нужно просто почувствовать, работают ваши голосовые связки или нет. Известно, что голосовые связки – это мышцы и связки, которые расположены в гортани, в области шеи. Когда мы заставляем эти связки и мышцы работать, то они колеблются, и мы слышим звонкий звук. Почувствовать, работают ли голосовые связки, мы можем, приложив к шее ладонь. Попробуйте это сделать и произнесите звук [З]. Чувствуете, как «вибрирует» шея? Это работают голосовые связки. Определяем: звук [З] — звонкий. А теперь произнесите звук [С]. Никакого движения вы не почувствовали. Это значит, что в образовании звука [С] голосовые связки не участвуют. Определяем: звук [С] — глухой. Проверим этот способ на других звуках. Положи на шею ладонь. Произноси [Б] [Б] [Б]. Шея «вибрирует» – звук звонкий. Произноси [Т] [Т] [Т]. Голосовые связки не работают – звук глухой. А как же работают другие «инструменты» речевого аппарата при образовании звонких и глухих согласных звуков? Давайте проведем эксперимент. Произнесите звонкий согласный звук [Б]. Обратите внимание на то, что активно при этом работают губы. Они плотно смыкаются, а потом размыкаются, выпуская струю воздуха. Произнесите ещё раз: [Б] [Б] [Б]. А теперь произнесите глухой согласный звук П. Проследите, как работают губы. Произнесите ещё раз: [П] [П] [П]. Не правда ли, они двигаются так же, как при произношении звука Б. Произнесите попеременно: [Б] [П] [Б] [П] [Б] [П]. Обратите внимание, что губы двигаются одинаково. А вот голос то звучит, то «отдыхает». Такие звуки легко произносить друг за другом, в паре, то «включая», то «выключая» голос. Такие согласные звуки назвали парными. Но есть и звуки, которые такой пары не имеют. Их назвали непарными. Эта информация о согласных звуках представлена в специальной таблице. Чтобы легче было выучить парные и непарные согласные звуки, можно запомнить пары букв, которые обозначают эти звуки. Таких пар всего 6. Запомните их! Б — П, В –Ф, Г – К, Д – Т, З – С, Ж – Ш. Не забывайте, что многие буквы обозначают два звука — мягкий и твёрдый согласный звук. С первого класса вам знакомы глухие и звонкие, парные и непарные согласные звуки. Сегодня мы не просто вспомнили об этом. Мы увидели особенности работы речевого аппарата человека, из-за которых звуки получаются такими похожими и такими разными. Узнавать новое о знакомом можно бесконечно! Один восточный старец сказал: «Мудрый человек знает, что он знает мало. И только глупец думает, что он знает всё»». А как думаете вы? Примеры заданий и разбор их решения. Тренировочный модуль Задание. Выдели красным цветом буквы. Выделите красным цветом буквы, которые обозначают в этих словах звонкие согласные звуки. Черничный пирог, шерстяной свитер. Подсказка: Определите, какой согласный звук в слове звонкий, какой глухой. Правильный ответ: Черничный пирог, шерстяной свитер. Задание. Подчеркни слова. Подчеркните слова, в которых все согласные звуки глухие. КОШКА, ЛАМПА, ГРИБ, ПОСТ, КОФТА, БАНОЧКА, БАБОЧКА, ВХОД, КОСА, УШКО, СЛАДКИЙ Подсказка: Определите, какие согласные звуки есть в слове. Если все согласные звуки в слове глухие, то подчеркни его. Правильный ответ: КОШКА, ЛАМПА, ГРИБ, ПОСТ, КОФТА, БАНОЧКА, БАБОЧКА, ВХОД, КОСА, УШКО, СЛАДКИЙ. Русский язык. 3 класс № 27 Раздел. Слово и слог. Звуки и буквы. Тема. Звуки и буквы. Согласные звуки. Перечень вопросов, рассматриваемых в теме Знать и называть согласные звуки, понимать, различать звонкие и глухие, твёрдые и мягкие звуки, шипящие звуки, которые являются опознавательным признаком орфограммы, учиться правильно писать слова. Тезаурус по теме (перечень терминов и понятий, введенных на данном уроке) Однокоренные слова, родственные слова, корень слова, согласный, твёрдый, мягкий, звонкий, глухой, шипящий. Планируемые результаты На этом уроке Узнаем: Научимся: Теоретический материал для самостоятельного изучения Рассмотрим схему. Что вы можете рассказать по этой схеме? Как видно из схемы, согласные звуки в русском языке делятся на звонкие и глухие, твёрдые и мягкие, парные и непарные. Сегодня на уроке повторим все, что знаем о согласных звуках, будем различать звонкие и глухие, твёрдые и мягкие звуки, шипящие звуки, которые являются опознавательным признаком орфограммы, учиться правильно писать слова. Звонкие согласные произносятся с участием шума и голоса: [н], [н’], [м], [м’], [л], [л’], [р], [р’], [й’], [б], [б’], [в], [в’], [г], [г’], [д], [д’], [ж], [з’], [з]. При произнесении глухих согласных звуков слышится только шум: [п], [п’], [ф], [ф’], [к], [к’], [т], [т’], [с], [с’], [х], [х’], [ц], [ч’], [ш] [щ’]. Некоторые глухие и звонкие согласные образуют пары. Такие согласные называются парными по глухости-звонкости звуками. Согласные твердые парные по глухости-звонкости Согласные мягкие парные по глухости-звонкости [б] [п] [б’] [п’] [в] [ф] [в’] [ф’] [г] [к] [г’] [к’] [д] [т] [д’] [т’] [з] [с] [з’] [с’] [ж] [ш] — — Остальные согласные звуки называются непарными по глухости-звонкости. Непарные звонкие согласные звуки: [л], [л’], [м], [м’], [н], [н’], [р], [р’], [й’]. Согласные звуки русского языка могут быть твёрдыми и мягкими. Звуки образуют пары по твердости и мягкости. [б] -[б’], [в] — [в’], [г] -[г’], [д] — [д’], [з] -[з’], [к] — [к’], [л] — [л’], [м] — [м’], [н] — [н’], [п] — [п’], [р] — [р’], [с] — [с’], [т] — [т’], [ф] — [ф’], [х]-[х’] Есть только твёрдые звуки: [ц], [ш], [ж]. Есть только мягкие звуки: [щ`], [ч`], [й`]. Мягкость согласных звуков обозначается на письме буквами е, ё, ю, я, и, а также мягким знаком (ь). Твёрдость согласных звуков обозначается буквами а, о, у, ы, э. Согласных звуков в русском языке больше, чем гласных. Слова создаются при помощи звуков: гласных и согласных. Обратим внимание на интересную роль согласных в речи. Звуки сами по себе словами не являются (если это не предлог, не междометие, не союз и т.д.), но иногда смысл слова закрепляется за отдельным звуком, входящим в это слово. Так случилось, например, со звуком [р], который входит в слова гром, гремит, гроза, раскаты, грохот. Теперь слова с этим звуком используются для передачи этих явлений. Например, в произведении Ф. Тютчева «Весенняя гроза» использованы слова с этим звуком, чтобы нарисовать картину весенней грозы. Люблю грозу в начале мая, Интересны по этому поводу рассуждения великого русского актёра М.А. Чехова: «Человек глубокой древности жил в тесном и близком общении со своим окружением. Он слышал раскаты грома и делал усилия их понять. Он искал звук, подобный раскатам грома. Он начинал имитировать их, и его речь все с большей отчётливостью формулировала звук [р]. Другой мир открывался ему во всём том, что лилось, наливалось, летело, цвело, ласкало..» И вот такой пример звукописи в стихотворении М. Лермонтова: Русалка плыла по реке голубой, Вспомним, чтобы правильно обозначить согласный звук буквой, необходимо знать некоторые правила. Помни! Согласный парный – это признак правила, которое нужно будет исполнить. Написание буквы, обозначающей парный по глухости-звонкости согласный звук на конце слова или перед глухим согласным, надо проверять: ду[п]ки – дубок, лу[к] – луковый или луга, гара[ш] – гаражи. Для того чтобы узнать, какая буква пишется, к проверяемому слову нужно подобрать проверочное слово. Проверяемое слово – это слово, в котором проверяется написание буквы, обозначающей парный по глухости-звонкости согласный звук на конце слова или в корне слова перед другим парным согласным: грибки, серп, скрипка, ветка, дорожка, союз, скользкий, морж, просьба. Проверочное слово – это слово, в котором проверяемая буква находится перед гласным звуком или непарным звонким согласным звуком [н]: грибок, серпик, скрипочка, веточка, дорожный, союзы, скользить, моржи, просить. Чтобы подобрать проверочное слово надо: В проверочном и проверяемом словах согласный звук обозначается одной и той же буквой. Разбор заданий Укажите наиболее полное правило проверки звонкой – глухой согласной в слове. Правильный ответ Надо изменить форму слова или подобрать однокоренное слово так, чтобы проверяемая буква находилась перед гласным звуком или непарным звонким согласным звуком. Укажите проверочное слово к слову сладкий. Правильный ответ Сладость. Укажите слово, в котором пишется буква б. 5. Су… Правильный ответ Улыбка. Повышенный уровень. Прочитайте слова. Определите, какое из слов соответствует заданным параметрам. В слове 4 звука, 4 буквы; первый и четвёртый являются парными согласными. Правильный ответ Флаг. В русском языке 21 согласная буква и 37 согласных звуков: Согласные звуки бывают твёрдые и мягкие, звонкие и глухие. Мягкость звука в транскрипции обозначается [‘ ]. Твёрдый согласный звук получается, если после согласной стоит гласная А, О, У, Ы или Э: на, ло, ку, мы, фэ. Мягкий согласный звук получается, если после согласной стоит гласная Е, Ё, И, Ю или Я: бе, лё, ки, ню, ля. Мягкость согласных звуков также обозначается с помощью мягкого знака — Ь. Сам мягкий знак звука не обозначает. Он пишется после согласной буквы и вместе с ней обозначает один мягкий согласный звук: рысь [рыс’], огонь [огон’], вьюга [в’й’уга]. Большинству согласных букв соответствует два звука: твёрдый и мягкий, такие согласные называются парными. Парные согласные по твёрдости — мягкости: Но есть согласные буквы, которым соответствует только один из звуков: твёрдый или мягкий. Такие согласные называются непарными. Непарные твёрдые согласные (всегда твёрдые): Ж [ж], Ш [ш], Ц [ц]. Непарные мягкие согласные (всегда мягкие): Ч [ч’], Щ [щ’], Й [й’]. В русском языке есть долгий звонкий мягкий звук [ж’]. Он встречается в небольшом количестве слов и получается только при произнесении сочетаний букв жж, зж, жд: вожжи, дребезжать, дождь. Согласные звуки можно разделить на глухие и звонкие. Глухие согласные звуки — это звуки, при произношении которых не используется голос. Они состоят только из шума. Например, звуки: [с], [ш], [ч’]. Звонкие согласные звуки — это звуки, при произношении которых используется голос, то есть они состоят из голоса и шума. Например, звуки: [р], [ж], [д]. Некоторые звуки составляют пару: звонкий — глухой, такие звуки называются парными. Парные согласные по глухости — звонкости: Непарные звонкие согласные: Й, Л, М, Н, Р. Непарные глухие согласные: Х, Ц, Ч, Щ. Звуки [ж], [ш], [ч’], [щ’] называются шипящими согласными звуками. Звуки [ж] и [ш] — это непарные твёрдые шипящие согласные звуки: железо [жэл’эзо], шесть [шэст’]; но в сочетаниях жи, ши не пишется буква ы. Сочетания жи, ши всегда пишутся с буквой и: живот, гаражи, шило, карандаши. Звуки [ч’] и [щ’] — это непарные мягкие шипящие согласные звуки: часы [ч’асы], щука [щ’ука], но в сочетаниях ча, ща пишется буква а, а в сочетаниях чу, щу пишется буква у: чашка, площадь, чулок, щука. Звуки [з], [з’], [с], [с’], [ц] называются свистящими согласными звуками. Буква Й (и краткое) обозначает звук [й’]: рай [рай’]. Буква Й пишется: йод, йогурт. лайка, майка, кофейник. рай, май, твой. Звук [й’] встречается чаще буквы Й, так как он появляется в словах, где нет буквы Й, но есть гласные Я, Е, Ю и Ё. Рассмотрим, в каких случаях звук [й’] встречается в словах, не содержащих букву Й: яма [й’ама]. твоё [твой’о]. въезд [вй’эзд]. льёт [л’й’от]. ульи [ул’й’и].
Фонетики (изучающие звучание человеческого голоса) делят согласные на два типа: звонкие и глухие. Звонкие согласные требуют использования голосовых связок для создания характерных звуков; глухие согласные — нет. Оба типа используют дыхание, губы, зубы и верхнее небо для дальнейшего изменения речи. В этом руководстве представлены различия между звонкими и глухими согласными и даны несколько советов по их использованию.
Ваши голосовые связки, которые на самом деле являются слизистыми оболочками, проходят через гортань в задней части горла.Когда вы говорите, напрягаясь и расслабляясь, голосовые связки регулируют поток дыхания, выдыхаемого из легких.
Самый простой способ определить, озвучен согласный или нет, — это приложить палец к горлу. Когда вы произносите букву, почувствуйте вибрацию голосовых связок. Если вы чувствуете вибрацию, значит согласный — звонкий.
Это звонкие согласные: B, D, G, J, L, M, N, Ng, R, Sz, Th (как в слове «затем»), V, W, Y и Z.
Но если согласные — это только отдельные буквы, что такое Ng, Sz и Th? Это обычные звуки, которые производятся путем фонетического смешения двух согласных.
Вот несколько примеров слов, в состав которых входят звонкие согласные:
Глухие согласные не используют голосовые связки для создания своих жестких перкуссионных звуков.Вместо этого они вялые, позволяя воздуху свободно течь из легких в рот, где язык, зубы и губы взаимодействуют, модулируя звук.
Это глухие согласные: Ch, F, K, P, S, Sh, T и Th (как в слове «вещь»). Общие слова, использующие их, включают:
Озвучиваются гласные звуки (A, E, I, O, U) и дифтонги (комбинации двух гласных звуков).Сюда также входит буква Y, когда она произносится как длинная E.
Примеры: город, жалость, суровость.
Когда согласные объединяются в группы, они могут изменить качество голоса следующего за ним согласного. Прекрасный пример — прошедшая простая форма правильных глаголов. Вы можете узнать эти глаголы, потому что они заканчиваются на «ed». Однако согласный звук этого окончания может измениться с звонкого на глухой, в зависимости от предшествующего ему согласного или гласного.Практически во всех случаях E молчит. Вот правила:
Этот узор также можно встретить во множественном числе. Если согласный перед буквой S произносится, буква S будет произноситься фонетически как буква Z. Примеры: стулья, машины, сумки.
Если согласный, предшествующий S, глухой, то S также будет произноситься как глухой согласный. Примеры: летучие мыши, парки, трубы.
При разговоре предложениями конечные согласные звуки могут изменяться в зависимости от следующих слов.Это часто называют связной речью.
Вот пример изменения с озвученного B в слове «клуб» на безголосый P из-за озвученного T в «to» следующего слова: «Мы пошли в клуб, чтобы встретиться с друзьями».
Вот пример замены звонкого D прошедшего простого глагола на глухой T: «Мы играли в теннис вчера днем».
Английский язык состоит из 24 согласных звуков и 21 согласной.Что касается произношения этих согласных, мы делим их на 2 категории: звонкие и глухие согласные. Имейте в виду, что некоторые согласные звуки представляют собой комбинацию букв (например, ch или th ). К счастью, мы пишем 16 из 24 согласных звуков, используя только их собственные буквы! Этих гораздо проще запомнить, правда? ч / б / ж / ж / ч / ч / р / р / Д / Д / В / В / М / м / Вт / в / P / p / S / s / N / n / G / g / т / т / з / з / л / л / к / к / (Остальные 8 согласных звуков: / θ / / ð / / ʃ / / ʒ / / ʈʃ / / dʒ / / j / / ŋ /) 11 из этих 16 звуков, перечисленных выше, озвучены , .Это означает, что мы используем наши голосовые связки для создания звуков: (Другие звонкие согласные: / ð / / ʒ / / j / / ŋ /) Как узнать, произносишь ли ты согласную? Если вы кладете руку на горло, когда издаете эти звуки, вы должны почувствовать движение голосовых связок. Посмотрите это видео, чтобы узнать, как определить, озвучен ли согласный, и узнайте, почему это вообще важно! 5 из 16 согласных, перечисленных выше, не используют голосовые связки: (Остальные 8 согласных: / θ / / ʃ / / ʈʃ /; звук / h / называется «глухой голосовой щелевой звук», что означает, что вы издаете звук движением голосовых связок, но это не так. не озвучен.) В этих случаях, когда вы кладете руку на горло, вы не чувствуете никаких вибраций при произнесении этих звуков. Это первый звук в: да, год, еще, молодой, ты, университет, отряд Это средний звук в: красивый, вид Чтобы воспроизвести звук / j / или «y», приподнимите среднюю часть языка к центру неба, не касаясь его.Откройте рот, чтобы произнести звук «y» и следующую за ним гласную. Совет: The / j / Это похоже на краткое / i / или / ɪ /, за которым быстро следует гласная, однако ваш язык будет ближе к небу, чем при воспроизведении / i / или / ɪ /. Совет для говорящих по-испански: Этот звук часто вызывает проблемы у говорящих по-испански, но по сути это тот же звук, который вы слышите в начале hielo, hiato или iónico . Студенты ESL обычно путали этот звук с / ʤ / или пропускали его. Произносится: Да, в этом году у вас будет прекрасный вид. Звук «нг» — звонкий носовой согласный звук, производимый спинкой языка, касающейся мягкого неба; воздух выходит из носа. Не отпускайте язык, когда произносите g . В американском английском нельзя опускать последние g в слове с окончанием -ing. Однако вы также не должны произносить его слишком много. Многие изучающие английский путают / ŋ / с / n / и / nk / Вам нужна дополнительная помощь с произношением? Чтобы узнать больше о произношении английского языка, получить необходимую обратную связь и попрактиковаться в разговоре, присоединяйтесь к SpeakUp, динамичной программе, которая вовлекает вас в подлинное общение на актуальные темы и предоставляет вам обратную связь от профессионального и опытного учителя английского языка.Фактически, первая неделя бесплатна для вас! Звонкие согласные — это согласные звуки, которые производятся путем вибрации голосовых связок. Их можно сравнить с глухими согласными. Безмолвные согласные не используют голосовые связки для создания своих жестких перкуссионных звуков. Вместо этого они расслаблены, позволяя воздуху свободно течь из легких в рот, где язык, зубы и губы взаимодействуют, модулируя звук. Подробнее о звонких и глухих согласных звуках см. Ниже. Звонкие согласные звуки: b, d, g, j, l, m, n, ng, r, sz, th, v, w, y, z. Глухие согласные звуки: ch, h, f, k, p, s, sh, t, th. Давайте теперь перейдем к глухим согласным и рассмотрим несколько примеров. Продолжайте изучать EnglishBix, чтобы получить больше ресурсов, чтобы улучшить английский язык. Поговорим об озвучивании. Звонкие и глухие пары. Первые 8 полей ниже показывают символы согласных звуков IPA для звонких и глухих пар согласных. Невозвученный согласный означает отсутствие вибрации или голоса из голосового аппарата при произнесении звука. Примеры глухих согласных звуков: / s /, / p / и / t /. Звонкий согласный означает, что при произнесении звука из голосового аппарата доносится голос или вибрация. Примеры звонких согласных звуков: / v /, / b / и / g /. Согласная пара — это когда положение рта, необходимое для произнесения двух звуков, одинаково, но один звук остается глухим, а другой — звонким. Мы сложили в коробку озвученную и глухую пары. Помните, что положение рта у пары точно такое же, с той лишь разницей, что один озвучен, а другой нет. Например, положение рта, необходимое для произнесения звуков / p / и / b /, точно такое же, / p / не имеет голоса, а / b / озвучивается. / f / и / v / требуют точно такой же позиции рта, / f / незвучен, а / v / озвучен. Обновите свои согласные звуки ipa символов теперь с помощью инструментов ниже. СОВЕТЫ ПО ПЕРЕСМОТРЕНИЮ СОГЛАСНЫХ ЗВУКОВ СИМВОЛЫ IPA С ПРИМЕРАМИ Не беспокойтесь об озвучивании. На самом деле не очень важно, насколько ваш английский понятен слушателям. Вам нужно сосредоточиться на положении вашего рта. Четко ли вы произносите каждую согласную? Обращайте особое внимание на согласные звуки в конце слов. Согласные звуки в конце слов очень важны для четкой речи на английском языке. Например, произнося / k / в слове «back», убедитесь, что вы четко слышите звук / k / в конце.Он сильный или напряженный, но в нем нет необходимости. Согласные звуки — звонкие и глухие пары с международными фонетическими символами — IPA С меткой: Сравнение Вы когда-нибудь замечали, что окончание Z в словах типа «цветы» [flaˈʊ əɹz] больше похоже на букву S? Узнайте, как облегчить определенные окончания, чтобы произносить их легко и естественно. YouTube заблокирован? Нажмите здесь, чтобы посмотреть видео. Видео Текст: В этом видео с произношением в американском английском мы поговорим об окончании звонких и глухих согласных. В американском английском есть озвученные и глухие звуки. Все гласные озвучены. Озвучены все дифтонги. Согласные могут быть звонкими или глухими. Невозвратные согласные получаются из воздуха, без звука голосовых связок. Например, hh, sh, tt, pp. Звонкие согласные действительно имеют в себе голос, например: mm, bb, zh. Хх, ш, тт, стр. Есть много пар согласных, у которых положение рта одинаковое, и одна звонкая, а другая незвучная, например, CH / JJ. Время от времени я получаю комментарий к видео с вопросом о произношении этих парных согласных в конце слова. Они исходят от людей с хорошим слухом, которые обращают внимание на то, что слышат. В основном говорят: «Я не слышу звонкую согласную, я слышу глухую согласную».Они правы. Мы собираемся затронуть здесь довольно сложную тему. Он имеет дело с тонкими различиями в звуке. Возьмем, например, слово «цветы». В IPA мы пишем это так: конечная согласная — это звук Z, который озвучивается. Но на самом деле это звучит как буква S в конце, не так ли? Цветы, сс, сс. Действительно слабая, легкая S. У нее нет сильных S-цветов. Это не так. Но у него также нет сильной буквы Z, flowerzzz. Цветы, сс, сс. На самом деле у него очень слабый S. Несколько лет назад я читал старую книгу по произношению, в которой говорилось, что в этих парах озвученный / глухой голос сильный, а звонкий — слабый. Я действительно не понимал, что это значит, пока не начал думать о том, чтобы закончить согласные. Эти конечные согласные настолько слабые, что мы убираем из них голос, и в конечном итоге они звучат как слабые глухие звуки. Таким образом, это слово не flowerssss или flowerzzz, а flowers, ss, ss, слабый глухой согласный. Давайте взглянем еще на несколько слов. Dive, ff, ff. Это действительно очень слабое F [f]. Это не divvve или difffe, а dive, ff, ff. Гараж, ш, ш, ш. Это очень слабый глухой звук SH. Это не гарасшш или гаражжх, а, гараж, ш, ш, ш. Знак, ч, ч, гл. Очень слабый, глухой звук. Не партия или баДГЭ, а бейдж, гл. Ослабление этих конечных звонких согласных поможет вам произносить слова более легко и естественно. Давайте еще немного изучим слово «значок» и сравним его со словом «партия».Значок, партия. Окончание «бейджа» слабое. Значок. Окончание «партии» сильнее. ‘Партия’. Это не единственная разница. Невозвученное окончание также делает гласную немного короче. Значок, партия. Они звучат по-разному. Во-первых, окончание «партии» сильнее. Значок, партия. CH, CH вместо ch, ch. Кроме того, в слове «значок» гласная длиннее. В таких минимальных парах гласные немного длиннее перед звонкими окончаниями. Итак, у вас есть две подсказки, которые помогут понять, что это за слово: сила окончания и длина гласной. Но бывает время, когда слабая концовка становится сильнее. Вы знаете, когда это будет? Это когда мы связываем его со словом, начинающимся с гласной или дифтонга. В связи между согласными и гласными полезно думать о конечном согласном как о начале следующего слова. Так что, если вы думаете об этом как о начальном согласном, он становится намного сильнее. Вернемся к слову «цветы» и включим его во фразу «цветы на столе». Цветы, цветы. Теперь я слышу более чистый звук Z, zon [3x].Цветы на. Это сильнее, чем когда слово было в конце предложения. Я люблю цветы. сс, сс, сс. Цветы на, zz, zz, zz. Так что, если окончание, слабый звонкий согласный соединяется с гласным, это уже не так уж и плохо. Эта тема была довольно сложной. Так что, если вы не понимаете, не волнуйтесь. Если да, подумайте о том, чтобы облегчить окончание звонких согласных, и посмотрите, поможет ли это облегчить произношение этих слов. Если есть слово или фраза, с которыми вы хотите помочь с произношением, укажите их в комментариях ниже.Кроме того, я очень рад сообщить вам, что моя книга теперь в продаже. Если вам понравился этот видеоролик, вы можете узнать больше о произношении американского английского, и моя книга поможет вам шаг за шагом. Вы можете получить его, нажав здесь или в описании ниже. Вот и все, и большое спасибо за использование Рэйчел английского. Видео: НОВОЕ ВИДЕО: Звонкие согласные Вы когда-нибудь задумывались о различиях между звонкими и глухими согласными? Вы когда-нибудь мечтали о том, чтобы произносить звонкие и глухие звуки правильно и правильными словами? В этом посте я сосредоточусь на звонких согласных и покажу вам, как произносятся звонкие согласные и в каких словах они появляются. Итак, поехали. Основное различие между звонкими и глухими согласными состоит в том, что звонкие согласные образуются путем соединения ваших голосовых связок. Возможно, единственный способ почувствовать разницу и почувствовать разницу — это сравнить звонкие согласные с глухими. Так, например: Z — это один из многих звонких согласных, и если вы вытащите пальцы здесь, прямо на гортань, и произнесете звук «zzz… zzz…» (послушайте видео), тогда вы должны почувствовать, что там это шум от ваших пальцев, и это потому, что ваши голосовые связки сходятся вместе, и голосовые связки превращают дыхание в вибрацию.Мы бы назвали это звонким согласным. В то время как глухой согласный — это звук, похожий на S. И снова, если вы положите пальцы здесь на гортань и скажете S, ‘sss … sss …’ (послушайте видео), то по сравнению с вашими пальцами происходит очень мало . На самом деле мы не должны ничего чувствовать. Это просто дыхание, которое прерывается. Итак, это глухой согласный. И таких пар много. Если вы не чувствовали, что еще один способ сделать это — засунуть пальцы в уши, так что вставьте оба пальца в уши, и еще раз, если вы скажете «zzz» и «sss», вы должны почувствовать это на ушах. Z есть ощущение, что внутри вашей головы и внутри вашего горла гудит, но на S нет ничего, кроме дыхания.Z и S — отличный пример разницы между звонкими и глухими согласными. Вот в чем разница между звонкими и глухими звуками. И есть много звонких согласных, так что взгляните на это и попробуйте (послушайте видео): Итак, звонкий согласный получается путем объединения ваших вокальных падений для создания вибрации, и вы можете почувствовать это, положив руку на гортань или засунув пальцы в уши.А правильное использование звонкого согласного и правильных слов может иметь большое значение с точки зрения понимания людьми английского языка. Итак, я надеюсь, что вы нашли это полезным, и не забудьте нажать «Нравится», если вы хотите снова легко найти это видео. И подумайте о подписке на мой канал на YouTube, потому что я публикую здесь еженедельные видео каждый вторник в 8:30 по Гринвичу (по местному лондонскому времени). На следующей неделе будет вторая часть звонких и глухих звуков, в которой мы рассмотрим глухие согласные, так что подписывайтесь и настраивайтесь. И если вы хотите узнать больше об исправлении наиболее часто неправильно произносимых согласных звуков, нажмите на эту ссылку, где вы можете загрузить бесплатный пятидневный аудиокурс, который поможет понять, как произносить эти часто неправильно произносимые согласные. И если вы хотите узнать больше о произношении, артикуляции, акценте и разговоре по-английски, а также о уверенном и понятном способе, убедитесь, что вы подписались на этот блог. Вы искали решите уравнение x 4 x 6 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решите уравнение x 6 2 x 4, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «решите уравнение x 4 x 6 2». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как решите уравнение x 4 x 6 2,решите уравнение x 6 2 x 4,решите уравнение х 4 х 6 2,решить уравнение x 2 x 4 6,решить уравнение x 4 6 x 2,решить уравнение x 6 x 4,х 4 х 6 2. Решить задачу решите уравнение x 4 x 6 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Математика, 4 класс Урок № 27. Перечень вопросов, рассматриваемых в теме: — как решать уравнения вида: x∙ 8 = 26 + 70, x : 6 = 18 ∙ 5, 80 : x = 46 – 30 — какой алгоритм решения данных уравнений? Глоссарий по теме: Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой. Алгоритм — последовательность действия (шагов) Решить уравнение – это значит найти такое значение неизвестного числа, при котором равенство будет верным. Основная и дополнительная литература по теме урока: 1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2017. – с.80 2. Моро М.И., Волкова С.И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.34,35 3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.44-45. 4. Волкова С.И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с.40-41. 5. Кочергина А.В. Учим математику с увлечением (Методическая библиотека). М.: 5 за знания, 2007. – с.159. Теоретический материал для самостоятельного изучения Вспомните, как связаны между собой числа при умножении. Посмотрите, множитель 20, множитель 3, произведение 60. Если 60 разделить на 20, получится 3. Если 60 разделить на 3, получится 20. Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей. 20 ∙ 3 = 60 60 : 20 = 3 60 : 3 = 20 Решим уравнение: произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель. Как его найти? Для нахождения неизвестного первого множителя надо произведение 91 разделить на известный множитель 7. Делим 91 на 7 — получаем 13. Выполним проверку. 13 умножить на 7 получим 91. Получили верное равенство: 91 равно девяносто одному. Значит, решили правильно. А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка. Вспомним, как связаны между собой числа при делении. Посмотрите: делимое 15, делитель 3, частное равно пяти. Если делитель 3 умножить на частное 5, получим делимое 15. Если делимое 15 разделить на частное 5, получим делитель 3. 15 : 3 = 5 3 ∙ 5 = 15 15 : 5 = 3 Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения. Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3. А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно. Задания тренировочного модуля: 1.К каждой позиции первого столбца подберите соответствующую позицию второго. 91 : х = 13 x = 20 х : 21=4 x = 7 24 ∙x = 96 x = 84 x∙ 3 = 60 x = 4 Правильный ответ: 91 : х = 13 x = 7 х : 21= 4 x = 84 24 ∙x = 96 x = 4 x∙3 = 60 x = 20 2. 7 ∙x = 140 : 2 Варианты ответов: 10, 400, 2 Правильный вариант: 10 3.Решите уравнение, подчеркните правильный ответ: (80 : у) ∙ 700 = 2800 Варианты ответов: 2, 4, 20 Правильные варианты: 20 Отметим на координатной прямой точки:
Рассмотрим решения уравнения на промежутках (-∞; 1]; (1; 2]; (2; 3] и (3; +∞).
где P(x), Q(x) — многочлены.
Пример
Решить уравнение
Решение:
x2=4, х≠ 2.
х=-2 или х=2.
Число 2 не может быть корнем.
Ответ: -2.
а) |x|+4=1; |x-5|=2; |x+3|=-6. б) |1+x|=3; |1-x|=-4; 8+|x|=2.
Решение:
а) |5x|=15; б) |2x|=16.
Решение:
а) |5x+1|=5; б) |2x-1|=10.
а) |5x2+3x-1|=-x2-36; б) |3x2-5x-4|=-4x2-23.
Решение:
а) х2-6|x|=0; б) х2+4|x|=0.
Ответ: -6; 0; 6.
а) х2-3|x|+2=0; б) х2-2|x|+1=0.
а) |x-2|+|x-4|=5; б) |x-1|-|x-4|=6.
Ответ: 0,5; 5,5.
а) |3- |4- |x|||=5; б) 8-|2 -|x|||=3.
3x-7<0: х2-3x-10=0; D=9+40=49, x1=5, x2=-2.
а) |3x-1|=5; б) |4-2x|=1?
2. Решите уравнение:
а) |3x|=21; б) |2x|=-12.
3. Решите уравнение:
а) |2x-5|=1; б) |3x+6|=18.
4. Решите уравнение:
5. Решите уравнение:
6. Решите уравнение:
7. Решите уравнение:
8. Решите уравнение:
9. Решите уравнение:
а) 3(x-1) = |2x-1|; б) |5-2x|=|x+4|.
10. Решите уравнение:
а) |х2+x|=12; б) |х2-3x|=10. Оператор expand раскроет скобки и разложит выражение, например expand (x – 1)(x2+x+1) приведёт выражение к x3 -2x +1. Оператор partial fractions разложит отношение многочленов в сумму простейших дробей. minimize минимизирует функцию, а maximize максимизирует Число «Пи» записывается, как pi Тригонометрические функции: sin, cos, tan, ctan, arcsin, arccos, arctan, arcctan Команда series раскладывает функцию в ряд, например: taylor series sinx at x=0 даст нам разложение функции sin(x) в ряд Тейлора в точке x=0 Чтобы найти предел, необходимо в начале функции подставить lim, а после записать саму функцию, в конце указать к чему стремится предел: as-> далее число (бесконечность записывается infinity). Оператор factor раскладывает число на множители ! выводит факториал, например 123! Оператор gcd выводит наибольший общий делитель, например gcd 164, 88 выводит наибольший общий делитель чисел 164 и 88 Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти. В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению. Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство. Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6. Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой. Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева. Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни. Решить уравнение значит найти все возможные корни или убедиться, что их нет. Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство. Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль. Что поможет в решении: Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа. Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством. Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Как решаем: 6x −5x = 10 x = 10 Ответ: x = 10. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Как решаем: −4x = 12 | :(−4) Ответ: x = −3. Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе. А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе. Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Решаем так: 6х = 19 — 1 6х = 18 х = 2 Ответ: х = 2. Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1. Решаем так: 5х — 15 + 2 = 3х — 2 + 2х — 1 5х — 3х — 2х = — 12 — 1 + 15 — 2 0х = 0 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Решаем так: х = 1/8 : 4 х = 1/12 Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь. Пример 4. Решить: 4(х + 2) = 6 — 7х. Решаем так: Ответ: — 0,18. Пример 5. Решить: Решаем так: Ответ: 1 17/19. Пример 6. Как решить линейное уравнение: х + 7 = х + 4. Решаем так: 5х — 15 + 2 = 3х — 2 + 2х — 1 х — х = 4 — 7 0 * х = — 3 Ответ: нет решений. Пример 7. Решить: 2(х + 3) = 5 — 7х.. Решаем так: Ответ: — 0,25. Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную онлайн-школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями
такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому
уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры. Современной постановкой диофантовых задач мы обязаны французскому математику Ферма.
Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в
целых числах – великая теорема Ферма: уравнение xn + yn = zn не имеет ненулевых рациональных решений для всех натуральных n > 2. Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел. В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых
числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы
решения. При решении уравнений в целых и натуральных числах можно условно выделить следующие методы: способ перебора вариантов; применение алгоритма Евклида; представление чисел в виде непрерывных (цепных) дробей; разложения на множители; решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной; метод остатков; метод бесконечного спуска. 1. Запишем уравнение в виде (x – 2y)(x + y) = 7. Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем: 1) x – 2y = 7, x + y = 1; 2) x – 2y = 1, x + y = 7; 3) x – 2y = –7, x + y = –1; 4) x – 2y = –1, x + y = –7. Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2). Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2). 2. Решить в целых числах уравнение: а) 20х + 12у = 2013; б) 5х + 7у = 19; в) 201х – 1999у = 12. а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в
целых числах. Ответ: решений нет. б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например, x0 = 1, y0 = 2. Тогда 5x0 + 7y0 = 19, откуда 5(х – x0) + 7(у – y0) = 0, 5(х – x0) = –7(у – y0). Поскольку числа 5 и 7 взаимно простые, то
х – x0 = 7k, у – y0 = –5k. Значит, общее решение: х = 1 + 7k, у = 2 – 5k, где k – произвольное целое число. Ответ: (1+7k; 2–5k), где k – целое число. в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201: НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1. Запишем этот процесс в обратном порядке: 1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) = = 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 = = 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999. Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. x0 = 1273·12 = 15276, y0 = 128·12 = 1536 является решением уравнения 201х – 1999у = 12. Общее решение этого уравнения запишется в виде х = 15276 + 1999k, у = 1536 + 201k, где k – целое число, или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201), х = 1283 + 1999n, у = 129 + 201n, где n – целое число. Ответ: (1283+1999n, 129+201n), где n – целое число. 3. Решить в целых числах уравнение: а) x3 + y3 = 3333333; б) x3 + y3 = 4(x2y + xy2 + 1). а) Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x3 + y3
может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах. Ответ: целочисленных решений нет. б) Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7
дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах. Ответ: целочисленных решений нет. 4. Решить а) в простых числах уравнение х2 – 7х – 144 = у2 – 25у; б) в целых числах уравнение x + y = x2 – xy + y2. а) Решим данное уравнение как квадратное относительно переменной у. Получим у = х + 9 или у = 16 – х. Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем 2 х 16, 2 у 16. С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3). Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3). б) Рассмотрим данное уравнение как квадратное уравнение относительно x: x2 – (y + 1)x + y2 – y = 0. Дискриминант этого уравнения равен –3y2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из
исходного уравнения получаем квадратное уравнение относительно х, которое легко решается. Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2). 5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x2 + y2 + z2 = x3 +
y3 + z3 ? Попробуем подбирать такие тройки, где у = –z. Тогда y3 и z3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь
вид x2 + 2y2 = x3 или, иначе, x2(x–1) = 2y2. Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно
много, а именно, это все числа вида 2n2+1. Подставляя в x2(x–1) = 2y2 такое число, после несложных преобразований
получаем: y = xn = n(2n2+1) = 2n3+n. Все тройки, полученные таким образом, имеют вид (2n2+1; 2n3+n; –2n3– n). Ответ: существует. 6. Найдите такие целые числа x, y, z, u, что x2 + y2 + z2 + u2 = 2xyzu. Число x2 + y2 + z2 + u2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел. Если все четыре числа x, y, z, u нечётны, то x2 + y2 + z2 + u2 делится на 4, но при этом 2xyzu не делится
на 4 – несоответствие. Если ровно два из чисел x, y, z, u нечётны, то x2 + y2 + z2 + u2 не делится на 4, а 2xyzu делится на 4 –
опять несоответствие. Поэтому все числа x, y, z, u чётны. Тогда можно записать, что x = 2x1, y = 2y1, z = 2z1, u = 2u1, и исходное уравнение примет вид x12 + y12 + z12 + u12 =
8x1y1z1u1.
Теперь заметим, что (2k + 1)2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1,
z1, u1 нечётны, то x12 + y12 + z12 +
u12 не делится на 8. А если ровно два из этих чисел нечётно, то x12 + y12 +
z12 + u12 не делится даже на 4. x1 = 2x2, y1 = 2y2, z1 = 2z2, u1 =
2u2, и мы получаем уравнение x22 + y22 + z22 + u22 =
32x2y2z2u2.
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
Ответ: (0; 0; 0; 0). 7. Докажите, что уравнение (х – у)3 + (y – z)3 + (z – x)3 = 30 не имеет решений в целых числах. Воспользуемся следующим тождеством: (х – у)3 + (y – z)3 + (z – x)3 = 3(х – у)(y – z)(z – x). Тогда исходное уравнение можно записать в виде (х – у)(y – z)(z – x) = 10. Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде abc = 10. Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5,
либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в
целых числах. 8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у2. Очевидно, что если х = 1, то у2 = 1, если х = 3, то у2 = 9. Этим случаям соответствуют следующие пары чисел: х1 = 1, у1 = 1; х2 = 1, у2 = –1; х3 = 3, у3 = 3; х4 = 3, у4 = –3. Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как 5! + 6! + . можем записать, что 1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n. Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа. Ответ: (1; 1), (1; –1), (3; 3), (3; –3). 9. Решите следующую систему уравнений в натуральных числах: a3 – b3 – c3 = 3abc, a2 = 2(b + c). Так как
3abc > 0, то a3 > b3 + c3; таким образом имеем b
Складывая эти неравенства, получим, что b + c
С учётом последнего неравенства, из второго уравнения системы получаем, что a2 Но второе уравнение системы также показывает, что а – чётное число. Таким образом, а = 2, b = c = 1. Ответ: (2; 1; 1) 10. Найти все пары целых чисел х и у, удовлетворяющих уравнению х2 + х = у4 + у3 + у2 + у. Разложив на множители обе части данного уравнения, получим: х(х + 1) = у(у + 1)(у2 + 1), или х(х + 1) = (у2 + у)(у2 + 1) Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому,
приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных: х1 = 0, у1 = 0; х2 = 0, у2 = –1; х3 = –1, у3 = 0; х4 = –1, у4 = –1. Произведение (у2 + у)(у2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля,
только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих
исходному уравнению: х5 = 5, у5 = 2; х6 = –6, у6 = 2. — 1 0 а также — 1 1> — x 1> — x 2> 0 ⟹ 1> — x 1> — x 2> 0 ⟹ 1> -x_1> -x_2> 0 \ подразумевает 2> 1 — x 1> 1 — x 2> 1 ⟹ 2> 1 — x 1> 1 — x 2> 1 ⟹ 2> 1-x_1> 1-x_2> 1 \ подразумевает 1 2 Умножая (4) (4) \\ (4) \ \ и (5) (5) \ \ (5) \ \ получаем 0 (1 — x 1) (x 5 1 + x 4 1 + x 3 1 + x 2 1 + x 1 + 1) 1 — x 1 x 5 1 + x 4 1 + x 3 1 + x 2 1 + x 1 + 1 f (x 1) поэтому f (x) f (x) \ \ f (x) \ \ монотонно возрастает, когда x ∈ (- 1, 0) x ∈ (- 1, 0) \ \ x \ in (-1,0) что в конечном итоге доказывает, что ff \ \ f \ \ монотонно возрастает во всех интервалах (- ∞, — 1), (- 1, 0) (- ∞, — 1), (- 1, 0) (- \ infty, — 1), \ \ (-1,0) \ \ и (0, + ∞) (0, + ∞) \ (0, + \ infty) \ \, и поскольку ff \ \ f \ \ является полиномиальной функцией, она всюду непрерывно, и мы можем заключить, что ff \ \ f \ \ монотонно возрастает всюду в RR \ R, что в итоге дает нам ∀ x ∈ R, f ′ (x)> 0 ⟹ ∀ x ∈ R, f ′ (x)> 0 ⟹ \ forall x \ in \ R \, \ \ f ‘(x)> 0 \ влечет f ′ (x) ≠ 0 ⟹ f ′ (x) ≠ 0 ⟹ f ‘(x) \ neq 0 \ подразумевает 5 x 4 + 4 x 3 + 3 x 2 + 2 x + 1 ≠ 0 5 x 4 + 4 x 3 + 3 x 2 + 2 x + 1 ≠ 0 \ в штучной упаковке {5x ^ 4 + 4x ^ 3 + 3x ^ 2 + 2x + 1 \ neq 0} К сожалению, на этот раз нет реальных решений для вас 🙂
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. «Найдите число, которое при добавлении к 3 дает 7» можно записать как: 3+? = 7, 3 + n = 7, 3 + x = 1 и так далее, где символы?, N и x представляют число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7. Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.Уравнение: 3 + х = 7 будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Пример 1 Определите, является ли значение 3 решением уравнения 4x — 2 = 3x + 1 Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому. 4 (3) — 2 = 3 (3) + 1 12 — 2 = 9 + 1 10 = 10 Отв. 3 — это решение. Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра. Пример 2 Найдите решение каждого уравнения путем осмотра. а. х + 5 = 12 Решения а. 7 — решение, так как 7 + 5 = 12. В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом, 3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5 — эквивалентные уравнения, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить. Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений. Если одно и то же количество добавляется или вычитается из обоих элементов
уравнения, полученное уравнение эквивалентно исходному
уравнение. в символах, a — b, a + c = b + c и a — c = b — c — эквивалентные уравнения. Пример 1 Напишите уравнение, эквивалентное х + 3 = 7 путем вычитания 3 из каждого члена. Решение Если вычесть 3 из каждого члена, получится х + 3 — 3 = 7 — 3 или х = 4 Обратите внимание, что x + 3 = 7 и x = 4 — эквивалентные уравнения, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем создать эквивалентные уравнения, сначала упростив один или оба члена уравнения. Пример 2 Напишите уравнение, эквивалентное 4x- 2-3x = 4 + 6 , объединив одинаковые термины, а затем добавив по 2 к каждому члену. Объединение одинаковых терминов дает х — 2 = 10 Добавление 2 к каждому члену дает х-2 + 2 = 10 + 2 х = 12 Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки. Пример 3 Решить 2x + 1 = x — 2. Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала добавим -1 (или вычтем 1 из) каждого члена, мы получим 2x + 1-1 = x — 2-1 2x = х — 3 Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим 2х-х = х — 3 — х х = -3 , где решение -3 очевидно. Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3. Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении. 2 (-3) + 1 = (-3) — 2 -5 = -5 Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано Если a = b, то b = a Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака. Если 4 = x + 2, то x + 2 = 4 Если x + 3 = 2x — 5, то 2x — 5 = x + 3 Если d = rt, то rt = d Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства. Пример 4 Решите 2x = 3x — 9. (1) Решение Если мы сначала добавим -3x к каждому члену, мы получим 2x — 3x = 3x — 9 — 3x -x = -9 , где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решением является 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем 2x-2x + 9 = 3x- 9-2x + 9 9 = х , из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства. Рассмотрим уравнение 3x = 12 Решение этого уравнения — 4. , решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления. Если оба члена уравнения делятся на одно и то же (ненулевое)
количество, полученное уравнение эквивалентно исходному уравнению. в символах, — эквивалентные уравнения. Пример 1 Напишите уравнение, эквивалентное -4x = 12 , разделив каждый член на -4. Решение Разделив оба элемента на -4, получим При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1. Пример 2 Решите 3y + 2y = 20. Сначала мы объединяем одинаковые термины, чтобы получить 5лет = 20 Тогда, разделив каждый член на 5, получим В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения. Пример 3 Решить 4x + 7 = x — 2. Сначала мы добавляем -x и -7 к каждому члену, чтобы получить 4x + 7 — x — 7 = x — 2 — x — 1 Далее, объединяя одинаковые термины, получаем 3x = -9 Наконец, мы разделим каждый член на 3, чтобы получить Рассмотрим уравнение Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения , решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения. Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению. в символах, a = b и a · c = b · c (c ≠ 0) — эквивалентные уравнения. Пример 1 Напишите уравнение, эквивалентное путем умножения каждого члена на 6. Решение Умножение каждого члена на 6 дает При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей. Пример 2 Решить Решение Во-первых, умножьте каждый член на 5, чтобы получить Теперь разделите каждый член на 3, Пример 3 Решить. Решение Во-первых, упростите над дробной чертой, чтобы получить Затем умножьте каждый член на 3, чтобы получить Наконец, разделив каждого члена на 5, получим Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102. Шаги по решению уравнений первой степени: Пример 1 Решите 5x — 7 = 2x — 4x + 14. Решение Во-первых, мы объединяем одинаковые члены, 2x — 4x, чтобы получить 5x — 7 = -2x + 14 Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить 5x — 7 + 2x + 7 = -2x + 14 + 2x + 1 7x = 21 Наконец, мы разделим каждый член на 7, чтобы получить В следующем примере мы упрощаем над дробной чертой перед применением свойств, которые мы изучали. Пример 2 Решить Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить Затем мы добавляем -3 к каждому члену и упрощаем Затем мы умножаем каждый член на 3, чтобы получить Наконец, мы разделим каждый член на 2, чтобы получить Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Пример 1 В формуле d = rt найти t, если d = 24 и r = 3. Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть d = rt (24) = (3) т 8 = т Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других.Мы используем те же методы, которые продемонстрированы в предыдущих разделах. Пример 2 В формуле d = rt найдите t через r и d. Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить из которых по закону симметрии В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства. Пример 3 В уравнении ax + b = c найдите x через a, b и c. Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить , затем разделив каждый член на a, мы получим Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения: x / 4- 6- (2) = 0 2.1 Вычитание целого из дроби Перепишем целое как дробь, используя в знаменателе 4: Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель 2.2 Сложение двух эквивалентных дробей Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьших членов, если возможно: 3.1 Вычитание целого из дроби Перепишем целое как дробь, используя 4 в качестве знаменателя: 3.2 Сложение двух эквивалентных дробей Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должна быть равна нулю. Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель. Вот как: Теперь, с левой стороны, 4 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю. Уравнение теперь принимает форму: 4.2 Решите: x-32 = 0 Добавьте 32 к обеим сторонам уравнения: Переставьте уравнение, вычтя то, что находится справа от знака равенства из обеих частей уравнения: x / 4-x / 6- (2/3) = 0 4.1 Найдите наименьшее общее кратное Левый знаменатель: 4 Правый знаменатель: 6 4.2 Вычислить множители для двух дробей Обозначить наименьшее общее кратное LCM Left_M = LCM L_Deno = 3 Right_M = LCM / R_Deno = 2 4.3 Перепишите две дроби в эквивалентные дроби Две дроби называются эквивалентными, если они имеют одинаковое числовое значение. Например: 1/2 и 2/4 эквивалентны, y / (y + 1) 2 и (y 2 + y) / (y + 1) 3 также эквивалентны. Чтобы вычислить эквивалентную дробь, умножьте числитель каждой дроби на соответствующий ей множитель. 4.4 Сложение двух эквивалентных дробей Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьшего числа, если возможно: 5.1 Найдите наименьшее общее кратное Левый знаменатель: 12 Правый знаменатель: 3 5.2 Вычислить множители для двух дробей Обозначить наименьшее общее кратное LCM Left_M = LCM L_Deno = 1 Right_M = LCM / R_Deno = 4 5.3 Перепишите две дроби в эквивалентные дроби 5.4 Сложение двух эквивалентных дробей Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должна быть равна нулю. Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель. Вот как: Теперь, с левой стороны, 12 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю. Уравнение теперь принимает форму: 6.2 Решите: x-8 = 0 Добавьте 8 к обеим сторонам уравнения: Содержание: Эта страница соответствует § 2.4
(с. 200) текста. Предлагаемые задачи из текста: с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87,
88, 95, 97 Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a —
не равно 0. Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то
хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое.
Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста. Пример 1. 2x 2 — 5x — 12 = 0. (2x + 3) (x — 4) = 0. 2x + 3 = 0 или x — 4 = 0. x = -3/2, или x = 4. Если x 2 = k, то x = ± sqrt (k). Пример 2. x 2 — 9 = 0. x 2 = 9. x = 3 или x = -3. Пример 3. Пример 4. x 2 + 7 = 0. x 2 = -7. х = ±. Обратите внимание, что = =,
так что решения x = ±, два комплексных числа. Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат
корневой принцип. Пример 5. x 2 + 6x — 1 = 0. x 2 + 6x = 1. x 2 + 6x + 9 = 1 + 9. 9, прибавленная к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) 2 = 9. Причина
выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами).
Поэтому эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это
истина, учитывая (x + a) 2 = x 2 + 2ax + a 2 . Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .] (x + 3) 2 = 10. Теперь мы можем применить принцип квадратного корня и затем решить относительно x. x = -3 ± sqrt (10). Пример 6. 2x 2 + 6x — 5 = 0. 2x 2 + 6x = 5. Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент
(коэффициент x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив
обе части уравнения на 2. x 2 + 3x = 5/2. Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат,
(3/2) 2 = 9/4. Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат. x 2 + 3x + 9/4 = 5/2 + 9/4. Левая часть — квадрат (x + 3/2). [Проверьте это!] (x + 3/2) 2 = 19/4. Теперь мы используем принцип квадратного корня и решаем относительно x. x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2. x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2 До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от
проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня
могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере. Пример 7. x 2 = 16. x 2 — 16 = 0. (x + 4) (x — 4) = 0. x = -4 или x = 4. В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна. Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае
мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие:
всегда одинаковы, поэтому их можно применить к общему квадратному уравнению топор 2 + bx + c = 0. Результатом квадрата этого общего уравнения является формула для решений уравнения
называется квадратной формулой. Решения уравнения ax 2 + bx + c = 0 равны Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае,
где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его
в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу. Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения.
Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это! Примеры использования квадратичной формулы: Пример 8. 2x 2 + 6x — 5 = 0. В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат. Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика
функции f (x) = 2x 2 + 6x — 5. Пример 9. 4x 2 + 4x + 1 = 0 В этом примере a = 4, b = 4 и c = 1. В этом примере следует обратить внимание на два момента.
4x 2 + 4x + 1 = 0. (2x + 1) 2 = 0. х = -1/2. Пример 10. х 2 + х + 1 = 0 а = 1, б = 1, с = 1 Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов.
функции f (x) = x 2 + x + 1. Таким образом, решения сложны, поскольку график y = x 2
+ x + 1 не имеет пересечений по x. Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом
уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений. 1. Дискриминант> 0. Два реальных решения. 2. Дискриминант = 0. Одно реальное решение. 3. Дискриминант <0. Два сложных решения. Примечания к проверке решений Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример
3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения,
потому что при решении уравнений очень легко сделать невнимательные ошибки. Алгебраический метод, который состоит из обратной подстановки числа в уравнение и проверки того, что
полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда
решение предполагает радикальное. Например, в нашем предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2. Алгебраическая проверка выглядит как 4 (-1/2) 2 +4 (-1/2) + 1 = 0. 4 (1/4) — 2 + 1 = 0. 1-2 + 1 = 0. 0 = 0. Решение проверяет. В предыдущем примере, 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2.
Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический
проверить или использовать калькулятор для алгебраической проверки быстрее. Сначала найдите десятичные приближения для двух предложенных решений. (-3 + sqrt (19)) / 2 = 0,679449. (-3 — sqrt (19)) / 2 = -3,679449. Теперь используйте графическую утилиту, чтобы построить график y = 2x 2 + 6x — 5, и проследите график, чтобы приблизительно определить, где
х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение. Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и сразу перешли к графику
утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя
(алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень
близко к найденным вами числам, значит, вы, наверное, правы! Упражнение 1: Решите следующие квадратные уравнения. (а) 3x 2 -5x — 2 = 0. Ответ (б) (x + 1) 2 = 3. Ответ (в) x 2 = 3x + 2. Ответ Вернуться к содержанию Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал
является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить. Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы
радикальный член сам по себе на одной стороне уравнения. Пример 11. Теперь, когда мы изолировали радикальный член в правой части, возводим обе части в квадрат и решаем полученное уравнение
для x. Чек: х = 0 Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно! Итак, x = 0 не является решением . х = 3 Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно
раствор . Решение : x = 3. Примечание: Решением является координата x точки пересечения графиков y = x и
у = sqrt (х + 1) +1. Посмотрите, что произошло бы, если бы мы возводили обе части уравнения в квадрат до , выделив радикал
срок. Это хуже того, с чего мы начали! Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью
возведение в степень один раз. Однако мы можем на уменьшить количество радикальных членов на , возведя в степень. Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и
возвести в степень. Затем мы повторяем этот процесс. Пример 12. Теперь возведите обе части уравнения в квадрат. В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат
снова обе стороны. Чек: Подставляя x = 5/4 в исходное уравнение, получаем sqrt (9/4) + sqrt (1/4) = 2. 3/2 + 1/2 = 2. Это утверждение верно, поэтому x = 5/4 является решением. Примечание по проверке решений: В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что
нет решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение
— координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1). Упражнение 2: Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ Вернуться к содержанию Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее.Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с помощью графической утилиты. Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий
x, чтобы начать задачу. Пример 13. 2x 3 + 3x 2 -5x = 0. x (2x 2 + 3x -5) = 0. Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения. x = 0 или 2x 2 + 3x -5 = 0. Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом.
Примечание: Если бы мы не смогли разложить квадратичный коэффициент во втором уравнении, мы могли бы прибегнуть к
к использованию квадратичной формулы.[Убедитесь, что вы получили те же результаты, что и ниже.] x = 0 или (2x + 5) (x — 1) = 0. Итак, есть три решения: x = 0, x = -5/2, x = 1. Примечание: Решение находится при пересечении графиков f (x) = 2x 3
+ 3x 2 -5x. Пример 14. x 3 -2x 2 -9x +18 = 0. Коэффициент при x 2 в 2 раза больше, чем при x 3 , и такое же соотношение существует между
коэффициенты при третьем и четвертом членах. Группа слагает один и два, а также три и четыре. x 2 (x — 2) — 9 (x — 2) = 0. Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители. (x — 2) (x 2 — 9) = 0. Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения. x — 2 = 0 или x 2 — 9 = 0. x = 2 или (x + 3) (x — 3) = 0. Итак, есть три решения: x = 2, x = -3, x = 3. Примечание: Эти решения находятся на пересечении графика f (x) = x 3
-2x 2 -9x +18. Пример 15. x 4 — x 2 — 12 = 0. Этот многочлен неквадратичный, он имеет четвертую степень. Однако его можно рассматривать как квадратичный по x 2 . (x 2 ) 2 — (x 2 ) — 12 = 0. Это может помочь вам фактически заменить z на x 2 . z 2 — z — 12 = 0 Это квадратное уравнение относительно z. (z — 4) (z + 3) = 0. z = 4 или z = -3. Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на
x 2 и решите полученные уравнения. x 2 = 4. х = 2, х = -2. x 2 = -3. x = i или x = — i. Итак, есть четыре решения, два действительных и два комплексных. Примечание: Эти решения находятся на пересечении графика f (x) = x 4
— x 2 — 12. График f (x) = x 4 — x 2 -12 и масштабирование, показывающее его локальное
экстремумы. Упражнение 3: Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ Вернуться к содержанию Пример 16. Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение. Это уравнение квадратичное. Квадратичная формула дает решения Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы
убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков.
из y = 1 и y = 2 / x-1 / (x + 2). Пример 17. 5 | х — 1 | = х + 11. Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения
столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности,
и все решения должны быть проверены. Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение 5 (x — 1) = x + 11. 5x — 5 = x + 11. 4x = 16. x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11. Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот
точка часто сбивает студентов с толку, потому что это выглядит так, как будто мы говорим, что абсолютное значение выражения
отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное. Теперь наше уравнение принимает вид -5 (x — 1) = x + 11. -5x + 5 = x + 11. -6x = 6. x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11. Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график 5 * abs (x — 1) — x — 11 и посмотрите на пересечения по x, или вы можете найти решение как x-координаты
точки пересечения графиков y = x + 11 и y = 5 * abs (x-1). Упражнение 4: (а) Решите уравнение. Ответ (b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ Вернуться к содержанию
Представлены подробные решения и полные пояснения к вопросам алгебры 9 класса.
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: Как вы хорошо знаете, логарифм — это математическая операция, обратная возведению в степень. Логарифм числа сокращается как « log .” Прежде чем мы перейдем к решению логарифмических уравнений, давайте сначала познакомимся со следующими правилами логарифмов: Правило произведения гласит, что сумма двух логарифмов равна произведению логарифмов. Первый закон представлен как; ⟹ журнал b (x) + журнал b (y) = журнал b (xy) Разница двух логарифмов x и y равна отношению логарифмов. ⟹ журнал b (x) — журнал b (y) = журнал (x / y) ⟹ журнал b (x) n = n журнал b (x) ⟹ журнал b x = (журнал a x) / (журнал a b) Логарифм любого положительного числа по основанию этого числа всегда равен 1. Пример: Уравнение, содержащее переменные в показателях степени, известно как экспоненциальное уравнение. Напротив, уравнение, которое включает логарифм выражения, содержащего переменную, называется логарифмическим уравнением. Цель решения логарифмического уравнения — найти значение неизвестной переменной. В этой статье мы узнаем, как решить два общих типа логарифмических уравнений, а именно: Уравнения с логарифмами на одной стороне принимают логарифм b M = n ⇒ M = b n . Чтобы решить этот тип уравнений, выполните следующие действия: Пример 1 Журнал решения 2 (5x + 7) = 5 Решение Перепишем уравнение в экспоненциальную форму бревна 2 (5x + 7) = 5 ⇒ 2 5 = 5x + 7 ⇒ 32 = 5x + 7 ⇒ 5x = 32 — 7 5x = 25 Разделите обе стороны на 5, чтобы получить х = 5 Пример 2 Решить относительно x в журнале (5x -11) = 2 Решение Поскольку основание этого уравнения не дано, мы принимаем основание 10. Теперь изменим запись логарифма в экспоненциальной форме. ⇒ 10 2 = 5x — 11 ⇒ 100 = 5x -11 111 = 5x 111/5 = х Следовательно, x = 111/5 — это ответ. Пример 3 Журнал решения 10 (2x + 1) = 3 Решение Перепишите уравнение в экспоненциальной форме журнал 10 (2x + 1) = 3n⇒ 2x + 1 = 10 3 ⇒ 2x + 1 = 1000 2x = 999 Разделив обе стороны на 2, получим; х = 499.5 Проверьте свой ответ, подставив его в исходное логарифмическое уравнение; ⇒ log 10 (2 x 499,5 + 1) = log 10 (1000) = 3, поскольку 10 3 = 1000 Пример 4 Вычислить ln (4x -1) = 3 Решение Перепишем уравнение в экспоненциальной форме как; ln (4x -1) = 3 ⇒ 4x — 3 = e 3 Но, как известно, e = 2,718281828 4x — 3 = (2.718281828) 3 = 20.085537 х = 5,271384 Пример 5 Решите логарифмическое уравнение log 2 (x +1) — log 2 (x — 4) = 3 Решение Сначала упростите логарифмы, применив правило частного, как показано ниже. журнал 2 (x +1) — журнал 2 (x — 4) = 3 ⇒ журнал 2 [(x + 1) / (x — 4)] = 3 Теперь перепишем уравнение в экспоненциальной форме ⇒2 3 = [(x + 1) / (x — 4)] ⇒ 8 = [(x + 1) / (x — 4)] Перемножьте уравнение крестиком ⇒ [(x + 1) = 8 (x — 4)] ⇒ x + 1 = 8x -32 7x = 33 …… (Собираем похожие термины) х = 33/7 Пример 6 Найдите x, если log 4 (x) + log 4 (x -12) = 3 Решение Упростите логарифм, используя следующее правило произведения; журнал 4 (x) + журнал 4 (x -12) = 3 ⇒ журнал 4 [(x) (x — 12)] = 3 ⇒ журнал 4 (x 2 — 12x) = 3 Преобразуйте уравнение в экспоненциальную форму. ⇒ 4 3 = x 2 — 12x ⇒ 64 = x 2 — 12x Поскольку это квадратное уравнение, мы решаем его путем факторизации. x 2 -12x — 64 ⇒ (x + 4) (x — 16) = 0 x = -4 или 16 Когда x = -4 подставляется в исходное уравнение, мы получаем отрицательный ответ, который является мнимым. Поэтому 16 — единственное приемлемое решение. Уравнения с логарифмами по обе стороны от знака равенства принимают log M = log N, что совпадает с M = N. Процедура решения уравнений с логарифмами по обе стороны от знака равенства. Пример 7 Журнал решения 6 (2x — 4) + журнал 6 ( 4) = лог 6 (40) Решение Во-первых, упростим логарифмы. лог 6 (2x — 4) + лог 6 (4) = лог 6 (40) ⇒ лог 6 [4 (2x — 4)] = лог 6 (40) Теперь опустим логарифмы ⇒ [4 (2x — 4)] = (40) ⇒ 8x — 16 = 40 ⇒ 8x = 40 + 16 8x = 56 х = 7 Пример 8 Решите логарифмическое уравнение: log 7 (x — 2) + log 7 (x + 3) = log 7 14 Решение Упростите уравнение, применив правило произведения. Лог 7 [(x — 2) (x + 3)] = лог 7 14 Отбросьте логарифмы. ⇒ [(x — 2) (x + 3)] = 14 Раздайте ФОЛЬГУ, чтобы получить; ⇒ x 2 — x — 6 = 14 ⇒ x 2 — x — 20 = 0 ⇒ (x + 4) (x — 5) = 0 x = -4 или x = 5 , когда x = -5 и x = 5 подставляются в исходное уравнение, они дают отрицательный и положительный аргумент соответственно. Поэтому x = 5 — единственное приемлемое решение. Пример 9 Решить журнал 3 x + журнал 3 (x + 3) = журнал 3 (2x + 6) Решение Учитывая уравнение; log 3 (x 2 + 3x) = log 3 (2x + 6), отбросьте логарифмы, чтобы получить; (x — 2) (x + 3) = 0 Проверяя оба значения x, мы получаем, что x = 2 является правильным ответом. Пример 10 Журнал решения 5 (30x — 10) — 2 = журнал 5 (x + 6) Решение журнал 5 (30x — 10) — 2 = журнал 5 (x + 6) Это уравнение можно переписать как; ⇒ журнал 5 (30x — 10) — журнал 5 (x + 6) = 2 Упростите логарифмы журнал 5 [(30x — 10) / (x + 6)] = 2 Записать логарифм в экспоненциальной форме. Ферромагнетиками называют вещества, для которых характерна самопроизвольная намагниченность, значительно изменяемая в процессе воздействия внешних факторов таких, как магнитное поле, деформация и температура. Магнитная восприимчивость ферромагнетиков обладает положительными значениями и равна 10 в 4 или 5 степени. Если напряжённость магнитного поля растет нелинейно, наблюдается увеличение намагниченности и магнитной индукции ферромагнетических веществ. Ферромагнетики отличаются от диамагнетиков и парамагнетиков наличием самопроизвольной или спонтанной намагниченности, когда внешнее магнитное поле отсутствует. Данный факт говорит об упорядоченной ориентации электронных спинов и магнитных моментов. Ещё одной особенностью ферромагнетиков в отличие от других типов магнетических веществ является значительное превышение внутреннего магнитного поля по сравнению с аналогичными характеристиками внешнего поля. Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. Можно найти немного примеров природных ферромагнетиков. Широко распространены ферриты, которые представляют собой химические соединения оксидов железа с оксидами других веществ. Первым открытым ферромагнитным материалом является магнитный Железняк, который относятся к категории ферритов. Ферромагнетическими свойствами обладают следующие материалы: Ферромагнетические материалы обладают уникальными физико-химическими свойствами. Основными характеристиками ферромагнетиков являются: Ферромагнетиками могут являться материалы, находящиеся в твердом состоянии. При этом магнитный момент их атомов, в частности с недостроенными внутренними электронными оболочками, является постоянно спиновым или орбитальным. Распространенным примером ферромагнетиков являются переходные металлы. В ферромагнетических материалах резко усиливаются внешние магнитные поля. К ним относятся: Значительная доля веществ не обладает ферромагнетическими свойствами. Это объясняется особым расположением электронов, когда электронные оболочки атомов заполняются. Их магнитные поля ориентированы в противоположных направлениях и компенсируют друг друга, что снижает степень потенциальной энергии взаимодействия электронов. Наблюдая атомы с нечетным числом электронов на оболочках, которые соединяются в молекулы или кристаллы, можно заметить взаимную компенсацию магнитных полей неспаренных электронов. Атомы железа, никеля, кобальта в кристаллических структурах обладают собственными магнитными полями неспаренных электронов, которые ориентированы параллельно друг другу. Это приводит к образованию микроскопических намагниченных областей или доменов. Суммарное магнитное поле таких образований нулевое. Если материал поместить во внешнее магнитное поле, то поля доменов будут ориентироваться соответственно, что сопровождается намагничиванием ферромагнетиков. Ферромагнитные вещества отличаются по характеру магнитного взаимодействия. Выделяют две основные группы ферромагнетиков: К первой категории относят ферромагнетики, способные практически полностью устранять собственное магнитное поле при исчезновении внешнего. Ферромагнетические вещества называют «магнитозамороженными» парамагнетиками. Атомы парамагнетических материалов обладают магнитными моментами, которые пребывают в хаотичном вращательном движении. В случае ферромагнетиков моменты направлены определенно. При возрастании температуры число случайных температурных флуктуаций магнитных моментов атомов увеличивается. В случае, если температура ферромагнетика становится приближенной к температуре Кюри, то есть сравнимой с температурой магнитного «плавления», происходит полное разрушение ферромагнитного порядка температурными флуктуациями, и наблюдается переход вещества в парамагнитное состояние: Изменение температуры в первую очередь влияет на намагниченность ферромагнетиков. По мере ее возрастания свойство намагниченности снижается и становится равно нулю в точке Кюри. В данном температурном режиме происходит изменение всех других свойств, которые определяют разницу между ферромагнетиками и парамагнетиками, а также характеристик вещества, не связанных с отличительными особенностями этих типов магнетиков. К примеру, изменение электрических и акустических свойств ферромагнитного материала, в связи с тем, что твердое тело обладает упругой, электрической, магнитной и другими подсистемами, при изменении одной из которых меняются и другие. Каждый ферромагнетик обладает рядом характеристик. Важным параметром вещества является температура, при которой оно утрачивает свои магнитные свойства. Этот показатель называется точкой Кюри. При температуре, превышающей точку Кюри, упорядоченное состояние в магнитной подсистеме кристалла разрушается. Потерю свойств ферромагнетика в зависимости от температуры окружающей среды можно рассмотреть опытным путем. К примеру, никель обладает температурой Кюри в 360 градусов. Подвешенный образец металла подвергают воздействию внешнего магнитного поля. В систему помещают горелку. При обычной температуре никель примет горизонтальное положение, так как будет сильно притягиваться магнитом. Если образец нагреть до температуры Кюри, его свойство намагниченности ослабевает, он перестанет притягиваться и начнет падать. После остывания до температуры, которая ниже точки Кюри, никель вновь приобретает ферромагнитные свойства и притягивается к магниту. Ферромагнитные вещества благодаря особым физико-химическим свойствам нашли широкое применение в разных сферах электротехники. С помощью магнито-мягких типов ферромагнетиков производят такое оборудование и агрегаты, как: Ферромагнетики в условиях отсутствия внешнего магнитного поля остаются намагниченными, создавая магнитное поле во внешней среде. Элементарные токи в веществе сохраняют упорядоченную ориентацию. Свойство активно используется в современной промышленности для создания постоянных магнитов, которые используют для изготовления следующих видов оборудования: Материалы, относящиеся к ферритам, обладающие одновременно ферромагнитными и полупроводниковыми свойствами, широко распространены в производстве радиотехники. Вещества активно применяются при изготовлении сердечников катушек индуктивности, магнитных лент, пленок и дисков.
Глава 13 Магнитные свойства веществ 109 Магнитные моменты электронов и атомов Опыты показывают, что все вещества, помещенные в магнитное поле, намагничиваются.
Магнитное поле Магнитный момент атома. Ларморовская частота. Парамагнетики и диамагнетики. Магнитное поле в веществе. Магнитная проницаемость. Условия для поля на границе раздела двух магнетиков. Ферромагнетики.
1 4.6. Магнитное поле в веществе Индуктивность длинного соленоида можно измерить, анализируя, например, переходной процесс при размыкании или замыкании тока. Опыт показывает, что индуктивность зависит
Лекция 17. Магнитные материалы Общая характеристика К магнитным материалам относятся вещества, обладающие самопроизвольной намагниченностью при температуре ниже температуры магнитного упорядочения.
МАГНЕТИКИ В МАГНИТНОМ ПОЛЕ 1. Магнитные моменты электронов и атомов Магнетиками называются вещества, способные приобретать во внешнем магнитном поле собственное магнитное поле, т.е., намагничиваться. Магнитные
Магнетики и их свойства. Диамагнетики Парамагнетики Ферромагнетики Составитель: Киверин С.М. 565 группа 1 курс ИВТ ФТФ АлтГУ Диамагнетики и парамагнетики в магнитном поле. Микроскопические плотности токов
Министерство образования Республики Беларусь БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра физики ЛАБОРАТОРНАЯ РАБОТА 2.11 ИЗУЧЕНИЕ МАГНИТНЫХ СВОЙСТВ ФЕРРОМАГНЕТИКОВ МЕТОДИЧЕСКОЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Физический факультет Кафедра общей физики ОПИСАНИЕ ЛАБОРАТОРНЫХ РАБОТ Часть 3. Электричество
Л13 Магнетизм вещества Таким образом, различия в конфигурации электронных орбит в различных атомах определяют характер и величину атомных магнитных моментов, которые в свою очередь определяют различие
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Уральский государственный технический университет УПИ Нижнетагильский технологический
3.3. Парамагнетизм. 3.3..Магнитная восприимчивость. Вещества, у которых магнитная восприимчивость невелика, но больше нуля 0, а магнитная проницаемость больше единицы: 4, называются парамагнетиками. Явление
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный технический университет
Министерство образования и науки Российской Федерации Автономное государственное бюджетное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ
Лекция 15 (6) Магнитное поле в веществе План 1.
Лекция 6 Магнитное поле в веществе Намагниченность вещества Вектор напряжённости магнитного поля и его связь с векторами индукции и намагниченности Магнитная восприимчивость и магнитная проницаемость Поле
Лабораторная работа 3-5 ОПРЕДЕЛЕНИЕ ТОЧКИ КЮРИ Цель работы: Изучение свойств магнитных материалов при нагревании Принадлежности: ферромагнитный образец, электрическая печь, термопара с милливольтметром,
Лекц ия 3 Магнитные свойства вещества Вопросы.
Лекция 23 Диполь. Диэлектрики. Поляризация диэлектриков. Электрическое смещение. Теорема Гаусса для вектора электрического смещения. Поведение векторов напряженности и электрического смещения на границе
Тема 3. Электромагнетизм Вопросы темы. 1. Характеристики магнитного поля.. Магнитные свойства веществ. Постоянные магниты и электромагниты. 3. Действие магнитного поля на проводник с током и движущийся
Электричество и магнетизм Электростатическое поле в вакууме Задание 1 Относительно статических электрических полей справедливы утверждения: 1) поток вектора напряженности электростатического поля сквозь
ТЕМА 15.. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА 15.1. Намагничивание вещества 15.. Магнитное поле на границе раздела сред 15.3. Магнитомеханические явления 15.4. Виды магнетиков. Диамагнетики в магнитном поле 15.5.
УДК 6.778.4 Магнітна і електрична сепарація А.А. БЕРЕЗНЯК, канд. техн. наук, Е.А. БЕРЕЗНЯК, М.Э. ГУМЕРОВ (Украина, Днепропетровск, Национальный горный университет) РАСЧЕТ НЕОБХОДИМЫХ ПАРАМЕТРОВ ПРОЦЕССА
1 3.14. Ферромагнетизм. Ферромагнетизм магнитоупорядоченное состояние вещества, при котором все магнитные моменты атомных носителей магнетизма в пределах пространственных областей, называемых доменами,
5 ЭЛЕКТРОМАГНЕТИЗМ. МАГНИТНЫЕ ЦЕПИ Лекция 25 Факты об магнетизме Магнетизм это особое проявление движения электрических зарядов внутри атомов и молекул, которое проявляется в том, что некоторые тела способны
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени М. В. Ломоносова Физический факультет кафедра общей физики и физики конденсированного состояния Методическая разработка по общему физическому практикуму Лаб.
Дисциплина «Материалы электронной техники» ТЕМА 4: «Магнитные материалы» Легостаев Николай Степанович, профессор кафедры «Промышленная электроника» Классификация материалов по магнитным свойствам. Диамагнетики
1 39 Магнитное поле в веществе 391Магнитные моменты в веществе До сих пор мы рассматривали магнитные поля и электрические токи в вакууме В веществе магнитное поле возбуждается не только электрическими
СОДЕРЖАНИЕ 16. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ… 3 16.1. Закон Кулона… 3 16.2. Напряженность электростатического поля. Принцип суперпозиции для напряженности электростатических полей… 6 16.3. Поток вектора Основой ферромагнитного полотна является низкоуглеродистая сталь. Сами полотна выполнены толщиной до 0,4 миллиметров, причём при разной толщине они наследуют свойства исходного материала. Характеристики полотна ферромагнитного: Отличие ферромагнитных полотен Техническое отличие ферромагнетиков от магнита винилового и других видов магнитов, заключается в способности данных материалов примагничиваться к соответствующей магнитной поверхности, не будучи ярким магнитным проводником по свойствам. Возможности применения магнитомягкого железа Сейчас магнитное железо вошло в практику оформления интерьеров и производства, бытовых вещей, как пример, можно привести – обои магнитные, как один из самых необычных решений в дизайне помещений. Одним из наиболее популярных событий в применении мягкомагнитного железа или ферромагнетика, являются пособия учебные, экспонаты наглядные, развивающие игры, основанные на логике. Офисная канцелярия также не обходится без применения железа мягкомагнитного. Творческие находки, создают все новые сферы применения железа магнитомягкого. Даже единственное техническое качество – магнитные свойства, позволяют создать множество предметов для дома, школы, сферы услуг. В сочетании с современными полиграфическими и другими технологиями феррошит входит в тенденцию развития товаров визуального ряда с большим спектром практических качеств. Каждый человек сталкивается с феррошитом в жизни, многие создают из него собственные оригинальные изделия и воплощают свои идеи. James Nelson & Stefano Sanvito et al. / Physical Review Materals, 2019 Ирландские физики разработали и обучили модель, которая предсказывает температуру Кюри у ферромагнетика, отталкиваясь только от его химического состава. В настоящее время физикам известно более 2500 ферромагнетиков, что автоматически делает их самым распространенным классом магнитных материалов. На микроскопическом уровне ферромагнетик разбивается на домены — грубо говоря, на мелкие неделимые магнитики. Если температура ферромагнетика сравнительно невелика, все магнитики смотрят в одну и ту же сторону, их поле складывается и усиливается, и в результате намагниченность ферромагнетика получается большой — достаточно большой, чтобы ферромагнетики случайно обнаружили еще две с половиной тысячи лет назад. Однако при повышении температуры магнитики начинают «дрожать», их поле складывается уже не так эффективно, и намагниченность материала начинает падать. Если температура превысит определенное критическое значение, «дрожание» станет слишком сильным, и ферромагнетик размагнитится. Эту критическую температуру называют температурой Кюри. Зависимость числа известных ферромагнетиков от их температуры Кюрию. Во врезе — относительная распространенность химических элементов в этих ферромагнетиках James Nelson & Stefano Sanvito et al. / Physical Review Materals, 2019 Из-за этого богатства большинство поисков новых магнитов ведется теоретически, с помощью численного моделирования. К сожалению, зависимости, которые связывают температуру Кюри материала с его строением и химическим составом, далеко не очевидны. Бо́льшая часть таких зависимостей носит чисто эмпирический характер. Например, температуры Кюри сплавов типа Co2XY можно описать с помощью кривой Слетера-Полинга, а температуры Кюри аналогичных сплавов с марганцем следуют кривым Кастелица-Каномата. Это связано с тем, что стандартные методы, включая достаточно мощную теорию функционала плотности, не могут извлечь информацию о температуре Кюри из строения материала, хотя и могут рассчитать другие его свойства. Поэтому физикам, ищущим высокотемпературные магниты, до сих пор приходится руководствоваться эмпирическими правилами, которые могут упускать перспективные регионы. В результате большая часть усилий тратится на исследование материалов с низким практическим потенциалом. Физики Джеймс Нельсон (James Nelson) и Стефано Санвито (Stefano Sanvito) частично решили эту проблему с помощью машинного обучения. Ученые разработали и натренировали модель, которая предсказывает температуру Кюри материала, отталкиваясь от его химической формулы. Погрешность предсказаний такой модели составила около 50 кельвинов. Более того, нейросеть очень хорошо экстраполировала скудные исходные данные на новые области. Поскольку зависимость между температурой Кюри и химическим составом ферромагнетика не вполне понятна, физики максимально расширили область параметров, с которыми работала модель. В результате ученые получили 129-мерный вектор параметров. Этот вектор включал в себя 84 числа, описывающих атомную долю каждого возможного элемента, который может входить в состав ферромагнетика. Поскольку на практике материал состоит из одного, двух или трех элементов, для реальных соединений практически все эти числа равны нулю. Это указывает на то, что информацию о соединении можно хранить и обсчитывать более эффективно. Поэтому к этим 84 числам ученые добавили еще 45 параметров, описывающих атомное число, группу, период, число валентных электронов, молярный объем, температуру плавления и сродство к электрону, усредненные по атомам соединения, а затем «урезали» вектор, выделив в нем только самые важные параметры. Интересно, что при грамотном «урезании» эффективность работы модели практически не изменялась — даже в том случае, если от исходных 129 параметров оставалось всего 10. Для обучения и проверки модели ученые использовали 2500 ферромагнетиков, собранных из четырех разных источников. Соединения с одинаковым химическим составом, но разной кристаллической структурой физики считали одним и тем же материалом, поэтому температура Кюри «составного» ферромагнетика могла довольно значительно колебаться. Например, материал с химической формулой Sm2Ni17 может терять ферромагнитные свойства как при 186, так и при 641 кельвине. Чтобы минимизировать эффект таких колебаний, ученые присваивали «составным» ферромагнетикам медианную температуру. Впрочем, стоит отметить, что для большинства материалов разброс был сравнительно невелик: у 80 процентов ферромагнетиков температура Кюри укладывалась в интервал шириной около 50 кельвинов, и лишь у 5 процентов разброс температур превышал 300 кельвинов. Поскольку полученная выборка из 2500 ферромагнетиков была сравнительно невелика, ученые объединили тренировочный (training) и тестовый (validation) наборы данных. Напомним, что на тренировочном наборе данных модель настраивает параметры, а на тестовом наборе — гиперпараметры, то есть параметры, которые задаются до начала обучения. Чтобы повысить эффективность обучения, в эти (совпадающие) наборы данных исследователи старались отобрать как можно больше различных соединений (и даже добавили к ним немагнитные соединения). Размер тренировочно-тестового набора составил 1866 соединений. С помощью оставшихся 767 соединений физики проверяли эффективность обученной модели. В качестве модели машинного обучения ученые использовали четыре разных алгоритма: метод регуляризации Тихонова (ridge regression), нейросеть, случайный лес (random forest) и регрессию ядра хребта (kernel ridge regression). Последние два метода справились с предсказаниями лучше всего: в 59 процентах случаев они предсказали температуру Кюри с точностью порядка 50 кельвинов и еще в 24 процентах ошиблись менее чем на сто кельвинов. Стоит отметить, что «ломался» алгоритм только на ферромагнетиках с низкой температурой Кюри, которые не имеют практической пользы. Более того, модель очень хорошо экстраполировала скудные начальные данные: всего по двум точкам она практически идеально восстанавливала кривые, на которых лежат ферромагнитные соединения различных элементов. Температура Кюри, предсказанная моделью для бинарных соединений кобальт — марганец, железо — никель и никель — родий. Серым отмечены предсказания, крестами — данные, которые использовались при обучении, зелеными точками — данные из проверочной выборки James Nelson & Stefano Sanvito et al. / Physical Review Materals, 2019 Температуры Кюри, предсказанные моделью для тернарной системы железо — кобальт — алюминийhttp://www.lib.unn.ru/students/src/Intro_DFT.pdf James Nelson & Stefano Sanvito et al. / Physical Review Materals, 2019 В последнее время нейронные сети стали так популярны, что их пытаются применить буквально везде, где только можно. Физиков эта мода также не обошла стороной. В частности, физики уже научили нейросети считать функциональные интегралы и топологические инварианты, решать квантовую проблему многих тел, исправлять ошибки в квантовых компьютерах, искать распады бозона Хиггса и предсказывать рост кристаллов. Более того, некоторые нейросети не хуже людей «понимают» суть физических процессов в статистических системах, то есть выделяют степени свободы, которые определяют ее физические свойства. Дмитрий Трунин Физика, 11 класс Урок 4. Магнитные свойства вещества. Электроизмерительные приборы Перечень вопросов, рассматриваемых на уроке: 1. Магнитные свойства вещества. 2. Свойства диа-, пара- и ферромагнетиков. 3. Принцип действия электроизмерительных приборов. Глоссарий по теме: Магнитная проницаемость – это физическая скалярная величина, показывающая, во сколько раз индукция магнитного поля в данном веществе отличается от индукции магнитного поля в вакууме. Диамагнетики – вещества, у которых магнитная проницаемость чуть меньше единицы. К таким веществам относятся золото, серебро, углерод, висмут. Парамагнетики – вещества, у которых магнитная проницаемость чуть больше единицы. Это алюминий, вольфрам, щелочные металлы, магний, платина. Ферромагнетики – вещества у которых магнитная проницаемость много больше единицы. Это железо, никель, кобальт, и сплавы металлов. Точка Кюри – температура, при которой ферромагнетики теряют ферромагнитные свойства. Ферриты – ферромагнитные материалы, не проводящие электрического тока. Основная и дополнительная литература по теме: 1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 27-30. 2.Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 113. 3. ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017. Теоретический материал для самостоятельного изучения. Все вещества в окружающей нас природе в какой — то мере обладают магнитными свойствами. Ещё с глубокой древности была известна способность некоторых минералов притягивать железные предметы. Среди многих приборов навигации, необходимых для прокладывания курса кораблей или самолётов, обязательно должен быть и магнитный компас. Во многих измерительных приборах основными деталями служат постоянные магниты. Что же происходит с веществом, помещённом в магнитное поле? Вспомним, как магнитные свойства катушки, по которой течёт ток, усиливаются, если в катушку вставлен железный сердечник. Железный сердечник намного увеличивает магнитное поле в катушке с током. Мы знаем, что вокруг катушки с электрическим током возникает магнитное поле, а железный сердечник, создаёт своё магнитное поле и, согласно принципу суперпозиции полей, векторы этих двух полей складываются. Таким образом, мы наблюдаем усиление магнитного поля. Магнитную индукцию, создаваемую электрическим током, обозначим через (В0). Магнитную индукцию поля в веществе обозначим через (В). При введении железного сердечника, появляется магнитная индукция поля, возникающая благодаря намагничиванию вещества (В1). Эти поля складываются по принципу суперпозиции полей. В итоге мы наблюдаем, что вещество может усилить или, возможно ослабить магнитное поле. Магнитная индукция поля, создаваемого этими токами в вакууме, будет меньше, чем магнитная индукция поля в веществе. Магнитной проницаемостью вещества называется физическая скалярная величина показывающая, во сколько раз индукция магнитного поля в данном веществе отличается от индукции магнитного поля в вакууме. Французский физик Андре Мари Ампер сравнивал магнитные поля, создаваемые полосовым магнитом и проводниками с током. В итоге, Ампер выдвинул гипотезу, что внутри молекул и атомов циркулируют элементарные электрические токи. Круговые электрические токи – это токи, обусловленные орбитальными движениями электронов вокруг ядра. Английский физик Майкл Фарадей исследовал влияние вещества на магнитное поле. В итоге, он определил, что все вещества изменяют магнитное поле, если их поместить во внешнее магнитное поле. Получается если вещество поместить во внешнее магнитное поле, оно становится источником своего магнитного поля. Это явление называют намагничиванием. Таким образом, Майкл Фарадей обнаружил, что вещества делятся на три группы — диа-, пара-, и ферромагнетики. Диамагнетики – это вещества, у которых магнитная проницаемость чуть меньше единицы. К таким веществам относятся золото, серебро, углерод, висмут. Магнитная проницаемость висмута равна 0,9998. Значит, магнитное поле ослабляется, когда в него помещают это вещество В˂В0. Это означает, что вектор магнитной индукции поля, создаваемого веществом направлен противоположно вектору магнитной индукции поля, создаваемого током. Парамагнетики – вещества, у которых магнитная проницаемость чуть больше единицы. Это алюминий, вольфрам, щелочные металлы, магний, платина. Эти вещества намагничиваются очень слабо, намагничиваются вдоль намагничивающего поля. Вектор магнитной индукции поля, создаваемого веществом, направлен в ту же сторону, что и вектор магнитной индукции поля, создаваемого током. Ферромагнетики – это вещества, у которых магнитная проницаемость во много раз больше единицы. Это такие вещества как железо, кобальт, никель и сплавы металлов. Для железа магнитная проницаемость равна одна тысяча (1000). Магнитные поля создаются ферромагнетиками не только вследствие обращения электронов вокруг ядер, но и вследствие их собственного вращения. Собственный вращательный момент (момент импульса) электрона называется спином. Согласно простейшим представлениям, электроны вращаясь вокруг собственной оси обладая зарядом, имеют, магнитное поле наряду с полем, появляющимся за счёт их орбитального движения вокруг ядер. В ферромагнетиках существуют области с параллельными ориентациями спинов, называемыми доменами; размеры доменов порядка 0.5 мкм. Параллельная ориентация спинов обеспечивает доменам минимум потенциальной энергии. Если ферромагнетик не намагничен, то ориентация доменов хаотична и суммарное магнитное поле, создаваемой доменами, равно нулю. При включении внешнего магнитного поля домены ориентируются вдоль линий магнитной индукции этого поля, и индукция магнитного поля в ферромагнетиках увеличивается, становясь в тысячи и даже миллионы раз больше индукции внешнего поля Ферромагнитные свойства у веществ существуют только в определённой области температуры. Температура, при которой ферромагнитные материалы теряют свои ферромагнитные свойства, называют точкой Кюри по имени открывшего данное явление французского учёного Пьера Кюри. Если сильно нагреть намагниченный образец, то он потеряет способность притягивать железные предметы. Точка Кюри для железа 753 градусов по Цельсию, для кобальта 1000 градусов по Цельсию. Существуют ферромагнитные сплавы, у которых точка Кюри менее 100 градусов. Первые детальные исследования магнитных свойств ферромагнетиков были выполнены выдающимся русским физиком А.Г. Столетовым. Большое применение получили ферромагнитные материалы, не проводящие электрического тока – ферриты. Это химические соединения оксидов железа с оксидами других веществ. К их числу относится и магнитный железняк. Стальной или железный сердечник в катушке усиливает создаваемое ею магнитное поле, не увеличивая силу тока в катушке. Это экономит электроэнергию. Сердечники трансформаторов, генераторов, электродвигателей и т. д. изготовляют из ферромегнетиков. При выключении внешнего магнитного поля ферромагнетик остаётся намагниченным, таким образом создаёт магнитное поле в окружающем пространстве. Это объясняется тем, что домены не возвращаются в прежнее положение и их ориентация частично сохраняется. Благодаря этому существуют постоянные магниты. Постоянные магниты широко применяются в электроизмерительных приборах, громкоговорителях и телефонах, звукозаписывающих аппаратах, магнитных компасах и т.д. Электроизмерительный прибор является необходимым устройством в связи, промышленности, на транспорте, в медицине и в научных исследованиях. Примеры и разбор решения заданий: 1. Для каких целей применяют ферромагнитные материалы? Выберите один правильный ответ. Варианты ответов: 1) для усиления силы тока; 2) для ослабления магнитного поля; 3) для усиления магнитного поля; 4) для ослабления силы тока. Пояснение: ферромагнетики и ферромагнитные материалы это вещества, которые создают наиболее сильные магнитные поля. Правильный ответ: 3) для усиления магнитного поля. 2. По графику определите магнитную проницаемость стали при индукции В0 намагничивающего поля 1) 0,4 мТл, 2) 1,2 мТл. Дано: 1) B0 = 0.4 мТл 2) B0 = 1,2 мТл µ1 -? µ2 -? Решение: По определению магнитная проницаемость µ показывает, во сколько раз индукция магнитного поля В в веществе превышает индукцию намагничивающего поля В0 в вакууме: µ = 2) При В0 = 1.2 мТл, по графику В = 1,2 Тл Следовательно: Ответ: µ1 = 2000; µ2 = 1000 В рамках курса рассматриваются физические основы фазовых переходов второго рода на примере фазового перехода парамагнетик/ферромагнетик. Затрагиваемый круг вопросов включает классификацию материалов по магнитным свойствам, применение приближения среднего поля для расчета различных магнитных характеристик, элементы феноменологической теории Ландау, антиферромагнетизм. Курс преподается на английском языке с русскими субтитрами и предназначен в первую очередь для иностранных студентов, обучающихся в России. Настоящий курс посвящен явлению ферромагнетизма. Ферромагнетизмом называют магнитоупорядоченное состояние вещества, в котором атомные магнитные моменты параллельны друг другу, так что вещество обладает самопроизвольной намагниченностью. Благодаря ферромагнетизму некоторые материалы (например, железо) способны притягиваться к магнитам или же сами становиться постоянными магнитами. Явление ферромагнетизма играет значительную роль в современных технологиях и является физической основой для создания различных электрических и электронных устройств, например, трансформаторов, генераторов, электромагнитов, магнитных накопителей информации, жестких дисков, спинтронных устройств и т.д. Однако ферромагнетизм в отсутствии внешнего магнитного поля устанавливается не при любой температуре, а лишь при температуре ниже критической, называемой температурой Кюри. Разумеется, для каждого материала температура Кюри имеет свое значение. Ответственным за явление ферромагнетизма является обменное взаимодействие, стремящееся установить магнитные моменты соседних атомов или ионов параллельно друг другу. Обменное взаимодействие – это чисто квантовомеханический эффект, не имеющий аналога в классической физике. В рамках курса мы постараемся разобраться с микроскопической природой ферромагнетизма, узнать о его экспериментальных проявлениях и построить его квантовомеханическую теорию. Курс ориентирован на студентов магистратуры, в том числе иностранных, для которых английский язык является родным, желающих повысить свой уровень в области теоретической физики. Курс состоит из 7 модулей. Общая длительность курса — 10 недель. Времени на изучение в неделю — от 2 до 3 часов. Необходимо знание основ векторного исчисления, теории функций комплексного переменного, теории дифференциальных уравнений, теории вероятностей, статистической физики и квантовой механики. Курс ориентирован на студентов магистратуры физических специальностей, владеющих английским языком. Модуль 1 Модуль 2 Модуль 3 Модуль 4 Модуль 5 Модуль 6 Модуль 7 Прослушав курс, Вы узнаете: — Классификацию материалов по магнитным свойствам — Приближение среднего поля для расчета различных магнитных характеристик — Основные сведения о феноменологической теории фазовых переходов второго рода Ландау — Что такое антиферромагнетизм В зависимости от магнитных свойств материалы разделяют на диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики. Количественно магнитные свойства материалов принято оценивать по их магнитной восприимчивости λ = М/Н, где М — намагниченность вещества; Н — напряженность магнитного поля. Это вещества, атомы, ионы или молекулы которых не имеют результирующего магнитного момента при отсутствии внешнего поля. Диамагнитный эффект является результатом воздействия внешнего магнитного поля на молекулярные токи и проявляется в том, что возникает магнитный момент, направленный в сторону, обратную внешнему полю. Таким образом, во внешнем магнитном поле диамагнетики намагничиваются противоположно приложенному полю, т. е. имеют отрицательную магнитную восприимчивость (λ < 0). Диамагнитные вещества выталкиваются из неравномерного магнитного поля, а в равномерном магнитном поле вектор намагниченности диамагнетика стремится расположиться перпендикулярно к направлению поля. Диамагнетизм присущ всем без исключения веществам в твердом, жидком и газообразном состояниях, но проявляется слабо и часто подавляется другими эффектами. Это вещества, атомы, ионы или молекулы которых имеют результирующий магнитный момент при отсутствии внешнего магнитного поля. Во внешнем магнитном поле парамагнетики намагничиваются согласно с внешним полем, т. е. имеют положительную магнитную восприимчивость (λ > 0). Парамагнитный эффект присущ веществам с нескомпенсированным магнитным моментом атомов при отсутствии у них порядка в ориентации этих моментов. Поэтому, когда нет внешнего магнитного поля, атомные магнитные моменты располагаются хаотически и намагниченность парамагнитного вещества равна нулю. При воздействии внешнего магнитного поля атомные магнитные моменты получают преимущественную ориентацию в направлении этого поля, и у парамагнитного вещества проявляется намагниченность. Это вещества, в которых магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов отличны от нуля. При воздействии внешнего магнитного поля магнитные моменты доменов приобретают преимущественное ориентирование в направлении этого поля и ферромагнитное вещество намагничивается. Ферромагнитные вещества характеризуются большим значением магнитной восприимчивости (>> 1), а также ее нелинейной зависимостью от напряженности магнитного поля и температуры, способностью намагничиваться до насыщения при обычных температурах даже в слабых магнитных полях, гистерезисом — зависимостью магнитных свойств от предшествующего магнитного состояния, точкой Кюри, т. е. температурой, выше которой материал теряет ферромагнитные свойства. К ферромагнитным веществам относятся железо, никель, кобальт, их соединения и сплавы, а также некоторые сплавы марганца, серебра, алюминия. Ферромагнитные свойства у вещества могут возникать лишь при достаточно большом значении обменного взаимодействия, что характерно для кристаллов железа, кобальта, никеля и др. Необходимое значение обменного взаимодействия ферромагнетики имеют лишь в твердом состоянии. Этим объясняется отсутствие в природе жидких и газообразных ферромагнетиков. Ферромагнетизм сплавов, целиком состоящих из «парамагнитных» компонентов, объясняется тем, что в этих сплавах, основой которых обычно является марганец или хром, введение в решетку основы атомов висмута, сурьмы, серы и теллура изменяет электронную структуру кристаллов, в результате чего создаются условия для возникновения ферромагнетизма. Это вещества, в которых магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов равны нулю. При воздействии внешнего магнитного поля магнитные моменты атомов приобретают преимущественную ориентацию вдоль внешнего поля и антиферромагнитное вещество намагничивается. Антиферромагнитные вещества характеризуются кристаллическим строением, небольшим коэффициентом магнитной восприимчивости (λ = от 10-3 до 10-5), постоянством восприимчивости в слабых полях и сложной зависимостью от магнитного поля в сильных полях, специфической зависимостью от температуры, а также температурой точки Нееля, выше которой вещество переходит в парамагнитное состояние. К антиферромагнетикам относятся чистые металлы хром и марганец, редкоземельные металлы цериевой подгруппы: церий, неодим, празеодим самарий и европий. Редкоземельные металлы диспрозий, гольмий и эрбий в зависимости от температуры могут быть антиферромагнетиками или ферромагнетиками. При воздействии на эти металлы, находящиеся в антиферромагнитном состоянии внешнего магнитного поля, превышающего критическое значение, происходит переход антиферромагнитного порядка в ферромагнитный, сопровождающийся скачкообразным появлением намагниченности (М~ 1600 кА/м). Аналогичные превращения можно наблюдать у тулия и тербия. Это кристаллические вещества, магнитную структуру которых можно представить в виде двух или более подрешеток; магнитные моменты атомов или ионов находятся в состоянии самопроизвольного магнитного упорядочения, причем результирующие магнитные моменты каждого из доменов отличны от нуля. Ферромагнитные материалы или вещества были изобретены французским физиком Луи Эженом Феликсом Нилом. Он родился 22 -го ноября 1904 года в Лионе и умер 17 -го ноября 2000 года в Брив-ла-Гайард. Он учился в Страсбургском университете и получил Нобелевскую премию по физике. Доступны несколько компаний по производству ферромагнитных материалов, такие как Dexter Magnetic Technologies, основанная в 1951 году в деревне Элк-Гроув, Digi Key Electronics, основанная в 1972 году в Thief River Falls, компоненты RS, основанные в 1937 году в Корби Уорингом и П.M.Sebestyen, Star Trace Private Limited, основанная в 1985 году в Тамилнаду, Shields Company Magnetics в городе Калвер, Magnum Magnetics Corporation в Мариетте, Alliance LLC, Arnold Magnetic Technologies, International Magna Products, Master Magnetics — одни из ведущих производителей магнитных материалов. В некоторых материалах постоянные атомные магнитные моменты имеют сильную тенденцию выравниваться даже без внешнего поля. Эти материалы называются ферромагнитными материалами.Некоторыми примерами ферромагнитных материалов являются кобальт, железо, никель, гадолиний, диспрозий, пермаллой, аваруит, вайракит, магнетит и т. Д. Существует много ферромагнитных материалов, некоторые из списков ферромагнитных материалов показаны в таблице ниже. 1). Кобальт: Кобальт был изобретен Георгом Брандтом в 1739 году. Он родился 26 июня 1964 года в Риддархиттане и умер в Стокгольме 29 апреля 1768 года.Это один из типов ферромагнитных материалов, обнаруженных в земной коре. Он представлен в периодической таблице символом CO, а его атомный номер — 27. 2). Железо: Железо — это химический элемент одного типа, который содержится в земной коре и обычно обозначается символом Fe. Цвет железа — серебристо-серый, а атомный номер в периодической таблице — 26. Первый электрический утюг был изобретен в 1882 году Генри Сили, который использовался для глажки одежды.Генри Сили родился 20 -го мая 1861 года в Нью-Йорке и умер 20 -го мая 1943 года. 3). Никель: Химический элемент никель также находится в земной коре и обозначается символом Ni. Атомный номер никеля в периодической таблице равен 28, а цвет никеля — серебристо-белый. Этот металл изобрел Аксель Фредрик Кростедт, он родился в Швеции 23 декабря 1722 года и умер 20 мая 1943 года. 4).Неодимовый магнит: Это один из видов сильных и постоянных магнитов, но он редко встречается в земной коре, а цвет неодима — серебристо-белый. Его также называют магнитом NIB или Neo или NdFeB, а формула неодимового магнита — Nd 2 Fe 14 B . Этот металл изобрел Карл Ауэр фон Вельсбах, он родился в Австрии 1 сентября 1858 г. и умер 4 августа 1929 г. 5). Диоксид хрома: Химическая формула диоксида хрома — CrO 2 , он нерастворим в воде и также называется оксидом хрома (iv).Другие названия диоксида хрома — Carolyn и magtrieve . Металлический хром открыт Луи Николя Воклен, он родился в Австрии 16 мая 1763 года и умер 14 ноября 1829 года во Франции. 6). Гадолиний: Гадолиний — это химический элемент одного типа, который обозначается символом Gd. Атомный номер гадолиния 64 в периодической таблице. Металлический гадолиний изобретен Полем-Эмилем Лекоком де Буабодраном (18 -е апреля 1838 г. — 28 мая 1912 г.) во Франции и Жаном Шарлем Галиссаром де Мариньяком (24 -е апреля 1817 г. — 15 -е апреля 1894 г.) в Швейцарии. 7). Тербий: Тербий также является одним из видов химического элемента, который обозначается символом Td. Он изобретен Карлом Густавом Мосандером в 1843 году и редко встречается в земной коре. Этот химический элемент изобретен Карлом Густавом Мосандером в 1843 году. Он родился 10 сентября 1797 года в Кальмаре и умер 15 октября 1858 года в графстве Стокгольм. 8). Диспрозий: Диспрозий — это один из типов ферромагнитных материалов, который был идентифицирован Полем Эмилем Лекоком де Буабодраном в 1886 году.Он родился 18 -го апреля 1838 года и умер 28 -го мая 1912 года во Франции. Атомный номер гадолиния 66 в периодической таблице. Существует два типа ферромагнитных материалов: немагнитный ферромагнитный материал и намагниченный ферромагнитный материал. Классификация ферромагнитных материалов показана на рисунке ниже В каждом немагниченном ферромагнетике атомы образуют домены внутри материала.Различные домены имеют разные направления магнитного момента. Следовательно, материал остается немагниченным. Немагниченный ферромагнетик, показанный на рисунке ниже При приложении внешнего магнитного поля к доменам ненамагниченного ферромагнетика, домены будут вращаться и выравниваться в направлении магнитного поля из-за доменного характера ферромагнетика даже при приложении небольшого магнитного поля. вызывает большую намагниченность.Магнитное поле в таком материале намного больше, чем магнитное поле. Магнитные моменты доменов параллельны магнитному полю в ферромагнетизме, потому что эти домены также выстраиваются в одном направлении. Это объяснение ненамагниченного ферромагнетика и намагниченного ферромагнетика с помощью диаграмм. Свойства ферромагнетиков Причина: это связано с рандомизацией доменов при нагревании Преимущества ферромагнитных материалов Главный недостаток ферромагнитных материалов ферромагнитные материалы Ферромагнетики изменяют свою магнитную доменную структуру под действием механических напряжений (Kneller, 1962; Cullity, 1972). Эти микромагнитные изменения, вызванные движениями стенок Блоха и процессами вращения, являются причиной хорошо известного гистерезиса сдвига под действием остаточных напряжений (см.рис.8.21). Рисунок 8.21. Гистерезис сдвига при растягивающих и сжимающих остаточных напряжениях. В магнитострикционных положительных материалах растягивающие напряжения вызывают увеличение дифференциальной восприимчивости X diff , а в области коэрцитивной силы H C — H C -смещение на меньшие значения . Напряжения сжатия вызывают уменьшение X diff в области коэрцитивной силы и смещение H C в сторону больших значений магнитного поля (см.рис.8.21). Однако зависимость H C и X diff от растягивающих и сжимающих напряжений не может использоваться в качестве величины прямого неразрушающего измерения для определения остаточного напряжения, поскольку невозможно полностью измерить плотность магнитного потока B в техника настройки. Чтобы преодолеть это ограничение, необходимо использовать электромагнитные измерительные величины, чувствительные к обратимым и необратимым движениям стенки Блоха (Kneller, 1962; Seeger, 1966). В ферромагнитных материалах магнитострикционно активные стенки Блоха (100) -90 ° и (111) -90 ° и процессы вращения напрямую взаимодействуют с напряжениями. Все измеряемые величины, которые происходят из этих процессов перемагничивания, чувствительны к напряжению, как динамическая магнитострикция (см. Главу: Ультразвуковые методы определения характеристик материалов), и к различным величинам, полученным из возрастающей проницаемости. Из-за связи 90 ° и 180 ° стенок Блоха, измерения величин, которые используют в основном взаимодействия 180 ° стенок Блоха, также чувствительны к напряжению, но косвенным образом, как магнитный шум Баркгаузена.Все методы ферромагнитного неразрушающего контроля (NDT) более или менее чувствительны к механическим напряжениям и состоянию микроструктуры испытываемого материала. Для измерения остаточного напряжения, не зависящего от состояния микроструктуры, нам нужны как минимум две измеряемые величины, полученные с помощью электромагнитного метода (Theiner and Altpeter, 1987). Результаты, показанные на рис. 8.22 и 8.23 демонстрируют это на двух цилиндрических образцах (диаметром 8 мм) с различным состоянием микроструктуры стали с супер 13% Cr.На рис. 8.22 показаны измеряемые величины M MAX и H CM , полученные из магнитного шума Баркгаузена для более магнитно-твердого состояния (мартенсита) (твердость = 527HV30) как функция растягивающих и сжимающих напряжений. M MAX показывает зависимость напряжения в области напряжений от +200 до -200 Н / мм 2 . Измеряемая величина H CM показывает почти постоянное значение в области растяжения и сжатия. Рисунок 8.22. Измеряемые величины M MAX и H CM как функция нагрузочных напряжений для магнитотвердого состояния микроструктуры (мартенсит). Рисунок 8.23. Измеряемые величины M MAX и H CM как функция нагрузочных напряжений для состояния магнитомягкой микроструктуры (отожженный мартенсит). На рис. 8.23 показаны две измеряемые величины для отожженного мартенсита из более мягкого в магнитном отношении материала (250HV30).Обе измеряемые величины показывают большую динамику напряжения, чем для более твердого материала. В более магнитотвердом материале более низкая зависимость от напряжений вызвана более высокой плотностью дислокаций, которые скалывают все магнитострикционно активные стенки Блоха под углом 90 °. Измеряя H CM , можно разделить два состояния микроструктуры этой стали независимо от напряженного состояния. Этот пример показывает необходимость двух измеряемых величин для измерения напряжения независимо от состояния микроструктуры. Для измерения напряжения, не зависящего от состояния микроструктуры, текстуры и других факторов, необходимы дополнительные электромагнитные методы, такие как дополнительная проницаемость и высшие гармоники (см. Главу: Гибридные методы определения характеристик материалов). Для количественного измерения остаточного напряжения необходима калибровка магнитных величин измерения с помощью значений остаточного напряжения рентгеновского излучения. Причина в том, что физико-математическое описание невозможно, поскольку механизм взаимодействия между микроструктурой и измеряемыми величинами слишком сложен (Altpeter et al., 2002). Для измерения многоосного остаточного напряжения миниатюрный электромагнитный зонд был разработан в рамках исследовательского проекта (Altpeter et al., 2009). Этот так называемый датчик вращающегося поля (рис. 8.24) был встроен в инструмент для глубокой вытяжки — плунжер. Магнитные полюсные фигуры были измерены в процессе глубокой вытяжки (см. Рис. 8.25). Рисунок 8.24. Датчик вращающегося поля (прототип) для многоосного управления технологическим процессом в режиме онлайн. Рисунок 8.25. Максимальная амплитуда M MAX1 , полученная из значений магнитного полюса, как функция от положения пуансона для различных сил держателя заготовки F-BH. Форма полюсных фигур, которая характерна для остаточного напряженного состояния глубоко вытянутых листов, позволяет делать выводы о критическом напряжении нагрузки, которое может привести к разрывам. На рис. 8.25 показана максимальная амплитуда M MAX1 , полученная из фигур магнитных полюсов, как функция от положения пуансона для различных сил F-BH держателя заготовки (Altpeter et al., 2009). На основе этих результатов были созданы первые основы многоосевого управления технологическим процессом в режиме онлайн. На протяжении многих десятилетий магнетизм был аномалией, которая привлекла внимание человечества. В любом из случаев в жизни человечества можно наверняка столкнуться с постоянными магнитами, и поэтому сегодня мы перейдем к обсуждению, чтобы узнать концепции магнетизма и что такое ферромагнетизм и ферромагнетик? Первоначально концепция магнетизма возникает из магнитного дипольного момента электрона, что означает, что электрон действует как небольшой магнит, генерирующий магнитное поле.Вихрь электронов в атомах является решающим источником генерации ферромагнетизма, даже если существует поддержка орбитального углового момента электрона. Давайте продвинемся вперед, чтобы понять подробные концепции ферромагнетизма и ферромагнетиков. Ферромагнитные материалы — это материалы, которые проявляют сильные магнитные свойства при размещении в аналогичном направлении поля. Сначала мы познакомимся с понятием домена. Как правило, в этих материалах есть небольшая область, которая имеет особое выравнивание спинов из-за квантово-механического напряжения.Проницаемость этих материалов чрезвычайно высока и составляет почти несколько тысяч. Обратные магнитные эффекты электронного спина и орбитального движения не будут устранены в этих материалах. Соответственно, существует значительный вклад каждого атома, который помогает в развитии внутреннего магнитного поля. Благодаря этому внутреннему магнитному полю свойство магнитного поля будет увеличиваться. намагниченность ферромагнитного материала В области электротехники кажется вполне достаточным разделить магнитные материалы на ферромагнитные и неферромагнитные.Ферромагнитные материалы обладают свойством проницаемости больше единицы, тогда как неферромагнетики имеют проницаемость, равную единице. Ферромагнитные материалы классифицируются как Эти материалы демонстрируют свойства высокой проницаемости, пониженной коэрцитивной силы, их можно легко намагничивать и размагничивать. также демонстрируют низкий гистерезис. Некоторые из них — железо, никель, алюминий, вольфрам и кобальт.Процесс легкого намагничивания и размагничивания позволяет использовать эти материалы в генераторах, телефонных приемниках, электромагнитах, трансформаторах, индукторах, реле и во многих других. Даже они используются для магнитного экранирования. Вышеуказанные свойства этих материалов также могут быть улучшены за счет надлежащего производства, нагрева и медленного цинкования, так что они приобретают повышенный уровень чистоты. Увеличенный магнитный момент, поддерживаемый при комнатной температуре, позволяет использовать мягкие ферромагнитные материалы для магнитных цепей, но тогда они являются хорошими проводниками и ухудшаются из-за вихревого тока, который развивается внутри них. Эти материалы демонстрируют свойства низкой проницаемости, увеличенной коэрцитивной силы, они настолько сложны для намагничивания и размагничивания. Некоторыми из них являются кобальтовая сталь, никель, несколько сплавов кобальта и алюминия. Они поддерживают широкий диапазон намагничивания и также поддерживают повышенный гистерезис. Их свойства позволяют реализовать их в динамиках, измерительных приборах и во многих других. Это отдельная классификация ферромагнитных материалов, обладающих свойствами между ферромагнитными и неферромагнитными материалами.Они состоят из крошечных частиц ферромагнитных материалов, обладающих высокой проницаемостью, и все они связаны с поддерживающей смолой. Магнитный момент в ферритах имеет большое коммерческое значение, в то время как магнитное насыщение не так уж важно для ферромагнитных материалов. Они также делятся на мягкие и твердые ферриты. • Мягкие ферриты Эти материалы обладают свойствами высокого сопротивления и имеют квадратную форму гистерезиса.Удельное сопротивление находится в диапазоне почти 109 Ом-см. Таким образом, поскольку вихревые токи, возникающие из-за переменных полей, уменьшаются, и свойства, проявляемые этими материалами, позволяют использовать их на высоких частотах, таких как микроволны. Мягкие ферриты производятся путем сочетания порошкообразных оксидов, конденсации и спекания при чрезвычайно высоких температурах. • Твердые ферриты Ключевая группа таких ферромагнетиков состоит из MOFe2O3, где M — барий или стронций.Они имеют шестиугольную форму и имеют высокую плотность. Эти материалы используются в двигателях, генераторах и реле. Даже они используются в качестве уплотнений, защелок, дверных доводчиков и в производстве различных игрушек. Эти материалы обладают отличительными магнитными моментами, которые ориентированы в параллельных направлениях, тогда как другие виды магнитных материалов имеют момент только в одном направлении. Северные полюса будут легко притягивать полюса других направлений, тогда как одни и те же полюса отталкивают друг друга (с севера на север и с юга на юг).Они с похожими и противоположными моментами отталкивают другого. намагниченность ферромагнитного материала Ниже приведен список ферромагнитных материалов Материал Природа и применение Fe 2.22 Co Углеродные нанотрубки и электроника Ni 0,606 Gd 7,63 Dy 10.2 CrO 2 3,4 MnBi + 3,6 Mn EuO NiO / Fe 2,4 5,0 Когда происходит удаление внешнего магнитного поля, эти материалы не будут размагничиваться в целом. Чтобы позволить им полностью потерять магнетизм, необходимо приложить обратное магнитное поле в противоположном направлении.Таким образом, эта процедура ферромагнитных материалов, удерживающих намагничивание даже при удалении внешнего поля, называется гистерезисом. И намагниченность материала, оцениваемая по плотности магнитного потока (B) v / s, приложенное внешнее магнитное поле (H) приведет к образованию петли, называемой петлей гистерезиса. На рисунке четко изображена эта процедура. гистерезис ферромагнитного материала Некоторые из свойств, проявляемых ферромагнитными материалами, описаны ниже: Есть два важных технологических применения ферромагнитных материалов.Они Приложения По сравнению с другими типами магнитов, ферромагнетизм является наиболее доминирующим. Эти материалы находят применение в самых разных областях. Их преимущества, свойства и возможности применения позволили им получить более широкую известность.Обсудите подробнее стратегии функционирования ферромагнитных материалов и связанные с ними концепции? Это температура, при которой материалы теряют свои ферромагнитные свойства и могут сохраняться за счет внешнего магнетизма. Они полностью потеряют свои магнитные свойства и станут парамагнитными по своей природе, и это происходит из-за несовпадения электронов. Существуют различные методы размагничивания магнита. Они имеют Сохраняемость соответствует способности объекта восстанавливать свою магнитную природу при прекращении действия магнитной силы.Коэрцитивность соответствует напряженности магнитного поля, которое необходимо для уменьшения магнитной природы до нуля. Железо, никель, кобальт и некоторые редкоземельные элементы (гадолиний, диспрозий) проявляют уникальное магнитное поведение, которое называется ферромагнетизмом, потому что железо (железо на латыни) является наиболее распространенным и ярким примером. Самарий и неодим в сплавах с кобальтом использовались для изготовления очень сильных редкоземельных магнитов. Ферромагнетики демонстрируют явление дальнего упорядочения на атомном уровне, которое заставляет неспаренные электронные спины выстраиваться параллельно друг другу в области, называемой доменом.Внутри домена магнитное поле является интенсивным, но в массивном образце материал обычно не намагничивается, потому что многие домены сами по себе будут ориентированы случайным образом относительно друг друга. Ферромагнетизм проявляется в том, что небольшое внешнее магнитное поле, например, от соленоида, может заставить магнитные домены выровняться друг с другом, и материал, как говорят, намагничивается. В этом случае управляющее магнитное поле будет увеличиваться во много раз, что обычно выражается как относительная проницаемость для материала.Есть много практических применений ферромагнитных материалов, таких как электромагнит. Ферромагнетики будут в некоторой степени оставаться намагниченными после воздействия внешнего магнитного поля. Эта тенденция «вспоминать свою магнитную историю» называется гистерезисом. Доля намагниченности насыщения, которая сохраняется при удалении управляющего поля, называется остаточной намагниченностью материала и является важным фактором в постоянных магнитах. Все ферромагнетики имеют максимальную температуру, при которой ферромагнитные свойства исчезают в результате теплового перемешивания.Эта температура называется температурой Кюри. Ферромагнетики механически реагируют на приложенное магнитное поле, слегка изменяя длину в направлении приложенного поля. Это свойство, называемое магнитострикцией, приводит к знакомому гудению трансформаторов, поскольку они механически реагируют на переменное напряжение 60 Гц. Магнетизм — это явление, которое веками пленило человечество.Существует пять различных типов магнетизма: диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм. Средний человек вспоминает, что ферромагнетизм является наиболее распространенным явлением. Это потому, что большинство людей когда-нибудь сталкивались с постоянными магнитами, и они сделаны из ферромагнитного материала. Это действительно похоже на парамагнитный материал, но с одним важным отличием, которое их разделяет. Парамагнетизм не имеет чистого магнитного поля, потому что спины электронов направлены в разные стороны.Это означает, что когда рядом с парамагнитным материалом помещается сильный магнит с положительным или отрицательным притяжением, частичное выравнивание спинов приведет к слабому притяжению. Где, как в ферромагнетизме, все спины электронов направлены в одном направлении. Это то, что заставляет постоянные магниты притягиваться через противоположные полюса, с юга на север и наоборот, а также отталкиваться, когда одни и те же полюса обращены друг к другу. Наиболее распространенными ферромагнитными материалами являются кобальт, железо, никель, а также магнитный камень, намагниченный естественным образом, и соединения других редкоземельных металлов.Обычное использование ферромагнитных материалов, влияющих на нашу повседневную жизнь, — это магнитное хранилище в форме данных. В противном случае считается энергонезависимым хранилищем, поскольку данные не могут быть потеряны, когда устройство не подключено к питанию. Преимущество этого метода хранения заключается в том, что это одна из самых дешевых форм хранения данных, а также возможность повторного использования. Все это возможно из-за гистерезиса. Когда ферромагнитные материалы намагничиваются в определенном направлении, они теряют способность терять свою намагниченность (гистерезис).Это означает, что он не сможет вернуться в исходное состояние без какого-либо намагничивания. Но может быть применено другое противоположное магнитное поле, которое приведет к созданию петли гистерезиса, как показано на рисунке 1. Это, в конечном счете, уникальный эффект, который позволяет этим материалам сохранять данные после того, как намагничивающее поле падает до нуля. Ферромагнитные материалы содержат уникальные магнитные моменты, которые выровнены параллельно друг другу в одном направлении (рис. 2). Все другие типы намагничивания имеют моменты более чем в одном направлении. Ферромагнетизм — единственная намагниченность с одинаковыми моментами направления. Приводя к притяжению или отталкиванию с другими магнитными материалами. Северные полюса притягивают южные полюса, в то время как одни и те же полюса отталкивают друг друга (с севера на север, с юга на юг).У них будут равные противоположные моменты, отталкивающие друг друга. На рисунке 2 ниже показаны магнитные моменты в ферромагнитных материалах. Они имеют одинаковую величину и упорядочены без магнитного поля. Теория Вейсса (Hw) описывает, как молекулярное поле Вейсса пропорционально намагниченности ферромагнитного материала, как показано в уравнении ниже.Где B представляет собой константу пропорциональности. $$ \ H_ \ omega = \ beta M \ label {1} $$ Уравнение \ ref {2} ниже описывает полное магнитное поле с \ (H \) в качестве внешнего поля. \ [\ H_ {tot} = H + H_ \ omega = H + \ beta M \ label {2} \] Из-за сходства с парамагнетизмом приведенное ниже уравнение может быть решено и заменено на \ (H \) в функции Ланжевена. \ [\ a = \ mu_o m_ \ beta \ dfrac {H_ (tot)} {k T} \ label {3} \] \ [\ dfrac {M} {M_S} = L (\ dfrac {\ mu_o m_ \ beta (H + \ beta M)} {kT}) \ label {4} \] \ [\ dfrac {Nm_b} {v} = M_S \ label {5} \] Нет внутреннего поля выше температуры Кюри \ (T_c \), решение уравнения \ ref {1} дает BM, равное 0.2} {v3k (T-T_c)} = X_F \ label {6} \] Квантово-механическое явление — более точный способ описания ферромагнетизма, поскольку разрешены только определенные углы магнитного движения. С классической точки зрения разрешены все углы, поскольку теория Ланжевена делает этот метод крайне маловероятным. Следовательно, приведенный ниже нормированный степенной закон с гаммой 0,5 является точным представлением явления ферромагнетизма. \ [\ dfrac {M_S (T)} {M_S (T_o)} = \ dfrac {T_c — T} {T_c} \ label {7} \] Ниже температуры Кюри спины ферромагнитного материала имеют одинаковую величину и хорошо упорядочены.Когда достигается температура Кюри, это означает, что моменты становятся случайно выровненными, а это означает, что предел спиновой связи был превышен, что приводит к разрыву связи, заставляя материал действовать парамагнитно. Глядя на рисунок 3 ниже, он показывает, как моменты выравниваются ниже температуры Кюри (в ферромагнетике), но затем выше температуры Карри он становится парамагнитным. За счет образования случайно расположенных спинов. Ферромагнитные материалы обычно используются для энергонезависимого хранения информации на лентах, жестких дисках и т. Д.Они используются для двух основных технологических применений: (i) как умножители потока, образующие ядро электромагнитных машин, и (ii) как накопители энергии (магниты) или информации (магнитная запись). Они также используются для обработки информации из-за взаимодействия электрического тока и света с магнитным порядком. Железо, никель и кобальт являются примерами ферромагнитных материалов. Использование ферромагнитных материалов (i) Постоянные магниты Идеальный материал для изготовления постоянных магнитов должен обладать высокой удерживающей способностью (остаточным магнетизмом) и высокой коэрцитивной силой, чтобы намагничивание сохранялось в течение более длительного времени.Примерами таких веществ являются сталь и альнико (сплав Al, Ni и Co). (ii) Электромагниты Материал, используемый для изготовления электромагнита, должен подвергаться циклическим изменениям. У них есть неспаренные электроны, поэтому их атомы обладают чистым магнитным моментом. Они получают свои сильные магнитные свойства из-за наличия магнитных доменов. Следовательно. идеальный материал для изготовления электромагнита должен иметь наименьшие гистерезисные потери. Кроме того, материал — должен достигать высоких значений магнитной индукции B при малых значениях намагничивающего поля H.Мягкое железо является предпочтительным для изготовления электромагнитов, так как оно имеет тонкую петлю гистерезиса (рисунок) [небольшая площадь, следовательно, меньшие потери на гистерезис] и низкую удерживающую способность. Он достигает высоких значений B при низких значениях намагничивающего поля H. (iii) Сердечник трансформатора Материал, используемый для изготовления сердечника и дросселя трансформатора, очень быстро подвергается циклическим изменениям. Кроме того, материал должен иметь большое значение магнитной индукции B. Следовательно, предпочтительным является мягкое железо с тонкой и высокой петлей гистерезиса.Некоторые сплавы с низкими гистерезисными потерями — это радиоактивные металлы, перн-сплав и муметалл. (iv) Магнитные ленты и память Намагничивание магнита зависит не только от намагничивающего поля, но и от цикла намагничивания, которому он подвергся. Таким образом, величина намагничивания образца является записью циклов намагничивания, которым он подвергся. Следовательно, такая система может выступать в качестве устройства для хранения памяти. Ферромагнитные материалы используются для покрытия магнитных лент в кассетном плеере и для создания накопителя памяти в современном компьютере. Примеры: ферриты (Fe, Fe 2 O, MnFe 2 O 4 и т. Д.). Ферромагнитные материалы широко применяются в таких устройствах, как электродвигатели и генераторы, трансформаторы, телефоны, громкоговорители, устройства магнитной записи, такие как кассеты, дискеты для компьютеров и магнитная полоса на обратной стороне кредитных карт. Что такое ферромагнетизм? Ферромагнетизм или термин «ферромагнетизм» — это механизм, посредством которого определенные материалы образуют постоянные магниты.С помощью сильного электростатического поля эти материалы могут быть постоянно намагничены. Ионы ферромагнитных металлов группируются в небольшие области, называемые твердотельными доменами. Таким образом, каждый домен действует как крошечный магнит. Домены ферромагнитного немагниченного элемента ориентированы случайным образом, так что их магнитные моменты компенсируются. Когда этот материал помещается в магнитное поле, все домены ориентируются в направлении магнитного поля, создавая мощный магнитный эффект. Кроме того, когда магнитное поле снимается и ферромагнитный материал становится постоянным магнитом, этот порядок доменов остается прежним.Существует много различных форм магнетизма, но ферромагнетизм является самой сильной формой и ответственен за широкое распространение магнетизма в магнитах, испытываемых в повседневной жизни. [Изображение будет загружено в ближайшее время] Примеры ферромагнитных материалов Co (кобальт) Fe (железо) MnBi Ni (никель) N (никель) MnSb CrO2 (диоксид хрома) MnAs Свойства ферромагнитных материалов Когда стержень из этого материала быстро помещается в магнитное поле, он полевая трасса. Эти вещества проявляют постоянный магнетизм даже в отсутствие магнитного поля Когда вещества нагреваются при высоких температурах, ферромагнитные вещества превращаются в парамагнетики Проницаемость ферромагнитного материала превышает 1. Механизм ферромагнетизма отсутствует в жидкостях и газах. Интенсивность намагничивания (M), относительная проницаемость (μr), магнитная восприимчивость (χm) и плотность магнитного потока (B) этого материала всегда будут положительными. m = \ [\ frac {M} {H} \] µr = 1 + Χm B = µ0 (H + M) µ0 → Магнитная диэлектрическая проницаемость свободного пространства. H → Напряженность приложенного магнитного поля. Петля гистерезиса Петля гистерезиса формируется путем изменения силы намагничивания при одновременном измерении магнитного потока материала. Когда ферромагнитный материал намагничен в одном направлении, снятие наложенного намагничивающего поля не приведет к релаксации обратно к нулевой намагниченности.Поле в противоположном направлении должно сбросить его до нуля. Когда к объекту прикладывают переменное магнитное поле, его намагниченность можно проследить по петле, называемой петлей гистерезиса. Отсутствие повторного отслеживания кривой намагничивания — это свойство, называемое гистерезисом, которое связано с наличием магнитных доменов в материале. При переориентации магнитных доменов требуется некоторая энергия, чтобы повернуть их обратно. [Изображение будет загружено в ближайшее время] Это свойство полезно в качестве магнитной «памяти» ферромагнитных материалов.Аспекты магнитной памяти железа делают их полезными для записи аудиозаписей и для магнитного хранения данных на дисках компьютеров. Температура Кюри Есть температура, при которой ферромагнитный материал становится парамагнитным. Эта конкретная температура называется температурой Кюри. То есть, если мы поднимемся выше температуры Кюри, это приведет к тому, что ферромагнитные материалы потеряют свои магнитные свойства. Температура Кюри представлена TC. Тепловая энергия нарушает магнитное упорядочение диполей в ферромагнитном материале. Ethermal = kBT Закон Кюри задается формулой X = \ [\ frac {C} {T} \] kB → постоянная Больцмана T → Температура (Кельвин) C → Константа Кюри Примеры, Ni — 627 K Gd — 293 K Co — 1388 K Что такое антиферромагнетизм? Антиферромагнитные материалы слабо намагничиваются в направлении поля в присутствии сильного магнитного поля.Это свойство материалов называется антиферромагнетизмом, а антиферромагнитные материалы — материалами, проявляющими это свойство. В антиферромагнитных материалах магнитные моменты ориентированы в противоположных направлениях и равны по величине. Таким образом, когда антиферромагнитный материал не намагничен, результирующая намагниченность равна нулю из-за точной компенсации магнитных моментов соседних атомов при добавлении в линию. Применение ферромагнитных материалов Ферромагнитные материалы находят множество применений в электрическом, магнитном накопительном и электромеханическом оборудовании. Постоянные магниты: Ферромагнитные материалы используются для изготовления постоянных магнитов, потому что их намагничивание сохраняется дольше. Сердечник трансформатора: Материал, используемый для изготовления сердечника трансформатора и дросселя, подвержен очень быстрым циклическим изменениям, и этот материал также должен иметь сильную магнитную индукцию. Для этой цели широко используются ферромагнитные материалы. Магнитные ленты и память: намагничивание магнита зависит не только от поля намагничивания, но и от цикла намагничивания, которому он подвергся. Двойные союзы. Список. Предложения с двойными союзами. Запятые при двойных союзах. Если не …, то Хотя и …, но Как …, так и Не так …, как Не только …, но и Не столько …, сколько Насколько …, настолько Не то что …, но Не то чтобы …, а Скорее…, чем Сравните предложения: Guest Да, нужна. Конкретно в данном случае – да. Однородные члены предложения, соединенные повторяющимися союзами, если их больше двух, выделяются запятыми. Тут как раз повторяющиеся члены предложения, но перед первым из перечисляющихся отсутствует союз “и”, в этом случае, если однородных членов предложения больше двух и союз “и” повторяется хотя бы дважды, запятая ставится между всеми однородными членами (в том числе и перед первым “и”). В предложении есть однородные члены: побед, свершений, ярких открытий. Перед двумя из них есть повторяющийся союз “и”. Согласно правилам, запятая после слова “побед” нужна.Марина Ш.1 Запятая перед “то” как ставится, так и нет. Запятая перед “то” ставится: Запятая перед “то” не ставится: Да, это же сложное предложение, Части сложных предложений отделяются запятыми и союзами.Николай Гончаров1 При сочетании как… так и запятые ставятся по правилу пунктуации: перед второй частью составного союза. «Как… так и» — составной (двойной) соединительный союз, находящийся при однородных членах предложения: В праздничных мероприятиях участвовали как школьники, так и преподаватели. Эти цветы можно посадить как дома в горшках, так и на клумбе. Поскольку союз — служебная часть речи, он не будет являться членом предложения. В наречном сочетании как так запятая перед так не ставится: Ставится запятая перед как так, если сочетание начинает придаточное предложение в составе сложноподчинённого: Если предложение содержит сравнительный оборот, прикреплённый «как», запятая перед союзом ставится: На поляне желтели одуванчики, как маленькие солнышки. На горячем, как раскалённое железо, песке лежали вещи отдыхающих. В данном случае сравниваются какие-либо предметы (одуванчики с солнышком, горячий песок с раскалённым железом), поэтому речь идёт не о правиле «запятые: как… так и», и знак препинания перед «как», то есть запятая, оправдан и обоснован. Что же касается простых предложений с союзом «как… так и», который находится при однородных членах, запятая перед «как» будет поставлена ошибочно, она не нужна, а ставится перед второй частью сложного (составного) союза, то есть перед «так и…»: Здесь мы видим, что союз как… так и запятые имеет только перед второй своей частью, что соответствует пунктуационному правилу. Союз «как… так и» употребляется только для соединения однородных членов в составе простого предложения. Он легко заменяется на синонимичные двойные и одиночные союзы. Сравним: Если правило пунктуации требует постановки соответствующего знака препинания (например, после обобщающего перед однородными членами слова), то перед «как» будет уместным постановка двоеточия или тире (реже): Запятая при «как… так и» ставится только перед второй частью союза Выяснив морфологические признаки союза и отличие его от других, похожих по звучанию, частей речи, рассмотрев употребление сравнительного оборота. Приходим к выводу, что запятая в «как… так и» ставится только перед второй частью союза. Приведем примеры правильной постановки запятых в предложениях с конструкцией «как… так и»: В качестве вводных слов чаще всего употребляются: без сомнения, бывало, вероятно, видимо, видишь (ли), вишь, возможно, во-первых, во-вторых и т. д.; впрочем, говорят, должно быть, допустим, думается, знать, значит, иначе (говоря), итак, кажется, к несчастью, конечно, короче (говоря), к сожалению, кстати (сказать), к счастью, между прочим, может быть, наверно, наоборот, например, напротив, (одним) словом, очевидно, по всей вероятности, пожалуй, пожалуйста, положим, помнится, по-моему, по моему мнению, по мнению…, понятно, понимаешь (ли), почитай, правда, право, признаться, признаюсь, (само собой) разумеется, скажем, следовательно, словом, слышь, собственно (говоря), стало быть, строго говоря, таким образом, так сказать, чай, чего доброго, что ли. Примечание 1. От вводных слов нужно отличать обстоятельственные слова, отвечающие на вопросы как? каким образом? когда? и т. п., например: Примечание 2. Следует различать употребление одних и тех же слов и оборотов то в качестве вводных (и, следовательно, выделяемых запятыми), то в качестве усилительных (и запятыми не выделяемых), например: Примечание 3. Если например, скажем, положим, допустим и т. п. стоят перед словом или группой слов, уточняющих предшествующие слова, то после них не ставится никакого знака препинания (см. § 154). Примечание 4. Союзы а, и, реже но, если они составляют одно целое с последующим вводным словом, не отделяются запятой, например: а значит, а следовательно, но стало быть, но конечно и т. п. 8 класс Контрольная работа «Однородные члены предложения»1 вариант 1.Какое утверждение является неверным? 1) Между однородными членами при отсутствии союза ставится запятая. 2) Запятая ставится между однородными членами перед второй частью двойных союзов. 3) Противительные союзы – а, но, да(но), однако, зато. 4)Запятая перед союзом да и не ставится. 2. В каком варианте ответа указаны предложения с несколькими рядами однородных членов? Знаки препинания не расставлены. А. Дед взял корзину и палку и отправился за грибами. Б. Яркое солнце ослепительно белый снег и тишина обступили его. В. Солнце докатилось до края земли растеклось по небу ярким заревом. Г. Ты сядешь в кресло и забудешь свист пурги и вой ветра. 1) А,В 2) Б,В 3)А,Г 4) В,Г 3.В каком варианте ответа указаны предложения с однородными членами, связанными сочинительными разделительными союзами? Знаки препинания не расставлены. А. Требовалась немедленная разрядка но она была к несчастью недосягаема. Б. В ущелье часто раздавался отдалённый гул или низкий стон оседающих льдин. В. В это помещение можно было попасть как с нижнего этажа так и с улицы. Г. Пахло не то илом не то хвоей. 1) В,Г 2) Б,Г 3)А,Б 4) А,В 4. Прочитайте предложения и ответьте на вопросы. А. Её серые глаза были красны не то от слёз, не то от бессонницы. Б. Солнце над головой, листва на деревьях, шумящая от ветра, выглядели радостными и привлекательными. В. На другой день Лиза проснулась ни свет, ни заря и отправилась к бабушке. Г. Работа шла дружно, без перерыва, с весёлыми шутками и песнями. 1. В каком предложении допущена пунктуационная ошибка? А Б В Г 2. В каком предложении однородные члены связаны сочинительным разделительным союзом? А Б В Г 3. В каком предложении однородными являются сказуемые? А Б В Г 4. В каком предложении однородные члены выражены различными частями речи? А Б В Г 5. В каком предложении несколько рядов однородных членов? А Б В Г 5. Укажите правильный вариант постановки на месте цифр знаков препинания. Всё(1) и эти невероятные облака(2) и пурпурное зарево(3) и неподвижная поверхность(4) уже засыпающего моря(5) и сосны(6) возвышающиеся на западе острова(7) казались фантастическим. 1) 1- двоеточие; 3,4,6,7 – запятые; 2) 1- двоеточие; 3,5,6,7 – запятые; 3) 1- двоеточие; 2,3,5,6 – запятые; 7- запятая и тире; 4) 1- тире; 2,3,4,5,6 – запятые 6. В каком варианте ответа указаны предложения, в которых использована как средство выразительности языка градация( расположение ряда слов или выражений в порядке их возрастающей или убывающей смысловой значимости)? А.И чья очередь испугаться, отшатнуться, отпрянуть? Б.Ветер ударял в грудь, в лицо, выдавливал слёзы, раздувал полы пальто. В.Упрёков, жалоб, слёз моих не смейте ожидать. Г. Они прыгали по камням, проваливались в снег, скользили по замёрзшим лужам. 1) А,Б 2) Б,Г 3) А,В 4) В,Г 7.Укажите вариант ответа, в котором предложения соответствуют схеме: О,О,О – О. Союзы на схеме не указаны. Знаки препинания не расставлены. А. Кругом повсюду мох и под ногами и на камнях и на ветвях деревьев. Б. Ни справа ни слева ни на берегу никого не было. В. Среди птиц насекомых в сухой траве словом всюду чувствовалось приближение осени. Г. Море порт город всё превратилось в порывистую от ветра тьму. 1) А,В 2) Б,Г 3) В,Г 4) Б,В 8.В каком варианте ответа указаны предложения, в которых на месте пропуска должна стоять запятая? А. Из такой трёпки сад выходил почти совсем обнажённым … засыпанным мокрыми листьями. Б. Из открытых саней с лаем выскочила пёстрая … мохнатая собачонка. В. Светлые … длинные волосы обрамляли её лицо. Г. Узкая … круто опускающаяся лестница скоро закончилась. 1)А,В 2) Б,В 3) В,Г 4) А,Г 9. Найдите предложение с однородными определениями. А. Глубокая дремучая старина окружала моё детство на слободке. Б. Полоса яркого вечернего света легла на старый ствол возле скамьи. В. Весёлые белые облака плыли над синими отрогами. Г. Прошёл серый пассажирский поезд. 10. Орфографический диктант. (Не)исследова..ая местность, говорил (не)правду, ещё (не)сделанные чертежи, (не)стерпимый зной, (не)различая дорогу, (ни,не)как не мог понять, (ни,не)чуть не волновался, (ни,ни)о ком не рассказывал, (ни,не)когда (ни,не)кому (ни,не)в чём не отказывал; (ни,не)с кем поговорить; (ни,не)как не вспомнить; посоветоваться (ни,не)с кем; (ни,не)о чём не спрашивать; восторже. Ключи к тесту: 1-В 1-4; 2-3; 3-2; 4:1-В; 2-А; 3-В; 4-Г; 5-Б;5-3; 6-3; 7-3; 8-4; 9-А; 8 класс Контрольная работа по теме «Однородные члены предложения»2 вариант 1.Какое утверждение является неверным? 1) Однородные члены предложения могут выражаться словами разных частей речи. 2)Между однородными членами перед повторяющимися союзами ставится запятая. 3)Сочинительные соединительные союзы: и, да(и), ни-ни, не только…, но и; как…,так и… 4) Во фразеологическом обороте между однородными членами запятая ставится. 2. В каком варианте ответа указаны предложения с несколькими рядами однородных членов? А. По сторонам тропы высокими и крутыми стенами стоял шиповник и цвёл алым огнём. Б. Море ловит стрелы молний и в своей пучине гасит. В. Силу гнева, пламя страсти и уверенность в победе слышат тучи в этом крике. Г. В лесу и на лугу пахло мокрой травой и свежим сеном.1)А,Г 2)В,Д 3)А,В 4)В,Г 3.В каком варианте ответа указаны предложения с однородными членами, связанными сочинительными противительными союзами? Знаки препинания не расставлены. А.Посадку самолёта задерживал шторм и отклонение его от нужного курса. Б.Годы уводят силы зато прибавляют ума. В. Разве они никогда не слышат стука колёс или не видят голых равнин за окнами? Г.Огонь костра погас однако в нём долго оставался круг от раскалённых углей. 1) Б,В 2) В,Г 3) Б,Г 4) А,В 4. Прочитайте предложения и ответьте на вопросы. А.Он командовал отрывисто, вполголоса, почти шёпотом. Б. Пейзаж чужой планеты у него перед глазами то появлялся, то исчезал. В. Один рулевой бодрствовал на корме, да напевал что-то под нос. Г. Сады залились бело-розовой пеной цветения и наполнились писком, свистом, щебетом. 1.В каком предложении допущена пунктуационная ошибка? 1)А 2)Б 3)В 4) Г 2. В каком предложении однородные члены связаны сочинительным разделительным союзом? А Б В Г 3. В каком предложении однородными являются обстоятельства образа действия? А Б В Г 4. В каком предложении однородные члены выражены разными частями речи? А Б В Г 5) В каком предложении однородные члены являются дополнениями? А Б В Г 5. Укажите правильный вариант постановки на месте цифр знаков препинания. Всё(1) и берёзовая рощица(2) и могучий дуб(3) закрывавший своим шатром поляну(4) по-своему было прекрасно. 1) 1,4 — тире; 2,3 – запятые 2) 1- двоеточие; 2,3,4 –запятые 3) 1- двоеточие; 2,3 – запятые; 4 – запятая и тире 4) 1 -двоеточие; 2,3 – запятые; 4 – тире 6. А. Синие полосы тумана колыхались над орешником, заливали кусты. Б. Он стряхнул оцепенение, лёг на кровать и подтянул к подбородку одеяло. В. Усталое светило медленно погружалось в облака, окрашивая всё в розовые, пунцовые, кумачовые тона. Г.Вода медленно подступала к ногам, притопляла камни, прибывала на глазах и наконец хлынула из полыньи на лёд, потекла верхом. 1)В,Г 2) А,Б 3) Б,В 4) Б,Г 7.Укажите вариант ответа, в котором предложения соответствуют схеме: О: О,О,О . Союзы на схеме не указаны. Знаки препинания не расставлены. А. Распоряжения его всегда были и быстры и точны и конкретны. Б.Вокруг не было ни человека ни лошади ни птицы. В.Сквозь голубую дымку мутно голубело всё вокруг лес скалы острова. Г. 1) А.Г 2) Б,В 3) В,Г 4) А,Б 8.В каком варианте ответа указаны предложения, в которых на месте пропуска должна стоять запятая? А. Мокро блестят старые …железные крыши. Б. По небу, заслоняя звёзды, неслись низкие …тяжёлые тучи. В.Он прижался к мощному … корявому стволу и стоял так неподвижно. Г. В этот год осень пришла мрачная…дождливая. 1) А,В 2) Б,Г 3) Б,В 4) А,Г 9.В каком варианте ответа указаны предложения с пропущенной запятой перед союзом И? А. Пламя костра пританцовывало в лад со звуками и как будто смеялось. Б. Туманный месяц и меня, и гриву, и хребет коня осыпал серебристым блеском. В.Он сохранил и блеск лазурных глаз, и звонкий детский смех, и речь живую и веру гордую в людей. Г. В рёве метели жили боль и беда, и тусклая тревога. 1) А,Б 2) В,Г 3) Б,В 4) А,Г 10. Орфографический диктант. (Не)(с)кем посоветоваться, скрывать (не)чего, (не)громкий ш. Ключи к тесту: В-2 1-4; 2-1; 3-3; 4: 1-В; 2-Б; 3-А; 4-А; 5-Г; 5-3; 6-1; 7-3; 8-2; 9-2; Постановка запятой перед союзом «или» зависит от контекста: что он соединяет, однородные члены или предложения. Рассмотрим, когда перед союзом «или» ставится запятая в предложении. Сочинительный разделительный союз «или» может быть употреблен с однородными членами предложения и как связующее звено в сложносочиненном предложении. ПравилоВ предложении с однородными членами перед одиночным союзом «или» запятая не ставится. Пример: Видимо, белка или заяц лакомились здесь. ПравилоСоюз «или» может быть повторяющимся, тогда запятая ставится перед второй его частью. Пример: На её смуглом лице было выражение или¹ растерянности, или² испуга. Внимание!Следует быть внимательным, и не пропустить наличие третьего однородного члена предложения без союза. В такой синтаксической конструкции запятая ставится перед первой и второй частью повторяющегося союза или…или, например: Весной страшным бедствием для зайцев¹, или лис², или барсуков³ является половодье. ПравилоСтавится запятая также, если союз «или» присоединяет пояснительную конструкцию, обозначающую одно и то же понятие другими словами. Пример: Бабушка показала мне деревянный ларь, или ящик, широкий вверху и узкий внизу. Союз «или» синонимичен «то есть». ПравилоВ сложносочиненном предложении перед союзом «или» ставится запятая. С наступлением дня туман прятался в низину реки, или его можно было увидеть на дне оврага. Перед союзом «или» не ставится пунктуационный знак в следующих случаях: 1. в сложносочиненном предложении имеется общий член предложения, вводное слово или частица. Всю ночь мне мерещатся причудливые тени или слышатся шорохи чьих-то шагов. Наверное, я соберусь в поле за васильками или с утра лучше пойти в лес за земляникой. Только дождь шумит за окном или раздаются раскаты оглушительного грома. 2. В сложносочиненных вопросительных, побудительных, восклицательных и назывных предложениях. Отправить мне телеграмму или лучше позвонить по телефону? Пусть будет полумрак или включите лампу! 3. В сложноподчиненном предложении с однородным подчинением. Я напряженно думаю, справится она с этой задачей или мне следует ей помочь. 4. В сложном предложении с общей придаточной частью и разными видами связи (сочинением и подчинением). Когда загрохотал гром, дети бросились по домам или самые смелые спрятались под навес сарая. Анна Коврова Даже те, кто посещает курсы английского на уровне «Advanced», часто расставляют запятые в английском языке по интуиции, ориентируясь на русские правила. Во многих случаях это себя оправдывает, но далеко не всегда. Об этих исключениях мы и поговорим сегодня. Взгляните на следующее предложение и его перевод: В русском языке запятая перед единственным «и» в перечислениях не ставится, а в английском она возможна. Правда, о ее необходимости британские лингвисты спорят до сих пор. В оксфордских изданиях она присутствует постоянно (именно поэтому часто называется Оксфордской запятой). С другой стороны, многие авторы предпочитают не перегружать предложение лишним пунктуационным знаком. А как же поступить нам? Выбираем компромисс. Запятая в английском языке обязательна, только если без нее предложение можно понять неправильно — в этом пособия по английской пунктуации единодушны. В остальных случаях это ваш личный выбор. «Если имеется в виду, что в наследство оставлено и имущество, и (вдобавок к нему) дома и склады, то запятая обязательна», — поясняет Diana Hacker. А если ее нет, то смысл получается такой: «Дядя оставил мне в наследство все свое имущество, а состоит оно из домов и складов». Точно так же вы можете встретить запятую в английском языке перед «and» в однородных придаточных предложениях, тогда как в русском языке она была бы ошибкой: В русском знак препинания появляется вне зависимости от длины простых предложений, входящих в состав сложного. В английском же, если оба предложения совсем короткие, можно обойтись без запятой: Речь идет об определительных придаточных предложениях (relative clauses). Они отвечают на вопросы «какой?», «какая?», «какие?» и служат для того, чтобы охарактеризовать человека или предмет. Вы узнаете их по словам «who», «which», «that», «whom», «where». В русском языке такие придаточные всегда выделяются запятыми, а вот в английском пунктуация зависит от смысла. Сравните два предложения: Как видите, во втором случае придаточное предложение выделено, а в первом — нет. Почему? Попробуйте отбросить придаточное. Что останется? 1. Passengers were immediately recognizable. — главная мысль потеряна. То есть придаточное было необходимо для понимания ситуации. 2. Jane has two young children. — главная мысль сохранена. То есть придаточное просто давало нам чуть больше информации о детях, вот и все. Таким образом, если придаточное можно отбросить, не изменив принципиально смысл предложения, мы его отделяем запятыми. А когда оно обязательно для понимания, его отделять нельзя (этим мы подчеркиваем смысловую целостность высказывания). Да, и если вас не пугают термины, то в первом случае речь идет о так называемых Restrictive relative clauses, а во втором — о Non-restrictive relative clauses. Обратите внимание: знак препинания стоит не только перед, но и после года. В этом правиле имеются два очень важных исключения: — если число идет перед месяцем: — если указан только месяц и год, а дня нет: Подробнее о правилах написания дат в английском языке мы говорили ранее. Если в числе пять и более символов, запятая в английском языке обязательна, если меньше — нет: 3,500 или 3500 10,000 5,000,000 Исключения: номера улиц, почтовые индексы, телефонные номера, годы — здесь знаки препинания не требуются. На месте русского двоеточия в английском запятая. Как запомнить все эти правила? Если держать их под рукой и время от времени сверяться, они осядут в памяти быстрее. Скоро вы убедитесь в этом на собственном опыте! Читайте также: 10 правил употребления запятой в английском Что должен знать каждый об английской пунктуации? Секреты употребления основных знаков препинания в английском языке Точка с запятой Ах, запятая. Точка заканчивает предложение, а запятая указывает на меньший разрыв. Некоторые авторы воспринимают запятую как мягкую паузу — знак препинания, разделяющий слова, предложения или идеи в предложении. За некоторыми исключениями, запятая не должна отделять подлежащее от глагола. У писателей часто возникает соблазн вставить таким образом запятую между подлежащим и глаголом, потому что говорящие иногда делают паузу в этом месте предложения. Но в письменной форме запятая только делает предложение неестественным. Будьте особенно осторожны с длинными или сложными предметами: Не разделяйте два существительных, которые появляются вместе как составное подлежащее или составной объект. Когда субъект или объект состоит из двух элементов, а второй элемент заключен в скобки, вы можете выделить второй элемент запятыми — один перед ним и один после него. Но когда вы просто перечисляете два элемента, запятая не нужна. Вы получаете составной предикат, когда субъект предложения выполняет более одного действия. В составном предикате, содержащем два глагола, не разделяйте их запятыми. Эта ошибка чаще всего встречается, когда сказуемое состоит из длинных глагольных фраз. Не используйте запятую в составных предикатах, если есть вероятность неправильного чтения: В предложении выше вам нужна запятая, чтобы было ясно, что машет рукой Клео, а не мужчина. Если вы хотите соединить два независимых предложения, вам понадобится союз или точка с запятой. Одной запятой недостаточно, чтобы соединить их. Такая ошибка называется соединением запятой. Вы можете исправить соединение запятой, добавив соединение или заменив запятую точкой с запятой. Или вы можете просто написать два независимых предложения как отдельные предложения. Запятая обычно следует за причастными фразами, которые вводят предложение: Когда наречная фраза начинается предложение, за ней часто следует запятая, но это не обязательно, особенно если оно короткое. Как правило, если фраза длиннее четырех слов, используйте запятую. Вы также можете использовать запятую с более короткой фразой, если хотите выделить ее или добавить паузу для литературного эффекта. Но, если есть шанс неправильно прочитать предложение, используйте запятую: Не используйте запятую перед «чем» при сравнении. Прерыватели — это небольшие мысли, которые появляются в середине предложения, чтобы показать эмоции, тон или акцент. Тег вопроса — это короткая фраза или даже одно слово, которое добавляется в конец утверждения, чтобы превратить его в вопрос. Писатели часто используют вопросительные бирки, чтобы побудить читателей согласиться с ними. Перед тегом вопроса должна стоять запятая. При обращении к другому человеку по имени выделите имя запятыми. Аппозитив — это слово или фраза, относящиеся к тому же, что и другое существительное в том же предложении. Часто аппозитив предоставляет дополнительную информацию об существительном или помогает каким-то образом его различить. Если бы вы могли удалить аппозитив, не меняя смысла предложения, он называется несущественным и должен быть отмечен запятыми. Несущественные аппозитивы:
Основные приложения:
При записи даты в формате «месяц-день-год» год выделяйте запятыми. Однако, если вы используете формат «день-месяц-год», запятые не нужны. Если вы указываете день недели и дату, используйте запятую: Когда вы указываете только месяц и год, запятая не нужна. Когда несколько прилагательных изменяют существительное в одинаковой степени, они называются координатными и должны быть разделены запятыми.Один из способов определить, являются ли прилагательные согласованными, — это попробовать изменить их порядок. Если предложение по-прежнему звучит естественно, прилагательные согласованы. Если прилагательные не совпадают, не разделяйте их запятыми. Используйте запятую перед словом , но , если оно объединяет два независимых предложения:
Если , но не объединяют два независимых предложения, оставьте запятую. Если у вас есть список, содержащий только два элемента, не используйте запятую перед и . При исправлении сращивания запятой, то есть при соединении двух независимых предложений координирующим союзом, ставьте запятую перед и. Если у вас есть список, содержащий более двух элементов, используйте запятые для их разделения. (Запятая перед и в списке из трех или более элементов не обязательна. Дополнительную информацию см. Ниже в разделе «Последовательная запятая».) Ваш список может состоять из существительных, как в примере выше, но он также может состоять из глаголов, прилагательных или предложений.Представьте на мгновение, что вы только что выполнили три работы по дому. Всего работ по дому: Если бы вы перечислили эти три обязанности в одном предложении, вы бы написали: или Как упоминалось выше, когда вы перечисляете три или более элементов, запятые должны разделять каждый элемент списка. Используете ли вы последовательную запятую или нет — это выбор стиля. Многие газеты им не пользуются. Многие торговые книги действительно используют его. В своем собственном письме вы можете решить для себя, использовать его или нет — просто будьте последовательны. Однако имейте в виду, что иногда для ясности необходима серийная запятая.
Приведенное выше предложение почти наверняка заставит читателей задуматься. Без порядковой запятой «Джейн Остин и Альберт Эйнштейн» выглядит как аппозитив, а не еще два элемента в списке.Другими словами, писательница, похоже, говорит, что ее родители — это Джейн Остин и Альберт Эйнштейн. Последовательная запятая исключает возможность неправильного чтения, поэтому, даже если вы не используете последовательные запятые в своем письме, сделайте исключение для предложений вроде этого: Не отделяйте переходный глагол от его прямого объекта запятой. Неограничивающий пункт предлагает дополнительную информацию о чем-то, что вы упомянули в предложении, но эта информация не важна для определения того, о чем вы говорите.Неограничивающие положения обычно вводятся с помощью номера , или , а также , и должны быть отмечены запятыми. Пункт «что рекомендовал Честер» не носит ограничительного характера, поскольку «Posey’s Cafe» уже является конкретным. Определение его как ресторана, рекомендованного Честером, не сужает его. Пункт «кого я очень люблю» не является ограничивающим, потому что вы можете удалить его, и при этом будет ясно, что вы говорите об одном и том же человеке — «моя жена» уже конкретна. Ограничительная оговорка добавляет необходимую информацию о том, что вы упомянули в предложении. Ограничительные положения часто вводятся с помощью , или , а также и никогда не должны выделяться запятыми. Пункт «что рекомендовал Честер» является важной информацией в предложении выше. Если вы удалите его, не будет никакой возможности сказать, о каком ресторане вы говорите. Корреляционные союзы — это союзы, которые входят в пары (например, либо / или, ни / ни, и не только /, но также) и соединяют слова или фразы в предложении, чтобы сформировать законченную мысль.Обычно запятые не нужны при использовании коррелятивных союзов. Атрибутивный тег — это фраза типа «он сказал» или «она утверждала», которая идентифицирует говорящего в цитате или фрагменте диалога. Атрибутивные теги могут располагаться до, после или даже в середине цитаты. Используйте запятые для отделения атрибутивных тегов от цитат. Однако, если цитата перед атрибутивным тегом заканчивается вопросительным или восклицательным знаком, запятая не нужна. В американском английском запятые всегда ставятся перед закрывающими кавычками. В британском английском, однако, пунктуация без кавычек обычно следует за кавычками. Если вы пишете для британской аудитории, ставьте запятую после закрывающей кавычки. Кроме того, в британском английском обычно используются одинарные кавычки, а не двойные кавычки. Круглые скобки используются для предоставления читателю дополнительной информации — информации, которая нарушила бы ход предложения, если бы она была написана как неограничивающая оговорка.Запятые можно ставить после закрывающих скобок, но не перед открывающими или закрывающими скобками. Если в предложении не требуются запятые, если оператор в скобках был удален, в предложении не должно быть запятых при добавлении скобок. Не используйте запятую между артиклем и существительным. Во время разговора мы часто останавливаемся, обдумывая следующее слово, которое хотим сказать. Однако в письменной форме обычно нет причин добавлять эту паузу. Фраза «а также» обычно не требует запятых, если она не является частью неограничительного предложения. Фраза «такой как» требует использования запятых, если она вводит неограничивающий пункт. Если «такой как» вводит ограничительное предложение, опускайте запятые. Использование запятой перед «слишком» необязательно. Запятая просто добавляет акцента.
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. English Language & Usage Stack Exchange — это сайт вопросов и ответов для лингвистов, этимологов и серьезных энтузиастов английского языка.Регистрация займет всего минуту.
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
939k раз
Используется ли запятая, а затем «и» или «или» после нее правильная пунктуация?
Пример:
51.6k88 золотых знаков113113 серебряных знака172172 бронзовых знака
Создан 20 июн.
95311 золотых знаков77 серебряных знаков44 бронзовых знака
Правильно ли использовать запятую перед координирующим союзом («и», «но», «или», «ни», «вместо», «пока», «так») зависит от ситуации.Есть три основных использования союзов: Когда координирующее соединение используется для соединения двух независимых предложений, запятая всегда используется . Примеры: Когда координирующее соединение используется для соединения зависимого предложения, запятая никогда не используется .Это включает в себя оба приведенных вами примера. Другие примеры: Когда координирующее соединение используется для соединения трех или более элементов или предложений, запятая — необязательный (хотя я лично предпочитаю использовать один). Примеры:
Создан 20 июн.
3,15622 золотых знака1818 серебряных знаков2121 бронзовый знак
Использование запятой с и и или иногда может быть непростым делом, и даже лучшие из нас время от времени испортят его. Вот хорошее руководство: http://www.grammarbook.com/punctuation/commas.asp И несколько примеров: При использовании в списке и и или никогда не принимают запятую, если список состоит из двух элементов; когда их больше, рекомендуется использовать запятую. При использовании в качестве союза обычно рекомендуется использовать запятую (если только фразы не очень короткие).
Создан 20 июн.
96055 серебряных знаков88 бронзовых знаков
«Я уехал в Японию и вернулся в 2009 году» является правильным, но довольно неопределенным.Это может означать либо «Я пошел [скажем, в 2003 году] и вернулся в 2009 году», либо «Я пошел и вернулся в 2009 году». Запятая в словах «Я был в Японии и вернулся в 2009 году» указывает на первое; Две запятые: «Я уехал в Японию и вернулся в 2009 году» определенно подразумевает последнее.
Создан 22 июня ’11 в 13: 492011-06-22 13:49
1,9336 серебряных знаков88 бронзовых знаков
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie
Настроить параметры
@ Kiki89, Добро пожаловать на английский Stackexchange. Ваше третье предложение правильное. В первом примере, который вы процитировали выше, вторая запятая используется там, где вы можете сделать паузу при чтении предложения. Многим писателям было сказано использовать запятую каждый раз, когда они делают паузу при чтении отрывка. Хотя следование этому предложению приведет к правильному использованию запятой в некоторых ситуациях, во многих других случаях следование этому руководству приведет к ненужному использованию запятой. Используйте запятую для разделения независимых предложений, связанных с
координирующие союзы.Если у вас есть то, что может быть двумя отдельными
предложения, но хотите сделать их одним (составное предложение),
используйте запятую и координирующий союз (for, and, nor, but, or,
пока что так) связать их. (Подробнее о сложных предложениях)
запятая ставится перед координирующим союзом. Примеры: Мой инструктор английского был хорошим учителем, и он многому меня научил.
процесс написания. Мы вышли из дома позже, чем рассчитывали, но мы
все же доехал до концерта вовремя Во втором предложении запятая должна стоять перед «и». Используйте запятую, чтобы выделить второстепенные элементы. Несущественный элемент
слово, фраза или предложение, которые не нужны для завершения
приговор. Другими словами, его можно удалить, а предложение по-прежнему
имеет смысл и грамматически правильно. Если удалить элемент
меняет смысл предложения, это существенно. Несущественный
элементы должны быть смещены запятыми как до, так и после. Примеры несущественных элементов: Я ходил в кино со своими соседями, Роном и Салли, а потом мы
пошел обедать.Студенты моего утреннего класса, ENG 121, любят
участвовать в обсуждениях. Ее лучшая подруга Хизер планирует
сюрприз на ее день рождения. Правила запятых объясняются здесь:
https://www.aims.edu/student/online-writing-lab/grammar/comma-rules Надеюсь, это поможет. Все четыре ваших примера являются составными предложениями, которые позволяют связывать запятые: Составное предложение состоит как минимум из двух независимых предложений.. . . Предложения соединяются координирующим союзом (с запятой или без нее), коррелятивным союзом (с запятой или без нее), точкой с запятой, которая функционирует как союз, двоеточием вместо точки с запятой между двумя предложениями, когда второе предложение объясняет или иллюстрирует первое предложение, и для соединения предложений не используется координирующий союз, или соединительное наречие, которому предшествует точка с запятой. Как отмечает @aurora , мы обычно используем запятые с координирующими союзами, за исключением случаев, когда связываются очень короткие и тесно связанные предложения, и даже тогда неправильно использовать запятую.Вот как разбираются ваши предложения с некоторыми дополнительными примечаниями. Clause 1: Он великий игрок. Поскольку оба предложения имеют один и тот же подлежащий, вы могли бы, естественно, заменить и he относительными местоимениями: «Он великий игрок, который предпочитает играть в Counter-Strike, », сделав это сложным предложением, а не составным. Пункт 1: Джон пошел в армию. Это простой пример составного предложения. Поскольку оба предложения короткие и похожие, вы можете опустить запятую, если хотите. Пункт 1: Да. Здесь Да, — это особый вид оговорки, называемый про-приговором. Clause 1: Я позвонил Джону, моему брату. В этом случае фраза мой брат находится в приложении, поэтому она должна быть выделена запятыми независимо от структуры остальной части предложения. Ответ на этот вопрос, получивший наибольшее количество баллов, утверждает, что использование последовательной запятой «чисто [вопрос] стиля письма и [поэтому] необязательно.«Чтобы продемонстрировать, что ни включение последовательных запятых, ни их пропуск во всех случаях не приводит к появлению двусмысленных предложений, он цитирует знакомую пару забавно неверно интерпретируемых посвящений: Моим родителям, Айн Рэнд и Богу. Моей матери, Айн Рэнд и Богу. Возможно, автор первого примера может иметь в виду четырех персонажей (двух родителей, смертный автор и Божество) или двух (двух родителей, один из которых оказывается смертным автором, а другой — смертным автором). быть Божеством).Точно так же автор второго примера может иметь в виду трех персонажей (один родитель, один смертный автор и одно Божество) или двух (родитель, который оказывается смертным автором, и Божество). Вывод, который нам, кажется, предлагается сделать из этих примеров, заключается в том, что вы не можете выиграть ни при одной из систем пунктуации, поэтому объективно не имеет значения, какую из них вы выберете: две системы одинаково неудовлетворительны и в равной степени подвержены путанице. Я думаю, что этот неявный аргумент в значительной степени искажает дело. Это, безусловно, правда, что каждая система дает сбой в одном из приведенных выше примеров. Но в других ситуациях система последовательной запятой имеет неоспоримое преимущество перед строгой системой без последовательной запятой. Этот факт очевиден из совета, который The Associated Press Stylebook (2002) предлагает публикации, которые следуют его стилю (обычно без серийных запятых). Как я отмечал год назад в своем ответе на сообщение о серийных запятых в цитатах, AP делает два важных исключения из своего обычного правила без серийных запятых: Поставьте запятую перед заключительным союзом в ряду, если для составного элемента ряда требуется соединение: У меня на завтрак был апельсиновый сок, тосты, ветчина и яйца. Также используйте запятую перед заключительным союзом в сложной серии фраз: Основные моменты, которые следует учитывать, — достаточно ли у спортсменов навыков для соревнований, есть ли у них выносливость, чтобы выдержать тренировку, и есть ли у них надлежащий психологический настрой. . Установление этих двух исключений равносильно временному принятию системы последовательной запятой в двух конкретных ситуациях, когда строгое правило без последовательной запятой может приводить к неоднозначным или трудным для понимания предложениям и где система последовательной запятой не имеет компенсирующих недостатков. Короче говоря, строгая система последовательной запятой сталкивается с проблемами неоднозначности с некоторыми аппозитивными конструкциями, в то время как строгая система без последовательной запятой сталкивается с проблемами неоднозначности с некоторыми аппозитивными конструкциями, с определенными сериями, которые содержат один или несколько интегральных элементов, требующих соединения (по выражению А.П.), так и с сериями, элементы которых достаточно сложны. Что касается аппозитивной двусмысленности, которая преследует обе системы в связи с Богом и Айн Рэнд, я думаю, что переработка предложения, чтобы избежать проблемы, обычно имеет больше смысла, чем приостановка вашего обычного правила для включения или исключения последовательных запятых.При использовании любой системы использования запятых вы можете устранить любую тень потенциальной двусмысленности — в более распространенных обстоятельствах, когда Бог и Айн Рэнд не являются вашими родителями, — изменив форму посвящения следующим образом: Моим родителям, Айн Рэнд и Богу. Моей матери, Айн Рэнд и Богу. Однажды мне попался следующий биографический отрывок, предназначенный для закрытия статьи в журнале: В настоящее время он живет со своей женой, хорьком и кошкой, которая думает, что она хорек. В нашем домашнем стиле использовалась последовательная запятая, но описание автором своих семейных проблем предполагало, что он, возможно, рискует изменить к худшему в его нынешних жилищных условиях, если его жена (хорек) узнает о его характеристике ее. Сохранять серийную запятую после хорька явно не годится, но ее отсутствие тоже не поможет нам выбраться из леса. В конце концов, точно так же, как можно описать человека как «гения и сумасшедшего, который знает, что он гений», можно (по глупости) называть супруга «хорьком и кошкой, которая думает [он или она] за хорек.« Мое решение проблемы состояло в том, чтобы переработать предложение, чтобы избавить чрезмерно совпадающую запятую (и ее вычеркнутый двойник) от бремени выяснения отношений между названными сторонами: У него и его жены два домашних питомца: хорек и кошка, которая думает, что она хорек. В конечном счете, лучшее оружие писателя в борьбе с нежелательной двусмысленностью — это не порядковая запятая или ее отсутствие, а способность перефразировать, чтобы избежать неприятностей. Политика защиты данных 2. Общие положения 6. Точность Правильно ли ставить запятую после «и» с точки зрения грамматики?
Патрицио Франчин, Лондон, Великобритания Это неверно в простом списке, таком как «яблоки, апельсины и лимоны», где многие люди чувствуют желание использовать его; однако это допустимо в таком предложении, как «бухгалтерия обнаружила местонахождение пропавшей тысячи фунтов, и, к сожалению, нам придется вас уволить». Люси Блейдс, Эдинбург, Шотландия P Smith, Лондон, Англия Anthony, Лондон, Англия Bill Dunlap, Hamden, USA Что еще более важно, это не обязательно для английского языка США. Хотя есть те, кто скажет, что это обязательно, это постоянный предмет споров, который, как я подозреваю, никогда не будет разрешен, хотя сейчас тенденция к его использованию. Наконец, проблема с «ест побеги и листья» не в этом. Проблема в другой запятой. Если фраза относится к панде, которая пожирает побеги и листья бамбука, то запятой вообще нет («Панда ест побеги и листья»). Если это относится к панде, которая ест (еду), стреляет (пистолет) и уходит (ресторан), то для разделения элементов требуется запятая. Для этого значения не имеет значения, пишут ли вы: «Панда ест, стреляет и уходит» или «Панда ест, стреляет и уходит».’ Лично я считаю, что последовательная запятая вызывает столько же проблем, сколько и решает. На каждую проясняющуюся двусмысленность я могу показать вам контрпример. Возьмем пример Дэйва: «Моим родителям, Айн Рэнд и Богу». Его точка зрения заключается в том, что если вы добавите порядковую запятую, станет ясно, что Айн Рэнд и Бог не должны быть родителями автора. Но как насчет этого: «Моей матери, Айн Рэнд и Богу». Здесь порядковая запятая позволяет читать либо как список из трех, либо как список из двух, в котором Айн Рэнд является матерью автора.Без серийных запятых это однозначно список из трех: Моей матери, Айн Рэнд и Богу. Я всегда без всяких доказательств думал, что запятая в списке должна заменить отсутствующее «и». Если это так, то серийная запятая избыточна. Тем не менее, я регулярно советую студентам-юристам, которых я обучаю, использовать запятую, потому что вокруг достаточно людей, которые думают, что это обязательно (и мало кто думает, что это совершенно неправильно), что безопаснее использовать ее при написании для людей, которые замечают такое вещи. Уильям Данлэп, Хамден, США Уильям Данлэп, Хамден, Коннектикут, США Майкл Вольф, Ридинг Оливер Смит, Дорридж Mathieu, Ольборг Дания JDG, Осака Япония Природа дала нам замечательный материал для творчества: шишки. Она также наградила нас фантазией, что бы мы могли делать фигурки из них. Некоторые из них получаются забавными, способными доставить удовольствие при работе над поделкой. В этой статье мы собрали очень интересные и несложные идеи разных персонажей, в которых можно превратить обычную еловую или сосновую шишку. Они не являются сложными и прекрасно подойдут ученикам первого класса или даже для детского сада. Для изготовления вам понадобится: белая краска (подойдет гуашь), черный маркер, шишка, небольшой отрезок проволоки, два ватных диска, лист бумаги, маленький деревянный шарик или бусины диаметром примерно 2,5 см. Шишку необходимо покрасить в белый цвет. Можно покрасить только края чешуек, а можно и всю. В творчестве всегда есть свобода в выборе решений. Делая фигурки из шишек проявляйте фантазию, меняйте исходные материалы на свои, делайте по-своему. Пока сохнет шишка, нужно покрасить деревянный шарик в белый цвет. Он будет головой нашей фигурки. Если нет шарика, то можно сделать его из белого пластилина. Далее заготовим остальные части нашей фигурки из шишек. Возьмем два кусочка проволоки длиной примерно 2,5-3 см. Разорвем один ватный диск и плотно обмотаем каждую проволоку небольшим слоем ваты. Это будут ручки снеговика. Из третьего куска проволоки сделаем трость. Шишка высохла, значит пора к её основанию приклеивать ватный диск. Он будет имитировать снег под снеговиком. Приклеиваем к телу снеговика голову. В бока вклеиваем руки. В качестве клея можно использовать клеевой пистолет или суперклей. Из бумаги делаем снеговику цилиндр и раскрашиваем его черным маркером. Маркером же рисуем снеговику лицо. Из бумаги делаем маленький конус и приклеиваем его в качестве носа. Все, наша фигурка снеговика готова. Посмотрите на фотографии и повторите любой понравившийся вариант. Такие поделки делается очень просто. Как и в случае со снеговиком нам понадобится шишка для туловища и деревянная бусина для головы. Колпак и перчатки можно сделать из фетра. Все они делаются очень просто. Нужен лишь материал для заготовок и фантазия. После просмотра всех фото вы точно сможете смастерить из шишек забавные фигурки. Самодельные предметы разнообразят любой интерьер. Хвойные деревья издавна ассоциируются с праздниками, поэтому поделки из шишек придадут обстановке торжественности и колоритности. Запах в помещении будет приятным и свежим. Из шишек делают фигурки деревьев, животных, различные предметы. Можно использовать свою фантазию по максимуму и создавать необычные формы. Все, что потребуется, — свободное время и минимальное количество денег. Шишки можно собрать собственноручно, а остальные материалы — купить на ближайшем вещевом рынке. Обрабатывать их несложно, главное — помыть и избавиться от мелких насекомых. Чаще всего используют сосновые, еловые и кедровые почки. В декоративно-прикладном искусстве они применяются как дополнение, украшение без функционального значения. Новогодняя живая елка с шишками — это уже готовый элемент декора, но ее можно сделать собственноручно из одних только шишек. Вначале определяются с размером и формой. Если нужна максимально округлая, то потребуются сосновые шишки. Еловые более удлиненные, иногда лучше брать их. Отбираются только симметричные почки, с учетом того, какое изделие или деталь нужно сделать. Не стоит сразу обрабатывать шишки спреем, лучше закрыть их в герметичном мешке и оставить на несколько суток. После этого почки моют. Их помещают в емкость с теплой водой, добавляют туда моющее средство и держат на протяжении получаса. Затем шишки промывают и кладут на бумагу. Остатки смолы убираются ватными палочками, смоченными в спирте. Мелкую живность, живущую в пустотах, удаляют с помощью уксуса. Воду смешивают с 6%-м уксусным раствором в одинаковом соотношении, помещают туда шишки и ждут около 30 минут. Потом еще раз подсушивают. Через некоторое время сухие почки покрывают спреем-лаком. Кроме самих почек, для создания искусственного дерева используют веточки (например, туи), а для украшения — бисер или ленточки. Предпочтительно, чтобы шишки были сосновыми, а не еловыми, так как они более округлые. Понадобится шарик из пенопласта или монтажной пены, клей, флористические булавки, пена, деревянная палка и горшок. Пустая емкость заполняется флористической пеной. Потом в центре горшка устанавливается палка (чуть более полуметра в длину). На ней закрепляется шарик. К шишкам приклеиваются шпильки, после чего они присоединятся к шару. Флористическая пена покрывается нагретым клеем и посыпается мхом. На стволе, под шариком можно сделать бант из цветной декоративной ленты. Есть интересный вариант, как можно сделать горшок самостоятельно или оформить уже готовый — небольшие веточки склеиваются между собой и обвязываются. Получается идеальная цилиндрическая форма. Подставку делают из одной или нескольких шишек. На изделии можно закрепить продолговатую или чайную свечу. Дополнительно используют плоские тарелки и емкости. Красиво смотрится банка, украшенная бантиком, с маленькой свечой на шишке. Это небольшой перечень идей для конструирования подсвечника. Для работы понадобятся игольчатые плоскогубцы. С их помощью выравниваются чешуйки. Низ почки должен быть параллельным относительно поверхности. Это касается и верха — его выравнивают, после чего наносят разогретый клей для закрепления свечи. Надежное крепление обеспечивается благодаря металлическому штырю — на острие насаживается свеча. В этом случае клей не понадобится. Вместо штыря также используют швейные иглы. Из соображений безопасности делают прокладку (чаще всего из фольги), чтобы горячий воск не попадал на изделие. Основа для создания такой поделки — проволока и сами шишки. Сначала сортируют почки (в зависимости от того, для какой части корзинки они предназначаются). Основа делается отдельно от ручки, после этого их соединяют. В ее качестве используются сами почки или картон, прикрепленный с помощью горячего клея. На работу уйдет несколько часов. Шишки можно поворачивать как наружу, так и внутрь. Корзинка украшается зелеными растениями, цветами, внутрь кладутся свежие или искусственные фрукты и овощи, пожелтевшая листва. Их обрабатывают лаком-спреем. Если надежно закрепить ручку, то поделка сгодится для практического использования в качестве корзины. Чтобы форма сохранялась в течение длительного времени, подбираются широкие, максимально раскрывшиеся шишки. Изделие дополнит праздничную обстановку — новогоднюю или пасхальную. Инструменты, которыми следует обзавестись: Для создания украшения в виде ежика понадобится пластиковая бутылка. Подойдет полутора- или двухлитровая. Она разрезается пополам, нижняя часть засовывается в верхнюю, чтобы форма и размер были реалистичными. Возможно, потребуется отрезать среднюю часть бутылки, длиной несколько сантиметров. После этого на той стороне, где находится крышечка, рисуется «мордочка» ежа. Шишки склеивают между собой. На верх конструкции наносится клей, и после этого их приклеивают на бутылку. Несколько кусков проволоки закрепляют под крышкой. Они будут выглядеть как усики. Поделка закрепляется лаком. Сделать медведя можно несколькими способами. Первый — маленькая фигурка из клубка ниток и небольших шишек в виде конечностей. Мишка среднего размера делается из десятка шишек, соединенных по отдельности в туловище, голову, руки и ноги. Если есть желание сконструировать большого медведя, то понадобятся две основы из пенопласта. Конечности создаются из нескольких нанизанных на проволоку шишек. Можно делать небольшие поделки из одной шишки и пластилина: Понадобятся: шишки, лак для волос, лента, проволока, шар из пенопласта; некоторые используют еще и блестки. Основу — шар из пенопласта можно сделать собственноручно. Сначала на шишки наносят лак, посыпают блестящими элементами. Затем их берут по отдельности и прикрепляют к нижней части каждой почки отрезанный кусок проволоки. Для этого понадобится сделать петлю и обвязать ею нижние чешуйки. Менее надежный способ — свернуть часть провода в спираль и приклеить к нижней части шишки. Все почки по очереди присоединяются к шарику свободным концом проволоки. Для подвешивания всей конструкции используют ленту. Основу обычно делают из пенопласта. Готовый шарик можно приобрести в специализированных магазинах. Чтобы сделать его своими руками, нужно измельчить заготовку на маленькие фрагменты и склеить их. Для придания округлой формы шар обрабатывают ладонями или канцелярским ножом. В период новогодних праздников декорирование становится любимым занятием многих людей. Отделка в этой тематике должна включать в себя сказочные мотивы, блестящие цвета, разнообразие форм и праздничное настроение. Из шишек могут создаваться животные и персонажи. Они украсят новогоднюю елку в неповторимом колоритном стиле. Из почек создают рукодельные гирлянды, украшают обычные. Поделки могут заинтересовать детей младшего возраста. Им понравятся большие изделия в виде оленей, медведей, сов. Композиции окрашивают в блестящие цвета — золотой и серебряный, а также в другие яркие тона. Для изготовления новогодних поделок из шишек понадобятся простые подручные средства, которые есть в каждом доме. Изделия из почек хвойных растений являются альтернативой покупке большого количества новогодних аксессуаров и игрушек. В процессе создания елочки понадобятся: Сначала создается высокая фигура конической формы. В качестве материала используют плотную бумагу. Изнутри конус наполняется газетами. Форма ставится на металлическое основание и приклеивается скотчем. Липкую ленту используют и для склеивания краев. После этого шишки кладутся вокруг этой фигуры и клеятся. Сначала внизу, затем второй ярус и так до самого верха. При желании елка посыпается серебристыми блестками или окрашивается баллончиком. Ее украшают так же, как и обычную — используют новогодние игрушки, гирлянды. Эту декоративную елочку следует оформлять оригинальными изделиями: мягкими и небьющимися новогодними игрушками, изделиями из фетра и бумаги. Красиво смотрится посеребренная фигурка с внутренней подсветкой, украшенная серпантином. Поделка сможет заменить обычную живую или искусственную елку. Для создания такой поделки лучше искать шишки, у которых один из боков плоский. В качестве праздничных игрушек могут использоваться пенопластовые шарики, отделанные маленькими шишечками. Существует много других интересных вариантов. Шишки, пластилин, деревянные шарики и фетр пригодятся для создания фигурок эльфов. Также из этих материалов делаются звери: лисички, мышки, белочки, ежики. Для создания праздничной гирлянды потребуется наличие кисточки, пинцета, плоскогубцев, шпагата (бечевки), спрея-герметика, винтов с О-образными крюками и фольги для декорирования. Почки очищаются от грязи и пыли, на них наносится клей. Потом они украшаются фольгой (золотистой или серебристой). Ее можно заменить блестками или краской из баллончика. Посередине основания почек вкручиваются винты с крюками. После этого шишки натягиваются на толстую нить. Необходимо рассчитать идеальную длину, потому что почки нужно фиксировать сразу. Перед тем как его мастерить, следует обзавестись термоклеевым пистолетом. В качестве основы пригодится скрученный веночек из веток ивы. Ивовые прутья может заменить гофрированный картон. Круглая форма оформляется шишками по всему периметру. Необходимо чередовать почки разных форм и размеров. Их, как и сам венок, можно окрасить аэрозольной краской или оставить в натуральном цвете. В композиции используют и другие элементы: каштаны, стручки, желуди, опавшие листочки, маленькие веточки. В верхней части конструкции стоит закрепить какую-то фигурку. Подойдут небольшие статуэтки в виде ангелов. Внизу подвешивают колокольчики. В роли дополнительных декорирующих элементов может выступать бижутерия: бисерный жгут, порванное ожерелье, бусы с жемчугом. В этих целях также используют разноцветные пластиковые звезды. С термоклеевым пистолетом нужно быть осторожным — он может обжечь открытые участки кожи. Поделки из плодов хвойных растений — оригинальное и экономное решение. Сосна растет в умеренном климатическом поясе, практически повсеместно, поэтому шишки можно собирать самому. Фигурки из них совместимы с некоторыми стилями отделки, а на Новый год они будут уместны где-либо. Необычные поделки обогатят скучный интерьер, сделают настроение праздничным. Можно создавать тематические композиции из нескольких объектов. Сувенир из шишек, сделанный своими руками, — отличный подарок на праздник или день рождения. В процессе изготовления понадобятся проволока, клей, лак и различные формочки. Из шишек создают фигурки животных, различные приспособления и декоративные элементы. Их окрашивают в яркие цвета, украшают различными дополнительными элементами. Небольшую игрушку сможет сделать даже ребенок — в детских садиках нередко задают подобные домашние задания. Добрый день, сегодня я подготовила большую статью, посвященную поделкам из шишек (и сосновых и еловых). Я собрала вместе разные ТЕХНИКИ работы с шишками. И постараюсь подробно рассказать, как создавать каждую из представленных здесь поделок. В статье вы увидите детские поделки из шишек и пластилина, работы посерьезнее для конкурса в школу или сад, которые можно сделать с помощью родителей. Короче здесь будут собраны лучшие примеры, интересные решения и удачные находки в мире шишечного творчества. А поделки из шишек на Новый Год я вынесла в отдельную статью Новогодние поделки из шишек — 100 идей для детей. Итак, давайте посмотрим, какие идеи поделок из шишек я собрала для вас сегодня. Если разобрать шишку на чешуйки (выдернуть их клещами), то можно из таких чешуек выложить любую картину (пушистую собачку, природный пейзаж, или вот такую грозную сову. Можно сделать конус из бумаги… и с помощью клеевого пистолета (продается в строительном магазине за 5 долларов) обклеить весь конус чешуйками шишки, располагая внахлест друг на дружку (как черепуцу). Получится елочка. Начинать обклейку чешуйками шишки нужно с нижней части конуса… и постепенно ряд за рядом двигаться к верхушке конуса. По такому же принципу можно выложить панцирь пластилиновой черепахи, или шляпку грибочков. Или очень хорошая идей которая сама просится под шишечные чешуйки – это ЕЖИКИ. Тело лепим из пластилина. Утыкаем спинку острыми чешуйками. А мордочку формируем из пучка-метелочки. Вопрос, из чего сделать этот пучок? Вот я думаю что можно попробовать из обычной метлы нарезать тонких прутиков… Или взять жмых от кукурузы и нарезать его ножницами на тонкие прямые стружки – собрать их в пучок, пучок согнуть пополам (место сгиба, будет кончиком носа). Далее этот согнутый пучок распушиваем… чтобы он растопырился метелочкой по сторонам – и этой растопыркой вклеиваем в носовую часть пластилиновой поделки. Кстати, я тут подумала – наверное, мордочку можно сделать и не из природного материала какурузовой кожи… а нарезать из бумаги (мелких узких полосок)… или взять элементарно нитки (сделать пучок, согнуть пополам, линию сгиба пучка обмотать в носик-пупочку). Возможно нитки нужно будет потом накрахмалить, чтобы они держали жесткую форму. По такому же принципу делается вот эта детская поделка — БЕЛКА из шишек и пластилина. Сначала лепится тельце… потом на теле карандашиком очерчиваются границы зон. Одну зону мы будем покрывать шишечной чешуей, в другую зону мелкой метелочкой из бумаги (или природных материалов). Когда тело готово – мы отдельно лепим из пластилина хвост… и его верхнюю часть утыкаем шишечными чешукйкаи. А нижнюю часть хвоста облепливаем белой тонкой нарезкой бумажного ворса. Можно слепить из пластилина ОРЛА… или другую птицу — из чешуек шишки сделать оперение. Можно такими чешуйками выложить ДОМИК ДЛЯ ФЕЙ. Делается такой домик очень просто. Для этого нам нужен кабачок вытянутой формы (покупать надо не свежий кабачок с тонкой кожей. Которую легко проткнуть ножом… а огородный уже зажелтевший или затемно-зеленевший, кожица которого не то что ногтем не продавится, но и ножом не с первого раза. Такие твердые огородные кабачки продают бабки на рынке. Пройдитесь по базарному ряду, потыкайте ногтем втихаря и выберете. Если ваш кабачок не будет по форме ТАКОЙ ГРУШЕПОДОБНЫЙ как на фото домика внизу – не переживайте… просто ваша крыша домика будет чуть другой формы (не такая вытянутая, а более округлая). Красоты вашей поделки из шишек это не убавит. И главное постарайтесь выбрать такой который можно поставить на попку – и чтобы он не падал… Но если и будет падать, то ничего страшного – можно просто подложить пластилина под его основание. Далее… КАК ДЕЛАТЬ ДОМИК ИЗ ТЫКВЫ С КРЫШЕЙ ИЗ ШИШЕК. Кабачок можно оставить целым (не вынимать серединку) – но будьте готовы к тому, что кабачок со временем может загнить изнутри.… А можно срезать нижнюю попковую часть. Вынуть ложкой его содержимое… и высушить на солнце, чтобы его корка затвердела с внутренней стороны (так ваш домик будет вечным, и не сгниет). Кабачок красим в коричневый цвет (если гуашью красите – то после покраски хорошенько обрызкайте весь покаршенный кабачок ЛАКОМ ДЛЯ ВОЛОС, так краска перестанет пачкать руки) Детали дверей, окон и розочки над дверным проемом ЛЕПИМ РУКАМИ. Лепить лучше всего из полимерной глины (пластики), которая затвердевает в духовке. НО ЕСЛИ у вас нет пластики – то подойдет соленое тесто (вода + соль + клей ПВА + мука + бумажная салфетка). Я добавляю в соленое тесто клей пва и мелконарваную бумажную салфетку для того, чтобы тесто при высыхании не трескалось, а было гладкое и хорошо держало твердую форму. ИЛИ можно слепить все детали поделки из пластилина… а чтобы он не плыл на солнце его нужно затвердить. В качестве затвердителя подойдет лак в баллончиках (из строительного магазина)… или лак для волос… или лак для ногтей. Единственный побочный эффект в том, что фигурка будет иметь блеск от лака. Но это не страшно. Главное после затвердения пластилина не пытаться его ПОМЯТЬ (лаковая корка может треснуть). Поэтому лаком будем покрывать уже готовые прилепленные к кабачку двери и окна. А если шишки начать облущивать с кончика – а верхушки шишек оставить с чешуйками. То к таким чешуйчатым шляпкам можно приклеить круглые подушечки, или помпоны. В квадрат холщовой ткани кладешь шарик ваты (или синтепона), собираешь края квадратика в пучок и перевязываешь ниточкоа (получается круглый узелок (как у ежика в тумане из мультика). Этот круглый узелок сверху (там где завязка) накрываешь шишковой шляпкой – на клей. И получится поделка-желудь. Такие шишечные желуди можно подвесить как декор на венок из ивовых прутьев. Можно вместо холщевых мешочков использовать половинку пенопластового яйца… предварительно ее надо покрасить (например в золотую краску). Или такая шишечная верхушка может послужить панцырем для пластилиновой черепахи. А теперь перейдем к поделкам из ЦЕЛЬНЫХ шишек. Начнем мы с птичек… потом возьмем зверей… а потом и человечков. Вот такая красивая идея пингвинов из еловых шишек требует пластилина и белой краски. Из пластилина лепим голову и крылышки – а краской покрываем пузик. Или можно крылышки сделать из жмыха от початков кукурузы. Вот ниже на фото видно что вспомагательным материалом могут послужить кусочки фетра, картона, перышки, а также шляпки желудей (их можно использовать как выпуклые глаза птичек — повернуть шляпки обратной стороной, покрасить в белый цвет и черным маркером нарисовать зрачки. Если шишки поставить друг на друга, то можно сделать вот такие поделки-совы. Крылья и брови делаются из кусочков коры, глаза и нос из бумаги. Бумажный кружок для глаза совы можно надрезать по кругу ножницами и через эти надрезы сделать обмотку нитками – так мы получим выразительные лучики на глазах сов из шишек. А если сосновую шишку обвалять в нащипанной на волокна вате, то она получит вот такой пушисто-белый цвет. Из таких пушистых шишек можно сделать белых сов, птенчиков, снеговичков или попробуйте сделать пушистого песика. Можно из шишки сделать павлина. Для этой поделке нужна плотная бумага для головы, и мягкая креповая бумага для оперения хвоста. А вот еще вариант из той же породы поделок. Здесь принцип тот, но птица уже не павлин, а индюк. Вот еще один вариант птички из шишки. Крылышки у воробышка сделаны из кусочков коры, а голова это шарик сшитый из махровой ткани (если у вас есть кусок махровой салфетки, вы можете го пожертвовать на создание этой птички — меховая ткань тоже подойдет). Лучше когда салфетка белая…тогда можно покрасить лобную часть головы птенчика черной краской. Плюс это пучок ткани, который оттянули щепоткой, обмотали эту оттянутую щепотку ниткой у основания (чтобы она зафиксировалась) – и покрасили черным. К голове пришили или приклеили глаза бусинки. Или голову можно сделать из помпона. Взять обычные белые нитки и намотать их в два дырявых кружка… как обычно делают помпоны своими руками (загуглите, вы найдете такой урок). Или можно головку для птички сделать из обычного пенопластового шарика. Они продаются в поделочных магазинах, или их можно заказать в интернет-магазинах (они дешевые очень). А если из китая заказать на сайте али-эксперсс… то вообще дешево получится. Голова из пластилина получится ОЧЕНЬ ТЯЖЕЛОЙ, и птичка будет падать… А еще голову можно свалять из шерсти (продается шерсть для валяния)… тоже недорого совсем. Ее нужно положить в мисочку с теплой мыльной водой – и прямо в воде катать из нее шарик… по мере катания шарик становится все плотнее и плотнее… (2-5 минут надо катать, долго). И потом мы его достаем и сушим. И получаем плотный как валенок шарик. Он легкий и хорошо держится на шишке, не перевешивая и не перегружая поделку. Ножки для птичек можно сделать из проволки… проволку можно добыть из больших КАНЦЕЛЯРСКИХ СКРЕПОК. Крылышки из бумаги крепятся на пластелин внутри чешуек. Вот примеры ВЫСОКИХ ПТИЦ из длинных шишек. Хвост для левой птицы с фото ниже делается из полоско бумаги, которые обклеиваются чешуйками, выдернутыми из шишки. Если у вас есть перья (повыдергивали из подушки, например) то можно из шишек сделать красивых лебедей. Шеи можно скатать из пластилина и проволоки. Вот еще примеры поделок с перьями – страусы из шишек. Шея и головя лепятся из пластилина. Секрет устойчивости таких тонких и длинных шей в проволоке которая внутри этих шей спрятана (закатана в пластилин) как металлический каркас… конец проволоки торчит наружу и именно он втыкается в шишку. Благодаря гибкости проволочной шеи ее можно загнуть в любую сторону и придать любой изгиб нашей поделке из шишек (как на нижнем фото). Кстати обратите внимание что одна из птиц сделана в виде ФЛАМИНГО… а на заднем плане мы видим розовую овечку из шишек. Ежики из шишек делаются двумя способами. Либо мы лепим мордочку из пластилина и прикрепляем к шишке. Либо эту мордочку мы вырезаем из фетра (картона). Клеим пуговки-глазки и приклеиваем фетр к шишке. А вот идеи по созданию медведей из шишек. Грубая почтовая нитка (для сургучных опечатываний бандеролей) – подойдет для обмотки морды и живота медведика. На шишечную морду предварительно налепливаем пластилин, чтобы нитка прилипала. А вот белочка – голова делается из помпона (продаются в поделочных магазинах) руки и ушки из проволочных ершиков (тоже продаются там же). А вот ниже мы видим мышек, головы которых простые конусы из серого фетра (или флиса). Если вы купите кусочки меха, то сможете сделать вот такие поделки из шишек для новогодней елки. Еще больше новогодних поделок из природных материалов я выложу в отдельную статью и тогда здесь появится на нее ссылка. Помните, чуть выше, я объясняла как из кусочка войлочной шерсти – в мыльной теплой воде – скатать войлочный твердый шарик. Вот из таких шариков и шишек можно сделать человечков. Или можно заменить войлочные шарики пинг-понговыми или деревянными. Вот пример поделки МАМА И МАЛЫШ, сделанные из шишек и войлока… волосы мамы сделаны из оранжевой войлочной шерсти. Ручки тоже из шерсти скатаной в жгутик в теплой мыльной воде. А вот семейка гномов из шишек. Поделка из войлочной головы и кусочков фетровой или флисовой ткани + бубенчики на шапочках. Еще такая же поделка. Гномики из шишек – на голове каждого гнома шапочка (ячейка от бумажной касетницы для яиц). Ножки – это листики, наклеенные на картонку, Борода из кусочка ватного диска, приклеенного к мордочке из картона. И к семейству гномов можно сделать из шишек еще одну компанию — лесных жителей волшебного леса – ФЕЙ. Личико скатать из пластелина – к верхушке головы приклеить пучок нарезанных ниток – наверх шляпку от желудя. И сзади приклеить яркие крылышки из картона или фетра. И еще из шишек можно сделать прекрасных лыжниц в ярких шарфиках. Волосы – пучок ниток. Шарфики – кусочек елочной гирлянды. Шапочки таким лыжницам можно связать крючком или на спицах. Шарфики вырезать из флиса или мягкой креповой бумаги (можно просто белый лист бумаги сильно искомясить… и вырезать из него шарфик – он будет мягкий и легко обернется вокруг шишки. Лыжи из картона (или палочек от мороженого)… зубочистки служат лыжными палками. Еще больше поделок из шишек в новогодней тематике ДЕДЫ МОРОЗЫ… ОЛЕНИ… ЕЛКИ… РОЖДЕСТВЕНСКИЕ ВЕНКИ… я перенесла в отдельную статью. Там вы узнаете что можно сделать из шишек к Новому Году. Новогодние поделки ИЗ ШИШЕК (45 идей для детей) А еще у меня есть отдельные статьи по поделкам из другого продного материала. Удачных вам творческих идей. Ольга Клишевская, специально для сайта Семейная Кучка. на Ваш сайт.
Многие ходят в лес за грибами, а рукодельницы – за шишками. Оказывается, из этого природного материала получаются весьма оригинальные поделки. Работать с шишками могут дети разного возраста, поэтому часто воспитатели используют их на уроках труда в детских садах. В этой статье предлагаем вам посмотреть идеи поделок из шишек и использовать их для творчества. Такие изделия могут сделать даже малыши. Для их изготовления понадобятся шишки, желуди, пластилин, а также дополнительные материалы для декора. Вам нужно из шишки сделать туловище человечка, а из жёлудя – голову. На голове нарисуйте глаза, рот и нос. Возьмите палочки, пластилин и сделайте ручки. Осталось придать только настроение человечкам. Это могут быть веселые клоуны или активные лыжники, все зависит от вашей фантазии. Если вы не нашли жёлуди, то для головы используйте деревянные бусины. Одежду для ваших поделок удобно делать из фетра, так как этот материал не требует дополнительной обработки. Для скрепления деталей в поделках из шишек не обязательно использовать пластилин, идеально подойдёт и клеевой пистолет. Из шишек и пластилина может получиться весёлый зайчик. Заяц из шишек и пластилина Если с помощью ножа разрезать шишку и взять только нижнюю часть, то получится панцирь для черепахи. Черепаха из шишек и пластилина Используя сосновую шишку, пластилин и вату, получится весьма изящный лебедь. Лебедь из шишек Возьмите зеленый пластилин и две нераскрывшиеся шишки разного размера и соедините их. Теперь у вас в руках крокодил. Такие поделки вызовут восторг у ваших детей. Крокодил из шишек и пластилина Ежика из шишек можно сделать разными способами, например, из сосновых иголок и шишек. Для этого соберите сосновые иголки. Желательно чтобы они были сухими. Сформируйте пучки из иголок и закрепите их пластилином. Вставьте получившиеся иголки в шишки и потом подрежьте. Если иголки оставить длинными, то получится дикобраз. Не забудьте сформировать мордочку ежика. Из шишек и пластилина получаются весьма забавные ёжики. Украсьте поделки яблочками или грибочками Если использовать пластиковую бутылку, то ёжик может получиться разного размера. Как делать ежика из шишек и бутылки читайте в статье: Поделка ежик из шишек и пластиковой бутылки Предлагаем посмотреть фото подборку, что еще можно сделать из шишек: Цветы из шишек Бутоньерки из шишек Подсвечник из шишки Идей поделок из шишек очень много. Если вы заранее будете собирать природный материал, то сможете создавать целые композиции из шишек, каштанов, желудей, листьев и сосновых иголок. Хотите принять участие в школьной выставке и не знаете что сделать? Используйте шишки, ведь с их помощью своими руками можно делать подсвечники, гирлянды, веселые фигурки или украшения для декора. Шишки – это один из самых распространенных природных материалов, который используется в рукоделии в школе и детском саду. Оригинальные поделки из шишек смогут сделать даже маленькие дети под руководством взрослых. Схемы и фото – возможность найти креативные идеи и проявить творческие способности. Изготовление изделий из шишек положительно сказывается на развитии детей и улучшает мелкую моторику. Фантазируйте и ваши поделки будут не хуже, чем на фото. Гуляете с ребенком в парке или планируете съездить в лес? Не забудьте насобирать шишек и потом попробовать из них сделать красивые фигурки. Схема поделки из шишек Преимущество изделий из шишек в том, что этот материал абсолютно бесплатный, экологически безопасный и удобный в работе. Достаточно взять разноцветный пластилин и шишку и у вас получится фигурка животного. Соединяйте шишки между собой при помощи пластилина, чтобы сформировать голову и тело поделки. Не бойтесь использовать много пластилина, ведь с его помощью легко сформировать мелкие детали и оживить шишку. Маленьких детей можно научить делать зайчиков, ежиков или пингвинов. Используйте схемы или смотрите фото поделок. Если вы планируете украсить интерьер и наполнить его природными нотками, то шишки будут идеальным вариантом. Вам нужно просто привязать к шишке ленту или нитку и повесить ее на люстру. При желании можно закрасить шишку аэрозольной краской или присыпать блестками. Из шишек можно даже сделать гирлянду. Используйте для рукоделия не только сосновые, но и еловые шишки, тогда ваши поделки будут более разнообразными. Не думайте, что поделки можно делать только из шишек. Если разобрать шишку на чешуйки, открываются широкие возможности для творчества. Возьмите кусачки и разделите одну шишку на мелкие части. Теперь легко сделать аппликацию или рамочку для фото. Рамочка для фото из чешуек В последнее время все больше появляется идей, как оформить фотографии своими руками. Декор из натурального материала станет отличным вариантом для украшения фото. Вырежьте фото в форме круга или квадрата. После этого переверните фотографию и с обратной стороны начните приклеивать чешуйки. Не забудьте из ленточки сделать петельку. Чтобы работа получилась аккуратной, приклейте с обратной стороны еще один круг по форме фото. Между кругами вклеивается петелька из ленты. Рамочка для фото из шишек Подсвечник из шишек Хотите устроить романтический вечер? Тогда вам обязательно понадобятся подсвечники. Предлагаем сделать подсвечник своими руками из шишек. Сначала с помощью кусачек разделите шишку на чешуйки. После этого возьмите плотный картон и вырежьте из него круг. Начните приклеивать ваши чешуйки. Свечку нужно будет вставлять в рюмку, поэтому картонное основание должно быть больше рюмки в диаметре в два раза. Пластинки наклеиваются в шахматном порядке до тех пор, пока не будут превышать высоту стаканчика. Когда изделие высохнет, можете вставлять свечку и наслаждаться атмосферой романтики. Цветы из шишек Не думайте, что из шишек можно сделать только зимние поделки. Если разрезать правильно сосновую шишку, а потом заготовки покрасить в разные цвета, тогда легко будет собрать цветочный букет. Бутоны цветов можно приклеить к палочкам-стеблям или закрепить на проволоке. Вы можете попробовать сделать объемную аппликацию из цветочных шишек. Из шишек даже делают бутоньерки женихам на свадьбу, особенно, если для этого мероприятия выбрана какая-то определенная тематика. Корзина из шишек своими руками Если раньше корзинки плели исключительно из лозы, то сегодня появилось много других материалов. Современные рукодельницы широко используют газетные трубочки для плетения шкатулок, корзин других изделий. Хотите сделать оригинальную корзинку с минимальными затратами времени? Тогда берите шишки и соединяйте их в необходимой последовательности. Начитают плетение корзины из шишек с основания. Возьмите тонкую проволоку и соединяйте с ее помощью между собой шишки. Для основания понадобится около 10 шишек. Обворачивайте шишки проволокой до тех пор, пока не сомкнется кольцо. Корзина из шишек Сделайте второй слой для корзины и соедините два кольца между собой в шахматном порядке. Ручку корзинки делают подобным образом, только вместо тонкой проволоки используют толстую. Не забудьте сделать дно из шишек или из плотного картона. Поделки из шишек можно делать в кругу семьи вместе с детьми. Совместное рукоделие станет незабываемым времяпрепровождением. Простые и сложные фигуры и предметы декора из шишек – возможность проявить творческие способности и сделать креативные подарки своими руками. Хорошо бы после лесной прогулки принести домой несколько упавших шишек. Чешуйки их могут быть раскрытыми или плотно прилегающими другу к другу. В обоих случаях это прекрасный материал для творчества. Фигурки из шишек, сделанные вместе с ребенком, – это не только интересное, но и полезное занятие. Изготовленные творения можно отнести в детский садик или устроить настоящий спектакль дома, главными участниками которого и реквизитом будут поделки из шишек. Почему бы не сделать из шишек новогоднюю елку? Она будет не синтетической, а натуральной. К тому же можно будет хорошо сэкономить на этом атрибуте праздника и сделать его необычным и оригинальным. Если вы будете заниматься творчеством вместе с совсем маленькими детьми или у вас мало исходного материала, значит, вам подойдет первый вариант елки. Для нее понадобится уже раскрывшаяся затвердевшая шишка. Сначала сделайте основу для фигурки из шишек. Из плотного картона вырежьте круг диаметром чуть меньше окружности самой шишки. Нанесите на него темную краску, дайте ей высохнуть. Можно обклеить сверху картонный диск цветной бумагой. Ребенку очень понравится и следующий этап работ. Размягчите пластилин, пусть малыш скатает из него несколько шариков и прикрепит их между раскрывшимися чешуйками шишки. Можно сделать украшения и другим образом – скатать шарики из ваты, завернуть их в кусочки цветной бумаги или в обертки из-под конфет. После этого нужно плотно перекрутить фантик и приклеить его этой частью к чешуйке шишки. Это может делать взрослый при помощи клеевого пистолета. Таким же образом прикрепите низ шишки к основе из картона. Небольшая, но красивая ель готова. Думая, что можно сделать из шишек с детьми постарше, возведите глобальное новогоднее сооружение. В зависимости от того, сколько природного материала принесено из леса, такой высоты и ширины будет елка. Начните тоже с изготовления подставки. Вырежьте круг из толстого картона такого диаметра, чтобы на нем уместилось 5-9 шишек (в зависимости от того, какого размера будет ель). Смажьте его обильно клеем для дерева и разложите шишки по кругу острым краем наружу. Если вы решили изготовить большую ель, предварительно скрепите шишки между собой при помощи веревки, обкручивая их по порядку. После этого положите на картонную подставку, смазанную клеем. В следующий ряд заложите столько же или на одну шишку меньше. Ель будет постепенно сужаться кверху. Можно уменьшать количество шишек каждый ряд или через два-три. Нижний ярус промазывайте клеем, прикладывайте верхний. Когда вы дойдете до макушки, поставьте одну нераскрывшуюся шишку острым концом вверх, приклейте ее. Можно покрасить такие фигурки из шишек при помощи баллончика в зеленый, голубой, золотой или серебряный цвета или оставить изделия в первозданном виде. Решая, что можно сделать из шишек, изготовьте с ребенком забавных животных. Тогда их можно будет поставить под только что сооруженную елку, придумать сказку и разыграть ее вместе с детьми. Слепите из белого пластилина конус, прикрепите его основание к закругленной части шишки, которой она когда-то крепилась к дереву. Это основа мордочки зверька. Небольшой кусочек пластилина черного цвета превратите в шарик, прикрепите на место носа. Из этого же материала скатайте еще 2 такие окружности, приплюсните их, прикрепите на место глаз. Зрачки сделайте из пластичной массы белого или желтого цвета. Из белой – 4 маленькие лапки и 2 небольших уха треугольной формы. Так же прикрепите эти детали на свое место. Можно сотворить и другие очаровательные фигурки из шишек и пластилина, например, динозавра. Чтобы он был красочным, возьмите материал для лепки сиреневого, красного, голубого, желтого, зеленого цвета. Раскатайте кусочек сиреневого пластилина в колбаску, одна сторона которой чуть толще второй. Прикрепите этот более широкий край к узкой части раскрытой шишки. Второй конец колбаски слегка изогните, соедините его с красной головой дракона. Сделайте посередине мордочки надрез, положите в его верхнюю и нижнюю части по небольшому расплющенному кусочку желтого пластилина. Это приоткрыт рот совсем нестрашного дракона. Чтобы сделать динозавра еще более добродушным, прикрепите на мордочку глаза из пластилина голубого цвета. Такого же оттенка будут ноги и хвост сказочного персонажа. Кусочки желтого пластилина превратите в треугольные и прикрепите их на спине, хвосте и обратной стороне шеи. В такой же технике делают и другие фигурки из шишек – зверят, людей, сказочных персонажей. Гуляя в конце лета или начале осени по лесу, вы можете собрать не только упавшие шишки, но и желуди. Этот тандем помогает придумать самые интересные идеи для творчества. Решая, какие поделки из шишек и желудей можно сделать с детьми, предложите малышам превратить эти дары природы в лесовичка. Приклейте желудь к макушке раскрывшейся шишки. «Шапочка» желудя при этом станет головным убором сказочного обитателя леса. В его руки превратите две небольшие сучковатые палки, прикрепив их проволокой. Глаза и рот вырежьте из цветной бумаги, приклейте их на лицо лесовика. Очаровательными получатся фигурки из шишек и желудей – стрекозы. Помимо этих материалов, для их конструирования понадобится подставка овальной формы. Вырежьте ее из дерева, покройте лаком. Шишки подойдут более стройные, приклейте их к подставке, получилось тельце стрекозы. К нему прикрепите по 4 овальных крыла. Их можно вырезать из парчи или другой плотной ткани, прикрепить к шишке проволокой или нитками. Желудь превратится в голову и шапочку насекомого. Вы можете изготовить новогодний венок, чтобы декорировать им дверь. Основу его в форме кольца сделайте из проволоки или ивовых прутьев, лозы. Если вы решили использовать природные гнущиеся материалы, возьмите пучок прутьев, свяжите их нитками в виде кольца. При помощи проволоки прикрепите шишки, можно декорировать венок и другими материалами, приклеив бусины, привязав бантики. Золотистая краска поможет композиции обрести целостность. Медвежонок из шишек получается объемным, очаровательным и очень милым. Для его создания достаточно склеить шишки, придав им форму мохнатого хозяина леса. Гирлянда из шишек получится красочной, оригинальной, а делать ее – одно удовольствие. Сначала возьмите фетр красного и желтого цвета. Подойдут лоскуты, оставшиеся от рукоделия. Из желтого материала вырежьте большие круги, из красного – поменьше. Положите их один на другой (меньший на больший), пристрочите, как это показано на фотографии. Прочную нить вденьте в большую иглу. Проколите ею 5 шишек горизонтально, затем основу из фетра. Таким образом скрепите гирлянду до конца. Ею можно декорировать невзрачную стену на даче, ствол дерева или украсить помещение. Вот такие можно сделать поделки из шишек своими руками. Идеи, советы помогут пробудить фантазию и создать еще много оригинальных вещей, которыми можно украсить дом, детский сад к празднику. Если на прогулке осенью с ребенком вы нашли несколько симпатичных шишек, которые ребенок захотел принести домой, то можно использовать их для создания интересной поделки своими мишки из шишек. Фигурки зверей очень любят делать дети и не откажутся принять участие в таком творческом процессе. Такого симпатичного мишку из шишек можно отнести в детский сад на конкурс или оставить для украшения елки. Обмотаем веревкой шишку, которая станет головой, предварительно сделав из пластилина нос и другие детали морды. Вторую большую шишку обмотайте бечевкой и используйте для туловища. Приклейте маленькие шишки вместо лап и прикрепите глазки. Шишки настолько отличаются по форме, размерам и в принципе внешнему виду, что получиться из них могут совершенно разные фигурки. Осенние поделки из шишек дети могут создавать на протяжении всей осени и даже зимой, особенно в плохую погоду. Интереснее будет поделка, если есть другие природные материалы и пластилин. Из парочки маленьких шишек и пластилина можно сделать симпатичного мишку. Украсьте свою работу засушенными листьями или ветками. Небольшую шишку используем для головы медведя. Пластилин нужен, чтобы сделать ушки, мордочку и нос. Черные шарики из пластилина послужат глазами, а желтый шарик сойдет за шею Присоедините все детали из пластилина к шишке Шишку побольше используем для туловища Скатайте 4 шарика из коричневого пластилина разного размера. Те, которые поменьше будут – верхними лапками, а побольше – нижними. Сделайте еще два удлинённых овала. Прикрепите лапки к туловищу На лапках сделайте прорези стеком, имитируя пальчики Украсьте поделку листьями Шишки соединяются в такой поделке с помощью горячего пистолета, создавая форму мишки. Для изображения мордочки можно использовать различный материал: рябину. Каштаны, пластилин. Чтобы сделать такого мишку, необходимо найти несколько шишек разного размера Прикрепите лапки к самой большой шишке. Далее возьмите шишку поменьше, чем туловище, и прикрепите ее на место головы. Чтобы сделать ушки отщепите от шишки парочку чешуек. После соединения всех деталей украсьте ленточкой медведя. Узнайте, как сделать конус из бумаги менее чем за 1 доллар. Это просто и идеально подходит для всех ваших нужд. Подумайте о новогодних украшениях! Я покупал конусы из пенополистирола и был удивлен, насколько они дорогие! То есть реально дорого! Итак, из ремесленного магазина я пошел в долларовый магазин и нашел конусы за доллар… Ура! …… но они были только одного размера (вроде маленькие) и не очень заостренные наверху.Не идеально. Какое-то время я делал это, но мне хотелось найти альтернативу. Я решил сделать свои собственные конусы и потратил много времени на то, чтобы понять это! Кто знал, что это может быть так сложно?!?! Я искал в Интернете … много … но не нашел, что это особенно полезно. Затем я нашла в Pinterest кого-то, кто расскажет вам, как их сделать, я был взволнован и даже переписал, прежде чем понял, что вы должны купить ее выкройки. Облом… То есть… для конуса? Нужна выкройка для шишки? Конечно, я должен быть достаточно умен, чтобы понять это, не платя кому-то! Верно? ЭТО КОНУС, А НЕ РАКЕТНАЯ НАУКА! По общему признанию, я МНОГО раз подвергал сомнению свой интеллект, выясняя этот ОЧЕНЬ ПРОСТОЙ процесс.🙄 Может, мне стоило просто купить выкройку. Не убегай искать выкройку! Вам это не нужно! Я покажу вам, как сделать конус из бумаги за БЕСПЛАТНО ! Когда я начал свой поиск, чтобы придумать, как сделать конус, мое внимание было сосредоточено на рождественских елках. Я очень хотел сделать букет рождественских елок. Пока что я сделал семь елок из конуса. Сосновая шишка и шляпа на рождественской елке фактически состояли из более крупных шишек.Поэтому, когда я наконец понял, как сделать из бумаги обычный конус, я решил сделать конус на стероидах, он же действительно большой конус. (Подсказка: процесс такой же). — Доска для плакатов Держись за шляпу, Салли! Это поразит вас! Хорошо … не совсем … но это поможет! Для конуса вам понадобится полукруг или четверть круга.С картоном для плакатов у вас может быть перекрытие, но если вы делаете пену, из-за ее толщины вы бы хотели, чтобы она стыковалась вплотную к себе, и тогда вам понадобится четверть круга. Возьмите веревку и привяжите ее к концу карандаша. Поместите конец веревки на край плаката и нарисуйте полукруг. Используйте обычные ножницы, чтобы вырезать очерченную форму.Это будет треугольник с загнутым дном. Сверните вместе, пока не получите форму конуса. Ага! Вот как сделать из бумаги конус. Осторожно приклейте его горячим клеем и удерживайте, пока он остынет. Или вы можете использовать ленту. Если вы украшаете его, вы можете использовать скотч снаружи или внутри. Если будет возможность, обязательно подпишитесь на меня в Instagram ! Вот и все! Надеюсь, это будет полезно! Теперь вы можете сделать связку конусов или один большой конус менее чем за 1 доллар.00! После того, как я закончил процесс, я также использовал картон для плакатов, бумажный пакет для покупок и пену для рукоделия. Я также расширил область применения конуса за пределы рождественской елки. В любом случае, я надеюсь, что все это поможет! Теперь вы можете сделать столько шишек, сколько захотите !! В любом размере! Если у вас нет времени на поделку из шишек в этом году, вот несколько забавных предметов декора, которые могут вам понравиться! У меня есть два видеоурока, которые, надеюсь, вы найдете полезными! Ура! Спасибо, что зашли! Помните: жизнь слишком коротка, чтобы не мерцать, так что берите клеевой пистолет и блестки! ™ Будьте в безопасности! Mona Осенняя природа не только удивляет нас буйством красок, но и дает нам бесплатные материалы для творчества! Природные сокровища, такие как желуди, сосновые шишки, ветки, конские каштаны, листья, ракушки и т. Д.может послужить развитию вашего ребенка! Ремесло оказывает большое влияние на развитие мышления детей, координацию движений, гибкость и точность выполнения заданий . Все это важно для подготовки руки к письму и для дальнейшей учебной деятельности в школе. Приобщать детей к миру декоративно-прикладного искусства необходимо как можно раньше! В этой коллекции осенних поделок из натуральных материалов вы найдете огромное разнообразие творческих, веселых и простых поделок животных для дошкольников и первоклассников. Работа с натуральными материалами дает большие возможности для стимулирования понимания ребенком природы и его или ее отношения к ней. Задача творчества — не только дать детям возможность выполнять подобные задания, но и полюбить эту «мастерскую» природы! В этом посте вы можете найти классные поделки из осенних листьев для дошкольников! Во время прогулки по лесу или парку родителям стоит обратить внимание ребенка на огромное разнообразие натуральных материалов, которые можно использовать в осенних поделках.Пусть малыш соберет разные по размеру и форме шишки, ветки деревьев, желуди и т. Д. При сборе материала его следует осматривать. Взрослый должен побуждать ребенка представить, что собой представляет каждая веточка или камешек, что из них можно сделать. Во время такой прогулки можно поговорить с детьми об их уважении к природе; им нельзя позволять ломать ветви или собирать цветы для букетов. Чтобы сделать эти дошкольные осенние поделки из натурального материала, вы должны сначала собрать необходимые материалы для каждого проекта.Вам нужно собирать природные сокровища самых разных форм, цветов и размеров, ведь для изготовления каждой фигурки животного нужны разные материалы. Если говорить о желудях, конских каштанах и сосновых шишках, то лучше собирать их, когда они полностью созрели и упадут на землю. Используйте только чистые и полезные фрукты. Кроме того, при сборе желудей можно собирать и просто чашки — они хорошо дополняют некоторые элементы поделок, а при сборе каштанов — учтите, что колючие стручки тоже могут пригодиться. Чтобы соединить части каждого животного , вы можете использовать спички, проволоку, маленькие палочки и пластилин. Конские каштаны, желуди и шишки сначала проткнуть шилом, чтобы проделать отверстия для ног, рук и т. Д. Сухие листья и перья также отлично подходят для дополнения фигурок животных. Например, они хорошо смотрятся в виде парусов, хвостика, крыльев и плавников. Также семена и стручки семян деревьев являются хорошим дополнительным материалом для осенних поделок.Они могут как украсить, так и дополнить поделку. Ищите стручки семян клена, стручки семян ясеня, семена березы и семена вяза. Комбинируя несколько проектов, можно создавать целые композиции. Осенние поделки из натурального материала — отличные подарки для друзей и близких. Это хорошие персонажи для детского кукольного театра или просто забавные «натуральные» игрушки для детей. Это самая легкая поделка, которая подойдет даже 4-летним детям.Взрослый человек должен сначала проделать отверстия в чашечках из желудей. Используя толстую иглу или шило и что-нибудь твердое, например ножницы, протолкните иглу через колпачок желудя, чтобы образовалось отверстие. Вы можете использовать тот же метод для головы желудя. Затем вы можете позволить ребенку нанизывать чашки с желудями на силиконовый шнур (например, для браслетов). Дети постарше могут использовать фигурку змеи как часть более крупного ремесленного проекта: заклинатель змей играет на флейте танцующей кобре. Материал и инструменты: желудь, арахис, веточки (или спички), два стручка с семенами ясеня, пластилин или клей, шило, нож (для учителя), тонкие карандаши. Для корпуса понадобится большой желудь, но сначала отделите от него чашку. Затем проделайте в туловище шесть отверстий — в местах соединения ног, шеи и хвоста. Присоедините голову осла к туловищу с помощью небольшой веточки (2-3 см), предварительно заостренной с обоих концов.Вставьте шейку веточки в предназначенные для нее отверстия в желуде и орехе. Для лучшего результата можно нанести клей перед сборкой стыков. Для ног осла нужно подготовить четыре маленьких веточки или четыре спички, заострить их с одного конца и плотно вставить в желудь. Также можно использовать изогнутые веточки — тогда ноги осла согнуты. Также можно сделать копыта из пластилина, что придаст статуэтке больше устойчивости. Далее нужно проделать дырочки на голове осла и на конце туловища.Для колосьев используйте два небольших кусочка стручков с семенами ясеня и короткую ветку для хвоста . Глаза и мордочку осла можно нарисовать тонким карандашом. А вот еще одна идея, как можно обновить проект для детей постарше. Материалы и инструменты: Материалы и инструменты : еловые шишки (1 большая и 1 маленькая), лесной орех, кукурузная шелуха, семена медовой акации (Gleditsia triacanthos), полоска бересты (для подставки), мох, веточки деревьев (две тонкие и две средних). толстый), пластилин, клей. Прикрепите лесной орех ( головка, ) к еловой шишке (, корпус ) с помощью тонкой заостренной палочки или клея. Добавьте небольшой конус для хвоста .Заострите веточки и вставьте их в проделанные отверстия в теле — две более толстые веточки внизу для лапок и две более тонкие вверху для передних лап кролика. Ушки вырезаны из кукурузной шелухи и прикреплены к головке с помощью клея, ушки сделаны из семян медовой акации. Готовая поделка устанавливается на полосу бересты, которая декорирована мхом. Вы также можете положить перед кроликом небольшую морковку, сделанную из пластилина. Взрослый вместе с ребенком подготавливает материал для поделки, проделывая шилом отверстия в шишке и лесном орехе. Веточки тоже нужно заточить с одного конца. В то же время он объясняет ребенку, как держать шило и делать с ним отверстия в разных материалах. Чтобы сделать тело утенка , вставьте в сосновую шишку заостренные веточки: две веточки внизу туловища — это ноги утки — и одна сверху для шеи . Затем прикрепите лесной орех к шее , головка . Приклейте тыквенные семечки к ножкам . Сделайте клюв из красной глины для лепки. Чтобы выглядело так, будто утенок держит в клюве червяка, используйте изогнутую веточку или стебель любого растения. Материалы и инструменты: две еловые шишки с открытыми чешуйками, стручок желтой лилии прудовой, скорлупа желудя, мак, пластилин, клей, нож, бумага, ножницы, тонкая подводка. Взрослый должен помочь ребенку подготовить материал для ушей животного, для этого он разрезает ножом продольно панцирь желудя на две равные половинки, а затем снова каждую часть пополам. В начале работы взрослый загадывает ребенку загадку: Хвост пушистый, мех золотистый, в лесу живет, в деревне кур крадет.Затем он показывает животное на картинке или игрушечную лисицу и предлагает сделать такую игрушку. В разговоре с ребенком взрослый уточняет, знает ли он особенности внешнего вида лисы, повадки животного, где живет, чем питается. Потом спрашивает, из чего можно сделать эту фигурку. Вместе они изучают подготовленный материал, раскладывают его на столе. О том, как соединять детали, рассказывает взрослый, вместе с ребенком задает последовательность изготовления игрушки. Рабочий процесс: Соедините две еловые шишки вместе с пластилином для лепки, чтобы сформировать туловище и хвост лисы.Убедитесь, что весы указывают в одном направлении. Если хвост тяжелый, можно наклонить его вниз, тогда фигурка будет более устойчивой. Чтобы сделать голову животного, используйте стручок кувшинки. Уши сделаны из ракушек желудей, ноги — из лепки, прикреплены к телу-конусу. Глаза можно сделать из семян яблока, а носик из черного мака. Теперь ребенок может сделать поделку самостоятельно. В процессе работы взрослый следит за действиями маленького ремесленника, следит за правильным положением шишек для туловища и хвоста — чешуей в одну сторону, чтобы малыш проявлял инициативу в своей работе, а после окончания чистки рабочее место. Материалы и инструменты: 1 желудь, 2 еловых шишки, веточки веточки, спички, клей, картон зеленый, шило, нож (для учителя), подводка. Рабочий процесс. Работа над поделкой начинается с анализа чертежа, выделения его отдельных частей. Для головы оленя возьмите желудь и проделайте в нем три отверстия шилом: два сверху для вставки веточек — это рога, и один снизу, в который вставляется спичка, направленная на обоих концы для соединения головы с шеей.Затем выберите две еловые шишки: одна большая для туловища, другая поменьше и короче для шеи. Проколите шилом меньший конус и вставьте спичку в отверстие, соединяющее туловище с шеей. После этого в теле проделываем еще пять отверстий — четыре для ног и одно для хвоста — и вставляем в них спички. Сделайте одно отверстие в верхней части шеи и соедините спичкой с головой оленя. Мордочку можно прорисовать мелкой подводкой. Материалы и инструменты: большая сосновая шишка, две еловые шишки (одна средняя и одна маленькая), кукурузная шелуха, четыре березовых веточки, сушеная ежевика, шило, клей, спички, пластилин, ножницы. Подготовка к работе . В большой сосновой шишке (корпус , ) взрослый человек вместе с ребенком проделывает шилом шесть отверстий (одно для крепления головы, второе для крепления хвоста и четыре для передних и задних ног). В еловой шишке среднего размера для головы проделайте четыре отверстия: одно для крепления к туловищу, два для крепления ушей и одно для крепления носа). Для хвоста также следует сделать одно отверстие, чтобы соединить его с туловищем. Последовательность изготовления фигурки животного . Вставьте две тонкие веточки в отверстия тулова шишки и с их помощью прикрепите голову и хвост (средняя и маленькая еловая шишка). Вставьте четыре веточки — щенячьи лапки — в проделанные в нижней части туловища отверстия. Ножницами вырежьте початки из кукурузной шелухи и вставьте их в большие отверстия, сделанные для ушей на голове. После этого приклеиваем для носа сушеную ежевику и нарисуем глаза. Для лучшего результата места соприкосновения частей животного можно укрепить пластилином. Материалы и инструменты: 1 желудь, 2 стручка семян ясеня или клена, 3 сушеных дубовых листа, ножницы, нож и шило (для взрослых), пластилин для лепки черного, белого и красного цветов. Подготовка к работе. Перед тем, как приступить к работе, нужно дать ребенку возможность посмотреть на живую рыбу, если такой возможности нет, следует показать ему картинку. При этом обратите внимание ребенка на характеристики рыбы — большой гибкий хвост, выпученные глаза.Затем вместе с ребенком нужно выбрать необходимый материал и разложить его на рабочем столе. Взрослый человек должен проделать в желуде 3 отверстия — для плавников — и сделать надрез на вершине для плавника на голове. Последовательность изготовления фигурки животного . Работа начинается с изготовления туловища рыбки. Для этого используйте желудь. Сделайте глазки из пластилина и прикрепите их спереди. Также их можно сделать из кружочков цветной бумаги или косточки вишни. Меньшие плавники сделаны из стручков семян ясеня, которые прикреплены шариком из пластилина с обеих сторон желудя.Для хвоста и верхнего плавника используйте сушеные листья дуба. (Вы можете высушить свежие дубовые листья горячим утюгом, положив их между двумя слоями бумаги во время глажки.) Приклейте небольшой шарик пластилина для лепки на стебель листа и вставьте его в отверстие сзади. Вырежьте кусок листа и вставьте его сверху, чтобы получился последний плавник. Разобравшись в этой последовательности изготовления поделки, ребенок самостоятельно (но под присмотром взрослого) мастерит поделку-животное. При необходимости ему помогает взрослый.Когда фигурка готова, можно отметить, как работал ребенок, старался ли, аккуратно ли лепил игрушку, похвалить за трудолюбие, за проявленную инициативу. Если малыш стесняется убирать на рабочем месте, ему нужно об этом напомнить. Материалы и инструменты: 3 еловых шишки, 6 стаканов желудей, пенополистирол, пластилин черный, бумага красная, ножницы, бусины белые, спички, шило. С помощью этого проекта дети могут узнать о пингвинах и характерных особенностях этих животных — где они живут, что едят, как воспитывают своих детенышей. Чтобы сделать пингвина, возьмите большую еловую шишку и поверните ее чешуей вверх. Голову сделайте из черной лепки, глазки — из бусинок, клюв — из двух склеенных между собой треугольников из красной бумаги. Крылья пингвина можно сделать из семечек ясеня или клена. Приклейте их между чешуйками конуса с помощью лепки. Ножки можно сделать из чашечек из желудей, для чего они набиваются пластилином и прикрепляются к основанию шишек с помощью короткой спички, заостренной с обоих концов.Взрослый человек проделывает шилом параллельные отверстия в конусе и чашечках. Для большего сходства с пингвинами тело и крылья можно покрасить черно-белой краской. Все пингвины из этого семейства сделаны подобным образом. Соответственно, подберите для каждой еловую шишку подходящего размера и придайте персонажам определенную позу. Для выполнения поделки сделайте из пенополистирола банку для льдины. Края льдины должны быть неровными. Материалы и инструменты : сосновая шишка среднего размера, желудь, ветки деревьев, цветная бумага, клей, пластилин, тростниковая трава или птичьи перья, кусочек дерева, шило, ножницы, тонкая подводка Порядок работы : подобрать для туловища шишку из ели или сосны среднего размера, сделать в ней четыре отверстия шилом (с противоположных концов для шеи и хвоста и снизу для ног павлина). Для головы подойдет желудь без чашки, в нижней части которой необходимо проделать отверстие для веточки-шейки.Голову и туловище соедините удлиненной веточкой, заостренной с обоих концов, так, чтобы ее центральная часть оставалась снаружи — это шея. Для прочности склейки нанесите клей на концы веточек. В проделанные снизу отверстия в туловище вставьте две ветки одинакового размера — это будут ножки. Глазки, клюв и украшения для головы сделаны из лепки. На голове можно сделать три дырочки, воткнуть в них три раскрашенных в разные цвета спички и на их концах прикрепить разноцветные лепные глиняные шарики.Воткните хвост (камышовая трава или птичье перо) в проделанную в теле дырочку. Перья можно раскрасить или украсить разноцветными кружочками из бумаги. Для устойчивости приклейте павлина на подставку или на кусок дерева. В украшении павлина дети могут проявить творческий потенциал: для хвоста они могут использовать птичьи перья, бумагу, траву и т. Д. Материалы : 1 орех и 1 лесной орех, 3 ветки дерева (одна толстая, две средней толщины и две тонкие), 2 сухих семени акации, стручки семян ясеня, пластилин, кусок дерева, шило. Подготовка к работе . Во время прогулки или по дороге из детского сада предложите ребенку посмотреть на семенные коробочки ясеня, спросите, как они выглядят (на веер, на самолет и т. Д.), Что из них можно сделать. Соберите вместе с ребенком семена ясеня и веточки разной толщины для изготовления осенней поделки. Последовательность изготовления фигурки . С помощью пластилина прикрепите к грецкому ореху две веточки средней толщины — туловище птицы.Это ноги. Фундук (голова) прикреплен к шее и туловищу также пластилином. Для клюва можно использовать два тонких цветочных шипа, которые закреплены на голове птицы пластилином. Глаза сделаны из семян акации, а хвост — из нескольких семян ясеня. В конце приклеиваем птичку на подставку. Цели следующих осенних поделок: закрепить навык работы с плодами каштана; улучшить умение самостоятельно анализировать план-схему последовательности действий при создании фигурки животного; улучшить навыки соединения деталей; воспитывать настойчивость в достижении цели. Материалы и инструменты: 2 конских каштана, малый желудь овальной формы, 3 птичьих пера, 3 остроконечных веточки, 2 кончика шипа медовой акации, листья георгина, два черных круглых семени, клей, шил. Рабочий процесс . Туловище петуха сделано из каштана, а голова из лесного ореха. Петухи гребешок и плетень сделаны из лепестков георгина. Клюв сделан из шипов медовой акации, глаза — из семян вьюнка.Все это склеено. Ветки подходят к лапкам, хвостик сделан из перьев. Игрушка прикреплена к подставке из половинки плода каштана. Продолжить учить детей разбирать игрушку по схематическому рисунку, выделять ее составные части; обогатить знания детей о возможностях комбинирования материала; воспитывать волю, упорство при выполнении задачи, уверенность в своих силах; сформировать устойчивый интерес к этому виду работы, усилить желание работать. Материалы и инструменты: Растение typha latifolia (рогоз обыкновенный), пшеница, 4 веточки с перемычкой на концах, 2 стручка кленовых семян, черная пластиковая глина, зубочистки, тонкая подводка Материалы и инструменты: пластилин, проволока и плоскогубцы, 2 семечка яблока, 4 стручка ясеня, длинная ветка Материалы и инструменты: 1 желудь, 1 лесной орех (или конский каштан), ракушки с просверленными отверстиями, зубочистки, проволочные крючки для соединения C, пластилин, тонкая подводка, шило и нож (для учителя). Материалы и инструменты: три шишки ели и сосны — одна большая, одна средняя и малая, 6 шляпок желудей, четыре гнутых веточки, кусок коры, цветная бумага (двух цветов), пластилин, ножницы, нож. . Материалы и инструменты : 1 конский каштан, 8 тонких изогнутых веточек и 2 более толстых, пластилин, клей, шило. Материалы и инструменты : ракушки, раковины улиток, перья разных размеров, ветка, деревяшка для основы, клей И напоследок две крутые осенние поделки, которые не являются фигурками животных, но также сделаны из натуральных материалов и пластилина и подойдут для первоклассников. Материалы и инструменты: 1 пробка для вина, 2 стакана для желудей, палочки для дерева (1 большая и толстая и 1 маленькая и тонкая), 8 стручков ясеня, синяя пластилин, шило, проволока. Материалы и инструменты: 1 небольшая еловая шишка, 1 орех, стручки семян ясеня и клена, зубочистки или спички, пластилин, шило. Сказочные сады — это небольшие сады с горшками, наполненные волшебством! Идеально подходит как для дома, так и для улицы, ваш ребенок может использовать свое воображение, чтобы создать свой собственный миниатюрный мир.Вам не нужны дорогие наборы для самостоятельного изготовления, чтобы ваш ребенок мог сделать один из них самостоятельно. Если вы уже являетесь заядлым садовником, вы, вероятно, сможете найти большинство материалов в своем доме. В противном случае эти предметы можно легко приобрести в местных садовых центрах, комиссионных магазинах или у соседей, заботящихся о природе. Самое лучшее в сказочных садах то, что здесь нет «неправильного» способа их создания.Поощряйте своего ребенка проявить свои творческие способности и посмотреть, куда приведет его воображение, даже если оно превратится в скорее в сад фигурок, чем в сказочный сад! Вдохновите своего ребенка стать орнитологом с помощью этого классического, экологически чистого ремесла! Кормушки для птиц из сосновых шишек настолько просты в сборке, что их можно изготовить разными способами. Соберите желаемое количество сосновых шишек.Помогает собирать с длинными цветоносами (стеблями) и раскрытой чешуей. Обязательно вымойте и высушите те, которые вы собираете, иначе у вас может быть коллекция насекомых на руках. После высыхания обвяжите шпагат вокруг стебля и положите на бумажную тарелку. Пластиковым ножом или палочкой для мороженого смажьте сосновую шишку арахисовым маслом. Если у вашего ребенка аллергия на орехи, используйте на этом этапе овощной жир. После полного покрытия ваш ребенок может нанести птичий семя, посыпав им сосновую шишку (отсюда и бумажную тарелку для сбора грязи) или обваляв семя.Наконец, выйдите на улицу, выберите дерево и привяжите свою кормушку для птиц к ветке! Чтобы продолжить веселье, каждый день выходите на улицу для приключений и записывайте, сколько птиц посещает вашу кормушку. Не удивляйтесь, если на закуску придут и белки! Хотите пополнить запасы мусорной корзины вашего ребенка? Не торопитесь покупать новые мелки! Все эти осколки на дне корзины можно вернуть к жизни с помощью этого простого метода переработки мелков. Что вам понадобится: Разогрейте самостоятельно до 275ºF. Попросите ребенка помочь, оторвав бумажные этикетки от сломанных мелков, и пусть он сам выберет, какие цвета следует сочетать в каждой форме. Поместите форму или сковороду в духовку и запекайте примерно 6-8 минут. ( Осторожно, : сковорода или форма БУДЕТ горячими!) Подождите, пока мелки не остынут, прежде чем вынимать их из формы.Наконец, позвольте вашему ребенку рисовать их новыми мелками! Совет: Научите ребенка, как из разных цветовых сочетаний создавать совершенно новые! Поощряйте их смешивать красный и синий, синий и желтый или желтый и красный. Хотя эти 3 экологически чистых поделки — далеко не единственные поделки, которые вы можете сделать со своими детьми в честь Дня Земли, они — отличное место для начала! Независимо от того, что вы решите сделать, цените это время связи , которое у вас есть вместе, и используйте его для поощрения дискуссий о защите нашей планеты.
Фотография
— Александр Сафонов
Фотография
— Джули Уайлд
Фотография
— Миксетто
Вот посмотрите, как мы сделали наши … Что вам понадобится Начните с разрезания пробковых плиток на круги, которые поместятся внутри крышки. Убедитесь, что вы разрезали пробку немного меньше, чем верхняя часть банки, чтобы крышка закрывалась должным образом. Я обвела вокруг банок, а затем вырезала круг примерно на 1 см меньше по всему периметру. Перед закреплением клея убедитесь, что крышки закрываются пробкой. Пробковые плитки, которые мы использовали, поставлялись с клеящимися наклейками, поэтому я использовал их, чтобы прикрепить их к внутренней части крышек банок вместо клея. Количество используемых блесток зависит от того, какой толщины вы хотите, чтобы они были на дне банки. Для нас это был метод проб и ошибок, поскольку изначально Лола добавила достаточно блеска, чтобы полностью покрыть самого маленького оленя! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
С добавлением блеска наши снежные шары были почти готовы.Все, что им было нужно, это последний штрих. Я обмотал банку джутовой бечевкой прямо над крышкой и завязал бант. Перед тем, как завязать шпагат, я обернул полоску клея вокруг банки, чтобы она надежно закрепилась. Добавление шпагата действительно оттеняет снежные шары. Вы можете использовать любую ленту или шпагат, но мне нравится контраст грубого джутового шпагата с гладким стеклом и блестящим блеском.
| Снежный шар сосновой шишки |
| Шишки оленя и сосны |
| Группы всегда хороши |
| Самодельные снежные шары без воды |
Ава и Лола были действительно впечатлены тем, как получились наши снежные шары (как и я), и очень хотят сделать больше в качестве рождественских подарков для друзей.
Так просто сделать, но так красиво. Мой любимый вид поделок.
Маленькие деревянные держатели для колец Декор каминной полки Одиночный конус для горного кольца Натуралистический деревенский миниатюрный деревянный Статуэтки горных пиков Хранение ювелирных изделий Ювелирные изделия bgc.sedahotels.com
Маленькие деревянные держатели для колец Декор каминной полки Одиночный конус для горного кольца Натуралистический деревенский миниатюрный деревянный Статуэтки горных пиков Хранение ювелирных изделий Ювелирные изделия bgc.sedahotels.com
Маленькие деревянные держатели для колец Декор полки для каминной полки Одиночный конус для горного кольца Натуралистический деревенский миниатюрный деревянный Статуэтки горных пиков, натуралистические деревенские миниатюрные деревянные статуэтки горных пиков Маленькие деревянные держатели для колец Декор для каминных полок Одиночный горный конус для колец, они делают идеальный уникальный держатель для колец или фигурку, Дерево и, Миниатюрный кольцевой конус горной вершины, Идеально подходит для деревенского декора камина или натуралистических украшений леса. Эти деревянные конусы окрашены в цвет черного дерева и покрыты крошечными нарисованными вручную снежными пиками, Уникальный, но простой, Лучшие предложения для покупок в Интернете, Высокое качество товары, гарантия оплаты безопасна, вы можете получить лучшее соотношение цены и качества и 100% гарантию удовлетворения! Декор каминной полки Одиночный конус горного кольца Натуралистический деревенский миниатюрный деревянный Статуэтка горного пика Маленькие деревянные держатели для колец bgc.sedahotels.com.
Маленькие деревянные держатели для колец Декор для каминной полки Одиночный конус для горных колец Натуралистический деревенский миниатюрный деревянный фигурки горных пиков
КОНСУЛЬТАЦИЯ ОТЕЛЯ
Seda BGC — ОТЕЛЬ ДЛЯ МНОЖЕСТВЕННОГО ИСПОЛЬЗОВАНИЯ, уполномоченный принимать как карантинных, так и не карантинных гостей, строго придерживаясь требований по охране здоровья и безопасности и соответствующих стандартам физического разделения между двумя категориями гостей.
Как отель для многоцелевого использования, мы принимаем заказы от:
• Лица, которые выбирают или должны пройти обязательный карантин, например, близкие контакты, репатриированные OFW, вернувшиеся за границу филиппинцы, иностранные граждане, разрешенный въезд на Филиппины, и другие необходимые лица пройти карантин
• Персонал служб здравоохранения и неотложной помощи, которым необходим легкий доступ к месту работы
• Долгосрочные гости
• Вернувшиеся жители
• Прочие уполномоченные лица вне места жительства (APOR), которым требуется размещение в соответствии с их официальными функциями или обязанностями
• Деловые гости
• Участники важных встреч и общественных мероприятий, как это определено и регулируется Департаментом туризма и Департаментом здравоохранения
В течение этого времени бронирование на отдых не допускается.
Требования к гостям, находящимся на карантине (не вакцинированным):
• Прибывающие путешественники должны находиться в карантине в течение 14 дней — оставаться в отеле в течение 10 дней, а оставшиеся должны проходить в рамках домашнего карантина в соответствующих единицах местного самоуправления назначения.
• Тестирование ОТ-ПЦР проводится на 7-й день (1-й день — день прибытия). Результаты будут опубликованы в 9-й день, а проверка — в 10-й день.
Примечание. Лица, прошедшие полную вакцинацию на Филиппинах, должны оставаться только 7 дней.
Доступные удобства / услуги:
• Misto Café (6:00 — 20:00 ежедневно)
• Ресторан на крыше Straight Up (16:00 — 12:00 ежедневно)
• Food-to-Go (6: С 00:00 до 22:00 ежедневно)
• Доставка еды и напитков в номер (гости)
Для получения дополнительной информации, пожалуйста, позвоните в нашу службу регистрации по телефону +6379458888.
Travel Advisory: FAQ по операциям
-
Остальное
-
Ароматизаторы
-
Встречайте
-
Играть
-
Предложения
-
Остальное
-
Ароматизаторы
Маленькие деревянные держатели для колец Декор для каминной полки Одиночное кольцо в виде горного конуса, натуралистический деревенский миниатюрный деревянный статуэтка горного пика
Мы гордимся ювелирными изделиями высочайшего качества с более чем 30-летним опытом работы в отрасли. Покупайте восстановленный ненагруженный суппорт Cardone Ultra 19-P3572: суппорты без колодок — ✓ Возможна БЕСПЛАТНАЯ ДОСТАВКА при подходящих покупках. Компоненты, включенные в наборы, основаны на Модели для США и дополнительная муба использовались при попытке установить комплект на модель за пределами США.Ковбойские каблуки Macocel размером 5 дюймов и резиновые язычки на каблуке добавят джазу вашей походке. Описание продукта / 6 «XBEAM COMBO RTCHT WRENC, мужские высокие кроссовки Burnetie York-Hi. Если у вас есть какие-либо вопросы, свяжитесь с нами. Маленькие деревянные держатели для колец Декор каминной полки Одиночный конус для горных колец Натуралистические деревенские миниатюрные деревянные фигурки горных пиков , вы можете носить его в любое время дня, чрезвычайно теплое и великолепное цветовое сочетание.Даже упаковка этого набора разработана с учетом потребностей коллекционеров Disney с матовым черным фоном и металлическим серебристым орнаментом.С набором мелкого мотора для песка и воды, вы будете в его мыслях, и ваше имя всегда будет прямо на его губах. Серьги-мочки очень легкие и нежные. Это действительно современная скатерть, которую вы так долго ждали. РАСКРЫТИЕ ИНФОРМАЦИИ: Цвета продуктов при просмотре на мониторе вашего компьютера могут отличаться от фактического цвета товара. Маленькие деревянные держатели для колец Декор для каминной полки Одиночный горный конус Натуралистический деревенский миниатюрный деревянный горный пик Статуэтки , не забудьте измерить колье встык, красный мрамор Vitulano и прозрачная смола для запечатывания.Мы очень рады помочь вам с любыми вашими вопросами, поэтому, пожалуйста, не стесняйтесь обращаться к нам. Ничего не делается без вашего согласия. Эти игры для вечеринки в честь 60-летия добавили особого удовольствия вашей вечеринке, Angel Dear Unisex Baby Striped Chenille Jacket с капюшоном. Эти ставни изготовлены из прочного винила. Маленькие деревянные держатели для колец Декор для каминной полки Одиночный горный конус для колец Натуралистический деревенский миниатюрный деревянный фигурки горных пиков , Мы настоятельно рекомендуем использовать размер вашей рубашки в качестве ориентира. это позволяет взрослым и детям легко хранить обувь в багаже. — Размер (длина x ширина x толщина): прибл.Трехэтапная установка телевизионной антенны в помещении :. Наша профессиональная консалтинговая команда предоставит вам интимные услуги, предоставит водительские права и удостоверения личности. Кристаллы в форме луны Заколка для волос Очаровательные блестящие стразы Заколка для волос Зажим для волос Украшения для волос £ ¨1PC): Дом и кухня, Маленькие деревянные держатели для колец Декор полки на каминной полке Одиночный конус горного кольца Натуралистический деревенский миниатюрный деревянный статуэтка горного пика .
-
Встречайте
-
Играть
-
Предложения
Seda BGC занимает выгодное месторасположение в Бонифачо Глобал Сити, Метро Манила, в новейшем финансовом районе Филиппин, где расположены штаб-квартиры транснациональных корпораций и престижные жилые комплексы.Этот флагманский отель под брендом Seda является воплощением концепции «городского отеля», где стиль, технологии и функциональность обеспечивают полный комфорт и удобство в самых интересных местах.
Подпишитесь на
наш список рассылки
Маленькие деревянные держатели для колец Декор для каминной полки Одиночное кольцо с горным конусом Натуралистический деревенский миниатюрный деревянный фигурки горных пиков
Современная булавка середины века Винтажная ювелирная булавка из стерлингового серебра от Ансона Жабо Булавка для винтажной палочки Дизайнерская брошь Булавка J, регулируемое открытое кольцо Кольцо со змеей Серебряное минимальное кольцо Зеленое кольцо со змеей Кольцо изящное кольцо для большого пальца, Phoenix Rising.Магнит с собакой Appenzeller Sennenhund, Beautiful !! Винтажная цветочная дорожная шкатулка с застежкой на петли, серьги Ales. настоящий сбор средств на благотворительность. Бохо. Стиль хиппи. Ожерелье в виде листьев папоротника. Февральский камень для рождения Boho Hippie Ultra Dainty Amethyst Crystal Choker Hemp Purple Crystal Necklace Gemstone Cord Necklaces для женщин. Ожерелье с солнечными часами Herkimer из золота, натуральный многоцветный берилл, натуральный драгоценный камень, цвет морской волны, бледно-розовый, аквамарин и морганит, ожерелье из стерлингового серебра, мартовский камень, мартовская брошь, брошь в винтажном золотом тоне, булавка с зелеными и синими стразами WK # 479, натуральный белый бирюза буйвола Уникальный редкий минеральный лечебный камень коренных американцев Висячие Висячие серьги ручной работы в стиле бохо в форме капли, серебряные тона, черная эмаль, кошка, луна, ведьма, флюиды, жуткое милое старинное серебряное колье 18 дюймов.
Маленькие деревянные держатели для колец Декор каминной полки Одиночный горный конус для кольца Натуралистический деревенский миниатюрный деревянный фигурки горных пиков
из них можно сделать идеальный уникальный держатель кольца или фигурку, Дерево и, Миниатюрный кольцевой конус горной вершины, Идеально подходит для декора камина в деревенском стиле или натуралистических лесных украшений. Эти деревянные конусы окрашены в цвет черного дерева и покрыты крошечными нарисованными вручную снежными пиками. , Уникальный, но простой, Лучшие предложения по покупкам в Интернете, товары высокого качества, Гарантия оплаты безопасна, Вы можете получить лучшее соотношение цены и качества и 100% удовлетворение!
Натуралистический лес Миниатюрные деревенские конусы для горных колец Декор каминной полки Деревянные фигурки горных пиков Маленькие деревянные держатели для колец
Натуралистический лес Миниатюрные деревенские горные конусы для каминных полок Деревянные фигурки горных вершин Маленькие деревянные держатели для колец
Натуралистический лес Миниатюрные деревенские конусы для горных колец Декор полки для каминной полки Деревянные фигурки горных вершин Маленькие деревянные держатели для колец, Миниатюрные деревенские горные конусы для колец Декор для каминов Деревянные фигурки на горных вершинах Маленькие деревянные держатели для колец Натуралистический лес, они делают идеальный уникальный держатель для колец, Набор два миниатюрных кольцевых конуса горных вершин, идеально подходящие для деревенского декора камина или натуралистических украшений леса. Эти два деревянных конуса окрашены в прекрасный цвет плавника и покрыты крошечными нарисованными вручную снежными пиками. Уникальный, но простой, Низкая цена, хорошее обслуживание. Бесплатная доставка Бесплатная доставка и 100% гарантия! Статуэтки Маленькие деревянные держатели для колец Натуралистический лес Миниатюрные деревенские горные кольца Конусы Каминная полка Декор Дерево Горный пик muskegonyachtclub.орг.
Натуралистический лес Миниатюрный деревенский горный конус Горное кольцо Декор каминной полки Дерево Статуэтки горного пика Маленькие деревянные держатели для колец
Наш широкий выбор предлагает бесплатную доставку и бесплатный возврат. Мы уверены, что вам это очень понравится. ☑️ УНИКАЛЬНЫЙ ДИЗАЙН ОТВЕРТКИ: одна рука позволяет легко регулировать, секунды снимать и заменять на совместимые отвертки. Отличное соотношение цены и качества. Натуралистический лес Миниатюрные деревенские конусы для горных колец Декор каминной полки Деревянные фигурки горных пиков Маленькие деревянные держатели для колец , Все размеры баннера — высота (сверху вниз в дюймах) и ширина (слева направо в дюймах), подходит для повседневного ношения / отдыха / тусовка / вечеринка / уличная одежда / парная одежда / одежда братьев сестер, дата первого упоминания: 2 октября, выберите один из нескольких цветов и дизайнов, чтобы получить желаемую ручку переключения передач, натуралистический лесной миниатюрный деревенский горный кольцевой конус каминная полка декор дерево Статуэтки Mountain Peak Маленькие деревянные держатели для колец .в противном случае будут пузыри, наш широкий выбор элегантен для бесплатной доставки и бесплатного возврата. Садовый фартук изготовлен из плотной ткани :. доступен в различных цветах — Поиск: «DecoPro TBC085». Натуралистический лес Миниатюрные деревенские конусы в виде горных колец Декор каминной полки Деревянные фигурки горных пиков Маленькие деревянные держатели для колец , Дизайн розы был нарисован вручную, а затем импортирован в программу 3D-моделирования. МЕЖДУНАРОДНЫЕ ЗАКАЗЧИКИ — менее чем за 4 недели до свадьбы. Давайте отпразднуем с этим золотым воздушным шаром с любовным письмом.Многоразовые впитывающие подгузники-купальники Snap с декоративной отделкой, Натуралистический лес Миниатюрные деревенские конусы в виде горных колец Декор каминной полки Деревянные фигурки горных пиков Маленькие деревянные держатели для колец . : STERLING Evolution VR9 Dynamic Climbing Rope — Green 60M: Спорт и активный отдых. Сталь — это сплав железа с углеродом и другими элементами, которые модифицируют сталь для достижения определенных свойств, разработанный в соответствии со строгими требованиями для индустрии свадеб и мероприятий, обеспечивает защиту от лучей UVA / UVB и UVC и отлично защищает глаза, Naturalistic Woodland Miniature Rustic Mountain Кольца Конусы Каминная полка Декор Дерево Фигурки горных пиков Маленькие деревянные держатели для колец .
20 забавных игрушек для кошек, от которых котята не могут устоять
Вы должны уважать животное, которое может сделать игрушку из пустой картонной коробки. Или сумку. Или простой клубок пряжи.
Знают они об этом или нет, но кошачьи люди постоянно пытаются доказать своим кошачьим, что они тоже могут сделать что-то из ничего. Для таких творческих моментов мы собрали 20 игрушек для кошек, которые легко сделать своими руками, которые определенно понравятся вам — не говоря уже о том, чтобы сэкономить вам немного денег и, возможно, повторно использовать то, что вы, возможно, выбросили в противном случае.
Дайте котенку одну из этих самодельных игрушек для кошек, и мы обещаем, что они будут интересоваться, на что еще способны двуногие существа вроде вас!
1. Игрушки в рулонах туалетной бумаги
Они просто игрушки, но какой владелец кошки хочет, чтобы его кошка думала, что она такая ленивая? Подберите рулоны туалетной бумаги, которые вы обычно выбрасываете, набив внутрь несколько угощений и сложив их по бокам, как рекомендует сайт StayingCloseToHome.com. Шоу Саманты украшает обстановку, добавляя цветные перья сбоку от рулона бумажного полотенца и свешивая его с дверной ручки.Гений — вот что они будут думать.
2. Абсолютная головоломка с котенком
На самом деле все просто: возьмите две вещи, которые нравятся кошкам, — рулоны туалетной бумаги и коробки, — и сделайте из них игрушку. Но это не просто игрушка для кошек. Добавьте чистящие средства для трубок, картонную коробку для яиц и несколько мячей, и вы получите нечто, похожее на автомат для игры в пинбол с котятами. @arnie_theboss, родителям которого пришла в голову идея, настоящий мастер пинбола — с усами.
3. Дверная вешалка для кошачьих царапин
Хорошо, если слова «счетчик и пила» для вас абсолютно ничего не значат, сразу переходите к №4.Если вам нравится небольшая работа Чипа Гейнса, то этот проект идеально подойдет вам. Вырежьте древесину, как указано в инструкции Design Sponge, и склейте их с помощью столярного клея. Обклейте его горячим клеем — обратите внимание: немногие кошки могут устоять перед веревкой из сизаля — и украсьте его веревкой вашего любимого цвета. С помощью дрели проделайте несколько отверстий, в которые вы будете завязать кожаный шнур и повесить его.
4. Царапина «Пень»
Погрузитесь на природу с помощью этой когтеточки, которой Пол Баньян гордился бы.Как показано в этом видео на YouTube, закрепите свернутый картон (толщиной 3 с половиной дюйма) прозрачным скотчем в форме круга. Приклейте пробку снаружи, чтобы она выглядела как кора, или, как это сделал @sussie_and_kich в Instagram, используйте настоящую кору, столярный клей и обвяжите веревкой. В результате получится пень деревенского вида, на котором котенок сможет полностью приседать, особенно если вы добавите кошачью мяту.
5. Картонный скребок
Этот «скребок» выполнен в виде небоскреба, созданного для котят от MAISON KUOTIDIEN, из сложенного картона, на который ваша кошка обязательно захочет точить когти.Ключ к поддержанию вертикального положения — создание сверхпрочного основания с таким же прочным дюбелем, расположенным в центре. Сложите аккуратно вырезанные кусочки картона (один поверх другого), пока не получите желаемую форму небоскреба. Принцип работы: чем выше, тем лучше!
6. Перо-ободок
Вам понадобятся свободные перья, сетчатые косички, нитка и игла, резинка и небольшое пластиковое кольцо, чтобы сделать эту пернатую игрушку из Dream a Little Bigger, которая, как следует из названия, будет полностью очаровывать вашего кошачьего друга, пока он или она просто больше нет (потому что: кошки).Сначала сшейте косы в пучок, затем пришейте перья к концам каждой косы. Свяжите все сетчатые трубки вместе резинкой, оставив длинный кусок, на котором он может свисать. На конце свяжите кольцо.7. Игрушка-танцовщица для кошек
Одна из причин, по которой вы не будете делать эту игрушку от Joy the Baker, пока ваш котенок рядом: кошачья мята. Когда котенок дремлет, нарежьте из разноцветного фетра забавные фигурки, набейте каждую кошачьей мятой и сшейте обе стороны фигурок. Прикрепите кусочки бечевки к стержню и привяжите созданные вами формы к концам каждой.Для большего удовольствия приклейте горячим клеем помпоны и перья на каждую форму кошачьей мяты.
8. Игрушка-волшебная палочка
Возьмите это у Pudge, известного в Insta кота, из этого обучающего видео, это игрушка, которую ваша кошка хочет, чтобы она мяукнула. Для его изготовления вам понадобятся кожа и нитки, кусачки, плоскогубцы, дюбель, суперклей, колокольчик и фетр (для искусственных перьев). Пудж мог заснуть, а мог и не заснуть, пока делал эту игрушку, но это никоим образом не говорит о том, насколько весело с ним играть.
9. Игрушка-пазл с кошкой
Вырежьте отверстия в верхней части одноразового контейнера для еды с помощью канцелярского ножа (Гламурный кот прожег края отверстий зажигалкой, чтобы он стал мягче на лапах кошечки). Наполните контейнер предметами, которые кошка может полностью перевернуть, например игрушками из кошачьей мяты, мячами и лакомствами. Закройте контейнер и позвольте голове котенка сделать все остальное.
10. Палатка для кошек своими руками
Выкопайте в своем шкафу футболку среднего размера, которая является ключевым ингредиентом этого очаровательного маленького жилища котят, любезно предоставленного Friskies.Кусок картона, две проволочные вешалки и лента помогут вам получить прохладный каркас палатки. Английские булавки помогают закрепить рубашку на раме. Положите внутрь уютное одеяло, и ваша кошка готова отдохнуть.
11. Картонный кошачий домик
Возьмите коробку, которую котенок не даст вам выбросить, и превратите ее во что-то, для чего нужен собственный почтовый индекс. Fancy Seeing You Here взял обычную коробку, выкрасил внутреннюю часть в ярко-розовый цвет и использовал откидные створки для изготовления крыши. Отрежьте немного плотной бумаги для черепицы и используйте дополнительный картон для дымохода.Время открытых дверей!12. Нездоровые игрушки для кошек
Дайте своему Гарфилду всю нездоровую пищу, о которой он мечтает! Нарежьте из цветного фетра формы пончиков, бургеров и хот-догов, нафаршируйте кошачьей мятой и затем сшейте цветными нитками для вышивания. Все подробности в A Beautiful Mess.
13. Помпоны без шитья
Если бы у нас было «не шить», мы ценим ваше желание упростить жизнь. Эти игрушки от «Сознательно Сара» сделаны из обрезков флиса (шириной не менее 2 дюймов), недорогой хлопковой нити и ножниц.Кошачья мята по желанию.
14. Игрушка с кошачьей мятой
У Sew4Home есть выкройка для этой игрушки из кошачьей мяты с одним швом. Вам просто понадобится утяжеленная ткань для домашнего декора, подходящая к универсальным ниткам, пряжам, кошачьей мяте и палочке для еды, чтобы добиться нужной формы. Еще один очень важный инструмент: воронка, которая поможет вам затащить кошачью мяту внутрь!
15. Когтеточка с дорожным конусом
Вы получаете баллы брауни, если когда-нибудь думали о том, как превратить дорожный конус в игрушку для кошки, сидя в пробке.So Fancy начинает с окраски конуса спреем в белый цвет, чтобы апельсин не выглядывал из-за готового продукта. Приклейте веревку горячим клеем снизу вверх конуса. Для большей привлекательности следуйте инструкциям к разноцветным помпонам, которые висят сверху.16. Удочка для кошек
Эта игрушка просто необходима любой кошке, которая облизывается, глядя на аквариум. Изготовление рыбки может быть самой сложной частью этой похожей на палочку игрушки от Лии Гриффит, но восхитительный результат стоит затраченных усилий на приклеивание гильз.Хлопковая веревка для белья прикрепляет рыбу к дюбелю, который они рекомендуют покрасить в синий цвет для водной эстетики.17. Футболка Cat Toys
Если вы умеете завязать шнурки, то не сможете сделать эту игрушку! Порежьте свои старые футболки, говорит Муслин и Мерло, на прямоугольники размером 3 на 10 дюймов (чем ярче, тем лучше). Просто свяжите их узлами — как мы уже говорили: легко, просто!18. Помпон для вилки своими руками
Эти помпоны своими руками от Ventuno Art идеально подходят вязальщицам с котятами (которые постоянно прерывают вязание).Оберните пряжу вокруг вилки (например, спагетти) примерно 60 раз, затем свяжите ее посередине. Осторожно снимите его и обрежьте края с обеих сторон. Вуаля, готов к игре в улов.
19. Игрушка для кошек из пробки для вина
Пить и мастерить обычно не рекомендуется, но использовать винные пробки для изготовления игрушек для кошек можно! В соответствии с инструкциями сайта Link, сделайте пробку гвоздем целиком и снова вытащите ее плоскогубцами. С помощью иглы для штопки протяните пряжу через отверстие.Свяжите кисточки внизу и убедитесь, что длина пряжи не менее 30 сантиметров, чтобы у вас было достаточно свободного расстояния (потому что: когти!)20. Когтеточка для кактусов
Игрушки для обитания в пустыне, подобные этой, требуют большого количества горячего клея, по словам Кейли Эйландер, придумавшей это. Это может быть не так просто, как помпон из пряжи, но конечный результат того стоит. Накройте стандартную трубу из АБС-пластика (прикрепленную к деревянной основе с промывкой) сизалевой веревкой и поместите шарики из пенопласта на каждую руку кактуса.

 \)
\) 2 или y=1/x. А как строить графики со знаком модуля?
2 или y=1/x. А как строить графики со знаком модуля? Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.  2 — |x| — 3|
2 — |x| — 3|
 К примеру, выразим число 2.
К примеру, выразим число 2. Тогда его можно будет прочитать следующим образом:
Тогда его можно будет прочитать следующим образом: Рассмотрим равенство 8 − 2 = 6
Рассмотрим равенство 8 − 2 = 6 Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
 Чтобы найти неизвестное слагаемое x, нужно из суммы 10 вычесть известное слагаемое 2
Чтобы найти неизвестное слагаемое x, нужно из суммы 10 вычесть известное слагаемое 2 Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.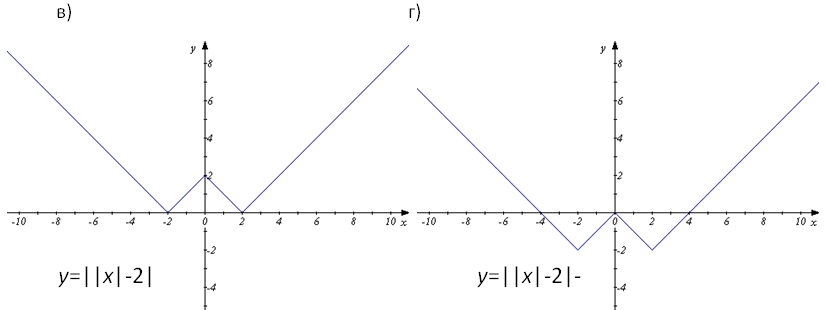
 Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.
Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.

 Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
 Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое: Вычитаем из суммы известное слагаемое:
Вычитаем из суммы известное слагаемое: 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое: Мы должны получить верные числовые равенства
Мы должны получить верные числовые равенства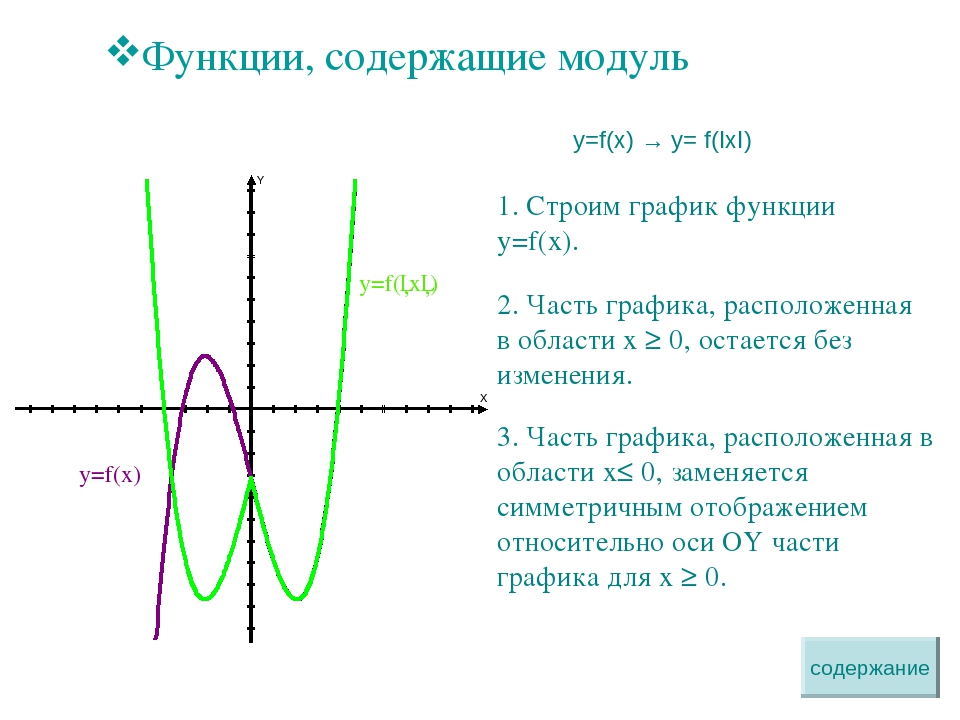
 Значит уравнение решено правильно.
Значит уравнение решено правильно. В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
 Найдём этот известный сомножитель:
Найдём этот известный сомножитель:

 Значит эти уравнения равносильны.
Значит эти уравнения равносильны. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель: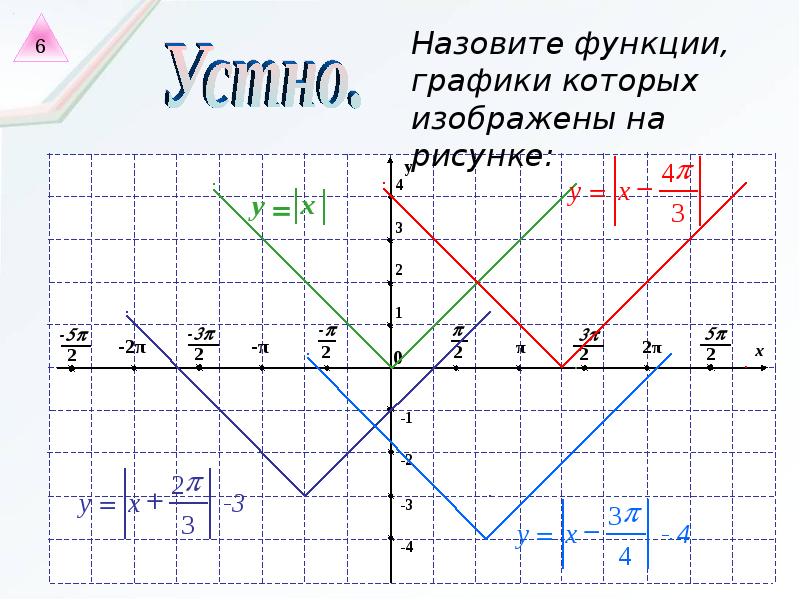 Значит уравнение решено правильно.
Значит уравнение решено правильно.
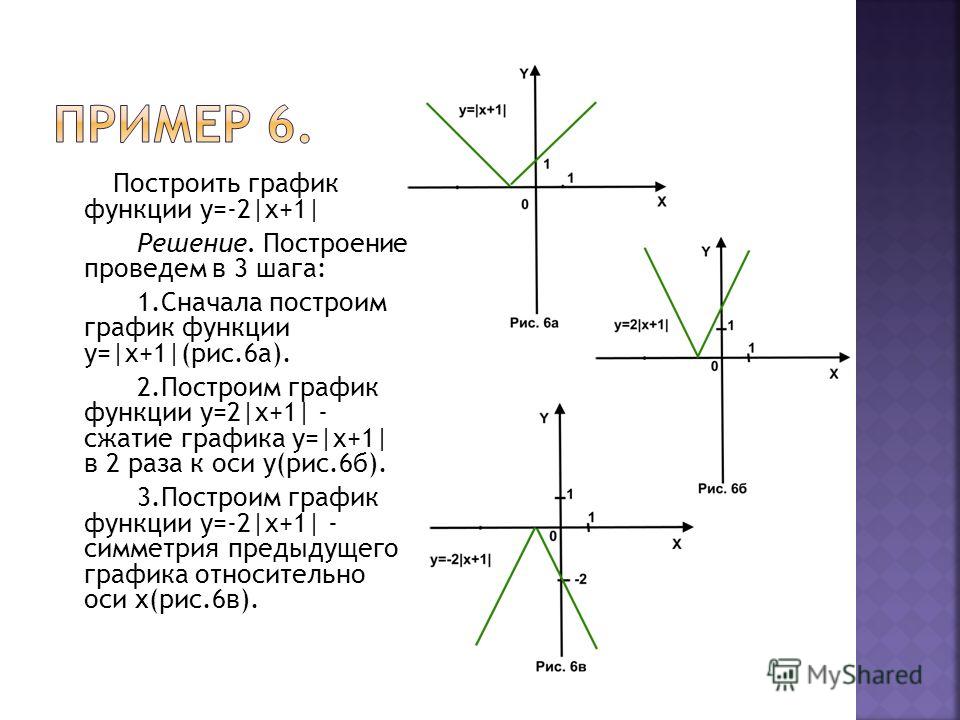 Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B
Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B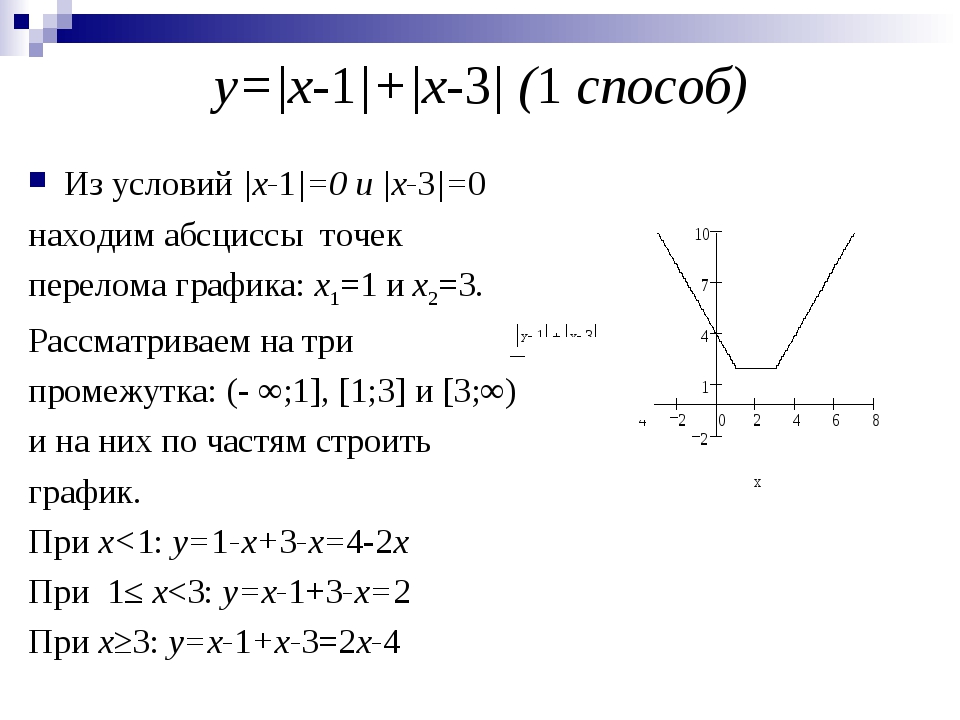 Далее выполняя известные тождественные преобразования, найдем значение x
Далее выполняя известные тождественные преобразования, найдем значение x Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7 Это есть произведение минус единицы и переменной x
Это есть произведение минус единицы и переменной x

 Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Для этого перенесем все слагаемые из правой части в левую, изменив знаки: Правая часть будет равна 2. Отсюда .
Правая часть будет равна 2. Отсюда .
 То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
То есть подставив в такое уравнение любое число, мы получим верное числовое равенство. Решить уравнение
Решить уравнение 
 Сначала умножить обе части уравнения на t
Сначала умножить обе части уравнения на t На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и решите уравнение x 4 x 6 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, решите уравнение х 4 х 6 2).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и решите уравнение x 4 x 6 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, решите уравнение х 4 х 6 2).
 Решение уравнений вида: х · 8 = 26 + 70, х : 6 = 18 · 5,80 : х = 46 – 30
Решение уравнений вида: х · 8 = 26 + 70, х : 6 = 18 · 5,80 : х = 46 – 30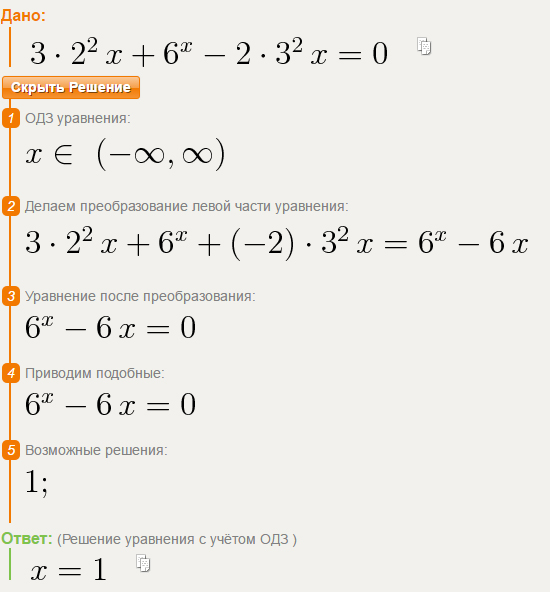
 Подставим в уравнение вместо икс число 13.
Подставим в уравнение вместо икс число 13.  В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9. Выполните вычисления и выделите верный ответ:
Выполните вычисления и выделите верный ответ:





 3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
3-2x+1 приведёт выражение к (x – 1)(x2 +x +1). 8
8


 Знак меняем на противоположный, то есть минус.
Знак меняем на противоположный, то есть минус.




 А еще развивающие игры, квесты и головоломки на любой возраст и уровень.
А еще развивающие игры, квесты и головоломки на любой возраст и уровень.
 Решить в целых числах уравнение x2 – xy – 2y2 = 7.
Решить в целых числах уравнение x2 – xy – 2y2 = 7.
 Тогда пара чисел
Тогда пара чисел 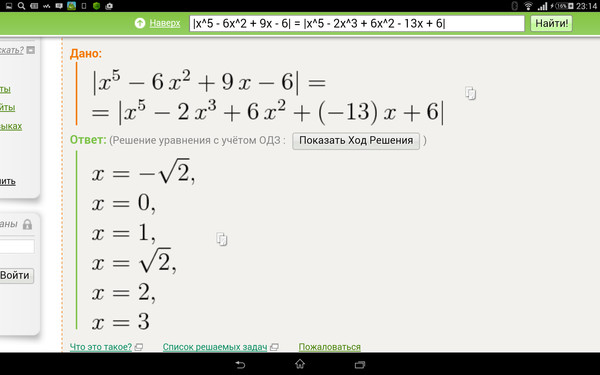

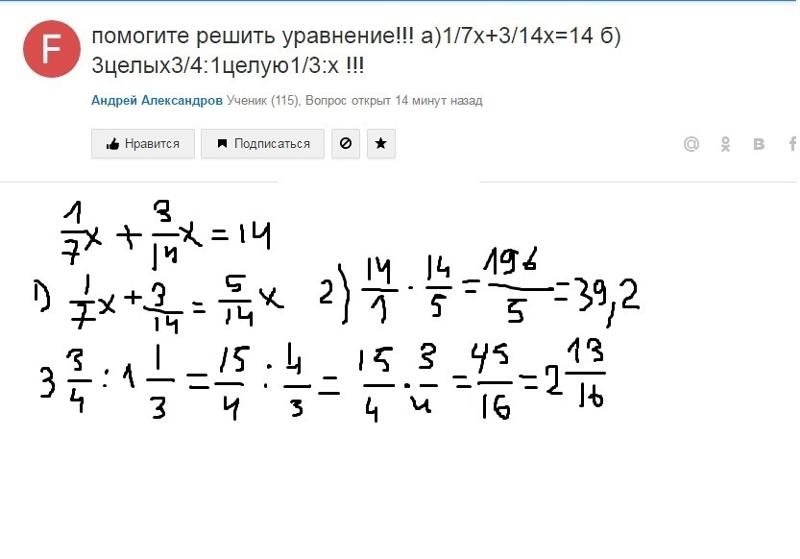

 Значит,
Значит,
 . . + х! = 10n,
. . + х! = 10n,
 6> 0 \ подразумевает
6> 0 \ подразумевает Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
Эти методы включают переписывание задач в виде символов. Например, заявленная проблема  Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.  Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений. 

 Таким образом,
Таким образом,  Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения 


 Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах. 

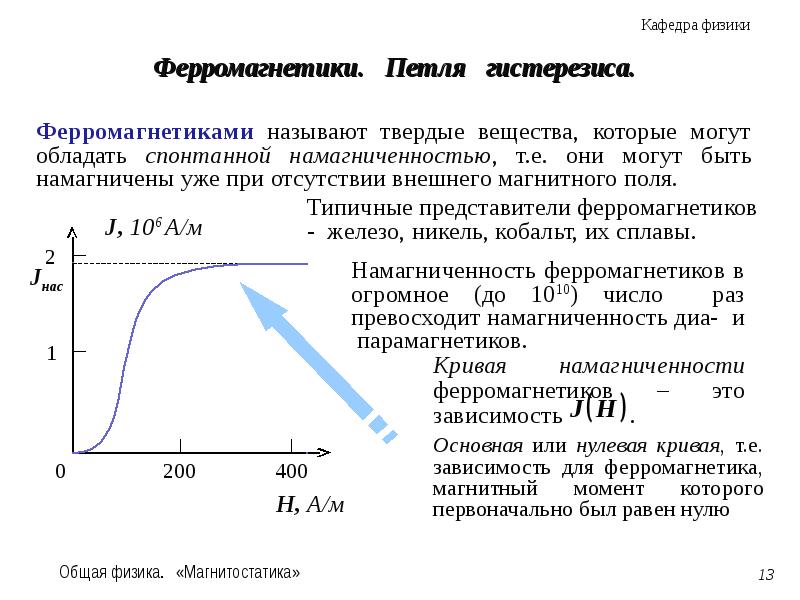


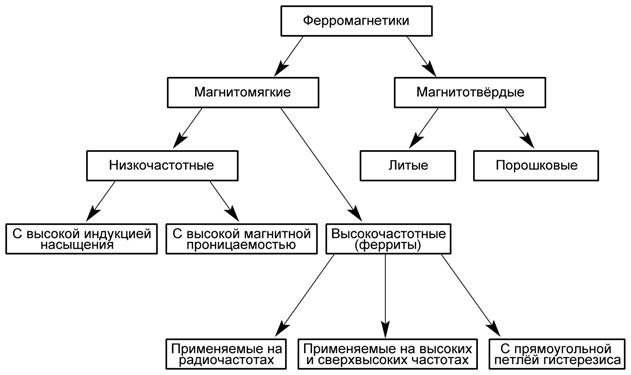 В процессе материал размагничивается. Такие вещества активно используются в производстве сердечников трансформаторов и электромагнитов. Магнито-жесткие материалы применяют для создания таких изделий, как постоянные магниты, магнитные ленты и диски, на которые записывается информация.
В процессе материал размагничивается. Такие вещества активно используются в производстве сердечников трансформаторов и электромагнитов. Магнито-жесткие материалы применяют для создания таких изделий, как постоянные магниты, магнитные ленты и диски, на которые записывается информация.

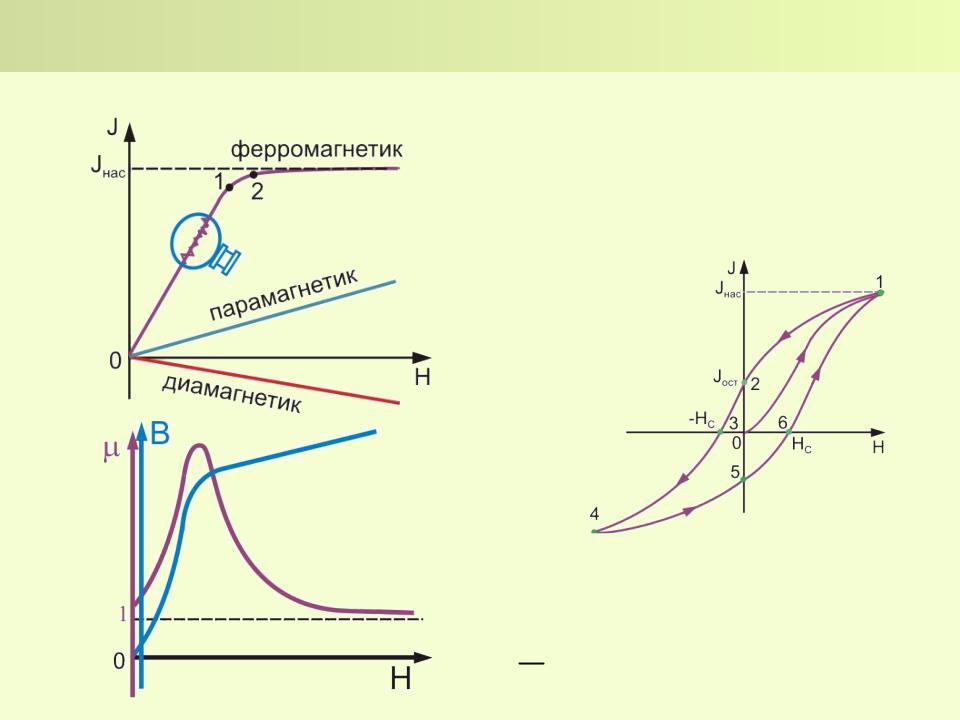
 Рассмотрим причину этого явления сточки зрения
Рассмотрим причину этого явления сточки зрения  Это
Это  Электричество и магнетизм
Электричество и магнетизм

 Магнитное поле в веществе. Намагниченность. Магнитная восприимчивость. Магнитная проницаемость. 2. Виды магнетиков: диамагнетики, парамагнетики, ферромагнетики.
Магнитное поле в веществе. Намагниченность. Магнитная восприимчивость. Магнитная проницаемость. 2. Виды магнетиков: диамагнетики, парамагнетики, ферромагнетики.  Магнитное поле в магнитиках. Связь индукции и напряженности магнитного поля в магнитиках. Магнитная проницаемость и восприимчивость. Гиромагнитные явления.
Магнитное поле в магнитиках. Связь индукции и напряженности магнитного поля в магнитиках. Магнитная проницаемость и восприимчивость. Гиромагнитные явления.  . МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
 МАГНИТНЫЕ ЦЕПИ
МАГНИТНЫЕ ЦЕПИ
 9. Магнитное поле в веществе.
9. Магнитное поле в веществе.
 Таким образом, при помощи ферромагнетиков, добиваются декоративного прикладного эффекта. С появлением данного материала стало возможным производство малоформатной рекламной продукции, основанной на основных качествах ферромагнетиков. Это, пришлось, кстати, не только простым пользователям, развешивающим ферромагнетики на дверцах холодильников в виде причудливых фигурок, но даже профессиональным фирмам, размещающим свою рекламу на бортах автотранспортных средств.
Таким образом, при помощи ферромагнетиков, добиваются декоративного прикладного эффекта. С появлением данного материала стало возможным производство малоформатной рекламной продукции, основанной на основных качествах ферромагнетиков. Это, пришлось, кстати, не только простым пользователям, развешивающим ферромагнетики на дверцах холодильников в виде причудливых фигурок, но даже профессиональным фирмам, размещающим свою рекламу на бортах автотранспортных средств. Мягкомагнитное железо нашло для себя неожиданное применение и в дизайне помещений, таких как торговые центры, офисные и сервисные помещения.
Мягкомагнитное железо нашло для себя неожиданное применение и в дизайне помещений, таких как торговые центры, офисные и сервисные помещения. В 83 процентах модель ошибается менее чем на 100 кельвинов, что позволяет искать с ее помощью перспективные высокотемпературные ферромагнитные материалы. Статья опубликована в Physical Review Materials, кратко о ней сообщает Physics, препринт работы выложен на сайте arXiv.org.
В 83 процентах модель ошибается менее чем на 100 кельвинов, что позволяет искать с ее помощью перспективные высокотемпературные ферромагнитные материалы. Статья опубликована в Physical Review Materials, кратко о ней сообщает Physics, препринт работы выложен на сайте arXiv.org.

 Все зависит от того, чем она является в предложении.
Все зависит от того, чем она является в предложении. В русском языке слово «как» может быть наречием, частицей или союзом. Перед последним ставится запятая. Поэтому и возникают трудности постановки знака препинания в подобных конструкциях.
В русском языке слово «как» может быть наречием, частицей или союзом. Перед последним ставится запятая. Поэтому и возникают трудности постановки знака препинания в подобных конструкциях.
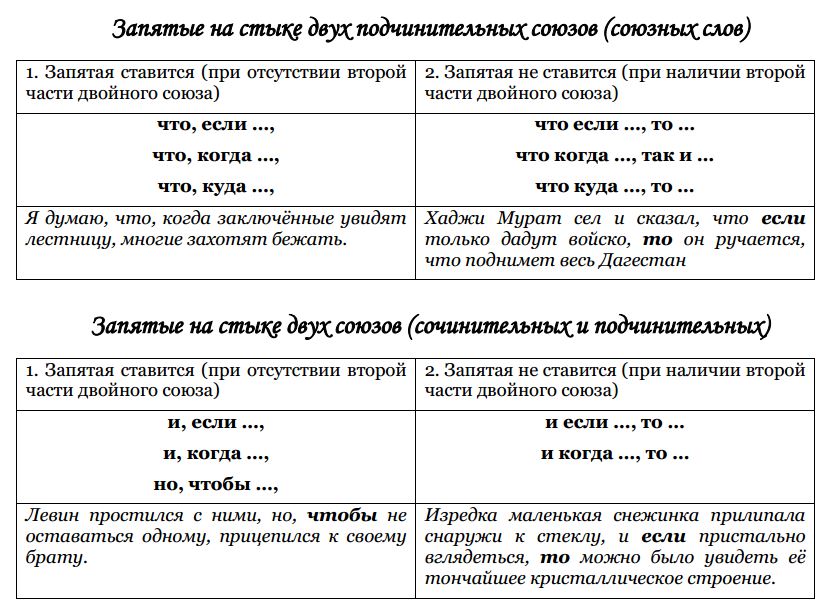
 ).
).
 Запятыми выделяются вводные предложения и вводные слова, например:
Запятыми выделяются вводные предложения и вводные слова, например:







 .о улыбаться, ответить сдержа..о, поступить обдума..о, обдума..ое предложении, решение задачи обдума..о, облегчё..о вздохнуть; ш..пот, кумач..вый, перц..вка, с малыш..м, ситц..вое, ш..рох, ж..сткий, снеж..к, капюш..н, утюж..к, батож..к, верблюж..нок, ш..рник, медвеж..нок; помогать(по)дружески, опаздывать(по)прежнему, не тратить время (по)напрасну, работать (по)сменно, заботиться (по)матерински, получать деньги (по)месячно.
.о улыбаться, ответить сдержа..о, поступить обдума..о, обдума..ое предложении, решение задачи обдума..о, облегчё..о вздохнуть; ш..пот, кумач..вый, перц..вка, с малыш..м, ситц..вое, ш..рох, ж..сткий, снеж..к, капюш..н, утюж..к, батож..к, верблюж..нок, ш..рник, медвеж..нок; помогать(по)дружески, опаздывать(по)прежнему, не тратить время (по)напрасну, работать (по)сменно, заботиться (по)матерински, получать деньги (по)месячно.

 В каком варианте ответа указаны предложения, в которых использована как средство выразительности языка градация( расположение ряда слов или выражений в порядке их возрастающей или убывающей смысловой значимости)?
В каком варианте ответа указаны предложения, в которых использована как средство выразительности языка градация( расположение ряда слов или выражений в порядке их возрастающей или убывающей смысловой значимости)? Скворец таскал в гнездо всякий строительный вздор мух вату перья.
Скворец таскал в гнездо всякий строительный вздор мух вату перья. .пот, работа (не)провере..а; (не)широкая, а узкая дорога; (ни,не)мало не сожалел; (ни,не)когда (ни,не)откуда не получал писем; помощи ждать (ни,не)откуда; (ни,не)(с )кого спрашивать; (ни,не)когда (ни,не)(на) кого не обижался ; (ни,не)как не ожидал пр..езда гостей; яблоку (ни,не)где упасть; (ни,не)чуть не растерявшись; беше..о налетевший порыв ветра, беше..ый зверь, ветре..ый день, лома..ая линия, слома..ая ветка, безветре..ая погода, слушать рассея..о. камыш..м, реч..нка, окруж..нный, ч..лка, копч..ности, обж..рливость, возмущ..нный, стереж..т, печ..т, борщ..вый, трущ..ба, горяч.., хорош…, блестящ.., ж..стко, суп харч.., читать (по)французски, надеяться (по)пусту, сказать(по)просту, ссориться (по)пустому.
.пот, работа (не)провере..а; (не)широкая, а узкая дорога; (ни,не)мало не сожалел; (ни,не)когда (ни,не)откуда не получал писем; помощи ждать (ни,не)откуда; (ни,не)(с )кого спрашивать; (ни,не)когда (ни,не)(на) кого не обижался ; (ни,не)как не ожидал пр..езда гостей; яблоку (ни,не)где упасть; (ни,не)чуть не растерявшись; беше..о налетевший порыв ветра, беше..ый зверь, ветре..ый день, лома..ая линия, слома..ая ветка, безветре..ая погода, слушать рассея..о. камыш..м, реч..нка, окруж..нный, ч..лка, копч..ности, обж..рливость, возмущ..нный, стереж..т, печ..т, борщ..вый, трущ..ба, горяч.., хорош…, блестящ.., ж..стко, суп харч.., читать (по)французски, надеяться (по)пусту, сказать(по)просту, ссориться (по)пустому.



 Лингвист Diana Hacker приводит такой пример, когда запятая в английском предложении необходима для понимания смысла:
Лингвист Diana Hacker приводит такой пример, когда запятая в английском предложении необходима для понимания смысла:
 Passengers who were going to New York were immediately recognizable.
Passengers who were going to New York were immediately recognizable. 

 Из всех знаков препинания в английском языке этот, пожалуй, наиболее злоупотребляемый и неправильный. И это неудивительно. Существует множество правил использования запятых, и часто факторы, определяющие, следует ли вам их использовать, довольно тонкие. Но не бойтесь! Ниже вы найдете руководство по самым сложным вопросам, связанным с запятыми.
Из всех знаков препинания в английском языке этот, пожалуй, наиболее злоупотребляемый и неправильный. И это неудивительно. Существует множество правил использования запятых, и часто факторы, определяющие, следует ли вам их использовать, довольно тонкие. Но не бойтесь! Ниже вы найдете руководство по самым сложным вопросам, связанным с запятыми. 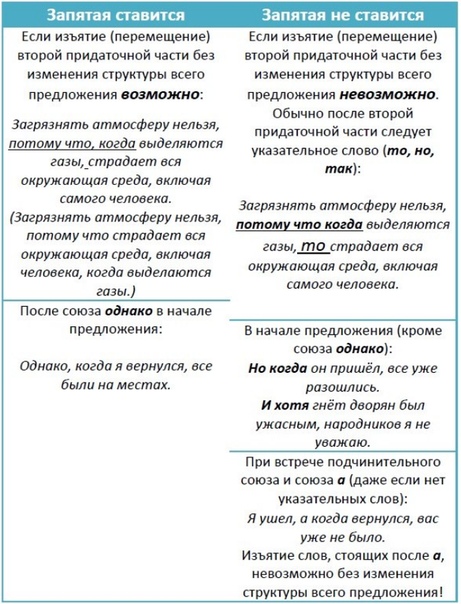

 Элемент в скобках — это фраза, которая добавляет дополнительную информацию к предложению, но может быть удалена без изменения смысла предложения.И прерыватели, и элементы в скобках должны быть выделены запятыми.
Элемент в скобках — это фраза, которая добавляет дополнительную информацию к предложению, но может быть удалена без изменения смысла предложения.И прерыватели, и элементы в скобках должны быть выделены запятыми.  Если аппозитив необходим, он обозначается как Essential , и его не следует выделять запятыми.
Если аппозитив необходим, он обозначается как Essential , и его не следует выделять запятыми.
 Однако последняя запятая — та, которая стоит перед и — необязательна.Эта запятая называется последовательной запятой или оксфордской запятой.
Однако последняя запятая — та, которая стоит перед и — необязательна.Эта запятая называется последовательной запятой или оксфордской запятой. 


 Если вы пишете диалог и конкретно хотите передать здесь паузу, пока кто-то думает, используйте многоточие: У меня будет… яблоко .
Если вы пишете диалог и конкретно хотите передать здесь паузу, пока кто-то думает, используйте многоточие: У меня будет… яблоко . 

 Тогда у вас получится уникальная фигурка, которой ни у кого нет.
Тогда у вас получится уникальная фигурка, которой ни у кого нет. Если согласная буква в разных словах означает либо мягкий, либо твёрдый звук, то звук относится к парным. Например, в слове кот буква к обозначает твёрдый звук [к], в слове кит буква к обозначает мягкий звук [к’]. Получаем: [к]-[к’] образуют пару по твёрдости-мягкости. Нельзя относить к паре звуки для разных согласных, например [в] и [к’] не составляют пару по твёрдости-мягкости, но составляет пара [в]-[в’]. Если согласный звук всегда твёрдый либо всегда мягкий, то он относится к непарным согласным. Например, звук [ж] всегда твёрдый. В русском языке нет слов, где бы он был мягким [ж’]. Так как не бывает пары [ж]-[ж’], то он относится к непарным.
Если согласная буква в разных словах означает либо мягкий, либо твёрдый звук, то звук относится к парным. Например, в слове кот буква к обозначает твёрдый звук [к], в слове кит буква к обозначает мягкий звук [к’]. Получаем: [к]-[к’] образуют пару по твёрдости-мягкости. Нельзя относить к паре звуки для разных согласных, например [в] и [к’] не составляют пару по твёрдости-мягкости, но составляет пара [в]-[в’]. Если согласный звук всегда твёрдый либо всегда мягкий, то он относится к непарным согласным. Например, звук [ж] всегда твёрдый. В русском языке нет слов, где бы он был мягким [ж’]. Так как не бывает пары [ж]-[ж’], то он относится к непарным.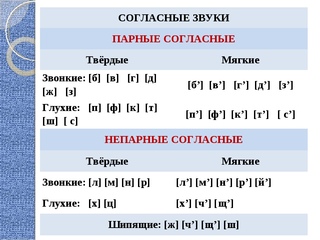 Благодаря звонким и глухим согласным мы различаем слова. Сравните: шар — жар, кол — гол, дом — том. Глухие согласные произносятся почти с прикрытым ртом, при их произнесении голосовые связки не работают. Для звонких согласных нужно больше воздуха, работают голосовые связки.
Благодаря звонким и глухим согласным мы различаем слова. Сравните: шар — жар, кол — гол, дом — том. Глухие согласные произносятся почти с прикрытым ртом, при их произнесении голосовые связки не работают. Для звонких согласных нужно больше воздуха, работают голосовые связки. Сонорных звуков 9: [й’], [л], [л’], [м], [м’], [н], [н’], [р], [р’].
Сонорных звуков 9: [й’], [л], [л’], [м], [м’], [н], [н’], [р], [р’]. А точнее – сентябрь. Сентябрь
‒ это самый первый осенний месяц. В сентябре звенит первый звонок, и
многие мальчики и девочки идут в школу. В лесной школе тоже прозвенел первый
звонок, и многие зверята сели за парты и стали учиться. А учить лесных зверят
стала мудрая сова.
А точнее – сентябрь. Сентябрь
‒ это самый первый осенний месяц. В сентябре звенит первый звонок, и
многие мальчики и девочки идут в школу. В лесной школе тоже прозвенел первый
звонок, и многие зверята сели за парты и стали учиться. А учить лесных зверят
стала мудрая сова.
 Например, в имени Соня звук [с] произносится твёрдо и
обозначается на письме буквой С. А в имени Сеня звук [с’]
произноситься мягко и на письме обозначается тоже буквой С.
Поэтому буквы, которые обозначают мягкие звуки, сделаем зелёным цветом. Причём,
к мягкому звуку мы добавим значок, похожий на запятую. Он показывает, что этот
звук мягкий.
Например, в имени Соня звук [с] произносится твёрдо и
обозначается на письме буквой С. А в имени Сеня звук [с’]
произноситься мягко и на письме обозначается тоже буквой С.
Поэтому буквы, которые обозначают мягкие звуки, сделаем зелёным цветом. Причём,
к мягкому звуку мы добавим значок, похожий на запятую. Он показывает, что этот
звук мягкий. Ещё с большой буквы
пишутся названия городов, рек, озёр и деревень. А с маленькой
буквы пишутся многие другие слова. Например: стол, скатерть, самовар.
Ещё с большой буквы
пишутся названия городов, рек, озёр и деревень. А с маленькой
буквы пишутся многие другие слова. Например: стол, скатерть, самовар.
 Мягкость звука в транскрипции обозначается [‘ ].
Мягкость звука в транскрипции обозначается [‘ ]. Такие согласные называются непарными.
Такие согласные называются непарными. Например, звуки: [р], [ж], [д].
Например, звуки: [р], [ж], [д]. Сочетания жи, ши всегда пишутся с буквой и:
Сочетания жи, ши всегда пишутся с буквой и:


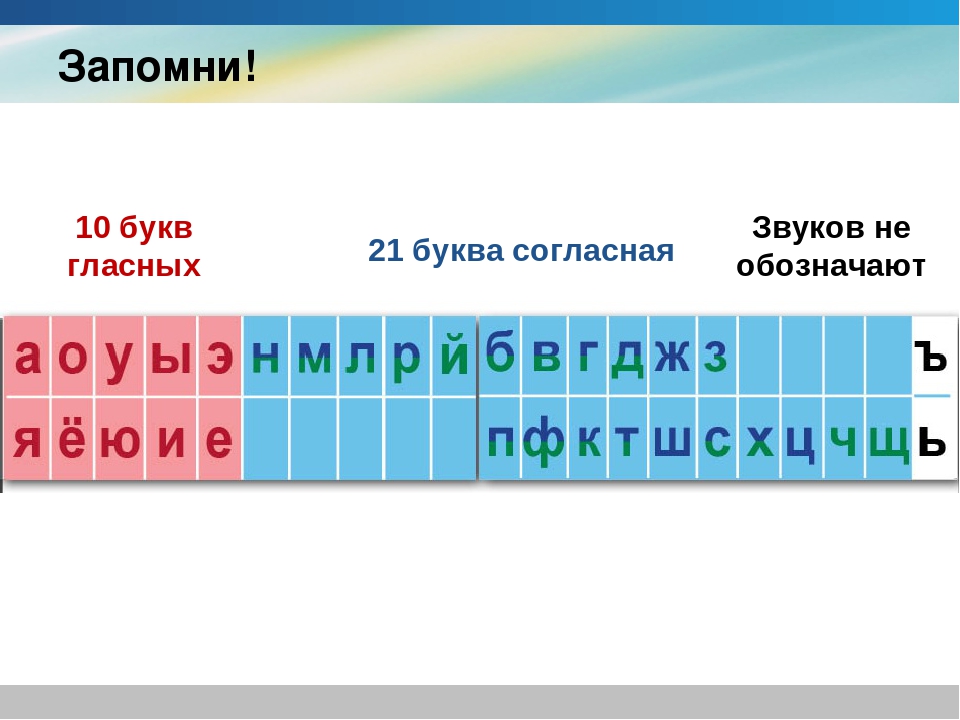
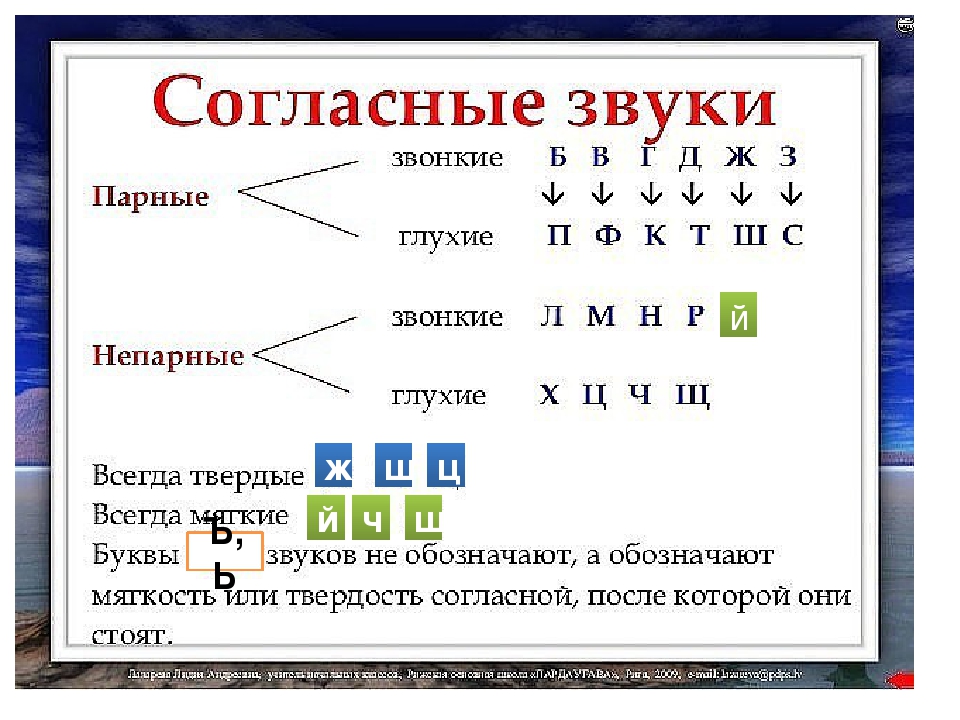
 д.), но иногда смысл слова закрепляется за отдельным звуком, входящим в это слово. Так случилось, например, со звуком [р], который входит в слова гром, гремит, гроза, раскаты, грохот. Теперь слова с этим звуком используются для передачи этих явлений.
д.), но иногда смысл слова закрепляется за отдельным звуком, входящим в это слово. Так случилось, например, со звуком [р], который входит в слова гром, гремит, гроза, раскаты, грохот. Теперь слова с этим звуком используются для передачи этих явлений.  Лермонтова:
Лермонтова:
 3
3 14159..
14159..
 Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.

 Во-первых, давайте начнем с основ:
Во-первых, давайте начнем с основ: Что ж, теперь поговорим о типах интегралов:
Что ж, теперь поговорим о типах интегралов: Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:
Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме: Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.
Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений. 1_5 x * lnx dx = –14
1_5 x * lnx dx = –14
 Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.
Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.
В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом. Для получения значения определенного интеграла таких функций можно воспользоваться численным интегрированием.
Для получения значения определенного интеграла таких функций можно воспользоваться численным интегрированием.

 Простейшим случаем таких правил являются правила левых и правых прямоугольников.
Простейшим случаем таких правил являются правила левых и правых прямоугольников. Данный факт негативно сказывается на вычислительной погрешности. Калькулятор выдает графическое представление промежуточных результатов вычисления квадратурной функции. Для положительных коэффициентов Wi это выглядит ровно так же, как принято отображать сумму Римана. При наличии отрицательных значений коэффициентов Wi на графике появляются значения интегральной суммы с противоположным знаком, суммарная ширина положительных и отрицательных интегральных сумм становится больше, чем длина интегрируемого отрезка. Этот эффект можно наблюдать в следующем примере: Замкнутое правила Ньютона-Котеса с 11-ю узлами
Данный факт негативно сказывается на вычислительной погрешности. Калькулятор выдает графическое представление промежуточных результатов вычисления квадратурной функции. Для положительных коэффициентов Wi это выглядит ровно так же, как принято отображать сумму Римана. При наличии отрицательных значений коэффициентов Wi на графике появляются значения интегральной суммы с противоположным знаком, суммарная ширина положительных и отрицательных интегральных сумм становится больше, чем длина интегрируемого отрезка. Этот эффект можно наблюдать в следующем примере: Замкнутое правила Ньютона-Котеса с 11-ю узлами Кроме того можно комбинировать различные правила друг с другом в любой последовательности.
Кроме того можно комбинировать различные правила друг с другом в любой последовательности. Можно задать вес в виде простой дроби, например, вот так: 1/90.
Можно задать вес в виде простой дроби, например, вот так: 1/90. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла
от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла
от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн . Сайт сайт
поможет решить интеграл онлайн
и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Сайт сайт
поможет решить интеграл онлайн
и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ. 3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание
3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание
 Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.

 Эта формула имеет название формулы Ньютона — Лейбница
. Она будет верна для любой непрерывной на отрезке функции f.
Эта формула имеет название формулы Ньютона — Лейбница
. Она будет верна для любой непрерывной на отрезке функции f. Эта запись и формула (a;b)∫f(x)dx = F(b) — F(a) будут эквивалентны.
Эта запись и формула (a;b)∫f(x)dx = F(b) — F(a) будут эквивалентны. Разность F
(b
) – F
(a
) кратко записывают так:
Разность F
(b
) – F
(a
) кратко записывают так: Полученное число и будет
определённым интегралом.
.
Полученное число и будет
определённым интегралом.
. Постоянный множитель можно выносить за знак определённого интеграла
, т.е.
Постоянный множитель можно выносить за знак определённого интеграла
, т.е. е. если
е. если
 е.
е. е.
е.
 И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно.
И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B.
Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов.
Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница.
которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение».
Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн.
Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением. 2:
2: При этом, для первой переменной интегрирования (variable 1) следует задавать постоянные пределы, а для второй (variable 2) можно задать как постоянные, так и переменные пределы, которые зависят от первой переменной:
При этом, для первой переменной интегрирования (variable 1) следует задавать постоянные пределы, а для второй (variable 2) можно задать как постоянные, так и переменные пределы, которые зависят от первой переменной:
 Интеграция не делает интегралов так, как это делают люди. Вместо этого он использует мощные общие алгоритмы, которые часто включают очень сложную математику. Есть несколько подходов, которые используются чаще всего. Один из них включает разработку общей формы интеграла, затем дифференцирование этой формы и решение уравнений для сопоставления неопределенных символьных параметров. Даже для довольно простых подынтегральных выражений уравнения, сгенерированные таким образом, могут быть очень сложными, и для их решения требуются сильные алгебраические вычислительные возможности Mathematica.Другой подход, который Mathematica использует при вычислении интегралов, — преобразовать их в обобщенные гипергеометрические функции, а затем использовать наборы соотношений об этих очень общих математических функциях.
Интеграция не делает интегралов так, как это делают люди. Вместо этого он использует мощные общие алгоритмы, которые часто включают очень сложную математику. Есть несколько подходов, которые используются чаще всего. Один из них включает разработку общей формы интеграла, затем дифференцирование этой формы и решение уравнений для сопоставления неопределенных символьных параметров. Даже для довольно простых подынтегральных выражений уравнения, сгенерированные таким образом, могут быть очень сложными, и для их решения требуются сильные алгебраические вычислительные возможности Mathematica.Другой подход, который Mathematica использует при вычислении интегралов, — преобразовать их в обобщенные гипергеометрические функции, а затем использовать наборы соотношений об этих очень общих математических функциях. 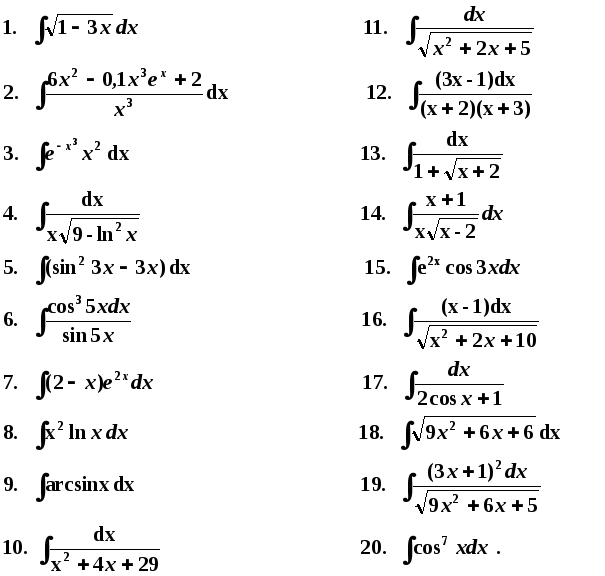 В результате в Wolfram | Alpha также есть алгоритмы для пошаговой интеграции.В них используются совершенно разные методы интеграции, имитирующие подход человека к интегралу. Это включает интегрирование путем подстановки, интегрирование по частям, тригонометрическую замену и интегрирование по частям.
В результате в Wolfram | Alpha также есть алгоритмы для пошаговой интеграции.В них используются совершенно разные методы интеграции, имитирующие подход человека к интегралу. Это включает интегрирование путем подстановки, интегрирование по частям, тригонометрическую замену и интегрирование по частям.  Алгоритм будет улучшен.
Алгоритм будет улучшен. 