Трапеция прямоугольная равнобедренная: Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
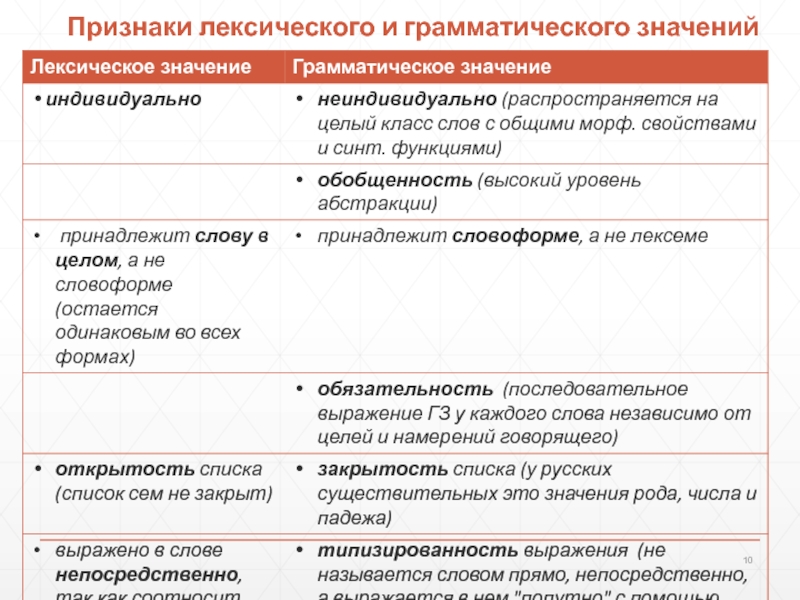
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.| Рис.1 |
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий: 1. В тапеции есть два смежных прямых угла:∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:a = b + d cos α = b + c ctg α = b + √d 2 — c2
b = a — d cos α = a — c ctg α = a — √d 2 — c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
Формулы длины оснований через стороны, диагонали и угол между ними:| a = | d1d2 | · sin γ — b = | d1d2 | · sin δ — b |
| c | c |
| b = | d1d2 | · sin γ — a = | d1d2 | · sin δ — a |
| c | c |
| a = | 2S | — b b = | 2S | — a |
| c | c |
c = √d 2 — (a — b)2 = (a — b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
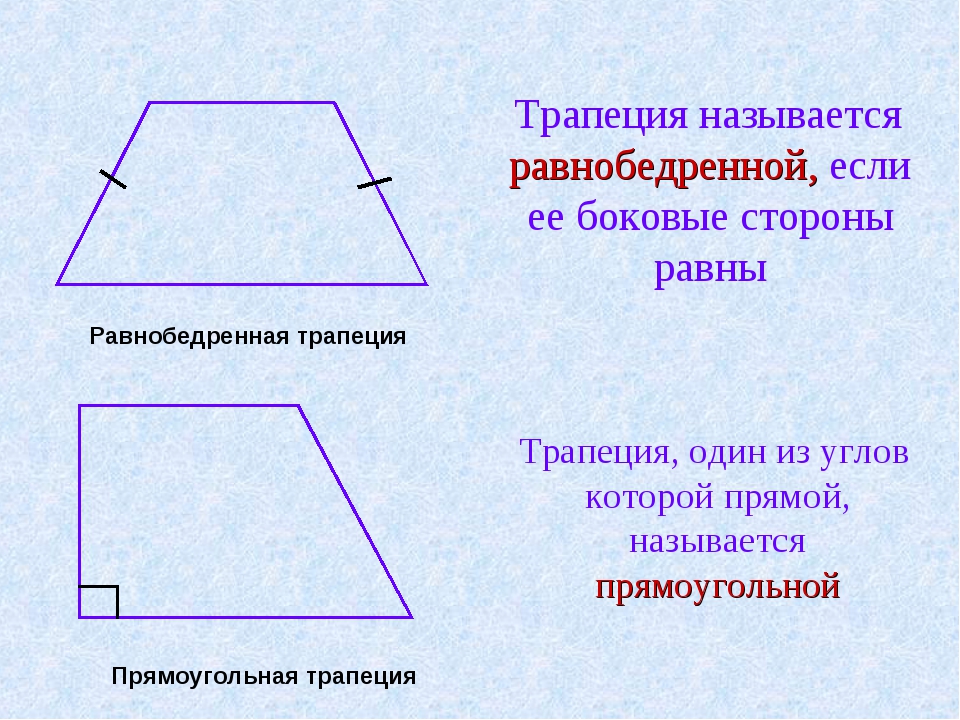 Формулы боковой стороны через площадь, основы и угол при нижнем основании:
Формулы боковой стороны через площадь, основы и угол при нижнем основании:| d = | S | = | 2S |
| m sin α | (a + b) sin α |
| d = | a — b | = | c | = | h | = √c2 + (a — b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:| m = | a — h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
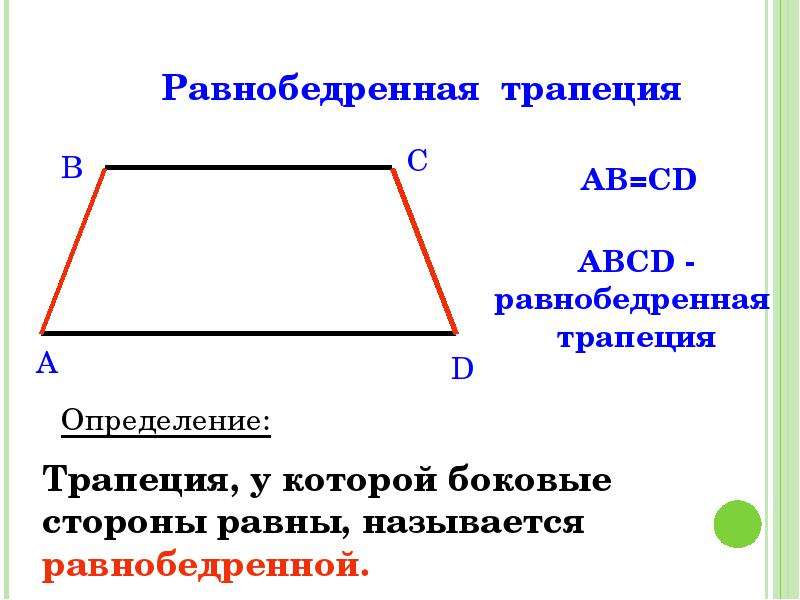 Формулы средней линии через основания и боковые стороны сторону:
Формулы средней линии через основания и боковые стороны сторону:| m = | a — | √d 2 — c2 | = | b + | √d 2 — c2 |
| 2 | 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Определение, признаки и свойства произвольной, равнобедренной и прямоугольной трапеции
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет.
Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже.
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу,
- боковые стороны AB и CD — два непараллельных элемента,
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры,
- высота трапеции CH — перпендикулярный основаниям отрезок,
- средняя линия EF — линия, соединяющая середины боковых сторон.

Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
- Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
- Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
- Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
- Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
- Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.

Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
- При проведении диагоналей образуются 4 треугольника, из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции.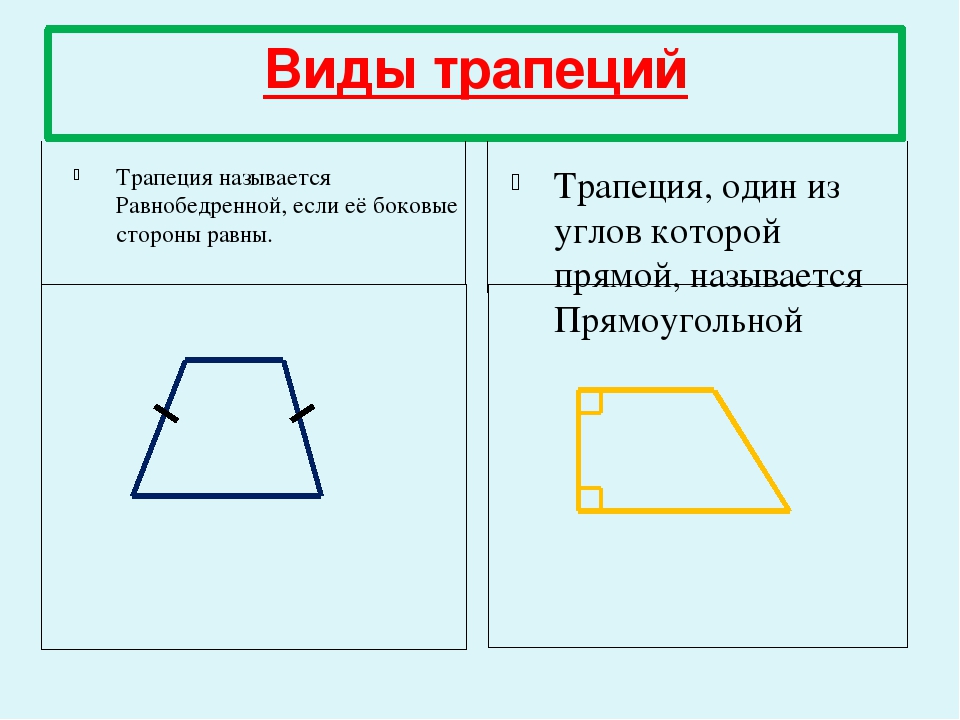 Другие свойства равнобедренной трапеции:
Другие свойства равнобедренной трапеции:
- Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
- Углы, лежащие при любых основаниях, попарно равны.
- Длины диагоналей совпадают.
- Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
- Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Что такое трапеция: определение, виды, свойства
В данной публикации мы рассмотрим определение, виды и свойства (касательно диагоналей, углов, средней линии, точки пересечения боковых сторон и т.д.) одной из основных геометрических фигур – трапеции.
Определение трапеции
Трапеция – это четырехугольник, две стороны которого параллельны, а остальные две – нет.
Параллельные стороны называются основаниями трапеции (AD и BC), две другие стороны – боковыми (AB и CD).
Угол при основании трапеции – внутренний угол трапеции, образованный ее основанием и боковой стороной, например, α и β.
Трапеция записывается путем перечисления его вершин, чаще всего, это ABCD. А основаниям обозначаются маленькими латинскими буквами, например, a и b.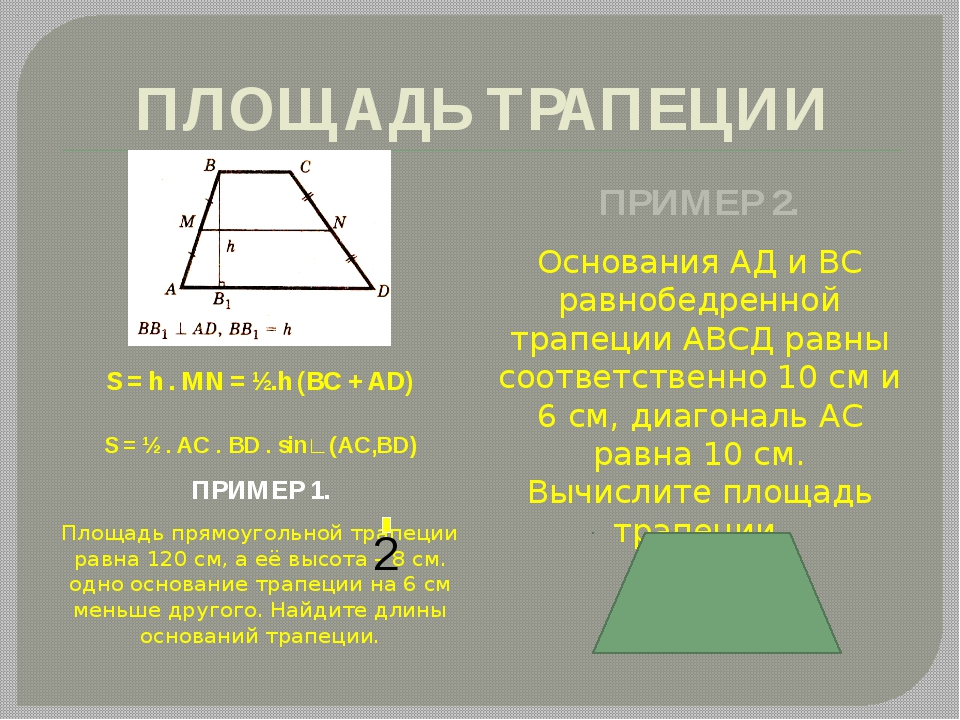
Средняя линия трапеции (MN) – отрезок, соединяющий середины ее боковых сторон.
Высота трапеции (h или BK) – это перпендикуляр, проведенный от одного основания к другому.
Виды трапеций
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной (или равнобокой).
AB = CD
Прямоугольная трапеция
Трапеция, у которой оба угла при одной из ее боковых сторон прямые, называется прямоугольной.
∠BAD = ∠ABC = 90°
Разносторонняя трапеция
Трапеция является разносторонней, если ее боковые стороны не равны, и ни один из углов при основании не является прямым.
Свойства трапеции
Перечисленные ниже свойства применимы к любым видам трапеций. Свойства равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Свойство 1
Сумма углов трапеции, прилежащих к одной и той же боковой стороне, равна 180°.
α + β = 180°
Свойство 2
Средняя линия трапеции параллельна ее основаниям и равняется половине их суммы.
Свойство 3
Отрезок, который соединяет середины диагоналей трапеции, лежит на ее средней линии и равняется половине разности оснований.
- KL – отрезок, соединяющий середины диагоналей AC и BD
- KL лежит на средней линии трапеции MN
Свойство 4
Точки пересечения диагоналей трапеции, продолжений ее боковых сторон и середин оснований лежат на одной прямой.
- DK – продолжение боковой стороны CD
- AK – продолжение боковой стороны AB
- E – середина основания BC, т.е. BE = EC
- F – середина основания AD, т.е. AF = FD
Если сумма углов при одном основании равняется 90° (т.е. ∠DAB + ∠ADC = 90°), значит продолжения боковых сторон трапеции пересекаются под прямым углом, а отрезок, который соединяет середины оснований (ML) равняется половине их разности.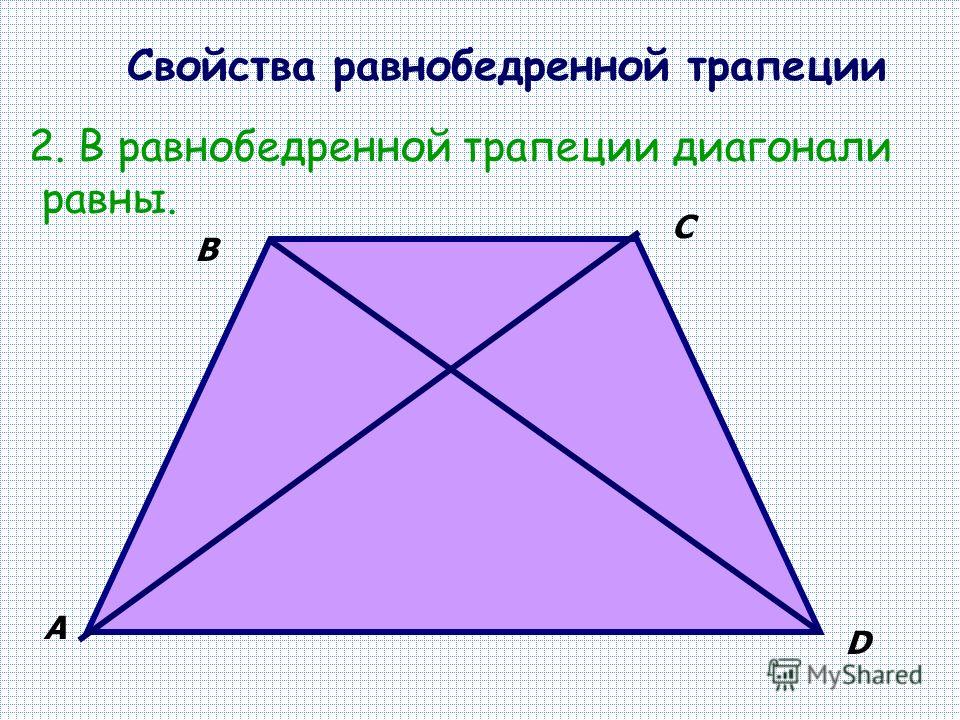
Свойство 5
Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях) подобны, а два других (при боковых сторонах) равны по площади.
- ΔAED ~ ΔBEC
- SΔABE = SΔCED
Свойство 6
Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, можно выразить через длины оснований:
Свойство 7
Биссектрисы углов трапеции при одинаковой боковой стороне взаимно перпендикулярны.
- AP – биссектриса ∠BAD
- BR – биссектриса ∠ABC
- AP перпендикулярна BR
Свойство 8
В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон.
Т.е. AD + BC = AB + CD
Радиус вписанной в трапецию окружности равен половине ее высоты: R = h/2.
свойства и признаки: площадь, средняя линия прямоугольной, равнобедренной, как найти высоту
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые параллельны друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет высотой. Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
[stop]Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.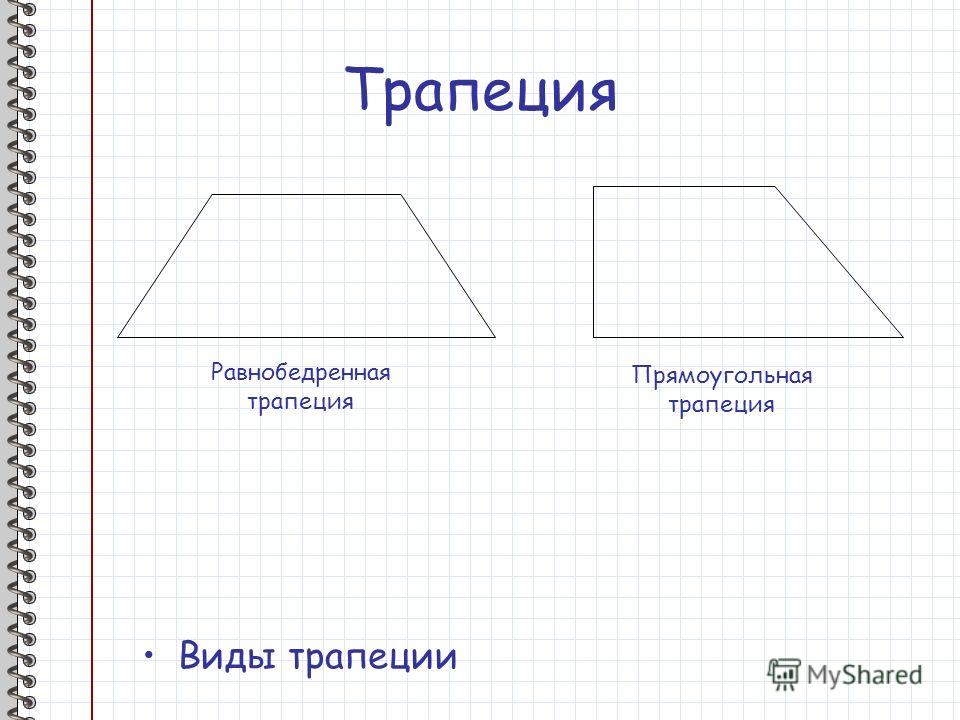 [/stop]
[/stop]
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.

- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить окружность.
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции:
- Если диагонали пересекаются под углом, то половина суммы оснований будет равна длине высоты.
- В случае, когда в правильную трапецию построена, или может быть построена, окружность, то квадрат высоты равен произведению величин оснований.
- Ось симметрии и средняя линия трапеции являются одним и тем же ГМТ.
- Когда диагонали пересекаются под прямым углом, тогда для вычисления площади потребуется формула:
- Окружность вписанная в трапецию, делает величину средней линии равной боковой.

Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
[stop]Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.[/stop]
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения.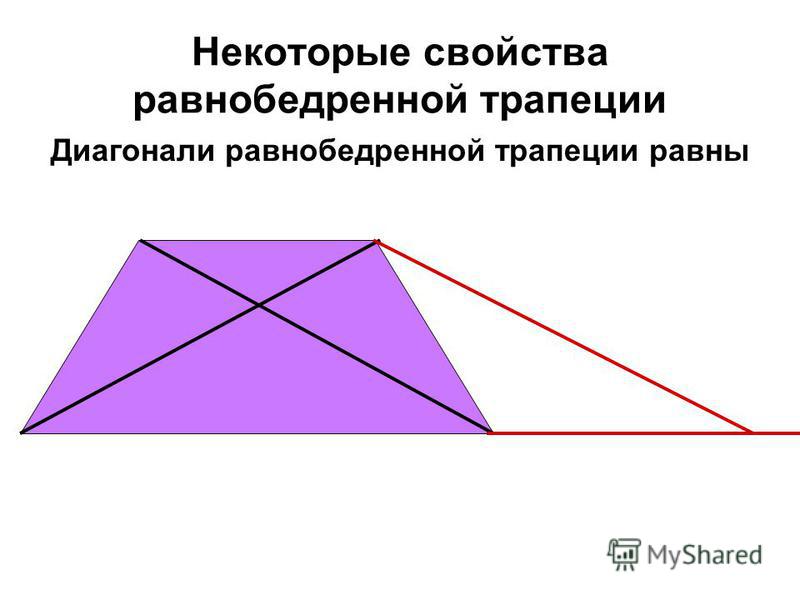 Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Решение:
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда
.Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
[stop]Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.[/stop]
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как:
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
youtube.com/embed/4wkb-2eDf1c» frameborder=»0″ allowfullscreen=»allowfullscreen»><span data-mce-type=»bookmark» style=»display: inline-block; width: 0px; overflow: hidden; line-height: 0;» class=»mce_SELRES_start»></span>
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
Трапеция. Свойства и элементы трапеции
Виды трапеций
Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная.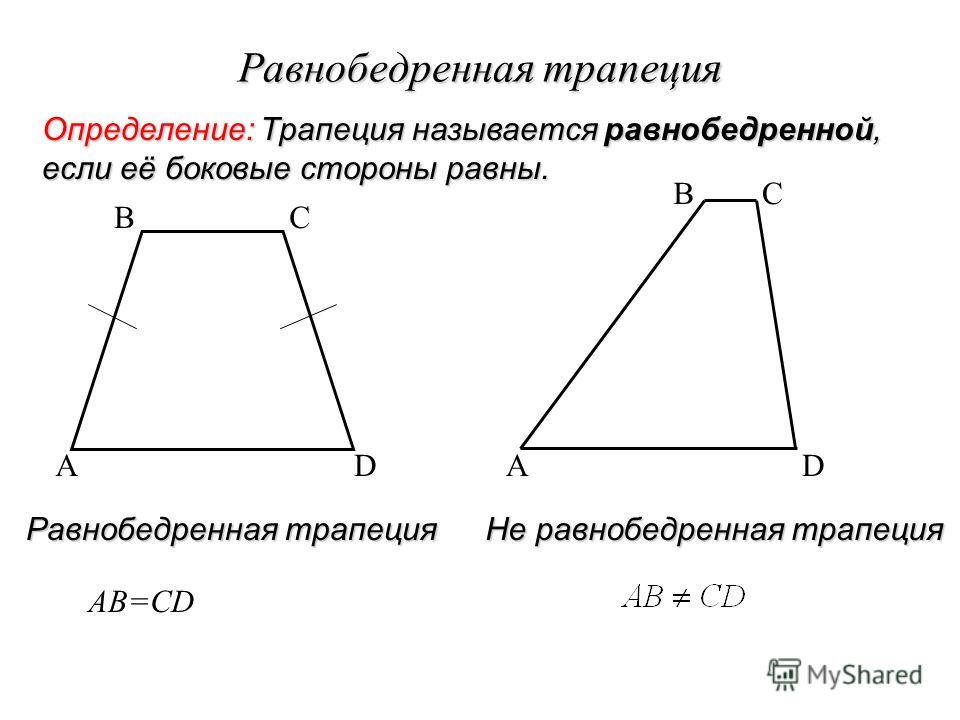
Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b),
m, n — боковые стороны трапеции,
d1, d2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h: S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h: S = MN\cdot h
- Через диагонали d1, d2 и угол (\sin \varphi) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{\circ}:
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами. {2}.
{2}.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Описанная около трапеции окружность
Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.
Вписанная в трапецию окружность
Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.
Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.
«Трапеция. Равнобедренная и прямоугольная трапеция»
План урока.
Урок № 37 по математике в 8 классе.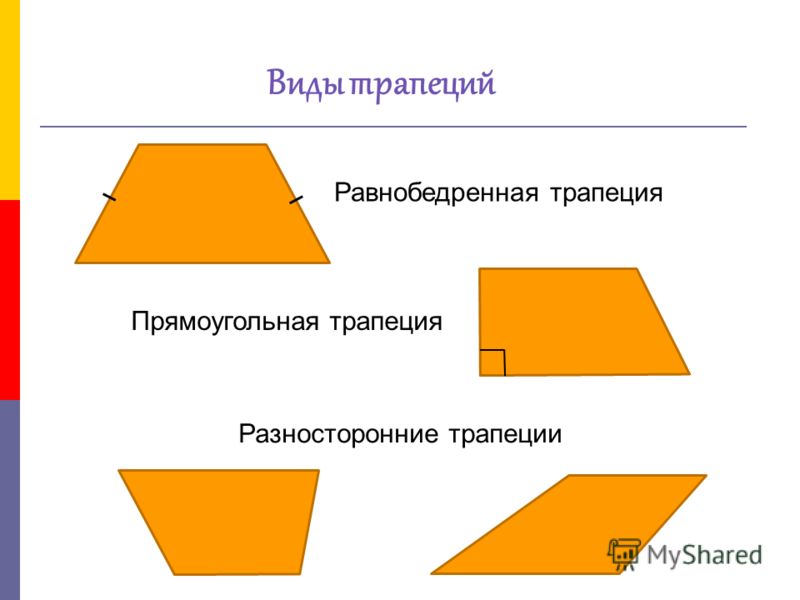
Трапеция. Равнобедренная и прямоугольная трапеция.
Цель урока
Создать условия для формирования понятия «Трапеция», «Равнобедренная трапеция», «Прямоугольная трапеция», элементов и видов трапеций; для рассмотрения решения задач, в которых раскрываются свойства трапеции.
Планируемые образовательные результаты
1. Предметные умения: умеют объяснять, какой многоугольник называется трапецией (равнобедренной и прямоугольной), знать элементы трапеций, знать свойства и признаки равнобедренной трапеции, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологией.
2. формирование у учащихся понятия “трапеция”; умений называть элементы и виды трапеции; умений называть свойства и признаки трапеции и применять эти свойства при решении простейших задач.
Метапреметные:
Познавательные: проводят информационно-смысловой анализ текста и лекции, осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно — следственные связи.
Регулятивные: принимают и сохраняют учебную задачу.
Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе.
Личностные: умеют контролировать процесс и результат математической деятельности.
Основные понятия.
Трапеция, основания трапеции, боковые стороны трапеции, равнобедренная и прямоугольная трапеция.
Трудовые действия учителя
1.Разработка технологической карты урока. 2. Подготовка презентаций к уроку, наглядных пособий, демонстративного материала, раздаточного материала.
Учебно-методическое обеспечение (средства, оборудование)
Для учителя
1. учебник; 2. индивидуальные задания; 3. презентация; 4. компьютер; 5. интерактивная доска.
Для обучающихся
1. учебник;
2. тестовые задания;
3. цветные карточки;
цветные карточки;
4. листы самооценивания;
Этап (ход) урока, включая демонстрируемые трудовые действия учителя.
Для учителя
Для обучающихся
1. Организационный этап.
Взаимное приветствие. Учитель предлагает определить готовность к уроку. Создает условия для возникновения у обучающихся внутренней потребности включения в учебную деятельность. Знакомит с эпиграфом урока.
Три пути ведут к знанию: путь размышления – это путь благородный, путь подражания – это путь самый легкий; путь опыта – это путь самый горький.(Слайд 1)
Ученики рассаживаются по местам. Проверяются наличие принадлежностей, знакомятся с листами самооценки.
2. Этап актуализация знаний по теме «Четырехугольники»; Подведение учащихся к новой теме.
Предлагает вспомнить ранее изученный материал. 1. Устная работа по готовым чертежам.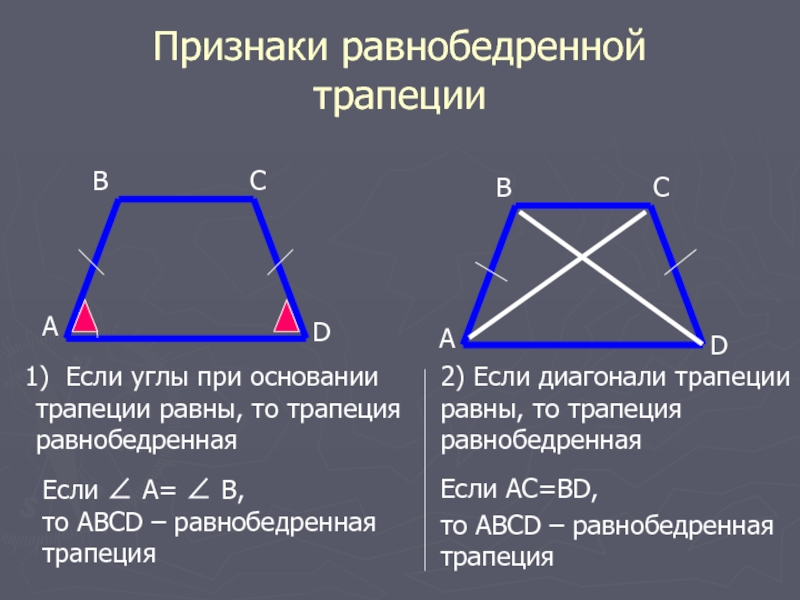 На слайде изображены различные выпуклые четырёхугольники. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция) (слайд 2) — Вспомните, с какими четырехугольниками и их свойствами вы хорошо знакомы? 2. Геометрическая разминка. — Выберите верные утверждения: (слайд 3,4) 1.Параллелограмм — это четырехугольник, у которого стороны попарно равны? (да) 2. Сумма углов четырехугольника 1800? (нет) 3. Противоположные углы параллелограмма равны? (да) 4. Диагонали параллелограмма равны? (нет). 5. Диагонали ромба пересекаются и точкой пересечения делятся пополам? (да) 6. Квадрат является ромбом? (да) 7. Диагонали прямоугольника равны? (да) 8. Диагонали ромба являются биссектрисами его углов? (да)
На слайде изображены различные выпуклые четырёхугольники. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция) (слайд 2) — Вспомните, с какими четырехугольниками и их свойствами вы хорошо знакомы? 2. Геометрическая разминка. — Выберите верные утверждения: (слайд 3,4) 1.Параллелограмм — это четырехугольник, у которого стороны попарно равны? (да) 2. Сумма углов четырехугольника 1800? (нет) 3. Противоположные углы параллелограмма равны? (да) 4. Диагонали параллелограмма равны? (нет). 5. Диагонали ромба пересекаются и точкой пересечения делятся пополам? (да) 6. Квадрат является ромбом? (да) 7. Диагонали прямоугольника равны? (да) 8. Диагонали ромба являются биссектрисами его углов? (да)
По ходу работы идет проверка ответов (слайд 5) и выставление баллов в оценочные листы.
Называют четырехугольники.
Выбирают верные утверждения. Работают с сигнальными карточками; зелёные карточки — верно, красные – неверно.
Работают с сигнальными карточками; зелёные карточки — верно, красные – неверно.
3. Этап целеполагания и планирования.
1. Ответы на вопросы по слайду 6:
— Среди представленных фигур, что вы заметили?
— Что общего у этих фигур?
—Чем отличается выделенный четырехугольник от других?
—А кто знает, как называется этот четырехугольник?
-Эта фигура называется трапецией.
-Как вы думаете какова тема сегодняшнего урока?
— Ребята, подумайте, чему бы вы сегодня хотели научиться и что хотели бы узнать нового на уроке о данном четырехугольнике?
— Как вы считаете, какой будет цель нашего урока?
— Какие нужно поставить задачи для достижения нашей цели?
— Записываем в тетрадь дату и тему сегодняшнего урока: «Трапеция».
Ответ: «Фигура стоящая справа незакрашена». Ответ: «Все фигуры являются четырехугольниками». Ответ: «Не является параллелограммом. У него две стороны параллельные, а две другие нет».) Ученики либо отвечают, либо нет.
Учащиеся формулируют тему урока.
Ученики ставят перед собой цели урока: — Сформировать понятие трапеции. — Научиться определять виды трапеции, находить её элементы. — Научиться изображать трапецию. — Выяснить свойства и признаки равнобедренной трапеции. — Научиться применять полученные знания в процессе решения задач. Формулируют задачи урока.
Записывают дату и тему урока.
3. Поисковая деятельность по открытию новых знаний.
1. Изображение трапеции. Практическая работа.
Начертите четырехугольник, у которого две стороны параллельны, а две другие – не параллельны (на доске и в тетрадях должен появиться рис.1) — На что похожа эта фигура? —Да, и в правду она похожа на стол и в переводе означает стол.
 Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.
— Как он называется? — Сформулируем точное определение.
3. Элементы трапеции. Учитель предлагает по учебнику (п.44, стр. 103) проверить выдвинутую гипотезу, а также по тексту ознакомиться с элементами трапеции. (слайд 8) 4. Работа по готовым чертежам. Предлагает задание для обсуждения в группах: — Определите, какие из предложенных четырехугольников являются трапециями и почему? (слайд 9) 5.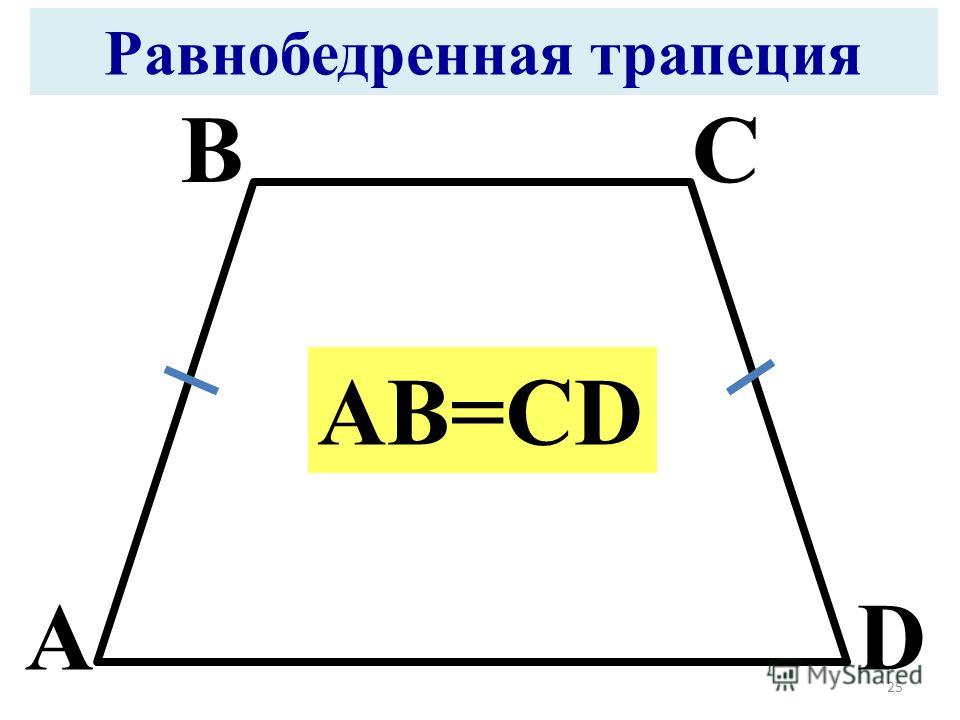 Виды трапеции. — Найдите отличия в представленных трапециях и предложите название каждому виду трапеции (слайд 10.)
Виды трапеции. — Найдите отличия в представленных трапециях и предложите название каждому виду трапеции (слайд 10.)
6. Свойства и признаки равнобедренной трапеции.
Учитель предлагает поделится на группы и провести исследовательскую работу. Задание: исследовать углы и диагонали равнобедренной трапеции, сформулировать свойства и признаки. (слайд 11)
Строят четырехугольник, у которого две стороны параллельны, а две другие – не параллельны.
Ответ: на стол
Идет обсуждение в группах.
Результат работы: учащиеся дают определение трапеции, ключевым моментом в котором должны быть слова «четырехугольник, у которого только одна пара противолежащих сторон параллельна».
Работают по тексту учебника.
Данные слайда учащиеся заносят в конспект.
Каждая группа называет по одной трапеции и объясняет ответ.
Учащиеся обсуждают задание в группах и делают выводы: «что трапеция ABCD содержит прямые углы, а трапеция KLMN имеет равные боковые стороны». Дают предполагаемые названия видов трапеций.
Информация со слайда заносится учащимися в конспект.
Обсуждают в группах и один ученик из группы делает вывод и формулирует свойство равнобедренной трапеции.
Из выясненных свойств ученики составляют признаки равнобедренной трапеции.
4. Физкульминутка.
Используется методика здоровьесберегающей технологий «зрительные метки».
Учитель обращает внимание учащихся на развешанные по периметру класса цветные фигурки четырехугольников и дает задание отыскать среди них трапеции (все фигурки пронумерованы) (слайд 12)
Учащиеся дают в ответ № четырехугольника, который является трапецией.
5. Этап первичного закрепления и применения новых знаний.
1. Решение задач по готовым чертежам. Учитель предлагает обсудив в парах решить задачи: №1 (устно). Один из углов равнобедренной
трапеции равен 68°. Найдите остальные углы трапеции. №2 (письменно). Дана ABCD – трапеция, ВЕ||CD, АВЕ=75, ВАЕ=40. Найти углы трапеции.
2. Вывод.
—Чему равна сумма двух углов при боковых сторонах трапеции?
— Как найдем второй угол, если первый известен?
Учитель предлагает оценить свою работу и проставить баллы в оценочные листы.
Ученики решают задачи и свои ответы обсуждают в парах. Один ученик решает задачу с комментариями у доски.
Решают задачу в тетрадях , записывают ответы и проверяют свои ответы с ответом ученика, решивший задачу у доски. По ходу решения задач ученики выясняют и делают вывод, что сумма двух углов при боковой стороне трапеции равна 1800 . В оценочных листах проставляют баллы за правильно решенные задачи.
6. Самоконтроль изученного материала.
Самоконтроль изученного материала.
1. Тест.
— А теперь проведем самоконтроль изученного материала. Учитель предлагает ответить на вопросы теста по теме «Трапеция» (приложение № 2).
Выполняют тест, ответы заносят в оценочные листы и проставляют баллы за правильные ответы.
7. Подведение итогов. Оценивание.
1. Подведение итогов урока. Фронтальный опрос (слайд 21):
Какой четырехугольник называется трапецией?
Назовите элементы трапеции и ее виды.
3. Вспомните свойства равнобедренной трапеции.
2. Самооценка.
— Учитель предлагает просуммировать набранные баллы и используя шкалу перевести баллы в оценку за урок.
Отвечают на вопросы, называют основные понятия нового материала.
Заполняют листы самооценки: суммируют полученные баллы за урок и используя шкалу, переводят баллы в оценку.
8. Рефлексия.
Учитель задает вопросы о цели урока, побуждает учащихся к высказыванию мнения, чему они научились на уроке. — Как вы думаете, нам удалось достичь поставленной цели?
Предлагает продолжить предложения. На уроке я узнал…
Мне было интересно, что …
Я разобрался в том, что…
Мне стало понятно ,что…
Мне было увлекательно…
Я познакомился …
Формулируют конечный результат своей работы на уроке. Подводят итог урока.
9. Домашнее задание
Домашнее задание.
п. 44, выучить конспект по рабочей тетради.
Ответить на контрольные вопросы
Решить задачи №386, 387.
Творческое задание. Сделать презентацию на тему «Трапеция в жизни человека»
Записывают домашнее задание в дневники.
Приложение №1
Оценочный лист по теме «Трапеция»
ученика 8 класса _____________________________________________ дата __________
Этап урока
Вид задания
Правильные ответы
Количество баллов
Актуализация.
1.____ 2.____ 3.____ 4.____
5.____ 6.____ 7.____ 8.____
3 б. — за 8-7 правильных ответов
2 б. — за 6-5 правильных ответов
1 б. — за 4-3 правильных ответа
Закрепление и применение новых знаний.
Решение задач.
№1. Ответ:_____________________
№2. Ответ:_____________________
Самоконтроль изученного материала.
Тест
1.___ 2.___ 3.___ 4.___ 5.___
Оценка за урок
Критерии выставления оценок:
«5» – 9 -10 баллов,
«4» – 7-8 баллов,
«3» – 5 -6 баллов.
Приложение №2
Тест по теме «Трапеция»1. Укажите верное утверждение: трапеция – это…
1) параллелограмм;
2) четырехугольник, у которого две стороны равны;
3) четырехугольник, у которого две стороны параллельны;
4) четырехугольник, у которого только две противоположные стороны параллельны.
2. Продолжите определение: трапеция называется равнобедренной, если…
1) две ее боковые стороны равны;
2) две ее соседние стороны равны;
3) любые две стороны трапеции равны;
4) другой ответ.
3. Укажите верное утверждение:
1) Только в прямоугольной трапеции углы при основании равны;
2) Углы при основании равны в любой трапеции;
3) Если трапеция равнобедренная, то противолежащие углы ее равны;
4) У равнобедренной трапеции углы при основании равны.
4. Укажите верное утверждение:
1) Сумма углов, прилежащих к одной стороне трапеции равна 180 градусов;
2) Сумма углов трапеции зависит от ее вида;
3) Сумма углов, прилежащих к боковой стороне и равна 180 градусов;
4) В трапеции сумма углов равна 180 градусов.
5. Укажите верное утверждение:
1) Трапеция может быть только прямоугольной и равнобедренной;
2) Трапеция может быть прямоугольной, равнобедренной;
3) Любой разносторонний четырехугольник можно назвать трапецией;
4) Четырехугольник с параллельными противолежащими сторонами называется трапецией.
Приложение 3
Ключи к тесту «Трапеция»
Правильныйответ
1.
4
2.
1
3.
4
4.
3
5.
4
Запоминаем и применяем свойства трапеции
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции.
 Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k2. - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
- Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 1800: α + β = 1800 и γ + δ = 1800.
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 900 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь.
 Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны. - Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 1800 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям.
 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. - На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне.
 В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). - Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.

- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*SАМЕ.
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b.
 Радиус окружности можно вычислить по формуле: r = √ab.
Радиус окружности можно вычислить по формуле: r = √ab. - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.

- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 1800 — МЕТ = 1800 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 1500 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 1800. Поэтому КАН = 300 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 300.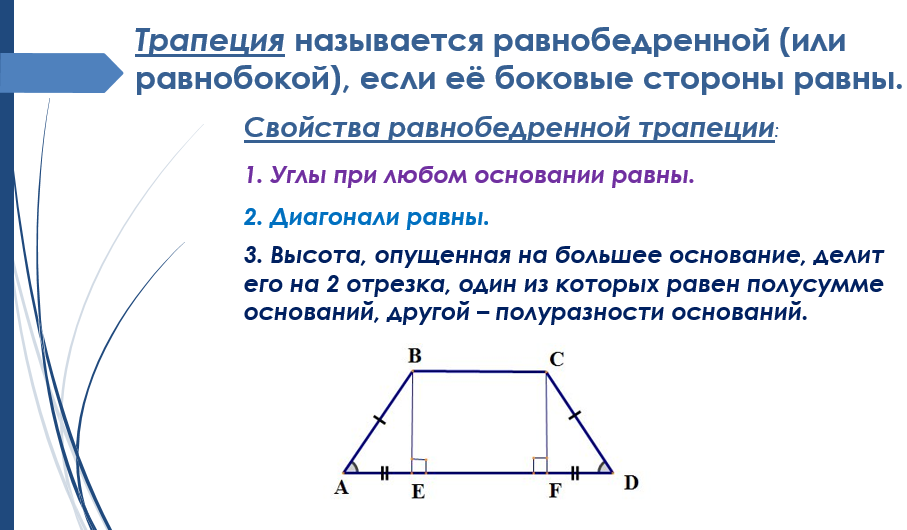 Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: SАКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см2.
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Площадь трапеции — пояснения и примеры
Напомним, трапеция , также называемая трапецией , — это четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.
В трапеции параллельные стороны называются основаниями, а пара непараллельных сторон — ногами. Расстояние по перпендикуляру между двумя параллельными сторонами трапеции называется высотой трапеции.
Проще говоря, основание и высота трапеции перпендикулярны друг другу.
Трапеции могут быть как правыми трапециями (два угла 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины). Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, образуя два прямых угла одновременно.
Из этой статьи вы узнаете:
- Как найти площадь трапеции,
- Как получить формулу площади трапеции и,
- Как найти площадь трапеции с помощью трапеции формула площади.
Как найти площадь трапеции?
Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости. Это пространство, заключенное в 2D-геометрии.
На рисунке выше трапеция состоит из двух треугольников и одного прямоугольника. Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.
Вывести формулу площади трапеции
Площадь трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x CD x EC )
= ( ¹ / ₂ × AB × h ) + ( BC × h ) + (¹ / ₂ × CD × h )
= ¹ / ₂ × h × ( AB + 2 BC + CD )
= ¹ / ₂ × h × ( FE + AD )
Но, FE = b 1 и AB = b 2
Следовательно, Площадь a трапеция ADEF ,
= ¹ / ₂ × h × (b 1 + b 2 ) ……………….(Это формула площади трапеции)
Формула площади трапеции
Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.
Площадь = ½ x (сумма параллельных сторон) x (расстояние по перпендикуляру между параллельными сторонами).
Площадь = ½ h (b 1 + b 2 )
Где h — высота, а b 1, и b 2 — параллельные стороны трапеции.
Как определить площадь неправильной трапеции?
Неправильная трапеция имеет непараллельные стороны неравной длины. Чтобы найти его площадь, нужно найти сумму оснований и умножить ее на половину высоты.
В вопросе иногда не хватает высоты, что можно найти с помощью теоремы Пифагора.
Как найти периметр трапеции?
Вы знаете, что периметр — это сумма всех длин внешнего края фигуры.Следовательно, периметр трапеции — это сумма длин всех 4 сторон.
Пример 1
Рассчитайте площадь трапеции, высота которой составляет 5 см, а основания — 14 см и 10 см.
Решение
Пусть b 1 = 14 см и b 2 = 10 см
Площадь трапеции = ½ h (b 1 + b 2 ) см 2
= ½ x 5 (14 + 10) см 2
= ½ x 5 x 24 см 2
= 60 см 2
Пример 2
Найдите площадь трапеции с высота 30 мм, а основания 60 мм и 40 мм.
Раствор
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
= ½ x 30 x (60 + 40) мм 2
= ½ x 30 x 100 мм 2
= 1500 мм 2
Пример 3
Площадь трапеции составляет 322 квадратных дюйма. Если длины двух параллельных сторон трапеции составляют 19 дюймов и 27 дюймов, найдите высоту трапеции.
Раствор
Площадь трапеции = ½ часа (b 1 + b 2 ) кв.единицы измерения.
⇒ 322 квадратных дюйма = ½ x в x (19 + 27) кв. дюймов
⇒ 322 квадратных дюйма = ½ x h x 46 кв. дюймы
⇒ 322 = 23h
Разделите обе стороны на 23.
h = 14
Итак, высота трапеции составляет 14 дюймов.
Пример 4
Учитывая, что высота трапеции составляет 16 м, а длина одного основания — 25 м. Рассчитайте размер другого основания трапеции, если его площадь составляет 352 м 2 .
Решение
Пусть b 1 = 25 м
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
⇒ 352 м 2 = ½ x 16 м x (25 m + b 2 ) кв. Единиц
⇒ 352 = 8 x (25 + b 2 )
⇒ 352 = 200 + 8b 2
Вычтите 200 с обеих сторон.
⇒ 152 = 8b 2
Разделите обе части на 8, чтобы получить;
b 2 = 19
Следовательно, длина другого основания трапеции составляет 19 м.
Пример 5
Рассчитайте площадь трапеции, показанной ниже.
Решение
Поскольку стороны (непараллельные стороны) трапеции равны, высоту трапеции можно рассчитать следующим образом;
Чтобы получить основание двух треугольников, вычтите 15 см из 27 см и разделите на 2.
⇒ (27-15) / 2 см
⇒ 12/2 см = 6 см
12 2 = h 2 + 6 2 По теореме Пифагора высота (h) рассчитывается как;
144 = h 2 + 36.
Вычтем 36 с обеих сторон.
h 2 = 108.
h = 10,39 см.
Следовательно, высота трапеции 10,39 см.
Теперь вычислите площадь трапеции.
Площадь трапеции = ½ ч (b 1 + b 2 ) кв. единицы измерения.
= ½ x 10,39 x (27 + 15) см 2 .
= ½ x 10,39 x 42 см 2 .
= 218,19 см 2 .
Пример 6
Одно основание трапеции на 10 м больше высоты.Если другое основание составляет 18 м, а площадь трапеции равна 480 м 2 , найдите высоту и основание трапеции.
Решение
Пусть высота = x
Другая база равна 10 м, чем высота = x + 10.
Площадь трапеции = ½ h (b 1 + b 2 ) Кв. единицы измерения.
Путем подстановки
480 = ½ * x * (x + 10 + 18)
480 = ½ * x * (x + 28)
Удалите скобки с помощью свойства распределения.
480 = ½x 2 + 14x
Умножьте каждый член на 2.
960 = x 2 + 28x
x 2 + 28x — 960 = 0
Решите квадратное уравнение, чтобы получить;
x = — 48 или x = 20
Подставьте положительное значение x в уравнение высоты и основания.
Высота: x = 20 м.
Другая база = x + 10 = 10 + 20 = 30 м.
Следовательно, другое основание и высота трапеции равны 30 и 20 м соответственно.
Практические задачи- Найдите площадь трапеции, у которой есть параллельные основания длиной 9 единиц и 12 единиц, а высота равна 15 единицам.
- Для трапециевидной фигуры сумма параллельных оснований составляет 25 м, а высота — 10 м. Определите площадь этой фигуры.
- Рассмотрим трапецию площадью 112b квадратных футов, где b — более короткая базовая длина. Какова высота этой трапеции, если длины двух параллельных оснований таковы, что одно основание в два раза больше другого основания?
Форма: трапеция — элементарная математика
Значение
Трапеция — четырехугольник, по крайней мере, с одной парой параллельных сторон.Никакие другие особенности не имеют значения. (В англоязычных странах за пределами Северной Америки эквивалентным термином является трапеция.)
Параллельные стороны могут быть вертикальными, горизонтальными или наклонными. Фактически, по определению, даже это трапеция, потому что у нее есть «по крайней мере одна пара параллельных сторон» (и никакие другие особенности не имеют значения) как есть. На этих фигурах две другие стороны также параллельны, и поэтому они удовлетворяют не только требованиям для того, чтобы быть трапецией (четырехугольник, по крайней мере, с одной парой параллельных сторон), но также и требованиям для того, чтобы быть параллелограммом.
Приведенное выше определение принято в математическом сообществе и, все чаще, в образовательном сообществе. Многие источники, связанные с K-12 образованием, исторически ограничивали определение трапеции, требуя ровно одной пары параллельных сторон. Этот более узкий вид исключает параллелограммы как подмножество трапеций и оставляет только такие фигуры, как, и. Это более узкое определение трактует трапеции, как если бы они были треугольниками с «одной вершиной, отрезанной параллельно противоположной стороне.«Даже с ограниченным определением для учащихся важно видеть нестандартные примеры — асимметричные, как примеры зеленого и коричневого, и в нестандартных ориентациях, как красный пример, — чтобы создаваемое ими изображение фокусировалось на Существенная особенность: пара параллельных сторон.
Классифицирующие трапеции
Параллелограммам с особыми характеристиками, такими как прямые углы или все совпадающие стороны (или и то и другое), даны собственные отличительные имена: прямоугольник, ромб и квадрат.Единственная особенность трапеции , которой присвоено собственное отличительное имя, — это вторая пара параллельных сторон, которая превращает специальную трапецию в параллелограмм. Когда две стороны (кроме оснований) имеют одинаковую длину, трапеция называется равнобедренной («равнобедренная трапеция»), так же как треугольники с двумя сторонами равной длины (кроме основания) называются равнобедренными треугольниками. Никакие другие отличительные названия не используются для трапеций с особыми характеристиками (например, прямые углы или три совпадающие стороны).
Что одним словом?
Суффикс -оид предполагает, что он «похож» на что-то, но не является тем же самым: сфероид похож на сферу, но не обязательно на идеальную сферу; гуманоид похож на человека, но не на человека; и трапеция имеет форму трапеции, но не трапеция. Современное значение трапеции предполагает цирковые качели ( часто имеет трапециевидную форму, сиденье расположено параллельно перекладине, на которой свисает трапеция), но trapeze первоначально означало «стол», из tra ( «четыре», как в tetra- ) pez («нога» или «ступня», которые мы чаще видим как ped как в pedal или pedestrian ).
Как найти длину диагонали трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Трапеция
Трапеция — это четырехугольник с одной парой параллельных сторон. На рисунке ниже показано несколько различных типов трапеций.
Примечание. Некоторые определяют трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон, подразумевая, что он может содержать две пары параллельных сторон, что сделало бы его параллелограммом.В рамках данной статьи мы определим трапецию как четырехугольник с одной парой параллельных сторон.
Грани трапеции
Параллельные стороны трапеции называются ее основаниями. Непараллельные стороны называются ножками. Высота (или высота) — это отрезок линии, используемый для измерения кратчайшего расстояния между двумя основаниями.
Углы трапеции
В трапеции пара углов, имеющих общее основание, называется базовыми углами.Для трапеций, показанных на диаграмме ниже, A и ∠D — это базовые углы, а ∠B и ∠C — базовые углы. Пара углов рядом с опорой дополнительные: ∠A + ∠B = 180 ° и ∠C + ∠D = 180 °.
Срединный отрезок трапеции
Середина трапеции — это отрезок прямой, соединяющий середину ее ног. Средний сегмент параллелен основаниям и имеет длину, равную половине суммы двух оснований.
На рисунке выше средний сегмент EF делит ветви AB и CD пополам и
Площадь трапеции
Площадь А трапеции равна половине произведения суммы ее оснований и ее высоты.
, где h — высота, а b 1 и b 2 — базовые длины.
Классификация трапеций
Трапеции можно классифицировать как разносторонние или равнобедренные в зависимости от длины ног. Если ноги и углы основания трапеции совпадают, это равнобедренная трапеция. В остальном это разносторонняя трапеция.
| Чешуйчатая трапеция | Равнобедренная трапеция |
|---|---|
| Ноги или углы основания не совпадают | Конгруэнтные ножки и углы основания |
Трапеции также можно классифицировать как прямые трапеции или тупые трапеции в зависимости от их углов.Если одна из ножек перпендикулярна основанию, трапеция представляет собой прямую трапецию. В противном случае трапеция должна содержать два тупых угла и называется тупой трапецией.
| Правая трапеция | Тупая трапеция |
|---|---|
| Одна нога перпендикулярна основаниям. | Два угла тупые. |
Равнобедренные трапеции
Равнобедренная трапеция — это особая трапеция с совпадающими сторонами и углами основания.Он обладает следующими свойствами.
- Две диагонали равнобедренной трапеции совпадают. Они также образуют совпадающие треугольники. На изображенной ниже равнобедренной трапеции диагонали AC и BD совпадают. Поскольку ноги равнобедренной трапеции конгруэнтны, а следующие пары треугольников имеют общее основание, △ ABD ≅ DCA и △ ABC ≅ △ DCB согласно постулату Сторона-Сторона-Сторона.
- Соотношение сегментов, составляющих диагонали трапеции, пропорционально. На диаграмме выше AE = DE, BE = CE и
- Равнобедренная трапеция имеет одну линию симметрии: высоту, разделяющую ее основания пополам.На рисунке выше высота FE делит пополам основания AD и BC. Отражение равнобедренной трапеции ABCE поперек FE сохраняет его, делая FE линией симметрии.
Типы четырехугольников | Бесплатная помощь с домашним заданием
Обзор: что такое четырехугольник?
Четырехугольники — это многоугольники с четырьмя сторонами. Они классифицируются по равным углам и равным сторонам. Есть семь различных типов четырехугольников: параллелограмм, ромб, прямоугольник, квадрат, воздушный змей, трапеция и равнобедренная трапеция.Типы четырехугольников часто пересекаются, поэтому фигура, подходящая к одной категории, может подходить и к другой. У каждого есть свои особенности.
Определения
Четырехугольник называется параллелограммом, если обе пары его противоположных сторон параллельны. Ромб — это четырехугольник со всеми сторонами одинаковой длины. Прямоугольник имеет 4 прямых угла, а квадрат — четыре равные стороны и четыре прямых угла. Эти определения существуют в иерархии отношений. Например, каждый квадрат также является параллелограммом, потому что обе пары его противоположных сторон равны, но каждый параллелограмм не является квадратом.Точно так же каждый квадрат также является ромбом, потому что все четыре стороны имеют одинаковую длину, но каждый ромб не является квадратом. Точно так же каждый квадрат также является прямоугольником, потому что прямоугольник имеет 4 прямых угла, но каждый прямоугольник не является квадратом.
Воздушный змей
Воздушный змей — это особый тип четырехугольника с двумя разными парами последовательных сторон одинаковой длины. Поскольку у ромбов и квадратов также есть стороны одинаковой длины, они тоже воздушные змеи, но обратное неверно. Не каждый воздушный змей — это ромб, потому что все стороны воздушного змея не равны.Точно так же каждый воздушный змей не является параллелограммом, потому что противоположные стороны воздушного змея не обязательно параллельны.
Трапеции
Трапеции — это четырехугольники, у которых одна пара параллельных сторон. Параллельные стороны называются основаниями. Если углы основания равны, трапеция относится к особому типу, называемому равнобедренной трапецией. Прямоугольники — это особый тип равнобедренных трапеций с параллельными противоположными сторонами и равными углами.
Диагонали
Четырехугольники имеют две диагональные линии.В воздушном змее диагональ, соединяющая концы, образует линию симметрии. В ромбе обе диагонали образуют линии симметрии. Линии симметрии обладают мощными свойствами, которые помогают измерять углы, площадь и отношения между геометрическими фигурами.
Заинтересованы в репетиторстве по геометрии? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.
SchoolTutoring Academy — ведущая компания в области образовательных услуг для школьников и школьников. Мы предлагаем репетиторские программы для учащихся K-12, AP и колледжей.Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Ньюарке, Калифорния, посетите: Репетиторство в Ньюарке, Калифорния
Решатель задач геометрии — трапеция
Решатель задач с геометрией
Трапеция
| равнобедренная трапеция | трапеция прямоугольная |
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Трасса 1
Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Рассчитайте периметр и площадь трапеции.
Колея 2
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 80 см, имеет меньшее основание 50 см. Рассчитайте периметр.
Трасса 3
Прямоугольная трапеция имеет высоту 40 м, основание большее 80 м, меньшее основание 50 м.Рассчитайте периметр и площадь трапеции.
Трасса 4
Равнобедренная трапеция с основанием больше 80 см, имеет меньшее основание 50 см, имеет площадь 1300 см. Рассчитайте высоту трапеции.
Колея 5
Прямоугольник в форме трапеции имеет площадь 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Колея 6
Равнобедренная трапеция имеет площадь 1500 см; имеет высоту 30 см.Вычисляет сумму двух оснований.
Колея 7
Равнобедренная трапеция имеет периметр 150 см; имеет основание больше 50 см; имеет меньшую базу 30 см. Рассчитайте длину скошенной стороны.
Направляющая 8
Равнобедренная трапеция имеет периметр 150 см, меньшее основание 30 см, наклонную сторону 35 см. Рассчитайте длину более длинного основания.
Колея 9
Равнобедренная трапеция имеет периметр 150 см, основание больше 50 см, наклонную сторону 35 см.Рассчитайте длину более короткого основания.
Колея 10
Прямоугольная трапеция имеет основание больше 50 см, имеет меньшее основание 30 см; имеет наклонную сторону 35 см. Рассчитайте периметр и площадь.
Колея 11
Прямоугольник трапеции имеет периметр 180 см; имеет основание больше 60 см, имеет наклонную сторону 50 см; имеет высоту 40 см. Рассчитайте длину более короткого основания.
Колея 12
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет высоту 40 см.Рассчитайте длину более длинного основания.
Колея 13
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет высоту 40 см; имеет базу больше 60 см. Рассчитайте длину скошенной стороны.
Колея 14
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет базу больше 60 см. Рассчитывает длину высоты.
Колея 15
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет высоту 4 см.Рассчитайте меньшую базу.
Колея 16
Равнобедренная трапеция имеет меньшее основание 14 см; имеет скошенную сторону 5 см; имеет высоту 4 см. Вычисляет большую базу.
Колея 17
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет выступ скошенной стороны на большее основание 3 см. Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет меньшее основание 14 см; имеет наклонную сторону 5 см. Имеет экранирование наклонной стороны на большем основании 3 см.Рассчитайте периметр.
Трасса 19
Равнобедренная трапеция имеет площадь 2400 см, высоту 40 см, основы составляют треть от другой. Определите периметр.
Дорожка 20
Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, вычислите площадь трапеции.
Колея 21
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание больше 90 см, имеет меньшее основание, равное 2/3 большего основания.Рассчитайте периметр.
Колея 22
Прямоугольная трапеция эквивалентна 1/4 квадрата с периметром 160 см. Учитывая, что высота трапеции составляет 20 см и 6 см, вычислите площадь прямоугольника, размеры которого совпадают с размерами оснований трапеции.
Направление 23
Прямоугольник в форме трапеции, описанный по кругу, длина скошенной стороны составляет 40 см, а высота равна 3/5 наклонной стороны.Рассчитайте периметр и площадь трапеции.
Дорожка 24
Площадь трапециевидного прямоугольника составляет 2250 см. Зная, что разница размеров проекции наклонной стороны на большее основание и высоты составляет 15 см, а их соотношение составляет 3/4, рассчитайте периметр трапеции.
Трасса 25
Периметр равнобедренной трапеции 250 см, высота 30 см, меньшее основание на 4/7 от большего, равного наклонной стороне.Вычислите площадь трапеции.
Колея 26
Большая база прямоугольной формы трапеции со скошенной стороной под углом 45; зная, что основания 25 см и 15 см, вычисляет площадь трапеции.
Трасса 27
Равнобедренная трапеция ABCD образована тремя равнобедренными равнобедренными треугольниками, периметр каждого из которых равен 170 см, а наклонная сторона составляет 6/5 основания. Рассчитайте периметр трапеции.
Дорожка 28
Равнобедренная трапеция ABCD имеет площадь 900 см. Основание AB является двойным, его высота составляет 20 см. Определите площадь треугольника ACD
Track 29
В равнобедренной трапеции площадь равна 1032 см, а два основания имеют размер 61 см и 25 см соответственно. Вычислите меру высоты и периметра.
Колея 30
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30.Две базы размером 50 см и 30 см соответственно определяют периметр и площадь трапеции.
Дорожка 31
В равнобедренной трапеции сумма и разница размеров двух оснований составляет соответственно 74 см и 14 см. Вычисляет площадь и периметр трапеции, зная, что наклонная сторона равна 25 см.
Колея 32
Периметр равнобедренной трапеции 176 см. Зная, что меньшее основание составляет 4/3 наклонной стороны, а большее основание составляет 19/10 меньшего основания, вычисляется площадь трапеции.
Трасса 33
Каждая из наклонных сторон равнобедренной трапеции составляет треть меньшего основания. Зная, что периметр равен 230 см, а наибольшее основание — 105 см, вычисляется размер меньшего основания и площадь трапеции.
Колея 34
В прямоугольной трапеции нижняя диагональ перпендикулярна наклонной стороне. Зная, что эта диагональная линия и наклонная сторона 24 см и 18 см соответственно, найдите периметр и площадь трапеции.
Колея 35
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Рассчитайте периметр трапеции, зная, что высота 11,56 см, а площадь 462,42 см.
Направляющая 36
В трапеции главное основание и вспомогательное основание имеют длину 55 см и 30 см, а периметр — 140 см. Определяет длину наклонных сторон, зная, что одна составляет 6/5 другой.
Колея 37
Разница между основаниями равнобедренной трапеции составляет 30 см, меньшее основание — 5/8 большего основания, периметр — 180 см.Рассчитывает размер наклонных сторон.
Колея 38
Из равнобедренной трапеции вы знаете, что: а) высота составляет 20 см. б) разница между двумя базами 30 см. в) основание больше 80 см. Рассчитайте периметр и площадь трапеции.
Трасса 39
Периметр трапеции, имеющей высоту 34,60 см, составляет 203,49 см. Вычислите площадь трапеции, зная, что наклонные стороны образуют с большим основанием острые углы шириной 45 и 60.
Дорожка 40
Площадь трапециевидного прямоугольника составляет 1080 квадратных сантиметров, а высота — 24 см. Рассчитайте размеры двух оснований, зная, что периметр равен 140 см.
Колея 41
Периметр равнобедренной трапеции составляет 152 см, а длина скошенной стороны — 26 см. Вычислите высоту и площадь трапеции, зная, что меньшее основание имеет длину 40 см.
Направляющая 42
В прямоугольной трапеции основное основание, меньшее основание и высота имеют длину соответственно 60 см, 50 см и 24 см.Вычисляет площадь и периметр трапеции.
Дорожка 43
Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, что, в свою очередь, равно высоте, составляющей 50 см.
Трасса 44
Сумма оснований трапеции 80 см, основание 5/3 другого, высота 2/3 вспомогательного основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что одна диагональ равна 25/16 другой.
Дорожка 45
Трапеция образована квадратом со стороной 48 см и двумя треугольниками, катет которых совпадает с одной из двух противоположных сторон квадрата. Гипотенуза двух треугольников составляет 60 см и 50 см соответственно. Рассчитайте периметр и площадь трапеции.
Колея 46
Разносторонняя трапеция имеет периметр 180 см; вычисляет все стороны, зная, что AB = 8/5 DC, DC — AB = 30 см, AD = 2/5 DC.
Дорожка 47
У равнобедренной трапеции ABCD основание CD составляет 15/22 большего основания, наклонные стороны превышают 7 см 3/5 меньшего основания, периметр составляет 124 см. Какой район?
Направляющая 48
Увеличенное основание, высота и наклонная сторона прямоугольника к трапеции, соответственно размером 80 см, 48 см и 50 см. Рассчитайте периметр и площадь трапеции.
Колея 49
Окружность имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют размер соответственно 96 см и 28 см.Вычисляет площадь и периметр трапеции, в основе которой лежат две хорды.
Трасса 50
Равнобедренная трапеция имеет высоту 20 м, основание больше 80 м, меньшее основание 50 м. Вычислите радиус окружности, описанной трапецией.
Трасса 51
Трапеция имеет основания для диаметра окружности длиной 50 см и параллельную ей веревку длиной 30 см. Рассчитайте периметр и площадь трапеции.
Дорожка 52
В круге с радиусом 50 см сделайте две параллельные хорды, расположенные на противоположных сторонах относительно центра и на расстоянии 14 см и 48 см от него соответственно. Вычисляет площадь и периметр трапеции, у которой есть основания для двух струн.
Колея 53
Прямоугольник и равнобедренная трапеция равны по высоте, периметр прямоугольника 140 см, разница размеров прямоугольника между ними 30 см, наклонная сторона трапеции 25 см.Вычислить:
размер оснований прямоугольника;
протяженность оснований трапеции;
площадь трапеции и прямоугольника;
периметр трапеции.
Направляющая 54
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует наклонной стороне, зная, что площадь трапеции составляет 1320 см.
Дорожка 55
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 28 и 8 см.Вычислите периметр, площадь и две диагонали.
Направляющая 56
Прямоугольная трапеция имеет высоту 24 см и основания соответственно 18 и 10 см. Вычислите периметр, площадь и две диагонали.
Колея 57
Прямоугольная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Трасса 58
Равнобедренная трапеция, сумма оснований 110 см, высота 24 см.Рассчитывает площадь.
Трасса 59
Равнобедренная трапеция имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Дорожка 60
Прямоугольник трапеции имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Колея 61
Равнобедренная трапеция имеет большее основание 50 см, меньшее основание 30 см. Рассчитайте высоту, зная, что наклонная сторона равна 26 см.
Колея 62
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте радиус круга, вписанного в трапецию, зная, что высота 24 см.
Колея 63
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 64
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см.Рассчитайте радиус круга, вписанного в трапецию, зная, что высота 24 см.
Колея 65
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Дорожка 66
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Рассчитайте диаметр круга на трапеции, зная, что высота равна 48.75 дюймов.
Колея 67
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите длину круга, окружающего трапецию, зная, что высота составляет 48,75 дюйма.
Колея 68
Равнобедренная трапеция имеет основание большее 80 см, меньшее основание 50 см. Вычислите площадь описанной круговой трапеции, зная, что высота составляет 48,75 дюйма.
Колея 69
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см.Вычислите:
площадь круга, описанного трапецией, зная, что высота составляет 48,75 дюйма;
расстояние от центра хорды AB;
расстояние каната от центра CD;
длина дуги АВ;
длина дуги CD;
центральный угол АОБ;
центральный угол ХПК;
площадь кругового сектора AOB; площадь кругового сектора наложенным платежом.
Направляющая 70
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1320 см.
Направляющая 71
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 1320 см.
Направляющая 72
Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см.Вычислите радиус окружности, соответствующей трапеции.
Направляющая 73
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Колея 74
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 75
Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Дорожка 76
Прямоугольник трапеции имеет большое основание 60 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь круга, окружность которого изопериметрическая трапеция.
Направляющая 77
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Колея 78
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 79
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 80
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует малой диагонали, зная, что площадь трапеции составляет 1320 см.
Трасса 81
Равнобедренная трапеция имеет высоту 10 см и основания, которые являются одним из 7/17 другого.Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 240 см.
Направляющая 82
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Трасса 83
Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Дорожка 84
Прямоугольник в форме трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Трасса 85
Равнобедренная трапеция имеет площадь 240 см и основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 86
Равнобедренная трапеция имеет периметр 186 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см.Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Трасса 87
Равнобедренная трапеция имеет большое основание 70 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь круга, окружность которого изопериметрическая трапеция.
Track 88
Рассчитайте площадь и периметр разносторонней трапеции, зная, что большее основание составляет 80 см, а меньшее основание — 50 см, а наклонные стороны имеют длину соответственно 30 см и 20 см.
Направляющая 89
Равнобедренная трапеция имеет меньшее основание 8,4 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 90
Прямоугольная трапеция имеет меньшее основание 19,2 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 91
Прямоугольник в форме трапеции имеет наклонную сторону 18 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 92
Равнобедренная трапеция имеет наклонную сторону 18 см и выступание наклонной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 93
Равнобедренная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 94
Прямоугольная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 95
Прямоугольная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 96
Равнобедренная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 97
Периметр равнобедренной трапеции составляет 204 см, а каждая наклонная сторона — 30 см.Вычислите площадь и протяженность оснований, зная, что большее — это 5/3 второстепенного.
Колея 98
Основание большей формы равнобедренной трапеции с наклонной стороной под углом 45; зная, что основания 35 см и 15 см, вычисляет площадь и периметр трапеции.
***********
Программа для решения задач может давать совершенно неверные ответы.
Что такое трапеция? [Определение, факты и пример]
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.
Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.
Расстояние по перпендикуляру между параллельными сторонами называется высотой.
Примеры :
Без примеров :
Типы трапеций
Трапеция бывает трех типов, а именно
1. Правая трапеция : Имеет пару прямых углов.
2. Равнобедренная трапеция : имеет равную длину непараллельных сторон. На изображении стороны AD и BC равны.
3. Трапеция из чешуи : у нее нет равных углов и равных сторон.
Свойства трапеции
Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.
Трапеция — это квадрат, если обе пары его противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу.
Примеры из реальной жизни
Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов.
Интересные факты
| ||||||||||||||||||||||
| Линейный график для определения (k): | \ ([A] \) от времени | \ (\ ln [A] \) в зависимости от времени | \ (\ dfrac {1} {[A]} \) в зависимости от времени | |||||||||||||||||||
| Зависимость постоянной скорости от наклона прямой: | \ (\ {slope} = \ {-k} \) | \ (\ {slope} = \ {-k} \) | \ (\ {slope} = \ {k} \) | |||||||||||||||||||
| Период полураспада: | \ (\ dfrac {[A] _0} {2k} \) | \ (\ dfrac {\ ln2} {k} \) | \ (\ dfrac {1} {k [A] _0} \) |
Примеры задач
1.Определить скорость реакции
2. ВЕРНО или НЕВЕРНО: изменение температуры или введение катализатора повлияет на константу скорости реакции.
Для примеров задач 3-6 используйте Формулу 6 , чтобы ответить на вопросы
\ [H_2O \ longrightarrow 2H_2 + O_2 \ label {6} \]
* Предположим, реакция протекает при постоянной температуре
3. Для данной реакции укажите закон скорости.
4. Укажите общий порядок реакции.
5. Найдите коэффициент при k = 1,14 x 10 -2 и [H 2 O] = 2,04M
6. Найдите период полураспада реакции.
ответы
1. Скорость реакции является мерой изменения концентрации исчезновения реагентов или изменения концентрации появления продуктов в единицу времени.
2. НЕВЕРНО. Константа скорости не зависит от присутствия катализатора. Однако катализаторы могут влиять на общую скорость реакции.
3. \ (\ {Rate} = \ {k [H_2O]} \)
4. Первый — Заказ
5. 2,33 x 10 -2 с -1
6. 60,8 с ((t1 / 2 = ln 2 / k = ln 2 / 1,14 x 10 -2 = 60,8 с).
Список литературы
- Чанг, Раймонд. (2005). Физическая химия для биологических наук . Саусалито, Калифорния: Университетские научные книги.
- Кроу, Джонатан, Брэдшоу, Тони, МонкПол. (2006) Химия для биологических наук: основные концепции .Oxford Press.
- Айзекс, Н.С. (1995). Physical Organic Chemistry (второе издание). Харлоу Великобритания: Эдисон Уэсли Лонгман.
- Кеннет Коннорс. (1990). Химическая кинетика . Издательство ВЧ.
- Левин, Ира Н. (1988). Physical Chemistry (Третье издание). McGraw-Hill Inc.
- Сегель, Ирвин. (1993). Enzyme Kinetics . Библиотека Wiley Classics.
- Zumdahl, Steven S. и Zumdahl, Susan A. (2003) Chemistry (шестое издание).Houghton Mifflin Co.
- Шагури, Ричард. Химия 1A Книга лекций. 4-е изд. Публикация на заказ. 2006. Печать .
Авторы и авторство
Скоростей Реакции | Безграничная химия
Измерение скорости реакции
Скорость реакции определяется путем наблюдения за изменениями концентраций реагентов или продуктов в течение определенного периода времени.
Цели обучения
Составьте выражения скорости, когда даны химические реакции, и обсудите методы измерения этих скоростей
Основные выводы
Ключевые моменты
- Скорость реакции рассчитывается по формуле скорость = Δ [C] / Δt, где Δ [C] — изменение концентрации продукта за период времени Δt.
- Скорость реакции можно наблюдать, наблюдая за исчезновением реагента или появлением продукта с течением времени.
- Если в результате реакции образуется газ, такой как кислород или диоксид углерода, есть два способа измерения скорости реакции: использование газового шприца для измерения произведенного газа или расчет уменьшения массы реакционного раствора.
- Если в результате реакции образуется осадок, образовавшееся количество можно использовать для определения скорости реакции путем измерения того, сколько времени требуется, чтобы образовавшийся осадок скрыл видимость креста через коническую колбу.
Ключевые термины
- скорость реакции : насколько быстро или медленно происходит реакция.
- газовый шприц : Элемент лабораторного оборудования, используемый для отбора объема газа из замкнутой химической системы для измерения и / или анализа.
- продукт : Химическое вещество, образующееся в результате химической реакции.
Скорость реакции
За скоростью реакции обычно наблюдают, наблюдая за исчезновением реагента или появлением продукта в течение заданного периода времени.Возьмем химическую реакцию:
[латекс] \ text {A} + 2 \ text {B} \ rightarrow 3 \ text {C} [/ latex]
Здесь скорость появления продукта C на временном интервале Δt составляет:
[латекс] \ text {средняя скорость} = \ frac {\ Delta \ text {C}} {\ Delta \ text {t}} [/ latex]
Концентрация C [C] обычно выражается в моль / литр. Это средняя скорость появления C за интервал времени Δt. Предел этой средней скорости по мере того, как временной интервал становится меньше, называется скоростью появления C в момент времени t, и это наклон кривой [C] в зависимости от t в момент времени t.Этот мгновенный наклон или скорость записывается как [latex] \ frac {\ text {d} [\ text {C}]} {\ text {dt}} [/ latex]. Поскольку одна молекула A и две молекулы B расходуются на каждые три производимые молекулы C, скорости исчезновения и появления этих химических частиц различны, но связаны между собой.
Скорость исчезновения и появления химических частиц : Это выражение связывает скорости исчезновения и появления химических частиц в реакции A + 2B -> 3C.
Измерение скорости реакции
Способ измерения скорости реакции будет зависеть от того, что это за реакция и какой продукт образуется. В следующих примерах описаны различные способы измерения скорости реакции.
Реакции с образованием газов, таких как кислород или диоксид углерода
Перекись водорода разлагается с образованием кислорода:
[латекс] 2 \ text {H} _2 \ text {O} _2 (\ text {aq}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text {l}) + \ text {O } _2 (\ text {g}) [/ latex]
Объем произведенного кислорода можно измерить с помощью газового шприца.Газ собирается в шприце, давя на поршень. Объем произведенного газа можно определить по отметкам на шприце. Это изменение объема можно преобразовать в изменение концентрации ([латекс] \ Delta [\ text {C}] [/ latex]) и разделив его на время реакции ([латекс] \ Delta \ text {t } [/ latex]) даст среднюю скорость реакции.
Метод газового шприца : В реакции, в которой образуется газ, объем выделяемого газа можно измерить с помощью метода газового шприца.
Изменение массы
Скорость реакции, при которой образуется газ, также можно измерить, рассчитав потерю массы при образовании газа и его выходе из реакционной колбы. Этот метод можно использовать для реакций с образованием диоксида углерода или кислорода, но он не очень точен для реакций с выделением водорода, поскольку масса слишком мала для точного измерения. Измерение изменения массы также может быть подходящим для других типов реакций.
Реакция осаждения
В реакции, в которой образуется осадок, количество осадка, образовавшегося за период времени, можно использовать как меру скорости реакции.Например, когда тиосульфат натрия реагирует с кислотой, образуется желтый осадок серы. Эта реакция записывается так:
[латекс] \ text {Na} _2 \ text {S} _2 \ text {O} _3 (\ text {aq}) + 2 \ text {HCl} (\ text {aq}) \ rightarrow 2 \ text {NaCl } (\ text {aq}) + \ text {SO} _2 (\ text {aq}) + \ text {H} _2 \ text {O} (\ text {l}) + \ text {S} (\ text {s}) [/ латекс]
Один из способов оценить скорость этой реакции — провести исследование в конической колбе и подложить под ее дно лист бумаги с черным крестом.В начале реакции крестик будет хорошо виден, когда вы заглянете в колбу. Однако по мере того, как реакция прогрессирует и образуется больше осадка, крест постепенно становится менее четким и в конечном итоге полностью исчезнет. Используя секундомер, чтобы измерить, сколько времени нужно, чтобы крестик исчез, а затем взвесив количество осадка, образовавшегося за это время, можно рассчитать среднюю скорость реакции. Обратите внимание, что невозможно собрать газ SO 2 , который образуется в реакции, потому что он хорошо растворяется в воде.
Стехиометрия реакции
Стехиометрия реакции изучает количественные отношения между реагентами и продуктами в рамках данной химической реакции.
Цели обучения
Используйте стехиометрию, чтобы сбалансировать химические уравнения
Основные выводы
Ключевые моменты
- Стехиометрия происходит от греческих слов «стоихион» (элемент) и «метрон» (измерять). Таким образом, стехиометрия касается определения количества реагентов и продуктов, которые потребляются и производятся в рамках данной химической реакции.
- Стехиометрический коэффициент любого вещества, не участвующего в данной химической реакции, равен нулю.
- Принципы стехиометрии основаны на законе сохранения массы. Материя не может быть ни создана, ни разрушена, поэтому масса каждого элемента, присутствующего в продукте (ах) химической реакции, должна быть равна массе каждого элемента, присутствующего в реагенте (ах).
Ключевые термины
- Стехиометрия реакции : Описывает количественное соотношение между реагентами и продуктами в рамках данной химической реакции.
- Стехиометрическое число : Равно стехиометрическому коэффициенту в сбалансированном уравнении, но положительно для продуктов (потому что они производятся) и отрицательно для реагентов (поскольку они потребляются).
- стехиометрическое соотношение : положительное целочисленное соотношение, которое связывает количество молей реагентов и продуктов, участвующих в химической реакции; это соотношение можно определить из коэффициентов сбалансированного химического уравнения.
- сбалансированное уравнение : Когда количество каждого отдельного элемента равно в обеих частях уравнения.
Стехиометрия — это раздел химии, который имеет дело с относительными количествами реагентов и продуктов, которые потребляются / производятся в рамках данной химической реакции. Однако, чтобы сделать какие-либо стехиометрические определения, мы должны сначала обратиться к сбалансированному химическому уравнению. В сбалансированном химическом уравнении мы можем легко определить стехиометрическое соотношение между количеством молей реагентов и количеством молей продуктов, потому что это соотношение всегда будет положительным целым отношением.Рассмотрим реакцию газообразного азота и газообразного водорода с образованием аммиака (NH 3 ):
[латекс] \ text {N} _2 (\ text {g}) + 3 \ text {H} _2 (\ text {g}) \ rightarrow 2 \ text {NH} _3 (\ text {g}) [/ латекс]
Из сбалансированного уравнения видно, что стехиометрический коэффициент для азота равен 1, для водорода — 3, а для аммиака — 2. Следовательно, стехиометрическое соотношение часто называют просто «молярным соотношением» или « молярное соотношение ”между N 2 (г), H 2 (г) и NH 3 (г) составляет 1: 3: 2.В особом случае, когда реагенты объединены в их молярных соотношениях (в данном случае 1 моль N 2 (г) и 3 моля H 2 (г)), они будут полностью реагировать друг с другом, и реагент останется после того, как реакция завершится. Однако в большинстве реальных ситуаций реагенты не сочетаются в таких идеальных стехиометрических количествах. В большинстве случаев один реагент неизбежно будет первым, который полностью израсходуется в реакции, что приведет к остановке реакции.Этот реагент известен как ограничивающий реагент или ограничивающий реагент.
Из этого краткого описания мы видим, что стехиометрия имеет много важных приложений. Как мы увидим, балансируя химические уравнения и определяя стехиометрические коэффициенты, мы сможем определить количество молей продукта (ов), которые могут быть получены в данной реакции, а также количество молей реагента (s ), который будет использован. Стехиометрию также можно использовать для определения ограничивающих реагентов и для расчета количества избыточного реагента (ов), оставшегося после того, как данная реакция завершилась.
Основы стехиометрии
Наука о стехиометрии возможна, потому что она основана на законе сохранения массы. Поскольку материя не может быть ни создана, ни разрушена, ни химическая реакция не может преобразовать один элемент в другой элемент, мы можем быть уверены, что масса каждого отдельного элемента, присутствующего в реагенте (ах) данной реакции, обязательно должна быть учтена в продукты). Этот физический закон делает возможными все стехиометрические вычисления.Однако мы можем выполнить эти расчеты правильно только в том случае, если у нас есть сбалансированное химическое уравнение, с которым можно работать.
Interactive: стехиометрия и уравнения баланса : Для производства хлористого водорода или любого другого химического вещества существует только одно соотношение реагентов, которое работает так, что весь водород и хлор используются для производства хлористого водорода. Попробуйте несколько разных соотношений, чтобы увидеть, какие из них образуют полную реакцию без остатка. Какое самое простое соотношение водорода и хлора для образования хлористого водорода?
Балансировочные уравнения
Прежде чем выполнять какие-либо стехиометрические вычисления, мы должны сначала получить сбалансированное химическое уравнение.Возьмем, к примеру, реакцию газообразного водорода и кислорода с образованием жидкой воды:
[латекс] \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow \ text {H} _2 \ text {O} (\ text {l} ) [/ латекс]
Как здесь написано, мы должны заметить, что наше уравнение не сбалансировано, потому что у нас есть два атома кислорода в левой части уравнения, а только один в правой. Чтобы уравновесить это, нам нужно добавить стехиометрический коэффициент 2 перед жидкой водой:
[латекс] \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text {l }) [/ латекс]
Однако из-за этого наши водороды стали неуравновешенными.Чтобы завершить балансировку уравнения, мы должны добавить коэффициент 2 перед газообразным водородом:
[латекс] 2 \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text { л}) [/ латекс]
Как мы видим, стехиометрический коэффициент для любого данного реагента / продукта — это количество молекул, которые будут участвовать в реакции, как записано в сбалансированном уравнении. Однако имейте в виду, что в наших расчетах мы часто будем работать с молями, а не с молекулами.В нашем примере мы видим, что стехиометрический коэффициент для H 2 (г) равен 2, в то время как для O 2 (г) он равен 1, а для H 2 O (l) он равен 2. Иногда вы можете встретить термин стехиометрическое число, который связан со стехиометрическим коэффициентом, но это не то же самое.
Электролиз воды : Хотя это изображение иллюстрирует обратную реакцию [латекса] 2 \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text {l}) [/ latex], стехиометрические коэффициенты для каждого типа молекул остаются теми же.Вода — 2, водород — 2, кислород — 1.
Для реагентов стехиометрическое число является отрицательным значением стехиометрического коэффициента, в то время как для продуктов стехиометрическое число просто равно стехиометрическому коэффициенту, оставаясь положительным. Следовательно, в нашем примере стехиометрическое число для H 2 (г) равно -2, а для O 2 (г) — -1. Однако для H 2 O (л) он равен +2. Это связано с тем, что в этой реакции H 2 (г) и O 2 (г) являются реагентами, которые потребляются, тогда как вода является продуктом, который образуется.
Наконец, иногда вы можете встретить некоторые химические соединения, которые присутствуют во время реакции, но не потребляются и не образуются в ходе реакции. Катализатор — наиболее известный пример этого. Для таких видов их стехиометрические коэффициенты всегда равны нулю.
Пример
В уравнении h3 (g) + Cl2 (g) → 2 HCl (g), каково молярное соотношение (стехиометрическое соотношение) между h3 (g) и HCl (g)?
В нашем сбалансированном химическом уравнении коэффициент для h3 (g) равен 1, а коэффициент для HCl (g) равен 2.Следовательно, молярное соотношение между этими двумя соединениями составляет 1: 2. Это говорит нам о том, что на каждый 1 моль h3 (г), который расходуется в реакции, образуется 2 моля HCl (г).
Экспериментальное определение скорости реакции
Цель обучения
- Планируйте эксперименты, в которых используются химические или физические свойства для измерения скорости реакции
Ключевые моменты
- Физические измерения могут выполняться в системе, когда она реагирует.Преимущество этих измерений состоит в том, что они не нарушают работу системы, и их можно проводить во время реакции. Примерами этих измерений являются изменения объема, температуры и поглощения раствора.
- Химические методы измерения дают непосредственный выход концентраций. Небольшой образец извлекается из реакционной смеси, и реакция останавливается разбавлением, охлаждением смеси на время, достаточным для измерения концентраций, или добавлением другого реагента для остановки реакции.
- Для реакций нулевого порядка, график зависимости концентрации отпора получить линию с уклоном -к . Для реакций первого порядка изобразите логарифм концентрации в зависимости от времени, чтобы получить линию с наклоном -k . Для реакций второго порядка изобразите на графике обратную зависимость концентрации от времени, чтобы получить линию наклона -k .
Условия
- Закон Бера связывает ослабление света со свойствами материала, через который свет распространяется.
- абсорбция Логарифмическая мера количества света, поглощаемого при прохождении через вещество.
Экспериментальные методы измерения реакций
Чтобы экспериментально определить скорость реакции, нам необходимо измерить концентрации реагентов и / или продуктов в ходе химической реакции. Если мы знаем порядок реакции, мы можем построить график данных и применить наши интегрированные законы скорости. Например, если реакция первого порядка, график ln [A] по сравнению с t даст прямую линию с наклоном — k .
Существует два основных способа измерения концентраций в реакциях: путем измерения изменений наблюдаемых физических свойств или путем отбора проб реакционного раствора и непосредственного измерения концентрации.
Физические измерения
Физические измерения могут выполняться в системе, пока она реагирует. Преимущество этих измерений состоит в том, что они не мешают реагирующей системе, и их обычно можно измерить быстро. Например, если общее количество молей газа изменяется во время газовой реакции, ход реакции можно измерить, отслеживая изменение давления при постоянном объеме. Другие физические измерения включают оптические методы, такие как измерение изменения поляризации света, изменения показателя преломления раствора или, что довольно часто, изменения цвета раствора и, следовательно, спектра поглощения.Общие электрические методы включают изменение проводимости раствора, электрического потенциала в ячейке и масс-спектрометрию. Другие методы включают теплопроводность, вязкость, теплоту реакции и точки замерзания.
Химические измерения
Химические методы позволяют напрямую определять концентрации. Небольшой образец извлекается из реакционной смеси, и реакция останавливается либо разбавлением, либо охлаждением смеси, либо добавлением другого химического реагента для остановки реакции.Одним из недостатков этого метода является то, что удаление части реагирующей системы или добавление к ней дополнительного реагента постепенно меняет ее с течением времени. Кроме того, существует временная задержка между взятием пробы и измерением реакции, что снижает точность измерения.
Использование закона Пива для измерения концентрации во времени
Одной окисленной формой бакминстерфуллерена (C 60 ) является C 60 O 3 . Когда раствор C 60 O 3 нагревается, компаунд разлагается, высвобождая O 2 и создавая C 60 O.Реакцию дает:
[латекс] C_ {60} O_3 \ rightarrow O_2 + C_ {60} O [/ латекс]
За скоростью этой реакции можно следить, измеряя оптическую плотность раствора. Поглощение определяется законом Бера:
.[латекс] A = abC [/ латекс]
В этом уравнении a — это поглощающая способность данной молекулы в растворе, которая является константой, зависящей от физических свойств рассматриваемой молекулы, b — длина пути, который проходит через раствор, а C — концентрация раствора.Мы заинтересованы в определении C .
Запустив интересующую реакцию внутри спектрометра, можно измерить оптическую плотность раствора с течением времени. Затем данные могут быть нанесены на график.
Поглощение окисленного бакминстерфуллерена Поглощение пропорционально концентрации C 60 O 3 в растворе, поэтому наблюдение поглощения как функции времени по существу аналогично наблюдению концентрации как функции времени.По закону Бера оптическая плотность раствора прямо пропорциональна концентрации C 60 O 3 в растворе, поэтому наблюдение оптической плотности как функции времени, по сути, аналогично наблюдению концентрации как функции время. В этом случае тарифный закон определяется по формуле:
[латекс] коэффициент = k [C_ {60} O_3] [/ latex]
Следовательно, график зависимости скорости от оптической плотности даст прямую линию с наклоном k.
Скорость реакции vs.абсорбция абсорбция прямо пропорциональна концентрации, так что это просто график закона скорости, скорость = k [C 60 O 3 ], а наклон линии представляет собой константу скорости k.Построение законов интегрированной ставки для определения скорости реакции
Как обсуждалось в предыдущей концепции, графики, полученные из интегрированных законов скорости для различных порядков реакции, могут использоваться для определения константы скорости k . Напомним, что для реакций нулевого порядка график зависимости [A] от времени будет прямой линией с наклоном, равным — k .Для реакций первого порядка график зависимости ln [A] от времени дает прямую линию с наклоном — k , в то время как для реакции второго порядка график зависимости 1 / [A] от t дает прямую линию с уклоном к .
Показать источникиBoundless проверяет и курирует высококачественный контент с открытой лицензией из Интернета. Этот конкретный ресурс использовал следующие источники:
12.1 Скорость химических реакций — Химия
Цели обучения
К концу этого раздела вы сможете:
- Определите скорость химической реакции
- Выведите выражения для скоростей из сбалансированного уравнения данной химической реакции
- Рассчитать скорость реакции по экспериментальным данным
Оценка — это мера того, как какое-то свойство изменяется со временем.Скорость — это привычный показатель, который выражает расстояние, пройденное объектом за заданный промежуток времени. Заработная плата — это ставка, которая представляет собой сумму денег, заработанную человеком, работающим в течение определенного времени. Точно так же скорость химической реакции является мерой того, сколько реагента потребляется или сколько продукта производится в результате реакции за заданный промежуток времени.
Скорость реакции — это изменение количества реагента или продукта в единицу времени. Поэтому скорости реакции определяют путем измерения зависимости от времени некоторого свойства, которое может быть связано с количествами реагента или продукта.Например, скорость реакций, в которых потребляются или образуются газообразные вещества, удобно определять путем измерения изменений объема или давления. Для реакций с участием одного или нескольких окрашенных веществ скорость можно контролировать путем измерения поглощения света. Для реакций с участием водных электролитов скорость можно измерить по изменению проводимости раствора.
Для реагентов и продуктов в растворе их относительные количества (концентрации) удобно использовать для целей выражения скоростей реакции.Если мы измерим концентрацию перекиси водорода, H 2 O 2 , в водном растворе, мы обнаружим, что она медленно изменяется со временем, поскольку H 2 O 2 разлагается в соответствии с уравнением:
[латекс] 2 \ text {H} _2 \ text {O} _2 (aq) \; {\ longrightarrow} \; 2 \ text {H} _2 \ text {O} (l) \; + \; \ text {O} _2 (г) [/ латекс]
Скорость разложения пероксида водорода можно выразить через скорость изменения его концентрации, как показано здесь:
[латекс] \ begin {array} {r @ {{} = {}} l} \ text {rate \; of \; разложение \; of \; H} _2 \ text {O} _2 & — \ frac { \ text {изменение \; в \; концентрация \; \; реагента}} {\ text {время \; интервал}} \\ [0.5em] & — \ frac {[\ text {H} _2 \ text {O} _2] _ {t_2} \; — \; [\ text {H} _2 \ text {O} _2] _ {t_1}} { t_2 \; — \; t_1} \\ [0.5em] & — \ frac {{\ Delta} [\ text {H} _2 \ text {O} _2]} {{\ Delta} t} \ end {array} [/ латекс]
Это математическое представление изменения концентрации компонентов с течением времени является выражением скорости для реакции. Скобки указывают молярные концентрации, а символ дельта (Δ) указывает «изменение в». Таким образом, [латекс] [\ text {H} _2 \ text {O} _2] _ {t_1} [/ latex] представляет молярную концентрацию перекиси водорода в определенный момент времени t 1 ; аналогично [латекс] [\ text {H} _2 \ text {O} _2] _ {t_2} [/ latex] представляет молярную концентрацию перекиси водорода в более позднее время t 2 ; и Δ [H 2 O 2 ] представляет собой изменение молярной концентрации пероксида водорода в течение интервала времени Δ t (то есть t 2 — t 1 ).Поскольку концентрация реагента уменьшается по мере протекания реакции, Δ [H 2 O 2 ] является отрицательной величиной; мы ставим отрицательный знак перед выражением, потому что скорость реакции, по соглашению, является положительной величиной. На рисунке 1 приведен пример данных, собранных при разложении H 2 O 2 .
Рис. 1. Скорость разложения H 2 O 2 в водном растворе уменьшается с уменьшением концентрации H 2 O 2 .Чтобы получить табличные результаты для этого разложения, концентрацию перекиси водорода измеряли каждые 6 часов в течение дня при постоянной температуре 40 ° C. Скорости реакции были рассчитаны для каждого временного интервала путем деления изменения концентрации на соответствующий временной интервал, как показано здесь для первого 6-часового периода:
[латекс] \ frac {- {\ Delta} [\ text {H} _2 \ text {O} _2]} {{\ Delta} t} = \ frac {- (0.500 \; \ text {mol / L} \; — \; 1.000 \; \ text {mol / L})} {(6.00 \; \ text {h} \; — \; 0.{-1} [/ латекс]
Такое поведение указывает на то, что реакция постоянно замедляется со временем. Использование концентраций в начале и в конце периода времени, в течение которого скорость реакции изменяется, приводит к вычислению средней скорости для реакции за этот интервал времени. В любое конкретное время скорость, с которой протекает реакция, известна как ее мгновенная скорость . Мгновенная скорость реакции в «нулевой момент времени», когда реакция начинается, равна ее начальной скорости .Рассмотрим аналогию с автомобилем, который замедляется при приближении к знаку остановки. Начальная скорость транспортного средства — аналогично началу химической реакции — будет показанием спидометра в момент, когда водитель начинает нажимать на тормоза ( t 0 ). Несколько мгновений спустя мгновенная скорость в определенный момент — назовем ее t 1 — будет несколько ниже, о чем свидетельствуют показания спидометра в этот момент времени. По прошествии времени мгновенная скорость будет продолжать падать, пока не достигнет нуля, когда машина (или реакция) остановится.В отличие от мгновенной скорости, средняя скорость автомобиля не отображается на спидометре; но его можно рассчитать как отношение пройденного расстояния ко времени, необходимому для полной остановки транспортного средства (Δ t ). Подобно замедляющемуся автомобилю, средняя скорость химической реакции будет находиться где-то между начальной и конечной скоростью.
Мгновенную скорость реакции можно определить одним из двух способов. Если экспериментальные условия позволяют измерять изменения концентрации в течение очень коротких интервалов времени, тогда средние скорости, вычисленные, как описано ранее, обеспечивают достаточно хорошее приближение мгновенных скоростей.В качестве альтернативы может использоваться графическая процедура, которая, по сути, дает результаты, которые были бы получены, если бы были возможны измерения с короткими временными интервалами. Если мы построим график зависимости концентрации перекиси водорода от времени, мгновенная скорость разложения H 2 O 2 в любой момент времени t будет выражена наклоном прямой линии, касательной к кривой в это время ( Фигура 2). Мы можем использовать исчисление для оценки наклона таких касательных, но процедура для этого выходит за рамки этой главы.
Рис. 2. На этом графике показан график зависимости концентрации от времени для 1.000 M раствора H 2 O 2 . Скорость в любой момент равна величине, противоположной наклону линии, касательной к этой кривой в этот момент. Касательные показаны при t = 0 ч («начальная скорость») и при t = 10 ч («мгновенная скорость» в это конкретное время).Скорость реакции при анализе: тест-полоски для анализа мочи
Врачи часто используют одноразовые тест-полоски для измерения количества различных веществ в моче пациента (рис. 3).Эти тест-полоски содержат различные химические реагенты, встроенные в небольшие подушечки в различных местах вдоль полоски, которые меняют цвет при воздействии достаточных концентраций определенных веществ. В инструкциях по использованию тест-полосок часто подчеркивается, что правильное время считывания имеет решающее значение для получения оптимальных результатов. Такой акцент на времени считывания предполагает, что важными факторами являются кинетические аспекты химических реакций, происходящих на тест-полоске. {-} \; {\ xrightarrow [\ text {катализатор}] {}} \; \ текст {I} _2 \; + \; 2 \ text {H} _2 \ text {O} \; + \; \ text {O} _2 [/ latex]
Первое уравнение описывает окисление глюкозы в моче с образованием глюколактона и перекиси водорода.Полученная перекись водорода впоследствии окисляет бесцветный ион йодида с образованием коричневого йода, который можно обнаружить визуально. Некоторые полоски содержат дополнительное вещество, которое вступает в реакцию с йодом, вызывая более отчетливое изменение цвета.
Две показанные выше тестовые реакции по своей природе очень медленные, но их скорость увеличивается за счет специальных ферментов, встроенных в подушечку для тест-полосок. Это пример катализатора , тема которого обсуждается далее в этой главе. Обычной тест-полоске для определения глюкозы в моче требуется около 30 секунд для завершения реакции формирования цвета.Слишком раннее прочтение результата может привести к заключению, что концентрация глюкозы в образце мочи ниже, чем она есть на самом деле (ложноотрицательный результат ). Слишком долгое ожидание для оценки изменения цвета может привести к ложному положительному результату из-за более медленного (не катализируемого) окисления йодид-иона другими веществами, обнаруженными в моче.
Рис. 3. Тест-полоски обычно используются для определения наличия определенных веществ в моче человека. Многие тест-полоски имеют несколько подушечек, содержащих различные реагенты, что позволяет обнаруживать несколько веществ на одной полоске.(Источник: Икбал Осман)Скорость реакции может быть выражена через изменение количества любого реагента или продукта и может быть просто получена из стехиометрии реакции. Рассмотрим реакцию, представленную следующим уравнением:
[латекс] 2 \ text {NH} _3 (g) \; {\ longrightarrow} \; \ text {N} _2 (g) \; + \; 3 \ text {H} _2 (g) [/ latex]
Стехиометрические коэффициенты, полученные из этого уравнения, могут использоваться для связи скоростей реакции таким же образом, как они используются для соответствующих количеств реагента и продукта.Соотношение между скоростями реакции, выраженными в единицах производства азота и потребления аммиака, например, составляет:
[латекс] — \; \ frac {{\ Delta} \ text {mol \; NH} _3} {{\ Delta} t} \; \ times \; \ frac {1 \; \ text {mol \; N } _2} {2 \; \ text {mol \; NH} _3} = \ frac {{\ Delta} \ text {mol \; N} _2} {{\ Delta} t} [/ latex]
Мы можем выразить это проще, не показывая единиц стехиометрического фактора:
[латекс] — \; \ frac {1} {2} \; \ frac {{\ Delta} \ text {mol \; NH} _3} {{\ Delta} t} = \ frac {{\ Delta} \ текст {mol \; N} _2} {{\ Delta} t} [/ latex]
Обратите внимание, что был добавлен отрицательный знак для учета противоположных знаков двух изменений количества (количество реагента уменьшается, а количество продукта увеличивается).Если реагенты и продукты присутствуют в одном растворе, молярные количества могут быть заменены на концентрации:
[латекс] — \; \ frac {1} {2} \; \ frac {{\ Delta} [\ text {NH} _3]} {{\ Delta} t} = \ frac {{\ Delta} [\ текст {N} _2]} {{\ Delta} t} [/ latex]
Точно так же скорость образования H 2 в три раза превышает скорость образования N 2 , потому что три моля H 2 образуются за время, необходимое для образования одного моля N 2 :
[латекс] \ frac {1} {3} \; \ frac {{\ Delta} [\ text {H} _2]} {{\ Delta} t} = \ frac {{\ Delta} [\ text {N } _2]} {{\ Delta} t} [/ latex]
На рис. 4 показано изменение концентраций во времени разложения аммиака на азот и водород при 1100 ° C.{-6} \; M / \ text {s}} \; {\ приблизительно} \; 3 [/ латекс]
Рисунок 4. На этом графике показаны изменения концентраций реагентов и продуктов во время реакции 2NH 3 → 3N 2 + H 2 . Скорости изменения трех концентраций связаны их стехиометрическими факторами, как показано разными наклонами касательных при t = 500 с.Пример 1
Выражения для относительных скоростей реакций
Первым этапом производства азотной кислоты является сжигание аммиака:
[латекс] 4 \ text {NH} _3 (g) \; + \; 5 \ text {O} _2 (g) \; {\ longrightarrow} \; 4 \ text {NO} (g) \; + \ ; 6 \ text {H} _2 \ text {O} (g) [/ latex]
Напишите уравнения, связывающие скорости потребления реагентов и скорости образования продуктов.
Раствор
Учитывая стехиометрию этой гомогенной реакции, скорости расходования реагентов и образования продуктов составляют:
[латекс] — \ frac {1} {4} \; \ frac {{\ Delta} [\ text {NH} _3]} {{\ Delta} t} = — \ frac {1} {5} \; \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} = \ frac {1} {4} \; \ frac {{\ Delta} [\ text {NO}]} { {\ Delta} t} = \ frac {1} {6} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O}]} {{\ Delta} t} [/ latex]
Проверьте свои знания
Скорость образования Br 2 равна 6.{+}]} {{\ Delta} t} = \ frac {1} {3} \; \ frac {{\ Delta} [\ text {Br} _2]} {{\ Delta} t} = \ frac { 1} {3} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O}]} {{\ Delta} t} [/ latex]
Пример 2
Выражения скорости реакции для разложения H 2 O 2
График на рисунке 2 показывает скорость разложения H 2 O 2 во времени:
[латекс] 2 \ text {H} _2 \ text {O} _2 \; {\ longrightarrow} \; 2 \ text {H} _2 \ text {O} \; + \; \ text {O} _2 [/ латекс]
На основании этих данных, мгновенная скорость разложения H 2 O 2 при t = 11.{-1} [/ латекс]
Какова мгновенная скорость производства H 2 O и O 2 ?
Раствор
Используя стехиометрию реакции, мы можем определить, что:
[латекс] — \ frac {1} {2} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O} _2]} {{\ Delta} t} = \ frac {1} {2} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O}]} {{\ Delta} t} = \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} [/ латекс]
Следовательно:
[латекс] \ frac {1} {2} \; \ times \; 3. {- 1} = \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} [/ latex]
и
[латекс] \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} = 1.{-1} [/ латекс]
Проверьте свои знания
Если скорость разложения аммиака, NH 3 , при 1150 K составляет 2,10 × 10 −6 моль / л / с, какова скорость образования азота и водорода?
Ответ:
1,05 × 10 −6 моль / л / с, N 2 и 3,15 × 10 −6 моль / л / с, H 2 .
Скорость реакции может быть выражена либо через уменьшение количества реагента, либо через увеличение количества продукта в единицу времени.Соотношения между различными выражениями скорости для данной реакции выводятся непосредственно из стехиометрических коэффициентов уравнения, представляющего реакцию.
- относительная скорость реакции для [латекса] a \ text {A} \; {\ longrightarrow} \; b \ text {B} = — \ frac {1} {a} \; \ frac {{\ Delta} [\ текст {A}]} {{\ Delta} t} = \ frac {1} {b} \; \ frac {{\ Delta} [\ text {B}]} {{\ Delta} t} [/ latex]
Химия: упражнения в конце главы
- В чем разница между средней, начальной и мгновенной скоростью?
- Озон разлагается до кислорода в соответствии с уравнением [латекс] 2 \ text {O} _3 (g) \; {\ longrightarrow} \; 3 \ text {O} _2 (g) [/ latex].Напишите уравнение, связывающее выражения скорости этой реакции через исчезновение O 3 и образование кислорода.
- В ядерной промышленности трифторид хлора используется для получения гексафторида урана, летучего соединения урана, используемого для разделения изотопов урана. Трифторид хлора получают по реакции [латекс] \ text {Cl} _2 (g) \; + \; 3 \ text {F} _2 (g) \; {\ longrightarrow} \; 2 \ text {ClF} _3 ( г) [/ латекс]. Напишите уравнение, связывающее выражения скорости этой реакции с точки зрения исчезновения Cl 2 и F 2 и образования ClF 3 .
- Исследование скорости димеризации C 4 H 6 дало данные, представленные в таблице:
[латекс] 2 \ text {C} _4 \ text {H} _6 \; {\ longrightarrow} \; \ text {C} _8 \ text {H} _ {12} [/ латекс]Время (с) 0 1600 3200 4800 6200 [C 4 H 6 ] ( M ) 1,00 × 10 −2 5,04 × 10 −3 3.37 × 10 −3 2,53 × 10 −3 2,08 × 10 −3 Таблица 1. (a) Определите среднюю скорость димеризации от 0 до 1600 с и от 1600 до 3200 с.
(b) Оцените мгновенную скорость димеризации при 3200 с по графику зависимости времени от [C 4 H 6 ]. Какие единицы этой ставки?
(c) Определите среднюю скорость образования C 8 H 12 за 1600 с и мгновенную скорость образования через 3200 с из скоростей, найденных в частях (a) и (b).
- Исследование скорости реакции, представленной как [латекс] 2A \; {\ longrightarrow} \; B [/ latex], дало следующие данные:
Время (с) 0,0 5,0 10,0 15,0 20,0 25,0 35,0 [ A ] ( M ) 1,00 0,952 0,625 0,465 0,370 0,308 0.230 Таблица 2. (a) Определите среднюю скорость исчезновения A от 0,0 до 10,0 с и от 10,0 до 20,0 с.
(b) Оцените мгновенную скорость исчезновения A через 15,0 с по графику зависимости времени от [ A ]. Какие единицы этой ставки?
(c) Используйте скорости, найденные в частях (a) и (b), чтобы определить среднюю скорость образования B между 0.{+} (aq) \; {\ longrightarrow} \; 3 \ text {Br} _2 (aq) \; + \; 3 \ text {H} _2 \ text {O} (l) [/ latex]
Если скорость исчезновения Br — ( водн. ) в определенный момент реакции составляет 3,5 × 10 −4 M с −1 , то какова скорость появления Br 2 ( водн ) в тот момент?
Глоссарий
- средняя оценка
- скорость химической реакции, вычисляемая как отношение измеренного изменения количества или концентрации вещества к интервалу времени, в течение которого это изменение произошло
- начальная ставка
- мгновенная скорость химической реакции при т = 0 с (сразу после начала реакции)
- мгновенная скорость
- скорость химической реакции в любой момент времени, определяемая наклоном касательной к графику концентрации как функция времени
- скорость реакции
- Мера скорости, с которой протекает химическая реакция
- скорость выражения
- математическое представление, связывающее скорость реакции с изменениями количества, концентрации или давления реагентов или продуктов в единицу времени
Решения
Ответы на упражнения в конце главы по химии
1.Мгновенная скорость — это скорость реакции в любой конкретный момент времени, период времени, который настолько короткий, что концентрации реагентов и продуктов изменяются на незначительную величину. Начальная скорость — это мгновенная скорость реакции, когда она начинается (когда продукт только начинает образовываться). Средняя скорость — это средняя мгновенная скорость за период времени.
3. [латекс] \ text {rate} = + \ frac {1} {2} \; \ frac {{\ Delta} [\ text {CIF} _3]} {{\ Delta} t} = — \ frac {{\ Delta} [\ text {Cl} _2]} {{\ Delta} t} = — \ frac {1} {3} \; \ frac {{\ Delta} [\ text {F} _2]} { {\ Delta} t} [/ латекс]
5.(а) средняя скорость, 0 — 10 с = 0,0375 моль л −1 с −1 ; средняя скорость, 12 — 18 с = 0,0225 моль л −1 с −1 ; (б) мгновенная скорость, 15 с = 0,0500 моль л −1 с −1 ; (c) средняя скорость образования B = 0,0188 моль л -1 с -1 ; мгновенная скорость образования B = 0,0250 моль л −1 с −1
Определение тарифных законов и порядок реагирования
Все химические реакции имеют определенную скорость, которая определяет, насколько быстро реагенты превращаются в продукты.
Химические реакции регулируются двумя факторами: кинетикой и термодинамикой. Термодинамические факторы определяют, произойдет ли реакция, и будет ли она поглощать или выделять энергию во время процесса.
Кинетика означает скорость химической реакции и то, как быстро система достигает равновесия. Кинетика реакции описывается законом кинетической скорости, который определяет скорость на основе константы скорости реакции, концентрации компонентов и порядка реакции.
Это видео знакомит с кинетикой реакции с использованием уравнения скорости скорости и демонстрирует, как определить закон скорости для определенной реакции в лаборатории.
Для общей реакции скорость реакции равна константе скорости, умноженной на концентрации реагентов, каждая из которых повышена до порядка реакции. Константа скорости k является фиксированной для реакции при данной температуре.
Порядки реакций не зависят от стехиометрических коэффициентов. Вместо этого они зависят от механизма реакции и показывают, как скорость связана с концентрацией реагентов.Например, если скорость реакции не меняется при удвоении концентрации «А», то реакция не зависит от концентрации и порядок равен нулю.
Если скорость увеличивается вдвое, когда концентрация реагента «А» удваивается, тогда реакция идет первого порядка по «А». То же самое верно и для реагента «B». Общий порядок реакции — это сумма индивидуальных порядков реакции для каждого реагента.
Во время реакции концентрация реагентов изменяется со временем.Обратите внимание, что основное уравнение скорости не включает время как переменную и может связывать скорость и концентрацию только в определенный момент времени. Однако скорость изменяется по мере протекания реакции и истощения реагентов. Используя закон дифференциальной скорости, можно связать изменение концентрации со временем.
Закон скорости реакции должен быть определен экспериментально, где химическая реакция тщательно контролируется при постоянной температуре, а концентрация реагентов или продуктов измеряется через определенные промежутки времени.Поскольку измерения концентрации производятся в дискретные моменты времени, дифференциальный закон скорости трудно сопоставить с экспериментальными данными.
Интегрирование закона дифференциальной скорости приводит к более простому уравнению, называемому законом интегрированной скорости. Интегрированный закон скорости сравнивает концентрации реагентов в начале реакции и в заданное время.
Уравнение интегрированного закона скорости изменяется в зависимости от порядка реакции. Эти уравнения могут принимать линейный вид y = mx + b.Таким образом, график зависимости концентрации от времени дает линейный график для уравнения нулевого порядка, график натурального логарифма концентрации от времени дает линейный график для уравнения первого порядка и так далее. Подгоняя экспериментальные данные к этим уравнениям, можно легко определить порядок реакции. Затем можно определить константу скорости k, используя наклон линии. Наконец, единицы измерения k меняются в зависимости от порядка реакции. Для реакции нулевого порядка единицы измерения — моль на литр в секунду, для реакции первого порядка единицы — обратные секунды, а для реакции второго порядка единицы — литр на моль в секунду.
Теперь, когда были объяснены основы кинетических законов скорости, давайте посмотрим, как экспериментально определить закон скорости разложения перекиси водорода до воды и кислорода.
В этом эксперименте исследуется каталитическое разложение перекиси водорода над платиновым катализатором.
Сначала приготовьте 5 разведений перекиси водорода, как показано в таблице. В этом случае диапазон концентраций составляет 0,882–0,176 М при использовании 3% или 0,882 М исходного раствора.Дайте растворам уравновеситься до комнатной температуры.
Затем подготовьте реакционный сосуд с помощью пробирки. Сначала определите объем, наполнив водой большую пробирку доверху. Затем вставьте резиновую пробку с одним отверстием, пока она не станет плотно и вода не будет вытекать из отверстия через верх.
Снимите пробку и налейте воду в мерный цилиндр для точного измерения объема. Это объем реакционного сосуда.
Затем налейте 50 мл первого раствора перекиси водорода в пробирку и поместите пробирку в водяную баню с температурой 25 ° C.После уравновешивания добавьте реакционный диск с платиновым покрытием и закройте систему пробкой, соединенной с датчиком давления газа.
Так как одним из продуктов является газообразный кислород, повышение давления в системе используется для измерения увеличения кислорода. Настройте датчик давления для сбора данных по 2 точкам в секунду, затем запустите эксперимент в течение 120 секунд. Должны быть видны пузырьки, поскольку перекись разлагается на газообразный кислород и воду.
По окончании периода реакции сбросьте давление и утилизируйте раствор пероксида.Промойте трубку, затем заполните трубку следующим раствором перекиси водорода. Повторите измерение давления газа для всех растворов.
Постройте график зависимости давления от времени для каждого решения. Давление выделяемого кислорода прямо пропорционально количеству молей кислорода, образовавшихся согласно закону идеального газа. После химической реакции образующиеся моли кислорода можно использовать для расчета молей разложившейся перекиси водорода. Во-первых, предположим, что концентрация перекиси водорода существенно не изменилась в течение короткого периода эксперимента.Таким образом, нанесенные на график данные представляют только начальную область кинетического эксперимента.
Определите наклон каждого набора данных с помощью линейной регрессии. Наклон равен начальной скорости реакции в единицах давления кислорода в секунду.
Затем, график натурального логарифма начальной скорости реакции и натурального логарифма начальной концентрации пероксида. Наклон равен порядку реакции m и приблизительно равен единице. Следовательно, реакция первого порядка.
Скорость каждого испытания выражается в единицах давления в Торр в секунду.Чтобы определить константу скорости, сначала преобразуйте скорость в единицы атмосферы в секунду. Поскольку в водном растворе образовались пузырьки, вычтите давление водяного пара из давления в системе для каждого испытания. Таким образом, новая скорость отражает только давление, обусловленное выделением кислорода.
Примените закон идеального газа, чтобы преобразовать скорость из атмосфер как таковых в моль в секунду для каждого испытания. В соответствии со стехиометрией химической реакции, в два раза больше молей произведенного кислорода, чем молей разложившейся перекиси водорода.Затем используйте реакционный объем для перевода единиц скорости в молярность в секунду.
Определите константы скорости для каждого испытания, разделив скорость в молярности в секунду на начальную концентрацию. В этом эксперименте средняя константа скорости k составляет приблизительно 1,48 x 10-4 в секунду. Реакция первого порядка, известная из графика натурального логарифма — натурального логарифма, показанного ранее. Следовательно, скоростной закон можно записать, как показано.
Теперь, когда вы рассмотрели, как определить закон скорости химической реакции, давайте рассмотрим некоторые области, в которых применяется эта концепция.
Химические реакции используются в синтезе соединений и материалов, используемых в широком спектре научных приложений. Важно понимать скорость реакции на этих этапах синтеза, чтобы контролировать ход реакции.
Например, синтез нанокристаллов и наностержней селенида кадмия проходит через серию химических реакций. Каждая реакция имеет свою собственную дискретную скорость реакции, и поэтому стадия синтеза тщательно контролируется в зависимости от скорости реакции; некоторые медленные, а некоторые очень быстрые.
Закон скорости реакции также можно использовать для описания радиоактивного распада и определения периода полураспада радиоактивного материала. Период полураспада означает время, необходимое для того, чтобы концентрация материала упала до половины от его начальной концентрации.
Радиоактивность следует кинетике первого порядка, что означает, что время, необходимое для распада радиоактивного материала до безопасного уровня, может быть очень хорошо охарактеризовано, что обеспечивает надлежащую транспортировку и хранение радиоактивных материалов и радиоактивных отходов.
Подобно радиоактивным материалам, лекарства также имеют период полураспада и разлагаются в организме. Например, некоторые лекарства имеют высокие константы скорости, что означает, что они быстро разлагаются, и их нужно принимать часто. Знание этой скорости разложения позволяет определить подходящую дозировку, использование и способ доставки.
Вы только что посмотрели, как JoVE рассказала о скорости реакции. Теперь вы должны понимать различные порядки химических реакций, то, как они соотносятся со скоростью химических реакций, и как определить закон скорости для данной химической реакции в лаборатории.
Спасибо за просмотр!
12.1 Скорость химических реакций — Химия 2e
Цели обучения
К концу этого раздела вы сможете:
- Определите скорость химической реакции
- Выведите выражения для скоростей из сбалансированного уравнения данной химической реакции
- Рассчитать скорость реакции по экспериментальным данным
Оценка — это мера того, как какое-то свойство изменяется со временем. Скорость — это привычный показатель, который выражает расстояние, пройденное объектом за заданный промежуток времени.Заработная плата — это ставка, которая представляет собой сумму денег, заработанную человеком, работающим в течение определенного времени. Точно так же скорость химической реакции является мерой того, сколько реагента потребляется или сколько продукта производится в результате реакции за заданный промежуток времени.
Скорость реакции — это изменение количества реагента или продукта в единицу времени. Поэтому скорости реакции определяют путем измерения зависимости от времени некоторого свойства, которое может быть связано с количествами реагента или продукта.Например, скорость реакций, в которых потребляются или образуются газообразные вещества, удобно определять путем измерения изменений объема или давления. Для реакций с участием одного или нескольких окрашенных веществ скорость можно контролировать путем измерения поглощения света. Для реакций с участием водных электролитов скорость можно измерить по изменению проводимости раствора.
Для реагентов и продуктов в растворе их относительные количества (концентрации) удобно использовать для целей выражения скоростей реакции.Например, концентрация перекиси водорода H 2 O 2 в водном растворе медленно изменяется со временем, поскольку он разлагается в соответствии с уравнением:
2h3O2 (водн.) ⟶2h3O (l) + O2 (г) 2h3O2 (водн.) ⟶2h3O (l) + O2 (г)Скорость разложения пероксида водорода можно выразить через скорость изменения его концентрации, как показано здесь:
скорость разложения h3O2 = −изменение концентрации реагента временной интервал = — [h3O2] t2− [h3O2] t1t2 − t1 = −Δ [h3O2] Δtrate of h3O2 = −изменение концентрации реагента временной интервал = — [h3O2] t2− [h3O2] t1t2 − t1 = −Δ [h3O2] ΔtЭто математическое представление изменения концентрации компонентов во времени является выражением скорости реакции.Скобки указывают молярные концентрации, а символ дельта (Δ) указывает «изменение в». Таким образом, [h3O2] t1 [h3O2] t1 представляет собой молярную концентрацию пероксида водорода в определенный момент времени t 1 ; аналогично, [h3O2] t2 [h3O2] t2 представляет собой молярную концентрацию пероксида водорода в более позднее время t 2 ; и Δ [H 2 O 2 ] представляет собой изменение молярной концентрации пероксида водорода во временном интервале Δ t (то есть t 2 — t 1 ).Поскольку концентрация реагента уменьшается по мере протекания реакции, Δ [H 2 O 2 ] является отрицательной величиной. Скорости реакции обычно являются положительными величинами, поэтому это отрицательное изменение концентрации умножается на -1. На рисунке 12.2 представлен пример данных, собранных во время разложения H 2 O 2 .
Рис. 12.2. Скорость разложения H 2 O 2 в водном растворе уменьшается с уменьшением концентрации H 2 O 2 .
Чтобы получить табличные результаты для этого разложения, концентрацию перекиси водорода измеряли каждые 6 часов в течение дня при постоянной температуре 40 ° C. Скорости реакции были рассчитаны для каждого временного интервала путем деления изменения концентрации на соответствующий временной интервал, как показано здесь для первого 6-часового периода:
−Δ [h3O2] Δt = — (0,500 моль / л − 1.000 моль / л) (6,00 ч − 0,00 ч) = 0,0833 моль · л − 1ч − 1 − Δ [h3O2] Δt = — (0,500 моль / л − 1.000 моль / L) (6,00 ч-0,00 ч) = 0.0833 моль · л − 1 · ч − 1Обратите внимание, что скорости реакции меняются со временем, уменьшаясь по мере протекания реакции. Результаты за последние 6 часов дают скорость реакции:
. −Δ [h3O2] Δt = — (0,0625 моль / л − 0,125 моль / л) (24,00 ч − 18,00 час) = 0,010 моль − 1 час − 1 − Δ [h3O2] Δt = — (0,0625 моль / л − 0,125 моль / L) (24,00 ч-18,00 ч) = 0,010 моль-1 ч-1Это поведение указывает на то, что реакция постоянно замедляется со временем. Использование концентраций в начале и в конце периода времени, в течение которого скорость реакции изменяется, приводит к вычислению средней скорости реакции за этот интервал времени.В любое конкретное время скорость, с которой протекает реакция, называется ее мгновенной скоростью. Мгновенная скорость реакции в «нулевой момент времени», когда реакция начинается, является ее начальной скоростью. Рассмотрим аналогию с автомобилем, который замедляется при приближении к знаку остановки. Начальная скорость автомобиля — аналогичная началу химической реакции — будет показанием спидометра в момент, когда водитель начинает нажимать на тормоза ( т 0 ). Несколько мгновений спустя мгновенная скорость в определенный момент — назовем ее t 1 — будет несколько ниже, о чем свидетельствуют показания спидометра в этот момент времени.По прошествии времени мгновенная скорость будет продолжать падать, пока не достигнет нуля, когда машина (или реакция) остановится. В отличие от мгновенной скорости, средняя скорость автомобиля не отображается на спидометре; но его можно рассчитать как отношение пройденного расстояния ко времени, необходимому для полной остановки транспортного средства (Δ t ). Подобно замедляющемуся автомобилю, средняя скорость химической реакции будет находиться где-то между начальной и конечной скоростью.
Мгновенную скорость реакции можно определить одним из двух способов.Если экспериментальные условия позволяют измерять изменения концентрации в течение очень коротких интервалов времени, тогда средние скорости, вычисленные, как описано ранее, обеспечивают достаточно хорошее приближение мгновенных скоростей. В качестве альтернативы может использоваться графическая процедура, которая, по сути, дает результаты, которые были бы получены, если бы были возможны измерения с короткими временными интервалами. На графике зависимости концентрации перекиси водорода от времени мгновенная скорость разложения H 2 O 2 в любой момент времени t задается наклоном прямой линии, касательной к кривой в это время. (Рисунок 12.3). Эти наклоны касательной можно оценить с помощью расчетов, но процедура для этого выходит за рамки данной главы.
Рис. 12.3 На этом графике показан график зависимости концентрации от времени для 1.000 M раствора H 2 O 2 . Скорость в любой момент равна отрицательному значению наклона касательной к кривой в этот момент. Касательные показаны при t = 0 ч («начальная скорость») и t = 12 часов («мгновенная скорость» через 12 часов).
Химия в повседневной жизни
Скорость реакции в анализе: тест-полоски для анализа мочи
Врачи часто используют одноразовые тест-полоски для измерения количества различных веществ в моче пациента (рис. 12.4). Эти тест-полоски содержат различные химические реагенты, встроенные в небольшие подушечки в различных местах вдоль полоски, которые меняют цвет при воздействии достаточных концентраций определенных веществ. В инструкциях по использованию тест-полосок часто подчеркивается, что правильное время считывания имеет решающее значение для получения оптимальных результатов.Такой акцент на времени считывания предполагает, что важными факторами являются кинетические аспекты химических реакций, происходящих на тест-полоске.
Тест на глюкозу в моче основан на двухэтапном процессе, представленном химическими уравнениями, показанными здесь:
C6h22O6 + O2 → катализатор C6h20O6 + h3O2C6h22O6 + O2 → катализатор C6h20O6 + h3O2 2h3O2 + 2I− → катализаторI2 + 2h3O + O22h3O2 + 2I− → катализаторI2 + 2h3O + O2Первое уравнение описывает окисление глюкозы в моче с образованием глюколактона и перекиси водорода.Полученная перекись водорода впоследствии окисляет бесцветный ион йодида с образованием коричневого йода, который можно обнаружить визуально. Некоторые полоски содержат дополнительное вещество, которое вступает в реакцию с йодом, вызывая более отчетливое изменение цвета.
Две показанные выше тестовые реакции по своей природе очень медленные, но их скорость увеличивается за счет специальных ферментов, встроенных в подушечку для тест-полосок. Это пример катализатора , тема которого обсуждается далее в этой главе. Обычной тест-полоске для определения глюкозы в моче требуется около 30 секунд для завершения реакции формирования цвета.Слишком раннее прочтение результата может привести к выводу, что концентрация глюкозы в образце мочи ниже, чем она есть на самом деле (ложноотрицательный результат ). Слишком долгое ожидание для оценки изменения цвета может привести к ложному положительному результату из-за более медленного (не катализируемого) окисления иодид-иона другими веществами, обнаруженными в моче.
Рис. 12.4 Тест-полоски обычно используются для определения наличия определенных веществ в моче человека. Многие тест-полоски имеют несколько подушечек, содержащих различные реагенты, что позволяет обнаруживать несколько веществ на одной полоске.(Источник: Икбал Осман)
Относительные скорости реакции
Скорость реакции может быть выражена как изменение концентрации любого реагента или продукта. Для любой данной реакции все эти выражения скорости просто связаны друг с другом в соответствии со стехиометрией реакции. Скорость общей реакции
можно выразить через уменьшение концентрации A или увеличение концентрации B. Эти два выражения скорости связаны стехиометрией реакции:
скорость = — (1a) (ΔAΔt) = (1b) (ΔBΔt) скорость = — (1a) (ΔAΔt) = (1b) (ΔBΔt)Рассмотрим реакцию, представленную следующим уравнением:
2Nh4 (г) ⟶N2 (г) + 3h3 (г) 2Nh4 (г) ⟶N2 (г) + 3h3 (г)Соотношение между скоростями реакции, выраженными в единицах производства азота и потребления аммиака, например, составляет:
−Δмоль Nh4Δt × 1 мольN22 мольNh4 = ΔmolN2Δt − Δmol Nh4Δt × 1 мольN22 мольNh4 = ΔmolN2ΔtЭто может быть представлено в сокращенном формате, опуская единицы стехиометрического фактора:
−12ΔmolNh4Δt = ΔmolN2Δt − 12ΔmolNh4Δt = ΔmolN2ΔtОбратите внимание, что отрицательный знак был включен в качестве фактора для учета противоположных знаков двух изменений количества (количество реагента уменьшается, а количество продукта увеличивается).Для гомогенных реакций и реагенты, и продукты присутствуют в одном растворе и, таким образом, занимают один и тот же объем, поэтому молярные количества могут быть заменены молярными концентрациями:
−12Δ [Nh4] Δt = Δ [N2] Δt − 12Δ [Nh4] Δt = Δ [N2] ΔtАналогично, скорость образования H 2 в три раза выше скорости образования N 2 , потому что на каждый моль полученного N 2 образуется три моля H 2 .
13Δ [h3] Δt = Δ [N2] Δt13Δ [h3] Δt = Δ [N2] ΔtРисунок 12.5 иллюстрирует изменение концентраций во времени разложения аммиака на азот и водород при 1100 ° C. Наклон касательных линий при t = 500 с показывает, что мгновенные скорости, полученные от всех трех частиц, участвующих в реакции, связаны их стехиометрическими факторами. Например, скорость производства водорода в три раза выше, чем скорость производства азота:
2,91 × 10–6М / с 9,70 × 10–7М / с ≈ 32,91 × 10–6М / с 9,70 × 10–7М / с ≈3 Рисунок 12.5 Изменение концентраций реагента и продуктов реакции 2Nh4⟶N2 + 3h3,2Nh4⟶N2 + 3h3. Скорости изменения трех концентраций связаны стехиометрией реакции, как показано разными наклонами касательных при t = 500 с.Пример 12.1
Выражения для относительных скоростей реакций
Первым этапом производства азотной кислоты является сжигание аммиака: 4Nh4 (г) + 5O2 (г) ⟶4NO (г) + 6h3O (г) 4Nh4 (г) + 5O2 (г) ⟶4NO (г) + 6h3O (г)Напишите уравнения, связывающие скорости потребления реагентов и скорости образования продуктов.
Решение
Учитывая стехиометрию этой гомогенной реакции, скорости потребления реагентов и образования продуктов составляют: −14Δ [Nh4] Δt = −15Δ [O2] Δt = 14Δ [NO] Δt = 16Δ [h3O] Δt − 14Δ [Nh4] Δt = −15Δ [O2] Δt = 14Δ [NO] Δt = 16Δ [h3O] ΔtПроверьте свои знания
Скорость образования Br 2 составляет 6,0 × 10 −6 моль / л / с в реакции, описываемой следующим чистым ионным уравнением: 5Br− + BrO3− + 6H + ⟶3Br2 + 3h3O5Br− + BrO3− + 6H + ⟶3Br2 + 3h3OНапишите уравнения, связывающие скорости потребления реагентов и скорости образования продуктов.
Ответ:
−15Δ [Br−] Δt = −Δ [BrO3−] Δt = −16Δ [H +] Δt = 13Δ [Br2] Δt = 13Δ [h3O] Δt − 15Δ [Br−] Δt = −Δ [BrO3−] Δt = −16Δ [H +] Δt = 13Δ [Br2] Δt = 13Δ [h3O] Δt
Пример 12.2
Выражения для скорости реакции разложения H
2 O 2 График на рисунке 12.3 показывает скорость разложения H 2 O 2 во времени: 2h3O2⟶2h3O + O22h3O2⟶2h3O + O2 На основании этих данных, мгновенная скорость разложения H 2 O 2 при t = 11.1 час определяется как
3,20 × × 10 −2 моль / л / ч, то есть:
Какова мгновенная скорость производства H 2 O и O 2 ?
Решение
Стехиометрия реакции показывает, что −12Δ [h3O2] Δt = 12Δ [h3O] Δt = Δ [O2] Δt − 12Δ [h3O2] Δt = 12Δ [h3O] Δt = Δ [O2] ΔtСледовательно:
12 × 3,20 × 10–2 моль – 1 ч – 1 = Δ [O2] Δt12 × 3,20 × 10–2 моль – 1 ч – 1 = Δ [O2] Δtи
Δ [O2] Δt = 1,60 × 10−2 моль-1 · ч − 1Δ [O2] Δt = 1.60 × 10−2моль · л − 1 · ч − 1Проверьте свои знания
Если скорость разложения аммиака, NH 3 , при 1150 K составляет 2,10 × × 10 −6 моль / л / с, какова скорость образования азота и водорода?Ответ:
1,05 × × 10 −6 моль / л / с, N 2 и 3,15 × × 10 −6 моль / л / с, H 2 .
12.1 Скорость химических реакций — Химия 112 — Главы 12-17 OpenStax General Chemistry
Цели обучения
К концу этого раздела вы сможете:
- Определите скорость химической реакции
- Выведите выражения для скоростей из сбалансированного уравнения данной химической реакции
- Рассчитать скорость реакции по экспериментальным данным
Оценка — это мера того, как какое-то свойство изменяется со временем.Скорость — это привычный показатель, который выражает расстояние, пройденное объектом за заданный промежуток времени. Заработная плата — это ставка, которая представляет собой сумму денег, заработанную человеком, работающим в течение определенного времени. Точно так же скорость химической реакции является мерой того, сколько реагента потребляется или сколько продукта производится в результате реакции за заданный промежуток времени.
Скорость реакции — это изменение количества реагента или продукта в единицу времени. Поэтому скорости реакции определяют путем измерения зависимости от времени некоторого свойства, которое может быть связано с количествами реагента или продукта.Например, скорость реакций, в которых потребляются или образуются газообразные вещества, удобно определять путем измерения изменений объема или давления. Для реакций с участием одного или нескольких окрашенных веществ скорость можно контролировать путем измерения поглощения света. Для реакций с участием водных электролитов скорость можно измерить по изменению проводимости раствора.
Для реагентов и продуктов в растворе их относительные количества (концентрации) удобно использовать для целей выражения скоростей реакции.Если мы измерим концентрацию перекиси водорода, H 2 O 2 , в водном растворе, мы обнаружим, что она медленно изменяется со временем, поскольку H 2 O 2 разлагается в соответствии с уравнением:
[латекс] 2 \ text {H} _2 \ text {O} _2 (aq) \; {\ longrightarrow} \; 2 \ text {H} _2 \ text {O} (l) \; + \; \ text {O} _2 (г) [/ латекс]
Скорость разложения пероксида водорода можно выразить через скорость изменения его концентрации, как показано здесь:
[латекс] \ begin {array} {r @ {{} = {}} l} \ text {rate \; of \; разложение \; of \; H} _2 \ text {O} _2 & — \ frac { \ text {изменение \; в \; концентрация \; \; реагента}} {\ text {время \; интервал}} \\ [0.5em] & — \ frac {[\ text {H} _2 \ text {O} _2] _ {t_2} \; — \; [\ text {H} _2 \ text {O} _2] _ {t_1}} { t_2 \; — \; t_1} \\ [0.5em] & — \ frac {{\ Delta} [\ text {H} _2 \ text {O} _2]} {{\ Delta} t} \ end {array} [/ латекс]
Это математическое представление изменения концентрации компонентов с течением времени является выражением скорости для реакции. Скобки указывают молярные концентрации, а символ дельта (Δ) указывает «изменение в». Таким образом, [латекс] [\ text {H} _2 \ text {O} _2] _ {t_1} [/ latex] представляет молярную концентрацию перекиси водорода в определенный момент времени t 1 ; аналогично [латекс] [\ text {H} _2 \ text {O} _2] _ {t_2} [/ latex] представляет молярную концентрацию перекиси водорода в более позднее время t 2 ; и Δ [H 2 O 2 ] представляет собой изменение молярной концентрации пероксида водорода в течение интервала времени Δ t (то есть t 2 — t 1 ).Поскольку концентрация реагента уменьшается по мере протекания реакции, Δ [H 2 O 2 ] является отрицательной величиной; мы ставим отрицательный знак перед выражением, потому что скорость реакции, по соглашению, является положительной величиной. На рисунке 1 приведен пример данных, собранных при разложении H 2 O 2 .
Рис. 1. Скорость разложения H 2 O 2 в водном растворе уменьшается с уменьшением концентрации H 2 O 2 .Чтобы получить табличные результаты для этого разложения, концентрацию перекиси водорода измеряли каждые 6 часов в течение дня при постоянной температуре 40 ° C. Скорости реакции были рассчитаны для каждого временного интервала путем деления изменения концентрации на соответствующий временной интервал, как показано здесь для первого 6-часового периода:
[латекс] \ frac {- {\ Delta} [\ text {H} _2 \ text {O} _2]} {{\ Delta} t} = \ frac {- (0.500 \; \ text {mol / L} \; — \; 1.000 \; \ text {mol / L})} {(6.00 \; \ text {h} \; — \; 0.{-1} [/ латекс]
Такое поведение указывает на то, что реакция постоянно замедляется со временем. Использование концентраций в начале и в конце периода времени, в течение которого скорость реакции изменяется, приводит к вычислению средней скорости для реакции за этот интервал времени. В любое конкретное время скорость, с которой протекает реакция, известна как ее мгновенная скорость . Мгновенная скорость реакции в «нулевой момент времени», когда реакция начинается, равна ее начальной скорости .Рассмотрим аналогию с автомобилем, который замедляется при приближении к знаку остановки. Начальная скорость транспортного средства — аналогично началу химической реакции — будет показанием спидометра в момент, когда водитель начинает нажимать на тормоза ( t 0 ). Несколько мгновений спустя мгновенная скорость в определенный момент — назовем ее t 1 — будет несколько ниже, о чем свидетельствуют показания спидометра в этот момент времени. По прошествии времени мгновенная скорость будет продолжать падать, пока не достигнет нуля, когда машина (или реакция) остановится.В отличие от мгновенной скорости, средняя скорость автомобиля не отображается на спидометре; но его можно рассчитать как отношение пройденного расстояния ко времени, необходимому для полной остановки транспортного средства (Δ t ). Подобно замедляющемуся автомобилю, средняя скорость химической реакции будет находиться где-то между начальной и конечной скоростью.
Мгновенную скорость реакции можно определить одним из двух способов. Если экспериментальные условия позволяют измерять изменения концентрации в течение очень коротких интервалов времени, тогда средние скорости, вычисленные, как описано ранее, обеспечивают достаточно хорошее приближение мгновенных скоростей.В качестве альтернативы может использоваться графическая процедура, которая, по сути, дает результаты, которые были бы получены, если бы были возможны измерения с короткими временными интервалами. Если мы построим график зависимости концентрации перекиси водорода от времени, мгновенная скорость разложения H 2 O 2 в любой момент времени t будет выражена наклоном прямой линии, касательной к кривой в это время ( Фигура 2). Мы можем использовать исчисление для оценки наклона таких касательных, но процедура для этого выходит за рамки этой главы.
Рис. 2. На этом графике показан график зависимости концентрации от времени для 1.000 M раствора H 2 O 2 . Скорость в любой момент равна величине, противоположной наклону линии, касательной к этой кривой в этот момент. Касательные показаны при t = 0 ч («начальная скорость») и при t = 10 ч («мгновенная скорость» в это конкретное время).Скорость реакции при анализе: тест-полоски для анализа мочи
Врачи часто используют одноразовые тест-полоски для измерения количества различных веществ в моче пациента (рис. 3).Эти тест-полоски содержат различные химические реагенты, встроенные в небольшие подушечки в различных местах вдоль полоски, которые меняют цвет при воздействии достаточных концентраций определенных веществ. В инструкциях по использованию тест-полосок часто подчеркивается, что правильное время считывания имеет решающее значение для получения оптимальных результатов. Такой акцент на времени считывания предполагает, что важными факторами являются кинетические аспекты химических реакций, происходящих на тест-полоске. {-} \; {\ xrightarrow [\ text {катализатор}] {}} \; \ текст {I} _2 \; + \; 2 \ text {H} _2 \ text {O} \; + \; \ text {O} _2 [/ latex]
Первое уравнение описывает окисление глюкозы в моче с образованием глюколактона и перекиси водорода.Полученная перекись водорода впоследствии окисляет бесцветный ион йодида с образованием коричневого йода, который можно обнаружить визуально. Некоторые полоски содержат дополнительное вещество, которое вступает в реакцию с йодом, вызывая более отчетливое изменение цвета.
Две показанные выше тестовые реакции по своей природе очень медленные, но их скорость увеличивается за счет специальных ферментов, встроенных в подушечку для тест-полосок. Это пример катализатора , тема которого обсуждается далее в этой главе. Обычной тест-полоске для определения глюкозы в моче требуется около 30 секунд для завершения реакции формирования цвета.Слишком раннее прочтение результата может привести к заключению, что концентрация глюкозы в образце мочи ниже, чем она есть на самом деле (ложноотрицательный результат ). Слишком долгое ожидание для оценки изменения цвета может привести к ложному положительному результату из-за более медленного (не катализируемого) окисления йодид-иона другими веществами, обнаруженными в моче.
Рис. 3. Тест-полоски обычно используются для определения наличия определенных веществ в моче человека. Многие тест-полоски имеют несколько подушечек, содержащих различные реагенты, что позволяет обнаруживать несколько веществ на одной полоске.(Источник: Икбал Осман)Скорость реакции может быть выражена через изменение количества любого реагента или продукта и может быть просто получена из стехиометрии реакции. Рассмотрим реакцию, представленную следующим уравнением:
[латекс] 2 \ text {NH} _3 (g) \; {\ longrightarrow} \; \ text {N} _2 (g) \; + \; 3 \ text {H} _2 (g) [/ latex]
Стехиометрические коэффициенты, полученные из этого уравнения, могут использоваться для связи скоростей реакции таким же образом, как они используются для соответствующих количеств реагента и продукта.Соотношение между скоростями реакции, выраженными в единицах производства азота и потребления аммиака, например, составляет:
[латекс] — \; \ frac {{\ Delta} \ text {mol \; NH} _3} {{\ Delta} t} \; \ times \; \ frac {1 \; \ text {mol \; N } _2} {2 \; \ text {mol \; NH} _3} = \ frac {{\ Delta} \ text {mol \; N} _2} {{\ Delta} t} [/ latex]
Мы можем выразить это проще, не показывая единиц стехиометрического фактора:
[латекс] — \; \ frac {1} {2} \; \ frac {{\ Delta} \ text {mol \; NH} _3} {{\ Delta} t} = \ frac {{\ Delta} \ текст {mol \; N} _2} {{\ Delta} t} [/ latex]
Обратите внимание, что был добавлен отрицательный знак для учета противоположных знаков двух изменений количества (количество реагента уменьшается, а количество продукта увеличивается).Если реагенты и продукты присутствуют в одном растворе, молярные количества могут быть заменены на концентрации:
[латекс] — \; \ frac {1} {2} \; \ frac {{\ Delta} [\ text {NH} _3]} {{\ Delta} t} = \ frac {{\ Delta} [\ текст {N} _2]} {{\ Delta} t} [/ latex]
Точно так же скорость образования H 2 в три раза превышает скорость образования N 2 , потому что три моля H 2 образуются за время, необходимое для образования одного моля N 2 :
[латекс] \ frac {1} {3} \; \ frac {{\ Delta} [\ text {H} _2]} {{\ Delta} t} = \ frac {{\ Delta} [\ text {N } _2]} {{\ Delta} t} [/ latex]
На рис. 4 показано изменение концентраций во времени разложения аммиака на азот и водород при 1100 ° C.{-6} \; M / \ text {s}} \; {\ приблизительно} \; 3 [/ латекс]
Рисунок 4. На этом графике показаны изменения концентраций реагентов и продуктов во время реакции 2NH 3 → 3N 2 + H 2 . Скорости изменения трех концентраций связаны их стехиометрическими факторами, как показано разными наклонами касательных при t = 500 с.Таким образом, для химической реакции:
aA + bB → cC + dD
скорость реакции может быть выражена как:
[латекс] \ text {скорость реакции} = — \ frac {1} {a} \; \ frac {{\ Delta} [A]} {{\ Delta} t} = — \ frac {1} {b } \; \ frac {{\ Delta} [B]} {{\ Delta} t} = \ frac {1} {c} \; \ frac {{\ Delta} [C]} {{\ Delta} t} = \ frac {1} {d} \; \ frac {{\ Delta} [D]} {{\ Delta} t} [/ latex]
Пример 1
Выражения для относительных скоростей реакций
Первым этапом производства азотной кислоты является сжигание аммиака:
[латекс] 4 \ text {NH} _3 (g) \; + \; 5 \ text {O} _2 (g) \; {\ longrightarrow} \; 4 \ text {NO} (g) \; + \ ; 6 \ text {H} _2 \ text {O} (g) [/ latex]
Напишите уравнения, связывающие скорости потребления реагентов и скорости образования продуктов.
Раствор
Учитывая стехиометрию этой гомогенной реакции, скорости расходования реагентов и образования продуктов составляют:
[латекс] — \ frac {1} {4} \; \ frac {{\ Delta} [\ text {NH} _3]} {{\ Delta} t} = — \ frac {1} {5} \; \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} = \ frac {1} {4} \; \ frac {{\ Delta} [\ text {NO}]} { {\ Delta} t} = \ frac {1} {6} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O}]} {{\ Delta} t} [/ latex]
Пример 2
Выражения скорости реакции для разложения H 2 O 2
График на рисунке 2 показывает скорость разложения H 2 O 2 во времени:
[латекс] 2 \ text {H} _2 \ text {O} _2 \; {\ longrightarrow} \; 2 \ text {H} _2 \ text {O} \; + \; \ text {O} _2 [/ латекс]
На основании этих данных, мгновенная скорость разложения H 2 O 2 при t = 11.{-1} [/ латекс]
Какова мгновенная скорость производства H 2 O и O 2 ?
Раствор
Используя стехиометрию реакции, мы можем определить, что:
[латекс] — \ frac {1} {2} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O} _2]} {{\ Delta} t} = \ frac {1} {2} \; \ frac {{\ Delta} [\ text {H} _2 \ text {O}]} {{\ Delta} t} = \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} [/ латекс]
Следовательно:
[латекс] \ frac {1} {2} \; \ times \; 3. {- 1} = \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} [/ latex]
и
[латекс] \ frac {{\ Delta} [\ text {O} _2]} {{\ Delta} t} = 1.{-1} [/ латекс]
Это означает, что если мы знаем скорость изменения одного химического вещества (реагента или продукта) в реакции, мы сможем вычислить скорость изменения для всех других химикатов.
Скорость реакции может быть выражена либо через уменьшение количества реагента, либо через увеличение количества продукта в единицу времени. Соотношения между различными выражениями скорости для данной реакции выводятся непосредственно из стехиометрических коэффициентов уравнения, представляющего реакцию.
- относительная скорость реакции для [латекса] a \ text {A} \; {\ longrightarrow} \; b \ text {B} = — \ frac {1} {a} \; \ frac {{\ Delta} [\ текст {A}]} {{\ Delta} t} = \ frac {1} {b} \; \ frac {{\ Delta} [\ text {B}]} {{\ Delta} t} [/ latex]
Озон разлагается до кислорода согласно уравнению [латекс] 2 \ text {O} _3 (g) \; {\ longrightarrow} \; 3 \ text {O} _2 (g) [/ latex]. Напишите уравнение, связывающее выражения скорости этой реакции через исчезновение O 3 и образование кислорода.
В ядерной промышленности трифторид хлора используется для получения гексафторида урана, летучего соединения урана, используемого для разделения изотопов урана. Трифторид хлора получают по реакции [латекс] \ text {Cl} _2 (g) \; + \; 3 \ text {F} _2 (g) \; {\ longrightarrow} \; 2 \ text {ClF} _3 ( г) [/ латекс]. Напишите уравнение, связывающее выражения скорости этой реакции с точки зрения исчезновения Cl 2 и F 2 и образования ClF 3 .
Исследование скорости димеризации C 4 H 6 дало данные, представленные в таблице:
[латекс] 2 \ text {C} _4 \ text {H} _6 \; {\ longrightarrow} \; \ text {C} _8 \ text {H} _ {12} [/ latex]
| Время (с) | 0 | 1600 | 3200 | 4800 | 6200 |
| [C 4 H 6 ] ( M ) | 1.00 × 10 −2 | 5,04 × 10 −3 | 3,37 × 10 −3 | 2,53 × 10 −3 | 2,08 × 10 −3 |
| Таблица 1. | |||||
(a) Определите среднюю скорость димеризации от 0 до 1600 с и от 1600 до 3200 с.
(b) Оцените мгновенную скорость димеризации при 3200 с по графику зависимости времени от [C 4 H 6 ].Какие единицы этой ставки?
(c) Определите среднюю скорость образования C 8 H 12 за 1600 с и мгновенную скорость образования через 3200 с из скоростей, найденных в частях (a) и (b).
Исследование скорости реакции, представленной как [латекс] 2A \; {\ longrightarrow} \; B [/ latex], дало следующие данные:
| Время (с) | 0,0 | 5,0 | 10,0 | 15,0 | 20,0 | 25.0 | 35,0 |
| [ A ] ( M ) | 1,00 | 0,952 | 0,625 | 0,465 | 0,370 | 0,308 | 0,230 |
| Таблица 2. | |||||||
(a) Определите среднюю скорость исчезновения A от 0,0 до 10,0 с и от 10,0 до 20,0 с.
(b) Оцените мгновенную скорость исчезновения A через 15.{+} (aq) \; {\ longrightarrow} \; 3 \ text {Br} _2 (aq) \; + \; 3 \ text {H} _2 \ text {O} (l) [/ latex]
Если скорость исчезновения Br — ( водн. ) в определенный момент реакции составляет 3,5 × 10 −4 M с −1 , то какова скорость появления Br 2 ( водн ) в тот момент?
Глоссарий
- средняя оценка
- скорость химической реакции, вычисляемая как отношение измеренного изменения количества или концентрации вещества к интервалу времени, в течение которого это изменение произошло
- начальная ставка
- мгновенная скорость химической реакции при т = 0 с (сразу после начала реакции)
- мгновенная скорость
- скорость химической реакции в любой момент времени, определяемая наклоном касательной к графику концентрации как функция времени
- скорость реакции
- Мера скорости, с которой протекает химическая реакция
- скорость выражения
- математическое представление, связывающее скорость реакции с изменениями количества, концентрации или давления реагентов или продуктов в единицу времени
Решения
Ответы на упражнения в конце главы по химии
1.Мгновенная скорость — это скорость реакции в любой конкретный момент времени, период времени, который настолько короткий, что концентрации реагентов и продуктов изменяются на незначительную величину. Начальная скорость — это мгновенная скорость реакции, когда она начинается (когда продукт только начинает образовываться). Средняя скорость — это средняя мгновенная скорость за период времени.
3. [латекс] \ text {rate} = + \ frac {1} {2} \; \ frac {{\ Delta} [\ text {CIF} _3]} {{\ Delta} t} = — \ frac {{\ Delta} [\ text {Cl} _2]} {{\ Delta} t} = — \ frac {1} {3} \; \ frac {{\ Delta} [\ text {F} _2]} { {\ Delta} t} [/ латекс]
5.(а) средняя скорость, 0 — 10 с = 0,0375 моль л −1 с −1 ; средняя скорость, 12 — 18 с = 0,0225 моль л −1 с −1 ; (б) мгновенная скорость, 15 с = 0,0500 моль л −1 с −1 ; (c) средняя скорость образования B = 0,0188 моль л -1 с -1 ; мгновенная скорость образования B = 0,0250 моль л −1 с −1
.
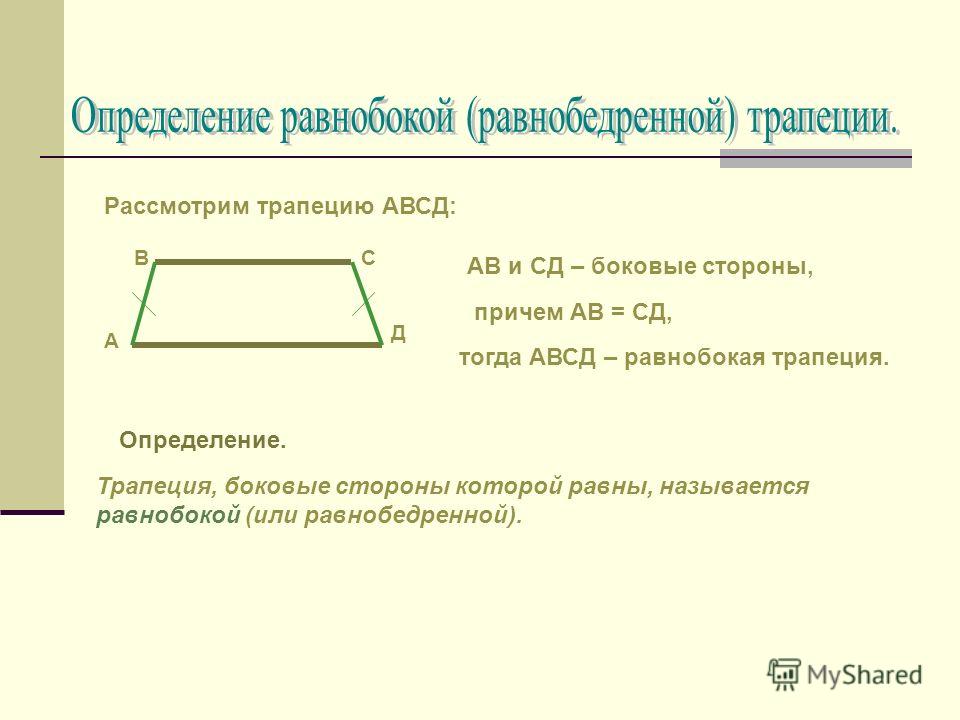 Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.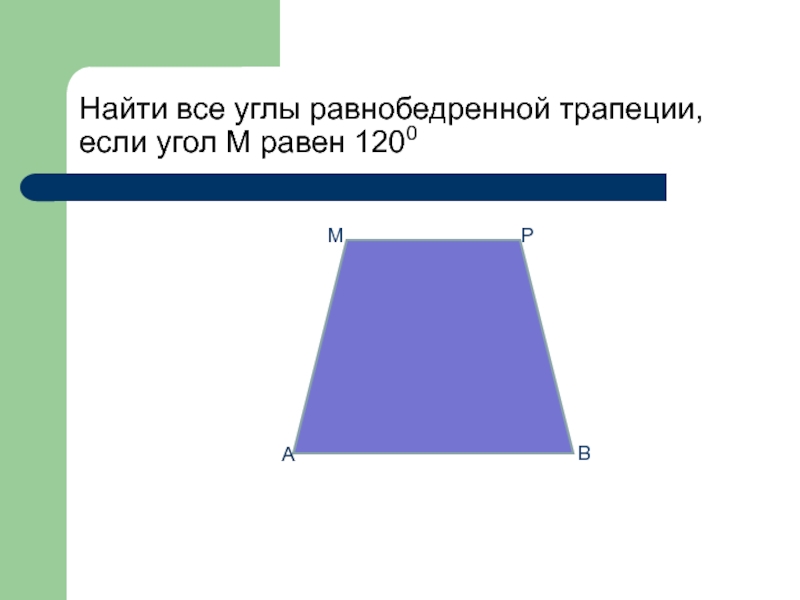

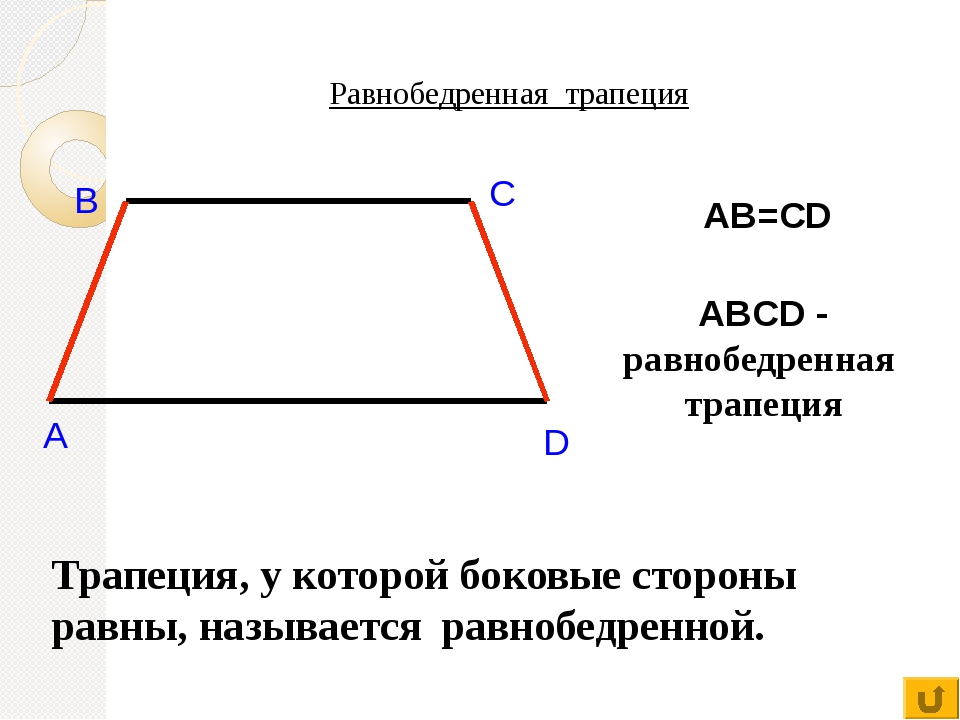

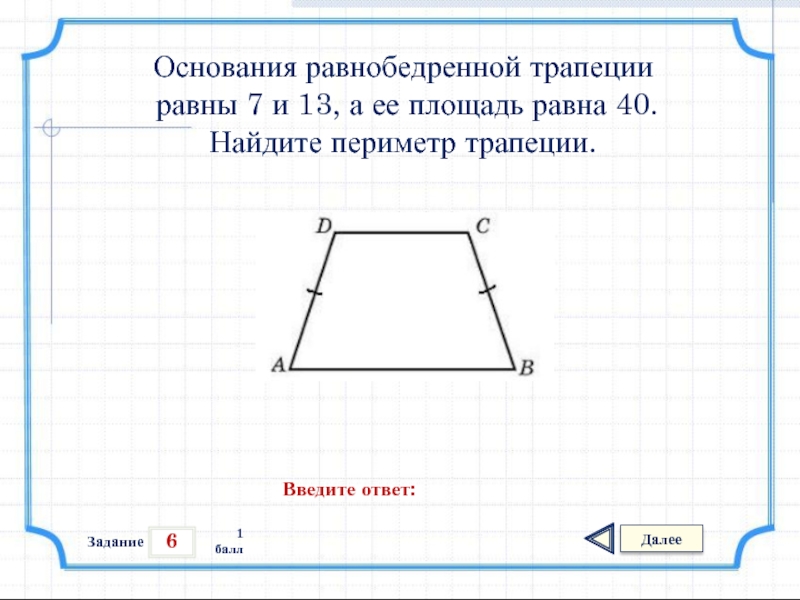 Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.  Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.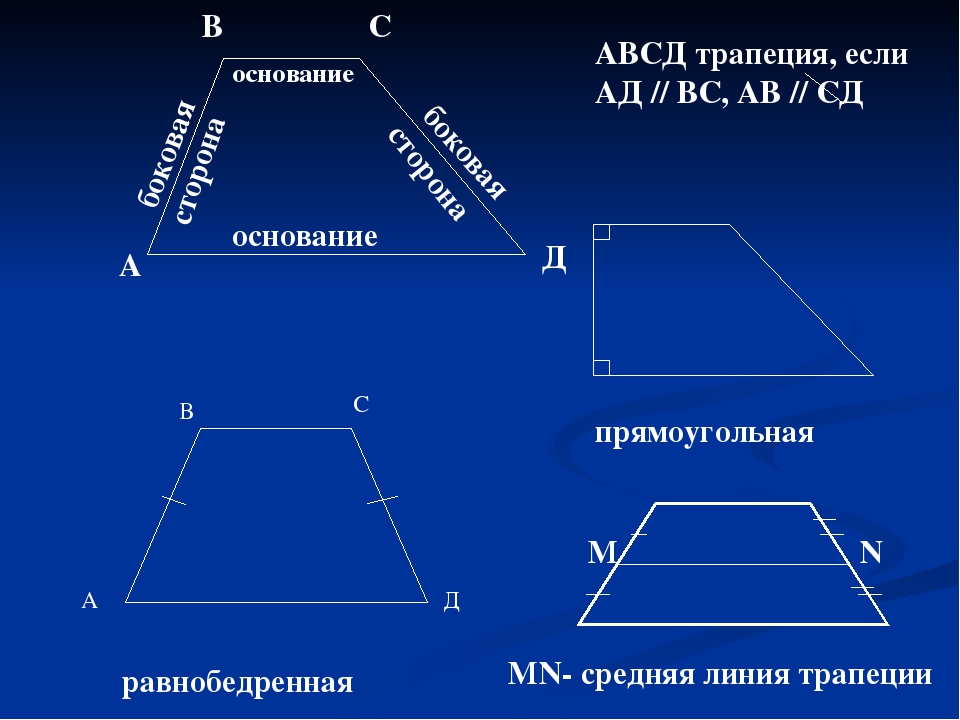
 Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны. И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
 Радиус окружности можно вычислить по формуле: r = √ab.
Радиус окружности можно вычислить по формуле: r = √ab.


 8. Как вычислить площадь фигуры с помощью определённого интеграла?
8. Как вычислить площадь фигуры с помощью определённого интеграла?
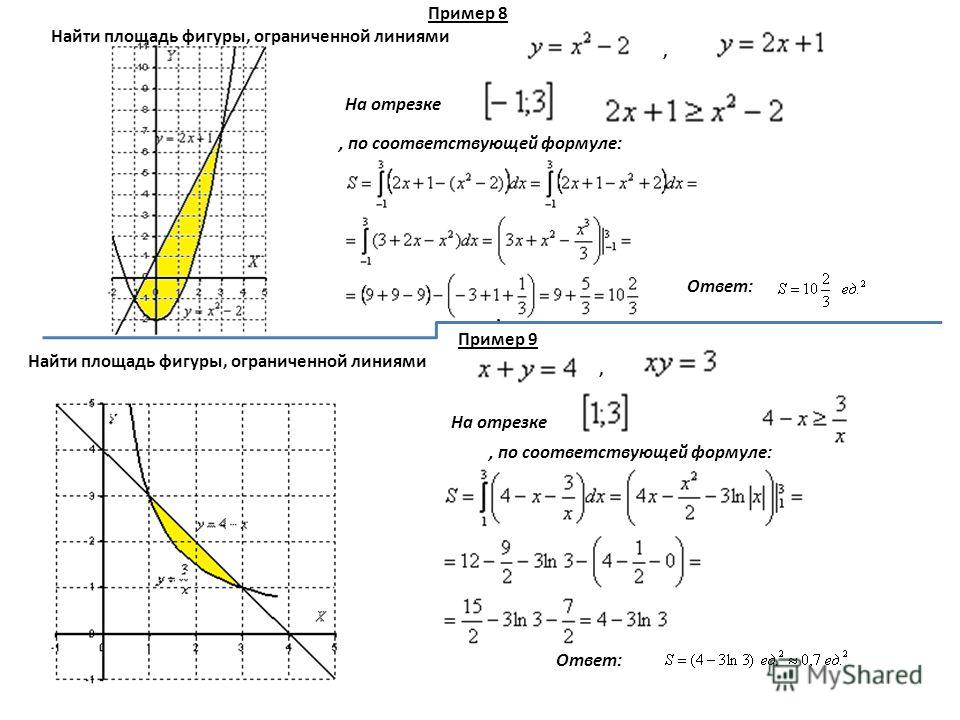 На отрезке график функции расположен над осью , поэтому искомая площадь:
На отрезке график функции расположен над осью , поэтому искомая площадь: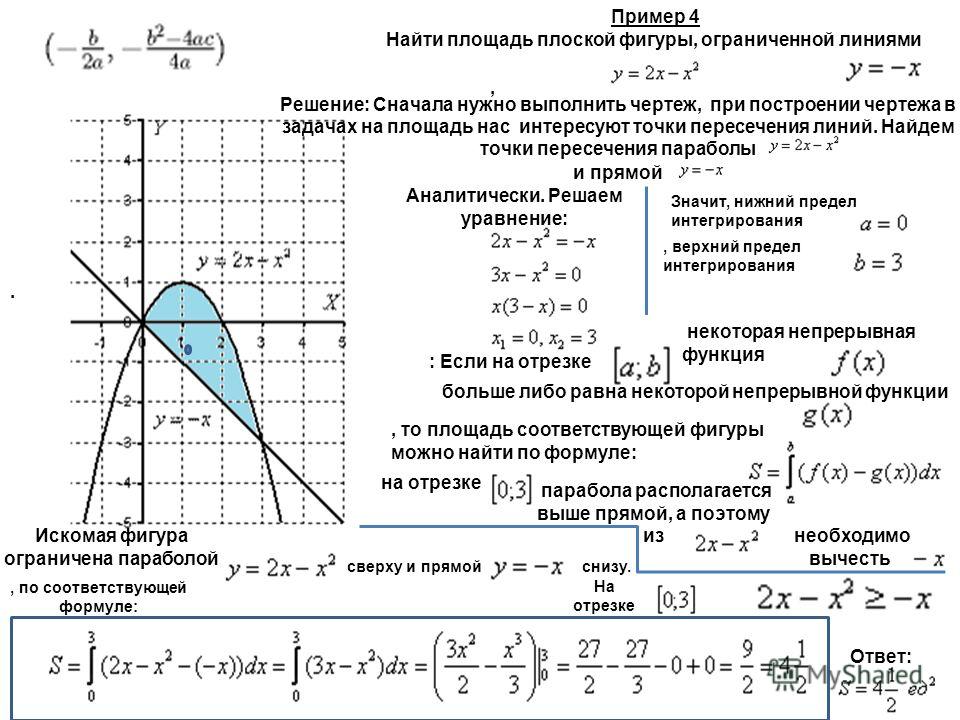
 Составим и решим уравнение:
Составим и решим уравнение:
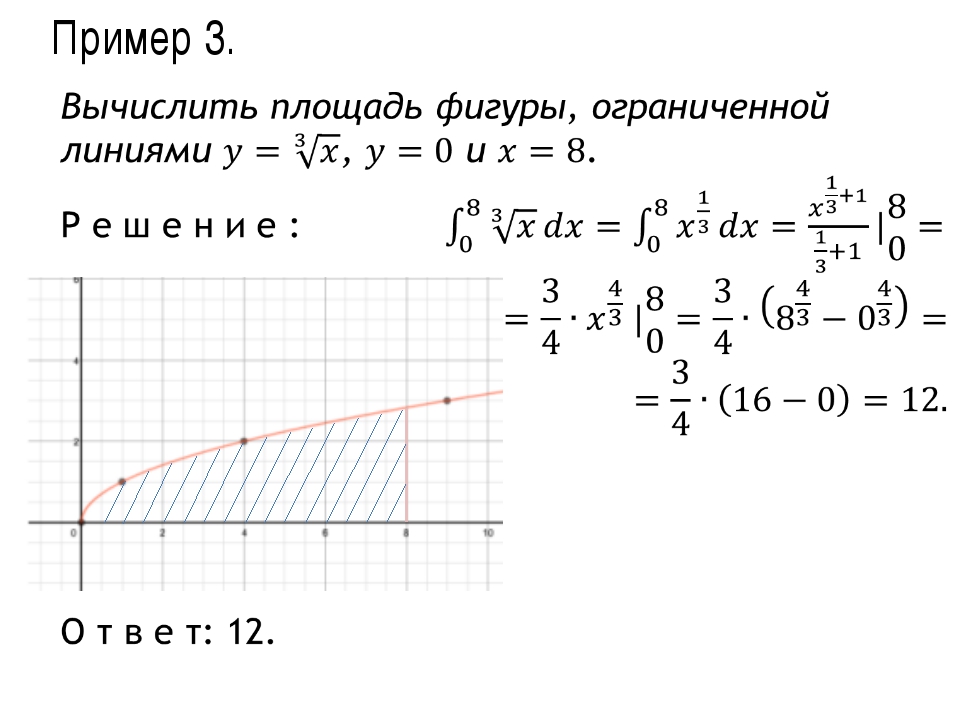 Вот реальный случай из жизни:
Вот реальный случай из жизни:
 В таких случаях следует использовать аналитический метод, составляем уравнение:
В таких случаях следует использовать аналитический метод, составляем уравнение: Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.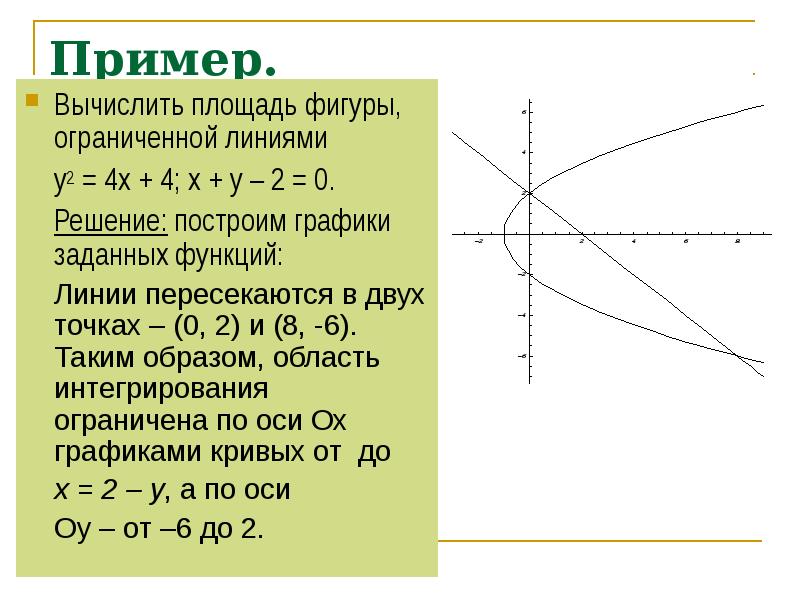
 Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление площади фигуры ограниченной линиями,вычисление площади фигуры ограниченной линиями онлайн,вычислите площадь фигуры,вычислите площадь фигуры ограниченной,вычислите площадь фигуры ограниченной линиями,вычислите площадь фигуры ограниченной линиями y,вычислите площадь фигуры ограниченной линиями y 0 x 1 y x,вычислите площадь фигуры ограниченной линиями онлайн,вычислите площадь фигуры ограниченной линиями онлайн решение,вычислите площадь фигуры ограниченной линиями у 1 x y 2 x 2,вычислить онлайн площадь ограниченную линиями,вычислить площади фигур ограниченных линиями,вычислить площадь ограниченную линиями,вычислить площадь ограниченную линиями онлайн,вычислить площадь плоской фигуры ограниченной заданными кривыми онлайн,вычислить площадь плоской фигуры ограниченной линиями,вычислить площадь плоской фигуры ограниченной линиями онлайн с решением,вычислить площадь фигур ограниченных линиями онлайн,вычислить площадь фигуры,вычислить площадь фигуры ограниченной,вычислить площадь фигуры ограниченной графиками функций,вычислить площадь фигуры ограниченной графиками функций онлайн,вычислить площадь фигуры ограниченной графиками функций онлайн решение,вычислить площадь фигуры ограниченной линиями,вычислить площадь фигуры ограниченной линиями y,вычислить площадь фигуры ограниченной линиями y x 2 1 y x 1,вычислить площадь фигуры ограниченной линиями y x 2 y 2 x,вычислить площадь фигуры ограниченной линиями y x 2 y x,вычислить площадь фигуры ограниченной линиями онлайн,вычислить площадь фигуры ограниченной линиями онлайн калькулятор,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с графиком,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с решением,вычислить площадь фигуры ограниченной линиями онлайн подробное решение,вычислить площадь фигуры ограниченной линиями онлайн с решением калькулятор,вычислить площадь фигуры ограниченной линиями примеры решения,вычислить площадь фигуры ограниченной указанными линиями сделать чертеж,вычислить площадь фигуры онлайн,заштрихуй фигуры ограниченные двумя линиями,заштрихуй фигуры ограниченные линиями,как найти площадь фигуры ограниченной графиками функций,как найти площадь фигуры ограниченной линиями,калькулятор вычислить площадь фигуры ограниченной линиями онлайн с решением,калькулятор онлайн площадь фигуры,найдите площадь плоской фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями y 5 x 2 y 1,найдите площадь фигуры ограниченной линиями y x 2 1 y 1 x,найдите площадь фигуры ограниченной линиями онлайн,найдите площадь фигуры ограниченной линиями онлайн калькулятор,найдите площадь фигуры ограниченной указанными линиями,найти площадь криволинейной трапеции ограниченной линиями онлайн,найти площадь криволинейной трапеции онлайн,найти площадь области ограниченной линиями онлайн,найти площадь ограниченной фигуры,найти площадь ограниченную линиями,найти площадь ограниченную линиями онлайн калькулятор,найти площадь плоской фигуры ограниченной линиями,найти площадь плоской фигуры ограниченной линиями онлайн,найти площадь фигуры,найти площадь фигуры ограниченной,найти площадь фигуры ограниченной графиками функций,найти площадь фигуры ограниченной кривыми,найти площадь фигуры ограниченной линиями,найти площадь фигуры ограниченной линиями онлайн,найти площадь фигуры ограниченной линиями онлайн калькулятор,найти площадь фигуры ограниченной линиями онлайн калькулятор подробно,найти площадь фигуры ограниченной линиями онлайн решение,найти площадь фигуры ограниченной линиями онлайн с подробным решением,найти площадь фигуры ограниченной линиями примеры решения,найти площадь фигуры ограниченной линиями с помощью определенного интеграла сделать иллюстрацию,найти площадь фигуры ограниченной указанными линиями,найти площадь фигуры онлайн,нахождение площади фигуры ограниченной линиями,нахождение площади фигуры ограниченной линиями онлайн,онлайн вычисление площади фигуры ограниченной линиями,онлайн вычислить площадь фигуры ограниченной графиками функций онлайн,онлайн калькулятор площадь фигуры ограниченной линиями,онлайн нахождение площади фигуры ограниченной линиями,онлайн площадь фигуры,площадь криволинейной трапеции онлайн,площадь ограниченная линиями,площадь плоской фигуры ограниченной линиями онлайн,площадь под графиком,площадь фигуры ограниченной графиками функций,площадь фигуры ограниченной линиями,площадь фигуры ограниченной линиями онлайн,площадь фигуры ограниченной линиями онлайн калькулятор,площадь фигуры онлайн,построить фигуру ограниченную линиями онлайн,сделайте чертеж и вычислите площадь фигуры ограниченной данными линиями,фигуры ограниченные двумя линиями,фигуры ограниченные линиями.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление площади фигуры ограниченной линиями,вычисление площади фигуры ограниченной линиями онлайн,вычислите площадь фигуры,вычислите площадь фигуры ограниченной,вычислите площадь фигуры ограниченной линиями,вычислите площадь фигуры ограниченной линиями y,вычислите площадь фигуры ограниченной линиями y 0 x 1 y x,вычислите площадь фигуры ограниченной линиями онлайн,вычислите площадь фигуры ограниченной линиями онлайн решение,вычислите площадь фигуры ограниченной линиями у 1 x y 2 x 2,вычислить онлайн площадь ограниченную линиями,вычислить площади фигур ограниченных линиями,вычислить площадь ограниченную линиями,вычислить площадь ограниченную линиями онлайн,вычислить площадь плоской фигуры ограниченной заданными кривыми онлайн,вычислить площадь плоской фигуры ограниченной линиями,вычислить площадь плоской фигуры ограниченной линиями онлайн с решением,вычислить площадь фигур ограниченных линиями онлайн,вычислить площадь фигуры,вычислить площадь фигуры ограниченной,вычислить площадь фигуры ограниченной графиками функций,вычислить площадь фигуры ограниченной графиками функций онлайн,вычислить площадь фигуры ограниченной графиками функций онлайн решение,вычислить площадь фигуры ограниченной линиями,вычислить площадь фигуры ограниченной линиями y,вычислить площадь фигуры ограниченной линиями y x 2 1 y x 1,вычислить площадь фигуры ограниченной линиями y x 2 y 2 x,вычислить площадь фигуры ограниченной линиями y x 2 y x,вычислить площадь фигуры ограниченной линиями онлайн,вычислить площадь фигуры ограниченной линиями онлайн калькулятор,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с графиком,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с решением,вычислить площадь фигуры ограниченной линиями онлайн подробное решение,вычислить площадь фигуры ограниченной линиями онлайн с решением калькулятор,вычислить площадь фигуры ограниченной линиями примеры решения,вычислить площадь фигуры ограниченной указанными линиями сделать чертеж,вычислить площадь фигуры онлайн,заштрихуй фигуры ограниченные двумя линиями,заштрихуй фигуры ограниченные линиями,как найти площадь фигуры ограниченной графиками функций,как найти площадь фигуры ограниченной линиями,калькулятор вычислить площадь фигуры ограниченной линиями онлайн с решением,калькулятор онлайн площадь фигуры,найдите площадь плоской фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями y 5 x 2 y 1,найдите площадь фигуры ограниченной линиями y x 2 1 y 1 x,найдите площадь фигуры ограниченной линиями онлайн,найдите площадь фигуры ограниченной линиями онлайн калькулятор,найдите площадь фигуры ограниченной указанными линиями,найти площадь криволинейной трапеции ограниченной линиями онлайн,найти площадь криволинейной трапеции онлайн,найти площадь области ограниченной линиями онлайн,найти площадь ограниченной фигуры,найти площадь ограниченную линиями,найти площадь ограниченную линиями онлайн калькулятор,найти площадь плоской фигуры ограниченной линиями,найти площадь плоской фигуры ограниченной линиями онлайн,найти площадь фигуры,найти площадь фигуры ограниченной,найти площадь фигуры ограниченной графиками функций,найти площадь фигуры ограниченной кривыми,найти площадь фигуры ограниченной линиями,найти площадь фигуры ограниченной линиями онлайн,найти площадь фигуры ограниченной линиями онлайн калькулятор,найти площадь фигуры ограниченной линиями онлайн калькулятор подробно,найти площадь фигуры ограниченной линиями онлайн решение,найти площадь фигуры ограниченной линиями онлайн с подробным решением,найти площадь фигуры ограниченной линиями примеры решения,найти площадь фигуры ограниченной линиями с помощью определенного интеграла сделать иллюстрацию,найти площадь фигуры ограниченной указанными линиями,найти площадь фигуры онлайн,нахождение площади фигуры ограниченной линиями,нахождение площади фигуры ограниченной линиями онлайн,онлайн вычисление площади фигуры ограниченной линиями,онлайн вычислить площадь фигуры ограниченной графиками функций онлайн,онлайн калькулятор площадь фигуры ограниченной линиями,онлайн нахождение площади фигуры ограниченной линиями,онлайн площадь фигуры,площадь криволинейной трапеции онлайн,площадь ограниченная линиями,площадь плоской фигуры ограниченной линиями онлайн,площадь под графиком,площадь фигуры ограниченной графиками функций,площадь фигуры ограниченной линиями,площадь фигуры ограниченной линиями онлайн,площадь фигуры ограниченной линиями онлайн калькулятор,площадь фигуры онлайн,построить фигуру ограниченную линиями онлайн,сделайте чертеж и вычислите площадь фигуры ограниченной данными линиями,фигуры ограниченные двумя линиями,фигуры ограниченные линиями.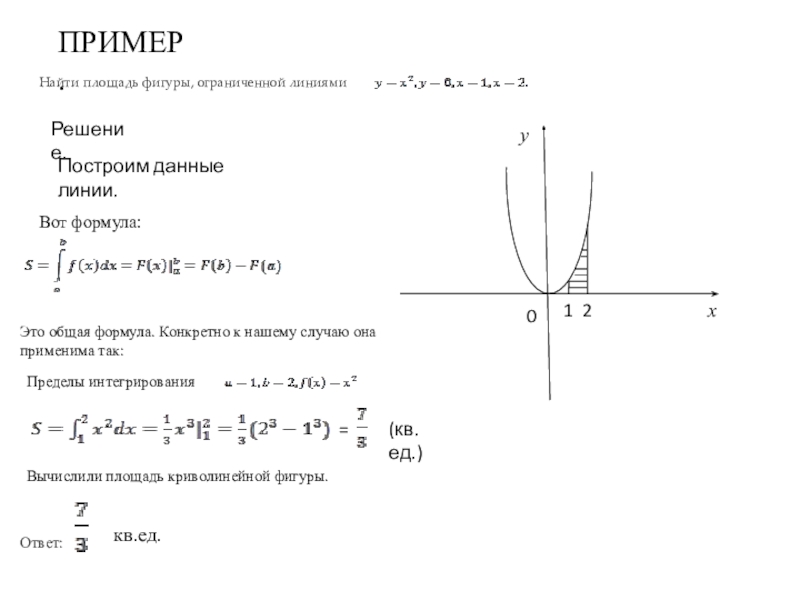 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление площади фигуры ограниченной линиями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислите площадь фигуры).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление площади фигуры ограниченной линиями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислите площадь фигуры). Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
 Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования. Как сельские школьники будут сдавать ЕНТ по новому формату?
Как сельские школьники будут сдавать ЕНТ по новому формату? Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
 В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам. 2}{6}\) .
2}{6}\) . Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.
Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.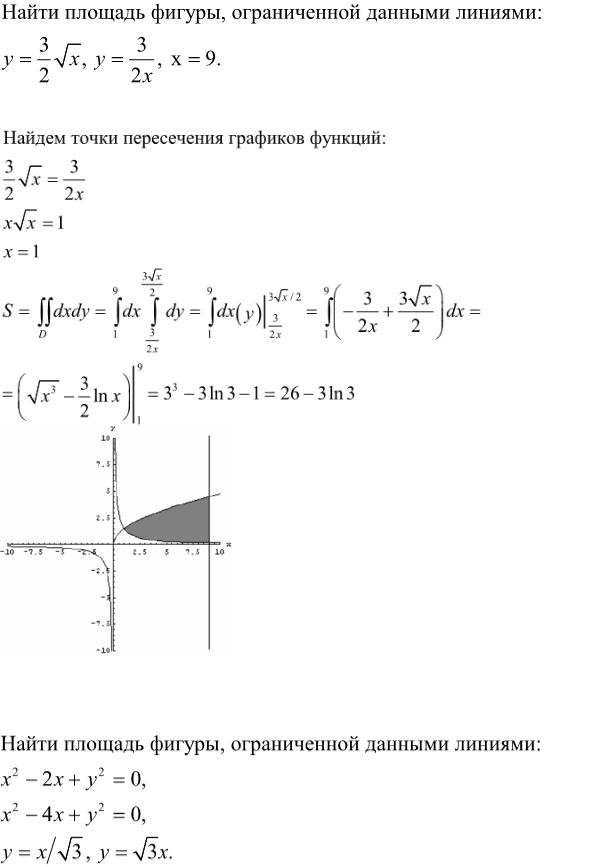
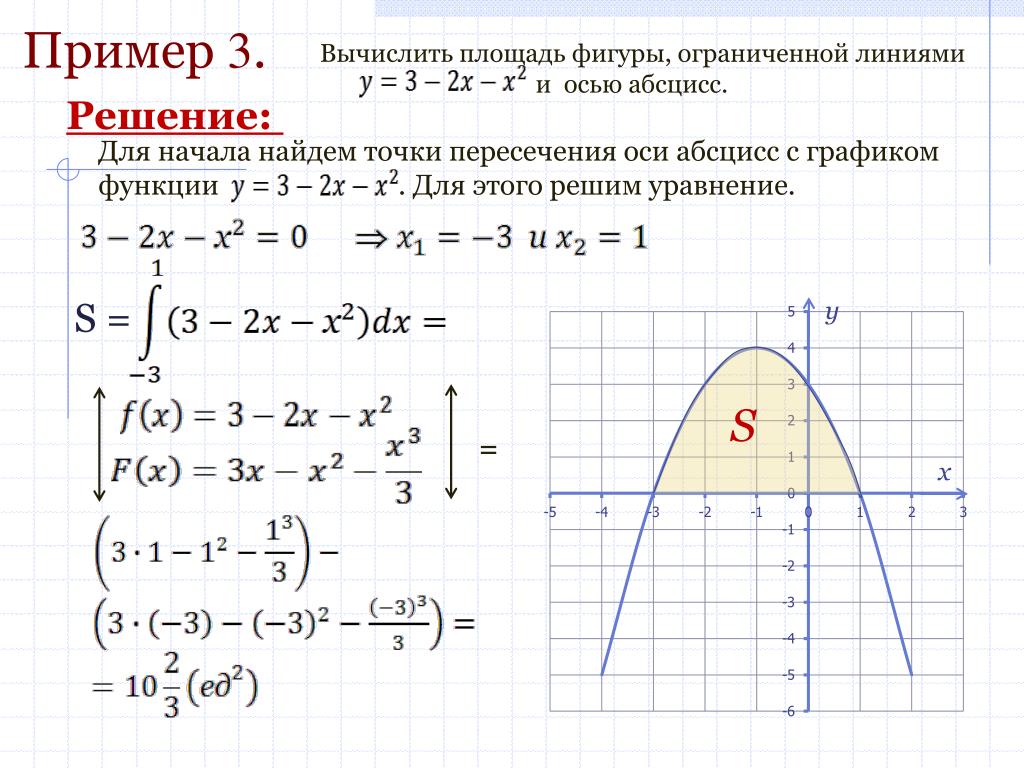 (3/2)) = 59/6.
(3/2)) = 59/6. Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два.
Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два. 1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс ( у = 0 ), прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b. При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница:
1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс ( у = 0 ), прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b. При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница: Ну и у = 0, она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница.
Ну и у = 0, она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница. Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1]. Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале.
Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1]. Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале. Вы должны использовать исчисление, иначе вы не получите никаких кредитов!
Вы должны использовать исчисление, иначе вы не получите никаких кредитов!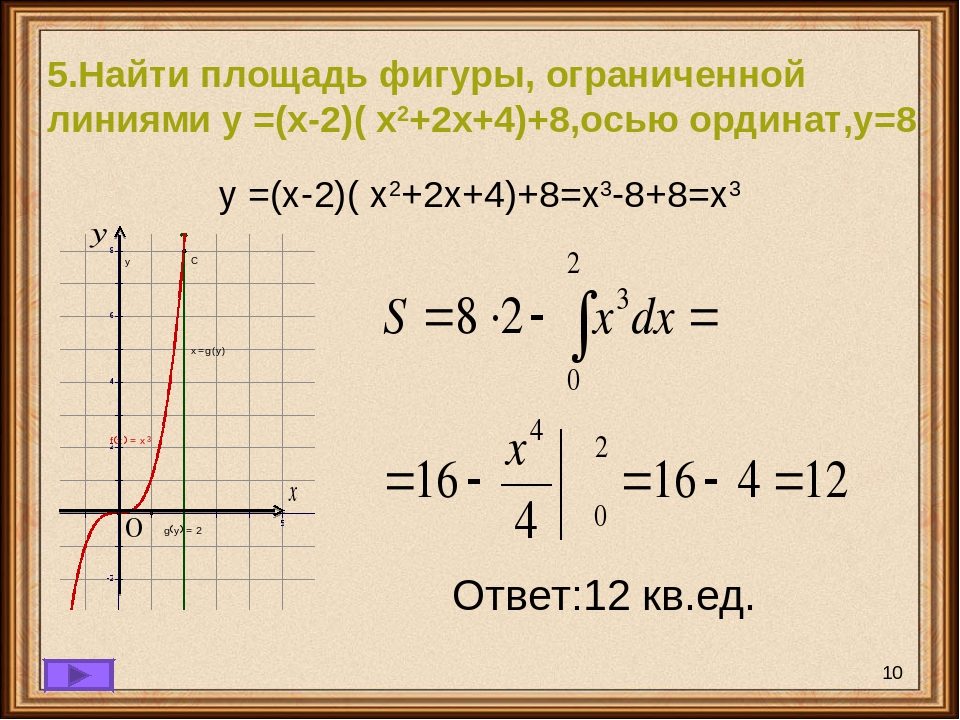 Д.
Д.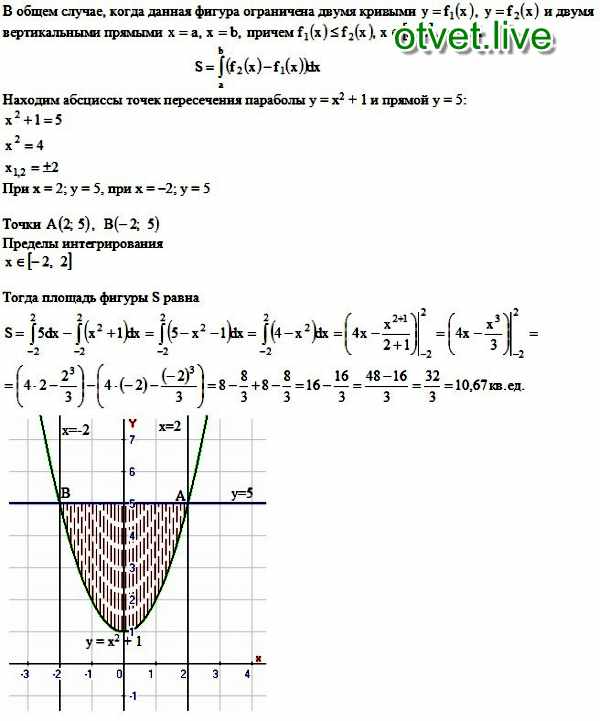 Иногда бывает. На самом деле, это зависит от того, на какую часть треугольника мы смотрим. Если мы разрежем эту область в точке пересечения \ (y = 3x \) и \ (y = 2 \), то часть, которая находится слева от разреза, будет ограничена сверху \ (y = 3x \). Часть справа от разреза ограничена сверху \ (y = 2 \).Позвольте мне показать вам, что я имею в виду:
Иногда бывает. На самом деле, это зависит от того, на какую часть треугольника мы смотрим. Если мы разрежем эту область в точке пересечения \ (y = 3x \) и \ (y = 2 \), то часть, которая находится слева от разреза, будет ограничена сверху \ (y = 3x \). Часть справа от разреза ограничена сверху \ (y = 2 \).Позвольте мне показать вам, что я имею в виду: Формула площади требует определенного интеграла , а это означает, что нам нужны пределы интегрирования (также известные как «границы»). Что ж, помните, что наши границы — это просто значения \ (x \), которые говорят нам, где область начинается и заканчивается. Чтобы найти их, давайте еще раз посмотрим на график:
Формула площади требует определенного интеграла , а это означает, что нам нужны пределы интегрирования (также известные как «границы»). Что ж, помните, что наши границы — это просто значения \ (x \), которые говорят нам, где область начинается и заканчивается. Чтобы найти их, давайте еще раз посмотрим на график: Для левой части получаем:
Для левой части получаем: b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}} = {F \ left (b \ right) — G \ left (b \ right) — F \ left (a \ right) + G \ left (a \ right),} \]
b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}} = {F \ left (b \ right) — G \ left (b \ right) — F \ left (a \ right) + G \ left (a \ right),} \]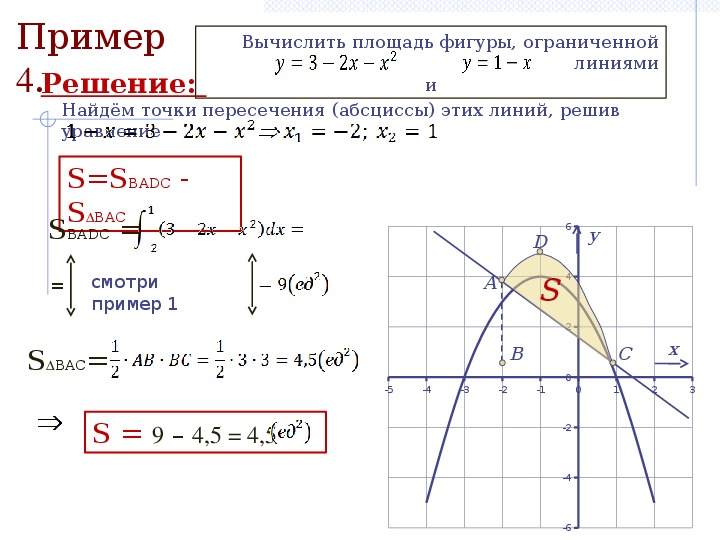 2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)
2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \) } \]
} \]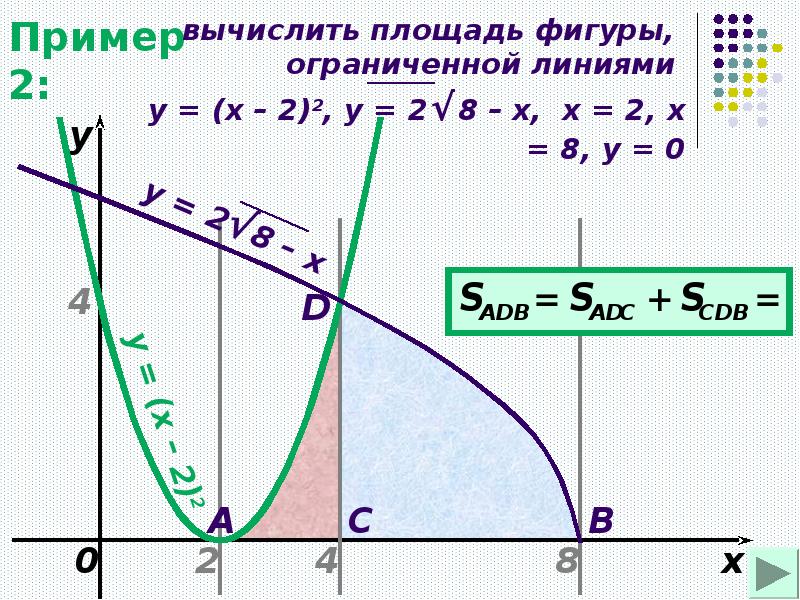 {2 \ pi} {\ left ({3 + 4 \ cos \ theta + \ cos 2 \ theta} \ right) d \ theta}} = {\ frac {1} {4} \ left.{2 \ pi}} = {\ frac {3} {{16}} \ cdot 2 \ pi} = {\ frac {{3 \ pi}} {8}} \]
{2 \ pi} {\ left ({3 + 4 \ cos \ theta + \ cos 2 \ theta} \ right) d \ theta}} = {\ frac {1} {4} \ left.{2 \ pi}} = {\ frac {3} {{16}} \ cdot 2 \ pi} = {\ frac {{3 \ pi}} {8}} \]
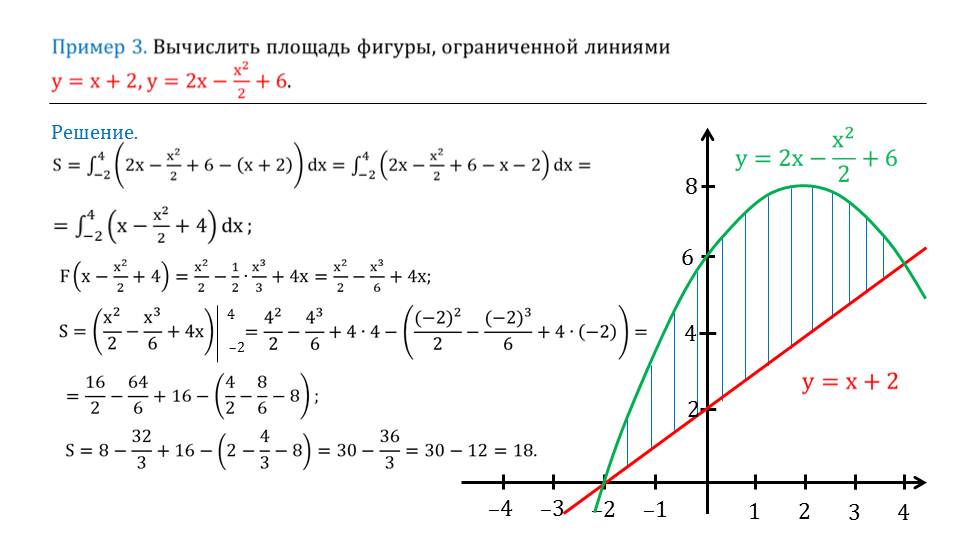 2} \) и \ (y = \ sqrt x \).Показать решение
2} \) и \ (y = \ sqrt x \).Показать решение 2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \]
2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \] 2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -.
Показать решение
2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -.
Показать решение 2} — 4x — 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x — 3} \ right) & = 0 \ end {align *} \]
2} — 4x — 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x — 3} \ right) & = 0 \ end {align *} \] Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы больше не будем утруждать себя поиском точек пересечения.
Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы больше не будем утруждать себя поиском точек пересечения. 2} — 2y — 8 \\ 0 & = \ left ({y — 4} \ right) \ left ({y + 2} \ right) \ end {align *} \]
2} — 2y — 8 \\ 0 & = \ left ({y — 4} \ right) \ left ({y + 2} \ right) \ end {align *} \] {{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) — \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ ]
{{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) — \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ ] 2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \]
2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \] Сначала мы должны определить, что такое твердое тело революции. Чтобы получить твердое тело вращения, мы начинаем с функции \ (y = f \ left (x \ right) \) на интервале \ (\ left [{a, b} \ right] \).
Сначала мы должны определить, что такое твердое тело революции. Чтобы получить твердое тело вращения, мы начинаем с функции \ (y = f \ left (x \ right) \) на интервале \ (\ left [{a, b} \ right] \).
 Имея это в виду, мы можем отметить, что первое уравнение — это просто парабола с вершиной \ (\ left ({2,1} \ right) \) (вы помните, как получить вершину параболы справа?) И открывается вверх. и поэтому нам действительно не нужно тратить много времени на его набросок.
Имея это в виду, мы можем отметить, что первое уравнение — это просто парабола с вершиной \ (\ left ({2,1} \ right) \) (вы помните, как получить вершину параболы справа?) И открывается вверх. и поэтому нам действительно не нужно тратить много времени на его набросок.
 Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.
Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.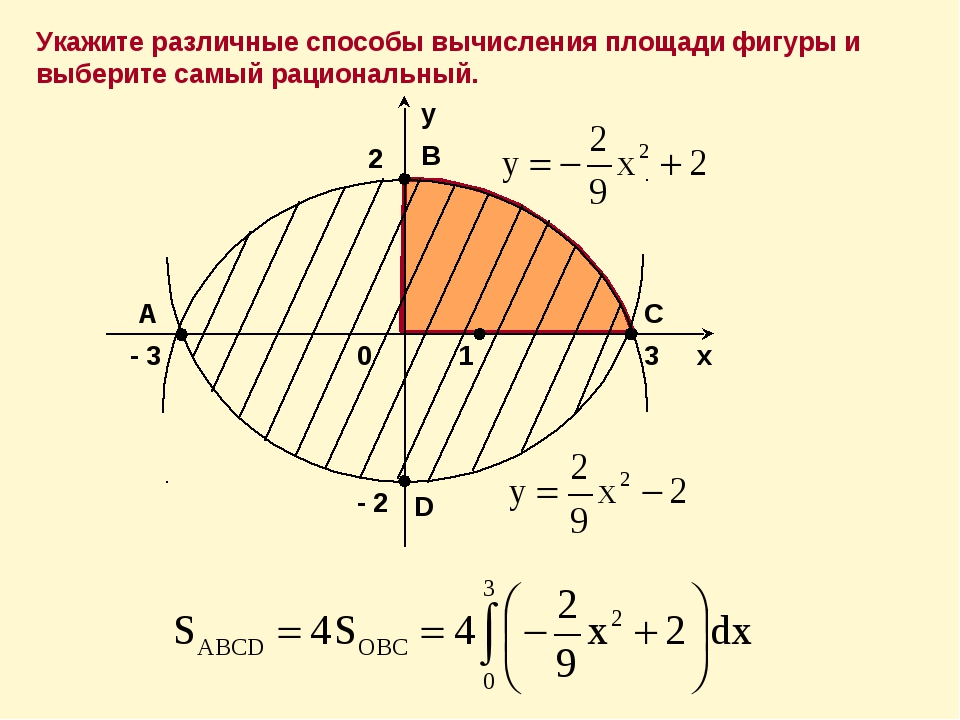
 Как показано на рисунке, внешний край кольца находится ниже оси \ (x \), и в этой точке значение функции будет отрицательным, поэтому, когда мы выполняем вычитание в формуле для внешнего радиуса, мы фактически вычитаем от отрицательного числа, которое имеет чистый эффект прибавления этого расстояния к 4 и дает правильный внешний радиус.3 \\ & = \ frac {{153 \ pi}} {5} \ end {align *} \]
Пример 4 Определите объем твердого тела, полученного вращением области, ограниченной \ (y = 2 \ sqrt {x — 1} \) и \ (y = x — 1 \), вокруг линии \ (x = — 1 \) .
Показать решение
Как показано на рисунке, внешний край кольца находится ниже оси \ (x \), и в этой точке значение функции будет отрицательным, поэтому, когда мы выполняем вычитание в формуле для внешнего радиуса, мы фактически вычитаем от отрицательного числа, которое имеет чистый эффект прибавления этого расстояния к 4 и дает правильный внешний радиус.3 \\ & = \ frac {{153 \ pi}} {5} \ end {align *} \]
Пример 4 Определите объем твердого тела, полученного вращением области, ограниченной \ (y = 2 \ sqrt {x — 1} \) и \ (y = x — 1 \), вокруг линии \ (x = — 1 \) .
Показать решение Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.
Набросок слева включает заднюю часть объекта, чтобы дать небольшой контекст рисунку справа.
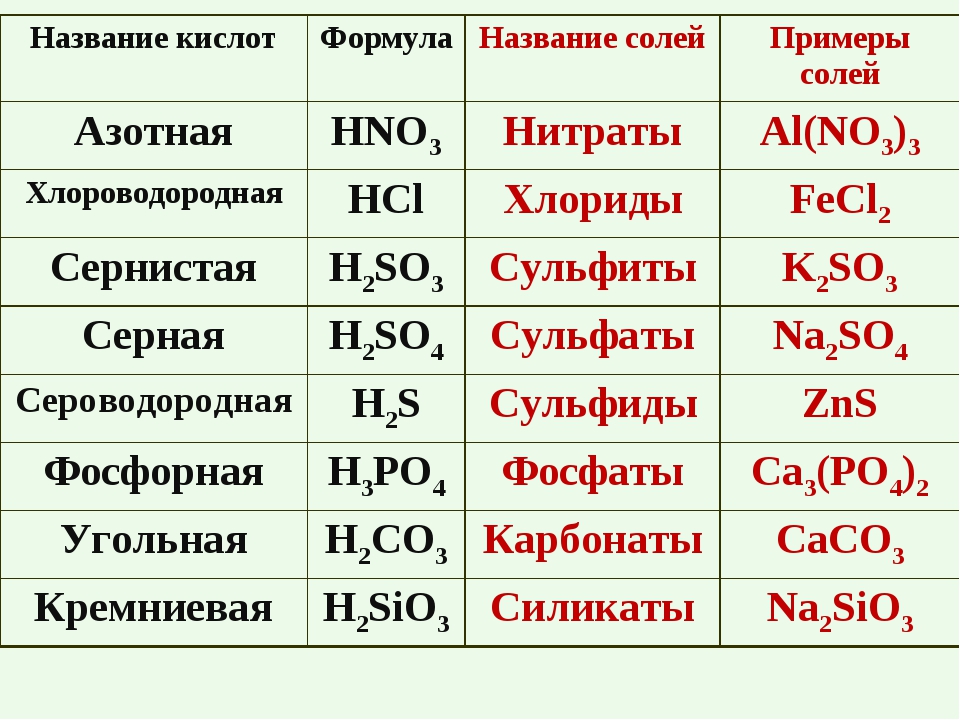
 В. Еремина.
В. Еремина.

 ст. Температура воздуха 273,15 K = 0°C) кислоты чаще жидкости, хотя встречаются и твердые вещества: например ортофосфорная H3PO4 или кремниевая H2SiO3.
ст. Температура воздуха 273,15 K = 0°C) кислоты чаще жидкости, хотя встречаются и твердые вещества: например ортофосфорная H3PO4 или кремниевая H2SiO3.
 Запомните, что лакмус в кислой среде краснеет.
Запомните, что лакмус в кислой среде краснеет.
 Химия, 8–9 класс: уроки, тесты, задания.
Химия, 8–9 класс: уроки, тесты, задания.




 д.
д. Хотя в молекуле этой кислоты — четыре атома водорода, только один из них (входящий в состав группы СООН) может быть замещён металлом. Поэтому кислотный остаток уксусной кислоты является одновалентным.
Хотя в молекуле этой кислоты — четыре атома водорода, только один из них (входящий в состав группы СООН) может быть замещён металлом. Поэтому кислотный остаток уксусной кислоты является одновалентным.
 )
) Такой знак отражает обратимость диссоциации слабых кислот — в их случае сильно выражен обратный процесс объединения катионов водорода с кислотными остатками:
Такой знак отражает обратимость диссоциации слабых кислот — в их случае сильно выражен обратный процесс объединения катионов водорода с кислотными остатками: Связано такое явление с увеличением заряда кислотных остатков, вследствие чего возрастает прочность связи между ними и положительными ионами H+.
Связано такое явление с увеличением заряда кислотных остатков, вследствие чего возрастает прочность связи между ними и положительными ионами H+. Например:
Например: Взаимодействие кислот с основаниями и амфотерными гидроксидами
Взаимодействие кислот с основаниями и амфотерными гидроксидами

 В отличие от других галогеноводородных кислот ее могут окислить даже оксид и соли трехвалентного железа.
В отличие от других галогеноводородных кислот ее могут окислить даже оксид и соли трехвалентного железа. Hortobagyi
et al. – JAMA, 2017 ].
Hortobagyi
et al. – JAMA, 2017 ].
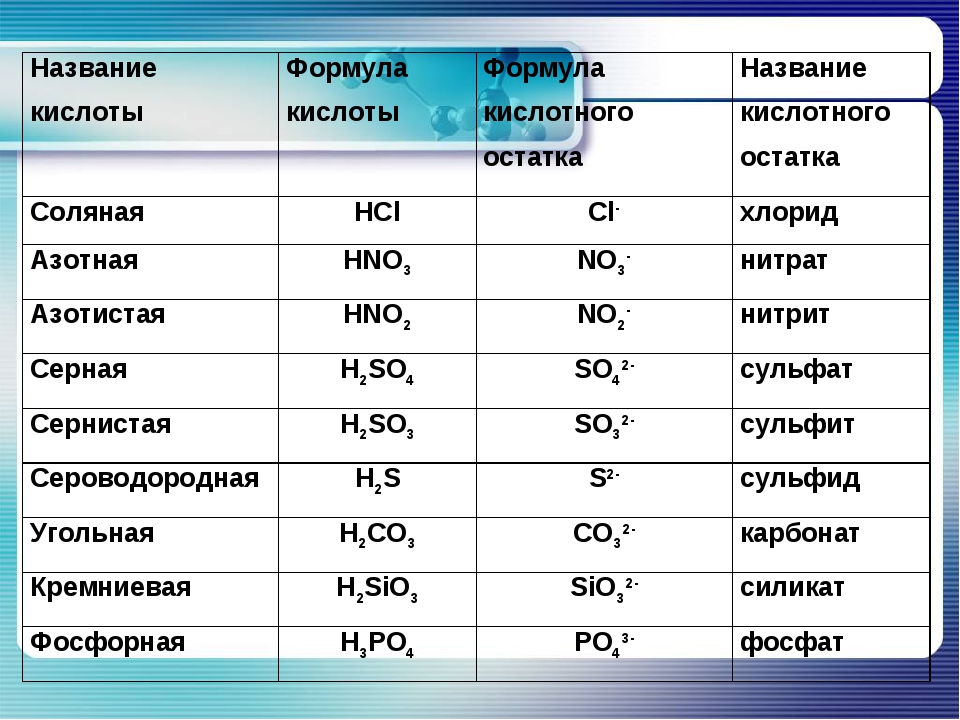

 Дольки измельчают небольшими кубиками или полосками. Фруктовую нарезку складывают в кастрюлю и заливают небольшим количеством воды. Варить массу нужно под плотно закрытой крышкой на среднем огне 10 минут. Готовые кусочки вынимают из миски с помощью шумовки и перетирают до однородной консистенции. Отвар в дальнейшем можно использовать для приготовления вкусного витаминного компота или киселя.
Дольки измельчают небольшими кубиками или полосками. Фруктовую нарезку складывают в кастрюлю и заливают небольшим количеством воды. Варить массу нужно под плотно закрытой крышкой на среднем огне 10 минут. Готовые кусочки вынимают из миски с помощью шумовки и перетирают до однородной консистенции. Отвар в дальнейшем можно использовать для приготовления вкусного витаминного компота или киселя.

 2 г.
2 г. Учитывая наличие клетчатки, при употреблении грушевого пюре в пищу происходит очистка организма от продуктов распада, что помогает улучшить работу пищеварительной системы.
Учитывая наличие клетчатки, при употреблении грушевого пюре в пищу происходит очистка организма от продуктов распада, что помогает улучшить работу пищеварительной системы. Кроме этого, его применяют для приготовления разнообразных десертов, напитков, джемов и варений.
Кроме этого, его применяют для приготовления разнообразных десертов, напитков, джемов и варений. Далее следует груши нарезать, положить ее в таком виде в кастрюлю, залить водой, чтобы она полностью покрывала фрукты, и поставить на огонь на 15 минут. В процессе варки плоды хорошо размягчатся. После того, как груши остынут, их необходимо раздавить вилкой или измельчить при помощи блендера, что позволит достичь однородной консистенции.
Далее следует груши нарезать, положить ее в таком виде в кастрюлю, залить водой, чтобы она полностью покрывала фрукты, и поставить на огонь на 15 минут. В процессе варки плоды хорошо размягчатся. После того, как груши остынут, их необходимо раздавить вилкой или измельчить при помощи блендера, что позволит достичь однородной консистенции. Как только смесь забурлит, всыпать туда сто двадцать пять граммов сахара, около восьми граммов кислоты лимонной и оставить томиться еще минут пятнадцать, регулярно помешивая. Готовое грушевое пюре на зиму разлить по простерилизованной таре и закупорить.
Как только смесь забурлит, всыпать туда сто двадцать пять граммов сахара, около восьми граммов кислоты лимонной и оставить томиться еще минут пятнадцать, регулярно помешивая. Готовое грушевое пюре на зиму разлить по простерилизованной таре и закупорить. В чашу электроприбора налить пять стаканов холодной очищенной водички, насыпать сто граммов сахара и включить программу «Тушение». Как только сахар полностью исчезнет, в мультиварку необходимо выложить три килограмма мытых, очищенных от кожуры и семян спелых груш. Масса должна потушиться около получаса. Затем фруктовое пюре перелить в блендер и взбить до однородности, добавив половину чайной ложечки молотой корицы. Когда масса закипит, грушевое пюре разлить по простерилизованным баночкам и герметично закупорить.
В чашу электроприбора налить пять стаканов холодной очищенной водички, насыпать сто граммов сахара и включить программу «Тушение». Как только сахар полностью исчезнет, в мультиварку необходимо выложить три килограмма мытых, очищенных от кожуры и семян спелых груш. Масса должна потушиться около получаса. Затем фруктовое пюре перелить в блендер и взбить до однородности, добавив половину чайной ложечки молотой корицы. Когда масса закипит, грушевое пюре разлить по простерилизованным баночкам и герметично закупорить. Далее фруктовую массу распределить по простерилизованной таре и закупорить. Грушевое пюре для грудничка на зиму готово.
Далее фруктовую массу распределить по простерилизованной таре и закупорить. Грушевое пюре для грудничка на зиму готово. Фруктовые кусочки выложить в мультиварку, налить четверть стакана водички и установить режим «Тушение» на полчаса. Затем яблочно-грушевую массу перемолоть блендером до состояния пюре, после добавить туда банку молока сгущенного, вновь включить режим «Тушение» минут на тридцать. По завершении программы фруктовое пюре распределить по простерилизованной таре и герметично закупорить. Грушевое пюре со сгущенкой на зиму готово.
Фруктовые кусочки выложить в мультиварку, налить четверть стакана водички и установить режим «Тушение» на полчаса. Затем яблочно-грушевую массу перемолоть блендером до состояния пюре, после добавить туда банку молока сгущенного, вновь включить режим «Тушение» минут на тридцать. По завершении программы фруктовое пюре распределить по простерилизованной таре и герметично закупорить. Грушевое пюре со сгущенкой на зиму готово. Если вы вводите пюре в рацион ребенка, делайте это постепенно, так как реакция организма на такой прикорм может быть разной.
Если вы вводите пюре в рацион ребенка, делайте это постепенно, так как реакция организма на такой прикорм может быть разной. Яблоки и груши являются низкоаллергенными плодами наравне с другими фруктами, поэтому пюре на их основе просто идеально для малышей. Также оно подойдет для диабетиков или людей, которые ограничивают себя в порциях сахара с целью снижения веса.
Яблоки и груши являются низкоаллергенными плодами наравне с другими фруктами, поэтому пюре на их основе просто идеально для малышей. Также оно подойдет для диабетиков или людей, которые ограничивают себя в порциях сахара с целью снижения веса.
 Чем мельче будут нарезаны плоды, тем быстрее они станут мягкими в период варки.
Чем мельче будут нарезаны плоды, тем быстрее они станут мягкими в период варки.
 Во время загрузки пюре в банки следите, чтобы не было пузырьков воздуха. Баночки моментально закупорьте крышками как можно туже, остудите до комнатной температуры, после поставьте в холодильник.
Во время загрузки пюре в банки следите, чтобы не было пузырьков воздуха. Баночки моментально закупорьте крышками как можно туже, остудите до комнатной температуры, после поставьте в холодильник.
 Именно так поступила моя сестра Екатерина и заготовила массу самых разных фруктовых и овощных детских пюре для своего малыша. И уже с 4-5 месячного возраста начала прикармливать его домашним вкусным пюре.
Именно так поступила моя сестра Екатерина и заготовила массу самых разных фруктовых и овощных детских пюре для своего малыша. И уже с 4-5 месячного возраста начала прикармливать его домашним вкусным пюре. У Кати на всь объём варки ушло около 400 мл. воды. Вы сами решайте, какой густоты сделать фруктовое пюре, но не стоит оставлять его слишком густым и делать слишком жидким.
У Кати на всь объём варки ушло около 400 мл. воды. Вы сами решайте, какой густоты сделать фруктовое пюре, но не стоит оставлять его слишком густым и делать слишком жидким. Времени это не займёт много, зато вы будете знать, что кормите свою любимку настоящим фруктовым пюре, из фруктов, что вырастили сами.
Времени это не займёт много, зато вы будете знать, что кормите свою любимку настоящим фруктовым пюре, из фруктов, что вырастили сами. Они должны быть сладкими, спелыми и сочными. Учитывая, что это будет пюре из груш на зиму для ребенка, плоды следует собирать в чистом месте, вдалеке от заводов и автомобильных трасс. В зависимости от сладости плодов, можно регулировать количество сахара-песка в рецепте. Самое вкусное пюре получается из спелых, слегка мягких груш, сохранивших свою текстуру и форму.
Они должны быть сладкими, спелыми и сочными. Учитывая, что это будет пюре из груш на зиму для ребенка, плоды следует собирать в чистом месте, вдалеке от заводов и автомобильных трасс. В зависимости от сладости плодов, можно регулировать количество сахара-песка в рецепте. Самое вкусное пюре получается из спелых, слегка мягких груш, сохранивших свою текстуру и форму. | Приготовление 40 мин.
| Приготовление 40 мин.
 0
0 Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними Как вычислить площадь фигуры. Формулы площади трапеции
Как вычислить площадь фигуры. Формулы площади трапеции Площадь помещения любой формы и размера, так или иначе, поддается вычислению.
Площадь помещения любой формы и размера, так или иначе, поддается вычислению.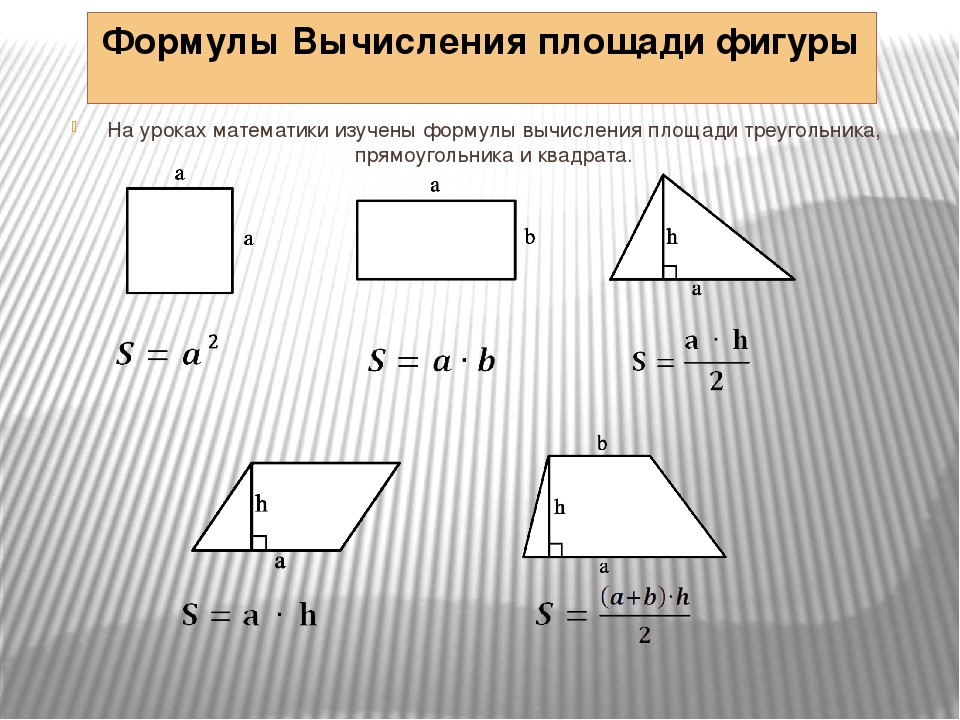 Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками:
Если такой возможности у вас нет, тогда воспользуйтесь следующими методиками: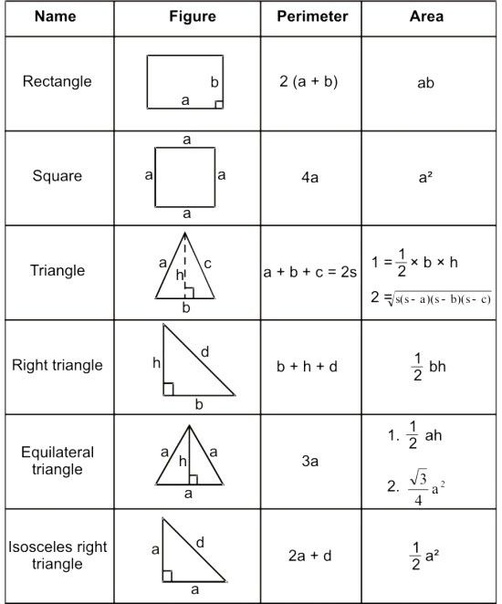 Их площадь необходимо отнять от получившегося значения.
Их площадь необходимо отнять от получившегося значения. Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.
Если ваше помещение имеет строго квадратную или прямоугольную форму, то этот этап можно пропустить.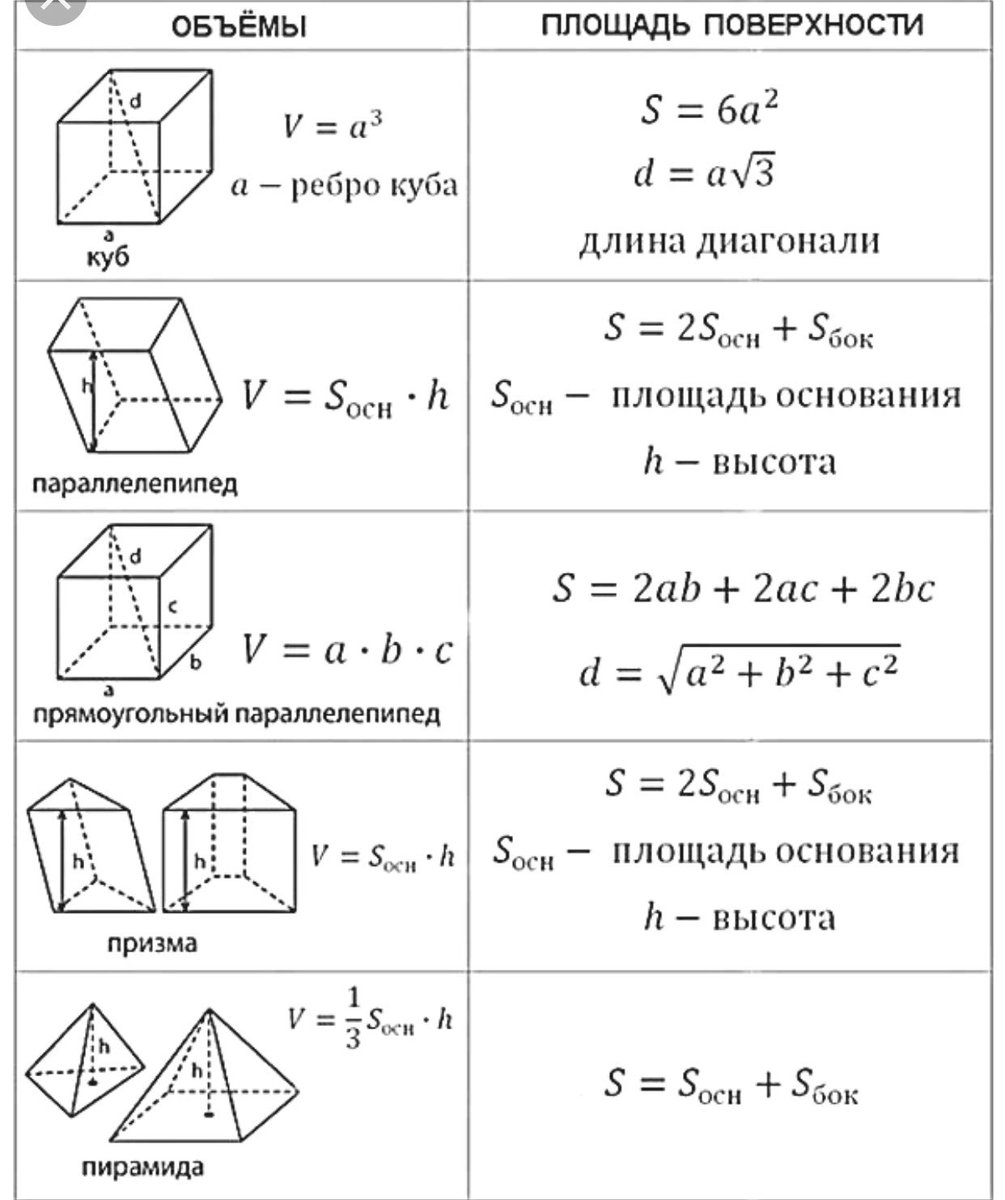




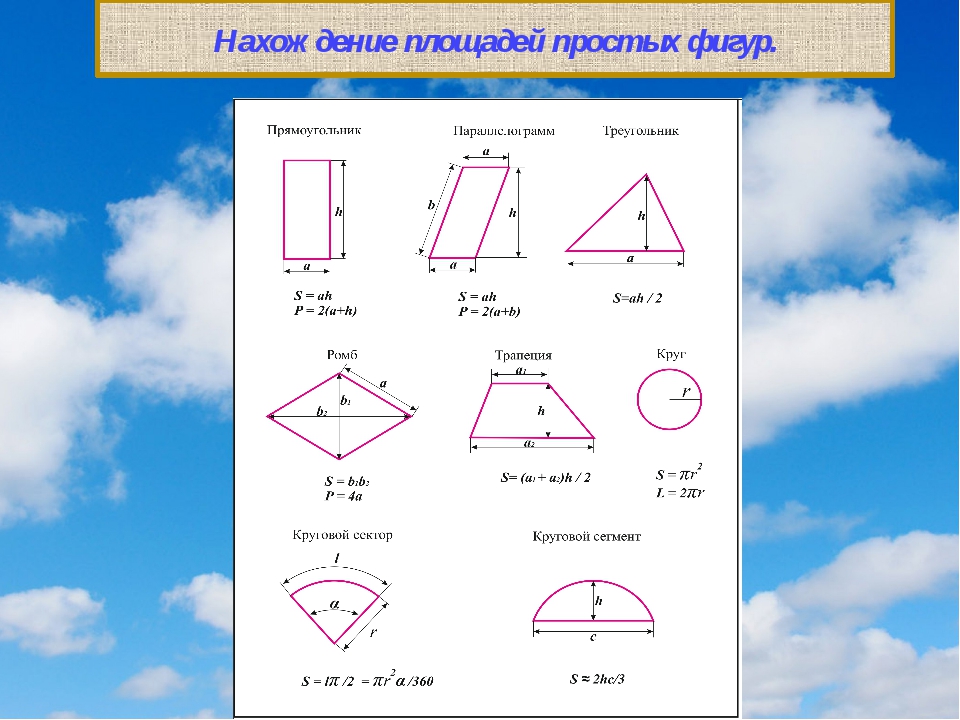 Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.
Не обойтись без этих знаний и при составлении или проверке смет на ремонт помещений, расчета количества необходимых расходных материалов. Поэтому давайте разберемся, как находить площади разных фигур.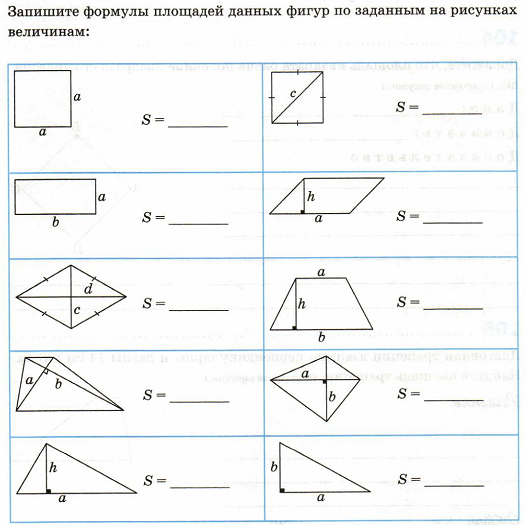

 Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо.
Площадь сложной фигуры определяется как сумма или разность составляющих площадей. Рассмотрим, к примеру, кольцо. Скажем так, «рамку» маленького квадрата. Для этого:
Скажем так, «рамку» маленького квадрата. Для этого: Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника: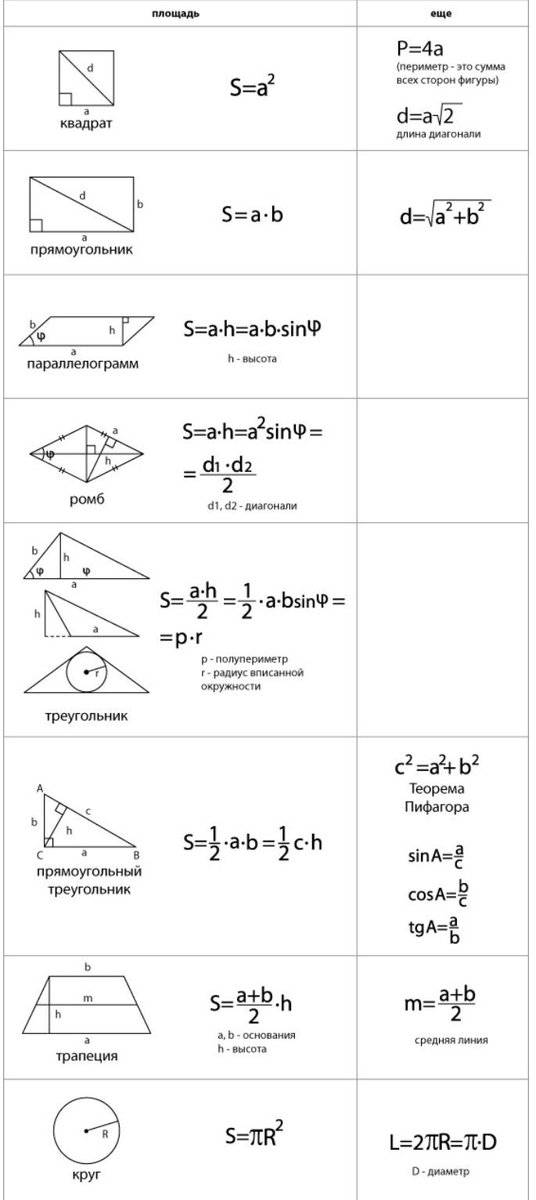 Такая формула площади прямоугольника имеет вид:
Такая формула площади прямоугольника имеет вид:
 При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.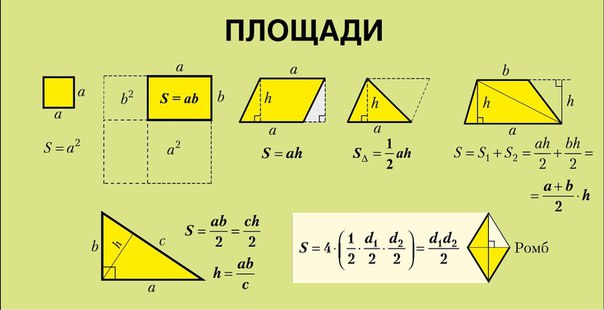 Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
 Найдём площадь параллелограмма:
Найдём площадь параллелограмма: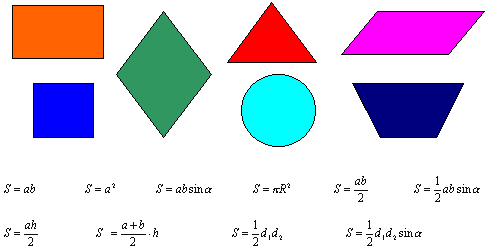 Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах. Успехов вам!
Успехов вам! Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.
Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота. Значение sin γ для конкретного угла можно посмотреть в специальной таблице.
Значение sin γ для конкретного угла можно посмотреть в специальной таблице.












 Площадь выпуклого четырёхугольника можно найти по формуле
Площадь выпуклого четырёхугольника можно найти по формуле
 Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
 Химические свойства — Взаимодействует с основными и амфотерными оксидами, водой и щелочами
Химические свойства — Взаимодействует с основными и амфотерными оксидами, водой и щелочами 
 » – Яндекс.Кью
» – Яндекс.Кью ru
ru С основными оксидами образует фосфаты.[3]
С основными оксидами образует фосфаты.[3]
 В условиях слабокислой реакции среды, именно в них возделываются растения, наиболее распространен и доступен первый ион, в меньшей степени второй и практически недоступен третий. Однако люпин, гречиха, горчица, горох, донник, конопля и другие растения способны усваивать фосфор из трехзамещенных фосфатов.[4]
В условиях слабокислой реакции среды, именно в них возделываются растения, наиболее распространен и доступен первый ион, в меньшей степени второй и практически недоступен третий. Однако люпин, гречиха, горчица, горох, донник, конопля и другие растения способны усваивать фосфор из трехзамещенных фосфатов.[4]

 К ним относится золото Аu и некоторые другие. Оксиды этих элементов получают косвенным путём.
Химическая природа оксидов проявляется в их отношении к кислотам и щелочам.
В связи с этим оксиды можно разделить на следующие группы
— солеобразующие, которые реагируют с образованием солей с кислотами или щелочами;
— несолеобразующие, которые не образуют солей с кислотами или щелочами.
В свою очередь, солеобразующие оксиды подразделяются на кислотные (реагируют со щелочами), основные (реагируют с кислотами) и амфотерные (реагируют как с кислотами, так и с щелочами).
Кислотные оксиды — это оксиды, которые реагируют со щелочами с образованием соли и воды, но они не реагируют с кислотами. Например, при взаимодействии кислотного оксида – оксида углерода (IV) с гидроксидом натрия образуются карбонат натрия и вода:
CO2 + 2NaOH = Na2CO3 + h3O
К кислотным оксидам относятся, как правило, оксиды неметаллов (например, SO2, CO2, P2O5), и те оксиды металлов, в которых металл находится в валентности более III (например, Mn2O7, CrO3).
К ним относится золото Аu и некоторые другие. Оксиды этих элементов получают косвенным путём.
Химическая природа оксидов проявляется в их отношении к кислотам и щелочам.
В связи с этим оксиды можно разделить на следующие группы
— солеобразующие, которые реагируют с образованием солей с кислотами или щелочами;
— несолеобразующие, которые не образуют солей с кислотами или щелочами.
В свою очередь, солеобразующие оксиды подразделяются на кислотные (реагируют со щелочами), основные (реагируют с кислотами) и амфотерные (реагируют как с кислотами, так и с щелочами).
Кислотные оксиды — это оксиды, которые реагируют со щелочами с образованием соли и воды, но они не реагируют с кислотами. Например, при взаимодействии кислотного оксида – оксида углерода (IV) с гидроксидом натрия образуются карбонат натрия и вода:
CO2 + 2NaOH = Na2CO3 + h3O
К кислотным оксидам относятся, как правило, оксиды неметаллов (например, SO2, CO2, P2O5), и те оксиды металлов, в которых металл находится в валентности более III (например, Mn2O7, CrO3). Кислотным оксидам соответствуют кислоты. Оксиду серы (IV) соответствуют сернистая кислота, оксиду углерода(IV) — угольная, оксиду фосфора(V) – ортофосфорная, оксиду марганца(VII) – марганцовая, оксиду хрома(VI) – хромовая.
Основные оксиды — это оксиды, которые реагируют с кислотами с образованием соли и воды, но не реагируют со щелочами. Например, при взаимодействии оксида магния с соляной кислотой образуются хлорид магния и вода:
MgO + 2HCl = MgCl2 + h3O
Основные оксиды образуют, как правило, металлы с валентностью – I, II или III. Основным оксидам соответствуют основания. Например, оксиду натрия соответствует гидроксид натрия NaOH, оксиду бария – гидроксид бария, оксиду меди(II) – гидроксид меди(II).
Третья группа солеобразующих оксидов – амфотерные оксиды. Эти оксиды проявляют двойные свойства, т.е свойства и кислотных, и основных оксидов. Значит, они способны реагировать как со щелочами, так и с кислотами.К амфотерным оксидам относятся, например, оксид алюминия, оксид цинка, оксид бериллия, оксид хрома(III):Al2O3, ZnO, BeO, Cr2O3
Несолеобразующие, или безразличные оксиды не реагируют с образованием солей ни с кислотами, ни со щелочами.
Кислотным оксидам соответствуют кислоты. Оксиду серы (IV) соответствуют сернистая кислота, оксиду углерода(IV) — угольная, оксиду фосфора(V) – ортофосфорная, оксиду марганца(VII) – марганцовая, оксиду хрома(VI) – хромовая.
Основные оксиды — это оксиды, которые реагируют с кислотами с образованием соли и воды, но не реагируют со щелочами. Например, при взаимодействии оксида магния с соляной кислотой образуются хлорид магния и вода:
MgO + 2HCl = MgCl2 + h3O
Основные оксиды образуют, как правило, металлы с валентностью – I, II или III. Основным оксидам соответствуют основания. Например, оксиду натрия соответствует гидроксид натрия NaOH, оксиду бария – гидроксид бария, оксиду меди(II) – гидроксид меди(II).
Третья группа солеобразующих оксидов – амфотерные оксиды. Эти оксиды проявляют двойные свойства, т.е свойства и кислотных, и основных оксидов. Значит, они способны реагировать как со щелочами, так и с кислотами.К амфотерным оксидам относятся, например, оксид алюминия, оксид цинка, оксид бериллия, оксид хрома(III):Al2O3, ZnO, BeO, Cr2O3
Несолеобразующие, или безразличные оксиды не реагируют с образованием солей ни с кислотами, ни со щелочами. К такому виду оксидов относятся, например, оксиды азота N2O и NO, оксид углерода(II) – СО.
л
2.просмотрите видео урок
К такому виду оксидов относятся, например, оксиды азота N2O и NO, оксид углерода(II) – СО.
л
2.просмотрите видео урок
 Водный раствор кислоты изменяет окраску индикаторов на красный:
Водный раствор кислоты изменяет окраску индикаторов на красный: При нагревании ортофосфорная кислота постепенно превращается в метафосфорную кислоту:
При нагревании ортофосфорная кислота постепенно превращается в метафосфорную кислоту: Применяется как регулятор кислотности в газированных напитках.
Применяется как регулятор кислотности в газированных напитках. Лишь инертные газы не могут образовывать данные соединения.
Лишь инертные газы не могут образовывать данные соединения. В несолеобразующих оксидах элемент проявляет переменную (не постоянную) валентность.
В несолеобразующих оксидах элемент проявляет переменную (не постоянную) валентность. Например:
Например: Основной оксид + кислота (образуется соль + вода)
Основной оксид + кислота (образуется соль + вода)



 ВaО
ВaО


 п.
п.

 Однако все они будут реагировать с основаниями, такими как гидроксид натрия, с образованием солей, таких как сульфат натрия.
Однако все они будут реагировать с основаниями, такими как гидроксид натрия, с образованием солей, таких как сульфат натрия. Он является основным, поскольку содержит ион оксида, O 2-, который является очень сильным основанием с высокой тенденцией к соединению с ионами водорода.
Он является основным, поскольку содержит ион оксида, O 2-, который является очень сильным основанием с высокой тенденцией к соединению с ионами водорода. Чтобы их сломать, требуется больше энергии.
Чтобы их сломать, требуется больше энергии. Например, он реагирует с теплой разбавленной соляной кислотой с образованием раствора хлорида магния.
Например, он реагирует с теплой разбавленной соляной кислотой с образованием раствора хлорида магния. Я не смог установить, связано ли это поглощение только с такими вещами, как водородные связи, или происходит настоящая химическая реакция с образованием какого-то гидроксида. Если у вас есть надежная информация по этому поводу, не могли бы вы связаться со мной по адресу, указанному на странице об этом сайте.
Я не смог установить, связано ли это поглощение только с такими вещами, как водородные связи, или происходит настоящая химическая реакция с образованием какого-то гидроксида. Если у вас есть надежная информация по этому поводу, не могли бы вы связаться со мной по адресу, указанному на странице об этом сайте.



 Ниже).
Ниже). Все, что вам действительно нужно знать по этой теме, это то, что чем ниже значение pK a , тем сильнее кислота.
Все, что вам действительно нужно знать по этой теме, это то, что чем ниже значение pK a , тем сильнее кислота. 

 В каждом случае это просто зависит от пропорций двух используемых вами реагентов.
В каждом случае это просто зависит от пропорций двух используемых вами реагентов. Знайте, как их решить, если вам нужно.
Знайте, как их решить, если вам нужно.  Именно его мы выясняем, когда встречаем незнакомое слово. А вот объяснить, что такое грамматическое значение, несколько сложнее.Очень здорово это получается с помощью, например, лингвистической сказки Людмилы Петрушевской («Сяпала калуша по напушке»), или знаменитой фразы Льва Владимировича Щербы:
Именно его мы выясняем, когда встречаем незнакомое слово. А вот объяснить, что такое грамматическое значение, несколько сложнее.Очень здорово это получается с помощью, например, лингвистической сказки Людмилы Петрушевской («Сяпала калуша по напушке»), или знаменитой фразы Льва Владимировича Щербы: За основой находится информация о том, как слово изменяется, какую грамматическую форму оно приняло сейчас. Существительное изменяется по числам и падежам, и за основой, в окончании, будет информация о том, в какой форме оно сейчас находится (например, окончание -ами за основой будет указывать на множественное число и творительный падеж, окончание -ов — на родительный падеж множественного числа).
За основой находится информация о том, как слово изменяется, какую грамматическую форму оно приняло сейчас. Существительное изменяется по числам и падежам, и за основой, в окончании, будет информация о том, в какой форме оно сейчас находится (например, окончание -ами за основой будет указывать на множественное число и творительный падеж, окончание -ов — на родительный падеж множественного числа). Такие суффиксы, не входящие в основу, не образующие новых слов, а выражающие только грамматические значения, называются «формообразующими» (в противопоставление остальным, словообразовательным, которые образуют новые слова, а не изменяют форму).
Такие суффиксы, не входящие в основу, не образующие новых слов, а выражающие только грамматические значения, называются «формообразующими» (в противопоставление остальным, словообразовательным, которые образуют новые слова, а не изменяют форму). И увазила Бутявку, и волит:
И увазила Бутявку, и волит: 




 Пустыня внемлет богу
Пустыня внемлет богу Результаты исследования показали, что слово является минимальной единицей языка, обладающей позиционной самостоятельностью. Значение слова в речи формируется с учетом лексического и грамматического аспектов, которые являются взаимозависимыми и дополняют друг друга. Таким образом, слово в речевой цепи несет в себе не только понятийную нагрузку, дополненную социальными и культурными аспектами, но, с точки зрения системного подхода, отражает характерные признаки существующей структуры и иерархии языка, а также исторические изменения грамматического строя.
Результаты исследования показали, что слово является минимальной единицей языка, обладающей позиционной самостоятельностью. Значение слова в речи формируется с учетом лексического и грамматического аспектов, которые являются взаимозависимыми и дополняют друг друга. Таким образом, слово в речевой цепи несет в себе не только понятийную нагрузку, дополненную социальными и культурными аспектами, но, с точки зрения системного подхода, отражает характерные признаки существующей структуры и иерархии языка, а также исторические изменения грамматического строя. The research is based on the British social and political mass media texts, namely, from such magazines as the Economist, the Week and the Spectator. The results have shown that a word is a minimal positionally independent linguistic unit. The meaning of the word in speech includes lexical and grammatical meanings, which are interrelated and complete each other. As a result, the word in the speech flow has the conceptual meaning including social and cultural aspects, and, according to the systematic approach, it reflects the features of the language structure, hierarchy and history.
The research is based on the British social and political mass media texts, namely, from such magazines as the Economist, the Week and the Spectator. The results have shown that a word is a minimal positionally independent linguistic unit. The meaning of the word in speech includes lexical and grammatical meanings, which are interrelated and complete each other. As a result, the word in the speech flow has the conceptual meaning including social and cultural aspects, and, according to the systematic approach, it reflects the features of the language structure, hierarchy and history.
 В свою очередь, составную часть лексемы представляет собой парадигма, которая является системой форм. Таким образом, А.И. Смирницкий пишет о том, что в слове можно выделить парадигму и основу слова, а связь между основой и парадигмой обеспечивается через определенные словоформы. [Смирницкий, 2007].
В свою очередь, составную часть лексемы представляет собой парадигма, которая является системой форм. Таким образом, А.И. Смирницкий пишет о том, что в слове можно выделить парадигму и основу слова, а связь между основой и парадигмой обеспечивается через определенные словоформы. [Смирницкий, 2007]. ) связей. Слово необходимо для создания синтаксических единиц (словосочетания, предложения, текст) и находятся в парадигматических (грамматических) и синтагматических (грамматическо-фонетическая сочетаемость) отношениях с другими единицами языка [Глухов, 2007].
) связей. Слово необходимо для создания синтаксических единиц (словосочетания, предложения, текст) и находятся в парадигматических (грамматических) и синтагматических (грамматическо-фонетическая сочетаемость) отношениях с другими единицами языка [Глухов, 2007].