Концентрированная соляная кислота: Кислота соляная — производство и применение
Кислоты в лаборатории — правила работы c кислотами в обзорной статье Глювекс
Кислоты часто используются в большинстве химических лабораторий. Прежде чем покупать, хранить, использовать и утилизировать кислоты, важно изучить их свойства, риски и правила работы с кислотами в лаборатории.
Свойства
|
Кислотность |
Химическая формула |
Молекулярный вес по формуле соединения |
Удельная плотность |
Концентрированная кислота |
|
|
Массовая доля кислоты (в %) |
Молярность |
||||
|
Уксусная кислота |
HC2h4O2 |
60,05 |
1,05 |
99,8 |
17,4 |
|
Соляная кислота |
HCL |
36,46 |
1,19 |
37,2 |
12,1 |
|
Азотная кислота |
HNO3 |
63,02 |
1,42 |
69,5 |
15,8 |
|
Фосфорная кислота |
h4PO4 |
98,00 |
1,70 |
86 |
14,8 |
|
Серная кислота |
h3SO4 |
98,08 |
1,84 |
96 |
18,0 |
Меры предосторожности
Концентрированные кислоты оказывают сильное разъедающее воздействие на все ткани организма, в особенности на глаза и кожу. Концентрированные кислоты очень токсичны из-за своей чрезвычайно высокой коррозионной активности. Соляная и уксусная кислоты также токсичны при вдыхании. Другие факторы риска перечислены в этом обзоре. При работе с концентрированными кислотами в лаборатории или растворами всегда носите закрытые очки для защиты от агрессивных жидкостей, химически стойкие перчатки и химически стойкий фартук. Пожалуйста, ознакомьтесь с действующими паспортами безопасности материалов, чтобы узнать подробную информацию о технике безопасности, правилах обращения и утилизации.
Концентрированные кислоты очень токсичны из-за своей чрезвычайно высокой коррозионной активности. Соляная и уксусная кислоты также токсичны при вдыхании. Другие факторы риска перечислены в этом обзоре. При работе с концентрированными кислотами в лаборатории или растворами всегда носите закрытые очки для защиты от агрессивных жидкостей, химически стойкие перчатки и химически стойкий фартук. Пожалуйста, ознакомьтесь с действующими паспортами безопасности материалов, чтобы узнать подробную информацию о технике безопасности, правилах обращения и утилизации.
Покупка
Покупайте, по возможности, разбавленные кислоты для лаборатории. По сравнению с концентрированными кислотами, разбавленные кислотные растворы проще и безопаснее в использовании, хранении и обращении. При работе с растворами вы не потеряете драгоценное время на подготовку.
Покупайте кислоту всегда в небольших количествах. В этом случае кислота не испортится раньше времени, а сам процесс хранения и обработки станет более безопасным и легким. Разлив кислоты в количестве 100 мл ликвидировать намного легче, чем в объеме 2,5 л.
Разлив кислоты в количестве 100 мл ликвидировать намного легче, чем в объеме 2,5 л.
Всегда покупайте концентрированные кислоты в стеклянных бутылках с защитным ПВХ-покрытием. При падении такие бутылки не разобьются, а кислота из них не выльется. ПВХ создает своеобразную пластиковую защитную оболочку, что значительно уменьшает риск разлива и повреждения. ПВХ-покрытие может со временем обесцвечиваться, особенно если подвергается воздействию паров соляной кислоты. Это изменение цвета не влияет на ПВХ-покрытие или качество кислоты внутри бутылки.
Условия хранения
Храните все кислоты в специальном шкафу для сильнодействующих веществ или кислот. Самые лучшие шкафы для хранения кислот в лаборатории изготавливают из дерева, потому что металлические шкафы быстро корродируют под воздействием кислотных паров. Деревянные шкафы обеспечивают безопасное и надежное хранение кислот на протяжении многих лет. Шкаф должен находиться в закрываемом на ключ складе химических реагентов. В противном случае сам шкаф должен закрываться на замок.
В противном случае сам шкаф должен закрываться на замок.
Разрешается хранить кислоты и основания все вместе в одном шкафу для агрессивных веществ. При этом на бутылках может образоваться налет из хлорида аммония под воздействием паров соляной кислоты и аммиака. Промойте шкаф и бутылки при помощи тринатрийфосфата или другого сильного растворителя, чтобы удалить белую пленку.
Если у вас нет специального шкафа для хранения кислот, храните концентрированную кислоту в кубических контейнерах. Такие кубы обеспечивают надежное хранение кислот в лаборатории за счет дополнительной защитной оболочки.
Прежде чем поместить подготовленные растворы кислот на хранение, промаркируйте их с указанием как минимум следующей информации: название кислоты, концентрация кислоты, предупреждение об опасности или о вредном воздействии на организм человека, дата.
Техника безопасности при работе с кислотами
Всегда закрывайте бутылки с концентрированной кислотой крышками с соответствующей цветовой маркировкой. Никогда не используйте эти крышки на других бутылках. Цветовая маркировка является дополнительной мерой безопасности и позволяет идентифицировать концентрированные кислоты в тех случаях, когда этикетка была удалена или повреждена.
Никогда не используйте эти крышки на других бутылках. Цветовая маркировка является дополнительной мерой безопасности и позволяет идентифицировать концентрированные кислоты в тех случаях, когда этикетка была удалена или повреждена.
Если при работе с кислотой в лаборатории крышка на бутылке треснула или потеряла изначальный цвет, замените крышку на новую с соответствующей цветовой маркировкой.
Учитывая то, что концентрированная соляная кислота постоянно испаряется, при хранении следует предусмотреть отвод возникающих паров. Эти пары являются главным виновником повреждений на вашем складе химических реагентов, вызванных коррозией. Хранение соляной кислоты в деревянном шкафу для кислот является обязательным требованием. Пары соляной кислоты быстро разъедают металлические шкафы.
Азотная кислота является сильным окислителем. Концентрированную азотную кислоту следует хранить в отдельном непроницаемом для жидкостей отсеке внутри шкафа для кислот. Если смешать азотную кислоту с горючим органическим соединением, например, уксусной кислотой, то тепла, образовавшегося от реакций окисления и нейтрализации, будет достаточно для воспламенения этого соединения. Азотная кислота также способна медленно разрушать красную пластиковую крышку бутылки. Азотная кислота может также со временем желтеть вследствие выделения диоксида азота под действием света.
Азотная кислота также способна медленно разрушать красную пластиковую крышку бутылки. Азотная кислота может также со временем желтеть вследствие выделения диоксида азота под действием света.
Ледяная уксусная кислота является горючей жидкостью. Ледяную уксусную кислоту следует хранить в шкафу для кислот, в месте, защищенном от возможного контакта с азотной кислотой. Ледяная уксусная кислота замерзает при температуре +16,6 ° C. Кислота может кристаллизоваться на холодном складе. Если это произошло, дайте бутылке нагреться до температуры окружающей среды (+25 °C).
Концентрированная серная кислота является сильным обезвоживающим агентом. Сильной способностью поглощать воду объясняется и обугливание многих органических веществ, например, сахара, древесины, бумаги, при действии на них концентрированной серной кислоты. Если серная кислота приобрела коричневый цвет, значит, скорее всего, она была загрязнена органическими веществами и больше уже не является чистой.
Концентрированная фосфорная кислота имеет температуру плавления, близкую к температуре окружающей среды, и также может кристаллизоваться на холодном складе. Фосфорная кислота гигроскопична и имеет свойство впитывать влагу из воздуха. Храните емкости с фосфорной кислотой плотно закрытыми.
Фосфорная кислота гигроскопична и имеет свойство впитывать влагу из воздуха. Храните емкости с фосфорной кислотой плотно закрытыми.
Транспортировка
Вторичная защитная оболочка имеет решающее значение для предотвращения крупных разливов или аварий при транспортировке кислот. Храните кислоты в бутылках с ПВХ-покрытием или на небьющихся держателях для бутылок.
Возьмите себе за правило проверять наличие трещин на бутылке с кислотой, прежде чем прикасаться к ней или брать ее. Проверьте также, не пролилась ли кислота на ручку или бутылку.
Носите 2,5-литровые бутылки с кислотой, взявшись одной рукой за дно бутылки, а другой рукой обхватив горлышко или углубление для пальцев. В этом случае вы будете держать бутылку ближе к телу, и опасность разбить или повредить бутылку при контакте с острыми предметами, например, при ударе об угол стола, будет снижена.
При транспортировке кислот из одной лаборатории в другую или из кладовой (склада) в лабораторию, следует использовать пластиковые или резиновые защитные держатели для бутылок.
Если вы используете тележку для перевозки опасных химических веществ (например, кислот), поместите совместимые химические вещества во вторичный защитный контейнер, изготовленный из небьющихся материалов, например, в пластиковый лоток. Тележка должна иметь защитное ограждение, чтобы не допустить соскальзывания пластиковых лотков или бутылок.
Если опасные химические вещества перемещаются с одного этажа на другой, используйте, по возможности, лифт. И даже несмотря на то, что несчастные случаи в лифтах происходят редко, соблюдайте необходимую предосторожность. Если утечка материала в лифте все же произойдет, последствия для пассажиров, находящихся в кабине лифта, могут оказаться весьма плачевными.
Подготовка раствора
- Добавьте необходимое количество кислоты — примерно 2/3 от заданного количества дистиллированной или деионизированной воды.
- Всегда добавляйте кислоту в воду! Работая с кислотами в лаборатории, никогда не добавляйте воду в концентрированные кислоты.
 Кислота может начать разбрызгиваться с выделением кислотных паров.
Кислота может начать разбрызгиваться с выделением кислотных паров. - Всегда используйте посуду из боросиликатного стекла.
- Перемешайте раствор.
- Как только раствор остынет до температуры окружающей среды, разбавьте его водой до нужного объема.
- Используйте мерную лабораторную колбу, чтобы точно определить необходимое количество.
- При разбавлении серной кислоты, поместите боросиликатный стакан или колбу в ледяную ванну. Не забывайте о том, что разбавление серной кислоты всегда сопровождается выделением большого количества тепла. Пластиковые контейнеры под воздействием тепла могут расплавиться, а стеклянная посуда, изготовленная не из боросиликатного стекла, может треснуть.
Использование и дозирование кислот
Перед каждым использованием любого опасного материала в лаборатории следует внимательно ознакомиться с паспортом безопасности материала.
Разливайте кислоты из небольших бутылок, чтобы ограничить возможные утечки и испарения.
При дозировании кислот, используйте лабораторные коврики и/или пластиковые лотки для сбора случайно пролившейся кислоты.
Дозирование кислот, особенно соляной, азотной и уксусной, производите в функционирующем вытяжном шкафу.
В процессе лабораторных работ установите бутылку с кислотой на центральную площадку дозирования и поставьте градуированный цилиндр или контрольную пробирку в зону дозирования. Это поможет минимизировать разливы и несчастные случаи, а также ограничить количество кислоты, возвращаемой обратно на лабораторный стенд.
Вылейте необходимое для эксперимента количество кислоты из бутылки с реактивом. Запрещается помещать химические вещества обратно в бутылку с реактивом.
Держите наготове материалы для ликвидации разливов кислот при работе с ними.
Кислоты являются химически агрессивными веществами и разъедают большинство тканей, в результате чего на одежде образуются небольшие дырки. Этот процесс происходит не сразу, а в течение нескольких часов и может не проявляться до тех пор, пока одежда не будет постирана. При работе с кислотами всегда носите химически стойкий фартук или лабораторный халат.
При работе с кислотами всегда носите химически стойкий фартук или лабораторный халат.
Средства индивидуальной защиты и инструкции по технике безопасности
Перчатки из нитрильного каучука устойчивы к воздействию кислот и являются оптимальным средством защиты при работе с концентрированными кислотами. Однако любые полимерные или виниловые перчатки способны обеспечить некоторую защиту от случайных брызг, небольших разливов, которые могут возникнуть при использовании или дозировании кислот.
Средства для аварийного промывания глаз должны быть доступны в любом кабинете или лаборатории, в которых проводятся работы с кислотами или растворами кислот. Средство для аварийного промывания глаз должно обеспечивать промывку обоих глаз и подачу чистой питьевой воды как минимум в течение 15-20 минут.
При работе с кислотами в лаборатории или кислотными растворами следует носить закрытые очки для защиты от агрессивных жидкостей. Защитные очки не являются надлежащим средством индивидуальной защиты.
Следует обеспечить надлежащую вентиляцию при работе с соляной, азотной или уксусной кислотами.
Прежде чем работать с кислотами или кислотными растворами, убедитесь в наличии подходящих материалов и средств для ликвидации разливов (песок, абсорбент и нейтрализующий агент).
Меры по оказанию первой помощи
- Всегда обращайтесь за профессиональной медицинской помощью, если вы подверглись воздействию любого опасного химического вещества, особенно концентрированных кислот в лаборатории.
- При любом химическом воздействии на ткани тела или глаза лучше всего немедленно промыть их водой.
- Если кислота попала в глаза, промывайте глаза в течение как минимум 15-20 минут, воспользовавшись средством аварийного промывания глаз. Держите веки открытыми, чтобы тщательно промыть глаза.
- Если кислота попала на открытые участки кожи, промывайте их водой не менее 15-20 минут.
- Если брызги кислоты попали на одежду, сразу же снимите ее, не допуская проникновение кислоты через одежду и контакта с кожей.
 Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов.
Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов. - При попадании кислоты в желудок, первое, что нужно предпринять, — это попытаться разбавить кислоту в желудке и предотвратить дальнейшие травмы, вызванные рвотой. Если пострадавший находится в сознании, немедленно попросите его прополоскать рот водой. Попросите пострадавшего выпить одну или две чашки воды или молока. Можно также дать пострадавшему антациды, т. е. препараты для нейтрализации желудочной кислоты. Не вызывайте рвоту, не пытайтесь нейтрализовать кислоту сильным основанием и не давайте пострадавшему бикарбонат натрия или газированные напитки. Позвоните в скорую помощь и следуйте их указаниям.
Комплексное оснащение химических лабораторий
Компания Gluvex выполняет проектирование и комплексное оснащение химических лабораторий всеми видами качественного лабораторного оборудования. Возможно расширение функционала текущих отделений или организация новых. Гарантируется полное соответствие всем нормативно-правовым актам страны клиента и международным стандартам GLP, ISO/IEC 17025, ISO 15189, ISO 7218-2015 и другим.
Возможно расширение функционала текущих отделений или организация новых. Гарантируется полное соответствие всем нормативно-правовым актам страны клиента и международным стандартам GLP, ISO/IEC 17025, ISO 15189, ISO 7218-2015 и другим.
Ваши преимущества с Gluvex:
- Грамотная разработка проектной документации.
- Тесное сотрудничество с клиентом и его подрядчиками.
- Создание лабораторий «под ключ».
- Возможность интеграции в существующую среду.
- Оснащение ведущим европейским оборудованием.
- Доставка в любой регион РФ.
- Установка, наладка и калибровка всех устройств.
- Оптимизация под бюджет клиента без потери качества.
- Последовательное обучение персонала.
- Гарантия и фирменный сервис.
- Расходные материалы всегда в наличии.
- Быстрая поставка запасных частей.
- Своевременные консультации и техническая поддержка.
Специалисты Gluvex уверенно решают задачи любой сложности.Свяжитесь с нами по телефону +7 (499) 270-16-62 и убедитесь в этом!
Соляная кислота (хлористоводородная кислота) – водный раствор хлористого водорода HCl, представляет собой прозрачную бесцветную жидкость с острым запахом хлористого водорода.
Соляная кислота (хлористоводородная кислота) – водный раствор хлористого водорода HCl, представляет собой прозрачную бесцветную жидкость с острым запахом хлористого водорода.
Техническая кислота имеет желтовато-зеленый цвет из-за примесей хлора и солей железа. Максимальная концентрация соляной кислоты около 36% HCl, такой раствор имеет плотность 1,18 г/см3. Концентрированная кислота на воздухе «дымит», так как выделяющийся газообразный HCl образует с водяным паром мельчайшие капельки соляной кислоты.
Максимальная концентрация соляной кислоты около 36% HCl, такой раствор имеет плотность 1,18 г/см3. Концентрированная кислота на воздухе «дымит», так как выделяющийся газообразный HCl образует с водяным паром мельчайшие капельки соляной кислоты.
⠀
Соляная кислота не горюча, не взрывоопасна. Она является одной из самых сильных кислот, растворяет все металлы. Получают соляную кислоту растворением в воде хлористого водорода, который синтезируют или непосредственно из водорода и хлора или получают действием серной кислоты на хлорид натрия.
⠀
Выпускаемая техническая соляная кислота имеет крепость не менее 31% HCl (синтетическая) и 27,5% HCl (из NaCI). Торговую кислоту называют концентрированной, если она содержит 24% и больше HCl, если содержание HCl меньше, то кислота называется разбавленной.
⠀
Соляную кислоту применяют для получения хлоридов различных металлов, органических полупродуктов и синтетических красителей, уксусной кислоты, активированного угля, различных клеев, гидролизного спирта, в гальванопластике. Ее применяют для травления металлов, для очистки различных сосудов, обсадных труб буровых скважин от карбонатов, окислов и др. осадков и загрязнений. В металлургии кислотой обрабатывают руды, в кожевенной промышленности – кожу перед дублением и крашением. Соляную кислоту применяют в текстильной, пищевой промышленности, в медицине и т.д. Транспортируют соляную кислоту в стеклянных бутылях или гуммированных металлических сосудах, а также в полиэтиленовой посуде.
Ее применяют для травления металлов, для очистки различных сосудов, обсадных труб буровых скважин от карбонатов, окислов и др. осадков и загрязнений. В металлургии кислотой обрабатывают руды, в кожевенной промышленности – кожу перед дублением и крашением. Соляную кислоту применяют в текстильной, пищевой промышленности, в медицине и т.д. Транспортируют соляную кислоту в стеклянных бутылях или гуммированных металлических сосудах, а также в полиэтиленовой посуде.
Наши контакты:
Приемная: +998781479090
Отдел маркетинга: +998781474004
Email: [email protected]
Email: [email protected]
Опыты по химии. Соляная кислота
Чтобы поделиться, нажимайте
Получение соляной кислоты (практическая работа)
Соляная кислота HCl получается при растворении газа хлороводорода воде.
Хлороводород можно получить действием концентрированной серной кислоты на поваренную соль.
NaCl + H2SO4 = HCl ↑ + Na2HSO4
Направим поток хлороводорода в пробирку с водой. Этот газ легко растворяется в воде: до 450 объемов хлороводорода — в одном объеме воды. В пробирке образуется соляная кислота – раствор хлороводорода в воде.
Этот газ легко растворяется в воде: до 450 объемов хлороводорода — в одном объеме воды. В пробирке образуется соляная кислота – раствор хлороводорода в воде.
Оборудование: пробирка, штатив для пробирок, пробирка с газоотводной трубкой, штатив, химические стаканы, воронка.
Техника безопасности. Соблюдать правила работы с нагревательными приборами. Необходима особая осторожность при работе с концентрированной серной кислотой. Недопустимо попадание выделяющегося хлороводорода в дыхательные пути. Опыт следует проводить под тягой.
Постановка опыта – Елена Махиненко, текст – к.п.н. Павел Беспалов.
Химические свойства соляной кислоты (практическая работа)
Соляная кислота это раствор хлороводорода в воде. Чтобы получить кислоту, получим хлороводород взаимодействием растворов поваренной соли и серной кислоты.
NaCl + H2SO4 = HCl + Na2HSO4.
Растворим хлороводород в воде, получится кислота. Соляная кислота – сильная кислота с типичными для кислот свойствами. Соляная кислота взаимодействует с основаниями с образованием солей и воды. В стакане со щелочью при добавлении соляной кислоты происходит реакция нейтрализации ‑ цвет индикатора изменяется, указывая на появление нейтральной среды.
HCl + NaOH = NaCl+ H2O
Проведем качественную реакцию на хлорид-ион – реакцию с нитратом серебра.
Образуется нерастворимая соль – хлорид серебра.
HCl + AgNO3 = AgCl ↓ + HNO3
Соляная кислота взаимодействует с активными металлами: Когда цинк попадает в раствор соляной кислоты – начинается бурное выделение водорода.
2HCl + Zn = ZnCl2 + H2 ↑
Мы убедились в том, что соляная кислота реагирует с металлами, основаниями, солями.
Оборудование: спиртовка, шпатель, пробирка, штатив для пробирок, пробирка с газоотводной трубкой, штатив, химические стаканы, воронка.
Техника безопасности. Следует соблюдать правила работы с растворами кислот и щелочей. Избегать попадания кислот, щелочей, нитрата серебра на кожу и слизистые оболочки.
Постановка опыта – Елена Махиненко, текст – к.п.н. Павел Беспалов.
Растворение хлороводорода в воде
youtube.com/embed/QGNf3tNBqls?feature=oembed» frameborder=»0″ allowfullscreen=»»/>
Как хранить кислоту❓ Серную, соляную, азотную ⚗️ Материалы сосуда и пробки
Однажды для целей экспериментов с гальваникой и паяльными флюсами в домашних условиях были закуплены три вида кислот: соляная, серная, азотная. Все концентрированные, химически чистые. Все они были в одинаковых небольших пластиковых флакончиках миллилитров на 100. Позже выяснилось, что материал этих флаконов — полиэтилен высокой плотности (PEHD). Казалось, что раз в таких ёмкостях эти кислоты продают, то и хранить их можно таким же образом сколь угодно долго. Тем более, что в интернейтах этих ваших всяких пишут, что полиэтилен и полипропилен химически стойки к кислотам. Но… жизнь показала, где тут крабы зимуют:
Коричневый флакон слева на фото хранил в себе соляную кислоту (чда) 2 года. Флакон справа — для сравнения, таким матово-белым он был изначально. Кроме того, весь это флакон снаружи покрылся росой, пахнущей соляной кислотой, и вообще вонь распространялась вокруг, из-за чего этот (и другой, с азотной кислотой) забытый было уже флакон и был обнаружен.
Оказалось, что соляная кислота просачивается через полиэтилен (PE) и полипропилен (PP), причём целиком (т. е. вся молекула HCL проходит), поэтому долгосрочно (более года) в такой таре хранить её нельзя. Кислота была перелита в стеклянную тару, но с полиэтиленовой крышкой. Через два года:
В общем-то, капелек кислоты на поверхности крышки не наблюдается, но запах снаружи есть. Т. е. теперь проблема в подборе материала крышки-пробки. Кто-то в Сети написал, что достаточно пробки из мягкой резины… пробуем:
Хрен-то с два — это фото сделано уже через неделю. Активно испаряющаяся кислота сконденсировалась у пробки и явно реагирует с ней, судя по пузырькам и тёмно-жёлтому цвету. Часть пробки, побывавшая внутри, бодро изменила цвет:
Неполучи… лося. Походу хранить её можно только в стеклянной колбе со стеклянной плотно притёртой пробкой:
Но такой в наличии нет… Не совсем понятно, каким образом стеклянная пробка может герметично закрыть отверстие. Наверное, её нужно ещё смазывать таким веществом, с которым данная кислота реагирует с образованием в итоге такого другого вещества, которое плотно-непроницаемо заполнит промежуток между пробкой и горлышком. Какую смазку для какой кислоты лучше использовать — тема отдельного исследования.
Наверное, её нужно ещё смазывать таким веществом, с которым данная кислота реагирует с образованием в итоге такого другого вещества, которое плотно-непроницаемо заполнит промежуток между пробкой и горлышком. Какую смазку для какой кислоты лучше использовать — тема отдельного исследования.
С серной кислотой никаких проблем не возникло. Её продают в магазинах типа «Автозапчасти» в 6-литровых полипропиленовых (PP) канистрах (аккумуляторный электролит), из этого же материала сделаны корпуса автомобильных аккумуляторов, и храниться в таких ёмкостях данная кислота может десятилетиями. Она почти не испаряется, поэтому не пахнет, даже если её кипятить (а если кипятить, то испаряется вода, концентрация кислоты повышается, температура её кипения возрастает и испарительные способности при комнатной температуре падают совсем до нуля). Так что с хранением серной кислоты проблем нет, лишь бы не разлить её и не испачкаться ею. Соответственно, хранить серную кислоту лучше как раз не в стеклянной (бьющейся) таре, а в PP (правда сильно концентрированную советуют хранить всё-таки в стекле с PP-пробкой, т. к. полипропилен со временем этой кислотой обугливается).
к. полипропилен со временем этой кислотой обугливается).
А вот с азотной кислотой совсем всё плохо получилось. Хотя цвет флакона со временем не изменился, эта кислота тоже просочилась через PEHD и воняла, и это испарение её вредно для здоровья. Провёл эксперимент: положил флакон во внешнюю бочку, в которую напихал бумажки. Через некоторое время все бумажки в бочке стали влажными и покоричневели. Интернет нам говорит по этому поводу, что хранить азотную кислоту можно только в стеклянном сосуде, со стеклянной пробкой. За неимением таковой тары, пришлось сей флакон выбросить (азотную кислоту, предварительно разбавив, можно вылить в землю, там с неё получится много разных азотных удобрений, которые очень любят все растения).
Профессиональное хранение
Но давайте разберёмся, в чём советуют хранить эти кислоты в промышленности (помимо стекла). Вот что гласят инструкции от производителей химреактивов по этому поводу.
Серная кислота
- Может перевозиться в бочках и цистернах из коррозионно-стойкой стали марки 06ХН28МДТ.
 На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается.
На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается. - Полиэтилен высокой плотности (PEHD), полипропилен (PP), тефлон (он же polytetrafluoroethylene = PTFE, он же фторопласт-4).
На практике концентрированная серная кислота приводит к коричневению (обугливанию изнутри) PEHD и PP, что, по всей видимости, портит её чистоту. Но зато она через эти пластики не проникает. Тефлон… надо проверять, да и дороговат он. Серная кислота аккумуляторной концентрации (1.27-1.28 г/см3) может в PP-канистре храниться многие годы, канистра не коричневеет, количество кислоты не уменьшается (если, конечно, крышка нормально-плотно завинчена).
Соляная кислота
- В стальных гуммированных (покрытых изнутри резиной) бочках и цистернах.
- UPVC (Unplasticized Polyvinyl Chloride — непластифицированный поливинилхлорид, нПВХ), упрочнённый (снаружи) оболочкой из пропитанного эпоксидной смолой стекловолокна.
- Полиэтилен высокой плотности, HDPE.

- Полипропилен, PP, упрочнённый пропитанным эпоксидной смолой стекловолокном.
Как показал опыт и эксперименты, все эти промышленные методы хранения годятся только для непродолжительного хранения или транспортировки («в бочках и цистернах»). Сохранить в течение многих лет соляную кислоту, наверное, получится только в стеклянной таре со стеклянной же пробкой (и непонятно какой смазкой: кто-то использует силиконовое масло).
Через фторопласт (= тефлон, PTFE) соляная кислота просачивается, также как и через PP/PEHD, и оный тоже коричневеет.
Азотная кислота
- Концентрации более 92% — в алюминиевых бочках и цистернах. Алюминий либо чистый, либо сплав, не содержащий меди. А также из нержавеющих сталей марок (импортных) 304L и DIN 1.4361.
- Концентрация 60-70% — в бочках и цистернах из коррозионно-стойкой российской стали марки Х18Н9Т, импортные — 304L, 316L, 321.
- Оказывается даже обычная стеклянная тара не годится для хранения особо чистой азотной кислоты (имеет место быть реакция и кислота загрязняется) — нужно кварцевое стекло или окварцованное изнутри силикатное бутылочное стекло (внутренняя поверхность химически обрабатывается в течение 6-12 часов кипящей 70%-ной азотной кислотой с последующим прокаливанием при температуре 400-500°С в течение 3 ч).
- Поливинилхлорид (PVC). Точнее нПВХ — непластифицированный поливинилхлорид, в котором нет пластификаторов. Укреплённый стекловолокном, пропитанным полиэфирной/эпоксидной смолой.
- Поливинилиденфторид (PVDF).
- Этиленхлортрифторэтилен (ECTFE).
- Тефлон (он же политетрафторэтилен = PTFE — polytetrafluoroethylene, он же фторопласт-4).
Банальные ПВХ, фторопласт, алюминий — вот в чём, оказывается, надо хранить азотную кислоту. В тефлоновых контейнерах ещё (бывают такие, но они маленькие и почти непрозрачны). Или тогда уж проще купить стеклянный флакон с тефлоновой пробкой. И совсем уж просто и дёшево — тефлоновую пробку. Или самому вырезать нужной формы и диаметра на токарном станке из PTFE-стержня.
Что используют в лабах
Помимо стеклянных бутылок со стеклянными пробками, на случайных фотках различных лабораторий наиболее часто наблюдаются вот такие бутыли:
Установлено, что эти красные (иногда серые) пробки сделаны из полипропилена.
Также продают разноцветные крышки для разных кислот (видимо, сделаны из разных материалов; точнее, наверное, прокладка в них из подходящего материала):
По [ссылке] с картинки — КУПИТЬ их
Ещё бывают стеклянные бутылки, обтянутые полиэтиленовой оболочкой:По [ссылке] продают КИСЛОТЫ в этих бутылках
Если такая бутылка упадёт и разобьётся, то вся кислота останется внутри PE-мешка.Такие дела… А как храните кислоты вы?
Свойства алюминия
Свойства алюминия
Отличительные особенности алюминия — высокая электропроводимость, теплопроводность, коррозионная стойкость, малая плотность и отличная обрабатываемость давлением в холодном состоянии. **Физические свойства алюминия [2-6]**Плотность (99,996% А1), г/см3, при температуре: |
|
| 20 °С | 2,6989 |
| 1000 °С | 2,289 |
Температура, °С: |
|
| плавления | 660 |
| кипения | ~2452 |
Теплота кДж/моль: |
|
| плавления | 10,55 |
| испарения | 291,4 |
Давление пара, Па, при температуре: |
|
| 660 °С | 0,266 |
| 1123 °С | 13 3 |
| 1279 °С | 133 |
Удельная теплоемкость, Дж/(кг*К), при температуре: |
|
| 20 °С | 929,46 |
| 100 °С | 931,98 |
| Коэффициент линейного расширения при температуре 20-100 °С, К-1 | 24,58*10-6 |
Теплопроводность, Вт/( м*К), при температуре: |
|
| 20 °С | 217 |
| 190 °С | 343 |
| Электропроводность по отношению к меди при температуре 20 °С | 65,5% |
| Удельное электросопротивление, мк*Ом*м | 0.0265 |
| Температурный коэффициент электросопротивления | 0,042 |
Динамическая вязкость (99,85% А1), Н*с/м2, при температуре: |
|
| 800 °С | 2*10-3 |
| 1123 °С | 1,540-3 |
| 1279 °С | 1,3*10-3 |
Модуль нормальной упругости Е, МПа, при температуре: |
|
| 180 °С | 7,8*104 |
| 20 °С | 7,1*104 |
| 100 °С | 7,0*104 |
| 200 °С | 6,6*104 |
| 400 °С | 5,6*104 |
| 500 °С | 5,0*104 |
| 600 °С | 4,4*104 |
| Модуль сдвига при температуре 20 °С | 2,7*104 МПа |
| Магнитная характеристика алюминия | Слабо парамагнитен |
Временное сопротивление разрыву σв,МПА: |
|
| в отожженном состоянии | 50 |
| в деформированном (холоднокатаном) состоянии | 115 |
Предел текучести s 0,2 : |
|
| в отожженном состоянии | 50-80 |
| в деформированном состоянии | 120 |
Предел усталости (500*10 6 циклов),σ -1: |
|
| в отожженном состоянии | 40 |
| в деформированном состоянии | 50 |
Предел ползучести, при температуре: |
|
| 15 °С | 50 |
| 100 °С | 27 |
| 200 °С | 7 |
Предел прочности при срезе,σ ср: |
|
| в отожженном состоянии | 60 |
| в деформированном состоянии | 100 |
Относительное удлинение,δ: |
|
| в отожженном состоянии | 30-40% |
| в деформированном состоянии | 5-10% |
Относительное сужение, ψ: |
|
| в отожженном состоянии | 70-90% |
| в деформированном состоянии | 50-60% |
| Ударная вязкость при температуре 20 °С aм | 140 |
Твердость по Бринеллю, НВ: |
|
| в отожженном состоянии | 25 |
| в литом состоянии | 20 |
| в деформированном состоянии | 30-35 |
| Состояние | Содержание Аl, % | Предел прочности при растяжении σв2МПа | Предел текучести при растяжении σ.00,2, МПа | Относительное удлинение δ, % | Твердость по Бринеллю, НВ |
| Литой в землю | 99,996 | 50 | — | 45 | 13-15 |
| Литой в землю | 99,5 | 75 | — | 29 | 20 |
| Литой в землю | 99.0 | 85 | — | 20 | 25 |
| Литой в кокиль | 99,0 | 90 | — | 25 | 25 |
| Деформированный и отожженный | 99.0 | 90 | 30 | 30 | 25 |
| Деформированный | 99,0 | 140 | 100 | 12 | 32 |
| Литой в землю | 98,0 | 90 | 35 | 12,5 | 28 |
| Температура | °С |
| литья горячей обработки отжига отпуска Линейная усадка, % Допускаемая деформация (холодная и горячая), % Начало рекристаллизации, °С Жидкотекучесть, мм. |
690-710 350-450 370-400 150 2,7 75-90 150 317 |
Насосы Lutz для кислот | ЕТ-Сервис
Для перекачки высококонцентрированной серной кислоты особенно хорошо подходят насосы из сплавов нержавеющей стали, так как они образуют пассивный слой, защищающий от коррозии. В этом материальном исполнении можем предложить:
Перекачивать высоко агрессивную разбавленную серную кислоту лучше всего насосами из фторопласта (PVDF).
Lutz может предложить различные по конструкции насосы из этого материала. В зависимости от задачи перекачивания вы можете выбрать:
Для дозирования серной кислоты в большой концентрации свыше 40% подходят дозирующие насосы LUTZ-JESCO с корпусом из нержавеющей стали, а в малой концентрации можно выбрать любой насос, исходя из задачи.
Скрыть
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Концентрат соляной кислоты | 38282
Концентрат соляной кислоты | 38282 | Honeywell Research ChemicalsПохоже, в вашем браузере отключен JavaScript. Для максимального удобства работы на нашем сайте обязательно включите Javascript в своем браузере.
Мы используем выбранное вами местоположение, чтобы персонализировать контент на нашем веб-сайте и предоставлять вам актуальную информацию о ценах на продукты и их наличии.
{{еще}}{{{title.snippet}}} ({{total_results}})
{{/если}} {{else ifEq this.searchTypeValCheck «product»}} {{#if cas_number_all.snippet}} {{#ifEq cas_number_all.snippet «НЕ ПРИМЕНИМО»}}{{{имя.сниппет}}} | {{{short_description.snippet}}} ({{total_results}})
{{еще}}{{{name.snippet}}} | {{{short_description.snippet}}} | {{{cas_number_all.snippet}}} ({{total_results}})
{{/ ifEq}} {{еще}}{{{name.snippet}}} | {{{short_description.snippet}}} ({{total_results}})
{{/если}} {{/ ifEq}} {{иначе ifEq this.multiSearchCheck false}} {{#ifEq this.searchTypeValCheck «aem»}} {{#if resource_type.snippet}}{{{dc_title.snippet}}}
{{еще}}{{{title.snippet}}}
{{/если}} {{else ifEq this.searchTypeValCheck «product»}} {{#if cas_number_all.snippet}} {{#ifEq cas_number_all.snippet «НЕ ПРИМЕНИМО»}}{{{name.snippet}}} | {{{short_description.snippet}}}
{{еще}}{{{имя.сниппет}}} | {{{short_description.snippet}}} | {{{cas_number_all.snippet}}}
{{/ ifEq}} {{еще}}{{{name.snippet}}} | {{{short_description.snippet}}}
{{/если}} {{/ ifEq}} {{/ ifEq}} {{/каждый}}Из-за бездействия вы выйдете из системы через 0: 0.
для 1 л стандартного раствора, 1.0 M HCl (1.0 N)
Синоним (ы)Раствор соляной кислоты; Раствор хлористого водорода
XВойдите, чтобы просмотреть цены и доступность для конкретного аккаунта.
Цены, указанные в каталоге, не включают действующие налоги.
Войдите в систему или создайте учетную запись
Общая информация:- Лидирующий в отрасли более 65 лет
- Honeywell теперь поставляет неорганические реагенты премиум-класса Fluka ™ по всему миру — с гарантированной консистенцией, чистотой и точностью
| Бренд Fluka | Код UNSPSC 12352301 | Номера CAS (все) | Линейная формула HCl | Номер MDL |
| Молярный246 г / моль | Синонимы Раствор соляной кислоты; Раствор хлороводорода |
Технические характеристики
| Свойство | Значение | |
|---|---|---|
| Фактор | 0,998-1,002 | |
| BAM / EMPA | ||
| TraceabletoNISTSRM | эффективный |
Свойства
| Свойство | Значение | Значение | |
|---|---|---|---|
| Температура самовоспламенения | / | Температура кипения | 10092 | Не горюч. (1.013 гПа) |
| Сертификация | Отслеживается до SRM от NIST | ||
| Цвет | Бесцветный | ||
| Коррозионная активность | Коррозионно по отношению к металлам | ||
| Плотность | 1,010 г / см3 (20 ° C) | ||
| Температура воспламенения | Неприменимо | ||
| Форма | Жидкость | ||
| Марка | Объемный концентрат | ||
| Несовместимые материалы | Этиленимин, аммиак, хлорсульфоновая кислота, серная кислота, сильные окислители основания, уксусный ангидрид, амины, металлы | ||
| Нижний предел взрываемости | Неприменимо | ||
| Точка плавления / диапазон | 0 ° C | ||
| Коэффициент распределения | Нет данных | ||
| Растворимость в воде | Полностью смешивается | ||
| Верхний предел взрываемости | Неприменимо | ||
| Давление пара | Аналогично воде | ||
| Вязкость | Нет данных | ||
| Значение pH | 1 | ||
| Температура хранения | Окружающая среда |
Информация по технике безопасности
| Свойство | Значение | ||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Класс опасности | 8 | ||||||||||||||||||||||||||||||||||||||
| Группа упаковки | III | ||||||||||||||||||||||||||||||||||||||
| UN ID | UN178916 | ||||||||||||||||||||||||||||||||||||||
Соляная кислота Хлористый водород | |
Х.ч. конц. HCl содержит HCl | |
Концентрированная кислота выделяет HCl при т.кип. 110 ° C, т.пл. -24 ° C, т.кип. -85 ° C, т.пл. -114 ° C Смешивается с водой | |
Резкий раздражающий запах Резкий раздражающий запах | |
1,27 (воздух = 1,0) | LD 50 перорально (кролик) 900 мг / кг LC 50 ингалято (крыса) 3124 ppm (1 ч) PEL (OSHA) 5 ppm (7 мг / м 3 ; потолок) ПДК (ACGIH) 5 частей на миллион (7,5 мг / м 3 ; потолок) | Сильно агрессивный; вызывает сильные ожоги при попадании в глаза и на кожу, а также при вдыхании газа. | Соляная кислота и газообразный хлористый водород являются очень едкими веществами, которые могут вызвать серьезные ожоги при контакте с тканями тела. Водная кислота и газ — сильные раздражители глаз и слезоточивые средства. Попадание концентрированной соляной кислоты или концентрированных паров HCl в глаза может привести к серьезным травмам, что приведет к необратимому ухудшению зрения и возможной слепоте, а контакт с кожей приведет к тяжелым ожогам. Проглатывание может вызвать серьезные ожоги полости рта, горла и желудочно-кишечного тракта и привести к летальному исходу.Вдыхание газообразного хлористого водорода может вызвать сильное раздражение и травму верхних дыхательных путей и легких, а воздействие высоких концентраций может вызвать смерть. Считается, что газ HCl обладает адекватными предупреждающими свойствами. Не было обнаружено, что хлористый водород является канцерогенным и не проявляет токсичности для репродуктивной системы или развития человека. |
Негорючие, но при контакте с металлами может образовываться легковоспламеняющийся газообразный водород. | |
Соляная кислота и хлористый водород бурно реагируют со многими металлами с образованием легковоспламеняющегося газообразного водорода, который может взорваться.Реакция с окислителями, такими как перманганаты, хлораты, хлориты и гипохлориты, может привести к образованию хлора или брома. | |
С соляной кислотой следует обращаться в лаборатории в соответствии с «основными принципами осторожности», описанными в главе 5.C. При работе с этой кислотой следует использовать защитные очки и резиновые перчатки, а контейнеры с HCl следует хранить в хорошо вентилируемом месте, изолированном от несовместимых металлов. Ни в коем случае нельзя добавлять воду в HCl, поскольку это может привести к разбрызгиванию; всегда добавляйте кислоту в воду.Емкости с соляной кислотой следует хранить во вторичных пластиковых лотках, чтобы избежать коррозии металлических полок для хранения из-за капель или разливов. С газообразным хлористым водородом следует обращаться в лаборатории, используя «основные разумные методы», описанные в главе 5.C, дополненные процедурами, описанными в главе 5.H для работы со сжатыми газами. Баллоны с хлороводородом следует хранить в прохладном, сухом месте, отдельно от щелочных металлов и других несовместимых веществ. | |
При попадании на кожу снять загрязненную одежду и немедленно промыть проточной водой не менее 15 мин. В случае попадания в глаза немедленно промыть большим количеством воды не менее 15 минут, удерживая веки открытыми. Обратитесь за медицинской помощью. В случае проглатывания не вызывать рвоту. Дайте большое количество воды или молока и доставьте в медицинское учреждение. В случае вдыхания вынести на свежий воздух и обратиться за медицинской помощью. Тщательно нейтрализуйте пролитую соляную кислоту подходящим средством, например порошкообразным бикарбонатом натрия, затем разбавьте абсорбирующим материалом, поместите в соответствующий контейнер и утилизируйте должным образом. Разбавление водой перед нанесением твердого адсорбента может быть эффективным средством уменьшения воздействия паров хлористого водорода. В случае большого разлива или выброса в замкнутом пространстве может потребоваться защита органов дыхания. Утечки газообразного HCl проявляются в образовании плотных белых паров при контакте с атмосферой.Небольшие утечки можно обнаружить, подержав открытый контейнер с концентрированным гидроксидом аммония рядом с местом предполагаемой утечки; густые белые пары подтверждают наличие утечки. В случае случайного выброса газообразного хлористого водорода, например, из протекающего баллона или связанного с ним устройства, эвакуируйте зону и устраните источник утечки, если это можно сделать безопасно. Переместите баллон в вытяжной шкаф или в удаленное место, если его нельзя отключить. Может потребоваться полная защита органов дыхания и защитная одежда для борьбы с выбросом хлористого водорода. | |
Во многих местах соляная кислота или остатки разлива могут быть сброшены в канализацию после соответствующего разбавления и нейтрализации. В противном случае соляную кислоту и отходы, содержащие это вещество, следует поместить в соответствующий контейнер, четко помеченный, и обращаться с ними в соответствии с инструкциями по утилизации отходов вашего учреждения. Избыток хлористого водорода в баллонах следует вернуть производителю. | |
Информация в этом LCSS была собрана комитетом Национального исследовательского совета по литературным источникам и материалам Паспорта безопасности и считается точным по состоянию на июль 1994 года.Это резюме предназначено для использования обученным лабораторным персоналом. в сочетании с отчетом NRC Prudent Практика в лаборатории: обращение с химическими веществами и их утилизация . Этот LCSS представляет собой краткую краткое изложение информации по безопасности, которое должно быть достаточным для большинства лабораторное использование указанного вещества, но в некоторых случаях может рекомендуется ознакомиться с более подробными ссылками. Эта информация не следует использовать в качестве руководства для внелабораторного использования этого химический. Copyright 1995 Национальная академия наук.Все права защищены. | |
Производство соляной кислоты | KBR
Работа с кислотой требует современных технологий. Наши индивидуальные установки для обработки кислот и отходов производства соляной кислоты удовлетворяют особым требованиям, сочетая самые современные технологии с проверенными материалами.
KBR предлагает полный спектр обработки и обработки соляной кислотой (HCl), начиная от простой перегонки над ректификацией до экстрактивной ректификации и ректификации с двойным давлением, для достижения любой чистоты и концентрации во всем диапазоне вплоть до почти полного отсутствия воды, 100% сухой газ.Кроме того, предлагается противоположная абсорбция сухого газообразного HCl для достижения желаемой более низкой концентрации HCl.
«Что касается обработки соляной кислоты, мы специализируемся на обработке кислот и потоков отходов, что обеспечивает экономические и экологические преимущества».
Мы предлагаем технологические решения и технологии для концентрирования побочного продукта HCl от химического процесса, такого как фосгенирование, для рециркуляции или продажи третьим сторонам, для концентрирования разбавленных потоков HCl из вентиляционных скрубберов и удаления HCl из сточных вод по соображениям производительности или защиты окружающей среды.Мы также разрабатываем новые приложения нашей технологии и управляем лабораторией с пилотными установками, которые позволяют нам разрабатывать и масштабировать такие новые приложения очень надежно и эффективно для наших клиентов.
Мы проектируем малогабаритные установки, на которых восстанавливается всего несколько сотен килограммов кислоты в час, вплоть до установок мирового масштаба.
Предварительное концентрирование
Предварительное концентрирование используется для обработки сырой соляной кислоты с низким содержанием HCl для достижения концентрации HCl до 24% по весу. Воду удаляют ректификацией, а азеотроп вода / соляная кислота удаляют в нижнем потоке.В зависимости от рабочего давления азеотропная концентрация HCl составляет от 18 до 24 мас.%. Летучие и нелетучие примеси также удаляются из потока HCl во время предварительного концентрирования.
Средняя концентрация
Соляная кислота с концентрацией 30–35 мас.% Может быть произведена из любой разбавленной сырой соляной кислоты. При экстракционной ректификации слабая соляная кислота смешивается с экстракционным агентом и подается в ректификационную колонну. Вода абсорбируется экстрагирующим агентом, и летучесть потока соляной кислоты увеличивается.В верхней части колонны очищают соляную кислоту средней концентрации. Разбавленный экстракционный агент собирается в отстойнике, повторно концентрируется во внешнем испарителе и подается обратно в колонну. CaCl2, MgCl2 или h3SO4 могут использоваться в качестве экстрактивных агентов для удаления воды. Процесс двойного давления также доступен для производства соляной кислоты средней концентрации. На первом этапе предварительно сконцентрированная кислота с содержанием HCl 22–24 мас.% Разделяется на головной продукт с примерно 30–35 мас.% HCl и азеотропную кислоту отстойного продукта с использованием ректификации под давлением.На втором этапе азеотропная кислота восстанавливается путем испарения воды в условиях вакуума до 22–24 мас.% HCl, а затем возвращается на первую стадию. В качестве альтернативы азеотропная кислота может быть повторно усилена с помощью концентрированного газообразного HCl.
Высокая концентрация
Чтобы производить газообразный HCl с высокой концентрацией до 100% по весу HCl, можно применять ту же конфигурацию процесса для средней концентрации, изменяя при этом рабочие условия.
Очистка
Отработанные соляные кислоты различного происхождения, содержащие органические и неорганические примеси, могут быть извлечены и очищены с использованием технологии KBR PLINKE.
СОП: Разбавление концентрированной соляной кислоты
Решить переменные, которые нужно изменить и измерить в честных тестах, и наблюдать, измерить и записать данные с точностью, используя цифровые технологии, в зависимости от ситуации Решить переменные, которые необходимо изменить и измерить в честных тестах, и наблюдать, измерить и записать данные с точностью, используя цифровые технологии в зависимости от ситуации Навыки — Планирование и проведение — Участвовать в исследованиях и делать наблюдения с помощью органов чувств — Общение — Обмен наблюдениями и идеями — Задавать вопросы и предсказывать — Ставить вопросы о знакомых объектах и событиях и отвечать на них — Обработка и анализ данных и информации — Участвуйте в обсуждениях наблюдений и представляйте идеи-Наука как человеческое усилие — Природа и развитие науки — Наука включает в себя наблюдение, постановку вопросов и описание изменений в объектах и событиях-Наука Понимание — Физические науки — Способ движения объектов зависит от множества факторов, включая их размер и форму — Биологические науки- — У живых существ есть базовые потребности, включая пищу и воду — Науки о Земле и космосе — Ежедневные и сезонные изменения в нашей окружающей среде влияют на повседневную жизнь — Химические науки — Объекты сделаны из материалов, которые обладают наблюдаемыми свойствами1-Понимание науки — Биологические науки — Живые существа имеют множество внешних характеристик — Живые существа живут в разных местах, где их потребности удовлетворяются — Химические науки — Повседневные материалы можно физически изменять различными способами — Физические Науки — Свет и звук производятся различными источниками и могут быть восприняты — Науки о Земле и космосе — Наблюдаемые изменения происходят в небе и ландшафте — Наука как деятельность человека — Природа и развитие науки — — Наука включает в себя наблюдение, постановку вопросов и описание изменений в объектах и событиях — Использование и влияние науки — Люди используют науку в своей повседневной жизни, в том числе при заботе об окружающей среде и живых существах — Навыки исследования науки — Вопросы и прогнозы Инг — Ставьте вопросы и отвечайте на вопросы, а также делайте прогнозы относительно знакомых объектов и событий — Планирование и проведение — Участвуйте в управляемых исследованиях, чтобы исследовать и отвечать на вопросы, используя неформальные измерения для сбора и записи наблюдений, используя при необходимости цифровые технологии- —Участвовать в контролируемых исследованиях, чтобы изучить и ответить на вопросы, используя неформальные измерения для сбора и записи наблюдений, используя при необходимости цифровые технологии — Обработка и анализ данных и информации — Использование ряда методов для сортировки информации, включая чертежи и предоставленные таблицы и посредством обсуждения сравнивать наблюдения с прогнозами — использовать ряд методов для сортировки информации, включая рисунки и предоставленные таблицы, а также путем обсуждения сравнивать наблюдения с прогнозами — оценка — сравнивать наблюдения с наблюдениями других — общение— -Представлять и передавать наблюдения и идеи различными способами 2-Понимание науки — Биологические науки — — Живые существа растут, изменяются и имеют потомство, похожее на самих себя — Химические науки — Различные материалы можно комбинировать для определенной цели — Физические науки — Толчок или притяжение влияет на то, как объект движется или меняет форму — Науки о Земле и космосе — Ресурсы Земли используются различными способами — Наука как деятельность человека — Природа и развитие науки — Наука включает в себя наблюдение, постановку вопросов и описание изменений в объектах и событиях — Использование науки и ее влияние — Люди используют науку в своей повседневной жизни, в том числе при заботе об окружающей среде и живых существах. Навыки исследования науки — Задавать вопросы и делать прогнозы — Ставить вопросы и отвечать на них, а также делать прогнозы относительно знакомых объектов и события — Обработка и анализ данных и информации — Используйте ряд методов для сортировки информации, включая рисунки и предоставленные таблицы, а также путем обсуждения, сравнивайте наблюдения с прогнозами — Используйте ряд методов для сортировки информации, в том числе dr обзоров и предоставленных таблиц, а также в ходе обсуждения сравните наблюдения с прогнозами — Планирование и проведение — Участвуйте в управляемых исследованиях, чтобы исследовать и отвечать на вопросы, используя неофициальные измерения для сбора и записи наблюдений, при необходимости используя цифровые технологии — Участвуйте в управляемых исследованиях исследовать и отвечать на вопросы, используя неформальные измерения для сбора и записи наблюдений, используя при необходимости цифровые технологии — Оценка — Сравнение наблюдений с наблюдениями других — Общение — Представлять и передавать наблюдения и идеи различными способами3-Наука Понимание — Биологические науки — Живые существа можно сгруппировать на основе наблюдаемых характеристик и отличить от неживых существ — Физические науки — Тепло может производиться разными способами и может переходить от одного объекта к другому — Химические науки — Изменение состояния между твердым и жидким телом может быть вызвано добавлением или удалением тепла — Науки о Земле и космосе — Ea Вращение rth вокруг своей оси вызывает регулярные изменения, в том числе дневные и ночные — Наука как человеческое усилие — Использование и влияние науки — Научные знания помогают людям понять эффект своих действий — Природа и развитие науки — Наука включает в себя прогнозирование и описание закономерностей и взаимосвязей — Навыки исследования науки — Опрос и прогнозирование — Под руководством вы определяйте вопросы в знакомых контекстах, которые можно исследовать с научной точки зрения, и делать прогнозы на основе предшествующих знаний — Обработка и анализ данных и информации — —Сравните результаты с прогнозами, предлагая возможные причины выводов — Используйте ряд методов, включая таблицы и простые столбчатые диаграммы, для представления данных и выявления закономерностей и тенденций — Планирование и проведение — Рассмотрите элементы объективных тестов и использовать формальные измерения и цифровые технологии по мере необходимости для точного проведения и записи наблюдений — Планируйте и проводите научные исследования под руководством найти ответы на вопросы, учитывая безопасное использование соответствующих материалов и оборудования — Оценка — Обдумайте исследования, в том числе, был ли тест справедливым или нет — Общение — Представляйте и сообщайте наблюдения, идеи и результаты, используя формальные и неформальные формы Представления4-Понимание науки — Биологические науки — Живые существа зависят друг от друга и окружающей среды, чтобы выжить — У живых существ есть жизненные циклы — Химические науки — Природные и обработанные материалы имеют ряд физических свойств, которые могут влиять их использование — Науки о Земле и космосе — Поверхность Земли изменяется с течением времени в результате естественных процессов и деятельности человека — Физические науки — Силы могут быть применены одним объектом к другому посредством прямого контакта или с расстояния — Наука как человеческое усилие — Использование и влияние науки — Научные знания помогают людям понять эффект своих действий — Природа и развитие науки — Наука включает в себя предсказания и описание закономерности и взаимосвязи — Навыки исследования науки — Обработка и анализ данных и информации — Сравнение результатов с прогнозами, указание возможных причин для выводов — Использование ряда методов, включая таблицы и простые столбчатые диаграммы, для представления данных и выявления закономерностей и тенденции — Опрос и прогнозирование — Под руководством выявляйте вопросы в знакомых контекстах, которые можно исследовать с научной точки зрения, и делать прогнозы на основе предшествующих знаний — Планирование и проведение — Рассмотрение элементов честных тестов и использование формальных измерений и цифровых технологий по мере необходимости, точно производить и записывать наблюдения — Под руководством, планировать и проводить научные исследования, чтобы найти ответы на вопросы, учитывая безопасное использование соответствующих материалов и оборудования — Оценка — Обдумайте исследования, в том числе, было ли испытание справедливо или нет — Общение — Представлять и сообщать наблюдения, идеи и выводы, используя формальные и неформальные представления5-Sci Понимание — Биологические науки — У живых существ есть структурные особенности и приспособления, которые помогают им выживать в окружающей среде — Химические науки — Твердые тела, жидкости и газы имеют разные наблюдаемые свойства и ведут себя по-разному — Земля и Космос Науки — Земля является частью системы планет, вращающихся вокруг звезды (Солнца) — Физические науки — Свет от источника образует тени и может поглощаться, отражаться и преломляться — Наука как человеческое усилие — Использование и влияние науки — Научные знания используются для решения проблем и информирования людей и решений сообщества — Научное понимание, открытия и изобретения используются для решения проблем, которые непосредственно влияют на жизнь людей — Природа и развитие науки — -Важный вклад в развитие науки внесли люди, принадлежащие к разным культурам — Наука включает проверку предсказаний путем сбора данных и использования доказательств для разработки объяснений событий и явлений и т. Д. отражает исторический и культурный вклад — Навыки исследования науки — Планирование и проведение — Решите, какую переменную следует изменить и измерить с помощью объективных тестов, и точно наблюдать, измерять и записывать данные, используя при необходимости цифровые технологии — Определить, спланировать и применить элементы научных исследований для ответов на вопросы и решения проблем с безопасным использованием оборудования и материалов и выявления потенциальных рисков — Определение, планирование и применение элементов научных исследований для ответа на вопросы и решения проблем с безопасным использованием оборудования и материалов и выявления потенциальных рисков — Обработка и анализ данных и информации — Сравнение данных с прогнозами и использование в качестве доказательства при разработке объяснений — Создание и использование ряда представлений, включая таблицы и графики, для представления и описания наблюдений, закономерностей или взаимосвязей в данных с использованием цифровых технологий при необходимости — Оценка — Обдумайте и предложите улучшения в научных исследованиях tions — Общение — Передача идей, объяснений и процессов с использованием научных представлений различными способами, включая мультимодальные тексты — Вопросы и прогнозы — Под руководством задавайте уточняющие вопросы и делайте прогнозы относительно научных исследований6-Понимание науки — Биологические науки — Физические условия окружающей среды влияют на рост и выживание живых существ — Химические науки — Изменения материалов могут быть обратимыми или необратимыми — Физические науки — Электрическая энергия может передаваться и преобразуется в электрические цепи и может генерироваться из ряда источников — Электроэнергия может передаваться и преобразовываться в электрических цепях и может вырабатываться из ряда источников — Науки о Земле и космосе — Внезапные геологические изменения и экстремальные погодные явления могут повлиять на поверхность Земли — Наука как человеческое усилие — Использование и влияние науки — Научные знания используются для решения проблем и информирования людей и решения сообщества — Научное понимание, открытия и изобретения используются для решения проблем, которые напрямую влияют на жизнь людей — Природа и развитие науки — Важный вклад в развитие науки внесли люди, принадлежащие к разным культурам — Наука включает в себя проверку предсказаний путем сбора данных и использования доказательств для разработки объяснений событий и явлений и отражает исторический и культурный вклад. — Навыки исследования науки — Оценка — Обдумывайте и предлагайте улучшения в научных исследованиях — Планирование и проведение — — Решите, какая переменная должна быть изменена и измерена в честных тестах, и точно наблюдать, измерять и записывать данные, используя при необходимости цифровые технологии — Выявлять, планировать и применять элементы научных исследований для ответа на вопросы и решения проблем с использованием оборудования и материалов безопасно и выявить потенциальные риски — Определить, спланировать и применить элементы научных исследований для реагирования Решайте вопросы и решайте проблемы, используя оборудование и материалы безопасно и выявляя потенциальные риски — Общение — Передача идей, объяснений и процессов с использованием научных представлений различными способами, включая мультимодальные тексты — Обработка и анализ данных и информации — -Сравнить данные с прогнозами и использовать их в качестве доказательств при разработке объяснений — Построить и использовать ряд представлений, включая таблицы и графики, для представления и описания наблюдений, закономерностей или взаимосвязей в данных с использованием цифровых технологий в зависимости от обстоятельств — Опрос и прогнозирование- — Под руководством задавайте уточняющие вопросы и делайте прогнозы относительно научных исследований7 — Понимание науки — Биологические науки — Взаимодействия между организмами, включая последствия деятельности человека, могут быть представлены пищевыми цепями и пищевыми цепями — Классификация помогает организовать разнообразная группа организмов — Химические науки — Смеси, включая растворы, содержат комбинацию p Вещества, которые можно разделить с помощью ряда методов — Физические науки — Изменение движения объекта вызвано несбалансированными силами, в том числе гравитационным притяжением Земли, действующими на объект — Гравитация Земли притягивает объекты к центру Земля — Науки о Земле и космосе — Некоторые ресурсы Земли являются возобновляемыми, включая воду, циркулирующую в окружающей среде, но другие невозобновляемые — Вода является важным ресурсом, который циркулирует в окружающей среде — Предсказуемые явления на Земля, включая времена года и затмения, вызваны относительным положением Солнца, Земли и Луны — Наука как человеческое усилие — Природа и развитие науки — Научное знание изменило представление людей о мире и усовершенствовано как становятся доступными новые данные — Научные знания могут развиваться посредством сотрудничества между научными дисциплинами и вклада людей из разных культур — Использование науки и влияние — Люди нас Понимание науки и навыки в своей профессии, и они повлияли на развитие практики в областях человеческой деятельности — Люди используют понимание и навыки из разных научных дисциплин в своей профессии — Решения современных проблем, которые обнаруживаются с помощью науки и технологии могут влиять на другие области общества и могут включать этические соображения — Навыки исследования в области науки — Задавать вопросы и прогнозировать — Выявлять вопросы и проблемы, которые можно исследовать с научной точки зрения, и делать прогнозы на основе научных знаний — Обработка и анализ данных и информации — Обобщайте данные, полученные из собственных исследований учащихся и из вторичных источников, и используйте научное понимание для выявления взаимосвязей и делайте выводы на основе доказательств — Создавайте и используйте ряд представлений, включая графики, ключи и модели для представления и анализа закономерностей или взаимосвязи в данных с использованием цифровых технологий в зависимости от ситуации — Оценка — Размышляйте о науке Научные исследования, включая оценку качества собранных данных и выявление улучшений — Использование научных знаний и результатов исследований для оценки заявлений, основанных на доказательствах — Планирование и проведение — Измерение и контроль переменных, выбор оборудования, подходящего для задачи и собирать данные с точностью — Совместно и индивидуально планировать и проводить ряд типов исследований, включая полевые работы и эксперименты, обеспечивая соблюдение правил безопасности и этических норм — Общение — Обмен идеями, выводами и основанными на фактах решениями проблем с использованием научных язык и представления с использованием цифровых технологий в зависимости от ситуации8-Понимание науки — Биологические науки — Многоклеточные организмы содержат системы органов, которые выполняют специализированные функции, которые позволяют им выживать и воспроизводиться — Клетки являются основными единицами живых существ и имеют специализированные структуры и функции — Химические науки — Свойства различных состояния материи можно объяснить с точки зрения движения и расположения частиц — Различия между элементами, соединениями и смесями можно описать на уровне частиц — Химические изменения включают вещества, вступающие в реакцию с образованием новых веществ — Физические науки — -Энергия проявляется в различных формах, включая движение (кинетическая энергия), тепло и потенциальная энергия, а преобразования и передачи энергии вызывают изменения внутри систем — Науки о Земле и космосе — Осадочные, магматические и метаморфические породы содержат минералы и образуются в результате процессов, которые происходят на Земле в различных временных масштабах — Наука как человеческое усилие — Природа и развитие науки — Научное знание изменило понимание мира людьми и уточняется по мере появления новых данных — Научное знание может развиваться посредством сотрудничества через научные дисциплины и вклад людей из разных культур — Использование и влияние науки — Люди используют понимание и навыки ls из разных научных дисциплин в своей профессии — Решения современных проблем, которые обнаруживаются с помощью науки и техники, могут повлиять на другие области общества и могут включать этические соображения — Люди используют научные знания и навыки в своей профессии, и эти повлияли на развитие практики в областях человеческой деятельности — Навыки проведения научных исследований — Планирование и проведение — Совместно и индивидуально планировать и проводить ряд типов исследований, включая полевые работы и эксперименты, обеспечивая соблюдение правил безопасности и этических норм — В ходе честных испытаний измеряйте и контролируйте переменные и выбирайте оборудование для сбора данных с точностью, соответствующей задаче — Измеряйте и управляйте переменными, выбирайте оборудование, соответствующее задаче, и собирайте данные с точностью — Обработка и анализ данных и информации — -Создать и использовать ряд представлений, включая графики, ключи и модели для представления и анализа закономерностей или отношений в d ata, используя при необходимости цифровые технологии — Обобщайте данные, полученные из собственных исследований учащихся и из вторичных источников, и используйте научное понимание для выявления взаимосвязей и делайте выводы на основе доказательств — Общение — Обмен идеями, выводами и решениями, основанными на фактах к проблемам с использованием научного языка и представлений с использованием цифровых технологий по мере необходимости — Опрос и прогнозирование — Определение вопросов и проблем, которые можно исследовать с научной точки зрения, и делать прогнозы на основе научных знаний — Оценка — Использование научных знаний и результатов исследований для оценивать утверждения, основанные на доказательствах — Обдумывать научные исследования, включая оценку качества собранных данных и выявление улучшений9-Понимание науки — Науки о Земле и космосе — Теория тектоники плит объясняет глобальные закономерности геологической активности и движения континентов —Биологические науки — Экосистемы состоят из сообществ интерд независимые организмы и абиотические компоненты окружающей среды; материя и энергия проходят через эти системы — Многоклеточные организмы полагаются на скоординированные и взаимозависимые внутренние системы, чтобы реагировать на изменения в окружающей их среде — Химические науки — Химические реакции, включая горение и реакции кислот, важны как в неживые и живые системы и включают передачу энергии — Химические реакции включают перегруппировку атомов с образованием новых веществ; во время химической реакции масса не создается и не разрушается — Вся материя состоит из атомов, которые состоят из протонов, нейтронов и электронов; естественная радиоактивность возникает в результате распада ядер в атомах — Физические науки — Передача энергии через различные среды может быть объяснена с помощью моделей волн и частиц — Наука как человеческое усилие — Природа и развитие науки — Научное понимание, в том числе модели и теории, оспариваются и со временем уточняются в процессе обзора научным сообществом — Прогресс в научном понимании часто зависит от технологических достижений и часто связан с научными открытиями — Использование и влияние науки — Люди использовать научные знания, чтобы оценить, принимают ли они утверждения, объяснения или прогнозы, а достижения в науке могут повлиять на жизнь людей, в том числе создать новые возможности для карьерного роста — Ценности и потребности современного общества могут повлиять на направленность научных исследований — Люди используют научные знания для оценки того, принимают ли они утверждения, объяснения или прогнозы, а достижения науки могут повлиять на жизнь людей, в том числе Создание новых возможностей для карьерного роста — Навыки проведения научных исследований — Планирование и проведение — Выбор и использование соответствующего оборудования, включая цифровые технологии, для систематического и точного сбора и записи данных — Планирование, выбор и использование соответствующих типов исследований, включая полевые работы и лабораторные эксперименты для сбора надежных данных; оценивать риски и решать этические проблемы, связанные с этими методами — Обмен информацией — Обмен научными идеями и информацией для конкретной цели, включая построение доказательных аргументов и использование соответствующего научного языка, условностей и представлений — Обработка и анализ данных и информации — —Анализ закономерностей и тенденций в данных, включая описание взаимосвязей между переменными и выявление несоответствий — Использование знаний о научных концепциях, чтобы делать выводы, согласующиеся с доказательствами — Вопросы и прогнозы — Формулировать вопросы или гипотезы, которые можно исследовать с научной точки зрения — Оценка — Оценить выводы, включая определение источников неопределенности и возможных альтернативных объяснений, и описать конкретные способы повышения качества данных — Критически проанализировать достоверность информации в первичных и вторичных источниках и оценить подходы, используемые для решать проблемы10-Понимание науки — Физические науки ences — Движение объектов можно описать и спрогнозировать с помощью законов физики — Сохранение энергии в системе можно объяснить описанием передачи и преобразований энергии — Науки о Земле и космосе — Глобальные системы, включая углерод цикла, полагаться на взаимодействия с участием биосферы, литосферы, гидросферы и атмосферы — Вселенная содержит особенности, включая галактики, звезды и солнечные системы, и теорию Большого взрыва можно использовать для объяснения происхождения Вселенной — Химические науки — Атомная структура и свойства элементов используются для организации их в Периодической таблице — Различные типы химических реакций используются для производства ряда продуктов и могут происходить с разной скоростью — Биологические науки — Передача наследственных характеристик от поколения к поколению включает ДНК и гены. Теория эволюции путем естественного отбора объясняет разнообразие живых существ и поддерживается рядом научных данных. человеческое усилие — Использование и влияние науки — Люди используют научные знания, чтобы оценить, принимают ли они утверждения, объяснения или прогнозы, а достижения науки могут повлиять на жизнь людей, включая создание новых карьерных возможностей — Люди используют научные знания для оценить, принимают ли они утверждения, объяснения или прогнозы, и могут ли достижения в науке влиять на жизнь людей, в том числе создавать новые возможности для карьерного роста — Ценности и потребности современного общества могут влиять на направленность научных исследований — Природа и развитие науки — -Научное понимание, включая модели и теории, является спорным и со временем уточняется в процессе обзора научным сообществом — Достижения в научном понимании часто зависят от технологических достижений и часто связаны с научными открытиями -Навыки исследования науки — Общение — передача научных идей и информации для определенной цели, включая сбор доказательств. -основанные аргументы и использование соответствующего научного языка, условностей и представлений — Планирование и проведение — Планировать, выбирать и использовать соответствующие типы исследований, включая полевые работы и лабораторные эксперименты, для сбора надежных данных; оценивать риски и решать этические проблемы, связанные с этими методами — Выбирать и использовать соответствующее оборудование, включая цифровые технологии, для систематического и точного сбора и записи данных — Обработка и анализ данных и информации — Использовать знания научных концепций, чтобы делать выводы которые согласуются с доказательствами — Анализировать закономерности и тенденции в данных, включая описание взаимосвязей между переменными и выявление несоответствий — Ставить под сомнение и прогнозировать — Формулировать вопросы или гипотезы, которые можно исследовать с научной точки зрения — Оценка — Критически анализировать достоверность информации в первичных и вторичных источниках и оценка подходов, используемых для решения проблем — Оценка выводов, включая определение источников неопределенности и возможных альтернативных объяснений, и описание конкретных способов повышения качества данных —Химические науки — Науки о Земле и космосе — Физические науки ces-Наука как человеческое усилие — Использование и влияние науки — Природа и развитие науки — Навыки исследования науки — Коммуникация — Планирование и проведение — Обработка и анализ данных и информации — Опрос и прогнозирование — Оценка
.
Понятие знаки препинания: 2. Понятие знака препинания, основные функции
Понятие о синтаксисе и пунктуации — Уроки Русского
Рассмотрим текст.
День был солнечный жаркий. Но только мы подошли к лесу, вдруг набежала синяя тучка и из неё посыпался частый крупный дождь. А солнце всё продолжало светить. Дождевые капли падали на землю, тяжело шлепались о листья. Они повисали на траве, на ветвях кустов и деревьев. В каждой капле отражалось солнце.
Перед нами текст. Он состоит из шести предложений. В каждом предложении можно выделить словосочетания.
Строение словосочетаний и предложений изучает раздел науки о языке синтаксис.
Изучая синтаксис, мы узнаём, как устанавливать смысловые и грамматические связи между словами, т. е. по каким правилам соединяются слова в словосочетания и предложения. Знаки препинания помогают правильно понять смысл написанного.
Правила употребления знаков препинания изучает пунктуация.
Пунктуация – это раздел науки о языке, изучающий систему знаков препинания и правила их постановки.
Чтобы правильно уметь формулировать свои мысли и грамотно их излагать на письме, нужно изучать как синтаксис, так и пунктуацию.
У Самуила МАРШАКА есть стихотворение про знаки препинания:
ЗНАКИ ПРЕПИНАНИЯ
У последней ТОЧКИ
На последней строчке
Собралась компания
Знаков препинания
Прибежал Чудак —
ВОСКЛИЦАТЕЛЬНЫЙ ЗНАК.
Никогда он не молчит,
Оглушительно кричит:
-Ура! Долой! Караул! Разбой!
Притащился кривоносый ВОПРОСИТЕЛЬНЫЙ ЗНАК:
-Кто? Кого? Откуда? Как?
Явились ЗАПЯТЫЕ,
Девицы завитые,
Живут они в диктовке
На каждой остановке.
Прискакало ДВОЕТОЧИЕ,
Прикатило МНОГОТОЧИЕ,
И прочие,
И прочие,
И прочие…
Заявили запятые:
-Мы — особы занятые,
Не обходится без нас
Ни диктовка, ни рассказ.
Отозвалась с той же строчки
Тетя ТОЧКА С ЗАПЯТОЙ:
-Если нет над вами точки,
Запятая — знак пустой!
В русском языке 10 знаков препинания. Они выполняют разную роль. Это
. – точка
? – вопросительный знак
! – восклицательный знак
…— многоточие
, — запятая
; — точка с запятой
: — двоеточие
– -тире
( ) – скобки двойные (круглые)
« » — кавычки двойные
Видно, что знаки препинания могут быть одиночными и парными. Одиночные знаки препинания отделяют члены предложения и предложения друг от друга. Например:
Одиночные знаки препинания отделяют члены предложения и предложения друг от друга. Например:
Ветер бросал горстки листьев на стол, на койку, на пол, на книги.
В этом предложении запятые отделяют друг от друга однородные члены предложения.
Парные знаки препинания выделяют какие-либо части текста. Всегда парным знаком являются кавычки, обычно выделяющие прямую речь. Например:
Васенька вскочил с места и звонко прокричал: «Ребята, идём на каток!»
Знаки препинания помогают пишущему выразить свои мысли и чувства, а читающему – точнее понять текст и выразительно прочитать его.
Повторим
Синтаксис – это раздел науки о языке, который изучает строение словосочетаний и предложений.
Пунктуация – это раздел науки о языке, изучающий систему знаков препинания и правила их постановки.
В русском языке 10 знаков препинания.
. – точка
? – вопросительный знак
! – восклицательный знак
…— многоточие
, — запятая
; — точка с запятой
: — двоеточие
– -тире
( ) – скобки двойные (круглые)
« » — кавычки двойные
Одиночные знаки препинания отделяют члены предложения и предложения друг от друга.
Парные знаки препинания выделяют какие-либо части текста. Всегда парным знаком являются кавычки, обычно выделяющие прямую речь.
Знаки препинания помогают пишущему выразить свои мысли и чувства, а читающему – точнее понять текст и выразительно прочитать его.
Знаки препинания при обособленных членах предложения (обобщение) | ЕГЭ по русскому языку
1. Обособленные определения
Обособленные определения в предложении могут быть выражены:
1) причастным оборотом;
Например: В дальнем краю парка, заросшего высокой травой и кустарником, находилась аллея.
2) одиночными причастиями или прилагательными.
Например: Небо, хмурое и неприветливое, накрывало город.
3) прилагательным с зависимыми словами
Например: На столе я увидел книгу, похожую на древнюю энциклопедию.
2. Обособленные приложения
Обособленные приложения синтаксически являются определениями.
Обособленные приложения в предложении могут быть выражены:
1) именами существительными;
Например: Мы, школьники, устали от экзаменов.
2) именами существительными с зависимыми словами;
Например: Петр Иванович, добрый наш друг, оказал нам помощь.
3. Обособленные обстоятельства
Обособленные обстоятельства в предложении могут быть выражены:
1) одиночными деепричастиями;
Например: Танцуя и кружась, она смотрела на меня.
2) деепричастным оборотом;
Например: Проехав несколько километров, я увидел на обочине путника.
4. Уточняющие, пояснительные и присоединительные члены предложения
1) Уточняющие члены предложения
Уточняющие члены предложения сужают понятие, уточняют его. Как правило они представлены обстоятельствами места, времени, образа действия, степени, меры.
Например: В лесу, за дорогой, есть ромашковая поляна.
2) Пояснительные члены предложения
Пояснительные члены предложения называют по-другому те понятия, к которым относятся, представляют собой еще одно название этих понятий.
Часто пояснительные члены сопровождаются союзами: то есть, именно, а именно, или в значении «то есть» Например: Бегемот, или гиппопотам, вызывает интерес ученых.
3) Присоединительные члены предложения
Присоединительные члены предложения передают добавочную информацию. Такие члены обычно вводятся словами и сочетаниями слов: даже, в особенности, особенно, главным образом, в том числе, в частности, например, и притом, и потому, да и, да и только, да и вообще, и, тоже, и тоже, причем и др.
Например: В людях есть много благородства, особенно в женщинах.
5. Сравнительные обороты
Сравнительные обороты, начинающиеся сравнительными союзами будто, словно, точно, чем, нежели, как будто, подобно, что, равно как и и др., выделяются запятыми Например: Он, как вихрь, залетел в комнату.
Контрольная работа по русскому языку Разделы языкознания 10 класс
Контрольная работа по русскому языку Разделы языкознания, Понятие литературного языка, Нормы литературного языка, Единицы языка для учащихся 10 класса. Работа включает в себя 2 варианта в каждом варианте 3 части (Часть А, Часть В, и Часть С).
Часть А — 6 заданий (с выбором ответа)
Часть В — 5 задания (с кратким ответом)
Часть С — 1 задание (сочинение)
1 вариант
А1. Укажите неверное утверждение.
1) В литературный язык не входят диалекты, жаргоны (в том числе профессиональный), просторечие.
2) Литературный язык существует в письменной и устной форме.
3) Разговорный стиль литературного языка может быть представлен как в устной, так и в письменной форме.
4) «Синтаксис» — раздел языкознания, в котором изучаются правила расстановки знаков препинания.
А2. Какая из названных единиц языка не обладает каким-либо значением?
1) слово
2) слог
3) морфема
4) словосочетание
А3. Укажите тип словаря из которого взят фрагмент
аге́нт, -а / об аге́нте [ньть] ! неправ. а́гент
1) толковый
3) фразеологический
2) этимологический
4) орфоэпический
А4.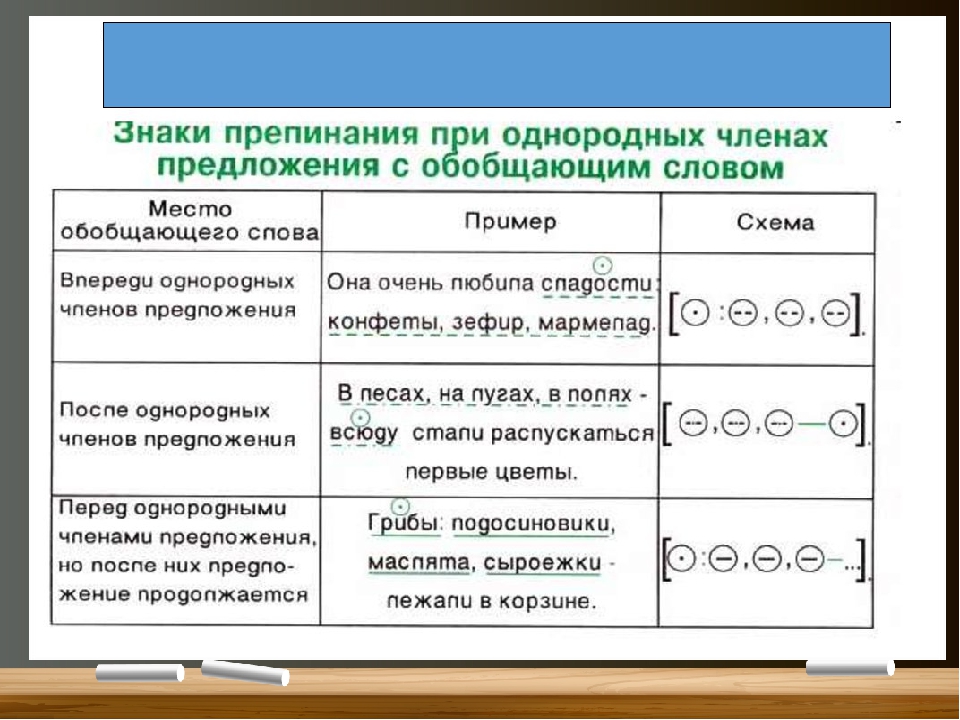 В каком ряду все слова согласно литературной норме имеют ударение на втором слоге, независимо от их лексического значения?
В каком ряду все слова согласно литературной норме имеют ударение на втором слоге, независимо от их лексического значения?
1) начать, передан, орган
2) цемент, светло, раджа
3) торец, оптовый, звонит
4) (вы) правы, досуг, диспансер
А5. Укажите слово, образованное приставочно-суффиксальным способом.
1) недалеко
2) невинный
3) поспешность
4) подписывать
Прочитайте предложение и выполните задания А6, B1.
Если вы бывали в Одессе, вы должны помнить эти медные сумерки, когда акации сереют от пыли и в море лежит тишина. (К. Паустовский)
А6. Какое средство выразительности, характерное для художественного стиля, используется в предложении?
1) аллитерация
2) сравнение
3) эпитет
4) инверсия
В1. Выпишите слова, образованные от прилагательных.
В2. Укажите, какие суффиксы входят в глаголы:
а) претерпевать
б) разогревать
в)горевать
г) зевать
1) -ева-
2) -е- и -ва-
3) -ва-
4) -а-
Прочитайте текст (в предложениях расставлены не все знаки препинания). Выполните задания B3-B5.
Выполните задания B3-B5.
Больш_нство древних письменностей из всех знаков пр_пинания знало только «абзац» и «точку». Графически они выр_жались (по)разному, хотя (по)видимому точка и была самой распространё_ой формой. В (древне)русской письменности самым ч_стотным знаком так(же) была точка употребляемая в основном в роли нашей запятой и разделяющ_ текст на синтагмы — отрезки речи, образующие смысловое и интонационное единство.
В3. Напишите 10 выделенных курсивом слов, вставляя пропущенные буквы и раскрывая скобки.
В4. Напишите те слова, после которых нужно поставить запятую.
В5. Выберите из данного ниже списка термины, характеризующие стиль (подстиль) этого текста и тип (подтип) речи, который используется в нём. Напишите номера выбранных терминов через запятую.
Стиль
1) официально-деловой
научный:
2) научно-деловой
3) научно-учебный
4) научно-популярный
5) публицистический
6) художественный
7) разговорный
Тип речи
описание:
8) описание предмета
9) описание явления
10) повествование рассуждение:
11) рассуждение-доказательство
12) обсуждение-объяснение
13) рассуждение-размышление
С1.
Напишите кратко (1-3 фразы) о том, как изменялась роль точки в истории письменности.
2 вариант
А1. Укажите неверное утверждение.
1) Литературным языком называется язык литературных произведений.
2) Литературный язык представлен разными стилями, которые подразделяются на книжные (научный, публицистические и др.) и разговорный.
3) Грамматические ошибки проявляются как в письменной, так и в устной речи.
4) «Морфология» — раздел языкознания, в котором рассматриваются формы слова, словоизменение.
А2. Какая из названных морфем обладает только грамматическим значением?
1) приставка
2) корень
3) суффикс
4) окончание
А3. Укажите тип словаря, из которого взят фрагмент:
ДЕМАГО́Т. Заимствовано из греч. яз. в конце XVIII в. Греч. — образовано на базе греч. «народ» и «ведущий», первоначально «народный вождь» > «своекорыстный искатель народной популярности» (сначала о Клеоне, Аристиде и др. в употреблении их врагов). — Укр. демагог, бел. дэмагог, польск. demagog, чешек. demagog, словацк. demagog, болг. демаго́г.
в употреблении их врагов). — Укр. демагог, бел. дэмагог, польск. demagog, чешек. demagog, словацк. demagog, болг. демаго́г.
1) толковый
2) этимологический
3) фразеологический
4) орфоэпический
А4. В каком ряду все слова согласно литературной норме имеют ударение на первом слоге, независимо от их лексического значения?
1) судно, рапорт, св(е/ё)кла
2) отзыв, орден, преданный
3) мало, (в) скольких (случаях), компас
4) ордер, эксперт, оптом
А5. Укажите слово, образованное приставочно-суффиксальным способом.
1) подарок
2) невиновный
3) подорожник
4) небрежность
Прочитайте предложение и выполните задания А6, B1.
Это было пенистое, веселое море — родина крылатых кораблей и отважных мореплавателей. Изумрудами горели на его берегах маяки. (К. Паустовский)
А6. Какое из указанных средство выразительности, характерных для художественного стиля, не используется в предложении?
1) олицетворение
2) сравнение
3) эпитет
4) антитеза
В1. Выпишите непроизводное прилагательное, образуйте от него отвлечённое (абстрактное) существительное.
Выпишите непроизводное прилагательное, образуйте от него отвлечённое (абстрактное) существительное.
В2. Укажите, какие суффиксы входят в глаголы:
а) вызревать
б) преодолевать
в) клевать
г) ночевать
1) -ева-
2) -е-и -ва-
3) -ва-
4) -а-
Прочитайте текст (в предложениях расставлены не все знаки препинания). Выполните задания В3-В5.
Совреме_ая европейская пунктуация, в том числе и русская во_ходит к началу книгопечатания. Однако правила ра_тановки знаков уст_новились не сразу и в разных языках значительно разнятся, (при)чём можно выделить две группы: францу_кий (английский, итальянский и т.д.) и немецкий (чешский, русский и т.д.). В первой например, реже чем во второй ставит_ся тире, то(же) относит_ся и к употр_блению запятых.
В3. Напишите 9 выделенных курсивом слов, вставляя пропущенные буквы и раскрывая скобки.
В4. Напишите те слова, после которых нужно поставить запятую.
В5. Выберите из данного ниже списка термины, характеризующие стиль (подстиль) этого текста и тип (подтип) речи, который используется в нём. Напишите номера выбранных терминов через запятую.
Стиль
1) официально-деловой
научный:
2) научно-деловой
3) научно-учебный
4) научно-популярный
5) публицистический
6) художественный
7) разговорный
Тип речи
описание:
8) описание предмета
9) описание явления
10) повествование рассуждение:
11) рассуждение-доказательство
12) обсуждение-объяснение
13) рассуждение-размышление
С1. Напишите кратко (1-3 фразы) о том, как возникли правила пунктуации русского языка.
Ответы на контрольную работу по русскому языку Разделы языкознания, Понятие литературного языка, Нормы литературного языка, Единицы
1 вариант
А1. 4
4
А2. 2
А3. 4
А4. 3
А5. 2
А6. 3
В1. сереют, тишина
В2. 2314
В3. Больши_нство, препинания, выражались, по-разному, по-видимому, распространённой, древнерусской, частотным, также, разделяющая
В4. хотя, по-видимому, точка
В5. 3. 12
С1. Самый древний знак, сначала употреблялась и в роли запятой (между синтагмами), сейчас обозначает границу между повествовательными предложениями.
2 вариант
А1. 1
А2. 4
А3. 2
А4. 1
А5. 3
А6. 4
В1. весёлое, веселье (весёлость)
В2. 3241
В3. Современная, восходит, расстановки, уста_новились, причём, французский, ставится, то_же, относится, употреблению
В4. русская,первой,реже,второй
В5. 3, 12
С1. Главные правила пунктуации сложились при развитии книгопечатания, но в разных европейских языках разнятся; русская пунктуация ближе к немецкой.
Примеры и определение знаков препинания
Определение знаков препинания
Знаки пунктуации — это набор знаков, которые регулируют и поясняют значения различных текстов. Термин «пунктуация» произошел от средневекового латинского слова « pūnctuātiōn », что означает маркировку или знаки.
Термин «пунктуация» произошел от средневекового латинского слова « pūnctuātiōn », что означает маркировку или знаки.
Назначение знаков препинания — прояснить значения текстов путем связывания или разделения слов, фраз или предложений. Например, в предложении «Вчера дождь-туман; сегодня мороз-туман.Но как интересно каждое »( На рубеже года, Фиона Маклеод), дефисы используются для разделения составных слов, а запятые — для разделения фраз.
Типы пунктуации
В грамматике английского языка существует пятнадцать основных знаков препинания. К ним относятся точка, запятая, восклицательный знак, вопросительный знак, двоеточие, точка с запятой, маркер, тире, дефис, круглые скобки, скобки, фигурные скобки, многоточие, кавычки и апостроф. Ниже приведены несколько примеров использования этих знаков в предложении.
Кронштейны и эллипсы
“Mr. Бамбл сказал «осел», а не «осел» в «Оливер Твист». … [В цитате одним] вариантом могло быть «Закон — это [н] жопа», хотя это было бы снисходительным тоном sic flag, подразумевая, что мы умнее Диккенса ». ( Придирчивые цитаты , Блер Шевчук)
( Придирчивые цитаты , Блер Шевчук)
В этом примере посмотрите на использование квадратных скобок ([]) и многоточия («…»). Автор использовал квадратные скобки для объяснения технического описания и многоточие, чтобы показать пропуск слов.
Тире и круглые скобки
«Причина и причина скорпиона — как он попал на борт и выбрал свою комнату, а не кладовую (это было темное место и к чему скорпион был бы неравнодушен), и как, черт возьми, ему удалось утонуть в чернильнице его письменного стола, — это его бесконечно мучило ». ( Тайный участник , Джозеф Конрад)
Здесь Конрад использовал тире для краткого изложения основного предложения. Он также использовал круглые скобки или изогнутые обозначения для дальнейшего объяснения идеи.
Bullet Points
«Идея состоит в том, чтобы закончить просто по замыслу, а не по умолчанию, и любой из следующих способов поможет:
- В своих заметках следите за потенциально драматичными заключительными материалами.

- Оставьте место для развернутой концовки.
- Сделайте завершение достойным работы.
- Избегайте дрейфа к шаблонному финалу ».
( Spunk & Bite , Артур Плотник)
Здесь автор использовал маркеры, чтобы отобразить свой список идей.
Апострофы и кавычки
«А под парнем на изображении лошади всегда написано:« С 1888 года мы превращали мальчиков в прекрасных, здравомыслящих молодых людей »…»
«Нет, сэр, Я с ними не общался ».
( Над пропастью во ржи , Дж. Д. Сэлинджер)
В этом отрывке Сэлинджер использовал апостроф, который позволяет удалять буквы из слова, так что слово все еще имеет смысл. Он также использует пару кавычек вокруг предложения, чтобы процитировать утверждение другого персонажа.
Двоеточие и полуколонки
«Город — территория термитов: тысячи упорных рабочих, служащих непризнанной королеве, двигатель страха, спрятанный глубоко в сердце этого места».
( Отключите свет для территории , Иэн Синклер)
«Прошлое — это чужая страна; там они делают по-другому ».
( The Go-Between , L.P. Hartley)
Здесь в первом примере появляется двоеточие. Он используется для объяснения основного предложения.Во втором примере точка с запятой соединяет два независимых предложения.
Вопросы и восклицательные знаки
ЛАВИНИЯ — (испуганно — взволнованно)
«Отец? Нет! … Да! Он знает — что-то в его лице — должно быть, поэтому у меня возникло странное чувство, что я знала его раньше … О! Я не поверю! Вы, должно быть, ошибаетесь, Сет! … »
( Mourning Becomes Electra , Юджин О’Нил)
В этих строках восклицательный знак«! » указывает на внезапное проявление эмоций, а знак вопроса «?» используется, чтобы задать вопрос.
Периоды
ЭСТРАГОН:
«Я помню карты Святой Земли. Цветные они были. Очень хорошенькая. Мертвое море было бледно-голубым. От самого его вида меня захотелось пить ».
( В ожидании Годо , Сэмюэл Беккет)
Беккет использовал пять точек в приведенных выше предложениях. Использование точки указывает на конец мысли. Точку также можно использовать как паузу после мысли.
Использование точки указывает на конец мысли. Точку также можно использовать как паузу после мысли.
Функция
Знаки препинания служат в качестве паузы в предложении, что часто необходимо, чтобы выделить определенные фразы или слова, чтобы помочь читателям и слушателям лучше понять, что писатель или оратор пытается передать.Таким образом, основная функция пунктуации — сделать ударение на определенных частях предложения.
Знаки препинания также используются для разделения текста на слова и фразы, когда это необходимо, чтобы лучше прояснить значение этих слов или фраз. Напротив, неправильное использование знаков препинания может передать совершенно иное значение предложения, чем оно было изначально задумано.
Подробное руководство по пунктуации | Thesaurus.com
В это трудно поверить, но было время, когда вы, взяв книгу, могли расшифровать текст без помощи прописных букв, знаков препинания или (ужас!) Пробелов.Можешь представить? Одно слово переходило в другое, не говоря уже о целых предложениях и абзацах.
Мы очень благодарны за то, что пунктуация существует — даже если это означает, что мы должны испытывать незначительные неудобства, связанные с определением того, какую из них использовать в тех сложных случаях, которые могут вызвать жаркие споры по грамматике.
Если вам тоже нравится небольшая пунктуация в словах, вы можете начать здесь, чтобы изучить не только основы, но и нюансы каждого вида знаков.
Типы знаков препинанияДавай вернемся в наши школьные годы, ладно? Это основные отметки, которые мы выучили, когда только начинали читать и писать.Но наше обучение на этом не закончилось. Каждый тип знаков препинания имеет уникальное применение, которое мы изучали на более поздних курсах грамматики — или собираемся открыть!
- Точки, вопросительные и восклицательные знаки
- Запятые, двоеточия и точки с запятой
- Дефисы и дефисы
- Кавычки и эллипсы
- Скобки, скобки и круглые скобки
Начнем с того, что эти три знака препинания используются в конце предложений. У каждого есть конкретная цель, и все они достаточно распространены, и мы полагаемся на них каждый день. Вот почему мы включаем их в руководство «6 распространенных типов знаков препинания», где вы можете узнать больше о каждом из них.
У каждого есть конкретная цель, и все они достаточно распространены, и мы полагаемся на них каждый день. Вот почему мы включаем их в руководство «6 распространенных типов знаков препинания», где вы можете узнать больше о каждом из них.
Точки ставятся в конце повествовательного предложения, когда утверждение не требует ответа. Конечно, они также используются для обозначения некоторых аббревиатур и инициалов. Но знаете ли вы, что этот период находится в центре споров поколений о интервалах?
Знаки вопроса (?)Вопросительные знаки используются в конце предложения после прямого вопросительного заявления или одного, выражающего сомнение.Вам может быть любопытно, стоит ли ставить вопросительный знак внутри или вне кавычек. Британский и американский английский дают разные ответы на этот непростой вопрос.
Восклицательный знак (!) Восклицательный знак используется, чтобы показать удивление, недоверие, похвалу, команду — в основном, он показывает эмоции в заявлении. У него также есть несколько специальных применений: он может заменить вопросительный знак, когда имеется в виду ирония или подчеркнутый тон, например, Как ты мог! Вам может быть интересно, используется ли этот знак препинания по-разному в формальном и неформальном (т.е., текстовые сообщения) написание. Ответ положительный! (Или да !!!)
У него также есть несколько специальных применений: он может заменить вопросительный знак, когда имеется в виду ирония или подчеркнутый тон, например, Как ты мог! Вам может быть интересно, используется ли этот знак препинания по-разному в формальном и неформальном (т.е., текстовые сообщения) написание. Ответ положительный! (Или да !!!)
Когда студенты овладевают основными знаками препинания, они должны понимать разницу между запятыми, двоеточиями и точками с запятой, которые часто сбивают с толку даже самых опытных писателей. К счастью, у нас есть необходимые вам руководства по использованию.
Запятые (,) Запятая чаще всего используется для разделения или зачета элементов, которые в противном случае могли бы быть неправильно поняты, например: элементы серии, которая включает и , или , или или ; две глагольные фразы в предложении; или аппозитив.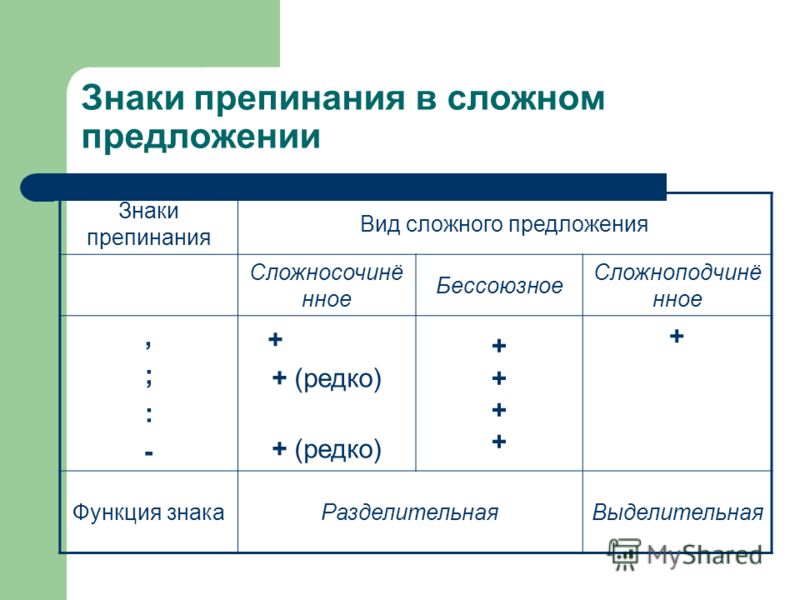 Запятые также используются в диалогах и ставятся перед цитатой после вступительной фразы, например, Она тихо сказала: «Я люблю тебя».
Запятые также используются в диалогах и ставятся перед цитатой после вступительной фразы, например, Она тихо сказала: «Я люблю тебя».
Конечно, у запятых бесчисленное множество применений — и у писателей возникает бесчисленное количество вопросов о том, как использовать запятую: вы за оксфордскую запятую или нет? Как они используются с союзами? Как они используются в приветствиях? У нас тоже есть эти гиды.
Двоеточие (:) Двоеточие может вводить пояснительную информацию и списки.Например, оно используется перед последним предложением, которое объясняет или расширяет что-то в этом предложении, например, Диссертация требует доработки: в ней отсутствует поток . Ряд или итоговый оператор также может быть введен с двоеточием, например, В нашем списке мест для go находится следующее: продуктовый магазин, магазин игрушек, магазин пончиков. Вы захотите узнать, как писать после двоеточия с заглавной буквы и как отличать их от запятых и точек с запятой.
Иногда эта пунктуация рассматривается как слабая точка или сильная запятая и используется аналогично точкам и запятым.Вот почему это может сбивать с толку некоторых писателей; точка с запятой может выполнять несколько задач. Например, он отмечает конец предложения и указывает, что следующее предложение тесно связано с ним. Или он может разделить предложение, чтобы прояснить его значение. Прежде чем погрузиться в споры о том, как его использовать, с другими любителями грамматики, убедитесь, что вы знаете все тонкости этого знака.
Дефисы и дефисыВам будет важно научиться различать все тире.Кто-то может сказать, что дефис, наряду с его родственниками, длинное и длинное тире, может быть самым неправильно понятым из всех знаков препинания.
Дефис (-) Дефис — это короткая линия, соединяющая части составного слова или слова, разделенного для какой-либо цели. Они также могут сами соединять слова. Например, во фразе современные технологии мы ставим дефис до , чтобы обозначить, что эти три слова следует читать как одно понятие.Вы не поверите, но использование дефиса со временем сильно изменилось — такие слова, как завтра , когда-то переносились через дефис ( завтра ).
Они также могут сами соединять слова. Например, во фразе современные технологии мы ставим дефис до , чтобы обозначить, что эти три слова следует читать как одно понятие.Вы не поверите, но использование дефиса со временем сильно изменилось — такие слова, как завтра , когда-то переносились через дефис ( завтра ).
Следующее (по длине) — короткое тире. Этот знак обозначает диапазон (например, чисел) или соединяет конечные точки маршрута. Он также может показать контраст или связь между двумя словами. Существует множество вариантов использования и тире , поэтому самый простой способ узнать о них больше — прочитать исчерпывающую статью, посвященную этой строке.
Длинное тире (-) Если вы состоите в фан-клубе em dash , вам, вероятно, не нужно представлять. (Некоторые заявили о своей любви к этому знаку препинания с помощью татуировок тире ). Этот знак удобен для писателей, поскольку предлагает способ выделить слово или предложение для выделения. Или он может сигнализировать о прерывании (подробнее об этом читайте в нашей статье о прерывании предложений!) Или об усилении идеи. Но не верьте нам на слово — прочтите об этом здесь!
Этот знак удобен для писателей, поскольку предлагает способ выделить слово или предложение для выделения. Или он может сигнализировать о прерывании (подробнее об этом читайте в нашей статье о прерывании предложений!) Или об усилении идеи. Но не верьте нам на слово — прочтите об этом здесь!
Кавычки выделяют прямые цитаты — это то, что мы называем предложениями, которые указывают на то, что кто-то в книге или статье, например, цитируется точно так, как написано.Цитата начинается и заканчивается кавычками: «Я забеспокоился, — сказал он, — что она не позвонила». Конечно, это не единственное их использование, и работа с кавычками может быть проблематичной (особенно при попытке решить, находится ли другой знак препинания внутри или за пределами кавычек). Мы рассмотрели эту и другие темы в нашем руководстве по кавычкам.
Скобки и скобки Скобки, фигурные скобки и круглые скобки смещают дополнительную информацию, которая может состоять из числа или слова или нескольких предложений. Многие из этих знаков также появляются в информатике и программировании, где они выполняют уникальные роли. Наше руководство по скобкам и скобкам объясняет разницу между этими часто путающими знаками.
Многие из этих знаков также появляются в информатике и программировании, где они выполняют уникальные роли. Наше руководство по скобкам и скобкам объясняет разницу между этими часто путающими знаками.
Угловая скоба или шеврон чаще всего используется в сложных математических задачах. Как они связаны с козами? Вам нужно будет прочитать больше, чтобы узнать!
Квадратные скобки ({}) Квадратные скобки используются внутри круглых скобок для обозначения чего-либо, подчиненного придаточному предложению.Вот пример из 13-го издания Chicago Manual of Style : «Во время длительного визита в Австралию, Глейк и его помощник (Джеймс Грин, который позже должен был провести собственное исследование нелетающей птицы [киви] в Нью-Йорке). Зеландия) провела несколько трудных месяцев, наблюдая за выживанием казуаров и эму ».
Фигурные скобки имеют разные названия; они называются скобками , фигурными скобками или волнистыми скобками .Обычно такие скобки используются для списков, но в Интернете они также означают объятие при электронном общении. (Ой!)
Круглые скобки ()Круглые скобки всегда появляются парами, чтобы выделить часть предложения или обсуждения. Иногда их используют там, где уместны запятые. Скобки также можно использовать в качестве прерывания в предложениях, чтобы создать более неформальный и непринужденный стиль письма. Прежде чем добавлять слишком много из них в свой текст, убедитесь, что вы их правильно используете.
Апострофы и косые черты Апостроф (‘) Апостроф может указывать на владение или на пропущенные буквы или цифры. Например: Я не могу вместо Я не могу, давайте танцевать вместо , давайте , и это прекрасный день вместо это . Апостроф также может указывать на владение. Помимо этого обычного использования, апостроф также сопровождает отдельные буквы и цифры, обозначающие десятилетия.(Апостроф также создает некоторые острые проблемы: это День ветеранов или День ветеранов?)
Апостроф также может указывать на владение. Помимо этого обычного использования, апостроф также сопровождает отдельные буквы и цифры, обозначающие десятилетия.(Апостроф также создает некоторые острые проблемы: это День ветеранов или День ветеранов?)
Косую черту также иногда называют косой чертой , косой чертой , косой или косой . (Как вам такое для причудливых имен?) Он может представлять слово, которое было пропущено. Например, он может заменять союзы ( твое / мое, , любовь / ненависть, ) и сопровождать союзы ( и / или ).У него много применений; вы также захотите отметить разницу между прямой и обратной косой чертой.
Знак препинания — обзор
«ПАРАДОКС ОБЕЗЬЯН»
Не все находят определение Шеннона интуитивно понятным. Это своего рода «парадокс», что это означает, что произведения Шекспира содержат меньше информации, чем случайная перестановка букв и знаков препинания. Существует хорошо известная история, которую обычно приписывают Олдосу Хаксли, 5 , о том, что 100 обезьян, набирающих случайным образом в течение достаточно долгого времени, в конечном итоге (благодаря чистой случайности и статистике) напечатали все произведения Шекспира.В большинстве случаев обезьяна набирает полную чушь, но иногда она набирает Hamlet . Конечно, Гамлет будет появляться снова и снова из этого «тумана» печати (как и « Sound and the Fury » Фолкнера, и колонка мисс Мэннерс из газеты прошлых выходных и т. Д.), Но подавляющее преобладание будет совершенно бессмысленно.
Существует хорошо известная история, которую обычно приписывают Олдосу Хаксли, 5 , о том, что 100 обезьян, набирающих случайным образом в течение достаточно долгого времени, в конечном итоге (благодаря чистой случайности и статистике) напечатали все произведения Шекспира.В большинстве случаев обезьяна набирает полную чушь, но иногда она набирает Hamlet . Конечно, Гамлет будет появляться снова и снова из этого «тумана» печати (как и « Sound and the Fury » Фолкнера, и колонка мисс Мэннерс из газеты прошлых выходных и т. Д.), Но подавляющее преобладание будет совершенно бессмысленно.
«Парадокс обезьян», как я его называю, состоит в том, что полная чушь большей части этого набора текста будет содержать больше информации, чем то небольшое количество времени, в течение которого может появиться Hamlet . 6
С одной стороны, может показаться, что когда обезьяна печатает сцены из «Гамлета», персонажи более предсказуемы, чем когда они печатают полную ерунду. Мы знаем, что пробелы встречаются довольно часто, что большая часть строк между пробелами (словами) встречается в относительно небольшом словаре, что слова «Гамлет» и «Офелия» встречаются с некоторой относительной частотой и т.д. Разве эта полная чушь несет в себе больше информации, чем слова великого автора.
Мы знаем, что пробелы встречаются довольно часто, что большая часть строк между пробелами (словами) встречается в относительно небольшом словаре, что слова «Гамлет» и «Офелия» встречаются с некоторой относительной частотой и т.д. Разве эта полная чушь несет в себе больше информации, чем слова великого автора.
Я считаю, что есть несколько поэтапных ответов на этот предполагаемый «парадокс» (и, следовательно, на цитаты). Во-первых, предположим, что обезьяна печатает наугад. Тогда на самом деле вероятность того, что он наберет 18-символьную строку «ничего не означающую», не больше, чем строка «gnihton gniyfingis» (последняя является просто перестановкой первой). Это похоже на тот факт, что если обезьяна набрала 3 буквы «а», это никоим образом не увеличивает вероятность того, что следующим символом будет «а» — это не больше, чем (справедливо) подброшенная монета 3 раза «орел». подряд увеличивают вероятность того, что следующая подбрасывание будет «орлом».«В действительно случайных последовательностях узоры возникают в сознании смотрящего.
В недавней статье Далкилик и др. , [2006] разработали компьютерную программу, которая может распознавать «аутентичные тексты» как те, которые попадают в «золотую середину» между полной случайностью и полной предсказуемостью.
Конечно, закономерности могут возникать из-за скрытых причинных влияний. Мне вспоминается история о Раймонде Смулляне, первоклассном фокуснике, а также первоклассном логике, который, обучая класс элементарной вероятности, вытащил колоду карт и приступил к раздаче флеш-рояля.Раймонд сказал классу, что, как это ни удивительно, эта рука так же вероятна, как и любая другая. И, конечно же, он повторял эту процедуру, производя один флеш-рояль за другим, пока класс не рассмеялся.
Может ли предсказуемая последовательность действительно предоставить важную информацию? Рассмотрим следующее, основанное на реальных событиях. 7 Во время Второй мировой войны союзники взломали немецкий код «Энигма». Но немцы использовали определенные специальные кодовые названия для кораблей, поэтому не имело значения, если кто-то расшифровал кодовое имя — это все равно было кодовое имя. Но у союзников были веские причины предполагать, что определенное кодовое имя было именем определенного корабля, который они знали. Поэтому они отправили сообщение с низким уровнем шифрования, в котором упоминалось кое-что интересное об этом корабле. Они прислушивались к немецкому трафику, и, как и предполагалось, эта информация была отправлена при упоминании этого корабля под его кодовым названием. Это, конечно, подтвердило правильность прогноза. Таким образом, даже несмотря на то, что считалось весьма вероятным, что у союзников было правильное кодовое имя, и, следовательно, весьма вероятно, что оно появится в немецкой передаче, похоже, что оно все же содержало важную информацию, когда это было.
Но у союзников были веские причины предполагать, что определенное кодовое имя было именем определенного корабля, который они знали. Поэтому они отправили сообщение с низким уровнем шифрования, в котором упоминалось кое-что интересное об этом корабле. Они прислушивались к немецкому трафику, и, как и предполагалось, эта информация была отправлена при упоминании этого корабля под его кодовым названием. Это, конечно, подтвердило правильность прогноза. Таким образом, даже несмотря на то, что считалось весьма вероятным, что у союзников было правильное кодовое имя, и, следовательно, весьма вероятно, что оно появится в немецкой передаче, похоже, что оно все же содержало важную информацию, когда это было.
Я так понимаю, что то, что было значительно увеличено, не было фактической информацией. Вероятность того, что кодовое имя является названием этого конкретного корабля, существенно не изменилась с чисто числовой точки зрения. Риск снизился.
Общепризнанно, что концепция риска включает в себя как вероятность, так и стоимость последствий, а стандартная математизация «риска», используемая страховыми компаниями (и фактически всеми, кто участвует в так называемой «оценке риска»), включает в себя функции в обеих этих переменных. Стандартное представление состоит в том, что риск события является продуктом вероятности и стоимости последствий, и те из нас, кто рационально использует это понятие на ежедневной основе, имея очень приблизительное представление как о вероятности, так и о стоимости. данного события.
Стандартное представление состоит в том, что риск события является продуктом вероятности и стоимости последствий, и те из нас, кто рационально использует это понятие на ежедневной основе, имея очень приблизительное представление как о вероятности, так и о стоимости. данного события.
Я предполагаю, что какое-то подобное сложное понятие связано с тем, что мы могли бы назвать «значимостью» части информации. Я не уверен, как лучше всего это математизировать, но, по крайней мере, в первом приближении, я предлагаю просто умножить обратную вероятность на стоимость.
Пунктуация: примеры и определение
1. Что такое пунктуация?
Пунктуация — это набор знаков, которые мы используем, чтобы предложения текли гладко и четко выражали смысл. Он говорит нам, когда нужно сделать паузу или добавить определенное чувство к нашим словам; он разделяет идеи так, чтобы предложения были ясными, выделяет заголовки, цитаты и другие ключевые элементы языка — пунктуация важна!
Изначально пунктуация использовалась только для речи, а не для письма. Писатели разработали его так, чтобы люди знали, когда нужно сделать паузу, остановиться или сделать что-то другое, когда они говорят. Это не было частью литературы, потому что у большинства людей не было даже доступа к печатным работам. Но в настоящее время, поскольку все читают, а печатная литература доступна для всех, мы используем знаки препинания в письменной форме, чтобы предложения читались так же, как мы говорим. Знание того, как, когда и зачем использовать знаки препинания, теперь является стандартной частью письма на английском языке.
Писатели разработали его так, чтобы люди знали, когда нужно сделать паузу, остановиться или сделать что-то другое, когда они говорят. Это не было частью литературы, потому что у большинства людей не было даже доступа к печатным работам. Но в настоящее время, поскольку все читают, а печатная литература доступна для всех, мы используем знаки препинания в письменной форме, чтобы предложения читались так же, как мы говорим. Знание того, как, когда и зачем использовать знаки препинания, теперь является стандартной частью письма на английском языке.
2.Примеры знаков препинания
Знаки пунктуации являются частью каждого предложения и многих других слов в письменной речи. Вы, наверное, знаете большинство типов. Здесь подчеркнуты некоторые разные части пунктуации:
ЭТО ЗАГЛАВНЫЕ БУКВЫ.
Точка заканчивает это предложение.
Вот запятая, но видели ли вы вопросительный знак?
Восклицательный знак — это здорово!
«Это кавычки», — сказал я.
3. Типы пунктуации
Есть много типов пунктуации, и каждый имеет свое назначение и правила.Вот ключевые типы, которые мы используем постоянно:
a. Использование заглавных букв
Использование заглавных букв — это когда вы используете заглавную форму буквы (A вместо a). Первая буква предложения ВСЕГДА пишется с заглавной буквы, будь то одна буква, например, я пошел или собака, или первая буква слова, например. Кроме того, в начале предложения мы используем заглавные буквы для имен собственных, таких как места, имена людей, титулы и бренды. В диалоге заглавные буквы обычно означают, что говорящий кричит.
Лисица по имени мистер Браун была быстрой. «БЕГ MR. ЛИСА!» крикнула белка.
г. Конечные знаки
Конечные знаки — это типы знаков препинания, которые ставятся в конце предложения. В каждом предложении есть одно (и только одно), но его тип зависит от тона предложения.
Период
Точка (.) Означает остановку, и она всегда идет только в конце предложения. Действительно, любое предложение может заканчиваться точкой (если это не вопрос), но это не всегда означает, что это лучшая оценка.Однако точка является стандартной отметкой в конце предложения:
Действительно, любое предложение может заканчиваться точкой (если это не вопрос), но это не всегда означает, что это лучшая оценка.Однако точка является стандартной отметкой в конце предложения:
- Лисица была оранжево-белой.
- Он был опытным бегуном .
Восклицательный знак
Восклицательный знак (!) Добавляет к предложению сильные чувства, такие как радость или страх. «Воскликнуть» — значит сказать что-то с волнением, и это именно то, что делает восклицательный знак — он восклицает! Поскольку они добавляют азарта, также важно не злоупотреблять ими. Вот пример:
- Лисица была быстрее ветра!
Подобно этому предложению, восклицательный знак может подчеркнуть значение предложения в целом.Здесь мы осознаем, что лиса действительно быстро бегает, и это кажется важным.
Знак вопроса
Знак вопроса (?) Используется в конце каждого вопроса. Он используется только для того, чтобы показать, что предложение — это вопрос.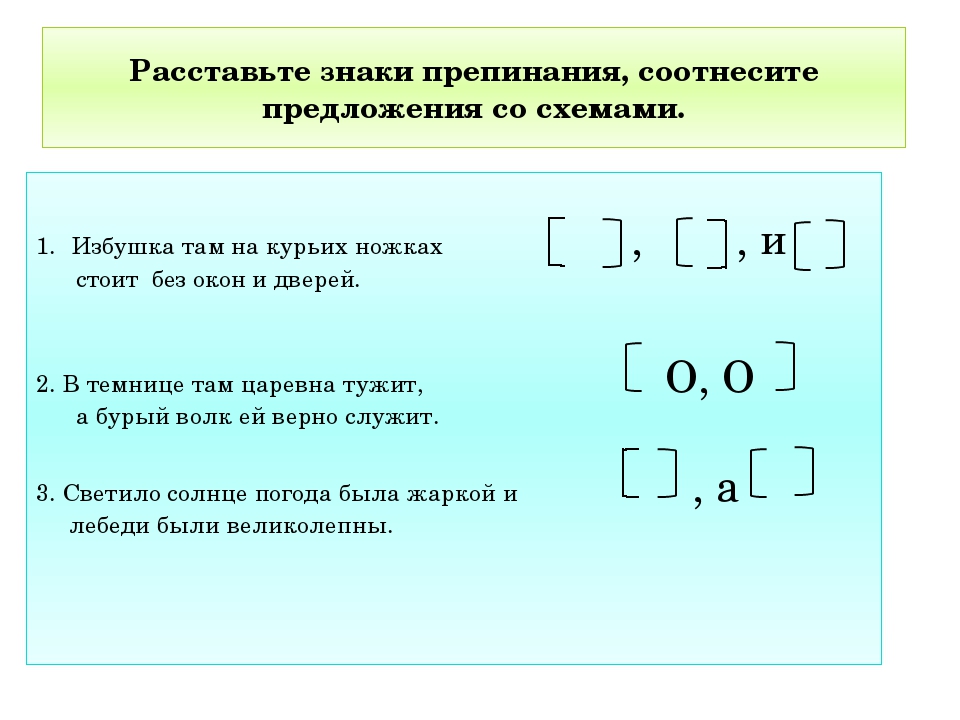
Многоточие
Многоточие (…) (многоточие во множественном числе) — это момент, который следует продолжить, в конце предложения, например:
Но многоточие особенное, потому что оно также может использоваться внутри предложения, обычно, чтобы сделать акцент на том, что будет дальше.Когда вы видите многоточие, это обычно знак того, что следующее за ним слово или предложение будет важным. Прочтите эти два предложения:
- Итак, единственное, что могла сделать лиса, — это бежать.
*** - Итак, лиса могла сделать только одно… убежать.
Как видите, многоточие во втором предложении делает его немного более захватывающим, чем первое. Это помогает создать некоторое напряжение для читателя, вместо того, чтобы давать всю информацию за один раз.
г. Запятая
Запятая (,) указывает читателю, когда следует сделать паузу в предложении. Самое главное, запятые помогают прояснить суть предложения.
Они могут разделить идеи или события:
- Лис побежал, а потом напился воды.

Мы также используем их для перечисления вещей:
- Один, два, три, четыре и пять.
Во многих предложениях нужны запятые — это одни из наиболее часто используемых знаков препинания.Но запятые также все время используются неправильно. Когда вы используете запятую, помните, что она означает «пауза», поэтому попробуйте прочитать предложение вслух, чтобы увидеть, если вы делаете паузу в нужное время. Например, если вы прочитаете это предложение вслух:
- Лис побежал, а затем напился воды.
Вы можете слышать, что паузы в этом предложении появляются не в то время. Значит, нам нужно переместить запятые:
- Лиса побежала, а потом попила воды.
Или,
- Лиса побежала, а потом напилась воды.
Хорошее общее правило, которое следует запомнить: когда вы перечисляете более двух вещей, вам, вероятно, придется использовать запятую, например:
- Лисица была быстрой, хитрой и тихой в лесу.
 ПРАВИЛЬНО
ПРАВИЛЬНО - Лисица была быстрой, хитрой и тихой в лесу. ПРАВИЛЬНО
- Лисица в лесу шла быстро, коварно и тихо. НЕПРАВИЛЬНО
- Лисица была быстрой, хитрой и тихой в лесу. НЕПРАВИЛЬНО
Иногда, стоит ли использовать запятую, зависит от автора и его стиля. Первые два предложения верны — использование одной или двух запятых зависит от автора. Третье предложение без запятой и последнее предложение со слишком большим количеством запятых неверны. При двух или меньшем количестве вещей запятая не нужна, например:
- Лисица была быстрой и хитрой в лесу. ПРАВИЛЬНО
- Лисица была быстрой и хитрой в лесу. НЕПРАВИЛЬНО
d. Апостроф
Апостроф (’) делает две важные вещи.
Во-первых, мы используем его, чтобы показать владение:
- «Шубка лисицы была оранжевой».
Во-вторых, мы используем его для сокращений, таких как превращение «не могу» в «не могу» или «ты есть» в «ты».
Самая большая ошибка, которую люди делают с апострофами, — это использовать их для создания множественного числа — это НЕПРАВИЛЬНО.Например, «собаки» означает несколько собак, но «собака» означает что-то, что принадлежит этой собаке.
e. Цитаты
Цитаты («») используются для множества вещей, но, вероятно, наиболее важный способ использования цитат — это «цитировать» чьи-то точные слова:
- Свидетели говорят, что они слышали крик лисы «Я люблю блины! ”
Или,
- В газетной статье говорилось, что «главный источник пищи лисы — блины».
Точно так же они показывают, что персонаж говорит (диалог):
- «Я люблю блины», — сказал лис.
Цитаты также могут показать, что автор использует жаргонное или необычное слово:
- Лисица не знала, что такое «вилка».
Мы также используем цитаты для названий стихов, статей, названий песен и фирменных наименований вещей, таких как «Сонет 18» Шекспира и бургер «Биг Мак».
e. Двоеточие и двоеточие
Двоеточие
Двоеточие (:) говорит, что автор собирается дать список:
- Лисе нравились три вещи: блины, сироп и масло.
Двоеточие также может разделять два предложения, где второе предложение дает больше информации о первом:
Лисица умела прятаться: человек никогда его не видел.
Точка с запятой
Точка с запятой (;) может соединять два независимых предложения, связанных друг с другом:
- Лисица любила блины; он ел их каждый день на завтрак.
Точку с запятой можно комбинировать с переходом, например «но», чтобы соединить два связанных предложения:
- Лисица любила блины; но он не мог их есть без сиропа и масла.
Точка с запятой также может разделять элементы в списке, которые могут сбивать с толку:
Лиссабон, Португалия; Барселона, Испания; Венеция, Италия; Париж, Франция; и Берлин, Германия — популярные места для посещения в Европе.
ф. Круглые скобки
Круглые скобки () содержат дополнительную информацию, которую авторы хотят использовать в качестве отступления, например:
- Лисица любила блины (он ел их каждое утро), и у него был отличный рецепт для них.
Важная информация — лиса любит блины и имеет хороший рецепт.Но автор также хочет сделать заметку для читателей, что он ест их каждое утро — это подчеркивает, насколько лиса любит блины, а также дает читателю больше информации.
Или вы можете использовать скобки для пояснения, например:
- Лисица заплатила много денег за хороший кленовый сироп (50 долларов за бутылку).
Здесь писатель хочет сказать, что сироп дорогой, но читатель может не знать, сколько денег это много. Ввод цены в круглые скобки показывает, что 50 долларов — это то, что автор имеет в виду под «большими деньгами».”
Кроме того, в этих предложениях вы также можете увидеть, что: a. если информация в круглых скобках идет в конце предложения, знак конца выходит за скобки; и б. запятые обычно ставятся после скобок.
если информация в круглых скобках идет в конце предложения, знак конца выходит за скобки; и б. запятые обычно ставятся после скобок.
4. Как использовать (и не использовать) знаки препинания
В предложении пунктуация может иметь такое же значение, как и слова, которые вы используете! Это важная и ключевая часть каждого предложения. Представьте записку от девушки своему парню:
Пример AДорогой Джек, Мне жаль, что я люблю тебя. От Джилл | Пример BУважаемый Джек, Мне жаль, я люблю тебя. От Джилл | Пример CУважаемый Джек, Мне очень жаль. Я люблю вас. От Джилл |
Буква A имеет другое значение, чем буквы B и C. Буква A имеет отрицательное значение; выражая, что Джилл сожалеет о том, что влюблена в Джека. Однако в письмах B и C Джилл извиняется перед Джеком, а затем говорит ему, что любит его. Итак, вы можете увидеть, насколько простая запятая может повлиять на смысл предложения.
Итак, вы можете увидеть, насколько простая запятая может повлиять на смысл предложения.
Когда мы говорим каждый день, легко изменить голос и выделить разные слова, чтобы смысл был понятен. Но письменно нужно отметить места, где должны произойти эти изменения. Вот три предложения, похожих на приведенный выше комикс «Бабушка», которые покажут вам, почему:
Без правильной пунктуации
- Хочешь съесть Салли?
- Я хочу съесть Салли.
- Поедим Салли!
С правильной пунктуацией
- Хочешь поесть, Салли?
- Я хочу поесть, Салли.
- Едем, Салли!
Как вы можете видеть во всех приведенных выше примерах, если вы забудете использовать знаки препинания или неправильные знаки в неправильное время, это может запутать предложение или даже полностью изменить его значение. Здесь запятая определяет разницу между едой Салли и едой с Салли!
Полное руководство по 12 английским знакам препинания
Пунктуация — это основной метод различения различных фрагментов текста, который делает процесс чтения более легким и информативным. Некоторые знаки препинания используются интуитивно, в то время как другие часто используются неправильно и требуют изучения. Мы создали полное руководство, чтобы научить вас основам использования 12 наиболее распространенных знаков препинания.
Некоторые знаки препинания используются интуитивно, в то время как другие часто используются неправильно и требуют изучения. Мы создали полное руководство, чтобы научить вас основам использования 12 наиболее распространенных знаков препинания.
Научное определение пунктуации — это набор символов, которые могут прояснять значение фраз и предложений, разделять их различные части и подчеркивать значение слов и словосочетаний. При правильном использовании знаки препинания могут обогатить ваш текст и сделать его полным и разборчивым.В английском языке используются 12 наиболее распространенных знаков препинания, и вот советы по использованию каждого из них.
Полная остановка или период
Точка является одним из наиболее широко используемых знаков препинания в английском языке и фактически является одним из знаков, используемых интуитивно. Точка не используется для выделения смысла или повышения стиля текста; его единственная цель — сигнализировать о завершении предложения.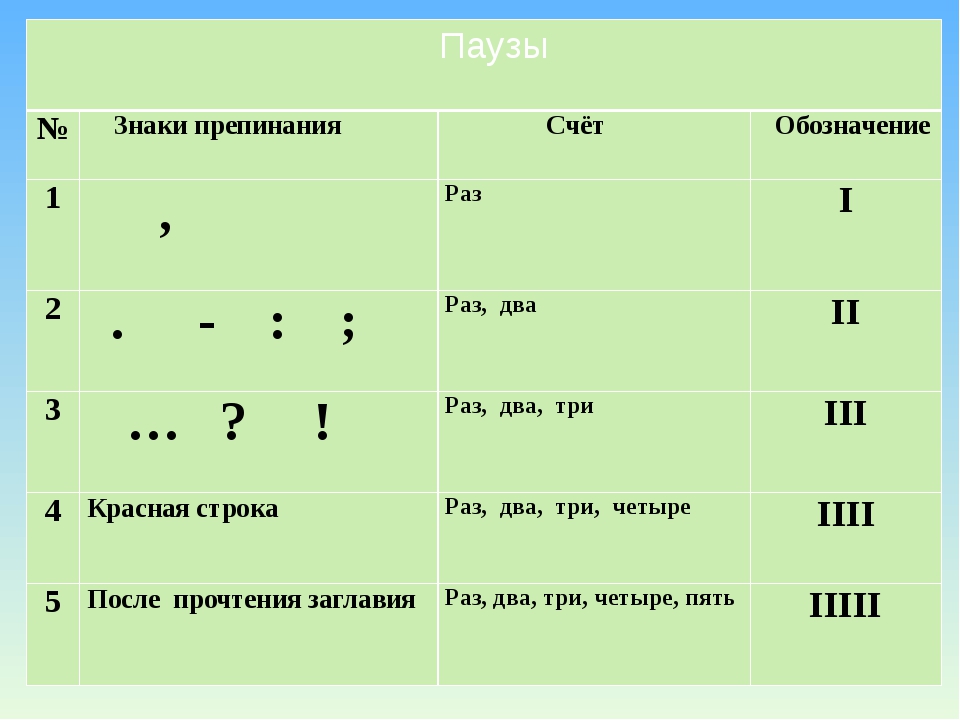
Вопросительный знак
Каждое предложение, в конце которого есть прямой вопрос, также будет содержать вопрос после последнего слова, но это верно только для прямых вопросов.Предложения, содержащие косвенные вопросы, не требуют вопросительного знака. Точно так же, если предложение классифицируется как запрос, сформулированный как вопрос, ему не нужен вопросительный знак в конце. В то же время длинные и сложные вопросы, часто встречающиеся в периодических изданиях, всегда должны сопровождаться вопросительным знаком. Если в предложении есть вопрос, например, если оно заключено в кавычки или скобки, всегда нужен вопросительный знак.
Восклицательный знак
Роль восклицательного знака является стилистической: это инструмент, который используется для передачи эмоций, таких как волнение, а также для указания на срочность или драматичность предложения.Использование восклицательного знака при необходимости — верный способ привлечь внимание к вашему тексту.
Менее распространенные случаи использования восклицательного знака включают выражение сарказма или случаи, когда восклицательный знак используется вместе с вопросительным знаком, чтобы продемонстрировать удивление. Использование нескольких восклицательных знаков недопустимо в литературе и в профессиональной среде, но совершенно нормально в неформальном письме.
Использование нескольких восклицательных знаков недопустимо в литературе и в профессиональной среде, но совершенно нормально в неформальном письме.
запятая
Запятая — один из самых разнообразных знаков препинания с несколькими важными целями.Чаще всего запятая используется для разделения различных элементов предложения, таких как прилагательные или элементы списка. Когда необходимо создать логическую паузу между двумя частями предложения, следует также использовать запятую. Другой случай, когда запятая широко используется, — это когда вы записываете дату или хотите отделить название города от названия страны.
точка с запятой
Есть несколько случаев, когда точка с запятой оказывается обязательной в тексте.Первый — когда вы хотите убрать союз из длинного предложения, чтобы улучшить его читаемость. Еще одна причина использовать точку с запятой — это когда у вас есть два связанных коротких предложения, которые вы хотите объединить в одну фразу. Еще одно допустимое использование точки с запятой — разделение элементов в списке.
Колон
Знак препинания с двоеточием обычно стоит перед списком элементов. Когда вы пишете предложение с двумя независимыми предложениями, где второе предложение иллюстрирует первое, также используйте двоеточие.Иногда двоеточия используются как синонимы длинного тире, чтобы обозначить конец предложения.
Круглые скобки
Круглые скобки обычно используются в двух случаях: когда вам нужно добавить в предложение запоздалую мысль и когда вам нужно дать пояснение. В обоих случаях очень важно, чтобы предложение было логичным и информативным, а также имело смысл, даже без текста в круглых скобках. Другими словами, круглые скобки не должны изменять структуру или смысл предложения и должны предоставлять только дополнительную информацию.
Дефис
Дефис чаще всего используется в составных словах или словах, состоящих из двух или более слов, представляющих отдельную идею. Однако не все составные слова пишутся через дефис; некоторые из них могут открывать или закрывать сложные слова. Другой распространенный случай, когда необходимо использовать дефис, — числа, записанные в виде слов.
En Dash
Очень важно различать дефис и короткое тире. Наиболее распространенное использование короткого тире — это диапазон чисел, расстояния или отношений.Первые два примера достаточно ясны, но третий довольно сложен. Диапазон отношений, которые могут быть обозначены коротким тире, включает связь, конфликт и расстояние.
Эм Даш
Длинное тире — один из самых распространенных знаков препинания в профессиональной письменной форме. В зависимости от контекста длинное тире может использоваться вместо круглых скобок, запятой или точки с запятой. Основное назначение длинного тире — сделать стилистически обоснованный перерыв в тексте.
Одинарные кавычки
Одиночные кавычки — менее распространенный знак препинания, который может быть очень полезен в следующих ситуациях:
- Показать владение;
- Чтобы показать сокращения;
- Чтобы ввести цитату в предложение.
Двойные кавычки
Единственный случай, когда используются двойные кавычки, — это сигнализация наличия кавычек. Нет других ситуаций, когда использование кавычек оправдано, будь то акцент или выделение названия книги или фильма.
Что такое пунктуация? — Правила и знаки — Видео и стенограмма урока
Правила для часто используемых знаков препинания
Давайте взглянем на некоторые правила для наиболее распространенных знаков препинания в американском английском:
Период
Используйте точки (.) в конце предложений, чтобы указать точку, как в предложении:
Используйте точки для создания сокращений. Например:
- Мистер сокращенно Мистер — как у мистера Джонсона .
Запятая
Используйте запятую (,) после вводных фраз в списках для разделения трех или более элементов в серии, а также в качестве индикатора, обозначающего независимые и зависимые предложения.
В предложении:
- Мытье машины — тяжелая работа, но награда того стоит.
запятая разделяет предложения. В предложении:
- Чтобы хорошо поработать, вам понадобятся мыло, вода, тряпки для мытья посуды и средство для мытья окон.
первая запятая отделяет вступительную фразу от остальной части предложения, а последние три запятые отделяют отдельные элементы в списке.
Используйте запятую для разделения названий городов и штатов, а также между датой и годом:
- Миннеаполис, Миннесота
- 4 апреля 2013 г.
Например, обратите внимание на запятую между Миннеаполисом и Миннесотой и запятую между датой (4 апреля) и годом (2013).Однако, если вы просто используете месяц и год (как в апреле 2013 года), запятая не используется.
Вопросительный знак
Используйте вопросительный знак (?), Когда задаете прямой вопрос , , конкретный вопрос, который задается, но не косвенный вопрос , повторение ранее заданного вопроса. Например:
— это прямой вопрос, поэтому в нем используется вопросительный знак. Однако предложение:
- Он спросил меня, куда я иду.
повторяет то, что сказал кто-то другой, и, таким образом, является косвенным вопросом, что делает его предложением, требующим точки, а не вопросительного знака.
Дополнительные правила пунктуации
Точка с запятой
Используйте точку с запятой (;) для разделения независимых предложений, для разделения элементов в серии, когда есть дополнительная пунктуация и когда есть переходная фраза (например: в результате, даже если , по сути) между независимыми предложениями.
В этом предложении:
- Члены прибыли из Фарго, Северная Дакота; Юнона, Аляска; Олбани, Нью-Йорк; Майами, Флорида; и Ньюпорт, Род-Айленд.
Точка с запятой разделяет серии элементов с дополнительной пунктуацией. В предложении:
- Все больше людей усыновляют собак; на самом деле местный приют пуст.
точка с запятой ставится сразу после первого независимого предложения.
Восклицательный знак
Используйте восклицательных знаков (!) Для выделения, команд или демонстрации крайних эмоций. Например, восклицательный знак используется в предложении:
, потому что это команда.Пока в предложении:
- Ух ты! Это отличная песня.
восклицательный знак используется для выделения.
Одинарные кавычки
Используйте одинарные кавычки (»), чтобы выделить фразу или слово, например, в предложении:
- Он был полностью честен, говоря нам «хорошее, плохое и уродливое». ‘
Апостроф
Используйте апострофы (‘), где буквы были опущены, чтобы создать сокращение, показать владение или прояснить множественное число.В предложении:
«не могу» является сокращением слова «не могу». Апостроф указывает на то, что буквы были удалены. В предложении:
- Тоби получил все пятерки в этом квартале.
апостроф разъясняет множественное число. В:
апостроф обозначает владение.
Двоеточие
Используйте двоеточие (:) после независимого предложения (предложение, которое может стоять само по себе), чтобы указать, что за ним последует объяснение или список.Давайте посмотрим на несколько примеров использования двоеточия в действии:
- Он понял, что осталось сделать только одно: упаковать чемоданы.
- Персонал нашей школы состоит из следующих людей: директор, заместитель директора, учителя, библиотекарь, секретарь и дворники.
Круглые скобки
Используйте круглые скобки (), чтобы заключить в них материал, который менее важен, чем остальная часть предложения. В предложении:
- Макс попросил немного подумать (но долго не думал), а затем согласился.
«но он недолго думал» добавляет к предложению некоторые дополнительные детали, но это не является необходимой информацией.
длинное тире
Используйте тире длинное тире (-), длинное тире, чтобы выделить список элементов или задать краткую мысль. Посмотрите, как длинное тире используется в этих двух предложениях, чтобы выделить некоторую информацию:
- Все мальчики — Дэйв, Марк, Макс и Сэм — ушли сегодня утром.
- Вы можете положить в эту комнату свое пальто и шляпу, но не сумочку.
En Dash
Используйте тире en dash (-), короткое тире, чтобы отметить промежуток между годами и отрезками времени, например, при написании:
Краткое содержание урока
В английском языке используются самые разные знаки препинания. . Эти знаки препинания , некоторые из которых представляют собой точку, запятую и двоеточие, являются символами, которые выполняют важные функции, обеспечивая четкость и понятность нашего письма. Изучение правил, связанных с различными знаками препинания, не только поможет вам лучше понимать то, что вы читаете, но и сделает вас более сильным писателем.
Грамматика и пунктуация — Профессиональное общение
По завершении этой главы вы сможете
- переписывать грамматически неправильные предложения, чтобы прояснить смысл сообщений,
- объясняют различные способы, которыми грамматика может влиять на значение или прием письменных сообщений на рабочем месте,
- демонстрируют, когда использовать разные, но подходящие знаки препинания в письменной форме,
- объяснить влияние использования неправильной пунктуации при общении на рабочем месте,
- переписывают предложения, исправляя ошибки пунктуации, а
- применяют правильную пунктуацию, чтобы передать истинное значение сообщений.
Введение
Чтобы обеспечить ясность и правильность написания сообщений, у вас есть возможность обновить и попрактиковаться в грамматике и пунктуации.
Если вы уже являетесь гуру грамматики (или, если вы стали гуру после использования дополнительного пакета грамматики), вы можете сразу же погрузиться в следующую главу, чтобы узнать о пяти распространенных рабочих документах: стандартные деловые письма, титульные листы по факсу, служебные записки и т. Д. короткие отчеты и электронные письма.
Скорее всего, если вы когда-либо читали или комментировали что-либо в разделе онлайн-комментариев, вы, вероятно, сталкивались с «полицией грамматики».«Это люди, которые быстро игнорируют значение того, что вы сказали, и сосредотачиваются исключительно на том, правильно ли вы сделали это с грамматической точки зрения. Для наших целей определение грамматики — это «набор фактических или предполагаемых предписывающих понятий о правильном использовании языка».
Люди, чей родной язык — английский, могут постоянно делать грамматические ошибки. Часто условности речи не соответствуют правилам грамматики. Пока все вокруг совершают ту же ошибку, это не звучит неправильно, и нет никаких проблем, пока они не встретят людей, которые научились иначе.От региона к региону и даже от рабочего места к рабочему месту могут быть небольшие, но ощутимые различия в том, как люди используют грамматику, поскольку английский язык продолжает развиваться. Вообще говоря, правила грамматики помогают всем нам понять, как правильно использовать английский язык. Каким бы раздражающим или педантичным ни казалось изучение и применение грамматики, грамматические нормы важны для эффективного и ясного общения.
Аналогичным образом, пунктуация определяется как «знаки, такие как точка, запятая и круглые скобки, используемые в письменной форме для разделения предложений и их элементов и для пояснения смысла.«Пунктуация иногда воспринимается как должное или используется неправильно, особенно в цифровой коммуникации, такой как обмен текстовыми сообщениями и социальные сети.
Как писатель и коммуникатор, стремящийся быть ясным и точным, вам могут быть полезны повторения по грамматике и пунктуации, что и даст вам этот раздел.
Грамматические ошибки могут помешать аудитории ясно понять ваше сообщение или могут просто отвлечь от вашего сообщения. Кроме того, грамматические ошибки часто могут ослабить доверие к автору, потенциально заставляя вашу аудиторию не воспринимать ваше сообщение всерьез.
В этом разделе мы дадим обзор частей речи, типов предложений и ошибок модификаторов. В качестве напоминания, вот некоторые основы грамматики:
Части речи«Части речи» — это основные типы слов в английском языке. В большинстве учебников грамматики говорится, что существует восемь частей речи: существительных, глаголов, прилагательных, наречий, местоимений, союзов, предлогов, и междометий. Добавим еще один тип: статьи.
Важно уметь распознавать и идентифицировать различные типы слов в английском языке, чтобы вы могли понимать грамматические объяснения и использовать правильную словоформу в нужном месте. Вот краткое объяснение частей речи:
Если вы хотите попрактиковаться в распознавании различных частей речи, вы можете попробовать это интерактивное упражнение:
Виды приговоровКогда мы говорим о грамматике, мы обычно говорим о том, как язык формируется на уровне предложения.Слова являются основой предложений, и в предыдущем разделе мы узнали о том, какие типы слов составляют основную часть речи. Здесь мы сосредотачиваемся на том, как мы соединяем эти слова, чтобы попытаться создать смысл. В будущих главах мы продолжим опираться на это, чтобы узнать о абзацах и о том, как мы затем используем их в различных форматах, таких как письма, заметки и отчеты.
Первая часть этого обзора будет посвящена трем основным типам предложений: простым, составным и сложным предложениям.
Простые предложения
Простые предложения содержат одну пару подлежащее – глагол и выражают законченную мысль.Они могут содержать более одной темы, как в следующем примере:
Мы с женой поженились в Японии.
Простые предложения могут также содержать более одного глагола, как в следующем примере:
Он косил траву и отложил газонокосилку.
Вот еще несколько примеров простых предложений и их сочетаний «подлежащее – глагол»:
Фильм был не очень интересным. (подлежащее, глагол)
Мне и моим друзьям фильм не понравился. (подлежащее, подлежащее, глагол)
Мы с друзьями готовили и ели вместе.(подлежащее, подлежащее, глагол, глагол)
Я могу посмотреть телевизор или почитать книгу после обеда. (подлежащее, глагол, глагол)
Сложные приговоры
Второй тип предложения, составное предложение , состоит из двух простых предложений, соединенных координирующим союзом .
Есть семь координирующих союзов: для, и, ни, но, или, все же, так. Запятая предшествует координирующему союзу, который соединяет два простых предложения.
Не путайте координирующий союз в составном предложении и составной глагол в простом предложении.Внимательно изучите следующие примеры.
Мой друг играет на гитаре и пишет музыку.
Это простое предложение, содержащее подлежащее (друг) и составной глагол (играет / пишет).
Мой друг играет на гитаре и пишет музыку.
Это составное предложение — два простых предложения, соединенных запятой и координирующим союзом. Подлежащее первого простого предложения — друг, а глагола — игры. Подлежащее второго простого предложения — он, а глагол — пишет.
Сложные предложения
Предложения — это группы слов, которые содержат подлежащие и глаголы. Есть два типа: независимых (основных) предложений и зависимых (подчиненных) предложений. Независимое придаточное предложение, помимо подлежащего и глагола, выражает законченную мысль и может стоять отдельно как простое предложение. Само по себе зависимое предложение — это просто часть предложения или фрагмента. Его необходимо присоединить к независимому пункту, чтобы он имел смысл и представлял читателю полную мысль.
Есть три типа зависимых предложений: прилагательные, наречия и существительные. Когда вы соединяете зависимые и независимые предложения вместе, вы создаете сложных предложений. Изучите приведенные ниже примеры.
Сложное предложение с придаточным зависимым прилагательным:
| Пример | Пояснение |
| В Ванкувере есть много интересных мест для покупок. | отдельная оговорка или простое предложение |
| самый большой город Британской Колумбии | зависимое прилагательное придаточное |
| Ванкувер, крупнейший город Британии. Колумбия, есть много интересных мест для покупок. | сложное предложение |
Сложное предложение с зависимым наречием от времени:
| Пример | Пояснение |
| Я расскажу ей новости. | отдельная оговорка или простое предложение |
| как только увижу ее | зависимое наречие предложение времени |
| Как только я увижу ее, я расскажу ей новости. | сложное предложение |
Сложное предложение с зависимым наречием с условием причины:
| Пример | Пояснение |
| Я рано лег спать. | отдельная оговорка или простое предложение |
| потому что я устал | зависимое наречие придаточное слово причины |
| Я рано лег спать, потому что устал. | сложное предложение |
Сложное предложение с использованием придаточного предложения зависимого существительного:
| Пример | Пояснение |
| Я уже знаю. | отдельная оговорка или простое предложение |
| что вы сказали | зависимое существительное придаточное положение |
| Я уже знаю, что вы сказали. | сложное предложение |
Запятая с придаточным зависимым наречием
Если зависимое предложение наречия стоит перед независимым предложением в предложении, они разделяются запятой.Однако, если за независимым (основным) предложением следует предложение зависимого наречия, запятая не используется.
Используйте запятую, когда зависимое предложение является первым:
Пока мы ужинали, кто-то позвонил в дверь.
Не используйте запятую, когда главное предложение стоит первым:
Кто-то позвонил в дверь, когда мы ужинали.
Если вы уверены, что усвоили урок, можете продолжить это упражнение:
Согласование и параллелизмУ вас, вероятно, достаточно хорошо развито чувство того, правильно ли звучит предложение.Фактически, это одна из основных причин, по которой вы должны иметь привычку читать свои черновики вслух, прежде чем отправлять их на рассмотрение коллегам или инструкторам. Или еще лучше, попросите друга прочитать вам черновик. Вы удивитесь, сколько неосторожных ошибок вы поймаете, просто услышав их.
Один из ключевых аспектов, из-за которого предложение может звучать некорректно, — несовпадение подлежащего и глагола. В правильно написанных предложениях подлежащее и глаголы должны совпадать по количеству и лицу. Согласование числа означает, что подлежащее множественного числа соответствует форме множественного числа глагола.Хотя множественное число существительного часто оканчивается на -s, это единственное число глагола, которое обычно оканчивается на -s.
Примеры:
Кролик прыгает по клетке. (подлежащее и глагол в единственном числе)
кроликов прыгают по клетке. (подлежащее и глагол множественного числа)
Соглашение лично означает, например, что существительное от третьего лица должно сочетаться с правильным глаголом от третьего лица. На этой диаграмме показаны первые, вторые и третьи лица для нескольких глаголов в настоящем времени.Как видите, большинство глаголов одинаковы во всех столбцах, за исключением третьего лица единственного числа. Глагол быть внизу также меняется в столбце единственного числа от первого лица. Таким образом, чтобы сопоставить подлежащие и глаголы по людям, вы можете, например, сказать «Я есть», но не «Я есть».
Глаголы настоящего времени
| Первое лицо Единственное число: I | 1-е лицо Множественное число: We | 2-е лицо в единственном числе: Вы | 2-е лицо Множественное число: You | Третье лицо Единственное число: Он, Она, Оно | 3-е лицо Множественное число: они |
| ходьба | прогулка | прогулка | прогулка | прогулки | прогулка |
| смеяться | смеяться | смеяться | смеяться | смеется | смеяться |
| погремушка | погремушка | погремушка | погремушка | погремушки | погремушка |
| падение | осень | осень | осень | водопад | осень |
| думаю | думаю | думаю | думаю | думает | думаю |
| утра | это | это | это | это | это |
Примеры:
Хрипит от ветра.(подлежащее и глагол от третьего лица)
Я считаю себя забавным человеком. (подлежащее и глагол от первого лица)
Каждое из следующих предложений представляет собой типичную ошибку согласования. Объяснение и исправление ошибки следуют каждому примеру:
Пит и Тара — братья и сестры.
Пояснение: Подлежащее, которое включает слово «и», обычно принимает глагол множественного числа, даже если два существительных в единственном числе.
Исправление : Пит и Тара — братья и сестры.
Мой любимый завтрак — печенье с подливкой.
Пояснение: Иногда слово «и» связывает два слова, которые образуют подлежащее и на самом деле являются одним целым. В данном случае «бисквиты с подливкой» — это одно блюдо. Таким образом, даже если есть два существительных, связанных словом «и», это субъект единственного числа и должен принимать глагол единственного числа.
Поправка: Бисквиты с соусом — мой любимый завтрак.
К работающим здесь женщинам относятся хорошо.
Объяснение : Относительные местоимения (тот, кто и который) могут быть в единственном или множественном числе, в зависимости от их предшественников (слов, которые они обозначают). Местоимение имеет тот же номер, что и антецедент. В этом случае «who» означает «женщины», а «женщины» — во множественном числе, поэтому глагол должен быть во множественном числе.
Исправление: С работающими здесь женщинами обращаются хорошо.
Одна из девушек поет в хоре.
Объяснение : Субъект единственного числа отделяется фразой, оканчивающейся на существительное во множественном числе.Этот образец заставляет людей думать, что существительное во множественном числе (в данном случае «девушки») является подлежащим, которому они должны соответствовать глаголу. Но на самом деле глагол («петь») должен соответствовать единственному подлежащему («один»).
Исправление: Одна из девушек поет в хоре.
Данные неясны.
Пояснение: Слова «данные» и «носитель» всегда считаются множественным числом, когда используются в академическом письме. В более повседневном письме некоторые люди используют версию двух слов в единственном числе.
Поправка: Данные нечеткие.
Баскетболисты, пользующиеся наибольшим спросом в этом месяце, — это студенты колледжей, играющие в турнире «Финал четырех».
Объяснение: В некоторых предложениях, подобных этому, глагол стоит перед подлежащим. Порядок слов может вызвать путаницу, поэтому вам нужно найти подлежащее и глагол и убедиться, что они совпадают.
Исправление: Баскетболисты, пользующиеся наибольшей прессой в этом месяце, — это студенты колледжей, играющие в турнире «Финал четырех».
Я готов к работе.
Объяснение : Подлежащее и глагол должны согласовываться лично. В этом случае «I» — существительное от первого лица, а «is» — глагол от третьего лица.
Исправление : Я готов к работе.
Мы думаем, что Клайд Делбер должен немедленно уйти в отставку.
Пояснение: Слова, начинающиеся с «что», могут принимать глагол единственного или множественного числа в зависимости от того, понимается ли «что» в единственном или множественном числе.В этом случае «мы» все вместе думаем об одном, поэтому глагол должен быть в единственном числе, даже если «мы» во множественном числе.
Исправление: Мы думаем, что Клайд Делбер должен немедленно уйти в отставку.
Либо собака, либо кошки проводят время на этом сиденье у окна, когда меня нет.
Пояснение: Слово «или» обычно указывает на подлежащее единственного числа, даже если вы видите два существительных. Это предложение является исключением из этого правила, потому что по крайней мере один из подлежащих стоит во множественном числе.Когда это происходит, глагол должен согласовываться с подлежащим, к которому он ближе всего.
Исправление: Собака или кошки проводят время на этом сиденье у окна, когда меня нет.
Молли или Гек хранят книги для клуба, так что один из них узнает.
Пояснение: Слово «или» обычно указывает на подлежащее единственного числа, даже если вы видите два существительных. Исключением из этого правила является то, что если одно из подлежащих стоит во множественном числе, глагол должен согласовываться с подлежащим, к которому он ближе всего.
Исправление: Молли или Гек хранят книги для клуба, так что один из них будет знать.
Пустыня пугает меня, когда я думаю о том, чтобы выйти в одиночестве.
Объяснение: Когда существительное в единственном числе заканчивается на -s, вы можете запутаться и подумать, что это существительное во множественном числе.
Исправление: Пустыня пугает меня, когда я думаю о том, чтобы выйти в одиночестве.
Каждая из девушек счастлива быть здесь.
Пояснение: Неопределенные местоимения (любой, каждый, любой, все и все) всегда в единственном числе.Поэтому их всегда нужно использовать с глаголами единственного числа.
Исправление: Каждая из девушек рада быть здесь.
Согласование местоимений — еще один важный аспект при составлении предложений. Сопоставление местоимения с его антецедентом с точки зрения числа (единственного или множественного числа) может быть непростым, о чем свидетельствуют такие предложения, как это:
Так как ученик — единственное число, ему должно соответствовать местоимение единственного числа. Правильная, но довольно неуклюжая версия предложения следующая:
Чтобы избежать проблем с местоимением и антецедентом, вам следует предпринять три шага:
Определите антецедент.
Определите, является ли антецедент единственным или множественным числом.
Убедитесь, что антецедент и местоимение совпадают, желательно сделать оба числа множественным числом, если это возможно.
Использование единственного числа они / их широко оспаривается, и многие руководства по стилю письма теперь считают это приемлемым. Английский язык постоянно развивается, и мы думаем, что стоит отметить, что эта конструкция, хотя и не является параллельной или грамматически правильной с традиционной точки зрения (согласование местоимений), возможно, более эффективно, чем использование традиционных гендерных конструкций «он или она» и «его или». ее.Иногда контекст подсказывает, с чем лучше работать. В этом конкретном модуле мы используем единственное число они / их, потому что контекст заставляет нас ссылаться на общие обозначения людей, такие как начальник, работодатель, сотрудник, ученик, учитель, писатель, читатель и т. Д .; использование традиционных местоимений единственного числа каждый раз в предложениях, таких как «Ваш начальник может попросить вас написать письмо от его или ее имени», привело бы к утомительному электронному тексту! Так что иногда ваш контекст письма будет влиять на нормы, соглашения и правила, которых вы придерживаетесь — или отклоняетесь!
Антецедентная идентификацияАнтецедент — это существительное, которое местоимение представляет в предложении.Когда вы видите местоимение, вы сможете понять его значение, посмотрев на остальную часть предложения. Посмотрите на следующее предложение:
- Смиты часами собирали яблоки и складывали их в большие ящики.
- Антецедент слова «они» — «Смиты». Антецедент слова «они» — «яблоки».
Прочтите каждое из следующих предложений и отметьте антецедент для каждого местоимения.
- Бет упала на пол и обнаружила, что это было труднее, чем она думала.
- ит — пол; она — Бет
- Женщины болтали как , они бегали трусцой вместе с своими домашними животными.
- они — женщины; их — женщин
- Когда Эйб потерял своих перчаток, он вернулся в поисках их.
- его — Эйба; он — Абэ; им — перчатки
По мере того, как предложения становятся более сложными или задействуются целые абзацы, определение предшествующих местоимений также может усложняться. Однако, если местоимения и антецеденты используются правильно, вы сможете найти антецедент для каждого местоимения.Прочтите следующие предложения и отметьте антецедент для каждого местоимения.
Оригинал: Древние майя наметили 12 декабря 2012 года как знаменательный день, знаменующий конец 5126-летней эры. Сегодня ученые размышляют о том, что майя ожидали в этот день, и видели ли они в нем время празднования или страха. Некоторые говорят, что конец эпохи был бы поводом для празднования. Другие рассматривают это как надвигающуюся зловещую ситуацию из-за ее неизвестной природы.В любом случае, вы можете быть уверены, что многие ученые обратят внимание на приближающуюся дату.
С объяснением: Древние майя планировали 12 декабря 2012 года как знаменательный день, знаменующий конец 5126-летней эры. Сегодня ученые размышляют о том, что майя ожидали в этот день, и видели ли они (майя) это (12 декабря 2012 года) как время для празднования или страха. Некоторые говорят, что конец эпохи был бы поводом для празднования.Другие считают это (12 декабря 2012 г.) надвигающейся зловещей ситуацией из-за ее (12 декабря 2012 г.) неизвестной природы. Во всяком случае, вы (читатель) можете быть уверены, что многие ученые обратят внимание на приближающуюся дату.
Антецеденты единственного и множественного числа
Когда вы пишете и используете местоимения и антецеденты, начните с определения того, является ли антецедент единственным или множественным числом. Как вы можете видеть из следующей таблицы, сделать это иногда не так просто, как может показаться.
| Предыдущий | Единственное или множественное число? | Пояснение |
| собака | Особое число | Существительные в единственном числе являются антецедентами единственного числа. |
| певцов | Множественное число | Существительные общего множественного числа служат антецедентами множественного числа. |
| все | Особое число | Неопределенные местоимения иногда выступают в качестве антецедентов.Поскольку они относятся к неспецифическим вещам или людям, их количество может быть неоднозначным. Чтобы решить эту проблему, неопределенные местоимения обрабатываются как единственное число. Другие неопределенные местоимения включают любой , каждый, каждый , кто-то , никто , никто , что-то и ничего . |
| команда | Особое число | Слова, обозначающие одну группу, используются в единственном числе, даже если в группу входит множественное число. |
| членов команды | Множественное число | По самому определению, члены в группе состоят более чем из одного, поэтому этот термин имеет множественное число. |
| пальто и шапка | Множественное число | Когда два или более существительных соединяются с помощью «и», они образуют множественное число. |
| пальто или шляпа | Особое число | Когда два или более существительных соединены словом «или», определение такого антецедента в единственном или множественном числе основывается на последнем упомянутом существительном.В этом случае «шляпа» упоминается последней и используется в единственном числе. Итак, антецедент — единственное число. |
| пальто или головные уборы | Множественное число | Поскольку последнее упомянутое существительное в этом наборе является множественным, в качестве антецедента этот набор будет множественным. |
| пальто или шапка | Особое число | Поскольку последнее упомянутое существительное в этом наборе является единственным, в качестве антецедента этот набор будет единственным, даже если набор включает существительное во множественном числе.(Примечание: с точки зрения стиля постарайтесь избежать такой расстановки, используя последовательность «[единственное число] или [множественное число]» для ваших антецедентов.) |
Соответствие предшествующего и местоимения
Антецеденты и местоимения должны совпадать с точки зрения числа (единственного или множественного числа) и пола. Для ясности постарайтесь расположить местоимение относительно близко к его антецеденту. Если антецедент не сразу ясен, внесите изменения, например переставьте слова, заменив единственное число на множественное или заменив местоимение существительным.В каждом из следующих предложений есть проблема сопоставления предшествующего и местоимения. Прочтите каждое предложение и подумайте о проблеме. Затем просмотрите ниже каждый пример для исправления и объяснения.
Певец держал под табуреткой бутылку с водой.
Пояснение: Поскольку «певец» — единственное число, местоимение должно быть единственного числа. В этой ситуации сказать «его или ее» звучит странно, поэтому лучше всего будет пересмотреть предложение, чтобы уточнить пол певца.
Исправление: Певица Анджела держала под табуретом бутылку с водой.
Каждый студент должен завершить регистрацию на следующий семестр к 5 октября. * (См. Также объяснение на стр. 19)
Пояснение: Часто, как и в этой ситуации, лучшим решением является переключение предмета с единственного на множественное число, чтобы вы можете избежать использования «его или ее».
Исправление: Студенты должны завершить регистрацию на следующий семестр до 5 октября.
Каждый должен делать то, что считает лучшим.
Explanation: Неопределенные местоимения в английском языке рассматриваются как единственное число, даже если они имеют предполагаемое значение множественного числа.Вы должны либо использовать местоимение единственного числа, либо изменить предложение, чтобы исключить неопределенное местоимение как антецедент.
Исправление: Каждый должен делать то, что считает лучшим.
ИЛИ Все сотрудники должны делать то, что они считают лучшим.
Чтобы принять участие в праздничном турнире, команда совершила свой первый полет в группе.
Пояснение: Собирательные существительные в единственном числе, так как они представляют, например, одну команду, одну группу или одну семью. Хотя местоимение «оно» используется для обозначения нечеловеческого характера, оно также может использоваться для обозначения единственного собирательного существительного, в котором участвуют люди.
Исправление: Для участия в праздничном турнире команда совершила свой первый полет на авиалинии в составе группы.
Ни Кэти, ни Петерсоны не хотели уступать свое место в очереди.
Объяснение : В ситуациях, связанных с «или» или «ни», антецедент должен соответствовать существительному, ближайшему к местоимению, которым в данном случае является Петерсонс. Поскольку Петерсонс имеет множественное число, местоимение должно быть множественным.
Исправление: Ни Кэти, ни Петерсоны не хотели уступать свое место в очереди.
Собаки и кошка сразу съели всю пищу.
Пояснение: При соединении с «и» составные антецеденты имеют множественное число и, следовательно, образуют местоимение множественного числа.
Исправление: Собаки и кошка съели всю свою еду сразу.
Каждый член несет ответственность за свои взносы и регистрацию.
Пояснение: Использование «он», «его» или «его» в качестве универсального местоимения единственного числа больше не приемлемо. Либо используйте местоимения мужского и женского рода, как в первой редакции, либо измените существительное на множественное число и используйте местоимение множественного числа, как во второй редакции.Стилистически предпочтительнее множественное число.
Исправление: Каждый участник несет ответственность за свои взносы и регистрацию. ИЛИ Члены несут ответственность за свои взносы и регистрацию.
Параллелизм — это представление идей равной значимости в одинаковой грамматической манере. Этот принцип письма подпадает под действие грамматики, стиля, риторики и содержания. Параллелизм важен в различных типах предложений.
Вы можете этого не осознавать, но когда мы пишем, мы часто включаем списки. Списки должны быть параллельны, чтобы предложение было грамматически правильным и чтобы читатель получал удовольствие от его чтения. Все элементы в списке должны быть грамматически параллельны. Например, если в вашем предложении перечислены действия, все элементы должны начинаться с глаголов одного и того же времени и падежа.
Пример:
После работы Логан купил продукты, приготовил ужин и посмотрел телевизор.
Купил, сделал и смотрел — все глаголы совершенного прошедшего времени, в результате получается параллельный список.
Помните также, что когда вы соединяете даже два элемента с помощью соединения, эти два элемента должны быть параллельны. Параллельные списки особенно важны в хорошо написанных резюме. Когда вы перечисляете свои рабочие обязанности в записи о занятости, убедитесь, что каждый пункт в вашем списке начинается со слов, которые совпадают в части речи, времени и, если применимо, падеже.
Однако достижение параллелизма выходит за рамки технических деталей простого списка. Это совпадение следует иметь в виду, когда вы пишете на более глубокие темы или рассчитаны на то, чтобы убедить аудиторию.При правильном использовании параллелизм может улучшить понимание и оценку темы вашими читателями (и даже вашими собственными). Самая известная строка из инаугурационной речи Джона Ф. Кеннеди дает еще один пример (особый вид перестановки фраз, известный как антиметаболе ): «Не спрашивайте, что ваша страна может сделать для вас. Спросите, что вы можете сделать для своей страны ». Вы столкнетесь с параллелизмом не только в политике, но и в рекламе, религии и поэзии:
- «Достаточно крепкий для мужчины, но сделанный для женщины.”
- «Поступайте с другими так, как хотите, чтобы другие поступали с вами».
- «Некоторые говорят, что мир погибнет в огне, / Некоторые говорят, что наступит лед».
Параллелизм необходим для хорошо продуманных, хорошо построенных и легко читаемых предложений и абзацев.
Проверьте свое пониманиеУкажите, параллельны ли следующие предложения. В случаях, когда они не параллельны, перепишите предложение, чтобы сделать его параллельным.
- Вы можете ответить на наш опрос по телефону, посетить любое из наших 10 офисов или написать электронное письмо.
- Эта позиция представляет собой динамичную, перспективную, динамичную и ориентированную на клиента возможность.
- Проблема была в производстве, а не в планировании.
- Джереми получает звание лучшего сотрудника месяца, потому что он умен, внимателен, честен и много работает.
Предлоги
Предлоги — это слова, которые показывают отношения между двумя или более другими словами. Выбор правильных предлогов может быть сложной задачей, но следующие примеры помогут прояснить, как использовать некоторые из наиболее распространенных предлогов.
| Типы предлогов | Примеры предлогов | Как использовать | Предлоги, используемые в предложениях |
| Время | при | Используйте с часами дня и этими словами, обозначающими время дня: рассвет , полночь , ночь и полдень. | Съедим в 11:30. Мы съедим в полдень. |
| по | Используется со словами времени для обозначения определенного времени. | Я буду там к 5:00 . Я закончу к октября. | |
| дюйм | Используйте с , и следующие слова времени суток: после полудня , вечером и утром. Используется отдельно с месяцами, временами года и годами. | Старт утра . Сезон дождей начинается в июне . | |
| по | Используется с днями недели. | Увидимся в пятницу . | |
| Расположение | при | Используется для обозначения конкретного места. | Остановлю у химчистки . |
| дюйм | Используется, когда указывается, что объект или человек находится в заданных границах. | Мой билет , в кармане . | |
| по | Используется для обозначения «рядом с определенным местом». | Мой стол у задней двери . | |
| по | Используется для обозначения поверхности или участка, на котором что-то стоит или находится. | Поместите на стол , пожалуйста. Мой офис на бульваре Линкольн . | |
| Логические отношения | из | Используется для обозначения части целого. Используется для обозначения содержимого или макияжа. | Я съел половину бутерброда . Принес сумку фишек . |
| для | Используйте, чтобы показать цель. | Джейк использует свой фартук для приготовления на гриле . | |
| Состояние жизни | в | Используется для обозначения состояния бытия. | Боюсь, что у меня беда . |
Соединения
Союзы известны как «соединительные» слова. Они соединяют два слова, фразы или предложения вместе. Это классическое видео иллюстрирует функцию союзов, которые являются либо координирующими союзами (и, но, для, ни, или, так, пока), либо коррелятивными союзами (оба… и, либо… или, как… так, ни… ни, не… но не только… но и то ли… или).
Проверьте свое понимание Ошибки модификатора и инфинитивы разделенияРассмотрим это предложение: «На день рождения Меган подарила привлекательный женский портфель.Модификатор «привлекательный» находится в неудобном положении. Человек, написавший это предложение, скорее всего, намеревался предположить, что портфель был привлекательным. Однако люди, читающие или слушающие его, могут легко предположить, что портфель был предназначен (или уже принадлежал) привлекательной женщине.
Три категории проблем с модификаторами включают неуместных модификаторов, висячие модификаторы, и разделенных инфинитивов. Эти три категории, объясненные в следующих подразделах, похожи, потому что все они включают неправильные слова или фразы.Понимание различий между этими категориями должно помочь вам следить за такими ошибками в вашем письме и в письмах ваших коллег.
Неуместные модификаторы
Самый простой способ уточнить, какое слово в предложении модифицируется — это поместить модификатор рядом со словом, которое оно изменяет. По возможности лучше всего размещать модификатор непосредственно перед измененным словом или после него.
Прочтите следующий пример неуместного модификатора, обратите внимание на путаницу и просмотрите исправление.
Пример:
Неисправный телефон ученика пищал во время урока.
Модификатор неверно размещен : «неисправен»
Изменение: «телефон» (не «студент»)
Замешательство: Писатель хочет сказать, что у ученика был неисправный телефон, который пищал во время урока, а не то, что ученик был неисправен.
Исправление: Неисправный телефон ученика издал звуковой сигнал во время урока.
Висячие модификаторы
Часто висячий модификатор модифицирует подлежащее предложения, но размещение модификатора создает впечатление, будто он изменяет другое существительное в предложении. В других случаях модификатор dangling на самом деле модифицирует кого-то или что-то, кроме субъекта предложения, но формулировка создает впечатление, что модификатор dangling изменяет субъект. Полученное в результате изображение часто может быть довольно запутанным, юмористическим или просто смущающим.
Прочтите следующие примеры висящих модификаторов, отметьте, что вызывает путаницу в каждом случае, и просмотрите возможные исправления.Обратите внимание, что часто существует более одного правильного способа переписать каждое предложение.
Пример 1
Ребенок перелезал через забор, что всегда казалось приключением.
Неуместный модификатор : «это всегда казалось авантюрным»
Изменение: «ребенок» (не «забор»)
Замешательство: формулировка звучит так, как будто забор — это приключения, а не ребенок.
Исправление: Ребенок, который всегда казался предприимчивым, перелезал через забор.ИЛИ Отважный ребенок перелезал через забор.
Пример 2
Читая в качелях на крыльце, на меня напали гигантские комары.
Модификатор неуместен: «Чтение на качелях на крыльце»
Изменение: Неявное «I» (не «комары»)
Замешательство: Из-за формулировки предложение звучит так, как будто комары читают на качелях на крыльце, а не из динамика.
Поправка: Пока я читал на качелях на крыльце, на меня напали гигантские комары.ИЛИ Гигантские комары напали на меня, когда я читал на качелях на крыльце.
Пример 3
Найденный в стиральной машине пес нетерпеливо играл со своей любимой жевательной игрушкой.
Неуместный модификатор : «После обнаружения в стиральной машине»
Изменение : «игрушка» (не «собака»)
Замешательство: Предполагается, что в этом предложении говорится, что в стиральной машине была найдена игрушка, а не собака.
Исправление: После того, как любимая игрушка собаки была найдена в стиральной машине, он нетерпеливо поиграл с ней.ИЛИ Собака жадно играла со своей любимой игрушкой для жевания после того, как она была найдена в стиральной машине.
Разделение инфинитивов
Разделение инфинитивов означает размещение слова между «to» и глаголом, как в «Мисс Кларк намеревалась четко определить проблему». Технически не следует помещать слово «четко» между «до» и «определять». Это грамматическое правило появилось в восемнадцатом веке, когда люди считали латынь стандартом языка. Поскольку в латыни не было инфинитивов из двух слов, таких как «to define», грамматики хотели сохранить единство инфинитивов из двух слов, чтобы сделать английский язык более похожим на латынь.Однако использование разделенных инфинитивов становится все более распространенным на протяжении десятилетий (например, «смело идти туда, где еще никто не ступал» — «Звездный путь», 1966). Фактически, разделенные инфинитивы получают признание и в профессиональной, и в академической литературе. Для ваших целей знание того, что такое разделенные инфинитивы, поможет вам узнать свои варианты как писатель.
Пример 1
Я быстро сбегу в магазин, так что вернусь, когда ты вернешься домой.
Инфинитивная ссылка: «запустить»
Разветвитель: «быстро»
Исправление: Я быстро сбегу в магазин, поэтому вернусь, когда вы вернетесь домой.
Пример 2
Хелен подумала, что мистер Бид сказал громко петь, но на самом деле он сказал гордо петь.
Инфинитивная ссылка : «петь» (дважды)
Разветвитель: «громко»; «Гордо»
Исправление: Хелен подумала, что мистер Бид сказал громко петь, но на самом деле он сказал петь гордо.
Проверьте свое понимание ПунктуацияПредположим, вы произносите речь.Если вы говорите слишком быстро, ваша аудитория не поймет, что вы говорите. Чтобы этого не произошло, вы останавливаетесь и несколько раз делаете вдох во время чтения. Но как узнать, где сделать паузу, где изменить голос и где остановиться? Конечно же, с пунктуацией!
Знаки препинания дают читателям визуальные подсказки, рассказывающие им, как им следует читать предложение. Некоторые знаки препинания говорят вам, что вы читаете список элементов, а другие знаки говорят вам, что предложение содержит две независимые идеи.Знаки препинания говорят вам не только о том, когда предложение заканчивается, но и о том, какое предложение вы прочитали. В этой главе рассматриваются различные типы знаков препинания и их использование.
Начнем с трех знаков препинания, которые вам, вероятно, уже знакомы.
Периоды
Точка (.) — очень распространенный знак препинания, обозначающий конец повествовательного предложения. Точка также может использоваться в конце повелительного предложения.
Примеры:
Концерт начнется через два часа.
Следите за встречным движением.
Вопросительные знаки
Вопросительный знак (?) используется в конце вопросительного предложения, указывая на то, что предложение является вопросом.
Пример:
Сейчас идет снег?
Восклицательный знак
Восклицательный знак (!) Ставится в конце восклицательного предложения, указывая на то, что предложение является восклицательным. Знак также может использоваться в конце повелительного предложения для обозначения команды.
Пример:
Это лучший день в моей жизни!
Прекратите то, что вы делаете прямо сейчас!
запятые
Один из знаков препинания при чтении, с которым вы можете столкнуться, — это запятая (,). Запятая указывает на паузу в предложении или разделение элементов в списке. Есть много способов использовать запятую. Вот несколько:
- Вступительное слово (например, наречие в предложении) : Лично я считаю, что практика полезна.
- Списки : Сарай, сарай для инструментов и заднее крыльцо были разрушены ветром.
- Координационные прилагательные : Он устал, голоден и опоздал.
- Союзы в сложных предложениях : Дверь спальни была закрыта, поэтому дети знали, что их мать спит.
- Прерывание слов : Я, конечно, знал, где это спрятано, но я хотел, чтобы они сами нашли это.
- Даты, адреса, приветствия и письма : Письмо было проштамповано 8 декабря 1945 года.
Запятые после вводного слова или фразы
Эта запятая позволяет читателю узнать, где заканчивается вводное слово или фраза и начинается основное предложение.
Пример:
Не портя сюрприз, мы должны сказать ей, чтобы она сохранила дату
.В этом предложении «не испортить сюрприз» — это вступительная фраза, а «мы должны сказать ей, чтобы она сохранила дату» — это основное предложение.
Запятые в списке
Если вы хотите перечислить несколько существительных в предложении, разделяйте каждое слово запятой. Это позволяет читателю определить, какие слова включены в группировку. Когда вы перечисляете элементы в предложении, ставьте запятую после каждого существительного, затем добавляйте и перед последним элементом.
Пример:
Пицца будет украшена оливками, перцем и кусочками ананаса.
Запятые и согласованные прилагательные
Вы можете использовать запятые для перечисления как прилагательных, так и существительных. Строка прилагательных, описывающих существительное, называется координирующими прилагательными. Они идут перед изменяемым существительным и разделяются запятыми. В отличие от списка существительных, слово и не всегда должно стоять перед последним прилагательным.
Пример:
Был ясный, ветреный, ясный день.
Запятые перед союзами в составных предложениях
Иногда для разделения двух независимых предложений используются запятые. Запятая ставится после первого независимого предложения, за ней следует союз, например for, and или but.
Пример:
Он пропустил урок сегодня и думает, что тоже выйдет завтра.
Запятые до и после прерывающих слов
В разговоре вы можете прервать ход своих мыслей, чтобы сообщить подробности.В предложении вы можете прервать ход своих мыслей прерывающими словами . Они могут быть в начале или в середине предложения. Когда прерывающие слова появляются в начале предложения, после слова или фразы появляется запятая.
Пример:
Если вы можете в это поверить, когда-то люди думали, что Солнце и планеты вращаются вокруг Земли.
Когда прерывающие слова находятся в середине предложения, они отделяются от остальной части предложения запятыми.Вы можете определить, где должны располагаться запятые, посмотрев на несущественную часть предложения.
Пример:
Итальянский астроном Галилей доказал, что Земля вращается вокруг Солнца.
Запятые в датах, адресах, а также в начале и в конце писем
Вы также используете запятые при написании даты, например, в сопроводительных письмах и электронных письмах. Запятые используются, когда вы пишете дату, когда указываете адрес и когда кого-то приветствуете.
Если вы пишете полную дату, добавьте запятую после дня и перед годом.Вам не нужно добавлять запятую, когда вы пишете месяц и день или когда вы пишете месяц и год. Если вам нужно продолжить предложение после добавления даты, которая включает день и год, добавьте запятую после конца даты.
Примеры:
Письмо отгружено по почте 4 мая 2001 г.
Ее день рождения 5 мая.
Я зарегистрировался на конференцию 7 марта 2010 г., так что скоро мы получим билеты.
Вы также используете запятые, когда указываете адреса и местоположения. Когда вы включаете адрес в предложение, не забудьте поставить запятую после улицы и после города. Не ставьте запятую между провинцией и почтовым индексом. Как и в случае с датой, если вам нужно продолжить предложение после добавления адреса, просто добавьте запятую после адреса.
Примеры:
Мы переехали на 4542 Boxcutter Lane, Оттава, Онтарио, K1R 6h3.
Переехав в Оттаву, Онтарио, Эрик добирался до работы на общественном транспорте.
Приветствия также разделяются запятыми. Когда вы пишете электронное письмо или письмо, вы добавляете запятую после слова приветствия или имени человека. Вам также необходимо поставить запятую после закрытия, то есть слово или фразу, которые вы ставите перед своей подписью.
Пример:
Здравствуйте,
Я хотел бы получить больше информации о вашей вакансии.
Спасибо,
Анита Аль-Сайф
точка с запятойДругой знак препинания, с которым вы столкнетесь, — это точка с запятой (;) .Точка с запятой указывает на разрыв предложения, но работает иначе, чем точка или запятая. Когда вы встречаете точку с запятой при чтении вслух, это указывает на место, где можно остановиться и перевести дух.
Точка с запятой для объединения двух независимых статей
Используйте точку с запятой для объединения двух тесно связанных независимых предложений, если использование точки для разделения их на два более коротких предложения может сделать ваше письмо прерывистым, а использование запятой приведет к объединению запятой или продолжению предложения (соединение двух независимых предложений с просто запятая — ошибка).
Пример:
Неправильно : На собеседование обязательно наденьте чистую, хорошо выглаженную одежду, внешность важна. (неверно из-за сращивания запятой / бесконечного предложения)
Choppy: Обязательно приходите на собеседование в чистой, хорошо выглаженной одежде. Внешний вид важен.
Правильно: Обязательно приходите на собеседование в чистой, хорошо выглаженной одежде; внешность важна.
Здесь правильно писать независимые предложения в виде двух предложений, разделенных точкой.Однако использование точки с запятой для объединения предложений может сделать ваше письмо более интересным, создавая предложения различной длины и структуры, сохраняя при этом поток идей.
Точка с запятой для присоединения элементов к списку
Вы также можете использовать точку с запятой для объединения элементов в списке, когда элементы в списке уже имеют свои собственные запятые (так называемая «внутренняя пунктуация» — по крайней мере, один из элементов сам является отдельным списком). Точка с запятой помогает читателю различать группы элементов.
Пример:
Неправильно: Мы можем выбирать из следующих цветовых комбинаций: черный, белый и серый, зеленый, коричневый и черный или красный, зеленый и коричневый.
Правильно: Цветовые комбинации, которые мы можем выбрать: черный, белый и серый; зеленый, коричневый и черный; или красный, зеленый и коричневый.
Используйте точку с запятой для соединения двух основных предложений. Не используйте точки с запятой в координирующих союзах, таких как и, или, и но.
ДвоеточиеДвоеточие (:) используется для введения списков, цитат, примеров и объяснений.Вы также можете использовать двоеточие после приветствия в деловых письмах и служебных записках.
Примеры:
Уважаемый менеджер по найму:
Кому: отдел кадров
Откуда: Дина Дин
Двоеточие для введения в список
Используйте двоеточие, чтобы ввести список элементов. Внесите в список независимое предложение.
Пример:
Команда совершит поездку по трем штатам: Нью-Йорк, Пенсильвания и Мэриленд.
В этом семестре мне нужно пройти четыре класса: композиция, статистика, этика и итальянский.
Двоеточие для введения предложения
Вы можете использовать двоеточие, чтобы ввести цитату.
Пример:
Лучше всего об этом сказал Марк Твен: «Если сомневаешься, говори правду».
Если цитата длиннее 40 слов, пропустите строку после двоеточия и отступите левое поле цитаты на пять пробелов. Поскольку в кавычках длиннее 40 слов для обозначения кавычек используется межстрочный интервал и отступ, кавычки не требуются.
Пример:
Мой отец всегда любил слова Марка Твена:
В основном есть два типа людей.Люди, которые добиваются чего-то, и
человека, которые утверждают, что чего-то добились. Первая группа менее многолюдна.
Длинные цитаты, состоящие из 40 слов и более, называются блочными цитатами. Блочные цитаты часто появляются в более объемных эссе и исследовательских статьях
Двоеточие для введения примеров или объяснений
Используйте двоеточие, чтобы ввести пример или пояснить идею, представленную в первой части предложения. Первая часть предложения всегда должна быть независимым предложением; то есть оно должно стоять отдельно как законченная мысль с подлежащим и глаголом.Не ставьте двоеточие после таких фраз, как, например, или, например.
Пример:
Неправильно: Наша компания предлагает множество издательских услуг, таких как написание, редактирование и рецензирование.
Правильно: Наша компания предлагает множество издательских услуг: написание, редактирование и рецензирование.
Используйте заглавную букву после двоеточия для имени собственного, начала цитаты или первой буквы другого независимого предложения. НЕ используйте заглавные буквы, если информация, следующая за двоеточием, не является полным предложением.
Примеры:
Существительное собственное : Мы посетили три страны: Белиз, Гондурас и Сальвадор.
Начало цитаты : Моя мать любила эту строчку из Гамлета: «Самому себе будь правдивым».
Два независимых пункта : Существуют недостатки современных технологий: у моего брата сломался мобильный телефон, и он потерял много телефонных номеров.
Неправильно: Рецепт простой: помидоры, базилик и авокадо.
Проверьте свое понимание КотировкиКавычки («») отделяют группу слов от остального текста.Используйте их, чтобы указать прямые цитаты или указать заголовок. Кавычки всегда появляются парами.
Прямые предложения
Прямая цитата — это точное описание того, что кто-то сказал или написал. Чтобы включить прямую цитату в свой текст, заключите слова в кавычки. Косвенная цитата — это повторение того, что кто-то сказал или написал, и не использует точные слова человека. Вам не нужно использовать кавычки для косвенных цитат.
Примеры:
Прямая цитата : Карли сказала: «Я больше туда не вернусь».
Косвенная цитата: Карли сказала, что никогда не вернется туда.
Письмо на рабочем местеБольшинство текстовых редакторов предназначены для выявления ошибок в грамматике, орфографии и пунктуации. Хотя этот инструмент может быть полезным, у него есть серьезные ограничения. Лучше хорошо знать правила пунктуации, чем оставлять все мысли на компьютере.Правильно пунктированное письмо ясно передаст ваш смысл. Обратите внимание на незначительные сдвиги в значениях следующих предложений:
Примеры:
Клиент сказал, что считает нашу рукопись мусором.
Клиент сказал: «Он думал, что наша рукопись — мусор.
Первое предложение читается как косвенная цитата, в которой клиенту не нравится рукопись. Но действительно ли он использовал слово «мусор» или говорящий перефразировал (и преувеличил) слова клиента?
Второе предложение читается как прямая цитата клиента.Но кто в этом предложении «он»? Это третья сторона?
Программа обработки текстов не обнаружит и не пометит это, потому что предложения грамматически неверны. Однако значения предложений не совпадают, но программа проверки грамматики не может определить, передают ли слова на экране предполагаемое значение. Когда вы понимаете пунктуацию, вы можете писать то, что имеете в виду, и в этом случае избавляетесь от лишней путаницы в офисе.
Прямое предложение с пунктуацией
Кавычки показывают читателям точные слова другого человека.Часто вам нужно определить, кто говорит. Вы можете сделать это в начале, середине или конце цитаты. Обратите внимание на использование запятых и прописных слов.
Примеры:
Начало : Мэдисон сказала: «Давайте остановимся на фермерском рынке, чтобы купить свежих овощей на ужин».
Посередине: «Давайте остановимся на фермерском рынке, — сказал Мэдисон, — чтобы купить свежих овощей на ужин».
Конец: «Давайте остановимся на фермерском рынке, чтобы купить свежих овощей на ужин», — сказал Мэдисон.
Спикер не указан : «Давайте остановимся на фермерском рынке, чтобы купить свежих овощей на ужин».
Всегда используйте заглавную первую букву цитаты, которая является полным предложением, даже если это первое слово не является первым словом исходного предложения. При использовании ваших собственных поясняющих слов в середине цитаты, начало второй части цитаты не нужно писать с заглавной буквы.
Примеры:
«Регулярные упражнения, — добавил он, — повышают уровень вашей энергии и улучшают ваше общее настроение.(Определение слов разбивает цитату.)
«Вы должны начать читать ребенку простые книги как можно раньше — желательно в младенчестве», — проинструктировал психолог, добавив, «задолго до того, как ваш ребенок поймет или заговорит на языке!»
Когда цитата играет грамматическую роль в предложении (т. Е. Является частью грамматической структуры остальной части предложения), цитируемая часть должна начинаться со строчной буквы. Другими словами, когда цитируемый материал завершает грамматический состав всего утверждения, включая ваши собственные идентифицирующие или сообщающие слова, не делайте первую букву заглавной.В большинстве случаев цитируемый материал такого рода представляет собой фрагмент предложения (а не полное предложение).
Примеры:
Мой друг сказал: «В Луиджи подают лучшую лазанью во всем городе». (Цитируемый материал представляет собой полное предложение и не играет грамматической роли.)
Мой друг сказал, что в ресторане Luigi’s «лучшая лазанья во всем городе». (Цитируемый материал не является законченным предложением, но необходим для завершения грамматической структуры остальной части предложения.)
Он сказал ей: «Практикуйся больше, потому что практика ведет к совершенству.(Цитируемый материал не влияет на грамматическую структуру всего предложения.)
Он посоветовал ей «практиковаться больше, потому что практика ведет к совершенству». (Цитируемый материал завершает грамматическую структуру остальной части предложения.)
Используйте запятые между определяющими словами и кавычками. Кавычки необходимо ставить после запятых и точек. Ставьте кавычки после вопросительных знаков и восклицательных знаков, только если вопрос или восклицательный знак являются частью цитируемого текста.
Примеры:
Вопрос является частью цитируемого текста: Новый сотрудник спросил: «Когда обед?»
Вопрос не является частью цитируемого текста: Вы слышали, как она говорила, что вы «следующий Пикассо»?
Восклицательный знак является частью цитируемого текста: Мой руководитель просиял: «Спасибо за вашу тяжелую работу!»
Восклицательный знак не является частью цитируемого текста : Он сказал, что я «в одиночку спас компании тысячи долларов»!
Ценовое предложение внутри Ценового предложения
Используйте одинарных кавычек (‘’) , чтобы показать цитату внутри цитаты.
Примеры:
Тереза сказала: «Я хотела взять свою собаку на фестиваль, но человек у ворот сказал:« Собаки не допускаются »».
«Когда вы говорите:» Я ничего не могу с собой поделать «, что именно это означает?»
«В инструкции сказано:« Затягивайте винты по одному »».
Заголовки
Используйте кавычки вокруг названий коротких письменных произведений, таких как эссе, статьи, названия отдельных сообщений в блогах, песни, стихи, рассказы и главы в книгах.Обычно названия более длинных произведений, таких как книги, журналы, альбомы, газеты и романы, а также названия веб-сайтов выделяются курсивом.
Примеры:
«Аннабель Ли» — одно из моих любимых романтических стихотворений.
The New York Times издается с 1851 года.
Письмо на рабочем месте
Во многих компаниях разница между точной формулировкой и перефразированием чрезвычайно важна. В юридических целях или для правильного выполнения работы важно точно знать, что сказал клиент, заказчик или руководитель.Иногда детали могут быть потеряны при перефразировании инструкций. Используйте кавычки, чтобы указать точные слова, где это необходимо, и пусть ваши коллеги знают источник цитаты (клиент, покупатель, коллега и т. Д.).
Проверьте свое понимание АпострофыАпостроф (’) — это знак препинания, который используется с существительным, чтобы показать владение или указать, где буква была пропущена, чтобы сформировать сокращение.
Владение
Апостроф и буква s указывают, кому или чем что-то принадлежит.Чтобы показать владение существительным в единственном числе, добавьте ‘s.
Примеры:
Танцы Джен заворожили всех в комнате.
Поводок собаки висит на крючке у двери.
Сестра Джесс тоже придет на вечеринку.
Обратите внимание, что существительные в единственном числе, оканчивающиеся на s, по-прежнему имеют окончание апострофа (ов), чтобы показать владение.
Чтобы показать владение существительным во множественном числе, оканчивающимся на s, просто добавьте апостроф (’). Если существительное во множественном числе не оканчивается на s, добавьте апостроф и s.
Примеры:
Существительное множественного числа, оканчивающееся на с: все палочки барабанщиков двигались в одном ритме, как машина.
Существительное множественного числа, не оканчивающееся на s: Народные голоса ясно показали, что никто не поддержал решение руководства.
схватки
Сокращение — это слово, образованное путем объединения двух слов. В сокращении апостроф показывает, где одна или несколько букв были пропущены. Сокращения обычно используются в неформальной письменной форме, но не в официальной.
Примеры:
Не люблю мороженое.
Не люблю мороженое.
Обратите внимание, как слова сочетаются и не объединяются, чтобы образовать сокращение «нет». Апостроф показывает, где упущено o in not.
Примеры:
Увидимся позже.
Увидимся позже.
Посмотрите на таблицу несколько примеров часто используемых сокращений.
| Сокращение | Фраза |
| — это не | не |
| не могу | не может |
| не | не |
| не | не |
| не | не |
| он будет | он будет |
| Я | Я буду |
| она | она будет |
| они | они будут |
| вы будете | вы будете |
| это | он есть, в нем |
| давайте | давайте |
| она | она есть, у нее |
| есть | есть, там |
| кто | кто есть, у кого |
Будьте осторожны, не перепутайте его со своим.Это сокращение слов он и есть. Это притяжательное местоимение.
На улице холодно и дождливо. (На улице холодно и дождливо.)
Кот гнался за своим хвостом. (Показывает, что хвост принадлежит кошке.)
Если есть сомнения, замените слова в предложении. Если предложение по-прежнему имеет смысл, используйте сокращение.
Проверьте свое понимание СкобкиКруглые скобки () — это знаки препинания, которые всегда используются парами и содержат второстепенный материал по отношению к значению предложения.Скобки никогда не должны содержать подлежащее или глагол предложения. Предложение по-прежнему будет иметь смысл, если вы удалите любой текст в круглых скобках и скобках.
Примеры:
Атака картофеля-убийцы , наверное, худший фильм, который я видел (пока).
Ваш салат из шпината и чеснока — один из самых вкусных (и питательных) продуктов, которые я когда-либо пробовал!
ПрочеркДлинное тире (-) — это знак препинания, используемый для выделения информации в предложении для выделения.Вы можете заключить текст между двумя тире или использовать только один тире. Чтобы создать тире в Microsoft Word, введите два дефиса вместе, и программа автоматически преобразует их в тире. Не ставьте пробел между тире и текстом.
Примеры:
Приходите на собеседование рано, но не слишком рано.
Любой из костюмов, кроме пурпурного, должен подойти.
дефис (-) используется для разделения элементов в диапазоне. Это могут быть диапазоны чисел, диапазоны дат или диапазоны школьных оценок (например,г., 4–7 классы). Вы также можете использовать тире при отображении оценок (например, победа 5–0), сравнений или между двумя элементами, которые связаны между собой (отношения США и Канады).
ДефисДефис (-) похож на тире, но он короче и используется по-другому.
Дефис между двумя прилагательными, которые работают как одно целое
Используйте дефис, чтобы объединить слова, которые работают вместе, чтобы сформировать единое описание.
Примеры:
55-летний спортсмен был так же квалифицирован для марафона, как и его более молодые соперники.
Мой врач не рекомендовал принимать какие-либо лекарства, вызывающие привыкание.
Моя исследовательская группа сосредоточилась на подготовке к среднегодовому обзору.
* Примечание: Знаете ли вы, что существительное + причастие прилагательное перед изменяемым существительным должно быть перенесено через дефис, но должно быть оставлено «открытым», если оно стоит после существительного? Примеры: лекарство вызывает привыкание.
Лекарство, вызывающее привыкание, слишком сильное для безрецептурного использования.
Мой врач посоветовал не принимать лекарства, которые могут вызвать привыкание.
Дефис при разрыве слова в конце строки
Используйте дефис, чтобы разделить слово на две строки текста. Вы можете заметить, что большинство текстовых редакторов сделают это за вас. Если вам нужно вручную вставить дефис, поместите дефис между двумя слогами. Если вы не знаете, где разместить дефис, обратитесь к словарю или переместите все слово на следующую строку.
Пример:
Мой руководитель был обеспокоен встречей команды —
ing будет конфликтовать со встречей с клиентом.
Заключение
В этом разделе вы вернулись к основам грамматики и пунктуации.
В разделе грамматики вы рассмотрели типы предложений, такие как простые и сложные предложения. Вы продолжили смотреть на такие вещи, как согласование подлежащих и глаголов и параллелизм. Затем вы просмотрели предлоги и союзы и завершили раздел ошибками модификаторов и разделенными инфинитивами.
В разделе о пунктуации сначала были рассмотрены некоторые из наиболее распространенных и правильно используемых знаков препинания, таких как точки, вопросительные знаки, восклицательные знаки и запятые.Затем вы немного углубились в более сложные знаки препинания, такие как точка с запятой, двоеточие, кавычки, апострофы, круглые скобки, тире и дефисы.
Усиление слабых мест в грамматике или пунктуации поможет вам стать лучше писателем и коммуникатором.
- Сопоставьте местоимения и антецеденты по числу (единственному или множественному) и полу.
- Коллективные существительные и неопределенные местоимения считаются единственными, даже если они относятся к нескольким членам или компонентам.
- Превращение субъекта единственного числа во множественное число часто является лучшим способом решения числовой проблемы между подлежащим и местоимением.
- Неуместные модификаторы могут затуманивать смысл предложения из-за неправильного размещения ключевых фраз в предложении.
- Висячие модификаторы приписывают описание неправильному существительному из-за того, что оно помещено в неправильное место в предложении.
- Разделенные инфинитивы допустимы во многих письменных ситуациях, но вы должны понимать их, чтобы избежать их, когда вам нужно.
Проверьте свое понимание
Если вы хотите узнать больше о грамматике и пунктуации, посетите следующий сайт:
Грамматика. (без даты) В Оксфордских словарях. Получено с http://www.oxforddictionaries.com/definition/english/grammar
. Заявление об авторстве (грамматика и пунктуация)Эта глава представляет собой ремикс, содержащий контент из различных источников, опубликованный под различными открытыми лицензиями, включая следующие:
Содержание главы
Оригинальный контент, предоставленный командой разработчиков OER Olds College из Olds College в открытый учебный план по профессиональным коммуникациям в соответствии с CC-BY 4.0 лицензия
частей речи, по учебной зоне, Центр английского языка, Университет Виктории, опубликовано по адресу http://web2.uvcs.uvic.ca/elc/studyzone/330/grammar/parts.htm в соответствии с CC BY-NC-SA 4.0 Международная лицензия
Обзор типов предложений, по учебным зонам, Центр английского языка, Университет Виктории, опубликованный по адресу http://web2.uvcs.uvic.ca/courses/elc/studyzone/490/grammar/review-of-sentence-types.htm по международной лицензии CC BY-NC-SA 4.0
Контент, созданный Anonymous для обеспечения согласия субъектов и глаголов; в Writers ’Handbook, опубликованном по адресу http: // 2012books.lardbucket.org/books/writers-handbook/s19-03-making-sure-subjects-and-verbs.html под лицензией CC BY-NC-SA 3.0
Контент, созданный Anonymous для четкой связи местоимений и антецедентов; в Writers ’Handbook, опубликованном по адресу http://2012books.lardbucket.org/books/writers-handbook/s19-06-connecting-pronouns-and-antece.html под лицензией CC BY-NC-SA 3.0
Контент, созданный Anonymous для параллелизма; в Writers ’Handbook, опубликованном по адресу http: // 2012books.lardbucket.org/books/writers-handbook/s20-04-using-parallelism.html по лицензии CC BY-NC-SA 3.0
Контент, созданный Anonymous для предлогов и предложных фраз; в Writers ’Handbook, опубликованном по адресу http://2012books.lardbucket.org/books/writers-handbook/s25-17-prepositions-and-prepositional.html под лицензией CC BY-NC-SA 3.0
Контент, созданный Anonymous для ошибок модификаторов и разделенных инфинитивов; в Writers ’Handbook, опубликованном по адресу http: // 2012books.lardbucket.org/books/writers-handbook/s19-04-avoiding-misplaced-modifiers-d.html под лицензией CC BY-NC-SA 3.0
Контент, созданный Anonymous для знаков препинания в Справочнике писателей; в Writers ’Handbook, опубликованном по адресу http://2012books.lardbucket.org/books/english-for-business-success/s06-punctuation.html под лицензией CC BY-NC-SA 3.0
Проверьте свое понимание
.
Карлики и великаны: Карлики и великаны
Великан и карлики — Константин Ушинский
- Подробности
- Категория: Константин Ушинский
Страница 1 из 3
Великан и карлики (сказка)
Глава I
Житье-бытье великана и карликов
Лет тысяч пять или шесть тому назад, когда на белом свете водилось еще много различных чудес, жил-был где-то очень далеко отсюда, посреди жаркой Африки, огромный великан. По соседству с великаном находилось целое царство удивительно маленьких человечков. Великана звали Антеем, маленьких человечков – Пигмеями. Антей и Пигмеи были детьми одной и той же матери, нашей общей старой бабушки-земли. Они считались братьями и жили дружно, по-братски. Пигмеи были такие крошки, жили за такими пустынями и горами, что неудивительно, если в сотни лет ни одному человеку не пришлось разу увидать их. Великана, правда, можно было бы рассмотреть и за сотни верст, но благоразумие приказывало держаться от него подальше.
Пигмей в пять или шесть вершков [Вершок – старинная мера длины, равная 4,4 см. ] росту считался между Пигмеями великаном. Из этого вы можете судить, какие это были маленькие человечки. Приятно было бы посмотреть на маленькие города Пигмеев, где улицы были шириною в пять или шесть четвертей, мостовые из крошечных камешков, а самый большой дом не больше беличьей клетки. Дворец пигмейского короля был очень велик – выше даже нашего стула! Стоял он посредине такой обширной площади, что ее, может быть, не закрыть бы и заслонкой из кухонной печи. Главный пигмейский храм был величиною с детский комод, и Пигмеи смотрели с гордостью на это величественное здание. Вообще Пигмеи были очень искусные строители и строили свои дома почти так же, как птички вьют свои гнезда: из соломы, перьев, яичных скорлупок и других не слишком тяжелых материалов. Все это скреплялось вместо извести вишневым клеем, и когда такое величественное здание высыхало на солнце, то карлики находили его и красивым и удобным.
] росту считался между Пигмеями великаном. Из этого вы можете судить, какие это были маленькие человечки. Приятно было бы посмотреть на маленькие города Пигмеев, где улицы были шириною в пять или шесть четвертей, мостовые из крошечных камешков, а самый большой дом не больше беличьей клетки. Дворец пигмейского короля был очень велик – выше даже нашего стула! Стоял он посредине такой обширной площади, что ее, может быть, не закрыть бы и заслонкой из кухонной печи. Главный пигмейский храм был величиною с детский комод, и Пигмеи смотрели с гордостью на это величественное здание. Вообще Пигмеи были очень искусные строители и строили свои дома почти так же, как птички вьют свои гнезда: из соломы, перьев, яичных скорлупок и других не слишком тяжелых материалов. Все это скреплялось вместо извести вишневым клеем, и когда такое величественное здание высыхало на солнце, то карлики находили его и красивым и удобным.
Вокруг пигмейского города расстилались поля. Самое большое из них было не больше нашего цветника. На этих полях маленькие человечки садили пшеничные, ячменные и ржаные зерна, и когда из этих зерен вырастали колосья, то для Пигмеев казались они огромными деревьями. На жатву трудолюбивые крошки выходили с топориками и без устали рубили зрелые колосья, как рубим мы сосны и березы. Случалось иногда, что неосторожно срубленный колос с тяжелой головкой падал на Пигмея, и всякий раз из этого выходила весьма неприятная история: если Пигмей и оставался жив, то, по крайней мере, долго стонал и охал. Вот каковы были отцы и матери Пигмеев; представьте же себе, каковы у них были детки! Целая толпа пигмейских ребятишек могла бы удобно расположиться спать в нашем башмаке или играть в жмурки в старой перчатке; годового Пигмейчика вы без труда накрыли бы наперстком.
Забавные малютки, как я уже сказал, жили по соседству с великаном. А великан был действительно великан! Отправляясь гулять, он вырывал целую сосну сажен [Сажень – старинная мера длины, равная 2,13 м.] в десять высотою и помахивал ею, как мы машем тросточкою. Самый зоркий Пигмей без подзорной трубы не мог видеть ясно головы Антея. Иногда же, в туманную погоду, Пигмеям видны были только страшные ножищи великана, которые двигались будто сами собою. Но в ясный день, когда солнышко блистало ярко, Антей шутил с Пигмеями очень мило: стоит, бывало, подбоченясь, гора горою, и его широкое лицо ласково улыбается маленьким братцам, а единственный глаз, величиною в каретное колесо, торчавший у Антея посреди самого лба, дружески мигает разом всему пигмейскому народу. Пигмеи любили поболтать с своим братцем. Иной пятьдесят раз в день подбежит, бывало, к ногам великана, задерет кверху головку, приложит кулак ко рту и закричит, как в трубу, изо всей мочи: «Го-го, братец Антей! Как поживаешь, мой милый?» И если тоненький писк достигал до слуха великана, то он, бывало, непременно ответит: «Спасибо, братец Пигмей, живу помаленьку», но ответит так, что даже пигмейские дома задрожат.
Большим счастьем было для Пигмеев, что Антей был с ними дружен. Если бы он так же злился на них, как злился на всякое другое живое существо, то одним пинком мог бы перевернуть все их царство кверху ногами; стоило ему ступить на пигмейский город, и следа бы его не осталось. Но Антей любил своих крохотных братцев, насколько мог любить такой грубый великан, а они платили ему такою любовью, какая только могла поместиться в их крошечных сердечках. Великан как добрый брат и хороший сосед не раз оказывал Пигмеям большие услуги. Если ветряные мельницы их переставали вертеться за недостатком ветра, то стоило только Антею подышать на крылья, и мельницы принимались молоть; жгло ли крошек солнце слишком сильно, Антей садился на землю, и тень его закрывала все их царство из конца в конец; но вообще Антей был довольно умен, чтобы не мешаться в дела крошек, и предоставлял им самим управляться, как знают.
Пигмеи жили недолго, жизнь Антея была длинна, как его тело. Много пигмейских поколений сменилось на глазах Антея. Самые почтенные и седые Пигмеи не слыхали от своих предков, когда началась их дружба с Антеем. Никто из Пигмеев не помнил, чтобы они когда-нибудь ссорились с громадным братом. Дружба их шла ненарушимо с незапамятных времен. Однажды только Антей по неосторожности сел разом на пять тысяч Пигмеев, собравшихся на великолепный парад. Но это было одно из тех печальных событий, которых никто не может предвидеть, а потому Пигмеи не рассердились на Антея и только попросили его, чтобы вперед он осторожнее выбирал место, где ему захочется усесться; на месте же печального события Пигмеи воздвигнули пирамиду четверти в три вышиною.
Приятно было думать, что существа, столь различные по величине, питали друг к другу такую нежную братскую любовь. Эта дружба была счастьем для Пигмеев, но она была также счастьем и для великана. Может быть, Пигмеи были даже нужнее своему длинному братцу, чем он Пигмеям. Не будь у Антея его маленьких братьев, и у него решительно не было бы ни одного друга в целом мире. В целом мире не было ни одного великана, похожего на Антея, и когда Антей стоял, как громадная башня, а голова его уходила в облака, то он был страшно одинок. Да и нрава Антей был неуживчивого: встреться он с подобным ему великаном, то, вероятно, начал бы с ним драку не на живот, а на смерть. Им вдвоем показалось бы тесно жить на белом свете. Но с Пигмеями Антей был самым добродушным, ласковым великаном.
Маленькие приятели Антея, как вообще все маленькие люди, были о себе очень высокого мнения и, говоря о великане, принимали покровительственный тон.
– Бедное доброе созданье, – говорили они об Антее. – Пропал бы он без нас, бедняга! Ему одному, должно быть, ужасно как скучно. Уделим же минутку нашего драгоценного времени и позабавим милого дружка. Поверьте, что он очень нуждается в нас и далеко не так весел, как мы. Спасибо матушке-земле, что она не создала нас такими же великанами!
По праздникам Пигмеи превесело играли с Антеем. Он, бывало, растянется на земле и займет собою такое пространство, что для коротенького Пигмея пройти от Антеевой головы до его ног было весьма порядочной прогулкой. Крошечные человечки весело перепрыгивали у него с пальца на палец, смело запрятывались в складки его одежды, взбирались к нему на голову и не без ужаса заглядывали в его широкий рот – страшную пропасть, куда могли бы провалиться сотни две Пигмеев разом. Дети играли в прятки в волосах и бороде Антея, а большие держали пари, кто скорее обежит вокруг его единственного глаза. Иные молодцы со всего размаха даже прыгали с носа Антея на его верхнюю губу.
Говоря откровенно, Пигмеи иногда препорядочно надоедали своему братцу, как надоедают нам мухи и комары, но Антей принимал их шутки очень добродушно. Смотрит-смотрит, бывало, на все их проказы и расхохочется. Да так расхохочется, что весь пигмейский народ закроет себе уши, чтобы не оглохнуть.
– Хо, хо, хо! – проревет Антей, колыхаясь, как огнедышащая гора при извержении. – Право, недурно быть таким крошкой, и не будь я Антеем, я пожелал бы быть Пигмеем!
Когда обе враждебные армии сходились к битве, то журавли кидались вперед и, махая крыльями, вытягивая шеи, старались выхватить кого-нибудь из пигмейских рядов своими длинными носами. Грустно было видеть, как иногда маленький человечек, барахтаясь, дрыгая ножками, исчезал мало-помалу в длинном журавлином горле. Но герой, как вы знаете, должен быть готов к случайностям всякого рода, и, без сомнения, слава утешала Пигмеев даже в журавлином зобу. Если Антей замечал, что битва становится уже слишком жарка и что его маленьким приятелям приходится плохо, то он только махнет, бывало, своей дубиной, и журавли с криком, перегоняя друг друга, убираются восвояси. Тогда пигмейская армия возвращалась с торжеством, конечно, приписывая победу своей собственной храбрости искусству своих полководцев. Долго после того по улицам пигмейских городов ходили торжественные процессии, горели блестящие иллюминации и фейерверки, задавались великолепные публичные обеды, выставлялись статуи героев во весь их маленький рост. Если же какому-нибудь Пигмею удавалось вытащить перо из журавлиного хвоста, то это перо гордо колыхалось на его шляпе; за три, за четыре таких пера храбрец делался даже предводителем пигмейской армии.
Так-то жили и благоденствовали маленькие Пигмеи возле своего громадного брата, и дружба их, может быть, продолжалась бы и до сих пор, если б не случилось одного печального происшествия, о котором я расскажу вам в следующей главе.
И карлики, и великаны — AgroXXI
Среди ранних динозавров были особи самых разных размеров одного и того же вида
Люди бывают разного роста — от очень высоких баскетболистов до очень маленьких танкистов. Как выяснили палеонтологи, точно такой же была ситуация и среди первых динозавров. Индивидуальные размеры особей у них варьировались намного шире, чем у близкородственных динозаврам птиц или крокодилов.
Возможно, как раз такая вариативность позволила первым динозаврам успешно приспособиться к непростым условиям жизни триасового периода и в итоге стать властелинами суши, удерживающими свое господство на протяжении полутора сотен миллионов лет.
Если сегодня мы выглянем в окно, то скорее всего увидим там и высоких, и низкорослых людей. Более того, мы вполне можем увидеть подростка, превосходящего многих взрослых длиной своего тела, или маленькую сухонькую старушку.
Исследуя триасовых динозавров, живших от 210 млн до 201 млн лет назад, палеонтологи Политехнического университета Виргинии Кристофер Гриффин (Christopher Griffin) и Стерлинг Несбит (Sterling Nesbitt) столкнулись примерно с такой же ситуацией, пишет paleonews.ru со ссылкой на статью в PNAS.
«Мы обнаружили, что самые ранние динозавры имели гораздо более высокий уровень различий в моделях роста между отдельными особями, чем крокодилы и птицы, их ближайшие родственники, — рассказал доктор Гриффин. — Мало того, что у них имелось много различных путей, чтобы вырасти от детеныша до взрослой особи, существовало еще и невероятное количество вариаций в размерах тела, когда некоторые мелкие особи оказывались гораздо более зрелыми, чем другие, более крупные, а некоторые крупные особи — более незрелыми, чем мы могли бы представить себе, если судили бы только по размеру тела».
Исследование Гриффина и Несбита фокусировалось на целофизисах (Coelophysis) – ранних динозаврах, чьи многочисленные остатки исчисляются сотнями почти полных скелетов хорошей сохранности. Палеонтологи работали со 174 экземплярами, захороненными наводнением на территории современного Нью-Мексико.
«По мере того, как эти животные росли, следы прикрепления мышц к костям конечностей у них сливались вместе, подобно тому, как кости черепа человеческого ребенка объединяются в единое целое во время его взросления, — говорит Гриффин, поясняя, как именно они определяли возраст давно вымерших ящеров. — Окаменелости даже неполного скелета раннего динозавра исключительно редки, так что заполучить для исследования целую группу представителей одного вида, которые жили и умерли вместе, оказалось уникальной возможностью для изучения роста ранних динозавров».
Восстановив последовательность онтогенетических изменений для Coelophysis и сравнив их с аналогичными последовательностями двух видов птиц и одного вида крокодилов, ученые пришли к выводу, что ранние динозавры заметно отличались от своих родственников. Кстати, различия между скелетами ранних динозавров замечали и раньше, но, как правило, их истолковывали как разницу между самцами и самками.
«Широкая вариативность ранних динозавров, возможно, позволила им пережить суровые экологические проблемы, такие как засушливый климат и высокие уровни содержания углекислого газа в атмосфере, — предположил Несбитт. — Понимание того, почему динозавры оказались настолько успешными, пока остается великой тайной, и высокая изменчивость, возможно, была одним из тех признаков динозавров, которые привели их к успеху. Пока трудно сказать, появилось ли это их свойство под влиянием окружающей среды, или просто удача улыбнулась динозаврам, дав возможность жить и процветать, доминируя над наземными позвоночными в течение 150 миллионов лет».
Интересна тема? Подпишитесь на персональные новости в .ДЗЕН или Pulse или .Новости.
Было бы несправедливо забыть об этом захватывающем детском соревновании. Особенно часто его проводят на новогодних праздниках в детском саду. Описание игры Правила игры Двум соперникам дают очень большие взрослые валенки. Дети утопают в них, и действительно они похожи на мальчиков-с -пальчиков в сапогах — скороходах Людоеда.
«Карлики» и «великаны» Веселая и интересная игра для ваших детей. Описание игры Правила игры Дети стоят вокруг ведущего, который рассказывает, что есть на свете совсем маленькие люди — карлики, а есть громадные — великаны.
|
Литцман В. Великаны и карлики в мире чисел. — 1959 // Библиотека Mathedu.Ru
Литцман В. Великаны и карлики в мире чисел. — 1959
ПодготовкатекстаПодготовка
текста
Содержание
Загрузкаструктуры
Информация
Загрузкаописаний
Справка
Загрузкасправки
Поиск
Страниц найдено: 1
Если строка в кавычках «…», то найдутся страницы со словосочетанием в точно такой форме.
Если слова указаны через пробел или оператор «&», то найдутся страницы, содержащие все введенные слова в одном предложении.
Если указано несколько слов через оператор «|», то найдутся страницы, содержащие любое из введенных слов.
Если указано два слова через оператор «~», то найдутся страницы, содержащие первое, но не содержащие второе слово в одном предложении.
По вашему запросу ничего не найдено.
Убедитесь, что слова написаны без ошибок или попробуйте выбрать другие значения.
null
Подождите,пожалуйста…
Печать
Обложка1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768Обложка (с. 4)
Подготовка [0%]…
Отмена
{«root»:»text»,»url»:»litczman_velikany_i_karliki_v_mire_chisel_1959″,»surl-package»:»\/text\/%PACKAGE%\/?query=%QUERY%»,»surl-page»:»\/text\/%PACKAGE%\/p%PAGE%\/?query=%QUERY%»,»query»:»\»\»»,»section»:»library»,»mode-gfx»:true,»mode-html»:true,»mode-prefer»:»gfx»,»layout-prefer»:»1×1″,»zoom»:{«1×1»:{«level»:100,»_w»:false,»_h»:true},»2×1″:{«level»:100,»_w»:true,»_h»:false},»html»:{«level»:100}},»textsize-prefer»:»2″,»textfont-prefer»:»a»,»tree-type»:»ajax»,»tree-state»:»visible»,»printbox-state»:»hidden»,»print-allowed»:»1″,»searchbox-state»:»hidden»,»searchbox-type»:»inline»,»goto-pageno»:null,»goto-page»:-1,»defw»:»800″,»defh»:»1311″,»minh»:1311,»maxh»:1311,»fixeven»:null,»package»:»left»,»sitemode»:»live»,»user»:{«uuid»:»»}}
Удерживайте правую кнопку мыши для выделения группы страниц.
Удерживайте клавишу Shift для выделения диапазона страниц.
Удерживайте клавишу Ctrl для перехода к странице без её выделения.
Позволяет находить заданные слова и словосочетания в тексте публикации.
Поиск поддерживает кириллический и латинский алфавиты.
Переключайте вид списка результатов поиска кнопками «Список» и «Карта».
Функция печати/скачивания доступна только зарегистрированным пользователям.
Пожалуйста, зарегистрируйтесь или авторизуйтесь.
Выбор оформления (светлое/тёмное) доступен только зарегистрированным пользователям.
Пожалуйста, зарегистрируйтесь или авторизуйтесь.
Игра Карлики и великаны | KidsClever.ru
На данной странице вы найдете правила игры в Карлики и великаны, вам обязательно пригодится эта информация для общего развития.
Описание игры
Дети стоят вокруг ведущего, который рассказывает, что есть на свете совсем маленькие люди — карлики, а есть громадные — великаны. Когда ведущий произносит: «Карлики!», он присаживается на четвереньки, опускает руки, всем своим видом показывая, какие это маленькие люди. Даже слово «карлики» он произносит тоненьким голосом — вот такие они крохотные.
А когда говорит «Великаны!», голос его грубеет, ведущий встает во весь рост, да еще руки вытягивает вверх — такие они громадные. Детям эта игра ведущего очень нравится, они смеются и тоже вытягиваются во весь рост — «великаны» и садятся на четвереньки — «карлики».
Когда ребята научились правильно выполнять команды, ведущий предупреждает, что сейчас он увидит, кто самый внимательный.
Ведущий: Запомните, дети, правильные команды: «Карлики!» и «Великаны!». Все остальные мои команды выполнять не надо. Тот, кто ошибется, — выбывает из игры.
Сначала ведущий дает правильные команды, а потом слова «карлики» и «великаны» заменяет на похожие. Побеждает тот, кто меньше всех ошибся.
Правила игры
1. Дети стоят вокруг ведущего, который рассказывает, что есть на свете совсем маленькие люди — карлики, а есть громадные — великаны.
2. Когда ведущий произносит: «Карлики!», он присаживается на четвереньки, опускает руки, всем своим видом показывая, какие это маленькие люди. Даже слово «карлики» он произносит тоненьким голосом — вот такие они крохотные.
А когда говорит «Великаны!», голос его грубеет, ведущий встает во весь рост, да еще руки вытягивает вверх — такие они громадные.
3. Детям эта игра ведущего очень нравится, они смеются и тоже вытягиваются во весь рост — «великаны» и садятся на четвереньки — «карлики».
4. Когда ребята научились правильно выполнять команды, ведущий предупреждает, что сейчас он увидит, кто самый внимательный.
5. Ведущий: Запомните, дети, правильные команды: «Карлики!» и «Великаны!». Все остальные мои команды выполнять не надо. Тот, кто ошибется, — выбывает из игры.
Сначала ведущий дает правильные команды, а потом слова «карлики» и «великаны» заменяет на похожие.
6. Побеждает тот, кто меньше всех ошибся.
Дорохов, Алексей Алексеевич — Карлики и великаны [Текст] ; Сердце на ладони. Город твоих друзей / [Предисл. Л. Кассиля] ; [Ил.: Б. Рытман]
Поиск по определенным полям
Чтобы сузить результаты поисковой выдачи, можно уточнить запрос, указав поля, по которым производить поиск. Список полей представлен выше. Например:
author:иванов
Можно искать по нескольким полям одновременно:author:иванов title:исследование
Логически операторы
По умолчанию используется оператор AND.
Оператор AND означает, что документ должен соответствовать всем элементам в группе:
исследование разработка
author:иванов title:разработка
оператор OR означает, что документ должен соответствовать одному из значений в группе:исследование OR разработка
author:иванов OR title:разработка
оператор NOT исключает документы, содержащие данный элемент:исследование NOT разработка
author:иванов NOT title:разработка
Тип поиска
При написании запроса можно указывать способ, по которому фраза будет искаться. Поддерживается четыре метода: поиск с учетом морфологии, без морфологии, поиск префикса, поиск фразы.
По-умолчанию, поиск производится с учетом морфологии.
Для поиска без морфологии, перед словами в фразе достаточно поставить знак «доллар»:
$исследование $развития
Для поиска префикса нужно поставить звездочку после запроса:исследование*
Для поиска фразы нужно заключить запрос в двойные кавычки:«исследование и разработка«
Поиск по синонимам
Для включения в результаты поиска синонимов слова нужно поставить решётку «#» перед словом или перед выражением в скобках.
В применении к одному слову для него будет найдено до трёх синонимов.
В применении к выражению в скобках к каждому слову будет добавлен синоним, если он был найден.
Не сочетается с поиском без морфологии, поиском по префиксу или поиском по фразе.
#исследование
Группировка
Для того, чтобы сгруппировать поисковые фразы нужно использовать скобки. Это позволяет управлять булевой логикой запроса.
Например, нужно составить запрос: найти документы у которых автор Иванов или Петров, и заглавие содержит слова исследование или разработка:
author:(иванов OR петров) title:(исследование OR разработка)
Приблизительный поиск слова
Для приблизительного поиска нужно поставить тильду «~» в конце слова из фразы. Например:
бром~
При поиске будут найдены такие слова, как «бром», «ром», «пром» и т.д.Можно дополнительно указать максимальное количество возможных правок: 0, 1 или 2.4 разработка По умолчанию, уровень равен 1. Допустимые значения — положительное вещественное число.
Поиск в интервале
Для указания интервала, в котором должно находиться значение какого-то поля, следует указать в скобках граничные значения, разделенные оператором TO.
Будет произведена лексикографическая сортировка.
author:[Иванов TO Петров]
Будут возвращены результаты с автором, начиная от Иванова и заканчивая Петровым, Иванов и Петров будут включены в результат.author:{Иванов TO Петров}
Такой запрос вернёт результаты с автором, начиная от Иванова и заканчивая Петровым, но Иванов и Петров не будут включены в результат.Для того, чтобы включить значение в интервал, используйте квадратные скобки. Для исключения значения используйте фигурные скобки.
эссе, 1960–1990: Блум, Аллан Дэвид: 9780671707774: Amazon.com: Книги
Еженедельно от издателей
Профессор Чикагского университета Блум (автор скандального бестселлера «Закрытие американского разума») собрал здесь 19 впечатляющих, ранее опубликованных эссе. Научными, но доступными серьезным и целеустремленным читателям являются 11 комментариев к Аристофану, Платону, Руссо, Свифту и Шекспиру и три — к учителям — влиятельному политическому теоретику Лео Штраусу; Раймон Арон, «последний из либералов»; и Александр Кожев, «самый блестящий человек, которого я когда-либо встречал.«Последние пять эссе посвящены коммерции и« культуре »: Макиавелли и изучение текстов, теория справедливости Джона Ролза, кризис гуманитарного образования и демократизация университета. Сборник является заметной демонстрацией широты знаний Блума. .Первый сериал к комментарию; права на книгу в мягкой обложке на Touchstone; альтернативный вариант BOMC.
Copyright 1990 Reed Business Information, Inc.
Из библиотечного журнала
Блум снова критикует историзм, культурный релятивизм и позитивизм за то, что они способствуют ослаблению наших традиционных представлений о добре и зле, особенно в применении к политической философии.В отличие от его бестселлера «Закрытие американского разума» (LJ 5/1/87), этот сборник возвращается к исходным текстам, на которых основаны многие его идеи: Платону, Шекспиру, Руссо и Лео Штраусу и другим. Краткая статья под названием «Western Civ» отвечает его критикам, особенно левым, которые почти повсеместно отвергали его раннюю книгу как ошибочный рецепт реформирования американского высшего образования. Эссе в этой антологии сложны и, вероятно, не являются бестселлером.Тем не менее, в этих произведениях предпринимаются усилия по рассмотрению серьезных идей, которые, по мнению Блума, были искажены или превращены в догмы, в результате чего у нас осталось слишком мало универсальных ценностей, на которых можно было бы построить теорию социальной справедливости. Предварительно просмотрено в Prepub Alert, LJ 15.06.90.
— Ричард Х. Куэй, Майами Univ. Libs., Оксфорд, Огайо
Авторские права, 1990 г., Reed Business Information, Inc.
гномов или гигантов? Звездные металлы и расстояния от ugrizG Многополосная фотометрия
На рисунке 3 схематически представлен алгоритм, который мы разработали.Этот алгоритм использует только фотометрические данные, описанные в предыдущем разделе, чтобы сначала отделить гигантов от карликов с помощью классификатора случайного леса (RFC; Breiman 2001), как подробно описано в разделе 3.2. После завершения этой классификации два набора искусственных нейронных сетей (ИНС), один для звезд, идентифицированных как карлики (раздел 3.3.1), а другой для звезд, идентифицированных как гиганты (раздел 3.3.2), используются для определения фотометрических характеристик. металличность. Наконец, еще два набора ИНС используются для определения абсолютной величины двух групп звезд в полосе G .
Увеличить Уменьшить Сбросить размер изображения
Рисунок 3. Схема алгоритма, описанного в Разделе 3. Входными параметрами являются фотометрические измерения из различных съемок, описанных в Разделе 2. Параметры, выделенные красным цветом, используются для обучения. Классификация карликовых гигантов выполняется с использованием RFC. Для каждого класса используется набор ИНС для вычисления фотометрической металличности. Затем другой набор ИНС используется для вычисления абсолютной звездной величины в полосе G , которая обеспечивает расстояния до звезд.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияДля расчета неопределенностей по различным параметрам, оцененным с помощью нашего алгоритма ( P Dwarf , P Giant , [Fe / H] и M G ), вызванных фотометрическими неопределенностями различных полос, мы генерируем 20 реализаций Монте-Карло для каждой звезды. Мы также провели 100 и 1000 реализаций Монте-Карло для подвыборки из 50 000 случайно выбранных звезд.Для них мы получили окончательные неопределенности, которые обычно на <1% отличались от того, что мы получали с использованием всего 20 реализаций. Таким образом, мы приступили к 20 реализациям Монте-Карло для всей выборки, чтобы сэкономить дорогостоящее время вычислений. Для каждой реализации мы выбираем величину в каждой полосе из распределения Гаусса с центром на указанной величине и со стандартным отклонением, равным неопределенности величины. Неопределенности производных параметров устанавливаются равными стандартному отклонению для каждого параметра из этих 20 реализаций.
След CFIS- u , который определяет пространственный охват этого исследования, включает большое количество звезд, наблюдаемых SDSS / SEGUE (Янни и др., 2009b), по которым доступны спектроскопические данные. Мы используем эти звезды с качественными спектроскопическими измерениями в качестве обучающих выборок для первых двух компонентов нашего алгоритма. Выгодно использовать как можно большую обучающую выборку; поэтому мы выбрали 74 442 звезды SDSS / SEGUE, присутствующие в следе CFIS- u , которые имеют спектроскопическое отношение сигнал / шум (S / N) ≥ 25.Этот порог был выбран потому, что при более низком S / N распределение неопределенностей по параметрам, заданным конвейером SEGUE Stellar Parameters Pipeline (SSPP) как функция S / N, является нерегулярным, что указывает на то, что параметры плохо определены. Более того, более 96% звезд с отношением S / N <25 имеют измерения параллакса с плохой точностью (> 20%), и они не будут использоваться для калибровки отношения фотометрических расстояний, даже если они пройдут разрез S / N. Для третьего компонента нашего алгоритма (определение абсолютной величины) мы используем информацию о параллаксе из Gaia (обсуждается позже).
Сначала мы выполняем разрез по цвету, чтобы удалить звезды A-типа (которые лежат в области «запятой» на диаграмме цвета и цвета на рис. 4) и белые карлики, что определяется при осмотре рис. 4 и показан в оранжевом поле. Наличие бальмеровского скачка в полосе u для этих звезд означает, что они имеют более сложное фотометрическое поведение по сравнению с другими звездами, представленными на этой цветно-цветной диаграмме, и алгоритмы значительно упрощаются, если мы исключим их из рассмотрения.Отметим, что звезды A-типа в CFIS были подробно изучены в предыдущих работах (Thomas et al. 2018, 2019), а анализ белых карликов находится в стадии подготовки (N. Fantin et al. 2019, в стадии подготовки). Наложение этого цвета – выбор цвета 11 на спектрах SDSS / SEGUE привели к каталогу из ~ 42 800 звезд, по которым у нас есть астрометрическая, фотометрическая и спектроскопическая информация. Этот цветовой разрез представляет собой первый шаг нашей процедуры и применяется как к тестовой / обучающей выборке, так и к окончательному основному каталогу (см. Раздел 4.4).
Увеличить Уменьшить Сбросить размер изображения
Рис. 4. Цветовая диаграмма звезд SDSS / SEGUE с отношением S / N ≥ 25. Оранжевый многоугольник соответствует геометрическому месту звезд MS и RGB в этой цветно-цветной плоскости. Это поле выбора удаляет звезды A-типа и белые карлики из последующего анализа.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияЗдесь мы описываем метод, используемый для отделения звезд ветви красных гигантов (RGB) от звезд ГП. 12 Для выполнения этой классификации мы используем RFC, входными данными которого являются ( u — g ) 0 , ( g — r ) 0 , ( r — i ) 0 , ( i — z ) 0 и ( u — G ) 0 цветов, нормализованных так, чтобы среднее значение равно нулю и стандартное отклонение, равное единице, а выходные данные представляют собой вероятность каждый будет карликом, P карликом , или гигантом, P гигантом ≡ 1 — P карликом .Здесь стоит отметить, что RFC не обязательно требует нормализации входных данных, но настоятельно рекомендуется для ИНС. Поэтому, чтобы соответствовать различным шагам алгоритма, мы используем нормализованные входные данные для классификации карликов / гигантов.
По данным Lee et al. (2008), типичная внутренняя неопределенность, полученная SSPP для принятой поверхностной силы тяжести (loggadop), составляет ~ 0,19 dex. Поэтому мы оставляем только звезды SDSS / SEGUE, которые имеют неопределенности δ log ( g ) ≤0.2. Окончательный каталог SDSS / SEGUE, использованный для обучения / тестирования классификатора карликовых гигантов, содержит 41 062 звезды. Этот каталог показан в виде диаграммы Киля на рисунке 5, где мы определяем звезды, лежащие в оранжевом многоугольнике, как гиганты, а все другие звезды как карлики. Обратите внимание, что в принципе мы могли бы использовать измерения параллакса Gaia DR2 для классификации звезд как карликов или гигантов; однако, как мы покажем позже, измерения параллакса Gaia DR2 недостаточно точны, особенно для звезд с [Fe / H] <−1.0, многие из которых обычно расположены на больших расстояниях и имеют низкую точность параллакса.
Увеличить Уменьшить Сбросить размер изображения
Рис. 5. Диаграмма Киля , показывающая распределение звезд в каталоге SDSS / SEGUE, используемом для классификации карликов и гигантов. Оранжевый многоугольник показывает те звезды, которые мы «определяем» как гиганты.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияОтметим, что наша «гигантская» выборка содержит подавляющее большинство звезд RGB, но также и субгигантские звезды с эффективной температурой между 5000 ≤ T eff (K) ≤ 6000 и силой тяжести на поверхности между 3.2 ≤ log ( г ) ≤ 3,9. Даже на диаграмме Киля трудно определить строгий предел между карликами, субгигантами и гигантами, особенно когда мы включаем неопределенности в поверхностной гравитации, которые действуют, размывая любые границы, которые мы принимаем. Добавление субгигантского класса увеличивает сложность алгоритма и не решает основную проблему «нечеткости» между классами. По этой причине мы не рассматриваем конкретный класс звезд-субгигантов. Отметим также, что наше определение гигантов не включает большинство звезд асимптотической ветви гигантов (AGB).Однако в каталоге SDSS / SEGUE очень мало звезд AGB, поэтому мы не можем обучить алгоритм для их идентификации. Как и все алгоритмы контролируемого машинного обучения, мы в конечном итоге ограничены репрезентативным характером нашей обучающей выборки. Однако звезды AGB очень редки, и поэтому их отсутствие в нашем обучающем наборе не оказывает большого статистического влияния на наши результаты.
Мы создаем обучающий и тестовый набор из каталога SDSS / SEGUE, состоящий из случайно выбранных 80% и 20% выборки соответственно.Обучающий набор используется для поиска наилучшей архитектуры с помощью метода перекрестной проверки k раз и с пятью подвыборками. Затем он используется для поиска лучших параметров RFC, которые затем применяются к набору тестов для проверки сходства статистики двух выборок. Эта техника предотвращает переобучение тренировочной выборки. Мы используем пакет python sklearn, чтобы найти лучший параметр RFC.
Полнота и чистота классов карликов и гигантов (заселены звездами с P карликом / P гигантом > 0.5) для тестового набора показаны в таблице 1. Значения для двух классов аналогичны значениям для обучающего набора, что указывает на отсутствие переобучения данных. RFC правильно классифицирует подавляющее большинство карликов (96%) с менее чем 7% -ным загрязнением гигантскими звездами (обратите внимание, что, поскольку карлики составляют 86% нашей обучающей / тестовой выборки, это означает улучшение в 2 раза по сравнению со случайным ). Для гигантов правильно классифицировано чуть больше половины с относительно низким уровнем загрязнения ~ 30%.Таким образом, наша полнота примерно в 4 раза лучше, чем «случайная», а наша загрязненность почти в 3 раза ниже, чем «случайная». На рисунке 6 представлена диаграмма Киля ожидаемой / предсказанной вероятности того, что каждая звезда будет карликом, и мы видим, что большая часть загрязнения карликами происходит от субгигантов, которые предпочтительно классифицируются как карлики, а не гиганты.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 6. Кильских диаграмм, где каждая точка соответствует звезде в тестовом наборе, имеющем цветовую кодировку в зависимости от вероятности того, что она является карликом. Ожидаемая вероятность или фактический класс звезд отображается на левой панели, а прогнозируемая вероятность из нашего алгоритма показана на правой панели.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияТаблица 1. Полнота и чистота классов карликов и гигантов для тестовой выборки
| Класс | Фракция | Полнота | Чистота |
|---|---|---|---|
| Карлик | 0.86 | 0,96 | 0,93 |
| Гигант | 0,14 | 0,57 | 0,70 |
Примечание. Результаты статистически одинаковы для обучающей выборки, демонстрируя, что мы не переобучаем обучающую выборку. Первый столбец относится к истинной доле звезд, фактически классифицированных как карлики или гиганты в тестовой выборке.
Скачать таблицу как: ASCIITypeset image
Здесь ничего не стоит отметить, что на рисунке 6 поверхностная гравитация от SDSS / SEGUE уменьшается с температурой для звезд ГП с эффективной температурой ниже 4800 К.Это неожиданно по сравнению с теоретическими предсказаниями и, вероятно, является следствием плохого определения силы тяжести на поверхности SSPP в этой области. Однако это не влияет на нашу классификацию, поскольку все звезды в этой области правильно определены алгоритмом как карлики.
Подробные характеристики нашей классификационной схемы в зависимости от металличности, поверхностной силы тяжести, эффективной температуры и цвета ( u — G ) 0 показаны на рисунке 7.Полнота и загрязнение в основном постоянны в диапазоне температуры и цвета, охватываемого гигантами. Полнота и загрязнение также постоянны с металличностью до [Fe / H] -1,2, после чего полнота быстро падает (с 70% при [Fe / H] = -1,3 до 20% при [Fe / H] = -1,0 ), что коррелирует с резким увеличением загрязнения. Мы пришли к выводу, что классификация хорошо работает для гигантов с металличностью ниже [Fe / H] = -1,2, но не может идентифицировать гигантов с наибольшим содержанием металлов.Также наблюдается падение полноты гигантов при поверхностной гравитации log ( g ), равной 3,3, что соответствует субгигантам, которые предпочтительно классифицируются как карлики.
Увеличить Уменьшить Сбросить размер изображения
Рис. 7. Полнота (синий) и загрязнение (оранжевый) звезд, классифицированных RFC как гиганты в тестовой выборке, в зависимости от (а) спектроскопической металличности, (b) поверхностной силы тяжести, (c) эффективной температуры, и (d) цвет ( u — G ) 0 .
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияОтносительная важность каждого фотометрического цвета в схеме классификации, вычисленная с использованием метода важности признаков, реализованного в пакете sklearn, показана на рисунке 8. Этот метод использует вес каждой особенности в каждом узле различных деревьев RFC для измерить относительную важность такого признака для классификации. Самая важная особенность — это цвет ( r — i ) 0 , при этом около четверти информации, используемой для классификации звезд, исходит от него.Это неудивительно, поскольку этот цвет является хорошим показателем эффективной температуры; поэтому мы предполагаем, что этот цвет используется для выбора диапазона температур, в котором преимущественно присутствуют гиганты (4900 K ≤ T eff ≤ 5500 K). Вторая по важности характеристика — ( u — g ) 0 , которая имеет тесную корреляцию с металличностью звезд ГП (Ивезич и др., 2008; Ибата и др., 2017b). Аналогичная корреляция существует для гигантов, хотя и с другой нулевой точкой (Ibata et al.2017b). Другие цвета, на которые приходится ~ 50% относительной важности, по-видимому, дают дополнительную незначительную дополнительную информацию (о металличности, температуре и поверхностной гравитации), чтобы отделить карликов от гигантов с использованием полной формы SED.
Увеличить Уменьшить Сбросить размер изображения
Рис. 8. Относительное значение каждого цвета в классификации карликов и гигантов RFC.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияИз рисунка 8 мы заключаем, что классификация карликов / гигантов в основном использует фотометрические особенности, которые отслеживают температуру и металличность. Это становится более ясным на рисунке 9, где геометрическое место гигантов очевидно на диаграмме эффективной температуры-металличности (левые панели) или на диаграмме цвет-цвет с использованием двух наиболее важных фотометрических характеристик, ( r — i ) 0 и ( u — g ) 0 цветов (правые панели).Две верхние панели рисунка 9 ясно показывают, что образец SDSS / SEGUE не содержит большого количества малометаллических карликов в температурном диапазоне, который перекрывается с большинством гигантов (4900 K ≤ T eff ≤ 5500 K ). Критерии выбора для SDSS / SEGUE обычно сложны (Yanny et al. 2009a). Однако отсутствие малометаллических карликов усугубляется относительно небольшой глубиной набора данных SDSS / SEGUE, который не содержит звезд слабее G 18 mag.Это означает, что карлики обычно находятся довольно близко и поэтому предпочтительно выбираются из диска, который в среднем намного более богат металлами, чем ореол.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 9. Левая панель: диаграммы эффективная температура – металличность; правые панели: ( u — g ) 0 — ( r — i ) 0 диаграмма. Верхние панели: распределение истинных карликов (красные) и гигантов (синие) тестовой выборки.Нижние панели: те же распределения, но звезды имеют цветовую кодировку в зависимости от их вероятности быть карликами в соответствии с алгоритмом.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияКак следствие этого, доля истинных карликов, ошибочно идентифицированных как гиганты, резко возрастает с металличностью в этой области температур, как показано на рисунке 10. Большинство истинных карликов с [Fe / H] <-1,5 классифицируются как гиганты по алгоритм.Это следует сравнивать с общей выборкой, в которой доля неправильно идентифицированных карликов никогда не превышает 0,2 (и которая почти постоянна для металличности ниже [Fe / H] = -1,0). Интересно отметить, что даже в диапазоне температур, включающем гигантов, более 50% настоящих карликов (и настоящих гигантов) правильно идентифицируются между -1,45 ≤ [Fe / H] ≤ -1,1. Это демонстрирует, что для классификации карликов и гигантов алгоритмом используются дополнительные функции, а не только те, которые относятся к температуре и металличности.Кажется разумным предположить, что эти особенности напрямую связаны с поверхностной гравитацией звезд, например линии Пашена, присутствующие в полосах i , z и G , или линии поглощения Ca H и K в полосах u , g и G (см. Starkenburg et al.2017).
Увеличить Уменьшить Сбросить размер изображения
Рис. 10. Доля настоящих карликов, ошибочно идентифицированных как гиганты в зависимости от металличности, для всего тестового образца (красный) и для более узкого диапазона эффективных температур между 4900 K ≤ T eff ≤ 5500 K (что является температурным диапазоном гигантов).Серой заштрихованной областью выделена область металличности, в которой правильно идентифицировано более 50% карликов и гигантов.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияНаш вывод частично противоречит Lenz et al. (1998), которые показали, что невозможно одновременно разделить чисто звезд по температуре, металличности и поверхностной гравитации с помощью набора фильтров SDSS (которые в целом аналогичны фильтрам CFIS и PS1), за заметным исключением A звезды типа.Однако их анализ не учитывал возможные нелинейные связи между фотометрическими цветами и соответствующими параметрами звезды. По своей конструкции наш RFC учитывает нелинейность этих отношений, что позволяет нам использовать фотометрию для лучшего предсказания вероятности того, что звезда будет карликом или гигантом. Отметим также, что мы экспериментировали с различными методами классификации карликов и гигантов, включая ИНС и анализ главных компонентов (PCA). Мы обнаружили, что ИНС дает те же результаты, что и RFC, но результаты было труднее интерпретировать; PCA не дал хороших результатов из-за требований линейности.
С появлением новых спектроскопических исследований в северном полушарии, таких как WEAVE и SDSS-V, количество малометаллических карликов с эффективной температурой между 4900 K ≤ T eff ≤ 5500 K, имеющих спектры, увеличится. скорее всего увеличится. Эти будущие данные станут отличным обучающим набором для улучшения классификации карликов / гигантов. Более того, мы обсудим позже другие проблемы с обучающими / тестовыми наборами, для которых будущие наборы спектроскопических данных, вероятно, внесут существенные улучшения.
Важно помнить, что гигантская выборка, полученная с помощью алгоритма, может содержать незначительную часть реальных бедных металлами карликов, поскольку в любом обзоре карликов обычно больше, чем гигантов. Однако в критическом диапазоне температур (4900 K ≤ T eff ≤ 5500 K) разница в абсолютной величине между истинным карликом и истинным гигантом того же цвета составляет не менее 3 звезд, что эквивалентно неверному расстоянию в не менее 150% (эта ошибка еще больше для более красных звезд).Таким образом, многие из неправильно идентифицированных карликов в нашем обзоре можно легко идентифицировать, рассматривая их собственные движения Gaia .
Следующим шагом алгоритма является определение независимо для каждого из двух классов фотометрической металличности и абсолютной звездной величины (и, следовательно, расстояния) каждой звезды.
Было проведено множество исследований, оценивающих фотометрический параллакс звезд, особенно звезд ГП (Лэрд и др., 1988; Юрич и др., 2008; Ивезич и др., 2008; Ибата и др.).2017b; Андерс и др. 2019). Это возможно, потому что локус MS имеет четко определенное соотношение цвет – яркость. Используя это свойство, Юрич и др. (2008) определили расстояния от 48 миллионов звезд, присутствующих в следе SDSS DR8, до расстояний ~ 20 кпк, используя только фотометрию в диапазонах r и i . Однако в этом исследовании не принималось во внимание влияние металличности, которая изменяет светимость для данного цвета: более богатые металлами звезды были ярче, чем бедные металлами (Laird et al.1988; но также см. рис. 3 из Gaia Collaboration et al. 2018b). Возраст оказывает меньшее влияние на фотометрический параллакс, потому что его эффект заключается в уменьшении заселения более голубых звезд при сохранении формы локуса ГП для более красных звезд.
Хорошо известно, что можно определить фотометрическую металличность звезды, измерив ее УФ-избыток (Wallerstein & Carlson 1960; Wallerstein 1962; Sandage 1969), поскольку бедные металлами звезды имеют более сильный УФ-избыток, чем богатые металлами. звезды. Карни (1979) показывает, что можно измерить металличность звезды с точностью до 0.2 dex для звезд с фотометрией лучше 0,01 dex в фильтрах Johnson UBV . Совсем недавно Ivezić et al. (2008) показали, что можно получить аналогичную точность с фильтрами SDSS ugr и использовали его для получения фотометрического параллакса 2 миллионов карликов F / G до 8 кпк, где порог расстояния ограничен точностью диапазон SDSS и (см. также Ибата и др., 2017b).
В этом разделе мы основываемся на этой литературе и представляем основанный на данных метод оценки металличности и расстояний до карликовых звезд (Раздел 3.3.1) и гиганты (раздел 3.3.2).
3.3.1. Карликовые звезды
Мы сначала определяем фотометрическую металличность карликов, прежде чем вычислять расстояние до этих звезд. Для определения расстояния мы предпочитаем использовать абсолютную светимость, полученную с использованием параллаксов Gaia , а не самих параллаксов, учитывая, что большое количество параллаксов Gaia является отрицательным из-за стохастичности обзора (Luri et al. 2018). По построению, использование абсолютной величины приводит к полученным расстояниям, которые всегда положительны.
Существует вырождение между металличностью, светимостью и цветами, особенно для звезд с высокой металличностью (Ленц и др., 1998). Как указывает Ибата и др. (2017b), пренебрежение влиянием металличности на полученную абсолютную звездную величину может привести к серьезным ошибкам, делая полученные расстояния недействительными. В принципе, должно быть возможно получить металличность и абсолютную величину карликов одновременно, за один шаг. Однако, как описано ниже, только около половины карликов, у которых есть хорошие измерения металличности, также имеют достаточно хорошие измерения параллакса, чтобы оценить их абсолютные величины.Чтобы использовать максимальный объем доступной информации, мы решили использовать два шага: первый для определения фотометрической металличности, а второй — для оценки абсолютной звездной величины.
Чтобы оценить фотометрическую металличность карликов, мы построили набор из пяти независимых ИНС, на входах которых используются те же цвета, что и для классификации карликов-гигантов. Использование набора независимых ИНС, а не только одной, предпочтительнее, потому что это позволяет нам оценивать систематические ошибки на предсказанных значениях, сгенерированных алгоритмом.Используя подвыборку обучающего набора, мы обнаружили, что пять независимых ИНС дают аналогичные систематические ошибки для набора из 10 или 15. Более того, это также предотвращает любое возможное переобучение. Пять ИНС, построенные с использованием пакета Keras (Chollet 2015), имеют разные индивидуальные архитектуры и состоят из двух-пяти скрытых слоев. Что касается RFC, обучающий набор используется для поиска лучшей архитектуры каждой ИНС с помощью k-кратного метода перекрестной проверки с пятью подвыборками, где мы предполагаем, что каждая ИНС имеет независимую архитектуру.Параметры, используемые для обучения / тестирования 13 ИНС — это принятые спектроскопические металличности из SSPP (FeHadop) и их неопределенности для ~ 35 000 карликов из набора данных SDSS / SEGUE. Упомянутые ранее методы оценки металличности по фотометрическим полосам пропускания имеют типичную погрешность δ [Fe / H] 0,2 (относительно спектроскопических измерений). К набору спектроскопических данных применяется качественная обрезка, чтобы использовать только карлики с принятой неопределенностью спектроскопической металличности δ [Fe / H] spectro ≤ 0.2. Отметим, что этот критерий очень мало влияет на каталог карликов SDSS / SEGUE, так как он удаляет ~ 100 звезд.
Функция потерь (или стоимости), используемая для обучения ИНС, представляет собой модифицированную среднеквадратичную функцию, которая включает неопределенности в отношении металличности:
, где y истинно, i и δy i i спектроскопическая металличность и ее неопределенность для звезды i , соответственно, и y pred, i — соответствующая металличность, предсказанная алгоритмом.
После обучения каждой ИНС мы определяем металличность карликов ([Fe / H] Карлик ) как среднее значение выходных данных пяти ИНС, а систематическую ошибку — как их стандартное отклонение. Разница между фотометрической и спектроскопической металличностью показана на двух верхних панелях рисунка 11 и составляет σ [Fe / H] = 0,15 dex. Это умеренное улучшение метода Ibata et al. (2017b) ( σ [Fe / H] = 0,20 dex). Обратите внимание, что невязки не показывают какой-либо значимой тенденции с металличностью, за исключением наиболее бедных металлами звезд ([Fe / H] <−2), для которых фотометрическая металличность имеет тенденцию быть выше, чем спектроскопические измерения.Отметим, что невязки увеличиваются с уменьшением металличности, указывая на то, что предсказанные фотометрические металличности менее надежны для звезд с металличностью ниже [Fe / H] <−2.0. Частично это будет из-за меньшего количества звезд, присутствующих в обучающей выборке при этой металличности, чем при более высокой металличности. Средняя неопределенность спектроскопической металличности карликов составляет δ [Fe / H] = 0,04, а систематическая ошибка составляет δ [Fe / H] Dwarf, sys = 0.02. Таким образом, большая часть разброса в наших измерениях металличности связана с внутренним видимым изменением цвета карликов с аналогичной металличностью.
Увеличить Уменьшить Сбросить размер изображения
Рис. 11. Сравнение «истинной» и производной металличности для карликов (верхние панели), а также истинной и производной абсолютных величин для карликов (нижние панели). На левых панелях показаны графики зависимости истинных и производных величин друг от друга.Показана взаимно однозначная зависимость (сплошные линии), а штриховые и пунктирные линии соответствуют отклонениям 1 σ и 2 σ соответственно. Правые панели показывают распределение разностей между истинными и производными величинами с наложенной гауссовой аппроксимацией. Горизонтальные панели показывают остаток между количеством, предсказанным алгоритмом, и «истинными» значениями. Линии такие же, как на левых панелях. Красные полосы ошибок показывают разброс полученных параметров в разных местах.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияКак только металличность определена, она используется в сочетании с цветами для оценки абсолютной величины каждого карлика и, следовательно, расстояния до него. Что касается металличности, создается набор из пяти ИНС, где входные данные имеют те же цвета, которые использовались ранее, в дополнение к производной металличности. Результатом является абсолютная величина в заданном диапазоне. Мы решили использовать полосу Gaia G в качестве эталона, поскольку это фильтр с самой низкой фотометрической неопределенностью при данной звездной величине.
Абсолютные звездные величины карликов в каталоге SDSS / SEGUE вычисляются на основе параллаксов Gaia ( ) согласно
. Стоит отметить, что Gaia имеет тенденцию занижать параллаксы, и поэтому мы исправляем все параллаксы на глобальное смещение 0 = 0,029 мсек, как было предложено Lindegren et al. (2018). Luri et al. (2018) показывают, что инверсия параллакса для получения расстояния (и, следовательно, абсолютной звездной величины) действительна только для звезд с низкими относительными неопределенностями параллакса, обычно / δ ≥ 5 (относительная точность ≤20% ).В этих случаях функция распределения вероятностей (pdf) абсолютной звездной величины может быть аппроксимирована гауссовой величиной с центром по ширине, так что
На карликах SDSS / SEGUE выполняется качественная обрезка, чтобы сохранить только те звезды с относительной величиной. Gaia Измерение параллакса лучше 20%. С этим критерием средняя точность относительного параллакса спектроскопической выборки карлика составляет ~ 10%, что соответствует средней неопределенности абсолютной величины mag. Набор спектральных карликовых данных, используемый для обучения / тестирования набора ИНС, состоит из 18 930 звезд и является хорошим представлением распределения металличностей и абсолютных величин в исходном наборе данных (охватывающий диапазон металличности −3.0 dex <[Fe / H] Spectro <0,5 dex, диапазон по абсолютной величине 3 < M G <7,5 и 600 звезд с [Fe / H] spectro <−2,0 с хорошей точность параллакса).
Набор из пяти ИНС, используемых для получения абсолютной величины, имеет структуру, отличную от набора, используемого для оценки металличности, с четырьмя или пятью скрытыми слоями и большим количеством нейронов на слой, чем раньше. Однако функция потерь остается той же, где y true , δy и y pred теперь соответствуют, и, соответственно.Мы определяем прогнозируемую абсолютную звездную величину в полосе G карликов () как медианное значение выходных сигналов пяти ИНС, а систематическую ошибку ( δ ) как их стандартное отклонение. Как показано на нижних панелях рисунка 11, предсказанная абсолютная величина показывает разброс магнитуды по сравнению с абсолютной величиной, вычисленной из параллаксов Gaia . Это соответствует относительной точности на расстоянии 15%, что очень похоже на точность, обнаруженную Ivezić et al.(2008). Стоит отметить, что разброс почти постоянен в диапазоне абсолютной звездной величины, за исключением области вокруг, где несколько звезд имеют тенденцию иметь более высокую прогнозируемую абсолютную величину, чем наблюдаемая. Эти звезды, вероятно, являются молодыми звездами (<5 млрд лет) на повороте ГП (MSTO). Поскольку CFIS проводит наблюдения на высокой галактической широте (), их количество незначительно, и мы ожидаем, что эта недооценка светимости более молодых звезд должна иметь незначительное влияние на статистические исследования распределения расстояний.
3.3.2. Giant Stars
Метод определения металличности и абсолютной звездной величины для гигантов аналогичен методу для карликов, с первым набором ИНС для получения металличности и вторым набором ИНС для оценки абсолютной величины. Архитектура двух наборов ИНС точно такая же, как у карликов.
Принятые металличности и неопределенности для спектроскопических гигантов используются для обучения / тестирования первого набора ИНС. Опять же, мы применяем качественное сокращение металличности, которое использует только 5670 гигантов с точностью металличности лучше, чем δ [Fe / H] spectro ≤ 0.2 (этот качественный разрез удаляет менее 0,5% первоначальной гигантской пробы). Используемая процедура в точности такая же, как и для карликов, а предсказанная металличность гигантов ([Fe / H] Giant ) равна медиане пяти выходов ИНС и систематическим ошибкам ( δ [Fe / H] Giant, sys ) — стандартное отклонение этих выходных данных. Как показано на двух верхних панелях рисунка 12, разница между фотометрической и спектроскопической металличностью составляет σ [Fe / H] = 0.16 dex и не показывает какой-либо тенденции с металличностью, за исключением звезд с [Fe / H] <−2.0, как для карликов. Это очень значительное улучшение по сравнению с предыдущими исследованиями, в которых гиганты не рассматривались отдельно от карликов, что привело к завышению их металличности на [Fe / H] = 0,16 dex (Ибата и др., 2017b).
Увеличить Уменьшить Сбросить размер изображения
Рисунок 12. То же, что и рисунок 11, но для гигантов.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияВ отличие от карликов, невозможно удержать только гигантов с относительной точностью параллакса Gaia 20%. При одинаковой светимости гиганты более далеки от карликов, что приводит к большей неопределенности их параллакса. Принятие того же выбора, что и для карликов, создает набор данных только из 1000 звезд, общее распределение металличности которых сильно отличается от общего распределения металличности гигантов.Действительно, подавляющее большинство этих звезд (~ 670) имеют металличность выше, чем [Fe / H]> -1, в то время как 3/4 всего набора данных спектроскопических гигантов имеет металличность ниже, чем [Fe / H] <-1. с пиком около [Fe / H] -1,4 (см. нижнюю панель рисунка 13). Вдобавок более 60% гигантов с точностью параллакса 20% кажутся субгигантскими звездами, ошибочно идентифицированными нашим классификатором карликовых гигантов.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 13. МДФ карликов (верхняя панель) и гигантов (нижняя панель). Серые гистограммы — это спектроскопические MDF из каталога SDSS / SEGUE, использующие металличность, принятую из SSPP. Синяя и красная гистограммы представляют собой предсказанные фотометрические MDF для звезд, где синие и красные линии соответствуют звездам с достоверностью 0,5 и 0,7 соответственно для карлика / гиганта. Избыток карликов около [Fe / H] -0,5 и истощение гигантов, более богатых металлами, чем [Fe / H] = -1,0, являются следствием неправильной классификации настоящих богатых металлами гигантов алгоритмом.
Загрузить рисунок:
Стандартный образ Изображение высокого разрешенияОколо 2/3 спектроскопических гигантов имеют относительную точность измерения параллакса более 20%. Следовательно, PDF их абсолютной величины не может быть аппроксимирован гауссианом, как это было в случае карликов. Как показали Luri et al. (2018), их PDF-файл асимметричен, и максимум не сосредоточен на «истинной» абсолютной величине. Использование максимума PDF в этих случаях приводит к недооценке расстояния и, следовательно, к занижению абсолютной величины.В зависимости от точности относительного параллакса «истинная» абсолютная величина может быть более чем на 1 σ от значения максимального правдоподобия.
В принципе, мы могли бы выполнить расширение данных набора спектроскопических гигантских данных, чтобы учесть неопределенности различных параметров, особенно параллакса. Это может быть выполнено методом Монте-Карло выборки спектроскопических гигантских данных в диапазоне 2,5 σ –3 σ вокруг максимального правдоподобия наблюдаемых .Чтобы не вносить смещения, это распределение должно быть симметричным относительно максимальной вероятности различных параметров. Однако, чтобы физическая величина оставалась абсолютной, параллаксы должны быть положительными. Это приводит к набору данных, состоящему из звезд с — 2,5 δ > 0, резко сокращая количество звезд, используемых для обучения модели, что также смещает выборку в сторону гораздо более богатых металлами звезд, аналогично эффекту сокращение неопределенностей параллакса, описанных выше.
По этим причинам мы используем все спектроскопические гиганты, у которых есть положительное измерение параллакса. Следуя Hogg et al. (2019) мы применяем качественный отбор по параллаксу, чтобы оставить только гигантов с неопределенностью по параллаксу δ <0,1 мсек. Дуги, чтобы у нас не преобладали звезды с чрезвычайно плохими измерениями. Окончательный набор данных, используемый для обучения / тестирования набора ИНС, состоит из 3497 гигантов. Однако мы обнаружили, что для этой гигантской выборки параллаксы Gaia должны быть скорректированы смещением 0 = 0.033 мсек. Дуги, чтобы получить разумные расстояния для шаровых скоплений (ШС; см. Раздел 4.3). Это смещение немного выше, чем для карликов ( 0 = 0,029 мсек. Дуги), но ниже смещения 0 = 0,048 мсек. Дуги, найденного Hogg et al. (2019) для звезд красных гигантов.
Из-за отсутствия точных параллаксов, точный PDF (и, следовательно, неопределенности) абсолютной звездной величины (вычисленной с использованием уравнения (2)) не может быть известен для большинства гигантов без принятия априорной точки зрения на распределение плотности гигантов. в Млечном Пути.Следовательно, мы не можем оценить неопределенности абсолютной величины с помощью уравнения (3). По этой причине функция потерь, используемая в качестве метрики для ИНС, представляет собой стандартное среднеквадратичное значение, которое не принимает во внимание неопределенности абсолютной величины.
Разброс абсолютной величины, показанный на левой панели рисунка 12, равен dex со смещением ~ -0,28 dex, аналогичным медиане остатков (Me (Δ M G ) = — 0,28). Это смещение является следствием недооценки расстояния до гигантов с использованием значений, заданных максимумом PDF.Средняя невязка больше, потому что на нее влияют звезды с наибольшими невязками, что является результатом ограниченной статистической выборки.
Действительно, параллаксы Gaia этих звезд неточны, а расстояния, полученные путем инвертирования параллакса, как правило, занижают истинное расстояние до этих звезд (Лури и др., 2018). Таким образом, абсолютные величины, используемые для обучения связи, неточны и, вероятно, недооценены. Поэтому невозможно использовать разброс между предсказанной абсолютной величиной и абсолютной величиной, полученной из параллакса Gaia , чтобы проверить правильность предсказанных расстояний с помощью этого метода.Однако, как мы покажем в Разделе 4.3, используя глобальные скопления, присутствующие в следе CFIS, расстояния до гигантов, определенные таким образом, дают хорошие оценки их реальных расстояний, несмотря на отсутствие точности абсолютных величин, используемых для обучения связи.
Классификация полевых карликов и гигантов в RAVE и ее использование для обнаружения звездных потоков
Аннотация
Образцы ярких звезд, полученные в результате таких обзоров, как RAVE, содержат сопоставимые доли карликовых и гигантских звезд.Поэтому эффективное разделение этих двух классов светимости важно, особенно для исследований, в которых расстояния оцениваются с помощью фотометрических соотношений параллакса. Мы используем доступные спектральные оценки log g из второго выпуска данных RAVE (DR2), чтобы присвоить каждой звезде вероятность быть карликом или субгигантом / гигантом на основе модели смеси, которая соответствует распределению log g в различных цветовых диапазонах. Мы также пытаемся использовать эти звезды в качестве помеченного обучающего набора, чтобы классифицировать звезды, у которых отсутствуют оценки log g, на карликов и гигантов с помощью алгоритма машины опорных векторов.Мы оцениваем эффективность этой классификации в сравнении с различными вариантами входного вектора признаков. В частности, мы используем различные комбинации приведенных собственных движений, видимых звездных величин 2MASS JHK, DENIS IJK и USNO-B B2R2. Наше исследование показывает, что — для наших цветовых диапазонов — одни только инфракрасные диапазоны не предоставляют важной информации для разделения карликов и гигантов. Даже если добавить оптические полосы и уменьшенные собственные движения, доля настоящих гигантов, классифицируемых как карлики (загрязнение), остается выше 20%.Используя только карлики с доступными спектральными картами g и оценками расстояния (последнее из Breddels et al.), Мы затем повторяем поиск потока Klementet al. (KFR08), который предположил, что все звезды были карликами, и заявил об открытии нового звездного потока на V ≈ -160 км с -1 в выборке из 7015 звезд из RAVE DR1. Существование потока KFR08 было подтверждено двумя недавними исследованиями с использованием других независимых наборов данных. Наш повторный анализ выборки чистого карлика DR2 показывает, что плотность пяти звезд в фазовом пространстве потока KFR08, с распределением металличности, кажется несовместимым с распределением звезд со сравнительно низкими скоростями вращения.По сравнению с несколькими моделями сглаженного Млечного Пути, среднее стандартизованное отклонение потока KFR08 незначительно и составляет 1,6 ± 0,4. Таким образом, наши данные не позволяют сделать определенные выводы о его существовании, но будущие выпуски данных RAVE и другие (лучшие спектроскопические) обзоры помогут решить эту проблему.
(PDF) Идентификация полевых карликов и гигантов во втором выпуске данных экспериментов по радиальной скорости
448 S. Bilir et al.
Вкладка 2. Количество звезд в шести подвыборках, исследованных в нашей работе, и в тех, которые фигурируют в Ammons et al. (2006). В последних трех столбцах указано число
звезд с отношением S / N меньше 13 и 33 соответственно, а также диапазон χ2.
Ammons et al. (2006) Bilir et al. (2006) Отношение сигнал / шум
Dwarf Giant Dwarf Giant S / N ≤13 S / N ≤33
Подвыборка Процент Процент Всего КПД Процент Всего NNχ2 Диапазон
Ia 48 98 2 4 50 92 95 5 5 97 2 31 [240, 22 502]
Ib 276 98 5 2 281 423 98 10 2 433 7 86 [074, 10 579]
Ic 1335 99 12 1 1347 2005 99 16 1 2021 13 329 [075, 11 826 ]
II 118 04 3237 96 3355 484 12 3567 88 4051 18 428 [024, 16 633]
III 2938 98 46 2 2984 4357 99 51 1 4408 47 950 [046, 13 029]
IV 80 35 146 65 226 211 46 249 54 460 10 90 [045, 09585]
Всего 4795 100 3448 100 8243 7572 100 3898 100 11470 97 1914
276 карликов и пять гигантов Аммонса и др.(2006) с 3 <
log g≤3,5 и J − H≤0,4 занимают карликовую и гигантскую полуплоскости,
соответственно, на рис. 4 (b). Это подтверждает, что 423 звезды с одинаковыми значениями силы тяжести и цвета поверхности
в нашей работе, которые занимают полуплоскость карлика
, являются карликами. На рис. 3 (b) есть 10 звезд (2% от общего числа
звезд), которые занимают гигантскую полуплоскость и должны быть
гигантами.
В разделе 3 мы отметили, что большинство звезд с 3.5 4andJ − H≤0,4 должны быть карликами. Фактически, карлики 2005 г., взятые у Аммонса и др. (2006), с той же плотностью поверхности и цветов, подтверждают наше предположение (рис. 4c). Кроме того, 12 из 16 звезд (рис. 3c), которые были классифицированы как гиганты в Ammons et al. (2006), занимают гигантскую полуплоскость, подтверждая процедуру, согласно которой разделяет карликов и гигантов с помощью двух полос. Данные Ammons et al. (2006) также подтверждают результаты, полученные и отмеченные в разделе 3 для подвыборок II (log g≤4, J-H> 0.4), III (log g> 4, J − H≤0,4) и IV (log g> 4, J − H> 0,4). То есть звезды, идентифицированные как карлики и гиганты в Ammons et al. (2006) занимают карликовые и гигантские полуплоскости на рис. 4 (d), 4 (e) и 4 (f), соответственно. На рис. 4 (г) преобладают гиганты, тогда как большинство из звезд на рис. 4 (д) являются карликами. Как и ожидалось, рис. 4 (f) включает в себя популяций (гигантов и карликов) в большом количестве. В таблице 2 значения в двух столбцах перед последним столбцом обозначают количество звезд с S / N ≤33 и S / N ≤13, что соответствует среднему значению S / N −1σ и S / N ≤ . / N −2σ, соответственно, где σ = 20 — стандартное отклонение S / N.Эти звезды не показывают какой-либо систематической разницы положения относительно звезд с более высоким отношением S / N, в диаграмме J − V с двумя звездными величинами. Наконец, значения в последнем столбце являются значениями CHISQ (подробности см. В разделе 5). 4.2 Подтверждение с помощью диаграммы поверхностная гравитация – цвет Мы наносим все подвыборки звезд (Ia, Ib, Ic, II, III и IV) на диаграмму log gsurface Gravity и J − Hцветную диаграмму и обсуждаем их идентификации (Рисунок.5). Кроме того, на данные накладываются изохроны , чтобы различить карликовую область на диаграмме J− Hversus log gdiagram. Изохроны взяты из базы данных Padova (Мариго и др., 2008) с использованием веб-интерфейса.2 Для нашей выборки звезд мы приняли изохроны с металличностью −2≤ [M / H] ≤ +0.2 dex с интервалами 0,5 dex для возрастов 1, 5 и 10 млрд лет. Всего на диаграмме log gversus J − H нанесено 18 изохрон (рис.5). Большинство звезд в подвыборке II (log g≤4, J − H> 0,4) должны быть красными гигантами. Это случай на рис. 2 (b), где 3567 гигантов и 484 2 http://stev.oapd.inaf.it/cgi-bin/cmd карликов могут быть идентифицированы в соответствии с их положением в Jversus Диаграмма Vmagnitude. Карлики соответствуют только 12 процентам от общей подвыборки . Другое подтверждение можно легко сделать для звезд в подвыборке III (log g> 4, J − H≤0.4). Большая поверхностная сила тяжести и их положения на изохронах населения дисков этих звезд указывают на , что они должны быть карликами. Фактически, количество карликов, идентифицированных по положению на рис. 2 (c) , составляет 99% от общего числа звезд этой подвыборки. Почти половина звезд в подвыборке IV (log g> 4, J − H> 0,4) лежит на главной последовательности изохрон. Следовательно, эти звезды с большой поверхностной силой тяжести должны быть карликами.Разрыв в изохронах при J − H> 0,4 между карликовой ветвью (показанной на рис. 5, панель IV) и ветвью гиганта (гиганты показаны на рис. не должно быть звезд с J − H> 0,4 и 4 Рис. 5 показывает, что данные существуют в этом регионе. Скорее всего, являются результатом ошибок измерения на log g. RAVE DR2 log g ошибок по консервативной оценке равны 0.5 dex для среднего значения S / N ∼40. Это достаточно велико, чтобы у карликов с log g> 4,5 можно было измерить , чтобы иметь log g> 4, а у гигантов с log g <4 можно было измерить , чтобы получить log g <4,5. Это согласуется с нашим аргументом, что количество карликов и гигантов в подвыборке IV почти равно (рис. 2d). Нелегко подтвердить карликов и гигантов, идентифицированных двумя полосами , J и V, для подвыборок Ia и Ib с диаграммой зависимости поверхностной силы тяжести от цвета (рис.5). Хотя 95% из звезд в подвыборке Ia (log g≤3, J − H≤0,4) занимают карликовую полуплоскость , их поверхностная сила тяжести мала. Это почти то же самое для звезд в подвыборке Ib (3 поверхностной силы тяжести имеют верхний предел log g = 3,5. Большинство звезд в подвыборке Ic (J − H≤0,4, 3,5 изохрон, что указывает на то, что они скорее субгиганты , чем карлики.Следовательно, мы должны добавить еще одну процедуру к процедуре Bilir et al. (2006), чтобы отделить субгигантов от карликов и гигантов. 4.3 Число звезд для разных популяций оценивается с использованием модели Галактики Мы используем модель Галактики Безансон (Робин и др., 2003) для оценки количества звезд для разных популяций (т. Е. Карлика, субгиганта и гигант) в нашей выборке. Мы сравниваем их с полученными с использованием процедуры Bilir et al.(2006). Модель синтеза звездного населения Галактики Безансон представляет собой инструмент моделирования, используемый для проверки сценариев эволюции Галактики путем сравнения звездных распределений , предсказанных этими сценариями, с наблюдениями, такими как фотометрические C 2011 Авторы, MNRAS 418, 444–455 Ежемесячные уведомления Королевского астрономического общества C 2011 RAS Загружено с https://academic.oup.com/mnras/article-abstract/418/1/444/962782 гостем 10 сентября 2018 г. Патагония стала означать «Страна Большоногих», но это миф, что был домом гигантских человеческих существ В Южной Америке живут две из самых больших популяций карликов в мире Бернар o Уссе был первым ученым в Латинской Америке, удостоенным Нобелевской премии Хосе Дантас де Соуза Лейте получил международное признание благодаря своему вкладу в первоначальное описание Акромегалии Цель Данная статья представляет собой исторический обзор гигантов и карликов, живущих в Южной Америке, и вклад южноамериканских исследователей в научные достижения в области гормона роста (GH) и заболеваний человека, связанных с избытком GH и дефицитом GH (GHD).Мы вернулись в прошлое, чтобы исследовать факты и мифы, вытекающие из бесчисленных сообщений о гигантах, которые жили в регионе Патагония, сосредоточив внимание на том, что в настоящее время известно о гигантизме в Южной Америке. Кроме того, мы рассмотрели исключительную работу, выполненную в двух крупнейших в мире когортах карликовости, связанных с осью GH-IGF: одна из них живет в Итабаианинья, Бразилия, страдает тяжелым GHD из-за мутации рецептора GHRH ( GHRHR ). ген, и другие, живущие в провинциях Эль-Оро и Лоха в Эквадоре, которые являются носителями мутации гена рецептора GH, вызывающей полную нечувствительность к GH (синдром Ларона).Важно отметить, что мы представляем обзор выдающегося медицинского вклада Хосе Дантаса де Соуза Лейте, бразильского врача, описавшего первые случаи акромегалии, и Бернардо Альберто Хусая, аргентинского исследователя, удостоенного Нобелевской премии, который был одним из первых ученых, получивших Нобелевскую премию. установить связь между GH и метаболизмом глюкозы. Гигантизм Акромегалия Карликовость Дефицит гормона роста Синдром Ларона Изолированный дефицит гормона роста, тип II История медицины Рекомендуемые статьи Поиск Поиск Поиск У слонов глаза маленькие, пропорциональные размеру их головы: довольно сложно найти их глазницы по бокам черепа.Напротив, их большая носовая полость прямо в центре их лба, отверстие, в котором начинается их хобот, очень очевидно. На Сицилии когда-то жили два вида слонов: Elephas falconeri , вымершие полмиллиона лет назад, и Elephas mnaidriensis , обитавшие на острове до 40 миллионов лет назад. Они были небольшого размера: первый был около метра в высоту, а второй — не более двух метров. Слоны прибыли на Сицилию по суше, когда уровень Средиземного моря упал на много метров во время последнего ледникового периода.Затем, когда уровень моря снова начал подниматься, слоны, выброшенные на остров, продолжали размножаться, но по мере смены поколений их становилось все меньше: это явление, хорошо известное в биологии, называется островной карликовостью . Для крупных видов, прибывающих на остров, может быть выгодно становиться меньше по мере того, как поколения следуют друг за другом, чтобы оптимизировать ограниченные ресурсы ограниченной окружающей среды. Более того, отсутствие крупных хищников, которым нужны огромные охотничьи территории, помогает сделать сверхбольшие размеры излишними как средство защиты.Островная карликовость характерна не только для слонов: Флорес — небольшой остров, принадлежащий вулканическому архипелагу Зунда в Индонезии. Люди, живущие на Флоресе в деревне Рампасаса, крошечные, их средний рост составляет 145 сантиметров. В 2003 году в пещере недалеко от Рампасасы были найдены очень интересные окаменелые человеческие останки. Это был частичный скелет гоминина ростом едва ли один метр и с плоскостопием. Сразу же в шутку идентифицированный как один из хоббитов, о которых писал Толкин, человек Флореса не является предком пигмеев, живущих в настоящее время на острове: Homo floresiensis принадлежит к другому виду, обнаруженному совсем недавно, обитающему на Флоресе до 17 тысяч человек. много лет назад.Это были маленькие люди, не выше современного ребенка в возрасте около четырех лет, но они уже могли разжигать огонь, создавать каменные орудия и обращаться с ними для охоты и разделки животных, которые зачастую были крупнее их. Комодский дракон Островная карликовость часто сопровождается противоположным явлением: островной гигантизм , который, напротив, определяет огромные размеры животных, которые на континенте обычно малы. На острове, где нет крупных хищников, маленькие размеры излишни, потому что нет необходимости убегать от когтей и бивней, прячась в норах.По этой причине на некоторых островах можно встретить гигантских животных, таких как галапагосские черепахи и драконы Комодо. Большинство островных гигантов вымерли, когда сюда прибыли люди со своими домашними хищниками: собаками, кошками и крысами. Однако карлики больших размеров, такие как гигантская крыса Тенерифе, размером с кролика, и гигантский лемур на Мадагаскаре, размером с гориллу, когда-то были очень распространены. Было время, когда на Сицилии тоже жили гиганты. Это были циклопы, дети Гайи, богини-матери-Земли, и Урана, бога-отца-Неба, и они были кузнецами, живущими ниже горы Этна, где они выковали молнии для Зевса и Гефеста, бога огня и обработки металлов.Основной характеристикой циклопов, помимо гигантизма, был единственный глаз в центре лба. Они не были дикими и примитивными, именно так их описал Гомер: его Полифем был жестоким гигантом, пещерным пастухом, неравнодушным к поеданию людей. От карликов до гигантов: вклад Южной Америки в историю гормона роста и связанных с ним заболеваний
Основные моменты
Аннотация
Ключевые слова
Рекомендуемые статьи
Ссылки на статьи
Перейти к основному содержанию
Поиск
Быстрый поиск где угодно
Пропустить основную навигацию Закрыть меню ящика Открыть меню ящика Домой Тарифы, заказы
и платежи
Карлики и гиганты островов
Карлики и гиганты островов

И поэтому запятая: «Поэтому»: запятая нужна или нет?
запятые — Нужна ли запятая после «поэтому»? (2)
Поэтому когда речь заходит об обновлении, подразумевается вовсе не обновление, а обновление нашего понимания.
В данном предложении запятую после наречия поэтому не ставим, так как переставить придаточное нельзя (у него здесь фиксированная позиция).
По смыслу текста придаточное должно стоять на первом месте (идет повтор слов: об обновлении, но подразумевается не обновление…).
В других же случаях постановка запятой после наречия поэтому перед союзом факультативная, например:
Поэтому, когда Тома была маленькой, она была уверена, что Павел Алексеевич любит её больше, чем Таню. [Людмила Улицкая. Казус Кукоцкого 2000]
Поэтому, когда осенью 1984 года в Большом театре был организован вечер памяти великого певца, снова был аншлаг. [И. К. Архипова. Музыка жизни (1996)]
И поэтому когда Христос даёт нам заповедь, Он нам не только указывает, что делать; [митрополит Антоний (Блум). О жизни христианской (1990)]
О жизни христианской (1990)]
ДОПОЛНЕНИЕ 1
1) Мне кажется некорректной такая перестановка: Поэтому подразумевается вовсе не обновление, а обновление нашего понимания, когда речь заходит об обновлении.
2) Но есть еще зависимость от контекста, для окончательного решения нужен фрагмент текста.
3) Обратите внимание на вставочную интонацию при обособлении придаточного: ударение на наречии, выделение придаточного паузами, произношение с понижением тона: ПоЭтому, когда речь заходит об обновлении, подразумевается вовсе не обновление, а обновление нашего понимания.
4) Если Вас всё это устраивает, то вы можете принять свое авторское решение обособить придаточное, правилами это не запрещено. К сожалению, у Розенталя нет примеров СПП с эти наречием.
ДОПОЛНЕНИЕ 2
Хотелось бы подробнее раскрыть тему о факультативности обособления придаточного после наречия поэтому.
Скорее всего, здесь надо учитывать ряд факторов, а не только формальную перестановку придаточного. Многое зависит от структуры предложения, а также от предыдущего текста.
При обособлении мы дополнительно выделяем придаточное предложение в отдельную структуру, а всегда ли нужно такое дробление? Предложение может и так состоять из нескольких фраз, придаточное в них просто затеряется. Если это уточнение, то хорошо, а если нет? Тогда важные отношения между прждложениями могут уйти с первого плана.
Надо ли выделять ударением наречие, что неизбежно при обособлении? Если до этого подробно раскрывалась какая-то тема, то наречие укажет на нее, тогда это положительный момент, а если нет, то такая ударная позиция будет казаться неоправданной.
В целом это действительно факультативное решение, рассчитанное на интуицию автора, и тогда важной становится ориентация на интонацию. Прочитайте предложение дважды в разных вариантах. Правильным будет тот, который обеспечивает легкое прочтение и быстрое понимание текста.
Прочитайте предложение дважды в разных вариантах. Правильным будет тот, который обеспечивает легкое прочтение и быстрое понимание текста.
ставится ли запятая перед или после слова
Многим непонятно, где ставить знаки препинания в контекстах с выражением «поэтому». В первую очередь стоит определить, какая это часть речи.
Нормативные источники относят слово «поэтому» к наречиям (местоименным). Неправильно считать его союзом, т.к. эта часть речи не выражает обстоятельственное значение. Не является выражение и союзным словом, потому что не включено в ряд местоименных слов вопросительного типа («каков», «откуда», «отчего» и др.).
Значит, «поэтому» – это аналог союза, который должен писаться слитно.
Вопрос, какой связью соединены такие предложения – подчинительной, сочинительной или бессоюзной, – остаётся дискуссионным. Тем не менее, большинство лингвистов считает, что это бессоюзная связь.
Когда запятая нужна
Правила пунктуационного оформления:
Перед лексемой «поэтому» ставится запятая, если она объединяет два и более простых предложения в сложной синтаксической конструкции, находясь на стыке частей. Примеры:
Примеры:
Когда лексеме предшествуют обособленные обороты (деепричастные, уточняющие), вводные сочетания или союзы, то запятая уместна после слова «поэтому». Примеры:
«Поэтому» реже может выступать обособленным обстоятельством, если автору важно объяснить причину. Пунктуационные знаки (тире, скобки) ставятся с двух сторон:
- Владислав мечтает стать профессиональным баскетболистом. И, поэтому, он каждое утро бегает, а потом выполняет сложный комплекс упражнений.
Требуется запятая перед «и поэтому», «и именно поэтому», если эти сочетания объединяют простые предложения в составе сложного:
- Женя хотел скрыть от друзей своё горе, и именно поэтому он долго избегал разговоров с ними.
Если фраза сочетается с союзами, которые относятся к подчинительным («когда», «если» и т.д.), то между ними и «поэтому» запятая уместна при логическом выделении слова.
Сравним:
- Поэтому, чтобы тебя любили, надо отдавать тепло взамен (выделяется действие).
- Поэтому чтобы прийти вовремя, необходимо встать в шесть часов (выделяется причина).
Когда запятая не нужна
Нередко выражение «поэтому» выделяют как вводное, но это неправильно. При обычных условиях оно обособляться не должно.
В начале и середине высказывания обстоятельство знаком не отделяется. Примеры:
Запятая перед «именно поэтому» и «и поэтому» не требуется, если эти фразы разделяют:
Однородные члены:
- Мария Ивановна была влюблена и поэтому глупа.
Простые синтаксические конструкции или однородные придаточные, которые имеют одну общую фразу (вводное сочетание или второстепенный член):
- Несомненно, мы хорошо выступили и именно поэтому организаторы мероприятия пригласят наш коллектив ещё.

Обособление в паре с другими словами
- Андрей заболел. Поэтому я считаю, что на день рождения он не придёт.
- Возможно, поэтому мама так и не смогла стать счастливой по-настоящему.
Примеры
«В основном» выделяется запятыми или нет?
Перед «в основном» ставится запятая, если это слово входят в присоединительный оборот. Чаще всего «в основном» не является вводным словом и не выделяется запятыми.
Чтобы узнать, требуется ли ставить запятую перед или после слова «в основном», определим его роль в предложении.
«В основном» не выделяется запятыми
Рассмотрим высказывание, в котором употребляется интересующее нас слово:
В течение дня ему приходилось в основном отвечать на звонки потенциальных клиентов.
Исследуемое слово не изменяется. В контексте оно зависит от глагола и обозначает обстоятельство, при котором совершается действие:
В контексте оно зависит от глагола и обозначает обстоятельство, при котором совершается действие:
приходилось отвечать как?
В предложении оно является полноправным членом предложения — обстоятельством. Это грамматические признаки самостоятельной части речи наречия. Это наречие не является вводным словом, так как грамматически связано со сказуемым. Поэтому нет никаких оснований выделять его запятыми ни вначале, ни в середине предложения.
Вывод
Слово «в основном» не является вводным, поэтому запятые не ставятся.
Примеры
В основном в этой деревне живут старики, а вся молодежь давно в городе.
По вечерам с детьми она в основном занималась английским языком.
На этой выставке представлены в основном работы художников прошлого века.
Укажем случаи, когда перед этим словом ставится запятая.
Перед «в основном» ставится запятая
Постановка запятой перед рассматриваемым словом возможна в том случае, если оно входит в присоединительный оборот.
На празднике города в легкоатлетическом забеге приняли участие многие горожане, в основном люди среднего возраста.
В этом высказывании сообщается о горожанах, которые участвовали в забеге, а затем уточняется их возраст с помощью присоединительного оборота, который начинается с исследуемого слова. Согласно правилу пунктуации обособляются слова и словосочетания, содержащие дополнительные замечания или разъяснения к тому, о чем ведется речь.
Вывод
Запятая ставится перед словом «в основном», входящим в присоединительный оборот.
Присоединительный оборот, как правило, находится в конце высказывания. Если предложение сложное, то оборот может оказаться в середине предложения и тогда с обеих сторон выделяется запятыми.
Примеры
Дожди пошли только в конце июля, в основном в последние два дня.
На столе стояло нехитрое угощение, в основном соленые огурцы, квашеная капуста и картошка.
Скачать статью: PDFВ этом краю много озер и речушек, в основном быстрых, с холодной водой, которая по вкусу не хуже родниковой.
| |||||||||||||||||||||||||||||||||||||||
| Top of Page | Разработано LiveJournal.com | ||||||||||||||||||||||||||||||||||||||
6 слов и сочетаний, после которых нужно ставить запятые (но не всегда!)
Вы, наверное, не раз замечали, что одни и те же слова в одних случаях могут выделяться запятыми, а в других (на первый взгляд очень похожих) — не обособляться. В новом выпуске разбираемся как раз с такими словами и сочетаниями: «наконец», «таким образом», «вообще», «правда» и другими.
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
Правда иногда бывает жестокой, но принимать её приходится — ничего не поделаешь. Так и с этим словом. Дело в том, что в предложении оно может играть три разные роли: быть вводным словом, частицей или союзом со значением уступки. Давайте разбираться.
«Здесь правда не нужна запятая?» — задаём мы вопрос в первом примере. Правда: в качестве частицы слово употребляется в значении «действительно» для выражения уверенности («Мне правда очень понравился подарок») или в вопросе, который требует подтверждения (как в нашем примере). В этих случаях запятыми оно, конечно, не выделяется.
Как вводное слово его употребляют в значении «не правда ли?» («Правда, отличные были выходные?») или в функции уступительного союза («Мне понравился подарок, правда, это не совсем то, что я хотел»). И тут уже запятые спешат на помощь.
На всякий случай обратим ещё раз ваше внимание на предложение про жестокую правду. Здесь «правда» — существительное, но его, надеемся, вы ни с чем не перепутаете.
Извините, что мы снова про жестокую правду, но, возможно, так правило запомнится лучше. Если сомневаетесь, нужно ли выделять запятыми слово «вообще», попробуйте мысленно заменить его на «вообще говоря». И если это легко получается, скорее всего, перед вами вводное слово: «Вообще, сидеть дома мне уже надоело».
В значениях «в общем, в целом» и «совсем, при всех условиях» обособлять запятыми слово не нужно: «В этом году учителя вообще не отдохнут». А ещё слово может быть междометием. Но тут вы его точно узнаете, потому что в этом случае оно выделяется как отдельное предложение: «Ну и времена настали! Вообще!»
Слово «наконец» тоже нужно выделять запятыми не всегда. Если оно указывает на то, что слово или выражение, которое идёт за ним, завершает мысль или станет последним, — вы имеете дело с вводным словом, которому очень нужны ваши запятые (второй пример у нас). А ещё его используют для выражения недовольства или нетерпения: «Приходи же в гости, наконец!»
Если же слово используется в значении «под конец», «в конечном итоге», «напоследок», оно не вводное и запятыми выделять его не нужно: «В августе выпускники наконец смогут расслабиться».
Согласны, есть случаи, когда сложно определить, будет ли это слово вводным. Зато в справочнике Розенталя можно найти отличную подсказку: попробуйте добавить частицу «-то» — в большинстве случаев с вводным словом это проделать не удастся.
Похожая ситуация с сочетанием «в конце концов». Если оно выражает нетерпение, недовольство или относится к какой-то заключительной мысли, — значит, сочетание вводное: «Я, в конце концов, два года не был за границей» или «Главное, в конце концов, что все живы и здоровы».
Если же сочетание используется в значении «в завершение, напоследок, после всего», оно не вводное и выделять запятыми его не нужно: «В конце концов мы решили поехать на море».
Ещё одно сложное слово в плане запятых — «значит». Если удаётся заменить его в предложении на «следовательно», «стало быть» — перед вами вводное слово: «Ты, значит, к нам ненадолго?» Ещё оно может соединять части предложения, выступая в роли союза: «Рюкзак небольшой — значит, он к нам ненадолго», «Небо звёздное — значит, завтра будет ясно». В этих случаях слово по значению близко к вводному и поэтому тоже выделяется запятыми.
В этих случаях слово по значению близко к вводному и поэтому тоже выделяется запятыми.
Что касается первого примера, то запятая в нём не нужна. Здесь сказуемое выражено неопределённой формой глагола, а «значит» используется в значении «это, есть» для связки подлежащего и сказуемого. В таком случае перед «значит» всегда ставится тире.
Нет, мы не ошиблись на картинке. Это действительно два одинаковых предложения, в одном из которых сочетание «таким образом» обособляется, а в другом нет. Рассказываем, в чём подвох.
В первом случае оно используется в значении «так, таким способом» — запятые тут не нужны. Во втором предложении это уже вводное сочетание со значением «итак» — то есть его используют, чтобы обозначить, что в предложении есть вывод, следствие того, о чём шла речь раньше. Согласны, случай сложный, зато шансы ошибиться близятся к нулю.
Запятая перед «и»: правила и примеры
Союзы сами по себе не являются поводом для употребления (или отсутствия) запятой. Поэтому соединительный «и» вызывает немало сомнений – нет единого правила, как для союзов «а», «но». В каких-то случаях запятая перед «и» нужна, в каких-то ее постановка неверна. Чтобы не запутаться, нужно запомнить несколько пунктуационных правил.
Поэтому соединительный «и» вызывает немало сомнений – нет единого правила, как для союзов «а», «но». В каких-то случаях запятая перед «и» нужна, в каких-то ее постановка неверна. Чтобы не запутаться, нужно запомнить несколько пунктуационных правил.
Когда нужна запятая
Первым делом нужно обозначить случаи, когда запятая перед «и» необходима:
- Простое предложение с перечислением, однородными членами. В каком случае перед «и» ставится запятая? Перед повторяющимся союзом: «и звери, и птицы, и люди радовались ранней весне».
- Сложноподчиненное предложение. Когда перед «и» ставится запятая? В тех случаях, если союз стоит перед однородными придаточными предложениями. «Я вспоминаю, и как мы познакомились, и как вместе съездили на Байкал, и как устраивали друг другу сюрпризы без повода».
- Сложносочиненное предложение. Когда перед «и» ставится запятая? Она обязательна между его частями: как с повторяющимся «и», так и с одиночным союзом. «Я увидел друга на набережной, и он меня заметил».
 «И я увидел друга на набережной, и он меня заметил».
«И я увидел друга на набережной, и он меня заметил». - Всегда нужна запятая перед «и», если он повторяющийся. В случае с ССП необходимо запомнить, что в большинстве случаев простые предложения всегда будут отделены друг от друга запятыми.
Когда запятая не нужна
Случаев, когда запятая перед «и» не требуется:
- Однородные члены простого предложения. Если союз один-единственный, запятая не нужна: «В музее мое внимание привлекло обмундирование римских легионеров и предметы быта варягов».
- Пары однородных конструкций в простом предложении. Союзы «и» могут повторяться: если они соединяют по два слова, запятые нужны только между парами. «Солнце и жара, море и песок, пляж и горы ждали нас на Крымском побережье».
- Обобщающее слово в составе сложносочиненного предложения. В ССП может быть употреблено общее слово для входящих в него простых предложений (чаще всего это обстоятельство). При его наличии запятая не нужна: «Вчера солнце светило ярко и облака не застилали небо».

- Вводное слово или предложение в ССП. Соблюдается та же логика, что и в случае с обобщающим словом. «К счастью, ценные экспонаты не сгорели и дорогостоящее оборудование не было повреждено». «Как мне рассказал брат, уже поспевает виктория и созрела жимолость».
- Сложносочиненное предложение с вопросительным или восклицательным знаком. Если поставлен «?» или «!» в конце ССП, между составляющими его предложениями, соединенными «и», запятая не нужна. «Кто этот путник и откуда он явился?» «Будет победа и воцарится мир!»
- Сложносочиненное побудительное предложение. Запятая перед «и» не требуется в случае, если эта конструкция состоит из двух простых предложений. «Пусть скорее уйдут тучи и закончится дождь».
- Назывные и безличные предложения в составе сложного. Если таких предложений, соединенных «и», не больше двух, запятая между ними не нужна. «Жара и солнце». «Необходимо заранее занять место и нужно доложить о своем визите».
- Однородное соподчинение в СПП. Запятая не нужна при соединении «и» двух простых зависимых предложений. Придаточные в таком случае схожей конструкции, отвечают на одинаковый вопрос. Еще одно условие: союз «и» не должен быть повторяющимся. «Он представлял, как поступит в институт и как будет жить в большом городе».
Данные правила запятых перед «и» требуется запомнить.
Если рассуждать логически, она не требуется в случаях, когда сложное предложение по своей структуре начинает напоминать простое с однородными членами. Тогда в его отношении действуют практически аналогичные пунктуационные правила.
Простое предложение
Правила запятых перед «и»: они не нужна в случае, когда союз единственный, больше не повторяется во фразе. Примеры:
- «Я купила яблоки, груши и сливы».
- «Наташа и Толя играют во дворе».
- «Мне нужно было сделать салат и сварить суп».
- «Вчера мы получили хорошие отметки по математике, обществознанию и химии».
- «Для своей коллекции он покупал, обменивал и ремонтировал старые телефоны».
- Когда перед «и» ставится запятая? Понадобится она только при повторении союза:
- «Мы купили и груши, и сливы, и яблоки».
- «И Наташа, и Саша, и Толя играют сегодня во дворе».
- «Мне нужно было и сварить суп, и сделать салат».
- «Вчера мы получили оценки и по математике, и по химии, и по обществознанию».
- «Для своей коллекции он и обменивал, и покупал, и ремонтировал старые телефоны».
Ставится ли запятая перед «и»? Запятой не будет только перед первым союзом. Перед всеми последующими, вне зависимости от их количества, она нужна.
Сложносочиненное предложение (ССП)
Запятая перед и после «и»: по основному правилу русского языка части сложных предложений отделяются друг от друга запятыми. Соединительный союз «и» не должен смущать.
Запятая перед ним не нужна только при одиночном соединении однородных конструкций простого предложения. В сложном она ставится обязательно (кроме случаев с обобщающими, вводными словом, вопросительными и восклицательными знаками, которые нужно запомнить).
Запятые в сложных предложениях перед союзом «и»:
- «Начиналась гроза, и вдали слышались раскаты грома». Два простых предложения: «Начиналась гроза. Слышались раскаты грома».
- «Наша команда проиграла, и сегодня мы снова встречаемся на поле с победителями». Запятая перед «и» в сложносочиненном предложении соединяет два простых предложения.
- «Я сегодня сделала много дел, и мама тоже была весь день занята». Почему перед «и» ставится запятая? Два простых предложения в составе сложносочиненного – требуется разделить их знаком препинания.
- «Костя быстрее других ребят справился с заданием, и учительница предложила ему решить более сложную задачку». «Костя справился» и «учительница предложила» — основы простых предложений. Запятая в сложносочиненном предложении перед союзом «и» нужна.
- «Он поделился с товарищем своими мыслями, и это помогло им избавиться от всех недомолвок». «Он поделился», «это помогло» — основы простых предложений в составе сложносочиненного – требуется запятая перед «и».
Так же, как и с однородными членами в простом предложении, требуется запятая перед «и» в сложном предложении при двукратном, многократном повторении союза:
- «И солнце светит, и птички поют, и на улице тепло».
- «И я не знал решения этой задачи, и мои друзья не помнили эту тему».
- «И времени не хватало, и новые возможности не появлялись».
Перед «и», соединяющим простые предложения в составе сложносочиненного, не нужна запятая в случае, когда эти конструкции объединены обобщающим словом. Пример: «К вечеру ожила рассада томатов и подняли свои бутончики пионы».
Нет запятой, потому что употреблено обобщающее слово «к вечеру». Оно объединяет два предложения: «к вечеру ожила рассада томатов» и «к вечеру подняли свои бутончики пионы». Поэтому запятая перед «и» между этими простыми предложениями в составе ССП не нужна.
Другие примеры:
- «С утра разразилась гроза и задул шквалистый ветер» (простые предложения объединяет «с утра» — запятая не нужна).
- «Сегодня мы сдали экзамен по математике и прошли тест по русскому языку» (есть объединяющее слово «сегодня», поэтому запятая перед «и» в сложносочиненном предложении не требуется).
- «Перед рассветом небо порозовело и появились оранжевые облачка» (простые предложения в ССП объединяет обстоятельство «перед рассветом» — нужно поставить знак препинания).
Когда перед союзом «и» ставится запятая? В примерах с ССП обязательно проверяют предложение на наличие обобщающего слова. Если его нет, то запятая нужна обязательно: как перед одиночным «и», так и перед повторяющимися.
Сложноподчиненное предложение
В такой синтаксической конструкции «и» соединяет схожие по структуре придаточные предложения. Если он единственный, то запятая перед союзом «и» не нужна:
- «Я заметил, как появились новые книги и как обновилась коллекция журналов».
- «Петр Васильевич забыл, что Антон Степанович нашел здание для клуба и что Сергей Васильевич на свои деньги купил оборудование».
- «Ему показалось, будто лес преклонился и будто трава расступилась».
- «Сегодня мы изучим, как делать хорошие снимки при ярком солнце и как обрабатывать вечерние кадры».
- «Мы понимаем, насколько тяжело было одобрить этот проект и насколько сложно воплотить его в жизнь».
Когда в предложении перед «и» ставится запятая? Придаточные конструкции в таком случае схожи друг с другом по структуре, напоминая однородные члены в составе сложного предложения, а союз повторяется два или более раз.
Запятая перед союзом «и» нужна:
- «Я сразу же заметил, и как появились новые энциклопедии, и как обновилась коллекция периодических изданий».
- «Петр Васильевич позабыл, и что Антон Степанович нашел отличное помещение для клуба, и что Сергей Александрович на собственные деньги купил мебель и технику».
- «Сегодня мы разберем, и как делать хорошие кадры при ослепительном солнце, и как ретушировать вечерние фото».
Когда перед союзом «и» ставится запятая? Тут опять же повторяется ситуация с однородными членами в простом предложении: если перед несколькими схожими конструкциями находится «и», они отделяются запятыми.
Запятая после «и»
Правил постановки запятой после союза «и» нет. Но есть случаи, когда знак препинания требуется, когда «и» выделяется с двух сторон запятой. Однако это не связано конкретно с союзом. Таким образом происходит выделение обстоятельств, определений, вводных слов, обособляются простые предложения в сложном.
Примеры случаев «запятая перед и после «и»»:
- «Я шла по берегу и, кажется, заметила чужой катер у дальнего берега». Запятыми здесь выделяется вводная конструкция «кажется».
- «Василий Иванович вышел из избы, и, когда он только подходил к забору, с огорода примчалась Жучка». Запятые здесь отделяют простые конструкции, составляющие сложное предложение. Запятые после «и» — это обособление придаточного «когда он только подходил к забору» (примчалась когда?).
- «Он снова не пришел на конференцию, и, понимаю, у него были веские причины пропустить это событие». Первая запятая отделяет простые предложения в составе ССП. Вторая – обособление конструкции «понимаю».
- «Мама купила свежие помидоры и, конечно же, не забыла взять оливковое масло для салата». Запятыми выделяется вводная конструкция «конечно же».
Когда ставить запятую перед «и»? Это соединительный союз, что не значит безусловно, что запятые перед ним не нужны. Они обязательны перед повторяющимся «и», между частями ССП. Есть случаи, когда постановку запятой нужно запомнить: в вопросительных и побудительных предложениях, при обобщающем слове или вводной конструкции. После «и» запятая нужна в случае, если за союзом следует конструкция, которую необходимо обособить.
Запятая перед союзом «И»
Cтраница 1 из 2
Союз «и» может соединять, во-первых, однородные члены предложения, во-вторых, простые предложения в составе сложного.
Чтобы правильно поставить запятую перед союзом «и», необходимо отличать структуру сложносочиненного предложения от простого предложения с однородными сказуемыми или подлежащими. Поэтому сначала напомним определения простого и сложносочинённого предложений.
Сложносочиненное предложение – предложение, в котором две и более грамматических основ связаны сочинительными союзами (например, и, а, но, однако, или и т.д.)
Простое предложение – предложение с одной грамматической основой.
Предложение с однородными сказуемыми, которые образуют сочинительную связь, не являются сложными.
Например: Жара и усталость взяли, однако ж, свое, и я заснул мертвым сном (две основы, сложносочиненное предложение). Огромная и ослепительно яркая луна стояла уже над горою и ясным зеленоватым светом заливала город (одна основа – подлежащее и два относящихся к нему сказуемых, простое предложение).
Запятая СТАВИТСЯ, если союз «И»
1) при однородных членах повторяется.
Например: А березка мила и при солнце, и в серый день, и при дожде.
2) связывает больше двух однородных членов.
Например: В лесу одному шумно, и жутко, и грустно, и весело.
Запятая НЕ СТАВИТСЯ, если однородные члены соединены попарно (отделяются друг от друга пары).
Например: На Крите жили привольно и весело, нараспашку и не таясь.
Постановка запятой перед союзом «И», соединяющим простые предложения в составе сложного.
Запятая СТАВИТСЯ, если
1) соединяются простые предложения в составе сложносочинённого: [ ], и [ ].
Например: Надвигалась гроза, и тучи заволокли всё небо.
2) после придаточной части предложения следует вторая часть двойного союза ТО, КАК или НО:
Например: Он носил тёмные очки, фуфайку, уши закладывал ватой, и когда садился на извозчика, то приказывал поднимать верх.
Изредка маленькая снежинка прилипала снаружи к стеклу, и если пристально вглядеться, то можно было увидеть её тончайшее кристаллическое строение.
Запятая НЕ СТАВИТСЯ, если
1) обе части сложносочиненного предложения имеют общий второстепенный член, чаще всего это обстоятельство места или времени, реже дополнение.
Например: Там (вот это общий второстепенный член) синь и полымя воздушней и легкодымней пелена.
У Ивана Ивановича (и это тоже он) большие выразительные глаза табачного цвета и рот несколько похож на букву ижицу
2) объединены два безличных предложения (то есть в предложении подлежащего нет), имеющие в своем составе синонимичные члены:
Например: Необходимо закутать горло шарфом и надо попытаться прополоскать его содой.
3) общее придаточное предложение.
Например: Если бы не было дождей, вся зелень давно высохла бы и земля лежала бы в морщинах и трещинах.
4) общее главное предложение.
Например: Ласточка простилась с Дюймовочкой, как только солнце пригрело и земля растаяла.
5) общее вводное слово (чаще всего это слово, указывающее на одинаковый для обеих частей источник сообщения.
Например: Словом, время уже истекло и пора было уже уходить. Вопреки всем предсказаниям синоптиков, небо уже прояснилось и дождь перестал.
6) объединены два вопросительных, побудительных, восклицательных или назывных предложения.
Например: Где же твоя деревня и ждут ли нас там?
Пусть кончится зима и наступят теплые деньки!
Важно!
В случаях постановки запятой перед союзом «и», соединяющим ПРОСТЫЕ ПРЕДЛОЖЕНИЯ В СОСТАВЕ СЛОЖНОПОДЧИНЁННОГО, логика постановки знака такая же, как при однородных членах.
Например: Чудилось, будто корчуют сразу весь лес и земля стонет от боли. (союз «и» одиночный)
Он вспоминал, как фашисты напали на них внезапно, и как они оказались в окружении, и как отряду все же удалось пробиться к своим. (союз «и» повторяется)
К сожалению, разделение правил на пунктуацию при однородных членах предложения, знаках в сложносочиненном предложении и работе со сложным предложением, включающим однородные придаточные, приводит к неумению многих заканчивающих курс русского языка ориентироваться в том, как и когда применяется то или иное правило. К тому же теоретические знания часто не позволяют правильно разобраться, какое из правил необходимо применить, поэтому даже при знании правил не все школьники способны употреблять их к месту и адекватно.
Поэтому мы предлагаем вам еще один путь усвоения данной пунктограммы, который был обозначен Николенковой Н.В.: идти от «внешних» признаков организации предложения, то есть от количества использованных союзов «и». Мы считаем, это позволит немного упростить работу по правильной расстановке знаков препинания.
Перейдите на вторую страницу по этой теме
НачалоПредыдущая 1 2 Следующая > Последняя >>
запятых с соединительными наречиями | AJE
Обычно мы думаем о наречиях как о модификаторах, но соединительных наречия представляют собой особую породу. Их функция — не изменять, а соединять. Таким образом, конъюнктивное наречие — это наречие, соединяющее два предложения. Конъюнктивные наречия показывают причину и следствие, последовательность, контраст, сравнение или другой тип отношений.
Примеры конъюнктивных наречий:
| соответственно, | кроме того, | кроме того, | аналогично, |
| также, | следовательно, | а именно, | по-прежнему, |
| в любом случае, | тем не менее, | тогда, | |
| далее, | кстати, | далее, | после этого, |
| конечно, | действительно, | тем не менее, | следовательно, |
| следовательно, | вместо этого, | между тем, | таким образом, |
| наконец, | аналогично, | в противном случае, | несомненно, |
Конъюнктивные наречия как вводные
Конъюнктивные наречия часто используются как вводные термины ; в этом случае после этих слов следует поставить запятую для ясности: Следовательно, всех подопытных животных были повторно обследованы.
Эта ситуация также применима к случаям, в которых конъюнктивное наречие является вводным словом второго независимого предложения: Джо забыл свои кроссовки , и, следовательно, он не мог участвовать в гонке. В этом предложении первая запятая используется для отделения первого независимого предложения от второго независимого предложения, а вторая запятая необходима после вводного слова , следовательно, . Вам не нужна третья запятая между и и , следовательно, .
Обратите внимание, что этот пример также можно записать следующим образом: Джо забыл свои кроссовки ; следовательно, он не мог участвовать в гонке. Использование точки с запятой для разделения двух независимых предложений часто предпочтительнее, когда второе предложение начинается с вводных наречий, таких как , таким образом, , , следовательно, , , но и действительно . Будьте осторожны, чтобы не ставить запятую при соединении двух независимых предложений конъюнктивным наречием:
- Неверно:
- Игра была почти проиграна, но наша команда забила гол.
- Игра была почти проиграна, но наша команда забила гол.
- Правильно :
- Игра была почти проиграна; Однако наша команда забила гол.
Другое применение
Когда конъюнктивные наречия не используются в качестве вводных слов, расстановка запятых зависит от того, является ли слово ограничивающим или существенным для значения; то есть, требуется ли слово для передачи правильного значения, или предложение останется нетронутым, если слово будет удалено? Если слово носит ограничительный характер, использовать запятые не следует; если слово неограниченное, запятые обязательны.
Вот пример, в котором , следовательно, является существенным по смыслу предложения: Студенты обманули и были , следовательно, дисквалифицированы. В этом предложении дисквалификация является прямым следствием мошенничества. Если бы , следовательно, было опущено, было бы неясно, связаны ли эти две проблемы.
Вот пример, в котором , следовательно, служит больше из в сторону или паузу : Все подопытные животные , следовательно, были повторно исследованы. В данном случае , следовательно, ограничено запятыми, чтобы отделить его от остальной части предложения и дать читателю паузу. Обратите внимание, что в этом предложении точка с запятой не нужна, потому что это не сложное предложение. В этом примере, если , следовательно, было перемещено и помещено в глагол , было повторно исследовано , оно будет рассматриваться как существенное (ограничивающее) наречие и не требует запятых: Все подопытные животные были , следовательно, повторных. -проверено.
Мы надеемся, что сегодняшняя статья расширила ваше понимание того, как использовать запятые с соединительными наречиями. Как всегда, с любыми вопросами пишите нам на [адрес электронной почты]. С наилучшими пожеланиями от AJE!
Поделитесь с коллегами
Как правильно ставить знаки препинания, следовательно, и более того
Как вы помечаете
, , , следовательно, и , а также ?Вопрос читателя: Я хотел бы знать правильную пунктуацию при использовании слов , тем не менее, и тем более.
Ответ: То, как вы расставляете эти слова, зависит от их положения и функции в предложении.
Мои рекомендации для таких слов, как , тем не менее, более того, следующие.
В начале предложения
Если вы используете эти слова в начале предложения, ставьте после них запятую.
Однако у нас все еще есть надежда.
Значит, приступим к заказу.
Причем менеджеры согласны.
Более того, вы знаете, что это правда.
Некоторые современные писатели теперь опускают запятую, но мне она все еще нравится, потому что она указывает на паузу.
Традиционное правило гласило, что , однако, , означающее «тем не менее», не должно использоваться в начале предложения. Большинство гидов по стилю считают это правило устаревшим.
В этой позиции предложения , но , , следовательно, , , а также и , следовательно, — наречия.
Объединение двух независимых статей
Используйте точку с запятой и запятую с , но , , кроме , , следовательно, и , а также , чтобы ввести новое независимое предложение в предложение. (Независимое предложение — это группа слов, которая содержит подлежащее и глагол и выражает законченную мысль.)
Мы планируем остаться еще на год ; однако Питер сейчас уезжает.
Вы получаете немедленный доступ при покупке онлайн-курса ; следовательно, вы можете начать сегодня.
Плавание не соответствует правилам ; кроме того, опасно.
Всегда соблюдает сроки ; кроме того, ее работа хороша.
Когда эти слова соединяют два независимых предложения, они известны как наречия союзы (или союзы наречий), потому что они являются наречиями, действующими как союзы.
Некоторые авторы сейчас трактуют , но , , следовательно, , m или и , кроме того, как союзы и просто используют запятую.
Планируем остаться еще на год, но Питер сейчас уезжает.
Я предпочитаю использовать точку с запятой и запятую или переписать предложение.
Планируем остаться еще на год , но Питер сейчас уезжает.
Планируем остаться еще на год . Однако , Питер сейчас уезжает.
Для усиления или для выделения
Когда вы используете , но , , а также , , а также или , следовательно, в качестве усилителей или акцентов, мы обычно ставим запятые по обеим сторонам от них.
Мы , однако не согласны с приговором.
Вы можете , следовательно, делать все, что хотите.
Это , притом правда.
Овощи , кроме того, полезны.
Однако как соединение
Вы также можете использовать , однако как союз, означающий «любыми средствами».
Меня не волнует , однако вы делаете это, просто сделайте это.
Подробнее о грамматике
Зарегистрируйтесь на мой онлайн-курс «Грамматика, пунктуация и употребление», чтобы узнать больше о грамматике.
И подпишитесь на мою ежемесячную электронную рассылку, чтобы получать советы по написанию и грамматике.
Следовательно, правила грамматики и пунктуации — Grammarist
Наречие , следовательно, следует использовать с осторожностью, так как оно часто находится в центре продолжающихся предложений. Следовательно, традиционно не считается союзом, поэтому он не может объединить два независимых предложения в одно предложение, как союзы, такие как и , , но и , потому что может. Например, следующие предложения являются повторением, потому что они используют , следовательно, как союз, вводящий независимое предложение:
Игроки были моими героями, поэтому мой отец был моим героем, потому что он был тренером. [расшифровано в Houston Chronicle]
Европейский центральный банк и сам ЕС не поставят под угрозу свое существование, поэтому они сделают все, что в их силах, для поддержания евро и, следовательно, платежеспособности Греции. [Wall Street Journal]
Тем не менее, у большинства людей меньше трудностей с выбором сети предпочтений, поэтому, безусловно, становится немного проще сузить выбор.[Заголовок новости]
Есть несколько способов исправить подобные предложения. Во-первых, сделайте предложение, начинающееся с , следовательно, отдельным предложением:
Игроки были моими героями. Поэтому папа был моим героем, потому что он был тренером.
Два, используйте точку с запятой вместо запятой:
Игроки были моими героями; поэтому мой папа был моим героем, потому что он был тренером.
Или три, добавьте союз, чтобы связать два независимых предложения:
Игроки были моими героями, и поэтому мой отец был моим героем, потому что он был тренером.
Но когда , следовательно, — наречие, оно отлично работает в середине предложения, например:
Дороги в Амстердаме более пустынны, и поэтому водители такси могут быстрее двигаться и маневрировать. [Calgary Herald]
Кэмерон находится под давлением со стороны правых тори за то, что он мягок, и поэтому пообещал более жесткие меры в отношении плохих парней из таблоидов. [Guardian]
Итак, они обсуждают, как они могут расположить его так, чтобы он служил максимальное время, тем самым уберегая его от улицы в будущем.[New York Daily News]
Следует ли начинать предложение со слова «поэтому»?
Когда вы пишете, поток может унести вас, и, прежде чем вы это заметите, вы сделали бы несколько глупых грамматических ошибок. Удивительно, но одна из наиболее распространенных ошибок часто случается в начале предложения.
Писатели часто спрашивают: «Могу ли я начать предложение со союза, числа или наречия?»
Многие из нас, возможно, выросли со строгими правилами, которые нам вручили, и именно поэтому возникает большая путаница.В этом посте мы рассмотрим, можно ли начинать предложение с наречия «, следовательно». И если вы это сделаете, будут ли последующие ужасные последствия?
Что именно значит?
Так как наречие , следовательно, работает, то наречие чаще встречается в центре предложения в виде прерывателя с запятой перед словом и после него. Это как-то работает аналогично соединению. Однако, в отличие от последнего, он не объединяет две независимые статьи.
Правильно: Следовательно, вы можете использовать это слово как прерыватель.
Однако , следовательно, также считается конъюнктивным наречием. Наречия описывают или изменяют глагол, и эта часть речи также делает то же самое с прилагательными, предлогами и союзами. Вы также должны помнить, что точка с запятой должна предшествовать конъюнктивному наречию, разделяющему два независимых предложения.
Прочтите больше сообщений в нашем блоге о других соединениях здесь .
Бегите от назойливых приговоров
Когда мы решаем использовать , следовательно, вместо обычного союза, мы получаем бесконечные предложения. Таким образом, при использовании вводит независимое предложение. См. Пример ниже:
Неправильно: Большинство собак приучены к туалету, поэтому им разрешено находиться в доме.
Это предложение можно исправить несколькими способами. Первый вариант — разместить , следовательно, в начале второго предложения (убедитесь, что после него стоит запятая).
Правильно: Большинство собак приучены к туалету. Поэтому их пустили в дом.
Если вы все еще не уверены в использовании , следовательно, в начале предложения, вы можете использовать точку с запятой и оставить предложение как единое целое:
Правильно: Большинство собак приучены к туалету; следовательно, им разрешили войти в дом.
Последний вариант — фактически использовать союз для связи двух независимых предложений следующим образом:
Правильно: Большинство собак приучены к туалету, и поэтому им разрешено находиться в доме.
Избегайте сращивания запятыми
Последний аспект при использовании , поэтому больше относится к его положению в центре слова. Часто, когда авторы помещают , следовательно, в предложение и путают его с координирующим союзом, возникает этот вопрос.
Неправильно: Писатель не спал всю ночь, чтобы закончить свою статью, поэтому он уложился в срок.
Здесь есть запятые по обе стороны от , следовательно, , что неверно.Это связано с тем, что каждое из предложений по обе стороны от , следовательно, является завершенным. Вместо этого вы можете начать второе предложение с .
Правильно: Писатель не спал всю ночь, чтобы дочитать статью. Таким образом, он смог уложиться в срок.
Дополнительные советы!
Также важно не запутаться в разнице соединительных наречий и координирующих союзов.Это больше проблема, когда союзное наречие появляется в середине предложения, когда следует использовать координирующий союз.
Использование , следовательно, вполне приемлемо, если вы используете правильную пунктуацию, хотя это может немного сбивать с толку, так как имеет разные применения. Вы можете поместить его в середине предложения с двумя запятыми, а также в начале предложения. Вам просто нужно убедиться, что предыдущее предложение по-прежнему актуально для второго.
Мы — компания по написанию контента, предоставляющая онлайн-компаниям платформу для покупки контента в Интернете. Теперь вы можете присоединиться к нашему пулу писателей, помочь нам предоставлять услуги по написанию контента нашим клиентам и в то же время решать грамматические трудности и совершенствовать себя как писатель. Зарегистрируйтесь сейчас и начните писать!
Когда использовать запятую перед «И»
Ставите ли вы запятую перед и , зависит от того, как вы используете и . Нет единого правила, применимого ко всем ситуациям.Обычно перед и ставится запятая, когда они соединяют два независимых предложения. Почти всегда необязательно ставить запятую перед и в списке.
Запятая перед
и в спискахМногие люди очень не любят ставить запятую перед и в списке. Трудно сказать, почему именно эта причуда использования запятой вызывает такие страсти; это просто одна из тех вещей. Если вы когда-нибудь слышали, чтобы кто-то спорил о последовательных запятых или оксфордских запятых , то это то, о чем они говорили.
Допустим, у вашей собаки столько замечательных качеств, что вам просто нужно рассказать миру. Когда вы перечисляете качества вашей собаки, вы должны ставить запятую после каждого качества, которое вы указываете , за исключением , которое стоит непосредственно перед и . Эта запятая не обязательна.Предложение правильное с запятой перед и или без нее. (Есть несколько исключений, которые требуют, чтобы вы использовали оксфордскую запятую в списке, но они довольно редки.) Просто будьте последовательны. Не переключайтесь в одном и том же документе между использованием оксфордской запятой и ее неиспользованием.
Кстати, это правило применяется только к спискам из трех и более пунктов. Не используйте запятую перед и , если вы упоминаете только два качества.
Это верно для имен собственных, обычных существительных, глаголов и всего остального.
Запятая перед
и , которая объединяет два независимых предложенияСлова и являются союзом, и когда союз объединяет два независимых предложения, вы должны использовать с ним запятую. Правильное место для запятой — перед союзом.
Приведенное выше предложение содержит два независимых предложения , поэтому перед и требуется запятая. (Между прочим, вы можете сказать, что это независимые предложения, потому что каждое из них может стоять само по себе как законченное предложение.)
Давайте посмотрим на другой пример.
И снова у нас есть два независимых пункта: На улице холодно плюс Я не могу найти свое пальто . Следовательно, нам нужна запятая перед и .
Не используйте запятую перед и , если одно из предложений, которое он связывает, является зависимым предложением .
Первое предложение, Сэм бросил мяч может стоять само по себе как законченное предложение, что означает, что это независимое предложение. Но второе предложение, наблюдало, как собака преследовала его , не может стоять само по себе как законченное предложение. Это означает, что это зависимое предложение, поэтому мы не должны использовать запятую перед и .
Исключения
Но подождите! Есть исключение. (Разве не всегда?) Когда у вас есть два независимых предложения, соединенных между собой и , большинство руководств по стилю говорят, что можно оставить запятую , если два независимых предложения очень короткие и тесно связаны между собой .Вот пример:
Нет ничего плохого в том, чтобы добавить запятую перед и в предложении выше, но это может сделать предложение немного прерывистым.
Хотите узнать о других способах использования запятой? Ознакомьтесь с нашим общим руководством по использованию запятых.
Знаки препинания с «однако» и «поэтому» — bigwords101
Действительно ли Декарт использовал здесь точку с запятой ??Слова , однако и , следовательно, являются наречиями. Однако (как вы можете видеть прямо здесь) они также соединяют слова, соединяя то, что идет прямо перед ними, с тем, что идет сразу после них.
Однако часто функционирует как конъюнктивное наречие , своего рода гибридной части речи! Согласно Вебстеру, , следовательно, — наречие, часто используемое с «соединительной силой».
Нет проблем, если эти два слова находятся в начале предложения. Обычно после них ставится запятая, и они относятся к предложению прямо перед ними:
Я провалил тест. Следовательно, придется брать еще раз.
Я сдал тест. А вот , в последний раз я его не взял.
Можно ли ставить перед ними точку с запятой, а не точку? Да, поскольку эти два предложения, скорее всего, будут тесно связаны, использование точки с запятой и строчной буквы также нормально:
Я провалил тест; значит , придется снова брать.
Я сдал тест; , однако, , когда в последний раз брал, не получилось.
Хорошо. Как насчет использования , следовательно, или , но в середине предложения и использования запятых вокруг него? Это правильно?
Иногда.По-разному. В приведенных выше примерах с точкой с запятой мы использовали , следовательно, и , однако в середине предложения; однако мы поставили перед ними точку с запятой. Запятая была бы неправильной.
Теперь посмотрим на эти предложения:
1. Куда бы вы ни пошли, однако ваши проблемы будут следовать за вами.
2. Я переезжаю на Восточное побережье, однако, и если мои проблемы последуют за мной, пусть будет так!
3. Мне нужна няня, и, следовательно, , , я не приду на свадьбу.
Это верно. Это неверно:
4. Я еду в Париж, , а моя сестра нет.
5. Нужна няня, поэтому не пойду.
В чем разница? В пяти приведенных выше примерах возьмите , но или , следовательно, . Если все правильно расставлено без этих слов, все в порядке. Однако, если у вас осталось продолжающееся предложение, вам понадобится точка или точка с запятой. Давайте проверим приведенные выше примеры, выбрав , а следовательно, или .
1. Куда бы вы ни пошли, проблемы будут следовать за вами. Это предложение подходит, поэтому вы можете спокойно поставить , но в запятых. Это просто прерыватель предложения.
2. Я переезжаю на Восточное побережье, и если мои проблемы последуют за мной, пусть будет так. Это предложение тоже нормально, поэтому можно использовать запятые около , но .
3. Мне нужна няня, и я не буду на свадьбе . Тоже все в порядке.
4.Я еду в Париж, моя сестра нет. Не нормально. Вы не можете использовать запятые около , но здесь . Вам нужны два отдельных предложения или точка с запятой (или союз).
5. Мне нужна няня, я не пойду. Не хорошо. Вы не можете использовать запятые около , поэтому здесь . Вам нужны два отдельных предложения, точка с запятой или добавление союза.
Кстати, многие совершают подобную ошибку со словом тогда. Тогда — наречие.Он говорит, когда. Это НЕ соединение и не может соединяться.
Я иду в кино, потом на ужин. Неправильно.
Я иду в кино, а потом поужинаю. Правильно.
Купите мои книги на Amazon!
Таким образом, следовательно, и, следовательно, на английском языке
Совет: См. Мой список самых распространенных ошибок на английском языке. Он научит вас избегать ошибок с запятыми, предлогами, неправильными глаголами и многим другим.
Поскольку вы читаете эту статью на английском языке, скорее всего, вы уже знаете, что означает союз «так». Вы, вероятно, также знаете, что «таким образом», «поэтому» и «следовательно» означают в основном то же самое, что и «так», и вам интересно, в чем разница. В таком случае эта статья специально для вас.
Перед тем, как перейти к конкретным словам, следует отметить, что «таким образом», «поэтому» и «следовательно» являются довольно формальными и гораздо более распространены в письменной форме, чем в повседневной беседе, где они почти всегда заменяются на «так ».
«То-то и то-то»
Наиболее важное различие между «таким образом» и «так» состоит в том, что «так» является союзом (означающим «и по этой причине», «и по этой причине»), тогда как «таким образом» является наречием (синонимом «следовательно »). Например, предложение
Его не устраивает, поэтому мы должны подготовить новое предложение.
можно переписать с помощью «таким образом» следующим образом:
правильно Не устраивает. Таким образом, мы должны подготовить новое предложение.
правильно Не удовлетворен; Таким образом, мы должны подготовить новое предложение.
правильно Он не удовлетворен, и (,) таким образом (,) мы должны подготовить новое предложение.
неверно Его это не устраивает, поэтому мы должны подготовить новое предложение.
«Таким образом» обычно отделяется от остальной части предложения запятыми, но запятые часто опускают, если это приведет к появлению трех запятых подряд (как в третьем примере).
Последний пример неверен, потому что «таким образом» не может соединить два независимых предложения.
«Таким образом» также имеет другое значение: «таким образом», «таким образом» (в этом случае предложение не вводится).Например:
Они разработали новую технологию, позволяющую снизить затраты.
Запятая здесь была подходящей, потому что то, что следует за «таким образом», не является предложением. Это просто выражение в скобках, расширяющее предыдущее предложение.
«Отсюда»
Как и «таким образом», «следовательно» является наречием, а не союзом, поэтому он не может соединять два независимых предложения (обратите внимание, что в формальном письме чаще опускают запятые вокруг «следовательно», чем после «таким образом»):
правильно Не устраивает.Следовательно (,) мы должны подготовить новое предложение.
правильно Не удовлетворен; следовательно (,) мы должны подготовить новое предложение.
неверно Он не удовлетворен, поэтому мы должны подготовить новое предложение.
«Следовательно», используемое в этом смысле, довольно необычно, и такое использование сохраняется в основном в специализированных областях, таких как научное письмо.
Однако есть другое, более распространенное значение слова «отсюда», которое заменяет глагол, но не является предложением само по себе и всегда отделяется от остальной части предложения запятой:
Наш сервер не работал, отсюда задержка ответа.
Химические вещества вызывают кислотный дождь, отсюда и термин «кислотный дождь».
Как видите, «следовательно» заменяет такие фразы, как «который ведет к» или «который является причиной».
«Поэтому»
Наконец, «поэтому» также является наречием, означающим «как логическое следствие». Он используется в основном в аргументации, когда одно утверждение логически следует из другого, и часто встречается в научной литературе.
Опять же, руководства по стилю обычно рекомендуют выделять его запятыми, но когда это нарушает естественный ход предложения, большинство авторов склонны опускать запятые:
правильно Две линии пересекаются.Следовательно (,) они не параллельны.
правильно Две линии пересекаются; следовательно (,) они не параллельны.
правильно Две прямые пересекаются, и (,), следовательно, (,) они не параллельны.
неверно Две линии пересекаются, поэтому они не параллельны.
Некоторые люди утверждают, что «следовательно» прекрасно работает как союз (например, «так»), и разделение его запятой вместо точки с запятой допустимо.Однако ни один из основных словарей английского языка (таких как Oxford English Dictionary или Merriam-Webster) не поддерживает такое использование.
Обратите внимание, что «поэтому» звучит неестественно, когда нет очевидной логической связи между двумя утверждениями, особенно в неформальном контексте. В таких случаях следует использовать «так»:
правильно Поездку отменили, поэтому я навестил бабушку.
неестественное Поездка отменена; поэтому вместо этого я навестил свою бабушку.
.
Синус тангенс котангенс косинус правила: Урок 30. определение синуса, косинуса и тангенса угла — Алгебра и начала математического анализа — 10 класс
Электронный справочник по математике для школьников тригонометрические функции острого угла синус косинус тангенс котангенс определения значения формулы
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.
Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
Рис.2
Синусом угла называют дробь:
Косинусом угла называют дробь:
Тангенсом угла называют дробь:
Котангенсом угла называют дробь:
Синус, косинус, тангенс и котангенс, и их комбинации называют тригонометрическими функциями. В данном разделе справочника тригонометрические функции вводятся для острых углов. В следующем разделе даётся определение тригонометрических функций для произвольных углов.
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения
sin α , cos α , tg α , ctg α
Рис.3
В соответствии с рисунком 3 справедливы формулы:
Следовательно,
Кроме того, справедливы формулы:
sin α = cos β, cos α = sin β, tg α = ctg β, ctg α = tg β,
которые можно переписать в виде:
sin α = cos (90° – α), cos α = sin (90° – α),
tg α = ctg (90° – α), ctg α = tg (90° – α).
ПРИМЕР. Найти тригонометрические функции углов 30°, 45°, 60°.
РЕШЕНИЕ. Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
Рис.4
Тогда
Поэтому
Кроме того
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).
Тогда
Поэтому
Определение тригонометрических функций произвольного угла приводится в разделе справочника «Тригонометрические функции произвольного угла».
Формулы приведения / Блог / Справочник :: Бингоскул
Таблица формул приведения
Два правила формул приведения
- при 900 и при 2700 (в виде (π/2 ±a) или (3*π/2 ±a)) — функция меняется на кофункцию (sin на cos либо в обратную сторону, tg на ctg либо в обратную).
- при 1800 и при 3600 (в виде (π ±a) или (2*π ±a)) — функция НЕ изменяется.
2 способа запоминания формул приведения
1. «Правило лошади»:
- Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
- Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
- Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
2. Использование четности и периодичности.
нечетная функция
- sin (-α) = -sin α
- tg (-α) = -tg α
- сtg (-α) = -сtg α
четная функция
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими:
- sin α, cos α — периодические функции с наименьшим положительным периодом 2π: sin(α+2kπ) = sin α,cos(α+2kπ) = cos α, k ∈ Z.
- tg α, ctg α — периодические функции с наименьшим положительным периодом π: tg(α+kπ) = tgα, ctg(α+kπ) = ctg α, k ∈ Z.
Формулы приведения в виде списка
sin
- sin(900 — α) = cos α
- sin (900 + α) = cos α
- sin (1800 — α) = sin α
- sin (1800 + α) = -sin α
- sin (2700 — α) = -cos α
- sin (2700 + α) = -cos α
- sin (3600 — α) = -sin α
- sin (3600 + α) = sin α
cos
- cos (900 — α) = sin α
- cos (900 + α) = -sin α
- cos (1800 — α) = -cos α
- cos (1800 + α) = -cos α
- cos (2700 — α) = -sin α
- cos (2700 + α) = sin α
- cos (3600 — α) = cos α
- cos (3600 + α) = cos α
tg
- tg(900 — α) = ctg α
- tg (900 + α) = -ctg α
- tg (1800 — α) = -tg α
- tg (1800 + α) = tg α
- tg (2700 — α) = ctg α
- tg (2700 + α) = -ctg α
- tg (3600 — α) = -tg α
- tg (3600 + α) = tg α
ctg
- ctg (900 — α) = tg α
- ctg (900 + α) = -tg α
- ctg (1800 — α) = -ctg α
- ctg (1800 + α) = ctg α
- ctg (2700 — α) = tg α
- ctg (2700 + α) = -tg α
- ctg (3600 — α) = -ctg α
- ctg (3600 + α) = ctg α
Угол альфа α находится в интервале 0 — 90°.
Знаки основных тригонометрических функций в зависимости от четверти
Дополнительный материал: Формулы тригонометрии
Смотри также: Основные формулы по математике
синуса, косинуса, тангенса и котангенса
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления. Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им. Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/х, а ctg α = х/y. Рассматривая углы в отрицательной системе координат, можно рассчитать, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Вычисления и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, можно вывести значения этих функций для некоторых углов.k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.
Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции.2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный.2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение
Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Инструкция
Воспользуйтесь знаниями планиметрии, чтобы выразить синус через косинус . Согласно определению, синус ом угла в прямоугольном треугольнике длины противолежащего к , а косинус ом – прилежащего катета к гипотенузе. Даже знание теоремы Пифагора позволит вам в некоторых случаях быстро искомое преобразование.
Выразите синус через косинус , воспользовавшись простейшим тригонометрическим тождеством, согласно которому сумма квадратов этих величин дает единицу. Обратите внимание, что корректно выполнить задание вы сможете, только если знаете, в четверти находится искомый угол, в противном случае вы получите два возможных результата – с положительным и знаком.
соs?=(b?+c?-а?)/(2*b*c)
Имеется треугольник со сторонами а, b, с, равными 3, 4, 5 мм, соответственно.
Найти косинус угла, заключенного между большими сторонами.
Обозначим противоположный стороне а угол через?, тогда, согласно выведенной выше формуле, имеем:
соs?=(b?+c?-а?)/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40=32/40=0,8
Ответ: 0,8.
Если треугольник прямоугольный, то для нахождения косинус а угла достаточно знать длины всего двух любых сторон (косинус прямого угла равен 0).
Пусть имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.
Рассмотрим все варианты:
Найти соs?, если известны длины сторон а и b ( треугольника)
Воспользуемся дополнительно теоремой Пифагора:
соs?=(b?+c?-а?)/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)
Чтобы правильность полученной формулы, подставим в нее из примера 1, т.е.
Проделав элементарные вычисления, получаем:
Аналогично находится косинус в прямоугольном треугольнике в остальных случаях:
Известны а и с (гипотенуза и противолежащий катет), найти соs?
соs?=(b?+c?-а?)/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.
Подставляя значения а=3 и с=5 из примера, получаем:
Известны b и с (гипотенуза и прилежащий катет).
Найти соs?
Произведя аналогичные (показанные в примерах 2 и 3 преобразования), получим, что в этом случае косинус в треугольнике вычисляется по очень простой формуле:
Простота выведенной формулы объясняется элементарно: фактически, прилежащий к углу? катет является проекцией гипотенузы, его длина равна длине гипотенузы, умноженной на соs?.
Подставляя значения b=4 и с=5 из первого примера, получим:
Значит, все наши формулы верны.
Для того чтобы получить формулу, связывающую синус и косинус угла, необходимо дать или вспомнить некоторые определения. Так, синус угла — это отношение (частное от деления) противолежащего катета прямоугольного треугольника к гипотенузе. Косинус угла — это отношение прилежащего катета к гипотенузе.
Инструкция
Полезный совет
Величина синуса и косинуса любого угла не может быть больше 1.
Синус и косинус — это прямые тригонометрические функции, для которых существует несколько определений — через окружность в декартовой системе координат, через решения дифференциального уравнения, через острые углы в прямоугольном треугольнике. Каждое из таких определений позволяет вывести зависимость между этими двумя функциями. Ниже приведен самый, пожалуй, простой способ выразить косинус через синус — через их определения для острых углов прямоугольного треугольника.
Инструкция
Выразите синус острого угла прямоугольного треугольника через длины сторон этой фигуры. Согласно определению, синус угла (α) должен быть отношению длины стороны (a), лежащей напротив него — катета — к длине стороны (c), противолежащей прямому углу — гипотенузы: sin(α) = a/c.
Найдите аналогичную формулу для косинус а того же угла. По определению эта величина должна выражаться отношением длины стороны (b), примыкающей к этому углу (второго катета), к длине стороны (c), лежащей напротив прямого угла: cos(а) = a/c.
Перепишите равенство, вытекающее из теоремы Пифагора, таким образом, чтобы в нем были задействованы соотношения между катетами и гипотенузой, выведенные на двух предыдущих шагах. Для этого сначала разделите обе исходного этой теоремы (a² + b² = c²) на квадрат гипотенузы (a²/c² + b²/c² = 1), а затем полученное равенство перепишите в таком виде: (a/c)² + (b/c)² = 1.
Замените в полученном выражении соотношения длин катетов и гипотенузы тригонометрическими функциями, исходя из формул первого и второго шага: sin²(а) + cos²(а) = 1. Выразите косинус из полученного равенства: cos(a) = √(1 — sin²(а)). На этом задачу можно решенной в общем виде.
Если кроме общего нужно получить численный результат, воспользуйтесь, например, калькулятором, встроенным в операционную систему Windows. Ссылку на его запуск в подразделе «Стандартные» раздела «Все программы» меню ОС. Эта ссылка сформулирована лаконично — «Калькулятор». Чтобы иметь возможность вычислять с этой программы тригонометрические функции включите ее «инженерный» интерфейс — нажмите комбинацию клавиш Alt + 2.
Введите в условиях значение синуса угла и кликните по кнопке интерфейса с обозначением x² — так вы возведете исходное значение в квадрат. Затем наберите на клавиатуре *-1, нажмите Enter, введите +1 и нажмите Enter еще раз — таким способом вы вычтите из единицы квадрат синуса. Щелкните по клавише со значком радикала, чтобы извлечь квадратный и получить окончательный результат.
Одной из фундаментальных основ точных наук является понятие о тригонометрических функциях. Они определяют простые отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Найти его, зная угол, можно большим количеством способов, включающих экспериментальные, вычислительные методы, а также использование справочной информации.
Вам понадобится
- — калькулятор;
- — компьютер;
- — электронные таблицы;
- — таблицы брадиса;
- — бумага;
- — карандаш.
Инструкция
Используйте с функцией вычисления синуса для получения нужных значений на основании знания угла. Подобный функционал сегодня имеют даже самые простые . При этом вычисления производятся с очень высокой степенью точности (как правило, до восьми и более знаков после запятой).
Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами подобных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в любую ячейку формулу, состоящую из вызова функции вычисления синуса с нужным аргументом. Нажмите Enter. В ячейке отобразится искомая величина. Преимуществом электронных таблиц является возможность быстрого расчета значений функций для большого набора аргументов.
Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками после запятой.
Найдите приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого необходимо найти. Начертите еще один отрезок, пересекающий первый в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два уже существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира.9)/9! — … Для повышения скорости расчетов записывайте текущее значение числителя и знаменателя последнего члена ряда, производя вычисление следующего значения на основе предыдущего. Увеличивайте длину ряда для получения более точной величины.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники. Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
tg \alpha \cdot ctg \alpha = 1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha} , а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha} — будет являться котангенсом.
Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .
Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом.
Зависимость между тангенсом и котангенсом
tg \alpha \cdot ctg \alpha=1
Данное тождество справедливо только для таких углов \alpha , которые отличны от \frac{\pi}{2} z . Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что tg \alpha = \frac{y}{x} , а ctg \alpha=\frac{x}{y} . Отсюда следует, что tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1 . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.{2} \alpha = 1 . Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14 .
По условию \frac{\pi}{2} . Во второй четверти косинус отрицателен, поэтому \cos \alpha = -\sqrt\frac14=-\frac12 .
Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.
ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.
1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус. И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются» : синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами». Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Синусы — «смешиваются» :
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать.°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Функция: Кофункция:
\(sin\) \(a\) \(→\) \(cos\) \(a\)
\(cos\) \(a\) \(→\) \(sin\) \(a\)
\(tg\) \(a\) \(→\) \(ctg\) \(a\)
\(ctg\) \(a\) \(→\) \(tg\) \(a\)
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс, он либо останется синусом, либо превратиться в косинус.°}}=\)
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
\(= 18\)
Записываем ответ
Ответ: \(18\)
Пример. Найдите значение выражения \(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}\)
Решение:|
\(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Рассмотрим первое слагаемое числителя: \(\sin(π-a)\). Воспользуемся формулами приведения, выведя ее самостоятельно:
Таким образом, \(\sin(π-a)=\sina\) |
|
|
\(=\frac{3 \sin{a}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Второе слагаемое числителя: \(\cos{(\frac{π}{2} + a)}\):
Таким образом, \(\cos{(\frac{π}{2} + a)}=-\sina\) |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Теперь знаменатель: \(\cos(\frac{3π}{2} — a)\). Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\) |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{-\sin {a}}=\) |
Раскрываем скобки и приводим подобные слагаемые. |
|
|
\(=\frac{3 \sin{a}+\sin{a}}{-\sin {a}}=\frac{4\sin{a}}{-\sin{a}}\) |
Сократив на \(\sin{a}\), получаем ответ. |
|
|
\(=\frac{4 }{-1}=\)\(-4\) |
Ответ: \(-4\)
Пример. Вычислить чему равен \(ctg(-a-\frac{7π}{2})\), если \(tg\) \(a=2\)
Решение:
|
\(ctg(-a-\frac{7π}{2}) =\) |
Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный. Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки. |
|
|
\(= ctg(-\frac{7π}{2}-a) =\) |
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента. |
|
|
\(= ctg(-(\frac{7π}{2}+a)) =\) |
Теперь вспомним о том, что котангенс – функция нечетная, то есть |
|
|
\(= — ctg(\frac{7π}{2}+a) =\) |
Несмотря на то, что точка привязки \(\frac{7π}{2}\) мы все равно можем использовать формулы приведения, потому что \(\frac{7π}{2}\) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже). \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) . |
|
|
\(= — (- tg\) \(a) = tg\) \(a = 2\) |
Готов ответ. |
Ответ: \(2\)
Еще раз проговорим этот важный момент: с точки зрения формулы приведения \(\frac{7π}{2}\) — это тоже самое, что и \(\frac{3π}{2}\). Почему? Потому что \(\frac{7π}{2}=\frac{3π+4π}{2}=\frac{3π}{2}+\frac{4π}{2}=\frac{3π}{2}+2π\). Иными словами, они отличаются ровно на один оборот \(2π\). А на значения тригонометрических функций количество оборотов никак не влияет:
\(cos\) \(t=cos (t+2π)=cos (t+4π)=cos (t+6π)= …=cos (t-2π)=cos (t-4π)=cos (t-6π)…\)
\(sin\) \(t=sin (t+2π)=sin (t+4π)=sin (t+6π)= …=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
Аналогично с тангенсом и котангенсом (только у них «оборот» равен \(π\)).
\(tg\) \(t=tg(t+π)=tg(t+2π)=tg(t+3π)= …=tg(t-π)=tg(t-2π)=tg(t-3π)…\)
\(ctg\) \(t=ctg(t+π)=ctg(t+2π)=ctg(t+3π)= …=ctg(t-π)=ctg(t-2π)=ctg(t-3π)…\)
Таким образом, \(-ctg(\frac{7π}{2}+a)=- ctg(\frac{3π}{2}+2π+a)=- ctg(\frac{3π}{2}+a)\).
То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).
Ответы на часто задаваемые вопросы
Вопрос: Есть ли формулы приведения с аргументами \((\frac{π}{3}-a)\),\((\frac{π}{4}+a)\),\((\frac{7π}{6}+a)\) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Смотрите также Как доказать тригонометрическое тождество?
Скачать статьюсинуса, косинуса, тангенса и котангенса
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Задача 6.12. Тот же вопрос, что и в предыдущей задаче, но для правильного пятиугольника (указание: см. задачу 3.5 ).
Задача 6.13. В задаче 4.8 было сказано, что в качестве приближенного значения косинуса малого угла α можно взять число 1, то есть значение функции косинус в нуле. Что, если в качестве приближенного значения для синуса малого угла α, не мудрствуя лукаво, взять 0 = sin 0? Чем это плохо?
Рис. 6.4. Точка M движется по циклоиде.
Задача 6.14. Рассмотрим колесо радиуса 1, касающееся оси абсцисс в начале координат (рис. 6.4 ). Предположим, что колесо покатилось по оси абсцисс в положительном направлении со скоростью 1 (т. е. за время t его центр смещается на t вправо).
а) Нарисуйте (примерно) кривую, которую будет описывать точка M, касающаяся в первый момент оси абсцисс.
б) Найдите, каковы будут абсцисса и ордината точки M через время t после начала движения.
Синус и косинус мы в этом параграфе определили геометрически, как ординату и абсциссу точки, а тангенс — алгебраически, как sin t/ cos t. Можно, однако, и тангенсу придать геометрический смысл.
Для этого проведем через точку с координатами (1; 0) (начало отсчета на тригонометрической окружности) касательную к тригонометрической окружности — прямую, параллельную оси
Рис. 6.5. Ось тангенсов.
ординат. Назовем эту прямую осью тангенсов (рис. 6.5 ). Название это оправдывается так: пусть M — точка на тригонометрической окружности, соответствующая числу t. Продолжим радиус SM до пересечения с осью тангенсов. Тогда оказывается, что ордината точки пересечения равна tg t.
В самом деле, треугольники NOS и MP S на рис. 6.5 , очевид-
но, подобны. Отсюда | ||||||||||
что и утверждалось. | или (0; −1), то пря- | |||||||||
Если точка M имеет координаты (0; 1) | ||||||||||
мая SM параллельна оси тангенсов, и тангенс нашим способом определить нельзя. Это и не удивительно: абсцисса этих точек равна 0, так что cos t = 0 при соответствующих значениях t, и tg t = sin t/ cos t не определен.
6.2. Знаки тригонометрических функций
Разберемся, при каких значениях t синус, косинус и тангенс положительны, а при каких — отрицательны. Согласно определению, sin t — это ордината точки на тригонометрической окружности, соответствующая числу t. Поэтому sin t > 0, если точка t на
Прежде чем перейти к этому разделу, напомним определения синуса и косинуса, изложенные в учебнике геометрии 7-9 классов.
Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):
Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):
Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.
Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).
Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс). А гипотенуза с равна радиусу окружности (R).
Таким образом, наши формулы обретают иной вид.
Так как b = y , a = x , c = R, то:
y x
sin t = — , cos t = —.
R R
Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.
Так как tg t = b/a, ctg t = a/b, то, верны и другие уравнения:
tg t = y /x ,
ctg = x /y .
Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:
y
sin t = — = y ,
1
x
cos t = — = x .
1
Так мы приходим к третьему, более простому виду тригонометрических формул.
Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).
Определения и формулы cos t, sin t, tg t, ctg t.
Из формул тангенса и котангенса следует еще одна формула:
Уравнения числовой окружности.
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть | |
Косинус и синус основных точек числовой окружности:
Как запомнить значения косинусов и синусов основных точек числовой окружности.
Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.
1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):
1 √2 √3
0; -; —; —; 1.
2 2 2
Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.
2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.
Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.
На концах оси косинусов (оси х ), разумеется, косинусы равны модулю 1 , а синусы равны 0.
На концах оси синусов (оси у ) синусы равны модулю 1 , а косинусы равны 0.
Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса 7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные. И тогда вы не ошибетесь со знаком 1.
3) Теперь перейдем к дробным значениям.
Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.
В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.
Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).
Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).
Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).
Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.
Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.
Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.
Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:
cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2
Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.
Важно знать :
Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).
В порядке убывания получается такое чередование значений:
√3 √2 1 1 √2 √3
1; —; —; -; 0; – -; – —; – —; –1
2 2 2 2 2 2
Возрастают они строго в обратном порядке.
Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.
Тангенс и котангенс основных точек числовой окружности.
Зная косинус и синус точек числовой окружности, легко можно вычислить их тангенс и котангенс. Делим синус на косинус — получаем тангенс. Делим косинус на синус — получаем котангенс. Результаты этого деления — на рисунке.
ПРИМЕЧАНИЕ : В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.
Как запомнить значение тангенсов и котангенсов основных точек числовой окружности.
Здесь такие же закономерности, что и с синусами и косинусами. И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
На концах осей координат – прочерки и нули. Прочерки означают, что в данных точках тангенс или котангенс не имеют смысла.
Как запомнить, где прочерки, а где нули? Поможет правило.
Тангенс – это отношение синуса к косинусу. На концах оси синусов (ось у ) тангенс не существует.
Котангенс – это отношение косинуса к синусу. На концах оси косинусов (ось х ) котангенс не существует.
В остальных точках идет чередование всего лишь трех чисел: 1, √3 и √3/3 со знаками плюс или минус. Как с ними разобраться? Запомните (а лучше представьте) три обстоятельства:
1) тангенсы и котангенсы всех середин четвертей имеют в модуле 1.
2) тангенсы и котангенсы ближайших к оси х точек имеют в модуле √3/3; √3.
3) тангенсы и котангенсы ближайших к оси у точек имеют в модуле √3; √3/3.
Не ошибитесь со знаками – и вы большой знаток.
Нелишне будет запомнить, как возрастают и убывают тангенс и котангенс на числовой окружности (см.числовую окружность выше или раздел «Возрастание и убывание тригонометрических функций»). Тогда еще лучше будет понятен и порядок чередования значений тангенса и котангенса.
Тригонометрические свойства чисел числовой окружности.
Представим, что определенная точка М имеет значение t.
Свойство 1 :
| | | |
Пояснение . Пусть t = –60º и t = –210º.
cos –60º равен 1/2. Но cos 60º тоже равен 1/2. То есть косинусы –60º и 60º равны как по модулю, так и по знаку: cos –60º = cos 60º.
cos –210º равен –√3/2. Но cos 210º тоже равен –√3/2. То есть: cos –210º = cos 210º.
cos (– t) = cos t.
sin –60º равен –√3/2. А sin 60º равен √3/2. То есть sin –60º и sin 60º равны по модулю, но противоположны по знаку.
sin –210º равен 1/2. А sin 210º равен –1/2. То есть sin –210º и sin 210º равны по модулю, но противоположны по знаку.
Таким образом, мы доказали, что sin (– t) = – sin t.
Посмотрите, что происходит с тангенсами и котангенсами этих углов – и вы сами легко докажете себе верность двух других тождеств, приведенных в таблице.
Вывод: косинус – четная функция, синус, тангенс и котангенс – нечетные функции.
Свойство 2: Так как t = t + 2πk , то:
| |
Пояснение : t и t + 2πk – это одна и та же точка на числовой окружности. Просто в случае с 2πk мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t. Значит, и равенства, изложенные в этой таблице, очевидны.
Свойство 3: Если две точки окружности находятся друг против друга относительно центра О, то их синусы и косинусы равны по модулю, но противоположны по знаку, а их тангенсы и котангенсы одинаковы как по модулю, так и по знаку.
| | | |
Пояснение : Пусть точка М находится в первой четверти. Она имеет положительное значение синуса и косинуса. Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности. Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Тангенс и котангенс точки М имеют положительное значение. А тангенс и котангенс точки N? Ответ простой: ведь тангенс и котангенс – это отношение синуса и косинуса. В нашем примере синус и косинус точки N – со знаком «минус». Значит:
–sin t
tg (t + π) = —- = tg t
–cos t
–cos t
ctg (t + π) = —- = ctg t
–sin t
Мы доказали, что тангенс и котангенс диаметрально противоположных точек окружности имеют не только одинаковое значение, но и одинаковый знак.
Свойство 4: Если две точки окружности находятся в соседних четвертях, а расстояние между точками равно одной четверти окружности, то синус одной точки равен косинусу другой с тем же знаком, а косинус одной точки равен синусу второй с противоположным знаком.
π | π |
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.
- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Формулы приведения, калькулятор онлайн, конвертер
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы тригонометрии
Тригонометрические формулы – список основных формул
Познакомьтесь с основными тригонометрическими формулами, перепишите себе все таблицы формул и всегда держите их перед глазами, изучая тригонометрию.
Основные тригонометрические тождества
Разберитесь с основными тригонометрическими тождествами, запомните формулы и рассмотрите их вывод.
Формулы приведения
Научитесь пользоваться формулами приведения, их запоминанию способствует мнемоническое правило, посмотрите на примеры применения формул приведения.
Формулы сложения в тригонометрии
Разберитесь в формулах сложения, рассмотрите их доказательство и конкретные примеры их применения.
Формулы двойного угла
Дан список формул двойного угла, приведено их доказательство и показаны примеры применения, перечислены формулы других кратных углов: тройного, четверного и т.д.
Формулы половинного угла
Запомните еще ряд формул тригонометрии — формулы половинного угла, рассмотрите решения примеров с их использованием.
Формулы понижения степени
Рассмотрите формулы, позволяющие понижать степень тригонометрических функций, ознакомьтесь с их применением на практике.
Формулы суммы и разности синусов и косинусов
Дан вывод формул суммы синусов, суммы косинусов, разности синусов и разности косинусов, разобрано как они применяются.
Формулы произведения синусов, косинусов и синуса на косинус
Приведен список формул произведения синусов, косинусов и синуса на косинус, показано их доказательство и примеры использования.
Универсальная тригонометрическая подстановка
Познакомьтесь с формулами, выражающими тригонометрические функции через тангенс половинного угла, разберите их применение на примерах.
Формулы с arcsin, arccos, arctg и arcctg
Рассмотрите основные формулы, использующиеся при работе с обратными тригонометрическими функциями.
Произведение тригонометрических функций
В предыдущем разделе, когда мы выводили ф-лы для вычисления суммы синусов и косинусов, мы сначала получали уравнения:
Далее мы производили замену переменных sи t. Однако давайте вместо этого просто поделим первые два уравнения на двойку, а третье – на (– 2):
В случае с последней формулой мы воспользовались правилом, по которому знак минус перед дробью можно убрать, если в числителе поменять местами вычитаемое и уменьшаемое.
Получили ф-лы, которые позволяют заменять произведение тригонометрических ф-ций их суммой.
Задание. Преобразуйте произведение в сумму:
Решение.
На этом наше знакомство с основными тригонометрическими формулами заканчивается. Ещё раз напомним, что в рамках школьного курса заучивать все ф-лы не нужно, можно при необходимости пользоваться смотреть в справочник. Тригон-кие преобразования помогут в будущем при решении сложных тригон-ких уравнений.
В самом конце приведем перечень всех формул, выведенными в этом уроке:
Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы
Формулы приведения для тригонометрических функций
Формулы приведения – это формулы, позволяющие упростить сложные выражения тригонометрической функции.
Выражения типа π + t, 3π/2 – t, π/2 + t и т.п. можно упростить настолько, что они будут состоять лишь из одного аргумента t. В предыдущих разделах мы имели дело с несколькими такими упрощениями – например, sin (π + t) = –sin t.
Формул приведения очень много. Запомнить их трудно – но самое главное, в этом нет необходимости. Достаточно запомнить одно-единственное правило – и вы легко сможете самостоятельно выводить формулы и упрощать выражения.
Правило приведения:
| Для выражений π + t, π – t, 2π + t, 2π – t | Для выражений π/2 + t, π/2 – t, 3π/2 + t, 3π/2 – t |
|
|
Обратите внимание: в левом и правом столбцах различаются только первые пункты правила. Вторые пункты абсолютно идентичны
Формулы приведения.
| cos (π + t) = –cos t | sin (π + t) = –sin t | tg (π + t) = tg t | ctg (π + t) = ctg t |
| cos (π – t) = –cos t | sin (π – t) = sin t | tg (π – t) = –tg t | ctg (π – t) = –ctg t |
| cos (2π + t) = cos t | sin (2π + t) = sin t | tg (2π + t) = tg t | ctg (2π + t) = ctg t |
| cos (2π – t) = cos t | sin (2π – t) = –sin t | tg (2π – t) = –tg t | ctg (2π – t) = –ctg t |
| cos (π/2 + t) = –sin t | sin (π/2 + t) = cos t | tg (π/2 + t) = –ctg t | ctg (π/2 + t) = –tg t |
| cos (π/2 – t) = sin t | sin (π/2 – t) = cos t | tg (π/2 – t) = ctg t | ctg (π/2 – t) = tg t |
| cos (3π/2 + t) = sin t | sin (3π/2 + t) = –cos t | tg (3π/2 + t) = –ctg t | ctg (3π/2 + t) = –tg t |
| cos (3π/2 – t) = –sin t | sin (3π/2 – t) = –cos t | tg (3π/2 – t) = ctg t | ctg (3π/2 – t) = tg t |
Примечание: Часто встречаются более сложные выражения, но они не меняют правила. Например, если cos (2π + t) = cos t, то cos (2π + 3t) = cos 3t.
Два правила формул приведения, примеры.
Формул приведения много, но все они подчиняются двум правилам:
Первое правило:
Для аргументов функция меняется на кофункцию, т.е. синус на косинус и наоборот, тангенс на котангенс и наоборот.
Для аргументов функция не меняется.
Примеры на первое правило:
Знак пока не учитываем, он определяется вторым правилом, пока важно понять, в каких случаях функция меняется на кофункцию, а в каких не меняется. 1)
1)
2)
3)
4)
Для аргументов вида наименование функции следует изменить на кофункцию.
5)
6)
7)
8)
Для аргументов вида наименование функции не меняется.
Второе правило (для знака приведенной функции, функции угла ).
1) Считаем угол острым,
2) Определяем четверть и знак в ней приводимой функции (функции слева).
3) Ставим этот знак перед приведенной к углу функцией (функцией справа).
Примечание: Угол может быть любым, острым мы его считаем условно, для применения правила.
Примеры на второе правило:
1)
Рис. 2.
Угол находится во второй четверти. Во второй четверти , ставим знак плюс.
2)
Рис
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
3)
Рис. 4.
Угол находится во второй четверти. Во второй четверти ставим знак минус.
4)
Рис. 5.
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
5)
Рис. 6.
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
6)
Рис. 7.
Угол находится во второй четверти, во второй четверти ставим знак минус.
7)
Рис. 8.
Угол находится во второй четверти. Во второй четверти ставим знак минус.
8)
Рис. 9.
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
Итак, мы рассмотрели различные примеры применения первого и второго правил формул приведения.
Формулы двойного и половинного аргумента
Теперь перейдем к формулам двойного аргумента и следствиям из них. Напомним:
Получить формулы для тангенса и котангенса двойного угла очень просто. Этот прием мы уже неоднократно использовали сегодня в уроке. Расписываем по определению:
По сути, мы получили формулу для тангенса двойного угла. Ее можно преобразовать и к другому виду, разделив числитель и знаменатель на :
Получилась многоэтажная дробь, разберем ее числитель и знаменатель отдельно:
В итоге тангенс двойного угла мы выразили только через тангенс одинарного.
Аналогичным образом можно поступить и с котангенсом.
Задание 7. Найти , если .
Решение
Обратим внимание, что аргументы отличаются в 2 раза. Значит, нам понадобятся формулы двойного угла или же следствия из них – формулы половинного угла
Способ 1. Попробуем использовать формулы двойного угла:
По условию, это выражение равно :
Тут у нас косинус квадрат и синус квадрат. Для них мы знаем еще одно соотношение – основное тригонометрическое тождество:
Из этих двух соотношений мы можем найти значения и . Сложив их, получим:
Тогда:
Требуется найти . Как обычно, расписываем по определению:
Способ 2. Можно использовать формулы половинного аргумента. Тогда и можно сразу выразить:
Ответ: .
Вторым способом получилось быстрее, но нужно помнить больше формул. Каждый сам может выбрать более удобный для себя способ решения: больше запоминать, но быстрее решать или же запоминать меньше, но тогда решение может оказаться длиннее.
Уметь применять формулы двойных аргументов нужно как слева направо, так и справа налево. Слева направо это сделать проще, а вот справа налево их нужно «увидеть». Вспомните: похожая ситуация была с формулами сокращенного умножения. Найти выражение вида просто: увидел – применил формулу. А вот в обратную сторону выражение вида нужно еще заметить.
Итак, посмотрим на правые части формул двойных аргументов и подумаем, на что же нам обращать внимание
Для синусов справа стоит произведение синуса и косинуса с одинаковыми аргументами
Именно на это мы будет обращать внимание. Умножить и разделить выражение на – это не проблема
Для косинусов справа стоит разность квадратов. Не путайте с основным тригонометрическим тождеством – там сумма квадратов.
Задание 8. Найти значение выражения:
Решение
Видим произведение косинуса и синуса одного аргумента. Это показатель того, что нужно применить формулу синуса двойного угла. Не хватает двойки перед выражением. Поэтому умножим и разделим выражение на :
Теперь можем применить формулу:
Далее нужно применить формулы приведения. Можете самостоятельно потренироваться это делать. В итоге вы должны получить ответ . Если ответ не совпал, смотрите решение ниже.
Ответ: .
Использование формул приведенияВыделим в дроби целую часть:
Тогда:
У нас по-прежнему в аргументе не острый угол. Попробуем еще раз выделить :
Осталось применить формулу приведения для отрицательных углов и найти значение по таблице:
Тогда:
Список литературы
- «Алгебра и начала математического анализа. 10-11 классы. Базовый и углубленный уровни. Учебник. ФГОС», АО «Издательство «Просвещение» Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и др. 10–11.
- «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа». 10-11 классы. Учебник для общеобразовательных организаций (базовый уровень). В 2 ч., ООО «ИОЦ МНЕМОЗИНА» Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г. 10–11.
- Алгебра и начала математического анализа. 10 класс, АО «Издательство «Просвещение» Никольский С.М., Потапов М.К., Решетников Н.Н. и др. 10.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал cleverstudents.ru
- Интернет-портал ru.solverbook.com
- Интернет-портал yaklass.ru
Домашнее задание
- Вычислить:
- Вычислить, если известно, что :
- Доказать тождество:
Формулы приведения. Как запомнить?
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
- задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
- задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
- задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
- стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов
Формулы приведения:
Угол альфа лежит пределах от 0 до 90 градусов.
Итак, необходимо уяснить «закон», который здесь работает:
Определите знак функции в соответствующей четверти.
Напомню их:
Запомните следующее:
Функция изменяется на кофункцию
Функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
- Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов.
- Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов.
- Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов.
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения.
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию.°-a). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Для начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс, он либо останется синусом, либо превратиться в косинус. А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.
Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
- как определить знак перед конечной функцией (плюс или минус)?
- как определить меняется ли функция на кофункцию или нет?
Основное тригонометрическое тождество
Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:
Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:
АВ2 + ОВ2 = ОА2
Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:
sin2α + соs2α = 1
Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.
Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?
Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:
sin2α + соs2α = 1
0,82 + соs2α = 1
0,64 + соs2α = 1
соs2α = 1 – 0,64
соs2α = 0,36
соsα = – 0,6 или соsα = 0,6
Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.
Ответ: 0,6.
Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:
По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.
Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.
Решение.
sin2α + соs2α = 1
0,282 + sin2α = 1
0,0784 + sin2α = 1
sin2α = 1 – 0,0784
sin2α = 0,9216
sin α = –0,96 или sin α = 0,96
Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.
Ответ: – 0,96.
Задание. Найдите tgα, если sinα = 5/13 и π/2
Решение. Здесь задача уже в два действия! Сначала определим соsα:
sin2α + соs2α = 1
соs2α = 1 – sin2α = 1 – (5/13)2 = 169/169 – 25/169 = 144/169
соsα = – 12/13 или соsα = 12/13
Условие π/2
Далее находим тангенс, просто деля синус на косинус:
tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12
Ответ: 5/12
Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.
Запишем тождество
sin2α + соs2α = 1
Далее поделим его на величину соs2α:
Крайнее левое слагаемое – это величина tg2α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:
В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin2α:
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.
Решение.
Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:
Так как угол относится к III четверти, где косинус отрицателен, то
соsα = – 0,8
Синус угла найдем, используя основное тригон-кое тождество:
sin2α + соs2α = 1
sin2α = 1 – соs2α = 1 – (– 0,8)2 = 1 – 0,64 = 0,36
sinα = – 0,6 или sinα = 0,6
С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6
Ответ: sinα = – 0,6; соsα = – 0,8.
Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin2α + соs2α = 1 несложно получить из выражения
sin2α = 1 – соs2α
и
соs2α = 1 – sin2α
которые помогают в работе с длинными ф-лами.
Задание. Упростите выражение
4sin2α + 9соs2α – 6
таким образом, чтобы в нем не содержалось синуса.
Решение. Произведем замену sin2α = 1 – соs2α:
4sin2α+ 9соs2α – 6 = 4(1 – соs2α)+ 9соs2α – 6 =
= 4 – 4 соs2α + 9соs2α – 6 = 5соs2α – 2
Видим, что получилось значительно более простое выражение.
Ответ: 5соs2α – 2.
Задание. Избавьтесь от синуса в выражении
sin4α – соs4α
Решение. Воспользуемся ф-лой :
sin4α – соs4α = (sin2α – соs2α)(sin2α + соs2α) = (sin2α – соs2α)•1 =
= 1 – соs2α– соs2α = 1 – 2 соs2α
Ответ:1 – 2 соs2α.
Задание. Упростите дробь
Решение.
Ответ: ctg6α.
Для достижения наилучшего результата важно структурировать знания. В этом вам помогут онлайн-курсы по математике
Формулы приведения. Быстро и легко!
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода.
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.
Разберем в каждой четверти функции sin(a) и cos(a). Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
В первой четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти. И функция cos(a)>0, потому что ось X положительна в этой четверти.
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).
Во второй четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
А функция cos(a)
В четвертой четверти видно, что функция sin(a)0, потому что ось X положительна в этой четверти.Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм:
- Четверть. (Всегда смотрите в какой вы четверти находитесь).
- Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
- Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется.
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
- Четверть первая.
- В первой четверти знак у функции косинуса положительный.
- В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90-α) = sin(α).
Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению…
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению…
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени. Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
К оглавлению…
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
ACT Тригонометрия: полное руководство
Тригонометрия — это раздел математики, который имеет дело с прямоугольными треугольниками и отношениями между их сторонами и углами. (Слово «триггер» связано со словом «треугольник», чтобы помочь вам запомнить.)
Обычно в тесте ACT есть около 4-6 вопросов, касающихся тригонометрии (официальные инструкции по тестированию ACT говорят, что задачи тригонометрии составляют 7% теста). На первый взгляд они могут показаться сложными, но большинство из них сводятся к нескольким простым концепциям.
Эта статья будет вашим исчерпывающим руководством по тригонометрии, которое вам нужно знать для ACT. Мы расскажем вам о значении тригонометрии, формулах и понимании, которые вам нужно знать, а также о том, как решать некоторые из самых сложных тригонометрических задач ACT.
Что такое тригонометрия и как ею пользоваться?
Тригонометрия изучает отношения между сторонами и углами прямоугольных треугольников. Соотношения между размерами сторон прямоугольного треугольника и размерами его углов постоянны, независимо от того, насколько большой или маленький треугольник.
Некоторые из множества различных возможных типов прямоугольных треугольников.
Если вы знаете размер одной стороны и один угол, отличный от 90 ° для прямоугольного треугольника, вы сможете определить остальные стороны и углы треугольника. А если у вас есть две стороны прямоугольного треугольника, вы сможете найти меру всех внутренних углов.
Если у нас есть две стороны, мы можем использовать теорему Пифагора, чтобы найти третью.2 = 340 $
$ c = √340 $ или $ c = 2√85 $
Но что, если у нас есть только одна длина стороны и мера одного из углов (не девяносто градусов)?
Даже если у нас есть длина только одной стороны, мы все равно можем найти другие, используя тригонометрию, потому что у нас есть мера одного из острых углов.
Итак, здесь мы могли бы сказать $ sin 34 ° = 12 / \ hypotenuse \ $
Итак, $ \ hypotenuse \ = 12 / {sin 34 °} $
Не волнуйтесь, если это еще не имеет для вас смысла! Мы разберем каждый шаг по мере продвижения в руководстве.
(Примечание: чтобы найти фактическую величину угла в градусах с использованием двух длин сторон, вам нужно будет выполнить вычисление обратной функции (также называемой функцией «дуги»). Но НЕ БОЙТЕСЬ — ACT никогда не заставит вас Сделайте это! Что касается вашей подготовки к математике ACT, поймите, что тест будет предлагать вам только вычислить достаточно далеко, чтобы сказать, например, «$ Cosinex = 4/5 $». Вам никогда не придется находить фактическую угловую меру из х по АКТ.
Мы находим эти меры, понимая отношение определенных сторон треугольника к их соответствующим углам. Это так называемые тригонометрические функции, и есть три, которые вы должны запомнить для ACT: синус, косинус и тангенс. Самый простой способ понять это — использовать мнемоническое устройство SOH, CAH, TOA , о котором мы поговорим чуть позже.> / P>
Тригонометрия широко используется в навигации, а также для расчета высот и расстояний. (На случай, если вам интересно, нужен ли вам триггер в реальной жизни.)
Наиболее распространенные триггерные вопросы ACT
Вопросы по тригонометрии в ACT можно разделить на несколько категорий.Мы предоставили несколько реальных математических примеров ACT, чтобы продемонстрировать каждую концепцию.
# 1: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла из заданной прямоугольной треугольной диаграммы.
# 2: Нахождение синуса, косинуса или тангенса прямоугольного треугольника из задачи со словами.
Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены?
А.10 $ tan23 ° $
Б. 10 $ sin23 ° $
C. 10 $ cos23 ° $
D. $ cos {10/23} $
E. $ sin {10/23}
$# 3: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла от заданного sin, cos или tan и диапазона, в который попадает угол.
Если $ tanΘ = 3/4 \ и 180 ° <Θ <270 ° $, что такое $ sinΘ $?
A. $ 4/3 $
Б. $ -4 / 3 $
C. $ -3 / 4 $
Д.$ 3/5 $
-3 Э. $ / 5
# 4: Определение периода или амплитуды графика.
Какова амплитуда графика?
А. 1
Б. 2
К. π
Д. 2π
E. 0
# 5: Закон синусов или закон косинусов.
Для такого вопроса, , они дадут вам формулы закона синусов или закона косинусов , так что вам не нужно беспокоиться об их запоминании.Однако наличие формулы вам не очень поможет, если она вам покажется или звучит как тарабарщина. По мере того, как вы будете изучать это руководство, выполнять практические вопросы по математике ACT, которые мы предоставили, и знакомиться с языком тригонометрии, используемым в этих вопросах, их станет намного легче решать.
Мы рассмотрим, как решить каждую из этих проблем, , но это даст вам представление о том, как будут выглядеть триггерные проблемы ACT в тесте.
SOH, CAH, TOA
Помните эту знаменитую мнемонику? Это спасет вашу жизнь.Давайте пройдемся по каждому.
SOH (синус)
Синус — это функция, в которой значение синуса (также называемого «грехом») угла тета может быть найдено с помощью отношения стороны треугольника, противоположной углу тета, к гипотенузе треугольника.
SOH : S in $ Θ $ = O одна сторона треугольника / H yпотенуза треугольника
Итак, в этом треугольнике $ sinΘ = b / c $, потому что сторона, противоположная углу $ Θ $, равна b , а гипотенуза — c .
CAH (косинус)
Косинус — это функция, в которой значение косинуса (также называемого «$ cos $») угла тета ($ Θ $) можно найти, используя отношение стороны треугольника, примыкающей к углу $ Θ $ (т. Е. не гипотенуза) над гипотенузой треугольника.
CAH : C os $ Θ $ = A соседняя сторона треугольника / H yпотенуза треугольника
Примечание: смежный означает, что сторона треугольника касается угла / помогает создать угол $ Θ $.
В этом же треугольнике $ cosΘ = a / c $, потому что сторона, примыкающая к углу $ Θ $, равна a , а гипотенуза — c .
TOA (касательная)
Касательная — это функция, в которой значение тангенса (также называемого «тангенс») угла тета может быть найдено с помощью отношения стороны треугольника, противоположной углу тета, по соседней стороне треугольника к тета (что не является гипотенуза).
TOA : T и $ $ = O заданная сторона треугольника / A смежная сторона треугольника.
В этом же треугольнике $ tanΘ = b / a $, потому что сторона, противоположная углу $ Θ $, равна b , а смежная сторона — a .
Теперь, когда вы знакомы со своими мнемоническими устройствами, вы можете составлять вопросы в несколько этапов. Например, немного более сложный вопрос может выглядеть примерно так:
Вам даны длины двух сторон треугольника, но для решения задачи требуется длина третьей стороны.2 = 21 $
$ x = √21 $
Теперь, когда у вас есть размер третьей стороны, вы можете найти $ tanB $.
$ TanB = \ напротив / \ Соседний $
$ TanB = √21 / 2 $
Итак, ответ: F , √21 $ / 2 $
Какие стороны противоположные или смежные?
Гипотенуза треугольника всегда остается неизменной, но противоположные или смежные стороны меняются в зависимости от угла фокусировки.
Например, если вы пытаетесь найти $ sin $ угла $ γ $, вы должны использовать соотношение $ b / c $; если вы пытаетесь найти грех угла $ ξ $, вы должны использовать соотношение $ a / c $.2 = 44 $
$ x = √44 $
Теперь $ sin $ = $ \ Against / \ hypotenuse $, поэтому $ sinM = √44 / 12 $.
Итак, ответ K.
Нет необходимости находить градусную меру (арксинус или обратный синус) угла M на вашем калькуляторе — это все, что вам нужно.
Вам также может быть предоставлено значение угла и длины стороны знаменателя вашего соотношения. В этом случае управляйте уравнением, как алгебраическим уравнением, и умножайте противоположную сторону на знаменатель.
$ sin Θ = \ напротив / \ гипотенуза $
$ гипотенуза $ * sinΘ = $ напротив
Поскольку вас спрашивают о длине лодки до дока, а эта сторона составляет против , угол 52 °, вы знаете, что вам понадобится либо sin, либо tan (cos использует смежную и гипотенузу, а не противоположную).
Вам также дается смежная длина , 30 миль, поэтому вы будете использовать tan. (Вы можете сказать, что эта сторона смежная, потому что сторона, противоположная углу 90 °, является гипотенузой, поэтому 30 миль должны быть еще одним катетом треугольника).
$ tanΘ = \ напротив / \ рядом $
So $ tan52 ° = x / 30 $
30 $ тан52 ° = x
долл. СШАИтак, ответ — франков, длина лодки до причала 30 тангенциальных 52 °.
И снова проблема со словом из ранее.
Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены?
А.10 $ загар23 ° $
Б. 10 $ sin23 ° $
C. 10 $ cos23 ° $
D. $ cos10 / 23 $
E. $ sin10 / 23 $
Во-первых, нарисуйте свою картинку, чтобы легче было представить, о чем вас просят.
Итак, расстояние между лестницей и землей составляет 23 ° $. Также мы работаем с длинами соседней стороны треугольника и гипотенузы. Это означает, что нам понадобится косинус, так как $ cosΘ = \ напротив / \ hypoteneuse $
Итак, $ cos23 ° = \ смежный / 10 $ (Почему 10? Длина лестницы 10 футов)
Это становится 10 $ cos23 ° = \ смежный $
Итак, ответ: C , 10 $ cos23 ° $
Придется ли мне определять угол?
Короткий ответ: нет, вас не попросят определить точную величину угла в градусах с помощью тригонометрии.2)}
долл. СШАКогда Sin, Cos и Tan являются положительными или отрицательными?
В зависимости от того, где расположен треугольник в двумерном пространстве, значения sin, cos и tan будут отрицательными или положительными.
В двухмерном пространстве четыре квадранта, разделенных по осям x и y.
- В квадранте I и x, и y положительны.
- В квадранте II x отрицателен, а y положителен
- В квадранте III оба значения x и y отрицательны
- А в квадранте IV x положителен, а y отрицателен
Как и в случае со значениями x и y, sin, cos и tan могут быть положительными или отрицательными в зависимости от квадранта, в котором находится треугольник / угол.
- В квадранте I все положительные
- В квадранте II sin положителен, а cos и tan отрицательны
- В квадранте II tan положительный, а sin и cos отрицательные
- В квадранте IV cos положительна, а sin и tan отрицательны
Хороший способ запомнить это — мнемоническое сокращение ASTC — A ll S tudents T ake C hemistry — чтобы увидеть, какая из функций является положительной в зависимости от квадранта.
Итак, A ll положительны в квадранте I, S in положительны в квадранте II, T an положительны в квадранте III, а C os положительны в квадранте IV
Если $ tanΘ = 3/4 $ и $ 180 ° <Θ <270 ° $, что такое $ sinΘ $?
A. $ 4/3 $
Б. $ −4 / 3 $
C. $ -3 / 4 $
D. $ 3/5 $
-3 Э. $ / 5
Чтобы решить эту проблему, сначала определите длины сторон треугольника, используя теорему Пифагора (или используя свои знания о 3-4-5 треугольниках).2 = 25 9000 долларов США 3
$ c = 5
$Итак, наша гипотенуза равна 5.
Мы знаем, что $ sin Θ = \ Against / \ hypotenuse $. Итак, $ sinΘ = 3/5 $.
Но подождите! Мы еще не закончили. Поскольку они сказали нам, что $ Θ $ лежит между $ 180 ° $ и $ 270 ° $, мы знаем, что значение sin для $ Θ $ отрицательно. Согласно ASTC, только тангенс угла $ Θ $ будет положительным между 180 ° $ и 270 ° $.
Итак, наш окончательный ответ — E, $ — 3/5 $
Вторичные триггерные функции
В редких случаях на ACT вам будет предложено указать одну из вторичных триггерных функций.Это косеканс, секанс и котангенс. Максимум один вопрос за тест.
Вы могли заметить, что они похожи на основные триггерные функции, которые вы изучили выше. Фактически, эти вторичные функции являются обратными (обратными) sin, cos и касательной.
Чтобы помочь вам запомнить, что есть что, обратите внимание на третью букву каждого слова:
- Co s ecant = величина, обратная s ine
- Se c ant = аналог c osine
- Co t Угол = величина, обратная t Угол
Косеканс
Косеканс — величина, обратная синусу.$ Косеканс Θ = \ гипотенуза / \ напротив $
Секант
Секанс — величина, обратная косинусу. $ Секанс Θ = \ гипотенуза / \ смежный $
Котангенс
Котангенс — величина, обратная касательной. $ Котангенс Θ = \ смежный / \ противоположный $
Полезные формулы с Sin, Cos и Tan
Есть две формулы, которые время от времени будут появляться в ACT. Если вы чувствуете, что не можете больше запоминать тригонометрию, не беспокойтесь об их запоминании — они когда-либо поднимут не более одного вопроса за тест .2 {x}) $, что также равно 1.
Итак, мы имеем 1 + 1 = 2
Окончательный ответ: H , 2.
$$ (sinΘ) / (cosΘ) = tanΘ $$
Это уравнение имеет логический смысл, если представить его в виде диаграммы. Допустим, у вас есть треугольник, который выглядит так
$ Sin Θ $ будет 5 $ / 13 $. $ Cos Θ $ будет $ 12/13 $. $ Tan Θ $ будет 5 долларов США / 12%.
Вы также можете сказать $ tanΘ = {sinΘ} / {cosΘ} = {5/14} / {12/13} = (5/13) (13/12) = 65/156 $ (вы также можете просто отменить обе 13s для упрощения) = 5 $ / 12 $
Графические триггерные функции
ACT не будет запрашивать у вас график триггерной функции, но вам нужно распознать, как каждая функция выглядит в виде графика.
Синус
Синусоидальный график пересекает начало координат в волновой структуре. Он всегда возрастает после $ x = 0 $, после пересечения начала координат.
Это «нечетная» функция, потому что она не симметрична относительно оси y.
Косинус
График косинусов также «волнистый», но не пересекает начало координат. Он спускается после $ x = 0 $.
Это может помочь вам запомнить, что косинус убывает после x = 0, если подумать, что « co — это low »
Косинус является «четной» функцией, потому что он симметричен относительно оси y.Это означает, что для всех значений $ x $ $ f (x) = f (-x) $.
Например, на графике выше $ y = 0,7 $ как при $ x = 1 $ , так и при $ x = -1 $
.Иногда все, что вам зададут, — это определить, является ли график четным или нечетным, а также является ли график sin или cos. Вам будет легко понять это, если вы помните основные элементы тригонометрических графиков.
Хотя вы можете понять этот вопрос из предоставленной информации, это займет гораздо меньше времени, если вы узнаете, что график является косинусным и, следовательно, четным.А на ACT время ограничено и ценно.
Касательная
Касательный график выглядит совсем иначе, чем графики sin и cos — вам просто нужно уметь распознавать касательный график, когда вы его видите.
Периоды и амплитуды
ACT иногда просит вас найти период или амплитуду синусоидального или косинусного графика.
Период
Период графика — это расстояние по оси x, с которого график начинает повторяться.Найдите расстояние по оси x, на котором точка возвращается в исходное положение после завершения полного цикла .
Период синусоидального графика здесь равен 2π. Он должен идти как вверх, так и вниз, прежде чем окончательно вернуться к $ y = 0 $.
Период косинусного графика здесь также равен 2π. Он должен сначала спуститься, а затем снова подняться, чтобы вернуться в исходное положение при $ y = 1 $.
Амплитуда
Амплитуда графика — это его высота от оси x, расстояние между его наивысшим значением $ y $ и $ x = 0 $.
Итак, чтобы использовать тот же график, что и выше:
И синус, и косинус имеют амплитуду 1 (и, опять же, период 2π).
Радианы
Радианы — это еще один (более точный) способ измерения расстояния по окружности, а не в градусах. Вместо градусов радианы выражаются через π (и доли π).
Если у вас есть полный круг, то это 360 градусов. Это также 2π радиан.
Почему 2π радиан? Что ж, придумайте формулу длины окружности. С = 2πr. Если ваш радиус равен 1, тогда ваша окружность равна 2π, что совпадает с вашей мерой в радианах.
Окружность с радиусом 1 и центром в начале координат называется «единичной окружностью». Радианы удобно рассматривать, помещая их на единичный круг.
Итак, если у вас есть полукруг, это 180 ° или π радиан.
И так далее. 90 ° — это $ π / 2 $ радиан, 270 ° — $ (3π) / 2 $ радиан.
Для преобразования градусов в радианы проще всего использовать преобразование между 180 ° и π .
Преобразовать 45 ° в радианы => $ (45) {π / 180} = π / 4 $ радиан
Преобразовать $ (3π) / 4 $ радиан в градусы => $ {(3π) / 4} (180 / π) $ = 135 °
Шаги к решению триггерного вопроса
Итак, давайте рассмотрим, как разбить триггерный вопрос
# 1: Определите, требует ли проблема тригонометрии. Вы можете сказать, что проблема потребует триггера, когда:
- Проблема упоминает sin, cos или tan в вопросе или в вариантах ответа
- Задача дает вам диаграмму или описывает прямоугольный треугольник, а затем просит вас найти значение, которое нельзя найти, используя только теорему Пифагора.
- Как мы видели в этой задаче ранее — вы можете использовать теорему Пифагора в задаче тригонометрии, но вы не можете решить задачу триггера с помощью только , используя теорему Пифагора.
- Проблема показывает вам «волнистый» график по осям x и y
- Задача запрашивает период или амплитуду графика
# 2: Помните SOH, CAH, TOA.2 {Θ} и др.
# 4 :. Вспомните, как выглядят графики синуса, косинуса и тангенса.
И знайте, что:
Период = горизонтальное расстояние
Амплитуда = вертикальное расстояние
# 5: Празднуйте, потому что вы ответили на триггерные вопросы ACT!
Итоги
Хотя тригонометрические задачи могут показаться устрашающими, почти каждый вопрос о тригонометрии ACT может быть решен, если вы знаете основные элементы тригонометрии.
Чтобы получить максимальную отдачу от подготовки к математике ACT, запомните эти три триггерные концепции: SOH, CAH, TOA, как управлять своими уравнениями и как распознавать графики функций. Если вы запомните их, вы обнаружите, что решаете практически все триггерные вопросы, которые ACT может бросить вам.
Что дальше?
Хотите больше математических стратегий и руководств ACT? Прочтите нашу статью по всем математическим темам, протестированным на ACT, чтобы убедиться, что вы их хорошо усвоили. Вы знаете твердотельную геометрию ACT? Не забудьте освежить в памяти все, что вам нужно.
Хотите получить высший балл по математике в ACT? Ознакомьтесь с нашей статьей о том, как набрать 36 баллов в разделе ACT Math от тестера ACT-Score.
Чувствуете себя подавленным? Не знаю, с чего начать? Не ищите дальше наших статей о том, что считается хорошей, плохой или отличной оценкой ACT. Не знаете, в какие дни проводится ACT? Ознакомьтесь с нашим полным списком дат тестирования ACT, чтобы найти подходящие для вашего расписания.
И если вы обнаружите, что у вас не хватает времени на математический раздел, посмотрите не дальше нашей статьи о том, как перестать не хватать времени на математику ACT.
Хотите улучшить свой результат SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.
Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.
Оцените нашу 5-дневную бесплатную пробную версию:
Косинус — математический способ
В прямоугольном треугольнике косинус угла θ определяется как отношение соседнего катета ( b ) к гипотенузе ( c ).
Это одно из тригонометрических соотношений.Их называют отношениями, потому что они выражаются как отношение двух сторон прямоугольного треугольника.
Его аббревиатура — cos (от латинского cosinus ).
Косинусы для специальных общих углов
В следующей таблице приведены значения косинусов для общих углов :
Свойства косинуса
Графическое представление функции косинуса
Косинус — это периодическая функция с периодом 2π радиан (360 градусов), поэтому этот участок графика будет повторяться в разные периоды.
Геометрическое представление косинуса
Связь между косинусом и другими тригонометрическими функциями
Есть несколько основных тригонометрических тождеств, включающих косинус :
(1) Примечание : знак зависит от квадранта исходного угла.
Тригонометрические тождества с функцией косинуса
Косинус дополнительных, дополнительных и сопряженных углов
Косинус отрицательных углов
Косинус углов, отличающихся на 90 ° или 180 °
Сумма, разность, двойной, полуугловой и тройной угол тождества для косинуса
Эти идентификаторы помогают преобразовать тригонометрическое выражение, представленное как произведение, в сумму или наоборот:
Закон косинусов (или правило косинусов ) связывает одну сторону треугольника с двумя другими и углом, который они образуют.Теорема утверждает, что:
Квадрат любой стороны ( a , b или c ) треугольника равен , равному сумме квадратов двух оставшихся сторон минус удвоенное их произведение на косинус угол ( A , B или C ) они образуют:
Закон косинусов является обобщением теоремы Пифагора , которая верна только для прямоугольных треугольников.Фактически, если A является прямым углом (90º), его косинус равен нулю и, следовательно, a 2 = b 2 + c 2 .
Если угол A тупой, то есть> 90º, то косинус отрицательный.
Другие тригонометрические соотношения
Тригонометрические отношения угла θ — это отношения, полученные между тремя сторонами прямоугольного треугольника. Это сравнение по частному его трех сторон: a , b и c .
- Синус — это отношение между длиной противоположного плеча ( a ), деленной на длину гипотенузы ( c ). В формуле это записывается просто как грех:
- Касательная — это отношение к между длиной противоположного участка ( a ), деленной на длину соседнего участка ( b ). В формуле это записывается просто как tan :
Тригонометрические соотношения для специальных общих углов
Тригонометрические отношения для наиболее распространенных углов (0º, 30º, 45º, 60º, 90º, 180º и 270º) составляют:
Взаимосвязи между тригонометрическими функциями
Любое тригонометрическое соотношение можно выразить через любое другое.В следующей таблице показаны формулы, с помощью которых каждая из них выражается как функция другой:
Примечание : знак + или — зависит от квадранта исходного угла.
Взаимные тригонометрические отношения — это мультипликативные обратные тригонометрические отношения. Это:
Тригонометрические функции
Тригонометрические функции также называются круговыми функциями. Причина в том, что в прямоугольном треугольнике, начерченном на координатной оси, с вершиной угла θ в центре круга ( O ), то есть в стандартном положении, его вершина B может идти через все точки этого круга.
тригонометрических функций и взаимных тригонометрических функций можно графически представить в прямоугольном треугольнике на окружности r = 1.
Искусство решения проблем
В геометрии тригонометрия — это изучение тригонометрических функций , функций , которые стремятся связать длины и углы треугольников. Тригонометрия является неотъемлемой частью геометрии, поскольку многие известные результаты были подтверждены с помощью тригонометрии.
В математике для соревнований использование тригонометрии не ограничивается только геометрией; проблемы, связанные с уравнениями с тригонометрическими функциями, очень распространены. Они часто решаются с помощью умного использования множества тождеств тригонометрических функций, которые значительно упрощают выражения.
Помимо математики соревнований, тригонометрия является основой большей части анализа, особенно анализа Фурье.
Определения
Тригонометрические функции имеют несколько определений.Определение, которое обычно преподается первым, — это определение прямоугольного треугольника из-за простоты доступа. Курс геометрии от среднего до олимпиадного обычно использует определение единичного круга тригонометрии. В комплексном анализе определение тригонометрии ряда Тейлора предпочтительнее для расширения тригонометрии на сложную область, хотя это выходит за рамки математики конкуренции.
Определение прямоугольного треугольника
Определение прямоугольного треугольника в тригонометрии включает отношения между краями прямоугольного треугольника по отношению к заданному углу.Приведенные ниже определения относятся к углу, длина сторон которого указана на схеме. Поскольку угол должен быть меньше, чем для того, чтобы треугольник оставался прямым, эти определения работают только для острых углов.
Обычный пневмонический знак, который следует запомнить, это SOH-CAH-TOA , где S ine = O pposite / H ypotenuse, C osine = A djacent / H ypotenuse, и H ypotenuse, и H ypotenuse angent = O pposite / A djacent
Более редкими являются значения, обратные тригонометрическим функциям, перечисленным ниже.
Это определение чаще всего преподается на вводных уроках геометрии из-за его простоты. Однако это ограничение. Он работает только в том случае, если он прав, а это означает, что тригонометрические функции определяются только при остром угле.
Определение единичной окружности
Рассмотрим единичный круг, круг радиуса один с центром в начале координат. Начиная с, пройдите расстояние против часовой стрелки вокруг единичного круга, как показано на схеме. Координаты этой точки определены как.
Что касается других тригонометрических функций, определяется как отношение к, а косеканс, секанс и котангенс определяются как обратные величины синуса, косинуса и тангенса соответственно.
Преимущество этого определения в том, что оно соответствует определению прямоугольного треугольника для острых углов, но расширяет их область от острых углов до всех действительных углов. Таким образом, это определение обычно предпочтительнее для промежуточных настроек геометрии олимпиады.
Определение серии Тейлора
Ряды Тейлора для синуса и косинуса используются в качестве определения синуса и косинуса в анализе, особенно в комплексном анализе.Такое определение тригонометрических функций дает конкретный способ расширить определение тригонометрии от действительных чисел до полной комплексной плоскости. Ряды Тейлора для синуса и косинуса показаны ниже: Эти определения не используются на олимпиадах по математике в старших классах; тем не менее, они участвуют в конкурсе Putnam и других университетских соревнованиях.
Приложения к геометрии
Тригонометрия находит широкое применение в промежуточной геометрии. Помимо возврата соотношений прямоугольных треугольников, тригонометрия может применяться ко всем треугольникам через закон синусов и закон косинусов.
Закон синусов
Закон синусов гласит, что в любом, где — сторона, противоположная, противоположная, противоположная, и — радиус описанной окружности. Закон синусов особенно удобен в задачах, связанных с радиусом описанной окружности, поскольку он чрезвычайно широко используется в промежуточной геометрии.
Закон косинусов
Закон косинусов гласит, что в любом, где — сторона, противоположная, противоположная и противоположная. Это обобщение теоремы Пифагора и используется для доказательства нескольких известных результатов, таких как формула Герона и теорема Стюарта.Однако он видит ограниченную применимость по сравнению с законом синусов, поскольку использование закона косинусов может быть очень сложным для алгебры. Полезно запоминать «хорошие» значения синуса и косинуса, поскольку это может пригодиться в соревнованиях, особенно если вы хотите применить либо этот закон, либо закон синусов.
Тригонометрические идентификаторы
Тригонометрические тождества — это выражения, включающие тригонометрические функции, которые верны для всех входных данных. Тригонометрические функции известны своим тождеством.Наиболее часто используемые идентичности в математике соревнований:
- Пифагорейские тождества
- Идентификаторы сложения углов
- Идентификаторы с двойным углом
- Идентификаторы половинного угла
- Идентификаторы суммы к продукту
- Идентификаторы произведения к сумме
См. Также
7.4: Другие тригонометрические функции
Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности.Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены. Обычно идентичность можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Пример \ (\ PageIndex {6} \): использование идентификаторов для упрощения тригонометрических выражений
Упростить \ (\ frac {\ sec t} {\ tan t}. \)
Решение
Мы можем упростить это, переписав обе функции в терминах синуса и косинуса.
\ [\ begin {array} {lll} \ dfrac {\ sec t} {\ tan t} & = \ dfrac {1 / \ cos t} {\ sin t / \ cos t} & \ text {Чтобы разделить функции, мы умножаем на обратную.} \\ \ text {} & = \ dfrac {1} {\ cos t} \ dfrac {\ cos t} {\ sin t} & \ text {Разделим косинусы.} \ \ \ text {} & = \ dfrac {1} {\ sin t} & \ text {Упростите и используйте идентичность.} \\ \ text {} & = \ csc t \ end {array} \]
Показав, что \ (\ frac {\ sec t} {\ tan t} \) можно упростить до \ (\ csc t \), мы фактически установили новую идентичность.2 t & = \ dfrac {25} {169} \\ \ sin t & = ± \ sqrt {\ dfrac {25} {169}} \\ \ sin t & = ± \ dfrac {\ sqrt {25}} { \ sqrt {169}} \\ \ sin t & = ± \ dfrac {5} {13} \ end {align} \]
Знак синуса зависит от значений y в квадранте, где расположен угол. Поскольку угол находится в квадранте IV, где значения y отрицательны, его синус отрицательный, \ (- \ frac {5} {13} \).
Остальные функции можно вычислить с помощью тождеств, связывающих их с синусом и косинусом.
\ [\ begin {align} \ tan t & = \ dfrac {\ sin t} {\ cos t} = \ dfrac {- \ frac {5} {13}} {\ frac {12} {13}} = — \ dfrac {5} {12} \\ \ sec t & = \ dfrac {1} {\ cos t} = \ dfrac {1} {\ frac {12} {13}} = \ dfrac {13} {12 } \\ \ csc t & = \ dfrac {1} {\ sin t} = \ dfrac {1} {- \ frac {5} {13}} = — \ dfrac {13} {5} \\ \ cot t & = \ dfrac {1} {\ tan t} = \ dfrac {1} {- \ frac {5} {12}} = — \ dfrac {12} {5} \ end {align} \]
Упражнение \ (\ PageIndex {7} \):
Если \ (\ sec (t) = — \ frac {17} {8} \) и \ (0 Решение \ (\ cos t = — \ frac {8} {17}, \ sin t = \ frac {15} {17}, \ tan t = — \ frac {15} {8} \) \ (\ csc t = \ frac {17} {15}, \ cot t = — \ frac {8} {15} \) Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция . Тригонометрические функции периодические. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или \ (2π \) приведет к одинаковым результатам для этих функций.А для тангенса и котангенса только половина оборота даст одинаковые результаты. Другие функции также могут быть периодическими. Например, продолжительность месяцев повторяется каждые четыре года. Если x x представляет собой продолжительность, измеряемую в годах, а \ (f (x) \) представляет количество дней в феврале, тогда \ (f (x + 4) = f (x) \). Этот образец повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и 4 годами ранее. Положительное число 4 — это наименьшее положительное число, которое удовлетворяет этому условию и называется периодом.Период — это самый короткий интервал, в течение которого функция выполняет один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней. СРОК РАБОТЫ Период \ (P \) повторяющейся функции f f — это число, представляющее интервал, такой что \ (f (x + P) = f (x) \) для любого значения \ (x \). Период функций косинуса, синуса, секанса и косеканса равен \ (2π \). Период функций касательной и котангенса равен \ (π \). Пример \ (\ PageIndex {8} \): поиск значений тригонометрических функций Найдите значения шести тригонометрических функций угла \ (t \) на основе рисунка \ (\ PageIndex {9} \) . Решение \ [\ begin {align *} \ sin t & = y = — \ dfrac {\ sqrt {3}} {2} \\ \ cos t & = x = — \ dfrac {1} {2} \\ \ tan t & = \ dfrac {\ sin t} {\ cos t} = \ dfrac {- \ frac {\ sqrt {3}} {2}} {- \ frac {1} {2}} = \ sqrt {3 } \\ \ sec t & = \ dfrac {1} {\ cos t} = \ dfrac {1} {- \ frac {1} {2}} = — 2 \\ \ csc t & = \ dfrac {1} {\ sin t} = \ dfrac {1} {- \ frac {\ sqrt {3}} {2}} = — \ dfrac {2 \ sqrt {3}} {3} \\ \ cot t & = \ dfrac {1} {\ tan t} = \ dfrac {1} {\ sqrt {3}} = \ dfrac {\ sqrt {3}} {3} \ end {align *} \] Упражнение \ (\ PageIndex {8} \) Найдите значения шести тригонометрических функций угла \ (t \) на основе рисунка \ (\ PageIndex {10} \) . Решение \ (\ begin {align} \ sin t & = — 1, \ cos t = 0, \ tan t = \ text {Undefined} \\ \\ sec t & = \ text {Undefined}, \ csc t = — 1, \ cot t = 0 \ end {align} \) Пример \ (\ PageIndex {9} \): поиск значения тригонометрических функций Если \ (\ sin (t) = — \ frac {\ sqrt {3}} {2} \) и \ (\ cos (t) = \ frac {1} {2} \), найдите \ (\ sec (t), \ csc (t), \ tan (t), \ cot (t). \) Решение \ [\ begin {align} \ sec t & = \ dfrac {1} {\ cos t} = \ dfrac {1} {\ frac {1} {2}} = 2 \\ \ csc t & = \ dfrac {1} {\ sin t} = \ dfrac {1} {- \ frac {\ sqrt {3}} {2}} — \ dfrac {2 \ sqrt {3}} {3} \\ \ tan t & = \ dfrac {\ sin t} {\ cos t} = \ dfrac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} = — \ sqrt {3} \\ \ cot t & = \ dfrac {1} {\ tan t} = \ dfrac {1} {- \ sqrt {3}} = — \ dfrac {\ sqrt {3}} {3} \ end {align} \] Упражнение \ (\ PageIndex {9} \): Если \ (\ sin (t) = \ frac {\ sqrt {2}} {2} \) и \ (\ cos (t) = \ frac {\ sqrt {2}} {2}, \) найти \ (\ sec (t), \ csc (t), \ tan (t), \) и \ (\ cot (t) \). Решение \ (\ sec t = \ sqrt {2}, \ csc t = \ sqrt {2}, \ tan t = 1, \ cot t = 1 \) Этот калькулятор тригонометрии поможет вам в двух популярных случаях, когда необходима тригонометрия. Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент — тоже беспроигрышный вариант! Введите 2–3 заданных значения во второй части калькулятора, и вы в мгновение ока найдете ответ.Прокрутите вниз, если хотите узнать больше о тригонометрии и о том, где ее можно применить. Есть много других инструментов, полезных при решении задач тригонометрии. Ознакомьтесь с двумя популярными тригонометрическими законами: калькуляторами закона синусов и закона косинусов, которые помогают решить любой тип треугольника. Если вы хотите узнать больше о тригонометрических функциях, перейдите к нашим специальным инструментам: Тригонометрия — это раздел математики. Само это слово происходит от греческого слова trignon (что означает «треугольник») и metron («мера»).Как следует из названия, тригонометрия имеет дело в основном с углами и треугольниками ; в частности, он определяет и использует отношения и соотношения между углами и сторонами в треугольниках. Таким образом, основное приложение — решение треугольников, в частности прямоугольных, а также любого другого типа треугольника, который вам нравится. Тригонометрия имеет множество приложений: от повседневных задач, таких как вычисление высоты или расстояния между объектами, до спутниковой навигационной системы, астрономии и географии.Кроме того, функции синуса и косинуса являются фундаментальными для описания периодических явлений — благодаря им мы можем описывать колебательные движения (как простой маятник) и волны, такие как звук, вибрация или свет. Тригонометрия и тригонометрические функции используются во многих различных областях науки и техники, если упомянуть лишь некоторые из них: музыка, акустика, электроника, медицина и медицинская визуализация, биология, химия, метеорология, электротехника, машиностроение и гражданское строительство, даже экономика. Тригонометрические функции действительно вокруг нас! Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах.Под калькулятором появятся шесть самых популярных триггерных функций — три основных: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. Кроме того, если угол острый, будет отображаться прямоугольный треугольник, который может помочь вам понять, как могут быть интерпретированы функции. Чтобы найти недостающие стороны или углы прямоугольного треугольника, все, что вам нужно сделать, это ввести известные переменные в калькулятор тригонометрии. Вам нужны только два заданных значения в случае: Помните, что если вы знаете два угла, этого недостаточно, чтобы найти стороны треугольника.Два треугольника, имеющие одинаковую форму (что означает, что они имеют равные углы), могут иметь разные размеры (не одинаковую длину стороны) — такая взаимосвязь называется сходством треугольника . Если стороны имеют одинаковую длину, то треугольники равны и соответствуют . Тригонометрия — это исследование отношений внутри треугольника . Для прямоугольных треугольников соотношение между любыми двумя сторонами всегда одинаково и задается в виде тригонометрических соотношений, cos, sin и tan.Тригонометрия также может помочь найти некоторую недостающую треугольную информацию , например, правило синуса. Поначалу тригонометрия может быть сложной задачей, но после некоторой практики вы ее освоите! Вот несколько советов по тригонометрии: Обозначьте гипотенузу, смежную и противоположную на вашем треугольнике, чтобы помочь вам выяснить, какую идентичность использовать, и запомните мнемонику SOHCAHTOA для тригонометрических отношений! Тригонометрия используется для поиска информации обо всех треугольниках и, в частности, прямоугольных треугольниках.Поскольку треугольников повсюду в природе , тригонометрия используется вне математики, в таких областях, как строительство, физика, химическая инженерия и астрономия. Поскольку тригонометрия — это соотношение между углами и сторонами треугольника, никто не придумал ее , она все равно была бы там, даже если бы об этом никто не знал! Первыми людьми, открывшими часть тригонометрии, были древние египтяне и вавилоняне , но Евклид и Архемид первыми подтвердили идентичность, хотя они сделали это с помощью форм, а не алгебры. Тригонометрия — это , которые обычно преподают подросткам в возрасте 13-15 лет , что составляет 8 и 9 классов в США и лет 9 и 10 в Великобритании. Точный возраст преподавания тригонометрии зависит от страны, школы и способностей учеников. Мнемоники триггеров, такие как SOH-CAH-TOA, сосредоточены на вычислениях, а не на концепциях: TOA объясняет касательную примерно так же, как $ x ^ 2 + y ^ 2 = r ^ 2 $ описывает окружность.Конечно, если вы математический робот, уравнения достаточно. Остальным из нас, с органическим мозгом, наполовину посвященным обработке зрения, кажется, нравятся образы. А «TOA» вызывает потрясающую красоту абстрактного соотношения. Думаю, вы заслуживаете большего, и вот что сделало триггерный клик для меня. Представьте себе Боба-инопланетянина, который посещает Землю, чтобы изучить наш вид. Без новых слов трудно описать людей: «Наверху есть сфера, которая иногда царапается» или «Два удлиненных цилиндра, кажется, обеспечивают движение». После создания конкретных терминов для анатомии Боб может записать типичные пропорции тела: Чем это полезно? Ну, когда Боб находит куртку, он может поднять ее, протянуть руки и оценить рост владельца.И размер головы. И шириной глаз. Один факт связан с множеством выводов. Еще лучше, человеческая биология объясняет человеческое мышление. У столов есть ноги, у организаций есть голова, у криминальных авторитетов есть мускулы. Наша биология предлагает готовые аналогии, которые появляются в созданных руками человека творениях. Теперь поворот сюжета: вы, — Боб-инопланетянин, изучающий существ в математической стране! Общие слова, такие как «треугольник», не слишком полезны. Но обозначение синуса, косинуса и гипотенузы помогает нам заметить более глубокие связи.И ученые могут изучать гаверсин, эксеканс и гамзин, как биологи, которые находят связь между вашей голенью и ключицей. И поскольку треугольники появляются в кругах… … и круги появляются циклически, наша терминология треугольников помогает описать повторяющиеся узоры! Trig — это книга по анатомии «математических» объектов. Если нам удастся найти метафорический треугольник, мы бесплатно получим армаду выводов. Вместо того, чтобы смотреть на треугольники сами по себе, как замороженный во льду пещерный человек, представьте их в сценарии охоты на этого мамонта. Представьте, что вы находитесь в центре купола и собираетесь повесить киноэкран. Вы указываете на некоторый угол «x», и именно там экран будет висеть. Угол, на который вы указываете, определяет: Хотите максимально большой экран? Укажите прямо вверх.Он находится в центре, на макушке вашей головы, но это большой дагнаббит. Хотите, чтобы экран находился как можно дальше? Конечно. Укажите прямо, 0 градусов. В этом положении экран имеет нулевую высоту и находится далеко, как вы и просили. Высота и расстояние меняются в противоположных направлениях: поднесите экран ближе, и он станет выше. Никто никогда не говорил мне, когда я учился в школе: синус и косинус — это проценты .Они варьируются от + 100% до 0 до -100% или от максимального положительного значения до нуля до максимального отрицательного. Допустим, я заплатил 14 долларов в виде налога. Вы понятия не имеете, дорого ли это. Но если я скажу, что заплатил 95% налога, вы знаете, что меня ограбят. Абсолютная высота бесполезна, но если ваше значение синуса 0,95, я знаю, что вы почти на вершине своего купола. Довольно скоро вы достигнете максимума, а затем снова начнете снижаться. Как вычислить процент? Просто: разделите текущее значение на максимально возможное (радиус купола, он же гипотенуза). Это , почему нам говорят: «Синус = Противоположность / Гипотенуза». Чтобы получить проценты! Лучшая формулировка: «Синус — это ваш рост в процентах от гипотенузы». (Синус становится отрицательным, если ваш угол указывает «под землю». Косинус становится отрицательным, когда ваш угол направлен назад.) Давайте упростим расчет, предположив, что мы находимся на единичной окружности (радиус 1). Теперь мы можем пропустить деление на 1 и просто сказать синус = высота. Каждый круг — это действительно единичный круг, увеличенный или уменьшенный до разного размера.Так что проработайте связи на единичном круге и примените результаты к вашему конкретному сценарию. Попробуйте: подключите угол и посмотрите, какой процент высоты и ширины он достигает: Линия роста синуса не является ровной. Первые 45 градусов покрывают 70% высоты, а последние 10 градусов (от 80 до 90) покрывают только 2%. Это должно иметь смысл: при 0 градусах вы двигаетесь почти вертикально, но когда вы добираетесь до вершины купола, ваша высота меняет свой уровень. Однажды ваш сосед ставит стену прямо рядом с от вашего купола. Ага, твой взгляд! Ваша стоимость при перепродаже! Но можем ли мы извлечь максимальную пользу из плохой ситуации? Конечно. Что, если мы повесим киноэкран на стену? Вы указываете под углом (x) и получаете: У нас есть новые причудливые термины.Представьте себе, что вы видите витрувианского «ДЖЕНТЛЬМЕНА», проецируемого на стену. Вы поднимаетесь по лестнице, чтобы убедиться, что вы можете «ВИДЕТЬ, НЕ МОЖЕТЕ?». (Да, он голый … не забудете аналогию, ладно?) Обратите внимание на касательную высоту экрана. Начинается с 0 и идет бесконечно высоко. Вы можете продолжать указывать на стену все выше и выше, чтобы получить бесконечно большой экран! (Это будет стоить вам.) Касательная — это просто увеличенная версия синуса! Она никогда не становится меньше, и хотя синусоида «достигает вершины» по мере изгиба купола, касательная продолжает расти. Как насчет секанса, лестничного расстояния? Помните, значения процентов . Если вы указываете под углом 50 градусов, tan (50) = 1.19. Ваш экран на 19% больше, чем расстояние до стены (радиус купола). (Подключите x = 0 и проверьте свою интуицию, что tan (0) = 0, а sec (0) = 1.) Удивительно, но теперь ваш сосед решает построить потолок на вершине вашего купола, далеко за горизонтом. ( Что с этим парнем? Ах, случай с голым мужчиной на стене… ) Что ж, пора построить пандус до потолка и немного поболтать.Вы выбираете угол для построения и тренировки: Касательная / секущая описывает стену, а СО-касательная и СО-секанс — потолок. Наши интуитивные факты аналогичны: Недавно у меня было ноль «интуитивных выводов» о косеканте. Но с метафорой купола / стены / потолка мы видим следующее: Ого, это тот же треугольник, только увеличенный до стены и потолка.2 $) мы видим, как связаны стороны каждого треугольника. И из сходства, отношения, такие как «высота к ширине», должны быть одинаковыми для этих треугольников. (Интуиция: отойдите от большого треугольника. Теперь он кажется меньше в вашем поле зрения, но внутренние соотношения не могли измениться.) Вот как мы находим «синус / косинус = тангенс / 1». Я всегда пытался запомнить эти факты, когда они просто выскакивают на нас при визуализации. 2 $, за исключением глупых тестов, которые ошибочно принимают пустяки за понимание.В этом случае потратьте минуту, чтобы нарисовать схему купола / стены / потолка, заполните метки (загорелый джентльмен, вы же видите, не так ли?) И создайте шпаргалку для себя. В дальнейшем мы узнаем о построении графиков, дополнениях и использовании формулы Эйлера, чтобы найти еще больше связей. Вы можете увидеть касательную, определяемую как длина касательной линии от круга до оси x (любители геометрии могут с этим справиться). Как и ожидалось, на вершине круга (x = 90) касательная линия никогда не может достигать оси x и является бесконечно длинной. Мне нравится эта интуиция, потому что она помогает нам запомнить название «касательная», и вот хорошее интерактивное руководство по триггерам для изучения: Тем не менее, очень важно расположить касательную вертикаль и распознать, что это просто синус, спроецированный на заднюю стену (вместе с другими соединениями треугольника). {- 1} $ или $ \ arcsin $ («арксинус»), и часто записываются как Если наша высота составляет 25% от купола, какой у нас угол? Если вставить asin (0,25) в калькулятор, получится угол 14,5 градусов. А что насчет чего-нибудь экзотического, например, обратной секущей? Часто он недоступен как функция калькулятора (даже тот, который я построил, вздох). Глядя на нашу шпаргалку по триггерам, мы находим простое соотношение, в котором мы можем сравнить секанс с 1. Например, секанс с 1 (гипотенуза по горизонтали) совпадает с 1 по косинусу: Предположим, что наш секанс равен 3.5, т.е. 350% радиуса единичной окружности. Какой угол к стене? Пример: найти синус угла x. Ack, какой скучный вопрос. Вместо того, чтобы «найти синус», подумайте: «Какая высота в процентах от максимума (гипотенузы)?». Во-первых, обратите внимание на треугольник, повернутый назад. Это нормально. У него все еще есть высота, зеленая. Какая максимальная высота? По теореме Пифагора мы знаем Хорошо! Синус — это высота в процентах от максимума, равная 3/5 или.60. Продолжение: Найдите угол. Конечно. У нас есть несколько способов. Теперь, когда мы знаем, что синус = 0,60, мы можем просто сделать: Вот еще один подход. Вместо использования синуса обратите внимание, что треугольник «упирается в стену», поэтому можно использовать касательную. Высота 3, расстояние до стены 4, поэтому касательная высота 3/4 или 75%. Мы можем использовать арктангенс, чтобы снова превратить процентное значение в угол: Пример: Сможете ли вы добраться до берега? Вы находитесь на лодке, у которой достаточно топлива, чтобы проплыть 2 мили.Сейчас вы находитесь в 0,25 милях от берега. Какой самый большой угол вы можете использовать и при этом дотянуться до земли? Кроме того, единственная доступная ссылка — это «Сборник арккосинов» Хуберта, 3-е изд. . (Поистине адское путешествие.) Хорошо. Здесь мы можем визуализировать пляж как «стену», а «расстояние по лестнице» до стены — это секущая. Во-первых, нам нужно все нормализовать в процентах. У нас есть 2 / 0,25 = 8 «единиц гипотенузы» топлива. Итак, наибольшая секущая, которую мы могли допустить, составляет 8-кратное расстояние до стены. Мы бы выбрали как , чтобы спросить: «Какой угол имеет секущую 8?». Но мы не можем, поскольку у нас есть только книга арккосинусов. Мы используем нашу шпаргалку, чтобы связать секанс с косинусом: А, я вижу, что «sec / 1 = 1 / cos», поэтому Секанс 8 означает косинус 1/8. Угол с косинусом 1/8 равен arccos (1/8) = 82,8 градуса, это самый большой угол, который мы можем себе позволить. Неплохо, правда? До аналогии купола / стены / потолка я бы тонул в беспорядке вычислений.Визуализация сценария позволяет легко и даже весело увидеть, какой приятель по триггеру может нам помочь. В своей задаче подумайте: меня интересует купол (sin / cos), стена (tan / sec) или потолок (cot / csc)? Счастливая математика. Обновление: Владелец Gray Matters собрал интерактивные диаграммы для аналогий (перетащите ползунок слева, чтобы изменить угол): Спасибо! Встречаются тригонометрические функции суммы или разности двух углов.
часто в приложениях.Есть несколько способов подтвердить
эти результаты. Следующие тождества верны для всех значений, для которых они
определено: Доказательство: Пусть $ P $ будет точкой с
координаты $ (1,0) $.Измеряется против часовой стрелки из точки $ P $, пусть
$ Q $ — точка, длина дуги которой равна $ A $, пусть $ R $ —
точка, длина дуги которой равна $ A + B $, и пусть $ S $ будет точкой, длина дуги которой равна
$ -B $. 2
\ end {уравнение *} Благодаря использованию симметричного и пифагорейского тождеств,
это упрощается и становится формулой суммы углов для косинуса. Доказательство формулы разности углов для
косинус выглядит следующим образом: Тогда, используя теорему о совместных функциях, мы можем
получить формулы для синуса: По результатам формул синуса и косинуса
можно вывести другие четыре формулы.♦ Формулы также можно выводить с помощью треугольников.
Хотя мы ссылаемся на следующий вывод как на доказательство, на самом деле
допустимые при выводе значения углов $ A $ и $ B $ весьма ограничены, а
на самом деле требуется более общее доказательство. Альтернативное подтверждение: Пусть положительный
углы $ A $ и $ B $, сумма которых меньше 90
градусов. Постройте отрезок $ PU $ длиной 1.
Построить треугольник $ TPU $ так, чтобы угол $ TPU $ был равен
угол $ A $, а угол $ TUP $ равен дополнению к $ A $.Построить
описанный прямоугольник $ PQRS $ так, чтобы угол $ QPT $ был равен углу $ B $, угол $ QPU $
равна сумме углов $ A $ и $ B $, точка $ T $ находится на
сегмент $ QR $ и $ U $ находится в сегменте $ RS $. Обратите внимание, что угол $ RTU $
также равен углу $ B $. У треугольника
Соотношения
Теорема, имеем: Доказательство тождества суммы углов для косинуса:
похожий.Идентификаторы угловой разницы могут быть получены напрямую
из того же рисунка, отождествив угол $ A $ с углом $ TPS $,
а также
угол $ B $ с углом $ TPU $. ♦ Есть несколько классов идентификаторов, которые
непосредственные следствия суммы углов и
Теорема о разности. 2 t} $ Доказательство: Доказательство двойного
Формула угла для синуса выглядит следующим образом: Доказательства формулы двойного угла для другого
пять функций аналогичны.2 t = \ dfrac {2} {1- \ cos 2t} долл. США Проба: Чтобы найти понижающий
формулу для синуса, мы начинаем с косинуса двойного
угол
формулу и замените член в квадрате косинуса, используя тождество Пифагора.
Полученное уравнение можно решить для члена с синусом в квадрате.
Доказательства степенных формул для остальных пяти функций
похожи. ♦ Следующие тождества верны для всех значений, для которых они
определено: Доказательство: Формулы полуугла для
синус и косинус находятся сразу после уменьшения мощности
формулы подстановкой и извлечением квадратного корня.2 t} {2 \ sin t \ cos t} = \ dfrac {\ sin t} {\ cos t} = \ tan t
\ end {align} Подстановка в этот результат дает касательную
формула полуугла. Доказательство формулы котангенса
аналогичный. ♦ Следующие ниже тождества верны для всех реальных ценностей. Доказательство: Расширение и упрощение
правая часть каждой формулы, используя угол
Сумма
и теорема разности даст левую часть.♦ Следующие ниже тождества верны для всех реальных ценностей. Доказательство: Путем замены переменных $ \ dfrac {A \ pm B} {2} $ в произведении на сумму
формулы, эти формулы могут быть выведены.. Простой способ найти sin, cos, tan, cot
Что такое тригонометрия?
Калькулятор триггеров нахождения sin, cos, tan, cot, sec, csc
Что такое тригонометрия?
Сложна ли тригонометрия?
Для чего используется тригонометрия?
Кто изобрел тригонометрию?
Какой уровень у тригонометрии?
Как научиться тригонометрии интуитивно — лучше объяснять
Мотивация: Триг — это анатомия
Синус / косинус: купол
Совет: триггерные значения — это проценты
Касательная / секущая: стена
Котангенс / косеканс: потолок
Визуализируйте связи
Приложение: Исходное определение тангенса
asin на различных языках программирования. Приложение: несколько примеров
Другие сообщения из этой серии
Идентификаторов суммы углов и разностей
Идентификаторов суммы углов и разностей
Мы используем MathJax Тождества суммы углов и разностей
Теорема о сумме и разности углов
$ \ sin (A \ pm B) = \ sin A \ cos B \ pm \ cos A \ sin B $ $ \ cos (A \ pm B) = \ cos A \ cos B \ mp \ sin A \ sin B $ $ \ tan (A \ pm B) = \ dfrac {\ tan A \ pm \ tan B} {1 \ mp \ tan A \ tan B} $ $ \ cot (A \ pm B) = \ dfrac {\ cot A \ cot B \ mp 1} {\ cot B \ pm \ cot A} $ $ \ sec (A \ pm B) = \ dfrac {\ sec A \ sec B \ csc A \ csc B} {\ csc A \ csc B \ mp \ sec A \ sec B} $ $ \ csc (A \ pm B) = \ dfrac {\ sec A \ sec B \ csc A \ csc B} {\ sec A \ csc B \ pm \ csc A \ sec B} $ $ \ csc 2t = \ dfrac {\ sec t \ csc t} {2} $ Теорема о половинном угле
$ \ sin \ dfrac {t} {2} = \ pm \ sqrt {\ dfrac {1- \ cos t} {2}} $ $ \ cos \ dfrac {t} {2} = \ pm \ sqrt {\ dfrac {1+ \ cos t} {2}} $ $ \ tan \ dfrac {t} {2} = \ dfrac {1- \ cos t} {\ sin t} $ $ \ cot \ dfrac {t} {2} = \ dfrac {\ sin t} {1+ \ cos t} $ $ \ sec \ dfrac {t} {2} = \ pm \ sqrt {\ dfrac {2 \ sec t} {\ sec t + 1}} $ $ \ csc \ dfrac {t} {2} = \ pm \ sqrt {\ dfrac {2 \ sec t} {\ sec t-1}} $ Теорема произведения к сумме
$ \ sin A \ sin B = \ dfrac12 [(\ cos (A-B) — \ cos (A + B)] $ $ \ sin A \ cos B = \ dfrac12 [(\ sin (A + B) + \ sin (A-B)] $ $ \ cos A \ cos B = \ dfrac12 [(\ cos (A + B) + \ cos (A-B)] $ Теорема о сумме-произведении
$ \ sin A \ pm \ sin B = 2 \ sin \ dfrac {A \ pm B} {2} \ cos \ dfrac {A \ mp B} {2} $ $ \ cos A + \ cos B = 2 \ cos \ dfrac {A + B} {2} \ cos \ dfrac {A-B} {2} $ $ \ cos A- \ cos B = -2 \ sin \ dfrac {A + B} {2} \ sin \ dfrac {A-B} {2} $
 Кислота может начать разбрызгиваться с выделением кислотных паров.
Кислота может начать разбрызгиваться с выделением кислотных паров. Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов.
Если брызги кислоты попали на кожу и одежду, немедленно промойте пораженные участки водой (аварийный душ идеально подходит для этих целей), после чего снимите загрязненную одежду. Не ограничивайте себя в средствах защиты перед потенциальной опасностью химических ожогов. Свяжитесь с нами по телефону +7 (499) 270-16-62 и убедитесь в этом!
Свяжитесь с нами по телефону +7 (499) 270-16-62 и убедитесь в этом! На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается.
На металле образуется пассивирующий слой и дальнейшее взаимодействие с контейнером прекращается.


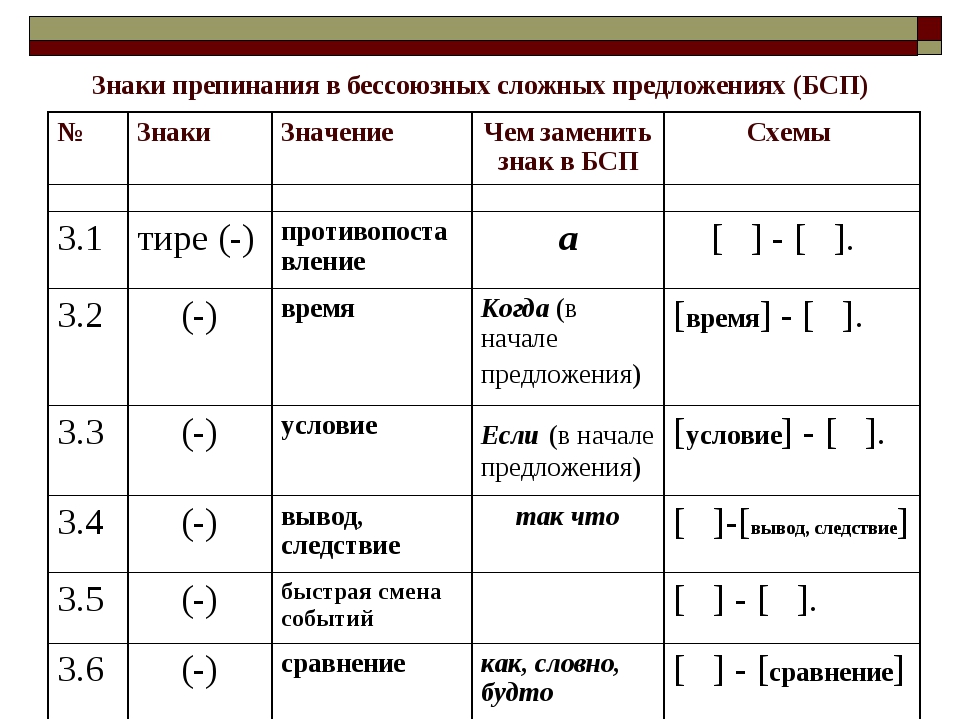 ПРАВИЛЬНО
ПРАВИЛЬНО 
 Спасибо заранее.
Спасибо заранее. Но зависит от того, отдельное это у вас предложение или часть сложного.
Но зависит от того, отдельное это у вас предложение или часть сложного. Ничего не поделать, время идет. Кроме того, тенденции к подобному решению даже у Розенталя уже просвечивали: у него не ставится запятая, если вводное внутри обособления, в начале или в конце предложения.
Ничего не поделать, время идет. Кроме того, тенденции к подобному решению даже у Розенталя уже просвечивали: у него не ставится запятая, если вводное внутри обособления, в начале или в конце предложения. «И я увидел друга на набережной, и он меня заметил».
«И я увидел друга на набережной, и он меня заметил».



 С. Тургенев).
С. Тургенев).

 Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.
Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.


 Решение. Находим определитель системы:
Решение. Находим определитель системы: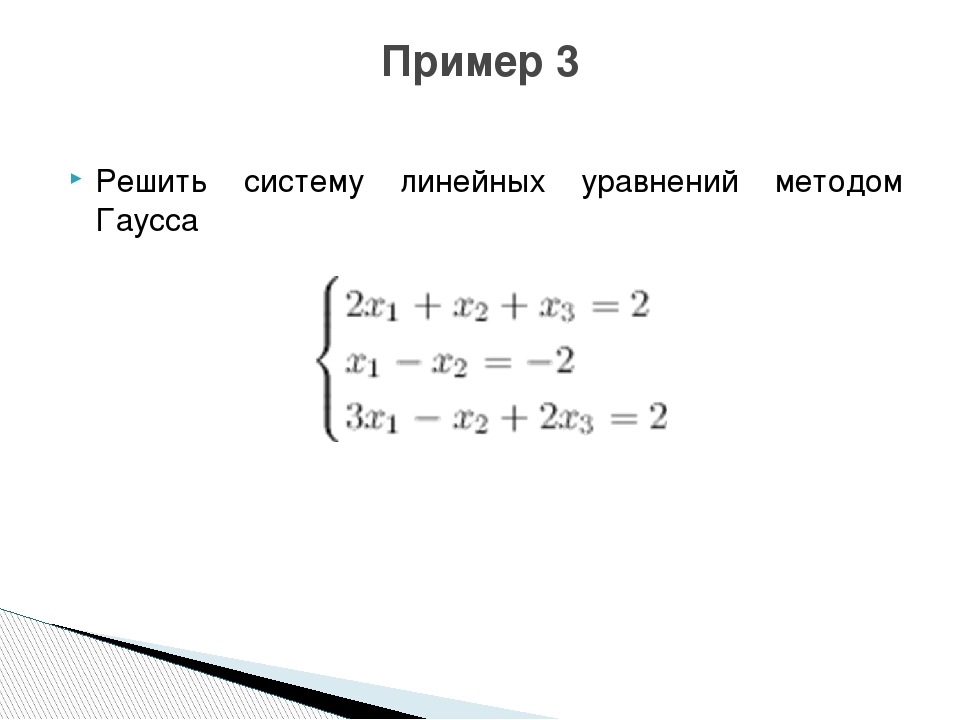 Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
 Это называется
Это называется
 е. подстановку в первое
е. подстановку в первое Запишем новую эквивалентную систему с учетом расширенной матрицыx 2 y 2z 3
Запишем новую эквивалентную систему с учетом расширенной матрицыx 2 y 2z 3

 Симметричными могут быть лишь квадратные матрицы.
Симметричными могут быть лишь квадратные матрицы.

 е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.